Adjusting to errors in arithmetic: a longitudinal investigation of metacognitive control in 7–9-year-olds

Introduction: Monitoring and controlling one's performance are essential skills for children's cognitive development and academic success. Metacognitive control, operationalized as post-error adjustments, is, however, often measured in conflict tasks, but the findings of such studies may not be readily generalizable to academic domains, such as arithmetic. Yet, investigating how children control their performance in arithmetic is crucial in understanding the large individual differences within this specific academic domain. This longitudinal study investigated how children control their performance through post-error slowing and accuracy improvement in arithmetic. We additionally examined this development of metacognitive control in a working memory task, to further unravel its domain-generality or the lack thereof.

Methods: A cohort of 127 typically developing children, followed up longitudinally from 7–8 years old (2nd grade of primary school) to 8–9 years old (3rd grade of primary school), completed an arithmetic and working memory task at two time points.

Results and discussion: Meticulous comparison of response times and accuracy rates following errors with those following correct answers revealed the presence of metacognitive control at each time point. We observed significant positive correlations between children's metacognitive control and their arithmetic accuracy at 7–8 years old, underscoring a possible adaptive role of metacognitive control in the learning phase of arithmetic. No correlations were found between the post-error adjustments in the arithmetic task and those in the working memory task, challenging previous evidence for domain-generality of post-error adjustments.

1 Introduction

Imagine a student taking a test. He feels confident answering the questions due to his thorough preparation. Yet, as the test progresses, he encounters a more challenging part, making him uncertain and less confident about his answers. The student, therefore, decides to slow down his thought process to answer the questions with increased focus. The awareness and regulation of one's own cognitive processes, as the student presented in this example, are also known as metacognitive monitoring and metacognitive control, respectively, both subskills of metacognitive regulation or procedural metacognition (Flavell, 1979; Nelson and Narens, 1990). Metacognitive regulation is thought to be of great importance to academic learning (e.g., Efklides and Misailidi, 2010). Yet, most of the existing body of work has examined metacognitive control in simple tasks, such as perceptual or conflict tasks, leaving it unresolved as to how it operates in academic tasks. The present study aimed to address this gap by exploring metacognitive control in the context of arithmetic.

Metacognitive control encompasses the actions individuals take to enable cognitive adaptations to increase task performance (Roebers et al., 2014). There are many possible manifestations of metacognitive control, such as allocation of study time and information-seeking, which occur during different stages of cognitive performances (Nelson and Narens, 1990). These manifestations of metacognitive control are often measured explicitly by giving participants the option to control their performance (e.g., asking participants whether they need help, Coughlin et al., 2015). It is, however, also possible to assess metacognitive control in an implicit way through post-error adjustments, which are thought to reflect the cognitive adaptations individuals make following errors (Danielmeier and Ullsperger, 2011). Two prominent manifestations of post-error adjustments are post-error slowing (PES) and post-error improvement in accuracy (PEIA). PES refers to the phenomenon that people tend to slow down their response speed after committing an error (Notebaert et al., 2009). PEIA is the phenomenon that individuals show increased accuracy in performance immediately after committing an error (Danielmeier and Ullsperger, 2011). It is important to note that PES and PEIA are often considered to be measures of cognitive control rather than metacognitive control due to their immediate nature, with the main difference between these two types of control being the consciousness involved in these processes (Roebers, 2017). However, the extent to which individuals consciously engage in these adjustments might vary, both across tasks and among people, making it possible that post-error adjustments are situated on a continuum from cognitive to metacognitive control. As it is beyond the scope of this study to disentangle these two conceptualizations, findings from both the cognitive and metacognitive control literature are integrated in the current study.

Although it is generally agreed that PES and PEIA reflect cognitive control, alternative interpretations especially regarding PES, have been suggested. Specifically, the orienting account posits PES as a reaction to a surprising event (i.e., an error) that prompts the individual to slow down (Notebaert et al., 2009). However, studies giving evidence for PES as an orienting response are restricted to conflict tasks (e.g., Fiehler et al., 2005; Hajcak and Simons, 2008; King et al., 2010; Notebaert et al., 2009; Notebaert and Verguts, 2011), in which opportunities for behavioral post-error adjustments are limited. This interpretation may, therefore, not apply to academic tasks, which have a more complex nature and, therefore, allow for multiple possible ways to adapt behavior following errors.

One such an academic domain is arithmetic. Studies investigating PES and PEIA in arithmetic are surprisingly scarce. The few studies that have examined this have found both PES and PEIA to be present in children (de Mooij et al., 2022) and adults (Desmet et al., 2012; Van der Borght et al., 2016). Both Desmet et al. (2012) and Van der Borght et al. (2016) studied PES and PEIA in a verification multiplication task in university students, and concluded that post-error adjustments can be observed in arithmetic in adults. Van der Borght et al. (2016) additionally highlighted the role of changing strategies after errors as a way to improve task performance in arithmetic. This finding suggests that, in contrast to conflict tasks, arithmetic does allow for multiple ways to adjust behavior after committing an error. Regarding post-error adjustments in children, to our knowledge, only one study has been performed in the domain of arithmetic. de Mooij et al. (2022) investigated PES in children from 5 to 13 years old in an adaptive learning environment including both mathematical and language activities. They found PES to be present in almost all learning activities, and found it to be positively associated with PEIA and the children's ability level. This latter finding suggests that PES could play an important role in explaining the large individual differences in mathematical ability, and more specifically in arithmetic skills.

While there is knowledge—albeit limited—on post-error adjustments in arithmetic, knowledge about its development in this particular domain is close to non-existent. Studies investigating the development of metacognitive control in other domains, such as spelling and memory, agree that metacognitive control undergoes substantial development during primary school (Krebs and Roebers, 2010; Roebers et al., 2014; Roebers and Spiess, 2017; Selmeczy et al., 2021), and continues to develop until late adolescence (Crone and Steinbeis, 2017). However, these studies investigated explicit operationalizations of metacognitive control, such as withdrawal of wrong answers and information-seeking. Findings regarding the development of post-error adjustments specifically remain to be mixed, as some studies found the magnitude of PES to decrease between 7 and 19 years old (Dubravac et al., 2022; Schachar et al., 2004), while Smulders et al. (2016) found it to remain stable across development until adulthood and Gupta et al. (2009) reported a non-linear developmental trend between the ages of 6 and 11. In the domain of arithmetic, there is, to our knowledge, only one study that examined the development of post-error adjustments. de Mooij et al. (2022) investigated PES cross-sectionally from 5 until 13 years old in mathematical activities. They found a non-linear developmental trend with an increase in PES from 6 to 9 followed by a decrease from 9 until 13 years old, suggesting that children from 6 to 9 years old are in an important developmental phase regarding metacognitive control in mathematical activities. The authors interpreted the decrease in PES from 9 to 13 years old as a shift from reactive control, which accounts for greater PES, to more proactive control, as previous research has provided evidence for such a shift around the age of 8 years old (Niebaum et al., 2021). Nevertheless, to our knowledge, no longitudinal investigations on metacognitive control in arithmetic have been performed as of now.

Another question that arises, especially in a developmental perspective, is whether post-error adjustments are domain-specific or domain-general. Research has only recently begun to address this question. Ger and Roebers (2023) and Dubravac et al. (2022) argue for a domain-general nature, as they found similarities in PES between different tasks at various ages ranging from 4 years old until adulthood. However, both of these studies compared conflict tasks. Studies examining this issue in academic tasks are scarce. van Loon et al. (2024) investigated the withdrawal of wrong answers as a measure of metacognitive control in three different language-based learning tasks in 8- to 12-year-olds. While they mainly observed evidence for a domain-general nature, they also found evidence for a task-specific factor. However, what is similar in all the above-described studies is that they all compared tasks that are different versions of the same task, and, therefore, are, quite similar in task-requirements and cognitive demands, for which reason correlations between tasks, which is taken as evidence for domain-generality, are likely to occur. To the best of our knowledge, studies investigating the domain-generality of metacognitive control in tasks that involve more distinct cognitive domains are non-existent. Such studies might provide a more appropriate test of the idea of domain-generality of metacognitive control, and more specifically of post-error adjustments. We will address this issue in the current study.

Extending the discussion of control as a separate skill, according to the theoretical framework of Nelson and Narens (1990), this skill is closely intertwined with monitoring, which involves the self-awareness and judgement of one's own task performance and has been shown to be a fundamental skill in diverse domains, such as memory, reading, spelling, and arithmetic (e.g., Bellon et al., 2019, 2020; Efklides and Misailidi, 2010; Rinne and Mazzocco, 2014; Schneider and Artelt, 2010; Touron et al., 2010). This theoretical assumption is supported by empirical evidence in adults. For example, adults allocate their study time based on how well they think they know the subject (Souchay et al., 2003), and seem to slow down more when they are uncertain about their answer (Dali et al., 2022). From a developmental perspective, however, the evidence for this hypothesis is less conclusive. While most studies have found an association between monitoring and control in primary school children between the ages of 8 and 12 (e.g., Destan et al., 2014; Hoffmann-Biencourt et al., 2010; Krebs and Roebers, 2010; Roebers and Spiess, 2017; Steiner et al., 2020; van Loon et al., 2024), a few studies have observed monitoring and control to operate independently from each other in that same age range (O'Leary and Sloutsky, 2017, 2019). In younger age groups, from 5 until 7 years old, most studies have failed to find an association between the two skills (e.g., Destan et al., 2014; Roebers and Spiess, 2017), while other studies observed an association between the two skills in even younger children in preschool (e.g., Coughlin et al., 2015; Gardier and Geurten, 2024). These findings suggest that, while it appears that monitoring and control become increasingly intertwined across development, their association is complex and results might depend on measurement methods, as the described studies used diverse measures of metacognitive control (e.g., Destan et al., 2014; Hoffmann-Biencourt et al., 2010; Krebs and Roebers, 2010; Roebers and Spiess, 2017). Furthermore, to our knowledge, no studies have investigated implicit measures, such as post-error adjustments, in relation to explicit metacognitive monitoring in academic tasks, which will be addressed in the current study. As a measure of metacognitive monitoring, the current study focuses on task-specific retrospective monitoring, identified as an important, unique predictor of children's concurrent (Bellon et al., 2019) and future arithmetic skills (Bellon et al., 2021; Rinne and Mazzocco, 2014). Assessing confidence judgements retrospectively is particularly interesting in relation to post-error adjustments, as this allows us to examine how these judgments are related to immediate subsequent behavior.

In the present study, we longitudinally examined metacognitive control, operationalized as PES and PEIA, in arithmetic in children of 7–9 years old, as this age range is considered an important developmental period for metacognitive regulation (de Mooij et al., 2022; Geurten et al., 2018). To do so, we had four aims. Firstly, we wanted to examine the presence of PES and PEIA during an arithmetic task in 7–8- and 8–9-year-olds, that is 2nd and 3rd grade of primary school (Research question 1). We expected to observe both PES and PEIA at both ages and predicted to observe greater PES and PEIA in 3rd grade than in 2nd grade. As an exploratory analysis, we additionally investigated the association between PES and PEIA to further unravel the underlying mechanisms of metacognitive control. Secondly, we wanted to investigate whether an association was present between PES and PEIA on the one hand and overall task performance on the other hand (Research question 2). We expected PES and PEIA to be positively correlated with overall task performance. Thirdly, we aimed to examine the association between metacognitive control (operationalized via PES and PEIA) and metacognitive monitoring (Research question 3). Given the age range of the children under study, we did not expect control to be correlated with monitoring. Fourth, the present study aimed to examine domain-generality of metacognitive control (Research question 4). To do so, we examined PES and PEIA in a working memory task to verify whether results differed with the ones found in the arithmetic task. Comparing two tasks that reflect distinct domains could yield new insights beyond those obtained from studies comparing tasks within similar domains (e.g., Dubravac et al., 2022; Ger and Roebers, 2023). While we expected to observe PES and PEIA in the working memory task as well as correlations with overall task performance, we did not expect correlations with PES and PEIA in the arithmetic task, challenging previous found evidence for domain-generality of post-error adjustments in children at this young age.

2 Methods

This study involves a secondary data analysis of the studies by Bellon et al. (2019, 2021). These studies focused on the cross-sectional associations of numerical magnitude processing, executive functions and metacognitive monitoring during arithmetic (Bellon et al., 2019) and the longitudinal associations between metacognitive monitoring, math anxiety and arithmetic (Bellon et al., 2021). None of these studies reported data on metacognitive control. As a result, measures of PES and PEIA, indices of metacognitive control, have never been analyzed and reported before, which makes the current study unique.

2.1 Participants

No a-priori sample size calculation was performed. At the outset of the longitudinal study, a total of 127 typically developing Flemish children from 2nd grade of primary school participated (64 girls; M_age = 7 years 11 months, SD = 4 months, range = 7 years 4 months to 8 years 5 months). Of these participants, 121 were followed up 1 year later in 3rd grade (63 girls; M_age = 8 years 8 months, SD = 3 months, range = 8 years 2 months to 9 years 2 months). None of them had a diagnosis of a developmental disorder, nor did any of them repeat a grade. All the participants had a predominantly middle- to high-socioeconomic background. Written informed parental consent was obtained for every participant. This study was approved by the social and societal ethics committee of KU Leuven.

2.2 Materials and measures

Materials consisted of custom computerized tasks designed with E-Prime 2.0 (Schneider et al., 2002) and a standardized paper-and-pencil test.

2.2.1 Arithmetic task

2.2.1.1 General performance

A single-digit computerized production task with addition and multiplication problems was administered. Because the accuracy rate of the addition problems was too high for the scope of this study, the current study focused only on the second part of this task, namely the multiplication problems. The multiplication problems consisted of all possible combinations of the numbers 2 through 9 as operands. Problems with 0 or 1 as one of the operands were excluded, yielding a total of 64 multiplication problems. To ensure the children were familiar with the task, six practice trials were performed at the start. After fixation, each item was presented in white on a black background for 2,000 ms. The children were instructed to respond verbally as quickly and accurately as possible as soon as the item was presented. Once the 2,000 ms passed, a black screen appeared, during which the children were still allowed to response. RTs and answers were registered by the experimenter through a key press on the computer. The task was pseudo-randomly divided into two blocks (i.e., no commutative pairs in the same block). During the first block the children were presented with the multiplication items as described above. During the second block, each arithmetic item was followed by a metacognitive monitoring measure (see below). The performance metric used was the average response time on correct multiplication trials and the total number of correct multiplication answers across the two blocks.

2.2.1.2 Metacognitive control

Metacognitive control was measured trough PES and PEIA in the computerized arithmetic task. Response times on a trial-by-trial basis were used to quantify PES. Trial-by-trial accuracy rates were used to quantify PEIA.

2.2.1.2.1 Post-error slowing

There are two prominent ways of measuring PES in the current body of literature, namely the traditional method and a robust method of Dutilh et al. (2012). The traditional method quantifies PES as the difference between the mean RT of correct trials following errors and the mean RT of correct trials following correct trials. However, according to Dutilh et al. (2012) this method can be biased because of fluctuations in attention and motivation during the task. Therefore, these authors proposed a more robust method, in which PES is quantified as the average difference between the RT of correct trials following errors and the RT of trials preceding an error. In the current study, however, the stimuli used in the computerized arithmetic task were multiplication problems, which are known to differ in the level of difficulty due to the problem size and interference effects (De Visscher et al., 2018; Imbo and Vandierendonck, 2008). This results in longer RTs and lower accuracy rates on harder problems compared to easier ones. Additionally, as Derrfuss et al. (2022) pointed out with congruent and incongruent trials in interference tasks, these differences in difficulty could account for imbalances in the percentage of post-correct, pre-error, and post-error trials. These two considerations call for the need of a quantification of PES that is corrected for these imbalances.

The current study, therefore, pioneers in using two quantifications of PES based on Derrfuss et al. (2022) in arithmetic: the corrected traditional method and the corrected robust method. This implied that we divided the multiplication problems in categories of equal difficulty based on the problem size effect (i.e., large problems are harder than small problems, Imbo and Vandierendonck, 2008) and the interference effect (i.e., problems that have more overlap in digits with previously learned problems are harder to retrieve than low interfering problems, De Visscher et al., 2018), resulting in three categories: (1) the easiest category, which consisted of problems with a problem size below or equal to 25 and an interference effect below 8, (2) the middle category, which included problems with a problem size below or equal to 25 and an interference effect above or equal to 8, or vice versa, and (3) the hardest category, which consisted of problems with a problem size above 25 and an interference effect above or equal to 8. For the corrected traditional method, PES was calculated by computing the difference between the mean RT of post-error correct trials and the mean RT of post-correct correct trials for each level of difficulty separately to control for imbalances in it, and then taking the average across these three measures for each participant. Similarly, the corrected robust method was calculated by computing the difference between the mean RT of post-error correct trials and the mean RT of pre-error correct trials for each level of difficulty separately, before averaging across these three measures for each participant. In order to not completely rely on these two quantifications of PES and because RT data are typically skewed with large variability, we additionally repeated the same quantifications making use of the median instead of the mean. This resulted in four different quantifications of PES for each participant in the computerized arithmetic task. However, during analyses we encountered some challenges related to the robust method, which are discussed in more detail in Section 3.

$PE{S}_{trad,corr}=\frac{{\displaystyle \sum ({\overline{RT}}_{PostErro{r}_{correct},dif{f}_i}-{\overline{RT}}_{PostCorrec{t}_{correct},dif{f}_i})}}{n_{diff}}$

$PE{S}_{robust,corr}=\frac{{\displaystyle \sum ({\overline{RT}}_{PostErro{r}_{correct},dif{f}_i}-{\overline{RT}}_{PreErro{r}_{correct},dif{f}_i})}}{n_{diff}}$

2.2.1.2.2 Post-error improvement in accuracy

As the above-described difficulty differences might also influence accuracy rates, PEIA in the computerized arithmetic task was quantified in a similar way to PES. We calculated the difference between the proportion of post-error trials that were answered correctly (out of the total number of post-error trials) and the proportion of post-correct trials that were answered correctly (out of the total number of post-correct trials). This was done for each difficulty level separately before averaging these differences to obtain a single PEIA measure for each participant controlled for the influence of difficulty differences.

$PEI{A}_{corr}=\frac{{\displaystyle \sum (\frac{n_{PostErro{r}_{correct},dif{f}_i}}{n_{PostErro{r}_{total},dif{f}_i}}-\frac{n_{PostCorrec{t}_{correct},dif{f}_i}}{n_{PostCorrec{t}_{total},dif{f}_i}})}}{n_{diff}}$

2.2.1.3 Metacognitive monitoring

Metacognitive monitoring was measured similarly to Rinne and Mazzocco (2014). In the second block of the computerized arithmetic task, a question was added after each item to measure task-specific retrospective metacognitive judgements. After each multiplication item, participants were asked to indicate their confidence in the accuracy of their answer. They did so by verbally choosing between “correct”, “not sure”, or “incorrect”. These three answer options were presented simultaneously on the screen accompanied by a happy, neutral, and sad smiley, respectively. The participants were presented with six practice trials to familiarize themselves with the task. Calibration of confidence scores, which represent the alignment between the participant's confidence and the actual accuracy of their arithmetic answer, were calculated on a trial-by-trial basis, as in Bellon et al. (2019, 2020, 2021). Participants got a score of 2 when they made a correct judgement (i.e., said they were correct when they were correct, or reversed), a score of 1 when they answered, “not sure”, and a score of 0 when they made an incorrect judgment (i.e., said they were correct when they were incorrect, or reversed). These scores were then averaged for each participant, yielding one calibration score per child.

2.2.2 Working memory task

2.2.2.1 General performance

Working memory was assessed using a standard 2-back task (adapted from Pelegrina et al., 2015). Participants were presented with a sequence of colored images on a computer screen. For each item, they needed to indicate whether the presented stimulus matched the one that occurred two trials back. To do so, participants pressed a green or red key, corresponding to “yes” or “no”, respectively. After fixation, the items were presented in the center of a white screen for 3,000 ms. This was followed by a black screen for 1,000 ms. The participants were allowed to answer both during the white screen and the black screen. They were instructed to answer as quickly and accurately as possible. In total, 40 items, divided into two blocks, were presented. An additional practice block of 20 trials was added to the beginning of the task to familiarize the children with the requirements. Each block started with three non-target trials (correct answer = no) and 30% of the trials in each block were target trials (correct answer = yes). The total number of correct answers served as a performance measure reflecting the participants' working memory skills.

2.2.2.2 Metacognitive control

Metacognitive control, measured trough PES and PEIA, was also assessed in the domain of working memory. Response times on a trial-by-trial basis of the 2-back task were used to quantify PES. Trial-by-trial accuracy rates were used to quantify PEIA.

2.2.2.2.1 Post-error slowing

PES in the 2-back task was quantified in the same ways as earlier described in the arithmetic task. However, as all the trials in the 2-back task are expected to be of a similar difficulty level, no correction for difficulty differences was applied. This resulted in four uncorrected measures of PES: the traditional method using the mean, the robust method using the mean, the traditional method using the median, and the robust method using the median.

2.2.2.2.2 Post-error improvement in accuracy

For the 2-back task, PEIA was quantified in the same way as in the computerized arithmetic task, except that we did not control for differences in difficulty. However, the quantification of PEIA in the 2-back task poses a challenge, as the accuracy on a trial directly depends on the participant's performance two trials before. Therefore, participants are not able to actively improve their accuracy on the trial immediately after the error but might be able to do so two or three trials after committing the error. Thus, PEIA in the 2-back task was quantified in two ways: (1) as the difference between the proportion of correct answers two trials after an error and the proportion of correct answers two trials after a correct answer, and (2) as the difference between the proportion of correct responses on trials that were completed three trials after an error and the proportion of correct answers three trials after a correct answer.

2.2.3 Control variables

The Raven's Standard Progressive Matrices (Raven et al., 1992) were used to assess intellectual ability. This standardized test was used as a control measure in our study to make sure that any associations observed between the various variables could not be explained by the intellectual ability of the children, as all of the variables of interest in our study are assumed to be associated with intellectual ability to some extent (e.g., Veenman and Spaans, 2005). Children were instructed to complete 60 patterns. To do so, they had to choose the correct answer out of the provided possibilities. The number of correctly solved patterns within the time limit of 40 min was the performance metric.

2.3 Procedure

The administered tasks were divided into three sessions. The first session was an individual session, in which each participant completed the arithmetic task. In the second session, groups of five children were tested individually on the working memory task. During this session the children were also administered other tasks, from which the data were not used in the current study. These tasks included a motor speed task, a symbolic numerical magnitude processing task, and three other executive functioning tasks. Lastly, there was a group-administered session for the intellectual ability task. This last session also included three other paper and pencil tasks, namely the Tempo Test Arithmetic, a metacognitive questionnaire, and a math anxiety questionnaire, from which the data were not used in the current study. All these sessions took place at the school of the participants during regular school hours. Each child went through the exact same order of tasks. The duration of the sessions was 40, 45, and 60 min, respectively. The participants were tested again 1 year later on the same tasks in the same order.

2.4 Analyses

We employed a combination of frequentist and Bayesian analyses to examine the data. For the Bayesian analyses, a default prior provided by the statistical program JASP (JASP Team, 2024) was used. Prior to conducting the main analyses, ANOVAs were performed to check whether the proposed difficulty categories in the arithmetic task differed in average RT and accuracy rate. The main analyses aimed to investigate the presence of PES and PEIA in primary school children in the domain of arithmetic. To do so, we ran one-sample t-tests for the various quantifications of PES and PEIA, and paired t-tests to assess developmental changes (Research question 1). Furthermore, we assessed correlations between post-error adjustments, calibration scores, and overall task performance (Research questions 2 and 3). Additionally, the same analyses were performed in the working memory task to assess the presence of metacognitive control and its correlations with overall task performance. These results were then compared with the results obtained in the arithmetic domain to investigate domain-generality of post-error adjustments (Research question 4).

3 Results

As the current study controlled for difficulty differences in the arithmetic task, we encountered some challenges during the analyses regarding the robust quantification of PES. The robust method proposed by Dutilh et al. (2012) assumes trials of similar difficulty levels, as each post-error trials needs to be compared with the pre-error trial of that same error. As there was not always a pre-error trial of the same difficulty level to compare with the post-error trials in the current study, this quantification resulted in few trials to compare within each participant, ultimately leading to a less reliable measure of PES compared to the traditional quantification. Therefore, only results from the traditional quantification are reported and discussed. Results regarding the robust method are available in the Supplementary material.

3.1 Preliminary analyses

Some participants were excluded from the analyses due to the following reasons. On the arithmetic task, 3 participants in 2nd grade and 13 participants in 3rd grade made no errors. Their data were, therefore, removed for the analyses regarding post-error adjustments. An additional 13 children committed only one error on the arithmetic task in 3rd grade, which poses an issue for the interpretation of the post-error adjustments, as PEIA would always be a positive value regardless of the actual presence of metacognitive control. These participants were, thus, also removed from the analyses of post-error adjustments. Due to a lot of participants who made only two errors on the arithmetic task in 3rd grade, possibly accounting for unreliable measures of post-error adjustments, we decided to repeat all the analyses after removing these participants. Results remained unchanged. Thus, all reported results include participants that made two or more errors on the computerized arithmetic task. Finally, data of 3 participants from 2nd grade on the 2-back task were removed due to too many non-responses.

Of the remaining participants in the computerized arithmetic task, the mean accuracy rate was 0.83 (SD = 0.38) in 2nd grade and 0.91 (SD = 0.28) in 3rd grade. A paired sample t-tests revealed significant improvement in overall accuracy from 2nd to 3rd grade on the arithmetic task [t₍₁₂₀₎ = −10.62, p < 0.001, Cohen's d = −0.97]. The mean RT was 9,243.11 ms (SD = 13,469.68) in 2nd grade and 5,161 ms (SD = 6,287.48) in 3rd grade. A paired sample t-test revealed a significant decrease in RT from 2nd to 3rd grade [t₍₁₂₀₎ = 10.70, p < 0.001, Cohen's d = 0.97]. The mean calibration of confidence score of the participants in the arithmetic task was 1.74 (SD = 0.18) in 2nd grade and 1.86 (SD = 0.13) in 3rd grade. In the 2-back task, participants had a mean accuracy rate of 0.71 (SD = 0.45) in 2nd grade and 0.75 (SD = 0.43) in 3rd grade, and a mean RT of 1,151.77 (SD = 490.57) in 2nd grade and 1,162.07 (SD = 585.12) in 3rd grade. A paired sample t-test revealed a significant improvement in accuracy from 2nd to 3rd grade on the 2-back task [t₍₁₁₈₎ = −4.51, p < 0.001, Cohen's d = −0.41].

Using ANOVA, we tested whether the chosen difficulty categories in which we divided the multiplication problems differed in RT and accuracy. The proposed difficulty categories based on the problem size and interference effect did indeed differ significantly in average RT, both in 2nd grade, F_{(2, 7, 933)} = 461.67, p < 0.001, η² = 0.10, and in 3rd grade, F_{(2, 6, 077)} = 312.94, p < 0.001, η² = 0.09. Post-hoc tests using Bonferroni correction indicated significant differences between all categories in both grades, with the slowest RTs in the hardest category and the fastest RTs in the easiest category. The results of these post-hoc tests can be found in Appendix A. The proposed difficulty categories also differed significantly in accuracy rate, both in 2nd grade, F_{(2, 7933)} = 284.88, p < 0.001, η² = 0.07 and in 3rd grade, F_{(2, 6077)} = 75.95, p < 0.001, η² = 0.02. Similar to the RTs, post-hoc tests using Bonferroni correction, of which the results can be found in Appendix A, revealed significant differences between all categories in both grades, with the lowest accuracy rate in the hardest category and the highest accuracy rate in the easiest category. These results indicate both the effectiveness of our categorization and the necessity of accounting for these differences when quantifying PES and PEIA.

3.2 Metacognitive control in arithmetic

3.2.1 Post-error slowing

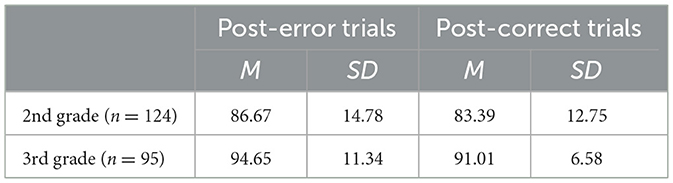
The mean and median RTs for post-error and post-correct trials at both time points are shown in Table 1 and Figure 1. To test whether there was PES in the arithmetic task (Research question 1), one-sample t-tests were performed for the different PES quantifications. When using the traditional quantification with the mean, there was no significant PES present, not in 2nd grade [t₍₁₂₃₎ = −0.38, p = 0.70, Cohen's d = −0.03], nor in 3rd grade [t₍₉₄₎ = 0.38, p = 0.70, Cohen's d = 0.04]. Thus, the children did not significantly respond slower on post-error trials compared to post-correct trials. The Bayes factor indicated moderate evidence in favor of the null hypothesis at both time points (0.10 <BF₁₀ <0.33). The corrected traditional quantification using the median, however, did reveal significant PES. This was the case in 2nd grade [t₍₁₂₃₎ = 3.12, p = 0.002, Cohen's d = 0.28], as well as in 3rd grade [t₍₉₄₎ = 3.49, p < 0.001, Cohen's d = 0.36]. Thus, using this metric, the children did significantly respond slower on post-error trials compared to post-correct trials. The Bayes factors indicated moderate to strong evidence for this effect in 2nd grade (BF₁₀ = 9.83), and very strong evidence in 3rd grade (BF₁₀ = 30.21).

Table 1

Table 1. Mean/median RT's (in ms) for post-error and post-correct trials of the arithmetic task.

Figure 1

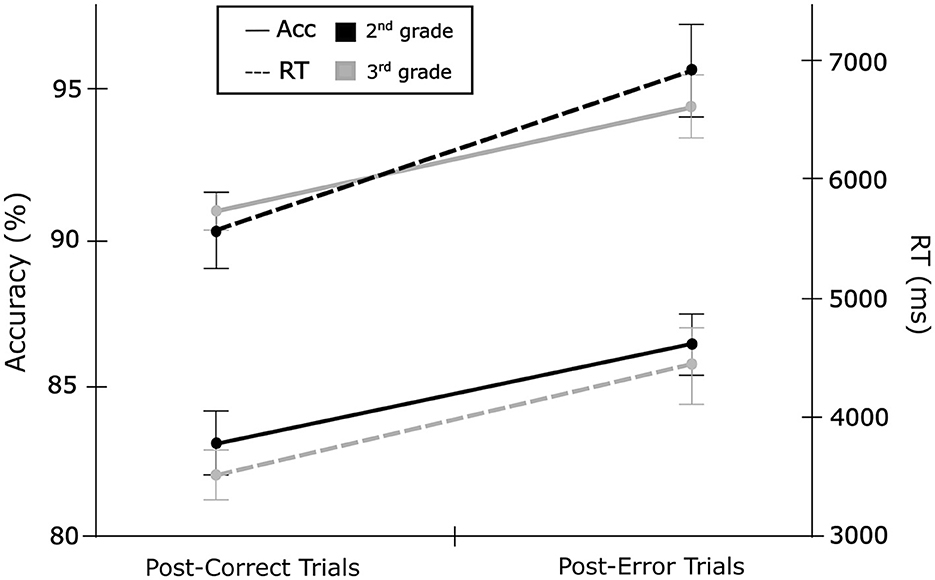
Figure 1. Mean accuracy rates and median response times after errors and corrects trials for 2nd and 3rd grade in the arithmetic task.

Using paired t-tests, we investigated whether the magnitude of PES changed from 2nd to 3rd grade. The analyses revealed no significant difference between the two time points, for neither of the traditional quantifications of PES [t₍₉₄₎ = –0.11, p = 0.91, Cohen's d = –0.01 for the corrected traditional method using the mean; t₍₉₄₎ = 1.22, p = 0.22, Cohen's d = 0.13 for the corrected traditional method using the median]. The Bayes factor indicated moderate evidence for the null hypothesis (0.10 <BF₁₀ <0.33) for both quantifications.

3.2.2 Post-error improvement in accuracy

Accuracy rates of post-error and post-correct trials at both time points are shown in Table 2 and Figure 1. To investigate the presence of PEIA in the arithmetic task (Research question 1), one-sample t-tests were performed. The analysis revealed significant PEIA in arithmetic, both in 2nd grade, t₍₁₂₃₎ = 3.12, p = 0.002, Cohen's d = 0.28, and in 3rd grade, t₍₉₄₎ = 3.32, p < 0.001, Cohen's d = 0.34. The children were, thus, significantly more accurate on trials following an error compared to trials following a correct response. The Bayes factor indicated moderate to strong evidence in 2nd grade (BF₁₀ = 9.64) and strong evidence in 3rd grade (BF₁₀ = 18.33). A paired t-test revealed that the magnitude of PEIA did not significantly change from 2nd to 3rd grade, t₍₉₄₎ = 0.08, p = 0.94, Cohen's d = 0.01. The Bayes factor (BF₁₀ = 0.11) indicated moderate evidence for the null hypothesis.

Table 2

Table 2. Accuracy rates (in %) for post-error and post-correct trials of the arithmetic task.

3.2.3 Correlations

Pearson correlation coefficients, controlled for performance on the Raven's Standard Progressive Matrices, were run to assess associations between PES, PEIA, calibration of confidence, and overall task performance in the arithmetic task. A full correlation matrix can be found in Appendix B. No significant correlations were found between PES and PEIA, neither in 2nd grade nor in 3rd grade (Research question 1). For each quantification at both time points, the Bayes factor indicated moderate evidence in favor of the null hypothesis (0.10 <BF₁₀ <0.33).

Regarding the association between metacognitive control and overall task performance (Research question 2), both the corrected traditional quantifications of PES were found to be positively correlated with the number of accurate answers on the arithmetic task in 2nd grade [r₍₁₂₁₎ = 0.22, p = 0.02 for the traditional quantification using the mean; r₍₁₂₁₎ = 0.21, p = 0.02 for the traditional quantification using the median]. The Bayes factor, however, indicated only anecdotal evidence for these associations (1 <BF₁₀ <3). The traditional quantification of PES using the median was also found to be positively correlated with the RT on correct trials in 3rd grade, r₍₉₂₎ = 0.21, p = 0.04, but the Bayes factor indicated no evidence either way (BF₁₀ = 1). No other significant correlations between PES or PEIA and overall task performance were found.

Moving on to the association between metacognitive monitoring and control (Research question 3), it is important to note that calibration of confidence is typically influenced by task performance (i.e., accurate responses are easier to judge than inaccurate responses, Fleming and Lau, 2014). This was also observable in the current study, as the mean calibration of correct trials was 1.91 (SD = 0.12) in 2nd grade and 1.91 (SD = 0.13) in 3rd grade, while for error trials this was only 0.82 (SD = 0.54) in 2nd grade and 0.93 (SD = 0.74) in 3rd grade. We, therefore, controlled for overall accuracy on the arithmetic task when running these correlations. No significant correlations were found between monitoring and post-error adjustments, not in 2nd grade nor in 3rd grade.

3.3 Metacognitive control in working memory

3.3.1 Post-error slowing

The mean and median RTs for post-error and post-correct trials at both time points are shown in Table 3 and Figure 2. One-sample t-tests revealed significant PES in the 2-back task for both traditional quantifications. This was the case in 2nd grade [t₍₁₂₃₎ = 10.14, p < 0.001, Cohen's d = 0.91 for the traditional quantification with the mean; t₍₁₂₃₎ = 9.70, p < 0.001, Cohen's d = 0.87 for the traditional quantification with the median] and also in 3rd grade [t₍₁₂₀₎ = 8.92, p < 0.001, Cohen's d = 0.81 for the traditional quantification with the mean; t₍₁₂₀₎ = 9.80, p < 0.001, Cohen's d = 0.89 for the traditional quantification with the median]. The Bayes factor indicated decisive evidence for both quantifications in both grades (BF₁₀ > 100).

Table 3

Table 3. Mean/median RT's (in ms) for post-error and post-correct trials on the 2-back task.

Figure 2

Figure 2. Mean accuracy rates and median response times after errors and correct trials for 2nd and 3rd grade in the working memory task.

Paired t-tests revealed that the magnitude of PES did not change significantly from 2nd to 3rd grade for neither of the quantifications [t₍₁₁₈₎ = −0.35, p = 0.73, Cohen's d = −0.03 for the traditional quantification with the mean; t₍₁₁₈₎ = 0.44, p = 0.66, Cohen's d = 0.04 for the traditional quantification with the median]. The bayes factor indicated moderate evidence in favor of the null hypothesis for both quantifications of PES (0.1 <BF₁₀ <0.33).

3.3.2 Post-error improvement in accuracy

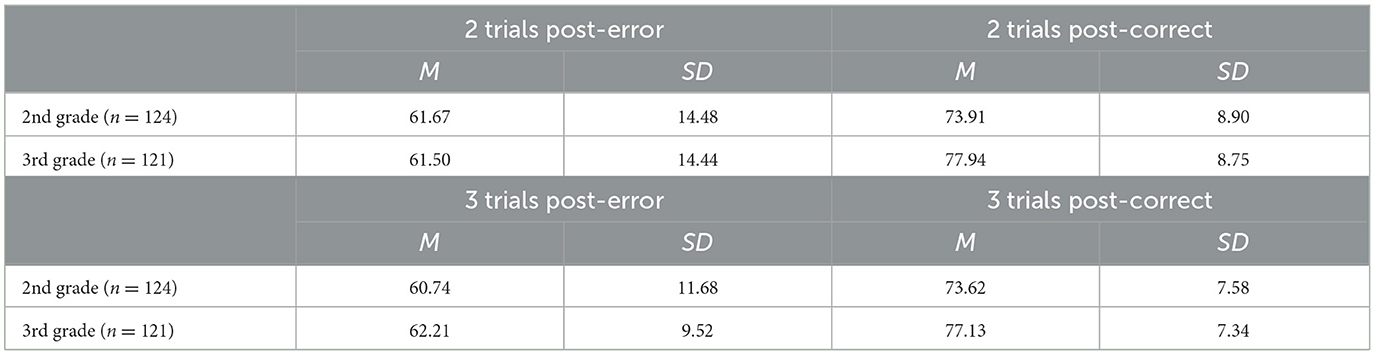
Accuracy rates of post-error and post-correct trials at both time points are shown in Table 4 and Figure 2. One-sample t-tests revealed no significant PEIA in the 2-back task, for neither of the quantifications of PEIA. To the contrary, for both quantifications, there was a significant decrease in accuracy. This was the case in 2nd grade as well as in 3rd grade [t₍₁₂₃₎ = −7.03, p < 0.001, Cohen's d = −0.63 for PEIA two trials after the error in 2nd grade; t₍₁₂₃₎ = −10.30, p < 0.001, Cohen's d = −0.92 for PEIA three trials after the error in 2nd grade; t₍₁₂₀₎ = −9.06, p < 0.001, Cohen's d = −0.82 for PEIA two trials after the error in 3rd grade; t₍₁₂₀₎ = −13.49, p < 0.001, Cohen's d = −1.23 for PEIA three trials after the error in 3rd grade]. The Bayes factor indicated decisive evidence for all these effects (BF₁₀ > 100).

Table 4

Table 4. Accuracy rates (in %) for post-error and post-correct trials on the 2-back task.

Paired t-tests revealed a significant difference in the magnitude of PEIA 2 trials after an error between 2nd and 3rd grade [t₍₁₁₈₎ = 2.48, p = 0.02, Cohen's d = 0.23]. However, the Bayes factor indicated only anecdotal evidence for this effect (BF₁₀ = 1.91). In contrast, no significant difference was found in the magnitude of PEIA 3 trials after an error between 2nd and 3rd grade [t₍₁₁₈₎ = 1.11, p = 0.27, Cohen's d = 0.10]. The Bayes factor indicated moderate evidence for the null hypothesis (BF₁₀ = 0.19).

3.3.3 Correlations

Pearson correlation coefficients, controlled for performance on the Raven's Standard Progressive Matrices, were run to assess associations between PES, PEIA, and overall task performance, as well as with PES and PEIA in the arithmetic task. A full correlation matrix can be found in Appendix C. The traditional quantification of PES with the mean was found to be negatively correlated with PEIA 2 trials after an error in 2nd grade [r₍₁₂₁₎ = −0.19, p = 0.03]. However, the Bayes factor indicated only anecdotal evidence (BF₁₀ = 1.02). No other significant correlations between the quantifications of PES and the two quantifications of PEIA were found, not in 2nd grade nor in 3rd grade.

Regarding the association between metacognitive control and overall task performance, no significant correlations between PES or PEIA and performance on the 2-back task were found in 2nd grade. Surprisingly, in 3rd grade, the two traditional quantifications of PES and PEIA 2 trials after an error were negatively correlated with performance on the 2-back task [r₍₁₁₈₎ = −0.20, p = 0.03 for the traditional quantification of PES using the mean; r₍₁₁₈₎ = −0.19, p = 0.04 for the traditional quantification of PES using the median; r₍₁₁₈₎ = −0.30, p < 0.001 for PEIA 2 trials after an error]. While the Bayes factor indicated anecdotal evidence for the null hypothesis for the correlations with PES (0.33 <BF₁₀ <1), it did reveal strong evidence for the correlation with PEIA (BF₁₀ = 24.37).

Moving on to the associations between metacognitive control in the working memory domain and metacognitive control in the arithmetic domain (Research question 4), PES in the 2-back task was not significantly correlated with PES in the arithmetic task, not in 2nd grade nor in 3rd grade, except for the traditional quantifications with the median in 2nd grade [r₍₁₁₈₎ = 0.20, p = 0.03]. However, the Bayes factor indicated only anecdotal evidence for this association (BF₁₀ = 1.30). The Bayes factor indicated moderate evidence in favor of the null hypothesis for most of the other correlations, both in 2nd and in 3rd grade (0.10 <BF₁₀ <0.33). For the correlation between the traditional quantifications with the mean in 3rd grade, the Bayes factor indicated only anecdotal evidence in favor of the null hypothesis (0.33 <BF₁₀ <1). Similarly, neither of the two quantifications of PEIA in the 2-back task were significantly correlated with PEIA in the computerized arithmetic task, not in 2nd grade nor in 3rd grade. The Bayes factor indicated moderate evidence in favor of the null hypothesis for these correlations in both grades (0.1 <BF₁₀ <0.33), except for the correlation with PEIA 3 trials after an error in the 2-back task in 3rd grade, for which the Bayes factor indicated only anecdotal evidence in favor of the null hypothesis (BF₁₀ = 0.64).

4 Discussion

This study longitudinally investigated metacognitive control, operationalized as post-error slowing (PES) and post-error improvement in accuracy (PEIA), in an arithmetic and working memory task in children from 2nd to 3rd grade of primary school. No strong evidence for PES in arithmetic was found, with only the traditional method using the median revealing significant PES effects. The great variability in the RT's between and within the children in the current study might explain why PES was only found when using the median. In contrast, we found strong evidence for PES in the working memory domain. This is a surprising result, as PES has previously been observed in children both in simple conflict tasks (e.g., Dubravac et al., 2022; Smulders et al., 2016), as well as in arithmetic (de Mooij et al., 2022).

There are two points worth mentioning regarding the absence of PES in arithmetic. First, previous studies that found PES in arithmetic, such as de Mooij et al. (2022) in children and Desmet et al. (2012) in adults, included feedback immediately following responses, while this was not the case in our study. One possibility is, therefore, that an external feedback signal after an error is necessary and a driving force for PES, especially in young children, who exhibit a stronger reaction to external feedback than adults (Ferdinand and Kray, 2014). We did, however, observe strong evidence for PES in the working memory task without feedback. Moreover, previous research has also observed PES in tasks without immediate feedback in adults (e.g., Allain et al., 2009; Houtman et al., 2012). Taken together, it is plausible that the necessity of feedback to elicit PES is greater in more complex tasks, such as arithmetic, and is, therefore, task-dependent. Research directly comparing the magnitude of PES between feedback vs. non-feedback conditions in arithmetic is, therefore, needed to gain more insights into the role of feedback in post-error adjustments.

Second, the absence of PES in arithmetic in combination with the presence of PEIA suggests that children might use control mechanisms other than slowing down to control their performance. A possibility could be that children decide to switch to a more effective strategy. Van der Borght et al. (2016) revealed that only adults who repeat the same strategy following an error exhibit PES. Adults that do not slow down after errors are the ones that change strategies after an error and are also the ones that are more accurate on post-error trials. Such patterns of performance might also be observed in children, as children have been shown to be able to select and switch strategies in arithmetic within the same task (Ardiale and Lemaire, 2013; Imbo and Vandierendonck, 2007), yet this has not been examined empirically. Studies investigating this in children are needed to obtain empirical evidence for this hypothesis. In the working memory task, individuals are more limited in post-error behavioral adjustments compared to the arithmetic task. Other than slowing down, there are not many other possibilities to control behavior in this task, which could explain why PES was observed in this domain in contrast to what was found in arithmetic.

Although we did not observe substantial evidence for the presence of PES in arithmetic, we did find strong evidence for PEIA in both grades. This suggests that children control their performance after committing errors, resulting in improved accuracy on the trial following the error. This aligns with de Mooij et al. (2022) who also revealed PEIA in children during mathematical activities. In contrast, many studies investigating PEIA in more simple tasks, such as conflict tasks, failed to observe PEIA (e.g., Hajcak and Simons, 2008; King et al., 2010; Notebaert and Verguts, 2011) or even found a decrease in accuracy on the trials following errors (e.g., Fiehler et al., 2005; Hajcak and Simons, 2008; Notebaert et al., 2009). The latter was also observed in the current study for the working memory domain. This discrepancy suggests that arithmetic allows for more ways to control behavior and improve accuracy following errors than more simple tasks. The fact that we observed a decrease in accuracy in the working memory task suggests that, in this specific task where performance on one trial is partly dependent of performance on another trial, children seem to lose control after committing an error or might be thrown off by their error, resulting in a pattern of subsequent errors after the initial error. However, it is important to note that PEIA measures in tasks where accuracy streaks are task-inherent (e.g., trials depending on each other) should be interpreted with caution (Danielmeier and Ullsperger, 2011).

PES and PEIA were not associated, neither in arithmetic nor in working memory, suggesting that slowing down is not effective in improving accuracy following errors. This is not a surprising finding considering the ongoing debate about the functionality of PES (Danielmeier and Ullsperger, 2011; Notebaert et al., 2009). The absence of an association between PES and PEIA might suggest that PES is not a reflection of cognitive control but rather a reaction to a surprising error prompting the individual to slow down, also referred to as the orienting account (Notebaert et al., 2009). Moreover, this interpretation can be backed-up with empirical evidence, as many studies have observed an absence of PEIA in combination with PES (e.g., Hajcak and Simons, 2008; King et al., 2010; Notebaert and Verguts, 2011) or a lack of association between these two post-error adjustments (e.g., King et al., 2010). What is, however, surprising is that the scarce studies in the domain of arithmetic have found PES and PEIA to be associated (Desmet et al., 2012), even in children (de Mooij et al., 2022). Moreover, most studies support the idea that PES only functions as an orienting response in simple tasks, such as conflict tasks, while it is more likely to reflect cognitive control in more complex tasks, such as arithmetic (e.g., de Mooij et al., 2022; Desmet et al., 2012). It is, therefore, plausible that the orienting account can explain the findings of the current study in the working memory domain, but not in the arithmetic domain. Perhaps more likely for the arithmetic domain is that children do slow down with the goal to control and improve their performance, but slowing down may not be the most effective way to do so. As mentioned previously, Van der Borght et al. (2016) found that switching strategies, rather than slowing down, is a more effective control mechanism in arithmetic in adults and does not necessarily occur in combination with PES.

We did not observe any developmental differences in the magnitude of the post-error adjustments between 2nd and 3rd grade, neither in arithmetic nor in working memory. While the 1-year follow-up period of the current study might be too short to capture any significant changes, as metacognitive regulation and post-error adjustments specifically are presumed to have a longer developmental trajectory (e.g., Dubravac et al., 2022), these findings are surprising. This is because previous research—albeit not all of them in the domain of arithmetic or working memory nor operationalized as post-error adjustments—have depicted the period of 7 until 9 years old as vital in the development of metacognitive control (de Mooij et al., 2022; Krebs and Roebers, 2010; Roebers et al., 2014; Roebers and Spiess, 2017; Selmeczy et al., 2021; Steiner et al., 2020). However, apart from Roebers and Spiess (2017) and Steiner et al. (2020), these studies all encompassed cross-sectional investigations rather than longitudinal ones, which could explain the difference in results with the current study. Moreover, while van Loon et al. (2024) did observe age-related differences in metacognitive control between the ages of 8 until 10 in one out of three tasks, these differences were not apparent in the other two. Steiner et al. (2020) also found age-related developmental differences to differ across tasks, suggesting that developmental differences could be task- and domain-specific.

It is, however, important to note that, while we did observe significant improvement in overall performance from 2nd to 3rd grade, the children in the current study got exactly the same tasks in 2nd grade as in 3rd grade. While other studies, although not in the domain of arithmetic, have also administered the exact same task to children from different ages and found age-related differences (e.g., Roebers and Spiess, 2017), the children in the current study were administered multiplication problems, which are known to go through major developmental progression in the age range under study in the Flemish school system. The 2nd graders in our study were still in a learning phase for multiplication, while the 3rd graders already automatized these multiplications, as is evidenced by the notable differences in accuracy rates and RTs between the two time points on the arithmetic task. More specifically, in 3rd grade we observed ceiling effects for many of the children. This could account for smaller PES and PEIA than what we might observe if the task was adjusted to their skill level. In other words, if the children were administered a task that reflected their increasing skill level, increases in the magnitude of PES and PEIA might have been observed. This hypothesis is strengthened by the study of de Mooij et al. (2022) who investigated PES in an adaptive learning environment and found the magnitude of PES to increase from the age of 6 until 9 years old. Moreover, they found PES to be greater in children that chose the highest difficulty level and, therefore, had the highest error rate.

The current study revealed a small association between PES and the overall accuracy on the arithmetic task in 2nd grade, even after controlling for intellectual ability. No such association was found in 3rd grade. The latter finding is not surprising, given that previous research suggests that metacognitive control, although not operationalized as PES or PEIA, at a young age is not always associated with overall task performance (Ger and Roebers, 2023), and that this association only emerges from the age of 10 years old onwards (van Loon and Oeri, 2023). While de Mooij et al. (2022) found PES to be positively associated with ability level in mathematical activities between the ages of 5 and 13 years old, they did not investigate the influence of age on this association, leaving it unresolved whether this association is present throughout this whole age range or, for example, only in older children. The current study found an association between PES and overall task performance in 2nd grade. Even though no strong conclusions can be drawn from this result, as the Bayes factor only indicated anecdotal evidence, there are two plausible explanations for the difference in results between 2nd and 3rd grade. First, the ceiling effects observed in 3rd grade, as mentioned earlier, could explain the lack of association between PES and overall accuracy. Second, as mentioned before, 2nd graders in Flemish schools are still in the learning phase regarding single-digit multiplication. It could, therefore, be that slowing down following errors helps children learn and memorize the material better, resulting in greater ability and better overall task performance. This hypothesis is strengthened by the findings from de Mooij et al. (2022), who, as mentioned before, found an association with ability level; importantly, they found this association in an adaptive environment that is more focused on learning than performance. Research specifically investigating post-error adjustments in an arithmetic learning protocol could provide more insights into how these behavioral adjustments might support the learning process for new arithmetic problems.

Regarding the working memory domain, the current study revealed a negative association between PEIA two trials after an error and performance on the working memory task, indicating that children who are more accurate two trials after an error perform worse on the task. This is a surprising result considering that PEIA is thought to reflect cognitive control with the goal to increase overall task performance (Danielmeier and Ullsperger, 2011). One possibility is that children might notice the error, resulting in an orientation toward and increased recall of the presented item, which ultimately results in better performance two trials later, as that trial is inherently dependent on the trial two steps before. This could, however, ultimately result in worse task performance overall, as an increased orientation to the error might make it harder for the child to regain focus on the other trials (Notebaert et al., 2009). In this situation, PEIA is, thus, not a reflection of cognitive control but rather an orienting response to the error.

Moving on to the association between metacognitive control and metacognitive monitoring, no significant associations were found. These results align with previous research, as studies suggest that an association between monitoring and control is only just emerging at this age (Hoffmann-Biencourt et al., 2010; Roebers and Spiess, 2017). A hypothesis for the lack of association between monitoring and PES is that other skills, such as executive functions, are needed to slow down after committing an error. Given that these types of skills are still developing in this age group (Diamond, 2013), children who pick up on their errors might not be able to translate this in an immediate control response, resulting in a lack of association between these two skills.

The discussion up until this point made clear that findings regarding post-error adjustments in arithmetic and post-error adjustments in working memory differed. Furthermore, we also found measures of PES and PEIA in arithmetic to be uncorrelated with PES and PEIA in working memory. These results challenge previous evidence for domain-generality of post-error adjustments found in studies by Dubravac et al. (2022) and Ger and Roebers (2023). A possible explanation for this discrepancy in results is that these studies compared different types of conflict tasks that reflect a similar domain, while the current study compared two tasks that reflect two distinct domains. Domain-generality of post-error adjustments might, therefore, only hold evidence when assessing and comparing relatively similar domains. It is, however, important to note that the two tasks used in the current study differed on more characteristics than solely the domain. First, as mentioned earlier, trials are dependent on each other in the 2-back task, while they are independent in the arithmetic task. To account for the dependency of trials in the 2-back task, we calculated PEIA in a different way than in the arithmetic task, raising challenges regarding the interpretation of the lack of association between the two tasks. Second, in contrast to the arithmetic task, PEIA was found to go in the opposite direction in the 2-back task, making the interpretation regarding correlations between the two more complicated. Such differences make it difficult to draw strong conclusions on the domain-generality of post-error adjustments and the results should, therefore, be interpreted with caution. Research investigating and comparing tasks that reflect distinct domains but are similar in task-requirements is, thus, needed.

The findings of this study should be interpreted with knowledge about its limitations, which offer opportunities for future research. First, ceiling effects present in the arithmetic task in 3rd grade might have biased or hidden possible effects and correlations. Future studies investigating post-error adjustments should avoid high accuracy rates by using tasks that reflect the participants' skill level. Second, while the current study provides new insights in the development of post-error adjustments due to its longitudinal nature, it only covered a short developmental period, which might have been insufficient to capture developmental changes. Future longitudinal studies should cover a larger age range to capture the long developmental trajectory that metacognitive control is presumed to have. Third, while the current study provides insights into post-error adjustments in an academic task, the tasks were still to some extent controlled. Although the controlled nature of the tasks is needed to isolate and obtain a clear understanding of metacognitive processes, it should be noted that there are still differences with tasks used in real classroom settings. Finally, the provided hypotheses regarding the underlying mechanisms of PES and PEIA could not be empirically evaluated in the current study. In other words, the design of this study did not allow us to investigate why children slow down or how they manage to improve their accuracy on trials. Moreover, these underlying mechanisms could be different depending on the task. Further research investigating other post-error adjustments, such as strategy switches, in combination with PES and PEIA could provide more insight into the underlying mechanisms.

In summary, the current study provides some evidence for the presence of metacognitive control, as indicated by measures of PES and PEIA, among 7–8-year-old children who were longitudinally followed up until 8–9 years old, both in arithmetic and working memory tasks. Nevertheless, notable distinctions emerged between the two domains, challenging previous evidence for domain-generality of post-error adjustments. Modest associations between metacognitive control and overall task performance in arithmetic were found at 7–8 years old, suggesting a potential adaptive role of post-error adjustments in the learning phase of arithmetic. It is, however, yet to be empirically investigated what the precise underlying mechanisms of the observed post-error adjustments are. Further research is necessary to advance our understanding of metacognitive control in arithmetic.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://osf.io/943va/.

Ethics statement

The studies involving humans were approved by Social and Societal Ethics Committee KU Leuven. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin.

Author contributions

EJ: Conceptualization, Data curation, Formal analysis, Methodology, Visualization, Writing – original draft, Writing – review & editing. EB: Conceptualization, Data curation, Investigation, Methodology, Supervision, Writing – review & editing, Project administration. BD: Funding acquisition, Project administration, Supervision, Writing – review & editing, Conceptualization, Resources, Methodology.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was supported by a WEAVE project G.0041.23 of the Research Foundation Flanders (FWO) and Austrian Research Fund (FWF) and by the Research Fund KULeuven (METH/24/003). Elien Bellon was supported by a post-doctoral fellowship of the Research Foundation Flanders (FWO).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fdpys.2024.1424754/full#supplementary-material

References

Allain, S., Burle, B., Hasbroucq, T., and Vidal, F. (2009). Sequential adjustments before and after partial errors. Psychon. Bull. Rev. 16, 356–362. doi: 10.3758/PBR.16.2.356

PubMed Abstract | Crossref Full Text | Google Scholar

Ardiale, E., and Lemaire, P. (2013). Within-item strategy switching in arithmetic: a comparative study in children. Front. Psychol. 4:924. doi: 10.3389/fpsyg.2013.00924

PubMed Abstract | Crossref Full Text | Google Scholar

Bellon, E., Fias, W., and De Smedt, B. (2019). More than number sense: the additional role of executive functions and metacognition in arithmetic. J. Exp. Child Psychol. 182, 38–60. doi: 10.1016/j.jecp.2019.01.012

PubMed Abstract | Crossref Full Text | Google Scholar

Bellon, E., Fias, W., and De Smedt, B. (2020). Metacognition across domains: is the association between arithmetic and metacognitive monitoring domain-specific? PLoS ONE 15:e0229932. doi: 10.1371/journal.pone.0229932

PubMed Abstract | Crossref Full Text | Google Scholar

Bellon, E., Fias, W., and De Smedt, B. (2021). Too anxious to be confident? A panel longitudinal study into the interplay of mathematics anxiety and metacognitive monitoring in arithmetic achievement. J. Educ. Psychol. 113, 1550–1564. doi: 10.1037/edu0000704

Crossref Full Text | Google Scholar

Coughlin, C., Hembacher, E., Lyons, K. E., and Ghetti, S. (2015). Introspection on uncertainty and judicious help-seeking during the preschool years. Dev. Sci. 18, 957–971. doi: 10.1111/desc.12271

PubMed Abstract | Crossref Full Text | Google Scholar

Crone, E. A., and Steinbeis, N. (2017). Neural perspectives on cognitive control development during childhood and adolescence. Trends Cogn. Sci. 21, 205–215. doi: 10.1016/j.tics.2017.01.003

PubMed Abstract | Crossref Full Text | Google Scholar

Dali, G., Orr, C., and Hester, R. (2022). Error awareness and post-error slowing: the effect of manipulating trial intervals. Conscious. Cogn. 98:103282. doi: 10.1016/j.concog.2022.103282

PubMed Abstract | Crossref Full Text | Google Scholar

Danielmeier, C., and Ullsperger, M. (2011). Post-error adjustments. Front. Psychol. 2, 1–10. doi: 10.3389/fpsyg.2011.00233

PubMed Abstract | Crossref Full Text | Google Scholar

de Mooij, S. M., Dumontheil, I., Kirkham, N. Z., Raijmakers, M. E., and van der Maas, H. L. (2022). Post-error slowing: large scale study in an online learning environment for practising mathematics and language. Dev. Sci. 25:e13174. doi: 10.1111/desc.13174

PubMed Abstract | Crossref Full Text | Google Scholar

De Visscher, A., Vogel, S. E., Reishofer, G., Hassler, E., Koschutnig, K., De Smedt, B., et al. (2018). Interference and problem size effect in multiplication fact solving: individual differences in brain activations and arithmetic performance. Neuroimage 172, 718–727. doi: 10.1016/j.neuroimage.2018.01.060

PubMed Abstract | Crossref Full Text | Google Scholar

Derrfuss, J., Danielmeier, C., Klein, T. A., Fischer, A. G., and Ullsperger, M. (2022). Unbiased post-error slowing in interference tasks: a confound and a simple solution. Behav. Res. Methods 54, 1416–1427. doi: 10.3758/s13428-021-01673-8

PubMed Abstract | Crossref Full Text | Google Scholar

Desmet, C., Imbo, I., De Brauwer, J., Brass, M., Fias, W., and Notebaert, W. (2012). Error adaptation in mental arithmetic. Q. J. Exp. Psychol. 65, 1059–1067. doi: 10.1080/17470218.2011.648943

PubMed Abstract | Crossref Full Text | Google Scholar

Destan, N., Hembacher, E., Ghetti, S., and Roebers, C. M. (2014). Early metacognitive abilities: the interplay of monitoring and control processes in 5-to 7-year-old children. J. Exp. Child Psychol. 126, 213–228. doi: 10.1016/j.jecp.2014.04.001

PubMed Abstract | Crossref Full Text | Google Scholar

Diamond, A. (2013). Executive functions. Annu. Rev. Psychol. 64, 135–168. doi: 10.1146/annurev-psych-113011-143750

PubMed Abstract | Crossref Full Text | Google Scholar

Dubravac, M., Roebers, C. M., and Meier, B. (2022). Age-related qualitative differences in post-error cognitive control adjustments. Br. J. Dev. Psychol. 40, 287–305. doi: 10.1111/bjdp.12403

PubMed Abstract | Crossref Full Text | Google Scholar

Dutilh, G., Van Ravenzwaaij, D., Nieuwenhuis, S., Van der Maas, H. L., Forstmann, B. U., and Wagenmakers, E. J. (2012). How to measure post-error slowing: a confound and a simple solution. J. Math. Psychol. 56, 208–216. doi: 10.1016/j.jmp.2012.04.001

Crossref Full Text | Google Scholar

Efklides, A., and Misailidi, P. (2010). Trends and Prospects in Metacognition Research. New York, NY: Springer Science + Business Media.

PubMed Abstract | Google Scholar

Ferdinand, N. K., and Kray, J. (2014). Developmental changes in performance monitoring: how electrophysiological data can enhance our understanding of error and feedback processing in childhood and adolescence. Behav. Brain Res. 263, 122–132. doi: 10.1016/j.bbr.2014.01.029

PubMed Abstract | Crossref Full Text | Google Scholar

Fiehler, K., Ullsperger, M., and Von Cramon, D. Y. (2005). Electrophysiological correlates of error correction. Psychophysiology 42, 72–82. doi: 10.1111/j.1469-8986.2005.00265.x

PubMed Abstract | Crossref Full Text | Google Scholar

Flavell, J. H. (1979). Metacognition and cognitive monitoring: a new area of cognitive–developmental inquiry. Am. Psychol. 34:906. doi: 10.1037/0003-066X.34.10.906

Crossref Full Text | Google Scholar

Fleming, S. M., and Lau, H. C. (2014). How to measure metacognition. Front. Hum. Neurosci. 8:443. doi: 10.3389/fnhum.2014.00443

PubMed Abstract | Crossref Full Text | Google Scholar

Gardier, M., and Geurten, M. (2024). The developmental path of metacognition from toddlerhood to early childhood and its influence on later memory performance. Dev. Psychol. 60, 1244–1254. doi: 10.1037/dev0001752

PubMed Abstract | Crossref Full Text | Google Scholar

Ger, E., and Roebers, C. (2023). Hearts, flowers, and fruits: all children need to reveal their post-error slowing. J. Exp. Child Psychol. 226:105552. doi: 10.1016/j.jecp.2022.105552

PubMed Abstract | Crossref Full Text | Google Scholar

Geurten, M., Meulemans, T., and Lemaire, P. (2018). From domain-specific to domain-general? The developmental path of metacognition for strategy selection. Cogn. Dev. 48, 62–81. doi: 10.1016/j.cogdev.2018.08.002

Crossref Full Text | Google Scholar

Gupta, R., Kar, B. R., and Srinivasan, N. (2009). Development of task switching and post-error-slowing in children. Behav. Brain Funct. 5, 1–13. doi: 10.1186/1744-9081-5-38

PubMed Abstract | Crossref Full Text | Google Scholar

Hajcak, G., and Simons, R. F. (2008). Oops!.. I did it again: an ERP and behavioral study of double-errors. Brain Cognit. 68, 15–21. doi: 10.1016/j.bandc.2008.02.118

PubMed Abstract | Crossref Full Text | Google Scholar

Hoffmann-Biencourt, A., Lockl, K., Schneider, W., Ackerman, R., and Koriat, A. (2010). Self-paced study time as a cue for recall predictions across school age. Br. J. Dev. Psychol. 28, 767–784. doi: 10.1348/026151009X479042

PubMed Abstract | Crossref Full Text | Google Scholar

Houtman, F., Castellar, E. N., and Notebaert, W. (2012). Orienting to errors with and without immediate feedback. J. Cogn. Psychol. 24, 278–285. doi: 10.1080/20445911.2011.617301

Crossref Full Text | Google Scholar

Imbo, I., and Vandierendonck, A. (2007). The development of strategy use in elementary school children: working memory and individual differences. J. Exp. Child Psychol. 96, 284–309. doi: 10.1016/j.jecp.2006.09.001

PubMed Abstract | Crossref Full Text | Google Scholar

Imbo, I., and Vandierendonck, A. (2008). Effects of problem size, operation, and working-memory span on simple-arithmetic strategies: differences between children and adults? Psychol. Res. 72, 331–346. doi: 10.1007/s00426-007-0112-8

PubMed Abstract | Crossref Full Text | Google Scholar

JASP Team (2024). JASP (Version 0.19.0) [Computer software]. Available at: https://jasp-stats.org/

Google Scholar

King, J. A., Korb, F. M., von Cramon, D. Y., and Ullsperger, M. (2010). Post-error behavioral adjustments are facilitated by activation and suppression of task-relevant and task-irrelevant information processing. J. Neurosci. 30, 12759–12769. doi: 10.1523/JNEUROSCI.3274-10.2010

PubMed Abstract | Crossref Full Text | Google Scholar

Krebs, S. S., and Roebers, C. M. (2010). Children's strategic regulation, metacognitive monitoring, and control processes during test taking. Br. J. Educ. Psychol. 80, 325–340. doi: 10.1348/000709910X485719

PubMed Abstract | Crossref Full Text | Google Scholar

Nelson, T. O., and Narens, L. (1990). “Metamemory: a theoretical framework and some new findings,” in The Psychology of Learning and Motivation, ed. G. H. Bower (New York, NY: Academic Press), 125–173.

Google Scholar

Niebaum, J. C., Chevalier, N., Guild, R. M., and Munakata, Y. (2021). Developing adaptive control: age-related differences in task choices and awareness of proactive and reactive control demands. Cogn. Affect. Behav. Neurosci. 21, 561–572. doi: 10.3758/s13415-020-00832-2

PubMed Abstract | Crossref Full Text | Google Scholar

Notebaert, W., Houtman, F., Van Opstal, F., Gevers, W., Fias, W., and Verguts, T. (2009). Post-error slowing: an orienting account. Cognition 111, 275–279. doi: 10.1016/j.cognition.2009.02.002

PubMed Abstract | Crossref Full Text | Google Scholar

Notebaert, W., and Verguts, T. (2011). Conflict and error adaptation in the Simon task. Acta Psychol. 136, 212–216. doi: 10.1016/j.actpsy.2010.05.006

PubMed Abstract | Crossref Full Text | Google Scholar

O'Leary, A. P., and Sloutsky, V. M. (2017). Carving metacognition at its joints: Protracted development of component processes. Child Dev. 88, 1015–1032. doi: 10.1111/cdev.12644

PubMed Abstract | Crossref Full Text | Google Scholar

O'Leary, A. P., and Sloutsky, V. M. (2019). Components of metacognition can function independently across development. Dev. Psychol. 55, 315–328. doi: 10.1037/dev0000645

PubMed Abstract | Crossref Full Text | Google Scholar

Pelegrina, S., Lechuga, M. T., García-Madruga, J. A., Elosúa, M. R., Macizo, P., Carreiras, M., et al. (2015). Normative data on the n-back task for children and young adolescents. Front. Psychol. 6:1544. doi: 10.3389/fpsyg.2015.01544

PubMed Abstract | Crossref Full Text | Google Scholar

Raven, C. J., Court, J. H., and Raven, J. (1992). Standard Progressive Matrices. Oxford: Oxford Psychologist Press.

Google Scholar

Rinne, L. F., and Mazzocco, M. M. M. (2014). Knowing right from wrong in mental arithmetic judgments: calibration of confidence predicts the development of accuracy. PLoS ONE 9:e98663. doi: 10.1371/journal.pone.0098663

PubMed Abstract | Crossref Full Text | Google Scholar

Roebers, C. M. (2017). Executive function and metacognition: towards a unifying framework of cognitive self-regulation. Dev. Rev. 45, 31–51. doi: 10.1016/j.dr.2017.04.001

Crossref Full Text | Google Scholar

Roebers, C. M., Krebs, S. S., and Roderer, T. (2014). Metacognitive monitoring and control in elementary school children: their interrelations and their role for test performance. Learn. Individ. Differ. 29, 141–149. doi: 10.1016/j.lindif.2012.12.003

Crossref Full Text | Google Scholar

Roebers, C. M., and Spiess, M. (2017). The development of metacognitive monitoring and control in second graders: a short-term longitudinal study. J. Cognit. Dev. 18, 110–128. doi: 10.1080/15248372.2016.1157079

Crossref Full Text | Google Scholar

Schachar, R. J., Chen, S., Logan, G. D., Ornstein, T. J., Crosbie, J., Ickowicz, A., et al. (2004). Evidence for an error monitoring deficit in attention deficit hyperactivity disorder. J. Abnorm. Child Psychol. 32, 285–293. doi: 10.1023/B:JACP.0000026142.11217.f2

PubMed Abstract | Crossref Full Text | Google Scholar

Schneider, W., and Artelt, C. (2010). Metacognition and mathematics education. ZDM Int. J. Math. Educ. 42, 149–161. doi: 10.1007/s11858-010-0240-2

Crossref Full Text | Google Scholar

Schneider, W., Eschman, A., and Zuccolotto, A. (2002). E-Prime Computer Software and Manual. Pittsburgh, PA: Psychology Software Tools.

PubMed Abstract | Google Scholar

Selmeczy, D., Ghetti, S., Zheng, L. R., Porter, T., and Trzesniewski, K. (2021). Help me understand: adaptive information-seeking predicts academic achievement in school-aged children. Cogn. Dev. 59:101062. doi: 10.1016/j.cogdev.2021.101062

Crossref Full Text | Google Scholar

Smulders, S. F., Soetens, E., and van der Molen, M. W. (2016). What happens when children encounter an error?. Brain Cogn. 104, 34–47. doi: 10.1016/j.bandc.2016.02.004

PubMed Abstract | Crossref Full Text | Google Scholar

Souchay, C., Isingrini, M., Pillon, B., and Gil, R. (2003). Metamemory accuracy in Alzheimer's disease and frontotemporal lobe dementia. Neurocase 9, 482–492. doi: 10.1076/neur.9.6.482.29376

PubMed Abstract | Crossref Full Text | Google Scholar

Steiner, M., van Loon, M. H., Bayard, N. S., and Roebers, C. M. (2020). Development of children's monitoring and control when learning from texts: effects of age and test format. Metacognit. Learn. 15, 3–27. doi: 10.1007/s11409-019-09208-5

PubMed Abstract | Crossref Full Text | Google Scholar

Touron, D. R., Oransky, N., Meier, M. E., and Hines, J. C. (2010). Metacognitive monitoring and strategic behaviour in working memory performance. Q. J. Exp. Psychol. 63, 1533–1551. doi: 10.1080/17470210903418937

PubMed Abstract | Crossref Full Text | Google Scholar

Van der Borght, L., Desmet, C., and Notebaert, W. (2016). Strategy changes after errors improve performance. Front. Psychol. 6:2051. doi: 10.3389/fpsyg.2015.02051

PubMed Abstract | Crossref Full Text | Google Scholar

van Loon, M., Orth, U., and Roebers, C. (2024). The structure of metacognition in middle childhood: evidence for a unitary metacognition-for-memory factor. J. Exp. Child Psychol. 241:105857. doi: 10.1016/j.jecp.2023.105857

PubMed Abstract | Crossref Full Text | Google Scholar

van Loon, M. H., and Oeri, N. S. (2023). Examining on-task regulation in school children: interrelations between monitoring, regulation, and task performance. J. Educ. Psychol. 115, 446–459. doi: 10.1037/edu0000781

Crossref Full Text | Google Scholar

Veenman, M. V., and Spaans, M. A. (2005). Relation between intellectual and metacognitive skills: age and task differences. Learn. Individ. Differ. 15, 159–176. doi: 10.1016/j.lindif.2004.12.001

PubMed Abstract | Crossref Full Text | Google Scholar