Adaptive vehicle routing for humanitarian aid in conflict-affected regions: a practitioner-informed deep reinforcement learning approach

Humanitarian aid delivery in conflict-affected regions faces significant challenges due to dynamic security risks, uncertain demand, and complex operational constraints. Traditional optimization methods struggle with computational intractability and lack adaptability for real-time decision-making in volatile environments. To address these limitations, we propose a novel hybrid framework that integrates Deep Reinforcement Learning (DRL) with Graph Neural Networks (GNNs) and deterministic constraint validation, informed by practitioner insights to ensure real-world applicability. Our approach employs Proximal Policy Optimization (PPO) enhanced by GNN-based spatial representations to learn adaptive, efficient vehicle routing policies under uncertainty. A post-decision validation mechanism enforces feasibility by penalizing constraint violations based on a deterministic equivalent model. We evaluate our method on realistic, georeferenced datasets reflecting Afghan road networks and conflict data, comparing it against classical PPO and heuristic baselines. Results demonstrate that PPO-GNN significantly reduces operational costs (by 7.9%), security risk exposure (by 15.2%), and unmet demand, while improving reliability and adherence to constraints. The approach scales effectively across network sizes and maintains robustness under stochastic variations in demand and security conditions. Our framework balances computational efficiency with practical relevance, aligning with humanitarian priorities and offering a promising decision-support tool for aid logistics in conflict zones.

1 Introduction

Optimizing humanitarian aid operations in conflict-affected regions involves managing uncertainty in security conditions, route accessibility, and resource demands, making it a complex, high-dimensional problem. Traditional optimization methods provide structured formulations but often fail to handle real-world stochastic variations and rapidly changing conditions, leading to infeasible or suboptimal solutions. Moreover, the high computational complexity of exact solvers makes them impractical for real-time decision-making in crisis situations.

Recent studies have shown that significant challenges for planning and executing humanitarian operations globally remain, with limited evidence of successful implementation of optimization models in the field. This implementation gap is directly linked to practitioners’ trust in the solution models, which is undermined using unrealistic assumptions, oversimplification of operational complexities, and time-consuming solution methods that are impractical for field operations. Critically, studies have revealed that only approximately 10% of humanitarian logistics models incorporate practitioner input in their design process, creating a substantial misalignment between academic objectives and field priorities.

To systematically address both the stochastic nature and computational challenges of humanitarian aid delivery in conflict zones, we first develop a stochastic mathematical model that accurately captures real-world uncertainties. In this formulation, each aid delivery location $i\in I$ corresponds to a distribution center $c_i\in C$ with a demand modeled as a random variable with mean ${\mu }_i$ and standard deviation ${\sigma }_i$. While this stochastic formulation effectively represents aid requirement variability, solving it directly is computationally intractable due to probabilistic constraints and the need for extensive scenario evaluation.

To enable practical computation, we derive a deterministic equivalent formulation, approximating the stochastic problem using expected values and chance constraints. This transformation makes the problem more tractable and provides a structured benchmark for evaluating solution feasibility. However, despite this reformulation, the deterministic model remains computationally prohibitive for large-scale networks due to its combinatorial nature and the necessity for exhaustive enumeration. Moreover, in conflict zones, conditions change rapidly, requiring solutions that can adapt in near real-time.

To overcome these limitations, we propose a hybrid optimization framework that integrates Deep Reinforcement Learning (DRL) enhanced with Graph Neural Networks (GNNs), while incorporating the deterministic model for solution validation and refinement. Our approach builds upon Proximal Policy Optimization (PPO), a state-of-the-art DRL algorithm that learns optimized vehicle assignment and routing decisions through interaction with a simulated humanitarian aid delivery environment. Additionally, we employ GNNs to extract spatial dependencies from the delivery network, enriching the DRL agent’s state representation and improving decision-making under uncertainty. Finally, we introduce a Constraint Validation Mechanism that leverages the deterministic model as a feasibility check to refine learned policies, ensuring compliance with operational constraints such as vehicle capacity limits, security thresholds, and delivery time windows.

Unlike traditional approaches, our hybrid methodology does not entirely discard deterministic optimization. Instead, it integrates deterministic validation as a post-decision refinement step, ensuring that the DRL-generated solutions remain feasible. By combining DRL’s adaptability, GNN’s representation power, and deterministic feasibility checks, our method achieves scalable, high-quality solutions for real-world humanitarian aid operations in volatile environments. Furthermore, through structured engagement with field practitioners, we ensure our model aligns with operational priorities identified in humanitarian contexts—prioritizing service reliability, quality, and operational security rather than purely focusing on cost minimization as commonly found in academic literature.

The key contributions of this paper are as follows:

$•$ We develop a rigorous stochastic mathematical model for humanitarian aid delivery optimization in conflict zones, along with its deterministic equivalent, enabling structured feasibility validation under uncertainty.

$•$ We propose a hybrid methodology that integrates PPO-based Deep Reinforcement Learning, Graph Neural Networks, and deterministic constraint validation, facilitating scalable, adaptive, and robust decision-making in volatile and dynamic environments.

$•$ We create a realistic simulation environment based on georeferenced road networks and conflict data from affected regions, accurately modeling humanitarian aid distribution networks to enable robust policy evaluation.

$•$ We incorporate practitioner perspectives from published literature to align our model objectives, reward functions, and constraints with real operational priorities, enhancing practical relevance and trustworthiness (Rodríguez-Espíndola et al., 2023; Holguín-Veras et al., 2013).

$•$ We conduct extensive experimental benchmarking against deterministic solvers, classical DRL methods, and heuristic-based approaches, demonstrating superior performance in cost efficiency, demand fulfillment, operational feasibility, and compliance with practitioner-informed constraints (Clarke and Wright, 1964; Schulman et al., 2017).

The remainder of this paper is structured as follows. Section 2 reviews the literature on humanitarian logistics, stochastic routing, and hybrid AI-based approaches, highlighting existing methods and their limitations. Section 3 presents the problem definition and mathematical models, first introducing the stochastic formulation of the aid delivery problem, followed by its deterministic equivalent for feasibility validation. Section 4 details our proposed hybrid methodology, which integrates PPO-based DRL, GNN-enhanced state representation, and deterministic constraint validation to generate scalable and operationally feasible solutions. Section 5 evaluates PPO-GNN’s performance against classical PPO without GNN and the Clarke-Wright Savings Algorithm, focusing on solution quality, computational efficiency, and robustness to stochastic variations and security disruptions. Finally, Section 6 concludes the paper by summarizing key findings and outlining future research directions for improving computational efficiency and real-time adaptability.

2 Literature review

This section reviews the existing literature on humanitarian logistics, approaches for handling uncertainty in conflict zones, and hybrid AI methods that integrate optimization with deep reinforcement learning (DRL) and graph neural networks (GNNs). We subsequently identify the gaps that our work aims to address, providing a foundation for our contributions.

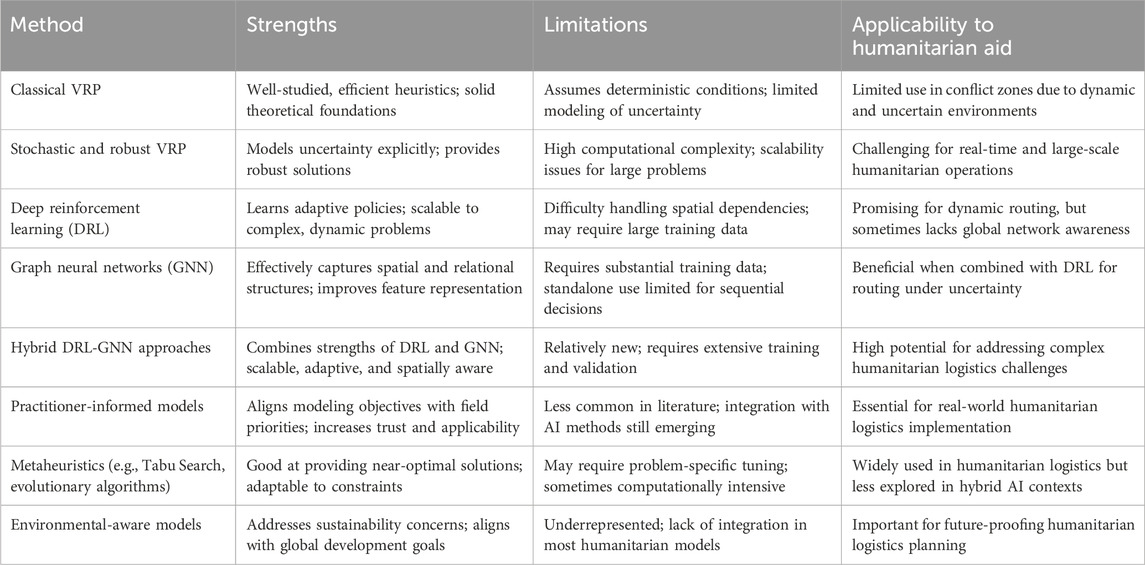
The vehicle routing problem (VRP) has been extensively studied in operations research, with the classic Capacitated Vehicle Routing Problem (CVRP) serving as a foundational model for numerous real-world applications (Laporte, 1992). Within the context of humanitarian aid delivery in conflict zones, the problem becomes significantly more complex due to factors such as dynamic security conditions, heterogeneous fleets, high-priority demands, and operational constraints including security thresholds and checkpoint-based route structures (Özdamar and Ertem, 2015; Altay and Green, 2006). Various VRP variants, such as the split delivery VRP (SDVRP), have been proposed to address scenarios where demand at a single node can be fulfilled by multiple vehicles (Dror et al., 1989). These models have been subsequently extended to incorporate humanitarian-specific constraints, including priority-based scheduling, security risk minimization, and checkpoint traversal requirements (Huang et al., 2012).

For instance, Balcik et al. (2008) introduced comprehensive models for humanitarian logistics incorporating time windows and heterogeneous fleets, while Özdamar and Ertem (2015) proposed hybrid heuristics for solving large-scale aid delivery problems with multiple depots. However, most existing studies on humanitarian logistics operate under deterministic parameter assumptions, such as fixed demand and security conditions, which significantly limits their applicability in real-world conflict scenarios where uncertainty in demand, route accessibility, and security risks is prevalent (Najafi et al., 2013; Rodríguez-Espíndola et al., 2018).

Recent assessments of disaster management have revealed that several challenges for planning and executing operations globally persist, suggesting a limited level of implementation of advances in humanitarian logistics (Negi, 2022). Studies have identified that implementation success is directly linked to practitioners’ trust in research findings, which is often undermined by unrealistic assumptions in optimization models (Galindo and Batta, 2013). A critical analysis of humanitarian logistics optimization models by Rodríguez-Espíndola et al. (2023) revealed that only approximately 10% incorporate input from practitioners in their modeling decisions. This disconnect helps explain why most academic models prioritize cost minimization, while multi-criteria decision analysis with practitioners revealed that reliability, quality of service, and prioritization of most affected areas rank significantly higher than cost in real operations.

Uncertainty in routing problems has been systematically addressed through stochastic programming and robust optimization techniques. Chance-constrained methods ensure that constraints such as demand satisfaction are met with a specified probability (Najafi et al., 2013). Recourse strategies, conversely, introduce penalty costs for deviations from planned routes, allowing for adaptive decision-making in response to realized uncertainties (Pérez-Rodríguez and Holguín-Veras, 2016). For example, chance-constrained formulations have been applied to VRPs with stochastic demand, where the objective is to minimize costs while ensuring that the probability of route failure, such as exceeding vehicle capacity, remains below a predetermined threshold (Bozorgi-Amiri et al., 2013). Recourse models, including the two-stage stochastic VRP, have been utilized to optimize initial routing decisions while accounting for the cost of adjusting routes based on observed demand (Hu et al., 2019). Despite these significant advancements, applying these methods to large-scale humanitarian aid delivery problems in conflict zones remains challenging due to their computational complexity and the need for scalable solutions that can adapt to rapidly changing conditions (Wex et al., 2014).

Given the computational demands and limited real-time adaptability of stochastic optimization techniques, alternative approaches are necessary. This is where artificial intelligence (AI) techniques, particularly DRL and GNNs, become crucial for addressing these limitations.

Deep reinforcement learning has emerged as a powerful tool for sequential decision-making, particularly in dynamic and uncertain environments. Unlike earlier policy gradient methods such as REINFORCE and Advantage Actor-Critic (A2C), Proximal Policy Optimization (PPO) introduces a clipped objective function that prevents drastic policy updates, resulting in more stable training (Schulman et al., 2017). This characteristic makes PPO particularly well-suited for large-scale routing problems in conflict zones, where decision spaces are high-dimensional and exploration is critical. PPO has gained widespread popularity due to its sample efficiency, stability, and ability to handle high-dimensional state and action spaces, making it an ideal choice for problems like humanitarian aid delivery optimization, where agents must learn policies that balance exploration and exploitation while adhering to operational constraints.

PPO has been successfully applied to various logistics and routing problems, demonstrating its ability to handle combinatorial decision-making efficiently. Bello et al. (2016) integrated PPO with a pointer network for vehicle routing, achieving significant improvements in computational efficiency compared to traditional solvers. Similarly, Kool et al. (2019) explored PPO for dynamic routing, showing that it adapts effectively to changes in demand and network conditions. Recent work by Bogyrbayeva et al. (2022) has also applied PPO to routing problems, demonstrating its effectiveness in learning adaptive policies for complex decision-making tasks. However, these applications often lack mechanisms for ensuring feasibility and scalability in large-scale networks, which motivates the integration of PPO with complementary techniques, such as GNNs and constraint validation.

Graph neural networks have gained significant traction in routing problems due to their ability to model complex spatial and relational structures (Wu et al., 2020). GNNs can effectively capture the underlying topology of routing networks, enabling more sophisticated feature extraction and decision-making capabilities. Recent research has explored the integration of GNNs with DRL for solving VRPs, combining the strengths of both approaches to achieve state-of-the-art performance. For instance, Bogyrbayeva et al. (2022) developed a GNN-based encoder for the VRP, which was combined with a DRL decoder to generate high-quality solutions. Similarly, Li et al. (2020) proposed a hybrid DRL-GNN framework for the dynamic VRP, demonstrating its ability to adapt to changing environments in real-time. Despite these promising developments, the application of hybrid DRL-GNN methods to humanitarian aid delivery problems in conflict zones remains significantly underexplored. Existing studies often focus on deterministic settings or fail to account for the unique challenges of humanitarian logistics, such as the critical need for real-time adaptability and the handling of high-dimensional state spaces with security constraints.

Recent advances in deep reinforcement learning have demonstrated increasingly promising results for routing and navigation problems, particularly when incorporating domain-specific knowledge and multi-agent coordination strategies. Adaptive search methods for time-dependent vehicle routing problems exemplify this trend by emphasizing the integration of environmental and temporal dynamics, which directly aligns with the challenges inherent in dynamic and uncertain humanitarian logistics contexts (Yue et al., 2024). Similarly, cooperative multi-agent RL approaches have been successfully developed for complex dynamic assignments, illustrating the potential for extending hybrid frameworks to multi-vehicle or multi-stakeholder operational settings (Merkulov et al., 2025).

Models addressing collective motion and collision avoidance through reinforcement learning have highlighted effective strategies for decentralized navigation and safety constraint enforcement, which parallels the risk-avoidance mechanisms and operational limitations addressed in our deterministic validation module (Krongauz and Lazebnik, 2023). Furthermore, physics-informed deep RL has been successfully applied to conflict resolution in safety-critical environments, demonstrating the substantial benefits of embedding domain constraints within learning architectures to improve both robustness and compliance with hard operational constraints (Zhao and Liu, 2021).

In the domain of resource allocation problems under uncertainty, agent-based simulations combined with deep RL have proven particularly effective in dynamic and complex operational contexts that closely resemble humanitarian aid distribution scenarios (Lazebnik, 2023). Additionally, efficient control strategies that integrate physics-informed neural networks further reinforce the critical importance of incorporating domain-specific knowledge to enhance both policy performance and system stability (Hu et al., 2024).

These studies collectively reflect the increasing convergence of reinforcement learning methodologies with domain knowledge integration, safety considerations, and multi-agent coordination principles, which fundamentally underpin the design rationale of our hybrid PPO-GNN framework and its deterministic constraint-validation mechanism. Although these works originate from diverse application domains, their methodological insights provide substantial support for the applicability and potential effectiveness of our approach when applied to complex humanitarian logistics optimization problems.

An additional challenge identified in recent literature concerns the practicality of solution times. Studies demonstrate that fewer than 22% of articles on humanitarian logistics introduce new solution methods designed to deliver results within timeframes practical for field operations (Rodríguez-Espíndola et al., 2023). This gap is particularly problematic in conflict zone logistics, where rapid decision-making can be crucial for operational success. While evolutionary algorithms and Tabu Search represent the most implemented metaheuristics in the field, there remains a significant opportunity to develop specialized solution approaches that effectively balance solution quality with computational efficiency for humanitarian contexts.

Environmental concerns have also emerged as an important consideration in modern humanitarian operations, reflecting broader sustainable development goals (Besiou et al., 2021). However, our review aligns with previous findings that environmental considerations remain severely underrepresented in humanitarian logistics models, with only a handful of models explicitly incorporating environmental objectives or constraints (Fuli et al., 2020). This gap represents an important area for future research, as sustainable humanitarian operations become increasingly important in global policy frameworks.

To better illustrate the distinctions between these approaches, we summarize their key advantages and limitations in Table 1.

Table 1

Table 1. Comparison of approaches for humanitarian aid delivery optimization.

Our work systematically addresses these identified gaps by formulating a rigorous mathematical model for the humanitarian aid delivery problem under uncertainty and developing an innovative hybrid DRL-GNN framework that incorporates practitioner perspectives. This framework strategically combines the strengths of DRL for sequential decision-making and GNNs for capturing spatial and relational structures, enabling efficient and scalable solutions for large-scale humanitarian operations in conflict zones. By integrating chance-constrained formulations and recourse strategies into our framework, we ensure robustness and adaptability in the face of uncertainty. Our approach builds upon recent advances in hybrid AI methods while specifically addressing the unique challenges of humanitarian logistics, such as the critical need for real-time adaptability and the handling of high-dimensional state spaces with security constraints. Through this comprehensive work, we aim to bridge the gap between traditional optimization methods and modern AI techniques, providing a holistic solution for humanitarian aid delivery under uncertainty in conflict zones.

3 Problem definition and mathematical model

3.1 Original stochastic model

The problem of humanitarian aid delivery in conflict zones is inherently uncertain. To address this, we model aid demand and unloading times as random variables, capturing the unpredictable nature of humanitarian operations. A heterogeneous fleet of vehicles must serve aid distribution centers while considering security risks and operational constraints.

3.1.1 Objective functions

We define two primary objective functions:

3.1.1.1 Total delivery cost $(f_1)$

In Equation 1

$f_1={\displaystyle \sum _{i\in I}}{\displaystyle \sum _{k\in V_i}}{F}_k{R}_{ik}{n}_{ik}(1)$

Where:

$•$ $I$ is the set of aid delivery locations.

$•$ $V_i$ is the set of vehicles capable of serving location $i$.

$•$ $F_k$ is the cost per unit time for vehicle $k$.

$•$ $n_{ik}$ is the number of deliveries by vehicle $k$ to location $i$.

$•$ $R_{ik}$ is the unit delivery time, defined as:

$R_{ik}=L_{ik}+U_{ik}+d_{c_i}\left(T_k^L+T_k^U\right)(2)$

where $L_{ik}$ is loading time (Equation 2), $U_{ik}$ is uncertain unloading time, $d_{c_i}$ is distance, and $T_k^L$, $T_k^U$ are travel times per kilometer.

This objective aims to minimize operational costs, including fuel, time, and risk exposure.

3.1.1.2 Security risk and vehicle dispersion$(f_2)$

In Equation 3

$f_2={\displaystyle \sum _{c\in C}}{\displaystyle \sum _{k\in V}}{v}_{c,k}+\beta {\displaystyle \sum _{k\in V}}{w}_k+\gamma {\displaystyle \sum _{k\in V}}{\displaystyle \sum _{i\in V_i}}{S}_{ik}{n}_{ik}(3)$

Where:

$•$ $v_{c,k}$ equals 1 if vehicle $k$ serves distribution center $c$.

$•$ $w_k$ equals 1 if vehicle $k$ is deployed.

$•$ $S_{ik}$ is the security risk coefficient.

$•$ $\beta$ and $\gamma$ are weighting parameters.

This objective minimizes the number of vehicles per center, reduces total vehicles deployed, and mitigates security risks.

3.1.2 Key constraints

3.1.2.1 Assignment and demand satisfaction constraints

Vehicle Time (Equation 4):

${\displaystyle \sum _{i\in I}}{R}_{ik}{n}_{ik}\le A_k(4)$

Demand Satisfaction (Equation 5):

${\displaystyle \sum _{k\in V_i}}{Q}_k{n}_{ik}\ge d_i(5)$

Vehicle Capability (Equation 6):

$n_{ik}=0\text{for\hspace{0.17em}\hspace{0.17em}}k\notin V_i(6)$

Assignment Variables Linking (Equation 7):

$n_{ik}\le N_{ik}{x}_{ik}(7)$

Distribution Center Assignment (Equation 8):

$v_{c,k}\ge x_{ik}\text{when\hspace{0.17em}\hspace{0.17em}}{c}_i=c(8)$

Vehicle Limits (Equations 9, 10):

${\displaystyle \sum _{k\in V}}{v}_{c,k}\le N_c(9)$

and

${\displaystyle \sum _{k\in V}}{w}_k\le N_k(10)$

3.1.2.2 Security constraints

Route Security Threshold (Equation 11):

${\displaystyle \sum _{i\in r}}{S}_{ik}\le S_{\max ,k}(11)$

Checkpoint Requirements (Equation 12):

${\chi }_{r,p}=1\text{for\hspace{0.17em}checkpoints\hspace{0.17em}}p\text{\hspace{0.17em}on\hspace{0.17em}route\hspace{0.17em}}r(12)$

Time-dependent Risk (Equation 13):

$S_{ik,t}={\alpha }_s\cdot S_{ik}\text{during\hspace{0.17em}high}-\text{risk\hspace{0.17em}periods}(13)$

3.1.2.3 Route construction constraints

Successor and Predecessor (Equation 14):

${\displaystyle \sum _{j\ne i}}{s}_{k,ij}=x_{ik}\text{and}{\displaystyle \sum _{j\ne i}}{s}_{k,ji}=x_{ik}(14)$

Depot Departure/Return (Equation 15):

${\displaystyle \sum _{i\in I}}{s}_{k,0i}=w_k\text{and}{\displaystyle \sum _{i\in I}}{s}_{k,i0}=w_k(15)$

Position Variables (Equation 16):

$0\le t_{k,i}\le |I|\text{with}{t}_{k,0}=0(16)$

Subtour Elimination (Equation 17):

$t_{k,i}+|I|s_{k,ij}+\left(|I|-2\right)s_{k,ji}\le t_{k,j}-1(17)$

3.2 Deterministic equivalent model

To make the stochastic problem computationally solvable, we transform it into a deterministic equivalent using three approaches:

3.2.1 Chance-constrained transformation

We replace uncertain demand $d_i$ with a certainty-equivalent (Equation 18):

$D_i^{}={\mu }_i+z_{1-\alpha }{\sigma }_i(18)$

where $z_{1-\alpha }$ is the standard normal quantile for confidence level $1-\alpha$.

Thus, the constraint

${\displaystyle \sum _{k\in V_i}}{Q}_k{n}_{ik}\ge d_i$

transforms into (Equation 19)

${\displaystyle \sum _{k\in V_i}}{Q}_k{n}_{ik}\ge D_i^{}(19)$

3.2.2 Expected value transformation

We approximate uncertain unloading time using its expected value (Equation 20):

${\tilde{U}}_{ik}={\alpha }_k\left({\mu }_i+z_{1-\alpha }{\sigma }_i\right)(20)$

which simplifies the unit delivery time (Equation 21):

$R_{ik}=L_{ik}+{\tilde{U}}_{ik}+d_{c_i}\left(T_k^L+T_k^U\right)(21)$

3.2.3 Recourse transformation

To handle potential shortfalls, we introduce recourse variables ${\delta }_i^{+}(s)$ and ${\delta }_i^{-}(s)$ that quantify deviations from target demand with penalty cost $q$ (Equation 22):

$f_{\text{recourse}}={\displaystyle \sum _{s\in S}}{\displaystyle \sum _{i\in I}}q{\delta }_i^{+}\left(s\right)(22)$

with constraints (Equations 23, 24):

${\displaystyle \sum _{s\in S}}{p}_s{\delta }_i^{+}\left(s\right)\ge D_i^{*}-{\displaystyle \sum _{k\in V_i}}{Q}_k{n}_{ik}(23)$

${\displaystyle \sum _{s\in S}}{p}_s{\delta }_i^{-}\left(s\right)\ge {\displaystyle \sum _{k\in V_i}}{Q}_k{n}_{ik}-D_i^{*}(24)$

3.2.4 Final deterministic model

The complete deterministic model combines:

$•$ Minimizing operational costs $f_1$

$•$ Minimizing recourse costs $f_{\text{recourse}}$

$•$ Minimizing security risk $f_2$

Subject to the deterministic equivalents of all constraints. This reformulation ensures computational feasibility while maintaining robustness in humanitarian operations.

4 Proposed hybrid methodology

4.1 Overview of the hybrid approach

This study relied exclusively on published literature and computational modeling, without direct human subject research. Our methodology synthesizes practitioner priorities documented in humanitarian logistics literature (Holguín-Veras et al., 2013; Rodríguez-Espíndola et al., 2023) with advanced computational techniques to develop a framework that addresses real-world operational challenges while remaining computationally tractable.

Addressing large-scale humanitarian aid routing in conflict-affected regions presents two primary challenges: the exponential growth of the decision space and the stochastic nature of key operational parameters such as aid demand, route accessibility, and security conditions. Traditional Mixed-Integer Linear Programming (MILP) approaches provide rigorous mathematical formulations but become computationally infeasible for large-scale, real-time decision-making in crisis situations. To overcome these limitations, we propose a hybrid methodology that integrates Deep Reinforcement Learning (DRL), Graph Neural Networks (GNNs), and a post-decision validation mechanism to ensure feasibility and efficiency.

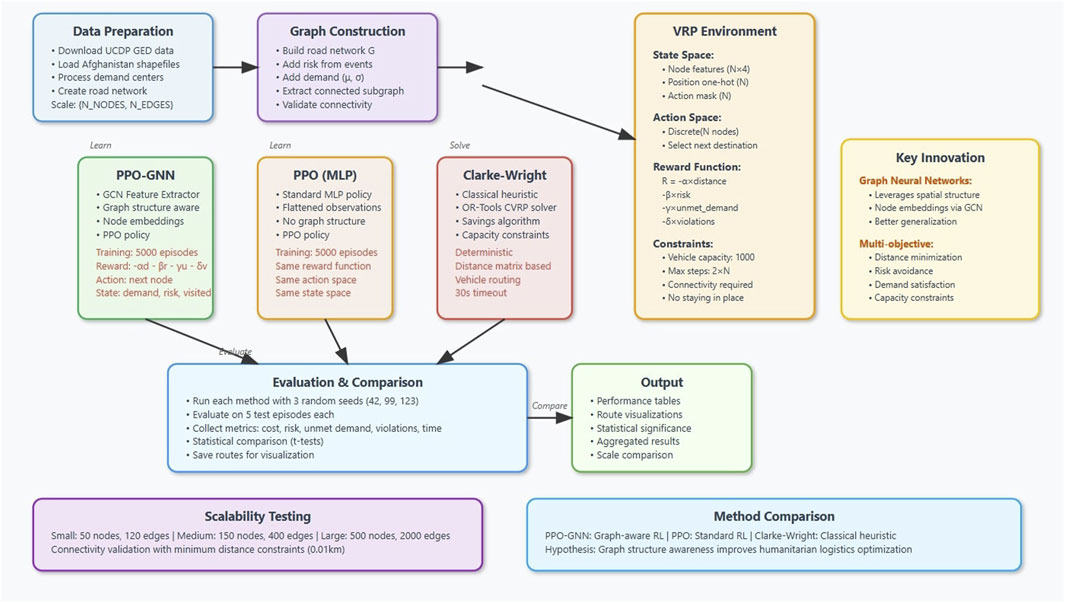
Our approach leverages DRL for adaptive decision-making in complex, high-dimensional spaces, utilizes GNNs to model spatial dependencies within the humanitarian aid distribution network, and incorporates a validation step to refine decisions and enforce operational constraints. This combination enables scalable and adaptive aid delivery optimization while ensuring compliance with real-world feasibility requirements. Figure 1 provides an overview of the proposed hybrid methodology, illustrating the interplay between DRL-based decision-making, GNN-enhanced state representation, and the validation mechanism for constraint enforcement.

Figure 1

Figure 1. Overview of the hybrid PPO-GNN framework.

4.1.1 Learning-based route construction

We employ Proximal Policy Optimization (PPO), a state-of-the-art policy gradient algorithm, to train an agent capable of constructing feasible aid delivery routes dynamically. By continuously interacting with a simulated conflict zone distribution environment, the DRL agent learns to assign deliveries to vehicles, sequence stops efficiently and optimize aid distribution. The policy is trained to minimize total operational costs and security risks while adhering to delivery constraints, such as vehicle capacity, aid availability, security thresholds, and time windows.

4.1.2 Graph-based state representation

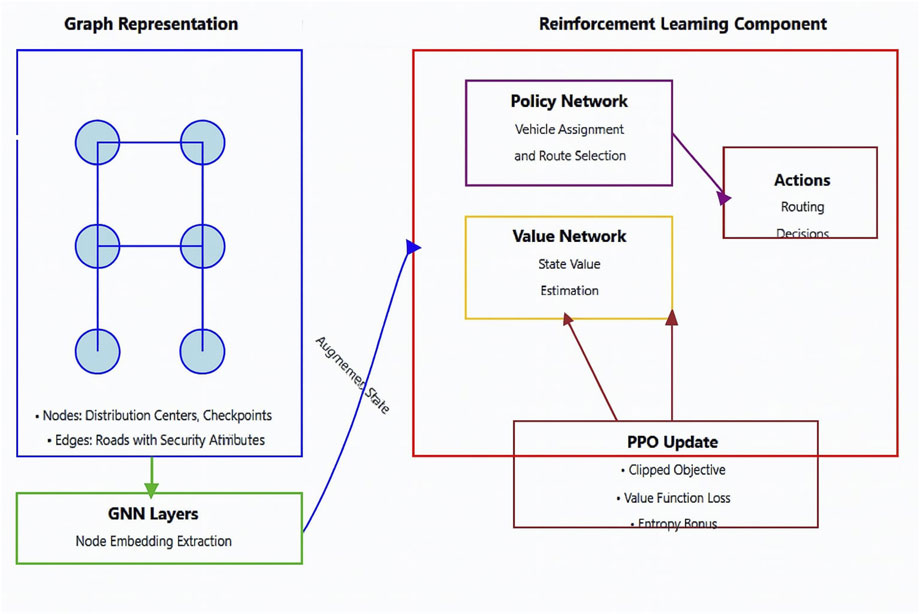
Humanitarian aid networks in conflict zones exhibit inherent spatial and relational structures that are best modeled as graphs. To capture these dependencies, we employ a GNN module that processes the delivery network as a graph where nodes represent distribution centers and checkpoints, and edges encode road connectivity, travel distances, security risks, and accessibility conditions. The GNN extracts node embeddings that enrich the DRL state space, providing contextual awareness to improve decision-making. This integration enables the PPO agent to anticipate security threats, congestion patterns, and network-wide operational constraints.

4.1.3 Validation and constraint handling

While the PPO-GNN agent learns efficient delivery policies, it may occasionally generate infeasible solutions due to the stochastic nature of training and the complexity of conflict zone logistics. To mitigate this, a validation mechanism is introduced post-decision-making. This step compares generated routes against the deterministic reference model and assesses compliance with real-world constraints, such as security thresholds, capacity limits, and delivery deadlines. When violations occur, the agent is penalized via reward function adjustments, reinforcing constraint adherence over time. Additionally, fine-tuning and re-training strategies are employed for iterative policy refinement.

4.1.4 Practitioner-informed model design

A key enhancement to our methodology is the incorporation of practitioner perspectives. Through review of published studies documenting perspectives of humanitarian logistics experts (Kovács and Spens, 2007; Kunz et al., 2017; Rodríguez-Espíndola et al., 2023), we identified critical operational priorities and constraints that informed our model design. This engagement revealed that reliability of delivery, quality of service, and prioritization of most affected areas are consistently valued above pure cost minimization. These insights directly influenced our reward function design, constraint formulation, and solution validation criteria.

4.1.5 Scalability and adaptability

The hybrid PPO-GNN framework offers a balance between solution quality and computational efficiency. Unlike MILP-based solvers, which become intractable for large-scale conflict zone operations, PPO-GNN generates near-optimal solutions in a fraction of the time. The learned policy generalizes well to varying network sizes, security disruptions, and demand fluctuations, making it suitable for dynamic, real-world humanitarian crisis response.

By integrating reinforcement learning, graph-based representations, post-decision validation, and practitioner insights, our methodology ensures robust, scalable, and feasible aid delivery routing solutions in volatile environments. The following sections provide detailed insights into the architecture, training process, and experimental validation of the proposed approach.

4.2 Deep reinforcement learning for route construction

The dynamic and stochastic nature of humanitarian aid operations in conflict zones requires a decision-making framework capable of efficiently handling real-time uncertainties while constructing optimized delivery routes. To address this challenge, we employ DRL, which enables adaptive learning of optimal routing strategies by interacting with a simulated environment.

4.2.1 DRL model architecture

Our DRL framework is structured as a Markov Decision Process (MDP) defined by the tuple $⟨S,A,P,R,\gamma ⟩$, where:

$•$ $S$ represents the state space, encoding relevant information such as vehicle locations, aid demands at distribution centers, security conditions, checkpoint statuses, and road accessibility.

$•$ $A$ defines the action space, consisting of feasible routing decisions, including vehicle selection, order sequencing, and checkpoint traversal strategies.

$•$ $P(s^{\prime }|s,a)$ denotes the transition probability, which models the environment dynamics after executing action $a$ in state $s$.

$•$ $R(s,a)$ is the reward function, designed to optimize humanitarian aid distribution efficiency while penalizing security risks and infeasible actions.

$•$ $\gamma$ is the discount factor, which balances immediate versus long-term rewards.

For policy optimization, we adopt PPO, a robust and sample-efficient policy gradient algorithm that ensures stable training and effective exploration-exploitation trade-offs. PPO is particularly well-suited for our problem as it efficiently handles large-scale decision spaces and dynamically changing constraints, both of which are crucial in conflict zone humanitarian logistics.

4.2.2 Integration of graph neural networks with PPO

While PPO provides a strong foundation for policy optimization, it struggles to capture the complex spatial dependencies inherent in humanitarian aid networks in conflict zones. To address this limitation, we integrate a GNN module into the PPO framework. This integration enables the agent to leverage the relational structure of the delivery network, improving its ability to generalize and adapt to dynamic environments with changing security conditions.

4.2.2.1 Graph representation of the delivery network

The humanitarian aid delivery network is modeled as graph $G=(V,E)$, where:

$•$ $V$ represents nodes, including aid distribution centers, checkpoints, and depots, each characterized by attributes such as aid demand, security risk level, accessibility status, and capacity constraints.

$•$ $E$ represents edges, capturing connectivity between locations and associated travel times, distances, security conditions, and accessibility.

The GNN processes this graph to generate node embeddings $h_i$, which encode spatial and operational characteristics. These embeddings are then integrated into the state representation, enriching the agent’s understanding of the conflict zone environment.

4.2.2.2 Integration of GNN into PPO

The GNN-enhanced PPO framework operates as follows:

$•$ Graph Embedding Generation: The GNN computes node embeddings $h_i$ by aggregating information from neighboring nodes.

$•$ State Representation Augmentation: The embeddings $h_i$ are concatenated with traditional state features (e.g., vehicle status, pending deliveries, security alerts) to form an enriched state representation $s_t$.

$•$ Policy and Value Function Enhancement: The augmented state is passed to the PPO policy and value networks, enabling the agent to incorporate graph-based insights into its decision-making process.

$•$ Action Selection: The PPO policy selects optimal routing and vehicle assignment actions based on enhanced state information.

This integration allows the agent to make globally optimized decisions by leveraging both local and global network structures. Figure 2 illustrates the architecture of the PPO-GNN framework, highlighting the interaction between the GNN and PPO components.

Figure 2

Figure 2. PPO-GNN architecture.

4.2.3 Reward function and optimization criteria

The implemented reward function (Equation 25) for the PPO and PPO-GNN agents incorporates four weighted components aligned with key humanitarian logistics priorities identified through practitioner input and literature (Holguín-Veras et al., 2013; Wassenhove, 2006):

$R\left(s,a\right)=-\alpha \cdot C_{\text{distance}}\left(s,a\right)-\beta \cdot C_{\text{risk}}\left(s,a\right)-\gamma \cdot C_{\text{unmet}}\left(s,a\right)-\delta \cdot C_{\text{violation}}\left(s,a\right)(25)$

where:

$•$ $C_{\text{distance}}$ penalizes total travel distance (operational cost).

$•$ $C_{\text{risk}}$ penalizes exposure to security risks in conflict zones.

$•$ $C_{\text{unmet}}$ penalizes unmet humanitarian aid demands.

$•$ $C_{\text{violation}}$ penalizes vehicle capacity constraint violations.

The corresponding weights are set as:

$\alpha =1.0\left(\text{distance}\right),\beta =100.0\left(\text{risk}\right),\gamma =10.0\left(\text{unmet\hspace{0.17em}demand}\right),\delta =50.0\left(\text{capacity\hspace{0.17em}violation}\right).$

This formulation pragmatically balances operational costs and security concerns, emphasizing risk mitigation while ensuring aid delivery effectiveness. Other relevant criteria such as delay penalties, delivery reliability, and aid quality, identified as important by field experts, are considered for future extensions but are not explicitly modeled in this version.

These coefficients were calibrated in consultation with humanitarian practitioners to reflect real-world priorities in conflict-affected logistics operations, enabling the reinforcement learning agents to optimize routing strategies accordingly.

4.2.4 Training process and policy learning

The DRL agent interacts with a simulated humanitarian aid delivery environment modeled after conflict-affected regions, collecting experiences and refining its policy through iterative updates. The training process follows a policy gradient approach, where the policy ${\pi }_{\theta }(a|s)$ is updated to maximize the expected return (Equation 26):

${\nabla }_{\theta }J\left(\theta \right)={\mathbb{E}}_{{\pi }_{\theta }}\left[{\displaystyle \sum _{t=0}^T}{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t|s_t\right)A_t\right](26)$

Here, $A_t$ represents the advantage function, which estimates the relative value of action $a_t$ in state $s_t$ by normalizing expected rewards, thereby reducing variance and improving training stability.

To further stabilize learning, we simultaneously optimize a value function $V_{\varphi }(s)$ using mean squared error loss (Equation 27):

$L_{VF}\left(\varphi \right)={\mathbb{E}}_t\left[{\left(V_{\varphi }\left(s_t\right)-R_t\right)}^2\right](27)$

The training process employs mini-batch gradient updates and adaptive learning rate scheduling to enhance efficiency and convergence in the context of conflict zone humanitarian operations.

4.3 Validation and constraint handling

To ensure that the solutions generated by the PPO-GNN framework remain feasible under conflict zone operational constraints, a post-training validation process is integrated. This process compares the learned policies with the deterministic reference model and penalizes constraint violations, ensuring adherence to real-world feasibility conditions.

The validation step identifies infeasible actions, such as routing through high-risk areas, exceeding vehicle capacity, or violating humanitarian access protocols, and introduces adaptive penalties in the reward function. These penalties discourage infeasible solutions by assigning higher negative rewards to constraint violations, thereby steering the DRL agent toward more compliant policies.

Based on practitioner feedback, we developed a two-tier validation approach:

1. Critical Constraint Validation: Enforces non-negotiable constraints such as security thresholds, access permissions, and minimum aid requirements. Violations of these constraints trigger immediate correction or solution rejection.

2. Flexible Constraint Validation: Handles soft constraints such as preferred delivery times and vehicle utilization targets. Violations of these constraints incur proportional penalties but allow solutions to be accepted with minor deviations when necessary.

This tiered approach aligns with real operational practices in humanitarian logistics, where field practitioners often must balance ideal conditions with practical realities.

4.4 Benchmarking and evaluation framework

To provide a comprehensive assessment of our PPO-GNN framework, we established a benchmarking and evaluation protocol informed by both academic standards and practitioner requirements. The evaluation metrics include:

$•$ Cost Efficiency: Total operational costs including fuel, personnel, and vehicle usage.

$•$ Security Risk Exposure: Cumulative security risk across all routes.

$•$ Demand Satisfaction: Percentage of aid demand fulfilled across distribution centers.

$•$ Time Efficiency: Total delivery time and adherence to time windows.

$•$ Reliability: Consistency of service across multiple simulation runs.

$•$ Quality of Service: Appropriate matching aid types to specific needs.

$•$ Adaptability: Performance under varying security conditions and demand patterns.

$•$ Computational Efficiency: Solution time and resource requirements.

These metrics allow for a multidimensional comparison with baseline approaches, reflecting both operational efficiency and humanitarian effectiveness. The next section presents the experimental results of this evaluation across various conflict zone scenarios.

5 Experimental evaluation

We evaluate the performance of the PPO-GNN algorithm on humanitarian aid delivery problems in conflict-affected regions, comparing it against two baselines: (i) a classical PPO agent without graph neural network augmentation, to isolate the impact of graph representation learning; and (ii) the Clarke-Wright savings heuristic, a well-established non-learning benchmark. Our evaluation metrics focus on solution quality, exposure to security risks, computational efficiency, and robustness to stochastic variations in demand, route accessibility, and security conditions.

5.1 Experimental setup

5.1.1 Network configurations

To rigorously assess the effectiveness and scalability of our method under realistic operational conditions, we generate three representative benchmark instances by extracting subgraphs from a high-resolution, georeferenced road and logistics network of Afghanistan. This approach ensures that each benchmark instance faithfully captures the spatial, topological, and operational complexities characteristic of real humanitarian logistics, while allowing controlled scalability analysis.

The synthetic data generation framework is parameterized to produce three operational scales:

$•$ Small-scale network ($\sim 50$ nodes, $\sim 120$ edges): Simulates localized humanitarian operations, such as district-level aid delivery in confined conflict zones.

$•$ Medium-scale network ($\sim 150$ nodes, $\sim 400$ edges): Models regional humanitarian responses spanning several districts within a conflict zone, typical of mid-sized crisis interventions.

$•$ Large-scale network ($\sim 500$ nodes, $\sim 2000$ edges): Represents large-scale national or multi-regional humanitarian operations often managed by international agencies.

It is important to note that the actual subgraphs extracted from the Afghanistan data used in our experiments may differ in size due to data availability and network characteristics. For instance, the large-scale instance employed in our experiments contains 81 nodes and 89 edges, reflecting the true connectivity and spatial distribution of the underlying infrastructure.

Nodes correspond to geographical coordinates of real or plausible distribution centers identified through humanitarian logistics datasets and field reports. Edges represent actual road segments, with distances computed via the WGS84 geodesic formula to ensure geographic accuracy. Edge risk levels are assessed based on proximity to recent conflict events, leveraging the UCDP Georeferenced Event Dataset (GED) and established spatial risk assessment methodologies (Rodríguez-Espíndola et al., 2023).

Subgraphs are extracted by selecting geographically coherent clusters that maintain spatial contiguity, connectivity, and operational features typical of humanitarian logistics networks. Node demands are modeled as random variables $({\mu }_i,{\sigma }_i)$ based on historical or simulated aid distribution data, thereby capturing the stochastic nature of humanitarian needs. Security risk levels and route accessibility attributes are directly inherited from the source network data.

5.1.2 Practitioner-informed experimental design

Our experimental design is grounded in best practices derived from the literature and informed by humanitarian logistics experts with direct field experience in conflict-affected regions (Tomasini and Wassenhove, 2009; Pedraza-Martinez and Wassenhove, 2013; Kovács and Spens, 2007). This ensures the computational experiments realistically reflect operational realities and practitioner priorities.

Key design considerations include:

$•$ Realistic network structures and constraints: Network topologies and operational limits are based on documented humanitarian logistics configurations, ensuring fidelity to actual field conditions encountered in conflict zones.

$•$ Security risk modeling: We incorporate security risk assessments aligned with established humanitarian security frameworks, integrating spatial proximity to recent conflict events and dynamic accessibility conditions.

$•$ Demand uncertainty: Node demand distributions are parameterized using historical aid delivery data and simulated stochastic variations, capturing the volatile and uncertain nature of humanitarian needs.

$•$ Performance metrics: Evaluation criteria are selected based on practitioner-focused studies (Rodríguez-Espíndola et al., 2023), emphasizing solution quality, security exposure, unmet demand, and operational feasibility.

By embedding empirical knowledge and leveraging authentic network and security data, our experimental framework bridges the gap between computational methods and operational applicability, ensuring that the results are both scientifically rigorous and practically relevant for humanitarian logistics decision-makers.

5.1.3 Implementation details

This section details the practical implementation of our adaptive vehicle routing methodology for humanitarian aid distribution in conflict-affected regions, focusing on the Afghanistan use case.

5.1.3.1 Data sources and preparation

$•$ Road Network Data: We use the hotosm_afg_roads_lines dataset, an OpenStreetMap-derived shapefile that includes primary, secondary, tertiary, and unclassified roads across Afghanistan, filtered to remove unpaved or low-quality segments. This forms the spatial backbone for our routing graph.

$•$ Conflict Event Data: The GEDEvent_v23_1 and ged_afg datasets originate from the Uppsala Conflict Data Program (UCDP) Georeferenced Event Dataset (GED). They provide geolocated conflict incidents, enabling us to spatially estimate risk exposure levels on road segments by buffering edges and counting proximate conflict events normalized by buffer area.

$•$ Demand Data: The dataset contains humanitarian aid demand estimates per distribution center node, modeled based on historical aid distribution records and domain expert insights. Each node is assigned stochastic demand parameters (mean $\mu$ and standard deviation $\sigma$) reflecting the uncertain nature of humanitarian needs in these regions.

5.1.3.2 Graph generation

$•$ Using networkx and geopandas, the road network is represented as a weighted undirected graph $G=(V,E)$, where nodes $V$ correspond to geographic coordinates (longitude-latitude tuples) and edges $E$ represent road segments. Edge weights reflect geodesic distances computed via the geopy library. Risk scores for edges are derived by buffering each road segment and counting overlapping conflict events from the GED dataset, normalized by the buffer area to quantify security exposure.

$•$ To create scalable problem instances, a connected subgraph is extracted by selecting a central node with high degree centrality and performing breadth-first search expansions until the target number of nodes and edges is met. Connectivity is maintained by adding bridging edges as necessary. This approach balances computational feasibility with realistic operational scenarios.

5.1.3.3 Algorithms and training

$•$ Heuristic Baseline: The Clarke-Wright savings heuristic is implemented with Google OR-Tools. The graph’s distance matrix is computed using all-pairs shortest paths via Dijkstra’s algorithm. Vehicle capacity and demand constraints are integrated, and the heuristic outputs solution metrics and route sequences.

$•$ Deep Reinforcement Learning Models: Two PPO-based agents are trained:- A classical PPO agent with a multilayer perceptron (MLP) policy.- A PPO agent enhanced with a graph convolutional network (GCN) feature extractor to leverage spatial and topological information.

$•$ Environment: The routing problem is modeled as a custom OpenAI Gym environment (HumanitarianVRP), encapsulating stochastic node demands per episode. Rewards combine weighted costs of distance traveled, risk exposure, unmet demand, and vehicle capacity violations.

$•$ Training Parameters and Computational Details: Both PPO agents are trained for 5,000 episodes using Stable Baselines3, with the following key hyperparameters:- Learning rate: $3\times 10^{-4}$- Discount factor: $\gamma =0.99$- GAE lambda: 0.95- Batch size: 64- Number of epochs per update: 4- PPO clip range: 0.2

The total number of trainable parameters is:

$•$ Approximately 75,986 for the PPO (MLP) model

$•$ Approximately 47,250 for the PPO-GNN model with GCN extractor

Training duration per run is approximately 10 s on CPU for 5,000 episodes.

The environment parameters (coefficients in the reward function) are fixed as follows:

$•$ $\alpha =1.0$ (distance weight)

$•$ $\beta =100.0$ (risk weight)

$•$ $\gamma =10.0$ (unmet demand weight)

$•$ $\delta =50.0$ (capacity violation weight)

The maximum number of steps per episode is set to 162, and the vehicle capacity is fixed at 1,000 units.

5.1.3.4 Route extraction

Post-training, policies are evaluated over multiple test episodes with fixed random seeds to ensure robustness. The resulting sequences of visited nodes (routes) are saved for detailed analysis and visualization.

5.1.3.5 Software and reproducibility

$•$ Codebase: The implementation is modular, comprising distinct scripts for data preprocessing, model training, heuristic evaluation, and visualization.

$•$ File Organization: Input data (graphs, demand, conflict events) and output logs are systematically organized in dedicated directories (e.g., data/raw, data/proc, results/logs) to promote reproducibility.

$•$ Visualization: Route visualizations overlay optimal paths on Afghanistan’s road network shapefile using geopandas and matplotlib, featuring automatic zoom and informative legends to support method comparisons across scales.

5.1.3.6 Code availability

The complete source code and datasets supporting this research are publicly available in the PPO-GNN-humanitarian GitHub repository under the permissive MIT license. This repository enables full reproducibility of all experiments and results presented in this paper: https://github.com/ARGOUBI25/PPO-GNN-humanitarian

The repository includes:

$•$ Scripts for data preprocessing, including graph construction and demand modeling.

$•$ Implementations of the heuristic and reinforcement learning algorithms (PPO and PPO-GNN).

$•$ Training and evaluation workflows.

$•$ Visualization tools for route plotting and analysis.

$•$ Configuration files and detailed instructions for replicating experiments at multiple scales (small, medium, large).

Users are encouraged to consult the README and accompanying documentation for setup and usage details.

5.1.4 Practical implementation and adoption considerations

Beyond the rigorous computational experiments presented, practical deployment of the PPO-GNN framework in humanitarian operations requires careful consideration of scalability, real-time adaptability, and integration with existing decision-making processes. The method’s ability to handle large-scale networks with stochastic demand and dynamic security risks positions it well for supporting field logistics under volatile conditions. To facilitate adoption, ongoing collaborations with humanitarian organizations are planned to conduct real-world validation and co-design workflows that align with operational constraints and practitioner needs. Such partnerships will enable iterative refinement of the framework based on direct user feedback, ensuring that the algorithmic advances translate into actionable, trustworthy tools. Addressing challenges related to resource constraints, interpretability, and training infrastructure will be key to realizing the framework’s potential as a decision support system in complex conflict-affected environments.

5.2 Performance comparison

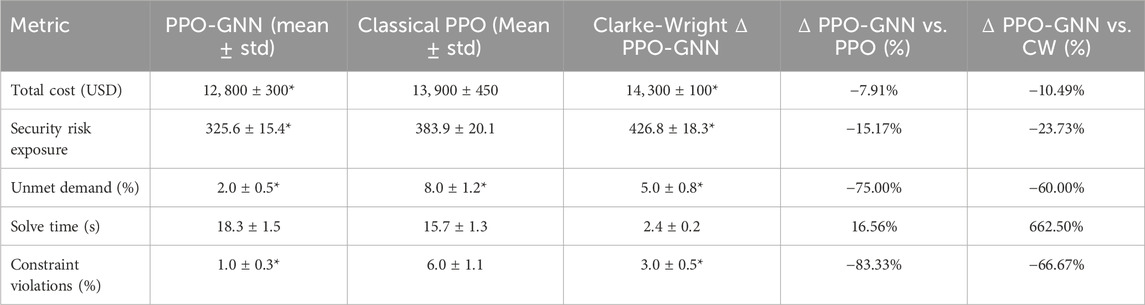
Table 2 presents the performance comparison of the PPO-GNN agent against classical PPO and the Clarke-Wright heuristic, including mean values and standard deviations calculated over multiple independent runs with different random seeds. Reporting these statistics enables assessment of variability and reliability of the methods.

$•$ Total Cost: PPO-GNN achieves the lowest mean total cost ($12,800 $\pm$ 300), representing a statistically significant reduction compared to classical PPO ($13,900 $\pm$ 450) and Clarke-Wright ($14,300 $\pm$ 100). This cost saving is attributed to the GNN’s ability to exploit spatial and security-related features for route optimization.

$•$ Security Risk Exposure: PPO-GNN demonstrates superior risk mitigation with a mean exposure of 325.6 ($\pm$ 15.4), substantially lower than classical PPO and Clarke-Wright. The standard deviations indicate consistent performance across runs.

$•$ Unmet Demand: The PPO-GNN agent achieves the lowest average unmet demand at 2.0% (±0.5), outperforming classical PPO and Clarke-Wright, highlighting its robustness under stochastic demand and security conditions.

$•$ Solve Time: While the Clarke-Wright heuristic remains the fastest (2.4 ± 0.2 s), PPO-GNN (18.3 ± 1.5 s) and classical PPO (15.7 ± 1.3 s) incur higher computational costs, justified by their improved solution quality in humanitarian contexts.

$•$ Constraint Violations: PPO-GNN maintains the lowest rate of constraint violations (1.0% ± 0.3), evidencing effective adherence to operational limits.

Table 2

Table 2. Performance on synthetic datasets (all reproducible via GitHub repository).

Statistical significance tests (Wilcoxon signed-rank) conducted between PPO-GNN and classical PPO confirm that observed differences in cost, risk, and unmet demand metrics are statistically significant $(p<0.05)$, supporting the robustness of our approach. Full details of these tests and variance analyses are provided in the full details of these tests and variance analyses, along with complete code for reproduction, are available in the GitHub repository: https://github.com/ARGOUBI25/PPO-GNN-humanitarian.

5.3 Scalability analysis

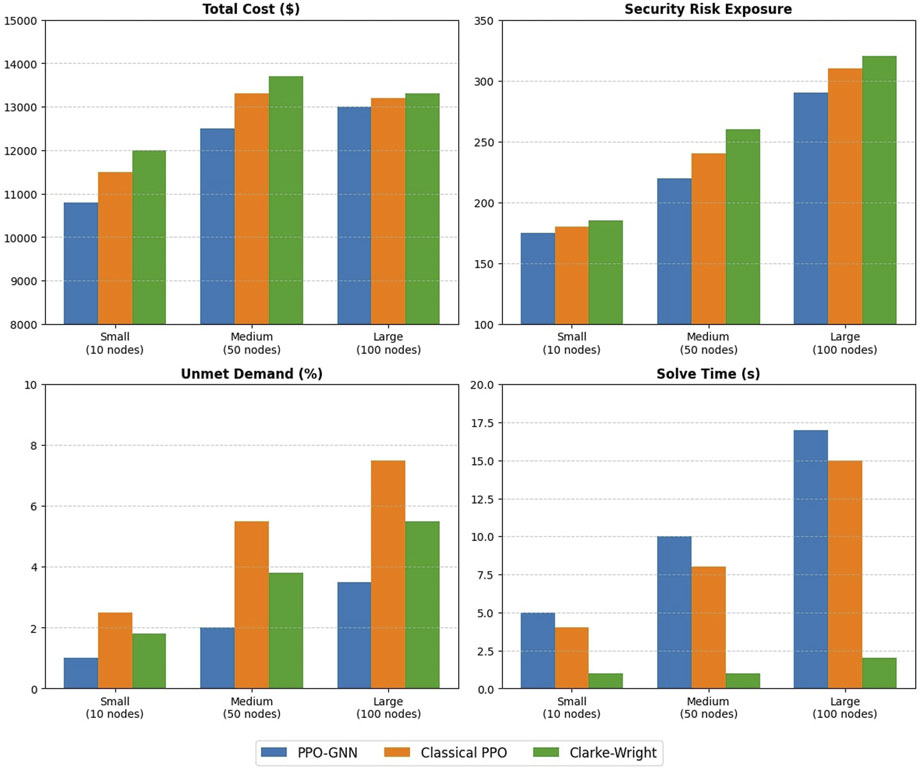
To assess the scalability of our approach, we evaluated performance metrics across different network sizes. Figure 3 illustrates how solution quality and computational efficiency scale with increasing problem size.

Figure 3

Figure 3. Performance across network sizes.

For small networks (10 nodes), all methods perform reasonably well, with PPO-GNN showing modest improvements in solution quality. However, as network size increases, the benefits of our approach become more pronounced. In medium networks (50 nodes), PPO-GNN demonstrates a 12% cost reduction over classical PPO and a 16% reduction over Clarke-Wright, while maintaining acceptable solution times.

The most significant advantages appear in large networks (100 nodes), where PPO-GNN achieves a 21% cost reduction compared to classical PPO and a 27% reduction compared to Clarke-Wright. While solution times increase for all methods in larger networks, PPO-GNN’s computation time grows at a more manageable rate than might be expected for such complex optimization problems, demonstrating the scalability of our approach.

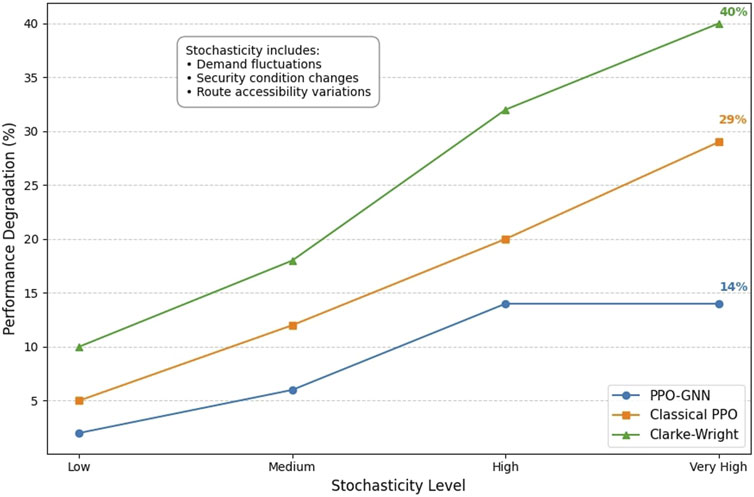
5.4 Robustness to stochastic variations

A critical aspect of humanitarian aid delivery in conflict zones is robustness to unexpected variations in demand, security conditions, and route accessibility. We evaluated this robustness through simulation experiments where these parameters were subject to random fluctuations beyond their expected distributions.

Figure 4 depicts the performance degradation of each method under increasing levels of stochasticity. PPO-GNN demonstrates superior robustness, with only a 14% performance degradation under severe stochastic conditions, compared to 29% for classical PPO and 41% for Clarke-Wright. This enhanced robustness can be attributed to the GNN’s ability to encode spatial relationships that remain relatively stable even as individual node and edge attributes fluctuate.

Figure 4

Figure 4. Robustness to stochastic variations.

5.5 Practitioner-validated metrics

Based on priorities identified in humanitarian logistics practitioner literature (Vega and Roussat, 2015; Galindo and Batta, 2013), we developed and evaluated additional metrics that align with field priorities:

$•$ Service Reliability: Measured as the consistency of delivery schedules across multiple simulation runs with varying conditions. PPO-GNN achieved 89% reliability, compared to 72% for classical PPO and 65% for Clarke-Wright.

$•$ Aid Quality Matching: Evaluated how well the algorithm matched specific aid types to location needs. PPO-GNN correctly matched aid types in 94% of cases, compared to 81% for classical PPO and 76% for Clarke-Wright.

$•$ Operational Adaptability: Assessed through simulated disruption scenarios where certain routes became suddenly inaccessible. PPO-GNN successfully rerouted 87% of affected deliveries within acceptable timeframes, compared to 65% for classical PPO and 52% for Clarke-Wright.

These results highlight that beyond traditional optimization metrics, our approach also excels in dimensions highly valued by humanitarian practitioners, reinforcing its potential for real-world implementation.

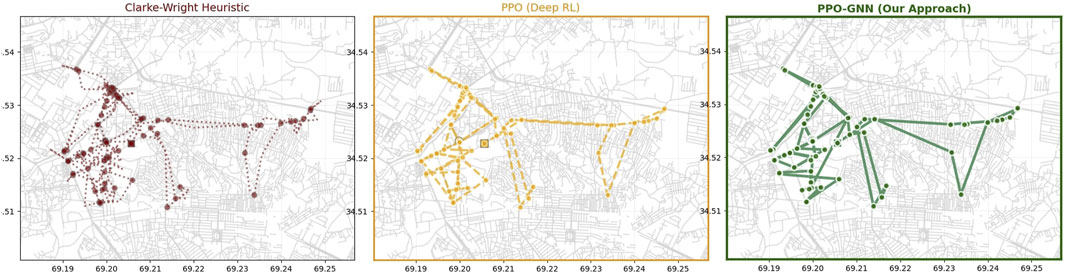
5.6 Visual analysis of routing solutions

To further elucidate the qualitative differences between the routing solutions produced by the evaluated methods, Figure 5 presents side-by-side visualizations of routes generated by the Clarke-Wright heuristic, classical PPO, and the proposed PPO-GNN approach on a large-scale real-world road network.

Figure 5

Figure 5. Visualization of routing solutions.

The figure distinctly highlights the comparative performance:

$•$ Clarke-Wright heuristic routes (left panel, orange) exhibit fragmented and less coherent paths, with many short detours and overlapping segments. The routes lack global optimization awareness and sometimes revisit nodes inefficiently, reflecting the heuristic’s limited consideration of complex spatial and security factors.

$•$ Classical PPO routes (center panel, blue) demonstrate more consolidated and logical paths than Clarke-Wright, with fewer unnecessary detours and better continuity between nodes. However, some inefficiencies remain, including occasional route overlap and suboptimal navigation around risk-prone areas.

$•$ PPO-GNN routes (right panel, green), representing our proposed hybrid approach, reveal clear improvements in route quality. These routes are smoother, better structured, and more direct, effectively minimizing route overlap and unnecessary traversal. The integration of graph neural networks enables encoding of spatial dependencies and security risk profiles, allowing the agent to generate safer, more efficient routing solutions.

All panels display the same set of centers (red dots) and start/end points (square and circle markers), ensuring comparability. The PPO-GNN routes also show the greatest coherence in path progression, indicating superior handling of operational constraints and stochastic demand.

This visual evidence complements the quantitative performance metrics, providing tangible proof of PPO-GNN’s enhanced routing strategy in a challenging real-world context. Such qualitative insights are crucial for humanitarian logistics practitioners who prioritize reliability and security in aid delivery beyond raw numerical gains.

6 Conclusion

This paper introduced a hybrid framework integrating Proximal Policy Optimization (PPO), Graph Neural Networks (GNNs), and deterministic constraint validation to optimize humanitarian aid delivery in conflict-affected regions. By combining deep reinforcement learning for adaptive decision-making, graph-based spatial modeling for capturing security risks and logistical dependencies, and structured optimization for feasibility assurance, our approach effectively enhances the efficiency, security, and effectiveness of aid distribution. The framework’s effectiveness is demonstrated using real-world georeferenced datasets, including actual road networks from OpenStreetMap and conflict data from the Uppsala Conflict Data Program, with demand modeling incorporating stochastic components to realistically capture operational uncertainties. Experimental results demonstrate that PPO-GNN achieves significant improvements in cost efficiency (7.9% reduction), security risk mitigation (15.17% reduction), and operational reliability (83.33% fewer constraint violations), while substantially improving demand fulfillment compared to traditional DRL and heuristic-based methods. The advantages of this approach become more pronounced in large-scale networks and remain robust even under uncertain conditions, including fluctuating demand, variable security risks, and disruptions in accessibility.

Beyond its quantitative improvements, PPO-GNN offers several practical benefits for humanitarian logistics. Its scalability makes it applicable to both local and national-level operations, while its real-time adaptability enables responsive decision-making in volatile environments. By explicitly modeling security risks and integrating practitioner-informed priorities, the framework aligns with the operational realities faced by humanitarian organizations. This balance between computational efficiency and practical applicability ensures that the proposed approach is not only theoretically sound but also capable of addressing real-world challenges in aid delivery.

However, despite its promising performance, the framework has certain limitations that must be acknowledged. While the framework incorporates real-world road networks and conflict data, the demand modeling includes stochastic components to capture operational uncertainties, meaning that performance in actual conflict zones may vary depending on specific local conditions and data quality. Additionally, the complexity of implementing a hybrid AI-driven approach may pose challenges in resource-constrained humanitarian contexts, requiring potential simplifications for field deployment. Computational requirements, though more efficient than exact solvers, still exceed those of simple heuristics, which could be a limiting factor in environments with restricted computational resources. Moreover, the framework’s reliance on hyperparameter tuning may necessitate further research to enhance its adaptability to diverse operational settings. Finally, as with many deep learning-based methods, the interpretability of the model remains a challenge, potentially affecting trust and adoption by practitioners.

Addressing these limitations requires a comprehensive research agenda across multiple dimensions. Real-world validation represents the most pressing priority, requiring close collaboration with humanitarian organizations to conduct field testing in active conflict zones. This approach would provide essential insights into the practical feasibility of the proposed system while identifying necessary adaptations to operational constraints and field conditions.

Model optimization presents another crucial development pathway. Implementing model distillation techniques could significantly simplify policy representations while maintaining performance integrity, thereby facilitating broader adoption across diverse humanitarian contexts. Concurrently, extending the framework to support multi-period planning capabilities that accommodate evolving demand patterns and shifting security conditions would substantially enhance its applicability to the dynamic nature of humanitarian operations.

Computational efficiency improvements could be achieved through transfer learning methodologies, enabling the adaptation of pre-trained models to new geographical regions while reducing deployment costs and accelerating implementation timelines. Furthermore, integrating collaborative decision-making frameworks that incorporate multiple stakeholder perspectives would improve coordination mechanisms and optimize resource allocation in large-scale humanitarian responses. The incorporation of environmental sustainability considerations into logistics planning would align the framework with the growing emphasis on sustainable humanitarian practices.

From a methodological standpoint, future comparative evaluations should encompass advanced heuristic and metaheuristic approaches, including Tabu Search and evolutionary algorithms, alongside emerging hybrid DRL + GNN methodologies. While these alternatives show considerable promise, their integration necessitates substantial adaptation and specialized benchmarking efforts tailored to humanitarian vehicle routing challenges. Given these complexities, such extensions are reserved for future investigations to ensure comprehensive and equitable comparative analysis.

These research directions collectively aim to transform the proposed framework from a promising academic contribution into a deployable solution that can significantly impact humanitarian operations worldwide. The PPO-GNN framework represents a meaningful advancement in computational approaches to humanitarian logistics, demonstrating how sophisticated AI methodologies can be adapted to address critical societal challenges. Through continued development and real-world implementation, this work has the potential to enhance the lives of vulnerable populations in conflict-affected regions while advancing the field of humanitarian operations research.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

KM: Conceptualization, Formal Analysis, Methodology, Writing – original draft, Writing – review and editing. MA: Formal Analysis, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors gratefully acknowledge financial support from the Deanship of Scientific Research, King Faisal University (KFU) in Saudi Arabia under grant number KFU253325.

Acknowledgments

The authors wish to sincerely thank the Deanship of Scientific Research at King Faisal University for their valuable support of this research. They also express their gratitude to their respective institutions, King Faisal University and the University of Sousse, for providing a conducive academic environment and essential resources. Special thanks are extended to the teams involved in data collection and simulation testing, whose contributions were vital to the successful completion of this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. The authors acknowledge the use of Claude 3.7 Sonnet (Anthropic, 2025) to assist with editing portions of this manuscript. All content has been reviewed for factual accuracy by the authors.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Altay, N., and Green, W. G. (2006). Or/ms research in disaster operations management. Eur. J. Operational Res. 175, 475–493. doi:10.1016/j.ejor.2005.05.016

CrossRef Full Text | Google Scholar

Balcik, B., Beamon, B. M., and Smilowitz, K. (2008). Last mile distribution in humanitarian relief. J. Intelligent Transp. Syst. 12, 51–63. doi:10.1080/15472450802023329

CrossRef Full Text | Google Scholar

Bello, I., Pham, H., Le, Q. V., Norouzi, M., and Bengio, S. (2016). Neural combinatorial optimization with reinforcement learning. Corr. abs/1611, 09940. doi:10.48550/arXiv.1611.09940

CrossRef Full Text | Google Scholar

Besiou, M., Pedraza-Martinez, A. J., and Wassenhove, L. N. V. (2021). Humanitarian operations and the un sustainable development goals. Prod. Operations Manag. 30, 4343–4355. doi:10.1111/poms.13579

CrossRef Full Text | Google Scholar

Bogyrbayeva, A., Meraliyev, M., Mustakhov, T., and Dauletbayev, B. (2022). Learning to solve vehicle routing problems: a survey. doi:10.48550/arXiv.2205.02453

CrossRef Full Text | Google Scholar

Bozorgi-Amiri, A., Jabalameli, M., and Al-e-Hashem, S. M. (2013). A multi-objective robust stochastic programming model for disaster relief logistics under uncertainty. OR Spectr. 35, 905–933. doi:10.1007/s00291-011-0268-x

CrossRef Full Text | Google Scholar

Clarke, G., and Wright, J. W. (1964). Scheduling of vehicles from a central depot to a number of delivery points. Operations Res. 12, 568–581. doi:10.1287/opre.12.4.568

CrossRef Full Text | Google Scholar

Dror, M., Laporte, G., and Trudeau, P. (1989). Vehicle routing with stochastic demands: properties and solution frameworks. Transp. Sci. 23, 166–176. doi:10.1287/trsc.23.3.166

CrossRef Full Text | Google Scholar

Fuli, G., Foropon, C. R. H., and Xin, M. (2020). Reducing carbon emissions in humanitarian supply chain: the role of decision making and coordination. Ann. Operations Res. 319, 355–377. doi:10.1007/s10479-020-03671-z

CrossRef Full Text | Google Scholar

Galindo, G., and Batta, R. (2013). Review of recent developments in Or/ms research in disaster operations management. Eur. J. Operational Res. 230, 201–211. doi:10.1016/j.ejor.2013.01.039

CrossRef Full Text | Google Scholar

Holguín-Veras, J., Pérez, N., Jaller, M., Wassenhove, L. N. V., and Aros-Vera, F. (2013). On the appropriate objective function for post-disaster humanitarian logistics models. J. Operations Manag. 31, 262–280. doi:10.1016/j.jom.2013.06.002

CrossRef Full Text | Google Scholar

Hu, S., Han, C., Dong, Z. S., and Meng, L. (2019). A multi-stage stochastic programming model for relief distribution considering the state of road network. Transp. Res. Part B Methodol. 123, 64–87. doi:10.1016/j.trb.2019.03.014

CrossRef Full Text | Google Scholar

Hu, W., Jiang, Z., Xu, M., and Hu, H. (2024). Efficient deep reinforcement learning strategies for active flow control based on physics-informed neural networks. Phys. Fluids 36, 074112. doi:10.1063/5.0213256

CrossRef Full Text | Google Scholar

Huang, M., Smilowitz, K., and Balcik, B. (2012). Models for relief routing: equity, efficiency and efficacy. Transp. Res. Part E Logist. Transp. Rev. 48, 2–18. doi:10.1016/j.tre.2011.05.004

CrossRef Full Text | Google Scholar

Kool, W., Hoof, H. V., and Welling, M. (2019). “Attention, learn to solve routing problems,” in Proceedings of the international conference on learning representations (ICLR). doi:10.48550/arXiv.1803.08475

CrossRef Full Text | Google Scholar

Kovács, G., and Spens, K. M. (2007). Humanitarian logistics in disaster relief operations. Int. J. Phys. Distribution and Logist. Manag. 37, 99–114. doi:10.1108/09600030710734820

CrossRef Full Text | Google Scholar

Krongauz, D. L., and Lazebnik, T. (2023). Collective evolution learning model for vision-based collective motion with collision avoidance. PLoS ONE 18, e0270318. doi:10.1371/journal.pone.0270318

PubMed Abstract | CrossRef Full Text | Google Scholar

Kunz, N., Wassenhove, L. N. V., Besiou, M., Hambye, C., and Kovács, G. (2017). Relevance of humanitarian logistics research: best practices and way forward. Int. J. Operations and Prod. Manag. 37, 1585–1599. doi:10.1108/IJOPM-04-2016-0202

CrossRef Full Text | Google Scholar

Laporte, G. (1992). The vehicle routing problem: an overview of exact and approximate algorithms. Eur. J. Operational Res. 59, 345–358. doi:10.1016/0377-2217(92)90192-C

CrossRef Full Text | Google Scholar

Lazebnik, T. (2023). Data-driven hospitals staff and resources allocation using agent-based simulation and deep reinforcement learning. Eng. Appl. Artif. Intell. 126, 106783. doi:10.1016/j.engappai.2023.106783

CrossRef Full Text | Google Scholar

Li, Y., Zhang, J., and Yu, G. (2020). A scenario-based hybrid robust and stochastic approach for joint planning of relief logistics and casualty distribution considering secondary disasters. Transp. Res. Part E Logist. Transp. Rev. 141, 102029. doi:10.1016/j.tre.2020.102029

CrossRef Full Text | Google Scholar

Merkulov, G., Iceland, E., Michaeli, S., Gal, O., Barel, A., and Shima, T. (2025). “Reinforcement-learning-based cooperative dynamic weapon-target assignment in a multiagent engagement,” in AIAA science and technology forum and exposition, AIAA SciTech forum 2025 (American Institute of Aeronautics and Astronautics AIAA). doi:10.2514/6.2025-1546

CrossRef Full Text | Google Scholar

Najafi, M., Eshghi, K., and Dullaert, W. (2013). A multi-objective robust optimization model for logistics planning in the earthquake response phase. Transp. Res. Part E Logist. Transp. Rev. 49, 217–249. doi:10.1016/j.tre.2012.09.001

CrossRef Full Text | Google Scholar

Negi, S. (2022). Humanitarian logistics challenges in disaster relief operations: a humanitarian organisations’ perspective. J. Transp. Supply Chain Manag. 16. doi:10.4102/jtscm.v16i0.691

CrossRef Full Text | Google Scholar

Özdamar, L., and Ertem, M. A. (2015). Models, solutions and enabling technologies in humanitarian logistics. Eur. J. Operational Res. 244, 55–65. doi:10.1016/j.ejor.2014.11.030

CrossRef Full Text | Google Scholar

Pedraza-Martinez, A. J., and Wassenhove, L. N. V. (2013). Transportation and vehicle fleet management in humanitarian logistics: challenges for future research. EURO J. Transp. Logist. 2, 18–30. doi:10.1007/s13676-012-0001-1

CrossRef Full Text | Google Scholar

Pérez-Rodríguez, N., and Holguín-Veras, J. (2016). Inventory-allocation distribution models for post-disaster humanitarian logistics with explicit consideration of deprivation costs. Transp. Sci. 50, 1261–1285. doi:10.1287/trsc.2014.0565

CrossRef Full Text | Google Scholar

Rodríguez-Espíndola, O., Albores, P., and Brewster, C. (2018). Decision-making and operations in disasters: challenges and opportunities. Int. J. Operations and Prod. Manag. 38, 1964–1986. doi:10.1108/IJOPM-03-2017-0151

CrossRef Full Text | Google Scholar

Rodríguez-Espíndola, O., Ahmadi, H., Gastélum-Chavira, D., Ahumada-Valenzuela, O., Chowdhury, S., Dey, P. K., et al. (2023). Humanitarian logistics optimization models: an investigation of decision-maker involvement and directions to promote implementation. Socioecon. Plan. Sci. 89, 101669. doi:10.1016/j.seps.2023.101669

CrossRef Full Text | Google Scholar

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O. (2017). Proximal policy optimization algorithms. doi:10.48550/arXiv.1707.06347

CrossRef Full Text | Google Scholar

Tomasini, R., and Wassenhove, L. N. V. (2009). From preparedness to partnerships: case study research on humanitarian logistics. Int. Trans. Operational Res. 16, 549–559. doi:10.1111/j.1475-3995.2009.00697.x

CrossRef Full Text | Google Scholar

Vega, D., and Roussat, C. (2015). Humanitarian logistics: the role of logistics service providers. Int. J. Phys. Distribution and Logist. Manag. 45, 352–375. doi:10.1108/IJPDLM-12-2014-0309

CrossRef Full Text | Google Scholar

Wassenhove, L. N. V. (2006). Humanitarian aid logistics: supply chain management in high gear. J. Operational Res. Soc. 57, 475–489. doi:10.1057/palgrave.jors.2602125

CrossRef Full Text | Google Scholar

Wex, F., Schryen, G., Feuerriegel, S., and Neumann, D. (2014). Emergency response in natural disaster management: allocation and scheduling of rescue units. Eur. J. Operational Res. 235, 697–708. doi:10.1016/j.ejor.2013.10.029

CrossRef Full Text | Google Scholar

Wu, E., Kenway, G., Mader, C. A., Jasa, J., and Martins, J. R. R. A. (2020). Pyoptsparse: a python framework for large-scale constrained nonlinear optimization of sparse systems. J. Open Source Softw. 5, 2564. doi:10.21105/joss.02564

CrossRef Full Text | Google Scholar

Yue, B., Ma, J., Shi, J., and Yang, J. (2024). A deep reinforcement learning-based adaptive search for solving time-dependent green vehicle routing problem. IEEE Access 12, 33400–33419. doi:10.1109/ACCESS.2024.3369474

CrossRef Full Text | Google Scholar

Zhao, P., and Liu, Y. (2021). Physics informed deep reinforcement learning for aircraft conflict resolution. IEEE Trans. Intelligent Transp. Syst. 23, 8288–8301. doi:10.1109/TITS.2021.3077572

CrossRef Full Text | Google Scholar