- Advanced Architecture Research, NPU IP, Intel Corporation, Santa Clara, CA, United States
This paper introduces FlexNPU, a Flexible Neural Processing Unit, which adopts agile design principles to enable versatile dataflows, enhancing energy efficiency. Unlike conventional convolutional neural network accelerator architectures that adhere to fixed dataflows (such as input, weight, output, or row stationary) to transfer activations and weights between storage and compute units, our design revolutionizes by enabling adaptable dataflows of any type through configurable software descriptors. Considering that data movement costs considerably outweigh compute costs from an energy perspective, the flexibility in dataflow allows us to optimize the movement per layer for minimal data transfer and energy consumption, a capability unattainable in fixed dataflow architectures. To further enhance throughput and reduce energy consumption in the FlexNPU architecture, we propose a novel sparsity-based acceleration logic that utilizes fine-grained sparsity in both the activation and weight tensors to bypass redundant computations, thus optimizing the convolution engine within the hardware accelerator. Extensive experimental results underscore a significant improvement in the performance and energy efficiency of FlexNPU compared to existing DNN accelerators.
1 Introduction
The landscape of machine learning is experiencing an unprecedented surge, with a multitude of artificial intelligence (AI) networks proposed along with the development of numerous hardware platforms dedicated to accelerating Deep Neural Network (DNN) inference tasks. As the field progresses, the complexity of DNNs continues to grow, resulting in the handling of large amounts of tensor data that exhibit diverse shapes and dimensions across different layers of existing networks. Moreover, with the continuous introduction of new networks, the dimensions of these tensor data are in constant flux. Consequently, there is a pressing need to engineer hardware accelerators with the flexibility to efficiently process network layers of varying dimensions (Raha et al., 2023, 2021b).
Furthermore, the proliferation of edge devices, including wearables, smart cameras, smartphones, and surveillance platforms, underscores the importance of energy efficiency in the design of DNN accelerators (Ghosh et al., 2023). In this work, efficiency refers primarily to energy savings achieved through optimal scheduling (dataflow) strategies that minimize data movement and enhance data reuse at all levels of the memory hierarchy. Since tensor operations frequently span multiple memory levels, reducing unnecessary data transfers and maximizing reuse and compute resource utilization are essential to significantly improve the energy efficiency of DNN accelerators (Raha et al., 2021a).
However, established canonical accelerators for DNN execution—such as Eyeriss (Chen et al., 2016c) and TPU (Jouppi et al., 2017)—represent two foundational dataflow strategies: row stationary and weight stationary, respectively. These architectures have not only pioneered critical memory hierarchy and data reuse principles but also serve as the underlying blueprints for a majority of modern accelerator designs. In fact, most recent accelerators, academic or commercial, can be viewed as derivatives or targeted refinements of these two archetypes. For this reason, we adopt Eyeriss and TPU as the principal baselines in our evaluations, providing a meaningful and representative comparison point rooted in the architectural lineage. Although newer accelerators continue to emerge, their innovations often build upon the same dataflow philosophies introduced by these early systems. To acknowledge this evolution and provide a comprehensive view, we discuss several prominent and highly cited recent accelerators in detail later in Section 6. As DNN models and workloads continue to evolve, there is growing interest in exploring novel architectures and strategies that can better adapt to the evolving demands of DNN inference while simultaneously improving energy efficiency across a range of edge devices and AI applications.
The energy consumption for each layer in DNN inference is heavily influenced by the movement of data across the memory hierarchy and the level of reuse within the processing units. Previous studies have attempted to characterize energy efficiency through analytical models while stressing the importance of allowing flexibility in scheduling tensors of varying dimensions (Kwon et al., 2019). This flexibility involves optimizing the ordering, blocking, and partitioning of tensors to maximize reuse from the innermost memory hierarchy, where the energy cost per unit of data moved is minimized. However, most existing DNNs, such as ResNet, YOLO, VGG, and GoogLeNet, comprise tens to hundreds of layers, each with different preferences for scheduling to achieve energy optimality. Fixed-schedule DNN accelerators can only offer optimal data reuse and resource utilization for a subset of DNN layers, thus limiting overall energy efficiency. Moreover, these accelerators exhibit strong network dependencies, which poses challenges in adapting to the rapidly evolving landscape of DNNs. Existing DNN accelerator designs from both industry and academia predominantly employ fixed schedules, such as input stationary (IS), weight stationary (WS), output stationary (OS), non-local reuse (NR), and row stationary (RS) (Chen et al., 2016b,c). The fixed dataflow characteristic of these accelerators originates from their tensor data distribution modules, which perform addressing to on-die storage, data transfer to processing engine arrays, and data storage to SRAM banks in a predetermined manner. As a result, these accelerators lack the flexibility to implement different schedules (i.e., dataflows). Although software solutions on general-purpose CPUs and GPUs can reshape and load tensor data, fixed-function accelerators do not support flexibility. FPGAs, although offering flexibility, cannot alter the hardware configuration during execution from one layer to another.
In contrast to previous approaches, this paper proposes a dataflow-aware flexible DNN accelerator that leverages schedule information from DNN layers to adapt tensor data shape and internal compute configuration per layer. This enables the compiler to configure the DNN accelerator optimally for handling tensor operations based on tensor dimensions. The key advantage of our proposed accelerator design lies in its ability to switch among multiple schedules based on layer characteristics, thereby minimizing memory accesses for a given tensor operation and resulting in significant energy savings at the accelerator level.
To further enhance performance and increase energy efficiency in the accelerator, we capitalize on the inherent sparsity in DNNs. Due to the nature of DNNs, the weights associated with the network are often “sparse,” which means that they contain a significant number of zeros generated during the training phase (Parashar et al., 2017; Ghosh et al., 2024). These zero-valued weights do not contribute to the accumulation of partial sums during multiply-and-accumulate (MAC) operations. Additionally, highly sparse weights cause activations to become sparse in subsequent layers of the DNN after passing through non-linear activation functions like ReLU. Furthermore, network quantization (INT8/INT4) for edge device inference also results in a high number of zeros in both weights and activations. This fine-grained unstructured sparsity in weights and activations offers potential for improved energy efficiency and processing speed in two ways: (1) MAC computation can be gated or skipped, and (2) weights and activations can be compressed to reduce storage and data movement. The former reduces energy consumption, while the latter reduces both energy consumption and processing cycles. However, designing DNN accelerators to harness these benefits from sparsity is challenging due to irregular access patterns, workload imbalances, and under-utilization of MAC-based processing elements (Chen et al., 2019). Hence, in this paper, we develop a novel sparsity acceleration logic capable of skipping computation of zero-valued compressed data while simultaneously identifying non-zero elements in both activation and weight tensors. This will facilitate the implementation of an efficient convolution engine in the hardware accelerator at the edge, enabling efficient utilization of resources and enhancing overall performance and energy efficiency.
In this paper, we introduce FLEXNPU, a Flexible Neural Processing Unit, designed with agile principles to support versatile dataflows, thereby improving energy efficiency. Recognizing that data movement costs significantly outweigh compute costs in terms of energy consumption, the flexibility in dataflow enables us to optimize data transfer per layer, leading to minimal data movement and reduced energy consumption, an advantage not achievable in fixed dataflow architectures. Furthermore, to further boost throughput and reduce energy consumption within the FLEXNPU architecture, we propose an innovative sparsity-based acceleration logic. This logic harnesses fine-grained sparsity in both activation and weight tensors to bypass redundant computations, effectively optimizing the convolution engine within the hardware accelerator. In summary, this paper makes the following contributions.
• This paper introduces a novel DNN accelerator, FLEXNPU, designed to be sensitive to dataflow, offering flexibility by integrating DNN layer scheduling insights. By dynamically adjusting tensor data shape and internal compute configuration for each layer, the accelerator allows the compiler to optimize its performance in handling tensor operations, tailoring its configurations based on tensor dimensions for diverse neural network architectures.
• We introduce a novel sparsity acceleration logic that capitalizes on the unstructured fine-grained sparsity present in incoming activation and weights, thereby expediting inference execution within the DNN accelerator. Data are maintained in a zero-compressed format to mitigate storage and data movement expenses. Weights and activations are mapped while considering sparsity to enhance reuse, thus enhancing overall performance.
• Extensive experimental evaluations conducted on six distinct DNNs that span both image classification and object detection tasks highlight the transformative impact of our accelerator. Specifically, our architecture showcases substantial improvements over fixed-schedule accelerators for ResNet101 and YOLOv2, demonstrating up to 77% and 62% energy reduction over Eyeriss and TPU, respectively. Furthermore, our accelerator achieves notable sparsity improvements for four additional DNNs, namely ResNet50, MobileNetV2, GoogLeNet, InceptionV3. Across these benchmarks, FLEXNPU achieves a speedup of 1.8 × –3.3 × over dense accelerators and 1.7 × –2.0 × over semi-sparse accelerators with weight-sparsity support. For four transformer models, namely DETR-ResNet50, T5, MobileBERT, DistilBERT, FLEXNPU provides 1.4 × –4.2 × and upto 2.2 × speedup over dense and weight-sparse accelerators, respectively. Sparsity support also provides 1.7 × –3.0 × and 1.6 × –1.8 × improvement in energy efficiency compared to dense and weight-sparse accelerator. The savings for transformers amount to 1.3 × –3.6 × and 1.0 × –2.0 × . These results underscore the profound impact of our accelerator in enabling efficient execution of sparse and compact DNNs, significantly enhancing both speed and energy consumption metrics.
The remainder of the paper is organized as follows. Section 2 delineates the need for flexible dataflow and efficient two-sided sparsity acceleration logic. Section 3 describes the microarchitectural details of the proposed FLEXNPU accelerator. Section 4 presents the experimental setup followed by the results in Section 5. The prior art in this domain is described in Section 6. Finally, Section 7 concludes the paper.
2 Motivation
In this section, we delve into the fundamental motivations driving the design and development of our accelerator architecture, focusing on two key aspects: the paramount importance of flexibility and the critical need for efficient sparsity acceleration. By addressing these critical considerations, our accelerator aims to revolutionize the landscape of deep learning (DL) hardware, offering unparalleled versatility and performance across a wide range of DNNs and applications. We explore how these foundational principles drive innovation and shape the architectural decisions that lead to the design of FLEXNPU.
2.1 Importance of flexibility
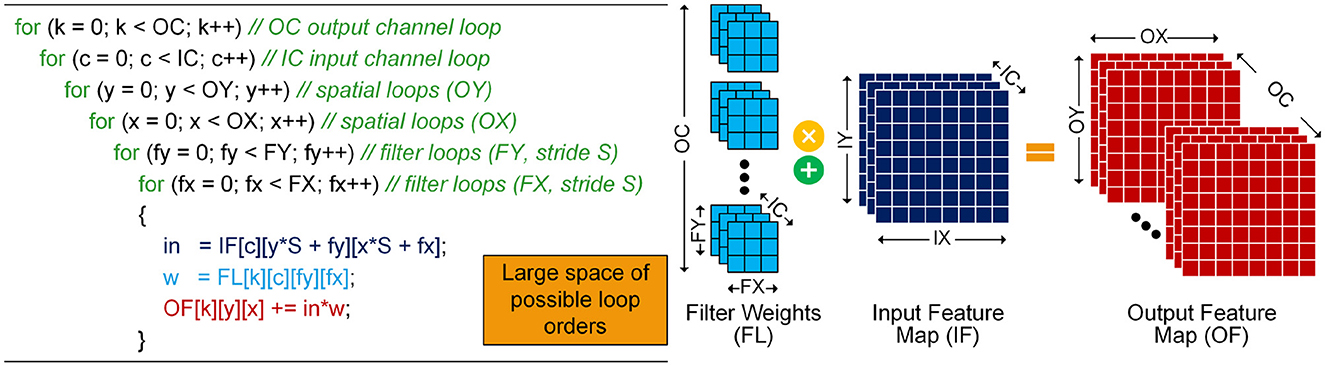
Numerous DNN accelerators utilize spatial architectures comprised of arrays of processing elements (PEs) alongside local storage, such as register files (RFs), for those PEs, and external storage, such as SRAM banks. In inference tasks, trained weights, or filters (FL), must be loaded into PE arrays from storage sources such as DRAMs and SRAM buffers. Input images, referred to as input activations or features (IFs), are also transferred to PE arrays, where MAC operations occur across multiple input channels (ICs) between activations and weights, generating output activations or features (OFs). Multiple sets of weight tensors (OCs) are commonly used against a specific set of activations to produce an output tensor volume. Finally, a non-linear function (e.g., ReLU) is applied to the output activations, which then become the input activations for the subsequent layer. Tensor processing involved in a convolution operation, as shown in Figure 1, shows convolution layers comprising six nested loops. These layers generate an output tensor, OF map, from multiple kernel feature maps, FLs, operating on one or more input tensors, IF map. Each point in the output volume undergoes a MAC operation during the calculation. For instance, a 1 × 1 convolution layer, such as the second convolution layer in ResNet50, illustrates IF map dimensions of IX = 56, IY = 56, IC = 64, and the filters dimensions of FX = 1, FY = 1, IC = 64, OC = 256. These dimensions convolve (with a batch size of 1) to produce an OF map with dimensions OX = 56, OY = 56, OC = 256, accompanied by appropriate padding values.
The dimensions of the input tensor undergo changes as they transition from one layer to another within a DNN and across various DNNs. Consequently, the development of flexible hardware accelerators becomes crucial to maintaining high utilization of compute units across network layers with arbitrary dimensions. Attempting to map various tensor dimensions to a fixed PE array with a consistent tensor mapping pattern can lead to decreased array utilization. To improve performance and energy efficiency, it is imperative to minimize data movement by maximizing data reuse from local memory and improving resource utilization. This optimization is particularly vital, as the cost of memory accesses often exceeds that of computing, as illustrated in Figure 2. Numerous existing DNN accelerators, such as Eyeriss (Chen et al., 2019), TPU (Jouppi et al., 2017), and SCNN (Parashar et al., 2017), implement novel memory hierarchies and fixed dataflows, influencing the movement of tensors for activations and weights within the processing units and the workload assigned to each PE. A fixed dataflow constrains the types of data movement across the memory hierarchy, limiting the degree of reuse within processing units. The movement of IFs, FLs, and partial sums (psums), as well as the order of reuse, directly impact the energy consumption of each layer. In the literature (Kwon et al., 2019), inference accelerators are classified into IS, WS, OS, and RS based on dataflow. The data reuse scheme is based on loop order, loop blocking, and loop partitioning for tensor processing, collectively called a “schedule,” as depicted in Figure 3. This schedule is described in relation to the dimensions of the tensors in a convolutional neural network. The loop order dictates the relative order of IX, IY (spatial), and IC dimensions for activations, and FX, FY, IC, and OC dimensions for filters when loading these data into the accelerator. Loop partitioning dictates how the overall convolution operation is distributed among the PEs in the PE array, whereas loop blocking governs the allocation of multiple points in each dimension to the same PE. This optimization is particularly vital, as the cost of memory accesses often exceeds that of computing, as illustrated in Figure 2. To maintain high compute unit utilization across layers with arbitrary and irregular shapes—not necessarily powers of two—it is essential to design accelerators that support flexible scheduling. This includes the ability to adapt loop blocking, partitioning, and tensor mapping at a per-layer level, allowing efficient mapping of diverse layer configurations while minimizing under-utilization.
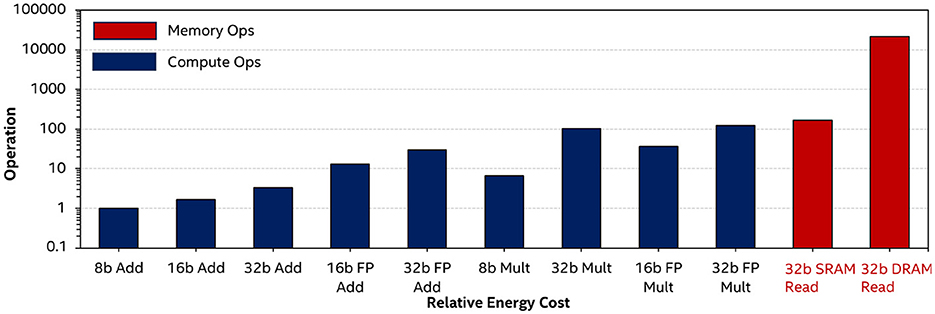
Figure 2. Relative energy costs of different compute and memory operations at various precisions in 45 nm technology (Horowitz, 2014). Note that x-axis is in logarithmic scale.
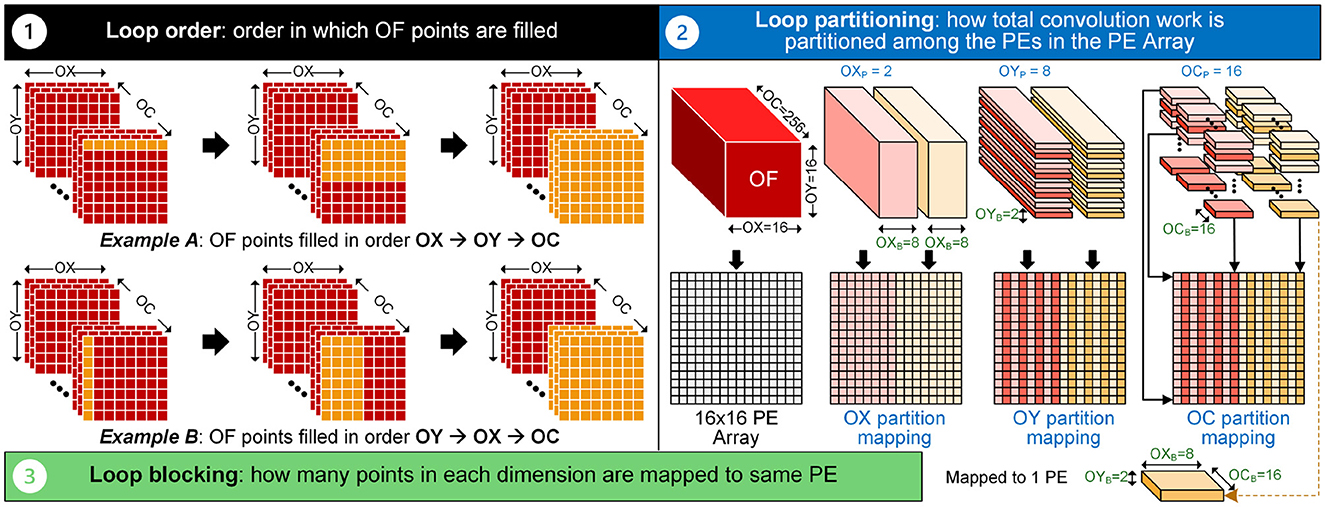
Figure 3. Illustration of (1) loop order, (2) loop partitioning, and (3) loop blocking—referred to collectively as schedule—for optimizing data loading and distribution in the accelerator.
All existing inference engines operate with fixed loop orders, blocking, and partitioning for convolution operations. Consequently, each accelerator can execute only one predetermined dataflow, where the data remain stationary in a single aspect. Various schedules require that IFs, FLs, and OFs/psums be mapped and accessed from local RF storage differently, depending on the type of schedule being computed. For example, in the IS scenario, a single point within the IF RF must undergo multiplication and accumulation against multiple points in the FL RF. The frequency of this repetition of operations varies on the basis of the schedule. Similarly, in the WS situation, a single point within the FL RF must be multiplied and accumulated against multiple points in the IF RF. Lastly, for OS schedules, the same psum in the OF RF must be retained and used to accumulate the results of multiplication between distinct IF and FL RF points over multiple cycles. Furthermore, when SRAM size imposes limitations on the number of IC points that can be stored, incomplete OF points in the form of psums must be transferred to a higher-level memory hierarchy (DRAM) for subsequent retrieval into PE RFs to complete OF computation across all ICs.
Previous research aimed at characterizing the energy efficiency of DNN accelerators by constructing analytical models underscores the need to introduce flexibility in scheduling tensor operations of various dimensions to maximize reuse from the innermost memory hierarchy, where the energy cost per unit of data moved is minimized (Kwon et al., 2019). However, as mentioned in Section 1, fixed dataflows can only cater to optimal data reuse and resource utilization for a limited subset of DNN layers. To address this flexibility challenge, the proposed tensor data computing PE array offers a practical solution with minimal hardware overhead. Implementing a flexible dataflow accelerator requires a dataflow-aware tensor distribution unit that can exploit layer-specific optimal schedules and dataflow information to distribute data throughout the array. Moreover, the accelerator should inherently support flexible mapping and execution of these data within each PE.
Motivation 1: It is important to develop a flexible dataflow in order to minimize data movement and maximize reuse in the PE array.
2.2 Importance of sparsity acceleration
Sparse input features are a common characteristic of modern DNNs, driven by activation functions and architectural choices. One primary cause is the widespread use of ReLU as an activation function, which zeros out negative values, resulting in high activation sparsity. This is especially pronounced in deeper layers of convolutional networks like ResNet50, InceptionV3, MobileNetV2/V3, and newer architectures such as EfficientNet and ConvNeXt, where sparsity can exceed 90%. Sparsity is also prevalent in convolutional encoder-decoder style networks, such as U-Net, DeepLabv3+, and SegFormer, commonly used in semantic segmentation and image generation tasks. These networks employ convolutional up-sampling through techniques such as transposed convolution or zero-insertion, which significantly increase the proportion of zero-valued activations, often surpassing 75%.
The trend of activation sparsity is not limited to vision models, but also evident in transformers/Large language models (LLMs). For example, ReLU-based OPT model shows >90% activation sparsity in Feed Forward Network layers (Mirzadeh et al., 2023). While many LLMs (e.g., PaLM, LLaMA, Falcon) use smooth activations like GELU or SiLU that lack inherent sparsity, recent works have reintroduced sparsity through techniques such as ReLU/Squared ReLU replacements and activation regularization (Liu et al., 2024; Luo et al., 2024). Moreover, recent work such as ProSparse (Song et al., 2024) reports up to 89.3% sparsity in modified LLaMA2-7B/13B models with minimal accuracy loss. To support these trends, Figure 4 presents layer-wise activation sparsity, averaged across corresponding datasets for representative CNNs (dataset: ImageNet) and transformers (datasets: MS COCO, Glue SST2, Glue MNLI).
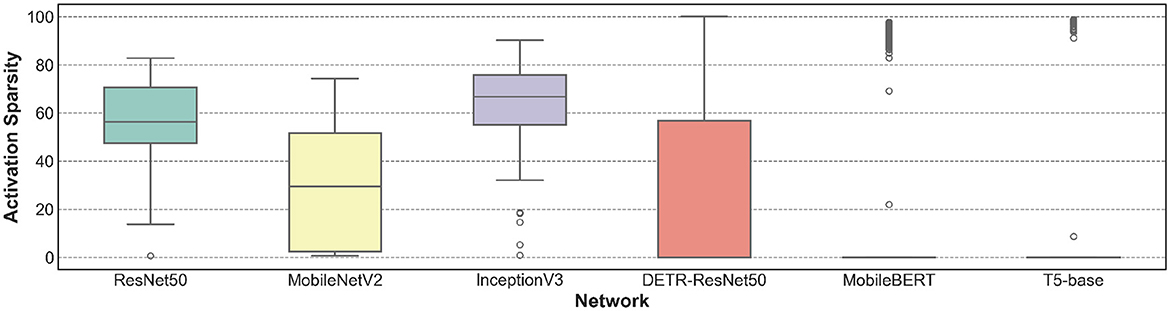
Figure 4. Activation sparsity of different pretrained DNN benchmarks. First 3 networks are traditional CNNs, last 3 networks are transformers. Sparsity measured at input of all convolution/matmul layer.
Furthermore, weight sparsity has also been a major target of optimization in both traditional CNNs and transformers. Numerous structured and unstructured pruning techniques have been proposed to eliminate redundant weights without degrading model accuracy. Pruning methods typically rely on criteria such as magnitude, saliency, gradient sensitivity, or energy impact to identify and remove less critical weights. As a result, these pruned networks exhibit weight sparsity levels of up to 90% (Gale et al., 2019; Hoefler et al., 2021; Frantar and Alistarh, 2023; Li et al., 2023). Taken together with activation sparsity, these trends underscore the need for accelerator designs that can fully exploit both static (weight) and dynamic (activation) sparsity for maximal performance and energy efficiency.
The observed sparsity in weights and activations presents a compelling opportunity to improve both energy efficiency and processing speed. However, designing DNN accelerators capable of effectively harnessing these characteristics remains a formidable challenge. Computation gating emerges as a promising technique for converting sparsity in both IFs and FLs into energy savings. The implementation involves recognizing whether either the weight or activation is zero and clock-gating the datapath switching and memory accesses accordingly, achieving cost-effective solutions. To optimize throughput while conserving energy, skipping cycles of processing MACs with zero weights or activations becomes desirable. Yet, this necessitates intricate read logic to locate the next non-zero value without expending cycles on zeros. A natural solution entails maintaining FLs and IFs in a compressed format indicating the next non-zero location relative to the current one. However, compressed formats, often of variable length, pose challenges for parallel processing across PEs without compromising compression efficiency. Additionally, simultaneous recognition of sparsity in both weights and activations complicates matters, as efficiently “looking ahead” (e.g., skipping non-zero weights when the corresponding activation is zero) proves challenging with many compression formats. The irregularity introduced by such jumps precludes the use of pre-fetching to enhance throughput. Consequently, the control logic for processing compressed data becomes complex, adding overhead to the PEs. Addressing these complexities is vital to realize the full potential of sparsity in DNN accelerators.
As a result, hardware solutions in this domain have been limited. For example, Cnvlutin (Albericio et al., 2016) exclusively facilitates skipping cycles for activations without compressing weights, while Cambricon-X (Zhang et al., 2016) lacks the ability to maintain activations in compressed format. Given the intricacies involved in skipping cycles for both weights and activations, existing hardware designed for sparse processing tends to be tailored to specific layer types. For example, EIE (Han et al., 2016) is tailored for fully connected (FC) layers, while SCNN (Parashar et al., 2017) is optimized for convolutional (CONV) layers. This specialization underscores the need for further innovation in developing versatile hardware architectures capable of efficiently handling sparsity across various layer types in diverse DNNs.
Introducing computation skipping for sparse data fundamentally alters the workload distribution across PEs, as the workload at each PE becomes contingent on sparsity levels. As the count of non-zero values fluctuates across diverse layers, data types, or even within specific regions within the same filter or feature map, it endangers an inherent imbalance in workload distribution across PEs (Chen et al., 2019). Consequently, the throughput of the entire DNN accelerator becomes constrained by the PE processing the highest number of non-zero MAC operations. This imbalance inevitably results in reduced PE utilization, thereby impeding the overall efficiency and performance of the DNN accelerator. Addressing this challenge requires innovative strategies to optimize workload distribution and improve PE utilization, thus maximizing the potential benefits of computation skipping for sparse data.
Motivation 2: It is important to develop an acceleration logic that can leverage both unstructured IF and FL sparsity, in zero-compressed format.
3 Microarchitecture design
In this section, we present the microarchitecture of the proposed FLEXNPU accelerator, beginning with its integration into a heterogeneous compute system. We then delve into the core architecture, emphasizing flexible dataflow and support for fine-grained sparsity acceleration that enable efficient DNN execution.
3.1 System-level integration
To contextualize the design of FLEXNPU accelerator, we adopt a system-level perspective commonly seen in heterogeneous System-on-Chip (SoC) designs (Raha et al., 2023). As shown in Figure 5, the accelerator is integrated alongside a scalar host processor, a vector DSP, and a dedicated DMA engine. The scalar core orchestrates control flow and data movement across off-chip memory (DRAM), on-chip SRAM, and compute units, issuing instructions via a shared Network-on-Chip (NoC).
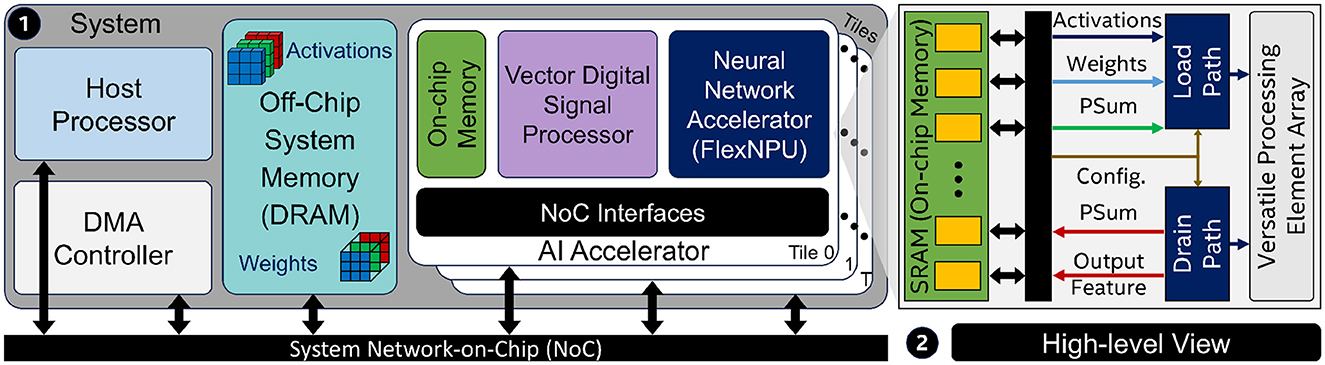
Figure 5. (1) Integration of FLEXNPU accelerator in heterogeneous computing system. (2) High-level schematic of FLEXNPU showing PE array, load and drain paths, and flow of DNN activations and weights.
A lightweight DMA engine enables data transfers between DRAM and SRAM, decoupling memory access from compute and minimizing load/store overhead on the scalar processor. The vector DSP handles operations unsuitable for direct mapping on the accelerator, such as complex non-linear activation functions (e.g., GeLU, Swish, SoftMax), normalization layers (e.g., LayerNorm), other control-flow and pre/post-processing operations (e.g., Slice, Gather, Concatenate, Reshape, Padding) common in CNNs and transformers, while FLEXNPU is optimized for high-throughput, energy-efficient execution of core DNN layers (e.g., convolution, matrix multiplication, elementwise, pool). Due to its limited arithmetic resources and memory reuse, the vector DSP operates at lower performance and is used only when necessary. This design hierarchy ensures that the accelerator is utilized for the most compute-intensive layers, maximizing overall system efficiency.
In the remainder of this paper, we focus entirely on the microarchitectural innovations of the FLEXNPU accelerator, which accounts for the majority of compute and energy consumption in the system.
3.2 Overview of flexNPU accelerator
The proposed FLEXNPU accelerator supports flexible and reconfigurable dataflow to accommodate various DNN workloads. Although it is capable of executing any valid schedule, performance and energy efficiency are maximized by selecting optimal schedules tailored to each layer of the neural network. To this end, we employ a cycle-accurate cost model—similar to prior works (Yang et al., 2020; Kwon et al., 2020)—which evaluates candidate schedules and selects the one that minimizes latency and energy for each layer. Further details are provided in Section 4.2. The choice of schedule directly impacts the opportunities for data reuse across memory hierarchies, thereby influencing efficiency. To support this, the accelerator employs a carefully designed three-level memory hierarchy, illustrated in Figures 5.2, 6, which is critical for maximizing reuse and minimizing energy consumption during DNN execution. (1) The first level consists of internal register files within each PE. The second level comprises an on-chip SRAM, serving as a small L1 cache for input activations, filter weights, partial sums, output features, and layer configuration metadata. The third level is system DRAM, providing high-capacity storage for large models and spilled output activations. For brevity, we omit DRAM-level implementation specifics and assume that the SRAM's capacity is sufficient to accommodate all input, intermediate activations, and weights.
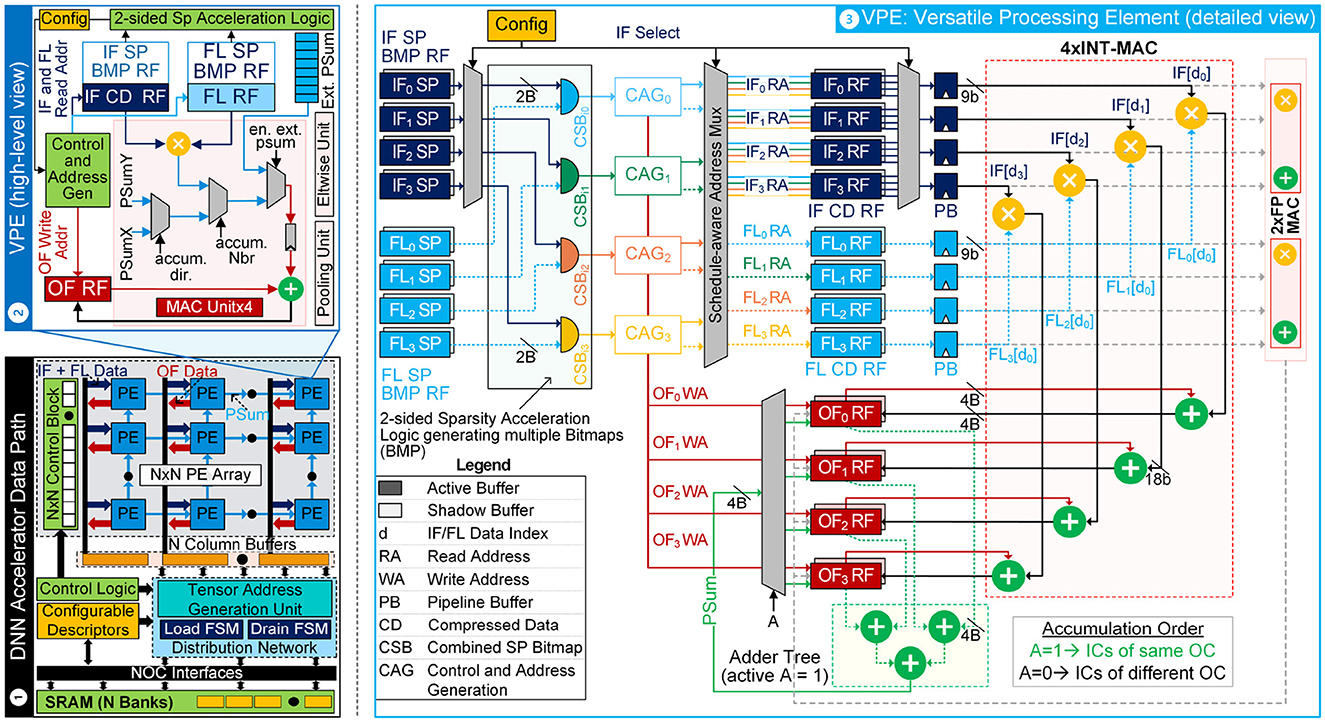
Figure 6. Top-level schematic of the FLEXNPU accelerator: (1) System-level view showing interconnect pathways within the PE array (arranged in N columns), the data distribution network, control block, and SRAM. (2) High-level view of a single VPE, highlighting data storage (IF/FL/OF RF), sparsity bitmap registers (IF/FL SP BMP RF), and the MAC unit. (3) Detailed VPE view, showcasing internal interconnects, sparsity acceleration logic, and control units, while illustrating support for two accumulation orders.
The FLEXNPU accelerator supports multiple datatypes, such as, INT8, U8, FP16, and BF16 and comprises three primary subsystems that are detailed in the following sections: the Processing Element Array/inter-PE mesh (Section 3.3), a schedule-aware load path (Section 3.4.1) for distributing activations/psums and weights from SRAM to PEs and drain path (Section 3.4.2) for writing output features/psums in SRAM.
3.3 Versatile processing element
The inter-PE mesh forms the core compute fabric of the FLEXNPU accelerator and consists of an N × M array of Versatile Processing Elements (VPEs). The array dimensions are parameterized at design time, typically via synthesis parameters. For simplicity and streamlined control logic, we adopt a square configuration (N × N) with N = 16, where each column comprises N VPEs and is managed by a dedicated control unit. The VPE is the fundamental computational unit within the accelerator. Each VPE performs MAC operations between IF and FL points for channel-wise and depth-wise convolutions and supports the accumulation of both internal and external psums (Mohapatra et al., 2020; Hsu et al., 2021; Raha et al., 2021d). Designed for flexibility, the VPE dynamically selects the appropriate compute template based on the optimal schedule per layer, optimizing the reuse of IF, FL, and OF data.
Figure 6.1 illustrates the schematic of the DNN inter-PE mesh. While the diagram depicts an N × N control block for clarity, in practice, each column of VPEs is paired with a control unit composed of N individual control blocks, one per VPE. Each VPE, as demonstrated in Figures 6.2, 3, consists of register files, MAC unit, configuration logic to iterate over the inputs as well as 2-sided sparsity acceleration logic to skip computations that results in zero product. Each VPE consists of four sub-banks of four 4R1W IF compressed data (CD) RFs to store input features (IF0RF to IF3RF), 1R1W FL CD RF to store weights (FL0RF to FL3RF), and 1R1W OF RF (OF0RF to OF3RF) to store output values (OF/psum). Each IF and FL data sub-bank can store upto 16 × 9bit entries. Both IF and FL are stored in INT9 precision after zero point subtraction. The OFRF sub-banks can each hold 4 × 32bit entries. In addition, each VPE consists of 4 sub-banks of 1R1W RFs to store sparsity bitmaps (SP BMP), namely IF SP BMP RF and FL SP BMP RF, with 16 × 1bit size. During a typical MAC operation, the input operands are fetched from the IF and FL RFs, based on the stored bitmaps, the sparsity acceleration logic (described later in Section 3.5), and the addresses generated by control and address generation (CAG) unit. The operation output is accumulated within the OF RF. Note that for stall-free high-performance execution, we introduced double buffers (active + shadow) in IF, FL, and OF RFs.
Figure 6.3 shows the detailed microarchitecture view of VPE that executes computations on the IF, FL, and OF/psum tensor data based on the optimal schedule of the current layer. VPE dynamically adjusts the loading and access patterns of the IF, FL, and OF/psum tensor data within the PE RFs to maximize reuse of the tensor data. The PE's microarchitecture is crafted to effectively utilize sparsity within both IF and FL. As illustrated in the figure, the PE comprises registers dedicated to storing sparsity data from incoming IF and FL streams, represented as bitmaps (IF SP BMP RF and FL SP BMP RF). These bitmaps are merged using a sparsity acceleration logic (further elaborated in Section 3.5), resulting in a combined sparsity bitmap (CSB). This unified bitmap serves as input to the CAG unit, facilitating the generation of participating non-zero IF and FL read addresses. N control blocks in each PE column updates the configuration descriptors inside individual PE at the onset of each convolution layer based on the optimal layer schedule, guiding data redirection during load, compute, and drain operations throughout the lifetime of the input tensor data. The PE finite-state machine (FSM) guides internal counters and logic in the CAG unit to generate read and write control signals for IF, FL, and OF RFs, along with multiplexer control signals to route data from the RFs to the appropriate units based on the template, viz., vector-vector (V × V) or matrix-matrix (M × M) or operation type, viz., MAC/Eltwise/Pooling and tensor dimension. The Floating Point MAC (FPMAC) sits in parallel with the Integer MAC, as illustrated in Figure 6.3, and both units share the same load, compute, and drain register files within the FLEXNPU architecture (Kaul et al., 2019).
Assisted by the PE FSM, internal registers within the CAG unit track the total number of PE blocks (or OF/psum points) produced, aiding in addressing IF/FL/OF RFs. Additionally, counters like ifcount, wcount, and ofcount manage the addresses/indexes for IF, FL, and OF RFs, increasing or clearing based on the number of input activations and weights required to calculate each OF point or psum block. The layer schedule determines the type and extent of IF/FL/OF RF data reuse, regulated by internal IF/FL/OF block counters controlling the loading of new IF/FL data and draining OF data each round, as per the layer's optimal schedule. These internal structures and associated control logic are crucial to supporting flexible schedules within the VPE. The critical role of VPE in facilitating flexible blocking within the DNN accelerator is realized by dividing the RF into multiple subbanks (X) and incorporating X MACs (e.g., X = 4) alongside multiplexers, allowing the implementation of V × V, V × M, and M × M templates (Mohapatra et al., 2022b), based on layer's optimal blocking factor (ICB, OCB, OXB, OYB), as shown in Figure 7.
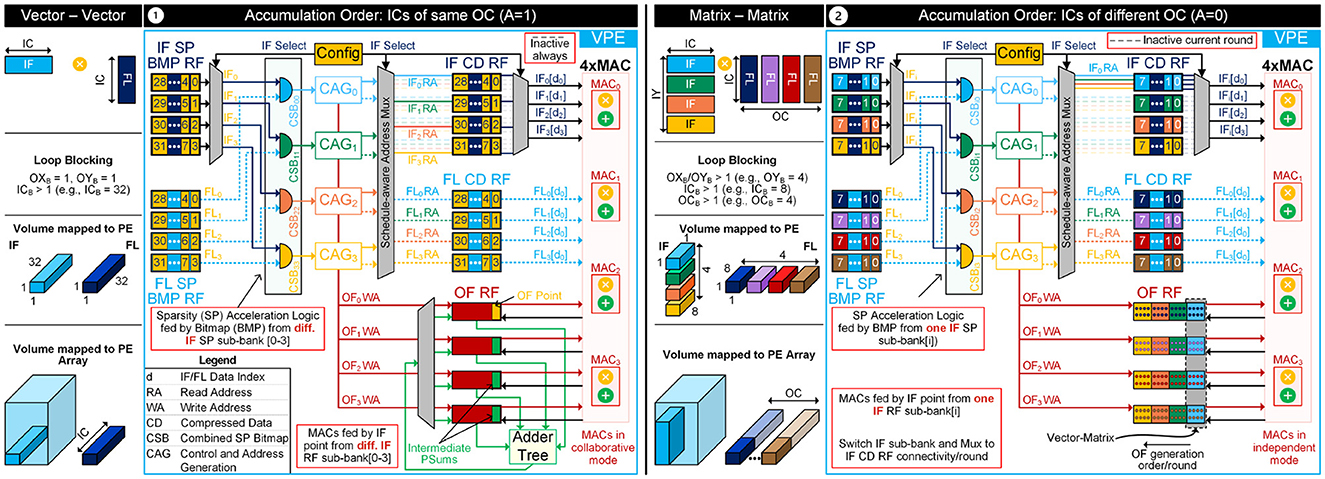
Figure 7. Versatile Processing Element (VPE) accommodating (1) V×V and (2) M×M templates. In V×V, accumulation involves Input Channel (IC) of the same Output Channel (OC) of weights (FL), while M×M entail accumulation of ICs from different OCs. M×M involves different V×M each round. Illustration presents schedule-aware flexible dataflow along with loop blocking and partitioning. Weight dimensions assumed: FX = 1 and FY = 1. Shadow, pipeline buffers, signal width, FPMAC not shown for clarity.
Although the adder datapath in the VPE includes four independent partial sum adders and a reduction adder tree, not all adders are utilized concurrently in every clock cycle. This design reflects a deliberate architectural trade-off: the inclusion of seven adders supports both accumulator update and cross-MAC reduction modes, enabling greater flexibility in scheduling while avoiding pipeline stalls under varying sparsity patterns. While the peak adder utilization may be bounded by 4/7, the additional hardware simplifies the datapath and reduces control overhead compared to a multiplexed alternative. During execution, the adders operate in one of two modes—collaborative or independent—selected per layer based on the schedule. This choice prioritizes energy efficiency and schedule adaptability over peak instantaneous utilization, which is a key design objective in latency- and power-constrained inference scenarios.
To aid clarity of the VPE microarchitecture, Figure 6.3 demonstrates signal widths and register configurations across all data paths. Each OFRF sub-bank consists of four entries, each 32 bits wide, corresponding to the output precision of the partial sum adders. The four 18-bit multipliers inside the VPE compute independent products which are accumulated into 32-bit partial sums, and these results are stored directly into dedicated OFRF sub-banks. The datapath shows that the adder tree reads directly from these sub-banks. Input/output port widths for all adders in the accumulation network have been annotated to be 32 bits, consistent with the partial sum precision. Additionally, read port widths have been annotated on the IF and FL compressed data RFs, as well as the sparsity bitmap RFs, to improve dataflow transparency. For completeness, Figure 6.3 also illustrates the dual-bank structure (active and shadow) within each RF to support double buffering. This enables stall-free operation during overlapping load, compute, and drain phases of execution. These enhancements collectively provide a more detailed view of the memory and accumulation subsystems within the VPE, which are essential for implementing the layer-wise flexible dataflow and high-throughput execution modes central to the FLEXNPU design.
For specific schedules, the convolution operation can be partitioned to split across multiple VPEs based on the number of ICs. Consequently, DNN computations that generate psums across different sets of ICs for a particular OF point should be mapped to a single column or row of VPEs. External psum accumulation enables the summation of all ICs partitioned into multiple VPEs to generate the final OF point. The inter-PE mesh facilitates the transmission of psums formed within the PE to its right or top neighbor, which is essential for the psum accumulation in inter-PE mesh. To mitigate wire congestion and routing complexity, interconnections between PEs are restricted to their top and right neighbors. As shown in Figure 6.2, three multiplexers are used with control signal accum_dir selecting the neighbor, accum_Nbr and en_ext_psum selecting between external accumulation and internal MAC accumulation. Note that these multiplexers are not shown in Figures 6.3, 7 for clarity. This architectural decision inherently influences how work is partitioned among different PEs, mainly in the IC dimension.
In certain optimal schedules, all ICs are not accumulated simultaneously. Instead, a portion of the IC set is initially loaded into the PE RFs, and the computed psum is extracted to the SRAM (or even DRAM) to be brought back into the PE RFs later when the remaining ICs are accumulated. External partial sum accumulation necessitates a 32-bit wide read and write direct bypass to and from the SRAMs. Sharing arithmetic units for MAC and Eltwise computation, along with multiplexer control logic routing appropriate tensor data into these units, reduces area overhead by enhancing hardware reuse efficiency within the PE. Residual networks such as ResNet require element-wise operations, such as the addition of OFs from two convolution layers. To support such operations while maximizing hardware resource reuse, OFs from two different layers are routed into the PE, using existing load and drain paths. The Eltwise field in the programmable descriptor signals an eltwise operation, bypassing the multiply operation within the PE and performing an eltwise addition of the two IF inputs.
Illustrative example: The FLEXNPU PE demonstrates flexibility by executing V × V and M × M MAC operations, exploiting sparsity in both scenarios, as illustrated in Figures 7.1, 2 respectively. The PE adapts this flexibility in its operation based on the optimal schedule selected for each specific layer. Let us first delve into the V × V operation scenario, where ICs within the same OC are accumulated and the MACs are operating in collaborative mode (A = 1). In this example with ICB = 32, 32 IFs and FLs are assigned to the PE for computation, corresponding to 32 distinct ICs but belonging to the same OC (represented by a single yellow color). Since these values exhibit sparsity, the sparsity bitmaps of IF and FL are stored in the respective registers IF SP BMP RF and FL SP BMP RF. The IF select signal retrieves the bitmaps from the first IF register (IF0) and the first FL register (FL0), transmitting them to the two-sided combined sparsity acceleration logic, which produces CSB00. This logic identifies the non-zero activations and weight addresses through the CAG unit. These addresses guide the IF and FL CD RFs that store zero-compressed IF and FL values and provide precise values for MAC operations. Simultaneously, this process repeats for the other IFs (IF1 to IF3) and FL registers (FL1 to FL3), thus feeding the MACs with IF/FL points from different IF/FL RF subbanks and generating four psums concurrently in each case, within the OF RFs. These psums aggregate to produce a single OF point upon completion of the computation using the adder tree fed directly by the OFRFs. This cycle is iterated until all 32 ICs are processed. Subsequently, the next set of 32 ICs is loaded, and this process continues until all OF points for that OC are computed.
Now, let us dive into the second scenario of M × M operations, focusing on the computation of ICs across different OCs within the PE, where the MACs are operating in independent mode (A = 0). Here, IF SP BMP RFs and IF CD RFs receive bitmaps and input features that correspond to four distinct OCs, each represented by a different color. Similarly, the corresponding FL SP BMP RFs are loaded with four different FLs. During computation, in the initial round (i), only elements from the first IF SP BMP RF are provided as input to all CAGs along with four different FL bitmap values for the four OCs. Consequently, the CAG generates addresses only corresponding to IF0 following a two-sided sparsity acceleration logic (CSB00−CSB03). Subsequently, after obtaining the participating non-zero IFs and FLs from the compressed RFs, the MAC operation partially generates each of the four OC points in the first round, each denoted by a distinct color. Notably, in this case, MACs draw input exclusively from one IF RF subbank at a time, unlike the previous scenario in which they obtained IFs from all sub-banks simultaneously. In this mode, the adder tree is inactive as illustrated in the figure. In the subsequent round, IF RF subbanks are switched using appropriate MUXing logic, consequently switching the compressed IF RF bank to acquire non-zero IF points for that specific round. Thus, contingent on the optimal layer schedule, the sparse PE efficiently conducts both V × V and M × M operations, capitalizing on both-sided sparsity in activations and weights.
3.3.1 Schedule-aware flexible depth adder tree (FlexTree)
Our FLEXNPU accelerator's core features a tree-based architecture named FlexTree, designed for psum accumulation across numerous PEs within the inter-PE mesh to generate the final output point (Mohapatra et al., 2022a). The distinguishing feature of FlexTree is its ability to dynamically adapt the depth of the adder tree, allowing the compiler to create flexible schedules for network layers of varying dimensions. This hardware enhancement allows the compiler/scheduler to discover highly compute-efficient schedules. Before delving into the FlexTree architecture, it is essential to understand the concept of Input Channel Partition (ICP), similar to OF channel partition as illustrated earlier in Figure 3. ICP denotes how many ICs are assigned to a single PE in the inter-PE mesh. Consequently, this also denotes the number of PEs that participate in the partial sum accumulation. Let us elucidate ICP using an example of 64 ICs. When ICP = 1, the computation involves only one PE, denoted PE1. All 64 ICs undergo pointwise multiplication and accumulation within PE1, producing the final output. When ICP = 2, 64 ICs are evenly divided between PE1 and PE2, each processing 32 ICs. PE1 accumulates psums from channels 0 to 31, while PE2 accumulates those from channels 32 to 63, forming the final output collectively. Similarly, for ICP = 4, the channels are distributed in PE1, PE2, PE3, and PE4, each PE handling 16 ICs. These psums of the respective sets of ICs are accumulated within each PE to generate the final output. Essentially, ICP × ICB = IC.
Figure 8 illustrates the FlexTree architecture, which receives 16 inputs from the 16 PEs within a column of the PE array in the DNN accelerator. ICP supported by the adder tree network ranges from 1 to 16, inclusively. Even if ICP=2, the output of the computation must still pass through the adder tree network before producing the final OF output. This ensures a reduction in hardware overhead by simplifying hardware design and achieving uniformity across all ICP values. It is noteworthy that our FlexTree architecture can accommodate ICP values that are not powers of 2 by entering zeros into the FlexTree network of PEs that do not align with powers of 2. Each module marked with a “+” sign comprises both the INT8 adder and the FP16 adder to support convolution layers of different precision (Raha et al., 2022a). Depending on the input precision (INT8 vs. FP16), the psum output from the PEs is routed to the appropriate hardware resource within FlexTree. In Figure 8, for ICP values of [1, 2], the flops [A, B, C, D, E, F, G, H] at level 1 serve as the final OF output tap points. For ICP = [4], the flops [I, J, K, L] at level 2 act as the final OF output tap points. Similarly, for ICP values of [8] and [16], the flops [M, N] at level 3 and [O] at level 4, respectively, serve as the final OF output tap points. Therefore, the total number of FlexTree output tap points varies for different ICP values. Therefore, for ICP values of [1, 2, 4, 8, 16], the total number of FlexTree output tap points is [8, 8, 4, 2, 1], respectively. To simplify the extraction of final OF points from the FlexTree module into the drain module, we allow a maximum of four OF points to be extracted from FlexTree in one round. The figure illustration assumes IC = 64, ICP = 16, and therefore Port O is active.
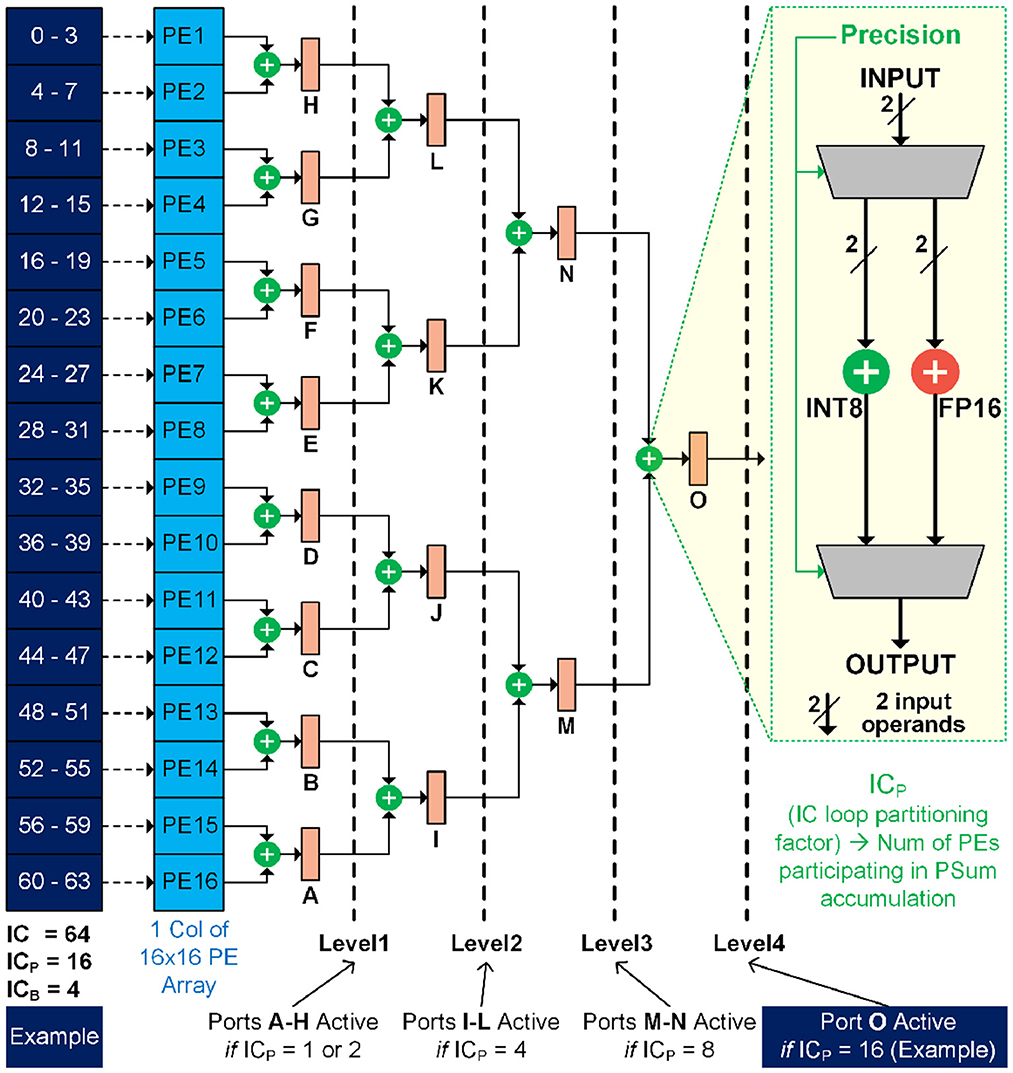
Figure 8. FlexTree architecture details with illustration using 64 input channels and 16 input channel partition factor.
As is evident from the above discussion, FlexTree achieves dynamic reconfiguration of the depth of the adder tree. This configurable feature is aided by software-programmable configuration registers. Unlike existing DNN accelerators where partial sum accumulation occurs by moving psums among neighboring PEs, FlexTree's innovative tree-based architecture significantly enhances partial sum accumulation efficiency (up to 2.14× speedup). In contrast to state-of-the-art DNN accelerators with fixed schedules and adder tree-based architectures, where the adder tree depth remains fixed at design time, our FlexTree technique offers dynamic reconfiguration capabilities, achieving speedups of up to 4× –16 ×, across seven DNNs, namely, ResNet50, GoogleNet, InceptionV2, MobileNetV2, MobileNetV3, SqueezeNet1.1, and MobileNet_SSD. Thus, our proposed FlexTree architecture enhances compute efficiency by allowing superior psum accumulation techniques across a wide range of layers found in modern DNNs.
3.4 Schedule-aware tensor distribution network
The Schedule-aware Tensor Distribution Network (SDN) serves as one of the fundamental architectural innovations of the proposed FLEXNPU accelerator, tasked with efficiently transferring input data between on-chip memory (SRAM) and inter-PE mesh, and vice versa, adhering to the optimal layer schedule (Chinya et al., 2024). These data include configuration settings, activation and kernel data (IF & FL), sparsity encodings, as well as bias & scale factors essential for calculation within the PE array. Additionally, the SDN manages the transportation of computational results, including output activation (OF) and partial sums, from the PE array's internal storage structure (RF) back to the SRAM, ensuring that the layout facilitates subsequent tensor layer acceleration. During the operational phases, the input side of the distribution network is termed the “load/fill” phase, while the output side is termed the “drain” phase. In fixed hardware accelerators, the pre-determined data layout in SRAM simplifies the load and drain phases, but compromises flexibility and optimization in operations. This rigidity restricts reuse potential, escalates memory accesses, and significantly increases overall energy and power consumption. Flexible hardware demands dynamic changes in the SRAM data layout, contingent on the type of reuse and optimal schedule (blocking and partitioning) for the layer.
3.4.1 Load path
The usual design consideration revolves around simplifying one of load or drain phase, while the other phase manages the complexities associated with rearranging the data to adhere to the optimal schedule. When the SRAM data layout remains fixed, the loading process must handle the complexity associated with unpacking the fixed layout data and arranging it according to the predetermined order and sequence dictated by the optimal schedule. Furthermore, the loading process must be hierarchical: initially organizing the input in a manner consumable by a column of PEs based on the partitioning factor and then, within the column, determining which input byte corresponds to which PE based on the blocking factor through a series of multiplexers (Mathaikutty et al., 2022a,b). For activation data, this involves retrieving data from memory in a predetermined order and distributing the IX, IY, and IC in the sequence and quantity specified by the reuse factor of the optimal schedule. Throughout the reuse process, one set of input remains resident, while the other circulates multiple times. Typically, the optimal schedule strives to maximize reuse, thereby reducing the frequency of fetching from SRAM. Ideally, a fully flexible DNN accelerator would allow partitioning in both the incoming activation and weights. However, this approach introduces a significant rise in MUXing complexity, along with its accompanying overheads, resulting in a convoluted routing process in the load, circular buffer, and PE FSM. To mitigate these challenges, we restrict weight partitioning within column and activation partitioning across column of the PE array. This strategy aims to streamline routing complexities and enhance operational efficiency within the accelerator architecture.
Figure 9.1 illustrates the crucial load path of FLEXNPU, spanning from SRAM to PEs. Central to this pathway is the load FSM, which interfaces with SRAM, the circular buffer FSM, sparse byte select modules, and PE columns. Activation of the load FSM is initiated by a start signal, indicating that all configuration register values have been appropriately set by the schedule descriptor based on the optimal schedule. Optionally, this start signal can also serve as the reset input for the load FSM, ensuring the removal of any outdated register values from previous layers. Once the FSM is active and space becomes available within the circular buffer, the FSM transmits fetch address and bank select signals to SRAM, and the IF and FL NoCs commence the transmission of IF and FL data to their respective circular buffers. Concurrently, each PE within the PE columns returns credits to the load FSM as space becomes available in the any of the double-buffered IF/FL data RF. Upon receipt, the FSM directs read requests to the circular buffer FSM. Within the circular buffer FSM, metadata is managed and data are dequeued in response to load FSM requests, signaling when the buffer is empty.
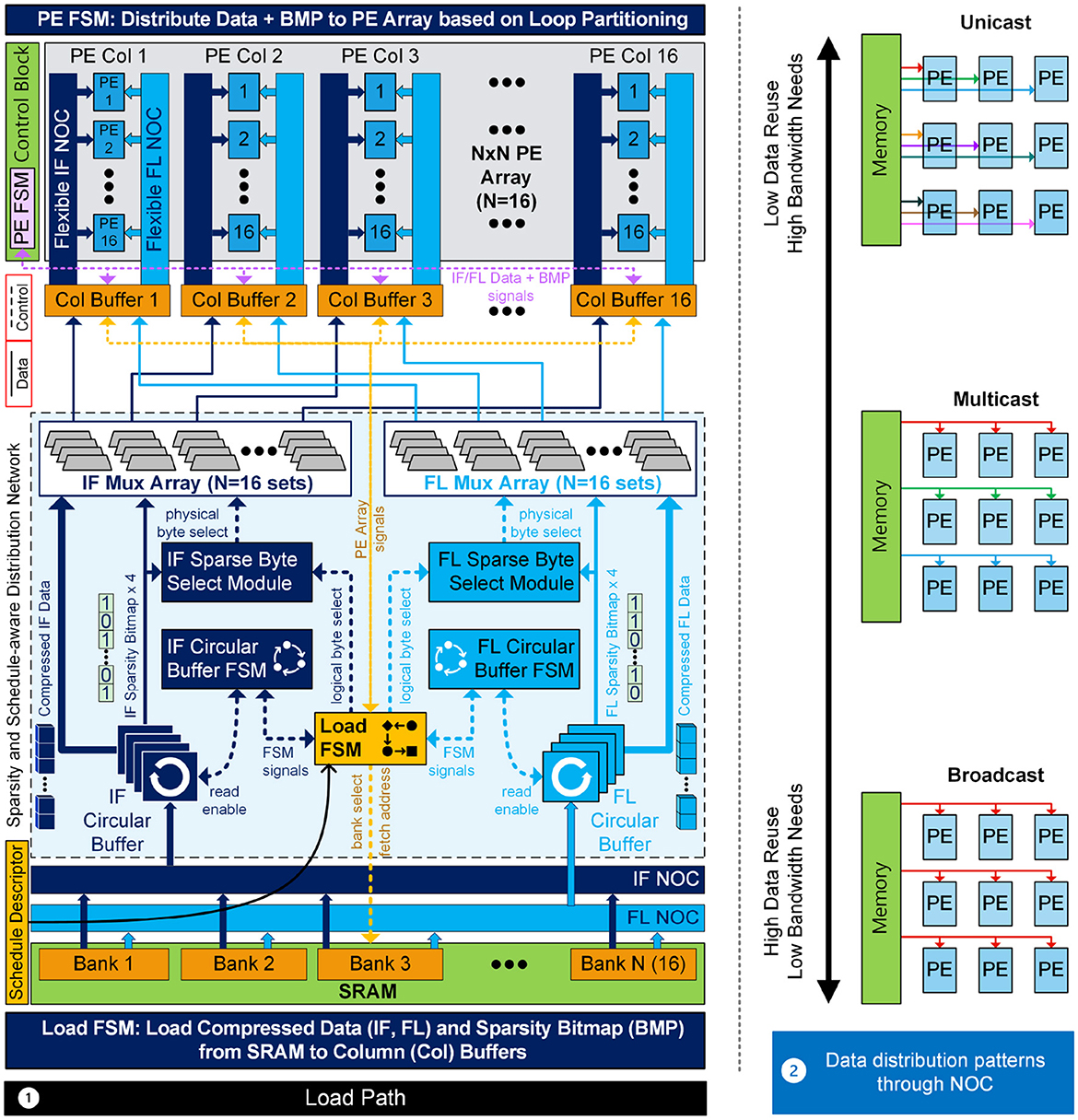
Figure 9. (1) FLEXNPU accelerator load path. Compressed activations (IF) and weights (FL) along with sparsity bitmaps are fetched from SRAM and delivered to PE array via the NoC interfaces. Flexible schedule support is integrated in Load FSM, Circular Buffer FSM, and PE FSM. OF NoC (part of drain) not shown inside PE array for clarity. (2) Illustration of different data distributions adopted by IF, FL, OF NoC for optimizing reuse and minimizing SRAM accesses.
In cases where valid compressed IF/FL data and corresponding sparsity bitmaps are present in the buffers, the circular buffer FSM initiates bitmap transmission to the sparse byte select module and compressed IF/FL data transmission to the IF/FL multiplexer (mux) array. The load FSM calculates logical byte select signals based on current load counter values and configuration registers. These signals are utilized by the byte select modules, along with sparsity bitmaps, to determine physical byte select signals, which control the IF and FL mux arrays for data routing, accounting for potential compression. These mux arrays facilitate data routing between the circular buffers and the column buffers associated with each PE column. It is important to note that when communicating with the PE, control signals pass through the distribution network, utilizing a specific number of staging buffers to meet timing requirements. The Load FSM remains active, fetching data until the entire load volume is processed, at which point clock gating is initiated.
Another critical aspect of the distribution network is the interconnect or Network-on-Chip used to link the PE array to the drain and load blocks in the design. NoC must have the ability to unicast, multicast, or broadcast the input data to one or more PEs based on the order specified by the optimal schedule, as demonstrated in Figure 9.2. This maximizes reuse and minimizes the number of SRAM accesses, improving overall efficiency, as defined in existing research (Kwon et al., 2018). As shown in Figure 9.1, when valid compressed data are loaded into column buffers, IF and FL NoCs distribute data to the appropriate PEs.
3.4.2 Drain path
One of the core innovations within the FLEXNPU architecture is FLEXDRAIN, an efficient framework for processing OF maps across various schedules. Systematically drains OF maps, specifically tailored for flexible schedule-based DNN accelerators. Focusing on MAC operations along the IC dimension, the fixed drain pattern ensures consistent extraction of OF points in an IC-major fashion, regardless of the current layer schedule. This design choice capitalizes on the understanding that sparse compression in DNN accelerators predominantly occurs along the IC dimension. Implementing this fixed draining methodology simplifies drain design, integrating schedule awareness into load logic with minimal overhead. This novel approach holds promise for advancing DNN accelerators, enhancing reuse, reducing memory traffic, and improving energy efficiency.
The FLEXDRAIN datapath encompasses several agents distributed across the PE compute array subsystem. Figure 10 provides a high-level depiction of these components and their respective functions. The components constituting the drain data path are: (1) Local Drain (LD): Instantiated on a per-column basis, the LD is responsible for extracting the output activation or psums from the PE, facilitating their transfer to the Super Column Drain Concatenator (SCDC). (2) SCDC: Implemented on a per-super column basis, the SCDC is tasked with concatenating data from the output column buffers of all 4 columns within a super column using psum-NoC. Subsequently, it transmits this concatenated data to the Global Drain (GD) via the super-column NoC. (3) GD: Serving as a central agent, it plays a pivotal role in rearranging SCDC data in a 1 × 1 × Z manner, which further encodes/compresses these data and writes them to the SRAM.
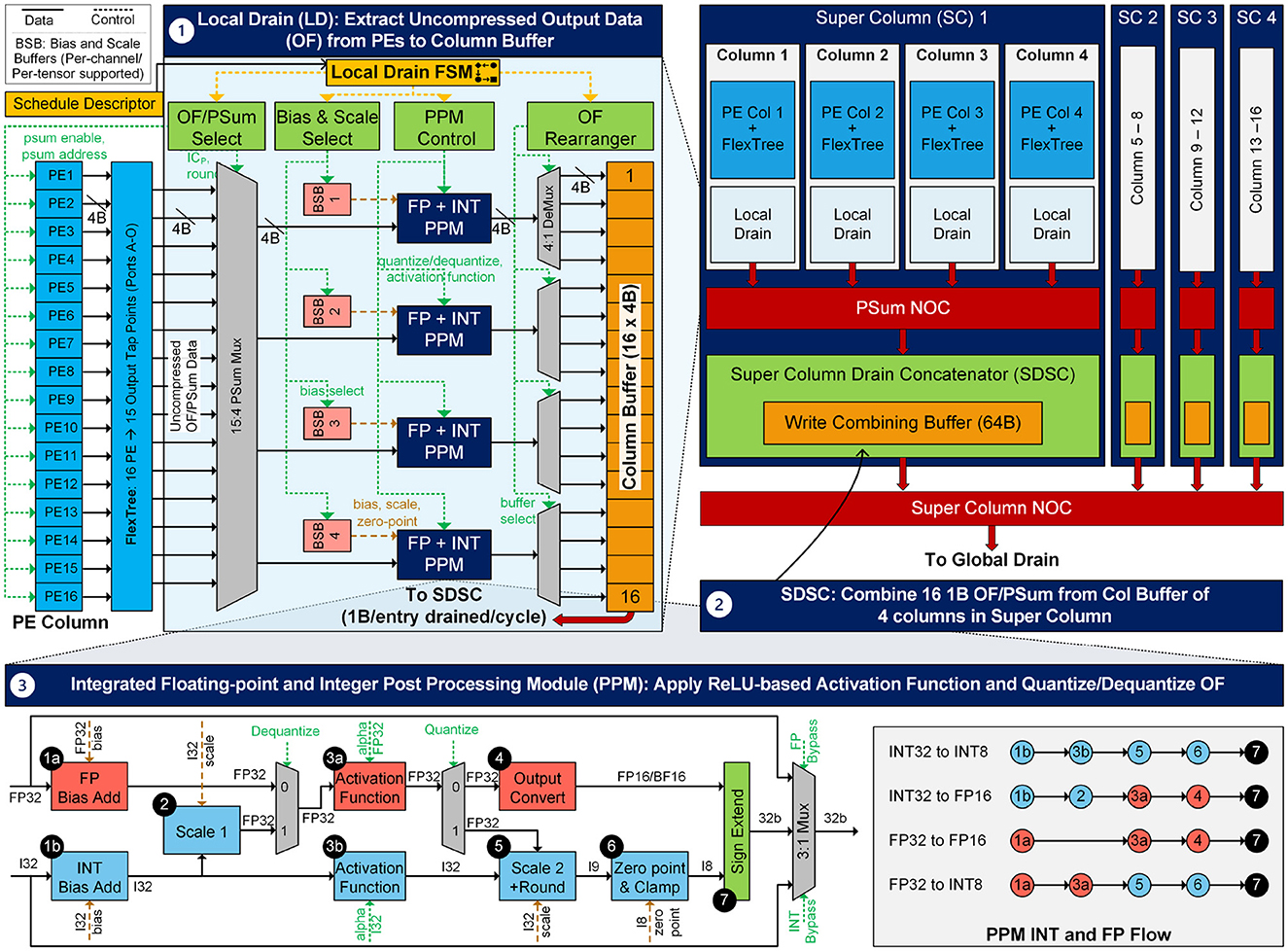
Figure 10. FLEXNPU accelerator local drain path, showing (1) local drain path routing output activations/partial sums from each PE inside a PE column to column buffer. Group of 4 columns organized into the super column. (2) SDSC per super column routes data from the local to global drain. (3) Detailed architecture of the post-processing module showing both floating-point and integer paths.
Local drain: The Local Drain (LD) operates to extract output activation data from the PEs within a column, forwarding them to the Post Processing Modules (PPMs), and then directing the PPM outputs to the column's output buffer, subsequently routed to the centralized GD. An overview of the local drain datapath is depicted in Figure 10. The accompanying block diagram illustrates the various components of the Local Drain at a high level, each of which will be elaborated upon in subsequent sections. As previously outlined, each PE can generate up to 16 OF points per round for a given set of input data, with the exact count contingent upon the layer and input tensor parameters. Upon readiness, these OF points transition from the active OF RF to the shadow OF RF. Following this transfer, the PE signals to the Accumulate Finite State Machine (AccumFSM), a part of local drain FSM, that the associated Local Drain is primed to extract the OF points from the PEs.
Flow of Control: Based on the layers and tensor parameters configured in the registers, it is possible to determine whether AccumFSM needs to consume data for accumulation across PEs, particularly if ICs are distributed across different PEs. In such scenarios, the LD waits for the AccumFSM to complete processing these OF points before proceeding. When AccumFSM is active, the LD streamlines the flow, refraining from extracting OF points until the accumulation is complete. In contrast, when AccumFSM is not required prior to LD operations, the PEs trigger the extraction process to the LD. The extraction sites and the number of points in each PE with a valid OF point to be extracted are determined using configuration registers. This information guides the sequential extraction of OF points from the shadow OF RF. Upon completing the extraction from the shadow OF RF, the LD indicates to the PEs that the shadow OF RF is fully utilized and prepared for the next round of transfers from the active OF RF.
OF Select to PPM: The OF outputs accumulated from the FlexTree flexible adder architecture (Section 3.3.1), multiplexed (MUXed) using a 15:4 MUX, are fed into each PPM. LD orchestrates the selection of inputs for the psum-MUX in a round-robin manner, facilitating the transfer of input data into the PPM. The LD assumes the responsibility of steering the data path for the PPM, issuing input data alongside bias/scale values, and subsequently extracting the output data to feed into the output column buffer.
Post-Processing Module (PPM): The PPM performs various post-processing operations on the OF points of each layer. It includes two primary data paths: an INT path and an FP path, as illustrated in Figure 10.3. The INT path is primarily used for quantized convolution/matmul workloads. It processes INT32 accumulator outputs through a sequence of operations: bias addition, activation function, quantization, rounding, zero-point adjustment, and clamping, to produce INT8 outputs. The FP path is used for floating-point convolutions/matmuls. It applies bias addition, activation functions, and output format conversion (e.g., from FP32 to FP16/BF16). Additionally, the PPM supports mixed-precision modes: for instance, in FP-to-INT8 conversion, the FP path handles bias and activation, while the INT path applies scaling and zero-point adjustment. Similarly, INT-to-FP conversions are also supported, where dequantization is applied before activation in the FP path. Note that PPM also supports bypass mode for draining partial sums when the final OF is not generated in the current computation round. All functions and modes are controlled via a dedicated bank of configuration registers, which dictate processing behavior, scale selection, and bias application. The PPM natively supports multiple ReLU variants for quantized inference, programmable through descriptor-based control logic. For more complex activation functions such as GELU or Swish—which are not natively implemented—the FLEXNPU system provides a fallback mechanism via a tightly integrated on-chip DSP processor (as shown in Figure 5). In such cases, OF points are routed directly to the DSP in floating-point precision (FP16/BF16 or FP32 using bypass mode), and the processed outputs are seamlessly reintegrated into the accelerator pipeline.
OF Rearranger: The PPM data output links to the column OF buffer entries through a 4:1 DeMUX, configured by LD FSM based on the drained OF point context. LD directs the PPM output to the appropriate buffer entry. In layers where certain PEs yield no OF points, LD ensures that 0 values populate the corresponding buffer entries, facilitating seamless data drainage by GD. For floating-point cases, data must be outputted in high-low pattern for seamless processing by both GD and Sparse Encoder.
Taking into account the area and performance specifications of the accelerator, it has been established that each column, comprising 16 PEs, should integrate 4 PPMs. This configuration includes 4 INT PPMs and 4 FP PPMs, activated when FPMACs are enabled. Each of these PPMs is exclusively allocated to serve 4 PEs, ensuring optimized resource utilization and efficient processing capabilities.
Super Column Drain Concatenator (SCDC): The Super Column Drain Concatenator (SCDC) plays a pivotal role in consolidating data from the output column buffers of all 4 columns within a super column and forwarding it to the centralized GD via the Super Column NoC (SC-NoC). Each output column buffer within a column is 4 bytes wide and 16 entries deep. Once all round-required entries are filled in individual column buffers, LD in each column transmits 16 bytes of data from its column buffer to the SCDC through the psum agent packet NoC (psum-NoC) per round. SDSC combines these 4 × 16B values into 64B data. A 2-bit super-column ID (SCID) is appended to create a 514-bit data packet for GD, which is subsequently transferred to the GD via the SC-NoC. Thus, the SDSC serves as a crucial link between the LD and the GD. Note that when PPM is enabled, each generated output activation is 1 byte for INT8 precision or 2 bytes for FP16/BF16 precision. In both cases, data from the column buffer is dispatched to the SCDC in 16-byte chunks, formed by 1byte from the 16 different entries of the buffer. Thus, the SDSC drains outs INT8 OF in 1 cycle, FP16/BF16 OF in 2 cycles, and FP32/INT32 PSUM in 4 cycles in bypass mode.
Global Drain: The Global Drain (GD), as demonstrated in Figure 11 (left side), serves as the central hub within the PE array subsystem, tasked with gathering output activation points from PEs across all columns. Its primary function involves rearranging these activations into a 1 × 1 × Z format, where Z represents the OC dimension for the current layer (or the IC dimension for the subsequent layer). Subsequently, the GD encodes these activations and writes them to the SRAM for further processing or storage. The GD comprises the following components: (1) A 256B input buffer called the Drain Staging Buffer (DSB) where the output activations from all PEs are staged. 64B data from each Super Column are transmitted to the GD via the SC-NoC, and concatenated into the DSB, thereby generating 256B for processing. (2) Global Drain Mux (GDM) network consisting of 4 sets of multiplexer arrays that rearrange the staged output activations from DSB into the Drain Banks. (3) Sixty four Drain Banks (DB) organized as 4 groups of 16 entries, with each Drain Bank of size 16B, for a total of 1KB. These buffers serve as a pre-final staging area for output activations from PEs before encoding and writing to SRAM. Each 16B bank can hold 16 OCs for the next layer, controlled by GDM for writing and DAGU for reading. (4) Drain Address Generator Unit (DAGU), which computes the x, y, z coordinates of the points in the DBs that will be written into the SRAM. The read signals drive a drain bank reader (not shown in figure) to get the data out of the DBs. (5) A bank of four Sparse Encoders (SE), which encode the data to be written to the SRAM. (6) Four Write combining buffers that allow the writing of compressed data and the corresponding sparsity bitmaps into the SRAMs. Among the six components, the Global Drain Mux and Sparse Encoder are the most important elements of the GD. Detailed explanations of these components are provided below.
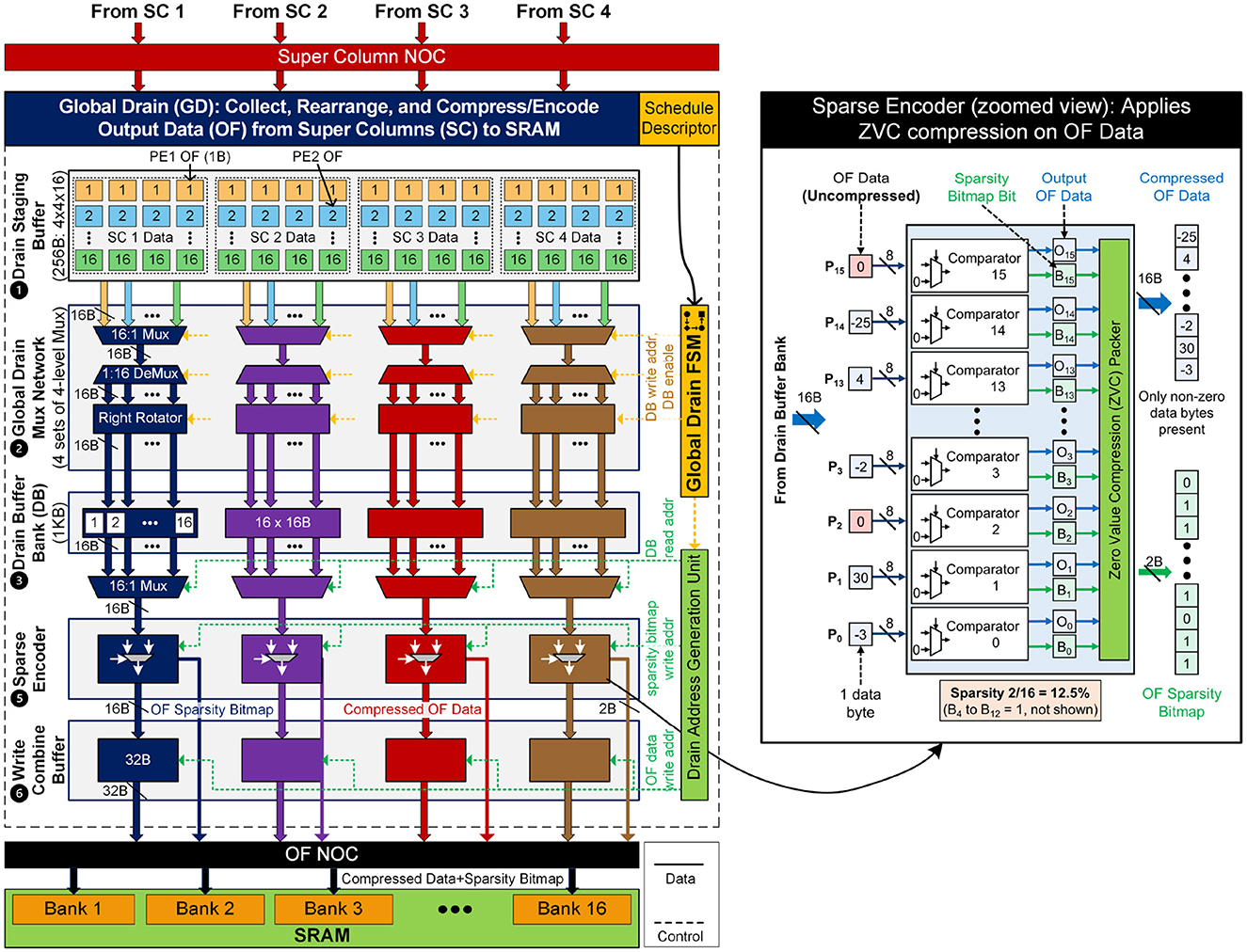
Figure 11. FLEXNPU global drain path, showing (1) drain staging buffer, (2) global drain mux network, (3) drain buffer banks, (4) drain address generation unit, (5) sparse encoders, and (6) write combining buffers. Collectively, these units drain uncompressed data from local drains and writes compressed data to SRAM. Illustration of sparse encoder performing zero-valued compression provided on the right.
Global Drain Mux: The role of the GD Mux control logic is to manage the selection process across the various mux stages to drain data from the DSB. There are a total of four GDMs, each capable of independently accessing DSB entries but restricted to writing solely to its designated group of DBs. Let us dive into each stage of the GDM: Stage S1: Entry Select: This stage involves choosing 16B of the DSB data. Following the configuration registers, the GD Mux control logic adopts a row-wise selection approach from the DSB, utilizing a 16:1 entry selects Mux capable of picking any of the 16 row entries. Stage S2: Bank Select: The 64 drain banks (DBs) are grouped into four sets, each containing 16 entries. The bank select function determines to which of the 16 entries the data will be written to. Notably, data can be written to multiple entries, potentially all 16 entries in an extreme scenario. The bank select or bank enable ensures proper multicasting of data to the DBs. Stage S3: Right Rotator: After each GDM multicasts the selected DSB entry to one or more DBs, it assigns an appropriate right rotation value specific to each DB. This step is crucial to align and concatenate consecutive Zs within a single DB. Stage S4: Byte Enable: Finally, this serves as the write byte enable, ensuring that the correct set of bytes from DSB line is written to the DB.
Sparse Encoder: This is a pivotal element within the global drain, crucial for leveraging data sparsity to enhance the speed of inference processing in FLEXNPU. Figure 11 (right side) provides a schematic representation of the SE block. Its primary function is to compress dense data streams by discarding zero values, thereby outputting a compressed data representation accompanied by a sparsity bitmap. The drain buffer acts as a staging area for the data before they are written to SRAM, providing the SE with input. Each DB bank is allocated to store data corresponding to a unique output context (OX, OY) point, with a 16B payload containing the OC data for that specific OX, OY coordinate pair. A single context, representing one data stream, may extend across multiple banks and up to 16 contexts can be processed concurrently within a group. The GDM ensures that banks flagged with valid bits, indicating that their data has yet to be processed by the SE, are protected from being overwritten. The SE itself operates on 16B granularity, compressing the data for each distinct context contained within the DB. The degree of sparsity dictates the number of input lines that the SE must handle before it can produce a compressed 16B output line for a particular context. Alongside the compressed data, the SE generates a unique sparsity bitmap for each context, which is then sent to SRAM through the OF-NoC. The address for writing the bitmap to SRAM is determined by DAGU. As elements within a context stream may be received over several cycles, the SE is designed to manage context switching efficiently by preserving the state of each context and retrieving it when necessary to continue processing. Note that the sparse encoder is bypassed when the final output activation point is not generated in the current computation round and instead partial sums are drained out to SRAM.
3.5 Two-sided sparsity acceleration
In the proposed FLEXNPU accelerator, our aim is to harness the sparsity in both FLs and IFs to enhance not only energy efficiency but also DNN inference throughput. Throughout the accelerator, the data remains compressed until reaching the PE. Operating within the compressed domain offers advantages, such as reducing on-chip bandwidth requirements and storage demands. However, handling compressed data, which often varies in length, poses challenges in terms of data manipulation, such as distributing data across PEs and implementing sliding window processing within the PE (Raha et al., 2022c). In this section, we will introduce an innovative two-sided sparsity acceleration logic capable of processing sparse data within the compressed domain to achieve higher throughput (Chinya et al., 2021; Raha et al., 2021c, 2022b; Kundu et al., 2024). This logic spans multiple units including VPE, load and drain path.
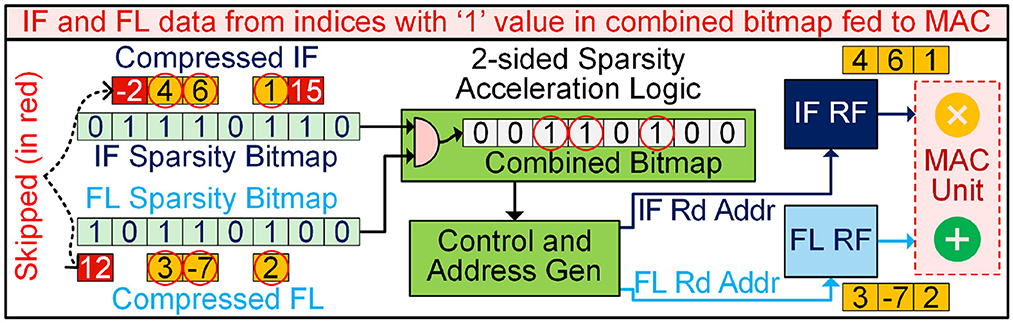
The core idea is that IFs or FLs with a value of 0 do not contribute to non-zero outcomes during MAC operations, allowing them to be skipped during both the compute and storage phases (Connor et al., 2020). As explained in Section 3.4.1, SRAM serves as storage for zero-value compressed input activations (IF) and weights (FL), which are delivered to each column buffer in batches through the load path in SDN (Chinya et al., 2023; Raha et al., 2021c). The PE FSM then transmits the compressed IF and FL to their respective buffers (CD RF) in each PE. Along with these, the corresponding bitmaps are also transferred to IF and FL sparsity bitmap buffers, respectively.
As illustrated in Figure 6.3, the two-sided sparsity acceleration module in FLEXNPU receives bitmaps as inputs, each consisting of 1-bit entries that denote whether a corresponding value in the original activation (IF) or weight (FL) vector is non-zero. A “1” represents a meaningful non-zero entry, while a “0” indicates a zero value that has been removed through zero-value compression (ZVC). These compressed vectors and their associated bitmaps are loaded into dedicated register files and buffers within each Processing Element (PE). This logic operates over a fixed-size compute window—such as 16 activations and 16 weights. Rather than decompressing the data or performing all possible multiply-accumulate (MAC) operations, the accelerator uses a dedicated find-first sparsity logic to identify only those positions where both activation and weight are non-zero. This produces a combined sparsity map that directly indicates the valid compute pairs—those that will contribute to non-zero partial sums. To execute this efficiently, the system maintains a tracking mechanism to keep record of which pairs have already been processed. In each cycle, it scans for the next unprocessed valid pair—i.e., the earliest position in the window where a non-zero activation aligns with a non-zero weight. This is done through a low-latency circuit implemented in combinational logic. Once identified, the logic computes the internal offset within the compressed data and retrieves the corresponding values from the register files. These values are then fed into the MAC unit via the CAG unit, contributing to the generation of the output feature maps, as demonstrated in Figure 12. After each MAC operation, the tracking state is updated, and the system proceeds to the next valid pair. This continues until all meaningful activation-weight pairs in the window are processed. Critically, the design ensures that each cycle performs exactly one useful computation, dynamically adapting to sparsity and skipping ineffectual MACs without wasting compute resources. Once the computations are complete, the output feature maps flow through post-processing stages such as activation functions and scaling. They are then passed through another ZVC module that removes zero-valued elements and generates updated bitmaps for the outputs. These compressed feature maps are stored in SRAM or DRAM for further use in downstream layers, preserving compression throughout the end-to-end inference pipeline. By tightly integrating sparsity-aware decoding, dynamic compute scheduling, and output compression, this combined logic significantly improves the performance and energy efficiency of FLEXNPU. It reduces the number of cycles to match the actual number of useful computations, minimizes data movement, and maintains a lean, compression-aware memory footprint—making the architecture especially suited for efficient deep learning inference in energy-constrained environments.
4 Experimental setup
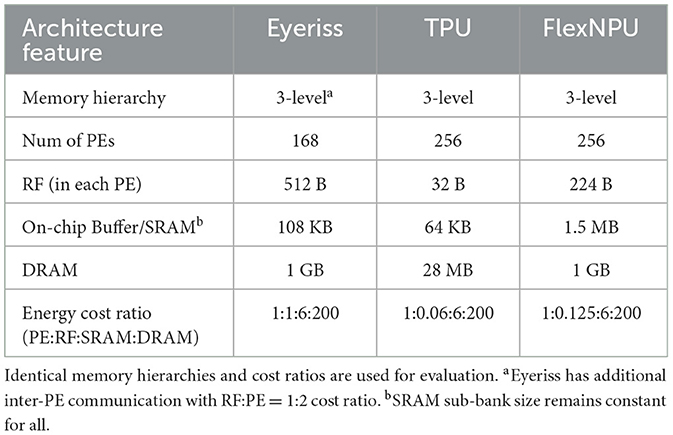
To evaluate the efficiency of the proposed accelerator, we implemented FLEXNPU in Chisel 3.0, with the generated RTL simulated in Synopsys VCS®. We chose Chisel because of its ability to facilitate the generation of parametrizable designs featuring multiple variations of PE, allowing easy modification of RF size, number of MAC units, etc. As mentioned in Section 3.2, the accelerator supports UINT8, INT8, FP16, BF16 precision. Subsequently, the RTL undergoes synthesis in the Synopsys Design Compiler (DC), utilizing one of the industry's most advanced process technology nodes, (based on 7 nm), to generate the Gate-Level Netlist (GLS) and corresponding area for each accelerator component. To estimate the power consumption within the proposed FLEXNPU accelerator, we employed Synopsys Verdi to generate an activity file (Switching Activity Interchange Format: SAIF), using test benches for assistance. The accelerator netlist, coupled with the activity file, serves as input to Synopsys PrimeTimePX (PTPX), enabling power estimation at the gate level for both block and full-chip designs of the FLEXNPU accelerator. The FLEXNPU architecture comprises a unified tile of 256 PEs organized in a 16 × 16 grid (16 columns with each column having 16 individual PEs), featuring 8 MAC units within each PE, resulting in a total of 2048 MACs. This tile encompasses 1.5 MB of SRAM equipped with 32-byte read/write ports. The PE consists of 4 × 16 9bit IF Data RF Register File (RF), 4 × 16 9bit FL Data RF, and 16 × 4 B OF RF. In addition, each PE also consists of 4 × 2B IF sparsity bitmap RF and 4 × 2B FL sparsity bitmap RF, which is 1/8th the size of data RF, as 1 bit in bitmap is used to represent 1 entry in IF/FL. Together, these RFs contribute to 224B RF per PE. The precision of the IF and FL is INT9 and OF points is FP32/INT32. The memory hierarchy of our design is illustrated in Table 1. Operating at a frequency of 2.4 GHz and 0.65 volts, the accelerator boasts a dense peak Trillion Operations Per Second (TOPS) performance, reaching 7.37 TOPS, with efficiency metrics of 5 TOPS/watt and 4.6 TOPS/mm2.
4.1 Datasets and benchmarks
We conducted a comparative analysis of the performance of FLEXNPU in conjunction with two state-of-the-art dense accelerators, namely Eyeriss (Chen et al., 2016c) and TPU (Jouppi et al., 2017). The comparison considered various design specifications described in Table 1. Furthermore, we evaluated the performance of FLEXNPU on sparse DNN workloads using state-of-the-art networks: ResNet50, MobileNetV2, InceptionV3, and GoogLeNet trained on the ImageNet dataset (Krizhevsky et al., 2012). The first three models were compressed using (i) Quantization-Aware Training (QAT) to quantize weights/activations to INT8 precision and (ii) unstructured pruning using the regularization-based sparsity algorithm (RB-sparsity). GoogLeNet was quantized in the same way, but filter pruning with geometric median criterion was applied. The compressed models were obtained from Intel's Neural Network Compression Framework (NNCF) (Kozlov et al., 2020). Per-layer and overall network weight sparsity were obtained from these models. Furthermore, all models were subjected to inference on the entire ImageNet2012 validation dataset (50,000 images) and activation sparsity at input and output of each layer was calculated using PyTorch hooks. The average activation sparsity across the entire dataset, weight sparsity, and layer statistics were fed into a framework of FLEXNPU, which was used to obtain the layer-wise and overall network compute acceleration and total energy consumption of the accelerator, reported in Section 5. In addition to traditional CNNs, we considered 4 state-of-the-art transformer based models and corresponding application/dataset. DETR-ResNet50 was evaluated on MS-COCO dataset for object detection. For Question Answering tasks, we employed DistilBERT-base on the SQuAD1.1 dataset. Lastly, for Sentiment Classification, we utilized T5-base on the Glue SST2 dataset, and MobileBERT on the Glue MNLI dataset. Weights of all these models were compressed to FP16 format, targeting evaluation of the FP MAC path in our accelerator.
To ensure accurate modeling of activation sparsity, we adopted a symmetric quantization scheme (for 4 CNNs) with a 0 zero-point for the outputs of convolution layers followed by ReLU-type activations. This choice preserves true zeros in the quantized domain, thereby retaining the sparsity induced by the activation functions. Using a non-zero zero-point could otherwise obscure zero activations, reducing sparsity and degrading the effectiveness of our two-sided sparsity-aware engine. This design choice ensures that the sparsity measurements and acceleration results reported in Section 5 faithfully reflect the actual sparsity distribution in the models. Specifically, we compared the performance of FLEXNPU, which uses two-sided combined sparsity, against dense accelerators without any sparsity support and those capable of exploiting fixed weight-sided sparsity (Chen et al., 2016c; Park et al., 2020). The framework was modified to evaluate the latency and energy of a dense variant and a weight-sided variant of FLEXNPU to allow fair comparison.
4.2 FlexNPU cost model
To evaluate the performance of the proposed FLEXNPU accelerator, we developed a cycle-accurate analytical cost model calibrated using RTL simulations. This model is used to estimate compute and memory latency per layer and to generate the total end-to-end cycle counts reported in Section 5. Note that compute acceleration metrics are reported only for FLEXNPU, while reference architectures such as Eyeriss (Chen et al., 2016c) and TPU (Jouppi et al., 2017) are evaluated purely in their dense configurations. Since their RTL models and sparse execution logic are not publicly available, they are modeled under identical memory and energy assumptions, but without sparsity-induced acceleration. For FLEXNPU, the cost model was calibrated using detailed RTL simulations of our architecture. The RTL was written in Chisel and simulated using Synopsys VCS. Functional and switching activity traces were collected to estimate dynamic behavior, and synthesis was performed using Synopsys Design Compiler. A broad sweep of representative DNN layers was simulated, spanning various tensor shapes, sparsity levels, and schedule configurations, ensuring the analytical model captures realistic microarchitectural behavior across different scenarios. The model accounts for:
• Sparse MAC compute cycles, based on activation and weight bitmaps.
• Memory access cycles across hierarchy levels, including overhead for bitmap-based compression and decompression for sparsity acceleration logic.
• Load/compute/drain phase transitions, governed by the FSM in each PE column.
• Control logic and flow dependencies, including two-sided sparsity traversal and operand gating.
Optimal layer schedules—defining the loop ordering, blocking factors, and data reuse strategy are evaluated to select the configuration that minimizes combined compute and memory cycles. The analytical model incorporates FLEXNPU's two-sided sparsity support, which dynamically identifies valid operand pairs at runtime, enabling zero-skipping in both activations and weights as described in Section 3.5. The compute engine avoids unnecessary MAC operations using this mechanism, and the model accurately captures this benefit in per-layer cycle estimation. By using consistent modeling assumptions across baselines and validating against RTL simulations, we ensure that performance and energy comparisons in Section 5 are both fair and grounded in architectural reality.
5 Experimental results
In this section, we present a comprehensive evaluation of the proposed FlexNN accelerator, including test chip measurements and post-synthesis results. The evaluation begins with area and power breakdowns at the chip and PE levels, followed by a comparison with Eyeriss and TPU under dense inference to highlight the benefits of flexible dataflow. We then demonstrate the gains from two-sided sparsity acceleration across several CNN and transformers models, showing improvements in energy and performance.
5.1 flexNPU test chip implementation and evaluation
This section presents the implementation details of the FLEXNPU test chip fabricated in Intel's 7nm technology node, followed by the power and area evaluation using both synthesis results and post-silicon measurements.
5.1.1 Test chip design and layout
Figures 13.2, 3 illustrates the logical and physical layouts of the FLEXNPU test chip prototype. The chip instantiates four FLEXNPU columns, constrained by the available test chip area. Within each column, sixteen VPEs are deployed. The place and route layout in Figure 13.4 highlights individual PEs with different colors, IF/FL load buffers, and the local drain in a single VPE column, which follows the architecture described in Section 3.3. As illustrated, the NoC includes routers that facilitate data movement between the four columns, load (Section 3.4.1), the checker, which is a simplified version of the global drain. This module aggregates output data from the columns and compares it against precomputed reference results stored in a programmable logic array (PLA). Detailed chip parameters and area metrics are presented in Table 2. The aspect ratio, total area, operating frequencies, and memory hierarchies used are summarized to aid in contextualizing the power and area efficiency of the design.
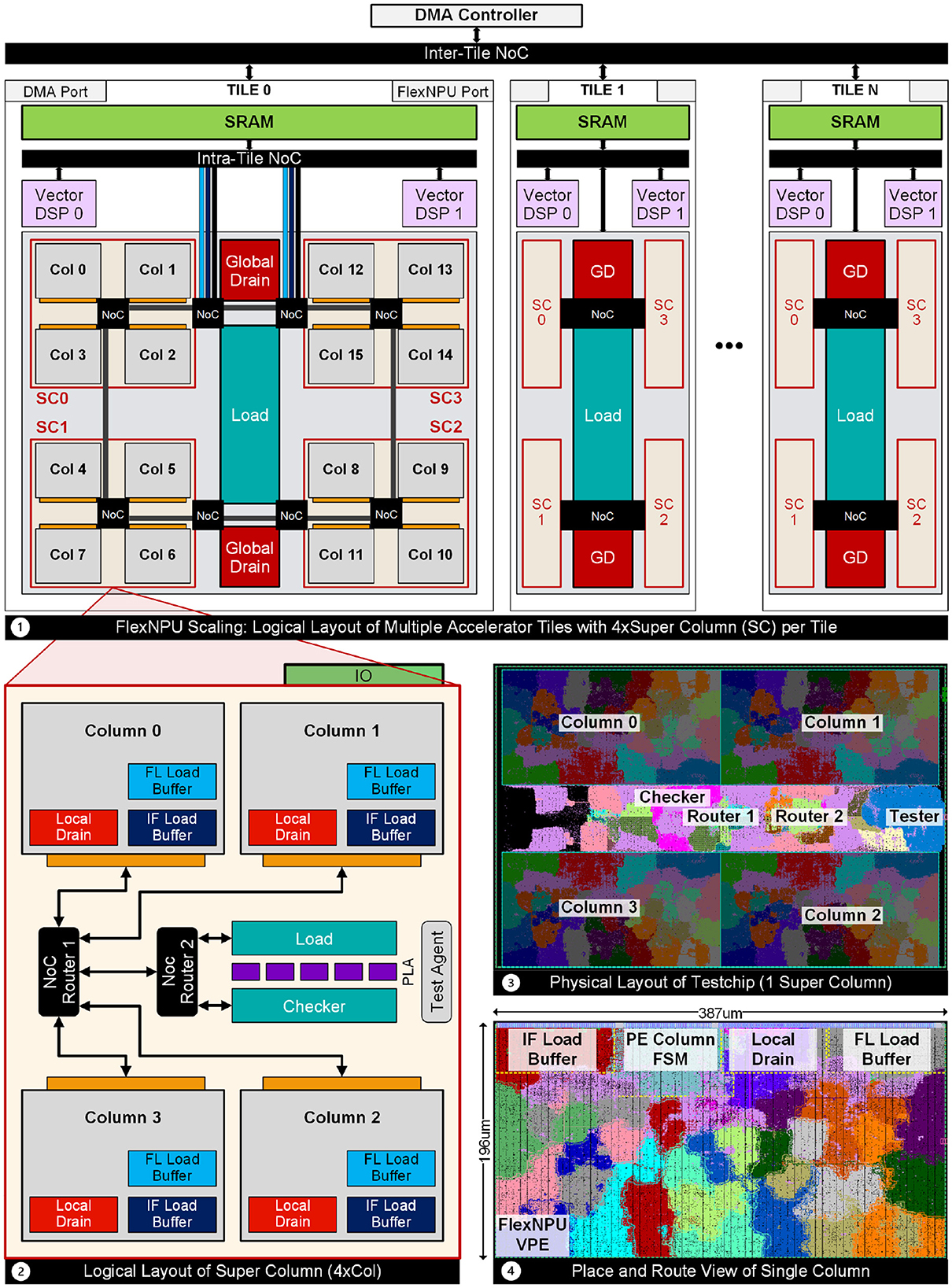
Figure 13. FLEXNPU test chip layout details and modular scaling layout. (1) Organization of accelerator tiles and four super column (16 VPE columns)/tile for scaling FLEXNPU TOPs. (2) Logical layout of a single super column with four VPE columns. (3) Physical floorplan of test chip. (4) Place and route view of single FLEXNPU VPE column with highlighted PEs, buffers, and local drain.
5.1.2 Power and area characterization
The power and area distributions for the FLEXNPU accelerator are presented in Figure 14. The top row (1–4) visualizes the area breakdown across different architectural hierarchies, while the bottom row (5–8) reports the corresponding power consumption.
1. Synthesis results: In the synthesized design, the PE-level area is dominated by MAC units, accounting for 54% of the PE column area (Plot 1), followed by RFs used for IF/FL/OF data and sparsity bitmaps, jointly consuming 33% (data: 28%, bitmap: 5%). Control and sparsity acceleration logic modules contribute minimally. At the system level (Plot 2), inter-PE mesh consisting of 16 × 16 PE array dominates both area and power, contributing more than 80%. Similarly, in power breakdown (Plot 5), MAC operations consume 46%, while data storage and movement use 26% (data: 22%, bitmap: 4%), reflecting efficient data reuse. Control and sparsity logic accounts for remaining 24% power.
2. Post-silicon test chip results: Power was measured by executing integer and floating-point test configurations with identical dimensions and durations, and averaging the results over the active execution window. PE-level measurements (Plots 3 and 7) closely match synthesis trends, with MAC units occupying 56% (FP: 30%, INT: 26%) of area and 43% (FP: 25%, INT: 18%) of power. The PE column in the test chip (Plots 4 and 8) shows high efficiency: 16 PEs consume 85% of the area, with remaining modules (local drain, FlexTree, control/buffers) using 15%. Inside the drain, PPM modules contribute 6.4% of the total column area. Note that, power consumption in the PE column is overwhelmingly dominated by the compute engine (98%), validating the minimal overhead from control and data movement logic. The critical path, identified through test chip measurements, lies within the FPMAC unit of the FLEXNPU FLEXNPU, where computations are performed using activations and weights from the IF/FL RF and results are written back to the OF RF.
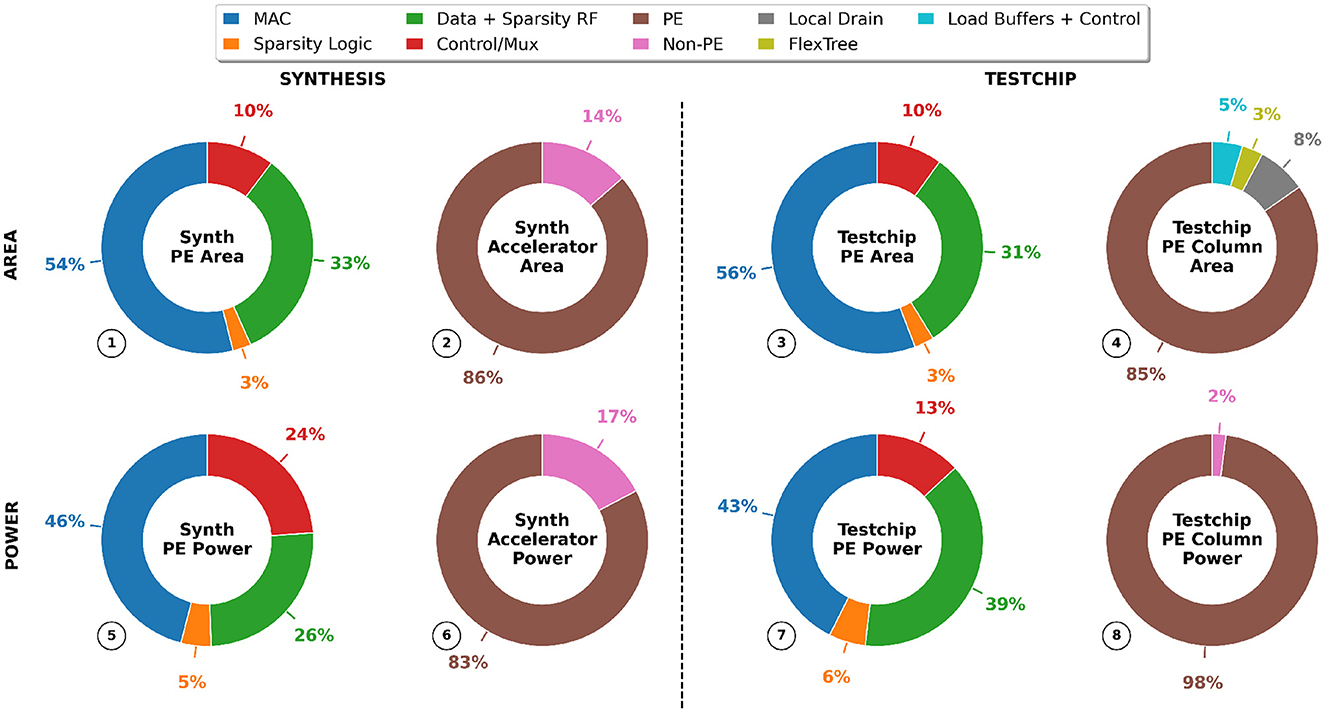
Figure 14. Area (top row) and power (bottom row) breakdown of synthesized and FLEXNPU test chip. (1, 5) PE breakdown in synthesis, (2, 6) full accelerator breakdown in synthesis, (3, 7) PE breakdown in test chip, and (4, 8) single column breakdown in test chip.
5.1.3 Scaling flexNPU for high TOPS
To meet higher TOPS demands, the FLEXNPU architecture adopts a hierarchical and modular scaling strategy—one that goes beyond simply increasing the number of PEs. A naive scale-up of PEs would eventually lead to routing congestion, bandwidth bottlenecks, and diminishing returns due to the centralized resource contention. Instead, FLEXNPU employs a structured, congestion-aware design, as illustrated in Figure 13.1. At the lowest level, individual PEs are organized into vertical columns, optimized for local data reuse and pipelined computation. Next, four such PE columns are grouped to form a Super Column, which integrates localized interconnect and shared control. We then stamp out four super columns to construct a single FLEXNPU tile, which acts as an independently schedulable compute unit with its own dataflow control and buffer hierarchy. This tiling approach ensures that data movement and scheduling remain manageable even as the architecture grows. Finally, multiple FLEXNPU tiles are instantiated to form the complete FLEXNPU accelerator. At this top level, workload distribution occurs across tiles, each of which executes its assigned partition independently. This hierarchical scale-out method allows FLEXNPU to achieve higher compute throughput while maintaining area efficiency, predictable routing, and scalable memory bandwidth—crucial for deployment in constrained edge or mobile form factors.
5.2 Comparison with SOTA fixed schedule accelerators
Figure 15 shows the improvement in energy efficiency of our flexible schedule DNN accelerator FLEXNPU over two prominent fixed-schedule designs, Eyeriss (Chen et al., 2016c) and TPU (Jouppi et al., 2017) assuming identical memory hierarchies. These results are obtained for two DNNs used in image classification and object detection, ResNet101 and YOLOv2, using our custom DNN accelerator energy estimation framework. We have used dense models (i.e., with 0 weight sparsity) for these results. Note that we have scaled the memory hierarchy of the two accelerators to the same level as FLEXNPU for a fair comparison. In this figure, Here, the y-axis represents a % reduction in energy consumption of FLEXNPU compared to these two designs. The left subplot depicts the layer-wise energy reduction for all layers, sorted in increasing order of reduction. In the right subplot, we summarize the distribution of reduction across all layers. The x-axis shows the two comparative accelerators. Compared to Eyeriss, FLEXNPU results in 40%–77% reduction for ResNet101 and 45%–77% for YOLOv2. Compared to TPU, FLEXNPU provides up to 62% and 58% energy savings for ResNet101 and YOLOv2, respectively. While it is true that in certain layers, FLEXNPU exhibits a slight energy increase (indicated by a negative energy reduction) compared to TPU, this is primarily attributed to the optimized dataflow in TPU for specific layers, particularly 20 layers in ResNet101 and 4 layers in YOLOv2. However, on average, FLEXNPU still provides notable advantages, offering average energy savings of 14% and 22% for these respective DNN architectures over TPU. It is important to note that the increased energy consumption in these layers comes from the robust support for flexibility within DNN, which inherently introduces slightly higher overhead. On the other hand, we see an average improvement of 57% and 69% over Eyeriss. Despite occasional spikes in energy consumption for select layers, FLEXNPU consistently outperforms these fixed-schedule accelerators, showcasing its superior efficiency and overall cost-effectiveness.
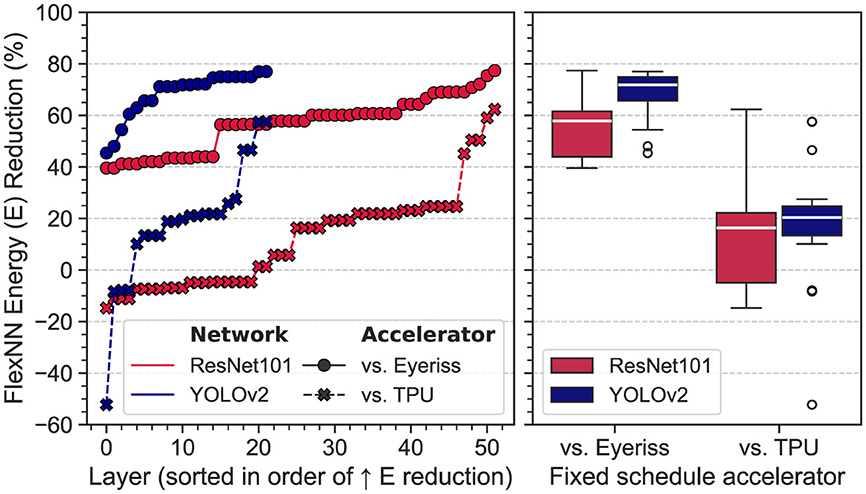
Figure 15. Layer-wise distribution of % energy improvement of FLEXNPU over fixed schedule DNN accelerators (Table 1) for ResNet101 and YOLOv2 (dense models). Optimal schedule used for each layer in FLEXNPU accelerator.
5.3 Sparsity benefits using FLEXNPU
In this section, we present a comprehensive analysis of the layer-wise and overall network speed-up achieved by FLEXNPU compared to two prominent counterparts: a dense accelerator without any sparsity acceleration support and a fixed weight-sided sparse accelerator. Figures 16.1–4 presents the layer-wise compute acceleration (y-axis) provided by weight-sided and FLEXNPU in comparison with the dense accelerator, for few representative layers (x-axis) of 4 DNN benchmarks. Note that the activation sparsity numbers reported in the following discussion are averaged across the entire dataset. For a fair comparison, benchmarking was performed using the same optimal schedule for all accelerator types.
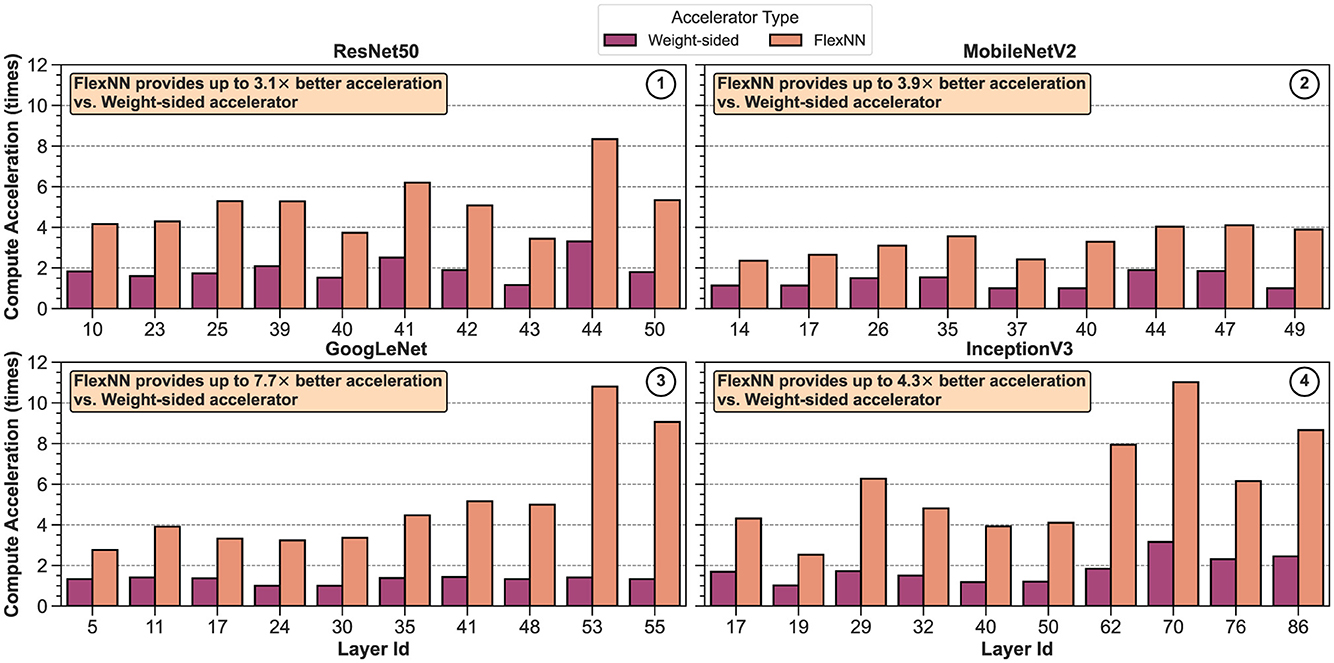
Figure 16. Comparison of layerwise compute acceleration of FLEXNPU and Weight-sided (one-sided) sparse accelerator over dense accelerator (no sparsity support) benchmarked with (1) ResNet50, (2) MobileNetV2, (3) GoogLeNet, (4) InceptionV3. Few representative layers are presented for each DNN.
5.3.1 ResNet50
The sparse ResNet50 model has 5%–88% unstructured weight sparsity, weight_splayer, resulting in up to 8.1% acceleration across layers in weight-sided accelerator. However, except before the first conv layer, ResNet50 has a high activation sparsity, act_splayer, at the input of every convolution layer due to the presence of the ReLU activation function. On average across the entire ImageNet validation dataset, this amounts to act_splayer = 14%–83% sparsity. FLEXNPU conveniently leverages both weight and activation sparsity to provide up to 10.3% compute acceleration, as shown in Figure 16.1. Overall, FLEXNPU gives up to 3.1× better acceleration than the weight-sided accelerator for ResNet50.
5.3.2 GoogLeNet
Since GoogLeNet was filter-pruned, maximum weight_splayer = 30%. This contributed to maximum 1.4× speed-up in weight-sided accelerator. In contrast, the maximum measured act_splayer = 91% resulted in a maximum acceleration 10.8× in FLEXNPU. Figure 16.3 shows that FLEXNPU provides up to 7.7× better compute acceleration compared to fixed weight-sided accelerator, even for networks with low weight sparsity.
5.3.3 InceptionV3
This model is very sparse with a maximum weight_splayer = 96%. There are many layers with large dimensions and filter sizes; therefore, both the weight-sided accelerator and FLEXNPU can leverage weight sparsity and provide up to 24.7× speed-up for Mixed.7a.branch3x3.2.conv, Layer Id: 72 (not shown in figure). Although act_splayer for this layer is 78%, FLEXNPU cannot provide any additional speed-up for this layer. However, there are many other layers with activation sparsity higher than weight sparsity, allowing FLEXNPU to leverage both. As depicted in Figure 16.4, FLEXNPU provides a high level of compute acceleration. Among such layers with sparsity skewed toward activations, the maximum speed-up is 11.3×. Therefore, the proposed design can take the best of both worlds and give better savings than the weight-sided accelerator. Across all layers, FLEXNPU is up to 4.3 × faster than the weight-sided accelerator, clearly demonstrating superior performance.
5.3.4 MobileNetV2
MobileNetV2 is a compact and lightweight model compared to the other benchmarks discussed earlier. Although sparse MobileNetV2 consists up to 70% weight_splayer, the maximum speed-up provided by the weight-sided accelerator is only 3.3× (last linear layer). Interestingly, the weight sparsity of all conv layers, except features.18.0, Layer Id: 51 is <50% leading to a low overall speed-up. However, FLEXNPU leveraging activation sparsity (maximum act_splayer = 74%) in addition to weights can provide up to 4.1× acceleration. Figure 16.2 indicates that even for compact models with small layer sizes, FLEXNPU is superior to the weight-sided accelerator by 3.9×.
5.3.5 Overall network acceleration
The compute acceleration obtained by dense, weight-sided and our proposed accelerator for the entire end-to-end network inference, depicted in Figure 17.1 reveal a significant acceleration advantage conferred by FLEXNPU across all evaluated networks. Here, the y-axis represents the acceleration, whereas the x-axis represents benchmarks. The dense accelerator does not provide any acceleration as it cannot leverage weight or activation sparsity, denoted by values 1. Evidently, the speed-up for weight-sided accelerator is proportional to the overall network weight sparsity. Across all these networks, the weight-sided accelerator provides 1.01 × –1.79 × speed-up. On the contrary, the acceleration obtained in FLEXNPU is proportional to the relative distribution of weight and activation sparsity. For ResNet50, weight_spnetwork, act_spnetwork = 61%, 55% and FLEXNPU takes advantage of them to provide 3.11 × speed-up. MobileNetV2 and GoogLeNet has weight_spnetwork, act_spnetwork = 52%, 30% and weight_spnetwork, act_spnetwork = 24%, 58%, respectively. These results in 1.81 × and 2.63 × speed-up in FLEXNPU, respectively. Clearly, even with these two networks with low sparsity on one side, FLEXNPU provides a significant amount of computation due to two-sided sparsity support. Finally, InceptionV3 has weight_spnetwork, act_spnetwork = 61%, 63% contributing to 3.3×, which is the maximum across the 4 networks. As evident from these results, our accelerator consistently outperforms both dense and weight-sided architectures in terms of compute acceleration. This substantial improvement, 2.6 × vs. dense and 1.8 × vs. weight-sided accelerator (geomean), underscores the efficacy of our proposed approach in enhancing overall network speed-up, demonstrating its superiority in accelerating DNN inference computations. Furthermore, the observed acceleration benefits are valid across the various architectural complexities and model sizes represented by the diverse DNNs considered in our evaluation. This robust performance underscores the versatility and effectiveness of two-sided sparsity acceleration support in FLEXNPU across a spectrum of DL models.
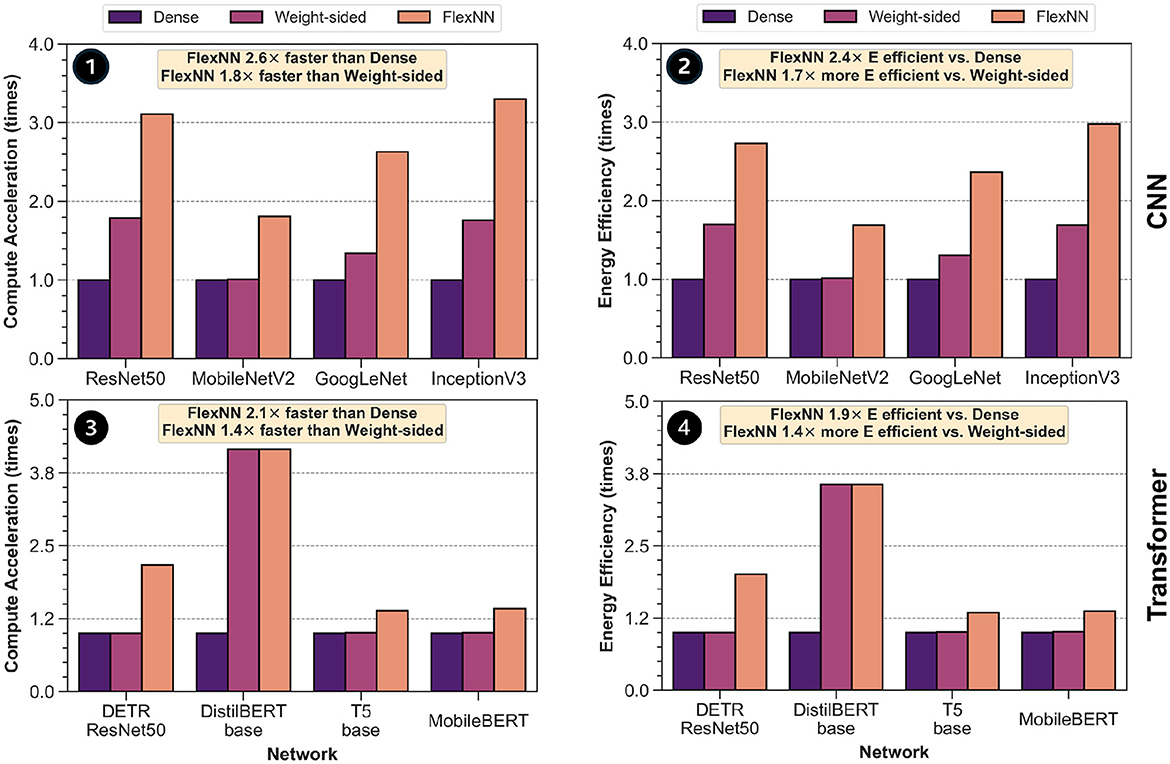
Figure 17. Comparison of (1, 3) compute acceleration and (2, 4) energy efficiency for full network inference in FLEXNPU over dense and weight-sided accelerator benchmarked with 4 CNNs and 4 transformers.
We further validate the generality of our approach on Transformer-based architectures, as illustrated in Figure 17.3. For models such as T5 and MobileBERT, our proposed accelerator achieves 1.4 × speed-up, even in scenarios with relatively modest activation sparsity. In DETR-ResNet50, the benefits increase to 2.2 × due to presence of high activation sparsity, while DistilBERT demonstrates the highest acceleration of 4.15×, primarily due to pronounced 50% structured weight sparsity. Notably, while weight-sided acceleration saturates in DistilBERT, FLEXNPU still provides further gains by leveraging concurrent activation sparsity. On average, our accelerator achieves 2.1 × speed-up over dense baselines and 1.4 × over weight-sided designs, highlighting its adaptability to both CNNs and Transformers. These results establish that our method not only sustains its efficacy across conventional CNNs, but also seamlessly scales to Transformer workloads—a critical requirement for modern AI deployments.
5.3.6 Energy efficiency improvement
Figure 17.2 presents the improvement in energy efficiency of 3 different accelerator architectures (y-axis) while evaluating 4 DNN benchmarks (x-axis) on the ImageNet validation dataset. We considered dense accelerator energy consumption as the baseline. As evident in the figure, these results largely correlate with overall network compute acceleration in Figure 17.1 since the accelerator circuits are active for a reduced amount of time. Furthermore, compared to the weight-sided accelerator, FLEXNPU allows for substantial reduction in memory cycle count as ZVC compressed data flows through the different memory hierarchies, resulting in reduced memory energy consumption. This is enabled by the sparsity-aware load and drain path, as explained in Section 3.4. Note that DRAM transactions are not considered in these results. Across all 4 benchmarks, FLEXNPU is 2.4 × and 1.7 × more energy efficient than the dense and weight-sided accelerators, respectively.
We observe a similar trend in energy efficiency across Transformer models, as shown in Figure 17.4. For instance, FLEXNPU achieves 1.9 × energy efficiency improvement over dense baselines and 1.4 × over weight-sided accelerators. DistilBERT shows the highest gain, reaching 3.6×, due to pronounced weight sparsity. Even models like T5 and Mobilebert, which have lower absolute sparsity show 1.35 × efficiency gains, demonstrating the versatility of the proposed sparsity-aware datapath. These results underscore the robustness of our energy savings, not only across diverse CNNs but also across modern Transformer architectures—establishing FLEXNPU as a generalized solution for efficient DNN inference across modalities.
In conclusion, our comprehensive evaluation showcases not only the substantial compute acceleration achieved by our proposed accelerator, but also its remarkable energy efficiency improvements compared to existing dense and weight-sided architectures. This underscores the pivotal role of our approach in addressing the dual challenges of performance enhancement and energy conservation in DNN accelerators, paving the way for sustainable and efficient AI hardware solutions.
6 Related work
The design of DNN accelerators has evolved around optimizing data movement, which remains the primary bottleneck in both energy consumption and performance on edge devices. Most accelerator architectures rely on a fixed dataflow model, hardwiring their compute and memory hierarchies to a single pattern of data reuse. This limits their adaptability to the heterogeneity present across different layers of modern neural networks, especially when layer-wise reuse profiles vary significantly.
Among the earliest and most influential dataflow paradigms is the weight stationary (WS) model, which aims to maximize the reuse of weights by statically holding them in local buffers while streaming activations and accumulating outputs. This strategy forms the basis of designs such as DaDianNao (Chen et al., 2016a), Origami (Cavigelli and Benini, 2016), Cambricon-X (Zhang et al., 2016), EIE (Han et al., 2016), Samsung's NPU (Jang et al., 2021), NeuFlow (Farabet et al., 2011), ISAAC (Shafiee et al., 2016), and the Google TPU (v1–v3) (Jouppi et al., 2017; Norrie et al., 2021; Jouppi et al., 2020). These architectures frequently employ systolic or spatially tiled compute topologies, where the reuse pattern is baked into the interconnect and register allocation. In this work, we group these designs under the term TPU-like, using them as a canonical baseline for WS execution models.
A second widely studied approach is the row stationary (RS) dataflow, pioneered by Eyeriss (Chen et al., 2016c) and later extended in SCNN (Parashar et al., 2017) and AMD's xVDPU (Jia et al., 2024; Rico et al., 2024). RS attempts to minimize total data movement—including inputs, weights, and partial sums—by balancing reuse across all three tensor domains. This is accomplished through carefully choreographed mapping strategies that exploit on-chip storage locality and inter-PE communication, often within a hierarchical memory system. RS dataflows are particularly effective in reducing accesses to global buffers and DRAM, and Eyeriss remains one of the most cited and architecturally foundational RS accelerators.
Alternatively, there exists a third major dataflow strategy is output stationary (OS), which holds the output activations (or partial sums) in local accumulators for the duration of a kernel operation. OS excels in scenarios with low input channel counts or spatially sparse computations, such as depthwise separable convolutions. Architectures such as ShiDianNao (Du et al., 2015), NVDLA (Zhou et al., 2018), Intel's Core Ultra 1 (Meteor Lake) (Intel, 2024), Core Ultra 2 (Lunar Lake) (Intel, 2024), Movidius VPU2 (KeemBay), and NullHop (Aimar et al., 2018) employ OS scheduling to minimize output writeback bandwidth and leverage accumulator locality in sparse execution patterns. Though less emphasized in academic taxonomies, OS remains a key strategy in production-grade embedded inference pipelines.
Despite their architectural diversity, all of these accelerators are fundamentally limited by rigid PE array microarchitectures that are tightly bound to a single dataflow model. These processing elements are not schedule-aware, and lack the capability to adapt to different reuse-optimal execution orders. As a result, when the data reuse pattern required by a layer deviates from the hardware's fixed dataflow, developers must either accept non-optimal reuse (leading to increased memory accesses and reduced PE utilization) or resort to software-based data reshaping, which is costly in energy and often impractical on resource-constrained platforms. Programmable platforms such as FPGAs offer some level of dataflow flexibility, but suffer from coarse-grained reconfiguration granularity—once programmed, the dataflow remains fixed throughout the DNN execution (Mousouliotis and Petrou, 2018). Their general-purpose routing and logic fabric also yield lower energy efficiency than ASIC-based accelerators, especially for high-throughput convolutional operations. Recent efforts have sought to introduce some level of configurability into fixed-function accelerators. For example, Gemmini (Genc et al., 2021) provides compile-time configurable systolic mappings, enabling weight and output stationary dataflows. However, it lacks support for row stationary execution and therefore cannot adaptively optimize reuse across all three data domains.
While prior efforts—including recent reconfigurable accelerators (Du et al., 2023)—have attempted to introduce mode-switching capabilities, these architectures typically support only a small number of coarse-grained hardwired schedules, such as toggling between weight and output stationary modes. In contrast to these architectures, FLEXNPU provides fine-grained, compiler-defined control over dataflow at the granularity of individual layers. Each layer is compiled into a custom dataflow schedule that specifies loop ordering, spatial tiling, and memory access patterns, enabling the PE array to execute the optimal schedule—be it weight, input, output stationary, or a hybrid variant—based on the layer's shape, reuse profile, and sparsity structure. Beyond dataflow flexibility, FLEXNPU incorporates FlexTree, a reconfigurable partial sum (psum) accumulation network that dynamically adjusts its depth and reduction structure according to the input channel partitioning factor (ICP) of each layer. This allows the compute pipeline to maintain high utilization and balanced fan-in across layers with varying reduction dimensions—capabilities not available in prior accelerators. Furthermore, FLEXNPU uniquely supports two-sided unstructured sparsity in both activations and weights, leveraging zero-aware compute skipping and compressed memory access to improve energy and memory efficiency in sparse workloads. Together, these features establish FLEXNPU as a more expressive and efficient design than existing reconfigurable accelerators, making it especially well-suited for deployment in energy-constrained, workload-diverse edge environments.
7 Conclusion
In this paper, we proposed a flexible schedule-aware DNN accelerator FLEXNPU, which can adapt its internal dataflow to the optimal schedule of each layer in DNNs. Our proposed solution maximizes data reuse at each memory level, resulting in significant energy savings arising from optimal data reuse. Note that flexibility works seamlessly on top of existing performance-enhancing features such as sparsity acceleration and low-precision logic, and it does not diminish their impact in any manner. It is evident that this flexibility comes at the cost of additional area overhead compared to fixed dataflow accelerators, but it also enables us to achieve significant energy savings on average across a myriad of DNN layers. Furthermore, we propose a novel approach to improve throughput and reduce energy usage in the FLEXNPU architecture. Taking advantage of fine-grained sparsity in both activation and weight tensors, we optimize the inference engine within the hardware accelerator. Experimental results demonstrate significant improvements in both performance and energy efficiency compared to existing DNN accelerators. This research contributes to ongoing efforts to develop more efficient hardware accelerators for executing deep neural networks.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
AR: Conceptualization, Investigation, Methodology, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. DM: Conceptualization, Investigation, Methodology, Supervision, Validation, Writing – original draft, Writing – review & editing. SK: Investigation, Methodology, Validation, Writing – original draft, Writing – review & editing. SG: Investigation, Validation, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Acknowledgments
We would like to sincerely thank Gautham Chinya, Debebrata Mohapatra, Huichu Liu, Moongon Jung, Sang Kyun Kim, Guruguhanathan Venkataramanan, Raymond Sung, Hong Wang, and Cormac Brick for their contributions to this work during their time at Intel Corporation.
Conflict of interest
AR, DM, SK, and SG were employed by Intel Corporation.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aimar, A., Mostafa, H., Calabrese, E., Rios-Navarro, A., Tapiador-Morales, R., Lungu, I.-A., et al. (2018). Nullhop: a flexible convolutional neural network accelerator based on sparse representations of feature maps. IEEE Trans. Neural Netw. Learn. Syst. 30, 644–656. doi: 10.1109/TNNLS.2018.2852335
Albericio, J., Judd, P., Hetherington, T., Aamodt, T., Jerger, N. E., and Moshovos, A. (2016). Cnvlutin: ineffectual-neuron-free deep neural network computing. ACM SIGARCH Comput. Architect. News 44, 1–13. doi: 10.1145/3007787.3001138
Cavigelli, L., and Benini, L. (2016). Origami: a 803-gop/s/w convolutional network accelerator. IEEE Transactions Circ. Syst. Video Technol. 27, 2461–2475. doi: 10.1109/TCSVT.2016.2592330
Chen (2019). Eyeriss v2: a flexible accelerator for emerging deep neural networks on mobile devices. IEEE Journal on Emerging and Selected Topics in Circuits and Systems 9, 292–308. doi: 10.1109/JETCAS.2019.2910232
Chen, Y., Chen, T., Xu, Z., Sun, N., and Temam, O. (2016a). Diannao family: energy-efficient hardware accelerators for machine learning. Commun. ACM 59, 105–112. doi: 10.1145/2996864
Chen, Y.-H., Emer, J., and Sze, V. (2016b). Eyeriss: a spatial architecture for energy-efficient dataflow for convolutional neural networks. ACM SIGARCH Comput. Architec. News 44, 367–379. doi: 10.1145/3007787.3001177
Chen, Y.-H., Krishna, T., Emer, J. S., and Sze, V. (2016c). Eyeriss: an energy-efficient reconfigurable accelerator for deep convolutional neural networks. IEEE J. Solid-State Circ. 52, 127–138. doi: 10.1109/JSSC.2016.2616357
Chinya, G., Liu, H., Raha, A., Mohapatra, D., Brick, C., and Hacking, L. (2024). Schedule-aware tensor distribution module. US Patent 11,907,827.
Chinya, G., Mathaikutty, D., Venkataramanan, G., Mohapatra, D., Jung, M., Kim, S. K., et al. (2021). Accelerated loading of unstructured sparse data in machine learning architectures. US Patent App. 17/081,509.
Chinya, G., Mohapatra, D., Raha, A., Liu, H., and Brick, C. (2023). Methods, systems, articles of manufacture, and apparatus to decode zero-value-compression data vectors. US Patent 11,804,851.
Connor, F., Bernard, D., and Hanrahan, N. (2020). Dot product calculators and methods of operating the same. US Patent 10,768,895.
Du, C.-Y., Tsai, C.-F., Chen, W.-C., Lin, L.-Y., Chang, N.-S., Lin, C.-P., et al. (2023). “A 28nm 11.2 tops/w hardware-utilization-aware neural-network accelerator with dynamic dataflow,” in 2023 IEEE International Solid-State Circuits Conference (ISSCC) (IEEE), 1–3. doi: 10.1109/ISSCC42615.2023.10067774
Du, Z., Fasthuber, R., Chen, T., Ienne, P., Li, L., Luo, T., et al. (2015). “Shidiannao: shifting vision processing closer to the sensor,” in Proceedings of the 42nd Annual International Symposium on Computer Architecture, 92–104. doi: 10.1145/2749469.2750389
Farabet, C., Martini, B., Corda, B., Akselrod, P., Culurciello, E., and LeCun, Y. (2011). “Neuflow: a runtime reconfigurable dataflow processor for vision,” in CVPR 2011 WORKSHOPS, 109–116. doi: 10.1109/CVPRW.2011.5981829
Frantar, E., and Alistarh, D. (2023). “Sparsegpt: massive language models can be accurately pruned in one-shot,” in International Conference on Machine Learning (PMLR), 10323–10337.
Gale, T., Elsen, E., and Hooker, S. (2019). The state of sparsity in deep neural networks. arXiv preprint arXiv:1902.09574.
Genc, H., Kim, S., Amid, A., Haj-Ali, A., Iyer, V., Prakash, P., et al. (2021). “Gemmini: enabling systematic deep-learning architecture evaluation via full-stack integration,” in 2021 58th ACM/IEEE Design Automation Conference (DAC) (IEEE), 769–774. doi: 10.1109/DAC18074.2021.9586216
Ghosh, S. K., Kundu, S., Raha, A., Mathaikutty, D. A., and Raghunathan, V. (2024). “Harvest: towards efficient sparse DNN accelerators using programmable thresholds,” in 2024 37th International Conference on VLSI Design and 2024 23rd International Conference on Embedded Systems (VLSID) (IEEE), 228–234. doi: 10.1109/VLSID60093.2024.00044
Ghosh, S. K., Raha, A., and Raghunathan, V. (2023). Energy-efficient approximate edge inference systems. ACM Trans. Embedded Comput. Syst. 22, 1–50. doi: 10.1145/3589766
Han, S., Liu, X., Mao, H., Pu, J., Pedram, A., Horowitz, M. A., et al. (2016). Eie: efficient inference engine on compressed deep neural network. ACM SIGARCH Comput. Archit. News 44, 243–254. doi: 10.1145/3007787.3001163
Hoefler, T., Alistarh, D., Ben-Nun, T., Dryden, N., and Peste, A. (2021). Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks. JMLR 22, 10882–11005. doi: 10.5555/3546258.3546499
Horowitz, M. (2014). “1.1 computing's energy problem (and what we can do about it),” in 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC) (IEEE), 10–14. doi: 10.1109/ISSCC.2014.6757323
Hsu, S., Agarwal, A., Mohapatra, D., Raha, A., Jung, M., Chinya, G., et al. (2021). Multi-buffered register files with shared access circuits. US Patent App. 17/132,895.
Jang, J.-W., Lee, S., Kim, D., Park, H., Ardestani, A. S., Choi, Y., et al. (2021). “Sparsity-aware and re-configurable NPU architecture for Samsung flagship mobile SOC,” in 2021 ACM/IEEE 48th Annual International Symposium on Computer Architecture (ISCA) (IEEE), 15–28. doi: 10.1109/ISCA52012.2021.00011
Jia, X., Zhang, Y., Liu, G., Yang, X., Zhang, T., Zheng, J., et al. (2024). XVDPU: a high-performance CNN accelerator on the Versal platform powered by the AI engine. ACM Trans. Reconfigurable Technol. Syst. 17, 1–24. doi: 10.1145/3617836
Jouppi, N. P., Yoon, D. H., Kurian, G., Li, S., Patil, N., Laudon, J., et al. (2020). A domain-specific supercomputer for training deep neural networks. Commun. ACM 63, 67–78. doi: 10.1145/3360307
Jouppi, N. P., Young, C., Patil, N., Patterson, D., Agrawal, G., Bajwa, R., et al. (2017). “In-datacenter performance analysis of a tensor processing unit,” in Proceedings of the 44th Annual International Symposium on Computer Architecture, 1–12.
Kaul, H., Anders, M., Mathew, S., Kim, S., and Krishnamurthy, R. (2019). “Optimized fused floating-point many-term dot-product hardware for machine learning accelerators,” in 2019 IEEE 26th Symposium on Computer Arithmetic (ARITH) (IEEE), 84–87. doi: 10.1109/ARITH.2019.00021
Kozlov, A., Lazarevich, I., Shamporov, V., Lyalyushkin, N., and Gorbachev, Y. (2020). Neural network compression framework for fast model inference. arXiv preprint arXiv:2002.08679.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “ImageNet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems, 25.
Kundu, S., Raha, A., Mathaikutty, D. A., and Basu, K. (2024). “RASH: reliable deep learning acceleration using sparsity-based hardware,” in 2024 25nd International Symposium on Quality Electronic Design (ISQED) (IEEE), 1–10. doi: 10.1109/ISQED60706.2024.10528741
Kwon, H., Chatarasi, P., Pellauer, M., Parashar, A., Sarkar, V., and Krishna, T. (2019). “Understanding reuse, performance, and hardware cost of DNN dataflow: a data-centric approach,” in Proceedings of the MICRO, MICRO '52 (New York, NY, USA: Association for Computing Machinery), 754–768. doi: 10.1145/3352460.3358252
Kwon, H., Chatarasi, P., Sarkar, V., Krishna, T., Pellauer, M., and Parashar, A. (2020). Maestro: a data-centric approach to understand reuse, performance, and hardware cost of DNN mappings. IEEE Micro 40, 20–29. doi: 10.1109/MM.2020.2985963
Kwon, H., Samajdar, A., and Krishna, T. (2018). Maeri: enabling flexible dataflow mapping over DNN accelerators via reconfigurable interconnects. ACM SIGPLAN Notices 53, 461–475. doi: 10.1145/3296957.3173176
Li, Y., Niu, L., Zhang, X., Liu, K., Zhu, J., and Kang, Z. (2023). E-sparse: boosting the large language model inference through entropy-based n: M sparsity. arXiv preprint arXiv:2310.15929.
Liu, J., Ponnusamy, P., Cai, T., Guo, H., Kim, Y., and Athiwaratkun, B. (2024). Training-free activation sparsity in large language models. arXiv preprint arXiv:2408.14690.
Luo, Y., Song, C., Han, X., Chen, Y., Xiao, C., Liu, Z., et al. (2024). Sparsing law: towards large language models with greater activation sparsity. arXiv preprint arXiv:2411.02335.
Mathaikutty, D., Raha, A., Sung, R., Mohapatra, D., and Brick, C. (2022a). Sparsity-aware datastore for inference processing in deep neural network architectures. US Patent App. 17/524,333.
Mathaikutty, D. A., Raha, A., Sung, R. J.-H., and Mohapatra, D. (2022b). Data reuse in deep learning. US Patent App. 17/684,764.
Mirzadeh, I., Alizadeh, K., Mehta, S., Del Mundo, C. C., Tuzel, O., Samei, G., et al. (2023). Relu strikes back: exploiting activation sparsity in large language models. arXiv preprint arXiv:2310.04564.
Mohapatra, D., Raha, A., Chinya, G., Liu, H., Brick, C., and Hacking, L. (2020). Configurable processor element arrays for implementing convolutional neural networks. US Patent App. 16/726,709.
Mohapatra, D., Raha, A., Mathaikutty, D., Sung, R., and Brick, C. (2022a). Schedule-aware dynamically reconfigurable adder tree architecture for partial sum accumulation in machine learning accelerators. US Patent App. 17/520,281.
Mohapatra, D., Raha, A., Mathaikutty, D. A., Sung, R. J.-H., and Brick, C. M. (2022b). Runtime configurable register files for artificial intelligence workloads. US Patent App. 17/530,156.
Mousouliotis, P. G., and Petrou, L. P. (2018). “Squeezejet: high-level synthesis accelerator design for deep convolutional neural networks,” in International Symposium on Applied Reconfigurable Computing (Springer), 55–66. doi: 10.1007/978-3-319-78890-6_5
Norrie, T., Patil, N., Yoon, D. H., Kurian, G., Li, S., Laudon, J., et al. (2021). The design process for Google's training chips: TPUV2 and TPUV3. IEEE Micro 41, 56–63. doi: 10.1109/MM.2021.3058217
Parashar, A., Rhu, M., Mukkara, A., Puglielli, A., Venkatesan, R., Khailany, B., et al. (2017). Scnn: An accelerator for compressed-sparse convolutional neural networks. ACM SIGARCH Comput. Architec. News 45, 27–40. doi: 10.1145/3140659.3080254
Park, J., Yoon, H., Ahn, D., Choi, J., and Kim, J.-J. (2020). Optimus: optimized matrix multiplication structure for transformer neural network accelerator. Proc. Mach. Learn. Syst. 2, 363–378.
Raha, A., Anders, M. A., Sung, R. J.-H., Mohapatra, D., Mathaikutty, D. A., Krishnamurthy, R. K., et al. (2022a). Floating point multiply-accumulate unit for deep learning. US Patent App. 17/688,131.
Raha, A., Ghosh, S., Mohapatra, D., Mathaikutty, D. A., Sung, R., Brick, C., et al. (2021a). “Special session: approximate TINYML systems: full system approximations for extreme energy-efficiency in intelligent edge devices,” in 2021 IEEE 39th International Conference on Computer Design (ICCD) (IEEE), 13–16. doi: 10.1109/ICCD53106.2021.00015
Raha, A., Kim, S. K., Mathaikutty, D. A., Venkataramanan, G., Mohapatra, D., Sung, R., et al. (2021b). “Design considerations for edge neural network accelerators: an industry perspective,” in 2021 34th International Conference on VLSI Design and 2021 20th International Conference on Embedded Systems (VLSID) (IEEE), 328–333. doi: 10.1109/VLSID51830.2021.00061
Raha, A., Langhammer, M., Mohapatra, D., Tunali, N., and Wu, M. (2022b). Methods and apparatus to perform low overhead sparsity acceleration logic for multi-precision dataflow in deep neural network accelerators. US Patent App. 17/709,337.
Raha, A., Mathaikutty, D., Mohapatra, D., Kim, S. K., Chinya, G., and Brick, C. (2021c). Methods and apparatus to load data within a machine learning accelerator. US Patent App. 17/359,392.
Raha, A., Mohapatra, D., Chinya, G., Venkataramanan, G., Kim, S. K., Mathaikutty, D., et al. (2021d). Performance scaling for dataflow deep neural network hardware accelerators. US Patent App. 17/246,341.
Raha, A., Mohapatra, D., Mathaikutty, D. A., Sung, R. J.-H., and Brick, C. M. (2022c). System and method for balancing sparsity in weights for accelerating deep neural networks. US Patent App. 17/534,976.
Raha, A., Sung, R., Ghosh, S., Gupta, P. K., Mathaikutty, D. A., Cheema, U. I., et al. (2023). “Efficient hardware acceleration of emerging neural networks for embedded machine learning: an industry perspective,” in Embedded Machine Learning for Cyber-Physical, IoT, and Edge Computing: Hardware Architectures (Springer), 121–172. doi: 10.1007/978-3-031-19568-6_5
Rico, A., Pareek, S., Cabezas, J., Clarke, D., Ozgul, B., Barat, F., et al. (2024). AMD XDNA™ NPU in Ryzen™ AI processors. IEEE Micro. 44, 73–82. doi: 10.1109/MM.2024.3423692
Shafiee, A., Nag, A., Muralimanohar, N., Balasubramonian, R., Strachan, J. P., Hu, M., et al. (2016). “ISAAC: a convolutional neural network accelerator with in-situ analog arithmetic in crossbars,” in 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), 14–26. doi: 10.1109/ISCA.2016.12
Song, C., Han, X., Zhang, Z., Hu, S., Shi, X., Li, K., et al. (2024). Prosparse: introducing and enhancing intrinsic activation sparsity within large language models. arXiv preprint arXiv:2402.13516.
Yang, X., Gao, M., Liu, Q., Setter, J., Pu, J., Nayak, A., et al. (2020). “Interstellar: using halide's scheduling language to analyze DNN accelerators,” in Proceedings of the Twenty-Fifth International Conference on Architectural Support for Programming Languages and Operating Systems, 369–383. doi: 10.1145/3373376.3378514
Zhang, S., Du, Z., Zhang, L., Lan, H., Liu, S., Li, L., et al. (2016). “Cambricon-x: an accelerator for sparse neural networks,” in 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), 1–12. IEEE. doi: 10.1109/MICRO.2016.7783723
Zhou, G., Zhou, J., and Lin, H. (2018). “Research on nvidia deep learning accelerator,” in 2018 12th IEEE International Conference on Anti-counterfeiting, Security, and Identification (ASID) (IEEE), 192–195. doi: 10.1109/ICASID.2018.8693202
Appendix A: Schedule examples demonstrating flexNPU flexibility
This appendix presents two worked examples that demonstrate flexNPU's flexible scheduler and dataflow engine. Each example highlights how flexNPU efficiently maps irregular-shaped layers to its 2D PE array while maintaining high MAC utilization.
Example A1: ResNet layer with non-power-of-two dimensions
We consider a layer from ResNet50 with the following configuration:
• Activation: OX = 56, OY = 56, IC = 64.
• Weight: OC = 256, FX = FY = 1.
Fixed dataflow accelerator schedule:
• Inner loop: OX/1/14, OY/1/14, IC/64/1, OC/1/1.
→ Each PE processes 64 ICs for a 1 × 1 XY tile; 14 × 14 = 196 PEs used.
• Outer loop: OC/256/1, OX/4/1, OY/4/1.
MAC utilization: ~77% (196 out of 256 PEs active)
flexNPU schedule (Matrix × Matrix Template):
• Inner loop: OX/2/4, OY/2/4, OC/4/16, IC/16/1.
→ All 256 PEs are active, each PE computes 2 × 2 × 4 partial sums.
• Outer loop: IC/4/1, OC/4/1, OX/7/1, OY/7/1.
MAC utilization: 100%
Example A2: Low-channel, high-spatial layer (early CNN stage)
This example considers a challenging layer with small input channels and large spatial dimensions:
• Input activation: OX = 112, OY = 112.
• Filter: FX = 7, FY = 7, IC = 3, OC = 64.
flexNPU schedule (vector × matrix template):
• Inner loop: IC/1, OC/4/16, OX/4/4, OY/1/4.
→ 16 PEs process a 4 × 4 spatial tile across 64 OCs.
• Each PE receives 3 inputs and 4 weights → 12 MACs used per PE (out of 16).
• Outer loop: FX/7, FY/7, OX/28, OY/112.
MAC utilization: 75%
Commentary: This is a particularly difficult case for fixed accelerators, which often:
• Require SIMD-friendly IC counts (e.g., 4, 8, 16), wasting compute on zero-padding.
• Fail to map large spatial extents efficiently.
flexNPU, in contrast, dynamically configures the compute template, loop blocking, and PE-level data mapping to maximize MAC utilization despite low IC and high FX/FY. These examples demonstrate how flexNPU can consistently adapt to diverse layer shapes using its flexible architecture, loop scheduler, and modular PE configuration.
Keywords: deep neural network accelerator, flexible data flow, sparsity acceleration, energy efficiency, edge intelligence
Citation: Raha A, Mathaikutty DA, Kundu S and Ghosh SK (2025) flexNPU: a dataflow-aware flexible deep learning accelerator for energy-efficient edge devices. Front. High Perform. Comput. 3:1570210. doi: 10.3389/fhpcp.2025.1570210
Received: 03 February 2025; Accepted: 04 June 2025;
Published: 26 June 2025.
Edited by:
Jaime H. Moreno, IBM Research, United StatesCopyright © 2025 Raha, Mathaikutty, Kundu and Ghosh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arnab Raha, YXJuYWIucmFoYUBpbnRlbC5jb20=
 Arnab Raha
Arnab Raha Deepak A. Mathaikutty
Deepak A. Mathaikutty