Using statistical population reconstruction to estimate the effect of pelt prices on river otter abundance and harvest vulnerability in Kentucky

Introduction: Accurately estimating the abundance, survival rates, and harvest vulnerability of harvested populations of North American river otters (Lontra canadensis) is essential for their effective management and conservation. Monitoring these rates over time allows for more informed decision-making regarding harvest regulations such as quotas, bag limits, and season lengths, and can also be used to evaluate the impact of various anthropogenic stressors such as rising pelt prices and increased trapper effort.

Methodology: We used age-at-harvest, catch-effort, and radio-telemetry data to parameterize a second-stage statistical population reconstruction model with both fixed and linear effects to estimate abundance and harvest vulnerability of river otter in Kentucky, USA from 2012 to 2023. We then used this model to investigate the effect that interannual fluctuations in pelt prices during this time likely had on the population in terms of both harvest mortality and overall abundance.

Results: Our results suggest that the measurable decline in overall abundance from 2012 to 2016 was caused by higher pelt prices from 2012 to 2014, which resulted in above-average harvest intensity during those three years. Our results also suggest that although higher pelt prices resulted in more catch-effort, they may have counterintuitively decreased the likelihood of a river otter being harvested per additional unit of catch-effort, possible attributable to more casual or inexperienced trappers shifting their focus to river otters to maximize profits.

Discussion: Our findings illustrate the utility of using statistical population reconstruction with linear effects to help management agencies better understand the likely driving forces behind observed interannual fluctuations in abundance, survival, and harvest vulnerability of river otters and other furbearer species that are in high demand by the public.

1 Introduction

The North American river otter (Lontra canadensis) is a medium-sized semi-aquatic carnivore whose pre-European distribution encompassed most major drainages in Canada and the continental United States, all the way from Alaska to parts of Texas and Florida, with large populations in the Great Lakes region and glaciated areas of New England (Hall, 1981; Melquist and Hornocker, 1983; Mason, 1990). However, unregulated hunting and trapping combined with ongoing changes to riparian habitats caused by anthropogenic disturbance resulted in river otters being extirpated from many parts of their distribution in the early 1900s. Widespread and highly successful reintroduction efforts have since then allowed river otters to recover and reclaim much of their historic range (Raesly, 2001; Bricker et al., 2022), to the point that regulated harvest opportunities became available in many states, including Kentucky, Ohio, Illinois, and Indiana (Ellington et al., 2018; Rutter, 2018; Berg and Palmer, 2021; Berg, 2023). Monitoring and regulating this harvest to ensure a sustainable population and to prevent overharvest remains a key management focus for these and other state wildlife management agencies.

In Kentucky, river otters likely occupied every major watershed in the state before being extirpated from all but the most extreme western portion in the Jackson Purchase Region by the 1950s (Barbour and Davis, 1974; Cramer, 1995). From 1982 to 1983, the Tennessee Valley Authority (TVA) and the Kentucky Department of Fish and Wildlife Resources (KDFWR) conducted an experimental restocking of river otters in the Land Between-the-Lakes area of western Kentucky. High survival rates among the 11 released animals suggested that rivers otters were capable of repopulating and expanding their range beyond the Jackson Purchase Region (Cramer, 1995). This prompted a larger restoration effort that released 355 river otters across 14 sites in the central and eastern regions of the state from 1991 to 1994. In the years since the reintroduction, sightings of river otters, reports of damage to personal property and state fish hatcheries, and sign surveys demonstrated that river otters were once again present in all major watersheds in Kentucky (Barding et al., 2010; Barding, 2011). This prompted the KDFWR to implement a restricted harvest season (with a bag limit of five) in 2004 within the 13 counties west of and including the main stem of the Tradewater River. The harvest season was then expanded statewide (with a bag limit of six) in 2006, followed by the establishment of two zones in 2010 and an increase to a bag limit of ten otters in the western zone. Although KDFWR has monitored the number, age structure, and spatial distribution of harvested river otter over several years, a robust estimate of their overall abundance and harvest vulnerability throughout the state is still lacking. Such estimates are critical for effective management because they allow for more informed decision-making regarding harvest regulations such as quotas, bag limits, season lengths, zones, and number of licenses.

Statistical population reconstruction (SPR) using integrated population models (IPMs) provides a flexible framework for estimating the abundance, harvest vulnerability, and non-harvest survival of harvested wildlife populations by integrating age-at-harvest data with estimates of catch-effort and any available auxiliary information from radio-telemetry, mark-recapture, and aerial surveys (Gove et al., 2002; Skalski et al., 2007; Broms et al., 2010; Gast et al., 2013a; Terhune et al., 2017). These models produce reliable and cost-effective estimates of multiple demographic parameters and their uncertainties through time and can be implemented over the large spatial scales (e.g., states) at which harvest management decisions are typically made (Clawson et al., 2013; Berg et al., 2017, 2024). If sufficient data are available, they can also incorporate fixed effects to provide separate harvest and survival estimates for different ages and sexes (Broms et al., 2010; Skalski et al., 2011), as well as random effects that allow for interannual fluctuations in these estimates (Gast et al., 2013a, b). These models have already been used to help estimate population dynamics of river otter in Kentucky (Berg and Palmer, 2021) and neighboring Ohio (Ellington et al., 2018) and Indiana (Berg, 2023), as well as of other harvested furbearer species such as the American marten (Skalski et al., 2011; Berg et al., 2017), fisher (Bellier et al., 2024; Berg et al., 2025), and bobcat (Murphy et al., 2022; Berg et al., 2024).

Although most SPR models assume that harvest vulnerability and other demographic rates are constant over time, this approach is unable to account for the interannual fluctuations that these parameters undoubtedly experience due to various anthropogenic and environmental factors (Gast, 2012, 2013a). For example, fluctuations in non-harvest survival rates may occur because of annual changes in environmental factors such as winter severity, prey abundance, and disease prevalence. Similarly, we can expect harvest mortality to vary from year to year not just because of fluctuations in the number of trappers (i.e., catch-effort), but also in response to changes in other anthropogenic factors such as pelt prices, bag limits, and season lengths. To account for these and other potential anthropogenic covariates, Gast 2002 recommended incorporating linear effects directly into the model definition of harvest mortality, thereby providing a mechanism with which to separate the influence of a chosen covariate from interannual fluctuations in catch-effort. This modeling framework was recently used to demonstrate how decreasing season lengths in Minnesota, as an anthropogenic factor, may have counterintuitively increased the likelihood of a fisher being harvested per additional unit of effort (Berg et al., 2025). These results, which were attributed to trappers adjusting their strategy to maximize harvest during the shortened periods, illustrated the utility of using SPR models with linear effects to help management agencies better understand the impact of various anthropogenic factors on the demographic trends of harvested wildlife populations.

In this study, we use age-at-harvest and catch-effort data collected in Kentucky alongside radio-telemetry data from nearby states to parameterize an updated SPR model to estimate the abundance and harvest vulnerability of river otters in Kentucky from 2012 to 2023 and to explore how changes in fur prices during these years likely impacted these demographic trends. Although some of these data were already used in the earlier SPR model of river otters in Kentucky (Berg and Palmer, 2021), we incorporated five additional years of harvest and effort data and included more precise age-at-harvest data that separated harvested animals by age rather than age-class (i.e., young-of-the-year, yearlings, and adults). Further, this updated model employed a second-stage abundance estimate procedure that, rather than estimating abundance directly within the modeling framework, instead estimates abundance outside the model by adjusting the observed harvest counts using a Horvitz-Thompson type estimator (Gast, 2012). This second-stage approach substantially reduces the number of parameters that need to be directly estimated by the model and has been shown to produce less biased estimates of overall abundance and more optimal confidence interval coverage when compared to the one-stage approach (Gast et al., 2013a, b). Because there were no auxiliary data available for river otters specific to Kentucky, we included radio-telemetry data on non-harvest survival of river otter collected in neighboring Ohio and nearby Minnesota. Finally, we incorporated linear effects into the model that allowed us to test how interannual fluctuations in pelt prices both in Kentucky and the greater United States likely influenced harvest vulnerability of river otter over time.

2 Materials and methods

2.1 Study area

To demonstrate how SPR models with linear effects can be used to evaluate the impact of various anthropogenic factors on harvest vulnerability, we used data from a harvested population of river otter in Kentucky, USA. During the course of our reconstruction, this area was largely under private ownership (Morgan et al., 2019) and comprised about 150,000 km of streams, 23 major reservoirs, and over 200,000 farm ponds (Berg and Palmer, 2021). Kentucky’s climate was moderate and humid, with temperatures that ranged from an average low of 5 °C in January to an average high of 31 °C in July, with an average annual precipitation of 120 cm (Runkle et al., 2017). Although most of Kentucky was below 300 m above sea level, the landscape varied greatly across the state, from forested mountains and coalfields in the east to floodplain forests and wetlands along the Mississippi River in the west (Jones, 2005).

2.2 Available demographic data

From 2012 to 2023, the KDFWR recorded all river otter harvested in Kentucky during the regulated harvest season, which runs from mid-November until the end of February, and aged harvested otter that were voluntarily submitted by trappers (mean percentage aged annually = 15.7%, range = 7.5 – 21.6%) using microscopic counts of cementum annuli (Table 1). KDFWR also mailed a voluntary annual furbearer trapping survey to all individuals who purchased a trapping license (mean response rate = 30.3%, range = 19.5 – 39.8%), to estimate trap-nights as a measure of annual catch-effort (Table 2).

Table 1

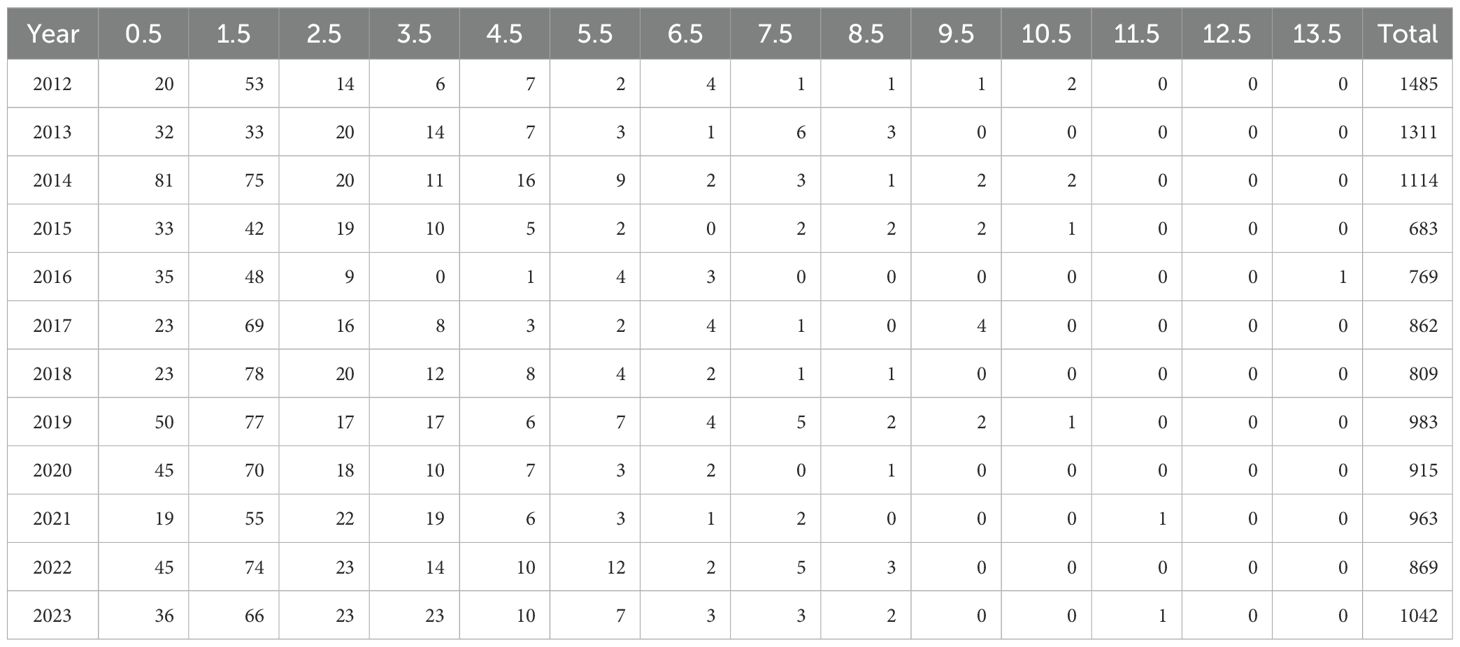
Table 1. Number of North American river otter that were harvested and successfully aged in Kentucky, USA from 2012 to 2023, as well as the total number of harvested animals.

Table 2

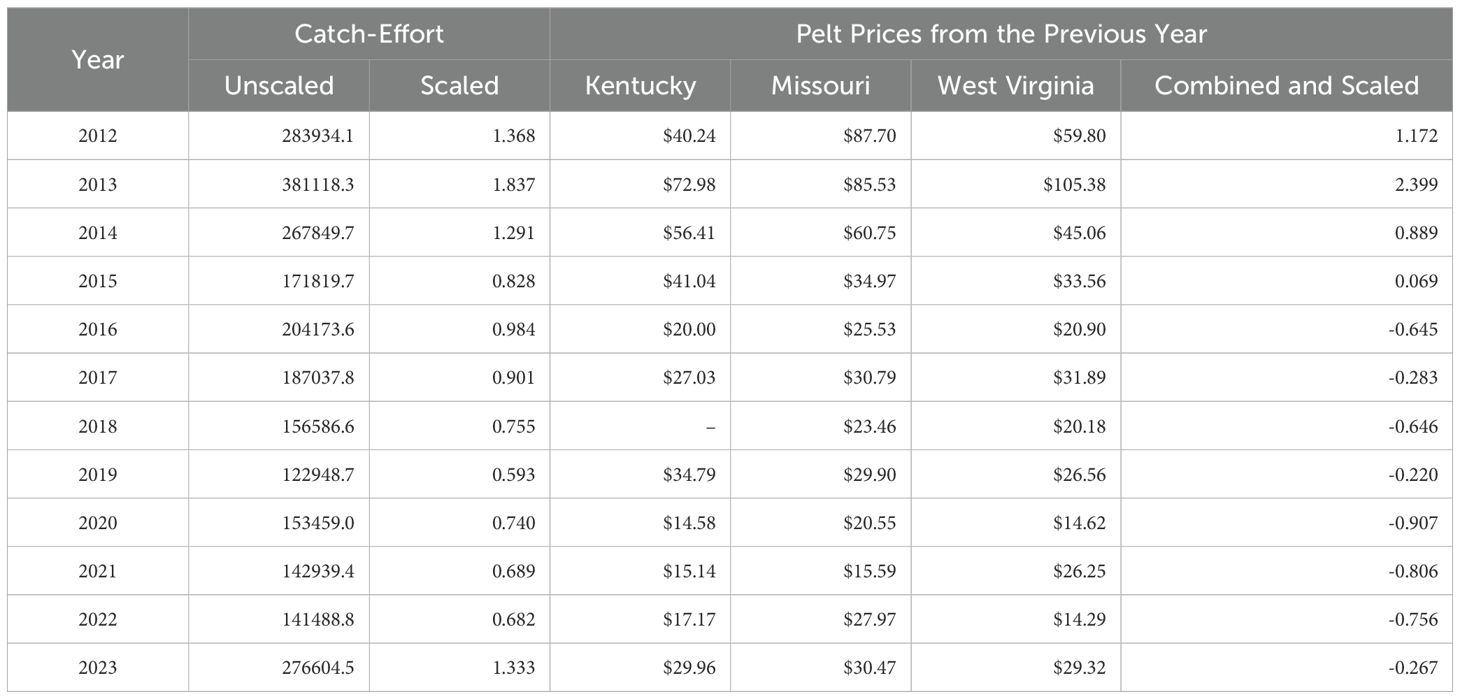
Table 2. Estimated catch-effort in terms of trap-nights (both unscaled and scaled to a mean of one prior to analysis) for North American river otter in Kentucky, USA from 2012 to 2023, alongside corresponding pelt prices from the previous year (in USD) from Kentucky, Missouri, and West Virginia (both unscaled and combined and scaled to a mean of zero prior to analysis).

To evaluate what effect pelt prices from the prior season had on both catch-effort and vulnerability during this time, we also used fur buyer reports to estimate the average price of river otter pelts sold in Kentucky from 2011 to 2022. Because of the low number of licensed fur buyers and lack of data for some years (mean number sold annually = 129.5, range = 0 – 354), we also used data on average prices of pelts sold in neighboring Missouri and West Virginia. Average annual pelt prices in these three states were highly correlated (Pearson correlation coefficient, r = 0.83 – 0.89), so we combined these three estimates into a single standardized measure of pelt prices for this region of the United States (Table 2).

In addition to these age-at-harvest, catch-effort, and pelt price data, we used information from radio-collared river otters with known fates (i.e., right-censored) to help estimate model parameters (Gove et al., 2002; Berg et al., 2017). However, because no such data were available for river otters in Kentucky, we instead used telemetry data that were collected from 2002 to 2004 in neighboring Ohio (Ellington et al., 2018) and in nearby Minnesota (Gorman et al., 2008) by their Departments of Natural Resources (ODNR and MNDNR, respectively). Although harvest rates undoubtedly varied between these different states and Kentucky because of differences in quotas, number of licenses, and season lengths, we assumed that non-harvest survival rates would be similar across this region of North America. As such, we only used these data to help estimate non-harvest survival and excluded any animals that died because of harvest. We also excluded any river otters that died within 14 days of capture, for a total sample size of 53 unique animals across the two states (Table 3).

Table 3

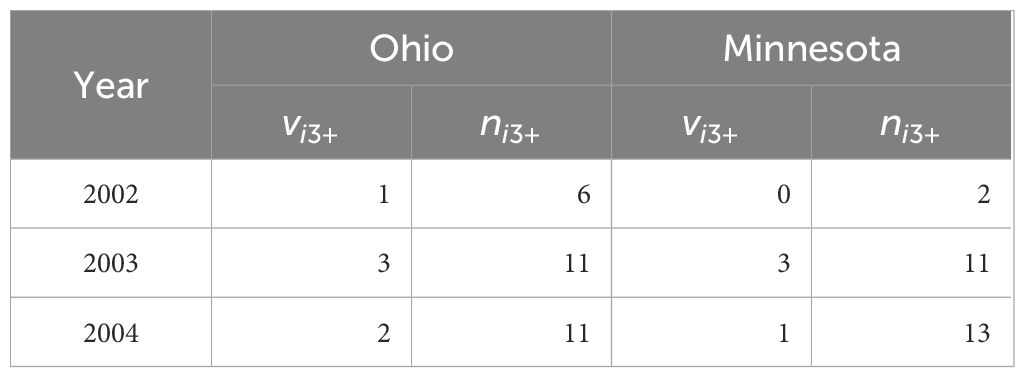
Table 3. Radio-telemetry data on non-harvest mortalities $v_{ij}$ and associated at-risk counts $n_{ij}$ for each year $i$ for adult ($j=3+$) river otter in Ohio and Minnesota, USA from 2002 to 2004.

2.3 SPR model

SPR models typically begin by considering the age-at-harvest matrix $h$(Table 1) where each value of $h_{ij}$ denotes the number of animals that were harvested in year $i$ ($i=1,\dots ,Y$) of age $j$ ($j=1,\dots ,A$). Each diagonal (e.g., $h_{1,12}$, $h_{2,13}$, and $h_{3,14}$) in the matrix represents a distinct cohort of animals that were born during the same year, survived to recruitment, and were then subjected to both harvest and non-harvest mortality during each subsequent year. Using a second-stage estimation procedure, we can use a series of probability mass functions (PFMs) to describe the distribution of harvest counts in each of these diagonal cohorts as being conditional on the total harvest of that cohort (Gast, 2012; Gast et al., 2013a, b).

Under this framework, we can write the PMF for the diagonal cohort that begins with 13-year-old animals harvested during the first year (i.e., $h_{1,13}$ and $h_{2,14}$) as

$$PM{F}_{1,13}=\left(\begin{array}{c}{h}_{1,13}+h_{2,14}\\ h_{1,13},h_{2,14}\end{array}\right)\times {\left(\frac{P_{1,13}}{P_{1,13}+Q_{1,13}{S}_{1,13}{P}_{2,14}}\right)}^{h_{1,13}}\times {\left(\frac{Q_{1,13}{S}_{1,13}{P}_{2,14}}{P_{1,13}+Q_{1,13}{S}_{1,13}{P}_{2,14}}\right)}^{h_{2,14}},$$

where $P_{ij}$ is the probability of an animal being harvested, $Q_{ij}$ is the probability of an animal not being harvested (i.e., $Q_{ij}=1-P_{ij}$), and $S_{ij}$ is the probability of an animal that is not harvested surviving until the onset of harvest the following year (Gast, 2012; Gast et al., 2013a). Similarly, we can write the PMF for the next diagonal cohort that begins with 12-year-old animals harvested during the first year (i.e., $h_{1,12}$, $h_{2,13}$, and $h_{3,14}$) as

$$\begin{array}{l}PM{F}_{1,12}=\left(\begin{array}{c}{h}_{1,12}+h_{2,13}+h_{3,14}\\ h_{1,12},h_{2,13},h_{3,14}\end{array}\right)\\ \times {\left(\frac{P_{1,12}}{P_{1,12}+Q_{1,12}{S}_{1,12}{P}_{2,13}+Q_{1,12}{S}_{1,12}{Q}_{2,13}{S}_{2,13}{P}_{3,14}}\right)}^{h_{1,12}}\\ \times {\left(\frac{Q_{1,12}{S}_{1,12}{P}_{2,13}}{P_{1,12}+Q_{1,12}{S}_{1,12}{P}_{2,13}+Q_{1,12}{S}_{1,12}{Q}_{2,13}{S}_{2,13}{P}_{3,14}}\right)}^{h_{2,13}}\\ \times {\left(\frac{Q_{1,12}{S}_{1,12}{Q}_{2,13}{S}_{2,13}{P}_{3,14}}{P_{1,12}+Q_{1,12}{S}_{1,12}{P}_{2,13}+Q_{1,12}{S}_{1,12}{Q}_{2,13}{S}_{2,13}{P}_{3,14}}\right)}^{h_{3,14}}\end{array}$$

By defining similar PMFs for each of the other diagonal cohorts in the age-at-harvest matrix, we can write the joint PFM for the entire age-at-harvest matrix as

$$PM{F}_{AAH}={\displaystyle \prod }_{i=1}^{Y}PM{F}_{i1}\times {\displaystyle \prod }_{j=2}^{A}PM{F}_{1j}.$$

The probability of harvest $P_{ij}$ and the probability of non-harvest survival $S_{ij}$ in this function represent the parameters that can be directly estimated by the model via maximum likelihood estimation.

However, rather than estimating the probability of harvest directly, we instead modeled it as a function of the observed annual catch-effort (Table 2) as

$$P_{ij}=1-e^{-f_i{C}_j},$$

where $f_i$ is the catch-effort in year $i$ and $C_j$ is the age-specific harvest vulnerability coefficient that is to be estimated as a parameter in place of the probability of harvest (Skalski et al., 2007; Broms et al., 2010; Clawson et al., 2013). Similarly, we modeled non-harvest survival as a function of the non-harvest survival coefficient $B_j$, but assumed that it was constant through time as

$$S_j=\frac{e^{B_j}}{1+e^{B_j}}.$$

This formulations aids in the numerical fitting of SPR models by bounding the non-harvest survival rate $S_j$ within the interval from 0 to 1 (Gast, 2012).

To account for anthropogenic factors that may directly influence mean harvest vulnerability (e.g., interannual fluctuations in pelt prices), we incorporated a linear effect into the harvest probability as

$$P_{ij}=1-e^{-e^{(C_j+L_1{z}_i)}{f}_i},$$

where $z_i$ represents the value of the anthropogenic covariate in year $i$ and $L_1$ is the corresponding linear regression parameter that is estimated by the model (Gast, 2012).

Because not all harvested river otter were successfully aged, we included an additional PMF to model the probability of aging a harvested animal as a binomial process as

$$PM{F}_{AGE}={\displaystyle \prod }_{i=1}^Y\left(\begin{array}{c}{x}_i\\ h_i\end{array}\right){(R_i)}^{h_i}{(1-R_i)}^{x_i-h_i},$$

where $R_i$ is the probability of aging an animal in year $i$, $x_i$ is the total number of animals harvested that year, and $h_i$ is the corresponding total number that were successfully aged (Skalski et al., 2011; Gast et al., 2013a). Combining this aging PMF with the age-at-harvest PMF defined earlier, we can write the joint PMF as

$$PMF=PM{F}_{AAH}\times PM{F}_{AGE},$$

where $C_j$, $B_j$, $L_1$, and $R_i$ again represent the parameters that can be directly estimated by the model via maximum likelihood estimation.

Unfortunately, age-at-harvest and catch-effort data alone are often insufficient to uniquely and accurately estimate each of the underlying model parameters (Gove et al., 2002; Skalski et al., 2007; Clawson et al., 2013; Berg et al., 2024). As such, we used information from radio-collared river otters with known fates from neighboring Ohio and nearby Minnesota (Table 3) to help estimate non-harvest survival rates. By assuming that the number of animals that die from non-harvest sources each year follows a binomial distribution, we can write the PMF for these data as

$$PM{F}_{TEL}={\displaystyle \prod }_{i=1}^Y{\displaystyle \prod }_{j=1}^A\left(\begin{array}{c}{n}_{ij}\\ v_{ij}\end{array}\right){(1-S_j)}^{v_{ij}}{(S_j)}^{n_{ij}-v_{ij}},$$

where $v_{ij}$ represents the number of radio-collared animals that died from causes other than harvest in year $i$ of age $j$, and $n_{ij}$ is the corresponding number of collared animals at risk (Gove et al., 2002; Broms et al., 2010; Berg et al., 2017).

Incorporating this telemetry PMF into the joint PMF defined earlier, we can write the expanded joint PMF as

$$PMF=PM{F}_{AAH}\times PM{F}_{AGE}\times PM{F}_{TEL}.$$

We then estimated the corresponding model parameters $C_j$, $B_j$, $L_1$, and $R_i$ by numerically maximizing this joint objective function given the observed values of $h_{ij}$, $f_i$, $z_i$, $x_i$, $v_{ij}$, and $n_{ij}$. We used Program R (R Core Team, 2022) to implement this joint objective function and a combination of particle swarm optimization (Kennedy and Eberhart, 1995) and the Broyden-Fletcher-Goldfarb-Shanno algorithm (Shanno, 1970) to estimate model parameters. We then calculated standard errors for each parameter by using a numerical estimate of the inverse Hessian (Fieberg et al., 2010; Skalski et al., 2012b; Berg et al., 2017).

Next, rather than estimating the abundance directly, we instead used a Horvitz-Thompson type estimator to estimate the annual pre-harvest abundance of each age by inflating the observed age-at-harvest counts $h_{ij}$ by the model-estimated harvest probability $P_{ij}$ as

$$N_{ij}=\frac{h_{ij}}{P_{ij}}$$

where $N_{ij}$ is the number of animals that are alive immediately before the onset of harvest in year $i$ of age $j$ (Gast et al., 2013a, b). We then derived 95% confidence intervals for these abundance estimates using Monte Carlo simulations. This second-stage approach to estimating pre-harvest abundance results in an SPR model with fewer parameters when compared to the single-stage approach that estimates abundance directly as a model parameter (e.g., Gove et al., 2002; Skalski et al., 2007; Broms et al., 2010). This requires less data for proper parameterization, is more likely to provide unbiased estimates of annual population abundance, and produces more optimal interval coverage (Gast, 2012; Gast et al., 2013a, b; Berg et al., 2025).

2.4 SPR model of river otter in Kentucky

We examined four alternative models for the river otter reconstruction, using Akaike’s Information Criterion (AIC; Burnham and Anderson, 2002) to determine whether fixed effects are needed to provide separate harvest vulnerability and non-harvest survival coefficients for young-of-the-year, yearlings, and adults. We then used a Wald test to investigate if interannual fluctuations in pelt prices from previous years had a significant effect on river otter vulnerability to harvest (i.e., if the corresponding linear effect was significantly different from zero). Because our radio-telemetry data did not come directly from Kentucky, we repeated this process with every possible combination of available data from the nearby states to determine how robust our results were to their inclusion or exclusion. All resulting models and corresponding demographic parameter estimates were also evaluated for biological realism prior to any further analysis (Skalski et al., 2012a; Johnson et al., 2019; Berg et al., 2024).

3 Results

Our best-fit reconstruction model included fixed effects for the harvest vulnerability coefficient but not for the non-harvest survival coefficient, indicating that although non-harvest survival of river otter in the state did not differ by age, their vulnerability to harvest did. Using this best-fit reconstruction model, we estimated that pre-harvest river otter abundance experienced a steady decline from an estimated 6120 (95% CI = 5196 – 7390) animals in 2012 to a low of 3917 (95% CI = 3338 – 4721) in 2016. This was followed by a rapid increase to a high of 8357 (95% CI = 7409 – 9545) in 2019, and then another decline back to 4312 (95% CI = 3791 – 4977) by 2023. During this time, the total number of harvested animals varied from a high of 1485 in 2012 to a low of 683 in 2015 (Figure 1). The next best model (ΔAIC = 3.32) included additional fixed effects for the non-harvest survival coefficient, produced similar relative trends in population growth, and resulted in an overall abundance that was only 3.7% lower than the best-fit model.

Figure 1

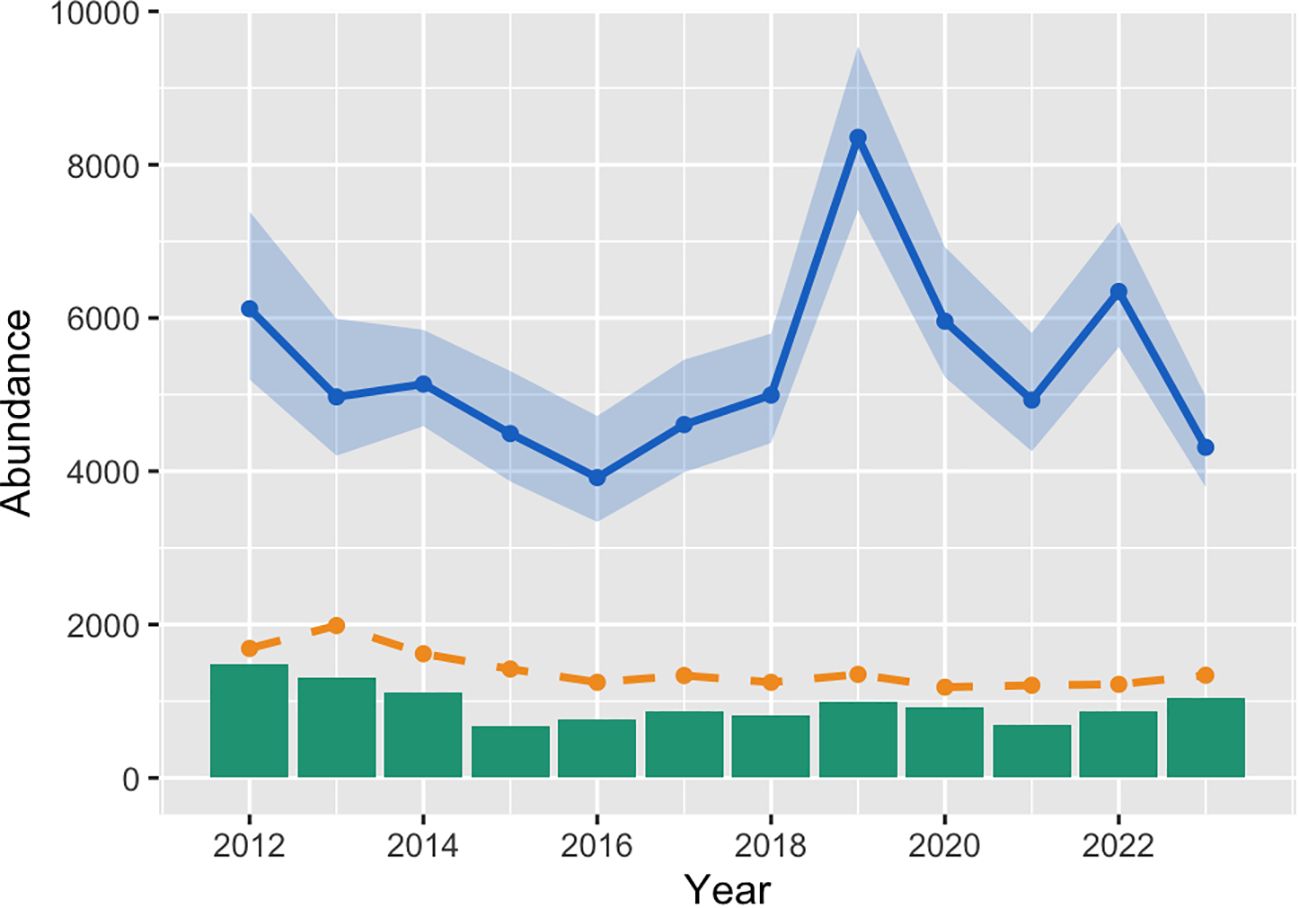
Figure 1. Estimated pre-harvest abundance of North American river otter in Kentucky, USA from 2012 to 2023 based on the best available reconstruction model (solid line), along with associated confidence intervals (shaded areas), number of animals harvested each year (vertical bars), and mean pelt prices from the previous year (scaled to a mean of zero; dotted line).

During these 12 years of reconstruction, we estimated mean harvest vulnerability coefficients of $C_1$= -1.836 (SE = 0.026), $C_2$= -0.939 (SE = 0.027), and $C_3$= -1.812 (SE = 0.037) for young-of-the-year, yearlings, and adults, respectively, which resulted in a higher baseline harvest probability for yearlings than young-of-the-year and older animals (0.324 versus 0.144 and 0.151, respectively). Catch-effort during this time ranged from an estimated high of 381,118 trap-nights in 2013 to a low of 122,949 in 2019 and was highly correlated with pelt prices from the previous season (Pearson correlation coefficient, r = 0.87), which ranged in Kentucky from a high of $72.98 in 2012 to a low of $14.58 in 2019. We found a significant negative linear effect of increased pelt prices during these years ($L_1$= -0.055, SE = 0.013, Z = -4.23, p< 0.001), which, when combined with annual changes in catch-effort, resulted in harvest probability that ranged from 0.091 to 0.226, 0.209 to 0.467, and 0.093 to 0.231 for young-of-the-year, yearlings, and adults, respectively. We also estimated a mean non-harvest survival coefficient of 1.618 (SE = 0.044), which resulted in an annual non-harvest survival rate of 0.835 that did not vary by age.

Including or excluding different combinations of radio-telemetry did not alter our choice of the best-fit model and resulted in only minor differences to parameter and abundance estimates, indicating that model results were robust to whether or not these auxiliary data were included.

4 Discussion

4.1 Linear effects of pelt prices on catch-effort, vulnerability, and mortality

Our results demonstrate the utility of incorporating linear effects into SPR models of river otter and other harvested species of furbearers to explore how various anthropogenic stressors directly impact harvest vulnerability and mortality, as well as the corresponding trends in overall abundance. As expected, pelt prices from the previous year were strongly and positively correlated with the number of trap nights that trappers devoted to harvesting river otter in Kentucky, indicating that higher pelt prices increased interest among trappers for this furbearer during the following year. This finding supports the previous use of pelt prices as an index of trapper effort (e.g., Ellington et al., 2018) and suggests that management agencies may be able to use pelt prices from the current year to predict the likely amount of catch-effort that river otters will be subjected to during the following year. This information could then be used to make any necessary adjustments to harvest regulations (e.g., quotas, bag limits, season lengths, and number of licenses) ahead of the start of the next harvest season if there are concerns regarding, for example, above-average effort negatively impacting an already declining population.

Although our results indicate that pelt prices had a strong and positive effect on the amount of effort that trappers devoted to harvesting river otters, it is important to recognize that other anthropogenic factors (e.g., quotas, bag limits, season lengths, and number of licenses) may also have played a role. For example, even though neither season length (range = 105–111 days) nor bag limits (10 otters per person) changed substantially from 2012 to 2023, the number of trapping licenses sold did vary from a low of 2403 in 2016 to a high of 3635 in 2023. Although these licenses weren’t exclusively for harvesting river otters, a higher number of licensed trappers could have resulted in a higher number of trap nights devoted to river otter. Similarly, increased awareness of river otter as a valuable furbearer or of the damage they can cause to personal property and state fish hatcheries may have encouraged more licensed trappers to focus on this furbearer during some years, thereby also increasing trap nights. Finally, we acknowledge that there may have also been changes in harvest effort that are not captured by trap nights, including pre-baiting of trap sites before the start of the season (Berg et al., 2025) or the use of different types of traps or trapping techniques. As such, we encourage future research to explore a wider range of anthropogenic factors and to quantify their likely effects on harvest effort.

Our SPR model also suggests that although higher pelt prices resulted in more catch-effort during the following year, the likelihood of a river otter being harvested per additional unit of effort actually decreased at the same time. For example, when average pelt prices in Kentucky increased almost two-fold in 2012 from $40.24 to $72.98, catch-effort during the following year increased from 283,934 to 381,118 trap nights. The harvest vulnerability, however, which converts hunter effort into a harvest probability, counterintuitively decreased that year from -1.876 to -1.944, -1.003 to -1.071, and -1.900 to -1.968 for young-of the-year, yearlings, and adults, respectively. We suggest that this may have been caused by higher pelt prices encouraging more casual or inexperienced trappers, who otherwise harvest other furbearers, to shift their focus more to river otter during the following year. Although this would lead to a higher number of trappers and, by extension, a higher number of trap nights, it could result in an effort pool of trappers who, on average, are less effective at trapping river otters. When pelt prices began to fall, on the other hand, this may have discouraged participation by these more casual trappers, thereby leading to an effort pool that was mostly comprised of dedicated trappers who were more effective at trapping river otters per unit of effort. It is important to note, however, that although this effect was consistent and significant within our SPR model, its magnitude was much smaller than that of the corresponding increase in catch-effort. This would suggest that higher pelt prices will still result in higher harvest rates, even if at a slightly less-than-proportional amount.

4.2 Age-specific trends in harvest and non-harvest mortality

Although our SPR model estimated three separate harvest vulnerability coefficients for young-of-the-year, yearling, and adult river otter, it is important to note that the estimates for young-of-the-year and adults were almost identical and that most of the differences were due to the much higher vulnerability experienced by yearlings. This finding is consistent with the results of the SPR model of river otter in Indiana, which also found a significantly higher vulnerability for yearlings (Berg, 2023) and is also reflective of our age-at-harvest data, where the number of yearlings harvested each year often exceeded the corresponding combined number of older animals. We suggest that this heightened vulnerability was likely caused by the increased movements commonly observed during this age as river otters disperse from their natal range or expand their home range beyond their natal range boundaries (Melquist and Hornocker, 1983; Blundell et al., 2002). These higher and more expansive movement rates could increase the rate at which dispersing river otter encounter traps, thereby producing the higher harvest vulnerability suggested by our model. Other potentially additive reasons for this higher vulnerability among yearlings include higher nutritional demands, less suspicion of novel objects, and a recent release from parental protection, all of which could increase their likelihood of encountering a trap. Regardless of the exact reason, this result suggests that any changes in harvest pressure (e.g., through increased pelt prices or adjustments to harvest regulations) are likely to have a larger effect on these younger river otters that are critical to maintaining a stable population. Because yearlings represent the future reproductive segment of the population, disproportionate harvest of these individuals can depress future reproductive potential and thereby hinder population replacement rates.

Our SPR model also estimated a single non-harvest survival coefficient that did not differ by age and corresponded to an annual non-harvest survival rate of 0.835. This value is consistent with estimates of non-harvest survival rates of river otter in other nearby states (range = 0.76 – 0.89; Gorman et al., 2008; Ellington et al., 2018; Berg, 2023), supporting our original assumption that non-harvest survival of river otter likely does not differ substantially throughout this region of North America. It is important to note, however, that our model did not include the decreased survival due to senescence included in the SPR model of river otter in Ohio, which began when river otters reached the age of 12 (Ellington et al., 2018). As more age-at-harvest and other data continue to be collected in Kentucky and other nearby states, a more detailed assessment of how survival declines as river otters approach senescence could yield additional insights into their population dynamics.

4.3 Temporal trends in overall statewide abundance

Inflating the number of animals harvested each year by the model-derived age-specific harvest probabilities indicated that the river otter population in Kentucky experienced a steady decline in pre-harvest abundance during the first half of our reconstruction from an estimated high of just over 6000 animals in 2012 to a low of just under 4000 in 2016. These years of decrease coincided with the three highest harvest counts observed during the entire 12 years of reconstruction, suggesting that above-average harvest intensity (particularly from 2012 to 2014) may have been responsible for the observed decline. As the number of river otters harvested was cut in half by 2016, the population was able to recover to a pre-harvest high of over 8000 by 2019. However, that year also saw a return to above-average harvest counts, which likely led to the population decline that began the following year and continued until reaching a low of just under 4500 by 2023. We recommend that management agencies continue to update this SPR model as new years of age-at-harvest and catch-effort data become available to ensure that the most recent decline in abundance does not continue. Further, given the high degree of correlation between pelt prices and the following year’s catch-effort, we recommend that agencies explore preemptively adjusting harvest regulations (i.e., quotas, season lengths, and number of licenses) following years of unusually high demand for river otter pelts.

The relative trends in these estimates of abundance compare favorably to those derived by the earlier SPR model of river otters in Kentucky (Berg and Palmer, 2021), which only reconstructed abundance from 2012 to 2018. This earlier model also suggested that river otter abundance decreased steadily during the first few years of reconstruction, again likely due to the above-average harvest counts observed during those years, before rebounding somewhat as the harvest counts decreased. Our updated model, however, suggests that absolute (not relative) abundance during these years may have been much lower than originally estimated. For example, our current model estimated a pre-harvest abundance of just over 6000 animals in 2012, compared to the approximately 22000 estimated by the earlier model – a difference of almost 250%. Such a large difference drastically changes any conclusions regarding the rate at which river otters were removed from this population via harvest, which can in turn severely impact management decisions regarding quotas and other harvest regulations. Fortunately, KDFWR has maintained a very conservative approach to harvest regulations since the river otter season was reopened in 2004 and did not make any adjustments to bag limits or season lengths based on these earlier overestimates, instead choosing to wait until additional years of data became available.

These new estimates of river otter abundance in Kentucky do compare favorably with estimates derived from SPR models developed in both Ohio and Indiana, two states that neighbor Kentucky and that experienced similar historic trends in overharvesting, season closure, reintroduction, and the eventual reinstatement of otter harvesting. Ellington et al. (2018), for example, estimated pre-harvest abundances in Ohio ranged from 4000 and 6000 animals from 2006 to 2008, just two to four years after restricted and limited harvest began in 2005. Similarly, estimates in Indiana ranged from approximately 6500 in 2015 when river otter harvest was first reinstated to just over 8000 animals six years later in 2020 (Berg, 2023). By comparison, our estimate of just over 6000 animals in 2012 occurred eight years after river otter harvest in Kentucky was reinitiated in 2004, reinforcing our conclusion that this updated SPR model provides a more robust and accurate estimate of absolute river otter abundance across the state.

We suggest three potentially additive reasons for why the original SPR model severely overestimated the absolute abundance of river otters in the state. First, the original model was based on only seven years of data compared to the 12 years of data used in the updated model. Previous studies have consistently shown that the duration of available age-at-harvest and catch-effort data has a significant effect on the precision of reconstruction estimates (Laake, 1992; Gast, 2012; Berg et al., 2024), which suggests that the original seven years of data may not have been sufficient to accurately reconstruct trends in absolute abundance. Further, the variability in the catch-effort data available for the original reconstruction was minimal, with only a two-and-half-fold difference between years of highest and lowest effort. Given previous cautions against using SPR models when catch-effort data are relatively constant over time (Laake, 1992; Skalski et al., 2007; Clawson et al., 2013), cautions that were later confirmed by simulation studies (Berg et al., 2024), this lack of variability likely compounded the issues caused by the few years of data. Finally, the original model was based on a single-stage approach where abundance was estimated as a parameter directly within the modeling framework, whereas the updated model uses a second-stage estimation procedure. This approach, which instead produces a Horvitz-Thompson estimate of abundance by inflating the observed harvest counts by the model-derived estimates of harvest probability, has been shown to significantly improve model accuracy and precision (Gast et al., 2013a, b). These findings further reinforce previous recommendations that management agencies carefully evaluate all relevant aspects of the available data, as well as the specific means with which they are integrated into the SPR model, before using the results of these models to aid in setting harvest regulations and other management decisions.

4.4 Model limitations and future directions

One overall caution is that using age-at-harvest data where not every animal is successfully aged assumes that the corresponding age distribution is representative of the entire population of harvested animals. This assumption is less critical for states like Indiana, where mandatory submission of harvested river otters by trappers resulted in an average of 98% of all harvested animals being successfully aged every year (range = 94 – 100%; Berg, 2023). Kentucky, on the other hand, relied on voluntary submission of teeth by trappers, which not only resulted in relatively lower proportions of harvested animals being successfully aged (mean = 16%, range = 7 – 22%), but may also have skewed the resulting age distribution if trappers were less likely to submit a particular age class over another. Given that previous research has identified accurately estimating the harvest age distribution as a critical consideration of accurately estimating furbearer abundance (Murphy et al., 2022), we recommend increasing the proportion of harvested animals that are aged each year through increased trapper outreach, education, and incentives.

Another important consideration that may limit the reliability of our results is that there were no radio-telemetry data available on river otter in Kentucky to help estimate either harvest vulnerability or non-harvest survival coefficients. Previous studies have consistently demonstrated that including such data, however limited they may be, can significantly improve both the accuracy and precision of SPR models (Clawson et al., 2013; Berg et al., 2017, 2024). Given these potential improvements, we incorporated radio-telemetry data on river otter that were collected in nearby states, but only to help estimate non-harvest survival. Because harvest rates and regulations undoubtedly differed between these states, we did not use any radio-telemetry data from other states to help estimate harvest vulnerability. Simulation studies conducted by Berg et al. (2017), however, indicated that most of the improvements from telemetry data actually comes from incorporating information on harvest rather than non-harvest mortality. As such, collecting such data in the future could greatly improve the performance of these SPR models and provide a clearer and more complete picture of river otter vulnerability throughout the state.

This lack of available radio-telemetry data on both harvest and non-harvest mortality also prevented us from incorporating random effects into our SPR model that would have allowed for the natural fluctuations that these parameters undoubtedly experienced from year to year (Gast, 2012; Gast et al., 2013a). For example, even if non-harvest survival did not differ by age from 2012 to 2023, it likely differed from year to year because of annual changes in weather, prey abundance, or other external environmental factors. Having additional auxiliary data to help estimate these natural interannual fluctuations in parameter values would not only improve our understanding of river otter mortality throughout the state, but could also help confirm if the observed differences in harvest vulnerability were truly due to changes in pelt prices or if they could be explained by other factors.

Despite these limitations, we believe that this updated SPR model provides a robust and more accurate estimate of river otter abundance, harvest vulnerability, and non-harvest survival throughout Kentucky. In addition to confirming that higher pelt prices from previous years are a good indicator of increased catch-effort and, by extension, harvest counts, our model suggested that some of this increase will be offset by the lower harvest vulnerability caused by less experienced trappers switching to river otters. Accurately estimating and identifying the driving forces behind these interannual trends in harvest mortality and other demographic parameters remains critical for ensuring effective management of river otter throughout North America. As such, we continue to encourage management agencies to explore using SPR models, whether with fixed, linear, or random effects, to provide robust estimates of these parameters and to better understand the role that anthropogenic stressors such as pelt prices can have on furbearer populations that are in high demand by the public.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Ethics statement

Ethical approval was not required for the study involving animals in accordance with the local legislation and institutional requirements because all trapping, handling, and data collection was conducted by licensed fur trappers and the Kentucky Department of Fish and Wildlife Resources, Ohio Department of Natural Resources, and Minnesota Department of Natural Resources.

Author contributions

SB: Methodology, Conceptualization, Software, Writing – original draft, Investigation, Writing – review & editing, Visualization, Formal Analysis, Validation. LP: Data curation, Validation, Project administration, Resources, Funding acquisition, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research and/or publication of this article. This study was supported by the Wildlife Restoration Act and by the Commonwealth of Kentucky under Vendor Contract No. PON2 660 2500001923.

Acknowledgments

We are grateful to Kentucky fur trappers who continuously donate tooth samples year after year for river otter research and management projects. We thank the Kentucky Department of Fish and Wildlife Resources wildlife biologists and technicians for coordinating tooth sample donations and processing samples from harvested river otters. Radio-telemetry data were provided by the Ohio and Minnesota Departments of Natural Resources, and we are especially grateful to Katie Dennison, Chris Dwyer, Hance Ellington, and John Erb for providing these data. We also thank Holly Morris and Nate Bowersock for providing pelt price data for West Virginia and Missouri, respectively, and Geriann Albers, Matt Peek, and John Erb for their helpful feedback and suggestions on our analysis.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barbour R. W. and Davis W. H. (1974). Mammals of Kentucky (Lexington, Kentucky, USA: University Press of Kentucky).

Google Scholar

Barding E. E. (2011). The Recovery of the River Otter (Lontra canadensis) in Kentucky: Status, Distribution, Diet, Reproductive Characteristics, and Management of a Reintroduced Species (Lexington, Kentucky, USA: University of Kentucky).

Google Scholar

Barding E. E., Lacki M. J., and Patton L. L. (2010). “Recovery of the river otter to Kentucky,” in Proceedings of the Annual Conference of the Southeastern Association of Fish and Wildlife Agencies. 112–117.

Google Scholar

Bellier E., Ferreira D. C., Kalb D. M., Ganoe L. S., Mayer A. E., and Gerber B. D. (2024). A statistical population reconstruction model for wildlife populations: A case study with white-tailed deer and fisher. Ecosphere 15, e4878. doi: 10.1002/ecs2.4878

Crossref Full Text | Google Scholar

Berg S. S. (2023). Utility of particle swarm optimization in statistical population reconstruction. Mathematics 11, 827–854. doi: 10.3390/math11040827

Crossref Full Text | Google Scholar

Berg S. S., Erb J. D., Fieberg J. R., and Forester J. D. (2017). Utility of radio-telemetry data for improving statistical population reconstruction. J. Wildl. Manage. 81, 535–544. doi: 10.1002/jwmg.21212

Crossref Full Text | Google Scholar

Berg S. S., Erb J. D., Kostynick E. E., Snider B. A., Anderson J. D., and Guo H. (2025). Using statistical population reconstruction to estimate effects of changing harvest regulations on fisher in Minnesota. J. Wildl. Manage. 89 (7), e70060. doi: 10.1002/jwmg.70060

Crossref Full Text | Google Scholar

Berg S. S., Erb J. D., and Westphal A. K. (2024). The effects of variability in catch effort on the precision of statistical population reconstruction. Wildlife Biol. 2028 (2), e01288. doi: 10.1002/wlb3.01288

Crossref Full Text | Google Scholar

Berg S. S. and Palmer L. L. (2021). A comparison of multinomial likelihood and chi-square approaches to statistical population reconstruction. J. Biol. Syst. 29, 543–559. doi: 10.1142/S0218339021400106

Crossref Full Text | Google Scholar

Blundell G. M., Ben-David M., Groves P., Bowyer R. T., and Geffen E. (2002). Characteristics of sex-biased dispersal and gene flow in coastal river otters: implications for natural recolonization of extirpated populations. Mol. Ecol. 11, 289–303. doi: 10.1046/j.0962-1083.2001.01440.x

PubMed Abstract | Crossref Full Text | Google Scholar

Bricker E. A., Serfass T. L., Hanley Z. L., Stevens S. S., Pearce K. J., and Bohrman J. A. (2022). “Conservation status of the North American river otter in the United States and Canada: Assessing management practices and public perceptions of the species,” in Small carnivores: Evolution, ecology, bheaviour, and conservation. Eds. San E. D. L., Sato J. J., Belant J. L., and Somers M. J. (John Wiley and Sons, New Jersey, USA), 509–535.

Google Scholar

Broms K., Skalski J. R., Millspaugh J. J., Hagen C. A., and Schulz J. H. (2010). Using statistical population reconstruction to estimate demographic trends in small game populations. J. Wildl. Manage. 74, 310–317. doi: 10.2193/2008-469

Crossref Full Text | Google Scholar

Burnham K. P. and Anderson D. R. (2002). Model selection and multimodel inference (New York, New York, USA: Springer-Verlag).

Google Scholar

Clawson M. V., Skalski J. R., and Millspaugh J. J. (2013). The utility of auxiliary data in statistical population reconstruction. Wildlife Biol. 19, 147–155. doi: 10.2981/12-076

Crossref Full Text | Google Scholar

Cramer M. S. (1995). River otter (Lontra canadensis) restoration in Kentucky: final report (Frankfurt, Kentucky, USA: Kentucky Department of Fish and Wildlife Resources).

Google Scholar

Ellington E. H., Flournoy P. D., Dwyer C. P., Witt M. D., and Gehrt S. D. (2018). Assessment of river otter abundance following reintroduction. Wildl. Res. 45, 490–499. doi: 10.1071/WR17164

Crossref Full Text | Google Scholar

Fieberg J. R., Shertzer K. W., Conn P. B., Noyce K. V., and Garshelis D. L. (2010). Integrated population modeling of black bears in Minnesota: implications for monitoring and management. PloS One 5, e12114. doi: 10.1371/journal.pone.0012114

PubMed Abstract | Crossref Full Text | Google Scholar

Gast C. M. (2012). Fixed and Random Effects Models and Multistage Estimation Procedures for Statistical Population Reconstructions (Seattle, Washington, USA: University of Washington).

Google Scholar

Gast C. M., Skalski J. R., and Beyer D. E. (2013a). Evaluation of fixed- and random-effects models and multistage estimation procedures in statistical population reconstruction. J. Wildl. Manage. 77, 1258–1270. doi: 10.1002/jwmg.576

Crossref Full Text | Google Scholar

Gast C. M., Skalski J. R., Isabelle J. L., and Clawson M. V. (2013b). Random effects models and multistage estimation procedures for statistical population reconstruction of small game populations. PloS One 8, e65244. doi: 10.1371/journal.pone.0065244

PubMed Abstract | Crossref Full Text | Google Scholar

Gorman T. A., McMillan B. R., Erb J. D., Deperno C. S., and Martin D. J. (2008). Survival and cause-specific mortality of a protected population of river otters In Minnesota. Am. Midl. Nat. 159, 98. doi: 10.1674/0003-0031(2008)159[98:SACMOA]2.0.CO;2

Crossref Full Text | Google Scholar

Gove N. E., Skalski J. R., Zager P., and Townsend R. L. (2002). Statistical models for population reconstruction using age-at-harvest data. J. Wildl. Manage. 66, 310–320. doi: 10.2307/3803163

Crossref Full Text | Google Scholar

Hall E. R. (1981). The Mammals of North America. 2nd Edn (New York, USA: John Wiley and Sons).

Google Scholar

Johnson R. D., Jenks J. A., Tucker S. A., and Wilckens D. T. (2019). Mountain Lion (Puma concolor) population characteristics in the Little Missouri Badlands of North Dakota. Am. Midl. Nat. 181, 207. doi: 10.1674/0003-0031-181.2.207

Crossref Full Text | Google Scholar

Jones R. L. (2005). Plant Life of Kentucky: An illustrated Guide to the Vascular Flora (Lexington, Kentucky, USA: University Press of Kentucky).

Google Scholar

Kennedy J. and Eberhart R. (1995). “Particle swarm optimization,” in Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia. 1942–1948.

Google Scholar

Laake J. L. (1992). Catch-effort Models and their Application to Elk in Colorado (Fort Collins, Colorado, USA: Colorado State University).

Google Scholar

Mason C. (1990). “An introduction to the otters,” in Proceedings of the International Union for the Conservation of Nature, Otter Specialist Group Meeting, Gland, Switzerland. 4–7.

Google Scholar

Melquist W. E. and Hornocker M. G. (1983). Ecology of river otters in West Central Idaho. Wildlife Monogr. 83, 3–60.

Google Scholar

Morgan J. J., Rhoden C. M., White B., and Riley S. P. (2019). A state assessment of private lands wildlife conservation in the United States. Wildlife Soc. Bull. 43, 328–337. doi: 10.1002/wsb.997

Crossref Full Text | Google Scholar

Murphy S. M., Eriksen-Meier S., Robertson L., and Elbroch L. M. (2022). Is unreliable science guiding bobcat management in Wyoming and other western U.S. states? Ecol. Sol. Evidence 3, e12116. doi: 10.1002/2688-8319.12116

Crossref Full Text | Google Scholar

Raesly E. J. (2001). Progress and status of river otter reintroduction projects in the United States. Wildlife Soc. Bull. 29, 856–862.

Google Scholar

R Core Team (2022). R: A language and environment for statistical computing. Available online at: http://www.R-project.org (Accessed March 6, 2025).

Google Scholar

Runkle J., Kunkel K. E., Champion S., Frankson R., and Stewart B. C. (2017). Kentucky State Climate Summary. NOAA Technical Report NESDIS 149-KY, Silver Spring, Maryland, USA.

Google Scholar

Rutter A. U. (2018). Survival and cause-specific mortality of river otters in southern Illinois. Am. Midl. Nat. 180, 160–167. doi: 10.1674/0003-0031-180.1.160

Crossref Full Text | Google Scholar

Shanno D. F. (1970). Conditioning of quasi-newton methods for function minimization. Math. Comp. 24, 647–656. doi: 10.1090/S0025-5718-1970-0274029-X

Crossref Full Text | Google Scholar

Skalski J. R., Clawson M. V., and Millspaugh J. J. (2012a). Model evaluation in statistical population reconstruction. Wildlife Biol. 18, 225–234. doi: 10.2981/11-080

Crossref Full Text | Google Scholar

Skalski J. R., Millspaugh J. J., and Clawson M. V. (2012b). Comparison of statistical population reconstruction using full and pooled adult age-class data. PloS One 7, e33910. doi: 10.1371/journal.pone.0033910

PubMed Abstract | Crossref Full Text | Google Scholar

Skalski J. R., Millspaugh J. J., Clawson M. V., Belant J. L., Etter D. R., Frawley B. J., et al. (2011). Abundance trends of American martens in Michigan based on statistical population reconstruction. J. Wildl. Manage. 75, 1767–1773. doi: 10.1002/jwmg.227

Crossref Full Text | Google Scholar

Skalski J. R., Townsend R. L., and Gilbert B. A. (2007). Calibrating statistical population reconstruction models using catch-effort and index data. J. Wildl. Manage. 71, 1309–1316. doi: 10.2193/2005-707

Crossref Full Text | Google Scholar

Terhune T. M., Malone K. M., Sisson D. C., and Martin J. A. (2017). Statistical population reconstruction using wings from harvested Northern Bobwhites can inform management. NQSP 8, 241–247. doi: 10.7290/nqsp08u8gq

Crossref Full Text | Google Scholar