- 1School of Medicine, Baylor College of Medicine, Houston, TX, United States
- 2Department of Biomedical Engineering, The University of Texas at Austin, Austin, TX, United States
- 3Department of Aerospace Engineering and Engineering Mechanics, The University of Texas at Austin, Austin, TX, United States
- 4Department of Mechanical Engineering, The University of Texas at Austin, Austin, TX, United States
- 5Department of Obstetrics and Gynecology, Division of Pediatric and Adolescent Gynecology, Baylor College of Medicine, Houston, TX, United States
- 6Department of Surgery, Division of Pediatric Surgery, Texas Children’s Hospital, Houston, TX, United States
Finite element modeling (FEM) is a critical tool in biomechanics and biomedical engineering, offering valuable insights where in vivo or ex vivo investigations are not possible. This review specifically highlights the diverse applications of FEM within obstetrics and gynecology through a comprehensive analysis of the literature. We explore the past use of FEM in analyzing complications affecting pelvic floor structures, urinary continence, and reproduction. The potential contributions of FEM in addressing these challenges are summarized and future directions for its application in obstetrics and gynecology are highlighted.
1 Introduction
Finite element modeling (FEM) is a powerful numeric simulation tool that can solve complex mechanical problems. That is, it can predict stress and strain in a deformable body in response to internal and external forces. It is important to note that accurately modeling the stress–strain response of soft tissues is challenging due to their complex composition; failure to account for characteristics such as viscoelastic behavior and anisotropy may compromise the accuracy of finite element model predictions. FEM predicts stress and strain by solving the balance of linear momentum equation, which governs the deformation of solids, including the soft and hard tissues (1, 2). In contrast to other numerical approaches, it is applicable even for arbitrarily complex geometries and material behaviors. Therefore, FEM is uniquely well suited for applications in biomechanics in general and soft tissue biomechanics in particular (2). Fundamentally, FEM breaks down geometries into so-called “finite elements,” thereby reducing a generally unsolvable differential equation into a system of solvable, algebraic equations (1). FEM is especially useful where in vitro or in vivo experimentation is not possible, unethical, or too expensive. In those scenarios, it can provide insight into the underlying mechanics of tissues, organs, and device-organ interfaces that is otherwise inaccessible. Its inverse counterpart, inverse finite element analysis (iFEA), is also informative, focusing on the estimation of material parameters. Using known variables, it applies an algorithmic and iterative approach to determine material constants for various constitutive models (3).
FEM is an indispensable tool in engineering disciplines, used in modeling of continuum mechanics and macroscopic material behavior, including biomechanics and biomedical engineering. Its use has contributed significant insights to fields like cardiology (4), orthopedics (5), and dentistry (6)—particularly in addressing pathologies that are dictated by complex biomechanical phenomena. Over the past 20 years, FEM has been adopted to understand similar functions within obstetrics and gynecology, thereby deepening our understanding of conditions impacting pelvic floor health, ranging from pelvic floor dysfunction (PFD) to obstetric complications. In doing so, FEM has addressed the unique mechanical stressors affecting the pelvic floor, where forces arise from gravitational load, are amplified during physiologic events like childbirth, and accumulate through repeated increases in intra-abdominal pressure during activities such as coughing or lifting. These stressors are further compounded by age-related changes in tissue structure, including collagen degradation and hormonal shifts associated with menopause.
Conditions impacting the pelvic floor and pregnancy have devastating consequences for women. Specifically, PFD impacts around 25% of women (7), with an estimated cost of 1.5 billion dollars for surgical repair of prolapse alone in the United States (8). Unfortunately, damage sustained during labor and delivery leads to pelvic floor dysfunction in up to 10% of women following childbirth (9). Additionally, as many as 26% of women suffer from urinary incontinence following childbirth (10). During pregnancy, cervical insufficiency is a significant cause of preterm birth and may be responsible for up to 20% of second trimester losses (11). The field of gynecology has made progress in identifying risk factors (10, 12, 13) and imaging techniques (14, 15) to assess pelvic pathologies. However, these approaches have not yet identified clear mechanisms behind many of these conditions, which has limited efforts to identify targeted solutions for them. The use of FEM may offer an additional understanding of the mechanical environments surrounding these disorders, which combined with other methods may enable more effective treatments. By integrating patient-specific data, FEM can help explore the pathophysiology and potential treatments of pelvic disorders. It allows researchers to manipulate specific biomechanical variables, such as tissue elasticity, loading conditions, or anatomical structures, and observe how these changes influence mechanical stress, strain distributions, and organ displacement. This capability has contributed to answering key questions about the magnitude and location of strains required to produce symptoms in various pelvic pathologies. While reviews have addressed FEM applications in either gynecology (16–19) or obstetrics (20, 21) this review systematically examines both fields to highlight methodological advances, synthesize insights into key pathologies, and illustrate FEM’s broad and evolving role in women’s health.
2 Methods
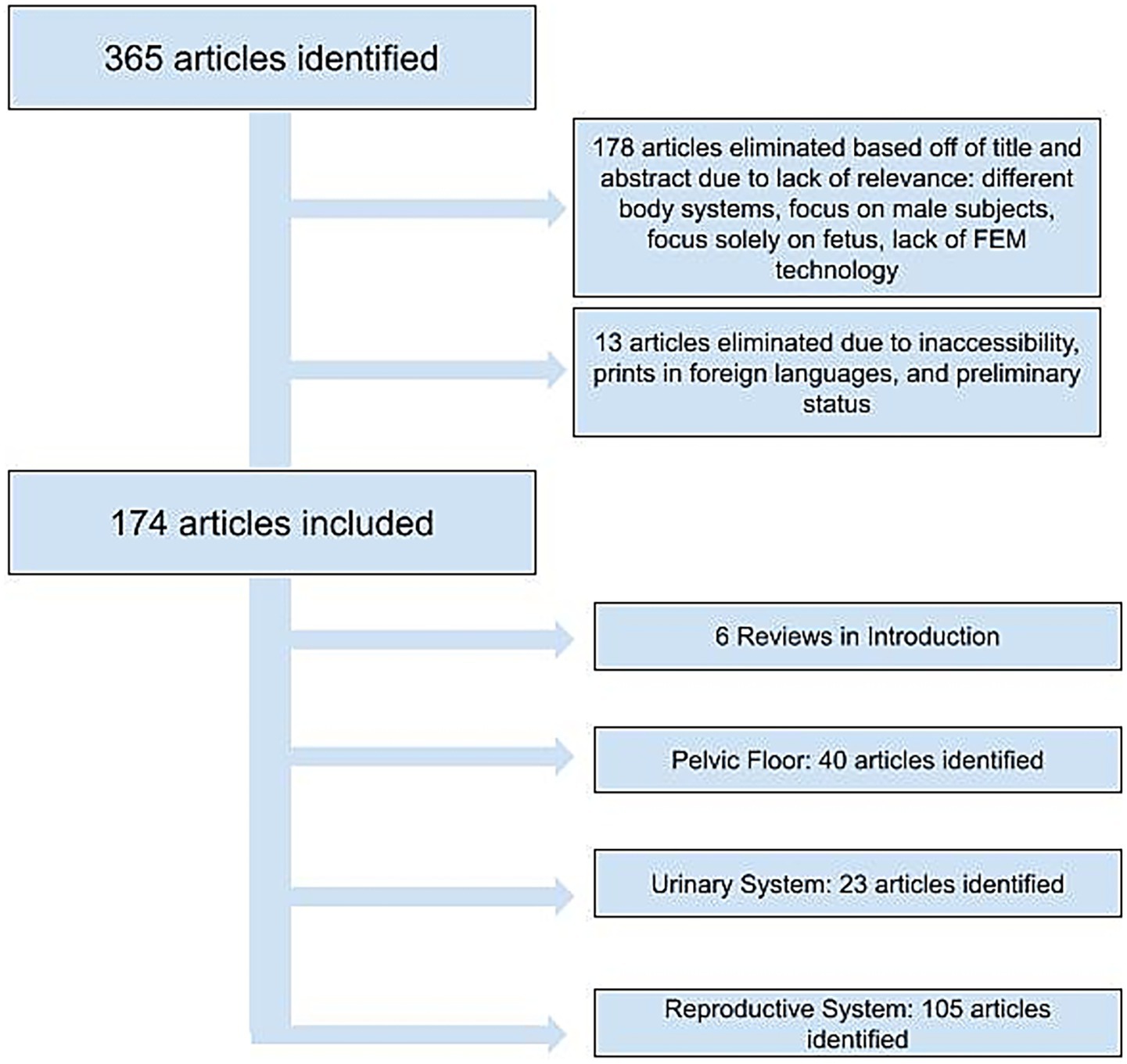
We performed a literature search in pubmed using the terms “finite element” and (“gynecology” or “gynaecology” or “vagina” or “uterus” or “cervix” or “obstetric” or “pelvic floor” or “incontinence” or “urethra”) on 6/19/24. This resulted in 365 articles. 178 were eliminated due to lack of relevance, meaning they focused on non-gynecological body systems, focused solely on the fetus, or lacked finite element modeling. Of the remaining 187 articles, 13 were eliminated due to language, preprint status or inaccessibility (Figure 1). Each of the included articles was grouped by subject area (pelvic floor, urinary system, or reproductive system). Then each subject area was reviewed to identify FEM related contributions.
3 Pelvic floor
3.1 Anatomy and tissue modeling
FEM has enhanced our understanding of the pelvic floor’s structural system, which suspends and supports organs essential to reproduction and urination (22). Figure 2 illustrates the anatomical organization of the pelvic floor. We identified 40 articles in this topic area. Initial work created geometric meshes of the pelvic floor using data from magnetic resonance (MR) imaging, computed tomography (CT), and cadaveric analysis (23–25). To simulate the biomechanical behavior of the pelvic floor structures, researchers developed constitutive models that characterize the soft tissue mechanics. Several models incorporated hyperelastic behavior into musculature and ligaments (26–29), with some employing hyperelastic material laws, such as Mooney–Rivlin formulations, to describe the nonlinear behavior of these structures (28, 29). Other work acknowledged the hyperelastic nature of fascia but implemented simplified linear elastic properties in the finite element model (30). Simulations have continued to employ additional, informative modeling techniques. For example, to help estimate the material properties of the pelvic floor, iFEA has been used as a key tool by refining material constants through deformation-based experiments (31). To characterize the behavior of pelvic fascia, one study applied mixture theory, using Voigt’s isostrain model to represent the fascia’s composition of collagen-elastin fibers, adipose tissue, and smooth muscle (32). The development of pelvic floor models have enabled the simulation of normal physiological movements that occur in the pelvic floor. For example, Noakes et al. modeled the Valsalva maneuver (i.e., forcibly expiring against a closed airway leading to increased intrathoracic and intraabdominal pressure (33)) from live patient data to improve the general understanding of levator ani muscle (LAM) group function during this process, using FEM to solve the proposed governing equations of finite elasticity (34). These models paved the way for the adoption of FEM to study gynecologic and obstetric challenges.
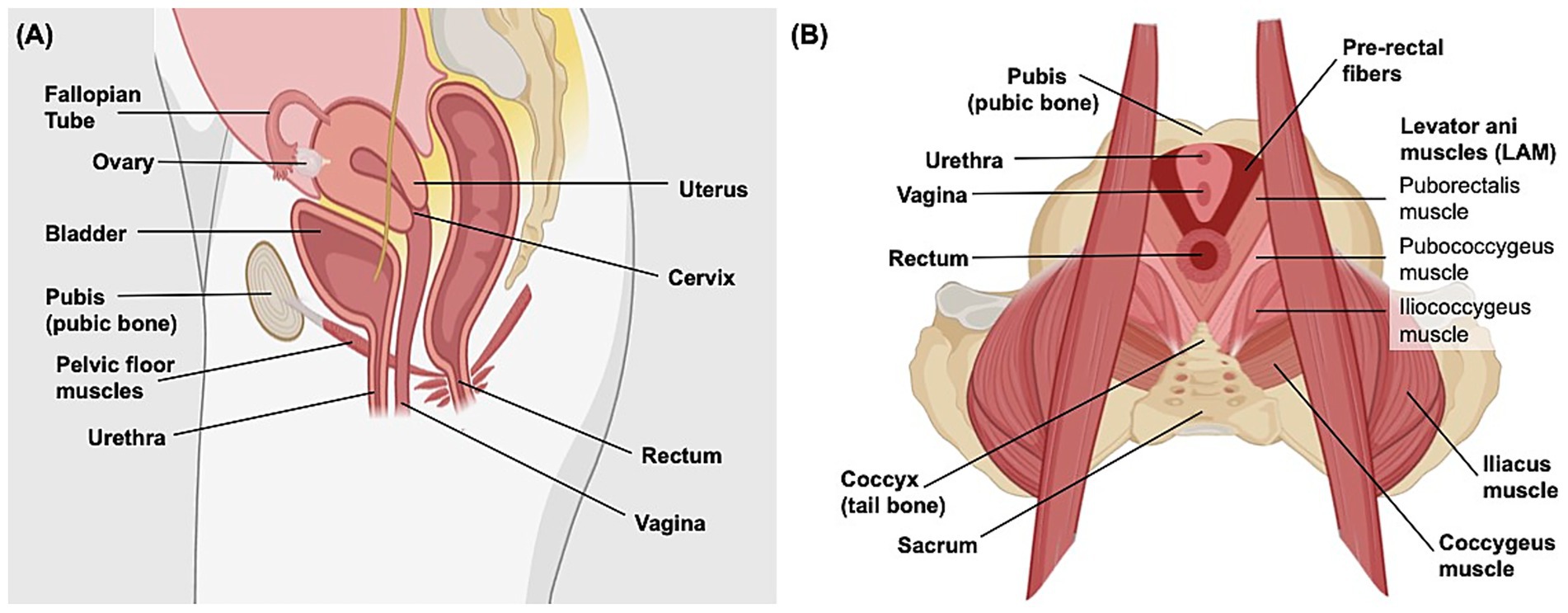
Figure 2. Anatomy of the human female pelvis. (A) Sagittal view of the female abdomen demonstrating the general position and orientation of the bladder, rectum, and reproductive organs. (B) Superior transverse view of the organization of female pelvic floor muscles, including the levator ani muscle group that is primarily involved in urination, defecation, sexual activity, and supporting pelvic organs. Created in Biorender. (195).
3.2 Pathology, injury and pelvic organ prolapse
The pelvic floor not only suspends organs against the force of gravity but also supports the primary function of preventing pelvic organ prolapse (POP). Unfortunately, stressors such as obesity, age, LAM injury, and parity (35) cause critical lapses in tissue integrity and compromise this role, leading to pelvic organ herniation. Historically, risk factors for POP were ascertained through correlational studies of women in which prolapse had occurred (35). However, use of FEM has allowed many groups to simulate the effect of potential pelvic floor injuries and determine how the severity and location of these injuries may manifest into POP at different areas within the pelvis, which could not be performed clinically. Newer FEM methodologies introduced anatomically accurate 3D models based on MRI (36, 37), incorporating detailed structures such as the vaginal lumen (38), pelvic floor muscles, and ligaments such as the cardinal and uterosacral ligaments. Xu et al. used a different modality, the Chinese Visible Human (CVH) dataset, to construct their model and further augment anatomical accuracy. The CVH dataset is an anatomical dataset derived from ultra-thin cadaveric sections (39). Through each of these strategies, simulations improved the fidelity of anatomical attachments and boundary conditions. As shown by Mayeur et al., such improvements may significantly enhance the accuracy of pelvic floor displacement models—even more so than variations in soft tissue material properties (40).
In addition, models simulated increased intra-abdominal pressure and revealed potential sites of vulnerability within the pelvis, including ligaments at connection points (36, 38) and the upper anterior vaginal wall (36, 37) in anterior vaginal wall prolapse. Chanda et al. similarly identified stress concentration along the anterior vaginal wall (AVW) when simulating bladder filling using FEM, employing an innovative forced thermal expansion technique to examine the effects of vaginal tissue stiffening in cases of pelvic organ prolapse (41). Their findings revealed that while bladder filling alone led to a relatively uniform stress distribution along the AVW, increasing vaginal tissue stiffness resulted in a growing zone of concentrated stress, particularly at the mid-vagina. Notably, the peak stress levels remained relatively unchanged despite the enlargement of this high-stress zone. This suggested that as prolapse progresses and vaginal tissue stiffens, discomfort may intensify due to the increasing area of strain, even if conventional clinical assessments fail to detect significant changes in stress at the AVW. These results highlight the value of subject-specific computational modeling in identifying subtle biomechanical changes that may not be apparent through standard imaging techniques, potentially aiding clinicians in determining the need for early intervention.
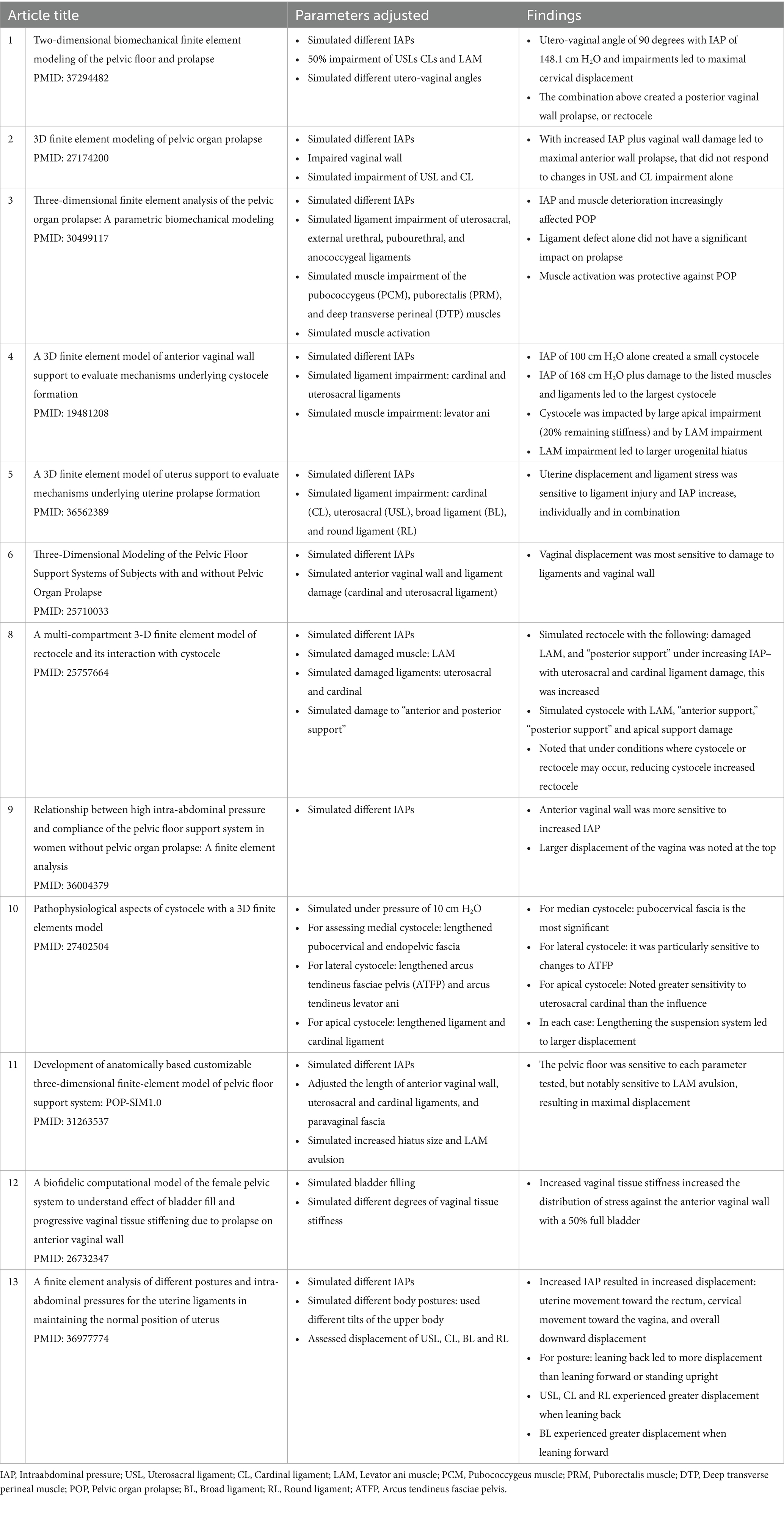
The effects of increased pressures on displacement of pelvic floor-supported organs were assessed by systematically varying: (1) loading conditions, (2) the modeled material properties of the pelvic floor, and (3) the degree of damage to supportive ligaments (Table 1). For example, pairing damage to the anterior vaginal wall with different degrees of intra-abdominal pressure (IAP) identified the amount of pressure needed to produce anterior prolapse (42). Simulations also showed that solely weakening the apical ligaments did not lead to prolapse in several cases (42, 43). Instead, anterior prolapse emerged from specific combinations of apical ligament changes (uterosacral and cardinal ligaments), fascial and muscle damage, and increased IAP (38, 44). By modeling increased IAP and tissue strain across various conditions (Table 1), FEM studies have demonstrated the potential contributions of specific pelvic floor components—such as differences in the levator ani muscle, apical ligaments, and vaginal wall—to the development of organ prolapse (36–38, 41–49).
Interestingly, FEM also revealed a slight paradoxical protection of cystocele against rectocele and vice versa by assessing the impacts of one form of prolapse upon another (45, 50). FEM demonstrated that the presence of either a cystocele or rectocele restricted the other by showing that when one was removed from simulation, the other grew slightly more pronounced (45).
3.2.1 The levator ani muscle role in prolapse
Within the pelvic floor, the levator ani muscles (LAM) have been modeled extensively using FEM and examined with iFEA. The LAM are a group of muscles that form a hammock-like support of the pelvic floor, serving as the limiting factor to preventing POP through the hiatal opening (51). To better understand the impact of LAM damage on pelvic floor function, Silva et al. developed and analyzed comparative models of both healthy patients and those with pelvic floor pathologies, including urinary incontinence and POP (52, 53). Using iFEA, they assessed the pubovisceralis muscle and found higher material parameters in hyperelastic constitutive models derived from patients with POP, indicating increased tissue stiffness, along with greater force generation. These differences were hypothesized to result from changes in muscle fiber size and collagen content (52). Such findings highlight the utility of iFEA in identifying patient-specific material alterations associated with pelvic floor dysfunction.
The LAM’s passive (34, 52, 54, 55) and active (29, 52, 56) movements during activities such as the Valsalva maneuver or contracting the pelvic floor have also been explored with FEM and iFEA. Demonstrating similar results to imaging studies (57), the LAM hiatus was observed to reduce under active contraction. With FEM, the impact of these contractions under increased pressure could be compared to a pelvis at rest. Higher pressures increased the hiatal opening; however, activation of the LAM reduced these changes (26, 58, 59). Using FEM to simulate LAM damage validated the significance of this muscle group. Specifically, under increased IAP, models with LAM damage had larger hiatal openings (46, 47), avulsion (46), and more significant prolapse (43, 45–47). Adding apical ligament damage to the model caused significant posterior vaginal wall strain, resulting in a rectocele (37, 45). For both POP and LAM impairment, FEM revealed that damage to specific supportive ligaments results in an adverse, additive effect—a finding that could not have been evaluated experimentally.
3.3 Surgical and device interventions
FEM has also been used to analyze medical interventions aimed at treating and reducing prolapse. A few studies have modeled surgical mesh repair and assessed the resultant reduction in displacement of the vagina (60, 61). FEM also helped evaluate the optimal mesh structure suture type (single vs. continuous) (61), mesh porosity (62), and suture number (63) to minimize movement and stress. With regards to suture type, the mesh was anchored at discrete nodes to represent the distinct fixation points of the simple stitch. For the continuous stitch, anchoring occurred across a continuous line of nodes, akin to running sutures. They found that while both the simple stitch and continuous stitch improved displacement, the continuous stitch reduced the supero-inferior movement of the uterus and vaginal wall (61), and an increased number of stitches did not produce reduced mobility (63). Similarly, FEM also assessed the efficacy of sacrospinous fixation and the optimal anchorage location to reduce pelvic organ displacement (64). Lastly, FEM was used to improve non-surgical options such as modeling underwear supporting the bladder neck (65) and ways to reduce movement of vaginal pessaries to make them more comfortable (66).
4 Urinary system
4.1 Modeling urinary mechanics and continence
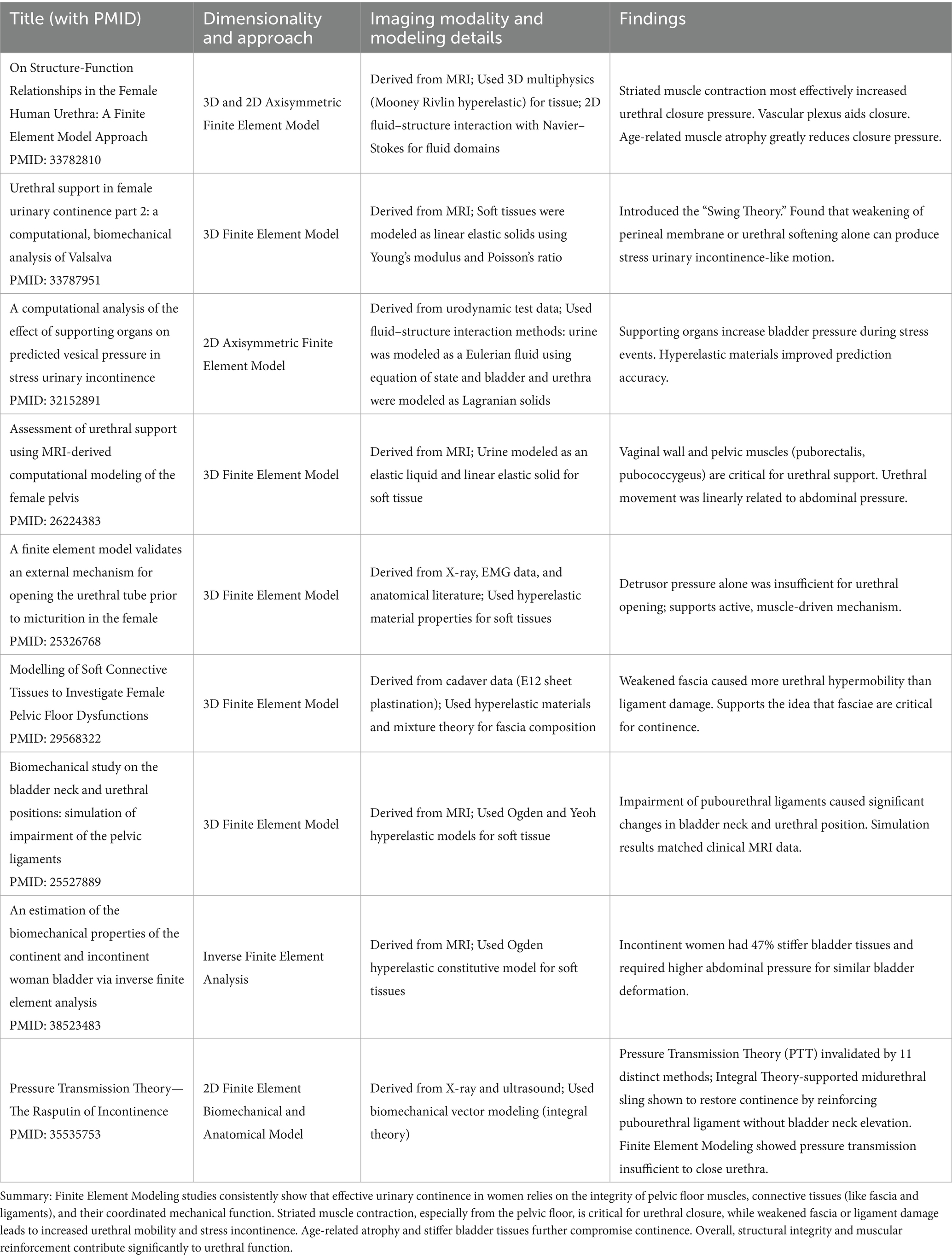
The mechanisms behind urinary incontinence have also been explored using FEM. We identified 23 articles on the application of FEM to the urinary system. In addition to developing bladder filling and displacement models (67–71), simulations have been used to demonstrate the impact of increased IAP on the bladder and urethra (72) as well as coordination and support from structures within the urinary system (73) and surrounding pelvic floor. By strategically altering the location and constitutive properties of urinary organs, FEM has been used to identify interconnected functions of the urinary tract and supporting structures, including the vascular plexus (74), levator ani (32, 75, 76), perineal membrane, and surrounding pelvic tissue (76, 77). For example, simulating urinary tract structures revealed that the urethra does not open independently at normal detrusor pressures. Instead, the inferior motion that occurs with LAM contraction enables urethra opening (75). The relationship between continence and LAM activity was also supported by pathological models using FEM and iFEA. For instance, modeling urinary tract structures based on women with incontinence and those with continence produced differences in the displacement (53) and angle of the LAM during Valsalva (32). Finally, by incorporating fluid–structure interaction (FSI)—a modeling method that assesses the interplay between fluids and solids—the model by Attari et al. was able to evaluate the urethral vascular plexus, surrounding structures and continence in greater detail. This coupling allowed the simulation to capture how changes in blood and urine pressures deformed the tissue. A reduction in urethra muscle stiffness in combination with altered vasculature impacted urethral sphincter closure pressure by compromising its ability to maintain a seal, and reducing urethral length (74), potentially impacting continence. Table 2 highlights several urinary continence mechanisms identified through FEM studies, including the roles of striated muscle contraction, vascular support, ligament integrity, and connective tissue behavior.
Outside of the urethra, simulating weakening of the LAM, paraurethral and pubourethral ligaments and supporting fascia showed that these vulnerabilities may produce urethral and bladder neck deformation during straining conditions such as increased IAP or during the Valsalva maneuver (32, 76–78). Silva et al. utilized both FEM and iFEA to investigate biomechanical differences in bladder function between continent and incontinent women. Through iFEA, they identified higher Ogden hyperelastic material parameters in incontinent women, indicating increased bladder tissue stiffness. FEM simulations, supported by MRI data, revealed greater bladder neck displacement in these women, highlighting both tissue-level and structural contributors to stress urinary incontinence (79). Finally, FEM also was utilized to model and evaluate several interventions to address urinary incontinence, including laser treatments (80, 81), single incision slings (82), MiniSlings (83), spinal cord epidural stimulation (84), and midurethral slings (85, 86).
4.2 Athletic activity and urinary continence
FEM was also utilized to understand the role of athletic activity in urinary continence. Comparing continent female athletes to incontinent female athletes, FEM revealed no significant difference in the displacement of the pelvic floor muscles during pelvic floor contraction, despite thicker pubovisceral muscles in incontinent women (87). FEM also simulated the urinary tract during a jump to assess which variables (height of jump, fullness of bladder) produced the most urinary leakage (88), as well as the precise malformations to the bladder throughout the activity (89). Two studies noted deformation within the pelvis during jump landings, involving both the pelvic bones (88) and the bladder itself (89). Interestingly, neither identified levator ani muscle (LAM) weakness as a primary cause of incontinence during this activity. Instead, both studies emphasized dynamic factors—specifically, asymmetric deformation between the anterior and posterior pelvis (88) and significant increases in IAP (89)—as key contributors to stress urinary incontinence.
5 Reproductive system
5.1 Reproductive tissue characterization
In addition to addressing gynecologic concerns, FEM served as a valuable tool to investigate challenges impacting reproductive organs and their respective functions. We identified 105 articles in this area. Similarly to the pelvic floor structures, mechanical experiments established and refined tissue parameters of the cervix, vagina (90, 91), and uterus (92–94). FEM and iFEA were also applied at the cellular and tissue level to characterize abnormal mechanical and biophysical properties in pathological tissues, such as those found in cancer (95, 96), endometriosis (97), and cysts such as cortical inclusion cysts in the ovary (98). FEM and iFEA have been also extensively used to ascertain cervical tissue properties, including electrical impedance (99–104) hydration (105), compressibility (106), and tissue stiffness (106–115)—measurements that could be used to characterize cervical changes during pregnancy. Furthermore, some studies have used FEM to demonstrate the process of pregnancy-related cervical swelling (116), integrating several of these properties in its analysis. Understanding these properties may be particularly useful in assessing cervical insufficiency, a condition with no clear etiology.
To investigate potential maladaptive conditions contributing to cervical strain, FEM was used to simulate different anatomical and material parameters, including IAP, cervical length, tissue scarring, and fiber orientation (117–119). These models revealed that under pressure akin to that experienced during labor contractions, areas of high strain were located at the inner os of the cervix (117, 118). By manipulating cervical length, an established risk factor for cervical insufficiency, Westervelt et al. identified specific changes to the strain patterns of the cervical os. Interestingly, shortening the cervical length from 4 to 2.5 cm in the model caused changes in both stress and strain—but only when simulating softer cervical tissue (117). In fact, softer tissue alone led to increased tissue strain within the cervix, and this effect was further amplified when combined with other factors such as cervical length. When simulating an incompetent cervix (<2.5 cm), stress was distributed more broadly across the cervix, extending beyond the internal os, unlike in models with normal cervical lengths, where stress was more concentrated near the internal os (118). This suggests that a shorter cervix experiences a more widespread mechanical load, potentially contributing to its increased susceptibility to deformation.
Using FEM, tissue structures within the pelvic floor were manipulated in ways that would be impossible in vivo. Specifically, altering the alignment of the uterocervical canal to the uterus (117) affirmed the benefit of proper cervical placement; tilting the cervix posteriorly increased the stretch at the cervical os. Also, adjusting the adhesion and thickness of fetal membranes (117) demonstrated that fetal membranes reduce strain on the uterus by redistributing the load of the fetus. Therefore, having thicker and more adherent tissue resulted in less uterine strain.
5.2 Fertility and conception models
FEM-based simulation has also greatly advanced our understanding of obstetrics from conception to contractions to delivery. Early studies demonstrated the applicability of FEM in simulating the uterus and adnexa (120). Over time, FEM has been adapted to model various morphological changes in the fallopian tubes (121) and sperm (122), as well as to assess the impact of those changes on fertility. Models captured age-related changes in the tubes, including reduced tubal diameter and cilia (121). In addition, they examined various components of sperm quality, adjusting the size of sperm tails and heads (121, 122). Such models were novel in capturing a range of sperm morphologies and tubal parameters, and in their ability to predict fertility success. Furthermore, by simulating aging reproductive tracts (122) and adjusting sperm motility and number (121), FEM demonstrated the potential to create personalized fertility models that could optimize reproductive outcomes.
5.3 Pregnancy and labor simulations
Following conception, FEM and iFEA have advanced existing pregnancy models—for example by identifying constitutive parameters of the uterus (92, 93, 123, 124) and placenta (125, 126) and simulating a pregnant uterus at-term (194). These advancements have enhanced progress toward creating physiologically accurate models. Beyond the uterus, FEM has also been applied to explore the mechanical behavior of the pelvic floor during labor (128–130). For instance, Li et al. developed a subject-specific model of the pelvic floor to evaluate how different constitutive laws affect predictions of childbirth mechanics. They found that using a nonlinear exponential model, as opposed to a neo-Hookean one, led to significantly higher predicted delivery forces and altered stretch distributions in the LAM, highlighting the need for high-strain material data (129). In a related simulation, they also examined the role of mechanical anisotropy in the LAM and showed that increased fiber-direction stiffness (relative to cross-fiber stiffness) reduced the required delivery force and decreased peak muscle stretch (130). Parente et al. explored parameters; they demonstrated how variations in material parameters—even within the same constitutive model—substantially affected predicted pelvic floor strains, emphasizing FEM sensitivity to parameter choice (131).
FEM also progressed our understanding of the strains, forces, and injuries that occur during childbirth. Table 3 outlines key variables explored in these models—including labor duration, fetal size and position, and maternal pushing strategies—highlighting their influence on pelvic floor stress and injury. One such study, by Lepage et al., modeled localized strain on the uterosacral ligaments during delivery and found significant deformation—around 30%—was observed, with important implications for pelvic organ prolapse (132). As expected, multiple models identified significant stress on the perineum (133–137) and LAM during labor (127, 129, 135, 138–143), with several simulations localizing stress to the puborectalis (138, 141, 142, 144), pubococcygeal muscles (139, 142, 143, 145) and attachment sites to the bone (145–147). However, through FEM, researchers were able to assess the interplay between these structures. As models simulated the loosening (134) and removal (135) of the perineum, they demonstrated a decrease in LAM stress during labor, affirming the perineum as a significant source of tension on the LAM.
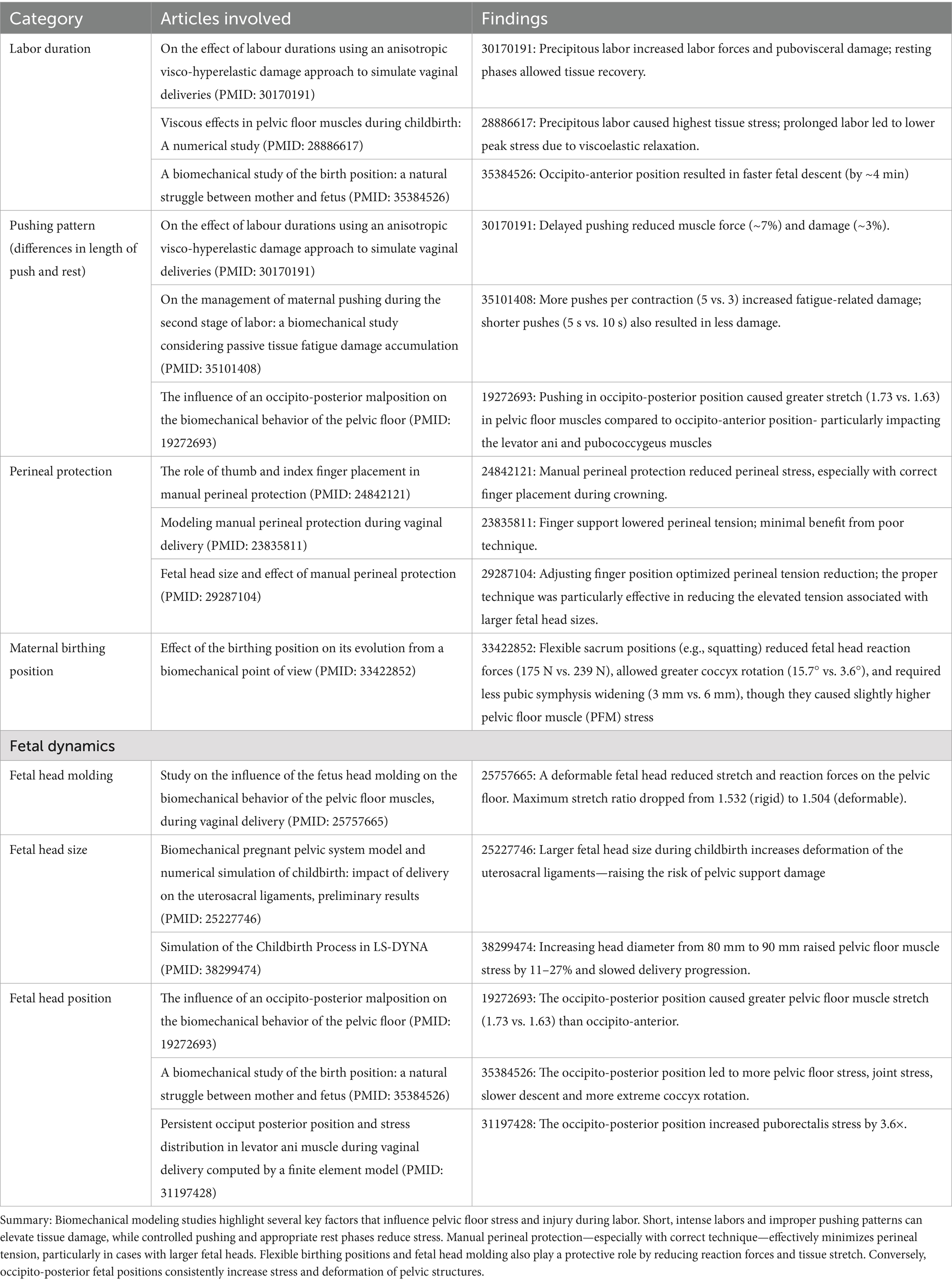
Table 3. Biomechanical factors influencing pelvic floor stress and injury during labor and delivery.
FEM has been useful in advancing our understanding of how fetal position, head size, and pelvic anatomy interact to influence maternal tissue strain during childbirth. Investigations focused on fetal positioning, comparing occiput anterior (OA) and occiput posterior (OP) presentations during descent (139, 140, 148). The OP position was found to place greater strain on the LAM, yielding higher maximal principal stresses. FEM allowed for a more detailed characterization of OP-related stress, fostering analysis of stress distribution across different fetal head descent stations during labor (140) and revealing its potential impact on fetal head molding (148). Beyond positioning, FEM was applied to assess the effect of fetal head size on maternal tissue strain. Several studies reported that larger fetal head diameters correlated with increased stress on the pelvic floor muscles (145, 149, 150). Notably, Yan et al. further developed a partial least squares regression model to predict key deformation metrics during childbirth (149). Meanwhile, Tao and Grimm found that uterine stress was minimally affected by head size, in contrast to the fetal neck and pelvic floor, where stress increased (150). Finally, FEM was applied to evolutionary questions regarding pelvic design. Although the human pelvis is not optimized in all respects, increasing its size or altering its anterior shape was found to impair delivery mechanics and reduce overall mobility (151, 152).
FEM models have advanced significantly in simulating fetal dynamics during labor, including fetal head molding and the cardinal movements—flexion, internal rotation, extension, and external rotation—during vaginal delivery (153). These advancements enhanced our understanding of strain patterns on maternal tissues. For example, a 3D FEM model was used to evaluate varying degrees of fetal head flexion. The results showed that greater flexion was associated with reduced pelvic floor stress and a shift in peak stress to lower stations within the birth canal (154). In another study, simulations of fetal head molding demonstrated a notable reduction in pelvic floor muscle strain and stretch, with the most pronounced effect observed in the levator ani muscle during vertical descent (155).
Incorporating visco-hyperelastic material properties into FEM models has added significant value by accounting for the time-dependent behavior of tissues under stress. This approach enables a more accurate representation of how strain accumulates over time. One study used this method to evaluate the effects of different maternal pushing patterns on pelvic floor strain, comparing 1, 3, and 5 pushes per contraction, with push durations of 5 and 10 s. The results showed that the least tissue damage occurred with three 5-s pushes per contraction, while the most damage resulted from five 5-s pushes. The study also found that the most damage was sustained during active pushing efforts, rather than being solely related to the total duration of labor (156). However, it is important to note, excessively rapid labor is not ideal for minimizing strain. Precipitous labor—defined as delivery within 3 h of regular contractions (157)—was associated with higher reaction forces compared to normal or prolonged labor (138, 158). Furthermore, brief rest intervals between contractions were shown to increase mechanical strain on pelvic tissues, while longer rests helped reduce maximal reaction force (158, 159).
In addition to identifying factors that increase stress on the pelvic floor, FEM was used to examine other mechanisms that reduced stress and stretch. For instance, FEM revealed that organized fiber orientation in scar tissue minimized stress (160). Birthing positions were also assessed; simulations of different maternal birthing positions found that kneeling or squatting enhanced the flexibility of the coccyx, reduced widening of the pubic symphysis, and alleviated strain on the pubic ligaments (161). Additionally, finite element simulations showed that external rotation of the femurs—by inducing lateral expansion of the ilia and increasing tension in the ilio-sacro-transverse and axial ligaments—leads to a measurable enlargement of the pelvic inlet area. This mechanism may be clinically useful in situations where increased inlet space is beneficial, such as in cases of obstructed labor or shoulder dystocia (162). Athletic status did not appear to have a large impact on stretch, but athletic women appeared to produce more force in one simulation (147). From a clinical perspective, simulations have also reinforced actionable insights for physicians by demonstrating the protective effects of manual perineal support—identifying optimal finger placements to reduce high-strain areas in the perineum (163, 164) and confirming this method’s utility across a range of fetal head sizes (165). Finally, FEM models optimized the angle and length of episiotomies to reduce strain, particularly in the more strenuous occiput posterior (OP) fetal positioning (166–169).
5.4 Modeling uterine contractions
Finite element modeling of uterine contractions has progressed significantly through the incorporation of greater physiological detail and structural complexity, enabling more accurate simulation of uterine stress and function. FEM models have been significantly refined by integrating detailed physiological mechanisms, including uterine smooth muscle cell electrical activity, intracellular calcium dynamics, myosin phosphorylation, and filament sliding (170). Enhancements have allowed for more realistic simulations of contractile behavior by incorporating both active contractile elements and passive tissue properties (150, 171). Additionally, the anatomical accuracy of the models was improved by expanding the fiber architecture of the uterine wall to include three simulated fiber directions: longitudinal, circumferential, and normal (150, 172). Using magnetomyography data, FEM was also employed to compute the lead-field matrix that maps uterine electrical activity to the magnetic fields detected by sensors, in order to better understand patterns of uterine activity (173). Finally, FEM also facilitated evaluation of how different contraction patterns affect uterine stress. Notably, simulations revealed that tachysystole elevated stress levels during relaxation, while shortened resting intervals between contractions resulted in the highest overall stress levels (159).
5.5 Device testing and clinical applications
FEM was used to improve technology that could benefit from non-invasive methods, such as pregnancy-related trauma, training, and device testing. After developing a novel balloon dilator to expand the cervix, Filipovic et al. employed FEM to evaluate differences in strain on the cervix non-invasively (174). Similarly, Asiedu et al. applied FEM to assess the safety of competing designs and materials for a new, pen-sized colposcope before human use (175). FEM was also used to improve the safety of therapies, including hyperthermic treatments for cancer (176–178), endometrial ablation (179, 180), as well as assessing the impacts of the heat produced by transvaginal transducers (181). To support training and simulation, FEM was used to help identify the ideal material for physical training models (182). FEM also helped lay the groundwork for creating hysteroscopy (183–185), childbirth (186) and gynecological surgical simulations. Finally, FEM has been used to simulate dangerous situations, including the responses of pregnant women and fetuses in road accidents (187–192) and military blasts (193), enabling the analysis of tissue and fluid responses to trauma as well as fetal injury.
6 Summary and future directions
FEM is a powerful tool with wide-ranging applications across the field of obstetrics and gynecology. FEM has facilitated the recreation and manipulation of complex pelvic structures to better characterize the biomechanics underlying pathologies of the pelvic floor, pregnancy, and childbirth. Although informative, it is important to note that FEM simulations have limitations.
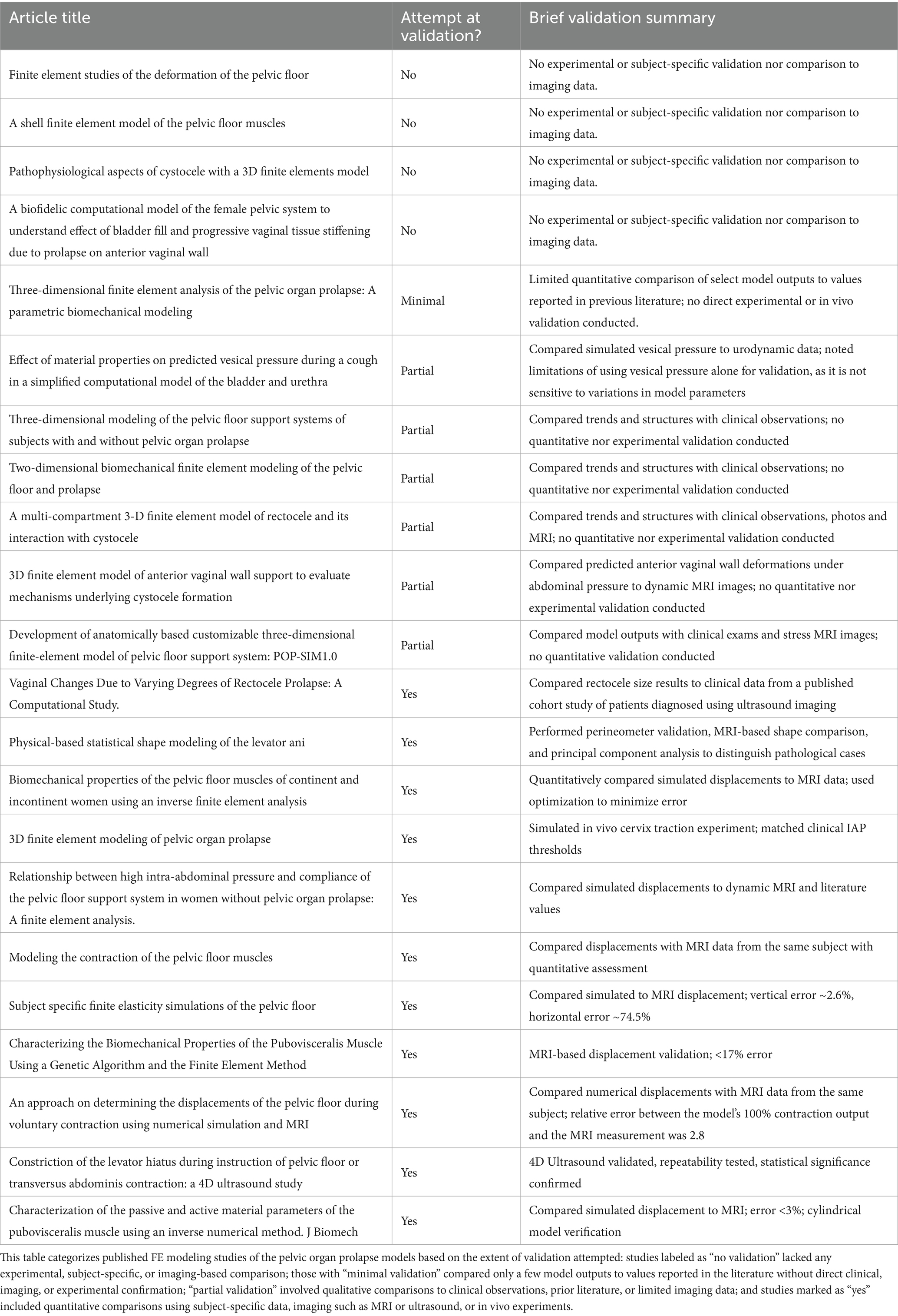
First, many simulations lacked validation against imaging studies or experimental data. In several cases, this was due to ethical and technical constraints. For example, in vivo assessment of tissue damage during pregnancy or labor was limited by concerns for patient comfort and safety. As demonstrated in Table 4, which focused on validation of pelvic organ prolapse simulations, validation methods varied considerably. While several studies incorporated mesh convergence, sensitivity analysis, or qualitative comparison to clinical trends, only a few performed quantitative validation using MRI-based displacement or statistical assessments. Several models had no direct validation attempts. This variability highlights the ongoing challenge of achieving both anatomical fidelity and experimental validation.
Second, FEM is a simulation tool sensitive to its inputs, including boundary conditions, anatomical anchoring points or pressures applied to the model, as well as constitutive assumptions and formulations. For example, in pelvic floor modeling, while some teams chose to model each muscle of the LAM group, others simulated it as a singular entity—an approach that may have impacted the precision of the results. Further, many models of the pelvic floor simplified or excluded structural supports such as ligaments or fascia, reducing the accuracy of boundary constraints, which are inherently influenced by adjacent anatomical supports. In urinary system models, common simplifications included modeling the bladder as a spherical structure or omitting urine flow entirely. In childbirth simulations, several models omitted key aspects of fetal dynamics by modeling only the fetal head while excluding the body, or by representing the head as rigid without accounting for molding Across each of these systems discussed, several studies relied on cadaveric or animal-derived tissue properties, which may not have reflected the mechanical behavior of living human tissue under physiological conditions. Of course, it is important to acknowledge that increasing model complexity and anatomical accuracy often requires greater time and resource investment—striking the right balance between model fidelity and feasibility remains a persistent challenge.
Evidently, there is no established standard for pelvic floor models. Models are oftentimes developed to address a specific need and validated, if at all, using individualized patient data. Therefore, the specificity of these unique models often limits their generalizability.
However, while specificity is a limitation for widespread application, it also aligns with one of FEM’s greatest strengths: its capacity for subject-specific modeling. Using geometric meshes constructed from medical imaging, FEM offers the ability to subject-specific solutions. Future applications of these models could include guiding the design of patient-specific pessaries for pelvic organ prolapse, identifying targeted stretching protocols for individuals with hypertonic pelvic floor dysfunction, optimizing cerclage techniques based on patient-specific biomechanics, and determining ideal positioning strategies for individuals with restricted mobility or those preparing for labor.
Beyond current applications, FEM could create detailed simulations supporting the development of new treatment and diagnostic strategies. Given its ability to model mechanical strain and predict tissue displacement, FEM could be leveraged to assess the risk of ovarian torsion in cases where the ovary is enlarged due to cysts, tumors, or other adnexal masses. By incorporating anatomical data—such as ovary size, vascular pedicle length, mass location, and tissue properties—acquired through medical imaging, FEM can simulate the mechanical forces acting on the adnexa and identify conditions that may predispose to torsion. This predictive approach could aid in clinical risk stratification and guide surgical planning, particularly for patients who are not ideal candidates for immediate or exploratory surgery. With regards to obstetrics, by applying advanced FEM methods (i.e., computational fluid dynamics) to study blood flow during pregnancy, simulations of placental development and vasculature could be generated, which could deepen our understanding of conditions such as placental insufficiency or pre-eclampsia. Once models are created, their use could be extended to develop treatments or even ways to prevent these conditions.
Finally, FEM could help in understanding the impact of pelvic tissue scarring—especially in patients with profibrotic conditions, such as pelvic inflammatory disease (PID), Asherman’s syndrome, or those undergoing oncologic treatments. Models could simulate the fibrotic barriers that hinder ovum transport, and design stents or other devices that optimize the passage of the egg, improving fertility outcomes. Within the vagina, FEM could address post-surgical or radiation vaginal stenosis by aiding in the design of custom degradable stents with the necessary stiffness to interrupt the progression of tissue damage and maximize therapeutic benefit. FEM could accelerate the development of stents, dilators, and other personalized devices by reducing the need for repeated physical prototyping and minimizing dependence on animal models.
In summary, FEM has the potential to significantly enhance our understanding and treatment of conditions in obstetrics and gynecology, ultimately helping to preserve quality of life for patients with pelvic pathologies. To fully harness this potential, future efforts should prioritize model standardization, rigorous validation, and integration into clinical workflows. With continued refinement, FEM holds great promise for transforming diagnostics, uncovering the biomechanics underlying common disorders, and improving patient outcomes across the field.
Author contributions
TM: Conceptualization, Writing – original draft, Writing – review & editing. AH: Conceptualization, Visualization, Writing – review & editing. EC-H: Conceptualization, Writing – review & editing. MR: Conceptualization, Writing – review & editing. JH: Conceptualization, Writing – review & editing, Supervision.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the National Institutes of Health (R01 HD116968, R21 HD104059), and by the Research Vision program at Texas Children’s Hospital.
Acknowledgments
This manuscript was written with the support of a science writer, Ariel M. Lyons-Warren, MD, PhD.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The authors declare that Gen AI was used in the creation of this manuscript. Generative AI was used to assist in editing the paper, specifically to improve grammar and syntax.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Zienkiewicz, OC, Taylor, RL, and Zhu, JZ. The finite element method: its basis and fundamentals. 7th ed. Amsterdam: Elsevier, Butterworth-Heinemann (2013). 714 p.
2. Freutel, M, Schmidt, H, Dürselen, L, Ignatius, A, and Galbusera, F. Finite element modeling of soft tissues: material models, tissue interaction and challenges. Clin Biomech (Bristol). (2014) 29:363–72. doi: 10.1016/j.clinbiomech.2014.01.006
3. Halloran, JP, and Erdemir, A. Adaptive surrogate modeling for expedited estimation of nonlinear tissue properties through inverse finite element analysis. Ann Biomed Eng. (2011) 39:2388–97. doi: 10.1007/s10439-011-0317-2
4. Doost, SN, Ghista, D, Su, B, Zhong, L, and Morsi, YS. Heart blood flow simulation: a perspective review. Biomed Eng Online. (2016) 15:101. doi: 10.1186/s12938-016-0224-8
5. Saha, S, and Roychowdhury, A. Application of the finite element method in orthopedic implant design. J Long-Term Eff Med Implants. (2009) 19:55–82. doi: 10.1615/JLongTermEffMedImplants.v19.i1.70
6. Shivakumar, S, Kudagi, V, and Talwade, P. Applications of finite element analysis in dentistry: a review. J Int Oral Health. (2021) 13:415. doi: 10.4103/JIOH.JIOH_11_21
7. Wu, JM, Vaughan, CP, Goode, PS, Redden, DT, Burgio, KL, Richter, HE, et al. Prevalence and trends of symptomatic pelvic floor disorders in U.S. women. Obstet Gynecol. (2014) 123:141–8. doi: 10.1097/AOG.0000000000000057
8. St Martin, B, Markowitz, MA, Myers, ER, Lundsberg, LS, and Ringel, N. Estimated national cost of pelvic organ prolapse surgery in the United States. Obstet Gynecol. (2024) 143:419–27. doi: 10.1097/AOG.0000000000005485
9. DeLancey, JOL, Masteling, M, Pipitone, F, LaCross, J, Mastrovito, S, and Ashton-Miller, JA. Pelvic floor injury during vaginal birth is life-altering and preventable: what can we do about it? Am J Obstet Gynecol. (2024) 230:279–294.e2. doi: 10.1016/j.ajog.2023.11.1253
10. Dai, S, Chen, H, and Luo, T. Prevalence and factors of urinary incontinence among postpartum: systematic review and meta-analysis. BMC Pregnancy Childbirth. (2023) 23:761. doi: 10.1186/s12884-023-06059-6
11. Meserve, EE, Parast, MM, and Boyd, TK. Gestational diseases and the placenta. In: CP Crum, MR Nucci, BE Howitt, SR Granter, MM Parast, and TK Boyd editors. Diagnostic Gynecologic and Obstetric Pathology. 3rd ed. (2018) 1219–49. doi: 10.1016/B978-0-323-44732-4.00033-9
12. Han, Y, Li, M, Ma, H, and Yang, H. Cervical insufficiency: a noteworthy disease with controversies. J Perinat Med. (2020) 48:648–55. doi: 10.1515/jpm-2020-0255
13. Meng, L, Öberg, S, Sandström, A, Wang, C, and Reilly, M. Identification of risk factors for incident cervical insufficiency in nulliparous and parous women: a population-based case-control study. BMC Med. (2022) 20:348. doi: 10.1186/s12916-022-02542-7
14. Law, YM, and Fielding, JR. MRI of pelvic floor dysfunction: review. AJR Am J Roentgenol. (2008) 191:S45–53. doi: 10.2214/AJR.07.7096
15. Habib, VVF, Araujo Júnior, E, Sun, SY, Júnior, DF, Mattar, R, Szejnfeld, J, et al. Early indicators of cervical insufficiency assessed using magnetic resonance imaging of the cervix during pregnancy. J Matern Fetal Neonatal Med. (2015) 28:626–31. doi: 10.3109/14767058.2014.928858
16. Easley, DC, Abramowitch, SD, and Moalli, PA. Female pelvic floor biomechanics: bridging the gap. Curr Opin Urol. (2017) 27:262–7. doi: 10.1097/MOU.0000000000000380
17. Brandão, S, Da Roza, T, Parente, M, Ramos, I, Mascarenhas, T, and Natal Jorge, RM. Magnetic resonance imaging of the pelvic floor: from clinical to biomechanical imaging. Proc Inst Mech Eng H. (2013) 227:1324–32. doi: 10.1177/0954411913502952
18. Yang, M, Chen, C, Wang, Z, Long, J, Huang, R, Qi, W, et al. Finite element analysis of female pelvic organ prolapse mechanism: current landscape and future opportunities. Front Med (Lausanne). (2024) 11:1342645. doi: 10.3389/fmed.2024.1342645
19. Peng, Y, Miller, BD, Boone, TB, and Zhang, Y. Modern theories of pelvic floor support: a topical review of modern studies on structural and functional pelvic floor support from medical imaging, computational modeling, and electromyographic perspectives. Curr Urol Rep. (2018) 19:9. doi: 10.1007/s11934-018-0752-9
20. Li, X, Kruger, JA, Nash, MP, and Nielsen, PMF. Modeling childbirth: elucidating the mechanisms of labor. Wiley Interdiscip Rev Syst Biol Med. (2010) 2:460–70. doi: 10.1002/wsbm.65
21. Westervelt, AR, and Myers, KM. Computer modeling tools to understand the causes of preterm birth. Semin Perinatol. (2017) 41:485–92. doi: 10.1053/j.semperi.2017.08.007
22. Strohbehn, K. Normal pelvic floor anatomy. Obstet Gynecol Clin N Am. (1998) 25:683–705. doi: 10.1016/S0889-8545(05)70037-1
23. Noakes, KF, Bissett, IP, Pullan, AJ, and Cheng, LK. Anatomically based computational models of the male and female pelvic floor and anal canal. Conf Proc IEEE Eng Med Biol Soc. (2006) 2006:3815–8. doi: 10.1109/IEMBS.2006.259886
24. Noakes, KF, Bissett, IP, Pullan, AJ, and Cheng, LK. Anatomically realistic three-dimensional meshes of the pelvic floor & anal canal for finite element analysis. Ann Biomed Eng. (2008) 36:1060–71. doi: 10.1007/s10439-008-9471-6
25. Zhang, Y, Sweet, RM, Metzger, GJ, Burke, D, Erdman, AG, and Timm, GW. Advanced finite element mesh model of female SUI research during physical and daily activities. Stud Health Technol Inform. (2009) 142:447–52. doi: 10.3233/978-1-58603-964-6-447
26. d’Aulignac, D, Martins, J a C, Pires, EB, Mascarenhas, T, and Jorge, RMN. A shell finite element model of the pelvic floor muscles. Comput Methods Biomech Biomed Engin. (2005) 8:339–47. doi: 10.1080/10255840500405378
27. Brandão, S, Parente, M, Silva, E, Da Roza, T, Mascarenhas, T, Leitão, J, et al. Pubovisceralis muscle fiber architecture determination: comparison between biomechanical Mmdeling and diffusion tensor imaging. Ann Biomed Eng. (2017) 45:1255–65. doi: 10.1007/s10439-016-1788-y
28. Venugopala Rao, G, Rubod, C, Brieu, M, Bhatnagar, N, and Cosson, M. Experiments and finite element modelling for the study of prolapse in the pelvic floor system. Comput Methods Biomech Biomed Engin. (2010) 13:349–57. doi: 10.1080/10255840903251270
29. Lee, SL, Tan, E, Khullar, V, Gedroyc, W, Darzi, A, and Yang, GZ. Physical-based statistical shape modeling of the levator ani. IEEE Trans Med Imaging. (2009) 28:926–36. doi: 10.1109/TMI.2009.2012894
30. Cosson, M, Rubod, C, Vallet, A, Witz, JF, Dubois, P, and Brieu, M. Simulation of normal pelvic mobilities in building an MRI-validated biomechanical model. Int Urogynecol J. (2013) 24:105–12. doi: 10.1007/s00192-012-1842-8
31. Haridas, B, Hong, H, Minoguchi, R, Owens, S, and Osborn, T. Pelvic Sim--a computational-experimental system for biomechanical evaluation of female pelvic floor organ disorders and associated minimally invasive interventions. Stud Health Technol Inform. (2006) 119:182–7.
32. Bhattarai, A, and Staat, M. Modelling of soft connective tissues to investigate female pelvic floor dysfunctions. Comput Math Methods Med. (2018) 2018:1–16. doi: 10.1155/2018/9518076
33. Pstras, L, Thomaseth, K, Waniewski, J, Balzani, I, and Bellavere, F. The Valsalva manoeuvre: physiology and clinical examples. Acta Physiol (Oxf). (2016) 217:103–19. doi: 10.1111/apha.12639
34. Noakes, KF, Pullan, AJ, Bissett, IP, and Cheng, LK. Subject specific finite elasticity simulations of the pelvic floor. J Biomech. (2008) 41:3060–5. doi: 10.1016/j.jbiomech.2008.06.037
35. Schulten, SFM, Claas-Quax, MJ, Weemhoff, M, van Eijndhoven, HW, van Leijsen, SA, Vergeldt, TF, et al. Risk factors for primary pelvic organ prolapse and prolapse recurrence: an updated systematic review and meta-analysis. Am J Obstet Gynecol. (2022) 227:192–208. doi: 10.1016/j.ajog.2022.04.046
36. Liu, X, Rong, Q, Liu, Y, Wang, J, Xie, B, and Ren, S. Relationship between high intra-abdominal pressure and compliance of the pelvic floor support system in women without pelvic organ prolapse: a finite element analysis. Front Med (Lausanne). (2022) 9:820016. doi: 10.3389/fmed.2022.820016
37. Xue, X, Wang, H, Xie, J, Gao, Z, Shen, J, and Yao, T. Two-dimensional biomechanical finite element modeling of the pelvic floor and prolapse. Biomech Model Mechanobiol. (2023) 22:1425–46. doi: 10.1007/s10237-023-01729-y
38. Ren, S, Xie, B, Wang, J, and Rong, Q. Three-dimensional modeling of the pelvic floor support systems of subjects with and without pelvic organ prolapse. Biomed Res Int. (2015) 2015:845985. doi: 10.1155/2015/845985
39. Xu, Z, Chen, N, Wang, B, Yang, J, Liu, H, Zhang, X, et al. Creation of the biomechanical finite element model of female pelvic floor supporting structure based on thin-sectional high-resolution anatomical images. J Biomech. (2023) 146:111399. doi: 10.1016/j.jbiomech.2022.111399
40. Mayeur, O, Witz, JF, Lecomte, P, Brieu, M, Cosson, M, and Miller, K. Influence of geometry and mechanical properties on the accuracy of patient-specific simulation of women pelvic floor. Ann Biomed Eng. (2016) 44:202–12. doi: 10.1007/s10439-015-1401-9
41. Chanda, A, Unnikrishnan, V, Richter, HE, and Lockhart, ME. A biofidelic computational model of the female pelvic system to understand effect of bladder fill and progressive vaginal tissue stiffening due to prolapse on anterior vaginal wall. Int J Numer Method Biomed Eng. (2016) 32:e02767. doi: 10.1002/cnm.2767
42. Yang, Z, Hayes, J, Krishnamurty, S, and Grosse, IR. 3D finite element modeling of pelvic organ prolapse. Comput Methods Biomech Biomed Engin. (2016) 19:1772–84. doi: 10.1080/10255842.2016.1186662
43. Babayi, M, Azghani, MR, Hajebrahimi, S, and Berghmans, B. Three-dimensional finite element analysis of the pelvic organ prolapse: a parametric biomechanical modeling. Neurourol Urodyn. (2019) 38:591–8. doi: 10.1002/nau.23885
44. Lamblin, G, Mayeur, O, Giraudet, G, Jean Dit Gautier, E, Chene, G, Brieu, M, et al. Pathophysiological aspects of cystocele with a 3D finite elements model. Arch Gynecol Obstet. (2016) 294:983–9. doi: 10.1007/s00404-016-4150-6
45. Luo, J, Chen, L, Fenner, DE, Ashton-Miller, JA, and DeLancey, JOL. A multi-compartment 3-D finite element model of rectocele and its interaction with cystocele. J Biomech. (2015) 48:1580–6. doi: 10.1016/j.jbiomech.2015.02.041
46. Gordon, MT, DeLancey, JOL, Renfroe, A, Battles, A, and Chen, L. Development of anatomically based customizable three-dimensional finite-element model of pelvic floor support system: POP-SIM1.0. Interface Focus. (2019) 9:20190022. doi: 10.1098/rsfs.2019.0022
47. Chen, L, Ashton-Miller, JA, and DeLancey, JOL. A 3D finite element model of anterior vaginal wall support to evaluate mechanisms underlying cystocele formation. J Biomech. (2009) 42:1371–7. doi: 10.1016/j.jbiomech.2009.04.043
48. Chen, J, Zhang, J, and Yu, C. A 3D finite element model of uterus support to evaluate mechanisms underlying uterine prolapse formation. Comput Methods Biomech Biomed Engin. (2023) 26:1930–9. doi: 10.1080/10255842.2022.2159759
49. Chen, J, Zhang, J, and Wang, F. A finite element analysis of different postures and intra-abdominal pressures for the uterine ligaments in maintaining the normal position of uterus. Sci Rep. (2023) 13:5082. doi: 10.1038/s41598-023-32368-z
50. Chanda, A, Meyer, I, Richter, HE, Lockhart, ME, Moraes, FRD, and Unnikrishnan, V. Vaginal changes due to varying degrees of rectocele prolapse: a computational study. J Biomech Eng. (2017) 139:101001. doi: 10.1115/1.4037222
51. Gowda, SN, and Bordoni, B. Anatomy, abdomen and pelvis: levator ani muscle In: Stat pearls. Treasure Island (FL): StatPearls Publishing (2024)
52. Silva, MET, Parente, MPL, Brandão, S, Mascarenhas, T, and Natal Jorge, RM. Characterization of the passive and active material parameters of the pubovisceralis muscle using an inverse numerical method. J Biomech. (2018) 71:100–10. doi: 10.1016/j.jbiomech.2018.01.033
53. Silva, MET, Brandão, S, Parente, MPL, Mascarenhas, T, and Natal Jorge, RM. Biomechanical properties of the pelvic floor muscles of continent and incontinent women using an inverse finite element analysis. Comput Methods Biomech Biomed Engin. (2017) 20:842–52. doi: 10.1080/10255842.2017.1304542
54. Silva, E, Parente, M, Brandão, S, Mascarenhas, T, and Natal, JR. Characterizing the biomechanical properties of the pubovisceralis muscle using a genetic algorithm and the finite element method. J Biomech Eng. (2019) 141:081002. doi: 10.1115/1.4041524
55. Silva, MET, Brandão, S, Parente, MPL, Mascarenhas, T, and Natal Jorge, RM. Establishing the biomechanical properties of the pelvic soft tissues through an inverse finite element analysis using magnetic resonance imaging. Proc Inst Mech Eng H. (2016) 230:298–309. doi: 10.1177/0954411916630571
56. Saleme, CS, Parente, MPL, Natal Jorge, RM, Pinotti, M, Silva-Filho, AL, Roza, T, et al. An approach on determining the displacements of the pelvic floor during voluntary contraction using numerical simulation and MRI. Comput Methods Biomech Biomed Engin. (2011) 14:365–70. doi: 10.1080/10255842.2010.482045
57. Bø, K, Braekken, IH, Majida, M, and Engh, ME. Constriction of the levator hiatus during instruction of pelvic floor or transversus abdominis contraction: a 4D ultrasound study. Int Urogynecol J Pelvic Floor Dysfunct. (2009) 20:27–32. doi: 10.1007/s00192-008-0719-3
58. Martins, JAC, Pato, MPM, Pires, EB, Jorge, RMN, Parente, M, and Mascarenhas, T. Finite element studies of the deformation of the pelvic floor. Ann N Y Acad Sci. (2007) 1101:316–34. doi: 10.1196/annals.1389.019
59. Brandão, FSQ d S, Parente, MPL, Rocha, PAGG, Saraiva, MT d QEC d M, Ramos, IMAP, and Natal Jorge, RM. Modeling the contraction of the pelvic floor muscles. Comput Methods Biomech Biomed Engin. (2016) 19:347–56. doi: 10.1080/10255842.2015.1028031
60. da Silva, MET, Bessa, JNM, Rynkevic, R, Parente, MPL, Saraiva, MT d QECM, Natal Jorge, RM, et al. Simulation of vaginal uterosacral ligament suspension damage, mimicking a mesh-augmented apical prolapse repair. Proc Inst Mech Eng H. (2022):9544119221074567. doi: 10.1177/09544119221074567
61. Silva, MET, Bessa, JNM, Parente, MPL, Mascarenhas, T, Natal Jorge, RM, and Fernandes, AA. Effect of mesh anchoring technique in uterine prolapse repair surgery: a finite element analysis. J Biomech. (2021) 127:110649. doi: 10.1016/j.jbiomech.2021.110649
62. Knight, KM, Moalli, PA, and Abramowitch, SD. Preventing mesh pore collapse by designing mesh pores with auxetic geometries: a comprehensive evaluation via computational Modeling. J Biomech Eng. (2018) 140:0510051–8. doi: 10.1115/1.4039058
63. Jeanditgautier, E, Mayeur, O, Brieu, M, Lamblin, G, Rubod, C, and Cosson, M. Mobility and stress analysis of different surgical simulations during a sacral colpopexy, using a finite element model of the pelvic system. Int Urogynecol J. (2016) 27:951–7. doi: 10.1007/s00192-015-2917-0
64. Lallemant, M, Shimojyo, AA, Mayeur, O, Ramanah, R, Rubod, C, Kerbage, Y, et al. Mobility analysis of a posterior sacrospinous fixation using a finite element model of the pelvic system. PLoS One. (2024) 19:e0299012. doi: 10.1371/journal.pone.0299012
65. Tawara, D, Nishiki, T, Ninomiya, S, Okayama, H, Naito, K, and Morikawa, S. Development of primary design guidelines for supportive underwear to elevate the bladder neck in women based on finite element analysis of the pelvis. Proc Inst Mech Eng H. (2022) 236:269–78. doi: 10.1177/09544119211047058
66. Roshanfar, M, Fatehi, E, Torkaman, T, Ashouri, N, Lalani, I, Khademi, S, et al. Toward patient-specific pessary to manage pelvic organ prolapse: design and simulation. Annu Int Conf IEEE Eng Med Biol Soc. (2023) 2023:1–4. doi: 10.1109/EMBC40787.2023.10340082
67. Dunne, E, Santorelli, A, McGinley, B, Leader, G, O’Halloran, M, and Porter, E. Image-based classification of bladder state using electrical impedance tomography. Physiol Meas. (2018) 39:124001. doi: 10.1088/1361-6579/aae6ed
68. Xiong, L, Viswanathan, A, Stewart, AJ, Haker, S, Tempany, CM, Chin, LM, et al. Deformable structure registration of bladder through surface mapping. Med Phys. (2006) 33:1848–56. doi: 10.1118/1.2198192
69. Chai, X, van Herk, M, Hulshof, MCCM, and Bel, A. A voxel-based finite element model for the prediction of bladder deformation. Med Phys. (2012) 39:55–65. doi: 10.1118/1.3668060
70. Beekman, C, van Beek, S, Stam, J, Sonke, JJ, and Remeijer, P. A biomechanical finite element model to generate a library of cervix CTVs. Med Phys. (2020) 47:3852–60. doi: 10.1002/mp.14349
71. Beekman, C, Schaake, E, Sonke, JJ, and Remeijer, P. Deformation trajectory prediction using a neural network trained on finite element data-application to library of CTVs creation for cervical cancer. Phys Med Biol. (2021) 66:215004. doi: 10.1088/1361-6560/ac2c9b
72. Spirka, T, Kenton, K, Brubaker, L, and Damaser, MS. Effect of material properties on predicted vesical pressure during a cough in a simplified computational model of the bladder and urethra. Ann Biomed Eng. (2013) 41:185–94. doi: 10.1007/s10439-012-0637-x
73. Barzegari, M, Vahidi, B, Safarinejad, MR, and Ebad, M. A computational analysis of the effect of supporting organs on predicted vesical pressure in stress urinary incontinence. Med Biol Eng Comput. (2020) 58:1079–89. doi: 10.1007/s11517-020-02148-2
74. Attari, A, DeLancey, JO, and Ashton-Miller, JA. On structure-function relationships in the female human urethra: a finite element model approach. Ann Biomed Eng. (2021) 49:1848–60. doi: 10.1007/s10439-021-02765-4
75. Bush, MB, Liedl, B, Wagenlehner, F, and Petros, P. A finite element model validates an external mechanism for opening the urethral tube prior to micturition in the female. World J Urol. (2015) 33:1151–7. doi: 10.1007/s00345-014-1419-x
76. Peng, Y, Khavari, R, Nakib, NA, Boone, TB, and Zhang, Y. Assessment of urethral support using MRI-derived computational modeling of the female pelvis. Int Urogynecol J. (2016) 27:205–12. doi: 10.1007/s00192-015-2804-8
77. Routzong, MR, Martin, LC, Rostaminia, G, and Abramowitch, S. Urethral support in female urinary continence part 2: a computational, biomechanical analysis of Valsalva. Int Urogynecol J. (2022) 33:551–61. doi: 10.1007/s00192-021-04694-1
78. Brandão, S, Parente, M, Mascarenhas, T, da Silva, ARG, Ramos, I, and Jorge, RN. Biomechanical study on the bladder neck and urethral positions: simulation of impairment of the pelvic ligaments. J Biomech. (2015) 48:217–23. doi: 10.1016/j.jbiomech.2014.11.045
79. da Silva, MET, Pinheiro, FAT, Ferreira, NM, Brandão, FSQ d S, Martins, PAL d S, Parente, MPL, et al. An estimation of the biomechanical properties of the continent and incontinent woman bladder via inverse finite element analysis. Proc Inst Mech Eng H. (2024) 238:598–607. doi: 10.1177/09544119241237356
80. Hardy, LA, Chang, CH, Myers, EM, Kennelly, MJ, and Fried, NM. Computer simulations of thermal tissue remodeling during transvaginal and transurethral laser treatment of female stress urinary incontinence. Lasers Surg Med. (2017) 49:198–205. doi: 10.1002/lsm.22491
81. Hardy, LA, Chang, CH, Myers, EM, Kennelly, MJ, and Fried, NM. Laser treatment of female stress urinary incontinence: optical, thermal, and tissue damage simulations. Proc SPIE Int Soc Opt Eng. (2016) 9689:96891R. doi: 10.1117/12.2208126
82. Peng, Y, Khavari, R, Nakib, NA, Stewart, JN, Boone, TB, and Zhang, Y. The single-incision sling to treat female stress urinary incontinence: a dynamic computational study of outcomes and risk factors. J Biomech Eng. (2015) 137:0910071–7. doi: 10.1115/1.4030978
83. Staat, M, Trenz, E, Lohmann, P, Frotscher, R, Klinge, U, Tabaza, R, et al. New measurements to compare soft tissue anchoring systems in pelvic floor surgery. J Biomed Mater Res B Appl Biomater. (2012) 100:924–33. doi: 10.1002/jbm.b.32654
84. Herrity, AN, Aslan, SC, Mesbah, S, Siu, R, Kalvakuri, K, Ugiliweneza, B, et al. Targeting bladder function with network-specific epidural stimulation after chronic spinal cord injury. Sci Rep. (2022) 12:11179. doi: 10.1038/s41598-022-15315-2
85. Brandão, S, Parente, M, Da Roza, TH, Silva, E, Ramos, IM, Mascarenhas, T, et al. On the stiffness of the mesh and urethral mobility: a finite element analysis. J Biomech Eng. (2017) 139:e02778. doi: 10.1115/1.4036606
86. Petros, P. Pressure transmission theory-the Rasputin of incontinence. Neurourol Urodyn. (2022) 41:1216–23. doi: 10.1002/nau.24938
87. Roza, TD, Brandão, S, Oliveira, D, Mascarenhas, T, Parente, M, Duarte, JA, et al. Football practice and urinary incontinence: relation between morphology, function and biomechanics. J Biomech. (2015) 48:1587–92. doi: 10.1016/j.jbiomech.2015.03.013
88. Zhang, Y, Kim, S, Erdman, AG, Roberts, KP, and Timm, GW. Feasibility of using a computer modeling approach to study SUI induced by landing a jump. Ann Biomed Eng. (2009) 37:1425–33. doi: 10.1007/s10439-009-9705-2
89. Dias, N, Peng, Y, Khavari, R, Nakib, NA, Sweet, RM, Timm, GW, et al. Pelvic floor dynamics during high-impact athletic activities: a computational modeling study. Clin Biomech (Bristol). (2017) 41:20–7. doi: 10.1016/j.clinbiomech.2016.11.003
90. Ferreira, JPS, Rynkevic, R, Martins, PALS, Parente, MPL, Famaey, NM, Deprest, J, et al. Predicting the mechanical response of the vaginal wall in ball burst tests based on histology. J Biomed Mater Res B Appl Biomater. (2020) 108:1925–33. doi: 10.1002/jbm.b.34534
91. Martins, PALS, Jorge, RMN, Ferreia, AJM, Saleme, CS, Roza, T, Parente, MMP, et al. Vaginal tissue properties versus increased intra-abdominal pressure: a preliminary biomechanical study. Gynecol Obstet Investig. (2011) 71:145–50. doi: 10.1159/000315160
92. Fang, S, McLean, J, Shi, L, Vink, JSY, Hendon, CP, and Myers, KM. Anisotropic mechanical properties of the human uterus measured by spherical indentation. Ann Biomed Eng. (2021) 49:1923–42. doi: 10.1007/s10439-021-02769-0
93. Kauer, M, Vuskovic, V, Dual, J, Szekely, G, and Bajka, M. Inverse finite element characterization of soft tissues. Med Image Anal. (2002) 6:275–87. doi: 10.1016/S1361-8415(02)00085-3
94. Tillier, Y, Paccini, A, Durand-Reville, M, and Chenot, JL. Finite element modeling for soft tissue surgery based on linear and nonlinear elasticity behavior. Comput Aided Surg. (2006) 11:63–8. doi: 10.3109/10929080600628605
95. Gandhi, MSA, Zhao, Y, Fu, HY, and Li, Q. A highly versatile porous core photonic quasicrystal fiber based refractive index terahertz sensor. Sensors (Basel). (2022) 22:3469. doi: 10.3390/s22093469
96. Arifler, D, Guillaud, M, Carraro, A, Malpica, A, Follen, M, and Richards-Kortum, R. Light scattering from normal and dysplastic cervical cells at different epithelial depths: finite-difference time-domain modeling with a perfectly matched layer boundary condition. J Biomed Opt. (2003) 8:484–94. doi: 10.1117/1.1578640
97. Ukai, T, Tanaka, Y, Fukuda, T, Kajikawa, T, Miura, H, and Terada, Y. Softness sensing probe with multiple acoustic paths for laparoscopic surgery. Int J Comput Assist Radiol Surg. (2020) 15:1537–47. doi: 10.1007/s11548-020-02207-x
98. Fleszar, AJ, Walker, A, Kreeger, PK, and Notbohm, J. Substrate curvature induces fallopian tube epithelial cell invasion via cell-cell tension in a model of ovarian cortical inclusion cysts. Integr Biol (Camb). (2019) 11:342–52. doi: 10.1093/intbio/zyz028
99. Gandhi, SV, Walker, D, Milnes, P, Mukherjee, S, Brown, BH, and Anumba, DOC. Electrical impedance spectroscopy of the cervix in non-pregnant and pregnant women. Eur J Obstet Gynecol Reprod Biol. (2006) 129:145–9. doi: 10.1016/j.ejogrb.2005.12.029
100. Wang, JY, Healey, T, Barker, A, Brown, B, Monk, C, and Anumba, D. Magnetic induction spectroscopy (MIS)-probe design for cervical tissue measurements. Physiol Meas. (2017) 38:729–44. doi: 10.1088/1361-6579/aa6b4e
101. Ge, W, Brooker, G, Woo, J, Rae, W, Liu, Y, and Hyett, J. Magnetorheological gel mimicking cervical ripening as a potential model for evaluating shear wave elastography. Ultrasound Med Biol. (2020) 46:2472–80. doi: 10.1016/j.ultrasmedbio.2020.05.002
102. Gandhi, SV, Walker, DC, Brown, BH, and Anumba, DOC. Comparison of human uterine cervical electrical impedance measurements derived using two tetrapolar probes of different sizes. Biomed Eng Online. (2006) 5:62. doi: 10.1186/1475-925X-5-62
103. Walker, DC, Brown, BH, Blackett, AD, Tidy, J, and Smallwood, RH. A study of the morphological parameters of cervical squamous epithelium. Physiol Meas. (2003) 24:121–35. doi: 10.1088/0967-3334/24/1/309
104. González-Correa, CA, Brown, BH, Smallwood, RH, Walker, DC, and Bardhan, KD. Electrical bioimpedance readings increase with higher pressure applied to the measuring probe. Physiol Meas. (2005) 26:S39–47. doi: 10.1088/0967-3334/26/2/004
105. Choi, H, Barker, E, Abduljabar, AA, Anumba, D, and Porch, A. Cervical tissue hydration level monitoring by a resonant microwave coaxial probe. Sensors (Basel). (2022) 22:9527. doi: 10.3390/s22239527
106. Fang, S, Shi, L, Vink, JSY, Feltovich, H, Hall, TJ, and Myers, KM. Equilibrium mechanical properties of the nonhuman primate cervix. J Biomech Eng. (2024) 146:081001. doi: 10.1115/1.4064558
107. Yao, W, Yoshida, K, Fernandez, M, Vink, J, Wapner, RJ, Ananth, CV, et al. Measuring the compressive viscoelastic mechanical properties of human cervical tissue using indentation. J Mech Behav Biomed Mater. (2014) 34:18–26. doi: 10.1016/j.jmbbm.2014.01.016
108. Torres, A, Palmeri, ML, Feltovich, H, Hall, TJ, and Rosado-Mendez, IM. Shear wave dispersion as a potential biomarker for cervical remodeling during pregnancy: evidence from a non-human primate model. Front Phys. (2021) 8:606664. doi: 10.3389/fphy.2020.606664
109. Shi, L, and Myers, K. A finite porous-viscoelastic model capturing mechanical behavior of human cervix under multi-step spherical indentation. J Mech Behav Biomed Mater. (2023) 143:105875. doi: 10.1016/j.jmbbm.2023.105875
110. Palmeri, ML, Feltovich, H, Homyk, AD, Carlson, LC, and Hall, TJ. Evaluating the feasibility of acoustic radiation force impulse shear wave elasticity imaging of the uterine cervix with an intracavity array: a simulation study. IEEE Trans Ultrason Ferroelectr Freq Control. (2013) 60:2053–64. doi: 10.1109/TUFFC.2013.2796
111. Maurer, MM, Badir, S, Pensalfini, M, Bajka, M, Abitabile, P, Zimmermann, R, et al. Challenging the in-vivo assessment of biomechanical properties of the uterine cervix: a critical analysis of ultrasound based quasi-static procedures. J Biomech. (2015) 48:1541–8. doi: 10.1016/j.jbiomech.2015.02.038
112. Badir, S, Bajka, M, and Mazza, E. A novel procedure for the mechanical characterization of the uterine cervix during pregnancy. J Mech Behav Biomed Mater. (2013) 27:143–53. doi: 10.1016/j.jmbbm.2012.11.020
113. Yoshida, K, Mahendroo, M, Vink, J, Wapner, R, and Myers, K. Material properties of mouse cervical tissue in normal gestation. Acta Biomater. (2016) 36:195–209. doi: 10.1016/j.actbio.2016.03.005
114. Shi, L, Yao, W, Gan, Y, Zhao, LY, Eugene McKee, W, Vink, J, et al. Anisotropic material characterization of human cervix tissue based on indentation and inverse finite element analysis. J Biomech Eng. (2019) 141:0910171–09101713. doi: 10.1115/1.4043977
115. Briggs, BN, Stender, ME, Muljadi, PM, Donnelly, MA, Winn, VD, and Ferguson, VL. A Hertzian contact mechanics based formulation to improve ultrasound elastography assessment of uterine cervical tissue stiffness. J Biomech. (2015) 48:1524–32. doi: 10.1016/j.jbiomech.2015.03.032
116. Gou, K, Topol, H, Demirkoparan, H, and Pence, TJ. Stress-swelling finite element modeling of cervical response with homeostatic collagen fiber distributions. J Biomech Eng. (2020) 142:081002. doi: 10.1115/1.4045810
117. Westervelt, AR, Fernandez, M, House, M, Vink, J, Nhan-Chang, CL, Wapner, R, et al. A parameterized ultrasound-based finite element analysis of the mechanical environment of pregnancy. J Biomech Eng. (2017) 139:0510041–05100411. doi: 10.1115/1.4036259
118. Fernandez, M, House, M, Jambawalikar, S, Zork, N, Vink, J, Wapner, R, et al. Investigating the mechanical function of the cervix during pregnancy using finite element models derived from high-resolution 3D MRI. Comput Methods Biomech Biomed Engin. (2016) 19:404–17. doi: 10.1080/10255842.2015.1033163
119. Moghaddam, AO, Lin, Z, Sivaguru, M, Phillips, H, McFarlin, BL, Toussaint, KC, et al. Heterogeneous microstructural changes of the cervix influence cervical funneling. Acta Biomater. (2022) 140:434–45. doi: 10.1016/j.actbio.2021.12.025
120. Hutter, R, Schmitt, KU, and Niederer, P. Mechanical modeling of soft biological tissues for application in virtual reality based laparoscopy simulators. Technol Health Care. (2000) 8:15–24. doi: 10.3233/THC-2000-8102
121. Nassir, M, Levi, M, Wiser, A, and Shaked, NT. Evaluation of women’s aging influence on sperm passage inside the fallopian tube using 3D dynamic mechanical modeling. Front Bioeng Biotechnol. (2024) 12:1324802. doi: 10.3389/fbioe.2024.1324802
122. Nassir, M, Levi, M, and Shaked, NT. Dynamic 3D modeling for human sperm motility through the female cervical canal and uterine cavity to predict sperm chance of reaching the oocyte. Cells. (2023) 12:203. doi: 10.3390/cells12010203
123. Vila Pouca, MCP, Ferreira, JPS, Oliveira, DA, Parente, MPL, Mascarenhas, MT, and Natal Jorge, RM. Simulation of the uterine contractions and foetus expulsion using a chemo-mechanical constitutive model. Biomech Model Mechanobiol. (2019) 18:829–43. doi: 10.1007/s10237-019-01117-5
124. Sharifimajd, B, Ölvander, J, and Stålhand, J. Identification of the mechanical parameters for the human uterus in vivo using intrauterine pressure measurements. Int J Numer Method Biomed Eng. (2017) 33:10821. doi: 10.1002/cnm.2778
125. Pérès, J, Thollon, L, Delotte, J, Tillier, Y, Brunet, C, Kayvantash, K, et al. Material properties of the placenta under dynamic loading conditions. Comput Methods Biomech Biomed Engin. (2014) 17:958–64. doi: 10.1080/10255842.2012.727403
126. Lecarpentier, E, Bhatt, M, Bertin, GI, Deloison, B, Salomon, LJ, Deloron, P, et al. Computational fluid dynamic simulations of maternal circulation: wall shear stress in the human placenta and its biological implications. PLoS One. (2016) 11:e0147262. doi: 10.1371/journal.pone.0147262
127. Sindhwani, N, Bamberg, C, Famaey, N, Callewaert, G, Dudenhausen, JW, Teichgräber, U, et al. In vivo evidence of significant levator ani muscle stretch on MR images of a live childbirth. Am J Obstet Gynecol. (2017) 217:194.e1–8. doi: 10.1016/j.ajog.2017.04.014
128. Melchert, F, Wischnik, A, and Nalepa, E. The prevention of mechanical birth trauma by means of computer aided simulation of delivery by means of nuclear magnetic resonance imaging and finite element analysis. J Obstet Gynaecol (Tokyo 1995). (1995) 21:195–207. doi: 10.1111/j.1447-0756.1995.tb01093.x
129. Li, X, Kruger, JA, Nash, MP, and Nielsen, PMF. Effects of nonlinear muscle elasticity on pelvic floor mechanics during vaginal childbirth. J Biomech Eng. (2010) 132:111010. doi: 10.1115/1.4002558
130. Li, X, Kruger, JA, Nash, MP, and Nielsen, PMF. Anisotropic effects of the levator ani muscle during childbirth. Biomech Model Mechanobiol. (2011) 10:485–94. doi: 10.1007/s10237-010-0249-z
131. Parente, MPL, Natal Jorge, RM, Mascarenhas, T, Fernandes, AA, and Martins, J a C. The influence of the material properties on the biomechanical behavior of the pelvic floor muscles during vaginal delivery. J Biomech. (2009) 42:1301–6. doi: 10.1016/j.jbiomech.2009.03.011
132. Lepage, J, Jayyosi, C, Lecomte-Grosbras, P, Brieu, M, Duriez, C, Cosson, M, et al. Biomechanical pregnant pelvic system model and numerical simulation of childbirth: impact of delivery on the uterosacral ligaments, preliminary results. Int Urogynecol J. (2015) 26:497–504. doi: 10.1007/s00192-014-2498-3
133. Moura, R, Oliveira, DA, Parente, MPL, Kimmich, N, and Natal Jorge, RM. A biomechanical perspective on perineal injuries during childbirth. Comput Methods Prog Biomed. (2024) 243:107874. doi: 10.1016/j.cmpb.2023.107874
134. Jing, D, Ashton-Miller, JA, and DeLancey, JOL. A subject-specific anisotropic visco-hyperelastic finite element model of female pelvic floor stress and strain during the second stage of labor. J Biomech. (2012) 45:455–60. doi: 10.1016/j.jbiomech.2011.12.002
135. Cechova, H, Kalis, V, Havelkova, L, Rusavy, Z, Fiala, P, Rybarova, M, et al. Finite element modeling of maximum stress in pelvic floor structures during the head expulsion (FINESSE) study. Int Urogynecol J. (2021) 32:1997–2003. doi: 10.1007/s00192-021-04769-z
136. Hynčík, L, Čechová, H, Jansová, M, Lv, W, Hympánová, LH, and Krofta, L. In silico prediction of maximum perineal muscle strain during vaginal delivery by design of experiment. Comput Methods Prog Biomed. (2023) 242:107835. doi: 10.1016/j.cmpb.2023.107835
137. Rusavy, Z, Kalis, V, Aglyamov, S, and Egorov, V. Feasibility and safety of antepartum tactile imaging. Int Urogynecol J. (2021) 32:1785–91. doi: 10.1007/s00192-020-04552-6
138. Vila Pouca, MCP, Ferreira, JPS, Oliveira, DA, Parente, MPL, Mascarenhas, T, and Natal Jorge, RM. On the effect of labour durations using an anisotropic visco-hyperelastic-damage approach to simulate vaginal deliveries. J Mech Behav Biomed Mater. (2018) 88:120–6. doi: 10.1016/j.jmbbm.2018.08.011
139. Parente, MPL, Jorge, RMN, Mascarenhas, T, Fernandes, AA, and Martins, J a C. The influence of an occipito-posterior malposition on the biomechanical behavior of the pelvic floor. Eur J Obstet Gynecol Reprod Biol. (2009) 144:S166–9. doi: 10.1016/j.ejogrb.2009.02.033
140. Havelková, L, Krofta, L, Kochová, P, Liška, V, Kališ, V, and Feyereisl, J. Persistent occiput posterior position and stress distribution in levator ani muscle during vaginal delivery computed by a finite element model. Int Urogynecol J. (2020) 31:1315–24. doi: 10.1007/s00192-019-03997-8
141. Oliveira, DA, Parente, MPL, Calvo, B, Mascarenhas, T, and Natal Jorge, RM. Numerical simulation of the damage evolution in the pelvic floor muscles during childbirth. J Biomech. (2016) 49:594–601. doi: 10.1016/j.jbiomech.2016.01.014
142. Krofta, L, Havelková, L, Urbánková, I, Krčmář, M, Hynčík, L, and Feyereisl, J. Finite element model focused on stress distribution in the levator ani muscle during vaginal delivery. Int Urogynecol J. (2017) 28:275–84. doi: 10.1007/s00192-016-3126-1
143. Berardi, M, Martinez-Romero, O, Elías-Zúñiga, A, Rodríguez, M, Ceretti, E, Fiorentino, A, et al. Levator ani deformation during the second stage of labour. Proc Inst Mech Eng H. (2014) 228:501–8. doi: 10.1177/0954411914533678
144. Jean Dit Gautier, E, Mayeur, O, Lepage, J, Brieu, M, Cosson, M, and Rubod, C. Pregnancy impact on uterosacral ligament and pelvic muscles using a 3D numerical and finite element model: preliminary results. Int Urogynecol J. (2018) 29:425–30. doi: 10.1007/s00192-017-3520-3
145. Xuan, R, Yang, M, Gao, Y, Ren, S, Li, J, Yang, Z, et al. A simulation analysis of maternal pelvic floor muscle. Int J Environ Res Public Health. (2021) 18:10821. doi: 10.3390/ijerph182010821
146. Parente, MPL, Jorge, RMN, Mascarenhas, T, Fernandes, AA, and Martins, J a C. Deformation of the pelvic floor muscles during a vaginal delivery. Int Urogynecol J Pelvic Floor Dysfunct. (2008) 19:65–71. doi: 10.1007/s00192-007-0388-7
147. Li, X, Kruger, JA, Chung, JH, Nash, MP, and Nielsen, PMF. Modelling childbirth: comparing athlete and non-athlete pelvic floor mechanics. Med Image Comput Comput Assist Interv. (2008) 11:750–7. doi: 10.1007/978-3-540-85990-1_90
148. Moura, R, Borges, M, Oliveira, D, Parente, M, Kimmich, N, Mascarenhas, T, et al. A biomechanical study of the birth position: a natural struggle between mother and fetus. Biomech Model Mechanobiol. (2022) 21:937–51. doi: 10.1007/s10237-022-01569-2
149. Yan, X, Kruger, JA, Nielsen, PMF, and Nash, MP. Effects of fetal head shape variation on the second stage of labour. J Biomech. (2015) 48:1593–9. doi: 10.1016/j.jbiomech.2015.02.062
150. Tao, R, and Grimm, MJ. Simulation of the childbirth process in LS-DYNA. J Biomech Eng. (2024) 146:061002. doi: 10.1115/1.4064594
151. Stansfield, E, Kumar, K, Mitteroecker, P, and Grunstra, NDS. Biomechanical trade-offs in the pelvic floor constrain the evolution of the human birth canal. Proc Natl Acad Sci USA. (2021) 118:e2022159118. doi: 10.1073/pnas.2022159118
152. Stansfield, E, Fischer, B, Grunstra, NDS, Pouca, MV, and Mitteroecker, P. The evolution of pelvic canal shape and rotational birth in humans. BMC Biol. (2021) 19:224. doi: 10.1186/s12915-021-01150-w
153. Lapeer, R, Gerikhanov, Z, Sadulaev, SM, Audinis, V, Rowland, R, Crozier, K, et al. A computer-based simulation of childbirth using the partial Dirichlet-Neumann contact method with total Lagrangian explicit dynamics on the GPU. Biomech Model Mechanobiol. (2019) 18:681–700. doi: 10.1007/s10237-018-01109-x
154. Parente, MP, Natal Jorge, RM, Mascarenhas, T, Fernandes, AA, and Silva-Filho, AL. Computational modeling approach to study the effects of fetal head flexion during vaginal delivery. Am J Obstet Gynecol. (2010) 203:217.e1–6. doi: 10.1016/j.ajog.2010.03.038
155. Silva, MET, Oliveira, DA, Roza, TH, Brandão, S, Parente, MPL, Mascarenhas, T, et al. Study on the influence of the fetus head molding on the biomechanical behavior of the pelvic floor muscles, during vaginal delivery. J Biomech. (2015) 48:1600–5. doi: 10.1016/j.jbiomech.2015.02.032
156. Vila Pouca, MCP, Ferreira, JPS, Parente, MPL, Natal Jorge, RM, and Ashton-Miller, JA. On the management of maternal pushing during the second stage of labor: a biomechanical study considering passive tissue fatigue damage accumulation. Am J Obstet Gynecol. (2022) 227:267.e1–267.e20. doi: 10.1016/j.ajog.2022.01.023
157. Suzuki, S. Clinical significance of precipitous labor. J Clin Med Res. (2015) 7:150–3. doi: 10.14740/jocmr2058w
158. Vila Pouca, MCP, Ferreira, JPS, Oliveira, DA, Parente, MPL, and Natal Jorge, RM. Viscous effects in pelvic floor muscles during childbirth: a numerical study. Int J Numer Method Biomed Eng. (2018) 34. doi: 10.1002/cnm.2927
159. Fidalgo, DS, Borges, M, Pouca, MCPV, Oliveira, DA, Malanowska, E, and Myers, KM. On the effect of irregular uterine activity during a vaginal delivery using an electro-chemo-mechanical constitutive model. J Mech Behav Biomed Mater. (2022) 131:e2927. doi: 10.1016/j.jmbbm.2022.105250
160. Fidalgo, DS, Pouca, MCPV, Oliveira, DA, Malanowska, E, Myers, KM, Jorge, RMN, et al. Mechanical effects of a maylard scar during a vaginal birth after a previous caesarean. Ann Biomed Eng. (2021) 49:3593–608. doi: 10.1007/s10439-021-02805-z
161. Borges, M, Moura, R, Oliveira, D, Parente, M, Mascarenhas, T, and Natal, R. Effect of the birthing position on its evolution from a biomechanical point of view. Comput Methods Prog Biomed. (2021) 200:105921. doi: 10.1016/j.cmpb.2020.105921
162. Frémondière, P, Thollon, L, Marchal, F, and Desseauve, D. The impact of femoral rotation on sacroiliac articulation during pregnancy. Is there evidence to support Farabeuf’s hypothesis by finite element modelization? Eur J Obstet Gynecol Reprod Biol. (2023) 290:78–84. doi: 10.1016/j.ejogrb.2023.08.381
163. Jansova, M, Kalis, V, Lobovsky, L, Hyncik, L, Karbanova, J, and Rusavy, Z. The role of thumb and index finger placement in manual perineal protection. Int Urogynecol J. (2014) 25:1533–40. doi: 10.1007/s00192-014-2425-7
164. Jansova, M, Kalis, V, Rusavy, Z, Zemcik, R, Lobovsky, L, and Laine, K. Modeling manual perineal protection during vaginal delivery. Int Urogynecol J. (2014) 25:65–71. doi: 10.1007/s00192-013-2164-1
165. Jansova, M, Kalis, V, Rusavy, Z, Räisänen, S, Lobovsky, L, and Laine, K. Fetal head size and effect of manual perineal protection. PLoS One. (2017) 12:e0189842. doi: 10.1371/journal.pone.0189842
166. Oliveira, DA, Parente, MPL, Calvo, B, Mascarenhas, T, and Jorge, RMN. A biomechanical analysis on the impact of episiotomy during childbirth. Biomech Model Mechanobiol. (2016) 15:1523–34. doi: 10.1007/s10237-016-0781-6
167. Oliveira, DA, Parente, MPL, Calvo, B, Mascarenhas, T, and Natal Jorge, RM. A holistic view of the effects of episiotomy on pelvic floor. Int J Numer Method Biomed Eng. (2017) 33:e2892. doi: 10.1002/cnm.2892
168. Oliveira, D, Pouca, MV, Ferreira, J, and Mascarenhas, T. Episiotomy: the biomechanical impact of multiple small incisions during a normal vaginal delivery. Interface Focus. (2019) 9:20190027. doi: 10.1098/rsfs.2019.0027
169. Oliveira, DA, Parente, MPL, Calvo, B, Mascarenhas, T, and Jorge, RMN. The management of episiotomy technique and its effect on pelvic floor muscles during a malposition childbirth. Comput Methods Biomech Biomed Engin. (2017) 20:1249–59. doi: 10.1080/10255842.2017.1349762
170. Sharifimajd, B, Thore, CJ, and Stålhand, J. Simulating uterine contraction by using an electro-chemo-mechanical model. Biomech Model Mechanobiol. (2016) 15:497–510. doi: 10.1007/s10237-015-0703-z
171. Nguyen, TNT, Ballit, A, Lecomte-Grosbras, P, Colliat, JB, and Dao, TT. On the uncertainty quantification of the active uterine contraction during the second stage of labor simulation. Med Biol Eng Comput. (2024) 62:2145–64. doi: 10.1007/s11517-024-03059-2
172. Tao, R, and Grimm, M. Simulation of uterus active contraction and fetus delivery in ls-dyna. J Biomech Eng. (2024) 146:101002. doi: 10.1115/1.4065341
173. Zhang, M, La Rosa, PS, Eswaran, H, and Nehorai, A. Estimating uterine source current during contractions using magnetomyography measurements. PLoS One. (2018) 13:e0202184. doi: 10.1371/journal.pone.0202184
174. Filipovic, N, Nikolic, D, Saveljic, I, Tanaskovic, I, Zdravkovic, N, Zivanovic, A, et al. Computer simulation of cervical tissue response to a hydraulic dilator device. Theor Biol Med Model. (2013) 10:64. doi: 10.1186/1742-4682-10-64
175. Asiedu, MN, Agudogo, J, Krieger, MS, Miros, R, Proeschold-Bell, RJ, Schmitt, JW, et al. Design and preliminary analysis of a vaginal inserter for speculum-free cervical cancer screening. PLoS One. (2017) 12:e0177782. doi: 10.1371/journal.pone.0177782
176. Debicki, MP, Mrozowski, M, Debicki, PS, Zielinski, J, Piotrkowicz, N, and Petrovich, Z. Localized current field hyperthermia in carcinoma of the cervix: 3-D computer simulation of SAR distribution. Int J Hyperth. (1999) 15:427–40. doi: 10.1080/026567399285611
177. Salgaonkar, VA, Prakash, P, and Diederich, CJ. Temperature superposition for fast computation of 3D temperature distributions during optimization and planning of interstitial ultrasound hyperthermia treatments. Int J Hyperth. (2012) 28:235–49. doi: 10.3109/02656736.2012.662666
178. Chen, X, Diederich, CJ, Wootton, JH, Pouliot, J, and Hsu, IC. Optimisation-based thermal treatment planning for catheter-based ultrasound hyperthermia. Int J Hyperth. (2010) 26:39–55. doi: 10.3109/02656730903341332
179. Baldwin, SA, Pelman, A, and Bert, JL. A heat transfer model of thermal balloon endometrial ablation. Ann Biomed Eng. (2001) 29:1009–18. doi: 10.1114/1.1415521
180. Kanaoka, Y, Hirai, K, and Ishiko, O. Microwave power and duration without extrauterine thermal damage in microwave endomyometrial ablation at 2.45 GHz. J Obstet Gynaecol Res. (2005) 31:359–67. doi: 10.1111/j.1447-0756.2005.00303.x
181. Calvert, J, Duck, F, Clift, S, and Azaime, H. Surface heating by transvaginal transducers. Ultrasound Obstet Gynecol. (2007) 29:427–32. doi: 10.1002/uog.3973
182. Nadhif, MH, Irsyad, M, and Ocviyanti, D. Biomechanically compliant gynecologic training simulator. Simul Healthc. (2023) 18:135–43. doi: 10.1097/SIH.0000000000000654
183. Sierra, R, Zátonyi, J, Bajka, M, Székely, G, and Harders, M. Hydrometra simulation for VR-based hysteroscopy training. Med Image Comput Comput Assist Interv. (2005) 8:575–82. doi: 10.1007/11566489_71
184. Weiss, S, Bajka, M, Nava, A, Mazza, E, and Niederer, P. A finite element model for the simulation of hydrometra. Technol Health Care. (2004) 12:259–67. doi: 10.3233/THC-2004-12305
185. Niederer, P, Weiss, S, Caduff, R, Bajka, M, Szekély, G, and Harders, M. Uterus models for use in virtual reality hysteroscopy simulators. Eur J Obstet Gynecol Reprod Biol. (2009) 144:S90–5. doi: 10.1016/j.ejogrb.2009.02.009
186. Buttin, R, Zara, F, Shariat, B, Redarce, T, and Grangé, G. Biomechanical simulation of the fetal descent without imposed theoretical trajectory. Comput Methods Prog Biomed. (2013) 111:389–401. doi: 10.1016/j.cmpb.2013.04.005
187. Moorcroft, DM, Stitzel, JD, Duma, GG, and Duma, SM. Computational model of the pregnant occupant: predicting the risk of injury in automobile crashes. Am J Obstet Gynecol. (2003) 189:540–4. doi: 10.1067/S0002-9378(03)00519-2
188. Tanaka, K, Motozawa, Y, Takahashi, K, Maki, T, and Hitosugi, M. Factors affecting the severity of placental abruption in pregnant vehicle drivers: analysis with a novel finite element model. Healthcare (Basel). (2021) 10:27. doi: 10.3390/healthcare10010027
189. Irannejad Parizi, M, Ahmadian, MT, and Mohammadi, H. Rigid-bar loading on pregnant uterus and development of pregnant abdominal response corridor based on finite element biomechanical model. Int J Numer Method Biomed Eng. (2020) 36:e3284. doi: 10.1002/cnm.3284
190. Pearlman, MD, Klinich, KD, Schneider, LW, Rupp, J, Moss, S, and Ashton-Miller, J. A comprehensive program to improve safety for pregnant women and fetuses in motor vehicle crashes: a preliminary report. Am J Obstet Gynecol. (2000) 182:1554–64. doi: 10.1067/mob.2000.106850
191. Auriault, F, Thollon, L, Peres, J, Delotte, J, Kayvantash, K, Brunet, C, et al. Virtual traumatology of pregnant women: the PRegnant car occupant model for impact simulations (PROMIS). J Biomech. (2014) 47:207–13. doi: 10.1016/j.jbiomech.2013.09.013
192. Auriault, F, Thollon, L, and Behr, M. Development of a gravid uterus model for the study of road accidents involving pregnant women. J Biomech Eng. (2016) 138:011009. doi: 10.1115/1.4032055
193. Arias, J, Kurgansky, G, Wei, OC, Chan-Akeley, R, and Toma, M. Fluid-structure interaction analysis of amniotic fluid with fetus and placenta inside uterus exposed to military blasts. Injury. (2023) 54:110843. doi: 10.1016/j.injury.2023.110843
194. Louwagie, EM, Rajasekharan, D, Feder, A, Fang, S, Nhan-Chang, CL, Mourad, M, et al. Parametric solid models of the at-term uterus from magnetic resonance images. J Biomech Eng. (2024) 146:071008. doi: 10.1115/1.4065109
195. Hicks, A. Available online at: https://BioRender.com/69o1r1o (2025).
Keywords: pelvic floor, computational modeling, incontinence, pelvic floor dysfunction, vagina, uterus, labor
Citation: Moseley T, Hicks AJ, Cosgriff-Hernandez EM, Rausch MK and Hakim J (2025) Finite element modeling in obstetrics and gynecology: advances, applications, and challenges. Front. Med. 12:1606989. doi: 10.3389/fmed.2025.1606989
Edited by:
A. Seval Ozgu-Erdinc, Ankara Bilkent City Hospital University, TürkiyeReviewed by:
Wenle Lv, Tianjin University of Science and Technology, ChinaDivya Rajasekharan, Stanford University, United States
Copyright © 2025 Moseley, Hicks, Cosgriff-Hernandez, Rausch and Hakim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Julie Hakim, anVsaWUuaGFraW1AYmNtLmVkdQ==
 Taylor Moseley
Taylor Moseley Ashley J. Hicks
Ashley J. Hicks Elizabeth M. Cosgriff-Hernandez
Elizabeth M. Cosgriff-Hernandez Manuel Karl Rausch
Manuel Karl Rausch Julie Hakim5,6*
Julie Hakim5,6*