Sticker-and-spacer model for amyloid beta condensation and fibrillation

A major pathogenic hallmark of Alzheimer's disease is the presence of neurotoxic plaques composed of amyloid beta (Aβ) peptides in patients' brains. The pathway of plaque formation remains elusive, though some clues appear to lie in the dominant presence of Aβ₁₋₄₂ in these plaques despite Aβ₁₋₄₀ making up approximately 90% of the Aβ pool. We hypothesize that this asymmetry is driven by the hydrophobicity of the two extra amino acids that are incorporated in Aβ₁₋₄₂. To investigate this hypothesis at the level of single molecules, we have developed a molecular “sticker-and-spacer lattice model” of unfolded Aβ. The model protein has a single sticker that may reversibly dimerise and elongate into semi-flexible linear chains. The growth is hampered by excluded-volume interactions that are encoded by the hydrophilic spacers but are rendered cooperative by the attractive interactions of hydrophobic spacers. For sufficiently strong hydrophobicity, the chains undergo liquid-liquid phase-separation (LLPS) into condensates that facilitate the nucleation of fibers. We find that a small fraction of Aβ₁₋₄₀ in a mixture of Aβ₁₋₄₀ and Aβ₁₋₄₂ shifts the critical concentration for LLPS to lower values. This study provides theoretical support for the hypothesis that LLPS condensates act as a precursor for aggregation and provides an explanation for the Aβ₁₋₄₂-enrichment of aggregates in terms of hydrophobic interactions.

1. Introduction

Alzheimer's disease (AD), the most common cause of dementia (60–80% of cases Abeysinghe et al., 2020), and is a fatal neurodegenerative disease causing severe and devastating cognitive impairment. Age is the biggest risk factor for AD, of which, most cases are sporadic (around 95%) and occur over the age of 65 (Abeysinghe et al., 2020; Zhang et al., 2020; Zhao et al., 2020; Ayodele et al., 2021). The exact cause of AD is not fully understood and with better living conditions meaning average life expectancy in developed countries is increasing, the number of cases and the burden of neurodegenerative disease is increasing worldwide. As of 2018, an estimated 50 million people worldwide suffer from dementia, with this number expected to triple by 2050 (Patterson, 2018).

A major pathogenic hallmark in AD brains is the presence of extracellular neurotoxic plaques made up of amyloid beta (Aβ) (Stelzmann et al., 1995; Breijyeh and Karaman, 2020). Aβ is produced from amyloid precursor protein (APP) which is cleaved by α, β and γ secretases (Chen et al., 2017; Guo et al., 2020; Hampel et al., 2021). APP proteolytic cleavage can be separated into non-amyloidogenic and amyloidogenic pathways. We will focus on the amyloidogenic pathway as it is relevant to AD. First APP is cleaved by β secretase into soluble APPβ and a 99 amino acid C-terminal fragment (C99). C99 is then cleaved by γ secretase at multiple sites giving rise to Aβ of multiple lengths ranging from 39-51 amino acids (Zhang et al., 2011; Haass et al., 2012). After cleavage, Aβ is secreted from the cell where it can then form oligomers, fibrils, and finally plaques. The amyloid cascade hypothesis suggests that the deposition of Aβ into senile plaques is critical for AD pathology (Hardy and Higgins, 1992; Karran et al., 2011; Castellani et al., 2019) but the exact mechanism and change in AD brains that lead to this neurotoxic aggregation is not fully understood. Recently, this hypothesis has been called into question based on amounting evidence in disagreement. Amyloid deposition does not correlate with neuronal loss (Kametani and Hasegawa, 2018) and amyloid burden can be identified in cognitively unimpaired individuals (Arenaza-Urquijo and Vemuri, 2018; Dubois et al., 2021). Furthermore, clinical trials using therapeutics that target Aβ for degradation have been ineffective thus far (Ricciarelli and Fedele, 2017). A particular issue for anti-Aβ therapeutics is that most treatments focus on clearing insoluble aggregates (Tolar et al., 2019) with increasing evidence suggesting that pre-fibrillar soluble oligomers are orders of magnitude more toxic than fibrils and plaques (Chafekar et al., 2008; Ono et al., 2009; Sengupta et al., 2016; Huang and Liu, 2020). Unlike plaques, oligomers have been shown to impair both synaptic function and structure (Selkoe and Hardy, 2016; Kametani and Hasegawa, 2018). A recent study by Ghadami et al. (2020) has demonstrated that transthyretin is neuroprotective which is achieved by binding to Aβ oligomers, inhibiting primary and secondary nucleation without altering elongation, ephasising the role of oligomers in Aβ-mediated neurotoxicity. Consequently, understanding the role of pre-fibrillar Aβ species such as soluble oligomers and their contribution to AD pathology have gained significant interest in recent years.

The most predominant Aβ species is 40 amino acids long (Aβ₁₋₄₀) and makes up ~90% of the Aβ pool. A less prevalent 42 amino acid long species of Aβ (Aβ₁₋₄₂), which accounts for ~10 % of the Aβ population is of particular importance to AD due to a higher aggregation propensity. Compared to Aβ₁₋₄₀, Aβ₁₋₄₂ has a longer chain length that increases a repulsive excluded-volume interaction but adds an attractive hydrophobic interaction due to the addition of two C-terminal hydrophobic amino acids. As such, Aβ₁₋₄₂ has increased aggregation propensity and is a predominant component of senile plaques (Iwatsubo et al., 1994; Tamaoka et al., 1994; Gu and Guo, 2021). Familial AD mutations in APP, PSEN1, and PSEN2, cause increased production of Aβ, with abnormally high levels of Aβ₁₋₄₂ relative to Aβ₁₋₄₀ (Scheuner et al., 1996; Hecimovic et al., 2004; Kumar-Singh et al., 2006; Chávez-Gutiérrez and Szaruga, 2020). Recent work shows that the ratio of Aβ₁₋₄₂:Aβ₁₋₄₀ in plasma and cerebrospinal fluid can be used as a biomarker for AD diagnosis (Baldeiras et al., 2018; Lehmann et al., 2018; Nakamura et al., 2018; Zetterberg, 2019; Doecke et al., 2020; Mahaman et al., 2022; Teunissen et al., 2022) as it correlates with Aβ deposition (Fandos et al., 2017) and cognitive decline (Yaffe et al., 2011; Pérez-Grijalba et al., 2019; Giudici et al., 2020; Lim et al., 2020). This evidence suggests that an increased ratio of Aβ₁₋₄₂:Aβ₁₋₄₀ may promote the formation of neurotoxic aggregation and the progression of AD.

Hence, in summary, while the physico-chemical properties of Aβ remains subject to debate, these properties appear to correlate with the structural properties of the aggregates. In this study, we focus our attention on the pathway of self-assembly (Michaels et al., 2020), and aim to understand how this pathway is affected by the molecular properties of Aβ, such as hydrophobicity and intrinsic disorder. We hypothesize that when Aβ₁₋₄₂ interacts with Aβ₁₋₄₀ sufficient hydrophobicity is added to enhance self-assembly, while the excluded volume interaction is limited. We will model this on a molecular level by describing the intrinsically disordered protein as chains with hydrophilic and hydrophobic segments, as well as ‘sticky' building blocks that may reversibly self-ensemble into needle-like aggregates.

The aggregation of intrinsically disordered poly-peptides (IDPs) is an important topic in the biological physics of vital intracellular and extracellular processes. In particular, this class of proteins is known to undergo liquid-liquid phase separation (LLPS) to serve biological functionality, such as the (temporary) formation of membraneless organelles (Shin and Brangwynne, 2017; Jin et al., 2021), but also appears responsible to form large droplet-like precursors for the aggregation of the tau protein (Wegmann et al., 2018), which is another hallmark for AD. Large structures (possibly micellar) of approximately 50 Aβ molecules that are speculated to facilitate Aβ aggregation have also been observed (Wegmann et al., 2018). In the present study, we analyse the self-assembly of single peptides to address the current lack of physical models that explain both the formation of large agglomerates and the transition into fibrillar structures in terms of the molecular properties of the IDPs.

We argue that the general mechanism of coupled LLPS and aggregation is an example of physics that emerges from simple concepts such as (non-specific) hydrophobic interactions, excluded volume, and specific interactions. This is a hopeful scenario, as it implies that we may gain relevant molecular insight into this mechanism using strongly coarse-grained molecular models, rather than full atomistic molecular-dynamics simulations that are computationally too demanding to reach the relevant timescales. A commonly used coarse-graining approach to capture both the polymer physics of the polypeptide and the localized formation of reversible non-covalent bonds is to develop a sticker-and-spacer model. Such models were originally developed for synthetic associating polymers (Leibler et al., 1991), and were later adopted for disordered, multivalent proteins, including natural silk (Schaefer et al., 2020; Schaefer and McLeish, 2022) and scaffolding proteins in biological condensates (Shin and Brangwynne, 2017 and Choi et al., 2019, 2020). Typical simulation approaches solve the Brownian dynamics of the proteins using simulation software packages such as MARTINI or LAMMPS. A major challenge, which is receiving wide attention from the modeling community (Gissinger et al., 2017; Cui et al., 2018; Raffaelli et al., 2020; Schaefer and McLeish, 2022), remains to couple the (continuum-time) conformational dynamics to model the stochastic (instantaneous) association and dissociation of reversible bonds between the molecules. To circumvent the current methodological challenges, in the present study, we will employ the fully stochastic Bond-Fluctuation Model (Carmesin and Kremer, 1988, 1990), which by modeling the molecular dynamics on a 3D lattice successfully describes the (self-avoiding) random walk statistic of flexible and persistent chains (Bates, 2002; Feric et al., 2016; Harmon et al., 2017), LLPS, Reister et al. (2001), Reister and Müller (2003), ring-polymers (Subramanian and Shanbhag, 2009), and cross-linking reactions (Trautenberg et al., 1995). Crucially, as the dynamics are fully stochastic and discrete, they can be addressed using previously developed kinetic Monte Carlo (kMC) schemes (Lukkien et al., 1998).

In the following, we will present a simple sticker-and-spacer model for the dimerisation and (linear) oligomerisation of unfolded Aβ, where the cooperativity of growth is determined both by the chain conformation (i.e., intrinsic disorder) and by the binding energies for dimerisation/nucleation, ε_n, and elongation, ε_e, and where hydrophobic interactions are modeled using a short-ranged interaction energy, ε_H. Subsequently, we will present the bond-fluctuation model (BFM) using which we simulate the aggregation of the Aβ. In our analysis, we first investigate how the hydrophobic interactions affect the partial collapse of the molecule, and how it may lead to LLPS. We then show that these interactions facilitate dimerisation, as well as the further cooperative growth into longer oligomers. Finally, we demonstrate that increasing Aβ₁₋₄₂ relative to Aβ₁₋₄₀ promotes aggregation.

2. Theory and method

2.1. Introduction: Equilibrium statistics of self-assembly

The irreversible formation of Aβ aggregates is nucleated by oligomers, which themselves are reversible and on most occasions re-dissolve into Aβ monomers (Michaels et al., 2020). The formation of oligomers can on a coarse-grained scale, be described by chemical-reaction equations of the form A₁⇌A_n, where n > 1 is the order of the reaction. This reaction order gives a measure for the size of the oligomers but does not provide any structural information [e.g., whether the oligomers are amorphous clusters, rings, or linear chains, and if there are parallel or anti-parallel assemblies of poly-peptide sequences (Miller et al., 2010)]. While this structural information is typically studied at the level of single amino acids and atoms, the observations on the intrinsic disorder in Aβ through its random-coil conformations through both circular dichroism (Danielsson et al., 2005) and nuclear magnetic resonance spectroscopy (Wälti et al., 2015; Roche et al., 2016), begs the question of to what extent concepts from coarse-grained polymer physics can be used to understand the difference in self-assembly behavior of Aβ₁₋₄₀ and Aβ₁₋₄₂. The key idea that we explore is that the specific binding between substrands of the chain leads to interactions between the intrinsically disordered parts of the protein. These include both repulsive excluded-volume interactions and attractive hydrophobic interactions, (Figure 1); their contributions grow non-linearly with the size of the oligomer.

FIGURE 1

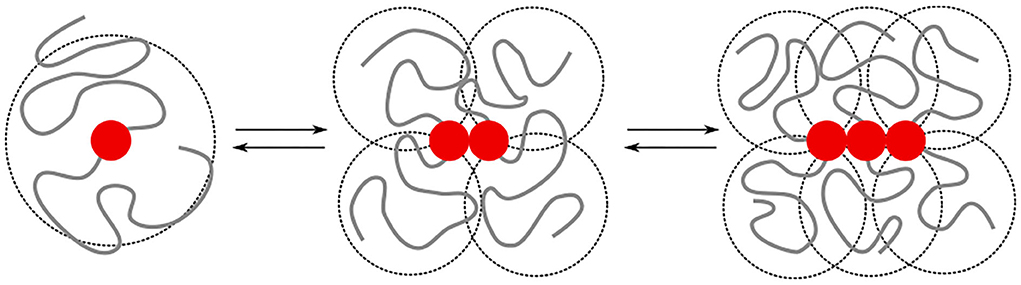
Figure 1. We model the growth of an oligomer through reversible bonds between bivalent stickers (red bead). The cooperativity is controlled by a difference in the binding energy for dimerisation/nucleation (ε_n) and elongation (ε_e). The total binding energy is further affected by repulsive excluded volume interactions between beads, as well as attractive hydrophobic interactions (ε_H) between beads within a short interaction range. The excluded volume interactions and hydrophobic interactions depend on the overlap (indicated by the dashed circles) of the intrinsically disordered sequences; the amount of overlap non-linearly increases with the length of the chains. In this study, we study how the added hydrophobic interactions and increased chain length of Aβ₁₋₄₂ compared to Aβ₁₋₄₀ affects the self-assembly into oligomers.

To investigate these ideas, we will describe both species as a randomly coiled polymer that is composed of hydrophilic and hydrophobic beads, as well as one ‘sticker' bead. This sticker bead forms reversible intermolecular bonds and leads to the formation of an oligomer. In general, any two oligomers of size m ≥ 1 and n ≥ 1 may reversibly assemble into an aggregate of size m + n through the chemical equilibrium equation (Martin, 1996; van der Schoot, 2005; de Greef et al., 2009).

$\begin{array}{ll}{A}_m+{\text{A}}_n\rightleftharpoons {\text{A}}_{m+n}.& (1)\end{array}$

The equilibrium constants of the reactions are non-universal and may be different for each oligomerisation step due to the formation of rings (Cates and Candau, 1990) or due to detailed phenomena, such as the parallel and anti-parallel assembly of poly-peptides. These different mechanisms may be summarised into generic schemes of (anti-)cooperative growth, where in the anti-cooperative case the nucleus is stable and only grows into larger species at high chemical potentials, whereas in the cooperative case, the nucleus is unstable and, once formed, either re-dissolves or rapidly grows into larger (stable) species. As the exact nature of the Aβ species is still under debate, we here represent these overall ideas by a simple ‘dimerisation-and-elongation' model (de Greef et al., 2009; Kulkarni et al., 2017), where we have a precise in silico control over the cooperativity of growth. We discuss this binding mechanism of the stickers in detail in Section 2.5. First, we will discuss the parametrisation of the protein as a randomly colloid polymer, discuss the Bond-Fluctuation model by which we simulate its equilibrium statistics, and the simple hydrophobicity model.

2.2. Parametrisation of unfolded Aβ

Random walk statistics of polymers typically emerge when the contour length is more than 10 times its persistence length and can be modeled using the ‘Bond-Fluctuation Model' (refer to next Section). The smallest length scale of this model is the persistence length which for polypeptides is one or a few amino acids. Using these considerations, we have chosen to use 20 beads to model Aβ₁₋₄₀ and 21 beads to model Aβ₁₋₄₂. Within our model, a bead may either be hydrophilic, hydrophobic, or may be a sticker. We have parameterised this model using the sequence of amino acids in Aβ₁₋₄₂, (Figure 2A), which displays the hydrophilic residues in red, the neutral ones in black, and the hydrophobic ones in blue. Our model for Aβ (Figure 2B) was based on the structure of Aβ₁₋₄₂ in Zhu et al. (2012). The first eight gray beads represent the first 16 amino acids corresponding to the hydrophilic N-terminal region. The central hydrophobic core is modeled as two blue (hydrophobic) beads representing amino acids 17-21. A red ‘sticky' bead which is capable of dimerising with other red beads was added into the turn region to recapitulate the intra- and inter-chain salt bridges that can occur in this region. The remaining hydrophobic beads represent the C-terminal region with Aβ₁₋₄₂ containing one extra bead to account for the addition of two hydrophobic amino acids. In principle, the properties of the beads may be informed from MD simulations or structural information. However, at this high level of coarse graining the exact sequence is not expected to qualitatively alter the conclusions of our study, in which we have only observed the formation of linear oligomers (i.e., the stickers bind into supramolecular chains) and droplets, but in which no higher-order self-assembled structures such as micelles or membranes were formed (see Results). These may be expected if the hydrophobic/hydrophilic beads would have been arranged into a co-block configuration, and/or if the stickers would have been placed at the chain ends.

FIGURE 2

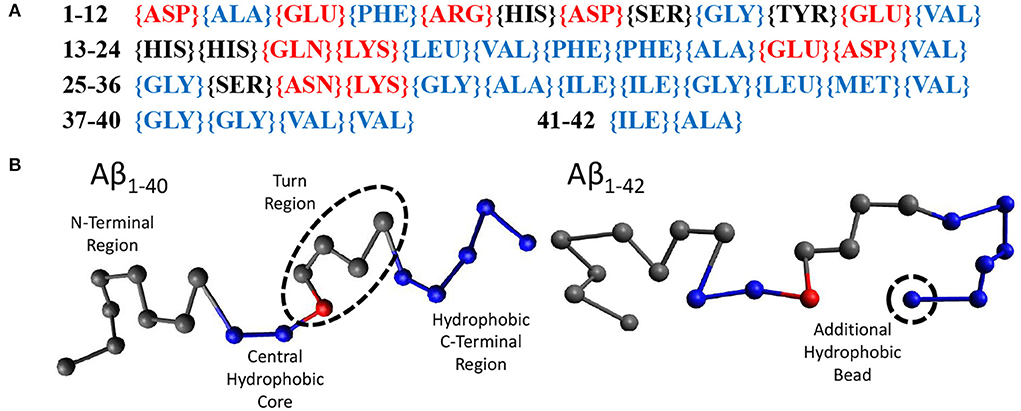
Figure 2. (A) The amino acid sequence of Aβ₁₋₄₂. Amino acids labeled red are hydrophilic, black are neutral, and blue are hydrophobic. (B) Our beads on a string model for both Aβ₁₋₄₀ and Aβ₁₋₄₂ with the N-terminus to the C-terminus going from left to right. Each bead represents 2 amino acids. Gray beads are inert, representing the N-terminus (1–16) and the turn region (24–27). Blue beads are hydrophobic, representing the central hydrophobic core (17–21), the second hydrophobic region (29–35) and the hydrophobic C-terminus (36–40/42). Red beads are capable of dimerising with other red beads.

2.3. Method: Bond-fluctuation model

We model the chain conformations by placing the polymer segments on the sites of a discrete lattice, following the so-called Bond-Fluctuation Model (BFM) (Carmesin and Kremer, 1988, 1990). This approach originates from the success of lattice models to predict phenomena such as LLPS, including in conditions near the critical point where the correlation-length diverges and mean-field models break down (Hohenberg and Halperin, 1977; Schaefer, 2018; Schaefer et al., 2019). Similarly, the lattice models have provided computationally efficient means to sample the configuration space of polymers. Early lattice models for polymers place polymer segments on a single lattice site (Binder, 1987) but underestimated the Rouse dynamics of the chains due to kinetically trapped states. This was remedied in the BFM by letting a segment occupy 8 sites on a 3D cubic lattice (4 sites on a 2D square lattice) and where the bond lengths can fluctuate from 2 to $\sqrt{10}$ in lattice units (Carmesin and Kremer, 1988, 1990). This approach was proven competitive with off-lattice models both in terms of computational convenience and in physical accuracy in (and beyond) the examples mentioned in the Introduction (Trautenberg et al., 1995; Reister et al., 2001; Bates, 2002; Reister and Müller, 2003; Subramanian and Shanbhag, 2009; Choi et al., 2019).

Within the BFM, the polymer conformations and/or dynamics are modeled using kinetic Monte Carlo (kMC) time steps in which a monomer may move in 6 directions on the lattice if this does not (1) overstretch or understretch the bond between two monomers within the chain or (2) lead to double-occupied lattice sites. This leads to a list of N_enabled ≤ 6N_monomers possible processes that may occur during the time step, of which only one (or none) may take place. Which process, i, may take place is selected using the rate,

$\begin{array}{ll}{\nu }_i=\{\begin{array}{l}{\nu }_0,\text{if}\text{Δ}{E}_{\text{i}}\le 0\\ {\nu }_0\exp (\text{−Δ}{E}_{\text{i}}/kT),\text{if}\text{Δ}{E}_{\text{i}}>0,\end{array}& (2)\end{array}$

where ν₀ is an elementary rate (typically of the order 1 − 100μs⁻¹) and where ΔE_i is the change in energy. In the algorithm that we use, a process is randomly selected out of the N_enabled list of processes. The process is then executed if the system energy is unchanged or decreases ΔE_i ≤ 0. However, if the energy would increase, the process is only executed with a probability p = exp(−ΔE_i/kT) and rejected otherwise; this decision is carried out using random numbers drawn using a SIMD-oriented Fast Mersenne Twister (Saito and Matsumoto, 2008). Regardless, if the process is accepted or rejected, the time is increased with Δt = 1/(N_enabledν₀). The computational efficiency of the method relies on the fact that following a Monte Carlo step during which monomer moves, only the rates of monomers in the vicinity of this monomer need to be recalculated (Lukkien et al., 1998).

2.4. Parametrisation: Hydrophobicity of spacers

To model the attraction between two hydrophobic monomers we follow the approach by Reister et al., and use a square-well potential (Reister et al., 2001).

$\begin{array}{ll}U(r)=\{\begin{array}{l}-{\epsilon }_{\text{H}},\text{ for }r\le \sqrt{10},\hfill \\ 0,\text{ otherwise},\hfill \end{array}& (3)\end{array}$

where r is the distance (in units of the lattice spacing) between the two monomers, and where ε_H describes non-specific (e.g., hydrophobic) interactions (Reister et al., 2001). This interaction energy enables the parametrisation of intrinsically disordered poly-peptides through the radius of gyration, and may in principle depend on conditions such the temperature and the ionic strength (Müller-Späth et al., 2010; Wuttke et al., 2014). This parametrisation is done using the Flory exponent υ, which describes the swelling of a polymer through the radius of gyration as $R_{\text{g}}=l{N}^{\upsilon }/\sqrt{6}$, with l the step length between segments. In good solvent conditions, the chain is swollen due to intramolecular self-excluded volume interactions and υ = 0.588. Completely insoluble chains, described with a large value of ε_H, collapse to a compact sphere with υ = 1/3. At θ conditions, the hydrophobic interactions exactly cancel the excluded-volume interactions and the chain obeys random-walk statistics, which are characterized by υ = 1/2. To find the θ-condition, we measure the radius of gyration for chains with various chain length, N, as a function of ε_H (Paul et al., 2005; Steinhauser, 2005). As $R_{\text{g}}^2/N$ is independent of the chain length at the theta condition, the ε_H value at which all curves intersect represents the θ condition. From Figure 3, we find that this occurs at ε_H/k_BT ≈ 0.27 for (homopolymer) chains with identical subunits.

FIGURE 3

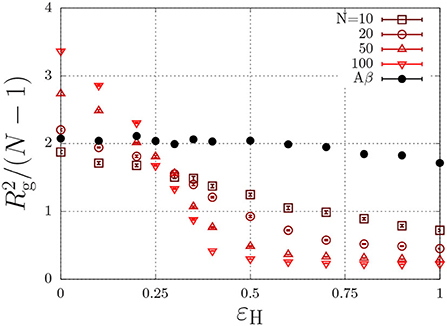
Figure 3. Polymer size, $R_{\text{g}}^2/(N-1)$, (R_g is the radius of gyration in units of the lattice spacing) as a function of the hydrophobic interaction energy ε_H/k_BT for a various number of beads per chain, N. The Aβ model has a total of N = 20 beads, of which 7 are hydrophobic.

As discussed in the previous section, our model for Aβ describes the protein as a copolymer with both hydrophilic and hydrophobic units. The solid circles in Figure 3 show that the radius of gyration, $R_{\text{g}}=l{N}^{\upsilon }/\sqrt{6}$ of this model polypeptide is relatively insensitive to the hydrophobic interaction parameter. To estimate the overlap concentration above which the intramolecular excluded-volume interactions are screened, we use the end-to-end distance, given by $R_{\text{e}}=l{N}^{\upsilon } \approx 3.3$ nm, where Aβ has N = 40 amino acids, and where l = 0.36 nm is the typical step length of amino acids (Müller-Späth et al., 2010; Wuttke et al., 2014). Using the molecular volume $V_{\text{m}}=(4/3)\pi R_{\text{e}}^3$, we find an overlap concentration of c_* = M_w/(N_AV_m) ≈ 100 mg/ml = 0.025 M, where we used M_w = 4.5 kg/mol. In typical experiments, aggregation is observed well below the overlap concentration (e.g., Aβ₁₋₄₀ aggregates below 1 mg/ml Hortschansky et al., 2005 and Aβ₁₋₄₂ aggregates at concentrations as low as 90 nM Novo et al., 2018).

While those experimental conditions may suggest dilute conditions in which excluded-volume interactions are unimportant, inside LLPS condensates the concentration is signicantly higher, and may in fact exceed the overlap concentration. To identify LLPS in our simulations, we focus on structural coarsening phenomena such as Ostwald or Lifshitz-Slyozov-Wagner (LSW) ripening and/or Brownian coalescence (Bray, 2002). The dynamics of coarsening are typically associated with a characteristic length scale (e.g., the radius of a droplet) that grows with the one-third power of time as R^*−R⁰ ∝ t^1/3 with R₀ the initial length scale, which may emerge through nucleation or spinodal decomposition. In our simulations, we determine R* using the following recipe (Singh et al., 2012; Schaefer, 2018; Schaefer et al., 2019): For a given time, t, we calculate the order-parameter field ψ(r_i), with r_i the spatial coordinate of a lattice site with i the index of a lattice site. The value of ψ(r_i) is set to 1 if the site is occupied by a hydrophobic monomer, and to −1 otherwise. We then calculate the 3D Fourier transform $\widehat{\psi }(\text{q})$ and obtain the structure factor $S(q)=\langle |\widehat{\psi }(q){|}^2\rangle$, where 〈.〉 is the spherical/angular average. Next, we obtain the spatial correlation function C(R) as the inverse Fourier transform of S(q). As discussed previously (Singh et al., 2012; Schaefer, 2018; Schaefer et al., 2019), numerically robust measures for the characteristic length scale R^* are the first root (i.e., given by C(R^*) = 0) and the first minimum for which C(R^*) < 0 and C′(R^*) = 0. In our analysis, we will use both measures to assess if structural coarsening occurs in our simulations.

2.5. Parametrisation: Binding of stickers

As motivated in Section 2.1, we will model oligomerisation through the reversible binding of divalent stickers through a ‘dimerisation-and-elongation' mechanism, where each sticker can either form a single bond or two bonds with other stickers. The dimerisation reaction is

$\begin{array}{ll}2{\text{A}}_1\stackrel{K_{\text{n}}}{\rightleftharpoons }{\text{A}}_2,& (4)\end{array}$

where

$K_{\text{n}}=\frac{1}{\upsilon }\exp \left(-\text{Δ}{H}_{\text{n}}/k_{\text{B}}T+\text{Δ}{S}_{\text{n}}/k_{\text{B}}\right),(5)$

is the equilibrium constant for nucleation, with υ the characteristic volume, ΔH < 0 is the binding enthalpy and with ΔS_n > 0 the entropic penalty of dimerisation. In this equation, ΔH_n is controlled by the binding energy ε_n > 0 and the hydrophobic interaction strength ε_H. In the absence of hydrophobic interactions, ΔH_n = −ε_n is exact. The entropic penalty essentially originates from an excluded-volume interaction due to a limitation of the internal degrees of freedom (DOF) of two chains that undergo dimerisation (refer to Section 3.1). In that section, we will show that these internal DOF are affected by the hydrophobicity (an increased hydrophobicity partially collapses the chain and limits the DOF prior to dimerisation), and by the concentration (above the overlap concentration the free chains have fewer DOF prior to dimerisation), such that an increasing hydrophobicity and concentration reduce the entropic penalty and enhance dimerisation.

For subsequent oligomerisation steps, i.e., for n > 1, we describe the equilibrium statistics using

$\begin{array}{ll}{A}_1+{\text{A}}_n\stackrel{K_{\text{e}}}{\rightleftharpoons }{\text{A}}_{n+1}& (6)\end{array}$

with

$K_{\text{e}}=\frac{1}{\upsilon }\exp \left(-\text{Δ}{H}_{\text{e}}/k_{\text{B}}T+\text{Δ}{S}_{\text{e}}/k_{\text{B}}\right),(7)$

in which ΔH_e/k_BT = −ε_n+U_hydrophobic+U(θ) is composed of an oligomeration/elongation energy, ε_n > 0, and hydrophobic interactions as before. The free energy of binding is modeled as completely entropic using a square-well bending potential (BFM simulations with smoother potentials were previously discussed in the literature, refer to Weber et al., 1999; Bates, 2002; Paul et al., 2005).

$\begin{array}{ll}U(\theta )=\{\begin{array}{l}\infty ,\text{ for }|\theta -\pi |\le {\theta }_{\text{max}},\hfill \\ 0,\text{ otherwise, }\hfill \end{array}& (8)\end{array}$

for the angle, θ, between the intermolecular bonds between stickers. Here, θ = π represents fully extended bonds. Hence, for small values of θ_max, the persistence length increases and the chain of stickers approaches a rigid rod. In our simulations, we set θ_max = π/18 (equivalent to 10 degrees), which ensures sufficient rigidity to avoid ring formation but sufficient flexibility to avoid lattice artifacts.

One of the key predictions of our simulations will be the dependence of the fraction of aggregated material on the concentration and hydrophobicity. We will interpret these findings using analytical predictions in the limit where hydrophobic interactions are absent and where the entropic penalties are constant. In this limit, there exist some known analytical predictions (van der Schoot, 2005). The starting point to obtain these is by writing the equilibrium constants as $K_{\text{n}}=\left[{\text{A}}_2\right]/{\left[{\text{A}}_1\right]}^2$ and as K_e = [A_n+1]/[A_n][A₁], which are constant for all n ≥ 2, so that the concentration of any aggregate [A_n] with n ≥ 2, can be expressed in terms of the concentration of unbound Aβ, [A₁], as

$K_{\text{e}}[{\text{A}}_n]=\sigma {(K_{\text{e}}[{\text{A}}_1])}^n,(9)$

with σ ≡ K_n/K_e the so-called cooperativity factor.

The concentrations of unbound Aβ is obtained from the mass balance,

$\begin{array}{l}\rho ={\displaystyle \sum _{n=1}^{\infty }n}[A_n]\Rightarrow K_{\text{e}}\rho =K_{\text{e}}[{\text{A}}_1]+\sigma {\displaystyle \sum _{n=2}n{(K_{\text{e}}[{\text{A}}_1])}^n}\\ =\sigma \frac{K_{\text{e}}[{\text{A}}_1]}{{(1-K_{\text{e}}[{\text{A}}_1])}^2},& (10)\end{array}$

where ρ is the (experimentally-controlled) overall concentration of Aβ. Using the standard sum $\sum _{n=1}^{\infty }n{x}^n=x/{(1-x)}^2$ for |x| < 1 and the fraction of aggregated molecules, f ≡ 1−[A₁]/ρ, this mass balance can be written as Martin (1996) and de Greef et al. (2009).

$\begin{array}{ll}0=-f+\sigma \frac{K_{\text{e}}\rho {[1-f]}^2(2-K_{\text{e}}\rho [1-f])}{{(1-K_{\text{e}}\rho [1-f])}^2},& (11)\end{array}$

which provides an implicit dependence of f on ρ.

This equation has three asymptotic limits of interest, namely the strongly anti-cooperative case where dimers do not grow into larger aggregates, K_e → 0 (resulting in σ → ∞) leads to Martin (1996).

$\begin{array}{ll}f=1-\frac{-1+\sqrt{1+8K_{\text{n}}\rho }}{4K_{\text{n}}\rho }.& (12)\end{array}$

In the non-cooperative case, or “isodesmic” case (Smulders et al., 2010), K ≡ K_e = K_n (Martin, 1996),

$\begin{array}{ll}f=1-\frac{1+2K\rho -\sqrt{1+4K\rho )}}{2{(K\rho )}^2},& (13)\end{array}$

and in the strongly cooperative case, σ → 0 (van der Schoot, 2005; Smulders et al., 2010), we have f = 0 for K_eρ < 0 and

$\begin{array}{ll}f=1-\frac{1}{K_{\text{e}}\rho },& (14)\end{array}$

for K_eρ ≥ 0. These equations show that from the anti-cooperative to the cooperative case, the transition from unbound to aggregated material becomes increasingly sharp. In the following, we will discuss the influence of hydrophobic and excluded-volume interactions on self-assembly in terms of the elongation constant K_e and the cooperativity factor, σ.

3. Results and discussion

3.1. Dimerisation and LLPS

To investigate how hydrophobic and steric interactions affect dimerisation, we have compared the self-assembly of chains with such interactions to the completely hydrophilic counterpart with ε_H = 0, and disabled oligomerisation (i.e., ε_e = 0). We have then simulated the molecular self-assembly of 100 chains in a periodic simulation box with sizes ranging from 50 × 50 × 50 to 1,000 × 1,000 × 1,000, with dimerisation energies ranging from ε_n = 2 to 10k_BT. The resulting fraction of dimerised chains, f, against the number density ρ (in the number of molecules per box size), is represented by the symbols in Figure 4A.

FIGURE 4

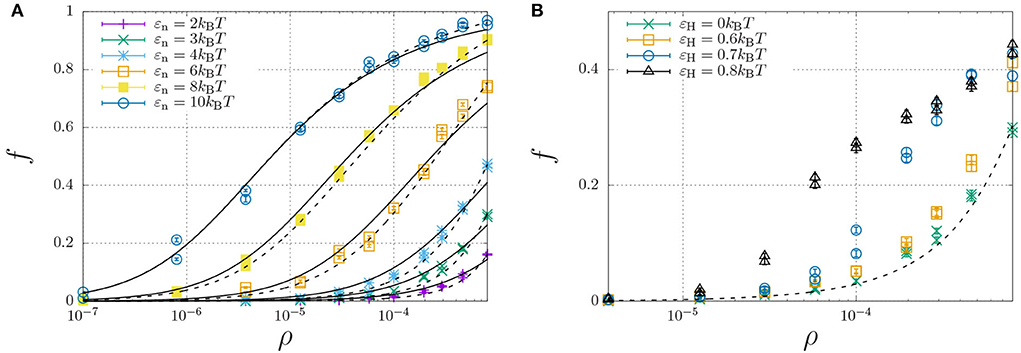
Figure 4. Fraction of dimerised Aβ, f, plotted against the number density, ρ (in units of the lattice spacing). Well below the overlap concentration of ρ = 10⁻⁴ (corresponds roughly to 100 mg/ml, refer to main text) the solution can be considered dilute, while at higher concentrations excluded volume interactions become important. (A) The dimerisation energy ε_n is varied from 2 to 10k_BT without hydrophobic interactions (ε_H = 0). The solid curves are individual fits using Equation (12) with a dimerisation constant K_n = K_n,0 exp(ε_n) with a non-constant K_n,0 (Table 1), while the dashed curves represent a simultaneous fit of all data using K_n,0 = K_n,00 exp[(∂[ΔS_n/k_B]/∂ρ)ρ] with constant K₀₀ = 6.85 and an entropic excluded-volume correction $(\partial \left[\Delta S_{\text{n}}/k_{\text{B}}\right]/\partial \rho )=1.3·10^3$. (B) The dimerisation energy is fixed ε_n = 3k_BT, while the hydrophobicity is increased from 0 up to ε_H = 0.8. The dashed and dotted curve are calculated using K_n = 6.85 exp(3+1300ρ) and K_n = 6.85 exp(3.6+1300ρ), respectively. The data for ε_H = 0.7 and 0.8 are underestimates, as ongoing LLPS enables the slow increase of aggregate sizes.

We have curve fitted each data set with fixed dimerisation energy, ε_e, using the dimerisation model of Equation (12) (solid curves) with the equilibrium constant K_n = K_n,0 exp(ε_n). While K_n,0 is explicitly independent of ε_n, the curve fits yielded the apparent dependence ln K_n,0 ≈ 3.0 − 1.1ε_n (Table 1). This is caused by the fact that the dimerization concentration (characterized by the inflection point of the self-assembly curve) shifts to higher concentrations (above the overlap concentration of ρ ≈ 10⁻⁴, see Section 2.4) for decreasing interaction strengths. Following Flory's approach to self-avoiding walk statistics, we modify the entropy for excluded-volume interactions using a mean-field description, ΔS_n = ΔS_n,0+(∂ΔS_n/∂ρ)ρ, and write K_n = K_n,00 exp(ε_n+(∂[ΔS_n/k_B]/∂ρ)ρ. Using this modification, we have been able to capture all dimerisation curves in Figure 4A with fixed K₀₀ = 6.85 and excluded-volume correction $(\partial \left[\Delta S_{\text{n}}/k_{\text{B}}\right]/\partial \rho )=1.3·10^3$ (dashed curves). As expected, this correction is insignificant below the overlap concentration, ρ < 10⁻⁴, but significantly affects the self-assembly curves at higher concentrations.

TABLE 1

Table 1. Values for the equilibrium constant K_n,0 determined by curve-fitting Equation 12 to the simulated data for various values of the dimerisation energy ε_n.

We now focus our attention on the dimerisation curve with ε_n = 3k_BT, which has a very low fraction of dimers below the overlap concentration but a finite fraction of dimers at higher concentrations, and increase the hydrophobic-interaction parameter, ε_H, from 0 to 0.8k_BT (Figure 4B). We find that up to a value of 0.6k_BT, the hydrophobicity appears to only modestly modify the equilibrium constant as K_n ≈ 6.85 exp(ε_n + ε_H + 1300ρ); we speculate that only the central hydrophobic beads contribute to the enhancement of dimerisation. For stronger hydrophobic interactions, however, the shape of the self-assembly curve can no longer be described using the simple dimerisation model.

In fact, the datapoint for ε_H ≥ 0.7 in Figure 4B is not fully converged, and the fraction of dimers increases in a slow process, as indicated in Figure 5A. This figure shows that the fraction of dimers, f, reaches a plateau at f ≈ 0.2 for times t > 100 up to t ≈ 3, 000, but then slowly increases up to f ≈ 0.4 at t = 10⁵ without any sign of convergence to a higher plateau value. This process is a consequence of the slow formation of large structures, as indicated by the typical length scales in the system Figure 5B, which increase as R^*−R⁰ ∝ t^1/3, which is a hallmark of LLPS, refer to Section 2.4. Here, we determined R^* using the structure factor S(q, t) (top right), and its corresponding spatial correlation function, C(R, t), (bottom right). We quantified R^* using the first root (C(R^*, t) = 0, R⁰ = 8) and the first minimum (C(R_*, t) < 0 and ∂C/∂R = 0, R⁰ = 12).

FIGURE 5

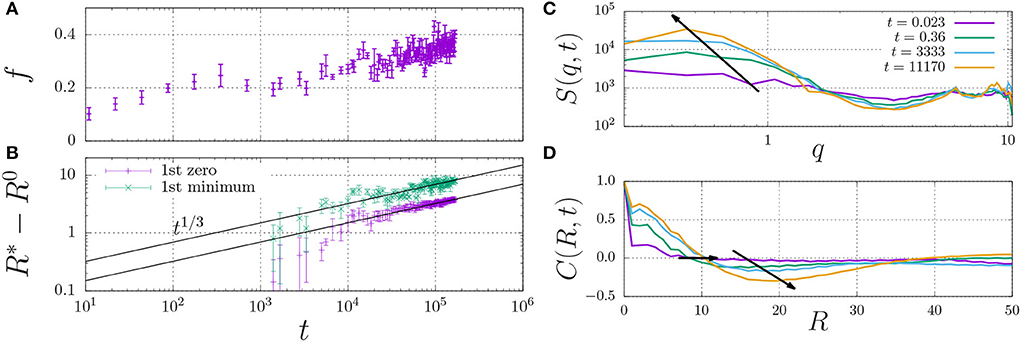
Figure 5. Fraction of dimerised material, f, (A) and characteristic length scale, R^*−R⁰ (B) against time. The characteristic length scale, R^* is determined by i) calculating the dynamic structure factor, S(q) (C), ii) taking the inverse Fourier transform to obtain the radial correlation function, C(R, t) (D), and iii) determining its first root C = 0 (here, we use the initial offset R⁰ = 8) and first minimum for which C < 0 (here, R⁰ = 12). The arrows indicate the time dependence of the dominant wavenumber q (C) and the two measures for R^* (D).

These findings indicate that sufficiently strong hydrophobic interactions may lead to the formation of droplets through LLPS, which inside the droplets increases the concentration of dimerising units beyond the overlap concentration (which screens the excluded-volume interactions), and provides the mass action needed to induce dimerisation.

3.2. Oligomerisation

Now that we have investigated the dimerisation of Aβ, we will investigate the growth of larger oligomers. For that purpose, we again first focus on the case without any hydrophobic interactions, as this enables us to isolate the impact of excluded-volume interactions on the (anti-)cooperativity of self-assembly. This also enables us to select nucleation and elongation energies of interest in the subsequent simulations, in which we do switch on hydrophobic interactions. Akin to the dimerisation case, we have simulated the self-assembly of 100 Aβ₁₋₄₀ chains in box sizes ranging from 36 × 36 × 36 to 500 × 500 × 500. In these simulations, we have switched off the non-specific/hydrophobic interactions ε_H = 0 and varied the nucleation energies in the range ε_n = 1 − 9k_BT and the elongation energies in the range ε_e = 8 − 14k_BT.

The simulations yielded the fraction of aggregated material, f, as a function of the concentration, to which we have curve fitted the theoretical model of Equation (11). From the curve-fits, we have extracted the cooperativity factor σ and the equilibrium constant K_e,0 as a function of the dimerisation energy. Here, K_e,0 is defined by

$K_{\text{e}}={\upsilon }^{-1}\exp (\text{−Δ}{H}_{\text{e}}+\text{Δ}{S}_{\text{e}}/k_{\text{B}})\equiv K_{\text{e},0}\exp ({\epsilon }_{\text{e}}/k_{\text{B}}T).(15)$

The results are tabulated in Table 2 and plotted in Figures 6B,C (discussed below).

TABLE 2

Table 2. Shown are the results from varying ε_n for multiple different values of ε_e, in the absence of hydrophobic interactions i.e., ε_H = 0k_BT.

FIGURE 6

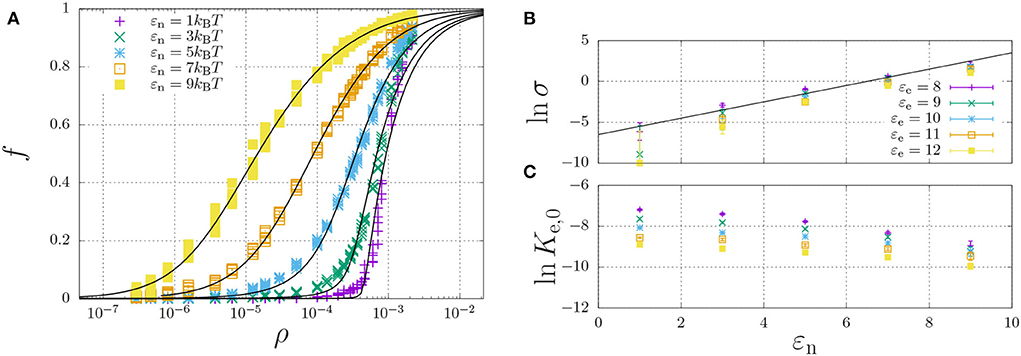
Figure 6. Self-assembly of a hydrophilic chain (ε_H = 0) for a fixed elongation energy ε_e = 9k_BT and varying dimerisation energy ε_n. (A) The fraction of aggregated material is plotted against the concentration. For each value of ε_n, the data was curve-fitted using Equation (11) with cooperativity factor σ (B) and the equilibrium constant K_e = K_e,0 exp(ε_e) (C) as fitting parameters. For (B,C), each point represents the mean and standard error of 5 simulations.

A representative self-assembly curve, obtained for fixed ε_e = 9k_BT, is shown in Figure 6A. This panel shows the fraction of aggregated material, f, increases with an increasing number density, ρ. The sigmoidal curve becomes increasingly sharp with decreasing dimerisation energy, which, as expected (refer to Section 2.5), indicates increasing cooperativity of self-assembly. Indeed, Figure 6B shows that the logarithm of the cooperativity factor increases linearly with increasing dimerisation energy, as expected. On the other hand, the elongation constant K_e,0 is in principle expected to be independent of the dimerisation energy; however, Figure 6C shows it apparently decreases with increasing dimerisation energy. We attribute this apparent dependence to the excluded-volume interactions becoming more present at higher concentrations, as we found above in the dimerisation curves of Figure 4.

To investigate the effect of non-specific hydrophobic interaction on oligomerisation, we have used the parameters ε_n = 3k_BT and ε_e = 9k_BT of a hydrophilic chain that cooperatively self-assembles at reasonably high concentrations. This ensured that low-concentration structuring due to hydrophobic interactions would not necessitate larger (and computationally expensive) box sizes. We have then used the sequences for the Aβ₁₋₄₀ and Aβ₁₋₄₂ chains and varied the hydrophobic interaction energy ε_H from 0.4 to 0.7k_BT. We have again simulated 100 chains in box sizes ranging from 36 × 36 × 36 to 500 × 500 × 500 lattice sites.

We have presented the results in Figures 7A,B, displaying the fraction of aggregated material f against the number density ρ for Aβ₁₋₄₀ (Figure 7A) and Aβ₁₋₄₂ (Figure 7B). In line with our results on dimerisation, we find that increasing hydrophobic interaction energy shifts the aggregation concentration to a lower concentration and that the transition to the aggregates state becomes sharp. For these higher hydrophobicities, we again find a slow ongoing increase of the fraction of aggregated material due to Ostwald ripening and/or rare events of fusion of condensates. After close inspection of Figures 7A,B, we observe that the transition occurs for Aβ₁₋₄₂ at lower concentrations than for Aβ₁₋₄₀, which we attribute to a larger number of hydrophobic interactions for the longer chain. Indeed, Figure 7C shows that the mean aggregate size at ρ = 2·10⁻⁴ sharply increases at ε_H = 0.6 for the longer chain and at ε_H = 0.65 for the shorter chain. The mean values of the aggregate size are biased by the presence of small oligomers; Figure 7D reveals the presence of aggregates with 8 or more chains.

FIGURE 7

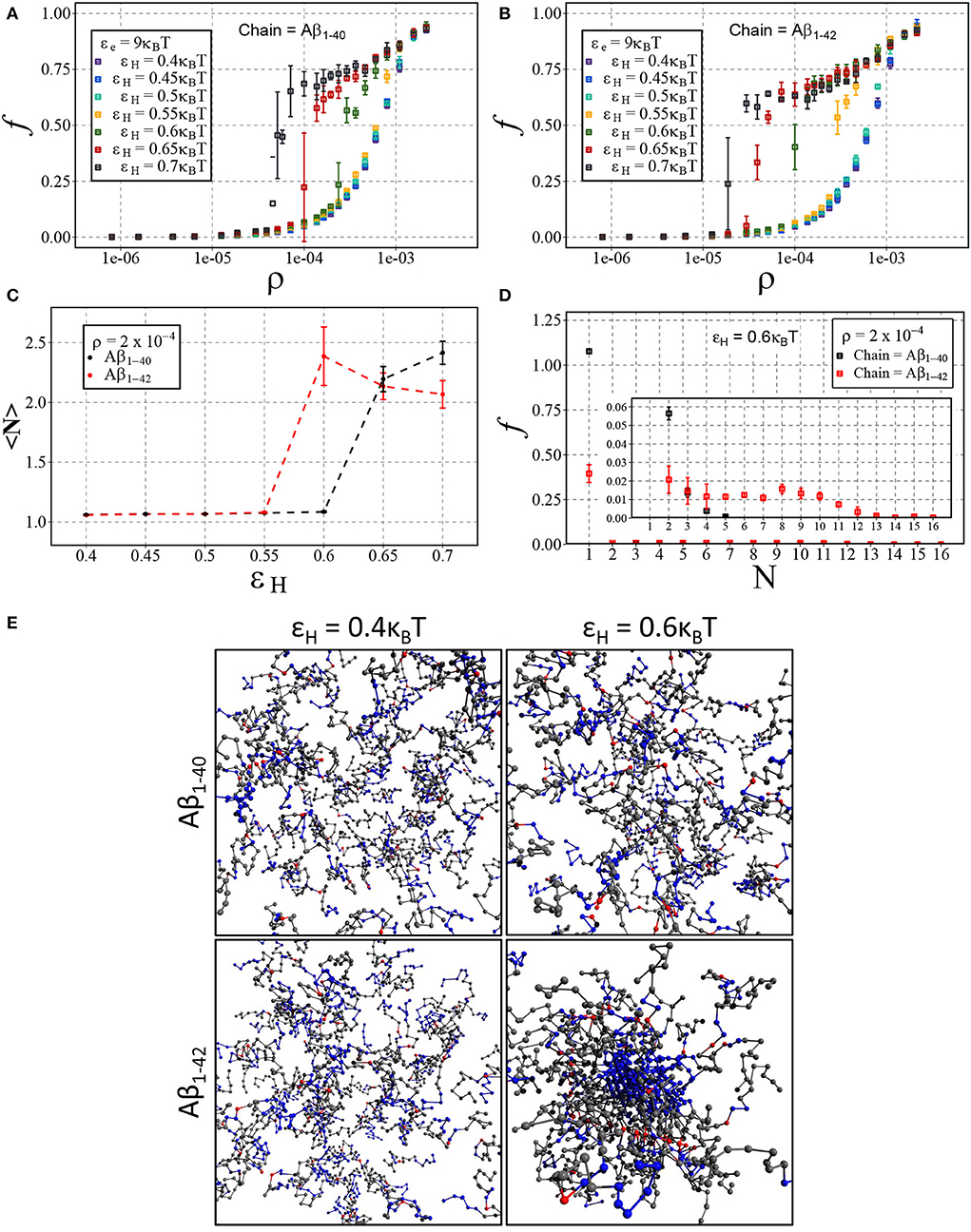
Figure 7. Aβ aggregation with dimerisation (nucleation) energy ε_n = 3k_BT and elongation energy ε_e = 9k_BT. Each point represents the mean and standard deviation of 3 simulations. The fraction of aggregated material, f, is plotted against the number density, ρ (in units of the lattice spacing), for varying values of ε_H using either (A) Aβ₁₋₄₀ and (B) Aβ₁₋₄₂. (C) Displays the change in mean cluster size, 〈N〉, against varying hydrophobic interaction energy, ε_H, at a concentration of ρ = 2·10⁻⁴. (D) A size distribution plot with the fraction of material, f, plotted against the cluster size, N, with a fixed hydrophobicity of ε_H = 0.6k_BT at a concentration of ρ = 2·10⁻⁴. (E) Shown are snapshots taken from the end point of the simulation for Aβ₁₋₄₀ and Aβ₁₋₄₂ at low (ε_H = 0.4k_BT) and high (ε_H = 0.6k_BT) hydrophobicity.

3.3. Aggregation of mixed Aβ₁₋₄₀ and Aβ₁₋₄₂

The difference in the critical concentration for condensation of Aβ₁₋₄₀ and Aβ₁₋₄₂, begs the question of to what extent our simple model can capture the reported observation of Aβ₁₋₄₂-enhanced aggregation in mixtures of Aβ₁₋₄₀ and Aβ₁₋₄₂ (Kumar-Singh et al., 2006; Zetterberg, 2019). To investigate this, we have carried out in silico mixing experiments for two different values of hydrophobicity. First, we have chosen ε_H = 0.4k_BT as it previously appeared to not have led to different aggregation dynamics of Aβ₁₋₄₂ and Aβ₁₋₄₀. Second, we have chosen ε_H = 0.6k_BT, as this value showed the largest difference in the aggregation propensity of the two chains (refer to Figure 7).

In Figure 8, we plot the fraction of aggregated material (Figure 8A) and the mean aggregate size (Figure 8B) against the fraction of Aβ₁₋₄₂ in a mixture of Aβ₁₋₄₂ and Aβ₁₋₄₀. Having in mind that for strong hydrophobicity, structural coarsening renders the system out-of-equilibrium even at long time scales, and thermal equilibrium may never be reached (refer to Figure 5), we have plotted the results after time $4·10^6{\nu }_0^{-1}$ and after $4·10^7{\nu }_0^{-1}$. As expected, for low hydrophobicity (ε_H = 0.4k_BT), almost no aggregation takes place and the fraction of aggregated materials is ≈ 0.1, independently of the fraction of long chains. However, for higher hydrophobicity (ε_H = 0.6k_BT) aggregation occurs rapidly for mixtures with 20% Aβ₁₋₄₂ (solid lines), while at long timescale mixtures with 10% Aβ₁₋₄₂ start to aggregate (dotted lines). In qualitative agreement with the experimental observations by Kuperstein et al. (2010), the critical point is strongly biased to a low fraction of Aβ₁₋₄₂ in the mixture (< 10% in our simulations). The slow dynamics are expected, as it is typical for first-order phase separation near the critical point (Hohenberg and Halperin, 1977). However, we observe another slow process beyond the critical point, namely the increase of the aggregate size at high concentrations of Aβ₁₋₄₂ (panel B). We attribute these to rare events of aggregate fusion.

FIGURE 8

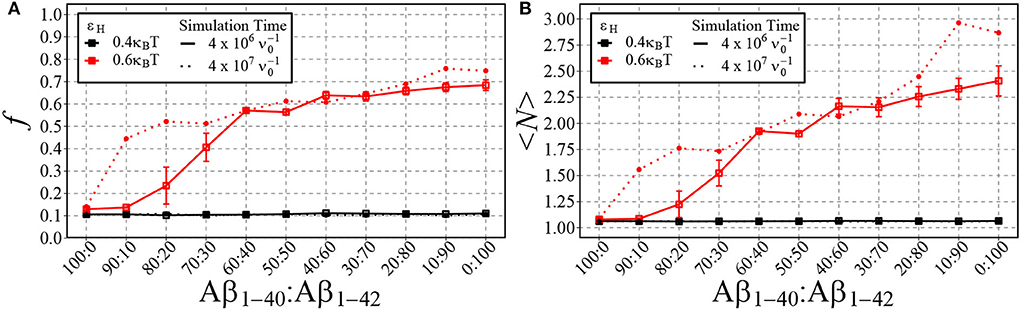
Figure 8. Shown are the fraction of aggregated material, f, (A) and the mean cluster size, 〈N〉, (B) using different ratios of Aβ₁₋₄₀ and Aβ₁₋₄₂ chains for two different values of ε_H. 100 total chains were used in each simulation. A consistent box size of 80 × 80 × 80 (approximately 200 uM) was used in all simulations, with ε_e = 9k_BT and ε_n = 3k_BT. For typical simulation times (4·10⁶ in units of ${\nu }_0^{-1}$; reached in 5·10¹⁰ timesteps), each point represents the mean and standard error of 3 simulations. For longer simulation times (4·10⁷ ${\nu }_0^{-1}$), each data point represents the result from a single simulation.

4. Discussion and conclusion

Our study has contributed a molecular modeling approach to address (1) the observation of Aβ₁₋₄₂-enhanced toxic plaques associated with Alzheimer's disease, despite being the less concentrated species of Aβ, and (2) the hypothesis of condensate-precursors for fibrillation. Here, we sought a molecular explanation for the different self-assembly behavior of Aβ₁₋₄₀ and Aβ₁₋₄₂ using sticker-and-spacer models that capture the intrinsic disorder and the effect of hydrophobicity. while the two extra amino acids in Aβ₁₋₄₂ elongate the chain length, they also add hydrophobicity.

The model predicts a rich range of phenomena due to the interplay between the nucleation and elongation of aggregates with the LLPS of condensates, driven by hydrophobic or other non-specific interactions, which we have summarised in Figure 9. The high concentration inside the condensates enhances the rate of nucleation through the formation of dimers. Furthermore, at these high concentrations the excluded-volume interactions, which in dilute conditions would hamper the growth of aggregates, are screened, such that the cooperativity of oligomerisation is enhanced. Consequently, we find a sharp transition from the unbound to the aggregated state. However, the dynamics by which aggregates may form are slow close to the critical conditions for LLPS. At concentrations above the critical concentration, the growth of aggregates is slow due to the relatively slow dynamics of Ostwald ripening and/or fusion events.

FIGURE 9

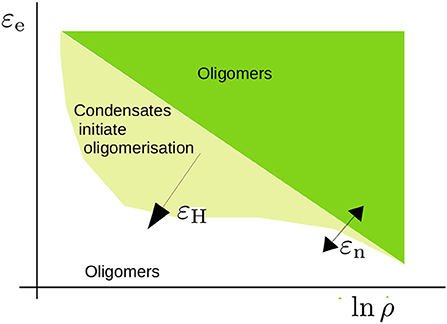
Figure 9. Schematic representation of the phase diagram that we have studied in the present study. The critical concentration for oligomerisation is roughly given by ln ρ_crit ∝ ε_e/k_BT with ε_e the elongation energy. This critical concentration is affected by excluded volume effects near the overlap concentration and leads to an apparent dependence on the nucleation energy ε_n (refer to Section 3.1). For a sufficiently high hydrophobic interaction energy ε_H, condensates form. The concentration is high within these condensates and promotes oligomer formation. The shape of this region is a qualitative estimate that acknowledges that phase separation takes place within a limited concentration range.

A similar secondary-nucleation mechanism was discussed previously by Cohen et al. (2013) and Michaels et al. (2020), and it was found that the rate constants for primary nucleation, elongation, and secondary nucleation are 100-, 10-, and 3-fold greater, respectively, for Aβ₁₋₄₂ compared to Aβ₁₋₄₀ (Meisl et al., 2014). This provides evidence that the addition of two c-terminal hydrophobic amino acids promotes aggregation propensity, in particular, the rate of primary nucleation. This is in agreement with Roche et al. (2016) who propose that the primary nucleation of Aβ is driven by non-specific hydrophobic interactions which explain the difference in the aggregation rates of Aβ₁₋₄₀ and Aβ₁₋₄₂.

Despite its simplicity, the model also predicts that a small fraction (< 10%) of Aβ₁₋₄₂ in a mixture of Aβ₁₋₄₂ and Aβ₁₋₄₀ shifts the critical concentration for the LLPS of condensates to lower values, which in turn leads to the nucleated self-assembly of fibrillar oligomers at reduced concentrations. This finding is qualitatively consistent with Kuperstein et al. (2010) who found that even a small change from a 1:9 to a 3:7 ratio of Aβ₁₋₄₂:Aβ₁₋₄₀ caused a dramatic change in the aggregation kinetics and toxicity of the two mixtures in vitro and in vivo. This 3:7 ratio is of particular importance as it reflects the ratio of Aβ₁₋₄₂:Aβ₁₋₄₀ observed in familial AD patients (Scheuner et al., 1996) suggesting that maintaining a physiological ratio of Aβ₁₋₄₂:Aβ₁₋₄₀ is of great importance and may be an effective therapeutic target.

Whether Aβ₁₋₄₀ and Aβ₁₋₄₂ can co-fibrilise is still under debate, Cukalevski et al. (2015) found that mixing Aβ₁₋₄₀ and Aβ₁₋₄₂ leads to the generation of separate homomolecular fibrils. In contrast, studies have shown that mixing Aβ₁₋₄₀ and Aβ₁₋₄₂ leads to the formation of mixed oligomers and fibrils (Cerofolini et al., 2020; Gu and Guo, 2021). However, it is accepted that Aβ₁₋₄₀ and Aβ₁₋₄₂ interact at the molecular level with increased levels of Aβ₁₋₄₀ inhibiting fibril formation and increased levels of Aβ₁₋₄₂ promoting aggregation (Hasegawa et al., 1999; Yan and Wang, 2007; Jan et al., 2008; Pauwels et al., 2012). Despite studies disagreeing on co-fibrilisation, they agree that prefibrillar intermediates consisting of both Aβ₁₋₄₀ and Aβ₁₋₄₂ exist. Our findings suggest that Aβ₁₋₄₂ interacts with Aβ₁₋₄₀, facilitating its aggregation. When only Aβ₁₋₄₀ chains are present and ε_H = 0.6k_BT, approximately 10% of the chains are aggregated. However, with 4·10⁶ ${\nu }_0^{-1}$, when Aβ₁₋₄₀ and Aβ₁₋₄₂ are mixed at a 60:40 ratio, f increases to approximately 60%. If only Aβ₁₋₄₂ chains are capable of aggregation, f = 40% at maximum. As this is not the case, it demonstrates that the addition of Aβ₁₋₄₂ is sufficient to promote the aggregation of Aβ₁₋₄₀ under these conditions. One explanation may be that when the more aggregation prone Aβ₁₋₄₂ is present, it forms the primary nuclei overcoming the initial energy barrier that then enables Aβ₁₋₄₀ to aggregate. This theory is supported by Cukalevski et al. (2015) who showed that upon mixing Aβ₁₋₄₂ and Aβ₁₋₄₀ it is Aβ₁₋₄₂ that aggregates first, followed by Aβ₁₋₄₀.

In conclusion, we have presented a simple sticker-and-spacer lattice model that captures a wide range of molecular phenomena of relevance to the literature on Aβ aggregation, which enables us to interpret those phenomena in terms of the simple concepts of nucleation-elongation models and hydrophobicity and polymeric excluded-volume effects at the level of coarse-grained sticky-polymer models. We hope this approach will lead to further (quantitative) refinements to the understanding of typical experimental time and length scales of Aβ aggregation in few-component in vitro and complex multi-component in vivo studies.

Data availability statement

The datasets generated/analyzed presented in this study are available on Zenodo https://doi.org/10.5281/zenodo.7053937. The simulation code is available on request.

Author contributions

CS and JC collected the data, performed the analysis, and wrote the first draft of the manuscript. CS administered the project and developed, coded the model, and the simulation algorithm. All authors conceived and designed the study, contributed to manuscript revision, read, and approved the submitted version.

Funding

JC acknowledges financial support from the Physics of Life UK. SQ acknowledges support from Alzheimer's Research UK (RF2019-A-001). CS acknowledges support from the Engineering and Physical Sciences Research Council [Grant No. EPSRC (EP/N031431/1)].

Acknowledgments

CS thanks Dr. Ed Higgins, Mitch Aitchison, Thibault Delpech, and Arsenii Zats for their assistance in the development and implementation of the model. CS and JC are grateful for computational support from the University of York Research and High Performance Computing service, The Viking Cluster.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abeysinghe, A. A. D. T., Deshapriya, R. D. U. S., and Udawatte, C. (2020). Alzheimer's disease; a review of the pathophysiological basis and therapeutic interventions. Life Sci. 256, 117996. doi: 10.1016/j.lfs.2020.117996

PubMed Abstract | CrossRef Full Text | Google Scholar

Arenaza-Urquijo, E. M., and Vemuri, P. (2018). Resistance vs resilience to Alzheimer disease: clarifying terminology for preclinical studies. Neurology 90, 695–703. doi: 10.1212/WNL.0000000000005303

PubMed Abstract | CrossRef Full Text | Google Scholar

Ayodele, T., Rogaeva, E., Kurup, J. T., Beecham, G., and Reitz, C. (2021). Early-onset Alzheimer's disease: what is missing in research? Curr. Neurol Neurosci. Rep. 21, 4. doi: 10.1007/s11910-020-01090-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Baldeiras, I., Santana, I., Leitão, M. J., Gens, H., Pascoal, R., Tábuas-Pereira, M., et al. (2018). Addition of the Aβ42/40 ratio to the cerebrospinal fluid biomarker profile increases the predictive value for underlying Alzheimer's disease dementia in mild cognitive impairment. Alzheimers Res. Therapy 10, 33. doi: 10.1186/s13195-018-0362-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Bates, M. A. (2002). Coarse grained models for flexible liquid crystals: parameterization of the bond fluctuation model. J. Chem. Phys. 120, 3986–3997. doi: 10.1063/1.1634551

PubMed Abstract | CrossRef Full Text | Google Scholar

Binder, K. (1987). Dynamics of phase separation and critical phenomena in polymer mixtures. Colloid Polymer Sci. 265, 273–288. doi: 10.1007/BF01417926

PubMed Abstract | CrossRef Full Text | Google Scholar

Bray, A. J. (2002). Theory of phase-ordering kinetics. Adv. Phys. 51, 481–587. doi: 10.1080/00018730110117433

CrossRef Full Text | Google Scholar

Breijyeh, Z., and Karaman, R. (2020). Comprehensive review on Alzheimer's disease: causes and treatment. Molecules 25, 5789. doi: 10.3390/molecules25245789

PubMed Abstract | CrossRef Full Text | Google Scholar

Carmesin, I., and Kremer, K. (1988). The bond fluctuation method: a new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules 21, 273–288. doi: 10.1021/ma00187a030

CrossRef Full Text | Google Scholar

Carmesin, I., and Kremer, K. (1990). Static and dynamic properties of two-dimensional polymer melts. J. Phys. 51, 915–932. doi: 10.1051/jphys:019900051010091500

CrossRef Full Text | Google Scholar

Castellani, R. J., Plascencia-Villa, G., and Perry, G. (2019). The amyloid cascade and Alzheimer's disease therapeutics: theory versus observation. Lab. Invest. 99, 958–970. doi: 10.1038/s41374-019-0231-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Cates, M. E., and Candau, S. J. (1990). Statics and dynamics of worm-like surfactant micelles. J. Phys. 2, 6869–6892. doi: 10.1088/0953-8984/2/33/001

CrossRef Full Text | Google Scholar

Cerofolini, L., Ravera, E., Bologna, S., Wiglenda, T., Böddrich, A., Purfürst, B., et al. (2020). Mixing Aβ (1–40) and Aβ(1–42) peptides generates unique amyloid fibrils. Chem. Commun. 56, 8830–8833. doi: 10.1039/D0CC02463E

PubMed Abstract | CrossRef Full Text | Google Scholar

Chafekar, S. M., Baas, F., and Scheper, W. (2008). Oligomer-specific Aβ toxicity in cell models is mediated by selective uptake. Biochim. Biophys. Acta 1782, 523–531. doi: 10.1016/j.bbadis.2008.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Chávez-Gutiérrez, L., and Szaruga, M. (2020). Mechanisms of neurodegeneration-Insights from familial Alzheimer's disease. Seminars Dev. Biol. 105, 75–85. doi: 10.1016/j.semcdb.2020.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, G.-f., Xu, T.-,h., Yan, Y., Zhou, Y.-r., Jiang, Y., Melcher, K., et al. (2017). Amyloid beta: structure, biology and structure-based therapeutic development. Acta Pharmacol Sin. 38, 1205–1235. doi: 10.1038/aps.2017.28

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, J.-M., Dar, F., and Pappu, R. V. (2019). LASSI: a lattice model for simulating phase transitions of multivalent proteins. PLoS Comput. Biol. 15, e611095. doi: 10.1101/611095

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, J.-M., Holehouse, A. S., and Pappu, R. V. (2020). Physical principles underlying the complex biology of intracellular phase transitions. Annu. Rev. Biophys. 49, 107–133. doi: 10.1146/annurev-biophys-121219-081629

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, S. I. A., Linse, S., Luheshi, L. M., Hellstrand, E., White, D. A., Rajah, L., et al. (2013). Proliferation of amyloid-β42 aggregates occurs through a secondary nucleation mechanism. Proc. Natl. Acad. Sci. U.S. A. 110, 9758–9763. doi: 10.1073/pnas.1218402110

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, G., Boudara, V. A. H., Huang, Q., Baeza, G. P., Wilson, A. J., Hassager, O., et al. (2018). Linear shear and nonlinear extensional rheology of unentangled supramolecular side-chain polymers. J. Rheol. 62, 1155–1174. doi: 10.1122/1.5012349

CrossRef Full Text | Google Scholar

Cukalevski, R., Yang, X., Meisl, G., Weininger, U., Bernfur, K., Frohm, B., et al. (2015). The Aβ40 and Aβ42 peptides self-assemble into separate homomolecular fibrils in binary mixtures but cross-react during primary nucleation. Chem. Sci. 6, 4215–4233. doi: 10.1039/C4SC02517B

PubMed Abstract | CrossRef Full Text | Google Scholar

Danielsson, J., Jarvet, J., Damberg, P., and Gräslund, A. (2005). The alzheimer β-peptide shows temperature-dependent transitions between left-handed 31-helix, β-strand and random coil secondary structures. FEBS J. 272, 3938–3949. doi: 10.1111/j.1742-4658.2005.04812.x

PubMed Abstract | CrossRef Full Text | Google Scholar

de Greef, T. F. A., Smulders, M. M. J., Wolffs, M., Schenning, A. P. H. J., Sijbesma, R. P., and Meijer, E. W. (2009). Supramolecular polymerization. Chem. Rev. 109, 5687–5754. doi: 10.1021/cr900181u

PubMed Abstract | CrossRef Full Text | Google Scholar

Doecke, J. D., Pérez-Grijalba, V., Fandos, N., Fowler, C., Villemagne, V. L., Masters, C. L., et al. (2020). Total Aβ42/Aβ40 ratio in plasma predicts amyloid-PET status, independent of clinical AD diagnosis. Neurology 94, e1580–e1591. doi: 10.1212/WNL.0000000000009240

PubMed Abstract | CrossRef Full Text | Google Scholar

Dubois, B., Villain, N., Frisoni, G. B., Rabinovici, G. D., Sabbagh, M., Cappa, S., et al. (2021). Clinical diagnosis of Alzheimer's disease: recommendations of the International Working Group. Lancet Neurol. 20, 484–496. doi: 10.1016/S1474-4422(21)00066-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Fandos, N., Pérez-Grijalba, V., Pesini, P., Olmos, S., Bossa, M., Villemagne, V. L., et al. (2017). Plasma amyloid β 42/40 ratios as biomarkers for amyloid β cerebral deposition in cognitively normal individuals. Alzheimers Dement. 8, 179–187. doi: 10.1016/j.dadm.2017.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Feric, M., Vaidya, N., Harmon, T. S., Mitrea, D. M., Zhu, L., Richardson, T. M., et al. (2016). Coexisting liquid phases underlie nucleolar sub-compartments. Cell 165, 1686–1697. doi: 10.1016/j.cell.2016.04.047

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghadami, S. A., Chia, S., Ruggeri, F. S., Meisl, G., Bemporad, F., Habchi, J., et al. (2020). Transthyretin inhibits primary and secondary nucleations of Amyloid-β peptide aggregation and reduces the toxicity of its oligomers. Biomacromolecules 21, 1112–1125. doi: 10.1021/acs.biomac.9b01475

PubMed Abstract | CrossRef Full Text | Google Scholar

Gissinger, J. R., Jensen, B. D., and Wise, K. E. (2017). Modeling chemical reactions in classical molecular dynamics simulations. Polymer 128, 211–217. doi: 10.1016/j.polymer.2017.09.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Giudici, K. V., de Souto Barreto, P., Guyonnet, S., Li, Y., Bateman, R. J., Vellas, B., and MAPT/DSA Group (2020). assessment of plasma amyloid-β42/40 and cognitive decline among community-dwelling older adults. JAMA Network Open 3, e2028634. doi: 10.1001/jamanetworkopen.2020.28634

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, L., and Guo, Z. (2021). Alzheimer's Aβ42 and Aβ40 form mixed oligomers with direct molecular interactions. Biochem. Biophys. Res. Commun. 534, 292–296. doi: 10.1016/j.bbrc.2020.11.092

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, T., Zhang, D., Zeng, Y., Huang, T. Y., Xu, H., and Zhao, Y. (2020). Molecular and cellular mechanisms underlying the pathogenesis of Alzheimer's disease. Mol. Neurodegener. 15, 40. doi: 10.1186/s13024-020-00391-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Haass, C., Kaether, C., Thinakaran, G., and Sisodia, S. (2012). Trafficking and proteolytic processing of APP. Cold Spring Harbor Perspect. Med. 2, a006270. doi: 10.1101/cshperspect.a006270

PubMed Abstract | CrossRef Full Text | Google Scholar

Hampel, H., Hardy, J., Blennow, K., Chen, C., Perry, G., Kim, S. H., et al. (2021). The amyloid-β pathway in Alzheimer's disease. Mol. Psychiatry 26, 5481–5503. doi: 10.1038/s41380-021-01249-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardy, J. A., and Higgins, G. A. (1992). Alzheimer's disease: the amyloid cascade hypothesis. Science 256, 184–185. doi: 10.1126/science.1566067

PubMed Abstract | CrossRef Full Text | Google Scholar

Harmon, T. S., Holehouse, A. S., Rosen, M. K., and Pappu, R. V. (2017). Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. Elife 6, e30294. doi: 10.7554/eLife.30294

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasegawa, K., Yamaguchi, I., Omata, S., Gejyo, F., and Naiki, H. (1999). Interaction between A beta(1-42) and A beta(1-40) in Alzheimer's beta-amyloid fibril formation in vitro. Biochemistry 38, 15514–15521. doi: 10.1021/bi991161m

PubMed Abstract | CrossRef Full Text | Google Scholar

Hecimovic, S., Wang, J., Dolios, G., Martinez, M., Wang, R., and Goate, A. M. (2004). Mutations in app have independent effects on aβ and ctf? generation. Neurobiol. Dis. 17, 205–218. doi: 10.1016/j.nbd.2004.04.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Hohenberg, P. C., and Halperin, B. I. (1977). Theory of dynamic critical phenomena. Rev. Mod. Phys. 49, 435–479. doi: 10.1103/RevModPhys.49.435

CrossRef Full Text | Google Scholar

Hortschansky, P., Schroeckh, V., Christopeit, T., Zandomeneghi, G., and Fändrich, M. (2005). The aggregation kinetics of Alzheimer's β-amyloid peptide is controlled by stochastic nucleation. Protein Sci. 14, 1753–1759. doi: 10.1110/ps.041266605

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Y.-R., and Liu, R.-T. (2020). The toxicity and polymorphism of β-amyloid oligomers. Int. J. Mol. Sci. 21, 4477. doi: 10.3390/ijms21124477

PubMed Abstract | CrossRef Full Text | Google Scholar

Iwatsubo, T., Odaka, A., Suzuki, N., Mizusawa, H., Nukina, N., and Ihara, Y. (1994). Visualization of A beta 42(43) and A beta 40 in senile plaques with end-specific A beta monoclonals: evidence that an initially deposited species is A beta 42(43). Neuron 13, 45–53. doi: 10.1016/0896-6273(94)90458-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Jan, A., Gokce, O., Luthi-Carter, R., and Lashuel, H. A. (2008). The ratio of monomeric to aggregated forms of Aβ40 and Aβ42 Is an important determinant of amyloid-β aggregation, fibrillogenesis, and toxicity *. J. Biol. Chem. 283, 28176–28189. doi: 10.1074/jbc.M803159200

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, X., Li, J.-E., Schaefer, C., Luo, X., Luo, X., Wollman, A. J. M., et al. (2021). Membraneless organelles formed by liquid-liquid phase separation increase bacterial fitness. Sci. Adv. 7, eabh2929. doi: 10.1126/sciadv.abh2929

PubMed Abstract | CrossRef Full Text | Google Scholar

Kametani, F., and Hasegawa, M. (2018). Reconsideration of amyloid hypothesis and tau hypothesis in Alzheimer's disease. Front. Neurosci. 12, 25. doi: 10.3389/fnins.2018.00025

PubMed Abstract | CrossRef Full Text | Google Scholar

Karran, E., Mercken, M., and Strooper, B. D. (2011). The amyloid cascade hypothesis for Alzheimer's disease: an appraisal for the development of therapeutics. Nat. Rev. Drug Discovery 10, 698–712. doi: 10.1038/nrd3505

PubMed Abstract | CrossRef Full Text | Google Scholar

Kulkarni, C., Meijer, E. W., and Palmans, A. R. A. (2017). Cooperativity scale: a structure-mechanism correlation in the self-assembly of benzene-1,3,5-tricarboxamides. Acc. Chem. Res. 50, 1928–1936. doi: 10.1021/acs.accounts.7b00176

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar-Singh, S., Theuns, J., Van Broeck, B., Pirici, D., Vennekens, K., Corsmit, E., et al. (2006). Mean age-of-onset of familial alzheimer disease caused by presenilin mutations correlates with both increased Aβ42 and decreased Aβ40. Human Mutation 27, 686–695. doi: 10.1002/humu.20336

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuperstein, I., Broersen, K., Benilova, I., Rozenski, J., Jonckheere, W., Debulpaep, M., et al. (2010). Neurotoxicity of Alzheimer's disease Aβ peptides is induced by small changes in the Aβ42 to Aβ40 ratio. EMBO J. 29, 3408–3420. doi: 10.1038/emboj.2010.211

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmann, S., Delaby, C., Boursier, G., Catteau, C., Ginestet, N., Tiers, L., et al. (2018). Relevance of Aβ42/40 ratio for detection of Alzheimer disease pathology in clinical routine: the PLMR scale. Front Aging Neurosci. 10, 138. doi: 10.3389/fnagi.2018.00138

PubMed Abstract | CrossRef Full Text | Google Scholar

Leibler, L., Rubinstein, M., and Colby, R. H. (1991). Dynamics of reversible networks. Macromolecules 24, 4701–4707. doi: 10.1021/ma00016a034

CrossRef Full Text | Google Scholar

Lim, Y. Y., Maruff, P., Kaneko, N., Doecke, J., Fowler, C., Villemagne, V. L., et al. (2020). Plasma Amyloid-β biomarker associated with cognitive decline in preclinical Alzheimer's disease. J. Alzheimers Dis. 77, 1057–1065. doi: 10.3233/JAD-200475

PubMed Abstract | CrossRef Full Text | Google Scholar

Lukkien, J. J., Segers, J. P. L., Hilbers, P. A. J., Gelten, R. J., and Jansen, A. P. J. (1998). Efficient monte carlo methods for the simulation of catalytic surface reactions. Phys. Rev. E 58, 2598–2610. doi: 10.1103/PhysRevE.58.2598

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahaman, Y. A. R., Embaye, K. S., Huang, F., Li, L., Zhu, F., Wang, J.-Z., et al. (2022). Biomarkers used in Alzheimer's disease diagnosis, treatment, and prevention. Ageing Res. Rev. 74, 101544. doi: 10.1016/j.arr.2021.101544

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, R. B. (1996). Comparisons of indefinite self-association models. Chem. Rev. 96, 3044–3064. doi: 10.1021/cr960037v

PubMed Abstract | CrossRef Full Text | Google Scholar

Meisl, G., Yang, X., Hellstrand, E., Frohm, B., Kirkegaard, J. B., Cohen, S. I. A., et al. (2014). Differences in nucleation behavior underlie the contrasting aggregation kinetics of the Aβ40 and Aβ42 peptides. Proc. Natl. Acad. Sci. U.S.A. 111, 9384–9389. doi: 10.1073/pnas.1401564111

PubMed Abstract | CrossRef Full Text | Google Scholar

Michaels, T. C. T., Saric, A., Curk, S., Bernfur, K., Arosio, P., Meisl, G., et al. (2020). Dynamics of oligomer populations formed during the aggregation of Alzheimer's Aβ42 peptide. Nat. Chem. 12, 445–451. doi: 10.1038/s41557-020-0452-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, Y., Ma, B., and Nussinov, R. (2010). Polymorphism in Alzheimer Aβ amyloid organization reflects conformational selection in a rugged energy landscape. Chem. Rev. 110, 4820–4838. doi: 10.1021/cr900377t

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller-Späth, S., Soranno, A., Hirschfeld, V., Hofmann, H., Rüegger, S., Reymond, L., et al. (2010). Charge interactions can dominate the dimensions of intrinsically disordered proteins. Proc. Natl. Acad. Sci. U.S.A. 107, 14609–14614. doi: 10.1073/pnas.1001743107

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, A., Kaneko, N., Villemagne, V. L., Kato, T., Doecke, J., Dore, V., et al. (2018). High performance plasma amyloid-β biomarkers for Alzheimer's disease. Nature 554, 249–254. doi: 10.1038/nature25456

PubMed Abstract | CrossRef Full Text | Google Scholar

Novo, M., Freire, S., and Al-Soufi, W. (2018). Critical aggregation concentration for the formation of early amyloid-β (1–42) oligomers. Sci. Rep. 8, 1783. doi: 10.1038/s41598-018-19961-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Ono, K., Condron, M. M., and Teplow, D. B. (2009). Structure-neurotoxicity relationships of amyloid β-protein oligomers. Proc. Natl. Acad. Sci. U.S.A. 106, 14745–14750. doi: 10.1073/pnas.0905127106

PubMed Abstract | CrossRef Full Text | Google Scholar

Patterson, C. (2018). World Alzheimer Report 2018. The State of the Art of Dementia Research: New Frontiers. An Analysis of Prevalence, Incidence, Cost and Trends. Alzheimer's Disease International.

Google Scholar

Paul, W., Muller, M., Binder, K., Stukan, M. R., and Ivanov, V. A. (2005). Computer Simulations of Liquid Crystals and Polymers: Monte Carlo Simulations of Semi-Flexible Polymers. Dordrecht: Kluwer Academic Publisher.

Google Scholar

Pauwels, K., Williams, T. L., Morris, K. L., Jonckheere, W., Vandersteen, A., Kelly, G., et al. (2012). Structural basis for increased toxicity of pathological Aβ42:Aβ40 ratios in Alzheimer disease. J. Biol. Chem. 287, 5650–5660. doi: 10.1074/jbc.M111.264473

PubMed Abstract | CrossRef Full Text | Google Scholar

Pérez-Grijalba, V., Romero, J., Pesini, P., Sarasa, L., Monleón, I., San-José, I., et al. (2019). Plasma Aβ42/40 ratio detects early stages of Alzheimer's disease and correlates with CSF and neuroimaging biomarkers in the AB255 study. J. Prevent. Alzheimers Dis. 6, 34–41. doi: 10.14283/jpad.2018.41

PubMed Abstract | CrossRef Full Text | Google Scholar

Raffaelli, C., Bose, A., Vrusch, C. H. M. P., Ciarella, S., Davris, T., Tito, N. B., et al. (2020). “Rheology, rupture, reinforcement and reversibility: computational approaches for dynamic network materials,” in Self-Healing and Self-Recovering Hydrogels, Vol. 285, eds C. Creton and O. Okay (Cham: CRC Press).

Google Scholar

Reister, E., and Müller, M. (2003). Formation of enrichment layers in thin polymer films: the influence of single chain dynamics. J. Chem. Phys. 118, 8476–8488. doi: 10.1063/1.1565105

CrossRef Full Text | Google Scholar

Reister, E., Müller, M., and Binder, K. (2001). Spinodal decomposition in a binary polymer mixture: dynamic self-consistent-field theory and monte carlo simulations. Phys. Rev. E 64, 041804. doi: 10.1103/PhysRevE.64.041804

PubMed Abstract | CrossRef Full Text | Google Scholar

Ricciarelli, R., and Fedele, E. (2017). The amyloid cascade hypothesis in Alzheimer's disease: it's time to change our mind. Curr. Neuropharmacol. 15, 926–935. doi: 10.2174/1570159X15666170116143743

PubMed Abstract | CrossRef Full Text | Google Scholar

Roche, J., Shen, Y., Lee, J. H., Ying, J., and Bax, A. (2016). Monomeric Aβ1–40 and Aβ1–42 peptides in solution adopt very similar ramachandran map distributions that closely resemble random coil. Biochemistry 55, 762–775. doi: 10.1021/acs.biochem.5b01259

PubMed Abstract | CrossRef Full Text | Google Scholar

Saito, M., and Matsumoto, M. (2008). “Simd-oriented fast mersenne twister: a 128-bit pseudorandom number generator,” in Monte Carlo and Quasi-Monte Carlo Methods 2006, eds A. Keller, S. Heinrich and H. Niederreiter (Berlin; Heidelberg: Springer Berlin Heidelberg), 607–622.

Google Scholar

Schaefer, C. (2018). Structuring of fluid adlayers upon ongoing unimolecular adsorption. Phys. Rev. Lett. 120, 036001. doi: 10.1103/PhysRevLett.120.036001

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaefer, C., Laity, P. R., Holland, C., and McLeish, T. C. B. (2020). Silk protein solution: a natural example of sticky reptation. Macromolecules 53, 2669–2676. doi: 10.1021/acs.macromol.9b02630

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaefer, C., and McLeish, T. C. B. (2022). Theoretical rheo-physics of silk: Intermolecular associations reduce the critical specific work for flow-induced crystallization. J. Rheol. 66, 515–534. doi: 10.1122/8.0000411

CrossRef Full Text | Google Scholar

Schaefer, C., Paquay, S., and McLeish, T. C. B. (2019). Morphology formation in binary mixtures upon gradual destabilisation. Soft Matter. 15, 8450. doi: 10.1039/C9SM01344J

PubMed Abstract | CrossRef Full Text | Google Scholar

Scheuner, D., Eckman, C., Jensen, M., Song, X., Citron, M., Suzuki, N., et al. (1996). Secreted amyloid beta-protein similar to that in the senile plaques of Alzheimer's disease is increased in vivo by the presenilin 1 and 2 and APP mutations linked to familial Alzheimer's disease. Nat. Med. 2, 864–870. doi: 10.1038/nm0896-864

PubMed Abstract | CrossRef Full Text | Google Scholar

Selkoe, D. J., and Hardy, J. (2016). The amyloid hypothesis of Alzheimer's disease at 25 years. EMBO Mol. Med. 8, 595–608. doi: 10.15252/emmm.201606210

PubMed Abstract | CrossRef Full Text | Google Scholar

Sengupta, U., Nilson, A. N., and Kayed, R. (2016). The role of Amyloid-β oligomers in toxicity, propagation, and immunotherapy. EBioMedicine 6, 42–49. doi: 10.1016/j.ebiom.2016.03.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Shin, Y., and Brangwynne, C. P. (2017). Liquid phase condensation in cell physiology and disease. Cell. Biophys. 357, 1253. doi: 10.1126/science.aaf4382

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, A., Puri, S., and Dasgupta, C. (2012). Growth kinetics of nanoclusters in solution. J. Phys. Chem. B 116, 4519. doi: 10.1021/jp211380j

PubMed Abstract | CrossRef Full Text | Google Scholar

Smulders, M., Nieuwenhuizen, M., de Greef, T., van der Schoot, P., Schenning, A., and Meijer, E. (2010). How to distinguish isodesmic from cooperative supramolecular polymerisation. Chem. A Eur. J. 16, 362–367. doi: 10.1002/chem.200902415

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinhauser, M. O. (2005). A molecular dynamics study on universal properties of polymer chains in different solvent qualities. Part I. a review of linear chain properties. J. Chem. Phys. 122, 094901. doi: 10.1063/1.1846651

PubMed Abstract | CrossRef Full Text | Google Scholar

Stelzmann, R. A., Norman Schnitzlein, H., and Reed Murtagh, F. (1995). An english translation of alzheimer's 1907 paper, “über eine eigenartige erkankung der hirnrinde”. Clin. Anat. 8, 429–431. doi: 10.1002/ca.980080612

PubMed Abstract | CrossRef Full Text | Google Scholar

Subramanian, G., and Shanbhag, S. (2009). Conformational free energy of melts of ring-linear polymer blend. Phys. Rev. E 80, 041806. doi: 10.1103/PhysRevE.80.041806

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamaoka, A., Kondo, T., Odaka, A., Sahara, N., Sawamura, N., Ozawa, K., et al. (1994). Biochemical evidence for the long-tail form (A beta 1-42/43) of amyloid beta protein as a seed molecule in cerebral deposits of Alzheimer's disease. Biochem. Biophys. Res. Commun. 205, 834–842. doi: 10.1006/bbrc.1994.2740

PubMed Abstract | CrossRef Full Text | Google Scholar

Teunissen, C. E., Verberk, I. M. W., Thijssen, E. H., Vermunt, L., Hansson, O., Zetterberg, H., et al. (2022). Blood-based biomarkers for Alzheimer's disease: towards clinical implementation. Lancet Neurol. 21, 66–77. doi: 10.1016/S1474-4422(21)00361-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Tolar, M., Abushakra, S., and Sabbagh, M. (2019). The path forward in Alzheimer's disease therapeutics: reevaluating the amyloid cascade hypothesis. Alzheimers Dement. 16, 1553–1560. doi: 10.1016/j.jalz.2019.09.075

PubMed Abstract | CrossRef Full Text | Google Scholar

Trautenberg, H. L., Sommer, J.-U., and Goritz, D. (1995). Structure and swelling of end-linked model networks. J. Chem. Soc. Faraday Trans. 91, 2649–2653. doi: 10.1039/FT9959102649

PubMed Abstract | CrossRef Full Text | Google Scholar

van der Schoot, P. (2005). “Theory of supramolecular polymerization,” in Supramolecular Polymers, 2nd Edn, eds A. Ciferri (Boca Raton: CRC Press), 77–106.

Google Scholar

Wälti, M. A., Orts, J., Vögeli, B., Campioni, S., and Riek, R. (2015). Solution NMR studies of recombinant Aβ(1-42): from the presence of a micellar entity to residual β-sheet structure in the soluble species. ChemBioChem 16, 659–669. doi: 10.1002/cbic.201402595

PubMed Abstract | CrossRef Full Text | Google Scholar

Weber, H., Paul, W., and Binder, K. (1999). Monte carlo simulation of a lyotropic first-order isotropic-nematic phase transition in a lattice polymer model. Phys. Rev. E 59, 2168–2174. doi: 10.1103/PhysRevE.59.2168

CrossRef Full Text | Google Scholar

Wegmann, S., Eftekharzadeh, B., Tepper, K., Zoltowska, K. M., Bennett, R. E., Dujardin, S., et al. (2018). Tau protein liquid-liquid phase separation can initiate tau aggregation. EMBO J. 37, e98049. doi: 10.15252/embj.201798049

PubMed Abstract | CrossRef Full Text | Google Scholar

Wuttke, R., Hofmann, H., Nettels, D., Borgia, M. B., Mittal, J., Best, R. B., et al. (2014). Temperature-dependent solvation modulates the dimensions of disordered proteins. Proc. Natl. Acad. Sci. U.S.A. 11, 5213–5218. doi: 10.1073/pnas.1313006111

PubMed Abstract | CrossRef Full Text | Google Scholar

Yaffe, K., Weston, A., Graff-Radford, N. R., Satterfield, S., Simonsick, E. M., Younkin, S. G., et al. (2011). Association of plasma beta-amyloid level and cognitive reserve with subsequent cognitive decline. JAMA 305, 261–266. doi: 10.1001/jama.2010.1995

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, Y., and Wang, C. (2007). Aβ40 protects non-toxic Aβ42 monomer from aggregation. J. Mol. Biol. 369, 909–916. doi: 10.1016/j.jmb.2007.04.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Zetterberg, H. (2019). Blood-based biomarkers for Alzheimer's disease-an update. J. Neurosci. Methods 319, 2–6. doi: 10.1016/j.jneumeth.2018.10.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q., Sidorenko, J., Couvy-Duchesne, B., Marioni, R. E., Wright, M. J., Goate, A. M., et al. (2020). Risk prediction of late-onset Alzheimer's disease implies an oligogenic architecture. Nat. Commun. 11, 4799. doi: 10.1038/s41467-020-18534-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y.-W., Thompson, R., Zhang, H., and Xu, H. (2011). APP processing in Alzheimer's disease. Mol. Brain 4, 3. doi: 10.1186/1756-6606-4-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, N., Ren, Y., Yamazaki, Y., Qiao, W., Li, F., Felton, L. M., et al. (2020). Alzheimer's risk factors age, APOE genotype, and sex drive distinct molecular pathways. Neuron 106, 727.e6–742.e6. doi: 10.1016/j.neuron.2020.02.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, X., Bora, R. P., Barman, A., Singh, R., and Prabhakar, R. (2012). Dimerization of the full-length Alzheimer amyloid β-peptide (Aβ42) in explicit aqueous solution: a molecular dynamics study. J. Phys. Chem. B 116, 4405–4416. doi: 10.1021/jp210019h

PubMed Abstract | CrossRef Full Text | Google Scholar