Efficient Low Threshold Frequency Conversion in AlGaAs-On-Insulator Waveguides

A design study is presented for an efficient, compact and robust device to convert the frequency of single-photons from the near-infrared to the telecom C-band. The material platform aluminum gallium arsenide (AlGaAs)-on-insulator, with its relatively large second-order nonlinearity, is used to create highly confined optical modes. This platform can feasibly incorporate single-photon emitters such as indium arsenide (InAs) on gallium arsenide (GaAs), paving the way towards direct integration of single-photon sources and nonlinear waveguides on the same chip. In this design study, single-pass difference-frequency generation (DFG) producing C-band single-photons is enabled via form birefringent phase-matching between a 930 nm single-photon pump and continuous wave (CW) idler at 2,325 nm. In particular the idler and single-photons are combined with an on-chip directional coupler, and then tapered to a single waveguide where the three modes are phase-matched. The design is studied at a special case, showing high fabrication tolerances, and an internal conversion efficiency up to 41%.

1 Introduction

Single-photon sources are beneficial for applications such as random number generation, quantum metrology, quantum lithography (Giovannettil et al., 2004), and quantum information such as quantum computations and quantum key distribution (QKD) (Eisaman et al., 2011; O’Brien, 2007). One of the leading techniques to efficiently generate single-photons, is to optically pump semiconductor quantum-dots (QD) (Uppu et al., 2020a; b, 2021). It is desired to have QD emission at 1,550 nm to make use of common and optimized optical components and to support long-range quantum networks in the telecom band. This spectral range is essential for optical networks, where ultra-low propagation losses only occur in the telecom C-band (1,530–1,565 nm) (Kao, 2010). In particular, large-scale quantum networks based on entanglement distribution requires highly indistinguishable single-photon sources without post-selection (Srocka et al., 2020). Single-photon sources emitting directly in the telecom bands are advancing. However, the more efficient quasi-deterministic sources emitting mainly in the visible (VIS) or near-infrared (NIR) spectrum (Cao et al., 2019) are still preferred for several of their properties such as high indistinguishability, high purity, and being semi-deterministic (Müller et al., 2018; Cao et al., 2019; Paesani et al., 2020; Stachurski et al., 2022).

As an alternative to direct telecom emission, second-order nonlinear frequency conversion can transfer the quantum properties and states of the single-photons emitted by the quantum dots to the single-photons in the C-band (Kumar, 1990; Huang and Kumar, 1992; Singh et al., 2019). In recent years, this has been thoroughly investigated for both entangled photon-pairs and nonlinear conversion of the VIS/NIR to the C-band (Senellart et al., 2017). This also supports a denser communication scheme in the case of optical communication through wavelength division multiplexing (Fisher et al., 2021). However, the second-order nonlinear conversion of single-photons has only been shown for difference frequency generation (DFG) in periodically poled lithium niobate (PPLN) waveguides (De Greve et al., 2012; Bock et al., 2018; Dréau et al., 2018; Zhang et al., 2020; Da Lio et al., 2022). Lithium niobate (LN) is a mature material for frequency conversion, exhibiting strong second-order nonlinearities and low losses from VIS to mid-IR (Kores et al., 2021). Still, efficient frequency conversion in LN requires periodic poling to create quasi-phase-matching (QPM). Although this phase-matching technique has been transferred to thin-film PPLN-on-insulator, significantly improving the nonlinear conversion efficiency, LN still has a relatively low second-order optical susceptibility and weak optical confinement compared to semiconductor nonlinear crystals as gallium phosphide (GaP), indium gallium phosphide (InGaP), gallium arsenide (GaAs), and AlGaAs (Adachi, 1989; Chen et al., 2019; Wilson et al., 2020; Poulvellarie et al., 2021).

This study focus on designing DFG in zinc-blende materials. The material AlGaAs is recently getting more attention as an integrated quantum platform, to generate entangled photon-pairs in the C-band using, e.g. spontaneous parametric down-conversion (SPDC). (Placke and Ramelow, 2020). In this paper AlGaAs is studied for DFG with an indium arsenide (InAs) QD source emitting single-photons near λ_p = 930 nm. These can be converted to a signal at λ_s = 1,550 nm, by DFG with an idler wavelength ${\lambda }_{\text{i}}={(1/{\lambda }_{\text{p}}-1/{\lambda }_{\text{s}})}^{-1}=\mathrm{2,325}$ nm. This is a wavelength that can be generated with frequency conversion, or gallium antimonide (GaSb) based laser diodes (Joullié and Christol, 2003; Boehm et al., 2011; Spott et al., 2017; Wang et al., 2018). Single-photon sources and detectors have been demonstrated on a variety of platforms, and there is a clear integration roadmap to combine these technologies on the same platform with the semiconductor nonlinear waveguides (Kahl et al., 2015; McDonald et al., 2019; Paesani et al., 2020). Furthermore, integrating these III-V materials on silica with a silicon substrate will further improve the conversion efficiency, by giving a strong confinement of the modes (Chang et al., 2016; Guo et al., 2016; Roland et al., 2016). A special interest is given to AlGaAs as the second-order nonlinear material to leverage a higher effective nonlinearity compared to conventional single-photon frequency conversion in PPLN.

The paper is organized as follows. In the next section, the case of DFG in crystals belonging to the zinc-blende point group is shown, explaining the required optical polarization and crystal orientation. This is followed by an analytical expression for the conversion efficiency in the case of DFG with the consideration of a weak pump, propagation losses, imperfect phase-matching, and strong confinement in the waveguides. Next, a DFG waveguide is designed in AlGaAs and the analytical model derived for DFG in zinc-blende is employed to simulate the conversion process. From these results, a design with an on-chip optical combiner is proposed and followed by a discussion of the design trade-offs.

2 Theory

2.1 Design

As the base material for the nonlinear conversion Al_xGa_1−xAs is considered with an aluminum mole fraction x = 0.2. This value is chosen to increase the bandgap energy and thus reduce one- and two-photon absorption at the signal wavelength. In addition, it is a mature material for integrated photonics and can be grown on GaAs, with a large second-order nonlinear coefficient. Using Kleinmann symmetry, the effective nonlinear d coefficient can be found as d_eff = d₁₄ ≈ 110  pm/V (Ohashi et al., 1993; Shoji et al., 1997).

For achieving efficient frequency conversion, the pump, signal, and idler wavelengths must all be phase-matched. Because cubic crystals are isotropic, birefringent phase-matching generally cannot occur in bulk forms of these crystals. A waveguide structure can be used to induce form birefringence and obtain phase-matching (Tien, 1971; Van der Ziel, 1975; Fiore et al., 1998). AlGaAs-on-insulator can achieve phase-matching for DFG when the pump is polarized along the [001] crystal axis for normal material dispersion, as shown in Figure 1. The pump mode has a quasi-transverse-magnetic (TM) polarization for this geometry. The direction of propagation z is along $[1\bar{1}0]$. The idler and signal are then quasi-transverse-electric (TE) modes, polarized along [110].

FIGURE 1

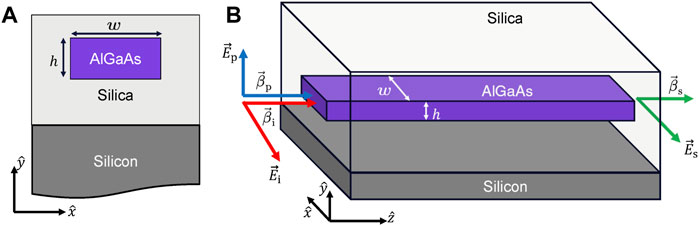
FIGURE 1. Schematic of the waveguide, (A) cross-section with the material layer stack and illustration of the simulated geometry, and of the (B) conversion of a pump single-photon to a signal, using DFG in an AlGaAs-on-insulator waveguide. AlGaAs is grown along the $\widehat{y}=[001]$ crystal axis. The signal and idler are polarized along $\widehat{x}=$[110] and the pump along $\widehat{y}$. The direction of propagation is along $\widehat{z}=[1\bar{1}0]$.

2.2 Conversion Efficiency

The complex electric fields ${\vec{\mathcal{E}}}_{\nu }$ for the optical waves involved in the DFG process can be expressed as (Yariv, 1973):

${\vec{\mathcal{E}}}_{\nu }\left(\vec{r},t\right)={\mathcal{Z}}_{\nu }\left(z\right){\vec{\mathit{E}}}_{\nu }\left(x,y\right)e^{i{k}_{\nu }z}{e}^{-i{\omega }_{\nu }t},(1)$

where the subscript ν apply for the pump (p), the signal (s) and the idler (i), ω_ν is the angular frequency, and the slowly-varying complex amplitude ${\mathcal{Z}}_{\nu }$ allows for mode coupling along the direction of propagation z. The nonlinear waveguide length is L, and starts at z = 0. ${\vec{\mathit{E}}}_{\nu }$ relates to the mode profile. The complex wavenumber is defined as: k_ν = β_ν + iα_ν/2, where β_ν is the wavenumber, and α_ν is the attenuation coefficient. The coupled amplitude equations can be solved assuming these boundary conditions: ${\mathcal{Z}}_{\text{s}}(0)=0$, ${\mathcal{Z}}_{\text{p}}(0)\equiv {\mathcal{Z}}_{\text{p},0}$, and ${\mathcal{Z}}_{\text{i}}(0)={\mathcal{Z}}_{\text{i}}(L)$ (Armstrong et al., 1962). It is assumed that the idler is strong compared to the single-photon pump and signal, and that the idler experiences small losses α_iL ≪ 1. The details of these derivations can be found in (Ulsig et al., 2022).The conversion efficiency can be defined as the fraction of pump power that is converted to the signal after propagating through the nonlinear waveguide: η_P ≡ P_s(L)/P_p(L). It is practical in the particular case of single-photons to redefine the conversion efficiency, as the fraction of pump photons converted to signal photons:

$\eta \equiv N_{\text{s}}\left(L\right)/N_{\text{p}}\left(L\right)={\eta }_{\text{max}}\left|{\gamma }^2{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}}^2\left(\xi L/2\right)\right|L^2{e}^{-L\left(\mathrm{\Delta }\alpha +2{\alpha }_{\text{s}}\right)/2},(2)$

where ξ is defined as:

${\xi }^2\equiv 4{\gamma }^2+{\left(\mathrm{\Delta }k+i{\alpha }_{\text{i}}\right)}^2,(3)$

and involves the wavenumber-mismatch Δk ≡ k_p − k_i − k_s, and the loss-mismatch is Δα ≡ α_p − α_s − α_i. The complex field is only of interest for a single polarization, and will from here be referred to as E_ν,x and E_ν,y for the x (TE) and y (TM) components, respectively. The nonlinear gain parameter γ is defined from:

${\gamma }^2\equiv \frac{8{\omega }_{\text{s}}{\omega }_{\text{p}}}{c^2}\frac{{\kappa }_{\text{s}}{\kappa }_{\text{p}}{P}_{\text{i}}}{{\iint }_{{\mathbb{R}}^2}{E}_{\mathrm{i},x}{H}_{\mathrm{i},y}^{\ast }\text{d}x\text{d}y}.(4)$

where c is the speed of light in vacuum, and P_i is the idler power. The double integral is performed over transverse xy − plane. κ_s and κ_p are coupling coefficients defined as:

${\kappa }_{\text{s}}\equiv \frac{{\iint }_{{\mathbb{R}}^2}d\left(x,y\right)E_{\text{p},y}{E}_{\text{i},x}^{\ast }{H}_{\text{s},y}^{\ast }\text{d}x\text{d}y}{n_{\text{s\hspace{0.17em}}}{\iint }_{{\mathbb{R}}^2}{E}_{\mathrm{s},x}{H}_{\mathrm{s},y}^{\ast }\text{d}x\text{d}y}(\mathrm{5a})$

${\kappa }_{\text{p}}\equiv \frac{{\iint }_{{\mathbb{R}}^2}d\left(x,y\right)E_{\text{i},x}{E}_{\text{s},x}{H}_{\text{p},x}^{\ast }\text{d}x\text{d}y}{n_{\text{p}}{\iint }_{{\mathbb{R}}^2}{E}_{\mathrm{p},x}{H}_{\mathrm{p},y}^{\ast }\text{d}x\text{d}y},(\mathrm{5b})$

where the effective refractive indices for the fundamental mode of the signal and pump are n_s and n_p, respectively. d(x, y) is spatially varying and has the value of d_eff where there material has an appreciable second-order susceptibility, and it is negligible elsewhere. In this case only the nonlinear waveguide core contributes to the conversion. The upper bound for the conversion efficiency is set by the effective modal-overlap with the waveguide:

${\eta }_{\text{max}}=\left|\frac{n_{\text{p}}{\iint }_{{\mathbb{R}}^2}d\left(x,y\right)E_{\mathrm{p},y}{E}_{\mathrm{i},x}^{\ast }{H}_{\mathrm{s},y}^{\ast }\text{d}x\text{d}y}{n_{\text{s}}{\iint }_{{\mathbb{R}}^2}d\left(x,y\right)E_{\mathrm{i},x}{E}_{\mathrm{s},x}{H}_{\mathrm{p},x}^{*}\text{d}x\text{d}y}\right|.(6)$

The maximal conversion efficiency is investigated further in the discussion section.

3 Simulation

Typical models of the refractive index of each material are used to simulate the optical fields and effective refractive indices for optimizing the geometry for form birefringent phase-matching (Malitson, 1965; Weber, 1990; Tan, 1998; Papatryfonos et al., 2021). A 2-dimensional finite-difference method (FDM) eigenmode solver is used to simulate the waveguide (EMode Photonix, 2022). A cross-section of the layer stack and waveguide geometry is seen in Figure 1A), with the relevant mode profiles of the electric fields in Figure 2). The conversion efficiency Eq. 2 can be calculated assuming propagation losses of α_p = 15 dB/cm, α_s = 2 dB/cm, α_i = 1 dB/cm from previous demonstrations at similar wavelengths in comparable materials (Porkolab et al., 2014; Ottaviano et al., 2016; Chiles et al., 2019; Stanton et al., 2020; Xie et al., 2022). This can be seen in Figure 3 at two different idler input powers of 15 and 60 mW, and as a function of the waveguide length. The single-photons are converted to the C-band with a probability depending on the idler power while propagating in the waveguide. However, back-conversion can dominate the process because the phase-matching condition is satisfied for both DFG and sum-frequency generation (SFG). After depletion of the pump, the 1,550 nm photons will be back-converted to 930 nm. The oscillating behavior of the conversion process depends on the waveguide length and the parameter ξ that depends on the intensity of the idler. This is shown for the two cases of different idler intensities, demonstrating how to minimize the back-conversion by changing the intensity of the idler. Assuming a non-depleted signal, the length-normalized conversion efficiency can also be calculated: η_n = 2,560/(W ⋅cm²). An upper cap is shown as a function of the maximal conversion efficiency and propagation losses, with perfect phase-matching and negligible loss, approximately given as:

${\eta }_{\text{peak}}\approx {\eta }_{\text{max}}{e}^{-L\left(\mathrm{\Delta }\alpha +2{\alpha }_{\text{s}}\right)/2}.(7)$

However, the peak value is also affected by the sinc² dependence shown in Eq. 2, and is thus seen to vary from Eq. 7 due to imperfect phase-matching and losses.

FIGURE 2

FIGURE 2. Simulated mode profile for the pump (930 nm), idler (2,325 nm) and signal (1,550 nm) for h = 144 nm and w = 2,285 nm.

FIGURE 3

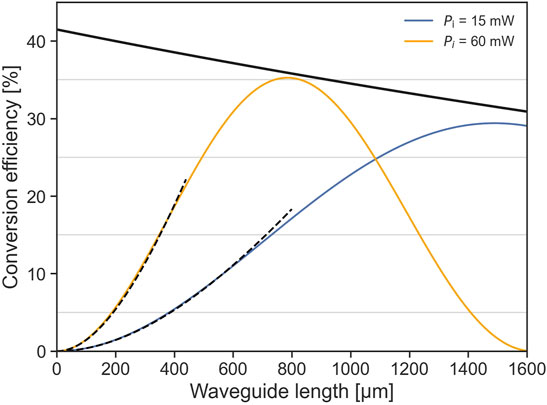
FIGURE 3. Conversion efficiency calculated as a function of the waveguide length for two values of idler power P_i. Dashed lines represent the non-depleted case. The thick black line represents an upper cap for the conversion efficiency from Eq. 2 The peak conversion efficiency Eq. 7, is limited here due to the mismatch in modal overlap and propagation losses.

DFG using form birefringent phase-matching is very sensitive to variations in the waveguide height, as well as the width and length. For longer waveguides, a lower optical power is needed for complete frequency conversion. However, there is a limit where the conversion efficiency does not increase with length due to propagation losses and degradation of phase-matching because of fabrication variation. A waveguide length of 1.6 mm is chosen in this study from a practical perspective, which needs an approximate input power of 15 mW to reach the peak conversion efficiency. Perfect phase-matching is calculated in Figures 4A,B by sweeping over the core width and height, respectively. The full-width half-maximum (FWHM) of the conversion efficiency is indicated by the shaded area and plotted in Figure 4C for different core heights, at their respective widths resulting in perfect phase-matching. It can be seen that the tolerance of the width increases with larger heights. A core height of 144 nm is taken as a special case throughout this study. This is due to the similar widths (2,025–2,640 nm) that allow for perfect phase-matching at the heights h = 143–145 nm. Furthermore, a narrower waveguide introduces more significant sidewall scattering, whereas a wider allows for higher-order modes to be excited, making it more challenging to use in practice. The phase-matching, and thus conversion efficiency, is also dependent on the wavelengths as seen in Figure 5 as a function of the signal wavelength. The pump is fixed at 930 nm, where the signal, and correspondingly idler are changing in wavelength. This demonstrates a fine-tuning for small fabrication variations, and returns a bandwidth defined from the FWHM of the signal: Δλ = 2.6 nm.

FIGURE 4

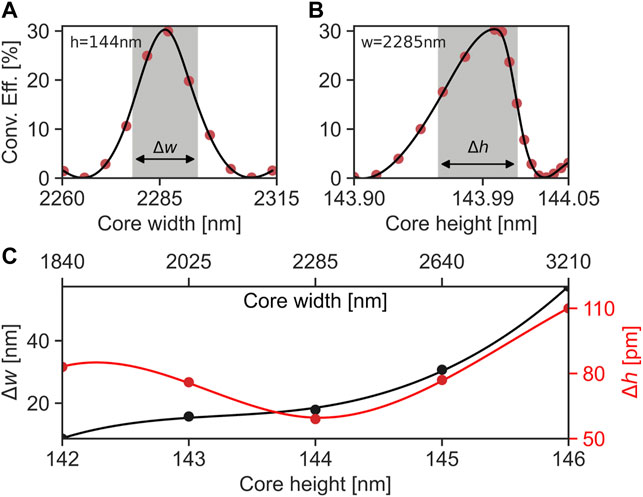
FIGURE 4. Conversion efficiency simulated as a function of (A), for the core width, (B) for the core height. The points are simulated, where the curve is interpolated by a spline function. The grey area indicates the FWHM. (C) show the FWHM of the widths and heights corresponding to near perfect phase-matching.

FIGURE 5

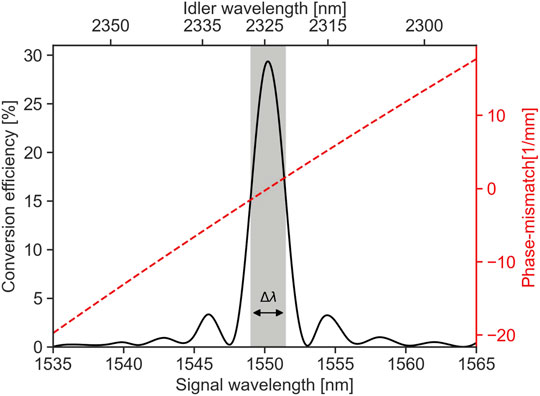
FIGURE 5. Conversion efficiency (left axis, black) calculated as a function of the signal wavelength, and corresponding idler wavelength. The phase-mismatch (Δβ) is seen as a function of the signal and idler wavelengths (right axis, red). The FWHM of 2.6 nm of the signal is indicated by the grey area.

3.1 Directional Coupler

For the design presented here, the strong idler is coupled to the nonlinear platform from a separate source and combined with the pump from an on-chip single-photon source. An on-chip directional coupler is needed to merge these two inputs to one nonlinear waveguide. Losing single-photons represents a loss of signal, whereas a loss of idler-photons only changes the power in the waveguide and modify the conversion efficiency. The idler power may be compensated by just increasing the power from the idler source. It is therefore desired to convert the single-photons before they propagate too far in the waveguide and experience significant total loss from scattering and absorption mechanisms. The coupler is designed with an AlGaAs thickness h = 144 nm and a fixed waveguide width w = 2,000 nm. After the coupling section, the waveguide containing both modes is tapered to the width that satisfies perfect phase-matching.

The device is seen in Figure 6 with two input waveguides separated by 150 μm to allow the coupling of two lensed fibers. The idler is coupled into the left bent waveguide where it is guided into a specified gap g, of the parallel waveguide containing the single-photons. The distance from the coupling edges, to where the waveguides are parallel is 150 μm, and the bending radius is 75 μm. The case of g = 400 nm is chosen as an example and simulated with an eigenmode-expansion (EME) solver (Ansys-Lumerical). The supermodes of the idler (top insets) and pump (bottom insets) are simulated and shown evidently before transitioning out to a straight waveguide. It is only the final modes indicated by c, where the waveguides are parallel, that the pump photons are significantly perturbed by the other waveguide. The idler is less confined than the pump because of the large wavelength difference as well as polarization, resulting in a much weaker coupling for the single-photons compared to the strong coupling for the idler. This is demonstrated in Figure 7, where the coupling is plotted as a function of the gap. The coupling length is defined as the propagation distance required for a complete power-transfer of the idler waveguide to the single-photon waveguide, and the crosstalk is the probability for a single-photon to couple into the other waveguide. The gap is changed at the idler and pump wavelength, for waveguide thickness variations of ±1% of the target height of h = 144 nm, to validate the design’s robustness to fabrication uncertainties. The errorbars show the tolerances to the coupling length, for having more than 95% of the idler coupled to the single-photon waveguide. The coupling length tolerances increase with larger gaps, however this comes at a price of larger variations to waveguide heights and propagation losses. The graph suggests that single-photons can be effectively retained in their own waveguide, while the idler is also transferred to it, assuming typical fabrication tolerances. The coupling length is around 250 μm, where probability for a single-photon coupling to the other waveguide is below 0.01% For the special case g = 400 nm.

FIGURE 6

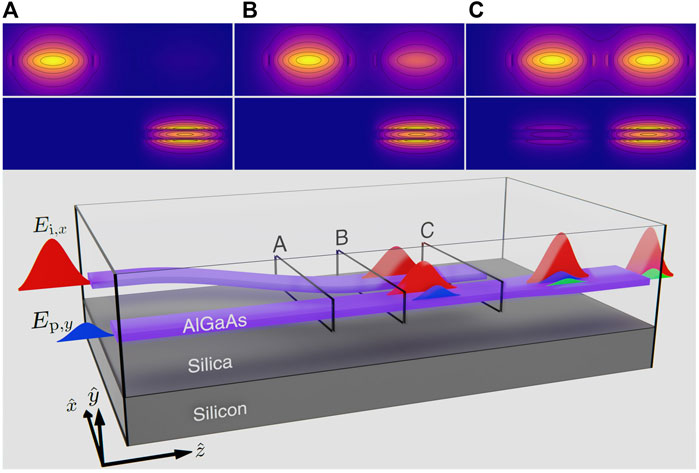
FIGURE 6. Schematic of the device frequency converter integrated on silicon. The strong idler (red wave) and weak pump (blue wave) are combined in one AlGaAs waveguide. Both modes interact with the waveguide and convert the frequency to the signal (green wave). The supermodes of the idler (top) and pump (bottom) is simulated, for the position labeled (A–C) of the coupling section.

FIGURE 7

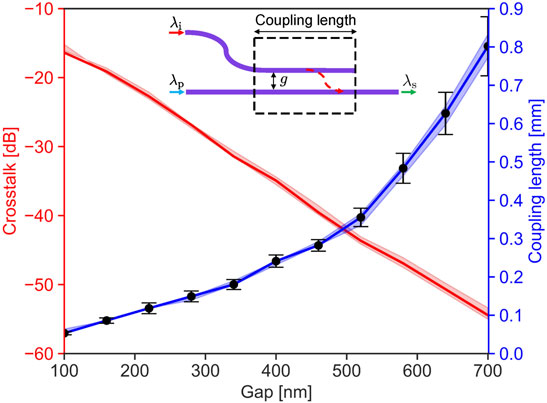
FIGURE 7. Crosstalk (left axis, in red) and corresponding coupling length (right axis, in blue) simulated as a function of the gap. Shaded areas represent the impact generated by a deviation of ± 1% from the target waveguide height. Errors bars gives the coupling length tolerances of having 95% or more of the idler coupled.

4 Discussion

The conversion was shown to be efficient with a small optical input power of the idler, as well as a short waveguide length. However, the current design is limited to $\sim 41\%$ in Figure 3 from the analytical function of the maximal conversion efficiency η_max. The parameter is investigated as a function of the nonlinear core-confinement, and modal overlap at different core heights, with the results plotted in Figure 8. The optical modes of the pump are shown at three different heights, where the yellow inset b is the 144 nm height used throughout this study. The modal overlap is relatively constant, but will set the upper limit of the conversion efficiency for thick waveguide cores. The current limitation is from the confinement of the pump, which can greatly improve the conversion efficiency with a higher confinement to the nonlinear core. However, the form birefringent phase-matching method makes use of the optical mode, with lowest wavelength is not entirely confined to the core. Other phase-matching schemes such as automatic phase-matching (Arabì et al., 2020), QPM or counter-propagating phase-matching could allow for a better confinement and overlap, resulting in higher conversion efficiencies.

FIGURE 8

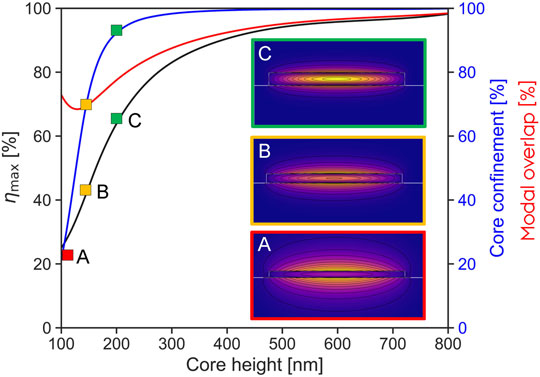
FIGURE 8. Maximum conversion efficiency from Eq. 6 plotted on the left axis, as a function of waveguide core height. The confinement of the pump in the core is plotted in blue. The modal overlap is plotted in red, is seen to dominate the conversion limitation at thicker waveguides. Insets show the corresponding pump mode profile labeled by (A–C) for 100 nm, 144 nm, and 200 nm core height.

Another aspect of the nonlinear conversion is the phase ϕ_ν of the sources. The phase information resides in the complex slowly-varying amplitude ${\mathcal{Z}}_{\nu }=\left|{\mathcal{Z}}_{\nu }\right|e^{i{\varphi }_{\nu }}$. The frequency conversion can induce a nonlinear phase-shift, resulting in the signal obtaining a phase based on the phase difference of the pump and idler ϕ_s(z) = ϕ_p(z) − ϕ_i(z). However, for an initial and fixed phase of the pump and idler, the change in phase is constant at the phase-matched condition (Eto and Hirano, 2021).

The current approach of PPLN can theoretically allow for almost perfect conversion of the single-photons from 930 nm to the telecom C-band. This is also shown experimentally where state-of-the-art for the internal conversion efficiency have been measured up to η ≈ 95%, with an external conversion efficiency up to about 41% (Da Lio et al., 2022). High power CW lasers, reaching up to 100–300 mW, or pulsed sources are needed for conversion in PPLN waveguides of several centimeters. PPLN-on-insulator are appearing for QFC and drastically reducing the required optical power, as well as simplifying the coupling for integrated platforms (Chen et al., 2021). The specific case of L = 1.6 mm and g = 400 nm for the coupling was investigated, assuming the conservative propagation losses and without coupling loss. An end-to-end conversion efficiency of 31%, is obtained. This is mainly due to η_max = 41%, and the losses from the idler traversed the coupling section and nonlinear waveguide. High fabrication tolerances were shown, especially for the coupling section but also for the width of the nonlinear waveguide core. The height is the most critical parameter, but with a tunable idler and several waveguide structures spanning different sections of a wafer, phase-matching is attainable.

5 Conclusion

This study investigates and validates the concept of an on-chip single-photon source heterogeneously integrated with a nonlinear waveguide to convert single-photons to the C-band using DFG. Furthermore, an integrated circuit in AlGaAs-on-insulator is investigated for the practical implementation of single-photon DFG. The theory for DFG in the case of a weak pump-power and phase-loss mismatch is revisited, where an analytical formulation is derived for the maximum conversion. This allows to optimize the design of nonlinear waveguides using form birefringent phase-matching. A design is proposed with two input waveguides and an optimized directional coupler to retain the single-photons in its own waveguide. Simulations show that power transfer between two straight waveguides is feasible, allowing for an idler beam at a longer wavelength to be combined with a pump of shorter wavelength in a single waveguide. Phase-matching is shown for single-pass DFG in a AlGaAs waveguide, with an internal maximum conversion efficiency of nearly 41%, limited by the modal overlap, the interaction of the modes with the nonlinear waveguide and linear losses.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

EU conceptualized the manuscript and figures. ID-E conceptualized and verified the coupling design. ES has contributed to the discussion and simulations. NV contributed to the theory and supervised the project. All of the authors have approved the final submission.

Funding

We acknowledge support from Innovation Fund Denmark.

Conflict of Interest

Author ES was employed by EMode Photonix

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adachi, S. (1989). Optical Dispersion Relations for GaP, GaAs, GaSb, InP, InAs, InSb, AlxGa1−xAs, and In1−xGaxAsyP1−y. J. Appl. Phys. 66, 6030–6040. doi:10.1063/1.343580

CrossRef Full Text | Google Scholar

Arabì, C. M., Parra-Rivas, P., Ciret, C., Gorza, S.-P., and Leo, F. (2020). Modeling of Quasi-Phase-Matched Cavity-Enhanced Second-Harmonic Generation. Phys. Rev. A 101, 043818. doi:10.1103/physreva.101.043818

CrossRef Full Text | Google Scholar

Armstrong, J. A., Bloembergen, N., Ducuing, J., and Pershan, P. S. (1962). Interactions between Light Waves in a Nonlinear Dielectric. Phys. Rev. 127, 1918–1939. doi:10.1103/physrev.127.1918

CrossRef Full Text | Google Scholar

Bock, M., Eich, P., Kucera, S., Kreis, M., Lenhard, A., Becher, C., et al. (2018). High-fidelity Entanglement between a Trapped Ion and a Telecom Photon via Quantum Frequency Conversion. Nat. Commun. 9, 1998. doi:10.1038/s41467-018-04341-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Boehm, G., Bachmann, A., Rosskopf, J., Ortsiefer, M., Chen, J., Hangauer, A., et al. (2011). Comparison of InP- and GaSb-Based VCSELs Emitting at 2.3 μm Suitable for Carbon Monoxide Detection. J. Cryst. Growth 323, 442–445. doi:10.1016/j.jcrysgro.2010.11.174

CrossRef Full Text | Google Scholar

Cao, X., Zopf, M., and Ding, F. (2019). Telecom Wavelength Single Photon Sources. J. Semicond. 40, 071901. doi:10.1088/1674-4926/40/7/071901

CrossRef Full Text | Google Scholar

Chang, L., Li, Y., Volet, N., Wang, L., Peters, J., and Bowers, J. E. (2016). Thin Film Wavelength Converters for Photonic Integrated Circuits. Optica 3, 531–535. doi:10.1364/optica.3.000531

CrossRef Full Text | Google Scholar

Chen, J.-Y., Li, Z., Ma, Z., Tang, C., Fan, H., Sua, Y. M., et al. (2021). Photon Conversion and Interaction on Chip. ArXiv:2105.00275.

Google Scholar

Chen, J.-y., Meng Sua, Y., Ma, Z.-h., Tang, C., Li, Z., and Huang, Y.-p. (2019). Efficient Parametric Frequency Conversion in Lithium Niobate Nanophotonic Chips. OSA Contin. 2, 2914–2924. doi:10.1364/osac.2.002914

CrossRef Full Text | Google Scholar

Chiles, J., Nader, N., Stanton, E. J., Herman, D., Moody, G., Zhu, J., et al. (2019). Multifunctional Integrated Photonics in the Mid-infrared with Suspended AlGaAs on Silicon. Optica 6, 1246–1254. doi:10.1364/optica.6.001246

CrossRef Full Text | Google Scholar

Da Lio, B., Faurby, C., Zhou, X., Chan, M. L., Uppu, R., Thyrrestrup, H., et al. (2022). A Pure and Indistinguishable Single‐Photon Source at Telecommunication Wavelength. Adv. Quantum Tech. 5, 2200006. doi:10.1002/qute.202200006

CrossRef Full Text | Google Scholar

De Greve, K., Yu, L., McMahon, P. L., Pelc, J. S., Natarajan, C. M., Kim, N. Y., et al. (2012). Quantum-dot Spin-Photon Entanglement via Frequency Downconversion to Telecom Wavelength. Nature 491, 421–425. doi:10.1038/nature11577

PubMed Abstract | CrossRef Full Text | Google Scholar

Dréau, A., Tchebotareva, A., El Mahdaoui, A., Bonato, C., and Hanson, R. (2018). Quantum Frequency Conversion of Single Photons from a Nitrogen-Vacancy Center in Diamond to Telecommunication Wavelengths. Phys. Rev. Appl. 9, 064031. doi:10.1103/physrevapplied.9.064031

CrossRef Full Text | Google Scholar

Eisaman, M. D., Fan, J., Migdall, A., and Polyakov, S. V. (2011). Invited Review Article: Single-Photon Sources and Detectors. Rev. Sci. Instrum. 82, 071101. doi:10.1063/1.3610677

PubMed Abstract | CrossRef Full Text | Google Scholar

[Dataset] EMode Photonix (2022). EMode Photonix. Available at: https://www.emodephotonix.com/.

Google Scholar

Eto, Y., and Hirano, T. (2021). Effect of Cascaded Nonlinear Phase Shift on Pulsed Second-Harmonic Generation Using Periodically Poled Waveguide: a Comparison of Experimental and Numerical Results. Jpn. J. Appl. Phys. 60, 052001. doi:10.35848/1347-4065/abf49e

CrossRef Full Text | Google Scholar

Fiore, A., Berger, V., Rosencher, E., Bravetti, P., and Nagle, J. (1998). Phase Matching Using an Isotropic Nonlinear Optical Material. Nature 391, 463–466. doi:10.1038/35091

CrossRef Full Text | Google Scholar

Fisher, P., Cernansky, R., Haylock, B., and Lobino, M. (2021). Single Photon Frequency Conversion for Frequency Multiplexed Quantum Networks in the Telecom Band. Phys. Rev. Lett. 127, 023602. doi:10.1103/PhysRevLett.127.023602

PubMed Abstract | CrossRef Full Text | Google Scholar

Giovannetti, V., Lloyd, S., and Maccone, L. (2004). Quantum-enhanced Measurements: Beating the Standard Quantum Limit. Science 306, 1330–1336. doi:10.1126/science.1104149

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, X., Zou, C., and Tang, H. X. (2016). Second-harmonic Generation in Aluminum Nitride Microrings with 2500%/W Conversion Efficiency. Optica 3, 1126–1131.

Google Scholar

Huang, J., and Kumar, P. (1992). Observation of Quantum Frequency Conversion. Phys. Rev. Lett. 68, 2153–2156. doi:10.1103/physrevlett.68.2153

PubMed Abstract | CrossRef Full Text | Google Scholar

Joullié, A., and Christol, P. (2003). GaSb-based Mid-infrared 2–5 μm Laser Diodes. C. R. Phys. 4, 621–637. doi:10.1016/s1631-0705(03)00098-7

CrossRef Full Text | Google Scholar

Kahl, O., Ferrari, S., Kovalyuk, V., Goltsman, G. N., Korneev, A., and Pernice, W. H. (2015). Waveguide Integrated Superconducting Single-Photon Detectors with High Internal Quantum Efficiency at Telecom Wavelengths. Sci. Rep. 5, 10941. doi:10.1038/srep10941

PubMed Abstract | CrossRef Full Text | Google Scholar

Kao, C. K. (2010). Nobel Lecture: Sand from Centuries Past: Send Future Voices Fast. Rev. Mod. Phys. 82, 2299–2303. doi:10.1103/revmodphys.82.2299

CrossRef Full Text | Google Scholar

Kores, C. C., Canalias, C., and Laurell, F. (2021). Quasi-phase Matching Waveguides on Lithium Niobate and KTP for Nonlinear Frequency Conversion: A Comparison. Apl. Photonics 6, 091102. doi:10.1063/5.0060096

CrossRef Full Text | Google Scholar

Kumar, P. (1990). Quantum Frequency Conversion. Opt. Lett. 15, 1476–1478. doi:10.1364/ol.15.001476

PubMed Abstract | CrossRef Full Text | Google Scholar

Malitson, I. H. (1965). Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 55, 1205–1209. doi:10.1364/josa.55.001205

CrossRef Full Text | Google Scholar

McDonald, C., Moody, G., Nam, S. W., Mirin, R. P., Shainline, J. M., McCaughan, A., et al. (2019). III-V Photonic Integrated Circuit with Waveguide-Coupled Light-Emitting Diodes and Wsi Superconducting Single-Photon Detectors. Appl. Phys. Lett. 115, 081105. doi:10.1063/1.5108893

CrossRef Full Text | Google Scholar

Müller, T., Skiba-Szymanska, J., Krysa, A., Huwer, J., Felle, M., Anderson, M., et al. (2018). A Quantum Light-Emitting Diode for the Standard Telecom Window Around 1550 Nm. Nat. Commun. 9, 862. doi:10.1038/s41467-018-03251-7

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Brien, J. L. (2007). Optical Quantum Computing. Science 318, 1567–1570.

PubMed Abstract | Google Scholar

Ohashi, M., Kondo, T., Ito, R., Fukatsu, S., Shiraki, Y., Kumata, K., et al. (1993). Determination of Quadratic Nonlinear Optical Coefficient of Al_x Ga_1−x as System by the Method of Reflected Second Harmonics. J. Appl. Phys. 74, 596–601. doi:10.1063/1.355272

CrossRef Full Text | Google Scholar

Ottaviano, L., Pu, M., Semenova, E., and Yvind, K. (2016). Low-loss High-Confinement Waveguides and Microring Resonators in Algaas-On-Insulator. Opt. Lett. 41, 3996–3999. doi:10.1364/ol.41.003996

PubMed Abstract | CrossRef Full Text | Google Scholar

Paesani, S., Borghi, M., Signorini, S., Maïnos, A., Pavesi, L., and Laing, A. (2020). Near-ideal Spontaneous Photon Sources in Silicon Quantum Photonics. Nat. Commun. 11, 2505. doi:10.1038/s41467-020-16187-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Papatryfonos, K., Angelova, T., Brimont, A., Reid, B., Guldin, S., Smith, P. R., et al. (2021). Refractive Indices of MBE-Grown Al_xGa_(1−x)As Ternary Alloys in the Transparent Wavelength Region. AIP Adv. 11, 025327. doi:10.1063/5.0039631

CrossRef Full Text | Google Scholar

Placke, M., and Ramelow, S. (2020). Engineering AlGaAs-On-Insulator toward Quantum Optical Applications. Opt. Lett. 45, 6763–6766. doi:10.1364/ol.406152

PubMed Abstract | CrossRef Full Text | Google Scholar

Porkolab, G. A., Apiratikul, P., Wang, B., Guo, S., and Richardson, C. J. (2014). Low Propagation Loss Algaas Waveguides Fabricated with Plasma-Assisted Photoresist Reflow. Opt. Express 22, 7733–7743. doi:10.1364/oe.22.007733

PubMed Abstract | CrossRef Full Text | Google Scholar

Poulvellarie, N., Arabi, C. M., Ciret, C., Combrié, S., De Rossi, A., Haelterman, M., et al. (2021). Efficient Type II Second Harmonic Generation in an Indium Gallium Phosphide on Insulator Wire Waveguide Aligned with a Crystallographic axis. Opt. Lett. 46, 1490–1493. doi:10.1364/ol.418064

PubMed Abstract | CrossRef Full Text | Google Scholar

Roland, I., Gromovyi, M., Zeng, Y., El Kurdi, M., Sauvage, S., Brimont, C., et al. (2016). Phase-matched Second Harmonic Generation with On-Chip GaN-on-Si Microdisks. Sci. Rep. 6, 34191. doi:10.1038/srep34191

PubMed Abstract | CrossRef Full Text | Google Scholar

Senellart, P., Solomon, G., and White, A. (2017). High-performance Semiconductor Quantum-Dot Single-Photon Sources. Nat. Nanotechnol. 12, 1026–1039. doi:10.1038/nnano.2017.218

PubMed Abstract | CrossRef Full Text | Google Scholar

Shoji, I., Kondo, T., Kitamoto, A., Shirane, M., and Ito, R. (1997). Absolute Scale of Second-Order Nonlinear-Optical Coefficients. J. Opt. Soc. Am. B 14, 2268–2294. doi:10.1364/josab.14.002268

CrossRef Full Text | Google Scholar

Singh, A., Li, Q., Liu, S., Yu, Y., Lu, X., Schneider, C., et al. (2019). Quantum Frequency Conversion of a Quantum Dot Single-Photon Source on a Nanophotonic Chip. Optica 6, 563–569. doi:10.1364/optica.6.000563

CrossRef Full Text | Google Scholar

Spott, A., Stanton, E. J., Volet, N., Peters, J. D., Meyer, J. R., and Bowers, J. E. (2017). Heterogeneous Integration for Mid-infrared Silicon Photonics. IEEE J. Sel. Top. Quantum Electron. 23, 1–10. doi:10.1109/jstqe.2017.2697723

CrossRef Full Text | Google Scholar

Srocka, N., Mrowiński, P., Große, J., von Helversen, M., Heindel, T., Rodt, S., et al. (2020). Deterministically Fabricated Quantum Dot Single-Photon Source Emitting Indistinguishable Photons in the Telecom O-Band. Appl. Phys. Lett. 116, 231104. doi:10.1063/5.0010436

CrossRef Full Text | Google Scholar

Stachurski, J., Tamariz, S., Callsen, G., Butté, R., and Grandjean, N. (2022). Single Photon Emission and Recombination Dynamics in Self-Assembled gan/aln Quantum Dots. Light Sci. Appl. 11, 114. doi:10.1038/s41377-022-00799-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Stanton, E. J., Chiles, J., Nader, N., Moody, G., Volet, N., Chang, L., et al. (2020). Efficient Second Harmonic Generation in Nanophotonic GaAs-On-Insulator Waveguides. Opt. Express 28, 9521–9532. doi:10.1364/oe.389423

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, C. (1998). Determination of Refractive Index of Silica Glass for Infrared Wavelengths by IR Spectroscopy. J. Non. Cryst. Solids 223, 158–163. doi:10.1016/s0022-3093(97)00438-9

CrossRef Full Text | Google Scholar

Tien, P. K. (1971). Light Waves in Thin Films and Integrated Optics. Appl. Opt. 10, 2395–2413. doi:10.1364/ao.10.002395

PubMed Abstract | CrossRef Full Text | Google Scholar

Ulsig, E. Z., Degli-Eredi, I., and Volet, N. (2022). Efficient Frequency Conversion of Low-intensity Light in AlGaAs-On-Insulator Waveguides. SPIE Proc. 11985, 68–78. doi:10.1117/12.2607179

CrossRef Full Text | Google Scholar

Uppu, R., Eriksen, H. T., Thyrrestrup, H., Uğurlu, A. D., Wang, Y., Scholz, S., et al. (2020a). On-chip Deterministic Operation of Quantum Dots in Dual-Mode Waveguides for a Plug-And-Play Single-Photon Source. Nat. Commun. 11, 3782. doi:10.1038/s41467-020-17603-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Uppu, R., Midolo, L., Zhou, X., Carolan, J., and Lodahl, P. (2021). Quantum-dot-based Deterministic Photon–Emitter Interfaces for Scalable Photonic Quantum Technology. Nat. Nanotechnol. 16, 1308–1317. doi:10.1038/s41565-021-00965-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Uppu, R., Pedersen, F. T., Wang, Y., Olesen, C. T., Papon, C., Zhou, X., et al. (2020b). Scalable Integrated Single-Photon Source. Sci. Adv. 6, eabc8268. doi:10.1126/sciadv.abc8268

PubMed Abstract | CrossRef Full Text | Google Scholar

Van der Ziel, J. (1975). Phase-matched Harmonic Generation in a Laminar Structure with Wave Propagation in the Plane of the Layers. Appl. Phys. Lett. 26, 60–61. doi:10.1063/1.88055

CrossRef Full Text | Google Scholar

Wang, R., Sprengel, S., Vasiliev, A., Boehm, G., Van Campenhout, J., Lepage, G., et al. (2018). Widely Tunable 2.3 μm III-V-On-Silicon Vernier Lasers for Broadband Spectroscopic Sensing. Photonics Res. 6, 858–866. doi:10.1364/prj.6.000858

CrossRef Full Text | Google Scholar

Weber, J.-P. (1990). Propagation of Light in Periodic Structures: Application to the Surface-Emitting Laser-Diode. Berkeley: University of California. Ph.D. thesis.

Google Scholar

Wilson, D. J., Schneider, K., Hönl, S., Anderson, M., Baumgartner, Y., Czornomaz, L., et al. (2020). Integrated Gallium Phosphide Nonlinear Photonics. Nat. Photonics 14, 57–62. doi:10.1038/s41566-019-0537-9

CrossRef Full Text | Google Scholar

Xie, W., Xiang, C., Chang, L., Jin, W., Peters, J., and Bowers, J. E. (2022). Silicon-integrated Nonlinear III-V Photonics. Photonics Res. 10, 535–541. doi:10.1364/prj.446898

CrossRef Full Text | Google Scholar

Yariv, A. (1973). Coupled-mode Theory for Guided-Wave Optics. IEEE J. Quantum Electron. 9, 919–933. doi:10.1109/jqe.1973.1077767

CrossRef Full Text | Google Scholar

Zhang, K., He, J., and Wang, J. (2020). Two-way Single-Photon-Level Frequency Conversion between 852 Nm and 1560 Nm for Connecting Cesium D2 Line with the Telecom C-Band. Opt. Express 28, 27785–27796. doi:10.1364/oe.402355

PubMed Abstract | CrossRef Full Text | Google Scholar