Self-chaotic microlasers for random bit generation

Semiconductor lasers with optical feedback can produce plentiful non-linear dynamics, including periodic and chaotic oscillations, which are usually applied to microwave signals and physical random number generation, respectively. Chaotic semiconductor lasers are especially successful in generating random numbers compared with pseudorandom numbers generated by a computing process. We report a self-chaotic microlaser based on the internal mode interaction of nearly degenerate modes. A special resonator is designed and demonstrated with the two modes’ frequency intervals on the order of GHz. These modes with strong mode beating result in chaos, and physical random bits are obtained from the laser output power at 10 Gb/s. Our proposals provide a novel scheme to generate laser chaos for high-speed random number generation.

1 Introduction

Non-linear dynamics in semiconductor lasers have been widely investigated for basic research and specific applications (Ohtsubo, 2008; Uchida et al., 2008; Reidler et al., 2009; Ke et al., 2018; Wang et al., 2020; Li et al., 2020; Wang et al., 2021). In particular, random number generation utilizing chaotic semiconductor lasers has realized a breakthrough in the generation rate due to the high bandwidth of the lasers (Uchida et al., 2008; Reidler et al., 2009; Wang et al., 2020). Many strategies have been proposed and demonstrated to generate specific non-linear dynamics by external perturbations to prevent the lasers settle down to a constant output (Mukai and Otsuka, 1985; Mork et al., 1990; Sciamanna and Shore, 2015; Zhao et al., 2020). Under continuous perturbations of delayed optical feedback or external optical injection (Wang et al., 2020), semiconductor lasers can exhibit strong non-linear dynamics, such as periodic and chaotic oscillations. However, the implementations of external perturbations are always accompanied by some deficiencies. For example, chaos derived from delayed optical feedback has obvious correlation peaks relative to the external feedback loop time (Rontani et al., 2007; Albert et al., 2011), which reduces the randomness and security in random number generation and chaotic communications. Besides, the dynamical behaviors are sensitive to the parameters of the perturbations and precise adjustment is essential to realize specific non-linear dynamics of interest.

Whispering-gallery mode (WGM) resonators, such as microdisk (McCall et al., 1992), microtoroid (Jiang et al., 2017), microring (Ma et al., 2014), and polygonal resonators (Lin et al., 2011) have attracted a great deal of attention in the past decades for potential device applications. Optical chaos is expected to occur in a suitable multimode laser. The longitudinal mode intervals are inversely proportional to the resonator size, hence, small-dimension microresonators are easy to realize single longitudinal mode operation. Single-transverse mode operations were easy to realize for hexagonal resonator microlasers (Lin et al., 2011). Compared with longitudinal modes, the transverse modes wavelength intervals are much smaller. By modifying the hexagon to a circular-side hexagonal resonator (CSHR), the Q factors of different transverse modes can be approximated, and then the multi-transverse modes can be realized. Recently, we realized dual-mode lasing with an adjusting interval in a square microcavity laser (Long et al., 2015) and demonstrated the enhancements of mode Q-factors and intervals in circular-side square microcavities (Weng et al., 2017). Circular sides were also applied to a hexagonal microcavity for enhancing mode Q factors and adjusting mode intervals (Xiao et al., 2017; Yang et al., 2019). In a multi-transverse mode microlaser, mode beating can lead to oscillations of the photon density and carrier density caused by stimulated emission (Ma et al., 2022).

Due to the laser diodes’ merits in intensity and bandwidth, the laser chaos signal has been proven to be an excellent entropy source for physical random bit generation (RBG). The early chaotic semiconductor lasers with external cavities are demonstrated with random bit rates of up to 1.7 Gbps in 2008 (Uchida et al., 2008). Polarized chaotic output was caused by non-linear mode competition between two elliptically polarized modes induced by the carrier spin-flip relaxation process for a quantum-dot vertical-cavity surface-emitting laser (Sanmiguel et al., 1995; Virte et al., 2013). Recently a microcavity was designed for lasing of multiple transverse modes with distinct field patterns occupying different regions of the microcavity (Bittner et al., 2018), and a specially designed laser diode was demonstrated for massively parallel ultrafast random bit generation caused by Spatio-temporal interference of many lasing modes with stochastic spontaneous noises(Kim et al., 2021). A chaotic solitary laser is the most promising configuration for random number generation due to its simple scheme and robustness.

In this Letter, a detailed description of the manipulation design of the fundamental mode and first-order transverse mode of the laser resonant cavity is reported. Using a CSHR microlaser, we demonstrate non-linear dynamical states including periodic and chaotic oscillations and realize physical random number generation. The chaotic microlaser has the potential application for chaos communication using the principle of chaos synchronization.

2 Materials and methods

2.1 Resonator design

Based on the previous study on hexagonal microlasers with the flat sides replaced by circular sides (Xiao et al., 2018), the circular sides can influence lasing mode spectra and greatly enhance the mode Q factors, since the circular sides can prove the mechanism of the concave mirrors. For the simulation of the resonator, a two−dimensional (2D) finite element method (FEM) (COMSOL Multiphysics 5.0) is utilized to calculate the mode Q factor, mode wavelength, and coupling efficiency to the output waveguide. As shown in Figure 1, a deformation amplitude δ is defined as $\delta =r-\sqrt{r^2-{\left(a/2\right)}^2}$, where r and a are the radius of the circular arc, the hexagonal flat-side length, and θ and w are the acute angle between the waveguide and the diagonal of the hexagon and the width of the output waveguide, respectively. The CSHR with an AlGaInAs/InP laser wafer has a fixed refractive index of 3.2 and is laterally confined by divinylsiloxane-bisbenzocyclobutene (BCB) with a refractive index of 1.54, which is coated for the planarization of the fabricated microlasers.

FIGURE 1

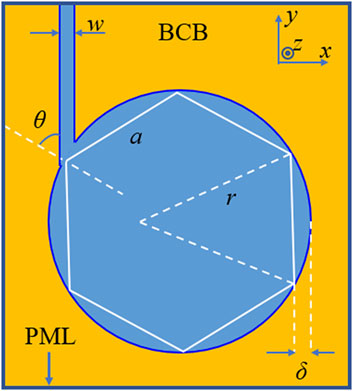
FIGURE 1. Diagram of the model used for the simulation of the circular-side hexagonal resonator laser (CSHR) laser.

Four high-Q modes with mode frequency intervals in the order of GHz, i.e., the fundamental and first-order transverse modes and their degenerate modes, are calculated within the same longitudinal mode order. To simplify the description, the degenerate modes are ignored because they have nearly the same Q factor and mode frequency compared with the corresponding transverse modes. The mode Q factor for the fundamental transverse mode (H₀) and the first-order transverse mode (H₁) and the interval frequency between the two modes (Δf) versus deformation amplitude δ for a = 10 μm and w = 1.5 μm are plotted in Figure 2. The simulation results show that the mode Q factors of the H₀ mode and H₁ mode decrease with the increase of the deformation amplitude δ, except that the Q factor has a slight enhancement near the δ = 1.015 μm. The resonator produces a focusing effect at the deformation amplitude of 1.015 μm, which reduces the mode loss and achieves a higher Q factor. With the increase of the deformation amplitude δ from 1.0 μm to 1.03 μm, the Q factor of H₀ (H₁) mode decreases from 7.8 × 10⁵ (4.5 × 10⁵) to 8.8 × 10⁴ (2.0 × 10⁴). In addition, the Δf decreases from 36.7 GHz to −43.2 GHz, and Δf is almost linear with the deformation amplitude δ. Considering that the H₀ and H₁ modes have similar mode frequencies at a deformation amplitude of 1.015 µm and that the H0 mode has a high Q factor, the δ = 1. Considering that the H0 and H1 modes have similar mode frequencies at a deformation amplitude of 1.015 µm and that the H0 mode has a high Q factor, the δ = 1.015 µm is selected as an optimized value.

FIGURE 2

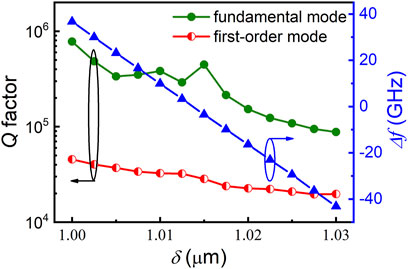
FIGURE 2. The mode Q factor for the fundamental transverse mode (H₀) and the first-order transverse mode (H₁) and the interval frequency between the two modes (Δf) versus deformation amplitude δ for a = 10 μm and w = 1.5 μm.

The mode Q factor of H₀ is much higher than that of H₁, which means the power radiated from the fundamental mode is lower than that radiated from the first-order transverse mode. To make the output power of the two modes similar, and achieve efficient interaction between different modes, it is required that the proportion of the power radiated from H₀ coupled into the waveguide is higher than that of H₁, that is, the fundamental mode has a higher waveguide coupling output efficiency than that of the first-order transverse mode. However, when the deformation amplitude is 1.015 μm, the waveguide coupling output efficiency (η) of H₀ is 7.5%, which is much lower than 43% of H₁, as shown in Figure 3A. By adjusting the output waveguide connection angle (θ) of the output waveguide, the waveguide coupling output efficiency of the CSHR microlaser can be greatly improved. Here we simulated the effect of θ on η of H₀ and H₁ in the CSHR microlaser with δ = 1.015 μm, and the results are shown in Figure 3A. The η of H₁ remains about 40% when θ is less than 45°, decreases to 14% when θ = 50°, and then increases with the increase of θ. The η of H₀ generally shows an increasing trend with the increase of θ, the maximum value of 51% at θ = 55° is obtained, and its value of H₀ is greater than that of H₁ for θ > 45°.

FIGURE 3

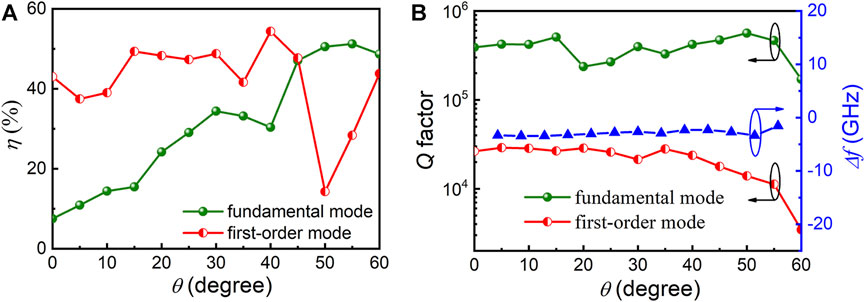
FIGURE 3. (A) The waveguide coupling output efficiency (η) of H₀ and H₁ in the CSHR microlaser with δ = 1.015 μm versus the output waveguide connection angle θ, and (B) The mode Q factor and the interval frequency between the two modes (Δf) versus the output waveguide connection angle θ for a = 10 μm and w = 1.5 μm and δ = 1.015 μm.

The effect of the connection angle θ on the Q factor of the two modes and the frequency interval Δf between H₀ and H₁ modes is shown in Figure 3B. It can be seen from Figure 3B that, the Δf changes slightly with θ, and almost remains at about −3 GHz when θ is less than 55°. The Q factor of H₀ remains above 10⁵ with the change of θ; The Q factor of H₁ changes slightly in the range of θ < 35°, and decreases slowly with the increase of θ in the range of 35°<θ < 55°, decreases from 2.6 × 10⁴ to 1.1 × 10⁴, and decreases sharply to 3.4 × 10³ at θ = 60°. Considering the waveguide coupling output efficiency, and Q factor of H₀ and H₁, the optimal value of θ is 55°.

2.2 Ring current injection window design

To realize the tunability of the interval frequency between the two transverse modes of the CSHR microlaser, we design a ring current injection window. The schematic diagram of which is shown in Figure 4A, where d is the width of the ring injection window. The carrier concentration and temperature are higher in the injection window area than that in the non-injection area due to non-uniform injection current density. As the refractive index changes with the carrier concentration and temperature, the non-uniform injection current may also modulate the refractive index distribution (Long et al., 2015). Assume the refractive index is n of the non-injection window area, and the refractive index of the injection window area is n+Δn. For a CSHR with a = 10 μm, w = 1.5 μm, δ = 1.015 μm, θ = 55°, and d = 5 μm, the mode Q factors of H₀ and H₁, and the frequency intervals of the two modes (Δf) vary with the refractive index difference Δn, as shown in Figure 4B. When Δn. Increases from −8 × 10⁻³ to 8 × 10⁻³, the Δf increases from −10.3 GHz to 15.6 GHz, and the mode Q factors of H₁ remain unchanged, while the mode Q factor of H₀ first increases and then decreases and remains above 1.3 × 10⁵. To reduce the computational effort, the results in Figure 4B are based on the simulation of the two-dimensional structure, which only includes the loss of the mode in the horizontal direction. According to the previous simulation structure, the Q factor corresponding to the vertical loss of the transverse electromagnetic mode is around 1.0 × 10⁴. The Q factor of the fundamental mode is mainly determined by the Q factor in the vertical direction. The simulation results show that the non-uniform refractive index distribution caused by non-uniform injection can adjust Δf without affecting the lasing characteristics of the two modes.

FIGURE 4

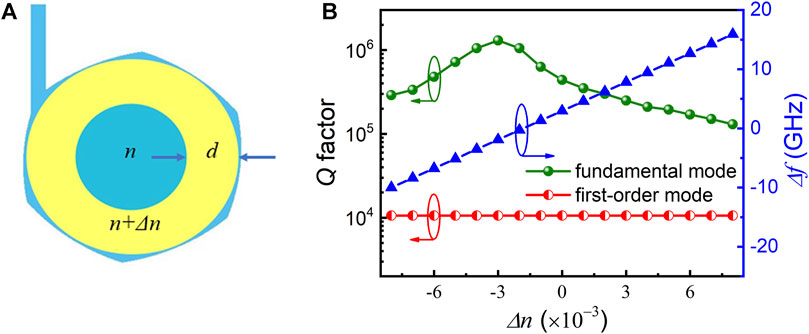
FIGURE 4. (A) Schematic diagram of ring current injection window, and (B) The mode Q factors of H₀ and H₁, and the frequency intervals of the two modes (Δf) vary with the refractive index difference Δn, for a CSHR with a = 10 μm, w = 1.5 μm, δ = 1.015 μm, θ = 55°, and d = 5 μm.

3 Results and discussion

3.1 The characteristics of the lasing spectrum

The CSHR microlasers are fabricated by a planar lithography process using an AlGaInAs/InP epitaxial wafer (Xiao et al., 2017), then the wafer is cleaved along the direction perpendicular to the output waveguide and bonded on an AlN submount and mounted on a thermoelectric cooler (TEC) to control the substrate temperature. The threshold current of the CSHR microlaser is 4 mA, and the laser spectra are characterized using an optical spectrum analyzer (OSA) with a resolution of 0.02 nm. And the bandwidth of the RF spectrum analyzer is set 100 kHz.

Non-linear states similar to the chaos in semiconductor lasers with optical feedback were observed at different injection currents (Zou et al., 2015), including chaotic, periodic states. A comprehensive rate equation for the CSHR microlaser was introduced to describe the periodic and chaotic states generated from the two-mode beating (Ma et al., 2022). The CSHR microlaser output light coupled into lensed single-mode fiber and the optical spectra at the injection current of 23 and 32 mA are plotted in Figures 5A, B and the corresponding RF spectra are present in Figures 5C, D, respectively. At the injection current of the CSHR microlaser at 23 mA, the optical spectrum is shown in Figure 5A. The optical spectrum is broadened, and the lasing peak is hard to be distinguished in the whole observed spectrum range. And the corresponding RF spectrum in Figure 5C shows a large bandwidth without any significant narrow peak. The gray line denotes the background noise. When the injection current of the CSHR microlaser is 32 mA, its optical spectrum is shown in Figure 5B, the wavelengths of the two lasing modes are 1566.55 and 1566.72 nm, respectively, and two weaker intensity modes exist at the wavelengths of 1566.38 and 1566.89 on both sides of the two lasing peaks, with the two adjacent peak wavelengths separated by 0.17 nm. The CSHR microlaser is in a periodic state, and the corresponding RF spectrum has a peak at 20.86 GHz with a magnitude about 35 dB higher than the background as shown in Figure 5D.

FIGURE 5

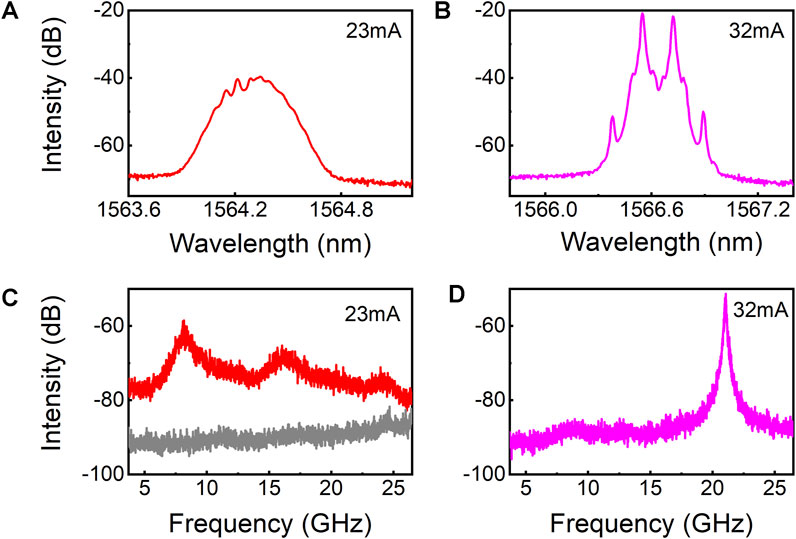
FIGURE 5. Lasing spectra at the injection current of (A) 23 mA, (B) 32 mA, and output RF spectra of a CSHR microlaser (C), (D), at the corresponding injection current.

The frequency interval of the two modes is tunable by varying the laser injection current, and Figure 6A gives the frequency interval and the variation of the intensity ratio of the two modes near 1568 nm with the injection current. When the injection current of the CSHR microlaser is varied in the range of 30 mA–40 mA, the laser is in a periodic oscillations state, the frequency interval of the two main peaks is varied in a range from 14.6 to 21.5 GHz, and the intensity ratio of the excitation peaks is maintained 2 dB. The output RF spectra of the CSHR microlaser at the injection current of 31, 35, 39, and 41 mA are given in Figure 6B, and the frequency-tunable RF signals were successfully obtained by varying the laser injection current.

FIGURE 6

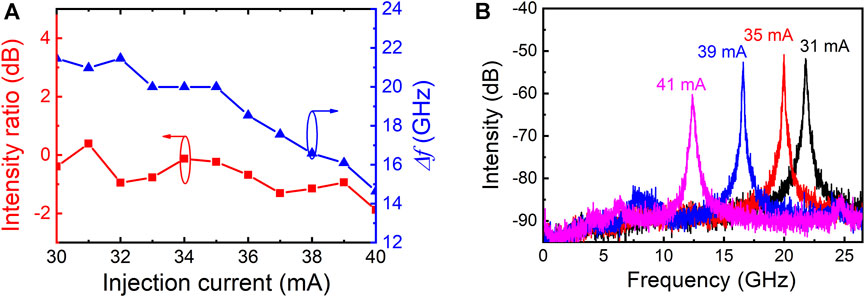
FIGURE 6. (A) The interval frequency and intensity ratio between the two modes versus injection current, and (B) output RF spectra of the CSHR microlaser at an injection current of 31, 35, 39, and 41 mA.

3.2 Random bit generation

Based on the previous experimental results, the CSHR microlaser evolves into a chaotic state at the injection current of 23 mA, and the laser temperature is stabilized at 288 K. The CSHR microlaser output is coupled into a single-mode fiber then amplified by an erbium-doped fiber amplifier (EDFA), and converted to an electronic signal by a broadband photodiode (PD), and the electrical signal enters a broadband digital oscilloscope (R&S RTO1024, 10 GSa/s sampling rate, 2-GHz analog bandwidth) to acquire the electrical signal. The electrical signal is also monitored by an optical spectrum analyzer and an RF spectrum analyzer. The output power of the CSHR microlaser is −16 dBm, and the output power of about 8 dBm is obtained by EDFA amplification into the PD for optical-to-electrical conversion. The converted electrically chaotic waveform is quantized by an 8-bit ADC in the oscilloscope, generating random bits by retaining the 2 least significant bits (LSBs) of each sample. The sampling rate of the oscilloscope is set to 5 GSa/s.

The experimental time series of the chaotic signal is shown in Figure 7A, which shows the intensity oscillations similar to noise on sub-nanosecond time scales. The probability density distribution of the time series is given in Figure 7B (blue solid line). The red dashed line represents the Gaussian fitting curve. Compared experimental results with the Gaussian fitting curve, the probability density distribution of the time series has a slight difference from the Gaussian distribution. Using Wolf’s algorithm (Wolf et al., 1985), we find a positive maximum Lyapunov exponent (λ_max) from the experimental time series as shown in Figure 7C.

FIGURE 7

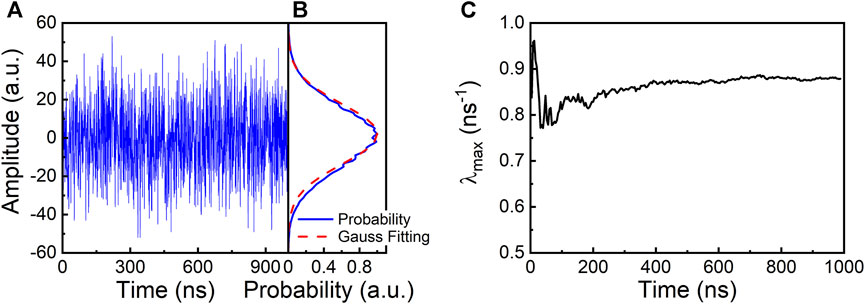
FIGURE 7. (A) Experimental time series, (B) probability density distribution of the generated chaotic waveform, and (C) estimation of largest Lyapunov exponent for the time series in (A).

The autocorrelation trace is shown in Figure 8. Unlike the presence of a time-delay signature of chaos generated by external optical feedback or optical injection laser, there is no significant peak in the time delay range of 6 μs. Due to the presence of relaxation oscillations in the semiconductor laser, a series of sidelobes with a full-width half-maximum of 1 ns appear around the main peak in the zoom-in autocorrelation curve, as shown in Figure 8B. These peaks, caused by the inherent characteristics of the laser, induce weak periodicity and are not conducive to the generation of high-quality random numbers. Post-data processing, such as exclusive or operation, can be used to eliminate them.

FIGURE 8

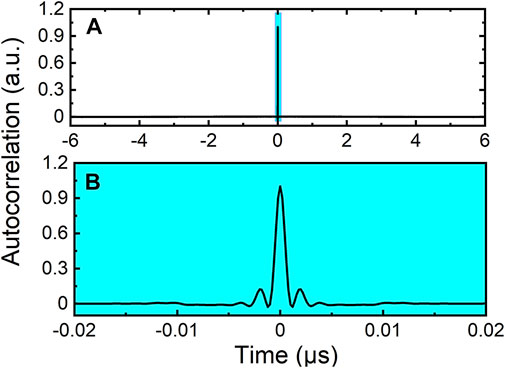
FIGURE 8. (A) Autocorrelation function of the generated broadband chaotic waveform, (B) zoom-in view of Autocorrelation function.

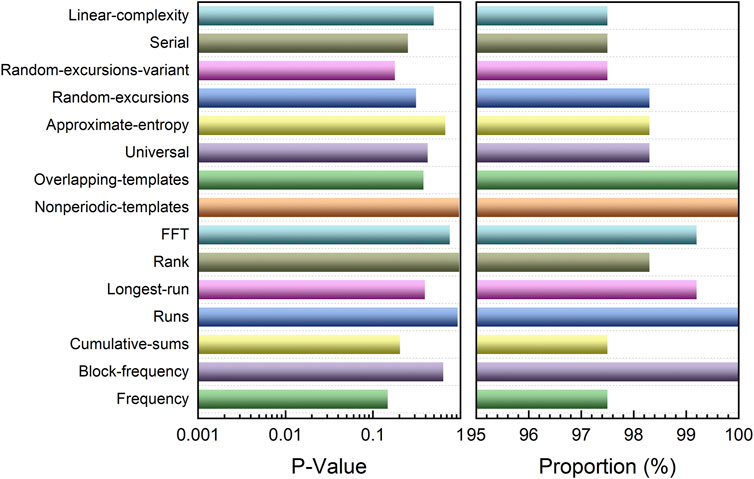
The 120 sequence signals obtained by the digital oscilloscope at a sampling rate of 5 GSa/s were converted to 8-bit binary codes, each sequence having a size of 1 Mbit, and the 2 least significant bit groups (LSBs) were selected. The results of the randomness test on the random bit sequences using the National Institutes of Standards and Technology Special Publication 800–22 statistical test suite are shown in Figure 9. The random bits generated at a bit rate of 10 Gbit/s (5 GSa/s × 2 bits) passed the test.

FIGURE 9

FIGURE 9. Result of the NIST special publication 800–22 statistical tests.

4 Conclusion

Compared with the conventional optical feedback and optical injection to generate laser chaos, the self-chaotic microcavity laser does not require external perturbation. Using the fundamental transverse mode and the first-order transverse mode in the resonant cavity to generate intense interactions between photons and carriers when the mode interval is close to the relaxation oscillation frequency of the lasers, the non-linear dynamics such as laser periodic oscillations and chaotic states by adjusting the injection current through mode interactions in the resonant cavity can be achieved. The optimized hexagonal resonator design and the introduction of ring electrodes enable to obtain dual-mode with high Q factor, meanwhile, its mode frequency interval is tunable in the order of GHz. The mode interval tuning is achieved utilizing adjusting the injection current, and experimentally plentiful non-linear dynamic states, including chaotic and periodic states in the solitary microlaser, are observed. Physical random numbers of 10 Gb/s and frequency-tunable RF signals were achieved using the output of the microlaser. The solitary self-chaotic microlasers provide a more simple and robust chaotic laser source compared with chaotic lasers caused by external optical feedback or optical injection.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

J-LX: Device fabrication and characterization, draft preparation. Z-XX, device fabrication, and characterization, figures preparation. C-GM: Data curation on the physical random number. Y-LL: Simulation of the resonator. Y-ZHa, Y-DY: Device fabrication. Y-ZHu: Conceptualization, conducted project supervision, reviewing, and edition of the final manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (61935018, 12274407, 61874113), the Strategic Priority Research Program, Chinese Academy of Sciences (XDB43000000).

Conflict of interest

Author Z-XX is employed by Microelectronics Center Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albert, F., Hopfmann, C., Reitzenstein, S., Schneider, C., Hofling, S., Worschech, L., et al. (2011). Observing chaos for quantum-dot microlasers with external feedback. Nat. Commun. 2, 366. doi:10.1038/ncomms1370

PubMed Abstract | CrossRef Full Text | Google Scholar

Bittner, S., Guazzotti, S., Zeng, Y. Q., Hu, X. N., Yilmaz, H., Kim, K., et al. (2018). Suppressing spatiotemporal lasing instabilities with wave-chaotic microcavities. Science 361 (6408), 1225–1231. doi:10.1126/science.aas9437

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, X. F., Shao, L. B., Zhang, S. X., Yi, X., Wiersig, J., Wang, L., et al. (2017). Chaos-assisted broadband momentum transformation in optical microresonators. Science 358 (6361), 344–347. doi:10.1126/science.aao0763

PubMed Abstract | CrossRef Full Text | Google Scholar

Ke, J., Yi, L., Xia, G., and Hu, W. (2018). Chaotic optical communications over 100-km fiber transmission at 30-Gb/s bit rate. Opt. Lett. 43 (6), 1323–1326. doi:10.1364/OL.43.001323

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, K., Bittner, S., Zeng, Y., Guazzotti, S., Hess, O., Wang, Q. J., et al. (2021). Massively parallel ultrafast random bit generation with a chip-scale laser. Science 371 (6532), 948–952. doi:10.1126/science.abc2666

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S. S., Zou, X. H., Wang, L. S., Wang, A. B., Pan, W., and Yan, L. S. (2020). Stable period-one oscillations in a semiconductor laser under optical feedback from a narrowband fiber Bragg grating. Opt. Express 28 (14), 21286–21299. doi:10.1364/oe.396180

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, J. D., Huang, Y. Z., Yang, Y. D., Yao, Q. F., Lv, X. M., Xiao, J. L., et al. (2011). Single transverse whispering-gallery mode AlGaInAs/InP hexagonal resonator microlasers. IEEE Photonics J. 3 (4), 756–764. doi:10.1109/jphot.2011.2163498

CrossRef Full Text | Google Scholar

Long, H., Huang, Y. Z., Ma, X. W., Yang, Y. D., Xiao, J. L., Zou, L. X., et al. (2015). Dual-transverse-mode microsquare lasers with tunable wavelength interval. Opt. Lett. 40 (15), 3548–3551. doi:10.1364/ol.40.003548

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, C. G., Xiao, J. L., Xiao, Z. X., Yang, Y. D., and Huang, Y. Z. (2022). Chaotic microlasers caused by internal mode interaction for random number generation. Light-Science Appl. 11 (1), 187. doi:10.1038/s41377-022-00890-w

CrossRef Full Text | Google Scholar

Ma, X. W., Lv, X. M., Huang, Y. Z., Yang, Y. D., Xiao, J. L., and Du, Y. (2014). Mode characteristics for unidirectional-emission microring resonator lasers. J. Opt. Soc. Am. B-Optical Phys. 31 (11), 2773–2778. doi:10.1364/josab.31.002773

CrossRef Full Text | Google Scholar

McCall, S. L., Levi, A. F. J., Slusher, R. E., Pearton, S. J., and Logan, R. A. (1992). Whispering-gallery mode microdisk lasers. Appl. Phys. Lett. 60 (3), 289–291. doi:10.1063/1.106688

CrossRef Full Text | Google Scholar

Mork, J., Mark, J., and Tromborg, B. (1990). Route to chaos and competition between relaxation oscillations for a semiconductor-laser with optical feedback. Phys. Rev. Lett. 65 (16), 1999–2002. doi:10.1103/PhysRevLett.65.1999

PubMed Abstract | CrossRef Full Text | Google Scholar

Mukai, T., and Otsuka, K. (1985). New route to optical chaos - successive-subharmonic-oscillation cascade in a semiconductor-laser coupled to an external cavity. Phys. Rev. Lett. 55 (17), 1711–1714. doi:10.1103/PhysRevLett.55.1711

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohtsubo, J. (2008). Semiconductor lasers stability, instability and chaos. Springer-Verlag, Berlin Heidelberg.

Google Scholar

Reidler, I., Aviad, Y., Rosenbluh, M., and Kanter, I. (2009). Ultrahigh-speed random number generation based on a chaotic semiconductor laser. Phys. Rev. Lett. 103 (2), 024102. doi:10.1103/PhysRevLett.103.024102

PubMed Abstract | CrossRef Full Text | Google Scholar

Rontani, D., Locquet, A., Sciamanna, M., and Citrin, D. S. (2007). Loss of time-delay signature in the chaotic output of a semiconductor laser with optical feedback. Opt. Lett. 32 (20), 2960–2962. doi:10.1364/ol.32.002960

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanmiguel, M., Feng, Q., and Moloney, J. V. (1995). Light-polarization dynamics in surface-emitting semiconductor-lasers. Phys. Rev. A 52 (2), 1728–1739. doi:10.1103/PhysRevA.52.1728

PubMed Abstract | CrossRef Full Text | Google Scholar

Sciamanna, M., and Shore, K. A. (2015). Physics and applications of laser diode chaos. Nat. Photonics 9 (3), 151–162. doi:10.1038/nphoton.2014.326

CrossRef Full Text | Google Scholar

Uchida, A., Amano, K., Inoue, M., Hirano, K., Naito, S., Someya, H., et al. (2008). Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photonics 2 (12), 728–732. doi:10.1038/nphoton.2008.227

CrossRef Full Text | Google Scholar

Virte, M., Panajotov, K., Thienpont, H., and Sciamanna, M. (2013). Deterministic polarization chaos from a laser diode. Nat. Photonics 7 (1), 60–65. doi:10.1038/nphoton.2012.286

CrossRef Full Text | Google Scholar

Wang, L., Wang, D., Gao, H., Guo, Y., Wang, Y., Hong, Y., et al. (2020a). Real-time 2.5-Gb/s correlated random bit generation using synchronized chaos induced by a common laser with dispersive feedback. IEEE J. Quantum Electron. 56 (1), 1–8. doi:10.1109/jqe.2019.2950943

CrossRef Full Text | Google Scholar

Wang, X. G., Zhao, B. B., Deng, Y., Kovanis, V., and Wang, C. (2021). Nonlinear dynamics of a quantum cascade laser with tilted optical feedback. Phys. Rev. A 103 (2), 023528. doi:10.1103/PhysRevA.103.023528

CrossRef Full Text | Google Scholar

Wang, Y. X., Jia, Z. W., Gao, Z. S., Xiao, J. L., Wang, L. S., Wang, Y. C., et al. (2020b). Generation of laser chaos with wide-band flat power spectrum in a circular-side hexagonal resonator microlaser with optical feedback. Opt. Express 28 (12), 18507–18515. doi:10.1364/oe.395434

PubMed Abstract | CrossRef Full Text | Google Scholar

Weng, H. Z., Huang, Y. Z., Yang, Y. D., Ma, X. W., Xiao, J. L., and Du, Y. (2017). Mode Q factor and lasing spectrum controls for deformed square resonator microlasers with circular sides. Phys. Rev. A 95 (1), 013833. doi:10.1103/PhysRevA.95.013833

CrossRef Full Text | Google Scholar

Wolf, A., Swift, J. B., Swinney, H. L., and Vastano, J. A. (1985). Determining lyapunov exponents from a time-series. Phys. D. 16 (3), 285–317. doi:10.1016/0167-2789(85)90011-9

CrossRef Full Text | Google Scholar

Xiao, J. L., Ma, C. G., Xiao, Z. X., Yang, Y. D., and Huang, Y. Z. (2018). “Random bit generation in dual transverse mode microlaser without optical injection or feedback,” in 2018 IEEE International Semiconductor Laser Conference), Santa Fe, NM, USA, 16-19 September 2018 (IEEE), 171–172.

CrossRef Full Text | Google Scholar

Xiao, Z. X., Huang, Y. Z., Yang, Y. D., Xiao, J. L., and Ma, X. W. (2017). Single-mode unidirectional-emission circular-side hexagonal resonator microlasers. Opt. Lett. 42 (7), 1309–1312. doi:10.1364/ol.42.001309

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y. D., Tang, M., Wang, F. L., Xiao, Z. X., Xiao, J. L., and Huang, Y. Z. (2019). Whispering-gallery mode hexagonal micro-/nanocavity lasers Invited. Photonics Res. 7 (5), 594–607. doi:10.1364/prj.7.000594

CrossRef Full Text | Google Scholar

Zhao, A. K., Jiang, N., Chang, C. C., Wang, Y. J., Liu, S. Q., and Qiu, K. (2020). Generation and synchronization of wideband chaos in semiconductor lasers subject to constant-amplitude self-phase-modulated optical injection. Opt. Express 28 (9), 13292–13298. doi:10.1364/oe.393276

PubMed Abstract | CrossRef Full Text | Google Scholar

Zou, L. X., Huang, Y. Z., Liu, B. W., Lv, X. M., Long, H., Yang, Y. D., et al. (2015). Nonlinear dynamics for semiconductor microdisk laser subject to optical injection. IEEE J. Sel. Top. Quantum Electron. 21 (6), 506–513. doi:10.1109/jstqe.2015.2414097

CrossRef Full Text | Google Scholar