- 1Department of Biomedical Sciences for Health, University of Milan, Milan, Italy
- 2Department of Cardiothoracic, Vascular Anesthesia and Intensive Care, IRCCS Policlinico San Donato, Milan, Italy
- 3BIOtech, Department of Industrial Engineering, University of Trento, Trento, Italy
- 4IRCS PAT-FBK, Trento, Italy
- 5Department of Electronics Information and Bioengineering, Politecnico di Milano, Milan, Italy
- 6Department of Emergency and Intensive Care, San Gerardo Hospital, Monza, Italy
- 7IRCCS Fondazione Salvatore Maugeri, Milan, Italy
- 8Department of Emergency, L. Sacco Hospital, Milan, Italy
- 9Department of Anesthesia and Intensive Care, IRCCS Humanitas Clinical and Research Center, Rozzano, Italy
A full decomposition of the predictive entropy (PE) of the spontaneous variations of the heart period (HP) given systolic arterial pressure (SAP) and respiration (R) is proposed. The PE of HP is decomposed into the joint transfer entropy (JTE) from SAP and R to HP and self-entropy (SE) of HP. The SE is the sum of three terms quantifying the synergistic/redundant contributions of HP and SAP, when taken individually and jointly, to SE and one term conditioned on HP and SAP denoted as the conditional SE (CSE) of HP given SAP and R. The JTE from SAP and R to HP is the sum of two terms attributable to SAP or R plus an extra term describing the redundant/synergistic contribution to the JTE. All quantities were computed during cardiopulmonary loading induced by −25° head-down tilt (HDT) via a multivariate linear regression approach. We found that: (i) the PE of HP decreases during HDT; (ii) the decrease of PE is attributable to a lessening of SE of HP, while the JTE from SAP and R to HP remains constant; (iii) the SE of HP is dominant over the JTE from SAP and R to HP and the CSE of HP given SAP and R is prevailing over the SE of HP due to SAP and R both in supine position and during HDT; (iv) all terms of the decompositions of JTE from SAP and R to HP and SE of HP due to SAP and R were not affected by HDT; (v) the decrease of the SE of HP during HDT was attributed to the reduction of the CSE of HP given SAP and R; (vi) redundancy of SAP and R is prevailing over synergy in the information transferred into HP both in supine position and during HDT, while in the HP information storage synergy and redundancy are more balanced. The approach suggests that the larger complexity of the cardiac control during HDT is unrelated to the baroreflex control and cardiopulmonary reflexes and may be related to central commands and/or modifications of the dynamical properties of the sinus node.
Introduction
Head-down tilt (HDT) is an experimental maneuver inducing an increase of the venous return, central blood volume, and central venous pressure (London et al., 1983; Nagaya et al., 1995). The resulting loading of the cardiopulmonary receptors in the right atrium and pulmonary veins leads to a sympatho-inhibitory response increasing the forearm blood flow (London et al., 1983; Nagaya et al., 1995; Tanaka et al., 1999) and decreasing the forearm vascular resistance (London et al., 1983; Nagaya et al., 1995; Tanaka et al., 1999), total peripheral resistance (Nagaya et al., 1995) and efferent muscle sympathetic nerve activity (Nagaya et al., 1995; Tanaka et al., 1999). Since the reduction of venous return and the consequent sinoaortic and carotid baroreceptor unloading during head-up tilt leads to a vagal withdrawal and sympathetic activation (Cooke et al., 1999; Marchi et al., 2013), to an engagement of the arterial baroreflex (Taylor and Eckberg, 1996; Porta et al., 2011) and to a reduction of the importance of the cardiopulmonary pathway (Porta et al., 2012b), it can be hypothesized that the acute central circulatory hypervoleamia induced by HDT produces the opposite cardiovascular response. Indeed, a reduced involvement of the cardiac baroreflex and an improved relevance of the cardiopulmonary circuits during HDT would explain the previously observed increase of respiratory sinus arrhythmia and the decrease of arterial pressure variability especially in the low frequency band (Porta et al., 2014b).
In the field of information dynamics multivariate tools have been recently devised that allow the quantitative description of the dynamical interactions among time series (McGill, 1954; Schreiber, 2000; Barnett et al., 2009; Faes et al., 2011, 2013, 2015; Lizier et al., 2011; Wibral et al., 2011, 2014; Chicharro and Ledberg, 2012; Stramaglia et al., 2012; Kugiumtzis, 2013; Porta et al., 2014a, 2015; Barrett, 2015). These tools have been successfully applied to disentangle physiological mechanisms from the spontaneous variability of the heart period (HP), systolic arterial pressure (SAP), and respiration (R). For example, the predictive entropy (PE) of HP assessed in the universe of knowledge Ω = {HP,SAP,R}, measuring the decline of uncertainty about the present HP due to the knowledge of the past history of HP, SAP, and R series, was taken as a measure of the loss of complexity of the cardiac neural regulation. Indeed, the PE of HP increased during the vagal withdrawal induced by an orthostatic challenge (Faes et al., 2015; Porta et al., 2015) and during an experimental maneuver imposing the regularization of the respiratory sinus arrhythmia (i.e., controlled respiration at slow breathing rate; Faes et al., 2015). The transfer entropies (TEs) from SAP to HP and from R to HP in Ω, denoting the portion of PE of HP solely attributable to past values of SAP and R respectively, were taken respectively as measures of the degree of involvement of the cardiac baroreflex and cardiopulmonary reflexes in controlling HP. Indeed, the TE from SAP to HP in Ω gradually augmented when the baroreflex was challenged in proportion to an orthostatic stimulus (Porta et al., 2015) and the TE from R to HP in Ω progressively decreased with age (Nemati et al., 2013; Porta et al., 2014a) as a likely consequence of the gradual vagal withdrawal inducing a progressive decoupling between HP variations and respiratory centers (Seals and Esler, 2000; Eckberg, 2003). Unfortunately, the full exploitation of this approach in assessing cardiovascular control is limited by the incomplete decomposition of PE of HP (McGill, 1954; Chicharro and Ledberg, 2012; Stramaglia et al., 2012; Barrett, 2015; Faes et al., 2015). Indeed, usually the full decomposition of PE is given for bivariate interactions (e.g., HP and R) (Faes et al., 2015) or limited to the TE term (Chicharro and Ledberg, 2012; Stramaglia et al., 2012; Barrett, 2015), while the full decomposition of the self-entropy (SE) has never been investigated.
The aim of this study is to provide a decomposition of PE including that of both TE and SE terms when the assigned target dynamic is HP and the two exogenous signals are SAP and R. The proposed decomposition is applied to elucidate the response of the cardiovascular control to HDT. We utilized: (i) the PE of HP as a global descriptor of the HP dynamic; (ii) the TEs from SAP to HP and from R to HP in Ω as markers of the degree of involvement of the cardiac baroreflex and cardiopulmonary reflexes, respectively; (iii) the SE of HP as a measure of the information stored into HP; (iv) the part of the SE of HP excluding the contributions of SAP and R as an index of the information stored into HP that cannot be explained by SAP and R; (v) the SAP-R interaction terms as measures of the redundant/synergistic contributions of SAP and R to the information transfer and storage. Results, over the same protocol exclusively relevant to the TEs from SAP to HP and from R to HP in Ω were presented to the EMBC 2014 (Porta et al., 2014b).
Methods
Modeling the Linear Variability Interactions Among HP, SAP, and R Series
In the following we consider HP = y = {y(n), n = 1, …, N} as an effect series driven by a pair of exogenous series, SAP = x1 = {x1(n), n = 1,…,N}, and R = x2 = {x2(n), n = 1,…,N} where N is the series length and n is the progressive cardiac beat counter. The series y, x1, and x2 form the universe of knowledge Ω = {y,x1,x2} about the short-term control of the HP variability exploited in this study (Porta et al., 2012a). The samples of all series in Ω are normalized by subtracting the mean value and by dividing the result by the standard deviation, in such a way that y, x1, and x2 have zero mean and unit variance. We also define the following restricted universes of knowledge obtained from Ω by excluding both exogenous signals, i.e., Ω\x1,x2 = {y}, or one exogenous signals i.e., Ω\x1= {y, x2} and Ω\x2 = {y, x1}.
The open loop autoregressive (AR) model with two exogenous (X) inputs (ARX1X2) describes the dependence of the current value of y, y(n), on past values of the same signal and past values of the exogenous inputs x1 and x2 as
where aj, b1j, and b2j, with 1 ≤ j ≤ p, are the constant coefficients of the regression of y on past values of y, x1, and x2 respectively, p is the order of the regressions, τ1 and τ2 are the delays of the action from x1 and x2 to y respectively, and wARX1X2(n) is zero mean white Gaussian noise with variance . In addition to the ARX1X2 model, four structures, all derived from the ARX1X2 model, are of interest in this study: (i) the ARX1 model in which the exogenous input x2 is disregarded by ignoring the regression of y on x2; (ii) the ARX2 model in which the exogenous input x1 is disregarded by ignoring the regression of y on x1; (iii) the X1X2 model in which the AR part is disregarded by ignoring the auto-regression of y; (iv) the AR model in which only the AR part is considered by ignoring both regressions of y on x1 and x2.
The one-step-ahead prediction of y, ŷ(n∕n−1), based on the ARX1X2 model is given by
where the coefficients âj, , and , with 1 ≤ j ≤ p, are estimated according to an optimization criterion (here the least squares approach minimizing the variance of wARX1X2) (Soderstrom and Stoica, 1988). According to the same optimization criterion the one-step-ahead prediction of the considered simplified versions of the ARX1X2 model (i.e., the ARX1, ARX2, X1X2, and AR structures) can be analogously obtained after a new identification of the regression coefficients. The prediction error is defined as the difference between y(n) and ŷ(n∕n−1). The ability of the model to describe the dynamic of y is quantified by the variance of the prediction error. It is bounded between 0 and the variance of y, σ2. Given the normalization of the series, the variance of the prediction error actually ranges between 0 and 1, where 0 indicates perfect prediction (the entire σ2 is explained by the model), and 1 indicates null prediction (no fraction of σ2 is explained by the model). In the following we will indicate the variances of the prediction error of the ARX1X2, ARX1, ARX2, X1X2, and AR models as , , , , and respectively.
Definition of the Information-theoretic Quantities
Under the hypothesis of linearity and Gaussianity of the dynamics, the Shannon entropy (ShE) of the normalized series y is ShEy = 0.5 · log(2πe) (McEliece, 2002), where log is the natural logarithm, and the conditional entropy (CE) of y in Ω is . ShEy and CEy measure, respectively, the total amount of information carried by y and its remaining portion that cannot be resolved using past samples of all signals present in Ω (Barnett et al., 2009). We define the PE of y in Ω (Chicharro and Ledberg, 2012; Faes et al., 2015) as
quantifying the portion of uncertainty of y that has been resolved in Ω (i.e., PEy = ShEy−CEy); the SE of y in Ω\x1,x2 (Lizier et al., 2012; Wibral et al., 2014) as
measuring the part of uncertainty of y that has been resolved in Ω\x1,x2, (i.e., solely using past values of y); the conditional SE (CSE) of y given x1 and x2 (Porta et al., 2015) as
measuring the part of information carried by y that can be explained in Ω, above and beyond the one that can be resolved using past values of x1 and x2 (Figure 1); the conditional self-entropy (CSE) of y given x1 in Ω\x2 (Faes et al., 2015) as
measuring the part of uncertainty of y that has been resolved in Ω\x2 (i.e., without accounting for the possible influences of the exogenous signal x2) above and beyond the one that can be resolved using past values of x1; the cross-entropy (C) from x1 to y in Ω\x2 (Faes et al., 2015) as
measuring the fraction of information carried by y that can be explained in Ω\x2 given past values of x1; the joint TE (JTE) from x1 and x2 to y (Porta et al., 2015) as
measuring the fraction of uncertainty of y that has been resolved in Ω above and beyond the one that can be resolved in Ω\x1,x2; the TE from x1 to y in Ω (i.e., by accounting for the possible influences of x2 on y) (Schreiber, 2000; Lizier and Prokopenko, 2010; Kugiumtzis, 2013), denoted here as the conditional JTE (CJTE) from x1 and x2 to y given x2 (Porta et al., 2015), as
measuring the reduction of uncertainty of y that can be achieved when Ω\x1 is completed with the introduction of x1 (Figure 1); the TE from x1 to y in Ω\x2 (i.e., without accounting for the possible influences of x2 on y) (Faes et al., 2015) as
measuring the reduction of uncertainty of y that can be achieved when Ω\x1,x2 is enlarged with the introduction of x1. By reversing the role between x1 and x2, CSEy|x2, Cx2→y, CJTEx1, x2→y|x1 (Figure 1), and TEx2→y can be computed as well.
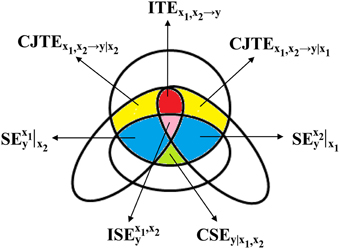
Figure 1. A mnemonic Venn diagram, redrawn from Porta et al. (2015), of the information-theoretic quantities contributing to the decomposition of PEy in Ω = {y, x1, x2}. The diagram is devised to represent in the information domain the terms whose sum gives the JTEx1, x2→y according to Equation (21), i.e., CJTEx1, x2→y|x1 (yellow area), CJTEx1, x2→y|x2 (yellow area), and ITEx1, x2→y (red area), and the terms whose sum gives the SEy according to Equation (22), i.e., CSEy|x1, x2 (green area), (blue area), (blue area), and (pink area).
Redundant/Synergistic Contribution of x1 and x2 to JTE
The interactive TE (ITE) of y is defined as the variation between the sum of the information individually transferred from x1 to y and from x2 to y and the quote jointly transferred (McGill, 1954; Stramaglia et al., 2012) (Figure 1). Therefore, the following equality
provides a relation among the information jointly transferred from x1 and x2 to y, JTEx1, x2→y, the quantities individually transferred from x1 to y, TEx1→y, and from x2 to y, TEx2→y and the ITEx1, x2→y. ITEx1, x2→y < 0 implies synergy of x1 and x2 in contributing to JTEx1, x2→y, indicating that the information jointly transferred from x1 and x2 to y is larger than the sum of the information transferred from x1 to y and from x2 to y when x1 and x2 are taken individually. Therefore, the ITEx1, x2→y measures the redundant or synergistic contribution of x1 and x2 to JTEx1, x2→y. The smaller and negative the ITEx1, x2→y, the more relevant the synergy of x1 and x2 in reducing the uncertainty about the present of y above and beyond the contribution of past values of y. ITEx1, x2→y>0 implies redundancy of x1 and x2 in contributing to JTEx1, x2→y, indicating that the information jointly transferred from x1 and x2 to y is smaller than the sum of the information transferred from x1 to y and from x2 to y when x1 and x2 are taken individually. Therefore, the larger and positive the ITEx1, x2→y, the more relevant the redundancy of x1 and x2 in reducing the uncertainty about the present of y above and beyond the contribution of past values of y. The ITEx1, x2→y can be easily estimated as
Equation (12) clearly indicates that the information transferred to y in Ω\x2 might be larger or smaller than that in Ω depending on whether redundancy or synergy occurs. From Equation (12) it is clear that the sign of ITEx1, x2→y depends on the balance between two quantities that are larger than 1: (i) ; (ii) . If >, redundancy is present. Conversely, if <, synergy is detected. Since ITEx1, x2→y is symmetric in x1 and x2, the abovementioned considerations hold by reversing the role of x1 and x2. The ITEx1, x2→y can be also expressed as a percent value with respect to JTEx1, x2→y. This quantity will be denoted as ITE%x1, x2→y.
Redundant/Synergistic Contributions of x1 and x2 to SE
The SEy can be seen as
where
represents the synergistic/redundant contribution of x1 and x2 to SEy (Figure 1). If >0, then SEy > CSEy|x1, x2. This indicates that past values of y and of the exogenous sources, when taken together, contribute redundantly to resolve the uncertainty of y because the joint consideration of past values of y and of the exogenous sources worsens predictability of y compared to their separated observations. Conversely, if < 0, the joint knowledge of past values of y and of the exogenous sources improves prediction compared to their separated consideration, thus indicating that past values of y and of the exogenous sources contribute synergistically to reduce the uncertainty of y. The can be also expressed as a percent value with respect to SEy. This quantity will be denoted as .
Defined the redundant/synergistic contributions of x1 and x2 to SEy when x1 and x2 are individually considered as
and
the equality
formally corresponds to Equation (11) as far as the information storage in y is concerned, where ISE stands for the interactive SE and represents the redundant/synergetic contributions of x1 and x2 to the information stored in y. At difference from Equation (11), where the ITEx1, x2→y is the unique synergistic/redundant term, in Equation (17) all parts might be positive or negative depending on whether x1 and x2, taken individually or jointly, contribute redundantly or synergistically to the information storage of y.
By substituting Equations (13), (15), and (16) into Equation (17) it can be easily demonstrated that the
thus leading to the following equality
that provides a viable estimate of .
Full Decomposition of PE of y in Ω
By following the definitions given in the previous sections it can be easily verified that the PEy in Ω can be fully decomposed (Figure 1) as
with
and
where and represent the synergistic/redundant contribution of x1 conditioned on x2 and vice versa to SEy in Ω (Figure 1). It is remarkable that the synergistic/redundant contribution of x1 and x2 to SEy, measured by , depends on the balance among the synergistic/redundant contributions of one of the exogenous inputs conditioned on the other, i.e., and , and on the synergistic/redundant contribution of x1 and x2 when they are jointly considered (i.e., ). Even though Equation (23) formally corresponds to Equation (21) as far as the information storage in y is concerned, Equations (21) and (23) are structurally very different. Indeed, while all the terms in Equation (23) can be positive or negative, CJTEx1, x2→y|x2 and CJTEx1, x2→y|x1 in Equation (21) are positive (or null).
Experimental Protocol and Data Analysis
Experimental Protocol
We studied 13 healthy men aged from 41 to 71 years (median: 59 years). A detailed medical history and examination excluded the evidence of any disease. The subjects did not take any medication nor did they consume any caffeine or alcohol containing beverages in the 24 h before the recording. The study adhered to the principles of the Declaration of Helsinki for medical research involving human subjects. The human research and ethical review board of the “L. Sacco” Hospital approved the protocol. All subjects gave their written informed consent. Electrocardiogram (ECG) and noninvasive finger blood pressure (Nexfin, BMEYE, Amsterdam, The Netherlands) were recorded during the experiments. Signals were sampled at 400 Hz. Each experiment consisted of 10 min of baseline recording at rest in supine position (REST) followed by 10 min of recording during HDT with a table inclination of −25°. Before REST we allowed 15 min of stabilization. The recordings of the HDT session started 5 min after tilting the table. During the protocol, the subjects breathed according to a metronome at 16 breaths.min−1 to prevent modifications of the magnitude of the respiratory sinus arrhythmia owing to the changes of the breathing rate as much as possible (Hirsch and Bishop, 1981; Brown et al., 1993). All experiments were carried out in the afternoon in the same temperature-controlled room and the subjects were not allowed to talk during the protocol. Original data are available through the corresponding author.
Extraction of the Beat-to-Beat Variability Series
After detecting the R-wave on the ECG and locating the R-wave peak using parabolic interpolation, the temporal distance between two consecutive R-wave apexes was computed and utilized as an approximation of HP. The maximum of arterial pressure inside the n-th HP [i.e., HP(n)] was taken as the n-th SAP [i.e., SAP(n)]. R signal was obtained from the respiratory-related amplitude modulation of the ECG. The amplitude of the first QRS complex delimiting HP(n), taken as the difference between the R-wave apex and the isoelectric line, was taken as the n-th R [i.e., R(n)]. The occurrences of R-wave and SAP peaks were carefully checked to avoid erroneous detections or missed beats. If isolated ectopic beats affected HP and SAP values, these measures were linearly interpolated using the closest values unaffected by ectopic beats. HP, SAP, and R sequences of 256 consecutive synchronous measures were chosen inside the REST and HDT periods, thus focusing on short-term cardiovascular regulatory mechanisms (Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996). The random selection of the onset of analysis within the overall REST and HDT periods made this preprocessing step operator-independent. The series were linearly detrended before multivariate linear regression analysis. If evident nonstationarities, such as very slow drifting of the mean or sudden changes of the variance, were visible despite the linear detrending, the random selection was carried out again. The HP and SAP means and the HP and SAP variances were indicated as μHP, μSAP, and and expressed in ms, mmHg, ms2, and mmHg2 respectively.
Power Spectral Analysis
The power spectrum was estimated according to an univariate parametric approach fitting the series according to the AR model (Kay and Marple, 1981). The Levinson-Durbin recursive algorithm was utilized to estimate the coefficients of the AR model and the variance of the white noise. The number of coefficients p was chosen according to the Akaike's figure of merit in the range from 8 to 14. The power spectral density was computed from the AR coefficients and from the variance of the white noise according to the maximum entropy spectral estimation approach (Kay and Marple, 1981). The AR spectral density was factorized into spectral components, the sum of which provides the entire power spectral density (Baselli et al., 1997). The AR spectral decomposition provided power and central frequency of the components of the AR spectral density. The central frequency of the components expressed in cycles.beats−1 was converted into Hz by dividing the values by μHP. A spectral component was labeled as low frequency (LF) or high frequency (HF) if its central frequency ranged between 0.04 and 0.15 Hz or was in the range of ±0.05 Hz around the paced breathing rate respectively. The LF and HF powers were computed as the sum of the powers of all LF and HF spectral components respectively. The HF power of the HP series, expressed in absolute units (i.e., ms2) and labeled as HFaHP, was utilized as a marker of vagal modulation directed to the heart (Akselrod et al., 1981), while the LF power of the SAP series, expressed in absolute units (i.e., mmHg2) and labeled as LFaSAP, was utilized as a marker of sympathetic modulation directed to vessels (Pagani et al., 1986).
Construction of Surrogates and Surrogate Analysis
We tested the null hypotheses of HP-SAP and HP-R coupling without or with preservation of the HP information storage. This test was performed by creating two sets of surrogates.
The first set was composed by the original SAP and R series, while the HP sequence was substituted with a series obtained by randomly shuffling the HP samples (Palus, 1997). The shuffling procedure was performed according to one of the N! permutations of the HP samples. As a consequence the SAP and R series were fully uncoupled to the HP shuffled dynamics and the original HP information storage was destroyed, while preserving the distribution of all series and the repetitive dynamical structures of SAP and R. This surrogate will be referred to as HP-shuffled surrogate.
The second set was composed by time-shifted versions of the original series (Andrzejak et al., 2003). While the HP series was left unmodified, the SAP and R sequences were shifted according to a delay much larger than the maximal order of the multivariate model (i.e., 50 cardiac beats), thus destroying the short-term temporal correspondence of the SAP and R samples to HP values, while preserving the HP information storage. The delays from SAP and R to HP were independently chosen. The values at the end of the SAP and R sequences were wrapped to their onset. This surrogate will be referred to as time-shifted surrogate.
For each triplet of original HP, SAP, and R series we created a triplet of HP-shuffled and time-shifted surrogates. If the values derived from the original data were significantly different from those obtained from the surrogate sets the null hypothesis of HP-SAP and HP-R coupling without or with preservation of the HP information storage was rejected.
Surrogate data are available through the corresponding author.
Calculation of the Information-theoretic Quantities
The HP series was modeled via ARX1X2, ARX1, ARX2, X1X2, and AR models where X1 = SAP and X2 = R. The delays from SAP and R to HP, τSAP and τR, were set to 0 to allow the description of the fast vagal reflex (within the current HP) capable to modify HP in response to changes of SAP and R (Eckberg, 1976; Baselli et al., 1994; Porta et al., 2012a). The coefficients were identified via a traditional least squares approach and Cholesky decomposition method (Soderstrom and Stoica, 1988; Baselli et al., 1997). The AR and X parts had the same model order p. The model order was optimized in the range from 4 to 16 according to the Akaike figure of merit for multivariate processes (Akaike, 1974) over the most complex model structure (i.e., the ARX1X2, model). The whiteness of the HP prediction error and its mutual uncorrelation, even at zero lag, with the SAP and R series was checked over the same model (Baselli et al., 1997; Porta et al., 2012a). All remaining model structures were separately identified using the optimal order of the ARX1X2 model. After the identification of the model coefficients the variances of the prediction errors were computed and the indexes PEHP, SEHP, JTESAP, R → HP, CJTESAP, R → HP|R, CJTESAP, R → HP|SAP, ITESAP, R → HP, CSEHP|SAP, R, , , , , ITE%SAP, R → HP, and were evaluated.
Statistical Analysis
We performed paired t-tests to check the significance of the difference between time, frequency and PEHP indexes derived at REST and during HDT. If the normality test (Kolmogorov-Smirnov test) was not fulfilled, the Wilcoxon signed rank test was utilized. The same test was exploited to check the difference between original and surrogate sets. Differences among the terms of the decompositions of PEHP (i.e., SEHP and JTESAP, R → HP), of JTESAP, R → HP (i.e., CJTESAP, R → HP|R, CJTESAP, R → HP|SAP, and ITESAP, R → HP), of SEHP (i.e., CSEHP|SAP, R and ) and of (i.e., , , and ) were assessed within the index and experimental condition via two-way repeated measures analysis of variance (Holm-Sidak test for multiple comparisons). The same test was utilized to compare ITE%SAP, R → HP and in both experimental conditions. Statistical analysis was carried out using a commercial statistical program (Sigmaplot, ver.11.0, Systat Software, San Jose, CA, USA). A p < 0.05 was always considered as significant.
Results
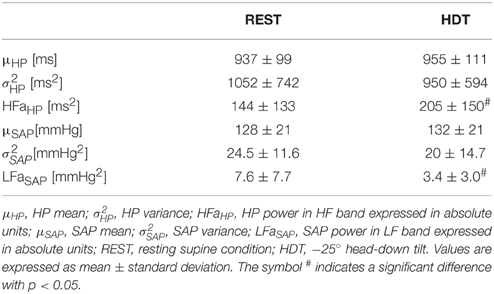
Table 1 summarizes the results relevant to the time and frequency domain analyses of the HP and SAP series. HDT did not affect the time domain parameters of both HP and SAP series (i.e., μHP, σ, μSAP, and σ). Conversely, the frequency domain indexes were significantly modified. Indeed, HFaHP increased during HDT, while LFaSAP significantly declined.
The bar graph shown in Figure 2 compares PEHP computed at REST and during HDT. PEHP was significantly decreased during HDT. The full decomposition of PEHP into more specific quantities is given in Figures 3–6.
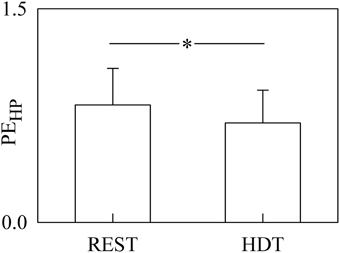
Figure 2. The bargraph shows the PEHP assessed at REST and during HDT. The values are reported as mean plus standard deviation. The symbol * indicates a significant difference with p < 0.05.
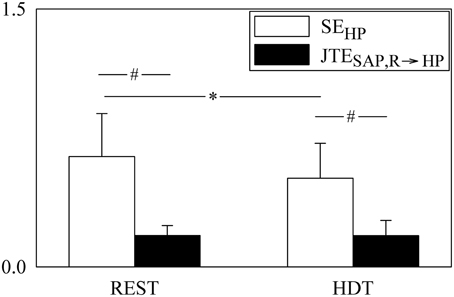
Figure 3. The grouped bargraph shows the SEHP (white bars) and JTESAP, R → HP (black bars) assessed at REST and during HDT. SEHP and JTESAP, R → HP are the two terms of the PEHP decomposition according to Equation (20). The values are reported as mean plus standard deviation. The symbol * indicates a significant difference between experimental conditions within the same index, while the symbol # indicates a significant difference between indexes within the same experimental condition with p < 0.05.
The grouped bar graph of Figure 3 shows the two terms forming PEHP according to Equation (20) (i.e., SEHP, white bars, and JTESAP, R → HP, black bars). SEHP was markedly larger than JTESAP, R → HP in both conditions. SEHP significantly decreased during HDT, while JTESAP, R → HP was not affected by the posture modification.
The grouped bar graph of Figure 4 depicts the three constituents of JTESAP, R → HP according to Equation (21) (i.e., CJTESAP, R → HP|R, white bars, CJTESAP, R → HP|SAP, gray bars, and ITESAP, R → HP, black bars). None of the terms forming JTESAP, R → HP were modified by HDT. At REST CJTESAP, R → HP|R, CJTESAP, R → HP|SAP, and ITESAP, R → HP were similar, while during HDT ITESAP, R → HP was significantly smaller than CJTESAP, R → HP|R. It is remarkable that ITESAP, R → HP was larger than 0 in all subjects regardless of the experimental condition, suggesting that SAP and R contributed redundantly to JTESAP, R → HP both at REST and during HDT.
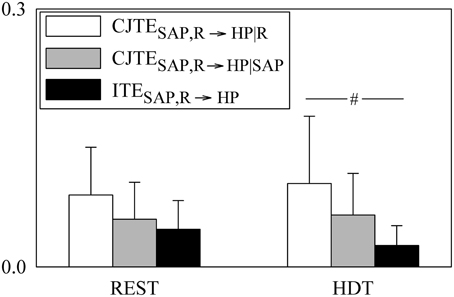
Figure 4. The grouped bargraph shows the CJTESAP, R → HP|R (white bars), CJTER, SAP → HP|SAP (gray bars) and ITESAP, R → HP (black bars) assessed at REST and during HDT. CJTESAP, R → HP|R, CJTER, SAP → HP|SAP, and ITESAP, R → HP are the three terms of the JTESAP, R → HP decomposition according to Equation (21). ITESAP, R → HP is the synergistic/redundant term of the JTESAP, R → HP decomposition. The values are reported as mean plus standard deviation. The symbol # indicates a significant difference between indexes within the same experimental condition with p < 0.05.
The grouped bar graph of Figure 5 shows the two terms forming SEHP according to Equation (13) (i.e., CSEHP|SAP, R, white bars, and , black bars). CSEHP|SAP, R significantly decreased during HDT, while was not affected by the posture modification. was significantly smaller than CSEHP|SAP, R in both experimental conditions. The average value of was larger than 0 indicating that, on average, SAP and R contributed redundantly to the information storage in HP. However, was negative in 31% and 46% of subjects at REST and during HDT respectively, thus indicating that at the level of the information storage in HP synergy between SAP and R occurred frequently.
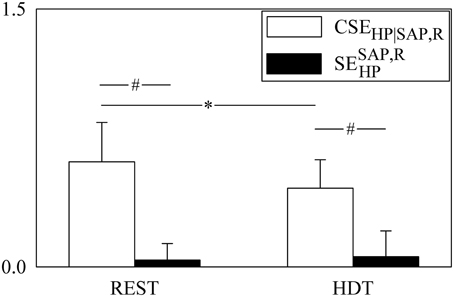
Figure 5. The grouped bargraph shows the CSEHP|SAP, R (white bars) and (black bars) assessed at REST and during HDT. CSEHP|SAP, R and are the two terms of the SEHP decomposition according to Equation (13). is the synergistic/redundant term of the SEHP decomposition. The values are reported as mean plus standard deviation. The symbol * indicates a significant difference between experimental conditions within the same index, while the symbol # indicates a significant difference between indexes within the same experimental condition with p < 0.05.
The grouped bar graph of Figure 6 depicts the synergistic/redundant terms present in the decomposition of SEHP according to Equation (22) (i.e., , white bars, , gray bars, and , black bars). No significant difference was detected within indexes given REST or HDT or within experimental conditions given the index. On average, , , and were positive at REST, but indexes were negative in 54%, 31%, and 54% of subjects respectively. On average during HDT and remained positive, while became negative. , , and were negative in 77%, 38%, and 38% of subjects respectively during HDT. These results stressed that at the level of the information storage in HP synergy between SAP and R was commonly present both at REST and during HDT, even though it did not take priority over redundancy.
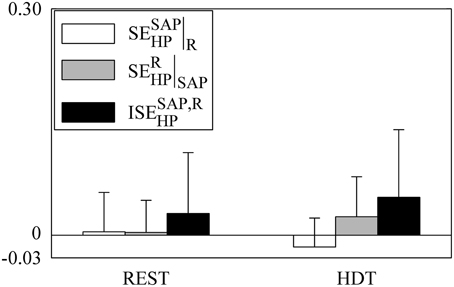
Figure 6. The grouped bargraph shows the (white bars), (gray bars), and (black bars) assessed at REST and during HDT. , , and are the three synergistic/redundant terms of the SEHP decomposition according to Equation (22). The values are reported as mean plus standard deviation.
The contributions of the redundant/synergistic terms to JTESAP, R → HP and SEHP (i.e., ITESAP, R → HP and ) are compared in Figure 7 after expressing them as ITE%SAP, R → HP and . Since ITE%SAP, R → HP was larger than 20% at REST, ITESAP, R → HP represented a sizable amount of JTESAP, R → HP. Conversely, was significantly smaller (about 3%), being a negligible quantity compared to SEHP. Both ITE%SAP, R → HP and were not affected by HDT. Remarkably, while ITE%SAP, R → HP was consistently positive in all subjects, the variability of was much higher due to the presence of both negative and positive values.
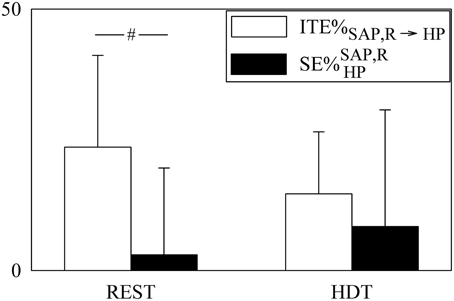
Figure 7. The grouped bargraph shows the ITE%SAP, R→HP (white bars) and (black bars) assessed at REST and during HDT. ITE%SAP, R → HP and measure the percent redundant/synergistic contributions of SAP and R to JTESAP, R → HP and SEHP respectively. The values are reported as mean plus standard deviation. The symbol # indicates a significant difference between indexes within the same experimental condition with p < 0.05.
For the surrogate analysis, the PEHP was significantly larger when computed over the original series than over both types of surrogates. This result held in the case of any term of the JTESAP, R → HP decomposition according to Equation (21). The SEHP and, more specifically, CSEHP|SAP, R was significantly larger over the original data than HP-shuffled surrogates. Conversely, the terms of the decomposition according to Equation (23) computed over the original data were similar to those calculated over both types of surrogates.
Discussion
The methodological findings of this study can be summarized as follows: (i) the study proposes a full decomposition of PE of y in Ω = {y,x1,x2} that includes the decomposition of SE of y in addition to the known decomposition of JTE from x1 and x2 to y; (ii) both JTE and SE decompositions include a term describing redundancy/synergy of x1 and x2 in contributing to the information carried by y and the redundant/synergistic term of SE has a more complex structure; (iii) the utility of the JTE and SE decompositions is demonstrated in the field of cardiovascular control analysis to disentangle physiological mechanisms from spontaneous variations and clarify the origin of the increase of respiratory sinus arrhythmia during HDT.
The experimental findings of this study can be summarized as follows: (i) in agreement with the literature we confirm the increase of respiratory sinus arrhythmia after acute cardiopulmonary loading induced by HDT; (ii) the PE of HP decreases during HDT, thus suggesting a larger complexity of the cardiac control and a vagal enhancement; (iii) the SE of HP is larger than the JTE from SAP and R to HP and the SE of HP due to SAP and R is negligible compared to the CSE of HP given SAP and R both at REST and during HDT, thus emphasizing the relevance of physiological mechanisms other than those mediated by SAP and R changes in governing the HP dynamics; (iv) the invariance of the CJTE from SAP and R to HP given R and CJTE from SAP and R to HP given SAP during HDT suggests a limited involvement of the baroreflex and cardiopulmonary pathway in controlling the HP dynamic during HDT; (v) the decrease of the CSE of HP given SAP and R in response to HDT suggests that the increase of respiratory sinus arrhythmia might be the consequence of modifications of the sinus node dynamical properties and/or an enhanced activity of the respiratory centers occurring independently of the cardiac baroreflex and cardiopulmonary circuits; (vi) SAP and R contribute redundantly to the information jointly transferred to HP, while, at the level of the information storage into HP, redundancy and synergy are more balanced; (vii) the amount of synergy or redundancy of SAP and HP to the information transfer and storage in HP is not affected by HDT, thus again stressing that the response to HDT is not mediated by a strong involvement of the cardiac baroreflex and cardiopulmonary circuits; (viii) surrogate analysis indicates that the terms of the JTE decomposition detect significant HP-SAP and HP-R interactions and the CSE of HP given SAP and R measures a significant HP information storage both at REST and during HDT.
Methodological Findings
Decomposition of PE of y in Ω = {y,x1,x2}
The study proposes a viable approach to tackle the issue of the PE decomposition of a target signal y affected by two exogenous signals, x1 and x2. The PE, measuring the reduction of uncertainty about the present of y when past samples of y, x1, and x2 are given (Chicharro and Ledberg, 2012; Faes et al., 2015), can be decomposed into the information jointly transferred from x1 and x2 to y and the information stored into y. The information stored into y estimates the amount of uncertainty about the present of y that can be resolved using only past values of y (Lizier et al., 2012; Wibral et al., 2014), while the JTE from x1 and x2 to y quantifies the reduction of uncertainty about the present value of y when past samples of x1 and x2 are given above and beyond the information stored into y (Porta et al., 2015). The decomposition of JTE from x1 and x2 to y into two terms considering the contribution of x1 to y given x2 and that of x2 to y given x1plus an additional term describing the balance between redundancy and synergy to the joint information transfer (i.e., the ITE) was originally proposed in (Stramaglia et al., 2012) by generalizing to the conditional case the notion of interaction information (McGill, 1954). Conversely, the full decomposition of SE of y is original, thus completing the PE decomposition of y in Ω = {y,x1,x2}. The SE is first decomposed into two terms: (i) the first term is the SE of y conditioned on the exogenous sources (i.e., the CSE of y given x1 and x2) assessing the information storage not attributable to SAP and R influences; (ii) the second term is a synergistic/redundant term indicating whether past values of y and of both exogenous signals, when jointly considered, contribute synergistically or redundantly to resolve the uncertainty of y (i.e., the SE of y due to x1 and x2). The SE of y due to x1 and x2 can be decomposed further into two terms considering the unique contribution of x1 and x2 plus an extra term describing the joint contribution of x1 and x2 (i.e., the ISE). We stress that, while in the decomposition of JTE from x1 and x2 to y given in Equation (21) the synergistic/redundant term is only one (i.e., ITE), in the decomposition of SE of y given in Equation (22) only one term is definitely larger than or equal to zero (i.e., the CSE of y given x1 and x2). Indeed, the SE of y due to x1 and x2 can be positive or negative and, consequently, the SE of y larger or smaller than the CSE of y given x1 and x2, depending on the balance among synergistic/redundant behaviors of past values of y and x1, past values of y and x2 and past values of y and both x1 and x2 in reducing the uncertainty of y.
Both JTE and SE of y in Ω = {y,x1,x2} Feature Redundant/Synergistic Terms
The JTE decomposition includes a term describing the redundant or synergistic contribution of x1 and x2 to JTE (McGill, 1954; Stramaglia et al., 2012; Barrett, 2015; Wibral et al., 2015). This term indicates that the single contributions of x1 and x2 to JTE do not invariably contain duplicate information (i.e., redundant contribution) about the present value of y, but, conversely, the contemporaneous knowledge of x1 and x2 might lead to extra information (i.e., synergistic contribution). The inclusion of any new additional exogenous signal in the universe of knowledge (e.g., x2 in Ω\x2) leading to synergy means to improve the prediction of y well above the one obtained when the exogenous signals are taken individually. Through, the SE decomposition this study proves that the notion of synergy or redundancy applies to the information storage as well. Information storage depends on the action of exogenous inputs (Lizier et al., 2012; Wibral et al., 2014) and the significance of the contribution of the exogenous signals to SE of y has been proved experimentally in the context of cardiovascular control analysis (Porta et al., 2015). The SE decomposition indicates that x1 and x2 might contribute redundantly or synergistically to the information storage. The study of the synergistic/redundant contributions of x1 and x2 to the information stored in y is more complex because the assessment of synergy/redundancy should take into account not only the ability of past values of x1 and x2 to reduce the uncertainty of y but also that of past values of y, thus increasing the number of synergistic/redundant terms. Conversely, in the case of the information transfer synergy/redundancy is exclusively attributable to past values of x1 and x2 since the contribution of past values of y is conditioned out. The multiplicity of terms describing redundancy/synergy at the level of the information storage has been spelled out in Equation (23) and viable estimators for their computation were provided.
JTE and SE Decompositions in Network Physiology
Our approach is framed into the emerging field of network physiology describing the complexity of aggregates of parts and their interactions as a network of nodes with interconnections (Bashan et al., 2012). This feature is in common with other approaches adopting the same logic for representing complex interactions among subsystems regardless of the scale (David et al., 2006; Bressler and Seth, 2011; Bashan et al., 2012; Iatsenko et al., 2013; Kralemann et al., 2014; Stankovski et al., 2015; Porta and Faes, 2016). This description might involve the utilization of raw data (David et al., 2006; Bressler and Seth, 2011), realizations of point processes or series of events (Porta and Faes, 2016) or phase evolutions estimated from raw data or series of events (Iatsenko et al., 2013; Kralemann et al., 2014; Stankovski et al., 2015). The functionals exploited to assess the strength of the interconnections among nodes might be fully adherent to the Wiener-Granger principle (Granger, 1963) if their calculation is based on a direct comparison of indexes computed in the unrestricted and restricted universes of knowledge via metrics assessing the predictability improvement (Bressler and Seth, 2011; Porta and Faes, 2016) and/or uncertainty decrement (Schreiber, 2000; Hlavackova-Schindler et al., 2007; Porta and Faes, 2016), or based on the explicit computation of coupling functions (Iatsenko et al., 2013; Kralemann et al., 2014; Stankovski et al., 2015), or the estimation of coupling coefficients of an assigned model (David et al., 2006). The approach devised in this study is fully consistent with the Wiener-Granger principle in the information domain, where functionals assess the uncertainty decrement and account for conditioning variables according to a multivariate approach. As such, some analogs can be found with fully multivariate methods based on the explicit calculation of coupling functions (Kralemann et al., 2014; Stankovski et al., 2015) and on its decomposition into self-, direct, and indirect components (Stankovski et al., 2015). Nevertheless, in the present study the proposed decomposition is achieved in a completely different framework (i.e., the Wiener-Granger one) and it is expressively devised for the identification of synergistic/redundant components, rather than for the exclusive separation of the direct influences from the indirect ones.
Experimental Findings
Time and Frequency Domain Analyses of HP Dynamics during HDT
Time and frequency domain parameters confirmed that HDT does not significantly affect the HP and SAP means (Harrison et al., 1986; Nagaya et al., 1995; Kardos et al., 1997; Tanaka et al., 1999) but it increases the HF power of HP (Kardos et al., 1997) and decreases the LF power of SAP (Weise et al., 1995). These findings were interpreted as a sign of the involvement of the autonomic nervous system in adjusting HP and SAP in response to the posture challenge and, more specifically, as an indication of the increased vagal modulation directed to the sinus node and the decreased sympathetic modulation directed to the vessels during HDT (Nagaya et al., 1995; Weise et al., 1995; Tanaka et al., 1999). Unfortunately, time and frequency domain analyses exploited in this study, and traditionally utilized to understand the physiological adaptation to acute central circulatory hypervolaemia (Weise et al., 1995; Kardos et al., 1997), are not helpful to clarify the origin of the increase of respiratory sinus arrhythmia during HDT. This limitation can be primarily attributable to the univariate nature of these classical time and frequency domain analyses and to their inability to interpret causality, thus preventing the possibility of disentangling the HP response to HDT driven by changes of SAP and R from the one independent of them. This limitation is tackled by the proposed multivariate approach grounded in the framework of information dynamics.
Information Dynamics Approach to the Assessment of the Cardiovascular Control during HDT
The involvement of the cardiovascular control in regulating the HP dynamic during HDT is clearly suggested by the significant decrease of PE of HP. Since we reported earlier that the level of predictability of HP based on past samples of HP, SAP and R is under vagal control being increased during head-up tilt and high dose administration of atropine (Porta et al., 2012c), the decrease of the amount of uncertainty about the present of HP that can be resolved by past values of HP, SAP, and R, as measured by the PE of HP, suggests a larger complexity of the cardiac control and an increased vagal regulation during HDT. Even though based on multivariate analysis, this finding is useless in explaining the mechanisms underpinning vagal activation and the increase of respiratory sinus arrhythmia because PE is a global parameter vaguely linked to physiological mechanisms. We need to directly exploit the decomposition of JTE of SAP and R to HP and SE of HP to try to elucidate the origin of the increase of respiratory sinus arrhythmia during HDT.
The information stored into HP, as measured by the SE of HP, is significantly larger than the JTE of SAP and R to HP. This finding suggests that, even though the knowledge of SAP and R is really helpful in resolving the uncertainty of HP, the contribution of these two signals is significantly smaller compared to the ability of past HP values in predicting the current HP. The relevance of the information storage in HP as the likely consequence of the importance of signals driving HP dynamics independently of SAP and R, such as modulation of efferent cardiac neural activity driven by central commands, originating from respiratory and vasomotor centers in the brainstem, and independent of afferent inputs (Preiss and Polosa, 1974; Valentinuzzi and Geddes, 1974; Preiss et al., 1975; Koepchen, 1984; Dick et al., 2009). Also the dynamical properties of the sinus node (i.e., how it responds to changes of sympathetic and vagal inputs) might play an important role in setting the magnitude of the information stored in HP because they directly affect the memory of HP over its past values (Chess and Calaresu, 1971; Berger et al., 1989; Porta et al., 2003). In addition to the dynamical response of receptors, the self-storage of information into HP depends on the type of neurotransmitters, their concentration, rate of release, degradation and removal and sympatho-vagal interactions (Kawada et al., 1996; Nakahara et al., 1998, 1999; Porta et al., 2003).
Remarkably, we found that the SE of HP and, more specifically, the CSE of HP given SAP and R decreased during HDT, while the JTE of SAP and R to HP remained unmodified. The reduction of the CSE of HP given SAP and R supports the central drive hypothesis as a possible explanation for the increase of respiratory sinus arrhythmia during HDT. Indeed, the activation of a central mechanism, independent of the cardiac baroreflex and cardiopulmonary stimulation, could limit the ability of past values of HP in reducing the uncertainty of the current HP value. For example, if the respiratory centers improved their activity (Valentinuzzi and Geddes, 1974; Dick et al., 2009), the resulting augmented modulation of the cardiovagal motorneuron responsiveness would produce an increase of respiratory sinus arrhythmia (Eckberg, 2003) and make cardiac regulation more complex (Porta et al., 2012c).
The invariance of JTE from SAP and R to HP during HDT is not a sufficient condition to exclude the role of the cardiac baroreflex and cardiopulmonary reflexes in the rise of respiratory sinus arrhythmia during HDT. Indeed, during graded head-up tilt we found that the invariance of JTE from SAP and R to HP hides the progressive increase of the information transferred from SAP to HP in Ω, as quantified by the CJTE from SAP and R to HP given R, and the decrease of the information transferred from R to HP in Ω, as quantified by the CJTE from SAP and R to HP given SAP, with the magnitude of the orthostatic challenge and baroreflex unloading (Porta et al., 2015). Therefore, it is necessary to check the trend of CJTE from SAP and R to HP given R and CJTE from SAP and R to HP given SAP during HDT to better characterize the involvement of the baroreflex and cardiopulmonary pathway in controlling HP dynamics. Given the invariance of the CJTE from SAP and R to HP given R and CJTE from SAP and R to HP given SAP during HDT we conclude that the amount of information transferred along the cardiac baroreflex and cardiopulmonary reflexes is not significantly different from that observed at REST and, thus, we exclude again the cardiac baroreflex control and cardiopulmonary reflexes as possible physiological mechanisms underpinning the observed increase of respiratory sinus arrhythmia.
The opposite influences on the venous return, central blood volume and central venous pressure during head-up tilt and HDT, leading to baroreflex unloading, sympathetic activation, and vagal withdrawal in the case of the head-up tilt (Montano et al., 1994; Cooke et al., 1999; Furlan et al., 2000; Marchi et al., 2013) and cardiopulmonary loading and sympathetic inhibition in the case of HDT (Nagaya et al., 1995; Tanaka et al., 1999), might suggest opposite effects on the degree of involvement of the baroreflex control of HP and cardiopulmonary neural circuits. Contrary to this expectation, while head-up tilt maneuver led to an augmented involvement of the baroreflex control of HP and a reduced participation of the cardiopulmonary reflexes (Porta et al., 2012b, 2015), the invariance of the information transferred along the cardiac baroreflex and cardiopulmonary pathway observed in the present study suggests that the physiological response to acute central circulatory hypervolaemia during HDT cannot be simply deduced from the knowledge of the response to acute central circulatory hypovolemia during head-up tilt.
Redundancy and Synergy of SAP and R in Contributing to the Information Transferred and Stored in HP Dynamics
SAP and R contribute redundantly to the information jointly transferred to HP. This means that SAP and R hold common information about the present value of HP above and beyond that derived from past values of HP. Remarkably, this quantity is important since it explains more than 20% of JTE from SAP and R to HP. The redundant nature of the SAP and R contributions to the information transferred to HP is not surprising. Indeed, R can directly modulate SAP by modifying venous return, pressure gradients over large arteries in the thorax and stroke volume via respiratory-related changes of the intrathoracic pressure (Innes et al., 1993; Toska and Eriksen, 1993; Caiani et al., 2000). However, the redundant contribution of SAP and R to JTE from SAP and R to HP might also come from more complex interactions and integrations between vasomotor and respiratory centers occurring at the brain stem level. This amount of redundancy might accomplish a principle of fault tolerance and harmonization of neural responses. In this specific experimental protocol the amount of redundancy of SAP and R to the information transferred to HP was not significantly varied during HDT, again confirming that HDT did not affect quantities closely linked to the functioning of the cardiac baroreflex and cardiopulmonary reflexes.
Even though on average SAP and R contribute redundantly to the information storage into HP, we cannot conclude that redundancy is prevailing over synergy as far as the information storage of HP is concerned. Indeed, the SE of HP due to SAP and R, measuring the balance between redundancy and synergy at the level of the information storage at REST, is quite small (i.e., 3% of the SE of HP) and in 31% of subjects synergistic behaviors between SAP and R in contributing to the SE of HP were observed. As a result of the presence of both redundancy and synergy inside the group of subjects in both experimental conditions, indexes describing the synergistic/redundant behavior of SAP and R to the information storage of HP are characterized by greater variability compared to the index describing the synergistic/redundant behavior of SAP and R to the information transferred into HP. The amount of redundancy of SAP and R to the information storage of HP was not significantly varied during HDT, thus again stressing that HDT did not affect quantities linked to the functioning of the cardiac baroreflex and cardiopulmonary circuits even when the action of these reflexes is mediated by memory effects of HP on its own past.
Surrogate Analysis
Surrogate data were constructed with the main aim to test the significance of the proposed indexes as markers of the strength of the HP-SAP and HP-R coupling in absence or presence of a significant amount of information stored in HP. According to this idea two types of surrogates, both destroying the HP-SAP and HP-R coupling are generated. The first type, the HP-shuffled surrogates, wiped out the HP autocorrelation function, while the second type, the time-shifted surrogates, preserved it. Remarkably, all indexes derived from the decomposition of JTE from SAP and R to HP both at REST and during HDT were significantly larger from those derived from surrogates, regardless of the type. This result indicates that both at REST and during HDT the HP-SAP and HP-R interactions are significant as well as the detected redundancy of SAP and R in contributing to the JTE from SAP and R to HP, suggesting that indexes derived from the JTE decomposition are helpful to detect physiological interactions from spontaneous variations. The SE of HP and, more specifically, the CSE of HP given SAP and R, was significantly larger in the original data than in the HP-shuffled surrogates both at REST and during HDT. This result suggests that the information stored into the HP dynamics is significant in both experimental conditions. Conversely, the terms of the decomposition of SE of HP due to SAP and R computed over the original data were indistinguishable from those calculated over surrogate data regardless the type of surrogate both at REST and during HDT. We suggest two possible explanations for this finding: (i) the contributions of SAP and R to the SE of HP did not reach the level of significance both at REST and during HDT; (ii) the surrogate analysis proposed in the present study is not suitable to test the significance of the causal interactions from SAP and R to HP at the level of the SE decomposition.
Significance of the Study and Future Perspectives
A full decomposition of the amount of uncertainty about a target signal that can be resolved based on two presumed driving signals is provided. The decomposition is relevant to the information jointly transferred from the two driving signals to the target one and to the information stored into the destination signal. Terms describing the balance between redundancy and synergy of the two driving series in resolving the uncertainty of the target signal have been highlighted and viable estimators have been proposed. The application to the experimental data suggests the relevance of the approach in dissecting out cardiovascular control mechanisms with the aim of accepting or rejecting physiological hypotheses. Since the proposed quantities are highly specific and take the form of indexes that can be computed very efficiently and robustly via a traditional multivariate regression analysis of spontaneously varying variables, they appear to be suitable candidates for large scale applications to clinical databases recorded even under uncontrolled conditions. Due to the generality of the approach it might be applied not only to cardiovascular physiology and neuroscience, but also in any field of science in which interactions among systems, or constituents of the same system, are under evaluation. Future studies should extend the decomposition to model-free frameworks to account for the possible presence of nonlinear dynamics disregarded by the present approach. In addition, given that in the present contribution the interaction terms actually represent the balance between redundancy and synergy, future studies might test different information decomposition strategies (Barrett, 2015; Wibral et al., 2015) and extend the proposed decomposition of SE to allow the coexistence of both redundancy and synergy as independent positive quantities. We also advocate studies devoted to the improvement of the physical/physiological interpretation of the parts of the JTE and SE decompositions that can be achieved by extending the application of these decompositions to new experimental conditions, proposing new experiments aimed at modulating the terms of the decompositions, comparing this approach to different techniques for the quantification of the coupling strength, developing new strategies for the construction of ad-hoc surrogate sets and designing specific simulation studies.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Akaike, H. (1974). A new look at the statistical novel identification. IEEE Trans. Autom. Cont. 19, 716–723. doi: 10.1109/TAC.1974.1100705
Akselrod, S., Gordon, D., Ubel, F. A., Shannon, D. C., Berger, R. D., and Cohen, R. J. (1981). Power spectrum analysis of heart rate fluctuations: a quantitative probe of beat-to-beat cardiovascular control. Science 213, 220–223. doi: 10.1126/science.6166045
Andrzejak, R. G., Kraskov, A., Stögbauer, H., Mormann, F., and Kreuz, T. (2003). Bivariate surrogate techniques: necessity, strengths, and caveats. Phys. Rev. E 68:066202. doi: 10.1103/physreve.68.066202
Barnett, L., Barrett, A. B., and Seth, A. K. (2009). Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 103:238701. doi: 10.1103/PhysRevLett.103.238701
Barrett, A. B. (2015). Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 91:052802. doi: 10.1103/physreve.91.052802
Baselli, G., Cerutti, S., Badilini, F., Biancardi, L., Porta, A., Pagani, M., et al. (1994). Model for the assessment of heart period and arterial pressure variability interactions and respiratory influences. Med. Biol. Eng. Comput. 32, 143–152. doi: 10.1007/BF02518911
Baselli, G., Porta, A., Rimoldi, O., Pagani, M., and Cerutti, S. (1997). Spectral decomposition in multichannel recordings based on multivariate parametric identification. IEEE Trans. Biomed. Eng. 44, 1092–1101. doi: 10.1109/10.641336
Bashan, A., Bartsch, R. P., Kantelhardt, J. W., Havlin, S., and Ivanov, P. C. (2012). Network physiology reveals relations between network topology and physiological function. Nat. Commun. 3, 702. doi: 10.1038/ncomms1705
Berger, R. D., Saul, J. P., and Cohen, R. J. (1989). Transfer function analysis of autonomic regulation I. Canine atrial rate response. Am. J. Physiol. 256, H142–H152.
Bressler, S., and Seth, A. K. (2011). Wiener-Granger causality: a well-established methodology. Neuroimage 58, 323–329. doi: 10.1016/j.neuroimage.2010.02.059
Brown, T. E., Beightol, L. A., Kob, J., and Eckberg, D. L. (1993). Important influence of respiration on human RR interval power spectra is largely ignored. J. Appl. Physiol. 75, 2310–2317.
Caiani, E., Turiel, M., Muzzupappa, S., Porta, A., Baselli, G., Pagani, M., et al. (2000). Evaluation of respiratory influences on left ventricular function parameters extracted from echocardiographic acoustic quantification. Physiol. Meas. 21, 175–186. doi: 10.1088/0967-3334/21/1/321
Chess, G. F., and Calaresu, F. R. (1971). Frequency response model of vagal control of heart rate in the cat. Am. J. Physiol. 220, 554–557.
Chicharro, D., and Ledberg, A. (2012). Framework to study dynamic dependencies in networks of interacting processes. Phys. Rev. E 86:041901. doi: 10.1103/physreve.86.041901
Cooke, W. H., Hoag, J. B., Crossman, A. A., Kuusela, T. A., Tahvanainen, K. U. O., and Eckberg, D. L. (1999). Human responses to upright tilt: a window on central autonomic integration. J. Physiol. 517, 617–628. doi: 10.1111/j.1469-7793.1999.0617t.x
David, O., Kiebel, S. J., Harrison, L. M., Mattout, J., Kilner, J. M., and Friston, K. J. (2006). Dynamic causal modeling of evoked responses in EEG and MEG. Neuroimage 30, 1255–1272. doi: 10.1016/j.neuroimage.2005.10.045
Dick, T. E., Baekey, D. M., Paton, J. F. R., Lindsey, B. G., and Morris, K. F. (2009). Cardiorespiratory coupling depends on the pons. Resp. Physiol. Neurobi. 168, 78–85. doi: 10.1016/j.resp.2009.07.009
Eckberg, D. L. (1976). Temporal response patterns of the human sinus node to brief carotid baroreceptor stimuli. J. Physiol. 258, 769–782. doi: 10.1113/jphysiol.1976.sp011445
Eckberg, D. L. (2003). The human respiratory gate. J. Physiol. 548, 339–352. doi: 10.1113/jphysiol.2002.037192
Faes, L., Nollo, G., and Porta, A. (2011). Information-based detection of nonlinear Granger causality in multivariate processes via a nonuniform embedding technique. Phys. Rev. E 83:051112. doi: 10.1103/physreve.83.051112
Faes, L., Porta, A., and Nollo, G. (2015). Information decomposition in bivariate systems: theory and application to cardiorespiratory dynamics. Entropy 17, 277–303. doi: 10.3390/e17010277
Faes, L., Porta, A., Rossato, G., Adami, A., Tonon, D., Corica, A., et al. (2013). Investigating the mechanisms of cardiovascular and cerebrovascular regulation in orthostatic syncope through an information decomposition strategy. Auton. Neurosci. Basic Clin. 178, 76–82. doi: 10.1016/j.autneu.2013.02.013
Furlan, R., Porta, A., Costa, F., Tank, J., Baker, L., Schiavi, R., et al. (2000). Oscillatory patterns in sympathetic neural discharge and cardiovascular variables during orthostatic stimulus. Circulation 101, 886–892. doi: 10.1161/01.CIR.101.8.886
Granger, C. W. J. (1963). Economic processes involving feedback. Inf. Cont. 6, 28–48. doi: 10.1016/S0019-9958(63)90092-5
Harrison, M. H., Rittenhouse, D., and Greenleaf, J. E. (1986). Effect of posture on arterial baroreflex control of heart rate in humans. Eur. J. Appl. Physiol. 55, 367–373. doi: 10.1007/BF00422735
Hirsch, J. A., and Bishop, B. (1981). Respiratory sinus arrhythmia in humans: how breathing pattern modulates heart rate. Am. J. Physiol. 241, H620–H629.
Hlavackova-Schindler, K., Palus, M., Vejmelka, M., and Bhattacharya, J. (2007). Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 441, 1–46. doi: 10.1016/j.physrep.2006.12.004
Iatsenko, D., Bernjak, A., Stankovski, T., Shiogai, Y., Owen-Lynch, P. J., Clarkson, P. B. M., et al. (2013). Evolution of cardio-respiratory interactions with age. Phil. Trans. R. Soc. A 371:20110622. doi: 10.1098/rsta.2011.0622
Innes, J. A., De Cort, S. C, Kox, W., and Guz, A. (1993). Within-breath modulation of left ventricular function during normal breathing and positive-pressure ventilation in man. J. Physiol. 460, 487–502. doi: 10.1113/jphysiol.1993.sp019483
Kardos, A., Rudas, L., Simon, J., Gingl, Z., and Csanády, M. (1997). Effect of postural changes on arterial baroreflex sensitivity assessed by the spontaneous sequence method and Valsalva manoeuvre in healthy subjects. Clin. Auton. Res. 7, 143–148. doi: 10.1007/BF02308842
Kawada, T., Ikeda, Y., Sugimachi, M., Shishido, T., Kawaguchi, O., Yamazaki, T., et al. (1996). Bidirectional augmentation of heart rate regulation by autonomic nervous system in rabbits. Am. J. Physiol. 271, H288–H295.
Kay, S. M., and Marple, S. L. (1981). Spectrum analysis: a modern perspective. Proc. IEEE 69, 1380–1418. doi: 10.1109/PROC.1981.12184
Koepchen, H. P. (1984). “History of studies and concepts of blood pressure waves,” in Mechanisms of Blood Pressure Waves eds K. Miyakawa, C. Polosa, and H. P. Koepchen (Berlin: Springer-Verlag), 3–23.
Kralemann, B., Pikovsky, A., and Rosenblum, M. (2014). Reconstructing effective phase connectivity of oscillator networks from observations. New J. Phys. 16:085013. doi: 10.1088/1367-2630/16/8/085013
Kugiumtzis, D. (2013). Direct-coupling information measure from nonuniform embedding. Phys. Rev. E 87:062918. doi: 10.1103/physreve.87.062918
Lizier, J. T., Atay, F. M., and Jost, J. (2012). Information storage, loop motifs, and clustered structure in complex networks. Phys. Rev. E 86:026110. doi: 10.1103/physreve.86.026110
Lizier, J. T., Heinzle, J., Horstmann, A., Haynes, J.-D., and Prokopenko, M. (2011). Multivariate information-theoretic measures reveal directed information structure and task relevant changes in fMRI connectivity. J. Comput. Neurosci. 30, 85–107. doi: 10.1007/s10827-010-0271-2
Lizier, J. T., and Prokopenko, M. (2010). Differentiating information transfer and causal effect. Eur. Phys. J. B. 73, 605–615. doi: 10.1140/epjb/e2010-00034-5
London, G. M., Levenson, J. A., Safar, M. E., Simon, A. C., Guerin, A. P., and Payen, D. (1983). Hemodynamic effects of head-down tilt in normal subjects and sustained hypertensive patients. Am. J. Physiol. 245, H194–H202.
Marchi, A., Colombo, R., Guzzetti, S., Bari, V., Bassani, T., Raimondi, F., et al. (2013). Characterization of the cardiovascular control during modified head-up tilt test in healthy adult humans. Auton. Neurosci.-Basic Clin. 179, 166–169. doi: 10.1016/j.autneu.2013.08.071
McEliece, R. J. (2002). The Theory of Information and Coding. Cambridge: Cambridge University Press.
McGill, W. J. (1954). Multivariate information transmission. Psychometrika 19, 97–116. doi: 10.1007/BF02289159
Montano, N., Gnecchi-Ruscone, T., Porta, A., Lombardi, F., Pagani, M., and Malliani, A. (1994). Power spectrum analysis of heart rate variability to assess changes in sympatho-vagal balance during graded orthostatic tilt. Circulation 90, 1826–1831. doi: 10.1161/01.CIR.90.4.1826
Nagaya, K., Wada, F., Nakamitsu, S., Sagawa, S., and Shiraki, K. (1995). Responses of the circulatory system and muscle sympathetic nerve activity to head-down tilt in humans. Am. J. Physiol. 268, H1289–H1294.
Nakahara, T., Kawada, T., Sugimachi, M., Miyano, H., Sato, T., Shishido, T., et al. (1998). Cholinesterase affects dynamic transduction properties from vagal stimulation to heart rate. Am. J. Physiol. 275, R541–R547.
Nakahara, T., Kawada, T., Sugimachi, M., Miyano, H., Sato, T., Shishido, T., et al. (1999). Neural uptake affects dynamic characteristics of heart rate response to sympathetic stimulation. Am. J. Physiol. 277, R140–R146.
Nemati, S., Edwards, B. A., Lee, J., Pittman-Polletta, B., Butler, J. P., and Malhotra, A. (2013). Respiration and heart rate complexity: effects of age and gender assessed by band-limited transfer entropy. Resp. Physiol. Neurobi. 189, 27–33. doi: 10.1016/j.resp.2013.06.016
Pagani, M., Lombardi, F., Guzzetti, S., Rimoldi, O., Furlan, R., Pizzinelli, P., et al. (1986). Power spectral analysis of heart rate and arterial pressure variabilities as a marker of sympatho-vagal interaction in man and conscious dog. Circ. Res. 59, 178–193. doi: 10.1161/01.RES.59.2.178
Palus, M. (1997). Detecting phase synchronisation in noisy systems. Phys. Lett. A 235, 341–351. doi: 10.1016/S0375-9601(97)00635-X
Porta, A., Bassani, T., Bari, V., Pinna, G. D., Maestri, R., and Guzzetti, S. (2012a). Accounting for respiration is necessary to reliably infer Granger causality from cardiovascular variability series. IEEE Trans. Biomed. Eng. 59, 832–841. doi: 10.1109/TBME.2011.2180379
Porta, A., Bassani, T., Bari, V., Tobaldini, E., Takahashi, A. C. M., Catai, A. M., et al. (2012b). Model-based assessment of baroreflex and cardiopulmonary couplings during graded head-up tilt. Comput. Biol. Med. 42, 298–305. doi: 10.1016/j.compbiomed.2011.04.019
Porta, A., Castiglioni, P., di Rienzo, M., Bari, V., Bassani, T., Marchi, A., et al. (2012c). Short-term complexity indexes of heart period and systolic arterial pressure variabilities provide complementary information. J. Appl. Physiol. 113, 1810–1820. doi: 10.1152/japplphysiol.00755.2012
Porta, A., Catai, A. M., Takahashi, A. C. M., Magagnin, V., Bassani, T., Tobaldini, E., et al. (2011). Causal relationships between heart period and systolic arterial pressure during graded head-up tilt. Am. J. Physiol. 300, R378–R386. doi: 10.1152/ajpregu.00553.2010
Porta, A., and Faes, L. (2016). Wiener-Granger causality in network physiology with applications to cardiovascular control and neuroscience. Proc. IEEE (accepted).
Porta, A., Faes, L., Bari, V., Marchi, A., Bassani, T., Nollo, G., et al. (2014a). Effect of age on complexity and causality of the cardiovascular control: comparison between model-based and model-free approaches. PLoS ONE 9:e89463. doi: 10.1371/journal.pone.0089463
Porta, A., Faes, L., Nollo, G., Bari, V., Marchi, A., De Maria, B., et al. (2015). Conditional self-entropy and conditional joint transfer entropy in heart period variability during graded postural challenge. PLoS ONE 10:e0132851. doi: 10.1371/journal.pone.0132851
Porta, A., Marchi, A., Bari, V., Catai, A. M., Guzzetti, S., Raimondi, F., et al. (2014b). “Directionality in cardiovascular variability interactions during head-down tilt test,” in Proceedings of the 36th Annual International Conference of the IEEE EMBS, 2014 August 26-30 (Chicago, IL: IEEE Press), 6008–6011.
Porta, A., Montano, N., Pagani, M., Malliani, A., Baselli, G., Somers, V. K., et al. (2003). Non-invasive model-based estimation of the sinus node dynamic properties from spontaneous cardiovascular variability series. Med. Biol. Eng. Comput. 41, 52–61. doi: 10.1007/BF02343539
Preiss, G., Kirchner, F., and Polosa, C. (1975). Patterning of sympathetic preganglionic neuron firing by the the central respiratory drive. Brain Res. 87, 363–374. doi: 10.1016/0006-8993(75)90434-5
Preiss, G., and Polosa, C. (1974). Patterns of sympathetic neuron activity associated with Mayer waves. Am. J. Physiol. 226, 724–730.
Schreiber, T. (2000). Measuring information transfer. Phys. Rev. Lett. 85, 461–464. doi: 10.1103/PhysRevLett.85.461
Seals, D. R., and Esler, M. D. (2000). Human ageing and sympathoadrenal system. J. Physiol. 528, 407–417. doi: 10.1111/j.1469-7793.2000.00407.x
Stankovski, T., Ticcinelli, V., McClintock, P. V. E., and Stefanovska, A. (2015). Coupling functions in networks of oscillators. New J. Phys. 17:0350022. doi: 10.1088/1367-2630/17/3/035002
Stramaglia, S., Wu, G.-R., Pellicoro, M., and Marinazzo, D. (2012). Expanding the transfer entropy to identify information circuits in complex systems. Phys. Rev. E 86:066211. doi: 10.1103/physreve.86.066211
Task Force of the European Society of Cardiology the North American Society of Pacing Electrophysiology (1996). Heart rate variability - Standards of measurement, physiological interpretation and clinical use. Circulation 93, 1043–1065. doi: 10.1161/01.CIR.93.5.1043
Tanaka, H., Davy, K. P., and Seals, D. R. (1999). Cardiopulmonary baroreflex inhibition of sympathetic nerve activity is preserved with age in healthy humans. J. Physiol. 515, 249–254. doi: 10.1111/j.1469-7793.1999.249ad.x
Taylor, J. A., and Eckberg, D. L. (1996). Fundamental relations between short-term RR interval and arterial pressure oscillations in humans. Circulation 93, 1527–1532. doi: 10.1161/01.CIR.93.8.1527
Toska, K., and Eriksen, M. (1993). Respiration-synchronous fluctuations in stroke volume, heart rate and arterial pressure in humans. J. Physiol. 472, 501–512. doi: 10.1113/jphysiol.1993.sp019958
Valentinuzzi, M. E., and Geddes, L. A. (1974). The central component of the respiratory heart rate response. Cardiovasc. Res. Center B. 12, 87–103.
Weise, F., London, G. M., Guerin, A. P., Pannier, B. M., and Elghozi, J.-L. (1995). Effect of head-down tilt on cardiovascular control in healthy subjects: a spectral analytic approach. Clin. Sci. 88, 87–93. doi: 10.1042/cs0880087
Wibral, M., Lizier, J. T., and Priesemann, V. (2015). Bits from brains for biologically-inspired computing. Front. Robot. Artif. Intell. 2:5. doi: 10.3389/frobt.2015.00005
Wibral, M., Lizier, J. T., Vögler, S., Priesemann, V., and Galuske, R. (2014). Local active information storage as a tool to understand distributed neural information processing. Front. Neuroinf. 8:1. doi: 10.3389/fninf.2014.00001
Keywords: information dynamics, multivariate linear regression analysis, blood pressure variability, heart rate variability, baroreflex, cardiopulmonary coupling, autonomic nervous system
Citation: Porta A, Faes L, Marchi A, Bari V, De Maria B, Guzzetti S, Colombo R and Raimondi F (2015) Disentangling cardiovascular control mechanisms during head-down tilt via joint transfer entropy and self-entropy decompositions. Front. Physiol. 6:301. doi: 10.3389/fphys.2015.00301
Received: 10 July 2015; Accepted: 12 October 2015;
Published: 27 October 2015.
Edited by:
Zbigniew R. Struzik, The University of Tokyo, JapanReviewed by:
Tomislav Stankovski, Lancaster University, United KingdomBenjamin Vandendriessche, Case Western Reserve University, USA
Copyright © 2015 Porta, Faes, Marchi, Bari, De Maria, Guzzetti, Colombo and Raimondi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alberto Porta, YWxiZXJ0by5wb3J0YUB1bmltaS5pdA==
 Alberto Porta
Alberto Porta Luca Faes
Luca Faes Andrea Marchi
Andrea Marchi Vlasta Bari
Vlasta Bari Beatrice De Maria
Beatrice De Maria Stefano Guzzetti
Stefano Guzzetti Riccardo Colombo
Riccardo Colombo Ferdinando Raimondi
Ferdinando Raimondi