- 1Department of Mechanical and Process Engineering, Institute of Fluid Dynamics, ETH Zurich, Zurich, Switzerland
- 2Department of Physiology, University of Arizona, Tucson, AZ, United States
- 3Institute of Pharmacology and Toxicology, University of Zurich, Zurich, Switzerland
Capillary dysfunction impairs oxygen supply to parenchymal cells and often occurs in Alzheimer's disease, diabetes and aging. Disturbed capillary flow patterns have been shown to limit the efficacy of oxygen extraction and can be quantified using capillary transit time heterogeneity (CTH). However, the transit time of red blood cells (RBCs) through the microvasculature is not a direct measure of their capacity for oxygen delivery. Here we examine the relation between CTH and capillary outflow saturation heterogeneity (COSH), which is the heterogeneity of blood oxygen content at the venous end of capillaries. Models for the evolution of hemoglobin saturation heterogeneity (HSH) in capillary networks were developed and validated using a computational model with moving RBCs. Two representative situations were selected: a Krogh cylinder geometry with heterogeneous hemoglobin saturation (HS) at the inflow, and a parallel array of four capillaries. The heterogeneity of HS after converging capillary bifurcations was found to exponentially decrease with a time scale of 0.15–0.21 s due to diffusive interaction between RBCs. Similarly, the HS difference between parallel capillaries also drops exponentially with a time scale of 0.12–0.19 s. These decay times are substantially smaller than measured RBC transit times and only weakly depend on the distance between microvessels. This work shows that diffusive interaction strongly reduces COSH on a small spatial scale. Therefore, we conclude that CTH influences COSH yet does not determine it. The second part of this study will focus on simulations in microvascular networks from the rodent cerebral cortex. Actual estimates of COSH and CTH will then be given.
Introduction
Microvessels are the primary site of gas exchange in the vertebrate microvascular system due to their large surface area. Energy metabolism is largely dependent on a continuous oxygen supply from the microcirculation which is actively regulated by the microvasculature. For instance, in the cerebral cortex, dilations of pial arteries (Chen et al., 2011) and penetrating arterioles (Tian et al., 2010) are essential components of neurovascular coupling. The smallest blood vessels are also involved in these processes. Capillary hyperemia was shown to occur prior to dilation of pial arteries (Hillman, 2014) and pericyte-mediated capillary dilations were observed to actively regulate cerebral blood flow (Hall et al., 2014). Therefore, an efficient and robust regulation of oxygen supply is highly dependent on the healthy function of microvessels.
Malfunctions in the microvasculature occur in many diseases and conditions. Cerebral small vessel disease plays a crucial role in stroke, dementia and aging (Pantoni, 2010). Cerebral pericytes, which were reported to regulate capillary diameter during functional activation (Hall et al., 2014), are susceptible to damage in ischemia (Yemisci et al., 2009) and to loss or degeneration in conditions such as aging, hypertension and diabetes (Østergaard et al., 2015). Exposure to β-amyloid is toxic to pericytes and amyloid accumulation often occurs in relation to Alzheimer's disease (Hamilton et al., 2010). These deposits characterize cerebral amyloid angiopathy which is associated with cerebral blood flow disturbance (Thal et al., 2009). Therefore, the study of these conditions requires a proper understanding of the consequences of capillary dysfunction on oxygen transport.
Capillary dysfunction can be quantified by capillary transit time heterogeneity (CTH) which is the standard deviation of the transit time distribution. In their seminal study, Jespersen and Østergaard (2012) showed using a theoretical model that the efficacy of oxygen extraction decreases with CTH. In particular, disturbed capillary flow patterns can decrease oxygen extraction even in the absence of changes in mean flow. CTH was linked to a number of diseases and conditions such as Alzheimer's disease (Østergaard et al., 2013a), stroke-like symptoms (Østergaard et al., 2013b), traumatic brain injury (Østergaard et al., 2014a) and ischemic heart disease (Ostergaard et al., 2014b).
In the study by Jespersen and Østergaard (2012), CTH was related to the oxygen extraction fraction by extending the Bohr-Kety-Crone-Renkin model which assumes homogeneous oxygen partial pressure (PO2) in the extravascular compartment. This flow diffusion equation relates the decrease in blood oxygen concentration to the capillary transit time and the oxygen partial pressure drop across the capillary wall by means of a single rate constant. This constant was fitted to yield a resting oxygen extraction fraction value of 0.3 and the tissue PO2 was required as a model input. Angleys et al. (2015) refined this model to determine tissue PO2 values that match metabolic oxygen consumption and the oxygen extraction fraction values predicted by the Bohr-Kety-Crone-Renkin model.
The distribution of PO2 levels at the distal ends of capillaries is a key determinant of tissue oxygenation. Even if blood flow to a given region is adequate to meet the oxygen needs of the tissue, a maldistribution of flow can lead to wide variations of end-capillary PO2. If the PO2 distribution is highly heterogeneous, low values in some capillaries can cause tissue hypoxia, whereas a uniform distribution of end-capillary PO2 tends to minimize tissue hypoxia, for a given overall oxygen supply. The heterogeneity of end-capillary PO2 can equivalently be expressed in terms of the heterogeneity of hemoglobin saturation (HS), which is functionally dependent on PO2 according to the oxy-hemoglobin saturation curve. This study therefore focuses on capillary outflow saturation heterogeneity (COSH), a measure of the variability of blood oxygen content at the distal end of capillaries where blood flows into venules. Elevated COSH may imply that a fraction of microvessels cannot supply oxygen to their surrounding tissue even if the average saturation is sufficiently high.
In previous modeling works (Jespersen and Østergaard, 2012; Angleys et al., 2015), the effects of CTH on brain oxygenation were quantified using blood oxygen levels. Both tissue PO2 and capillary HS were shown to depend on transit times through the erythrocyte velocity. Like other microvascular beds, the brain microvasculature has a heterogeneous geometric structure and hemodynamics, with substantial variability in path lengths, vessel diameters, flow rates, hematocrit, and tissue volumes supplied by individual capillaries. In parallel capillary arrays, the interaction among vessels reduces the heterogeneity of PO2 when RBC velocity and inlet oxygen concentration take different values in each capillary (Popel et al., 1986; Salathe, 2003). Besides, in the absence of CTH, irregular capillary spacings lead to a more heterogeneous oxygenation compared to regularly spaced arrays (Hoofd and Turek, 1996), which also affects the distribution of HS. Therefore, multiple factors beside CTH contribute to COSH, and CTH by itself does not provide a sufficient basis for understanding and predicting tissue oxygenation. The present study addresses the factors determining COSH and its relation to CTH, using theoretical models.
To compute COSH, models that describe the evolution of HSH in single and multiple capillaries are developed. Diffusive oxygen transfer among RBCs is shown to be the main physical mechanism for the reduction of HSH. The diffusive interaction between RBCs in single capillaries and between parallel capillaries is modeled based on ordinary differential equations. These interaction models are validated for a large range of physiological parameters using a computational model with individual moving RBCs (Lücker et al., 2014). Explicit formulas for the associated length and time scales are given and the resulting values are compared to RBC transit times and path lengths in capillaries. The modeling of COSH is an essential step toward an actual understanding of CTH and its relation to oxygen transport in MVNs. The resulting insights have potentially broad implications in the study of capillary dysfunction and related conditions.
Materials and Methods
Models for the diffusive interaction between RBCs in single capillaries and between multiple capillaries were developed based on ordinary differential equations that extend those used in Lücker et al. (2017). The interaction models were compared to our previously developed oxygen transport model with individual moving RBCs (Lücker et al., 2014).
Based on the observation that the RBC transit time is only one of multiple parameters that determine HS (Lücker et al., 2017), we asked the question: “Which phenomena cause a difference between CTH and COSH?” Two representative situations that contribute to a reduction of HSH were identified. The first one pertains to branchings where two capillaries with different HS levels are converging. This heterogeneity, which may result from different transit times, causes the rates of oxygen unloading from individual RBCs to differ. The second situation concerns parallel capillaries with different HS. In this case, the tissue volume supplied by each capillary can differ.
Diffusive interaction models are derived for these two representative situations. These simplified models directly highlight the variables that influence most the reduction of HSH. Then, the employed computational model (Lücker et al., 2014) is briefly outlined.
Models for Hemoglobin Saturation Based on Ordinary Differential Equations
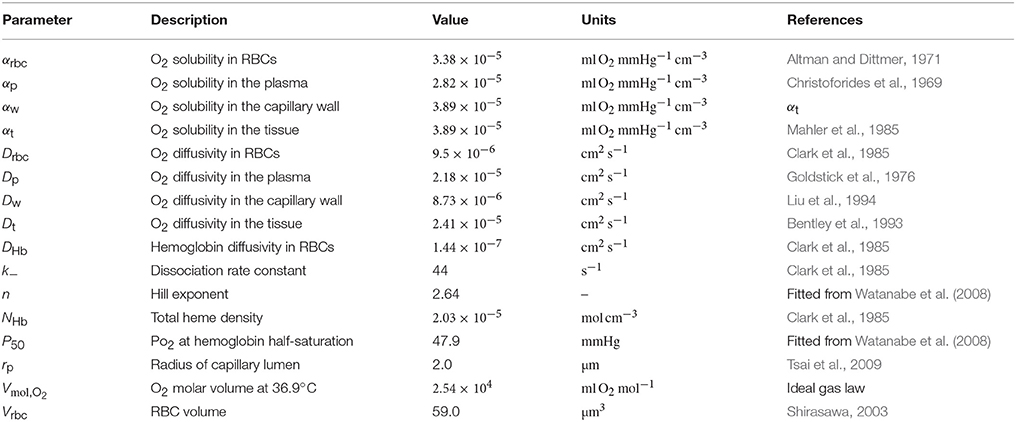
The interaction models developed in this study are all formulated in an axisymmetric geometry with four distinct regions: RBCs, plasma, capillary endothelium and tissue, denoted by the indices c, p, w, and t, respectively. Cylindrical RBCs with radius rc and volume Vrbc are employed. The domain geometry is described by its length L, the plasma radius rp, the outer capillary wall radius rw and the tissue radius rt(x) which may be a function of the axial position x (Figure 1A). The arterial and venous capillary ends (also referred to proximal and distal ends) are denoted by the indices a and v.
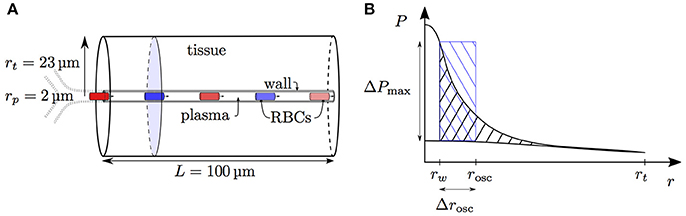
Figure 1. Schematics for RBC diffusive interaction. (A) Cylindrical domain used for the study of RBC diffusive interaction. In the modeled scenario, RBCs are flowing from a converging bifurcation into the domain with different HS values. The shaded tissue slice has area , where rt is the tissue cylinder radius and rw is the capillary endothelium radius. The term jt defined in Equation (5) corresponds to the metabolic oxygen consumption in the tissue slice at a given axial position x. The plasma radius is denoted by rp and the domain axial length by L. (B) Sketch for the definition of the integral spreading distance of PO2 oscillations (Equation 21). The top and bottom radial profiles indicate the maximal and minimal values of PO2 as RBCs are passing. The integral in cylindrical coordinates of the blue rectangle with width Δrosc is equal to that of the black hatched area.
In capillaries, RBCs flow in a single file with velocity vrbc and the RBC linear density is defined to be the ratio of the length occupied by the RBCs to the total vessel length. It is related to the tube hematocrit HT by
The equilibrium curve for hemoglobin and oxygen is modeled using the Hill equation
where n is the Hill exponent and P50 the oxygen partial pressure at half-saturation. The inverse form of this equation
will often be required. Since the Hill equation is known to be inaccurate at low PO2 values, the more complex Adair equation (Popel, 1989) will also be used to estimate diffusive interaction between parallel capillaries.
The models developed here are based on the neglect of axial diffusion and the use of steady-state equations. These common assumptions (Hellums, 1977; Roy and Secomb, 2014; Lücker et al., 2017) reduce the evolution of HS to an ordinary differential equation. Based on the absence of axial diffusion, the oxygen outflux from the capillary at the axial position x is balanced by the metabolic oxygen consumption integrated over the tissue slice normal to the capillary at x, which is denoted by jt(x). The mass balance between the capillary and the tissue is given by
where f(S) is the convective oxygen flux through the capillary. Oxygen consumption is assumed to occur at a rate per unit volume M0 which is independent from tissue PO2. This simplification allows the existence of an analytical expression for PO2 in the tissue. Based on this assumption, the oxygen consumption in the tissue slice normal to x becomes
as illustrated in Figure 1A.
Oxygen in the blood is present bound to hemoglobin in RBCs and dissolved in both plasma and RBCs. The total convective flux is given by
where C0 = NHbVmol,O2 is the product of the heme concentration and the molar volume of oxygen, and PIV is the intravascular PO2 which needs to be modeled. Here, the Fåhraeus effect is neglected, hence the discharge hematocrit HD is set to HT. The effective oxygen solubility is defined by αeff = HTαc + (1 − HT)αp. The first term in the right-hand side of Equation (6) thus accounts for oxygen bound to hemoglobin and the second one represents dissolved oxygen in the capillary. The average RBC oxygen partial pressure Pc is assumed to be in equilibrium with HS, that is, Pc = Peq(S); in the plasma, the oxygen partial pressure is set to be constant and equal to Pw, the oxygen partial pressure at the capillary outer wall. As in Lücker et al. (2017), we use the intravascular resistance coefficient KIV defined by
Values of KIV can be fitted from numerical simulations or obtained using an analytical formula (Lücker et al., 2017). This yields
We can now summarize the above equations to obtain the evolution equation for HS. For brevity, we define total oxygen convective capacity as
Equations (4), (6) and (8) result in
When the tissue domain is a straight cylinder, the last term vanishes. If the tissue radius is not constant, this term is nonzero but was found to be negligible. Therefore, it will be omitted in further derivations. However, this term was included in all numerical computations for completeness. Equation (10) can be recast in terms of the capillary transit time τ and integrated as
Thus, HS on the distal side is influenced by the RBC transit time, the oxygen consumption per unit length, hematocrit and vessel diameter. This description of distal blood oxygen concentration is more complete than the previously used Bohr-Kety-Crone-Renkin equation (Jespersen and Østergaard, 2012; Angleys et al., 2015). The BKCR model uses the normalized coordinate and reads
where C is the bound oxygen concentration in RBCs, B is the maximal amount of oxygen bound to hemoglobin and Ct the oxygen concentration in the tissue. The model constant k was adjusted to obtain an oxygen extraction fraction of 0.3 in Jespersen and Østergaard (2012) and Angleys et al. (2015). In Equation (10), the counterpart of k is the inverse of QO2(S) (Equation 9) which is an explicit function of hematocrit and the vessel geometry.
Given the sink term jt(x), Equation (10) can be integrated numerically using a standard differential equation solver. The implementation in SciPy (Jones et al., 2001) of an explicit Runge-Kutta method of order 4(5) was used (Hairer et al., 1993).
In the modeling of diffusive integration between parallel capillaries, knowledge of the PO2 in the tissue will be required. This is achieved using the intravascular resistance coefficient and the Krogh model. From the HS S at an axial position x, the average RBC oxygen partial pressure Pc is obtained using Equation (3). The oxygen partial pressure Pw at the capillary outer wall is then given by Equation (7). Finally, the Krogh model for the oxygen partial pressure at a distance r from the capillary centerline reads
Diffusive Interaction Between RBCs in a Single Capillary
Capillary networks in the cerebral microvasculature form a mesh-like structure (Lorthois and Cassot, 2010; Blinder et al., 2013) with both diverging and converging bifurcations. At converging bifurcations, RBCs from either inflow branch may have different HS, for instance due to different transit times or hematocrit values. Here, we derive an interaction model for the evolution of HS saturation in a single capillary.
To describe this fluctuation, the HS is treated as a random variable S. The RBC interaction model is based on Fick's law as follows: the oxygen flux out of the capillary is assumed to be proportional to the oxygen partial pressure difference between the RBC and the tissue. In other words, we assume that
where rs is a radial position which is independent from the fluctuations of S and where the PO2 fluctuations in the tissue are small (Figure 1B), and C is a proportionality factor that will be derived. From now on, averaged quantities will be denoted by an overline. In the next steps, the nonlinearity in S of the total convective oxygen capacity QO2(S) (Equation 9) will be ignored, which allows the simplification . Based on this, the averaged mass balance is given by
The averaging of Equation (14) combined with Equation (15) yields an expression for C which can be inserted into Equation (14). The terms can be rearranged as
The oxygen partial pressure P(rs) still needs to be modeled. This is achieved by introducing the resistance coefficient for RBC diffusive interaction , which is the only parameter of this model. Thus, the model equation for randomly distributed HS in a single capillary is given by
By a suitable linearization, the nonlinear Equation (17) can be further simplified to an evolution equation for the standard deviation of S. Here, we again assume that the function Peq (Equation 3) is linear around and that the derivative can be neglected. It follows that
Using the above assumptions, the standard deviation of HS σS satisfies the differential equation
This equation can be solved numerically given the average HS which is itself obtained by integrating Equation (10).
The resistance coefficient KRI describes the resistance to the PO2 drop between the RBC and a location in the tissue where PO2 oscillations are small. Since oscillations resulting from fluctuating capillary PO2 decay exponentially with distance into the tissue, there is no precise definition of this location and no exact formula for KRI can be derived. However, this coefficient can be fitted based on numerical simulations and compared to a measure for the spreading distance of PO2 oscillations into the tissue. First, KRI is decomposed as KRI = KIV + KOS, where KIV is the intravascular resistance coefficient (Lücker et al., 2017) and KOS represents the extravascular contribution to KRI. Second, we define a characteristic penetration radius rosc for PO2 oscillations by
where ΔP is the radially varying fluctuation in tissue PO2 (Figure 1B). Finally, the integral oscillation spreading distance Δrosc is defined as
This quantity can be obtained from the results of the computational model. We will show that Δrosc is an accurate predictor for the model coefficient KOS.
Diffusive Interaction Between Parallel Capillaries
Having examined the diffusive interaction between heterogeneously saturated RBCs in the same capillary, we now consider the diffusive interaction between capillaries with different saturation levels. For our analysis, four parallel capillaries with concurrent blood flow are considered where both pairs of diagonally opposed capillaries will be denoted by the indices ϕ and ψ, respectively (Figure 2).
Figure 2. Schematics for capillary diffusive interaction. (A) Sketch of the geometry with four parallel capillaries. (B) Transverse view of the computational domain with four parallel capillaries. The shaded areas represent the tissue regions supplied by each capillary. Solid lines: boundary of the representative domain with periodic boundary condition; dash-dotted lines: actual computational domain with symmetry boundary condition; dotted lines: boundary of the tissue region supplied by each capillary. (C) Sketch of the tissue PO2 between two capillaries with different RBC PO2 values Pc,ϕ (red dot) and Pc,ψ (blue dot). The colored circles indicate the locations of the capillaries ϕ and ψ. Solid line: continuous PO2 profile with adapted tissue radii rt,ϕ and rt,ψ; dashed line: discontinuous PO2 profile under the assumption of equal oxygen fluxes out of the capillaries.
Given different HS values Sϕ,a, Sψ,a at the proximal inlets, we aim to derive the evolution of S in both capillaries. To do this, the tissue region supplied by each capillary is approximated by a cylinder with varying radius which will be determined using the continuity of tissue PO2. As above, the neglect of axial diffusion allows tissue slices that are orthogonal to the capillary to be decoupled. Let A be the area of the normal domain slice supplied by the two model capillaries ϕ and ψ. Mass conservation implies that the oxygen flux at x out of both model capillaries balances the metabolic oxygen consumption in the tissue slice normal to x:
Using the intravascular resistance coefficient and the Krogh model (Equation 13), the continuity of tissue PO2 at the interface between the Krogh cylinders is given by
where ΔPEV(jt) is the extravascular PO2 drop associated to the local oxygen outflux jt. Based on the right-hand side of Equation (13), it is given by
Given Pc,ϕ and Pc,ψ, the nonlinear equation system formed by Equation (22) and (23) can be solved numerically for jt, ϕ and jt,ψ. Then, Equation (10) is solved in both model capillaries one step forward using an explicit differential equation integrator. This model will be referred to as nonlinear Krogh-based model and can be applied to capillaries with different flows and radii. Cases where one capillary is supplied with oxygen by the other (for instance, jt,ψ < 0) are captured by this formulation.
A slight simplification in Equation (23) provides an explicit expression for the oxygen flux out of both model capillaries. Under the assumption that both capillaries have the same geometry and linear density, the intravascular resistance coefficient KIV takes the same value in both capillaries, so Equation (23) can be rearranged as
The assumption that
where , yields an explicit expression for the oxygen outflux
and a similar expression for jt,ψ(x). We now define the resistance coefficient KCI for diffusive interaction between capillaries as
By using the average oxygen outflux , the evolution equations for HS in both model capillaries become
This model will be referred to as explicit Krogh-based model. To derive this equation, the respective linear densities in both capillaries were assumed to be equal. However, the respective RBC velocities were still allowed to be different. Under the assumption that vrbc is equal in both capillaries, the linearization of Peq around the average HS yields the following evolution equation for the saturation difference ΔS = Sϕ − Sψ between both model capillaries:
This third model will be referred to as linearized capillary interaction model. This equation leads to the definition of the characteristic length scale LCI for diffusive interaction between parallel capillaries
Similarly, the characteristic time scale τCI is defined as
Thus it is independent from the RBC velocity and depends on linear density, the average HS and the geometry. These characteristic quantities will be compared to fits obtained using the computational model presented below.
Computational Model
The results of the models for RBC and capillary diffusive interactions were compared with numerical solutions to the advection-diffusion-reaction equations for oxygen and hemoglobin. The reaction rates between both quantities are coupled based on Clark et al. (1985) with
where k− is the reaction rate. Metabolic oxygen consumption was modeled using zero-th order kinetics as
This was chosen instead of the commonly used Michaelis-Menten kinetics to facilitate the comparison between the interaction models and the computational model. The oxygen transport equation is given by
where v is the plasma velocity. In RBCs, the evolution of HS follows
where DHb is the diffusion coefficient of hemoglobin in RBCs.
For simulations in a single capillary or parallel capillaries, these equations were solved using the finite-volume method with moving RBCs (Lücker et al., 2014).
Model Parameters
The heterogeneity of HS was investigated in different computational domains. The physiological parameters were chosen to match the mouse cerebral cortex. The diffusive interaction between RBCs was studied in a two-dimensional cylindrical domain with radius rt = 23 μm, which corresponds to the distances between nuclei of neurons and capillaries (Tsai et al., 2009). Unless stated otherwise, a domain length L = 100 μm was chosen. This length is smaller than the average capillary path length of 343 μm measured by Sakadžić et al. (2014). The domain length influence will be addressed below. Cylindrical RBCs with volume Vrbc = 59 μm3 and radius rc = 1.5 μm were employed. The capillary lumen diameter was set to rp = 2.0 μm, which is typical in the rodent cerebral cortex (Tsai et al., 2009), and the endothelium thickness to 0.6 μm (Bertossi et al., 1997), so that the endothelium radius was rw = 2.6 μm. At the tissue boundary, the gradient of the PO2 field was set to zero. In this domain, the grid cell size was set to Δx = Δy = 0.3 μm in the capillary. The radial grid spacing in the tissue was smoothly increased to save computational effort, so that Δy was four times higher at the tissue boundary than in the capillary. The grid spacing in the RBC meshes was set to Δxrbc = Δyrbc = 0.1 μm. The time step size was set to Δt = Δx/vrbc. All simulations were ran until a statistical steady state was reached.
The diffusive interaction between capillaries was investigated in an array with four parallel capillaries with radius rp = 2.0 μm. The symmetry of the domain allowed that only one quarter of each capillary had to be simulated (Figure 2B). The normal PO2 gradient was set to zero at each boundary plane. A spacing of 40 μm between the capillaries was chosen, which yields an averaged supplied tissue volume per capillary very close to that of a cylinder with radius rt = 23 μm. In these simulations, the RBC radius was set to rc = 1.6 μm and the endothelium radius to rw = 2.5 μm. For this three-dimensional domain, a coarser grid spacing than in the two-dimensional cylinder was chosen. The grid cell size in the tissue away from the capillaries was set to 1 μm. At ≤ 8 μm from the capillaries, the grid was refined by a factor two to better resolve the high oxygen gradients in and close to the capillaries. The grid cell size in the RBCs was set to Δxrbc = 0.25 μm and the time step to Δt = Δx/vrbc. Since the HS difference ΔSv between the venous ends of the capillaries is our main quantity of interest here, the grid spacing needs to be sufficiently high to accurately resolve this quantity. A grid convergence study showed that doubling the spatial resolution in each dimension and reducing the time step correspondingly increases ΔSv by < 2.2%. Therefore, all simulations were run with the grid resolution described above, since it provides a good compromise between accuracy and run time (~20 h per simulation on a single core). The coarser grid resolution in the tissue was found not to affect the values of ΔS.
The metabolic rate of oxygen consumption was set to 10−3 μm3 O2 μm−3 s−1, which is within the range of values measured in the anesthetized rodent cerebral cortex (Zhu et al., 2013), using a brain density of 1.05 g cm−3 and the ideal gas law at body temperature for the molar volume of oxygen (2.544 × 104 ml O2/(mol O2)). The intravascular resistance coefficient, which is used for the model coefficients KRI and KCI (Equation 29), was determined using the formula KIV = 0.5KIV, 0.5/μLD (Lücker et al., 2017), with the difference that convective transport of dissolved oxygen content was included in Equation (10). For rc = 1.5 μm, the value of KIV, 0.5 was 5.15 mmHg μm s/(μm3 O2). In parameter studies, the RBC velocity will be varied between 0.4 and 2.0 mm/s and the linear density between 0.2 and 0.6. When these parameters are fixed, vrbc will be set to 1.0 mm/s and μLD to 0.3. For rc = 1.5 μm, this yields a RBC flow equal to vrbcμLD/Lrbc = 40.7 cells/s. These values are typical for the rodent brain (Parpaleix et al., 2013; Lyons et al., 2016). The other physiological parameters are given in Table 1.
Equations (37) and (38) were solved using a custom written extension of the open-source computational fluid dynamics library OpenFOAM 2.3.0 (Weller et al., 1998). The equations were discretized as explained in Lücker et al. (2014).
Results
The evolution of HSH was simulated in the geometries shown in Figure 1A, 2A, and compared to the RBC and capillary interaction models.
Diffusive Interaction Between RBCs
The diffusive interaction between RBCs with different HS was investigated in a cylindrical tissue domain (Figure 1A). This single-capillary setup with differently saturated RBCs aims to represent a capillary after a converging bifurcation where RBCs with different transit times are flowing in. The simplest model for the inlet HS of RBCs is when erythrocytes alternatingly take two fixed saturation values (one value per upstream branch). Figure 3 shows the evolution of HS in a capillary with length L = 300 μm with inlet values S = 0.8 and 0.6. The standard deviation σS,v of the HS from the numerical model at the venous end is approximately seven times lower than at the inlet. The values of σS from the RBC interaction model is almost indistinguishable from the numerical results (Figure 3B) when the model coefficient KRI is fitted to match the standard deviation from the computational model (here, KRI = 11.1 mmHg μm s/(μm3 O2)). The coefficient was fitted to minimize the model error . The linearized RBC diffusive interaction model with the same value of KRI also agrees very well with the numerical results, although it very slightly underestimates σS. The simulated values of σS were also fitted with a single exponential function of the form f(x) = a exp(x/LRI). Since this fit is also very good, our results can be expressed in terms of the characteristic decay length LRI and the related decay time τRI = LRI/vrbc. These first results suggest that HSH can be considerably reduced by diffusive interaction between RBCs within a single capillary.
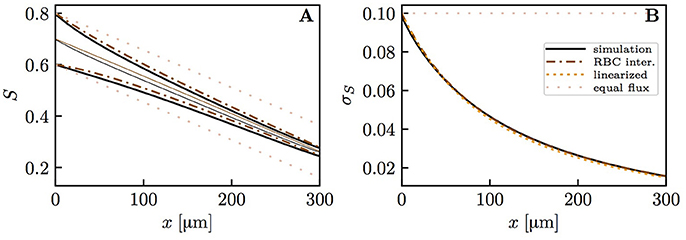
Figure 3. Hemoglobin saturation profiles with alternating inlet values in the cylindrical geometry. μLD = 0.3; vrbc = 1.0 mm/s. Solid lines: numerical simulation; dash-dotted lines: RBC interaction model; dotted line: linearized RBC interaction model; pale dotted lines: assumption of equal oxygen flux out of the RBCs. (A) HS profile of heterogeneously saturated RBCs (thin line: average). (B) Standard deviation profile of S.
To reduce the computational effort in further parameter studies, we compared the results obtained with domain lengths of 100 μm (Sa = 0.6 and 0.4) and 300 μm (Sa = 0.8 and 0.6, respectively). The fitted value of KRI in the short domain was only 4.6% lower than in the long domain. Therefore, the domain length does not have a major influence on the results and from now on we will use L = 100 μm. In the mouse cerebral cortex, an average capillary path length of 343 μm was measured by Sakadžić et al. (2014). The similar values of KRI with L = 100 μm and 300 μm show that it is not necessary to simulate whole capillary paths to estimate the model coefficient KRI, which in turn determines LRI and τRI. Additionally, a uniform random distribution of HS at the inflow of a 2 × 2 parallel capillary array yields very similar results (Figure S1). To investigate the dependence on the considered organ, a simulation was run with parameters for the working hamster retractor muscle as in Eggleton et al. (2000). The resulting evolution of HSH is qualitatively the same as with physiological parameters for the mouse cerebral cortex (Figure S2). This shows model robustness with respect to the inflow value of S, the boundary condition for tissue PO2 and the considered organ.
We now examine the influence of model parameters such as linear density, RBC velocity, oxygen consumption rate and HS difference at the inlet on the results. Figure S3 shows that the RBC interaction models with fitted KRI perform very well across a wide range of parameters. The relative model error in σS,v normalized by the standard deviation drop from the numerical model σS,a − σS,v is ≤ 2% for the initial model and ≤ 4% for the linearized model across the whole parameter range. Additionally, the exponential fit to the numerical results also matches very well the numerical results (< 2% error), which confirms that the decay length LRI and decay time τRI introduced above can used to compare results. The decay time τRI decreases from 206 to 157 ms when vrbc increases from 0.4 to 2.0 mm/s, but is rather insensitive to the linear density (10.2% decrease when μLD increases from 0.2 to 0.6, Figure 4). The oxygen consumption rate has an even smaller influence on τRI (6.3% variation), while the inlet standard deviation of HS almost does not affect it (1.2% variation).
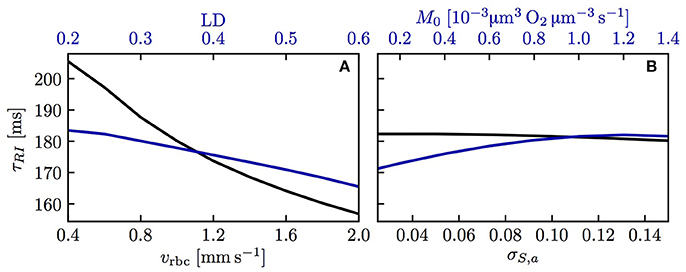
Figure 4. Decay time scale τRI for RBC diffusive interaction. The time scale τRI was obtained with an exponential fit of the standard deviation of HS from simulations across a range of parameters. (A) Linear density and RBC velocity; (B) oxygen consumption rate and standard deviation of HS at the inlet.
The above results show that the RBC interaction models agree closely with numerical simulations when using fitted values of KRI. To show the models' predictive power, it is necessary to characterize this model coefficient which was decomposed as KIV + KOS, where KOS was related to the spreading distance of PO2 oscillations in the tissue due to individual passing erythrocytes. Figure 5A shows the dependence of KOS on linear density and RBC velocity. The plot of Δrosc against KOS for all the simulated values of linear density and RBC velocity (Figure 5B) shows a strong correlation between these two quantities (Pearson's correlation coefficient r = 0.989). Therefore, consistently with our initial assumption (Equation 14), the model coefficient for RBC diffusive interaction is closely related to the PO2 oscillations in the tissue.
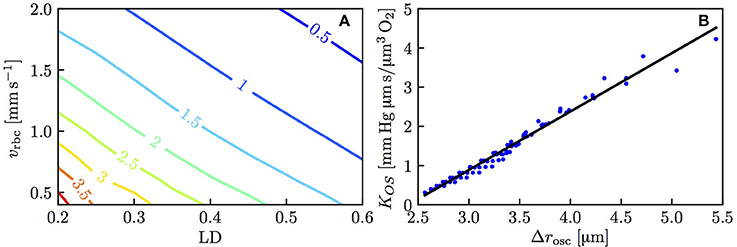
Figure 5. Model coefficient KOS for RBC diffusive interaction. (A) KOS in mmHg μm s/(μm3 O2) as a function of linear density and RBC velocity. (B) KOS as a function of the integral spreading distance of PO2 oscillations defined in Equation (21); solid line: linear fit with slope 1.49 and intercept −3.58.
Diffusive Interaction Between Parallel Capillaries
The capillary diffusive interaction models are now compared to our computational model for oxygen transport. Numerical simulations were run in an array of four straight, parallel capillaries (Figure 2A). In the two pairs of diagonally opposed capillaries, two different inlet values of HS Sa,ϕ, Sa,ψ were chosen. The evolution of Sϕ, Sψ and the HS difference ΔS = |Sϕ − Sψ| were computed with the numerical model and compared to predictions from the three interaction models for the oxygen flux out of the capillaries (nonlinear Krogh-based model, explicit model and linearized model for ΔS). Additionally, theoretical results based on the assumption of equal oxygen outflux will be shown to highlight the effects of capillary diffusive interaction. Unless otherwise stated, the average value of Sa over all capillaries was 0.7 and the capillaries were 40 μm apart. The linear density and the erythrocyte velocity were set to 0.3 and 1.0 mm/s, respectively.
Figure 6 shows HS profiles along both capillary pairs from the numerical model and the interaction models. The mean HS from the models matches very well the simulated results, which shows that mass conservation is fulfilled (the nonlinear and explicit Krogh-based models yield the same mean S, hence only the former is shown). In this setup, the HS difference between both capillary pairs drops by ~ 50% over 100 μm. This decrease is captured well by each interaction model, albeit slightly underestimated by the explicit Krogh-based model and the linearized model. Figure 6 also illustrates that the assumption of equal oxygen outfluxes cannot be used in the present context. As above, the underestimation of S by the interaction models away from the domain ends is caused by the absence of axial diffusion (Lücker et al., 2017). These first results suggest a strong reduction of HSH between parallel capillaries.
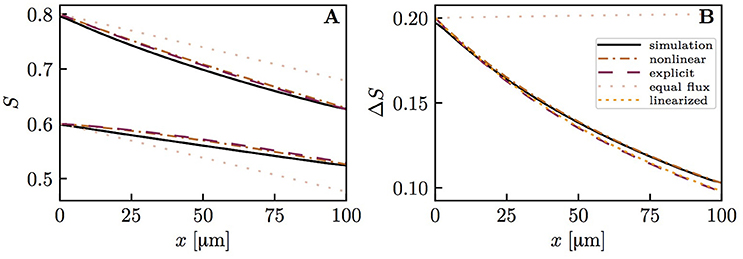
Figure 6. Hemoglobin saturation profiles in parallel capillaries. μLD = 0.3; vrbc = 1.0 mm/s. Solid lines: numerical simulation; dash-dotted lines: nonlinear Krogh-based model; dashed lines: explicit Krogh-based model; dotted line: linearized model for ΔS; pale dotted lines: equal outflux assumption. (A) HS profile in both model capillaries. (B) HS difference between both capillaries.
To show model robustness, several input parameters were varied and the predicted drop in HS difference ΔSa − ΔSv was compared to numerical simulation results. The spacing between capillaries, the oxygen consumption rate, the RBC velocity and linear density were investigated (Figure S4). In almost all cases, the nonlinear Krogh-based model shows the best agreement with numerical results (relative error ≤ 4% except at very low oxygen consumption rates). The explicit Krogh-based model and the linearized model perform almost equally well, with relative errors ≤ 8%. Similarly, simulations with physiological parameters for the working hamster retractor muscle yield results that are very similar to those with parameters for the mouse cerebral cortex (Figure S5). These parameter studies show that capillary diffusive interaction models perform well over a large range of physiological parameters.
The capillary interaction models rely on a single model parameter KCI defined in Equation (29). Unlike the coefficient KRI for RBC diffusive interaction, the expression for KCI only depends on the intravascular resistance coefficient KIV which can be determined based on numerical simulations (Lücker et al., 2017). Therefore, given a suitable value of KIV and mean HS , the decay length and time scales LCI and τCI (Equations (33) and (34), respectively) can be computed analytically. Figure 7A shows values of τCI for a range of linear densities and mean HS values. The decay time scale increases with linear density and attains its highest values at S ≃ 0.3, where dPeq/dS attains its minimum with the employed parameters for the Hill equation (Equation 2). Similarly to RBC diffusive interaction, the simulated values of ΔS are very well fitted by exponential decays. Figure 7B,C show a comparison of the analytical and the fitted decay time scale τCI for different values of capillary spacing, oxygen consumption rate, RBC velocity and linear density. For the analytical time scale, the simulated value of at x = L/2 was employed. Over the investigated range of parameters, the analytical estimates of τCI overestimate the fitted values by at most 12 ms (relative error of ≤ 7.2%). This shows that the variations in τCI that occur in the investigated parameter range can be entirely explained by the dependency of the analytical τCI on μLD and . The decay length scale LCI is equally well predicted by the analytical formulation. Besides, the interaction models have so far employed the Hill equation (Equation 2) to model the equilibrium curve between oxygen and hemoglobin. To examine model robustness, we computed the decay time scale τCI using the Adair equation (Popel, 1989) which is more accurate for S ≤ 0.3. The resulting values of τCI are at most 10% smaller at low HS, so the inaccuracy introduced by the Hill equation stays moderate (Figure S6). The structure of the microcirculation in the brain is heterogeneous, and estimates of several relevant parameters such as blood flow rate, capillary spacing and oxygen consumption rate are subject to uncertainties of considerably more than 10%. Therefore, the quantitative errors introduced by the use of the Hill equation are not significant with regard to the analysis of oxygen transport in vivo. The main conclusion of this study, namely that diffusive interaction between capillaries can significantly reduce COSH, is not affected by the assumption of the Hill equation.
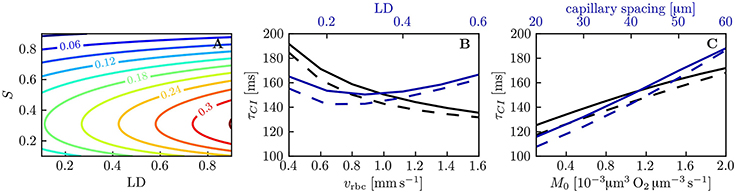
Figure 7. Decay time scale τCI for capillary diffusive interaction. (A) Theoretical decay time scale for capillary diffusive interaction. The contour values were obtained with Equation (34) for a capillary spacing of 40 μm (rt,mean = 22.6 μm, rc = 1.6 μm, rp = 2.0 μm, rw = 2.5 μm). (B,C) Decay time scale τCI of the HS difference between parallel capillaries across a range of parameters: linear density, RBC velocity (B), capillary spacing and metabolic consumption rate of oxygen (C). Solid lines: exponential fit to the simulated ΔS; dashed lines: theoretical value obtained with Equation (34) and the same parameters as in (A).
The previous results all assumed the same RBC velocity, flow direction and hematocrit in each capillary. These assumptions are now dropped to further examine model robustness. First, simulations with countercurrent flow instead of concurrent flow were run. Namely, the flows in both pairs of diagonally opposite capillary were set to opposite directions with the same RBC velocity. The HS difference between the venous capillary ends turned out to be practically the same as with concurrent flow (Figure S7). Then, actual CTH was introduced by setting different RBC velocities in the pairs of diagonally opposite capillaries (Figure 8). Similarly, different values of linear density were set in these capillary pairs (Figure 9). The RBC flow was also varied by modifying both RBC velocity and linear density (Figure S8). In all cases, the simulated distal HS difference was considerably lower than under the assumption of equal fluxes. When linear density is heterogeneous, diffusive interaction leads to a stronger reduction of HSH (84.4% in Figure 9) than in the presence of heterogeneous RBC velocities (41.8% in Figure 8). When the RBC flow is varied by modifying both of these parameters, the resulting reduction of HSH (64.5% in Figure S8) falls between the values obtained above. However, the differential equation models were more inaccurate in these cases and significantly overestimated the distal HS difference. Although the interaction models are not as accurate as before with heterogeneous RBC velocities and linear densities, our conclusions about the reduction of HSH still hold in the presence of CTH or hematocrit heterogeneity.
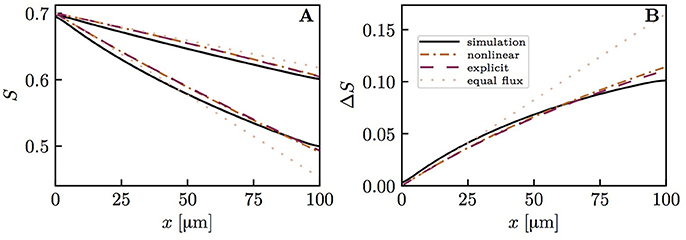
Figure 8. Capillary diffusive interaction with different RBC velocities (vrbc = 1.5 and 0.5mm/s). Solid lines: numerical model; dash-dotted lines: nonlinear Krogh-based model; dashed lines: explicit Krogh-based model; dotted lines: equal oxygen flux assumption. (A) HS profiles; (B) HS difference between both capillary pairs. The simulated final HS difference ΔSv with vrbc = 1.5 mm/s and 0.5 mm/s, respectively, is 41.8% lower than if the oxygen fluxes out of the capillaries are assumed to be equal. The overestimation of ΔSv by the nonlinear and explicit Krogh-based models is 18.8 and 15.8%, respectively. For smaller differences in vrbc, the model errors are in the same range.
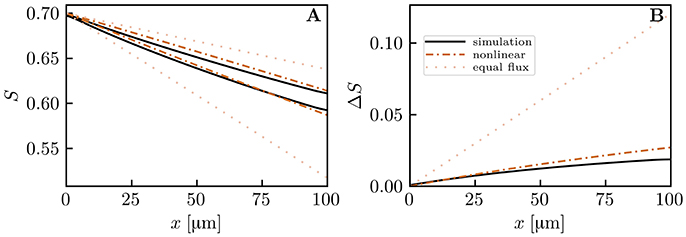
Figure 9. Capillary diffusive interaction with different linear densities (μLD = 0.6 and 0.2). Solid lines: numerical model; dash-dotted lines: nonlinear Krogh-based model; dotted lines: equal oxygen flux assumption. (A) HS profiles; (B) HS difference between both capillary pairs. The simulated distal HS difference is 84.4% lower than under the assumption of equal oxygen fluxes. The nonlinear Krogh-based model overestimates ΔSv by 44.4%.
Discussion
We identified two diffusive interaction mechanisms that cause a large reduction of HSH in capillary networks, developed associated interaction models and validated them using a computational model with individual moving RBCs. The interaction models provide explicit formulas for the reduction of HSH and the associated decay exponents, which gives more insight than a purely computational approach. This work shows that CTH only partially reflects the actual heterogeneity of blood oxygen content and that estimating HSH solely based on CTH may lead to considerable overestimation.
Diffusive interaction between RBCs in a single capillary occurs when two branches with different HS levels converge. This phenomenon is therefore more prevalent in the presence of multiple converging bifurcations along RBC paths. In the mouse cerebral cortex, Sakadžić et al. (2014) estimated the number of capillary branches between arterioles and venules to be 5.9 ± 2.1, with mean segment lengths between 65.6 and 81.4 μm. Since cortical capillary beds have a mesh-like structure (Lorthois and Cassot, 2010; Blinder et al., 2013), each RBC will on average travel through several converging bifurcations. According to the interaction models developed here and the numerical simulations, the standard deviation of HS decays exponentially (Equation 19) with a time scale between 0.15 and 0.21 s (Figure 4). This is slightly below the diffusion time scale given by . The time scale τRI was also shown not to depend on the length of the computational domain. Therefore, the RBC interaction time scale is not directly affected by the RBC transit time through the computational domain (although it depends on the RBC velocity). However, τRI can be compared to experimentally measured transit times to examine whether RBC diffusive interaction has enough time to occur while RBCs flow through capillaries. The obtained values of τRI are considerably lower than mean capillary transit times measured using bolus tracking (Gutiérrez-Jiménez et al., 2016) (0.81 ± 0.27 s at baseline, 0.69 ± 0.18 s during activation). These obtained time scales are also smaller than the transit times computed by Schmid et al. (2017) in five analysis layers at different depths in the mouse parietal cortex (0.19 to 0.79 s). Therefore, in the presence of converging bifurcations, this analysis indicates that RBCs spend sufficient time in capillary branches for the HSH to significantly drop.
While the standard deviation of HS in a single capillary generally decreases, our results show that the average value of S in a single capillary is not affected by fluctuations of S. Since the PO2 oscillations caused by the individual erythrocytes do not spread far into the tissue (see values of Δrosc in Figure 5B), tissue oxygenation is likely not adversely affected by the fluctuations in HS observed here. This provides a justification for the oxygen transport models based on a continuum approach for S (Goldman and Popel, 1999; Secomb et al., 2000), if the HS downstream of a converging bifurcation is set to the RBC-flow-weighted average of S in the upstream branches. Nevertheless, we postulate that the homogenization of S in individual vessels is beneficial for oxygen transport, since it reduces the probability of RBCs with very low saturation. Indeed, hypoxia as well as large tissue PO2 fluctuations are most likely to occur near vessels with low RBC flow. The homogenization of HS makes it less probable that RBCs with low oxygen content enter such vessels.
Diffusive interaction between capillaries is the second reduction mechanism of HSH that was investigated here. While RBC diffusive interaction primarily occurs downstream of converging bifurcations, capillary diffusive interaction is a more general phenomenon since it does not require the presence of branchings. Our results qualitatively agree with the computations by Popel et al. (1986) in parallel capillary arrays with heterogeneous inlet PO2 and erythrocyte velocities. Salathe (2003) performed similar computations in a 5 × 5 capillary array and reported that modeling interaction between functional units smooths out the oxygen concentration differences between capillaries and delays the onset of anoxia. Our results confirm the trends observed in these studies and shed further light on the physiological parameters involved in capillary diffusive interaction.
The range of distances between capillaries (20 to 60 μm) that was examined in our simulations in parallel capillary arrays corresponds to Krogh cylinder radii between 11.3 and 33.8 μm. This includes the mean Krogh radii of the reconstructed MVNs in Fraser et al. (2013) (21.3 ± 2.1 μm to 25.6 ± 3.9 μm) and in Sakadžić et al. (2014) (22.3 ± 1.2 μm to 24.2 ± 2.2 μm) which were obtained by approximating the tissue volume closest to each capillary segment by a cylinder. In our simulations, although the intercapillary distance was tripled, the decay time of the HS difference between parallel capillaries only increased from 0.115 to 0.188 s. This weak dependence on capillary spacing is explained by the formulas for the decay time scale τCI (Equation 34) and the model coefficient KCI (Equation 29) which only depend on the logarithm of the ratio between the mean Krogh radius and the capillary endothelium radius. These time scale values are lower than the decay time scale τRI for RBC diffusive interaction and also significantly smaller than the capillary transit times reported above. Additionally, our theoretical analysis showed that the HS difference between parallel capillaries decays exponentially (Equation 32). This provides compelling evidence that diffusive interaction between capillaries is a strong mechanism for the reduction of HSH at the scale of neighboring capillaries. Its occurrence regardless of the presence of converging bifurcations suggests that this is a more general phenomenon than RBC diffusive interaction. Finally, unlike the latter mechanism, capillary diffusive interaction strongly influences the mean HS drop along microvessels and thus affects more significantly tissue oxygenation.
Having shown the importance of diffusive interaction mechanisms, it is natural to ask up to which length scale they can act. While RBC interaction is confined to single capillaries, hence very local, it is not evident how far reaching capillary interaction can be. The weak dependence of the decay time scale τCI on capillary spacing (Equation (34) and Figure 7C) suggests that this oxygen transfer mechanism can be relevant for capillary distances above 50 μm, which is higher than typical inter-capillary spacings in the cerebral cortex (Tsai et al., 2009) or muscles (Ellsworth et al., 1988). To determine the maximal length scale of capillary diffusive interaction, it will be necessary to understand how capillaries with irregular spacings (see Hoofd and Turek, 1996) influence each other's supplied tissue regions. We propose the concept of diffusive interaction length scale as a tool to compare CTH and COSH. Our results provide strong evidence that HSH on the scale of the inter-capillary distance is efficiently damped by diffusive interaction. Whether this still holds for medium or large-scale HSH is an open question. Its answer is essential to assess the consequences of disturbed capillary flow patterns on oxygen transport based on their spatial scale.
The models for RBC and capillary diffusive interactions enable the computation of mean HS and its heterogeneity in single and parallel vessels, respectively. Previously, the relation between CTH and oxygen extraction fraction was studied by Jespersen and Østergaard (2012) using the Bohr-Kety-Crone-Renkin equation and extended by Angleys et al. (2015) Their approach does not account for the heterogeneity of hematocrit, vessel size and spacing which occurs in capillary networks. Our approach takes into account each of these parameters and shows that distal HS is not only a function of the transit time (Equation 11). In particular, it includes the influence of hematocrit which was shown to have a paramount influence on tissue PO2 (Lücker et al., 2017). Another major advance in this work is the modeling of interaction between capillaries through the presence of converging bifurcations and diffusive oxygen transfer. Instead of dealing with idealized distributions of capillaries with independent supplied tissue regions, the models developed here lay the ground for a refined analysis of HSH in realistic MVNs. This is an essential step to assess the actual consequences of CTH on oxygen transport and availability in the microcirculation.
The diffusive interaction models consist in ordinary differential equations that can be easily integrated. The simplifications done in their derivation give rise to slight inaccuracies with respect to the computational model. The errors of the RBC and capillary diffusive interaction models are ≤ 4% (Figure S3) and ≤ 8% (Figure S4), respectively. The main sources of inaccuracy are the linearization of the terms dPeq/dS (Equation 15) and Peq (Equation 18) as well as the neglect of axial diffusion. For capillary diffusive interaction, the approximation of the supplied tissue region by a cylinder (Figure 2B) and Equation (27) are additional sources of inaccuracy. Since these errors originate in the reduction of nonlinearly coupled partial differential equations to ordinary differential equations, these inaccuracies are a very moderate price to pay.
The limitations to our diffusive interaction models include the oxygen-independent metabolic consumption term M0, which provides an analytical solution to the radial oxygen transport equation in the tissue. At low tissue PO2, metabolic oxygen consumption modeled with Michaelis-Menten kinetics may produce higher tissue PO2 and thus influence the supplied tissue cylinder radii in capillary diffusive interaction. However, the choice of this consumption model over constant oxygen consumption only has a limited influence on the oxygen profiles in a cylindrical geometry (Grimes et al., 2014). Similarly, metabolic oxygen consumption is expected to vary spatially, as suggested by the depth-dependent neuron density in the mouse cerebral cortex (Tsai et al., 2009). Heterogeneous oxygen demand may result in an increase or a decrease in COSH, depending on its covariation with blood flow and vessel spacing. As a further limitation, the Bohr effect was not modeled. Since the derived equations for the evolution of HSH (Equations (19) and (32)) and the characteristic scales LCI and τCI (Equations (33) and (34)) explicitly depend on the derivative of the equilibrium curve Peq(S), its shift may influence the reduction mechanisms of HSH. Likewise, the inaccuracy of the Hill equation at low HS also has an influence, albeit in a limited way (Figure S6). Finally, since we focused on physiological parameters typical for the cerebral cortex, myoglobin-facilitated diffusion of oxygen in tissue was not considered. Its inclusion into our models would decrease the time scales for capillary diffusive interaction (Equations (29) and Equation (34)).
This study extensively investigates HSH in a Krogh cylinder geometry and parallel capillary arrays. Thus, our conclusions are currently limited to tissues with approximately parallel and straight capillaries such as striated muscles. The next step is to verify whether our theoretical predictions hold when blood vessels are interconnected, tortuous and have variable spacings. In a follow-up article, we are going to present simulations of oxygen transport in microvascular networks from the mouse somatosensory cortex. The distribution of capillary transit times will be compared to that of outflow HS. Then, the interaction models will be used to quantify how much diffusive interaction reduces COSH. The spatial scale up to which diffusive interaction acts also requires further investigation. This could be performed using parallel capillary arrays with more vessels or large realistic microvascular networks. In addition to numerical simulations, experimental data are needed to confirm our theoretical predictions. To achieve this, measurements of CTH based on bolus tracking (Gutiérrez-Jiménez et al., 2016) could be combined with intravascular measurements of capillary PO2 using two-photon phosphorescence laser microscopy (Finikova et al., 2008).
In conclusion, this study lays the theoretical basis for the analysis of HSH in MVNs. It is a substantial improvement over previous approaches in the brain that were limited to independent, identical capillaries without branchings. Models for RBC and capillary diffusive interactions were developed and successfully validated using a detailed computational model in simplified geometries. The following conclusions can be drawn: (1) diffusive interaction leads to a strong reduction of small-scale HSH caused by CTH or other factors; (2) HSH can arise in the absence of CTH, for instance due to differences in hematocrit or supplied tissue volume; (3) CTH influences COSH, but does not determine it. Thus, this modeling work is a major step to better understand the actual effects of CTH on blood oxygen content. This has potential implications in the study of all conditions where capillary dysfunction and CTH are thought to be involved, such as Alzheimer's disease (Østergaard et al., 2013a), stroke (Østergaard et al., 2015), traumatic brain injury (Østergaard et al., 2014a) and ischemic heart disease (Ostergaard et al., 2014b).
Author Contributions
AL conceived of the study, developed the theoretical models, implemented the algorithms, ran the simulations, interpreted the data and drafted the manuscript. TS contributed the initial idea for the study. BW and PJ conceived of the study and participated in its design.
Funding
This research was funded by the Swiss National Science Foundation under the grant No. 140660.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are grateful for the valuable discussions with Franca Schmid.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2018.00420/full#supplementary-material
Abbreviations
COSH, capillary outflow saturation heterogeneity; CTH, capillary transit time heterogeneity; HS, hemoglobin saturation; HSH, hemoglobin saturation heterogeneity; RBC, red blood cell.
References
Altman, P. L., and Dittmer, D. S. (eds.). (1971). Respiration and Circulation. Bethesda, MD: Federation of American Societies for Experimental Biology.
Angleys, H., Østergaard, L., and Jespersen, S. N. (2015). The effects of capillary transit time heterogeneity (CTH) on brain oxygenation. J. Cereb. Blood Flow Metab. 35, 806–817. doi: 10.1038/jcbfm.2014.254
Bentley, T. B., Meng, H., and Pittman, R. N. (1993). Temperature dependence of oxygen diffusion and consumption in mammalian striated muscle. Am. J. Physiol. Heart Circ. Physiol. 264, H1825–H1830. doi: 10.1152/ajpheart.1993.264.6.H1825
Bertossi, M., Virgintino, D., Maiorano, E., Occhiogrosso, M., and Roncali, L. (1997). Ultrastructural and morphometric investigation of human brain capillaries in normal and peritumoral tissues. Ultrastruct. Pathol. 21, 41–49. doi: 10.3109/01913129709023246
Blinder, P., Tsai, P. S., Kaufhold, J. P., Knutsen, P. M., Suhl, H., and Kleinfeld, D. (2013). The cortical angiome: an interconnected vascular network with noncolumnar patterns of blood flow. Nat. Neurosci. 16, 889–897. doi: 10.1038/nn.3426
Chen, B. R., Bouchard, M. B., McCaslin, A. F., Burgess, S. A., and Hillman, E. M. (2011). High-speed vascular dynamics of the hemodynamic response. Neuroimage 54, 1021–1030. doi: 10.1016/j.neuroimage.2010.09.036
Christoforides, C., Laasberg, L. H., and Hedley-Whyte, J. (1969). Effect of temperature on solubility of O2 in human plasma. J. Appl. Physiol. 26, 56–60. doi: 10.1152/jappl.1969.26.1.56
Clark, A., Federspiel, W., Clark, P., and Cokelet, G. (1985). Oxygen delivery from red cells. Biophys. J. 47, 171–181. doi: 10.1016/S0006-3495(85)83890-X
Eggleton, C., Vadapalli, A., Roy, T., and Popel, A. (2000). Calculations of intracapillary oxygen tension distributions in muscle. Math. Biosci. 167, 123–143. doi: 10.1016/S0025-5564(00)00038-9
Ellsworth, M. L., Popel, A. S., and Pittman, R. N. (1988). Assessment and impact of heterogeneities of convective oxygen transport parameters in capillaries of striated muscle: experimental and theoretical. Microvasc. Res. 35, 341–362. doi: 10.1016/0026-2862(88)90089-1
Finikova, O. S., Lebedev, A. Y., Aprelev, A., Troxler, T., Gao, F., Garnacho, C., et al. (2008). Oxygen microscopy by two-photon-excited phosphorescence. ChemPhysChem 9, 1673–1679. doi: 10.1002/cphc.200800296
Fraser, G. M., Goldman, D., and Ellis, C. G. (2013). Comparison of generated parallel capillary arrays to three-dimensional reconstructed capillary networks in modeling oxygen transport in discrete microvascular volumes. Microcirculation 20, 748–763. doi: 10.1111/micc.12075
Goldman, D., and Popel, A. (1999). “Computational modeling of oxygen transport from complex capillary networks,” in Oxygen Transport to Tissue XXI, Volume 471 of Advances in Experimental Medicine and Biology, eds A. Eke and D. T. Delpy (Boston, MA: Springer), 555–563.
Goldstick, T. K., Ciuryla, V. T., and Zuckerman, L. (1976). “Diffusion of oxygen in plasma and blood,” in Oxygen Transport to Tissue – II, eds J. Grote, D. Reneau, and G. Thews (Boston, MA: Springer), 183–190.
Grimes, D. R., Fletcher, A. G., and Partridge, M. (2014). Oxygen consumption dynamics in steady-state tumour models. R. Soc. Open Sci. 1:140080. doi: 10.1098/rsos.140080
Gutiérrez-Jiménez, E., Cai, C., Mikkelsen, I. K., Rasmussen, P. M., Angleys, H., Merrild, M., et al. (2016). Effect of electrical forepaw stimulation on capillary transit-time heterogeneity (CTH). J. Cereb. Blood Flow Metab. 36, 2072–2086. doi: 10.1177/0271678X16631560
Hairer, E., Wanne, G., and Nørsett, S. P. (1993). Solving Ordinary Differential Equations I. Berlin; Heidelberg: Springer.
Hall, C. N., Reynell, C., Gesslein, B., Hamilton, N. B., Mishra, A., Sutherland, B. A., et al. (2014). Capillary pericytes regulate cerebral blood flow in health and disease. Nature 508, 55–60. doi: 10.1038/nature13165
Hamilton, N. B., Attwell, D., and Hall, C. N. (2010). Pericyte-mediated regulation of capillary diameter: a component of neurovascular coupling in health and disease. Front. Neuroenerg. 2:5. doi: 10.3389/fnene.2010.00005
Hellums, J. (1977). The resistance to oxygen transport in the capillaries relative to that in the surrounding tissue. Microvasc. Res. 13, 131–136. doi: 10.1016/0026-2862(77)90122-4
Hillman, E. M. (2014). Coupling mechanism and significance of the BOLD signal: a status report. Annu. Rev. Neurosci. 37, 161–181. doi: 10.1146/annurev-neuro-071013-014111
Hoofd, L., and Turek, Z. (1996). Realistic Modelling of Capillary Spacing in Dog Gracilis Muscle Greatly Influences the Heterogeneity of Calculated Tissue Oxygen Pressures. Boston, MA: Springer.
Jespersen, S. N., and Østergaard, L. (2012). The roles of cerebral blood flow, capillary transit time heterogeneity, and oxygen tension in brain oxygenation and metabolism. J. Cereb. Blood Flow Metab. 32, 264–277. doi: 10.1038/jcbfm.2011.153
Jones, E., Oliphant, T., and Peterson, P. (2001). SciPy: Open Source Scientific Tools For Python. Available online at: https://www.scipy.org/citing.html (Accessed November 24, 2017).
Liu, C. Y., Eskin, S. G., and Hellums, J. D. (1994). “The oxygen permeability of cultured endothelial cell monolayers,” in Advances in Experimental Medicine and Biology, eds P. Vaupel, R. Zander, and D. F. Bruley (Boston, MA: Springer Nature), 723–730.
Lorthois, S., and Cassot, F. (2010). Fractal analysis of vascular networks: insights from morphogenesis. J. Theor. Biol. 262, 614–633. doi: 10.1016/j.jtbi.2009.10.037
Lücker, A., Secomb, T. W., Weber, B., and Jenny, P. (2017). The relative influence of hematocrit and red blood cell velocity on oxygen transport from capillaries to tissue. Microcirculation 24:e12337. doi: 10.1111/micc.12337
Lücker, A., Weber, B., and Jenny, P. (2014). A dynamic model of oxygen transport from capillaries to tissue with moving red blood cells. Am. J. Physiol. Heart Circ. Physiol. 308, H206–H216. doi: 10.1152/ajpheart.00447.2014
Lyons, D. G., Parpaleix, A., Roche, M., and Charpak, S. (2016). Mapping oxygen concentration in the awake mouse brain. eLife 5:e12024. doi: 10.7554/eLife.12024
Mahler, M., Louy, C., Homsher, E., and Peskoff, A. (1985). Reappraisal of diffusion, solubility, and consumption of oxygen in frog skeletal muscle, with applications to muscle energy balance. J. Gen. Physiol. 86, 105–134. doi: 10.1085/jgp.86.1.105
Østergaard, L., Aamand, R., Gutiérrez-Jiménez, E., Ho, Y.-C. L., Blicher, J. U., Madsen, S. M., et al. (2013a). The capillary dysfunction hypothesis of Alzheimer's disease. Neurobiol. Aging 34, 1018–1031. doi: 10.1016/j.neurobiolaging.2012.09.011
Østergaard, L., Engedal, T. S., Aamand, R., Mikkelsen, R., Iversen, N. K., Anzabi, M., et al. (2014a). Capillary transit time heterogeneity and flow-metabolism coupling after traumatic brain injury. J. Cereb. Blood Flow Metab. 34, 1585–1598. doi: 10.1038/jcbfm.2014.131
Østergaard, L., Engedal, T. S., Moreton, F., Hansen, M. B., Wardlaw, J. M., Dalkara, T., et al. (2015). Cerebral small vessel disease: capillary pathways to stroke and cognitive decline. J. Cereb. Blood Flow Metab. 36, 302–325. doi: 10.1177/0271678X15606723
Østergaard, L., Jespersen, S. N., Mouridsen, K., Mikkelsen, I. K., Jonsdottír, K. Ý., Tietze, A., et al. (2013b). The role of the cerebral capillaries in acute ischemic stroke: the extended penumbra model. J. Cereb. Blood Flow Metab. 33, 635–648. doi: 10.1038/jcbfm.2013.18
Ostergaard, L., Kristiansen, S. B., Angleys, H., Frøkiær, J., Hasenkam, J. M., Jespersen, S. N., et al. (2014b). The role of capillary transit time heterogeneity in myocardial oxygenation and ischemic heart disease. Basic Res. Cardiol. 109:409. doi: 10.1007/s00395-014-0409-x
Pantoni, L. (2010). Cerebral small vessel disease: from pathogenesis and clinical characteristics to therapeutic challenges. Lancet Neurol. 9, 689–701. doi: 10.1016/S1474-4422(10)70104-6
Parpaleix, A., Houssen, Y. G., and Charpak, S. (2013). Imaging local neuronal activity by monitoring PO2 transients in capillaries. Nat. Med. 19, 241–246. doi: 10.1038/nm.3059
Popel, A. S., Charny, C. K., and Dvinsky, A. S. (1986). Effect of heterogeneous oxygen delivery on the oxygen distribution in skeletal muscle. Math. Biosci. 81, 91–113. doi: 10.1016/0025-5564(86)90164-1
Roy, T. K., and Secomb, T. W. (2014). Theoretical analysis of the determinants of lung oxygen diffusing capacity. J. Theor. Biol. 351, 1–8. doi: 10.1016/j.jtbi.2014.02.009
Sakadžić, S., Mandeville, E. T., Gagnon, L., Musacchia, J. J., Yaseen, M. A., Yucel, M. A., et al. (2014). Large arteriolar component of oxygen delivery implies a safe margin of oxygen supply to cerebral tissue. Nat. Commun. 5:5734. doi: 10.1038/ncomms6734
Salathe, E. P. (2003). Mathematical analysis of oxygen concentration in a two dimensional array of capillaries. J. Math. Biol. 46, 287–308. doi: 10.1007/s00285-002-0175-5
Schmid, F., Kleinfeld, D., Blinder, P., Jenny, P., and Weber, B. (2017). Depth-dependent flow and pressure characteristics in cortical microvascular networks. PLoS Comput. Biol. 13:e1005392. doi: 10.1371/journal.pcbi.1005392
Secomb, T. W., Hsu, R., Beamer, N., and Coull, B. (2000). Theoretical simulation of oxygen transport to brain by networks of microvessels: effects of oxygen supply and demand on tissue hypoxia. Microcirculation 7, 237–247. doi: 10.1111/j.1549-8719.2000.tb00124.x
Shirasawa, T. (2003). Oxygen affinity of hemoglobin regulates O2 consumption, metabolism, and physical activity. J. Biol. Chem. 278, 5035–5043. doi: 10.1074/jbc.M211110200
Thal, D. R., Capetillo-Zarate, E., Larionov, S., Staufenbiel, M., Zurbruegg, S., and Beckmann, N. (2009). Capillary cerebral amyloid angiopathy is associated with vessel occlusion and cerebral blood flow disturbances. Neurobiol. Aging 30, 1936–1948. doi: 10.1016/j.neurobiolaging.2008.01.017
Tian, P., Teng, I. C., May, L. D., Kurz, R., Lu, K., Scadeng, M., et al. (2010). Cortical depth-specific microvascular dilation underlies laminar differences in blood oxygenation level-dependent functional MRI signal. Proc. Natl. Acad. Sci. U.S.A. 107, 15246–15251. doi: 10.1073/pnas.1006735107
Tsai, P. S., Kaufhold, J. P., Blinder, P., Friedman, B., Drew, P. J., Karten, H. J., et al. (2009). Correlations of neuronal and microvascular densities in murine cortex revealed by direct counting and colocalization of nuclei and vessels. J. Neurosci. 29, 14553–14570. doi: 10.1523/JNEUROSCI.3287-09.2009
Watanabe, T., Takeda, T., Omiya, S., Hikoso, S., Yamaguchi, O., Nakano, Y., et al. (2008). Reduction in hemoglobin–oxygen affinity results in the improvement of exercise capacity in mice with chronic heart failure. J. Am. Coll. Cardiol. 52, 779–786. doi: 10.1016/j.jacc.2008.06.003
Weller, H. G., Tabor, G., Jasak, H., and Fureby, C. (1998). A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12:620. doi: 10.1063/1.168744
Yemisci, M., Gursoy-Ozdemir, Y., Vural, A., Can, A., Topalkara, K., and Dalkara, T. (2009). Pericyte contraction induced by oxidative-nitrative stress impairs capillary reflow despite successful opening of an occluded cerebral artery. Nat. Med. 15, 1031–1037. doi: 10.1038/nm.2022
Keywords: blood flow, capillary transit time heterogeneity, computational modeling, hematocrit, hemoglobin saturation, microcirculation, oxygen transport, red blood cells
Citation: Lücker A, Secomb TW, Weber B and Jenny P (2018) The Relation Between Capillary Transit Times and Hemoglobin Saturation Heterogeneity. Part 1: Theoretical Models. Front. Physiol. 9:420. doi: 10.3389/fphys.2018.00420
Received: 28 November 2017; Accepted: 04 April 2018;
Published: 26 April 2018.
Edited by:
Joseph L. Greenstein, Johns Hopkins University, United StatesReviewed by:
Ranjan K. Dash, Medical College of Wisconsin, United StatesDaniel Goldman, University of Western Ontario, Canada
Leif Østergaard, Center of Functionally Integrative Neuroscience and MINDLab, Denmark
David Robert Grimes, Queen's University Belfast, United Kingdom
Copyright © 2018 Lücker, Secomb, Weber and Jenny. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adrien Lücker, bHVlY2tlckBpZmQubWF2dC5ldGh6LmNo
 Adrien Lücker
Adrien Lücker Timothy W. Secomb
Timothy W. Secomb Bruno Weber
Bruno Weber Patrick Jenny1
Patrick Jenny1