Imputation models and error analysis for phase contrast MR cerebral blood flow measurements in heterogeneous pediatric and adult populations

Cerebral blood flow (CBF) supports brain function and health. Cerebral blood flow is affected by normal brain development, disease, medications use, and other interventions. One method to measure CBF is phase contrast magnetic resonance (PC MR) imaging, a particularly fast and reliable method to measure blood flow through major arteries such as the internal carotid (ICA) or vertebral arteries (VA). Unfortunately, sometimes PC MR can be compromised due to errors by the technologist during image acquisition, patient movement, or complex vessel structures. Our goal was to develop mathematical models to estimate CBF for a wide age range of patients whenever 1 or more vessels are not correctly measured. To investigate this, we studied a set of 258 PC MR acquisitions from a group of 196 patients with one or three acquisitions per subject (165 single images, 31 acquisitions of 3 images) ranging in age from 0.4 to 61.3 years (mean [μ] = 13.1, standard deviation [σ] = 12.3). We deliberately excluded measurements from one or more arteries in each volunteer to mimic situations with low image quality. Subsequently, we developed mathematical models to predict the missing data. Our predictive models performed well; across the human lifespan when at least one ICA measurement was available, our normalized root mean squared error values were low (<0.137), our R-squared values were high (>0.91), and we observed high intra-class correlation coefficients (>0.951). In summary, these imputation models are effective in estimating CBF in children and adults.

1 Introduction

Maintaining an adequate blood supply to meet the brain’s energy demand is essential for its health. The brain consumes 20% of the body’s total energy, necessitating a considerable supply of blood which constitutes 12% of the heart’s total cardiac output (Hall et al., 2012; Mink et al., 1981). Both total cerebral blood flow (CBF [mL/min]) and relative CBF adjusted by brain volume [rCBF, mL/min/100 g] also change across the lifespan, and can become impaired by injury or disease (Liu et al., 2019; Paniukov et al., 2020; Oshima et al., 2002). In children, CBF is influenced by normal brain maturation and pathological conditions such as congenital heart defects (De Silvestro et al., 2023; Lim et al., 2016), meningitis (Ashwal et al., 1992), Moyamoya (Sun et al., 2018), metabolic disorders (Qi et al., 2023), and hydrocephalous (Hirabuki et al., 2000). In adults, alterations in CBF are associated with cardiovascular risk (Hirabuki et al., 2000; Jennings et al., 2013; King et al., 2018; Varela et al., 2012), small vessel disease including Alzheimer’s dementia (Yu et al., 2020; Leijenaar et al., 2017), white matter lesions (Hanaoka et al., 2016), anemia (Borzage et al., 2016), stroke risk in sickle cell disease (Prohovnik et al., 2009; Vernooij et al., 2008), and higher risk of non-cardiovascular mortality in the elderly (Sabayan et al., 2013).

Non-invasive assessment of CBF is attractive for diagnosing and monitoring disease status. Phase contrast (PC) magnetic resonance (MR) imaging can measure flow through the internal carotid arteries (ICA) and vertebral arteries (VA). PC MR imaging provides a reproducible (intra-class correlation coefficient (ICC) 0.97–0.99, coefficient of variation 4%–9%), robust measurement of CBF that can be normalized to estimate rCBF [mL/min/100 g] (Liu et al., 2014; Sakhare et al., 2019; Koerte et al., 2013; MacDonald and Frayne, 2015). PC MR is robust to parameter variations including encoding velocity, number of signal averages, voxel size, flip angle, slice thickness, and imaging acceleration (Greil et al., 2002; Correia de Verdier et al., 2024; Thunberg et al., 2003). Furthermore, PC acquisitions remain accurate despite practical acquisition challenges such as differing study sites, slice inclination, and breathing motion (Greil et al., 2002; Andersson et al., 2016; Summers et al., 2005). Because velocity is directly encoded in the moving blood, post-processing is straightforward and does not rely on complex modelling or assumptions that may differ between subjects who have normal or pathologic flow. By following well-established scanning norms such as minimizing repetition time and echo time, setting the encoding velocity to a value moderately above the fastest expected flow for a given clinical scenario, and selecting voxels sufficiently small to fit inside the vessel lumen, a robust PC protocols can be deployed in clinical environments across a wide age range (Greil et al., 2002; Correia de Verdier et al., 2024; Lagerstrand et al., 2020).

However, the clinical use of PC MR imaging to measure CBF is hampered when PC images from one or more vessels cannot quantify flow. Factors such as normal variation in vessel size, tortuosity of the ICAs and VAs, patient motion, and operator facility may contribute to an unsuccessful image acquisition. While automated techniques have been developed by researchers to overcome some of these challenges, they have not been implemented by vendors for use in standard clinical imaging environments (Liu et al., 2014). Our prior research in adults reported flow measurements in each vessel are sufficiently correlated with one another that imputation can compensate for measurements corrupted by anatomical variation, motion or obliquity, or improper placement (Shah et al., 2023). We previously reported that flow through any one vessel is highly correlated with CBF due to the left-right symmetry in arterial flows and the constant ratio between anterior and posterior flows, which lead to excellent imputation models in adults. This study extends the feasibility of imputation to a wider age range by examining these correlations in both children and adults. We developed new mathematical models using a combination of age and arterial blood flows to impute the CBF across the human lifespan.

2 Materials and methods

2.1 Patient demographics

This study includes 258 single-slice phase contrast images that were obtained from a total of 196 subjects (N = 108 children and N = 88 adults), across two studies. One study population comprised pediatric patients from a study approved by the Children’s Hospital Los Angeles Committee on Clinical Investigations (CCI 18–00493). Assent was obtained from the parents of patients (N = 67, all children) recruited between 2020 and 2023. These patients ranged from 0.4–11.9 years (μ = 2.7, σ = 1.6, 37M, 30F). This cohort included patients with seizures and epilepsy (N = 23), neoplasms (N = 14), developmental delay or regression (N = 7), cerebral palsy (N = 3), and other visit reasons (N = 20). All (N = 67) children were anesthetized with propofol (100%); some of these children also received dexmedetomidine (43%), sevoflurane (4%), or ketamine (1%). Their hematocrit levels were (μ = 35.9, σ = 3.2).

The other study population comprised unsedated patients and volunteers with ages ranging from adolescence through adulthood. This was a secondary analysis of existing data, which was originally approved by the Children’s Hospital Los Angeles Committee on Clinical Investigations (CCI 11–00083). Informed consent was obtained from 129 patients (N = 41 children and N = 88 adults) recruited between 2012 and 2017. These patients ranged from 9–61 years (μ = 23.5, σ = 9.7, 59M, 70F). This cohort included patients with sickle cell disease (N = 55), patients with other hemoglobinopathies (N = 32), and healthy control volunteers (N = 42). Their hematocrits levels were (μ = 32.9, σ = 7.2); some patients 33% of the adult cohort (N = 42) received chronic transfusions (Borzage et al., 2016). All subjects were free of known cerebral vessel steno-occlusive disease.

2.2 Image acquisition

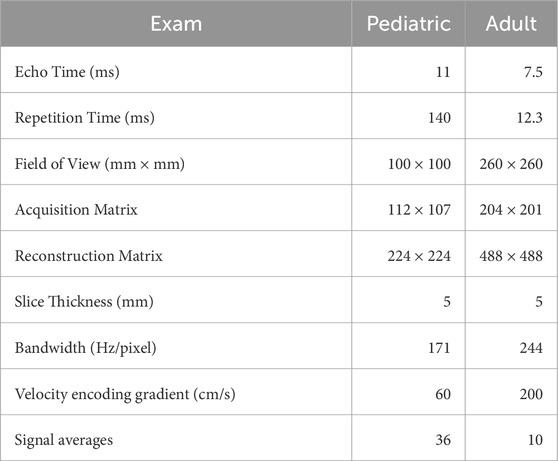
The imaging methods are reported elsewhere in detail and summarized here (Borzage et al., 2016). We obtained all images for both groups with 3T Philips MRI systems (Ingenia, Ingenia CX, or Achieva) equipped with an eight-element head coil. We localized the vessels in the neck with a magnetic resonance angiogram, and then placed a PC MR imaging plane approximately 1 cm above the carotid bifurcation. In the pediatric population, the angiogram was collected in the sagittal plane; in the adult population, it was collected in the axial plane with inline reformatting into sagittal and coronal planes to facilitate orthogonal placement of the PC imaging plane. Because flow values are similar with and without cardiac gating, no gating was used (Nordmeyer et al., 2010). Imaging parameters for both protocols were similar (Table 1). Each pediatric patient yielded 1 to 3 PC MR images (36 scans yield 1 image each, 31 scans yielded 3 images each).

Table 1

Table 1. Summary of relevant MR imaging parameters for pediatric and adult cohorts.

2.3 Image processing

PC images were processed to quantify flow rate through each of the four major cerebral arteries. We performed all PC image analysis using ImageJ (National Institutes of Health, Bethesda, MD) and MATLAB (The MathWorks, Natick, MA) to quantify flow. The complex difference image was thresholded to identify moving voxels (defined as greater than the mean plus two standard deviations of stationary voxels sampled from a non-vascular region). Background phase was identified by fitting the phase differences of stationary voxels using a two-dimensional second-order polynomial and then removed. Vessel boundaries were automatically selected using a Canny edge-detector of the complex difference image, dilating the edge by a single voxel, creating a binary mask representing the inside of the vessel lumen, and then excluding any stationary voxels within the vessel mask. Blood flow in each artery was calculated by summing the blood velocities (cm/s) within the vessel multiplied by the voxel area (cm²). When the automatic edge detection failed (<5% of the time), the ICA or VA lumen boundaries were identified manually by an MR researcher (JCW) with 22 years of experience analyzing PC MR images. Images demonstrating successful acquisition and flow quantitation of the 4 vessels (2 ICAs, 2 VAs) underwent further processing and modelling.

2.4 Modeling cerebral blood flow as a function of vessels and age and other variables

We computed the mean and standard deviation for CBF, individual vessel flows, and anterior and posterior circulations. We evaluated all 4 blood flow ratios for left (L) and right (R) ICAs and VAs (LICA-CBF, RICA-CBF, LVA-CBF, RVA-CBF) as well as anterior-to-posterior and right-to-left flow ratios from both pediatric and adult volunteers with a two-way ANOVA. Post-hoc comparison of these groups was performed using a Wilcoxon Kruskal-Wallis test (Table 2).

Table 2

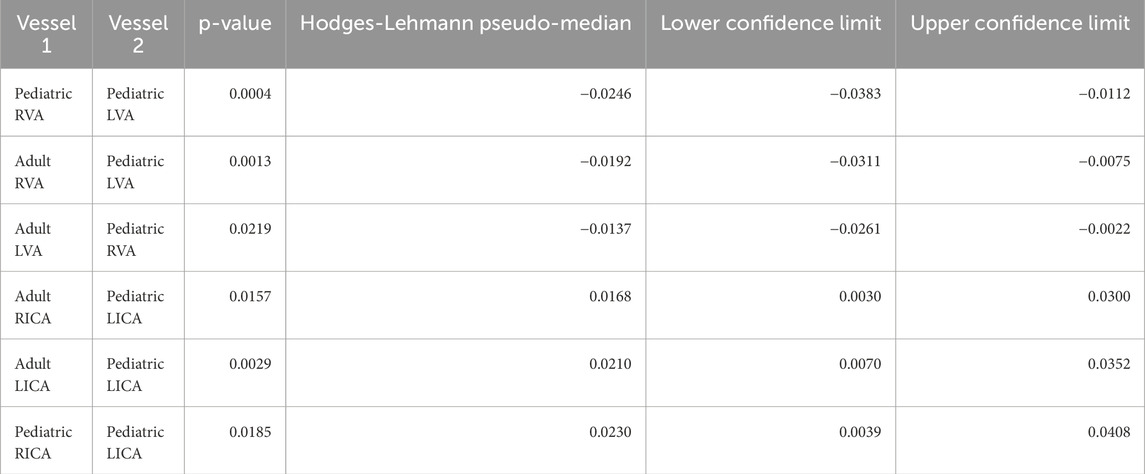
Table 2. Wilcoxon Kruskal-Wallis test results demonstrate statistical differences in vessel-to-CBF ratios. Despite the statistical difference, the effect size was small. The median difference between the vessels ranged from −2.5% (pediatric RVA versus pediatric RVA) to 2.3% (pediatric RICA vs. pediatric LICA) (mean [μ] = 0.05% standard deviation [σ] = 2.2%). This small effect does not justify the use imputation models, for which 32 unique combinations of pediatric or adult vessels would be presented as separate imputation models. Note that this table omits comparison of ICAs versus VAs, which are clearly different.

We systematically excluded flow data from one or more vessels to simulate the effects of a sub-optimal image acquisition. We analyzed the 8 scenarios wherein combinations of 2, 1, or 0 ICAs or VAs could be analyzed from an image. We applied a standard least-squares model to estimate CBF as a function of (1) the remaining vessels able to be analyzed, and (2) an age-dependent equation. The age-dependent equation was a single parsimonious model of CBF as a function of age across the human lifespan. To create this equation, we evaluated age-based models (polynomial, power, logistic, and combinations thereof) using MATLAB (R2021b, Mathworks, Natick, MA), and compared their performance using root mean squared error. In scenarios where either 2 ICAs or 2 VAs were analyzed, we reduced model complexity by calculating the total anterior (sum of ICAs) or posterior (sum of VAs) flow to reduce degrees of freedom. The age-based model was extended to include the following additional parameters: sex; sex and hematocrit; and sex, hematocrit, and total brain volume.

2.5 Assessing cerebral blood flow model quality

The quality of each imputation model was assessed using root mean squared error, R-squared statistic, and intra-class correlation coefficient (ICC). The ICC (2, 1) is a two-way random, single measures absolute agreement between model 0 (gold standard, all vessels present) and age-based models 1–8 (Table 3), calculated using MATLAB. We also performed Bland-Altman analyses of all age-based models compared to known CBF (model 0). We calculated the biases as the mean difference between model 0 and each other model, and the 95% limits of agreement were defined as twice the standard deviation of the differences of individual measurements between model 0 and each other model.

Table 3

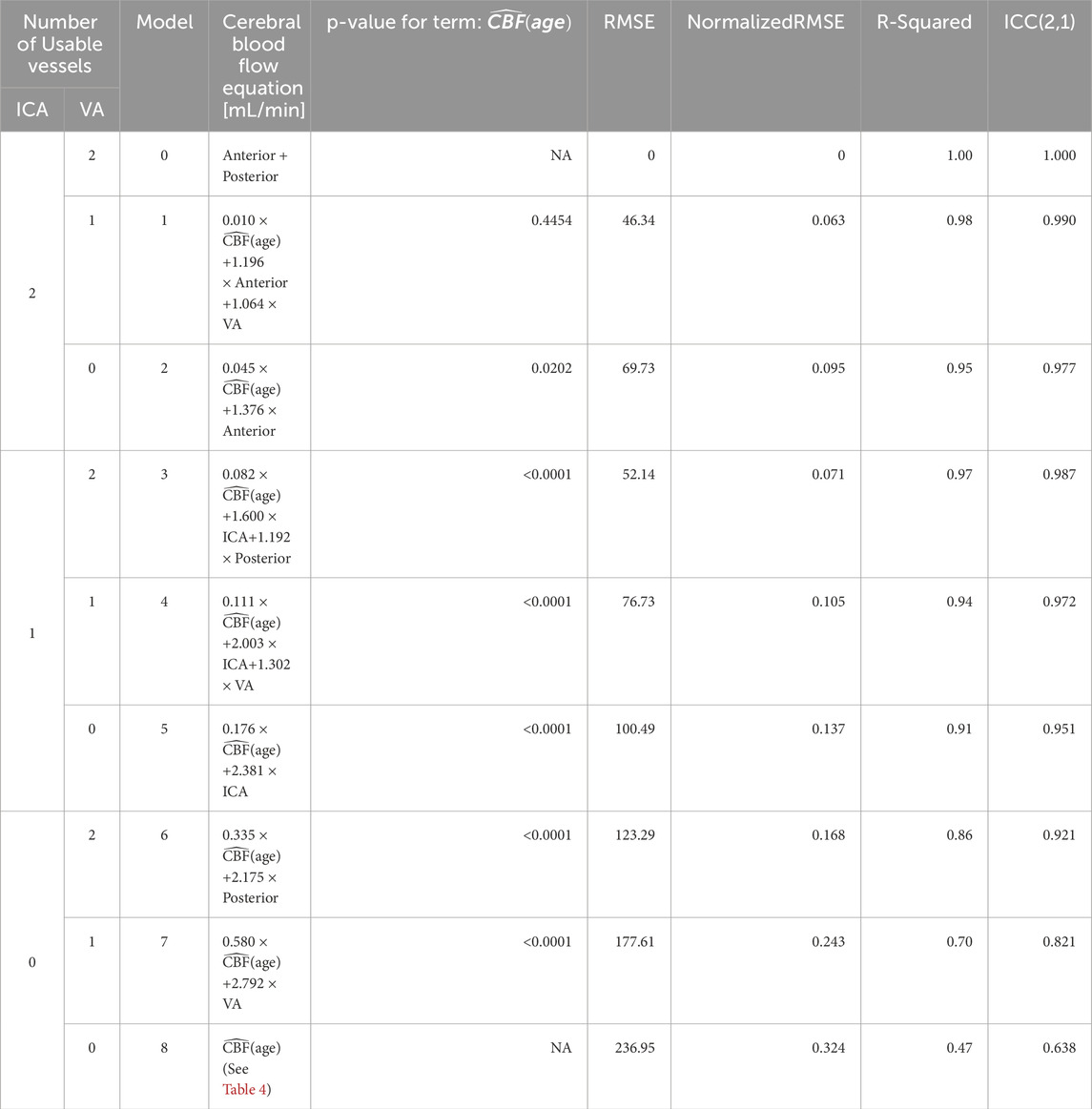
Table 3. Models for computing CBF when vessels are missing. The models are independent of the lateral location of the imputed vessel(s), allowing us to omit models for the combinations of different left versus right vessels (Figure 3). Models 1–7 use an age-dependent model of CBF, denoted $\widehat{CBF}\left(age\right)$ and defined as model 8, noted in Table 4 as model 8a; this is the most conservative of the vessel-independent CBF models. Overall, the models followed the anticipated pattern wherein missing ICAs contributed more error than missing VAs (e.g., model 3 versus 1). Age was useful in all models (p < 0.05), except model 1, for which it was not significant (p = 0.4454). Abbreviations cerebral blood flow (CBF), internal carotid artery (ICA), vertebral artery (VA), root mean square error (RMSE), intra-class correlation coefficient (ICC). An online calculator for these models is provided: https://brainflow.science/impute-cbf.

3 Results

In the pediatric volunteers, we report the following mean (μ) and standard deviation(σ) values for CBF (μ = 530.7, σ = 204.7), anterior flow (sum of ICAs, μ = 361.4, σ = 135.8), and posterior flow (sum of VAs, μ = 169.3, σ = 90.1). Flows in individual arteries were: LICA (μ = 176.4, σ = 75.3), RICA (μ = 184.9, σ = 73.3), LVA (μ = 90.4, σ = 51.2), and RVA (μ = 78.9, σ = 49.9).

In the adult volunteers, we report the CBF (μ = 930.6, σ = 298.0), anterior flow (μ = 650.5, σ = 209.4), and posterior flow (μ = 280.0, σ = 105.9). Flows in individual arteries were: LICA (μ = 326.8, σ = 111.0), RICA (μ = 323.7, σ = 106.1), LVA (μ = 145.5, σ = 76.7), and RVA (μ = 134.5, σ = 53.2). All values are shown in Figure 1. Ratios of anterior-to-posterior flow and right-to-left flow are shown in Figure 2. Ranges of CBF are similar to previous studies usings color duplex sonography and 4D flow MRI (Schöning and Hartig, 1996; Wu et al., 2016).

Figure 1

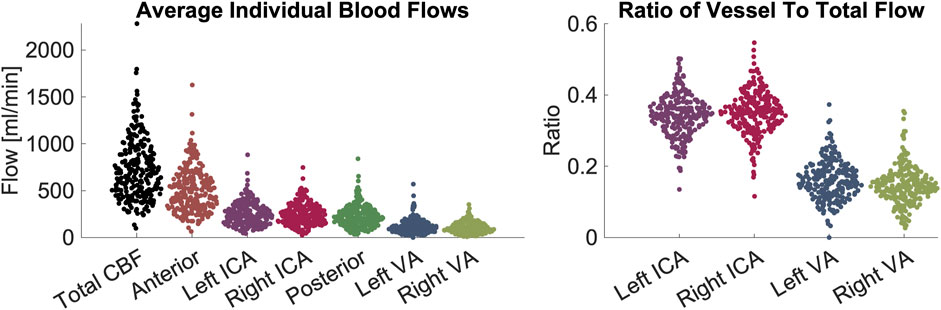
Figure 1. Demonstration of blood flow rates and ratios between vessels. Left panel: measurements of flow in units of mL/minute. From left to right the figures shows CBF contribution: total, anterior, left ICA, right ICA, posterior circulation, left VA, right VA. Right panel: ratios of flow in individual arteries versus CBF. From left to right the figure shows left ICA, right ICA, left VA, right VA. The figures demonstrate visually (1) the range of CBF (2), the contribution from individual arteries is predominantly from the anterior circulation, that flow through (3) ICAs and (4) VAs are symmetric on the left and right sides. Abbreviations cerebral blood flow (CBF), internal carotid artery (ICA), vertebral artery (VA).

Figure 2

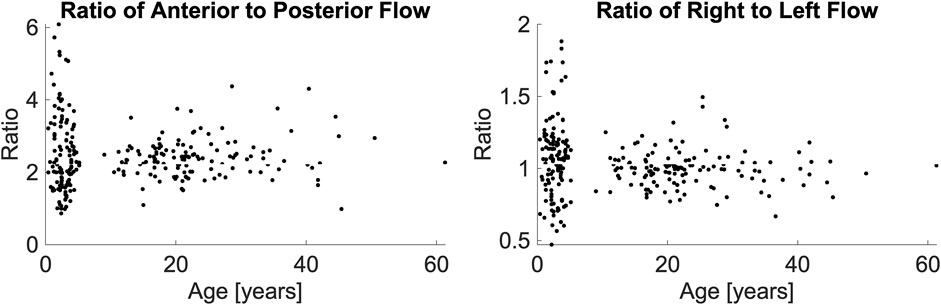
Figure 2. Anterior-to-posterior posterior ratio (left panel) and right-to-left ratio (right panel), presented as a function of their age. A Wilcoxon Kruskal-Wallace test demonstrated no difference between the pediatric and adult populations.

The two-way ANOVA determined that differences in flow ratios were particular to vessel types (p < 0.0001) and the interaction of vessel type and age (p = 0.0147) but not age alone (p = 0.9312). We performed post hoc comparisons of these ratios with Wilcoxon Kruskal-Wallis tests. We found that for most ratios, both the age-based comparisons (e.g., ratios of pediatric LVA versus adult LVA) and the lateral comparisons (e.g., pediatric LVA-CBF versus pediatric RVA-CBF) to be statistically similar (p > 0.05, statistically different vessels reported in Table 2). As expected, all comparisons of ICA-CBF ratios and VA-CBF ratios (e.g., pediatric VA-CBF versus pediatric ICA-CBF) were different (p < 0.0001). However, the size of differences in ratios between individual vessels and CBF were minor; the maximum ratio difference (pediatric RICA-CBF versus pediatric LICA-CBF) was very small, 0.023. Due to this small effect size, we simplified the models using equivalence of vessel-to-CBF ratios across age groups and left and right symmetry of vessels.

We evaluated the difference in anterior-to-posterior and right-to-left flow ratios as a function hematocrit and age group. There was no association in a linear regression between hematocrit and either the anterior-to-posterior ratio (p = 0.0595) or right-to-left ratio (p = 0.8292). There was no association between age and either anterior-to-posterior flow ratio (p = 0.1928) or the right-to-left ratio (p = 0.3261).

Table 3 demonstrates the performance of each imputation model as functions of the remaining vessels to be analyzed, and the age dependent equation. As anticipated, the error in imputation (RMSE) increased and the R-squared decreased from the model with the fewest to most missing vessels (model 1 to model 8). All models showed statistical significance (p < 0.0001); however the age term was not significant for model 1 (p = 0.4454), only marginally significant for model 2 (p = 0.0202), and significant for the remaining models (p < 0.0001). Table 4 demonstrates the vessel-free CBF models, using age, sex, hematocrit, and total brain volume. The age-logistic model to estimate age-related changes in CBF (Model 8a from Table 4, shown in Figure 3) was selected based on its superior performance over other tested models (Table 5). The same statistics were calculated for the original, age-independent imputation models (Table 6). Age-dependent models performed equivalently to the age-independent models in cases with 1 or 2 missing VAs, or 1 missing ICA with 1 or 2 VAs present (models 1, 2, 3, and 4), showing similar RMSE, normalized RMSE, ICC, and R-squared. In all other cases, the age-dependent models had lower RMSE and normalized RMSE, and higher R-squared correlations than the age-independent models.

Table 4

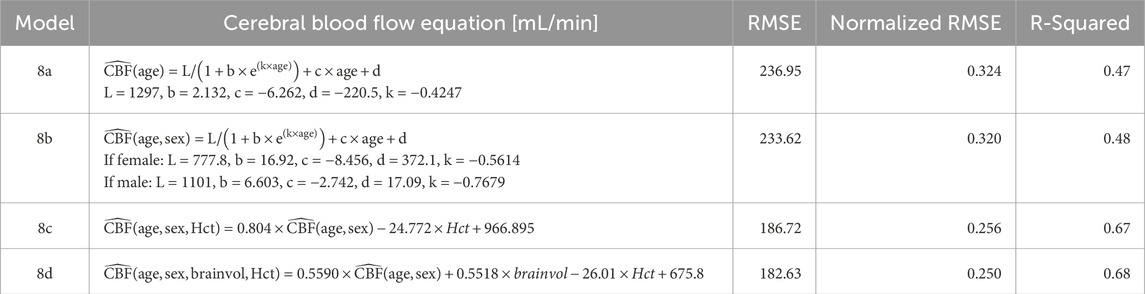
Table 4. Vessel-free models of CBF. The presented models take parameters of age (years), sex, Hct, brainvol. Abbreviations cerebral blood flow (CBF, mL/min), root mean square error (RMSE), hematocrit (Hct, percentage), and total brain volume (brainvol, cubic centimeters).

Figure 3

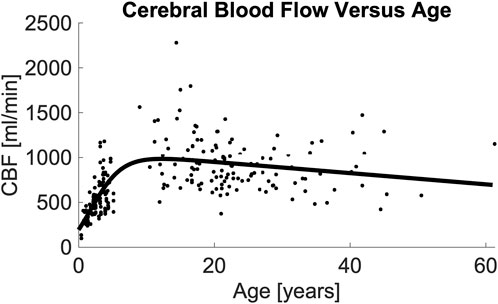
Figure 3. Image demonstrating total CBF vs. age and the resulting model. Regression analysis demonstrates that total CBF rises rapidly from birth through middle childhood followed by a slow decline from adolescence through adulthood. Regression line formula is noted in (Table 4, Model 8a). Abbreviations cerebral blood flow (CBF).

Table 5

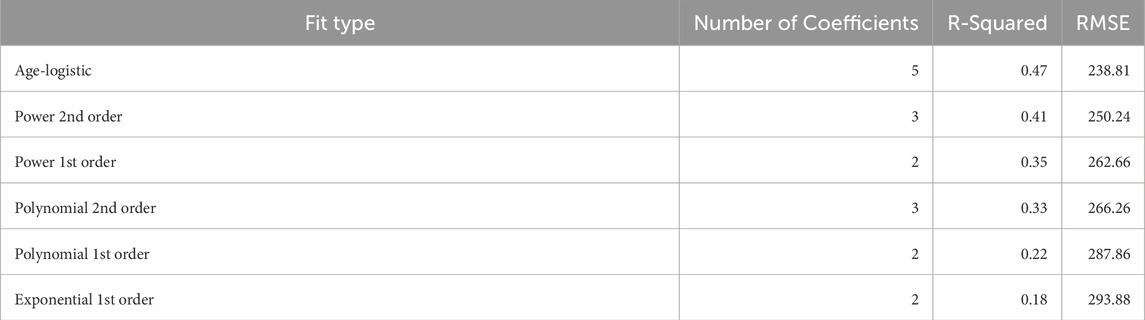
Table 5. Statistics comparing the performance of different models of cerebral blood flow as a function of age. The age-logistic model outperformed the other models, which failed to capture the rapid rise followed by slow decline of cerebral blood flow with age. Models are named by their corresponding fit type in MATLAB, while the age-logistic formula is presented in Table 4, Model 8a.

Table 6

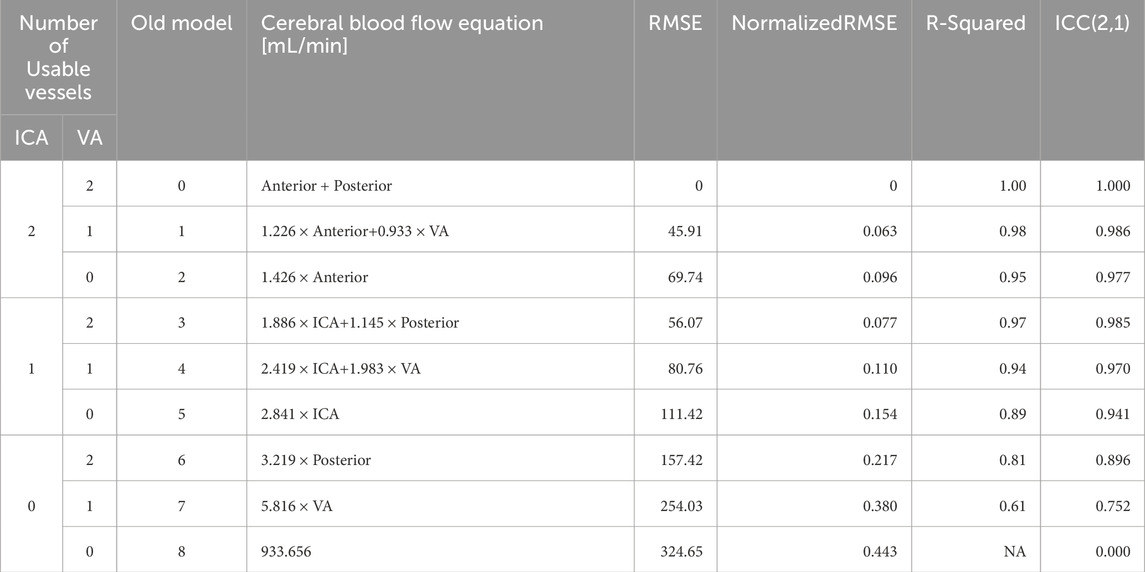
Table 6. Statistics for performance of age-independent models on adult and pediatric data. Models 1–7 use an age-independent model of CBF with the same configuration of missing vessels as Table 1; model 8 is defined as the population mean from the age-independent study. Performance of these models was equal to or worse than their corresponding age-dependent models. Abbreviations cerebral blood flow (CBF), internal carotid artery (ICA), vertebral artery (VA), root mean square error (RMSE), intra-class correlation coefficient (ICC).

We performed Bland-Altman analyses of models 1-8 compared to ground truth (model 0) (Figure 4). Models 1-5 were statistically unbiased (p > 0.05), while model 6 had a small yet significant bias (μ = −3.24%, p = 0.0045). Models 1-4 had narrow limits of agreement (σ = 6.06–11.62%) while models 5-6 and had wider limits of agreement (σ = 15.61–18.16%). Model 7, which was derived from a measurement in 1 VA, it performed exceptionally poorly (μ = −5.80%, σ = 24.64%, p = 0.0002), similar to model 8a (μ = −9.01%, σ = 32.80%, p < 0.0001) where CBF is estimated based on age alone.

Figure 4

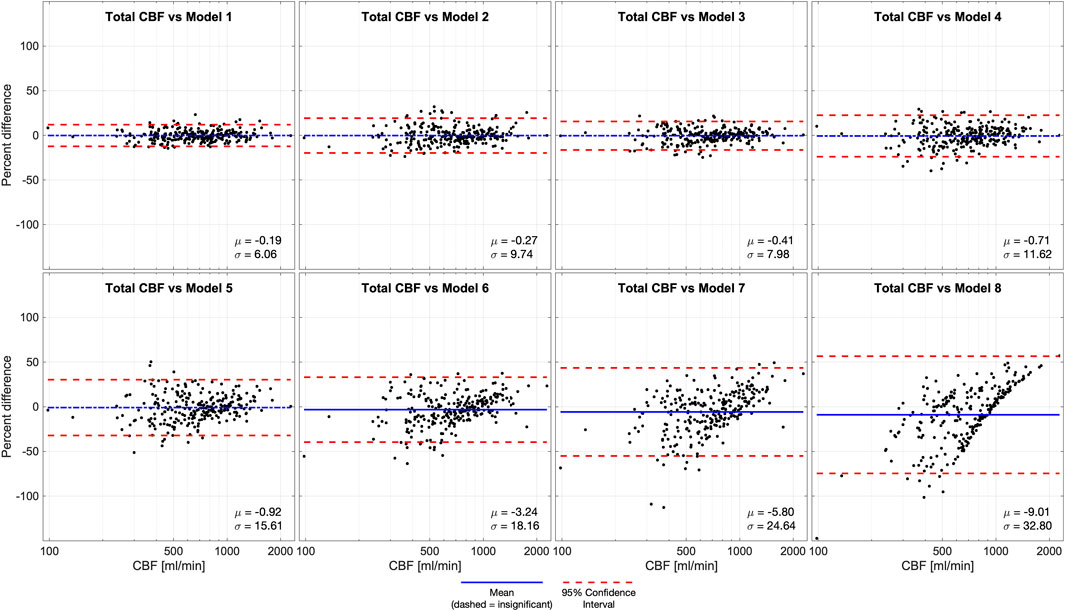
Figure 4. Bland-Altman analysis of total CBF quantified by phase contrast (PC) in 4 vessels (model 0) versus various models of 1 or more missing vessels. Blue line demonstrates bias, dashed blue line demonstrates insignificant (p > 0.05) bias, and red dash lines demonstrate 95% confidence intervals. These results suggest that it is important to successfully capture at least 1 ICA or 2 VAs to impute CBF measurements. Age-dependent model 4 was unbiased, improving performance compared the previously published age-independent model 4. Abbreviations cerebral blood flow (CBF).

4 Discussion

Cerebral blood flow varies considerably across the lifespan, especially across infancy and childhood. PC-based CBF measurements provide a robust and fast complement to both regional MR perfusion techniques, (arterial spin labelling and dynamic susceptibility contrast), bedside techniques (3D Doppler ultrasound), and radiologic approaches such as PET and SPECT (Clement et al., 2022; Shen et al., 2023, Catafau et al., 2001, Frackowiak et al., 1980). Two-dimensional PC methods require minimal scan time, complexity, or post-processing requirements, making them easier to deploy than more advanced 4D PC. We therefore sought to extend our previous imputation models by incorporating age-dependence and build models applicable across the human lifespan. The new age-based models meet or exceed the performance of the previously published age-independent models in all cases. We further evaluated other variables (hematocrit, sex, and brain volume) and present models that use these parameters to improve imputation. However, the presence of at least one well-resolved ICA remains crucial for performing high-accuracy imputation. In fact, when two ICAs and one VA were present, the age dependence in the imputation (model 1) was found to be statistically insignificant. Similarly, when both ICAs are present (model 2), the contribution of the age-dependent term was marginal. For the remaining models, the inclusion of age dependence was statistically significant and improved the quality of the models. Taken together, this suggests that imputation using age does not harm any of the models and may help improve accuracy, particularly when ICAs are not measured. The relatively modest effect of age in the modelling is attributable to the fact that anterior-to-posterior and right-to-left flow ratios do not change substantially with age, although total CBF does change with age, and these ratios have relatively high intra-subject variability unexplained by age.

Bland-Altman analysis of CBF versus imputed CBF demonstrated a similar trend. Models 1–5 were statistically unbiased and show similar 95% confidence intervals to the age-independent models. Despite the improved performance of all models, the Bland-Altman analysis still showed a significant bias for age-dependent models 6–8 with wide 95% confidence intervals. This confirms that failing to measure at least one ICA causes significant degradation of imputation performance. We included models 6 and 7 because they were valid correlates of CBF, and model 8a (CBF as a function of age) for completeness, but we recommend against using them for CBF imputation.

We anticipated and reported differences in vessel-to-CBF ratios for children and adults. However, these statistically significant differences were subtle, indicating only modest redistribution of flow patterns from childhood (when it is slightly more posterior) to adulthood (more anterior). This contrasted with our anticipation of a more profound change across development. The age-dependence of CBF follows a generally similar trend to total brain volume with age, peaking in late adolescence to early adulthood and slowly declining over the remainder of the human lifespan (Bethlehem et al., 2022; Borzage et al., 2014).

Although our models were intended for data imputation, they may also provide value in the case of the clinical setting. An unsuccessful acquisition would normally be repeated by a technician, however, occasionally an error is missed until after the patient is no longer being scanned, or repeating a scan is not possible because a patient is unstable. In these admittedly rare cases, our improved imputation provides more accurate results. A more likely application in a clinical setting is using our imputation after a successful acquisition. When all four vessels are acquired, our models can be used to evaluate potentially abnormal flow patterns due to intracranial arterial stenosis diminishing flow in one or more vessels (Kim et al., 2022; Craig et al., 1982). This evaluation comprises: calculating ground truth CBF (model 0), omitting one or more vessels and imputing CBF (model 1, 3), then comparing ground truth versus imputed CBF. Larger CBF discrepancies indicate flows that do not follow our established patterns. An alternative application in a clinical setting is detecting abnormal flow as a function of age, which may indicate impaired brain development.

5 Limitations

A key assumption of these models is that the cerebrovasculature is anatomically complete. The participants included in the modelling do not have steno-occlusive disease, and our imputation models are suitable for studying development and aging but will likely fail in subjects with dysfunctional vasculature, such as diminished flow through one or more vessels. Techniques such as arterial spin labelling will be more appropriate for quantifying blood flow and characterizing steno-occlusions in persons with vascular dysfunction. Brain volumes were not obtained in the analysis so rCBF [mL/min/100 g] cannot be reported; the process for brain volume normalization is presented in Supplementary Material for interested readers. The CBF imputation models presented assume that the anterior-to-posterior and right-to-left flow ratios are constant. Work is ongoing to determine whether these ratios, especially anterior-to-posterior flow, remain constant in the presence of anesthetics; application of these models will demonstrate increased error if the anterior-to-posterior ratio is modified by diseases or interventions. Furthermore, model 8a demonstrates that a smooth function with respect to age does not capture the high variation in CBF between two individuals. CBF is influenced by a wide variety of intrinsic and extrinsic factors, including key covariates such as sex and hematocrit (Borzage et al., 2016; Bush et al., 2016; Clement et al., 2018). The more complicated models presented (8b, 8c, 8d, Table 4) moderately improve performance by including hematocrit, sex, and total brain volume, but this limits their applicability to datasets which include these details. Our data were acquired with different protocols as a part of two separate projects with MR imaging for different indications. The pathologies and use of anesthesia in the younger group differed considerably from those in the older group. Therefore, we cannot exclude the possibility of important covariates or confounders that we cannot ascertain with this data. Average flow rates were assessed by our pipeline but peak flow rate data was not recorded. We also lack external data validation from other institutions. The full range of our data is 0.4–61.3 years, however most (95%) of our data spans 0.75–4.85 and 11.20–45.10 years, thus we recommend caution when attempting to extend this model into ages <0.75, 4.85–11.20, or >45.1 years, which represent an opportunity for future work. However, the effects of the limited data on the age-based CBF model are limited by the parsimonious nature of the equation. We also found only subtly different patterns of anterior and posterior flow in our two groups, which we omitted when modeling the ratio between CBF and vessel (Bethlehem et al., 2022). These limitations present opportunities for future research, particularly in studies that recruits volunteers with similar characteristics across the lifespan.

6 Conclusion

Phase contrast MR enables effective, robust estimation of CBF in both pediatric and adult populations. Our findings suggest that employing age-dependent imputation models, based on at least one ICA flow, offers a single, parsimonious approach to estimating CBF across the human lifespan when one or more vessels cannot be directly measured. This reduction in number of acquisitions and total scan time required for CBF estimation reduces the need for on-scanner quality control measures and mitigates attendant challenges.

PC MR imaging, combined with our methods for addressing missing data, provides valuable insights into CBF and the metabolic sustenance of the brain. This approach can complement other MR imaging techniques suited for assessing lung and heart efficiency in oxygenation and blood delivery, or for mapping the regional distribution of blood and oxygen consumption in the brain. Thus, PC MR fulfills a critical role in understanding brain physiology. Our imputation models demonstrate a significant advancement over previous approaches in describing vascular physiology. Our equations simplify CBF measurement across diverse ages groups and offers a solution to real-world acquisition challenges.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by Children’s Hospital Los Angeles Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin.

Author contributions

ED: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. IT: Investigation, Project administration, Writing – original draft, Writing – review and editing. JL: Software, Writing – original draft, Writing – review and editing. AK: Investigation, Writing – original draft, Writing – review and editing. SR: Writing – original draft, Writing – review and editing. BD: Investigation, Writing – original draft, Writing – review and editing. PS: Data curation, Formal Analysis, Investigation, Writing – original draft, Writing – review and editing. BP: Conceptualization, Writing – original draft, Writing – review and editing. JW: Conceptualization, Resources, Supervision, Writing – original draft, Writing – review and editing. MB: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Research reported in this publication was supported by The National Heart, Lung, and Blood Institute of the National Institutes of Health under award numbers 5K25HL153954, U01-HL-117718–01, and Minority Supplement to 1U01-HL-117718-01.

Acknowledgments

The authors would like to thank the NHLBI for funding this work and Children’s Hospital of Los Angeles for providing the research infrastructure to conduct this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2025.1527093/full#supplementary-material

References

Andersson C., Kihlberg J., Ebbers T., Lindström L., Carlhäll C. J., Engvall J. E. (2016). Phase-contrast MRI volume flow – a comparison of breath held and navigator based acquisitions. BMC Med. Imaging 16, 26. doi:10.1186/s12880-016-0128-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashwal S., Tomasi L., Schneider S., Perkin R., Thompson J. (1992). Bacterial meningitis in children. Neurology 42 (4), 739. doi:10.1212/WNL.42.4.739

PubMed Abstract | CrossRef Full Text | Google Scholar

Bethlehem R. a. I., Seidlitz J., White S. R., Vogel J. W., Anderson K. M., Adamson C., et al. (2022). Brain charts for the human lifespan. Nature 604 (7906), 525–533. doi:10.1038/s41586-022-04554-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Borzage M., Blüml S., Seri I. (2014). Equations to describe brain size across the continuum of human lifespan. Brain Struct. Funct. 219 (1), 141–150. doi:10.1007/s00429-012-0490-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Borzage M. T., Bush A. M., Choi S., Nederveen A. J., Václavů L., Coates T. D., et al. (2016). Predictors of cerebral blood flow in patients with and without anemia. J. Appl. Physiol. 120 (8), 976–981. doi:10.1152/japplphysiol.00994.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Bush A. M., Borzage M. T., Choi S., Václavů L., Tamrazi B., Nederveen A. J., et al. (2016). Determinants of resting cerebral blood flow in sickle cell disease. Am. J. Hematol. 91 (9), 912–917. doi:10.1002/ajh.24441

PubMed Abstract | CrossRef Full Text | Google Scholar

Catafau A. M. (2001). Brain SPECT in clinical practice. Part I: Perfusion. J. Nucl. Med. 42 (2), 259–271.

PubMed Abstract | Google Scholar

Clement P., Mutsaerts H. J., Václavů L., Ghariq E., Pizzini F. B., Smits M., et al. (2018). Variability of physiological brain perfusion in healthy subjects - a systematic review of modifiers. Considerations for multi-center ASL studies. J. Cereb. Blood Flow. Metab. 38 (9), 1418–1437. doi:10.1177/0271678X17702156

PubMed Abstract | CrossRef Full Text | Google Scholar

Clement P., Petr J., Dijsselhof M. B. J., Padrela B., Pasternak M., Dolui S., et al. (2022). A beginner’s guide to arterial spin labeling (ASL) image processing. Front. Radiol. 2, 929533. doi:10.3389/fradi.2022.929533Available online at: https://www.frontiersin.org/journals/radiology/articles/10.3389/fradi.2022.929533/full.

PubMed Abstract | CrossRef Full Text | Google Scholar

Correia de Verdier M., Berglund J., Wikström J. (2024). Effect of MRI acquisition parameters on accuracy and precision of phase-contrast measurements in a small-lumen vessel phantom. Eur. Radiol. Exp. 8, 45. doi:10.1186/s41747-024-00435-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Craig D. R., Meguro K., Watridge C., Robertson J. T., Barnett H. J., Fox A. J. (1982). Intracranial internal carotid artery stenosis. Stroke 13 (6), 825–828. doi:10.1161/01.str.13.6.825

PubMed Abstract | CrossRef Full Text | Google Scholar

De Silvestro A. A., Kellenberger C. J., Gosteli M., O’Gorman R., Knirsch W. (2023). Postnatal cerebral hemodynamics in infants with severe congenital heart disease: a scoping review. Pediatr. Res. 94 (3), 931–943. doi:10.1038/s41390-023-02543-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Frackowiak R. S. J., Lenzi G.-L., Jones T., Heather J. D. (1980). Quantitative measurement of regional cerebral blood flow and oxygen metabolism in man using 15O and positron emission tomography: theory, procedure, and normal values. J. Comput. Assist. Tomogr. 4 (6), 727.

PubMed Abstract | CrossRef Full Text | Google Scholar

Greil G., Geva T., Maier S. E., Powell A. J. (2002). Effect of acquisition parameters on the accuracy of velocity encoded cine magnetic resonance imaging blood flow measurements. Magn. Reson. Imaging 15 (1), 47–54. doi:10.1002/jmri.10029

PubMed Abstract | CrossRef Full Text | Google Scholar

Hall C., Lueshen E., Mošat’ A., Linninger A. A. (2012). Interspecies scaling in pharmacokinetics: a novel whole-body physiologically based modeling framework to discover drug biodistribution mechanisms in vivo. JPharmSci 101 (3), 1221–1241. doi:10.1002/jps.22811

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanaoka T., Kimura N., Aso Y., Takemaru M., Kimura Y., Ishibashi M., et al. (2016). Relationship between white matter lesions and regional cerebral blood flow changes during longitudinal follow up in Alzheimer’s disease. Geriatr. Gerontol. Int. 16 (7), 836–842. doi:10.1111/ggi.12563

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirabuki N., Watanabe Y., Mano T., Fujita N., Tanaka H., Ueguchi T., et al. (2000). Quantitation of flow in the superior sagittal sinus performed with cine phase-contrast MR imaging of healthy and achondroplastic children. AJNR Am. J. Neuroradiol. 21 (8), 1497–1501.

PubMed Abstract | Google Scholar

Jennings J. R., Heim A. F., Kuan D. C. H., Gianaros P. J., Muldoon M. F., Manuck S. B. (2013). Use of total cerebral blood flow as an imaging biomarker of known cardiovascular risks. Stroke 44 (9), 2480–2485. doi:10.1161/STROKEAHA.113.001716

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim J. H., Jung J. Y., Lee Y. B., Kang C. K. (2022). Investigation of flow changes in intracranial vascular disease models constructed with MRA images. Sensors 22 (6), 2302. doi:10.3390/s22062302

PubMed Abstract | CrossRef Full Text | Google Scholar

King K. S., Sheng M., Liu P., Maroules C. D., Rubin C. D., Peshock R. M., et al. (2018). Detrimental effect of systemic vascular risk factors on brain hemodynamic function assessed with MRI. Neuroradiol. J. 31 (3), 253–261. doi:10.1177/1971400917750375

PubMed Abstract | CrossRef Full Text | Google Scholar

Koerte I., Haberl C., Schmidt M., Pomschar A., Lee S., Rapp P., et al. (2013). Inter- and intra-rater reliability of blood and cerebrospinal fluid flow quantification by phase-contrast MRI. J. Magn. Reson Imaging 38 (3), 655–662. doi:10.1002/jmri.24013

PubMed Abstract | CrossRef Full Text | Google Scholar

Lagerstrand K. M., Svensson F., Polte C. L., Bech-Hanssen O., Starck G., Chodorowski A., et al. (2020). Reliable phase-contrast flow volume magnetic resonance measurements are feasible without adjustment of the velocity encoding parameter. J. Med. Imaging (Bellingham) 7 (6), 063502. doi:10.1117/1.JMI.7.6.063502

PubMed Abstract | CrossRef Full Text | Google Scholar

Leijenaar J. F., van Maurik I. S., Kuijer J. P. A., van der Flier W. M., Scheltens P., Barkhof F., et al. (2017). Lower cerebral blood flow in subjects with Alzheimer’s dementia, mild cognitive impairment, and subjective cognitive decline using two-dimensional phase-contrast magnetic resonance imaging. Alzheimers Dement. (Amst) 9, 76–83. doi:10.1016/j.dadm.2017.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim J. M., Kingdom T., Saini B., Chau V., Post M., Blaser S., et al. (2016). Cerebral oxygen delivery is reduced in newborns with congenital heart disease. J. Thorac. Cardiovasc Surg. 152 (4), 1095–1103. doi:10.1016/j.jtcvs.2016.05.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu P., Lu H., Filbey F. M., Pinkham A. E., McAdams C. J., Adinoff B., et al. (2014). Automatic and reproducible positioning of phase-contrast MRI for the quantification of global cerebral blood flow. PLOS ONE 9 (5), e95721. doi:10.1371/journal.pone.0095721

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu P., Qi Y., Lin Z., Guo Q., Wang X., Lu H. (2019). Assessment of cerebral blood flow in neonates and infants: a phase-contrast MRI study. Neuroimage. 185, 926–933. doi:10.1016/j.neuroimage.2018.03.020

PubMed Abstract | CrossRef Full Text | Google Scholar

MacDonald M. E., Frayne R. (2015). Phase contrast MR imaging measurements of blood flow in healthy human cerebral vessel segments. Physiol. Meas. 36 (7), 1517–1527. doi:10.1088/0967-3334/36/7/1517

PubMed Abstract | CrossRef Full Text | Google Scholar

Mink J. W., Blumenschine R. J., Adams D. B. (1981). Ratio of central nervous system to body metabolism in vertebrates: its constancy and functional basis. Am. J. Physiology-Regulatory, Integr. Comp. Physiology 241 (3), R203–R212. doi:10.1152/ajpregu.1981.241.3.R203

PubMed Abstract | CrossRef Full Text | Google Scholar

Nordmeyer S., Riesenkampff E., Crelier G., Khasheei A., Schnackenburg B., Berger F., et al. (2010). Flow-sensitive four-dimensional cine magnetic resonance imaging for offline blood flow quantification in multiple vessels: A validation study. J. Magn. Reson. Imaging 32 (3), 677–683. doi:10.1002/jmri.22280

PubMed Abstract | CrossRef Full Text | Google Scholar

Oshima T., Karasawa F., Satoh T. (2002). Effects of propofol on cerebral blood flow and the metabolic rate of oxygen in humans. Acta Anaesthesiol. Scand. 46 (7), 831–835. doi:10.1034/j.1399-6576.2002.460713.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Paniukov D., Lebel R. M., Giesbrecht G., Lebel C. (2020). Cerebral blood flow increases across early childhood. Neuroimage 204, 116224. doi:10.1016/j.neuroimage.2019.116224

PubMed Abstract | CrossRef Full Text | Google Scholar

Prohovnik I., Hurlet-Jensen A., Adams R., De Vivo D., Pavlakis S. G. (2009). Hemodynamic etiology of elevated flow velocity and stroke in sickle-cell disease. J. Cereb. Blood Flow. Metab. 29 (4), 803–810. doi:10.1038/jcbfm.2009.6

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi Y., Lin Z., Lu H., Mao J., Zhang H., Zhao P., et al. (2023). Cerebral hemodynamic and metabolic abnormalities in neonatal hypocalcemia: findings from advanced MRI. Am. J. Neuroradiol. 44, 1224–1230. doi:10.3174/ajnr.A7994Available online at: https://www.ajnr.org/content/early/2023/09/14/ajnr.A7994.

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabayan B., van der Grond J., Westendorp R. G., Jukema J. W., Ford I., Buckley B. M., et al. (2013). Total cerebral blood flow and mortality in old age: a 12-year follow-up study. Neurology 81 (22), 1922–1929. doi:10.1212/01.wnl.0000436618.48402.da

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakhare A. R., Barisano G., Pa J. (2019). Assessing test-retest reliability of phase contrast MRI for measuring cerebrospinal fluid and cerebral blood flow dynamics. Magn. Reson Med. 82 (2), 658–670. doi:10.1002/mrm.27752

PubMed Abstract | CrossRef Full Text | Google Scholar

Schöning M., Hartig B. (1996). Age dependence of total cerebral blood flow volume from childhood to adulthood. J. Cereb. Blood Flow. Metab. 16 (5), 827–833. doi:10.1097/00004647-199609000-00007

PubMed Abstract | CrossRef Full Text | Google Scholar

Shah P., Doyle E., Wood J. C., Borzage M. T. (2023). Imputation models and error analysis for phase contrast MR cerebral blood flow measurements. Front. Physiol. 14, 1096297. doi:10.3389/fphys.2023.1096297

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen G., Sanchez K., Hu S., Zhao Z., Zhang L., Ma Q. (2023). 3D Doppler ultrasound imaging of cerebral blood flow for assessment of neonatal hypoxic-ischemic brain injury in mice. PLOS ONE 18 (5), e0285434. doi:10.1371/journal.pone.0285434

PubMed Abstract | CrossRef Full Text | Google Scholar

Summers P. E., Holdsworth D. W., Nikolov H. N., Rutt B. K., Drangova M. (2005). Multisite trial of MR flow measurement: phantom and protocol design. Magn. Reson. Imaging 21 (5), 620–631. doi:10.1002/jmri.20311

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun W., Ruan Z., Dai X., Li S., Li S., Zhang J., et al. (2018). Quantifying hemodynamic changes in Moyamoya disease based on two-dimensional cine phase-contrast magnetic resonance imaging and computational fluid dynamics. World Neurosurg. 120, e1301–e1309. doi:10.1016/j.wneu.2018.09.057

PubMed Abstract | CrossRef Full Text | Google Scholar

Thunberg P., Karlsson M., Wigström L. (2003). Accuracy and reproducibility in phase contrast imaging using SENSE. Magnetic Reson. Med. 50 (5), 1061–1068. doi:10.1002/mrm.10634

PubMed Abstract | CrossRef Full Text | Google Scholar

Varela M., Groves A. M., Arichi T., Hajnal J. V. (2012). Mean cerebral blood flow measurements using phase contrast MRI in the first year of life. NMR Biomed. 25 (9), 1063–1072. doi:10.1002/nbm.2771

PubMed Abstract | CrossRef Full Text | Google Scholar

Vernooij M. W., van der Lugt A., Ikram M. A., Wielopolski P. A., Vrooman H. A., Hofman A., et al. (2008). Total cerebral blood flow and total brain perfusion in the general population: the Rotterdam Scan Study. J. Cereb. Blood Flow. Metab. 28 (2), 412–419. doi:10.1038/sj.jcbfm.9600526

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu C., Honarmand A. R., Schnell S., Kuhn R., Schoeneman S. E., Ansari S. A., et al. (2016). Age-related changes of normal cerebral and cardiac blood flow in children and adults aged 7 Months to 61 years. J. Am. Heart Assoc. 5 (1), e002657. doi:10.1161/JAHA.115.002657

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu C., Lu W., Qiu J., Wang F., Li J., Wang L. (2020). Alterations of the whole cerebral blood flow in patients with different total cerebral small vessel disease burden. Front. Aging Neurosci. 12, 175. doi:10.3389/fnagi.2020.00175

PubMed Abstract | CrossRef Full Text | Google Scholar