Seismic performance enhancement of three-dimensional frame structures via inerter-based control systems

Improving the seismic response of new and existing structures is a fundamental topic in civil engineering. Often, in structural mechanics this issue is addressed through low-dimensional mechanical models capable of capturing the primary dynamics of the structure. In contrast to most studies in the scientific literature that use two-dimensional models to describe structural behavior, this paper employs a low-dimensional, three-dimensional (3D) mechanical model to capture the seismic response of a structure, also accounting for its torsional effects. This low-dimensional model is used to investigate two different methods for improving seismic response. One approach involves inerter devices directly connected to the structure, while the other is based on connecting the structure to external auxiliary structures, equipped in turn with inerters. Therefore, in this case, the inerter devices are connected directly to the external structures. The responses of the original stand-alone frame structure and those with the two proposed methods are compared to assess the effectiveness of each approach. Three different earthquake records are used as base excitation. The results are presented in performance curves and maps, showing the response in terms of displacements of key points of the structure as various system parameters are varied. The results reveal the good performance of both methods over a wide range of parameters, with particularly favorable results for the approach using external structures equipped with inerter devices.

1 Introduction

Improving the seismic response of new and existing structures is a fundamental topic in civil engineering. Often, structural mechanics, this issue addressed through low-dimensional mechanical models capable of capturing the primary dynamics of the structure.

The seismic behavior of actual structures is often studied by using low-dimensional models. A general three-dimensional (3D), multi-degree-of-freedom (M-DOF) frame structure is modeled through a planar, two-degree-of-freedom (2-DOF) shear-type system. For instance, such low-dimensional model were employed to explore the conceptual aspects of the base isolation technique as proposed by (Kelly, 1995), as well as tuned mass damper (TMD) systems discussed in (Den Hartog, 1956; Rana and Soong, 1998; Miranda, 2005). Furtherly, (Tsai, 1995), and (Taniguchi et al., 2008) examined the reduction of base displacement in a base-isolated system using a TMD.

In recent years, the same approach utilizing low-dimensional models was employed to explore the application of TMDs as common techniques for protecting frame structures against earthquake. In (Dadkhah et al., 2020; Khatibinia et al., 2018; Kamgar et al., 2018; Kamgar et al., 2025), TMD systems were implemented to safeguard high-rise buildings, while in (Salimi et al., 2021; Kamgar et al., 2020) a friction TMD and a modified tuned liquid damper were used to enhance the seismic response of buildings. Additionally, in (Reggio and De Angelis, 2015; Fabrizio et al., 2017a; Fabrizio et al., 2019; Pagliaro and Di Egidio, 2022a; Wang et al., 2013; Pagliaro and Di Egidio, 2022a; Di Egidio et al., 2023), the use of an intermediate discontinuity as a non-conventional TMD was studied.

Typically, TMDs require a small mass to function effectively. However, when subjected to seismic excitation, the use of a small mass may hinder the TMD’s performance. This issue can be mitigated by coupling the TMD with an inerter device, which acts as a virtual mass to amplify inertial forces, as illustrated in (Marian and Giaralis, 2014). This combination led to the development of the Tuned Mass Damper Inerter (TMDI), a device that was extensively studied in various papers (Brzeski et al., 2015; Pietrosanti et al., 2017; De Domenico and Ricciardi, 2018; De Domenico et al., 2018; Giaralis and Taflanidis, 2018; Pietrosanti et al., 2020; Prakash and Jangid, 2022).

Different external devices that are suitable combinations of TMDs and inerters or that have hysteretic behavior were proposed to improve the seismic performances of structures. Also using low-dimensional mechanical models, recently in (Di Egidio and Contento, 2023; Di Egidio and Contento, 2022) a hysteretic device connecting the Tuned Mass Damper Inerter to the structure was used, referred to as the Hysteretic Mass Damper (HMDI), or in (Di Egidio et al., 2022a) where the connection of the frame structure with a short, hysteretic exoskeleton was considered.

Among the different possibilities to improve the seismic response of structures, one option is the regularization of torsional modes, particularly as architectural innovation increasingly prioritizes aesthetic asymmetry. Uncontrolled torsion during seismic or wind events amplifies localized damage, accelerates structural fatigue, and threatens life safety, as tragically illustrated by torsional failures in the 1985 Mexico City earthquake (Osteraas and Krawinkler, 1989). Contemporary building codes, such as ASCE 7–22 (2022) (American Society of Civil Engineers, 2022), now enforce stricter limits on torsional irregularities, reflecting lessons from past disasters.

Research on the regularization of torsional modes, aimed at mitigating vulnerabilities in asymmetric structures under seismic excitations, has evolved through analytical, experimental, and computational approaches. Early work by (Rutenberg, 1992) provided a critical review of nonlinear responses in asymmetric buildings, emphasizing the inadequacy of linear code provisions to address torsional coupling under extreme seismic demands. This work underscored the necessity of incorporating nonlinear behavior into design codes. Building on this, (Anagnostopoulos et al., 2015), expanded the discourse by systematically reviewing earthquake-induced torsion, highlighting challenges such as bidirectional excitation effects and the underestimation of torsional amplification in static code-based methods. Their synthesis advocated for dynamic analysis and performance-based design for torsionally irregular structures. Further analytical advancements were pioneered by De la Llera and Chopra (De la Llera and Chopra, 1995), who modeled the inelastic seismic behavior of asymmetric-plan buildings, demonstrating that torsional coupling amplifies ductility demands and interstory drift. Their findings necessitated code-compliant stiffness redistribution strategies. Subsequent studies, such as (Lim et al., 2018), empirically validated these analytical insights by analyzing a 3D asymmetric multi-story reinforced concrete structure. Their results showed that torsional irregularities exacerbate floor displacements and shear forces under bidirectional ground motions. Similarly, (Manish and Syed, 2017), compared symmetric and asymmetric buildings, revealing that even minor plan irregularities induce significant torsional responses, necessitating stricter code compliance.

The role of strong-motion duration in torsional response scaling was later investigated in (Málaga-Chuquitaype, 2021), revealing that prolonged seismic durations intensify torsional demands in systems with nonlinear behavior, particularly those experiencing strength and stiffness degradation. This work highlighted the need for duration-sensitive design criteria in modern codes. Analytical methods have also evolved to support regularization: (Zalka, 2001): introduced a simplified approach for calculating natural frequencies in wall-frame systems, enabling efficient preliminary assessments of torsional stiffness distribution. For nonlinear modeling, (Pelletier and Leger, 2017), developed a framework for reinforced concrete cores, capturing torsional-axial coupling effects and advocating for detailed 3D analysis to prevent premature damage.

Mitigation strategies have been explored across computational and experimental studies. In (Takewaki et al., 2012), the authors proposed a “worst-case scenario” framework for optimizing passive dampers, such as tuned mass dampers (TMDs), to decouple torsional and translational modes during earthquakes, thereby improving energy dissipation. Practical retrofitting techniques, such as stiffening and mass redistribution, were demonstrated by (Harbic et al., 2011) to reduce torsion in existing structures (Botis et al., 2018). extended these efforts by proposing layout optimization of shear walls in rectangular RC buildings to balance torsional resistance without compromising functionality. For new designs (Maske and Pajgade, 2013), emphasized symmetric stiffness distribution, showing that strengthening perimeter elements suppresses torsional vibrations.

Most of the mentioned contributions in the literature address the control of torsional modes by adding or strengthening elements within the structure to be protected. In contrast, this study adopts a different perspective; in particular, this paper extends the study presented in (Di Egidio et al., 2022b), which investigated the seismic response of a frame structure coupled with an external structure equipped with an inerter device. In that study, a general M-DOF frame structure was modeled as a 2-DOF shear-type system. Although the coupling with the external structures proved to be effective in reducing in-plane seismic effects, limited insight was obtained regarding torsional motion, which occurs in spatial frame structures during earthquake excitation. To overcome this limitation a low-dimensional spatial model is developed to investigate the seismic response of a general frame structure. This model is a two-level, spatial shear-type structure, in which it is assumed that the floor slabs are infinitely rigid within their own plane. Consequently, the model has six degrees of freedom, three for each level. While the two papers adopt conceptually similar approaches, employing inerter-based systems to enhance the seismic performance of frame structures, the present paper specifically focuses on mitigating torsional effects induced by asymmetric mass or stiffness distribution. This is achieved by strategically placing inertial devices to counteract rotational responses, whereas the previous study emphasizes the reduction of translational displacements and inter-storey drifts through coupling with an external, deformable structure.

The present study assumes linear behavior for both the structural system and the damping devices. While this simplification enables clearer interpretation of the fundamental dynamic mechanisms, particularly under moderate to strong excitations, it does not capture potential nonlinear effects such as yielding or stiffness degradation. The adoption of a linear model, widely accepted for preliminary design and parametric assessment, avoids the need to define a specific nonlinear formulation, which would require selecting a structural typology and significantly increasing the input data and model complexity, thus limiting generalizability.

Two distinct methods are proposed to enhance the seismic response of a three-dimensional (3D) frame structure. The first approach (System 1) integrates inerter devices directly into the structural system, whereas the second (System 2) couples the frame with external auxiliary structures incorporating inerters. The developed model facilitates a comprehensive assessment of torsional effects and evaluates the comparative efficacy of both systems in mitigating such responses. Using a Lagrangian formulation, the equations of motion are derived for three configurations: (i) the stand-alone frame structure, (ii) System 1, and (iii) System 2.

Three different earthquake records are used as base excitation to assess the effectiveness of each approach. An extensive parametric analysis is conducted by varying the fundamental parameters of the mechanical systems. Two performance indexes are introduced to evaluate the effectiveness of the proposed methods in comparison to the stand-alone frame structure. These indexes are defined as the ratios of the displacements or drifts of System one or System two and those of the stand-alone frame structure. A value of these indexes less than unity indicates that Systems one and two are effective in reducing the seismic effects on the frame structure. The results of the parametric analysis are presented in performance curves and maps that plot the performance indexes as functions of one or two parameters, respectively. Special attention is devoted to the effects of aligning the mass and stiffness centers at the first level in both System 1 and System 2.

2 Mechanical system

Two different methods are investigated to improve the seismic performance of a 3D frame structure. In the following analysis, a general spatial multi-degree-of-freedom (M-DOF) frame structure is consistently modeled as a two-level, three-dimensional shear-type system (see Figure 1).

Figure 1

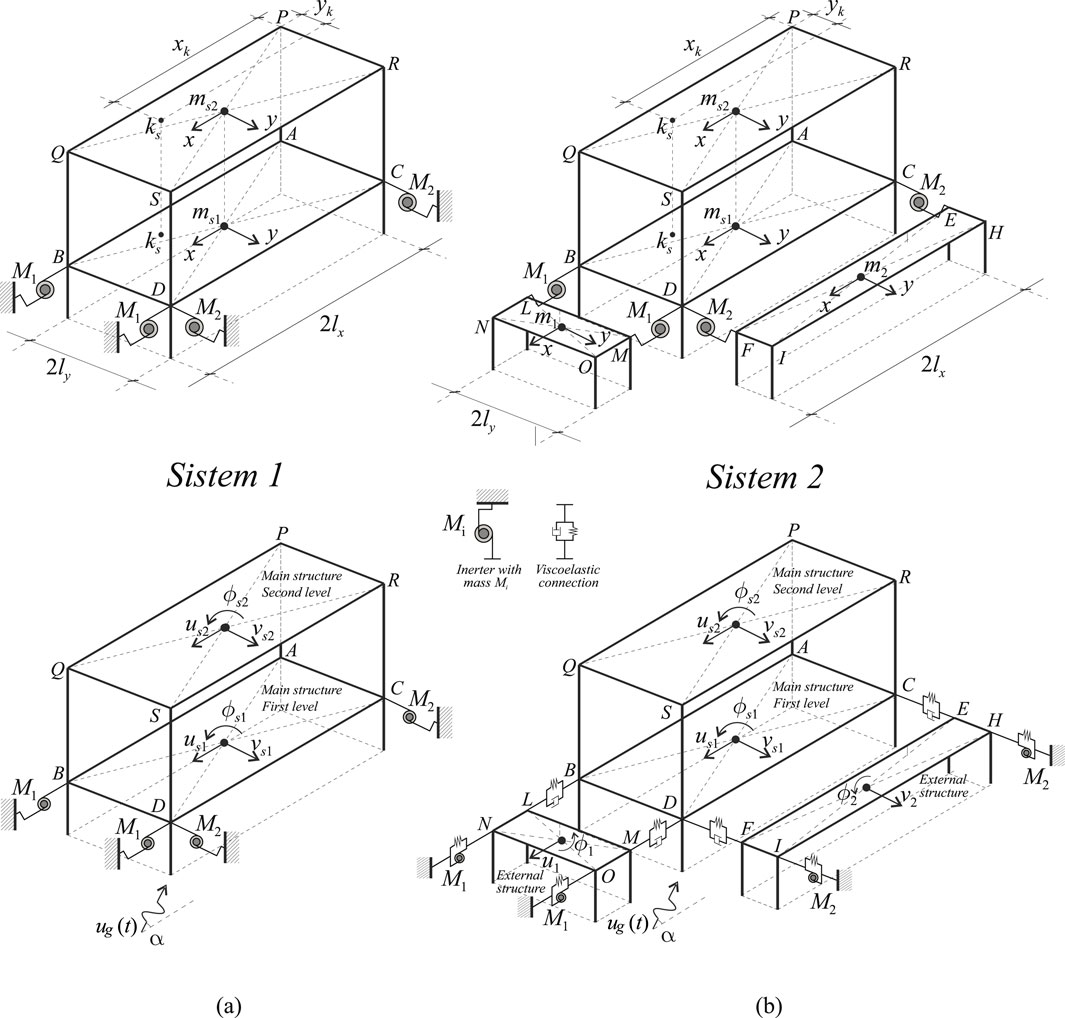
Figure 1. Mechanical systems: (a) System with only inerters (System 1); (b) System with external structures equipped with inerters (System 2).

Each level has the same dimensions $2l_x\times 2l_y$, is rectangular in shape, and is assumed to be rigid within its own plane. The assumption of infinitely rigid floor diaphragms is adopted to simplify the analysis and focus on the primary structural response mechanisms. Although in some structures, diaphragm flexibility and potential discontinuities can influence force distribution and dynamic characteristics, in the cases considered in this investigation, the floor slabs are relatively stiff compared to the lateral load-resisting elements, and the diaphragm spans are moderate (see Section 3.3), which reduces the significance of diaphragm deformation.

Additionally, the mass distribution is considered uniform, with the center of mass at each level located at the intersection of its diagonals. The masses of the levels are denoted as $m_{si}$, with $i=\mathrm{1,2}$. Hence, the kinematics of a level can be described by three displacement components. Since the adopted low-dimensional mechanical system consists of two levels, six Lagrangian parameters, $u_{si},v_{si},{\varphi }_{si}$, with $i=\{\mathrm{1,2}\}$, are required to fully describe the system’s kinematics. These Lagrangian parameters correspond directly to the displacement of the center of mass at each of the two levels of the structure.

The mechanical characteristics of the 6-DOF, 3D shear-type system are selected to be dynamically equivalent to a real M-DOF frame structure, utilizing the dynamic equivalence criterion developed in (Fabrizio et al., 2017a; Fabrizio et al., 2019; Fabrizio et al., 2017b). Specifically, since this criterion was originally formulated for 2D frame structures, it is applied here to define the total stiffness of the two levels of the 6-DOF shear-type system separately along the $x$- and $y$-directions. This choice yields a 3D model with equal stiffness along the two orthogonal directions. It is evident that, when the stiffness of a level is equally distributed among the four columns, the stiffness center of each level coincides with its corresponding mass center, provided the regularity in geometry and mass distribution mentioned before. Conversely, a non-uniform distribution of stiffness among the four columns (as in the case presented herein) would results in an irregular structure, where the stiffness and mass centers would not coincide. To simplify the derivation of the equations of motion, in each direction, the stiffness resulting from all the columns of each level has been modelled by springs located at two nodes of each level (see Figure 2). For example, all the stiffness of the columns of the first level along the $x$-direction is assumed to modeled by $k_{xA}$ and $k_{xC}$.

Figure 2

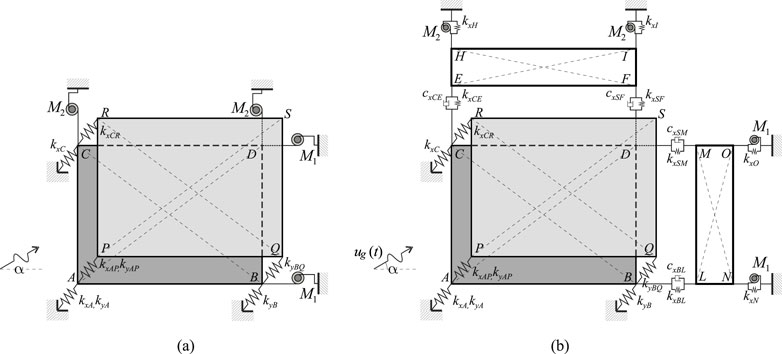
Figure 2. Mechanical systems, location of stiffness and damping elements: (a) System with only inerters (System 1); (b) System with external structures equipped with inerters (system 2).

The two investigated methods to improve the seismic performances of the frame structure both involve the use of inerter devices (see Section 2.4 for a brief description of these devices). In the case of System 1, the inerter devices are directly connected to the first level of the frame structure whose seismic performance is to be improved (see Figure 1a). Specifically, the two inerters $M_1$ operate along the $x$-direction, while the other two inerters $M_2$ operate along the $y$-direction. System 1 retains the same number of degrees of freedom as the stand-alone structure (without inerters), making it a 6-DOF mechanical system, as there is no need to associate additional degrees of freedom with the inerter devices. The Lagrangian parameters are the displacements $u_{si},v_{si},{\varphi }_{si}$ $(i=\{\mathrm{1,2}\})$ of the two levels.

In the case of System 2, the structure to be protected is connected at the first level to two external, auxiliary, rectangular-shaped structures with masses $m_1$ and $m_2$, through visco-elastic linear devices. These two external structures serve as TMDs for the studied structure. The mass distribution of the external structures is assumed to be uniform, with the center of mass located at the geometric center of the rectangle. The inerter devices are, in this case, connected to the auxiliary systems (see Figure 1b). As in the previous case, the two inerters $M_1$ operate along the $x$-direction, while the other two inerters $M_2$ operate along the $y$-direction. It is assumed that each external structure has two degrees of freedom (DOF): one associated with displacement along the smaller dimension and the other with torsion. The displacement along the greater dimension of the auxiliary structures is not considered as a Lagrangian parameter, as the stiffness in this direction is assumed to be very high, effectively preventing any significant interaction with the main dynamics of the coupled system. Consequently, the System 2 requires 10-DOF to fully describe its kinematics, 6-DOF for the two-level spatial shear-type system, and an additional 4-DOF $(u_1,{\varphi }_1,v_2,{\varphi }_2)$ for the two external auxiliary structures.

In both System 1 and System 2 the polar inertia of the sections of the columns are considered negligible. The equations of motion of both the System 1 and System 2 are obtained through a Lagrangian approach.

2.1 Damping of the 3D frame structure

The general equations of motion of the stand-alone, two-level, 3D shear-type system can be formally written as in Equation 1:

$\mathbf{M}\ddot{\mathbf{x}}+\mathbf{C}\dot{\mathbf{x}}+\mathbf{K}\mathbf{x}=-\mathbf{M}\mathbf{r}{\ddot{u}}_g\left(t\right),(1)$

where $\mathbf{M},\mathbf{C}$, and $\mathbf{K}$ are the mass, damping, and stiffness matrices of dimension $6\times 6$, respectively, the vector $\mathbf{x}={\left\{u_{s1},v_{s1},{\varphi }_{s1,}{u}_{s2},v_{s2},{\varphi }_{s2}\right\}}^T$ accounts the six Lagrangian parameters, and $u_g$ is the seismic input. As observed, the seismic excitation is applied along a direction inclined of angle $\zeta$ respective to the horizontal line (see Figure 1). In the paper, $\zeta$ is always set to $\zeta =45^{\text{o}}$. Since the mass matrix $\mathbf{M}$ is diagonal, the projection vector $\mathbf{r}={\left\{\cos (\zeta ),\sin (\zeta ),0,\cos (\zeta ),\sin (\zeta ),0\right\}}^T$. Although assuming a fixed angle may appear restrictive, preliminary analyses indicated that variations in this parameter have only a minor influence on the resulting maps, which remain qualitatively consistent. Therefore, only the results obtained with $\zeta =45^{\text{o}}$ are presented herein.

The damping matrix $\mathbf{C}$ is obtained from the stand-alone, two-level, 3D shear-type system, by a Rayleigh approach. Specifically, $\mathbf{C}$ is a linear combination of mass and stiffness matrices as:

$\mathbf{C}=\alpha \mathbf{M}+\beta \mathbf{K},(2)$

where coefficients $\alpha$ and $\beta$ are:

$\alpha =\xi \frac{2{\omega }_1{\omega }_2}{{\omega }_1+{\omega }_2},\beta =\xi \frac{2}{{\omega }_1+{\omega }_2}.(3)$

In Equation 3, ${\omega }_1$ and ${\omega }_2$ are the circular frequencies of the first two oscillation modes of the structure, whereas $\xi$ is the modal damping of such first two modes. In the analyses performed, it is always set $\xi =0.05$. The damping matrix $\mathbf{M}$ obtained from Equation 2 is used also to describe the damping properties of the 3D frame structure in System 1 and System 2.

2.2 System 1: 3D frame structure equipped with inerters

The equations of motion are obtained by a Lagrangian approach. To write the kinetic $T$ and potential $V$ energies, the displacements of the points labeled from $A$ to $D$ (vertexes of the first level) and from $P$ to $S$ (vertexes of the second level) needed to be written. In fact, the elastic springs and the virtual masses of the inerters are all applied in these points (see Figure 1a). With respect to coordinate systems that have origin in the mass centers of the two levels (intersection of the diagonals), such displacements read (Equation 4):

$\begin{array}{c}{x}_A=x_g+u_{s1}+{\varphi }_{s1}{l}_y,y_A=y_g+v_{s1}-{\varphi }_{s1}{l}_x,\hfill \\ x_B=x_g+u_{s1}+{\varphi }_{s1}{l}_y,y_B=y_g+v_{s1}+{\varphi }_{s1}{l}_x,\hfill \\ x_C=x_g+u_{s1}-{\varphi }_{s1}{l}_y,y_C=y_g+v_{s1}-{\varphi }_{s1}{l}_x,\hfill \\ x_D=x_g+u_{s1}-{\varphi }_{s1}{l}_y,y_D=y_g+v_{s1}+{\varphi }_{s1}{l}_x,\hfill \\ \cdots \hfill \\ x_P=x_g+u_{s2}+{\varphi }_{s2}{l}_y,y_P=y_g+v_{s2}-{\varphi }_{s2}{l}_x,\hfill \\ x_Q=x_g+u_{s2}+{\varphi }_{s2}{l}_y,y_Q=y_g+v_{s2}+{\varphi }_{s2}{l}_x,\hfill \\ x_R=x_g+u_{s2}-{\varphi }_{s2}{l}_y,y_R=y_g+v_{s2}-{\varphi }_{s2}{l}_x,\hfill \\ x_S=x_g+u_{s2}-{\varphi }_{s2}{l}_y,y_S=y_g+v_{s2}+{\varphi }_{s2}{l}_x,\hfill \end{array}(4)$

where $x_g=u_g\text{cos}(\alpha )$ and $y_g=u_g\sin (\alpha )$ are the components of the seismic input along the horizontal and vertical directions, respectively. The kinetic energy then reads (Equation 5):

$\begin{array}{ll}\hfill T& =\frac{1}{2}\left\{m_{s1}\left[{\left({\dot{x}}_g+{\dot{u}}_{s1}\right)}^2+{\left({\dot{y}}_g+{\dot{v}}_{s1}\right)}^2\right]+I_{s1}{{\dot{\varphi }}_{s1}}^2\right.\hfill \\ \hfill & +m_{s2}\left[{\left({\dot{x}}_g+{\dot{u}}_{s2}\right)}^2+{\left({\dot{y}}_g+{\dot{v}}_{s2}\right)}^2\right]+I_{s2}{{\dot{\varphi }}_{s2}}^2\hfill \\ \hfill & +\left.M_1\left[{\left({\dot{x}}_B-{\dot{x}}_g\right)}^2+{\left({\dot{x}}_D-{\dot{x}}_g\right)}^2\right]+M_2\left[{\left({\dot{y}}_C-{\dot{y}}_g\right)}^2+{\left({\dot{y}}_D-{\dot{y}}_g\right)}^2\right]\right\},\hfill \end{array}(5)$

where $I_{s1}$ and $I_{s2}$ are the polar moment of inertia of the two levels of the 3D frame structure. The potential energy reads (Equation 6):

$\begin{array}{c}V=\frac{1}{2}\left\{k_{xA}{\left(x_A-x_g\right)}^2+k_{xC}{\left(x_C-x_g\right)}^2+k_{yA}{\left(y_A-y_g\right)}^2+k_{yB}{\left(y_B-y_g\right)}^2\right.\hfill \\ \left.+k_{\mathit{xAP}}{\left(x_P-x_A\right)}^2+k_{\mathit{xCR}}{\left(x_R-x_C\right)}^2+k_{\mathit{yAP}}{\left(y_P-y_A\right)}^2+k_{\mathit{yBQ}}{\left(y_Q-y_B\right)}^2\right\},\hfill \end{array}(6)$

where $k_{xA}$ and $k_{xC}$ represent the sum of the stiffness of all the columns below the first level along horizontal lines passing through points $A$ and $C$, respectively. Similarly, $k_{yA}$ and $k_{yB}$ represent the sum of the stiffness of all the columns below the first level along vertical lines passing through points $A$ and $B$, respectively. The same meaning is associated to the other stiffnesses appearing in the potential energy. Specifically, $k_{\mathit{xAP}}$ and $k_{\mathit{xCR}}$ represent the sum of the stiffness of all the columns below the second level along horizontal lines passing through points $P$ and $R$, respectively. Similarly, $k_{\mathit{yAP}}$ and $k_{\mathit{yBQ}}$ represent the sum of the stiffness of all the columns below the second level along vertical lines passing through points $P$ and $Q$, respectively.

To account for the non-conservative forces due to the damping of the structure, their virtual work $\delta W$ needs to be computed (Equation 7). It reads:

$\delta W={\left(\mathbf{C}\dot{\mathbf{x}}\right)}^T\delta \mathbf{x},(7)$

where $\mathbf{C}$ is the damping matrix and $\mathbf{x}$ is the vector containing the six Lagrangian parameters, already described in Section 2.1. Finally, $\delta \mathbf{x}$ represents the virtual variation of the Lagrangian parameters.

By introducing the Lagrangian function $L=T-V$, the six equations of motion are then obtained through Equation 8:

$\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{\mathbf{x}}}\right)-\frac{\partial L}{\partial \mathbf{x}}=\mathbf{C}\dot{\mathbf{x}}.(8)$

The equations of motion are omitted for brevity, but all the equations presented in this section permit their derivation.

2.3 System 2: 3D frame structure coupled to an external apparatus with inerters

To derive the equations of motion of the System 2 (see Figure 1b), the displacements of all the vertexes of the 3D frame structure need to be evaluated. Their displacements are exactly equal to those written for System 1 and reported in Equation 4. Moreover, also the displacements of all the vertexes of the external auxiliary structures have to be written. With respect to coordinate systems that have origin in the mass centers of the two external structures (intersection of the diagonals, see Figure 1b), such displacements read as in Equation 9:

$\begin{array}{c}{x}_L=x_g+u_1+{\varphi }_1{l}_y,\hfill \\ x_M=x_g+u_1-{\varphi }_1{l}_y,\hfill \\ x_N=x_g+u_1+{\varphi }_1{l}_y,\hfill \\ x_O=x_g+u_1-{\varphi }_1{l}_y,\hfill \\ \cdots \hfill \\ y_E=y_g+v_2-{\varphi }_2{l}_x,\hfill \\ y_F=y_g+v_2+{\varphi }_2{l}_x,\hfill \\ y_H=y_g+v_2-{\varphi }_2{l}_x,\hfill \\ y_I=y_g+v_2+{\varphi }_2{l}_x,\hfill \end{array}(9)$

Then kinetic energy $T$ reads (Equation 10):

$\begin{array}{ll}\hfill T& =\frac{1}{2}\left\{m_{s1}\left[{\left({\dot{x}}_g+{\dot{u}}_{s1}\right)}^2+{\left({\dot{y}}_g+{\dot{v}}_{s1}\right)}^2\right]+I_{s1}{{\dot{\varphi }}_{s1}}^2\right.\hfill \\ \hfill & +m_{s2}\left[{\left({\dot{x}}_g+{\dot{u}}_{s2}\right)}^2+{\left({\dot{y}}_g+{\dot{v}}_{s2}\right)}^2\right]+I_{s2}{{\dot{\varphi }}_{s2}}^2\hfill \\ \hfill & +m_1{\left({\dot{x}}_g+{\dot{u}}_1\right)}^2+I_1{{\dot{\varphi }}_1}^2+m_2{\left({\dot{y}}_g+{\dot{v}}_2\right)}^2+I_2{{\dot{\varphi }}_2}^2\hfill \\ \hfill & +\left.M_1\left[{\left({\dot{x}}_L-{\dot{x}}_g\right)}^2+{\left({\dot{x}}_M-{\dot{x}}_g\right)}^2\right]+M_2\left[{\left({\dot{y}}_E-{\dot{y}}_g\right)}^2+{\left({\dot{y}}_F-{\dot{y}}_g\right)}^2\right]\right\},\hfill \end{array}(10)$

where $I_1$ and $I_2$ are the polar moment of inertia of the two auxiliary structures. The potential energy reads as in Equation 11:

$\begin{array}{c}V=\frac{1}{2}\left\{k_{xA}{\left(x_A-x_g\right)}^2+k_{xC}{\left(x_C-x_g\right)}^2+k_{yA}{\left(y_A-y_g\right)}^2+k_{yB}{\left(y_B-y_g\right)}^2\right.\hfill \\ \begin{array}{c}+k_{\mathit{xAP}}{\left(x_P-x_A\right)}^2+k_{\mathit{xCR}}{\left(x_R-x_C\right)}^2+k_{\mathit{yAP}}{\left(y_P-y_A\right)}^2+k_{\mathit{yBQ}}{\left(y_Q-y_B\right)}^2\hfill \\ +k_{xN}{\left(x_N-x_g\right)}^2+k_{xO}{\left(x_O-x_g\right)}^2+k_{yH}{\left(y_H-y_g\right)}^2+k_{yI}{\left(y_I-y_g\right)}^2\hfill \\ +\left.k_{\mathit{xBL}}{\left(x_L-x_B\right)}^2+k_{\mathit{xDM}}{\left(x_M-x_D\right)}^2+k_{\mathit{yCE}}{\left(y_E-y_C\right)}^2+k_{\mathit{yDF}}{\left(y_F-y_D\right)}^2\right\},\hfill \end{array}\hfill \end{array}(11)$

where $k_{\mathit{xBL}}$, $k_{\mathit{xDM}}$, $k_{\mathit{uCE}}$, and $k_{\mathit{yDF}}$ are the stiffness of the coupling visco-elastic devices that connects the 3D frame structure to the auxiliary structures (see Figure 1b).

To account for the non-conservative forces due to the damping of the structure, their virtual work $\delta W$ needs to be computed as in Equations 12, 13:

$\delta W={\left[\left({\mathbf{C}}_s+{\mathbf{C}}_{\mathit{ext}}\right)\dot{\widehat{\mathbf{x}}}\right]}^T\delta \widehat{\mathbf{x}},(12)$

where

${\mathbf{C}}_s=\left[\begin{array}{cc}\hfill \mathbf{C}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \end{array}\right],\widehat{\mathbf{x}}=\left\{\begin{array}{c}\hfill \mathbf{x}\hfill \\ \hfill {\mathbf{x}}_{\mathit{ext}}\hfill \end{array}\right\}.(13)$

Quantities $\mathbf{C}$ and $\mathbf{x}$ are the damping matrix and vector of the Lagrangian parameters of the 3D frame structure already introduced in Equation 7, and ${\mathbf{C}}_s$ is a $10\times 10$ matrix. Moreover, ${\mathbf{C}}_{\mathit{ext}}$ is still a $10\times 10$ matrix and accounts for the damping of the auxiliary structures and coupling visco-elastic devices. Vector ${\mathbf{x}}_{\mathit{ext}}={\left\{u_1,{\varphi }_1,v_2,{\varphi }_2\right\}}^T$ contains the Lagrangian parameters associated to the auxiliary structures. Due to the large dimensions of Matrix ${\mathbf{C}}_{\mathit{ext}}$ and by exploiting the symmetry properties, only its symmetric components $c_{ij}$ are reported in Equation 14:

$\begin{array}{c}{c}_{11}=-c_{\mathit{xBL}}-c_{\mathit{xDM}}\hfill \\ c_{21}=0,c_{22}=-c_{\mathit{yCE}}-c_{\mathit{yDF}}\hfill \\ c_{31}=c_{\mathit{xDM}}{l}_y-c_{\mathit{xBL}}{l}_y,c_{32}=c_{\mathit{yCE}}{l}_x-c_{\mathit{yDF}}{l}_x,\hfill \\ c_{33}=-c_{\mathit{xBL}}{l}_y^2-c_{\mathit{xDM}}{l}_y^2-c_{\mathit{yCE}}{l}_x^2-c_{\mathit{yDF}}{l}_x^2\hfill \\ c_{41}=0,c_{42}=0,c_{43}=0,c_{44}=0\hfill \\ c_{51}=0,c_{52}=0,c_{53}=0,c_{54}=0,c_{55}=0\hfill \\ c_{61}=0,c_{62}=0,c_{63}=0,c_{64}=0,c_{65}=0,c_{66}=0\hfill \\ c_{71}=c_{\mathit{xBL}}+c_{\mathit{xDM}},c_{72}=0,c_{73}=c_{\mathit{xBL}}{l}_y-c_{\mathit{xDM}}{l}_y,c_{74}=0,c_{75}=0,c_{76}=0,\hfill \\ c_{77}=-c_{\mathit{xBL}}-c_{\mathit{xDM}}-c_{xN}-c_{xO}\hfill \\ c_{81}=c_{\mathit{xBL}}{l}_y-c_{\mathit{xDM}}{l}_y,c_{82}=0,c_{83}=c_{\mathit{yDF}}{l}_x-c_{\mathit{yCE}}{l}_x,c_{84}=0,c_{85}=0,c_{86}=0,\hfill \\ c_{87}=-c_{\mathit{xBL}}{l}_y+c_{\mathit{xDM}}{l}_y-c_{xN}{l}_y+c_{xO}{l}_y,c_{88}=-c_{\mathit{xBL}}l{y}^2-c_{\mathit{xDM}}{l}_y^2-c_{xN}{l}_y^2-c_{xO}{l}_y^2\hfill \\ c_{91}=0,c_{92}=c_{\mathit{yCE}}+c_{\mathit{yDF}},c_{93}=c_{\mathit{yDF}}{l}_x-c_{\mathit{yCE}}{l}_x,c_{94}=0,c_{95}=0,c_{96}=0,\hfill \\ c_{97}=0,c_{98}=0,c_{99}=-c_{\mathit{yCE}}-c_{\mathit{yDF}}-c_{yH}-c_{yI}\hfill \\ c_{101}=0,c_{102}=c_{\mathit{yDF}}{l}_x-c_{\mathit{yCE}}{l}_x,c_{103}=c_{\mathit{yCE}}{l}_x^2+c_{\mathit{yDF}}{l}_x^2,c_{104}=0,c_{105}=0,\hfill \\ c_{106}=0,c_{107}=0,c_{108}=0,c_{109}=c_{\mathit{yCE}}{l}_x-c_{\mathit{yDF}}{l}_x+c_{yH}{l}_x-c_{yI}{l}_x,\hfill \\ c_{\mathrm{1010=}}-c_{\mathit{yCE}}{l}_x^2-c_{\mathit{yDF}}{l}_x^2-c_{yH}{l}_x^2-c_{yI}{l}_x^2\hfill \end{array}(14)$

Damping coefficients $c_{xN}$, $c_{xO}$, $c_{yH}$, and $c_{yI}$ are associated to the auxiliary structures and represent the viscous characteristic of the devices applied to the vertexes that correspond to the last subscript. As an instance, $c_{xN}$ is the damping coefficient that complete the description of the visco-elastic device applied at point $N$ and having stiffness $k_{xN}$. Note that in Figure 1 the visco-elastic properties associated to the elements of the structures are drawn only with springs for simplicity. Such dampings are conventionally defined as in Equation 15:

$\begin{array}{c}{c}_{xN}=c_{xO}=2{\omega }_{e1}{m}_1{\xi }_e,\hfill \\ c_{yH}=c_{yI}=2{\omega }_{e2}{m}_2{\xi }_e,\hfill \end{array}(15)$

where ${\omega }_{e1}=\sqrt{(k_{xO}+k_{xN})/m_1}$ and ${\omega }_{e2}=\sqrt{(k_{yH}+k_{yI})/m_2}$ are the frequencies of the two auxiliary structures assumed isolated. It is always considered ${\xi }_e=0.05$.

Damping coefficients $c_{\mathit{xBL}}$, $c_{\mathit{xDM}}$, $c_{\mathit{yCE}}$, and $c_{\mathit{yDF}}$ are instead associated to the coupling devices that connect the couple of vertexes corresponding to the last two subscripts. As an instance, $c_{\mathit{xBL}}$ is the damping coefficient that complete the description of the visco-elastic device connecting points $B$ and $L$ and of stiffness $k_{\mathit{xBL}}$. Such dampings are conventionally assumed as in Equation 16:

$\begin{array}{c}{c}_{\mathit{xBL}}=c_{\mathit{xDM}}=2{\omega }_{e1}{m}_1{\xi }_c,\hfill \\ c_{\mathit{yCE}}=c_{\mathit{yDF}}=2{\omega }_{e2}{m}_2{\xi }_c,\hfill \end{array}(16)$

where it is always considered ${\xi }_c=0.10$.

By introducing the Lagrangian function $L=T-V$, the ten equations of motion are then obtained through Equation 17:

$\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{\widehat{\mathbf{x}}}}\right)-\frac{\partial L}{\partial \widehat{\mathbf{x}}}=\left({\mathbf{C}}_s+{\mathbf{C}}_{\mathit{ext}}\right)\dot{\widehat{\mathbf{x}}},(17)$

and can be synthetically written as in Equation 18:

$\widehat{\mathbf{M}}\ddot{\widehat{\mathbf{x}}}+\widehat{\mathbf{C}}\dot{\widehat{\mathbf{x}}}+\widehat{\mathbf{K}}\widehat{\mathbf{x}}=-\widehat{\mathbf{M}}\widehat{\mathbf{r}}{\ddot{u}}_g\left(t\right).(18)$

The explicit expressions of such equations are presented in the Supplementary Appendix.

2.4 Inerter device

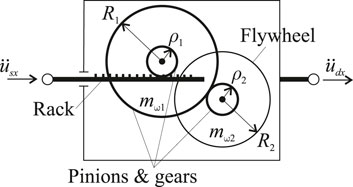
An inerter is a mechanical device designed to exert a force, $F_{ID}$, that is directly proportional to the relative acceleration between two connection points, or terminals. A common design approach involves using a rack-pinion-flywheel assembly, as depicted in Figure 3. In this configuration, the device’s primary components include two or more flywheels with radius $R_i$ and mass $m_{\omega i}$, which are linked to a linear rack through a pinion-gear mechanism. This arrangement allows the inerter to effectively translate relative accelerations into force outputs. The resisting force $F_{ID}$ of the inerter device is defined as in Equation 19 (Makris and Kampas, 2016; Thiers-Moggia and Málaga-Chuquitaype, 2018):

$F_{ID}=m_I\left({\ddot{u}}_{dx}-{\ddot{u}}_{sx}\right).(19)$

Here, $m_I$ represents the virtual mass (or inertance) of the inerter. This virtual mass can be increased by incorporating additional flywheels into the device. For an inerter device comprising $N$ flywheels, $m_I$ is given by Equation 20:

$\begin{array}{ll}\hfill m_I& =\frac{1}{2}{m}_{\omega 1}\frac{R_1^2}{{\rho }_1^2}+\frac{1}{2}{m}_{\omega 2}\frac{R_1^2{R}_2^2}{{\rho }_1^2{\rho }_2^2}+\cdots +\frac{1}{2}{m}_{\omega i}\frac{R_1^2{R}_2^2\cdots R_i^2}{{\rho }_1^2{\rho }_2^2\cdots {\rho }_i^2}+\cdots \hfill \\ \hfill & +\frac{1}{2}{m}_{\omega N}\frac{R_1^2{R}_2^2\cdots R_i^2\cdots R_N^2}{{\rho }_1^2{\rho }_2^2\cdots {\rho }_i^2\cdots {\rho }_N^2}.\hfill \end{array}(20)$

Figure 3

Figure 3. Rack-pinion-flywheel rotational inertia system.

The first two terms of Equation 20 define the virtual mass $m_I$ of the device shown in Figure 4. Importantly, in this type of inerter device, kinetic energy can transfer freely between the inerter and the structure due to the absence of clutches or other mechanisms that could restrict such energy exchange, as seen in (Makris and Kampas, 2016).

Figure 4

Figure 4. Periods and modal shapes of system 1 with only inerters.

3 Parametric analysis

An extensive parametric analysis is conducted by varying several parameters that characterize the coupled mechanical system. This analysis encompasses both System 1 and System 2 and aims to highlight the role of these parameters in promoting a more informed application of the proposed improvement methods.

3.1 Variable parameters for System 1

After selecting the frame characteristics for the parametric analysis, the fundamental parameter to consider as a variable is the value of the virtual mass provided by the inerters. The total virtual mass $M$ acting in both $x$ and $y$ directions thanks to the couples of equal inerters of virtual mass $M_1$ (acting along the $x$ direction) and $M_2$ (acting along the $y$ direction) (see Figure 1a) is parametrized with respect to the mass of the first level $m_{s1}$ as in Equation 21:

$M=\eta m_{s1}.(21)$

Therefore, for equal inerters along the $x$ and $y$ directions, follows that $M_1=M_2=M/2$. It is worth observing that, when the distribution of the virtual masses is uniform along the sides of the structures, as considered in this paper, the mass centers of both System one and System two coincide with the center of mass of the stand-alone frame structure.

3.2 Variable parameters for System 2

For System 2, a higher number of variable parameters than System 1 are investigated to analyse the performance of the protection method. The variable parameters considered in the analysis are.

$•$ The total virtual mass $M$ of the inerters in both the $x$ and $y$ directions (parametrized as before, Equation 22)

$M=\eta m_{s1}.(22)$

For equal inerters along the $x$ and $y$ directions, follows that $M_1=M_2=M/2$.

$•$The total stiffness $K_e$ of the external auxiliary structures along their shorter directions (assumed to be equal in both, Equation 23)

$K_e={\gamma }_e{K}_{x1}\text{\hspace{0.17em}or\hspace{0.17em}equivalently\hspace{0.17em}}{K}_e={\gamma }_e{K}_{y1},(23)$

where $K_{1x}=K_{1y}$ refers to the total stiffness of the first level of the 3D shear-type system, assumed equal in both directions. The stiffness $K_e$ is assumed to be uniformly distributed to align the centers of mass and stiffness within each auxiliary structure ($i.e$., $k_{xN}=k_{xO}=K_e/2$, $k_{yH}=k_{yI}=K_e/2$).

• The total stiffness $K_c$ of the coupling devices among the 3D shear-type system and the auxiliary structures (Equation 24)

$K_c={\gamma }_c{K}_{x1}\text{\hspace{0.17em}or\hspace{0.17em}equivalently\hspace{0.17em}}{K}_c={\gamma }_e{K}_{y1}.(24)$

The distribution of stiffness is considered variable to allow for adjusting the position of the stiffness center of the global coupled structure. Specifically (Equation 25):

$\begin{array}{c}{k}_{\mathit{xBL}}=\alpha K_c\text{,\hspace{0.17em}}{k}_{\mathit{xDM}}=\left(1-\alpha \right)K_c,\hfill \\ k_{\mathit{yCE}}=\beta K_c\text{,\hspace{0.17em}}{k}_{\mathit{xDF}}=\left(1-\beta \right)K_c.\hfill \end{array}(25)$

Coefficients $\alpha$ and $\beta$ are suitably selected to move the global stiffness center of the coupled structure in a desired point.

In all the analyses the mass of the auxiliary structures are considered fixed quantities, $m_1=m_2=0.1m_{s1}$.

3.3 Geometrical and mechanical characteristics of the 3D frame structure

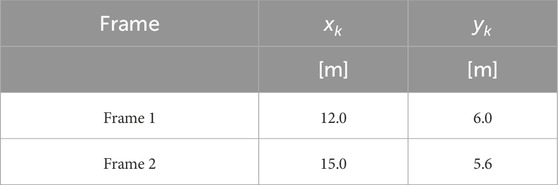
The parametric analyses are performed on two different frame structures. Table 1 shows the original geometrical characteristics of the studied M-DOF frame structures, that are then modeled by two-level, 3D shear-type systems. Specifically, the columns Storeys, Area, $2l_x$, and $2l_y$ refer to actual the M-DOF frame structures. The structure labeled as Frame 1 (first row of the Table) has four identical rectangular levels, each with an area of 300 ${\text{m}}^2$ and dimensions $20.0\times 15.0{\text{m}}^2$, while the other, labeled as Frame 2 (second row of the Table), has five identical rectangular levels, each measuring 350 ${\text{m}}^2$ and with dimensions $25.0\times 14.0{\text{m}}^2$. Both structures are assumed to have levels with uniform stiffness in both directions. Additionally, the mass centers at each level coincide, while the stiffness centers, although aligned with each other at the two levels, are offset from the mass centers.

Table 1

Table 1. Geometrical and mechanical characteristics of the two reference frame structures.

The remaining columns of Table 1 refer to the mechanical characteristics of the two-level, 3D shear-type systems, which are dynamically equivalent to the actual structures. The previously mentioned dynamic equivalence criterion ((Fabrizio et al., 2017a; Fabrizio et al., 2019; Fabrizio et al., 2017b)), used to assess the characteristics of the 3D shear-type systems, determines the values of masses and stiffnesses such that the first level corresponds to the first level of the actual structure, while the second level corresponds to the top level of the actual structure. Consequently, the displacement differences between the two levels serves as a measure of the drift in the actual structure. Columns $m_{s1}$ and $m_{s2}$ provide the masses associated to each level. It is worth noticing that in Frame 1, $m_{s2}$ is three times $m_{s1}$ since the second level of the 3D shear-type system has to represent all the levels above the first. The same thing occur for the Frame 2, where $m_{s2}$ is four times $m_{s1}$. Columns $K_{1x}=K_{1y}$ and $K_{2x}=K_{2y}$ are the total stiffness of the two levels of the 3D shear-type system along directions $x$ and $y$. Finally, the last column, Period, provides the fundamental oscillation period of the structures. The applied equivalence criterion ensures that both the actual structures and the 3D shear-type systems have the same oscillation period.

The position of the stiffness centers $k_s$ of the 3D shear-type systems, assumed coincident at each level, is reported in Table 2. The two columns provide the coordinates of $k_s$ with respect the structural vertex $A\equiv P$ (see Figure 1).

Table 2

Table 2. Position of the stiffness center of the two reference frame structure.

The eccentricity of the stiffness center with respect to the mass center is caused by the non-uniform distribution of stiffness among the columns along the two alignments parallel to the $x-$ and $y-$axes. Specifically, the position of the stiffness center in Table 2 is determined by the following stiffness distribution (Equation 26):

$\begin{array}{c}{k}_{xA}=0.60K_{1x},k_{xC}=0.40K_{1x}\hfill \\ k_{yA}=0.60K_{1y},k_{yB}=0.40K_{1y}\hfill \\ \dots \hfill \\ k_{\mathit{xAP}}=0.60K_{2x},k_{\mathit{xCR}}=0.40K_{2x}\hfill \\ k_{\mathit{yAP}}=0.60K_{2y},k_{\mathit{yBQ}}=0.40K_{2y}\hfill \end{array}(26)$

3.4 Performance indexes

To evaluate the performance of the proposed methods, two performance indexes are introduced (Equation 27). They read:

${\alpha }_1=\frac{\max \left|s_D\left(t\right)\right|}{\max \left|{\tilde{s}}_D\left(t\right)\right|},{\alpha }_2=\frac{\max \left|\mathrm{\Delta }{s}_{DS}\left(t\right)\right|}{\max \left|\mathrm{\Delta }{\tilde{s}}_{DS}\left(t\right)\right|}(27)$

where $s_D=\sqrt{u_D^2+v_D^2}$ is the displacement of point $D$ of System 1 or System 2, whereas ${\tilde{s}}_D$ is the displacement of the same point $D$ of the stand-alone frame structure. Similarly, $\mathrm{\Delta }{s}_{DS}=\sqrt{{(u_S-u_D)}^2+{(v_S-v_D)}^2}$ is the relative displacement (total drift) between points $S$ and $D$ of System 1 or System 2 (drift), whereas $\mathrm{\Delta }{\tilde{s}}_{DS}$ is the same drift evaluated on the stand-alone frame structure. Therefore, ${\alpha }_1$ refers to the displacement of the first level of the structures, whereas ${\alpha }_2$ refers to the drift between the top and the first levels.

Two additional performance indexes related to the torsion of the structure are used to assess the performance of the protection methods (Equation 28). They are defined as:

${\beta }_1=\frac{\max \left|{\varphi }_{s1}\left(t\right)\right|}{\max \left|{\tilde{\varphi }}_{s1}\left(t\right)\right|},{\beta }_2=\frac{\max \left|{\varphi }_{s2}\left(t\right)-{\varphi }_{s1}\left(t\right)\right|}{\max \left|{\tilde{\varphi }}_{s2}\left(t\right)-{\tilde{\varphi }}_{s1}\left(t\right)\right|},(28)$

where ${\varphi }_{s1}$ and ${\varphi }_{s2}$ are the rotations of the two levels of the System 1 or Sytem 2, whereas ${\tilde{\varphi }}_{s1}$ and ${\tilde{\varphi }}_{s2}$ are the corresponding rotations of the stand-alone frame structure. It is worth observing that ${\beta }_1$ refers to the torsion of the first level of the structures, whereas ${\beta }_2$ refers to torsional drift between the top and first levels.

With this formulation, the effectiveness of the external apparatus improves as the values of ${\alpha }_1$, ${\alpha }_2$ and ${\beta }_1$, ${\beta }_2$ decrease relative to unity. Although no absolute engineering threshold is imposed to quantify the effectiveness of the protection systems, a response ratio significantly lower than unity (typically below 0.8) can be considered as indicative of substantial improvement, with values approaching 0.6 or lower denoting particularly effective performance.

4 Spectral analysis

The first analysis aims to investigate the impact of the total virtual mass $M$ on the spectral characteristics of both System 1 and System 2. The periods and modal shapes of all the oscillation modes for System 1 and System 2 are obtained by varying $M$, then compared with those of the stand-alone structure, and the role of $M$ is discussed. All the results shown in this section refer to the 3D frame structure with geometrical and mechanical characteristics of Frame 1 (see the first row of Table 1).

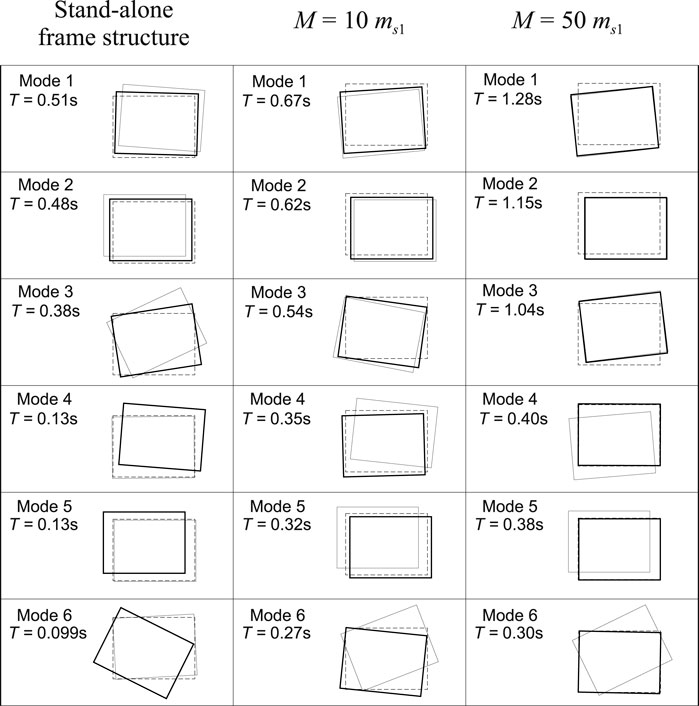
4.1 Periods and modes of System 1

Both the stand-alone 3D frame structure and System 1 are 6-DOF mechanical systems, therefore they admit six frequencies and oscillation modes. The results of the spectral analysis is reported in Figure 4, which shows the periods and modal shapes of the stand-alone frame structure (left columns), and those of the System 1 with two different total virtual mass $M$. Specifically, the middle column refers to the case with $M=10m_{s1}$ and the right column shows the case with $M=50m_{s1}$. In the modal shapes, the dashed line refers to the undeformed configuration, the thick solid line shows the modal displacement of the first level, whereas the thin solid line refers to the second level.The first observation concerns the fact that the mode periods increase as the virtual mass increases, producing effects similar to those achieved through base isolation (Mazza and Labernarda, 2022; Mazza et al., 2024). The other notable effect is related to the role played by the virtual mass $M$ on the modal shapes. As $M$ increases, a separation of effects on the oscillation modes can be observed. Specifically, for high values of $M$, only the first level exhibits significant modal displacement in the first three modes, while the second level is nearly superimposed on the first. In the second set of three modes, only the second level shows significant modal displacement, with the first level nearly superimposed on the undeformed configuration. This separation of effects between the two levels of the system clarifies the structure’s dynamic response, enabling a more straightforward design approach.

4.2 Periods and modes of System 2

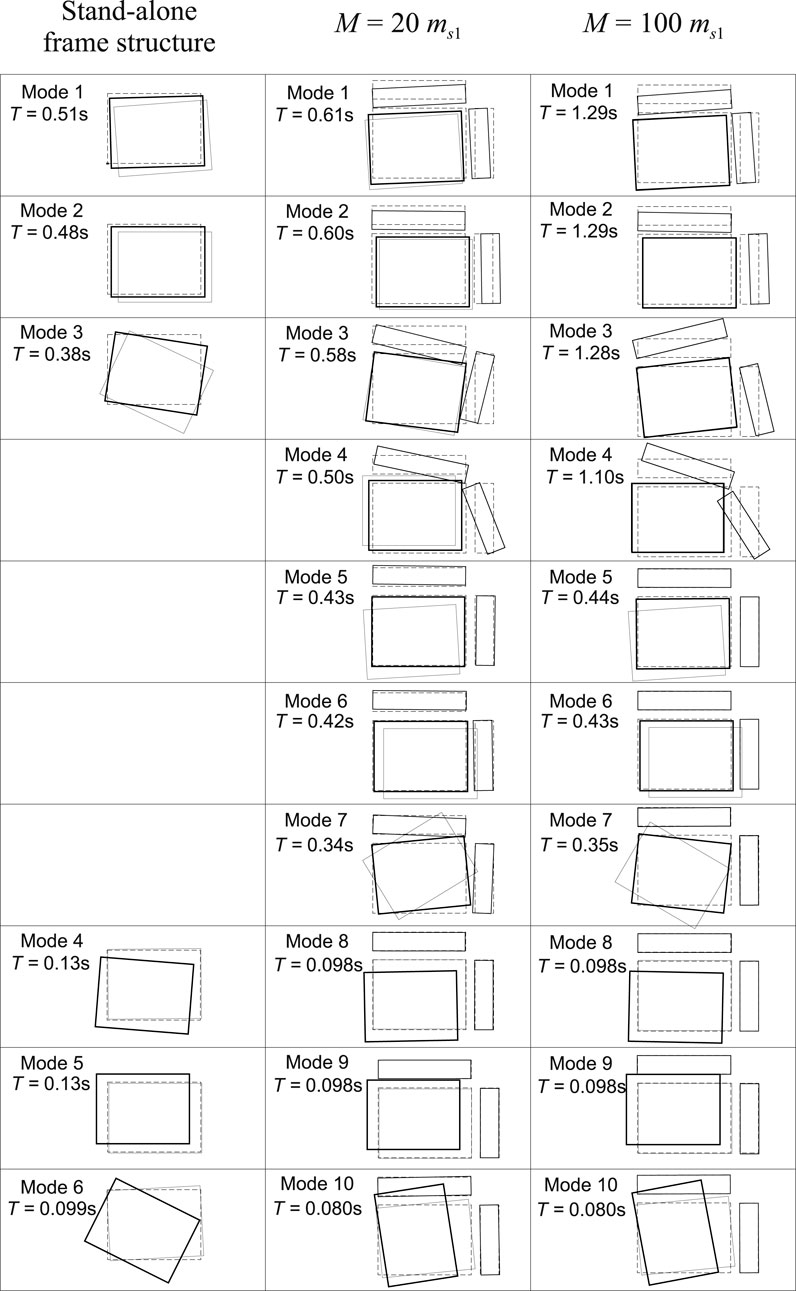
The spectral analysis on System 2 is performed under the hypothesis that ${\gamma }_e={\gamma }_c=1$ ($i.e$., $K_e=K_c=1.0K_{\mathit{xs1}}$, see Equations 23 and 24). Moreover, the stiffness of the coupling devices ($k_{\mathit{xBL}}$, $k_{\mathit{xDM}}$ and $k_{\mathit{yCE}}$, $k_{\mathit{yDF}}$) are distributed to align the stiffness and mass centers of the first level of the coupled structure. This can be obtained with specific values of $\alpha$ and $\beta$ in Equation 25: $\alpha =0.4$, $\beta =0.6$.

Figure 5 shows the frequencies and modal shapes of the stand-alone frame structure and of System 2 for two different values of $M$. The same graphical conventions as in Figure 4 are used: dashed lines represent the undeformed configuration, while thick and thin solid lines represent the first and second levels, respectively. Since the stand-alone and System 2 admit different number of modes (six and ten, respectively), in Figure 5 the modes of the stand-alone system and System 2 with similar shapes are arranged side by side.

Figure 5

Figure 5. Periods and modal shapes of system 2 with external structures equipped with inerters.

Figure 6

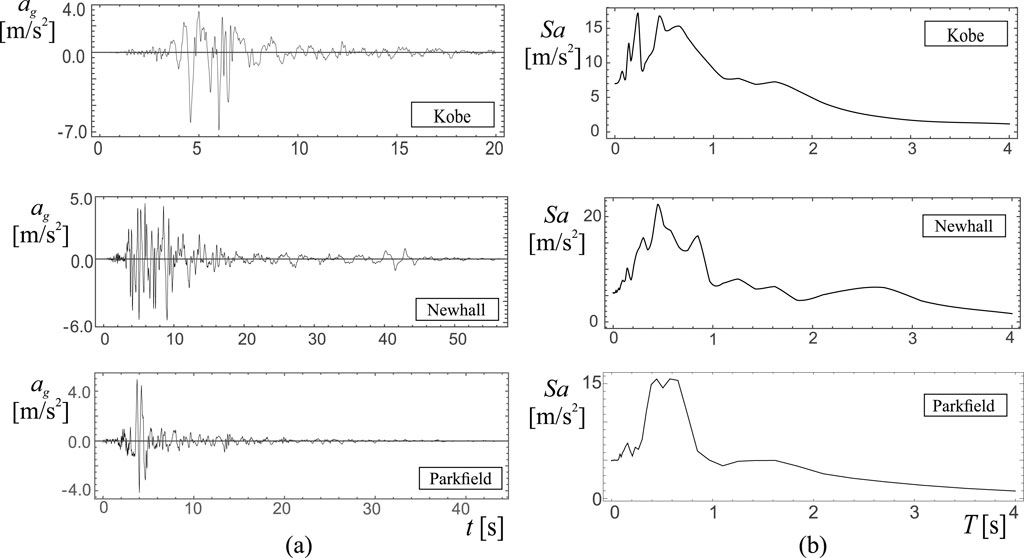
Figure 6. Records of kobe, newhall and parkfield events: (a) Time histories; (b) Pseudo-acceleration spectra.

For the smallest value of $M$, $M=20m_{s1}$, the first three modes of System 2 (middle column) show a slight increase in periods and exhibit shapes similar to those of the first three modes of the stand-alone structure. However, the modal amplitudes of the frame structure of System 2 are smaller than those of the stand-alone structure, with the predominant modal displacements occurring primarily in the external structures. The last three modes exhibit periods and modal shapes close to the last three of the stand-alone structure, with a negligible participation of the external auxiliary structures.

An increase of the virtual mass up to the value of $M=100m_{s1}$ results in a significant increase in the periods of the first three modes. Additionally, these modes primarily affect the first level, as the modal displacements at the second level are negligible, with predominant effects mainly occurring in the external structures. Modes 5, 6, and seven exhibit periods similar to those of the first three modes of the stand-alone structure, with the predominant modal displacements concentrated at the second level. This indicates a distinct separation of modal effects between the first and second levels, as previously discussed for System 1. Finally, the last three modes of System two have periods that closely match those of the last three modes of the stand-alone structure, albeit with slightly higher modal displacements at both levels. It is noteworthy that in modes 5 to 10, the external auxiliary structures are minimally involved due to their small modal displacements. As a final remark, mode four of System two does not have a direct correspondence with the modes of the stand-alone structure. It involves the frame structure through translational displacement and the external auxiliary structures through pure torsional displacement. Also in this case, distinguishing the modal effects at each system level enhances clarity in analyzing the structure’s dynamic response, thereby facilitating a more streamlined design process.

5 Seismic analysis

The seismic analysis is conducted by subjecting System 1 or System 2 to specific earthquake records and varying one or more parameters (see Section 3). Specifically, the parametric analysis on System 1 is carried out by evaluating the performance indexes ${\alpha }_1$ and ${\alpha }_2$ as the total virtual mass $M$ varies (Equation 22). In contrast, for System 2, the parametric analysis is conducted by creating performance maps that display the contour plot of the performance indexes in the parameter plane ${\gamma }_c-{\gamma }_e$ ($i.e$., the stiffness $K_c$ and $K_e$ are considered variable, see Equations 23 and 24), under a specific earthquake and keeping the total virtual mass $M$ fixed.

In the regions of the curves or maps where the performance indexes are less than unity, the seismic effects on System 1 and System 2 are smaller than those on the stand-alone frame structure.

5.1 Earthquake records

The following earthquake records are considered in this study (Figure 6).

(a) Kobe, 1995 Japan earthquake, Takarazuka station, 0 deg, ground level, position of the station: 34.8090N, 135.3440W;

(b) Northridge, Newhall, 1994 California earthquake,- LA County Fire station no.24279, 360 deg, position of the station: 34.387N, 118.530W;

(c) Parkfield, 1966 California earthquake, station no.013, comp N65E, position of the station: 35.726N, 120.287W.

For ease of reference, each record is labeled using the underlined name provided in the list.

The use of three natural earthquake records (Kobe, Newhall, and Parkfield) is driven by the need for an initial evaluation of the protection system’s performance under seismic inputs characterized by distinct spectral contents. These records are selected based on their effective use in prior studies by the authors, where they demonstrated marked differences in system dynamics due to variations in frequency content. This distinction is further supported by their pseudo-acceleration spectra, which highlight how different excitations can engage different modal responses of the structural system.

In this preliminary phase of the study, the earthquake records are used without scaling to a specific design spectrum or code-based intensity level. The aim is to qualitatively assess the sensitivity of the protection system to differences in seismic frequency content using natural, unmodified ground motions, thus preserving the intrinsic variability present in real earthquake data. This choice avoids potential distortions introduced by artificial scaling and is justified in the context of the linear structural model adopted in the study. Since the performance of the proposed systems is expressed through normalized response ratios (e.g., ${\alpha }_1$ and ${\alpha }_2$), applying uniform scaling to the input ground motions would not affect the results since both the numerator and denominator of the ratios would scale proportionally.Nonetheless, for a comprehensive assessment of practical applicability, especially for a specific structure or site, ground motions should be selected and scaled in accordance with seismic code provisions, hazard levels, and target spectra. Future developments of this research will include such extensions to enable a more rigorous, code-compliant performance evaluation of the proposed protection strategies.

5.2 Seismic response of System 1

The parametric seismic analysis involves evaluating the performance indices, ${\alpha }_1$ and ${\alpha }_2$, by varying the total virtual mass $M$ and using a single earthquake record. As a result, performance curves plotting the performance indexes against the total virtual mass $M$ are generated. Each graph also includes a line at unity to highlight the range of $M$ values where the proposed method effectively reduces the seismic effects on the frame structure. Specifically, in regions where the performance curves fall below this line, System one exhibits better seismic behavior than the stand-alone frame structure.

Figure 7 shows the results obtained by exciting Frame 1 (see Table 1) with the three selected earthquake records. Each graph displays two performance curves: the solid curve corresponds to the ${\alpha }_1$ index, while the dashed curve represents the ${\alpha }_2$ index. As can be observed, there are large ranges of $\eta$ ($i.e$., of $M$) where both the indexes are less than unity, assuring good performances of System 1 respective to the stand-alone frame structure. Notably, the best performances of the two levels (identified by the minimum values of ${\alpha }_1$ and ${\alpha }_2$) occur for different virtual mass $M$. Specifically, to ensure optimal seismic response at the first level, the value of $M$ must be higher than that required to achieve the best response at the second level. This can be explained by noting that, at the highest values of $M$, the system exhibits a separation in the dynamics between the first and second levels, as previously discussed. Furthermore, the modes primarily involving the first level acquire longer periods, thereby shifting the dynamics into the range of periods where the earthquakes exhibit lower spectral power. In contrast, the seismic response of the second level is associated with modes that have periods falling within the range where the earthquakes exhibit the highest spectral power. Conversely, the optimal seismic response at the second level, represented by ${\alpha }_2$, necessitates small values of $M$. However, these values are found in regions where the performance index ${\alpha }_1$ remains significantly greater than unity. Therefore, selecting an optimal value for the virtual mass $M$ must consider both performance indexes simultaneously. It is important to note that developing an optimal procedure for choosing the value of $M$ is not the focus of this paper. Finally, based on the results, it can be concluded that the performance trends of System one are qualitatively consistent across the three selected earthquake records, as evidenced by the similar shapes of the performance curves and the comparable ranges of the parameter $\eta$ in which optimal responses are observed in Figure 7. Nonetheless, some variation in the amplitude of the performance indexes is apparent, most notably for the Parkfield earthquake, where the range of $\eta$ values for which ${\alpha }_1$ exceeds unity is significantly narrower than in the other two cases.

Figure 7

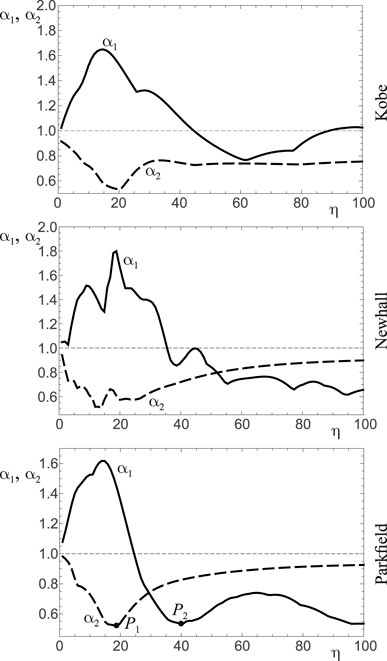
Figure 7. Performance curves ${\alpha }_1$ and ${\alpha }_2$ for system 1 under kobe, newhall, and parkfield earthquakes (Frame 1).

The time-histories of the total displacement $s_D$ and drift $\mathrm{\Delta }{s}_{DS}$ (see Section 3.4), for both System one and the stand-alone structure are obtained and compared in Figure 8. This figure shows the time-histories of the absolute value of $s_D$ and $\mathrm{\Delta }{s}_{DS}$ that refer to points labelled with letters $P_1$ and $P_2$ in Figure 7. Specifically, at point $P_1$, the performance index ${\alpha }_2$ reaches its minimum value, while at point $P_2$, the index ${\alpha }_1$ attains its minimum value. Each graph in Figure 8 contains two time-histories: one representing the stand-alone structure (thick grey line) and the other representing System 1 (thin black line). The system’s behavior at point $P_1$ (graphs in the first row of Figure 7) demonstrates that the maximum drift $\mathrm{\Delta }{s}_{DS}$ of System 1 is smaller than that of the stand-alone structure. Conversely, the maximum displacement $s_D$ is larger for System 1, aligning with the performance curves in Figure 7. The time-histories referring to point $P_2$ (second row of Figure 8) show that the maximum values of both $s_D$ and $\mathrm{\Delta }{s}_{DS}$ for System 1 are smaller than those for the stand-alone structure, consistent with the curves in Figure 7.

Figure 8

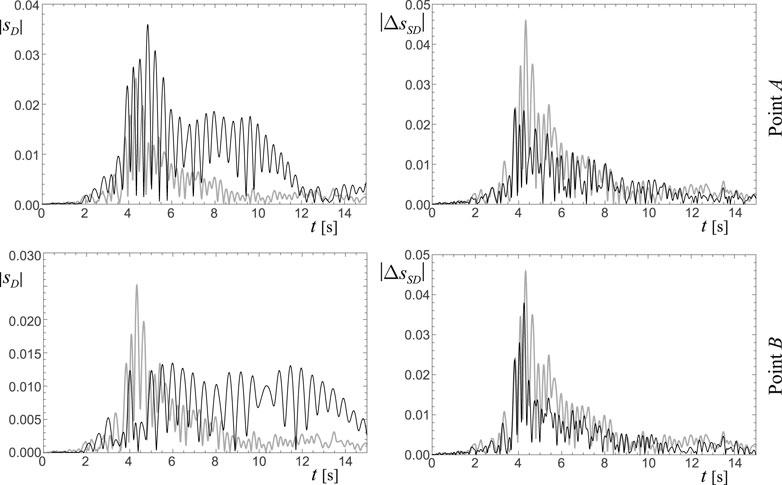
Figure 8. Time-histories of the system 1 under Parkfield earthquake (Frame 1, $M=30m_{s1}$, thin black line: System 1, thick grey line: stand-alone frame structure, $P_1\equiv (M=20.0);P_2\equiv (M=40.0)$.

The performance curves obtained from Frame 2 (see Table 1) and shown in Figure 9 are qualitatively similar to those referring to Frame one that are shown in Figure 7. Independently from the earthquake record, the performance index ${\alpha }_1$ acquires the minimum value for high values of the parameter $\eta$. Contrarily, the performance index ${\alpha }_2$ reaches its minimum value for small values of $\eta$. As a general observation, the efficiency of using inerter devices to enhance seismic behavior decreases as the dimensions of the frame structure, and in particular its height, increase. The observed reduction in performance is primarily associated with the relatively low installation level selected for the connection of the protection system. Inerters or auxiliary structural elements exert a direct influence on the displacement of the first storey, contributing to a modal regularization that effectively limits top-storey displacements. However, as the height of the structure increases (i.e., with a greater number of storeys), the influence of this indirect effect tends to diminish due to the increasing structural flexibility and mode complexity.

Figure 9

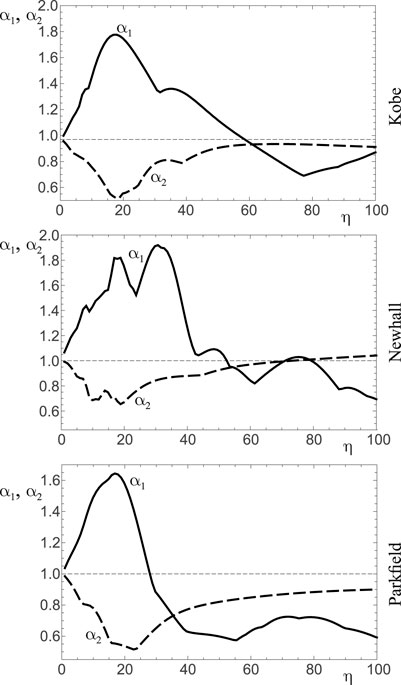
Figure 9. Performance curves ${\alpha }_1$ and ${\alpha }_2$ for system one under kobe, newhall, and parkfield earthquakes (Frame 2).

5.3 Seismic response of System 2

The parametric seismic analysis involves mapping the values of the performance indexes, ${\alpha }_1$ and ${\alpha }_2$ (or ${\beta }_1$ and ${\beta }_2$), onto the parameter plane defined by ${\gamma }_e$ and ${\gamma }_c$ (see Equations 23 and 24, respectively) using a single earthquake record and for a fixed value of the virtual mass $M$. This process generates performance maps, which are contour plots illustrating the distribution of ${\alpha }_1$ and ${\alpha }_2$ across the ${\gamma }_e-{\gamma }_c$ parameter’s plane. To enhance readability, the contour levels are delineated using a specific greyscale scheme, where lighter shades correspond to smaller values of the performance indices. A better seismic performance of System two than the stand-alone frame structure is observed within regions of the maps characterized by clearer greyscale tones. These areas indicate a superior system performance, as denoted by lower values of the performance indexes ${\alpha }_1$ and ${\alpha }_2$.

The first performance maps presented are those referring to Frame 1 (see Table 1), excited by Parkfield earthquake, are obtained. The stiffness of the coupling devices ($k_{\mathit{xBL}}$, $k_{\mathit{xDM}}$ and $k_{\mathit{yCE}}$, $k_{\mathit{yDF}}$) are distributed to align the stiffness and mass centers of the first level of the coupled structure. Since, the sum $K_c$ of these stiffnesses in each direction is related to the first-level stiffness, $K_{x1}$ (or $K_{y1}$) through the parameter ${\gamma }_c$ (see Equation 24), the distribution of the coupling stiffnesses directly depends on this parameter. Specifically, the parameters $\alpha$ and $\beta$ appearing in Equation 25 read (Equation 29):

$\alpha =0.5-\frac{0.1}{\gamma c},\beta =0.5+\frac{0.1}{\gamma c}.(29)$

Figure 10 shows the performance maps, arranged in matrix form. Specifically, along the rows the maps refer to different values of $M$, whereas along the columns the maps refer to the two performance indexes ${\alpha }_1$ and ${\alpha }_2$. In the regions colored with uniform grey the performance indexes are higher than unity, therefore no advantage in using the proposed method occurs. It should be noted that the grayscale levels used in the performance maps are independently scaled for each figure, as they are adapted to the specific range of values of the performance index displayed. Consequently, no uniform colormap bar is shown. These maps are intended to qualitatively highlight regions of improved performance, with lighter shades indicating lower index values relative to the stand-alone case, rather than to serve as absolute design charts. The analysis reveals that the size of the advantage regions, where the performance indexes are less than unity, as well as the values of the indexes themselves, depend on the virtual mass $M$. An increase in this parameter has opposing effects on the two indexes. Specifically, as $M$ increases, the advantage regions in the ${\alpha }_1$ map expand, while those in the ${\alpha }_2$ map contract. Additionally, an increase in $M$ generally leads to a decrease in the values of ${\alpha }_1$ and an increase in those of ${\alpha }_2$. The spectral analysis in Section 4 provides insights into the dependence of the maps on the value of $M$. For high values of $M$, there is a form of modal decoupling between the two levels of the frame system. The modes that primarily involve the first level acquire a longer period, shifting their dynamics outside the range where the earthquake has higher spectral power. Consequently, the seismic effects on the first level are less severe. Conversely, the modes involving the second level acquire periods that fall within ranges where the earthquake has higher spectral power, leading to more intense excitation. Therefore, in general, it is not possible to find a pair of values for the parameters ${\gamma }_c$ and ${\gamma }_e$ that minimize both performance indices simultaneously. The optimal results should be sought for moderate values of $M$, where the best trade-off between the performance indices can be achieved.

Figure 10

Figure 10. Performance maps ${\alpha }_1$ and ${\alpha }_2$ for system two under parkfield earthquake (Frame 1).

It is of great interest to evaluate the effects occurring from the coincidence between the stiffness and mass centers at the first level. Therefore, while the results shown in the previous Figure 10 are obtained considering this coincidence, in Figure 11 the performance maps with and without such coincidence are compared. The results refer to Frame 1, excited by Parkfield earthquake, and fixed $M=30m_{s1}$. Also in this figure a matrix arrangement of the maps is used. The first two rows (Figure 11a) refer to maps obtained with and without coincidence between the stiffness and mass centers. As observed, this coincidence primarily affects the drift of the frame structure, as the advantage region in the ${\alpha }_2$ map expands and the values of ${\alpha }_2$ decrease.

Figure 11

Figure 11. Effects of the centering of the mass and stiffness centers: (a) Performance maps ${\alpha }_1$ and ${\alpha }_2$ for System two under Parkfield earthquake; (b) Performance maps ${\beta }_1$ and ${\beta }_2$ for system two under Parkfield earthquake (Frame 1, $M=30m_{s1}$).

The coinciden\ce between the stiffness and mass centers at the first level has a limited effect on the ${\alpha }_1$ index, as the corresponding maps remain qualitatively similar in their overall trends and advantage regions. However, notably, the case without alignment shows a local minimum in the region of higher ${\gamma }_e$ and ${\gamma }_c$ values, suggesting the emergence of particularly favorable configurations in that portion of the parameter space. The performance indexes ${\beta }_1$ and ${\beta }_2$ provide interesting information about the torsion of the first level and the torsional drift of the second level of the frame structure. Figure 11b compares the performance ${\beta }_1$ and ${\beta }_2$ maps obtained with and without the coincidence between stiffness and mass centers. The results show that this coincidence significantly reduces the torsion at the first level, as the advantage region increases and the values of ${\beta }_1$ decrease. Conversely, the torsional drift, measured by ${\beta }_2$, remains largely unchanged. As expected, since the coincidence between the stiffness and mass centers occurs only at the first level, the improvement in torsional effects is primarily noticeable at the first level. Nevertheless, there is also a simultaneous, notable improvement in the overall drift of the frame structure.

To further assess the effectiveness of System two in mitigating seismic effects, Frame 1 with a total virtual mass of $M=30m_{s1}$ is also subjected to excitation from the Kobe and Newhall earthquake records. The corresponding performance maps, reported in Figure 12, complement the results previously obtained under the Parkfield earthquake and shown in Figure 10 (second row) and Figure 11a (second row). These additional maps confirm that System two maintains its protective capabilities across earthquakes characterized by distinct spectral contents. TextcolormagentaConsistently across the three seismic inputs, the maps reveal a broad region within the ${\gamma }_c$–${\gamma }_e$ parameter space where both performance indices ${\alpha }_1$ and ${\alpha }_2$ are significantly below unity, denoting a simultaneous reduction of first-level displacements and inter-storey drift. Although slight variations in the extent and location of these favorable regions are observed, likely due to the different dominant frequency bands of the earthquakes, the overall trend supports the robustness of the adopted protection strategy. TextcolormagentaMore specifically, the Kobe earthquake induces slightly larger values of the performance indices compared to Parkfield, with optimal regions shifting slightly toward higher values of ${\gamma }_c$. In contrast, the Newhall excitation produces performance contours similar in structure to those from the Parkfield case, although the drift index ${\alpha }_2$ exhibits more sensitivity to variations in the external structure stiffness ${\gamma }_e$. These findings emphasize the adaptability of System two under real earthquake conditions and reinforce the idea that optimal tuning of the auxiliary system can be maintained within practical ranges of stiffness ratios.

Figure 12

Figure 12. Performance maps ${\alpha }_1$ and ${\alpha }_2$ for System two under the Kobe and Newhall earthquakes (Frame 1, $M=30m_{s1}$).

The performance maps for Frame 2, subjected to seismic excitation from the three selected earthquakes, are presented in Figure 13. All results are obtained for a fixed value of the total virtual mass $M=50m_{s1}$. These maps provide a comprehensive overview of the performance of System two when applied to a taller frame structure. Across all earthquake scenarios, System two consistently demonstrates its ability to reduce both the displacement at the base level and the inter-storey drift, confirming its applicability beyond the smaller prototype frame.

Figure 13

Figure 13. Performance maps ${\alpha }_1$ and ${\alpha }_2$ for System two under Kobe, Newhall, and Parkfield earthquakes (Frame 5p, $M=50m_{s1}$).

Nonetheless, the maps also reveal that the regions of optimal performance vary depending on the specific performance index considered. In particular, the minima of the displacement performance index ${\alpha }_1$ and the drift performance index ${\alpha }_2$ do not coincide in the ${\gamma }_c$-${\gamma }_e$ parameter space. This divergence indicates that no single combination of coupling and external stiffness values simultaneously optimizes both metrics. As a result, the design strategy for System two must account for this inherent trade-off, selecting parameter configurations that balance the reduction in first-level displacements with the control of structural drift. Such balance is especially critical in taller buildings, where different vibration modes may dominate the response depending on the excitation frequency content and structural configuration.

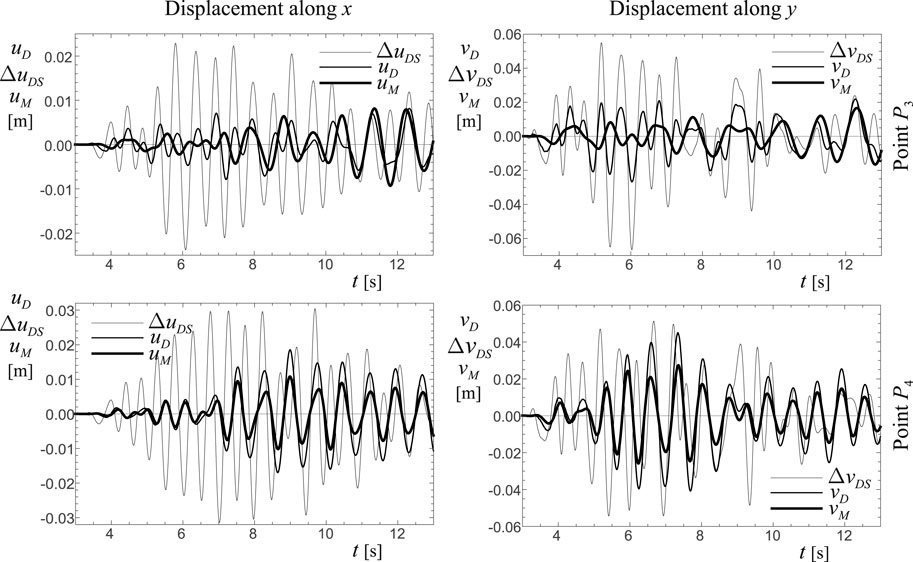
Finally, to understand how the coupling with external auxiliary structures works in reducing the seismic effects on frame structures, the time-histories of systems represented by labels $P_3$ and $P_4$ in Figure 13 are obtained and discussed. Figure 14 show such time-histories, arranged in matrix form. Specifically, rows refer to the different systems labeled with $P_3$ and $P_4$, while columns refer to displacements along the $x-$ or $y-$axis. Each graph contains three curves that represent the following: the displacement of point $D$ at the first level of the frame structure ($u_D$ in the $x$-direction and $v_D$ in the $y$-direction), the displacement of point $M$ on one of the external structures ($u_M$ in the $x$-direction and $v_M$ in the $y$-direction), and the drift between point $S$ at the second level of the frame structure and point $D$ ($\mathrm{\Delta }{u}_{DS}$ in the $x$-direction and $\mathrm{\Delta }{v}_{DS}$ in the $y$-direction). These points are all clearly indicated in Figure 1. As can be observed, at point $P_3$ on the map, the minimum value of the performance index ${\alpha }_1$ occurs. The time-histories show that the two levels of the frame structure move in-phase with each other, while the external auxiliary structure moves almost in counter-phase to the entire frame structure. In this case, the external structure works as a tuned mass damper for the structure being protected. Conversely, $P_4$ is located at a point of minimum value for the index ${\alpha }_2$. Here, the time-histories reveal that the first level and the external structure are in-phase with one another, whereas the second level moves primarily in counter-phase relative to all other components of System 2. Therefore, it can be concluded that both the first level and the external structure act as tuned mass dampers for the second level.

Figure 14

Figure 14. Time-histories of the System two under Newhall earthquake (Frame 5p, $M=50m_{s1}$, $P_3\equiv ({\gamma }_c=1.0,{\gamma }_e=0.5);P_4\equiv ({\gamma }_c=5.0;{\gamma }_e=1.6)$).

5.4 Final remarks

System one adds only the inerter devices to the stand-alone structure. By appropriately distributing the virtual masses along the sides of the frame, the structure’s center of mass can shift to any desired point. A notable choice could be to align the center of mass with the center of stiffness at the first level of the structure. Notably, base isolation has an opposite effect on the protected system, as it can shift the center of stiffness of the isolated level to align with the structure’s center of mass. However, the benefits provided by inerter devices are accompanied by certain limitations. Specifically, shifting the center of mass at the first level leaves the center of mass of the second level ($i.e$., of the superstructure) unchanged. As a result, the seismic inertial forces acting on the superstructure’s center of mass, which are eccentric relative to the seismic forces at the first level, induce significant torsional effects on the first level. Numerical simulations conducted to explore this aspect confirmed the validity of this conclusion. For the sake of brevity, these simulations are not presented in the paper.

In contrast, System two is derived from the stand-alone structure by adding both structural elements with appropriate stiffness and virtual masses through inerter devices. This approach enhances the ability to modify the characteristics of the coupled structure. Specifically, beyond the capacity to shift the mass center, as explained above, there is also the possibility to adjust the stiffness center to align it with the mass center of the structure. This coincidence can be achieved by appropriately distributing the stiffness of the external auxiliary structures. As previously mentioned, this mechanism is similar to that provided by base isolation. Such capability enhances the performance of System two compared to System 1, as confirmed by the numerical simulations shown in Section 5.3.

However, the virtual mass of the inerter device needs to be sufficiently large to significantly alter the structural modes. When the virtual mass reaches 50 times the mass of the first floor, it may correspond to 10 times the total mass of the structure. Even considering the mass amplification effect of the inerter device, achieving such magnitude is quite challenging. Additionally, employing additional stiffness or reducing stiffness (seismic isolation) may provide a more cost-effective and feasible means to adjust the center of stiffness. Consequently, the practical implementation of the studied protection strategy would be justified only in cases when interventions on the internal part of the building to be protected are prohibitive and there is a compelling need to operate on the outside of the structure.

6 Conclusion

Using low-dimensional mechanical models is a classical approach in Structural Mechanics to capture the predominant dynamic and seismic response of actual structures. Often, such models are employed to investigate the effectiveness of various external devices in enhancing the dynamic and seismic performance of different types of structures. Typically, these studies utilize planar models to capture the primary in-plane seismic response of frame structures.

In this paper, a low-dimensional spatial model has been used to investigate the seismic response of a general frame structure. This model represents a two-level frame structure, assuming the floor slabs are infinitely rigid within their own plane. Consequently, the model has six degrees of freedom, three for each level. The mechanical properties of the low-dimensional model have been calibrated to be dynamically equivalent to actual structures, using an established equivalence criterion.

Two different methods for enhancing the seismic response of a three-dimensional (3D) frame structure have been proposed. The first approach involves directly attaching inerter devices to the structure, while the second connects the structure to external auxiliary structures equipped with inerters. The developed 3D model enabled a detailed examination of the torsional effects acting on the frame structure and the effectiveness of both methods in reducing these torsional effects.

The equations of motion for three distinct mechanical systems have been derived using a Lagrangian approach. Specifically, the first system pertains to the stand-alone frame structure; the second incorporates inerter devices applied directly to the first level of the frame; and the third involves external auxiliary structures connected to the first level, each equipped with inerter devices.

The responses of the original stand-alone frame structure and those with the two proposed methods have been compared to assess the effectiveness of each approach. Three different earthquake records have been used as base excitation. These records were chosen due to their proven ability in previous studies by the authors to induce distinct dynamic responses, attributed to their differing spectral characteristics.

The results have been presented in performance curves and maps, illustrating the outcomes of an extensive parametric analysis in terms of the frame structure’s displacements and drifts.

The main elements of novelty of the proposed research can be summarised as follows.

• A low-dimensional, dynamically equivalent 3D mechanical model of an actual frame structure has been used to evaluate the seismic response, also accounting for the structural torsional motion.

•Two original, distinct structural schemes, both incorporating inerter devices, have been developed with the aim of reducing the seismic response of a frame structure.

•The effects on the seismic response due to the alignment of the stiffness and mass centers of the structure by adjusting the distribution of virtual mass and stiffness in the inerter devices and external auxiliary structures have been investigated.

The analyses performed to verify the effectiveness of the proposed protection methods led to the following relevant findings.

•Both the proposed structural schemes, named System one and System 2, perform efficiently since they both reduce the seismic response of the frame structure in a wide range of their mechanical parameters.

•The maximum reductions of the displacement of the first level (that is directly connected to the inerters or the external structure) and the drift of the superstructure never occur for the same values of the parameters. Therefore, design choices have to achieve a trade-off between these two objectives.

•The ability to align the mass center with the stiffness centers at the first level by appropriately adjusting the distribution of virtual masses provided by the inerters results in worse structural performance compared to the stand-alone frame structure.

•The capability offered exclusively by System two to align the stiffness and mass centers of the structure, achieved by appropriately distributing the stiffness of the external structures, leads to an improved seismic performance by reducing both displacements and torsional effects at each level.

For a comprehensive assessment of practical applicability on a specific structure, several limitations of the proposed approach should be addressed. In particular, ground motions should be selected and scaled according to seismic code provisions, hazard levels, and target spectra. Future research will address this by incorporating code-compliant inputs for more rigorous performance evaluation of the proposed protection systems. A second issued to be addressed is the assumption of infinitely rigid floor diaphragms that is not suitable for structure with significant floor deformability, such as structures having internal courts or timber structures. For these structures, the floor deformability makes the structure unsuitable for the proposed protection mechanism. Additionally, the current analysis assumes linear behavior for both the structure and damping devices to enable clearer interpretation of the fundamental mechanisms. While this is appropriate for preliminary studies, future work will consider nonlinear effects to improve realism and applicability under extreme seismic demands. Notably, the proposed strategy for enhancing the seismic performance of 3D frame structures could also be applied to improve the performance of piping systems, and ongoing studies are investigating this potential application.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AD: Writing – original draft, Formal Analysis, Writing – review and editing, Investigation, Software, Visualization, Conceptualization. AC: Visualization, Writing – review and editing, Formal Analysis, Investigation, Conceptualization, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is partially funded by the European Union - Next-Generation EU, Mission 4 Component 2 Investment 1.1, in the framework of the project PRIN 2022 PNRR, \P2022ZT5X5 - SmartUnder-Ground Infra-Structures for Secure Communities and Post-Disaster Emergency Response: Eco-Friendly Seismic Protection Solutions” (CUP: E53D2301762 0001, University of L'Aquila.The research in this paper was partially sponsored by the National Natural Science Foundation of China (Grant Nos. W2433120).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2025.1607520/full#supplementary-material

References

American Society of Civil Engineers (2022). Minimum design loads and associated criteria for buildings and other structures. Reston, Virginia. asce/sei 7-22 edition.

Google Scholar

Anagnostopoulos, S. A., Kyrkos, M., and Stathopoulos, K. (2015). Earthquake induced torsion in buildings: critical review and state of the art. Earthq. Struct. 8 (2), 305–377. doi:10.12989/eas.2015.8.2.305

CrossRef Full Text | Google Scholar

Botis, M. F., Cerbu, C., and Shi, H. (2018). “Study on the reduction of the general/overall torsion on multi-story, rectangular, reinforced concrete structures,” in Proceedings of the 3rd China-Romania science and technology seminar (CRSTS) (Brasov, Romania: Transilvania University).

Google Scholar

Brzeski, P., Kapitaniak, T., and Perlikowski, P. (2015). Novel type of tuned mass damper with inerter which enables changes of inertance. J. Sound Vib. 349, 56–66. doi:10.1016/j.jsv.2015.03.035

CrossRef Full Text | Google Scholar

Dadkhah, M., Kamgar, R., Heidarzadeh, H., Jakubczyk-Gałczyńska, A., and Jankowski, R. (2020). Improvement of performance level of steel moment-resisting frames using tuned mass damper system. Appl. Sci. 10 (10), 3403. doi:10.3390/app10103403

CrossRef Full Text | Google Scholar

De Domenico, D., Impollonia, N., and Ricciardi, G. (2018). Soil-dependent optimum design of a new passive vibration control system combining seismic base isolation with tuned inerter damper. Soil Dyn. Earthq. Eng. 105, 37–53. doi:10.1016/j.soildyn.2017.11.023

CrossRef Full Text | Google Scholar

De Domenico, D., and Ricciardi, G. (2018). An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq. Eng. Struct. Dyn. 47 (5), 1169–1192. doi:10.1002/eqe.3011

CrossRef Full Text | Google Scholar

De la Llera, J. C., and Chopra, A. K. (1995). Understanding the inelastic seismic behaviour of asymmetric-plan buildings. Earthq. Eng. and Struct. Dyn. 24 (4), 549–572. doi:10.1002/eqe.4290240407

CrossRef Full Text | Google Scholar

Den Hartog, J.-P. (1956). Mechanical vibrations. 4th edn. New York: McGraw-Hill.

Google Scholar

Di Egidio, A., and Contento, A. (2022). Improvement of the dynamic and seismic behaviour or rigid block-like structures with a hysteretic mass damper coupled with an inerter. Appl. Sci. 127 (22), 11527. doi:10.3390/app122211527

CrossRef Full Text | Google Scholar

Di Egidio, A., and Contento, A. (2023). Seismic benefits from coupling frame structures with a hysteretic mass damper inerter. Appl. Sci. 13 (8), 5017. doi:10.3390/app13085017

CrossRef Full Text | Google Scholar

Di Egidio, A., Pagliaro, S., and Contento, A. (2022a). Elasto-plastic short exoskeleton to improve the dynamic and seismic performance of frame structures. Appl. Sci. 12 (20), 10398. doi:10.3390/app122010398

CrossRef Full Text | Google Scholar

Di Egidio, A., Pagliaro, S., and Contento, A. (2022b). Seismic benefits of deformable connections between a frame structure and an external structure with inerter. Eng. Struct. 256, 114025. doi:10.1016/j.engstruct.2022.114025

CrossRef Full Text | Google Scholar

Di Egidio, A., Pagliaro, S., and Contento, A. (2023). Seismic performance of frame structure with hysteretic intermediate discontinuity. Appl. Sci. 13, 5373. doi:10.3390/app13095373

CrossRef Full Text | Google Scholar

Fabrizio, C., de Leo, A. M., and Di Egidio, A. (2017b). Structural disconnection as a general technique to improve the dynamic and seismic response of structures: a basic model. Procedia Eng. 199, 1635–1640. doi:10.1016/j.proeng.2017.09.086

CrossRef Full Text | Google Scholar

Fabrizio, C., de Leo, A. M., and Di Egidio, A. (2019). Tuned mass damper and base isolation: a unitary approach for the seismic protection of conventional frame structures. J. Eng. Mech. 145 (4). doi:10.1061/(asce)em.1943-7889.0001581

CrossRef Full Text | Google Scholar

Fabrizio, C., Di Egidio, A., and de Leo, A. M. (2017a). Top disconnection versus base disconnection in structures subjected to harmonic base excitation. Eng. Struct. 152, 660–670. doi:10.1016/j.engstruct.2017.09.041

CrossRef Full Text | Google Scholar

Giaralis, A., and Taflanidis, A. A. (2018). Optimal tuned mass-damper-inerter (TMDI) design for seismically excited MDOF structures with model uncertainties based on reliability criteria. Struct. Control Health Monit. 25 (2), e2082. doi:10.1002/stc.2082

CrossRef Full Text | Google Scholar

Harbic, C., Cismas, C., Dubasaru, V., and Botis, M. (2011). Aspects regarding reduction of general torsion in the structures of the braşov campus. Bull. Transilvania Univ. Braşov, Ser. I Eng. Sci. 4, 153–160. Available online at: https://webbut.unitbv.ro/index.php/Series_I/article/view/6200

Google Scholar

Kamgar, R., Dadkhah, M., Heidarzadeh, H., and Seidali Javanmardi, M. (2025). Utilizing tuned mass damper for reduction of seismic pounding between two adjacent buildings with different dynamic characteristics. Soil Dyn. Earthq. Eng. 188, 109036. doi:10.1016/j.soildyn.2024.109036

CrossRef Full Text | Google Scholar

Kamgar, R., Gholami, F., Zarif Sanayei, H. R., and Heidarzadeh, H. (2020). Modified tuned liquid dampers for seismic protection of buildings considering soil-structure interaction effects. Iran. J. Sci. Technol. Trans. Civ. Eng. 44 (1), 339–354. doi:10.1007/s40996-019-00302-x

CrossRef Full Text | Google Scholar

Kamgar, R., Samea, P., and Khatibinia, M. (2018). Optimizing parameters of tuned mass damper subjected to critical earthquake. Struct. Des. Tall Special Build. 27 (7), e1460. doi:10.1002/tal.1460

CrossRef Full Text | Google Scholar

Kelly, J. (1995). Base isolation: linear theory and design. Earthq. Spectra 6 (2), 223–244. doi:10.1193/1.1585566

CrossRef Full Text | Google Scholar

Khatibinia, M., Gholami, H., and Kamgar, R. (2018). Optimal design of tuned mass dampers subjected to continuous stationary critical excitation. Int. J. Dyn. Control 6 (3), 1094–1104. doi:10.1007/s40435-017-0386-7

CrossRef Full Text | Google Scholar

Lim, H. K., Kang, J. W., Pak, H., Chi, H. S., Lee, Y. G., and Kim, J. (2018). Seismic response of a three-dimensional asymmetric multi-storey reinforced concrete structure. Appl. Sci. 8, 479. [Green Version]. doi:10.3390/app8040479

CrossRef Full Text | Google Scholar

Makris, N., and Kampas, G. (2016). Seismic protection of structures with supplemental rotational inertia. J. Eng. Mech. 142 (11). doi:10.1061/(asce)em.1943-7889.0001152

CrossRef Full Text | Google Scholar

Málaga-Chuquitaype, C. (2021). Strong-motion duration and response scaling of yielding and degrading eccentric structures. Earthq. Eng. and Struct. Dyn. 50 (1), 123–137. doi:10.1002/eqe.3350

CrossRef Full Text | Google Scholar

Manish, A. K., and Syed, Z. I. (2017). Seismic analysis of torsional irregularity in multi-storey symmetric and asymmetric buildings. Eurasian J. Anal. Chem. 13, 286–292. Available online at: https://eurasianjournals.com/index.php/ej/article/view/847/847

Google Scholar

Marian, L., and Giaralis, A. (2014). Optimal design of a novel tuned mass-damper-inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Eng. Mech. 38, 156–164. doi:10.1016/j.probengmech.2014.03.007

CrossRef Full Text | Google Scholar

Maske, S. G., and Pajgade, P. S. (2013). Torsional behaviour of asymmetrical buildings. Int. J. Mod. Eng. Res. (IJMER) 3, 1146–1149. Available online at: http://www.ijmer.com.

Google Scholar

Mazza, F., Donnici, A., and Labernarda, R. (2024). Structural and non-structural numerical blind prediction of shaking table experimental tests on fixed-base and base-isolated hospitals. Earthq. Eng. and Struct. Dyn. 53 (10), 2961–2987. doi:10.1002/eqe.4146

CrossRef Full Text | Google Scholar

Mazza, F., and Labernarda, R. (2022). Internal pounding between structural parts of seismically isolated buildings. J. Earthq. Eng. 26 (10), 5175–5203. doi:10.1080/13632469.2020.1866122

CrossRef Full Text | Google Scholar

Miranda, J. C. (2005). On tuned mass dampers for reducing the seismic response of structures. Earthq. Engng. Struct. Dyn. 34 (7), 847–865. doi:10.1002/eqe.461

CrossRef Full Text | Google Scholar

Osteraas, J., and Krawinkler, H. (1989). The Mexico earthquake of september 19, 1985—behavior of steel buildings. Earthq. Spectra 5 (1), 51–88. doi:10.1193/1.1585511

CrossRef Full Text | Google Scholar

Pagliaro, S., and Di Egidio, A. (2022a). Archetype dynamically equivalent 3-d.o.f. model to evaluate seismic performances of intermediate discontinuity in frame structures. J. Eng. Mech. 148 (3). doi:10.1061/(asce)em.1943-7889.0002083

CrossRef Full Text | Google Scholar

Pelletier, K., and Leger, P. (2017). Nonlinear seismic modeling of reinforced concrete cores including torsion. Eng. Struct. 136, 380–392. doi:10.1016/j.engstruct.2017.01.042

CrossRef Full Text | Google Scholar

Pietrosanti, D., De Angelis, M., and Basili, M. (2017). Optimal design and performance evaluation of systems with tuned mass damper inerter (TMDI). Earthq. Eng. Struct. Dyn. 46 (8), 1367–1388. doi:10.1002/eqe.2861

CrossRef Full Text | Google Scholar

Pietrosanti, D., De Angelis, M., and Basili, M. (2020). A generalized 2-DOF model for optimal design of MDOF structures controlled by Tuned Mass Damper Inerter (TMDI). Int. J. Mech. Sci. 185, 105849. doi:10.1016/j.ijmecsci.2020.105849

CrossRef Full Text | Google Scholar

Prakash, S., and Jangid, R. S. (2022). Optimum parameters of tuned mass damper-inerter for damped structure under seismic excitation. Int. J. Dyn. Control 10, 1322–1336. doi:10.1007/s40435-022-00911-x

CrossRef Full Text | Google Scholar

Rana, R., and Soong, T. T. (1998). Parametric study and simplified design of tuned mass dampers. Eng. Struct. 20 (31), 193–204. doi:10.1016/s0141-0296(97)00078-3

CrossRef Full Text | Google Scholar

Reggio, A., and De Angelis, M. (2015). Optimal energy-based seismic design of non-conventional Tuned Mass Damper (TMD) implemented via inter-story isolation. Earthq. Eng. Struct. Dyn. 44 (10), 1623–1642. doi:10.1002/eqe.2548

CrossRef Full Text | Google Scholar

Rutenberg, A. (1992). Nonlinear response asymmetric building structures and seismic codes: a state of the art review. Amsterdam, Netherlands: Elsevier, 328–356.

Google Scholar

Salimi, R., Kamgar, M., and Heidarzadeh, H. (2021). An evaluation of the advantages of friction tmd over conventional tmd. Innov. Infrastruct. Solutions 6 (95), 95. doi:10.1007/s41062-021-00473-5

CrossRef Full Text | Google Scholar

Takewaki, I., Moustafa, A., and Fujita, K. (2012). Improving the earthquake resilience of buildings: the worst-case approach. Heidelberg, Germany: Springer.

Google Scholar

Taniguchi, T., Der Kiureghian, A., and Melkumyan, M. (2008). Effect of tuned mass damper on displacement demand of base-isolated structures. Eng. Struct. 30 (12), 3478–3488. doi:10.1016/j.engstruct.2008.05.027

CrossRef Full Text | Google Scholar

Thiers-Moggia, R., and Málaga-Chuquitaype, C. (2018). Seismic protection of rocking structures with inerters. Earthq. Eng. Struct. Dyn. 48 (5), 528–547. doi:10.1002/eqe.3147

CrossRef Full Text | Google Scholar

Tsai, H.-H. (1995). The effect of tuned-mass dampers on the seismic response of base-isolated structures. Int. J. Solid Struct. 32 (8/9), 1195–1210. doi:10.1016/0020-7683(94)00150-u

CrossRef Full Text | Google Scholar

Wang, J.-S., Hwang, S.-J., Chang, K.-C., Lin, M.-H., and Lee, B. H. (2013). Analytical and experimental studies on midstory isolated buildings with modal coupling effect. Earthq. Engng. Struct. Dyn., 42(2):201–219. doi:10.1002/eqe.2203

CrossRef Full Text | Google Scholar

Zalka, K. A. (2001). A simplified method for calculation of the natural frequencies of wall-frame buildings Eng. Struct. 23, 1544–1555. doi:10.1016/s0141-0296(01)00053-0

CrossRef Full Text | Google Scholar