A novel validation of satellite soil moisture using SM2RAIN-derived rainfall estimates

Despite the importance of soil moisture (SM) in various applications and the need to validate satellite SM products, the current in situ SM network is still inadequate, even for developed country such as the United States. Recently, SM2RAIN (Soil Moisture to Rain) algorithm has prominently emerged as a bottom-up approach to derive rainfall data from SM. In this study, we evaluated whether SM2RAIN algorithm and rain gauges, which are more abundant and readily available than in situ SM, can be used to validate satellite-based SMAP SM estimates. Since errors in SMAP SM propagate to SMAP-derived rainfall, the skills of SM2RAIN might be able to provide insights on the accuracy of SMAP SM observations. While the correlation between SM2RAIN skills and SMAP SM skills was found to be statistically significant, the strength of the correlation varied among different climate zones and annual rainfall classes. Specifically, weaker correlations were observed in arid and lower rainfall regions (median R value of 0.12), while stronger correlations were found in temperate and higher rainfall regions (median R value of 0.54). In term of over/under-estimation tendencies, 56% of the stations had the same tendencies (SM2RAIN skills and satellite SM skills both have positive or negative PBIAS value).

1 Introduction

Soil moisture (SM) is a key variable of the land-atmosphere interactions and provides valuable information for flood and drought monitoring (Lakshmi et al., 2023; Mishra et al., 2017; Sheffield et al., 2004), water resources management (López et al., 2017; Robinson et al., 2008; Vereecken et al., 2008), and agriculture applications (Hanson et al., 2000; Lawston et al., 2017). Over the past decades, satellite-based SM retrievals have been widely developed and utilized in numerous applications. These include SM retrieval from optical and thermal remote sensing instruments (e.g., Landsat, Moderate Resolution Imaging Spectroradiometer—MODIS) (Petropoulos et al., 2015), or from active/passive microwave instruments (e.g., Advanced Microwave Scanning Radiometer 2 (AMSR2) (Parinussa et al., 2015), Soil Moisture and Ocean Salinity (SMOS) (Kerr et al., 2012), and Soil Moisture Active Passive (SMAP) (Entekhabi et al., 2010). Additionally, other notable SM products are based on a merging scheme of multiple SM retrievals (Gruber et al., 2017; van der Schalie et al., 2017) or from assimilation of SM observations into hydrological or land surface model (Martens et al., 2017; Reichle et al., 2016).

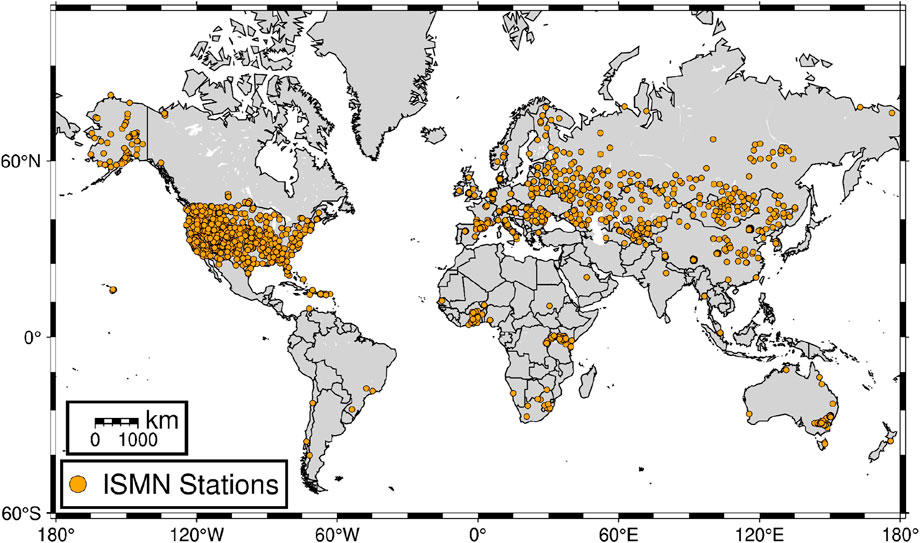
Numerous studies have validated different SM products using in situ SM measurement on both global and regional scale (Al-Yaari et al., 2019; Beck et al., 2021; Fang et al., 2020; Zhang et al., 2019a). These studies typically use the global network of SM measurement stations International Soil Moisture Network (ISMN) (Dorigo et al., 2011) The ISMN initiative is collaborative mechanism aimed at sharing and standardizing in situ SM data among worldwide researchers and organizations (Dorigo et al., 2011; Dorigo et al., 2021). However, the lack of in situ soil moisture data, especially in certain regions in the world, is primarily due to the higher costs associated with installing and maintaining SM stations compared to rain gauges (Du et al., 2022; Hrachowitz et al., 2013; Naeimi et al., 2013). Figure 1 shows the stations that have been included in the ISMN as of 2023. While certain areas such as Europe and the contiguous United States (CONUS) have dense and extensive networks of ground stations, regions like Southeast Asia, South America, and Africa have very few monitoring sites. Additionally, there is also a discrepancy in climate classes in ISMN datasets, with dominating number of stations and arid and cold region and limited number of stations in tropical and polar region (Beck et al., 2021).

Figure 1

Figure 1. Distribution of in situ stations in the International Soil Moisture Network (ISMN).

Triple collocation (Stoffelen, 1998), which can estimate the error variances of three or more geophysical measurement, has also been widely used to evaluate the relative uncertainties of SM products for global studies or for ungauged regions (Chen et al., 2018; Gruber et al., 2016; Xu et al., 2021). However, the assumptions of triple collocation (i.e., linearity, stationarity, error orthogonality, and zero cross-correlation) do not always hold true in practice (Gruber et al., 2016) and also generally underestimate the true random error of SM products (Yilmaz and Crow, 2014). Other notable approaches have relied on variables that have high correlations to SM such as remotely sensed vegetation greenness data (Tian et al., 2019) and evapotranspiration (Naeimi et al., 2013) for evaluation.

Among hydrological variables that can be used as proxy for SM evaluation, precipitation has been often used for indirect SM evaluation. Rain gauges, which are more affordable to set up and are received more attention than SM gauges, have been established for a longer time with better coverage across the globe (Menne et al., 2012a). Therefore, using rain gauge data can help with satellite SM evaluation in regions like South America or Southeast Asia where there are no or limited available in situ SM (Figure 1). While these regions are generally geopolitically ungauged or have a sparing network if in-situ data for both precipitation and SM, the lack of SM gauges is much more severe than that of rain gauges. Additionally, in data-rich regions like the CONUS and Europe, dense system of rain gauges can provide better evaluation for downscaled high-resolution SM products (Crow et al., 2022; Reichle et al., 2023). Past studies leveraged the inherent relationship between SM and rainfall to indirectly evaluate satellite SM. Notably, Crow (2007) and Crow et al. (2010) used the added value of SM assimilation for satellite precipitation correction to derive a linear proxy for true correlation. Additionally, Tuttle & Salvucci (2014) and Karthikeyan & Kumar (2016) used the natural sigmoidal relationship between SM and precipitation to derive mutual information which can be used to choose better SM products.

Additionally, another “bottom-up” approach called Soil Moisture to Rain (SM2RAIN) has been established to derive precipitation from satellite SM (Brocca et al., 2014; Brocca et al., 2015). As the soil can be considered a natural reservoir for measuring the amount of rainfall, SM2RAIN uses the soil water balance equation to estimate the rainfall rate from the changes in SM (Brocca et al., 2014). The method was applied to numerous satellite SM products such as Advanced SCATterometer (ASCAT) (Brocca et al., 2019) and SMAP (Koster et al., 2016) to derive continental- or global-scaled precipitation products. Nevertheless, to the best of our knowledge, no studies have utilized SM2RAIN for the evaluation of satellite SM. There existed studies that applied SM2RAIN to multiple sets of satellite SM products for the purpose of evaluating SM products’ skill in rainfall estimation and rainfall merging (Tarpanelli et al., 2017). However, these studies do not focus on the usage of SM2RAIN for satellite SM evaluation. From the past SM2RAIN studies, SM-derived rainfall provide good result in areas where SM retrievals are expected to be accurate (i.e., the skill of SM2RAIN is significantly dictated by the accuracy of SM retrieval) (Brocca et al., 2014).

In this study, we examined whether the relationship between SM2RAIN performance skill scores and satellite SM accuracy can be leveraged for evaluation of satellite SM without relying on in situ data. We chose CONUS as our study area due to the availability of in situ SM and rain gauges. SMAP Enhanced L2 Radiometer Half-Orbit 9 km SM product was chosen as satellite observations to evaluate. Additionally, while SM2RAIN algorithm has been extensively evaluated, most of the studies evaluated SM2RAIN with satellite SM (Brocca et al., 2019; Ciabatta et al., 2018; Koster et al., 2016). SM2RAIN studies using in-situ SM to validate the assumptions and inherent skills of the algorithm were only conducted in other region of the world (Brocca et al., 2015; Lai et al., 2022; Miao et al., 2023). In this study, we also focused on evaluating the skills of SM2RAIN algorithm using both in situ SM and satellite SM over the CONUS.

2 Data and methods

2.1 SMAP SM product

We used SMAP Enhanced L2 Radiometer Half-Orbit 9 km (SMAP_L2_SM_P_E) Version 3 SM as the satellite SM for evaluation in this study (ONeill et al., 2019). The SMAP mission from NASA, launched in 2015, is the first SM mission that contains both L-band radiometer and radar to combine active and passive microwave observations for high spatiotemporal resolution surface SM. Unfortunately, the active radar sensor on the SMAP satellite ceased operations a few months after its launch due to a component failure. Since then, various techniques have been developed to use multi-source data merging schemes to downscale SMAP SM observations to higher resolution (Brocca et al., 2023; Peng et al., 2017; Sabaghy et al., 2020). The SMAP_L2_SM_P_E product provides volumetric surface SM (0–5 cm) that is derived from SMAP brightness temperature (T_B) measurements. The product relies on the Backus-Gilbert interpolation method (Backus and Gilbert, 1967) to oversample SMAP T_B for higher spatial resolution and better accuracy. Downscaled SM is then derived from applying radiative transfer model to the downscaled 9-km T_B grid map (Chan et al., 2018). Before applying SM2RAIN to SMAP Enhanced Level 2 product, we filled the temporal gap in SM to obtain daily SMAP SM by discrete cosine transform and penalized least square regression (DCT-PLS) algorithm (Garcia, 2010). The algorithm has been widely used in other SM2RAIN studies for satellite SM gap filling (Miao et al., 2023; Saeedi et al., 2022). Both SMAP morning/descending (D) and afternoon/ascending (A) orbit retrievals, which have a temporal resolution of 2–3 days, were gap-filled and averaged to represent SMAP SM retrievals.

2.2 In situ SM measurements

We used in situ SM measurements (m³m⁻³) from the ISMN archive. ISMN is a global initiative dedicated to the collection, archiving, and dissemination of SM data for the purpose of scientific research and modelling (Dorigo et al., 2011; Dorigo et al., 2021). Different SM networks use different types of sensors [e.g., time domain-reflectometry, infrared thermometers, and capacitance censors (Vereecken et al., 2014; Walker et al., 2004)] and varying systems to measure and record observations. To standardize and insure the quality of SM records, the ISMN removes dubious and inconsistent SM observations and harmonizes data from different networks and organizations into the same time zone and measurement units (Dorigo et al., 2013). In addition to SM observations, some stations and networks also have soil and air temperature, precipitation, and snow water equivalent records.

In this study, in situ SM was obtained to both calibrate SM2RAIN parameters and evaluate satellite SM as benchmark for evaluation using SM2RAIN and rain gauge. We selected 775 stations (Figure 2) across the CONUS that contained at least 2 years of daily record length during either the SM2RAIN calibration (2011–2016) or the SM evaluation period (2017–2022). To calibrate and evaluate remote sensing SM which usually penetrate up to ∼5 cm of soil depth (Owe & Van De Griend, 1998), in situ SM measurements were selected only from sensors at a depth of $5cm\left(\pm 2cm\right)$ (Albergel et al., 2012; Beck et al., 2021; Wu et al., 2016). We also resampled SM records in the ISMN archive from their original hourly resolution to daily resolution. Along with SM records, the corresponding Koppen-Geiger climate classification and land cover of each station were provided by ISMN dataset. Information about in situ SM networks and stations selected in this study is summarized in Supplementary Table S1.

Figure 2

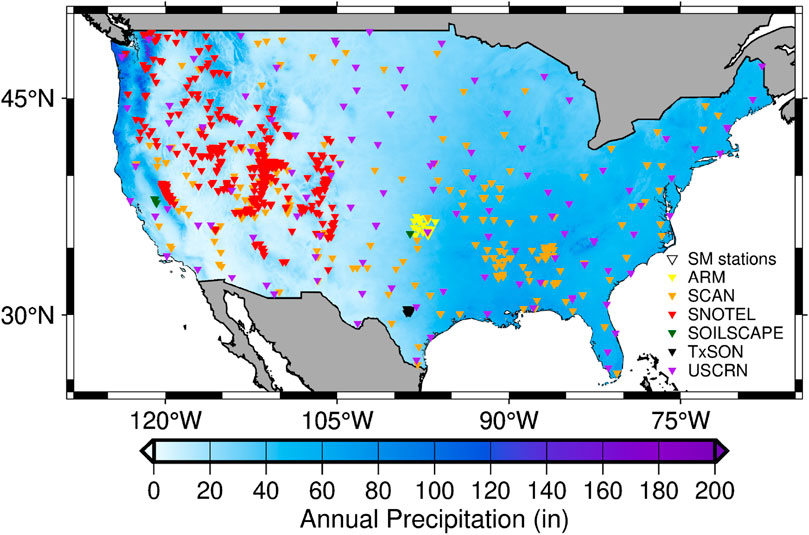
Figure 2. ISMN in situ SM networks and stations and the underlaying annual precipitation (Source: DAYMET) in CONUS. Darker blue color represents higher precipitation intensity.

2.3 Daymet dataset

We obtained in situ precipitation and temperature from the Daymet Version 3 data (accessed at https://daymet.ornl.gov/) (Thornton et al., 2016). Daymet dataset provides 1-km high resolution gridded daily surface weather data (e.g., precipitation, minimum and maximum temperature, vapor pressure) for North America from 1980 to present. The gridded output data is interpolated from in situ weather station data from the Global Historical Climatology Network-Daily (GHCN-Daily) (Menne et al., 2012b) by iterative estimation of local station density using the spatial convolution of a truncated Gaussian filter (Thornton et al., 1997).

2.4 SM2RAIN algorithm

Conventional methods for space-based rainfall estimation primarily rely on instantaneous data obtained from microwave radiometers, radars, and infrared sensor and use inversion techniques to correlate radiation with surface precipitation rates-a paradigm (Kidd and Levizzani, 2011). Such approaches, which can be referred to as “top-down,” require the merging of instantaneous rainfall measurements from multiple sensors. Therefore, the failure of one of the sensors may imply a significant degradation in the accuracy of the accumulated rainfall estimate due to the high temporal variability of rainfall (Trenberth and Asrar, 2012). Brocca et al. (2013) proposed a new “bottom-up” approach to quantify the rainfall estimates by observing the variation in time of the SM state called Soil Moisture To Rain (SM2RAIN). While top-down method might miss the peak precipitation event that occurs between satellite observations, SM2RAIN uses the soil as a natural gauge to indicate peak precipitation event (Saeedi et al., 2022). The algorithm was evaluated using in situ measurements (Brocca et al., 2014), and was applied to global satellite SM datasets and performed good results (Brocca et al., 2019; Filippucci et al., 2022; Koster et al., 2016). More information about SM2RAIN is available at http://hydrology.irpi.cnr.it/download-area/sm2rain-data-sets/and the code used in this study for SM2RAIN is found at https://github.com/IRPIhydrology/sm2rain.

The SM2RAIN algorithm has been formed based on the inversion of the soil water balance equation to estimate rainfall (Kirchner, 2009). The soil acts as a natural rain gauge, recording the quantity of rainfall that has fallen into the ground in which the expression of the equation is established as follows:

$nZ\frac{ds\left(t\right)}{dt}=p\left(t\right)-g\left(t\right)-r\left(t\right)-e\left(t\right)(1)$

with $n$ represents the soil porosity, $Z$ is the depth of soil layer with unit length L (mm), $s\left(t\right)$ is the relative saturation of the soil layer or relative SM, and $p\left(t\right),g\left(t\right),r\left(t\right),e\left(t\right)$ are precipitation, drainage, surface runoff, and evapotranspiration rate for each timestep $t$ of unit T (mm/day), respectively. SM2RAIN assumes that during a rainfall event, evapotranspiration rate is negligible (i.e., $e\left(t\right)=0$) and that all precipitation infiltrates into soil (i.e., $r\left(t\right)=0$) (Brocca et al., 2013). Surface runoff $r\left(t\right)$, drainage $g\left(t\right)$, and evapotranspiration rate $e\left(t\right)$ can be expressed as a function of precipitation $p\left(t\right)$ and SM $s\left(t\right)$ as followed:

$r\left(t\right)=p\left(t\right)s{\left(t\right)}^c(2)$

$g\left(t\right)=as{\left(t\right)}^b(3)$

$e\left(t\right)={ET}_{pot}\left(t\right)s\left(t\right)(4)$

${ET}_{pot}\left(t\right)=-2+1.26\left[\xi \left(0.46T_a\left(t\right)+8.13\right)\right](5)$

where a (L/T), b (−), and c (−) are the empirical parameters for calibration, and ${ET}_{pot}\left(t\right)$ is the potential evapotranspiration that depends on air temperature $T_a\left(t\right)$ (°C) and $\xi$ that represents the percentage of total daytime hours for the chosen period (daily or monthly) out of the entire daytime hours in a year (Brocca et al., 2015; Massari et al., 2017). To derive precipitation at each time step $p\left(t\right)$ from SM $s\left(t\right)$, Equation 1 can be arranged as:

$p\left(t\right)=\frac{Z^{*}\frac{ds\left(t\right)}{dt}+as{\left(t\right)}^b+{ET}_{pot}\left(t\right)s\left(t\right)}{1-s{\left(t\right)}^c}(6)$

where $Z^{*}$ is another parameter that represents soil layer water capacity that represents soil porosity $n$ and soil depth layer $Z$. With the assumption of negligible evapotranspiration and runoff, rainfall estimation can be simplified as:

$p\left(t\right)=Z^{*}\frac{ds\left(t\right)}{dt}+as{\left(t\right)}^b.(7)$

Generally, SM2RAIN parameters are often calibrated with satellite SM and interpolated and gridded in situ or satellite rainfall data using the simplified SM2RAIN equation assuming negligible runoff and evapotranspiration (Equation 7). In this study, we instead calibrated SM2RAIN parameters with point-based in situ SM to derive SM2RAIN parameters that can be applied to multiple satellite SM products, instead of deriving the parameters from satellite SM. As this study only focuses on exploring the capability of the novel idea of using SM2RAIN for SM evaluation, we only used one single SM product (i.,e., 9-km SMAP observation) for the evaluation. For future application however, with one single set of parameters calibrated using in-situ SM, SM2RAIN can be applied to multiple SM products to evaluate their observations’ accuracy. Additionally, to reduce noises and errors in satellite SM, exponential filtering is usually applied to SM data and introduces new parameters T_base and T_pot to SM2RAIN (Brocca et al., 2019; Wagner et al., 1999). Because we calibrated SM2RAIN on in situ SM, only three parameters (Z, a, b) in Equation 7 were considered in this study.

2.5 Evaluate satellite SM using SM2RAIN and rain gauge

Essentially, since the SM2RAIN parameters were calibrated from in situ SM and precipitation data, we wanted to investigate whether the deviation of satellite SM-derived rainfall from in situ precipitation is primarily a result of differences between in situ and satellite SM measurements. To assess this assumption, we evaluated SMAP Level 2 9 km SM in two different ways: (1) direct evaluation using in situ SM, and (2) proxy evaluation of SM by comparing rainfall derived from SM2RAIN to rain gauge.

Figure 3 shows the framework of this study to evaluate SMAP SM through SM2RAIN. In situ SM records were divided into two periods: the calibration period from 2011 to 2016 and the satellite SM proxy evaluation period from 2017 to 2022. A total of 788 and 607 stations were selected for the calibration and satellite SM evaluation periods respectively. Similar to previous SM2RAIN studies, we divided the in situ stations into six classes based on annual rainfall (Brocca et al., 2014) and calibrated a set of SM2RAIN parameters for each group (Table 1). The rain classes are determined so that there is a relatively equal number of stations in each class. Though a majority of stations overlapped between the two periods, the SM2RAIN parameters were calibrated for a group of stations’ data records within the same annual rainfall class, instead of for each single station. Air temperature from Daymet was obtained to exclude winter freezing period (${\mathrm{T}}_a<0°$C) whereas the physical relationship between SM and precipitation is unrealistic due to thawing and freezing (Tuttle and Salvucci, 2014). Similar to previous studies (Brocca et al., 2014; Koster et al., 2016), SM data at each station was normalized between 0 and 1 to address the difference in ranges and SM minima at different locations. Additionally, two daily records with a 5-day gap were also excluded to maintain the consistency in the relationship between SM change and precipitation in SM2RAIN. Because of the unrealistic behavior of SM and precipitation at some stations, we performed SM2RAIN calibration on each single station to determine its compatibility with SM2RAIN. For each annual rainfall class, only half of the stations with better SM2RAIN simulation results would be selected for SM2RAIN calibration for the class.

Figure 3

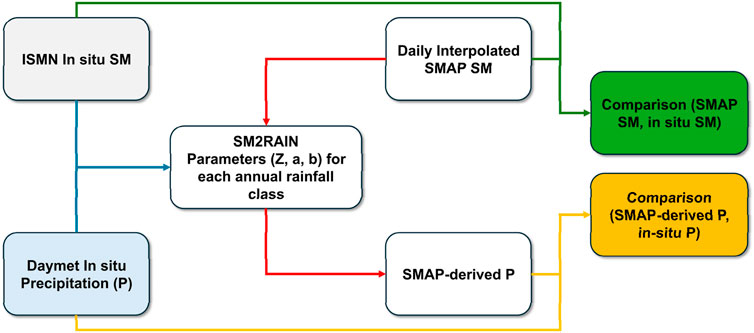
Figure 3. Proposed framework of evaluating SMAP SM using SM2RAIN and in situ precipitation (P). The actual skills of SMAP SM from using in situ SM are also obtained (green line). On the other hand, the skills of SMAP-derived P by applying SM2RAIN to SMAP SM is also derived (orange line). We investigate whether the skills of SMAP-derived P (orange box) can provide comparable performance on satellite SM skills (green box).

Table 1

Table 1. Number of stations in each annual rainfall classification for calibration period (2011–2016) and evaluation period (2017–2022).

As the study focuses on whether errors in SM2RAIN simulations can represent errors in satellite soil moisture (SM) data, we did not employ similar calibration approaches used in recent SM2RAIN studies that focus on producing the best SM-based rainfall estimates. In other studies, pixel-to-pixel calibration using satellite SM instead of annual rainfall classification was found to result in better rainfall estimates results (Filippucci et al., 2021; 2022). Nevertheless, as the study uses in-situ SM for calibration, pixel-to-pixel was not suitable and annual rainfall classification was selected.

We derived SM2RAIN SMAP precipitation during the evaluation period (2017–2022) by applying the rainfall class-specific calibrated SM2RAIN parameter values (Z, a, and b) to SMAP SM observations. Because SM2RAIN parameters were calibrated with daily in situ data, SMAP SM time series were also gap filled to daily temporal resolution using DCT-PLS algorithm. Daily rainfall simulations that were derived from SMAP SM using SM2RAIN algorithm (also known as SMAP-derived rainfall) were evaluated using daily DAYMET in situ precipitation at 607 available ISMN stations during the evaluation period (Table 1). Similar to the configuration for the calibration period, we excluded results at timesteps that have a gap of more than 5 days from the previous timestep and at timesteps with negative mean air temperatures (T_air from Daymet <0°C for the timestep). Additionally, because we wanted to use the evaluation of SMAP-derived rainfall as a potential substitute for in situ SM in validating satellite SM, two additional conditions were added to limit the inherent limitation of SM2RAIN and maximize the impacts of satellite SM accuracy on SMAP-derived rainfall’s skills. Firstly, precipitation simulations were aggregated by 3 days (i.e., the actual temporal resolution of SMAP SM) to minimize the errors and uncertainties in interpolated SMAP SM and SM2RAIN algorithm (Koster et al., 2016; Miao et al., 2023). Secondly, since SM2RAIN is known to underpredict the maximum rainfall after the soil is saturated, we excluded timesteps when in situ precipitation exceeds the maximum amount that SMAP-derived rainfall can simulate. The pair of in situ SM/SMAP SM and in situ precipitation/SMAP-derived precipitation were then evaluated separately. Finally, the results from the two evaluations were compared to assess whether the proxy evaluation using SM2RAIN rainfall can provide similar insights into SMAP SM performance as the direct evaluation using in situ SM.

We used three metrics in this study, including Pearson coefficient correlation (R), normalized Root Mean Square Error (NRMSE), and percent bias (PIBAS). The coefficient of correlation (R), ranging from −1 (perfect negative correlation) to 1 (perfect positive correlation), measures the strength and direction of the linear relationship between two variables and indicates how well the in situ data and simulation align in terms of temporal variability. The metric is widely used in both studies that evaluate satellite SM based on in situ records (Beck et al., 2021; Fang et al., 2020; Gruber et al., 2020) and studies that evaluate satellite precipitation and SM2RAIN rainfall products (Beck et al., 2017; Brocca et al., 2019). NRMSE is a metric that quantifies the magnitude differences between predicted and observed values, scaled to the range of observed values. This normalization allows for easy comparison of model performance across different datasets, providing a relative measure of prediction accuracy. Because SM and precipitation at different stations have varying ranges and distributions, RMSE must be normalized for evaluation across the CONUS. Additionally, because the errors from comparing SM to SM and precipitation to precipitation were being evaluated, the RMSE values from both evaluation methods needed to be normalized. Lastly, PBIAS quantifies the average tendency of predicted values to differ from observed values, expressed as a percentage, with positive values indicating overestimation and negative values indicating underestimation. Three metrics R, NRMSE, and PBIAS were used for both the calibration and SM proxy evaluation steps. In the calibration step, we used the mentioned metrics to evaluate SM2RAIN calibration and its skill. In the proxy evaluation, the metrics for both evaluation methods (i.e., from in situ SM, and from SM2RAIN SMAP-derived precipitation) were calculated and then compared.

3 Results and discussion

3.1 Evaluation of SM2RAIN model performance at each single station

Before recalibrating the parameters for six annual precipitation groups using only half of the stations with better performance, we applied SM2RAIN to daily SM records at each station that have at least 2 years of daily records during the 2011–2016 calibration period. Across 788 stations, the median R, NRMSE, and PBIAS of daily SM2RAIN simulations and observed precipitation are 0.54, 2.48, and −10%. The median correlation coefficient R is similar to that of previous studies that applied SM2RAIN on satellite SM for daily precipitation (Brocca et al., 2019; Ciabatta et al., 2016). Other studies that use in situ SM for SM2RAIN achieved higher R value by calibrating the parameters pixel-by-pixel wise with hourly SM and temporally aggregating rainfall simulation to daily timestep (Brocca et al., 2015; Miao et al., 2023). Nevertheless, since the SM2RAIN parameters would be then applied to daily satellite SM, we focused on the evaluation of SM2RAIN capacity on daily SM to daily precipitation timestep. The median PBIAS of −10% suggests that SM2RAIN generally underestimates rainfall amount. In theory, this could be due to the fact that at saturation, SM remains constant regardless of the rainfall event. Therefore, SM changes at saturation cannot capture the full amount of rainfall and generally underestimate precipitation (Brocca et al., 2014; Brocca et al., 2019). However, we found that the number of days that SM is saturated (higher than the 99.5% percentile) for consecutive days were minimal to make substantial impacts. Similar to previous studies (Brocca et al., 2019), for both in-situ and satellite SM data, we found the median number of consecutive days with saturated soil across all stations in a 6-year period (2017–2022) is 2 days across all stations. The underestimation of SM2RAIN is likely due to the noisy and volatile nature of SM when the soil is close to dry. When the parameters try to compensate for these durations (which occur more often than high rainfall event), it is difficult for SM2RAIN to simulate high rainfall rates.

We further divided the evaluation based on SM networks, climate classification, and annual rainfall class (Figure 4). Compared to the other selected SM networks, the Snow Telemetry (SNOTEL) Network (Leavesley et al., 2008) has a considerably lower median R value of 0.43. This could be the effect of rain gauges underestimating snowfall by up to 90% because of wind-induced undercatch in mountainous and snow-dominated regions (Beck et al., 2020; Rasmussen et al., 2012). Therefore, rainfall measurements at SNOTEL stations, which are located in remote, high-elevation mountain watersheds, can suffer from gauge undercatch and orographic effects, resulting in a discrepancy between SM and the rainfall records. Additionally, for these cold mountainous stations, snowmelt can significantly impact the skills of SM2RAIN estimates. After snow melts, SM increases, leading to false rainfall estimate by SM2RAIN. While timesteps with negative air temperatures were already excluded from the study, SM2RAIN performance following winter conditions can worsen due to snowmelt. On the other hand, Texas Soil Observation Network (TxSON) (Caldwell et al., 2019) presents the best R value (median R = 0.74) with low variance. However, this could also be due to the lower number of stations (n = 38) in the network during the calibration period. In terms of climate classification, SM2RAIN performs relatively better in temperate climate with median R of 0.64. This aligns with past studies’ findings, which could be ascribed to lower variations of SM in temperate climate resulting in better inversion of data through SM2RAIN algorithms (Brocca et al., 2015). Besides, SM2RAIN performance does not differ significantly among different annual rainfall classes. For all distributions of R values, we observed a long and narrow lower tail (i.e., extremely low correlation), indicating that there were a few stations where SM2RAIN could not capture the relationship between SM and precipitation or where there are significant issues with the reliability of in-situ SM data (e.g., missing data, sudden and drastic rise/drop in SM).

Figure 4

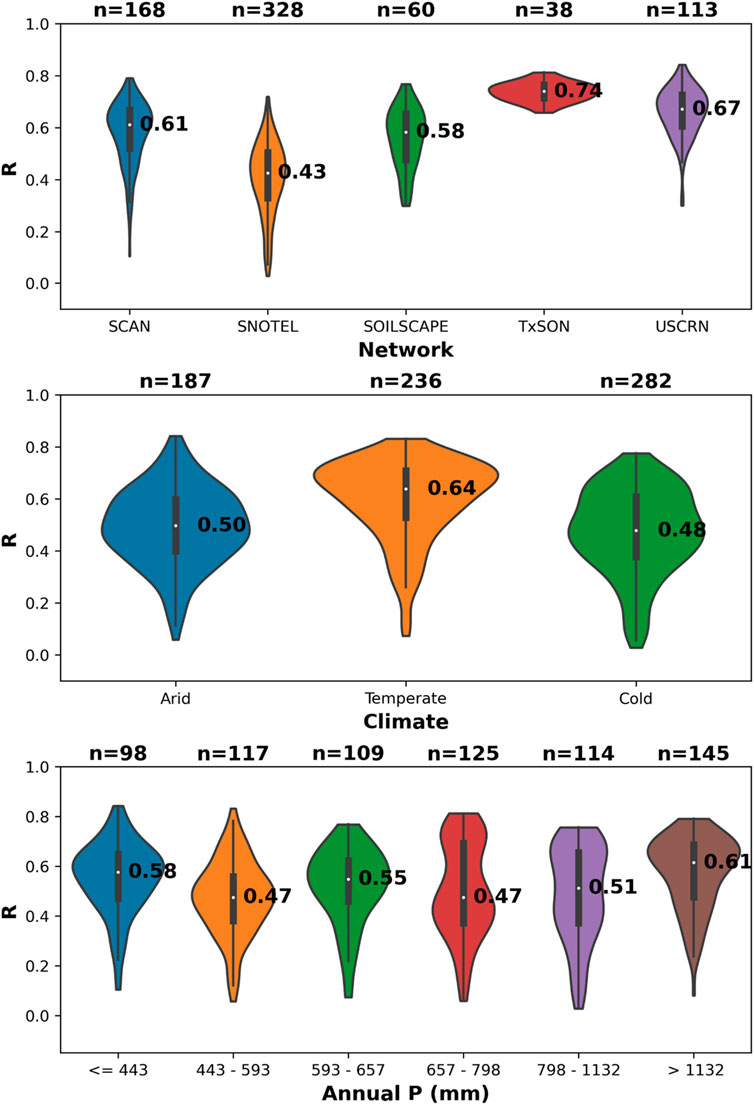
Figure 4. Violin plots of correlation coefficients (R) for SM2RAIN rainfall at each single station during the calibration period (2011–2016) for different networks, climate zones, and annual rainfall classes.

Figure 5 shows the spatial distribution of SM2RAIN skill metrics. Stations at temperate and cold climate regions in the east side of the U.S. achieved satisfactory results with good R value and low NRMSE. More variations in R and NRMSE metrics could be observed in the western U.S. due to more complex climate patterns and mountain ranges. Stations with the lowest R values could be observed along the Cascade and Sierra Mountain ranges and the Rocky Mountain ranges, which could be the result of high mountain rain gauge undercatch and the effect of snow on SM data quality (Ciabatta et al., 2016). We also noted that the stations with exceptionally high NRMSE (>5) at the Sierra Nevada mountain ranges near the southeastern border of California were mainly due to the very low annual precipitation at these stations (from 50 to 231 mm/year) and high elevation gauge undercatch. In terms of PBIAS, substantial underestimation of rainfall (negative PBIAS) was also observed at the mountain ranges. In addition, the majority of stations where SM2RAIN overestimated (positive PBIAS) could be observed mainly in temperate regions near the coast.

Figure 5

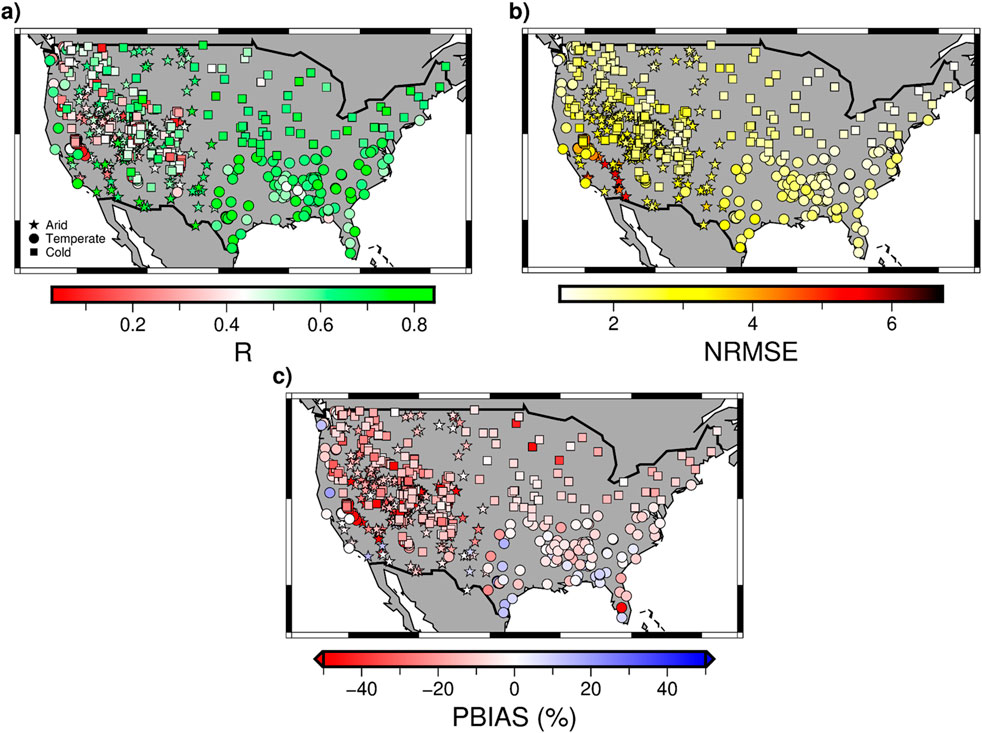
Figure 5. Spatial distribution of (A) correlation coefficient (R), (B) normalized root mean squared error (NRMSE), and (C) percent bias (PBIAS) for SM2RAIN rainfall at each single station during the calibration period (2011–2016). The stations are represented by their climate zone classification.

To investigate the stations where bad SM2RAIN results were achieved, we looked at the behavior between SM and precipitation. The relationship between two variable is expressed as E[P∣_SM], or the conditional expected value of precipitation given SM. From past studies, the expected value of mean precipitation based on SM should follow a steep, convex-concave shape of sigmoidal behavior with a convex shape at low SM and a concave shape at high SM (Karthikeyan & Kumar, 2016; Tuttle and Salvucci, 2014). This behavior is attributed to the cumulative effects of exponential growth curve dependence of evapotranspiration and surface runoff on SM. This behavior, consistent with the SM2RAIN soil water balance equation (Equations 1–6), was also observed when comparing the differences in the SM-precipitation relationship at stations where SM2RAIN performed well versus those where it did not.

Figure 6 shows the stations-wide average of mean-normalized precipitation conditionally averaged according to SM cumulative distribution at 50 stations with the highest R values and the 50 stations with the lowest R values of SM2RAIN calibration. The grey shading, which represents one standard error of the estimated mean precipitation at each SM percentile, is calculated as $\frac{{\sigma }_{Precip}}{\sqrt{N}}$, where N is the number of observations at each percentile). At the stations with good SM2RAIN results, the E[P∣_SM] curve follows the sigmoidal curve with minimal uncertainties, showing that SM-precipitation relationships follow the expected behavior, and that representation of evapotranspiration and runoff can be estimated by the exponential growth of SM. At these stations, the changes in SM are well represented by precipitation. On the other hand, at the 50 stations with the worst R values for SM2RAIN, we observed substantially more uncertainty and unrealistic SM-precipitation relationships. Though the steep convex-concave curve was still presented at high SM, changes in SM in the middle of the curve are shown to not be well represented by precipitation. This could be due to errors in in-situ SM data, especially in long-term and decade-old monitoring records. The in-situ SM records, which are less reliable than rainfall records due to the additional complexities in measuring SM, may suffer from incorrect instrument calibration, missing data, sudden record jumps, and unstable seasonal variability. While great efforts were made in ISMN’s quality control assurance (Dorigo et al., 2013; Dorigo et al., 2021), the potential errors from measurement and missing data can lead to unrealistic relationship between SM and precipitation records. The uncertainty and unrealistic behavior in SM-precipitation relationships could also be the results of high mountain rain gauge undercatch and snow effect.

Figure 6

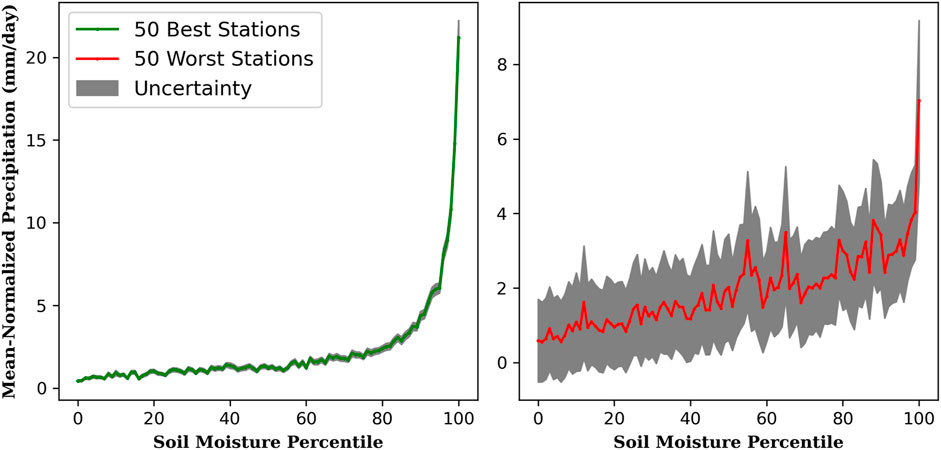
Figure 6. Station-wide average of all mean-normalized precipitation conditionally averaged according to soil moisture percentile E[P∣_SM] for 50 best stations with highest SM2RAIN R values (green line) and for 50 worst stations with lowest SM2RAIN R values. SM was transformed into 0–100 percentile (x-axis) and the curve represents the average expected value of precipitation across all stations (y-axis) for each SM percentile. The grey shading represents one standard error of the E[P∣_SM] at each percentile.

3.2 SM2RAIN calibration and SMAP-derived precipitation

To exclude stations with unrealistic SM-precipitation behavior and record errors, we only selected half of the stations of each annual rainfall class with the best R value for SM2RAIN calibration. Then, the SM2RAIN parameters were recalibrated using in-situ SM (from ISMN) and precipitation (from Daymet) during the 2011–2016 period. Table 2 shows the SM2RAIN parameter values (Z, a, and b) obtained from the recalibration using only the “better half” of the stations. The values of parameters Z and a generally increase with annual rainfall, which is expected since SM is normalized between 0 and 1. The value of parameter b, on the other hand, ranges from 1.15 to 3.93 depending on different rainfall classes. Similar to previous studies (Brocca et al., 2014), the values of a and b were obtained anomalously high for the lowest annual rainfall class, which are likely due to the smaller magnitude change in SM in these areas.

Table 2

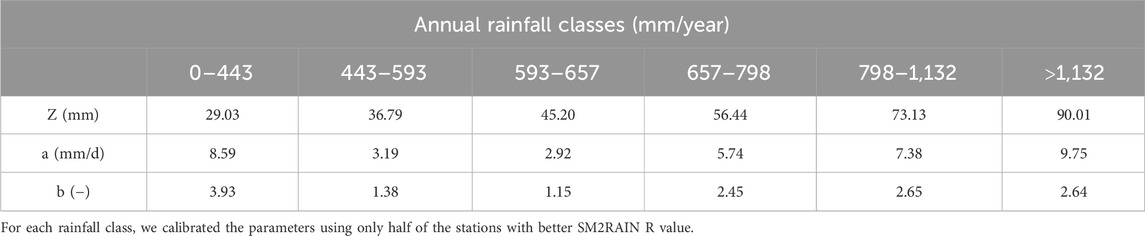
Table 2. SM2RAIN parameters Z, a, and b for different annual rainfall class that were calibrated using in situ SM and precipitation during the calibration period (2011–2016).

These parameters were then applied to SMAP SM during the evaluation period (2017–2022) to derive daily SMAP-derived precipitation. The median R, NRMSE, and PBIAS of daily SMAP-derived rainfall using SM2RAIN were 0.43, 2.74, and −16%, respectively, during the 2017–2022 period (Supplementary Figure S1). Compared to the SM2RAIN during calibration period (2011–2016) using in-situ SM, SM2RAIN during the evaluation period (2017–2022) using SMAP SM also has tendency to underestimate rainfall (negative PBIAS) but generally performs worse. The increase in errors of SMAP-derived SM2RAIN rainfall may come from many factors. Firstly, the spatial resolution mismatch during evaluation period (9 km SMAP SM versus point-scale in situ SM and 1 km DAYMET precipitation) can have substantial effects due to the spatial heterogeneity of SM (Grayson et al., 1997; Lei et al., 2014; Wang et al., 2016). Secondly, although SMAP SM was interpolated to daily timestep, the DCT-PLS gap filling could not fully capture the temporal variability of SM, leading to uncertainties that could propagate into SM2RAIN errors. Thirdly, the deviations of SMAP SM from in situ SM contributed to the deviation of SMAP-derived rainfall from in situ precipitation. In this study, we aimed to investigate whether these deviations of satellite SM from in situ SM had a substantial impact on SM2RAIN’s simulation accuracy. Our goal was to determine if evaluating satellite SM-derived precipitation could provide a reliable indication of the performance of satellite SM.

To alleviate the effects of DCT-PLS interpolation and SM2RAIN inherent limitation (e.g., underestimation of rainfall peak after soil is saturated), SMAP-derived simulated and observed precipitation were aggregated by 3 days and timesteps where in situ rainfall exceeded the SMAP-derived maximum rainfall were excluded (an average of less than 1% of timesteps excluded across all stations). The median R, NRMSE, and PBIAS of 3-day aggregated SMAP-derived rainfall with simulated maximum rainfall exclusion were 0.55, 1.65, and +7%. With the timestep aggregation, the errors in SM2RAIN and SMAP SM interpolation were reduced (Lai et al., 2022). More importantly, SMAP-derived rainfall simulations’ skill became more dependent on the accuracy of satellite SM. After excluding records that exceeded the maximum amount SM2RAIN could predict, the remaining SMAP-derived rainfall simulations were shown to have overestimation tendencies (positive PBIAS). These are more in line with SMAP SM’s overestimation trend when being compared to in situ SM (shown in Section 3.3). Figure 7 shows the violin plot of SMAP-derived rainfall R metrics when being compared to in situ precipitation (NRMSE and PBIAS metrics plots are shown in the Supplementary Material).

Figure 7

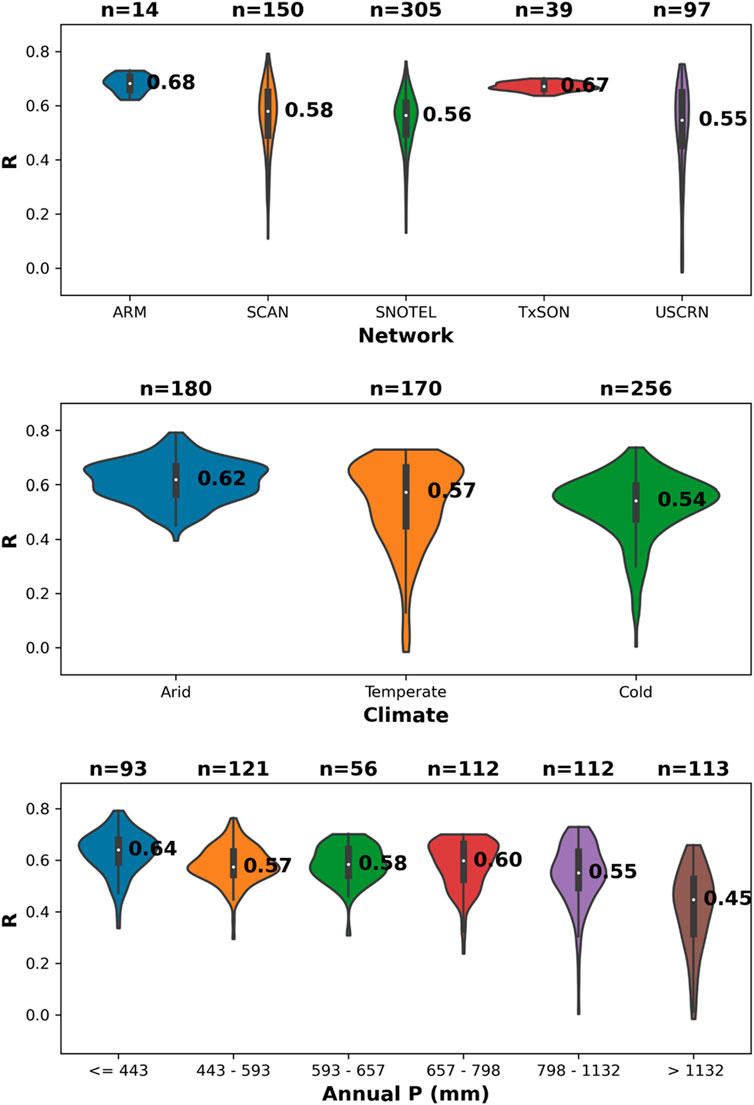
Figure 7. Violin plots of correlation coefficients (R) for 3-day aggregated and simulated maximum rainfall exclusion SMAP-derived precipitation for different networks, climate zones, and annual rainfall classes.

Long narrow tail for SCAN, SNOTEL, and USCRN networks suggest that even with the 3-day aggregation, there are some anomalous stations where it is extremely difficult to derive precipitation from SM. Better metrics and smaller variances among stations were observed for the ARM and TxSON networks; however, this could be due to the smaller sample sizes of stations in these two networks. While SM2RAIN performed better for temperate climate when using in situ SM, we observed better R value and less variances in skills in arid climate stations compared to stations in temperate and cold climates for SMAP-derived rainfall. This aligns with past studies that found SM2RAIN products (that use global satellite SM) performed better than other precipitation datasets in arid/semi-arid and low rainfall regions (Tran et al., 2023). However, slightly better NRMSE and PBIAS metrics were obtained for stations with temperate climates. In cold climate regions, we observed higher positive PBIAS (median PBIAS of +5%), which is likely the result of gauge undercatch in cold mountainous stations and the effect of snowmelt leading to false positive rainfall estimates. In terms of annual rainfall classes, lower rainfall classes (which mostly reside in arid climate) have better R value but have the tendencies to underestimate rainfall. On the other hand, SMAP-derived rainfall at stations in the highest annual rainfall classes (>800 mm/year) were found to have the worst R values and tendencies to overestimate.

Compared to the SM2RAIN results during the 2011–2016 period using in-situ SM (Figure 5 in Section 3.1), the SM2RAIN results using SMAP SM during the 2017–2022 period (3-day aggregated and simulated maximum rainfall exclusion) had better R value at high mountainous regions (Figure 8A). However, SM2RAIN simulation for stations in the cold climate eastern and northeastern CONUS which performed well during the calibration period had noticeably worse R and NRMSE values when we used SMAP SM during the evaluation period (Figures 8A, B). For evaluation period, we also observed anomalously high NRMSE values for stations near the border of California, which were likely due to both the limitations of SM2RAIN and the errors of SMAP observations in desert areas that simulated erroneous rainfall when observations are much lower (Brocca et al., 2014). In terms of PBIAS, as we excluded timesteps when observed rainfall was higher than the maximum rainfall SM2RAIN could simulate (to minimize the underestimation of SM2RAIN due to dry soil noisiness and soil saturation constraint), the majority of SMAP-derived rainfall was found to overestimate rather than underestimate (Figure 8C). Though many rainfall simulations were still found to underestimate (negative PBIAS), the shift from negative to positive PBIAS was prevalent, especially in regions with high annual rainfall like the western and southeastern CONUS (Figure 2).

Figure 8

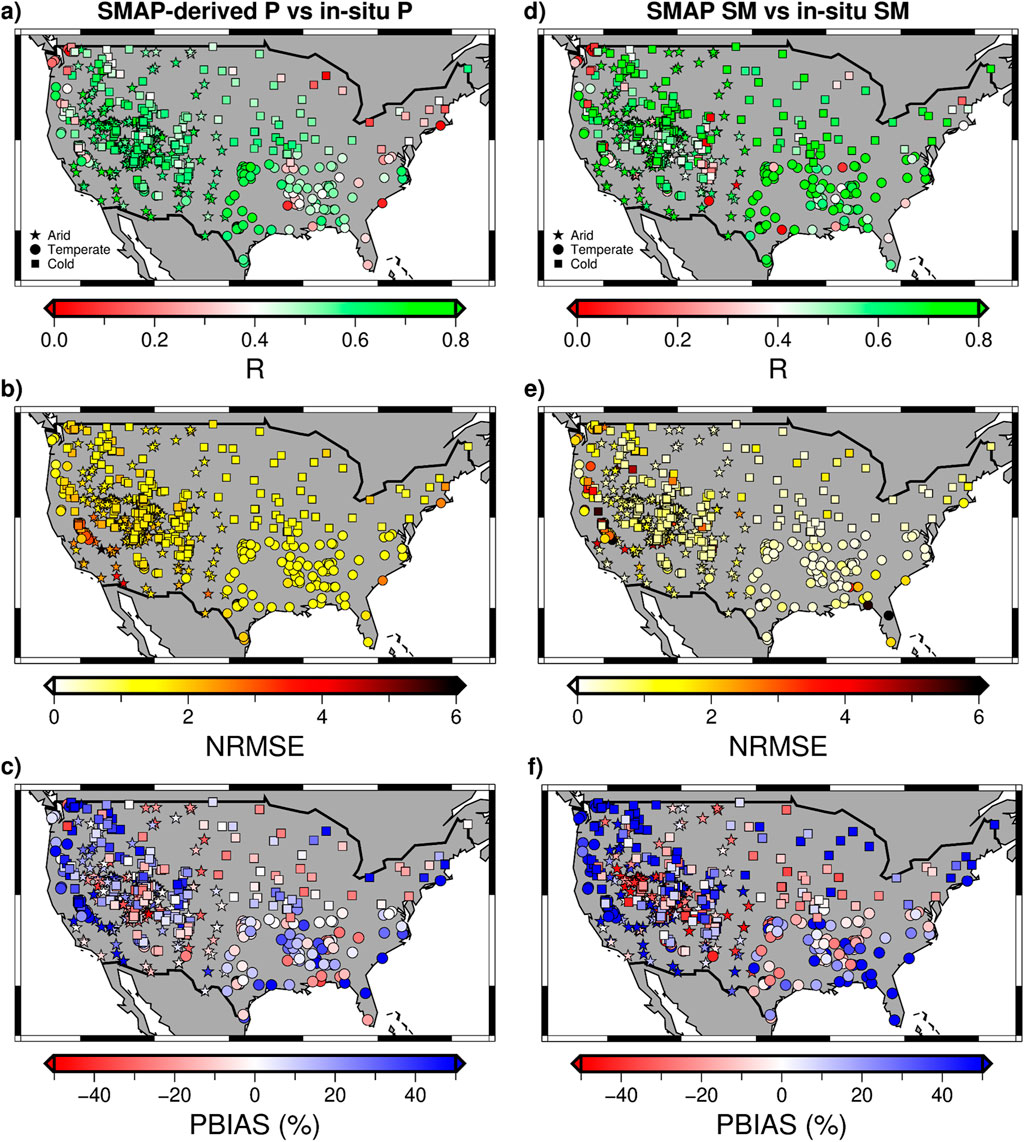
Figure 8. Spatial distribution of metrics for SM2RAIN skills (A–C) (i.e., SMAP-derived P (precipitation) versus in-situ P and for satellite SM skills (D–F) (i.e., SMAP SM versus in-situ SM). The stations are represented by their climate zone classification.

3.3 SMAP SM retrieval validation against in situ SM

We also evaluated daily interpolated SMAP SM data from SMAP 9 km Level 2 product using ISMN in situ records as a basis for actual SMAP SM performance. Since this evaluation using in situ SM was to be compared to the evaluation using SMAP-derived rainfall, we also excluded timesteps with negative air temperatures (${\mathrm{T}}_a<0°$C) for consistency. The median R, NRMSE, and PBIAS for SMAP SM at 607 ISMN stations during the evaluation period (2017–2022) are 0.67, 0.55, and +6.4%, respectively. SMAP SM achieved better results for temperate climate (Supplementary Figure S4) than arid and cold area (median R/NMRSE for temperate, arid, and cold climates are 0.76/0.33, 0.65/0.61, 0.65/0.55). This aligns with previous evaluation studies on SMAP and other satellite SM observations (Beck et al., 2021; Fang et al., 2020; Liu et al., 2018; Zhang et al., 2019b). Among the three climates, SMAP SM had moderate positive bias for temperate climate (median PBIAS of +3.19%), substantial positive bias for cold climate (median PBIAS of +8.68%). The superior performance of satellite SM in temperate regions and skill deterioration in cold regions are tied to vegetation effect, with lower vegetation attenuation in temperate climate region. For cold climate zones, the seasonally correlated trends of SM and vegetation density have substantial effects on the SMAP SM skills (Gruhier et al., 2008; Liu et al., 2018). The impacts of vegetation density are also illustrated by the skill differences among land cover/land type with much better metrics for stations with grassland land cover (median R and NRMSE of 0.75 and 0.41) than those with tree cover land cover (median R and NRMSE of 0.58 and 0.67) (Supplementary Figure S5). Figure 8 shows SMAP SM skills across the CONUS. Coefficient correlation R are generally good across the country with the exceptions of low R values in cold mountainous regions at the Cascade and Sierra Mountain ranges, Rocky Mountain ranges, and Coastal ranges in the northwestern region. More overestimations of SMAP SM observations can be seen in the eastern and western regions with the characteristics of higher precipitation rate/temperate climate or cold climate. In these regions, the overestimation can either be the effects of snowmelt (for cold climate) or the effects of wet canopy interfering with the observation. On the other hand, stations where SMAP SM was found to underestimate are located mostly in the central CONUS, with heavy underestimation tendencies at stations in arid climate.

3.4 Comparison of in situ SM evaluation and SMAP-derived rainfall

Figure 8 shows the R, NRMSE, and PBIAS metrics of SMAP-derived rainfall versus in situ precipitation (SM2RAIN skills) and SMAP SM versus in situ SM (satellite SM skills) side-by-side. We observed evident resemblance and correlation between the metrics of two evaluations. For correlation coefficient, both metrics have fairly good R values (>0.5) spreading across the CONUS, with a lower magnitude range of R for SM2RAIN skills (Figures 8A, D). However, differences exist between SM2RAIN skills and satellite SM skills at certain areas and stations. In the northeastern region, the R values of SMAP-derived rainfall deteriorated while SMAP-SM skills remained relatively good. As mentioned, SMAP SM was found to underperform cold mountainous regions at the central and western CONUS mountain ranges. We also observed similar patterns for SM2RAIN during the calibration period using in situ SM (Figure 5) and during the evaluation period using SMAP SM (Supplementary Figure S1) for daily rainfall simulation. With the 3-day aggregation and exclusion of timesteps when observed rainfall is higher than SM2RAIN can predict, SMAP-derived rainfall R values across the CONUS were significantly increased (Figure 8A). This brought the overall R value of SM2RAIN skills closer to those of satellite SM skills, especially in the eastern area. However, this improvement led to differences in skill at cold mountainous stations where SMAP SM showed bad R values (R < 0.2) while SMAP-derived rainfall showed higher correlation to in situ precipitation.

In terms of NRMSE, SMAP-derived rainfall generally has higher NRMSE value compared to SMAP SM (median NRMSE of 1.65 versus 0.55). This is mainly due to the high range of rainfall peaks and greater temporal variability in precipitation data, which leads to more errors in rainfall simulation. This can be seen in Figures 8B, E as higher NRMSE for SM2RAIN skills than for satellite SM skills was seen across the CONUS. For both metrics, stations with anomalously high errors (very high NRMSE) were observed at the Sierra Nevada mountain ranges. The two changes made to the evaluation of SMAP-derived rainfall to maximize the effects of SMAP SM accuracy on SM2RAIN skills were reflected most clearly in the PBIAS metrics. Without the changes, SM2RAIN was shown to significantly underestimate rainfall (Figure 5C; Supplementary Figure S1); however, PBIAS from SM2RAIN skills and satellite SM skills (Figures 8C, F) clearly had more resemblance and agreement after two proposed changes. Among 607 stations during evaluation period, 56% of the stations (343 stations) had the same over/under-estimation tendencies (SM2RAIN skills and satellite SM skills both have positive or negative PBIAS value). For the remaining stations, roughly half (133 stations) have SM2RAIN PBIAS skills being false negative (i.e., negative PBIAS for SMAP-derived rainfall but positive PBIAS for SMAP SM) and the other half (131 stations) have false positive SM2RAIN PBIAS skills (i.e., positive SMAP-derived rainfall PBIAS and negative SMAP SM PBIAS) (Figure 9). No clear distinction was found among annual rainfall, climate, or network class in relation to whether SM2RAIN PBIAS and satellite SM PBIAS skills match. However, we also observed differences in whether PBIAS skills agree for stations that are close together (e.g., clusters of SM stations in the central western CONUS). This is perhaps due to the high spatial variation for both precipitation and SM, while there is spatial resolution mismatch among satellite SM (9 km), in situ SM (point-based), and in situ precipitation (1 km).

Figure 9

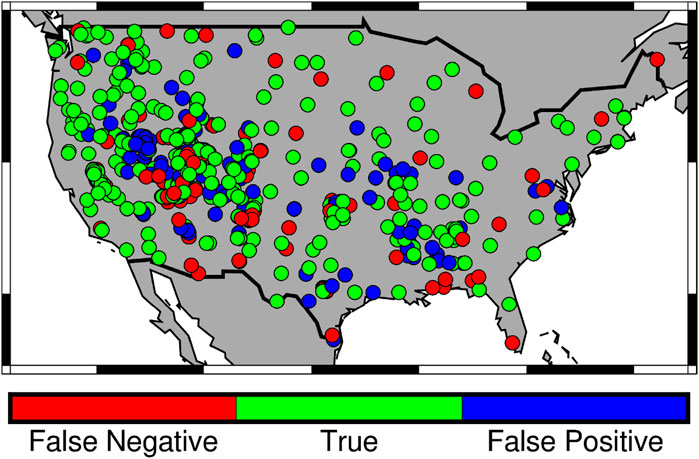
Figure 9. PBIAS direction correlation between SM2RAIN skills and satellite SM skills. True (green) stations have both PBIAS values indicating the same negative/positive direction. False negative (red) stations have negative SM2RAIN PBIAS and positive satellite SM PBIAS. False positive (blue) stations have positive SM2RAIN PBIAS and negative satellite SM PBIAS.

Table 3 shows the Pearson correlation coefficient and p-value between SM2RAIN metrics and satellite SM metrics, as well as the mean absolute error (MAE) and bias error (MBE) of SM2RAIN metrics compared to satellite SM metrics. We used both MAE and MBE to quantify the magnitude and direction of differences between two evaluations. Overall, the three metrics R, NRMSE, and PBIAS of the two skills have statistically significant correlations (p-value < 0.05), but the strength of the correlations is relatively weak (R value between 0.34 and 0.36). Among the climate zone and annual rainfall class however, there are clear distinctions in the correlation strength of SM2RAIN and satellite SM skills. We observed the strongest correlation between two evaluations for temperate climate and for higher rainfall classes (>657 mm/year). Moderately weak correlation was obtained for cold climate while very weak correlation with some statistically insignificant correlation (p-value > 0.05) was obtained for arid climate and for low annual rainfall classes.

Table 3

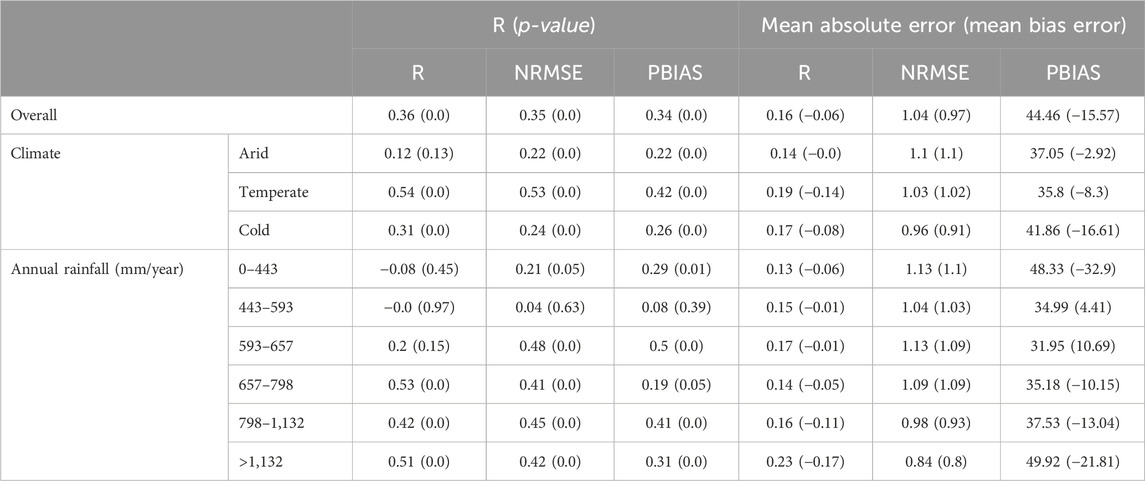
Table 3. Correlation coefficient and p-value along with mean absolute and mean bias error between SM2RAIN skills’ metrics and satellite SM skills’ metrics.

The MAE and MBE between SM2RAIN R values and SMAP SM R values are 0.16 and −0.06, respectively, suggesting R values from SM2RAIN are generally lower than those from satellite SM (Figures 8A, C). The errors were consistent across different climate zone and annual rainfall class, with slightly higher MAE observed in temperate climate and for the highest annual rainfall class (>1,132 mm/year). This is likely due to the high variability in precipitation along with the remaining effects of soi saturation and dry soil compensation on SM2RAIN skills.

Compared to R values, MAE and MBE for NRMSE values is generally similar. This suggests a consistent systematic bias of approximately +1 between SM2RAIN NRMSE values and satellite SM NRMSE values. For PBIAS, there are 56% of stations where both PBIAS values agree on the direction, 22% where SM2RAIN PBIAS values are false negatives, and 22% where SM2RAIN PBIAS values are false positives. In term of magnitude, the high MAE and MBE values in PBIAS were largely attributed to the range differences between SM2RAIN and SMAP SM PBIAS values. Due to the small range magnitude of SM, significantly larger PBIAS values could exist for satellite SM skills. Indeed, if the PBIAS values of two evaluations were normalized to the range of −100%–100%, the MAE and MBE were reduced to 22.81% and +2.42%.

Many factors could contribute to the relatively weak correlation and contradictory results at certain stations of SM2RAIN skills and satellite SM skills. The most substantial reason is the fact that SM2RAIN skills were influenced by other aspects than just the accuracy of satellite SM. Even though we attempted to maximize the impacts of SMAP SM skills by aggregating SMAP-derived rainfall by 3 days and excluding timesteps when observed rainfall is higher than SM2RAIN can predict, we still observed the impacts of SM2RAIN and rain gauge inherent limitations (e.g., soil saturation during extreme rainfall event, noisy SM during dry period, errors in SM gauges, high mountain gauge undercatch) (Beck et al., 2020; Brocca et al., 2014). In this study, we used the simplest version of SM2RAIN. Nevertheless, better SM2RAIN configurations with more calibrating parameters (Brocca et al., 2019), or with hybrid approaches to overcome the inherent limitations (Saeedi et al., 2022) can certainly improve the correlation of SM2RAIN skills and satellite SM skills. For example, adding a temporal filtering component to either the SM2RAIN calibration (through Tpot/Tbase parameters) or the satellite SM would improve the satellite noises and fluctuation that result in underestimation of rainfall estimates in SM2RAIN.

By addressing other aspects that affect SM2RAIN, the impact of SMAP SM skills would become more significant on SM2RAIN skills, thereby enhancing the correlation between the two evaluations. Another factor that impacted the correlation of SM2RAIN skills and satellite SM skills was the spatial resolution mismatch between datasets. Due to the spatial heterogeneity of both SM and precipitation, the difference between in situ SM resolution (point-based) compared to those of gridded products such as DAYMET would also have an impact on the correlation. Similarly, the spatial mismatch between in-situ soil moisture and satellite SM (9 km resolution in this case) is another substantial source of errors. Due to the heterogeneous nature of SM, point-based SM records may not represent the overall condition of surrounding area. With increasing focuses and studies in SM downscaling, this mismatch is expected to reduce greatly in the future. In terms of temporal sampling, the original 2–3 days sampling of SMAP SM (and most of satellite products) is not suitable to obtain daily SM2RAIN rainfall. While DCT-PLS was applied in this study to interpolate SMAP SM into daily resolution, the gap filling’s inability to fully capture the temporal variability of SM is another limitation of the approach. Additionally, the study uses in situ SM and annual rainfall classes for SM2RAIN calibration so the parameters can be applied to multiple satellite SM datasets. However, this approach is not the most optimized for SM2RAIN. If only one satellite SM product is considered, pixel-by-pixel calibration with 5 parameters (Z, a, b, Tpot, and c) (Brocca et al., 2019) using satellite SM instead of in-situ SM can substantially improve the performance of SM2RAIN. This improvement can certainly improve the agreement between the two comparisons. For future study, we are planning to incorporate this improved configuration of SM2RAIN and downscaled SMAP products to minimize the errors in SM2RAIN and the effect of spatial mismatch among data sources.

4 Conclusion

Despite current efforts in expanding field measurements through the International Soil Moisture Network, in situ SM data, which is necessary for evaluation satellite- and model-based SM products, remains inadequate. As rain gauges are more abundant and denser across the globe compared to in situ SM, we evaluated whether the bottom-up SM2RAIN algorithm could be utilized to use rain gauge for evaluation of satellite SM instead of relying on in situ SM. Additionally, SM2RAIN skills using in situ SM and satellite SM (i.e., SMAP) across CONUS were evaluated. The SM2RAIN parameters were calibrated using in situ SM and precipitation before being applied to SMAP SM to obtain SMAP-derived rainfall. We examined whether the SM2RAIN skills (SMAP-derived rainfall versus in situ precipitation) have good correlations to satellite SM skills (SMAP SM versus in situ SM) for the replacement of traditional SM evaluation methods.

SM2RAIN algorithm performed generally well across the CONUS during the calibration period when we evaluated each single station. The main limiting factors to the performance of SM2RAIN were shown to be parameters compensating for noisy and fluctuating SM during dry periods which leads to underestimation of rain peak, rain gauge undercatch for mountainous region, and unreasonable relationship between SM and precipitation at certain stations. The skills of SM2RAIN algorithm, however, could not be fully transferred when SMAP SM instead of in situ SM was being used, which lead to lower R values and higher NRMSE and PBIAS during the evaluation period. During the evaluation period, we also observed a reduction of SM2RAIN skills for temperate climate and high annual precipitation classes.

While the correlation of SM2RAIN skills and satellite SM skills are statistically significant, the overall strength of correlation is relatively weak with varying degree for different climate and annual rainfall classes. We observed a lower correlation between two evaluations for arid and lower rainfall classes and moderately strong correlation for temperate and higher rainfall classes. This is mainly due to other inherent limitations of SM2RAIN that take away the impacts of SMAP SM accuracy on SM2RAIN skills. Improvement on the SM2RAIN model to overcome its limitations (e.g., through better parameters and calibration configurations) can potentially improve the model’s capabilities in evaluate satellite SM observations. From there, SM2RAIN can be applied to multiple satellite SM products to evaluate and compare the accuracy of different satellite mission observations.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SD: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. T-N-DT: Conceptualization, Visualization, Writing–review and editing. M-HL: Conceptualization, Writing–review and editing. JB: Conceptualization, Writing–review and editing. VL: Project administration, Supervision, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Author M-HL was employed by Science Applications International Corporation (SAIC).

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2024.1474088/full#supplementary-material

References

Albergel, C., De Rosnay, P., Gruhier, C., Muñoz-Sabater, J., Hasenauer, S., Isaksen, L., et al. (2012). Evaluation of remotely sensed and modelled soil moisture products using global ground-based in situ observations. Remote Sens. Environ. 118, 215–226. doi:10.1016/j.rse.2011.11.017

CrossRef Full Text | Google Scholar

Al-Yaari, A., Wigneron, J.-P., Dorigo, W., Colliander, A., Pellarin, T., Hahn, S., et al. (2019). Assessment and inter-comparison of recently developed/reprocessed microwave satellite soil moisture products using ISMN ground-based measurements. Remote Sens. Environ. 224, 289–303. doi:10.1016/j.rse.2019.02.008

CrossRef Full Text | Google Scholar

Backus, G. E., and Gilbert, J. F. (1967). Numerical applications of a formalism for geophysical inverse problems. Geophys. J. Int. 13 (1–3), 247–276. doi:10.1111/j.1365-246x.1967.tb02159.x

CrossRef Full Text | Google Scholar

Beck, H. E., Pan, M., Miralles, D. G., Reichle, R. H., Dorigo, W. A., Hahn, S., et al. (2021). Evaluation of 18 satellite- and model-based soil moisture products using in situ measurements from 826 sensors. Hydrology Earth Syst. Sci. 25 (1), 17–40. doi:10.5194/hess-25-17-2021

CrossRef Full Text | Google Scholar

Beck, H. E., Vergopolan, N., Pan, M., Levizzani, V., van Dijk, A. I. J. M., Weedon, G. P., et al. (2017). Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrology Earth Syst. Sci. 21 (12), 6201–6217. doi:10.5194/hess-21-6201-2017

CrossRef Full Text | Google Scholar

Beck, H. E., Wood, E. F., McVicar, T. R., Zambrano-Bigiarini, M., Alvarez-Garreton, C., Baez-Villanueva, O. M., et al. (2020). Bias correction of global high-resolution precipitation climatologies using streamflow observations from 9372 catchments. J. Clim. 33, 1299–1315. doi:10.1175/JCLI-D-19-0332.1

CrossRef Full Text | Google Scholar

Brocca, L., Ciabatta, L., Massari, C., Moramarco, T., Hahn, S., Hasenauer, S., et al. (2014). Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 119 (9), 5128–5141. doi:10.1002/2014JD021489

CrossRef Full Text | Google Scholar

Brocca, L., Filippucci, P., Hahn, S., Ciabatta, L., Massari, C., Camici, S., et al. (2019). SM2RAIN–ASCAT (2007–2018): global daily satellite rainfall data from ASCAT soil moisture observations. Earth Syst. Sci. Data 11 (4), 1583–1601. doi:10.5194/essd-11-1583-2019

CrossRef Full Text | Google Scholar

Brocca, L., Massari, C., Ciabatta, L., Moramarco, T., Penna, D., Zuecco, G., et al. (2015). Rainfall estimation from in situ soil moisture observations at several sites in Europe: an evaluation of the SM2RAIN algorithm. J. Hydrology Hydromechanics 63 (3), 201–209. doi:10.1515/johh-2015-0016

CrossRef Full Text | Google Scholar

Brocca, L., Moramarco, T., Melone, F., and Wagner, W. (2013). A new method for rainfall estimation through soil moisture observations. Geophys. Res. Lett. 40 (5), 853–858. doi:10.1002/grl.50173

CrossRef Full Text | Google Scholar

Brocca, L., Zhao, W., and Lu, H. (2023). High-resolution observations from space to address new applications in hydrology. Innovation 4 (3), 100437. doi:10.1016/j.xinn.2023.100437

PubMed Abstract | CrossRef Full Text | Google Scholar

Caldwell, T. G., Bongiovanni, T., Cosh, M. H., Jackson, T. J., Colliander, A., Abolt, C. J., et al. (2019). The Texas soil observation network:A comprehensive soil moisture dataset for remote sensing and land surface model validation. Vadose Zone J. 18 (1), 1–20. doi:10.2136/vzj2019.04.0034

CrossRef Full Text | Google Scholar

Chan, S. K., Bindlish, R., O’Neill, P., Jackson, T., Njoku, E., Dunbar, S., et al. (2018). Development and assessment of the SMAP enhanced passive soil moisture product. Remote Sens. Environ. 204, 931–941. doi:10.1016/j.rse.2017.08.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, F., Crow, W. T., Bindlish, R., Colliander, A., Burgin, M. S., Asanuma, J., et al. (2018). Global-scale evaluation of SMAP, SMOS and ASCAT soil moisture products using triple collocation. Remote Sens. Environ. 214, 1–13. doi:10.1016/j.rse.2018.05.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciabatta, L., Brocca, L., Massari, C., Moramarco, T., Gabellani, S., Puca, S., et al. (2016). Rainfall-runoff modelling by using SM2RAIN-derived and state-of-the-art satellite rainfall products over Italy. Int. J. Appl. Earth Observation Geoinformation 48, 163–173. doi:10.1016/j.jag.2015.10.004

CrossRef Full Text | Google Scholar

Ciabatta, L., Massari, C., Brocca, L., Gruber, A., Reimer, C., Hahn, S., et al. (2018). SM2RAIN-CCI: a new global long-term rainfall data set derived from ESA CCI soil moisture. Earth Syst. Sci. Data 10 (1), 267–280. doi:10.5194/essd-10-267-2018

CrossRef Full Text | Google Scholar

Crow, W. T. (2007). A novel method for quantifying value in spaceborne soil moisture retrievals. J. Hydrometeorol. 8 (1), 56–67. doi:10.1175/jhm553.1

CrossRef Full Text | Google Scholar

Crow, W. T., Chen, F., and Colliander, A. (2022). Benchmarking downscaled satellite-based soil moisture products using sparse, point-scale ground observations. Remote Sens. Environ. 283, 113300. doi:10.1016/j.rse.2022.113300

CrossRef Full Text | Google Scholar

Crow, W. T., Miralles, D. G., and Cosh, M. H. (2010). A quasi-global evaluation system for satellite-based surface soil moisture retrievals. IEEE Trans. Geoscience Remote Sens. 48 (6), 2516–2527. doi:10.1109/tgrs.2010.2040481

CrossRef Full Text | Google Scholar

Dorigo, W., Himmelbauer, I., Aberer, D., Schremmer, L., Petrakovic, I., Zappa, L., et al. (2021). The international soil moisture network: serving earth system science for over a decade. Hydrology Earth Syst. Sci. 25 (11), 5749–5804. doi:10.5194/hess-25-5749-2021

CrossRef Full Text | Google Scholar

Dorigo, W., Wagner, W., Hohensinn, R., Hahn, S., Paulik, C., Xaver, A., et al. (2011). The international soil moisture network: a data hosting facility for global in situ soil moisture measurements. Hydrology Earth Syst. Sci. 15 (5), 1675–1698. doi:10.5194/hess-15-1675-2011

CrossRef Full Text | Google Scholar

Dorigo, W. A., Xaver, A., Vreugdenhil, M., Gruber, A., Hegyiova, A., Sanchis-Dufau, A. D., et al. (2013). Global automated quality control of in situ soil moisture data from the international soil moisture network. Vadose Zone J. 12 (3), 1–21. doi:10.2136/vzj2012.0097

CrossRef Full Text | Google Scholar

Du, T. L. T., Lee, H., Bui, D. D., Graham, L. P., Darby, S. D., Pechlivanidis, I. G., et al. (2022). Streamflow prediction in highly regulated, transboundary watersheds using multi-basin modeling and remote sensing imagery. Water Resour. Res. 58 (3), e2021WR031191. doi:10.1029/2021WR031191

PubMed Abstract | CrossRef Full Text | Google Scholar

Entekhabi, D., Njoku, E. G., O’Neill, P. E., Kellogg, K. H., Crow, W. T., Edelstein, W. N., et al. (2010). The soil moisture active passive (SMAP) mission. Proc. IEEE 98 (5), 704–716. doi:10.1109/JPROC.2010.2043918

CrossRef Full Text | Google Scholar

Fang, B., Lakshmi, V., Bindlish, R., Jackson, T. J., and Liu, P.-W. (2020). Evaluation and validation of a high spatial resolution satellite soil moisture product over the Continental United States. J. Hydrology 588, 125043. doi:10.1016/j.jhydrol.2020.125043

CrossRef Full Text | Google Scholar

Filippucci, P., Brocca, L., Massari, C., Saltalippi, C., Wagner, W., and Tarpanelli, A. (2021). Toward a self-calibrated and independent SM2RAIN rainfall product. J. Hydrology 603, 126837. doi:10.1016/j.jhydrol.2021.126837

CrossRef Full Text | Google Scholar

Filippucci, P., Brocca, L., Quast, R., Ciabatta, L., Saltalippi, C., Wagner, W., et al. (2022). High-resolution (1 km) satellite rainfall estimation from SM2RAIN applied to Sentinel-1: Po River basin as a case study. Hydrology Earth Syst. Sci. 26 (9), 2481–2497. doi:10.5194/hess-26-2481-2022

CrossRef Full Text | Google Scholar

Garcia, D. (2010). Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Statistics & Data Analysis 54 (4), 1167–1178. doi:10.1016/j.csda.2009.09.020

CrossRef Full Text | Google Scholar

Grayson, R. B., Western, A. W., Chiew, F. H. S., and Blöschl, G. (1997). Preferred states in spatial soil moisture patterns: local and nonlocal controls. Water Resour. Res. 33 (12), 2897–2908. doi:10.1029/97WR02174

CrossRef Full Text | Google Scholar

Gruber, A., De Lannoy, G., Albergel, C., Al-Yaari, A., Brocca, L., Calvet, J.-C., et al. (2020). Validation practices for satellite soil moisture retrievals: what are (the) errors? Remote Sens. Environ. 244, 111806. doi:10.1016/j.rse.2020.111806

CrossRef Full Text | Google Scholar

Gruber, A., Dorigo, W. A., Crow, W., and Wagner, W. (2017). Triple collocation-based merging of satellite soil moisture retrievals. IEEE Trans. Geoscience Remote Sens. 55 (12), 6780–6792. doi:10.1109/tgrs.2017.2734070

CrossRef Full Text | Google Scholar

Gruber, A., Su, C.-H., Zwieback, S., Crow, W., Dorigo, W., and Wagner, W. (2016). Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Observation Geoinformation 45, 200–211. doi:10.1016/j.jag.2015.09.002

CrossRef Full Text | Google Scholar

Gruhier, C., De Rosnay, P., Kerr, Y., Mougin, E., Ceschia, E., Calvet, J.-C., et al. (2008). Evaluation of AMSR-E soil moisture product based on ground measurements over temperate and semi-arid regions. Geophys. Res. Lett. 35 (10), 2008GL033330. doi:10.1029/2008GL033330

CrossRef Full Text | Google Scholar

Hanson, B. R., Orloff, S., and Peters, D. (2000). Monitoring soil moisture helps refine irrigation management. Calif. Agric. 54 (3), 38–42. doi:10.3733/ca.v054n03p38

CrossRef Full Text | Google Scholar

Hrachowitz, M., Savenije, H. H. G., Blöschl, G., McDonnell, J. J., Sivapalan, M., Pomeroy, J. W., et al. (2013). A decade of predictions in ungauged basins (PUB)—a review. Hydrological Sci. J. 58 (6), 1198–1255. doi:10.1080/02626667.2013.803183

CrossRef Full Text | Google Scholar

Karthikeyan, L., and Kumar, D. N. (2016). A novel approach to validate satellite soil moisture retrievals using precipitation data. J. Geophys. Res. Atmos. 121 (19). doi:10.1002/2016JD024829

CrossRef Full Text | Google Scholar

Kerr, Y. H., Waldteufel, P., Richaume, P., Wigneron, J. P., Ferrazzoli, P., Mahmoodi, A., et al. (2012). The SMOS soil moisture retrieval algorithm. IEEE Trans. Geoscience Remote Sens. 50 (5), 1384–1403. doi:10.1109/TGRS.2012.2184548

CrossRef Full Text | Google Scholar

Kidd, C., and Levizzani, V. (2011). Status of satellite precipitation retrievals. Hydrology Earth Syst. Sci. 15 (4), 1109–1116. doi:10.5194/hess-15-1109-2011

CrossRef Full Text | Google Scholar

Kirchner, J. W. (2009). Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 45 (2), 2008WR006912. doi:10.1029/2008WR006912

CrossRef Full Text | Google Scholar

Koster, R. D., Brocca, L., Crow, W. T., Burgin, M. S., and De Lannoy, G. J. M. (2016). Precipitation estimation using L -band and C -band soil moisture retrievals. Water Resour. Res. 52 (9), 7213–7225. doi:10.1002/2016WR019024

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai, Y., Tian, J., Kang, W., Gao, C., Hong, W., and He, C. (2022). Rainfall estimation from surface soil moisture using SM2RAIN in cold mountainous areas. J. Hydrology 606, 127430. doi:10.1016/j.jhydrol.2022.127430

CrossRef Full Text | Google Scholar

Lakshmi, V., Le, M.-H., Goffin, B. D., Besnier, J., Pham, H. T., Do, H.-X., et al. (2023). Regional analysis of the 2015–16 Lower Mekong River basin drought using NASA satellite observations. J. Hydrology Regional Stud. 46, 101362. doi:10.1016/j.ejrh.2023.101362

CrossRef Full Text | Google Scholar

Lawston, P. M., Santanello, J. A., and Kumar, S. V. (2017). Irrigation Signals Detected from SMAP soil moisture retrievals. Geophys. Res. Lett. 44 (23). doi:10.1002/2017GL075733

CrossRef Full Text | Google Scholar

Leavesley, G. H., David, O., Garen, D. C., Lea, J., Marron, J. K., Pagano, T. C., et al. (2008). A modeling framework for improved agricultural water supply forecasting. AGU Fall Meet. Abstr., C21A–C0497. Available at: https://ui.adsabs.harvard.edu/abs/2008AGUFM.C21A0497L/abstract.

Google Scholar

Lei, S., Bian, Z., Daniels, J. L., and Liu, D. (2014). Improved spatial resolution in soil moisture retrieval at arid mining area using apparent thermal inertia. Trans. Nonferrous Metals Soc. China 24 (6), 1866–1873. doi:10.1016/S1003-6326(14)63265-9

CrossRef Full Text | Google Scholar

Liu, Y., Yang, Y., and Yue, X. (2018). Evaluation of satellite-based soil moisture products over Four different continental in-situ measurements. Remote Sens. 10 (7), 1161. Article 7. doi:10.3390/rs10071161

CrossRef Full Text | Google Scholar

López, P., Sutanudjaja, E. H., Schellekens, J., Sterk, G., and Bierkens, M. F. P. (2017). Calibration of a large-scale hydrological model using satellite-based soil moisture and evapotranspiration products. Hydrology Earth Syst. Sci. 21 (6), 3125–3144. doi:10.5194/hess-21-3125-2017

CrossRef Full Text | Google Scholar

Martens, B., Miralles, D. G., Lievens, H., Van Der Schalie, R., De Jeu, R. A., Fernández-Prieto, D., et al. (2017). GLEAM v3: satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 10 (5), 1903–1925. doi:10.5194/gmd-10-1903-2017

CrossRef Full Text | Google Scholar

Massari, C., Crow, W., and Brocca, L. (2017). An assessment of the performance of global rainfall estimates without ground-based observations. Hydrology Earth Syst. Sci. 21 (9), 4347–4361. doi:10.5194/hess-21-4347-2017

CrossRef Full Text | Google Scholar

Menne, M. J., Durre, I., Korzeniewski, B., McNeal, S., Thomas, K., Yin, X., et al. (2012a). Global historical climatology network-daily (GHCN-Daily). NOAA Natl. Clim. Data Cent. Version 3. 10 (10.7289), V5D21VHZ. doi:10.7289/V5D21VHZ

CrossRef Full Text | Google Scholar

Menne, M. J., Durre, I., Vose, R. S., Gleason, B. E., and Houston, T. G. (2012b). An overview of the global historical climatology network-daily database. J. Atmos. Ocean. Technol. 29 (7), 897–910. doi:10.1175/jtech-d-11-00103.1

CrossRef Full Text | Google Scholar

Miao, L., Wei, Z., Zhong, Y., and Duan, Z. (2023). Improving the SM2RAIN-derived rainfall estimation using Bayesian optimization. J. Hydrology 622, 129728. doi:10.1016/j.jhydrol.2023.129728

CrossRef Full Text | Google Scholar

Mishra, A., Vu, T., Veettil, A. V., and Entekhabi, D. (2017). Drought monitoring with soil moisture active passive (SMAP) measurements. J. Hydrology 552, 620–632. doi:10.1016/j.jhydrol.2017.07.033

CrossRef Full Text | Google Scholar

Naeimi, V., Leinenkugel, P., Sabel, D., Wagner, W., Apel, H., and Kuenzer, C. (2013). Evaluation of soil moisture retrieval from the ers and metop scatterometers in the lower mekong basin. Remote Sens. 5 (4), 1603–1623. doi:10.3390/rs5041603

CrossRef Full Text | Google Scholar

Oneill, P. E., Chan, S., Njoku, E. G., Jackson, T., Bindlish, R., and Chaubell, M. J. (2019) SMAP enhanced L2 radiometer half-orbit 9 km EASE-grid soil moisture. Version 3. (Boulder, Colorado USA: NASA National Snow and Ice Data Center Distributed Active Archive Center). doi:10.5067/017XZSKMLTT2

CrossRef Full Text | Google Scholar

Owe, M., and Van De Griend, A. A. (1998). Comparison of soil moisture penetration depths for several bare soils at two microwave frequencies and implications for remote sensing. Water Resour. Res. 34 (9), 2319–2327. doi:10.1029/98WR01469

CrossRef Full Text | Google Scholar

Parinussa, R. M., Holmes, T. R. H., Wanders, N., Dorigo, W. A., and De Jeu, R. A. M. (2015). A preliminary study toward consistent soil moisture from AMSR2. J. Hydrometeorol. 16 (2), 932–947. doi:10.1175/JHM-D-13-0200.1

CrossRef Full Text | Google Scholar

Peng, J., Loew, A., Merlin, O., and Verhoest, N. E. C. (2017). A review of spatial downscaling of satellite remotely sensed soil moisture: downscale satellite-based soil moisture. Rev. Geophys. 55 (2), 341–366. doi:10.1002/2016RG000543

CrossRef Full Text | Google Scholar

Petropoulos, G. P., Ireland, G., and Barrett, B. (2015). Surface soil moisture retrievals from remote sensing: current status, products & future trends. Phys. Chem. Earth, Parts A/B/C 83–84, 36–56. doi:10.1016/j.pce.2015.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Rasmussen, R., Baker, B., Kochendorfer, J., Meyers, T., Landolt, S., Fischer, A. P., et al. (2012). How well are we measuring snow: the NOAA/FAA/NCAR winter precipitation test bed. Bull. Am. Meteorological Soc. 93 (6), 811–829. doi:10.1175/bams-d-11-00052.1

CrossRef Full Text | Google Scholar

Reichle, R., Lannoy, G. D., Koster, R., Crow, W., and Kimball, J. (2016). SMAP L4 global 9 km surface and Rootzone soil moisture land model constants. Object Object. Version 2. doi:10.5067/VBRUC1AFRQ22

CrossRef Full Text | Google Scholar

Reichle, R. H., Liu, Q., Ardizzone, J. V., Crow, W. T., De Lannoy, G. J., Kimball, J. S., et al. (2023). IMERG precipitation improves the SMAP Level-4 soil moisture product. J. Hydrometeorol. 24 (10), 1699–1723. doi:10.1175/jhm-d-23-0063.1

CrossRef Full Text | Google Scholar

Robinson, D. A., Campbell, C. S., Hopmans, J. W., Hornbuckle, B. K., Jones, S. B., Knight, R., et al. (2008). Soil moisture measurement for ecological and hydrological watershed-scale observatories: a review. Vadose Zone J. 7 (1), 358–389. doi:10.2136/vzj2007.0143

CrossRef Full Text | Google Scholar

Sabaghy, S., Walker, J. P., Renzullo, L. J., Akbar, R., Chan, S., Chaubell, J., et al. (2020). Comprehensive analysis of alternative downscaled soil moisture products. Remote Sens. Environ. 239, 111586. doi:10.1016/j.rse.2019.111586

CrossRef Full Text | Google Scholar

Saeedi, M., Kim, H., Nabaei, S., Brocca, L., Lakshmi, V., and Mosaffa, H. (2022). A comprehensive assessment of SM2RAIN-NWF using ASCAT and a combination of ASCAT and SMAP soil moisture products for rainfall estimation. Sci. Total Environ. 838, 156416. doi:10.1016/j.scitotenv.2022.156416

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheffield, J., Goteti, G., Wen, F., and Wood, E. F. (2004). A simulated soil moisture based drought analysis for the United States. J. Geophys. Res. 109 (D24), D24108. doi:10.1029/2004JD005182

CrossRef Full Text | Google Scholar

Stoffelen, A. (1998). Toward the true near-surface wind speed: error modeling and calibration using triple collocation. J. Geophys. Res. Oceans 103 (C4), 7755–7766. doi:10.1029/97JC03180

CrossRef Full Text | Google Scholar

Tarpanelli, A., Massari, C., Ciabatta, L., Filippucci, P., Amarnath, G., and Brocca, L. (2017). Exploiting a constellation of satellite soil moisture sensors for accurate rainfall estimation. Adv. Water Resour. 108, 249–255. doi:10.1016/j.advwatres.2017.08.010

CrossRef Full Text | Google Scholar

Thornton, P. E., Running, S. W., and White, M. A. (1997). Generating surfaces of daily meteorological variables over large regions of complex terrain. J. Hydrology 190 (3–4), 214–251. doi:10.1016/s0022-1694(96)03128-9

CrossRef Full Text | Google Scholar

Thornton, P. E., Thornton, M. M., Mayer, B. W., Wei, Y., Devarakonda, R., Vose, R. S., et al. (2016). Daymet: daily surface weather data on a 1-km grid for North America, version 3. ORNL DAAC, Oak Ridge, Tennessee, USA. USDA-NASS, 2019. 2017 Census Agric. Summ. State Data, Geogr. Area Ser. Part 51, AC-17-A 51. doi:10.3334/ORNLDAAC/2129

CrossRef Full Text | Google Scholar

Tian, S., Renzullo, L. J., Van Dijk, A. I., Tregoning, P., and Walker, J. P. (2019). Global joint assimilation of GRACE and SMOS for improved estimation of root-zone soil moisture and vegetation response. Hydrology Earth Syst. Sci. 23 (2), 1067–1081. doi:10.5194/hess-23-1067-2019

CrossRef Full Text | Google Scholar

Tran, T.-N.-D., Le, M.-H., Zhang, R., Nguyen, B. Q., Bolten, J. D., and Lakshmi, V. (2023). Robustness of gridded precipitation products for vietnam basins using the comprehensive assessment framework of rainfall. Atmos. Res. 293, 106923. doi:10.1016/j.atmosres.2023.106923

CrossRef Full Text | Google Scholar

Trenberth, K. E., and Asrar, G. R. (2012). “Challenges and opportunities in water cycle research: wcrp contributions,” in The Earth’s hydrological Cycle. Editors L. Bengtsson, R.-M. Bonnet, M. Calisto, G. Destouni, R. Gurney, J. Johannessenet al. (Netherlands: Springer), 46, 515–532. doi:10.1007/978-94-017-8789-5_3

CrossRef Full Text | Google Scholar

Tuttle, S. E., and Salvucci, G. D. (2014). A new approach for validating satellite estimates of soil moisture using large-scale precipitation: comparing AMSR-E products. Remote Sens. Environ. 142, 207–222. doi:10.1016/j.rse.2013.12.002

CrossRef Full Text | Google Scholar

van der Schalie, R., de Jeu, R. A. M., Kerr, Y. H., Wigneron, J. P., Rodríguez-Fernández, N. J., Al-Yaari, A., et al. (2017). The merging of radiative transfer based surface soil moisture data from SMOS and AMSR-E. Remote Sens. Environ. 189, 180–193. doi:10.1016/j.rse.2016.11.026

CrossRef Full Text | Google Scholar

Vereecken, H., Huisman, J. A., Bogena, H., Vanderborght, J., Vrugt, J. A., and Hopmans, J. W. (2008). On the value of soil moisture measurements in vadose zone hydrology: a review. Water Resour. Res. 44 (4). doi:10.1029/2008WR006829

CrossRef Full Text | Google Scholar

Vereecken, H., Huisman, J. A., Pachepsky, Y., Montzka, C., Van Der Kruk, J., Bogena, H., et al. (2014). On the spatio-temporal dynamics of soil moisture at the field scale. J. Hydrology 516, 76–96. doi:10.1016/j.jhydrol.2013.11.061

CrossRef Full Text | Google Scholar

Wagner, W., Lemoine, G., and Rott, H. (1999). A method for estimating soil moisture from ERS Scatterometer and soil data. Remote Sens. Environ. 70 (2), 191–207. doi:10.1016/S0034-4257(99)00036-X

CrossRef Full Text | Google Scholar

Walker, J. P., Willgoose, G. R., and Kalma, J. D. (2004). In situ measurement of soil moisture: a comparison of techniques. J. Hydrology 293 (1–4), 85–99. doi:10.1016/j.jhydrol.2004.01.008

CrossRef Full Text | Google Scholar

Wang, J., Ling, Z., Wang, Y., and Zeng, H. (2016). Improving spatial representation of soil moisture by integration of microwave observations and the temperature–vegetation–drought index derived from MODIS products. ISPRS J. Photogrammetry Remote Sens. 113, 144–154. doi:10.1016/j.isprsjprs.2016.01.009

CrossRef Full Text | Google Scholar

Wu, Q., Liu, H., Wang, L., and Deng, C. (2016). Evaluation of AMSR2 soil moisture products over the contiguous United States using in situ data from the International Soil Moisture Network. Int. J. Appl. Earth Observation Geoinformation 45, 187–199. doi:10.1016/j.jag.2015.10.011

CrossRef Full Text | Google Scholar

Xu, L., Chen, N., Zhang, X., Moradkhani, H., Zhang, C., and Hu, C. (2021). In-situ and triple-collocation based evaluations of eight global root zone soil moisture products. Remote Sens. Environ. 254, 112248. doi:10.1016/j.rse.2020.112248

CrossRef Full Text | Google Scholar

Yilmaz, M. T., and Crow, W. T. (2014). Evaluation of assumptions in soil moisture triple collocation analysis. J. Hydrometeorol. 15 (3), 1293–1302. doi:10.1175/JHM-D-13-0158.1

CrossRef Full Text | Google Scholar

Zhang, R., Kim, S., and Sharma, A. (2019a). A comprehensive validation of the SMAP Enhanced Level-3 Soil Moisture product using ground measurements over varied climates and landscapes. Remote Sens. Environ. 223, 82–94. doi:10.1016/j.rse.2019.01.015

CrossRef Full Text | Google Scholar

Zhang, R., Kim, S., and Sharma, A. (2019b). A comprehensive validation of the SMAP Enhanced Level-3 Soil Moisture product using ground measurements over varied climates and landscapes. Remote Sens. Environ. 223, 82–94. doi:10.1016/j.rse.2019.01.015

CrossRef Full Text | Google Scholar