- Department of Forest Engineering, Forest Management Planning and Terrestrial Measurements, Faculty of Silviculture and Forest Engineering, Transilvania University of Brasov, Brașov, Romania
Producing reliable log volume data is an essential feature in an effective wood supply chain, and LiDAR sensing, supported by portable platforms, is a promising technology for volume measurements. Computer-based algorithms like Poisson interpolation and Random Sampling and Consensus (RANSAC) are commonly used to extract volume data from LiDAR point clouds, and comparative studies have tested these algorithms for accuracy. To extract volume data, point clouds require several post-processing steps, while their outcome may depend largely on human input and operator decision. Despite the increasingly number of studies on accuracy limits, no paper has addressed the reliability of these procedures. This raises at least two questions: (i) Would the same person, working with the same data and using the same procedures get the same results? And (ii) How much would the results deviate when different people process the same data using the same procedures? A set of 432 poplar logs placed on the ground and spaced about 1 m apart, was scanned by a professional mobile LiDAR scanner in groups; the first 418 logs were then individually scanned using an iPhone-compatible app, with the remainder being excluded from this part of the study due to field time constraints and all the logs were manually measured to get the reference biometric data. Three researchers with different experiences processed the datasets produced by scanning twice, following a protocol that included shape reconstruction and volume calculation using Poisson interpolation and RANSAC algorithm for cylinders and cones. The intra- and inter-rater reliability were evaluated using a comprehensive array of statistical metrics. The results show that the most reliable estimates correlate with a greater experience. The Cronbach’s alpha metric at the subject level was high, with values of 0.902–0.965 for the most experienced subject, and generally indicated moderate to excellent intra-rater reliabilities. Moreover, working with Poisson interpolation and RANSAC cylinder shape reconstruction, respectively, indicated a moderate to excellent reliability. For the Poisson interpolation algorithm, the Intraclass Correlation Coefficient (ICC) ranged from 0.770 to 0.980 for multi-log datasets, and from 0.924 to 0.972 for single log datasets. For the same type of input datasets, the ICC varied between 0.761 and 0.855 and from 0.839 to 0.908 for the RANSAC cylinder, and from 0.784 to 0.869 and 0.843 to 0.893 for the RANSAC cone shape reconstruction algorithms, respectively. These values indicate a moderate to excellent inter-rater reliability. Similar to Cronbach’s alpha, the Root Mean Square Error (RMSE) was related in magnitude to the ICC. The results of this study indicate that, for improved reliability and efficiency, it is essential to automate point cloud segmentation using advanced machine learning and computer vision algorithms. This approach would eliminate the subjectivity in segmentation decisions and significantly reduce the time required for the process.
1 Introduction
In the wood supply chain, measurement of forest-related features such as standing trees, tree lengths and logs, is essential for practice and science. For practice, accurate estimates of the volume are important for wood transaction on the market (Davis et al., 2001; Gregory et al., 2003; Malinen et al., 2006; Moskalik et al., 2022), while for science, accurate estimates are required to support modelling and comparison, run wider system analyses (Janák, 2012), and generally to provide the data supporting informed decisions for management (Davis et al., 2001; Rauscher, 2005; Lauri et al., 2008).
Log measurement by manual means has long been used in forestry, but it requires important resources (Janák, 2007; 2012; Li et al., 2015; de Miguel-Díez et al., 2022; Niţă and Borz, 2023; Purfürst et al., 2023), and may generate bottlenecks within the supply chain (Berendt et al., 2021; de Miguel-Díez et al., 2021). Along with the introduction of Forestry 4.0 concepts in the wood supply chain (Feng and Audy, 2020; He and Turner, 2021), digitalization of operations and transactions has gained a lot of momentum (Feng and Audy, 2020; Müller et al., 2019), pushing the science and industry in exploring alternative ways of collecting wood biometric data. Various proximal sensing technologies supported by mobile platforms equipped with apps integrating the latest technologies, such as augmented reality and computer vision, were tested to determine how well they perform in obtaining reliable estimates on the main biometrics of the logs (Knyaz and Maksimov, 2014; Jodłowski et al., 2016; Kruglov, 2016; Chatzopoulos et al., 2017; Mehrentsev et al., 2019; Pasztory et al., 2019; Berendt et al., 2021; Panagiotidis and Abdollahnejad, 2021; Borz et al., 2022a; Purfürst et al., 2023). In this regard, several tests were carried out by dedicated studies to compare the log volume estimates produced by digital technologies to those obtained by water immersion (Ljubojević et al., 2011; Hohmann et al., 2017; de Miguel-Díez et al., 2022), or by manual measurement (Niţă and Borz, 2023).
Based on the most recent findings, the use of LiDAR-based platforms in collecting tree- and log-based biometric data seems to be a viable and feasible alternative due to the accuracy provided (Hyyppä et al., 2008; Chen, 2015; White et al., 2016; Beland et al., 2019; Alvites et al., 2022; de Miguel-Díez et al., 2022). In addition, the resources spent to procure the data, such as measurement time (Borz and Proto, 2022), were comparable to those of conventional log measurement methods. Moreover, LiDAR-based log measurement may remove important inconveniences of the manual log measurement methods, which typically relate to the safety and ergonomics of the work, environmental efficiency, labor shortage, skills and knowledge required, density of data sampling, and integration into technologies holding data flow capabilities along the supply chain.
In terms of safety and ergonomics, digital methods were shown to expose less their operators to postural risks (Borz et al., 2022b), which may also contribute to a less physical effort required when measuring; in addition, digital measurement does not require a direct contact with the work object, and therefore, it can prevent work-related accidents. Although the platforms used to collect data, such as smartphones, may require a wide range of resources and more complex manufacturing processes, by their material weight could be less resource-intensive compared to those required for manual measurement, which is typically done by a tape and a forest caliper. Frequently, such platforms are also multi-purpose devices storing the apps for different tasks in one place, hence the multi-function allocation from an environmental impact point of view. An important challenge that forest sector faces today is labor shortage (Proteau, 2008; Tsioras, 2010; 2012; Šporčić et al., 2024), with many choosing to work in other industrial sectors; this creates important problems and threatens the security of wood supply, at least at the operational level which, for log measurement, typically employs people that hold the knowledge and skills required to grade the logs and to record the data needed for volume estimates (Cown, 2005; Thomas and Bennett, 2017; TraitLab, 2024). Then, the estimates produced by manual methods are as good as the density used in sampling the data used to produce them, which is typically low; LiDAR measurement, on the other hand, can represent more accurately the objects in the three-dimensional space (White et al., 2016; Beland et al., 2019; Alvites et al., 2022), accounting for those variations that may make the difference in volume estimates. Last but not least, the advancements in computer vision and deep learning is likely to provide the tools needed for an automatic documentation and transfer of the data along the supply chain, removing the need for manual input of the data into a dedicated system (Gingras and Charette, 2017; Feng and Audy, 2020; Morin et al., 2020; He and Turner, 2021).
To extract meaningful data, currently the LiDAR point clouds require a workflow composed of several post-processing tasks. Most of these still require the human intervention over the point clouds to prepare them for the extraction of useful information. Software packages such as CloudCompare or Open 3D are equipped with such functionalities and are the main choices when one relies on open-source alternatives. In the CloudCompare app (CloudCompare, 2024), for instance, which is commonly used now in the related science, these functionalities include a manual segmentation, noise removal using a filtering tool, normalization using a given model, and shape reconstruction by various algorithms (Schnabel et al., 2007; Girardeau-Montaut, 2015; Girardeau-Montaut, 2016; Kazhdan et al., 2020; Panagiotidis and Abdollahnejad, 2021). As such, there can be a high subjectivity in the estimates, which may primarily come from the way in which the points assigned to logs are segmented out from a cloud containing all the data (i.e., log and the background). Typically, a human processor of such data, accounts for what the eyes can see in the cloud such as shapes and, when available, the color of the points. Assuming that a human processor would have to repeat the processing steps on the same cloud twice or more times, there is a degree of uncertainty in estimates as coming from the same source of processing error, since it is difficult for a human to make exactly the same cloud segmentation decision each time. Then, assuming that the same cloud would be processed by different persons, there is a degree of subjectivity that comes from how different people see and make decisions on what points should be included in processing following the segmentation.
Among the main concepts of digitization is that of a technology being sufficiently reliable for a given task (Wang et al., 2019a; Panagiotidis and Abdollahnejad, 2021) which comes from our understanding of systems design and analysis (Wasson, 2006). Since sourcing and processing data are integrant workflow steps, one would expect to get the same, readily usable estimates at the end of the process. If this would not be possible, then it is important to see how much such estimates may deviate due to the intra- or inter-person subjectivity, which are commonly known as intra- and inter-rater reliability, respectively (Gwet, 2001; 2008; Bonnet, 2023).
This study tried to quantify the reliability of log volume estimates sourced from LiDAR data, by employing the concepts of intra- and inter-rater variability and reliability. LiDAR point clouds are commonly sourced from mobile platforms such as smartphones or mobile professional scanners. This study employed both types of platforms because those from the first category are typically used for individual logs, while those from the second category are more effective for handling groups of logs. Therefore, the latter platforms produce increasingly crowded point clouds as the number of logs increases. Besides, different people can have different experience with the point cloud processing tasks and, as such, it is important to assess if significant deviations arise from this factor. The study aimed to answer the following questions: i) is the inter-person experience with point cloud processing—defined herein as an individual’s prior practical engagement, training, and familiarity with point cloud processing software (specifically CloudCompare) and related data manipulation tasks—a factor that may cause significant deviations in log volume estimates?, ii) are there significant deviations in log volume estimates related to the subjectivity of the same person when segmenting the point clouds?, and iii) which type of point clouds are likely to produce the most stable estimates: single or multiple log point clouds?
2 Materials and methods
2.1 Study site
The point clouds required by this study were collected in the Southern part of Romania, in the forests managed by the Regional State Directorate of Dolj, which is under the authority of National Forest Administration – RNP Romsilva. The Romanian forests are highly diverse (Ioras et al., 2009; Nicolescu, 2022) and distributed on altitudinal layers, starting from mountainous pure Norway spruce stands and ending with plain and meadow poplar forests (Toader and Dumitru, 2005; Stăncioiu et al., 2018). The Southern part of Romania is mostly bordered by the Danube River and poplar forests have an important share in the area. Data was collected by scanning with a ZEB-REVO Portable Scanning System and an iPhone 13 Pro Max (Figure 1), which was done at two yards (located 43°51′00″ N 23°06′53″ E and 43°51′20″ N 23°11′43″ E, respectively) that concentrated logs from several harvesting areas located nearby.

Figure 1. Examples from the field data collection activity showing (a) scanning of log groups by a ZEB-REVO Portable Scanning System (left), (b) individual log scanning by an iPhone 13 Pro Max (right), and (c) a schematic diagram illustrating the typical closed-loop scanning path for the iPhone around an individual log, maintaining an approximate 1m distance and varying sensor orientation.
The characteristics of the poplar logs used in this study revealed a diverse range of biometric attributes. The logs exhibited a length varying from 1.96 to 9.07 m, with an average value of 5.49 ± 1.23 m. At the small end, the diameter ranged from 11.50 to 68.00 cm, yielding an average value of 33.36 ± 8.93 cm. The large end diameter varied from 16.00 to 78.00 cm, averaging 41.43 ± 11.47 cm. Meanwhile, the diameter measured at the midpoint of the log varied from 15.50 to 67.00 cm, averaging 35.59 ± 8.62 cm.
2.2 Data collection and processing
A total of 432 logs were scanned using a ZEB-REVO Portable Scanning System (GeoSLAM Ltd and Ruddington, 2017). This handheld mobile LiDAR scanner, which uses Simultaneous Localization and Mapping (SLAM) technology for geo-referencing, was employed to capture 3D point cloud data of logs arranged in groups. The logs within each group were placed on the ground with an approximate spacing of 1 m between them. A total of 22 groups were considered, containing 14 to 26 logs (about 20 per group, on average). From this set, 418 logs were individually scanned using an iPhone 13 Pro Max equipped with its integrated LiDAR sensor and running the “3D Scanner App” (Laan, 2021a). This setup allowed for the direct generation of 3D point clouds from the LiDAR data. The iPhone 13 Pro Max performed adequately for capturing the geometry of individual logs at close range, providing sufficient point density for subsequent analysis. The remaining 14 logs, while scanned as part of a group with the ZEB-REVO system, were not scanned individually with the iPhone due to time limitations and were therefore excluded from the analyses pertaining to single-log datasets.
The scanning procedures and protocols used for the two mobile LiDAR platforms were comparable to those used in previous studies (Borz and Proto, 2022; Niţă and Borz, 2023). The two mobile LiDAR platforms differ in their sensing distances, and the typical workflows and algorithms used to reconstruct objects from the collected data depend on the reconstruction technology employed. The 3D Scanner App (Laan, 2021a) was pre-installed on the iPhone prior to field data collection. The app’s free version is currently available for download (Laan, 2021a). The 3D Scanner App facilitates real-time LiDAR scans and point cloud computation (Laan, 2021b; Gharge and Ali, 2024). The iPhone scanning process operated in a closed loop, commencing at one end of each log and involving data collection from approximately 1 m by moving forward and backward around the log at low speed (Figure 1, right). This was done while orienting the sensing devices toward the log from various positions and angles, as guided by the app’s interface. For this device and the associated app, the scans were conducted at medium density (MD), allowing the point clouds to effectively represent the logs. After scanning each log, an ID was assigned in the app, and the results were saved to the device’s memory before the operator proceeded to the next log. In contrast, the ZEB-REVO Portable Scanning System was used for scanning groups of logs (14–26 logs per group). The process involved walking around the logs and scanning them from approximately 2 m, starting and finishing at the same point, on a horizontally leveled platform. This device enables scanning at higher distances (up to 30 m), collects substantial amounts of data as spatially referenced point clouds, and is suitable for large-area scans (GeoSLAM Ltd and Ruddington, 2017). After each scanning session and based on external control, the device automatically processed and saved the point cloud data onto a USB stick (Forkuo and Borz, 2023). Both scanning platforms can output data in 3D file formats that are quite similar; specifically, these include files containing point clouds and images or media captured during scanning (Laan, 2021b). However, in this study, the point clouds captured by both platforms were exported in the office in a binary format specifically designed for storing LiDAR data (.LAS) (Laan, 2021b). Specifically, the point clouds from the iPhone equipped with the 3D Scanner App were exported at medium density, with the Z-axis oriented upwards, and in LAS format in meters with color settings.
Data collection, pre-processing and processing workflows are described in Figure 2 for the LiDAR-based data. The method for processing data and estimating log volumes in CloudCompare consists of several key steps, each designed to enhance the quality of the point cloud data and facilitate accurate shape reconstruction. The parameters used in the process were those described in Niţă and Borz (2023). Accordingly, noise was eliminated from the point cloud data to improve overall clarity and accuracy, using a k-Nearest Neighbors (kNN) algorithm specifically configured with a value of 60. This parameter aids in identifying and removing points that do not conform to the overall structure of the data, thereby enhancing the integrity of the subsequent analyses (Dong et al., 2023). Following noise removal, normalization of the point cloud was conducted to ensure consistent orientation and scaling, using a Least-Squares Method (LSM) with a quadric shape (Rusu et al., 2009), in combination with an automatically generated Octree structure and the same kNN value set at 60. Normalization is deemed very important in aligning the data for accurate comparative analysis and model fitting (Lin et al., 2022). Once normalization was completed, shape reconstruction was performed to accurately estimate the geometries of the logs, consisting of several sub-processes, starting with Poisson Surface Reconstruction. In this phase, the Poisson interpolation method was employed, with parameters set as follows: octree depth was set to 12, boundary to 3, samples per node to 6, point weight to 0, and 8 threads were used for parallel processing. This method is robust when reconstructing complex geometries from the point cloud, effectively capturing fine details (Kazhdan et al., 2006; Kazhdan et al., 2020). After the Poisson reconstruction, the RANSAC (Random Sample and Consensus) algorithm was used to fit cylindrical shapes to the point cloud data representing the logs, requiring a minimum of 500 support points for the algorithm to establish a reliable cylinder model, while the remaining RANSAC parameters were automatically adjusted to optimize the fitting process (Fischler and Bolles, 1981). Finally, a similar RANSAC approach was applied to fit conical shapes to the data, maintaining the same minimum support requirement of 500 points while using automatically configured parameters to enhance fitting accuracy. Collectively, these steps enabled the effective processing of LiDAR data in CloudCompare software, resulting in log volume estimates to five digits. The relevant inputs and outputs for data processing are shown in Figure 3. The initial point clouds sourced by both platforms were stored in a Google Drive data repository, along with a Microsoft Excel datasheet to support the collection of metadata for the processing effort.
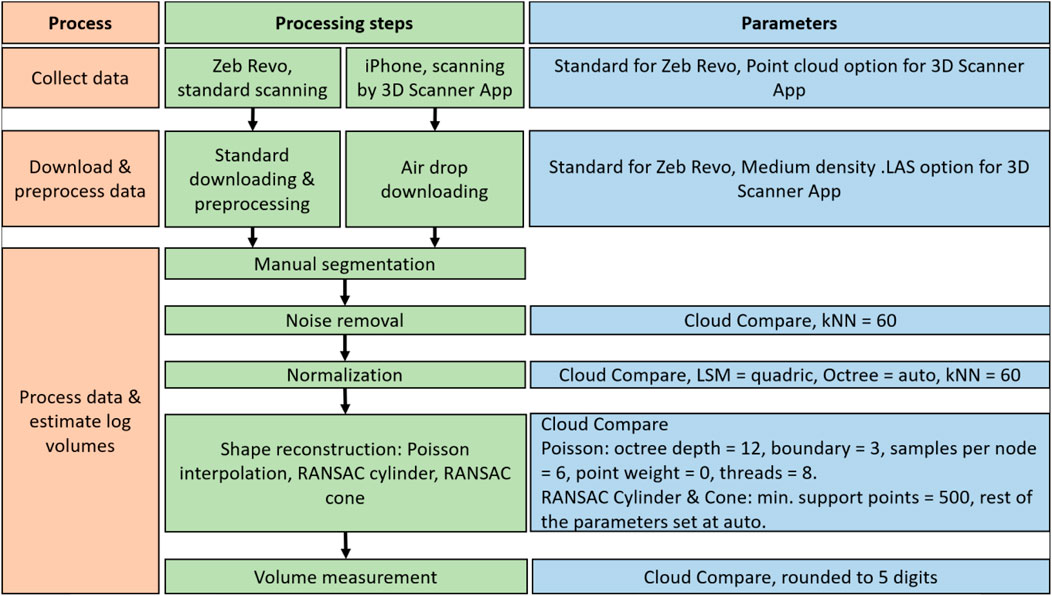
Figure 2. Description of the workflow used to collect, pre-process, process the data, and to get the log volume estimates.
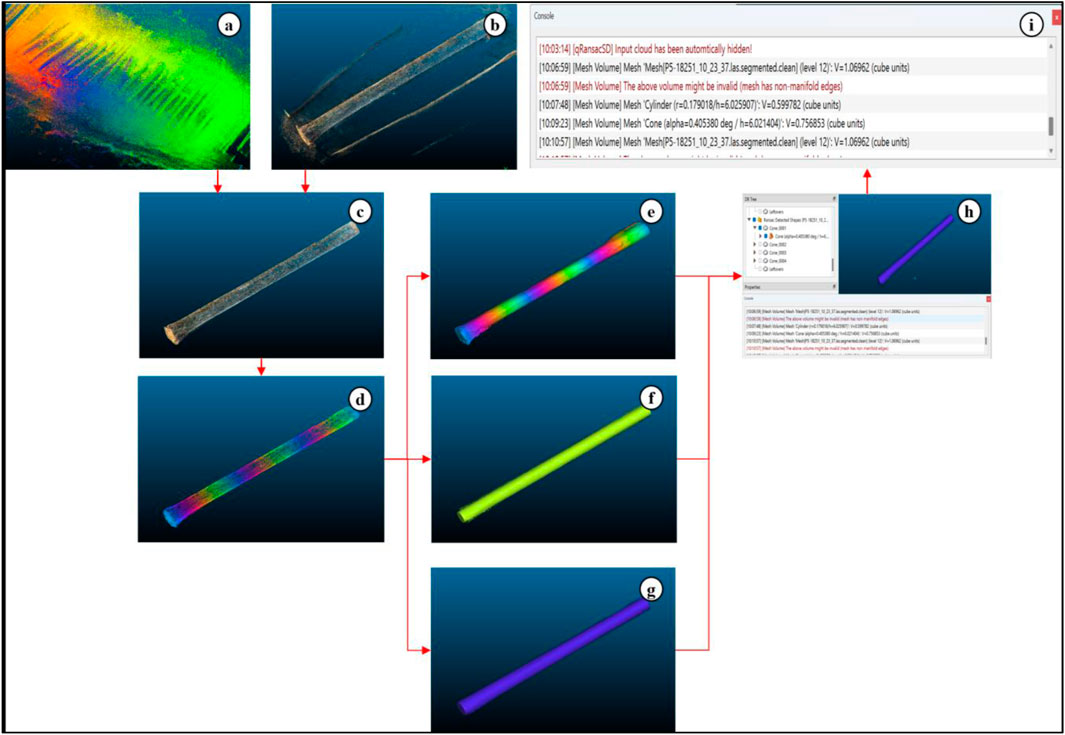
Figure 3. Steps used in data processing by CloudCompare. Legend: (a) – raw point cloud of a ZEB-REVO scan, (b) – raw point cloud of a iPhone scan, (c) – an example of a product after segmentation and noise removal, (d) – an example of a product after normalization, (e) – product after Poisson interpolation, (f) – product after RANSAC cylinder reconstruction, (g) – product after RANSAC cone reconstruction, (h) – an example of volume estimation (cone volume by RANSAC), (i) – volume display and visualization.
Reference data was collected as well, by manual measurements using a forestry tape and a caliper. Log diameters and lengths were measured to the nearest centimeter. Typically, this involved systematic measurements of diameters at a 0.5 m interval along the log, coupled with measurements of the log end and mid diameters and the length of the last segment of the log if it was shorter than 0.5 m. The manual measurements were then recorded on paper sheets. The concept used for manual measurement and volume estimation is fully described in Niţă and Borz (2023), as a part of the Hypercube 4.0 project (Hypercube 4.0, 2021). The reference volume for all logs was calculated based on the detailed manual field measurements (diameters at 0.5 m intervals along the log, end diameters, and total length), using established forestry formulas, primarily the section-wise truncated cone method for the highest accuracy, as detailed in Niţă and Borz (2023).
The Excel database included, among others, the metadata of each log such as the ID, group to which the log belonged when the case, platform used to collect the data, name of the person that processed the data, as well as the log volume estimates produced by the manual measurement. In addition, data fields such as the date of processing, time spent in processing, and volume estimates were included according to the workflows shown in Figures 2, 3. Repository of point clouds included a folder structure to contain all the intermediary processing products starting from the initial point clouds and ending with those used for volume estimation.
Data processing was performed by three persons with different experience (hereafter called subjects) who volunteered for the study. Subject 1 possessed substantial experience with CloudCompare and point cloud processing tasks, defined as over 2 years of consistent use in various research projects and formal training. In contrast, Subjects 2 and 3 were beginners, whose primary exposure consisted of an introductory tutorial and practice exercises provided specifically for this study before commencing data processing. To support the learning of the basic steps, a video tutorial developed in the framework of the Hypercube 4.0 (Hypercube 4.0, 2021) was used as a guiding reference. The subjects were provided with any other information and guidance as they asked for it in advance of the study, and they were allowed to experiment with some data as a training exercise.
2.3 Experimental design and data analysis
Volume data was used for comparison of differences and for checking the intra- and inter-rater reliability. To do so, the reference data coming from manual measurements was codded according to the method used to estimate the volume, and named hereafter RVHuber, RVSmalian, RVCil, and RVCone. These were used only to show the differences that can arise from the choice of measurement and estimation method applied to manual data. For the assessments done to check the intra- and inter-rater variability, the datasets were codded by abbreviations showing the shape reconstruction algorithm used, platform used to source the point clouds, processing attempt (repetition), and a number from 1 to 3 to designate the subject that carried out the processing tasks. Figure 4 shows the system used to code the two datasets: the dataset collected with Zeb Revo scanner and the dataset collected with iPhone.
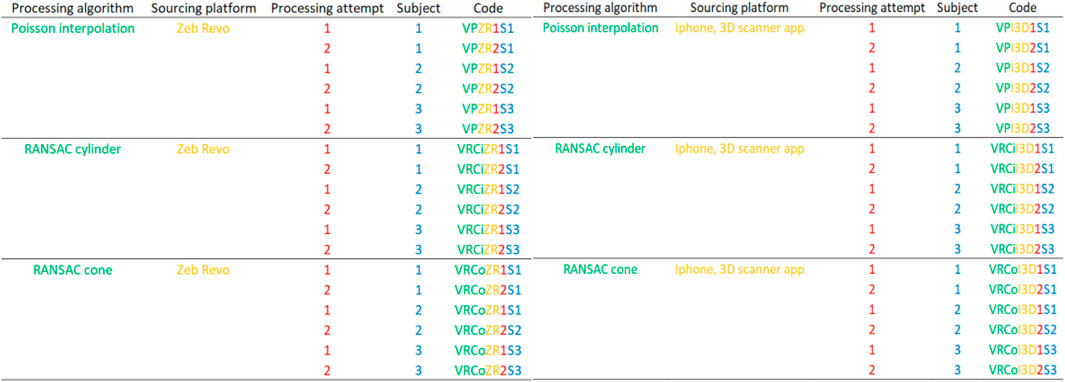
Figure 4. Description of the system used to code the datasets for intra- and inter-rater reliability analysis. The “Code” column shows the abbreviation for each dataset, where “VP” is Volume by Poisson, “VRCi” is Volume by RANSAC Cylinder, “VRCo” is Volume by RANSAC Cone; “ZR” denotes ZEB-Revo sourced data, “I3D” denotes iPhone 3D Scanner App sourced data; the number “1” or “2” immediately following the platform code indicates the first or second processing attempt (repetition) by the subject; “S1,” “S2,” or “S3” in the “Subject” part of the code refers to Subject 1 (experienced), Subject 2 (beginner), or Subject 3 (beginner), respectively. The left panel shows codes for datasets sourced by the ZEB Revo scanner, and the right panel for those sourced by the iPhone.
Subject 1 (coded as S1) was the individual with more experience with the use of Cloud Compare and LiDAR data, while subjects 2 and 3 were at their first experience with such tasks. Each subject worked twice with each dataset. In other words, the data was processed from end-to-end by each subject two times. This allowed to measure the intra-rater reliability (commonly known as internal consistency), which was measured using Cronbach’s alpha (Johnson, 2021; Revicki, 2023). This metric describes to what extent the measurements remain consistent over repeated trials ran under identical conditions, and the data is said to be reliable if the experiment yields consistent results on the same measure (Ferketich, 1990; Revicki, 2023). In this study, “identical conditions” refers primarily to the cloud segmentation step, as the input point cloud data was identical in each trail by the same subject. The parameters for subsequent steps, such as denoising and shape reconstruction, were also kept consistent as per the defined protocol. However, by different decisions on point selection, the outcomes of segmentation may affect the outcomes of the subsequent processing steps, therefore the volume estimates. Accordingly, if the decisions made on the points to include by segmentation led to identical point clouds for the following processing steps, then it is likely that the volume estimates would be identical and, as such, the results considered as being consistent between the trials. This part of the experiment led to the comparison of 18 datasets, coming from the platform used to collect the data (2), shape reconstruction algorithm used to process it (3) and the number of subjects (3).
The inter-rater reliability was measured using the inter-class correlation coefficient (ICC), which was adapted to the type of experiment conducted, as there are several classes and types of experiments (Bobak et al., 2018; Ten Hove et al., 2022). ICC assesses the reliability of ratings by comparing the variability of different ratings of the same observation against the variation of all ratings and observations. A class 2 experiment was setup in which a number of raters (subjects herein) are selected at random from a population of raters, and the selected raters rate all the observations (Koo and Li, 2016; Shieh, 2016). This part of the experiment used the data coming from same shape reconstruction procedure and platform used to collect it, but compared between each two possible subjects. This resulted in a number of 72 comparisons.
Analysis of the data was carried out in Microsoft Excel equipped with the Real Statistics (Zaiontz, 2023) add-in. Real Statistics is a tool that extends the capabilities of Microsoft Excel in statistical analysis and which provides dedicated functionalities for reliability assessments such as Cronbach’s alpha and ICC. The standard functionalities as included in Real Statistics were used in this study for analysis. Before running the analyses, the data on volume estimates was paired so as to remove those pairs which i) were commented by a given subject as unreliable in estimates, ii) had at least one data point missing in the pair due to various reasons and iii) had data that was showing contrasting differences which were less likely to occur solely due to a bad decision in segmenting the point clouds. A numerical description of the size of initial and compared datasets is provided in Supplementary Material (Supplementary Table S1).
The resulting datasets were also subjected to an advanced quantitative assessment of the differences. Error metrics such as the bias (BIAS), mean absolute error (MAE) and root mean squared error (RMSE) were computed for each dataset to characterize the deviation in volume estimates. These were used in conjunction with Cronbach’s alpha and ICC to characterize the reliability of estimates.
Bias (BIAS) is calculated as the average error, representing the difference between predicted (measured) and actual (reference) values (Willmott and Matsuura, 2005). It indicates whether the predictions are systematically higher or lower than the observed values. By definition, a positive bias value suggests underestimation, while a negative bias indicates overestimation. Bias is frequently used to assess also the accuracy of predictive models, particularly in fields such as forecasting and regression analysis (Hyndman and Koehler, 2006). Mean Absolute Error (MAE) is computed as the average of the absolute differences between actual and predicted values, providing a straightforward assessment of prediction accuracy by averaging the absolute errors (Willmott and Matsuura, 2005; Hyndman and Koehler, 2006). MAE is preferred in many analyses due to its reduced sensitivity to outliers, especially when compared to RMSE (Hyndman and Koehler, 2006). It is also commonly used in regression analysis and model evaluation to measure the average magnitude of prediction errors (Hyndman and Koehler, 2006). Root Mean Squared Error (RMSE) is calculated as the square root of the average of the squared differences between actual and predicted values (Chai and Draxler, 2014; Hodson, 2022). By squaring the differences, RMSE gives greater weight to larger errors (differences), thereby making it more sensitive to outliers compared to MAE (Armstrong, 2001; Chai and Draxler, 2014). RMSE offers a measure of the standard deviation of prediction errors and is also widely used in regression analysis, forecasting, and model validation to assess prediction accuracy (Li, 2017).
Cronbach’s alpha is derived by correlating the score for each scale item with the total score for each observation and comparing it with the variance of all individual item scores (Cronbach, 1951). This statistic measures the internal consistency or reliability of a set of items, where higher values indicate greater reliability (Tavakol and Dennick, 2011). Cronbach’s alpha is widely used in survey research and psychometrics to assess the reliability of scales and questionnaires (Tavakol and Dennick, 2011). It is particularly valuable in the process of designing and testing new survey or assessment instruments (Frost, 2022), and it is also well fitted to quantitative continuous data. The intraclass correlation coefficient (ICC) is calculated using variance components obtained from an analysis of variance (ANOVA) (Koo and Li, 2016). It measures the ratio of variance between groups to the total variance, thereby assessing the reliability of measurements or ratings for groups or clusters (Shrout and Fleiss, 1979). Higher ICC values indicate greater reliability and are commonly used in reliability studies, particularly in the context of repeated measurements or ratings by different observers (McGraw and Wong, 1996).
The complete statistical workflow included a test to check the normality of data, estimation of intra- and inter-rater reliability, and the estimation of BIAS, MAE and RMSE. Signed differences, absolute differences and squared differences between the observations of a given dataset used for comparison were included in the test for normality in data, and the results were presented in an aggregated form by considering i) the differences that occurred over all logs measured in the field by the manual method by taking one of the volume estimation method as a reference, ii) the intra-rater reliability, characterized qualitatively by bivariate plots showing the magnitude of differences, iii) the intra-rater reliability characterized, quantitatively by the Cronbach’s alpha, BIAS, MAE and RMSE, and iv) the inter-rater reliability, characterized quantitatively by the ICC, BIAS, MAE and RMSE.
3 Results and discussion
3.1 Agreement of log volume estimates based on manual measurement
The results of normality check indicated that none of the variables could be assumed to come from a normal distribution (data not shown herein). The data reported in Figure 5 indicate several degrees of agreement between the log volume estimates based on manually measured data. The methods that used finer sampling of the diameters produced more concordant results as shown by the trend equations included in the figure, a result that is consistent with previous findings (e.g., Niţă and Borz, 2023).
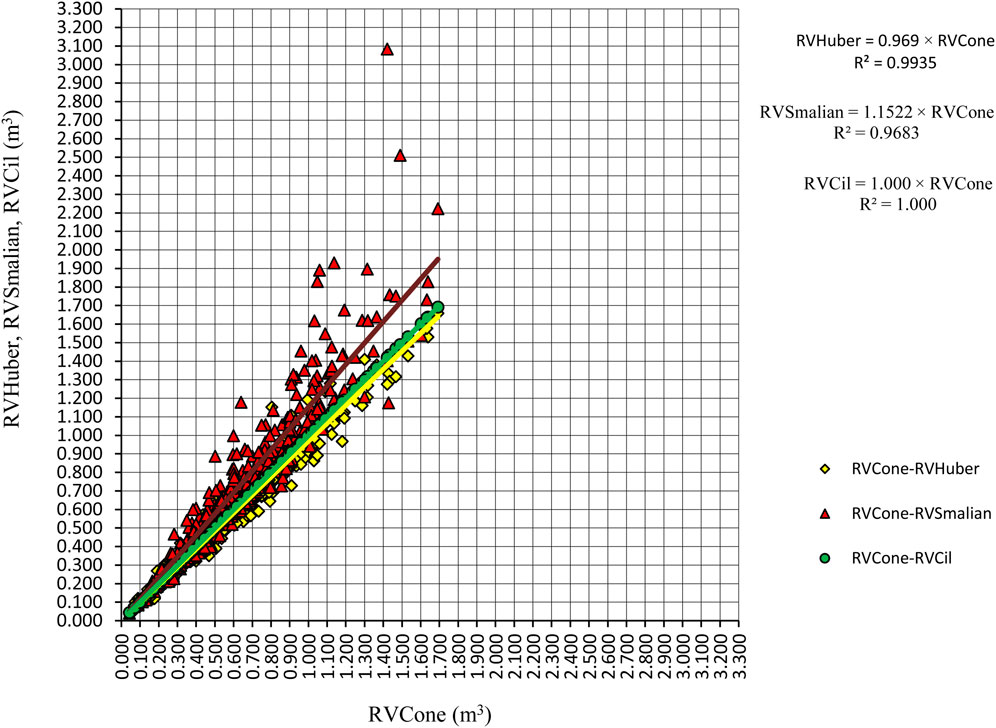
Figure 5. Agreement of log volume estimates based on the manual measurement methods. Legend: RVHuber - volume computed by Huber’s formula, RVSmalian - volume computed by Smalian’s formula, RVCil - volume computed by 0.5 m cylinders, RVCone - volume computed by 0.5 m truncated cones.
The analysis of different volume estimation methods highlights their tendencies to either overestimate or underestimate the log volumes. In this study, Smalian’s formula tends to overestimate volume when compared to the truncated cone (RVCone) method, as it is evident from the scatter plot showing that the trend line for RVSmalian is positioned above the diagonal. The overestimation arises because Smalian’s formula calculates volume based on the average of the cross-sectional areas at the ends of the log, which can be particularly inaccurate for tapering logs (de León and Uranga-Valencia, 2013; Li et al., 2015; Ahmad et al., 2020). In contrast, Huber’s formula tends to underestimate volume compared to the reference cone method used in this study, as the scatter plot indicates that the trend line for RVHuber appears slightly below the diagonal, expressed by the trend equation. This underestimation is a result of Huber’s calculation of volume based on the cross-sectional area at the midpoint of the log, which can lead to inaccuracies in cases of significant tapering or irregularities along the log (de León and Uranga-Valencia, 2013; Li et al., 2015; Ahmad et al., 2020). However, the reference cylinder method (RVCil), which calculated volume based on manually measured diameters at 0.5 m intervals, yielded estimates that showed extremely high agreement (R2 = 1.000) with the reference volumes derived from the section-wise truncated cone formula using the same detailed 0.5 m interval measurements. This high concordance, effectively a near 1:1 relationship, is due to the dense and comparable diameter sampling used in both the RVCil calculation and the most detailed reference method (Niţă and Borz, 2023). This method’s success is due to the diameter sampling procedure used, which was denser compared to that applied for Smalian’s and Huber’s formulae, an approach that better fitted the taper of the logs and had less residuals compared to the estimation of the logs’ segments volumes by truncated cones since the reference diameters used were the same.
Overall, these findings align with existing literature (e.g., Niţă and Borz, 2023), emphasizing the need to acknowledge inherent biases in various volume estimation methods based on their underlying assumptions and calculations, which is essential for selecting the appropriate method for accurate volume estimation in forestry and timber management.
3.2 Intra-rater reliability of log volume estimates
Figure 6 shows the bivariate plots of comparisons ran between the trials (repetitions) of the same subject processing the same dataset. The logic of this qualitative assessment is that, if there would be no differences between the estimates of a given dataset coming from separate trials, then all data points would distribute over the 1:1 identity line, which was not the case for any of the analyzed datasets. As a fact, there were important differences which seemed to depend on the level of experience with point cloud processing, type of input data (single log or group of logs) and, most importantly, the method used for shape reconstruction.
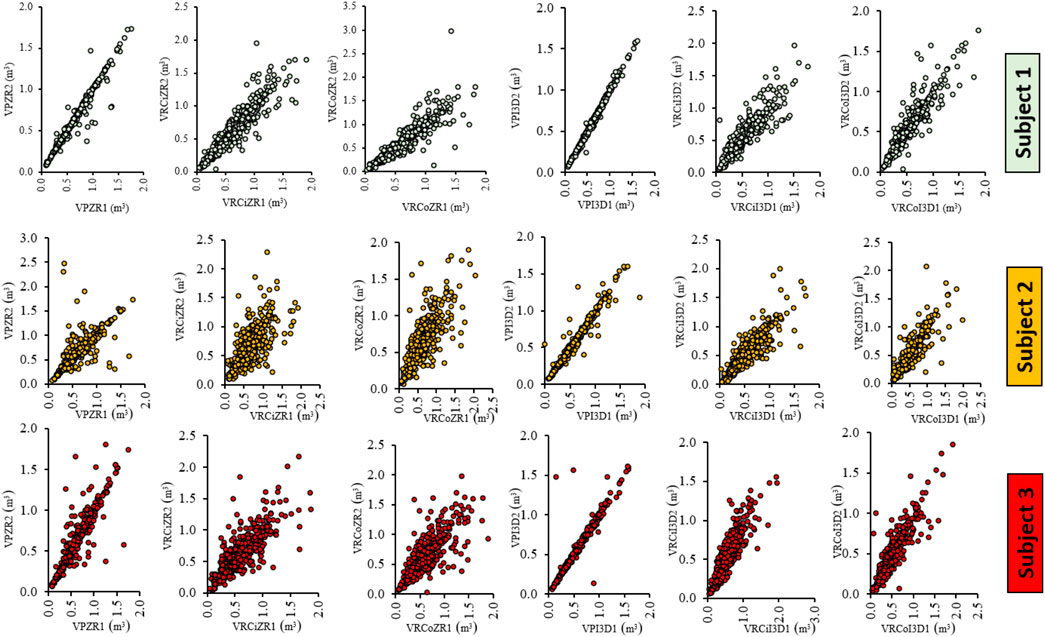
Figure 6. Intra-rater reliability described by bivariate plots. Legend: the color-coded bivariate plots represent different subjects.
Shape reconstruction using Poisson interpolation provided the highest intra-rater reliability, irrespective of the subject (Figure 6); however, it showed different degrees of reliability when the type of dataset was considered for the same subject. For instance, working with point clouds of single logs was more reliable compared to that of working with groups of logs, even if the Zeb Revo point clouds are often described as being accurate (Bauwens et al., 2016; Dewez et al., 2017; Sammartano and Spanò, 2018; Warchoł et al., 2023), hence there is a difference between accuracy and reliability. Then, intra-rater reliability depends on experience, as it can be seen when looking at the inter-subject plots of the same compared datasets. These results may have several explanations. For instance, Poisson surface reconstruction is a method used for shape reconstruction that is effective at reconstructing smooth surfaces from point clouds (Kazhdan et al., 2006; 2020); it can fill in gaps in the data to create a complete 3D model. One of the main advantages of Poisson interpolation is its resilience to data noise, as it considers all points at once without resorting to heuristic spatial partitioning or blending (Kazhdan et al., 2006; Kazhdan et al., 2020). However, Poisson interpolation may introduce artifacts if the point cloud is noisy or has outliers (Kazhdan et al., 2006; 2020). Additionally, it requires tuning parameters for the best results, which can be time-consuming and may require expertise (Kazhdan et al., 2006; Kazhdan et al., 2020).
RANSAC (Random Sample Consensus) cylinder reconstruction is another method used for shape reconstruction (Fischler and Bolles, 1981; Raguram et al., 2008; Cavalli et al., 2023); it is robust against outliers in the data, making it effective for modeling objects that are cylindrical in shape (Raguram et al., 2008; Niebles and Krishna, 2017). RANSAC cylinder reconstruction is relatively easy to implement and can handle a moderate percentage of outliers without significant computational cost (Bolles and Fischler, 1981; Niebles and Krishna, 2017). However, this method may not perform well with non-cylindrical shapes or if the cylinder axis is not well-defined by the data points (Niebles and Krishna, 2017). Additionally, while efficient, the method can become computationally expensive if the share of outliers is high (Niebles and Krishna, 2017). RANSAC cone reconstruction is suitable for objects with a conical shape and can handle noisy data points (Schnabel et al., 2007). It can be adapted to different shapes and sizes of cones, making it versatile for various applications (Schnabel et al., 2007; Niebles and Krishna, 2017). However, similar to RANSAC cylinder reconstruction, it may struggle with shapes that do not conform to an ideal cone (Niebles and Krishna, 2017). The accuracy of the reconstruction can also be sensitive to the parameters chosen for the RANSAC algorithm (Niebles and Krishna, 2017). Looking at the data outputted by these two shape reconstruction methods (Figure 6), it is evident that they had different degrees of disagreement. In addition, magnitude of disagreement seemed to increase as a function of log size, particularly for those logs that had an estimated volume which was higher than 0.5 m3.
The relevant quantitative measures of the intra-rater reliability are provided in Figure 7. As measured by Cronbach’s alpha at the subject level, the highest intra-rater reliability was that when working with data inputs on single logs and reconstructing the log shapes by Poisson interpolation. This was consistent among the subjects, although Cronbach’s alpha had different magnitudes among the subjects and assessments. At the dataset level, single log data and reconstruction by Poisson interpolation returned the best result for the first subject, with a maximum Cronbach’s alpha of 0.998. Next in line was the multi-log dataset of which the volume estimates were produced by Poisson reconstruction by the first subject, which returned a Cronbach’s alpha of 0.987, and the third and fourth best inter-rater reliabilities were found for the second and third subject based on single log data and Poisson reconstruction.

Figure 7. Intra-rater reliability measured by difference metrics and Cronbach’s alpha. Legend: reference and compared datasets are described in Figure 4, BIAS – bias, MAE – mean absolute error, RMSE – root mean squared error. Note: in green, yellow, orange and red, are provided the first, second, third and fourth-best results of all comparisons for the Cronbach’s alpha. The order of reliability is given from green to red for the compared datasets in terms of Cronbach’s alpha; for example green, yellow and red highlighting indicate the first-, second- and third-ranked intra-rater reliabilities for each subject, respectively. The rightmost column classifies the intra-rater reliability at subject level by the mean values of Cronbach’s alpha.
In general, the internal consistencies measured as the average values of Cronbach’s alpha at the subject level were high, with values of 0.902–0.965. However, the best intra-rater reliability was found for the first (experienced) subject, being followed by the third and the second subjects. The significance of these values can be understood by referring to the classifications of Cronbach’s alpha values. Cronbach’s alpha is a measure of internal consistency, which indicates how closely related a set of items are as a group (Cortina, 1993; Johnson, 2021). It is considered a measure of scale reliability (Tavakol and Dennick, 2011; Johnson, 2021). According to general guidelines, a Cronbach’s alpha value above 0.7 is considered acceptable, values above 0.8 are considered good, and values above 0.9 are considered excellent (Tavakol and Dennick, 2011; Johnson, 2021). In this study, the values between 0.902 and 0.965 indicate an excellent internal consistency, suggesting that the items used in the measurement are highly correlated and reliably measure the same construct. High values of Cronbach’s alpha imply that the measurements are consistent across different items, and the responses are reliable (Streiner, 2003; Tavakol and Dennick, 2011; Johnson, 2021). This level of internal consistency is important in ensuring the validity and reliability of the measurements, especially in research settings where accurate and consistent data are essential (Cortina, 1993; Taber, 2018; Johnson, 2021; Frost, 2022). In the context of this study, the high values of Cronbach’s alpha indicate that the log measurements taken by the subjects were generally consistent and reliable. The fact that the first (experienced) subject had the highest intra-rater reliability suggests that experience may play an important role in achieving more consistent and reliable estimates. This finding aligns with previous research that highlights the importance of experience and training in improving measurement accuracy and reliability (Hobbs-Murphy et al., 2024).
Also, the differences measured with BIAS, MAE and RMSE metrics were generally consistent with the assessments done by Cronbach’s alpha. For instance, the RMSE kept the same order of magnitude depending on the value of Cronbach’s alpha, with lower magnitudes in RMSE corresponding to higher values of Cronbach’s alpha, which was only partly true for MAE, and inconsistent for the BIAS, since this metric is signed and shows the direction of under- or over-estimation. The consistency among the outputs of BIAS, MAE, RMSE, and Cronbach’s alpha can be understood by examining how each metric interacts with the data. When the internal consistency is high, as indicated by Cronbach’s alpha, the errors in the measurements are likely to be smaller and the estimates more consistent (Goforth, 2024). This is reflected in lower values of RMSE and MAE. RMSE, in particular, is sensitive to larger differences, and its lower values correspond to higher values of Cronbach’s alpha, indicating that the measurements are more accurate, reliable and consistent (Singh, 2022; Goforth, 2024).
3.3 Inter-rater reliability of log volume estimates
Inter-rater reliability was measured by the intra-class correlation (ICC) and was complemented with the confidence intervals and the difference metrics, as shown in Figures 8–10. Figure 8 shows the results grouped by the Poisson interpolation algorithm, while Figures 9, 10 show the results based on RANSAC interpolation as cylinders and cones. Irrespective of the dataset, on average, the lowest ICC was consistently found for the multi-log datasets (Figures 8–10).
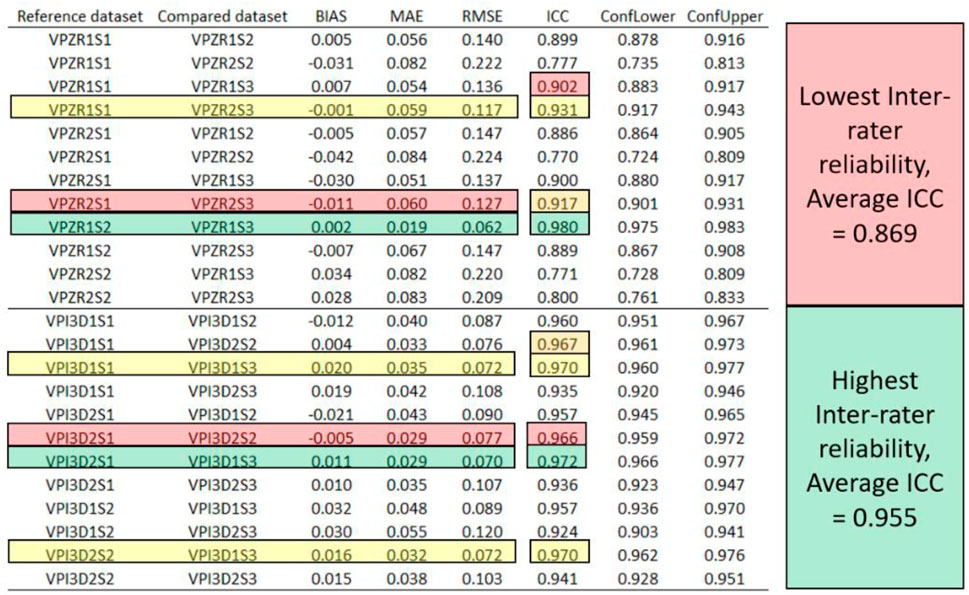
Figure 8. Inter-rater reliability for the Poisson shape reconstruction algorithm, measured by difference metrics and intra-class correlation (ICC). Legend: reference and compared datasets are described in Figure 4, BIAS – bias, MAE – mean absolute error, RMSE – root mean squared error. ConfLower and ConfUpper stand for the lower and upper confidence thresholds of the ICC. Note: in green, yellow, orange and red, are provided the first, second, third and fourth best results of all comparisons for the ICC. The order of reliability is given from green to red for the compared datasets in terms of ICC; for examplegreen, yellow and red highlighting indicate the first-, second- and third-ranked inter-rater reliabilities for each dataset. The rightmost column classifies the inter-rater reliability at dataset level by the mean values of ICC.
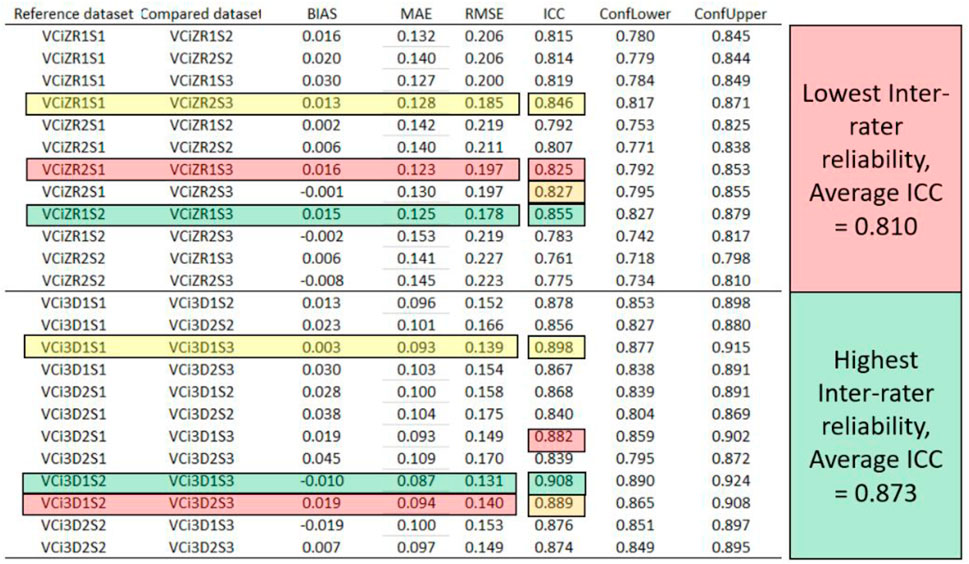
Figure 9. Inter-rater reliability for the RANSAC cylinder shape reconstruction algorithm, measured by difference metrics and intra-class correlation (ICC). Legend: reference and compared datasets are described in Figure 4, BIAS – bias, MAE – mean absolute error, RMSE – root mean squared error. ConfLower and ConfUpper stand for the lower and upper confidence thresholds of the ICC. Note: in green, yellow, orange and red, are provided the first, second, third and fourth best results of all comparisons for the ICC. The order of reliability is given from green to red for the compared datasets in terms of ICC, such as the green, yellow and red were the first, second and third ranked inter-rater reliabilities for each dataset. The rightmost column classifies the inter-rater reliability at dataset level by the mean values of ICC.

Figure 10. Inter-rater reliability for the RANSAC cone shape reconstruction algorithm, measured by difference metrics and intra-class correlation (ICC). Legend: reference and compared datasets are described in Figure 4, BIAS – bias, MAE – mean absolute error, RMSE – root mean squared error. ConfLower and ConfUpper stand for the lower and upper confidence thresholds of the ICC. Note: in green, yellow, orange and red, are provided the first, second, third and fourth best results of all comparisons for the ICC. The order of reliability is given from green to red for the compared datasets in terms of ICC, such as the green, yellow and red were the first, second and third ranked inter-rater reliabilities for each dataset. The rightmost column classifies the inter-rater reliability at dataset level by the mean values of ICC.
However, there was an order of magnitude in differences between the shape reconstruction algorithms used, with Poisson interpolation being ranked the first. For the Poisson interpolation algorithm, the ICC varied between 0.770 and 0.980 when working with multi-log datasets, and from 0.924 to 0.972 when working with single log datasets. For the same types of input datasets, it varied between 0.761 and 0.855 and from 0.839 to 0.908 for RANSAC cylinder, and from 0.784 to 0.869 and 0.843 to 0.893 for RANSAC cone shape reconstruction algorithms, respectively, indicating moderate to excellent inter-rater reliabilities. Similar to Cronbach’s alpha, RMSE was related in magnitude with ICC, with low values of RMSE being associated to high values in ICC.
The ICC plays an important role in delineating the reliability of measurements, with values indicating substantial reliability across various analyses (Chinn, 1991; Gisev et al., 2013; Koo and Li, 2016; Bruton et al., 2000). However, as with other reliability coefficients, there is no universally accepted level of reliability for the ICC (Bruton et al., 2000). The ICC ranges from 0 to 1, with values closer to one indicating a higher reliability. Chinn (1991) suggests that any measure should have an ICC of at least 0.6 to be considered useful, thus reinforcing the relevance of our findings. The ICC is particularly valuable when comparing the repeatability of measurements across different units, as it is a dimensionless statistic (Bruton et al., 2000). It is most effective when three or more sets of observations are collected, either from a single sample or from independent samples, according to Bruton et al. (2000). For instance, an average ICC of 0.900 was obtained from all the comparisons using the 3D Scanner App, whereas the average value of comparisons over the Zeb Revo data was much lower (0.833), indicating different degrees of reliability, and placing the comparisons on 3D Scanner App data in the category of excellent reliability (Bruton et al., 2000; Gisev et al., 2013). However, it is important to acknowledge certain limitations outlined by Rankin and Stokes (1998) that can render the ICC unsuitable for use in isolation. Specifically, when the ICC is applied to data from a diverse group of individuals exhibiting a wide range of the measured characteristic, the reliability may appear higher than when it is applied to a group with a narrow range of the same characteristic (Bruton et al., 2000). This underscores the need for caution when interpreting ICC values, particularly in contexts involving heterogeneous populations.
To answer the first question of the study, the inter-person experience is an important factor affecting the reliability of volume estimates. This is supported by both, the internal consistency of the assessments as well as by the intra-class correlation assessments, by which the second and third subjects, which were less experienced, performed poorer. Indeed, the differences in reliability were co-factored by the type of datasets used for segmentation, but still, there are important trends in data supporting the effect of experience on reliability. The question on whether the differences between the assessments are important and the assessments are still ranked as highly reliable is worth pursuing further. For instance, the experienced subject working on single log datasets achieved an internal consistency close to 1, meaning excellent reliability. However, the bias was positive, accounting for 0.010 m3, mean absolute error for 0.016 m3 and the root mean squared error for 0.027 m3, figures which some may interpret as big differences between the assessments.
Based on both the internal consistency and deviation metrics, the degree of deviation due to a person’s subjectivity may vary significantly, which answers to the second question of the study. Experienced persons are likely to come to more accurate, consistent and reliable estimates, which is less likely for unexperienced persons, therefore experience may be a co-factor in subjectivity when segmenting point clouds. In addition, the degree of reliability is also affected by the type of input dataset in question, with single log datasets generally improving the reliability of estimates.
The answer to the third question seems to be the most evident based on both types of reliability assessments. For the same person working on the same type of input dataset and with the same shape reconstruction method, the results indicate that working with single log input datasets produce the most reliable estimates. This is further supported by the results of inter-person assessment, consistently showing better outcomes when working with single log datasets. This may come from the fact that a given person can work more focused when the point clouds are not crowded and, as such, the geometry of the points is easier to understand by the human brain. Form our experience, working with point clouds of single logs can also prevent error in segmentation, and rendering the point clouds in natural colors may help deciding more accurately the boundaries of segmentation, which is a feature that can assist less experienced subjects.
Looking again at the data, it seems now that a new question may come up in relation to intra-rater reliability. By the Poisson interpolation, it seems that reliability of the estimates was consistently higher, irrespective of the type of dataset used and experience level of the subject. This should be explored in the future to check the degree at which the agreement and reliability of estimates may be related to the shape reconstruction method used since this study considered only the segmentation step of the process as being a subjective one.
Ideally, reliability figures should be built based on very large datasets containing both a high variability in log biometrics as well as in species and in the environment used for measurements, which could not be accommodated by this study. In addition, having much more subjects to make the assessments would contribute to a better understanding of the reliability of estimates, as well as to more representative figures under the statistical point of view. It is difficult, however, to run larger experiments, mainly due to the resources needed to accommodate them. As an example, the speed of processing depends largely on the architecture and power of the computers used to run the data processing steps. For instance, the experienced subject processed the data for both data processing attempts from 12 November 2023 to 9 February 2024, where the segmentation step took in between 2 and 3 min for one observation, meaning that for the data samples used in the study, this processing step alone took close to 60 h for one person. In addition, segmentation alone was the most time-consuming processing step (data not shown herein). Furthermore, while the data collection time was found to be comparable to conventional methods (Borz and Proto, 2022), future studies could explore alternative observation strategies to further enhance efficiency. For example, optimizing the scanning path or employing automated mobile platforms could significantly reduce the time required for data acquisition in the field, complementing the gains made by automating post-processing tasks.
Based on the findings of this study regarding reliability and the resources required to perform specific steps, there is a potential to improve both the efficiency and reliability. One suggested approach is to transfer the decision-making process for cloud segmentation to the computer. This would be the primary strategy to minimize the accuracy gap between novice and experienced operators, as it would effectively remove the human subjectivity identified as a key factor in our results (Hobbs-Murphy et al., 2024). By automating segmentation, the reliability of volume estimates would no longer depend on an operator’s experience level. As an intermediate step, the development of semi-automated tools and standardized, guided workflows within processing software could also help reduce inconsistencies. However, the most robust solution lies in leveraging advanced machine learning and computer vision algorithms (Guo et al., 2020; Sarker et al., 2024). Most likely, automated decisions will rely on the architecture of the point clouds and probably will use the color information contained in them. To do so, effective machine learning and computer vision algorithms will be required (e.g., Guo et al., 2020; GitHub, Inc, 2024; Sarker et al., 2024) since, for similar applications, several machine learning and computer vision algorithms have been proposed to perform point cloud data segmentation and shape reconstruction (Guo et al., 2020; Wang et al., 2020; Fang et al., 2023; Sarker et al., 2024). For example, PointNet (Qi et al., 2017) and DGCNN (Wang et al., 2019b) are state-of-the-art deep learning models for point cloud segmentation (GitHub, Inc, 2024). PointNet, for instance, takes a point cloud as the input and processes it directly with MLPs (multi-layer perceptron) layers, followed by a max-pooling layer for implicit global feature extraction (Qi et al., 2017), while DGCNN uses dynamic graph convolution to capture local geometric structures (Wang et al., 2019a). Another example is the 3D Convolutional Neural Network (3D CNN), that extracts features from the point cloud and then classifies each point on the basis of those features (Lee et al., 2022; Wang et al., 2018). More recently, advanced models that improve the results for point cloud segmentation by using mask-based learning approaches include MaskNet (Sarode et al., 2020) and MaskNet++ (Zhou et al., 2022). Besides, PCN (Point Completion Network) (Yuan et al., 2018) is a novel learning-based method for shape completion. Unlike previous shape reconstruction algorithms that usually require structural assumptions (such as symmetry) or annotations (such as semantic classes) regarding the underlying shape, PCN directly processes raw point clouds with no prior knowledge of the underlying shapes (Yuan et al., 2018). This reinforces that the outlook for AI techniques in the field of point cloud data processing is promising, with advancements in these deep learning models paving the way for more accurate and efficient point cloud segmentation and shape reconstruction. This class of computational approaches would likely solve the problem of accurate, consistent and reliable log segmentation from background data of point clouds.
4 Conclusion
Intra- and inter-rater reliability of log volume estimates based on LiDAR point clouds depends on experience of the person running the processing steps, in particular point cloud segmentation. Although the intra- and inter-rater figures indicate a moderate to excellent reliability, one must consider also other metrics such as those characterizing the deviation of the results. In other words, the magnitude of reliability, as indicated by figures such as the bias, mean absolute error and mean squared error, needs to be defined and categorized to serve the end users of the data. The potential to arrive at the same estimates lies in the way in which some of the point cloud processing steps are taken, particularly in the decision on how to segment the data characterizing the logs from the surrounding environment. Automation of these data processing steps may lead to a higher effectiveness in both reliability and resources spent.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
Written informed consent was not obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article because the person identifiable in photo is an author of this study.
Author contributions
GF: Data curation, Formal Analysis, Investigation, Resources, Software, Visualization, Writing – original draft, Writing – review and editing. SB: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work received funding from Romanian Ministry of Education and Research, CNCS – UEFISCDI, project number PN-IV-P8-8.1-PRE-HE-ORG-2023-0141, and project number PN-IV-P8-8.1-PRE-HE-ORG-2024-0186, within PNCDI IV.
Acknowledgments
The Authors acknowledge the support of the Department of Forest Engineering, Forest Management Planning and Terrestrial Measurements for supporting this study. Data collection and part of data processing tasks were supported by the Hypercube 4.0 Project - Moving Wood Measurement Towards a new Dimension (https://sites.google.com/view/hypercube40). The Authors would like to thank to Subject 2 and Subject 3 for their voluntary involvement in the study.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2025.1506838/full#supplementary-material
References
Ahmad, S. S. S., Mushar, S. H. M., Shari, N. H. Z., and Kasmin, F. (2020). A Comparative study of log volume estimation by using statistical method. Educ. - J. Sci. Math. Technol. 7 (1), 22–28. doi:10.37134/ejsmt.vol7.1.3.2020
Alvites, C., Marchetti, M., Lasserre, B., and Santopuoli, G. (2022). LiDAR as a tool for assessing timber assortments: a systematic literature review. Remote Sens. 14 (18), 4466. doi:10.3390/rs14184466
Armstrong, J. S. (2001). Selecting forecasting methods. Princ. Forecast. Int. Ser. Oper. Res. Manag. Sci. 30, 365–386. doi:10.1007/978-0-306-47630-3_16
Bauwens, S., Bartholomeus, H., Calders, K., and Lejeune, P. (2016). Forest inventory with terrestrial LiDAR: a comparison of static and hand-held mobile laser scanning. Forests 7 (6), 127. doi:10.3390/f7060127
Beland, M., Parker, G., Sparrow, B., Harding, D., Chasmer, L., Phinn, S., et al. (2019). On promoting the use of lidar systems in forest ecosystem research. For. Ecol. Manag. 450, 117484. doi:10.1016/j.foreco.2019.117484
Berendt, F., Wolfgramm, F., and Cremer, T. (2021). Reliability of photo-optical measurements of log stack gross volume. Silva Fenn. 55 (3), 1–13. doi:10.14214/sf.10555
Bobak, C. A., Barr, P. J., and O’Malley, A. J. (2018). Estimation of an inter-rater intra-class correlation coefficient that overcomes common assumption violations in the assessment of health measurement scales. BMC Med. Res. Methodol. 18, 93–11. doi:10.1186/s12874-018-0550-6
Bolles, R. C., and Fischler, M. A. (1981). A RANSAC-based approach to model fitting and its application to finding cylinders in range data. IJCAI 1981, 637–643.
Bonnet, A. (2023). Inter-rater reliability: definition, examples, calculation. Available online at: https://encord.com/blog/inter-rater-reliability/(Accessed July 13, 2024).
Borz, S. A., and Proto, A. R. (2022). Application and accuracy of smart technologies for measurements of roundwood: evaluation of time consumption and efficiency. Comput. Electron. Agric. 197, 106990. doi:10.1016/j.compag.2022.106990
Borz, S. A., Morocho Toaza, J. M., Forkuo, G. O., and Marcu, M. V. (2022a). Potential of Measure app in estimating log biometrics: a comparison with conventional log measurement. Forests 13 (7), 1028. doi:10.3390/f13071028
Borz, S. A., Papandrea, S. F., Marcu, M. V., Bacenetti, J., and Proto, A. R. (2022b). Postural assessment of three wood measurement options by the owas method: digital solutions seem to be better. Forests 13 (12), 2007. doi:10.3390/f13122007
Bruton, A., Conway, J. H., and Holgate, S. T. (2000). Reliability: what is it, and how is it measured? Physiother 86 (2), 94–99. doi:10.1016/s0031-9406(05)61211-4
Cavalli, L., Barath, D., Pollefeys, M., and Larsson, V. (2023). Consensus-adaptive RANSAC. arXiv Prepr. arXiv:2307.14030. doi:10.48550/arXiv.2307.14030
Chai, T., and Draxler, R. R. (2014). Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 7 (3), 1247–1250. doi:10.5194/gmd-7-1247-2014
Chatzopoulos, D., Bermejo, C., Huang, Z., and Hui, P. (2017). Mobile augmented reality survey: from where we are to where we go. IEEE Access 5, 6917–6950. doi:10.1109/ACCESS.2017.2698164
Chen, Q. (2015). Modeling aboveground tree woody biomass using national-scale allometric methods and airborne lidar. ISPRS J. Photogramm. Remote Sens. 106, 95–106. doi:10.1016/j.isprsjprs.2015.05.007
Chinn, S. (1991). Statistics in respiratory medicine. 2. Repeatability and method comparison. Thorax 46 (6), 454–456. doi:10.1136/thx.46.6.454
CloudCompare (2024). 3D Point cloud and mesh processing software open-source project. Available online at: https://www.danielgm.net/cc/(Accessed July 22, 2024).
Cortina, J. M. (1993). What is coefficient alpha? An examination of theory and applications. J. Appl. Psychol. 78 (1), 98–104. doi:10.1037/0021-9010.78.1.98
Cown, D. A. V. E. (2005). Understanding and managing wood quality for improving product value in New Zealand. N. Z. J. For. Sci. 35 (2/3), 205–220.
Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika 16, 297–334. doi:10.1007/BF02310555
Davis, L. S., Johnson, K. N., Bettinger, P., and Howard, T. (2001). Forest management: to sustain ecological, economic, and social values. 4th ed. Long Grove, IL: Waveland Press, Inc.
de León, G. C., and Uranga-Valencia, L. P. (2013). Theoretical evaluation of Huber and Smalian methods applied to tree stem classical geometries. Bosque 34 (3), 311–317. doi:10.4067/S0717-92002013000300007
de Miguel-Díez, F., Tolosana-Esteban, E., Purfürst, T., and Cremer, T. (2021). Analysis of the influence that parameters crookedness and taper have on stack volume by using a 3D-simulation model of wood stacks. Forests 12 (2), 238. doi:10.3390/f12020238
de Miguel-Díez, F., Reder, S., Wallor, E., Bahr, H., Blasko, L., Mund, J. P., et al. (2022). Further application of using a personal laser scanner and simultaneous localization and mapping technology to estimate the log’s volume and its comparison with traditional methods. Int. J. Appl. Earth Obs. Geoinf 109, 102779. doi:10.1016/j.jag.2022.102779
Dewez, T. J., Yart, S., Thuon, Y., Pannet, P., and Plat, E. (2017). Towards cavity-collapse hazard maps with Zeb-Revo handheld laser scanner point clouds. Photogramm. Rec. 32 (160), 354–376. doi:10.1111/phor.12223
Dong, S., Jiao, Z., Zhou, L., Yan, Q., and Yuan, Q. (2023). A novel filtering method of 3d reconstruction point cloud from tomographic SAR. Remote Sens. 15 (12), 3076. doi:10.3390/rs15123076
Fang, K., Xu, K., Wu, Z., Huang, T., and Yang, Y. (2023). Three-dimensional point cloud segmentation algorithm based on depth camera for large size model point cloud unsupervised class segmentation. Sensors 24 (1), 112. doi:10.3390/s24010112
Feng, Y., and Audy, J. F. (2020). Forestry 4.0: a framework for the forest supply chain toward Industry 4.0. Gestão and Produção 27 (4), e5677. doi:10.1590/0104-530X5677-20
Ferketich, S. (1990). Internal consistency estimates of reliability. Res. Nurs. Health 13 (6), 437–440. doi:10.1002/nur.4770130612
Fischler, M. A., and Bolles, R. C. (1981). Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 24 (6), 381–395. doi:10.1145/358669.358692
Forkuo, G. O., and Borz, S. A. (2023). Accuracy and inter-cloud precision of low-cost mobile LiDAR technology in estimating soil disturbance in forest operations. Front. For. Glob. Change 6, 1224575. doi:10.3389/ffgc.2023.1224575
Frost, J. (2022). Cronbach’s alpha: definition, calculations and example. Available online at: https://statisticsbyjim.com/basics/cronbachs-alpha/(Accessed August 21, 2024).
GeoSLAM Ltd Ruddington, N. (2017). ZEB-REVO user manual v3.0.0. Available online at: https://download.geoslam.com (Accessed July 18, 2024).
Gharge, P., and Ali, A. (2024). Best 3d scanner apps (android and iphone): 16 apps we love. Available online at: https://all3dp.com/2/best-3d-scanner-app-iphone-android-photogrammetry/(Accessed August 28, 2024).
Gingras, J. F., and Charette, F. (2017). “FP innovations forestry 4.0 initiative,” in Bangor: 2017 COFE annu. Meet. Available online at: http://blog.fpinnovations.ca/blog/2017/06/20/forestry-4-0-featured-as-part-of-cif-ifc-e-lecture-series/(Accessed July 27, 2024).
Girardeau-Montaut, D. (2015). CloudCompare: 3D point cloud and mesh processing software. Open Source Proj., 197.
Girardeau-Montaut, D. (2016). CloudCompare. Fr. EDF R&D Telecom ParisTech 11 (5). Available online at: https://www.eurosdr.net/sites/default/files/images/inline/04-cloudcompare_pcp_2019_public.pdf (Accessed July 22, 2024).
Gisev, N., Bell, J. S., and Chen, T. F. (2013). Interrater agreement and interrater reliability: key concepts, approaches, and applications. Res. Soc. Adm. Pharm. 9 (3), 330–338. doi:10.1016/j.sapharm.2012.04.004
GitHub, Inc (2024). Learning3D: a modern library for deep learning on 3d point clouds data. Available online at: https://github.com/vinits5/learning3d?tab=readme-ov-file (Accessed August 27, 2024).
Goforth, C. (2024). “Using and interpreting Cronbach's alpha,” in UVA library StatLab. Available online at: https://library.virginia.edu/data/articles/using-and-interpreting-cronbachs-alpha (Accessed August 12, 2024).
Gregory, S. A., Conway, M. C., and Sullivan, J. (2003). Econometric analyses of nonindustrial forest landowners: is there anything left to study? J. For. Econ. 9 (2), 137–164. doi:10.1078/1104-6899-00028
Guo, Y., Wang, H., Hu, Q., Liu, H., Liu, L., and Bennamoun, M. (2020). Deep learning for 3d point clouds: a survey. IEEE Trans. Pattern Anal. Mach. Intell. 43 (12), 4338–4364. doi:10.1109/tpami.2020.3005434
Gwet, K. L. (2001). Handbook of inter-rater reliability. Gaithersburg, MD: Stat. Publ. Co, 223–246. Available online at: https://agreestat.com/books/cac5/chapter1/chap1.pdf (Accessed July 20, 2024).
Gwet, K. L. (2008). Computing inter-rater reliability and its variance in the presence of high agreement. Br. J. Math. Stat. Psychol. 61 (1), 29–48. doi:10.1348/000711006x126600
He, Z., and Turner, P. (2021). A systematic review on technologies and Industry 4.0 in the forest supply chain: a framework identifying challenges and opportunities. Logist 5 (4), 88. doi:10.3390/logistics5040088
Hobbs-Murphy, K., Olmedo-Nockideneh, I., Brazile, W. J., Morris, K., and Rosecrance, J. (2024). Intra-rater and inter-rater reliability of 3D facial measurements. Appl. Ergon. 116, 104218. doi:10.1016/j.apergo.2023.104218
Hodson, T. O. (2022). Root mean square error (RMSE) or mean absolute error (MAE): when to use them or not. Geosci. Model Dev. Discuss. 2022, 5481–5487. doi:10.5194/gmd-15-5481-2022
Hohmann, F., Ligocki, A., and Frerichs, L. (2017). Harvester measuring system for trunk volume determination: comparison with the real trunk volume and applicability in the forest industry. Bull. Transilvania Univ. Brasov, Spec. Issue, Ser. II For. – Wood Ind. – Agric. Food Eng. 10 (59), 27–34.
Hyndman, R. J., and Koehler, A. B. (2006). Another look at measures of forecast accuracy. Int. J. Forecast. 22 (4), 679–688. doi:10.1016/j.ijforecast.2006.03.001
Hypercube 4.0 (2021). Hypercube 4.0 Project: moving wood measurement towards a new dimension. Available online at: https://sites.google.com/view/hypercube40/pagina-depornire (Accessed August 18, 2024).
Hyyppä, J., Hyyppä, H., Leckie, D., Gougeon, F., Yu, X., and Maltamo, M. (2008). Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 29 (5), 1339–1366. doi:10.1080/01431160701736489
Ioras, F., Abrudan, I. V., Dautbasic, M., Avdibegovic, M., Gurean, D., and Ratnasingam, J. (2009). Conservation gains through HCVF assessments in Bosnia-Herzegovina and Romania. Biodivers. Conserv. 18 (13), 3395–3406. doi:10.1007/s10531-009-9649-8
Janák, K. (2007). Differences in round wood measurements using electronic 2D and 3D systems and standard manual method. Drv. Ind. 58 (3), 127–133.
Janák, K. (2012). “Round wood measurement system. InTech Janeza Trdine. 9, 103–130. doi:10.5772/37519
Jodłowski, K., Moskalik, T., Tomusiak, R., and Sarzyński, W. (2016). “The use of photo-optical systems for measurement of stacked wood,” in Proceedings of the from theory to practice: challenges for forest engineering, Warsaw, Poland, 4–7 september 2016; department of forest utilization (Warsaw, Poland: Warsaw University of Life Sciences-SGGW), 306.
Johnson, E. (2021). “Cronbach’s alpha,” in Encycl. Autism spectr. Disord. Editor F. R. Volkmar (Cham: Springer), 1248–1249. doi:10.1007/978-3-319-91280-6_307
Kazhdan, M., Bolitho, M., and Hoppe, H. (2006). Poisson surface reconstruction. Proc. Eurogr. Symp. Geom. Process 7 (4), 61–70.
Kazhdan, M., Chuang, M., Rusinkiewicz, S., and Hoppe, H. (2020). Poisson surface reconstruction with envelope constraints. Compt. Graph. Forum 39 (5), 173–182. doi:10.1111/cgf.14077
Knyaz, V. A., and Maksimov, A. A. (2014). Photogrammetric technique for timber stack volume contol. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 40, 157–162. doi:10.5194/isprsarchives-XL-3-157-2014
Koo, T. K., and Li, M. Y. (2016). A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 15 (2), 155–163. doi:10.1016/j.jcm.2016.02.012
Kruglov, A. V. (2016). “Development of the rounded objects automatic detection method for the log deck volume measurement,” in First int. Workshop pattern recognit. Editors X. Jiang, G. Chen, G. Capi, and C. Ishll Tokyo, Japan: SPIE.
Laan, J. (2021a). “3d scanner app: capture anything in 3d,” in Laan labs. New York/Berlin/NOLA. Available online at: https://3dscannerapp.com/(Accessed August 28, 2024).
Laan, J. (2021b). 3d scanner app: how mobile lidar is redefining professional 3d workflows. New York/Berlin/NOLA: Laan Labs. Available online at: https://www.laan.com/case-studies/professional-workflows-iphone-lidar-3d-scanner-app.html (Accessed August 21, 2024).
Lauri, K., Jussi, P., Jukka, M., Aki, S., Matti, M., Petteri, P., et al. (2008). The use of airborne laser scanning to estimate sawlog volumes. Forestry 81 (4), 499–510. doi:10.1093/forestry/cpn018
Lee, J., Lee, H., and Mun, D. (2022). 3D convolutional neural network for machining feature recognition with gradient-based visual explanations from 3D CAD models. Sci. Rep. 12 (1), 14864. doi:10.1038/s41598-022-19212-6
Li, J. (2017). Assessing the accuracy of predictive models for numerical data: not r nor r2, why not? Then what? PLoS One 12 (8), e0183250. doi:10.1371/journal.pone.0183250
Li, C., Sidders, D., Barclay, H. J., and Hans, H. (2015). Estimation of log volumes: a comparative study (No. FI-X-11). Edmonton, AB, Canada: Nat. Resour. Can., Can. For. Serv. Available online at: https://oaresource.library.carleton.ca/wcl/2016/20160607/Fo148-1-11-eng.pdf (Accessed June 17, 2024).
Lin, Y. C., Shao, J., Shin, S. Y., Saka, Z., Joseph, M., Manish, R., et al. (2022). Comparative analysis of multi-platform, multi-resolution, multi-temporal LiDAR data for forest inventory. Remote Sens. 14 (3), 649. doi:10.3390/rs14030649
Ljubojević, S., Marčeta, D., and Kremenović, S. (2011). Conversion coefficients for distilling wood in running standards and everyday practice. South-East Eur. For. 2, 51–57. doi:10.15177/seefor.11-06
Malinen, J., Kilpeläinen, H., Wall, T., and Verkasalo, E. (2006). Variation in the value recovery when bucking to alternative timber assortments and log dimensions. For. Stud 45, 89–100.
McGraw, K. O., and Wong, S. P. (1996). Forming inferences about some intraclass correlation coefficients. Psychol. Methods 1 (1), 30–46. doi:10.1037/1082-989X.1.1.30
Mehrentsev, A. V., and Kruglov, A. V. (2019). The algorithm and software for timber batch measurement by using image analysis. Motion Imaging Data 842, 56–65. doi:10.1007/978-3-030-19816-9_5
Morin, M., Gaudreault, J., Brotherton, E., Paradis, F., Rolland, A., Wery, J., et al. (2020). Machine learning-based models of sawmills for better wood allocation planning. Int. J. Prod. Econ. 222, 107508. doi:10.1016/j.ijpe.2019.09.029
Moskalik, T., Tymendorf, Ł., van der Saar, J., and Trzciński, G. (2022). Methods of wood volume determining and its implications for forest transport. Sensors 22 (16), 6028. doi:10.3390/s22166028
Müller, F., Jaeger, D., and Hanewinkel, M. (2019). Digitization in wood supply–A review on how Industry 4.0 will change the forest value chain. Comput. Electron. Agric. 162, 206–218. doi:10.1016/j.compag.2019.04.002
Nicolescu, V. N. (2022). 1.1 Romanian forests and forestry: an overview. Plan B for Romania’s forests and society. Brașov, Romania: Universitatea “Transilvania”, 39–48. Available online at: https://tinyurl.com/3jy6jp6h (Accessed July 23, 2024).
Niebles, J. C., and Krishna, R. (2017). “Lecture: RANSAC and feature detectors,” in Stanford vision and learning lab. Available online at: http://vision.stanford.edu/teaching/cs131_fall1718/files/06_ransac.pdf (Accessed August 31, 2024).
Niţă, M. D., and Borz, S. A. (2023). Accuracy of a smartphone-based freeware solution and two shape reconstruction algorithms in log volume measurements. Comput. Electron. Agric. 205, 107653. doi:10.1016/j.compag.2023.107653
Panagiotidis, D., and Abdollahnejad, A. (2021). Reliable estimates of merchantable timber volume from terrestrial laser scanning. Remote Sens. 13 (18), 3610. doi:10.3390/rs13183610
Pasztory, Z., Heinzmann, B., and Barbu, M. C. (2019). Comparison of different stack measuring methods. Sib. J. For. Sci. 3, 5–13.
Proteau, E. (2008). Future shortage of forest workers drives home need for recruitment efforts. Link. Innov. Netw. Knowl. 9 (3), 1–3.
Purfürst, T., de Miguel-Díez, F., Berendt, F., Engler, B., and Cremer, T. (2023). Comparison of wood stack volume determination between manual, photo-optical, iPad-LiDAR and handheld-LiDAR based measurement methods. iForest - Biogeosc. For. 16 (4), 243–252. doi:10.3832/ifor4153-016
Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017). “Pointnet: deep learning on point sets for 3d classification and segmentation,” in Proc. IEEE conf. Comput. Vis. Pattern recognit., 652–660.
Raguram, R., Frahm, J. M., and Pollefeys, M. (2008). A comparative analysis of RANSAC techniques leading to adaptive real-time random sample consensus. Comput. Vis.–ECCV 2008 10th Eur. Conf. Comput. Vis. Marseille, Fr. Oct. 12-18, 2008, Proc. Part II. 10, 500–513. doi:10.1007/978-3-540-88688-4_37
Rankin, G., and Stokes, M. (1998). Reliability of assessment tools in rehabilitation: an illustration of appropriate statistical analyses. Clin. Rehabil. 12 (3), 187–199. doi:10.1191/026921598672178340
Rauscher, H. M., Reynolds, K., and Vacik, H. (2005). Decision-support systems for forest management. Comput. Electron. Agri. 49 (2005), 1–5. doi:10.1016/j.compag.2005.02.001
Revicki, D. (2023). “Internal consistency reliability,” in Encyclopedia of quality of life and well-being research. Editor F. Maggino (Cham: Springer), 3579–3580. doi:10.1007/978-3-031-17299-1_1494
Rusu, R. B., Blodow, N., and Beetz, M. (2009). “Fast point feature histograms (FPFH) for 3D registration,” in 2009 IEEE int. Conf. Robot. Autom. (IEEE), 3212–3217.
Sammartano, G., and Spanò, A. (2018). Point clouds by SLAM-based mobile mapping systems: accuracy and geometric content validation in multisensor survey and stand-alone acquisition. Appl. Geomat. 10 (4), 317–339. doi:10.1007/s12518-018-0221-7
Sarker, S., Sarker, P., Stone, G., Gorman, R., Tavakkoli, A., Bebis, G., et al. (2024). A comprehensive overview of deep learning techniques for 3D point cloud classification and semantic segmentation. Mach. Vis. Appl. 35 (4), 67. doi:10.1007/s00138-024-01543-1
Sarode, V., Dhagat, A., Srivatsan, R. A., Zevallos, N., Lucey, S., and Choset, H. (2020). “MaskNet: a fully-convolutional network to estimate inlier points,” in 2020 int. Conf. 3D vis. 3DV (IEEE), 1029–1038. doi:10.1109/3DV50981.2020.00113
Schnabel, R., Wahl, R., and Klein, R. (2007). Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 26, 214–226. doi:10.1111/j.1467-8659.2007.01016.x
Shieh, G. (2016). Choosing the best index for the average score intraclass correlation coefficient. Behav. Res. Methods 48, 994–1003. doi:10.3758/s13428-015-0623-y
Shrout, P. E., and Fleiss, J. L. (1979). Intraclass correlations: uses in assessing rater reliability. Psychol. Bull. 86 (2), 420–428. doi:10.1037/0033-2909.86.2.420
Singh, Y. (2022). 3 regression metrics you must know: MAE, MSE, and RMSE. Proclus Acad. Available online at: https://proclusacademy.com/blog/explainer/regression-metrics-you-must-know/(Accessed July 13, 2024).
Šporčić, M., Landekić, M., Šušnjar, M., Pandur, Z., Bačić, M., and Mijoč, D. (2024). Shortage of labour force in forestry of Bosnia and Herzegovina–forestry experts' opinions on recruiting and retaining forestry workers. Croat. J. For. Eng. 45 (1), 183–198. doi:10.5552/crojfe.2024.2345
Stăncioiu, P. T., Niță, M. D., and Lazăr, G. E. (2018). Forestland connectivity in Romania—implications for policy and management. Land Use Policy 76, 487–499. doi:10.1016/j.landusepol.2018.02.028
Streiner, D. L. (2003). Starting at the beginning: an introduction to coefficient alpha and internal consistency. J. Pers. Assess. 80 (1), 99–103. doi:10.1207/S15327752JPA8001_18
Taber, K. S. (2018). The use of Cronbach’s alpha when developing and reporting research instruments in science education. Res. Sci. Educ. 48 (6), 1273–1296. doi:10.1007/s11165-016-9602-2
Tavakol, M., and Dennick, R. (2011). Making sense of Cronbach's alpha. Int. J. Med. Educ. 2, 53–55. doi:10.5116/ijme.4dfb.8dfd
Ten Hove, D., Jorgensen, T. D., and van der Ark, L. A. (2022). Updated guidelines on selecting an intraclass correlation coefficient for interrater reliability, with applications to incomplete observational designs. Psychol. Methods 29. 967–979. doi:10.1037/met0000516
Thomas, R. E., and Bennett, N. D. (2017). An analysis of the differences among log scaling methods and actual log volume. For. Prod. J. 67 (3-4), 250–257. doi:10.13073/FPJ-D-16-00039
T. Toader, and I. Dumitru (2005). Romanian forests: national parks and natural parks (Bucharest: Tipografia Intact), 269.
TraitLab (2024). Career profile: log grader. Available online at: https://www.traitlab.com/occupations/log-grader (Accessed July 19, 2024).
Tsioras, P. A. (2010). Perspectives of the forest workers in Greece. iForest - Biogeosc. For. 3 (5), 118–123. doi:10.3832/ifor0547-003
Tsioras, P. A. (2012). Status and job satisfaction of Greek forest workers. Small-Scale For 11, 1–14. doi:10.1007/s11842-011-9164-0
Wang, L., Meng, W., Xi, R., Zhang, Y., Lu, L., and Zhang, X. (2018). “Large-scale 3D point cloud classification based on feature description matrix by CNN,” in Proc. 31st int. Conf. Comput. Animat. Soc. Agents, 43–47. doi:10.1145/3205326.32053
Wang, Y., Lehtomäki, M., Liang, X., Pyörälä, J., Kukko, A., Jaakkola, A., et al. (2019a). Is field-measured tree height as reliable as believed–A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. Remote Sens. 147, 132–145. doi:10.1016/j.isprsjprs.2018.11.008
Wang, Y., Sun, Y., Liu, Z., Sarma, S. E., Bronstein, M. M., and Solomon, J. M. (2019b). Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 38 (5), 1–12. doi:10.1145/3326362
Wang, L., Liu, Y., Zhang, S., Yan, J., and Tao, P. (2020). Structure-aware convolution for 3D point cloud classification and segmentation. Remote Sens. 12 (4), 634. doi:10.3390/rs12040634
Warchoł, A., Karaś, T., and Antoń, M. (2023). Selected qualitative aspects of LiDAR point clouds: GeoSLAM ZEB-REVO and faro focus 3D X130. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. - ISPRS Arch. 48, 205–212. doi:10.5194/isprs-archives-XLVIII-1-W3-2023-205-2023
Wasson, C. S. (2006). System analysis, design and development. Concepts, principles and practices. Hoboken, New Jersey: John Whiley and Sons Inc, 832p.
White, J. C., Coops, N. C., Wulder, M. A., Vastaranta, M., Hilker, T., and Tompalski, P. (2016). Remote sensing technologies for enhancing forest inventories: a review. Can. J. Remote Sens. 42 (5), 619–641. doi:10.1080/07038992.2016.1207484
Willmott, C. J., and Matsuura, K. (2005). Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 30 (1), 79–82. doi:10.3354/cr030079
Yuan, W., Khot, T., Held, D., Mertz, C., and Hebert, M. (2018). “PCN: point completion network,” in 2018 int. Conf. 3D vis. (3DV) (IEEE), 728–737. doi:10.1109/3DV.2018.00088
Zaiontz, C. (2023). Real statistics using excel. Real Statistics. Available online at: https://real-statistics.com/appendix/citation-real-statistics-software-website/(Accessed August 30, 2024).
Keywords: lidar sensing, big data, measurement, post-processing, comparison, experience, point cloud, segmentation
Citation: Forkuo GO and Borz SA (2025) Intra- and inter-rater reliability in log volume estimation based on LiDAR data and shape reconstruction algorithms: a case study on poplar logs. Front. Remote Sens. 6:1506838. doi: 10.3389/frsen.2025.1506838
Received: 06 October 2024; Accepted: 28 August 2025;
Published: 12 September 2025.
Edited by:
Nan Xu, Hohai University, ChinaReviewed by:
Yaohui Liu, Shandong Jianzhu University, ChinaFan Mo, Ministry of Natural Resources of the People’s Republic of China, China
Ahmed C. Kadhim, University of Technology, Iraq
Copyright © 2025 Forkuo and Borz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stelian Alexandru Borz, c3RlbGlhbi5ib3J6QHVuaXRidi5ybw==
 Gabriel Osei Forkuo
Gabriel Osei Forkuo Stelian Alexandru Borz
Stelian Alexandru Borz