Using seafloor echo-integrated backscatter for monitoring single beam echosounder calibration

Introduction: In recent years, methods have been developed to calibrate seafloor backscatter measurements from hydrographic multibeam echosounders. Some of these methods involve the use of well-characterized reference areas that consistently exhibit stable backscatter levels over the years. This study investigates the potential of measuring seafloor backscatter over such a known stable area with vertical single beam echosounders, to provide a straightforward monitoring of their calibration.

Methods: We propose a methodology for calculating standard seafloor surface backscattering at normal incidence, utilizing the standard volume backscattering echo-integration technique commonly used in fishery echosounders, which is also applicable to wideband frequency modulation (FM) transmissions. We explain how this technique compares to the typical multibeam echosounder computation, which is based on samples of maximum amplitude.

Results: The operational accuracy of seafloor backscatter measurements taken over a known stable area is presented, with data collected over several years from various single-beam systems primarily calibrated using the sphere method.

Discussion: The repeatability of the results suggests that such natural seafloor reference areas can serve as a secondary calibration reference for quickly monitoring single-beam echosounders, through a straightforward acquisition and processing approach. While this method may not provide access to all the echosounder features controlled by sphere calibration, it can be used to adjust standard volume and surface backscattering measurements.

1 Introduction

Reliable quantitative measurement of acoustic backscatter levels is essential for single-beam echosounders used in applications such as fishery stock assessment surveys (Simmonds et al., 2007). As equipment is subject to manufacturing variability, aging, and changes in performance due to environmental factors like temperature and pressure (Demer, D. A. et al., 2015; Demer and Renfree, 2008) a backscatter calibration procedure must be performed before any acquisition that involves quantitative analysis of acoustic backscatter levels. This calibration process corrects possible bias in quantitative data collected by the echosounders and ensures their performance and proper functioning. Any significant change in echosounder calibration parameters, if not related to environmental conditions such as temperature, indicates a change in the equipment. This change could be gradual due to aging, as shown in (Knudsen, 2009), or could signal more severe malfunctions, such as transducer damage or failure of electronic components. Decisions regarding whether to maintain, repair, or replace the echosounder depend on the expected impact on its performance.

A standard method for performing calibration is the sphere calibration protocol, which involves comparing Target Strength measurements obtained from a metallic reference sphere placed at a known distance from the echosounder to the theoretical value (Demer, D. A. et al., 2015). Scientific echosounders, such as the Simrad EK80, include a built-in calibration program that acquires sphere target data, calculates calibration offsets, and provides an evaluation of measurement accuracy.

Carrying out this procedure at sea for vessel-mounted echosounders requires a suitable anchoring area and favorable environmental conditions, including sufficient water depth, sheltered area with calm seas, low wind speed and low currents. Operating on large platforms may require dedicated poles and winches to manage the suspension lines for the sphere (Demer, D. A. et al., 2015). The complete operation can take several hours, depending on the number of echosounders and modes of operation to be calibrated.

Meeting these operational requirements, especially during an ongoing survey, is challenging, and the process becomes even more burdensome if calibration quality is found to be poor when environmental conditions are not optimal, requiring the protocol to be repeated at a later time. This situation can arise when large variability in the sphere measurements is observed, as indicated by a high standard deviation of the measured target strength, which is a quality factor provided by the EK80 calibration program. Values exceeding 0.4 dB are generally regarded as unsatisfactory, particularly if they are associated with suspicious parameter outputs, such as for beam opening angles, acoustic axis offsets, or gain values.

Given the operational constraints of the sphere calibration protocol and the benefits of regular calibration checks, it would be highly advantageous to have a cost-effective and convenient method for secondary checks on echosounder calibration. Zhu et al. (2024) used seafloor backscatter along specific transects to intercalibrate fishing echosounders with sphere-calibrated echosounders. A more general approach is developed here that uses specific seafloor areas as reference calibration targets, similar to methods proposed for backscatter calibration of hydrographic multibeam echosounders (Eleftherakis et al., 2018). Sphere calibration can be difficult for these systems due to their large transversal swath and the lack of a method to locate targets in the along-ship direction. However, multibeam systems can readily provide seafloor backscatter, which naturally leads to the search for seafloor areas that could serve as appropriate reference calibration targets. These areas must have specific geomorphological characteristics to be suitable for calibration (Roche et al., 2018), such as stability over time, homogeneity, isotropism, flat bathymetry, and accessibility (ideally near regular vessel routes). Most importantly, they must exhibit stable surface backscattering over various time scales, including daily, seasonal, and annual periods. Reference surface backscattering for such areas can be initially established using a calibrated EK80, with appropriate frequencies and different tilt angles, as described in (Eleftherakis et al., 2018; Ladroit et al., 2018). These calibrated values are then compared to multibeam echosounder measurements, which can be adjusted to fit the reference values.

An area with these characteristics is presented in (Roche et al., 2018), and its potential for the proposed single-beam quick calibration check is explored here, based on data observed over several years, across different systems and frequencies. A method for extracting seafloor surface backscattering values from the EK80 output is detailed in (Eleftherakis et al., 2018) similar to the procedure used for hydrographic multibeam systems. An alternative processing approach is also proposed here, which estimates the same surface backscattering physical quantity using the native EK80 volume backscattering strength output, and the typical echo-integration processing used for fish abundance estimation. This allows the use of existing processing tools to provide seafloor surface backscattering measurements that can be compared against the reference area data.

2 Materials and methods

2.1 Study area

The reference area used to investigate the accuracy of the EK80 calibration secondary check is Carré Renard, located in the Bay of Brest (Figure 1). The water depth is approximately 20 m, varying with tides. The bathymetry is generally flat, with variations less than 1 m over the 0.5 km² surface area. Features analyzed in (Roche et al., 2018) indicate that the substrate consists of relatively rough sediment composed of coarse sand and gravel within a mud matrix, mixed with larger elements such as pebbles and shells (Figure 2). The area is home to a population of small echinoderms.

Figure 1

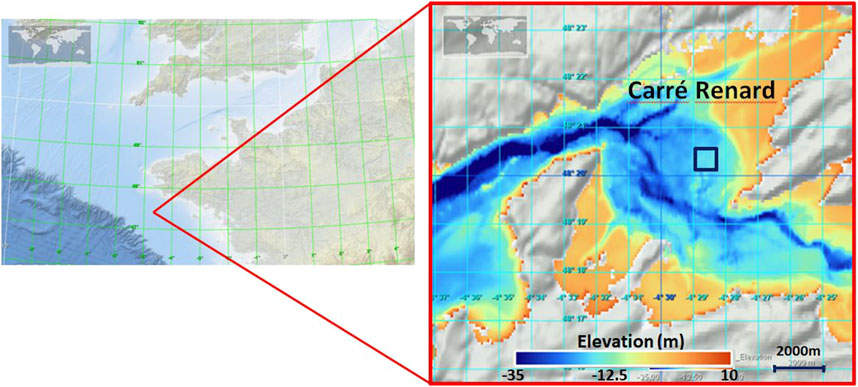
Figure 1. Location of Carré Renard reference area in the Grande Rade de Brest (France). Central coordinates of the area: 48°20.419′N–4°28.770′W. Background: EMODnet bathymetry (Thierry et al., 2019).

Figure 2

Figure 2. Carré Renard ground-truth observations from the RV Belgica cruise #2015/16, 11 June 2015. (a) Video images (variable scale, Ophiocomina nigra rigid central disc diameter = 2–3 cm). (b) Reineck box-corer samples. Excerpt from (Roche et al., 2018) Figure 4, used with permission from the authors.

Extensive acoustic multibeam surveys analyzed in (Roche et al., 2018) demonstrated that the seafloor surface backscattering strength is homogeneous across the area, independent of transect direction, and stable over the years. Surveys were confined to a 0.5NM x 0.5NM area, centered at 48°20.419′N–4°28.770′W, with preferential transects oriented East-West or North-South, focusing on the central region.

2.2 Single beam echosounders

The repeatability of seafloor surface backscatter measurements obtained using different calibrated single-beam echosounders has been analyzed through a series of acquisitions conducted over several years, frequencies, and pulse durations, as detailed in Table 1. Earlier surveys were carried out with Simrad EK60 single-beam echosounders using General Purpose Transceivers (GPT) electronics. More recent surveys utilized EK80 Wide Band Transceivers (WBT) electronics (Demer, D. A. et al., 2017). All acquisitions were performed with downward-looking echosounders using continuous wave (CW) transmission pulses and were previously calibrated according to the sphere calibration protocol. Details of the systems and calibration values can be found in the Supplementary Material.

Table 1

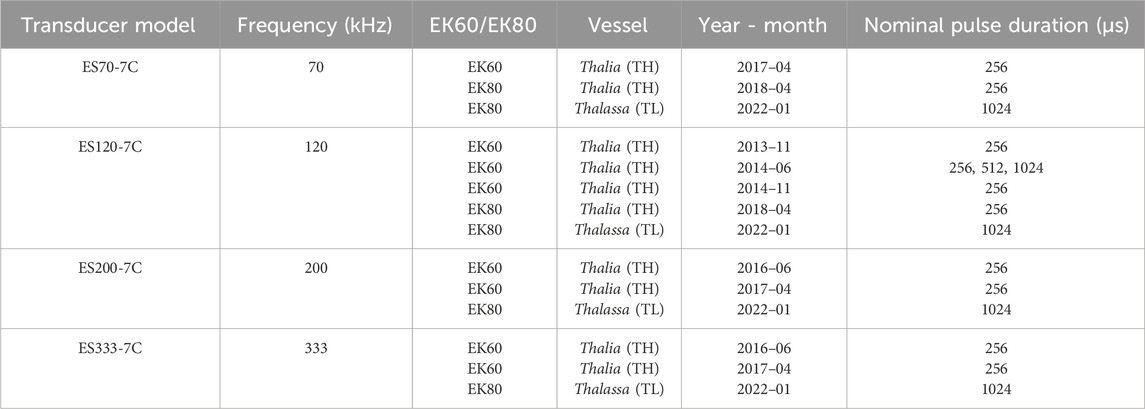
Table 1. Surveys and echosounders characteristics. All transducers have 7° circular one-way beamwidth.

2.3 Seafloor backscatter computation

Depending on the physical nature of the target (single reflector, surface, or volume), different physical backscatter indices can be calculated: single target strength, surface backscattering strength, and volume backscattering strength (Lurton, 2010). These three indices characterize the ratio of the acoustic power backscattered per steradian by the target, relative to the incident acoustic intensity. The latter two indices are compensated for the backscattering surface or volume that contributed to the backscattered signal. Therefore, calculating these quantities requires modelling the surface or volume of the reflectors that contributed to the acoustic power received by the echosounder at a given time.

In this context, we consider the seafloor as a surface reflector and the main contributor to backscatter during seabed echo reception, while neglecting the volume backscatter potentially generated by water column echoes or sub-bottom penetration.

By analyzing the acoustic signal received over time by a downward-looking single-beam echosounder over a flat seafloor, we observe that the extent of the bottom echo corresponds to different parts of the seafloor that successively reflect the propagated pulse (Lurton, 2010). The surface area of the elements reflecting the acoustic pulse must also be weighted by the corresponding acoustic beam shape.

When the contributing reflectors are initially located in the water column, the echo level is weak (Figure 3a). The echo level increases as the transmitted pulse reaches the seafloor (Figure 3b) and continues to grow as the surface intercepted by the pulse expands (Figure 3c), convolved with the beam directivity (Figure 4A). Once the pulse footprint becomes an annular shape (Figure 3d) and extends beyond the main lobe of the sounder (Figure 3e), the backscattered signal begins to decrease. Figure 4B presents a typical single-beam echogram including the bottom echo. The successive data levels corresponding to the subsets described in Figure 3 are highlighted in Figure 4C on a single echogram slice.

Figure 3

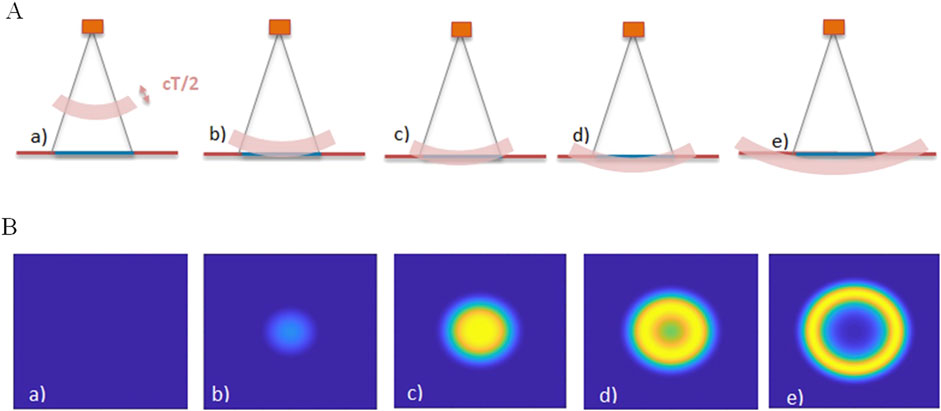
Figure 3. (A) Physical extent of a transmitted pulse of duration T, propagating through time. (B) Seafloor reflectors contributing to backscattered signal through time, weighted with the pulse amplitude. Successive footprints correspond to a) to e) situations shown in Figure 3A. Combination with beam directivity (Figure 4A) is not represented in these figures.

Figure 4

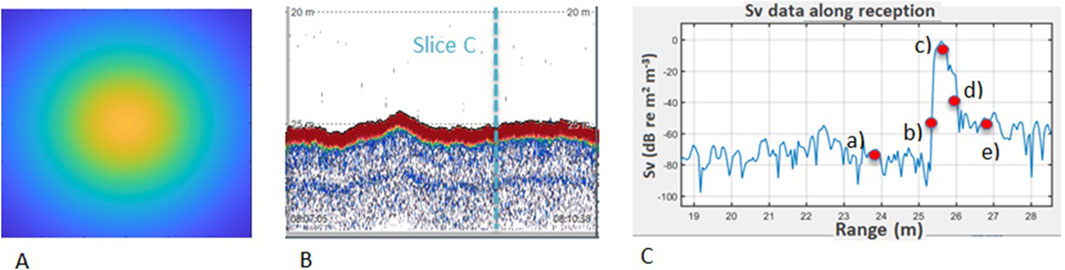
Figure 4. Beam directivity projected on the seafloor (A), EK80 echogram (B), EK80 reception signal for transmission (C), with echo levels corresponding to a) to e) situations shown in Figure 3.

To extract the seafloor backscatter index, various options can be considered depending on the time sample and the surface contributors selected for computation. Based on this choice, the level of the selected sample will vary, along with the associated insonified surface; however, the process should yield the same surface backscattering strength if properly compensated. Two approaches are presented in the following sections.

Note that the term seafloor surface backscattering strength (dB re 1 m² m^-2) is used here in accordance with the definitions, notation, and units provided by (Demer et al., 2015) in the context of acoustic instrument calibration, ensuring consistency with the volume backscattering strength also defined therein. The symbol $BS$ will be used to denote seafloor surface backscattering strength, following the convention adopted by (Eleftherakis et al., 2018; Roche et al., 2018). It is important to note, however, that various equivalent terms and notations are used throughout the acoustic literature that specifically address this quantity, such as bottom scattering strength, denoted $S_b$, and typically expressed in decibels (dB), as seen in (Jackson and Richardson, 2007; Lurton et al., 2015).

2.4 Seafloor surface backscattering strength computation from maximum echo level (MAX $\mathit{B}\mathit{S}$ extraction)

A common method used by hydrographic multibeams to determine seafloor surface backscattering in the case of normal incidence, when the bottom echo is brief and strong, is to determine the time and intensity of the maximum echo level (Hammerstad, 2000). It is assumed that the contributing seafloor reflectors correspond to the projection of the beam’s main lobe, fully covered by the effective pulse footprint (Figure 3c).

Since the EK80 acquisition software natively provides the volume backscattering strength $Sv$ (dB re 1 m² m^-3)) over time (Demer, D. A. et al., 2015), the seafloor surface backscattering strength $BS$ (dB re 1 m² m^-2) is then calculated using Equation 1.

$BS={Sv}_{\mathit{max}}+10\log V-10\log A(1)$

With:

- ${Sv}_{\mathit{max}}$ (dB re 1 m² m^–3) the maximum $Sv$ value observed over seafloor echo

- $A$ (m²) the surface ensonified by the pulse at this specific time

- $V$ (m³) the volume insonified by the pulse

It is commonly assumed that the surface corresponding to the maximum backscattered level at normal incidence represents the effective beam footprint, given by $\psi .r^2$, $\psi$ (sr) being the equivalent two-way beam angle and $r$ (m) the range corresponding to the acoustic sample. Accordingly to (Demer, D. A. et al., 2015) the volume $V$ (m³) insonified by the pulse equals $\psi .r^2.c\frac{T_{eff}}{2}$, with $T_{eff}$ (s) the effective pulse duration, and Equation 1 simplifies into Equation 2.

$BS={Sv}_{\mathit{max}}+10\log \left(\frac{c.T_{eff}}{2}\right)(2)$

This expression implies that the beam footprint is fully ensonified by the transmitted pulse. However, specific cases may arise where the transmitted pulse is too short to fully cover at once the entire beam footprint or the seafloor roughness, resulting in an effective ensonified area that is smaller than expected. These situations are further discussed in Section 4.4.

2.5 Seafloor surface backscattering strength computation from echo-integration over bottom echo (EI $\mathit{B}\mathit{S}$ extraction)

Another approach to calculating seafloor backscatter involves considering all the samples corresponding to the bottom echo. As with the previous method, we assume that the surface backscattering coefficient is constant within the beam footprint and equal to $bs$ (m²m^-2), expressed in linear units. The ratio of acoustic power backscattered per steradian by an elementary surface element $dx.dy$, relative to incident acoustic intensity is $bs.dx.dy$.

For a bottom echo sample at time $t$, the total backscattered power per steradian $P_{bs}$ (W sr⁻¹) is integrated over the footprint on the seafloor, as shown in Equation 3.

$P_{bs}\left(t\right)=I_{inc}.{\int }_{X,Y}bs.{\tau \left(x,y,t\right)}^2.d\left(x,y\right).dx.dy(3)$

Where:

- $I_{inc}$ (W m-²) is the incident acoustic intensity corresponding to beam axis and maximum pulse amplitude

- $\tau \left(x,y,t\right)$ (s) is the shaping value (normalized to 1) of acoustic signal amplitude at time $t$ and position $\left(x,y\right)$ on the seafloor. It corresponds to illustrations in Figure 3. Value is 0 for points that are not covered by incident pulse.

- $d\left(x,y\right)$ (dimensionless) is the beam 2-way directivity factor corresponding to $\left(x,y\right)$ position on the seafloor.

If we integrate $\frac{P_{bs}}{I_{inc}}$ over bottom echo duration $BT$ (Equation 4), we get from Equation 3:

${\int }_{BT}\frac{P_{bs}\left(t\right)}{I_{inc}}.dt={\int }_{X,Y,BT}bs.{\tau \left(x,y,t\right)}^2.d\left(x,y\right).dx.dy.dt(4)$

For every $\left(x,y\right)$ position, the integral of ${\tau \left(x,y,t\right)}^2$ through time is $T_{eff}$, since each seafloor element will reflect every part of transmit signal at some time. Integration of beam directivity projected normally on the seafloor at a distance $R$ is $\psi .R^2$. Equation 4 results in Equation 5.

${\int }_{BT}\frac{P_{bs}}{I_{inc}}\left(t\right).dt=bs.T_{eff}.\psi .R^2(5)$

Changing integration variable from time to range, with $r=c.t/2$ , and $BR$ the bottom echo range interval corresponding to $BT$, $bs$ can be expressed as in Equation 6.

$bs={\int }_{BR}\frac{\frac{P_{bs}}{I_{inc}}\left(r\right)}{\psi .R^2\frac{c.T_{eff}}{2}}dr={\int }_{BR}\frac{r^2}{R^2}{s}_v\left(r\right).dr(6)$

With $s_v$ (m² m^-3) the volume backscattering coefficient, corresponding to the EK80 volume backscattering strength output, expressed in linear unit.

For beamwidth of a few degrees, the seafloor echo length remains brief, and the range $r$ of successive bottom echoes will remain very close to seafloor distance $R$. Equation 6 can hence be simplified and seafloor backscatter can be computed through usual $sv$ echo-integration (Simmonds et al., 2007) over bottom echo range interval $BR$ (Equation 7).

$bs={\int }_{BR}{s}_v\left(r\right).dr(7)$

In other words, area backscattering strength $S_a$ (dB re m² m^-2), commonly used in fishery acoustic surveys (Simmonds et al., 2007), namely corresponds to seafloor surface backscattering strength $BS$ (dB re m² m^-2) issued by hydrographic multibeams at normal incidence, if computed over bottom echo range (Equation 8).

$BS=S_a=10.{\mathit{log}}_{10}\left({\int }_{BR}{s}_v\left(r\right).dr\right)(8)$

This approach to compute seafloor $BS$ with echo-integration (EI extraction) has been applied to the different survey lines on the reference area. Seafloor $BS$ values have been extracted over single pings, with an integration layer extending from 1 m above detected bottom to 3 m beneath, so as to ensure the entire bottom echo is encompassed.

Initial volume backscatter data ($Sv$) were acquired with EK60/EK80 Simrad software and logged in HAC format using Ifremer Hermes software (Trenkel et al., 2009). Echo-integration was then performed using python Moviesd3D library (“pymovies_3d,” 2024).

3 Results

We applied the echo-integration (EI $BS$) and maximum extraction (MAX $BS$) methods, through Equation 8 and Equation 2 respectively, to compute seafloor backscatter ($BS$) from data collected on the reference area Carré Renard. Surveys were conducted between 2013 and 2022, using various equipment, pulse lengths, and frequencies. The mean BS results for the 70kHz, 120kHz, 200kHz, and 333kHz frequencies are shown in Figures 5-8, respectively. Averaging is performed on linear values and the mean result is expressed in decibels. For the 70 kHz data, mean $BS$ values for both EI and MAX extraction methods across the different surveys are displayed in Figure 5a. Surveys transects are shown in Figure 5b. The distributions of $BS$ values are detailed in violin plots (Figures 5c,d), which include the minimum and maximum values, as well as the 25th and 75th percentiles and the mean. The distribution of the echosounder’s attitude angle, relative to the vertical, is also shown (Figure 5e), calculated as ${\cos }^{-1}\left[\cos \left(roll\right).\cos \left(pitch\right)\right]$.

Figure 5

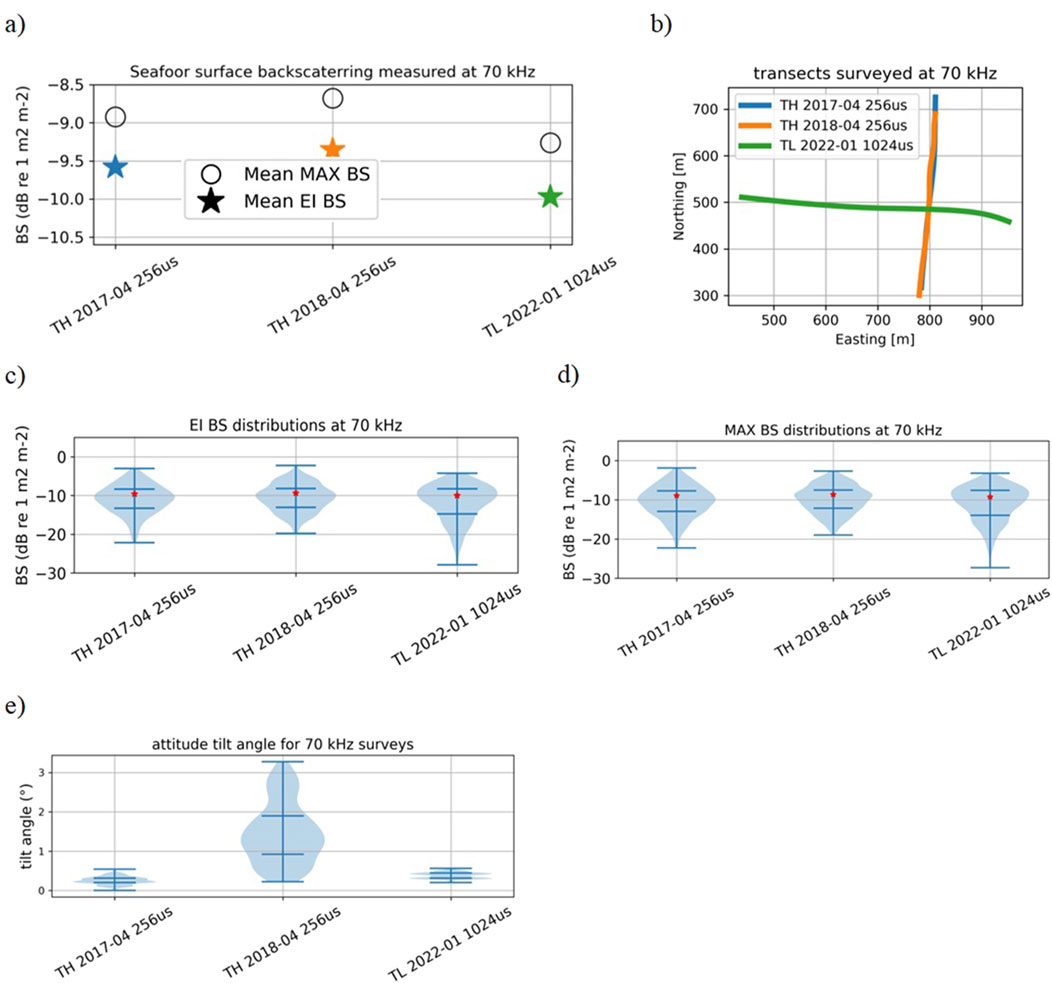
Figure 5. Results for 70 kHz surveys: (a) Mean $\mathit{B}\mathit{S}$ values for MAX extraction (circles) and EI extraction (stars). Star colors refer to corresponding tracks in panel b. (b) Transects relative tracks. (c) Single EI $\mathit{B}\mathit{S}$ distributions. (d) Single MAX $\mathit{B}\mathit{S}$ distributions. (e) Attitude tilt angle distributions. Violin plots in figures c, d, and e are indexed with minimum value, maximum value, 25% and 75% quantiles, and $\mathit{B}\mathit{S}$ mean as red dot.

Figure 6

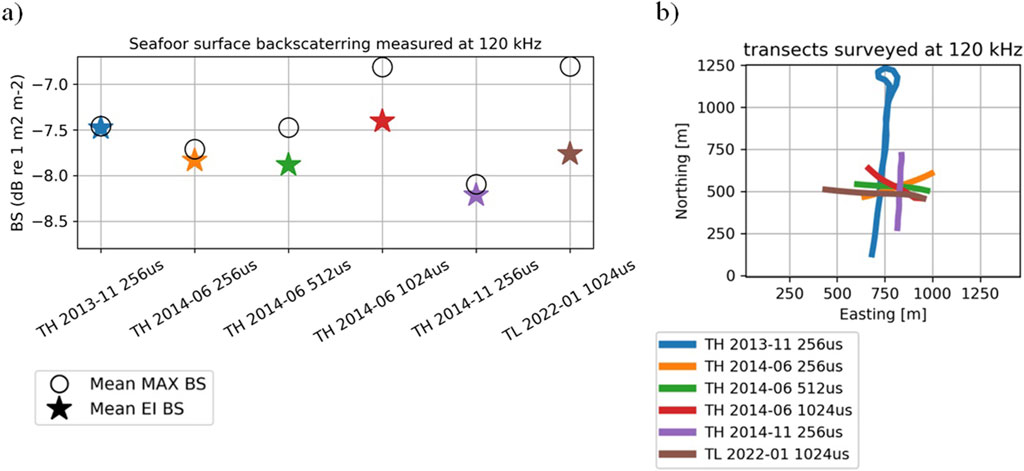
Figure 6. Results for 120 kHz surveys: (a) Mean $\mathit{B}\mathit{S}$ values for MAX extraction (circles) and EI extraction (stars). Star colors refer to corresponding tracks in panel b. (b) Transects relative tracks.

Figure 7

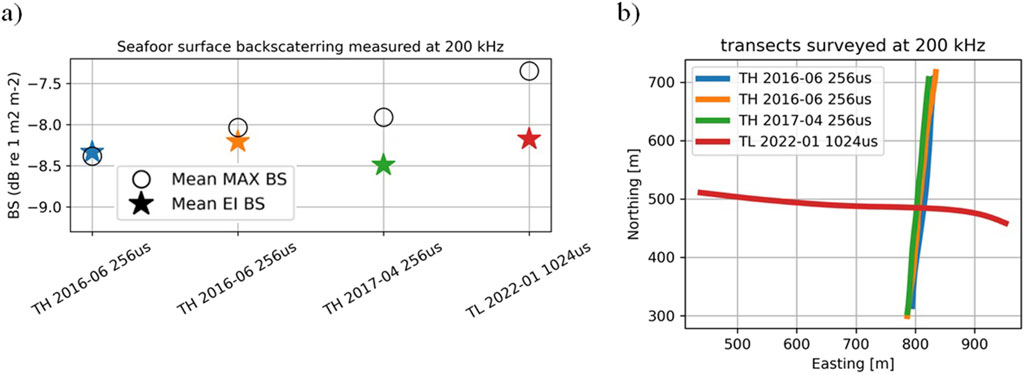
Figure 7. Results for 200 kHz surveys: (a) Mean $\mathit{B}\mathit{S}$ values for MAX extraction (circles) and EI extraction (stars). Star colors refer to corresponding tracks in panel b. (b) Transects relative tracks.

Figure 8

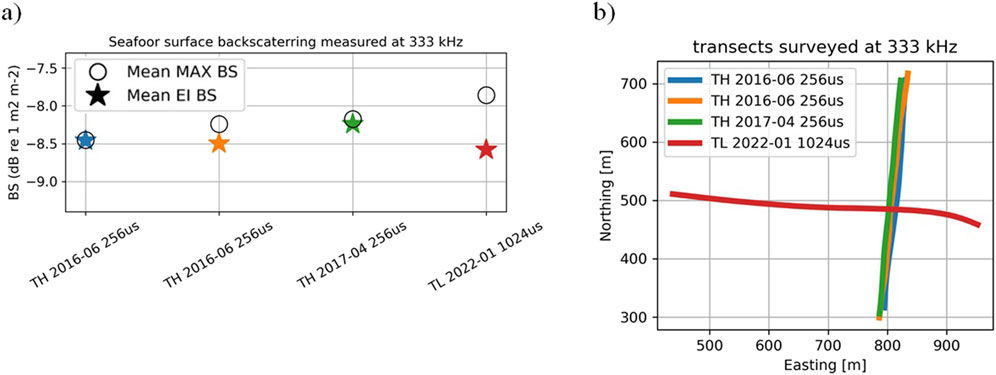
Figure 8. Results for 333 kHz surveys: (a) Mean $\mathit{B}\mathit{S}$ values for MAX extraction (circles) and EI extraction (stars). Star colors refer to corresponding tracks in panel b. (b) Transects relative tracks.

The stability of seafloor backscatter values on Carré Renard over the period 2013–2022, computed using the EI approach, is within 0.7 dB for the 70 kHz and 120 kHz echosounders. The stability of EI backscatter is better for higher frequencies (200 kHz and 333 kHz), varying by 0.3 dB.

The MAX $BS$ values, computed through maximum extraction, show greater variability, with changes of 1 dB for the 120 kHz echosounder and 0.5 dB for the 200 kHz and 333 kHz systems. MAX $BS$ values also appear to be more sensitive to pulse length, with higher values obtained for pulse durations of 1,024 µs compared to 256 µs.

4 Discussion

Carré Renard is an area that has been found to remain stable over the years (Roche et al., 2018). Measurements of seafloor $BS$ using the EI extraction method with different single-beam echosounders have shown an overall variability of 0.7 dB. This result suggests that it is possible to monitor the calibration gain of the echosounders within a 0.35 dB range by surveying the area.

4.1 Impact of initial calibration accuracy

The echosounders had been initially calibrated using the sphere method, but it is challenging to determine how much of the final $BS$ variability can be attributed to calibration accuracy. The sphere calibration procedure includes a quality factor based on the variability of sphere measurements. A quality factor of 0.25 dB or less is considered a good calibration. However, with averaging, the accuracy of the final gain is likely to be lower than this. Knudsen (2009) evaluated this over a time series of calibration gains measured over several years on the R/V “GO Sars” and the dispersion of gain values over a 5 years period was around 0.3 dB for the 70 kHz transducer and 0.5 dB for the 120 kHz and 200 kHz frequencies.

While it is difficult to separate calibration accuracy from seafloor backscatter stability, it can be stated that these two variables are independent. Their effects are summed in the seafloor $BS$ measurement, meaning that the variance of this sum is the sum of the variances of each component. As a result, the intrinsic stability of seafloor surface backscattering is higher than the measured stability, which is potentially further obscured by calibration uncertainty.

Beyond calibration accuracy, other factors that can impact backscatter measurements are further discussed.

4.2 Impact of attitude

The influence of platform movements during data acquisition on backscatter values can be questioned, as the seafloor backscatter index depends on the incident angle (Lurton, 2010; Kloser et al., 2010), as well as the insonified area (Lurton, 2010).

The seafloor is a directional reflector, and $BS$ values measured away from normal incidence can decrease rapidly due to the specular effect (Lurton, 2010). The amplitude of this specular effect depends on seafloor roughness, micro-bathymetry, and acoustic wavelength. In the Carré Renard area, the decrease in angular backscatter away from normal incidence is gradual at the considered frequencies. Eleftherakis et al. (2018) observed a decrease of less than 0.2 dB at ±3° for the 200 kHz frequency.

A second impact arises from the surface area of the reflectors contributing to acoustic reflection, which affects the backscatter level. The $BS$ computation method used in this study compensates for the insonified area at normal incidence, which is the projected surface of the beam pattern on the seafloor. For near-normal incidence angles θ, this surface is modified by a 1/cos(θ) factor, which is negligible for typical attitude movements. However, this would not necessarily be the case for a tilted single-beam system, as used in (Eleftherakis et al., 2018) where the factor becomes cos(tilt_angle)/cos(tilt_angle+θ).

During the different surveys, echosounder attitudes remained within ±2° for 75% of the data, and no significant impact is expected based on the phenomena described above.

The “TH 2018 256µs” survey showed much greater attitude dispersion than the “TH 2017 256µs” survey (Figure 5e), but the BS distributions, whether using the EI or MAX extraction methods, were similar for both surveys (Figures 5c,d for EI BS and MAX BS, respectively).

Seafloor backscatter measurements from the “TH 2018 256µs” rolling acquisition line were further averaged within 0.2° attitude intervals, and Figure 9 shows no noticeable trend with the attitude angle.

Figure 9

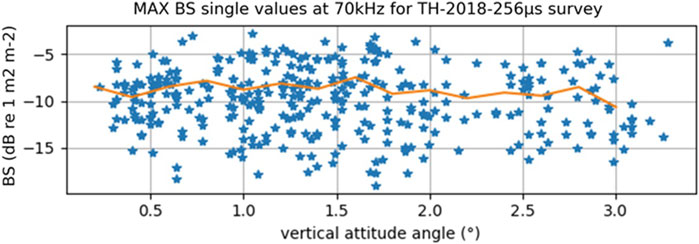
Figure 9. MAX $\mathit{B}\mathit{S}$ single measurements of 70 kHz “TH 2018 256µs” survey, averaged within 0.2° attitude intervals (orange line).

Further processing could be applied to adjust the insonified area computation based on attitude or simply filter out data with attitudes deviating from the vertical. However, since the impact of attitude is found to be minimal, we have kept the processing as simple as possible. This approach is straightforward to implement, using the standard echo-integration method, which is available in various single-beam echosounder analysis software, such as Echoview, ESP3, Matecho, LSSS, and Movies (González-Máynez et al., 2024).

4.3 Impact of frequency

The stability of the seafloor $BS$ values over Carré Renard improves at higher frequencies for both the EI and MAX computation methods. For the 256µs pulse duration, the variability of the EI $BS$ is around 0.7 dB for 70 kHz and 120 kHz, and it decreases to 0.3 dB for 200 kHz and 333 kHz. All echosounders, however, have the same 7° one-way beam aperture and use the same pulse durations. Therefore, no geometric factors can explain this phenomenon, especially considering that calibration accuracy is expected to be better for lower frequencies (Knudsen, 2009). Our hypothesis is that sub-bottom penetration is greater at lower frequencies, leading to more variable contributions from the volume component, which interferes with the more homogeneous surface reflectors. This is an interesting aspect for checking the calibration gains at higher frequencies, since calibration with spheres becomes more challenging as the frequency increases, due to greater interference from the net used for suspending the sphere below the transducer (Renfree et al., 2020).

4.4 Seafloor surface backscatter: EI versus MAX computations

Seafloor $BS$ values obtained through EI and MAX extraction methods are similar but not identical, with MAX generally yielding higher values and a maximum difference of 1 dB. It is not surprising that processing data in different ways can lead to varying estimates. Any operation, such as filtering, selecting, smoothing, or averaging, can influence the result depending on the statistical distribution of the data being processed. In this regard, the computational chain used to estimate a physical quantity from equipment output is an integral part of the measurement process (Lurton et al., 2015). In this study, the simple maximum echo extraction (MAX $BS$) is a basic approach. Hydrographic multibeam data would typically undergo further refinement with bottom echo smoothing or center of gravity estimation, but such operations can affect the final values. Here, we focused on the most straightforward processes to minimize dependence on refinements in the processing chain. The goal was to develop a method that is simple and accessible yet robust. In this respect, the echo-integration method (EI $BS$) was not sensitive to the tuning parameters, such as the exact extent of the echo-integration layer, as contributions from samples in the water column or below the bottom are not significant compared to the seafloor echo. For the 120 kHz survey set, the echo-integration layer width above the bottom detection was reduced from 1 m to 0. The resulting difference in mean echo-integrated backscattering strength EI $BS$ computed over each survey line was less than 0.001 dB, with no noticeable change in the distribution of individual EI $BS$ values. Below the bottom detection, the layer width was reduced from 3 m to 1 m. This adjustment resulted in a mean EI $BS$ difference of less than 0.001 dB for 256 µs and 512 µs pulse durations, and less than 0.11 dB for the 1,024 µs pulse duration. Further reducing the layer width below the bottom to 0.5 m had a significant impact, causing a difference of several decibels for the 1,024 µs pulse, due to the layer no longer fully encompassing the pulse length and bottom echo.

Based on these results, an operational recommendation for setting the echo-integration layer would be to maintain a 1-m margin above the detected bottom to avoid overreliance on the precision of bottom detection, and to ensure the layer fully encompasses the bottom echo, whose width varies with pulse length, beam width, depth, and seafloor characteristics.

Beyond the statistical impact of the processing chain, both MAX and EI approaches do not reflect the exact same physical phenomena nor imply same echosounder features. The EI method uses all the samples involved in the seafloor echo, potentially giving more weight to the volume backscattering component associated with sub-bottom penetration. The MAX method, on the other hand, decompensates the effective pulse duration $T_{eff}$ applied to the initial $Sv$ data (Equation 2) meaning that this echosounder feature is not included in the MAX $BS$ measurement, when it is in the EI $BS$.

The MAX $BS$ extracted for 70 kHz is consistently 0.5 dB higher than the EI $BS$, regardless of the echosounder model and pulse duration. While it is unlikely that this is due to a systematic overestimation of the effective pulse length, our main hypothesis is that the sub-bottom penetration component plays a role here, though there is no clear explanation for why it would result in lower values for the EI $BS$.

It is worth noting that 1,024 µs pulses show higher MAX $BS$ values compared to 256 µs pulses. A possible explanation is that while the 256 µs pulse is sufficient to cover the entire beam’s main lobe footprint on the seafloor at a 20m depth, the shape of the pulse causes its amplitude to decrease within the footprint. A longer 1,024 µs pulse ensures that the acoustic footprint is fully covered by the maximum pulse amplitude, which may not be the case for shorter pulses (Lurton et al., 2015). This is a common shortcoming of the MAX $BS$ computation, which assumes that the pulse length is adequate to insonify the entire beam lobe at once, though this is often not true for shorter pulses. For example, in Figure 10A simulating the intersection of a 64 µs pulse on a flat seafloor, the insonified area becomes an annulus before fully covering the beam footprint, leading to an underestimation of the seafloor backscatter strength with MAX $BS$. Such a situation also arises when bottom micro-bathymetry has depth variations greater than the pulse length, preventing the seafloor surface from being insonified at once, as shown in Figure 10B. EI $BS$ estimation, through time integration, ensures that even in these cases, the entire projected beam pattern is covered, minimizing the variation in $BS$ estimates with pulse length.

Figure 10

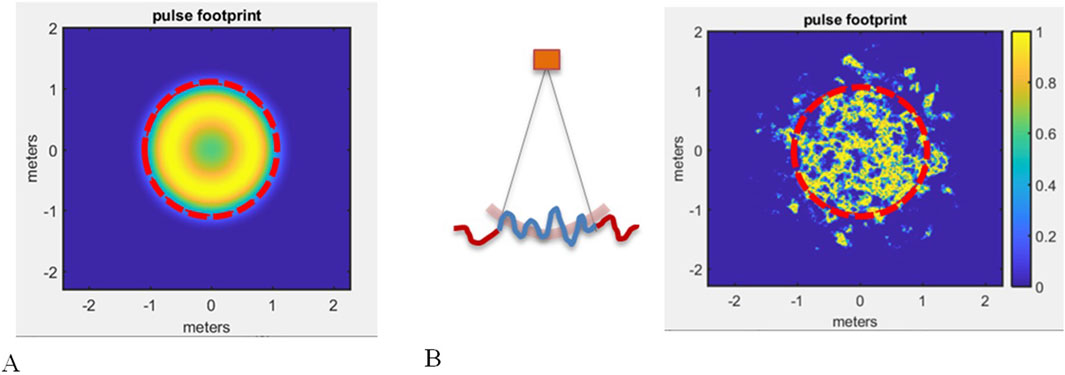
Figure 10. Cases where beam footprint is never fully insonified by the acoustic pulse: (A)- The 64µs pulse with sin² shaping becomes annulus before covering a 5° two-way beam lobe at 25m depth (dashed). (B)- The 64µs pulse is too short to insonify at once a surface with 5 cm micro-bathymetry.

The distribution and variability of individual $BS$ measurements are comparable for both methods over the same line (Figures 5c,d). It might have been expected that EI $BS$ would benefit from some smoothing by using all available bottom echoes, thus reducing the variance of the resulting distribution. However, for a normal incidence case, the seafloor echo is brief. The energetic part that mostly influences the echo-integration results corresponds to the pulse insonifying the entire beam footprint, that is the maximum value. Individual BS measurements obtained through either the maximum or echo-integration methods are highly correlated, as shown in Figure 11. While a shift between the mean values may occur, it affects all measurements uniformly and does not arise from different distribution shapes or outliers.

Figure 11

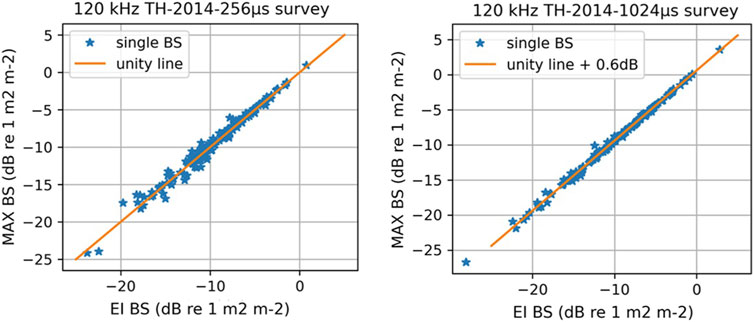
Figure 11. Comparison of single $\mathit{B}\mathit{S}$ measurements through echo-integration or maximum extraction, for 120 kHz “TH 2014 256 µs” survey (mean $\mathit{B}\mathit{S}$ Max - mean $\mathit{B}\mathit{S}$ EI = 0.02 dB) and “TH 2014 1024 µs” survey (mean $\mathit{B}\mathit{S}$ Max - mean $\mathit{B}\mathit{S}$ EI = 0.6 dB).

4.5 Wideband FM seafloor backscatter spectrum through echo-integration

A significant benefit of the echo-integration approach is that it allows for a direct estimation of the spectral seafloor backscattering coefficient $BS\left(f\right)$ (dB re m²/m²) for frequencies $f$ (Hz) covered by modulated (FM) wideband pulses. Computing seafloor $BS\left(f\right)$ for such transmission types is uncommon in the hydrographic community and requires careful control over the amplitude normalization in spectral analysis, as well as consideration of the variation in echosounder opening angles and calibration gains with frequency. Additionally, it is important to account for the pulse length achieved through the spectral process (Weber and Ward, 2015). However, these elements have been thoroughly described and calibrated for the use of broadband pulses in fishery science, allowing for the output of the spectral volume backscattering coefficient $sv\left(f\right)$ (m²/m³) (Demer, 2017). Since quantified $sv\left(f\right)$ outputs, along with the spectral echo-integration tool, are commonly available in standard single-beam analysis software (González-Máynez et al., 2024), users can directly access quantitative seafloor $BS\left(f\right)$ spectra through the EI approach. An example of the continuous $BS\left(f\right)$ spectrum over Carré Renard is shown in Figure 12. The line was surveyed in a row with the TL-2022–01 CW line, and the results are compared to CW EI $BS$. The same processing used for CW is applied, that is $BS\left(f\right)$ spectra are obtained from single pings through direct $sv\left(f\right)$ broadband echo-integration, performed over a layer extending from 1 m above the detected bottom to 3 m below it. A mean spectrum is then calculated by averaging the results from the single pings in linear values.

Figure 12

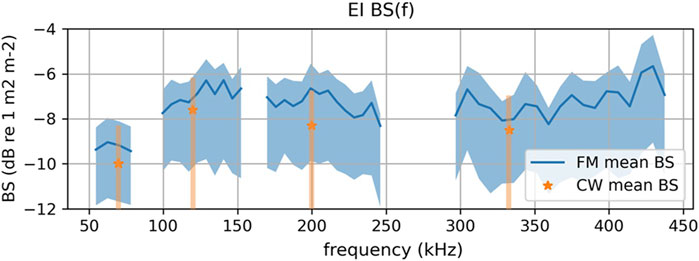
Figure 12. Seafloor backscatter spectrum over Carré Renard obtained through bottom echo-integration in FM mode, and comparison with EI $\mathit{B}\mathit{S}$ CW results (orange stars). 25%–75% quantiles of $\mathit{B}\mathit{S}$ spectrum are filled with blue for FM and orange for CW (25% quantiles are below −12 dB for CW).

$BS$ estimates for CW pulses are expected to align with FM $BS\left(f\right)$ for their respective frequencies $f_{CW}$. The correspondence is within 0.5 dB, except at 200 kHz, where it reaches 1 dB. However, FM gain in this range is uncertain (Figure 13A), as it is near a null in the Target Strength spectrum of the 38.1 mm tungsten sphere. Backscatter variations in the 300 kHz–450 kHz range also correspond to calibration gain uncertainties due to sphere TS nulls (Figure 13B). A detailed analysis of FM EI $BS\left(f\right)$ spectra would require further work and additional acquisitions. From a calibration perspective, it should be emphasized that measuring $BS\left(f\right)$ over a known reference area with FM pulses would provide a calibration method that is not affected by the nulls present in the sphere spectrum at various frequencies.

Figure 13

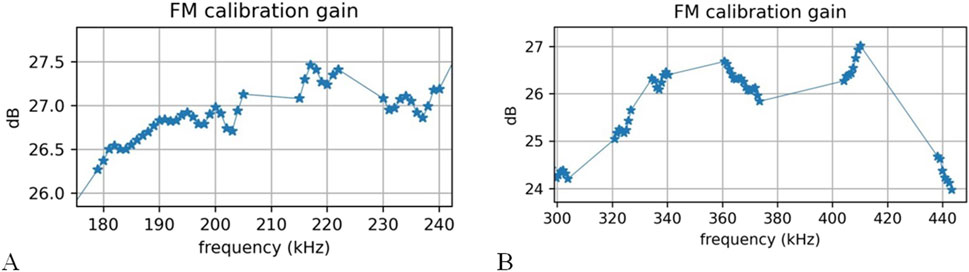
Figure 13. Calibration gains measured on 38.1 mm Tungsten sphere in ES200-7C (A) and ES333-7C (B) bandwidths.

4.6 Calibration monitoring over reference area and sphere calibration

The proposed method for measuring reference seafloor backscatter is not intended to replace a thorough sphere calibration protocol. The latter provides essential individual characteristics of the echosounder, such as on-axis gain, effective pulse duration, and the 2D beam pattern. These parameters are mandatory for applying the sonar equation and obtaining quantitative measurements of reflecting targets. The calibration check through seafloor $BS$ measurement only monitors the overall output of the equipment. Changes in the equivalent beam angle, on-axis gain, and effective pulse length (for EI $BS$ only), will result in variations in the measured seafloor $BS$. This offset can be used to correct the echosounder’s volume and surface backscattering data, as illustrated in Figure 14 but it does not allow for the identification of the specific parameter that has changed. Sphere calibration also provides insight into the proper functioning of the different split-beam quadrants by tracking the sphere’s coherent localization as it moves, and it helps estimate the measurement accuracy of the echosounder through the dispersion of the sphere’s Target Strength across the beam.

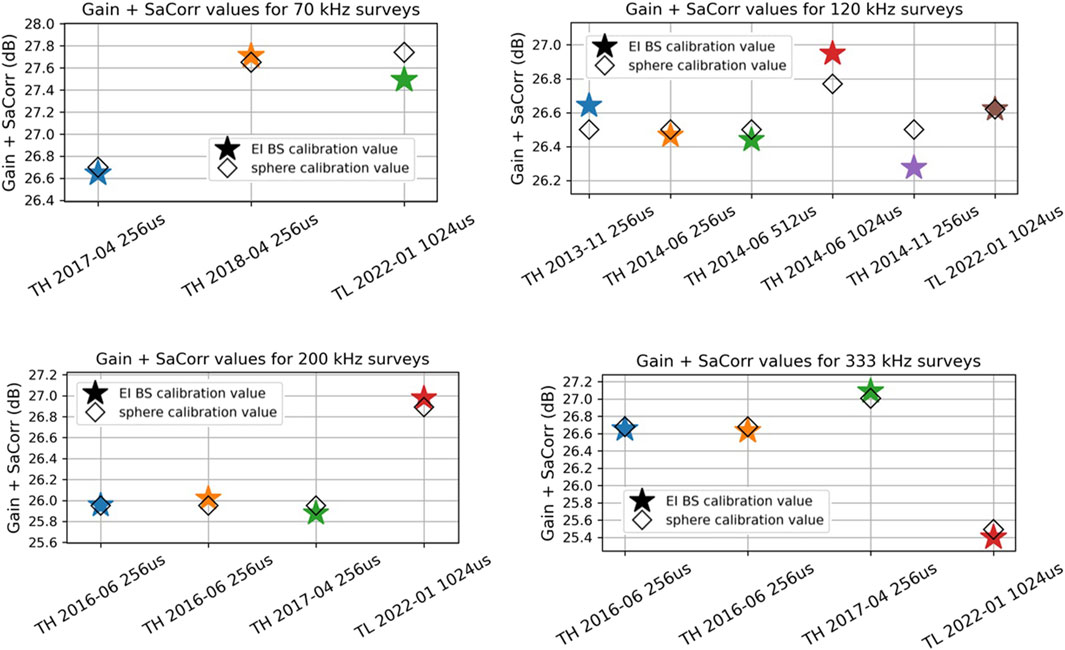
Figure 14

Figure 14. $\mathit{G}\mathit{a}\mathit{i}\mathit{n}+\mathit{S}\mathit{a}\mathit{C}\mathit{o}\mathit{r}\mathit{r}$ calibration values obtained with sphere calibration (diamond) or seafloor $\mathit{E}\mathit{I}\mathit{B}\mathit{S}$ measurement over Carré Renard (stars), for the different echosounders and frequencies.

For these reasons, sphere calibration is recommended for full equipment validation after its initial integration onto a platform, or before undertaking a critical survey requiring reliable quantitative acoustic measurements, such as fishery stock assessment surveys. However, regularly surveying an appropriate transect and measuring its seafloor surface backscattering offers an easy way to quickly monitor the equipment’s stability. This rapid check can also enhance confidence in the sphere-based calibration parameters used, particularly if, due to circumstances such as adverse weather conditions, the sphere calibration quality or results were unsatisfactory and could not be repeated. This method is also straightforward for ensuring consistent data comparison with different platforms. For instance, this assurance is crucial when conducting vessel intercalibration processes (De Robertis and Handegard, 2013) to assess the impact of target avoidance by the platform. Finally, this approach can serve as an alternative for correcting quantitative acquisitions when sphere calibrations cannot be performed due to logistical or time constraints, especially when using multiple opportunistic platforms like commercial fishing vessels, or when the involved single-beam echosounders lack split-beam capabilities.

We illustrate in Figure 14 the calibration results that would be extracted for each echosounder through the different surveys, using seafloor surface backscattering measured over Carré Renard, and we compare it to parameters obtained with sphere calibration. To do so we assume that the Carré Renard reference seafloor backscattering value, ${BS}_{ref}$, is the average of the results obtained from successive surveys. We then compute the calibration values that would be derived for each echosounder to make their $BS$ measurement (${BS}_{\mathit{MAX}BS}$ or ${BS}_{EIBS}$) match the ${BS}_{ref}$ value. As previously mentioned, various features of the echosounder can impact the $BS$ measurement, but any offset toward ${BS}_{ref}$ is attributed solely to calibration gain for MAX $BS$ extraction (Equation 10), and to the sum of calibration gain and Simrad $SaCorr$ values for EI $BS$ extraction (Equation 11). $SaCorr$ (dB) is a calibration parameter provided by the EK60 sphere calibration software, which adjusts the effective pulse duration $T_{eff}$ from the nominal pulse duration $T$ (Equation 9). It is combined as a sum with the gain in $Sv$ (dB re m²/m³) output from the echosounder, and subsequently used in the EI $BS$ extraction. Equations are given for MAX $BS$ and EI $BS$ extractions, but only EI $BS$ results are given in Figure 14, as this method provided the most stable measurements of surface backscattering.

$T_{eff}=T.{10}^{\frac{2\times SaCorr}{10}}(9)$

${Gain}_{\mathit{MAX}BS}={Gain}_{acq}+\left({{BS}_{\mathit{MAX}BS}-BS}_{ref}\right)/2(10)$

${\left(Gain+SaCorr\right)}_{EIBS}={\left(Gain+SaCorr\right)}_{acq}+\left({{BS}_{EIBS}-BS}_{ref}\right)/2(11)$

Gain and $SaCorr$ values used during acquisition to compute the initial echosounder $Sv$ values are denoted with the subscript $acq$.

4.7 Determination and use of reference seafloor transect

Unlike sphere calibration, where reference Target Strength is ensured by the physical characteristics of the target (such as its dimensions and material), reference seafloor surface backscattering is established using primary acoustic measurements from calibrated echosounders. If the $BS$ value of a transect is intended to be used as a long-term reference, significant acquisition time series are required to build confidence in the stability of the seafloor surface backscattering and its resilience to environmental events, such as storms, sedimentary accretion, or changes in benthic populations. The interest in calibrated seafloor surface backscattering is relatively recent, so definitive guidelines are not yet available, but research on reference areas for multibeam monitoring by (Roche et al., 2018; Eleftherakis et al., 2018), as well as features observed in (Kloser et al., 2010), can help in avoiding unfavorable geological facies. Rocky areas do not present homogeneous enough seafloor backscattering, while soft sediments, such as sand and mud, exhibit strong directionality around normal incidence (specular reflection) and are subject to frequent changes in microbathymetry and the orientation of micro ripples, which can significantly impact their backscattering at normal incidence. Currently, the backscattering areas that have been found sufficiently stable over the years are characterized by a sandy gravel type substrate.

When selecting a reference transect, it is also recommended to perform a full bathymetric survey of the surrounding area, with different line orientations, to ensure the homogeneity of seafloor backscattering, the absence of any orientation dependence of backscatter related to microbathymetry (Lurton et al., 2018), and the flatness of the topography.

When monitoring echosounder calibration over an established reference line, if the $BS$ measurement offset exceeds the dispersion observed in the validation time series (approximately 1 dB for Carré Renard), it should raise concerns about the echosounder’s performance and the validity of the calibration parameters, prompting a full sphere calibration check. Of course, it cannot be ruled out that the seafloor $BS$ has changed, which would be confirmed if changes are observed concurrently across several echosounders operating at different frequencies. In this case, the area would unfortunately no longer be considered a suitable seafloor reference, but it would provide valuable insight into geological phenomena that could be monitored through calibrated seafloor backscatter measurements.

5 Conclusion

This paper explored the possibility of quickly monitoring the calibration of vertical single-beam echosounders by regularly acquiring seafloor surface backscattering data over a reference area, such as Carré Renard. Time series of acquisitions conducted with different equipment and frequencies showed that this method is an effective way to monitor the validity of echosounder measurements within an interval of better than 1 dB.

The paper proposed using the widely employed volume backscattering echo-integration process, performed on bottom echoes, to compute the seafloor surface backscattering $BS$ at normal incidence. A comparison with a more traditional maximum echo extraction method validated the consistency of this approach, which also demonstrated improved stability and robustness.

By leveraging existing echo-integration tools commonly used in fishery acoustics, this method also facilitates the straightforward measurement of the seafloor backscatter spectrum $BS\left(f\right)$ from broadband FM pulses.

While $BS$ measurements over a reference area are not meant to provide the same insights as the sphere calibration protocol for echosounders, they offer a way to estimate calibration gain for systems that cannot easily use the sphere method. This approach could be applied to non-split-beam echosounders or equipment installed on opportunistic platforms, such as commercial fishing fleets, which often lack the time and resources for sphere deployment.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

NL: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Writing – original draft, Writing – review and editing. LB: Investigation, Supervision, Writing – review and editing. RF: Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

We thank the reviewers involved in this submission and in a previous attempt for their encouragement and constructive comments, which have greatly contributed to improving the manuscript and bringing it to publication standards.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. ChatGPT was used to correct english writing occasionnaly, from already written sentences. No result, no method, nor any analysis was extracted from generative AI.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2025.1549238/full#supplementary-material

References

Demer, D. A., Andersen, L. N., Bassett, C., Berger, L., Chu, D., Condiotty, J., et al. (2017). USA–Norway EK80 Workshop Report: evaluation of a wideband echosounder for fisheries and marine ecosystem science. ICES Coop. Res. Re-port No. 336. doi:10.17895/ices.pub.2318

CrossRef Full Text | Google Scholar

Demer, D. A., Berger, L., Bernasconi, M., Bethke, E., Boswell, K., Chu, D., et al. (2015). Calibration of acoustic instruments (report). ICES Coop. Res. Rep. (CRR). doi:10.17895/ices.pub.5494

CrossRef Full Text | Google Scholar

Demer, D. A., and Renfree, J. S. (2008). Variations in echosounder–transducer performance with water temperature. ICES J. Mar. Sci. 65, 1021–1035. doi:10.1093/icesjms/fsn066

CrossRef Full Text | Google Scholar

De Robertis, A., and Handegard, N. O. (2013). Fish avoidance of research vessels and the efficacy of noise-reduced vessels: a review. ICES J. Mar. Sci. 70, 34–45. doi:10.1093/icesjms/fss155

CrossRef Full Text | Google Scholar

Eleftherakis, D., Berger, L., Le Bouffant, N., Pacault, A., Augustin, J.-M., and Lurton, X. (2018). Backscatter calibration of high-frequency multibeam echosounder using a reference single-beam system, on natural seafloor. Mar. Geophys Res. 39, 55–73. doi:10.1007/s11001-018-9348-5

CrossRef Full Text | Google Scholar

González-Máynez, V. E., Morales-Bojórquez, E., Nevárez-Martínez, M. O., and Villalobos, H. (2024). Application of fisheries acoustics: a review of the current state in Mexico and future perspectives. Fishes 9, 387. doi:10.3390/fishes9100387

CrossRef Full Text | Google Scholar

Hammerstad, E. (2000). Backscattering and seabed image reflectivity. EM technical note.

Google Scholar

Jackson, D. R., and Richardson, M. D. (2007). High-frequency seafloor acoustics. New York, NY: Springer. doi:10.1007/978-0-387-36945-7

CrossRef Full Text | Google Scholar

Kloser, R. J., Penrose, J. D., and Butler, A. J. (2010). Multi-beam backscatter measurements used to infer seabed habitats. Cont. Shelf Res. 30, 1772–1782. doi:10.1016/j.csr.2010.08.004

CrossRef Full Text | Google Scholar

Knudsen, H. P. (2009). Long-term evaluation of scientific-echosounder performance. ICES J. Mar. Sci. 66, 1335–1340. doi:10.1093/icesjms/fsp025

CrossRef Full Text | Google Scholar

Ladroit, Y., Lamarche, G., and Pallentin, A. (2018). Seafloor multibeam backscatter calibration experiment: comparing 45°-tilted 38-kHz split-beam echosounder and 30-kHz multibeam data. Mar. Geophys Res. 39, 41–53. doi:10.1007/s11001-017-9340-5

CrossRef Full Text | Google Scholar

Lurton, X. (2010). “An introduction to underwater acoustics: principles and applications,” in Springer-Praxis books in geophysical sciences. Second edition. Berlin Heidelberg Dordrecht London New York: Springer.

Google Scholar

Lurton, X., Eleftherakis, D., and Augustin, J.-M. (2018). Analysis of seafloor backscatter strength dependence on the survey azimuth using multibeam echosounder data. Mar. Geophys Res. 39, 183–203. doi:10.1007/s11001-017-9318-3

CrossRef Full Text | Google Scholar

Lurton, X., Lamarche, G., Brown, C., Lucieer, V., Rice, G., Schimel, A., et al. (2015). Backscatter measurements by seafloor-mapping sonars - guidelines and Recommendations. pymovies_3d. Available online at: https://gitlab.ifremer.fr/fleet/movies/pymovies_3d.

Google Scholar

Renfree, J. S., Andersen, L. N., Macaulay, G., Sessions, T. S., and Demer, D. A. (2020). Effects of sphere suspension on echosounder calibrations. ICES J. Mar. Sci. 77, 2945–2953. doi:10.1093/icesjms/fsaa171

CrossRef Full Text | Google Scholar

Roche, M., Degrendele, K., Vrignaud, C., Loyer, S., Le Bas, T., Augustin, J.-M., et al. (2018). Control of the repeatability of high frequency multibeam echosounder backscatter by using natural reference areas. Mar. Geophys Res. 39, 89–104. doi:10.1007/s11001-018-9343-x

CrossRef Full Text | Google Scholar

Simmonds, J., and Maclennan, D. N. (2007). Fisheries acoustics: theory and practice: second edition. Fisheries acoustics. Theory Pract. Second Ed., 1–252. doi:10.1002/9780470995303

CrossRef Full Text | Google Scholar

Thierry, S., Dick, S., George, S., Benoit, L., and Cyrille, P. (2019). “EMODnet Bathymetry a compilation of bathymetric data in the European waters,” in Oceans 2019 - marseille. Presented at the OCEANS 2019 - marseille, 1–7. doi:10.1109/OCEANSE.2019.8867250

CrossRef Full Text | Google Scholar

Weber, T. C., and Ward, L. G. (2015). Observations of backscatter from sand and gravel seafloors between 170 and 250 kHz. J. Acoust. Soc. Am. 138, 2169–2180. doi:10.1121/1.4930185

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y., Kenji, M., Tokeshi, T., Nishiyama, Y., Kasai, A., Matsuura, M., et al. (2024). Calibration of commercial fisheries echo sounders using seabed backscatter for the estimation of fishery resources. PLoS ONE 19, e0301689. doi:10.1371/journal.pone.0301689

PubMed Abstract | CrossRef Full Text | Google Scholar