- 1Johns Hopkins University Applied Physics Laboratory, Space Exploration Sector, Space Science and Instrumentation Branch, Laurel, MD, United States
- 2Johns Hopkins University Applied Physics Laboratory, Space Exploration Sector, Space Systems and Analysis Branch, Laurel, MD, United States
Molten Regolith Electrolysis, as an in situ resource utilization (ISRU) technology, has the potential to enable the production of oxygen and metallic alloys on the Lunar surface; opening new doors in Cis-Lunar, and eventually Martian space exploration. This research studies the fundamental physics which govern the formation, growth, detachment, and rise of electrolytic bubbles. To this end, computational fluid dynamic (CFD) models were developed and run, to simulate water electrolysis, molten salt electrolysis (MSE), and molten Lunar regolith (MRE) electrolysis across multiple reduced gravity levels. The results demonstrate that reduced gravity, electrode surface roughness (possibly due to surface degradation), fluid properties, and electrode orientation can all affect electrolytic efficiency and possibly even stall electrolysis by delaying bubble detachment. The findings of this research must be considered when designing and operating electrolysis systems at reduced gravity levels.
1 Introduction and importance of work
In the current decade, the National Aeronautics and Space Administration (NASA), other national space agencies, and private companies plan to establish a sustained presence on the Lunar surface. While the exploration plans include crewed missions, a strategic focus in the coming years of Lunar exploration will be on uncrewed missions and operations. These uncrewed mission plans include rovers, autonomous habitats, robotic landers, power-generation stations, and in situ resource utilization (ISRU) systems. In the context of continued robotic missions to Mars and possible crewed missions to Mars, multiphase fluid systems are set to play a pivotal role in the future of spaceflight operations, both on the Lunar and Martian surfaces. A wide range of critical systems are expected to be developed for exploration of the Moon and Mars, including cryogenic fuel management, heat exchangers, microfluidics, phase separators, in situ sample collection and analysis tools, environmental control and life-support systems (ECLSS), and ISRU systems. One area of particular interest to this work is electrolysis systems. Whether it is a basic water electrolysis system or more complex reactions like molten regolith electrolysis (MRE) or molten salt electrolysis (MSE) at high temperatures, many of the fundamental physics and unanswered questions remain. These questions often fall within the broader field of reduced-gravity fluid physics, covering phenomena like bubble growth and detachment, convective heat transfer, or surface-tension driven flows. Reduced gravity fluid physics continues to be an active area of research.
Extensive research has been conducted to study fluid dynamics in microgravity environments; however, our understanding of fluid behavior under the influence of partial gravity, such as the Moon’s 1/6th g or Mars’ 3/8th g, remains limited and poorly characterized. In the familiar 1 g environment on Earth, multiphase fluid behavior is primarily influenced by buoyancy. However, in microgravity, surface tension dominates fluid flows. Thus, understanding the fundamental physics underlying both surface tension and buoyancy is paramount, particularly when it comes to studying fluid systems operating within partial gravity, between microgravity and 1 g. This partial gravity regime includes both the Lunar and Martian gravity levels.
Since nearly the start of the space race, fluid systems operating in reduced gravity have encountered unanticipated problems, sometimes leading to system failures (Kamotani et al., 1996; 1995; 1994a; 1994b; Burgess, 2016). Experiments conducted aboard the International Space Station (ISS) have revealed unexpected issues related to bubble nucleation and transport (Qiu et al., 2000). These issues have manifested as the destruction of microfluidic biological samples, decreased heat transfer in heat exchangers, reduced flow rates in heat pipes, and the formation of bubbles in intravenous medical systems (Chiaramonte and Joshi, 2004; Dhir et al., 2007; Herman, 2013; Burke, 2021). To this day, problems encountered by the ISS ECLSS systems are unable to be replicated in terrestrial laboratories, operating under 1 g conditions (Hurlbert et al., 2004; Burke, 2021).
Reduced gravity fluid behavior has been modeled and experimentally studied by several researchers. Using reduced gravity environments produced by parabolic flights, Kim found that there exists a nonlinear and discontinuous relationship between gravity-level and heat flux of a water-submerged boiling heat exchanger (Kim et al., 2002; Kim and Raj, 2014). Lomax similarly used parabolic flights to conduct a study on water electrolysis at Lunar gravity levels (Lomax et al., 2022). It was found that oxygen-generating water electrolysis is 11% less efficient in Lunar gravity than on Earth (Lomax et al., 2022). Through the development of Computational Fluid Dynamic (CFD) models, Burke identified a power-law relationship between gravity level and bubble volume generated by a submerged orifice (Burke and Dunbar, 2021). Considering the scarcity of experimental platforms capable of simulating partial gravity and the recent expansion of CFD investigations, several unanswered questions remain with respect to partial gravity fluid physics (Pamperin and Rath, 1995; Tsuge et al., 1997; Welch, 1998).
Electrolysis, specifically, has been studied experimentally under variable gravity environments as well. Using parabolic flights and drop towers, water electrolysis in microgravity has been studied by multiple researchers (Mandin et al., 2008; Brinkert and Mandin, 2022). Using experimental parabolic flights, it was found that current density decreases and resistance increases under microgravity, due to the layer of gas bubbles on the electrode (Derhoumi et al., 2013; Lomax et al., 2022). Mandin and others also convey that systems and processes which rely on electrochemical techniques, such as purification or electrodeposition, must consider the effects gravity has on fluid behavior (Mandin et al., 2007; Akay et al., 2022; Brinkert and Mandin, 2022). Past experimental studies have stressed the importance of improved modeling techniques, which can capture the unique fluid transport mechanisms which are prevalent in microgravity (Derhoumi et al., 2013; Brinkert and Mandin, 2022).
Molten regolith electrolysis (MRE) has emerged as a technology of significant interest within the in situ resource utilization (ISRU) community. Its ability to generate oxygen and metallic alloys holds immense importance for Lunar exploration efforts and has even been identified by space agencies and companies as a potential part of the future Cis-Lunar economy (Sibille et al., 2009). While molten salt electrolysis (MSE), an Earth-based MRE analog, has produced viable amount of oxygen, questions of MRE viability remain.
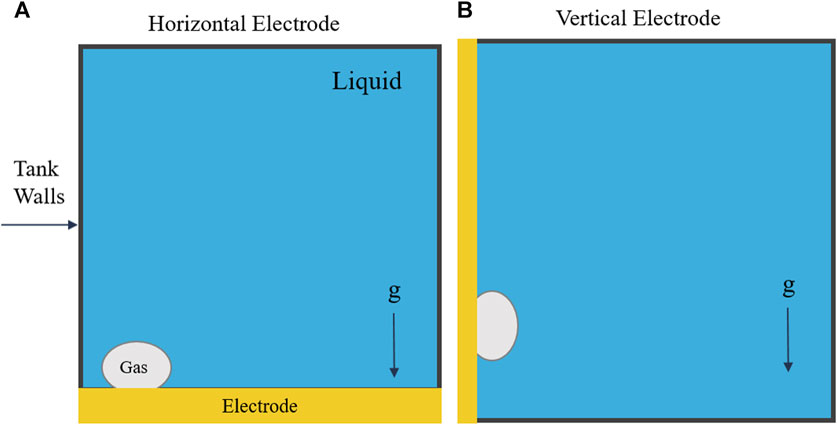
MRE’s viability could be affected by several factors. Not only will these systems typically be expected to operate autonomously for long periods of time, they will also operate in extreme and non-Earth-like environments. With reduced gravity (on the Moon or Mars), comes reduced buoyancy. A reduction in buoyancy leads to lower bubble detachment rates, which could possibly stall electrolysis or reduce its efficiency (Figure 1). In their partial gravity water electrolysis experiments, Lomax observed a larger bubble froth layer on the electrode surface, caused by reduced bubble detachment rates (Lomax et al., 2022). This froth layer increased ohmic resistance and decreased efficiency of the overall system. Derhoumi et al. found similar results in microgravity using parabolic flights (Derhoumi et al., 2013). Unlike water electrolysis, MRE systems have never been tested in reduced gravity environments, due to safety concerns on board parabolic flights. As modeling is still in its infancy, the lack of empirical data in partial gravity represents a critical gap in our understanding of MRE’s performance in the unique Lunar environment. Most researchers are relying solely on Earth-based experiments (operating in 1 g) to determine the efficacy and design of MRE systems, which will eventually be operating in Lunar gravity.
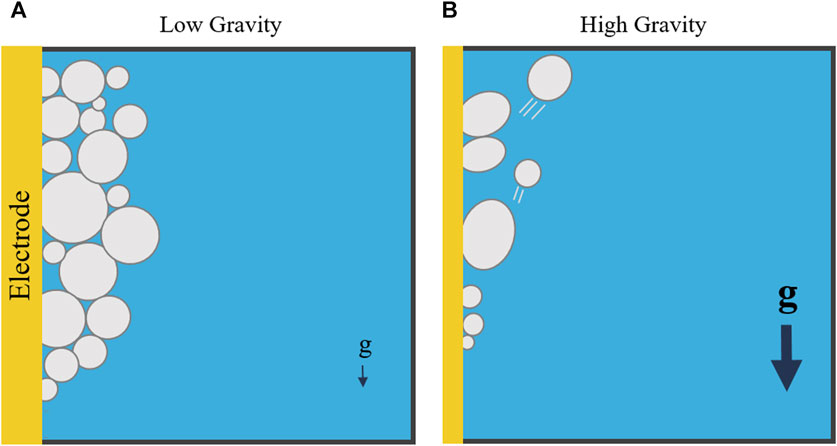
Figure 1. Bubbles forming on an electrode in low gravity (A) and high gravity (B). In low gravity regimes, bubbles may not detach and could stall electrolysis by covering the electrode’s surface. Based on image by Lomax et al. (Lomax et al., 2022), licensed CC-BY-4.0.
The research presented in this work aims to apply several well-established CFD methodologies, such as volume of fluid interface tracking and fluid property/material property variation, in new and novel ways. Modeling a single bubble, in order to study the detailed, fundamental growth and detachment mechanisms has been performed by a limited number of fluid physicists (Fritz and Ende, 1936; Chesters, 1978; Kim et al., 2002; Kulkarni and Joshi, 2005; Burke, 2021; Iwata et al., 2021). After an extensive literature review and prior experience, the authors believe this is the most expansive parameter space, related to the modeling of molten regolith and salt electrolysis. The work presented includes several variations in gravity level, electrolyte, electrode surface roughness, and electrode orientation, with all combinations of parameters being modeled. Finally, due to a lack of experimental platforms in partial gravity, it is common to only model fluid processes in Earth’s gravity (1 g) and microgravity. This work is one of a small collection of studies which present model or experimental results at multiple reduced gravity levels, enabling analysis into the scaling of fluid behavior across gravity levels (Tsuge et al., 1997; Qiu et al., 2000; Di Bari et al., 2013; Kim and Raj, 2014; Burke et al., 2023).
2 Methodology
2.1 Scope of computational fluid dynamic (CFD) models
The experimental and computational study of bubbles is far from simple. Exhaustive studies remain difficult, complex, and dependent upon factors which cannot typically be controlled. Bubbles which detach from a solid surface are highly sensitive to several interdependent forces and factors. These include: electrode surface properties (including any imperfections or inclusions), bubble-to-bubble interactions, chamber wall effects, and fluid composition (including any contaminants). Empirical and computational bubble studies are also limited by the very small time and length scales over which bubbles form, grow, and detach (Di Bari et al., 2013; Burke, 2021).
When studying bubble behavior and related phenomena (such as electrolysis), a common approach is to simplify and isolate individual bubble parameters and behaviors to model and analyze. In order to understand the fundamental physics affecting bubbles formed via electrolysis and with consideration to limited computational resources, the modeling effort described in this research follows the aforementioned approach.
Therefore, the research presented herein examines the formation, growth, detachment, and rise of oxygen gas bubbles formed via water electrolysis, MRE, and MSE across various gravity levels. To this end, a simplified electrolysis process was modeled. The model includes an individual bubble forming at a single, isolated nucleation site on an electrode. Modeling single bubble growth is a common assumption when studying phenomena such as boiling, electrolysis, and submerged orifices (Cooper, 1982; Di Bari et al., 2013). Although not realistic for an operational electrolysis system, a single bubble nucleation site allows for the careful study of bubble behavior throughout the entire process of bubble formation, growth, necking, detachment, and rise.
2.2 CFD solver
All CFD models developed and presented in this research use OpenFOAM, an open-source CFD toolbox (Greenshields, 2023). Specifically, the interFoam solver, a two-phase, isothermal, incompressible, transient, immiscible, volume of fluid (VOF) solver, was used to develop and run all models. The solver is a VOF, Euler-Euler solver. The VOF method is an efficient free surface modeling method used to track the fluid’s free surface using the concept of volume fraction and immiscible fluids (Hirt and Nichols, 1981; Hamdan et al., 2020). An independent solver then computationally solves the Navier-Stokes equations (Hirt and Nichols, 1981; Heyns and Oxtoby, 2014). All other assumptions of this solver (two-phase, isothermal, incompressible, etc.) are reasonable assumptions for a gas bubble forming and rising in a homogeneous melt.
The interFoam solver uses the below constant-density continuity equation.
The momentum equation is represented by the interFoam solver by the below equation, where density, surface tension, and curvature are defined in the subsequent equations (Brackbill et al., 1992; Heyns and Oxtoby, 2014).
Finally, the VOF solver tracks the phase interface using the interphase equation below.
2.3 Model geometry and meshing
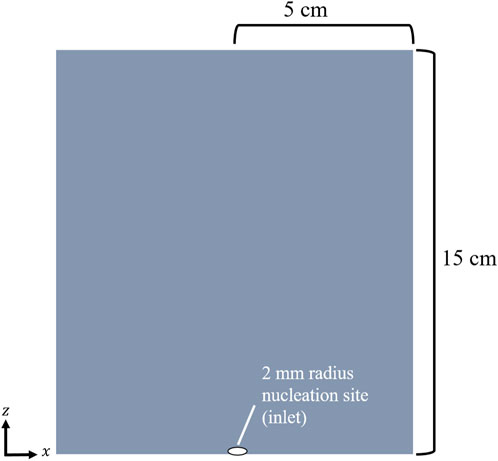
Gmsh was used to develop the model’s geometry and mesh. Gmsh is an open source 3-dimensional and 2-dimensional finite-element geometry and mesh generator. The model contained a structured mesh. The geometry primarily includes a fluid chamber (Figure 2). The chamber consists of an electrode (containing the single 2-mm radius bubble nucleation site) on one of the chamber walls and an outlet on the top of the chamber. The chamber dimensions are 15 cm tall by 10 cm by 10 cm. The width of the chamber walls was chosen to be wide enough as to mitigate any wall effects on the bubble’s shape or size during bubble formation and growth (Albadawi et al., 2013).
To ensure a satisfactory level of mesh refinement, a simple mesh refinement study was performed (Prakash and Ethier, 2000). The model’s mesh was gradually refined from coarse mesh to highly refined mesh. A standard case was run across all meshes and the bubble volume was measured for each case. The mesh was considered to be sufficiently refined when the bubble volume remained constant, even with increasing mesh refinement. This mesh refinement study is critical to ensuring consistent results, while maintaining computational efficiency (Prakash and Ethier, 2000; Contreras et al., 2002).
2.4 Computational resources
All models were run in parallel across six cores. The runs were conducted using OpenFOAM version 9 on high-performance computing resources at the Johns Hopkins University Applied Physics Laboratory.
2.5 Variables tested
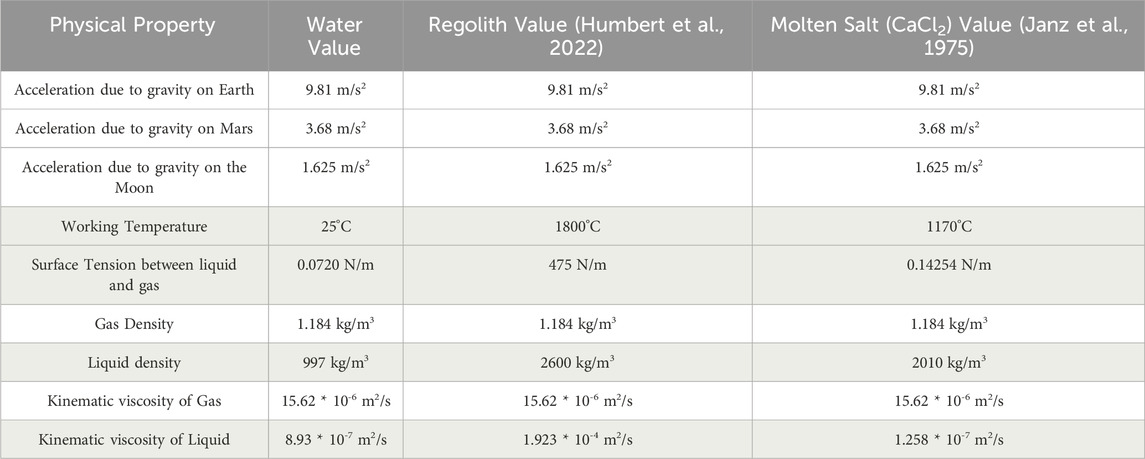
The primary aim of this research was to explore the influence common design choices and environmental factors could have on oxygen gas bubbles formed via electrolysis. Four primary variables were tested by the models: choice of fluid, electrode orientation (Figure 3), electrode surface roughness, and gravity level. Models were developed and run for water, molten Lunar regolith, and molten salt (CaCl2). All liquids were run in 1 g, Martian gravity, and Lunar gravity. The electrode orientation and surface properties were varied across all liquids. Models for water, MRE, and MSE were run with both horizontal (perpendicular to the gravity vector) and vertical (parallel to the gravity vector) electrode orientations. Three electrode surface roughness values were tested: smooth, medium, and rough. Specific values for all variables will be detailed in subsequent sections.
2.6 Boundary conditions
Standard boundary conditions were used in the model. Wall boundary conditions were used for all chamber walls and the electrode. The wall boundary condition includes conditions of fixed flux pressure and no slip. Using the zero-gradient pressure condition, the outlet was modeled as a fluid open to ambient atmosphere. This ensures that no pressure ever builds up in the chamber as gas bubbles are produced. All parts of the model include an isothermal boundary condition, as well.
The bubble nucleation site was modeled as a gas inlet with a constant and uniform velocity profile. For the horizontal electrode configuration, the inlet is directed vertically into the fluid chamber and is located on the electrode in the center of the chamber. For the vertical electrode orientation, the inlet is located on a vertical electrode and directed horizontally into the fluid chamber. A very low volumetric flow rate (7.16*10−7 m3/s) was chosen for the inlet, to emulate quasi-steady bubble growth.
As mentioned above, the electrode’s surface roughness was varied during this modeling effort. To account for this, an apparent Sessile drop contact angle boundary condition was used on the electrode’s surface. The Wenzel equation below relates the intrinsic contact angle (on a theoretically smooth surface) to the apparent contact angle (on a rough surface) (Wenzel, 1936). As described by the Wenzel relation, the apparent contact angle increases with rougher electrode surfaces (Wenzel, 1936). This is due to the fact that rougher surfaces provide more liquid-solid interfacial area per unit length than a smooth surface (Wolansky and Marmur, 1999; Li et al., 2021). Figure 4 illustrates that liquids are most likely to spread on smooth electrode surfaces. Using contact angle boundary conditions allows for the generalization of electrode material selection, since no material properties are needed as inputs into the model. Using real-world fluid and electrode material properties, actual surface roughness values could be calculated from these contact angle boundary conditions. Although the bubbles never come in contact with the fluid chamber walls, it is important to note that the surface roughness of the fluid chamber walls remained constant at a 40⁰ contact angle.
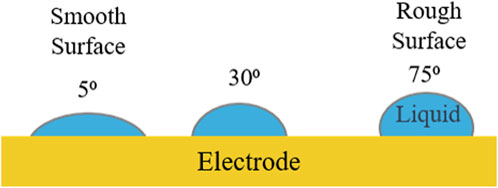
Figure 4. The three different electrode surface roughness values which were tested. The surface roughness was modeled via a Sessile drop contact angle boundary condition.
2.7 Physical properties of fluids tested
The physical properties which were used as inputs into the model (either as initial conditions or boundary conditions) were collected from tabulated references. All physical properties used are displayed in Table 1. While it is a limitation of the current model implementation, in order to study the effects of only the variables of keen interest (electrolyte selection, gravity level, and surface roughness), gaseous fluid properties were kept constant for all runs.
2.8 Post-analysis methodology
All post-processing and model analysis was conducted using ParaView version 5.6. ParaView is an open-source data analysis and visualization software. The primary uses of ParaView in this research included mesh visualization and data collection via visualization and bubble volume measurements.
2.9 Model limitations and assumptions
Multiple simplifying assumptions were made in this model. First, the developed model is a computational fluid dynamic model, not a multiphysics simulation. As opposed to multiphysics models, this CFD model is not able to model the spontaneous nucleation of gas bubbles across several points on the electrode’s surface. Instead, the model was designed to study the formation, growth, spreading, detachment, and rise of a single oxygen bubble from a carefully-placed nucleation site on the electrode. Concentrating on a single gas bubble’s formation, growth, and detachment allows for measurements and physical analysis which would not be possible if dozens to hundreds of bubbles were nucleating and growing at the same time. The lack of multiphysics modeling also means that the precipitation of any metals during MRE is also not able to be modeled.
Beyond the above assumptions, the model assumes uniform temperature fields, thus the model does not resolve the temperature field. The model also assumes homogeneous melts for water electrolysis, MRE, and MSE.
Lastly, the model assumes a constant contact angle boundary condition on the electrode. The constant contact angle boundary condition limits the model in two ways. First, it does not account for any degradation of the electrode, which is likely to occur with time, especially at high temperatures. However, the timescales over which electrode degradation are likely to occur are orders of magnitude longer than the growth and detachment of a single bubble. Thus, this is a fair assumption when using the model to study a single bubble’s growth and detachment. Secondly, the constant contact angle boundary condition limits the model by not modeling the change in contact angle which would result from the applied potential. When a potential is applied to an electrolyte, its surface tension and contact angle with the electrode both decrease. This was first described by Lippmann (Lippmann, 1875). If the electrolytic system was potentiostatic, then the voltage would remain constant and the electrolyte’s surface tension and contact angles would not change with time. However, if the system used a galvanostatic technique, applying a constant current, the potential would increase/decrease as the electrode’s resistance increased/decreased (with changing amounts of bubble coverage). With a changing potential, the electrolyte’s contact angle with the electrode would become time-dependent, affecting the time to detachment and bubble volume at detachment. The model presented in this research assumes a constant contact angle, and thus a potentiostatic electrolytic reaction.
3 Results
3.1 Water electrolysis
Results have been obtained for water electrolysis at 1 g, Martian gravity, and Lunar gravity. The results also include variation in electrode orientation and surface roughness. The results are presented in Table 2.
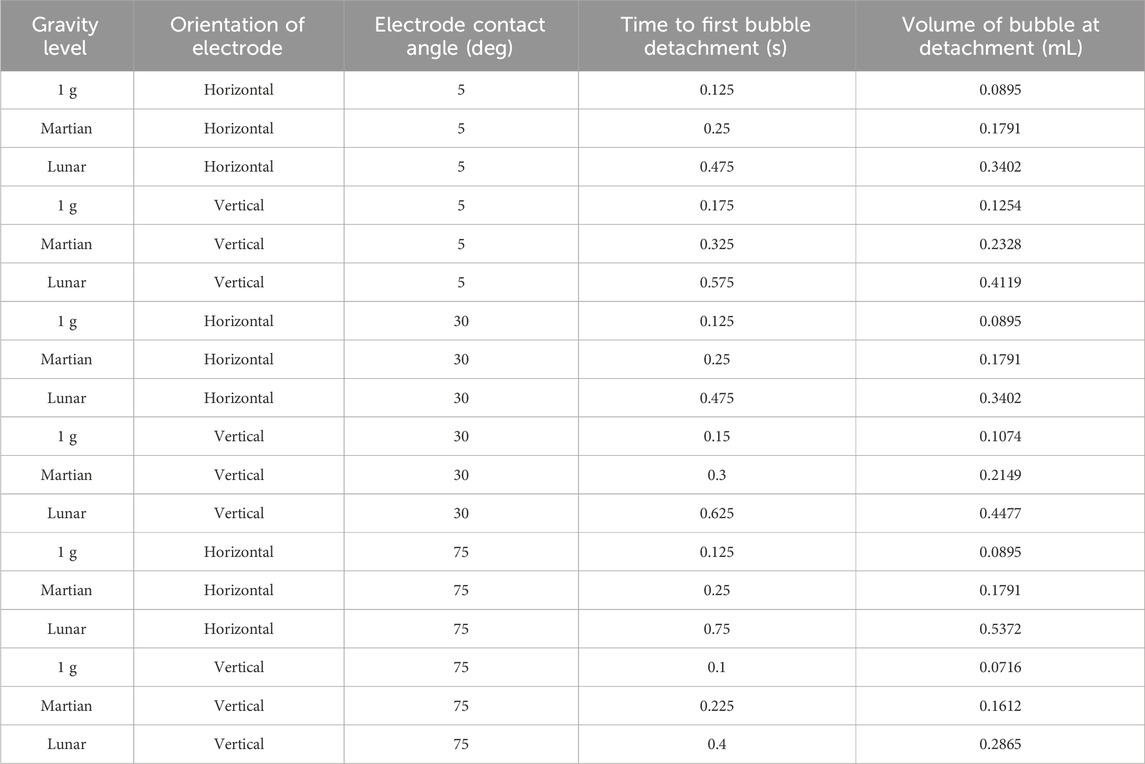
Table 2. Water electrolysis results across three gravity levels, two electrode orientations, and three electrode surface roughness values. The larger the contact angle value, the rougher the electrode surface.
3.2 Molten regolith electrolysis (MRE)
Results have been obtained for molten Lunar regolith electrolysis at 1 g, Martian gravity, and Lunar gravity. The results also include variation in electrode orientation and surface roughness. The results are presented in Table 3. It is important to note that due to limited computational resources, bubbles forming in MRE on very rough electrodes were not observed to detach after dozens of seconds. With longer computational runs, it is expected that the bubbles will eventually detach from the rough electrodes.
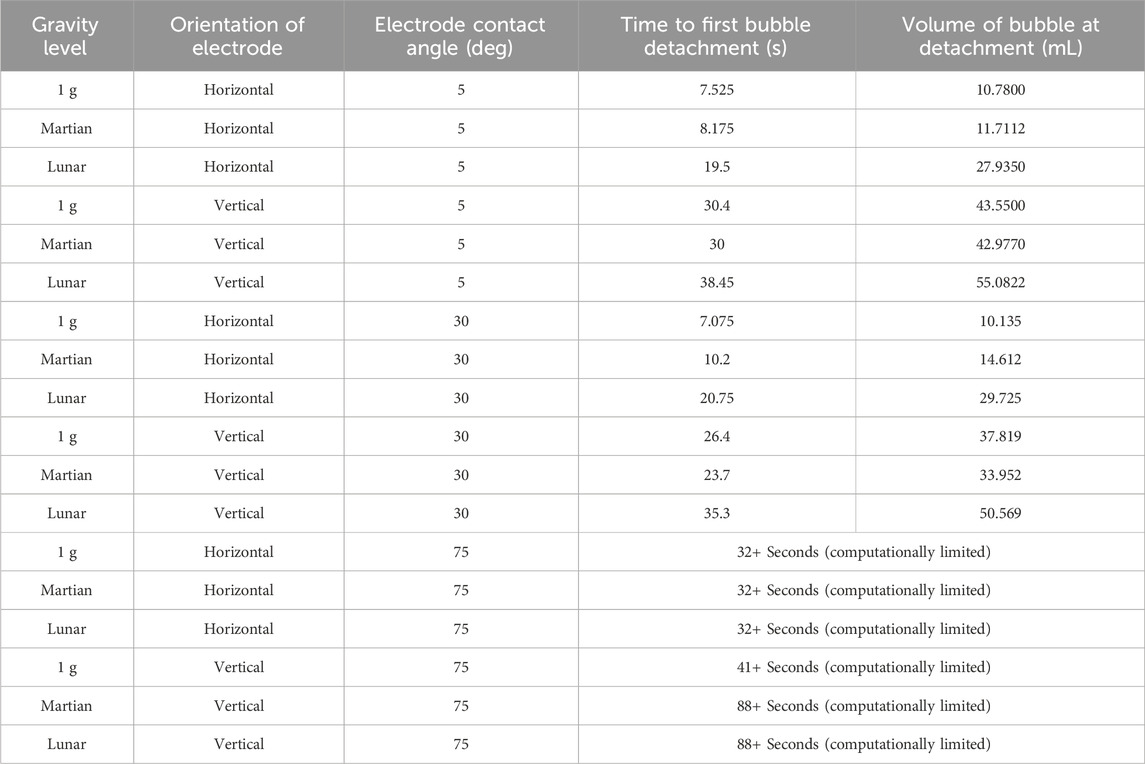
Table 3. Molten regolith electrolysis results across three gravity levels, two electrode orientations, and three electrode surface roughness values. The larger the contact angle value, the rougher the electrode surface.
3.3 Molten salt electrolysis (MSE)
Results have been obtained for molten salt (CaCl2) electrolysis at 1 g, Martian gravity, and Lunar gravity. The results also include variation in electrode orientation and surface roughness. The results are presented in Table 4.
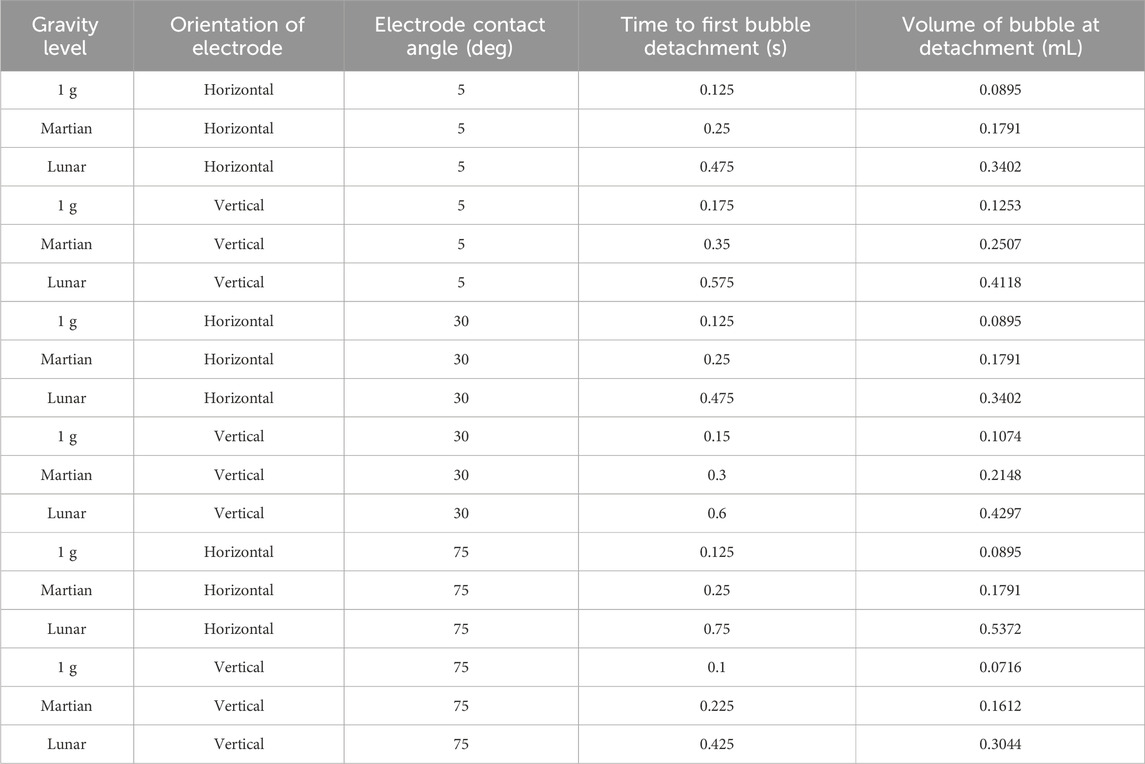
Table 4. Molten salt (CaCl2) electrolysis results across three gravity levels, two electrode orientations, and three electrode surface roughness values. The larger the contact angle value, the rougher the electrode surface.
3.4 Visualization of results
Sample visual representations of the bubble growth, detachment, and rise are displayed in Figures 5–8.
Videos of molten salt electrolysis models at various gravity levels and electrode orientations are available as Supplementary Material.

Figure 5. Visual CFD model results for water electrolysis in Lunar gravity using a horizontal electrode.

Figure 6. Visual CFD model results for water electrolysis in Lunar gravity using a vertical electrode.

Figure 8. Visual CFD model results for MSE in Martian gravity using a horizontal electrode at times: (A) 0.05 s, (B) 0.15 s, (C) 0.225 s, and (D) 0.25 s.
4 Discussion
4.1 Effects of reduced gravity
For all liquids and electrode properties tested, it was observed that a decrease in gravitational acceleration results in delayed bubble detachment and thus, larger bubble volumes at detachment. A decrease in gravitational acceleration causes a decrease in bubble buoyancy, according to the below equation.
A reduced buoyancy force decreases bubble detachment forces. With lowered bubble detachment forces, bubbles stay attached to the electrode and continue to grow larger in volume for longer periods of time.
The modeling data suggests that bubbles forming in MRE are less dependent upon gravity levels than bubbles forming in MSE or water electrolysis. For the case of the horizontal electrode with medium surface roughness, bubbles detaching in water or molten salt are 3.8 times larger in Lunar gravity than they are in 1 g. For bubbles rising in molten Lunar regolith, however, the detachment volumes are only 2.9 times larger in Lunar gravity than in 1 g.
Of particular interest is the relationship between scaling gravity levels and bubble detachment time/volume. A nonlinear, power-law trend is observed when bubble detachment volume is scaled from 1 g to Lunar gravity. Figures 9–11 display plots, exhibiting the relationship between bubble detachment volume and gravity level for horizontal and vertical electrodes with medium surface roughness. The nonlinear trend exhibited by the models agree well with other research conducted on scaling bubble behavior across variable gravity levels, including submerged orifice bubble growth, boiling, and water electrolysis (Burke and Dunbar, 2021; Lomax et al., 2022).
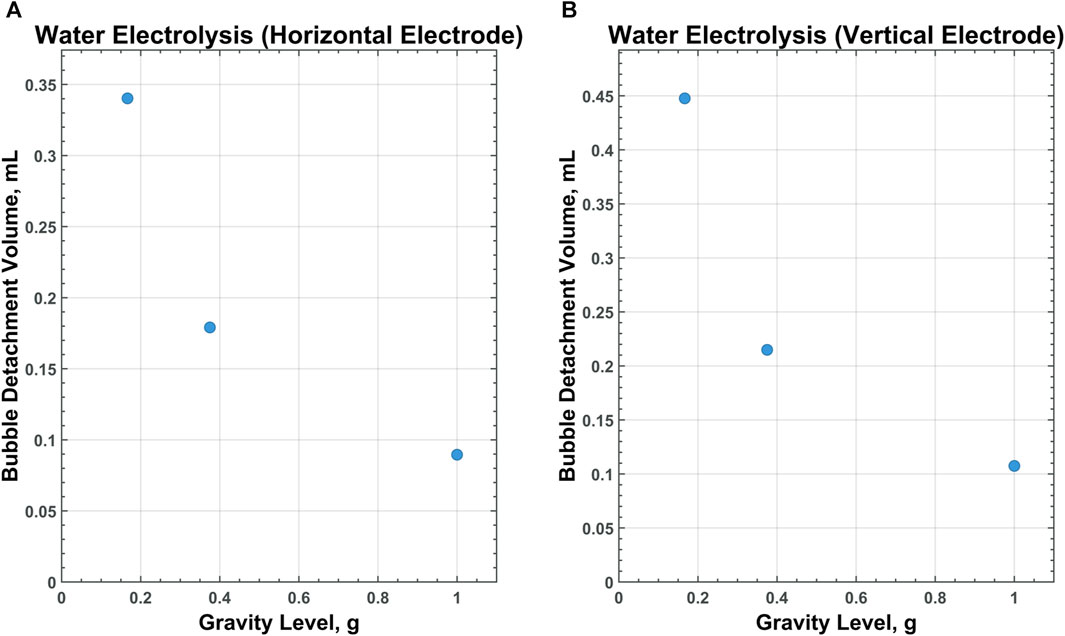
Figure 9. CFD data for water electrolysis on a horizontal (A) and vertical (B) electrode with medium-surface roughness across all gravity levels tested.
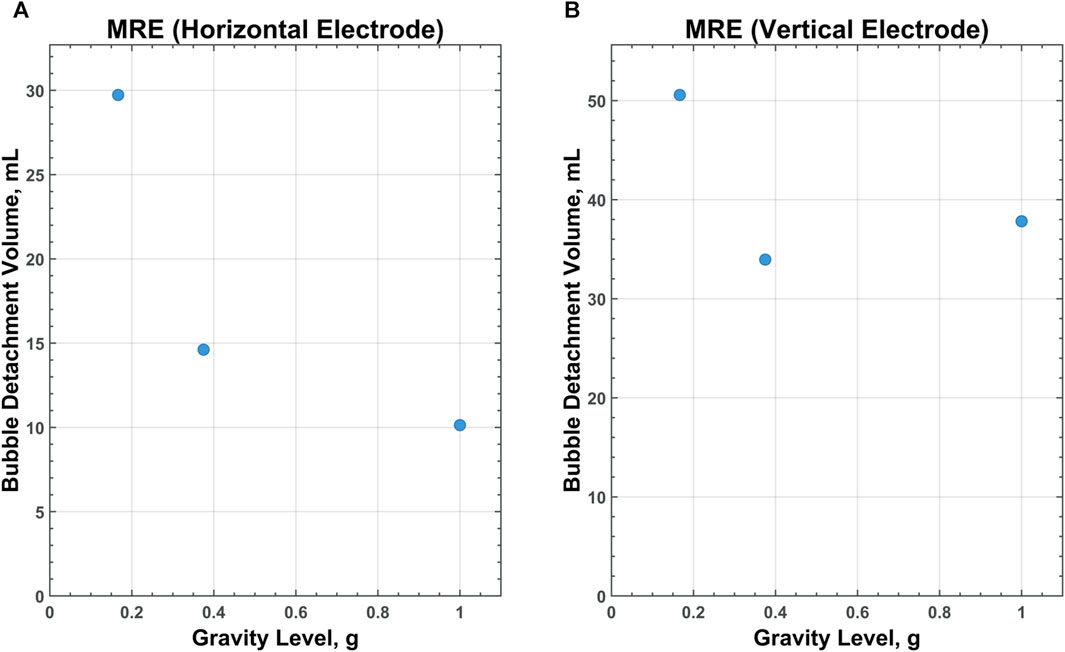
Figure 10. CFD data for MRE on a horizontal (A) and vertical (B) electrode with medium-surface roughness across all gravity levels tested.
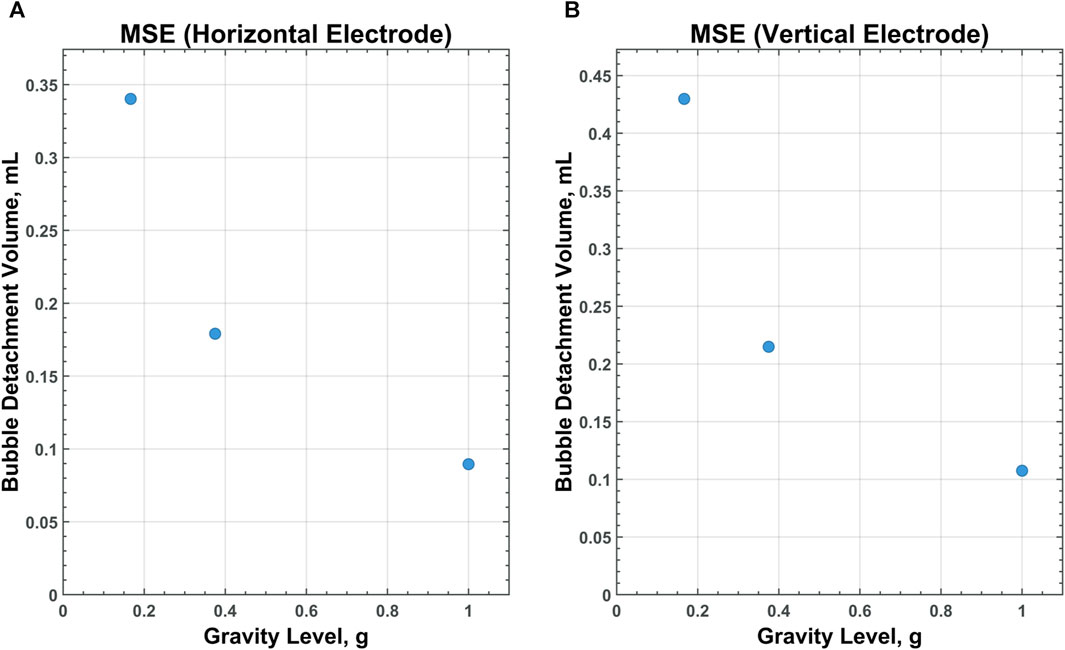
Figure 11. CFD data for MSE on a horizontal (A) and vertical (B) electrode with medium-surface roughness across all gravity levels tested.
4.2 Effects of fluid properties
Fluid properties can affect the rate at which bubbles grow and detach from an electrode. As mentioned previously, the physical properties used as inputs into the model are summarized in Table 1. Despite large differences in working temperatures and densities, water and molten salt have relatively similar surface tensions and viscosities. Potentially due to these similar fluid properties, water electrolysis and MSE exhibited bubble detachment volumes and time to detachments in the same order of magnitude.
Molten regolith electrolysis, however, saw bubble volumes and time to detachments at least two orders of magnitude larger than water electrolysis and MSE. The largest differences in fluid properties between these liquids are molten regolith’s very high viscosity, density, and surface tension. With high viscosity and surface tension, bubbles neck, detach, and rise at lower rates.
4.3 Effects of electrode orientation
The orientation of the electrode was observed to effect bubble detachment volume and time to detachment. For all liquids and nearly all electrode surface roughness values, bubbles forming and detaching from vertical electrodes were found to be larger in volume and detach later, compared to horizontal electrodes. At vertical electrode orientations, bubbles appear to spread vertically along the electrode’s surface, due to the upward buoyancy force (Figure 6). As the bubble spreads along the electrode’s surface, its contact area with the surface increases. Surface tension is directly related to bubble contact area (see below equation) and is an attachment force, opposing bubble detachment. Thus, increasing the bubble contact area via spreading would increase the surface tension force (increasing attachment forces between the bubble and electrode) and delay bubble detachment. It must be noted, however, that when several bubbles form on an electrode, instead of single bubble, rising bubbles and bubble-to-bubble interactions are expected to induce early detachment of other surrounding bubbles.
4.4 Effects of electrode surface properties
Surface roughness of the electrode was also observed to effect bubble detachment volume and time to detachment. At high surface roughness values, bubbles were observed to grow larger in volume and detach at lower rates. This is especially true for MRE. In molten regolith, bubbles remain attached to the electrode for extended amounts of time.
Similar to electrode orientation, this trend is hypothesized to be caused by varying amounts of bubble spreading along the electrode surface. At high values of surface roughness, the liquid melt does not spread across the electrode’s surface. The bubble, instead, spreads along the electrode. It has been shown that increased bubble spreading increases the surface tension forces between the bubble and the electrode, delaying bubble detachment (Burke and Dunbar, 2021).
Some surface roughness will always be present on an electrode. A manufactured electrode for instance, no matter how precise the manufacturing process, will have some degree of surface roughness. Surface defects, such as impurities, can also be expected to contribute to surface roughness. Surface roughness does not only come from manufacturing processes, however. When an electrode is used for extended amounts of time in extreme conditions, such as high-temperature molten regolith, its surface typically degrades. This surface degradation could unpredictably cause an increase in surface roughness.
No matter how surface roughness is introduced, a highly rough electrode will allow electrolytic bubbles to spread and remain attached, potentially stalling electrolysis completely. Even if the electrolytic process is not stalled, its efficiency could be negatively affected. As discussed in prior assumptions, if the model is used to predict the electrolytic production of oxygen over long timescales, modifications would have to be made to account for the slow, but significant degradation of the electrode’s surface. A time-variant contact angle boundary condition would most likely be chosen.
4.5 Future work
The results suggest a few gaps which should be investigated by further research and modeling. The model should be improved to a more realistic, operational design. This could include multiple nucleation sites and a larger fluid chamber/electrode. The variable parameter space could also be expanded to include more types molten regolith or other electrode orientations (possibly a 45⁰ angle). Lastly, mitigation techniques could be studied, if determined to be necessary. While electrolysis in Lunar gravity may be a viable form of oxygen production, it is possible that the reduced gravity and other effects discussed above detrimentally limit the efficiency of electrolysis in Lunar gravity. If that is the case, it would be advantageous to study various mitigation techniques. These could possibly include: induced cross flow over the electrode, vibrations, or electrode surface coatings to encourage bubble detachment.
5 Conclusion
The results presented by this research convey important insights into electrolysis in reduced gravity. Gravity level affects bubble detachment volume and time to detachment. At reduced gravity levels, bubble detachment is delayed and bubbles continue to grow larger. The relationship between bubble volume and gravity level follows a non-linear power-law trend. This trend emphasizes the importance of considering gravity level when designing and testing systems which rely on multiphase fluid flows. If the system is designed and tested in Earth’s gravity, one cannot expect similar, or even linearly scalable, results in Lunar gravity.
When bubbles spread along an electrode, bubble detachment is delayed. This is due to the fact that when bubbles spread along the electrode, the surface tension force (keeping the bubble attached to the electrode) increases. Bubble spreading can be caused by various factors. Vertical electrodes cause bubbles to spread (due to vertical buoyancy force) more than horizontal electrodes. Rough electrodes also cause increased bubble spreading, due to liquid-solid wetting properties. MRE in particular, is very dependent upon electrode surface properties, particularly surface roughness.
This research provides important insights into the feasibility of electrolytic processes (water, molten regolith, and molten salt) in reduced gravity environments, such as those of the Lunar or Martian surfaces. Molten regolith’s unique physical properties, especially high surface tension and viscosity, causes MRE to produce very large gas bubbles. These bubbles can remain attached and grow on the electrode for so long that electrolysis could possibly be stalled or decrease in efficiency, especially at reduced gravity levels.
This study has identified some characteristics which are important to control and consider, when designing or operating an electrolysis system in reduced gravity. First, the influence of electrode orientation should be taken into account when designing any future electrolysis system. The electrode’s surface properties, most importantly surface roughness, should also be considered. Smoother electrodes will best allow for the release of bubbles. Finally, when designing electrolysis systems, or any multiphase fluid system, expected to operate in reduced gravity, the nonlinear scaling relationship between fluid behavior and gravity level must not be overlooked. Success on Earth does not equate to success on the Moon or Mars.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
PB: Conceptualization, Formal Analysis, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. MN: Conceptualization, Resources, Supervision, Writing–review and editing. CH: Conceptualization, Funding acquisition, Project administration, Supervision, Writing–review and editing. JB: Project administration, Supervision, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported and paid for by NASA’s Space Technology Mission Directorate (STMD) via the Lunar Surface Innovation Initiative (LSII) task within Johns Hopkins University Applied Physics Laboratory. The LSII contract number is: 80MSFC20D0004.
Acknowledgments
The authors would like to acknowledge the Lunar Surface Innovation Consortium (LSIC) in-situ Resource Utilization (ISRU) Focus Group for expert inputs and insight on Molten Regolith Electrolysis.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frspt.2024.1304579/full#supplementary-material
Supplementary Video S1 | Model of bubbles forming, detaching, and rising via molten salt electrolysis in 1 g on a horizontal electrode with medium surface roughness.
Supplementary Video S2 | Model of bubbles forming, detaching, and rising via molten salt electrolysis in 1 g on a vertical electrode with medium surface roughness.
Supplementary Video S3 | Model of bubbles forming, detaching, and rising via molten salt electrolysis in Martian gravity on a horizontal electrode with medium surface roughness.
Supplementary Video S4 | Model of bubbles forming, detaching, and rising via molten salt electrolysis in Martian gravity on a vertical electrode with medium surface roughness.
Supplementary Video S5 | Model of bubbles forming, detaching, and rising via molten salt electrolysis in Lunar gravity on a horizontal electrode with medium surface roughness.
Supplementary Video S6 | Model of bubbles forming, detaching, and rising via molten salt electrolysis in Lunar gravity on a vertical electrode with medium surface roughness.
References
Akay, Ö., Poon, J., Robertson, C., Abdi, F. F., Cuenya, B. R., Giersig, M., et al. (2022). Releasing the bubbles: nanotopographical electrocatalyst design for efficient photoelectrochemical hydrogen production in microgravity environment. Adv. Sci. 9, 2105380. doi:10.1002/advs.202105380
Albadawi, A., Donoghue, D. B., Robinson, A. J., Murray, D. B., and Delauré, Y. M. C. (2013). On the analysis of bubble growth and detachment at low Capillary and Bond numbers using Volume of Fluid and Level Set methods. Chem. Eng. Sci. 90, 77–91. doi:10.1016/j.ces.2012.12.004
Brackbill, J. U., Kothe, D. B., and Zemach, C. (1992). A continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354. doi:10.1016/0021-9991(92)90240-Y
Brinkert, K., and Mandin, P. (2022). Fundamentals and future applications of electrochemical energy conversion in space. Npj Microgravity 8, 52–59. doi:10.1038/s41526-022-00242-3
Burgess, C. (2016). Aurora 7: the mercury SPaceflight of M. Scott carpenter. Bangor, NSW, Australia: Springer.
Burke, P. (2021). Computational fluid dynamic (CFD) modeling and experimental study of the formation and buoyancy-driven detachment of bubbles in variable gravity environments (PhD). College Station, TX, USA: Texas A&M University.
Burke, P. A., and Dunbar, B. J. (2021). “Development of computational fluid dynamic (CFD) models of the formation and buoyancy-driven detachment of bubbles in variable gravity environments,” in AIAA scitech 2021 forum, AIAA SciTech forum (American Institute of Aeronautics and Astronautics). ,Reston, VI, USA doi:10.2514/6.2021-1838
Burke, P. A., Nord, M. E., Berdis, J., and Hibbitts, C. (2023). “Oxygen production on the lunar surface: modeling molten regolith electrolysis and water electrolysis at reduced gravity levels,” in Ascend 2023 (American Institute of Aeronautics and Astronautics). Reston, VI, USA, doi:10.2514/6.2023-4793
Chesters, A. K. (1978). Modes of bubble growth in the slow-formation regime of nucleate pool boiling. Int. J. Multiph. Flow. 4, 279–302. doi:10.1016/0301-9322(78)90003-4
Chiaramonte, F., and Joshi, J. (2004). Workshop on critical issues in microgravity fluids, transport, and reaction processes in advanced human support technology. Washington, DC: National Aeronautics and Space Administration.
Contreras, J., Corral, R., Fernández Castañeda, J., Pastor, G., and Vasco, C. (2002). Semi-unstructured grid methods for turbomachinery applications. Amsterdam, Netherlands: ASME. doi:10.1115/GT2002-30572
Cooper, M. G. (1982). Growth and departure of individual bubbles at a wall. Appl. Sci. Res. 38, 77–84. doi:10.1007/BF00385939
Derhoumi, Z., Mandin, P., Roustan, H., and Wüthrich, R. (2013). Experimental investigation of two-phase electrolysis processes: comparison with or without gravity. J. Appl. Electrochem. 43, 1145–1161. doi:10.1007/s10800-013-0598-2
Dhir, V. K., Abarajith, H. S., and Li, D. (2007). Bubble dynamics and heat transfer during pool and flow boiling. Heat. Transf. Eng. 28, 608–624. doi:10.1080/01457630701266421
Di Bari, S., Lakehal, D., and Robinson, A. J. (2013). A numerical study of quasi-static gas injected bubble growth: some aspects of gravity. Int. J. Heat. Mass Transf. 64, 468–482. doi:10.1016/j.ijheatmasstransfer.2013.04.002
Fritz, W., and Ende, W. (1936). Über den Verdampfungsvorgang nach kinematographischen Aufnahmen an Dampfblasen. Phys. Z 37, 391–401.
Greenshields, C., 2023. OpenFOAM v11 user guide [WWW document]. CFD Direct. URL https://doc.cfd.direct/openfoam/user-guide-v11/index (Accessed 9.23).
Hamdan, M., Sebastia-Saez, D., Hamdan, M., and Arellano-Garcia, H. (2020). “CFD analysis of the use of desert sand as thermal energy storage medium in a solar powered fluidised bed harvesting unit,” in Computer aided chemical engineering, 30 European symposium on computer aided process engineering. Editors S. Pierucci, F. Manenti, G. L. Bozzano, and D. Manca (Elsevier), Amsterdam, Netherlands, 349–354. doi:10.1016/B978-0-12-823377-1.50059-8
Herman, C. (2013). Bubble Formation and coalescence under the influence of electric fields. Heat Transf. Therm. Eng. 8C, IMECE2013. doi:10.1115/IMECE2013-64991Volume
Heyns, J. A., and Oxtoby, O. F. (2014). Modelling surface tension dominated multiphase flows using the VOF approach. Barcelona, Spain: World Congress on Computational Mechanics.
Hirt, C. W., and Nichols, B. D. (1981). Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225. doi:10.1016/0021-9991(81)90145-5
Humbert, M. S., Brooks, G. A., Duffy, A. R., Hargrave, C., and Rhamdhani, M. A. (2022). Thermophysical property evolution during molten regolith electrolysis. Planet. Space Sci. 219, 105527. doi:10.1016/j.pss.2022.105527
Hurlbert, K. M., Witte, L. C., Best, F. R., and Kurwitz, C. (2004). Scaling two-phase flows to Mars and Moon gravity conditions. Int. J. Multiph. Flow. 30, 351–368. doi:10.1016/j.ijmultiphaseflow.2004.01.004
Iwata, R., Zhang, L., Wilke, K. L., Gong, S., He, M., Gallant, B. M., et al. (2021). Bubble growth and departure modes on wettable/non-wettable porous foams in alkaline water splitting. Joule 5, 887–900. doi:10.1016/j.joule.2021.02.015
Janz, G. J., Tomkins, R. P. T., Allen, C. B., Downey, J. R., Garner, G. L., Krebs, U., et al. (1975). Molten salts: volume 4, part 2, chlorides and mixtures—electrical conductance, density, viscosity, and surface tension data. J. Phys. Chem. Ref. Data 4, 871–1178. doi:10.1063/1.555527
Kamotani, Y., Chang, A., and Ostrach, S. (1996). Effects of heating mode on steady axisymmetric thermocapillary flows in microgravity. J. Heat. Transf. 118, 191–197. doi:10.1115/1.2824034
Kamotani, Y., Ostrach, S., and Pline, A. (1994a). Analysis of velocity data taken in surface tension driven convection experiment in microgravity. Phys. Fluids 6, 3601–3609. doi:10.1063/1.868432
Kamotani, Y., Ostrach, S., and Pline, A. (1994b). “Some results from the surface tension driven convection experiment aboard USML-1 spacelab,” in 32nd aerospace sciences meeting and exhibit, aerospace sciences meetings (American Institute of Aeronautics and Astronautics). Reston, VI, USA, doi:10.2514/6.1994-238
Kamotani, Y., Ostrach, S., and Pline, A. (1995). A thermocapillary convection experiment in microgravity. J. Heat. Transf. 117, 611–618. doi:10.1115/1.2822621
Kim, J., Benton, J. F., and Wisniewski, D. (2002). Pool boiling heat transfer on small heaters: effect of gravity and subcooling. Int. J. Heat. Mass Transf. 45, 3919–3932. doi:10.1016/S0017-9310(02)00108-4
Kim, J., and Raj, R. (2014). Gravity and heater size effects on pool boiling heat transfer. Cleveland, OH: National Aeronautics and Space Administration Glenn Research Center.
Kulkarni, A. A., and Joshi, J. B. (2005). Bubble Formation and bubble rise velocity in Gas−Liquid systems: a review. Ind. Eng. Chem. Res. 44, 5873–5931. doi:10.1021/ie049131p
Li, C., Zhang, J., Han, J., and Yao, B. (2021). A numerical solution to the effects of surface roughness on water–coal contact angle. Sci. Rep. 11, 459. doi:10.1038/s41598-020-80729-9
Lomax, B. A., Just, G. H., McHugh, P. J., Broadley, P. K., Hutchings, G. C., Burke, P. A., et al. (2022). Predicting the efficiency of oxygen-evolving electrolysis on the Moon and Mars. Nat. Commun. 13, 583. doi:10.1038/s41467-022-28147-5
Mandin, Ph., Cense, J. M., Georges, B., Favre, V., Pauporté, Th., Fukunaka, Y., et al. (2007). “Prediction of the electrodeposition process behavior with the gravity or acceleration value at continuous and discrete scale,” in Electrochimica Acta, ELECTROCHEMICAL PROCESSING OF TAILORED MATERIALS Selection of papers from the 4th International Symposium (EPTM 2005), Kyoto, Japan, 233–244. doi:10.1016/j.electacta.2007.01.044Electrochim. Acta3-5 October 200553
Mandin, P., Matsushima, H., Fukunaka, Y., Wüthrich, R., Calderon, E. H., and Lincot, D. (2008). One to two-phase electrolysis processes behavior under spatial conditions. Sayama, Japan: The Japan Society of Microgravity Application.
Pamperin, O., and Rath, H.-J. (1995). Influence of buoyancy on bubble formation at submerged orifices. Chem. Eng. Sci. 50, 3009–3024. doi:10.1016/0009-2509(95)00140-Z
Prakash, S., and Ethier, C. R. (2000). Requirements for mesh resolution in 3D computational hemodynamics. J. Biomech. Eng. 123, 134–144. doi:10.1115/1.1351807
Qiu, D., Dhir, V. K., Hasan, Md.M., Chao, D., Neumann, E., Yee, G., et al. (2000). Dynamics of bubble growth on a heated surface under low gravity conditions. AIP Conf. Proc. 504. doi:10.2514/6.2000-852
Sibille, L., Sadoway, D., Sirk, A., Tripathy, P., Melendez, O., Standish, E., et al. (2009). “Recent advances in scale-up development of molten regolith electrolysis for oxygen production in support of a lunar base,” in 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Aerospace Sciences Meetings, Orlando, Florida (American Institute of Aeronautics and Astronautics). doi:10.2514/6.2009-659
Tsuge, H., Terasaka, K., Koshida, W., and Matsue, H. (1997). Bubble formation at submerged nozzles for small gas flow rate under low gravity. Chem. Eng. Sci. 52, 3415–3420. doi:10.1016/S0009-2509(97)00159-0
Welch, S. W. J. (1998). Direct simulation of vapor bubble growth. Int. J. Heat. Mass Transf. 41, 1655–1666. doi:10.1016/S0017-9310(97)00285-8
Wenzel, R. N. (1936). RESISTANCE OF SOLID SURFACES TO WETTING BY WATER. Ind. Eng. Chem. 28, 988–994. doi:10.1021/ie50320a024
Wolansky, G., and Marmur, A. (1999). Apparent contact angles on rough surfaces: the Wenzel equation revisited. Colloids Surf. Physicochem. Eng. Asp. 156, 381–388. doi:10.1016/S0927-7757(99)00098-9
Nomenclature
Keywords: ISRU, reduced gravity, electrolysis, molten regolith electrolysis, CFD, molten salt electrolysis, lunar regolith, oxygen production
Citation: Burke PA, Nord ME, Hibbitts CA and Berdis JR (2024) Modeling electrolysis in reduced gravity: producing oxygen from in-situ resources at the moon and beyond. Front. Space Technol. 5:1304579. doi: 10.3389/frspt.2024.1304579
Received: 29 September 2023; Accepted: 12 February 2024;
Published: 02 April 2024.
Edited by:
Philipp Reiss, Technical University of Munich, GermanyReviewed by:
Philippe Mandin, Université Bretagne Sud, FranceShrihari Sankarasubramanian, University of Texas at San Antonio, United States
Authored by Paul A. Burke, Michael E. Nord, Charles A. Hibbitts and Jodi R. Berdis. © 2024 The Johns Hopkins University Applied Physics Laboratory LLC. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Paul A. Burke, cGF1bC5idXJrZUBqaHVhcGwuZWR1
 Paul A. Burke
Paul A. Burke Michael E. Nord2
Michael E. Nord2