- Environmental Sciences Division, Oak Ridge National Laboratory, Oak Ridge, TN, United States
Efforts to include more detailed representations of biogeochemical processes in basin-scale water quality simulation tools face the challenge of how to tractably represent mass exchange between the flowing channels of streams and rivers and biogeochemical hotspots in the hyporheic zones. Multiscale models that use relatively coarse representations of the channel network with subgrid models for mass exchange and reactions in the hyporheic zone have started to emerge to address that challenge. Two such multiscale models are considered here, one based on a stochastic Lagrangian travel time representation of advective pumping and one on multirate diffusive exchange. The two models are formally equivalent to well-established integrodifferential representations for transport of non-reacting tracers in steady stream flow, which have been very successful in reproducing stream tracer tests. Despite that equivalence, the two models are based on very different model structures and produce significantly different results in reactive transport. In a simple denitrification example, denitrification is two to three times greater for the advection-based model because the multirate diffusive model has direct connections between the stream channel and transient storage zones and an assumption of mixing in the transient storage zones that prevent oxygen levels from dropping to the point where denitrification can progress uninhibited. By contrast, the advection-based model produces distinct redox zonation, allowing for denitrification to proceed uninhibited on part of the hyporheic flowpaths. These results demonstrate that conservative tracer tests alone are inadequate for constraining representation of mass transfer in models for reactive transport in streams and rivers.
Introduction
Efforts to understand and model the fate and transport of solutes through streams and rivers have focused much attention on regions of stagnant or relatively slow-moving water known as transient storage zones. Transient storage zones include in-stream eddies and pools, biofilms, vegetation beds and especially the regions of saturated sediment below and surrounding the flowing channel known as hyporheic zones. Hyporheic zones in particular are widely recognized as biogeochemical hotspots where transformation and retention rates of solutes are elevated relative to the flowing channel (Boano et al., 2014; Ward, 2016). Hyporheic exchange flow (HEF), the movement of water from the channel into the hyporheic zone and back, allows solutes to access those reactive zones. As a result, hyporheic exchange flow is important in the biogeochemical processing of nutrients (Duff and Triska, 2000; Böhlke et al., 2004; Mulholland et al., 2008), organic carbon (Grimm and Fisher, 1984; Battin et al., 2008), metals (Bourg and Bertin, 1993; Fuller and Harvey, 2000; Palumbo-Roe et al., 2012), and organic contaminants (Kim et al., 1995; Conant et al., 2004; Schaper et al., 2018).
Despite the disproportionate role played by hyporheic exchange flow in regulating downstream water chemistry, the representation of the effects of HEF in watershed- and basin-scale models of biogeochemical processing and water quality remains a challenge. Helton et al. (2011) evaluated common modeling approaches for modeling biogeochemistry in stream networks using scaling of in situ denitrification from headwater streams to river networks as a concrete example. They identify the need to include hydrologic exchanges between the stream channel and subsurface waters coupled to more mechanistic representations of coupled biogeochemical cycles and conclude that limitations in our current modeling approaches “restrict our ability to simulate biogeochemical dynamics among diverse river networks.”
Models for transport of non-reacting tracers in stream corridors have progressed from the classical transient storage model (TSM) (Bencala and Walters, 1983) which conceptualizes a single well-mixed transient storage zone coupled to the stream channel by first-order mass exchange, to integrodifferential models that accommodate a diversity of hyporheic flowpaths with a distribution of travel times (Haggerty et al., 2002; Wörman et al., 2002; Gooseff et al., 2003; Marion et al., 2008; Liao and Cirpka, 2011; Lemke et al., 2013; Liao et al., 2013). The integrodifferential models have been highly successful at representing results of in-stream tracer tests. In particular, they are able to reproduce late-time tailing of breakthrough curves, which is commonly observed in stream tracer tests, important biogeochemically, and not represented by the TSM. However, the integrodifferential approach uses a convolution of the in-stream solute concentration with the hyporheic travel-time distribution to represent exchange of solutes between the stream and multiple hyporheic zone flowpaths, an approach that does not generalize to nonlinear multicomponent chemistry.
Recognizing the advantages of a travel-time-based model for representing the diversity of hyporheic flowpaths and the limitations of the integrodifferential models for reactive transport, Painter (2018) introduced an alternative formulation that uses the standard one-dimensional advection-dispersion-reaction equation for the channel and couples that equation at each channel location to a one-dimensional advection-reaction subgrid model. Written in Lagrangian form, each subgrid model represent an ensemble of streamlines that are diverted into the hyporheic zone before returning to the channel. That approach, which is referred to here as ADELS (Advection Dispersion Equation with Lagrangian Subgrid), is formally equivalent to the integrodifferential model for non-reacting tracers and steady channel discharge. However, the ADELS approach generalizes to nonlinear reactive chemistry, and thus provides a tractable method for multicomponent reactive transport in fluvial corridors from reach to river basin scales.
Motivated by similar considerations, Fang et al. (2020) coupled a generalization of the TSM to the geochemical reaction model PFLOTRAN (Hammond et al., 2014). Like ADELS, the TSM model and generalizations are readily coupled to full multicomponent reaction models. The TSM has been linked, for example, to the equilibrium geochemistry code MINTEQ (Allison et al., 1991) to form the OTIS/OTEQ model (Runkel et al., 1996). As noted already, the single-zone TSM is not able to represent the long-time behavior of breakthrough curves with slowly decaying tails, which is particularly problematic for understanding nutrient processing in streams, as the longer travel time pathways are responsible for denitrification (e.g., Zarnetske et al., 2012). Fang et al. (2020) addressed that limitation by adopting a multirate generalization of the TSM. Multirate mass transfer models were developed for the study of transport in porous media (Haggerty and Gorelick, 1995; Carrera et al., 1998; Haggerty et al., 2000; Wang et al., 2005; Gouze et al., 2008; Benson and Meerschaert, 2009) including multicomponent reactive transport (Donado et al., 2009). Multirate mass transfer models have been used previously to model non-reacting transport in fluvial corridors (Silva et al., 2009; Anderson and Phanikumar, 2011; Haggerty, 2013). Those Multirate Transient Storage Models (mTSM) use multiple transient storage zones, each with its own coefficient for mass transfer with the stream channel. Importantly, mTSM and integrodifferential models are equivalent for non-reactive tracers in steady flow with a known relationship between the distribution of rate constants and the hyporheic travel time distribution (Haggerty et al., 2000; Wang et al., 2005; Silva et al., 2009).
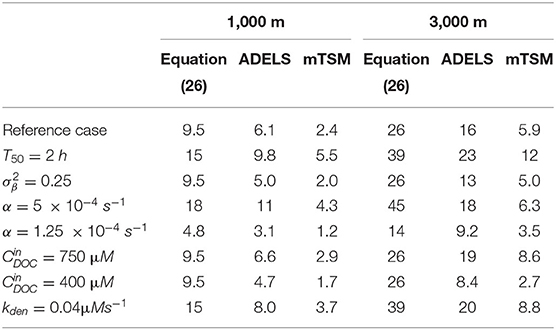
Since both are equivalent to the integrodifferential model for non-reacting tracers in steady flow, the ADELS and mTSM are thus equivalent in that situation. Unlike the integrodifferential form, both generalize to fully nonlinear chemical reaction models and provide tractable strategies for basin-scale simulation without sacrificing fidelity to contemporary process understanding. However, the two models use fundamentally different conceptualizations of the hyporheic zone and hyporheic exchange flow, as shown schematically in Figure 1. In mTSM, the hyporheic zone is represented as multiple well-mixed stagnant zones, each connected by diffusive (first-order reversible) exchange with the channel but not to each other. In contrast, the ADELS model conceptualizes an ensemble of one-dimensional hyporheic pathways that each takes its upstream boundary condition from the channel and provides a mass flux back to the channel at its outlet as in the advective pumping model. Once discretized for computation, computational cells representing the hyporheic zone in mTSM are connected in parallel to the channel while in ADELS they are connected in series. Because of that difference in model structure, it is not clear that the two approaches would produce the same results for reactive transport even though they are equivalent for non-reactive transport.
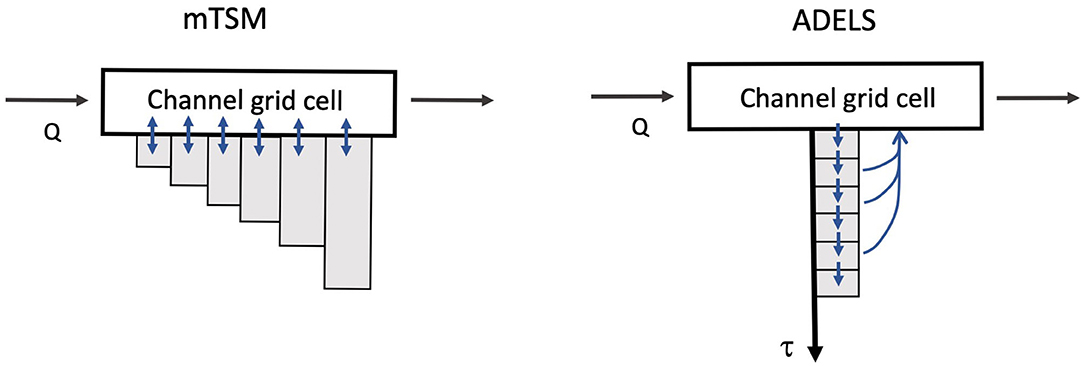
Figure 1. Schematic showing mesh topology for two approaches for representing the effects of hyporheic exchange in models of reactive transport in stream and river corridors. The multirate Transient Storage Model (mTSM) considers multiple transient storage zones of different sizes that are each coupled to the channel by first-order reversible mass exchange. The ADELS model represent an ensemble of streamlines that are diverted into the hyporheic zone before returning to the stream channel using a one-dimensional advection-reaction equation written in Lagrangian form with hyporheic age τ replacing the spatial coordinate. The two conceptualizations are equivalent for non-reacting tracer transport, but not for reactive transport.
Here we explore the field-scale reactive transport implications of different conceptualizations of the hyporheic zone that are equivalent for non-reactive transport. Specifically, we compare the ADELS and mTSM conceptualizations using denitrification as a concrete example. Results are also compared to a simple estimate (Painter, 2018) that accounts for hyporheic exchange but treats denitrification as a first-order kinetic process. The objectives are to identify conditions where the two models produce similar results and where they differ and to explore implications for the development of reactive transport models applicable to stream and river corridors. The focus here is on steady channel flow conditions. However, mTSM and to a limited extend ADELS are generalizable to unsteady flow conditions in contrast to convolution-based models.
The effect of hyporheic-zone model structure on transport of reactive solutes has been explored previously. Kerr et al. (2013) adopted 2-zone variants (Briggs et al., 2009) of the TSM and explored differences between nested (series) and competing (parallel) configurations focusing on transport with first-order degradation. Kelleher et al. (2019) compared reactive tracer transport assuming 1-zone and 2-zone TSMs. Yakirevich et al. (2017) compared reactive tracer transport assuming 2-zone and 3-zone TSMs. Here we go beyond the 2- and 3-zone TSM and focus on methods (ADELS and mTSM) that provide flexible representations of hyporheic residence times resulting from diverse flowpaths and include nonlinear reactive chemistry.
Methods
Transport of Non-reacting Solutes
ADELS
A recently introduced multiscale approach (Painter, 2018) uses a one-dimensional advection-dispersion-reaction equation for the channel and couples that equation at each channel location to a one-dimensional advection-reaction subgrid model representing an ensemble of streamlines that are diverted into the hyporheic zone before returning to the channel. The ADELS model adopts a Lagrangian travel time framework for the hyporheic subgrid models. Here we refer to hyporheic age τ as the time elapsed by a tracer since it starts moving on a hyporheic streamline and hyporheic lifetime or travel time T as the total time spent on a given hyporheic streamline. Thus, each streamline has a single value of T and τ replaces the spatial coordinate on that streamline with 0 ≤ τ ≤ T. Noting that the streamlines all have the same upstream boundary condition, which is governed by the concentration in the stream channel, the concentration vs. age are the same along the streamlines. Computationally, we thus need consider reactive transport along only one representative streamline. Solute flux from the hyporheic zone to the stream channel can then be computed from results at intermediate locations along that representative streamline, properly weighted by the probability density for hyporheic travel time ϕ(T). The concentration in the channel Cch is then a function of position x along the channel and time t, Cch = Cch(t, x), whereas the concentration Chz in the hyporheic zone is a function of x, t and the hyporheic age, Chz = Chz(t, x, τ).
The model for non-reacting tracers on a single reach is expressed mathematically as
plus initial conditions and suitable boundary conditions on the stream channel (x = 0 and x = L). Here the transport operator is used to simplify the notation. Note that the accumulation term was previously (Painter, 2018) included in . The accumulation term is written separately from the transport operator here to facilitate a more compact representation of reactive transport. Equation 3 and the last term in Equation (1) provide the coupling between the channel and hyporheic zone, with the latter acting as a solute source to the channel and the channel concentration providing the upstream boundary condition on the canonical streamline for the hyporheic zone. The constant α [1/s] is the rate constant for hyporheic exchange. Physically it is the volumetric flowrate for recirculating water in the hyporheic zone per unit channel volume.
An important numerical detail is how to calculate the integral in Equation (1). The integral can be efficiently approximated by considering Chz(t, x, T) as piecewise constant over N subintervals with the subintervals selected to be equally spaced in probability. That is, the i-th subinterval is the quantile interval from Ti−1 to Ti with . In that interval Chz(t, x, T) is approximated as Chz(t, x, Ti−1/2). Here Φ(T) is the cumulative lifetime distribution and Φ−1 its inverse. Noting that our choice of Ti means we have.
Numerical tests with conservative tracers on single reaches showed (Painter, 2018) this representation to be highly efficient in that it converges quickly as N increases, thus reducing the size of the number of unknowns in the the subgrid representation.
mTSM
The multirate generalization of the TSM represents a transient storage zone not as one zone but as a collection of sub-zones that are each exchanging mass with the flowing channel with different rate constants. This multirate TSM model is conceptually equivalent to multirate sorption models used to represent subsurface transport. They can represent an arbitrary residence time distribution by proper choice of the distribution of rate constants and are formally equivalent to convolution (Haggerty et al., 2000; Pruess and Wang, 2001; Wang et al., 2005) and thus to our multiscale model for non-reacting tracers and in steady flow. Although equivalent for non-reacting transport, the two conceptualizations differ in how the mass exchange is represented, which has consequences for reactive transport. In the multirate TSM conceptualization, all computational cells in the hyporheic zone exchange mass with the channel. That is, all reaction cells in the hyporheic zone are coupled in parallel to the channel. By contrast, the ADELS conceptualization couples a one-dimensional advection reaction system to each channel grid cell, thus connecting hyporheic grid cells in series, consistent with advective pumping. Here we explore how that difference in mass exchange representations results in different results reactive transport using a model denitrification system.
We adopt a parsimonious version of the multirate TSM. For a single non-reacting species, a continuous version of the multirate model can be written
where γ is the ratio of hyporheic zone volume to channel volume and f(β) is the probability density for the hyporheic exchange coefficients β. Here the explicit dependence of Cch and Chz on time t and position x are suppressed for clarity.
Following the same type of approximation used for Equation (4), a discrete version of the mTSM can be obtained by approximating Chz(β) as piecewise constant over N subintervals with the subintervals selected to be equally spaced in probability. That is, the i-th subinterval is the quantile interval from βi−1 to βi where . The interval on the right in Equation (6) then becomes
A discrete mTSM is then given by
Equivalence Between the ADELS and mTSM Models
Assuming, for the purposes of this comparison, that solute concentration in the hyporheic zone is initially zero, the continuous version of the multirate model has an equivalent convolution form (e.g., Wang et al., 2005), which can be written
where the hyporheic lifetime density ϕ(t) is the derivative of the so-called memory function (Carrera et al., 1998; Haggerty et al., 2000) normalized by the mean exchange rate constant 〈β〉. The hyporheic lifetime density is explicitly related to f(β) (e.g., Wang et al., 2005)
Equation 10 is equivalent to the ADELS model when the hyporheic exchange rate is α = γ 〈β〉 and hyporheic lifetime density is given by Equation (13).
The discrete forms of the ADELS and mTSM models can be related by selecting the quantiles Ti of the hyporheic lifetime distribution in ADELS based on the distribution of rate constants in mTSM. The hyporheic lifetime quantile Ti in the ADELS model [see Equation (5)].
Integrating both sides of Equation (13) with respect to t from 0 to Ti−1/2 gives
Given a probability density for the exchange rate constants in the mTSM f(β), Equation (15) can be solved for each i = 1, N to determine the hyporheic lifetime quantiles Ti−1/2 for use in the ADELS model.
Multicomponent Reactive Transport
Both ADELS and mTSM generalize to general multicomponent reactive transport. To keep things simple, we assume the reaction system is completely kinetically controlled. Although not addressed here, large reaction systems involving a combination of kinetically controlled and equilibrium reactions are easily accommodated by placing the system in canonical form (Lichtner, 1985, 1996) where algebraic mass action equations replace the differential equations for a subset of the species.
ADELS
Although mathematically equivalent to a convolution in the case of steady flow and no reactions, the Lagrangian subgrid formulation generalizes to include nonlinear reactions (Painter, 2018) while the convolution does not. Neglecting non-reactive zones for clarity (although easily included) and adopting the quadrature Equations (4), (5) the reactive transport system can be written
Here bold quantities represent column vectors, Cch(t, x) and Chz(t, x, τ) contain the species concentrations in the channel and hyporheic zones, respectively, Sch is the direct solute source to the channel, B is a column vector with elements equal to 1 for mobile species and 0 for immobile species, and the operator ° denotes element-wise multiplication. The element-wise multiplications by B ensure that immobile species are not transported and not transferred between the hyporheic zone and channel. The vector-valued vector functions Pch(Cch) and Phz(Chz) describe the transformation (production/consumption) rates caused by reactions as functions of local concentrations. Note that each species depends on all the other species through the reaction terms.
mTSM
The mTSM model generalizes to multicomponent reactive transport in a similar way:
Here the element-wise multiplication with B again prevents immobile species from being transported and transferred between the storage zones and the channel.
Model Reaction System
A simple denitrification example is used here to compare how different representations of hyporheic exchange impact reactive transport simulations. The denitrification example tracks a single representative dissolved organic carbon (DOC) species with chemical composition CH2O, dissolved oxygen, and nitrate with aerobic respiration and denitrification reactions
in the subgrid system, but not in the channels. Dissolved oxygen is held constant in the channel to represent re-aeration. Nitrate and DOC are introduced at the upstream boundary of the channel reach and tracked throughout. Carbon released from buried particulate organic carbon is neglected here. This example uses an implicit representation of microbially mediated denitrification. That is, the dynamics of microbial biomass is not explicitly simulated. Instead, the net effects of those reactions are described by dual-Monod kinetics with oxygen inhibiting denitrification. Explicit representations of microbial dynamics are available (e.g., Sanz-Prat et al., 2015) and have been used in the ADELS framework by Painter (2018). Implicit variants with more complete description of the reaction system are also available (e.g., Fang et al., 2020). For the purposes of our comparison, we adopt a simple but still nonlinear version. Production rates are represented as
Here M represents Monod kinetics or an inhibition function, depending on the order of concentration and model parameter in the argument list. That is, if C is a concentration and K is a constant, then M(C, K) represents Monod kinetics with Monod half-saturation K. Switching the order of the arguments, M(K, C), defines an inhibition function with the constant K taking the role of inhibition constant. Symbol definitions and reaction parameter values for the reference case are defined in Table 1. The rate constants kaer and kden were selected to make the half-lives for oxygen consumption and denitrification to be 1 and 5 h, respectively (Gomez-Velez et al., 2015). The Monod parameters are from Gu et al. (2007).
Numerical Experiments
Several numerical experiments with different physical hydrology parameters and different assumptions about the geochemical inputs exemplify sensitivity of reactive transport to how hyporheic exchange is represented. In these examples, the two-point flux finite-volume method was used for spatial discretization of the discrete-rate form of the mTSM and ADELS. The resulting system of nonlinear ordinary differential equations where then solved using the NDSolve routine in Mathematica™. In all examples, the channel was discretized into 50 computational cells. No significant differences were found in mesh convergence tests with 25 cells (not shown).
Channel parameters for the reference case are Q = 1 m3/s, A = 1.1 m2, D = 2 m2/s, and channel width of 2.78 m. The channel area A and width w were chosen to be consistent with well-known hydraulic geometry rating curves (Leopold and Maddock, 1953) and the assumed discharge Q. Empirical relationships shown graphically in Figure 1 of Gomez-Velez and Harvey (2014) were then used to select values for the hyporheic exchange coefficient α and median hyporheic lifetime that are consistent with the discharge and channel width. The reference case values α = 2.5 ×10−4s−1 and median lifetime of 1 h correspond to a median grain size of ~1.5 mm and geomorphic features dominated by dune-shaped bedforms. Note that Figure 1 of Gomez-Velez and Harvey, 2014, uses hyporheic flux qhz instead of our hyporheic exchange coefficient; the two are related as α = qhz/d where d is water depth in the channel.
To complete the physical hydrology model, a distribution of the exchange rate constant β is needed for the mTSM model and a corresponding set of hyporheic lifetime quantiles Ti is needed for the ADELS model. A distribution shape was first assumed for the mTSM model. Then Equation (15) was used to calculate the corresponding hyporheic lifetime quantiles Tis for use in the ADELS model. A log normal distribution with log-variance of 1.0 was used for the reference case. The arithmetic mean was selected as 0.38 hr−1 to make the median hyporheic lifetime 1 h. Finally, the hyporheic volume fraction γ for use in the mTSM model was then selected as γ = α/〈β〉 to make the two models equivalent (see Section “Equivalence Between the ADELS and mTSM Models”).
A variant case with Q = 10 m3/s and A = 1.1 m2 is also considered. For this case, the hyporheic exchange coefficient is α = 1.0 ×10−3s−1 and the median hyporheic lifetime is 0.5 h, correspond to a median grain size of ~3 mm and geomorphic features dominated by submerged alternate bars (Gomez-Velez and Harvey, 2014).
Figure 2 shows the resulting cumulative distribution of hyporheic lifetimes, as calculated from Equation (15) for the reference case with log-variance and a variant case with log-variance . The geometric mean exchange rate was selected to keep the median hyporheic lifetime T50 to same at 1 h. The variant case with lacks the slowly decaying tail of the reference case.
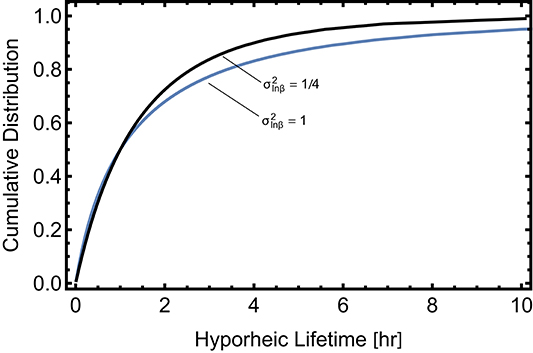
Figure 2. Cumulative distribution of hyporheic lifetime for two choices of the distribution of β, the hyporheic exchange rate coefficient, as calculated from Equation (15). The blue curve is for the reference case, a log-normal distribution of β with with log-variance of 1. The black curve uses a narrower distribution with log-variance 0.25. In both cases, the median travel time was constrained to be 1 h.
Several variant cases illustrate sensitivities, including different mean and log-variance for the exchange rate coefficient distribution, different median travel times, different DOC concentration, and different Monod parameters. In each case, denitrification result for the ADELS and mTSM models are compared to a first-order kinetic estimate (Painter, 2018) that neglects carbon limitations and assumes the entire hyporheic zone is active in denitrification
where is one-half the ratio of hyporheic exchange flux to channel discharge, Da = λT50 is the Damköhler number for the hyporheic flowpath, T50 is the median hyporheic lifetime, and is the first-order decay constant for nitrate removal.
Results
Conservative Tracer Transport
Figure 3 shows concentration in the stream channel as calculated by the mTSM and ADELS models assuming a hypothetical tracer test in a single reach of length 3,000 m. In these examples, a conservative tracer is injected into a steady stream discharge for a period of 12 h. Solid curves are the concentration in the channel at 3,000 m assuming the ADELS model and the dashed curve are from the equivalent mTSM model. The three cases shown are for different values of the exchange coefficient α. The tailing in all three cases is caused by solutes returning to the channel from the hyporheic zone after the solute injection is finished, the result of exchange with the hyporheic zone. Larger α results in more pronounced tailing. As expected, results from the two models overlay each other and are indistinguishable on this scale. The cases in Figure 3 and all cases shown here used N = 50. When smaller N = 25 is used, corresponding to fewer transient storage zones in the mTSM model and coarser discretization of the hyporheic lifetime, relatively small differences between the two models are apparent in the extreme tail of the breakthrough curve (result not shown). Although the mTSM and ADELS models are equivalent in their continuous versions, their discrete versions are not guaranteed to be equivalent unless N is large.
Figure 3. Channel concentration at 3 km relative to the inlet concentration for a conservative tracer test for three values of α, the hyporheic exchange rate constant. The solid curves are for the ADELS model and the dashed curves are for the mTSM.
Reference Case Reactive Transport
Although the mTSM and ADELS model can be made equivalent for conservative tracers by appropriate choice of the mass exchange coefficients in the mTSM model, the two models have different connectivity to the stream channel, which has the potential to affect biogeochemical processes. Here we use denitrification as an example to explore the biogeochemical consequences of that difference in coupling between transient storage zones and the flowing channel.
The fraction of the initial nitrate removed is shown vs. distance in Figure 4 for the mTSM (dashed) and ADELS models (solid). Figure 4A is for the reference case and Figure 4B is or the case Q = 10 m3/s. In these examples, the hyporheic zone and channel were initially free of solutes. At t = 0, the upstream boundary conditions shown in Table 1 were imposed and the system was then allowed to come to steady state. The mTSM model predicts nitrate removal that is approximately one-third that of the ADELS model at 3 km despite the fact that conservative transport is identical. Moreover, the difference is increasing downstream and would be larger when modeling larger sections of streams and rivers.
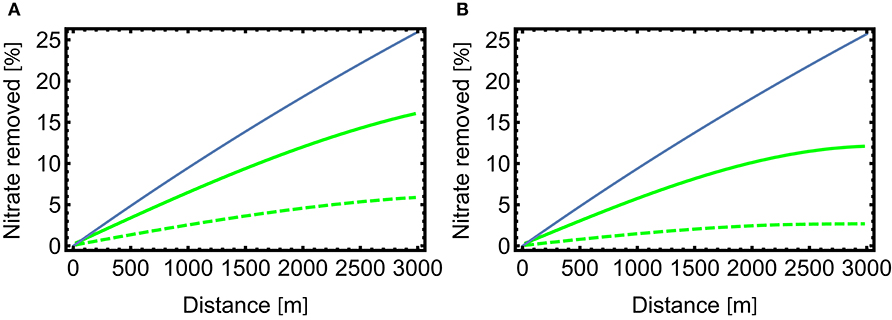
Figure 4. Percentage of incoming nitrate removed vs. travel distance for the ADELS model (solid curve) and the mTSM model (dashed curve) for reference case assumptions (A) and a variant case with channel discharge of 10 m3/s (B). The blue line is a first-order estimate that neglects reactant depletion and oxygen inhibition.
The reason for the lower denitrification rates in the mTSM model can be seen by examining DOC, oxygen and nitrate concentrations in the hyporheic zone, as shown in Figure 5. Concentrations are shown vs. hyporheic age for the ADELS model. The mTSM does not have a direct equivalent to hyporheic age. For comparison purposes the half-life for storage zone i, that is ln2/βi, is used for the characteristic time. The channel location in this case is 1.5 km from the inlet. The LS model shows the classic pattern of redox zonation with oxygen dropping to negligible levels after about 1 h of hyporheic age. Oxygen is resupplied to the transient storage subzones in the mTSM through direct diffusive exchange with the channel. As a result, oxygen is never completely consumed in the mTSM and oxygen concentrations remain above value of the inhibition constant , which partially suppresses denitrification. As a result, denitrification rates are lower in the mTSM model, as shown in Figure 4.
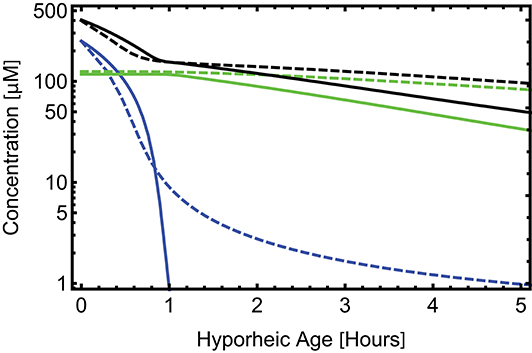
Figure 5. Hyporheic zone concentration for the ADELS model (solid curves) and the mTSM (dashed curves). The blue curve represents oxygen concentration, the green curve nitrate, and the black curve DOC. The x-axis is hyporheic age in the ADELS model and a characteristic time related to the exchange coefficient in the mTSM. Note that oxygen concentrations in the mTSM model do not drop below the inhibition constant for denitrification, thus partially inhibiting denitrification in the mTSM model.
In Figure 4, the first-order model predicts larger denitrification rates than ADELS for both the Q = 1 and Q = 10 cases. Those differences are partly due to the fact that the short-lifetime part of the hyporheic lifetime distribution experiences only aerobic conditions and thus does not contribute to denitrification, a process that is accounted for in ADELS but not in the first-order model. The other contributing factor is carbon limitation, which is modest on the upstream side of the reach but becomes more important moving downstream as DOC is consumed, causing the nitrate removal to depend nonlinearly on distance downstream in Figure 4 for ADELS.
Sensitivity to Model Parameters and Environmental Conditions
Shown in Table 2 are percent of nitrate removed at 1 and 3 km for different assumed values for α, the β distribution, and selected chemical parameters. In all cases examined, ADELS predicts significantly greater removal of nitrate, further emphasizing the sensitivity of reactive transport to model structure. Relative differences between the two models is not particularly sensitive to the physical or biogeochemical assumptions, with mTSM predicting nitrate removal that is 32–55% that of ADELS. The linear first-order model predicts significantly greater denitrification compared to ADELS, highlighting the role of the non-idealities noted above (i.e., carbon limitations and inhibition of denitrification by oxygen) that are not accounted for in the first-order estimate.
Nitrate removal in the ADELS model is sensitive to the nitrate/DOC ratio if that ratio is below a threshold value. Increasing the incoming DOC concentration by 50% compared to the reference case results in a modest increase in denitrification (Table 2). However, decreasing the incoming DOC concentration by 20% results in a significant decrease in denitrification. That asymmetric sensitivity indicates the reference case condition is at the threshold for carbon limitation.
Figure 6 shows nitrate removal as a function of distance along the reach for the ADELS and mTSM models when the incoming DOC concentration is increased by 50% over the reference case. In this case, the nitrate removal in the ADELS model is close to linear with distance and tracks closer to the first-order estimate. As in the reference case, the ADELS model is predicting significantly greater removal of nitrate.
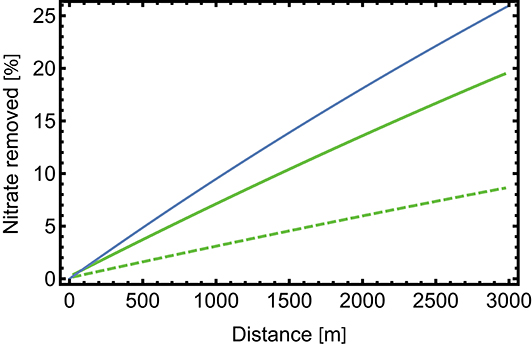
Figure 6. Percentage of incoming nitrate removed vs. travel distance for the ADELS model (solid curve) and the mTSM model (dashed curve) for a variant case with higher incoming DOC.
Figure 7 shows calculated concentrations vs. distance for the same high DOC case. With sufficient DOC, the ADELS model shows redox zonation with oxygen dropping to negligible levels after about 1 h of hyporheic age and nitrate dropping to negligible levels after approximately 10 h. By contrast the mTSM model does not produce complete redox zonation.
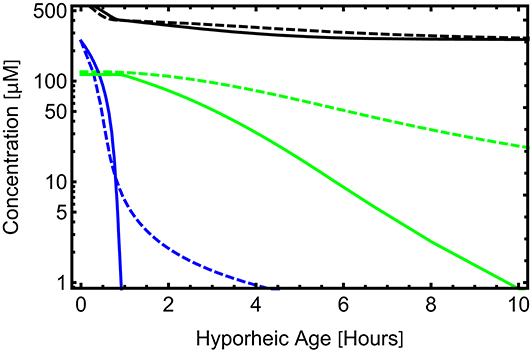
Figure 7. Hyporheic zone concentration for the ADELS model (solid curves) and the mTSM (dashed curves). The blue curve represents oxygen concentration, the green curve nitrate, and the black curve DOC. The x-axis is hyporheic age in the ADELS model and a characteristic time related to the exchange coefficient in the mTSM.
Discussion and Conclusions
In the situation of conservative tracers and steady stream discharge, the two models compared here, mTSM and ADELS, are equivalent to well-known integrodifferential representations of tracer transport, which have been very successful in reproducing results of conservative tracer tests. Unlike the integrodifferential formulations, mTSM and ADELS generalize to multicomponent reactive transport. It was shown here that although the two model structures produce equivalent results for conservative tracers, they predict very different results for reactive transport.
Significantly, distinct redox zonation did not fully develop in any of the mTSM cases considered here despite the fact that a significant fraction of the hyporheic lifetimes were long enough to consume oxygen. That significant oxygen remains is a result of the mTSM model structure, which assumes that each transient storage zone is well mixed and imposes direct connections between the channel and each transient storage subzone, effectively mixing waters of different hyporheic ages and preventing oxygen from being fully consumed. By contrast, the ADELS model produces the expected redox zonation in the hyporheic zone submodel with complete consumption of oxygen and, when sufficient DOC is available, complete consumption of nitrate. As a result of its inability to represent distinct redox zonation with full consumption of oxygen, the mTSM model does not fully activate denitrification and results in significantly smaller reach-scale denitrification as compared to ADELS.
The ADELS and the mTSM model both produced smaller nitrate removal as compared to the linear first-order model. Deviations from the linear first-order model have two causes in these examples. First, the linear first-order model does not account for the portion of the hyporheic lifetime distribution that lies in the aerobic range and thus does not contribute to denitrification. Second, carbon limitations become important in these examples as we move downstream, which are accounted for in both multiscale models, but not in the first-order estimate. Of course, that carbon limitation may not be relevant in systems where DOC is produced by dissolution of buried particulate organic carbon, which is important in some systems (e.g., Gu et al., 2007; Zarnetske et al., 2011). Overall, both ADELS and mTSM are able to represent a richer range of physical phenomena, as compared to a simple first-order denitrification model.
The inability of the mTSM model to represent redox zonation has implications for the ability of that model to represent the processing of other redox-sensitive contaminants. An important example is the methylation of inorganic mercury to the neurotoxin methylmercury, which requires fully anaerobic conditions. Given environmental conditions favorable for methylation—sufficiently long hyporheic lifetimes and sufficient DOC—the ADELS model will generate fully anaerobic local conditions in the long-lifetime portion of the hyporheic subgrid model.
Efforts to include more detailed representations of biogeochemical processes in basin-scale water quality simulation tools naturally lead to multiscale models that use relatively coarse representations of the channel network with subgrid models for mass exchange with, and reactions in, transient storage zones. A wide variety of model structures could be imagined for such multiscale models, depending on the mesh topology and whether the mass exchange is diffusive or advective. The two model structures explored here may be regarded as end members of such multiscale models. The mTSM is consistent with diffusively controlled exchanges between the channel and multiple well-mixed and mutually independent transient storage subzones. The ADELS model is based on advective exchange between the channel and hyporheic zone and an ensemble of one-dimensional flowpaths through the hyporheic zone.
Given that the two conceptualizations predict different results for reactive transport, an obvious question is how to constrain the model structure. At a conceptual level, ADELS is consistent with advective pumping through channel bedforms, pool-rifle complexes, alternating point bars, and meander bends, well-established processes for many streams. The diffusion-controlled exchange implicit in the mTSM model is consistent with low-permeability sediments and is thus also relevant for many streams and rivers. The well-mixed approximation for each subzone in mTSM is arguably difficult to reconcile with physical intuition especially for transient storage zones that have long residence times, where we would expect significant gradients to exist in the subzones. Indeed, the neglect of those gradients is the reason the mTSM fails to represent fully developed redox zonation. An extension of multirate models that represents one-dimensional diffusion into transient storage subzones instead of well-mixed subzones would resolve that inconsistency. Another potential model structure would be to combine diffusion- and advection-based conceptualizations.
Questions about model structure in multiscale models for reactive transport in stream corridors must be decided from available data. It might be expected that model structure for mass transfer could be resolved from conservative tracer tests alone leaving only reaction processes and parameters to be inferred by other means. However, these results show the opposite: conservative tracer tests alone are insufficient for distinguishing between different conceptualizations of mass transfer for use in reactive transport models and must be augmented by other types of data. Clearly, reactive or “smart” tracers have an important role to play, as do insights gained from sampling along hyporheic flowpaths and detailed three-dimensional simulations of individual hydrogeomorphological structures. In addition, synoptic sampling of stream chemistry across multiple stream orders combined with uncertainty-aware inverse modeling will likely be necessary to reduce model structural uncertainty to acceptable levels in emerging multiscale models for reactive transport in stream corridors.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author/s.
Author Contributions
SP conceived the study, performed all the work, and wrote the paper.
Funding
This work was funded by the U.S. Department of Energy, Office of Science, Biological and Environmental Research, Subsurface Biogeochemical Research (SBR) Program, and is a product of the SBR Science Focus Area (SFA) at ORNL and the IDEAS-Watersheds project.
Licenses and Permissions
This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paidup, irrevocable, world-wide license to publish, or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author is grateful to Saubhagya Rathore for careful review of the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2020.595538/full#supplementary-material
Mathematica™ (Wolfram Research, 2014) scripts used to generate the figures may be found in the supporting information.
References
Allison, J. D., Brown, D. S., and Novo-Gradac, K. J. (1991). MINTEQA2/PRODEFA2, a Geochemical Assessment Model for Environmental Systems: Version 3.0 User's Manual. Athens, GA: Environmental Research Laboratory, Office of Research and Development.
Anderson, E. J., and Phanikumar, M. S. (2011). Surface storage dynamics in large rivers: comparing three-dimensional particle transport, one-dimensional fractional derivative, and multirate transient storage models. Water Resour. Res. 47. doi: 10.1029/2010WR010228
Battin, T. J., Kaplan, L. A., Findlay, S., Hopkinson, C. S., Marti, E., Packman, A. I., et al. (2008). Biophysical controls on organic carbon fluxes in fluvial networks. Nat. Geosci. 1, 95–100. doi: 10.1038/ngeo101
Bencala, K. E., and Walters, R. A. (1983). Simulation of solute transport in a mountain pool-and-riffle stream: a transient storage model. Water Resour. Res. 19, 718–724. doi: 10.1029/WR019i003p00718
Benson, D. A., and Meerschaert, M. M. (2009). A simple and efficient random walk solution of multi-rate mobile/immobile mass transport equations. Adv. Water Resour. 32, 532–539. doi: 10.1016/j.advwatres.2009.01.002
Boano, F., Harvey, J. W., Marion, A., Packman, A. I., Revelli, R., Ridolf, I, L., et al. (2014). Hyporheic flow and transport processes: mechanisms, models, and biogeochemical implications. Rev. Geophy. 52, 603–679. doi: 10.1002/2012RG000417
Böhlke, J. K., Harvey, J. W., and Voytek, M. A. (2004). Reach-scale isotope tracer experiment to quantify denitrification and related processes in a nitrate-rich stream, midcontinent United States. Limnol. Oceanogr. 49, 821–838. doi: 10.4319/lo.2004.49.3.0821
Bourg, A. C., and Bertin, C. (1993). Biogeochemical processes during the infiltration of river water into an alluvial aquifer. Environ. Sci. Technol. 27, 661–666. doi: 10.1021/es00041a009
Briggs, M. A., Gooseff, M. N., Arp, C. D., and Baker, M. A. (2009). A method for estimating surface transient storage parameters for streams with concurrent hyporheic storage. Water Resour. Res. 45. doi: 10.1029/2008WR006959
Carrera, J., Sánchez-Vila, X., Benet, I., Medina, A., Galarza, G., and Guimerà, J. (1998). On matrix diffusion: formulations, solution methods and qualitative effects. Hydrogeol. J. 6, 178–190. doi: 10.1007/s100400050143
Conant, B. Jr, Cherry, J. A., and Gillham, R. W. (2004). A PCE groundwater plume discharging to a river: influence of the streambed and near-river zone on contaminant distributions. J. Contamin. Hydrol. 73, 249–279. doi: 10.1016/j.jconhyd.2004.04.001
Donado, L. D., Sanchez-Vila, X., Dentz, M., Carrera, J., and Bolster, D. (2009). Multicomponent reactive transport in multicontinuum media. Water Resour. Res. 45. doi: 10.1029/2008WR006823
Duff, J. H., and Triska, F. J. (2000) “8 - Nitrogen biogeochemistry and surface–subsurface exchange in streams,” in Streams and Ground Waters, eds Jones, J. B. and Mulholland, P. J. (San Diego, CA: Academic Press). 197–220. doi: 10.1016/B978-012389845-6/50009-0
Fang, Y., Chen, X., Gomez Velez, J., Zhang, X., Duan, Z., Hammond, G. E., et al. (2020). A multirate mass transfer model to represent the interaction of multicomponent biogeochemical processes between surface water and hyporheic zones (SWAT-MRMT-R 1.0). Geosci. Model Dev. 13, 3553–3569. doi: 10.5194/gmd-2019-301
Fuller, C. C., and Harvey, J. W. (2000). Reactive uptake of trace metals in the hyporheic zone of a mining-contaminated stream, Pinal Creek, Arizona. Environ. Sci. Technol. 34, 1150–1155. doi: 10.1021/es990714d
Gomez-Velez, J. D., and Harvey, J. W. (2014). A hydrogeomorphic river network model predicts where and why hyporheic exchange is important in large basins. Geophys. Res. Lett. 41, 6403–6412. doi: 10.1002/2014GL061099
Gomez-Velez, J. D., Harvey, J. W., Cardenas, M. B., and Kiel, B. (2015). Denitrification in the Mississippi River network controlled by flow through river bedforms. Nat. Geosci. 8:941. doi: 10.1038/ngeo2567
Gooseff, M. N., Wondzell, S. M., Haggerty, R., and Anderson, J. (2003). Comparing transient storage modeling and residence time distribution (RTD) analysis in geomorphically varied reaches in the Lookout Creek basin, Oregon, USA. Adv.Water Resour. 26, 925–937. doi: 10.1016/S0309-1708(03)00105-2
Gouze, P., Melean, Y., Le Borgne, T., Dentz, M., and Carrera, J. (2008). Non-Fickian dispersion in porous media explained by heterogeneous microscale matrix diffusion. Water Resour. Res. 44. doi: 10.1029/2007WR006690
Grimm, N. B., and Fisher, S. G. (1984). Exchange between interstitial and surface water: implications for stream metabolism and nutrient cycling. Hydrobiologia 111, 219–228. doi: 10.1007/BF00007202
Gu, C., Hornberger, G. M., Mills, A. L., Herman, J. S., and Flewelling, S. A. (2007). Nitrate reduction in streambed sediments: effects of flow and biogeochemical kinetics. Water Resour. Res. 43. doi: 10.1029/2007WR006027
Haggerty, R. (2013). Analytical solution and simplified analysis of coupled parent-daughter steady-state transport with multirate mass transfer. Water Resour. Res. 49, 635–639. doi: 10.1029/2012WR012821
Haggerty, R., and Gorelick, S. M. (1995). Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Water Resour. Res. 31, 2383–2400. doi: 10.1029/95WR10583
Haggerty, R., Mckenna, S. A., and Meigs, L. C. (2000). On the late-time behavior of tracer test breakthrough curves. Water Resour. Res. 36, 3467–3479. doi: 10.1029/2000WR900214
Haggerty, R., Wondzell, S. M., and Johnson, M. A. (2002). Power-law residence time distribution in the hyporheic zone of a 2nd-order mountain stream. Geophys. Res. Lett. 29, 18-1-18-4. doi: 10.1029/2002GL014743
Hammond, G. E., Lichtner, P. C., and Mills, R. T. (2014). Evaluating the performance of parallel subsurface simulators: an illustrative example with PFLOTRAN. Water Resour. Res. 50, 208–228. doi: 10.1002/2012WR013483
Helton, A. M., Poole, G. C., Meyer, J. L., Wollheim, W. M., Peterson, B. J., Mulholland, P. J., et al. (2011). Thinking outside the channel: modeling nitrogen cycling in networked river ecosystems. Front. Ecol. Environ. 9, 229–238. doi: 10.1890/080211
Kelleher, C., Ward, A., Knapp, J. L., Blaen, P. J., Kurz, M. J., Drummond, J. D., et al. (2019). Exploring tracer information and model framework trade-offs to improve estimation of stream transient storage processes. Water Resour. Res. 55, 3481–3501. doi: 10.1029/2018WR023585
Kerr, P., Gooseff, M., and Bolster, D. (2013). The significance of model structure in one-dimensional stream solute transport models with multiple transient storage zones–competing vs. nested arrangements. J. Hydrol. 497, 133–144. doi: 10.1016/j.jhydrol.2013.05.013
Kim, H., Hemond, H. F., Krumholz, L. R., and Cohen, B. A. (1995). In-situ biodegradation of toluene in a contaminated stream. Part 1. Field studies. Environ. Sci. Technol. 29, 108–116. doi: 10.1021/es00001a014
Lemke, D., Liao, Z., Wöhling, T., Osenbrück, K., and Cirpka, O. A. (2013). Concurrent conservative and reactive tracer tests in a stream undergoing hyporheic exchange. Water Resour. Res. 49, 3024–3037. doi: 10.1002/wrcr.20277
Leopold, L. B., and Maddock, T. (1953). The Hydraulic Geometry of Stream Channels and Some Physiographic Implications. Professional Paper. Washington, D.C: U.S. Government Printing Office. doi: 10.3133/pp252
Liao, Z., and Cirpka, O. A. (2011). Shape-free inference of hyporheic traveltime distributions from synthetic conservative and “smart” tracer tests in streams. Water Resour. Res. 47, doi: 10.1029/2010WR009927
Liao, Z., Lemke, D., osenbrück, K., and Cirpka, O. A. (2013). Modeling and inverting reactive stream tracers undergoing two-site sorption and decay in the hyporheic zone. Water Resour. Res., 49, 3406–3422. doi: 10.1002/wrcr.20276
Lichtner, P. C. (1985). Continuum model for simultaneous chemical reactions and mass transport in hydrothermal systems. Geochim. Cosmochim. Acta 49, 779–800. doi: 10.1016/0016-7037(85)90172-3
Marion, A., ZAramella, M., and Bottacin-Busolin, A. (2008). Solute transport in rivers with multiple storage zones: The STIR model. Water Resour. Res. 44, doi: 10.1029/2008WR007037
Mulholland, P. J., Helton, A. M., Poole, G. C., Hall, R. O., Hamilton, S. K., Peterson, B. J., et al. (2008). Stream denitrification across biomes and its response to anthropogenic nitrate loading. Nature 452:202. doi: 10.1038/nature06686
Painter, S. L. (2018). Multiscale framework for modeling multicomponent reactive transport in stream corridors. Water Resour. Res. 54, 7216–7230. doi: 10.1029/2018WR022831
Palumbo-Roe, B., Wragg, J., and Banks, V. J. (2012). Lead mobilisation in the hyporheic zone and river bank sediments of a contaminated stream: contribution to diffuse pollution. J. Soils Sediment. 12, 1633–1640. doi: 10.1007/s11368-012-0552-7
Pruess, K., and Wang, J. S. Y. (2001). Numerical Modeling of Isothermal and Nonisothermal Flow in Unsaturated Fractured Rock: A Review. Flow and Transport Through Unsaturated Fractured Rock. Washington, DC: American Geophysical Union.
Runkel, R. L., Bencala, K. E., Broshears, R. E., and Chapra, S. C. (1996). Reactive solute transport in streams: 1. Development of an equilibrium-based model. Water Resour. Res. 32, 409–418. doi: 10.1029/95WR03106
Sanz-Prat, A., Lu, C., Finkel, M., and Cirpka, O. A. (2015). On the validity of travel-time based nonlinear bioreactive transport models in steady-state flow. J. Contamin. Hydrol. 175–176, 26–43. doi: 10.1016/j.jconhyd.2015.02.003
Schaper, J. L., Posselt, M., MCcallum, J. L., Banks, E. W., Hoehne, A., Meinikmann, K., et al. (2018). Hyporheic exchange controls fate of trace organic compounds in an urban stream. Environ. Sci. Technol. 52, 12285–12294. doi: 10.1021/acs.est.8b03117
Silva, O., Carrera, J., Dentz, M., Kumar, S., Alcolea, A., and Willmann, M. (2009). A general real-time formulation for multi-rate mass transfer problems. Hydrol. Earth Syst. Sci. 13, 1399–1411. doi: 10.5194/hess-13-1399-2009
Wang, P. P., Zheng, C., and Gorelick, S. M. (2005). A general approach to advective–dispersive transport with multirate mass transfer. Adv. Water Resour. 28, 33–42. doi: 10.1016/j.advwatres.2004.10.003
Ward, A. S. (2016). The evolution and state of interdisciplinary hyporheic research. WIREs Water 3, 83–103. doi: 10.1002/wat2.1120
Wolfram Research, I. (2014). Mathematica Version 10, 10th Edn. Champaign, IL: Wolfram Research, Inc.
Wörman, A., Packman, A. I., Johansson, H., and Jonsson, K. (2002). Effect of flow-induced exchange in hyporheic zones on longitudinal transport of solutes in streams and rivers. Water Resour. Res. 38, 2-1-2-15. doi: 10.1029/2001WR000769
Yakirevich, A., Shelton, D., Hill, R., Kiefer, L., Stocker, M., Blaustein, R., et al. (2017). Transport of conservative and “smart” tracers in a first-order creek: role of transient storage type. Water 9:485. doi: 10.3390/w9070485
Zarnetske, J. P., Haggerty, R., wondzell, S. M., and Baker, M. A. (2011). Labile dissolved organic carbon supply limits hyporheic denitrification. J. Geophys. Res. Biogeosci. 116. doi: 10.1029/2011JG001730
Keywords: hyporheic zone, reactive transport, multiscale modeling, stochastic hydrological modeling, contaminant transport
Citation: Painter SL (2021) On the Representation of Hyporheic Exchange in Models for Reactive Transport in Stream and River Corridors. Front. Water 2:595538. doi: 10.3389/frwa.2020.595538
Received: 17 August 2020; Accepted: 02 December 2020;
Published: 03 February 2021.
Edited by:
Tim Scheibe, Pacific Northwest National Laboratory (DOE), United StatesReviewed by:
Reza Soltanian, University of Cincinnati, United StatesClare Robinson, Western University, Canada
Copyright © 2021 Painter. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Scott L. Painter, cGFpbnRlcnNsQG9ybmwuZ292
 Scott L. Painter
Scott L. Painter