Computational Microfluidics for Geosciences

Computational microfluidics for geosciences is the third leg of the scientific strategy that includes microfluidic experiments and high-resolution imaging for deciphering coupled processes in geological porous media. This modeling approach solves the fundamental equations of continuum mechanics in the exact geometry of porous materials. Computational microfluidics intends to complement and augment laboratory experiments. Although the field is still in its infancy, the recent progress in modeling multiphase flow and reactive transport at the pore-scale has shed new light on the coupled mechanisms occurring in geological porous media already. In this paper, we review the state-of-the-art computational microfluidics for geosciences, the open challenges, and the future trends.

1. Introduction

Since their appearance in the early eighties, microfluidic experiments have revolutionized the knowledge in porous media research. They brought new insights into the debates that drive the community for decades including the controversial use of Darcy's law for modeling multiphase flow and the understanding of the complex feedback between hydro-bio-chemical systems. The most famous example is the work of Lenormand et al. (1988) who identified different flow instabilities in unsaturated porous systems according to the fluid pair and the flow rates using micromodels. These microfluidic devices enable direct visualization of the flow, transport, and chemical processes in rock microstructure replica sandwiched between two parallel plates separated by a small distance (Jahanbakhsh et al., 2020; Morais et al., 2020). Classically, a representation of the pore space is etched on a substrate made of silicon, glass or polymeric materials and covered by a transparent material. Recently, 3D printing has been used for fast and robust micromodel fabrication (Watson et al., 2019), allowing to conduct many flow experiments at lower cost for 2D to complex 3D geometry, although for now resolution is not as accurate as etched 2D micromodels. Coupled with high-resolution imaging both in space and time, microfluidic experiments have shed new light on the key mechanisms controlling subsurface flow. For example, particle image velocimetry has highlighted internal fluid eddies within droplets trapped by capillary forces whose large scale impact is not included in multiphase Darcy's law (Kazemifar et al., 2016; Roman et al., 2016, 2020; Zarikos et al., 2018). Microfluidics also led to substantial advancements in the understanding of reactive systems as the most recent microchips involve reactive materials to investigate dissolution and precipitation of solid minerals in fractured porous media (Zhang et al., 2013; Song et al., 2014; Porter et al., 2015; Osselin et al., 2016; Soulaine et al., 2017, 2018; Yoon et al., 2019; Agrawal et al., 2020; Poonoosamy et al., 2020; Yun et al., 2020). In just a few decades, microfluidics has become an indispensable tool in geosciences to decipher the complex mechanisms that occur in porous systems and the discipline keeps improving.

Computational microfluidics is the digital counterpart of microfluidic experiments. Like any modeling approach, it is a natural companion of laboratory experiments as it can be used to perform sensitivity analysis for identifying the key parameters of the underlying processes or to explore ranges of conditions including pressure and temperature that are difficult to reach in the laboratory without dedicated equipment. Moreover, computational microfluidics can also assist in the design of micromodels. Unlike pore-network modeling—a widely used approach for describing pore-scale physics (Fatt, 1956)—that relies on an approximation of the pore geometries and on pore-averaged physical laws, computational microfluidics solves the fundamental equations of continuum mechanics in the exact microstructure geometry. Historically, this kind of simulations was considered computationally expensive and almost impossible to run on complex and large domains. The enormous progress in high-resolution numerical simulation of complex flow and high-performance computing techniques, however, makes it possible to perform routinely computational microfluidics for single-phase flows on domains that reach the size of a Representative Elementary Volume (Roman et al., 2016). Although it heavily relies on advanced and modern approaches for simulating fluid dynamics, computational microfluidics for geosciences has its own challenges related to the complexity of natural systems including the heterogeneity of geological porous media, the evolving porous microstructure along with geochemical processes, and the complex description of interfacial phenomena at the mineral surfaces (Meakin and Tartakovsky, 2009).

The recent improvements in computational microfluidics for geosciences enable the modeling of multiphase flow and reactive transport. Current capabilities capture many of the mechanisms observed experimentally. For example, two-phase flow simulations in micromodels describe the complex interplay between viscous, capillary, and gravity forces leading to viscous fingerings if a fluid drains another fluid (Ferrari and Lunati, 2013; Alpak et al., 2016; Chen et al., 2019; Zhao et al., 2019), or to the trapping of carbon dioxide droplets in the pore space (Chen et al., 2015; Hu et al., 2017). Computational microfluidics allows the understanding of subsurface processes by identifying key mechanisms. Hence, the integrated usage of computational and experimental microfluidics led (Roman et al., 2017) to highlight that snap-off events, i.e., the break-up of the invading fluid at the entrance of a pore-throat, can be followed by a reconnection to the flowing phase. They observed and characterized cycles of snap-off and reconnection events that contradict the criteria that are generally used to assess the storage capacity by capillary trapping. Another example is the study of Ferrari and Lunati (2014) which establishes that inertial forces arise during pore invasion—a statement also supported by glass bead experiments (Moebius and Or, 2012) and interface tracking in micromodels (Roman et al., 2016)—suggesting that creeping flow assumption for the derivation of multiphase Darcy's law is erroneous. Moreover, as computational microfluidics provides a mapping of pressure, velocity, species concentration, and mineral distribution, the characterization of constitutive laws using volume averaging is straightforward. For instance, Soulaine et al. (2017) used computational microfluidics to compute the accessible reactive surface area of a rock sample. A more comprehensive review of the state-of-the-art including the authors' contributions, as well as the remaining challenges that need to be solved for being truly predictive, are presented in section 3.

Our definition of computational microfluidics goes beyond the modeling of flow and geochemical processes in micromodels as it can also be applied to complex 3D structures. In this sense, computational microfluidics for geosciences is intimately linked to Digital Rock Physics, an emerging technology concerned with the estimation of effective upscaled parameters (e.g., permeability, dispersion tensor) in three-dimensional images of rock samples (Blunt et al., 2013). In Digital Rock Physics, these properties can be calculated using different techniques, such as pore network analysis (Andre et al., 2013a,b) or closure problem approaches (Whitaker, 1999; Soulaine et al., 2013). Alternatively, computational microfluidics can be used to directly solve the flow and transport equations within the pore-space and compute the desired upscaled properties. Although it is often restricted to small micro-CT images (<300³ voxels) or to single-phase flow due to high computing cost, computational microfluidics is also well-suited to investigate pore-to-pore physics (Ferrari and Lunati, 2014; Pavuluri et al., 2020) with the objective of improving upscaling techniques (e.g., pore entry pressure for pore network modeling). A major asset of microfluidics is the ability to design well-controlled experiments and obtain high-resolution measurements—both in space and time—of the velocity fields (Roman et al., 2016), phase distribution, film thickness (Roman et al., 2017), aqueous species concentrations (Chang et al., 2017), and mapping in mineral changes (Poonoosamy et al., 2020). Microfluidics is inestimable to verify the numerical models using direct comparison with microfluidic experiments (Willingham et al., 2008; Yoon et al., 2012; Chapman et al., 2013; Oostrom et al., 2016; Roman et al., 2017; Soulaine et al., 2018). Therefore, the combination of computational and experimental microfluidics promotes the development of robust and validated numerical models for pore-scale modeling.

Exposing simulation results to experimental data, however, is not always an easy task as it raises questions regarding the measurement resolution and also questions on the modeling spatial description. Micromodels are often referred to as “two-dimensional” objects by opposition to real geological objects or their reproduction using 3D printing. This qualification is somewhat imprecise as the micromodels are made of the assembly of two parallel plates and that important physical phenomena occur in the confined space between the plates. This confusion leads many scientists to use two-dimensional models for representing their microfluidic experiments numerically. In most cases, however, 2D simulations are not able to reproduce the experiments. Even in cases for which the micromodel depth is much larger than the smallest pore-throat diameter the two-dimensional hypothesis breaks down because physical events are not uniform in the thickness. For example, reactive particles can nucleate in the mid-plane or at the solid walls (Beuvier et al., 2015) and instabilities in the liquid films that wet the top and bottom plates can lead to the formation of bubbles in the bulk (Hansen and Toong, 1971; Zhao et al., 2018). The systematic usage of 3D models, however, is computationally intensive. To reduce the computational efforts, 2D depth-integrated models are an interesting alternative for solving flow in microfluidic chips. These approaches, however, can have strong limitations. In section 2, we present depth-integrated models for single-phase, two-phase, and species transport, and we discuss their range of validity.

This paper aims at reviewing the modeling approaches in computational microfluidics for geosciences and their open challenges, as well as the authors' contributions to this emerging scientific discipline. It is organized as follows. First, we introduce the fundamental equations used in computational microfluidics (section 2.1) and the common numerical approaches to solve them (section 2.2). We also present models that solve directly for the depth-averaged variables at a reduced simulation cost (section 2.3). Then, we summarize the main advances in modeling multiphase flow (section 3.1) and reactive transport (section 3.2), and we discuss future lines of research.

2. Mathematical Models and Numerical Solutions

In this section, we introduce the fundamental equations used in computational microfluidics for solving flow and transport. We also discuss the standard numerical approaches for solving these equations.

2.1. Fundamental Governing Equations

Computational microfluidics relies on the fundamental equations of continuum mechanics for fluid flow, namely the Navier-Stokes equations, solved in the exact geometry of the pore space. They are composed of a set of mass and momentum balance equations combined with boundary conditions at the solid surface.

2.1.1. Flow Equations

For single-phase flow, the conservation of mass reads,

$\begin{array}{ll}\frac{\partial \rho }{\partial t}+\nabla .\left(\rho v\right)=0,& (1)\end{array}$

where ρ and v are the fluid density and velocity, respectively. For liquids, it is common to assume that the fluid is incompressible, and the mass balance equation (Equation 1) reduces to the divergence-free velocity,

$\begin{array}{ll}\nabla .v=0.& (2)\end{array}$

In an Eulerian frame, the momentum balance writes,

$\begin{array}{ll}\frac{\partial \rho v}{\partial t}+\nabla .\left(\rho vv\right)=-\nabla p+\rho g+\nabla .\mu \left(\nabla v+{\nabla }^{t}v\right),& (3)\end{array}$

where p is the pressure field, g is the gravity, and μ is the fluid viscosity. The left-hand side corresponds to the inertial effects. As mass flow rates in the soils and the subsurface are usually low, it is common to neglect this term and to use Stokes instead of the Navier-Stokes momentum equation. On the right-hand side, the first term is the pressure gradient, the second is the gravity acceleration and the third term is the viscous dissipation. The latter characterizes the internal friction of the fluid particles with each other. The higher the viscosity, the larger the pressure gradient has to be to initiate the fluid movement. At the pore-scale, it is also common to neglect the gravity term.

For multiphase flow, the mass and momentum equations, Equations (1)–(3) apply to each fluid phase. Alternative forms of the Navier-Stokes equations including non-Newtonian and compressible fluids as well as descriptions of the equations in a Lagrangian frame are found in any fluid mechanics textbook (e.g., Landau and Lifshitz, 1987; Caltagirone, 2013).

2.1.2. Boundary Conditions at the Solid Walls

The flow equations are supplemented with boundary conditions at the solid surface that arise from particle/solid molecular interactions. Because the fluid molecules cannot penetrate into the impermeable boundary, the mass flux at the solid surface is null and the normal component of the velocity is zero, i.e., n.v = 0. For viscous flow, it is common to consider that the fluid molecules adhere to the surface due to molecular interactions including van der Waals or Coulombic forces. Because of this adherence, the fluid particles at the solid wall cannot slide on the surface and the tangential component of the velocity is null, leading to the no-slip condition,

$\begin{array}{ll}v=0.& (4)\end{array}$

The no-slip boundary condition is valid for most of the Newtonian liquids flowing through porous media with pore-throats larger than 100 nm. Although widely used in fluid dynamics, the no-slip condition is not always valid in geological systems. In particular, in complex fluids involving colloids or polymers, the fluid elements adjacent to the surface can travel along the surface by rolling or sliding. In such cases, the fluid in contact with the solid surface slide over it with a finite value. Moreover, the no-slip condition poses a problem in viscous flow theory at the place where an interface between two fluids meets a solid boundary. Instead, the so-called partial slip condition,

$\begin{array}{ll}v=\beta \left(I-nn\right).\left(n.\left(\nabla v+{\nabla }^{t}v\right)\right),& (5)\end{array}$

proposed by Navier (1823) and later revisited by Maxwell (1879), relates the tangential velocity to the strain rate. In this relation, n is the normal vector at the solid surface and β is called the slip length and is typically of the order of ten nanometers.

The description of boundary conditions at the solid walls for multiphase flow is discussed in section 3.1.

2.1.3. Interfacial Conditions Between Two Fluids

The interface between two fluid phases (labeled fluid 1 and fluid 2, respectively) is a discontinuity on which boundary conditions are applied. The interface deforms with the fluid motion and moves at the interface velocity, w. The latter is obtained using the conservation of mass at the vicinity of the interface,

$\begin{array}{ll}{n}_{12}.{\rho }_1\left(v_1-w\right)=n_{12}.{\rho }_2\left(v_2-w\right),& (6)\end{array}$

where n₁₂ is the normal at the interface separating the two fluids, and ρ_i and v_i are the density and velocity of phase i, respectively. If there is no phase change, the interface velocity and the fluid velocity balance each other at the interface and n₁₂.v₁ = n₁₂.v₂.

The normal stress balance at the interface gives (Landau and Lifshitz, 1987),

$\begin{array}{l}{n}_{12}.\left[-p_{1}I+\left({\mu }_1\nabla v_1+{\nabla }^t{v}_1\right)\right]\\ =n_{12}.\left[-p_{2}I+\left({\mu }_2\nabla v_2+{\nabla }^t{v}_2\right)\right]+\sigma \kappa ,& (7)\end{array}$

where p_i is the fluid pressure in fluid i, σ is the surface tension, and κ is the interface curvature. At equilibrium, this condition becomes Laplace law.

An overview of the simulation techniques used in computational microfluidics to solve Navier-Stokes equations along with the interfacial conditions is given in section 3.1.

2.1.4. Solute Transport

In its simplest form, the transport of a species i in a fluid phase is modeled by an advection-diffusion equation:

$\begin{array}{ll}\frac{\partial C_i}{\partial t}+\nabla .\left(v{C}_i\right)=\nabla .\left(D_i\nabla C_i\right),& (8)\end{array}$

where the first term is the accumulation term, the second term is the advection term and the right-hand side corresponds to diffusion effects where D_i is the diffusion coefficient of species i into the fluid phase. More complex forms of the solute transport includes multi-component diffusion, thermal diffusion and electrostatic gradients (Bird et al., 2002).

As for flow equations, the solute balance equation is supplemented by boundary conditions at the solid walls. For a passive tracer the no flux condition writes,

$\begin{array}{ll}n.D_i\nabla C_i=0.& (9)\end{array}$

If the species reacts with the solid surface the reactive flux condition is,

$\begin{array}{ll}n.D_i\nabla C_i=r_m\left(C_i\right),& (10)\end{array}$

where r_m is a source or sink term that describes kinetic reactions or adsorption phenomena (Molins et al., 2014).

It is also common to consider that the species satisfies thermodynamics equilibrium condition with the solid wall using,

$\begin{array}{ll}{C}_i=C_i^{eq},& (11)\end{array}$

where $C_i^{eq}$ is a fixed value imposed by thermodynamics equilibrium.

2.2. Numerical Engines for Solving Navier-Stokes Equations

Solving Navier-Stokes equations in complex geometries is not trivial, and except in very few situations, there are no analytical solutions. Computational microfluidics uses numerical approximations to solve the flow within the pore space. Complexities include the pressure-velocity coupling and the non-linearity due to the inertial term in the momentum equation. In this section, we introduce some of the standard approaches for solving Navier-Stokes equations. Specific techniques for multiphase flow and reactive transport are introduced and discussed in section 3.

2.2.1. Computational Fluid Dynamics

In Computational Fluid Dynamics (CFD), the Navier-Stokes equations are solved by discretizing the spatial differential operators on an Eulerian grid using techniques such as the finite difference method (FDM), the finite volume method (FVM), or the finite element method (FEM) (Ferziger and Peric, 2002). In principle, the three families of techniques yield the same solution if the computational grid is fine enough. For fluid flow, however, FVM is usually preferred as it is locally conservative and deals with unstructured grids by construction. In FVM, the domain is subdivided into a finite number of contiguous control volumes whereby the integral form of the conservation laws is applied. Modern gridders generate meshes that follow the complex boundaries of the microstructure (see Figure 1). Nowadays, all the commercial or open-source CFD simulators embed very efficient Navier-Stokes solvers that can deal with very large grids and complex geometries using multigrid strategies and High-Performance Computing. Solution algorithms usually rely on predictor-corrector methods to solve for the pressure-velocity coupling. The Pressure-Implicit with Splitting of Operators (PISO) algorithm is one of the most popular for solving transient flow (Issa, 1985). Algorithms such as Semi-Implicit Method for Pressure Linked Equations (SIMPLE) solve directly for steady-state flow (Patankar, 1980).

FIGURE 1

Figure 1. Example of finite-volume grid used in computational microfluidics.

2.2.2. Lattice Boltzmann Method

The lattice Boltzmann method (LBM) is an alternative CFD technique to solve fluid flow at the pore-scale. The popularity of LBM comes from the ease to program massively parallel codes. Unlike traditional CFD approaches that solve for Navier-Stokes equations, LBM is based on the Boltzmann equation that describes the probability of finding a given particle at a given position with a given velocity. This is a statistical approach and the averaged behavior approximates the continuum mechanics described by the Navier-Stokes equations. In LBM, a discrete Boltzmann equation is solved on a lattice where the particles can only move along a finite number of directions. The degree of freedom is determined by the nature of the lattice classified with the nomenclature DnQm where n corresponds to the dimension of the lattice (n = 2 for two-dimensional simulations, n = 3 for three-dimensional simulations) and m stands for the number of directions. The Boltzmann equation involves a collision operator that describes the change in the probability distribution function induced by the collisions between particles. In the Lattice Boltzmann method, the boundary conditions are described in terms of probability distribution functions. The description of the wall conditions corresponds actually to the physical model of boundary events proposed by Maxwell (1879). For a no-slip, the bounce-back condition is used where the particles are reflected at the wall. Hence, the net average flow rate at the solid surface is zero. Slip conditions can be obtained using specular reflections (Succi, 2002). Partial slip is modeled with a mix of bounceback and specular reflections. The implementation of boundary conditions in LBM can become very complex when the solid surface is not aligned with the lattice.

2.2.3. Smoothed-Particle Hydrodynamics

Smoothed-Particle Hydrodynamics (SPH) is a mesh-free modeling technique that describes fluids as a set of discrete moving particles in a Lagrangian framework. The method was initially developed to model the interaction of stars in astrophysics (Gingold and Monaghan, 1977; Lucy, 1977) and is now being used increasingly in real-time animation and video games. The particles have a spatial distance over which their properties are smoothed by a kernel function centered on the particles. This distance defines the sphere of influence for each particle and is used to reconstruct continuous variables such as fluid density. The SPH particles are then used as interpolation points to discretize and solve the governing equations. SPH has several benefits over traditional grid-based methods. First, it is meshless and there is no need to go through complex gridding processes. Second, it explicitly conserves mass and momentum. Because the method is Lagrangian, there is no non-linear term in the momentum equation and that allows an accurate description of the advection terms when dealing with high flow rates. Third, the SPH Lagrangian framework allows for the modeling of moving and deformable boundaries without using complex tracking algorithms. SPH has also important drawbacks. Although the SPH algorithms due to their simplicity and structure are easy to program, the implementation of boundary conditions can be tricky. Moreover, for the same accuracy, SPH is more computationally intensive than FVM or FEM because it requires much more neighboring particles than the tensile of grid-based methods. Nevertheless, because SPH can be easily paralleled, the rise of parallel computing including Graphical Processing Units makes SPH a promising technique (Vacondio et al., 2020).

2.3. Depth-Averaged Models: 2D vs. 3D

Most of the time, measurements in microfluidic experiments relate to depth-averaged values. For example, even though micro-Particle Image Velocimetry that uses confocal microscopy or laser pretends to measure the velocity profiles in a cross-section, these techniques do measure values averaged in a thickness of the order of few micrometers that corresponds to the laser thickness or the close surrounding of the focal plan (Roman et al., 2016). Likewise, microfluidic experiments using optical luminescence for measuring a concentration profile (Watson et al., 2019) or mapping the water distribution (Zhao et al., 2016; Roman et al., 2017) provides values that are averaged along the micromodel depth, h, without information of the depth profile of the species concentration or water saturation. The depth-averaged variables are defined as the vertical integration of the 3D fields,

$\begin{array}{ll}{\overline{v}}^{2D}=\frac{1}{h}{\displaystyle {\int }_0^h}v\left(x,y,z\right)dz.& (12)\end{array}$

In this section, we present depth-averaged models that directly provide the solution for the depth-averaged velocity, ${\overline{v}}^{2D}$, pressure, ${\overline{p}}^{2D}$, and concentration, ${\overline{C_i}}^{2D}$, fields without solving 3D problems. These models result from the integration of the fundamental equations described in section 2.1 along the depth axis and can significantly reduce the simulation costs. They have, however, ranges of validity that are discussed below.

2.3.1. Single-Phase Flow

The integration of Navier-Stokes momentum equation over the micromodel depth along with the assumption that a parabolic profile approximates the flow in the thickness gives,

$\begin{array}{l}\frac{\partial \rho {\overline{v}}^{2D}}{\partial t}+\nabla .\left(\rho {\overline{v}}^{2D}{\overline{v}}^{2D}\right)=-\nabla {\overline{p}}^{2D}+\nabla .\mu \left(\nabla {\overline{v}}^{2D}+{\nabla }^t{\overline{v}}^{2D}\right)\\ -\mu \frac{12}{h^2}{\overline{v}}^{2D},& (13)\end{array}$

where the last term of the right-hand side, $\mu \frac{12}{h^2}{\overline{v}}^{2D}$, is the Hele-Shaw correction (Lamb, 1906), i.e., a drag force related to the friction of the fluid along the micromodel top and bottom plates. Numerical implementation of Equation (13) has been reported using CFD (Roman et al., 2016) and LBM (Venturoli and Boek, 2006; Laleian et al., 2015). The Hele-Shaw correction is similar to a Darcy law for which the permeability is $k=\frac{h^2}{12}$ and the porosity is ϕ = 1. This simple depth-integration was historically the first step toward the derivation of Darcy's law from Stokes equation (Vasil'ev, 2009). Actually, for micromodels with a low aspect ratio between the cell thickness and the pore-throat size, h/d ≪ 1, the drag force is the dominant force and Equation 13 can be replaced by Darcy's law for Hele-Shaw cells,

$\begin{array}{ll}{\overline{v}}^{2D}=-\frac{h^2}{12\mu }\nabla {\overline{p}}^{2D}.& (14)\end{array}$

Theoretically, the hypothesis that flow sandwiched in between two parallel plates obey a parabolic profile is only valid for infinite plates—their dimensions are much larger than the space between them. Micromodels mimicking rock porous structures, however, contain pillars that violate this assumption with three-dimensional flowlines at the vicinity of the corner formed by the pillars and the top and bottom plates. Nonetheless, in practice, Equation (13) is a very good approximation of the flow behavior in Hele-Shaw cells. In Roman et al. (2016), the very good agreement in the comparison of the velocity profiles obtained experimentally with micro-PIV and numerically solving Equation (13) illustrates that the depth-averaged flow model is relevant for micromodels. This statement is verified numerically in the simulation results presented in Figure 2 for which the velocity profile in a micromodel was computed based on 2D, 2D depth-integrated, or 3D simulations for different micromodel thickness. For 3D simulations, the 2/3 factor in the velocity magnitude of the 3D depth-integrated profile with respect to the mid-plane value is representative of a parabolic profile in the third dimension. The 2D Navier-Stokes model only tends to the 3D solution if h/d > 1 and corresponds to the 3D mid-plane profile. In this case, the scales separation hypothesis leading to Darcy's law is not satisfied and the 2D Darcy solution cannot describe the flow through the micromodel. If h/d < 1, the friction of the fluid along the top and bottom plates are the dominant resistance to the flow. In such a case, the 3D flow tends to the 2D Darcy solution whereas the 2D Navier-Stokes solution—that corresponds to an infinite thickness—is completely off the reference data. The 2D depth-averaged simulations remain consistent with the 3D solution regardless of the aspect ratio.

FIGURE 2

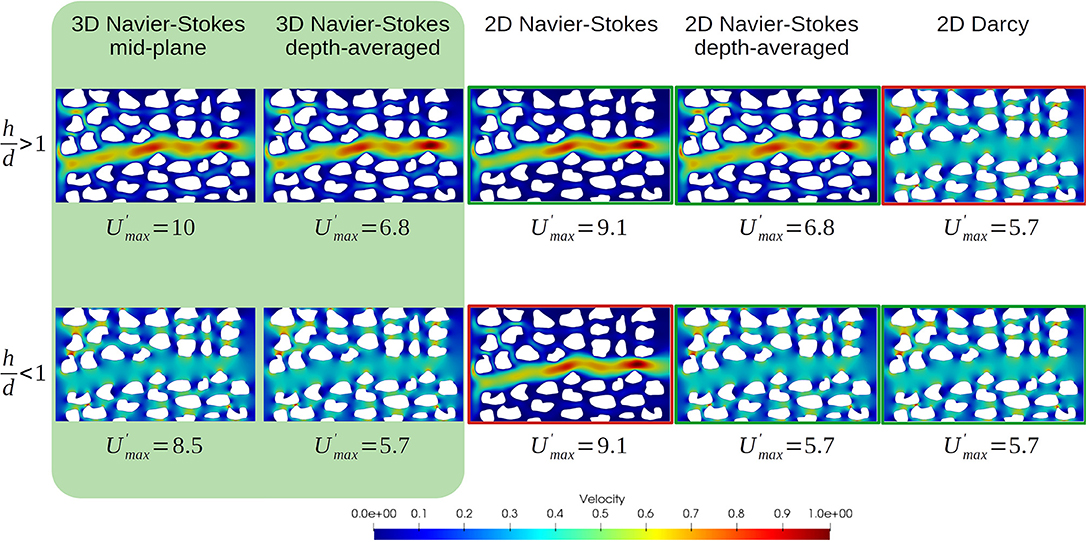
Figure 2. Single-phase flow simulations using 3D, 2D, and 2D-depth-averaged models for different aspect ratio between the micromodel thickness, h and the smallest pore-throat, d. The computational domain is gridded with 1.4 × 10⁵ cells for the 2D cases and 11.4 × 10⁵ × 10 for the 3D cases. The typical pore-throat size is $d_{typ}=4\times 10^{-3}m$, the largest is $d_{large}=12\times 10^{-3}m$ and the smallest is d = 0.5 × 10⁻³ m. We used two different depth thickness, namely h = 10⁻² m and h = 10⁻⁴ m. Simulations are performed with OpenFOAM. For each simulation, the velocity profile is normalized by the maximum value, and we indicate the maximum value normalized by the inlet velocity. If $\frac{h}{d}>1$, 2D Navier-Stokes simulations tend toward the mid-plane 3D Navier-Stokes solution and 2D Darcy is far from the reference solution. If $\frac{h}{d}<1$, 2D Darcy captures the 3D reference solution whereas 2D Navier-Stokes breaks down. The 2D depth-integrated Navier-Stokes model captures the 3D flow behavior regardless the micromodel thickness.

2.3.2. Single-Phase Scalar Transport

The integration of an advection-diffusion equation for the transport of a scalar—e.g., species concentration or temperature– across the micromodel thickness gives,

$\begin{array}{ll}\frac{\partial {\overline{C}}^{2D}}{\partial t}+\nabla .\left({\overline{v}}^{2D}{\overline{C}}^{2D}\right)=\nabla .\left(D\left(t\right).\nabla {\overline{C}}^{2D}\right),& (15)\end{array}$

where ${\overline{v}}^{2D}$ is obtained using Equation (13), and $D(t)$ is a time-dependent dispersion tensor. Because of the parabolic velocity profile in the micromodel depth, there are hydrodynamic dispersion effects that must be considered even if the aspect ratio between the pore-throat size and micromodel thickness is lower than one, h/d > 1. For transport in between two parallel plates, the dispersion tensor exactly writes (Dentz and Carrera, 2007),

$\begin{array}{ll}D\left(t\right)=D_{i}I+\frac{h^2}{4D_i}{\overline{v}}^{2D}{\overline{v}}^{2D}\left(\frac{2}{105}-{\displaystyle \sum _{n=1}^{\infty }}\frac{18}{{\left(n\pi \right)}^6}exp\left(-4{\left(\frac{n\pi }{h}\right)}^2{D}_{i}t\right)\right),& (16)\end{array}$

where the first term is the molecular diffusion and the second term corresponds to Taylor-Aris dispersion in the direction of the flow (Taylor, 1953; Aris, 1956)—notes that ${\overline{v}}^{2D}{\overline{v}}^{2D}$ is a tensor. The time-dependent infinite series accounts for the pre-asymptotic regime at early time and tends toward zero at long time. In practice, only the two first terms of the series are necessary.

Hydrodynamic dispersion effects are characterized by the Peclet number, $P{e}_h=\frac{hU}{D}$, that compares the transport by advection and the transport by diffusion. They are illustrated in the simulation results of Figure 3 that solve the transport of a scalar using 3D, 2D, and 2D depth-averaged models for Peclet numbers ranging from 0.1 to 10⁴. The deviations between mid-plane and depth-averaged values of the 3D simulations illustrate the hydrodynamic dispersion when advection is the dominant transport mechanism. Experimentally, the measurement of species concentration using optical index corresponds to depth-averaged values (Watson et al., 2019). Confusion regarding the nature of measured value may lead to misinterpretations of the comparison between experiments and 3D simulations. For transport dominated by diffusion, Pe_h < 1, the concentration profile is flat over the micromodel depth. Therefore, there are no dispersion effects and the 2D models are in good agreement with 3D simulations. If the advection takes over, Pe_h > 1, hydrodynamic dispersion becomes important and 2D model breaks down. The two-dimensional depth-averaged simulations using the time-dependant dispersion tensor approximate well the depth-integrated solution of the 3D simulations, regardless the Peclet number. Figure 4 highlights the importance of considering the pre-asymptotic regime. Neglecting the dispersion (i.e., $D(t)$ = D_i$I$) or considering only the asymptotic Taylor-Aris dispersion (i.e., $D(t)=D_{i}I+\frac{h^2{\overline{v}}^{2D}{\overline{v}}^{2D}}{210D_i}$) tends to overdisperse the solute. Likewise, it is crucial to consider the product ${\overline{v}}^{2D}{\overline{v}}^{2D}$ as a tensor and not as a scalar $|{\overline{v}}^{2D}{|}^2$ because Taylor-Aris dispersion in microfluidic devices is not isotropic and occurs in the direction of the flow.

FIGURE 3

Figure 3. Transport of a scalar in a micromodel with aspect ratio h/d > 1. We use 3D, 2D, and 2D-depth-averaged models for different Péclet number by varying the diffusion. The results correspond to isocontour of the concentration for C = 0.2 (blue), C = 0.5 (green), C = 0.8 (orange) at t = 42 s. 2D models without dispersion break down for Pe_h > 10.

FIGURE 4

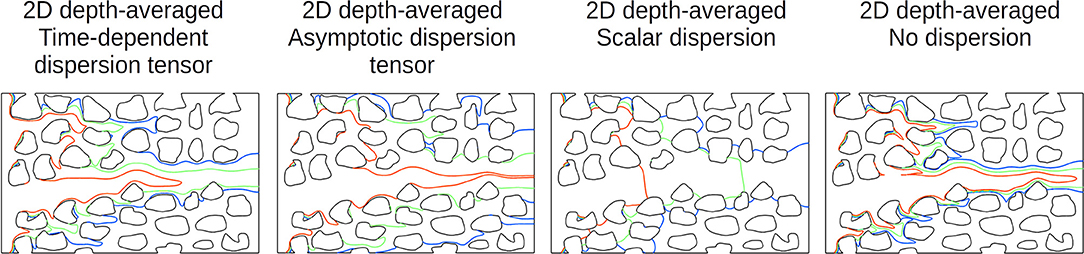
Figure 4. Comparison of the transport of a scalar at Pe = 10³ in a micromodel with aspect ratio h/d > 1 using 2D depth-averaged models including time-dependent dispersion tensor, the asymptotic dispersion tensor, isotropic dispersion, and no dispersion. The results correspond to isocontour of the concentration for C = 0.2 (blue), C = 0.5 (green), C = 0.8 (orange) at t = 42 s. Neglecting the dispersion [i.e., $D(t)$ = D_i$I$] or considering only the asymptotic Taylor-Aris dispersion [i.e., $D(t)=D_{i}I+\frac{h^2{\overline{v}}^{2D}{\overline{v}}^{2D}}{210D_i}$] tends to overdisperse the solute. Isotropic dispersion cannot capture the transport of scalars in micromodels.

2.3.3. Two-Phase Flow

Simulation of two-phase flow processes in microfluidic cells using 2D depth-averaged models is challenging as the fluid-fluid interface has two curvature radii: one in the micromodel plane, another in the micromodel thickness. Horgue et al. (2013) proposes 2D depth-averaged equations in which they integrated the interface curvature along the micromodel thickness in addition to the Hele-Shaw correction. Their model, however, is limited to cases for which no liquid films are flowing on the top and bottom plates, and cannot capture phenomena such as snap-off. Alternatively, Cueto-Felgueroso and Juanes (2014) proposes a Darcy-like model to simulate two-phase flow in Hele-Shaw cells that accounts for water films flowing on the top and bottom plates using relative permeabilities. The applicability of their model, however, is restricted to aspect ratios between the micromodel thickness and the pore-throat size smaller than one, h/d ≪ 1. In absence of reliable 2D depth-integrated models for two-phase flow, it is recommended to use 3D rather than 2D simulations since the former can capture the impact of wetting films along the top and bottom plates as well as corner flows (Zhao et al., 2019). Moreover, phenomena such as snap-off can only be captured if the two curvature radii are considered (Roman et al., 2017).

2.4. Multi-Scale Approach

Multi-modal pore-size distributions are quite common in geological porous media. This special feature appears, for example, in porous fractured media for which the width of a fracture is orders of magnitude larger than the typical pore throat diameter in the porous matrix. In such a case, a full Navier-Stokes modeling approach requires to resolve all the porosity explicitly and leads to tremendous computational grid size. Alternative approaches including micro-continuum models propose to model only the flow in the fracture using Navier-Stokes while the flow in the matrix is described by Darcy's law (Soulaine and Tchelepi, 2016). Micro-continuum approach relies on a hybrid-scale flow model based on the Darcy-Brinkman-Stokes equation (Brinkman, 1947; Neale and Nader, 1974) discretized with the Finite-Volume Method. All the geometric structures below a threshold that corresponds to the spatial resolution of the simulation is filtered and modeled as a porous medium. The momentum equation reads

$\begin{array}{ll}\frac{1}{\varphi }\left(\frac{\partial \rho \overline{v}}{\partial t}+\nabla .\left(\frac{\rho }{\varphi }\overline{v}\overline{v}\right)\right)=-\nabla \overline{p}+\nabla .\frac{\mu }{\varphi }\left(\nabla \overline{v}+{\nabla }^t\overline{v}\right)-\mu k^{-1}\overline{v},& (17)\end{array}$

where the overline notation denotes filtered variables, ϕ is porosity field, and k is the local permeability of the porous regions. Recent studies show that the micro-continuum framework is well-suited to solve problems involving two characteristic length-scales (e.g., fractured media, micro-porous rocks) (Arns et al., 2005; Scheibe et al., 2015; Soulaine et al., 2016, 2021; Carrillo et al., 2020; Menke et al., 2020; Poonoosamy et al., 2020) and also to describe the movement of fluid/solid interfaces caused by dissolution/erosion and precipitation/deposition (Soulaine and Tchelepi, 2016; Soulaine et al., 2017; Molins et al., 2020) or by solid deformation due to swelling or fracturing (Carrillo and Bourg, 2019). Micro-continuum models are also able to simulate two-phase flow processes (Soulaine et al., 2018, 2019; Carrillo et al., 2020).

3. Application to Geosciences and Open Challenges

In this section, we review the main advances in computational microfluidics involving multiphase flow and reactive transport including the authors' own contributions. We also discuss the open-challenges and the current and future lines of research in this area.

3.1. Modeling of Immiscible Two-Phase Flow

Modeling immiscible multi-phase flow is one the biggest challenge in the porous media community. Despite a very large usage in subsurface engineering, many studies have emphasized the limits of Darcy's law for two or more fluids (Danis and Quintard, 1984; Rose, 2000; Cinar et al., 2009). An accurate description of the flow mechanisms in porous media is challenged by the complex interplay between capillary, viscous, and gravitational forces that may lead to highly unstable flow and trapping mechanisms. The heterogeneous nature of geological formations further complicates the development of predictive models.

Computational microfluidics for multiphase flow offers an appealing framework to probe the underlying mechanisms in unsaturated porous media. Despite enormous improvements, however, the numerical modeling of multi-phase flow remains challenging. The difficulties are twofold: on the one hand, numeric must be improved (for calculating the interface curvature dynamically, for tracking the composition of the fluids, for speeding-up the simulation times); on the other hand, the physical description of interfacial properties is still not well-established (e.g., wettability conditions, thin films). Current research intends to address these open-challenges by developing reliable and efficient multi-phase flow simulators at the pore-scale.

3.1.1. Efficient Numerical Solvers for Capillary-Dominated Flow

The standard approaches for tracking the interface movement of two immiscible fluids rely on solving single-field equations for the single-field variables, i.e., variables that includes the contribution of each phase. Whether the modeling is grid-based or particle-based, a phase indicator function maps the distribution of the fluids within the pore-space and evolves as the fluid-fluid interface propagates along with hydrodynamic forces. This function denotes either the fluid volume fraction in every grid cells for the Volume-of-Fluid (VOF, Hirt and Nichols, 1981) and phase-field (PF, Jacqmin, 1999) approaches, a distance to the fluid interface for Level-Set (LS, Sussman et al., 1994) approaches, or a color function for Smooth Particles Hydrodynamics (SPH, Tartakovsky and Meakin, 2005) and Lattice Boltzmann Methods (LBM, Gunstensen et al., 1991). The literature also reports on modeling based on the Density Functional Theory for hydrodynamics (Demianov et al., 2014). A review of approaches is found in Wörner (2012). The phase indicator function is used to define single-field variables by weighting the fluid properties (e.g., viscosity, density) according to the distribution of fluid phases. Its gradient is also used to calculate the interface curvature. Today, none of the existing approaches can solve two-phase flow problems accurately and efficiently for a wide range of flow regimes (Abadie et al., 2015). One of the bottlenecks is the existence of spurious velocities near the interface attributed to inaccuracies in the calculation of the interface curvature, regardless of the computational approach. This problem acknowledged for more than 30 years (Brackbill et al., 1992), is particularly limiting for capillary-dominated flow (Scardovelli and Zaleski, 1999) that are the dominant regimes in many subsurface systems (Cinar and Riaz, 2014). An important part of the current research in computational microfluidics for two-phase flow consists in developing robust solvers that minimize these numerical issues (Pavuluri et al., 2018).

One of the popular approach in computational microfluidics is the algebraic VOF approach. This is the technique used in the simulations that illustrate the application section. In this technique, the phase indicator functions, α_l and α_g, described the volume fraction of each fluid within each cell of the computational domain and the governing equations are obtained by volume averaging the Navier-Stokes equations over a control volume (Maes and Soulaine, 2020). For incompressible fluids, the continuity equation writes,

$\begin{array}{ll}\nabla .v=0,& (18)\end{array}$

the mass balance equation for the liquid phase is

$\begin{array}{ll}\frac{\partial {\alpha }_l}{\partial t}+\nabla .\left({\alpha }_{l}v\right)+\nabla .\left({\alpha }_l{\alpha }_g{v}_r\right)=0,& (19)\end{array}$

and the momentum equation writes

$\begin{array}{ll}\frac{\partial \rho v}{\partial t}+\nabla .\left(\rho vv\right)=-\nabla p+\rho g+\nabla .\left(\mu \left(\nabla v+{\nabla }^{t}v\right)\right)+F_c,& (20)\end{array}$

where v_r and F_c are sub-grid models that describe the fluid-fluid interactions in cells that contain the interface. They represent the relative velocity and the surface tension force due to the curvature of the interface, respectively. Although other methods such as CFD with level-set (Sussman et al., 1994; Abu AlSaud et al., 2017, 2018) or combinations of LBM and level-set (McClure et al., 2016) can provide a more accurate description of the sharp interface, the VOF method is attractive due to its flexibility, robustness in terms of mass conservation, and adaptability to more complex physic (e.g., multi-component mass transfer). Because the derivation of the governing equations relies on volume averaging principles, algebraic VOF methods are the cornerstone of multi-scale solvers for two-phase flow using micro-continuum (Soulaine et al., 2018, 2019; Carrillo et al., 2020).

3.1.2. Modeling of Wettability and Interfacial Properties

Wettability plays a key role in multiphase flow in porous media (De Gennes, 1985; Singh et al., 2018). Accurate prediction of multiphase flow in the soils and the subsurface for geo-environmental issues including Carbon Capture and geological Storage, water resources remediation, or Enhanced Oil Recovery requires an in-depth understanding at the pore-scale of the key mechanisms that influence the fluid displacements and dynamics including viscous and capillary forces but also the solid surface wettability. Recent studies have shown that the spatial distribution of wettability play a crucial role (AlRatrout et al., 2018; Yesufu-Rufai et al., 2020). The rock wettability and the resulting multiphase flow can be modified by a change in pore water composition (pH, salinity) and interfacial physicochemical properties. For example, an oil droplet trapped within a pore may be more easily remobilized using low salinity water (Jackson et al., 2016). Accurate modeling of wettability conditions at the mineral surface is therefore crucial to develop efficient and reliable computational microfluidics for two-phase flow.

Traditionally, wettability is described considering that the fluid-fluid interface and the solid surface form a contact angle (see Figure 5). The value of the contact angle is provided from static measurements that described the contact angle at the nanoscale. In computational microfluidics, the cell size near the solid surface is usually orders of magnitude larger than nanometers. Therefore, upscaled laws including the Cox-Voinov model estimates an apparent dynamic contact angle that depends on the interface velocity near the solid surface and accounts for viscous bending (Voinov, 1976; Cox, 1986). The alteration of interfacial and solid surface properties due to a change of pH and salinity requires constitutive laws for modifying the contact angle accordingly (Maes and Geiger, 2018). Moreover, flow models based on contact angles break down in the presence of thin water films on the mineral surface (Starov et al., 2007).

FIGURE 5

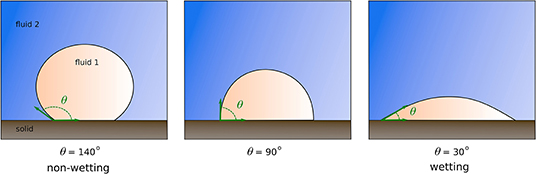
Figure 5. The contact angle, θ, is the angle formed by the tangent to the solid surface and the tangent to the fluid-fluid interface. For values smaller than 90°, a droplet lying on a solid substrate tends to spread over the surface. The fluid within the droplet is the wetting fluid with respect to the other fluid and the solid surface. For values larger than 90°, the droplet is the non-wetting phase and tends to minimize its surface area in contact with the solid substrate.

Alternative flow models including lubrication theory offer an appealing framework to account for physicochemical mechanisms controlling the wettability of rocks according to pore water chemistry and surface roughness for instance (Abu AlSaud et al., 2017, 2020). Instead of using a contact angle, lubrication theory provides a partial differential equation governing the evolution of the film thickness, δ, on the solid surface including molecular forces (Pahlavan et al., 2018). It reads,

$\begin{array}{ll}\frac{\partial \delta }{\partial t}+\frac{1}{{\mu }_w}\nabla .\left[\left(\frac{{\delta }^3}{3}\nabla \left(\sigma \kappa -\Pi \left(\delta \right)\right)\right)+\frac{{\delta }^2\tau }{2}\right]=0,& (21)\end{array}$

where μ_w is the water viscosity, σ is the surface tension, κ is the interface curvature, Π(δ) is the disjoining pressure term, and τ is the shear-stress exerted on the film surface. The disjoining –or Derjaguin– pressure includes attractive (e.g., van der Waals) and repulsive (e.g., electrostatic) forces that change with the ionic strength, i.e., pH and salinity. The film equation is solved on the solid surface and is coupled with the two-phase Navier-Stokes solver in the volume of the pore. By getting rid of the concept of contact angle, it is believed that simulators using lubrication models are more realistic and mechanistic for the description of multiphase systems in geological formations for energy and environmental issues. Applications include the modeling of wettability alteration measured in supercritical CO₂ stored in deep saline aquifers (Wan et al., 2014) and the detachment of crude oil from mineral surface observed when changing the brine from high to low salinity (Berg et al., 2010). The state-of-the-art computational microfluidics using lubrication theory, however, is limited to flat solid boundaries (Abu AlSaud et al., 2017, 2020). Recent work considers curvilinear surfaces on cylindrical solids (Qin et al., 2020). However, pore-scale multiphase flow solvers with lubrication models on generic solid geometries are still under development.

3.1.3. Modeling of Species Transfer Across Fluid-Fluid Interfaces

In many subsurface processes including the injection and sequestration of supercritical carbon dioxide (sCO₂) into deep geological formations, there is a transfer of species across the fluid-fluid interface. Moreover, the ability to track the composition of fluids in two-phase flow is crucial for modeling efficiently the change of wettability conditions with pH evolution (Maes and Geiger, 2018). The Continuous Species Transfer (CST) approach allows tracking multicomponent multiphase flow at the pore-scale (Haroun et al., 2010; Marschall et al., 2012). In this approach, the thermodynamic equilibrium at the interface is described by a partitioning relationship such as Henry's law (Henry, 1803) and the continuity of mass fluxes is guaranteed while the interface evolves in the pore-space due to fluid displacements including drainage and imbibition (see Figure 6).

FIGURE 6

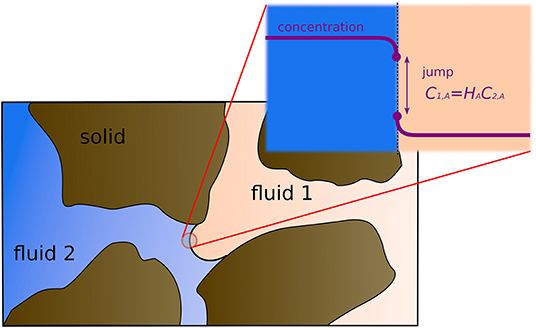
Figure 6. Illustration of multicomponent mass transfer in two-phase flow at the pore-scale. Thermodynamic equilibrium at the fluid/fluid interface obeys a partitioning relationship such as Henry's law.

CST is a single-field approach along the same lines as the Volume-Of-Fluid technique used for simulating immiscible two-phase flow, i.e., a unique partial differential equation solves for a single-field concentration regardless of the content of a grid block. It reads,

$\begin{array}{ll}\frac{\partial C_A}{\partial t}+\nabla .\left(v{C}_A\right)=\nabla .\left(D_A^{*}\left(\nabla C_A+{\Phi }_A\right)\right),& (22)\end{array}$

where $D_A^{*}$ is the weighted-average of the diffusion coefficients in both fluids and Φ_A is the CST flux enforcing the concentration discontinuity due to Henry's law. Graveleau et al. (2017) derived a boundary condition on a wetted wall for the CST and used the modeling approach to upscale the rate of mass transfer in unsaturated porous media as a function of the flow rates. Yang et al. (2017), however, pointed out that when convection dominates diffusion locally near the interface, the CST method generates large numerical errors. They show that in order to capture the species concentration discontinuity accurately, the mesh should be extremely refined at the vicinity of the interface. This workaround, however, increases dramatically the computational cost, especially for advection-dominated systems. The CST derivation was carefully revisited using the method of volume averaging (Maes and Soulaine, 2018b) leading to a new approach without limitation on the transport regimes or the grid refinement level—referred to as Compressive-CST or simply C-CST—that is fully consistent with the phase advection scheme unlike the standard CST scheme that was causing unbalanced mass transfer. C-CST can simulate the mass transfer of a passive scalar in a dynamic system (see Figure 7), and therefore, enable the assessment of the mean rate of mass transfer in unsaturated porous media in terms of saturation, flow rates and interfacial area. C-CST can be used to evaluate the role played on the mass transfer by the internal re-circulation within the trapped droplets that was observed experimentally using microfludics (Roman et al., 2016, 2020; Zarikos et al., 2018).

FIGURE 7

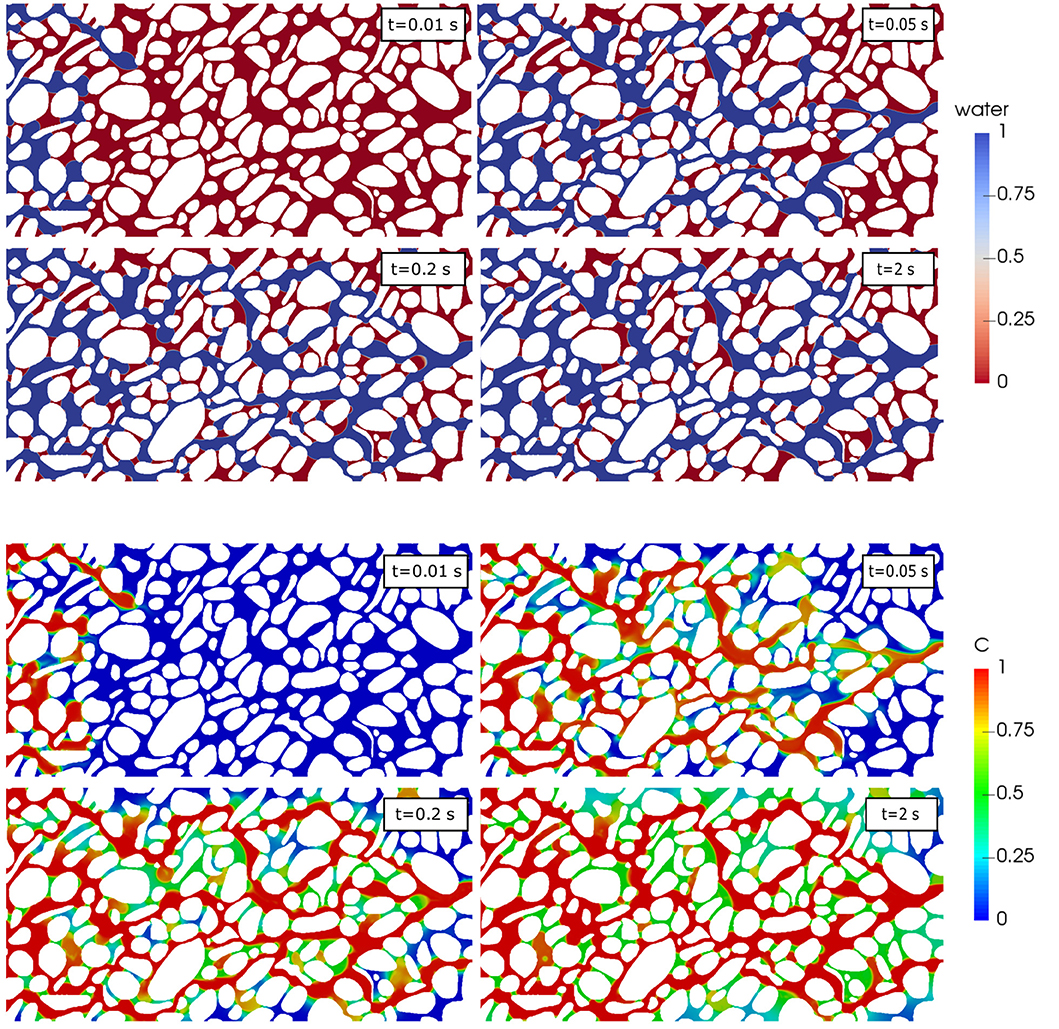
Figure 7. Simulation results of drainage of oil (wetting phase) by water with multi-component mass transfer at the pore-scale. The white pillars correspond to the solid grains. Top: distribution of the fluid phases during the drainage at different timestep. Bottom: concentration profile in the system (adapted from Maes and Soulaine, 2018b).

In more recent work, the C-CST has been extended for modeling cases for which the species transfer across the fluid-fluid interface is no longer passive but leads to local volume changes (Maes and Soulaine, 2020). Such situations happen, for example, when a soda can is opened, the pressure in the headspace falls abruptly and Henry's law is no longer satisfied. To re-establish equilibrium, the carbon dioxide concentration in water decreases by forming gas bubbles. During their travel toward the surface, gas bubbles grow because of the diffusive flux from the carbon dioxide dissolved in the liquid (Power et al., 2009). The other way around occurs in carbon sequestration processes when sCO₂ is stored in deep saline aquifers by capillary effects and trapped sCO₂ droplets dissolve into the surrounding brine (Kim et al., 2012). As a consequence, the volume of droplets decreases, and the equilibrium of hydrodynamic forces that was maintaining the sCO₂ trapped in the pore-space is displaced, eventually leading to a mobilization of the droplets. Computational microfluidics using C-CST for phase change can estimate the volume of CO₂ trapped in the porous structure and assess the timescale of potential remobilization.

3.1.4. Multi-Scale Two-Phase Flow

The micro-continuum approach for two-phase flow enables the simultaneous modeling of multiphase flow at two different length scales: (i) a Darcy-scale where sub-voxel fluid-fluid and fluid-solid interactions within a porous medium are modeled through relative permeability and capillary constitutive models, (ii) a pore-scale (or Navier-Stokes scale) where the solid material is non-porous and fluid-fluid interactions are described through a continuum representation of the Young-Laplace equation. The model combines the Volume-of-Fluid approach for tracking the fluid-fluid interface in regions free of solid and the Darcy-Brinkman-Stokes equation for modeling flow in porous regions (Soulaine et al., 2019). It includes classic concepts such as saturation, relative permeability, and capillary pressure curves in the porous matrix (Carrillo et al., 2020). This multiscale approach offers new possibilities in computational microfluidics to investigate multiphase flow in fractured porous media including the fracture-matrix interactions and to study the role played by microporosity in processes such as imbibition and drainage.

For example, the two-phase micro-continuum model was used to simulate the expulsion of methane stored in microporous matrix into a soaked fracture (see Figure 8). The results highlight two completely different expulsion flow regimes whether the fracture boundaries are hydrophobic or hydrophilic. On the one hand, there is a continuous gas production, and on the other hand a bubbly regime because the surface tension effects at the wet fracture boundary generate an energetic barrier that tends to form gas bubbles as far as the pressure in the microporous regions is sufficient to inflate them. This kind of simulations enables the assessment of the rate of hydrocarbon recovery in shale gas according to the spatial distribution of the kerogen (hydrophobic) and clay (hydrophilic) in the vicinity of the micro-cracks (Soulaine et al., 2019).

FIGURE 8

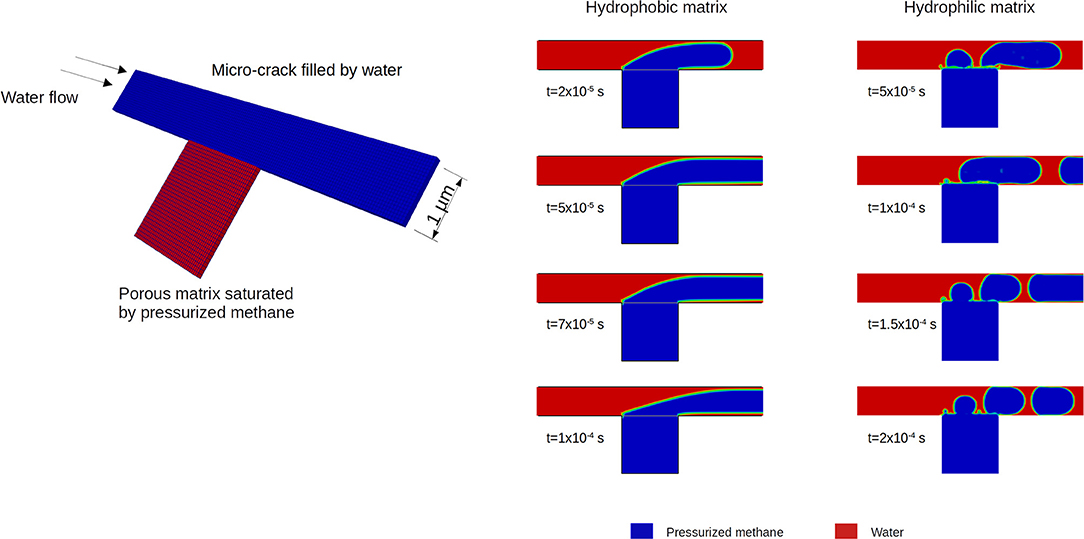
Figure 8. Multi-scale simulations of the expulsion of methane stored in a microporous matrix into a soaked fracture. We investigated two scenarios: the fracture/matrix interface is non-wetting and the methane production is continuous, and the fracture/matrix interface is wetting and the gas is produced in a bubbly flow regime. The simulation setup is fully described in Soulaine et al. (2019).

3.1.5. Three-Phase Flow

Computational microfluidics for three-phase flow (e.g., gas-water-oil) are still scarce in the literature because the community focuses mostly on two-phase flow simulators for which the open challenges discussed in previous sections are still limiting the predictive capabilities. Such a tool is crucial to understand fully the underlying mechanisms of non-aqueous phase liquid (e.g., hydrocarbon, chlorinated solvents) trapped in the unsaturated zone by capillary effects and to propose innovative remediation strategies. In the literature, Bayestehparvin et al. (2015) use a Volume-of-Fluid approach, Helland et al. (2017) and Mohammadmoradi and Kantzas (2017) use quasi-static displacement using a Level-Set method, Tartakovsky and Panchenko (2016) use Smooth Particle Hydrodynamics, Dinariev and Evseev (2016) use a phase-field method and van Kats and Egberts (1999) and Jiang and Tsuji (2017) use a lattice-Boltzmann method to investigate three-phase Navier-Stokes flow at pore scale. The development of efficient three-phase flow simulators at the pore-scale is still under development and microfluidic experiments will help to assess the robustness of the computational models.

3.2. Reactive Transport Modeling at the Pore-Scale

Most of computational microfluidics developments so far have been devoted to solve the Navier-Stokes equations under single (Spanne et al., 1994; Bijeljic et al., 2013; Guibert et al., 2015; Soulaine et al., 2016) and two-phase flow conditions (Horgue et al., 2013; Raeini et al., 2014; Graveleau et al., 2017; Maes and Soulaine, 2018a; Pavuluri et al., 2020). Flow in geological porous media, however, has the distinctive feature to interact chemically with the solid walls. The consideration of surface reactions in computational microfluidics requires inclusion of comprehensive reaction networks along with flow and transport, an approach known as Reactive Transport Modeling (Steefel et al., 2005). Despite the growing investment in the development of RTM at the pore-scale—pioneer simulators date back to the late 90s (Békri et al., 1995, 1997)—the field is still in its infancy. The main challenge consists in moving the fluid/solid boundary with respect to chemical reactions at the mineral surfaces. A large variety of methodologies has been proposed by the community to solve this problem and a comprehensive review can be found in Molins et al. (2020). They include Level-Set (Molins et al., 2014, 2017), or phase-field (Xu and Meakin, 2008, 2011) techniques in a Eulerian grid, LBM (Kang et al., 2003; Szymczak and Ladd, 2009; Prasianakis et al., 2013; Chen et al., 2014b; Yoon et al., 2015), SPH (Tartakovsky et al., 2007), and Arbitrary Lagrangian-Eulerian (Oltéan et al., 2013; Starchenko et al., 2016) frameworks. Another family of methods for displacing the mineral interface uses the micro-continuum approach (Soulaine and Tchelepi, 2016; Soulaine et al., 2017).

3.2.1. Modeling of Dissolution Processes

The modeling of pore-scale dissolution is the most advanced of the reactive transport processes using computational microfluidics. In this case, the solid mineral dissolves into the fluid phase according to thermodynamics and chemical reactions at the solid surface. High-resolution data of well-controlled microfluidic experiments have highlighted that the shape of a cylindrical crystal evolves into an elongated profile due to non-uniform distribution of the solute along the solid surface leading to faster dissolution rates upstream than downstream (Soulaine et al., 2017; Dutka et al., 2020) as illustrated in Figure 9. The elongated profile of the crystal as it dissolved in the acid flowing solution illustrates well the complex coupling between streamlines, solute transport, and surface reaction. The state-of-the-art of computational microfluidics for reactive transport using different techniques including micro-continuum, Level-Set, LBM, moving grids with conformal mapping, and Vortex methods can reproduce the shape evolution of the dissolving crystal with great fidelity (Molins et al., 2020). This success leads to the strong conclusion that pore-scale technologies for moving fluid-solid boundaries along with geochemical reactions are now mature enough to be used as predictive tools. Current development uses computational microfluidics along with geochemical packages to model comprehensive reaction networks.

FIGURE 9

Figure 9. Experimental (top) and computational (bottom) microfluidics images of calcite dissolution process at different time steps during the injection of 0.05% HCl at a mean velocity of 1.16 × 10⁻³ m/s flow rate from the left to the right (Reprinted with permission from Soulaine et al., 2017, Copyright Cambridge University Press 2017).

Computational microfluidics was used to investigate the dissolution of micro-model pore networks (Szymczak and Ladd, 2009; Kang et al., 2014; Molins et al., 2017; Soulaine et al., 2017). Five different dissolution regimes are observed according to the constant of reaction at the mineral surface and the injection mass flow rate as illustrated in Figure 10. For a given fluid, these two effects are characterized by the Damkohler number Da_I (i.e., ratio of the characteristic timescale of transport and surface reaction) and the Peclet number Pe (i.e., ratio of advection and diffusion), respectively. These regimes are: compact dissolution (Pe < 10⁻² and Da_I > 1), conical dissolution (1 > Pe > 10⁻² and Da_I > 1), dominant wormhole (10 > Pe > 1 and Da_I > 1), ramified wormholes (Pe > 10 and Da_I > 1) and uniform dissolution (Da_I < 1 and regardless the Peclet number). Because computational microfluidics provides a full mapping of the species and mineral evolution in the system, macroscopic properties can be obtained directly by averaging the simulation results, something that is barely achievable experimentally. For example, knowing the exact distribution of solute concentration including the local mass flux at the mineral surface (Soulaine et al., 2017) volume-averaged the pore-scale results and proposed a new law for quantifying the accessible reactive surface area, A, based on the transport and reactivity conditions. It reads

$\begin{array}{ll}\frac{A}{A_0}=1-exp\left(-P{e}^{-n}D{a}_I^{-m}\right),& (23)\end{array}$

where A₀ is the geometric surface area of the porous sample and n and m are model parameters. Similar relations that reduce the accessible surface area based on hydrodynamics conditions were used to reconcile experimental or numerical data at the larger scales (Wen and Li, 2017; Deng et al., 2018).

FIGURE 10

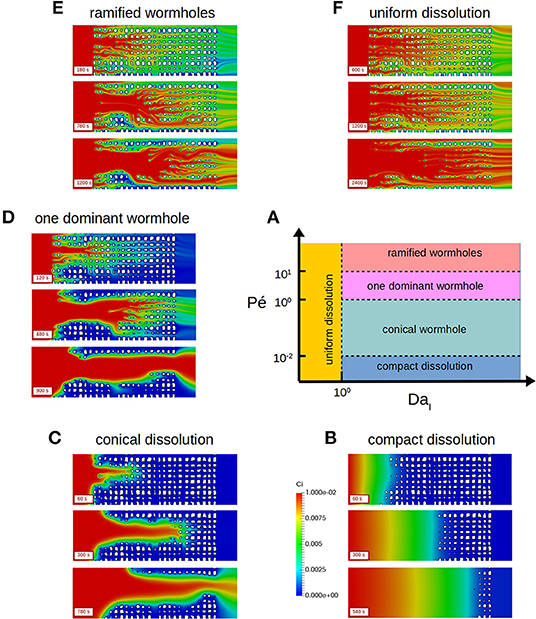
Figure 10. Prediction of the evolution of the pore space of a micromodel for different values of the constant of reaction and of the diffusion coefficient. Five different dissolution regimes are identified (A) namely compact dissolution (B), conical dissolution (C), one dominant wormhole (D), ramified wormholes (E), and uniform dissolution (F) (Reprinted with permission from Soulaine et al., 2017, Copyright Cambridge University Press 2017).

3.2.2. Modeling of Precipitation Processes

Although computational microfluidics for simulating precipitation processes are reported in the literature (Tartakovsky et al., 2007; Li et al., 2008; Yoon et al., 2012; Huber et al., 2014; Chen et al., 2015; Prasianakis et al., 2017; Ray et al., 2019), the field is still scarce and more development and verification are required to reach predictive capabilities. Pore-scale precipitation cannot be treated simply as the reverse problem of dissolution. Indeed, the creation of the solid phase during the precipitation of minerals needs to consider the nucleation of mineral at the solid surface. Moreover, the development of depth-averaged model for precipitation is challenging because in microfluidic experiments it is possible that precipitate preferentially form either on the top and bottom plates or in the bulk (Beuvier et al., 2015; Yoon et al., 2019). Model verification will use the ability of microfluidics to design well-controlled experiments along with high-resolution imaging and chemical characterization (Poonoosamy et al., 2020).

3.2.3. Multi-Scale Reactive Transport Models

Hybrid-scale models have been proposed to describe reactive systems that include multiple characteristic length-scales for which some regions are described using pore-scale modeling while others are modeled with continuum approaches (Liu and Ortoleva, 1996; Liu et al., 1997). Two kinds of approaches solve hybrid-scale problems. On the one hand, the domain decomposition technique solves different physics on separate domains—one for Darcy flow, another for Stokes flow—linked together through appropriate boundary conditions (Tartakovsky et al., 2008; Molins et al., 2019). On the other hand, micro-continuum models use a single set of partial differential equations throughout the computational domain regardless of the content of a grid block (Steefel et al., 2015; Soulaine and Tchelepi, 2016). The latter approach is particularly well-suited to capture the dynamic displacement of the interface between the porous and solid-free regions without involving complex re-meshing strategies. For example, micro-continuum models have been used successfully to simulate the formation and growth of wormholes in acidic environments (Ormond and Ortoleva, 2000; Golfier et al., 2002; Soulaine and Tchelepi, 2016; Faris et al., 2020).

3.2.4. Two-Phase Flow in Reactive Environments

The dynamics modeling of multiphase flow phenomena in reactive environments is quite complex because it involves tracking multiple interfaces that evolve as a function of the details of the reactive transport: on the one hand, the fluid/fluid interface is subject to surface tension forces, on the other hand, the fluid/solid interface moves with chemical reactions at the surface of the solid minerals. The modeling is complicated by the dynamics of the contact line or thin films along the solid walls, and by the transfer of mass across interfaces. Few research works have been devoted to the modeling of multiphase flow with solid boundaries that evolve with chemical reactions. Parmigiani et al. (2011) have proposed an LBM approach to study the evolution of capillary fingers in a porous medium that dynamically evolves with the melting of the solid phase. Later, LBM has been extended to multicomponent multiphase fluid flow and applied to reactive transport with dissolution and precipitation (Chen et al., 2013, 2015). LBM-based approaches, however, are unstable for high-density ratios between the liquid and the gas (Chen et al., 2014a), which, therefore, limits the predictive aspects of such modeling frameworks.

Alternatively, multicomponent multiphase reactive transport can be modeled using the Volume Of Fluid method to track the fluid/fluid interface and the C-CST approach to model the transport of reactive species in the system, including the effect of speciation and surface reactions (Maes and Menke, 2020). Maes and Geiger (2018) used this model to track pH, solid surface potential and contact angle alteration during injection of low-salinity water in micromodels and were able to observe and characterize for the first time the effect of secondary and tertiary low-salinity flooding at the pore-scale (Figure 11). Moreover, Soulaine et al. (2018) proposes new computational microfluidics to simulate mineral dissolution in unsaturated porous media. The model combines the reactive micro-continuum approach developed in Soulaine et al. (2017) with the VOF and C-CST methods. Chemical reactions and wettability conditions at the mineral surface are described as immersed boundaries that evolve with the dissolution of the solid phase. Microfluidic experiments that consist of a calcite crystal dissolving in a microchannel after the injection of an aqueous solution containing up to 1% of hydrochloric acid were used to verify the predictive aspect of the model (see Figure 12).

FIGURE 11

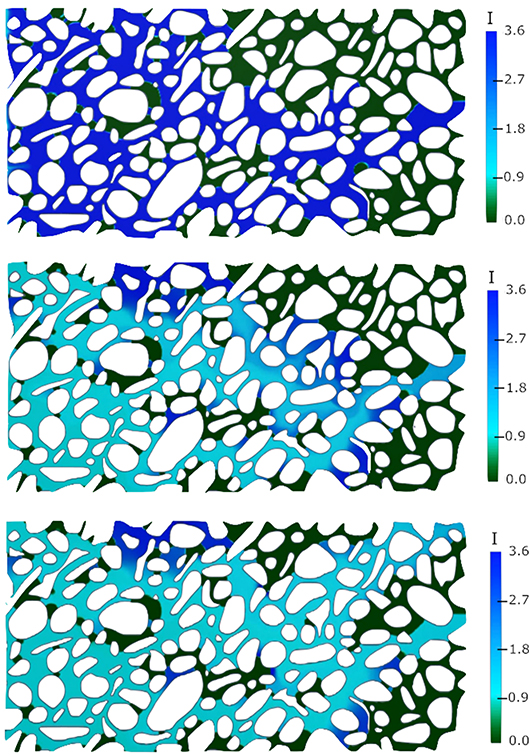
Figure 11. Numerical simulation of tertiary low-salinity flooding in a micromodel. The colormap corresponds to the ionic strength (mol/l) in the domain. The non-aqueous phase appears in green (I = 0), the high salinity water appears in dark blue (I = 3.6) and the low-salinity water appears in light blue (I = 0.9). The simulation parameters are fully described in Maes and Geiger (2018).

FIGURE 12

Figure 12. Comparison between experimental and computational microfluidics. A calcite crystal is dissolved in a flow of hydrochloric acid at atmospheric conditions. Carbon dioxide gas bubbles nucleate at the mineral surface, grow, coalesce, and eventually detach. The micro-continuum model for two-phase flow in reactive environments can reproduce accurately the microfluidic experiments. The microfluidic experiment and simulation are fully described in Soulaine et al. (2018).

The model has been used to investigate the effect of carbon dioxide production during the acidizing of carbonate formations. Results show that under single-phase flow conditions, i.e., when the dissolution time of CO₂ into the aqueous phase is instantaneous, the solid structure dissolves forming wormholes. However, if the characteristic time scale of CO₂ dissolving in brine is much longer compared to the rate of gas production, then CO₂ bubbles grow, coalesce and form flow barriers that limit the transport of the acid in the domain (see Figure 13). These flow barriers prevent the emergence of wormholes and limit significantly the overall dissolution rate. This finding is of great interest in acid stimulation processes for which a gas phase can be produced (Prutton and Savage, 1945; Thompson and Gdanski, 1993). Hence, the presence of a second fluid phase under the same flow conditions may lead to very different dissolution regimes, and the common behavior diagrams that characterize the dissolution pattern based on the Peclet and Damkohler numbers (Golfier et al., 2002) have to be complemented, at a minimum, by a third dimension that quantifies the solubility of the CO₂ in the aqueous phase.

FIGURE 13

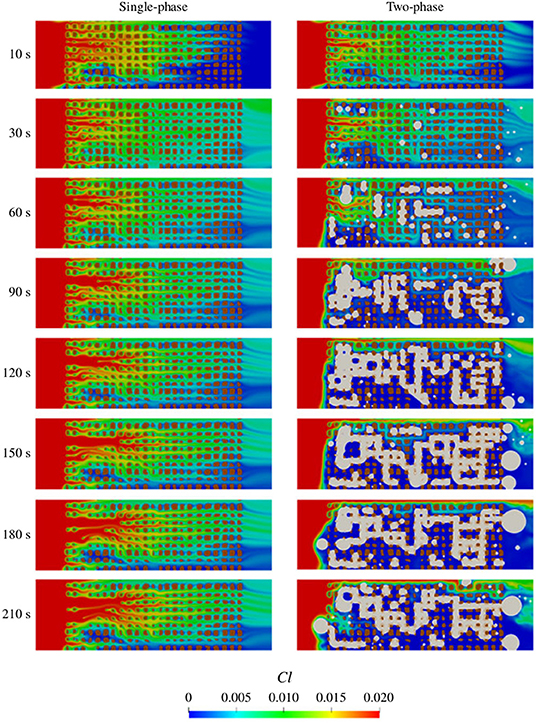
Figure 13. Evolution of a porous medium during the injection of acid. The color map corresponds to the concentration of acid in the domain. Solid grains are depicted in brown. (Left) Under single-phase flow conditions, the acid penetrates the domain and dissolves the solid grains producing wormholes. (Right) The mineral dissolution generates CO₂ gas that occupies the pore space, limits the dissolution process and prevents the development of wormholes (Reprinted with permission from Soulaine et al., 2018, Copyright Cambridge University Press 2018).

4. Conclusion and perspectives

Computational microfluidics for geosciences offers an appealing framework to investigate the coupled processes in geological porous media. The integrated usage of experimental and computational microfluidics is, therefore, a powerful approach to decipher the complex mechanisms that occur in the soils and the subsurface and to bring new insights into the open challenges associated with the continuum-scale modeling of flow and transport in geological systems. Microfluidic experiments provide valuable benchmark data sets, leading to more accurate and robust numerical solvers, while numerical simulations augment microfluidic experiments by providing high-resolution mapping of pressure and velocity profiles, solute concentration, and mineral distribution that are not easily measurable experimentally. Modern approaches can simulate pore-scale events over a wide range of conditions including multiphase flow and the microstructure evolution due to precipitation and dissolution. Combining experimental and computational microfluidics have led to new insights into complex subsurface processes, such as CO₂ geological storage, low salinity flooding and acid stimulation. The paper presents a snapshot of the current capabilities and discuss the validity of depth-averaged models.

The future of this emerging scientific discipline is guaranteed by the continuous improvements of numerical algorithms, modeling, and high-performance computing. The next generations of computational microfluidics will be able to simulate the transport of particles including the micro-dynamics of colloids, their aggregation and stability, the attachment/detachment from the solid walls, and pore-clogging mechanisms according to pH ad salinity conditions. This will necessitate handling the strong coupling between hydro-electro-chemical effects. Important efforts will be dedicated to the consideration of biological processes including the growth of biofilms.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge the first reviewer for suggesting time-dependent dispersion. The research leading to these results has received support from the French Agency for Research (Agence Nationale de la Recherche, ANR) through the Equipex Planex ANR-11-EQPX-36, the Labex Voltaire ANR-10-LABX-100-01, the grant CATCH ANR-18-CE05-0035, and through the FraMatI project under contract ANR-19-CE05-0002. It has also received financial support from the CNRS through the MITI interdisciplinary programs, and from the UK EPSRC funded project on Direct Numerical Simulation for Additive Manufacturing in Porous Media (grant reference EP/P031307/1). Finally, SR and JM would like to thank ALLIANCE (Partenariat Hubert Curien) for the grant that enable the scholar exchange of scientists.

References

Abadie, T., Aubin, J., and Legendre, D. (2015). On the combined effects of surface tension force calculation and interface advection on spurious currents within volume of fluid and level set frameworks. J. Comput. Phys. 297, 611–636. doi: 10.1016/j.jcp.2015.04.054

CrossRef Full Text | Google Scholar

Abu AlSaud, M. O., Esmaeilzadeh, S., Riaz, A., and Tchelepi, H. A. (2020). Pore-scale study of water salinity effect on thin-film stability for a moving oil droplet. J. Colloid Interface Sci. 569, 366–377. doi: 10.1016/j.jcis.2020.02.044

PubMed Abstract | CrossRef Full Text | Google Scholar

Abu AlSaud, M. O., Popinet, S., and Tchelepi, H. A. (2018). A conservative and well-balanced17 surface tension model. J. Comput. Phys. 371, 896–913. doi: 10.1016/j.jcp.2018.02.022

CrossRef Full Text | Google Scholar

Abu AlSaud, M. O., Soulaine, C., Riaz, A., and Tchelepi, H. A. (2017). Level-set method for accurate modeling of two-phase immiscible flow with moving contact lines. arXiv[Preprint]. arXiv:1708.04771.

Google Scholar

Agrawal, P., Raoof, A., Iliev, O., and Wolthers, M. (2020). Evolution of pore-shape and its impact on pore conductivity during co2 injection in calcite: single pore simulations and microfluidic experiments. Adv. Water Resour. 136:103480. doi: 10.1016/j.advwatres.2019.103480

CrossRef Full Text | Google Scholar

Alpak, F., Riviere, B., and Frank, F. (2016). A phase-field method for the direct simulation of two-phase flows in pore-scale media using a non-equilibrium wetting boundary condition. Comput. Geosci. 20, 881–908. doi: 10.1007/s10596-015-9551-2

CrossRef Full Text | Google Scholar

AlRatrout, A., Blunt, M. J., and Bijeljic, B. (2018). Spatial correlation of contact angle and curvature in pore-space images. Water Resour. Res. 54, 6133–6152. doi: 10.1029/2017WR022124

CrossRef Full Text | Google Scholar

Andre, H., Combaret, N., Dvorkin, J., Glatt, E., Han, J., Kabel, M., et al. (2013a). Digital rock physics benchmarks Part I: imaging and segmentation. Comput. Geosci. 50, 25–32. doi: 10.1016/j.cageo.2012.09.005

CrossRef Full Text | Google Scholar

Andre, H., Combaret, N., Dvorkin, J., Glatt, E., Han, J., Kabel, M., et al. (2013b). Digital rock physics benchmarks Part II: computing effective properties. Comput. Geosci. 50, 33–43. doi: 10.1016/j.cageo.2012.09.008

CrossRef Full Text | Google Scholar

Aris, R. (1956). On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. A. 235, 67–77. doi: 10.1098/rspa.1956.0065

CrossRef Full Text | Google Scholar

Arns, C., Bauget, F., Limaye, A., Sakellariou, A., Senden, T., Sheppard, A., et al. (2005). Pore-scale characterization of carbonates using x-ray microtomography. SPE J. 10, 475–484. doi: 10.2118/90368-PA

CrossRef Full Text | Google Scholar

Bayestehparvin, B., Abedi, J., and Ali, S. M. F. (2015). “Dissolution and mobilization of bitumen at pore scale,” in SPE Canada Heavy Oil Technical Conference (Calgary, AL: Society of Petroleum Engineers). doi: 10.2118/174482-MS

CrossRef Full Text | Google Scholar

Békri, S., Thovert, J., and Adler, P. (1995). Dissolution of porous media. Chem. Eng. Sci. 50, 2765–2791. doi: 10.1016/0009-2509(95)00121-K

CrossRef Full Text | Google Scholar

Békri, S., Thovert, J.-F., and Adler, P. (1997). Dissolution and deposition in fractures. Eng. Geol. 48, 283–308. doi: 10.1016/S0013-7952(97)00044-6

CrossRef Full Text | Google Scholar

Berg, S., Cense, A., Jansen, E., and Bakker, K. (2010). Direct experimental evidence of wettability modification by low salinity. Petrophysics 51, 314–322.

Google Scholar

Beuvier, T., Panduro, E. A. C., Kwaśniewski, P., Marre, S., Lecoutre, C., Garrabos, Y., et al. (2015). Implementation of in situ saxs/waxs characterization into silicon/glass microreactors. Lab Chip 15, 2002–2008. doi: 10.1039/C5LC00115C

PubMed Abstract | CrossRef Full Text | Google Scholar

Bijeljic, B., Raeini, A., Mostaghimi, P., and Blunt, M. J. (2013). Predictions of non-fickian solute transport in different classes of porous media using direct simulation on pore-scale images. Phys. Rev. E 87:013011. doi: 10.1103/PhysRevE.87.013011

PubMed Abstract | CrossRef Full Text | Google Scholar

Bird, R. B., Stewart, W. E., and Lightfoot, E. N. (2002). Transport Phenomena, 2nd Edn. New York, NY: John Wiley Sons, Inc.

Google Scholar

Blunt, M. J., Bijeljic, B., Dong, H., Gharbi, O., Iglauer, S., Mostaghimi, P., et al. (2013). Pore-scale imaging and modelling. Adv. Water Resour. 51, 197–216. doi: 10.1016/j.advwatres.2012.03.003

CrossRef Full Text | Google Scholar

Brackbill, J. U., Kothe, D. B., and Zemach, C. (1992). A continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354. doi: 10.1016/0021-9991(92)90240-Y

CrossRef Full Text | Google Scholar

Brinkman, H. C. (1947). A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A 1, 27–34. doi: 10.1007/BF02120313

CrossRef Full Text | Google Scholar

Caltagirone, J.-P. (2013). Physique Des écoulements Continus. Berlin; Heidelberg: Springer. doi: 10.1007/978-3-642-39510-9

CrossRef Full Text | Google Scholar

Carrillo, F. J., and Bourg, I. C. (2019). A Darcy-Brinkman-Biot approach to modeling the hydrology and mechanics of porous media containing macropores and deformable microporous regions. Water Resour. Res. 55, 8096–8121. doi: 10.1029/2019WR024712

CrossRef Full Text | Google Scholar

Carrillo, F. J., Bourg, I. C., and Soulaine, C. (2020). Multiphase flow modeling in multiscale porous media: an open-source micro-continuum approach. J. Comput. Phys. X 8:100073. doi: 10.1016/j.jcpx.2020.100073

CrossRef Full Text | Google Scholar

Chang, C., Zhou, Q., Oostrom, M., Kneafsey, T. J., and Mehta, H. (2017). Pore-scale supercritical co2 dissolution and mass transfer under drainage conditions. Adv. Water Resour. 100, 14–25. doi: 10.1016/j.advwatres.2016.12.003

CrossRef Full Text | Google Scholar

Chapman, E., Yang, J., Crawshaw, J., and Boek, E. (2013). Pore scale models for imbibition of co2 analogue fluids in etched micro-fluidic junctions from micro-model experiments and direct lbm flow calculations. Energy Proc. 37, 3680–3686. doi: 10.1016/j.egypro.2013.06.262

CrossRef Full Text | Google Scholar

Chen, L., Kang, Q., Mu, Y., He, Y.-L., and Tao, W.-Q. (2014a). A critical review of the pseudopotential multiphase lattice Boltzmann model: methods and applications. Int. J. Heat Mass Transfer 76, 210–236. doi: 10.1016/j.ijheatmasstransfer.2014.04.032

CrossRef Full Text | Google Scholar

Chen, L., Kang, Q., Robinson, B. A., He, Y.-L., and Tao, W.-Q. (2013). Pore-scale modeling of multiphase reactive transport with phase transitions and dissolution-precipitation processes in closed systems. Phys. Rev. E 87:043306. doi: 10.1103/PhysRevE.87.043306

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Kang, Q., Tang, Q., Robinson, B. A., He, Y.-L., and Tao, W.-Q. (2015). Pore-scale simulation of multicomponent multiphase reactive transport with dissolution and precipitation. Int. J. Heat Mass Transfer 85, 935–949. doi: 10.1016/j.ijheatmasstransfer.2015.02.035

CrossRef Full Text | Google Scholar

Chen, L., Kang, Q., Viswanathan, H. S., and Tao, W.-Q. (2014b). Pore-scale study of dissolution-induced changes in hydrologic properties of rocks with binary minerals. Water Resour. Res. 50, 9343–9365. doi: 10.1002/2014WR015646

CrossRef Full Text | Google Scholar

Chen, Y., Valocchi, A. J., Kang, Q., and Viswanathan, H. S. (2019). Inertial effects during the process of supercritical CO2 displacing brine in a sandstone: lattice Boltzmann simulations based on the continuum-surface-force and geometrical wetting models. Water Resour. Res. 55, 11144–11165. doi: 10.1029/2019WR025746

CrossRef Full Text | Google Scholar

Cinar, Y., and Riaz, A. (2014). Carbon dioxide sequestration in saline formations: part 2-review of multiphase flow modeling. J. Petrol. Sci. Eng. 124, 381–398. doi: 10.1016/j.petrol.2014.07.023

CrossRef Full Text | Google Scholar

Cinar, Y., Riaz, A., and Tchelepi, H. A. (2009). Experimental study of Co2 injection into saline formations. SPE J. 14, 588–594. doi: 10.2118/110628-PA

CrossRef Full Text | Google Scholar

Cox, R. (1986). The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194. doi: 10.1017/S0022112086000332

CrossRef Full Text | Google Scholar

Cueto-Felgueroso, L., and Juanes, R. (2014). A phase-field model of two-phase hele-shaw flow. J. Fluid Mech. 758, 522–552. doi: 10.1017/jfm.2014.512

CrossRef Full Text | Google Scholar

Danis, M., and Quintard, M. (1984). Modélisation d'un écoulement diphasique dans une succession de pores. Oil Gas Sci. Technol. 39, 37–46. doi: 10.2516/ogst:1984003

CrossRef Full Text | Google Scholar

De Gennes, P. (1985). Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863. doi: 10.1103/RevModPhys.57.827

CrossRef Full Text | Google Scholar

Demianov, A., Dinariev, O., and Evseev, N. (2014). Introduction to the Density Functional Method in Hydrodynamics. Moscow: Fizmatlit.

PubMed Abstract | Google Scholar

Deng, H., Molins, S., Trebotich, D., Steefel, C., and DePaolo, D. (2018). Pore-scale numerical investigation of the impacts of surface roughness: Upscaling of reaction rates in rough fractures. Geochim. Cosmochim. Acta 239, 374–389. doi: 10.1016/j.gca.2018.08.005

CrossRef Full Text | Google Scholar

Dentz, M., and Carrera, J. (2007). Mixing and spreading in stratified flow. Phys. Fluids 19:017107. doi: 10.1063/1.2427089

CrossRef Full Text | Google Scholar

Dinariev, O., and Evseev, N. (2016). Multiphase flow modeling with density functional method. Comput. Geosci. 20, 835–856. doi: 10.1007/s10596-015-9527-2

CrossRef Full Text | Google Scholar

Dutka, F., Starchenko, V., Osselin, F., Magni, S., Szymczak, P., and Ladd, A. J. (2020). Time-dependent shapes of a dissolving mineral grain: Comparisons of simulations with microfluidic experiments. Chem. Geol. 540:119459. doi: 10.1016/j.chemgeo.2019.119459

CrossRef Full Text | Google Scholar

Faris, A., Maes, J., and Menke, H. P. (2020). “An investigation into the upscaling of mineral dissolution from the pore to the core scale,” in Proceedings of the 17th European Conference on the Mathematics of Oil Recovery (Endinburgh) doi: 10.3997/2214-4609.202035250

CrossRef Full Text | Google Scholar

Fatt, I. (1956). The network model of porous media. Petrol. Trans. AIME 207, 144–181. doi: 10.2118/574-G

CrossRef Full Text | Google Scholar

Ferrari, A., and Lunati, I. (2013). Direct numerical simulations of interface dynamics to link capillary pressure and total surface energy. Adv. Water Resour. 57, 19–31. doi: 10.1016/j.advwatres.2013.03.005

CrossRef Full Text | Google Scholar

Ferrari, A., and Lunati, I. (2014). Inertial effects during irreversible meniscus reconfiguration in angular pores. Adv. Water Resour. 74, 1–13. doi: 10.1016/j.advwatres.2014.07.009

CrossRef Full Text | Google Scholar

Ferziger, J., and Peric, M. (2002). Computational Methods for Fluid Dynamics, 3rd Edn. Berlin; Heidelberg; New York, NY: Springer. doi: 10.1007/978-3-642-56026-2

CrossRef Full Text | Google Scholar

Gingold, R. A., and Monaghan, J. J. (1977). Smoothed particle hydrodynamics: theory and application to non-spherical stars. Mnthy Notices R. Astron. Soc. 181, 375–389. doi: 10.1093/mnras/181.3.375

CrossRef Full Text | Google Scholar

Golfier, F., Zarcone, C., Bazin, B., Lenormand, R., Lasseux, D., and Quintard, M. (2002). On the ability of a darcy-scale model to capture wormhole formation during the dissolution of a porous medium. J. Fluid Mech. 457, 213–254. doi: 10.1017/S0022112002007735

CrossRef Full Text | Google Scholar

Graveleau, M., Soulaine, C., and Tchelepi, H. A. (2017). Pore-scale simulation of interphase multicomponent mass transfer for subsurface flow. Transport Porous Media 120, 287–308. doi: 10.1007/s11242-017-0921-1

CrossRef Full Text | Google Scholar

Guibert, R., Nazarova, M., Horgue, P., Hamon, G., Creux, P., and Debenest, G. (2015). Computational permeability determination from pore-scale imaging: sample size, mesh and method sensitivities. Transport Porous Media 107, 641–656. doi: 10.1007/s11242-015-0458-0

CrossRef Full Text | Google Scholar

Gunstensen, A. K., Rothman, D. H., Zaleski, S., and Zanetti, G. (1991). Lattice boltzmann model of immiscible fluids. Phys. Rev. A 43, 4320–4327. doi: 10.1103/PhysRevA.43.4320

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, R. J., and Toong, T. Y. (1971). Interface behavior as one fluid completely displaces another from a small-diameter tube. J. Colloid Interface Sci. 36, 410–413. doi: 10.1016/0021-9797(71)90014-2

CrossRef Full Text | Google Scholar

Haroun, Y., Legendre, D., and Raynal, L. (2010). Volume of fluid method for interfacial reactive mass transfer: application to stable liquid film. Chem. Eng. Sci. 65, 2896–2909. doi: 10.1016/j.ces.2010.01.012

CrossRef Full Text | Google Scholar

Helland, J. O., Pedersen, J., and Jettestuen, E. (2017). “Pore-scale simulation of three-phase capillary pressure and trapping on 3D rock images,” in IOR NORWAY 2017-19th European Symposium on Improved Oil Recovery (Stavanger).

Google Scholar

Henry, W. (1803). Experiments on the quantity of gases absorbed by water, at different temperatures, and under different pressures. Philos. Trans. R. Soc. Lond. 93, 29–42, 274–276. doi: 10.1098/rstl.1803.0004

CrossRef Full Text | Google Scholar

Hirt, C. W., and Nichols, B. D. (1981). Volume-Of-Fluid (VOF) method fior the dynamic of free boundaries. J. Comput. Phys. 39, 201–225. doi: 10.1016/0021-9991(81)90145-5

CrossRef Full Text | Google Scholar

Horgue, P., Augier, F., Duru, P., Prat, M., and Quintard, M. (2013). Experimental and numerical study of two-phase flows in arrays of cylinders. Chem. Eng. Sci. 102, 335–345. doi: 10.1016/j.ces.2013.08.031

CrossRef Full Text | Google Scholar

Hu, R., Wan, J., Kim, Y., and Tokunaga, T. K. (2017). Wettability effects on supercritical co2-brine immiscible displacement during drainage: pore-scale observation and 3d simulation. Int. J. Greenhouse Gas Control 60, 129–139. doi: 10.1016/j.ijggc.2017.03.011

CrossRef Full Text | Google Scholar

Huber, C., Shafei, B., and Parmigiani, A. (2014). A new pore-scale model for linear and non-linear heterogeneous dissolution and precipitation. Geochim. Cosmochim. Acta 124, 109–130. doi: 10.1016/j.gca.2013.09.003

CrossRef Full Text | Google Scholar

Issa, R. I. (1985). Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65. doi: 10.1016/0021-9991(86)90099-9

CrossRef Full Text | Google Scholar

Jackson, M. D., Al-Mahrouqi, D., and Vinogradov, J. (2016). Zeta potential in oil-water-carbonate systems and its impact on oil recovery during controlled salinity water-flooding. Sci. Rep. 6, 1–13. doi: 10.1038/srep37363

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacqmin, D. (1999). Calculation of two-phase Navier-Stokes flows using phase-field modeling. J. Comput. Phys. 155, 96–127. doi: 10.1006/jcph.1999.6332

CrossRef Full Text | Google Scholar

Jahanbakhsh, A., Wlodarczyk, K. L., Hand, D. P., Maier, R. R. J., and Maroto-Valer, M. M. (2020). Review of microfluidic devices and imaging techniques for fluid flow study in porous geomaterials. Sensors 20:4030. doi: 10.3390/s20144030

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, F., and Tsuji, T. (2017). Estimation of three-phase relative permeability by simulating fluid dynamics directly on rock-microstructure images. Water Resour. Res. 53, 11–32. doi: 10.1002/2016WR019098

CrossRef Full Text | Google Scholar

Kang, Q., Chen, L., Valocchi, A. J., and Viswanathan, H. S. (2014). Pore-scale study of dissolution-induced changes in permeability and porosity of porous media. J. Hydrol. 517, 1049–1055. doi: 10.1016/j.jhydrol.2014.06.045

PubMed Abstract | CrossRef Full Text | Google Scholar

Kang, Q., Zhang, D., and Chen, S. (2003). Simulation of dissolution and precipitation in porous media. J. Geophys. Res. Solid Earth 108, 1–5. doi: 10.1029/2003JB002504

CrossRef Full Text | Google Scholar

Kazemifar, F., Blois, G., Kyritsis, D. C., and Christensen, K. T. (2016). Quantifying the flow dynamics of supercritical CO2-water displacement in a 2d porous micromodel using fluorescent microscopy and microscopic PIV. Adv. Water Resour. 95, 352–368. doi: 10.1016/j.advwatres.2015.05.011

CrossRef Full Text | Google Scholar

Kim, Y., Wan, J., Kneafsey, T. J., and Tokunaga, T. K. (2012). Dewetting of silica surfaces upon reactions with supercritical CO2 and brine: pore-scale studies in micromodels. Environ. Sci. Technol. 46, 4228–4235. doi: 10.1021/es204096w

PubMed Abstract | CrossRef Full Text | Google Scholar

Laleian, A., Valocchi, A., and Werth, C. (2015). An incompressible, depth-averaged lattice boltzmann method for liquid flow in microfluidic devices with variable aperture. Computation 3, 600–615. doi: 10.3390/computation3040600

CrossRef Full Text | Google Scholar

Lamb, H. (1906). Hydrodynamics, 3rd Edn. Cambridge: Cambridge University Press.

Google Scholar

Landau, L., and Lifshitz, E. (1987). “Fluid mechanics,” in Course of Theoretical Physics, 2nd Edn, Vol. 6 (Oxford: Pergamon Press Inc.).

Google Scholar

Lenormand, R., Touboul, E., and Zarcone, C. (1988). Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech. 189, 165–187. doi: 10.1017/S0022112088000953

CrossRef Full Text | Google Scholar

Li, X., Huang, H., and Meakin, P. (2008). Level set simulation of coupled advection-diffusion and pore structure evolution due to mineral precipitation in porous media. Water Resour. Res. 44, 1–17. doi: 10.1029/2007WR006742

CrossRef Full Text | Google Scholar

Liu, X., Ormond, A., Bartko, K., Ying, L., and Ortoleva, P. (1997). A geochemical reaction-transport simulator for matrix acidizing analysis and design. J. Petrol. Sci. Eng. 17, 181–196. doi: 10.1016/S0920-4105(96)00064-2

CrossRef Full Text | Google Scholar

Liu, X., and Ortoleva, P. (1996). “A general-purpose, geochemical reservoir simulator,” in SPE Annual Technical Conference and Exhibition (Society of Petroleum Engineers). doi: 10.2118/36700-MS

CrossRef Full Text | Google Scholar

Lucy, L. B. (1977). A numerical approach to the testing of the fission hypothesis. Astron. J. 82, 1013–1024. doi: 10.1086/112164

CrossRef Full Text | Google Scholar

Maes, J., and Geiger, S. (2018). Direct pore-scale reactive transport modelling of dynamic wettability changes induced by surface complexation. Adv. Water Resour. 111, 6–19. doi: 10.1016/j.advwatres.2017.10.032

CrossRef Full Text | Google Scholar

Maes, J., and Menke, H. P. (2020). “A bespoke openfoam toolbox for multiphysics flow simulations in pore structures,” in Proceedings of the 17th International Conference on Flow Dynamics (ICFD2020) (Endinburgh).

Google Scholar

Maes, J., and Soulaine, C. (2018a). “Direct pore-scale modelling of dissolution and trapping of supercritical CO2 in reservoir brine,” in Proceedings of the 16th European Conference on the Mathematics of Oil Recovery (Barcelona). doi: 10.3997/2214-4609.201802238

CrossRef Full Text | Google Scholar

Maes, J., and Soulaine, C. (2018b). A new compressive scheme to simulate species transfer across fluid interfaces using the volume-of-fluid method. Chem. Eng. Sci. 190, 405–418. doi: 10.1016/j.ces.2018.06.026

CrossRef Full Text | Google Scholar

Maes, J., and Soulaine, C. (2020). A unified single-field volume-of-fluid-based formulation for multi-component interfacial transfer with local volume changes. J. Comput. Phys. 402:109024. doi: 10.1016/j.jcp.2019.109024

CrossRef Full Text | Google Scholar

Marschall, H., Hinterberger, K., Schüler, C., Habla, F., and Hinrichsen, O. (2012). Numerical simulation of species transfer across fluid interfaces in free-surface flows using openfoam. Chem. Eng. Sci. 78, 111–127. doi: 10.1016/j.ces.2012.02.034

CrossRef Full Text | Google Scholar

Maxwell, J. C. (1879). VII. On stresses in rarified gases arising from inequalities of temperature. Philos. Trans. R. Soc. Lond. 170, 231–256. doi: 10.1098/rstl.1879.0067

CrossRef Full Text | Google Scholar

McClure, J. E., Berrill, M. A., Gray, W. G., and Miller, C. T. (2016). Tracking interface and common curve dynamics for two-fluid flow in porous media. J. Fluid Mech. 796, 211–232. doi: 10.1017/jfm.2016.212

CrossRef Full Text | Google Scholar

Meakin, P., and Tartakovsky, A. M. (2009). Modeling and simulation of pore-scale multiphase fluid flow and reactive transport in fractured and porous media. Rev. Geophys. 47, 1–47. doi: 10.1029/2008RG000263

CrossRef Full Text | Google Scholar

Menke, H. P., Maes, J., and Geiger, S. (2020). Upscaling the porosity-permeability relationship of a microporous carbonate to the darcy scale with machine learning. Sci. Rep. 11, 1–10. doi: 10.1038/s41598-021-82029-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Moebius, F. Or D. (2012). Interfacial jumps and pressure bursts during fluid displacement in interacting irregular capillaries. J. Colloid Interface Sci. 377, 406–415. doi: 10.1016/j.jcis.2012.03.070

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadmoradi, P., and Kantzas, A. (2017). Toward direct pore-scale modeling of three-phase displacements. Adv. Water Resour. 110, 120–135. doi: 10.1016/j.advwatres.2017.10.010

CrossRef Full Text | Google Scholar

Molins, S., Soulaine, C., Prasianakis, N., Abbasi, A., Poncet, P., Ladd, A., et al. (2020). Simulation of mineral dissolution at the pore scale with evolving fluid-solid interfaces: review of approaches and benchmark problem set. Comput. Geosci. doi: 10.1007/s10596-019-09903-x

CrossRef Full Text | Google Scholar

Molins, S., Trebotich, D., Arora, B., Steefel, C. I., and Deng, H. (2019). Multi-scale model of reactive transport in fractured media: diffusion limitations on rates. Transport Porous Media 128, 701–721. doi: 10.1007/s11242-019-01266-2

CrossRef Full Text | Google Scholar

Molins, S., Trebotich, D., Miller, G. H., and Steefel, C. I. (2017). Mineralogical and transport controls on the evolution of porous media texture using direct numerical simulation. Water Resour. Res. 53, 3645–3661. doi: 10.1002/2016WR020323

CrossRef Full Text | Google Scholar

Molins, S., Trebotich, D., Yang, L., Ajo-Franklin, J. B., Ligocki, T. J., Shen, C., et al. (2014). Pore-scale controls on calcite dissolution rates from flow-through laboratory and numerical experiments. Environ. Sci. Technol. 48, 7453–7460. doi: 10.1021/es5013438

PubMed Abstract | CrossRef Full Text | Google Scholar

Morais, S., Cario, A., Liu, N., Bernard, D., Lecoutre, C., Garrabos, Y., et al. (2020). Studying key processes related to CO₂ underground storage at the pore scale using high pressure micromodels. React. Chem. Eng. 5, 1156–1185. doi: 10.1039/D0RE00023J

CrossRef Full Text | Google Scholar

Navier, C. (1823). Mémoire sur les lois du mouvement des fluides. Mémoires de l'Académie Royale des Sciences de l'Institut de France 6, 389–440.

Google Scholar

Neale, G., and Nader, W. (1974). Practical significance of brinkman's extension of darcy's law: coupled parallel flows within a channel and a bounding porous medium. Can. J. Chem. Eng. 52, 475–478. doi: 10.1002/cjce.5450520407

CrossRef Full Text | Google Scholar

Oltéan, C., Golfier, F., and Bués, M. A. (2013). Numerical and experimental investigation of buoyancy-driven dissolution in vertical fracture. J. Geophys. Res. Solid Earth 118, 2038–2048. doi: 10.1002/jgrb.50188

CrossRef Full Text | Google Scholar

Oostrom, M., Mehmani, Y., Romero-Gomez, P., Tang, Y., Liu, H., Yoon, H., et al. (2016). Pore-scale and continuum simulations of solute transport micromodel benchmark experiments. Comput. Geosci. 20, 857–879. doi: 10.1007/s10596-014-9424-0

CrossRef Full Text | Google Scholar

Ormond, A., and Ortoleva, P. (2000). Numerical modeling of reaction-induced cavities in a porous rock. J. Geophys. Res. Solid Earth 105, 16737–16747. doi: 10.1029/2000JB900116

CrossRef Full Text | Google Scholar

Osselin, F., Kondratiuk, P., Budek, A., Cybulski, O., Garstecki, P., and Szymczak, P. (2016). Microfluidic observation of the onset of reactive-infitration instability in an analog fracture. Geophys. Res. Lett. 43, 6907–6915. doi: 10.1002/2016GL069261

CrossRef Full Text | Google Scholar

Pahlavan, A. A., Cueto-Felgueroso, L., Hosoi, A. E., McKinley, G. H., and Juanes, R. (2018). Thin films in partial wetting: stability, dewetting and coarsening. J. Fluid Mech. 845, 642–681. doi: 10.1017/jfm.2018.255

CrossRef Full Text | Google Scholar

Parmigiani, A., Huber, C., Bachmann, O., and Chopard, B. (2011). Pore-scale mass and reactant transport in multiphase porous media flows. J. Fluid Mech. 686:40. doi: 10.1017/jfm.2011.268

CrossRef Full Text | Google Scholar

Patankar, S. V. (1980). Numerical Heat Transfer and Fluid Flow. Washington, DC: Taylor Francis.

Google Scholar

Pavuluri, S., Maes, J., and Doster, F. (2018). Spontaneous imbibition in a microchannel: analytical solution and assessment of volume of fluid formulations. Microfluid Nanofluid 22, 1–18. doi: 10.1007/s10404-018-2106-9

CrossRef Full Text | Google Scholar

Pavuluri, S., Maes, J., Yang, J., Regaieg, M., Moncorge, A., and Doster, F. (2020). Towards pore network modelling of spontaneous imbibition: contact angle dependent invasion patterns and the occurrence of dynamic capillary barriers. Comput. Geosci. 24, 951–969. doi: 10.1007/s10596-019-09842-7

CrossRef Full Text | Google Scholar

Poonoosamy, J., Soulaine, C., Burmeister, A., Deissmann, G., Bosbach, D., and Roman, S. (2020). Microfluidic flow-through reactor and 3d raman imaging for in situ assessment of mineral reactivity in porous and fractured porous media. Lab Chip. 20, 2562–2571. doi: 10.1039/D0LC00360C

PubMed Abstract | CrossRef Full Text | Google Scholar

Porter, M. L., Jimnez-Martinez, J., Martinez, R., McCulloch, Q., Carey, J. W., and Viswanathan, H. S. (2015). Geo-material microfluidics at reservoir conditions for subsurface energy resource applications. Lab Chip 15, 4044–4053. doi: 10.1039/C5LC00704F

PubMed Abstract | CrossRef Full Text | Google Scholar

Power, O. A., Lee, W. T., Fowler, A. C., Dellar, P. J., Schwartz, L. W., Lukaschuk, S., et al. (2009). “The initiation of guinness,” in Proceedings of the Seventieth European Study Group with Industry, (Limerick: Mathematics Applications Consortium for Science and Industry), 141–182.

Google Scholar

Prasianakis, N. I., Curti, E., Kosakowski, G., Poonoosamy, J., and Churakov, S. V. (2017). Deciphering pore-level precipitation mechanisms. Sci. Rep. 7, 1–9. doi: 10.1038/s41598-017-14142-0

CrossRef Full Text | Google Scholar

Prasianakis, N. I., Rosen, T., Kang, J., Eller, J., Mantzaras, J., and Bichi, F. N. (2013). Simulation of 3D porous media flows with application to polymer electrolyte fuel cells. Commun. Comput. Phys. 13, 851–866. doi: 10.4208/cicp.341011.310112s

CrossRef Full Text | Google Scholar

Prutton, C., and Savage, R. (1945). The solubility of carbon dioxide in calcium chloride-water solutions at 75, 100, 120 and high pressures. J. Am. Chem. Soc. 67, 1550–1554. doi: 10.1021/ja01225a047

CrossRef Full Text | Google Scholar

Qin, Z., Esmaeilzadeh, S., Riaz, A., and Tchelepi, H. A. (2020). Two-phase multiscale numerical framework for modeling thin films on curved solid surfaces in porous media. J. Comput. Phys. 413:109464. doi: 10.1016/j.jcp.2020.109464

CrossRef Full Text | Google Scholar

Raeini, A. Q., Blunt, M. J., and Bijeljic, B. (2014). Direct simulations of two-phase flow on micro-CT images of porous media and upscaling of pore-scale forces. Adv. Water Resour. 74, 116–126. doi: 10.1016/j.advwatres.2014.08.012

CrossRef Full Text | Google Scholar

Ray, N., Oberlander, J., and Frolkovic, P. (2019). Numerical investigation of a fully coupled micro-macro model for mineral dissolution and precipitation. Comput. Geosci. 23, 1173–1192. doi: 10.1007/s10596-019-09876-x

CrossRef Full Text | Google Scholar

Roman, S., Abu-Al-Saud, M. O., Tokunaga, T., Wan, J., Kovscek, A. R., and Tchelepi, H. A. (2017). Measurements and simulation of liquid films during drainage displacements and snap-off in constricted capillary tubes. J. Colloid Interface Sci. 507, 279–289. doi: 10.1016/j.jcis.2017.07.092

PubMed Abstract | CrossRef Full Text | Google Scholar

Roman, S., Soulaine, C., AlSaud, M. A., Kovscek, A., and Tchelepi, H. (2016). Particle velocimetry analysis of immiscible two-phase flow in micromodels. Adv. Water Resour. 95, 199–211. doi: 10.1016/j.advwatres.2015.08.015

CrossRef Full Text | Google Scholar

Roman, S., Soulaine, C., and Kovscek, A. (2020). Pore-scale visualization and characterization of viscous dissipation in porous media. J. Colloid Interface Sci. 558, 269–279. doi: 10.1016/j.jcis.2019.09.072

PubMed Abstract | CrossRef Full Text | Google Scholar

Rose, W. (2000). Myths about later-day extensions of Darcy's law. J. Petrol. Sci. Eng. 26, 187–198. doi: 10.1016/S0920-4105(00)00033-4

CrossRef Full Text | Google Scholar

Scardovelli, R., and Zaleski, S. (1999). Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 31, 567–603. doi: 10.1146/annurev.fluid.31.1.567

CrossRef Full Text | Google Scholar

Scheibe, T. D., Perkins, W. A., Richmond, M. C., McKinley, M. I., Romero-Gomez, P. D. J., Oostrom, M., et al. (2015). Pore-scale and multiscale numerical simulation of flow and transport in a laboratory-scale column. Water Resour. Res. 51, 1023–1035. doi: 10.1002/2014WR015959

CrossRef Full Text | Google Scholar

Singh, K., Menke, H. P., Andrew, M., Rau, C., Bijeljic, B., and Blunt, M. J. (2018). Time-resolved synchrotron x-ray micro-tomography datasets of drainage and imbibition in carbonate rocks. Sci. Data 5:180265. doi: 10.1038/sdata.2018.265

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, W., de Haas, T. W., Fadaei, H., and Sinton, D. (2014). Chip-off-the-old-rock: the study of reservoir-relevant geological processes with real-rock micromodels. Lab Chip 14, 4382–4390. doi: 10.1039/C4LC00608A

PubMed Abstract | CrossRef Full Text | Google Scholar

Soulaine, C., Creux, P., and Tchelepi, H. A. (2019). Micro-continuum framework for pore-scale multiphase fluid transport in shale formations. Transport Porous Media 127, 85–112 doi: 10.1007/s11242-018-1181-4

CrossRef Full Text | Google Scholar

Soulaine, C., Davit, Y., and Quintard, M. (2013). A two-pressure model for slightly compressible single phase flow in bi-structured porous media. Chem. Eng. Sci. 96, 55–70. doi: 10.1016/j.ces.2013.03.060

CrossRef Full Text | Google Scholar

Soulaine, C., Gjetvaj, F., Garing, C., Roman, S., Russian, A., Gouze, P., et al. (2016). The impact of sub-resolution porosity of x-ray microtomography images on the permeability. Transport Porous Media 113, 227–243. doi: 10.1007/s11242-016-0690-2

CrossRef Full Text | Google Scholar

Soulaine, C., Pavuluri, S., Claret, F., and Tournassat, C. (2021). porousMedia4Foam: multi-scale open-source platform for hydro-geochemical simulations with OpenFOAM. Earth Space Sci. Open Arch. 1–23. doi: 10.1002/essoar.10505772.1

CrossRef Full Text | Google Scholar

Soulaine, C., Roman, S., Kovscek, A., and Tchelepi, H. A. (2017). Mineral dissolution and wormholing from a pore-scale perspective. J. Fluid Mech. 827, 457–483. doi: 10.1017/jfm.2017.499

CrossRef Full Text | Google Scholar

Soulaine, C., Roman, S., Kovscek, A., and Tchelepi, H. A. (2018). Pore-scale modelling of multiphase reactive flow. Application to mineral dissolution with production of CO₂. J. Fluid Mech. 855, 616–645. doi: 10.1017/jfm.2018.655

CrossRef Full Text | Google Scholar

Soulaine, C., and Tchelepi, H. A. (2016). Micro-continuum approach for pore-scale simulation of subsurface processes. Transport Porous Media 113, 431–456. doi: 10.1007/s11242-016-0701-3

CrossRef Full Text | Google Scholar

Spanne, P., Thovert, J., Jacquin, C., Lindquist, W., Jones, K., and Adler, P. (1994). Synchrotron computed microtomography of porous media: topology and transports. Phys. Rev. Lett. 73:2001. doi: 10.1103/PhysRevLett.73.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Starchenko, V., Marra, C. J., and Ladd, A. J. (2016). Three-dimensional simulations of fracture dissolution. J. Geophys. Res. Solid Earth 121, 6421–6444. doi: 10.1002/2016JB013321

CrossRef Full Text | Google Scholar

Starov, V. M., Velarde, M. G., and Radke, C. J. (2007). Wetting and Spreading Dynamics. Boca Raton, FL: CRC Press. doi: 10.1201/9781420016178

CrossRef Full Text | Google Scholar

Steefel, C. I., Beckingham, L. E., and Landrot, G. (2015). Micro-continuum approaches for modeling pore-scale geochemical processes. Rev. Mineral Geochem. 80, 217–246. doi: 10.1515/9781501502071

CrossRef Full Text | Google Scholar

Steefel, C. I., DePaolo, D. J., and Lichtner, P. C. (2005). Reactive transport modeling: an essential tool and a new research approach for the earth sciences. Earth Planet. Sci. Lett. 240, 539–558. doi: 10.1016/j.epsl.2005.09.017

CrossRef Full Text | Google Scholar

Succi, S. (2002). Mesoscopic modeling of slip motion at fluid-solid interfaces with heterogeneous catalysis. Phys. Rev. Lett. 89:064502. doi: 10.1103/PhysRevLett.89.064502

PubMed Abstract | CrossRef Full Text | Google Scholar

Sussman, M., Smereka, P., and Osher, S. (1994). A level-set approach for computing solutions to incompressible tow-phase flow. J. Comput. Phys. 114, 146–159. doi: 10.1006/jcph.1994.1155

CrossRef Full Text | Google Scholar

Szymczak, P., and Ladd, A. (2009). Wormhole formation in dissolving fractures. J. Geophys. Res. Solid Earth 114, 1–22. doi: 10.1029/2008JB006122

CrossRef Full Text | Google Scholar

Tartakovsky, A., and Meakin, P. (2005). Modeling of surface tension and contact angles with smoothed particle hydrodynamics. Phys. Rev. E 72:026301. doi: 10.1103/PhysRevE.72.026301

PubMed Abstract | CrossRef Full Text | Google Scholar

Tartakovsky, A. M., Meakin, P., Scheibe, T. D., and West, R. M. E. (2007). Simulations of reactive transport and precipitation with smoothed particle hydrodynamics. J. Comput. Phys. 222, 654–672. doi: 10.1016/j.jcp.2006.08.013

CrossRef Full Text | Google Scholar

Tartakovsky, A. M., and Panchenko, A. (2016). Pairwise force smoothed particle hydrodynamics model for multiphase flow: surface tension and contact line dynamics. J. Comput. Phys. 305, 1119–1146. doi: 10.1016/j.jcp.2015.08.037

CrossRef Full Text | Google Scholar

Tartakovsky, A. M., Tartakovsky, D. M., Scheibe, T. D., and Meakin, P. (2008). Hybrid simulations of reaction-diffusion systems in porous media. SIAM J. Sci. Comput. 30, 2799–2816. doi: 10.1137/070691097

CrossRef Full Text | Google Scholar

Taylor, G. (1953). Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. Ser. A Math. Phys. 219, 186–203. doi: 10.1098/rspa.1953.0139

CrossRef Full Text | Google Scholar

Thompson, K., and Gdanski, R. (1993). Laboratory study provides guidelines for diverting acid with foam. SPE Product. Facil. 8, 285–290. doi: 10.2118/23436-PA

CrossRef Full Text | Google Scholar

Vacondio, R., Altomare, C., Leffe, M. D., Hu, X., Touzé, D. L., Lind, S., et al. (2020). Grand challenges for smoothed particle hydrodynamics numerical schemes. Comp. Part. Mech. 1–14. doi: 10.1007/s40571-020-00354-1

CrossRef Full Text | Google Scholar

van Kats, F. M., and Egberts, P. J. P. (1999). Simulation of three-phase displacement mechanisms using a 2d lattice-boltzmann model. Transport Porous Media 37, 55–68. doi: 10.1023/A:1006502831641

CrossRef Full Text | Google Scholar

Vasil'ev, A. (2009). From the Hele-Shaw experiment to integrable systems: a historical overview. Complex Anal. Operator Theory 3, 551–585. doi: 10.1007/s11785-008-0104-8

CrossRef Full Text | Google Scholar

Venturoli, M., and Boek, E. S. (2006). Two-dimensional lattice-boltzmann simulations of single phase flow in a pseudo two-dimensional micromodel. Phys. A Stat. Mech. Appl. 362, 23–29. doi: 10.1016/j.physa.2005.09.006

CrossRef Full Text | Google Scholar

Voinov, O. (1976). Hydrodynamics of wetting. Fluid Dyn. 11, 714–721. doi: 10.1007/BF01012963

CrossRef Full Text | Google Scholar

Wan, J., Kim, Y., and Tokunaga, T. K. (2014). Contact angle measurement ambiguity in supercritical CO2-water-mineral systems: mica as an example. Int. J. Greenhouse Gas Control 31, 128–137. doi: 10.1016/j.ijggc.2014.09.029

CrossRef Full Text | Google Scholar

Watson, F., Maes, J., Geiger, S., Mackay, E., Singleton, M., McGravie, T., et al. (2019). Comparison of flow and transport experiments on 3d printed micromodels with direct numerical simulations. Transport Porous media 129, 449–466. doi: 10.1007/s11242-018-1136-9

CrossRef Full Text | Google Scholar

Wen, H., and Li, L. (2017). An upscaled rate law for magnesite dissolution in heterogeneous porous media. Geochim. Cosmochim. Acta 210, 289–305. doi: 10.1016/j.gca.2017.04.019

CrossRef Full Text | Google Scholar

Whitaker, S. (1999). The Method of Volume Averaging, Theory and Applications of Transport in Porous Media. Dorderecht: Kluwer Academic. doi: 10.1007/978-94-017-3389-2

CrossRef Full Text | Google Scholar

Willingham, T. W., Werth, C. J., and Valocchi, A. J. (2008). Evaluation of the effects of porous media structure on mixing-controlled reactions using pore-scale modeling and micromodel experiments. Environ. Sci. Technol. 42, 3185–3193. doi: 10.1021/es7022835

PubMed Abstract | CrossRef Full Text | Google Scholar

Wörner, M. (2012). Numerical modeling of multiphase flows in microfluidics and micro process engineering: a review of methods and applications. Microfluid. Nanofluid. 12, 841–886. doi: 10.1007/s10404-012-0940-8

CrossRef Full Text | Google Scholar

Xu, Z., and Meakin, P. (2008). Phase-field modeling of solute precipitation and dissolution. J. Chem. Phys. 129:014705. doi: 10.1063/1.2948949

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Z., and Meakin, P. (2011). Phase-field modeling of two-dimensional solute precipitation/dissolution: solid fingers and diffusion-limited precipitation. J. Chem. Phys. 134:044137. doi: 10.1063/1.3537973

CrossRef Full Text | Google Scholar

Yang, L., Nieves-Remacha, M. J., and Jensen, K. F. (2017). Simulations and analysis of multiphase transport and reaction in segmented flow microreactors. Chem. Eng. Sci. 169, 106–116. doi: 10.1016/j.ces.2016.12.003

CrossRef Full Text | Google Scholar

Yesufu-Rufai, S., Rcker, M., Berg, S., Lowe, S. F., Marcelis, F., Georgiadis, A., et al. (2020). Assessing the wetting state of minerals in complex sandstone rock in-situ by atomic force microscopy (AFM). Fuel 273:117807. doi: 10.1016/j.fuel.2020.117807

CrossRef Full Text | Google Scholar

Yoon, H., Chojnicki, K. N., and Martinez, M. J. (2019). Pore-scale analysis of calcium carbonate precipitation and dissolution kinetics in a microfluidic device. Environ. Sci. Technol. 53, 14233–14242. doi: 10.1021/acs.est.9b01634

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoon, H., Kang, Q., and Valocchi, A. J. (2015). Lattice Boltzmann-based approaches for pore-scale reactive transport. Rev. Mineral. Geochem. 80, 393–431. doi: 10.2138/rmg.2015.80.12

CrossRef Full Text | Google Scholar

Yoon, H., Valocchi, A. J., Werth, C. J., and Dewers, T. (2012). Pore-scale simulation of mixing-induced calcium carbonate precipitation and dissolution in a microfluidic pore network. Water Resour. Res. 48:W02524. doi: 10.1029/2011WR011192

CrossRef Full Text | Google Scholar

Yun, W., Chang, S., Cogswell, D. A., Eichmann, S. L., Gizzatov, A., Thomas, G., et al. (2020). Toward reservoir-on-a-chip: rapid performance evaluation of enhanced oil recovery surfactants for carbonate reservoirs using a calcite-coated micromodel. Sci. Rep. 10, 1–12. doi: 10.1038/s41598-020-57485-x

CrossRef Full Text | Google Scholar

Zarikos, I., Terzis, A., Hassanizadeh, S. M., and Weigand, B. (2018). Velocity distributions in trapped and mobilized non-wetting phase ganglia in porous media. Sci. Rep. 8, 1–11. doi: 10.1038/s41598-018-31639-4

CrossRef Full Text | Google Scholar

Zhang, C., Liu, C., and Shi, Z. (2013). Micromodel investigation of transport effect on the kinetics of reductive dissolution of hematite. Environ. Sci. Technol. 47, 4131–4139. doi: 10.1021/es304006w

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, B., MacMinn, C. W., and Juanes, R. (2016). Wettability control on multiphase flow in patterned microfluidics. Proc. Natl. Acad. Sci. U.S.A. 113, 10251–10256. doi: 10.1073/pnas.1603387113

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, B., MacMinn, C. W., Primkulov, B. K., Chen, Y., Valocchi, A. J., Zhao, J., et al. (2019). Comprehensive comparison of pore-scale models for multiphase flow in porous media. Proc. Natl. Acad. Sci. U.S.A. 116, 13799–13806. doi: 10.1073/pnas.1901619116

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, B., Pahlavan, A. A., Cueto-Felgueroso, L., and Juanes, R. (2018). Forced wetting transition and bubble pinch-off in a capillary tube. Phys. Rev. Lett. 120, 1–9. doi: 10.1103/PhysRevLett.120.084501

PubMed Abstract | CrossRef Full Text | Google Scholar