Modeling of Thermal-Hydrological-Chemical (THC) Processes During Waste Rock Weathering Under Permafrost Conditions

The oxidation of sulfide minerals such as pyrite present in waste rock results in elevated sulfate, enhanced metal loadings and in many cases low pH conditions. Recently, many mines have opened in remote areas, including regions subject to permafrost conditions. In these regions, freeze-thaw cycles and the possible development of permafrost in mine waste add to the complexity of weathering processes, drainage volumes and mass loadings. To assess weathering in these waste rock piles, the reactive transport code MIN3P-HPC has been enhanced by implementing constitutive relationships related to freeze-thaw cycles that control flow patterns, solute transport, generation and transport of heat, as well as geochemical reactions and their rates. Simulations of a hypothetical pyrite-rich waste rock pile placed onto natural permafrost were conducted under reference climate conditions. Additionally, the effect of a warming climate was also studied through a sensitivity analysis. The simulation results indicate a potentially strong coupled effect of sulfide mineral weathering rates and a warming climate on the evolution and persistence of permafrost within waste rock piles and the release of acidic drainage. For relatively low sulfide mineral oxidation rates, the simulations indicate that permafrost can develop within waste rock piles, even under warming climate conditions. However, the results for low reactivity also show that mass loadings can increase by >50% in response to a slight warming of climate (3°C), relative to reference climate conditions. For the chosen reference reaction rates, permafrost develops under reference climate conditions in the simulated waste rock pile; however, permafrost cannot be maintained for a marginally warmer climate, leading to internal heating of the pile and substantially increased production of acidic drainage (>550%). For high reaction rates, the simulations suggest that internal heating takes place irrespective of climate conditions. Evaluation of thermal covers indicates that significant reductions of mass loadings can be achieved for piles with low and reference reactivity (91–99% in comparison to uncovered piles), but also suggest that thermal covers can be ineffective for piles with high sulfide content and reactivity. Together, these simulations provide insights into the complex interactions controlling waste rock weathering in cold-region climates.

Introduction

Mining activities can produce large amounts of waste rock which is commonly stored at the surface in partially water-saturated, porous stockpiles (Amos et al., 2012). When sulfide minerals such as pyrite are present, waste rock piles (WRPs) have the potential to generate acid rock drainage (ARD), characterized by high concentrations of sulfate, low pH, and metals (Lefebvre et al., 2001). Even in regions with cold and long winters, internal heating can be observed in WRPs (Gélinas et al., 1994), identified by localized high temperatures as high as 70°C, sparked by the exothermic oxidation of sulfide minerals. Resulting temperature gradients tend to draw more oxygen into the permeable material, which fuels further pyrite oxidation and additional heat generation (Lefebvre et al., 2001). However, it is more common to observe a frozen core within WRPs in cold regions, where low temperatures slow down the oxidation kinetics and also limit contaminant migration (MEND, 1996; Elberling et al., 2000; Neuner et al., 2013; Pham, 2013).

Within cold regions, the subsurface is often subject to permafrost, implying that soils remain perennially frozen for at least 2 consecutive years due to sub-zero average annual temperatures (Woo, 2012; Bell and Brown, 2018). However, seasonal thawing is experienced within the top layer of soils, facilitating the formation of an active layer (also termed as “seasonally frozen ground” or “annually thawed layer”). The thickness of this active layer depends on soil properties and climatic conditions (Figure 1) (Dobinski, 2011; Woo, 2012). The active layer controls near-surface water drainage pathways and water storage (Walvoord and Kurylyk, 2016). Permafrost extends from the base of the active layer to the depth where geothermal heat flux maintains ground temperature above freezing (Woo, 2012).

FIGURE 1

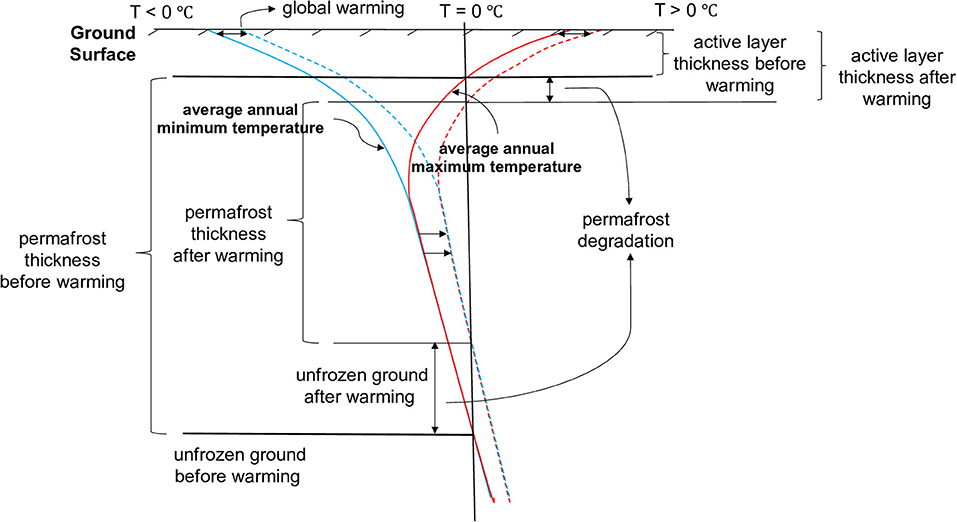
Figure 1. Permafrost degradation induced by a warming climate. Modified after Dobinski (2011). Dashed lines represent the temperature profiles for warmer climate conditions; an increase in temperature leads to permafrost degradation and an increase in active layer thickness.

Recent research in cold regions has revealed impacts of warming climate trends on permafrost stability. Specifically, increased temperatures can contribute to warming soil temperatures, increased active layer thickness, and thawing of underlying permafrost, termed “permafrost degradation” (Dobinski, 2011). If occurring in waste rock, an increase in active layer thickness can directly affect acid generation and water drainage from WRPs (MEND, 2011; Walvoord and Kurylyk, 2016; Rasmussen et al., 2018).

To evaluate the influences of climate change on flow and thermal regimes of WRPs located within permafrost regions, reactive transport modeling provides a versatile tool for analyzing the relevant coupled thermo-hydrological-chemical processes. Several reactive transport models have been developed or enhanced to simulate dynamic freeze-and-thaw processes in permafrost regions and have been applied at a range of sites (Zhao et al., 1997; Hansson et al., 2004; McKenzie et al., 2007; Li et al., 2008; Voss and Provost, 2010; Kurylyk and Watanabe, 2013; Walvoord and Kurylyk, 2016). However, few modeling studies have assessed processes controlling the evolution of mine waste in permafrost regions. To this end, our study aims to improve the understanding of strongly coupled hydrological, geochemical, and heat transport processes within WRPs in permafrost regions. Specific objectives of this work include: (1) development of capabilities for simulating freeze-thaw cycling in WRPs; (2) characterizing the potential impacts of various warming climate scenarios on WRP weathering and mass loadings; (3) assessment of the reactivity of sulfide minerals on mass loadings under reference and warming climate conditions; and (4) conceptual evaluation of cover reclamation approaches to limit ARD. Model results presented in this study were simulated using the multicomponent reactive transport code MIN3P-HPC (Mayer et al., 2002; Su et al., 2020a), which was enhanced as part of this work to include the effect of freeze-thaw cycles on flow, transport and reaction processes in order to meet these objectives.

Conceptual Model

The conceptual models in Figure 2 bracket the processes that can occur within sulfidic mine waste rock in permafrost environments with different outcomes. WRPs are often constructed above a layer of low-permeability material, which ensures that drainage water released from the mine waste is captured for treatment (Piteau Associates Engineering Ltd, 1991; Smith et al., 1995, 2013). The conceptual model in Figure 2A depicts a case with high sulfide mineral reactivity, leading to internal heating, thereby avoiding the development of permafrost within the pile. Sulfide mineral oxidation can be described by the following equation:

$\begin{array}{ll}{\text{FeS}}_2+3.{5\text{O}}_2+{\text{H}}_2\text{O }\to {\text{Fe}}^{2+}+2{\text{SO}}_4^{2-}+2{\text{H}}^{+}& (1)\end{array}$

Pyrite oxidation is strongly exothermic; in some instances, causing internal heat production, leading to temperature gradients driving heat conduction toward the surface of the pile. Another heat transfer mechanism in such WRPs is heat convection with pore water and pore gas, which is often seasonally controlled. Under arid conditions, the relatively low humidity in the atmosphere can lead to internal drying and removal of pore water by evaporation (Bea et al., 2012), while infiltration of relatively cold meteoric water may also affect the energy balance of a WRP.

FIGURE 2

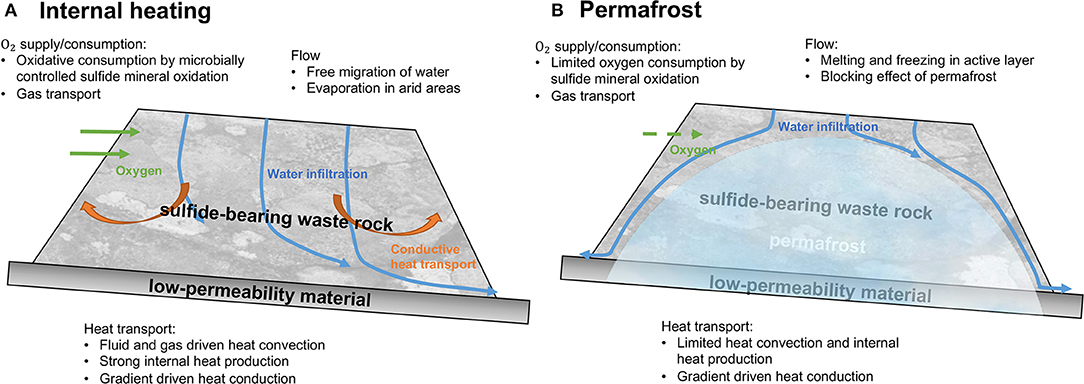
Figure 2. Coupled processes occurring within a waste rock pile for (A) internal heating and (B) permafrost conditions. Modified after Lefebvre et al. (2001) and Amos et al. (2015).

If heat production by pyrite oxidation is insufficient to cause substantial internal heating, permafrost can develop in cold regions. In this case, WRPs show different behavior in terms of pyrite oxidation, heat transfer, flow of water, and solute transport (Figure 2B). The presence of permafrost is often conceptualized as an impermeable barrier that inhibits deep infiltration and alters internal water routing (Walvoord and Kurylyk, 2016). Permafrost can be present in the core of a WRP, as shown in Figure 2B, while waste rock near the surface is subject to freeze-thaw cycles, hosting an active layer (Collette, 2017). In the active layer, water can flow freely during the warm season, but becomes immobile when frozen during the cold season. Since movement of water is both spatially and temporally constrained, release of reaction products from sulfide mineral oxidation is also more limited. Although heat production and convection are more limited due to restricted pyrite oxidation and limited water flow, respectively, heat conduction still can be driven by temperature gradients – especially during periods when the pile surface is heated during the summer months, while the pile core remains frozen.

Methodology

Model Development

MIN3P-HPC (Mayer et al., 2002; Su et al., 2020a) is a general purpose multicomponent reactive transport code designed for multi-dimensional and variably-saturated porous media. The code contains previous developments, including simulation capabilities for density dependent flow and heat transport (Henderson et al., 2009, Bea et al., 2012, 2016), in addition to basic reactive transport capabilities (Mayer et al., 2002). Recently parallel computing and unstructured grid capabilities have been added to the code (Su et al., 2020a). A brief summary of the governing equations of the MIN3P-HPC code is provided below with specific focus on the key model components, including variably saturated flow, multi-component reactive transport, and energy balance equations. Additional details can be found in Mayer et al. (2002), Henderson et al. (2009), Bea et al. (2012), and Su et al. (2017, 2020a,b). The code has been extensively applied to address problems related to environmental aspects of mine waste (Bea et al., 2012; Demers et al., 2013; Wilson et al., 2018b; Raymond et al., 2020; Seigneur et al., 2021).

For this study, several constitutive relationships were implemented to account for the effect of freeze-thaw cycles on flow, transport, and reaction processes. Parameters influenced by freeze-thaw cycles include hydraulic conductivity, kinetic rate coefficients, and specified heat sinks and sources. Although phase transformation between ice and water was not explicitly included, the code distinguishes between ice and water as a function of a user-specified freezing point. In addition, implementation of transient thermal boundary conditions facilitates capturing freeze-thaw cycles driven by seasonal temperature variations. These relationships are described in more detail below.

Variably-Saturated Flow Equation

The implementation of flow is based on the formulation of Richards equation (Richards, 1931):

$\begin{array}{ll}{\text{S}}_{\text{a}}{\text{S}}_{\text{s}}\frac{\text{∂h}}{\text{∂t}}+\text{ϕ}\frac{\text{∂}{\text{S}}_{\text{a}}}{\text{∂t}}=\nabla ·\left[{\text{k}}_{\text{ra}}\text{K}\nabla \text{h}\right]+{\text{Q}}_{\text{a}}& (2)\end{array}$

where t [T] is time, ϕ [L³ void L⁻³ porous medium] is porosity ${\text{S}}_{\text{a}}\left[{\text{L}}^3{\text{water L}}^{-3}\text{ void}\right]$ is the saturation of the aqueous phase (here including ice and water), ${\text{S}}_{\text{s}}\left[{\text{L}}^{-1}\right]$ is the specific storage coefficient, h [L] is hydraulic head, K [LT⁻¹] is the temperature-dependent hydraulic conductivity tensor, k_ra [-] is the relative permeability of the porous medium with respect to the aqueous phase, and Q_a [T⁻¹] is a source-sink term. The non-linear relationships between S_a, k_ra, and pressure head ψ_a = h−z [L] are accounted for through the functions given by Wösten and van Genuchten (1988):

$\begin{array}{lll}{\text{S}}_{\text{a}}& ={\text{S}}_{\text{ra}}+\frac{1-{\text{S}}_{\text{ra}}}{{(1+\text{α}{\text{ψ}}_{\text{a}}^{\text{n}})}^{\text{m}}}& (3)\end{array}$

$\begin{array}{ll}{\text{k}}_{\text{ra}}={\text{S}}_{\text{ea}}^{\text{l}}{\left[1-{\left(1-{{\text{S}}_{\text{ea}}^{\text{l}}}^{\frac{1}{\text{m}}}\right)}^{\text{m}}\right]}^2& (4)\end{array}$

where z is the elevation with respect to a given datum. S_ra [-] defines the residual saturation of the aqueous phase. α [L⁻¹], m, n, l are the soil hydraulic function parameters with m defined by m = 1−1/n. S_ea defines the effective saturation of the aqueous phase defined by:

$\begin{array}{ll}{\text{S}}_{\text{ea}}=\frac{{\text{S}}_{\text{a}}-{\text{S}}_{\text{ra}}}{1-{\text{S}}_{\text{ra}}}& (5)\end{array}$

Phase transformations between water and ice are not considered in the current formulation. Instead, the current formulation accounts for the effect of freezing by drastically reducing the hydraulic conductivities (see for details below). For illustrate purposes, the code distinguishes between ice and water saturations. Aqueous phase saturations are reported as water saturations S_w [-] above freezing, while they are reported as ice saturations S_ice [-] below freezing.

Reactive Transport Equations

The mass conservation equations for multicomponent reactive transport can be written as Mayer et al. (2002):

$\begin{array}{l}\frac{\text{∂}}{\text{∂t}}\left[{\text{S}}_{\text{a}}\text{ϕ}{\text{T}}_{\text{j}}^{\text{a}}\right]+\frac{\text{∂}}{\text{∂t}}\left[{\text{S}}_{\text{g}}\text{ϕ}{\text{T}}_{\text{j}}^{\text{g}}\right]+\frac{\text{∂}{\text{T}}_{\text{j}}^{\text{s}}}{\text{∂t}}+\nabla ·\left[{\text{q}}_{\text{a}}{\text{T}}_{\text{j}}^{\text{a}}\right]\\ -\nabla ·\left[{\text{S}}_{\text{a}}\text{ϕ}{\text{D}}_{\text{a}}{\nabla \text{T}}_{\text{j}}^{\text{a}}\right]-\nabla ·\left[{\text{S}}_{\text{g}}\text{ϕ}{\text{D}}_{\text{g}}{\nabla \text{T}}_{\text{j}}^{\text{g}}\right]-{\text{Q}}_{\text{j}}^{\text{a},\text{m}}\\ -{\text{Q}}_{\text{j}}^{\text{a},\text{ext}}-{\text{Q}}_{\text{j}}^{\text{g},\text{ext}}=0\text{ i}=1,{\text{N}}_{\text{c}}& (6)\end{array}$

where ${\text{S}}_{\text{g}}\left[{\text{L}}^3\text{ gas }{\text{L}}^{-3}\text{ void}\right]$ is the saturation of the gaseous phase, ${\text{T}}_{\text{j}}^{\text{a}}\left[\text{mol }{\text{L}}^{-3}{\text{H}}_2\text{O}\right]$ and ${\text{T}}_{\text{j}}^{\text{g}}\left[\text{mol }{\text{L}}^{-3}\text{gas}\right]$ are the total aqueous and gaseous component concentrations for component ${\text{A}}_{\text{j}}^{\text{c}}$, ${\text{T}}_{\text{j}}^{\text{s}}$ [mol L⁻³ bulk] are the total concentration of adsorbed species. q_a is the aqueous phase flux [LT⁻¹], D_a [L²T⁻¹] and D_g [L²T⁻¹] are the dispersion and diffusion tensors for the aqueous and gaseous phases, respectively. In this context, free phase diffusion coefficients for each phase are scaled by using ${\text{D}}_{\text{p}}={\text{τ}}_{\text{p}}{\text{D}}_{\text{p}}^0,$ in which p represents the phase, ${\text{D}}_{\text{p}}^0$ [L²T⁻¹] is the free-phase diffusion coefficient, and τ_p[-] is the phase-dependent tortuosity factor calculated after Millington (1959) (${\tau }_{\text{p}}={\text{S}}_{\text{p}}^{7/3}{\varphi }^{1/3}$. The scaled diffusion coefficients enter the dispersion and diffusion tensors D_a and D_g in Equation (6). ${\text{Q}}_{\text{j}}^{\text{a},\text{m}}$ [mol L⁻³ T⁻¹] is an internal source-sink term toward the total aqueous component concentrations due to kinetically controlled dissolution-precipitation reactions. ${\text{Q}}_{\text{j}}^{\text{a},\text{ext}}\text{ and }{\text{Q}}_{\text{j}}^{\text{g},\text{ext}}$ [mol L⁻³ T⁻¹] are external source-sink terms for the aqueous and gaseous phases, respectively. N_c defines the number of components in the system. Additional mass conservation equations used to describe the change of mineral quantities over time are defined by:

$\begin{array}{ll}\frac{\text{d}{\text{φ}}_{\text{i}}}{\text{dt}}={\text{V}}_{\text{i}}^{\text{m}}{\text{R}}_{\text{i}}^{\text{m}}\text{ i}=1,{\text{N}}_{\text{m}}& (7)\end{array}$

where φ_i [L³ mineral L⁻³ porous medium] is the volume fraction of the mineral, ${\text{V}}_{\text{i}}^{\text{m}}$ and ${\text{R}}_{\text{i}}^{\text{m}}$are the molar volume of the mineral [L³mineral mol⁻¹] and the corresponding overall dissolution-precipitation rate for the mineral [mol L⁻³porous medium T⁻¹]. N_m defines the number of minerals in the system.

Energy Balance Equation

The energy balance equation in MIN3P-HPC has been implemented by Bea et al. (2012) and is coupled with both the variably-saturated flow equation and the reactive transport equations:

$\begin{array}{l}\frac{\text{∂ϕ}{\text{c}}_{\text{a}}{\text{S}}_{\text{a}}{\text{ρ}}_{\text{a}}\text{T}}{\text{∂t}}+\frac{\text{∂ϕ}{\text{c}}_{\text{g}}{\text{S}}_{\text{g}}{\text{ρ}}_{\text{g}}\text{T}}{\text{∂t}}+\frac{\text{∂}(1-\text{ϕ}){\text{c}}_{\text{s}}{\text{ρ}}_{\text{s}}\text{T}}{\text{∂t}}+\frac{\text{∂}{\text{L}}_{\text{w}}\text{ϕ}{\text{S}}_{\text{g}}{\text{ρ}}_{\text{g}}}{\text{∂t}}\\ =\nabla ·{\text{J}}_{\text{e}}+{\text{Q}}_{\text{e}}^{\text{m}}& (8)\end{array}$

where ${\text{c}}_{\text{a}},{\text{c}}_{\text{g}},\text{and }{\text{c}}_{\text{s}}\left[\text{E }{\text{M}}^{-1}{\text{Θ}}^{-1}\right]$ are the heat capacities for aqueous, gaseous and solid phases, respectively, ${\text{L}}_{\text{w}}\left[\text{E }{\text{M}}^{-1}\right]$ is the latent heat of vaporization for water as a function of temperature T, ρ_gand ${\text{ρ}}_{\text{s}}\left[\text{M }{\text{L}}^{-3}\right]$ are the densities of gaseous and solid phases, $\nabla ·{\text{J}}_{\text{e}}\text{ and }{\text{Q}}_{\text{e}}^{\text{m}}\left[\text{E }{\text{L}}^{-3}{\text{T}}^{-1}\right]$ define the energy flux and the energy source-sink term due to heat production or consumption by mineral reactions. Details on the components of the energy flux can be found in Bea et al. (2012).

No attempt was made to distinguish between the energy fluxes and storage in water and ice due to the relatively low average ice and water contents relative to the solid phase content. The contribution of ice-water phase transition on the energy balance was not included explicitly due to its reversible nature that induces negligible impacts in the long-term behavior, and limited energy adsorption or production from melting or freezing in comparison to other energy transfer processes in the pile (e.g., heat production from pyrite oxidation).

Temperature-Dependent Constitutive Relationships

Freezing can result in a significant reduction in flow rates due to the formation of ice and blocking of flow channels. The cessation of flow as a function of freezing can be captured by a reduction of hydraulic conductivity as a surrogate for phase transformation (Azmatch et al., 2012; Zhao et al., 2013). Furthermore, the transition from unfrozen to frozen conditions occurs gradually over a temperature range, rather than following a sharp phase change (McCauley et al., 2002; Walvoord and Kurylyk, 2016). To capture these effects, the following relationship was modified based on Henderson et al. (2009) and Bea et al. (2012) and used to correct hydraulic conductivities as a function of temperature:

$\begin{array}{c}\text{β}={\text{β}}_{max}=1\text{ for T}>{\text{T}}_{\text{c}}\\ \text{K}=\text{β}\frac{\text{k}{\text{ρ}}_{\text{a}}\text{g}}{{\text{μ}}_{\text{a}}}\text{ with β}=\frac{({\text{β}}_{max}+{\text{β}}_{min})}{2}sin\left(\left(\frac{\text{π}}{{\text{T}}_{\text{c}}-{\text{T}}_{\text{m}}}\right)\left(\text{T}-\frac{({\text{T}}_{\text{c}}+{\text{T}}_{\text{m}})}{2}\right)\right)\\ +\frac{({\text{β}}_{max}+{\text{β}}_{min})}{2}\text{ for }{\text{T}}_{\text{m}}\le \text{T}\le {\text{T}}_{\text{c}}\\ \text{β}={\text{β}}_{min}=10^{-6}\text{ for T}<{\text{T}}_{\text{m}}& (9)\end{array}$

where T, T_c, T_m [Θ] are the current temperature, the temperature when water starts to freeze, and the temperature when all water is completely frozen; β [-] is the freezing correction coefficient, ${\text{μ}}_{\text{a}}\left[\text{M }{\text{L}}^{-1}{\text{T}}^{-1}\right]$ and ${\text{ρ}}_{\text{a }}\left[\text{M }{\text{L}}^{-3}\right]$ define the dynamic viscosity and density of the fluid, respectively, k is the intrinsic permeability tensor [L²], and g defines the gravitational acceleration [L T⁻²]. Above T_c, β = β_max is equal to 1, and K depends on μ_a and ρ_a, which are functions of temperature and total solute concentrations. Additional details on the controls of temperature on μ_a and ρ_acan be found in Henderson et al. (2009) and Bea et al. (2012). For completely frozen conditions below T_m, β is assigned a low value, β_min (e.g., 10⁻⁶) to effectively stop flow. Parameter assignments and a graphical representation of β as a function of temperature, as used in this study, are shown in the Supplementary Figure 1. This formulation provides an effective approach to capture the effect of freezing on flow processes, without the need to account for a phase change.

In reality, the oxidation of pyrite is a complex process affected by oxygen supply into the WRP and internal pore water chemistry; geochemical parameters such as pH and availability of dissolved ferric iron, which serves as a preferred oxidant, are known to affect sulfide oxidation rates (Singer and Stumm, 1970; Lefebvre et al., 2001; Palandri and Kharaka, 2004). Temperature is an additional important factor controlling the rate of pyrite oxidation, correlated to microbial activity (Lefebvre et al., 2001). Since the focus of this study is not on the detailed analysis of geochemical conditions within the pile, a simplified formulation for pyrite oxidation was used. It was assumed that the pile remains sufficiently aerated to sustain pyrite oxidation everywhere in the WRP, with reference reaction rates constrained by literature values, unaffected by geochemical variability. Under these conditions, the oxidation rate of pyrite can be expressed as a simple zero-order reaction:

$\begin{array}{ll}{\text{R}}_{\text{Fe}{\text{S}}_2}^{\text{m}}={\text{k}}_{\text{Fe}{\text{S}}_2}& (10)\end{array}$

where ${\text{R}}_{\text{Fe}{\text{S}}_2}^{\text{m}}\left[\text{mol }{\text{L}}^{-3}\text{porous medium }{\text{T}}^{-1}\right]$ represents the oxidation rate of pyrite by O_2(aq), and ${\text{k}}_{\text{Fe}{\text{S}}_2}\left[\text{mol }{\text{L}}^{-3}\text{porous medium }{\text{T}}^{-1}\right]$ is the corresponding rate coefficient that varies with temperature subject to the Arrhenius equation (Arrhenius, 1889). For moderate temperatures above freezing, the temperature-dependence of chemical reaction kinetics is adequately described by the Arrhenius equation; however, frozen conditions are expected to severely limit reaction progress (Stewart, 1988). Similarly, pyrite oxidation rates may also become impaired in high-temperature environments due to a reduction in microbial activity. The activity of most microorganisms increases to a maximum at an optimal temperature, while higher temperatures can lead to cell death by denaturing essential enzymes (Barton, 1979). As a result, microbially mediated reaction rates decline for temperatures exceeding an optimum temperature. The temperature-dependence of the rate of pyrite oxidation is here defined as:

$\begin{array}{c}{\text{k}}_{\text{Fe}{\text{S}}_2}=\text{γ}{\text{k}}_{\text{Fe}{\text{S}}_2}^{\text{ref}}\text{ with γ}={\text{e}}^{\left(\frac{-\text{Δ}{\text{E}}_{\text{a}}}{\text{R}}\left(\frac{1}{\text{T}}-\frac{1}{{\text{T}}_{\text{ref}}}\right)\right)}\frac{1}{1+{\text{e}}^{\text{δ}\left(\frac{\text{T}-{\text{T}}_{\text{o}}}{{\text{T}}_{\text{o}}}\right)}}\text{ for T}\ge {\text{T}}_{\text{f}}\\ \text{γ}=10^{-10}\text{ for T}<{\text{T}}_{\text{f}}& (11)\end{array}$

where k_FeS2 and ${\text{k}}_{\text{Fe}{\text{S}}_2}^{\text{ref}}\left[\text{mol }{\text{L}}^{-3}\text{porous medium }{\text{T}}^{-1}\right]$ are the rate coefficients at current temperature T, and reference temperature T_ref [Θ]. T_f [Θ] is the threshold temperature below which reaction progress immediately ceases. The selected T_f is within the range of T_m and T_c. γ [-] is the temperature correction coefficient, capturing the temperature dependence of the reaction rate. The term ${\text{e}}^{\left(\frac{-\text{Δ}{\text{E}}_{\text{a}}}{\text{R}}\left(\frac{1}{\text{T}}-\frac{1}{{\text{T}}_{\text{ref}}}\right)\right)}$ represents the contribution of the Arrhenius equation with $\text{Δ}{\text{E}}_{\text{a}}\left[\text{ΔE mo}{\text{l}}^{-1}\right]$ defining the activation energy which controls the rate as a function of temperature, with R [E mol⁻¹ T⁻¹] being the ideal gas constant. T_o [Θ] is the optimum temperature when microbial activity reaches the maximum (Xie et al., 2007) and δ [-] is an empirical parameter controlling the nature of rate decrease above T_o. The correction accounting for inhibition at elevated temperatures ($\frac{1}{1+{\text{e}}^{\text{δ}\left(\frac{\text{T}-{\text{T}}_{\text{o}}}{{\text{T}}_{\text{o}}}\right)}}$) is close to 1 when temperature is below T_o, ensuring that the temperature dependence follows the Arrhenius equation for temperatures between freezing and T_o. When temperature exceeds the optimal value, the function effectively suppresses the reaction rate, representing the decline in microbial activity (see Supplementary Figure 1, for parameterization and a graphical presentation of γ as a function of temperature).

Previous studies have shown that high temperatures can be naturally achieved in reactive waste rock due to the exothermic nature of oxidation processes (Lefebvre et al., 2001; Amos et al., 2015). A source-sink term, accounting for heat generation due to mineral dissolution-precipitation reactions, is therefore included in the energy balance equation:

$\begin{array}{ll}{\text{Q}}_{\text{e}}^{\text{m}}={\sum }_{\text{j}=1}^{{\text{N}}_{\text{m}}}(\text{Δ}{\text{E}}_{\text{r}}^{\ominus }){\text{R}}_{\text{i}}^{\text{m}}\text{ j}=1,{\text{N}}_{\text{m}}& (12)\end{array}$

where ${\text{E}}_{\text{r}}^{\ominus }\left[\text{E mo}{\text{l}}^{-1}\right]$ is the standard heat (i.e., heat produced or adsorbed for every mole of a mineral dissolved) of the j^th dissolution-precipitation reaction.

Model Verification

The verification and validation of the model developed here is challenging due to a lack of alternative models that are able to simulate the highly coupled THC processes in the context of mine waste weathering in permafrost environments. However, the implementation of the coupled THC processes, as implemented in the code, was previously verified by Bea et al. (2012, 2016). The code has also been verified by participating in a wide range of reactive transport benchmark benchmarks and code intercomparisons (e.g., Mayer and MacQuarrie, 2010; Alt-Epping et al., 2015; Poonoosamy et al., 2018). The modifications to account for the effect of freeze-thaw processes were limited to those described above (Section Temperature-Dependent Constitutive Relationships). In addition, a simple version of the relationship describing the reduction of hydraulic conductivity caused by freezing has been previously been successfully used for reactive transport modeling at the Diavik Mine, located in a typical permafrost region (Wilson et al., 2018a).

Modeling Approach

Since flow and transport processes in WRPs are predominantly vertical under temperate climate conditions, the domain may be simplified as a one-dimensional (1D) column composed of waste rock on natural terrain. The 1D simulations evaluate the new freeze-thaw capabilities developed for the model and assess the effect of different levels of sulfide mineral reactivity on the performance of a WRP for reference climate conditions and for a warming climate. However, this approach does not account for the diversion of vertical flow due to permafrost formation, blocking the percolation of infiltrating water. Following these 1D simulations, 2D flow and reactive transport simulations were conducted to further assess the dynamic interactions between flow, reactive transport and heat transport processes under cold climate conditions, accounting for the diversion of infiltration, leading to lateral flow and mass transport.

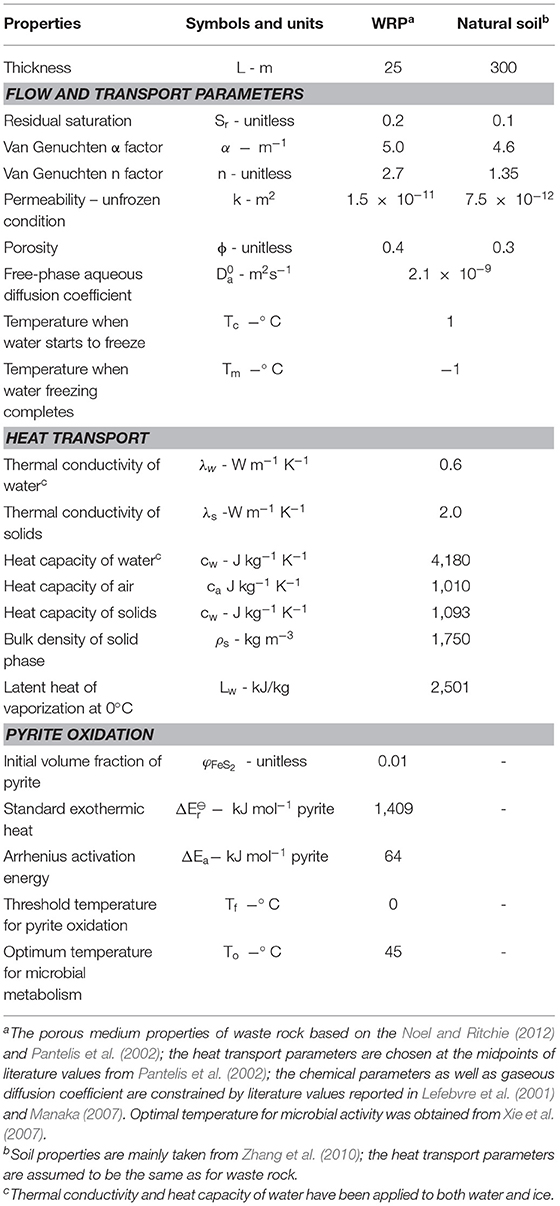
1D Model Description

Before waste rock placement, the active layer thickness present near the ground surface was assumed to be controlled by the local climate and soil properties. As conceptualized in Figure 3, after waste rock pile construction, permafrost encroaches into the waste rock pile, with the active layer now present in the shallow portion of the pile. For our conceptual simulations, a 25 m tall WRP was placed onto 300 m thick natural soil in a permafrost environment; with thicknesses constrained by the examples of Piteau Associates Engineering Ltd (1991) and Booshehrian et al. (2020), respectively. The domain was discretized in the vertical direction as 300 1 m and 250 0.1 m control volumes for the natural soil and the pile, respectively. Simulations were performed for 50 years, which was considered sufficient to characterize the long-term evolution of the pile and underlying soil. Physical, chemical, and thermal parameters used to parameterize the model and their sources are listed in Table 1. Physical parameters used for the WRP and underlying soil, including water retention curves, hydraulic conductivity and porosity, were constrained by literature data (Pantelis et al., 2002; Zhang et al., 2010; Noel and Ritchie, 2012; Wilson et al., 2018a), while parameters to control heat transport in WRPs were taken from Pantelis et al. (2002) and were assumed identical for the underlying soil. The volume fraction of pyrite was based on Lefebvre et al. (2001). Kinetic reaction parameters for pyrite oxidation under reference temperatures were slightly adjusted from reported values for the Doyon mine (Lefebvre et al., 2001) within ranges reported in the literature.

FIGURE 3

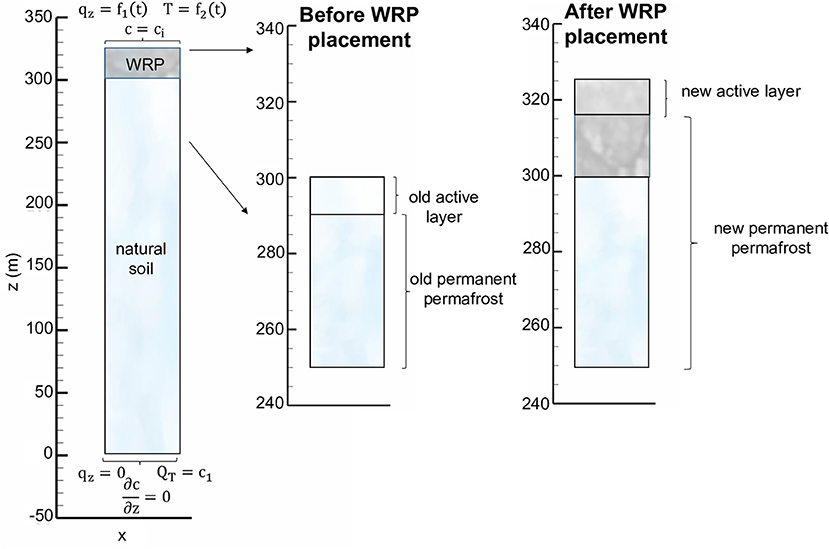
Figure 3. 1D conceptual model of waste rock placed on natural soil with corresponding boundary conditions.

TABLE 1

Table 1. Parameterization of 1D and 2D waste rock THC models.

Only the most relevant chemical components related to pyrite oxidation were considered in the model, including ${\text{SO}}_4^{2-}$, Fe²⁺, H⁺, and O_2(aq). The initial compositions of pore water within the waste rock and infiltrating water were similar to dilute rainwater (pH = 5.5). Pyrite was considered as the only reactive mineral present in the pile with a finite amount, and the underlying natural terrain was assumed as pyrite-free. Other complex chemical processes such as hydrolysis, aqueous complexation, dissolution of other primary minerals, and precipitation of secondary minerals were not considered in the model. As discussed above, pyrite oxidation was treated as a simple zero-order rate expression (Equation 10) without consideration of dynamic evolution of oxidation processes as a function of pore water geochemistry. Due the simplified geochemical reaction network, it was not possible to consider the different reaction pathways for pyrite oxidation (initiator reaction and propagation cycle). Sulfate was tracked and used as an indicator for the occurrence and progress of pyrite oxidation. Other chemical components were only included, since they are part of the reaction stoichiometry of pyrite oxidation but were not further evaluated in this study. In addition, it was assumed that the pile is well-aerated with respect to O₂ (pO₂ was fixed at 0.2 atm), in line with observations at WRPs with permafrost present (Pham et al., 2008; Wilson et al., 2018a). It is acknowledged that this assumption yields a worst-case scenario for situations with high pyrite reactivity and internal heating. Since O₂ concentrations are fixed at atmospheric levels throughout the entire pile, the simulations also neglect transport limitations related to gas advection and gas phase diffusion. The effect of ice formation and water accumulation at the base of the active layer on gas ingress was also neglected. However, since O₂ demand in permafrost is negligible, this simplification is unlikely to affect the results in a significant manner. Both pile and natural soil were assumed to possess homogeneous porosity and permeability. The effect of hydrodynamic dispersion and the impact of salinity on freezing point depression were assumed negligible. The resulting physical and geochemical is highly simplified in comparison to WRPs in the real world. However, these simplifications allow to focus the study on dynamics related to permafrost and active layer evolution for a variety of climate conditions and pyrite reactivities.

The initial conditions for water and ice content, as well as temperature are mainly controlled by air temperature, precipitation, and geothermal heat flux. These conditions have developed over long time frames and for the modeling, the following assumptions were made: First, a simulation subject to an annual infiltration rate of 280 mm year⁻¹ at the top and a constant head of 295 m at the base was run in the absence of the waste rock pile, until steady state was reached. The initial temperature distribution was subsequently determined by assigning a mean annual air temperature (MAAT) of −9°C at the surface (Pham, 2013) and a basal geothermal heat flux of 0.08 Wm⁻² (Booshehrian et al., 2020). For simplification, the initial temperature within the WRP after its placement was assumed to be the same as MAAT with permafrost present throughout the pile. Effects of pile construction during different seasons on the thermal regime of the pile was neglected.

Given these initial conditions, transient boundary conditions were then assigned at the surface, accounting for the occurrence of seasonal freeze-thaw cycles. A sine function was used to represent transient temperatures with a maximum temperature of 20°C and a minimum temperature of −38°C (Wilson et al., 2018b) (Figure 4). A constant geothermal flux of 0.08 Wm⁻² was retained as the boundary condition at the base of the domain. The annual infiltration rate was set to 280 mm year⁻¹ and was assumed to be seasonally controlled, correlating with fluctuating temperatures and also following a sine function, although infiltration was not permitted for surface temperatures below freezing (Figure 4). The impact of snowmelt on the annual distribution of infiltration was neglected for simplicity, which is justified considering the 50-year time frame of the simulations.

FIGURE 4

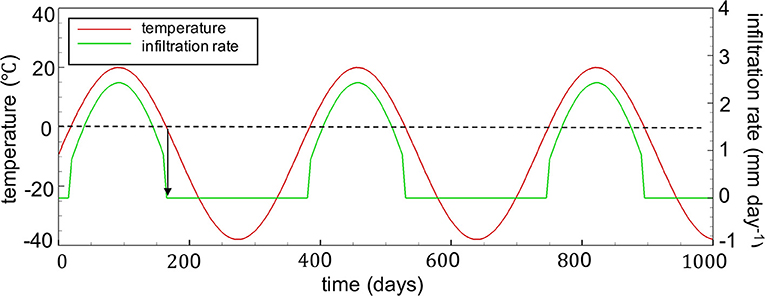
Figure 4. Seasonally controlled temperature profiles (mean annual air temperature is −9°C) and infiltration rates at the WRP surface boundary (annual infiltration rate is 280 mm yr⁻¹). The profile is assumed to repeat during the 50-year simulation period.

A warming of the MAAT of up to 4°C was forecast at 50N by the end of the century (Etkin et al., 1998). To evaluate the long-term effect of climate warming, the sine function for temperature in Figure 4 was modified by creating two alternative scenarios, increasing temperatures throughout the years by 1 and 3°C to delineate the potential warming scenarios in cold-climate regions in coming decades. These modified climate conditions were applied throughout the simulation. Accounting for the effects of gradual climate warming was beyond the scope of the present study. These simulations were then assigned with modified infiltration patterns, which followed the corresponding temperature functions, remaining sinuous and assuming the same annual infiltration rate for simplicity, although it is recognized that infiltration rates might also change with warming temperatures. Both infiltration and temperature patterns were assumed to be consistent over the 50-year simulation period and were repeated annually.

A scenario analysis in relation to pyrite reactivity and MAAT (Table 2) was conducted to evaluate the impacts of these parameters on weathering processes and mass loadings. The base case with reference pyrite reactivity includes three simulations under reference and future climate scenarios with MAATs of −9 and −8 or −6°C, respectively. Two additional cases were considered to investigate WRPs with lower and higher reactivity for the same temperature scenarios, which was achieved by decreasing or increasing the reference pyrite reaction rate constant by one order of magnitude, respectively. These modifications to the rate constant were selected based on literature values reported by Lefebvre et al. (2001) and Manaka (2007). All cases were simulated with for well-aerated conditions (assuming a fixed pO₂ at atmospheric levels). The simulations were run with the sequential version of the code, and the total runtime was <5 min on a PC equipped with an Intel® Core™ i7-8700K CPU @ 3.70 Ghz with 16 GB of RAM.

TABLE 2

Table 2. Parameters for sensitivity analyses of 1D and 2D simulations (k refers to ${\text{k}}_{\text{Fe}{\text{S}}_2}^{\text{ref}}$).

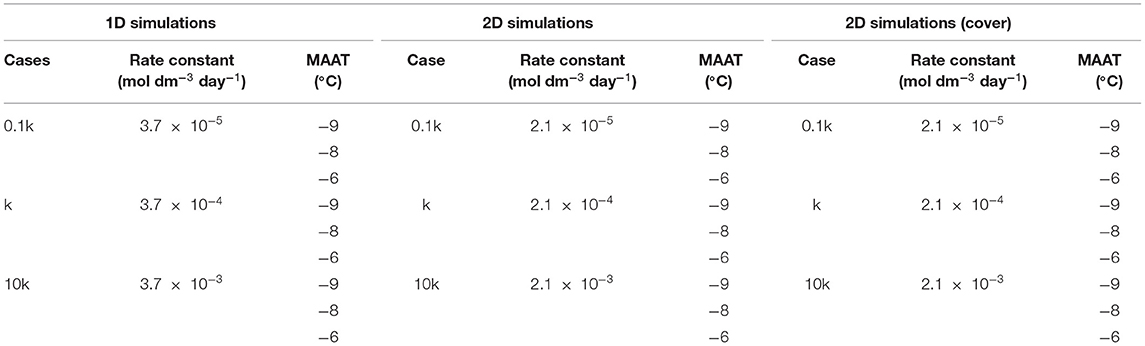
2D Model Description

To expand the analysis to more realistic conditions accounting for diversion of flow due to permafrost formation, a 2D-model was developed consisting of a 25 m tall WRP, overlying a 1.5 m thick low-permeability liner on top of natural soil (Figure 5A). The liner was considered to avoid the potential for infiltration of mine drainage into the natural soil. The simulated pile base and liner were 110 m long and the slopes of the pile were set at 35° (1.2 H: 1 V) (Smith et al., 2013). The pile was assumed to be located on an inclined ground surface with a slope of 5°. The domain containing natural soil below was extended laterally to 260 m in width and to 305 m in depth to minimize the horizontal temperature gradients near the lateral boundaries and to reasonably assign the base of the domain with geothermal heat flux, respectively. An unstructured grid method was used to discretize the domain using 17,206 nodes. Since the specific focus of the study is on the WRP, the unstructured grid was more refined for the WRP and the liner than for the underlying soil. The purpose of this discretization strategy was to allow an adequate representation of important processes occurring in the pile and to minimize grid effects on simulations results. The properties of both the pile and soil are given in Table 1. The low-permeability liner with no sulfide minerals has as significantly reduced permeability of 1.5 × 10⁻¹⁷ m² and a porosity of 0.15 constrained by data from Fetter (1994) and Brachman et al. (2017), representative for such materials.

FIGURE 5

Figure 5. (A) Geometry and discretization of 2D model, (B) Corresponding boundary conditions.

The reaction network considered was identical as for the 1D simulations. The initial conditions for the 2D domain were also calculated using the same method as for the 1D model. The same boundary conditions for flow, reactive transport, and temperature were assigned to the domain shown, as shown in Figure 5B, with the exception of the infiltration boundary assigned to the pile surface, which was modified to enable seepage when boundary nodes became saturated. Since infiltration into the soil on either side of the pile has little impact on processes in the WRP, only infiltration into the pile was taken into consideration for the simulations.

Analogous to the 1D modeling, a scenario analysis consisting of an additional set of 2D simulations was performed. Three cases with different levels of pyrite reactivity were simulated under reference and warming climate conditions (Table 2). The reference rate constant for the base case was slightly modified from 1D base case to best capture the long-term impacts of a warming climate for the more complex geometry. The modifications were necessary since the heat and flow transport processes differ as a function of dimensionality (lateral transport in 2D). Simplifications and assumptions for the 2D simulations are the same as for the 1D case. These simulations also assume that the WRP is well-aerated (at atmospheric pO₂ levels), providing worst-case scenarios in terms of sulfide oxidation and mass loadings. These simulations were carried out using the OpenMP parallel version of the code on the Optimum HPC Cluster at EOAS UBC using 20 processors (Intel's Ivy Bridge 2.8 GHz E5-2680v2 processor) and 128 GB memory, and the parallel runtime was about 48 h.

Thermal Cover

A thermal cover as an insulating barrier is one reclamation approach uniquely suited to permafrost environments to control contaminated drainage (Kyhn and Elberling, 2001; Coulombe et al., 2012; Boulanger-Martel et al., 2017; Stevens et al., 2018). Typically, thermal covers consist of locally sourced, non-acid-generating materials to encapsulate the mine waste, in order to maintain the active layer mostly within the cover material (Boulanger-Martel et al., 2017; Stevens et al., 2018). To assess the controls and functions of the thermal cover, additional 2D simulations were conducted as outlined in Table 2 for the same climatic conditions and pyrite reactivities as previously described. For these simulations, a WRP with the same geometry and parametrization as for the uncovered cases was considered, but capped with a 3.2 m-thick cover over the bench and slopes (Stevens et al., 2018). The domain of the bare waste rock was expanded to include the cover, and the new domain was discretized using 19,836 nodes. The simulations were subject to the same assumptions (e.g., a well-aerated pile) as the uncovered cases, and the same boundary conditions were used. The material properties of the cover were assumed to be the same as for waste rock, with the only difference that the cover was composed of non-acid generating material (i.e., sulfide-free).

Simulation Results

1D Modeling Analysis

Simulated seasonal temperature profiles for reference sulfide mineral oxidation rates are depicted in Figure 6A for the three climatic conditions considered. The temperature profiles were selected at the end of each season to provide good representation of permafrost degradation during thawing conditions (spring), maximum extent of thawing (summer), permafrost aggradation during freezing conditions (autumn), and maximum extent of freezing (winter). Under reference climate conditions (MAAT of −9°C), permafrost can be observed within the pile capped by an active layer extending to a depth of 2.5 m after 50 years. The temperatures in the active layer are strongly affected by seasonally controlled air temperatures. For this scenario, the temperature distribution within the waste rock column remains relatively unaffected for a slightly warmer climate with an increase in the MAAT by 1°C. The active layer thickness (3 m) for this scenario has increased only modestly in comparison to the base case scenario. However, if MAAT is increased from reference climate conditions by 3°C (MAAT of −6°C), the simulation results suggest that the temperature profile is significantly altered, showing dramatically increased temperatures reaching up to 60°C after 50 years with no permafrost present in the pile. For this simulation, the internal temperatures rapidly increase due to heat generation by sulfide mineral oxidation, causing permafrost to completely disappear throughout the pile during the first 5 years of the simulation (see Supplementary Figure 2). For these conditions, the active layer extends throughout the entire pile thickness and into the natural soil, allowing for pyrite oxidation to occur everywhere in the pile. The internal temperature remains high for the remainder of the simulation with a slight increasing trend, mainly due to constraints on microbial activity limiting the reaction rate along with heat production, especially in the core (see Supplementary Figure 2). For the reference reactivity scenario and an increase of MAAT by 1°C, pyrite oxidation remains restricted to the shallow active layer due to the persistence of permafrost deeper in the pile. This set of simulations demonstrates that under specific conditions, a relatively slight increase of the MAAT can severely affect the persistence or development of permafrost within a WRP with substantial effects on weathering processes.

FIGURE 6

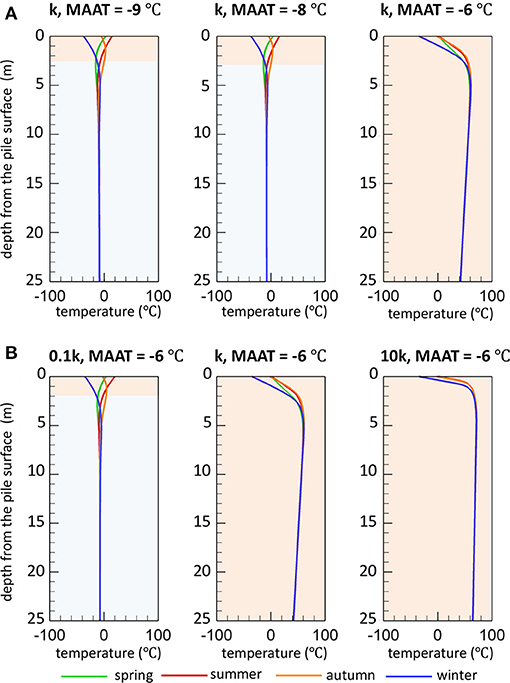
Figure 6. Spatial distribution of temperature (T) vs. depth in a WRP at the end of each season after 50 years, demonstrating the sensitivity of temperature profiles and permafrost development to (A) climate change and (B) pyrite reactivity. Based on the temperature profiles at the end of each season, the light orange and blue zones represent the estimated active layer thickness and continuous permafrost region, respectively (k refers to ${\text{k}}_{\text{Fe}{\text{S}}_2}^{\text{ref}}$).

Results for lower and higher pyrite reactivity were compared to the base case scenario to investigate the response of WRPs as a function of sulfide oxidation rates under the various climate conditions. The results show that for the lower reactivity scenario (0.1k), permafrost becomes established and remains long-term with an active layer thickness of about 2 m, even for the case with a more pronounced warming climate (Figure 6B), whereas the higher reactivity scenario (10k) does not allow for permafrost to develop under any conditions, including the reference climate. For higher reaction rates, temporary freezing only occurs in the uppermost waste rock layers during winter months, while pile-internal temperatures are higher than for the base case for all climate conditions.

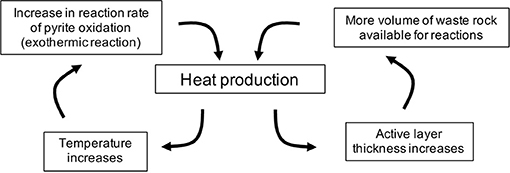
The increase in pile-internal temperatures are induced by a positive feedback termed as self-heating (Figure 7) (Rosenblum and Nesset, 2001), diminishing or preventing the formation of permafrost. The development of such conditions depends on the reactivity of sulfide minerals contained within the waste rock but can be aggravated by a warming climate. Simultaneously, the lack of permafrost formation caused by rising temperatures allows more volume of the waste rock exposed to water and oxygen, thus more pyrite is available for oxidation. The results of the scenario analysis illustrate how internal self-heating phenomena can become more likely in a warming climate.

FIGURE 7

Figure 7. Thermochemical processes contributing to self-heating.

2D Modeling Analysis

Base Case

For reference climate conditions and pyrite reactivity, contours for temperature, ice saturation, sulfate concentration, and volume fraction of pyrite are depicted in Figure 8 at t = 50 years at the end of the summer season (more detailed results on the temporal model evolution are provided in the Supplementary Material, Animation 1). Under the reference climate, a temperature gradient is observed near the pile surface reflecting seasonal heating from the surface. The depth of the 0°C isotherm represents the maximum extent of the active layer. The extent and configuration of permafrost within the pile are directly related to the pile shape and the frozen core of the pile is characterized by temperatures close to reference MAAT.

FIGURE 8

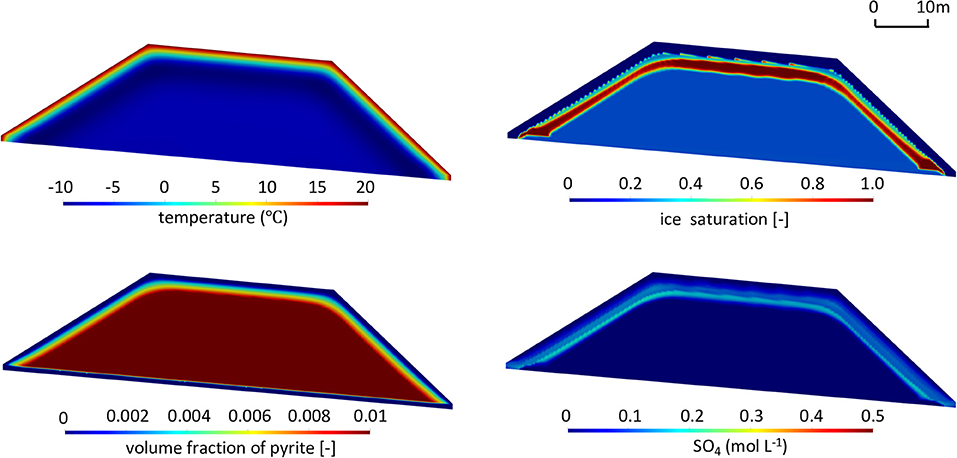
Figure 8. Contours of temperature (T), ice saturation (S_ice), residual volume fractions of pyrite (φ_pyrite), and sulfate concentrations (SO₄) in the waste rock pile in the summer of the 50th year for the base case (${\text{k}}_{\text{Fe}{\text{S}}_2}^{\text{ref}}$, MAAT = −9°C). The contours after 10 and 20 years are presented in Supplementary Figure 3.

Contours of ice saturation also reveal the transition from the active layer (shallow ice-free layer) to permafrost (ice-containing zone), which is bordered by a thin ice-saturated zone, a result of ice formation at the base of the active layer and the associated blocking effect of permafrost. The simulations predict that infiltration of water into deeper regions of the pile ceases, due to a strong decline in hydraulic conductivity in permafrost directly below the active layer, mimicking ice formation. The simulations illustrate the lateral redirection of flow paths through the active layer, indicating that seepage will exit the pile at the base of the slopes without passing through the core of the pile (Supplementary Figure 4A). The pronounced and continuous ice-saturated region in this simulation indicates the depth of the active layer under quasi steady-state conditions, while other less pronounced and discontinuous regions of elevated saturation above reflect the infiltration of snow melt and precipitation following the thawing front at the output time.

For the simulated conditions, sulfide mineral oxidation is restricted to the active layer, with no significant oxidation throughout the permafrost region, due to a strong decline of reaction rates under frozen conditions. For the relatively low pyrite content specified (1% volume fraction) and reference reactivity, the results show that pyrite is becoming depleted throughout the active layer 50 years after pile construction. Despite the assumption of well-aerated conditions throughout the pile, pyrite in the core of the pile remains stable and does not undergo oxidation. Sulfate release is controlled by sulfide oxidation in the near-surface active layer, occurring during the warm seasons. Sulfate accumulates in infiltrating water and is then partially released along lateral flow pathways toward the right and left toes of the slopes. The simulations also indicate that sulfate gets trapped at the interface between the active layer and permafrost in regions of lower hydraulic conductivity and ice formation. At the presented output time, highest sulfate concentrations occur in the lower part of the active layer, reflecting accumulation along the infiltration flow path as well as declining pyrite abundance and reactivity near the pile surface.

In summary, the simulation results suggest that permafrost can develop, despite the exothermic nature of pyrite oxidation. For the conditions simulated, the energy balance of the pile is dominated by seasonal temperature fluctuations and the geothermal heat flux coming from below, leading to permafrost development similar to natural soils. The effect of pyrite oxidation on the energy budget and system evolution is insufficient to substantially inhibit the development of permafrost within the WRP.

Climate Warming

The simulation results under future warming climates for reference pyrite reactivity are shown in Figure 9 (more detailed results on the temporal model evolution are provided in the Supplementary Material, Animations 2 and 3). A slight warming by 1°C (Figure 9A) still allows for the long-term establishment of permafrost with the active layer being restricted to zones near the pile surface, similar to the reference climate scenario (base case). However, the ice-saturated layer in this scenario is located deeper into the pile than for the reference climate scenario, due to the increased air temperature, implying a deeper extent of the active layer and partial permafrost degradation. As a result, more sulfide-bearing waste rock is accessible for oxidation, which is occurring under slightly warmer temperatures, leading to modestly increased mass loads of sulfate relative to the base case. Despite small changes relative to the base case in terms of active layer thickness, permafrost extent, pyrite oxidation and sulfate mass loadings, the overall evolution of the waste rock pile remains very similar to that of the base case scenario.

FIGURE 9

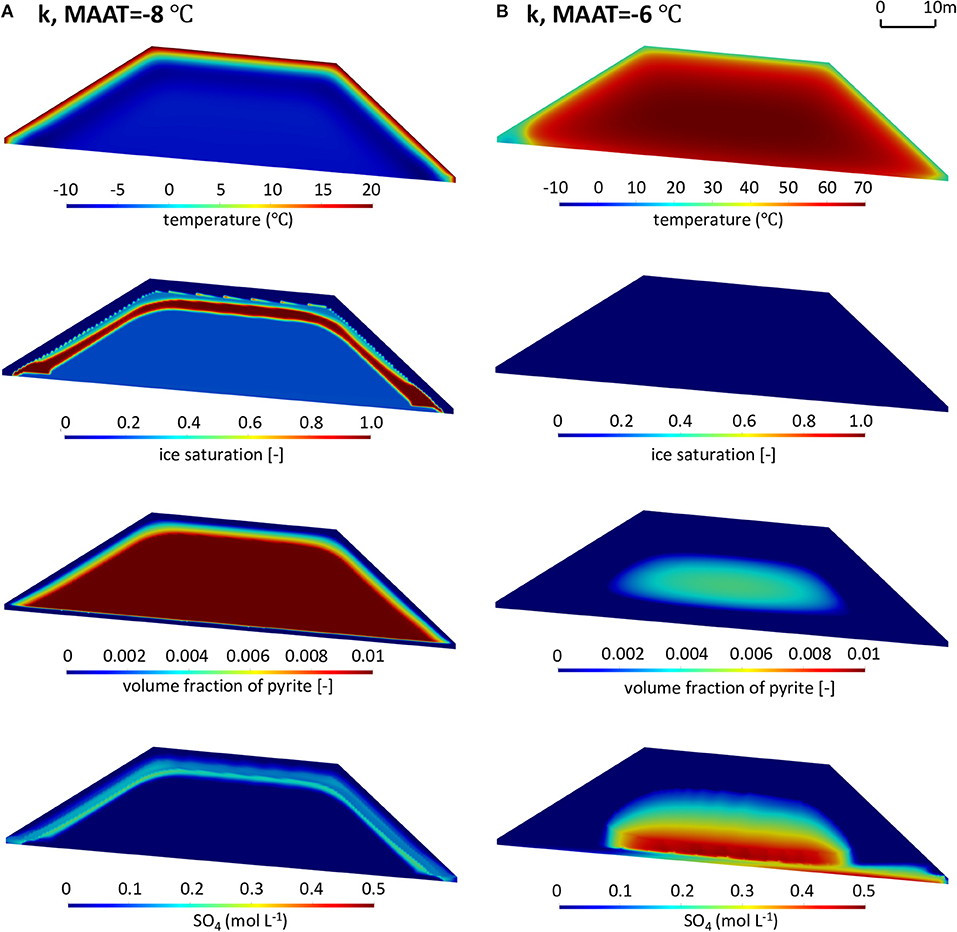
Figure 9. Contours of temperature (T), ice saturation (S_ice), residual volume fractions of pyrite (φ_pyrite), and sulfate concentrations (SO₄) in the waste rock pile in the summer of the 50th year for scenarios with reference pyrite reactivity (k refers to ${\text{k}}_{\text{Fe}{\text{S}}_2}^{\text{ref}}$) under warming climate conditions with (A) MAAT = −8°C and (B) MAAT = −6°C.

Considering a temperature increase of 3°C over the reference climate scenario; however, leads to a substantially different long-term evolution of the waste rock pile (Figure 9B). The temperature contours show that permafrost will not be present in the pile after 10 years. In fact, simulations indicate that pile-internal temperatures increase substantially above the MAAT, with core temperatures reaching up to 70°C, caused by internal heating due to the exothermic nature of pyrite oxidation. Ice formation as well as increased water saturations near the surface of the pile are no longer observed due to the complete disappearance of permafrost within the pile (Monthly changes of ice and water saturations are provided in the Supplementary Material, Animation 4). Without the barrier imposed by permafrost, infiltrating water can freely penetrate through the pile and forms a high water-saturation layer above the low-permeability liner near the base of the pile (Supplementary Figure 4B). As a result, the right toe becomes the main drainage location, receiving water that has passed through the core of the pile. These conditions can develop due to the exothermic nature of pyrite oxidation, leading to internal heating. Together with warmer climate conditions, pyrite oxidation rates and associated heat production had a pronounced effect on the energy balance of the waste rock pile, effectively leading to reaching a “tipping point” causing a gradual expansion of the active layer and ultimately the complete degradation of permafrost, while simultaneously promoting further self-heating. Under these conditions and assuming no oxygen limitation, oxidation of pyrite occurs throughout the pile at increased rates leading to enhanced sulfate release and higher concentrations. For the selected parameters, pyrite depletion occurs after 50 years within a large fraction of the pile with the exception of the core, where the temperatures are high and exceed the optimal temperature for microbially mediated pyrite oxidation, restricting reaction rates.

In summary, although the abovementioned three scenarios have the same initial reactivity of pyrite, the analysis demonstrates that climate warming has the potential to significantly change the thermal, hydrogeological and geochemical regimes of the entire system due to the self-heating. Warming by only a few degrees can enhance the heat production from pyrite oxidation so that permafrost degradation will occur. The higher air temperature more easily triggers self-heating, with pronounced effects on the pile's energy balance, flow system, sulfide oxidation, and mass loadings. In this context, it must be emphasized that rate parameters were purposefully chosen to induce this transition. These results are not predictive in nature for the chosen pile geometry and parameters, but they illustrate the possibility of reaching a tipping point and transitioning from a permafrost regime to a regime of internal heating.

Mass Loadings for Increased and Reduced Pyrite Reactivity

The results for sulfate mass loadings of low-reactivity and high-reactivity cases obtained by lowering or increasing the reference rate coefficient by a factor of 10 are summarized in Figure 10, in comparison to simulations performed for the base case reactivity. For a WRP with high reactivity (10k), all simulation cases show essentially the same elevated release of SO₄ over time, independent of the climate condition considered. The release of sulfate occurs only at the right toe of the WRP because pyrite oxidation takes place throughout the pile at significant rates, leading to rapid degradation of permafrost and transitioning to internal heating. For the 2D-cross section considered, the gently sloping ground surface enables drainage water to percolate toward a single focused discharge point. These results illustrate that the energy balance of the pile is dominated by heat generated from sulfide mineral oxidation, with limited impact of climate warming on the evolution of the pile and associated mass loadings.

FIGURE 10

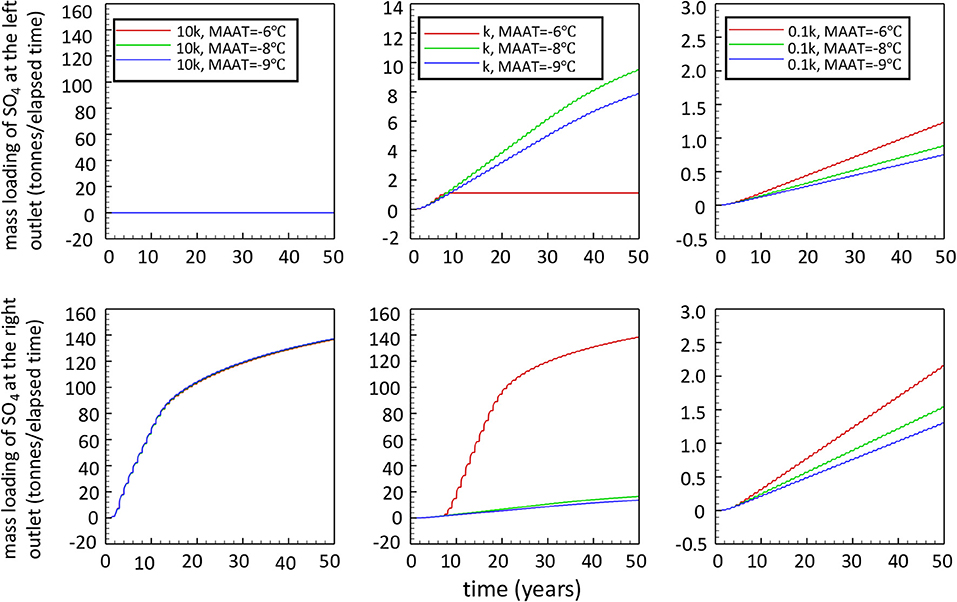
Figure 10. Total sulfate release over elapsed time at the two drainage locations at the toes of the waste rock pile for all scenarios (k refers to ${\text{k}}_{\text{Fe}{\text{S}}_2}^{\text{ref}}$).

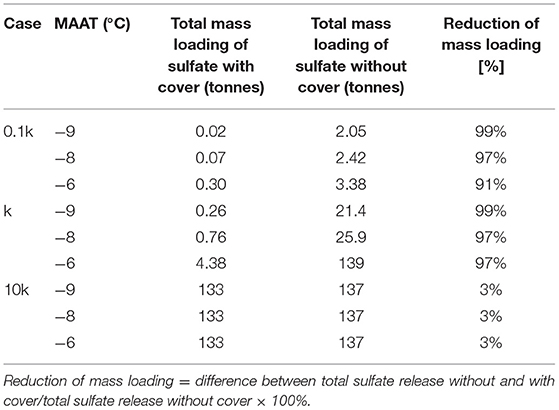
For conditions with lower reactivity (0.1k) of sulfide minerals, the long-term evolution of the pile is similar to that of the base case, with permafrost developing in the core of the pile, surrounded by an active layer. In this case the energy balance of the pile is dominated by climate conditions and the geothermal heat gradient, as discussed above for the base case. Considering the low reactivity of pyrite, it is not surprising that internal heating does not occur for any of the climate scenarios. Although effects of climate warming are not as dramatic as for the base case, marked differences can be observed for the different climate scenarios in terms of long-term mass loadings. For the lower pyrite reactivity, a warming climate enhances pyrite oxidation to generate more sulfate relative to the reference climate scenarios. Enhanced sulfate release is due to a thicker active layer, increasing access to pyrite, a longer duration of the warm season, and a marginally higher reaction rate due to a temperature-driven rate increase. Although mass loadings remain relatively low, these compounding effects lead to an increase in mass release over a 50-year time period of 18 or 65% for very modest MAAT increases of 1 and 3°C, respectively (Table 3).

TABLE 3

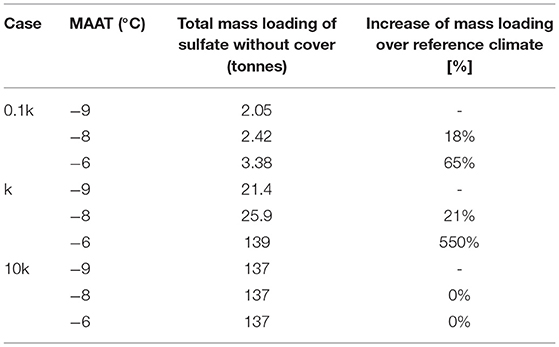
Table 3. Sensitivity analysis to climate warming for all simulation cases (k refers to ${\text{k}}_{\text{Fe}{\text{S}}_2}^{\text{ref}}$) (no cover).

The same effect can be seen for the base case reactivity, where a mild MAAT increase of 1°C leads to an increase of mass loadings by 21% relative to the reference climate scenario (Table 3). As discussed above, the development of internal heating for a MAAT increase of 3°C causes more drastic changes, increasing the mass loading by 550% of the reference climate scenario (assuming that O₂ does not become limiting).

Thermal Cover

Simulated sulfate mass loadings for the scenario with a thermal cover are summarized and compared to uncovered scenarios in Table 3. The factors of mass loading reduction for the covered cases vs. uncovered cases for lower and reference pyrite reactivities indicate that the insulating effects of the cover can dramatically decrease cumulative sulfate mass loadings, assuming the same initial conditions remain valid. The sulfide-free cover hosts most of the active layer, reducing accessibility to pyrite and temperatures in the pyrite-containing zone during the warm season, as well as the duration of above-freezing conditions in the portion of the active layer extending into the waste rock. Together these factors lead to a reduction in mass loadings of >90% for all cases considered (with reactivity of k and 0.1k), relative to the uncovered WRP (Table 4). For the reference reactivity scenario with an increase of the MAAT to −6°C, the total mass loadings reveal that in some select instances, the thermal cover can effectively prevent the development of internal heating and permafrost degradation, maintaining the long-term stability of permafrost within the pile (see Supplementary Figure 5), providing a pronounced reduction in mass loadings. In addition, examining these scenarios also shows that an increase of MAAT will tend to decrease the effectiveness of a thermal cover. This can most clearly be seen for the reactivity case with 0.1k, for which the cover is 99% effective at reducing sulfate release for the reference climate scenario, while it is only 91% effective for an increase of the MAAT of 3°C (Table 4). Although simulated mass loadings are quite low for these two covered cases (0.1k, MAAT of −9°C and MAAT of −6°C), it is notable that sulfate release for an increase in MAAT by 3°C increases by a factor of 13 relative to the reference climate (Supplementary Table 1). The decreases in the benefits and effectiveness of the cover caused by climate warming is due to a deeper extent of the active layer, reaching into the waste rock for cases with increased MAAT (see Supplementary Table 1).

TABLE 4

Table 4. Performance analysis of cover effectiveness for all simulation cases (k refers to ${\text{k}}_{\text{Fe}{\text{S}}_2}^{\text{ref}}$).

For the higher reactivity scenarios (10k), the simulations indicate that the placement of a thermal cover is ineffective in protecting the waste rock pile from self-heating and permafrost degradation. The reduction of mass loadings in this case is equally insignificant for all climate scenarios. Overall, the simulation results suggest that a thermal cover can provide a practical and effective option to control the release of contaminated drainage under many, but not all conditions.

Discussion

Climate Change and Effluent Quality

Simulated results demonstrate that a mild increase in air temperature can strongly influence the drainage water quality from a well-aerated pile in many cases, indicated by a substantial increase in sulfate mass loadings. The simulation results reveal that a series of phenomena caused by a warming climate enhance sulfate release from the active layer in the pile, including partial permafrost degradation, a deeper extent of the active layer, enhanced access to sulfide-bearing waste rock, and a marginally increased oxidation rate, which together pose risks to the persistence of permafrost within waste rock (MEND, 1996, 2011). In rare instances, a higher air temperature may lead to a transitioning of the pile to internal-heating conditions and alter the drainage evolution dramatically through the mechanisms described above (MEND, 1996). In these cases, the internal self-heating occurs because the pile's energy balance becomes dominated by the exothermic nature of sulfide oxidation (Rosenblum and Nesset, 2001; Arisoy and Beamish, 2015). As a result, permafrost cannot be sustained, resulting in more sulfide oxidation at enhanced rates occurring through the entirety of the pile. It is unlikely that such a drastic outcome is reached in many instances. Physical and geochemical conditions in a pile must be in a very narrow range to facilitate the transitioning from a permafrost-containing pile to an internal heating scenario. However, the more significant finding is that sulfide weathering and associated mass loadings can still increase significantly for lower reactivities, even if the increase in temperature is only relatively minor (1–3°C). This is due to the compounding effects of a warming climate on active layer thickness, reaction rates, and duration of the warm season. On the other hand, the simulations suggest that sulfate mass loading for highly reactive piles is not significantly affected by the climatic conditions; the strong exothermic nature of oxidation governs the energy balance and inhibit the development of the permafrost in the pile irrespective of climate conditions.

In real-world waste rock piles, the long-term evolution of the piles is likely more complex than simulated here due to additional factors that influence the effluent quality. Foremost, it must be noted that these findings are only valid if the system is supplied with sufficient oxygen. Oxygen availability can constrain the oxidation processes especially for high-reactivity piles. The inclusion of secondary mineral formation also tends to affect sulfate release and mass loadings of other elements. In addition, mineral precipitation reactions can as act as passivating agents for sulfide mineral oxidation. Physical heterogeneity and pile structure may also affect the basal drainage evolution and effluent quality, as are impacts from snowfall and snowmelt in the spring, affecting flow and heat transport dynamics. It must be acknowledged that the outcome of the simulations can be affected by the initial thermal conditions, which are highly simplified in the simulations presented here. These conditions are difficult to anticipate due to the duration of pile construction, typically spanning several years.

Considering the uncertainties with respect to material properties, placement of waste rock, and initial conditions, the models were designed in a simplified fashion to isolate the potential impacts of climate warming and sulfide reactivity on the weathering behavior of WRPs constructed in cold-region climates, specifically focusing on permafrost degradation and mass loadings in drainage. The results provide (1) a preliminary analysis of these complex systems, (2) a reference for assessing long-term weathering behavior, and (3) an aid to better understand the internal coupled processes. The results presented for low reactivity are least affected by the assumptions made, since the thermal regime within the pile is dominated by climate effects and the geothermal heat flux. It is therefore reasonable to expect that thermal conditions will evolve in a similar manner as simulated. On the other hand, the simulations for reference reactivity represent more unstable conditions, with the energy balance similarly affected by external forcing (climate and geothermal heat flux) and internal processes (exothermic nature of sulfide oxidation). These simulations must therefore be viewed as illustrations on how a waste rock pile could evolve under the given conditions, but not as predictions for a pile of the specified geometry and material properties. The simulations with reference reactivity for reference climate and a MAAT increase of 3°C conceptually bracket the outcomes for these unstable conditions. The simulations for high reactivity present worst-case scenarios, since the effect of O₂-limitation was not taken into consideration.

Cover Performance and Mass Loading Controls

Simulated sulfate mass loadings for the various cases suggest that the efficacy of thermal covers is maximized for piles with relatively low reactivity, especially for cases in which the active layer is completely or at least mostly maintained in the cover. For such cases, it may be possible to reduce mass loadings by >90%. The results also indicate that for some special scenarios, the cover can be used to prevent a WRP from transitioning into conditions of internal heating and reaching a tipping point, because the cover can suppress the contribution of exothermic sulfide oxidation in the pile's energy balance. Such conditions must be considered uncommon, as discussed above. The sulfate mass loading results also suggest that a warming climate, even if only by a few degrees, can substantially affect the cover performance. Depending on tolerable mass loadings and general water treatment needs, an appropriate increase in cover thickness could be considered to offset the decline in cover performance (MEND, 2009, 2011). Generally, it is advisable to take into account a safety factor related to potential hazards and challenges caused by climate warming during the construction of the cover (MEND, 2011). For a WRP containing material of known high reactivity, the simulation results suggest that a thermal cover design may be ineffective at controlling sulfate mass loadings. This can occur, if the active layer extends beyond the thickness of the cover, allowing the development of internal heating despite the presence of the cover. It may be possible to avert this situation by increasing the cover thickness. However, since in reality, both pile construction and cover placement take time, highly reactive piles may commence to weather during construction and accumulate internal heat prior to cover placement. In that case, even a thicker cover may fail to avoid progressive internal heating after cover installation.

Similar to the uncovered cases, the outcome of the simulations with reference and high reactivity are most strongly affected by underlying assumptions, in particular regarding the initial thermal conditions and O₂ limitations. For the simulations, it is difficult to take the duration of pile construction into consideration, and how sulfide oxidation, internal heating and permafrost development proceed during this period. Predictive modeling is difficult under such circumstances and site-specific conditions must be taken into consideration carefully. A purely thermal cover may be ineffective, if waste rock has already been affected by sulfide oxidation and internal heating prior to cover placement, which is not considered in our analysis. Irrespective of the uncertainties associated with the model, other cover options may provide useful alternatives to control the drainage quality, such as covers limiting oxygen ingress (Bussière, 2010).

Summary and Conclusions

Numerical modeling can be a useful tool to investigate processes in mine waste and forecast long-term behavior in these complex systems. In this study, a sensitivity analysis of waste rock weathering in a permafrost environment was performed using MIN3P-HPC. The overall simulation results and findings provide insights in the internal hydrogeological, chemical, and thermal evolutions of uncovered as well as covered piles for reference climatic conditions and warming climates. Scenario analyses were performed to test different hypotheses and different controls on the energy balance of WRPs affected by climate forcing, geothermal heat flux, and internal heating. Such model results are potentially useful to guide decision making on site-specific cover design to effectively and efficiently mitigate potential contaminated drainage.

The results also demonstrate the benefit of recent advances made in unstructured grid capabilities in MIN3P-HPC, enabling future users to simulate field-scale problems where the complex coupled THC processes requires high discretization, and to simulate other complex systems with irregular geometry, such as multi-lift waste rock stockpiles. Future work could also address other aspects such as effects of oxygen depletion, physical and chemical heterogeneities, more complex geochemical reaction networks, different initial conditions, and mass transfer between ice and liquid water. The evaluation of cover scenarios could also be expanded to improve the understanding of the functionality and effectiveness of thermal covers, providing information to help contrast different reclamation technique in the design planning stage.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XY, KM, and NS: conceptualization and result interpretation. XY, DS, and NS: code development. XY with guidance from DS and NS: computer simulations. XY and DS: visualization. XY: writing-original draft. KM: writing-review and editing and supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Natural Sciences and Engineering Research Council of Canada (NSERC) through the network grant Toward Environmentally Responsible Resource Extraction Network (TERRE-NET) (Program director D.W. Blowes), grant number 479708-2015.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Manuscript editing was additionally provided by K. Raymond at UBC.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2021.645675/full#supplementary-material

References

Alt-Epping, P., Tournassat, C., Rasouli, P., Steefel, C. I., Mayer, K. U., Jenni, A., et al. (2015). Benchmark reactive transport simulations of a column experiment in compacted bentonite with multispecies diffusion and explicit treatment of electrostatic effects. Comput. Geosci. 19, 535–550. doi: 10.1007/s10596-014-9451-x

CrossRef Full Text | Google Scholar

Amos, R. T., Bailey, B. L., Pham, H. N., Fretz, N., Hannam, S., Blowes, D. W., et al. (2012). Diavik waste rock project: northern aspects and scaling predictions. 19th British Columbia MEND Metal Leaching/Acid Rock Drainage Workshop. (Vancouver).

Google Scholar

Amos, R. T., Blowes, D. W., Bailey, B. L., Sego, D. C., Smith, L., and Ritchie, A. I. M. (2015). Waste-rock hydrogeology and geochemistry. Appl. Geochemistry 57, 140–156. doi: 10.1016/j.apgeochem.2014.06.020

CrossRef Full Text | Google Scholar

Arisoy, A., and Beamish, B. (2015). Mutual effects of pyrite and moisture on coal self-heating rates and reaction rate data for pyrite oxidation. Fuel 139, 107–114. doi: 10.1016/j.fuel.2014.08.036

CrossRef Full Text | Google Scholar

Arrhenius, S. (1889). Über die Dissociationswärme und den Einfluss der Temperatur auf den Dissociationsgrad der Elektrolyte. Zeitschrift für Phys. Chemie 4U, 96–116. doi: 10.1515/zpch-1889-0408

CrossRef Full Text | Google Scholar

Azmatch, T. F., Sego, D. C., Arenson, L. U., and Biggar, K. W. (2012). Using soil freezing characteristic curve to estimate the hydraulic conductivity function of partially frozen soils. Cold Reg. Sci. Technol. 83–84, 103–109. doi: 10.1016/j.coldregions.2012.07.002

CrossRef Full Text | Google Scholar

Barton, J. S. (1979). Denaturation at the optimum temperature. Biochem. Educ. 7, 13–14. doi: 10.1016/0307-4412(79)90013-X

CrossRef Full Text | Google Scholar

Bea, S. A., Mayer, U. K., and Macquarrie, K. T. B. (2016). Reactive transport and thermo-hydromechanical coupling in deep sedimentary basins affected by glaciation cycles: model development, verification, and illustrative example. Geofluids 16, 279–300. doi: 10.1111/gfl.12148

CrossRef Full Text | Google Scholar

Bea, S. A., Wilson, S. A., Mayer, K. U., Dipple, G. M., Power, I. M., and Gamazo, P. (2012). Reactive transport modeling of natural carbon sequestration in ultramafic mine tailings. Vadose Zo. J. 11:vzj2011.0053. doi: 10.2136/vzj2011.0053

CrossRef Full Text | Google Scholar

Bell, T., and Brown, T. M. (2018). From science to policy in the Eastern Canadian Arctic: an integrated regional impact study (IRIS) of climate change and moderization. ArcticNet (Quebec City, QC), 560. Available online at: https://arcticnet.ulaval.ca//pdf/media/29170_IRIS_East_full%20report_web.pdf

Google Scholar

Booshehrian, A., Wan, R., and Su, X. (2020). Hydraulic variations in permafrost due to open-pit mining and climate change: a case study in the Canadian Arctic. Acta Geotech. 15, 883–905. doi: 10.1007/s11440-019-00786-x

CrossRef Full Text | Google Scholar

Boulanger-Martel, V., Bussière, B., Côté, J., and Gagnon, P. (2017). “Design, construction,and preliminary performance of an insulation cover with capillary barrier effects at Meadowbank mine, Nunavut,” in 70th Can. Geotech. Conf (Ottawa, ON), 354.

Google Scholar

Brachman, R. W. I., Joshi, P., and Rowe, R. K. (2017). A new laboratory apparatus for measuring leakage through geomembrane holes beneath mine tailings. Can. Geotech. J. 54, 147–157. doi: 10.1139/cgj-2016-0333

CrossRef Full Text | Google Scholar

Bussière, B. (2010). Acid mine drainage from abandoned mine sites: problematic and reclamation approaches. Adv. Environ. Geotech. Proceedings of the International Symposium on Geoenvironmental Engineering in Hangzhou. 111–125. doi: 10.1007/978-3-642-04460-1_6

CrossRef Full Text | Google Scholar

Collette, L. (2017). Cryohydrogeology of a covered waste rock pile in permafrost environment: Large scale field experiment and freeze-thaw numerical investigations. Master's Thesis, University of British Columbia, Vancouver, BC, Canada.

Google Scholar

Coulombe, V., Bussière, B., Côté, J., and Garneau, P. (2012). “Performance of insulation covers to control acid mine drainage in cold environment,” in Proc. Int. Conf. Cold Reg. Eng. (Quebec City), 789–799. doi: 10.1061/9780784412473.078

CrossRef Full Text | Google Scholar

Demers, I., Molson, J., Bussière, B., and Laflamme, D. (2013). Numerical modeling of contaminated neutral drainage from a waste-rock field test cell. Appl. Geochemistry 33, 346–356. doi: 10.1016/j.apgeochem.2013.02.025

CrossRef Full Text | Google Scholar

Dobinski, W. (2011). Permafrost. Earth-Science Rev. 108, 158–169. doi: 10.1016/j.earscirev.2011.06.007

CrossRef Full Text | Google Scholar

Elberling, B., Schippers, A., and Sand, W. (2000). Bacterial and chemical oxidation of pyritic mine tailings at low temperatures. J. Contam. Hydrol. 41, 225–238. doi: 10.1016/S0169-7722(99)00085-6

CrossRef Full Text | Google Scholar

Etkin, D., Paoli, G., and Riseborough, D. (1998). Climate change impacts on permafrost engineering design. Environmental Adaptation Research Group, Atmospheric Environment Service. Available online at: https://www.researchgate.net/publication/259599095_Climate_Change_and_Permafrost_PERD (accessed March, 1998).

Google Scholar

Fetter, C. W. (1994). Applied Hydrogeology. 3rd Edn. New York, NY: Macmillan College Publishing Company.

Google Scholar

Gélinas, P., Lefebvre, R., Choquette, M., Isabel, D. L. J., and Guay, R. (1994). Monitoring and modeling of acid mine drainage from waste rocks dumps-La Mine Doyon case study. Canada Cent. Miner. Energy Technol. Available online at: http://mend-nedem.org/wp-content/uploads/1142g.pdf

Google Scholar

Hansson, K., Šimunek, J., Mizoguchi, M., Lundin, L.-C., and van Genuchten, M. T. (2004). Water flow and heat transport in frozen soil: numerical solution and freeze-thaw applications. Vadose Zo. J. 3, 693–704. doi: 10.2136/vzj2004.0693

CrossRef Full Text | Google Scholar

Henderson, T. H., Mayer, K. U., Parker, B. L., and Al, T. A. (2009). Three-dimensional density-dependent flow and multicomponent reactive transport modeling of chlorinated solvent oxidation by potassium permanganate. J. Contam. Hydrol. 106, 195–211. doi: 10.1016/j.jconhyd.2009.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurylyk, B. L., and Watanabe, K. (2013). The mathematical representation of freezing and thawing processes in variably-saturated, non-deformable soils. Adv. Water Resour. 60, 160–177. doi: 10.1016/j.advwatres.2013.07.016

CrossRef Full Text | Google Scholar

Kyhn, C., and Elberling, B. (2001). Frozen cover actions limiting AMD from mine waste deposited on land in Arctic Canada. Cold Reg. Sci. Technol. 32, 133–142. doi: 10.1016/S0165-232X(00)00024-0

CrossRef Full Text | Google Scholar

Lefebvre, R., Hockley, D., Smolensky, J., and Geélinas, P. (2001). Multiphase transfer processes in waste rock piles producing acid mine drainage. 1: Conceptual model and system characterization. J. Contam. Hydrol. 52, 137–164. doi: 10.1016/S0169-7722(01)00156-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, N., Chen, F., Xu, B., and Swoboda, G. (2008). Theoretical modeling framework for an unsaturated freezing soil. Cold Reg. Sci. Technol. 54, 19–35. doi: 10.1016/j.coldregions.2007.12.001

CrossRef Full Text | Google Scholar

Manaka, M. (2007). Comparison of rate laws for the oxidation of five pyrites by dissolved oxygen in acidic solution. J. Mineral. Petrol. Sci. 102, 24–38. doi: 10.2465/jmps.050302

CrossRef Full Text | Google Scholar

Mayer, K. U., Frind, E. O., and Blowes, D. W. (2002). Multicomponent reactive transport modeling in variably saturated porous media using a generalized formulation for kinetically controlled reactions. Water Resour. Res. 38, 13–1–13-21. doi: 10.1029/2001WR000862

CrossRef Full Text | Google Scholar

Mayer, K. U., and MacQuarrie, K. T. B. (2010). Solution of the MoMaS reactive transport benchmark with MIN3P-model formulation and simulation results. Comput. Geosci. 14, 405–419. doi: 10.1007/s10596-009-9158-6

CrossRef Full Text | Google Scholar

McCauley, C. A., White, D. M., Lilly, M. R., and Nyman, D. M. (2002). A comparison of hydraulic conductivities, permeabilities and infiltration rates in frozen and unfrozen soils. Cold Reg. Sci. Technol. 34, 117–125. doi: 10.1016/S0165-232X(01)00064-7

CrossRef Full Text | Google Scholar

McKenzie, J. M., Voss, C. I., and Siegel, D. I. (2007). Groundwater flow with energy transport and water-ice phase change: numerical simulations, benchmarks, and application to freezing in peat bogs. Adv. Water Resour. 30, 966–983. doi: 10.1016/j.advwatres.2006.08.008

CrossRef Full Text | Google Scholar

MEND (1996). Acid Mine Drainage in Permafrost Regions : Issues, Control Strategies and Research Requirements. Smithers, BC: MEND Project 1.61.2.

Google Scholar

MEND (2009). Mine Waste Covers in Cold Regions. Smithers, BC: MEND report 1.16.5a.

Google Scholar

MEND (2011). Climate Change and Acid Rock Drainage – Risks for the Canadian Mining Sector. Smithers, BC: MEND Report 1.61.7.

Google Scholar

Millington, R. J. (1959). Gas diffusion in porous media. Science 130, 100–102. doi: 10.1126/science.130.3367.100-a

CrossRef Full Text | Google Scholar

Neuner, M., Smith, L., Blowes, D. W., Sego, D. C., Smith, L. J. D., Fretz, N., et al. (2013). The Diavik waste rock project: water flow through mine waste rock in a permafrost terrain. Appl. Geochemistry 36, 222–233. doi: 10.1016/j.apgeochem.2012.03.011

CrossRef Full Text | Google Scholar

Noel, M. M., and Ritchie, A. I. M. (2012). Some physical properties of water transport in waste rock material. Mine Water Environ. 449–454. Available online at: https://www.imwa.info/docs/imwa_1999/IMWA1999_Noel_449.pdf

Google Scholar

Palandri, J. L., and Kharaka, Y. K. (2004). A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling. USGS Open File Rep. 2004–1068, 71. Available online at: https://pubs.usgs.gov/of/2004/1068/#pdf (accessed March, 2004).

Google Scholar

Pantelis, G., Ritchie, A. I. M., and Stepanyants, Y. A. (2002). A conceptual model for the description of oxidation and transport processes in sulphidic waste rock dumps. Appl. Math. Model. 26, 751–770. doi: 10.1016/S0307-904X(01)00085-3

CrossRef Full Text | Google Scholar

Pham, H. N. (2013). Heat Transfer in Waste Rock Piles Construted in a Contiuous Permafrost Region. Edmonton: Univ. Alberta.

Google Scholar

Pham, N. H., Sego, D. C., Arenson, L. U., Blowes, D. W., and Smith, L. (2008). “Convective heat transfer in waste rock piles under permafrost environment,” in Geoedmont. '08 61st Can. Geotech. Conf. (Edmonton), 940–947.

Google Scholar

Piteau Associates Engineering Ltd (1991). Mined rock and overburden piles - Investigation and design manual, British Columbia Mine Waste Rock Pile Research Committee. Available online at: https://www2.gov.bc.ca/assets/gov/farming-natural-resources-and-industry/mineral-exploration-mining/documents/mineral-titles/permitting/geotechnical-information/1991-05-00_minedrockoverburdenpile_investigationdesignmanual.pdf (accessed May, 1991).

Google Scholar

Poonoosamy, J., Wanner, C., Alt Epping, P., Águila, J. F., Samper, J., Montenegro, L., et al. (2018). Benchmarking of reactive transport codes for 2D simulations with mineral dissolution–precipitation reactions and feedback on transport parameters. Comput. Geosci. doi: 10.1007/s10596-018-9793-x

CrossRef Full Text | Google Scholar

Rasmussen, L. H., Zhang, W., Hollesen, J., Cable, S., Christiansen, H. H., Jansson, P. E., et al. (2018). Modelling present and future permafrost thermal regimes in Northeast Greenland. Cold Reg. Sci. Technol. 146, 199–213. doi: 10.1016/j.coldregions.2017.10.011

CrossRef Full Text | Google Scholar

Raymond, K. E., Seigneur, N., Su, D., Poaty, B., Plante, B., and Mayer, K. U. (2020). Numerical modeling of a laboratory-scale waste rock pile featuring an engineered cover system. Minerals 10, 1–25. doi: 10.3390/min10080652

CrossRef Full Text | Google Scholar

Richards, L. A. (1931). Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1, 318–333. doi: 10.1063/1.1745010

CrossRef Full Text | Google Scholar

Rosenblum, F., and Nesset, J. (2001). Evaluation and control of self-heating in sulphide concentrates. Cim.Org 94, 92–99. Available online at: https://www.researchgate.net/publication/299211950_Evaluation_and_control_of_self-heating_in_sulphide_concentrates (accessed November, 2001).

Google Scholar

Seigneur, N., Vriens, B., Beckie, R. D., and Mayer, K. U. (2021). Reactive transport modelling to investigate multi-scale waste rock weathering processes. J. Contam. Hydrol. 236:103752. doi: 10.1016/j.jconhyd.2020.103752

PubMed Abstract | CrossRef Full Text | Google Scholar

Singer, P. C., and Stumm, W. (1970). Acid mine drainage: the rate-determining step. Adv. Sci. 167, 1121–1123. doi: 10.1126/science.167.3921.1121

CrossRef Full Text | Google Scholar

Smith, L., López, D. L., Beckie, R., Morin, K., Dawson, R., and Price, W. (1995). Hydrogeology of Waste Rock Dumps. Smithers, BC: Mend Associate Project PA-1.115.

Google Scholar

Smith, L. J. D., Moncur, M. C., Neuner, M., Gupton, M., Blowes, D. W., Smith, L., et al. (2013). The Diavik waste rock project: design, construction, and instrumentation of field-scale experimental waste-rock piles. Appl. Geochemistry 36, 187–199. doi: 10.1016/j.apgeochem.2011.12.026

CrossRef Full Text | Google Scholar

Stevens, C. W., Shapka-Fels, T., and Rykaart, M. (2018). Thermal Cover Design for Mine Waste Facilities in Cold Regions. 13. Available online at: https://www.srk.com/en/publications/thermal-cover-design-for-mine-waste-facilities-in-cold-regions (accessed October, 2018).

Google Scholar

Stewart, B. A. (1988). Advances in Soil Science. New York, NY: Springer-Verlag. doi: 10.1007/978-1-4613-8771-8

CrossRef Full Text | Google Scholar

Su, D., Mayer, K. U., and MacQuarrie, K. T. B. (2020a). MIN3P-HPC: A High-Performance Unstructured Grid Code for Subsurface Flow and Reactive Transport Simulation. Berlin Heidelberg: Springer. doi: 10.1007/s11004-020-09898-7

CrossRef Full Text | Google Scholar

Su, D., Mayer, K. U., and MacQuarrie, K. T. B. (2020b). Numerical investigation of flow instabilities using fully unstructured discretization for variably saturated flow problems. Adv. Water Resour. 143:103673. doi: 10.1016/j.advwatres.2020.103673

CrossRef Full Text | Google Scholar

Su, D., Ulrich Mayer, K., and MacQuarrie, K. T. B. (2017). Parallelization of MIN3P-THCm: a high performance computational framework for subsurface flow and reactive transport simulation. Environ. Model. Softw. 95, 271–289. doi: 10.1016/j.envsoft.2017.06.008

CrossRef Full Text | Google Scholar

Voss, C. I., and Provost, A. (2010). SUTRA: a model for 2D or 3D saturated-unsaturated, Variable-density ground-water flow with solute or energy transport. USGS Water Resour. Investig. Available online at: https://www.usgs.gov/software/sutra-a-model-2d-or-3d-saturated-unsaturated-variable-density-ground-water-flow-solute-or (accessed September, 2010).

Google Scholar

Walvoord, M. A., and Kurylyk, B. L. (2016). Hydrologic impacts of thawing permafrost-a review. Vadose Zo. J. 15:vzj2016.01.0010. doi: 10.2136/vzj2016.01.0010

CrossRef Full Text | Google Scholar

Wilson, D., Amos, R. T., Blowes, D. W., Langman, J. B., Ptacek, C. J., Smith, L., et al. (2018a). Diavik waste rock project: a conceptual model for temperature and sulfide-content dependent geochemical evolution of waste rock – Laboratory scale. Appl. Geochemistry 89, 160–172. doi: 10.1016/j.apgeochem.2017.12.007

CrossRef Full Text | Google Scholar

Wilson, D., Amos, R. T., Blowes, D. W., Langman, J. B., Smith, L., and Sego, D. C. (2018b). Diavik Waste Rock Project: scale-up of a reactive transport model for temperature and sulfide-content dependent geochemical evolution of waste rock. Appl. Geochemistry 96, 177–190. doi: 10.1016/j.apgeochem.2018.07.001

CrossRef Full Text | Google Scholar

Woo, M. (2012). Permafrost Hydrology. Heidelberg: Springer. doi: 10.1007/978-3-642-23462-0

CrossRef Full Text | Google Scholar

Wösten, J. H. M., and van Genuchten, M. T. (1988). Using texture and other soil properties to predict the unsaturated soil hydraulic functions. Soil Sci. Soc. Am. J. 52, 1762–1770. doi: 10.2136/sssaj1988.03615995005200060045x

CrossRef Full Text | Google Scholar

Xie, X., Xiao, S., He, Z., Liu, J., and Qiu, G. (2007). Microbial populations in acid mineral bioleaching systems of Tong Shankou Copper Mine, China. J. Appl. Microbiol. 103, 1227–1238. doi: 10.1111/j.1365-2672.2007.03382.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Carey, S. K., Quinton, W. L., Janowicz, J. R., Pomeroy, J. W., and Flerchinger, G. N. (2010). Comparison of algorithms and parameterisations for infiltration into organic-covered permafrost soils. Hydrol. Earth Syst. Sci. 14, 729–750. doi: 10.5194/hess-14-729-2010

CrossRef Full Text | Google Scholar

Zhao, L., Gray, D. M., and Male, D. H. (1997). During infiltration into frozen ground. J. Hydrol. 200, 345–363. doi: 10.1016/S0022-1694(97)00028-0

CrossRef Full Text | Google Scholar

Zhao, Y., Nishimura, T., Hill, R., and Miyazaki, T. (2013). Determining hydraulic conductivity for air-filled porosity in an unsaturated frozen soil by the multistep outflow method. Vadose Zo. J. 12:vzj2012.0061. doi: 10.2136/vzj2012.0061

CrossRef Full Text | Google Scholar