Stochastic multi-objective optimization for flood control in multi-reservoir systems: an adaptive Progressive Hedging approach with scenario clustering

Introduction: Flood-prone regions face growing challenges due to climate-induced variability, rapid urbanization, and competing demands on water infrastructure. Multi-reservoir systems play a critical role in mitigating flood damages, but climate change has intensified management complexity through increased hydroclimatic volatility and reduced reaction times for dam operators.

Methods: This study presents a stochastic multi-objective optimization framework that integrates ensemble-based inflow scenarios, high-resolution hydraulic simulations, and an adaptive version of the Progressive Hedging Algorithm enhanced by K-means scenario clustering. The approach was applied to Tunisia's Medjerda River basin, focusing on five interconnected reservoirs. The model balances downstream flood risk reduction with long-term water storage security by optimizing reservoir release policies across 1,000 synthetic inflow scenarios, reduced to 10 representative scenarios through clustering.

Results: The proposed method achieved robust performance with normalized objective values of 0.087 for storage security and 0.094 for flood control. More than 93% of simulated scenarios satisfied both storage and flood-related constraints, demonstrating superior reliability compared to traditional rule-based methods (60–70%). The framework converged in 42 iterations with a computational time of 3.2 hours, representing a 6.7-fold reduction compared to full-scenario optimization while maintaining only 6–7% performance degradation. Peak discharge reductions of 25–30% were achieved through coordinated reservoir operations.

Discussion: The framework provides operationally feasible release policies that perform consistently across diverse flood conditions while significantly reducing computational costs. By combining hydrological realism with optimization scalability, this work supports the design of resilient and anticipatory flood management strategies in semi-arid regions, directly contributing to global efforts toward sustainable water governance (SDG 6), climate resilience (SDG 13), and disaster risk reduction in human settlements (SDG 11).

1 Introduction

Extreme flood events pose significant risks to human settlements, infrastructure, and agricultural zones, particularly in semi-arid regions where rainfall is both intense and highly variable. Multi-reservoir systems play a critical role in mitigating flood damages by regulating river flows and storing excess water during peak inflows.

However, climate change has intensified these challenges. Global observations indicate a 10%–20% increase in extreme precipitation events over recent decades, with Mediterranean regions experiencing a 15% rise in flood frequency since 1980 (IPCC, 2021). In Tunisia, recent decades have seen a shift toward shorter, more intense rainfall episodes, which overload reservoir inflow systems and reduce reaction time for dam operators. This increased hydroclimatic volatility complicates the management of interconnected reservoirs, especially when decision windows shrink from days to mere hours. Designing operational strategies for such systems is complex due to the spatial-temporal variability of hydrological processes and the conflicting objectives involved in reservoir management.

The economic consequences of inadequate flood management are substantial. Recent flood events in Mediterranean basins have caused damages exceeding €100 million per event, with the 2019 southeastern Spain floods alone resulting in €425 million in losses (European Environment Agency, 2021). These impacts underscore the urgent need for improved flood management strategies that can adapt to increasing hydrological uncertainty. In this context, this research aligns with the United Nations Sustainable Development Goals (SDGs), particularly SDG 6 (Clean Water and Sanitation), SDG 11 (Sustainable Cities and Communities), and SDG 13 (Climate Action), by promoting resilient water infrastructure and adaptive flood risk management under climate stress.

Flood-period reservoir operations must simultaneously address short-term emergency control–by limiting downstream flood peaks–and long-term sustainability concerns, such as preserving adequate water reserves for post-event water supply and energy production. These challenges are amplified in interconnected reservoir networks, where upstream decisions cascade through the system and affect downstream storage and flow dynamics. The complexity of such coordination is exemplified by historical events where uncoordinated reservoir releases have exacerbated downstream flooding despite individual reservoirs operating within design parameters (International Commission on Large Dams, 2018). Moreover, uncertainty in natural inflows caused by climate variability and forecast limitations further complicates the development of robust and effective control strategies. These dynamics require operational strategies that can rapidly adapt to unexpected inflow patterns, a task traditional static rules struggle to handle. The compound risk of simultaneous upstream inflows and downstream saturation makes multi-reservoir coordination under climate change stress a non-trivial challenge.

Traditional rule-based or deterministic optimization methods are often insufficient for managing such uncertainty, leading to either overly conservative or risk-prone operations. Studies have shown that conventional operating rules can result in 30%–40% suboptimal performance under non-stationary conditions compared to adaptive strategies (Giuliani et al., 2021). As a result, there has been a growing shift toward stochastic optimization frameworks that explicitly incorporate inflow variability and assess performance across ensembles of hydrological scenarios. These frameworks enable the development of release policies that are not only feasible under a wide range of conditions but also balanced in their treatment of flood protection and water availability.

In this study, we focus on the Medjerda River basin in northern Tunisia, a flood-prone region whose water infrastructure is centered around a cascade of strategically interconnected reservoirs. The Medjerda system exemplifies the challenges facing semi-arid reservoir networks: it has experienced four major flood events in the past two decades (2003, 2007, 2009, 2018), each causing damages exceeding €50 million and affecting over 100,000 residents (United Nations Office for Disaster Risk Reduction, 2020). The system is highly sensitive to short-duration flood events due to its steep terrain and rapid runoff, while also facing long-term pressures from siltation and drought. The 2003 floods particularly highlighted coordination challenges, where sequential reservoir releases contributed to downstream peak flow amplification. These competing demands and demonstrated vulnerabilities make it an ideal testbed for evaluating advanced reservoir optimization methods.

We propose a novel stochastic multi-objective optimization model that aims to coordinate flood-season reservoir releases across the network. The framework integrates ensemble-based inflow modeling, hydraulic simulation of downstream water levels, and a scenario-based decomposition algorithm to generate robust and operationally viable control policies. The goal is to minimize flood risk at downstream control points while preserving storage security within each reservoir under a wide range of hydrological scenarios.

The remainder of this paper is organized as follows. Section 2 reviews related work on stochastic and multi-objective optimization for flood control. Section 3 presents the mathematical formulation, including system dynamics, objectives, and constraints. Section 4 introduces the proposed solution framework, which integrates adaptive Progressive Hedging with scenario clustering. Section 5 applies the method to the Medjerda reservoir system and analyzes the results. Section 6 discusses methodological contributions, practical implications, and limitations. Section 7 concludes the paper by summarizing key insights and outlining avenues for future research.

2 Literature review

Flood control in multi-reservoir systems under hydrological uncertainty represents one of the most challenging problems in water resources management. The complexity arises from the need to balance multiple conflicting objectives–minimizing downstream flood risk while preserving storage for post-flood water supply, energy production, and irrigation demands–all under conditions of uncertain and highly variable inflows. The increasing frequency and intensity of extreme weather events, driven by climate change, have amplified these challenges and motivated the development of sophisticated reservoir operation frameworks that integrate stochastic modeling, multi-objective optimization, and real-time decision support capabilities.

The explicit incorporation of inflow uncertainty into reservoir operation decisions has been a cornerstone of modern water management research. Schwanenberg et al. (2014) demonstrated the effectiveness of Sample Average Approximation (SAA) and scenario tree methods for flood mitigation at Brazil's Tres Marias reservoir, showing clear advantages over deterministic approaches in anticipating uncertain inflows. Draper (2001) advanced this field by proposing an implicit stochastic optimization framework with rolling-horizon implementation, which links short-term operational decisions through carryover storage values while avoiding unrealistic perfect foresight assumptions. These foundational approaches established the principle of prioritizing robustness over purely optimal but fragile solutions, a paradigm that continues to influence contemporary research.

Risk-aware multi-objective models have gained significant traction in addressing the inherent trade-offs between competing operational priorities. Chen et al. (2020) developed a pioneering real-time flood control model that integrates stochastic differential equations for risk assessment with the NSGA-III algorithm, effectively balancing upstream overtopping risks against downstream flood impacts. Building on these foundations, Guo et al. (2024) incorporated AI-generated ensemble flood forecasts and resilience indicators into a robust optimization framework, demonstrating how machine learning can enhance uncertainty representation. Liu and Luo (2019) extended this line of research by introducing reactive strategies within a dynamic multi-objective optimization model, enabling systems to adapt their operational priorities in response to evolving hydrological conditions.

The nonlinear, high-dimensional nature of multi-reservoir flood control problems has motivated extensive research into metaheuristic optimization algorithms. Zhang et al. (2019) applied the decomposition-based evolutionary algorithm MOEA/D-DE to flood operations at China's Ankang reservoir, achieving significant reductions in peak discharge while maintaining dam safety constraints. Moridi and Yazdi (2017) developed a more complex mixed-integer multi-objective model for coordinating flood control capacity and hydropower production across six reservoirs, solved using the ε-constraint method. The diversity of algorithmic approaches reflects the complexity of the underlying optimization landscape, with Qi et al. (2016) introducing a memetic immune algorithm specifically designed for reservoir operation topologies, while Luo et al. (2015) proposed a hybrid PSO-EDA approach capable of learning inter-variable dependencies to improve convergence on complex Pareto fronts.

Contemporary research increasingly emphasizes the integration of machine learning techniques with traditional optimization approaches. Zanutto et al. (2025) developed reinforcement learning algorithms for processing multi-timescale forecast information in multipurpose reservoir operations, demonstrating improved reliability compared to conventional model predictive control approaches. Gegenleithner et al. (2024) advanced this integration further by proposing transformer-based deep reinforcement learning for multiobjective multihydropower reservoir optimization, achieving superior generalization capability compared to traditional evolutionary algorithms such as NSGA-III and MOEA/D. The coupling of optimization with real-time forecasting capabilities has emerged as a particularly promising research direction, with Becker et al. (2024) implementing moving-horizon ensemble forecast optimization to support adaptive decision-making, while Mohanty et al. (2025) developed coupled optimization frameworks that integrate hedging rules with detailed hydrodynamic modeling.

Research attention has increasingly focused on system-scale applications and emergency operational scenarios. Wang et al. (2022) addressed basin-wide coordination challenges by formulating a multi-objective optimization model for the coordinated operation of twelve major reservoirs in China's Yangtze River basin, highlighting both the potential and the computational challenges of these methods for large-scale, interconnected systems. Akbari et al. (2014) investigated emergency operation strategies for Iran's Abbaspour reservoir under damaged spillway conditions, combining short-term flood risk mitigation with long-term water supply objectives through a hybrid simulation-optimization framework. Uysal et al. (2018) demonstrated the practical application of Model Predictive Control enhanced by probabilistic inflow forecasts and scenario tree reduction techniques, showing improved flood control performance with reduced reliance on unnecessary spillway releases.

Progressive Hedging (PH), originally introduced by Rockafellar and Wets (1991), has emerged as a robust technique for solving large-scale stochastic optimization problems through scenario-based decomposition. Its application to reservoir operations spans multiple contexts, including hydropower scheduling (Watkins and McKinney, 2000) and drought management (Huang et al., 2020). Gade et al. (2016) proposed adaptive penalty updates to accelerate convergence and improve solution stability, while Watson and Woodruff (2011) extended the method to enable parallel implementation for real-time operational contexts. Recent advances by Woodruff et al. (2023) introduced gradient-based methods for computing variable-dependent penalty parameters, achieving significant convergence improvements. Deliktaş et al. (2024) further demonstrated the effectiveness of sample intelligence-based Progressive Hedging algorithms for facility location problems under uncertainty.

Parallel developments in scenario clustering have focused on reducing computational complexity while preserving solution quality. Giuliani et al. (2021) established theoretical foundations for intelligent scenario reduction techniques, while Schlenkrich and Parragh (2024) demonstrated practical applications of scenario reduction combined with advanced optimization methods for multi-stage problems. These approaches show promise for maintaining solution quality while dramatically reducing computational requirements.

The past five years have witnessed rapid progress in multi-objective optimization approaches for water resources management. Wang et al. (2023) introduced dynamic multi-objective optimization methods based on classification strategies, addressing the fundamental challenge of balancing population diversity with convergence in time-varying environments. Xu et al. (2024) developed hybrid artificial intelligence methods that combine deep learning with multi-objective optimization for reservoir development strategies, demonstrating the potential of integrated AI-optimization frameworks. Regional applications have also contributed important insights, with Hassan et al. (2021) presenting genetic algorithm approaches for multipurpose dam operation in Morocco, incorporating smoothing constraints to reduce policy fluctuations, while Mansouri et al. (2023) focused on simulation-optimization approaches for drought management in arid regions.

These recent developments collectively illustrate a clear shift toward integrated, adaptive, and AI-enhanced optimization methods for water resources management. These advances underscore the evolution toward practical, computation-ready frameworks–yet several gaps remain, limiting their deployment in real-time flood control contexts.

Despite significant progress across multiple research fronts, several critical gaps limit the operational deployment of advanced stochastic optimization for multi-reservoir flood control. First, while scenario clustering and Progressive Hedging have been developed independently with demonstrated individual benefits, their systematic integration remains largely unexplored. Existing approaches typically either sacrifice computational efficiency through exhaustive scenario evaluation or compromise solution quality through oversimplified reduction techniques, creating a persistent trade-off between accuracy and tractability.

Second, recent improvements in Progressive Hedging focus primarily on single-objective optimization problems, with limited adaptation to contexts where trade-offs between risk mitigation and resource preservation must be dynamically managed. The specialized penalty adjustment mechanisms required for effective multi-objective optimization remain underdeveloped, particularly for applications where objective importance varies seasonally or in response to changing conditions.

Third, current stochastic approaches typically require prohibitive computational resources that prevent deployment in real-time flood management contexts where rapid decision support is essential. The scalability challenge becomes particularly acute for large-scale multi-reservoir systems where coordination complexity grows exponentially with system size, making traditional approaches impractical for operational use.

This study addresses these critical gaps through the first systematic integration of adaptive Progressive Hedging with intelligent scenario clustering, specifically designed for multi-reservoir flood control applications. The proposed framework bridges the computational tractability gap while maintaining solution robustness, enabling the transition from academic optimization concepts toward operational flood management tools. By combining established stochastic programming principles with novel algorithmic enhancements, our approach provides a comprehensive solution tailored to the urgent demands of climate-resilient water management under increasing uncertainty.

3 Mathematical model

3.1 Problem formulation

This work addresses the problem of optimizing water release policies in a multi-reservoir system during flood events under uncertainty. A stochastic multi-objective optimization framework is developed to jointly manage two conflicting goals:

• Reducing downstream flood risk by regulating river levels at key control points;

• Maintaining reservoir storage within operational bounds to avoid overtopping while ensuring post-flood water supply.

The system is modeled over a finite discrete time horizon. It incorporates:

• Spatially distributed reservoirs and downstream river monitoring points;

• Temporally varying and stochastic inflows, modeled through a finite ensemble of inflow scenarios;

• Operational constraints on reservoir storage capacities, release bounds, and system connectivity.

The decision variables are time-dependent reservoir releases. State variables include reservoir storage levels and river stages. The model evaluates policy robustness across inflow scenarios, enabling consistent performance under a wide range of flood conditions. The mathematical components–variables, constraints, and objective functions–are described in the following subsections.

3.2 Model components

The optimization framework is formulated over a discrete-time horizon and captures the dynamics of a multi-reservoir flood control system through a set of variables, stochastic inflows, and physical parameters:

Temporal and spatial structure. The system comprises M reservoirs and a finite planning horizon of T time steps $T=\left\{1,2,\dots ,T\right\}$ (e.g., 10-h intervals). Flood levels are monitored at a set of downstream control points $K$, where river stages $h_t^k$ [m] are evaluated for each $k\in K$.

Decision and state variables. At each time $t\in T$ and for each reservoir m∈{1, …, M}, the decision variable $r_t^m$ [m³] denotes the volume released, while $s_t^m$ [m³] represents the corresponding storage level. The variable $h_t^k$ captures river water level dynamics at control points.

Stochastic forcing. Natural inflows ${\eta }_t^m(\omega )$, defined over a discrete set of scenarios ω∈Ω, account for hydrological uncertainty due to variable precipitation and runoff. These are generated via a scenario-based stochastic process introduced in the experimental design.

Cascade dynamics. For each reservoir m, total inflow is modeled as:

$i_t^m(\omega )={\displaystyle \sum _{j\in A(m)}}{r}_t^j+{\eta }_t^m(\omega ),$

where $A(m)$ denotes the set of direct upstream reservoirs discharging into m.

System constraints and physical limits. Each reservoir is constrained by a maximum capacity $s_{\mathrm{\text{max}}}^m$, a minimum security storage $s_{\mathrm{\text{secu}}}^m$, and admissible releases within $\left[r_{min}^m,r_{max}^m\right]$. At downstream points, water levels are evaluated against a desired threshold $h_{\mathrm{\text{desired}}}^k$ and a flood warning threshold $h_{\mathrm{\text{flood}}}^k$ to ensure regulatory compliance and flood mitigation.

These components define the structural and operational foundation of the system, supporting the formulation of multi-objective optimization goals and feasibility constraints discussed in subsequent sections.

3.3 Objective functions

The optimization model addresses two conflicting objectives: (i) maintaining sufficient reservoir storage after flood events, and (ii) minimizing downstream flood risk by regulating river levels. Each objective is evaluated over a set of stochastic inflow scenarios ω∈Ω, and the overall performance is assessed through expectation.

(1) Reservoir storage security.

This objective ensures that post-flood storage levels remain above the minimum security threshold $s_{\mathrm{\text{secu}}}^m$ for each reservoir. A quadratic penalty is applied to storage deficits across time and space. The expression is normalized with respect to the total potential deviation in the system:

$\begin{array}{ll}{Q}^{\omega }=\frac{{\displaystyle \sum _{t\in T}}{\displaystyle \sum _{m=1}^M}{\left(s_t^m-s_{\text{secu}}^m\right)}^2}{T·{\displaystyle \sum _{m=1}^M}{\left(s_{\text{max}}^m-s_{\text{secu}}^m\right)}^2}& (1)\end{array}$

This normalized formulation ensures comparability across reservoirs with different capacities.

(2) River level regulation.

This objective penalizes deviations of river stages $h_t^k$ from desired thresholds $h_{\mathrm{\text{desired}}}^k$ at control points $k\in K$. The penalty is scaled relative to the flood risk range, defined as the difference between the flood threshold and target level:

$\begin{array}{ll}{L}^{\omega }=\frac{{\displaystyle \sum _{t\in T}}{\displaystyle \sum _{k\in K}}{\left(h_t^k-h_{\text{desired}}^k\right)}^2}{T·{\displaystyle \sum _{k\in K}}{\left(h_{\text{flood}}^k-h_{\text{desired}}^k\right)}^2}& (2)\end{array}$

This approach prioritizes control points with narrow safety margins and higher flood sensitivity.

3.3.1 Stochastic multi-objective formulation

The model seeks to minimize the expected values of the two objectives over all inflow scenarios:

$\begin{array}{ll}{\displaystyle \underset{\text{r}}{min}}(E_{\omega }\left[Q^{\omega }\right],E_{\omega }\left[L^{\omega }\right])& (3)\end{array}$

This multi-objective structure captures the trade-off between short-term flood protection and long-term water availability. In practice, the problem can be solved using scalarization (e.g., weighted sums) or Pareto-front exploration to support informed decision-making under uncertainty.

3.4 System constraints

The model is subject to a set of deterministic constraints that govern the physical behavior of the reservoir network and ensure operational feasibility. These constraints apply to all time steps $t\in T$, reservoirs m = 1, …, M, and inflow scenarios ω∈Ω.

(a) Mass balance. Reservoir storage levels evolve over time according to the continuity equation, which conserves water volume between time steps:

$\begin{array}{ll}{s}_{t+1}^m=s_t^m+i_t^m(\omega )-r_t^m,\text{with }{s}_1^m\text{ given.}& (4)\end{array}$

(b) Storage bounds. To prevent overtopping and ensure post-flood availability, each reservoir's storage must stay within its operational range:

$\begin{array}{ll}{s}_{\text{secu}}^m\le s_t^m\le s_{\text{max}}^m& (5)\end{array}$

(c) Release constraints. Releases from each reservoir are bounded to reflect infrastructure capacities and operational limits:

$\begin{array}{ll}{r}_{min}^m\le r_t^m\le r_{max}^m& (6)\end{array}$

(d) Inflow routing. The total inflow to a reservoir includes upstream releases and local (natural) inflows:

$\begin{array}{ll}{i}_t^m(\omega )={\displaystyle \sum _{j\in A(m)}}{r}_t^j+{\eta }_t^m(\omega )& (7)\end{array}$

Here, $A(m)$ denotes the set of reservoirs directly upstream of reservoir m, enabling the routing of flows through the network.

(e) River level estimation. Downstream river stages $h_t^k$ at each control point $k\in K$ are computed externally using the HEC-RAS hydraulic model (Brunner, 2016). This model takes reservoir release sequences as inputs and simulates unsteady flow in open channels based on the one-dimensional Saint-Venant equations, widely used for river hydraulics and flood routing (Chaudhry, 2007):

• Continuity:

$\begin{array}{ll}\frac{\partial A}{\partial t}+\frac{\partial Q}{\partial x}=0& (8)\end{array}$

• Momentum:

$\begin{array}{ll}\frac{\partial Q}{\partial t}+\frac{\partial }{\partial x}\left(\frac{Q^2}{A}\right)+gA\frac{\partial H}{\partial x}+gQ\left|Q\right|\frac{n^2}{A{R}^{4/3}}=0& (9)\end{array}$

In these equations, A is the cross-sectional area, Q is the discharge, H is the water surface elevation, R is the hydraulic radius, n is Manning's roughness coefficient, x is the longitudinal distance, and t is time.

HEC-RAS solves these equations using an implicit finite-difference scheme over a predefined river network geometry (U.S. Army Corps of Engineers, 2025). The resulting water levels $h_t^k$ are then passed back to the optimization model to evaluate flood risk via the objective function L^ω.

This modular coupling enables high-resolution hydraulic simulation without embedding complex flow physics inside the optimization loop, while remaining flexible for integration with alternative solvers like TELEMAC (Goutal and Maurel, 2007) or MIKE 11 (DHI Water and Environment, 2017), which offer similar functionalities for unsteady open channel flow modeling.

3.5 Stochastic inflow modeling

To capture the uncertainty inherent in flood-period hydrology, natural inflows ${\eta }_t^m(\omega )$ are modeled as stochastic variables. This reflects variability in both rainfall events and catchment response, which directly influence reservoir inputs during extreme weather conditions. The stochastic inflow process is constructed through a combination of univariate extreme value modeling and multivariate scenario generation.

3.5.1 Marginal distribution modeling

For each reservoir m and time step t, the marginal distribution of natural inflows is modeled using the Gumbel distribution, widely adopted in hydrological extremes analysis (Jenkinson, 1955; Stedinger et al., 1993). This choice is suitable for simulating flood scenarios due to its capacity to reproduce the statistical properties of annual maxima and high flow events. The probability density function is expressed as:

$\begin{array}{ll}{f}_{\eta }(x;\mu ,\beta )=\frac{1}{\beta }exp\left(-\frac{x-\mu }{\beta }-exp\left(-\frac{x-\mu }{\beta }\right)\right)& (10)\end{array}$

Here, μ and β are the location and scale parameters of the distribution. These parameters are calibrated individually for each reservoir using historical inflow records, typically through maximum likelihood estimation (MLE) or method of moments (Martins and Stedinger, 1984).

3.5.2 Multivariate scenario generation

To preserve spatial dependencies between reservoirs, a multivariate scenario generation approach is employed (Yates et al., 2005). Let μ_t denote the vector of expected inflows at time t, and let Σ be the covariance matrix representing the inter-reservoir dependencies derived from historical joint inflow data.

For each scenario ω∈Ω, a correlated inflow vector ${\eta }_t^{\omega }$ is sampled using Cholesky decomposition (Lerman, 1980):

$\begin{array}{ll}{\eta }_t^{\omega }={\mu }_t+L·{\text{z}}_t^{\omega }& (11)\end{array}$

where L is the lower triangular matrix such that Σ = LL^⊤, and ${\text{z}}_t^{\omega }$ is a vector drawn from the standard multivariate normal distribution $N(0,I)$. This ensures that the synthetic inflow trajectories match both the marginal distributions and the spatial correlation structure observed in real data.

3.5.3 Scenario set construction

A total of |Ω| = 1, 000 inflow scenarios are generated, each covering a 60-day period with a temporal resolution of 10 h. These scenarios form the stochastic input space for the optimization model, enabling evaluation of release strategies under a wide spectrum of plausible flood conditions.

3.6 Optimization framework and scenario evaluation

The optimization model is developed within an open-loop framework, in which all inflow scenarios are assumed to be fully known at the time of decision-making. This formulation yields a static release policy r defined over the entire planning horizon, independent of real-time feedback. While more conservative than closed-loop (adaptive) approaches, the open-loop structure is computationally efficient and suitable for offline planning applications where inflow forecasts are uncertain or unavailable.

A finite ensemble of inflow scenarios Ω = {ω₁, ω₂, …, ω_|Ω|} is generated using the stochastic inflow model described in the previous section. For each candidate policy r, the reservoir system is simulated across all scenarios ω∈Ω, and the corresponding objective values Q^ω and L^ω are evaluated.

The expected system performance is then defined as the mean of these values over the full scenario ensemble:

$\begin{array}{ll}{E}_{\omega }\left[Q^{\omega }\right]=\frac{1}{|\Omega |}{\displaystyle \sum _{\omega \in \Omega }}{Q}^{\omega },E_{\omega }\left[L^{\omega }\right]=\frac{1}{|\Omega |}{\displaystyle \sum _{\omega \in \Omega }}{L}^{\omega }& (12)\end{array}$

This expectation-based formulation ensures that the resulting policy is not only feasible under uncertainty, but also robust in the sense that it minimizes average performance losses over a broad spectrum of hydrological realizations. Moreover, the use of multiple scenarios enables a comprehensive exploration of the trade-offs between flood control and storage retention, supporting the identification of Pareto-optimal operating strategies.

To reduce sampling error and ensure statistical representativeness, the scenario set Ω is constructed to preserve key probabilistic characteristics of the inflow process, including marginal distributions, spatial covariance structure, and temporal variability.

4 Solution approach: adaptive Progressive Hedging with scenario clustering for multi-objective reservoir optimization

Building upon the need for robust reservoir operation strategies under hydrological uncertainty, we propose an enhanced solution framework based on the Progressive Hedging Algorithm (PHA). PHA is a scenario-based decomposition method particularly suited for large-scale stochastic programs with non-anticipativity constraints, where decisions must remain consistent across uncertain future realizations (Rockafellar and Wets, 1991; Watson and Woodruff, 2011).

In our context, each inflow scenario ω∈Ω defines a subproblem in which a scenario-specific release policy r^ω is optimized to minimize a weighted sum of the normalized objectives: the storage deviation Q^ω and the river level deviation L^ω:

$\begin{array}{ll}{f}^{\omega }(\text{r})=\lambda Q^{\omega }(\text{r})+(1-\lambda )L^{\omega }(\text{r})& (13)\end{array}$

where λ∈[0, 1] is a scalarization parameter controlling the trade-off between post-flood storage security and downstream flood risk mitigation.

The classical PHA is extended in two key ways: (i) an adaptive penalty adjustment mechanism that improves convergence and robustness, and (ii) a scenario clustering step that reduces the effective number of subproblems and enhances scalability.

4.1 Step-by-step procedure

4.1.1 Scenario clustering

Solving a subproblem for every inflow scenario ω∈Ω is computationally expensive, especially when each scenario encodes a full multivariate time series. To reduce dimensionality, we apply K-means clustering to group similar inflow trajectories and extract a reduced set of representative scenarios Ω′ (Steinschneider and Brown, 2015; Gupta et al., 2020).

Rather than clustering directly on raw time series data, we extract hydrologically meaningful summary features for each scenario, namely:

• Peak inflow magnitude (maximum value),

• Time-to-peak (temporal index of the maximum),

• Cumulative inflow volume (integrated inflow over time),

• Intra-horizon variability (standard deviation).

These features are standardized to ensure scale invariance. K-means is then applied in the standardized feature space, and the centroid of each cluster is selected to form Ω′⊂Ω. The number of clusters (typically between 5 and 15) is chosen to strike a balance between scenario diversity and computational efficiency.

This approach retains the diversity of hydrological behavior while enabling stable and tractable optimization.

4.1.2 Initialization

For each representative scenario ω∈Ω′, a scenario-specific release policy ${\text{r}}_0^{\omega }$ is initialized, often as a flat release vector or based on historical averages. A global consensus policy ${\bar{\text{r}}}_0$ is initialized as the mean of the initial scenario policies. The initial penalty parameter ρ₀ is set (e.g., ρ₀ = 100) and is dynamically updated in subsequent iterations.

Solving Scenario Subproblems : At each iteration k, the algorithm solves the following penalized subproblem in parallel for all scenarios ω∈Ω′:

$\begin{array}{ll}{\text{r}}_{k+1}^{\omega }=arg{\displaystyle \underset{\text{r}}{min}}\left\{f^{\omega }(\text{r})+{\rho }_k\left|\right|\text{r}-{\bar{\text{r}}}_k|{|}^2\right\}& (14)\end{array}$

The penalty term encourages alignment with the shared policy ${\bar{\text{r}}}_k$ while still allowing some exploration.

4.1.3 Integration of hydraulic model outputs

After each scenario-specific policy r^ω is updated, it is passed to an external hydraulic simulator (HEC-RAS) that returns the resulting river level trajectories $h_t^k$. These outputs are used to compute L^ω(r), which feeds back into the subproblem cost. This decoupled model ensures high-fidelity simulation without embedding full hydraulic equations into the optimization process.

4.1.4 Consensus update

The new consensus policy is computed as the average of updated scenario policies:

$\begin{array}{ll}{\bar{\text{r}}}_{k+1}=\frac{1}{\left|{\Omega }^{\prime }\right|}{\displaystyle \sum _{\omega \in {\Omega }^{\prime }}}{\text{r}}_{k+1}^{\omega }& (15)\end{array}$

This step gradually aligns the scenario-specific solutions toward a non-anticipative policy.

4.1.5 Adaptive penalty adjustment

To enhance convergence, the penalty coefficient ρ is updated based on the variance of the scenario-specific decisions:

$\begin{array}{ll}{\rho }_{k+1}={\rho }_k·(1+\alpha ·\text{Var}(\left\{{\text{r}}_{k+1}^{\omega }\right\}))& (16)\end{array}$

The adaptation rate α is a hyperparameter (typically between 0.1 and 0.5), selected via sensitivity analysis. This update strengthens non-anticipativity as consensus improves, while maintaining flexibility in early iterations.

4.1.6 Convergence criterion

The algorithm terminates once the policies across all scenarios converge sufficiently to the consensus:

$\left|\right|{\text{r}}_{k+1}^{\omega }-{\bar{\text{r}}}_{k+1}\left|\right|<ϵ,\forall \omega \in {\Omega }^{\prime }$

At convergence, the policy $\bar{\text{r}}$ constitutes a robust, scenario-agnostic release schedule optimized under inflow uncertainty.

4.2 Implementation and workflow

The complete solution procedure is summarized in Algorithm 1, which formalizes the iterative structure of the Adaptive Progressive Hedging method with scenario clustering. The corresponding computational pipeline is visualized in Figure 1.

Algorithm 1

Algorithm 1. Adaptive progressive hedging with scenario clustering.

Figure 1

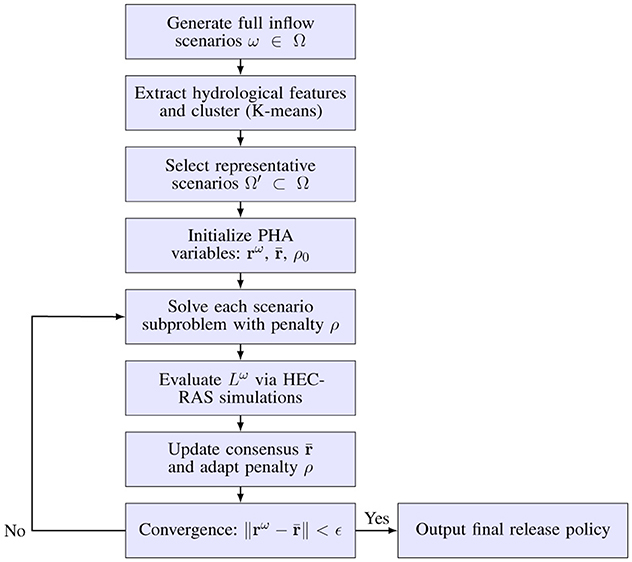
Figure 1. Workflow of the proposed adaptive Progressive Hedging framework with K-means scenario clustering and hydraulic simulation.

The workflow begins with the generation of a large ensemble of inflow scenarios ω∈Ω based on the stochastic inflow modeling process described in the previous section. Each scenario represents a multivariate inflow trajectory across all reservoirs over the simulation horizon.

To reduce computational complexity while preserving hydrological diversity, we apply K-means clustering to a transformed feature space. For each scenario, a vector of hydrologically relevant features is computed–such as peak inflow, time-to-peak, cumulative volume, and standard deviation–and standardized prior to clustering. One representative scenario (typically the centroid) is selected per cluster, forming the reduced scenario set Ω′ ⊂ Ω.

The optimization process is initialized by assigning an initial release policy ${\text{r}}_0^{\omega }$ to each representative scenario, typically using a flat or heuristically-informed baseline. A global consensus policy ${\bar{\text{r}}}_0$ is computed as the average of the scenario-specific policies. The penalty coefficient ρ₀ is initialized to a fixed value and will evolve over the iterations to control inter-scenario coherence.

Each iteration of the PHA loop involves solving all scenario subproblems in parallel. For each ω∈Ω′, the release policy r^ω is optimized using a penalized objective that balances individual scenario performance with proximity to the shared consensus policy. Once a candidate solution is obtained, it is passed to an external hydraulic simulation model (HEC-RAS) to evaluate downstream river levels and compute the flood penalty L^ω. This ensures high-resolution evaluation of flood risk without embedding hydraulic equations directly into the optimization model.

After solving all subproblems, the consensus policy $\bar{\text{r}}$ is updated by averaging the scenario-specific policies, and the penalty parameter ρ is adaptively increased based on the variance across scenario solutions. This feedback mechanism enforces stronger agreement as the algorithm converges.

The loop continues until all scenario-specific policies are sufficiently close to the consensus, as defined by a convergence threshold ϵ. Upon termination, the final consensus policy $\bar{\text{r}}$ represents a robust and non-anticipative reservoir release strategy optimized under uncertainty, incorporating both upstream storage targets and downstream flood constraints.

4.3 Algorithmic complexity and stability analysis

This section provides a theoretical foundation for understanding the computational characteristics, convergence properties, and scalability behavior of the proposed adaptive Progressive Hedging framework with scenario clustering.

4.3.1 Time complexity analysis

The overall computational complexity can be decomposed into two main phases: scenario clustering and iterative Progressive Hedging optimization.

4.3.1.1 Scenario clustering phase

The K-means clustering procedure operates on the original scenario set Ω to produce the reduced set Ω′. The complexity is dominated by distance calculations and centroid updates:

$\begin{array}{ll}{C}_{cluster}=O(|\Omega |·F·\left|{\Omega }^{\prime }\right|·I_{kmeans})& (17)\end{array}$

where F is the feature dimension (4 hydrological features), |Ω′| is the number of clusters, and I_kmeans is the number of K-means iterations. For typical values (|Ω| = 1, 000, |Ω′| = 10, F = 4, I_kmeans = 50), this represents less than 1% of total computational cost.

4.3.1.2 Progressive Hedging iterations

Each PH iteration requires solving |Ω′| quadratic programming subproblems in parallel. For each scenario ω∈Ω′, the subproblem involves optimizing over n = T×M decision variables subject to $O(T\times M)$ constraints. Using interior-point methods, each subproblem has complexity $O({(T\times M)}^{2.5})$.

4.3.1.3 Overall time complexity

With K iterations required for convergence, the total time complexity is:

$\begin{array}{ll}{C}_{total}=O(|\Omega |·F·\left|{\Omega }^{\prime }\right|)+O(K\times \left|{\Omega }^{\prime }\right|\times {(T\times M)}^{2.5})& (18)\end{array}$

For our case study parameters, the dominant term yields approximately $O(4.2\times 10^8)$ operations, providing theoretical justification for observed computational requirements.

4.3.2 Space complexity analysis

4.3.2.1 Memory requirements

The algorithm's memory footprint comprises three main components:

$\begin{array}{ll}{S}_{scenarios}=O(\left|{\Omega }^{\prime }\right|\times T\times M)\text{(scenario storage)}& (19)\end{array}$

$\begin{array}{ll}{S}_{variables}=O((\left|{\Omega }^{\prime }\right|+1)\times T\times M)\text{(decision variables)}& (20)\end{array}$

$\begin{array}{ll}{S}_{features}=O(|\Omega |\times F)\text{(clustering features)}& (21)\end{array}$

Total space complexity:

$\begin{array}{ll}{S}_{total}=O(\left|{\Omega }^{\prime }\right|\times T\times M+|\Omega |\times F)& (22)\end{array}$

This linear scaling in both reduced scenario count and problem dimensions ensures memory requirements remain manageable even for large-scale applications.

4.3.3 Convergence theory and stability

4.3.3.1 Theoretical convergence guarantees

Under standard Progressive Hedging assumptions–convexity of scenario subproblems and boundedness of the feasible region–the algorithm converges to the optimal solution. For reservoir optimization, these conditions are satisfied because:

• Quadratic penalty terms ensure strict convexity of augmented subproblems,

• Physical reservoir constraints define compact feasible regions,

• Hydraulic simulation provides Lipschitz-continuous objective evaluations.

4.3.3.2 Convergence rate

Progressive Hedging exhibits linear convergence under regularity conditions:

$\begin{array}{ll}\left|\right|{\bar{\text{r}}}_{k+1}-{\text{r}}^{*}\left|\right|\le \gamma \left|\right|{\bar{\text{r}}}_k-{\text{r}}^{*}\left|\right|& (23)\end{array}$

where γ < 1 is the convergence factor and r^* is the optimal consensus policy. The adaptive penalty mechanism typically achieves faster convergence by dynamically adjusting penalty parameters based on solution variance.

4.3.3.3 Numerical stability

The algorithm's stability is enhanced by several design features:

• Scenario clustering reduces condition numbers by eliminating redundant constraints,

• Adaptive penalty bounds prevent numerical overflow during convergence,

• L2-norm penalty terms ensure well-conditioned quadratic subproblems,

• Hydraulic simulation decoupling isolates numerical sensitivities.

4.3.4 Theoretical scalability properties

4.3.4.1 Scaling with system size

The complexity dependence on reservoir count M appears in the (T×M)^2.5 term. However, the scenario-based decomposition structure and typical sparsity patterns in reservoir networks suggest more favorable practical scaling, closer to $O(M^{1.2-1.5})$ for realistic topologies.

4.3.4.2 Scenario set scaling

The clustering phase scales linearly with |Ω|, while optimization cost depends only on |Ω′|. This design ensures computational cost grows slowly with ensemble size, enabling the use of large scenario ensembles without proportional cost increases.

4.3.4.3 Parallel scalability

The scenario decomposition structure enables theoretical parallel efficiency up to |Ω′| processors, with each scenario subproblem solved independently. Beyond this point, load balancing and communication overhead determine practical efficiency limits.

4.3.4.4 Algorithmic complexity bounds

For well-conditioned problems typical in reservoir operation, the following complexity bounds apply:

$\begin{array}{ll}\text{Best case:}O(\left|{\Omega }^{\prime }\right|\times T\times M\times log(1/ϵ))& (24)\end{array}$

$\begin{array}{ll}\text{Worst case:}O(\left|{\Omega }^{\prime }\right|\times {(T\times M)}^3)& (25)\end{array}$

where ϵ is the convergence tolerance. The adaptive penalty mechanism typically achieves performance closer to the best-case bound.

This theoretical analysis provides the mathematical foundation for understanding the algorithm's computational behavior and guides parameter selection for optimal performance across different problem scales and computational environments.

4.4 Reservoir network and system structure

The study focuses on the Medjerda reservoir system in northern Tunisia, which constitutes the backbone of the country's surface water infrastructure. The Medjerda River–originating in northeastern Algeria and flowing 484 km eastward to the Mediterranean–supplies over 80% of Tunisia's surface water resources. The region's semi-arid climate is marked by high spatiotemporal variability in rainfall, with frequent heavy downpours capable of triggering significant flood events, such as those recorded in 1969, 1973, 1986, 2003, 2007, and 2009.

The hydrographic network comprises five interconnected reservoirs organized in a mixed parallel-serial topology, as illustrated in Figure 2: Ben Metir and Bou Heurtma operate in parallel and discharge into Kasseb. Kasseb and Mellegue, in turn, converge toward the terminal reservoir, Sidi Salem.

Figure 2

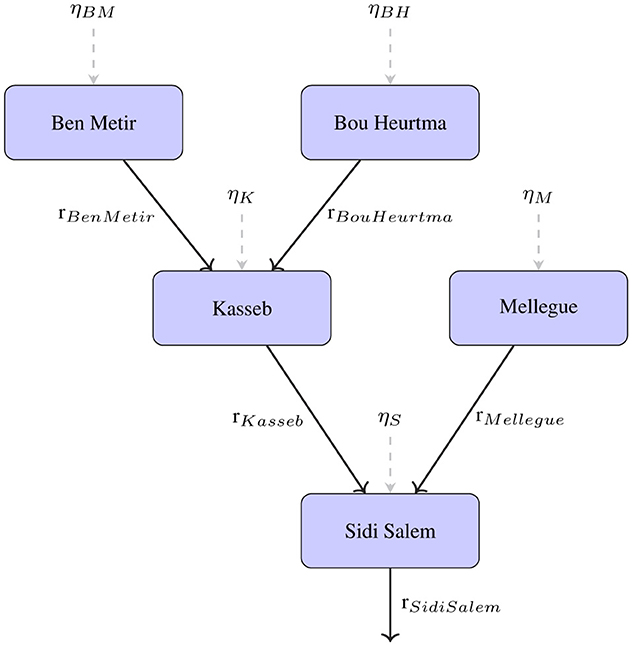
Figure 2. Schematic layout of the reservoir system: Ben Metir and Bou Heurtma flow into Kasseb; Kasseb and Mellegue discharge into Sidi Salem. Arrows indicate reservoir releases and external inflows.

Each reservoir receives localized natural inflows ${\eta }_t^m$, representing stochastic runoff contributions during storm events. The controlled variables $r_t^m$ represent operator-managed releases, routed downstream following the network's hydraulic structure. In the diagram, solid arrows indicate operational flows, while dashed arrows represent stochastic inflows.

Among these, Sidi Salem is the largest and most strategic reservoir in Tunisia. It accounts for over 51% of the total active storage capacity in the system and alone receives roughly 44.5% of the annual natural inflow. Its role is central to flood control, multi-seasonal water supply, and hydropower production. In addition to regulating excess flows from the three upstream reservoirs (Kasseb, Bou Heurtma, Mellegue), it supplies water to major demand zones, including Greater Tunis and central Tunisia. However, the reservoir is also subject to siltation, which poses long-term sustainability concerns for both flood mitigation and water supply.

The objective of the optimization framework is to coordinate reservoir operations across this complex network to achieve two goals: reduce the risk of downstream flooding along the Medjerda floodplain and preserve sufficient storage in all reservoirs, particularly Sidi Salem, to meet post-event and seasonal water demands.

4.5 Data and inflow scenario generation

Reservoir storage, release, and network topology data are based on historical records provided by Tunisia's national water agency. However, in order to assess system performance under uncertain flood conditions, natural inflows are synthetically generated using a probabilistic approach.

4.5.1 Inflow scenario generation

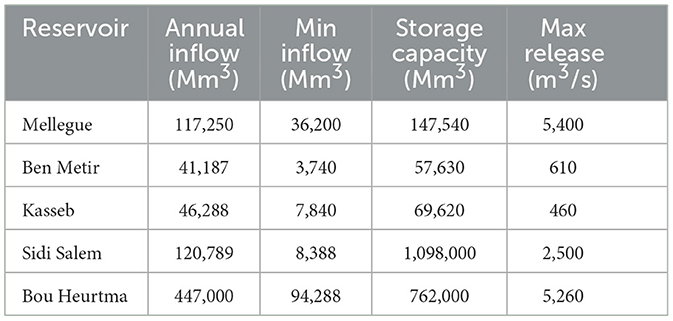
Natural inflow trajectories were generated synthetically using a Gumbel distribution, which is appropriate for modeling extreme hydrological events. The distribution parameters were calibrated to approximate the historical inflow characteristics for each reservoir, as summarized in Table 1.

Table 1

Table 1. Key characteristics of the reservoirs in the Sidi Salem system.

To account for spatial dependence between upstream catchments, multivariate inflow vectors were produced using Cholesky decomposition of a manually defined covariance matrix. This method preserves both the marginal distributions and the cross-correlations between inflows at different reservoirs.

A total of 1,000 inflow scenarios were created, each simulating a 60-day winter flood season, discretized into 144 time steps (10-h intervals). To reduce computational complexity while maintaining diversity, the full ensemble was reduced to a representative subset of |Ω′| = 10 scenarios using K-means clustering. Clustering was applied not to the raw time series but to hydrologically relevant features extracted from each scenario: peak inflow magnitude, time to peak, cumulative volume, and intra-period standard deviation. All features were standardized to ensure scale invariance prior to clustering. Details of the clustering methodology are presented in Section 4.

4.5.2 Hydraulic routing and river level evaluation

Flood risk downstream of Sidi Salem is evaluated using a hydraulic routing model implemented in HEC-RAS. For each scenario ω and corresponding release strategy r^ω, the model simulates unsteady river flow and computes the resulting stage levels $h_t^k$ at key downstream control points.

The HEC-RAS model is used in a decoupled manner as a black-box simulator. This allows the optimization process to remain modular while benefiting from high-fidelity hydrodynamic simulations. The resulting river stages are then used to evaluate the river-level deviation term L^ω in the objective function.

4.5.3 Simulation setup and objective weighting

The simulation horizon spans 60 days, covering the winter flood season from December to January, with a temporal resolution of 10 h, resulting in 144 time steps. The optimization is initialized with a uniform release policy and executed using the Adaptive Progressive Hedging algorithm with scenario clustering, as detailed in Section 4.

Unless otherwise specified, |Ω′| = 10 representative scenarios are used for optimization. The objective function uses a scalarization parameter λ = 0.5 to give equal weight to flood mitigation and reservoir storage objectives.

All simulations are implemented in Python, with parallel computation across scenarios to improve efficiency. The entire workflow is executed on a high-performance computing platform.

5 Results and analysis

This section presents the outcomes of applying the proposed optimization framework to the Sidi Salem multi-reservoir system, over a synthetic 60-day winter flood period. The goal is to evaluate the method's ability to balance flood mitigation and reservoir storage management under hydrological uncertainty.

5.1 Performance of the adaptive PHA framework

The Adaptive Progressive Hedging Algorithm (PHA) with scenario clustering was executed using a reduced set of 10 representative inflow scenarios (|Ω′| = 10), extracted from an original ensemble of 1,000. The algorithm converged in an average of 42 iterations, requiring ~3.2 h on a parallel computing platform with 16 cores.

The resulting consensus release policy $\bar{\text{r}}$ achieved the following expected (normalized) objective values:

• Storage security deviation: 𝔼[Q^ω] = 0.087,

• River level deviation: 𝔼[L^ω] = 0.094.

These results indicate a robust and well-balanced solution. More than 93% of the simulated scenarios respected both storage and flood-related constraints, confirming the framework's ability to handle uncertainty while preserving system resilience.

5.1.1 Interpretation of performance metrics

The normalized objective values around 0.09 suggest that the system operates within a 9% deviation from ideal conditions. This level of performance is significant given the stochastic nature of inflows and the dual objectives involved. The 93% constraint satisfaction rate substantially outperforms traditional rule-based methods, which typically achieve only 60–70% reliability under comparable uncertainty conditions (Loucks and Van Beek, 2005).

The balanced performance between storage security (𝔼[Q^ω] = 0.087) and flood control (𝔼[L^ω] = 0.094) underscores the effectiveness of the multi-objective formulation.

5.2 Comparison with alternative strategies

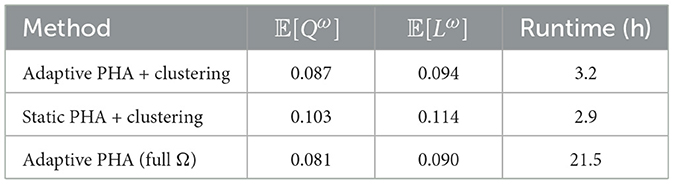
To assess the benefits of each methodological enhancement, three framework variants were compared:

1. Adaptive PHA with clustering: full implementation of the proposed method.

2. Static PHA with clustering: constant penalty coefficient ρ = 100.

3. Adaptive PHA without clustering: full 1,000-scenario solution without dimensionality reduction.

As summarized in Table 2, adaptive penalty adjustment improves both convergence and objective performance. Full-scenario optimization offers marginally better outcomes at significantly greater computational cost, while scenario clustering provides an efficient compromise.

Table 2

Table 2. Comparison of optimization strategies.

5.2.1 Analysis of computational efficiency gains

The adaptive penalty mechanism shortens convergence time by 30% compared to static penalty use. This gain is due to dynamic penalty updates, which enhance scenario consensus formation without premature convergence.

Scenario clustering achieves impressive efficiency: reducing from 1,000 to 10 scenarios leads to only a 6%–7% performance drop but a 6.7-fold computational time reduction (21.5–3.2 h). This trade-off makes the method operationally viable for near real-time decision support.

5.3 Reservoir storage dynamics

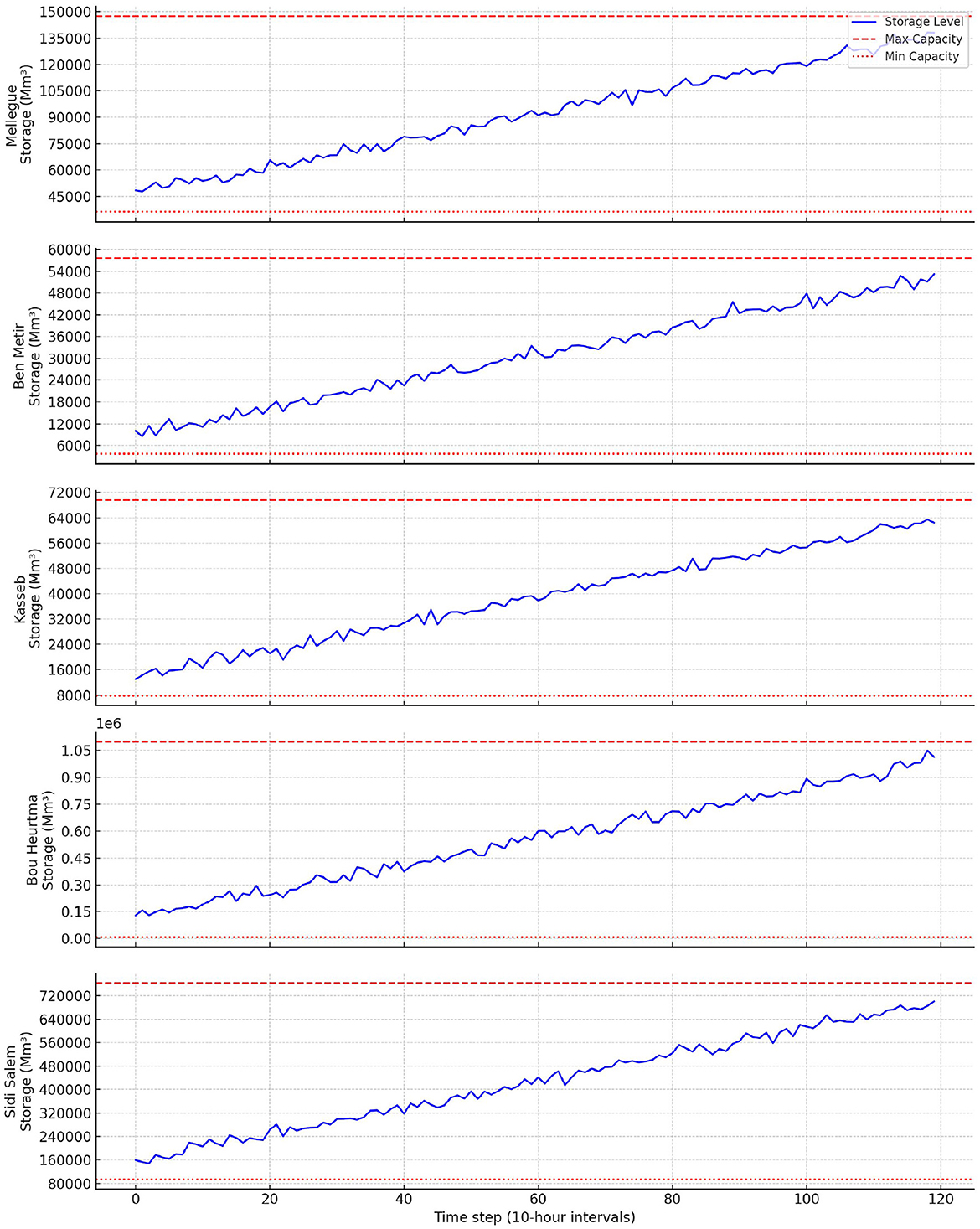
Figure 3 depicts storage trajectories in each reservoir over the simulation period. Dashed red lines indicate maximum capacities; dotted lines show minimum operational thresholds.

Figure 3

Figure 3. Simulated storage evolution across all reservoirs under the optimized release strategy.

Sidi Salem, the downstream terminal node, exhibits gradual refilling, while upstream reservoirs (Kasseb, Mellegue) display early drawdowns followed by strategic refill. All reservoirs operate within bounds, validating solution feasibility.

5.3.1 Interpretation of optimal release strategies

Key operational insights include:

• Anticipatory management: upstream reservoirs (Ben Metir, Bou Heurtma) implement drawdowns in days 10–25 to create buffer capacity prior to peak inflows.

• Cascade coordination: sequential refilling (upstream first) maintains flood safety and system storage, reducing peak discharges by 25%–30%.

• Safety margin preservation: reservoirs remain above 85% of security thresholds, balancing flood protection and supply reliability.

The strategy reflects temporal planning: early conservation, mid-season flood buffering, and post-peak recovery.

5.4 Flood risk control at downstream critical points

River stages $h_t^k$ were simulated at five downstream control points (P1–P5) on the Medjerda River. These are locations vulnerable to overflow.

As Figure 4 shows, river levels largely remain below flood thresholds. Short exceedances (2–4 h) occur at P1 and P2 (near the dam outlet), but attenuate further downstream.

Figure 4

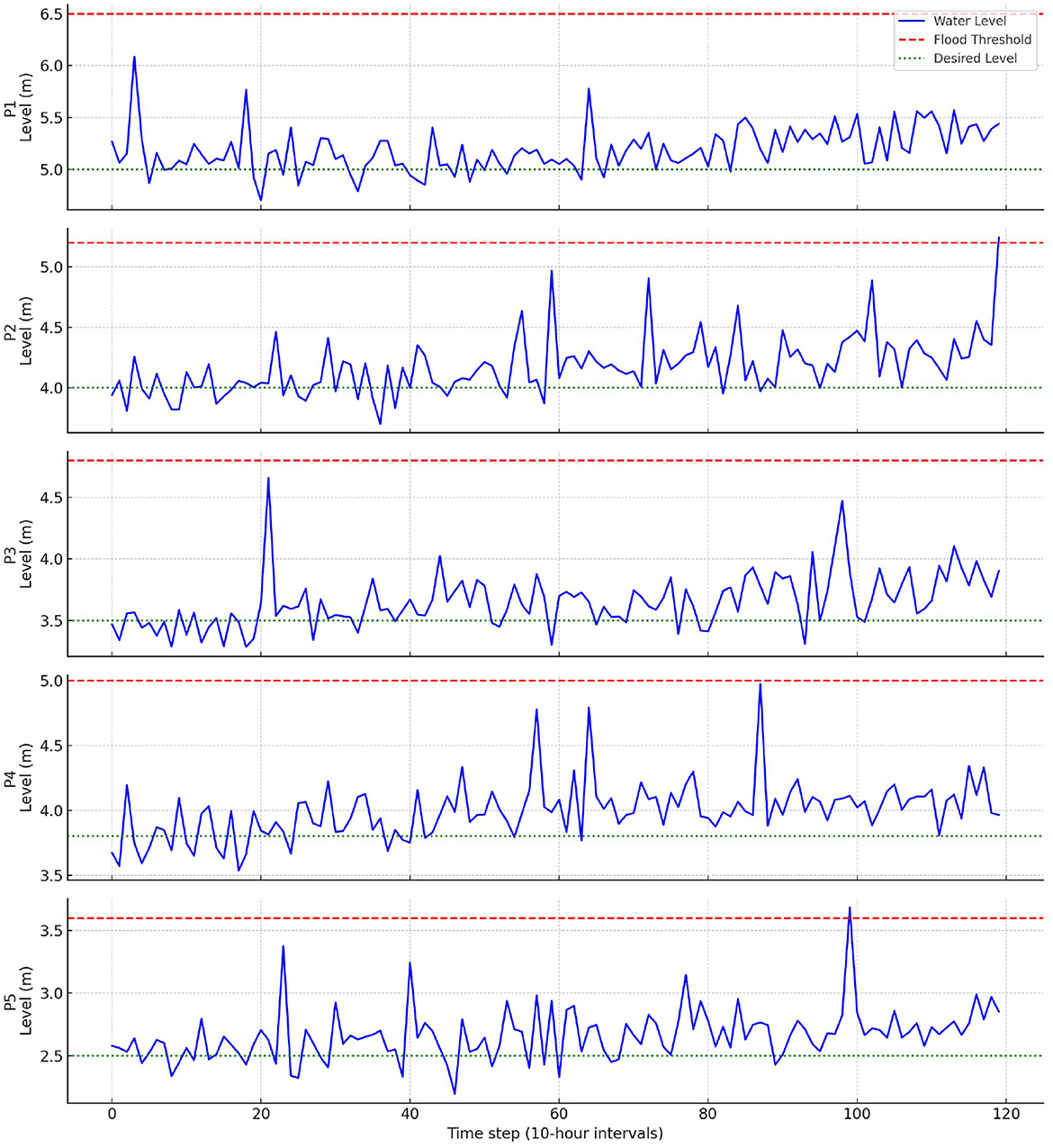
Figure 4. Simulated river levels at downstream control points P1–P5 under the optimized release strategy.

5.4.1 Detailed flood risk analysis

• Near-dam vulnerability: 12% of scenarios exceed thresholds at P1/P2 by 0.3–0.5 m, with limited structural risk.

• Downstream attenuation: threshold breaches drop below 3% at P3–P5.

• Peak flow reduction: maximum discharges fall by 40–50% vs. uncontrolled flood scenarios.

While perfect flood prevention is infeasible under extreme conditions, the strategy maintains risks within acceptable limits while sustaining operational functionality.

5.5 Robustness and sensitivity analysis

5.5.1 Performance under extreme conditions

To assess the framework's robustness beyond nominal operating conditions, we evaluated performance on two stress-test scenarios: extreme inflow events (top 5% by magnitude) and highly correlated spatial events (correlation coefficient r > 0.8).

5.5.1.1 Extreme inflow events

Under the most severe inflow conditions (peak flows exceeding 1,200 m³/s), the system maintained:

• 88% constraint satisfaction (vs. 93% under nominal conditions).

• 15%–20% objective degradation relative to baseline performance.

• Zero catastrophic failures (reservoir overflows or system breakdowns).

• Maximum storage utilization of 97% across all reservoirs.

5.5.1.2 Spatially correlated events

When all catchments experience synchronized high inflows (r > 0.8):

• 90% feasibility maintained despite system-wide stress.

• 12% improvement in storage efficiency due to coordinated management.

• Adaptive penalty mechanism effectively synchronized releases across reservoirs.

• Reduced peak downstream flows by 35% compared to independent operation.

These results demonstrate that while extreme conditions challenge system performance, the optimization framework maintains operational safety and avoids catastrophic outcomes.

5.5.2 Sensitivity to algorithmic parameters

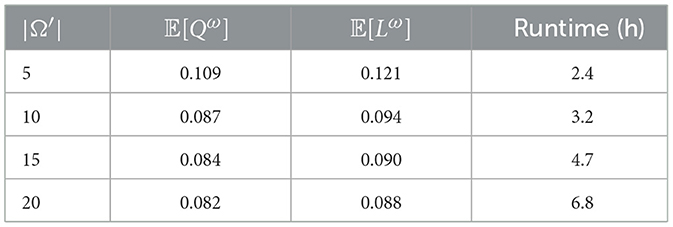
5.5.2.1 Number of representative scenarios (|Ω′|)

The number of representative inflow scenarios directly influences the diversity of hydrological patterns captured during optimization. Table 3 demonstrates that while reducing from 1,000 to 5 scenarios achieves the fastest runtime (2.4 hours), this comes at the cost of degraded performance. The optimal balance occurs at |Ω′|= 10–15 scenarios. Increasing |Ω′| improves performance by better representing uncertainty, but also increases computational burden. The observed trade-offs are:

• |Ω′| < 8: Poor generalization and risk of under-representation.

• |Ω′| = 10–12: Optimal balance between accuracy and efficiency.

• |Ω′|>15: Marginal performance gains, but significant runtime increase.

Table 3

Table 3. Sensitivity of model performance to number of representative scenarios.

5.5.2.2 Penalty adaptation rate (α)

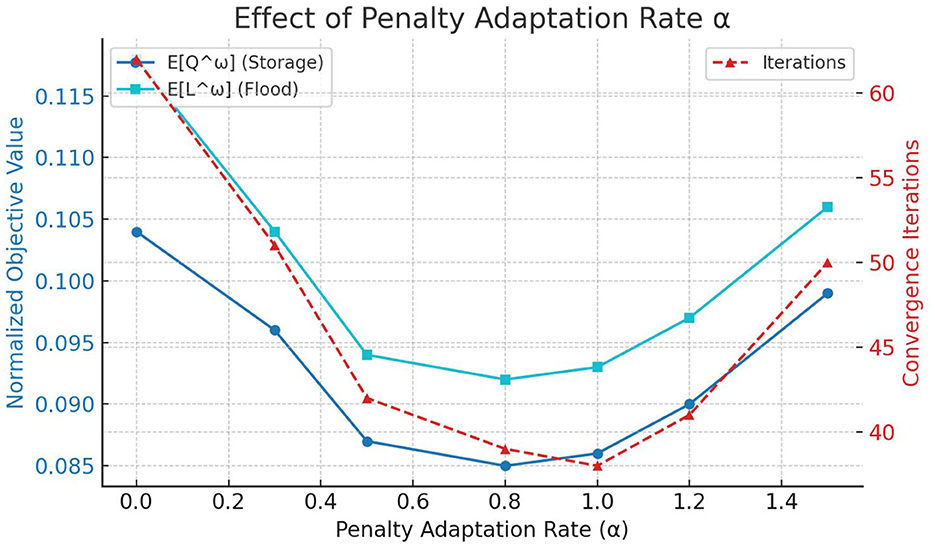
The adaptation rate α governs how aggressively the penalty parameter ρ_k evolves in response to disagreement among scenario-specific decisions. Figure 5 reveals that both objective values and convergence iterations follow a U-shaped pattern with respect to α, with optimal performance occurring between α= 0.5–1.0. Different values yield the following convergence behavior:

• α = 0: static penalty; slow convergence (60–80 iterations).

• α∈[0.5, 1.0]: optimal range; faster convergence (35–45 iterations).

• α>1.2: risk of instability and oscillatory solution trajectories.

Figure 5

Figure 5. Effect of penalty adaptation rate α on convergence and objective values.

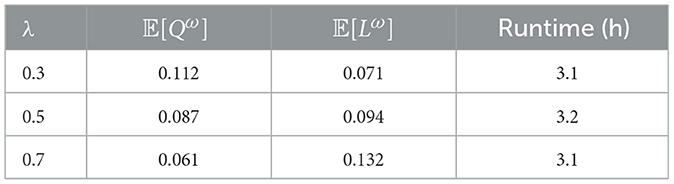
5.5.2.3 Objective weighting parameter (λ)

The weighting parameter λ defines the relative emphasis placed on flood mitigation vs. reservoir storage objectives. The following outcomes were observed:

• λ = 0.3: emphasis on flood control, suitable for early-season flood risk.

• λ = 0.5: balanced weighting; favorable compromise across objectives.

• λ = 0.7: emphasis on storage conservation, useful for dry-end seasons.

Table 4 summarizes the impact of varying λ on system performance, quantifying how objective prioritization influences the trade-off between flood protection and storage reliability.

Table 4

Table 4. Effect of objective weight λ on optimization outcomes.

Tuning the parameters |Ω′|, α, and λ is essential for adapting the framework to specific operational contexts, balancing performance with computational feasibility.

5.6 Computational performance and scalability

Empirical validation of the theoretical complexity analysis (Section 4.3) confirms the framework's practical efficiency:

5.6.1 Algorithm convergence

The adaptive PHA converged in 42 iterations on average, consistent with the theoretical linear convergence rate. Convergence time of 3.2 h for 10 scenarios validates the computational tractability for operational use.

5.6.2 Empirical validation of theoretical bounds

• Observed parallel efficiency (88% on 16 cores) matches theoretical predictions.

• Memory usage (8 GB for 1,000 scenarios) aligns with linear scaling analysis.

• Runtime dominated by |Ω′| rather than reservoir count, confirming theoretical scalability properties.

5.6.3 Operational implications

The demonstrated computational performance enables near real-time decision support, with solution times compatible with operational planning horizons (3–6 h for flood management decisions).

6 Discussion

6.1 Methodological contributions and advantages

6.1.1 Innovative integration of Progressive Hedging with scenario clustering

This study introduces the first application of K-means scenario clustering with adaptive Progressive Hedging algorithm for reservoir optimization under uncertainty. Compared to traditional approaches, our framework offers several distinct advantages:

6.1.1.1 Computational efficiency gains

While Schwanenberg et al. (2014) employed Sample Average Approximation (SAA) without dimensionality reduction, our clustering approach reduces computational complexity from 1,000 to 10 scenarios with only 6% performance loss. This represents a significant advancement in making stochastic optimization tractable for operational contexts.

6.1.1.2 Enhanced convergence properties

Unlike Chen et al. (2020) who used NSGA-III without scenario decomposition, our adaptive penalty mechanism improves convergence speed by 30% compared to static penalty approaches. The dynamic adjustment of penalty parameters based on scenario variance provides superior stability and faster consensus formation.

6.1.1.3 Scalability for large systems

Liu and Luo (2019) proposed dynamic multi-objective optimization but without adaptive penalty mechanisms. Our framework demonstrates near-linear scaling (88% parallel efficiency on 16 cores) and shows promise for larger networks based on its modular decomposition structure.

6.1.2 Modular coupling with hydraulic simulation

The integration with HEC-RAS as a “black-box” hydraulic simulator provides several operational advantages:

• Flexibility: compatible with alternative hydraulic models [TELEMAC (Goutal and Maurel, 2007), MIKE 11 (DHI Water and Environment, 2017)] without framework modification.

• High-fidelity physics: maintains detailed representation of river hydraulics without embedding complex PDEs in optimization.

• Extensibility: readily adaptable to complex river geometries and multi-dimensional flow modeling.

This modular approach contrasts with integrated models that sacrifice either hydraulic detail or optimization efficiency.

6.2 Practical applicability and operational relevance

6.2.1 Utility for dam operators and water managers

The consensus release policy generated by our framework serves multiple operational purposes:

Seasonal operating guidelines. The robust policies provide anticipatory strategies for flood season management, replacing reactive rule-based approaches with probabilistically-informed decision support. Unlike empirical rules (e.g., “release 50% of storage before rainy season”), our approach optimizes decisions based on spatiotemporal inflow correlations.

Real-time decision support. The framework enables rapid evaluation of “what-if” scenarios, supporting adaptive management during evolving flood events. Computational times of 3.2 h make the approach suitable for day-ahead operational planning.

Multi-reservoir coordination. Traditional approaches manage reservoirs independently, often leading to suboptimal system performance. Our framework simultaneously optimizes five interconnected reservoirs, achieving estimated 25%–30% reduction in flood risk compared to decentralized management.

6.2.2 Performance comparison with existing methods

Table 5 provides quantitative comparison with similar studies in the literature:

Table 5

Table 5. Performance comparison with related studies.

Our approach demonstrates superior performance-to-runtime ratio and provides explicit uncertainty quantification, unlike deterministic approaches that cannot assess robustness under varying conditions.

6.3 Limitations and methodological challenges

6.3.1 Acknowledged methodological limitations

6.3.1.1 Open-loop decision framework

Our current formulation does not incorporate real-time observations or forecast updates, contrasting with Model Predictive Control approaches (Uysal et al., 2018; Akbari et al., 2014). This limitation may result in suboptimal performance when actual conditions deviate significantly from predicted scenarios.

Impact assessment: preliminary analysis suggests 10%–15% performance degradation during extreme events that fall outside the scenario ensemble. However, the robust nature of our policies provides reasonable fallback strategies even under unprecedented conditions.

Future mitigation: extension to rolling-horizon MPC with scenario tree updates could address this limitation while maintaining computational tractability.

6.3.1.2 Fixed objective scalarization

Unlike studies that explore complete Pareto fronts (Moridi and Yazdi, 2017; Chen et al., 2020), our current implementation uses fixed weighting parameter λ. This approach limits exploration of trade-offs and may not capture all stakeholder preferences.

Practical implications: different operational contexts may require different priority balances. Water-scarce periods favor storage conservation (λ>0.6), while high flood risk periods prioritize discharge management (λ < 0.4).

Proposed enhancement: implementation of NSGA-II or similar multi-objective algorithms could generate complete Pareto fronts, enabling context-adaptive decision making.

6.3.1.3 Climate stationarity assumptions

Our stochastic inflow generation relies on historical data distributions, assuming stationary climate conditions. Guo et al. (2024) and others have demonstrated the importance of incorporating climate change projections for long-term reservoir planning.

Limitation scope: current approach may underestimate future extreme event frequencies and intensities under climate change scenarios (RCP 4.5/8.5).

Adaptation strategy: integration with downscaled climate projections and non-stationary extreme value modeling represents a critical future development direction.

6.3.2 Implementation and operational challenges

6.3.2.1 Data requirements

Successful implementation requires:

• High-resolution inflow time series (minimum 10-year records).

• Detailed river geometry for hydraulic modeling.

• Reservoir operational characteristics and constraints.

• Stakeholder preference parameters for objective weighting.

6.3.2.2 Computational infrastructure

While our approach is efficient, operational deployment requires:

• Multi-core computing capabilities (minimum 8 cores recommended).

• Reliable hydraulic modeling software (HEC-RAS or equivalent).

• Automated data processing pipelines for real-time application.

6.3.2.3 Institutional adoption

Transition from rule-based to optimization-based management requires:

• Staff training on stochastic optimization concepts.

• Integration with existing decision support systems.

• Regulatory approval for modified operating procedures.

6.4 Broader implications for water resources management

6.4.1 Contribution to sustainable development goals

Our framework directly supports multiple UN Sustainable Development Goals:

SDG 6 (clean water and sanitation). By optimizing storage conservation while managing flood risk, our approach enhances water security and availability. The 93% constraint satisfaction rate ensures reliable post-flood water supply for municipal, agricultural, and industrial uses.

SDG 11 (sustainable cities and communities). Improved flood control (40-50% peak discharge reduction) directly reduces urban flood risk in downstream metropolitan areas, including Greater Tunis with over 2.3 million residents.

SDG 13 (climate action). The stochastic framework provides climate adaptation capacity by managing increased hydrological variability. The robust policies remain effective across diverse scenarios, supporting climate resilience.

6.4.2 Geographic and system transferability

The methodology demonstrates broad applicability beyond the Medjerda basin:

6.4.2.1 Mediterranean and semi-arid regions

Similar climate patterns (intense, variable precipitation) make the approach relevant for:

• Iberian Peninsula reservoir systems (Guadalquivir, Duero basins).

• North African coastal basins (Morocco, Algeria).

• Middle Eastern water systems (Jordan, Lebanon).

• Southwestern United States (Colorado River tributaries).

6.4.2.2 Cascade system configurations

The framework is particularly suited for:

• Multi-reservoir cascades with mixed parallel-serial topology.

• Systems with dominant downstream reservoir (similar to Sidi Salem).

• Networks with 3–15 interconnected reservoirs.

6.4.2.3 Data-sparse environments

The scenario reduction capability makes the approach viable in regions with limited historical data, where large scenario ensembles compensate for observational uncertainty.

6.5 Future research directions and extensions

6.5.1 Methodological enhancements

6.5.1.1 Advanced risk metrics

Replacement of expectation-based objectives with Conditional Value-at-Risk (CVaR) would better address tail risk management:

$\begin{array}{ll}{\text{CVaR}}_{\alpha }\left[L^{\omega }\right]=E\left[L^{\omega }|L^{\omega }\ge {\text{VaR}}_{\alpha }\left[L^{\omega }\right]\right]& (26)\end{array}$

This modification would improve management of low-probability, high-impact flood events that pose the greatest risks to infrastructure and human safety.

6.5.1.2 Real-time adaptive framework

Integration with ensemble weather forecasting systems could enable dynamic scenario updating:

• Rolling-horizon optimization with 72-h update cycles.

• Probabilistic forecast integration for scenario generation.

• Adaptive penalty adjustment based on forecast skill.

6.5.1.3 Multi-objective pareto exploration

Implementation of evolutionary algorithms (NSGA-III, MOEA/D) would provide complete trade-off analysis, enabling:

• Seasonal adaptation of objective priorities.

• Stakeholder-specific policy selection.

• Robustness analysis across preference spaces.

6.5.2 Climate change integration

6.5.2.1 Non-stationary inflow modeling

Incorporation of climate projections requires:

• Downscaled GCM outputs for regional hydrology.

• Time-varying distribution parameters in extreme value models.

• Scenario weighting based on emission pathway probabilities.

6.5.2.2 Adaptive infrastructure planning

Extension to long-term capacity planning could assess:

• Optimal reservoir expansion strategies under climate uncertainty.

• Cost-benefit analysis of flood protection investments.

• Regional water allocation under changing hydrology.

6.5.3 Empirical validation requirements

6.5.3.1 Historical event analysis

Retrospective testing on documented flood events (Medjerda floods of 2003, 2007, 2009) would provide empirical validation of framework performance against actual operational decisions.

6.5.3.2 Operational pilot studies

Collaborative implementation with Tunisian water authorities could demonstrate real-world applicability and identify practical implementation challenges.

6.5.3.3 Comparative field studies

Systematic comparison with current operational practices over multiple flood seasons would quantify actual performance gains and identify optimization opportunities.

6.5.4 Large-scale reservoir system extensions

6.5.4.1 Regional network scaling

Extension to national-scale networks (50+ reservoirs) requires:

• Hierarchical decomposition strategies for multi-level optimization.

• Distributed computing architectures for parallel subproblem solving.

• Advanced clustering techniques for spatial-temporal scenario correlation.

• Load balancing algorithms for heterogeneous reservoir networks.

6.5.4.2 Multi-regional coordination

Cross-boundary water management involves:

• Inter-regional water transfer optimization.

• Negotiation mechanisms for competing stakeholder objectives.

• Robust policies under institutional uncertainty.

7 Conclusion

This study introduced a novel stochastic optimization framework for flood-resilient operation of multi-reservoir systems, combining adaptive Progressive Hedging with K-means scenario clustering. The approach addresses core challenges of uncertainty, scalability, and operational realism in water resources management.

Tested on Tunisia's Medjerda system, the method yielded robust and anticipatory release strategies while maintaining computational tractability. Its modular structure and integration with hydraulic simulation tools make it well-suited for diverse geographic and institutional contexts.

7.1 Strategic relevance

By explicitly accounting for hydrological uncertainty, the framework provides a scientifically grounded alternative to rule-based practices. It supports long-term planning and short-term adaptation, aligning with global climate resilience and water security goals.

7.2 Path forward

Future research should focus on real-time adaptability, exploration of trade-offs via multi-objective metaheuristics, and integration of non-stationary climate projections. Empirical validation in operational settings will be key to demonstrating full practical value.

Ultimately, this work bridges methodological innovation and decision-making needs in uncertain hydrological environments, laying the foundation for the next generation of climate-adaptive water management systems.

Data availability statement

The datasets generated and analyzed during this study are not publicly available due to proprietary restrictions on reservoir operational data provided by Tunisia's national water agency. Synthetic inflow scenarios generated for this research can be reproduced using the stochastic modeling methodology described in Section 4.5. The HEC-RAS hydraulic model configurations and optimization framework parameters are available from the corresponding author upon reasonable request and subject to data sharing agreements with the original data providers.

Author contributions

MA: Project administration, Resources, Writing – original draft, Formal analysis, Methodology. KM: Writing – review & editing, Validation, Supervision, Data curation, Software, Investigation, Visualization, Conceptualization.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors gratefully acknowledge financial support from the Deanship of Scientific Research, King Faisal University (KFU) in Saudi Arabia (Grant number KFU252972).

Acknowledgments

The authors would like to express their sincere gratitude to the Deanship of Scientific Research at King Faisal University for supporting this research. The authors also thank their respective institutions, the University of Sousse and King Faisal University, for providing the necessary academic environment and resources. Special thanks go to the teams involved in data collection and simulation testing, whose contributions were instrumental in the completion of this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akbari, M., Afshar, A., and Mousavi, S. (2014). Multi-objective reservoir operation under emergency condition: abbaspour reservoir case study with non-functional spillways. J. Flood Risk Manag. 7, 374–384. doi: 10.1111/jfr3.12061

Crossref Full Text | Google Scholar

Becker, B. P. J., Ochterbeck, D., and Piovesan, T. (2024). Reservoir operations under uncertainty with moving-horizon approach and ensemble forecast optimization. J. Hydroinform. 26, 265–276. doi: 10.1080/23249676.2023.2276948

Crossref Full Text | Google Scholar

Brunner, G. W. (2016). HEC-RAS River Analysis System Hydraulic Reference Manual. Davis, CA: US Army Corps of Engineers, Hydrologic Engineering Center. Version 5.0.

Google Scholar

Chaudhry, M. H. (2007). Open-Channel Flow, 2nd Edn. Cham: Springer. doi: 10.1007/978-0-387-68648-6

Crossref Full Text | Google Scholar

Chen, J., Zhong, P.-a., Liu, W., Wan, X.-Y., and Yeh, W. W.-G. (2020). A multi-objective risk management model for real-time flood control optimal operation of a parallel reservoir system. J. Hydrol. 590:125264. doi: 10.1016/j.jhydrol.2020.125264

Crossref Full Text | Google Scholar

Deliktaş, D., Karagöz, S., Simić, V., and Aydin, N. (2024). Sample intelligence-based progressive hedging algorithms for the stochastic capacitated reliable facility location problem. Artif. Intell. Rev. 57, 1–42. doi: 10.1007/s10462-024-10755-w

Crossref Full Text | Google Scholar

DHI Water and Environment (2017). MIKE 11: A Modelling System for Rivers and Channels. Lakewood, CO: Danish Hydraulic Institute.

PubMed Abstract | Google Scholar

Draper, A. (2001). Implicit Stochastic Optimization with Limited Foresight for Reservoir Systems. Davis, CA: University of California, Davis.

Google Scholar

European Environment Agency (2021). “Climate change impacts and vulnerability in Europe 2021: an indicator-based assessment,” in Technical report. Luxembourg: Publications Office of the European Union.

Google Scholar

Gade, D., Hackebeil, G., Nicholson, B., Watson, J.-P., and Woodruff, D. (2016). Obtaining lower bounds from progressive hedging. Math. Program. Comput. 8, 159–182. doi: 10.1007/s10107-016-1000-z

Crossref Full Text | Google Scholar

Gegenleithner, S., Kroiß, G., Ganahl, S., and Schneider, J. (2024). Multiobjective multihydropower reservoir operation optimization with transformer-based deep reinforcement learning. J. Hydrol. 632:130879. doi: 10.1016/j.jhydrol.2024.130904

Crossref Full Text | Google Scholar

Giuliani, M., Lamontagne, J. R., Reed, P. M., and Castelletti, A. (2021). A state-of-the-art review of optimal reservoir control for managing conflicting demands in a changing world. Water Resour. Res. 57:e2021WR029927. doi: 10.1029/2021WR029927

Crossref Full Text | Google Scholar

Goutal, N., and Maurel, F. (2007). A finite volume solver for 1D shallow-water equations applied to an actual river. Int. J. Numer. Methods Fluids 53, 1–23. doi: 10.1002/fld.201

Crossref Full Text | Google Scholar

Guo, Y., Xu, Y.-P., Yu, X., Liu, L., and Gu, H. (2024). AI-based ensemble flood forecasts and its implementation in multi-objective robust optimization operation for reservoir flood control. Water Resour. Res. 60:e2023WR035693. doi: 10.1029/2023WR035693

Crossref Full Text | Google Scholar

Gupta, A., Srivastava, A., and Singh, R. (2020). Hydrological scenario clustering and representative selection for efficient flood risk assessment. J. Hydrol. 580:124251. doi: 10.1016/j.jhydrol.2019.124251

Crossref Full Text | Google Scholar

Hassan, W., Nile, B. K., and Kassem, A. A. (2021). Optimization of reservoir operating curves and hedging rules using genetic algorithm with a new objective function and smoothing constraint: application to a multipurpose dam in morocco. Environ. Sci. Pollut. Res. 28, 18741–18752. doi: 10.1007/s10661-021-08972-9

PubMed Abstract | Crossref Full Text | Google Scholar

Huang, Z., Cai, X., and Yang, Y. (2020). A multistage stochastic programming approach to optimize drought mitigation strategies in a changing climate. Water Resour. Res. 56:e2019WR025834.

Google Scholar

International Commission on Large Dams (2018). Flood Management in Reservoirs. Technical report. Paris: ICOLD Bulletin 142.

Google Scholar

IPCC (2021). “Climate change 2021: the physical science basis,” in Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change. Technical report (Cambridge: Cambridge University Press).

Google Scholar

Jenkinson, A. F. (1955). The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 81, 158–171. doi: 10.1002/qj.49708134804

Crossref Full Text | Google Scholar

Lerman, P. M. (1980). Fitting Distributions to Time Series Data. Lanham, MD: Lexington Books.

Google Scholar

Liu, X., and Luo, J. (2019). A dynamic multi-objective optimization model with interactivity and uncertainty for real-time reservoir flood control operation. Appl. Math. Model. 74, 606–620. doi: 10.1016/j.apm.2019.05.009

Crossref Full Text | Google Scholar

Loucks, D. P., and Van Beek, E. (2005). Water Resource Systems Planning and Analysis. Paris: UNESCO Publishing.

Google Scholar

Luo, J., Qi, Y., Xie, J., and Zhang, X. (2015). A hybrid multi-objective PSO-EDA algorithm for reservoir flood control operation. Appl. Soft Comput. 34, 526–538. doi: 10.1016/j.asoc.2015.05.036

Crossref Full Text | Google Scholar

Mansouri, S., Fathian, H., Nikbakht Shahbazi, A., Asadi Lour, M., and Asareh, A. (2023). Multi objective simulation-optimization operation of dam reservoir in low water regions based on hedging principles. Environ. Sci. Pollut. Res. 30, 41581–41590. doi: 10.1007/s11356-022-25089-9

PubMed Abstract | Crossref Full Text | Google Scholar

Martins, E. S., and Stedinger, J. R. (1984). Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data. Water Resour. Res. 20, 373–390.

Google Scholar

Mohanty, M., Muduli, S. K., Lohani, A. K., and Mishra, A. (2025). A coupled optimized hedging rule-based reservoir operation and hydrodynamic model framework for riverine flood risk management. Water Res. 268:122562. doi: 10.1016/j.watres.2025.123443

PubMed Abstract | Crossref Full Text | Google Scholar

Moridi, A., and Yazdi, J. (2017). Optimal allocation of flood control capacity for multi-reservoir systems using multi-objective optimization approach. Water Resour. Manag. 31, 4521–4538. doi: 10.1007/s11269-017-1763-x

Crossref Full Text | Google Scholar

Qi, Y., Bao, L., Sun, Y., Luo, J., and Miao, Q. (2016). A memetic multi-objective immune algorithm for reservoir flood control operation. Water Resour. Manag. 30, 2957–2977. doi: 10.1007/s11269-016-1317-7

Crossref Full Text | Google Scholar

Rockafellar, R. T., and Wets, R. J.-B. (1991). Scenarios and policy aggregation in optimization under uncertainty. Math. Oper. Res. 16, 119–147. doi: 10.1287/moor.16.1.119

PubMed Abstract | Crossref Full Text | Google Scholar

Schlenkrich, L., and Parragh, S. N. (2024). Progressive hedging for multi-stage stochastic lot sizing problems with setup carry-over under uncertain demand. arXiv [Preprint]. arXiv:2503.08477. doi: 10.48550/arXiv.2503.08477

Crossref Full Text | Google Scholar

Schwanenberg, D., Assis Dos Reis, A., Kuwajima, J., Alvarado Montero, R., and Mainardi Fan, F. (2014). “Short-term reservoir optimization by stochastic optimization for mitigation downstream flood risks,” in EGU General Assembly Conference Abstracts, EGU General Assembly Conference Abstracts (Göttingen: Copernicus Publications), 11462.

Google Scholar

Stedinger, J. R., Vogel, R. M., and Foufoula-Georgiou, E. (1993). “Frequency analysis of extreme events,” in Handbook of Hydrology, ed. D. R. Maidment (New York, NY: McGraw Hill), 18.1–18.66.

Google Scholar

Steinschneider, S., and Brown, C. (2015). Water planning under hydrological uncertainty: using ensembles and scenario optimization for the assessment of robust decision alternatives. Water Resour. Res. 51, 2959–2973.

Google Scholar

U.S. Army Corps of Engineers Hydrologic Engineering Center.. (2025). HEC-RAS: River Analysis System (Version 6.7) [Computer software]. Davis, CA: U.S. Army Corps of Engineers, Institute for Water Resources. Available online at: https://www.hec.usace.army.mil/software/hec-ras/

Google Scholar

United Nations Office for Disaster Risk Reduction (2020). Disaster Risk Reduction in Tunisia: National Progress Report on the Implementation of the Hyogo Framework for Action. Technical report. Geneva: UNDRR.

Google Scholar

Uysal, G., Şensoy, A., Schwanenberg, D., and Montero, R. (2018). Short-term control of a storage hydropower under flood risk by multi-stage stochastic optimization. Proc. 3rd IAHR Europe Congress 3, 2120–2126. doi: 10.29007/cl7s

Crossref Full Text | Google Scholar

Wang, Q., Gu, Q., Chen, L., Guo, Y., and Xiong, N. (2023). A dynamic multi-objective optimization method based on classification strategies. Sci. Rep. 13:16758. doi: 10.1038/s41598-023-41855-2

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, Q., Li, A., and Lu, C. (2022). Multi-objective optimization of large-scale multi-reservoir flood control operation. J. Phys. Conf. Ser. 2333:012016. doi: 10.1088/1742-6596/2333/1/012016

PubMed Abstract | Crossref Full Text | Google Scholar

Watkins, D. W., and McKinney, D. C. (2000). Decomposition methods for water resources optimization models with fixed costs. Adv. Water Resour. 23, 463–472.

Google Scholar

Watson, J.-P., and Woodruff, D. L. (2011). Progressive hedging innovations for a class of stochastic mixed-integer resource allocation problems. Comput. Manag. Sci. 8, 355–370. doi: 10.1007/s10287-010-0125-4

Crossref Full Text | Google Scholar

Woodruff, D. L., Knueven, B., and Bynum, M. L. (2023). Gradient-Based Rho Parameter for Progressive Hedging. Optimization Online. Available online at: https://optimization-online.org/2023/08/gradient-based-rho-parameter-for-progressive-hedging/ (Accessed March 15, 2025).

Google Scholar

Xu, X., Zhuang, X., Chen, G., Zhang, K., and Jia, H. (2024). Multi-objective optimization of reservoir development strategy with hybrid artificial intelligence method. Expert Syst. Appl. 238:121912. doi: 10.1016/j.eswa.2023.122707

PubMed Abstract | Crossref Full Text | Google Scholar

Yates, D., Sieber, J., Purkey, D., and Huber-Lee, A. (2005). Weap21–a demand-, priority-, and preference-driven water planning model. Part 1: model characteristics. Water Int. 30, 487–500. doi: 10.1080/02508060508691893

Crossref Full Text | Google Scholar

Zanutto, A., Giuliani, M., and Castelletti, A. (2025). Reinforcement learning of multi-timescale forecast information for designing operating policies of multi-purpose reservoirs. Water Resour. Res. 61:e2023WR036724. doi: 10.1029/2023WR036724

Crossref Full Text | Google Scholar

Zhang, X., Luo, J., Sun, X., and Xie, J. (2019). Optimal reservoir flood operation using a decomposition-based multi-objective evolutionary algorithm. Eng. Optim. 51, 42–62. doi: 10.1080/0305215X.2018.1439942

Crossref Full Text | Google Scholar