SMamba-KAN: an advanced temporal-nonlinear model for precise water level prediction

Introduction: River water levels are influenced by a combination of meteorological and environmental factors. In recent years, with the widespread adoption of Transformer architectures in time series modeling, numerous structural variants have emerged, including Mamba based on structured state space models (SSM) and iTransformer, which employs a Variate Token Embedding strategy. Meanwhile, traditional multilayer perceptron (MLP) structures are increasingly being replaced by Kolmogorov–Arnold Networks (KAN) to enhance non-linear modeling capabilities.

Methods: Building upon the SMamba variant of Mamba, this study introduces a KAN module to construct a hybrid model named SMamba-KAN. The model is applied to multivariate hydrological and meteorological data from several stations in the Yangtze River Basin to forecast water levels at the Datong hydrological station over the next 15 days.

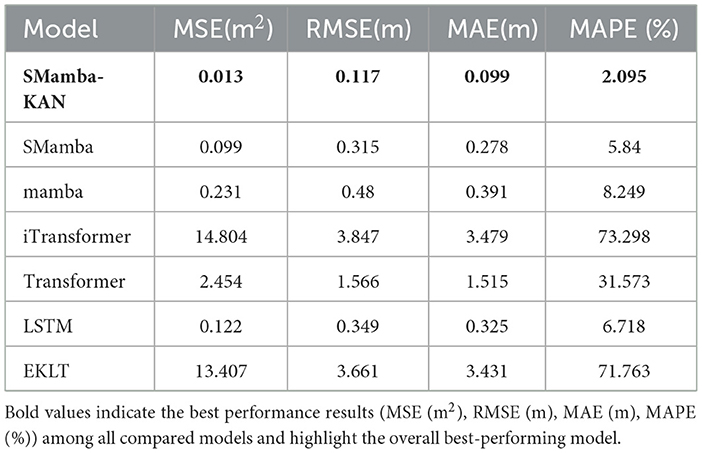
Results: Experimental results demonstrate that the proposed model achieves excellent performance across multiple evaluation metrics, with MSE, RMSE, MAE, and MAPE reaching 0.013, 0.117, 0.099, and 2.095%, respectively. Quantitative performance analysis demonstrates that SMamba-KAN exhibits substantial error reduction compared with the original Mamba, decreasing prediction errors by over 90% in MSE.

Discussion: Relative to its direct baseline SMamba, the incorporation of the KAN module facilitates a significant enhancement in predictive accuracy, further lowering MSE by 54% while maintaining consistent performance stability in MAPE metrics. These results verify the model's high accuracy and strong generalization ability in multivariate water level prediction tasks.

1 Introduction

Accurate water level prediction plays a crucial role in flood control operations, agricultural irrigation, and water resources management (Shekhar et al., 2020; Chang et al., 2024; Brunner et al., 2021). Water level fluctuations are influenced not only by local factors such as river channel topography but are also closely related to meteorological conditions and human activities (Hoque and Adhikary, 2020). Consequently, the development of efficient and precise predictive models has emerged as a critical research focus in the fields of water resource management, disaster prevention and mitigation, and ecological conservation.

At present, water level prediction methods can be broadly categorized into two groups: traditional models based on physical mechanisms and statistical laws, and advanced models driven by machine learning and deep learning techniques (Ozdemir et al., 2023; Yin et al., 2021; Zhang et al., 2025). Traditional hydrological models are typically constructed on the principles of fluid dynamics and hydrodynamics. These models offer strong physical interpretability and parameter realism, effectively reflecting the internal mechanisms of hydrological processes. However, they are often characterized by high dependency on parameters, structural complexity, and significant computational demands (Özdogan-Sarikoç and Dadaser-Celik, 2024; Carletti et al., 2022). Although these physically-based models demonstrate robust modeling capabilities in large-scale or topographically complex river basins, their adaptability and generalization capacity under extreme climatic events remain inadequate (Yang et al., 2025; Frame et al., 2022). Some models incorporate the coupling of multiple physical processes to simulate extreme conditions, but this often comes at the cost of increased computational burden (Doumbia et al., 2025; van Kempen et al., 2021). To enhance the timeliness and accuracy of predictions, recent studies have integrated data assimilation techniques to improve model responsiveness to uncertainty. Nevertheless, the broader application of these methods across diverse river basins still faces substantial challenges related to adaptability (Foroumandi et al., 2025). In comparison, traditional statistical models—such as autoregressive models and gray prediction methods—exhibit certain advantages in capturing linear trends within time series. However, their performance deteriorates significantly when confronted with data environments characterized by nonlinearity, multivariable interactions, and abrupt changes, rendering them insufficient for modeling complex hydrological processes (Chen et al., 2020; Guo et al., 2023; Nguyen, 2020). As a result, these methods are gradually being replaced by intelligent algorithms that are better suited to handling such complexities.

Machine learning methods have demonstrated excellent performance in problems characterized by clear patterns and distinct features, making them widely adopted in the field of water level time series prediction. For example, Support Vector Regression (SVR) and eXtreme Gradient Boosting (XGBoost) have been applied to groundwater level forecasting (Mahammad et al., 2023; Osman et al., 2021). Random Forest (RF) has also been widely adopted for modeling water levels in groundwater systems, lakes, and estuaries (Koch et al., 2019; Nhu et al., 2020; Hughes et al., 2022). Furthermore, Bayesian Model Averaging (BMA) has been shown to enhance the generalization performance of lake water level predictions (Li, G. et al., 2024). Ensemble learning methods have also demonstrated remarkable capacity to improve the accuracy and stability of water level forecasting; notably, a quad-meta model incorporating XGBoost, RF, GBM, and DT has markedly enhanced the prediction accuracy for water level fluctuations in glacier-fed lakes (Shah et al., 2025). Additionally, the emergence of AutoML platforms has streamlined the model construction process and demonstrated favorable performance in real-time forecasting scenarios (Li, S. et al., 2024; Han and Bae, 2025). However, traditional machine learning approaches rely heavily on manual feature engineering, which fundamentally limits their ability to model high-dimensional spatiotemporal features, thereby motivating researchers to explore more advanced deep learning approaches.

In recent years, deep learning has emerged as the dominant paradigm in water level prediction research, owing to its exceptional capabilities in modeling nonlinear relationships and handling high-dimensional data. Ehteram et al. (2021) enhanced prediction performance by integrating a Multilayer Perceptron (MLP), Adaptive Neuro-Fuzzy Inference System (ANFIS), and the Sunflower Optimization Algorithm. Similarly, Chen et al. (2021) developed a model based on spatiotemporal attention mechanisms, which significantly improved the accuracy of groundwater level prediction. Long Short-Term Memory (LSTM) networks, known for their strength in capturing long-term dependencies, have been extensively implemented in hydrological forecasting. The VMD-EF-OBiLSTM model developed by Tan et al. (2023) demonstrated outstanding performance in lake water level prediction, while Guo et al. (2021), Rochac et al. (2022) and Yang et al. (2024) achieved accurate streamflow forecasting under noisy conditions using ConvLSTM. In addition, the CNN-LSTM hybrid architecture proposed by Li et al. (2022) enhanced feature representation capabilities and improved the accuracy of river flow prediction.

Concurrent with purely data-driven methodologies, significant advancements have been observed in hydro–ML hybrid models and physics-informed machine learning (PIML) frameworks. Li et al. (2023) integrated hydrodynamic models with deep learning to predict water levels in ungauged river reaches; Huang et al. (2022) systematically incorporated machine learning methods into hydrodynamic models to improve river simulations under complex boundary conditions; and Feng et al. (2023) utilized physics-informed neural networks (PINNs) to embed the Saint-Venant equations into deep learning architectures, thereby facilitating enhanced interpretability and generalization of water-level-related variables.

The Transformer model, with its powerful long-range dependency modeling and parallel computation capabilities, has further advanced the field of water level prediction. Studies by Castangia et al. (2023), Xu et al. (2023), and Huang et al. (2024) based on historical water level data have validated the effectiveness of the Transformer architecture in time series modeling. Moreover, Ali et al. (2024) leveraged a hybrid architecture combining Transformer and LSTM models to achieve high-precision medium- and long-term groundwater level forecasting with notable improvements in accuracy metrics. The iTransformer model proposed by Liu et al. (2023) introduced an innovative variate tokenization approach, which effectively mitigates the compression of multivariate information commonly observed in conventional Transformer architectures. More recently, Liu et al. (2024) proposed Kolmogorov-Arnold Networks (KAN), which apply learnable activation functions to weights, significantly enhancing both the nonlinear modeling capacity and computational efficiency of the model. Granata et al. (2024) further validated the effectiveness of KAN in hydrological forecasting by comparing it with Transformer models for streamflow prediction in Central European rivers. Ren et al. (2025) further demonstrated the superior performance of the EKLT model, which combines KAN with Transformer and LSTM architectures in water level forecasting tasks.

However, Transformer models exhibit inherent limitations in computational complexity and long-range information processing. In hydrological forecasting, these constraints manifest as difficulties handling multi-year daily records and inadequate capture of critical seasonal or inter-annual dependencies, including hydrological regime transitions and cumulative meteorological effects. To address these limitations, Gu and Dao (2023) proposed the Mamba architecture based on structured state space models (SSMs), which significantly improves the accuracy and information retention in long-sequence forecasting tasks. Building upon this foundation, Wang et al. (2024) proposed the SMamba model by incorporating a variate tokenization strategy, which further enhanced the model's capacity to capture temporal structures and the dynamics of variable evolution. Despite its sequential modeling capabilities, SMamba demonstrates inherent constraints in nonlinear feature representation, which impede its performance in complex multivariate water level prediction tasks. In hydrological contexts, this limitation is reflected in the inadequate characterization of strongly nonlinear processes, including precipitation–runoff amplification during extreme events, thermal–hydrological interactions under heat waves, and abrupt impacts of anthropogenic interventions such as reservoir operations.

To address this limitation, this study proposes a novel integrated framework that combines the SMamba architecture with a specifically designed KAN module to compensate for SMamba's deficiencies in nonlinear feature modeling. By synergistically combining the flexible feature representation capability of KAN with the efficient temporal modeling capacity of SMamba, our proposed framework substantially enhance overall performance in multivariate water level forecasting while maintaining computational efficiency.

The main contributions of this study are summarized as follows:

1. We propose a novel and comprehensive water level forecasting framework (SMamba-KAN) that strategically integrates the SMamba architecture with a specialized KAN module, creating a synergistic modeling approach that simultaneously addresses the critical challenges of capturing long-range dependencies and modeling complex nonlinear interactions among hydrological variables. This integration significantly outperforms state-of-the-art models in both short-term and long-term forecasting scenarios.

2. We design an innovative lightweight KAN module that uniquely combines B-spline basis functions with the FullAttention mechanism, enabling controllable and computationally efficient nonlinear feature enhancement. This novel module not only improves the model's representation capacity but also demonstrates superior generalization capability across diverse hydrological conditions and geographical contexts, as validated through extensive cross-basin experiments.

The remainder of this paper is organized as follows. Section 2 describes the study area and data. Section 3 presents the proposed methodology. Section 4 reports the experimental results, including the experimental setup, evaluation metrics, and comparative analysis. Section 5 provides further discussion, covering ablation studies, generalization performance analysis, and window sensitivity analysis. Finally, Section 6 concludes the paper and outlines directions for future work.

2 Study area and data

To validate the effectiveness and generalization capability of the model proposed in this study for water level forecasting in the Yangtze River, the lower Yangtze River Basin was selected as the study area. As China's longest river and the third longest river worldwide, the Yangtze River encompasses a drainage area of approximately 1.8 million square kilometers, characterized by complex hydrological processes and significant seasonal variations in water levels. The downstream section exhibits distinct hydrological patterns throughout the annual cycle. From April to May, the Dongting Lake, Poyang Lake regions, and tributaries of the Yangtze enter the rising water period, leading to a short-term increase in the main channel water levels, known as the spring flood. Between June and September, the water levels experience substantial elevation intensified precipitation across the basin and augmented inflows from upstream watersheds, marking the primary flood season, with maximum water levels typically observed from July to September. By late October, precipitation diminishes considerably, resulting in a gradual recession of water levels, which signifies the conclusion of the flood season. The dry season begins in November. These pronounced temporal fluctuations in water levels represent critical dynamic characteristics that any effective forecasting model must accurately capture and predict. As illustrated in Figure 1, the dataset used in this study comprising water level records from representative hydrological stations in the lower Yangtze River Basin, along with multisource meteorological data, to thoroughly evaluate the model's performance in processing complex multivariate inputs. The Datong hydrological station serves as the core prediction target, providing daily water level time series as the primary forecasting objective. Additionally, water level data from three auxiliary stations—Jiujiang (Jiangxi), Anqing (Anhui), and Dangtu (Anhui)—are incorporated as supplementary features to enhance the model's spatial awareness of regional hydrodynamic patterns and inter-station correlations. The meteorological data are obtained from automatic weather stations operated by the China Meteorological Administration and include 10 key variables including temperature, humidity, air pressure, and wind speed. These data are collected from locations including Hefei, Huangshan, Nanjing, Jiujiang, and Quzhou. In total, 110 feature variables were constructed, covering the period from January 1, 2014 to December 31, 2021, resulting in 2,922 daily records.

Figure 1

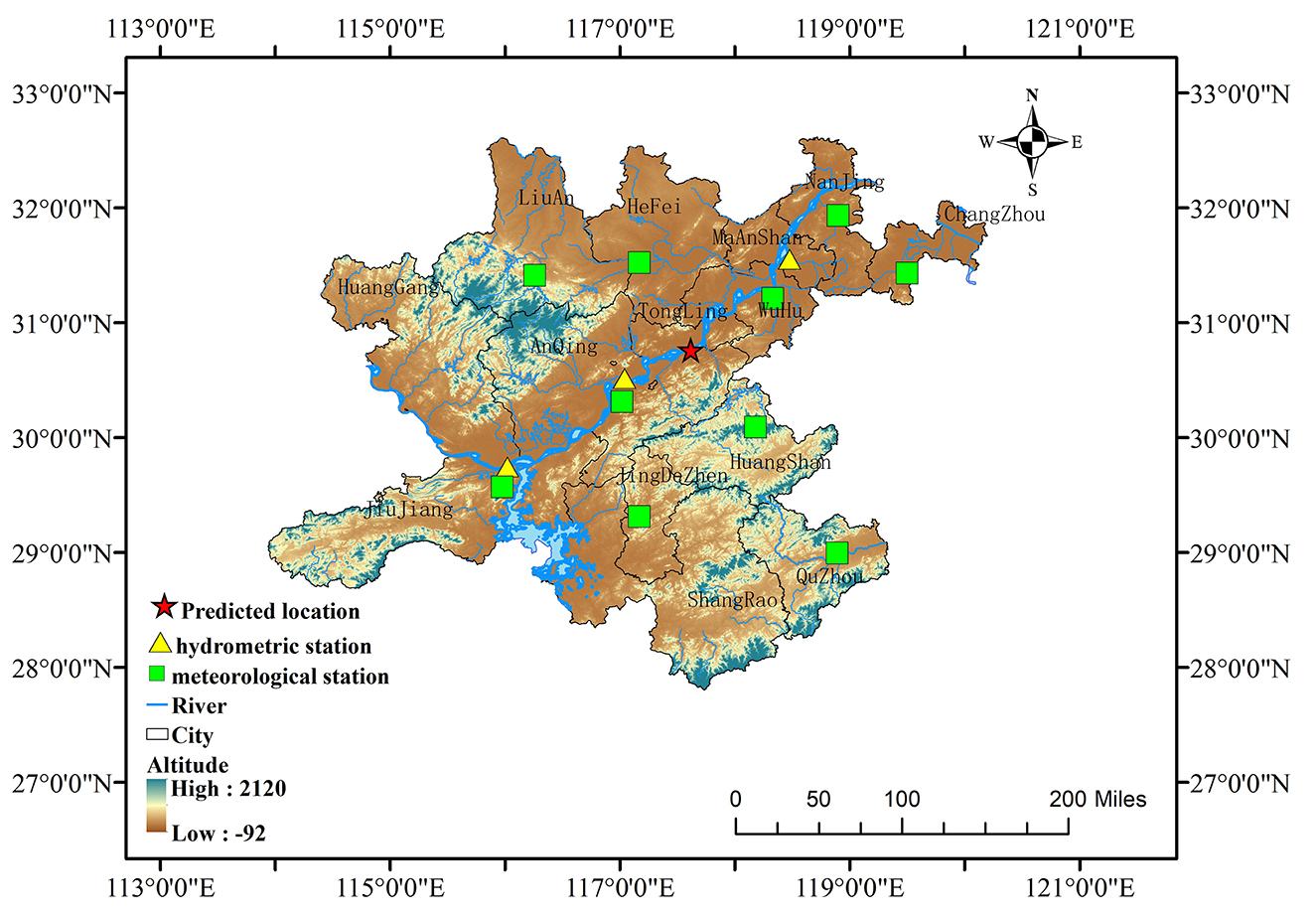
Figure 1. Geographical distribution of the study area. The red pentagram indicates the target hydrological station for prediction in this study; yellow triangles represent auxiliary hydrometric stations providing water level observations; green squares denote meteorological stations supplying variables such as temperature, precipitation, and wind speed. The map also shows major rivers, city locations, and regional topographic elevation, ranging from −92 to 2,120 meters.

All hydrological data utilized in this study were obtained from the National Hydrological Information Network of China (http://xxfb.mwr.cn), while the meteorological data were sourced from the China National Meteorological Data Center (https://data.cma.cn/data/detail/dataCode/A.0012.0001.html).

3 Method

3.1 Overall architecture

Based on the SMamba framework, we propose a multivariate time series prediction model that incorporates an explicit nonlinear modeling mechanism through the integration of KAN and FullAttention. As illustrated in Figure 2, the model is composed of the following key components, stacked in sequence, arranged sequentially: the Variate Token Embedding Layer, the Bidirectional Mamba Layer, the FullAttention Layer, the FFN Layer, and the Projection Layer.

Figure 2

Figure 2. The overall structure of the model.

Our proposed model abandons the conventional Transformer paradigm of token construction along the temporal axis, and instead adopts a Variate Token Embedding strategy that operates along the variable axis. In this design, each variable is treated as an individual token, thereby facilitating the modeling of inter-variable interactions. The embedded features are then fed into a bidirectional Mamba module, which captures temporal dependencies and long-range memory within the sequence. Building upon this, the FullAttention mechanism and KAN module are introduced to enhance the model's nonlinear representation capacity, enabling it to learn complex variable coupling relationships (e.g., wind speed + temperature → evaporation → water level decrease). Subsequently, a feed-forward neural network (FFN) layer is applied independently to each variable token for deep feature refinement, thus allowing the model to effectively capture dependencies across both spatial (variable-wise) and temporal dimensions simultaneously. Finally, the feature representations from all modules are mapped to the target prediction time step via a linear projection layer.

3.2 Variate token embedding layer

In conventional time series models, Transformer architectures typically treat the temporal dimension as the tokenization axis: for each time step t∈[1, L], the values of all N variables are aggregated into a single vector t∈ℝ^N. Consequently, the length of the token sequence corresponds to the length of the time series. In contrast, the Variate Token Embedding strategy constructs the token sequence along the variable axis, where each token corresponds to a specific variable, enabling the model to learn variable-wise feature representations. This structure is particularly advantageous for capturing inter-variable dependencies, and it enhances generalization performance in multivariate modeling scenarios. However, due to the restructured tokenization format, temporal dependency modeling must be explicitly handled by subsequent modules.

Specifically, given a multivariate input sequence ${\text{X}}_{\text{t}-\text{L}+1:\text{t}}\in {\text{ℝ}}^{B\times L\times N}$, where B denotes the batch size, L is the input sequence length, and N is the number of input variables, we first perform a dimension permutation to reorder the axes such that the variable dimension is moved to the front, resulting in a reshaped sequence ${\text{X}}_{\text{t-L+1}:\text{t}}^{\text{permut}}\in {ℝ}^{\text{B}\times \text{N}\times \text{L}}$. Subsequently, a linear projection is applied to each univariate sequence of length L, projecting it into a D-dimensional feature space. The resulting variable-level token representation is defined as:

$\begin{array}{ll}{\text{E}}_{\text{token}}=\text{Linear}\left({\text{X}}_{\text{t}-\text{L}+1:\text{t}}^{\text{permut}}\right)\in {\text{R}}^{\text{B}\times \text{N}\times \text{D}}& (1)\end{array}$

When additional temporal covariates C are available (such as timestamp information or periodic encodings), the covariate sequence X^mark∈ℝ^B×L×C is transposed in the same manner to obtain X^{mark, permut}∈ℝ^B×C×L. It is then concatenated with the original variable sequence along the variable dimension to form ${\text{X}}^{\text{concat}}=\left[X_{t-L+1:t}^{permut};X^{mark,permut}\right]\in {ℝ}^{B\times (N+C)\times L}$. A linear projection is then applied to X^concat, producing ${\text{E}}_{\text{token}}\in {ℝ}^{B\times (N+C)\times R}$.

Finally, dropout is applied to the result to promote generalization:

$\begin{array}{ll}{\text{E}}_{\text{final}}=\text{dropout}({\text{E}}_{\text{token}})\in {\text{R}}^{\text{B}\times \text{N}\times \text{D}}& (2)\end{array}$

3.3 Bidirectional Mamba layer

The Mamba model represents an efficient sequence modeling approach based on state space modeling (SSM). It incorporates an input-dependent parameter selection mechanism and a hardware-aware parallel computation design. This selective parameterization enables the model to dynamically adjust the state transition process according to the input content, thereby conferring greater flexibility in capturing long-term temporal dependencies. Furthermore, the Mamba module exhibits approximately linear time complexity, offering computational advantages over Transformers when handling long sequences. In the proposed architecture, the Mamba module serves to model long-range dependencies along the temporal dimension and is integrated with other components within the encoder layer.

To implement state-space modeling, the Mamba module initially performs linear expansion and local convolution on the input sequence to extract localized contextual features. Subsequently, a structured state transition matrix and an input-dependent learnable offset are computed. These parameters are passed through a Softplus activation function to generate the requisite parameter set for state evolution. The Selective SSM core module then executes hidden state recursion and output projection, ultimately producing a feature representation for each time step. The core computational process can be succinctly formulated by Equations 3, 4:

$\begin{array}{ll}{\text{h}}_{\text{t}}=\overline{\text{A}}·{\text{h}}_{\text{t}-1}+\overline{\text{B}}·{\text{x}}_{\text{t}}^{\prime }& (3)\end{array}$

$\begin{array}{ll}{\text{y}}_{\text{t}}^{\prime }=\text{C }·{\text{h}}_{\text{t}}& (4)\end{array}$

Here, h_t denotes the internal hidden state of the system at time step t, $x_t^{\prime }$ is the locally enhanced input feature, and y_t is the output.

Although the Mamba module is capable of efficiently modeling temporal dependencies in sequences, its state update mechanism relies solely on the current input and historical hidden states. As a result, it is inherently limited to unidirectional sequence modeling, making it difficult to capture future time-step dependencies, which may lead to degraded performance in complex water level forecasting tasks. To overcome this limitation, this study introduces a bidirectional attention mechanism based on the Mamba module. Specifically, after linear embedding and variate–time axis inversion, the model input is transformed into a three-dimensional tensor ${\text{E}}_{\text{token}}\in {ℝ}^{B\times N\times D}$, where each multivariate input token is unfolded along the temporal dimension to encode future-relevant information. The input sequence is then simultaneously passed into two parallel Mamba modules: one processes the sequence in the original chronological order, yielding $\vec{E}$ as the forward time-series processing result, while the other handles the time-reversed sequence, producing $\stackrel{⃖}{E}$ as the reverse time-series processing result. This allows the model to capture both forward and backward temporal dependencies, thereby improving its representational capacity and predictive accuracy. The overall process is formally described by the bidirectional Mamba structure, as defined in Equations 5–7.

$\begin{array}{ll}\vec{E}=\overrightarrow{\text{Mamba Block}}({\text{E}}_{\text{token}})& (5)\end{array}$

$\begin{array}{ll}\stackrel{⃖}{E}=\stackrel{⃖}{\text{Mamba Block}}({\text{E}}_{\text{token}})& (6)\end{array}$

$\begin{array}{ll}{E}_1=\vec{E}+\stackrel{⃖}{E}& (7)\end{array}$

In this layer, the bidirectional Mamba modules effectively capture inter-variable feature interactions at each time step, as well as their dynamic evolution across the temporal sequence. However, two significant limitations persist.

(1) The absence of local variable importance evaluation precludes explicit weighting of different variables, thereby limiting the model's ability to prioritize dominant factors. For example, it fails to distinguish the varying sensitivities of current water level to “previous-day precipitation” and “same-day wind speed.”

(2) The model exhibits insufficient capacity for modeling complex nonlinear cross-variable relationships. Due to the linear state evolution mechanism intrinsic to Mamba, it struggles to effectively represent nonlinear dependencies among variable combinations—exemplified by the joint influence of temperature and wind speed on evaporation rates in hydrological systems.

To address these limitations, an attention mechanism and a feed-forward network module are subsequently integrated to augment the model's capabilities in feature selection and nonlinear interaction modeling, thereby enhancing the prediction accuracy of future T-step water level forecasts.

3.4 FullAttention layer

To enhance the model's ability to capture nonlinear dependencies among variables, we apply a multi-head full attention mechanism prior to the KAN module, allowing the input tensor to be preprocessed based on classical full attention. This preprocessing step enhances the feature transformation capacity of KAN for modeling complex inter-variable relationships at finer granularity.

Given the input tensor sequence ${\text{E}}_{\text{token}}\in {ℝ}^{B\times N\times D}$, linear projections are first applied to generate the query (Q), key (K), and value (V) tensors, as defined in Equation 8:

$\begin{array}{ll}\text{Q},\text{K},\text{V}=\text{Linear}({\text{E}}_{\text{token}})\in {ℝ}^{\text{B}\times \text{N}\times \text{H}\times \text{d}}& (8)\end{array}$

Here, H denotes the number of attention heads, and d = D/H is the dimensionality per head. The scaled dot-product attention scores are then computed as shown in Equation 9:

$\begin{array}{ll}\text{S}=\frac{\text{Q }•{\text{K}}^{\top }}{\sqrt{\text{d}}}\in {\text{R}}^{\text{B}\times \text{H}\times \text{N}\times \text{N}}& (9)\end{array}$

Finally, the attention output is obtained by applying Softmax-based normalization to the attention scores, followed by weighting with V, and is then forwarded into the KAN network.

As illustrated in Figure 3, the traditional FullAttention mechanism fundamentally operates through a weighted summation process, wherein the attention output constitutes a linear combination of the value vectors weighted by Softmax coefficients. This linear formulation inherently constrains its ability to model complex nonlinear relationships among features. Even when implemented in a multi-head configuration, the representational capacity remains predominantly constrained by linear projections and the depth of stacked layers. In contrast, the integrated KAN module subsequently introduces nonlinear enrichment to the attention output by applying a set of explicitly controllable nonlinear transformations formulated via B-spline basis functions. This architectural enhancement enables KAN to approximate significantly more complex feature mappings and effectively compensates for the inherent representational limitations of traditional attention mechanisms—particularly when modeling nonlinear couplings among multiple variables, such as water levels that are jointly influenced by precipitation and temperature patterns through complex interactions.

Figure 3

Figure 3. Structure of the FullAttention layer.

3.5 KAN layer

Kolmogorov-Arnold Networks (KAN) constitutes a neural network architecture grounded in the Kolmogorov-Arnold representation theorem. They approximate arbitrary continuous functions through structured compositions of univariate functions, facilitating the modeling of complex nonlinear relationships with enhanced interpretability. Compared to conventional deep fully connected networks, KAN employs an explicit function approximation mechanism and exhibits superior generalization performance in modeling continuous dynamic processes. However, the original KAN architecture necessitates deeply nested compositions of univariate functions, resulting in high computational cost and structural complexity, thereby limiting its scalability in practical applications.

To address these constraints, we have developed a fused single-layer KAN module that integrates B-spline basis functions with the SiLU activation function for efficient feature extraction. A sparse masking matrix is implemented to enhance interpretability, and trainable scaling coefficients are utilized to regulate the response strength of different pathways. The module constrains the mapping between input and output features via a sparse connectivity mechanism, effectively reducing computational complexity. The architecture achieves flexible nonlinear transformations through least-squares-fitted B-spline functions, thereby providing stronger nonlinear approximation capacity, higher feature interpretability, and controllable modeling complexity and smoothness compared to conventional attention mechanisms. This architectural enhancement retains nonlinear expressiveness while significantly reducing redundant parameters, making it particularly advantageous for enhancing the linear projection modules in the original SMamba architecture and improving modeling performance in water level forecasting applications.

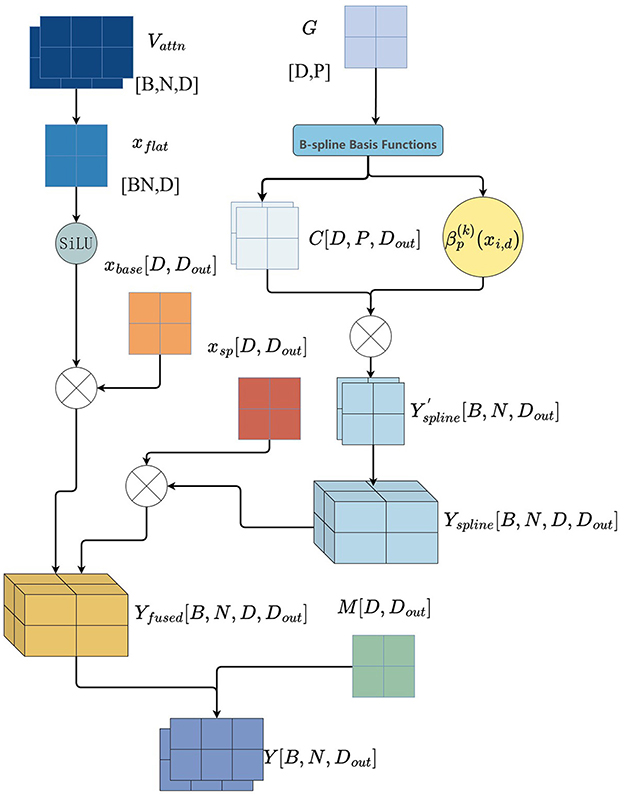
As illustrated in Figure 4, the KAN module takes the batch-wise input feature $V_{atten}\in {ℝ}^{B\times N\times D}$ as the basis. The input is first flattened and passed through a SiLU nonlinear activation function to extract basic feature representations. Subsequently, an explicit approximation mechanism based on B-spline basis functions is introduced to model higher-order nonlinear structures. Specifically, let G denote the spline node grid and k the spline order. For each input feature point, the effect of the p-th B-spline basis function of order k in the d-th dimension is evaluated at sample x_{i, d}, denoted as ${\beta }_p^{(k)}(x_{i,d})$. Combined with the predefined spline coefficient matrix C, the projection is defined as Equation 10:

$\begin{array}{ll}{\text{Y}}_{\text{spline}}\left[\text{i},{\text{d}}_{\text{out}}\right]={\displaystyle \sum _{\text{d}=1}^{\text{D}}}{\displaystyle \sum _{\text{p}=1}^{\text{P}}}{\beta }_{\text{p}}^{(\text{k})}({\text{x}}_{\text{i},\text{d}})•\text{C}\left[\text{p},\text{d},{\text{d}}_{\text{out}}\right]& (10)\end{array}$

After obtaining the spline projection output, the KAN module fuses it with the baseline activation pathway. Two learnable scaling matrices S_base and S_sp are introduced, and the fused result is given by Equation 11:

$\begin{array}{ll}\begin{array}{r}\hfill {\text{Y}}_{\text{fused}}\left[\text{b},\text{n},\text{i},\text{j}\right]={\text{S}}_{\text{base}}\left[i,j\right]•\varphi \left(\text{x}\left[\text{b},\text{n},\text{j}\right]\right)\\ \hfill +{\text{S}}_{\text{sp}}\left[\text{i}.\text{j}\right]•{\text{Y}}_{\text{spline}}\left[\text{b},\text{n},\text{i},\text{j}\right]\end{array}& (11)\end{array}$

To further enhance structural interpretability and computational efficiency, a sparse masking matrix $M\in {\left\{0,1\right\}}^{D\times D_{out}}$ is introduced during the fusion stage to select effective connections. The final output is computed as Equation 12:

$\begin{array}{ll}\text{Y}\left[\text{B},\text{N},{\text{D}}_{\text{out}}\right]={\displaystyle \sum _{\text{i}=0}^{\text{D}}}\text{M}\left[\text{i},\text{j}\right]•{\text{Y}}_{\text{fused}}\left[\text{b},\text{n},\text{i},\text{j}\right]& (12)\end{array}$

Finally, the second key latent representation ${\text{E}}_2\in {ℝ}^{B\times N\times D}$ is obtained from the transformed input:

$\begin{array}{ll}{\text{E}}_2=\text{ kan}\left(\text{FullAttention}({\text{E}}_{\text{token}})\right)\in {\text{R}}^{\text{B}\times \text{N}\times \text{D}}& (13)\end{array}$

Figure 4

Figure 4. Structure of the KAN layer.

3.6 FFN layer

Although long-range contextual dependencies have been captured by the Mamba module and local nonlinear transformations along each feature dimension have been modeled by the KAN module, both primarily focus on temporal or intra-feature modeling. To overcome these limitations, we introduce a feed-forward network (FFN) layer to enable cross-channel interactions among variables. This component compensates for the limitations of Mamba and KAN in modeling dependencies along the temporal or channel dimensions, and ensures that the final representations are more expressive and robust.

In this layer, we first apply a normalization step to standardize all variables E₁, E₂, E_tokentoward a Gaussian distribution. This process improves convergence and stabilizes the training of water-level-related data, mitigating discrepancies arising from inconsistencies in data balancing algorithms. Next, a FFN is applied to the sequential representations of each variable. The FFN layer utilizes densely connected nonlinear transformations to encode the observed historical sequences and decode the representations of future sequences. Throughout this process, the FFN implicitly encodes temporal dependencies by preserving sequential order.

Finally, an additional normalization layer is employed to further refine the future sequence representations.

$\begin{array}{ll}\text{E}=\text{FFN}({\text{E}}_1,{\text{E}}_2,{\text{E}}_{\text{token}})\in {\text{ℝ}}^{\text{B}\times \text{N}\times \text{D}}& (14)\end{array}$

Through these nonlinear transformations and cross-dimensional interactions, the model further enhances the representation of the fused features. At this point, the entire encoder module—composed of stacked layers—integrates the Bidirectional Mamba Layer, FullAttention layer, KAN layer, and FFN layer, thereby extracting the most discriminative representation tensor E for multivariate time series. This tensor serves as the final encoded output of the model and is passed to the subsequent projection head for the target sequence forecasting task.

3.7 Projection layer

The final representation tensor E∈ℝ^B×N×D produced by the encoder is passed through a linear projection layer to map the feature dimension to the prediction horizon, yielding the output for future time steps. Specifically, this projection layer performs a fully connected linear transformation that maps the hidden dimension D to the forecast length T. Subsequently, a transpose operation is applied to the result to generate the final prediction output.

4 Experiment results and analysis

4.1 Experimental environment and hyperparameter settings

All experiments were conducted on a Linux operating system with the following configuration: GPU: NVIDIA vGPU (32GB), Driver version: 560.35.03, CUDA version: 12.6. The implementation was based on Python 3.8.10. We utilized a look-back window of 90 time steps (corresponding to 90 days) and predicted the next 15 time steps (15 days) of river water level data. For all datasets, we allocated 80% of the data for training and the remaining 20% for testing.

For the single-step rolling prediction phase, we employed a sliding window approach. Specifically, the last 90 days of the training data were first extracted as the look-back window. At each iteration, the model forecasted the river water level for the next day based on the current window. The predicted value was then appended to the window while the oldest value was discarded, allowing the window to advance forward. This process was repeated iteratively until the forecasts for the next 15 days were obtained. The training dataset was constructed by excluding the last 15 days of the full dataset, which were reserved for rolling prediction evaluation.

To ensure fair comparability across different models under consistent data preprocessing and training strategies, and to evaluate the predictive performance of the proposed model under multivariate input conditions, we implemented a unified configuration for all models. Specifically, each model was trained with a fixed look-back window of 90 days, 100 training epochs, a hidden layer size of 64, an embedding dimension of 512, a batch size of 32, and a SiLU activation function, with a dropout rate set to 0.1. Since the proposed model utilized a single-encoder architecture, all baseline models built on encoder-decoder structures were configured with a single-layer decoder or projection head. This ensured consistency in model depth between encoders and decoders across all experimental comparisons.

4.2 Evaluation metrics

In the experiments, we employed four metrics to evaluate the performance of the proposed method: Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE). The definitions of these metrics are given as follows:

$\begin{array}{ll}\text{MSE}=\frac{1}{\text{n}}{\displaystyle \sum _{\text{i}=1}^{\text{n}}}{({\text{y}}_{\text{i}}-{\text{y}}_{\text{i}})}^2& (15)\end{array}$

$\begin{array}{ll}\text{MSE}=\sqrt{\frac{1}{\text{n}}{\displaystyle \sum _{\text{i}=1}^{\text{n}}}{({\text{y}}_{\text{i}}-{\text{y}}_{\text{i}})}^2}& (16)\end{array}$

$\begin{array}{ll}\text{MAE}=\frac{1}{\text{n}}{\displaystyle \sum _{\text{i}=1}^{\text{n}}}|{\text{y}}_{\text{i}}-{\text{y}}_{\text{i}}|& (17)\end{array}$

$\begin{array}{ll}\text{MAPE}=\frac{1}{\text{n}}{\displaystyle \sum _{\text{i}=1}^{\text{n}}}\left|\frac{{\text{y}}_{\text{i}}-{\text{y}}_{\text{i}}}{{\text{y}}_{\text{i}}}\right|\times 100\text{\%}& (18)\end{array}$

Here, y_i denotes the actual water level, y denotes the predicted water level, and y_i represents the average value.

RMSE represents the square root of MSE, which preserves the original units of the target variable, making it more interpretable in practice. It also quantifies the model's ability to capture extreme fluctuations in water levels. MSE emphasizes larger error terms and exhibits sensitivity to outliers, making it particularly suitable for measuring overall variance deviation. MAE measures the average absolute error, providing a robust and intuitive measure of prediction accuracy. MAPE assesses the prediction performance using standardized relative errors, thereby normalizing the influence of absolute water level magnitudes. By comprehensively analyzing these four metrics in conjunction, the model's predictive performance under varying water level conditions can be rigorously evaluated from multiple complementary perspectives.

4.3 Comparison methods

To validate the effectiveness and generalization capability of the proposed SMamba-KAN fusion model for multivariate time series forecasting, we systematically design and conduct a series of comparative experiments to evaluate its performance. We carefully select baseline models that are most relevant to our proposed method as fundamental references and compare them with several state-of-the-art hybrid models for water level prediction. The following six models were selected for comparison:

(1) SMamba (Wang et al., 2024): This model is derived from the Mamba framework with structural and parameter-level adjustments, specifically aiming to explore potential improvements based on the original architecture.

(2) Mamba (Gu and Dao, 2023): Serving as a baseline model, Mamba focuses solely on long-range dependency modeling. It does not incorporate the KAN module, the Variate Token Embedding layer, or any additional nonlinear enhancement, and was used to assess the necessity of introducing nonlinear mechanisms.

(3) iTransformer (Liu et al., 2023): A Transformer variant that adopts a Variate Token Embedding strategy, in which each token corresponds to a specific input variable. This embedding formulation directly inspired the design of the Variate Token Embedding layer proposed in this study.

(4) Transformer: The standard Transformer model that constructs tokens primarily along the temporal axis, implemented as a classical benchmark.

(5) LSTM: A time series forecasting model based on Long Short-Term Memory networks, implemented to verify sequential modeling capabilities.

(6) EKLT (Ren et al., 2025): A hybrid model that combines Transformer, LSTM, and KAN modules, designed to investigate the effectiveness of different module combinations in complex time series forecasting tasks.

4.4 Experimental results and analysis

Figure 5 illustrates the 15-day forecast sequences of different models in comparison with the observed water levels, and the corresponding error evaluation metrics are summarized in Table 1. It can be clearly observed that, compared to the baseline SMamba model, the SMamba-KAN model, which integrates the explicit nonlinear KAN module, demonstrates significant improvements across all error metrics. Specifically, the MSE decreased by approximately 87%, RMSE by 63%, MAE by 64%, and MAPE by 64%. This notable enhancement can be primarily attributed to the inclusion of the KAN module, which effectively enhances the model's ability to capture complex nonlinear relationships and long-term dependencies among multivariate inputs, thereby enabling more accurate river water level forecasting.

Figure 5

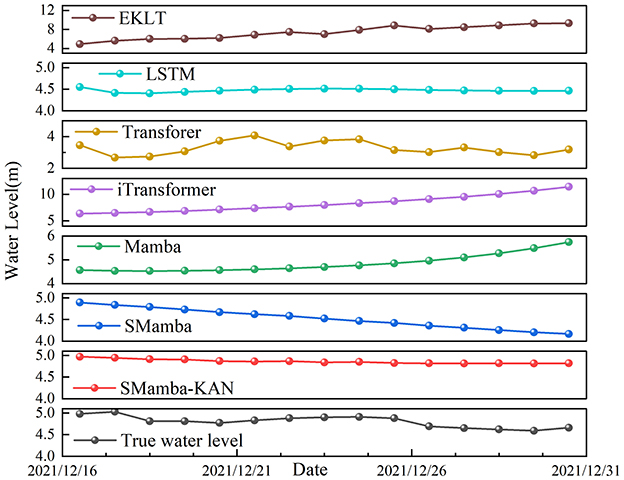
Figure 5. Comparison of predicted water levels and ground truth over a 15-day forecast horizon using a 90-day input window. The red solid line represents the SMamba-KAN model, the gray solid line indicates the true water level, and the remaining curves correspond to prediction sequences of various baseline models.

Table 1

Table 1. Performance metrics of different models (input window = 90 days).

In comparison with the conventional Mamba model, the advantages of the SMamba-KAN model are even more substantial. Specifically, the MSE decreased by approximately 94%, RMSE by 76%, MAE by 75%, and MAPE by 75%. The underlying mechanism lies in the fact that the SMamba-KAN model not only inherits the capability of the Mamba model in efficiently capturing long-term sequential dependencies, but also leverages the KAN module to explicitly model the nonlinear features in the data, enabling more effective learning of subtle yet critical interactions among variables.

Furthermore, comparison with the iTransformer model—which also adopts the Variate Token Embedding Layer—reveals that although iTransformer demonstrates clear advantages over the traditional Transformer in capturing inter-variable relationships (as discussed in Sections 5.2 and 5.3), it does not exhibit outstanding performance under conditions of high noise and variability. However, when its structural design is integrated into the SMamba-KAN model, the overall prediction accuracy is substantially enhanced, especially in terms of capturing long-term dependencies in multivariate inputs. This indicates that the Variate Token Embedding strategy itself can effectively augment the model's ability to perceive intrinsic variable relationships, and such advantages are further magnified when combined with the state-space memory mechanism and explicit nonlinear enhancement of the SMamba-KAN model.

In contrast, the traditional LSTM model and the hybrid model combining Transformer, LSTM, and KAN show significantly inferior overall performance, particularly under conditions with high variable complexity and noise levels. Although the LSTM model exhibits relatively strong robustness to noise—primarily due to its simpler architecture that enables the model to focus more on key signals and avoid overfitting—its limitations become increasingly apparent in scenarios involving long-term dependencies and complex nonlinear relationships. By comparison, the SMamba-KAN model, through the integration of the bidirectional Mamba module for long-sequence modeling and the KAN module for nonlinear feature learning, significantly mitigates the impact of noise and enhances the model's ability to capture the underlying trends in real-world data.

The superiority of the SMamba-KAN model manifests in the following aspects: first, the Mamba module efficiently captures long-range temporal dependencies, effectively mitigating the memory limitations faced by traditional sequence models when dealing with long sequences. Second, the KAN module explicitly models nonlinear interactions within the data, enabling the model to more precisely identify and capture key features. Additionally, by incorporating the Variate Token Embedding strategy, the SMamba-KAN model more accurately characterizes the strong upstream–downstream correlations and intrinsic relationships among variables, thereby achieving a significant performance advantage in prediction accuracy for water level forecasting tasks.

5 Discussion

5.1 Ablation experiment

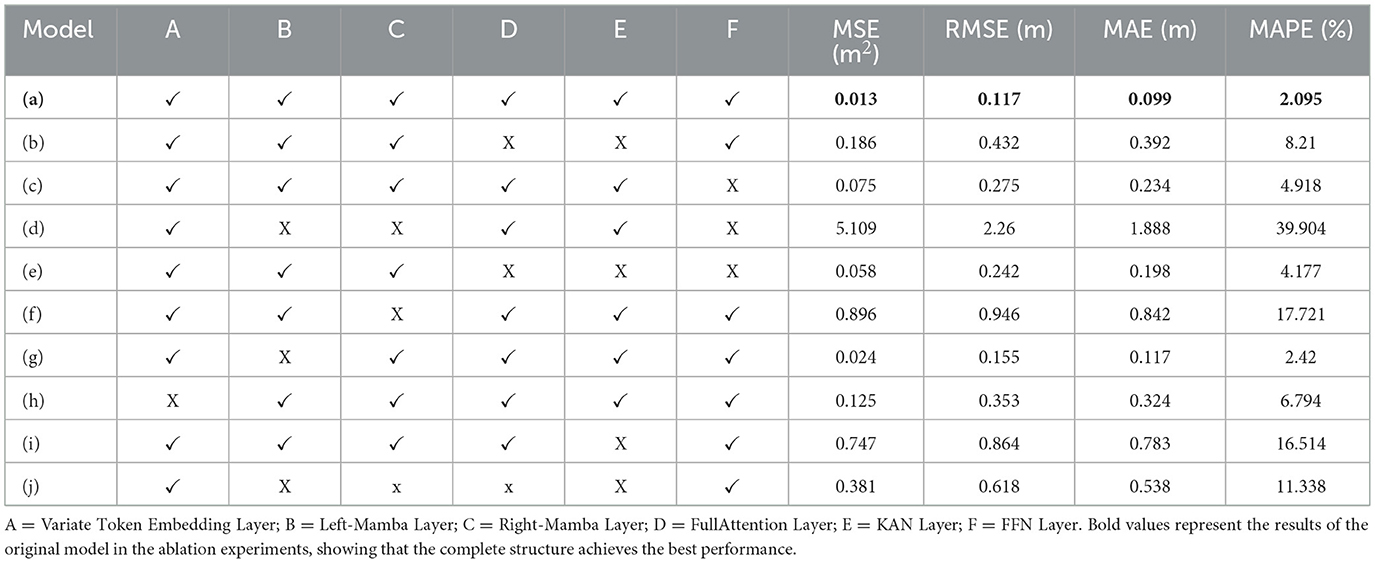
As shown in Table 2, we conducted ablation experiments using the full SMamba-KAN model as the baseline on a multivariate dataset that includes both water level and meteorological variables with a temporal input window of 90 days. We systematically performed ablation by removing or replacing individual components related to multivariate representation learning. The complete configuration includes the Variate Token Embedding Layer, Bidirectional Mamba Layer (comprising both the left-mamba and right-mamba layers), FullAttention Layer, KAN Layer, and FFN Layer. The complete model achieves significantly reduced errors. However, when certain modules are removed under identical experimental conditions, significant deterioration is observed in evaluation metrics. For example, removing the KAN module [variant (h)] leads to an increase in MSE by approximately 0.713, indicating the indispensable role of KAN in capturing complex nonlinear interactions among multivariate inputs.

Table 2

Table 2. Performance metrics of different model variants (input window = 90 days).

Furthermore, removing the Variate Token Embedding Layer [variant (g)] or the right-mamba layer [variant (f)] also causes notable performance degradation, suggesting that these components are crucial in the model's ability to interpret water level trends.

In experimental variant (d), only the Variate Token Embedding Layer and the FullAttention-KAN module are retained, while both the left and right Mamba layers and the FFN module are removed. Under this configuration, the model's performance metrics are substantially inferior to those of the full model. This result, along with the previously observed suboptimal performance in models combining KAN with LSTM or Transformer, indicates that the KAN module alone—or when improperly integrated—cannot fully exploit its modeling capacity. Only when the KAN module is appropriately integrated with other key components (such as Mamba, FullAttention, and FFN) can synergistic effects be achieved, wherein the overall performance significantly surpasses the sum of individual components acting independently.

Our analysis demonstrates that when only the left Mamba layer is removed [variant (f)], the model's prediction performance remains comparable to that of the full architecture. This suggests that the left Mamba layer functions analogously to the KAN module in capturing temporal information and variable interactions. However, when the left Mamba layer is used in conjunction with the KAN module, the model's ability to distinguish subtle variations in multivariate input data is further enhanced, thereby improving the overall robustness of the prediction.

Comprehensive examination of the different ablation variants reveals that when both the FullAttention and KAN modules are removed [variant (d)—which essentially approximates the original SMamba model, with only minor parameter modifications], the resulting MSE, RMSE, and MAE are relatively low. This may suggest that, in certain scenarios, exclusive reliance on these modules could introduce additional noise or interference, thereby affecting the model's ability to capture global trends. In contrast, the complete SMamba-KAN model achieves optimal performance equilibrium across all metrics, demonstrating the synergistic effect of the overall architecture. Although some ablated variants show sporadic improvements in individual metrics, the absence of specific modules—particularly the FFN, KAN, and Variate Token Embedding Layer—consistently leads to reduced robustness and accuracy in multivariate water level forecasting tasks. These ablation results strongly validate the superiority of the proposed model structure in capturing the complex nonlinear relationships between upstream and downstream water levels and associated meteorological variables.

5.2 Baseline analysis for upstream–downstream water level prediction

We additionally conducted extensive experiments on a low-noise, multivariate dataset that includes only upstream and downstream water level data. In this scenario, the multivariate inputs exhibit strong correlations and minimal interference, as the upstream and downstream water levels can effectively complement and enhance the prediction of the target station's water level trends. This setting provides more accurate and relevant supplementary information for the forecasting task.

Under this experimental configuration, the performance of each model differs significantly from that observed on datasets incorporating meteorological variables. In an environment with fewer variables and reduced interference, Figure 6 clearly demonstrates the structural advantages of the SMamba-KAN model.

Figure 6

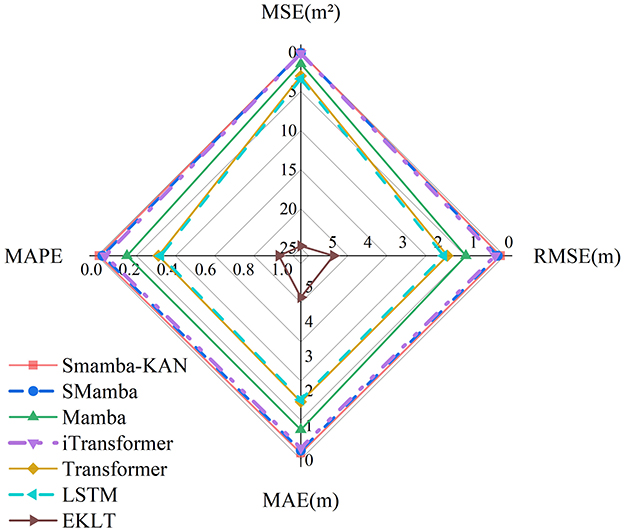
Figure 6. Radar chart comparing the prediction errors of different models on the upstream–downstream water level dataset (performance improves outward along each axis).

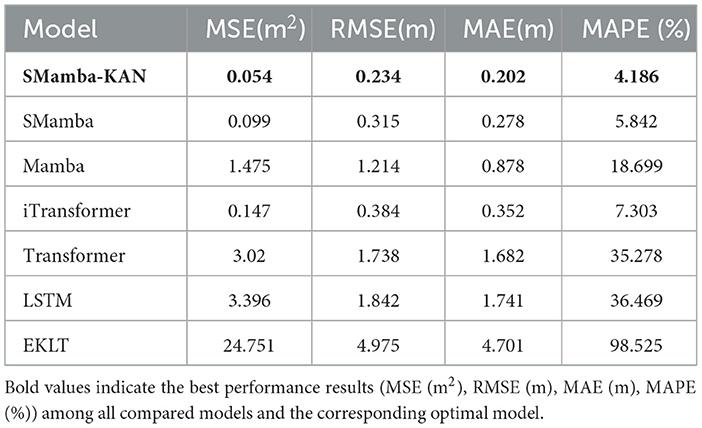
By reorienting the modeling focus from the temporal dimension to the variable dimension, the Variate Token Embedding Layer enables more accurate modeling of inter-variable relationships and dependencies across monitoring stations, thereby significantly mitigating prediction bias. As shown in Table 3, the SMamba-KAN model achieves MSE, RMSE, MAE, and MAPE values of 0.054, 0.234, 0.202, and 4.186%, respectively, significantly outperforming all other models. These results conclusively establish the effectiveness of integrating the Variate Token Embedding strategy with the bidirectional Mamba and the explicitly nonlinear KAN module, particularly in low-noise environments with fewer variables—highlighting this architectural combination as a key to achieving high-accuracy water level forecasting.

Table 3

Table 3. Model performance on upstream–downstream dataset (input window = 90 days).

5.3 Window sensitivity analysis

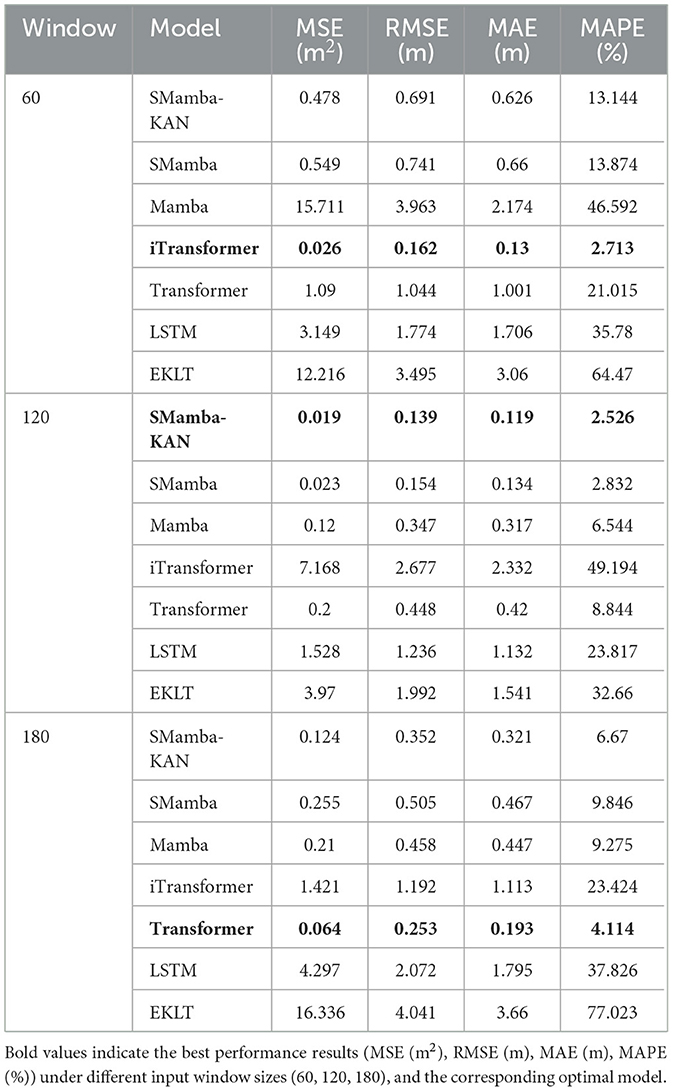
In the previous multivariate experiments using a 90-day input window as the baseline, we empirically assessed the model's predictive capability in assimilating comprehensive hydrological and meteorological information. To further investigate the impact of input window duration on forecasting performance, we systematically evaluated three additional settings with window sizes of 60, 120, and 180 days. Figure 7 depicts the fit between the predicted and observed values of the SMamba-KAN model under different input windows, while Table 4 summarizes the error metrics of all models across various window configurations. The results reveal that model performance exhibits differential sensitivity to input length, reflecting each model's efficacy in capturing short- and long-term dependencies. Notably, the proposed SMamba-KAN model demonstrates superior capability in adapting to longer input sequences.

Figure 7

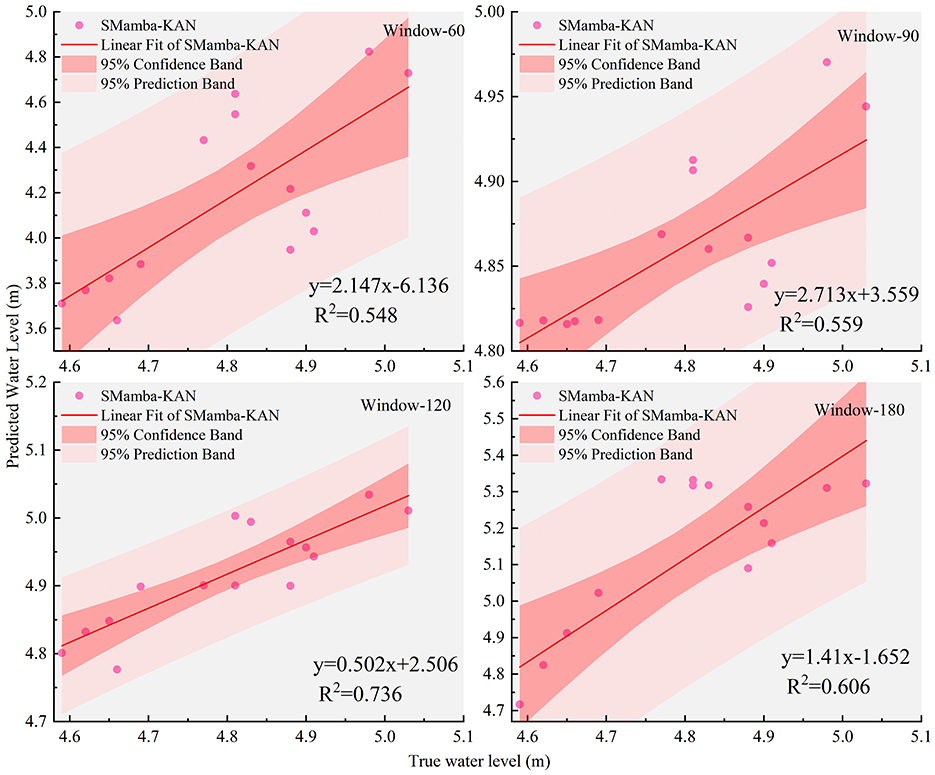
Figure 7. Scatter regression plots of predicted vs. observed values by the SMamba-KAN model under different input window lengths.

Table 4

Table 4. Performance comparison across different input window lengths.

As the input window extends from 60 to 120 days, the SMamba-KAN model exhibits a substantial reduction in prediction error—MSE, MAE, and MAPE decrease by nearly 96% under the same multivariate conditions, and the R² value increases markedly. However, when the window is further extended to 180 days, performance slightly deteriorates compared to the 120-day window. This indicates that SMamba-KAN can effectively leverage moderately extended temporal contexts to capture complex nonlinear interactions and long-term dependencies among variables, but excessively long windows may introduce redundancy or noise, thereby slightly compromising model stability. In contrast, conventional Transformer- and LSTM-based models show heightened sensitivity to window size. While some models (e.g., standard Transformer) benefit from longer input sequences, others—such as iTransformer—perform best under shorter windows, suggesting that the Variate Token Embedding structure may have inherent limitations in capturing long-range dependencies.

Overall, the window sensitivity analysis conclusively demonstrates that an appropriately selected input window-−120 days in this experimental context—can significantly improve forecasting accuracy, further corroborating the structural advantages of the SMamba-KAN model in multivariate settings.

5.4 Efficiency comparison of models

Empirical analysis of Table 5 reveals that SMamba-KAN, compared with SMamba, exhibits a marginal increase in training time, reaching 2.41 s per epoch vs. 1.45, and in inference latency, reaching 4.43 milliseconds per step vs. 4.30. This increase primarily originates from the introduction of the KAN and FullAttention modules. However, the model's parameter scale remains only 15.08 million, and its FLOPs amount to just 0.008 billion, which are still substantially lower than those of Mamba at 0.118 billion and LSTM at 0.038 billion. Thus, the overall computational burden remains within acceptable computational constraints.

Table 5

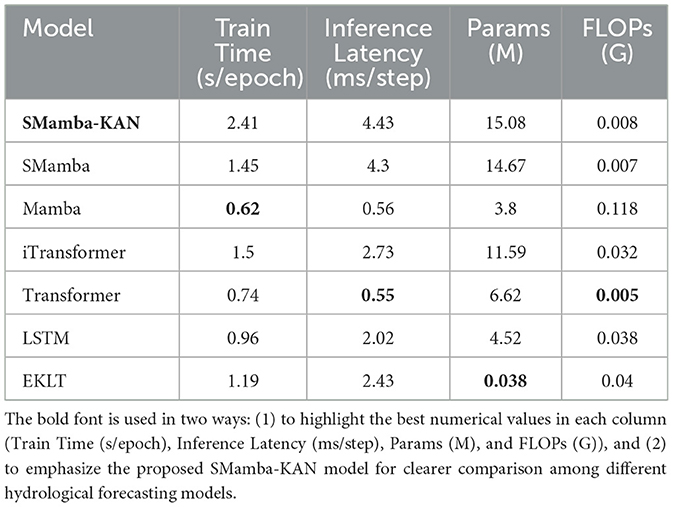
Table 5. Performance efficiency comparison of hydrological forecasting models (input window = 90 days).

Most notably, in terms of the efficiency-accuracy trade-off, SMamba-KAN demonstrates significant superiority. When juxtaposed with both Mamba and SMamba, it achieves improvements of more than 63 to 87 percent across all error metrics. Furthermore, in comparison to more complex hybrid models such as iTransformer and EKLT, SMamba-KAN delivers enhanced predictive accuracy while maintaining lower FLOPs and comparable inference speed. This indicates that the performance enhancements derive not from massive parameter counts or deep stacking, but rather from the synergistic computational capabilities of Mamba and KAN.

In operational hydrological forecasting contexts, models necessitate frequent retraining. The additional overhead of less than 1 s per epoch introduced by SMamba-KAN is negligible in practical applications, whereas its substantial improvements in predictive accuracy and robustness translate to significant benefits for scheduling and disaster prevention decisions. Therefore, the additional computational complexity is both justified and essential.

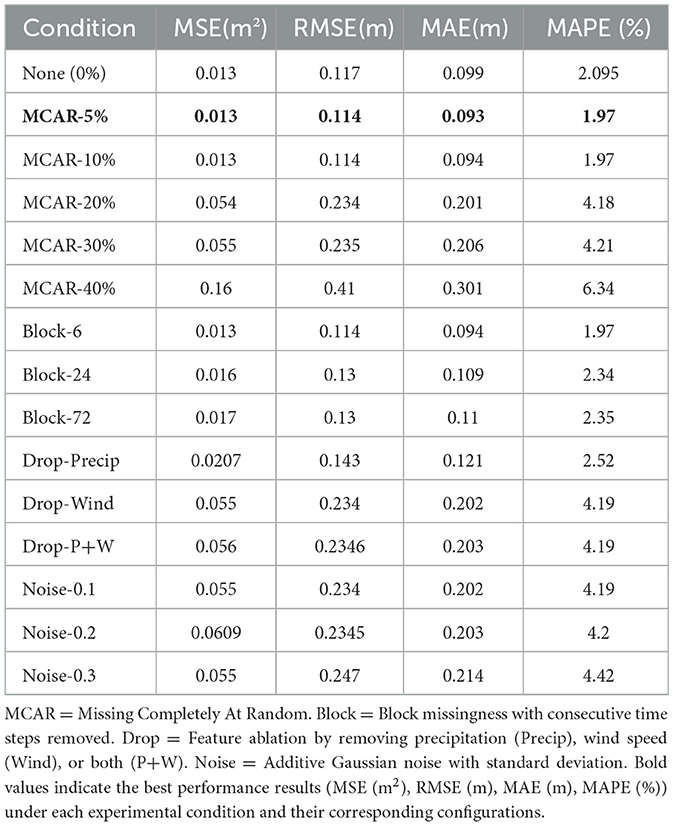
5.5 Performance under dataset complexity

As evidenced in Table 6, SMamba-KAN maintains stable performance under various scenarios of data quality degradation. For random missingness under the MCAR mechanism, the model exhibits exceptional robustness, showing negligible performance loss up to a 10% missing rate, and only moderate degradation at 20%, where predictive accuracy remains within acceptable parameters. Even when the missing rate increases to 40%, the error only rises to an MSE of 0.16 and a MAPE of 6.34%, which is still within tolerable operational thresholds. In the case of continuous block missingness, the model sustains superior predictive efficacy even when 72 consecutive time steps are absent, achieving a MAPE of 2.35%, which demonstrates its capacity to utilize historical context and multivariate relationships to compensate for sequence gaps.

Table 6

Table 6. Prediction errors of SMamba-KAN under different missingness and noise conditions.

Feature ablation reveals heterogeneous impacts across variables. Removing precipitation raises MAPE slightly from 2.1% to 2.5%, while excluding wind speed, either alone or with precipitation, increases it to about 4.2%. The overall degradation remains constrained, highlighting the model's robustness to partial feature loss. Under additive noise perturbations, when the noise standard deviation increases from 0.1 to 0.3, the error exhibits minimal fluctuation, with MAPE staying in the range of 4.2 to 4.4%, reflecting the model's substantial noise immunity.

The experimental results conclusively demonstrate that SMamba-KAN maintains high accuracy and stability under conditions such as random missingness, block missingness, feature ablation, and additive noise. The increase in error remains consistently bounded, indicating that the model possesses significant resilience to data quality degradation. This robustness suggests considerable potential for SMamba-KAN in addressing the practical requirements of hydrological and meteorological datasets, where missing values and noise disturbances are prevalent phenomena.

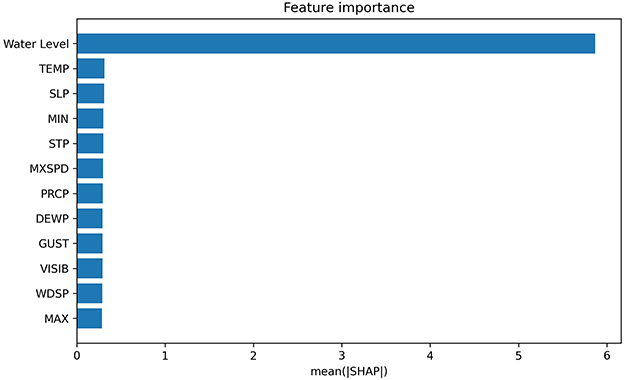
5.6 Interpretability analysis

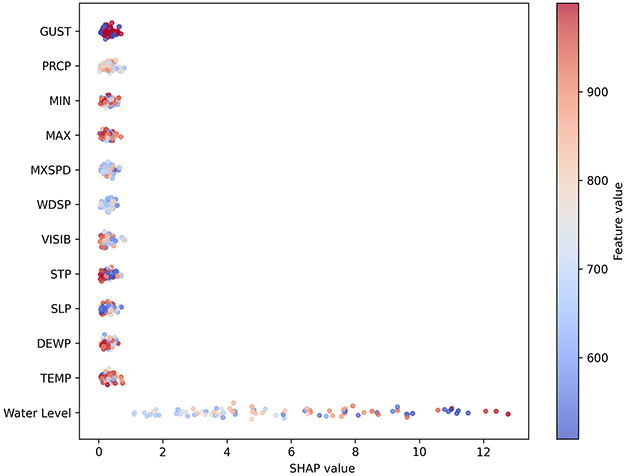
To systematically evaluate the interpretability of SMamba-KAN, we employed Gradient SHAP to quantify the importance of input features. As shown in Figure 8, the average contribution of upstream and downstream water levels reached approximately 5.87, which is significantly more pronounced than that of all meteorological factors, whose values ranged between 0.28 and 0.32. This marked predominance on target-site prediction aligns with established hydrological principles, whereby neighboring water levels constitute the primary determinants of short- to mid-term forecasting. Among meteorological variables, temperature recorded a mean_abs_shap value of about 0.312 and pressure about 0.309, both slightly higher than precipitation at around 0.294 and wind-related factors such as wind speed and maximum wind speed at approximately 0.288 and 0.298. These results indicate the differential significance of temperature and pressure as critical indicators during evapotranspiration, snowmelt, and extreme hydrological events.

Figure 8

Figure 8. Feature importance of input variables based on mean absolute SHAP values.

Figure 9 further elucidates the distribution of SHAP values, emphasizing the dominant role of water levels while revealing distinctive influences of meteorological drivers. Precipitation and wind-related variables exhibited substantial contribution to higher predicted water levels under extreme conditions, reflecting their nonlinear associations during flood or storm events. In contrast, pressure and temperature demonstrated more consistent effects, primarily functioning as regulatory mechanisms of hydrological processes. These patterns are consonant with fundamental hydrological theory, suggesting that SMamba-KAN captures not only the individual effects of features but also the complex interaction dynamics between water-level dynamics and meteorological variability.

Figure 9

Figure 9. SHAP beeswarm plot illustrating the distribution of feature contributions across samples.

The comprehensive SHAP analysis substantiates that SMamba-KAN effectively disentangles the hierarchical roles of water levels and meteorological factors, aligning its computational framework with hydrological processes and thereby enhancing predictive reliability. Leveraging the explicit nonlinear basis function mapping of the KAN module, the model facilitates quantification of variable interactions in a decomposable manner, conferring superior interpretability and transparency compared to conventional LSTM or Transformer architectures.

5.7 Cross-basin generalization experiments

To empirically validate the cross-basin transferability of the proposed model, we further selected the Kirin Zui hydrological station in the Zengjiang River Basin, located at 113.84011°E and 23.346278°N, together with five surrounding meteorological stations, as an independent validation domain. The dataset covers the period from January 1, 2014 to December 31, 2021, with a total of 2,922 daily records. Similar to the Yangtze River Basin experiments, the dataset includes multi-source meteorological and hydrological inputs, and the experimental procedure remained identical without additional parameter tuning. The model was implemented and evaluated directly on this basin to assess its generalization capability in a cross-basin context.

As quantitatively demonstrated in Table 7, SMamba-KAN continued to achieve the highest predictive accuracy in the new basin, with MSE of 0.023, RMSE of 0.151, MAE of 0.113, and MAPE of 1.38%, statistically outperforming all benchmark models. Using MSE as an example, the error was reduced by approximately 18% compared with SMamba, and by about 28% and 36% compared with Mamba and LSTM, respectively. In contrast, the traditional Transformer exhibited substantial performance degradation in this basin, with MAPE reaching as high as 4.31%.

Table 7

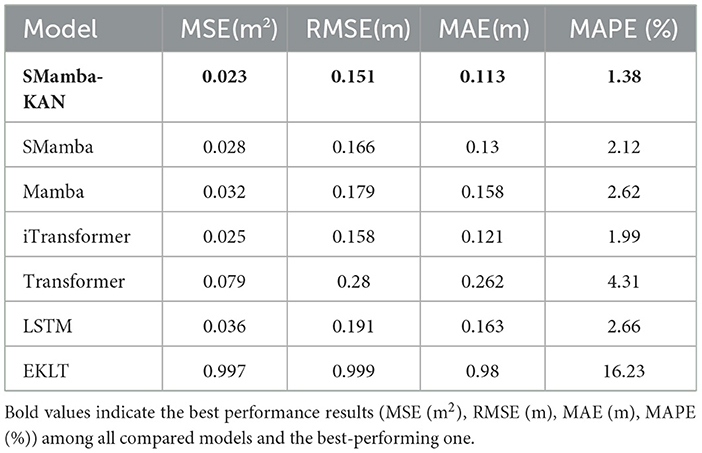
Table 7. Evaluation of cross-basin predictive performance at the Kirin Zui hydrological station (input window = 90 days).

The superior performance of SMamba-KAN is not limited to the Yangtze River Basin; it also demonstrates consistent predictive efficacy in different basins. Its cross-basin generalization advantage stems from the synergistic integration of Mamba's capacity for long-term dependency modeling and KAN's ability to capture nonlinear interactions, enabling the architecture to consistently extract key patterns under diverse hydrometeorological conditions.

6 Conclusion

To address the limitations of traditional water level forecasting models—specifically, their weak capacity in modeling long-term dependencies, restricted nonlinear feature representation, and insufficient ability to capture inter-variable interactions under multi-source hydrometeorological data—this study proposes a novel multivariate time series prediction model, Smamba-KAN, which integrates a bidirectional SMamba architecture with explicit nonlinear enhancement mechanisms. By constructing multi-dimensional time–variable interaction pathways, the proposed model significantly improves its capability in modeling complex hydrological systems. To further strengthen its nonlinear representation and variable coupling capacity, we design a lightweight KAN module and integrate it with a FullAttention mechanism, thereby enabling efficient perception and controllable transformation of multi-source input features. Comprehensive experiments across various scenarios and temporal scales demonstrate that Smamba-KAN consistently achieves superior forecasting accuracy, particularly exhibiting robust generalization and resilience in high-dimensional and long-range forecasting tasks.

The comprehensive experimental results demonstrate that the Smamba-KAN model combines efficient long-sequence memory with flexible nonlinear feature representation, showcasing remarkable advantages in complex multivariate time series modeling. It exhibits broad application potential in diverse domains such as river and lake water level forecasting, groundwater resource management, watershed flood early warning, and climate change impact analysis. By further enhancing variable interaction modeling and optimizing long-term dependency capture strategies, Smamba-KAN is expected to become a promising solution for high-precision, multi-source-integrated water level prediction tasks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XY: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. HZ: Conceptualization, Methodology, Resources, Validation, Writing – original draft. RZ: Project administration, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors sincerely thank the reviewers for their constructive feedback and insightful suggestions, which significantly improved the quality and clarity of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, A. J., Ahmed, A. A., and Abbod, M. F. (2024). Groundwater level predictions in the Thames Basin, London over extended horizons using transformers and advanced machine learning models. J. Clean. Prod. 484:144300. doi: 10.1016/j.jclepro.2024.144300

Crossref Full Text | Google Scholar

Brunner, M. I., Slater, L., Tallaksen, L. M., and Clark, M. (2021). Challenges in modeling and predicting floods and droughts: a review. WIREs Water 8:e1520. doi: 10.1002/wat2.1520

Crossref Full Text | Google Scholar

Carletti, F., Michel, A., Casale, F., Burri, A., Bocchiola, D., Bavay, M., et al. (2022). A comparison of hydrological models with different level of complexity in alpine regions in the context of climate change. Hydrol. Earth Syst. Sci. 26, 3447–3475. doi: 10.5194/hess-26-3447-2022

Crossref Full Text | Google Scholar

Castangia, M., Grajales, L. M. M., Aliberti, A., Rossi, C., Macii, A., Macii, E., et al. (2023). Transformer neural networks for interpretable flood forecasting. Environ. Modell. Softw. 160:105581. doi: 10.1016/j.envsoft.2022.105581

Crossref Full Text | Google Scholar

Chang, K-. H., Chiu, Y-. T., and Su, W-. R. (2024). A spatial–temporal deep learning-based warning system against flooding hazards with an empirical study in Taiwan. Int. J. Disaster Risk Reduction 102:104263. doi: 10.1016/j.ijdrr.2024.104263

Crossref Full Text | Google Scholar

Chen, C., Zhu, X., Kang, X., Zhou, H., Zhang, H., Chen, L., et al. (2021). “A deep learning algorithm for groundwater level prediction based on spatial-temporal attention mechanism,” in Proceedings of the 2021 IEEE International Conference on Dependable, Autonomic and Secure Computing, Pervasive Intelligence and Computing, Cloud and Big Data Computing, Cyber Science and Technology Congress (DASC/PiCom/CBDCom/CyberSciTech) (Calgary, AB: IEEE), 716–723.

Google Scholar

Chen, Y., Gan, M., Pan, S., Pan, H., Zhu, X., Tao, Z., et al. (2020). Application of auto-regressive (AR) analysis to improve short-term prediction of water levels in the Yangtze Estuary. J. Hydrol. 590:125386. doi: 10.1016/j.jhydrol.2020.125386

Crossref Full Text | Google Scholar

Doumbia, C., Rousseau, A. N., Başagaoglu, H., Baraer, M., and Chakraborty, D. (2025). Interpretation of glacier mass change within the Upper Yukon watershed from GRACE using explainable automated machine learning algorithms. J. Hydrol. 651:132519. doi: 10.1016/j.jhydrol.2024.132519

Crossref Full Text | Google Scholar

Ehteram, M., Ferdowsi, A., Faramarzpour, M., Gharabaghi, B., Al-Ansari, N., Sherif, M. M., et al. (2021). Hybridization of artificial intelligence models with nature inspired optimization algorithms for lake water level prediction and uncertainty analysis. Alex. Eng. J. 60, 2193–2208. doi: 10.1016/j.aej.2020.12.034

Crossref Full Text | Google Scholar

Feng, D., Tan, Z., and He, Q. Z. (2023). Physics-informed neural networks of the Saint-Venant equations for downscaling a large-scale river model. Water Resources Research, 59:e2022WR033168. doi: 10.1029/2022WR033168

Crossref Full Text | Google Scholar

Foroumandi, E., Moradkhani, H., Krajewski, W. F., and Ogden, F. L. (2025). Ensemble data assimilation for operational streamflow predictions in the Next Generation (NextGen) framework. Environ. Modell. Softw. 185:106306. doi: 10.1016/j.envsoft.2024.106306

Crossref Full Text | Google Scholar

Frame, J. M., Kratzert, F., Klotz, D., Gauch, M., Shalev, G., Gilon, O., et al. (2022). Deep learning rainfall–runoff predictions of extreme events. Hydrol. Earth Syst. Sci. 26, 3377–3392. doi: 10.5194/hess-26-3377-2022

Crossref Full Text | Google Scholar

Granata, F., Zhu, S., and Nunno, D. i. F. (2024). Advanced streamflow forecasting for central European rivers: the cutting-edge Kolmogorov–Arnold networks compared to transformers. J. Hydrol. 645:132175. doi: 10.1016/j.jhydrol.2024.132175

Crossref Full Text | Google Scholar

Gu, A., and Dao, T. (2023). Mamba: linear-time sequence modeling with selective state spaces. arXiv [Preprint]. arXiv:2312.00752. doi: 10.48550/arXiv.2312.00752

Crossref Full Text | Google Scholar

Guo, F., Yang, J., Li, H., Li, G., and Zhang, Z. (2021). A ConvLSTM conjunction model for groundwater level forecasting in a karst aquifer considering connectivity characteristics. Water 13:2759. doi: 10.3390/w13192759

Crossref Full Text | Google Scholar

Guo, S., Wen, Y., Zhang, X., and Chen, H. (2023). Runoff prediction of Lower Yellow River based on CEEMDAN–LSSVM–GM(1,1) model. Sci. Rep. 13:1511. doi: 10.1038/s41598-023-28662-5

PubMed Abstract | Crossref Full Text | Google Scholar

Han, J., and Bae, J. H. (2025). Developing an hourly water level prediction model for small- and medium-sized agricultural reservoirs using AutoML: case study of Baekhak Reservoir, South Korea. Agriculture 15:71. doi: 10.3390/agriculture15010071

Crossref Full Text | Google Scholar

Hoque, M. A., and Adhikary, S. K. (2020). “Prediction of groundwater level using artificial neural network and multivariate time series models,” in Proceedings of the 5th International Conference on Civil Engineering for Sustainable Development (ICCESD 2020) [Khulna: Department of Civil Engineering, Khulna University of Engineering & Technology (KUET)], 1–8.

Google Scholar

Huang, F., Ochoa, C. G., Li, Q., Shen, X., Qian, Z., Han, S., et al. (2024). Forecasting environmental water availability of lakes using temporal fusion transformer: case studies of China's two largest freshwater lakes. Environ. Monit. Assess. 196, 1–21. doi: 10.1007/s10661-024-12331-9

PubMed Abstract | Crossref Full Text | Google Scholar

Huang, S., Xia, J., Wang, Y., Wang, W., Zeng, S., She, D., et al. (2022). Coupling machine learning into hydrodynamic models to improve river modeling with complex boundary conditions. Water Resourc. Res. 58:e2022WR032183. doi: 10.1029/2022WR032183

Crossref Full Text | Google Scholar

Hughes, M. G., Glasby, T. M., Hanslow, D. J., West, G. J., and Wen, L. (2022). Random forest classification method for predicting intertidal wetland migration under sea level rise. Front. Environ. Sci. 10:749950. doi: 10.3389/fenvs.2022.749950

Crossref Full Text | Google Scholar

Koch, J., Berger, H., Henriksen, H. J., and Sonnenborg, T. O. (2019). Modelling of the shallow water table at high spatial resolution using random forests. Hydrol. Earth Syst. Sci. 23, 4603–4619. doi: 10.5194/hess-23-4603-2019

Crossref Full Text | Google Scholar

Li, G., Liu, Z., Zhang, J., Han, H., and Shu, Z. (2024). Bayesian model averaging by combining deep learning models to improve lake water level prediction. Sci. Total Environ. 906:167718. doi: 10.1016/j.scitotenv.2023.167718

PubMed Abstract | Crossref Full Text | Google Scholar

Li, G., Zhu, H., Jian, H., Zha, W., Wang, J., Shu, Z., et al. (2023). A combined hydrodynamic model and deep learning method to predict water level in ungauged rivers. J. Hydrol. 625:130025. doi: 10.1016/j.jhydrol.2023.130025

Crossref Full Text | Google Scholar

Li, S., Chen, K., Lei, X., Wang, B., Zhang, Y., Zhang, H., et al. (2024). Water level prediction model of the Upper Yangtze River by cloud computing and AutoML. J. Hydroinform. 26, 3192–3206. doi: 10.2166/hydro.2024.404

Crossref Full Text | Google Scholar

Li, X., Xu, W., Ren, M., Jiang, Y., and Fu, G. (2022). Hybrid CNN-LSTM models for river flow prediction. Water Supply 22, 4902–4919. doi: 10.2166/ws.2022.170

Crossref Full Text | Google Scholar

Liu, Y., Hu, T., Zhang, H., Wu, H., Wang, S., Ma, L., et al. (2023). iTransformer: inverted transformers are effective for time series forecasting. arXiv [Preprint]. arXiv:2310.06625. doi: 10.48550/arXiv.2310.06625

Crossref Full Text | Google Scholar

Liu, Z., Wang, Y., Vaidya, S., Ruehle, F., Halverson, J., Soljačić, M., et al. (2024). KAN: Kolmogorov-Arnold networks. arXiv [Preprint]. arXiv:2404.19756. doi: 10.48550/arXiv.2404.19756

Crossref Full Text | Google Scholar

Mahammad, S., Islam, A., Shit, P. K., Islam, A. R. M. T., and Alam, E. (2023). Groundwater level dynamics in a subtropical fan delta region and its future prediction using machine learning tools: sustainable groundwater restoration. J. Hydrol. Regional Stud. 47:101385. doi: 10.1016/j.ejrh.2023.101385

Crossref Full Text | Google Scholar

Nguyen, X. H. (2020). Combining statistical machine learning models with ARIMA for water level forecasting: the case of the Red River. Adv. Water Resour. 142:103656. doi: 10.1016/j.advwatres.2020.103656

Crossref Full Text | Google Scholar

Nhu, V-. H., Shahabi, H., Nohani, E., Shirzadi, A., Al-Ansari, N., Bahrami, S., et al. (2020). Daily water level prediction of Zrebar Lake (Iran): a comparison between M5P, random forest, random tree and reduced error pruning trees algorithms. ISPRS Int. J. Geo-Inform. 9:479. doi: 10.3390/ijgi9080479

Crossref Full Text | Google Scholar

Osman, A. I. A., Ahmed, A. N., Chow, M. F., Huang, Y. F., and El-Shafie, A. (2021). Extreme gradient boosting (Xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Eng. J. 12, 1545–1556. doi: 10.1016/j.asej.2020.11.011

Crossref Full Text | Google Scholar

Ozdemir, S., Yaqub, M., and Yildirim, S. O. (2023). A systematic literature review on lake water level prediction models. Environ. Modell. Softw. 163:105684. doi: 10.1016/j.envsoft.2023.105684

Crossref Full Text | Google Scholar

Özdogan-Sarikoç, G., and Dadaser-Celik, F. (2024). Physically based vs. data-driven models for streamflow and reservoir volume prediction at a data-scarce semi-arid basin. Environ. Sci. Pollut. Res. 31, 39098–39119. doi: 10.1007/s11356-024-33732-w

PubMed Abstract | Crossref Full Text | Google Scholar

Ren, D., Hu, Q., and Zhang, T. (2025). EKLT: Kolmogorov-Arnold attention-driven LSTM with transformer model for river water level prediction. J. Hydrol. 649:132430. doi: 10.1016/j.jhydrol.2024.132430

Crossref Full Text | Google Scholar

Rochac, J. F. R., Zhang, N., Deksissa, T., Xu, J., and Thompson, L. A. (2022). “A hybrid ConvLSTM deep neural network for noise reduction and data augmentation for prediction of nonlinear dynamics of streamflow,” in Proceedings of the 2022 IEEE International Conference on Data Mining Workshops (ICDMW) (Orlando, FL: IEEE), 1120–1127.

Google Scholar

Shah, S. A., Ai, S., and Yuan, H. (2025). Predicting water level fluctuations in glacier-fed lakes by ensembling individual models into a quad-meta model. Eng. Appl. Comput. Fluid Mech. 19:2449124. doi: 10.1080/19942060.2024.2449124

Crossref Full Text | Google Scholar

Shekhar, S., Kumar, S., Densmore, A., van Dijk, W., Sinha, R., Kumar, M., et al. (2020). Modelling water levels of northwestern India in response to improved irrigation use efficiency. Sci. Rep. 10:13452. doi: 10.1038/s41598-020-70416-0

PubMed Abstract | Crossref Full Text | Google Scholar

Tan, R., Hu, Y., and Wang, Z. (2023). A multi-source data-driven model of lake water level based on variational modal decomposition and external factors with optimized bi-directional long short-term memory neural network. Environ. Modell. Softw. 167:105766. doi: 10.1016/j.envsoft.2023.105766

Crossref Full Text | Google Scholar

van Kempen, G., van der Wiel, K., and Melsen, L. A. (2021). The impact of hydrological model structure on the simulation of extreme runoff events. Nat. Hazards Earth Syst. Sci. 21, 961–976. doi: 10.5194/nhess-21-961-2021

Crossref Full Text | Google Scholar

Wang, Z., Kong, F., Feng, S., Wang, M., Yang, X., Zhao, H., et al. (2024). Is Mamba effective for time series forecasting? Neurocomputing 619:129178. doi: 10.1016/j.neucom.2024.129178

Crossref Full Text | Google Scholar

Xu, J., Fan, H., Luo, M., Li, P., Jeong, T., Xu, L., et al. (2023). Transformer based water level prediction in Poyang Lake, China. Water 15:576. doi: 10.3390/w15030576

Crossref Full Text | Google Scholar

Yang, J., Zhang, T., Zhang, J., Lin, X., Wang, H., Feng, T., et al. (2024). A ConvLSTM nearshore water level prediction model with integrated attention mechanisms. Front. Mar. Sci. 11:1470320. doi: 10.3389/fmars.2024.1470320

Crossref Full Text | Google Scholar

Yang, X., Dai, C., Jing, J., Liu, Z., and Zhang, F. (2025). Study on the relationship between surface water and groundwater transformation in the middle and lower reaches of Songhua River Basin. Sci. Rep. 15:8088. doi: 10.1038/s41598-025-92801-3

PubMed Abstract | Crossref Full Text | Google Scholar

Yin, W., Fan, Z., Tangdamrongsub, N., Hu, L., and Zhang, M. (2021). Comparison of physical and data-driven models to forecast groundwater level changes with the inclusion of GRACE – A case study over the State of Victoria, Australia. J. Hydrol. 602:126735. doi: 10.1016/j.jhydrol.2021.126735

Crossref Full Text | Google Scholar

Zhang, J., Kong, D., Li, J., Qiu, J., Zhang, Y., Gu, X., et al. (2025). Comparison and integration of hydrological models and machine learning models in global monthly streamflow simulation. J. Hydrol. 650:132549. doi: 10.1016/j.jhydrol.2024.132549

Crossref Full Text | Google Scholar