Enhancing dissolved oxygen prediction in lake-reservoirs via a hybrid BO+SSA-driven backpropagation neural network

With the self-purification ability of lake-reservoir water body gradually weakened and the oscillation of dissolved oxygen (DO) concentration intensifying, the high-precision prediction of lake-reservoir DO is important to the aquatic ecological safety. Aiming at the key problem that the prediction precision is low, the model structure and hyperparameters of back propagation neural network (BPNN) are highly sensitive, and the global convergence is poor with high tendency to fall into local optima in traditional DO prediction. In this study, a new hybrid optimization technology called Bayesian Optimization (BO) + improved Sparrow Search Algorithm (SSA), named BO+SSA, is employed to optimize the hyperparameters of BPNN and search initial weights and thresholds to overcome such a problem. Chaotic initialization, adaptive weight adjustment, and dynamic search strategies are integrated to enhance global optimization capability and accelerate convergence of BPNN. Four representative monitoring sections (including Baiheshan and Luojiang) from lakes and reservoirs in the eastern Sichuan Basin, China, were selected for analysis. Based on correlation analysis and feature importance assessment, pH, water temperature (WT), air temperature (AT), and atmospheric pressure (AP) were identified as input variables for testing the predictive performance of the BO+SSA-BPNN model. The coefficient of determination (R²) for the test set ranged from 0.861 to 0.939. Furthermore, the improved BPNN model demonstrated a reduction of 30%−61% in Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE) compared to the original BPNN model. The result proves that the method of hybrid optimization of BO+SSA can better solve the problems of complex nonlinear relationship modeling and provide an efficient BPNN-based DO prediction model that can be applied to lake-reservoir dynamic monitoring and management.

Introduction

During the continuous process of urbanization and further agricultural nonpoint source pollution, small watershed water bodies with limited environmental capacity and multiple points of pollutant source have added additional risks, such as a quick change in dissolved oxygen (DO) concentration that impacts the regional water environmental security. Low DO concentrations in these small watershed water bodies can adversely affect aquatic ecosystems, destabilizing the system and depleting aquatic biological resources, thereby causing ecosystem imbalances (Lee et al., 2020). Consequently, it is imperative to identify and quantify the driving factors influencing water quality parameters, such as DO content, to develop effective water resource management strategies. Due to the lower flow speed of lake-reservoir type water bodies, which constrains natural oxygen exchange and inhibits the self-purification ability of water, a significantly lower rate of diffusion of DO is also a characteristic (Zhang et al., 2017). Under the condition of stagnation, the diffusion speed of oxygen between the surface and bottom layers is much lower than that in the moving water body. Therefore, for the lake-reservoir monitoring section, there may be situations where the dissolved oxygen is less than 5 mg/L.

In the past, the prediction of water quality usually depended on process-based modeling. However, due to the advancement of data availability, computational ability, machine learning techniques have shown promising potential in multiple fields (Bolick et al., 2023; Cojbasic et al., 2023; Kim and Ahn, 2022; Kozhiparamban et al., 2023). Following research about DO modeling and estimation aroused interest in artificial intelligence (AI) as a more robust alternative to traditional empirical and numerical models, which are subjected to errors, time-consuming, and expensive (Kumar et al., 2024; Liang et al., 2024). However, because the spatial and temporal patterns of DO will be affected by complicated nonlinear interactions of several environmental factors, such as pH value, water temperature, and weather conditions, the traditional statistical models and the single machine learning model usually show insufficient nonlinear relationship fit and a lack of generalization capabilities (Cojbasic et al., 2023; Liang et al., 2024).

The back propagation neural network (BPNN) has a strong non-linear mapping and approximation capability but is very sensitive to the selection of initial parameters and hyperparameters, which may lead to falling into the local optimum and generating the prediction bias of its output (Yu et al., 2022). Therefore, the performance of the BPNN for water quality prediction is inferior (Bao et al., 2024). For example, Li et al. (2022) demonstrated that while radial basis function neural network (RBFNN), support vector machine (SVM), and least squares support vector machine (LSSVM) achieved near-perfect correlation coefficients (0.99) for DO prediction in aquaculture systems, the BPNN showed markedly inferior performance with a low correlation coefficient of 0.60. The inferior performance of BPNN stems from its gradient-based optimization that easily stagnates in shallow local minima, coupled with high sensitivity to initial weight selection, which amplifies prediction variance in complex nonlinear systems like aquatic environments. In addition, despite the progress in neural-network-based prediction methods, there is still a notable research gap in addressing the limitations of traditional BPNN, particularly their susceptibility to local minima and slow convergence rates (Xue et al., 2024). Recently, some new techniques in the field of machine learning, such as Genetic Algorithm and Particle Swarm Optimization (PSO), BO, and others, have been introduced to improve the BPNN (Cai et al., 2022; Li C. X. et al., 2024). Li X. et al. (2024) showed that in predicting levee settlement caused by shield tunneling, the PSO-BPNN model exhibited optimal performance with the highest correlation coefficients (0.8831 in training and 0.8657 in testing) and the lowest errors (RMSE = 1.901, MAE = 0.8412), significantly outperforming comparative models such as random forest and support vector machine. Cui et al. (2023) demonstrated that in flood susceptibility mapping, the GQA-BPNN model outperformed both the pure BPNN and GA-BPNN, achieving superior performance in AUC, RMSE, Nash-Sutcliffe coefficient, and bias percentage, with more flood points identified in high-sensitivity zones, proving it the most effective method. Research (Cui et al., 2023) indicates that standalone optimization algorithms struggle to adequately enhance BPNN prediction accuracy, particularly when addressing complex nonlinear relationships, necessitating the development of advanced hybrid optimization architectures. Moreover, existing research predominantly focuses on rivers or open water bodies, with insufficient studies on BPNN model optimization and feature adaptation for the lake-reservoir monitoring section DO prediction.

This study introduces a novel hybrid BO+SSA framework to mitigate the hyperparameter sensitivity, susceptibility to local optima, and suboptimal convergence often encountered in traditional BPNN when predicting DO levels in lake-reservoir systems. The proposed framework integrates four key algorithmic enhancements into the SSA component: tent chaotic initialization, adaptive weights, Lévy flight mechanisms, and a dynamic spiral search strategy. These enhancements are designed to substantially improve the global optimization capabilities of the SSA for tuning BPNN weights and thresholds. Focusing on representative lake-reservoir monitoring sections in China (specifically, Baiheshan, Luojiang, Duoshipan, and Shangheba), we develop a DO prediction model based on four key water quality parameters, including pH and water temperature. The study systematically evaluates the performance of the BPNN both before and after optimization via the BO+SSA framework. The resulting optimized BO+SSA-BPNN model provides an efficient computational tool for dynamic water quality management, thereby advancing the application of hybrid optimization techniques in aquatic ecosystem monitoring.

Materials and methods

In the past 3 years, more frequent exceedances of DO were found in the eastern Sichuan basin. In order to analyze the DO exceedance causes for each section in the basin, this paper chose typical sections with excessive exceedance times as the Baiheshan (107.301740, 31.056889), Luojiang (107.562547, 31.314006), Duoshipan (107.157308, 31.033114), and Shangheba (107.455146, 30.787714), as represented rivers in eastern Sichuan and the sampling locations are shown in Figure 1.

Figure 1

Figure 1. Location map of water quality monitoring points for each section.

Four lake-reservoir monitoring sections (Baiheshan, Luojiang, Duoshipan, and Shangheba) in the eastern Sichuan basin were selected for analysis. Water quality parameters, including water temperature (WT), dissolved oxygen (DO), pH, ammonium nitrogen (NH₃-N), total nitrogen (TN), total phosphorus (TP), permanganate index (COD_Mn), conductivity (Ec), turbidity (NTU), atmospheric pressure (AP), and air temperature (AT), were monitored. All water quality data used in this study are time-series data, collected from June 2023 to June 2024 using professional water quality sensors installed at fixed stations (calibrated monthly to ensure accuracy) with a monitoring frequency of once every 4 h. The data were obtained from the Sichuan Dazhou Ecological Environment Monitoring Center. Due to equipment malfunctions and environmental interference, the raw data contained missing values and outliers, which were directly deleted to ensure data quality. The monitoring procedures conformed to the “Water Environment Monitoring Specifications” (SL 219-2013), and exceedance limits were determined based on the Class III criteria outlined in the “Surface Water Environmental Quality Standards” (GB 3838-2018).

Model input variable selection

In order to construct a high-performance and highly interpretable predictive model, this study used correlation analysis and feature importance for input variable selection. At the beginning, the Pearson correlation coefficient matrix was used to obtain primary features that are directly correlated with the target variable (p < 0.05). This linear correlation analysis provides an initial filter for potentially relevant features. On the basis of this, the Gini importance rank of random forest was adopted to model the non-linear interaction of features, thereby capturing more complex relationships beyond simple linear correlation, and then obtaining the feature importance.

Backpropagation neural network

ANN is a mathematical model representing the human brain in an attempt to replicate a vast network structure consisting of neurons in the human brain. ANN can have one or more hidden layers, multiple types of layers, and activation functions for classification, regression, and clustering. ANN is a generic term for different types of networks, such as multi-layer perceptron and a BPNN. Among the many algorithms in ANN, BPNN has attracted much attention due to its effectiveness and wide application. BPNN uses gradient descent to minimize the difference between network output and target output (Sun et al., 2021). In the BPNN model, each neuron in one layer is directly connected to the neurons of the subsequent layer with an activation function. In this study, we adopted the hyperbolic tangent function as the activation function of each neuron between the input and hidden layers, which is shown in Equation 1 (Sun et al., 2021):

$\begin{array}{ll}g(x)=\frac{2}{1+exp(-2x)}-1& (1)\end{array}$

Moreover, we adopted the linear function as the activation function of each neuron between the hidden and output layers:

$\begin{array}{ll}f(x)=x& (2)\end{array}$

Then the final output of a BPNN can be written as:

$\begin{array}{ll}Y(X)=f(W_{3,2}*g(W_{2,1}*X+b_1)+b_2)& (3)\end{array}$

where W_{2, 1} and W_{3, 2} are weight matrices and b₁ and b₂ are bias matrices, these four matrices store the coefficients of the BPNN model and should be optimized via the backpropagation algorithm, X and Y are the input and output variables.

The hyperbolic tangent function (tanh) was chosen for the hidden layer due to its desirable properties: it is zero-centered, aiding in convergence during training, and its output range (−1 to 1) can help mitigate the vanishing gradient problem compared to sigmoid functions. The linear function was used for the output layer because the task of predicting dissolved oxygen concentration is a regression problem, where the network needs to output continuous values without constraints imposed by non-linear activation functions like sigmoid or tanh.

Optimization model principles

First layer optimization: BO for hidden layer node number and learning rate as hyperparameters can effectively improve model effectiveness. When searching for hyperparameters, their values need to be optimized continuously to enhance the predictive effectiveness of the model. We first select BO to optimize the hyperparameters of the first layer and implement these specific steps: (1) Objective function f (x) and domain of x are defined. (2) A set of limited x is selected, and then the corresponding f (x) is solved as the observed value. (3) According to the observed value, use a Probability Surrogate Model to estimate the function and obtain the estimated target value f^*. (4) Through the rules of the Acquisition Function, the next observation point is determined to calculate. (5) Recursively repeat steps (2)–(4), check termination conditions, until the maximum number of observations is reached, and output the optimal results (see Supplementary Figure S1).

Second layer optimization: enhanced sparrow optimization algorithm

The traditional BPNN often relies on empirical determination of hyperparameters, initial weights, and thresholds, which may not meet the performance requirements of predictive models. Therefore, the second layer employs an improved sparrow algorithm to optimize initial weights and thresholds. This enhanced sparrow algorithm, designed with four key improvements (Ouyang et al., 2021).

Improvement 1: The tent chaotic mapping in the SSA generates population positions with high randomness, potentially leading to poor initial population quality and slower convergence. Introducing the tent mapping strategy makes population initialization more orderly and enhances algorithm controllability, as illustrated by the following equation:

$\begin{array}{ll}{Z}_{i+1}=\{\begin{array}{c}2Z_i+rand(0,1)\times \frac{1}{N},0\le Z\le \frac{1}{2}\\ 2(1-Z_i)+rand(0,1)\times \frac{1}{N},\frac{1}{2}\le Z\le 1\\ \end{array}& (4)\end{array}$

The expression after the Bernoulli transformation is

$\begin{array}{ll}{Z}_{i+1}=(2Z_i)mod1+rand(0,1)\times \frac{1}{N}& (5)\end{array}$

In Equation 5, N is the number of particles in the chaotic sequence. According to the characteristics of the tent mapping, the sequence flow for generating chaos in the feasible domain is as follows:

(1) Randomly generate the initial value z₀ in (0, 1), and let I = 1.

(2) Perform iteration by using that Equation 5 to generate a z sequence, and i is increased by 1.

(3) Stop if the number of iterations reaches the maximum, and store the generated z sequence.

Improvement 2: Adaptive weights are introduced to improve the quality of the discoverer's position, enabling other individuals to converge more rapidly to the optimal position and accelerating convergence speed. The equation for adaptive weights is as follows:

$\begin{array}{ll}\omega (t)=0.2cos(\frac{\pi }{2}•(1-\frac{t}{ite{r}_{max}}))& (6)\end{array}$

The meaning of Equation 6 is that w has the property of nonlinear change between [0, 1]. According to the characteristics of the cos function, the weight value is smaller at the beginning of the algorithm, but the optimization speed is faster, and the later weight value is larger, but the change speed is slower, so the convergence property of the algorithm is balanced. The improved discoverer location is updated as follows:

$\begin{array}{ll}{X}_{i,j}^{t+1}=\{\begin{array}{c}\omega (t)•X_{i,j}^t•exp(\frac{-i}{\alpha •ite{r}_{max}}),if{R}_2<ST\\ \omega (t)•X_{i,j}^t+Q•L,if{R}_2\ge ST\\ \end{array}& (7)\end{array}$

By introducing adaptive weights to dynamically adjust the position changes of sparrows, different guidance modes for the discoverer at different times make the algorithm search flexible. As the number of iterations increases, the individual sparrows converge toward the optimal position, and a larger weight makes the individual move faster, thus increasing the convergence speed of the algorithm.

Improvement 3: The Levy flight mechanism, based on the Levy distribution, generates random long and short-distance movements to cover the search space. Incorporating the Levy flight mechanism enhances the proposed algorithm's performance, with the position update equation as follows:

$\begin{array}{ll}{x}_t^{\prime }(t)=x_i(t)+l\oplus levy(\lambda )& (8)\end{array}$

In Equation 8, x_i(t) represents the position of the i-th individual in the t-th iteration, ⊕ is an arithmetic symbol representing point-to-point multiplication. l denotes a step length control parameter, which is obtained by this equation: l = 0.01[x_i(t)–x_p]. Levy (λ) is a path that obeys the Levy distribution, which represents the introduced Levy flight strategy and satisfies the following: levy u = t^−λ, 1 < λ ≤ 3.

Because the Levy distribution is very complex, the Mantegna algorithm is usually used to simulate it. The equation for calculating the step size is as follows:

$\begin{array}{ll}s=\frac{\mu }{|v{|}^{1/\gamma }}& (9)\end{array}$

$\begin{array}{ll}\mu ~N(0,{\sigma }_{\mu }^2)& (10)\end{array}$

$\begin{array}{ll}v~N(0,{\sigma }_v^2)& (11)\end{array}$

$\begin{array}{ll}{\sigma }_{\mu }={\left\{\frac{\Gamma (1+\gamma )sin(\pi \gamma /2)}{\gamma •\Gamma \left[(\gamma +1)/2\right]•2^{(\gamma +1)/2}}\right\}}^{1/\gamma }& (12)\end{array}$

Among them, σ_v = 1, and γ is generally 1.5.

The introduction of the Levy flight strategy makes the sparrows more flexible at this stage and can also lead other individuals to find a better location, free from the constraints of local extremes. Therefore, the combination of the Levy flight mechanism and adaptive weights balances the search method, and the quality of each solution obtained is improved to a certain extent, which greatly improves the search ability of the algorithm.

Improvement 4: The adaptive spiral search strategy introduces a flexible position update strategy for followers, developing various search paths for position updates and balancing global and local searches. The equation for the adaptive spiral position update strategy is as follows:

$\begin{array}{ll}{X}_{i,j}^{i+1}=\{\begin{array}{c}{e}^{zl}·cos(2\pi l)·Q·exp(\frac{X_{wost}^t-X_{i,j}^t}{i^2}),ifi>\frac{n}{2}\\ X_p^{t+1}+|X_{i,j}^t-X_p^{t+1}|·A^{+}·L·e^{zl}·cos(2\pi l),\\ otherwise\\ z=e^{k·cos(\pi ·(1-(i/i_{max})))}\\ \end{array}& (13)\end{array}$

In these equations, the z parameter varies with iteration count, dynamically adjusting the size and amplitude of the spiral according to the periodic characteristics of the cosine function. The k represents the change coefficient, set at k = 5; L is a uniformly distributed random number of [−1, 1]. The complete process of the optimized model is illustrated in Figure 2.

Figure 2

Figure 2. BO+SSA-BPNN process diagram.

Assess the quality of the model

To evaluate the performance of the proposed prediction model, we employed three widely recognized error metrics: mean absolute error (MAE), root mean square error (RMSE), and mean absolute percentage error (MAPE). MAE provides a straightforward measure of the average magnitude of prediction errors, offering an intuitive understanding of how close predictions are to actual values. RMSE emphasizes larger errors due to its quadratic nature, making it particularly suitable for applications where minimizing significant deviations is critical. MAPE provides a scale-invariant assessment of model accuracy by expressing prediction errors as a percentage of the actual values. By analyzing the results across these three complementary metrics, we provide a comprehensive validation of the models' performances, ensuring both accuracy and robustness in the predictions. The equations for these three error metrics are as follows:

$\begin{array}{ll}MAE=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{(x_i-{\widehat{x}}_i)}^2& (14)\end{array}$

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}(x_i-{\widehat{x}}_i)}& (15)\end{array}$

$\begin{array}{ll}MAPE=100{\%}^{*}\frac{1}{n}{\displaystyle \sum _{i=1}^n}\left|\frac{x_i-{\widehat{x}}_i}{x_i}\right|& (16)\end{array}$

where, n (n = 1,2,3,4......) represents the sample number; x_i denotes the original sample; and ${\widehat{x}}_{\text{i}}$ represents the predicted sample.

The coefficient of determination (R²), commonly referred to as the goodness of fit, is a statistical measure that evaluates how well a model fits the data. Ranging from 0 to 1, a value closer to 1 indicates a stronger explanatory power of the model, suggesting a greater influence of the independent variable on the dependent variable and a superior fitting effect. In this study, the R² value was determined using Origin 2024b.

Results

Statistical analysis of water quality parameters across monitoring sections

Table 1 shows the statistical results of water quality parameters among four sections, including Luojiang, Baiheshan, Duoshipan, and Shangheba section. For DO data, the average dissolved oxygen in the Luojiang section is 9.74 mg/L, and its minimum value is 3.29 mg/L; the average of the Baiheshan section is 7.04 mg/L, and its minimum value is 2.78 mg/L; the average of Duoshipan section and Shangheba section is 8.03 and 8.71 mg/L, and its minimum value is 2.58 and 4.45 mg/L, respectively. According to the standard dissolved oxygen (≥5 mg/L) for class III water bodies in the “Environment Quality Standard of Surface Water” (GB3838-2002), the average value in all sections met the standard, but the minimum value of DO in the Luojiang and Baiheshan sections was below the standard, indicating a potential risk of insufficient dissolved oxygen during certain periods. The observed DO minima falling below Class III standards (2.78–3.29 mg/L) highlight urgent management needs, where our high-precision model enables early warning systems to prevent aquatic hypoxia events. When the dissolved oxygen in each section is below 5 mg/L, the water temperature is approximately 15–35° C (Supplementary Figure S2). pH is all between neutral and slightly alkaline (7.69–8.23), the average values of TN and TP are 1.04–2.09 and 0.04–0.09 mg/L, respectively, and COD_Mn is 2.18–3.56 mg/L; the difference between sections of organic pollution intensity is small.

Table 1

Table 1. Statistics of water quality indicators for each section.

Figure 3, Supplementary Figures S3–S5 analyze the correlation between DO and the related water quality parameter in each section, respectively. A positive correlation between DO and pH was observed across sites, with correlation coefficients ranging from 0.66 in Duoshipan (Supplementary Figure S3) to 0.84 in Shangheba (Supplementary Figure S5), suggesting that increasing pH levels can promote DO concentrations. Conversely, water temperature is the reverse correlation to DO; the range of correlation coefficient is from −0.23 in Luojiang (Supplementary Figure S4) to −0.65 in Baiheshan (Figure 3), consistent with the physical law that high temperature will lead to reduced oxygen solubility in water. The correlation between AT and DO is generally poor, and it is usually negative, such as Duoshipan −0.34 (Supplementary Figure S3), indicating a weak influence of ambient temperature on the DO. The AP shows a relatively weak positive correlation with DO in Duoshipan and Shangheba (0.33 and 0.34; Supplementary Figures S3, S5), which may be due to the influence of changes in pressure in the water body on the oxygen exchange process. Overall, pH and water temperature are the main factors influencing the change trend of DO and should be focused on in subsequent water quality regulation work.

Figure 3

Figure 3. Correlation heatmap of various water quality indicators in Baiheshan.

The selection of input variables is critical in machine learning model development to ensure model stability and predictive performance. In this study, we utilized a Scree plot to determine the number of factors to retain. The Scree plot, with the number of features on the x-axis and feature importance on the y-axis, revealed that the first two features exerted considerable influence on feature importance and correlation (Figure 4). Specifically, for the Baiheshan, Duoshipan, and Shangheba sections, the water temperature and pH have the most important influence factors, while for the Luojiang section, the pH and total nitrogen are the most important influencing factors, which contributes much more to explain the correlation of features with the cumulative rate approximately 75%. Although parameters such as NH₃-N, TN, and TP were monitored, correlation analysis and feature importance assessments revealed weak or insignificant associations between these parameters and DO (Figure 3, Supplementary Figures S3–S5, and Figure 4). Furthermore, there is a time lag in laboratory analysis to determine NH₃-N, TN, and TP concentration. Therefore, subsequent modeling efforts prioritized pH, WT, AT, and AP as input variables for predicting DO.

Figure 4

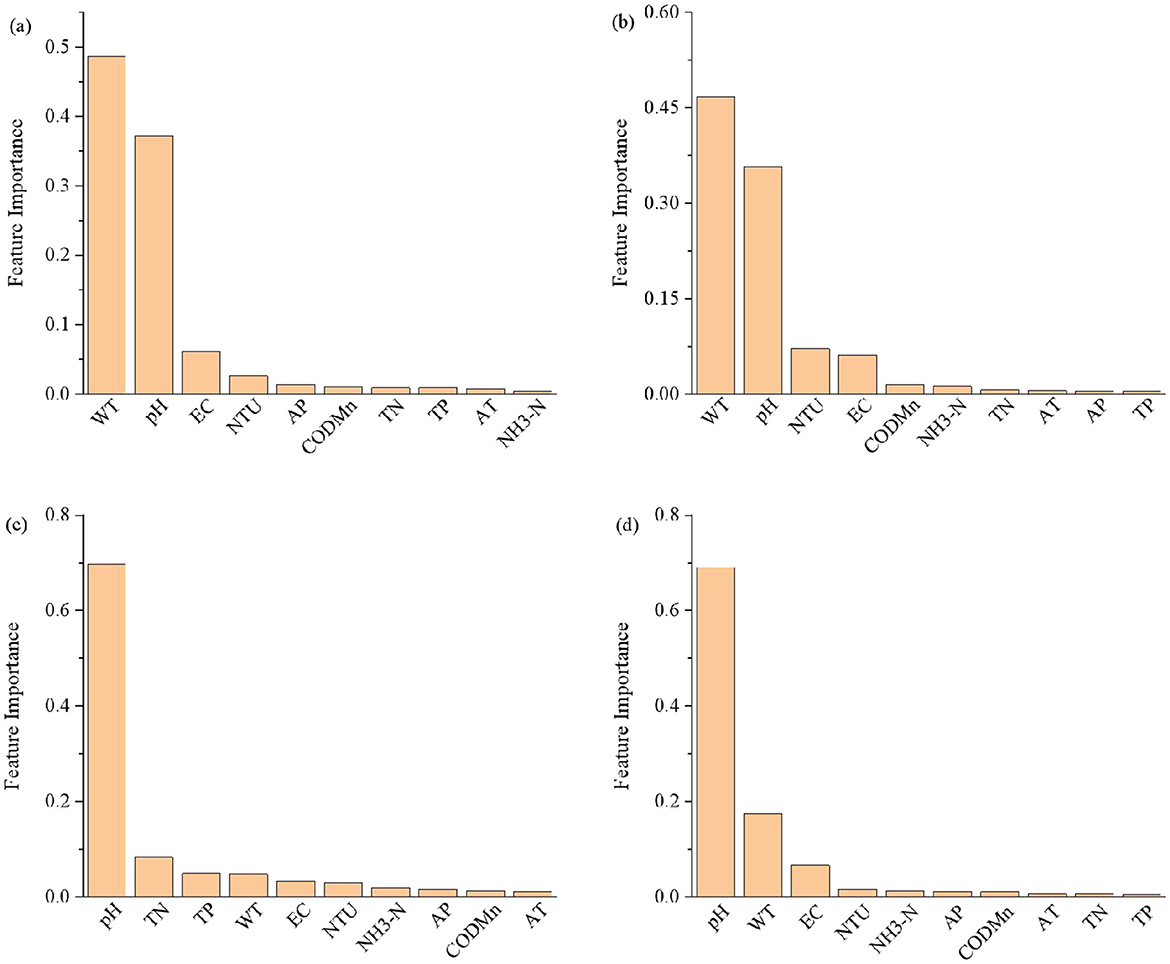
Figure 4. Importance of water quality index characteristics of various sections based on random forest. (a) Baiheshan, (b) Duoshipan, (c) Luojiang, (d) Shangheba.

Performance evaluation of the original BPNN model in DO prediction

Based on the analysis of data feature importance, correlation, and data acquisition difficulty, four factors—pH, WT, AT, and AP—were selected as input features, with DO as the output feature. The dataset was randomly divided into training and testing sets in a 7:3 ratio, and a BPNN was employed to establish the predictive model.

The relationship between the monitoring data and the BPNN prediction results based on the training data of the observation points of Baiheshan, Duoshipan, Luojiang, and Shangheba in the lake-reservoir monitoring section is shown in Supplementary Figure S6. The blue line represents the 1:1 line, while the red line is the fitted curve. A noticeable deviation of data points from the 1:1 line indicates suboptimal performance of the BPNN model across these four observation sections. The substantial angle between the 1:1 line and the fitted regression further suggests a weak correlation between observed and predicted values, with the model exhibiting a tendency to under-predict DO concentrations at higher levels and over-predict at lower levels. The predictive performance of the BPNN model for DO was relatively poor, evidenced by low correlation coefficients (r < 0.7) and coefficients of determination (R² < 0.5), with the Luojiang section exhibiting a particularly low R² of only 0.061 (Supplementary Figure S6c). The BPNN model did not work well on the monitoring test data either, with r being 0.685, 0.685, 0.238, and 0.528 for Baiheshan, Duoshipan, Luojiang, and Shangheba, and R² was 0.469, 0.470, 0.057, and 0.278 for these four points (Supplementary Figure S6). Therefore, the BPNN model for predicting the DO of the Lake-reservoir monitoring section is not good, which still needs to continue to explore or even adjust the model, or add feature variables to the model to achieve a more accurate effect.

Accuracy enhancement of BPNN via BO+SSA hybrid optimization

In order to enhance the predictive performance and accuracy of the BPNN model, a hybrid optimization algorithm of BO+SSA for BPNN model optimization was introduced. Figure 5 shows the correlation between the DO test values and the predicted values obtained from the training data of the same four monitoring sections using the optimized model. It can be seen from Figure 5 that the tested data points are mainly distributed along the 1:1 line, which shows that the optimized model has the ability of generalization in the same section. However, the angle between the blue and red lines is still observed to exhibit certain bias, and the optimized model exhibits a bias toward lower forecasts. The smaller the angle between the lines, the more the model becomes accurate. The optimized model presents the best performance in the Baiheshan section, followed by Shangheba. The correlation coefficients and R² values further illustrate the effectiveness of the optimized model, with r values of 0.969, 0.936, 0.957, and 0.928, and R² values of 0.939, 0.877, 0.915, and 0.861 for Baiheshan, Duoshipan, Shangheba, and Luojiang, respectively. The optimized model exhibits r values of more than 0.9 and R² values of above 0.85 in all sections, thus demonstrating a good performance and stability.

Figure 5

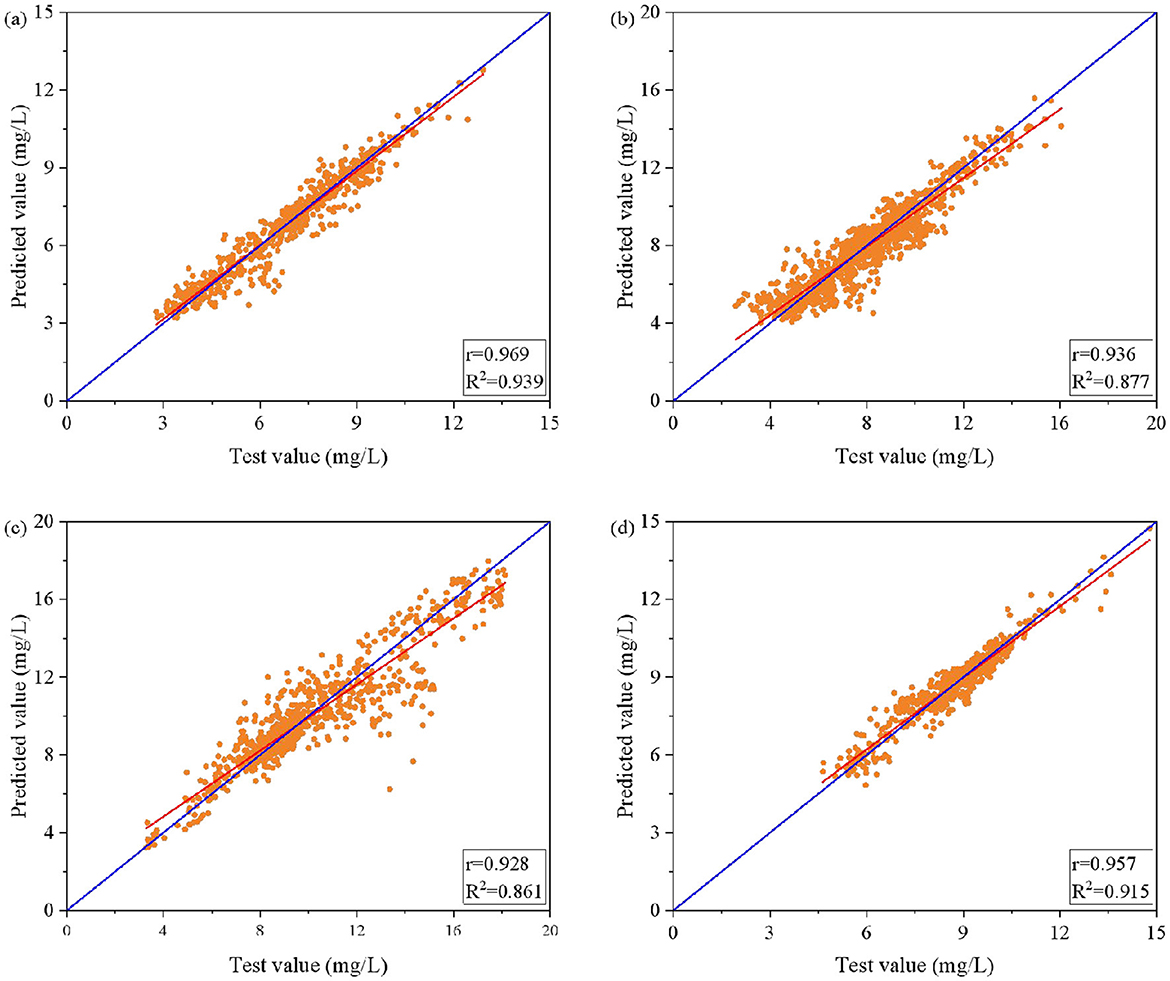
Figure 5. Bayesian optimization combined with the sparrow search algorithm to optimize the BP neural network for predicting the training set dissolved oxygen content: comparison of predicted and actual values. (a) Baiheshan, (b) Duoshipan, (c) Luojiang, (d) Shangheba. The blue line is a 1:1 line, and the red line is a fitted curve.

Comparison of model performance indicators

Figure 6 shows the evaluation of the BO+SSA-BPNN model on the test data of the lake-reservoir monitoring section, with the corresponding indices in Table 2. The data points of the test of DO and true value are scattered on the 1:1 line, which shows the good generalization ability of the model for the sections. However, the angle between blue and red lines denotes bias, with the smallest angles seen in the Baiheshan and Shangheba sections, where the model has a good performance, and r values of 0.949 and 0.941, respectively. These results demonstrate the effectiveness of the BO+SSA-BPNN model in predicting DO concentrations in the lake-reservoir monitoring section, particularly evident in the Baiheshan section (MAE = 0.37, RMSE = 0.53, and MAPE = 5.68% for the test set; MAE = 0.31, RMSE = 0.45, and MAPE = 4.94% for the training set) when compared to the standalone BPNN model. For Baiheshan, the training set metrics are MAE of 0.31, RMSE of 0.45, and MAPE of 4.94%; the test set metrics are MAE of 0.37, RMSE of 0.53, and MAPE of 5.68%. Compared to the BPNN model, the test set MAE for Baiheshan decreased by 59.67%, RMSE by 42.43%, and MAPE by 54.54%. Similarly, for Duoshipan, the test set MAE decreased by 41.34%, RMSE by 31.81%, and MAPE by 44.05%; for Luojiang, the test set MAE decreased by 45.24%, RMSE by 34.07%, and MAPE by 54.27%; and for Shangheba, the test set MAE decreased by 56.76%, RMSE by 31.94%, and MAPE by 61.00%. To further validate the stability and consistency of the optimized BO+SSA-BPNN model across different data subsets, Supplementary Figure S8 presents the comparison between predicted and actual DO values for the test set of the four monitoring sections (Baiheshan, Duoshipan, Luojiang, and Shangheba) using an alternative visualization format. Specifically, the concentration curve in Supplementary Figure S8 more intuitively reflects the prediction performance of the model for DO values, where the predicted values closely align with the observed data, further demonstrating that the hybrid optimization strategy effectively mitigates the systematic bias of the original BPNN model.

Figure 6

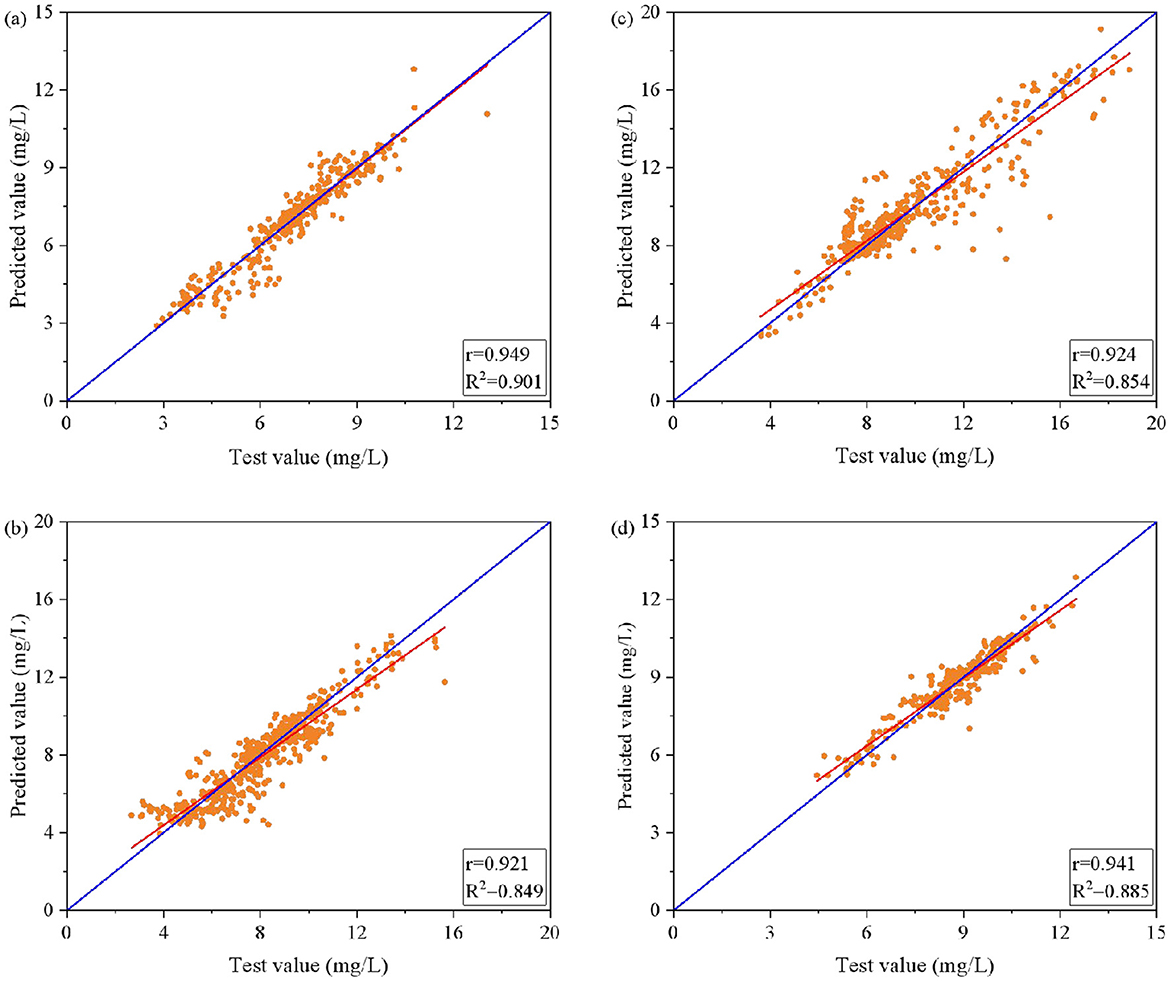
Figure 6. Bayesian optimization combined with the sparrow search algorithm to optimize the BP neural network for predicting the test set dissolved oxygen content: comparison of predicted and actual values. (a) Baiheshan, (b) Duoshipan, (c) Luojiang, (d) Shangheba. The blue line is a 1:1 line, and the red line is a fitted curve.

Table 2

Table 2. Model efficiency comparison.

Discussion

This study systematically analyzed water quality indicators at four monitoring sections: Luojiang, Baiheshan, Duoshipan, and Shangheba (Table 1). The findings show that the typical range of DO concentrations (7.04–9.74 mg/L) in every section surpasses the Class III water quality standard thresholds (≥5 mg/L) established by the Environmental Quality Standards for Surface Water (GB 3838-2018). However, the minimum DO levels at Baiheshan and Luojiang (2.78 and 3.29 mg/L, respectively) fall far lower than the normal level, indicating the occurrence of potential low oxygen risks at some time. The pH values in this study are generally within the neutral to slightly alkaline range, consistent with the characteristics of most freshwater ecosystems (Wu et al., 2019). TN and TP have mean concentration from 1.04 to 2.09 mg/L and from 0.04 to 0.09 mg/L, respectively. These TN and TP concentrations suggest a potential for eutrophication, given the observed increasing trends in nitrogen and phosphorus levels. The average TN value of Baiheshan (2.09 mg/L) is close to the threshold of eutrophication (2.0 mg/L), which may be influenced by natural conditions, external inputs, human activities, and the ecological characteristics of the lake itself (Shang et al., 2021; Su et al., 2022; Tong et al., 2019). The permanganate index (COD_Mn), ranging from 2.18 to 3.56 mg/L, indicated a low level of organic pollution along the sections, although the elevated mean value at Shangheba (3.56 mg/L) may be attributable to the agricultural non-point source pollution in that area.

Correlation analysis detailed the dynamics of links between DO and key environmental conditions. There is a strong positive correlation between DO and pH value (r = 0.66–0.84; Figure 3, Supplementary Figures S3–S5), which may be due to the favorable conditions for photosynthesis and oxygen production of phytoplankton under alkaline (i.e., higher pH) conditions (Parinet et al., 2004). Eze et al. (2021) found a positive correlation between dissolved oxygen and pH in aquaculture farms. Negative correlation between DO and water temperature (r = −0.23 to −0.65) was consistent with Henry's Law. The negative correlation between DO and water temperature was a well-documented phenomenon in aquatic ecosystems (Abdel-Wareth et al., 2024; Beshiru et al., 2018; Soltani et al., 2024). As water temperature increases, the solubility of oxygen decreases, leading to lower levels of dissolved oxygen. The effect of AT on DO was lower compared with pH and water temperature. The weak positive correlation between AP and DO (Duoshipan r = 0.33; Shangheba r = 0.34) may indicate enhanced oxygen exchange at the water surface with rising pressure. In summary, pH and water temperature are the main parameters controlling DO variation, and DO management should pay more attention to the joint effects of these factors (especially high-temperature season or large intensity of sudden increase in pollutant load).

The original BPNN was not applicable for predicting DO at reservoir-type monitoring sections. The R² values for training sets and testing sets were less than 0.5 (with the Luojiang testing set R² only 0.057; Supplementary Figures S6 and S7), which also suggested that nonlinear associations between input features (pH, water temperature, air temperature, and atmospheric pressure) and DO could not be well captured by the proposed model. Elkiran et al. (2019) used BPNN to predict the DO of three stations on the Yamuna River. Based on the DC values during the validation phase, the BPNN performance of the stations was 0.8149, 0.7259, and 0.6830, respectively, further indicating that a single BPNN has poor predictive performance for DO. Potential systematic prediction biases (under-prediction on the high-concentration side and over-prediction on the low-concentration side) could be explained due to the simple model structure, imperfect model hyperparameter optimization, as well as the data imbalance. After optimizing the BPNN using BO and the SSA, model performance was improved. The optimized BO+SSA-BPNN model exhibited substantially enhanced predictive capabilities, with R² values exceeding 0.85 in each section of the training set (Figure 5). This underscores the critical role of the optimization process in refining BPNN model accuracy. The superior performance of the optimized model demonstrates the feasibility of accurate DO prediction using this approach. Moreover, the improved performance on the testing sets indicates robust generalization ability, with correlation coefficients (r) exceeding 0.85 for Baiheshan and Shangheba sections, reaching 0.949 and 0.941, respectively (Figure 6). Corresponding reductions in MAE, RMSE, and MAPE by 30%−61% compared to the original BPNN model (Table 2) further suggest that BO+SSA effectively mitigated prediction bias and variance through global search and adaptive parameter adjustment.

The model comparison detailed in Supplementary Table S1 demonstrates the significant performance advantages of BO + SA-BPNN in DO prediction. Across the four monitoring sections—Baiheshan, Duoshipan, Luojiang, and Shangheba—BO + SA -BPNN consistently achieves the lower MAE, RMSE, and MAPE values, while maintaining high R² values (ranging from 0.85 to 0.90). Compared to models employing traditional single optimization algorithms [Particle Swarm Optimization (PSO)-BPNN and Genetic Algorithm (GA)-BPNN], BO + SA-BPNN, leveraging the synergistic effect of Bayesian optimization for hyperparameter tuning and the improved sparrow algorithm for weight adjustment, reduces MAE by 14%−59.8% and increases R² by 3%−5%. Furthermore, in prediction scenarios primarily influenced by static features, such as locations near river dams, BO + SA-BPNN demonstrates superior efficiency compared to time-series models like Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU), achieving a significantly lower MAPE (4.56%) than GRU (5.67%), highlighting the efficacy of the optimized feedforward network. While the model's performance is influenced by cross-sectional characteristics. Consequently, BO + SA-BPNN mitigates the local optima and hyperparameter sensitivity issues inherent in traditional BPNNs. This provides a high-precision and readily deployable solution for water quality prediction scenarios dominated by static features, such as lakes and reservoirs with infrequent monitoring, thereby validating the universality and practical value of this hybrid optimization strategy.

Conclusion

This study demonstrates the successful integration of BO+SSA to enhance the prediction accuracy of BPNN in modeling DO concentration dynamics in lakes and reservoirs. The resulting BO+SSA-BPNN model exhibits a robust global search capability and rapid self-adaptive parameter tuning, effectively mitigating the local optima convergence issues and limited generalization capacity often associated with traditional BPNN. The test-set R² reached the maximum value of 0.939, and the error index was decreased by more than 40%. This study finds that the pH and the temperature of the water are significant influence factors for DO variation, and the high prediction accuracy can still be achieved even though the feature input of the model is only static features, so that the model can be used under conditions of having less input data. Compared with single optimization algorithms and conventional machine learning models, the hybrid strategy is more efficient in improving the convergence rate and has excellent ability to eliminate bias, which also proves significantly superior to the individual algorithm. In the follow-up study, we may explore a hybrid strategy with more model algorithms by integrating time features to improve the stability of DO variation prediction in water bodies under extreme weather and sudden changes in pollutant load. This study provides effective scientific evidence and technical support for accurate and efficient prediction and ecological monitoring of DO variation in lake and reservoir water bodies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HL: Funding acquisition, Writing – original draft, Data curation, Validation, Conceptualization, Investigation, Writing – review & editing, Visualization, Methodology, Software. CC: Writing – review & editing, Writing – original draft, Data curation, Methodology, Funding acquisition, Conceptualization. JY: Writing – original draft, Writing – review & editing, Data curation, Methodology. LL: Validation, Writing – review & editing, Methodology, Writing – original draft. DF: Validation, Methodology, Writing – original draft, Writing – review & editing. ZT: Methodology, Validation, Writing – review & editing, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study was supported by Sichuan Dazhou Ecological Environment Science Research Institute (2024HX027), Key Laboratory of Exploitation and Study of Distinctive Plants in Education Department of Sichuan Province (TSZW2023ZB-11), and Dazhou City Science and Technology Plan Project (Key Research and Development Program) (24ZDYF0022).

Acknowledgments

The authors would like to express our gratitude to the Dazhou Ecological Environment Monitoring Center and the Dazhou Ecological Environment Research Institute for their invaluable technical assistance in this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2025.1655126/full#supplementary-material

References

Abdel-Wareth, M. T. A., Zanaty, N., Abd El-Hamid, R. M., and Saleh, H. A. (2024). Polychlorinated biphenyl congeners in water canals and their relationships with water quality parameters: Insights into their risk assessment. J. Environ. Sci. Health B 59, 263–276. doi: 10.1080/03601234.2024.2336859

PubMed Abstract | Crossref Full Text | Google Scholar

Bao, X. S., Jiang, Y. L., Zhang, L. T., Liu, B., Chen, L. J., Zhang, W. Q., et al. (2024). Accurate prediction of dissolved oxygen in perch aquaculture water by DE-GWO-SVR hybrid optimization model. Appl. Sci. 14:856. doi: 10.3390/app14020856

Crossref Full Text | Google Scholar

Beshiru, A., Okareh, O. T., Chigor, V. N., and Igbinosa, E. O. (2018). Assessment of water quality of rivers that serve as water sources for drinking and domestic functions in rural and pre-urban communities in Edo North, Nigeria. Environ. Monit. Assess. 190:387. doi: 10.1007/s10661-018-6771-7

PubMed Abstract | Crossref Full Text | Google Scholar

Bolick, M. M., Post, C. J., Naser, M. Z., and Mikhailova, E. A. (2023). Comparison of machine learning algorithms to predict dissolved oxygen in an urban stream. Environ. Sci. Pollut. Res. 30, 78075–78096. doi: 10.1007/s11356-023-27481-5

PubMed Abstract | Crossref Full Text | Google Scholar

Cai, B., Lin, X. Q., Fu, F., and Wang, L. (2022). Postfire residual capacity of steel fiber reinforced volcanic scoria concrete using PSO-BPNN machine learning. Structures 44, 236–247. doi: 10.1016/j.istruc.2022.08.012

Crossref Full Text | Google Scholar

Cojbasic, S., Dmitrasinovic, S., Kostic, M., Sekulic, M. T., Radonic, J., Dodig, A., et al. (2023). Application of machine learning in river water quality management: a review. Water Sci. Technol. 88, 2297–2308. doi: 10.2166/wst.2023.331

PubMed Abstract | Crossref Full Text | Google Scholar

Cui, H., Quan, H., Jin, R., and Lin, Z. (2023). Flood susceptibility mapping using novel hybrid approach of neural network with genetic quantum ensembles. Ksce J. Civil Eng. 27, 431–441. doi: 10.1007/s12205-022-0559-6

Crossref Full Text | Google Scholar

Elkiran, G., Nourani, V., and Abba, S. I. (2019). Multi-step ahead modelling of river water quality parameters using ensemble artificial intelligence-based approach. J. Hydrol. 577:123962. doi: 10.1016/j.jhydrol.2019.123962

Crossref Full Text | Google Scholar

Eze, E., Halse, S., and Ajmal, T. (2021). Developing a novel water quality prediction model for a South African aquaculture farm. Water 13:1782. doi: 10.3390/w13131782

Crossref Full Text | Google Scholar

Kim, K. M., and Ahn, J. H. (2022). Machine learning predictions of chlorophyll-a in the Han river basin, Korea. J. Environ. Manage. 318:115636. doi: 10.1016/j.jenvman.2022.115636

PubMed Abstract | Crossref Full Text | Google Scholar

Kozhiparamban, R. A. H., Swetha, P., and Harigovindan, V. P. (2023). Accurate dissolved oxygen prediction for aquaculture using stacked ensemble machine learning model. Natl. Acad. Sci. Lett. 46, 203–207. doi: 10.1007/s40009-023-01213-2

Crossref Full Text | Google Scholar

Kumar, V., Elkady, M. H., Misra, S., Odi, U., and Silver, A. (2024). Rapid production forecasting for heterogeneous gas-condensate shale reservoir. Geoenergy Sci. Eng. 240:213065. doi: 10.1016/j.geoen.2024.213065

Crossref Full Text | Google Scholar

Lee, J. W., Lee, S. W., An, K. J., Hwang, S. J., and Kim, N. Y. (2020). An estimated structural equation model to assess the effects of land use on water quality and benthic macroinvertebrates in streams of the Nam-Han River System, South Korea. Int. J. Environ. Res. Public Health 17:2116. doi: 10.3390/ijerph17062116

PubMed Abstract | Crossref Full Text | Google Scholar

Li, C. X., Li, Z. H., and Wu, M. (2024). The genetic algorithm and BP neural network in financial supply chain management under information sharing. Expert Syst. 41:e13273. doi: 10.1111/exsy.13273

Crossref Full Text | Google Scholar

Li, T. T., Lu, J., Wu, J., Zhang, Z. H., and Chen, L. W. (2022). Predicting aquaculture water quality using machine learning approaches. Water 14:2836. doi: 10.3390/w14182836

Crossref Full Text | Google Scholar

Li, X., Xue, Y., Kong, F., Li, Z., and Li, G. (2024). Analysis and prediction of the river levee settlement derived from shield tunneling considering the excavation face stability. Acta Geotech. 19, 3161–3184. doi: 10.1007/s11440-023-02048-3

Crossref Full Text | Google Scholar

Liang, X., Jian, Z. Q., Tan, Z. H., Dai, R., Wang, H. Z., Wang, J., et al. (2024). Dissolved oxygen concentration prediction in the pearl river estuary with deep learning for driving factors identification: temperature, pH, conductivity, and ammonia nitrogen. Water 16:3090. doi: 10.3390/w16213090

Crossref Full Text | Google Scholar

Ouyang, C., Qiu, Y., and Zhu, D. (2021). Adaptive spiral flying sparrow search algorithm. Sci. Program. doi: 10.1155/2021/6505253

Crossref Full Text | Google Scholar

Parinet, B., Lhote, A., and Legube, B. (2004). Principal component analysis: an appropriate tool for water quality evaluation and management-application to a tropical lake system. Ecol. Modell. 178, 295–311. doi: 10.1016/j.ecolmodel.2004.03.007

Crossref Full Text | Google Scholar

Shang, W., Jin, S., He, Y., Zhang, Y., and Li, J. (2021). Spatial-temporal variations of total nitrogen and phosphorus in poyang, dongting and taihu lakes from Landsat-8 data. Water 13:1704. doi: 10.3390/w13121704

Crossref Full Text | Google Scholar

Soltani, S., Ghatrami, E. R., Nabavi, S. M. B., Khorasani, N., and Naderi, M. (2024). The correlation between echinoderms diversity and physicochemical parameters in marine pollution: a case study of the Persian Gulf coastline. Mar. Pollut. Bull. 199:115989. doi: 10.1016/j.marpolbul.2023.115989

PubMed Abstract | Crossref Full Text | Google Scholar

Su, X., Steinman, A. D., Zhang, Y., Ling, H., and Wu, D. (2022). Significant Temporal and spatial variability in nutrient concentrations in a chinese eutrophic shallow lake and its major tributaries. Water 14:217. doi: 10.3390/w14020217

Crossref Full Text | Google Scholar

Sun, Z., Zhang, B., and Yao, Y. (2021). Improving the estimation of weighted mean temperature in china using machine learning methods. Remote Sens. 13:1016. doi: 10.3390/rs13051016

Crossref Full Text | Google Scholar

Tong, Y., Li, J., Qi, M., Zhang, X., Wang, M., Liu, X., et al. (2019). Impacts of water residence time on nitrogen budget of lakes and reservoirs. Sci. Total Environ. 646, 75–83. doi: 10.1016/j.scitotenv.2018.07.255

PubMed Abstract | Crossref Full Text | Google Scholar

Wu, S., Xia, P., Lin, T., Yang, J., Wang, R., Chen, Y., et al. (2019). Contents and distribution characteristics of nitrogen forms in sediments of Guizhou Lake Caohai under different water level levels. Hupo Kexue 31, 407–415. doi: 10.18307/2019.0210

Crossref Full Text | Google Scholar

Xue, K., Wang, J., Chen, Y., and Wang, H. (2024). Improved BP neural network algorithm for predicting structural parameters of mirrors. Electronics 13:2789. doi: 10.3390/electronics13142789

Crossref Full Text | Google Scholar

Yu, M. Y., Li, L. H., and Guo, Z. X. (2022). Model analysis of energy consumption data for green building using deep learning neural network. Int. J. Low-Carbon Technol. 17, 233–244. doi: 10.1093/ijlct/ctab100

Crossref Full Text | Google Scholar

Zhang, Y., Li, C., Gao, N., Shi, X., and Qiao, L. (2017). Effect of freezing on eutrophication in Lake Ulansuhai. Hupo Kexue 29, 811–818. doi: 10.18307/2017.0404

Crossref Full Text | Google Scholar