- 1Forschungszentrum Juelich GmbH, Agrosphere (IBG-3), Juelich, Germany
- 2Department Soil System Sciences, Helmholtz Centre for Environmental Research-UFZ, Halle, Germany
- 3Institute of Agricultural and Nutritional Sciences, Martin-Luther-University Halle-Wittenberg, Halle, Germany
- 4Institute of Crop Science and Resource Conservation (INRES), Soil Science and Soil Ecology, University Bonn, Bonn, Germany
In models of water flow in soil and roots, differences in the soil hydraulic properties of the rhizosphere and the bulk soil are usually neglected. There is, however, strong experimental evidence that rhizosphere and bulk soil hydraulic properties differ significantly from each other due to various root-soil interaction processes. Two such processes, which can also influence each other, are rhizosphere loosening or compaction and mucilage deposition. In this work, we identified realistic gradients in rhizosphere bulk density and mucilage concentration using X-ray CT imaging, respectively, model simulation for two different soil types and soil bulk densities and related them to soil hydraulic parameters. Using a 1D-single-root model, we then evaluated both the individual and combined effects of these gradients on soil water dynamics using scenario simulations. We showed that during soil drying, a lower rhizosphere bulk density leads to an earlier onset of water stress and to a reduced root water uptake that is sustained longer. The presence of mucilage led to a faster reduction of root water uptake. This is due to the stronger effect of mucilage viscosity on hydraulic conductivity compared to the mucilage- induced increase in water retention. Root water uptake was rapidly reduced when both mucilage and rhizosphere bulk density gradients were considered. The intensity of the effect of gradients in rhizosphere bulk density and mucilage concentration depended strongly on the interplay between initial soil hydraulic conditions, soil type and soil bulk densities. Both gradients in rhizosphere bulk density and mucilage concentration appear as a measure to sustain transpiration at a lower level and to avoid fast dehydration.
Introduction
The rhizosphere is defined as the small soil volume around the roots, whose physical, chemical, and biological properties are significantly influenced by the plant roots (Hinsinger et al., 2009). The properties of the rhizosphere soil are therefore significantly different to the properties of the bulk soil further away from the roots. When a root penetrates the soil, it alters the arrangement of soil particles and therefore the local compaction of the rhizosphere (Dexter, 1987; Koebernick et al., 2019). Growing roots furthermore release the organic compound mucilage that was shown to affect the water retention characteristics of the rhizosphere (Moradi et al., 2011; Ahmed et al., 2014). Both the local compaction of the rhizosphere as well as root mucilage deposition can thus be expected to have a significant impact on the water transport from the soil to the roots and therefore also on root water uptake (Whalley et al., 2005).
Recently, a lot of work has been published on the dynamic development of soil structure in the rhizosphere using non-invasive X-ray CT imaging. Several studies have found lower bulk densities in the immediate vicinity of the roots than further away in the bulk soil for different plant types, soil types and soil moisture contents (Helliwell et al., 2017, 2019; Koebernick et al., 2019; Lucas et al., 2019). It is assumed that the low point in bulk density in the immediate vicinity of the root is caused by the incomplete packing of the larger, incompressible mineral particles, which are displaced by the growing root (Koebernick et al., 2019). Furthermore, root shrinking due to soil drying, which causes a loss of contact between root and soil, may also play a role (Carminati et al., 2013; Koebernick et al., 2018). Helliwell et al. (2019), Koebernick et al. (2019), and Lucas et al. (2019) observed that this low point in bulk density close to the root was partly followed by a peak value before the density of the bulk soil was reached. Other studies predominantly observed a compaction of the rhizosphere close to the root (Bruand et al., 1996; Vollsnes et al., 2010; Aravena et al., 2011, 2014; Koebernick et al., 2017). Rhizosphere compaction can be justified by the fact that the volume occupied by a root must be compensated by a loss of the same volume of pore space of the surrounding soil (Dexter, 1987; Lucas et al., 2019). Lucas et al. (2019) found that rhizosphere compaction only developed at medium levels of soil bulk density and that its occurrence depends on the soil texture and on the particle size to which the soil was sieved. If the soil was too loose, the roots found their way through existing pores. If the soil was too dense, the roots could not overcome the mechanical stress and resorted to pre-existing pores.
Variations in bulk density have a direct impact on soil hydraulic parameters and can therefore be expected to affect soil water dynamics and root water uptake (Aravena et al., 2011, 2014; Daly et al., 2015; Koebernick et al., 2019). Daly et al. (2015) and Koebernick et al. (2019) investigated the structure of rhizosphere and bulk soil using X-ray CT imaging and related the changes in observed porosities to changes in soil hydraulic properties using the Young-Laplace equation, respectively, a homogenization method that allows deriving Darcy's law from Stoke's equations for fluid flow. However, the limited imaging resolution restricted the separation of the CT images into pore and solid phase and only allowed the description of the influence of the rhizosphere soil structure on the wet end of the water release characteristics (i.e., above −800 cm pressure head). Using X-ray CT imaging, Aravena et al. (2011) and Aravena et al. (2014) showed that in low-density soils, the compaction of the rhizosphere can increase the unsaturated hydraulic conductivity of the soil and thus the root water uptake due to an increased contact area between adjacent soil aggregates.
In recent years, many studies have shown the importance of root mucilage deposition for the water dynamics in the rhizosphere (Carminati et al., 2010, 2016b; Ahmed et al., 2014; Albalasmeh and Ghezzehei, 2014). It is a well-known phenomenon that mucilage increases the water retention due to its high water-holding capacity. The increased water content at a given pressure head then results in a higher unsaturated hydraulic conductivity (van Genuchten, 1980). However, mucilage also increases the water viscosity, and thereby decreases the unsaturated hydraulic conductivity at a given pressure head. Depending on the relative importance of the increase in water retention, respectively, in viscosity, hydraulic conductivity can either increase or decrease due to the impact of mucilage at a given pressure head (Moradi et al., 2011; Carminati et al., 2016b).
The actual extent of the impact of mucilage on soil water dynamics depends on its spatial distribution around the roots (Holz et al., 2018a). Due to the difficulty of imaging mucilage in soil non-invasively and quantitatively, knowledge about the spatial distribution of mucilage is very limited. Most modeling studies have therefore assumed constant mucilage concentrations in the rhizosphere (Carminati et al., 2016a; Schwartz et al., 2016) or linearly decreasing concentrations from the root surface to the bulk soil (Kroener et al., 2016). The radial extent of the rhizosphere affected by mucilage was assumed to be between 1 and 2 mm (Kroener et al., 2016; Schwartz et al., 2016). Recent studies, however, have shown that the radial gradients of mucilage distribution around a root are relatively steep and that the extent of the rhizosphere affected by mucilage was only about 0.6 mm (Zickenrott et al., 2016; Holz et al., 2018a). Furthermore, it is known that mucilage is secreted at the root tips and that its distribution varies along the root axis (Holz et al., 2018b; van Veelen et al., 2018). This has not been taken into account in previous modeling studies.
The aim of this modeling study was to assess how the individual and combined effects of variations in rhizosphere bulk density and mucilage concentration affect soil water dynamics and root water uptake in 2 soils with different hydraulic properties, namely loam and sand. These soils were furthermore compacted to two different bulk density levels. Variations in rhizosphere bulk density were measured experimentally using X-ray CT and were assumed to affect soil hydraulic parameters according to the empirical relations derived by Assouline (2006a,b). The distribution of mucilage in the rhizosphere of a growing root was predicted by solving the diffusion-reaction equation in a moving reference frame (Kim et al., 1999) using appropriate model input parameter values from the literature. The impact of mucilage concentration on soil hydraulic parameters was evaluated via the model proposed by Kroener et al. (2014) that was parameterized with optimized values from the literature. Using a 1D rhizosphere model, we then simulated a drying scenario to evaluate the individual and combined effects of rhizosphere bulk density and mucilage concentration on soil water dynamics and root water uptake. The workflow of the study is illustrated schematically in Figure 1.
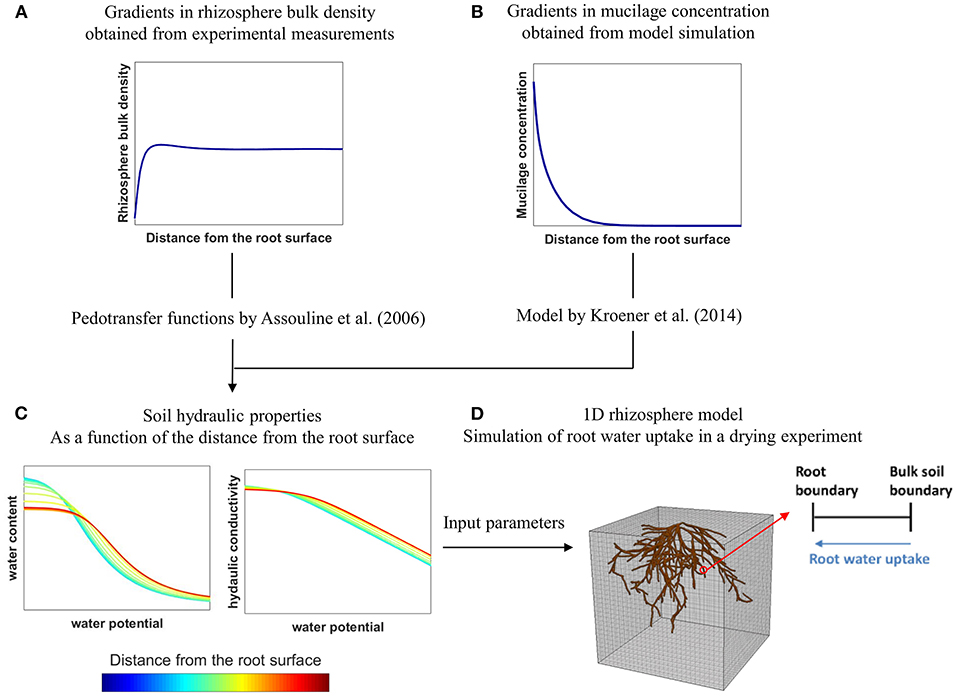
Figure 1. Schematic illustration of the workflow of the present study: Gradients in rhizosphere bulk density (A) were obtained from experimental measurements with X-ray CT and related to soil hydraulic properties using the pedotransfer functions by Assouline (2006a,b). Gradients in mucilage concentration (B) were obtained from model simulation and related to soil hydraulic properties using the model by Kroener et al. (2014). The obtained soil hydraulic properties (C) were then used as input parameters in a 1D-rhizosphere model (D) to evaluate the effects of rhizosphere bulk density and mucilage gradients on root water uptake in a drying experiment.
Materials and Methods
Analysis of the Rhizosphere Bulk Density
Experimental Setup and X-ray CT Imaging
The bulk density changes in the rhizosphere were investigated for 2 soils with differing textures, i.e., a loam and a sand that were compacted at two different bulk density levels (low and high). The loam was compacted to 1.26 and 1.36 g cm−3 whereas the sand was packed at 1.5 and 1.6 g cm−3, respectively. The loam was obtained from the upper 50 cm of a haplic Phaeozem soil profile, dried to 0.1 g g−1 gravimetric water content and then sieved down to <1 mm. The sand constitutes a mix of 83.3% quartz sand (WF 33, Quarzwerke Weferlingen, Germany) and 16.7% of the sieved loam. Details on chemical and physical properties are provided in Vetterlein et al. (2021).
Maize plants were grown in cylindrical containers of 18 cm height and 10 cm diameter over a period of 22 days in a climate chamber (Vötsch Industrietechnik GmbH). The columns were carefully watered from the top and from the bottom to an average volumetric water content of 0.22 cm3cm−3 and 0.18 cm3cm−3 for loam and sand, respectively. The climate chamber was set to 22 °C during the day and to 18°C at night with a 12 h light period, 350 μMm−2s−1 photosynthetically active radiation and a constant relative humidity of 65%. After 22 days of growth, the plants were harvested and undisturbed cylindrical soil samples (3 cm in height and diameter) were taken at depth −5, −10, and −15 cm from the soil surface.
X-ray tomography was performed with an industrial μCT scanner (X-TEK XTH 225, Nikon Metrology) operated at 130 kV and 150 μA. A total of 2,500 projections with an exposure time of 708 ms each were acquired during a full rotation of a sample. The obtained images were reconstructed into a 3D tomogram having a voxel size of 19 μm and an 8-bit greyscale via a filtered back projection algorithm with the CT Pro 3D software (Nikon metrology). After X-ray CT imaging, the images were visualized and the samples devoid of roots were not considered for further analysis. For the loam, 24 samples were analyzed per bulk density level. For the sand, 23 and 13 samples were analyzed for the low and high bulk density, respectively.
Analysis of Bulk Density Variation Around the Roots
The variation in rhizosphere bulk density around the roots was obtained from the X-ray CT images of the scanned samples. First, root segmentation of each sample was performed with a modified version of the segmentation algorithm Rootine v.2 (Phalempin et al., 2020) in order to distinguish root voxels from background voxels. After root segmentation, we computed the so-called “Root distance maps” on the segmented root system image using the “Euclidian Distance Transform (3D)” (EDT) plugin available in ImageJ (Schindelin et al., 2012). This resulted in images in which every soil voxel is assigned a value equal to its distance to the closest root in a 3D volume. The resulting images were then merged with the original gray scale data into one composite image. In this composite image, each voxel contains the root distance information in one channel and the gray value information in another channel. By looping over all x, y, and z coordinates and retrieving the value of each channel, we obtained the average gray value as a function of the distance from the root surface. The average gray value profile was thereafter normalized by division by the mean gray value of the image. Finally, the deviation from the mean gray value was used to derive rhizosphere bulk density properties for each sample and treatment. The rationale of the employed method is that gray value changes can be used as proxy for changes in soil bulk density that also considers sub-resolution differences, as already suggested by Lucas et al. (2019). The workflow used in this study to analyze the variation in rhizosphere bulk density around the roots is shown in Figure 2 for one small illustrative image of the loam low bulk density dataset.
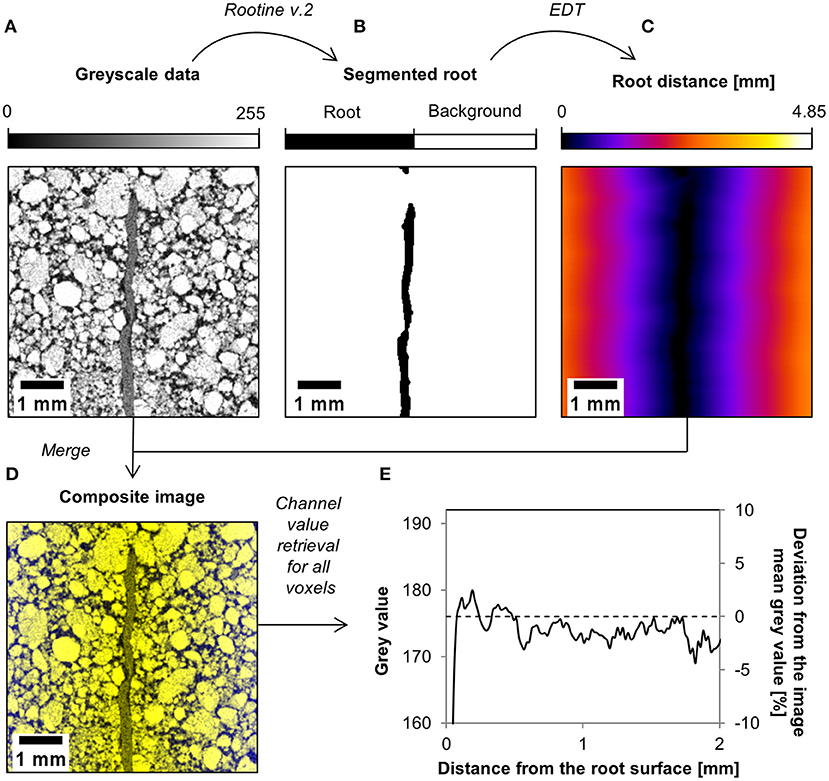
Figure 2. Workflow used to analyze the variation in rhizosphere bulk density around the roots. After root segmentation of the gray scale data (A), a root distance map is computed on the segmented root system (B). This root distance map (C) is then merged with the gray scale data into a composite image (D). This composite image is analyzed and the value of each of its channel is retrieved. This allows plotting the deviation from the mean gray value as a function of the distance from the root surface (E), which is further used to characterize the rhizosphere bulk density by simple scaling of the bulk soil bulk density.
Analysis of Mucilage Concentration in the Rhizosphere
The impact of mucilage on soil hydraulic parameters depends on the spatial distribution of mucilage in the soil. The spatial distribution of mucilage is a function of numerous factors such as mucilage deposition rate, root radius and root growth rate and it is extremely hard to measure those factors directly (Holz et al., 2018b). We therefore set up a 2D axi-symmetric simulation model in COMSOL Multiphysics (COMSOL, 2019) to predict the mucilage concentration profile around a root. We applied the diffusion-reaction equation in a moving reference frame so that the origin was always at the moving root tip. The root elongation was then implemented in analogy to the advection term (Kim et al., 1999):
with the boundary condition
where θ is the volumetric water content (cm3 cm−3), C is the concentration of mucilage (g g−1 dry soil), t is the time (d), r is the radial distance from the root axis (cm), z is the distance from the root tip (cm), v is the root elongation rate (cm d−1), K is the decomposition rate of mucilage at which fresh mucilage is decomposed to mucilage derivatives (d−1), htip (cm) is the zone behind the root tip where deposition occurs, E (μgd−1 per root tip) is the deposition rate, and D(θ) is the effective diffusion coefficient of mucilage in soil (cm2 s−1). The effective diffusion coefficient strongly depends on water content θ, i.e., with decreasing water contents the liquid phase becomes more and more tortuous and disconnected, which reduces effective diffusion. Several models (Millington and Quirk, 1961; Bresler, 1973; Papendick and Campbell, 1981) exist to estimate D(θ). Most of these models have been developed and tested for spreading of low molecular weight solutes. Mucilage also contains polymers of high-molecular weight, which may cause even more complex molecular transport dynamics within the soil pore space. Here, we chose the widely used empirical Millington and Quirk (1961) model to calculate D(θ) as
where D0 is the diffusion coefficient of mucilage in pure water (cm2s−1) and φ is the soil porosity (–). This model was tested against experimental datasets in various studies (e.g., Partridge et al., 1999; Moldrup et al., 2000; Chou et al., 2012). Considering that
where ρr is the soil bulk density in the rhizosphere and ρs is the soil particle density [set to ρs = 2.65 g cm−3 (Dexter, 1987)], we scaled the porosity with the measured rhizosphere bulk density gradients. Processes such as root water uptake, compaction and mucilage deposition change the soil water content locally. For reasons of simplicity, however, the radial spreading of mucilage around the root (Equations 1, 2) was computed using a constant soil water content of θ = 0.4 cm3cm−3. We chose two different mucilage deposition rates E (low and high) in the range of values found in literature (Chaboud, 1983; Zickenrott et al., 2016). All remaining model parameters were taken from our own measurements, respectively, from the literature and are listed in Table 1. At the top and the side boundaries of the domain, we assumed a zero gradient. The bottom boundary was set to zero flux.
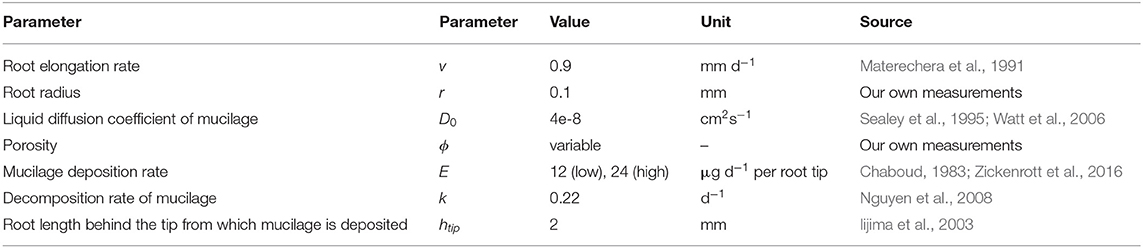
Table 1. Parameter values for the computation of the mucilage concentration profile around a single maize root.
According to Nguyen et al. (2008) and Mary et al. (1993), the decomposition half-life of the organic compounds of mucilage may vary between 3 and 11 days. Carminati (2013), however, have shown experimentally that mucilage-like substances have an impact on the water content in the rhizosphere of roots that were as old as 2–3 weeks. The reason may be that microbes do not only degrade mucilage, but also produce gel-like substances called bacterial exopolysaccharides (EPS) (Carminati and Vetterlein, 2013), which have similar physical properties as mucilage (Or et al., 2007). We therefore concluded that not only fresh mucilage, but also its derivatives alter soil hydraulic properties and further assumed that all of the degraded mucilage was converted to mucilage derivatives. Due to a lack of experimental data, we supposed that mucilage derivatives have the same impact on soil hydraulic properties as fresh mucilage. Albalasmeh and Ghezzehei (2014) suggested that dry mucilage is tightly bound to soil particles and no longer diffuses freely into the soil. This theory is supported by experimental findings by Carminati et al. (2010), who showed that the thickness of the rhizosphere of lupine roots did not significantly change within 1 week of observation using neutron radiography. We therefore assumed that the mucilage derivatives are irreversibly bound to the soil particles and can no longer move by diffusive transport. Based on these assumptions, the radial profile of the concentration of mucilage derivatives at a distance sufficiently far away from the root tip does not change anymore with time. Furthermore, hydrodynamic dispersion of mucilage was neglected, which we justified with the rather slow water fluxes.
Analysis of the Effect of Rhizosphere Bulk Density and Mucilage Concentration on Soil Hydraulic Parameters
The Effect of Rhizosphere Bulk Density on Soil Hydraulic Parameters
The pore space in aggregated soils can be classified into textural and structural pore space (Leij et al., 2002a,b). Textural pore space, which is determined by the distribution of soil primary particles, is relatively stable. Structural pore space, which is defined by the position and orientation of aggregates relative to one another, however, can easily be modified when exposed to external forces (Or et al., 2000; Leij et al., 2002a,b; Or and Ghezzehei, 2002). Following these considerations, we assume that all observed changes in rhizosphere bulk density are caused by modifications of the structural pore space. We used the pedotransfer functions by Assouline (2006a), Assouline (2006b) and Carman (1937) to relate the changes in rhizosphere bulk density to changes in soil hydraulic parameters. Assouline (2006a,b) calibrated and validated the relationships between soil hydraulic parameters and soil bulk density at various compaction levels between 0.68 and 1.59 g cm−3. The rhizosphere bulk density levels used in our study cover a range between 0.9 and 1.6 g cm−3 and are thus within this range.
The Effect of Mucilage Concentration on Soil Hydraulic Parameters
The high water adsorption capacity of mucilage leads to an increase in the water content of the rhizosphere for a given matric potential and thereby affects the water retention in the rhizosphere (Carminati et al., 2010). To simulate the effect of mucilage concentration on soil water retention, we used the model by Kroener et al. (2014)
where hm(θm) and h(θ) are the pressure heads with and without the impact of mucilage, θm and θ are the volumetric water contents with and without the impact of mucilage and ω0 and β are fitting parameters that describe how cw, the gravimetric mucilage concentration in water (g g−1), affects the overall water retention behavior. cw is thereby defined as
where C is the local gravimetric concentration of mucilage in the soil (g g−1), ρr is the local rhizosphere bulk density (g cm−3) and ρW is the density of water (1 g cm−3). Kroener et al. (2018) investigated the influence of soil texture on the mucilage-related increase in water content at a given water potential. They found that mucilage concentrations of 1 and 8 (mg g−1 dry soil) increase the water content by 0.5 and 6.6 % in coarse and fine sand and by 11.2 and 12.5 % in silty soil at a water potential of −500 cm. We assumed that the silty soil corresponds approximately to our loam. With the help of the simplex method (Nelder and Mead, 1965) and our soil hydraulic parameter sets, we then optimized the fitting parameters ω0 and β so that the findings by Kroener et al. (2018) were approximated as accurately as possible. We obtained and β = 4.1 for loam and and β = 2.99 for sand. These values are in good agreement with the parameters used in other studies (Carminati et al., 2016a; Kroener et al., 2016; Schwartz et al., 2016). ω0 can vary by some orders of magnitude because the fitted parameter ω0 is extremely sensitive to slight changes of the value of the fitted exponent β.
Due to its high viscosity, mucilage decreases the soil hydraulic conductivity. We approximated this decrease by the relation given by Ahmed et al. (2014):
where km and k (Equation 11) are the unsaturated hydraulic conductivities in soil with and without mucilage and μw and μ(cw) are the viscosities of water (μw = 1 mPa s−1) and mucilage, respectively. The latter is given as
where v = 566 and d = 1.4 are unitless fitting parameters given by Ahmed et al. (2014).
Analysis of Bulk Soil Hydraulic Parameters
We measured the soil water retention and soil hydraulic conductivity curves for both soils loam and sand at the low bulk density levels (ρ = 1.26 and 1.5 g cm−3 for loam and sand, respectively), with the HYPROP system (METER Group AG). Five 250 cm3 metal cylinder replicates were analyzed for each soil type. We then used the HYPROP-FIT software (Pertassek et al., 2015) to fit soil hydraulic parameters to these curves, which are used in the closed-form equations established by Mualem (1976) and van Genuchten (1980):
where h is the absolute value of the pressure head (cm), θs and θr are saturated and residual water content, respectively, α is the inverse of the air entry suction (cm−1), n is a shape parameter (–), Θ is the water saturation (–), l is the tortuosity (–), and K and Ks are unsaturated and saturated hydraulic conductivities (cm d−1), respectively. According to Mualem (1976), we assumed l = 0.5. Note that we have kept θs separated from the soil porosity φ, considering that θs may be smaller than φ due to air that is entrapped in the soil. All soil hydraulic parameters are given in Table 2.
1D Rhizosphere Model
To evaluate the impact of changes in water retention and hydraulic conductivity due to variations in rhizosphere bulk density and mucilage concentration on soil water dynamics and root water uptake, we set up a 1D rhizosphere model in COMSOL Multiphysics (COMSOL, 2019), which is schematically illustrated in Figure 3. This 1D model represents a radial cut through a soil cylinder surrounding a single root and thus contains a root and a bulk soil boundary. We prescribed the xylem water potential hx and computed the radial flux Jr at the root boundary as
where kr (d−1) is the radial root hydraulic conductivity and h (cm) is the soil water potential at the root surface. The xylem water potential hx applied by the plant was set to hx = −15,000 cm during the day and hx = 0 cm during night (Cai et al., 2018). To allow a smooth transition in pressure between day and night, we considered daily sinusoidal variations (Doussan et al., 2009). At the bulk soil boundary, we set a no-flux condition. The Richards equation was then solved in radial coordinates as
where r (cm) is the radial distance to the root surface. Assuming that the root is located vertically within the soil domain, gravity was neglected.
Scenario Description
We considered six different scenarios. In the control scenario, no impact of variations in rhizosphere bulk density or mucilage was considered. In the rhizosphere bulk density scenario, we only took into account variations due to gradients in rhizosphere bulk density. In the mucilage high scenario, we considered the impact of high mucilage deposition. In the mucilage low scenario, we took into account the influence of low mucilage deposition. In the rhizosphere bulk density and mucilage high, respectively, mucilage low scenarios, variations due to both rhizosphere bulk density and high, respectively, low mucilage depositions were considered. An overview with the respective symbols is given in Table 3.
Simulation Setup
We set up a virtual drying experiment. The root radius was set to 0.1 mm, which corresponds approximately to the median maize root radius found in the X-ray CT experiment. According to Gardner (1960), the maximum distance that water has to travel from any point in a soil domain to the nearest root is less than or equal to half the mean distance HMD between neighboring roots, which is calculated as
where RLD is the root length density (cm cm−3). An assumed root length density of RLD = 0.5 cm cm−3 leads to HMD = 0.8 cm, which was the radial extent of our soil domain. We used a radial root hydraulic conductivity of krad = 1.9e−4 d−1 (Meunier et al., 2018) and two different initial pressure heads Hini = −10 cm, a value that could be typically assumed directly after watering, and Hini = −100 cm, a value that is close to field capacity. All parameters are listed in Table 4. To catch all small-scale variations in soil hydraulic properties due to variations in rhizosphere bulk density and mucilage concentration, we discretized the soil domain into 1D elements of 1e−3 mm side length. We used adaptive time stepping with a relative tolerance of 0.0001 s convergence criteria. The simulations were run over 15 days.
Results
Gradients in Rhizosphere Bulk Density
Figure 4 shows the rhizosphere bulk density as a function of distance from the root surface for both soil types and soil bulk densities. Rhizosphere bulk density in the immediate vicinity of roots was lower than in the bulk soil for both loam and sand. Further away from the root surface, a minor soil compaction could be observed for loam. The shape of the rhizosphere bulk density variation is reminiscent of an oscillatory wave, which is caused by particle re-alignment when the root penetrates the soil (Suzuki et al., 2008; Koebernick et al., 2019). The low bulk density at the root-soil interface may also be caused by gap formation due to root shrinkage (Carminati et al., 2013; Koebernick et al., 2018).
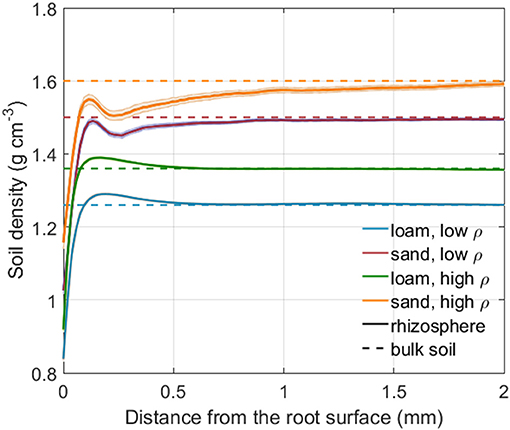
Figure 4. Rhizosphere bulk density as a function of the distance from the root surface for both soil types and bulk densities. The shaded area denotes the standard error of the mean for 24 (loam, low, and high density), 23 (sand, low bulk density), and 13 (sand, high bulk density) samples. The dashed lines represents the bulk soil density for each soil type and bulk density level.
Gradients in Mucilage Concentration
Figure 5A shows the concentration profiles of fresh mucilage and mucilage derivatives for the example of low density loam in soil with uniform rhizosphere bulk density simulated with a low and a high mucilage deposition rate (Table 1). For further model simulation of the impact of mucilage on root water uptake, we used the radial concentration profiles of mucilage derivatives at a distance sufficiently far away from the root tip since they can be considered as constant in time. For both low and high mucilage deposition rates, we computed radial mucilage concentration profiles for both soil types and soil bulk density levels as well as with and without rhizosphere bulk density gradients (Figures 5B,C). The radial mucilage concentration profiles differed slightly for the different soil types and more significantly in consideration of the radial gradients in rhizosphere bulk density: The low rhizosphere bulk density in the immediate vicinity of the root led to a larger mucilage concentration (mg mucilage g−1 dry soil) within a distance of 0- 0.1 mm from the root surface.
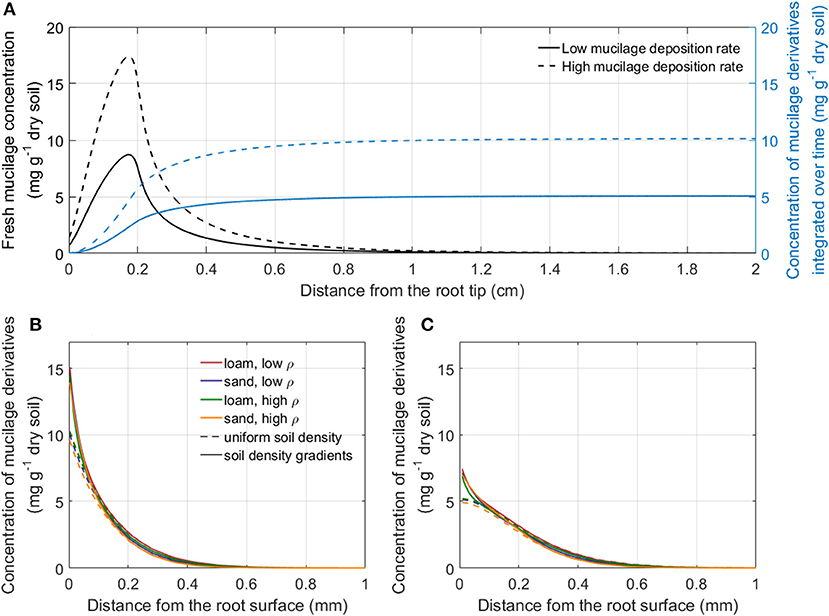
Figure 5. Concentration profiles of fresh mucilage and mucilage derivatives after a simulation time of 30 days: along the root axis for the example of low bulk density loam with uniform rhizosphere bulk density simulated with a low and a high mucilage deposition rate (A); radial concentration profile of mucilage derivatives sufficiently far away from the root tip for the high (B) and the low (C) mucilage deposition rate around a single maize root in loam and sand for both bulk densities with and without the consideration of radial gradients in rhizosphere bulk density.
Effect of Gradients in Rhizosphere Bulk Density and Mucilage Concentration on the Soil Hydraulic Parameters
From each of the radial rhizosphere bulk density respective mucilage concentration profiles shown in Figures 4, 5B,C, we took 500 values at a distance of 0–10 mm from the root surface. The 500 points were drawn in logarithmically spaced distances (many points near the root and fewer points further away), because both rhizosphere bulk density and mucilage concentrations near the root change strongly over small distances in the radial profiles. For each of the 500 rhizosphere bulk density values, we computed the soil hydraulic parameters. For each of the 500 mucilage concentration values, we computed soil water retention curves and estimated the corresponding soil hydraulic parameters.
Figure 6 shows the deviations in soil hydraulic parameters relative to the bulk soil values (Table 2) due to variations in rhizosphere bulk density for both loam and sand and low and high levels of soil bulk density. A decrease in rhizosphere bulk density led to an increase in saturated volumetric water content θs due to an increase in the fraction of large pores (Figure 6A, Assouline, 2006a, Equation 5). The residual water content θr in the rhizosphere slightly decreased due to the decrease in specific soil particle surface when rhizosphere bulk density decreased (Figure 6B, Assouline, 2006a, Equation 6). The inverse of the air entry suction α increased with a decrease in rhizosphere bulk density due to an earlier air entry point caused by the higher fractions of large pores (Figure 6C, Assouline, 2006a, Equation 15, converted from Brooks and Corey). Changes of the van Genuchten shape parameter n depend on the development of the pore size distribution: If the variance of the distribution of pore radii increases more than the mean pore radius, a decreased shape parameter n is to be expected. If the opposite is the case, the shape parameter n increases (Stange and Horn, 2005). We assumed that both the variance and the mean size of the pore radii increase uniformly and n therefore remained constant (Figure 6D). According to the Kozeny- Carman relation (Carman, 1937), the saturated soil hydraulic conductivity ks increases when rhizosphere bulk density decreases due to the increased volume of large pores (Figure 6E). Variations in rhizosphere bulk density give us information about the total change in the volume of voids, but not about the volume distribution of voids, i.e. the tortuosity or the aggregate connectivity (Assouline, 2006a). We therefore kept the tortuosity parameter constant at l = 0.5.
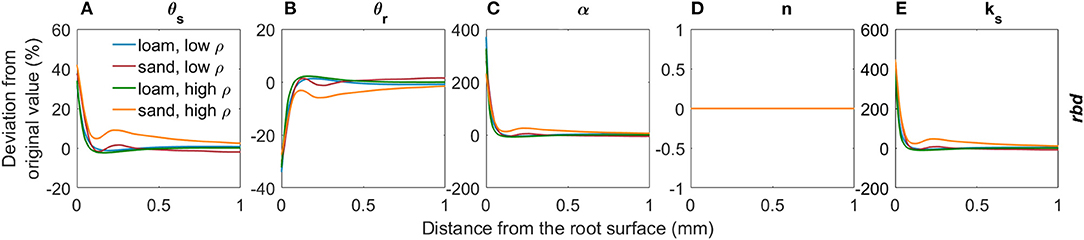
Figure 6. Relative changes in the van Genuchten parameters θs (A), θr (B), α (C), n (D), and ks (E) due to variations in rhizosphere bulk density for loam and sand and for low and high soil bulk density levels.
Figure 7 shows the deviations in soil hydraulic parameters relative to the bulk soil values (Table 2) due to variations in mucilage concentration (low and high concentrations according to the radial concentration profiles in Figures 5B,C) for both loam and sand and for both low and high levels of soil bulk density. Mucilage has no impact on the saturated water content θs and on the residual water content θr since it does not influence the pore size distribution (Figures 7A,B). Due to the high water adsorption capacity of mucilage, it is generally assumed that the inverse of the air entry suction α decreases with increasing mucilage concentration. With our parameterisation, however, α remained constant, which is in line with findings by Kroener et al. (2018) for coarse and medium textured soils (Figure 7C). The shape parameter n also decreased due to the high water adsorption capacity of mucilage, since for a given decrease in pressure head the water content decreases less than in soil without mucilage. It must be noted that this decrease in n was stronger in sand than in loam (Figure 7D). Considering that mucilage increases the viscosity, the saturated hydraulic conductivity decreased (Figure 7E). To date, it is not clear how mucilage affects soil pore tortuosity (Haupenthal et al., 2020). We therefore kept the tortuosity parameter constant at l = 0.5.
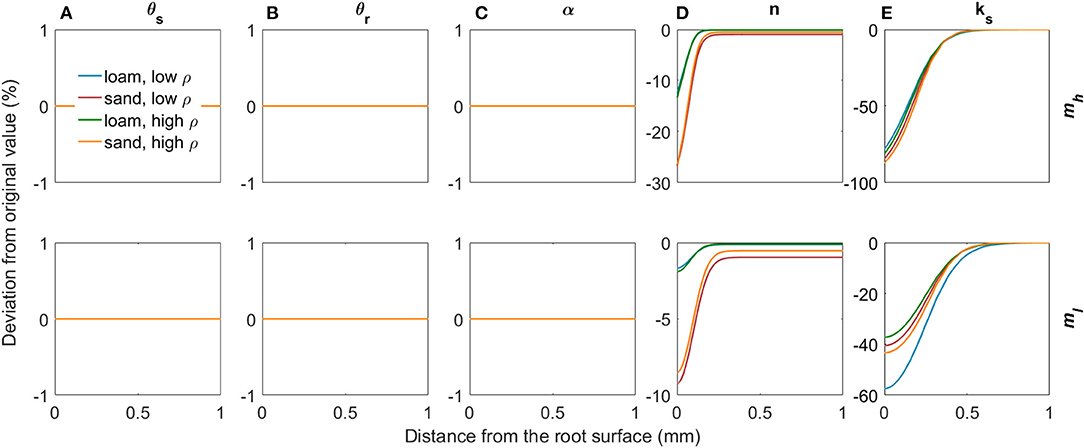
Figure 7. Relative changes in the van Genuchten parameters θs (A), θr (B), α (C), n (D), and ks (E) due to variations in mucilage concentration for loam and sand, for low and high soil bulk density, and for low and high mucilage deposition rates.
Subsequently, we combined the effects of variations in rhizosphere bulk density and mucilage concentration on soil hydraulic parameters assuming superposition. The effects of both gradients in rhizosphere bulk density and mucilage concentration on soil hydraulic parameters are shown in Figure 8. While the saturation and residual water content θs and θr are only influenced by rhizosphere bulk density, the shape parameter n depends only on the mucilage concentration (Figures 8A,B,D). The inverse of the air entry suction α as well as the saturated soil hydraulic conductivity ks are a function of both the rhizosphere bulk density and the mucilage concentration (Figures 8C,E). In our parameterization, mucilage had only a very small influence on α. Therefore, α increases in the rhizosphere due to the earlier air inflow caused by the higher fractions of large pores. Both rhizosphere bulk density and mucilage have a strong impact on ks. In the immediate vicinity of the root, the impact of rhizosphere bulk density is stronger and ks therefore increases, whereas at a distance of about 0.1 to 0.4 mm, mucilage formation is more important and ks decreases.
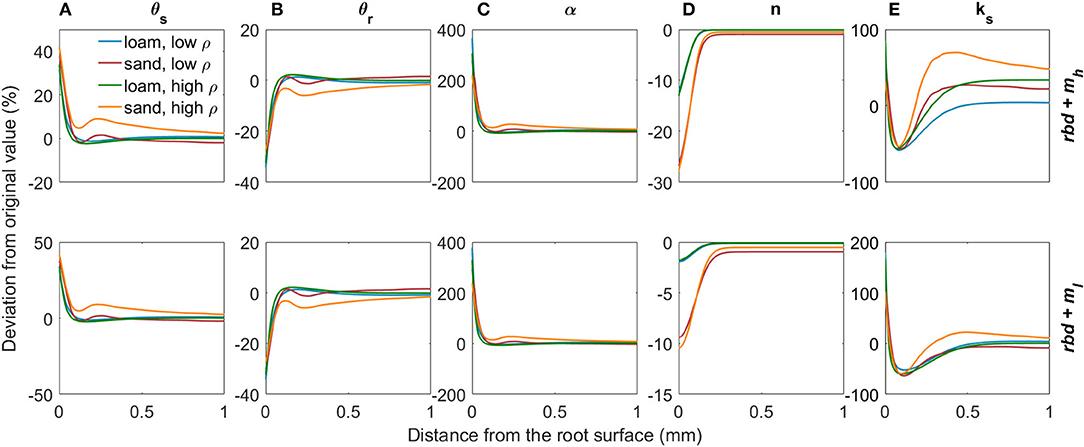
Figure 8. Relative changes in the van Genuchten parameters θs (A), θr (B), α (C), n (D), and ks (E) due to variations in rhizosphere bulk density and mucilage concentration for loam and sand, for low and high soil bulk density levels, and for low and high mucilage deposition rates.
Effect of Gradients in Rhizosphere Bulk Density and Mucilage Concentration on the Soil Water Retention and Soil Hydraulic Conductivity Curves
Using the previously computed soil hydraulic parameters, we computed soil water retention and soil hydraulic conductivity curves as a function of rhizosphere bulk density and mucilage concentration gradients for both loam and sand and for both low and high soil bulk density (Figures 9, 10). Reduced rhizosphere bulk density resulted in increased water content when the soil was wet and in decreased water content when the soil was dry. Similarly, soil hydraulic conductivity increased at pressure heads close to zero and decreased when the pressure head became more negative. Mucilage increased the water retention, especially in case of very negative pressure heads. For the low mucilage concentration, the increase in water retention was only very small and more pronounced in sand than in loam. While the hydraulic conductivity increased due to the higher retention of mucilage, it was simultaneously reduced due to the higher viscosity of mucilage. In loam, both high and low concentrations of mucilage led to a general decrease in the soil hydraulic conductivity. For low mucilage concentrations, the same was true in sand. However, high mucilage concentrations in sand led to increased hydraulic conductivity in dry soil. The simultaneous consideration of mucilage deposition and gradients in rhizosphere bulk density led to a higher mucilage concentration in the rhizosphere (Figures 5B,C), which in turn affected water retention and hydraulic conductivity. For the high mucilage concentration, the combined effect of mucilage and rhizosphere bulk density led to a general increase of retention in the whole saturation range. This was true for both loam and sand as well as low and high soil bulk density. For the low mucilage concentration, the combined effect of mucilage and rhizosphere bulk density led to a general increase of water retention in the wet range. In the dry range of loam, water retention was increased close to the root, but decreased further away. In the dry range of sand, it was generally decreased. The combined effect of mucilage and rhizosphere bulk density led to a general decrease in the soil hydraulic conductivity at pressure heads of less than approximately −10 cm. In general, rhizosphere bulk density had a stronger influence when saturation was high (h ≳ −10 cm), while the effect of mucilage concentration was higher in the negative range of pressure heads.
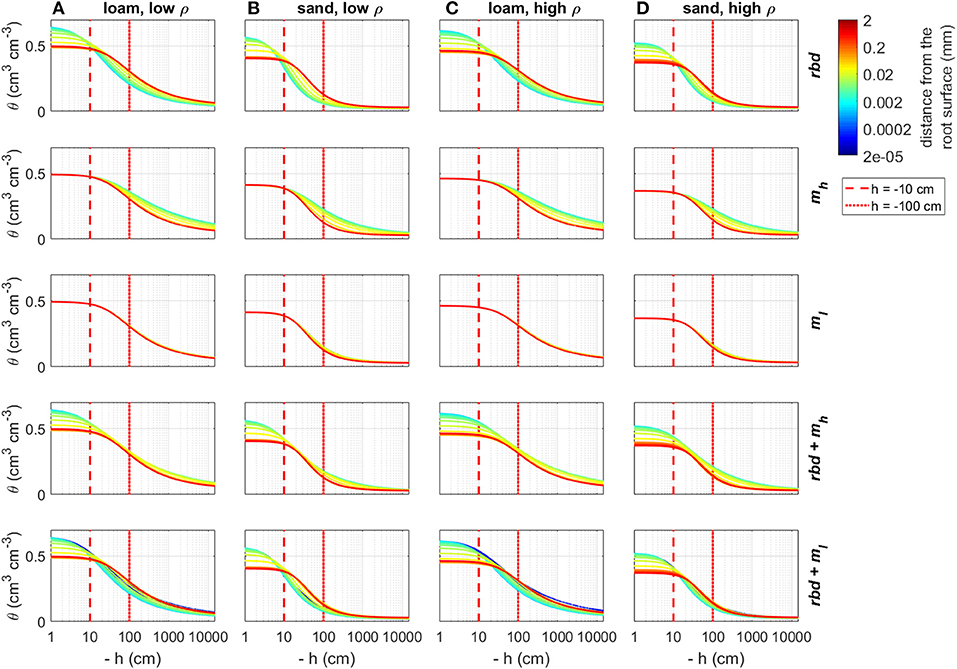
Figure 9. Changes in the soil water retention curves due to gradients in rhizosphere bulk density and/or mucilage concentration for loam and sand and low and high soil bulk density, the vertical red lines indicate the initial pressure heads used in the simulation Hini = −10 cm and Hini = −100 cm. (A) Loam, low ρ; (B) Sand, low ρ; (C) Low, high ρ; and (D) Sand, high ρ.
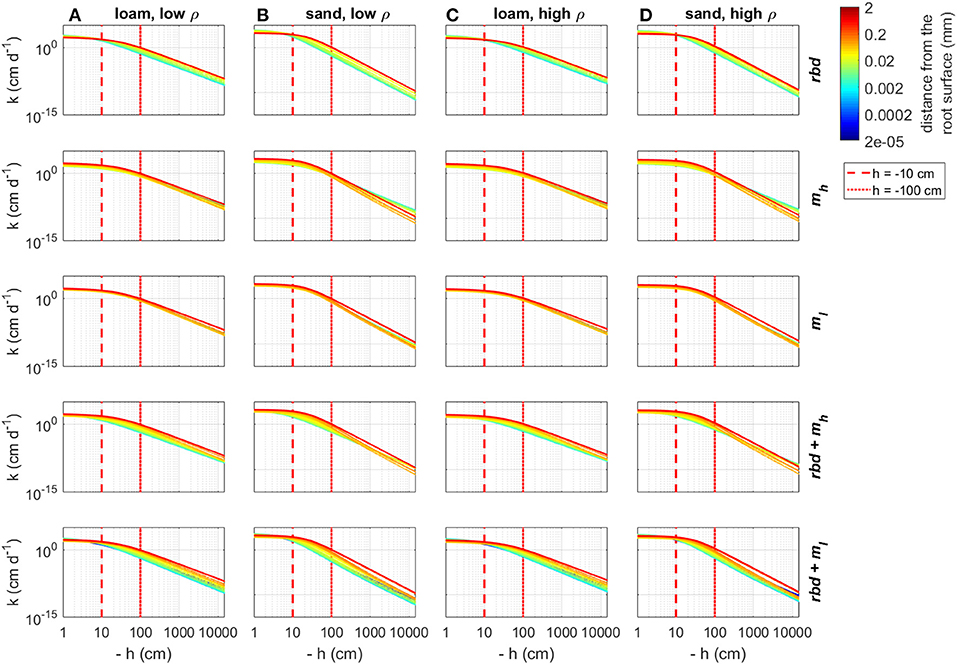
Figure 10. Changes in the hydraulic conductivity curves due to gradients in rhizosphere bulk density and/or mucilage concentration for loam and sand and low and high soil bulk density, the vertical red lines indicate the initial pressure heads used in the simulation Hini = −10 cm and Hini = −100 cm. (A) Loam, low ρ; (B) Sand, low ρ; (C) Loam, high ρ; and (D) Sand, high ρ.
Scenario Simulations
At the beginning of the simulation period, the pressure head was uniform. Due to the differences in soil hydraulic parameters, however, water content and soil hydraulic conductivity distribution in the rhizosphere varied for the different soil types, soil bulk density levels, initial conditions and scenarios (Figures 11, 12). For the subsequent drying experiment, the initial conditions are important since they determine the amount of water that is available in the soil domain.
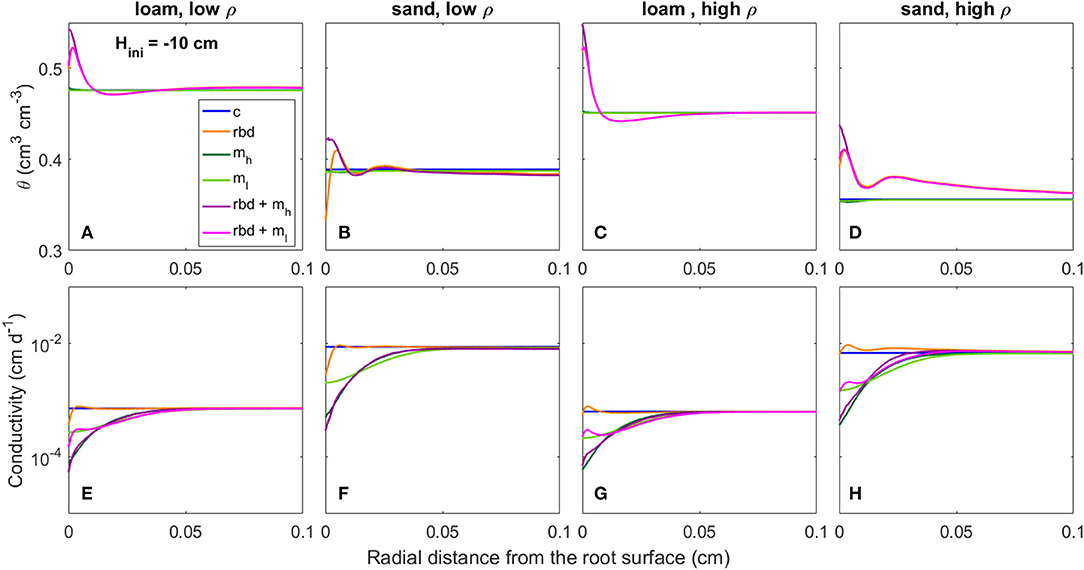
Figure 11. Radial gradients of water content (θ) (A–D) and soil hydraulic conductivity (E–H) at the start of the simulation period for loam and sand, for low and high soil bulk density, for the different scenarios (Table 3) and an initial pressure head of Hini = −10 cm.
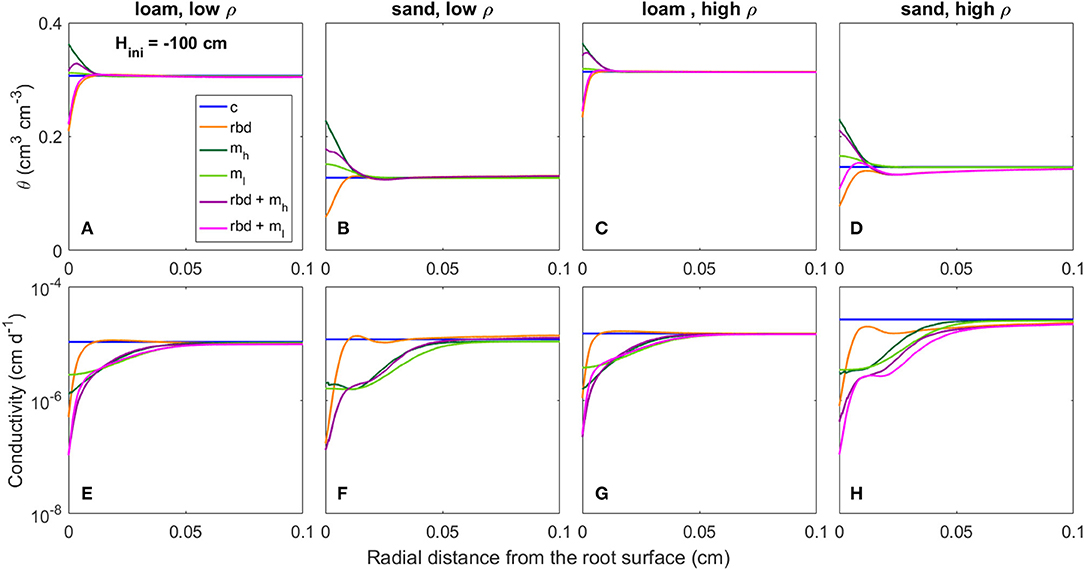
Figure 12. Radial gradients of water content (θ) (A–D) and soil hydraulic conductivity (E–H) at the start of the simulation period for loam and sand, for low and high soil bulk density, for the different scenarios (Table 3) and an initial pressure head of Hini = −100 cm.
At an initial pressure head of −10 cm, the low rhizosphere bulk density in the immediate vicinity of the root led to an increase in water content at the root boundary in loam for both bulk densities and the high density sand (Figures 11A,C,D) and to a decrease for the low-density sand (Figure 11B). At an initial pressure head of −100 cm, the low rhizosphere bulk density close to the root led to a decrease in soil water content for both soil types and bulk densities (Figures 12A–D). These differences as well as the irregular course of the water content curve can be explained by the differences in the inflection points of the water retention curves for the different soil types and bulk densities [Figure 9 (rbd)]. At an initial pressure head of −10 cm, mucilage did not have a significant impact on soil water content, since its effect on retention starts at lower pressure heads [Figure 9 (mh, ml), Figures 11A–D]. At an initial pressure head of −100 cm, the effect of mucilage is already visible through a higher water content at the root surface [Figure 9 (mh, ml), Figures 12A–D].
At an initial pressure head of −10 cm, the gradients in rhizosphere bulk density led to an increase in hydraulic conductivity in the immediate vicinity of the root in high-density loam and sand (Figures 11G,H), and to a decrease in low-density loam and sand (Figures 11E,F). At an initial pressure head of −100 cm, the gradients in rhizosphere bulk density led to a decrease in hydraulic conductivity at the root surface for both soil types and bulk densities (Figures 12A–D). At both initial pressure heads as well as for both soil types and bulk densities, mucilage led to a decrease in hydraulic conductivity in the immediate vicinity of the root due to the impact of viscosity (Figures 11E–H, 12E–H).
Figures 13, 14 show for the two initial pressure heads, soil types, soil bulk densities, and for all scenarios the net transpiration rate, the cumulative transpiration rate as well as the cumulative transpiration of the scenarios with rhizosphere bulk density and/or mucilage gradients relative to the control scenario. Due to the huge gradients in pressure head as well as in soil hydraulic conductivity in the rhizosphere, the simulation scenarios with low-density sand, including rhizosphere bulk density variation and low mucilage concentration [Figure 13B (rbd + ml) and Figure 14B (rbd + ml)] did not converge and were therefore omitted.
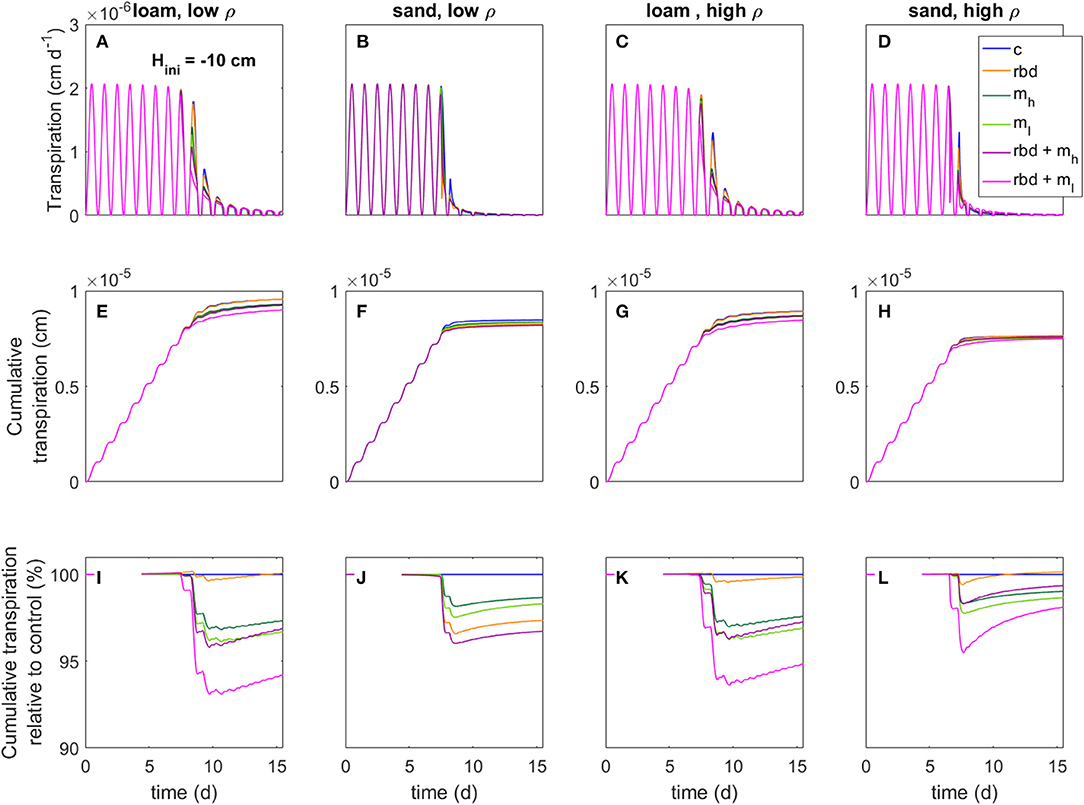
Figure 13. Transpiration rates (A–D), cumulative transpiration rates (E–H), and cumulative transpiration rate relative to the control scenario (I–L) for loam and sand as well as for low and high soil bulk density for an initial pressure head of Hini = −10 cm (for better visibility, we only show simulation day 7 to 15), an overview of the different scenarios is given in Table 3.
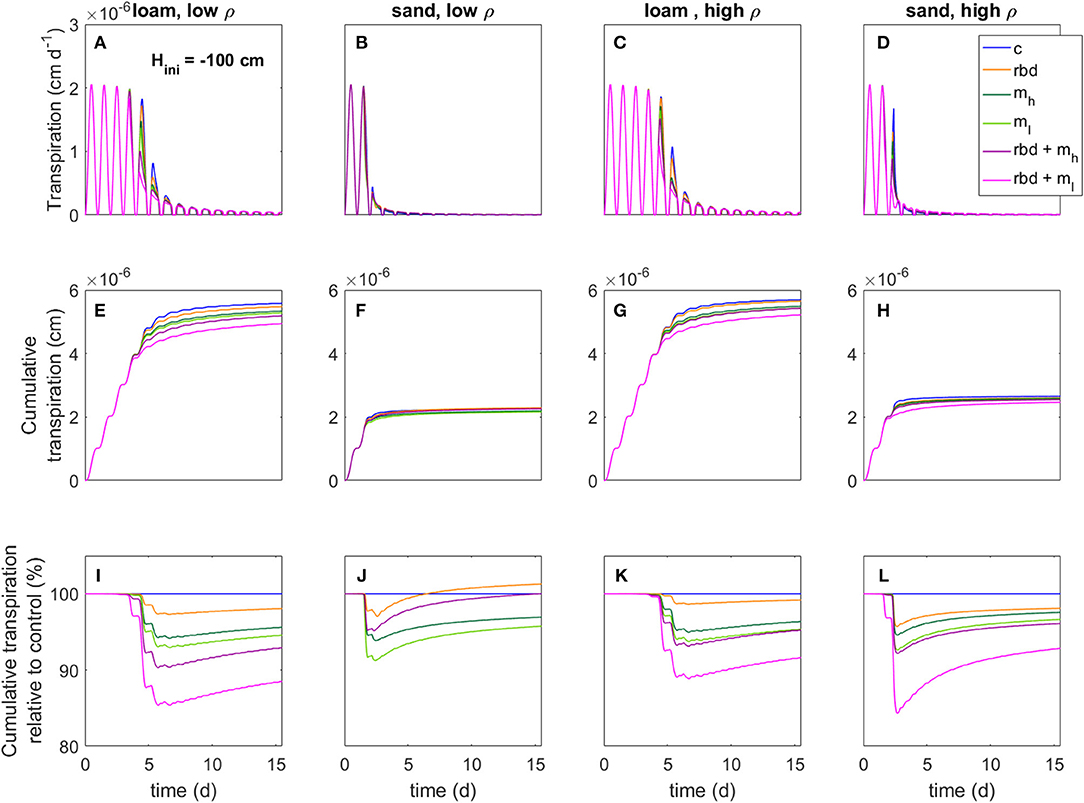
Figure 14. Transpiration rates (A–D), cumulative transpiration rates (E–H), and cumulative transpiration rate relative to the control scenario (I–L) for loam and sand as well as for low and high soil bulk density for an initial pressure head of Hini = −100 cm, an overview of the different scenarios is given in Table 3.
Compared to the control scenario, the rhizosphere bulk density gradient led to an earlier water stress onset and a higher reduction in the transpiration rate by 2–4% for both initial pressure heads, soil types and bulk densities (Figures 13, 14). This can be explained by the lower soil hydraulic conductivity at the root surface due to the drop in rhizosphere bulk density, which limited the water transport toward the root [Figure 10 (rbd)]. Over time, however, the cumulative transpiration in the rhizosphere bulk density scenarios approached that of the control scenario (Figures 13I–L, 14I–L). Due to the initially large amount of available water in the scenarios with loam and high-density sand at an initial pressure head of −10 cm (Figures 13I, L, K), the cumulative transpiration in the rhizosphere bulk density scenarios was even higher than in the control scenario at the end of the simulation.
The presence of mucilage also led to an earlier water stress onset and a higher reduction in the transpiration rate by 2–4% compared to the control scenario for both soil types and bulk densities (Figures 13, 14). The reason is again the lower soil hydraulic conductivity close to the root surface, which limited water transport [Figure 10 (mh, ml)]. Interestingly, in the scenarios with sand, at pressure heads < ~ −500 cm the soil hydraulic conductivity directly at the root surface was actually higher than in the control scenario for the high mucilage concentration [Figure 10 (B mh, D mh)]. However, this effect could not compensate for the lower hydraulic conductivity at a greater distance from the root surface, where the mucilage concentration was low and the effect of the viscosity was stronger than the effect of the increased water retention. The decrease in transpiration was stronger for the low than for the high mucilage concentration. This is because at low mucilage concentrations the increase in viscosity is more significant compared to the increase in water retention.
The combination of rhizosphere bulk density and mucilage gradients (scenarios rbd + mh, rbd + ml) led to an even earlier onset of water stress, respectively, an even higher reduction in transpiration rate by 5 to 8% (Figures 13, 14). Interestingly, this decrease was much more pronounced for the low than for the high mucilage concentration. This is because the combination of the rhizosphere bulk density gradient with a low mucilage concentration not only increased the viscosity but also decreased water retention in the rhizosphere, which was not the case with the high mucilage concentration [Figure 9 (rbd + mh, rbd + ml) and Figure 10 (rbd + mh, rbd + ml)]. This resulted in a drastic reduction of the pressure head and the soil hydraulic conductivity at the root-soil boundary.
The impact of gradients in rhizosphere bulk density was stronger when the soil was initially drier. This is caused by differences in the amount of available water, which depends on the initial pressure heads. The low rhizosphere bulk density in the immediate vicinity of the root led to an increased amount of available water if the initial pressure head was higher and to a decreased amount of available water if the initial pressure head was lower (Figures 13, 14).
The intensity of the effect of rhizosphere bulk density and mucilage gradients was different for the two different soil types and bulk densities. However, there could not be identified a general rule, for which soil type or bulk density the effect was greater. It all depended on the initial soil hydraulic conditions and therefore on the soil hydraulic properties of the specific soil.
Discussion
Gradients in Rhizosphere Bulk Density
The experimentally measured gradients of rhizosphere bulk density extended over a distance of 0.5 to 1 mm from the root surface for the loam and sand, respectively. A typical decrease in rhizosphere bulk density was observed in the immediate vicinity of the root and, in loam, a minor soil compaction was observed further away from the root (Figure 4). These observations agree well with previous findings (Helliwell et al., 2017, 2019; Koebernick et al., 2019; Lucas et al., 2019). The decrease in rhizosphere bulk density in the immediate vicinity of the root was assumed to originate from an increased number of larger pores. An increased number of larger pores again leads to a reduced retention and conductivity at intermediate to low water potentials, which is in line with experimental findings by Whalley et al. (2005). Radial soil compaction, such as described in many earlier studies (Bruand et al., 1996; Vollsnes et al., 2010; Aravena et al., 2011, 2014; Koebernick et al., 2017; Lucas et al., 2019), was much less significant than soil loosening in our experimental observations. A compaction of the rhizosphere associated with an increase in the number of smaller pores would lead to an increased retention and conductivity at medium to low water potentials, as observed by Aravena et al. (2014).
Gradients in Mucilage Concentration
We have used values from the literature to predict the distribution of mucilage in the rhizosphere of a maize plant. This was achieved by solving the diffusion-reaction equation. The most important parameters affecting the mucilage concentration in the diffusion-reaction equation are the mucilage deposition rate and the liquid diffusion coefficient of mucilage. According to the range of plausible literature values (Chaboud, 1983; Zickenrott et al., 2016), we used mucilage deposition rates of 12 (low) and 24 (high) μg d−1 per root tip. This led to maximum concentrations of mucilage derivatives between 5 and 10 mg g−1 dry soil, which is within the range of plausible mucilage concentration values of 0.05–50 mg g−1 dry soil specified by Zickenrott et al. (2016). Observed mucilage deposition rates of Zea mays are lower than those of other plants such as Vicia faba or Lupinus albus where values of up to 34 μg d−1 per root tip were measured (Zickenrott et al., 2016). Such high mucilage deposition rates would lead to a larger proportion of the root system being affected by mucilage and therefore to a larger impact of mucilage on root water uptake. The gradient in mucilage concentration from the root surface to the bulk soil as well as the extent of the rhizosphere that is affected by mucilage is determined by the liquid diffusion coefficient (Zickenrott et al., 2016; Holz et al., 2018b). However, mucilage diffusion can only be expected if the mucilage is freshly exuded. Dry mucilage has been shown to be firmly bound to soil particles, from where it cannot diffuse freely into the soil (Ahmed et al., 2014; Albalasmeh and Ghezzehei, 2014). We parameterized the liquid diffusion coefficient of mucilage with a value from literature (Sealey et al., 1995) and assumed that only fresh mucilage, but not mucilage derivatives can diffuse into the soil. Our simulation model predicted a rhizosphere thickness of ~0.6 mm, which corresponds well to the experimentally found values by Holz et al. (2018a).
Relation Between Rhizosphere Gradients and Soil Hydraulic Parameters
We used the pedotransfer functions by Assouline (2006a,b) and Carman (1937) to relate the changes in rhizosphere bulk density to changes in soil hydraulic parameters. These pedotransfer functions were originally developed based on differently compacted soil samples from the field. Due to a lack of more appropriate functions (Alaoui et al., 2011), we assumed that these pedotransfer functions are also valid at the rhizosphere scale. Further experimental studies on the effects of changes in pore size distribution on soil hydraulic properties at the rhizosphere scale are needed. In our model, we use the Richards equation to simulate water flow in soil at the continuum scale. The reduced rhizosphere bulk density at the root-soil interface is thereby accounted for by adjusting the van Genuchten parameters according to the pedotransfer functions by Assouline (2006a,b). In reality, it can be expected that the reduced rhizosphere bulk density at the root-soil interface is the result of averaging differences in rhizosphere bulk density on the pore scale i.e., averaging gaps and the density of unchanged soil aggregates (Carminati et al., 2013). Considering that the loss of root-soil contact not only reduces, but prevents water flow, the unsaturated hydraulic conductivity could be lower than predicted by the pedotransfer functions by Assouline (2006a,b). Carminati et al. (2008) predicted a decrease in unsaturated conductivity due to a loss of contact between soil aggregates by a few orders of magnitude. This would lead to a greater reduction in transpiration due to the gradient of rhizosphere bulk density than predicted by our simulation model. A possibility to take into account a stronger reduction in unsaturated conductivity due to a reduced contact area is the increase of the tortuosity parameter l (Equation 11) such as proposed by Schlüter et al. (2012) and Carminati et al. (2008). However, currently there are no pedotransfer functions to parameterize the tortuosity parameter when facing gap formation.
To evaluate the effect of mucilage concentration on the soil water retention curve and further on soil hydraulic parameters, we used the model by Kroener et al. (2014). Qualitatively, the impact of mucilage on soil hydraulic parameters matches well with findings from previous studies such as Carminati et al. (2010) and Carminati and Vetterlein (2013). Quantitatively, however, the effect depends much on the parametrization of the fitting parameters of this model. We chose these fitting parameters using experimental results on the influence of soil texture on the mucilage-related increase in water content at a given water potential from Kroener et al. (2018). However, this experimental information gives rather a plausible range than actual values for the fitting parameters and our parameter choice can be expected to have affected the simulation results.
Challenges of the Non-linearity of the Parameterization of the Mucilage Model
Several parameter functions show a huge non-linearity, e.g., the soil water retention and soil hydraulic conductivity functions of the Mualem-van Genuchten parameterisation, the Millington-Quirk model (Equation 3) and the models describing how rhizosphere bulk density and mucilage (Equation 5–8) alter hydraulic functions. These non-linearities could lead to convergence problems in the numerical scheme, especially if all feedback mechanisms between mucilage spreading and hydraulic dynamics were considered.
Therefore, we had to make a few simplifications in this study, namely: (a) to calculate the spreading of mucilage around a root, we assumed a water content that is constant in space and time; (b) we assumed a stationary radial mucilage distribution throughout the entire simulation period; (c) we neglected hydrodynamic dispersion of mucilage, which is quite reasonable due to the rather slow water fluxes; (d) We assumed superposition of the effects of rhizosphere bulk density and mucilage concentration on soil hydraulic parameters; this is possibly a simplification, because the effect of mucilage on soil hydraulic properties depends strongly on pore size.
Despite these simplifications, the results show very realistic distributions, indicating that this approach manages the challenge to be both reasonable and feasible at the same time. This approach to first simulate spreading of mucilage and then based on this the hydraulic dynamics allows to simulate the coupled physical processes and avoids several numerical convergence problems that could have been expectable due to the highly non-linear parameterisations and feedback mechanisms.
The Impact of Rhizosphere Gradients in Rhizosphere Bulk Density and Mucilage Concentration on Water Dynamics
We found that the gradients of rhizosphere bulk density and mucilage concentration have a significant influence on the hydraulic properties of the rhizosphere (Figures 9, 10). However, their influence on the absolute amount of water taken up by the root is–depending on the initial conditions and the duration of water absorption by the root–rather small (Figures 13E–H, 14E–H). The greatest effect of rhizosphere properties on root water uptake was observed in the scenarios in which gradients of rhizosphere bulk density and mucilage concentration were combined. While the lower rhizosphere bulk density led to a lower water retention, the presence of mucilage led to an increased viscosity. In combination, this significantly reduced the hydraulic conductivity of the soil and consequently resulted in an earlier water stress onset and a stronger reduction in the transpiration rate. However, considering that the limiting factor for root water uptake was not the available water volume but the reduced soil hydraulic conductivity, the process of root water uptake took longer, but the roots eventually took up the same amount of water. The gradients in rhizosphere bulk density and mucilage concentration therefore keep transpiration at a lower level for a longer time, which prevents fast dehydration and can be regarded as beneficial.
The initial soil hydraulic conditions had a strong effect on the scenarios with rhizosphere bulk density gradient. Our measured rhizosphere bulk density gradient led to a higher water retention when the soil was initially wet and to a lower water retention when the soil was drier, at field capacity. Depending on the initial pressure head, the water content in the rhizosphere was therefore either higher or lower than in the surrounding bulk soil at the start of the simulation. During a drying scenario, root water uptake could be maintained longer if the rhizosphere water content was initially higher.
The gradients in rhizosphere bulk density and mucilage concentration may play an important role in the distribution of root water uptake of an entire root system. To study this effect, however, a three-dimensional model of water flow in soil and roots (e.g., Mai et al., 2019) must be coupled with rhizosphere bulk density and mucilage concentration gradients along the root system. Such a model could then also be used to examine the effects of rhizosphere processes on soil water dynamics at a larger scale (e.g., field scale). For model validation, experimental measurements are needed, which take into account the spatial variability of water infiltration and soil hydraulic properties due to differences in the vegetation cover and therefore differences in mucilage release and soil bulk density. An appropriate method was proposed by Lassabatere et al. (2019). Combining a 3D rhizosphere model with further experimental measurements would provide important information on how rhizosphere processes can help achieve a resilient and healthy soil water system (Keesstra et al., 2018; Visser et al., 2019).
According to our simulation results, gradients in rhizosphere bulk density and mucilage concentration lead to an initially lower, but longer lasting root water uptake. A general statement on whether gradients in rhizosphere bulk density or mucilage concentration lead to a higher or lower root water uptake cannot be made, however, as this depends on the characteristics of the gradients, the initial soil hydraulic conditions, the soil type, the soil bulk density, the soil hydraulic properties, and–in the case of mucilage–on the model parameterization. Aravena et al. (2014) found that rhizosphere compaction leads to an increase in water flow toward the roots in a very loose soil. In our experiments, however, the predominant effect of the rhizosphere bulk density gradients was not a compaction, but a loosening of the rhizosphere, and our simulations therefore showed reduced water flow to the roots. Using model simulation, Schwartz et al. (2016) observed that the presence of mucilage in a sandy soil led to a delay in the onset of water stress and thus to a longer maintenance of higher transpiration rates. Our model simulations on a loamy and a sandy soil, however, led to contrasting observations, which has several reasons. Schwartz et al. (2016) assumed constant mucilage concentrations in the rhizosphere and did not consider radial gradients. The presence of radial gradients, however, has an enormous effect on soil hydraulic conductivity and consequently influences root water uptake (Figures 10, 13, 14). At low pressure heads, high mucilage concentrations lead to a larger soil hydraulic conductivity, while low mucilage concentrations lead to a lower soil hydraulic conductivity (Figure 10). When radial gradients are considered, the low mucilage concentration at the outer edge of the rhizosphere results in a low soil hydraulic conductivity, which limits water transport to the root. When no radial gradients are considered, the soil hydraulic conductivity of the entire rhizosphere is larger than that of the bulk soil and water transport to the root is promoted. This phenomenon of an earlier reduction in transpiration at low mucilage concentrations was also shown by Carminati et al. (2016a).
Conclusion
In this study, we used a mechanistic simulation model to evaluate the impact of gradients in rhizosphere bulk density and mucilage concentration on soil water dynamics. These gradients lead to differences in soil hydraulic properties and consequently to differences in root water uptake. Our simulations showed that the experimentally observed decrease in rhizosphere bulk density in the immediate vicinity of the root leads to an earlier onset of water stress and to lower transpiration rates. The decreasing radial mucilage concentrations increase the viscosity in the rhizosphere, which leads to a decrease in soil hydraulic conductivity. This in turn also leads to an earlier onset of water stress. When both gradients in rhizosphere bulk density and mucilage concentration are considered, root water uptake decreases even faster. However, considering that the limiting factor for root water uptake was not the available water volume but the reduced soil hydraulic conductivity, the process of root water uptake took longer, but the roots eventually took up the same amount of water. Gradients in rhizosphere bulk density and mucilage concentration thus appear as a measure to sustain transpiration at a lower level and to avoid fast dehydration.
Our simulations proved the importance of considering gradients in rhizosphere bulk density and mucilage concentration. Low values of rhizosphere bulk density and mucilage concentration lead to extremely low hydraulic conductivities, which are then the limiting factor for water flow to the roots. However, these lows in rhizosphere bulk density and mucilage concentration occur only in a limited portion of the rhizosphere and therefore cannot be accounted for with mean values of rhizosphere properties.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
ML and AS designed the study. ML performed the model simulations. MP carried out the analysis of the bulk density in the rhizosphere and the characterization of the bulk soil hydraulic properties. All authors have participated in the writing of the manuscript.
Funding
This project was carried out in the framework of the priority programme 2089 Rhizosphere spatiotemporal organization-a key to rhizosphere functions funded by the German Research Foundation DFG under the project numbers 403641034, 403640293, and 403801423.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Caroline Marcon and Frank Hochholdinger (University of Bonn) for providing the maize B73 seeds.
References
Ahmed, M. A., Kroener, E., Holz, M., Zarebanadkouki, M., and Carminati, A. (2014). Mucilage exudation facilitates root water uptake in dry soils. Funct. Plant Biol. 41, 1129–1137. doi: 10.1071/FP13330
Alaoui, A., Lipiec, J., and Gerke, H. H. (2011). A review of the changes in the soil pore system due to soil deformation: a hydrodynamic perspective. Soil Tillage Res. 115–116, 1–15. doi: 10.1016/j.still.2011.06.002
Albalasmeh, A. A., and Ghezzehei, T. A. (2014). Interplay between soil drying and root exudation in rhizosheath development. Plant Soil 374, 739–751. doi: 10.1007/s11104-013-1910-y
Aravena, J. E., Berli, M., Ghezzehei, T. A., and Tyler, S. W. (2011). Effects of root-induced compaction on rhizosphere hydraulic properties - X-ray microtomography imaging and numerical simulations. Environ. Sci. Technol. 45, 425–431. doi: 10.1021/es102566j
Aravena, J. E., Berli, M., Ruiz, S., Suárez, F., Ghezzehei, T. A., and Tyler, S. W. (2014). Quantifying coupled deformation and water flow in the rhizosphere using X-ray microtomography and numerical simulations. Plant Soil 376, 95–110. doi: 10.1007/s11104-013-1946-z
Assouline, S. (2006a). Modeling the relationship between soil bulk density and the hydraulic conductivity function contribution of the agricultural research organization, institute of soil, water and environmental sciences, Bet Dagan, Israel, No. 608/05. Vadose Zone J. 5, 697–705. doi: 10.2136/vzj2005.0084
Assouline, S. (2006b). Modeling the relationship between soil bulk density and the water retention curvecontribution of the agricultural research organization, institute of soil, water and environmental sciences, Bet Dagan, Israel, No. 607/05. Vadose Zone J. 5, 554–563. doi: 10.2136/vzj2005.0083
Bresler, E. (1973). Simultaneous transport of solutes and water under transient unsaturated flow conditions. Water Resour. Res. 9, 975–986. doi: 10.1029/WR009i004p00975
Bruand, A., Cousin, I., Nicoullaud, B., Duval, O., and Bégon, J. C. (1996). Backscattered electron scanning images of soil porosity for analyzing soil compaction around roots. Soil Sci. Soc. Am. J. 60, 895–901. doi: 10.2136/sssaj1996.03615995006000030031x
Cai, G., Vanderborght, J., Couvreur, V., Mboh, C. M., and Vereecken, H. (2018). Parameterization of root water uptake models considering dynamic root distributions and water uptake compensation. Vadose Zone J. 17:160125. doi: 10.2136/vzj2016.12.0125
Carman, P. C. (1937). Fluid flow through granular beds. Chem. Eng. Res. Design 75, S32–S48. doi: 10.1016/S0263-8762(97)80003-2
Carminati, A. (2013). Rhizosphere wettability decreases with root age: a problem or a strategy to increase water uptake of young roots? Front. Plant Sci. 4:298. doi: 10.3389/fpls.2013.00298
Carminati, A., Kaestner, A., Lehmann, P., and Flühler, H. (2008). Unsaturated water flow across soil aggregate contacts. Adv. Water Resour. 31, 1221–1232. doi: 10.1016/j.advwatres.2008.01.008
Carminati, A., Kroener, E., Ahmed, M. A., Zarebanadkouki, M., Holz, M., and Ghezzehei, T. (2016a). Water for carbon, carbon for water. Vadose Zone J. 15, 1–10. doi: 10.2136/vzj2015.04.0060
Carminati, A., Moradi, A. B., Vetterlein, D., Vontobel, P., Lehmann, E., Weller, U., et al. (2010). Dynamics of soil water content in the rhizosphere. Plant Soil 332, 163–176. doi: 10.1007/s11104-010-0283-8
Carminati, A., and Vetterlein, D. (2013). Plasticity of rhizosphere hydraulic properties as a key for efficient utilization of scarce resources. Ann. Bot. 112, 277–290. doi: 10.1093/aob/mcs262
Carminati, A., Vetterlein, D., Koebernick, N., Blaser, S., Weller, U., and Vogel, H. J. (2013). Do roots mind the gap? Plant Soil 367, 651–661. doi: 10.1007/s11104-012-1496-9
Carminati, A., Zarebanadkouki, M., Kroener, E., Ahmed, M. A., and Holz, M. (2016b). Biophysical rhizosphere processes affecting root water uptake. Ann. Bot. 118, 561–571. doi: 10.1093/aob/mcw113
Chaboud, A. (1983). Isolation, purification and chemical composition of maize root cap slime. Plant Soil 73, 395–402. doi: 10.1007/BF02184316
Chou, H., Wu, L., Zeng, L., and Chang, A. (2012). Evaluation of solute diffusion tortuosity factor models for variously saturated soils. Water Resour. Res. 48, 1–11. doi: 10.1029/2011WR011653
Daly, K. R., Mooney, S. J., Bennett, M. J., Crout, N. M., Roose, T., and Tracy, S. R. (2015). Assessing the influence of the rhizosphere on soil hydraulic properties using X-ray computed tomography and numerical modelling. J. Exp. Bot. 66, 2305–2314. doi: 10.1093/jxb/eru509
Dexter, A. R. (1987). Compression of soil around roots. Plant Soil 97, 401–406. doi: 10.1007/BF02383230
Doussan, C., Pagès, L., and Pierret, A. (2009). “Soil exploration and resource acquisition by plant roots: an architectural and modelling point of view,” in Sustainable Agriculture, eds. E. Lichtfouse, M. Navarrete, P. Debaeke, S. Véronique, and C. Alberola (Dordrecht: Springer), 583–600. doi: 10.1007/978-90-481-2666-8_36
Gardner, W. R. (1960). Dynamic aspects of water availability to plants. Soil Sci. 89, 63–73. doi: 10.1097/00010694-196002000-00001
Haupenthal, A., Bentz, J., Brax, M., Schuetzenmeister, K., Jungkunst, H., and Kroener, E. (2020). Plants Possibility to Control Soil Gas Exchanges via Mucilage. EGU General Assembly.
Helliwell, J. R., Sturrock, C. J., Mairhofer, S., Craigon, J., Ashton, R. W., Miller, A. J., et al. (2017). The emergent rhizosphere: imaging the development of the porous architecture at the root-soil interface. Sci. Rep. 7:14875. doi: 10.1038/s41598-017-14904-w
Helliwell, J. R., Sturrock, C. J., Miller, A. J., Whalley, W. R., and Mooney, S. J. (2019). The role of plant species and soil condition in the structural development of the rhizosphere. Plant Cell Environ. 42, 1974–1986. doi: 10.1111/pce.13529
Hinsinger, P., Bengough, A. G., Vetterlein, D., and Young, I. M. (2009). Rhizosphere: biophysics, biogeochemistry and ecological relevance. Plant Soil 321, 117–152. doi: 10.1007/s11104-008-9885-9
Holz, M., Leue, M., Ahmed, M. A., Benard, P., Gerke, H. H., and Carminati, A. (2018a). Spatial distribution of mucilage in the rhizosphere measured with infrared spectroscopy. Front. Environ. Sci. 6:87. doi: 10.3389/fenvs.2018.00087
Holz, M., Zarebanadkouki, M., Kaestner, A., Kuzyakov, Y., and Carminati, A. (2018b). Rhizodeposition under drought is controlled by root growth rate and rhizosphere water content. Plant Soil 423, 429–442. doi: 10.1007/s11104-017-3522-4
Iijima, M., Sako, Y., and Rao, T. P. (2003). A new approach for the quantification of root-cap mucilage exudation in the soil. Plant Soil 255, 399–407. doi: 10.1023/A:1026183109329
Keesstra, S., Mol, G., De Leeuw, J., Okx, J., De Cleen, M., and Visser, S. (2018). Soil-related sustainable development goals: four concepts to make land degradation neutrality and restoration work. Land 7:133. doi: 10.3390/land7040133
Kim, T. K., Silk, W. K., and Cheer, A. Y. (1999). A mathematical model for pH patterns in the rhizospheres of growth zones. Plant Cell Environ. 22, 1527–1538. doi: 10.1046/j.1365-3040.1999.00512.x
Koebernick, N., Daly, K. R., Keyes, S. D., Bengough, A. G., Brown, L. K., Cooper, L. J., et al. (2019). Imaging microstructure of the barley rhizosphere: particle packing and root hair influences. New Phytol. 221, 1878–1889. doi: 10.1111/nph.15516
Koebernick, N., Daly, K. R., Keyes, S. D., George, T. S., Brown, L. K., Raffan, A., et al. (2017). High-resolution synchrotron imaging shows that root hairs influence rhizosphere soil structure formation. New Phytol. 216, 124–135. doi: 10.1111/nph.14705
Koebernick, N., Schlüter, S., Blaser, S. R. G. A., and Vetterlein, D. (2018). Root-soil contact dynamics of vicia faba in sand. Plant Soil 431, 417–431. doi: 10.1007/s11104-018-3769-4
Kroener, E., Holz, M., Zarebanadkouki, M., Ahmed, M., and Carminati, A. (2018). Effects of mucilage on rhizosphere hydraulic functions depend on soil particle size. Vadose Zone J. 17:170056. doi: 10.2136/vzj2017.03.0056
Kroener, E., Zarebanadkouki, M., Bittelli, M., and Carminati, A. (2016). Simulation of root water uptake under consideration of nonequilibrium dynamics in the rhizosphere. Water Resour. Res. 52, 5755–5770. doi: 10.1002/2015WR018579
Kroener, E., Zarebanadkouki, M., Kaestner, A., and Carminati, A. (2014). Nonequilibrium water dynamics in the rhizosphere: how mucilage affects water flow in soils. Water Resour. Res. 50, 6479–6495. doi: 10.1002/2013WR014756
Lassabatere, L., Di Prima, S., Angulo-Jaramillo, R., Keesstra, S., and Salesa, D. (2019). Beerkan multi-runs for characterizing water infiltration and spatial variability of soil hydraulic properties across scales. Hydrol. Sci. J. 64, 165–178. doi: 10.1080/02626667.2018.1560448
Leij, F. J., and Ghezzehei, T. A. Or D. (2002a). Analytical models for soil pore-size distribution after tillage. Soil Sci. Soc. Am. J. 66, 1104–1114. doi: 10.2136/sssaj2002.1104
Leij, F. J., and Ghezzehei, T. A. Or D. (2002b). Modeling the dynamics of the soil pore-size distribution. Soil Till. Res. 64, 61–78. doi: 10.1016/S0167-1987(01)00257-4
Lucas, M., Schlüter, S., Vogel, H.-J., and Vetterlein, D. (2019). Roots compact the surrounding soil depending on the structures they encounter. Sci. Rep. 9:16236. doi: 10.1038/s41598-019-52665-w
Mai, T. H., Schnepf, A., Vereecken, H., and Vanderborght, J. (2019). Continuum multiscale model of root water and nutrient uptake from soil with explicit consideration of the 3D root architecture and the rhizosphere gradients. Plant Soil 439, 273–292. doi: 10.1007/s11104-018-3890-4
Mary, B., Fresneau, C., Morel, J. L., and Mariotti, A. (1993). C and N cycling during decomposition of root mucilage, roots and glucose in soil. Soil Biol. Biochem. 25, 1005–1014. doi: 10.1016/0038-0717(93)90147-4
Materechera, S. A., Dexter, A. R., and Alston, A. M. (1991). Penetration of very strong soils by seedling roots of different plant species. Plant Soil 135, 31–41. doi: 10.1007/BF00014776
Meunier, F., Zarebanadkouki, M., Ahmed, M. A., Carminati, A., Couvreur, V., and Javaux, M. (2018). Hydraulic conductivity of soil-grown lupine and maize unbranched roots and maize root-shoot junctions. J. Plant Physiol. 227, 31–44. doi: 10.1016/j.jplph.2017.12.019
Millington, R., and Quirk, J. (1961). Permeability of porous solids. Trans. Faraday Soc. 57, 1200–1207. doi: 10.1039/tf9615701200
Moldrup, P., Olesen, T., Schjønning, P., Yamaguchi, T., and Rolston, D. E. (2000). Predicting the gas diffusion coefficient in undisturbed soil from soil water characteristics. Soil Sci. Soc. Am. J. 64, 94–100. doi: 10.2136/sssaj2000.64194x
Moradi, A. B., Carminati, A., Vetterlein, D., Vontobel, P., Lehmann, E., Weller, U., et al. (2011). Three-dimensional visualization and quantification of water content in the rhizosphere. New Phytol. 192, 653–663. doi: 10.1111/j.1469-8137.2011.03826.x
Mualem, Y. (1976). A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 12, 513–522. doi: 10.1029/WR012i003p00513
Nelder, J. A., and Mead, R. (1965). A simplex method for function minimization. Comput. J. 7, 308–313. doi: 10.1093/comjnl/7.4.308
Nguyen, C., Froux, F., Recous, S., Morvan, T., and Robin, C. (2008). Net N immobilisation during the biodegradation of mucilage in soil as affected by repeated mineral and organic fertilisation. Nutr. Cycl. Agroecosyst. 80, 39–47. doi: 10.1007/s10705-007-9119-1
Or Ghezzehei, D. T. A. (2002). Modeling post-tillage soil structural dynamics: a review. Soil Till. Res. 64, 41–59. doi: 10.1016/S0167-1987(01)00256-2
Or Leij, D. F. J., Snyder, V., and Ghezzehei, T. A. (2000). Stochastic model for posttillage soil pore space evolution. Water Resour. Res. 36, 1641–1652. doi: 10.1029/2000WR900092
Or Phutane, D. S., and Dechesne, A. (2007). Extracellular polymeric substances affecting pore-scale hydrologic conditions for bacterial activity in unsaturated soils. Vadose Zone J. 6, 298–305. doi: 10.2136/vzj2006.0080
Papendick, R. I., and Campbell, G. S. C. (1981). “Theory and Measurement of Water Potential,” in Water Potential Relations in Soil Microbiology, eds J. Parr, W. Gardner, and L. Elliott. doi: 10.2136/sssaspecpub9.c1
Partridge, G. P., Lehman, D. M., and Huebner, R. S. (1999). Modeling the reduction of vapor phase emissions from surface soils due to soil matrix effects: porosity/tortuosity concepts. J. Air Waste Manage. Assoc. 49, 412–423. doi: 10.1080/10473289.1999.10463812
Phalempin, M., Lippold, E., Vetterlein, D., and Schlüter, S. (2020). An Improved Method for the Segmentation of Roots from X-ray Computed Tomography 3D Images: Rootine v.2. In Review. doi: 10.21203/rs.3.rs-96550/v1
Schindelin, J., Arganda-Carreras, I., Frise, E., Kaynig, V., Longair, M., Pietzsch, T., et al. (2012). Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682. doi: 10.1038/nmeth.2019
Schlüter, S., Vogel, H.-J., Ippisch, O., Bastian, P., Roth, K., Schelle, H., et al. (2012). Virtual soils: assessment of the effects of soil structure on the hydraulic behavior of cultivated soils. Vadose Zone J. 11:vzj2011.0174. doi: 10.2136/vzj2011.0174
Schwartz, N., Carminati, A., and Javaux, M. (2016). The impact of mucilage on root water uptake—a numerical study. Water Resour. Res. 52, 264–277. doi: 10.1002/2015WR018150
Sealey, L. J., McCully, M. E., and Canny, M. J. (1995). The expansion of maize root-cap mucilage during hydration. 1. Kinetics. Physiol. Plant. 93, 38–46. doi: 10.1034/j.1399-3054.1995.930107.x
Stange, C. F., and Horn, R. (2005). Modeling the soil water retention curve for conditions of variable porosity. Vadose Zone J. 4, 602–613. doi: 10.2136/vzj2004.0150
Suzuki, M., Shinmura, T., Iimura, K., and Hirota, M. (2008). Study of the wall effect on particle packing structure using X-ray micro computed tomography. Adv. Powd. Technol. 19, 183–195. doi: 10.1163/156855208X293817
van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44, 892–898. doi: 10.2136/sssaj1980.03615995004400050002x
van Veelen, A., Tourell, M. C., Koebernick, N., Pileio, G., and Roose, T. (2018). Correlative visualization of root mucilage degradation using X-ray CT and MRI. Front. Environ. Sic. 6:32. doi: 10.3389/fenvs.2018.00032
Vetterlein, D., Lippold, E., Schreiter, S., Phalempin, M., Fahrenkampf, T., Hochholdinger, F., et al. (2021). Experimental platforms for the investigation of spatiotemporal patterns in the rhizosphere – laboratory and field scale. J. Plant Nutr. Soil Sci. doi: 10.1002/jpln.202000079
Visser, S., Keesstra, S., Maas, G., and De Cleen, M. (2019). Soil as a basis to create enabling conditions for transitions towards sustainable land management as a key to achieve the SDGs by 2030. Sustainability 11:6792. doi: 10.3390/su11236792
Vollsnes, A. V., Futsaether, C. M., and Bengough, A. G. (2010). Quantifying rhizosphere particle movement around mutant maize roots using time-lapse imaging and particle image velocimetry. Eur. J. Soil Sci. 61, 926–939. doi: 10.1111/j.1365-2389.2010.01297.x
Watt, M., Silk, W. K., and Passioura, J. B. (2006). Rates of root and organism growth, soil conditions, and temporal and spatial development of the rhizosphere. Ann. Bot. 97, 839–855. doi: 10.1093/aob/mcl028
Whalley, W. R., Riseley, B., Leeds-Harrison, P. B., Bird, N. R. A., Leech, P. K., and Adderley, W. P. (2005). Structural differences between bulk and rhizosphere soil. Eur. J. Soil Sci. 56, 353–360. doi: 10.1111/j.1365-2389.2004.00670.x
Zickenrott, I.-M., Woche, S. K., Bachmann, J., Ahmed, M. A., and Vetterlein, D. (2016). An efficient method for the collection of root mucilage from different plant species—a case study on the effect of mucilage on soil water repellency. J. Plant Nutr. Soil Sci. 179, 294–302. doi: 10.1002/jpln.201500511
Keywords: mucilage, bulk density, rhizosphere model, root water uptake, COMSOL, rhizosphere
Citation: Landl M, Phalempin M, Schlüter S, Vetterlein D, Vanderborght J, Kroener E and Schnepf A (2021) Modeling the Impact of Rhizosphere Bulk Density and Mucilage Gradients on Root Water Uptake. Front. Agron. 3:622367. doi: 10.3389/fagro.2021.622367
Received: 28 October 2020; Accepted: 02 February 2021;
Published: 24 February 2021.
Edited by:
Antonio Rafael Sánchez-Rodríguez, University of Cordoba, SpainReviewed by:
Siul Ruiz, University of Southampton, United KingdomArtemi Cerdà, University of Valencia, Spain
Copyright © 2021 Landl, Phalempin, Schlüter, Vetterlein, Vanderborght, Kroener and Schnepf. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Magdalena Landl, bS5sYW5kbEBmei1qdWVsaWNoLmRl
†These authors have contributed equally to this work
 Magdalena Landl
Magdalena Landl Maxime Phalempin
Maxime Phalempin Steffen Schlüter
Steffen Schlüter Doris Vetterlein
Doris Vetterlein Jan Vanderborght
Jan Vanderborght Eva Kroener1,4
Eva Kroener1,4 Andrea Schnepf
Andrea Schnepf