- 1Department of Civil and Environmental Engineering, School of Engineering, Zhejiang University City College, Hangzhou, China
- 2State Key Laboratory of Internet of Things for Smart City, Department of Civil and Environmental Engineering, University of Macau, Macau SAR, China
- 3MOE Key Laboratory of Intelligence Manufacturing Technology, Department of Civil and Environmental Engineering, College of Engineering, Shantou University, Shantou, China
- 4State Key Laboratory of Internet of Things for Smart City, Department of Civil and Environmental Engineering, University of Macau, Macau SAR, China
- 5Laboratory of Geotechnics, Department of Civil Engineering, Faculty of Engineering and Architecture, University of Ghent, Ghent, Belgium
- 6Deltares, Delft, Netherlands
Tunneling-induced ground surface settlement is associated with many complex influencing factors. Beyond factors related to tunnel geometry and surrounding geological conditions, operational factors related to the shield machine are highly significant because of the complexity of shield-soil interactions. Distinguishing the most relevant factors can be very difficult, for all factors seem to affect tunneling-induced settlement to some degree, with none clearly the most influential. In this research, a machine learning method is adopted to intelligently select features related to tunneling-induced ground settlement based on measured data and form a robust non-parametric model with which to make a prediction. The recorded data from a real construction site were compiled and 12 features related to the operational factors were summarized. Using the intelligent method, two other features in addition to cover depth–pitching angle and rolling angle–were distinguished from among the 12 feature candidates as those most influencing the settlement trough. Another new finding is that advance rate does not emerge in the top 10 selected models from the observational data used. The generated non-parametric model was validated by comparing the measured data from the testing dataset and performance on a new dataset. Sensitivity analysis was conducted to evaluate the contribution of each factor. According to the results, engineers in general practice should attend closely to pitching angle during tunnel excavation in soft soil conditions.
1 Introduction
Underground tunneling is necessary for transportation in urban areas having a large population, and the shield tunnel boring machine (TBM) approach has become popular for its construction, having less effect on the surrounding environment, a relatively high construction rate and so forth. (Verruijt and Booker, 1996; Zheng et al., 2017; Zhou et al., 2017; Elbaz et al., 20182018; Wu et al., 2018; Chen et al., 2019; Lin et al., 2021; Yan et al., 2021; Elbaz et al., 2022; Shen et al., 2022). Nevertheless, ground surface deformations may have destructive effects on adjacent buildings and facilities, raising concerns for engineers and researchers (Leca and New, 2007; Marshall et al., 2010; Zhao et al., 2016; Soga et al., 2017; Zhao et al., 2017; Zhao et al., 2019a; Lu et al., 2019; Moeinossadat and Ahangari, 2019). Accordingly, engineers and researchers strive for reliable estimations of ground surface settlement and have gone to great lengths to model tunneling-induced deformation, including through use of empirical and analytical approaches (Loganathan and Poulos, 1998; Chou and Bobet, 2002; Wu et al., 2018), numerical methods (Maynar and Rodríguez, 2005; Paternesi et al., 2017; Yang et al., 2020; Lyu et al., 2022), and artificial intelligence methods (Santos and Celestino, 2008; Boubou et al., 2010; Zhang et al., 2019; Hajihassani et al., 2020; Lin et al., 2021).
Conventional empirical formulas (Attewell and Hurrell, 1985) present only a limited number of parameters for predicting ground surface settlement. For instance, Peck (Peck, 1969) adopted an inverse Gaussian probability distribution curve, which can be defined by a few parameters to describe the transverse deformation profile of tunneling-induced ground surface settlement based on field observations. Loganathan and Poulos (1998), finding these empirical solutions to lack sufficient influencing factors, introduced the concept of the “undrained gap parameter” with which to consider geometry and equivalent 3D elastic features in their proposed analytical predictions. Because their calculation method is valid only for homogeneous purely elastic clay, the observed settlement in uniform clay has mostly a narrower trough with a larger depth than in the Loganathan and Poulos method of calculation. In these analytical methods (Wu et al., 2015; Elbaz et al., 20182018; Xu and Bezuijen, 2018), each input variable has its own physical meaning and changes in tunneling-induced settlement are interpretable. Nevertheless, some ideal assumptions are inevitable in these analytical methods so as to obtain a closed form solution, potentially causing deviations from practical field measurements, as ideal assumptions could eliminate certain features used to estimate the settlements and also neglect plastic deformation in the soil. Considering the complexity of tunneling-induced settlement, some researchers (Ng et al., 2013; Ibrahim et al., 2015; Soranzo et al., 2015; Zhang et al., 2017; Alagha and Chapman, 2019; Lin et al., 2019) have turned to numeric simulations that integrate complicated boundary conditions, spatial variations of stratigraphy, and elasto-plastic soil behavior. Ng and Lee (2005) conducted a series of three-dimensional numerical simulations to evaluate ground deformations. Huang et al. (2015) used a simplified procedure to analyze the longitudinal performance of shield tunnels and investigated spatial variability using the finite element method. The limitation of numerical methods, however, lies in the evaluation of the input parameters involved in the constitutive models (Ninić et al., 2017). Besides, implementing all operational factors in numeric simulations simultaneously is challenging (Khisamitov and Meschke, 2018; Ren et al., 2018; Shen et al., 2019). However, these operational factors are significant for estimation of tunneling-induced ground surface settlement. Ren et al. (2018) (Ren et al., 2018) evaluated the gap area between the double-O-tube (DOT) shield machine by considering pitching, yawing, and rolling features. Shen et al. (2019) considered pitching angle and yawing angle to investigate shield-soil interactions and proposed a prediction model. Owing to the complexity of shield-soil interactions, data-driven models were triggered using artificial intelligence methods (Cho, 2009; Ochmański et al., 2015; Chen et al., 2016; Pooya Nejad and Jaksa, 2017; Qi and Tang, 2018). Through the flexibility of machine learning methods, some scholars have generated various models with which to make predictions (Shi et al., 1998; Mahdevari et al., 2012; Chen et al., 2016; Bouayad and Emeriault, 2017; Hajihassani et al., 2019). Neaupane and Adhikari (2006) adopted a multi-layer backpropagation neural network to predict tunneling-induced ground movement. Ahangari et al. (2015) adopted Adaptive Neuro-Fuzzy Inference System (ANFIS) and Gene Expression Programming (GEP) methods to establish the relationship between possible influencing factors and tunneling-induced settlement.
In these artificial intelligence methods, the features which is to say influencing factors used to predict ground surface settlement have been summarized chiefly based on experience, which is inherently subjective. Suwansawat and Einstein (2006) classified factors affecting the surface settlement into three categories: The first is related to tunnel geometry, such as tunnel depth and tunnel diameter. The second concerns geological conditions, such as geology at the tunnel crown and invert. The third comprises shield operation factors, such as face pressure, advance rate, pitching angle, etc. Their study provided a comprehensive understanding of possible influencing factors, which they integrated to form a neural network with which to make estimations. Ahangari et al. (2015) selected the same five features adopted in Darabi et al. (2012) to predict tunneling-induced settlement. Santos and Celestino (2008) found that it was not possible to establish a clear relationship between advance rate and surface settlement. Zhang (2019) introduced global sensitivity analysis for feature selection and evaluated the importance of each input variable. Introducing irrelevant input variables can distort the Euclidean distance between different points and degrade the flexibility of prediction. However, seldom have researchers extracted significant features and eliminated irrelevant input candidates so as to obtain a robust prediction model.
In recent decades, the Bayesian inference method has been widely applied in various fields of geotechnical engineering, such as for consolidation (Kelly and Huang, 2015), braced excavation (Qi and Zhou, 2017), pile engineering (Park et al., 2012), and soil nailing (Zhou et al., 2013). One merit of this approach lies in uncertainty quantification; (Phoon and Kulhawy, 1999) an other in model selection (Gamse et al., 2018; Tan et al., 2018; Zhou et al., 2018; Jin et al., 2019a; Jin et al., 2019b). These merits allow the selection of a set of suitable input parameters from designed candidates. Yuen and Ortiz (2016) proposed a novel algorithm, Bayesian nonparametric general regression (BNGR), with which to filter out unrelated input parameters from among possible candidates. This algorithm reformulated the general regression neural network under the Bayesian framework. Except for the ability to reduce unrelated input parameters, this method can preclude the effects of the prior distribution for the adopted regression coefficients–a common challenge in Bayesian frameworks. It provides the possibility of selecting suitable input parameters for complex problems involving many plausible input parameters, such as TBM tunneling projects.
In the present study, 12 possible input parameters potentially influencing maximum tunneling-induced settlement were selected based on engineers’ experience and concerns (Suwansawat and Einstein, 2006; Shen et al., 2019). The BNGR method was introduced to extract relevant features and form a data-driven optimal model, which was validated using the testing database. Sensitivity analysis was conducted to examine the selected inputs. The proposed model was conducted on the new introduced dataset and its performance was examined by comparison with observational measured data. Influencing factors associated with maximum ground settlement were analyzed and discussed.
2 Methodology and Database
2.1 Bayesian Nonparametric General Regression Framework
2.1.1 General Regression Neural Network
The GRNN method was proposed by Specht (1991) on the basis of the probabilistic neural network. This method can establish a non-linear relationship between inputs in multi-dimensional and corresponding outputs. Moreover, it is a one-pass learning algorithm without an iterative process, in contrast to the backpropagation process seen in other artificial neural network methods. It has been widely used in geotechnical engineering in recent decades (Theodosiou, 2011; Doulati Ardejanii et al., 2013; Zhao et al., 2019b), such as for spatial prediction of soil contamination (Kanevski, 1999), soil type inference (Kurup and Griffin, 2006), and static pile capacity prediction (Pal and Deswal, 2008). Chen et al. (2019) evaluated different machine learning methods for tunneling-induced settlement and indicated that the GRNN method outperformances the back-propagation neural network and radial basis neural network in prediction.
The GRNN method involves an input layer, pattern layer, weighted layer, and output layer. Supposing that s represents tunneling-induced maximum ground settlement, w is the designed inputs, and f (w, s) is the joint probability density function, the regression of s given w can be written as:
f (w, s) is usually estimated from a sample of the measured w and s using the kernel density approximation
where N is the number of measured samples and d is the dimension of input w. The smoothing parameter, σ, is the only unknown to be calculated. Combining Eq. (2) and Eq. (1), the desired conditional value of s can be written as:
To determine the appropriate value of
Through fitting the measurements, the optimal value of
The GRNN method bridges the designed inputs and the corresponding outputs. Nevertheless, the adopted designed inputs should be evaluated using experience or pre-judgment before being implemented in the GRNN method. The prior evaluation may bring uncertainties into the model inputs, which play an essential role in prediction. The ability to select models in Bayesian inferences allows selection of a suitable set of input variables from input candidates. Yuen and Ortiz (2016) proposed the innovative Bayesian nonparametric general regression (BNGR) algorithm, which can extract relevant input features for model prediction while simultaneously obtaining the non-parametric regression model. The BNGR algorithm is briefly introduced in the following section, but the detailed derivation process can be found in Yuen and Ortiz (2016).
2.1.2 General Regression Under the Bayesian Framework
Assuming that s is the tunneling-induced ground surface settlement, C denotes the general regression model with a specified set of inputs, and θ is the unknown parameter related to the smoothing parameter in GRNN method, then according to the Bayesian inference, the posterior PDF of θ can be written as:
where p (s|θ, w, C) is the likelihood function with which to reveal fit performance based on observational data given the parameter vector, θ. P (θ|C) is the prior PDF of the unknown parameter, θ. p (s|w, C) indicates the normalizing constant.
The chain rule of probability is used to develop the likelihood function and the product of conditional PDFs is:
where
where
Yuen and Ortiz (2016) introduced the smoothing scale parameter, v1, and the prediction error scale parameter, v2, to integrate the smoothing parameters
Then θ = (v1, v2) is the generated unknown parameters in the BNGR method. The posterior PDF of this parameter can be derived as:
where
The optimal value of v2 can be obtained using the following equation:
Based on a certain value of v1,
The parameter
After v1 and v2 are calculated, a general regression model is readily obtained. It should be noted that a regression model in this study means a non-parametric regression model with a subset of design variables. Suppose that d variables are included in the input domain, with different combinations of the designed variables, there will be Nc = (2d–1) subsets of input candidates. Bayesian model selection was applied to select the optimal model among the Nc model candidates. According to Bayes’s theorem, the plausibility of a model candidate can be expressed as:
where P (C(k)) = 1/Nc is the prior plausibility for a certain model C(k) (k = 1, 2, … , Nc) and this parameter is assumed to be the same for all models, while the evidence
This is the configuration of non-parametric regression under the Bayesian framework. Yuen and Ortiz (2016) identify two merits of the BNGR method. First, the variation of prior distribution in the regression coefficient, θ, has no impact on the model selection in Eq. 16. Second, in contrast to traditional regression approaches, the proposed method dramatically decreases the number of model candidates, for the network is automatically generated based on the GRNN method and development of different function forms using the same subset of inputs is not necessary.
2.2 Description of Case History
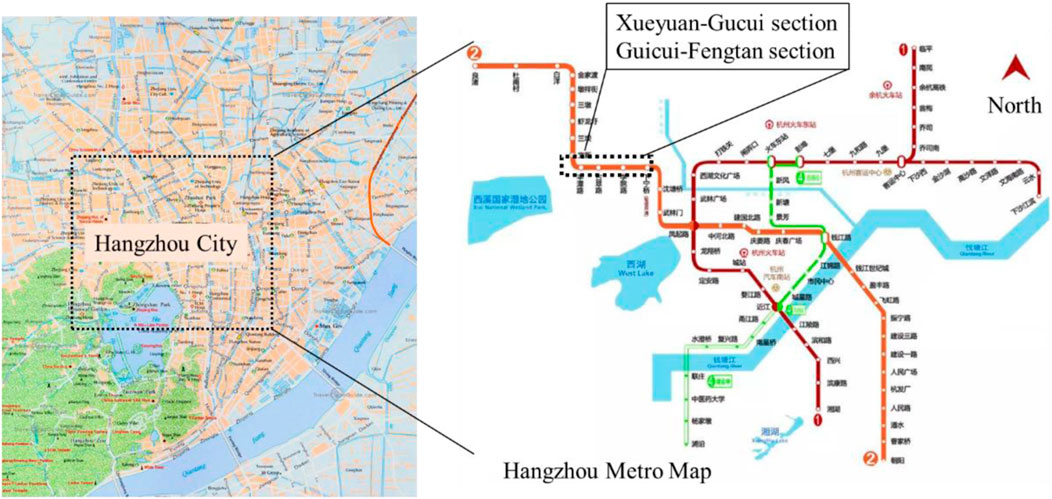
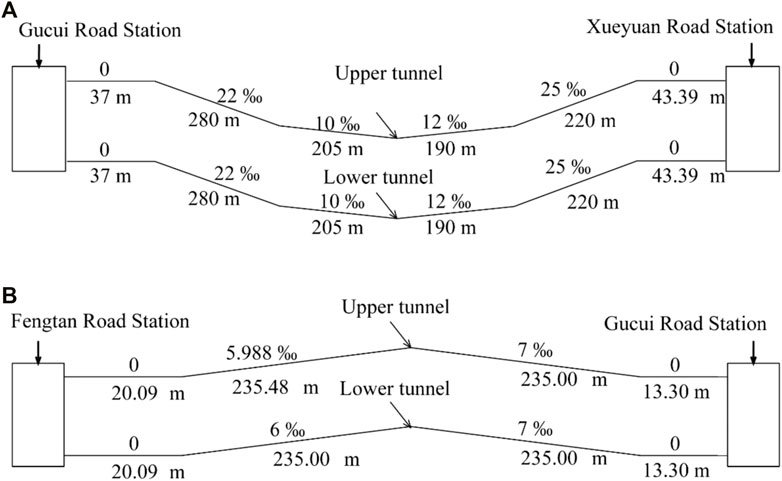
This study investigated tunneling-induced maximum ground settlement in the construction section from Xueyuan Road Station to Gucui Road Station (Xueyuan–Gucui section) as well as from Fengtan Road Station to Gucui Road Station (Gucui–Fengtan section) of Metro Line 2 in Hangzhou, China (Figures 1, 2). A photo of the construction site is shown in Figure 2A, and the adopted Earth pressure balance (EPB) shield machine, “Shichuandao”, is presented in Figure 2B. The length of the Xueyuan–Gucui section is 975.385 m; its cover depth varies from 10.641 to 18.701 m. By contrast, the length of the Gucui–Fengtan section is 503.866 m, and its cover depth varies from 8.566 to 9.976 m. The geometries of these two sections are shown in Figure 3. The inner diameter of the tunnel is 5.5 m, and its outer diameter is 6.2 m. The thickness and width of a tunnel segment are 0.35 and 1.2 m, respectively. Extensive in-situ explorations and laboratory experiments were conducted in this project, whose geological profile is illustrated in Figure 4. One can observe that the tunnel mostly advanced through the muddy silty clay layer, the muddy clay layer with silt, and the muddy silty clay layer with silt. A photo of the soils is shown in Figure 2C, and the soil properties of these three layers are presented in Supplementary Table S1 in the supplemental data. The undrained shear strength, Su, is obtained from the in-situ shear test, and the compression modulus is from the laboratory test of the remolded soil.
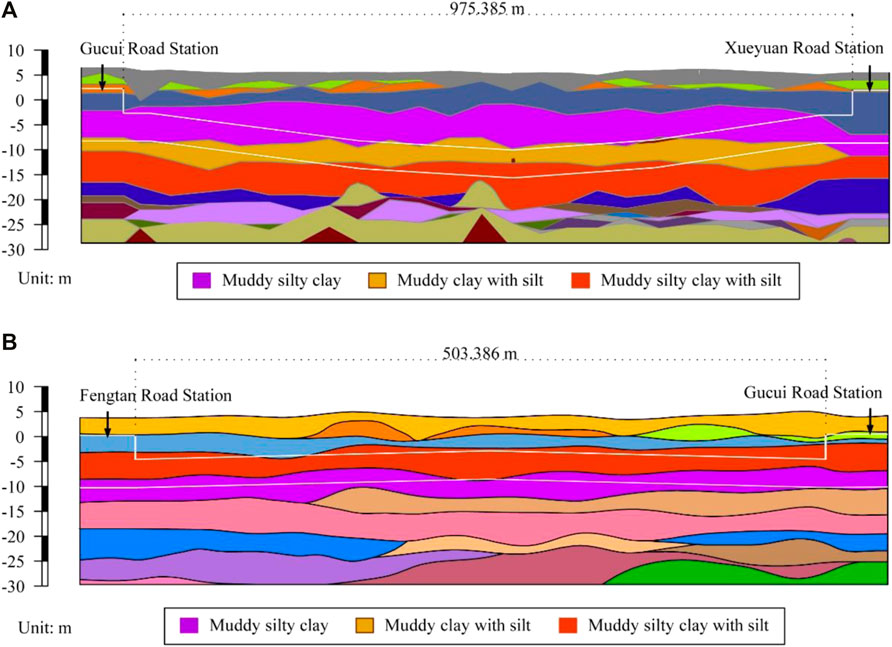
FIGURE 4. Geological profile of tunneling excavation section: (A) Gucui–Xueyuan section; (B) Fengtan–Gucui section.
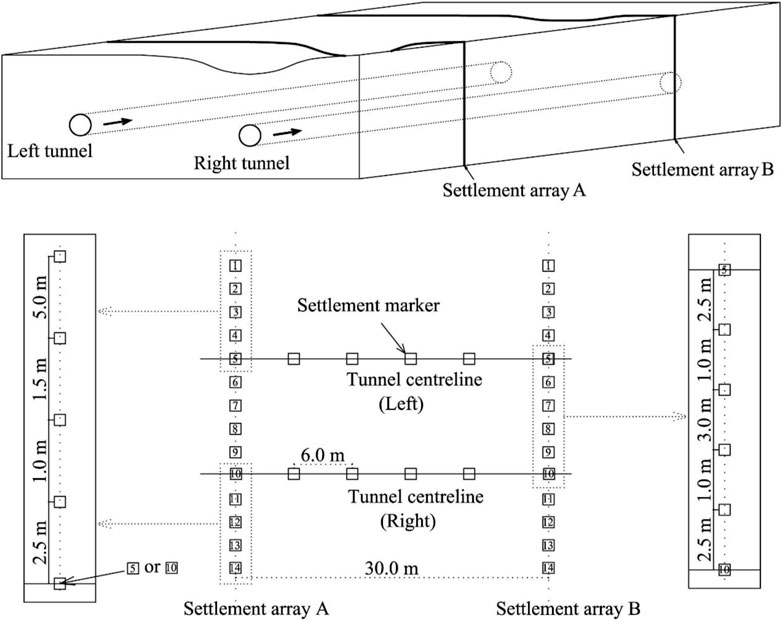
Along the tunnel alignment, the surface settlement markers were installed at approximately 6.0 m intervals (i.e., 5 segments) as shown in Figure 5. What’s more, perpendicular to the tunnel alignment, a settlement array was designed at roughly 30.0 m intervals (i.e., 25 segments), as presented in Figure 5. Fourteen measured points were set at each settlement array, with “Points 5” and “Point 10” positioned just above the left- and right-tunnel centerline, respectively. The measured points outside the two tunnel centerlines (left and right) were 2.5 m, 3.5 m, 5.0 m, and 10.0 m, respectively, from the tunnel centerlines, as shown in Figure 5. The distances of the four measured points between the tunnel centerlines are also presented in Figure 5. Settlement monitoring is conducted twice daily (8 a.m. and 3 p.m.). It should be noted that the observed ground settlement data above the right-tunnel line (excavated first) were applied in the present study and that data above the left-tunnel line were not introduced to prevent previously adjacent tunneling of the right-tunnel line from affecting ground settlement of the left-tunnel line. For each segment, the operational parameters, such as, face pressure, thrust, and torque, were automatically recorded. Based on the three categories of influencing factors suggested by Suwansawat and Einstein (2006), the following features may be associated with tunneling-induced maximum ground settlement:
• Advance rate (x1): calculated using the excavated distance over the total time in every excavation cycle;
• Cover depth (x2): the distance from the ground surface to the crown of the excavated tunnel;
• Pitching angle (x3): the discrepancy between the designed alignment and the central axial line of the shield machine (Figure 6);
• Rolling angle (x4): the slight rotation of the shield machine during the excavation process, as shown in Figure 6;
• Horizontal deviation (x5): the discrepancy between the designed tunnel alignment and the real tunnel centerline in the horizontal direction;
• Vertical deviation (x6): the discrepancy between the designed tunnel alignment and the real tunnel centerline in the vertical direction;
• Face pressure (upper) (x7): the soil pressure in the upper chamber (in this research, the face pressure was subdivided into face pressure (upper) and face pressure (Middle), as shown in Figure 6);
• Face pressure (middle) (x8): the average face pressure of the left and right chambers, as presented in Figure 6–monitored using Earth pressure cells installed inside the chambers;
• Thrust (x9): driven by hydraulic power; used to drive the shield ahead and control the pose of shield machine;
• Torque (x10): used to cut the soil at the front of shield machine; will develop shear deformation in the soil;
• Soil removal rate (x11): used to measure how quickly the excavated soil volume is transported from the shield face;
• Soil removal volume (x12): the excavated soil volume transported from the shield face by a balanced screw conveyor.
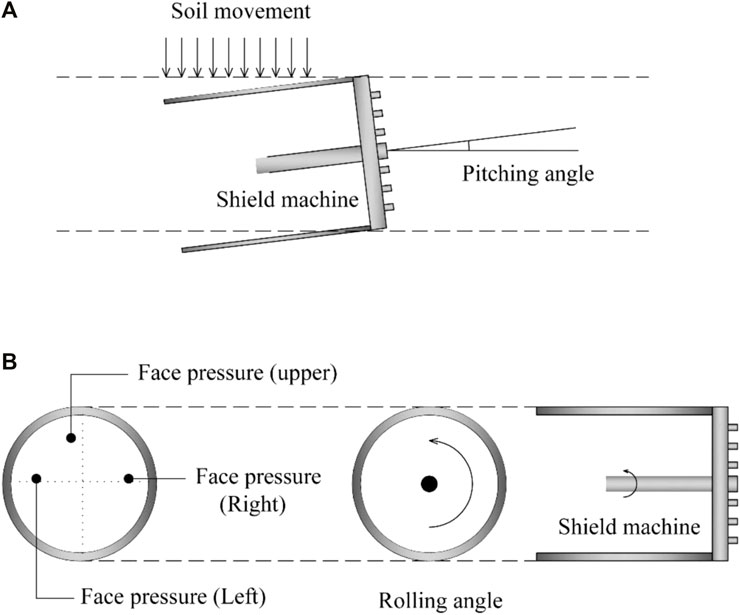
FIGURE 6. Features related to ground deformation: (A) pitching angle; (B) face pressure and rolling angle.
In the present tunneling project, a new mixture composition of grouting fill was designed, as shown in Supplementary Table S3 in the supplemental data. The lime was introduced as an additional component to accelerate the hardening and thus mitigate the uplift of the tunnel tube. Grouting pressure and filling were maintained around 0.35–0.36 MPa and 4.0–4.5 m3 per segment, respectively, and features related to grouting were not considered in the present study due to the tiny variations involved. Nevertheless, the present algorithm can be used to consider the grouting pressure and filling as input candidates when the record data are available. It should be noted that grouting pressure and filling have been found to be important parameters in tunnel excavation with which to control maximum ground surface settlement.
2.3 Preparation of Database
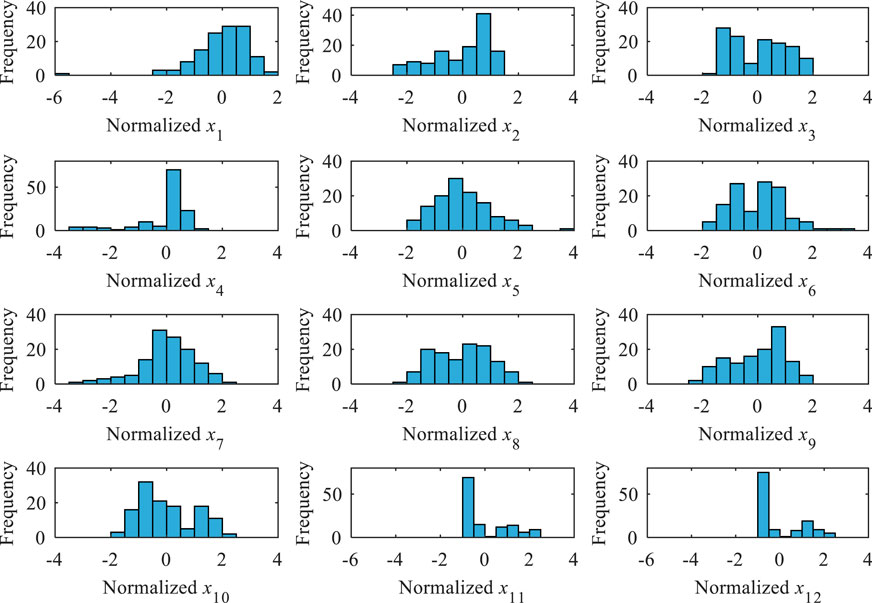
According to the classification proposed by Suwansawat and Einstein (2006), the features used to estimate the maximum ground settlement were separated into three categories: geological properties, tunnel geometry, and operation factors. The geological properties are closely related to the friction between shield and soil and were investigated by many researchers (Chen et al., 2019; Bouayad and Emeriault, 2017). The geological properties were evaluated according to the friction angle and cohesion as presented in Supplementary Table S1 in the supplemental data. The contact areas between the shield and different soil layers were considered as the weights to evaluate the geological index. Then, the geological index can be used as one influencing factors. Supplementary Table S1 in the supplemental data indicates that there is little variation of geological properties in the zone where the tunnel crossed, so that geological features can be neglected in the present study. Nevertheless, the geological variation is important for tunnelling induced settlement. The methodology proposed by Chen et al. (2019) is adopted to consider the geological variation. This novel approach associated the location and thickness of soil layers and the soil properties and these geological properties can be quantified using formulas. The detailed description is shown in the study of Chen et al. (2019). Furthermore, in the whole excavation section, the same shield tunnel boring machine was used, with uniform diameter maintained. Hence the cover depth is the only parameter in the category of tunnel geometry, with the overburden thickness at the middle of each segment collected to form a database of cover depth. It should be noted that the tunnel diameter is an important factors related to the ground maximum settlement. This can be a significant factors when the database contains varying diameter. Advance rate is calculated by advance distance over advance time in each segment. Average values in each segment were calculated for the other operational factors (Chen et al., 2019), with 12 features in total summarized in this tunnel project. 126 datasets were compiled, including input candidates and corresponding maximum ground surface settlement. Supplementary Table S2 in the supplemental data illustrates the statistic characteristics of these input candidates and the related maximum ground surface settlement.
3 Model Selection and Validation
The 126 observational data sets were randomly divided into a training dataset (70%), used for selecting optimal model and identifying parameters (i.e., smoothing scale parameter, and prediction error scale parameter), and a testing dataset (30%), used to examine the proposed model. All designed input candidates were normalized using the following equation:
where wm stands for the mean value of designed input candidates.

FIGURE 7. (A) Performance of optimal model on training and testing datasets; (B) Predicted error on testing dataset for optimal model.
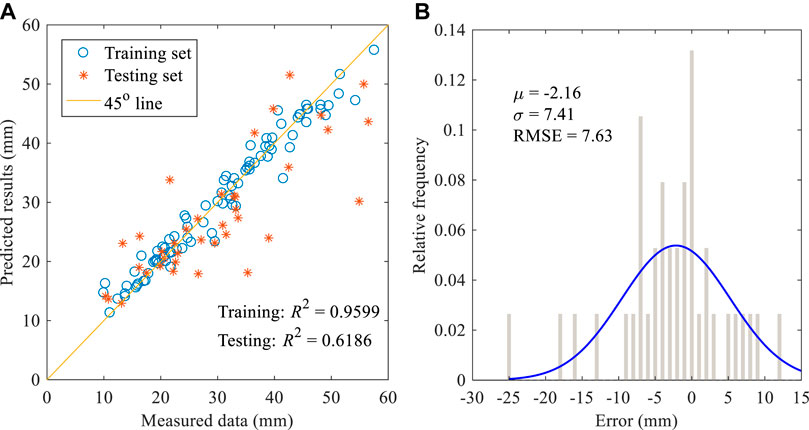
FIGURE 8. (A) Performance of model-2 on training and testing datasets; (B) Predicted error on testing dataset.
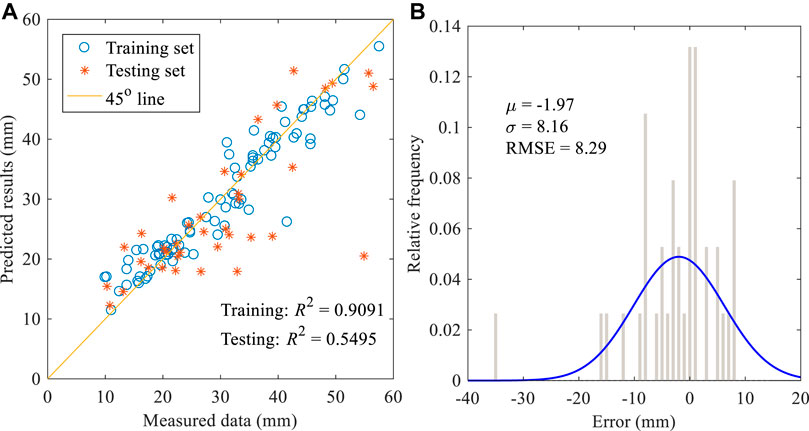
FIGURE 9. (A) Performance of model-3 on training and testing datasets; (B) Predicted error on testing dataset.
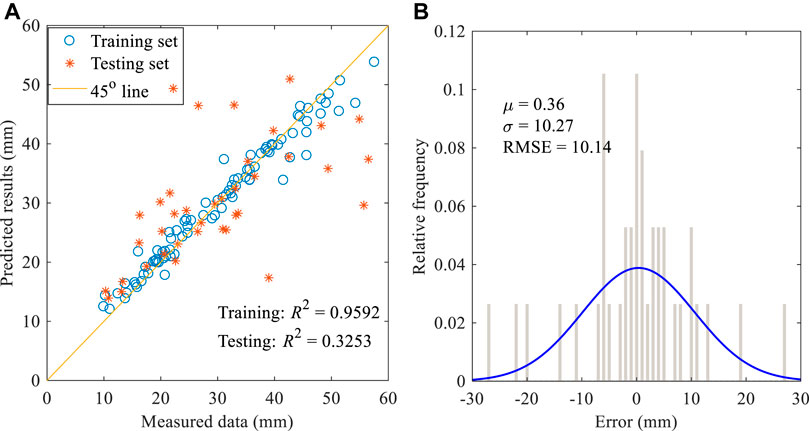
FIGURE 10. (A) Performance of model with all designed variables on training and testing datasets; (B) Predicted error on testing dataset for model with all designed variables.
4 Discussion
4.1 Feature Selection
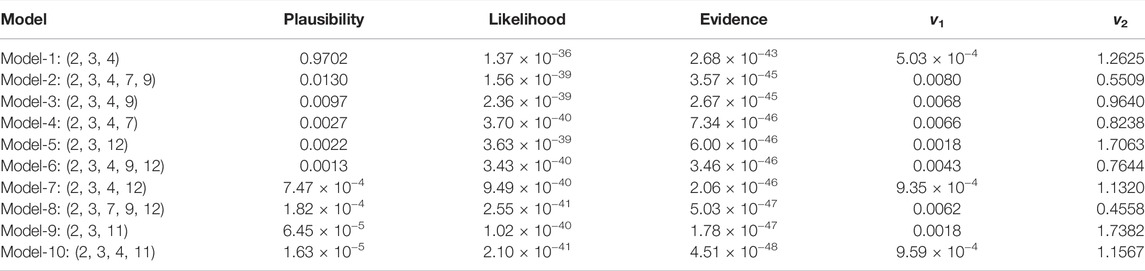
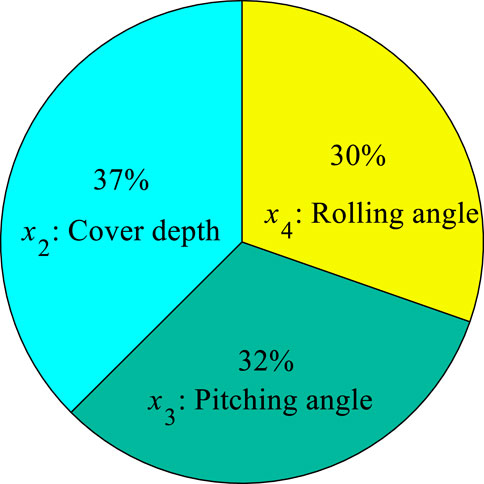
Based on the model selection results in Table 1, the overburden depth is the main feature associated with ground settlement, as has been recognized by many researchers. The pitching and rolling angles of the shield machine are included in the optimal model. Pitching angle represents the shield machine’s orientation during tunneling. Changes in pitching angle, which are inevitable, may create a gap between shield machine and surrounding soil, inducing ground deformation. Rolling angle evolves from the torque of the shield machine during excavation. To provide anti-support for the cutter-head torque, self-rotation may develop in the shield machine. Shear resistance between shield machine and surrounding soil may induce ground deformation. What’s more, as indicated by Supplementary Table S1 in the supplemental data, soft soil conditions surrounding the shield machine are sensitive to tunneling-induced disturbances. Shield-soil interactions generated from the pitching and rolling angles can significantly influence ground surface settlement in such soil conditions. All this may help in interpreting the selected three input variables in the optimal model. Pitching and rolling angles as features predicting ground settlement should be considered in future studies, especially those conducted under soft soil conditions. In the second-best model (model-2), in addition to the three selected input variables in the optimal model (i.e., cover depth, pitching angle, rolling angle), thrust and face pressure (upper) were extracted from the input candidates. This indicated that thrust and face pressure (upper) could influence tunneling-induced maximum ground settlement: thrust amplitude by influencing the movement of surrounding soil and inducing ground deformation and face pressure by maintaining excavation stability, with face pressure at the upper portion closely relationship to soil movement at the shield face.
Notably, despite being an input candidate, advance rate is not among the top 10 optimal models–consistent with the findings of Zhang et al.( 2019), in which advance rate ranked last among all model inputs in sensitivity analysis. In the present study, the advance rate is controlled to balance Earth pressure at the front interface of the shield machine. Undoubtedly, engineers and researchers are well aware that too small an advance rate may result in ground loss where too large a rate may generate high pressure at the front interface of the shield machine and cause ground heave. However, in this case study, advance rate is commonly carefully managed to avoid unacceptable excessive deformation. Hence advance rate may vary in a range that cannot be the dominant influencing factor for a certain project. Soil removal rate and removal volume are two factors closely related to advance rate. To maintain a desired face pressure at the front of the shield machine, soil removal rate and removal volume should be coordinated with the advance rate. As a result, these two features did not emerge in the top four models. The cutterhead torque of the shield machine can be affected by geological conditions, the opening ratio of the cutterhead, Earth pressure, tunnel diameter and the like. As a result of small variations in geological conditions, constant opening ratio, and tunnel diameter (for the same shield machine as in the present case history), the torque feature can have little impact on the ground surface settlement. Accordingly, this feature was not incorporated into the optimal model.
The relative importance of the various parameters depends on the tunneling procedure. For example, face pressure is highly determinant of the tunnel stability and settlement, as overly low face pressure may lead to collapse of the tunnel face. However, if during the period when these data sets were obtained face pressure was always sufficient, scant influence of face pressure will be evident in the data. As shown in Figure 11, normalized x7 (face pressure) was mostly in the range (-1, 1). Only when there is critically low face pressure in the data will this be evident as an important parameter. In general, a parameter is important in this procedure when it influences the settlement trough and is varied during the drive in a way that allows different outcomes of the settlement trough, such as the normalized x2 (cover depth) and x3 (pitching angle) illustrated in Figure 11, in which the frequencies in each interval are roughly equal. Important parameters that did not vary into critical ranges will not be recognized as important using this approach.
4.2 Sensitivity Analysis of Selected Features
Sensitivity analysis of the selected features in the optimal model was conducted to search for a dominant feature and evaluate relationships between tunneling-induced maximum ground settlement and the selected features. The sensitivity percentage of the ground settlement related to each input parameter is calculated using the equations:
where xi is the ith input variable and fmax (xi) and fmin (xi) denote the maximum and minimum predictions for ground settlement, respectively, by varying the ith input variable in its range while assuming other inputs to be at their mean values. Figure 12 gives the sensitivity percentage for each input variable, showing that cover depth had the dominant impact on ground settlement and that pitching angle ranked second. Feature selection of cover depth has been recognized as one important factor by many researchers, and sensitivity analysis further illustrates the significance of pitching angle and rolling angle.
4.3 Maximum Settlement Prediction Using the Bayesian Nonparametric General Regression Algorithm
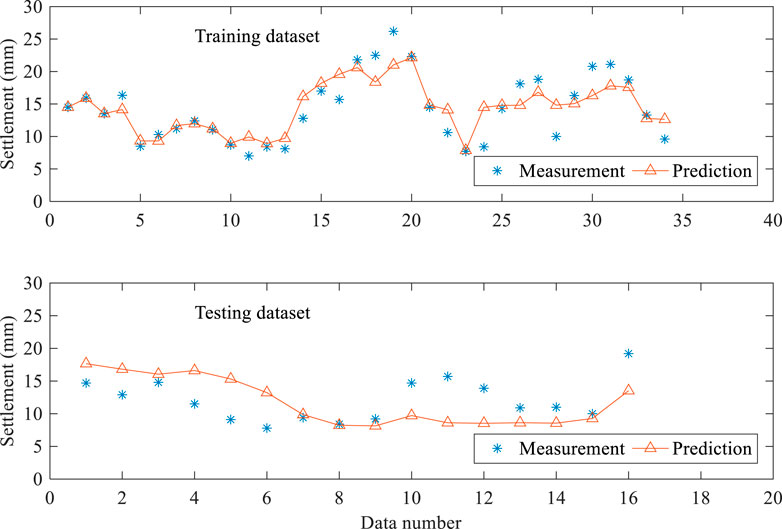
An additional database (50 sets of data points in total) collected from the Fengtan–Gucui section was used to assess prediction performance using the BNGR algorithm on new data. This database was manually divided into two subsets: one containing 34 data points collected from the beginning of the Fengtan–Gucui section, incorporated into the database of the Gucui–Xueyuan section to form an extended training dataset, and an other including 16 data points collected from the rest of the Fengtan–Gucui section, used to estimate maximum ground settlement. Inclusion of new data points into the existing training dataset was necessary to capture the specific characteristics of the new section (Chen et al., 2019). What’s more, inclusion of a new dataset can enlarge the ranges of the input variables essential for the BNGR algorithm. The geological condition of the Fengtan–Gucui section is illustrated in Figure 4B. Soil conditions at the site where the tunnel passes through contain mainly muddy silty clay layers, similar to those seen in the Gucui–Xueyuan section. Their properties are quite similar and are presented in Supplementary Table S1 in the supplemental data, indicating that the geological conditions of the Fengtan–Gucui section resemble those of the Gucui–Xueyuan section. What’s more, because the same shield machine was applied in these two sections, it is reasonable to combine the measured data from these two sections as a single training section. Figure 13 illustrates both measured and predicted data for the Fengtan–Gucui section. Figure 13A presents tunneling-induced maximum ground settlement at the beginning of this section. This dataset is part of the training dataset, and the estimated settlements are almost identical to the measured data except for some scattering data points. Figure 13B shows ground settlement in the second half of the Fengtan–Gucui section. It can be observed that estimated ground settlement using the BNGR method approximates the measured data points.
5 Conclusion
Based on the collected data from a construction site in Hangzhou, China, a general regression neural network under the Bayesian framework (BNGR) was used for feature selection and prediction of tunneling-induced maximum ground settlement in soft soils. Beyond overburden depth, two other features associated with ground settlement were selected in the optimal model: pitching angle and rolling angle. The optimal model was validated on the testing dataset and sensitivity analysis was conducted to examine the selected features. The estimation performance of the BNGR algorithm was evaluated on the new data set, with predictions found to be acceptable. Based on these findings, certain conclusions can be drawn:
5.1)The pitching and rolling angles of the shield machine directly control its orientation and significantly affect shield–soil interactions. In the present research, involving soft soils with lower strength and high compression, shield–soil interactions become particularly important and can cause relatively large disturbances to surrounding soil, consequently inducing ground surface settlement. Engineers should attend closely to operational factors associated with shield–soil interactions when tunneling in soft soils.
5.2)Thrust and face pressure (upper) emerged in the second-best model (model-2) in addition to the three features present in the optimal model. These two features, which have been discussed in the literature, play a significant role in controlling face stability during excavation process. Feature selection shows, however, that these two influencing factors are less evident than pitching angle and rolling angle for the present dataset perhaps as a result of the variation in face pressure applied within this dataset.
5.3)Advance rate is not selected in the top 10 models from the designed input candidates. But this does not mean the advance rate is not important and the advance rate can induce intolerant ground surface deformation when extremely large or small. In the present study, the advance rate is carefully controlled in practice and thus varies within a range in which it can have little effect on the surrounding soil. Accordingly, compared with other features, such as overburden depth, pitching angle, and rolling angle, this operational factor might not directly influence ground surface settlement.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
Writing: ZD, L-SZ; review and editing: W-HZ, AB.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors wish to thank the support funded by the Chinese National Natural Science Foundation (No. 42102308 and 51508506), the Research Funding of Shantou University for New Faculty Member (Grant No. NTF21008-2021), the Special Fund for Science and Technology of Guangdong Province in 2021 (STKJ2021168), the Science and Technology Development Fund, Macau SAR (File no. SKL-IOTSC-2018-2020 and FDCT/0035/2019/A1), the University of Macau Research Fund (MYRG 2018-00173-FST), and the Joint Fund of Zhejiang Provincial Natural Science Foundation (LHZ20E080001).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2022.848158/full#supplementary-material
References
Ahangari, K., Moeinossadat, S. R., and Behnia, D. (2015). Estimation of Tunnelling-Induced Settlement by Modern Intelligent Methods. Soils and Foundations 55, 737–748. doi:10.1016/j.sandf.2015.06.006
Alagha, A. S. N., and Chapman, D. N. (2019). Numerical Modelling of Tunnel Face Stability in Homogeneous and Layered Soft Ground. Tunnelling Underground Space Techn. 94, 103096. doi:10.1016/j.tust.2019.103096
Attewell, P. B., and Hurrell, M. R. (1985). Settlement Development Caused by Tunnelling in Soil. Gr Eng. 18, 17–20.
Bouayad, D., and Emeriault, F. (2017). Modeling the Relationship between Ground Surface Settlements Induced by Shield Tunneling and the Operational and Geological Parameters Based on the Hybrid PCA/ANFIS Method. Tunnelling Underground Space Techn. 68, 142–152. doi:10.1016/j.tust.2017.03.011
Boubou, R., Emeriault, F., and Kastner, R. (2010). Artificial Neural Network Application for the Prediction of Ground Surface Movements Induced by Shield Tunnelling. Can. Geotech. J. 47, 1214–1233. doi:10.1139/T10-023
Chen, D.-F., Feng, X.-T., Xu, D.-P., Jiang, Q., Yang, C.-X., and Yao, P.-P. (2016). Use of an Improved ANN Model to Predict Collapse Depth of Thin and Extremely Thin Layered Rock Strata during Tunnelling. Tunnelling Underground Space Techn. 51, 372–386. doi:10.1016/j.tust.2015.09.010
Chen, R.-P., Zhang, P., Kang, X., Zhong, Z.-Q., Liu, Y., and Wu, H.-N. (2019). Prediction of Maximum Surface Settlement Caused by Earth Pressure Balance (EPB) Shield Tunneling with ANN Methods. Soils and Foundations 59, 284–295. doi:10.1016/j.sandf.2018.11.005
Cho, S. E. (2009). Probabilistic Stability Analyses of Slopes Using the ANN-Based Response Surface. Comput. Geotechnics 36, 787–797. doi:10.1016/j.compgeo.2009.01.003
Chou, W.-I., and Bobet, A. (2002). Predictions of Ground Deformations in Shallow Tunnels in clay. Tunnelling Underground Space Techn. 17, 3–19. doi:10.1016/S0886-7798(01)00068-2
Darabi, A., Ahangari, K., Noorzad, A., and Arab, A. (2012). Subsidence Estimation Utilizing Various Approaches - A Case Study: Tehran No. 3 Subway Line. Tunnelling Underground Space Techn. 31, 117–127. doi:10.1016/j.tust.2012.04.012
Doulati Ardejanii, F., Rooki, R., Jodieri Shokri, B., Eslam Kish, T., Aryafar, A., and Tourani, P. (2013). Prediction of Rare Earth Elements in Neutral Alkaline Mine Drainage from Razi Coal Mine, Golestan Province, Northeast Iran, Using General Regression Neural Network. J. Environ. Eng. 139, 896–907. doi:10.1061/(ASCE)EE.1943-7870.0000689
Elbaz, K., Shen, S.-L., Cheng, W.-C., and Arulrajah, A. (2018). Cutter-disc Consumption during Earth Pressure Balance Tunnelling in Mixed Strata. Proc. Inst. Civil Eng. - Geotechnical Eng. 171 (4), 363–376. doi:10.1680/jgeen.17.0011710.1680/jgeen.17.00117
Elbaz, K., Yan, T., Zhou, A., and Shen, S.-L. (2022). Deep Learning Analysis for Energy Consumption of Shield Tunneling Machine Drive System. Tunnelling Underground Space Techn. 123, 104405. doi:10.1016/j.tust.2022.104405
Gamse, S., Zhou, W.-H., Tan, F., Yuen, K.-V., and Oberguggenberger, M. (2018). Hydrostatic-season-time Model Updating Using Bayesian Model Class Selection. Reliability Eng. Syst. Saf. 169, 40–50. doi:10.1016/j.ress.2017.07.018
Hajihassani, M., Abdullah, S. S., Asteris, P. G., and Armaghani, D. J. (2019). A Gene Expression Programming Model for Predicting Tunnel Convergence. Appl. Sci. 9, 4650. doi:10.3390/app9214650
Hajihassani, M., Kalatehjari, R., Marto, A., Mohamad, H., and Khosrotash, M. (2020). 3D Prediction of Tunneling-Induced Ground Movements Based on a Hybrid ANN and Empirical Methods. Eng. Comput. 36, 251–269. doi:10.1007/s00366-018-00699-5
Huang, H., Gong, W., Khoshnevisan, S., Juang, C. H., Zhang, D., and Wang, L. (2015). Simplified Procedure for Finite Element Analysis of the Longitudinal Performance of Shield Tunnels Considering Spatial Soil Variability in Longitudinal Direction. Comput. Geotechnics 64, 132–145. doi:10.1016/j.compgeo.2014.11.010
Ibrahim, E., Soubra, A.-H., Mollon, G., Raphael, W., Dias, D., and Reda, A. (2015). Three-dimensional Face Stability Analysis of Pressurized Tunnels Driven in a Multilayered Purely Frictional Medium. Tunnelling Underground Space Techn. 49, 18–34. doi:10.1016/j.tust.2015.04.001
Jin, Y.-F., Yin, Z.-Y., Zhou, W.-H., Yin, J.-H., and Shao, J.-F. (2019). A Single-Objective EPR Based Model for Creep index of Soft Clays Considering L2 Regularization. Eng. Geology. 248, 242–255. doi:10.1016/j.enggeo.2018.12.006
Jin, Y. F., Yin, Z. Y., Zhou, W. H., and Shao, J. F. (2019). Bayesian Model Selection for Sand with Generalization Ability Evaluation. Int. J. Numer. Anal. Methods Geomech 43, 2305–2327. doi:10.1002/nag.2979
Kanevski, M. F. (1999). The General Regression Neural Network—Rediscovered. Int. J. Syst. Res. Inf. Syst. 8Z, 241–256. doi:10.1016/S0893-6080(09)80013-0
Kelly, R., and Huang, J. (2015). Bayesian Updating for One-Dimensional Consolidation Measurements. Can. Geotech. J. 52, 1318–1330. doi:10.1139/cgj-2014-0338
Khisamitov, I., and Meschke, G. (2018). Variational Approach to Interface Element Modeling of Brittle Fracture Propagation. Comput. Methods Appl. Mech. Eng. 328, 452–476. doi:10.1016/j.cma.2017.08.031
Kurup, P. U., and Griffin, E. P. (2006). Prediction of Soil Composition from CPT Data Using General Regression Neural Network. J. Comput. Civ. Eng. 20, 281–289. doi:10.1061/(asce)0887-3801(2006)20:4(281)
Leca, E., and New, B. (2007). Settlements Induced by Tunneling in Soft Ground. Tunnelling Underground Space Techn. 22, 119–149. doi:10.1016/j.tust.2006.11.001
Lin, S.-S., Shen, S.-L., Zhang, N., and Zhou, A. (2021). Modelling the Performance of EPB Shield Tunnelling Using Machine and Deep Learning Algorithms. Geosci. Front. 12 (5), 101177. doi:10.1016/j.gsf.2021.101177
Lin, X.-T., Chen, R.-P., Wu, H.-N., and Cheng, H.-Z. (2019). Three-dimensional Stress-Transfer Mechanism and Soil Arching Evolution Induced by Shield Tunneling in sandy Ground. Tunnelling Underground Space Techn. 93, 103104. doi:10.1016/j.tust.2019.103104
Loganathan, N., and Poulos, H. G. (1998). Analytical Prediction for Tunneling-Induced Ground Movements in Clays. J. Geotechnical Geoenvironmental Eng. 124, 846–856. doi:10.1061/(asce)1090-0241(1998)124:9(846)
Lu, H., Shi, J., Wang, Y., and Wang, R. (2019). Centrifuge Modeling of Tunneling-Induced Ground Surface Settlement in Sand. Underground Space 4, 302–309. doi:10.1016/j.undsp.2019.03.007
Lyu, H.-M., Shen, S.-L., Zhou, A., and Yin, Z.-Y. (2022). Assessment of Safety Status of Shield Tunnelling Using Operational Parameters with Enhanced SPA. Tunnelling Underground Space Techn. 123, 104428. doi:10.1016/j.tust.2022.104428
Mahdevari, S., Torabi, S. R., and Monjezi, M. (2012). Application of Artificial Intelligence Algorithms in Predicting Tunnel Convergence to Avoid TBM Jamming Phenomenon. Int. J. Rock Mech. Mining Sci. 55, 33–44. doi:10.1016/j.ijrmms.2012.06.005
Marshall, A. M., Klar, A., and Mair, R. J. (2010). Tunneling beneath Buried Pipes: View of Soil Strain and its Effect on Pipeline Behavior. J. Geotech. Geoenviron. Eng. 136, 1664–1672. doi:10.1061/(ASCE)GT.1943-5606.0000390
Maynar, M. J., and Rodríguez, L. E. (2005). Discrete Numerical Model for Analysis of Earth Pressure Balance Tunnel Excavation. J. Geotech. Geoenviron. Eng. 131, 1234–1242. doi:10.1061/(asce)1090-0241(2005)131:10(1234)
Moeinossadat, S. R., and Ahangari, K. (2019). Estimating Maximum Surface Settlement Due to EPBM Tunneling by Numerical-Intelligent Approach - A Case Study: Tehran Subway Line 7. Transportation Geotechnics 18, 92–102. doi:10.1016/j.trgeo.2018.11.009
Neaupane, K. M., and Adhikari, N. R. (2006). Prediction of Tunneling-Induced Ground Movement with the Multi-Layer Perceptron. Tunnelling Underground Space Techn. 21, 151–159. doi:10.1016/j.tust.2005.07.001
Ng, C. W., and Lee, G. T. (2005). Three-dimensional Ground Settlements and Stress-Transfer Mechanisms Due to Open-Face Tunnelling. Can. Geotech. J. 42, 1015–1029. doi:10.1139/t05-025
Ng, C. W. W., Boonyarak, T., and Mašín, D. (2013). Three-dimensional Centrifuge and Numerical Modeling of the Interaction between Perpendicularly Crossing Tunnels. Can. Geotech. J. 50, 935–946. doi:10.1139/cgj-2012-0445
Ninić, J., Freitag, S., and Meschke, G. (2017). A Hybrid Finite Element and Surrogate Modelling Approach for Simulation and Monitoring Supported TBM Steering. Tunnelling Underground Space Techn. 63, 12–28. doi:10.1016/j.tust.2016.12.004
Ochmański, M., Modoni, G., and Bzówka, J. (2015). Prediction of the Diameter of Jet Grouting Columns with Artificial Neural Networks. Soils and Foundations 55, 425–436. doi:10.1016/j.sandf.2015.02.016
Pal, M., and Deswal, S. (2008). Modeling Pile Capacity Using Support Vector Machines and Generalized Regression Neural Network. J. Geotech. Geoenviron. Eng. 134, 1021–1024. doi:10.1061/(asce)1090-0241(2008)134:7(1021)
Park, J. H., Kim, D., and Chung, C. K. (2012). Implementation of Bayesian Theory on LRFD of Axially Loaded Driven Piles. Comput. Geotechnics 42, 73–80. doi:10.1016/j.compgeo.2012.01.002
Paternesi, A., Schweiger, H. F., and Scarpelli, G. (2017). Numerical Analyses of Stability and Deformation Behavior of Reinforced and Unreinforced Tunnel Faces. Comput. Geotechnics 88, 256–266. doi:10.1016/j.compgeo.2017.04.002
Peck, R. B. (1969). Deep Excavations and Tunneling in Soft Ground. 7th Int. Conf. Soil Mech. Found. Eng. Mexico City: The Sociedad Mexicana de Meca´nica de Suelos, 225–290.
Phoon, K.-K., and Kulhawy, F. H. (1999). Evaluation of Geotechnical Property Variability. Can. Geotech. J. 36, 625–639. doi:10.1139/t99-039
Pooya Nejad, F., and Jaksa, M. B. (2017). Load-settlement Behavior Modeling of Single Piles Using Artificial Neural Networks and CPT Data. Comput. Geotechnics 89, 9–21. doi:10.1016/j.compgeo.2017.04.003
Qi, C., and Tang, X. (2018). Slope Stability Prediction Using Integrated Metaheuristic and Machine Learning Approaches: A Comparative Study. Comput. Ind. Eng. 118, 112–122. doi:10.1016/j.cie.2018.02.028
Qi, X.-H., and Zhou, W.-H. (2017). An Efficient Probabilistic Back-Analysis Method for Braced Excavations Using wall Deflection Data at Multiple Points. Comput. Geotechnics 85, 186–198. doi:10.1016/j.compgeo.2016.12.032
Ren, D.-J., Shen, S.-L., Arulrajah, A., and Wu, H.-N. (2018). Evaluation of Ground Loss Ratio with Moving Trajectories Induced in Double-O-Tube (DOT) Tunnelling. Can. Geotech. J. 55, 894–902. doi:10.1139/cgj-2017-0355
Santos, O. J., and Celestino, T. B. (2008). Artificial Neural Networks Analysis of São Paulo Subway Tunnel Settlement Data. Tunnelling Underground Space Techn. 23, 481–491. doi:10.1016/j.tust.2007.07.002
Shen, S.-L., Elbaz, K., Shaban, W. M., and Zhou, A. (2022). Real-time Prediction of Shield Moving Trajectory during Tunnelling. Acta Geotech. doi:10.1007/s11440-022-01461-4
Shen, X., Yuan, D.-J., and Jin, D.-L. (2019). Influence of Shield Attitude Change on Shield-Soil Interaction. Appl. Sci. 9, 1812. doi:10.3390/app9091812
Shi, J., Ortigao, J. A. R., and Bai, J. (1998). Modular Neural Networks for Predicting Settlements during Tunneling. J. Geotechnical Geoenvironmental Eng. 124, 389–395. doi:10.1061/(asce)1090-0241(1998)124:5(389)
Soga, K., Laver, R. G., and Li, Z. (2017). Long-term Tunnel Behaviour and Ground Movements after Tunnelling in Clayey Soils. Underground Space 2, 149–167. doi:10.1016/j.undsp.2017.08.001
Soranzo, E., Tamagnini, R., and Wu, W. (2015). Face Stability of Shallow Tunnels in Partially Saturated Soil: Centrifuge Testing and Numerical Analysis. Géotechnique 65, 454–467. doi:10.1680/geot.14.P.123
Specht, D. F. (1991). A General Regression Neural Network. IEEE Trans. Neural Netw. 2, 568–576. doi:10.1109/72.97934
Suwansawat, S., and Einstein, H. H. (2006). Artificial Neural Networks for Predicting the Maximum Surface Settlement Caused by EPB Shield Tunneling. Tunnelling Underground Space Techn. 21, 133–150. doi:10.1016/j.tust.2005.06.007
Tan, F., Zhou, W.-H., and Yuen, K.-V. (2018). Effect of Loading Duration on Uncertainty in Creep Analysis of clay. Int. J. Numer. Anal. Methods Geomech 42, 1235–1254. doi:10.1002/nag.2788
Theodosiou, M. (2011). Disaggregation & Aggregation of Time Series Components: A Hybrid Forecasting Approach Using Generalized Regression Neural Networks and the Theta Method. Neurocomputing 74, 896–905. doi:10.1016/j.neucom.2010.10.013
Verruijt, A., and Booker, J. R. (1996). Surface Settlements Due to Deformation of a Tunnel in an Elastic Half Plane. Géotechnique 46, 753–756. doi:10.1680/geot.1996.46.4.753
Wu, H.-N., Shen, S.-L., Liao, S.-M., and Yin, Z.-Y. (2015). Longitudinal Structural Modelling of Shield Tunnels Considering Shearing Dislocation between Segmental Rings. Tunnelling Underground Space Techn. 50, 317–323. doi:10.1016/j.tust.2015.08.001
Wu, H.-N., Shen, S.-L., Yang, J., and Zhou, A. (2018). Soil-tunnel Interaction Modelling for Shield Tunnels Considering Shearing Dislocation in Longitudinal Joints. Tunnelling Underground Space Techn. 78, 168–177. doi:10.1016/j.tust.2018.04.009
Xu, T., and Bezuijen, A. (2018). Analytical Methods in Predicting Excess Pore Water Pressure in Front of Slurry Shield in Saturated sandy Ground. Tunnelling Underground Space Techn. 73, 203–211. doi:10.1016/j.tust.2017.12.011
Yan, T., Shen, S.-L., Zhou, A., and Lyu, H.-M. (2021). Construction Efficiency of Shield Tunnelling through Soft deposit in Tianjin, China. Tunnelling Underground Space Techn. 112, 103917. doi:10.1016/j.tust.2021.103917
Yang, J., Yin, Z.-Y., Liu, X.-F., and Gao, F.-P. (2020). Numerical Analysis for the Role of Soil Properties to the Load Transfer in clay Foundation Due to the Traffic Load of the Metro Tunnel. Transportation Geotechnics 23, 100336. doi:10.1016/j.trgeo.2020.100336
Yuen, K.-V., and Ortiz, G. A. (2016). Bayesian Nonparametric General Regression. Int. J. Uncertaintyquantification 6, 195–213. doi:10.1615/int.j.uncertaintyquantification.2016016055
Zhang, P. (2019). A Novel Feature Selection Method Based on Global Sensitivity Analysis with Application in Machine Learning-Based Prediction Model. Appl. Soft Comput. 85, 105859. doi:10.1016/j.asoc.2019.105859
Zhang, P., Chen, R.-P., and Wu, H.-N. (2019). Real-time Analysis and Regulation of EPB Shield Steering Using Random Forest. Automation in Construction 106, 102860. doi:10.1016/j.autcon.2019.102860
Zhang, Z. X., Liu, C., and Huang, X. (2017). Numerical Analysis of Volume Loss Caused by Tunnel Face Instability in Soft Soils. Environ. Earth Sci. 76, 1–19. doi:10.1007/s12665-017-6893-1
Zhao, L.-S., Zhou, W.-H., Geng, X., Yuen, K.-V., and Fatahi, B. (2019). A Closed-form Solution for Column-Supported Embankments with Geosynthetic Reinforcement. Geotextiles and Geomembranes 47 (3), 389–401. doi:10.1016/j.geotexmem.2019.01.006
Zhao, L.-S., Zhou, W.-H., and Yuen, K.-V. (2017). A Simplified Axisymmetric Model for Column Supported Embankment Systems. Comput. Geotechnics 92, 96–107. doi:10.1016/j.compgeo.2017.07.027
Zhao, L. S., Zhou, W. H., Fatahi, B., Li, X. B., and Yuen, K. V. (2016). A Dual Beam Model for Geosynthetic-Reinforced Granular Fill on an Elastic Foundation. Appl. Math. Model. 40 (21-22), 9254–9268. doi:10.1016/j.apm.2016.06.003
Zhao, L. S., Zhou, W. H., Su, L. J., Garg, A., and Yuen, K-V. (2019). Selection of Physical and Chemical Properties of Natural Fibers for Predicting Soil Reinforcement. J. Mater. Civ Eng. 31. doi:10.1061/(ASCE)MT.1943-5533.0002850
Zheng, G., Cui, T., Cheng, X., Diao, Y., Zhang, T., Sun, J., et al. (2017). Study of the Collapse Mechanism of Shield Tunnels Due to the Failure of Segments in sandy Ground. Eng. Fail. Anal. 79, 464–490. doi:10.1016/j.engfailanal.2017.04.030
Zhou, J., Sh, X., Du, K., Qiu, X., Li, X., and Mitri, H. S. (2017). Feasibility of Random-forest Approach for Prediction of Ground Settlements Induced by the Construction of a Shield-Driven Tunnel. Int. J. Geomech 17, 1–12. doi:10.1061/(ASCE)GM.1943-5622.0000817
Zhou, W.-H., Tan, F., and Yuen, K.-V. (2018). Model Updating and Uncertainty Analysis for Creep Behavior of Soft Soil. Comput. Geotechnics 100, 135–143. doi:10.1016/j.compgeo.2018.04.006
Keywords: tunneling-induced settlement, feature selection, non-parametric, pitching angle, operational factor
Citation: Ding Z, Zhao L-S, Zhou W-H and Bezuijen A (2022) Intelligent Prediction of Multi-Factor-Oriented Ground Settlement During TBM Tunneling in Soft Soil. Front. Built Environ. 8:848158. doi: 10.3389/fbuil.2022.848158
Received: 04 January 2022; Accepted: 21 February 2022;
Published: 05 April 2022.
Edited by:
Domenico Lombardi, The University of Manchester, United KingdomCopyright © 2022 Ding, Zhao, Zhou and Bezuijen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lin-Shuang Zhao, bHNoemhhb0BzdHUuZWR1LmNu
 Zhi Ding
Zhi Ding Lin-Shuang Zhao
Lin-Shuang Zhao Wan-Huan Zhou
Wan-Huan Zhou Adam Bezuijen5,6
Adam Bezuijen5,6