- 1College of Petroleum Engineering, Xi’an Shiyou University, Xi’an, China
- 2Shaanxi Key Laboratory of Advanced Stimulation Technology for Oil and Gas Reservoirs, Xi’an, China
- 3Shaanxi Future Energy Chemical Co., Ltd., Yu’lin, China
- 4No.8 Oil Extraction Plant, Changqing Oilfield Branch, PetroChina, Xi’an, China
In this paper, the GM(1,1) model with function
1 Introduction
When the temperature of crude oil containing wax is lower than the waxing point, the dissolved wax crystals will be deposited on the inner wall of the pipe; as the thickness of wax deposition increases, the pipe diameter decreases, the transmission capacity decreases, and the energy consumption increases (Alnaimat et al., 2020; Ridzuan et al., 2020; Zhou et al., 2016). In order to ensure the efficient and safe operation of the pipeline, regular pipe cleaning is adopted to reduce the wax deposition thickness. In the process of developing the pipe cleaning cycle, mastering the wax deposition law and accurately predicting the thickness of wax deposition are the prerequisites for developing the pipe cleaning cycle (Li et al., 2020; Duan et al., 2016). Over time, the wax deposit thickness will tend to grow, and shear stripping will occur after the wax deposit grows to a certain thickness. Lu et al. (Lu et al., 2012) proposed that there are three effects that affect the increase or decrease of wax deposition, and the wax deposition decreases with the increase of flow rate by flow loop device experiments. Jin et al. (Jin et al., 2018) analyzed the trend of wax deposition thickness under different time periods, divided the wax deposition process into three stages: rapid deposition, faster deposition, and slow deposition, and verified the feasibility of the model; the model is highly accurate and has good application value. Wang et al. (Wang et al., 2016) developed a wax deposition thickness prediction and economic pipe cleaning cycle prediction program for the Tieling-Xinmin section of the pipeline as an example, and the prediction effect of this program is more consistent with the actual thickness value of the pipeline in the field, and the program can only predict one-quarter at present. Leporini et al. (Leporini et al., 2019) fitted the laboratory wax deposition data with a mathematical model, and to verify the error of the predicted values of the mathematical model, the data were scaled up and compared with the field data in the oil field. It is finally concluded that the shear stripping mechanism must be initiated in the multiphase flow simulation. Jalalnezhad et al. (Jalalnezhad et al., 2016) developed the ANFIS model from experimental data, and the predictions of this model were closer to the experimental data. The ANFIS model was more accurate than the Halstensen model in predicting wax deposition thickness at single-phase turbulent flow rates. Saeedi Dehaghani et al. (Saeedi et al., 2017) developed an artificial neural network model (ANN) to predict the wax deposition thickness in single-phase turbulent flow and the ANN model was compared with the ANFIS model and the predicted values of the ANN model were closer to the experimental data. Alnaimat et al. (Alnaimat et al., 2020) comprehensively evaluated different techniques for wax deposition thickness prediction and compared with other models, the Matzain model gave better results for wax deposition thickness prediction, therefore, the optimized Matzain model can be studied in more depth. Gray system theory is the study of the exploitation of a small sample of partially known information to achieve the correct description and effective monitoring of evolutionary laws in the presence of a large lack or disorder of information (Julong., 1989). Scholars often refer to the GM(1,1) model in the gray model to predict the wax deposition thickness. While the traditional GM(1,1) model has some limitations, if the smoothness of the original series is low or there are extreme values, it will have a serious impact on the prediction accuracy.
In order to improve the prediction accuracy of the GM(1,1) model, researchers have improved the traditional GM(1,1) model. Wang et al. (Wang et al., 2014) established a new model by optimizing the background values in the gray model, and compared with the traditional GM(1,1) model, the new model has higher prediction accuracy. Xu et al. (Xu et al., 2021) used the function
In order to make the prediction of wax deposition thickness more accurate, new function transformations are proposed in this paper. The GM(1,1) model with function
2 Establish the model
The prediction principle of GM(1,1) model is to generate a new set of data series with obvious trend for a certain data series by accumulation, build a model for prediction according to the growth trend of the new data series, and then reverse the calculation by accumulation and subtraction to recover the original data series, and then get the prediction result.
2.1 Establish GM(1,1) model
1) Original data sequence:
Where:
2) Accumulate the data sequence
Where:
3) Generate mean sequence:
Where:
4) Establish the GM(1,1) model whitening differential equation:
5) Establish the GM(1,1) model gray differential equation:
Where:
Where:
6) The time response sequence equation is obtained by solving:
Where:
7) Reduction yields the model prediction sequence equation:
Where:
2.2 Establish the GM(1,1) model for the transformation of function
The function
1) Set the original sequence
Where:
2) The sequence
Where:
3) The sequence
Where:
4) Then reduce
5) The modeling process for the GM(1,1) model with function
2.3 Establish the GM(1,1) model for the transformation of function
In the literature (Liu et al., 2013), it was demonstrated theoretically that the smoothness of the original data series can be elevated when the function
1) Set the original sequence
where
2) The sequence
Where:
3) The sequence
4) Then reduce
5) The modeling process for the GM(1,1) model with function
3 Calculation example
To verify the accuracy of the models, GM(1,1) model, GM(1,1) model with function
3.1 Wax deposition thickness prediction model for indoor loop experiments
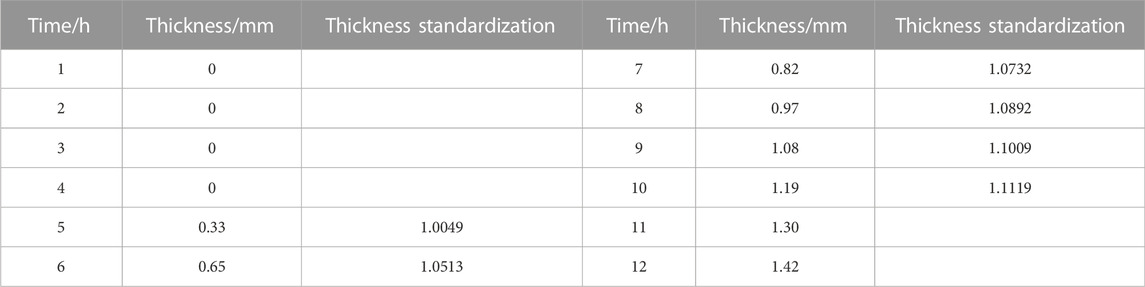
The indoor loop device can simulate the wax deposition phenomenon in the field pipeline more realistically. In the literature (Chen et al., 2015), an indoor loop experimental device was used to simulate the wax formation in the pipeline at different inlet fluid temperatures, and then the wax formation thickness of the pipe wall was calculated using the static differential pressure method. The wax deposition thickness data in the pipe at the inlet fluid temperature of 50°C in the literature (Chen et al., 2015) was taken as an example, and since the thickness was 0 for the first 4 h, the wax deposition thickness from 5 h to 10 h was used as the base data for modeling and prediction of the thickness within 11 h to 12 h. The standardized data for the GM(1,1) model with function
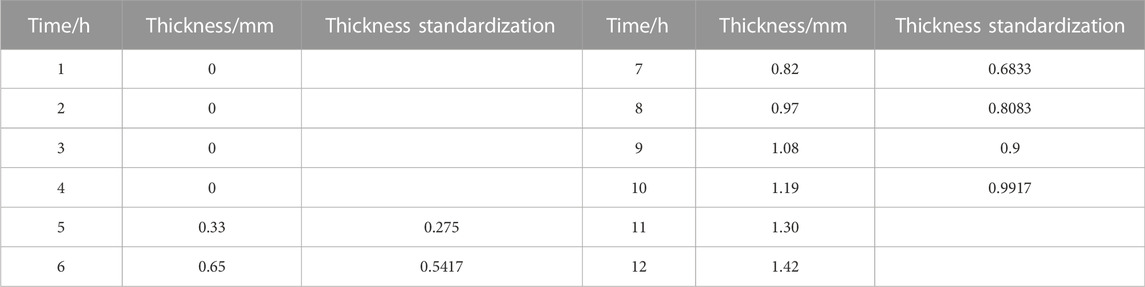
TABLE 1. Standardized data for the GM(1, 1) model with function
After obtaining the standardized data, GM(1,1) model, GM(1,1) model with function

TABLE 2. Prediction sequence formula for GM(1,1) model and GM(1,1) model with function
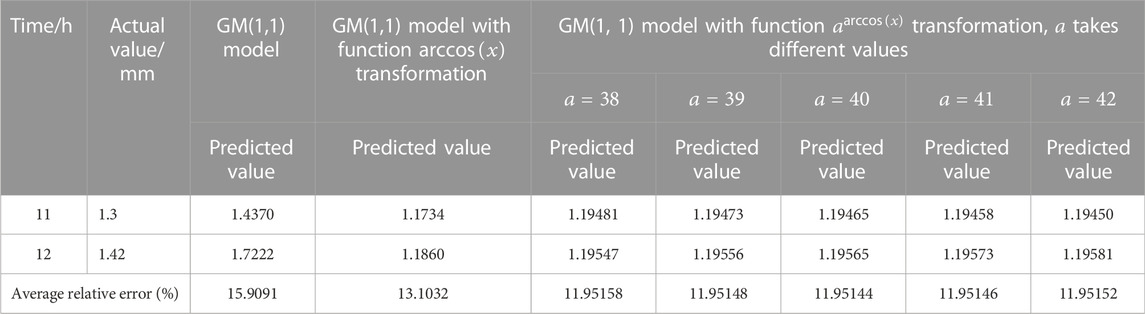
TABLE 3. Comparison of wax deposition thickness prediction results of GM(1,1) model and GM(1,1) model with function
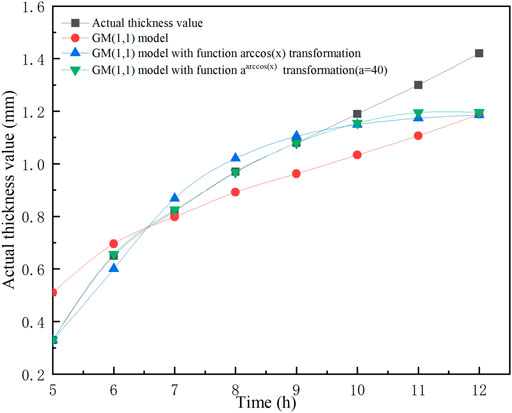
FIGURE 1. Comparison of predicted and actual values of wax deposition thickness for GM(1,1) model and GM(1,1) model with function
According to the results in Table 3, it can be found that the average relative errors of all three models are relatively large. In the GM(1,1) model with function
The standardized data for the GM(1,1) model with function
After obtaining the standardized data, GM(1,1) model, GM(1,1) model with function

TABLE 5. Prediction sequence equation for GM(1,1) model and GM(1,1) model with function
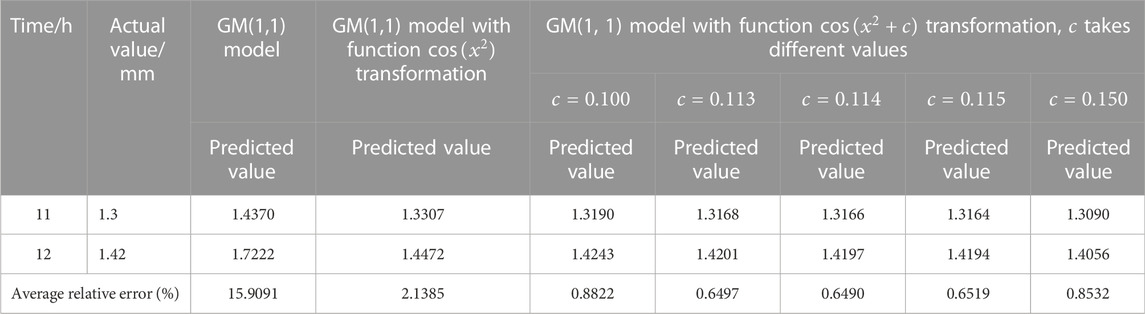
TABLE 6. Comparison of wax deposition thickness prediction results of GM(1,1) model and GM(1,1) model with function
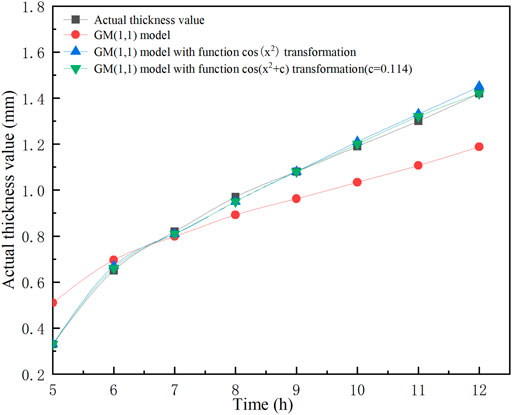
FIGURE 2. Comparison of predicted and actual values of wax deposition thickness for GM(1,1) model and GM(1,1) model with function
According to the results in Table 6, it can be found that the average relative error of wax deposition thickness shows a trend of decreasing and then increasing for different values of translation
3.2 Wax deposit thickness prediction model for field pipelines
In order to make the predicted wax deposition thickness of the improved model more consistent with the actual situation in the field pipeline, the wax deposition thickness data of a field pipeline in the literature (Xu et al., 2021) is taken as an example in this paper, and the wax deposition thickness of 1 day∼15 days is used as the base data for modeling to predict the wax deposition thickness of 18 days∼21 days. The standardized data for the GM(1,1) model, the GM(1,1) model with function
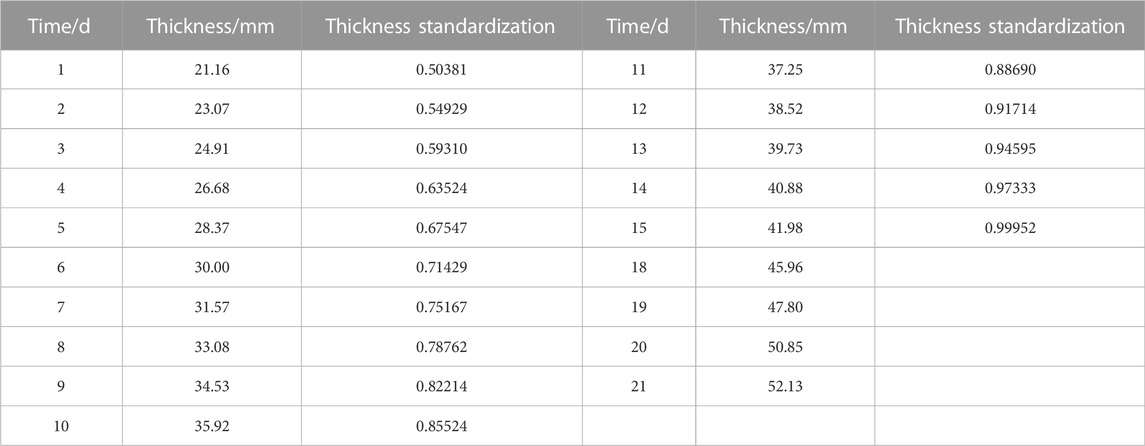
TABLE 7. Standardized data for the GM(1,1) model with functions
After obtaining the standardized data, the GM(1,1) model, GM(1,1) model with function

TABLE 8. Prediction sequence equation for GM(1,1) model and GM(1,1) model with function
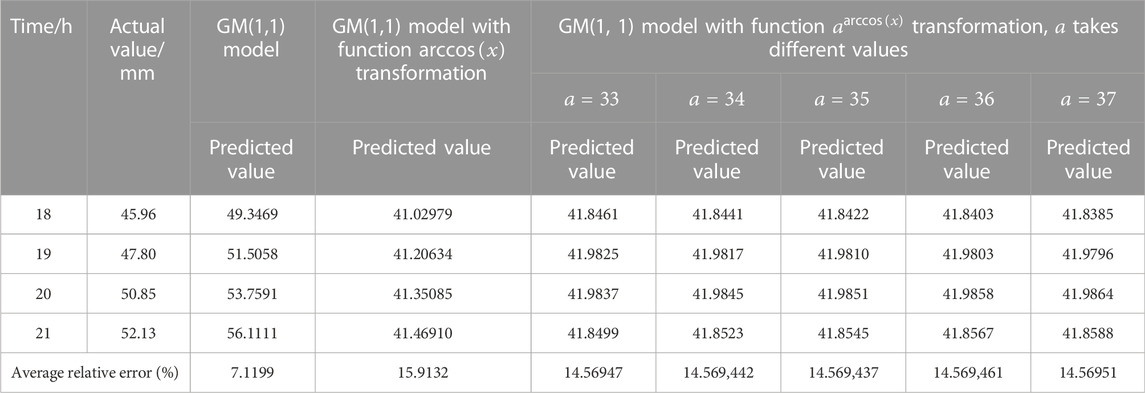
TABLE 9. Comparison of wax deposition thickness prediction results of GM(1,1) model and GM(1,1) model with function
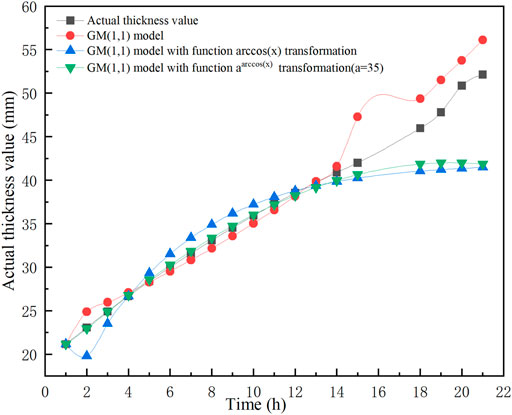
FIGURE 3. Comparison of predicted and actual values of wax deposition thickness for GM(1,1) model and GM(1,1) model transformed by functions
According to the results in Table 9, the average relative error of the GM(1,1) model is 7.1199%, which is the minimum average relative error value. In the GM(1,1) model with the function
The standardized data for the GM(1,1) model with function
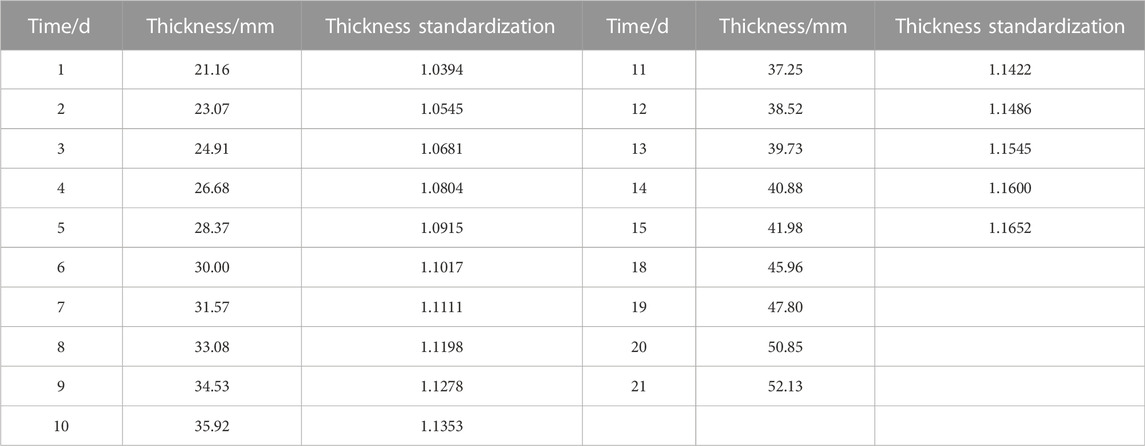
TABLE 10. Standardized data for the GM(1,1) model with function
After obtaining the standardized data, GM(1,1) model, GM(1,1) model with function
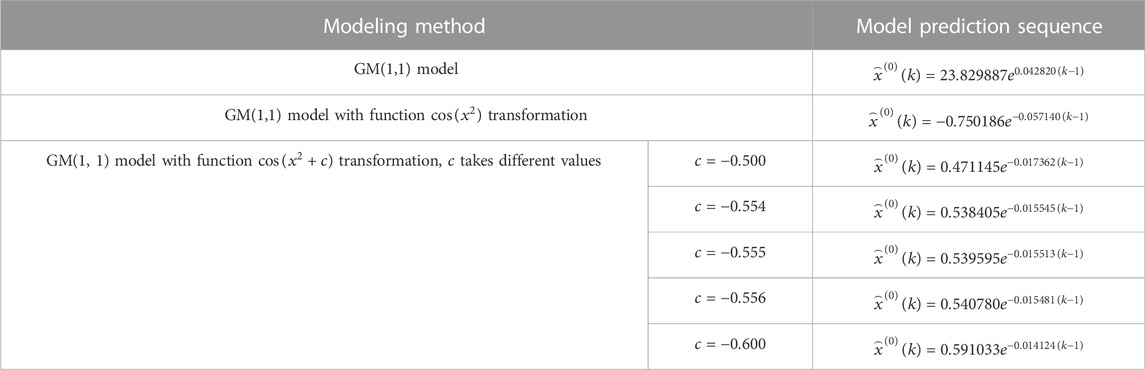
TABLE 11. Prediction sequence equation for GM(1,1) model and GM(1,1) model with function
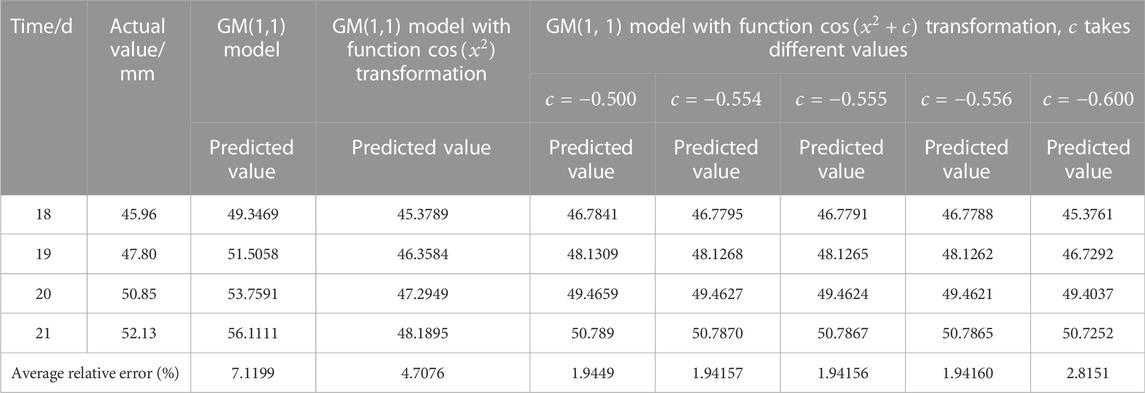
TABLE 12. Comparison of wax deposition thickness prediction results of GM(1,1) model and GM(1,1) model with function
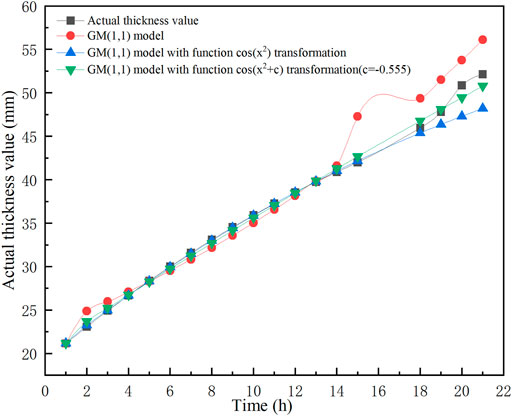
FIGURE 4. Comparison of predicted and actual values of wax deposition thickness for GM(1,1) model and GM(1,1) model with function
According to the results in Table 12, the average relative error in the GM(1,1) model with function
4 Conclusion and outlook
In this paper, the GM(1,1) model, the GM(1,1) model with function
1) The GM(1,1) model with function
2) The GM(1,1) model with function
3) In the GM(1,1) model with the function
4) The GM(1,1) model with function
5) As theoretical research continues, the results of different wax deposition thickness prediction models vary. At present, many experimental data are based on the indoor loop experimental simulation, and amplifying loop data to solve field pipeline problems has certain errors. Therefore, how to reasonably amplify the parameters and establish more accurate prediction models for application in actual pipelines is the direction of future research in this field.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
SX (corresponding author): contributed to the conception of the study, performed the data analyses and wrote the manuscript; CF: contributed significantly to analysis and manuscript preparation; PS: helped perform the analysis with constructive discussions. CL: added important references and checked and revised calculated data.
Conflict of interest
PS was employed by the company “Shaanxi Future Energy Chemical Co. Ltd.”. Author CL was employed by the company PetroChina.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alnaimat, F., and Ziauddin, M. (2020). Wax deposition and prediction in petroleum pipelines. J. Petroleum Sci. Eng. 184, 106385. doi:10.1016/j.petrol.2019.106385
Chen, Xiaoyu, Su, Xin, and Ling, Peiwen (2015). Comparative anal-ysis of wax deposition simulation and loop experiment. Oil-Gas Field Surf. Eng. (6), 13–15. doi:10.3969/j.issn.1006-6896.2015.6.006
Duan, J., Liu, H., Guan, J., Hua, W., Jiao, G., and Gong, J. (2016). Wax deposition modeling of oil/gas stratified smooth pipe flow. AIChE J. 62 (7), 2550–2562. doi:10.1002/aic.15223
Huanyong, Z., Aiping, Y., and Wenzhan, D. “Function x-ln x (x≥e) transformation for improving smooth degree and its application in grey modeling,” in Proceedigs of the 2007 IEEE International Conference on Grey Systems and Intelligent Services, Nanjing, China, 2007 November (IEEE), 1338–1342. doi:10.1109/GSIS.2007.4443491
Jalalnezhad, M. J., and Kamali, V. (2016). Development of an intelligent model for wax deposition in oil pipeline. J. Pet. Explor. Prod. Technol. 6 (1), 129–133. doi:10.1007/s13202-015-0160-3
Jin, W. B., Xiao, R. G., Xiao, Z. L., et al. (2018). A new method for predicting the wax deposition thickness based on various deposition stages. China Offshore Oil Gas 30 (5), 159–164. doi:10.11935/j.issn.1673-1506.2018.05.021
Jin, W., Quan, Q., Hui, X., Chen, J., and Qin, G. (2022). Prediction of wax deposition thickness on pipe wall by improved GM (1, 1) model based on data transformation method. Petroleum Sci. Technol. 40 (13), 1551–1566. doi:10.1080/10916466.2022.2046057
Leporini, M., Terenzi, A., Marchetti, B., Giacchetta, G., and Corvaro, F. (2019). Experiences in numerical simulation of wax deposition in oil and multiphase pipelines: Theory versus reality. J. Petroleum Sci. Eng. 174, 997–1008. doi:10.1016/j.petrol.2018.11.087
Li, H., Zhang, J., Xu, Q., Hou, C., Sun, Y., Zhuang, Y., et al. (2020). Influence of asphaltene on wax deposition: Deposition inhibition and sloughing. Fuel 266, 117047. doi:10.1016/j.fuel.2020.117047
Liu, X., Zhang, B., Zou, J., et al. (2013). Gray model based on cos(xα) transformation and it’s application in the prediction of gas concentration in transformer oil. J. Xihua Univ. Nat. Sci. (2), 79–83. doi:10.3969/j.issn.1673-159X.2013.02.019
Lu, Y., Huang, Z., Hoffmann, R., Amundsen, L., and Fogler, H. S. (2012). Counterintuitive effects of the oil flow rate on wax deposition. Energy fuels.. 26 (7), 4091–4097. doi:10.1021/ef3002789
Ridzuan, N., Subramanie, P., and Uyop, M. F. (2020). Effect of pour point depressant (PPD) and the nanoparticles on the wax deposition, viscosity and shear stress for Malaysian crude oil. Petroleum Sci. Technol. 38 (20), 929–935. doi:10.1080/10916466.2020.1730892
Saeedi Dehaghani, A. H. (2017). An intelligent model for predicting wax deposition thickness during turbulent flow of oil. Petroleum Sci. Technol. 35 (16), 1706–1711. doi:10.1080/10916466.2017.1358281
Shao, Y., Wei, Y., and Su, H. J. “An approach of the grey modeling based on ax+ b, sin x over x transformation,” in Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 2010 July (IEEE), 3455–3460. doi:10.1109/WCICA.2010.5553957
Wang, J., Wang, X., Baojain, H., et al. (2016). Calculation of wax deposit thickness and economic p-igging Period of waxy crude oil pipeline. Contemp. Chem. Ind. (3), 545–548. doi:10.13840/j.cnki.cn21-1457/tq.2016.03.035
Wang, Y., Liu, Q., Tang, J., Cao, W., and Li, X. (2014). Optimization approach of background value and initial item for improving prediction precision of GM (1, 1) model. J. Syst. Eng. Electron. 25 (1), 77–82. doi:10.1109/JSEE.2014.00009
Xu, S., Yin, Y., Lin, Q., et al. (2021). Research on prediction of wax deposition thickness on pipe wall based on improved grey model. J. Saf. Sci. Technol. (10), 32–38. doi:10.13637/j.issn.1009-6094.2021.1182
Yao-guo, D., Wu-yong, Q., and Qingfeng, W. (2009). An approach of the GM (1, 1) model based on linear transformation. J. Grey Syst. 21 (3), 279–290.
Zhang, J., Lü, X., Ran, M., and Han, G. (2016). DGM model based on anti-cotangent function and its application. J. Grey Syst. 28 (3), 63–74.
Zhou, Y., Gong, J., and Wang, P. (2016). Modeling of wax deposition for water-in-oil dispersed flow. Asia. Pac. J. Chem. Eng. 11 (1), 108–117. doi:10.1002/apj.1948
Nomenclature
Keywords: improved GM(1,1) model, smooth degree, translation transformation, wax deposition thickness, model accuracy
Citation: Xu S, Fan C, Song P and Liu C (2022) Prediction of wax deposit thickness in waxy crude oil pipelines using improved GM(1,1) model. Front. Chem. Eng. 4:1024259. doi: 10.3389/fceng.2022.1024259
Received: 21 August 2022; Accepted: 02 December 2022;
Published: 15 December 2022.
Edited by:
George Karapetsas, Aristotle University of Thessaloniki, GreeceReviewed by:
Jian Zhao, Northeast Petroleum University, ChinaBarbara Marchetti, University of eCampus, Italy
Copyright © 2022 Xu, Fan, Song and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shiqi Xu, NDE4OTAyNTE0QHFxLmNvbQ==
 Shiqi Xu
Shiqi Xu Chengyang Fan
Chengyang Fan Peijian Song3
Peijian Song3