- Santa Fe Institute, Santa Fe, NM, United States
Complexity science and machine learning are two complementary approaches to discovering and encoding regularities in irreducibly high dimensional phenomena. Whereas complexity science represents a coarse-grained paradigm of understanding, machine learning is a fine-grained paradigm of prediction. Both approaches seek to solve the “Wigner-Reversal” or the unreasonable ineffectiveness of mathematics in the adaptive domain where broken symmetries and broken ergodicity dominate. In order to integrate these paradigms I introduce the idea of “Meta-Ockham” which 1) moves minimality from the description of a model for a phenomenon to a description of a process for generating a model and 2) describes low dimensional features–schema–in these models. Reinforcement learning and natural selection are both parsimonious in this revised sense of minimal processes that parameterize arbitrarily high-dimensional inductive models containing latent, low-dimensional, regularities. I describe these models as “super-Humean” and discuss the scientic value of analyzing their latent dimensions as encoding functional schema.
1 Complex schemata and statistical manifolds
The passage from data to orderly knowledge resembles a sequence that starts with perception and measurement and concludes with concepts and rules. The philosopher Emmanuel Kant in the 1781 Critique of Pure Reason (Kant, 1908) described the mapping from sense impressions (direct or instrumentally mediated) to concepts, as a production of Schema. Schemata are rules that transform the rich world of input-data to an abstract domain of categories, where categories are the stuff of thought, theory, and science. The Kantian idea of the schema was adopted by both John Holland and Murray Gell-Mann in their definitions of complex systems. For Holland a schema is a binary string whose fixed elements (as opposed to wild cards) define an equivalence class of coordinates encoding optimal solutions in adaptive landscapes. Complex systems are for Holland agents in possession of map-like schemata (Holland, 2000). For Gell-Mann, schemata, which he also called the IGUS (Information Gathering Utilizing System) are compressed rule systems capable of receiving inputs from history and environment in order to predict and act on states of the world (Gell-Mann, 1995). These span genomes, nervous systems, and even material culture. In this way schema strongly resemble the emphasis placed on codes in “code biology” which draws parallels between culture and biology as two representational domains that consider mappings from syntactic marks to semantic symbols (Barbieri, 2015). James Hartle formalized the IGUS in order to explore the origin of the emergent concepts, present, past, and future, by placing an IGUS in Minkowski space in order to trace the emergence of “subjective” world lines (Hartle, 2005). In this way connecting complexity (agentic life) to simplicity (variational physics). We can say that complex reality evolves coding systems which retain a coarse-grained memory, or archive, of their adaptive histories. The underlying symmetries of physics are recurrently overlaid with fundamentally non-ergodic rule systems.
Schemata bear a striking resemblance to the idea of manifolds in data science, which are low dimensional geometric encodings, that capture stable relationships in high dimensional data sets (LawrenceSaul and Roweis, 2003). In moving from “measurement” to “concept”, machine learning algorithms continuously deform vector spaces in order to discover parsimonious manifolds. In this way learning in a neural network looks like it might be computing Holland/Gell-Mann schema and thereby creating complex systems directly from data. It is our purpose to extract scientific insights from these compressed simulacra.
Complexity science and machine learning are two of the more successful endeavors that seek to make discoveries in schema-rich phenomena. Their targets are not physical matter but teleonomic/purposeful matter. Both approaches have been promoted as providing insights and predictions for classes of phenomena that have been described as reflexive or agentic–systems that encode historical data sets for the purposes of adaptive decision-making. An open question is whether machine learning is in fact capable of discovering such adaptive schema. Several recent efforts provide clues about a few of the challenges that this project is likely to encounter and what human ideas and constraints need to be added to purely associative models in order that they provide intelligible generative outputs. We might describe these requirements in terms of priors, constraints, and strategies. All restrict configuration spaces in order to enhance processes of induction.
1.1 The need for knowledge-based priors
Neural networks are universal function approximators and can be trained to simulate dynamical systems (Narendra and Parthasarathy, 1990). The obvious way to do this is to latently encode second order differential equations of motion in a network and output velocities and momenta so as to conform to any desired trajectory. In large non-linear dynamical systems this leads to a rather complicated reward function which needs to provide gradient information to all relevant degrees of freedom. An alternative approach is to make use of physical constraints. In this case in the form of Hamiltonian mechanics which exploit propositional knowledge of differentiable manifolds–symplectic geometry. In recent work Miller and colleagues compare the performance of networks trained by exploiting prior knowledge of conservation laws through Hamiltonian-based feedback, versus those trained with no prior “knowledge” of the symmetries of physics (Miller et al., 2020). For both linear and non-linear oscillators, Hamiltonian Neural Networks (HNNs) scale in system size far more effectively than regular neural networks. Hence knowledge of a fundamental physical principle, the principle of least action, improves a purely correlational machine learning model by promoting more minimal and robust reward signals.
1.2 Sparsity constraints encoding reality statistics
A well documented fact of many natural signals, to include visual data and sound data, is that they are full of redundancies or are informationally sparse–much can be eliminated without loss of information. This is what makes lossy compression techniques for images (e.g., JPEG) and sound (e.g., MP3) possible. Compressed sensing techniques can input large machine-learned associative data sets (vectors in Rm) and reduce them to far smaller data sets (vectors in Rn where n ≪ m) (Donoho, 2006). These sparse encodings of the data are given by a relatively small set of dominant coefficients of a suitable orthonormal basis (e.g., Fourier basis). These bases are the naturally induced schema of large, sparse data sets. It has been shown that through the use of a suitable optimal algorithms for compressed sensing, n ≈ N log(m). Hence prior knowledge of basis might significantly accelerate the process of associative learning.
1.3 Strategic common knowledge
One of the interesting features of schema-rich systems is their “insider-ability” to encode other schema-rich systems. A compelling example for this is coordination in a Bayesian game played among agents with or without a common prior - a shared schema. Bayesian games are games of incomplete information where different players possess different private information. This private information relates to the particular subgame being played. Games are made up from multiple subgames (e.g., normal form bimatrix games) which are selected by a stochastic process described as “nature’s move”. There are distributions over these types. Actions within a subgame receive payoffs according to which typem or move, nature makes. For example, agents could be playing a cooperative game (CG) or a prisoner’s dilemma (PD) game. The actions for both subgames are shared knowledge (cooperate and defect) but the payoffs vary according to the subgame selected. In a one shot game the CC subgame will favor cooperation and the PD subgame defect. Dekel and colleagues argue that if the distribution over nature’s moves is not shared (the common prior) then an optimal Bayesian learner will not be able to learn the mixed Nash equilibrium over subgames (Dekel et al., 2004). This suggests a way that elementary forms of prior “social knowledge” might enhance strategically-deployed machine learning.
2 Wigner reversals and Feynman limits
Ernst Mach in The Economy of Science (Ernst, 1986) observed that “The sciences most developed economically are those whose facts are reducible to a few numerable elements of like nature. Such is the science of mechanics, in which we deal exclusively with spaces, times, and masses” and “Mathematics may be defined as the economy of counting”. The success of economical or parsimonious reasoning during the course of the scientific revolution lead Alfred North Whitehead to quip, “The history of the 17th century science reads as if it were some vivid dream of Plato or Pythagoras” (Alfred North Whitehead, 1956).
The authoritative statement on minimal math with a maximum of explanatory power was made by Eugene Wigner in 1960 (Wigner, 1990) in a paper on The Unreasonable Effectiveness of Mathematics in the Natural Sciences. Describing the success of mathematical models in accounting for both planetary motion using classical mechanics, and complex spectra and the Lamb shift using quantum mechanics, Wigner proposed an ”empirical” law of epistemology. The law describes a surprising correspondence between the deductive rules of mathematics and the laws of physics.
The philosopher of mathematics Marc Steiner refined Wigner’s insight in order to explain this epistemological law as a property of formal mathematical analogies for physical processes (Steiner, 1989). For example, the mathematical property of linearity can be analogized to the physical phenomenon of superposition. The key requirement is that physical processes are regular enough to be captured by relatively simple propositions.
When we turn to complex reality Wigner’s epistemological law unravels. There are few instances of a parsimonious mathematical theory in biology, anthropology, or economics, that rival the numerical precision of theories in mathematical physics. Wigner’s insight is effectively reversed, mathematics seems to be–at least by the standards of physics–unreasonably ineffective in the complex domain (see Figure 1). A partial answer for the “Wigner Reversal” was provided by Richard Feynman in his Lectures on Physics (Feynman et al., 1963) where he asks what is meant by understanding something in physics:
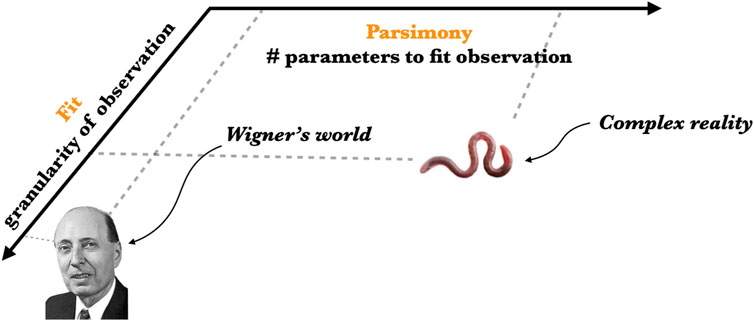
FIGURE 1. Fundamental physical theory achieves high granularity fits to observables with parsimonious theories. This is the phenomenology described by Eugene Wigner as “the unreasonable effectiveness of mathematics”–Wigner’s World. Complex reality does not achieve this degree of propositional compression and requires larger models (high description length) that fit coarse-grained observables–Complex reality.
We can imagine that this complicated array of moving things which constitutes “the world” is something like a great chess game being played by the gods, and we are observers of the game. We do not know what the rules of the game are; all we are allowed to do is to watch the playing … Of course, if we watch long enough, we may eventually catch on to a few of the rules. The rules of the game are what we mean by fundamental physics. Even if we knew every rule, however, we might not be able to understand why a particular move is made in the game, merely because it is too complicated and our minds are limited.”
The principal character of complex reality is that while it obeys the laws of physics it is not determined by the laws of physics. As Anderson made very clear in his foundational paper, More is Different (Anderson, 1972), the ontological character of complexity is an accumulation of broken symmetries, also called “frozen accidents”, that amass over the course of biological and cultural evolution. These broken symmetries impose a very restrictive upper bound on the power of parsimonious mathematics (Krakauer, 2023) typically suited for ergodic systems. Complex reality can be said to cross what I like to call a “Feynman Limit” where understanding the game of reality is dominated by decidably non-ergodic “moves” beyond which the fundamental rules or laws of physics lose much of their explanatory power. Complex reality evolves towards irreducibly high dimension and complication, with little of Mach’s “economy of counting” or Whitehead’s “vivid dream of Pythagoras”, and resembles far more the historically-encrypted natural histories of Linnaeus (Krakauer et al., 2017).
3 Ockham versus Meta-Ockham razors
Despite the apparent irreducibly of complexity, an intriguing feature of complex phenomena is the high information content of descriptive and predictive models, and the low information content of processes generating the same models. Two illustrative examples include the high information content of genomes and deep neural networks versus the relative simplicity of natural selection (NS) and reinforcement learning (RL). Both NS and RL can be used to evolve or train arbitrarily complicated agents and models. Stated differently, the Darwinian logic for the evolution of a bacterium or a mammal remains essentially invariant, as does the RL scheme for training a simple classifier versus a large language model. There is a Wigner-Reversal in terms of the many parameters required to fit observations but it is accompanied by a surprising simplicity in terms of the small number of parameters of the generative process. Ockham’s razor does not apply to complex systems and yet there is what we might call a Meta-Ockham’s razor applicable to constructing them. What is required is an historical process that can break symmetries and store these in suitable memories. And one consequence of these processes is that they typically result in schema (genes; circuits, modules) that encode a coarse-grained reflection of the world in which the model lives. We should think of Meta-Ockham as any parsimonious process or algorithm that is able to discover emergent forms of schema-rich effective theory.
This highlights a fundamental distinction between complexity science and machine-learning on the one hand and fundamental physical science on the other. In fundamental physics, Ockham’s razor applies to the structure of physical reality (e.g., the standard model), whereas theories that purport to explain the standard model, to include solutions to the “fine-tuning problem” (Donoghue, 2007), are often infinitely complicated. These include theories of the multiverse (infinite diversity from which we select our own Universe) (Carr and Ellis, 2008), Top Down Cosmology (infinite diversity of initial conditions) (Stephen, 2003), and simulation theory (an infinite regress on the weak anthropic principle) (Bostrom, 2003). This situation is illustrated in 2 in which complex reality maps to non-parsimonious models and meta-parsimonious (P2) processes, whereas physical reality maps to parsimonious models and non-meta-parsimonious processes (P1) (Figure 2).
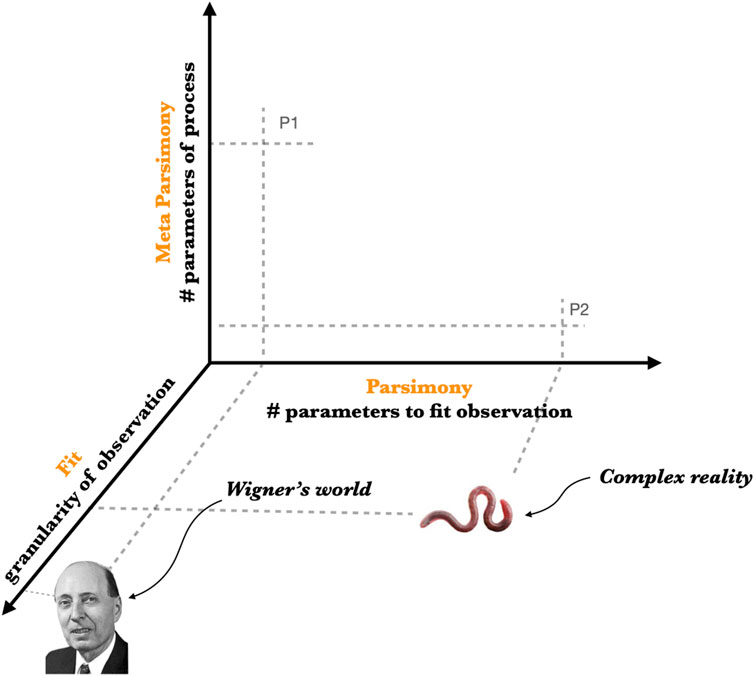
FIGURE 2. Wigner’s world is parsimonious at the level of observables but far from parsimonious in origin. The processes behind these worlds, often described as the fine-tuning of physical reality, are very large (P1) or effectively infinite in complication. Complex reality is not parsimonious but meta-parsimonious (P2). Processes like natural selection and reinforcement learning can scale to arbitrarily large models. Hence physical knowledge and complex knowledge achieve minimality in different domains of explanation.
4 Discovering schema in “super-humean” models
To make progress in our understanding of the complex domain I would like to suggest that it will be necessary to integrate the fine-grained paradigms of prediction provided by machine learning with the coarse-grained paradigms of understanding provided by complexity science. In Figure 3 I lay out four quadrants in a theory space described by two dimensions of model parameters and phenomenal dimensions. Physical theory (B), sensu Wigner and Mach, expresses low dimensional rule systems (e.g., gravitation) using fundamental parameters (e.g., the gravitational constant). Unnecessarily complicated models (A) are simplified by searching for more fundamental rules, invoking principles such as symmetry, thereby realizing Ockham’s razor. Irreducibly high dimensional phenomena are fit using effective parameters capturing innumerable higher order associations (C) or described with coarse-grained equalities among emergent schema (D). Finding schema in very large statistical associations goes beyond the application of Ockham’s razor (i.e., eliminating correlations below a certain threshold) to discovering new mechanical dependencies among effective degrees of freedom through processes like natural selection and reinforcement learning.
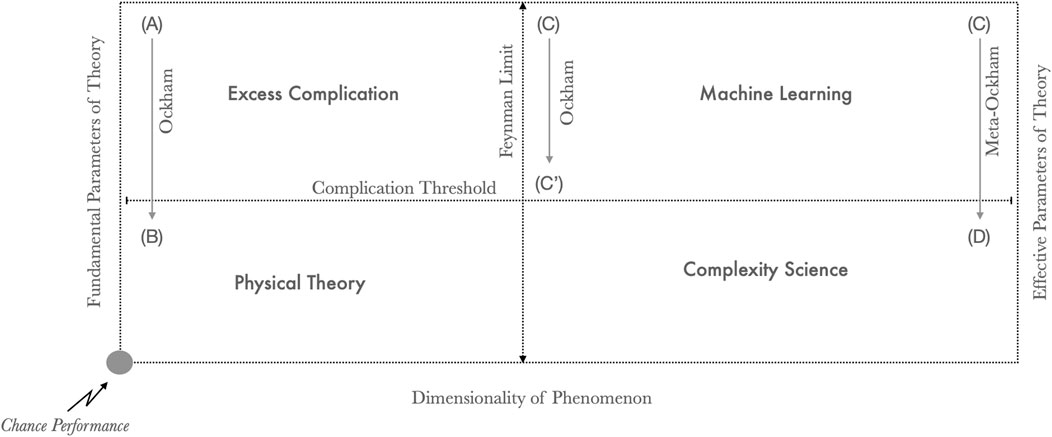
FIGURE 3. A categorical theory space for mathematical science. (B): physical theory describes low dimensional phenomena with a small number of fundamental parameters. (A): low dimensional phenomena often begin with theories of excessive complication above a Complication Threshold. Ockham’s razor is used to move theories into the space of parsimonious physical theory (A->B). (C): high dimensional phenomena can be described with large associative models capturing a variety of feature-rich manifolds. C’: these can be simplified by through lossy compression that prune sub-threshold parameters (C->C′). (D): through suitable coarse-graining and abstraction low dimensional constructs with effective parameters are discovered in machine learning models through the application of a Meta-Ockham’s razor.
Figure 4 plots a possible course for scientific discovery through theory space. All models begin with a suitable simplification of parts and their interactions such that complicated processes can be based on simple components - they are microscopically coarse-grained (MiC). In population genetics genes are encoded as simple linear or non-linear contributions to a global fitness function (Ewens, 2004); in physics particles are encoded as charges in suitable fields (Kosyakov, 2007), and in game theory agents are encoded as strategies and interactions as scalar payoffs (Osborne, 2004).
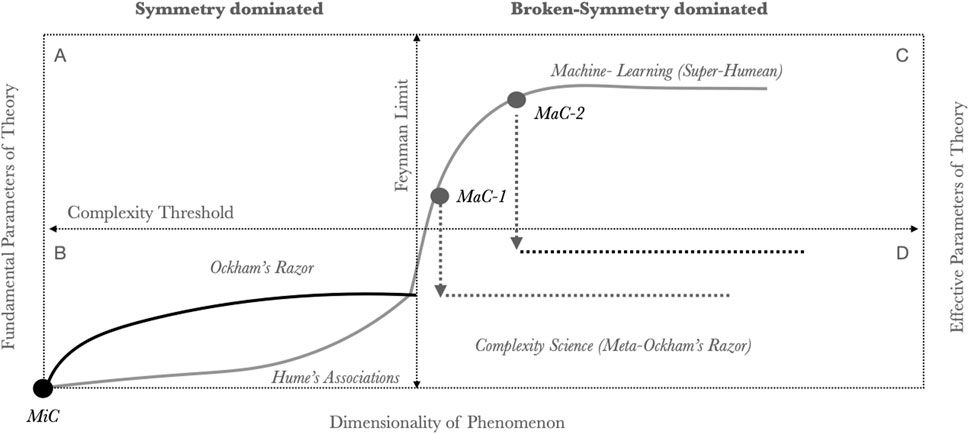
FIGURE 4. Paths through theory space. All theory starts with suitable microscopic coarse-graining (MiC) and increases in complication as the dimension of phenomena increase (Quadrant B). Physical theory saturates in complication by discovering fundamental symmetries. Hence further increases in dimension are not matched by an increase in fundamental parameters (e.g., the theory of gravity is not extensive in the number of massive objects). Statistical models control their size through appropriate penalties on parameter numbers. This scaling holds true up to a Feynman-Limit where broken symmetries and broken ergodicities dominate over fundamental regularities. Statistical models continue to grow without bound describing/fitting increasingly high dimensional phenomena whereas physical models cease to be informative. Very large statistical models (Quadrant C) achieve Super-Humean encodings of irreducible complex data sets. Through macroscopic coarse-graining (MaC1-2) statistical models of different ranks can be approximated through the discovery of schema that replace pure associations with causal mechanical dependencies. MaC-1 illustrates a relatively small statistical model in which model correlations allow for compression into a mechanical theory which remains insensitive to dimension (Quadrant D). MaC-2 describes the case where only very large statistical models yield to coarse-graining. This is a case where new mechanical theory can only be discovered once a suitable super-Humean model has been trained.
A suitable MiC is always necessary in order to explore collective properties of a given system. A good example is provided by neural network models in which neurons are encoded as rectified linear units (Arora et al., 2016) trained to encode very large data sets allowing for unprecedented “super-Humean” (after Hume for whom all knowledge is associative and causal mechanism nominal) inductive performance. This enables the discovery of regularities not present in smaller models. Evidence for such discontinuities in model scaling is now abundant and comes from the remarkable success of very large neural networks in a variety of complex domains, including performance on computer and combinatorial games (Schrittwieser et al., 2020), visual classification tasks (Chen et al., 2021), language production (Mitchell and Krakauer, 2023), and prediction in structural biology (Jumper et al., 2021).
What remains to be explored is the use of these models as auxiliaries for understanding complex reality. Complexity science can take as input large statistical models - constructed from simple (MiC) elements - in order to discover within them suitable macroscopic coarse-grainings (MaC). Whereas the MiC units are assumed in all scientific models and theories the MaC properties need to be found. The value of a MaC is that they provide the basis for development of low dimensional effective theories. In Figure 4 I illustrate the discovery of coarse-grained schema in statistical models (MaC1-2) associated with significant reductions in effective parameters.
Both physical models and statistical models are able to provide parsimonious descriptions of simple systems (Quadrant B). Physical models do so by finding minimal mechanisms and statistical models do so through suitable regularization. Physical mechanisms start losing their explanatory power when symmetry is broken–systems transition to non-ergodicity - wherein much of the phase-space of a system becomes localized. Physical theory does not stop working at this limit but offers few further predictions. For statistical models as dimensionality increases the number of effective parameters increases. This achieves better fits to data (Quadrant C). It is possible however for “effective degrees of freedom” to be discovered in large statistical models which are in effect induced MaCs of the underlying data sets produced by any algorithm that obeys the Meta-Ockham principle. That is a minimal process producing a maximal model with latent low-dimensional regularities. Two putative MaCs are illustrated in 4. I consider examples for Mac-1 (schema discovery in modest statistical models) and Mac-2 (schema discovery in super-Humean models).
4.1 Schema in MaC-1: latent states
Autoencoders and variational autoencoders provide means of compressing data sets by learning embeddings, or latent spaces, in unlabeled data sets (Dor Bank et al., 2020) typically using reinforcement learning. Linear autoencoders are in effect solving simple eigenvalue problems resembling principal component analysis. Variational autoencoders achieve more uniform encodings of data in latent space than “vanilla” autoencoders by adding explicit regularization terms (minimizing a similarity loss). In the language of this paper–autoencoders are discovering MaCs in data sets. With these in hand, such as with PCA, effective theories can be expressed in terms of a smaller number of latent variables. Whereas techniques of factor analysis, including PCA, are notoriously sensitive to the choice of variable and the order of observation, autoencoders are considerably more robust. In recent work exploring the effect of bottlenecks in variational autoencoders, it has been found that bottleneck-based coarse-graining is able to efficiently discover latent spaces for representing handwritten digits and visual images typical of Street View housing numbers (Wu and Flierl, 2020). And similar results have been discovered by stacking bottlenecked autoencoders in neural networks input with acoustic signals derived from speech (Gehring et al., 2013). Both studies illustrate how statistical models can be: 1) trained with a simple algorithm, and 2) manipulated in order to arrive at low dimensional encodings of data. These then become the basis for more traditional mechanical models. Increasing the size of data sets does not increase the dimensionality of these models as long as the underlying features are those used by the “real-world” system. A very nice example for this kind of hybrid approach comes from use of symbolic regression to extract algebraic laws for dark-matter dynamics from Graph Neural Networks (Cranmer et al., 2020). The project aligns the physical domain/problem (particle interaction) with a bias in network structure (graphs of interactions), and then finds closed form, interpretable expressions, capturing regularities in the data.
4.2 Schema in MaC-2: biological features and units
Living systems discover means of adapting and behaving in very complicated environments. A crucial aspect of these abilities is constructing schema, that in non-trivial ways, generate independent functional traits. Both cells and the nervous system, when analyzed at a sufficient remove from primary chemical and sensory inputs, are characterized by a range of efficient and composable low dimensional and mechanical units that can be aggregated into adaptive functions. Recurrent neural networks trained through reinforcement on very large chemical data-bases of molecules are able to generate idealized, highly coarse-grained molecules (schema-molecules), described with concatenated sequences of atoms. These are able to generate realistic distributions of molecular properties (Flam-Shepherd et al., 2022). Novel molecules can then be discovered by selecting an appropriate property from these distributions and extracting associated “schema-molecules”. Hence large data sets train generative neural networks to discover essential features of molecules which then become the coarse-grained basis for more traditional chemical models. Much as idealized molecules (e.g., strings of letters) are induced schema, so are dynamical trajectories through space produced by robotic limbs. Spatial autoencoders, trained on very large data sets–real world dynamical images–are able to acquire through reinforcement learning compact states whose activation trace out efficient robotic manipulation paths (Finn et al., 2016). Hence through a suitable process for inducing a MaC, very large machine learning models, might provide exactly the preprocessed data required by lower dimensional mechanical theories of function.
5 Conclusion
I propose that both machine learning and complexity science are in a fundamental sense in pursuit of functional schema. Both study the structure of machines that encode adaptive histories–from molecular sensors to language games. Fortunately, they do so in complementary ways, which we might think of as the machine-learning pre-processing of phenomena (encoding non-trivial dependencies), and the complexity science post-processing of encodings (coarse-graining into schema). Coarse-graining by virtue of revealing natural units provides gains in terms of computational efficiency (Israeli and Goldenfeld, 2006), limits combinatorial explosions (Feret et al., 2009), enables the analysis of behavior over long time-scales (Espanol, 2004), elucidates causal interactions (Flack, 2017), and can provide a principled compression for non-linear time series (Shalizi and Crutchfield, 2001).
The scientific revolution provides a useful analogy for this relationship in its connection of scientific instruments to theories. The light telescope captures and focuses visible wavelengths and provides these as inputs to a reduced mathematical theory, e.g., the theory of orbits. And reduced theories such as general relativity allows for the design of a gravitational wave detector on principles independent from optics. If we think of machine learning as an algorithmic telescope, and become expert in its modes of operation, there is a prospect of discovering entirely new rules and laws for noisy domains that through more direct observation have proven recalcitrant to simplification. And very large statistical models can provide, by virtue of Meta-Ockham processes, the foundation for entirely new mechanical theories in the complex domain.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
DK concieved and wrote the paper.
Funding
This work is in part supported by grant no. 20650 from the TWCF on Intelligence, Compositionality and Mechanism Design.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alfred North Whitehead (1956). Mathematics as an element in the history of thought. world Math. 1, 402–417.
Anderson, P. W. (1972). More is different. Science 177 (4047), 393–396. doi:10.1126/science.177.4047.393
Arora, R., Basu, A., Mianjy, P., and Mukherjee, A. (2016). Understanding deep neural networks with rectified linear units. arXiv preprint arXiv:1611.01491.
Bostrom, N. (2003). Are we living in a computer simulation? philosophical Q. 53 (211), 243–255. doi:10.1111/1467-9213.00309
Carr, B., and Ellis, G. (2008). Universe or multiverse? Astronomy Geophys. 49 (2), 2.29–2.33. doi:10.1111/j.1468-4004.2008.49229.x
Chen, L., Li, S., Bai, Q., Yang, J., Jiang, S., and Miao, Y. (2021). Review of image classification algorithms based on convolutional neural networks. Remote Sens. 13 (22), 4712. doi:10.3390/rs13224712
Cranmer, M., Sanchez-Gonzalez, A., Battaglia, P., Xu, R., Cranmer, K., David, S., et al. (2020). Discovering symbolic models from deep learning with inductive biases. arXiv preprint arXiv:2006.11287.
Dekel, E., Fudenberg, D., and Levine, D. K. (2004). Learning to play bayesian games. Games Econ. Behav. 46 (2), 282–303. doi:10.1016/s0899-8256(03)00121-0
Donoghue, J. F. (2007). The fine-tuning problems of particle physics and anthropic mechanisms. Universe or multiverse, 231–246.
Donoho, D. L. (2006). Compressed sensing. IEEE Trans. Inf. theory 52 (4), 1289–1306. doi:10.1109/tit.2006.871582
Espanol, P. (2004). “Statistical mechanics of coarse-graining,” in Novel methods in soft matter simulations (Springer), 69–115.
Feret, J., Danos, V., Krivine, J., Harmer, R., and Fontana, W. (2009). Internal coarse-graining of molecular systems. Proc. Natl. Acad. Sci. 106 (16), 6453–6458. doi:10.1073/pnas.0809908106
Feynman, R. P., Leighton, R. B., Sands, M., and Hafner, E. M. (1963). The feynman lectures on physics, Vol. i. Rading, Mass.: Addison-Wesley.
Finn, C., Tan, X. Y., Duan, Y., Darrell, T., Levine, S., and Abbeel, P. (2016). “Deep spatial autoencoders for visuomotor learning,” in 2016 IEEE International Conference on Robotics and Automation (ICRA) (IEEE), 512–519.
Flack, J. C. (2017). Coarse-graining as a downward causation mechanism. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 375 (2109), 20160338. doi:10.1098/rsta.2016.0338
Flam-Shepherd, D., Zhu, K., and Aspuru-Guzik, A. (2022). Language models can learn complex molecular distributions. Nat. Commun. 13 (1), 3293. doi:10.1038/s41467-022-30839-x
Gehring, J., Miao, Y., Metze, F., and Waibel, A. (2013). “Extracting deep bottleneck features using stacked auto-encoders,” in 2013 IEEE international conference on acoustics, speech and signal processing (IEEE), 3377–3381.
Gell-Mann, M. (1995). The quark and the jaguar: adventures in the simple and the complex. Macmillan.
Holland, J. H. (2000). Building blocks, cohort genetic algorithms, and hyperplane-defined functions. Evol. Comput. 8 (4), 373–391. doi:10.1162/106365600568220
Israeli, N., and Goldenfeld, N. (2006). Coarse-graining of cellular automata, emergence, and the predictability of complex systems. Phys. Rev. E 73 (2), 026203. doi:10.1103/physreve.73.026203
Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., et al. (2021). Highly accurate protein structure prediction with alphafold. Nature 596 (7873), 583–589. doi:10.1038/s41586-021-03819-2
Kant, I. (1908). Critique of pure reason. 1781. Modern classical philosophers. Cambridge, MA: Houghton Mifflin, 370–456.
Kosyakov, B. (2007). Introduction to the classical theory of particles and fields. Springer Science and Business Media.
Krakauer, D. C. (2023). Symmetry–simplicity, broken symmetry–complexity. Interface Focus 13 (3), 20220075. doi:10.1098/rsfs.2022.0075
Krakauer, D., Walker, S. I., Davies, P. C. W., and Ellis, G. F. R. (2017). Cryptographic nature. From matter to life: information and causality, 157. Cambridge: Cambridge University Press–173.
LawrenceSaul, K., and Roweis, S. T. (2003). Think globally, fit locally: unsupervised learning of low dimensional manifolds. J. Mach. Learn. Res. 4 (6), 119–155.
Miller, S. T., Lindner, J. F., Choudhary, A., Sinha, S., and Ditto, W. L. (2020). The scaling of physics-informed machine learning with data and dimensions. Chaos, Solit. Fractals X 5, 100046. doi:10.1016/j.csfx.2020.100046
Mitchell, M., and Krakauer, D. C. (2023). The debate over understanding in ai’s large language models. Proc. Natl. Acad. Sci. U. S. A. 120 (13), e2215907120. doi:10.1073/pnas.2215907120
Narendra, K. S., and Parthasarathy, K. (1990). Identification and control of dynamical systems using neural networks. IEEE Trans. neural Netw. 1 (1), 4–27. doi:10.1109/72.80202
Schrittwieser, J., Antonoglou, I., Hubert, T., Simonyan, K., Sifre, L., Schmitt, S., et al. (2020). Mastering atari, go, chess and shogi by planning with a learned model. Nature 588 (7839), 604–609. doi:10.1038/s41586-020-03051-4
Shalizi, C. R., and Crutchfield, J. P. (2021). Computational mechanics: pattern and prediction, structure and simplicity. J. Stat. Phys. 104, 817–879.
Steiner, M. (1989). The application of mathematics to natural science. J. philosophy 86 (9), 449–480. doi:10.2307/2026759
Wigner, E. P. (1990). “The unreasonable effectiveness of mathematics in the natural sciences,” in Mathematics and science (World Scientific), 291–306.
Keywords: complexity, machine learning, schema, ockham, parsimony, theory, manifold learning, simplicity
Citation: Krakauer DC (2023) Unifying complexity science and machine learning. Front. Complex Syst. 1:1235202. doi: 10.3389/fcpxs.2023.1235202
Received: 05 June 2023; Accepted: 03 October 2023;
Published: 18 October 2023.
Edited by:
Maxi San Miguel, Institute for Cross Disciplinary Physics and Complex Systems, IFISC (CSIC-UIB), SpainReviewed by:
Guido Fioretti, University of Bologna, ItalyAndrea Rapisarda, University of Catania, Italy
Copyright © 2023 Krakauer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David C. Krakauer, a3Jha2F1ZXJAc2FudGFmZS5lZHU=
 David C. Krakauer
David C. Krakauer