Bearing-Only Adaptive Formation Control Using Back-Stepping Method

1 Introduction

In recent years, formation control of multi-agent systems has attracted great attention due to its wide application in military, scientific research, and daily life. The information commonly used in the existing formation control are categorized into position, relative distance and relative bearing. In particular, the research on formation control based on position or relative distance are very rich (Lin et al., 2016; Ran et al., 2017; Han et al., 2019; Mehdifar et al., 2019; Sun et al., 2019; Zou et al., 2019; Chen et al., 2020; Liu et al., 2020; Mehdifar et al., 2020; Yu and Chen, 2020). Relatively speaking, there is a lack of researches on formation control based on relative bearing. However, compared to the formation control approaches that rely on position or relative distance, bearing-only formation control has lower requirements for sensors, so it reduces the production cost and has a wide range of application scenarios. Therefore, the research on bearing-only formation control is of great significance.

Zhao and Zelazo (2016) have put forward the definition of bearing rigidity for any dimension and proved the conditions of bearing rigidity, which greatly promoted the development of formation control based on relative bearing. Based on the definition, researchers have done a lot of research. For different agent models such as single integrators, double integrators and unicycles, Zhao et al. (2019) designed a series of bearing-only control laws, which can enable followers to track leaders and reach the specified formation, and proved its stability by use of the standard Lyapunov method. Li et al. (2021) solved the bearing-only formation control problem of the three-dimensional nonholonomic constraints system by transforming the three-dimensional nonholonomic model into Euler-Lagrange-like form and using the back-stepping design method. Zhao et al. (2021) considered the system with local reference frame, they synchronized the orientations of followers with the leader first, and then adopted bearing-only control law to solve the formation control problem of double-integrators without global reference coordinates. Yang et al. (2020) designed a relative position estimator, which uses the relative bearing and the linear velocity information of the leader to estimate the relative position of the leader, and designed a controller with the estimated relative position information to complete the task of tracking the leader. Since collision is devastating to the formation control system, Hu and Yang (2020) proposed a distributed cooperative consensus control algorithm, and proved that this control method can prevent agents from colliding effectively. Besides, Luo et al. (2020) used the maximal clique graph instead of infinitesimal rigidity to express the communication topology between multi-agent with non-holonomic constraints, and designed a bearing-only formation control law to solve the problem of how to achieve global stability without leaders. Compared with these existing research on bearing-only formation control, most of existing research are focused on linear system, while the system studied in this paper is a nonlinear system with unknown time-varying disturbance. Disturbance is inevitable in reality, so it seems of more practical significance to study nonlinear system.

The main contribution of this paper is to propose a novel bearing-only formation control law that can handle second-order system with unknown disturbance. The control algorithm based on the negative gradient method only uses the information of relative bearings between neighboring agents. The adaptive estimation method is introduced to counteract the unknown disturbance, and the back-stepping design method is used in the design process. Then, the global stability of the bearing-only formation system is demonstrated by use of the Barbalat’s Lemma.

2 Problem Statement

Consider a formation system comprising of n agents, and the model of each agent is as follows:

$\{\begin{array}{l}{\dot{r}}_i=v_i\\ {\dot{v}}_i=u_i+d_{ui}\end{array}(1)$

In the formula above, $r_i\in R^d$ stands for the position of agent i, and $v_i$ and $u_i$ represent velocity and control input of agent i, respectively. Here, $i=\mathrm{1,2},\cdots ,n$. $d_{ui}$ is the unknown disturbance, and we assume $\Vert d_{ui}\Vert \le D_{ui}$, $D_{ui}$ is unknown constant.

In this paper, we use an undirected graph $G=\left(V,E\right)$ to represent the communication relationship of the system. $V=\left\{\mathrm{1,2},\cdots ,n\right\}$ represents the set of agents in the system, and $E\subseteq V\times V$ represents the set of edges in the system. The edge $\left(i,j\right)\in E$ indicates that agent i can measure the relative bearing of agent j, and hence agent j is neighbor of i. Let $N_i=\left\{j\in V:\left(i,j\right)\in E\right\}$ denote the set of neighboring vertices of vertex i, and we also have $\left(i,j\right)\in E\iff \left(j,i\right)\in E$.

Define the edge vector and bearing vector, respectively:

$r_{ij}=r_i-r_j,g_{ij}=\frac{r_{ij}}{\Vert r_{ij}\Vert }$

As shown above, $\Vert r_{ij}\Vert$ stands for the Euclidean distance between agent i and agent j, $j\in N_i$ is neighbor of agent i. $g_{ij}$ means the bearing of $r_i$ relative to $r_j$. In this chapter, assuming that all agents can perceive the global coordinate system, there are $r_{ij}=-r_{ji}$, $g_{ij}=-g_{ji}$. Relative bearing of agents can usually be measured by onboard vision in practice.

In this paper, considering the control of formation without leader, the position information of multiple agents is $r={\left[r_1^T,\cdots ,r_n^T\right]}^T$. An oriented graph $\overrightarrow{G}$ is obtained by orienting each edge in the undirected graph G, that is, the direction of any edge in G is calibrated (Biggs, 1974). Define the edge in the graph G, tagging the order from 1 to m, m represents the total number of edges in graph G. Number the edges in $\overrightarrow{G}$ from $E_1$ to $E_m$, then get the corresponding incidence matrix $H=H\left(G\right)=\left(h_{ij}\right)\in R^{m\times n}$. The incidence matrix H is a matrix composed of 0, 1, and −1. The elements on the rows of the incidence matrix are indexed by edges $E\subseteq V\times V$, and the value elements on the columns are indexed by vertices $V=\left\{\mathrm{1,2},\cdots ,n\right\}$, namely: except for ${\left[H\right]}_{ki}$ and ${\left[H\right]}_{kj}$, all elements in the row k of the incidence matrix H are zero. Among them, when vertex i is the last vertex of edge k, ${\left[H\right]}_{ki}=-1$, and when vertex j is the first vertex of edge k, ${\left[H\right]}_{kj}=1$.

Therefore, the incidence matrix is defined as:

$e=H\otimes I_{d}r=\overline{H}r(2)$

where $\otimes$ denotes the Kronecker product, and $I_d\in R^{d\times d}$ is the identity matrix.

Assuming that the edge $\left(i,j\right)$ in the graph corresponds to the edge k in the directed graph, where $k\in \left\{1,\cdots ,m\right\}$. The edge and bearing vectors for the kth directed edge can be expressed as: $e_k=r_{ij}=r_i-r_j$, $g_k=e_k/\Vert e_k\Vert$, where $e={\left[e_1^T,\cdots ,e_m^T\right]}^T$, $g={\left[g_1^T,\cdots ,g_m^T\right]}^T$.

At the same time, assign an expected vector to each edge vector $g_{ij}$ in graph G, which is called $g_{ij}^{\ast }$. In the same way, define $g_k^{\ast }=g_{ij}^{\ast }$ and $g^{\ast }={\left[g_1^{\ast T},g_2^{\ast T},\cdots ,g_m^{\ast T}\right]}^T$.

In this paper, we use the infinitesimally bearing rigidity to express the communication topology of multi-agent systems. It means that the shape of the formation can be uniquely determined. Zhao and Zelazo (2016) put forward the definition of infinitesimally bearing rigidity for any dimension and proved the conditions of infinitesimally bearing rigidity, which is shown in the following lemma.

Lemma 1: (Zhao and Zelazo, 2016): A framework G in $R^d$ is infinitesimally bearing rigid if and only if rank $\left(R\left(r\right)\right)=dn-d-1$, where $R\left(r\right)=\frac{\partial F_B\left(r\right)}{\partial r}$, $F_B\left(r\right)={\left[g_1^T,g_2^T,\cdots g_m^T\right]}^T$.

In order to design the globally stable formation control strategy, we give the following assumption and the potential function.

Assumption 1: The initial positions of agents do not coincide, and neighboring agents will not collide during formation.

The potential function between agent i and its neighboring agent j is defined as follows:

$V_{ij}={\Vert g_{ij}-g_{ij}^{\ast }\Vert }^2\Vert r_{ij}\Vert (3)$

Define:

${\rho }_{ij}=\frac{\partial V_{ij}}{\partial r_{ij}}=2\left(g_{ij}-g_{ij}^{\ast }\right)(4)$

The definition of total potential function of agent i is

$V_i={\displaystyle \sum _{j\in N_i}{V}_{ij}}(5)$

The problem of the bearing-only formation control to be solved in this paper is formally described as follows.

Problem 1: Consider multi-agent systems of n agents with unknown disturbance, its communication topology is defined by infinitesimal bearing rigidity. For any initial condition other than coincidence $r_i\left(0\right)\in R^d$, $i=\mathrm{1,2},\cdots n$, design a bearing-only control law to control the relative bearings between agents reaches the desired value, and all agents are moving at the desired velocity $v^{\ast }$, which make the multi-agent systems form the specified formation, that is:

$\underset{t\to \infty }{\text{lim}}{g}_{ij}=g_{ij}^{\ast },\underset{t\to \infty }{\text{lim}}{v}_i=v^{\ast },\left(i=\mathrm{1,2},\cdots n,j\in N_i\right)$

3 Design of Global Stabilizer

Define ${\tilde{r}}_i=r_i-r^{\ast }$, ${\tilde{v}}_i=v_i-v^{\ast }$, ${\dot{r}}^{\ast }=v^{\ast }$, ${\tilde{u}}_i=u_i-{\dot{v}}^{\ast }$, then we have

$\{\begin{array}{l}{\dot{\tilde{r}}}_i={\tilde{v}}_i\hfill \\ {\dot{\tilde{v}}}_i={\tilde{u}}_i+d_{ui}\hfill \end{array}i=\mathrm{1,2},\cdots ,n(6)$

Also, let $\tilde{r}={\left[{\tilde{r}}_1^T,\cdots ,{\tilde{r}}_n^T\right]}^T,\tilde{v}={\left[{\tilde{v}}_1^T,\cdots ,{\tilde{v}}_n^T\right]}^T,\tilde{u}={\left[{\tilde{u}}_1^T,\cdots ,{\tilde{u}}_n^T\right]}^T$, $d_u=\left[d_{u1},\cdots ,d_{un}\right]$ , then ${\tilde{r}}_{ij}=r_{ij},{\tilde{v}}_{ij}=v_{ij}$, so the whole system can be written in the form as:

$\{\begin{array}{l}\dot{\tilde{r}}=\tilde{v}\hfill \\ \dot{\tilde{v}}=\tilde{u}+d_u\hfill \end{array}(7)$

Then, the control law is designed by use of the back-stepping design method.

Step 1:

Focus on the following subsystems of Eq. 7:

$\dot{\tilde{r}}=\tilde{v}(8)$

In this subsystem, $\tilde{v}=h\left(\tilde{r}\right)={\left[h_1^T,h_2^T,\cdots ,h_n^T\right]}^T$, and we use the feedback controller $h\left(\tilde{r}\right)$ to control the relative bearing.

The Lyapunov function candidate is chosen as follows:

$W_1\left(t\right)={\displaystyle \sum _{i=1}^n{V}_i}={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\in N_i}{V}_{ij}}}(9)$

Owing to $r_{ij}=-r_{ji}$, $V_i$ is symmetric about $r_{ij}$, we have $\partial V_{ij}/\partial r_{ij}=\partial V_{ij}/\partial r_i=-\partial V_{ij}/\partial r_j$, $j\in N_i$, then

${\dot{W}}_1\left(t\right)=\frac{d}{dt}{\displaystyle \sum _{i=1}^n{V}_i}=2{\displaystyle \sum _{i=1}^n{\tilde{v}}_i^T{\nabla }_{r_i}{V}_i}$

The virtual control law $\tilde{v}=h\left(\tilde{r}\right)$ is chosen as

$h_i\left(\tilde{r}\right)=-{\displaystyle \sum _{j\in N_i}2\left(g_{ij}-g_{ij}^{\ast }\right)}(10)$

$\tilde{v}=h\left(\tilde{r}\right)(11)$

and it follows that

${\dot{W}}_1\left(t\right)=2{\displaystyle \sum _{i=1}^n{\tilde{v}}_i^T{\nabla }_{r_i}{V}_i}=-2{\displaystyle \sum _{i=1}^n{\Vert {\displaystyle \sum _{j\in N_i}2\left(g_{ij}-g_{ij}^{\ast }\right)}\Vert }^2\le 0}(12)$

Step 2:

Then, introducing the error variable

$\overline{v}={\left[{\overline{v}}_1^T,{\overline{v}}_2^T,\cdots ,{\overline{v}}_n^T\right]}^T=\tilde{v}-h\left(\tilde{r}\right)(13)$

Take the derivative of the above equation, that is

$\{\begin{array}{l}\dot{\tilde{r}}=\overline{v}+h\left(\tilde{r}\right)\hfill \\ \dot{\overline{v}}=\tilde{u}+d_u-\dot{h}\left(\tilde{r}\right)\hfill \end{array}(14)$

For the above system, the Lyapunov function candidate is chosen as follows:

$\begin{array}{c}{W}_2\left(\tilde{r},\overline{v}\right)=W_1\left(t\right)+{\displaystyle \sum }_{i=1}^n\left[{\overline{v}}_i^T{\overline{v}}_i+\frac{1}{{\lambda }_i}{\left({\gamma }_i-{\widehat{\gamma }}_i\right)}^T\left({\gamma }_i-{\widehat{\gamma }}_i\right)\right]\end{array}(15)$

where ${\gamma }_i={\left[D_{ui},\cdots ,D_{ui}\right]}^T\in R^d$, ${\widehat{\gamma }}_i$ is the estimated value of ${\gamma }_i$ at time t.

Differentiate the function $W_2\left(\tilde{r},\overline{v}\right)$ with respect to time, we have

$\begin{array}{l}{\dot{W}}_2\left(\tilde{r},\overline{v}\right)=2{\displaystyle \sum _{i=1}^n{\left[{\displaystyle \sum _{j\in N_i}2\left(g_{ij}-g_{ij}^{\ast }\right)}\right]}^T{\overline{v}}_i}+{\displaystyle \sum _{i=1}^n{\left[{\displaystyle \sum _{j\in N_i}2\left(g_{ij}-g_{ij}^{\ast }\right)}\right]}^T{h}_i\left(\tilde{r}\right)}\hfill \\ +2{\displaystyle \sum _{i=1}^n{\overline{v}}_i^T{\tilde{u}}_i}+2{\displaystyle \sum _{i=1}^n{\overline{v}}_i^T{d}_{ui}}-2{\displaystyle \sum _{i=1}^n{\overline{v}}_i^T{\dot{h}}_i\left(\tilde{r}\right)}-\frac{2}{{\lambda }_i}{\displaystyle \sum _{i=1}^n\left[{\stackrel{.}{\widehat{{\gamma }_i}}}^T\left({\gamma }_i-{\widehat{\gamma }}_i\right)\right]}\hfill \end{array}(16)$

Motivated by Wang et al. (2015), the global stabilized formation control law is designed as follows

$\begin{array}{c}{\tilde{u}}_i=-{\overline{v}}_i+h_i\left(\tilde{r}\right)+{\dot{h}}_i\left(\tilde{r}\right)-B_i{\widehat{\gamma }}_i,i=\mathrm{1,2},\cdots ,n\end{array}(17)$

Because of $u_i={\tilde{u}}_i+{\dot{v}}^{\ast }$, the control law is as follows,

$\begin{array}{c}{u}_i=-{\overline{v}}_i+h_i\left(\tilde{r}\right)+{\dot{h}}_i\left(\tilde{r}\right)-B_i{\widehat{\gamma }}_i+{\dot{v}}^{\ast },i=\mathrm{1,2},\cdots ,n\end{array}(18)$

The adaptive law is shown as:

${\dot{\widehat{\gamma }}}_i={\lambda }_i{B}_i{\overline{v}}_i(19)$

Here $B_i=diag\left[\text{sgn}\left({\overline{v}}_{i1}\right),\cdots ,\text{sgn}\left({\overline{v}}_{id}\right)\right]$, where ${\overline{v}}_{id}$ represents the dth element in ${\overline{v}}_i$, $i=\mathrm{1,2},\cdots ,n$, and the sign function is shown as follows:

$\text{sgn}\left(x\right)=\{\begin{array}{c}1,\\ 0,\\ -1,\end{array}\begin{array}{c}x>0\\ x=0\\ x<0\end{array}$

Remark 1: ${\dot{h}}_i\left(\tilde{r}\right)=-{\displaystyle \sum _{j\in N_i}2{\dot{g}}_{ij}}$. In practice, $g_{ij}$ can generally be measured by onboard vision. At the same time, the rate of change of relative bearing can also be measured by onboard vision with optical flow technology, so ${\dot{g}}_{ij}$ can be measured.

Remark 2: The sign function in the control law would cause the chattering phenomenon. In simulation or engineering practice, the saturation function $sat\left(x/\mathit{\phi }\right)$ is usually used to replace the sign function to solve the problem of chattering. When $\left|s/\mathit{\phi }\right|\le 1$, $sat\left(x/\mathit{\phi }\right)=x/\mathit{\phi }$; when $\left|x/\mathit{\phi }\right|>1$, $sat\left(x/\mathit{\phi }\right)=sgn\left(x/\mathit{\phi }\right)$, where $\mathit{\phi }$ represents the width of the boundary layer. Whether the saturation function or the sign function is used, the results in engineering practice and simulation are unchanged.

4 Stability Analysis

The formation stability is analyzed as follows.

Theorem 1: Under the control law (Eq. 18), the multi-agent systems converges asymptotically to the desired shape and all agents move at the desired velocity $v^{\ast }$, and the closed-loop system is globally asymptotically stable.

Proof: The Lyapunov function candidate $W_2\left(\tilde{r},\overline{v}\right)$ is determined by Eq. 15, and note that $W_2$ is smooth and hence regular; its generalized gradient (Clarke, 1983) is a singleton which is equal to its usual gradient everywhere in the state space: $\partial W_2=\left\{\nabla W_2\right\}$ (Shevitz and Paden, 1993). Along with Eqs. 13–19, we can obtain

$\begin{array}{c}{\dot{W}}_2\left(\tilde{r},\overline{v}\right)=2{\displaystyle \sum _{i=1}^n{\left({\nabla }_{r_i}{V}_i\right)}^T{\overline{v}}_i}+{\displaystyle \sum _{i=1}^n\left[2{\overline{v}}_i^T{\dot{\overline{v}}}_i-\frac{2}{{\lambda }_i}{\dot{\widehat{{\gamma }_i}}}^T\left({\gamma }_i-{\widehat{\gamma }}_i\right)\right]}\\ =-2{{\displaystyle \sum _{i=1}^n\Vert {\displaystyle \sum _{j\in N_i}2\left(g_{ij}-g_{ij}^{\ast }\right)}\Vert }}^2-2{\displaystyle \sum _{i=1}^n{\overline{v}}_i^T{\overline{v}}_i}+2{\displaystyle \sum _{i=1}^n{\overline{v}}_i^T\left(d_{ui}-B_i{\gamma }_i\right)}\\ \le -2{{\displaystyle \sum _{i=1}^n\Vert {\displaystyle \sum _{j\in N_i}2\left(g_{ij}-g_{ij}^{\ast }\right)}\Vert }}^2-2{\displaystyle \sum _{i=1}^n{\overline{v}}_i^T{\overline{v}}_i}\\ \le 0\end{array}(20)$

the above inequality is obtained when ${\dot{\widehat{\gamma }}}_i={\lambda }_i{B}_i{\overline{v}}_i$.

Eq. 20 proves that $W_2\left(r_{ij}\left(t\right)\right)$ is non-increasing, and Eq. 15 shows that $W_2\left(r_{ij}\left(t\right)\right)$ greater than zero, so it can be inferred that it has a limit $W_2\left(r_{ij}\left(t\right)\left(\infty \right)\right)$. Define $T\left(g_{ij}\left(t\right)\right)=8{{\displaystyle \sum _{i=1}^n\Vert {\displaystyle \sum _{j\in N_i}\left(g_{ij}-g_{ij}^{\ast }\right)}\Vert }}^2$, so $T\left(g_{ij}\left(t\right)\right)\le -{\dot{W}}_2$. Integrating both sides of the equation, we have

$\underset{t\to \infty }{\text{lim}}{\displaystyle {\int }_0^{t}T\left(g_{ij}\left(\tau \right)\right)d\tau }\le -\underset{t\to \infty }{\text{lim}}{\displaystyle {\int }_0^t{\dot{W}}_2\left(r_{ij}\left(\tau \right)\right)d\tau }=W_2\left(r_{ij}\left(0\right)\right)-W_2\left(r_{ij}\left(\infty \right)\right)$

which means that ${\displaystyle {\int }_0^{t}T\left(g_{ij}\left(\tau \right)\right)d\tau }$ exists and is finite. Now we show that ${\displaystyle {\int }_0^{t}T\left(g_{ij}\left(\tau \right)\right)d\tau }$ is also uniformly continuous.

Since $g_{ij}=r_{ij}\text{/}\Vert r_{ij}\Vert$, $g_{ij}$ are bounded. It is concluded that ${\dot{g}}_{ij}=\frac{\left(I_d-g_{ij}{g}_{ij}^T\right)}{\Vert r_{ij}\Vert }{\dot{r}}_{ij}$ and $\Vert r_{ij}\Vert$ are not equal to zero because it is assumed that agents will not collide. So ${\dot{g}}_{ij}$ are bounded, which indicates $g_{ij}$ are uniformly continuous with $\forall t\in \left[0,+\infty \right)$. Since $T\left(g_{ij}\left(t\right)\right)$ is continuous, it is uniformly continuous with $\forall g_{ij}\left(t\right)$, so it can be deduced that $T\left(g_{ij}\left(t\right)\right)$ is uniformly continuous with $\forall t\in \left[0,+\infty \right)$. According to Barbalat’s lemma (Ge et al., 2002), we can get $\underset{t\to \infty }{\text{lim}}T\left(g_{ij}\left(t\right)\right)=0$, and we can deduce:

$\underset{t\to \infty }{\text{lim}}\left|\right|{\displaystyle \sum }_{j\in N_i}\left(g_{ij}-g_{ij}^{\ast }\right)|{|}^2=0$

In the same way

$\underset{t\to \infty }{\text{lim}}{\overline{v}}_i\left(t\right)=0$

That is ${\Vert {\displaystyle \sum _{j\in N_i}\left(g_{ij}-g_{ij}^{\ast }\right)}\Vert }^2=0\Rightarrow {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\in N_i}\left(g_{ij}-g_{ij}^{\ast }\right)=0}}$

In the following, put the above equation into matrix-vector form

${\overline{H}}^T\left(g_{ij}-g_{ij}^{\text{*}}\right)=0(21)$

Combining Eq. 2 and Eq. 21, we have:

$\begin{array}{c}{r}^T{\overline{H}}^T\left(g-g^{\ast }\right)=e^T\left(g-g^{\ast }\right)={\displaystyle \sum _{k=1}^m{e}_k^T\left(g_k-g_k^{\ast }\right)}={\displaystyle \sum _{k=1}^m\Vert e_k\Vert g_k^T\left(g_k-g_k^{\ast }\right)}\\ ={\displaystyle \sum _{k=1}^m\Vert e_k\Vert \left(1-g_k^T{g}_k^{\ast }\right)}=\frac{1}{2}{\displaystyle \sum _{k=1}^m\Vert e_k\Vert {\Vert g_k-g_k^{\ast }\Vert }^2}\\ =0\end{array}$

We can get $\underset{t\to \infty }{\text{lim}}\left(g_{ij}\left(t\right)-g_{ij}^{\ast }\left(t\right)\right)=0$. It means that all the relative bearing vectors $g_{ij}$ meet the expected value $g_{ij}^{\text{*}}$, that is, the multi-agent systems meets the expected formation, and the system is globally asymptotically stable.

So, $\underset{t\to \infty }{\text{lim}}{h}_i\left(\tilde{r}\right)=-\underset{t\to \infty }{\text{lim}}{\displaystyle \sum _{j\in N_i}2\left(g_{ij}-g_{ij}^{\ast }\right)=0}$. It can be seen from Eq. 13, $\underset{t\to \infty }{\text{lim}}{\tilde{v}}_i\left(t\right)=0$, that is to say, $\underset{t\to \infty }{\text{lim}}{v}_i=v^{\ast }$.

In summary, the system will converge to the following set:

$M=\{r_{ij},{\overline{v}}_i|g_{ij}=g_{ij}^{\ast },{\overline{v}}_i=0,j\in N_i,i=\mathrm{1,2},\cdots ,n\}$

That is, the relative bearings between agents reach the desired value, and all agents are moving at the same desired velocity; then the multi-agent systems achieve the desired formation shape.

5 Simulations

In the simulation, the dynamic model of agents is expressed by the following equation:

$\{\begin{array}{l}{\dot{r}}_i=v_i\\ {\dot{v}}_i=u_i+1.2\cos r_i\end{array}i=\mathrm{1,2},\cdots ,5$

Then, we prove the effectiveness of the control law through 2D and 3D simulation examples.

5.1 Simulation for 2-Dimensional

In simulation, we choose $D_i=1.2$, ${\widehat{\gamma }}_i\left(0\right)={\left[0.1,0\right]}^T$, ${\lambda }_i=2$, $i=1,\cdots ,5$. Set the initial position of each agent to $r_1={\left[\mathrm{1,2}\right]}^T$, $r_2={\left[\mathrm{2,1}\right]}^T$, $r_3={\left[3.5,2.5\right]}^T$, $r_4={\left[\mathrm{3,3}\right]}^T$, $r_5={\left[\mathrm{2,4}\right]}^T$, the initial velocities of the agents are set to $v_1={\left[\mathrm{1,1}\right]}^T$, $v_2={\left[0.5,0\right]}^T$, $v_3={\left[1,-1\right]}^T$, $v_4={\left[\mathrm{1,0.5}\right]}^T$, $v_5={\left[0,-1\right]}^T$. $g={\left[g_{12}^T,g_{13}^T,g_{14}^T,g_{15}^T,g_{23}^T,g_{34}^T,g_{45}^T\right]}^T$ is the desired relative bearing vector, where $g_{12}={\left[-\mathrm{1,0}\right]}^T$, $g_{13}={\left[-0.809,-0.588\right]}^T$, $g_{14}={\left[-0.309,-0.951\right]}^T$, $g_{15}={\left[0.309,-0.951\right]}^T$, $g_{23}={\left[-0.309,-0.951\right]}^T$, $g_{34}={\left[0.809,-0.588\right]}^T$, $g_{45}={\left[0.809,0.588\right]}^T$, and the desired velocity is $v^{\ast }={\left[\mathrm{2,2}\right]}^T$. The simulation results are shown in Figures 1–3.

FIGURE 1

FIGURE 1. The trajectories of agents.

FIGURE 2

FIGURE 2. The bearing errors.$\left|\left|g_{ij}-g_{ij}^{\text{*}}\right|\right|.$

FIGURE 3

FIGURE 3. The velocities of agents.

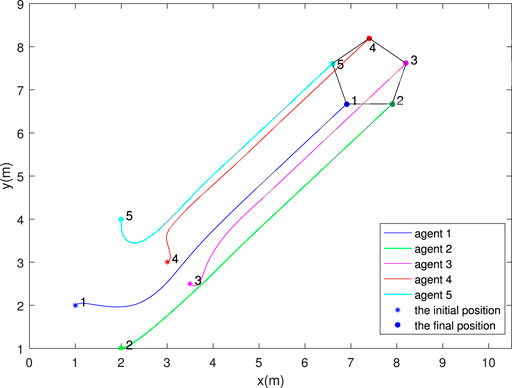
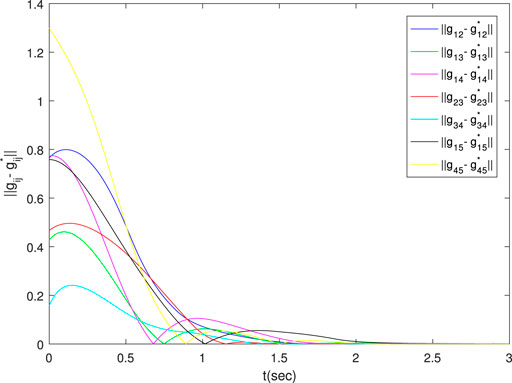
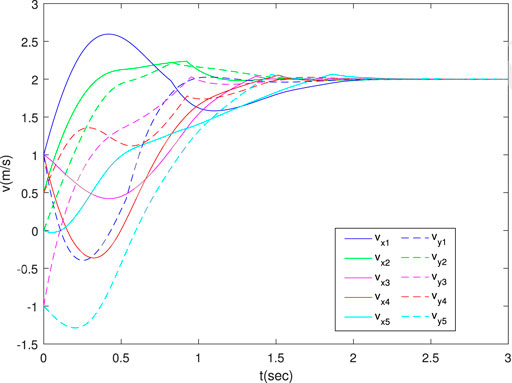
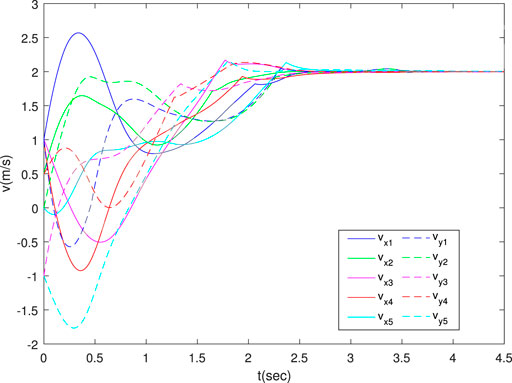
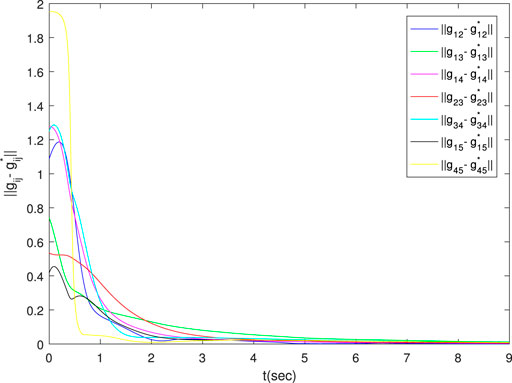
As is shown in Figure 1, the formation converges to the desired regular pentagon. Figure 2 shows the bearing errors converge to zero. Figure 3 illustrates that the velocities of agents converge to desired one. The above results prove the effectiveness of the proposed control law in two dimensions.

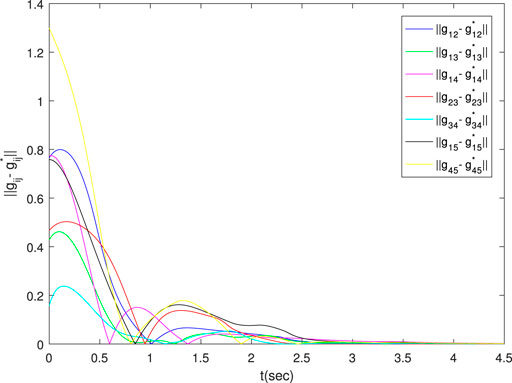
Increasing the disturbance by a factor of three, and comparing the results of Figures 4–6 with Figures 1–3, it can be seen that the magnitude of the disturbance will affect the time required for the system to reach stability. The larger the disturbance, the longer it takes to reach stability.

FIGURE 4

FIGURE 4. The trajectories of agents.

FIGURE 5

FIGURE 5. The bearing errors.$\left|\left|g_{ij}-g_{ij}^{\text{*}}\right|\right|.$

FIGURE 6

FIGURE 6. The velocities of agents.

5.2 Simulation for 3-Dimensional

In simulation, we choose $D_i=1.2$, ${\widehat{\gamma }}_i\left(0\right)={\left[0.1,\mathrm{0,0}\right]}^T$, ${\lambda }_i=2$, $i=1,\cdots ,5$. Setting the initial position of each agent to $r_1={\left[\mathrm{1,3,0}\right]}^T$, $r_2={\left[\mathrm{2,2,2}\right]}^T$, $r_3={\left[3.5,\mathrm{5,3}\right]}^T$, $r_4={\left[\mathrm{3,4,5}\right]}^T$, $r_5={\left[\mathrm{1,4,2}\right]}^T$, the initial velocities of the agents are set to $v_1={\left[\mathrm{5,4,6}\right]}^T$, $v_2={\left[\mathrm{0,2,0}\right]}^T$, $v_3={\left[\mathrm{2,7,1}\right]}^T$, $v_4={\left[\mathrm{4,3,2}\right]}^T$, $v_5={\left[\mathrm{3,5,7}\right]}^T$. $g={\left[g_{12}^T,g_{13}^T,g_{14}^T,g_{15}^T,g_{23}^T,g_{34}^T,g_{45}^T\right]}^T$ is the desired relative bearing vector, where $g_{12}={\left[-\mathrm{1,0,0}\right]}^T$, $g_{13}={\left[-0.707,-0.707,0\right]}^T$, $g_{14}={\left[0,-\mathrm{1,0}\right]}^T$, $g_{15}={\left[-0.408,-0.408,-0.816\right]}^T$, $g_{23}={\left[0,-\mathrm{1,0}\right]}^T$, $g_{34}={\left[\mathrm{1,0,0}\right]}^T$, $g_{45}={\left[-0.408,0.408,-0.816\right]}^T$, and the desired velocity is $v^{\text{*}}={\left[\mathrm{2,2,2}\right]}^T$. The simulation results are shown in Figures 7–9.

FIGURE 7

FIGURE 7. The trajectories of agents.

FIGURE 8

FIGURE 8. The bearing errors.$\left|\left|g_{ij}-g_{ij}^{\text{*}}\right|\right|.$

FIGURE 9

FIGURE 9. The velocities of agents.

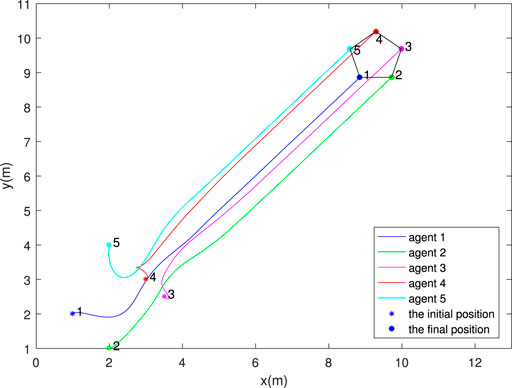
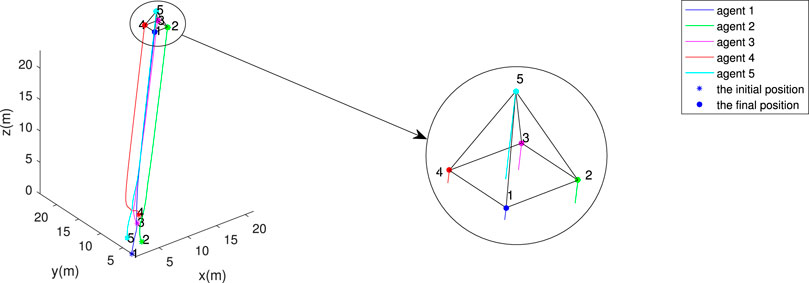
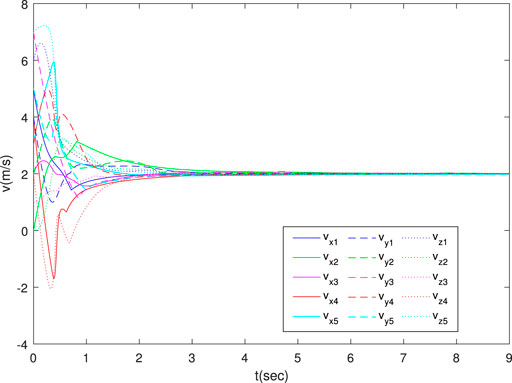
As shown in Figure 7, the formation converges to the desired right square pyramid. Figure 8 shows the bearing errors converge to zero. Figure 9 illustrates that the velocities of agents converge to desired one. The above results prove the effectiveness of the proposed control law in three dimensions.

6 Conclusion

This paper proposes an adaptive formation control algorithm based on negative gradient method to solve the formation problem of a class of second-order system with uncertain disturbances, and the control law only uses the information of relative bearing between neighboring agents. The algorithm introduces adaptive estimation to counteract unknown disturbances. Furthermore, the back-stepping design method is used in the design process. Then, the global stability of the whole formation system is proved by Barbalat’s lemma. In the end, the simulation results in 2D and 3D show the effectiveness of the algorithm.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SL contributed to the design of control law, simulation and writing of the original draft. QW helped with the methodology, guidance, review and editing. EW and YC helped with review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grants 61803331, 61873229, 61806175, and 61873346, in part by the Jiangsu Planned Projects for Postdoctoral Research Funds 1601024B.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Biggs, N. (1974). Algebraic Graph Theory. Cambridge: Cambridge University Press. doi:10.1017/cbo9780511608704

CrossRef Full Text

Chen, L., Mei, J., Li, C., and Ma, G. (2020). Distributed Leader-Follower Affine Formation Maneuver Control for High-Order Multiagent Systems. IEEE Trans. Automat. Contr. 65, 4941–4948. doi:10.1109/tac.2020.2986684

CrossRef Full Text | Google Scholar

Clarke, F. H. (1990). Optimization and Nonsmooth Analysis. New York: John Wiley & Sons. doi:10.1137/1.9781611971309

CrossRef Full Text

Ge, S. S., Hang, C. C., Lee, T. H., and Zhang, T. (2002). Stable Adaptive Neural Network Control. New York: Springer US. doi:10.1007/978-1-4757-6577-9

CrossRef Full Text

Han, Z., Guo, K., Xie, L., and Lin, Z. (2019). Integrated Relative Localization and Leader-Follower Formation Control. IEEE Trans. Automat. Contr. 64, 20–34. doi:10.1109/TAC.2018.2800790

CrossRef Full Text | Google Scholar

Hu, Z., and Yang, J. (2020). Collision Avoidance Cooperative Attack with Multiple Pursuers Based on Bearing-Only Measurements. J. Franklin Inst. 357, 437–456. doi:10.1016/j.jfranklin.2019.11.061

CrossRef Full Text | Google Scholar

Li, X., Wen, C., and Chen, C. (2021). Adaptive Formation Control of Networked Robotic Systems with Bearing-Only Measurements. IEEE Trans. Cybern. 51, 199–209. doi:10.1109/TCYB.2020.2978981

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, Z., Wang, L., Han, Z., and Fu, M. (2016). A Graph Laplacian Approach to Coordinate-free Formation Stabilization for Directed Networks. IEEE Trans. Automat. Contr. 61, 1269–1280. doi:10.1109/TAC.2015.2454711

CrossRef Full Text | Google Scholar

Liu, Y., Huang, P., Zhang, F., and Zhao, Y. (2020). Distributed Formation Control Using Artificial Potentials and Neural Network for Constrained Multiagent Systems. IEEE Trans. Contr. Syst. Technol. 28, 697–704. doi:10.1109/TCST.2018.2884226

CrossRef Full Text | Google Scholar

Luo, X., Li, X., Li, X., Yan, J., and Guan, X. (2020). Globally Stable Formation Control of Nonholonomic Multiagent Systems with Bearing-Only Measurement. IEEE Syst. J. 14, 2901–2912. doi:10.1109/JSYST.2019.2935162

CrossRef Full Text | Google Scholar

Mehdifar, F., Bechlioulis, C. P., Hashemzadeh, F., and Baradarannia, M. (2020). Prescribed Performance Distance-Based Formation Control of Multi-Agent Systems. Automatica 119, 109086. doi:10.1016/j.automatica.2020.109086

CrossRef Full Text | Google Scholar

Mehdifar, F., Hashemzadeh, F., Baradarannia, M., and de Queiroz, M. (2019). Finite-time Rigidity-Based Formation Maneuvering of Multiagent Systems Using Distributed Finite-Time Velocity Estimators. IEEE Trans. Cybern. 49, 4473–4484. doi:10.1109/TCYB.2018.2876608

PubMed Abstract | CrossRef Full Text | Google Scholar

Ran, D., Chen, X., Misra, A. K., and Xiao, B. (2017). Relative Position Coordinated Control for Spacecraft Formation Flying with Communication Delays. Acta Astronautica 137, 302–311. doi:10.1016/j.actaastro.2017.04.011

CrossRef Full Text | Google Scholar

Shevitz, D., and Paden, B. (1993). “Lyapunov Stability Theory of Nonsmooth Systems,” in Proceedings of 32nd IEEE Conference on Decision and Control, San Antonio, TX, December 15, 1993 (Piscataway, NJ: IEEE), 416–421. doi:10.1109/CDC.1993.325114

CrossRef Full Text | Google Scholar

Sun, Z., de Marina, H. G., Seyboth, G. S., Anderson, B. D. O., and Yu, C. (2019). Circular Formation Control of Multiple Unicycle-type Agents with Nonidentical Constant Speeds. IEEE Trans. Contr. Syst. Technol. 27, 192–205. doi:10.1109/TCST.2017.2763938

CrossRef Full Text | Google Scholar

Wang, Q., Zhu, Y., Li, J., and Hua, Q. (2015). “Globally Stable Rigid Formation Control for Multi-Robot Systems,” in 2015 34th Chinese Control Conference (CCC), Hangzhou, China, July 28–30, 2015 (Piscataway, NJ: IEEE), 7505–7510. doi:10.1109/ChiCC.2015.7260829

CrossRef Full Text | Google Scholar

Yang, Z., Zhu, S., Chen, C., Feng, G., and Guan, X. (2020). Leader-follower Formation Control of Nonholonomic mobile Robots with Bearing-Only Measurements. J. Franklin Inst. 357, 1628–1643. doi:10.1016/j.jfranklin.2019.11.025

CrossRef Full Text | Google Scholar

Yu, D., and Chen, C. L. P. (2020). Automatic Leader-Follower Persistent Formation Generation with Minimum Agent-Movement in Various Switching Topologies. IEEE Trans. Cybern. 50, 1569–1581. doi:10.1109/TCYB.2018.2865803

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, J., Yu, X., Li, X., and Wang, H. (2021). Bearing-only Formation Tracking Control of Multi-Agent Systems with Local Reference Frames and Constant-Velocity Leaders. IEEE Control. Syst. Lett. 5, 1–6. doi:10.1109/LCSYS.2020.2999972

CrossRef Full Text | Google Scholar

Zhao, S., Li, Z., and Ding, Z. (2019). Bearing-only Formation Tracking Control of Multiagent Systems. IEEE Trans. Automat. Contr. 64, 4541–4554. doi:10.1109/TAC.2019.2903290

CrossRef Full Text | Google Scholar

Zhao, S., and Zelazo, D. (2016). Bearing Rigidity and Almost Global Bearing-Only Formation Stabilization. IEEE Trans. Automat. Contr. 61, 1255–1268. doi:10.1109/TAC.2015.2459191

CrossRef Full Text | Google Scholar

Zou, Y., Wen, C., and Guan, M. (2019). Distributed Adaptive Control for Distance‐based Formation and Flocking Control of Multi‐agent Systems. IET Control. Theor. Appl. 13, 878–885. doi:10.1049/iet-cta.2018.6001

CrossRef Full Text | Google Scholar