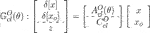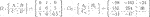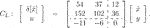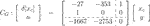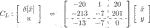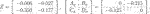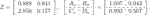- 1Aeronautical Technology Directorate, Japan Aerospace Exploration Agency, Tokyo, Japan
- 2Department of Intelligent and Control Systems, Kyushu Institute of Technology, Fukuoka, Japan
This paper considers the conversion problem from unstructured linear time-invariant (LTI) controllers to observer-structured LTI controllers, whose structure is similar to but not exactly the same as the so-called “Luenberger observer–based controllers,” for linear parameter-varying (LPV) plant systems. In contrast to Luenberger observer–based controllers, observer-structured LTI controllers can be defined and constructed even if the plant systems are given as LPV systems. In the conversion problem, the state-space matrices of the observer-structured LTI controller are parameterized with those of the given unstructured LTI controller, one free matrix, and a state transformation matrix. We also show a method to obtain the optimal state transformation matrix with respect to the convergence of the discrepancy between the plant state and the observer-structured controller state for a stochastically defined non-zero initial plant state. Several toy examples are included to illustrate the effectiveness and the usefulness of observer-structured LTI controllers, and the utility of the proposed conversion parametrization.
1 Introduction
It is well-known that H∞ control is a powerful tool for controlling plant systems with uncertainties (Zhou et al., 1996). At first, the Riccati equation–based synthesis approach is proposed (Doyle et al., 1989); however, the plant systems should satisfy several assumptions (the so-called “standard assumption”), and this restriction diminishes their applicability and usability. On this issue, after the paper by Sampei et al. (1990) which tackles H∞ controller synthesis with output feedback controllers in terms of linear matrix inequality (LMI), many research studies on LMI-based H∞ controller synthesis have been conducted (Gahinet and Apkarian, 1994; Iwasaki and Skelton, 1994; Masubuchi et al., 1998), and the applicability and usability of H∞ control have been extended. However, it is also well-known that H∞ controllers have a complicated structure; that is, H∞ controllers have no special structures as H2 controllers whose structure is composed of LQR controllers and observers. Due to this property, on-site engineers have a difficulty to understand the structure of H∞ controllers as well as the meaning of the figures of the state-space matrices of the designed H∞ controllers.
On this issue, Alazard has explored a new horizon in the studies of Alazard and Apkarian (1999) and Alazard (2012). In the study by Alazard and Apkarian (1999), for LTI plant systems with no direct feedthrough, the authors have proposed a conversion method from a priori designed unstructured LTI controllers to Luenberger observer–based LTI controllers by finding appropriate state transformation matrices for the controllers. Furthermore, in the study of Alazard (2012), the method in the study of Alazard and Apkarian (1999) is extended to the case in which a direct feedthrough exists. In those papers, the dimensions of the controllers are not restricted to be the same as those of the plant systems; that is, even if the dimensions of the controllers are different from those of the plant systems, appropriate state transformation matrices which render the unstructured LTI controllers to Luenberger observer–based controllers can be found by solving the generalized non-symmetric and rectangular Riccati equation. In summary, LTI controllers (including H∞ controllers) for LTI plant systems can be equivalently represented as Luenberger observer–based controllers using the methods in those papers. This achievement is very helpful for on-site engineers because a priori designed unstructured LTI controllers can be converted to well-known Luenberger observer–based controllers without deteriorating control performance as long as the plant systems are LTI systems. As an application example, the converted controllers can be used as “virtual sensors” (Goupil et al., 2014) for plant health monitoring, fault detection, etc., without any additional controllers or observers because the state of the converted controllers, i.e., Luenberger observer–based controllers, estimates the plant state faithfully. Some application examples can be found in the study of Alazard (2012). By considering the above, it is concluded that the conversion from unstructured LTI controllers to observer-based controllers is useful.
Although the methods in the studies of Alazard and Apkarian (1999) and Alazard (2012) are effective and attractive, there is a drawback that the methods cannot be applied to plant systems which are given as linear parameter-varying (LPV) systems. This is because Luenberger observer–based controllers need the nominal state-space matrices of the plant systems; however, as demonstrated by Peaucelle et al. (2017), Sato (2018), etc., the use of the nominal state-space matrices of plant systems does not always lead to the optimal H∞ control performance. This fact poses a simple question: “Under the supposition that LPV plant systems can be interpreted to be composed of their nominal LTI plant systems and norm bounded variations, do the methods in the studies of Alazard and Apkarian (1999) and Alazard (2012) give the state transformation matrices which minimize the discrepancies between plant systems’ state and converted controllers’ state even for LPV plant systems?” This question motivates us to try to extend the methods in the studies of Alazard and Apkarian (1999) and Alazard (2012) to the case in which the plant systems are given as LPV systems, and also to try to find the counterpart conversion method for LPV plant systems. That is, our addressed problem in this paper is the counterpart problem in the studies of Alazard and Apkarian (1999) and Alazard (2012) for LPV plant systems. To this end, we first propose observer-structured LTI controllers whose structure is similar to but not exactly the same as the so-called Luenberger observer–based controllers. By using the observer-structured controllers, we then propose a method producing appropriate state transformation matrices which convert the a priori designed unstructured LTI controllers to observer-structured LTI controllers. As a consequence, even if plant systems are given as LPV systems, we can use the converted controllers obtained by our proposed method as “virtual sensors” (Goupil et al., 2014) for plant health monitoring, fault detection, etc., without any additional controllers or observers.
This paper is structured as follows: In Section 2, we first give definitions of an LPV plant system with a direct feedthrough and strictly proper LTI controllers (an unstructured controller designed a priori and an observer-structured controller), then show our parameterization of the observer-structured controller with the state-space matrices of the unstructured controller, one free matrix and a state transformation matrix, and finally clarify the relation between our method and the method in the study of Alazard (2012) for the case that plant systems are given as LTI systems with direct feedthrough, and the dimensions of the controllers are the same as those of the LTI plant systems. In Section 3, we propose a method to obtain the optimal state transformation matrix, which gives the minimum convergence of the discrepancy between the plant state and the observer-structured controller state for a stochastically defined non-zero initial plant state, in terms of parameter-dependent linear matrix inequality (LMI). In Section 4, several toy examples are introduced to illustrate our contributions (i.e., proposition and parameterization of observer-structured controllers, and proposition of design method for state transformation matrices minimizing the estimation errors), and finally, we give concluding remarks in Section 5.
We summarize the notation used in this paper.
2 Proposed Parameterization
2.1 Linear Parameter-Varying Plant System
Let us suppose that the stabilization problem of the following LPV plant system is addressed:
where
Then, the following is also supposed:
2.2 Unstructured Linear Time-Invariant Controller
We next define an unstructured LTI controller which has already been designed:
where
Then, the closed-loop system comprising G(θ) and CG is straightforwardly derived as follows:
2.3 Observer-Structured Linear Time-Invariant Controller
We next define an observer-structured LTI controller inspired by Sato (2020a). In the DT case, only predictor form (Alazard, 2012) is considered hereafter:
where
Then, the closed-loop system comprising G(θ) and CO is straightforwardly derived as follows:
Remark 1. As is obvious, the controller
2.4 Parameterization of Observer-Structured Linear Time-Invariant Controller
By comparing
The last equation in Eq. 8 is equivalently represented as follows:
Then, we give one of our main results.
Theorem 1. The matrix
where matrices with superscript “†” denote the corresponding Moore–Penrose inverse matrices.
Proof 1. The corresponding assertion for constant matrices is easily proved by using Theorem 2.3.1 in the study of Skelton et al. (1998), and thus, our claim is also easily proved. However, for completeness, we give the detailed proof.We now prove that the following two statements are equivalent:
1) There exists a solution satisfying Eq. 9, and all the solutions are parameterized as in Eq. 10.
2)
This equation always holds as long as Z(θ) is set as XO. Thus, each XO satisfying Eq. 9 has each corresponding parameterization matrix Z(θ); that is, all solutions of Eq. 9 are parameterized as in Eq. 10. We have thus proved that the two statements, 1) and 2), are equivalent.As it is easily confirmed that 2) holds from Eq. 9, i.e.,
Remark 2. As the left-hand sides and the right-hand sides of all equations in Eq. 11 are, respectively, constant and parameter-dependent, in general, complicated constraints consequently arise for Z(θ). A simple solution to escape from the complicated constraints is to set Z(θ) to be constant, i.e., Z(θ) = Z. This setting reduces the generality; however, it also reduces numerical complexity when obtaining the state-space matrices Ao, Bo, Co, and Do in the next section.Note that matrices Ao, Bo, Co, and Do have freedom as in the last equation of Eq. 11; however, they must satisfy Eq. 9, i.e., the last equation of Eq. 8. That is, we would like to emphasize that even if they are chosen as desired matrices within the parameterization of Eq. 11, the input–output property of CO is the same as that of CG. Therefore, the essential freedom of the conversion from CG to CO is only the state transformation represented by T.In the next section, we propose a design method to obtain the optimal state transformation matrix with respect to the convergence of the discrepancy between the plant state and the observer-structured controller state for a stochastically defined non-zero initial plant state, and then we also propose a method to obtain matrices Ao, Bo, Co, and Do as close to as the designated matrices within the parameterization of the last equation of Eq. 11.
2.5 Relation Between Our Method and Existing Method for Linear Time-Invariant Plant Systems
In this subsection, we clarify the relation between our method and the method in the study of Alazard (2012) for LTI plant systems. For simplicity, nc is supposed to be equal to n; that is, only full-order controllers are considered. In the DT case, only predictor form (Alazard, 2012) is considered.
2.5.1 Brief Review of Existing Method in the Study of Alazard (2012)
Now, it is supposed that the plant system is given as an LTI system:
where
We define the observer-based controller as
where
The closed-loop system comprising G and CL is expressed as follows:
In order to make the closed-loop system
If an appropriate
i.e.,
The solution of Eq. 16 can be obtained by the following method (Alazard, 2012):
• Choose n closed-loop eigenvalues which are the eigenvalues of
• Find n-dimensional invariant subspace, i.e., matrices
where the eigenvalues of
• If the matrix U1 is confirmed to be non-singular, then the state transformation matrix is obtained as
By following the procedure for obtaining
2.5.2 Comparison of Our Method With Existing Method
Comparing CO in Eq. 6 and CL in Eq. 13 concludes that if matrices Ao, Bo, Co, and Do are set as A, B, C, and D, respectively, and gain matrices K and L are also set as
Furthermore, if the state transformation matrix T is set as
In summary, the observer-structured controller encompasses the expression of Luenberger observer–based controller, and the transformation from CG to CO also encompasses the corresponding one from CG to CL. Thus, we conclude that the observer-structured controller is a kind of generalization of the Luenberger observer–based controller, and the conversion from CG to CO is also a kind of generalization of the one from CG to CL.
3 Observer-Structured Controller With Optimal Estimation Error for Non-Zero Initial Plant State
In this section, we give a formulation to obtain the optimal state transformation matrix with respect to the convergence of the discrepancy between the plant state and the observer-structured controller state for a stochastically defined non-zero initial plant state.
We first define performance output to be evaluated. Now, the dimension of the unstructured controller is not always the same as that of the LPV plant system. We thus select nsl state variables of the LPV plant system to be estimated by the observer-structured controller and set the vector containing them as
Then, using
By considering that if xsl and
Problem 1. For
Here, it is supposed that the initial plant state x(0) is set as a stochastic variable which satisfies E[x(0)] = 0 and E[x(0) x(0)T] = In and that the initial controller states xc(0) and xo(0) are both set as 0.To address this problem, we define the following system which is composed of 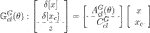 Note that the following hold, since xo = T−1xc is applied to
Note that the following hold, since xo = T−1xc is applied to
Then, the following theorem is proposed for Problem 1.
Theorem 2. If Eq. 21 is solved affirmatively, then
Proof 2. As the upper-left block of the left-hand side of Eq. 24 is negative-definite, the following are confirmed for all combinations of (θ, δ[θ]) ∈ Λ:
Since the positivity of
After
Then, the satisfaction of Eq. 18 is confirmed after consideration of the stability of
Remark 3. If
Assumption 1. All the parameter-dependent state-space matrices of G(θ) in Eq. 1 are supposed to be multi-affine with respect to θi; that is, they are represented as follows:
where
Lemma 1. Under Assumption 1, if Eq. 29 is solved affirmatively with multi-affine
In inequalities (Eqs 30–32),
If the initial plant state is given as a deterministic (but unknown) variable instead of a stochastic variable, and its region is supposed to be in a polytope
Lemma 2. Under Assumption 1, if Eq. 33 is solved affirmatively with multi-affine
By using Lemma 1 or Lemma 2, we can obtain an optimal constant state transformation matrix T for Problem 1. Although the essential freedom for the conversion from CG to CO is the state transformation matrix T, we still have freedom for the state-space matrices (i.e., Ao, Bo, Co, and Do) in an observer-structured controller CO. To address this issue, we propose the following problem to obtain the state-space matrices Ao, Bo, Co, and Do as close to as the designated ones after obtaining T. In our proposed optimization problem shown below, we set Z(θ) in Eq. 10 to be constant Z by considering Remark 2.
Problem 2. If Eq. 35 is solved affirmatively, then all the elements of the state-space matrices in the observer-structured controller CO satisfy
where ϒi,j represents the (i, j) element of the right-hand side of the last equation of Eq. 11 with constant
4 Numerical Examples
Several toy examples are introduced to clearly illustrate our contributions. To this end, we first confirm that our conversion method from CG to CO, i.e., Eq. 11, encompasses the method from CG to CL proposed in the study of Alazard (2012) for LTI plant systems and full-order unstructured LTI controllers. We next show the effectiveness of our method for state transformation matrices, i.e., Lemma 2, and our method for obtaining a priori designated matrices as the state-space matrices in CO, i.e., solving Eq. 35 in Problem 2. We finally show the effectiveness of Lemma 1 in CT and DT cases.
4.1 Confirmation of Relation Between the Method in the Study of Alazard (2012) and Our Method
We first confirm the relation of our method and the method in the study of Alazard (2012) using the following CT LTI plant and CT unstructured LTI controller. The controller is designed to assign the closed-loop poles at −7, −5, −3 ± i; that is, a stabilizing controller is designed:
By following the procedure in the study of Alazard (2012), if the poles −3 ± i are set to be the eigenvalues of
The state-space representation of CL is consequently obtained as follows:
We now obtain K and L in Eq. 11 by setting
Obviously, they are the same as the result obtained by the method in the study of Alazard (2012) because T is set as
Next, we obtain matrices Ao, Bo, Co, and Do in Eq. 11 with several Z, i.e., constant Z due to an LTI plant system and LTI controller. To this end,
Although the matrix XO above has corresponding figures in accordance with different Z, Ao + BoK + LCo + LDoK is calculated as
That is, we have confirmed that our parameterization encompasses the formulation in the study of Alazard (2012) regardless of the choice of Z.
4.2 Effectiveness Demonstration of Our Method for Linear Time-Invariant Plant System
We next consider the same example in the study of Alazard (2012), i.e., the following CT LTI plant:
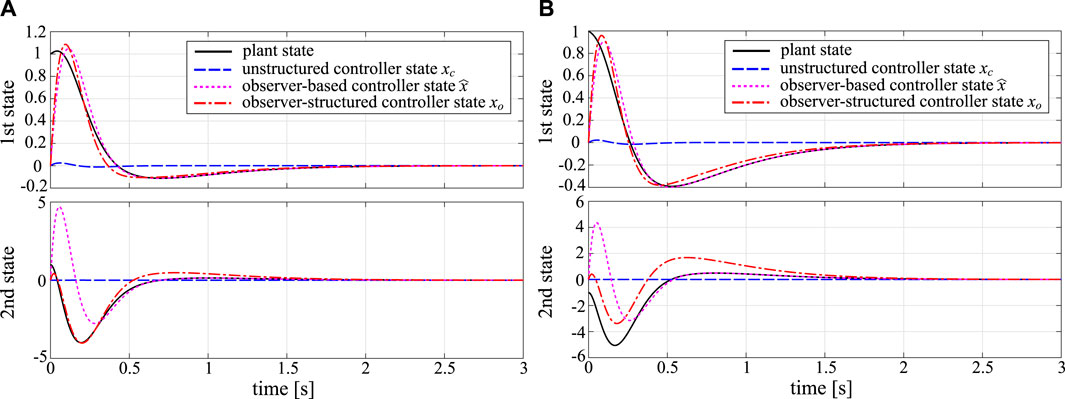
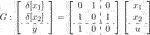 .We now suppose that the following CT unstructured LTI stabilizing controller, which is also borrowed from the study of Alazard (2012), has already been designed:
.We now suppose that the following CT unstructured LTI stabilizing controller, which is also borrowed from the study of Alazard (2012), has already been designed:
This controller assigns the closed-loop poles at −3, −4, −10 ± 10i. We now suppose that poles −3 and −4 are assigned by
The consequently calculated CL is given as
We now solve Eq. 33 in Lemma 2 for 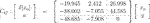 (38)
(38)
We show the simulation results using controllers CG, CL, and CO in Figure 1 and show the finite-time state estimation performance, i.e.,

TABLE 1. State estimation performance in Figure 1.
In contrast, the observer-structured controller CO has a much better state estimation performance as indicated in Table 1. This clearly illustrates the effectiveness of our method compared to the method in the study of Alazard (2012).
We next address Problem 2 with the following ϒdes and W using the above T:
where ∗ denotes the element of no interest. Solving Eq. 35 gives the following Z and the following corresponding state-space matrices of CO: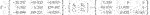 (40)
(40)
The transfer functions of CG in Eq. 36, CL in Eq. 37, and CO in Eq. 38 are all calculated as
4.3 Effectiveness Demonstration of Our Method for Linear Parameter-Varying Plant System
We finally consider the conversion problem for LPV plant systems. Note that the methods in the studies of Alazard and Apkarian (1999) and Alazard (2012) cannot be applied to the example shown below because the plant system is given as an LPV system.
4.3.1 CT Case
We first consider the following CT LPV system:
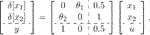 (41)where
(41)where
It is supposed that the following stabilizing controller is given as an unstructured controller: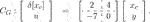 (42)
(42)
For this problem setup, we solve Eq. 29 in Lemma 1 with Csl = [1 0] and 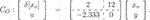 (43)
(43)
The simulation results with CG in Eq. 42 and CO in Eq. 43 are shown in Figure 2. It is confirmed that the state of CO faithfully represents the plant state x1 in both cases with x(0) = [1 0]T and x(0) = [0 1]T.
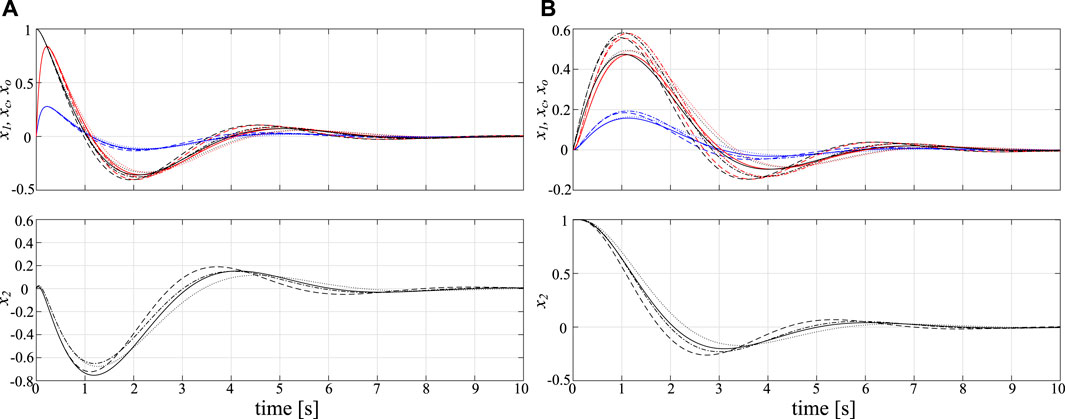
FIGURE 2. Simulation results with frozen
We next address Problem 2 with the following ϒdes and W using the above T:
where ∗ denotes the element of no interest. Solving Eq. 35 gives the following Z and the following corresponding state-space matrices of CO:
The transfer functions of CG in Eq. 42 and CO in Eq. 43 are both calculated as
4.3.2 DT Case
We next consider the discretized system of Eq. 41 by using Euler approximation with the sampling period ΔT = 0.1 (s):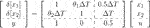 .(46)
.(46)
We now set that θ1 can vary arbitrarily fast within the interval; however, θ2 is set as frozen in the interval; that is, the following vertex sets are considered:
The controller in Eq. 42 is also discretized by using Euler approximation with the sampling period ΔT = 0.1 (s):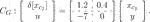 (47)
(47)
For this problem setup, we solve Eq. 29 in Lemma 1 with Csl = [1 0] and 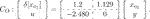 .(48)
.(48)
The simulation results with CG in Eq. 47 and CO in Eq. 48 are shown in Figure 3. It is indeed better to have simulations with varying θ1 within the interval [0.9, 1.1]; however, there are uncountable combinations for the variation of θ1. Thus, we conduct numerical simulations only with the fixed extreme points of θ1. It is confirmed that the state of CO faithfully represents the plant state x1 in both cases with x(0) = [1 0]T and x(0) = [0 1]T.
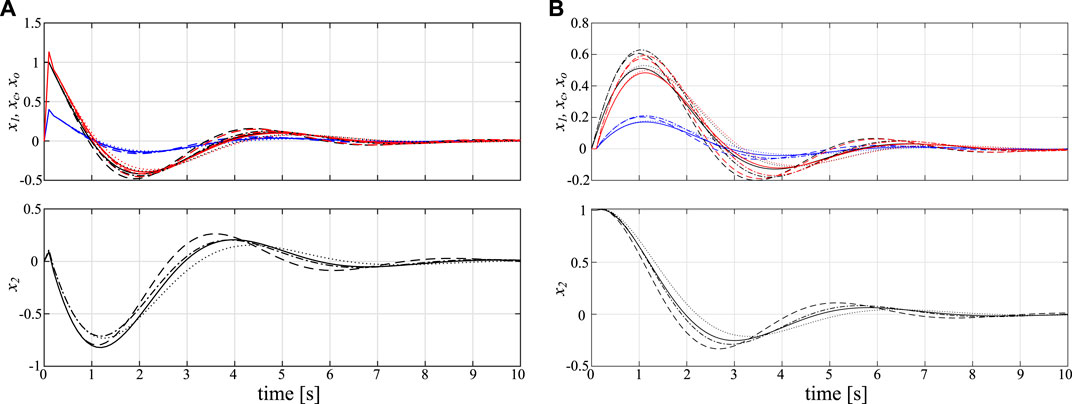
FIGURE 3. Simulation results with frozen
We next address Problem 2 with the following ϒdes and W using the above T:
In this case, we set ϒdes composed of the upper-left element of A(θ), the first element of B(θ), and the first element of C(θ) and D(θ) in the state-space matrices of Eq. 46. Our aim is to obtain matrices close to the nominal state-space matrices corresponding to the first-input-first-output system. We minimize the Frobenius norm for ϒ−ϒdes, and obtain the following Z and the corresponding state-space matrices:
In this case, in contrast to the previously shown examples, we cannot obtain the designated figures for the state-space matrices Ao, Bo, Co, and Do due to lack of enough freedom in Eq. 11.
The transfer functions of CG in Eq. 47 and CO in Eq. 48 are both calculated as
5 Conclusion
We address the conversion problem from unstructured LTI controllers to observer-structured LTI controllers, whose structure is similar to but not exactly the same as Luenberger observer–based controllers, for LPV systems with direct feedthrough. To this end, we first define observer-structured LTI controllers, then parameterize the state-space matrices with a priori designed unstructured LTI controller, one free matrix and a state transformation matrix, and finally propose a method which produces the optimal state transformation matrix with respect to the convergence of the discrepancy between the plant state and the observer-structured controller state for a stochastically defined non-zero initial plant state. Several toy examples are introduced to clearly illustrate the effectiveness and usefulness of observer-structured LTI controllers and the proposed method for obtaining optimal state transformation matrices with respect to the minimization between the discrepancies between the LPV plant state and the converted LTI controller state.
In this paper, we address the controller conversion problem in the case that only the stabilization problem of LPV plant systems is considered. As our next step, we are now tackling the same conversion problem in the case that some control performance criteria are also considered. Then, we will demonstrate the practicality of the conversion by using practical systems including H∞ performance.
In this paper, it is also supposed that LTI controllers are given for LPV plant systems; however, the usefulness and effectiveness of using LPV controllers for LPV plant systems are also well recognized. Thus, the extension of our results to LPV controllers is another future research topic.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
MS was in charge of theoretical development, numerical examples, and writing. NS supervised Sato’s work.
Funding
This work was conducted under the support of KAKENHI Grant Number 22K04176.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors give a sincere acknowledgement to Ms. Shikada for checking the numerical example results.
References
Alazard, D. (2012). Advances in Missile Guidance, Control, and Estmation. Boca Raton, FL: CRC Press. Chap. Control Designand Gain-Scheduling Using Observer-Based Structures. 77–128.
Alazard, D., and Apkarian, P. (1999). Exact Observer-Based Structures for Arbitrary Compensators. Int. J. Robust Nonlinear Control. 9, 101–118. doi:10.1002/(sici)1099-1239(199902)9:2<101::aid-rnc400>3.0.co;2-u
Amato, F., Mattei, M., and Pironti, A. (2005). Gain Scheduled Control for Discrete-Time Systems Depending on Bounded Rate Parameters. Int. J. Robust Nonlinear Control. 15, 473–494. doi:10.1002/rnc.1001
Chesi, G., Garulli, A., Tesi, A., and Vicino, A. (2003). Solving Quadratic Distance Problems: An LMI-Based Approach. IEEE Trans. Automat. Contr. 48, 200–212. doi:10.1109/TAC.2002.808465
de Oliveira, R. C. L. F., and Peres, P. L. D. (2007). Parameter-Dependent LMIs in Robust Analysis: Characterization of Homogeneous Polynomially Parameter-Dependent Solutions via LMI Relaxations. IEEE Trans. Automat. Contr. 52, 1334–1340. doi:10.1109/TAC.2007.900848
de Oliveira, M. C., Bernussou, J., and Geromel, J. C. (1999). A New Discrete-Time Robust Stability Condition. Syst. Control. Lett. 37, 261–265. doi:10.1016/S0167-6911(99)00035-3
Doyle, J. C., Glover, K., Khargonekar, P. P., and Francis, B. A. (1989). State-Space Solutions to Standard H/Sub 2/and H/Sub Infinity/Control Problems. IEEE Trans. Automat. Contr. 34, 831–847. doi:10.1109/9.29425
Gahinet, P., and Apkarian, P. (1994). A Linear Matrix Inequality Approach to H∞ Control. Int. J. Robust Nonlinear Control. 4, 421–448. doi:10.1002/rnc.4590040403
Goupil, P., Dayre, R., and Brot, P. (2014). “From Theory to Flight Tests: Airbus Flight Control System TRL5 Achievements,” in Proceedings of the 19th IFAC World Congress Cape Town, South Africa, 10562–10567. IFAC Proceedings Volumes. doi:10.3182/20140824-6-za-1003.0254747
Iwasaki, T., and Skelton, R. E. (1994). All Controllers for the General ∞ Control Problem: LMI Existence Conditions and State Space Formulas. Automatica 30, 1307–1317. doi:10.1016/0005-1098(94)90110-4
Masubuchi, I., Ohara, A., and Suda, N. (1998). LMI-Based Controller Synthesis: A Unified Formulation and Solution. Int. J. Robust Nonlinear Control. 8, 669–686. doi:10.1002/(sici)1099-1239(19980715)8:8<669::aid-rnc337>3.0.co;2-w
Parrilo, P. A. (2003). Semidefinite Programming Relaxations for Semialgebraic Problems. Math. Programming 96, 293–320. doi:10.1007/s10107-003-0387-5
Peacelle, D., and Ebihara, Y. (2018). “Affine versus Multi-Affine Models for S-Variable LMI Conditions,” in Preprints of the 9th IFAC Symposium on Robust Control Design Florianopolis, Brazil, 643–648.
Peaucelle, D., Arzelier, D., Bachelier, O., and Bernussou, J. (2000). A New Robust - stability Condition for Real Convex Polytopic Uncertainty. Syst. Control. Lett. 40, 21–30. doi:10.1016/S0167-6911(99)00119-X
Peaucelle, D., Ebihara, Y., and Hosoe, Y. (2017). Robust Observed-State Feedback Design for Discrete-Time Systems Rational in the Uncertainties. Automatica 76, 96–102. doi:10.1016/j.automatica.2016.10.003
Peaucelle, D., and Sato, M. (2009). LMI Tests for Positive Definite Polynomials: Slack Variable Approach. IEEE Trans. Automat. Contr. 54, 886–891. doi:10.1109/TAC.2008.2010971
Pipeleers, G., Demeulenaere, B., Swevers, J., and Vandenberghe, L. (2009). Extended LMI Characterizations for Stability and Performance of Linear Systems. Syst. Control. Lett. 58, 510–518. doi:10.1016/j.sysconle.2009.03.001
Sampei, M., Mita, T., and Nakamichi, M. (1990). An Algebraic Approach to H∞ Output Feedback Control Problems. Syst. Control. Lett. 14, 13–24. doi:10.1016/0167-6911(90)90075-6
Sato, M. (2020a). Observer-Based Robust Controller Design with Simultaneous Optimization of Scaling Matrices. IEEE Trans. Automat. Contr. 65, 861–866. doi:10.1109/TAC.2019.2919811
Sato, M. (2020b). One-Shot Design of Performance Scaling Matrices and Observer-Based Gain-Scheduled Controllers Depending on Inexact Scheduling Parameters. Syst. Control. Lett. 137, 104632. doi:10.1016/j.sysconle.2020.104632
Sato, M. (2018). Simultaneous Design of Discrete-Time Observer-Based Robust Scaled-H8 Controllers and Scaling Matrices. SICE J. Control Meas. Syst. Integration 11, 65–71. doi:10.9746/jcmsi.11.65
Skelton, R. E., Iwasaki, T., and Grigoriadis, K. (1998). A Unified Algebraic Approach to Linear Control Design. London, UK: Taylor & Francis.
Keywords: observer-based controller, observer-structured controller, LTI controller, conversion, LPV system
Citation: Sato M and Sebe N (2022) Conversion From Unstructured LTI Controllers to Observer-Structured Ones for LPV Systems. Front. Control. Eng. 3:804549. doi: 10.3389/fcteg.2022.804549
Received: 29 October 2021; Accepted: 26 January 2022;
Published: 29 August 2022.
Edited by:
Olivier Sename, Grenoble Institute of Technology, FranceReviewed by:
Natalia Alexandrovna Dudarenko, ITMO University, RussiaCopyright © 2022 Sato and Sebe. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Masayuki Sato, c2F0by5tYXNheXVraUBqYXhhLmpw
 Masayuki Sato
Masayuki Sato Noboru Sebe
Noboru Sebe