Introduction
This report describes a publicly available dataset of harmonic analyses of all Beethoven string quartets together with a new annotation scheme. The quantitative study of large datasets is gaining increasing importance in musicology, reflecting a global trend toward empirical corpus studies and big data methods in the sciences as well as the (digital) humanities. Several initiatives and publications exemplify these new developments (e.g., Mauch et al., 2007; Rohrmeier and Cross, 2008; Temperley, 2009; De Clercq and Temperley, 2011; Schubert and Cumming, 2015; Klauk and Zalkow, 2016; White and Quinn, 2016). Ever increasing digital music resources are available online in the form of large collections of audio recordings,1 scanned scores,2 or MIDI files.3 Furthermore, musicologists have produced collections of symbolic and audio music repositories, e.g., the Essen Folksong collection (Schaffrath, 1995), the score collection in Humdrum/KERN format4 (Huron, 1997; Sapp, 2014), and the corpora of audio resources of Non-Western classical music traditions gathered by the CompMusic project5 (Serra, 2014). However, raw audio or symbolic musical information is often insufficient to investigate more abstract structural properties of musical styles, such as harmony, counterpoint, or form. Sufficiently sophisticated and statistically fully reliable automated Music Information Retrieval (MIR) methods for structural inference are not yet available.
Despite the availability of raw audio material and the recent research initiatives mentioned above, digital musicology still lacks large labeled corpora combining score and harmonic annotations. These corpora are necessary as ground truth data for the minute investigation of structural dimensions of music such as harmony. As we elaborate below, our research addresses this gap by providing a large dataset of expert-generated harmonic labels in the stylistically coherent corpus of Ludwig van Beethoven's string quartets, the Annotated Beethoven Corpus (ABC). This corpus will be useful for the research purposes of empirical and digital musicology, such as deepening the understanding of musical syntax, voice-leading schemata, form, and style, as well as for the development and evaluation of computational models of harmony and musical structure in general.
Methods
Dataset
The dataset presented here consists of expert harmonic analyses of all Beethoven string quartets6, encoded in a human- and machine-readable format (MuseScore XML7). It includes common music theoretical harmonic features such as key, chordal root, chord inversion, chord extensions, suspensions, and others (see Annotation Standard). The dataset is licensed under Creative Commons License (v4.0, BY-NC-SA) and is hosted with version control in a GitHub repository.8 It is freely available for non-commercial academic, creative, or other uses.
Corpus selection
The present corpus was selected for several reasons. One was the major importance and influence of the composer in general as well as his inventiveness in the domain of harmony (Damschroder, 2016). Beethoven's string quartets in particular exercised a strong influence on the subsequent development of the genre history (Hefling, 2003; Jones, 2003). They cover a period of ca. 25 years (1800–1826), comprising the composer's middle and late creative phases, and hence both the high Classical and the early Romantic eras, which enables not only the study of the tonal system as such but also of stylistic change.
Data format
In order to use a graphical user interface to enter the annotation symbols, we chose the open source software MuseScore. In its generic format,9 this software allows for a detailed description of musical data which can be parsed automatically and displayed visually for human score-readers. This allows for simultaneously viewing and listening to the music while entering labels. At the same time, it is not necessary for annotators to possess detailed technical knowledge of the XML standard. Since the Music Encoding Initiative (MEI) scheme (Hankinson et al., 2011) permits chord symbols to be any string, our chord annotation standard could potentially be integrated in this framework.
Expert annotations
The XML files were split equally between two of the authors (MN and FM) who entered the annotations with MuseScore and mutually cross-checked their annotations. Each chord symbol in the corpus conforms to the annotation standard that was specified as a regular expression within the scope of this project (see next section). Typographical errors were identified by matching each chord symbol with the regular expression and subsequently corrected. The annotation process was based on elaborate guidelines detailing the annotation standard and addressing particular annotation challenges. The guidelines can be found in the same repository as the data. In the case of ambiguous harmonic events, the annotators opted in general for the more probable or plausible interpretation, although the annotation standard is capable of expressing multiple readings.
Annotation standard
There are various conventions to annotate harmony (cf. Harte et al., 2005; Harte, 2010), including Jazz lead sheet symbols (e.g., Dm7, G7, Cmaj7), Roman numerals (e.g., ii6, V7, V, I), and functional Riemannian notation (e.g., Tp, Sp, D7, T). Existing chord annotation systems in the literature range from notations containing only the 24 major and minor triads (Cruz-Alcázar et al., 2003; Unal et al., 2007) to more complex ones incorporating also various chord forms and bass notes (Harte et al., 2005; Cambouropoulos et al., 2014). The standard proposed by Harte et al. (2005), for instance, models lead sheet symbols (such as Db7#11) in absolute terms and thus does not incorporate information about key and modulation. It is therefore limited in its music theoretical applications.
Our proposed annotation format is based on standard Roman numeral notation, the internationally most common music theoretical notation system for harmonic analysis (e.g., Aldwell et al., 2011). We have refined and extended this notation, and formalized it as a regular expression (Wintner, 2010), incorporating not only the harmonic features key, scale degree, and figured bass, but also pedals (and harmonic motion over such a pedal), suspensions, and added notes. We offer a notation that is easily readable for humans and computers. At the same time, its applicability goes beyond classical music and extends well to many popular music genres.
The regular expression, shown in Figure 1A, defines the internal structure of valid chord symbols using the Perl-compatible regular expression syntax10 and operates on the following alphabets:
Key symbols: {ab, a, a#, bb, b, b#, cb, c, c#, db, d, d#, eb, e, e#, fb, f, f#, gb, g, g#, Ab, A, A#, Bb, B, B#, Cb, C, C#, Db, D, D#, Eb, E, E#, Fb, F, F#, Gb, G, G#}
Roman numerals (with possible alterations): {bi, i, #i, bii, ii, #ii, biii, iii, #iii, biv, iv, #iv, bv, v, #v, bvi, vi, #vi, bvii, vii, #vii, bI, I, #I, bII, II, #II, bIII, III, #III, bIV, IV, #IV, bV, V, #V, bVI, VI, #VI, bVII, VII, #VII, Ger, It, Fr}
Chord forms: {M, %, o, +}
Figured bass: {6, 64, 7, 65, 43, 2}
Extensions and suspensions (possibly altered): {2, 4, 6, 7, 9, 11, 13}
Special characters: {., +, /, \\}
Figure 1
Figure 1B illustrates how chord symbols are realized in a harmonic analysis by showing an excerpt from Beethoven's string quartet op. 127.
The regular expression for each chord symbol consists of nine parts whereof the declaration of the root (the third part of a chord symbol) is the only required part. Chordal roots and pedal tones are denoted by Roman numerals relative to the key of the respective chord symbol. Since the chord symbols are entered in MuseScore into the chord line, symbols beginning with a key symbol or a flattened Roman numeral had to be preceded by a period (.). Otherwise, MuseScore would interpret the character as the root of the chord.
In the first chord symbol of a piece, its first part (<key>) indicates the global key of the piece as a key symbol; it must be followed by a period (.). For instance, when the piece is in F minor, the first chord symbol has to start with “f.”. In all other chord symbols, the first part of the regular expression can indicate a key change as a Roman numeral relative to the global key. For example, a modulation to the dominant key would be indicated by “V.”. Uppercase key symbols indicate major keys, whereas lowercase key symbols indicate minor keys. Each chord symbol is interpreted as belonging to the most recently specified key.
The second part of the chord symbol (<pedal>) can indicate the beginning of a pedal tone by specifying its scale degree relative to the present key followed by an opening square bracket ([).
The third part of the chord symbol (<root>) is the only required part of any chord symbol; it denotes the root of the chord relative to the current key by a Roman numeral which can be preceded by an accidental (“b” or “#”). For instance, in a C-major context “bIII” denotes an E-flat major chord. Alternatively, the common symbols “Ger”, “It”, and “Fr” can substitute a Roman numeral, denoting a German, Italian, or French augmented sixth chord, respectively.
The chord form can be notated in the fourth part of the chord symbol (<chordform>). While uppercase and lowercase Roman numerals indicate major and minor triads, respectively, the characters “M”, “%”, “o”, and “+” denote major seventh, half-diminished, diminished and augmented chord forms, respectively (e.g., “iio” refers to the diminished triad on scale degree ii).
The inversion of a chord can be inferred from the figured bass information in the fifth part of the chord symbol (<figbass>); if this information is omitted, the chord is interpreted to be in root position. To illustrate, “ii6” is a minor triad on the second scale degree in first inversion, and “V43” is a dominant-seventh chord in second inversion. In combination with the root and key information, the figured bass allows to infer the bass note.
Additional changes to the chord, such as suspensions or added tones, can be specified in the sixth part of the symbol (<changes>) in parentheses. For example, in the key of C major, the symbol “V(64)” denotes the set of pitch classes G C E with the root and bass note G (and the C and E suspending the third and fifth of a G-major triad); by contrast, the symbol “V64” denotes G B D with the root G and bass note D. Therefore “V(64)” equals “I64” in terms of the denoted pitch elements, but there is a functional difference that can be inferred from the scale-degree information. Moreover, one can differentiate between suspensions and added notes by preceding the latter with a “+”. An example of a chord with an added ninth is “I(+9)”, where the plus indicates that the ninth is not a suspension, but an added note.
Furthermore, the root of the chord can be annotated in reference to another scale step that is indicated after a slash (/) in the seventh part (<relativeroot>). This notation is especially convenient for denoting applied dominants. For instance, in the key of C major an E major triad followed by an A minor triad would be encoded as “V/vivi”.
The penultimate part of the symbol (<pedalend>) can indicate the end of a pedal by a closing square bracket (]). All chord symbols in between the starting and ending brackets of a pedal are still interpreted in reference to the current key. For example, consider the sequence “.C.V[V6 ii V] I” which consists of four chord symbols in the key of C major. The first symbol “V[V6” indicates a G major triad in first inversion over the pedal tone G. The symbols “ii” and “V]” are interpreted as D minor and G major triads, still over the pedal G; the closing bracket indicates the end of the pedal. Therefore, “I” is interpreted as a C major triad in root position without the pedal tone.
The final part of a chord symbol (<phraseend>) can additionally annotate the ending of a phrase at this chord by a double backslash (\\). In ambiguous cases, two alternative interpretations can be annotated, separated by a hyphen (–). If an event cannot be interpreted in harmonic terms at all, the symbol “@none” can be chosen.
Summary statistics
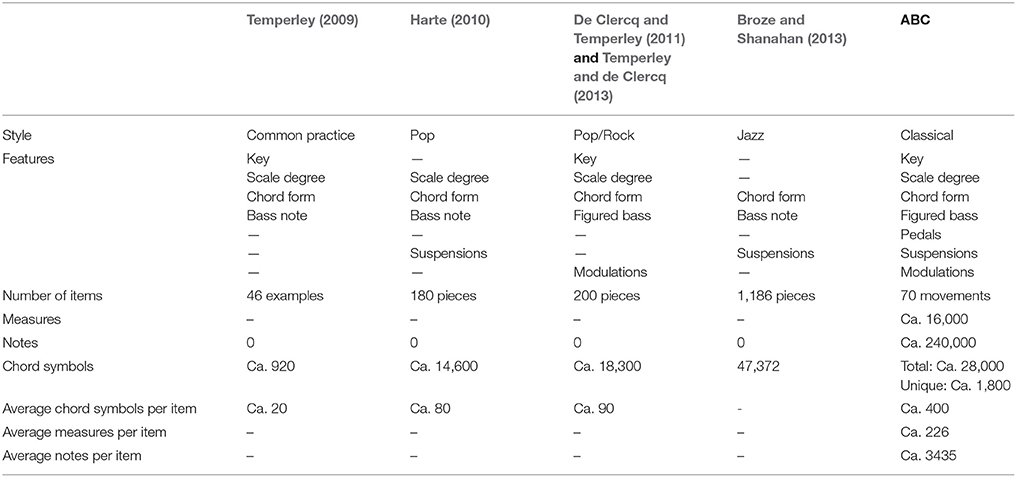
The ABC contains expert harmonic annotations of all sixteen string quartets (70 movements) by Beethoven: quartets nos. 1–6 (op. 18), nos. 7–9 (op. 59), no. 10 (op. 74), no. 11 (op. 95), no. 12 (op. 127) (four movements each quartet), no. 13 (op. 130; six movements), no. 14 (op. 131; seven movements), no. 15 (op. 132; five movements), and no. 16 (op. 135; four movements). In total, the ABC consists of 15,806 measures (240,462 notes) of music, which were annotated with 27,962 chord labels (1,753 unique). Table 1 describes our dataset in comparison to other corpora of symbolic harmonic labels with respect to style, structural features, and size (number of items, measures, and chord symbols) in the first six rows. The last three rows give more detailed information about the distribution of chord symbols in our string quartet corpus.
Table 1
| Temperley (2009) | Harte (2010) | De Clercq and Temperley (2011) and Temperley and de Clercq (2013) | Broze and Shanahan (2013) | ABC | |
|---|---|---|---|---|---|
| Style | Common practice | Pop | Pop/Rock | Jazz | Classical |
| Features | Key Scale degree Chord form Bass note — — — | — Scale degree Chord form Bass note — Suspensions — | Key Scale degree Chord form Figured bass — — Modulations | — — Chord form Bass note — Suspensions — | Key Scale degree Chord form Figured bass Pedals Suspensions Modulations |
| Number of items | 46 examples | 180 pieces | 200 pieces | 1,186 pieces | 70 movements |
| Measures | – | – | – | – | Ca. 16,000 |
| Notes | 0 | 0 | 0 | 0 | Ca. 240,000 |
| Chord symbols | Ca. 920 | Ca. 14,600 | Ca. 18,300 | 47,372 | Total: Ca. 28,000 Unique: Ca. 1,800 |
| Average chord symbols per item | Ca. 20 | Ca. 80 | Ca. 90 | - | Ca. 400 |
| Average measures per item | – | – | – | – | Ca. 226 |
| Average notes per item | – | – | – | – | Ca. 3435 |
Summary statistics of our dataset in comparison with other musical corpora.
Data usage and applications
The corpus is hosted at https://github.com/DCMLab/ABC. This repository contains all annotated XML files. To facilitate the usage of our dataset of harmonic labels, we additionally provide TSV files that contain the extracted annotations as dataframes. The column “chord” contains the chord label, whereas “altchord” contains alternative analyses (if provided by the annotator). The position of these labels in the dataset can be determined by the remaining columns “measure,” “beat,” “op,” “no,” and “mov,” describing the measure number, beat position, opus number, piece number, and movement, respectively. The time signature of the present measure is given in the “timesig” column.
The dataset presented here allows to examine a broad range of research issues. These include n-gram-based approaches to studying Beethoven's harmonic and key choices, for instance by analyzing the chord alphabet as well as the frequency of chord transitions. This may be done either from a synchronic or a diachronic perspective, the latter focusing the evolution of harmonic choices over Beethoven's middle and late periods (e.g., by comparing different subsets such as opp. 18 and 59 and the late quartets). Either perspective promises to give empirically grounded insights into the use of tonal harmony by a prominent composer. However, to date it is difficult to estimate the extent to which the harmonic choices in Beethoven's quartets are peculiar for this repertoire or his entire oeuvre, or whether they reflect trends in the classical style or even in the common-practice tonal system as a whole. To answer these questions in a scientifically reliable manner and to enable comparative studies, more corpora of harmonic labels need to be prepared using the standard proposed in this paper.
Statements
Author contributions
MN and FM annotated the corpus. DH programmed scripts for access and analysis and modeled the regular expression for chord symbols. MR and MN conceived the project. FM and DH were responsible for planning and organizing the project. All authors were involved in equal parts in the development of the guidelines and the annotation standard, and in the writing of the article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The reviewer BB and handling Editor declared their shared affiliation.
Footnotes
1.^Accessible via streaming services such as Spotify (http://www.spotify.com).
2.^E.g., International Music Score Library Project (http://www.imslp.org); Project Gutenberg (http://www.gutenberg.org/wiki/Gutenberg:The_Sheet_Music_Project).
3.^Classical Archives (http://www.classicalarchives.com/midi.html).
4.^http://www.musiccog.ohio-state.edu/Humdrum/; http://www.verovio.org/humdrum.xhtml
5.^http://compmusic.upf.edu/corpora
6.^Only the “Große Fuge” op. 133 was excluded because here contrapuntal principles largely prevail over harmony.
7.^The entire set of string quartets is publicly available under the Project Gutenberg License (http://www.gutenberg.org/wiki/Gutenberg:The_Sheet_Music_Project).
8.^https://github.com/DCMLab/ABC
References
1
AldwellE.SchachterC.CadwalladerA. (2011). Harmony and Voice Leading4th Edn. Beverly, MA: Wadsworth Publishing.
2
BrozeY.ShanahanD. (2013). Diachronic changes in Jazz harmony: A cognitive perspective. Music Percept.31, 32–45. 10.1525/mp.2013.31.1.32
3
CambouropoulosE.Kaliakatsos-PapakostasM.TsougrasC. (2014). An idiom-independent representation of chords for computational music analysis and generation, in Joint 40th International Computer Music Conference (ICMC) and 11th Sound and Music Computing (SMC) Conference (ICMC-SMC2014) (Athens).
4
Cruz-AlcázarP. P.Vidal-RuizE.Pérez-CortésJ. C. (2003). Musical style identification using grammatical inference: the encoding problem, in Iberoamerican Congress on Pattern Recognition, eds SanfeliuA.Ruiz-ShulcloperJ. (Berlin; Heidelberg: Springer), 375–382.
5
DamschroderD. (2016). Harmony in Beethoven.Cambridge: Cambridge University Press.
6
De ClercqT.TemperleyD. (2011). A corpus analysis of Rock harmony. Pop. Music30, 47–70. 10.1017/S026114301000067X
7
HankinsonA.RolandP.FujinagaI. (2011). The Music Encoding Initiative as a document-encoding framework, in 12th International Society for Music Information Retrieval Conference, ISMIR, Miami (FL), 293–298.
8
HarteC. (2010). Towards Automatic Extraction of Harmony Information From Music Signals. Doctoral dissertation. Available online at: http://qmro.qmul.ac.uk/jspui/handle/123456789/534
9
HarteC. A.SandlerM.AbdallahS.GómezE. (2005). Symbolic representation of musical chords: A proposed syntax for text annotations, in Proceedings of the 4th International Conference on Music Information Retrieval (ISMIR 2005) (London), 66–71.
10
HeflingS. E. (2003). The Austro-Germanic quartet tradition in the nineteenth century, in The Cambridge Companion to the String Quartet, ed StowellR. (Cambridge: Cambridge University Press), 228–249.
11
HuronD. (1997). Humdrum and kern: Selective feature encoding, in Beyond MIDI: The Handbook of Musical Codes, ed Selfridge-FieldE. (Cambridge: MIT Press), 375–401.
12
JonesD. W. (2003). Beethoven and the Viennese legacy, in The Cambridge Companion to the String Quartet, ed StowellR. (Cambridge: Cambridge University Press), 210–227.
13
KlaukS.ZalkowF. (2016). Das italienische Streichquartett im 18. Jahrhundert. Möglichkeiten der semiautomatisierten Stilanalyse, in Beitragsarchiv zur Jahrestagung der Gesellschaft für Musikforschung Halle/Saale 2015 – “Musikwissenschaft: die Teildisziplinen im Dialog,” eds AuhagenW.HirschmannW. (Mainz). Available online at: http://schott-campus.com/gfm-jahrestagung-2015.
14
MauchM.DixonS.HarteC. A.CaseyM.FieldsB. (2007). Discovering chord idioms through Beatles and Real Book songs, in Proceedings of the 8th International Conference on Music Information Retrieval (ISMIR 2007) (Vienna), 255–258.
15
RohrmeierM.CrossI. (2008). Statistical properties of harmony in Bach's Chorales, in Proceedings of the 10th International Conference on Music Perception and Cognition, ICMPC, eds MiyazakiK.HiragaY.AdachM.NakajimaY.TsuzakiM. (Sapporo), 619–627.
16
SappC. (2014). 371 Four-Part Chorales by J.S. Bach in the Humdrum File Format. Available online at: https://github.com/craigsapp/bach-371-chorales.
17
SchaffrathH. (1995). The Essen Folksong Collection. Doctoral dissertation. CCARHMenlo Park,CA.
18
SchubertP.CummingJ. (2015). Another lesson from Lassus: Using computers to analyse counterpoint. Early Music43, 577–586. 10.1093/em/cav088
19
SerraX. (2014). Creating research corpora for the computational study of music: The case of the CompMusic project, in Proceedings of the 53rd AES International Conference on Semantic Audio (London), 1–9.
20
TemperleyD. (2009). A Statistical Analysis of Tonal Harmony. Available online at: http://davidtemperley.com/kp-stats (Accessed November 17, 2016).
21
TemperleyD.de ClercqT. (2013). Statistical analysis of harmony and melody in Rock Music. J. New Music Res.42, 187–204. 10.1080/09298215.2013.839525
22
UnalE.GeorgiouP. G.NarayananS. S.ChewE. (2007). Statistical modeling and retrieval of polyphonic music, in 2007 IEEE, 9th International Workshop on Multimedia Signal Processing, MMSP 2007 (Crete), 405–409.
23
WhiteC.QuinnI. (2016). The Yale-classical archives corpus. Emp. Musicol. Rev.11, 50–58. 10.18061/emr.v11i1.4958
24
WintnerS. (2010). Formal language theory, in The Handbook of Computational Linguistics and Natural Language Processing, eds ClarkA.Chr. FoxLappinS. (Hoboken, NJ: Wiley-Blackwell), 11–42.
Summary
Keywords
music, digital musicology, corpus research, ground truth, harmony, symbolic music data, Beethoven
Citation
Neuwirth M, Harasim D, Moss FC and Rohrmeier M (2018) The Annotated Beethoven Corpus (ABC): A Dataset of Harmonic Analyses of All Beethoven String Quartets. Front. Digit. Humanit. 5:16. doi: 10.3389/fdigh.2018.00016
Received
03 April 2018
Accepted
11 June 2018
Published
03 July 2018
Volume
5 - 2018
Edited by
Xavier Serra, Universidad Pompeu Fabra, Spain
Reviewed by
Tim Crawford, Goldsmiths, University of London, United Kingdom; Baris Bozkurt, Universidad Pompeu Fabra, Spain
Updates
Copyright
© 2018 Neuwirth, Harasim, Moss and Rohrmeier.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Markus Neuwirth markus.neuwirth@epfl.ch
This article was submitted to Digital Musicology, a section of the journal Frontiers in Digital Humanities
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.