- 1 Department of Biostatistics, University of Alabama at Birmingham, Birmingham, AL, USA
- 2 Department of Biostatistical Sciences, Wake Forest University Health Sciences, Winston-Salem, NC, USA
Since the discovery of the ubiquitous contribution of copy number variation to genetic variability, researchers have commonly used metrics such as r2 to quantify linkage disequilibrium (LD) between copy number variants (CNVs) and single nucleotide polymorphisms (SNPs). However, these reports have been restricted to SNPs outside copy number variable regions (CNVR) as current methods have not been adapted to account for SNPs displaying variable copy number. We show that traditional LD metrics inappropriately quantify SNP/CNV covariance when SNPs lie within CNVR. We derive a new method for measuring LD that solves this issue, and defaults to traditional metrics otherwise. Finally, we present a procedure to estimate CNV–SNP allele frequencies from unphased CNV–SNP genotypes. Our method allows researchers to include all SNPs in SNP/CNV LD measurements, regardless of copy number.
Introduction
Examination of linkage disequilibrium (LD) between single nucleotide polymorphisms (SNPs) has played a key role in our understanding of worldwide patterns of genetic variation, including determining the extent of haplotype diversity (Conrad et al., 2006), detecting regions of positive selection (Sabeti et al., 2007), and guiding the design of most current genotyping arrays through the selection of appropriate haplotype tagging SNPs. Traditional pairwise metrics of LD, including r2, D, and D′, have been designed to quantify the degree of non-independence between neighboring genetic polymorphisms (Lewontin and Kojima, 1960; Lewontin, 1964; Hill and Robertson, 1968). With the current understanding that copy number variation (CNV) also significantly contributes to genetic variation (Redon et al., 2006), research has turned to the role for CNV in disease risk (Gonzalez et al., 2005; Aitman et al., 2006; McCarroll and Altshuler, 2007; Sebat et al., 2007), particularly as a partial explanation for the so-called missing heritability (Manolio et al., 2009; Eichler et al., 2010). Recently, genome-wide CNV surveys such as that performed by the Wellcome Trust Case Control Consortium (WTCCC) have concluded that common CNVs were adequately tagged by SNPs; and thus unlikely to substantially contribute to the genetic basis of common human diseases (Conrad et al., 2010; Wellcome Trust Case Control Consortium et al., 2010). However, current methods have restricted these studies to only include SNPs that fall outside of copy number variable regions (CNVR) – the ramifications being that more tagging SNPs are being missed, particularly in DNA segments of higher copy number.
In this paper, we explicitly derive the covariance between SNPs and CNVs under a range of scenarios where SNPs either fall inside (interior) or outside (exterior) of a CNVR. We find that traditional LD metrics are sufficient for exterior SNPs; however, these same metrics inappropriately quantify covariance for interior SNPs. Specifically, we show that the covariance estimated from common metrics using interior SNPs will: (1) always be non-zero at any polymorphic loci; (2) differ based upon the arbitrary choice of reference SNP allele; and (3) potentially lead to high values of LD despite any meaningful correlation between the copy number state and SNP allele. Based on this result, we modify traditional techniques to appropriately quantify the covariance in the case of SNPs residing within CNVRs.
Materials and Methods
We begin with a brief review of current statistical metrics for the quantification of LD, discuss their performance in the presence of CNV, and conclude with our proposed statistics based on CNV–SNP covariance.
Review of Current LD Metrics for SNPs and CNVs
In accordance with current LD metrics, let X denote the integer copy number state for a CNVR on a single maternal/paternal chromosome or haploid, where we assume for simplicity that X can take three values representing a deletion (0), normal copy number (1), and duplication (2). Similarly define Y as the count of reference alleles at a SNP on the same chromosome, where we arbitrarily label the SNP alleles as A (reference) and B. The marginal probability distributions for X and Y can then be defined as:
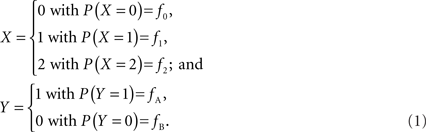
Assuming that the joint frequencies (fX,Y) are known, the covariance between X and Y can be written as:
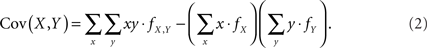
We consider this covariance between CNVs and SNPs in the following four scenarios.
Scenario 1a: The SNP is outside a CNVR (exterior SNP) that contains a normal (one copy) variant and deletion (zero copies). Then:
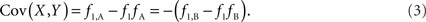
Scenario 1b: The SNP is outside a CNVR (exterior SNP) that contains a normal (one copy) variant and duplication (two copies). Then:
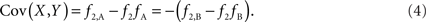
In both of the above scenarios, the covariance between the CNV and SNP will appropriately be zero when X and Y are independent (i.e., the joint frequency is equivalent to the product of the marginal frequencies). Also, any inference concerning the relationship between the CNV and SNP does not depend on as the choice of reference allele, since only the direction of the covariance differs. Given these features, traditional measurements of LD between CNVs and SNPs are sufficient for exterior SNPs.
Scenario 2a: The SNP is inside a CNVR (interior) that contains a normal (one copy) variant and deletion (zero copies). Table 1 provides definitions of CNV–SNP allele frequencies based on haploid, three copy number state model (zero to two copies per haploid). In situations where the SNP lies within the CNVR, SNP allele counts are dependent on copy number state. For example, whenever a deletion is present, both X and Y must be equal to zero. Thus,
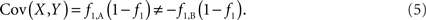
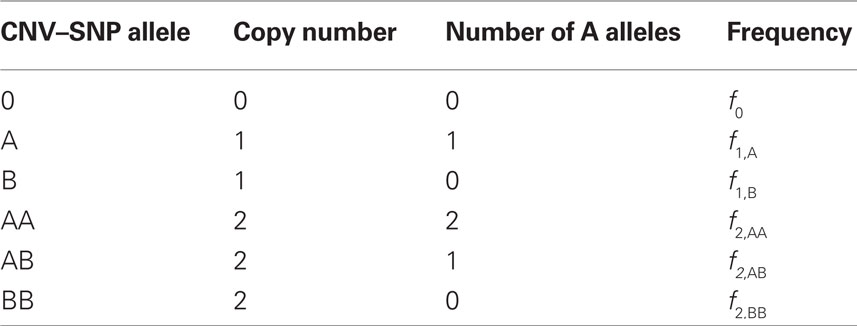
Table 1. Copy number variant–single nucleotide polymorphism (CNV–SNP) alleles based upon a haploid three copy number state model (zero to two copies per haploid).
Scenario 2b: The SNP is inside a CNVR (interior) that contains a normal (one copy) variant and duplication (two copies). This final scenario represents the most complex case. The sample space of Y needs to change to reflect the possibility of zero to two copies of the A allele. Namely:
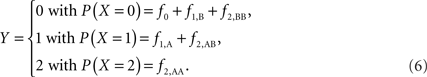
The covariance then becomes,
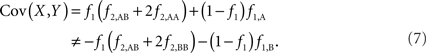
Based on the covariances calculated in scenarios 2a and 2b, we find two undesirable features of current metrics when used to assess LD between interior SNP and CNVs: (1) polymorphic SNPs inside CNVRs will never be uncorrelated with the CNV; and (2) the correlation between variants will differ based upon which SNP allele is considered as the reference. In these scenarios the use of traditional LD measurements could impact association results. Consider a population where a monomorphic SNP lies within a CNVR that includes a moderately frequent deletion (for instance: f0 = 0.1 and f1,A = 0.9). Traditional metrics would conclude that the SNP and CNV are in perfect LD; and that any inference based upon the SNP would apply to the CNV. However, in the absence of copy number data, an association analysis based upon the SNP would be completely uninformative – leading to, perhaps, the incorrect conclusion that CNV is also not associated with the trait. In general, we show that high values of r2 between an interior SNP and deletion are obtained whenever the SNP minor allele frequency is low (Figure 1). However, in the absence of CNV data, the same incorrect conclusion would again be applied to the CNV. In these situations we would hope LD measurements would conclude independence. However that is not the case. We also note the result that the correlation between the SNP and CNV depends on the SNP allele considered as the reference. We have provided an example in the results section signifying this property. Together, these features demonstrate that traditional LD metrics are inappropriate when applied to interior SNPs and CNVs.
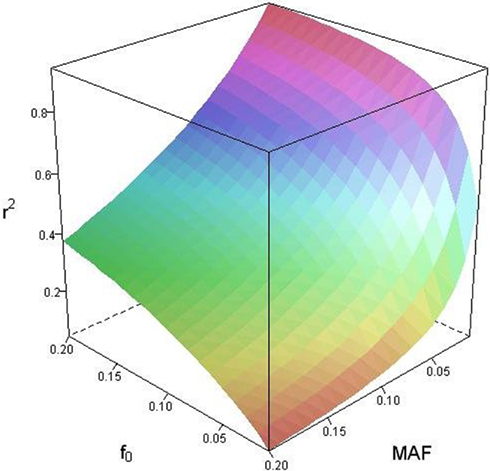
Figure 1. Linkage disequilibrium (r2) between copy number variants (CNVs) and single nucleotide polymorphisms (SNPs) within the copy number variable region as a function of deletion frequency (f0) and SNP minor allele frequency (MAF).
To address these deficiencies, we now propose a new metric to quantify LD between CNVs and SNPs that functions equivalently to traditional measures for exterior SNPs, and solves these issues for interior SNPs.
Derivation of New Proposed Statistic
We consider a bi-allelic SNP present within a CNVR with three potential haploid copy number states: zero, one, or two copies – although methods here can be expanded to higher copy number, or multiple SNP alleles (Kalinowski and Hedrick, 2001). Define the CNV–SNP allele at this locus to be a combination of the haploid copy number state and nucleotide frequency with two differing, generically labeled SNPs A and B. Then this model can be treated similar to a multiallelic locus with alleles: 0, A, B, AA, AB, and BB; where 0 represents a deletion (Table 1). Combined in pairs, these alleles form a CNV–SNP genotype which provides information on the total number of copies of each nucleotide (Table 2). This model is consistent with those in the majority of copy number calling algorithms for array-based CNV detection (Wang et al., 2007; Korn et al., 2008; Coin et al., 2010). Note, however, that while CNV–SNP genotypes can be inferred from common genotyping platforms (Korn et al., 2008; Coin et al., 2010), the phase, particularly in duplicated regions, may be ambiguous. For example, an AAB genotype may have either of the phased haploid configurations AA/B or AB/A.

Table 2. Copy number variant–single nucleotide polymorphism (CNV–SNP) genotypes based upon a haploid three copy number state model, CNV–SNP haploid configurations, and respective frequencies.
We note that in the case of interior SNPs, a deletion should not provide any information on the relationship between the copy number state and SNP allele(s) present. Therefore, let X be the integer haploid copy number state and Y represent the presence of a particular SNP allele, conditional on haploid copy number state not equal to zero, so that:
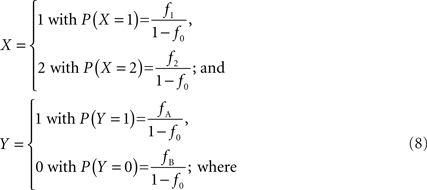
f1 = f1,A + f1,B; f2 = f2,AA + f2,AB + f2,BB; fA = f1,A + f2,AA + 1/2f2,AB; and fB = f1,B = f2,BB + 1/2f2,AB according to the CNV–SNP allele frequencies listed in Table 1. The covariance between X and Y then becomes,
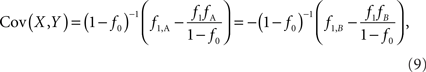
which does not depend on the particular choice of the reference allele. We denote the inner factor in formula {9} as DC, noting its equivalence to Lewontin’s D (Lewontin and Kojima, 1960) in situations for exterior SNPs. Specifically, let

where 
Similar to D, the range of values for DC is difficult to interpret without proper scaling. Therefore, we propose a method nearly identical to the construction of D′(Lewontin, 1964). Define the maximum value that DC can take based upon allele frequencies as 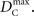 Then:
Then:
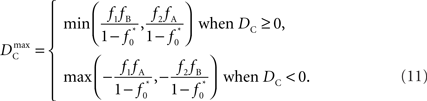
Finally, let

Meanwhile, we can also calculate the correlation between X and Y to be:

or, alternatively:

We again note that  and
and  are identical to the traditional LD measurements D′ and r2, respectively, for exterior SNPs; and both are an appropriate measurement for interior SNPs.
are identical to the traditional LD measurements D′ and r2, respectively, for exterior SNPs; and both are an appropriate measurement for interior SNPs.
Estimation of CNV–SNP Allele Frequencies
Calculation of  and
and 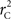 is straightforward when the CNV–SNP haplotype frequencies are known. However, current methods for array-based genotype/CNV calling do not directly infer the haploid configuration (phase), though methods for estimating this configuration have been recently proposed (Kato et al., 2008; Su et al., 2010). Here we present a novel method to estimate CNV–SNP allele frequencies based on unphased CNV–SNP genotypes. The method is a direct result of an EM algorithm and nearly identical in construction to the gene-counting, allele frequency estimation procedure in Ceppellini et al. (1955) and Smith (1957). Consider a CNVR with CNV–SNP haploid configurations S/T such that S, T ∈ {0, A, B, AA, AB, BB}. In the E-step, haploid configuration counts are estimated based on the expected counts from estimated CNV–SNP allele frequencies. That is, for each CNV–SNP haploid configuration S/T:
is straightforward when the CNV–SNP haplotype frequencies are known. However, current methods for array-based genotype/CNV calling do not directly infer the haploid configuration (phase), though methods for estimating this configuration have been recently proposed (Kato et al., 2008; Su et al., 2010). Here we present a novel method to estimate CNV–SNP allele frequencies based on unphased CNV–SNP genotypes. The method is a direct result of an EM algorithm and nearly identical in construction to the gene-counting, allele frequency estimation procedure in Ceppellini et al. (1955) and Smith (1957). Consider a CNVR with CNV–SNP haploid configurations S/T such that S, T ∈ {0, A, B, AA, AB, BB}. In the E-step, haploid configuration counts are estimated based on the expected counts from estimated CNV–SNP allele frequencies. That is, for each CNV–SNP haploid configuration S/T:

where NST is number of CNV–SNP genotypes that could possibly result in an S/T haploid configuration, fS/T, k is the estimated frequency of the S/T haploid configuration, and fS/T, k is the estimated frequency of CNV–SNP genotypes that could result in an S/T haploid configuration for the kth iteration. In the M-step, CNV–SNP allele frequencies estimates are updated:

as well as new CNV–SNP haploid configuration frequencies estimates:
The algorithm is based upon haploid configurations falling into their appropriate Hardy–Weinberg equilibrium proportions. As a result, this approach may perform poorly in de novo mutation hot-spots and CNVs found only in somatic cells.
Results
We provide calculations of 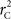 for various CNV–SNP allele frequencies and compare them to the traditional measurements for SNPs inside CNVRs (Table 3). We define,
for various CNV–SNP allele frequencies and compare them to the traditional measurements for SNPs inside CNVRs (Table 3). We define, 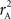 and
and 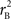 are the traditional metrics of LD using SNP allele A or B as the reference allele, respectively. Note how vastly different results can be obtained depending on which allele is used as the reference. The value of
are the traditional metrics of LD using SNP allele A or B as the reference allele, respectively. Note how vastly different results can be obtained depending on which allele is used as the reference. The value of 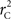 is the same irrespective of SNP allele considered as the reference allele.
is the same irrespective of SNP allele considered as the reference allele.
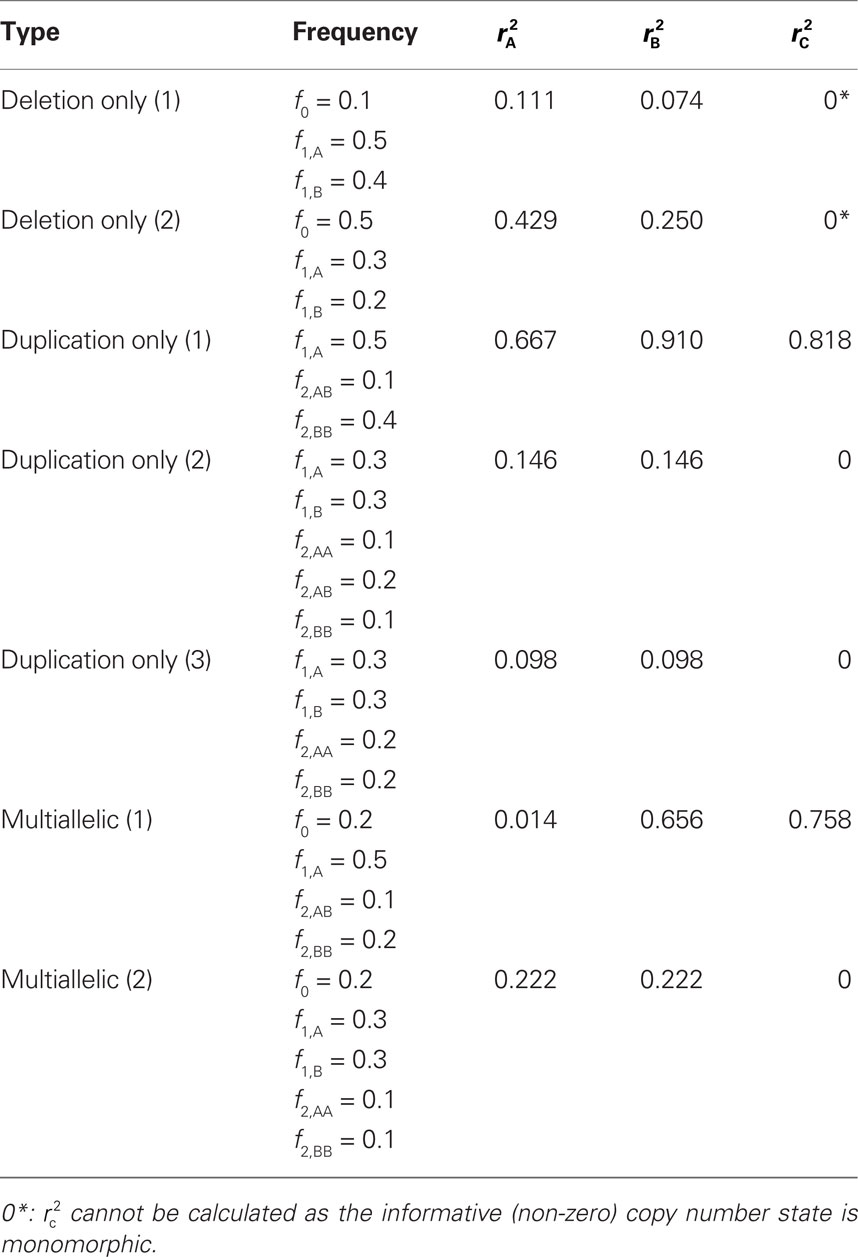
Table 3. Measurements of linkage disequilibrium (LD) between copy number variants and single nucleotide polymorphisms (SNPs) within the copy number variable region.
We theoretically demonstrated how current metrics of LD are inappropriate in certain cases and proposed a new method that solves these issues. Note that the CNV–SNP allele frequencies are critical in calculating 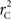 . We evaluated our method for estimating CNV–SNP allele frequencies via an EM algorithm, as described above in the methods section, using a simulation procedure. These results are provided in Table 4. In summary, our metric accurately and precisely measures SNP/CNV covariance, regardless of the location of the SNP and type of CNV. In particular, high values of
. We evaluated our method for estimating CNV–SNP allele frequencies via an EM algorithm, as described above in the methods section, using a simulation procedure. These results are provided in Table 4. In summary, our metric accurately and precisely measures SNP/CNV covariance, regardless of the location of the SNP and type of CNV. In particular, high values of 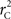 will always lead to a proper conclusion about role of CNVs from the study of SNPs. In CNVRs that only include a deletion, our proposed method will always correctly assign independence between interior SNPs and the CNV. Meanwhile, in duplicated regions our metric will provide a value that appropriately quantifies the correlation between SNP allele(s) and the number of copies present.
will always lead to a proper conclusion about role of CNVs from the study of SNPs. In CNVRs that only include a deletion, our proposed method will always correctly assign independence between interior SNPs and the CNV. Meanwhile, in duplicated regions our metric will provide a value that appropriately quantifies the correlation between SNP allele(s) and the number of copies present.

Table 4. Copy number variant–single nucleotide polymorphism (CNV–SNP) allele frequency estimation procedure diagnostics based upon 1,000 simulations of a sample size of 1,000 (2,000 haploids) and various CNV–SNP allele frequencies.
Discussion
We have provided rationale for why current metrics used to assess LD between CNVs and interior SNPs are inappropriate. Given that difficulties arise only for these SNPs, one potential solution, as previous studies have done, would be to rely upon exterior SNPs for tagging CNVs. Though this approach been successful for deletions, duplications tend to be in very low LD with exterior SNPs (Kato et al., 2010). It is possible that duplicate copies are not simply positioned in tandem next to a neighboring SNP in relation to the reference genome. The more extreme case arises when a duplicate copy has been translocated onto a different chromosome. In this situation an exterior SNP will be completely unlinked to the translocated duplicate. However, interior SNPs will segregate within the duplicate – particularly if this copy is not suitably matched for recombination. A similar argument can be made for duplicated segments inserted downstream of its reference location. A larger physical distance between the duplicated copies and an exterior SNP allows for a greater probability of recombination to eliminate LD. However, this distance will be irrelevant in regards to the allelic content within the duplicated genomic segment.
We have included a new method to quantify LD between CNVs and SNPs which provides accurate estimates for interior SNPs and defaults to the traditional measurements otherwise. As our methods require knowledge of CNV–SNP allele frequencies, we have provided an estimation procedure that performs well under a wide range of scenarios. We hope CNV researchers, particularly those hoping to draw conclusions about CNVs from SNPs, will use this method to identify tagging SNPs which may or may not exist within the CNV boundary.
Web Resources
R code to measure 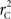 and CNV–SNP allele frequencies from CNV–SNP genotypes is available from the corresponding author upon request.
and CNV–SNP allele frequencies from CNV–SNP genotypes is available from the corresponding author upon request.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The work is supported in part by the University of Alabama at Birmingham’s Alumni Associations’ Marie and Emmett Carmichael Fund for Graduate Students in Biosciences, and NIH grants T32 HL-079888 and T32 HL-072757. The opinions expressed herein are those of the authors and not necessarily those of the NIH or any organization with which the authors are affiliated.
References
Aitman, T. J., Dong, R., Vyse, T. J., Norsworthy, P. J., Johnson, M. D., Smith, J., Mangion, J., Roberton-Lowe, C., Marshall, A. J., Petretto, E., Hodges, M. D., Bhangal, G., Patel, S. G., Sheehan-Rooney, K., Duda, M., Cook, P. R., Evans, D. J., Domin, J., Flint, J., Boyle, J. J., Pusey, C. D., and Cook, H. T. (2006). Copy number polymorphism in Fcgr3 predisposes to glomerulonephritis in rats and humans. Nature 439, 851–855.
Ceppellini, R., Siniscalco, M., and Smith, C. A. B. (1955). The estimation of gene frequencies in a random-mating population. Ann. Hum. Genet. 20, 97–115.
Coin, L. J., Asher, J. E., Walters, R. G., Moustafa, J. S., de Smith, A. J., Sladek, R., Balding, D. J., Froguel, P., and Blakemore, A. I. (2010). cnvHap: an integrative population and haplotype-based multiplatform model of SNPs and CNVs. Nat. Methods 7, 541–546.
Conrad, D. F., Jakobsson, M., Coop, G., Wen, X., Wall, J. D., Rosenberg, N. A., and Pritchard, J. K. (2006). A worldwide survey of haplotype variation and linkage disequilibrium in the human genome. Nat. Genet. 38, 1251–1260.
Conrad, D. F., Pinto, D., Redon, R., Feuk, L., Gokcumen, O., Zhang, Y., Aerts, J., Andrews, T. D., Barnes, C., Campbell, P., Fitzgerald, T., Hu, M., Ihm, C. H., Kristiansson, K., Macarthur, D. G., Macdonald, J. R., Onyiah, I., Pang, A. W., Robson, S., Stirrups, K., Valsesia, A., Walter, K., Wei, J., Wellcome Trust Case Control Consortium, Tyler-Smith, C., Carter, N. P., Lee, C., Scherer, S. W., and Hurles, M. E. (2010). Origins and functional impact of copy number variation in the human genome. Nature 464, 704–712.
Eichler, E. E., Flint, J., Gibson, G., Kong, A., Leal, S. M., Moore, J. H., and Nadeau, J. H. (2010). Missing heritability and strategies for finding the underlying causes of complex diseases. Nat. Rev. Genet. 11, 446–450.
Gonzalez, E., Kulkarni, H., Bolivar, H., Mangano, A., Sanchez, R., Catano, G., Nibbs, R. J., Freedman, B. I., Quinones, M. P., Bamshad, M. J., Murthy, K. K., Rovin, B. H., Bradley, W., Clark, R. A., Anderson, S. A., O’connell, R. J., Agan, B. K., Ahuja, S. S., Bologna, R., Sen, L., Dolan, M. J., and Ahuja, S. K. (2005). The influence of CCL3L1 gene-containing segmental duplications on HIV-1/AIDS susceptibility. Science 307, 1434–1440.
Hill, W. G., and Robertson, A. (1968). The effects of inbreeding at loci with heterozygote advantage. Genetics 60, 615–628.
Kalinowski, S. T., and Hedrick, P. W. (2001). Estimation of linkage disequilibrium for loci with multiple alleles: basic approach and an application using data from bighorn sheep. Heredity 87, 698–708.
Kato, M., Awaguchi, T., shikawa, S., Umeda, T., Nakamichi, R., Shapero, M. H., Jones, K. W., Nakamura, Y., Aburatani, H., and Tsunoda, T. (2010). Population-genetic nature of copy number variations in the human genome. Hum. Mol. Genet. 19, 761–773.
Kato, M., Nakamura, Y., and Tsunoda, T. (2008). An algorithm for inferring complex haplotypes in a region of copy-number variation. Am. J. Hum. Genet. 83, 157–169.
Korn, J. M., Kuruvilla, F. G., McCarroll, S. A., Wysoker, A., Nemesh, J., Cawley, S., Hubbell, E., Veitch, J., Collins, P. J., Darvishi, K., Lee, C., Nizzari, M. M., Gabriel, S. B., Purcell, S., Daly, M. J., and Altshuler, D. (2008). Integrated genotype calling and association analysis of SNPs, common copy number polymorphisms and rare CNVs. Nat. Genet. 40, 1253–1260.
Lewontin, R. C. (1964). The interaction of selection and linkage. I. General considerations; heterotic models. Genetics 49, 49–67.
Lewontin, R. C., and Kojima, K. (1960). The evolutionary dynamics of complex polymorphisms. Evolution 14, 458–472.
Manolio, T. A., Collins, F. S., Cox, N. J., Goldstein, D. B., Hindorff, L. A., Hunter, D. J., McCarthy, M. I., Ramos, E. M., Cardon, L. R., Chakravarti, A., Cho, J. H., Guttmacher, A. E., Kong, A., Kruglyak, L., Mardis, E., Rotimi, C. N., Slatkin, M., Valle, D., Whittemore, A. S., Boehnke, M., Clark, A. G., Eichler, E. E., Gibson, G., Haines, J. L., Mackay, T. F., McCarroll, S. A., and Visscher, P. M. (2009). Finding the missing heritability of complex diseases. Nature 461, 747–753.
McCarroll, S. A., and Altshuler, D. M. (2007). Copy-number variation and association studies of human disease. Nat. Genet. 39, S37–S42.
Redon, R., Ishikawa, S., Fitch, K. R., Feuk, L., Perry, G. H., Andrews, T. D., Fiegler, H., Shapero, M. H., Carson, A. R., Chen, W., Cho, E. K., Dallaire, S., Freeman, J. L., González, J. R., Gratacòs, M., Huang, J., Kalaitzopoulos, D., Komura, D., MacDonald, J. R., Marshall, C. R., Mei, R., Montgomery, L., Nishimura, K., Okamura, K., Shen, F., Somerville, M. J., Tchinda, J., Valsesia, A., Woodwark, C., Yang, F., Zhang, J., Zerjal, T., Zhang, J., Armengol, L., Conrad, D. F., Estivill, X., Tyler-Smith, C., Carter, N. P., Aburatani, H., Lee, C., Jones, K. W., Scherer, S. W., and Hurles, M. E. (2006). Global variation of copy number in the human genome. Nature 444, 444–454.
Sabeti, P. C., Varilly, P., Fry, B., Lohmueller, J., Hostetter, E., Cotsapas, C., Xie, X., Byrne, E. H., McCarroll, S. A., Gaudet, R., Schaffner, S. F., Lander, E. S., International HapMap Consortium, Frazer, K. A., Ballinger, D. G., Cox, D. R., Hinds, D. A., Stuve, L. L., Gibbs, R. A., Belmont, J. W., Boudreau, A., Hardenbol, P., Leal, S. M., Pasternak, S., Wheeler, D. A., Willis, T. D., Yu, F., Yang, H., Zeng, C., Gao, Y., Hu, H., Hu, W., Li, C., Lin, W., Liu, S., Pan, H., Tang, X., Wang, J., Wang, W., Yu, J., Zhang, B., Zhang, Q., Zhao, H., Zhao, H., Zhou, J., Gabriel, S. B., Barry, R., Blumenstiel, B., Camargo, A., Defelice, M., Faggart, M., Goyette, M., Gupta, S., Moore, J., Nguyen, H., Onofrio, R. C., Parkin, M., Roy, J., Stahl, E., Winchester, E., Ziaugra, L., Altshuler, D., Shen, Y., Yao, Z., Huang, W., Chu, X., He, Y., Jin, L., Liu, Y., Shen, Y., Sun, W., Wang, H., Wang, Y., Wang, Y., Xiong, X., Xu, L., Waye, M. M., Tsui, S. K., Xue, H., Wong, J. T., Galver, L. M., Fan, J. B., Gunderson, K., Murray, S. S., Oliphant, A. R., Chee, M. S., Montpetit, A., Chagnon, F., Ferretti, V., Leboeuf, M., Olivier, J. F., Phillips, M. S., Roumy, S., Sallée, C., Verner, A., Hudson, T. J., Kwok, P. Y., Cai, D., Koboldt, D. C., Miller, R. D., Pawlikowska, L., Taillon-Miller, P., Xiao, M., Tsui, L. C., Mak, W., Song, Y. Q., Tam, P. K., Nakamura, Y., Kawaguchi, T., Kitamoto, T., Morizono, T., Nagashima, A., Ohnishi, Y., Sekine, A., Tanaka, T., Tsunoda, T., Deloukas, P., Bird, C. P., Delgado, M., Dermitzakis, E. T., Gwilliam, R., Hunt, S., Morrison, J., Powell, D., Stranger, B. E., Whittaker, P., Bentley, D. R., Daly, M. J., de Bakker, P. I., Barrett, J., Chretien, Y. R., Maller, J., McCarroll, S., Patterson, N., Pe’er, I., Price, A., Purcell, S., Richter, D. J., Sabeti, P., Saxena, R., Schaffner, S. F., Sham, P. C., Varilly, P., Altshuler, D., Stein, L. D., Krishnan, L., Smith, A. V., Tello-Ruiz, M. K., Thorisson, G. A., Chakravarti, A., Chen, P. E., Cutler, D. J., Kashuk, C. S., Lin, S., Abecasis, G. R., Guan, W., Li, Y., Munro, H. M., Qin, Z. S., Thomas, D. J., McVean, G., Auton, A., Bottolo, L., Cardin, N., Eyheramendy, S., Freeman, C., Marchini, J., Myers, S., Spencer, C., Stephens, M., Donnelly, P., Cardon, L. R., Clarke, G., Evans, D. M., Morris, A. P., Weir, B. S., Tsunoda, T., Johnson, T. A., Mullikin, J. C., Sherry, S. T., Feolo, M., Skol, A., Zhang, H., Zeng, C., Zhao, H., Matsuda, I., Fukushima, Y., Macer, D. R., Suda, E., Rotimi, C. N., Adebamowo, C. A., Ajayi, I., Aniagwu, T., Marshall, P. A., Nkwodimmah, C., Royal, C. D., Leppert, M. F., Dixon, M., Peiffer, A., Qiu, R., Kent, A., Kato, K., Niikawa, N., Adewole, I. F., Knoppers, B. M., Foster, M. W., Clayton, E. W., Watkin, J., Gibbs, R. A., Belmont, J. W., Muzny, D., Nazareth, L., Sodergren, E., Weinstock, G. M., Wheeler, D. A., Yakub, I., Gabriel, S. B., Onofrio, R. C., Richter, D. J., Ziaugra, L., Birren, B. W., Daly, M. J., Altshuler, D., Wilson, R. K., Fulton, L. L., Rogers, J., Burton, J., Carter, N. P., Clee, C. M., Griffiths, M., Jones, M. C., McLay, K., Plumb, R. W., Ross, M. T., Sims, S. K., Willey, D. L., Chen, Z., Han, H., Kang, L., Godbout, M., Wallenburg, J. C., L’Archevêque, P., Bellemare, G., Saeki, K., Wang, H., An, D., Fu, H., Li, Q., Wang, Z., Wang, R., Holden, A. L., Brooks, L. D., McEwen, J. E., Guyer, M. S., Wang, V. O., Peterson, J. L., Shi, M., Spiegel, J., Sung, L. M., Zacharia, L. F., Collins, F. S., Kennedy, K., Jamieson, R., and Stewart, J. (2007). Genome-wide detection and characterization of positive selection in human populations. Nature 18, 913–918.
Sebat, J., Lakshmi, B., Malhotra, D., Troge, J., Lese-Martin, C., Walsh, T., Yamrom, B., Yoon, S., Krasnitz, A., Kendall, J., Leotta, A., Pai, D., Zhang, R., Lee, Y. H., Hicks, J., Spence, S. J., Lee, A. T., Puura, K., Lehtimäki, T., Ledbetter, D., Gregersen, P. K., Bregman, J., Sutcliffe, J. S., Jobanputra, V., Chung, W., Warburton, D., King, M. C., Skuse, D., Geschwind, D. H., Gilliam, T. C., Ye, K., and Wigler, M. (2007). Strong association of de novo copy number mutations with autism. Science 316, 445–449.
Su, S. Y., Asher, J. E., Jarvelin, M. R., Froguel, P., Blakemore, A. I., Balding, D. J., and Coin, L. J. (2010). Inferring combined CNV/SNP haplotypes from genotype data. Bioinformatics 26, 1437–1445.
Wang, K., Li, M., Hadley, D., Liu, R., Glessner, J., Grant, S. F., Hakonarson, H., Bucan, M., and Penn, C. N. V. (2007). an integrated hidden Markov model designed for high-resolution copy number variation detection in whole-genome SNP genotyping data. Genome Res. 17, 1665–1674.
Wellcome Trust Case Control Consortium, Craddock, N., Hurles, M. E., Cardin, N., Pearson, R. D., Plagnol, V., Robson, S., Vukcevic, D., Barnes, C., Conrad, D. F., Giannoulatou, E., Holmes, C., Marchini, J. L., Stirrups, K., Tobin, M. D., Wain, L. V., Yau, C., Aerts, J., Ahmad, T., Andrews, T. D., Arbury, H., Attwood, A., Auton, A., Ball, S. G., Balmforth, A. J., Barrett, J. C., Barroso, I., Barton, A., Bennett, A. J., Bhaskar, S., Blaszczyk, K., Bowes, J., Brand, O. J., Braund, P. S., Bredin, F., Breen, G., Brown, M. J., Bruce, I. N., Bull, J., Burren, O. S., Burton, J., Byrnes, J., Caesar, S., Clee, C. M., Coffey, A. J., Connell, J. M., Cooper, J. D., Dominiczak, A. F., Downes, K., Drummond, H. E., Dudakia, D., Dunham, A., Ebbs, B., Eccles, D., Edkins, S., Edwards, C., Elliot, A., Emery, P., Evans, D. M., Evans, G., Eyre, S., Farmer, A., Ferrier, I. N., Feuk, L., Fitzgerald, T., Flynn, E., Forbes, A., Forty, L., Franklyn, J. A., Freathy, R. M., Gibbs, P., Gilbert, P., Gokumen, O., Gordon-Smith, K., Gray, E., Green, E., Groves, C. J., Grozeva, D., Gwilliam, R., Hall, A., Hammond, N., Hardy, M., Harrison, P., Hassanali, N., Hebaishi, H., Hines, S., Hinks, A., Hitman, G. A., Hocking, L., Howard, E., Howard, P., Howson, J. M., Hughes, D., Hunt, S., Isaacs, J. D., Jain, M., Jewell, D. P., Johnson, T., Jolley, J. D., Jones, I. R., Jones, L. A., Kirov, G., Langford, C. F., Lango-Allen, H., Lathrop, G. M., Lee, J., Lee, K. L., Lees, C., Lewis, K., Lindgren, C. M., Maisuria-Armer, M., Maller, J., Mansfield, J., Martin, P., Massey, D. C., McArdle, W. L., McGuffin, P., McLay, K. E., Mentzer, A., Mimmack, M. L., Morgan, A. E., Morris, A. P., Mowat, C., Myers, S., Newman, W., Nimmo, E. R., O’Donovan, M. C., Onipinla, A., Onyiah, I., Ovington, N. R., Owen, M. J., Palin, K., Parnell, K., Pernet, D., Perry, J. R., Phillips, A., Pinto, D., Prescott, N. J., Prokopenko, I., Quail, M. A., Rafelt, S., Rayner, N. W., Redon, R., Reid, D. M., Renwick, Ring, S. M., Robertson, N., Russell, E., St Clair, D., Sambrook, J. G., Sanderson, J. D., Schuilenburg, H., Scott, C. E., Scott, R., Seal, S., Shaw-Hawkins, S., Shields, B. M., Simmonds, M. J., Smyth, D. J., Somaskantharajah, E., Spanova, K., Steer, S., Stephens, J., Stevens, H. E., Stone, M. A., Su, Z., Symmons, D. P., Thompson, J. R., Thomson, W., Travers, M. E., Turnbull, C., Valsesia, A., Walker, M., Walker, N. M., Wallace, C., Warren-Perry, M., Watkins, N. A., Webster, J., Weedon, M. N., Wilson, A. G., Woodburn, M., Wordsworth, B. P., Young, A. H., Zeggini, E., Carter, N. P., Frayling, T. M., Lee, C., McVean, G., Munroe, P. B., Palotie, A., Sawcer, S. J., Scherer, S. W., Strachan, D. P., Tyler-Smith, C., Brown, M. A., Burton, P. R., Caulfield, M. J., Compston, A., Farrall, M., Gough, S. C., Hall, A. S., Hattersley, A. T., Hill, A. V., Mathew, C. G., Pembrey, M., Satsangi, J., Stratton, M. R., Worthington, J., Deloukas, P., Duncanson, A., Kwiatkowski, D. P., McCarthy, M. I., Ouwehand, W., Parkes, M., Rahman, N., Todd, J. A., Samani, N. J., and Donnelly, P. (2010). Genome-wide association study of CNVs in 16,000 cases of eight common diseases and 3,000 shared controls. Nature 464, 713–720.
Keywords: copy number variation, linkage disequilibrium, CNV–SNP haplotype
Citation: Wineinger NE, Pajewski NM and Tiwari HK (2011) A method to assess linkage disequilibrium between CNVs and SNPs inside copy number variable regions. Front. Gene. 2:17. doi: 10.3389/fgene.2011.00017
Received: 20 January 2011; Accepted: 31 March 2011;
Published online: 25 April 2011.
Edited by:
Mingyao Li, University of Pennsylvania, USAReviewed by:
Yun Li, University of North Carolina, USAXiaofeng Zhu, Case Western Reserve University, USA
Copyright: © 2011 Wineinger, Pajewski and Tiwari. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with
*Correspondence: Nathan E. Wineinger and Hemant K. Tiwari, Section on Statistical Genetics, Department of Biostatistics, University of Alabama at Birmingham, 1665 University Boulevard, Birmingham, AL 35294, USA. e-mail:bndpbmVpbmdAdWFiLmVkdQ==;aHRpd2FyaUB1YWIuZWR1


