Multi-objective genetic algorithm for pseudoknotted RNA sequence design

RNA inverse folding is a computational technology for designing RNA sequences which fold into a user-specified secondary structure. Although pseudoknots are functionally important motifs in RNA structures, less reports concerning the inverse folding of pseudoknotted RNAs have been done compared to those for pseudoknot-free RNA design. In this paper, we present a new version of our multi-objective genetic algorithm (MOGA), MODENA, which we have previously proposed for pseudoknot-free RNA inverse folding. In the new version of MODENA, (i) a new crossover operator is implemented and (ii) pseudoknot prediction methods, IPknot and HotKnots, are used to evaluate the designed RNA sequences, allowing us to perform the inverse folding of pseudoknotted RNAs. The new version of MODENA with the new crossover operator was benchmarked with a dataset composed of natural pseudoknotted RNA secondary structures, and we found that MODENA can successfully design more pseudoknotted RNAs compared to the other pseudoknot design algorithm. In addition, a sequence constraint function newly implemented in the new version of MODENA was tested by designing RNA sequences which fold into the pseudoknotted structure of a hepatitis delta virus ribozyme; as a result, we successfully designed eight RNA sequences. The new version of MODENA is downloadable from http://rna.eit.hirosaki-u.ac.jp/modena/.

1. Introduction

Evolutionary related non-coding RNAs have their own characteristic secondary structure corresponding to each function, and it is well known that the secondary structures play key roles in the functions of the RNA sequences. This biochemical knowledge accumulated to date indicates that we can generate functional synthetic RNAs if we can control the secondary structure of the RNAs. In this context, various synthetic RNAs, such as ribozymes (Schultes and Bartel, 2000), micro RNAs (Schwab et al., 2006), riboswitches (Breaker, 2004), and RNA nano structures (Jaeger et al., 2001) have been successfully designed.

RNA inverse folding is a computational methodology for designing RNA sequences which fold into a given target structure (Hofacker et al., 1994). The name “inverse” comes from the reason that the inverse folding is defined as the inverse problem of RNA secondary structure prediction, where RNA secondary structure prediction problem is referred to as “direct problem”. Since usually there can be multiple solutions for an RNA inverse folding problem and we have no deterministic algorithm which can enumerate all solutions of a given RNA inverse folding problem, previous RNA inverse folding algorithms have adopted heuristic approaches to find desired RNA sequences. We can find the following six RNA inverse folding algorithms in literature: local search algorithms [RNAinverse (Hofacker et al., 1994), RNA-SSD (Andronescu et al., 2004), INFO-RNA (Busch and Backofen, 2006), Inv (Gao et al., 2010), design in NUPACK (Zadeh et al., 2011)] and a genetic algorithm [GA; MODENA (Taneda, 2011)]. The local search algorithms are well characterized by their initialization step and refinement step in the exploration procedures for obtaining desired RNA sequences. First, in these local search approaches, a single RNA sequence is generated. The pioneering RNA inverse folding algorithm, RNAinverse, uses a pure random initialization. RNA-SSD randomly initializes an RNA sequence in a more sophisticated manner, where a base composition and a tabu mechanism for avoiding undesired stem formation are taken into account. INFO-RNA utilizes a dynamic programming algorithm to obtain a good initial sequence for the RNA inverse folding, where the lowest energy RNA sequence determined assuming that the RNA sequence folds into a given structure is used as an initial sequence. In the refinement step after the initialization, RNAinverse performs adaptive walk to improve the initial sequence, and RNA-SSD and INFO-RNA use stochastic local search (Hoos and Stützle, 2004) to improve the initial sequence. In the refinement step, RNAinverse and RNA-SSD employ a structure decomposition strategy to reduce the number of folding calculations for a whole sequence. Inv and NUPACK also utilize structure decomposition strategies in their refinement step. Inv is an RNA inverse folding algorithm designed for a restricted pseudoknot class and can perform the inverse folding of pseudoknotted RNAs. NUPACK is a suite of programs for computational nucleic acid analysis and includes a program named design. Design generates the sequences by minimizing an ensemble defect (Zadeh et al., 2011); the value of ensemble defect becomes lower, the designed RNA sequence more specifically folds into a given target structure. MODENA is a multi-objective genetic algorithm (MOGA; Deb, 2001) for RNA inverse folding. As objective functions, MODENA uses two quantities, a structure similarity measure and a stability measure (e.g., free energy). By virtue of simultaneous optimization in these objective functions, MODENA can explore the sequence which not only folds into the desired target structure but has a high stability (= a low free energy).

Pseudoknots are important functional motifs in RNA structure (Staple and Butcher, 2005). In contrast to other RNA structure motifs such as hairpin loop, bulge loop, internal loop, and multibranch loop, where any two base pairs (i, j) and (k, l) do not have a relationship such that i < k < j < l (where i, j, k, and l are nucleotide positions), pseudoknots are defined as the structures which have base pairs satisfies the condition i < k < j < l. Since pseudoknots have various enzymatic functions (Staple and Butcher, 2005), they are intriguing targets of functional RNA design. However, in the previous RNA inverse folding algorithms, only Inv can design pseudoknots. Moreover, there is no algorithm which can design pseudoknotted RNAs with sequence constraints, which are an important feature for designing the molecule with a known functional sequence motif. For these reasons, development of a novel pseudoknotted RNA inverse folding algorithm is important in order to promote the sequence design of RNA pseudoknots.

In this paper, we present an extension of MODENA algorithm to the inverse folding of pseudoknotted RNAs. In MODENA algorithm, designed RNA sequences are evaluated by performing secondary structure prediction with an RNA folding program such as RNAfold (Hofacker, 2003), and we can easily substitute the RNA folding program by a different RNA folding program (in the context of inverse folding, we refer RNA structure prediction program as “direct problem solver”). This advantage of MODENA algorithm also remains in the case of pseudoknotted RNA inverse folding, where we have to use a pseudoknotted RNA secondary structure prediction program as direct problem solver. In the rest of the present paper, first, we describe the MODENA algorithm for pseudoknotted RNA design, where a multi-objective genetic algorithm is used in combination with the state of the art pseudoknotted RNA structure prediction programs. After that, the performance of MODENA algorithm is evaluated by benchmarks based on natural RNA secondary structures, where not only pseudoknotted structures but also pseudoknot-free structures are taken into account. Then, a sequence constraint function available in MODENA is demonstrated with a biological example taken from literature.

2. Materials and Methods

Since the detail of the MODENA algorithm for pseudoknot-free RNAs is described in Taneda (2011) and the present version for pseudoknot RNA design shares all parts of the previous pseudoknot-free version of MODENA, the algorithmically common parts between the two versions are briefly described below.

MODENA algorithm is an RNA inverse folding algorithm based on MOGA. GA is a population based algorithm for optimization and search (Goldberg, 1987), which is inspired from the mechanism of evolution. MOGA is a GA for exploring the objective function space consisting of multiple objective functions, while standard GA uses a single objective function. In MODENA algorithm, we use the following two objective functions, a structure stability score ϵ and a structure similarity score σ:

$\begin{array}{llll}& ϵ=-E,& & \text{(1)}\\ & \sigma =\left(N-d\right)∕N,& & \text{(2)}\end{array}$

where E is the lowest free energy of a designed sequence; N is the total number of nucleotides, and d is the structure distance between target and predicted structures (Taneda, 2011). Structure distance d is defined as the number of the bases which have a different base-paring status between the target structure and the structure predicted for the designed sequence.

In MODENA algorithm, we utilize multi-objective optimization (MOO; Deb, 2001) to explore solutions (i.e., RNA sequences) with better values of both of the two objective functions. In MOO, two solutions are compared based on their dominance. Let us consider two solutions, x_a and x_b. When “all objective function values of x_a are better than or equal to those of x_b” and “at least one objective function value of x_a is not equal to that of x_b”, x_a dominates x_b; a solution which is not dominated by any other solution is called a Pareto optimal solution. If “all objective function values of x_a are better than those of x_b”, x_a strongly dominates x_b; a weak Pareto optimal solution is defined as a solution which is not strongly dominated by any other solution. MODENA algorithm explores weak Pareto optimal solutions for RNA inverse folding problem (Taneda, 2011).

Since usually it is difficult to enumerate all (weak) Pareto optimal solutions for a given MOO problem, MOGA computes approximate set (partial solutions) of the (weak) Pareto optimal solutions. MODENA is developed based on one of the standard MOGA, non-dominated sorting genetic algorithm 2 (NSGA2; Deb, 2001). NSGA2 proceeds in accordance with the framework similar to that of standard GA, which is composed of initialization, evaluation, and reproduction for a population of solutions. In the initialization step, a user-defined number of solutions (RNA sequences) are randomly generated. In the present study, we use 50 or 100 solutions in one population.

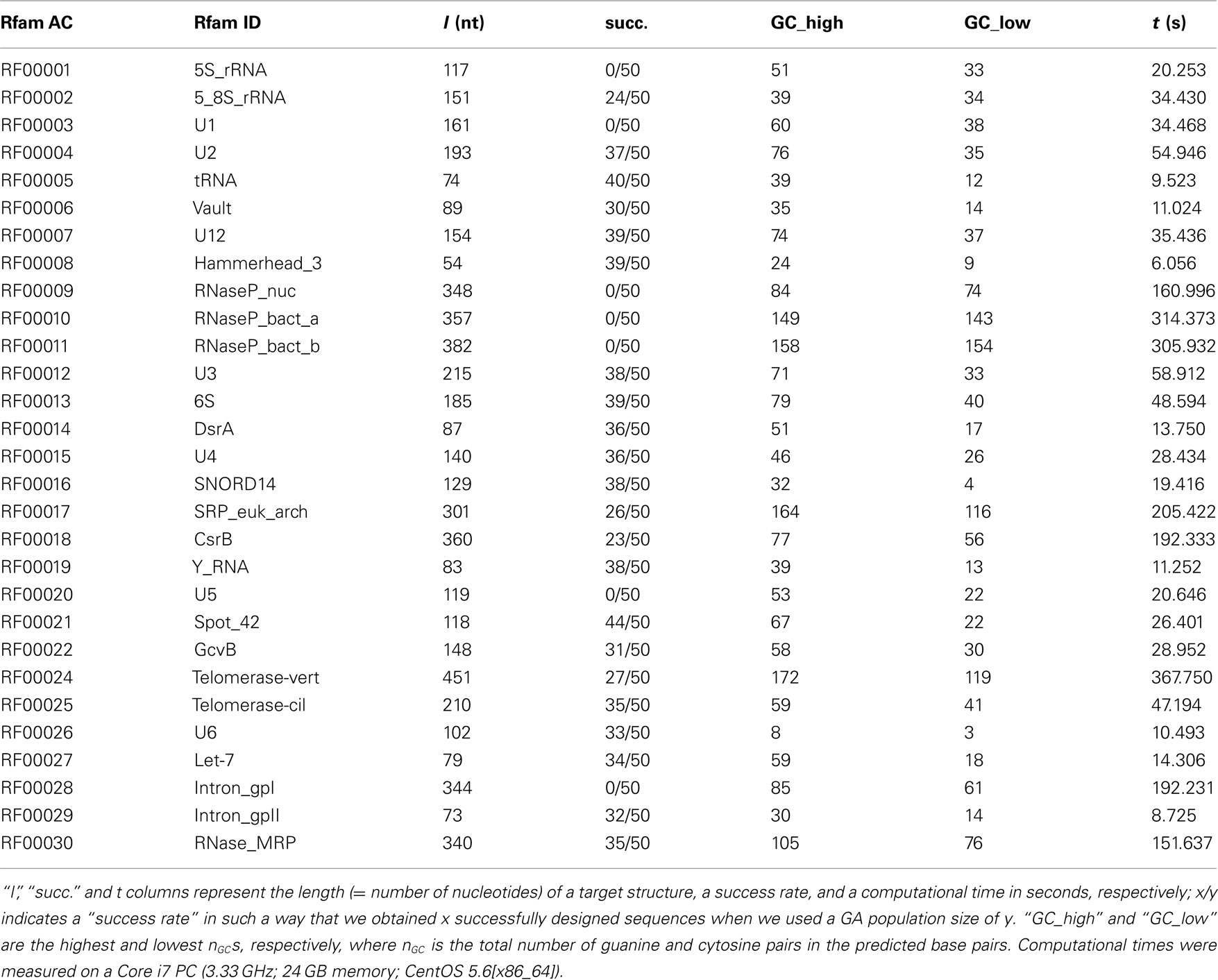
In the evaluation step, we perform an RNA structure prediction for each solution in the current generation, and then assign stability and similarity scores to the solutions. We use an RNA structure prediction program as a direct problem solver to obtain the objective function values. In MODENA, RNAfold (Hofacker, 2003), CentroidFold (Hamada et al., 2009), or UNAFold (Markham and Zuker, 2008) can be used as a direct problem solver for pseudoknot-free RNA design, and IPknot (Sato et al., 2011) or HotKnots (Ren et al., 2005) can be utilized for pseudoknotted RNA sequence design (in the present study, we used IPknot 0.0.2 and HotKnots 2.0). Since IPknot does not output a free energy or some quantity indicating stability of the predicted structure, instead of using Equation 1, we assign the total number of guanine and cytosine pairs in the predicted base pairs to each solution as a stability score when we use IPknot as a direct problem solver.

Based on the solutions of the current generation, reproduction step generates child solutions for the next generation. MODENA algorithm generates child solutions by invoking three GA operators with an equal probability: structural n-point crossover, point accepted mutation, and error diagnosis mutation (Taneda, 2011); structural n-point crossover generates a child solution by concatenating subsequences taken from two parent solutions; point accepted mutation randomly changes a nucleotide; error diagnosis mutation compares the predicted and target structures, and then changes the nucleotides which have different base pairs between the predicted and target structures.

Point accepted mutation and error diagnosis mutation can be applied to pseudoknotted RNA sequence design without any modification. Structural n-point crossover, however, has to be changed for pseudoknotted RNAs, since its original algorithm (Taneda, 2011) assumes no pseudoknot in a target structure (i.e., a nucleotide k, [i < k < j], never forms a base pair with a nucleotide l [l < i or j < l]). Structural n-point crossover is composed of four steps (Taneda, 2011, p. 5), and we modified Step 2 to take pseudoknots into account. After a crossover parameter n_c (= 2 in the present study) and a randomly determined x₀ (= 0 or 1) are given, structural n-point crossover allowing pseudoknots is performed as follows:

Step 1 Set l = 0 and set x_i= x₀ for all i (1 ≤ i ≤ N; N is a sequence length). Randomly select a base pair (i, j) (1 ≤ i < j ≤ N).

Step 2 For each x_k (i ≤ k ≤ j) which does not form a base pair with x_l (l < i or j < l) in the target structure, perform the following: if x_k is zero, change x_k to one, otherwise change x_k to zero. Then increment l by one.

Step 3 If l < n_c and “the number of the base pairs whose upstream nucleotide position m satisfies i < m (where m < N)” is larger than or equal to one, randomly select a base pair (i^new, j^new), where i < i^new < j^new ≤ N; then we set i = i^new and j = j^new, and move to Step 2; otherwise we go to Step 4.

Step 4 Generate a child solution according to x_i for all i (1 ≤ i ≤ N); if x_i= 0, copy the value of a nucleotide $s_i^{\text{A}}$ in parent A to the corresponding nucleotide $s_i^{\text{child}}$ of the child solution; if x_i= 1, the value of a nucleotide $s_i^{\text{B}}$ in parent B is copied to $s_i^{\text{child}}.$

It is noted that Step 1, Step 3, and Step 4 are exactly the same with those in Taneda (2011). By using this modified version, we can crossover two parent solutions without destructing any base complementarity in the target structure. An example of structural n-point crossover is depicted in Figure 1.

FIGURE 1

Figure 1. An example of structural n-point crossover operator for pseudoknotted target structure. Trgt and x_k indicate a target structure and a crossover position indicator, x_k, respectively. (A) An initial state. All x_ks are set to zero. (B) Position i is randomly selected. Position j is the position complementary to the position i. (C) The values of x_ks between i and j are changed to 1. The values in the pseudoknotted region are not changed. The positions whose x_k = 1 are shaded. We can use the x_ks obtained after this step as a crossover position indicator for a 4-point crossover. (D) In addition, we can randomly select one more position i to increase the crossover points. (E) In this example, as a result, we can obtain a crossover position indicator for a 6-point crossover, which is composed of 7 subsequence regions.

2.1. Sequence Constraints

Since the previous version of MODENA does not support sequence constraints, we have added the function to the present version of MODENA. The sequence constraints of MODENA can be specified in accordance with the IUPAC notation of nucleotide codes. By using the sequence constraints, user can design pseudoknotted RNA sequences with sequence motifs specified by the user.

2.2. A Note on Input Target Structure

In MODENA, user inputs a target structure using a bracket notation, where (), <>, {}, [], and alphabets (AaBbCcDdEe) are allowed to specify a base pair (where uppercase and lowercase alphabets indicate upstream and downstream nucleotide positions, respectively). User can freely input a target structure using these bracket notations, but it is noted that if the direct problem solver selected by the user cannot predict the class (e.g., Condon et al., 2004) of the input pseudoknot, the user never obtain the sequences folding into the target structure.

2.3. Dataset for Benchmark

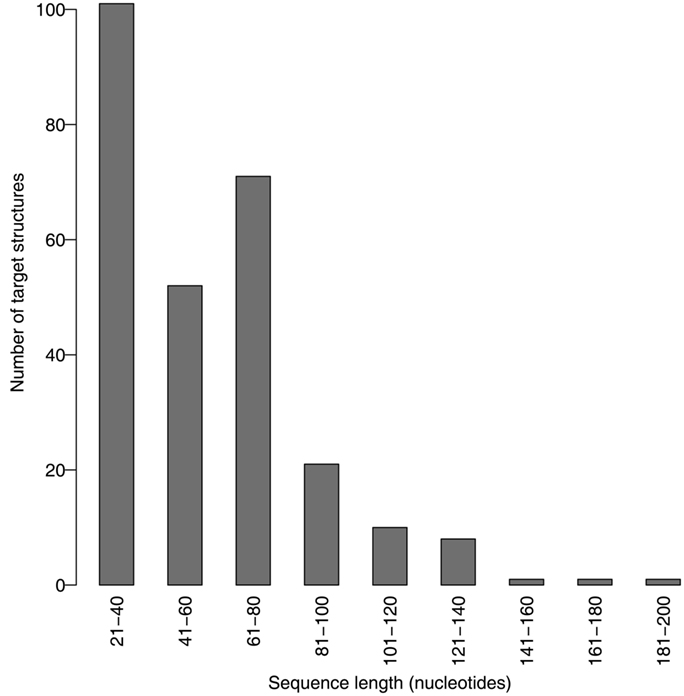
We evaluated the design performance of MODENA with a dataset which contains the natural pseudoknotted structures taken from Pseudobase (Batenburg et al., 2000). Since the original 342 pseudoknotted structures downloaded from Pseudobase are redundant, i.e., different Pseudobase entries can share strictly the same structure, we performed a non-redundant processing to guarantee that all structures are unique in our dataset. Consequently, we obtained 266 pseudoknotted structures for the performance evaluation. We refer to this dataset as the Pseudobase dataset.

In addition to the benchmark for the pseudoknotted target structures, we performed a benchmark for pseudoknot-free target structures, where the Rfam dataset of our previous paper (Taneda, 2011) was used. It is noted that a pseudoknot prediction method (IPknot) was used as a direct problem solver in this pseudoknot-free benchmark. The reason why we performed a benchmark for pseudoknot-free target structures in the present study is as follows. If we use a non-pseudoknot prediction method as a direct problem solver to design an RNA sequence, the designed RNA sequence may fold into a pseudoknotted structure when we fold the designed sequence with a pseudoknot prediction method. By using a pseudoknot prediction method as a direct problem solver for pseudoknot-free RNA sequence design, we can decrease the probability with which undesired pseudoknots accidentally form in the designed RNA sequence. That is, inverse folding of pseudoknotted RNAs is useful not only to design pseudoknotted RNA sequences but also to design pseudoknot-free ones.

3. Results

3.1. Benchmark Results

We evaluated the pseudoknot design performance of MODENA with the Pseudobase dataset, where IPknot and Hotknots were used as a direct problem solver. We set both a population size and maximum iteration number to 50 in our GA. In this performance evaluation, we obtained successfully designed RNA sequences for 207 and 198 pseudoknotted target structures by MODENA + IPknot and MODENA + HotKnot, respectively, in the 266 target structures of the Pseudobase dataset, where MODENA + IPknot and MODENA + HotKnots denote the sequence design utilizing IPknot and HotKnots as a direct problem solver, respectively (“successfully designed RNAs” mean the RNA sequences which fold into the input target structure). Inv obtained successfully designed RNAs for 181 pseudoknotted target structures with the same dataset. Figure 2 shows the sequence length dependence of the pseudoknot design performances for MODENA and Inv, where the performance is indicated by “the rate of successfully designed RNAs” = 100 × (number of the target structures for which a successfully designed RNA is obtained)/(total number of the target structures). The total number of the target structures included in each length bin is given in Figure 3. As can be seen from Figure 2, MODENA + IPknot outperforms Inv for all bins of sequence lengths. MODENA + IPknot showed the best performance for the length range between 21 and 60 nucleotides. For the range between 61 and 80 nucleotides, MODENA + IPknot and MODENA + HotKnots have comparable performances. For longer target structures with lengths from 81 to 140 nucleotides, MODENA + HotKnots gives the best results among MODENA + IPknot, MODENA + HotKnots, and Inv.

FIGURE 2

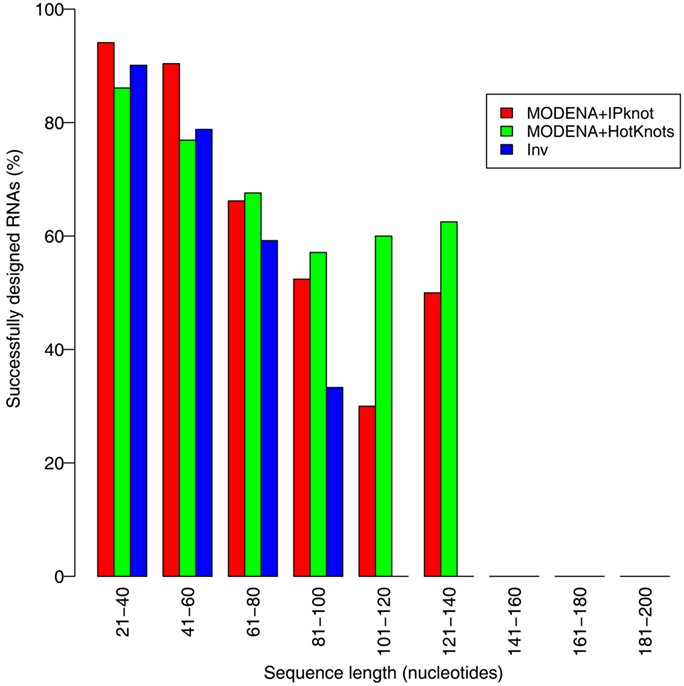
Figure 2. Sequence length dependence of the pseudoknot design performances for MODENA and Inv. “MODENA + IPknot” and “MODENA + HotKnots” denote the sequence designs using IPknot and HotKnots as a direct problem solver, respectively. In each bin, results for MODENA + IPknot, MODENA + HotKnots and Inv are shown from left to right.

FIGURE 3

Figure 3. Distribution of the target structures in the Pseudobase dataset.

For the target structures longer than 85 nucleotides, Inv completely failed to design pseudoknots. MODENA also could not obtain successfully designed pseudoknotted RNAs when the target structures have a length longer than 137 nucleotides. It is noted that the number of target structures longer than 81 nucleotides is much smaller than that of the other shorter target structures (Figure 3); a benchmark with more target structures with long lengths may give a different result. Details of the results for the Pseudobase dataset are tabulated in Table S1 in Supplementary Material, which is downloadable from the MODENA website.

To examine whether a larger calculation, where both a population size and an iteration number have a value of 100, improves the pseudoknot design performance or not, we performed the inverse folding of the 59 target structures which were failed to design when we used a value of 50. By using the larger parameter values, we successfully designed 15 pseudoknots (Pseudobase PKB-number: PKB00050, PKB00129, PKB00138, PKB00148, PKB00170, PKB00171, PKB00178, PKB00179, PKB00211, PKB00217, PKB00219, PKB00228, PKB00267, PKB00329, PKB00333) of the 59 target structures. These results indicate that a larger calculation can improve the design performance; it is noted that the computational time for the larger calculation becomes longer, i.e., there is a tradeoff between computational time and design performance.

The logarithm of the computational times needed for the Pseudobase benchmark of MODENA + IPknot, MODENA + HotKnots, and Inv is plotted in Figure 4. The computational times were measured on a Core i7 PC (3.33 GHz; 24 GB memory; CentOS 5.6[x86_64]). Since we performed fifty independent runs with Inv for each target structure, the mean computational times for the target structures are used as the computational time of Inv in Figure 4 (and in Table S1 in Supplementary Material). Figure 4 clearly reveals the difference between two direct problem solvers we used for MODENA in the present study; i.e., IPknot is much faster than HotKnots. For the target structures shorter than 50 nucleotides, Inv is faster than MODENA. However, in longer target structures, we found that Inv often becomes much slower than MODENA + IPknot. In addition, Inv completely failed to design the pseudoknotted RNAs longer than 85 nucleotides. Inv quickly terminates its calculation when the inverse folding of the input target structure is impossible (Inv analyzes the input target structure before performing a stochastic search). The results of such terminated calculations are not plotted in Figure 4; the computational times of the terminated Inv runs can be seen in Table S1 in Supplementary Material.

FIGURE 4

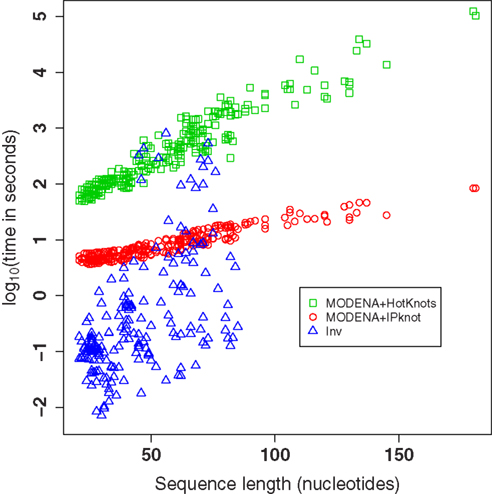
Figure 4. The logarithm of the computational times needed for the Pseudobase benchmark of MODENA + IPknot, MODENA + HotKnots, and Inv. Each symbol corresponds to one target structure. Each computational time for Inv is the mean over fifty independent runs. The results of failed Inv runs are not included in this figure.

To compare the convergence properties of different direct problem solvers, we averaged the converged GA iteration numbers for all target structures in the Pseudobase dataset (where we used the results for a population size and a maximum iteration number of 50). As convergence criterions, similar to Taneda (2011), the GA iteration stops when (i) the maximum iteration number is reached or (2) the number of weak Pareto optimal solutions is not changed during continuous 30 iterations. As a result, we found that MODENA needs 41.8 and 36.9 GA iterations when IPknot and HotKnots, respectively, are used as a direct problem solver.

The inverse folding results for the Rfam dataset, which is composed of pseudoknot-free target structures, are summarized in Table 1, where the results obtained by MODENA + IPknot alone are shown. This is because the target structure lengths of the Rfam dataset are too long for MODENA + HotKnots in terms of computational time, and Inv is limited to the application to the short target structures. In this benchmark for the pseudoknot-free target structures, MODENA successfully designed RNA sequences for 22 target structures. This result is comparable to our previous result (Taneda, 2011) obtained by using the direct problem solvers which cannot predict pseudoknots. The present result indicates that pseudoknot prediction methods are useful even for designing pseudoknot-free RNA sequences, by which we can reduce the possibility of an accidental pseudoknot formation when designing pseudoknot-free RNAs.

TABLE 1

Table 1. The benchmark results for the pseudoknot-free Rfam dataset.

3.2. Design with sequence constraints

To demonstrate the sequence constraint function in MODENA, we performed an RNA inverse folding with the secondary structure and sequence of a known hepatitis delta virus (HDV) self-cleaving ribozyme, which has been used as a prototype for generating artificial ribozymes (Schultes and Bartel, 2000). The pseudoknotted secondary structure and the sequence motifs (key nucleotides) of the HDV ribozyme design were taken from Figure 1 in the paper by Schultes and Bartel (2000). The key nucleotides, which are important for the activity of the ribozyme, were used as constraint sequences. By using MODENA + IPknot with a population size of 100 and an iteration number of 100, we successfully designed 8 RNA sequences folding into the structure of the prototype HDV ribozyme with the constraint sequence motifs. The designed 8 HDV ribozyme sequences are shown in Figure 5, in which the target structure, constraint sequences, and nucleotide positions are also indicated. As can clearly be seen from the figure, the designed 8 sequences share all constraint sequences. Moreover, interestingly, the designed 8 sequences are highly “conserved”. To illustrate the sequence conservation among the designed sequences, we drew the sequence logo of the 8 sequences by using WebLogo (Crooks et al., 2004; Figure 6). The low sequence conservation in the region between position 51 and 74 is mainly due to the seq3, since the seq3 has a very different subsequence from the other sequences in the region. This seq3 has a very similar sequence except for the region between position 51 and 74, hence we can guess that the seq3 shares an ancestral sequence with the other seven successfully designed sequences in our GA. In addition, the region between position 51 and 74 corresponds to a hairpin structure [the P4 stem + L4 loop (Schultes and Bartel, 2000)] of the HDV ribozyme. These results imply that the sequence difference between seq3 and the other seven successfully designed sequences in the region between position 51 and 74 was generated by structural n-point crossover in our GA.

FIGURE 5

Figure 5. Eight HDV ribozyme sequences designed by MODENA. The top eight rows are designed RNA sequences. Trgt and cnst rows correspond to the target pseudoknotted secondary structure in bracket notation and constraint sequences, respectively. A set of pos1 and pos2 indicates a nucleotide position.

FIGURE 6

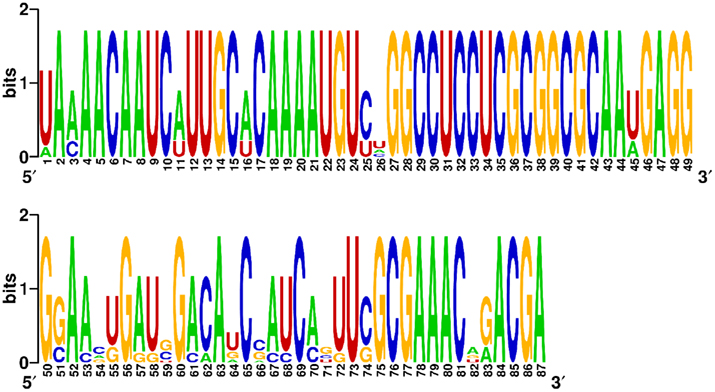
Figure 6. The sequence logo for the eight designed HDV ribozyme sequences. The sequence logo was generated by WebLogo (Crooks et al., 2004).

This constrained design of the HDV ribozyme is a relatively hard calculation; we could not design the HDV ribozyme with the constraints when we set a population size and an iteration number to a smaller value, 50; MODENA + HotKnots failed to design the pseudoknotted ribozyme even when we set both a population size and an iteration number to 100.

Discussion

We have proposed a multi-objective genetic algorithm for pseudoknotted RNA sequence design, which is a modified version of our previous pseudoknot-free RNA design algorithm. Important differences between the current version which can design pseudoknots and the previous pseudoknot-free version are as follows. (i) We utilize a new structural n-point crossover operator in the current version, by which we can generate child solutions without breaking complementary relationships in parent solutions even when pseudoknots are included in the target structure. (ii) We allow MODENA to use pseudoknotted RNA structure prediction methods as direct problem solver. As a result, the current version of MODENA can directly evaluate whether designed sequences have a desired pseudoknot structure or not. This feature is indispensable for the inverse engineering of pseudoknotted RNAs. (iii) The third important point introduced in the current version of MODENA is sequence constraint. Since the current version of MODENA can work as both pseudoknotted and pseudoknot-free RNA sequence designer, the sequence constraint function of MODENA can be utilized to design not only pseudoknotted RNAs but also pseudoknot-free ones.

The new version of MODENA, in which the new features for pseudoknot design are implemented, was tested with two benchmark datasets: the Pseudobase dataset, which is a non-redundant dataset and is composed of 266 target structures taken from the Pseudobase, and the Rfam dataset which does not contain pseudoknots. In both datasets, MODENA showed high sequence design performances. For the Pseudobase dataset, another pseudoknot design algorithm, Inv, was also benchmarked and it was found that MODENA can successfully design pseudoknotted RNAs for more target structures compared to Inv.

The sequence constraint function of MODENA was tested through the inverse folding of a HDV ribozyme. In this test, we successfully obtained 8 RNA sequences, which fold into the target pseudoknotted structure of the HDV ribozyme. All of the designed 8 RNA sequences have the key nucleotides important for the activity of the ribozyme, which were specified as sequence constraints when running MODENA.

The present results clearly indicate that multi-objective genetic algorithm is a promising approach for the inverse folding of pseudoknotted RNA. One important issue concerning the computational inverse folding is “Do the designed sequences truly fold into the target structure in vivo and/or in vitro?”, in other words, the reliability of the design. Although theorists have no answer to this question, it is noteworthy that the inverse folding methods can be improved accompanying improvement of structure prediction methods. In inverse folding, the prediction accuracy of direct problem solver (structure prediction method) determines the design reliability. As an extreme case, if we can use a perfect structure prediction method as a direct problem solver (where “perfect” means that the RNA sequence for which a structure is predicted strictly folds into the predicted structure in vivo and/or in vitro), the designed RNA sequence will perfectly fold into the target structure. Recent drastic progress in RNA structure prediction methods has enabled us to perform very accurate and efficient RNA structure prediction. Improvement of structure prediction methods will continue not only in a secondary structure level but also in a tertiary structure level (Das and Baker, 2007; Parisien and Major, 2008), and the design reliability of RNA inverse folding methods will also continue to be improved.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was partially supported by KAKENHI (22700304) and a “Grant for Hirosaki University Institutional Research”.

References

Andronescu, M., Fejes, A. P., Hutter, F., Hoos, H. H., and Condon, A. (2004). A new algorithm for RNA secondary structure design. J. Mol. Biol. 336, 607–624.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Batenburg, F. H. V., Gultyaev, A. P., Pleij, C. W., Ng, J., and Oliehoek, J. (2000). PseudoBase: a database with RNA pseudoknots. Nucleic Acids Res. 28, 201–204.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Breaker, R. R. (2004). Natural and engineered nucleic acids as tools to explore biology. Nature 432, 838–845.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Busch, A., and Backofen, R. (2006). INFO-RNA–a fast approach to inverse RNA folding. Bioinformatics 22, 1823–1831.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Condon, A., Davy, B., Rastegari, B., Zhao, S., and Tarrant, F. (2004). Classifying RNA pseudoknotted structures. Theor. Comp. Sci. 320, 35–50.

CrossRef Full Text

Crooks, G. E., Hon, G., Chandonia, J. M., and Brenner, S. E. (2004). WebLogo: a sequence logo generator. Genome Res. 14, 1188–1190.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Das, R., and Baker, D. (2007). Automated de novo prediction of native-like RNA tertiary structures. Proc. Natl. Acad. Sci. U.S.A. 104, 14664–14669.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deb, K. (2001). Multi-Objective Optimization using Evolutionary Algorithms. Chichester: John Wiley & Sons.

Gao, J. Z., Li, L. Y., and Reidys, C. M. (2010). Inverse folding of RNA pseudoknot structures. Algorithms Mol. Biol. 5, 27.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Goldberg, D. E. (1987). Genetic Algorithms in Search, Optimization and Machine Learning. New York: Addison-Wesley.

Hamada, M., Kiryu, H., Sato, K., Mituyama, T., and Asai, K. (2009). Prediction of RNA secondary structure using generalized centroid estimators. Bioinformatics 25, 465–473.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hofacker, I. (2003). Vienna RNA secondary structure server. Nucleic Acids Res. 31, 3429–3431.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hofacker, I., Fontana, W., Stadler, P., Bonhoeffer, L., Tacker, M., and Schuster, P. (1994). Fast folding and comparison of RNA secondary structures. Monatsh. Chem. 125, 167–188.

CrossRef Full Text

Hoos, H. H., and Stützle, T. (2004). Stochastic Local Search: Foundations and Applications. San Francisco: Elsevier/Morgan Kaufmann.

Jaeger, L., Westhof, E., and Leontis, N. B. (2001). TectoRNA: modular assembly units for the construction of RNA nano-objects. Nucleic Acids Res. 29, 455–463.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Markham, N. R., and Zuker, M. (2008). UNAFold: software for nucleic acid folding and hybridization. Methods Mol. Biol. 453, 3–31.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Parisien, M., and Major, F. (2008). The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data. Nature 452, 51–55.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ren, J., Rastegari, B., Condon, A., and Hoos, H. H. (2005). HotKnots: heuristic prediction of RNA secondary structures including pseudoknots. RNA 11, 1494–1504.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sato, K., Kato, Y., Hamada, M., Akutsu, T., and Asai, K. (2011). IPknot: fast and accurate prediction of RNA secondary structures with pseudoknots using integer programming. Bioinformatics 27, 85–93.

CrossRef Full Text

Schultes, E. A., and Bartel, D. P. (2000). One sequence, two ribozymes: implications for the emergence of new ribozyme folds. Science 289, 448–452.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schwab, R., Ossowski, S., Riester, M., Warthmann, N., and Weigel, D. (2006). Highly specific gene silencing by artificial microRNAs in Arabidopsis. Plant Cell 18, 1121–1133.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Staple, D. W., and Butcher, S. E. (2005). Pseudoknots: RNA structures with diverse functions. PLoS Biol. 3, e213. doi:10.1371/journal.pbio.0030213

CrossRef Full Text

Taneda, A. (2011). MODENA: a multi-objective RNA inverse folding. Adv. Appl. Bioinform. Chem. 4, 1–12.

Pubmed Abstract | Pubmed Full Text

Zadeh, J. N., Steenberg, C. D., Bois, J. S., Wolfe, B. R., Pierce, M. B., Khan, A. R., Dirks, R. M., and Pierce, N. A. (2011). NUPACK: analysis and design of nucleic acid systems. J. Comput. Chem. 32, 170–173.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text