- 1Department of Biostatistics, School of Medicine, Virginia Commonwealth University, Richmond, VA, USA
- 2College of Information Science and Engineering, Shandong University of Science and Technology, Qingdao, China
- 3Virginia Institute for Psychiatric and Behavioral Genetics, School of Medicine, Virginia Commonwealth University, Richmond, VA, USA
- 4Department of Biostatistics, University of Alabama, Birmingham, AL, USA
Meta-analysis of genome-wide association studies (GWAS) has become a useful tool to identify genetic variants that are associated with complex human diseases. To control spurious associations between genetic variants and disease that are caused by population stratification, double genomic control (GC) correction for population stratification in meta-analysis for GWAS has been implemented in the software METAL and GWAMA and is widely used by investigators. In this research, we conducted extensive simulation studies to evaluate the double GC correction method in meta-analysis and compared the performance of the double GC correction with that of a principal components analysis (PCA) correction method in meta-analysis. Results show that when the data consist of population stratification, using double GC correction method can have inflated type I error rates at a marker with significant allele frequency differentiation in the subpopulations (such as caused by recent strong selection). On the other hand, the PCA correction method can control type I error rates well and has much higher power in meta-analysis compared to the double GC correction method, even though in the situation that the casual marker does not have significant allele frequency difference between the subpopulations. We applied the double GC correction and PCA correction to meta-analysis of GWAS for two real datasets from the Atherosclerosis Risk in Communities (ARIC) project and the Multi-Ethnic Study of Atherosclerosis (MESA) project. The results also suggest that PCA correction is more effective than the double GC correction in meta-analysis.
Introduction
Genome-wide association studies (GWAS) are an important approach for identifying genetic variants associated with complex human diseases. Recently, meta-analysis of GWAS has been used to obtain collective evidence from the multiple GWAS studies (Lohmueller et al., 2003; Houlston et al., 2008; Zeggini et al., 2008; Lindgren et al., 2009; Lin and Zeng, 2010; Stahl et al., 2010; Willer et al., 2010; Nalls et al., 2011; Qayyum et al., 2012). Unfortunately population stratification in the studied samples can lead to spurious associations in disease studies (Cardon and Palmer, 2003; Freedman et al., 2004; Marchini et al., 2004; Price et al., 2006). To control the spurious associations caused by population stratification in meta-analysis of GWAS, genomic control (GC) correction within each study (which is referred to as single GC correction) has been used (Devlin and Roeder, 1999; Devlin et al., 2001; Reich and Goldstein, 2001; Devlin et al., 2004; Lindgren et al., 2009). However, the GC correction method cannot effectively control false positive rates and may lead to a loss in power (Price et al., 2006; Mägi and Morris, 2010; Willer et al., 2010). Therefore, a double GC correction method has been proposed and implemented in the widely used meta-analysis software METAL and GWAMA (Mägi and Morris, 2010; Willer et al., 2010). The double GC correction method adjusts the set of test statistics across all markers within each study by a GC inflation factor, calculates a combined statistic across studies at each marker, and then adjusts all combined statistics across the genome by the corresponding GC inflation factor. The double GC correction method has been used by many investigators in their meta-analyses (e.g., Lindgren et al., 2009; Mägi and Morris, 2010; Willer et al., 2010; Lettre et al., 2011). To adjust for stratification in meta-analysis of GWAS, another popular approach is the principal component analysis (PCA) correction method that adjusts for stratification by top principal components (PCs) of genotype data within each study (Price et al., 2006; Wang et al., 2009; Qayyum et al., 2012).
In this research, we compared the single GC correction, the double GC correction and PCA correction in meta-analysis by simulation studies and applied these methods to a meta-analysis of two real data sets from the Atherosclerosis Risk in Communities (ARIC) project and the Multi-Ethnic Study of Atherosclerosis (MESA) project. Results from simulations and real data analysis suggest that when population stratification exists, using double GC correction can have inflated false positive error rates at markers with significant allele frequency differentiation in the subpopulations (such as caused by recent strong selection), and can have lower power than using the PCA method for stratification correction in meta-analysis.
Materials and Methods
We consider K case–control studies with nk individuals in the kth study (k = 1,2,…,K) and N single nucleotide polymorphisms (SNPs) in each study. In the kth study, let Yik denote the disease status (1 = disease, 0 = no disease) of the ith individual, let gijk denote the additive genotype coding value (the count of reference alleles) at the jth SNP of ith individual (j = 1,2,…,N,i = 1,2,…,nk), and let Xik = (x1k,x2k,…,xsk)T denote a vector of s covariates.
In this research, we focus on fixed-effect meta-analysis, i.e., we assume that the allelic effects at a test marker are the same across all studies. In the kth study, we use the following logistic regression model
where α0k is the study-specific intercept, αk is the coefficient vector corresponding to covariate vector Xik, and βkj denote the genetic effect (log odds ratio) of the reference allele at the jth SNP in the kth study. We can estimate βkj and var(βkj) at the jth SNP based on the logistic model (Eq. 1). Thus, the combined allelic effect Bj at the jth SNP across K studies, can be calculated as
where wkj is a weight for the genetic effect and is the inverse of the variance of the estimated allelic effect in the kth study. The variance of Bj is estimated by and its estimated standard error SEj is the square root of variance Vj, i.e., . Therefore, the combined statistic has an approximate χ2 distribution with one degree of freedom (Mägi and Morris, 2010; Willer et al., 2010).
GC Correction in Meta-Analysis
To adjust for population stratification, in the kth study, we can calculate the statistic at the jth SNP (j = 1,2,,…,N), and then calculate a GC inflation factor λk that is the median of these statistics divided by its expectation under the null hypothesis of no association, which is 0.455 (Devlin and Roeder, 1999). To adjust for stratification within each study in the meta-analysis, we can calculate a corrected weight at the jth SNP in the kth study as (see also Section “Materials and Methods” for the calculation of wkj) and calculate the combined allelic effect Bj by using to replace wkj in Eq. 2 correspondingly, the variance of Bj can be calculated as . The combined statistic can be calculated for meta-analysis (j = 1,2,…,N).
Double GC Correction in Meta-Analysis
After GC correction in each individual study as described above, the combined statistics may still have over-dispersion which is caused by population stratification. Therefore, investigators proposed to further adjust the combined statistics by the corresponding GC inflation factor λ, which is the median of the combined statistics divided by 0.455 (Mägi and Morris, 2010; Willer et al., 2010). This process corrects for stratification twice and is called double GC correction.
PCA Correction in Meta-Analysis
Price et al. (2006) proposed to correct for stratification by PCA in GWAS analysis. For meta-analysis of GWAS with K (>1) case–control studies of population stratification, PCA has been used to correct for stratification within each of the K studies (Qayyum et al., 2012): for each of the K studies, we can calculate the PCs (Jackson, 2003) of genome-wide genotype values for each individual and use the top 10 PCs as covariates, as suggested in the literature (Price et al., 2006; Liu et al., 2011; Qayyum et al., 2012), to correct for population stratification by incorporating these covariates (top 10 PCs) into the logistic regression model (Eq. 1). Meta-analysis for the K studies can be conducted based on this modified model.
Simulation Studies
Data Simulation
To evaluate the performance of the single GC correction, double GC correction, and PCA correction in meta-analysis of data with population stratification, we simulated datasets on K case–control studies in a similar way to those described in Pritchard and Donnelly (2001) and Price et al. (2006). Individuals in each of the K case–control studies were sampled from two populations. For each dataset we simulated 100,000 independent random SNPs. To generate each of these SNPs, we used the Balding–Nichols model with FST = 0.01 (Balding and Nichols, 1995) to generate allele frequencies fs for populations s(s = 1, 2) which was drawn from a beta distribution with parameters fs(1 - Fst)/Fst and (1 - fs) (1 - Fst)/Fst. FST = 0.01 usually leads to allele frequency differences under 0.10 for typical common SNPs (Price et al., 2006). At each of the random SNPs, we assumed Hardy–Weinberg equilibrium in each population, and individuals from populations were assigned genotypic values of 0, 1, or 2 with probabilities , respectively. For the PCA correction, we used these 100,000 random SNPs to calculate the first 10 PCs, which were used as covariates in the analysis.
Meta-Analysis with Two Case–Control Studies (K = 2)
We first simulated two case–control studies. In each study, 60% of the cases and 40% of the controls were sampled from population 1 and the remaining cases and controls from population 2.
Meta-Analysis with K = 5 Case–Control Studies
To evaluate the performance of the three correction methods in meta-analysis with K (>2) studies, we simulated datasets on five case–control studies. Each of the five studies had 1000 cases and 1000 controls. For each case–control study, a proportion of cases and a proportion of controls were sampled from population 1, and the remaining cases and controls were sampled from the population 2: in the first study, 55% of the cases and 45% of the controls were sampled from population 1; in the second study, 70% of the cases and 30% of the controls; in the third study, 60% of the cases and 40% of the controls; in the fourth study, 70% of the cases and 30% of controls; in the fifth study, 60% of the cases and 40% of the controls.
Type I Error Rate Evaluation
To verify the effectiveness of the three stratification correction methods in meta-analysis, we simulated replicated data sets. Each data set contained 100,000 independent random SNPs (as described above) and an additional test SNP (which is not associated with the disease). We simulated the test SNP by the following four scenarios: in the first scenario, the test SNP was simulated in each individual by the same way as that for the random SNPs described above using the Balding–Nichols model with FST = 0.01; for the second, third, and fourth scenarios, we assumed that the test SNP had significant different allele frequencies in populations 1 and 2, which could be caused by recent strong selection (see also Price et al., 2006). In scenario 2, the frequencies in populations 1 and 2 were 0.4 and 0.2, respectively; in scenario 3, frequencies were 0.6 and 0.2; in scenario 4, frequencies were 0.8 and 0.2. For each scenario, we computed type I error rates of meta-analysis using the three correction methods (PCA, single GC correction, and double GC correction) separately, under a set of combination of parameters (numbers of cases and controls in the two studies). For each combination of these parameters, we simulated 108 replicated data sets to estimate the type I error rates at significance levels of 10–5 and 10–6. We did not use the significance level of 10–7 because estimating accurate type I error rates at this level requires at least 109 replicated data sets. This is computationally intensive.
Type I Error Rates for Meta-Analysis with Two Case–Control Studies (K = 2)
Detailed results are listed in Table 1, which shows that using PCA correction can control the type I error rates well. However, using the single GC correction or double GC correction, the type I error rates could be controlled only in the first scenario in which the test SNP was randomly generated with no association with disease. For other three scenarios in which populations 1 and 2 had significant different allele frequencies at the test SNPs, both single GC correction and double GC correction had inflated type I error rates; the type I error rates could increase to almost 1 when the allele frequency differences between populations 1 and 2 increased. For example, when both studies had 1000 cases and 1000 controls, the populations 1 and 2 had allele frequencies of 0.6 and 0.2 at the test SNP, respectively, and the nominal significance level was 10–6, the type I error rates of meta-analysis using the PCA correction, single GC correction, and double GC correction were 7.70 × 10–7, 0.585, and 0.591, respectively.
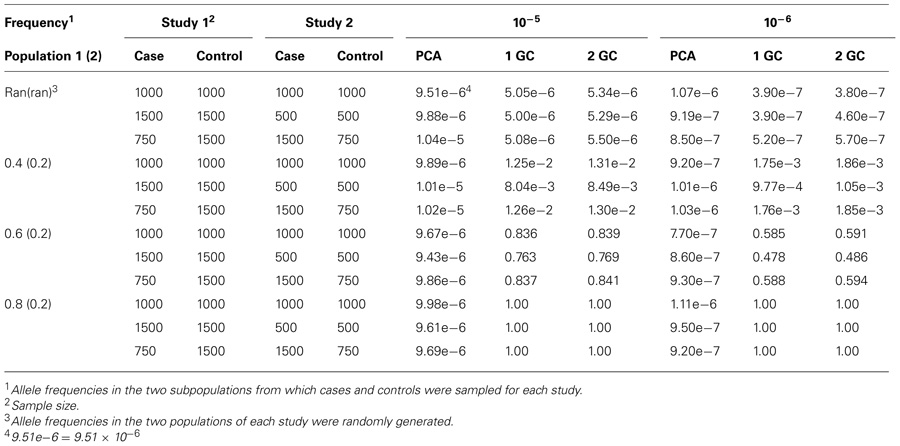
TABLE 1. Type I error rates of meta-analysis with two case–control studies for different allele frequencies in the two subpopulations.
Type I Error Rates for Meta-Analysis with Five Case–Control Studies (K = 5)
We estimated the type I error rates for meta-analysis with K = 5 case–control studies. The detailed results are shown in Table 2. We can see the type I error rates had similar pattern to that for meta-analysis with two case–control studies described above.
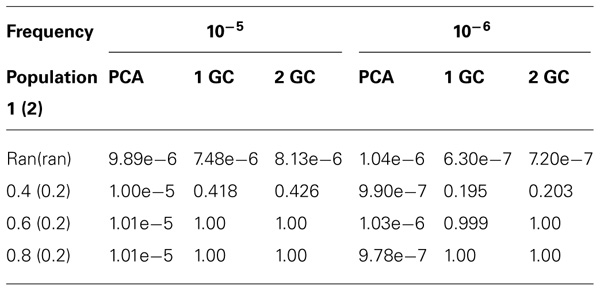
TABLE 2. Type I error rates of meta-analysis with five studies for different allele frequencies in the two subpopulations.
Power Evaluation
To evaluate power of meta-analysis using the three stratification correction methods, we simulated 10,000 replicated datasets. Each data set contained 100,000 independent random SNPs (described above) and a causal SNP. We simulated the causal SNP by a similar method of Price et al. (2006). We used the Balding–Nichols model with FST = 0.01 again to generate allele frequencies for populations 1 and 2. We generated genotypes at the causal SNP by using a multiplicative disease risk model with a relative risk (R) for the causal allele as follows: genotypic values of control individuals were generated as those for random SNPs described above. Case individuals were assigned genotypic values 0,1, or 2 with relative probabilities (1 + fs)2/S, 2Rfs(1 - fs)/S, or R2 fs2 /S, respectively, where S = (1 - fs)2 + 2Rfs(1 - fs) + R2 fs2 . The power of meta-analysis was estimated based on 10,000 replicated datasets at significance levels of 10–5, 10–6, and 10–7, respectively.
Power Evaluation for Meta-Analysis with Two Case–Control Studies (K = 2)
We considered various numbers of cases and controls and a set of relative risk values (R = 1.2, 1.3, 1.4, 1.5) at the causal SNP in the two studies. The results are summarized in Table 3. The power of meta-analysis using PCA correction is much higher than both that using single GC correction and that using double GC correction. For example, when Rs in the two studies were 1.3 and 1.4 and both studies had 1000 cases and 1000 controls, the power of meta-analyses using PCA correction, single GC correction, and double GC correction were 0.6386, 0.1709, and 0.18, respectively, at the significance level of 10–7.
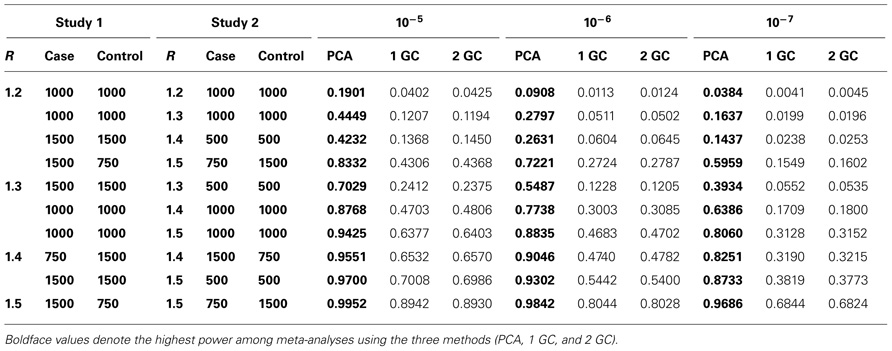
TABLE 3. Power of meta-analysis of GWAS for two studies using PCA correction, single GC correction (1 GC), and double GC correction (2 GC) at significance levels of 10−5, 10−6, and 10−7.
Power Evaluation Meta-Analysis with Five Case–Control Studies (K = 5)
For the meta-analysis with five case–control studies, we only considered eight combined relative risk values (see Table 4). Each of the five studies has 1000 cases and 1000 controls. The results from five case–control studies also demonstrated the power of meta-analysis using PCA correction is the highest among the meta-analysis using the three correction methods.
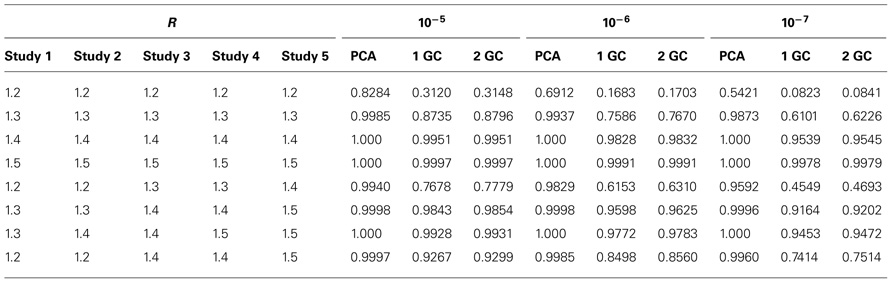
TABLE 4. Power of meta-analysis of GWAS for five studies using PCA correction, single GC correction (1 GC), and double GC correction (2 GC) at significance levels of 10−5, 10−6, and 10−7.
Analyses of Two Real Data Sets
We performed meta-analysis of GWAS for two real data sets on European Americans drew from the ARIC and the MESA projects. We chose hypertension as phenotype and gender, age, body mass index, waist circumference, and smoking status as covariates in the logistic regression model (Eq. 1). There were 9,526 subjects with 839,173 SNPs in ARIC project and 2,397 subjects with 577,627 SNPs in MESA project. We first extracted 414,363 SNPs with minor allele frequency ≥0.05 and shared by the two data sets, and focused our analyses on these SNPs. Among these 414,363 SNPs, 3,295 SNPs were not concordant in terms of positive or negative strand in the two data sets. So we flipped the strands for these SNPs in MESA. In our research, an individual was defined with hypertension if systolic blood pressure ≥140 mm Hg, diastolic blood pressure ≥90 mm Hg, a self-reported history of hypertension or current use of antihypertensive medications (Schroeder et al., 2003; Kramer et al., 2004; Mujahid et al., 2011). We removed the subjects with missing phenotypes and multiple copies of the same subject from ARIC and MESA datasets and excluded 212 subjects as outliers from ARIC and 19 subjects as outliers from MESA if at least one of the first 10 PCs of the subject is out of the interval [μ − 6σ,μ + 6σ], where μ and σ are the mean and standard deviation of a PC, respectively. Finally, there were 2,780 cases and 5,881 controls left in ARIC with GC inflation factor λ = 1.04967 and 920 cases and 1458 controls left in MESA with λ = 1.07127. As an ancillary illustration of population stratification in the two data sets, we plotted the first two PCs of all subjects in each data set (as shown in Figure 1). The figure indicates that there is stratification in these two data sets. In the data analysis, genotype coding value at each SNP was defined as the count of the reference allele.
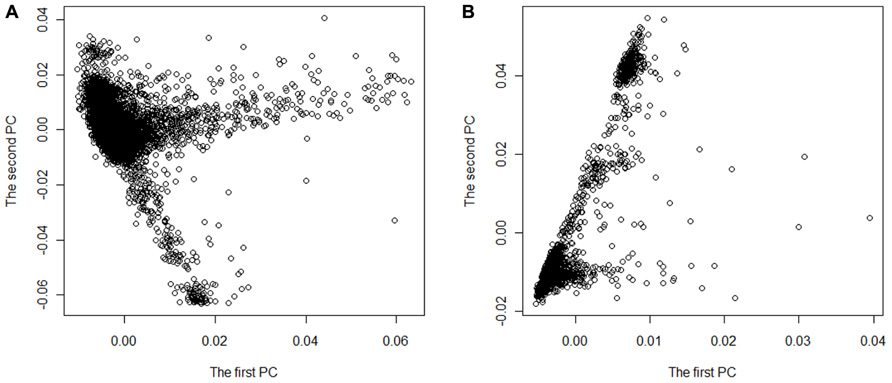
FIGURE 1. The stratification structure plotted by the first PC versus the second PC for the two data sets ARIC (A) and MESA (B).
In meta-analyses of GWAS for the two real data sets, we used PCA correction, single GC correction, and double GC correction for the stratification, separately. The top eight SNPs with p-values <10–5 in at least one of the three meta-analysis methods are displayed in Table 5. At each of the eight SNPs, meta-analysis with PCA correction had much smaller p-value than that with double GC. This may indicate that meta-analysis with double GC correction for stratification is not as effective as that with PCA.
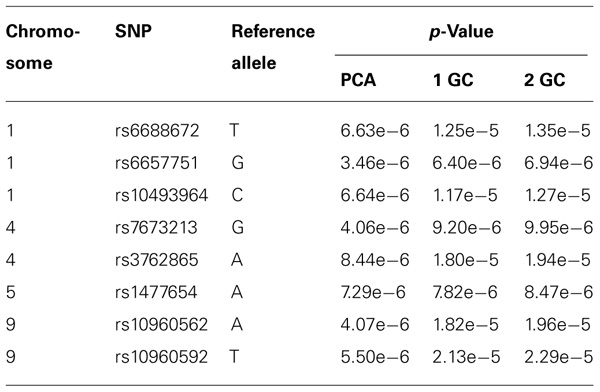
TABLE 5. Top SNPs with p-values <10−5 in a meta-analysis with PCA correction, single GC correction (1 GC), or double GC correction (2 GC).
Discussion
In this research, we evaluated the performance of three methods for correcting for population stratification (PCA correction, single GC correction, and double GC correction) in meta-analysis of GWAS by simulation studies. Our results demonstrate that both the single GC correction and the widely used double correction cannot control type I error rates in meta-analysis, when the test SNP has significant allele frequency differentiation in the subpopulations in the case–control data. On the other hand, the PCA correction can control type I error rates well. In addition, when population stratification exists in the case–control data, using double GC method usually results in much lower power than using the PCA correction in meta-analysis, even though the casual SNP does not have significant allele frequency differentiation in the subpopulations. We note that Price et al. (2006) reported similar results in single GWAS analysis. Therefore, the double GC method is not effective to correct for stratification in meta-analysis.
Although the PCA correction method works well for correction for stratification in meta-analysis, it may need more than 5,000 SNPs to calculate PCs for each individual (Price et al., 2006). This may be challenging in replication studies with meta-analysis in which usually only a small set of significant SNPs identified from previous meta-analysis are collected and tested. If population stratification exists in the data for replication meta-analysis, we would suggest collecting additional 5,000 or 10,000 independent SNPs to calculated PCs for each individual, and use these PCs to correct for population stratification when testing the small set of promising SNPs identified from previous meta-analysis. As can be seen from the results described above, using PCA correction controls type I error rates well, and more importantly can have increased power in meta-analysis compared to the widely used double GC correction.
When evaluating the three methods for correcting for stratification in meta-analysis for case–control studies, we only considered the fixed-effect model and the additive genetic model for case–control designs with binary traits. We expect that the conclusion will also hold for quantitative traits. We plan to consider random-effects model in meta-analysis and the dominant, recessive genetic models for evaluating the three methods for population stratification correction used in meta-analysis in our future study.
In our simulation studies, we did consider cryptic relatedness among individuals. Since GC method can be useful for controlling spurious association caused by relatedness in the data, investigators proposed a “PCA + double GC” method to control the spurious association findings in meta-analysis as follows: 1 to perform PCA adjustment for population stratification in the individual study association analysis, followed by a GC correction on the genome-wide results, 2 to perform a GC correction on the combined statistics over all studies by the corresponding GC inflation factor λ (see Materials and Methods). Although this “PCA + double GC” method may control type I error rate well, it may not maximize power to detect true associations in meta-analysis (Price et al., 2010). To adjust for the cryptic relatedness and population stratification in meta-analysis, a better choice may be using the mixed model approaches, such as the EMMAX and TASSEL software (Kang et al., 2010; Zhang et al., 2010).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by grants GM073766 and GM081488 from the National Institute of General Medical Science and U01HL101064 from the National Heart, Lung, and Blood Institute (NHLBI). Shudong Wang was partially supported by grant 61170183 from National Natural Science Foundation of China, BS2011SW025 from Excellent Young and Middle-Aged Scientists Fund of Shandong Province of China and SDUST Research Fund of China (2010 KYJQ104). The Atherosclerosis Risk in Communities Study is carried out as a collaborative study supported by NHLBI contracts (HHSN268201100005C, HHSN268201100006C, HHSN268201100007C, HHSN268201100008C, HHSN268201100009C, HHSN268201100010C, HHSN268201100011C, and HHSN268201100012C). The authors thank the staff and participants of the ARIC study for their important contributions. Funding for CARe genotyping was provided by NHLBI contract N01-HC-65226. MESA and the MESA SHARe project are conducted and supported by the NHLBI in collaboration with MESA investigators. Support for MESA is provided by contracts N01-HC-95159 through N01-HC-95169 and RR-024156. Funding for genotyping was provided by NHLBI contracts N02-HL-6-4278 and N01-HC-65226.
References
Balding, D. J., and Nichols, R. A. (1995). A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identify and paternity. Genetica 96, 3–12.
Cardon, L. R., and Palmer, L. J. (2003). Population stratification and spurious allelic association. Lancet 361, 598–604.
Devlin, B., Bacanu, S. A., and Roeder, K. (2004). Genomic control to the extreme. Nat. Genet. 36, 1129–1130.
Devlin, B., and Roeder, K. (1999). Genomic control for association studies. Biometrics 55, 997–1004.
Devlin, B., Roeder, K., and Wasserman, L. (2001). Genomic control, a new approach to genetic-based association studies. Theor. Popul. Biol. 60, 155–166.
Freedman, M. L., Reich, D., Penney, K. L., McDonald, G. J., Mignault, A. A., Patterson, N., et al. (2004). Assessing the impact of population stratification on genetic association studies. Nat. Genet. 36, 388–393.
Houlston, R. S., Webb, E., Broderick, P., Pittman, A. M., Di Bernardo, M. C., Lubbe, S., et al. (2008). Meta-analysis of genome-wide association data identifies four new susceptibility loci for colorectal cancer. Nat. Genet. 40, 1426–1435.
Kang, H. M., Sul, J. H., Service, S. K., Zaitlen, N. A., Kong, S., Freimer, N. B., et al. (2010). Variance component model to account for sample structure in genome-wide association studies. Nat. Genet. 42, 348–354.
Kramer, H., Han, C., Post, W., Goff, D., Diez-Roux, A., Cooper, R., et al. (2004). Racial/Ethnic differences in Hypertension and Hypertension treatment and control in the Multi-Ethnic Study of Atherosclerosis (MESA). Am. J. Hypertens. 17, 963–970.
Lettre, G., Palmer, C. D., Young, T., Ejebe, K. G., Allayee, H., Benjamin, E. J., et al. (2011). Genome-wide association study of coronary heart disease and its risk factors in 8,090 African Americans: the NHLBI CARe Project. PLoS Genet. 7:e1001300. doi: 10.1371/journal.pgen.1001300
Lin, D. Y., and Zeng, D. (2010). Meta-analysis of genome-wide association studies: no efficiency gain in using individual participant data. Genet. Epidemiol. 34, 60–66.
Lindgren, C. M., Heid, I. M., Randall, J. C., Lamina, C., Steinthorsdottir, V., Qi, L., et al. (2009). Genome-wide association scan meta-analysis identifies three loci influencing adiposity and fat distribution. PLoS Genet. 5:e1000508. doi: 10.1371/journal.pgen.1000508
Liu, N., Zhao, H., Patki, A., Limdi, N. A., and Allison, D. B. (2011). Controlling population structure in human genetic association studies with samples of unrelated individuals. Stat. Interface 4, 317–326.
Lohmueller, K. E., Pearce, C. L., Pike, M., Lander, E. S., and Hirschhorn, J. N. (2003). Meta-analysis of genetic association studies supports a contribution of common variants to susceptibility to common disease. Nat. Genet. 33, 177–182.
Mägi, R., and Morris, A. P. (2010). GWAMA: software for genome-wide association meta-analysis. BMC Bioinformatics 11:288 doi: 10.1186/1471-2105-11-288
Marchini, J., Cardon, L. R., Phillips, M. S., and Donnelly, P. (2004). The effects of human population structure on large genetic association studies. Nat. Genet. 36, 512–517.
Mujahid, M. S., Diez Roux, A. V., Cooper, R. C., Shea, S., and Williams, D. R. (2011). Neighborhood stressors and race/ethnic differences in hypertension prevalence (the Multi-Ethnic Study of Atherosclerosis). Am. J. Hypertens. 24, 187–193.
Nalls, M. A., Plagnol, V., Hernandez, D. G., Sharma, M., Sheerin, U. M., Saad, M., et al. (2011). Imputation of sequence variants for identification of genetic risks for Parkinson’s disease: a meta-analysis of genome-wide association studies. Lancet 377, 641–649.
Price, A. L., Patterson, N. J., Plenge, R. M., Weinblatt, M. E., Shadick, N. A., and Reich, D. (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 38, 904–909.
Price, A. L., Zaitlen, N. A., Reich, D., and Patterson, N. (2010). New approaches to population stratification in genome-wide association studies. Nat. Rev. Genet. 11, 459–63.
Pritchard, J. K., and Donnelly, P. (2001). Case–control studies of association in structured or admixed population. Theor. Popul. Biol. 60, 227–237.
Qayyum, R., Snively, B. M., Ziv, E., Nalls, M. A., Liu, Y. M., Tang, W. H., et al. (2012). A meta-analysis and genome-wide association study of platelet count and mean platelet volume in African Americans. PLoS Genet. 8:e1002491. doi: 10.1371/journal.pgen.1002491
Reich, D. E., and Goldstein, D. B. (2001). Detecting association in a case–control study while correcting for population stratification. Genet. Epidemiol. 20, 4–16.
Schroeder, E. B., Liao, D. P., Chambless, L. E., Prineas, R. J., Evans, G. W., and Heiss, G. (2003). Hypertension, blood pressure, and heart rate variability: the Atherosclerosis Risk in Communities (ARIC) study. Hypertension 42, 1106–1111.
Stahl, E. A., Raychaudhuri, S., Remmers, E. F., Xie, G., Eyre, S., Thomson, B. P., et al. (2010). Genome-wide association study meta-analysis identifies seven new rheumatoid arthritis risk loci. Nat. Genet. 42, 508–514.
Wang, D., Sun, Y., Stang, P., Berlin, J. A., Wilcox, M. A., and Li, Q. Q. (2009). Comparison of methods for correcting population stratification in a genome-wide association study of rheumatoid arthritis: principal-component analysis versus multidimensional scaling. BMC Proc. 3(Suppl. 7):S109. doi: 10.1186/1753-6561-3-S7-S109
Willer, C. J., Li, Y., and Abecasis, G. R. (2010). METAL: fast and efficient meta-analysis of genomewide association scans. Bioinformatics 26, 2190–2191.
Zeggini, E., Scott, L. J., Saxena, R., Voight, B. F., Marchini, J. L., Hu, T., et al. (2008). Meta-analysis of genome-wide association data and large-scale replication identifies additional susceptibility loci for type 2 diabetes. Nat. Genet. 40, 638–645.
Keywords: genome-wide association studies, meta-analysis, double genomic control correction, principal components analysis, population stratification
Citation: Wang S, Chen W, Chen X, Hu F, Archer KJ, Liu N, Sun S and Gao G (2012) Double genomic control is not effective to correct for population stratification in meta-analysis for genome-wide association studies. Front. Gene. 3:300. doi: 10.3389/fgene.2012.00300
Received: 18 September 2012; Paper pending published: 08 October 2012;
Accepted: 04 December 2012; Published online: 24 December 2012.
Edited by:
Jianzhong Ma, University of Texas MD Anderson Cancer Center, USAReviewed by:
Jian Li, Tulane University, USAJianzhong Ma, University of Texas MD Anderson Cancer Center, USA
Jian Wang, University of Texas MD Anderson Cancer Center, USA
Copyright: © 2012 Wang, Chen, Chen, Hu, Archer, Liu, Sun and Gao. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and subject to any copyright notices concerning any third-party graphics etc.
*Correspondence: Guimin Gao, Department of Biostatistics, School of Medicine, Virginia Commonwealth University, One Capitol Square, Room 730, 830 East Main Street, P.O. Box 980032, Richmond, VA 23298-0032, USA. e-mail:Z2dhbzNAdmN1LmVkdQ==
†ShudongWang andWenan Chen have contributed equally to this work.

 Wenan Chen1†
Wenan Chen1†

