- 1Division of Biostatistics, School of Public Health, University of Minnesota, Minneapolis, MN, USA
- 2School of Statistics, University of Minnesota, Minneapolis, MN, USA
In statistical data analysis, penalized regression is considered an attractive approach for its ability of simultaneous variable selection and parameter estimation. Although penalized regression methods have shown many advantages in variable selection and outcome prediction over other approaches for high-dimensional data, there is a relative paucity of the literature on their applications to hypothesis testing, e.g., in genetic association analysis. In this study, we apply several new penalized regression methods with a novel penalty, called Truncated L1-penalty (TLP) (Shen et al., 2012), for either variable selection, or both variable selection and parameter grouping, in a data-adaptive way to test for association between a quantitative trait and a group of rare variants. The performance of the new methods are compared with some existing tests, including some recently proposed global tests and penalized regression-based methods, via simulations and an application to the real sequence data of the Genetic Analysis Workshop 17 (GAW17). Although our proposed penalized methods can improve over some existing penalized methods, often they do not outperform some existing global association tests. Some possible problems with utilizing penalized regression methods in genetic hypothesis testing are discussed. Given the capability of penalized regression in selecting causal variants and its sometimes promising performance, further studies are warranted.
1. Introduction
Genome-wide association studies (GWAS) have uncovered many common variants (CVs) associated with complex diseases, but the proportion of variance explained by the identified CVs is often low (Maher, 2008). With the recent advance of sequencing technologies, analysis of rare variants (RVs) has become a feasible alternative. Recent studies have demonstrated that some RVs are associated with complex disease. For example, Kotowski et al. (2006) found that multiple RVs in gene PCSK9 are associated with plasma levels of low-density lipoprotein cholesterol.
In this study, we propose applying some new penalized regression methods to test for association between a quantitative trait and multiple RVs. Differing from the usual application of penalized regression methods to variable selection or risk prediction for high-dimensional data (Kooperberg et al., 2010; Austin et al., 2013), here we focus on their application to hypothesis testing on a quantitative trait in a relatively low-dimensional setting. In such a setting, one commonly used statistical test is the F-test in linear regression. For example, in simple regression, a trait Y is regressed on each of multiple variants sequentially. However, because of the extremely low minor allele frequency (MAF) of a RV, a test to detect the association between a trait and a single RV might be low powered. Also, this approach may be too conservative due to a stringent control for multiple testing, e.g., by the Bonferroni correction to control the family-wise error rate. In addition, ultimately, complex diseases are expected to be affected by a combination of multiple genetic variants. Thus an analysis in which a group of variants are tested simultaneously for their joint effects on the trait may be more powerful. In multiple regression, to assess any association between a trait and k RVs, all k RVs are added to a regression model. However, as k increases, the statistical power might decrease due to the cost of large degrees of freedom (DF), k. To avoid the large DF and to aggregate information across multiple RVs, one common strategy is to pool or collapse multiple RVs in a region or gene (Li and Leal, 2008; Madsen and Browning, 2009). One such attempt is the Sum test (Pan, 2009), which was developed to utilize joint effects of multiple variants while reducing the DF. With only 1 DF, the Sum test enhances power under some scenarios (Chapman and Whittaker, 2008; Pan, 2009). However, it is noted that the performance of the Sum test depends on the directions of the variants' associations with a trait. Thus, in an extreme case where a half of the variants are positively associated with the trait and the other half are negatively associated with similar effect sizes, the positive and negative effects may cancel out, leading to the poor performance of the Sum test and other burden tests (Han and Pan, 2010; Li et al., 2010). In addition, in the Sum test or other pooling-based burden tests, combining or collapsing all variants into just one group ignores the variants' possibly varying effect sizes, and thus may not work well in those situations. In particular, the Sum test and many burden tests perform poorly if many null (i.e., non-associated) RVs are present (Basu and Pan, 2011). Consequently, the Sum test and other pooled association tests might be low powered.
On the other hand, to deal with high-dimensional genetic and genomic data, penalized regression methods have received much attention, especially those based on the Lasso penalty (Tibshirani, 1996; Kooperberg et al., 2010). Penalized regression has been considered attractive for its potential of simultaneous variable selection and parameter estimation. In particular, several authors have studied the performance of penalized regression in genetic association analysis (Guo and Lin, 2009; Tzeng and Bondell, 2010; Zhou et al., 2011). However, the penalties used therein are typically based on the Lasso, which is known to give biased parameter estimates and possibly inconsistent variable selection. In contrast, one of the very recently developed state-of-the-art penalties, the truncated L1-penalty (TLP) (Shen et al., 2012), overcomes the above shortcomings of Lasso. The TLP approximates the L0-loss and reduces the bias of a parameter estimate from the popular Lasso or L1-penalty. To investigate whether an application of TLP would boost statistical power in genetic association testing, in this study we apply the TLP for variable selection, denoted TLP-S, and for both variable selection and parameter grouping (Zhu et al., 2013), denoted TLP-SG, in a data-adaptive way, to select and group variants to reduce the DF as in the Sum test, while reducing the downward bias of the parameter estimates based on an L1-type penalty. We compare the TLP-S and TLP-SG to the Lasso and graph-fused Lasso (gflasso) (Kim and Xing, 2009). The gflasso also pursues parameter grouping with an L1-penalty. Specifically, the gflasso shrinks two variants' effect sizes toward each other by penalizing their difference |βj − r(j, j′)βj′|, where either r(j, j′) = 1 (called gflassor = 1) or r(j, j′) is the sign of the correlation between the two variants j and j′ (called flassor = cor). There are two main differences between our proposed TLP-SG and gflasso. First, TLP-SG shrinks the absolute values of the two parameters toward each other by penalizing . In this way, it desirably allows two variants to have similar effect sizes but opposite association directions. However, such a penalty is non-convex and thus computationally more challenging. Second, by the use of TLP-based grouping (see details later), TLP-SG shrinks |βj| and |βj′| toward each other only if their difference is relatively small (as compared to a tuning parameter to be decided), thus, for example, avoiding severely biasing the estimate of the effect size of an associated variant toward 0 by shrinking it toward the null effect of a null variant. We note that, although penalized regression methods have been widely used and studied, their applications to the current context with RVs are much more limited; in particular, we are not aware of any applications of TLP-S, TLP-SG and gflasso to association testing of RVs.
This paper is organized in four sections. Section 2 provides a brief review of some existing association tests to be compared, and then introduces our proposed TLP-based tests. In section 3, we compare the performance of the methods with simulated data and with an application to the Genetic Analysis Workshop 17 (GAW17) sequence data (Almasy et al., 2011). Finally, the Discussion section summarizes the results, and suggests some potential problems for future study.
2. Methods
2.1. Some Existing Association Tests
We briefly review some existing global tests based on the ordinary least squares (OLS) estimates. Given n independent observations (Yi, Xi), i = 1, …, n, with Yi as a quantitative trait and a vector Xi = (Xi1, …, Xik) as genotypes of k variants for subject i, we would like to test for any possible association between the trait and genotypes. We use the dosage coding for Xij: Xij = 0, 1, or 2, representing the count number of one of the two alleles present in variant j of subject i. A multi-locus association analysis is based on fitting a linear model,
where the errors ϵi are assumed to be independently drawn from N(0, σ2), a Normal distribution with mean 0 and variance σ2. A global test of any possible association between the trait and k variants can be formulated as testing on the multiple parameters βjs for j = 1, …, k with null hypothesis H0: β = (β1, …, βk)′ = 0 by an F-test, which is based on the OLS estimates that minimize the residual sum of squares. A potential problem with the test is the power loss due to the large variance of j since the MAFs of RVs are small.
We also apply other four association tests: the Score, the sum of squared score (SSU), its weighted version SSUw (Pan, 2009), and the univariate minP (UminP) tests. The Score test is popular in general statistics while the UminP test is most widely used for CVs in GWAS; on the other hand, Basu and Pan (2011) showed that the SSU and SSUw tests were powerful in RV association testing for case-control studies. Here, as a secondary contribution, we extend the SSU and SSUw tests to the case with a quantitative trait. All the four tests are based on the score vector U and its covariance matrix V under H0:
where , and is the estimate of σ2 under H0. The corresponding four test statistics are
where Uj is the jth element of U and vj is the (j, j)th diagonal element of V. Under H0, asymptotically TScore has a χ2k distribution, each of TSSU and TSSUw has a mixture of chi-squared distributions (Pan, 2009), and the p-value of TUminP can be numerically obtained (Conneely and Boehnke, 2007).
Next, we extend the Sum test (Pan, 2009) and its modified version, a data-adaptive Sum (aSum) test (Han and Pan, 2010), to the case with a quantitative trait. The Sum test was originated to model multiple variants jointly while inducing a minimum number of DF: while including all the variants in the linear model, it assumes that the variants all have the same effect size (and direction), βc, as in the following model:
Fitting (Equation 2) is equivalent to conducting a simple regression of Y on a new covariate, the sum of the genotypes over the multiple variants. To address the question of whether any association between the disease and the variants exists, one simply needs to test H0 : βc = 0, without the need for multiple testing adjustment. The main advantage of the Sum test is that, because it tests on only one parameter βc, there will be no power loss due to the large DF. The common association parameter βc is a weighted average of the individual βM, 1, …, βM, k in the marginal models Yi = βM, 0 + XijβM, j + ϵij for j = 1, …, k (Pan, 2009). On the other hand, the main problem of the Sum test is its dependence on the signs of βM,js or on the coding of each variant (i.e., which allele is chosen as the reference category). If the signs are not the same, the test may have a quite small c and thus low power. To overcome the limitation of the Sum test, Han and Pan (2010) proposed the aSum test for a case-control study design, which can be equally applied to quantitative traits as the following. (1) For each variant j, flip its coding to X*.j = 2 − X.j if M,j < 0 and its p-value pM,j ≤ α0 in the marginal model; otherwise use the same coding X*.j = X.j. (2) Fit the model (Equation 2) with the new coding X*. To test H0 in the aSum test, we use a permutation-based log-likelihood ratio test (LRT), which is asymptotically equivalent to the score test. For the choice of α0, we use the same value as recommended by Han and Pan (2010), 0.1, to prevent reduced power when a too small or too large α0 is used.
While the F-test is based on OLS estimates, in next section we apply some penalized regression methods, the Lasso, gflasso and a recently developed TLP for either only variable selection (TLP-S) or both variable selection and parameter grouping (TLP-SG). In short, both the Lasso and TLP-S consider only variable selection, while the gflasso and TLP-SG pursue parameter grouping along with variable selection to improve power by striking a better balance between goodness-of-fit and reduced DF in the joint model (Equation 1).
2.2. Penalized Regression Based Tests
2.2.1. Parameter estimation from penalized regression
Given a vector of traits Y = (Y1, …, Yn)′ and a design matrix for k variants X = (X·1, …, X·k), the Lasso estimate of β is obtained from the penalized least squares function:
where a large λ automatically yields some components of as 0, realizing variable selection. While Lasso does effective variable selection, its estimates are always biased. To overcome the issue, Shen et al. (2012) proposed a truncated Lasso(L1)-penalty (TLP) , which, as τ → 0+, tends to the L0-loss, I(|x| ≠ 0). The degree of approximation by TLP is controlled by a tuning parameter, τ. See Figure 1 for a display over the different values of τ. Then the TLP-estimate is obtained from
and we denote (Equation 4) as TLP-S. The most interesting feature of the TLP is that only smaller |βj|'s less than a threshold τ are penalized, hence realizing variable selection (if some are shrunken to 0) while avoiding penalizing larger |βj|'s and thus leading to their almost unbiased estimates.
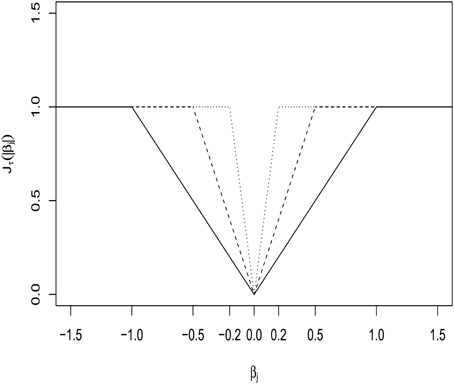
Figure 1. Truncated L1-penalty (TLP) function Jτ(|βj|) with τ = 0.2, 0.5, and 1 (as solid, dashed and dotted lines, respectively).
While both the Lasso and TLP-S consider only variable selection, an alternative way to reduce model complexity is grouping pursuit (Shen and Huang, 2010). To investigate the grouping effects on a test's power, we apply two recent penalized grouping methods, gflasso and TLP-SG. The β estimate from gflasso is based on the following objective function:
where the first penalty is used for variable selection and the second is to encourage parameter grouping. r(j, j′) is the sign of the correlation between two variants X·j and X·j′, which is used to approximate the target |βj| ≈ |βj′|; this method is denoted gflassor = cor. On the other hand, if r(j, j′) = 1 is used, the penalty targets βj ≈ βj′.
The TLP-SG estimate of β comes from
where the first penalty is for variable selection while the second shrinks the difference of |βj|'s if a difference is within the upper bound τ. The number of the groups of equal parameter estimates is a decreasing function of λ2. Thus, the tuning parameters (λ1, λ2, τ) are selected to balance between the model complexity and model goodness-of-fit, which presumably may contribute to enhanced power. As a comparison, in the Sum test all parameters (or variants) are forced to belong to the same single group even if the variants' associations with the trait are quite different both in effect sizes and directions; the TLP-SG method attempts to conduct a more precise grouping over all variants in a data-adaptive way.
To compute β in Lasso, gflasso, TLP-S and TLP-SG, we used the Feature Grouping and Selection Over an Undirected Graph (FGSG) package of Yang et al. (2012), which is a C library with interface to MATLAB and is quite fast to run. Its computing efficiency allowed us to estimate separate tuning parameters for each permuted dataset to control the type I error as explained in the next section.
2.2.2. Hypothesis testing
To test the null hypothesis H0 : β = 0 in Equation (1), we conduct a permutation-based test, in which the p-value is calculated by comparing a test statistic T applied to the original dataset to the ones T(b)0 applied to the B permuted datasets for b = 1, …, B. We use permutation to control the Type I error since the null distribution of a test statistic based on a penalized regression estimate is in general difficult to obtain. The permutation-based testing procedure follows:
Step 1. With the original data {(Yi, Xi)}, we solve a penalized regression problem to obtain in Equation (1).
Step 2. Calculate a test statistic T = T().
Step 3. By repeatedly permuting the observed Y of the original data, we obtain B sets of permuted data {(Y(b)i, Xi)} for b = 1, …, B. For each permuted data set, {(Y(b)i, Xi)}, we repeat the Steps 1 and 2, obtaining the null statistics T(b)0.
Step 4. The final p-value is .
We apply each of several test statistics in Step 2. First, across all penalized methods, we use a 1-df F-statistic (1-df) to test the association between Y and X, where is the penalized estimate of β in Step 1. Specifically, we fit a linear model
and test H′0 : α = 0. This 1-df test uses variable selection and possibly parameter grouping result from the corresponding penalized method, while allowing testing with only 1 DF. Second, for TLP-SG, we also apply the corresponding SSU and SSUw tests, where the test statistics TSSU and TSSUw are both based on the selected variables from the corresponding penalized estimates. Specifically,
where U* is a sub-component vector of the score vector U corresponding to |j| ≠ 0, and |j| > 0.001 is considered as non-zero. Similarly, V* is the corresponding sub-matrix of the covariance matrix V. Note that the grouping information is not used.
2.2.3. Selection of tuning parameters
To select the suitable tuning parameters, we apply a grid-search with Akaike's information criterion (AIC) (Akaike, 1974):
where log L = (−nlog(2) − n − p − 1)/2 is the log-likelihood with the penalized estimate plugged-into model (Equation 1), and . The effective number of the parameters, p, in AIC is computed as the number of non-zero |j|'s for Lasso and TLP-S, as the number of non-zero unique j's for gflassor = 1, and as the number of non-zero unique |j|'s for gflassor = cor and TLP-SG, respectively. For λ in Lasso, the one resulting in the smallest AIC out of 50 equally spaced points in [0.001,10] is selected. Similarly, the values of each of λ1, λ2 and τ in other methods are searched over five equally spaced grid points of [0.001, 1], [0.001, 0.5], and [0.001, 0.5], respectively. For each permuted dataset {(Y(b)i, Xi)} for b = 1, …, B, we also estimate its own (λ(b)1, λ(b)2, τ(b)) to properly control the type I error.
3. Results
3.1. Simulations
We consider two simulation schemes. In the first scheme, we generate only RVs with a total of 200 replicates and n = 400 in each replicate. The permutation size is set as B = 100. For each replicate, to generate k variants including six causal ones in linkage disequilibrium (LD), as in Wang and Elston (2007), two latent vectors from multivariate normal distribution MVN(0,R) are simulated, where R has a first order auto regressive (AR1) structure; the association between any two elements of the latent vector decreases by ρ = 0.8 times as 1 lag increases. Then, the vector is dichotomized to yield a haplotype with the minor allele frequency (MAF) of each variant randomly chosen between 0.005 and 0.01. The genotype data Xi = (Xi1, …, Xik)′ for sample i is obtained by adding two haplotypes together. Finally, Yi is generated from the randomly located six causal variants with σ2 = 2 in model (Equation 1), where the intercept β0 is set as 0.3 throughout the simulations. The considered three cases are:
In each case, we vary the number of non-causal RVs k-6 from 0 to 24 so that the total number of RVs, k, ranges from 6 to 30. The Type I error is computed from the Y under H0 : β = (0, …, 0)′.
In the second scheme, multiple RVs and two CVs are generated to mimic the GAW17 data we use later. The frequency of one allele for each CV is randomly distributed between 0.2 and 0.7, and CVs may or may not be chosen as a causal variant in each replicate. When a CV is randomly selected as a causal variant, its effect size βj is scaled down to βj/10 in the following cases to prevent its dominating association with the outcome. The considered three cases for mixed RVs and CVs are:
Figure 2 displays the TLP-S and TLP-SG solution paths of |j| over a tuning parameter given other(s), where two horizontal lines at 1.2 and 0 give the true parameter values for Case 2 set-up with only RVs. In contrast to piece-wise linear solution paths of the Lasso estimates, the TLP solution paths are like step functions as expected from an L0-penalty (i.e., best subset selection).
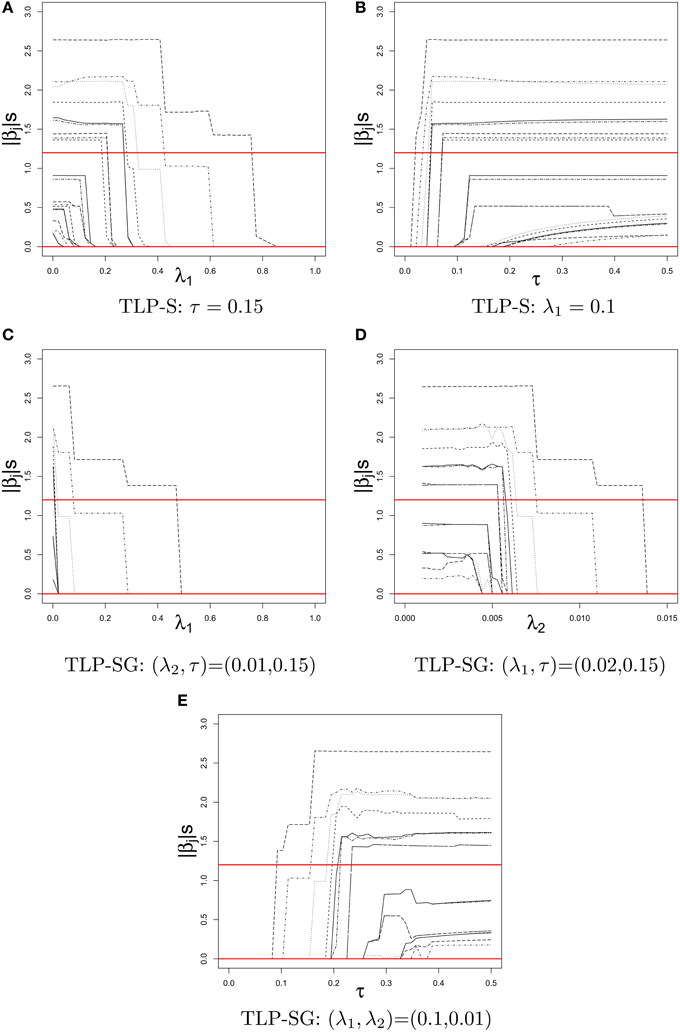
Figure 2. Solution paths of |j|'s in a simulated dataset of Case 2 with k = 22 RVs for TLP-S and TLP-SG over the values of a tuning parameter given other(s). The true values of |βj|'s at 1.2 and 0 are given by two horizontal lines. (A) TLP-S: τ = 0.15. (B) TLP-S: λ1 = 0.1. (C) TLP-SG: (λ2, τ) = (0.01, 0.15). (D) TLP-SG: (λ1, τ) = (0.02, 0.15). (E) TLP-SG: (λ1, λ2) = (0.1, 0.01).
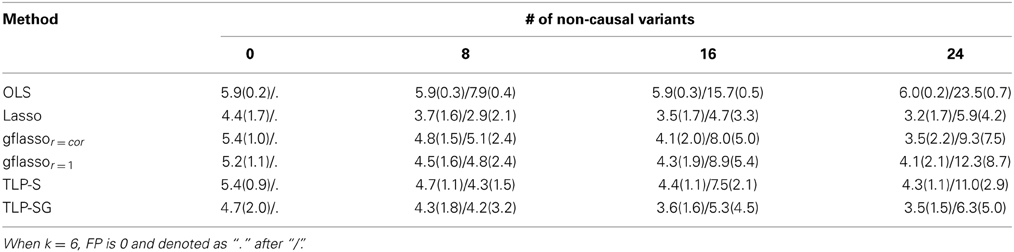
Table 1 presents the simulation results for the RVs only set-ups. The Type I error rates seem to be properly controlled under the null for all cases, though there are some slightly inflated numbers, possibly due to the relatively small number of replicates and/or permutation numbers. Under the alternative hypothesis, in Case 1 where the causal associations are all in the same direction, the Sum or aSum test beats other methods. Within the class of penalized regression methods, TLP-SG with the SSU or SSUw test statistics is most powerful; in particular, TLP-SG with the SSUw statistic performs better than the F-test regardless of the number of non-causal RVs included. There seems to be no gain with grouping in TLP-SG as compared to no grouping in TLP-S, and the 1df-test of TLP-SG works better than gflassor = cor unless the number of non-causal RVs is large at 24. Overall, penalized regression methods do not significantly outperform the power over the Sum and aSum tests. In Cases 2 and 3, where the causal effect directions are mixed, the Sum test works poorly as expected, while the aSum test has higher power. Overall, either the SSU or SSUw test is the winner. In particular, the TLP-S- and TLP-SG-based tests do not significantly improve over the SSU and SSUw tests, though they may perform better than those based on the Lasso and gflasso. Again, a comparison between TLP-S and TLP-SG reveals that parameter grouping does not seem to contribute much to increased power.
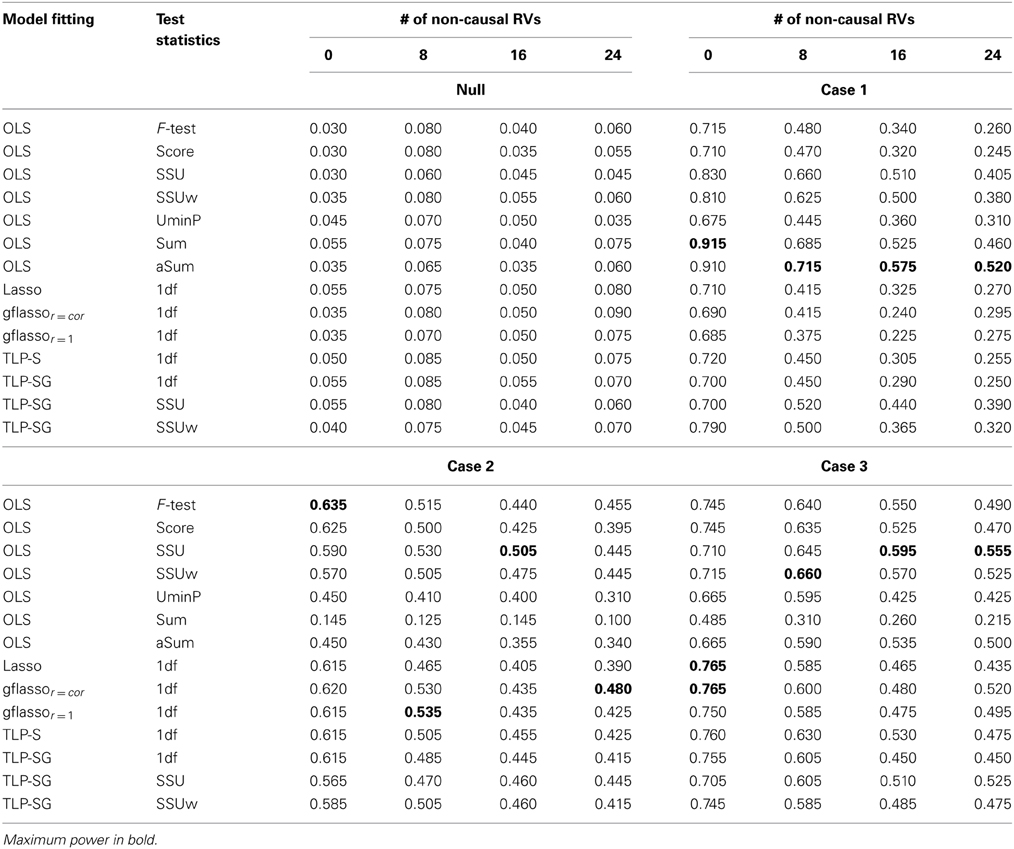
Table 1. Empirical Type I error and Power at the nominal level α = 0.05 based on 200 replicates for the RVs only set-ups with six causal RVs and a varying number of non-causal RVs.
The results of the mixed RVs and CVs set-ups are listed in Table 2. Note that, as discussed in Basu and Pan (2011), with mixed RVs and CVs, the SSU test might not perform well. Overall, the SSUw test is the winner. The penalized methods can perform well in some situations, but they do not always outperform the SSUw test. Among the penalized methods, the proposed TLP-S and TLP-SG are competitive against the Lasso and gflasso.
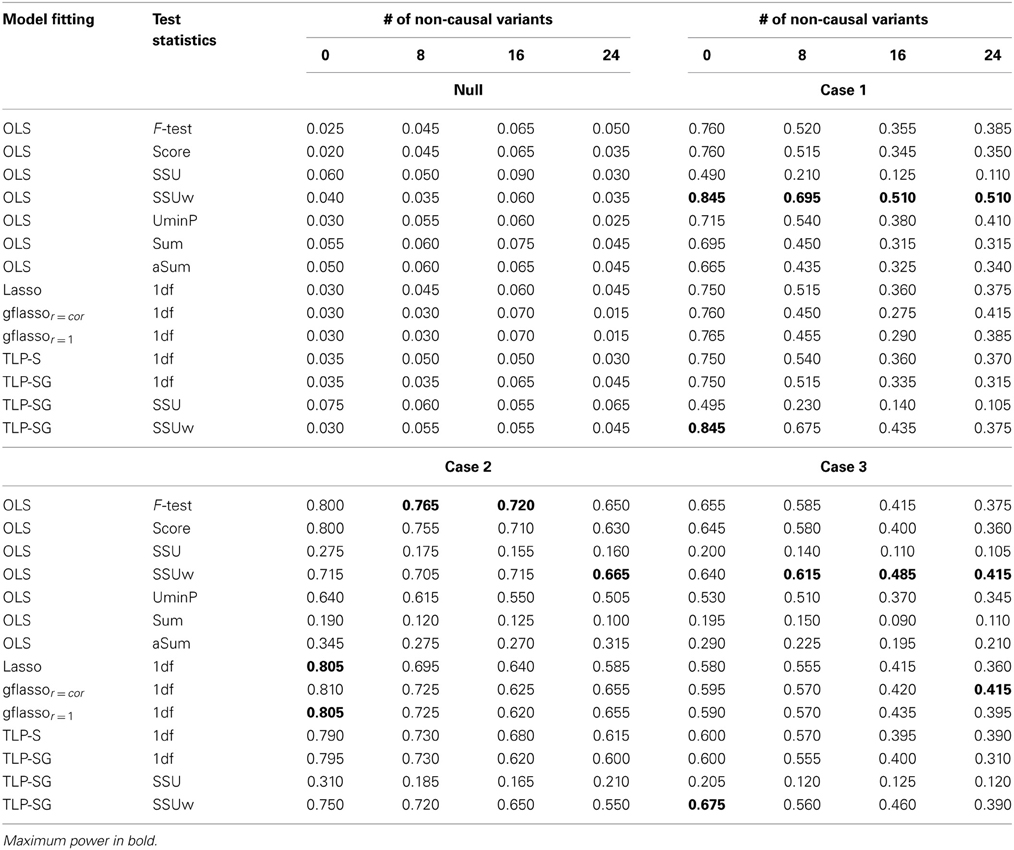
Table 2. Empirical Type I error and Power at the nominal level α = 0.05 based on 200 replicates for the RVs + CVs set-ups with six causal variants and a varying number of non-causal ones.
An advantage of penalized methods over global tests is the formers' ability for variable selection, narrowing down possible causal variants. We note that causal variant selection is an under-studied problem in genetics, which will become more important when we transition from association studies to causal inference. On the other hand, variable selection via penalized methods or any other methods has yet been fully investigated in the current context with large n, small k, and more importantly with RVs. In Table 3, we investigate their variable selection performance for one simulation set-up; the results for other set-ups are similar and thus omitted. We show the mean numbers of true positives (TP) and false positives (FP), where a |j| > 0.001 is counted as a positive (i.e., non-zero). As expected, the OLS estimates (and the global tests) cannot conduct variable selection with the mean TP and mean FP close to their maximum possible values. Among the penalized methods, a method tends to be either more conservative (fewer FP and fewer TP at the same time) or more liberal (higher FP and higher TP). If we look at the ratio of FP over TP, it seems that the Lasso and TLP-SG are best with the highest ratio, especially for a larger number of non-causal RVs.
We compare the performance of the parameter estimates in Table 4 for one simulation set-up; the results for other set-ups are similar and thus omitted. As expected, the OLS estimates are almost unbiased, but with the largest mean squared errors (MSEs) due to their large variability. The penalized estimates all have smaller MSEs and larger biases than the OLS estimates. Among the penalized methods, the TLP-S and TLP-SG estimates have much smaller biases, but larger variances and thus larger MSEs than those of Lasso and gflasso. In particular, for a causal effect (βc), Lasso and gflasso shrink it more toward 0, while TLP-S and TLP-SG give much less biased estimates.
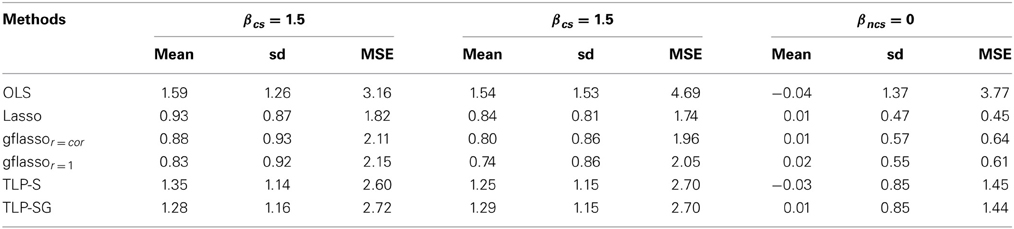
Table 4. Means, sd's and MSEs of some causal (βcs) and non-causal (βncs) variants' regression coefficient estimates when k = 30 in Case 2 with both RVs and CVs.
3.2. Mini-Exome Sequence Data
We apply the methods to the mini-exome sequence data from the GAW17 (Almasy et al., 2011). The data set consists of 3205 autosomal genes with 24,487 variants on 697 subjects. The genotypes are obtained from the sequence alignment files provided by the 1000 Genomes Project for the pilot 3 study. The GAW17 data include 200 replicates of three simulated quantitative traits named Q1, Q2, and Q4, where only Q1 and Q2 were influenced by genetic factors. Here we use Q2, which is determined by 72 variants in 13 genes. The true effect sizes of all variants range from 0.2 to 1.2; all variants are positively associated with the trait Q2 but in differential magnitudes.
In this study, we test on each of all causal genes (PLAT, SREBF1, SIRT1, VLDLR, VNN3, PDGFD, BCHE, INSIG1, LPL, RARB, VNN1, and VWF) except GCKR, which contains just one SNP. The number of causal variants (nC) in each gene affecting Q2, and some summary statistics of their MAFs and pairwise correlations (COR) are listed in Table 5. Within each gene, most variants are RVs, but a few are CVs with their MAFs larger than 5%. First, we test for any association between Q2 and all variants gene by gene as shown in Table 6, and then test on each gene without its CVs as shown in Table 7.
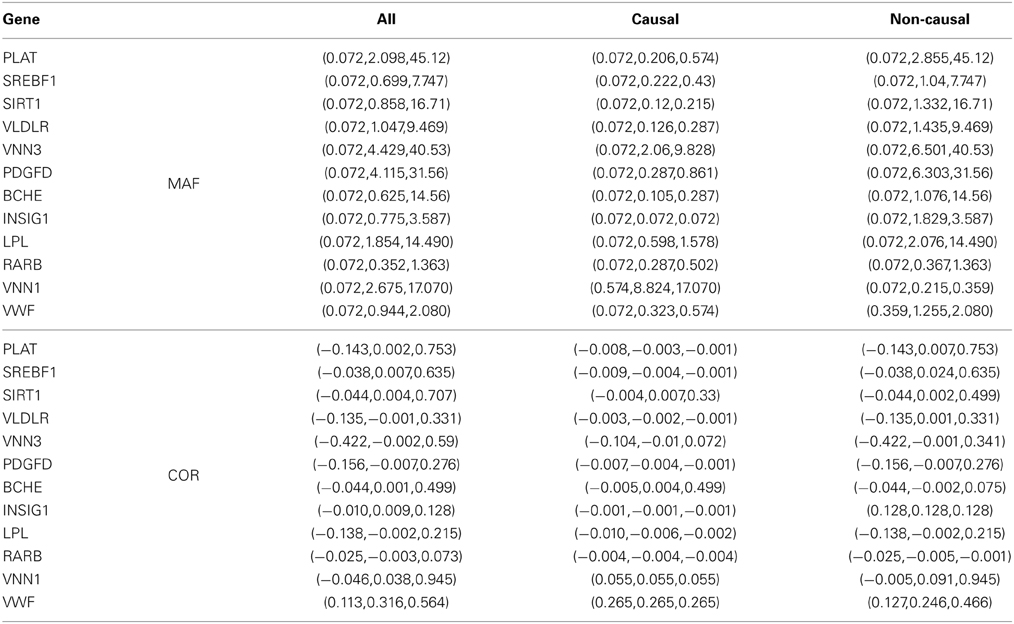
Table 5. MAFs (%) and pair-wise correlations (COR) in the values of (min, mean, max) for the 12 genes influencing the quantitative trait Q2 in the GAW17 data.
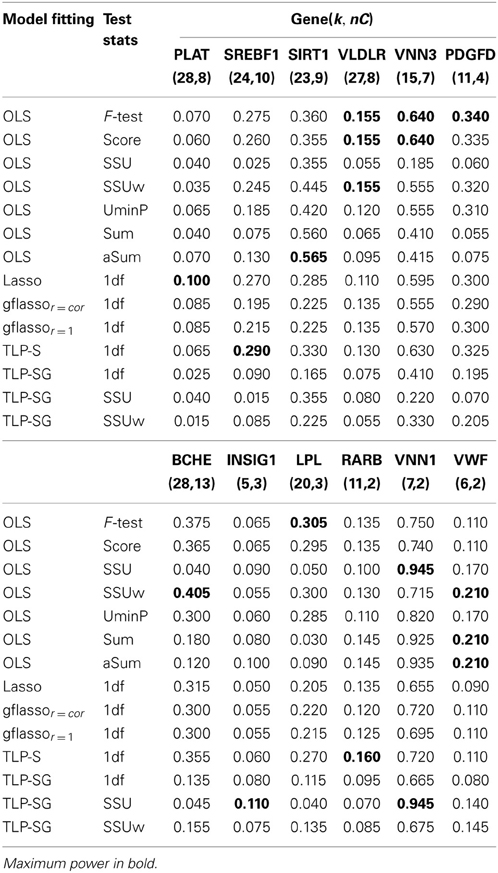
Table 6. Empirical power based on the GAW17 data from 200 replicates of Q2, k, and nC denote the numbers of the total and causal variants in a gene.
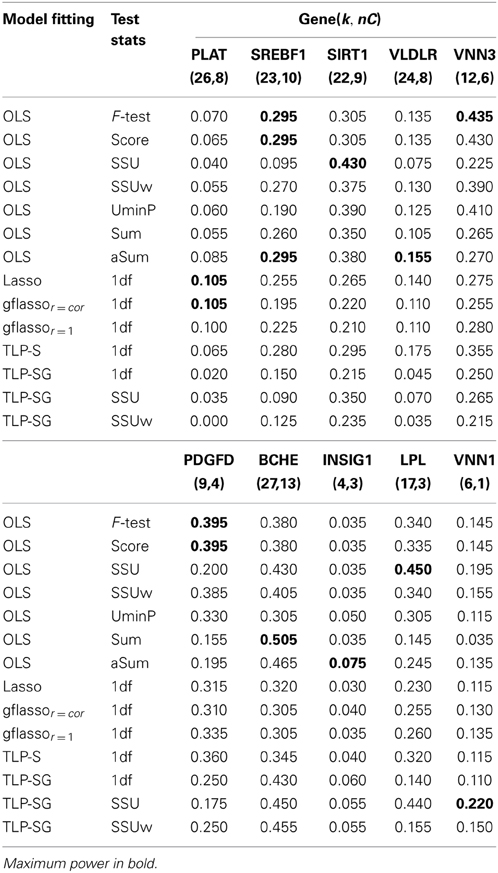
Table 7. Empirical power based on the GAW17 data without CVs from 200 replicates of Q2, k, and nC denote the numbers of the total and causal RVs in a gene.
In Table 6, when both RVs and CVs within a gene are included, the identity of the most powerful test differs across the genes: the F-test is the winner for the genes VLDLR, VNN3, PDGFD, and LPL; however, for the genes VLDLR, BCHE, VNN1, and VWF, the SSU or SSUw test is the best. The two gflasso-based tests work quite similarly over all genes. The TLP based tests perform best for the genes SREBF1, RARAB, VNN1, and INSIG1. After removing a few CVs in each gene (Table 7), the SSU test recovers good power for the genes PDGFD, BCHE and LPL. The Sum test is the winner for gene BCHE, while the F-test based on the OLS estimates perform best for genes VNN3, SREBF1, and PDGFD. For gene VNN1, the TLP-SG with the SSU statistic has the highest power.
A potential advantage of penalized regression is variable selection, which is missing from existing global tests. Table 8 shows the results of causal variant selection by the penalized methods. Overall, each penalized method could eliminate some non-associated variants at the cost of omitting some causal ones. In general, in agreement with simulated data, the Lasso and TLP-SG seem to select fewest variants, including both TPs and FP, while TLP-S and gflasso give higher numbers of both TPs and FPs.
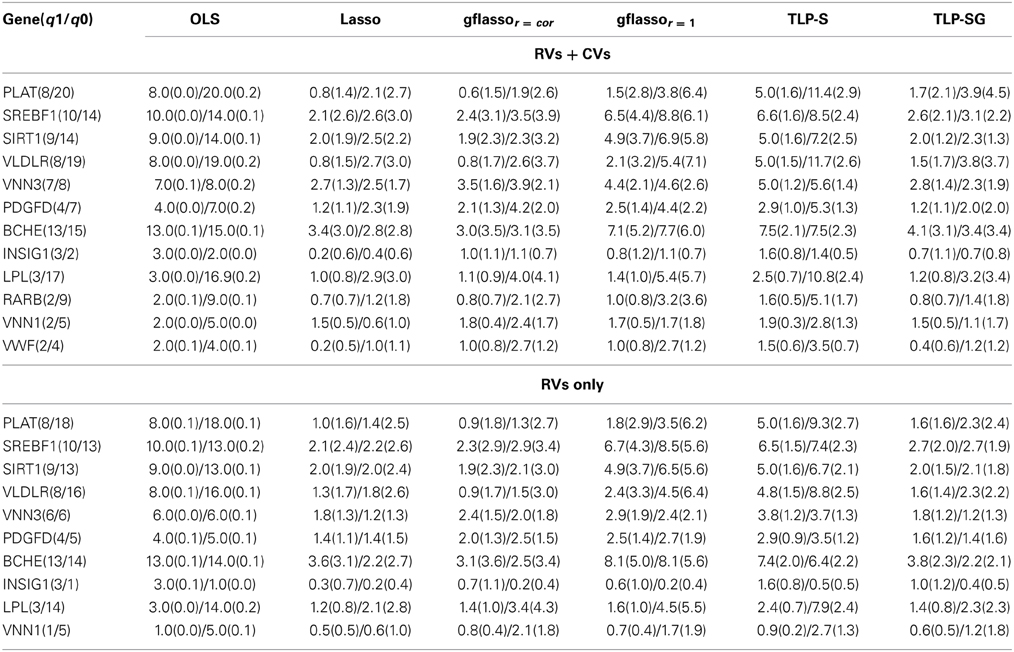
Table 8. Mean numbers of TP(sd)/FP(sd) in the GAW17 data, where q1 and q0 denote the numbers of the causal and non-causal variants in each gene.
4. Discussion
In this study we have conducted hypothesis testing to detect the association between a quantitative trait and multiple RVs based on some new penalized regression methods. In addition to the traditional use of penalized regression for variant selection, we have also considered several state-of-the-art grouping pursuit methods that smooth the effect sizes of the variants, either βi or |βi|, in a data-adaptive way, which can be considered as a generalization of the Sum and other genotype pooling/collapsing-based burden tests. In particular, our proposed TLP-SG overcomes several limitations of the Sum and other burden tests. First, by variable selection, the result of TLP-SG is presumably less influenced by the presence of many non-associated variants to be tested. Second, rather than pooling all the variants into a single group or two groups, TLP-SG automatically determines the number of groups to be formed based on the given data. Furthermore, since TLP-SG shrinks the effects sizes |βi|, not βi, toward each other, it is robust to varying association directions of the causal variants. However, based on our studies on both simulated and real sequence data, we found that TLP-SG and other penalized methods sometimes might be more powerful than some existing global tests, though they do not always outperform the SSU or SSUw test. The discovery of no uniform gain of penalized methods over existing global tests is interesting and even surprising, and can be due to non-optimal implementation of the penalized methods in several aspects. First, the selection of the tuning parameters based on the model selection criterion AIC may not be optimal. As an example, in a simulated dataset, when we set the tuning parameters to properly group the variants, the estimates were quite close to the true values, but the corresponding AIC was less desirable, leading to choosing other low performing tuning parameters. Importantly, there is no theory yet to justify the applicability of AIC for the gflasso- and TLP-based methods; in particular, it is unclear how to count the effective number of parameters in the AIC. Alternatively, one may want to try a more popular model selection method, multi-fold cross-validation. However, for RVs as considered here, if we divide the data into multiple folds, the training data may contain several monomorphic variants, causing non-identifiability of their corresponding effect sizes. Second, due to the repeated model-fitting with many permuted datasets, to save computing time, we only searched relatively few grid points for the tuning parameters, which might not have covered some suitable tuning parameter values. These are all issues to be addressed in the future.
Another non-convex penalty is SCAD (Fan and Li, 2001), which as TLP aims to reduce the biases of large coefficient estimates resulting from the Lasso or L1 penalty. Although SCAD can be equally applied and compared here, we chose the TLP as a representative of non-convex penalties for its good properties: as shown by Shen et al. (2012), L0 regularization is optimal in variable selection, and its computational surrogate, TLP, shares the same property for sufficiently small tau; furthermore, the variable selection consistency of TLP regularization also led to enhanced parameter estimation and prediction in numerical studies with finite sample sizes. Nevertheless, we note that, penalized regression methods have been intensively studied for high-dimensional data, but not for the type of data considered here, which are low dimensional but with RVs as sparse predictors.
In summary, the established benefit of penalized regression for variable selection and risk prediction for high-dimensional data (Kooperberg et al., 2010) did not seem to directly translate into substantial power gains in genetic association testing. In addition to the current work, there exist three recent reports (Croiseau and Cordell, 2009; Martinez et al., 2010; Basu et al., 2011) questioning the effectiveness of the Lasso penalized regression in hypothesis testing, while Basu et al. (2011) showed that several variable selection approaches did not outperform some global tests (e.g., the SSU or SSUw test) for association analysis of CVs. Due to the limitations mentioned above, we cannot conclude here that any penalized regression method would not outperform exiting global association tests; rather, further investigation on enhanced tuning parameter selection and better choice of the test statistic is warranted. Finally, we note that the capability of variable selection by penalized regression can be useful, e.g., in narrowing down causal variants.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the editor and reviewers for many helpful and constructive comments and suggestions. This research was supported by NIH grants R01HL65462, R01HL105397, R01GM081535, and R01HL116720, and by the Minnesota Supercomputing Institute.
References
Akaike, H. (1974). A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723. doi: 10.1109/TAC.1974.1100705
Almasy, L. A., Dyer, T. D., Peralta, J. M., Kent, J. W. Jr., Charlesworth, J. C., Curran, J. E., et al. (2011). Genetic analysis worksho p 17 mini-exome simulation. BMC Proc. 5(suppl. 9):S2. doi: 10.1186/1753-6561-5-S9-S2
Austin, E., Pan, W., and Shen, X. (2013). Penalized regression and risk prediction in Genome-Wide association studies. Stat. Anal. Data Min. 6, 315–328. doi: 10.1002/sam.11183
Basu, S., and Pan, W. (2011). Comparison of statistical tests for disease association with rare variants. Genet. Epidemiol. 35, 606–619. doi: 10.1002/gepi.20609
Basu, S., Pan, W., Shen, X., and Oetting, W. (2011). Multi-locus association testing with penalized regression. Genet. Epidemiol. 35, 755–765. doi: 10.1002/gepi.20625
Chapman, J. M., and Whittaker, J. (2008). Analysis of multiple SNPs in a candidate gene or region. Genet. Epidemiol. 32, 560–566. doi: 10.1002/gepi.20330
Conneely, K. N., and Boehnke, M. (2007). So many correlated tests, so little time! Rapid adjustment of p values for multiple correlated tests Am. J. Hum. Genet. 81, 1158–1168. doi: 10.1086/522036
Croiseau, P., and Cordell, H. J. (2009). Analysis of North American rheumatoid arthritis consortium data using a penalized logistic regression approach. BMC Proc. 3(Suppl. 7):S61. doi: 10.1186/1753-6561-3-S7-S61
Fan, J., and Li, R. (2001). Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96, 1348–1360. doi: 10.1198/016214501753382273
Guo, W., and Lin, S. (2009). Generalized linear modeling with regularization for detecting common disease rare haplotype association. Genet. Epidemiol. 33, 308–316. doi: 10.1002/gepi.20382
Han, F., and Pan, W. (2010). A data-adaptive sum test for disease association with multiple common or rare variants. Hum. Hered. 70, 42–54. doi: 10.1159/000288704
Kim, S., and Xing, E. P. (2009). Statistical estimation of correlated genome associations to a quantitative trait network. PLoS Genet. 5:e1000587. doi: 10.1371/journal.pgen.1000587
Kooperberg, C., LeBlanc, M. L., and Obenchain, V. (2010). Risk prediction using genome-wide association studies. Genet. Epidemiol. 34, 643–652. doi: 10.1002/gepi.20509
Kotowski, I. K., Pertsemlidis, A., Luke, A., Cooper, R. S., Vega, G. L., Cohen, J. C., et al. (2006). A spectrum of PCSK9 alleles contributes to plasma levels of low density lipoprotein cholesterol. Am. J. Hum. Genet. 78, 410–422. doi: 10.1086/500615
Li, B., and Leal, S. M. (2008). Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am. J. Hum. Genet. 83, 311–321. doi: 10.1016/j.ajhg.2008.06.024
Li, Y., Byrnes, A. E., and Li, M. (2010). To identify associations with rare variants, just WHaIT: weighted haplotype and imputation-based tests. Am. J. Hum. Genet. 87, 728–735. doi: 10.1016/j.ajhg.2010.10.014
Madsen, B. E., and Browning, S. R. (2009). A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 5:e1000384. doi: 10.1371/journal.pgen.1000384
Maher, B. (2008). Personal genomes: the case of the missing heritability. Nature 456, 18–21. doi: 10.1038/456018a
Malo, N., Libiger, O., and Schork, N. J. (2008). Accommodating linkage disequilibrium in genetic-association analyses via ridge regression. Am. J. Hum. Genet. 82, 375–385. doi: 10.1016/j.ajhg.2007.10.012
Martinez, J. G., Carroll, R. J., Muller, S., Sampson, J. N., and Chatterjee, N. (2010). A note on the effect on power of score tests via dimension reduction by penalized regression under the null. Int. J. Biostat. 6, 12. doi: 10.2202/1557-4679.1231
Pan, W. (2009). Asymptotic tests of association with multiple SNPs in linkage disequilibrium. Genet. Epidemiol. 33, 497–507. doi: 10.1002/gepi.20402
Roeder, K., Bacanu, S. A., Sonpar, V., Zhang, X., and Devlin, B. (2005). Analysis of single-locus tests to detect gene/disease associations. Genet. Epidemiol. 28, 207–219. doi: 10.1002/gepi.20050
Shen, X., and Huang, H.-C. (2010). Grouping pursuit through a regularization solution surface. J. Am. Stat. Associat. 105, 727–739. doi: 10.1198/jasa.2010.tm09380
Shen, X., Pan, W., and Zhu, Y. (2012). Likelihood-based selection and sharp parameter estimation. J. Am. Stat. Associat. 107, 223–232. doi: 10.1080/01621459.2011.645783
Tibshirani, R. (1996). Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. 58, 267–288.
Tibshirani, R., Saunders, M., Rosset, S., Zhu, J., and Knight, K. (2005). Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. B 67, 91–108. doi: 10.1111/j.1467-9868.2005.00490.x
Tzeng, J. Y., and Bondell, H. D. (2010). A comprehensive approach to haplotype specific analysis via penalized likelihood. Eur. J. Hum. Genet. 18, 95–103. doi: 10.1038/ejhg.2009.118
Wang, T., and Elston, R. C. (2007). Improved power by use of a weighted score test for linkage disequilibrium mapping. Am. J. Hum. Genet. 80, 353–360. doi: 10.1086/511312
Yang, S., Yuan, L., Lai, Y.-C., Shen, X., Wonka, P., and Ye, J. (2012). “Feature grouping and selection over an undirected graph,” in KDD'12 Proceedings of the 18th ACM SIGKDD International Conference On Knowledge Discovery and Data Mining (SIGKDD 2012) (New York, NY), 922–930. doi: 10.1145/2339530.2339675
Zhou, H., Alexander, D. H., Sehl, M. E., Sinsheimer, J. S., Sobel, E. M., and Lange, K. (2011). Penalized regression for genome-wide association screening of sequence data. Pac. Symp. Biocomput. 2011, 106–117. doi: 10.1142/9789814335058_0012
Keywords: GWAS, SSU test, SSUw test, Sum test, TLP
Citation: Kim S, Pan W and Shen X (2014) Penalized regression approaches to testing for quantitative trait-rare variant association. Front. Genet. 5:121. doi: 10.3389/fgene.2014.00121
Received: 01 March 2014; Accepted: 18 April 2014;
Published online: 13 May 2014.
Edited by:
Bingshan Li, Vanderbilt University, USACopyright © 2014 Kim, Pan and Shen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Pan, Division of Biostatistics, School of Public Health, University of Minnesota, Mayo Bldg/Delaware St SE, MMC 303, Minneapolis, MN 55455–0392, USA e-mail:d2VpcEBiaW9zdGF0LnVtbi5lZHU=
 Sunkyung Kim
Sunkyung Kim Wei Pan
Wei Pan Xiaotong Shen
Xiaotong Shen