- Radon Institute for Computational and Applied Mathematics, Austrian Academy of Sciences, Linz, Austria
A fundamental result in metabolic pathway analysis states that every flux mode can be decomposed into a sum of elementary modes. However, only a decomposition without cancelations is biochemically meaningful, since a reversible reaction cannot have different directions in the contributing elementary modes. This essential requirement has been largely overlooked by the metabolic pathway community. Indeed, every flux mode can be decomposed into elementary modes without cancelations. The result is an immediate consequence of a theorem by Rockafellar which states that every element of a linear subspace is a conformal sum (a sum without cancelations) of elementary vectors (support-minimal vectors). In this work, we extend the theorem, first to “subspace cones” and then to general polyhedral cones and polyhedra. Thereby, we refine Minkowski's and Carathéodory's theorems, two fundamental results in polyhedral geometry. We note that, in general, elementary vectors need not be support-minimal; in fact, they are conformally non-decomposable and form a unique minimal set of conformal generators. Our treatment is mathematically rigorous, but suitable for systems biologists, since we give self-contained proofs for our results and use concepts motivated by metabolic pathway analysis. In particular, we study cones defined by linear subspaces and nonnegativity conditions — like the flux cone — and use them to analyze general polyhedral cones and polyhedra. Finally, we review applications of elementary vectors and conformal sums in metabolic pathway analysis.
1. Introduction
Cellular metabolism is the set of biochemical reactions which transform nutrients from the environment into all the biomolecules a living cell consists of. Most metabolic reactions are catalyzed by enzymes, the expression and activity of which is controlled by gene and allosteric regulation, respectively.
A metabolic network together with enzymatic reaction rates gives rise to a nonlinear dynamical system for the metabolite concentrations. However, for genome-scale networks, quantitative knowledge of the underlying kinetics is not available, and a mathematical analysis is not practicable. Instead, one considers only stoichiometric information and studies the system of linear equalities and inequalities for the fluxes (net reaction rates), arising from the pseudo steady-state assumption and irreversibility constraints.
A metabolic network is given by n internal metabolites, r reactions, and the corresponding stoichiometric matrix N ∈ ℝn×r, which contains the net stoichiometric coefficients of each metabolite in each reaction. The set of irreversible reactions is given by ⊆ {1, …, r}. One is interested in the flux cone
which is a polyhedral cone defined by the null-space of the stoichiometric matrix and nonnegativity conditions. Its elements are called flux modes.
As a running example, we consider a small network, taken from Schuster et al. (2002), the corresponding stoichiometric matrix, and the resulting flux cone:
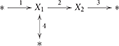
The network consists of two internal metabolites X1, X2 and four chemical reactions. Reaction 1 imports X1 from the environment (indicated by the symbol *) which yields the first column (1, 0)T of the stoichiometric matrix N. Reaction 2 transforms X1 into X2 which gives the column (−1, 1)T, and reaction 3 exports X2 which gives (0, −1)T. The first three reactions are assumed to be irreversible which yields the nonnegativity constraints f1, f2, f3 ≥ 0 in the definition of the flux cone C. Finally, reaction 4 is reversible and exports/imports X1.
Metabolic pathway analysis aims to identify biochemically/biologically/biotechnologically meaningful routes in a network, in particular, the smallest routes. Several definitions for minimal metabolic pathways have been given in the literature, with elementary modes (EMs) being the fundamental concept both biologically and mathematically Klamt and Stelling (2003); Llaneras and Picó (2010). Formally, EMs are defined as support-minimal (or, equivalently, support-wise non-decomposable) flux modes Schuster and Hilgetag (1994); Schuster et al. (2002). Clearly, a positive multiple of an EM is also an EM since it fulfills the steady-state condition and the irreversibility constraints.
In the example, the EMs are given by e1 = (1, 0, 0, 1)T, e2 = (0, 1, 1, −1)T, e3 = (1, 1, 1, 0)T, and their positive multiples. It is easy to check that e1, e2, and e3 are flux modes (elements of the flux cone) and support-minimal. Note that e3 = e1 + e2.
A fundamental result in metabolic pathway analysis states that every flux mode can be decomposed into a sum of EMs Schuster et al. (2002). However, only a decomposition without cancelations is biochemically meaningful, since a reversible reaction cannot have different directions in the contributing EMs. This essential requirement has been largely overlooked by the metabolic pathway community. Indeed, as we will show in this work, every flux mode can be decomposed into EMs without cancelations, that is,
(0) if a component of the flux mode is zero, then this component is zero in the contributing EMs,
(+) if a component of the flux mode is positive, then this component is positive or zero in the contributing EMs,
(−) if a component of the flux mode is negative, then this component is negative or zero in the contributing EMs.
In mathematical terms, every nonzero element of a “subspace cone” (defined by a linear subspace and nonnegativity conditions) is a conformal sum of elementary vectors, cf. Theorem 3. The result is stated in Urbanczik and Wagner (2005) and Urbanczik (2007); part (0) has been shown in Schuster et al. (2002) and guarantees a decomposition without cancelations in a weaker sense Llaneras and Picó (2010); Zanghellini et al. (2013).
In the example, the flux mode f = (2, 1, 1, 1)T can be decomposed into EMs in two ways:
The first sum involves a cancelation in the last component of the flux. The last reaction is reversible, however, it cannot have a net rate in different directions at the same time. Hence, only the second sum is biochemically meaningful. As stated above, a decomposition without cancelations is always possible.
In convex analysis, elementary vectors of a linear subspace were introduced as support-minimal vectors by Rockafellar in 1969. He proves that every vector is a conformal sum (originally called harmonious superposition) of elementary vectors (Rockafellar, 1969, Theorem 1). For proofs and generalizations in the settings of polyhedral geometry and oriented matroids (see Ziegler, 1995, Lemma 6.7) and (Bachem and Kern, 1992, Theorem 5.36). Rockafellar points out that this result is easily shown to be equivalent to Minkowski's theorem Minkowski (1896) for pointed polyhedral cones, stating that every nonzero vector is a nonnegative linear combination of extreme vectors. Moreover, the result immediately implies Carathéodory's theorem Carathéodory (1911), stating that the number of extreme vectors in such a nonnegative linear combination need not exceed the dimension of the cone. In fact, Rockafellar writes: “This is even a convenient route for attaining various important facts about polyhedral convex cones, since the direct proof […] for Theorem 1 is so elementary.”
In metabolic pathway analysis, decompositions without cancelations were introduced by Urbanczik and Wagner (2005). The corresponding elementary vectors are defined by intersecting a polyhedral cone with all closed orthants of maximal dimension. By applying Minkowski's theorem for pointed polyhedral cones, every vector is a sum of extreme vectors without cancelations. Urbanczik further extended this approach to polyhedra arising from flux cones and inhomogeneous constraints Urbanczik (2007).
In polyhedral geometry, it seems that conformal decompositions of general cones and polyhedra have not yet been studied. In this work, following Rockafellar, we first extend his result to cones defined by linear subspaces and nonnegativity conditions (Theorem 3). For subspace cones, support-minimality is equivalent to conformal non-decomposability. As it turns out, for general polyhedral cones, elementary vectors have to be defined as conformally non-decomposable vectors. However, these are in one-to-one correspondence with elementary vectors of a higher-dimensional subspace cone, and, by our result for subspace cones, we obtain a conformal refinement of Minkowski's and Carathéodory's theorems for polyhedral cones (Theorem 8). In particular, there is an upper bound on the number of elementary vectors needed in a conformal decomposition of a vector. Finally, by taking into account vertices and conformal convex combinations, we further extend our result to polyhedra (Theorem 13). We note that elementary vectors do not form a minimal generating set (of an s-cone, a general polyhedral cone, or a polyhedron). However, they form a unique minimal set of conformal generators (Proposition 17).
2. Definitions
We denote the nonnegative real numbers by ℝ≥. For x ∈ ℝn, we write x ≥ 0 if . Further, we denote the support of a vector x ∈ ℝn by supp(x) = {i ∣ xi ≠ 0}.
2.1. Sign Vectors
For x ∈ ℝn, we define the sign vector sign(x) ∈ {−, 0, +}n by applying the sign function component-wise, that is, sign(x)i = sign(xi) for i = 1, …, n. The relations 0 < − and 0 < + induce a partial order on {−, 0, +}n: for X, Y ∈ {−, 0, +}n, we write X ≤ Y if the inequality holds component-wise. For x, y ∈ ℝn, we say that x conforms to y, if sign(x) ≤ sign(y). For example, let x = (−1, 0, 2)T and y = (−2, −1, 1). Then,
that is, sign(x) ≤ sign(y), and x conforms to y. Let X ∈ {−, 0, +}n. The corresponding closed orthant O ⊂ ℝn is defined as O = {x ∣ sign(x) ≤ X}.
2.2. Convex Cones
A nonempty subset C of a vector space is a convex cone, if
or, equivalently, if
A convex cone C is called pointed if C∩−C = {0}. It is polyhedral if
that is, if it is defined by finitely many homogeneous inequalities. Hence, a polyhedral cone is pointed if and only if ker(A) = {0}.
2.3. Special Vectors
We recall the definitions of support-minimal vectors and extreme vectors, which play an important role in both polyhedral geometry and metabolic pathway analysis. We also introduce support-wise non-decomposable vectors, which serve as elementary modes for flux cones (in the original definition), and conformally non-decomposable vectors, which serve as elementary vectors for general polyhedral cones (see Subsection 3.2).
Let C be a convex cone. A nonzero vector x ∈ C is called
• support-minimal, if
• support-wise non-decomposable, if
• conformally non-decomposable, if
• and extreme, if
From the definitions, we have the implications
If x ∈ C is extreme, then {λx ∣ λ > 0} is called an extreme ray of C. In fact, C has an extreme ray if and only if C is pointed. If C is contained in a closed orthant (and hence pointed), we have the equivalence cND ⇔ EX.
3. Mathematical Results
We start by extending a result on conformal decompositions into elementary vectors from linear subspaces to special cases of polyhedral cones, including flux cones in metabolic pathway analysis.
3.1. Linear Subspaces and S-cones
We consider linear subspaces with optional nonnegativity constraints as special cases of polyhedral cones. Let S ⊆ ℝr be a linear subspace and 0 ≤ d ≤ r. We define the resulting s-cone (subspace cone, special cone) as
Clearly, C(S, 0) = S and .
Definition 1. Let C(S, d) be an s-cone. A vector e ∈ C(S, d) is called elementary if it is support-minimal.
For linear subspaces, the definition of elementary vectors (EVs) as SM vectors was given in Rockafellar (1969). For flux cones, where S = ker(N), the definition of elementary modes (EMs) as SM vectors was given in Schuster et al. (2002). Interestingly, the choice of the same adjective for the closely related concepts of elementary vectors and elementary modes was coincidental Schuster (2015).
In the proofs of Theorem 3 and Propositions 4 and 5, we use the following argument.
Lemma 2. Let C(S, d) be an s-cone and x, x′ ∈ C(S, d) be nonzero vectors which are not proportional. If supp(x′) ⊆ supp(x), then there exists a nonzero vector
such that
If sign(x′) ≤ sign(x), then λ > 0 in x″.
Proof. Clearly, x″ = x − λx′ is nonzero for all λ ∈ ℝ. There exists a largest λ > 0 (in case sign(−x′) ≤ sign(x) a smallest λ < 0) such that sign(x″) ≤ sign(x). For this λ, x″ ∈ C(S, d) and supp(x″) ⊂ supp(x). □
For linear subspaces, the following fundamental result was proved in Rockafellar (1969 Theorem 1). We extend it to s-cones.
Theorem 3. Let C(S, d) be an s-cone. Every nonzero vector x ∈ C(S, d) is a conformal sum of EVs. That is, there exists a finite set E ⊆ C(S, d) of EVs such that
The set E can be chosen such that its elements are linearly independent, in particular, they can be ordered such that every e ∈ E has a component which is nonzero in e, but zero in its predecessors (in the ordered set). Then, |E| ≤ dim(S) and |E| ≤ |supp(x)|.
Proof. We proceed by induction on the cardinality of supp(x).
Either, x is SM (and E = {x}) or there exists a nonzero vector x′ ∈ C(S, d) with supp(x′) ⊂ supp(x), but not necessarily with sign(x′) ≤ sign(x). However, by Lemma 2, there exists a nonzero vector x″ ∈ C(S, d) with sign(x″) ≤ sign(x) and supp(x″) ⊂ supp(x). By the induction hypothesis, there exists a SM vector e* with sign(e*) ≤ sign(x″) and hence sign(e*) ≤ sign(x). By Lemma 2 again, there exists a nonzero vector
such that sign(x*) ≤ sign(x) and supp(x*) ⊂ supp(x). By the induction hypothesis, there exists a finite set E* of SM vectors such that
and hence sign(e) ≤ sign(x). We have constructed a finite set E = E* ∪ {λe*} of SM vectors such that
By the induction hypothesis, the set E* can be chosen such that its elements are linearly independent and ordered such that every e ∈ E* has a component which is nonzero in e, but zero in all its predecessors. By construction, λe* has a component which is nonzero, but zero in x* and hence in all e ∈ E*. Obviously, the elements of E = E* ∪ {λe*} are linearly independent and can be ordered accordingly. □
The statement about the support of the EVs was too strong in Rockafellar (1969, Theorem 1). It was claimed that every EV has a nonzero component which is zero in all other EVs.*
Theorem 3 is a conformal refinement of Minkowski's and Carathéodory's theorems for s-cones. In fact, it remains to show that there are finitely many EVs.
Proposition 4. Let C(S, d) be an s-cone. If two SM vectors x, x′ ∈ C(S, d) have the same sign vector, sign(x) = sign(x′), then x = λx′ with λ > 0. As a consequence, there are finitely many SM vectors up to positive scalar multiples.
Proof. Assume there are two SM vectors with the same sign vector which are not proportional. Then, by Lemma 2, there exists a vector with smaller support. □
We conclude by showing that, for s-cones, EVs can be equivalently defined as SM, swND, or cND vectors.
Proposition 5. For an s-cone, support-minimality, support-wise non-decomposability, and conformal non-decomposability are equivalent. That is,
Proof. SM ⇒ swND: By definition.
swND ⇒ cND: Let C(S, d) be an s-cone and assume that x ∈ C(S, d) is conformally decomposable, that is, x = x1 + x2 with nonzero x1, x2 ∈ C(S, d), sign(x1), sign(x2) ≤ sign(x), and x1, x2 being not proportional. By Lemma 2, there exists a nonzero x′ = x − λx1 ∈ C(S, d) such that supp(x′) ⊂ supp(x). Hence supp(x′) ≠ supp(x1), and x = x′ + λx1 is support-wise decomposable.
cND ⇒ SM: Let C(S, d) be an s-cone and assume that x ∈ C(S, d) is not SM, that is, there exists a nonzero x ′ ∈ C(S, d) with supp(x ′) ⊂ supp(x). Then, there exists a largest λ > 0 such that and fulfill sign(x1), sign(x2) ≤ sign(x). For this λ, either supp(x1) ⊂ supp(x) or supp(x2) ⊂ supp(x); in any case, x1, x2 ∈ C(S, d) and supp(x1) ≠ supp(x2). Hence, x = x1 + x2 is conformally decomposable. □
If an s-cone is contained in a closed orthant, then further cND ⇔ EX, and all definitions of special vectors are equivalent.
3.2. General Polyhedral Cones
Let C be a polyhedral cone, that is,
For s-cones, we defined elementary vectors (EVs) via support-minimality which, in this case, turned out to be equivalent to conformal non-decomposability. For general polyhedral cones, only the latter concept allows to extend Theorem 3.
Definition 6. Let C be a polyhedral cone. A vector e ∈ C is called elementary if it is conformally non-decomposable.
In order to apply Theorem 3, we define an s-cone related to a polyhedral cone C. We introduce the subspace
with and the s-cone
Hence,
Moreover, the cND vectors of C and are in one-to-one correspondence.
Lemma 7. Let C = {x ∣ Ax ≥ 0} be a polyhedral cone and the related s-cone. Then,
Proof. First, we show the equivalence of the premises in the definitions of conformal non-decomposability for C and . Indeed,
Assuming x = x1 + x2 with x1, x2 ∈ C (and hence Ax1, Ax2, Ax ≥ 0), we have
It remains to show the equivalence of the conclusions in the two definitions. In fact,
□
Now, we can extend Theorem 3 to general polyhedral cones.
Theorem 8. Let C = {x ∣ Ax ≥ 0} be a polyhedral cone. Every nonzero vector x ∈ C is a conformal sum of EVs. That is, there exists a finite set E ⊆ C of EVs such that
The set E can be chosen such that |E| ≤ dim(C) and |E| ≤ |supp(x)| + |supp(Ax)|.
Proof. Let A ∈ ℝm×r. Define the subspace
and the s-cone
Let x ∈ C be nonzero. By Theorem 3, is a conformal sum of EVs. That is, there exists a finite set of EVs such that
By Lemma 7, the EVs of C and are in one-to-one correspondence. Hence, there exists a finite set ⊆ C of EVs such that
The set Ẽ (and hence E) can be chosen such that and . □
Theorem 8 is a conformal refinement of Minkowski's and Carathéodory's theorems for polyhedral cones. In fact, it remains to show that there are finitely many EVs.
Proposition 9. For a polyhedral cone, there are finitely many cND vectors up to positive scalar multiples.
Proof. Let C be a polyhedral cone and the related s-cone. By Lemma 7, the cND vectors of C and are in one-to-one correspondence. By Proposition 5, the cND and SM vectors of coincide, and by Proposition 4, there are finitely many SM vectors. □
In Urbanczik and Wagner (2005), EVs of a polyhedral cone C were equivalently defined as extreme vectors of intersections of C with closed orthants of maximal dimension. Indeed, the following equivalence holds for closed orthants, not necessarily of maximal dimension.
Proposition 10. Let C ⊆ ℝr be a polyhedral cone, x ∈ C, and O ⊂ ℝr a closed orthant with x ∈ O. Then,
Proof. We show the equivalence of the premises in the definitions of conformal non-decomposability for C and extremity for C ∩ O. (The conclusions are identical.) Indeed, assuming x = x1 + x2, we have
□
3.3. Polyhedra
Let P be a polyhedron, that is,
In order to extend Theorem 3 to polyhedra, we introduce corresponding special vectors.
3.3.1. Special Vectors
Let P be a polyhedron. A vector x ∈ P is called
• a vertex, if
• and convex-conformally non-decomposable, if
From the definitions, we have
For a polyhedral cone, we defined elementary vectors (EVs) via conformal non-decomposability. For a polyhedron, we require two sorts of EVs: convex-conformally non-decomposable vectors of the polyhedron and conformally non-decomposable vectors of its recession cone.
Definition 11. Let P = {x ∈ ℝr ∣ Ax ≥ b} be a polyhedron and Cr = {x ∈ ℝr ∣ Ax ≥ 0} its recession cone. A vector e ∈ Cr ∪ P is called an elementary vector of P if either e ∈ Cr is conformally non-decomposable or e ∈ P is convex-conformally non-decomposable.
In order to apply Theorem 3, we define an s-cone related to a polyhedron P = {x ∈ ℝr ∣ Ax ≥ b}. We introduce the homogenization
of the polyhedron, the subspace
with , and the s-cone
Hence,
Moreover, the cND vectors of Cr and the ccND vectors of P (as the cND vectors of Ch) are in one-to-one correspondence with the cND vectors of .
Lemma 12. Let P = {x ∣ Ax ≥ b} be a polyhedron, Cr = {x ∣ Ax ≥ 0} its recession cone, and
the related s-cone. Then,
and
Proof. See Appendix. □
Now, we can extend Theorem 3 to polyhedra.
Theorem 13. Let P = {x ∣ Ax ≥ b} be a polyhedron and Cr = {x ∣ Ax ≥ 0} its recession cone. Every vector x ∈ P is a conformal sum of EVs. That is, there exist finite sets and E1 ⊆ P of EVs such that
λe ≥ 0, and . (Hence, |E1| ≥ 1.)
The set E = E0 ∪ E1 can be chosen such that |E| ≤ dim(P) + 1 and |E| ≤ |supp(x)| + |supp(Ax)| + 1.
Proof. By defining an s-cone related to P, applying Theorem 3, and using Lemma 12. See Appendix. □
Theorem 13 is a conformal refinement of Minkowski's and Carathéodory's theorems for polyhedra. In fact, it remains to show that there are finitely many EVs.
Proposition 14. For a polyhedron, there are finitely many ccND vectors.
Proof. Let P be a polyhedron and the related s-cone. By Lemma 12, the ccND vectors of P are in one-to-one correspondence with a subset of cND vectors of . By Proposition 5, the cND and SM vectors of coincide, and by Proposition 4, there are finitely many SM vectors. □
EVs of a polyhedron P can be equivalently defined as vertices of intersections of P with closed orthants.
Proposition 15. Let P ⊆ ℝr be a polyhedron, x ∈ P, and O ⊂ ℝr a closed orthant with x ∈ O. Then,
Proof. We show the equivalence of the premises in the definitions of convex-conformal non-decomposability for P and of a vertex for P ∩ O. (The conclusions are identical.) Indeed, assuming x = λx1 + (1 − λ)x2 with 0 < λ < 1, we have
□
We conclude by noting that Theorem 8 is a special case of Theorem 13. If a polyhedron is also a cone, then P = Cr, E1 = {0}, and . However, we do not use Theorem 8 to prove Theorem 13. In classical proofs of Minkowski's and Carathéodory's theorems, one first studies polyhedral cones and then extends the results to polyhedra by a method called homogenization/dehomogenization; (see e.g., Ziegler, 1995).
3.4. Minimal Generating Sets
For a pointed polyhedral cone, the extreme rays form a minimal set of generators with respect to addition. The set is minimal in the sense that no proper subset forms a generating set and minimal in the even stronger sense that it is contained in every other generating set. Hence, the extreme rays form a unique minimal set of generators.
For a general polyhedral cone, there are minimal sets of generators (minimal in the sense that no proper subset forms a generating set), but there is no unique minimal generating set. However, there is a unique minimal set of conformal generators, namely the set of elementary vectors.
Recall that elementary vectors of a polyhedral cone are defined as conformally non-decomposable vectors. Indeed, every nonzero element of a polyhedral cone is a conformal sum of elementary vectors (Theorem 8), and every elementary vector is contained in a set of conformal generators.
We make the above argument more formal.
Definition 16. Let C be a polyhedral cone. A subset G ⊆ C is called a conformal generating set if (i) every nonzero vector x ∈ C is a conformal sum of vectors in G, that is, if there exists a finite set Gx ⊂ G such that
and (ii) if λ G = G for all λ > 0.
Proposition 17. Let C be a polyhedral cone, E ⊆ C the set of elementary vectors, and G ⊆ C a conformal generating set. Then, E ⊆ G.
Proof. Let e ∈ C be an elementary vector. Since G is a conformal generating set, we have
where we choose a nonzero and write . If |Ge| = 1, then h = 0 and e = g* ∈ G. Otherwise, since e is an elementary vector (a cND vector), we have h = λg* with λ > 0 and hence e = (1 + λ)g* ∈ G. □
Analogously, for a polyhedron, there is a unique minimal set of conformal generators, namely the set of elementary vectors.
3.5. Examples
We illustrate our results by examples of polyhedral cones and polyhedra in two dimensions, and we return to the running example from the introduction.
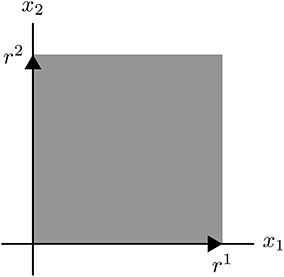
Example 1. The s-cone C = {x ∣ x1 ≥ 0, x2 ≥ 0}.
Its EVs (SM vectors) are elements of the rays and (indicated by arrows). Every nonzero vector x ∈ C is a conformal sum of EVs. That is,
where e1 ∈ r1 and e2 ∈ r2.
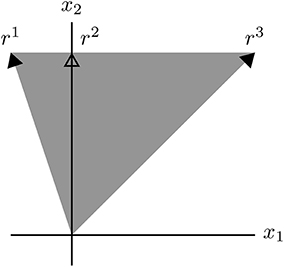
Example 2. The general polyhedral cone
Its EVs (cND vectors) are elements of the rays r1, r2, and r3. Note that r2 is not an extreme ray of C, but an extreme ray of , the intersection of the cone with the nonnegative orthant. Every nonzero vector x ∈ C is a conformal sum of EVs. In particular, if , then
where e2 ∈ r2 and e3 ∈ r3.
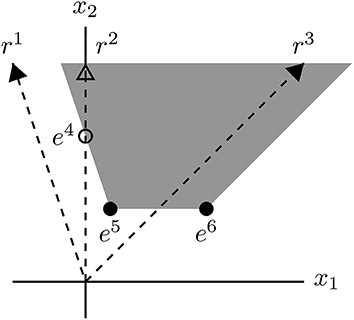
Example 3. The polyhedron
Its EVs are elements of the rays r1, r2, and r3 (cND vectors of the recession cone) and the vectors e4, e5, and e6 (ccND vectors of the polyhedron). Note that e4 is not a vertex of P, but a vertex of , the intersection of the polyhedron with the nonnegative orthant. Every vector x ∈ P is a conformal sum of EVs. In particular, if , then
where e2 ∈ r2, e3 ∈ r3 and λ4, λ5, λ6 ≥ 0 with λ4 + λ5 + λ6 = 1.
Finally, we return to the running example from the introduction. We restate the underlying network, the corresponding stoichiometric matrix and the resulting flux cone:
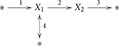
Its EVs (SM vectors) are
and their positive multiples. In other words, the EVs are elements of the rays r1 = {λe1 ∣ λ > 0}, r2 = {λe2 ∣ λ > 0}, and r3 = {λe3 ∣ λ > 0}.
The flux cone is defined by the stoichiometric matrix and the set of irreversible reactions. If additionally lower/upper bounds for the fluxes through certain reactions are known, then one is interested in the resulting flux polyhedron. In the example, we add an upper bound for the flux through reaction 1, in particular, we require f1 ≤ 2 and obtain the flux polyhedron
Its EVs are elements of the ray r2 = {λe2 ∣ λ > 0} (cND vectors of the recession cone) and the vectors e1, e3, e4 (ccND vectors of the polyhedron), where
Note that e3 is not a vertex of P, but a vertex of , the intersection of the polyhedron with the nonnegative orthant. Every vector x ∈ P is a conformal sum of EVs. In particular, if , then
where λ1, λ3, λ4 ≥ 0 with λ1 + λ3 + λ4 = 1. In other words, the polyhedron is a polytope.
In applications such as computational strain design, the set of EVs (the unique minimal set of conformal generators) is often more useful than a minimal set of generators. In the example, the set of EVs includes e3 which is a ccND vector, but not a vertex of P. If we delete reaction 4 by gene knockout, the new set of EVs consists of e3 and e4 (having zero flux through reaction 4), and the resulting flux polyhedron is the polytope generated by e3 and e4. Most importantly, we obtain the result without recalculating the set of generators (after deleting reaction 4).
4. Discussion
Metabolic pathway analysis aims to identify meaningful routes in a network, in particular, to decompose fluxes into minimal metabolic pathways. However, only a decomposition without cancelations is biochemically meaningful, since a reversible reaction cannot have a flux in different directions at the same time.
In mathematical terms, one is interested in a conformal decomposition of the flux cone and of general polyhedral cones and polyhedra. In this work, we first study s-cones (like the flux cone) arising from a linear subspace and nonnegativity conditions. Then, we analyze general polyhedral cones and polyhedra via corresponding higher-dimensional s-cones. Without assuming previous knowledge of polyhedral geometry, we provide an elementary proof of a conformal refinement of Minkowski's and Carathéodory's theorems (Theorems 3, 8, and 13): Every vector (of an s-cone, a general polyhedral cone, or a polyhedron) is a conformal sum of elementary vectors (conformally non-decomposable vectors), and there is an upper bound on the number of elementary vectors needed in a conformal decomposition (in terms of the dimension of the cone or polyhedron).
As a natural next question, one may ask: what is a minimal generating set of a polyhedral cone that allows a conformal decomposition of every vector? Clearly, such a set must contain all conformally non-decomposable vectors. Indeed, we show that the elementary vectors form a unique minimal set of conformal generators (Proposition 17). In metabolic pathway analysis, the question is: what is a minimal generating set of the flux cone that allows a biochemically meaningful decomposition of every flux mode? In this case, the elementary modes form a unique minimal set of generators without cancelations. This property distinguishes elementary modes as a fundamental concept in metabolic pathway analysis and may serve as a definition.
The correspondence of general polyhedral cones and polyhedra to higher-dimensional s-cones has also important consequences for the computation of elementary vectors. In particular, it allows to use efficient algorithms and software developed for elementary modes (see e.g., Zanghellini et al., 2013 and the references therein) for computing elementary vectors of general polyhedral cones and polyhedra.
In applications, decompositions without cancelations were first used in the study of the conversion cone Urbanczik and Wagner (2005), a general polyhedral cone obtained by flux cone projection Marashi et al. (2012). The approach was extended to polyhedra arising from the flux cone and inhomogeneous constraints, in particular, to describe the solution set of linear optimization problems encountered in flux balance analysis Urbanczik (2007). In analogy to s-cones, these sets could be called s-polyhedra. Recently, elementary vectors have been used to describe such polyhedra in the study of growth-coupled product synthesis Klamt and Mahadevan (2015). Interestingly, conformal decompositions of the flux cone itself appeared rather late. In fact, they have been used to characterize optimal solutions of enzyme allocation problems in kinetic metabolic networks Müller et al. (2014).
Minkowski's and Carathéodory's theorems (and their conformal refinements) are fundamental results in polyhedral geometry with important applications in metabolic pathway analysis. In subsequent work, we plan to revisit other results from polyhedral geometry and oriented matroids (like Farkas' lemma) and investigate their consequences for metabolic pathway analysis.
Author Contributions
The authors contributed equally to the work and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors acknowledge helpful comments from three reviewers. SM was supported by the Austrian Science Fund (FWF), project P28406. GR was supported by the FWF, project P27229.
Footnotes
* ^For a counterexample, consider the subspace S = ker(1, −1, −1, 1) ⊆ ℝ4. Its nonnegative EVs are
and their positive multiples. Then x = (1, 2, 3, 4)T is not a conformal sum of EVs with the claimed property. (Every conformal decomposition of x consists of at least 3 EVs, and every set of 3 EVs contains 1 EV which does not have a nonzero component which is zero in the other EVs.)
References
Bachem, A., and Kern, W. (1992). Linear Programming Duality. An Introduction to Oriented Matroids. Berlin: Springer-Verlag.
Carathéodory, C. (1911). Über den Variabilitätsbereich der Fourierschen Konstanten von positiven harmonischen Funktionen. Rend. Circ. Mat. Palermo, 32, 193–217.
Klamt, S., and Mahadevan, R. (2015). On the feasibility of growth-coupled product synthesis in microbial strains. Metab. Eng. 30, 166–178. doi: 10.1016/j.ymben.2015.05.006
Klamt, S., and Stelling, J. (2003). Two approaches for metabolic pathway analysis? Trends Biotechnol. 21, 64–69. doi: 10.1016/S0167-7799(02)00034-3
Llaneras, F., and Picó, J. (2010). Which metabolic pathways generate and characterize the flux space? A comparison among elementary modes, extreme pathways and minimal generators. J. Biomed. Biotechnol. 2010:753904. doi: 10.1155/2010/753904
Marashi, S.-A., David, L., and Bockmayr, A. (2012). Analysis of metabolic subnetworks by flux cone projection. Algorithms Mol. Biol. 7:17. doi: 10.1186/1748-7188-7-17
Müller, S., Regensburger, G., and Steuer, R. (2014). Enzyme allocation problems in kinetic metabolic networks: optimal solutions are elementary flux modes. J. Theor. Biol. 347, 182–190. doi: 10.1016/j.jtbi.2013.11.015
Rockafellar, R. T. (1969). “The elementary vectors of a subspace of RN,” in Combinatorial Mathematics and its Applications (Proc. Conf., Univ. North Carolina, Chapel Hill, N.C., 1967) (Chapel Hill, NC: Univ. North Carolina Press), 104–127.
Schuster, S., and Hilgetag, C. (1994). On elementary flux modes in biochemical reaction systems at steady state. J. Biol. Syst. 2, 165–182.
Schuster, S., Hilgetag, C., Woods, J. H., and Fell, D. A. (2002). Reaction routes in biochemical reaction systems: algebraic properties, validated calculation procedure and example from nucleotide metabolism. J. Math. Biol. 45, 153–181. doi: 10.1007/s002850200143
Urbanczik, R. (2007). Enumerating constrained elementary flux vectors of metabolic networks. IET Syst. Biol. 1, 274–279. doi: 10.1049/iet-syb:20060073
Urbanczik, R., and Wagner, C. (2005). Functional stoichiometric analysis of metabolic networks. Bioinformatics 21, 4176–4180. doi: 10.1093/bioinformatics/bti674
Zanghellini, J., Ruckerbauer, D. E., Hanscho, M., and Jungreuthmayer, C. (2013). Elementary flux modes in a nutshell: properties, calculation and applications. Biotechnol. J. 8, 1009–1016. doi: 10.1002/biot.201200269
Appendix
We prove the main results for polyhedra, Lemma 12 and Theorem 13.
Proof of Lemma 12. To prove the first equivalence, we note that is cND if and only if ∈ C′ is cND, where C′ = { ∈ ℝr+m ∣ Ax ≥ 0}, and apply Lemma 7.
To prove the second equivalence, we show the two implications separately:
(⇒) We assume that x ∈ P is ccND and first consider a conformal sum of the form
with x1 ∈ P, nonzero x2 ∈ Cr, and sign(x1), sign(x2) ≤ sign(x). Indeed, we also have with x1, x1 + 2x2 ∈ P and sign(x1), sign(x1 + 2x2) ≤ sign(x). By the assumption, x1 = x1 + 2x2, that is, x2 = 0, and it remains to consider a conformal sum of the form
with x1, x2 ∈ P, sign(x1), sign(x2) ≤ sign(x), and 0 < λ < 1. By the assumption, x1 = x2, and the first vector in the sum is a positive multiple of the second. That is,
with μ > 0. Hence, is cND.
(⇐) We assume that is cND and consider the convex-conformal sum
with x1, x2 ∈ P, sign(x1), sign(x2) ≤ sign(x), and 0 < λ < 1. Hence, we also have the conformal sum (+). By the assumption, we have equation (*) which implies x1 = x2. Hence, x ∈ P is ccND. □
Proof of Theorem 13. Let A ∈ ℝm×r and b ∈ ℝm. Define the homogenization
the subspace
and the s-cone
Let x ∈ P. By Theorem 3, is a conformal sum of EVs. That is, there exist finite sets of (normalized) EVs such that
with
λe ≥ 0, and . By Lemma 12, the EVs of P are in one-to-one correspondence with the EVs of . Hence, there exist finite sets and E1 = {e ∣ ∈ Ẽ1} ⊆ P of EVs such that
The set Ẽ = Ẽ0 ∪ Ẽ1 (and hence E = E0 ∪ E1) can be chosen such that and |E| = |Ẽ| ≤ |supp| = |supp(x)| + 1 +|supp(Ax − b)|. □
Keywords: Minkowski's theorem, Carathéodory's theorem, s-cone, polyhedral cone, polyhedron, conformal generators
Citation: Müller S and Regensburger G (2016) Elementary Vectors and Conformal Sums in Polyhedral Geometry and their Relevance for Metabolic Pathway Analysis. Front. Genet. 7:90. doi: 10.3389/fgene.2016.00090
Received: 29 November 2015; Accepted: 02 May 2016;
Published: 24 May 2016.
Edited by:
Alberto Marin-Sanguino, Technical University of Munich, GermanyReviewed by:
Jesus Picó, Universitat Politècnica de València, SpainRuriko Yoshida, University of Kentucky, USA
Carsten Wiuf, University of Copenhagen, Denmark
Copyright © 2016 Müller and Regensburger. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefan Müller, c3RlZmFuLm11ZWxsZXJAcmljYW0ub2Vhdy5hYy5hdA==
 Stefan Müller
Stefan Müller Georg Regensburger
Georg Regensburger