- 1Department of Statistical Science, School of Mathematics, Sun Yat-sen University, Guangzhou, China
- 2Center for Quantitative Medicine, Duke-National University of Singapore Medical School, Singapore, Singapore
- 3Department of Biostatistics, Harvard T.H. Chan School of Public Health, Harvard University, Boston, MA, United States
In recent years, a number of literatures published large-scale genome-wide association studies (GWASs) for human diseases or traits while adjusting for other heritable covariate. However, it is known that these GWASs are biased, which may lead to biased genetic estimates or even false positives. In this study, we provide a method called “BTOB” which extends the biased GWAS to bivariate GWAS by integrating the summary association statistics from the biased GWAS and the GWAS for the adjusted heritable covariate. We employ the proposed BTOB method to analyze the summary association statistics from the large scale meta-GWASs for waist-to-hip ratio (WHR) and body mass index (BMI), and show that the proposed approach can help identify more susceptible genes compared with the corresponding univariate GWASs. Theoretical results and simulations also confirm the validity and efficiency of the proposed BTOB method.
1. Introduction
Genome-wide association studies (GWASs) have been greatly successful in identifying tens of thousands susceptible genes for complex diseases or traits, revealing the genetic architectures of complex diseases or traits in question (Visscher et al., 2012, 2017). These large scale studies produce extremely valuable resource for further studies. However, due to the privacy concerns and other logistical considerations, most GWASs publish the summary association statistics rather than the individual-level data. This limitation motivates the rapid development of developing methods for analyzing the summary association statistics, such as conditional association analysis (Yang et al., 2012), gene-based association tests (Hu et al., 2013; Lee et al., 2013), jointly analyzing multiple traits (Zhu et al., 2015; Liu and Lin, 2018; Ray and Michael, 2018). A recent publication systematically reviews the development of summary association statistics-based methods (Pasaniuc and Price, 2017).
In this study, we mainly focus on the summary association statistics obtained from the GWASs of human diseases or traits while adjusting for heritable covariate, such as the GWAS of waist-to-hip ratio (WHR) after adjusting for BMI (Heid et al., 2010; Randall et al., 2013), the GWAS of fasting glycemic traits and insulin resistance after adjusting for BMI (Manning et al., 2012). However, it has been known that the results from these GWASs are biased, which may result in biased genetic estimates or even false positive genetic discoveries (Aschard et al., 2015). If the aim is to increase the statistical power, it is suggested to use the bivariate analyse of the trait (or disease) of interest and the corresponding heritable covariate (Aschard et al., 2015). However, the practical issue is still under addressed for this suggestion, that is how to extend the existing the biased GWAS to the bivariate analyse. Recent efforts have indicated that the multivariate GWAS can be conducted based on summary association statistics of the univariate GWASs (Zhu et al., 2015; Liu and Lin, 2018; Ray and Michael, 2018). However, these methods require the summary association statistics from the unbiased GWASs, that is the univariate GWASs without adjusting the heritable covariate. In reality, many studies only have the results from the GWAS after adjusting the heritable covariate. For example, in the GIANT (Genetic Investigation of ANthropometric Traits) consortium website, we can only download the summary association statistics for WHR adjusted BMI stratified by sex and age (Winkler et al., 2015). To obtain the results for WHR without adjusting for BMI, it needs to re-run a GWAS, which needs a great effort. To our best knowledge, there are no literatures addressing how to extend the biased GWAS to the bivariate GWAS.
In this paper, we develop a simple integration method called BTOB which extends the Biased GWAS TO Bivariate GWAS. We assess the valid and efficiency of BTOB using theoretical arguments and simulation studies. Finally, we apply the BTOB method to analyze the data downloaded from the GIANT consortium website.
2. Method
2.1. BTOB: Extending the Biased GWAS to Bivariate GWAS
Mathematically, the model used in the biased GWAS can be formulated as Y2 = Gβ2 + Y1γ1 + Z2ς2 + ε2, where Y2 is the trait or disease of interest, Y1 is the adjusted heritable covariate, G is the genotype score, and Z2 is the adjusted non-heritable covariates. In reality, many studies also had conducted additional GWAS for Y1, that is Y1 = Gβ1 + Z1ς1 + ε1. For example, the GIANT consortium had conducted the GWASs for WHR while adjusting for BMI, and the GWASs of BMI (Winkler et al., 2015). In addition, it is common that partial sample overlap between these two GWASs. For example, the sample size of the GWAS for BMI in men cohort with age greater than 50 is about 90,000, while the corresponding GWAS for WHR after adjusting BMI only use a sub-sample with about 60,000 sample. And the two studies may use different covariates adjustment strategies. In conclusion, the above real scenarios can be formulated as follows
Where and are the overlap sample of two phenotypes with genotypes Gc, is the unique sample only used in first model with genotypes , and and are the unique sample only used in second model with genotypes . Z1 and Z2 includes the intercept and covariates, which may consider different covariates for different GWAS. In Supplementary Theorem 1, we show that the estimates of the genetic effects and are independent. Under the null hypothesis H0: none of Y1 and Y1 associates with G, we have . Therefore, we can simply integrate the summary association statistics in model (1) and (2), that is
which is a test statistics about testing the null hypothesis H0: none of Y1 and Y2 associates with G. Hence the proposed procedure extends the biased GWAS to bivariate analyse, which is termed BTOB (extends the Biased GWAS to Bivariate GWAS).
2.2. Simulations
We simulate 1,000 replicates of correlated traits, the causal SNP G is generated with minor allele frequency of 0.3 assuming the Hardy Weinberg equilibrium. The traits are generated using a linear additive model
where follows multivariate normal distribution with mean 0 and covariance matrix Σ. We set the sample size of Y1 to be 5,000, and then vary the sample size of Y2 to be 5,000, 4,000, and 3,000. We consider three scenarios:(1) The tested variant affects the bivariate traits in the same direction. The tested variant explains 0.5% of the variance of Y1 and 0 to 0.5% of the variance of Y2, or the tested variant explains 0.5% of the variance of Y2 and 0 to 0.5% of the variance of Y1. The correlation was set to be low (ρ = 0.4), moderate (ρ = 0.6), or high (ρ = 0.8), where ρ was the correlation coefficient between Y1 and Y2. (2) The tested variant affects one phenotype only. Specifically, we considered the following two scenarios: the tested variant explains 0.5% of the variance of Y1 and 0% of the variance of Y2, or the tested variant explains 0.5% of the variance of Y2 and 0% of the variance of Y1. The correlation coefficient between Y1 and Y2 is varied from −0.9 to 0.9. (3) The test variant affects the bivariate traits in the opposite directions. The tested variant explains 0.3% of the variance of Y1 and 0.4% of the variance of Y2 with the opposite directions, or the tested variant explains 0.4% of the variance of Y1 and 0.3% of the variance of Y2 with the opposite direction. The correlation between Y1 and Y2 is varied from 0 to 0.9.
2.3. Study Decription
We download the gender and age specific summary association statistics for WHR after adjustment for BMI, and the marginal summary association statistics of BMI by the GIANT consortium from website http://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files (Winkler et al., 2015). We integrated the summary association statistics from the following univariate GWASs stratified by age and gender: BMI~SNP, WHR~SNP+BMI, resulting in the bivariate analysis of WHR and BMI. The aim of this study is to assess whether the proposed BTOB approach can contribute novel gene compared with the corresponding univariate GWASs. Hence, the gene is considered to be novel if the lead SNP in (or 400 KB flanking) a gene is genome-wide significant in the bivariate analysis, whereas none of the lead SNPs in (or 400 KB flanking) this gene reach genome-wide significance in the corresponding univariate GWASs. As we can only assess the HapMap II allele frequencies instead of pooled allele frequencies across all cohorts, we only included SNPs with sample size greater than 30,000, for which the HapMap allele frequencies may be representative.
3. Result
3.1. The Performance of BTOB in Integrating the Summary Association Statistics
For illustrate purpose, we conducted simulation studies to investigate the validity and efficiency of the proposed BTOB. As a comparison, we include the MANOVA method (Ray et al., 2016). Since MANOVA is not directly applicable to the summary association data, we use the overlap sample and re-run the multivariate association analysis using the MANOVA.
Supplementary Table 1 presents the type 1 error for BTOB, which shows that the proposed BTOB can control the type 1 error rate quite well. Figure 1 presents the power comparisons when the tested variant affects the bivariate phenotypes in the same direction. The tested variant explains 0.5% of the variance of Y1 and 0 to 0.5% of the variance of Y2. We can observe from Figure 1 that BTOB and MANOVA have nearly the same power when both phenotypes have the sample size 5,000, which indicates the validity and efficiency for BTOB. However, as the overlap sample size is set to be 4,000, BTOB performs much better than MANOVA. When the overlap sample size is set to be 3,000, the power discrepancy between BTOB and MANOVA is more obvious. This is expected as the sample size used in GWAS: Y1 = μ1 + β1G+Z1ς1 + ε1 is often larger than the sample size used in GWAS: Y2 = β2G+Y1γ1 + Z2ς2 + ε2. Traditional multivariate approaches, such as MANOVA, are only applicable to the overlap sample between Y1 and Y2. However, the proposed BTOB can make full use of the whole sample for Y1, hence boosting the power compared with MANOVA. The same phenomenons can be observed in Figures 1B,C with median and high correlation. In Figure 1, we also compare the power between the bivariate analysis and the univariate analysis after the Bonferroni correction. We can observe from Figure 1 that BTOB approach performs better than the univariate approach in most scenarios. It should be noted that there is a decrease of power for BTOB when the proportion of the test variant's variance for Y2 varies from 0 to a reasonably small value. This counterintuitive phenomenon can be explained by using the theoretical results given in a recent work (Guo et al., 2018). Supplementary Figures 1–3 present the power comparison for two other scenarios: the tested variant affects one trait only, and the tested variant affects the bivariate traits in the opposite direction. All of the simulated results indicate the superior performance for BTOB compared with MANOVA when the overlap sample size is set to be 4,000 and 3,000, and the superior power for BTOB compared with univariate analysis in most scenarios.
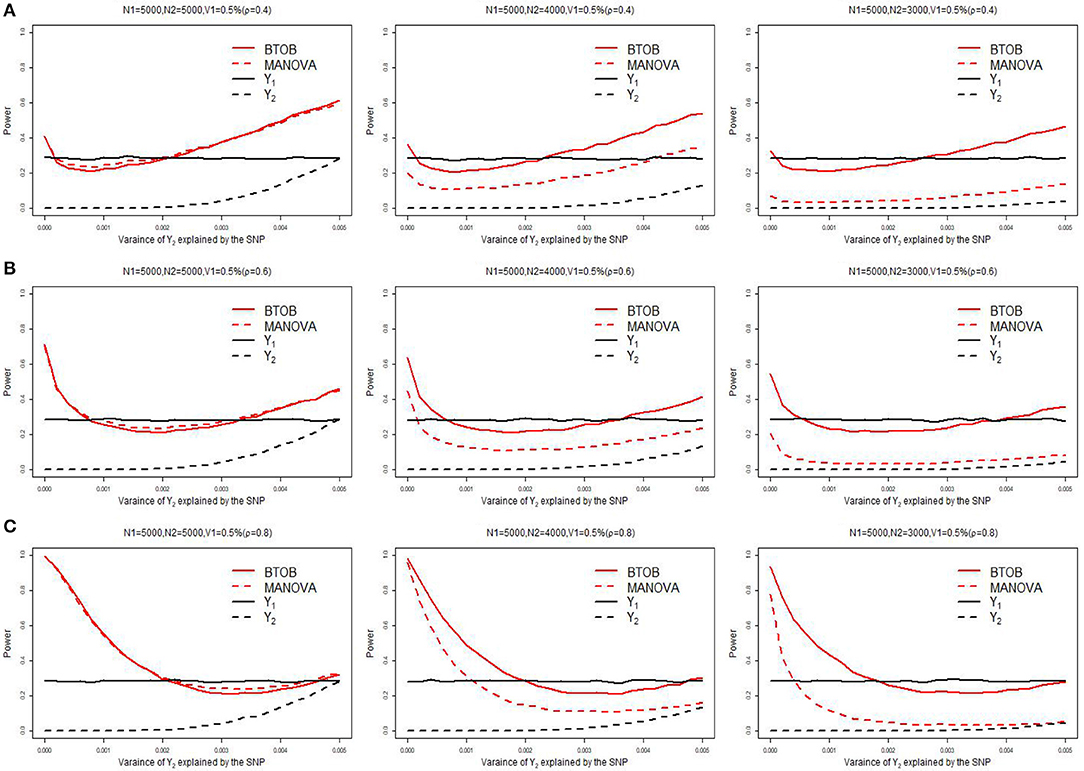
Figure 1. Power comparison of BTOB, MANOVA, and the univariate analysis. The test variant explains 0.5% of the variance of Y1, and the proportion of the test variant's variance for Y2 varies from 0 to 0.5%. The genetic effects of Y1 and Y2 are with the same direction. The sample size of Y1 is 5,000, and the sample size of Y2 is set to be 5,000, 4,000 and 3,000, respectively. Three levels of correlation between Y1 and Y2 are investigated: low correlation with ρ = 0.4 (A), moderate correlation with ρ = 0.6 (B), and high correlation with ρ = 0.8 (C).
3.2. Real Data Analysis
In total, 8 loci are novel compared with the univariate GWASs: 4 for bivariate analysis of WHR and BMI in the cohort of men aged over 50, and 4 for bivariate analysis of WHR and BMI in the cohort of women aged over 50 (Table 1). The genomic control (GC) inflation factors of these 4 bivariate analyses is presented in Supplementary Table 2.
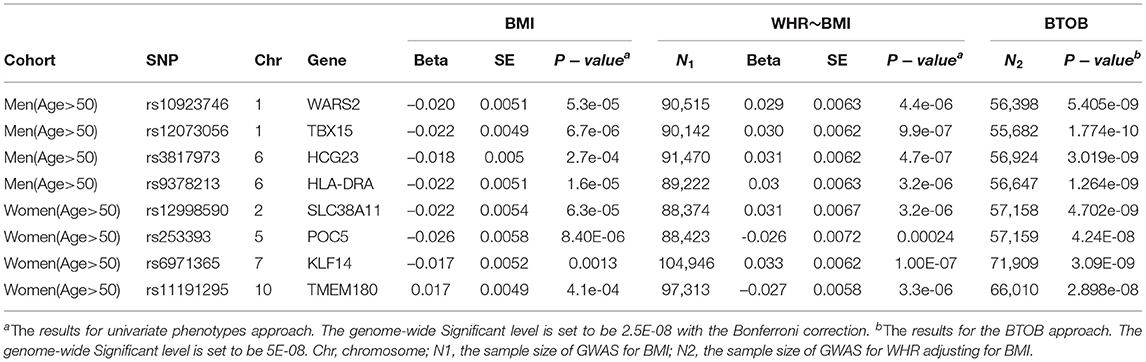
Table 1. The novel Genome-wide Significant loci which were identified by the proposed combining method but not found by the standard univariate approach for the analysis of WHR and BMI.
Firstly, for the analyses of WHR and BMI in the cohort of women aged over 50, we identified 4 novel genes compared with the univariate GWASs (WARS2, leading SNP: rs10923746, p-value = 5.405E-09; TBX15, leading SNP: rs10923715, p-value = 4.88E-11; HCG23, leading SNP: rs3817973, p-value = 3.019e-09; HLA-DRA, leading SNP: rs9378213, p-value = 1.264e-09) (Table 1). Even though these 4 leading SNPs show evidence of association in the univariate analyses: GWAS for WHR after adjusting BMI and GWAS for BMI, these univariate analyses have no enough power to reach the genome-wide significance. What is more, for the analyse of WHR and BMI in the cohort of women aged over 50, BTOB method identified 4 novel loci compared with the univariate GWASs (SLC38A11, leading SNP: rs12998590, p-value = 4.702e-09; POC5, leading SNP: rs253393, p-value = 4.24E-08; KLF14, leading SNP: rs6971365, p-value = 3.09E-09; TMEM180, leading SNP: rs11191295, p-value = 2.898e-08) (Table 1). The real data analysis suggested that the BTOB method is capable to integrate moderate signals from the corresponding univariate analyses, hence leading to the identification of novel genetic signals compared with the univariate analyses. Further, six identified loci from the BTOB method, including TBX15, WARS2, POC5, KLF14, HLA-DRA, SLC38A11, were confirmed in the follow-up GWASs with at least ten times larger sample size (Pulit et al., 2019; Zhu et al., 2020), suggesting BTOB can help identify novel genes in the GWASs when the sample size is limited.
Finally, several studies have suggested a potential causal role of these identified genes in adipose development and function. For example, animal models have demonstrated that the important role of WARS2 in regulating brown adipose tissue function and consequently lipid and glucose metabolism, by regulating mitochondrial respiration, leading to the increased glucose oxidation in brown adipose tissues (Pravenec et al., 2017; Ejarque et al., 2019). TBX15 encodes a T-box transcription factor (TF) that has shown to be involved in various aspects of adipose development and maintenance, also to be associated with body fat distribution (Singh et al., 2005; Zhang et al., 2020). It has also been implicated the transcription factor KLF14, a member of the Krupple-like factor family (KLF), plays a key role in energy homeostasis by regulating lipid and glucose metabolism, and adipogenesis via promoting adipocyte differentiation (Chen et al., 2005; Birsoy et al., 2008).
4. Discussion
There are several concerns that should be noted about multivariate approaches in GWAS. First, the proposed bivariate method or other multivaraite methods for summary association statistics from univariate GWASs have been shown to help identify novel genes compared with univariate GWASs. While the multivariate approaches can also fails some genes identified in the univariate GWASs. Hence, the multivaraite GWASs should be considered as a valuable compensation rather substitution for univariate GWASs. Second, there is no single multivariate method that is uniformly most powerful in all scenarios. Hence, it is valuable to try several candidate methods in real case.
In summary, our proposed approach provides an efficient shortcut for extending the existing biased GWASs to the bivariate GWAS. Considering a great amount of large scale biased GWASs have been published (Hancock et al., 2010; Kaplan et al., 2011; Randall et al., 2013; Loth et al., 2014; Winkler et al., 2015; Pulit et al., 2019; Zhu et al., 2020), the proposed BTOB method is expected to be of great practical utility.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Author Contributions
XG conceived the idea and conducted the simulation. JZ, WD, YW, and QF processed the data and conducted the real dataset experiments. XG and QF wrote the manuscript. XG, QF, JZ, and WD revised the manuscript. All authors read and approved the final manuscript.
Funding
XG's research was supported by the NSFC (11771463), the Pearl River S&T Nova Program (201806010142).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2021.654821/full#supplementary-material
References
Aschard, H., Vilhjálmsson, B. J., Joshi, A. D., Price, A. L., and Kraft, P. (2015). Adjusting for heritable covariates can bias effect estimates in genome-wide association studies. Am. J. Hum. Genet. 96, 329–339. doi: 10.1016/j.ajhg.2014.12.021
Birsoy, K., Chen, Z., and Friedman, J. (2008). Transcriptional regulation of adipogenesis by klf4. Cell Metab. 7, 39–347. doi: 10.1016/j.cmet.2008.02.001
Chen, Z., Torrens, J. I., Anand, A., Spiegelman, B. M., and Friedman, J. M. (2005). Krox20 stimulates adipogenesis via c/ebpβ-dependent and-independent mechanisms. Cell Metab. 1, 93–106. doi: 10.1016/j.cmet.2004.12.009
Ejarque, M., Ceperuelo-Mallafré, V., Serena, C., Maymo-Masip, E., Duran, X., Díaz-Ramos, A., et al. (2019). Adipose tissue mitochondrial dysfunction in human obesity is linked to a specific DNA methylation signature in adipose-derived stem cells. Int. J. Obes. 43, 1256–1268. doi: 10.1038/s41366-018-0219-6
Guo, X., Zhu, J., Fan, Q., He, M., Wang, X., and Zhang, H. (2018). A univariate perspective of multivariate genome-wide association analysis. Genet. Epidemiol. 42, 470–479. doi: 10.1002/gepi.22128
Hancock, D. B., Eijgelsheim, M., Wilk, J. B., Gharib, S. A., Loehr, L. R., Marciante, K. D., et al. (2010). Meta-analyses of genome-wide association studies identify multiple loci associated with pulmonary function. Nat. Genet. 42:45. doi: 10.1038/ng.500
Heid, I. M., Jackson, A. U., Randall, J. C., Winkler, T. W., Qi, L., Steinthorsdottir, V., et al. (2010). Meta-analysis identifies 13 new loci associated with waist-hip ratio and reveals sexual dimorphism in the genetic basis of fat distribution. Nat. Genet. 42, 949–960. doi: 10.1038/ng.685
Hu, Y.-J., Berndt, S. I., Gustafsson, S., Ganna, A., Mägi, R., Wheeler, E., et al. (2013). Meta-analysis of gene-level associations for rare variants based on single-variant statistics. Am. J. Hum. Genet. 93, 236–248. doi: 10.1016/j.ajhg.2013.06.011
Kaplan, R. C., Petersen, A.-K., Chen, M.-H., Teumer, A., Glazer, N. L., Döring, A., et al. (2011). A genome-wide association study identifies novel loci associated with circulating igf-i and igfbp-3. Hum. Mol. Genet. 20, 1241–1251. doi: 10.1093/hmg/ddq560
Lee, S., Teslovich, T. M., Boehnke, M., and Lin, X. (2013). General framework for meta-analysis of rare variants in sequencing association studies. Am. J. Hum. Genet. 93, 42–53. doi: 10.1016/j.ajhg.2013.05.010
Liu, Z., and Lin, X. (2018). Multiple phenotype association tests using summary statistics in genome-wide association studies. Biometrics 74, 165–175. doi: 10.1111/biom.12735
Loth, D. W., Artigas, M. S., Gharib, S. A., Wain, L. V., Franceschini, N., Koch, B., et al. (2014). Genome-wide association analysis identifies six new loci associated with forced vital capacity. Nat. Genet. 46, 669–677. doi: 10.1038/ng.3011
Manning, A. K., Hivert, M.-F., Scott, R. A., Grimsby, J. L., Bouatia-Naji, N., Chen, H., et al. (2012). A genome-wide approach accounting for body mass index identifies genetic variants influencing fasting glycemic traits and insulin resistance. Nat. Genet. 44, 659–669. doi: 10.1038/ng.2274
Pasaniuc, B., and Price, A. L. (2017). Dissecting the genetics of complex traits using summary association statistics. Nat. Rev. Genet. 18, 117–127. doi: 10.1038/nrg.2016.142
Pravenec, M., Zidek, V., Landa, V., Mlejnek, P., Šilhavỳ, J., Šimáková, M., et al. (2017). Mutant wars2 gene in spontaneously hypertensive rats impairs brown adipose tissue function and predisposes to visceral obesity. Physiol. Res. 66, 917–924. doi: 10.33549/physiolres.933811
Pulit, S. L., Stoneman, C., Morris, A. P., Wood, A. R., Glastonbury, C. A., Tyrrell, J., et al. (2019). Meta-analysis of genome-wide association studies for body fat distribution in 694 649 individuals of european ancestry. Hum. Mol. Genet. 28, 166–174. doi: 10.1093/hmg/ddy327
Randall, J. C., Winkler, T. W., Kutalik, Z., Berndt, S. I., Jackson, A. U., Monda, K. L., et al. (2013). Sex-stratified genome-wide association studies including 270,000 individuals show sexual dimorphism in genetic loci for anthropometric traits. PLoS Genet. 9:e1003500. doi: 10.1371/journal.pgen.1003500
Ray, D., and Michael, B. (2018). Methods for meta-analysis of multiple traits using GWAS summary statistics. Genet. Epidemiol. 42, 134–145. doi: 10.1002/gepi.22105
Ray, D., Pankow, J. S., and Basu, S. (2016). Usat: a unified score-based association test for multiple phenotype-genotype analysis. Genet. Epidemiol. 40, 20–34. doi: 10.1002/gepi.21937
Singh, M. K., Petry, M., Haenig, B., Lescher, B., Leitges, M., and Kispert, A. (2005). The t-box transcription factor tbx15 is required for skeletal development. Mech. Dev. 122, 131–144. doi: 10.1016/j.mod.2004.10.011
Visscher, P. M., Brown, M. A., McCarthy, M. I., and Yang, J. (2012). Five years of gwas discovery. Am. J. Hum. Genet. 90, 7–24. doi: 10.1016/j.ajhg.2011.11.029
Visscher, P. M., Wray, N. R., Zhang, Q., Sklar, P., McCarthy, M. I., Brown, M. A., et al. (2017). 10 years of GWAS discovery: biology, function, and translation. Am. J. Hum. Genet. 101, 5–22. doi: 10.1016/j.ajhg.2017.06.005
Winkler, T. W., Justice, A. E., Graff, M., Barata, L., Feitosa, M. F., Chu, S., et al. (2015). The influence of age and sex on genetic associations with adult body size and shape: a large-scale genome-wide interaction study. PLoS Genet. 11:e1005378. doi: 10.1371/journal.pgen.1005378
Yang, J., Ferreira, T., Morris, A. P., Medland, S. E., Madden, P. A., Heath, A. C., et al. (2012). Conditional and joint multiple-SNP analysis of GWAS summary statistics identifies additional variants influencing complex traits. Nat. Genet. 44:369. doi: 10.1038/ng.2213
Zhang, X., Ehrlich, K. C., Yu, F., Hu, X., Meng, X.-H., Deng, H.-W., et al. (2020). Osteoporosis-and obesity-risk interrelationships: an epigenetic analysis of GWAS-derived SNPs at the developmental gene tbx15. Epigenetics 15, 728–749. doi: 10.1080/15592294.2020.1716491
Zhu, X., Feng, T., Tayo, B. O., Liang, J., Young, J. H., Franceschini, N., et al. (2015). Meta-analysis of correlated traits via summary statistics from GWASs with an application in hypertension. Am. J. Hum. Genet. 96, 21–36. doi: 10.1016/j.ajhg.2014.11.011
Keywords: GWAS, bivariate GWAS, summary association statistics, heritable covariate, biased
Citation: Zhu J, Fan Q, Deng W, Wang Y and Guo X (2021) BTOB: Extending the Biased GWAS to Bivariate GWAS. Front. Genet. 12:654821. doi: 10.3389/fgene.2021.654821
Received: 17 January 2021; Accepted: 07 April 2021;
Published: 06 May 2021.
Edited by:
Zhonghua Liu, The University of Hong Kong, Hong KongReviewed by:
Lin Hou, Tsinghua University, ChinaDajiang Liu, Pennsylvania State University, United States
Copyright © 2021 Zhu, Fan, Deng, Wang and Guo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaobo Guo, Z3VveGIzQG1haWwuc3lzdS5lZHUuY24=
†These authors have contributed equally to this work
 Junxian Zhu
Junxian Zhu Qiao Fan2†
Qiao Fan2† Yimeng Wang
Yimeng Wang Xiaobo Guo
Xiaobo Guo