- 1Novartis Pharmaceuticals Corporation, East Hanover, NJ, United States
- 2Division of Biostatistics, Department of Population Health, New York University School of Medicine, East Hanover, NY, United States
- 3Center for Advanced Biotechnology and Medicine, Rutgers University, New Brunswick, NJ, United States
- 4Division of Intramural Research, Immunopathogenesis Section, NIAID, NIH, Bethesda, MD, United States
Dynamic changes of microbiome communities may play important roles in human health and diseases. The recent rise in longitudinal microbiome studies calls for statistical methods that can model the temporal dynamic patterns and simultaneously quantify the microbial interactions and community stability. Here, we propose a novel autoregressive zero-inflated mixed-effects model (ARZIMM) to capture the sparse microbial interactions and estimate the community stability. ARZIMM employs a zero-inflated Poisson autoregressive model to model the excessive zero abundances and the non-zero abundances separately, a random effect to investigate the underlining dynamic pattern shared within the group, and a Lasso-type penalty to capture and estimate the sparse microbial interactions. Based on the estimated microbial interaction matrix, we further derive the estimate of community stability, and identify the core dynamic patterns through network inference. Through extensive simulation studies and real data analyses we evaluate ARZIMM in comparison with the other methods.
Introduction
The human microbiota, a diverse array of microbial organisms living in and on human bodies, form a dynamic ecosystem that plays a critical role in human health. While temporally stable microbial communities are observed among healthy adults (Faith et al., 2013), the fluctuation of microbiome has been linked to increasing frailty (Jackson et al., 2016) and declining immune function of hosts (Claesson et al., 2012), and diseases such as inflammatory bowel disease (Martinez et al., 2008; Zuo and Ng, 2018), colorectal cancer (Scanlan et al., 2008; Uronis et al., 2009), and irritable bowel syndrome (Maukonen et al., 2006; Carroll et al., 2012). When a microbial community changes in response to an external perturbation, it undergoes a dynamic process and tends to evolve toward another stable state (Figure 1). This dynamic process is stochastic and varies according to the type and strength of perturbation, the community stability prior to the perturbation, and other subject-level relevant features. The recent rise in longitudinal studies, in which microbial samples are collected repeatedly over time, offers unique insights into the responses of such communities to perturbations and the associated dynamic patterns. For example, in our ongoing microbiome study evaluating the effects of antibiotic exposure as a short-term perturbation on microbial, immune, and metabolic physiology (MIME study), we are interested in determining how differently the microbial community responds to the antibiotic treatment.
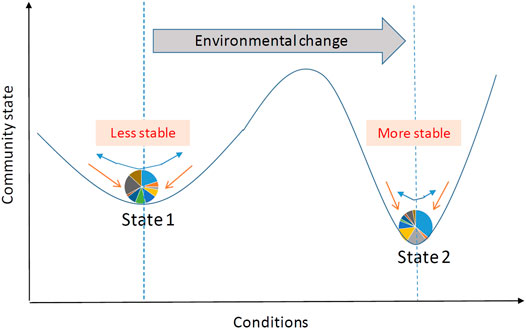
FIGURE 1. Schematic of the evolution of microbial community states in response to external perturbation. External perturbation (blue arrows) can affect microbial community composition (shown in a pie chart), defined as a community state. For each state, the ball-in-basin diagram portrays stability measured by the variance in the stationary distribution of the location of the ball. White arrows indicate the reaction of microbial community to the perturbation.
Human microbiota studies have been accelerated by the advent of next-generation sequencing technologies which enabled the quantification of the composition of microbiomes, often by two common sequencing approaches—16S rRNA marker gene sequencing and shotgun metagenomics sequencing (Woo et al., 2008). There are pros and cons to each of those techniques, which are discussed in recent reviews (Shankar, 2017; Gilbert et al., 2018). But for both methods, because of the varying sequencing read counts obtained across samples, it is necessary to employ various normalization tools to convert raw counts data into relative abundances (Knight et al., 2018). However, the dependency of the compositional components greatly hampers the interpretation of microbiota changes in longitudinal studies. There is reason to believe that the absolute abundances of bacteria are biologically meaningful measures, especially in the study of microbial interactions. Thus, in our MIME study, we use an independent quantitative polymerase chain reaction (qPCR) technology (Nadkarni et al., 2002; Ott et al., 2004; Kim et al., 2013) to quantify total bacterial load per unit sample, and then use these data to estimate absolute bacterial abundance by combining them with the relative abundance values obtained from 16S rRNA or shotgun sequencing methods. This MIME study motivated us to develop analytical methods to investigate microbial interaction and community stability after a strong external perturbation, and identify core active microbial taxa by modeling the absolute abundances of bacteria.
Although many well-developed statistical tools are widely used for assessing the diversity of microbial communities and its composition, there are only a few methods available for inferring the ecological networks of microbial communities. Here we briefly review the well-developed statistical methods for studying the dynamic microbial systems and their limitations.
A Bayesian network contains a set of multivariate joint distributions that exhibit certain conditional independences and a directed and acyclic graph that encodes conditional independences among random variables. If the dependence relationships repeat and the signals at a certain time point only depend on the signals from previous time points, then the whole network can be formulated as a dynamic Bayesian network (DBN) (Russell and Norvig, 2002) representation. McGeachie et al. (McGeachie, 2016) constructed a simplified two-stage DBN which uses a Markov assumption that the observed values at time
The classical Lotka-Volterra equation has been used to model simple system such as two species in a predator-prey relationship, where the interactions are strictly assumed to be competitive. The generalized Lotka-Volterra (gLV) equations extend the classical predator-prey (Lotka-Volterra) equations, where the interacting species might have a wide range of relationships including competition, cooperation, or neutralism. Assuming that the interaction (or the effect) of one species with another can be modeled by the corresponding coefficient in the equation, gLV equations provide a framework to analyze and simulate microbial populations. Mounier et al. used the gLV equations to model the interaction between bacteria and yeast in a cheese microbiome (Mounier et al., 2009). Other microbiome studies further extended and implemented the gLV equations (Marino et al., 2014; Dam et al., 2016; de Vos et al., 2017; Venturelli et al., 2018).
Many software are available for applying gLV modeling on microbial time series data, such as LIMITS (Fisher and Mehta, 2014), MetaMis (Shaw et al., 2016), and MDSINE (Bucci et al., 2016a). LIMITS and MetaMis can be implemented to construct microbial interactions using the longitudinal microbiome data from one subject. MDSINE can jointly analyze multiple time series, but requires Matlab programming. Web-gLV (http://web.rniapps.net/webglv) can be used for modeling, visualization, and analysis of microbial populations, but can only handle limited number of samples. In summary, there are several limitations of gLV in analyzing the longitudinal microbial data. 1) gLV based models capture the interactions using a single averaged effect, thus they are not well-suited for noisy data. 2) Some methods estimate almost all possible edges without incorporating variable selection techniques. 3) gLV estimates the growth rate of each taxon marginally, therefore, ignores the intrinsic dynamic correlations of the repeated measurements. 4) gLV does not account for random processes which form essential part of any biological system. 5) With the increased number of species and time span of prediction, the simulation output is prone to numerical errors. For example, Web-gLV can only simulate a maximum of 10 species at a time for at most 100 time points. 6) As DBN, gLV is not suitable for sparse, compositional, and irregular sampled microbiome data.
In Ives et al. (Ives et al., 2003), the stability of a microbial community is determined by three key interrelated components of microbial community structure: diversity, species composition, and interaction pattern among species. They viewed the dynamics of a microbial community as a stochastic process and proposed to use a first-order multivariate autoregressive process [MAR (1)] time-series model to disentangle the effects of these three components on community stability and to estimate the stability properties of a community by estimating the strengths of interactions between species. This method is widely used to estimate the stability of ecosystems (e.g., lake, ocean) based on culture-dependent microbial data (Carpenter et al., 2011; Shade et al., 2013). Usually a few (four or five) key microbes are detected with high frequency in each ecosystem in time-series measurements over a long period, and their abundances are rarely zero. In contrast, our MIME study will yield microbiome data from approximately nine time points over half a year from 80 subjects in three groups in the complete study—a relatively smaller number of repeated microbiome samples but from a relatively larger number of microbial communities (subjects) than what would be the case for an ecosystem study. Moreover, the 16S rRNA sequencing and qPCR methods used in this study provide absolute abundances for a staggering number of taxa, which include a large number of zero values. Because the MAR modeling methods require the normality assumption, they are not appropriate for analyzing data from sequence-based longitudinal microbiome studies. Therefore, we propose an autoregressive zero-inflated mixed effects model (ARZIMM) to address the special features of data instead. Its novelties are threefold. First, we propose to use a zero-inflated Poisson autoregressive model to model the excessive zero abundances and the non-zero abundances separately. Second, the random effects in the proposed model can investigate the underlining dynamic pattern shared within the group. Third, the employment of regularization techniques and network inference in our model enables the identification of the core dynamic patterns. The proposed ARZIMM estimates the strength of interactions between taxa, which is required to estimate the stability properties of a community, and identify key active taxa efficiently by using all of the longitudinal sequencing data. ARZIMM has been implemented in an open-source software package (https://github.com/Hlch1992/ARZIMM), and provides a useful tool for formulating, understanding, and implementing longitudinal microbiome data analysis.
In the following Material and Method section, we introduce the ARZIMM framework, discuss the quantification of microbial stability based on the estimated microbial interaction matrix, and investigate the conditions under which there exist a strict-sense stationary distribution. Then in the Result section, we evaluate ARZIMM using extensive simulation studies to show that it outperforms the conventional methods, and apply ARZIMM to the MIME study to illustrate network visualization and inference. In the end, we conclude with Discussion section.
Materials and Methods
ARIZMM Model
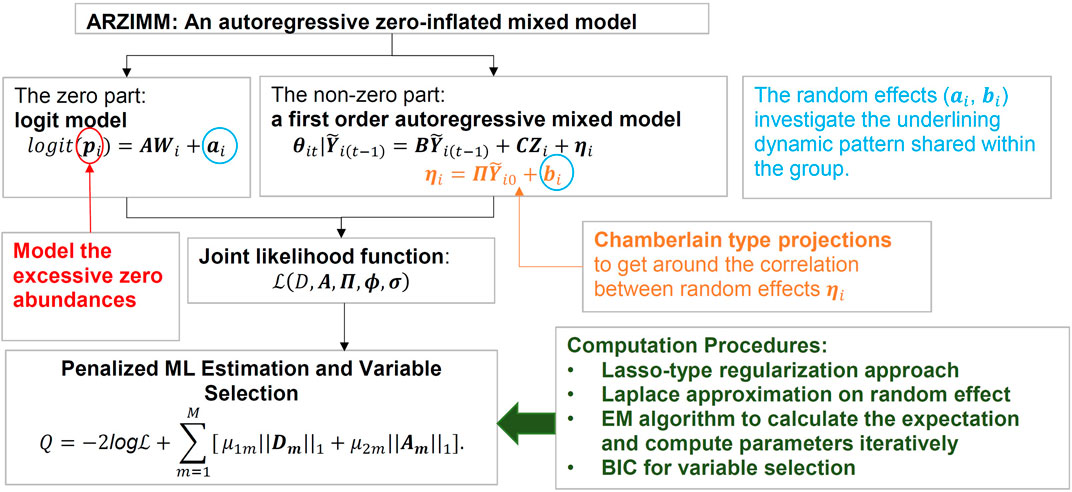
As illustrated in Figure 2, ARZIMM can be considered as a two-part model which comprises a logistic component and an autoregressive component. To address zero inflation, we consider the zero-inflated mixture model because it assumes both sampling zeros (due to the low sequencing depth) and structural zeros (being truly absent) exist in the data. Specifically, the logistic component models the structure zeros of taxa in the samples, and the autoregressive component models the non-structure-zero abundances of the taxa under the assumption that the changes in abundances from time
Notation and Model Specifications
Let
where
The mixture probability parameters
where
The canonical parameters for Poisson distribution is
where
where
In the model, our primary interest is to estimate matrix
Note that we choose Poisson distribution because of its nice stationary distribution property in the autoregressive model which is crucial for our following stability investigation. To deal with the over-dispersion of microbiome data, we implemented the quasi-Poisson model (Ver Hoef and Boveng, 2007) in the simulation and real data analysis.
Penalized ML Estimation and Variable Selection
To define the joint likelihood of the longitudinal microbial absolute abundance data
where
The function
Assuming that the true underlying fixed effects
Maximization of the penalized log-likelihood function corresponding to Eq. 7 with respect to
Stability Properties
The existence of a stationary distribution has been investigated for the log-linear Poisson auto-regression model based on the perturbation technique (Fokianos and Tjøstheim, 2011). Here, we prove the existence of a stationary distribution of a zero-inflated Poisson mixed-effect auto-regression model in Theorem 1 utilizing the theory of Markov chains which has been proposed to prove the existence of a stationary distribution of a general class of time series count models (Douc et al., 2013). The detailed proof is provided in the Supplementary Material Section S3.
Theorem 1 Assuming that time-independent parameters
Results
Simulation Study
We have conducted extensive simulation studies to evaluate the performance of ARZIMM in both model fitting and variable selection by comparing it with the competing methods: penalized Poisson auto-regression (Poisson), penalized log-normal multivariate auto-regression (MAR), and extended generalized Lotka-Volterra (gLV) equations using Bayesian algorithm (MDSINE) (Bucci et al., 2016b). The brief descriptions of these methods are provided in the Supplementary Material Section S2.
Simulation Design
We generated the longitudinal absolute abundances from zero-inflated Poisson distribution with parameters
The detailed values of
In each scenario, we generated 500 independent repetitions for
Simulation Results
We first compared the model fittings of ARZIMM, Poisson, and MAR methods using mean normalized squared error score (MNSES), as suggested in the prior studies (Carroll and Cressie, 1997; Liesenfeld et al., 2006; Czado et al., 2009; Tkacz et al., 2018a). MNSES is defined as
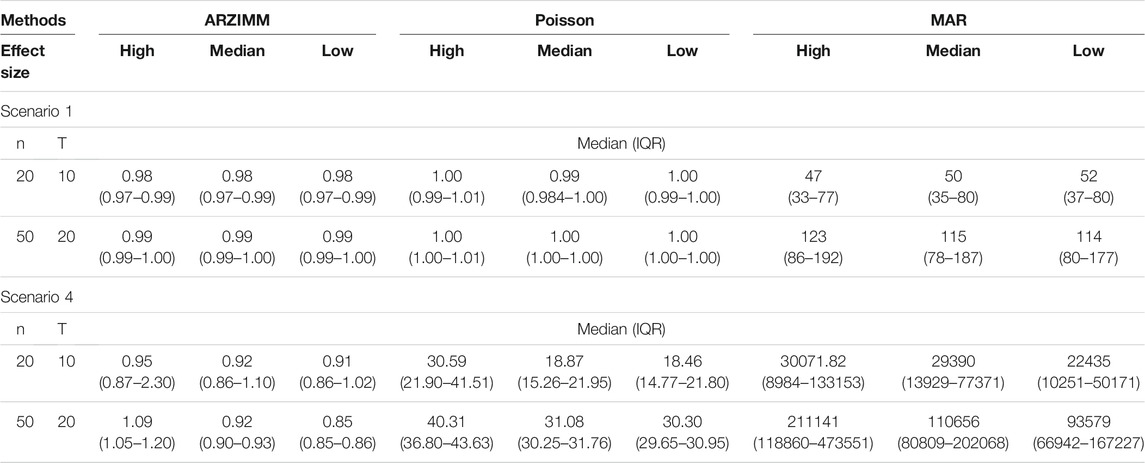
TABLE 1. Simulation results for all settings under scenario 1 and 4. Poisson refers to the penalized Poisson autoregression model and MAR refers to penalized log-normal multivariate autoregression model. The reported value is median (IQR) of mean normalized squared error score (MNSES) calculated over 500 simulations for each setting.
Next, we evaluated the variable selection performance for ARZIMM, Poisson, MAR, and MDSINE in terms of true positive rate (TPR; mathematically equals to the power) and false positive rate (FPR; mathematically equals to the type I error). Specifically, TPR quantifies the probability of a significant interaction identified by one method given that the interaction effect is truly nonzero; and FPR quantifies the probability of a significant interaction identified by one method given that the interaction effect is truly zero. The simulation results for 50 subjects with 20 time points are summarized in Figure 3 and all the other simulation results with different subject numbers and time points are deferred to Supplementary Figure S1, because they have a similar pattern as seen in Figure 3. Figure 3 shows that the FPRs of ARZIMM are all at or below the nominal level (5%) across different simulation regimes and effect sizes, and its TPR estimates exhibit a sensible and consistent pattern as they increase as the interaction effect gets stronger across four scenarios. As expected, the FPR and TRP estimates of Poisson and ARZIMM models are coincident under Scenario 1, because when subjects are homogeneous and taxa don’t have excess zeros, ARZIMM model is reduced to Poisson model. However, in Scenarios 2-4, because simple Poisson model fails to take care of the excess zeros or subject heterogeneity, it suffers from the inflated false positives, while ARZIMM does not. For the other two methods, both MAR and MDSINE perform poorly on controlling false positive rates for all simulation scenarios, because MAR fails to fit the skewed and highly sparse microbiome data, while MDSINE captures the interactions based on the averaged effect over subjects in a group but completely ignores the randomness at the subject level process which is the essential characteristic of any biological system. In summary, ARZIMM outperforms the other competitors in handling the excess zeros and subject heterogeneity well with controlled FPR and satisfactory TPR.
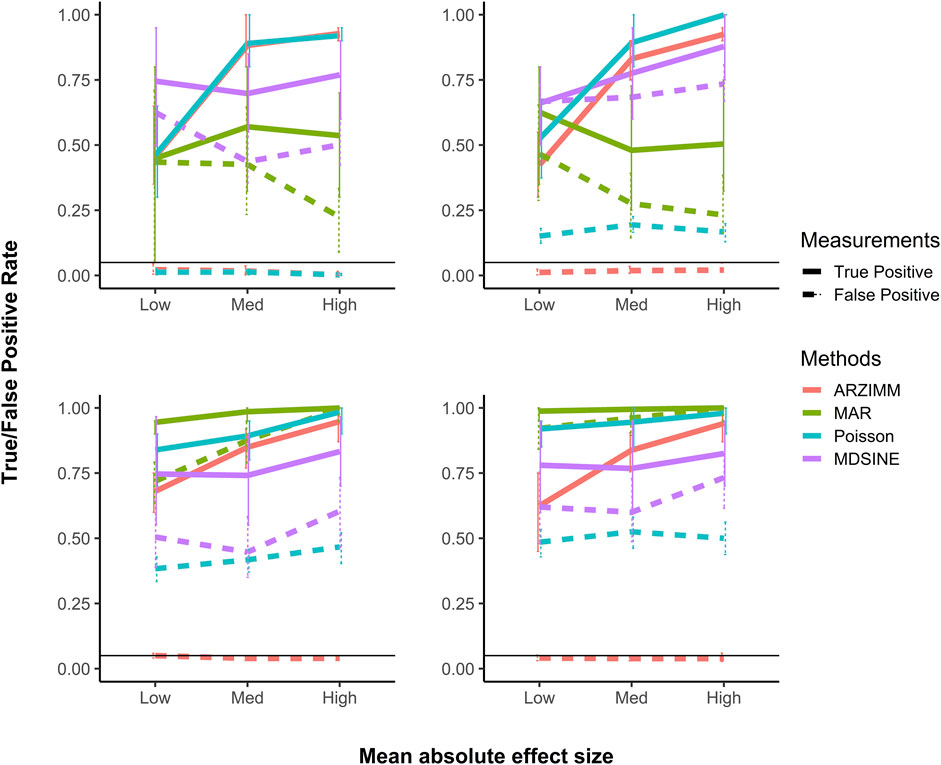
FIGURE 3. Simulation results of variable selection performance. Poisson refers to the penalized Poisson auto-regression model and MAR refers to penalized log-normal multivariate auto-regression model. MDSINE refers to the method with extended generalized Lotka-Volterra (gLV) equations using a Bayesian algorithm. Mean (and 95% confidence interval) of false positive and true positive rates are reported for 500 simulations with 50 subjects and 20 time points in four scenario: (A) no zero-inflated structure and no heterogeneity, (B) heterogeneity but no zero-inflated structure, (C) zero-inflated structure but no heterogeneity, and (D) both zero-inflated structure and heterogeneity.
To further investigate the performance of informative interaction selection, we calculate Matthew correlation coefficient (MCC), defined as
As for the computational cost, ARIZMM took about 2.4 h to complete the estimation and bootstrap inference for a simulated dataset with 50 subjects, 20 timepoints, and 20 taxa.
Real Data Application
We applied ARZIMM methods to the MIME study. The MIME study is an ongoing randomized trial on 80 healthy volunteers with one control group (ctrl) and two antibiotic groups (amoxicillin, amx, and azithromycin, azm); antibiotics are provided for a 1-week period at the start of the trial. The main microbiome research goal of the MIME study is to evaluate the effects of antibiotics on microbial profiles at both the community and taxonomical levels. With ARIZMM, we propose a different perspective to evaluate the effect of antibiotics through the investigation of microbial interaction and community stability across groups. Because the clinical trial is still ongoing and only partial data are available, the following data analysis is done on a subset of MIME data including only 11 subjects who were randomized to two groups: 4 ctrls and 7 azms. The main purpose of this analysis is to illustrate how to use ARIZMM, not for the scientific conclusion. For each subject, we collected two baseline microbiome samples, three samples during the course of antibiotics, and five post-antibiotic samples. The gut microbiota of these individuals were profiled using 16S rRNA gene targeted sequencing on the Illumina MiSeq platform. To obtain the microbial absolute abundances, we multiplied the relative abundances of OTUs by the sample density 1.1 g/cm3 and the number of universal 16S rRNA per gram measured using qPCR (Stein et al., 2013a). In our analysis, samples that collected before treatment in both antibiotic groups were excluded. The abundances of taxa were agglomerated at the genus level and taxa were further filtered if 1) the average relative abundances over all samples are less than 0.1%, and 2) the taxa are presented in less than 5 samples within each group.
First, Figure 4A shows a comparison of the relative abundance (top panel) and the absolute abundances determined by quantitative sequencing (bottom panel) of the dominant bacterial genera in 99 fecal samples from 11 subjects (blocks) across seven to nine time points (shown from left to right within each block) of this preliminary dataset. It is evident that the relative abundance and absolute abundance data present different information about the microbial profiles, and that the total bacterial load changes over time for each subject (i.e., within each block). Thus it is essential to study the microbial interactions using the absolute abundance data.
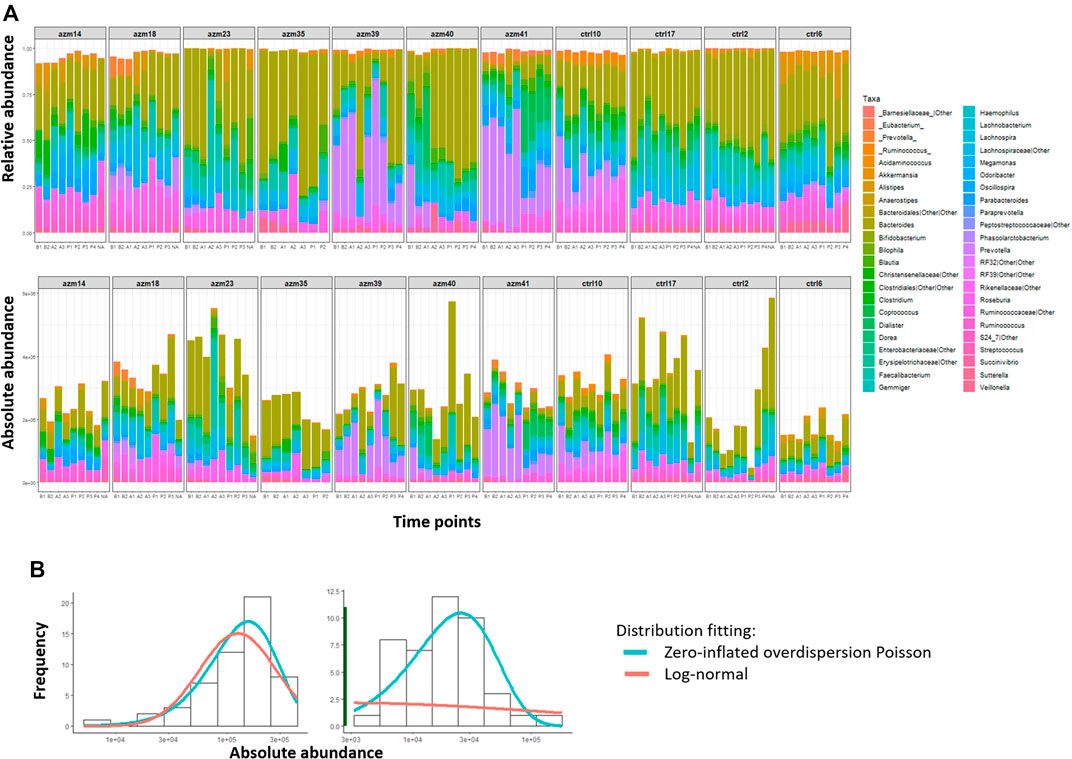
FIGURE 4. MIME study microbiome data. (A) Difference between relative abundances (top panel) and absolute abundances based on qPCR (bottom panel) of dominant genera in XX fecal samples obtained from 21 subjects (block) at 7–9 time points (x-axis) each. (B) Distribution of absolute abundances of two representative genera from the MIME study, shown in the left and right panels, respectively. For each genus, the absolute abundance is fitted with a log-normal distribution (red line) or a two-part distribution: a zero part (dark green line shown in right panel) and a non-zero part fitted with an over-dispersion Poisson distribution (blue line).
Then, we evaluate the model fitting of the log-normal distribution [used in MAR(1)] and zero-inflated over-dispersed Poisson distribution (used in ARZIMM) on the available subset of MIME data using chi-square goodness of fit test at 5% significance level taxon by taxon. Out of 45 taxa in the control group, 1 and 44 of their absolute abundances were fitted well (p > 0.05) by log-normal distribution and zero-inflated over-dispersed Poisson distribution respectively. The log-normal distribution fails to fit the data well when microbial taxa’s absolute abundance data are left-skewed and sparse (two examples are illustrated in Figure 4B).
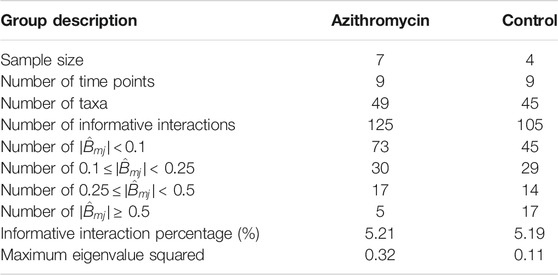
Next we demonstrate how to conduct inference for microbial interactions and community stability with ARZIMM on MIME data. First, we fit ARZIMM to ctrl and azm groups separately, adjusting for age, gender, and BMI, to get their estimated interaction matrix
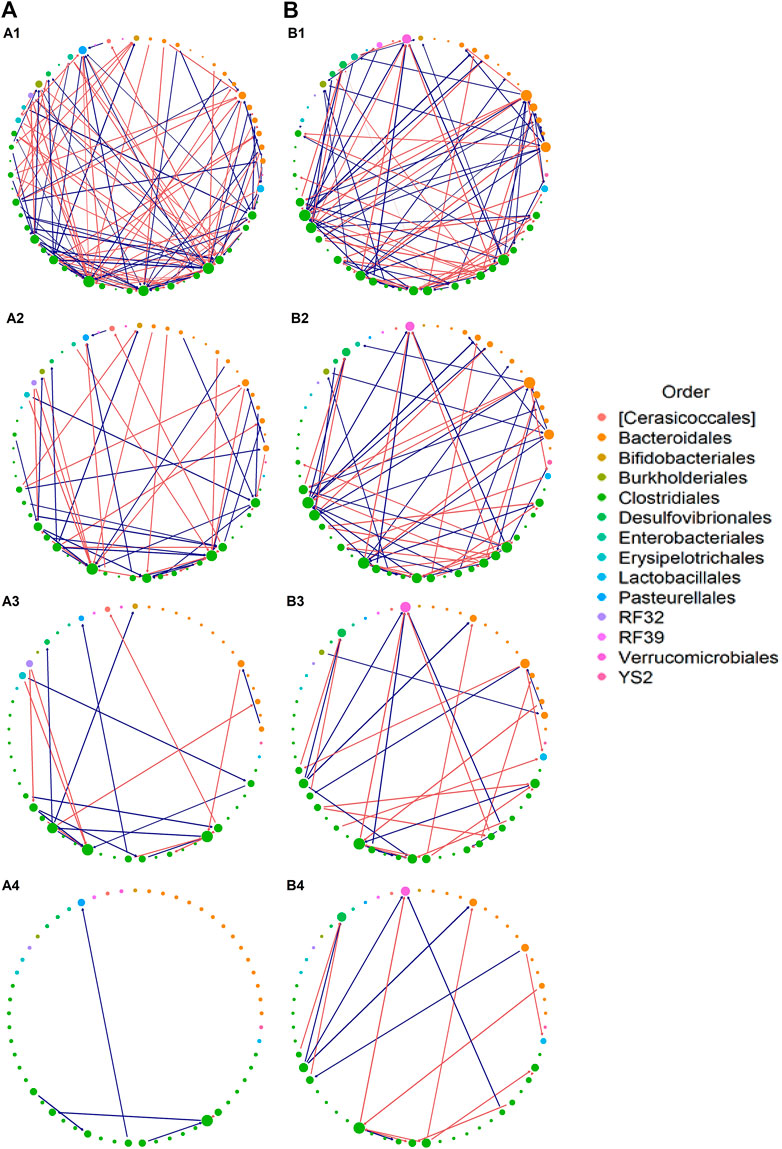
FIGURE 5. Interaction network. Estimated interaction network for: (A) azithromycin (azm), and (B) control groups, displaying (1) all selected interactions, (2) interactions with
Figure 6 provides additional information on the network feature comparison between ctrl and azm groups. Figure 6A displays the distribution of the positive and negative informative interaction estimates separately. The ratios between the numbers of positive and negative interactions are both around 1:1 in two groups. Figure 6B presents the frequency distribution of vertex degree of all the taxa in each group and they are all skew to the right. In the figure, a vertex represents a taxon in a community and its vertex degree is the number of informative interaction effect it has with the other taxa. By defining average neighbor degree as the average number of a given taxon’s neighbor vertices’ degrees, Figure 6C shows that the average neighbor degree is negatively correlated with the vertex degree in azm antibiotic treated group, but not in the control group. This indicates that there may be a group of taxa interacting with each other actively in the antibiotic group. It would be interesting to identify such sub-community with additional effort.
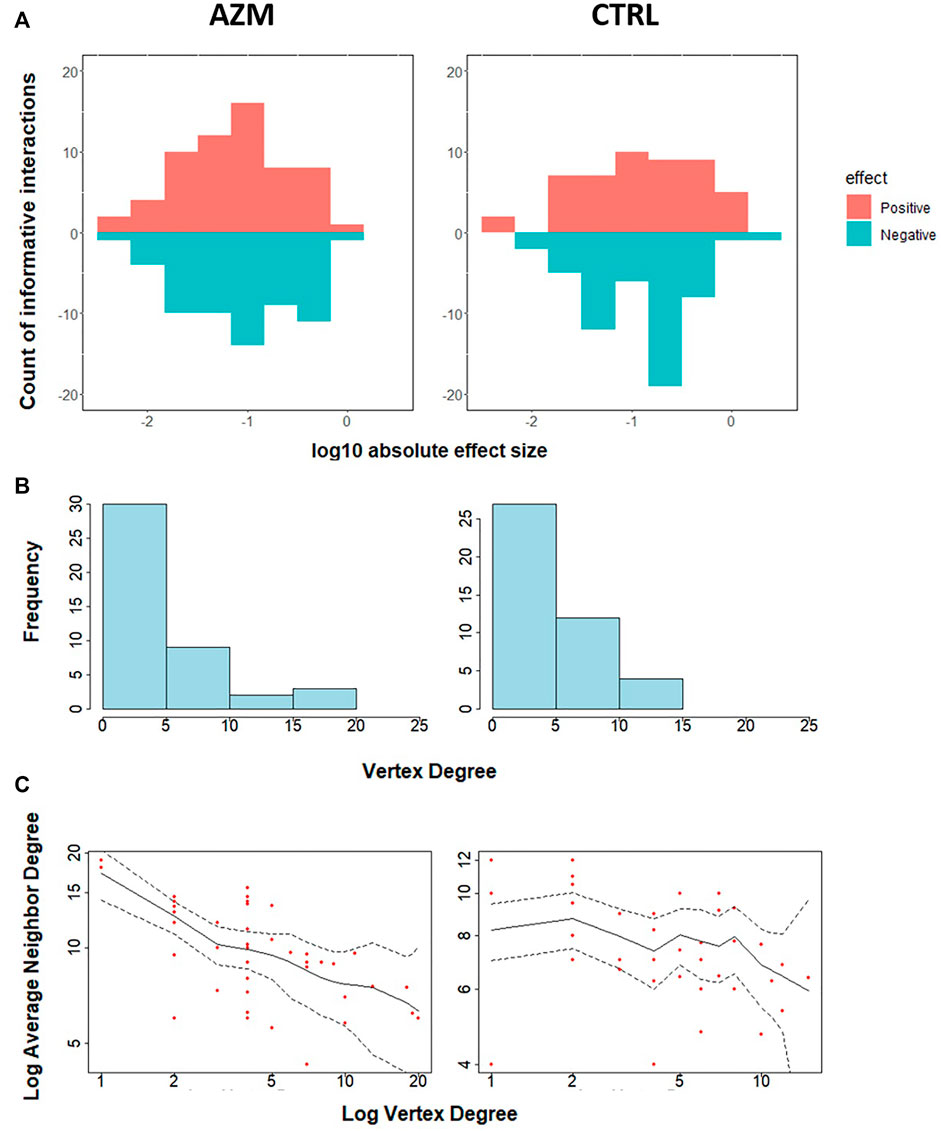
FIGURE 6. Characteristics of estimated interactions. (A) The effect size of estimated informative interactions, wherein the x-axis represents the log10 scaled absolute effect size, the y-axis represents the count of informative interactions, and the colors represent the positive or negative effects. (B) Histogram of vertex degree, wherein given a vertex, vertex degree is defined as the counts of edges upon the vertex. (C) The average neighbor degree (y-axis) versus vertex degree on a log-log scale (x-axis). The average neighbor degree is the average number of a given taxon’s neighbor vertices’ degrees. Dotted lines represent 95% confidence limits.
Discussion
In this paper, we propose ARZIMM, an analytic platform which estimates the microbial interactions and community stability using longitudinal microbiome data. ARZIMM tackles the zero-inflated absolute abundance with a mixture distribution of zero and exponential dispersion distribution family, and enhances statistical efficiency by utilizing a random-effects term to account for the correlations among repeated measurements.
It is well-known that microbial correlations calculated from relative abundances are distorted by the compositional nature of microbiome data, and are insufficient in tracking microbial dynamics(Gloor et al., 2017). We advocate to investigate the microbial correlations using longitudinal absolute abundances which can be determined by combining gene amplicon sequencing with auxiliary total DNA quantitation data. qPCR is one of the most commonly used strategies to quantify total DNA (Dannemiller et al., 2014) and has been implemented in various statistical analyses (Stein et al., 2013b). Other alternative methods to quantify the absolute abundances include the combination of the sequencing approach (16S rRNA gene) with robust single-cell enumeration technologies (flow cytometry) (Props et al., 2017) and the usage of synthetic chimeric DNA spikes (Tkacz et al., 2018b).
Plenty of zero-inflated mixed effects models have been recently proposed to handle the excess zeros in microbiome abundance data such as zero-inflated Poisson, negative binomial and quasi-Poisson models(Xia et al., 2018; Zhang et al., 2018). However, none of the existing methods estimates the microbial interactions and community stability. To fill this gap, we extended a zero-inflated Poisson model with auto-regression and random effects modeling, which plays crucial role in efficiently handling the individual heterogeneity and enable the investigation of microbial interactions.
We investigated two community stability measurements derived from ARZIMM: the return rate and reactivity, to further understand ecological dynamics. The estimated interaction matrix
It is worth noting that by utilizing the ARZIMM model framework, the time-dependent perturbation (for instance, diet) can also be assessed flexibly in both the autoregressive part and the logistic part in the model. However, the stability based on the microbial interactions has to be interpreted with caution, since the mean of stationary distribution changes along with the time-dependent covariates.
We have demonstrated that ARZIMM outperforms the competing methods and exhibits its feasibility for examining microbial interactions and stability based on longitudinal microbial data. We applied our method to a real human microbiome study of antibiotic treatment and elucidated the microbial interaction network of bacteria from antibiotic and non-antibiotic groups separately. The application of ARZIMM to temporal microbiome data shows great promise. Still, the development of accurate predictive models will require further developments. For example, the method used here to infer microbial interactions may be expanded by adding functional information as well as phylogenetic information. Although this method is primarily developed for the gut microbiota, it may be potentially applied to longitudinal data from any ecological systems. Since interactions between members of microbial communities are primary driving forces for the long-term stability(Ratzke et al., 2020), the corresponding stability properties will provide useful principles for community dynamics.
Note that the proposed ARIZMM assumes the probability of observing a zero count for a taxon is constant over time. The reason is two-fold. 1) One major goal of ARIZMM is to derive the inference on the stability of the microbial community over a certain period. With the constant probability of observing a zero count assumption, the stability inference will solely depend on the estimation of the taxon-by-taxon interaction matrix B. Otherwise, a stationary distribution will not exit. 2) Using the MIME data, we estimated the proportions of zeros (denoted as
The proposed method, ARZIMM has a few limitations and future works are needed to improve it. ARZIMM adopts a simple correlation structure that the random effects in the multivariate logistic component and the multivariate autoregressive component
Data Availability Statement
The data analyzed in this study is subject to the following licenses/restrictions: The motivating study is still ongoing. After it is closed, it will be uploaded to the public repository. Requests to access these datasets should be directed to bWFydGluLmJsYXNlckBjYWJtLnJ1dGdlcnMuZWR1.
Author Contributions
LH and HL developed the methodological ideas. LH implemented the methods, performed the simulations and real data analysis, and developed the software package. CW and JH contributed to the simulation design and real data analysis. ZG, EF, SH, and MB contributed to the acquisition of utilized real microbiome data. MB provided biological insights and interpretation of the real data analysis. LH and HL wrote the manuscript. All authors read, edited, and approved the final manuscript.
Funding
This work was supported in part by National Institutes of Health grants R01DK110014, P20CA252728, and U01AI22285.
Conflict of Interest
LH was employed by the company Novartis Pharmaceuticals Corporation.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2022.777877/full#supplementary-material
References
Bucci, V., Tzen, B., Li, N., Simmons, M., Tanoue, T., Bogart, E., et al. (2016). MDSINE: Microbial Dynamical Systems INference Engine for Microbiome Time-Series Analyses. Genome Biol. 17 (1), 121–217. doi:10.1186/s13059-016-0980-6
Bucci, V., Tzen, B., Li, N., Simmons, M., Tanoue, T., Bogart, E., et al. (2016). MDSINE: Microbial Dynamical Systems INference Engine for Microbiome Time-Series Analyses. Genome Biol. 17 (1), 121. doi:10.1186/s13059-016-0980-6
Carpenter, S. R., Cole, J. J., Pace, M. L., Batt, R., Brock, W. A., Cline, T., et al. (2011). Early Warnings of Regime Shifts: a Whole-Ecosystem experiment. Science 332 (6033), 1079–1082. doi:10.1126/science.1203672
Carroll, I. M., Ringel-Kulka, T., Siddle, J. P., and Ringel, Y. (2012). Alterations in Composition and Diversity of the Intestinal Microbiota in Patients with Diarrhea-Predominant Irritable Bowel Syndrome. Neurogastroenterology Motil. 24 (6), 521–e248. doi:10.1111/j.1365-2982.2012.01891.x
Carroll, S. S., and Cressie, N. (1997). Spatial Modeling of Snow Water Equivalent Using Covariances Estimated from Spatial and Geomorphic Attributes. J. Hydrol. 190 (1-2), 42–59. doi:10.1016/s0022-1694(96)03062-4
Chamberlain, G. (1982). Multivariate Regression Models for Panel Data. J. Econom. 18 (1), 5–46. doi:10.1016/0304-4076(82)90094-x
Claesson, M. J., Jeffery, I. B., Conde, S., Power, S. E., O’Connor, E. M., Cusack, S., et al. (2012). Gut Microbiota Composition Correlates with Diet and Health in the Elderly. Nature 488 (7410), 178–184. doi:10.1038/nature11319
Czado, C., Gneiting, T., and Held, L. (2009). Predictive Model Assessment for Count Data. Biometrics 65 (4), 1254–1261. doi:10.1111/j.1541-0420.2009.01191.x
Dam, P., Fonseca, L. L., Konstantinidis, K. T., and Voit, E. O. (2016). Dynamic Models of the Complex Microbial Metapopulation of lake mendota. NPJ Syst. Biol. Appl. 2 (1), 16007–7. doi:10.1038/npjsba.2016.7
Dannemiller, K. C., Lang-Yona, N., Yamamoto, N., Rudich, Y., and Peccia, J. (2014). Combining Real-Time PCR and Next-Generation DNA Sequencing to Provide Quantitative Comparisons of Fungal Aerosol Populations. Atmos. Environ. 84, 113–121. doi:10.1016/j.atmosenv.2013.11.036
de Vos, M. G. J., Zagorski, M., McNally, A., and Bollenbach, T. (2017). Interaction Networks, Ecological Stability, and Collective Antibiotic Tolerance in Polymicrobial Infections. Proc. Natl. Acad. Sci. USA 114 (40), 10666–10671. doi:10.1073/pnas.1713372114
Douc, R., Doukhan, P., and Moulines, E. (2013). Ergodicity of Observation-Driven Time Series Models and Consistency of the Maximum Likelihood Estimator. Stochastic Process. their Appl. 123 (7), 2620–2647. doi:10.1016/j.spa.2013.04.010
Faith, J. J., Guruge, J. L., Charbonneau, M., Subramanian, S., Seedorf, H., Goodman, A. L., et al. (2013). The Long-Term Stability of the Human Gut Microbiota. Science 341 (6141), 1237439. doi:10.1126/science.1237439
Faust, K., and Raes, J. (2012). Microbial Interactions: from Networks to Models. Nat. Rev. Microbiol. 10 (8), 538–550. doi:10.1038/nrmicro2832
Fisher, C. K., and Mehta, P. (2014). Identifying keystone Species in the Human Gut Microbiome from Metagenomic Timeseries Using Sparse Linear Regression. PloS one 9 (7), e102451. doi:10.1371/journal.pone.0102451
Fokianos, K., and Tjøstheim, D. (2011). Log-linear Poisson Autoregression. J. Multivariate Anal. 102 (3), 563–578. doi:10.1016/j.jmva.2010.11.002
Gerber, G. K. (2014). The Dynamic Microbiome. FEBS Lett. 588 (22), 4131–4139. doi:10.1016/j.febslet.2014.02.037
Gilbert, J. A., Blaser, M. J., Caporaso, J. G., Jansson, J. K., Lynch, S. V., and Knight, R. (2018). Current Understanding of the Human Microbiome. Nat. Med. 24 (4), 392–400. doi:10.1038/nm.4517
Gloor, G. B., Macklaim, J. M., Pawlowsky-Glahn, V., and Egozcue, J. J. (2017). Microbiome Datasets Are Compositional: And This Is Not Optional. Front. Microbiol. 8, 2224. doi:10.3389/fmicb.2017.02224
Hu, J. (2021). Joint Modeling of Zero-Inflated Longitudinal Proportions and Time-To-Event Data with Application to a Gut Microbiome Study. Biometrics 2, 2020. doi:10.1111/biom.13515
Ives, A. R., Dennis, B., Cottingham, K. L., and Carpenter, S. R. (2003). Estimating Community Stability and Ecological Interactions from Time-Series Data. Ecol. Monogr. 73 (2), 301–330. doi:10.1890/0012-9615(2003)073[0301:ecsaei]2.0.co;2
Ives, A. R., Klug, J. L., and Gross, K. (2000). Stability and Species Richness in Complex Communities. Ecol. Lett. 3 (5), 399–411. doi:10.1046/j.1461-0248.2000.00144.x
Jackson, M. A., Jeffery, I. B., Beaumont, M., Bell, J. T., Clark, A. G., Ley, R. E., et al. (2016). Signatures of Early Frailty in the Gut Microbiota. Genome Med. 8 (1), 8. doi:10.1186/s13073-016-0262-7
Kim, J., Lim, J., and Lee, C. (2013). Quantitative Real-Time PCR Approaches for Microbial Community Studies in Wastewater Treatment Systems: Applications and Considerations. Biotechnol. Adv. 31 (8), 1358–1373. doi:10.1016/j.biotechadv.2013.05.010
Knight, R., Vrbanac, A., Taylor, B. C., Aksenov, A., Callewaert, C., Debelius, J., et al. (2018). Best Practices for Analysing Microbiomes. Nat. Rev. Microbiol. 16 (7), 410–422. doi:10.1038/s41579-018-0029-9
Liesenfeld, R., Nolte, I., and Pohlmeier, W. (2006). Modelling Financial Transaction price Movements: a Dynamic Integer Count Data Model. Empirical Econ. 30 (4), 795–825. doi:10.1007/s00181-005-0001-1
Lugo-Martinez, J., Ruiz-Perez, D., Narasimhan, G., and Bar-Joseph, Z. (2019). Dynamic Interaction Network Inference from Longitudinal Microbiome Data. Microbiome 7 (1), 54–14. doi:10.1186/s40168-019-0660-3
Marino, S., Baxter, N. T., Huffnagle, G. B., Petrosino, J. F., and Schloss, P. D. (2014). Mathematical Modeling of Primary Succession of Murine Intestinal Microbiota. Proc. Natl. Acad. Sci. USA 111 (1), 439–444. doi:10.1073/pnas.1311322111
Martinez, C., Antolin, M., Santos, J., Torrejon, A., Casellas, F., Borruel, N., et al. (2008). Unstable Composition of the Fecal Microbiota in Ulcerative Colitis during Clinical Remission. Am. J. Gastroenterol. 103 (3), 643–648. doi:10.1111/j.1572-0241.2007.01592.x
Maukonen, J., Satokari, R., Mättö, J., Söderlund, H., Mattila-Sandholm, T., and Saarela, M. (2006). Prevalence and Temporal Stability of Selected Clostridial Groups in Irritable Bowel Syndrome in Relation to Predominant Faecal Bacteria. J. Med. Microbiol. 55 (5), 625–633. doi:10.1099/jmm.0.46134-0
McGeachie, M. J. (2016). Longitudinal Prediction of the Infant Gut Microbiome with Dynamic Bayesian Networks. Scientific Rep. 6 (1), 1–11. doi:10.1038/srep20359
Mounier, J., Monnet, C., Jacques, N., Antoinette, A., and Irlinger, F. (2009). Assessment of the Microbial Diversity at the Surface of Livarot Cheese Using Culture-dependent and Independent Approaches. Int. J. Food Microbiol. 133 (1-2), 31–37. doi:10.1016/j.ijfoodmicro.2009.04.020
Nadkarni, M. A., Martin, F. E., Jacques, N. A., and Hunter, N. (2002). Determination of Bacterial Load by Real-Time PCR Using a Broad-Range (Universal) Probe and Primers Set. Microbiology (Reading) 148 (Pt 1), 257–266. doi:10.1099/00221287-148-1-257
Ott, S. J., Musfeldt, M., Ullmann, U., Hampe, J., and Schreiber, S. (2004). Quantification of Intestinal Bacterial Populations by Real-Time PCR with a Universal Primer Set and Minor Groove Binder Probes: a Global Approach to the Enteric flora. J. Clin. Microbiol. 42 (6), 2566–2572. doi:10.1128/jcm.42.6.2566-2572.2004
Props, R., Kerckhof, F.-M., Rubbens, P., De Vrieze, J., Hernandez Sanabria, E., Waegeman, W., et al. (2017). Absolute Quantification of Microbial Taxon Abundances. Isme J. 11 (2), 584–587. doi:10.1038/ismej.2016.117
Ratzke, C., Barrere, J., and Gore, J. (2020) Strength of Species Interactions Determines Biodiversity and Stability in Microbial Communities. Nat. Ecol. Evol. 4, 376–383. doi:10.1038/s41559-020-1099-4
Russell, S., and Norvig, P. (2002). Artificial Intelligence: A Modern Approach. Englewood Cliffs, NJ: University of California at Berkeley.
Scanlan, P. D., Shanahan, F., Clune, Y., Collins, J. K., O'Sullivan, G. C., O'Riordan, M., et al. (2008). Culture-independent Analysis of the Gut Microbiota in Colorectal Cancer and Polyposis. Environ. Microbiol. 10 (3), 789–798. doi:10.1111/j.1462-2920.2007.01503.x
Shade, A., Gregory Caporaso, J., Handelsman, J., Knight, R., and Fierer, N. (2013). A Meta-Analysis of Changes in Bacterial and Archaeal Communities with Time. Isme J. 7 (8), 1493–1506. doi:10.1038/ismej.2013.54
Shankar, J. (2017). Insights into Study Design and Statistical Analyses in Translational Microbiome Studies. Ann. Transl. Med. 5 (12), 249. doi:10.21037/atm.2017.01.13
Shaw, G. T., Pao, Y. Y., and Wang, D. (2016). MetaMIS: a Metagenomic Microbial Interaction Simulator Based on Microbial Community Profiles. BMC bioinformatics 17 (1), 488–512. doi:10.1186/s12859-016-1359-0
Stein, R. R., Bucci, V., Toussaint, N. C., Buffie, C. G., Rätsch, G., Pamer, E. G., et al. (2013). Ecological Modeling from Time-Series Inference: Insight into Dynamics and Stability of Intestinal Microbiota. Plos Comput. Biol. 9 (12), e1003388. doi:10.1371/journal.pcbi.1003388
Stein, R. R., Bucci, V., Toussaint, N. C., Buffie, C. G., Rätsch, G., Pamer, E. G., et al. (2013). Ecological Modeling from Time-Series Inference: Insight into Dynamics and Stability of Intestinal Microbiota. Plos Comput. Biol. 9 (12), e1003388. doi:10.1371/journal.pcbi.1003388
Tkacz, A., Hortala, M., and Poole, P. S. (2018). Absolute Quantitation of Microbiota Abundance in Environmental Samples. Microbiome 6 (1), 110–113. doi:10.1186/s40168-018-0491-7
Tkacz, A., Hortala, M., and Poole, P. S. (2018). Absolute Quantitation of Microbiota Abundance in Environmental Samples. Microbiome 6 (1), 110. doi:10.1186/s40168-018-0491-7
Uronis, J. M., Mühlbauer, M., Herfarth, H. H., Rubinas, T. C., Jones, G. S., and Jobin, C. (2009). Modulation of the Intestinal Microbiota Alters Colitis-Associated Colorectal Cancer Susceptibility. PloS one 4 (6), e6026. doi:10.1371/journal.pone.0006026
Venturelli, O. S., Carr, A. C., Fisher, G., Hsu, R. H., Lau, R., Bowen, B. P., et al. (2018). Deciphering Microbial Interactions in Synthetic Human Gut Microbiome Communities. Mol. Syst. Biol. 14 (6), e8157. doi:10.15252/msb.20178157
Ver Hoef, J. M., and Boveng, P. L. (2007). Quasi-Poisson vs. Negative Binomial Regression: How Should We Model Overdispersed Count Data. Ecology 88 (11), 2766–2772. doi:10.1890/07-0043.1
Wang, C. (2021). Microbial Trend Analysis for Common Dynamic Trend, Group Comparison and Classification in Longitudinal Microbiome Study. BMC Genomics 15, 667. doi:10.1186/s12864-021-07948-w
Woo, P. C. Y., Lau, S. K. P., Teng, J. L. L., Tse, H., and Yuen, K.-Y. (2008). Then and Now: Use of 16S rDNA Gene Sequencing for Bacterial Identification and Discovery of Novel Bacteria in Clinical Microbiology Laboratories. Clin. Microbiol. Infect. 14 (10), 908–934. doi:10.1111/j.1469-0691.2008.02070.x
Xia, Y., Sun, J., and Chen, D.-G. (2018). Statistical Analysis of Microbiome Data with R, 847. Springer.
Zhang, X., Pei, Y.-F., Zhang, L., Guo, B., Pendegraft, A. H., Zhuang, W., et al. (2018). Negative Binomial Mixed Models for Analyzing Longitudinal Microbiome Data. Front. Microbiol. 9, 1683. doi:10.3389/fmicb.2018.01683
Keywords: autoregressive, longitudinal microbiome data, microbial community stability, mixed-effects model, zero-inflated, network analysis, microbial interaction, absolute abundance
Citation: He L, Wang C, Hu J, Gao Z, Falcone E, Holland SM, Blaser MJ and Li H (2022) ARZIMM: A Novel Analytic Platform for the Inference of Microbial Interactions and Community Stability from Longitudinal Microbiome Study. Front. Genet. 13:777877. doi: 10.3389/fgene.2022.777877
Received: 16 September 2021; Accepted: 31 January 2022;
Published: 25 February 2022.
Edited by:
Himel Mallick, Merck, United StatesReviewed by:
Boyu Ren, Dana–Farber Cancer Institute, United StatesSiyuan Ma, University of Pennsylvania, United States
Qiwei Li, The University of Texas at Dallas, United States
Copyright © 2022 He, Wang, Hu, Gao, Falcone, Holland, Blaser and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huilin Li, aHVpbGluLmxpQG55dWxhbmdvbmUub3Jn
 Linchen He
Linchen He Chan Wang2
Chan Wang2 Jiyuan Hu
Jiyuan Hu Zhan Gao
Zhan Gao Steven M. Holland
Steven M. Holland Huilin Li
Huilin Li