- 1Aarhus University, Center for Quantitative Genetics and Genomics, Aarhus, Denmark
- 2Viking Genetics, Randers, Denmark
Introduction: The use of automation and sensor-based systems in livestock production allows monitoring of individual cows in real-time and provides the possibility of early warning systems to take necessary management actions against possible anomalies. Among the different RT monitoring parameters, body weight (BW) plays an important role in tracking the productivity and health status.
Methods: In this study, various supervised learning techniques representing different families of methods in the machine learning space were implemented and compared for performance in the prediction of body weight from 3D image data in dairy cows. A total of 83,011 records of contour data from 3D images and body weight measurements taken from a total of 914 Danish Holstein and Jersey cows from 3 different herds were used for the predictions. Various metrics including Pearson’s correlation coefficient (r), the root mean squared error (RMSE), and the mean absolute percentage error (MAPE) were used for robust evaluation of the various supervised techniques and to facilitate comparison with other studies. Prediction was undertaken separately within each breed and subsequently in a combined multi-breed dataset.
Results and discussion: Despite differences in predictive performance across the different supervised learning techniques and datasets (breeds), our results indicate reasonable prediction accuracies with mean correlation coefficient (r) as high as 0.94 and MAPE and RMSE as low as 4.0 % and 33.0 (kg), respectively. In comparison to the within-breed analyses (Jersey, Holstein), prediction using the combined multi-breed data set resulted in higher predictive performance in terms of high correlation coefficient and low MAPE. Additional tests showed that the improvement in predictive performance is mainly due to increase in data size from combining data rather than the multi-breed nature of the combined data. Of the different supervised learning techniques implemented, the tree-based group of supervised learning techniques (Catboost, AdaBoost, random forest) resulted in the highest prediction performance in all the metrics used to evaluate technique performance. Reported prediction errors in our study (RMSE and MAPE) are one of the lowest in the literature for prediction of BW using image data in dairy cattle, highlighting the promising predictive value of contour data from 3D images for BW in dairy cows under commercial farm conditions.
Introduction
Over the past decades, one of the major changes the dairy sector has witnessed has been a reduction in the number of farms with a simultaneous increase in the average herd size (Lowder et al., 2016; Martin and Egon, 2018). With such increases in the average herd size, individual cow management, as well as measurement for traits of interest, is becoming more challenging and labor demanding (Barkema et al., 2015). As a result, the application of automation and sensor systems has increased among dairy farmers as a means to reduce labor costs and improve the management of large herds (Bewley, 2010; Eastwood et al., 2016; Milkevych et al., 2022).
The use of automation and sensor systems in livestock production, commonly termed precision livestock farming (PLF) (Friggens and Thorup, 2015; Berckmans, 2017), allows monitoring of individual cows in real time (RT) and provides the possibility of early-warning systems to take necessary management actions against possible anomalies (Song et al., 2018). Among the different RT-monitoring parameters, body weight (BW) plays an important role in tracking the productivity and health status and provides an insight into lactating cows’ energy balance of individual cows (Mäntysaari and Mäntysaari, 2015; Lassen et al., 2018). It is an integral trait determined mostly by an individual’s genetics and feeding conditions and is subject to temporal variability due to several factors such as physiological state (such as lactation), health status, and other environmental stressors (de Vries et al., 1999; Collard et al., 2000; Mäntysaari and Mäntysaari, 2015). Monitoring BW can allow farmers to make management decisions aimed at early interventions regarding cows’ health status (van der Tol and van der Kamp, 2010).
Several studies explored the possibility of predicting BW using animal morphological features acquired with novel approaches including computer-vision techniques (Song et al., 2018; Jang et al., 2020; Weber et al., 2020). Such approaches cover a variety of techniques to generate predictive features based on dairy cows’ morphology. In particular, contour data based on 2-dimensional (2D) vision (Weber et al., 2020), thermal vision (Stajnko et al., 2008), stereo vision using multiple calibrated 2D cameras (Tasdemir et al., 2011), and 3-dimensional (3D) vision using one or multiple 3D cameras have been previously explored (Marinello et al., 2015; Salau et al., 2016; Song et al., 2018; Jang et al., 2020). Investigation on the promise of computer vision for the prediction of BW in cattle remains a dynamic research topic where combined efforts promise better prediction accuracy toward mainstreaming image-based systems for prediction and monitoring BW in dairy cattle. However, a comparison across studies in predictive performance is hampered by the use of different data sizes and structures (time-series (TS), single-record samples, etc.), different breeds of cattle, inconsistent use of validation and data-split strategies, as well as metrics to compare model performance (Pearson’s correlation coefficient, R2, root mean squared error (RMSE), the mean absolute percentage error (MAPE), the average magnitude of error (MAE), etc.).
Additionally, previous studies on the prediction of BW in cattle based on digital image data mostly used general linear regression models (e.g., Tasdemir et al., 2011; Jang et al., 2020). However, the linear regression methods have been shown to have limitations in handling several predictors, as in the case of automated high-throughput phenotyping, with complex and often nonlinear relationships among these predictors (Comrie, 1997). In comparison, machine-learning (ML) techniques are shown to be better in handling big data and modeling several predictors simultaneously addressing the issue of non-linearity among variables (Shahinfar and Kahn, 2018). The ML is a fast evolving research area and numerous supervised and unsupervised learning techniques with potential application to livestock phenomics are proposed. Nonetheless, only a handful of such techniques are applied to the prediction of BW from image data in dairy cattle (Shine and Murphy, 2022). Moreover, the few studies available on prediction of BW in dairy cattle were breed-specific; all of which focused on the Holstein breed (Tasdemir et al., 2011; Kuzuhara et al., 2015; Hansen et al., 2018; Song et al., 2018). To the best of our knowledge, no study investigated predictive ability image data for BW in the Jersey dairy cattle or used a combined Jersey–Holstein dataset.
In this study, by using one of the largest training datasets used for the prediction of BW in the literature (> 80,000 records from two dairy cattle breeds and three different commercial farms), we investigate the performance of various supervised learning techniques in the prediction of dairy cattle BW using contour data from 3D images. We implement various data-filtering and -splitting methods that accommodate time-series data and used various metrics (Pearson’s correlation coefficient; RMSE, MAPE, etc.) for a robust evaluation of the prediction ability of the various supervised learning methods used in this study.
Materials and methods
Ethics approval statement
All procedures to collect 3D images and body weight data were based on non-invasive methods as part of routine farm management and hence, no specific permission was required.
The methods implemented in this study involved eight major steps for image acquisition and processing as well as data filtering and model fitting (Figure 1).
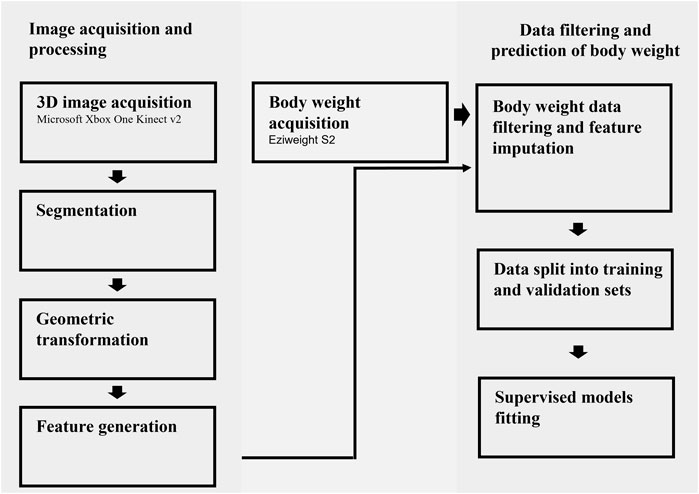
FIGURE 1. A flowchart of all the steps involved in the image acquisition, processing, and prediction of body weight.
Sampled cows and body weight data
Data used in this study included a total of 83,011 records of contour data from 3D images and BW measurements taken from a total of 914 Danish Holstein and Jersey lactating cows from three different herds (WO 2020260631A1, 2020). Of the 914 cows used for obtaining image and BW data, 521 cows were from the Danish Holstein and 393 from the Danish Jersey breeds. The data for the Jersey cows were from two different commercial farms while all the Holstein data came from a single separate farm in Denmark. The number of cows and the distribution (range and mean) of the number of records available per cow in each breed and in the combined Holstein–Jersey dataset are presented in Table 1. The age of the cows during the data collection ranged between 22 and 136 months. BW was measured using a weighing scale installed on the route after the milking parlor in such a way that the BW of passing individual cows is always recorded right after being milked.

TABLE 1. The number of cows and the distribution (min, mean, and max) of the number of records per cow in each breed and the combined dataset.
3D digital image acquisition and processing
The reference unit consists of a single 3D camera using Time of Flight technology (Microsoft Xbox One Kinect v2) to create a 3D image and a Radio Frequency Identification (RFID) reader (Agrident Sensor ASR550). A DELL T630 128 GB RAM server with a 3090 RTX graphics card was used for the data analysis. These were installed in a narrow corridor with a time-based trigger system that allocates all images taken within 3 s of reading an RFID to the associated ear tag. This system ensured that one reference image was obtained from each cow when they passed through the corridor. The corridor has been narrowed further than a normal exit corridor to avoid anomalies during image acquisition; for instance, two cows exiting together or cows turning around and exiting at oblique angles. The 3D camera was placed at a height of 3.4 m above floor level, directly above the passing cows. At the same position as the camera, a bespoke walking scale (Eziweight S2) was installed to make individual BW recordings of the cow that was passing. The scale was calibrated to 50 and 100 kg using two 50 kg blocks.
Before any cows enter the system, the fixed interior in the image of an empty corridor is annotated. In that way, anything that enters an image will be noticed as a change from the annotated picture and be considered a cow. The first step in the image process is to estimate features from the geometric information in the 3D images, which are useful for separating the individuals. All points within the cow circumference are located in a point cloud, so each pixel in this region of the 3D image is transformed into the corresponding spatial 3D coordinates. The calibration procedure is primarily done to remove distortions due to perspective.
The process starts by finding the circumference and spine of the cow in the raw uncorrected 3D images. The circumference is defined as the last pixel before the image sees the annotated floor. Across the back of the cow, the highest point is found and named the spine. This is simply the highest point across the whole corridor. Figure 2 presents an image of the corridor where 3D images are taken (A), an example cow in the corridor (B), and a heatmap of the highest point on the spine of the example cow (C). The feature generation process starts by finding the points on the corrected depth image lying 3, 5, 10, and 15 cm below the spine level of the cow. So how far left or right respectively should you go from the spine to drop 3, 5, 10 or 15 cm is given. This describes the contour of the back of each cow. Because of the length standardization descripted previously, 100 spots are placed for each of the 3, 5, 10, and 15 cm features. In total, 900 spots for each image. The variables used to predict BW are the distance between 3, 5, 10, and 15 cm, respectively, from left to right across the spine of the cow. The height is measured perpendicular to the spine of the cow to make the features invariant with respect to position and orientation. Cubic smooth splines are fitted to the points corresponding to each distance to reduce noise.

FIGURE 2. An illustration of the corridor where the 3D images are taken (A), an example cow in the corridor (B), and a heatmap of the highest point on the spine of the example cow (C).
An illustration of some of the acquired images and examples of these contours are presented in Figure 3. The raw spine features are generated by measuring the distance between the intersection of the spine normal and the spines on each side of the cow. The raw spine features are normalized to correct for anatomically differences. All programming was carried out using the Python software.

FIGURE 3. An illustration of the data from an image after correction for the annotated floor. All images are standardized in length and width. The highest point across the image is the spine and these points can be found all the way down the back. Afterward, the distance you have to go left or right respectively to drop 3, 5, 10 and 15 cm is found, and again, 100 points are found and noted. The data used to predict bodyweight are the distance from left to right between the 3, 5, 10 and 15 cm point.
Data filtering
Data used in this study include (i) the sets of individual time series (TS) of cows’ BW measurements and (ii) associated sets of contours (resulted from image processing) for each individual’s TS records. The data records include some proportion of unavoidable incorrect records due to on-site measurements (improper position of cows on weighing scale, malfunctions in the weighing scale, image quality, etc.). Therefore, implementation of data filtering, considered here as detection and removal and/or imputation of incorrect records, is an important primary step in the automated data processing pipeline.
The methods used in our study for filtering data were, to some extent, based on prior knowledge of BW characteristics in Jersey and Holstein dairy cows such as expected average of BW at a specific age and breed-specific growth rates. That means, the prior information was used in tuning and/or adapting the selected filtering methods to handle TS data of BW records. The records (of cows’ weights) are provided with (i) herd and farm conditions; (ii) animals’ ages; and (iii) breed-specific characteristics of growth dynamics.
Three different filtering approaches were used and tested for the best performance (filtering quality) in the study. The first approach was based on the modified Z-score (ZS) method (Iglewicz and Hoaglin, 1993).
The time-series body weight data for a specific cow is the sequence of records sampled continuously within a specified time interval
Assume that
where
The normalization constant 0.6745 is required because the expectation
Finally, the records are labeled outliers when the following condition is satisfied:
where
The second-implemented data-filtering approach (CL1) was based on the mean shift clustering (MSC) algorithm (Comaniciu and Meer, 2002). Here, the appropriate use of MSC in the case of
As in the case of the ZS method, we use only the
Finally, the resulting cluster is not labeled outlier when the following condition is satisfied:
where
The third data-filtering approach was based on clustering using the dynamic changes of animals’ weights, such as expected breed-, age-, and farm-specific daily weight gain (CL2).
Let us suppose that the initial record
Data clustering is realized by iterative calculation of the dynamical BW change for every pair
The following estimator is used to estimate the dynamical change of BW in
where
The resulting record is labeled outlier (inherited by the outlier cluster) when the following condition is satisfied:
where
The general overview of data filtering is represented in Figure 4 (and more details in Supplementary File S1). In order to determine the best performing data-filtering method, all three methods were implemented and analyzed with respect to the quality of outlier filtering. In this regard, three different simulation pipelines using three filtered datasets (generated according to the specific filtering method) were established. The pipelines involved training and validation of the range of selected models (see all details further in this section). The prediction results (BW for each dataset) were subjected to the quality assessment. Here, the assessment was based on Pearson’s correlations coefficients between the predicted and observed BW. Accordingly, results on the predictive performances of the different models presented in this study are based on the best-performing data-filtering technique (CL2) based on this preliminary assessment. A fully functional Python code for implementing the data-filtering techniques is presented in Supplementary File S2.
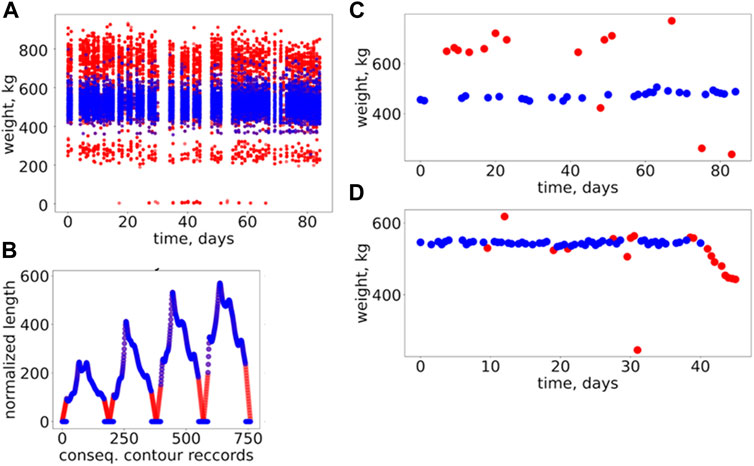
FIGURE 4. General overview of the results of data-filtering and imputation. (A) Changes of body weight over time for the combined datasets (all data depicted in the plot) for Jersey and Holstein; here the original (raw) data is represented by red dots; the same data but without outliers are represented by the blue dots; the outliers were filtered out using the CL2 method. (B) An example of imputation of contour data for a specific (randomly selected) cow; here, the blue dots indicate the original contour data resulting from the image processing; the red dots indicate an imputed data for the missing records in the original contour data; the plot depicts the complete dataset (for the selected cow) which will be used for modeling; the different colors shown in the plot are just to highlight the imputed part of the contour data. (C), (D) Two examples of body weight changes over time for the randomly selected cows; here, the original (depicted by the red dots) data and the data without outliers (the blue dots) are shown together.
In contrast to the BW records, the contour data have limited prior knowledge: all contours are expected to be closed, which means that the first and last records of a normalized distance (width) should approach zero. We used this information for contours’ records filtering and imputation (recover missing records). Because no additional information was available regarding the shape of the contours’ curves, we used simple linear approximation to detect outliers and complete (impute) the missing/incorrect contours’ records (Figure 4B).
Training and validation strategies
Predictive ability of contour data from 3D images for BW in dairy cows was first investigated separately within each breed and subsequently in the combined multi-breed (Holstein–Jersey) dataset. Within each dataset (Jersey, Holstein, and combined), splitting the data into training and test sets was the first step in the implementation of the prediction models. Accordingly, we implemented approaches including the traditional time-series approach (TS), a modified version of the time-series approach (TS2), and an approach randomly splitting data (RA) for splitting the data into training and test sets. The first two scenarios were based on time-series data splitting such that observations from the training set occurred before their corresponding test set. These were implemented in a two-step manner, such that, the first 80% of cows were randomly selected and records for each of these cows were sorted according to timestamps, while the remaining 20% cows were held out as the test set. Subsequently, for these randomly selected cows, 80% of the records with the earliest timestamps were selected for training. The remaining 20% records from these randomly selected cows were either discarded (TS) or added to the test set (TS2). Therefore, the main difference between scenario 1 (TS) and scenario 2 (TS2) was whether later records of cows in the training set were included in the test set. In addition, a third data-split scenario was implemented by randomly selecting 80% of individuals for training and excluding all their records from the test set, while the remaining 20% were used as the test set (RA).
In the traditional time-series prediction, usually a part at the end of each series is reserved and not used during model generation for later use in model evaluation. This is often called out-of-sample evaluation (Tashman, 2000). Whereas, in machine-learning studies, cross-validation is the most widely used tool in the evaluation of regression and classification methods; studies have demonstrated practical problems and violations of important assumptions such as stationarity in time-series data (Bergmeir and Benítez, 2012). Therefore, here in this study, we apply, in addition to the RA and TS approaches, a modified TS approach in a two-stage manner where we first take a random sub-sample of the data (80%) at a time and apply time-series approaches to split the data into training and test sets. That way, we were able to undertake repeated evaluations (replicates) and still use a part at the end of each series for validation. Except for the predictions using the linear regression techniques (LR, RR, and, to some extent, LA), the modified time-series approach (TS2) for splitting data into training and test sets resulted in higher correlation between predicted and observed BW and low RMSE and MAPE values across the datasets.
Supervised learning techniques
Several methods chosen to represent different families of techniques in the supervised learning space were compared for predictive performance of BW using contour data.
Linear regression
Here, we used the ordinary linear regression (LR) and the regularization techniques of ridge regression (RR) (Hoerl and Kennard, 1970) and the Least Absolute Shrinkage and Selection Operator regression (LASSO) (Tibshirani, 1996). The linear regression method is one of the most widely deployed tools for predicting a quantitative response (James et al., 2013), and is often used as a benchmark method in comparing the performance of other ML methods. The RR and LASSO are a family of the linear regression technique with regularization of parameters in the linear regression fit.
Tree-based regression
We have chosen the random forest (RF) (Ho, 1995) and decision tree (DT) regressors as well as boosting approaches as representatives of the tree-based family of supervised learning techniques. The tree-based methods are a group of supervised learning techniques that is getting increasing popularity in computational biology (Geurts et al., 2009) and represents the most frequent-used family of techniques in the ML applications to the livestock space (Shine and Murphy, 2022). Regression trees have previously been used for BW prediction in different livestock species including cattle (e.g. Topal et al., 2010). While regression trees are relatively simple for implementation and interpretation, prediction accuracies have often been lower than other supervised learning techniques (James et al., 2013). In contrast, methods such as random forests and boosting use trees as building blocks to construct more powerful prediction models by aggregating many decision trees. Therefore, in addition to the random forest model, we implement two boosting approaches (Adaptive Boosting (AB) and Catboost (CB)) in this study. Catboost (Ostroumova et al., 2018) is developed for an unbiased boosting with categorical features. However, studies have implemented and demonstrated how well-suited CatBoost is for regression problems involving time-series data (Kolesnikov et al., 2019; Hancock and Khoshgoftaar, 2020). For the RF and DT regressors, the sklearn ccp_alpha parameter for Minimal Cost-Complexity Pruning was optimized through cross-validation.
Support vector regression
Support vector (SV) machines (Vapnik and Lerner, 1963) have been extensively used in machine learning, primarily for classification, and are being increasingly applied for regression as well (Smola and Schölkopf, 2004).
All implemented supervised learning techniques, except the Catboost regressor, were imported from their corresponding packages available in the scikit learn website (https://scikit-learn.org). The Catboost regressor was imported from the open-source Catboost package (Ostroumova et al., 2018).
Evaluation of predictive performance
Predictive performances of the different models were quantified by using Pearson’s correlation coefficient (
where
The prediction was undertaken in ten replicates for each dataset (Jersey, Holstein, and combined) and data-split scenario (TS2, TS, and RA), and the average
Results
Descriptive statistics
Descriptive statistics of BW measured in dairy cows according to the breed and the combined dataset are presented in Table 2. The Jersey cows had a mean BW of 558.4 kg, while the Holstein cows had a mean BW of 690.3 kg. The coefficient of variability (CV) observed in BW measurements was comparable in the two breeds while a relatively higher CV was observed in the combined dataset. Figure 5 presents BW across ages of cows in the two breeds and the combined dataset.
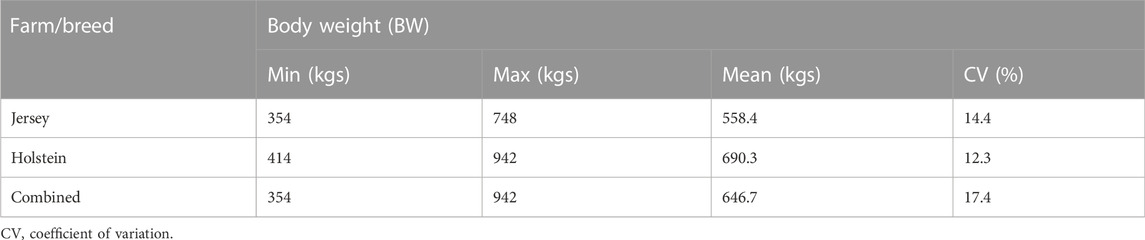
TABLE 2. Descriptive statistics of the BW measured in Jersey and Holstein cows, as well as the combined dataset.
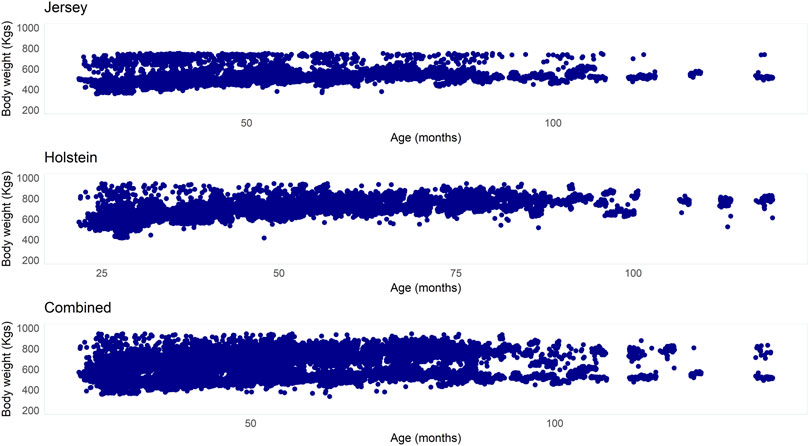
FIGURE 5. Bodyweight (kg) across ages (months) of cows from the three datasets (Jersey, Holstein, and combined breed).
Predictive performance of supervised learning techniques
Figures 6–8 present mean correlation coefficients (
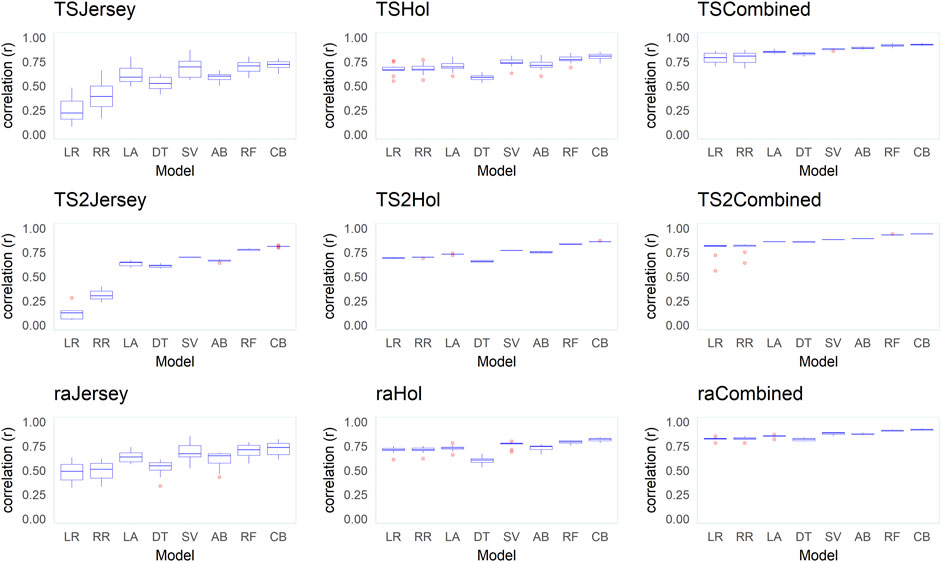
FIGURE 6. Box plots of correlations (r) between the observed and predicted body weight (BW) from predictions in 10 replicates across the different datasets (Jersey, Holstein, and combined), data-split scenarios (TS2, TS, and RA), and various supervised learning techniques (LR, linear regression; RR, ridge regression; LA, LASSO; DT, decision tree; SV, support vector machine; AB, Adaboost; RF, random forest; and CB, Catboost).
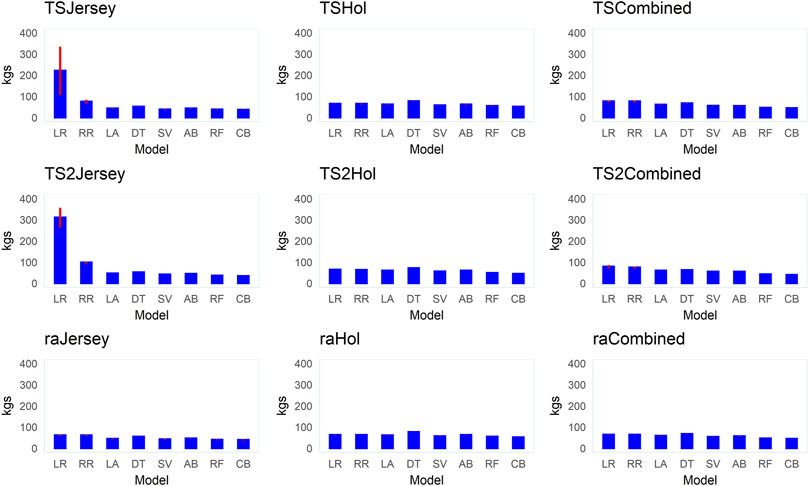
FIGURE 7. Bar plots of the mean root mean squared error (RMSE) values (+ standard error bars) for the different supervised learning techniques (LR, linear regression; RR, ridge regression; LA, LASSO; DT, decision tree; SV, support vector machine; AB, Adaboost; RF, random forest; and CB, Catboost) across the different datasets (Jersey, Holstein, and combined) and data-split scenarios (TS2, TS and RA).
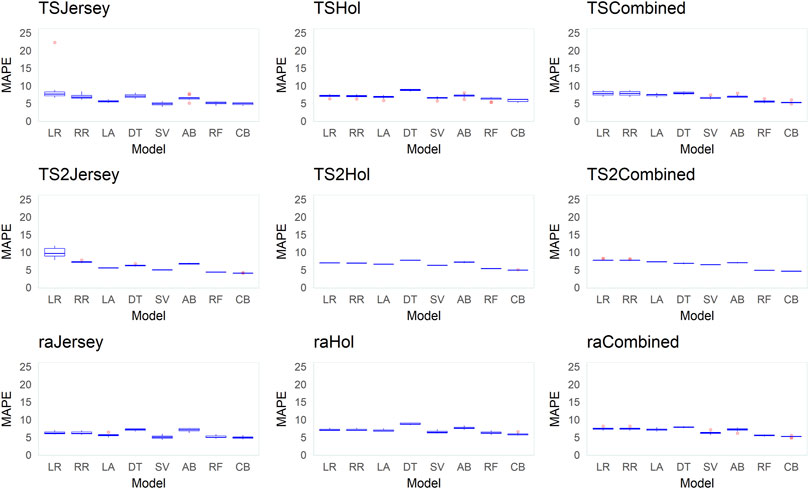
FIGURE 8. Box plots of the mean absolute percentage error (MAPE) between observed and predicted body weight (BW) from predictions in 10 replicates across the different datasets (Jersey, Holstein, and combined), data-split scenarios (TS2, TS, and RA), and various supervised learning techniques (LR, linear regression; RR, ridge regression; LA, LASSO; DT, decision tree; SV, support vector machine; AB, Adaboost; RF, random forest; and CB, Catboost).
Across all datasets and data-split scenarios, the tree-based group of supervised learning techniques (Catboost, AdaBoost, and random forest) resulted in the highest prediction performance in all the metrics used to evaluate the technique performance, followed by the support vector regression technique. The tree-based group of supervised learning techniques also resulted in the lowest standard deviation between the 10 replicates. Of the tree-based methods, Catboost resulted in the highest performance in all the metrics used, while the decision tree regressor resulted in the lowest prediction performance. In most instances (dataset and -split scenario), the support vector method outperformed the decision tree regressor. In the majority of the data-splitting scenarios and datasets, the linear regression methods (classical linear regression, ridge regression, and LASSO) resulted in the lowest prediction performance compared to the rest of families of supervised learning techniques. Within this family, classical linear regression showed the lowest performance in the majority of the scenarios (dataset and data-split method). The exception was in the Holstein dataset, where the decision tree regressor resulted in the lowest predictive performance. Prediction using the linear regression technique was worst in the dataset with the smallest number of records (Jersey) in terms of low Pearson’s correlation coefficient ( = 0.12–0.48) and high RMSE (60–309.8 kg) and MAPE values (6.2–9.8%) across different data-splitting scenarios.
In general, the predictive performance of supervised learning techniques varied according to the datasets. Overall, the highest discrepancy between the learning techniques in predictive performance was observed within the dataset with a relatively smaller number of records (Jersey) where the linear regression group of techniques showed poor performance while the tree-based models were shown to be highly predictive in terms of all metrics used to evaluate models. In the combined (Jersey–Holstein) dataset, where the largest number of records was used in training the supervised learning techniques, and differences in predictive performance between the various supervised learning techniques were modest. Predictive performance was the highest in the combined dataset compared to the single-breed Jersey and Holstein datasets across all implemented models. To test if the improvement in predictive ability in the combined dataset was due to the increase in dataset or due to the multi-breed nature of the combined dataset, we implemented an additional test where multi-breed data of similar sizes as the single-breed Jersey and Holstein datasets were used for prediction using 10 replicates. The results showed that prediction using multi-breed data of equal sizes to the single-breed datasets led to slightly lower prediction accuracies in terms of correlation between the predicted and observed BW. However, the differences were neither statistically nor significantly different except in the comparison in the Jersey dataset (combined multi-breed data with equal size as the Jersey breed dataset) using the LR models.
Predictive performance of the implemented supervised learning techniques also varied according to the data-split scenario used to create training and validation subsets (Supplementary Files S4–S6). In general, higher Pearson’s correlation coefficients and lower MAPE and RMSE values were obtained when supervised learning techniques were trained using the training subset created with the TS2 method, followed by TS in comparison to the approach of splitting training and testing subsets randomly (RA).
Discussion
Relative performance of different supervised learning techniques
Generally, our results indicate marked differences in the predictive abilities of various supervised learning techniques depending on the dataset (Jersey, Holstein, and combined data) and the data-splitting techniques followed. Relatively higher predictive performance was shown for the tree-based family of supervised learning techniques compared to a wide variety of other techniques implemented in this study to represent different families of methods in the ML space. Boosting methods such as Catboost as well as the random forest performed reasonably well in this study. A similar observation of the outstanding performance of the tree-based techniques in the prediction of cattle BW using various features including 3D image data is previously reported (e.g. Weber et al., 2020). The linear regression group of techniques (LR, RR, and LASSO) generally performed poorly in our study. In general, the relative performance and suitability of different supervised learning techniques may vary, among others, depending on the nature of the data and the relationship between predictors and between predictors and the outcome. The linear regression group of learning techniques tends to perform poorly when there is a nonlinear relationship between the predictors and the outcome (James et al., 2013). CatBoost is a gradient-boosted decision-tree implementation for supervised ML allowing ordered target statistics and ordered boosting (Hancock and Khoshgoftaar, 2020). Gradient boosting is a powerful supervised learning technique that remained an important method for learning problems with heterogeneous features, noisy data, and complex dependencies (Ostroumova et al., 2018).
Repeated records of BW from cows ranging between 22 and 136 months of age were used in training the supervised learning methods in our study. Moreover, the on-access setup of weighing scales along the path to milking parlors might cause some noise in the target variable (BW) in such a way that at times, cows might have placed only the front or rear legs at the time of weight reading and, in some cases, reading might belong to that of two cows both placing some of their legs on the floor attached to the weighing scale. All these combined can introduce heterogeneity and noise in the data. Different approaches have been followed to filter noise and enforce rigorous quality control before implementing the learning techniques. While such approaches can help detect and remove major outliers, it is not possible to eliminate all noise in the data. The differences in the predictive performance of the various learning techniques implemented in this study might largely be due to such unavoidable noises in the data used for training.
Data-splitting methods and validation metrics matter
Our results also showed differences in the predictive performance of the learning techniques according to the implemented data-split scenario. Except for the predictions using the linear regression techniques (LR, RR, and, to some extent, LA), the modified time-series approach (TS2) for splitting data into training and test sets resulted in higher correlation between predicted and observed BW and low RMSE and MAPE values across the datasets. While both the traditional and modified time-series data-splitting techniques accounted for the time-series nature of the data such that observations from the training set occur before their corresponding test set, they differed regarding the use of a part at the end of each series for validation. In the traditional time-series prediction, usually a part at the end of each series is reserved and not used during model generation for later use in model evaluation. This is often called out-of-sample evaluation (Tashman, 2000); whereas in machine-learning studies, cross-validation is the most widely used tool in the evaluation of regression and classification methods, studies have demonstrated practical problems and violations of important assumptions such as stationarity in time-series data (Bergmeir and Benítez, 2012). The modified-TS approach (TS2) implemented in this study allowed repeated evaluations while still using a part at the end of each series as it was applied in a two-stage manner where we first take a random sub-sample of the data (80%) at a time and apply time-series approaches to split the data into training and test sets. That way, we were able to undertake repeated evaluations (replicates) and still use a part at the end of each series for validation, and thus allowing for better predictive performance.
The comparison across the studies investigating predictive abilities of various supervised learning techniques for the prediction of cattle BW using image data is hampered by the use of different data sizes and structures (time-series, single-record samples, etc.), different validation and data-split strategies as well as the use of different metrics to compare model performances (r, RMSE, MAPE, etc.).
In our study, the combined use of three metrics (r, RMSE, and MAPE) to evaluate the different supervised learning techniques was chosen to ensure comparability with other studies and for a robust model evaluation as each has different advantages and limitations. In computational biology, it is common to use Pearson’s correlation coefficient (r) as a model selection criterion (González-Recio et al., 2014). However, a limitation is that Pearson’s correlation does not address the bias of predictions (González-Recio et al., 2014). The RMSE is the most popular measure of prediction error which has been used in several studies on the prediction of cattle BW using image data (e.g., Song et al., 2018; Jang et al., 2020; Weber et al., 2020). RMSE is however scale-dependent and hence, a comparison of results between variables or species is not possible. The mean absolute percentage error (MAPE) is, on the other hand, scale-independent and easy to interpret, making it one of the most popular measures of prediction accuracy (Byrne, 2012; Kim & Kim, 2016). In our study, the highest Pearson’s correlation between predicted and observed BW was observed in the combined Holstein–Jersey dataset. This is expected due to the large increase in training data from combining the datasets from the two breeds compared to the within-breed predictions. However, the lowest RMSE value was observed in the Jersey dataset where the smallest training data was used compared to the Holstein or combined datasets. This is due to the fact that Jersey cows are smaller in size when compared to Holstein cows as reflected in the mean BW from the two datasets and the scale-dependent nature of RMSE as an evaluation metric. This suggests the need for caution in the use of scale-dependent metrics such as RMSE for comparison of prediction performance even between different breeds of cattle of the same livestock species.
Combining datasets is advantageous
Generally, studies on the predictive ability of image data for BW in dairy cattle are scarce, and the few available studies have solely focused on the Holstein breed (Tasdemir et al., 2011; Kuzuhara et al., 2015; Hansen et al., 2018; Song et al., 2018). To the best of our knowledge, no study investigated the predictive ability of image data for dairy cattle BW using multi-breed data. Moreover, most studies relied on numerically small data (number of cows and records). For instance, the image data from 30 or a lower number of cows were used to predict the BW in Holstein cows in the studies of Song et al. (2018) and Kuzuhara et al. (2015). The study of Kuzuhara et al. (2015) used RMSE as the metric to evaluate predictive performance in a linear regression model and report an RMSE value of 42.65 kg while Song et al. (2018) reported the lowest RMSE of 41.2 kg and MAPE of 5.2%. Here in this study, we used a large dataset (> 80K records) across different breeds (Holstein, Jersey, and combined multi-breed data) from different commercial farms to investigate the predictive ability of 3D image data for BW in dairy cattle. We report one of the lowest RMSE (33 kg) and MAPE (4%) values in the literature available on the prediction of dairy cattle BW using contour data from 3D images, indicating that combining data (from different breeds or farms) to increase the size of learning data can improve prediction accuracies.
Often, combining multi-breed data for the prediction of phenotypes is challenging due to differences in the breeds. In this study, we show that the increase in data size due to combining different breeds might offset the disadvantage from the multi-breed nature of the combined dataset given that the combined data is substantially larger than the single-breed data. Several research groups have undertaken studies aimed at predicting BW in dairy cattle using morphometric measurements based on different systems, including 3D images. Across-population combined analysis using available data in the different research groups might substantially improve data size to train learning techniques with substantially reduced prediction errors. Publicly available repositories and databases that store images and corresponding biometrics have previously been suggested (Wang et al., 2021).
Practical implications and the way forward
In general, our study indicates the promising predictive value of contour data from 3D images for BW in dairy cows under commercial farm conditions. Depending on the supervised learning technique and the datasets used, we show reasonable predictive performances in terms of correlation between predicted and observed BW (r), RMSE, and MAPE, promising an automated and high-throughput prediction of BW in dairy cattle herds.
Use of image data for automated detection of anomalies in cows’ health status or monitoring other short-term changes in cows’ BW requires high sensitivity. While our study reports one of the lowest prediction errors (RMSE as low as 33 kg) in the literature on prediction of BW using image data for dairy cattle, these values might still be considered as high in light of early warning and monitoring systems. However, these RMSE values are in line with the expected fluctuation in body weight within a day for Holstein and Jersey cattle. For instance, dry-matter intake was reported to be approximately between 14 and 20 kg for Danish Holstein cows and between 11 and 16.7 kg for Danish Jersey cows (Li et al., 2016). In addition, the maximum average daily milk yield of 35 and 24 kg/day were reported for Danish Holstein and Jersey cows, respectively (Halachmi et al., 2011). A Holstein cow requires 4–5 kg of water per kg of milk yield (www.lely.com). Therefore, given all these factors introducing massive fluctuations of body weight within a day, the RMSE values reported in this study are within the expected daily weight fluctuations for Holstein and Jersey cows.
Of all potential reasons for higher prediction errors, erroneous records might be difficult to eliminate completely and thus cost prediction accuracies. In this study, we preliminarily assessed three different data-filtering techniques for prediction accuracy and presented results based on data-filtered using the high-ranking method (CL2). Despite a relatively better performance of this outlier detection technique compared to the other two implemented, some irregularities still persist in the filtered data. We used time-series data where some individuals have hundreds of records in different time periods whereas others have only one or few records. High variability was observed in the BW measurement in cows (records) measured at an early age compared to later ages (as shown in Figure 5). Efficient outlier detection and missing-value-interpolation techniques need to be developed to rigorously filter such time-series data. Furthermore, as previously suggested by Nir et al. (2018), considering additional features, based on the image or other data sources, and introducing deep artificial neural network algorithms might allow further improvement in the prediction accuracy of various livestock phenotypes using computer-vision.
Conclusion
Using a multi-breed dataset consisting of over 80,000 records of contour features from 3D images and BW data, our study reaffirms the promise of image data for rapid and high throughput prediction of BW in dairy cattle. The study implemented and compared the predictive performance of various supervised learning techniques using different metrics and in both within-breed and combined-breed datasets. Our results indicate that combining datasets from different breeds and farms allowed improved prediction accuracy. Our study also show that the tree-based learning techniques, including Catboost and random forest led to higher predictive performance, in terms of higher Pearson’s correlation coefficients between predicted and observed BW as well as lower RMSE and MAPE values. Reported prediction errors in our study (RMSE and MAPE) are one of the lowest in the literature for prediction of BW using image data in dairy cattle, highlighting the promising predictive value of contour data from 3D images for BW in dairy cows under commercial farm conditions. Further increasing training data size and development of efficient and tailored outlier detection techniques could allow further reduction of prediction error.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Ethics statement
Ethical review and approval was not required for the animal study because all procedures to collect 3D images and body weight data were based on non-invasive methods as part of routine farm management, and hence, no specific permission was required.
Author contributions
GG conceived the study, implemented the analyses, and drafted the manuscript. VM developed pipelines for the statistical analyses and contributed to drafting the manuscript. GS contributed to the discussion of the results and manuscript write-up. JL attracted funding and contributed to the manuscript write-up.
Funding
This work was carried out in the CFIT project (9090-00083B) funded by the Innovation Fund Denmark.
Conflict of interest
JL was employed by the company Viking Genetics.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2022.947176/full#supplementary-material
References
Barkema, H. W., Von Keyserlingk, M. A. G., Kastelic, J. P., Lam, T. J. G. M., Luby, C., Roy, J.-P., et al. (2015). Invited review: Changes in the dairy industry affecting dairy cattle health and welfare. J. Dairy Sci. 98, 7426–7445. doi:10.3168/jds.2015-9377
Berckmans, D. (2017). General introduction to precision livestock farming. Anim. Front. Front. 7, 6–11. doi:10.2527/af.2017.0102
Bergmeir, C., and Benítez, J. M. (2012). On the use of cross-validation for time series predictor evaluation. Inf. Sci. (N. Y). 191, 192–213. doi:10.1016/j.ins.2011.12.028
Bewley, J. (2010). “Precision dairy farming: Advanced analysis solutions for future profitability,” in Proc. First North American Conference on Precision Dairy Management, Toronto, Canada, March 2–5, 2010, 2–5.
Byrne, R. F. (2012). Beyond traditional time-series: Using demand sensing to improve forecasts in volatile times. J. Bus. Forecast. 31 (2), 13–19.
Collard, B. L., Boettcher, P. J., Dekkers, J. C. M., Petitclerc, D., and Schaeffer, L. R. (2000). Relationships between energy balance and health traits of dairy cattle in early lactation. J. Dairy Sci. 83, 2683–2690. doi:10.3168/jds.S0022-0302(00)75162-9
Comaniciu, D., and Meer, P. (2002). Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 24, 603–619. doi:10.1109/34.1000236
Comrie, A. C. (1997). Comparing neural networks and regression models for ozone forecasting. J. Air Waste Manag. Assoc. 47, 653–663. doi:10.1080/10473289.1997.10463925
de Vries, M. J., van der Beek, S., Kaal-Lansbergen, L. M., Ouweltjes, W., and Wilmink, J. B. (1999). Modeling of energy balance in early lactation and the effect of energy deficits in early lactation on first detected estrus postpartum in dairy cows. J. Dairy Sci. 82, 1927–1934. doi:10.3168/jds.S0022-0302(99)75428-7
Eastwood, C., Jago, J., Edwards, J., and Burke, J. (2016). Getting the most out of advanced farm management technologies: Roles of technology suppliers and dairy industry organisations in supporting precision dairy farmers. Anim. Prod. Sci. 56, 1752–1760. doi:10.1071/an141015
Friggens, N. C., and Thorup, V. M. (2015). From monitoring to precision phenotyping: Towards a systemic use of precision livestock measures in dairy herds. Proc. New Zeal. Soc. Anim. Prod. 75, 145–148.
Geurts, P., Irrthum, A., and Wehenkel, L. (2009). Supervised learning with decision tree-based methods in computational and systems biology. Mol. Biosyst. 5 (12), 1593–1605. doi:10.1039/b907946g
González-Recio, O., Rosa, G. J. M., and Gianola, D. (2014). Machine learning methods and predictive ability metrics for genome-wide prediction of complex traits. Livest. Sci. 166, 217–231. doi:10.1016/j.livsci.2014.05.036
Halachmi, I., Børsting, C. F., Maltz, E., Edan, Y., and Weisbjerg, M. R. (2011). Feed intake of Holstein, Danish Red, and Jersey cows in automatic milking systems. Livest. Sci. 138, 56–61. doi:10.1016/j.livsci.2010.12.001
Hancock, J. T., and Khoshgoftaar, T. M. (2020). CatBoost for big data: An interdisciplinary review. J. Big Data 7, 94. doi:10.1186/s40537-020-00369-8
Hansen, M. F., Smith, M. L., Smith, L. N., Jabbar, K. A., and Forbes, D. (2018). Automated monitoring of dairy cow body condition, mobility and weight using a single 3D video capture device. Comput. Ind. 98, 14–22. doi:10.1016/j.compind.2018.02.011
Ho, T. K. (1995). “Random decision forests,” in Proceedings of the International Conference on Document Analysis and Recognition, ICDAR (IEEE Computer Society), 278282. doi:10.1109/ICDAR.1995.598994
Hoerl, A. E., and Kennard, R. W. (1970). Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 12, 55–67. doi:10.1080/00401706.1970.10488634
Iglewicz, B., and Hoaglin, D. (1993). “The ASQC basic references in quality control: Statistical techniques,” in How to detect and handle outliers. Editor E. F. Mykytka (Milwaukee: ASQC Quality Press), 16.
James, G., Witten, D., Hastie, T., and Tibshirani, R. (2013). “Linear regression,” in An introduction to statistical learning (New York: Springer), 373–418.
Jang, D. H., Kim, C., Ko, Y. G., and Kim, H. Y. (2020). Estimation of body weight for Korean cattle using three-dimensional image. J. Biosyst. Eng. 45, 325–332. doi:10.1007/s42853-020-00073-8
Jensen, C., Østergaard, S., Bertilsson, J., and Weisbjerg, M. R. (2015). Responses in live weight change to net energy intake in dairy cows. Livest. Sci. 181, 163–170. doi:10.1016/j.livsci.2015.09.016
Kim, S., and Kim, H. (2016). A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 32 (3), 669–679. doi:10.1016/j.ijforecast.2015.12.003
Kolesnikov, A. A., Kikin, P. M., and Portnov, A. M. (2019). Diseases spread prediction in tropical areas by machine learning methods ensembling and spatial analysis techniques. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. XLII-3/W8, 221–226. doi:10.5194/isprs-archives-XLII-3-W8-221-2019
Kuzuhara, Y., Kawamura, K., Yoshitoshi, R., Tamaki, T., Sugai, S., Ikegami, M., et al. (2015). A preliminarily study for predicting body weight and milk properties in lactating Holstein cows using a three-dimensional camera system. Comput. Electron. Agric. 111, 186–193. doi:10.1016/j.compag.2014.12.020
Lassen, J., Thomasen, J. R., Hjort Hansen, R., Gunner Brink Nielsen, G., Olsen, E. V., Bolvig Stentebjerg, P. R., et al. (2018). “Individual measure of feed intake on in-house commercial dairy cattle using 3D camera system,” in Proceedings of the World Congress on Genetics Applied to Livestock Production, Auckland, New Zealand, February 11, 2018 (v. Technologies). Novel Phenotypes.
Li, B., Fikse, W. F., Lassen, J., Lidauer, M. H., Løvendahl, P., Mäntysaari, P., et al. (2016). Genetic parameters for dry matter intake in primiparous Holstein, Nordic Red, and Jersey cows in the first half of lactation. J. Dairy Sci. 99, 7232–7239. doi:10.3168/jds.2015-10669
Lowder, S. K., Skoet, J., and Raney, T. (2016). The number, size, and distribution of farms, smallholder farms, and family farms worldwide. World Dev. 87, 16–29. doi:10.1016/j.worlddev.2015.10.041
Mäntysaari, P., and Mäntysaari, E. A. (2015). Modeling of daily body weights and body weight changes of Nordic Red cows. J. Dairy Sci. 98, 6992–7002. doi:10.3168/jds2015-9541
Marinello, F., Pezzuolo, A., Cillis, D., Gasparini, F., and Sartori, L. (2015). “Application of Kinect-Sensor for three-dimensional body measurements of cows,” in 7th European Conference on Precision Livestock Farming, ECPLF, Milan, Italy, September 15–18, 2015, 661–669.
Martin, H. T., and Egon, B. N. (2018). Denmark national report: SUFISA, WP2- deliverable 2.2. Aarhus, Denmark: Aarhus University and University of Southern Denmark. Accessible at: https://www.sufisa.eu/wp-content/uploads/2018/09/D_2.2-Denmark-National-Report.pdf.
Milkevych, V., Villumsen, T. M., Løvendahl, P., and Sahana, G. (2022). Data synchronization for gas emission measurements from dairy cattle: A matched filter approach. Comput. Electron. Agric. 201, 107299. doi:10.1016/j.compag.2022.107299
Nir, O., Parmet, Y., Werner, D., Adin, G., and Halachmi, I. (2018). 3D Computer-vision system for automatically estimating heifer height and body mass. Biosyst. Eng. 173, 4–10. doi:10.1016/j.biosystemseng.2017.11.014
Ostroumova, L., Gusev, G., Vorobev, A., Dorogush, A. V., and Gulin, A. (2018). “Catboost: Unbiased boosting with categorical features,” in Advances in Neural Information Processing Systems. Editors S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Curran Associates, Inc), 31, 6638–6648.
Salau, J., Haas, J. H., Junge, W., and Thaller, G. (2016). Extrinsic calibration of a multi-Kinect camera scanning passage for measuring functional traits in dairy cows. Biosyst. Eng. 151, 409–424. doi:10.1016/j.biosystemseng.2016.10.008
Shahinfar, S., and Kahn, L. (2018). Machine learning approaches for early prediction of adult wool growth and quality in Australian Merino sheep. Comput. Electron. Agric. 148, 72–81. doi:10.1016/j.compag.2018.03.001
Shine, P., and Murphy, M. D. (2022). Over 20 Years of machine learning applications on dairy farms: A comprehensive mapping study. Sensors 22 (1), 52. doi:10.3390/s22010052
Smola, A., and Schölkopf, B. (2004). A tutorial on support vector regression. Statistics Comput. 14, 199–222. doi:10.1023/b:stco.0000035301.49549.88
Song, X., Bokkers, E. A. M., van der Tol, P. P. J., Koerkamp, P. W. G. G., and van Mourik, S. (2018). Automated body weight prediction of dairy cows using 3-dimensional vision. J. Dairy Sci. 101, 4448–4459. doi:10.3168/jds.2017-13094
Stajnko, D., Brus, M., and Hočevar, M. (2008). Estimation of bull live weight through thermographically measured body dimensions. Comput. Electron. Agric. 61, 233–240. doi:10.1016/j.compag.2007.12.002
Tasdemir, S., Urkmez, A., and Inal, S. (2011). Determination of body measurements on the Holstein cows using digital image analysis and estimation of live weight with regression analysis. Comput. Electron. Agric. 76 (2), 189–197. doi:10.1016/j.compag.2011.02.001
Tashman, L. J. (2000). Out-of-sample tests of forecasting accuracy: An analysis and review. Int. J. Forecast. 16 (4), 437–450.
Tibshirani, R. (1996). Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B B 58, 267–288. doi:10.1111/j.2517-6161.1996.tb02080.x
Topal, M., Aksakal, V., Bayram, B., and Yaganoglu, M. (2010). An analysis of the factor affecting birth weight and actual milk yield in Swedish red cattle using regression tree analysis. J. Animal Plant Sci. 20, 63–69.
van der Tol, P. P. J., and van der Kamp, A. (2010). “Time series analysis of live weight as health indicator,” in First North American Conference on Precision Dairy Management 2010, Toronto, Canada, March 2”5, 2010 (Madison, WI: Omnipress), 230–231.
Vapnik, V., and Lerner, A. (1963). Pattern recognition using generalized portrait method. Automation Remote Control 24, 774–780.
Wang, Z., Shadpour, S., Chan, E., Rotondo, V., Wood, K. M., and Tulpan, D. C. (2021). ASAS-NANP SYMPOSIUM: Applications of machine learning for livestock body weight prediction from digital images. J. Anim. Sci. 99, skab022. doi:10.1093/jas/skab022
Weber, V. A. M., de Lima, W. F., da Silva, O. A., Astolfi, G., Menezes, G. V., de Andrade Porto, J. V., et al. (2020). Cattle weight estimation using active contour models and regression trees Bagging. Comput. Electron. Agric. 179 (2020), 105804. doi:10.1016/j.compag.2020.105804
WO2020260631A1 (2020). Weight determination of an animal based on 3D imaging. Available at: https://patentscope.wipo.int/search/en/detail.jsf?docId=WO2020260631 (Accessed March, 2021).
Keywords: dairy cow, bodyweight, precision livestock farming (PLF), 3D images, machine learning (ML)
Citation: Gebreyesus G, Milkevych V, Lassen J and Sahana G (2023) Supervised learning techniques for dairy cattle body weight prediction from 3D digital images. Front. Genet. 13:947176. doi: 10.3389/fgene.2022.947176
Received: 18 May 2022; Accepted: 29 November 2022;
Published: 05 January 2023.
Edited by:
Juan Steibel, Iowa State University, United StatesReviewed by:
Gota Morota, Virginia Tech, United StatesGareth Frank Difford, Norwegian University of Life Sciences, Norway
Rik Van Der Tol, Wageningen University and Research, Netherlands
Copyright © 2023 Gebreyesus, Milkevych, Lassen and Sahana. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Grum Gebreyesus, Z3J1bS5nZWJyZXllc3VzQHFnZy5hdS5kaw==
 Grum Gebreyesus
Grum Gebreyesus Viktor Milkevych
Viktor Milkevych Jan Lassen1,2
Jan Lassen1,2 Goutam Sahana
Goutam Sahana