- ARC Centre of Excellence in Population Ageing Research, University of Melbourne, Melbourne, VIC, Australia
Sustained below replacement fertility leads to declining population size. Several countries in Asia have experienced below replacement fertility for many years. The paper applies a novel approach to examining the viability of using immigration to achieve zero population growth in six Asian countries: China, Japan, Republic of Korea, Thailand, Singapore and Australia. The novel approach is to estimate the level of immigration that would be required to maintain a constant annual number of births in the long term. Maintaining the number of births at the current level is the fastest way to achieve eventual zero population growth. A population with a constant annual number of births, labeled as a quasi-stationary population, also has a near-to constant age structure that is not excessively old. The study concludes that, for all countries except Australia, no reasonable level of immigration could produce a quasi-stationary population if fertility remains at the country's 2020 level. The constraining factors are the current population size and level of fertility and the extent to which there is acceptance of permanent immigrants in the country. If fertility were to increase over 15–20 years to 1.7 births per woman and the country was accepting of relatively large numbers of permanent immigrants, the quasi-stable outcome becomes potentially viable for all countries except China.
Introduction
Rapid aging, declining labor supply and declining population are serious issues faced by countries with very low fertility rates. Beyond a country's demography, these challenges can be addressed to some extent through increases in labor force participation rates, higher levels of labor productivity and greater efficiency in the delivery of health and aged care services. For example, using Australia as an example, McDonald and Kippen (1999) examined the impact on labor supply for Australia of increases in older-age, labor force participation rates and found that reasonable assumptions about future labor force participation at older ages had a substantial impact on labor supply. Subsequently, the Australian Government introduced a range of policies to stimulate older age labor force participation, including increases in the age at eligibility for the national Age Pension. These policies contributed to higher participation rates at older ages that had a large impact on the life cycle deficit in Australia (Temple et al., 2017). Incorporating migration, upon the request of the Australian Government, McDonald and Temple (2010) investigated the level of net international migration to Australia that optimized the growth rate of GDP per capita through the impact of immigration on the age structure of the population. In doing so, they assumed that the new immigrants had the same labor force participation rates as the total population and the same level of labor productivity. They produced an optimal range for net international migration and the Australian Government has set its international migration program within that range from 2011 onwards.
Extending their earlier work on Australia, McDonald and Kippen (2001) modeled the extent to which changes in labor force participation rates could moderate future labor supply for 16 developing countries including an assumed shift over 30 years for all countries to the then age and sex specific labor force participation rates for Sweden. The United Nations Population Division (2000) published a report on replacement migration as a policy approach to low fertility that showed, as we do in this paper, that migration was not usually a viable option. Other hypothetical modeling exercises of this nature have been published in the past two decades (Feld, 2005; Bijak et al., 2008). A recent paper by Marois et al. (2020) referring to 28 European countries applies the same assumption about future labor force participation that McDonald and Kippen had used in 2001 but adds the impact of applying Canada's net migration rate but assuming that only highly educated immigrants are admitted. Not unexpectedly based on previous research, their paper shows that these hypothetical assumptions would make a large difference to the impacts of population aging. The authors describe these policy approaches as “feasible public policies” with more hope of success than attempts to increase the fertility rate. Despite this, the most recent United Nations report on population policies (United Nations, 2021) shows that 18 of the 28 European countries included in the Marois et al. study had policies to raise the fertility rate. This suggests that the governments of these countries may be skeptical about the feasibility of increasing labor force participation rates to Swedish levels or having net migration at the level of Canada and even more skilled than migrants to Canada. Experience in the past two decades gives some credence to such skepticism. Since McDonald and Kippen (2001) demonstrated the value of increasing labor force participation rates to the levels of Sweden, none of the European countries included in their study has had any significant change in its labor force participation rates and, in some countries, attempts to raise participation at older ages have met with severe political resistance. We are also skeptical that many of the countries in the Marois et a. study would be able to increase migration to the Canadian level. Indeed, several have experienced net losses of population from migration throughout the past two decades.
We take the view that countries with aging populations should attempt to increase labor force participation rates and levels of labor productivity and introduce greater efficiency in the delivery of health and aged care services. We also consider that increased levels of migration, wherever feasible, are beneficial to countries with aging populations. However, it should also be pointed out from mathematical demography that, if the aim is to achieve zero population growth in the long term though a combination of below replacement fertility and positive net migration, the final stationary population size increases substantially as the fertility rate falls (see discussion of Table 3 below). Hence, if the aim is to have zero population growth in the long run but to limit the growth of the total population while this is being achieved, it will often be preferable to have a higher level of fertility than presently applies.
The Republic of Korea, one of the countries considered in this paper, has the highest level of female education in the world and the highest rates of older age, male labor force participation in the OECD countries. Its scope to increase labor force participation applies only to women and, under present working arrangements, higher female labor force participation would tend to lower its fertility rate when, at 0.8 births per woman, its current fertility rate is already the lowest in the world. The Republic of Korea also has relatively low per capita expenditure on the aged population compared with countries such as Japan, Sweden and Australia (McDonald, 2022). In simple terms, even in the context of its present high levels of labor force participation and labor productivity, we are not sanguine about the future of the Republic of Korea if its fertility rate continues to remain at 0.8 births per woman. Very low fertility is unsustainable in the long run because the population ages dramatically and the labor supply and the population size fall rapidly.
The scope of this paper is limited to the demographic components of the future. Implicitly, we assume that labor force participation rates and labor productivity remain constant into the future. Given current levels of fertility in the six Asian countries studied, we model the level of net migration that would produce a near-stationary population in the shortest possible time. We then consider the feasibility of that level of migration.
Migration and Below Replacement Fertility
The impact of immigration upon populations with below replacement fertility has been addressed in mathematical demography. Espenshade et al. (1982) demonstrated that, when fertility is below replacement, a constant number and age distribution of immigrants (with fixed fertility and mortality schedules) lead to a stationary population (a population with a zero rate of growth and constant numbers at each age for each sex). The interesting feature of this work is that it is constant numbers of immigrants by age and sex that are required, not constant age and sex specific migration rates.
This pioneering work was developed further by others as reviewed comprehensively in Parr (2021). Parr's article defines the terminal stationary population (TSP) as the size of the ultimate stationary population that results from constant fertility and mortality schedules and constant numbers of immigrants by age and sex. Using current rates of fertility and mortality and migration numbers by age and sex for 22 countries, Parr calculated that the TSP for most of these populations is very different to the present population size. For example, the TSP for Japan is 10.4 million, South Korea 6.5 million and New Zealand 40 million.
While this mathematical work is very interesting from a theoretical perspective, the times taken to reach the terminal stationary population are usually in the hundreds of years and the ultimate population size would often be unacceptably high or low for today's policy makers. This means that investigation of the effects of varying the level of migration is desirable.
A population that maintains a constant annual number of births will become “near-stationary” over about 80 years as it “loses” the impact of its age structure at the beginning. This is the fastest possible pathway to a stationary population from the present situation. It is “near stationary” because it will grow and change its age structure only through the effects of changing levels of mortality. These effects will be small and slow. In mathematical terms, it could be described as a quasi-stationary population. A quasi-stationary population will be only moderately old with no more than about 35 per cent being aged 65 years and over. If there was a level of immigration that could achieve a constant annual number of births in a relatively short time frame for populations with below replacement fertility, pursuing that level of migration would be a potential policy direction provided the level of migration was feasible.
In this paper, we first examine the level of migration that would be required to achieve a constant number of births in the relative short term and a roughly constant population size out into the long-term future for six Asian countries with below replacement fertility. In most cases, the level of migration required to achieve this result is beyond the realms of possibility. In these instances, only a higher level of fertility would produce a reasonable result and so the paper investigates what level of migration would be required to achieve near stationarity if the level of fertility increased from its 2020 level to 1.7 births per woman within 20 years. Again, consideration is given to the feasibility of this level of migration.
The six countries studied are China, Japan, Republic of Korea, Thailand, Singapore and Australia. These countries are chosen because they encapsulate a range of initial fertility rates, but all well below replacement level, and wide variation in their initial population size. They also have a relatively wide range of current levels of net international migration.
Materials and Methods
To find the level of migration required to keep the number of births constant across time, population projections using the standard component method are conducted iteratively continually increasing or decreasing the assumed level of migration until the desired result of a constant number of births across time is achieved. In some instances, there is a delay because the initial age structure of the population is conducive to an increasing number of births for a short period.
The modeled scenarios include several assumptions about the inputs to the population projection model that remain unchanged as the levels of migration and fertility are modified. These assumptions are:
1 Future mortality rates by age and sex in the six countries are assumed to follow the assumptions made for the United Nations World Population Prospects, 2019 Version (United Nations, 2019).
2 The sex ratio at birth is assumed to be 105 males per 100 females.
3 The age pattern of fertility is assumed to remain constant for each country at its 2020 pattern as estimated in World Population Prospects, 2019 Version.
4 Immigrants are assumed to have the same mortality and fertility as non-migrants. This assumption would only hold if the migrants have permanent residence in the destination country. Migrants who are temporary residents generally rarely have births and they leave the country before they age. This is important because, for most of the countries considered in this paper, a high proportion of migrants are temporary.
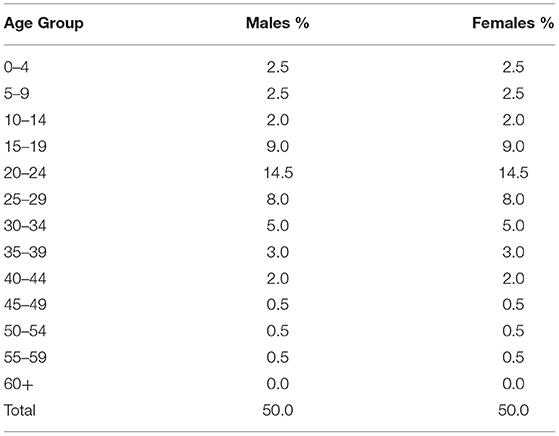
5 The age and sex pattern of net international migration is assumed to follow the same, “idealized” pattern for all countries with the distribution shown in Table 1. This distribution is considered “ideal” because it is heavily centered on young adults in the early childbearing ages and has an equal balance of the sexes. This means that the impacts on annual births are optimized and they occur rapidly. The assumed age pattern of migrants is not unrealistic as it is very close to the current pattern applying to Australia's net international migration.
Reasonable variations of the first four assumptions have only relatively minor impacts upon the projection results. The age and sex pattern of net international migration, however, can have a large impact on the results because it contributes significantly to the number of additional births that the population has because of migration. As demonstrated by Australia, the age and sex distribution in Table 1 is achievable through policy intervention. For these reasons, we have not modeled the effects of an older age distribution of immigrants. A detailed description of the projection methodology is provided in the Supplementary Material.
For all scenarios in the paper, the projections commence with the 2020 population age distributions for each country and the 2020 level of the Total Fertility Rate for each country, specifically: China 1.3; Japan 1.4; Republic of Korea 1.0; Singapore 1.1; Thailand 1.5 and Australia 1.65. For perspective, Table 2 shows the past history of fertility rates in the six countries as well as migration numbers and rates in a recent period. As Figure 1 shows, all the countries face hyper-aging and considerable population decline in the next 100 years unless this future can be modified through immigration or increases in fertility. Examining the feasibility of migration as a modifier of these futures is the rationale of this paper.
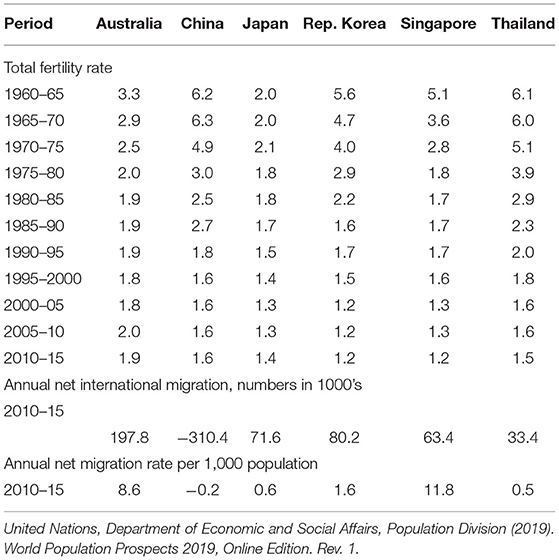
Table 2. Total fertility rates and annual net international migration, averages for 5-years periods, six countries.
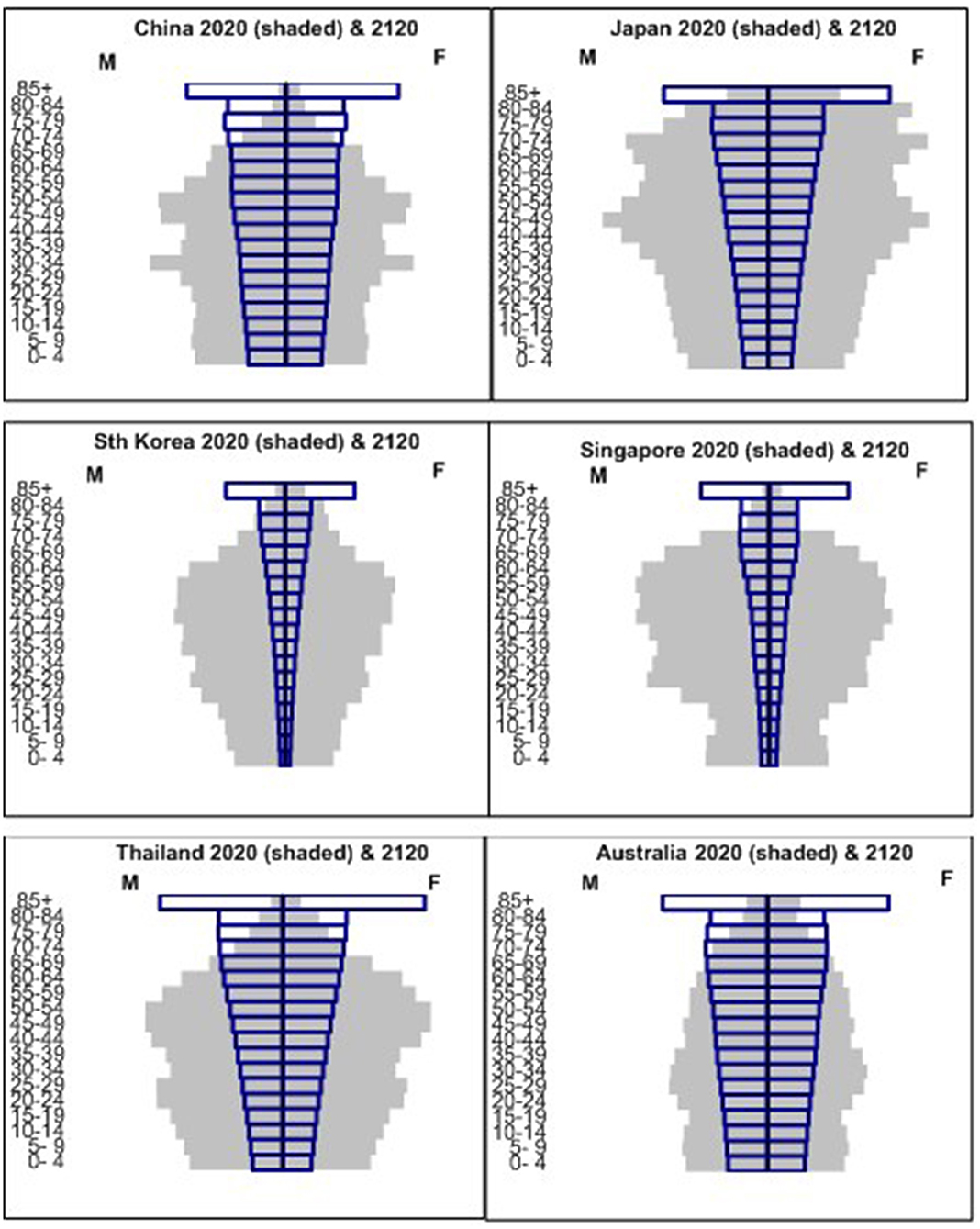
Figure 1. Age distributions (numbers) in 2020 and 2120 assuming constant fertility and zero migration (Scenario A in subsequent graphs). Singapore refers to Singapore residents only.
For each country other than Australia, four scenarios are shown:
Scenario A: TFR is unchanged at its 2020 level and net migration is zero across the 100 years of the projection.
Scenario B: TFR is unchanged at its 2020 level with net migration set at the level that achieves a constant number of births.
Scenario C: A phased in increase of TFR to 1.7 by 2040 with net migration set at the level that achieves a constant number of births.
Scenario D: A phased in increase of TFR to 1.7 by 2040 with net migration set to zero across the 100 years of the projection.
Comparing Scenario A with Scenario B shows the impact of immigration at current levels of fertility. Comparing Scenario C with Scenario D shows the impact of immigration when fertility rises to 1.7 by 2040.
Australia: An Example of Feasibility
Australia's Total Fertility Rate is the highest of the six countries and its 2020 age distribution (largely because of the impact of past migration on births) is already close to that of a stationary population (see Figure 1). Because of these characteristics, a constant annual number of births and, ultimately, near-zero population growth are produced easily with a combination of a constant TFR of 1.65 and annual net migration of 100,000. As Figure 2 shows, in Scenario B, the annual number of births remains constant at around 300,000 and the population rises slowly leveling off below 34 million, or eight million more than the 2020 population. By 2060, about 26 per cent of the population would be aged 65 years and over, about four percentage points lower than Scenario A that has zero annual net migration. At 26 per cent aged 65 and over, population aging would be manageable from the economic perspective.
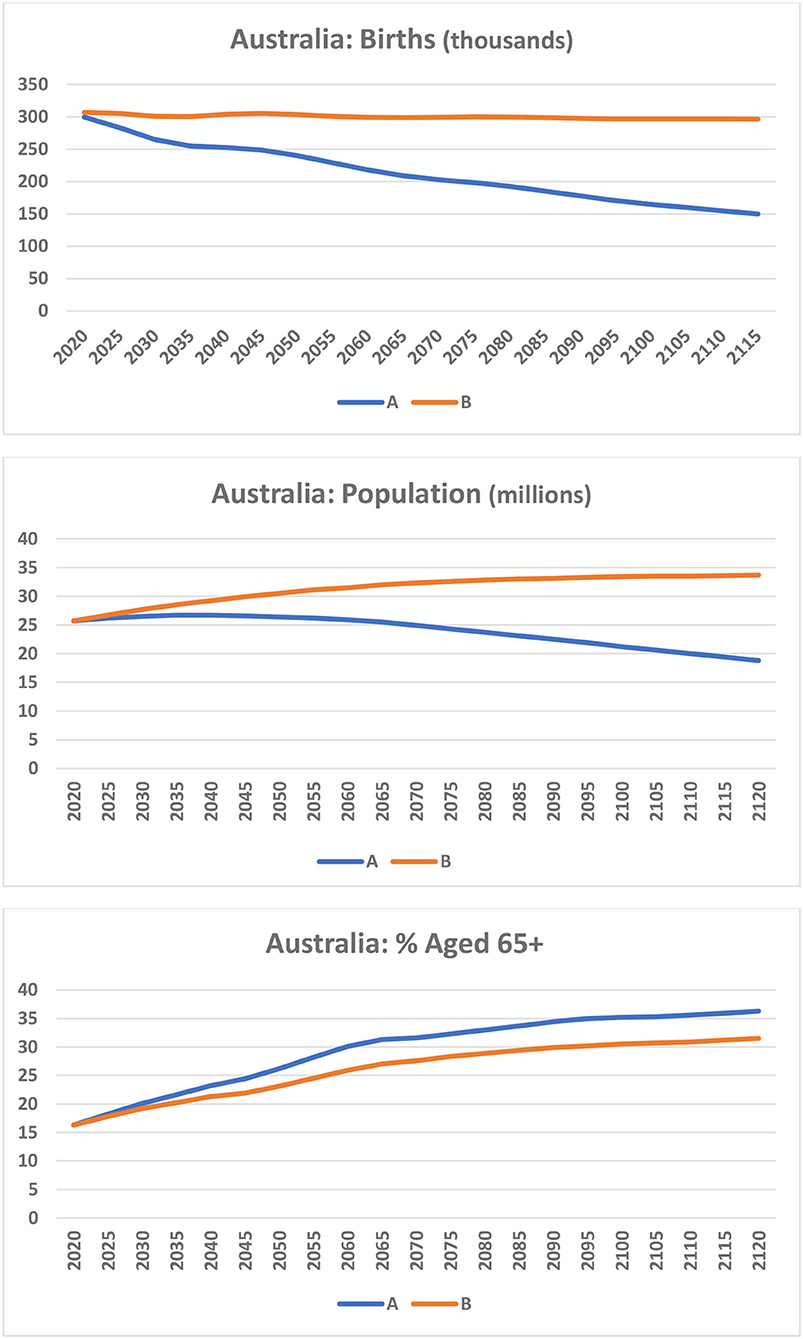
Figure 2. Australia: Projections of births, population and percent of population aged 65+. A: TFR = 1.65; Net migration = 0. B: TFR = 1.65; Net migration = 100,000.
As annual net migration to Australia has averaged around 200,000 per annum in recent years, 100,000 is clearly feasible. From a policy perspective for Australia, a reduction in migration from 100,000 to 200,000 would have to be accommodated by a considerable reduction in skilled migration as family and humanitarian migration (which are not easily reduced) would make up about two-thirds of the 100,000. This reduction in migration and, especially, the consequent change in composition would be counter to current Australian migration policy settings (Commonwealth of Australia, 2021). With 200,000 annual net migration, the annual number of births would continue to increase to 444,000 births per annum and the population to 49 million in 2120, but the percentage of the population aged 65 and over would be just 23 per cent in 2060.
Another measure of interest is that 46 per cent of the 2120 population based on Scenario B (100,000 net migration) would be due to the migrants arriving from 2020 onwards. This percentage is again well within the bounds of acceptability as, at present, around 50 per cent of the Australian population has at least one parent born outside of Australia.
Thus, for Australia, migration can comfortably make up for its below replacement level of fertility.
China: An Example of Infeasibility Even if Fertility Increases
At the other end of the feasibility spectrum is China. With a Total Fertility Rate of 1.3 and zero net migration (Scenario A in Figure 3), China would have 11.8 million births in 2020. With the same assumptions through to 2035, the number of births in China would fall to 10.3 million in 2035. Thus, even though the fertility rate would be very low over the next 15 years, the number of births does not fall dramatically because the 2020 China age structure is favorable to future births in the short term (see Figure 1). After 2035, however, the number of births would begin to fall sharply reaching just 6.2 million in 2065.
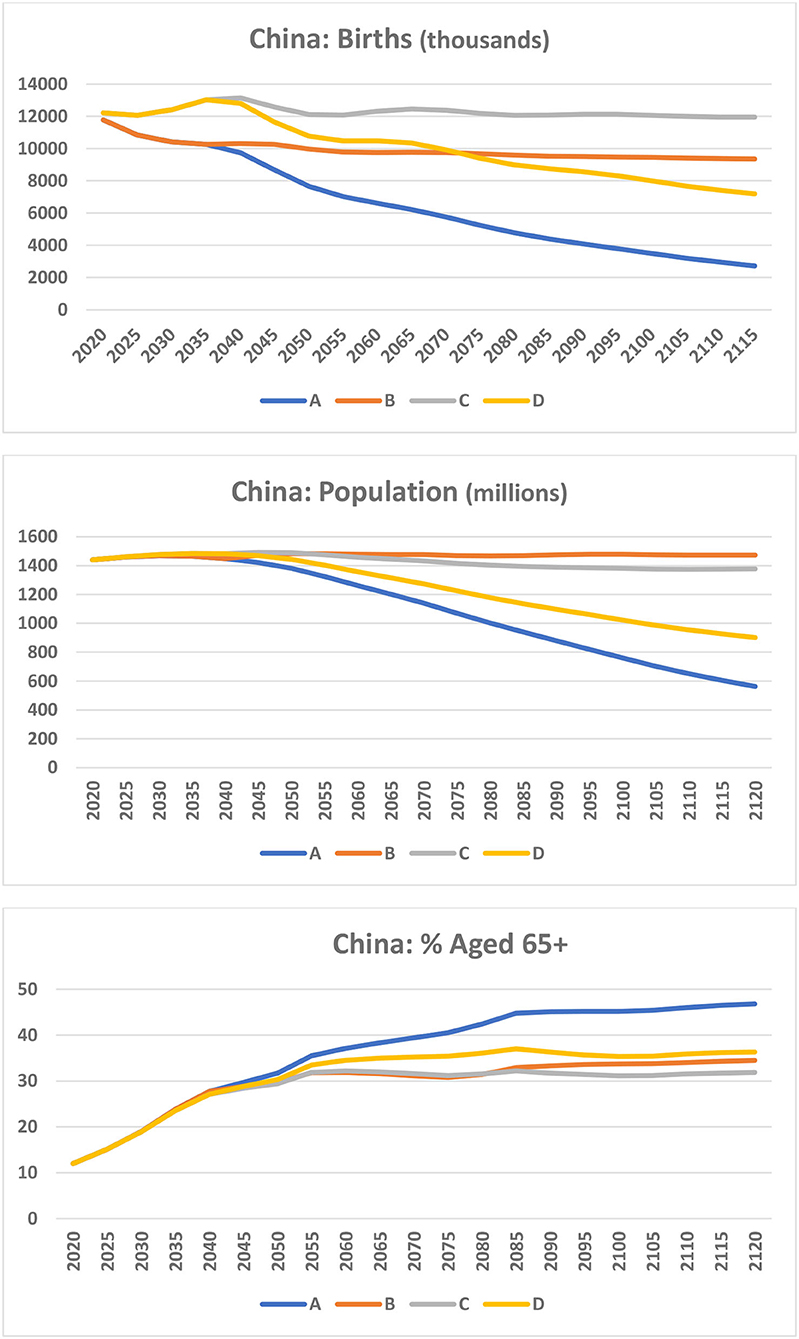
Figure 3. China: Projections of births, population and percent of population aged 65+. A: TFR = 1.3; Net migration = 0. B: TFR = 1.3; Net migration = 9 million from 2040. C: TFR rises from 1.3 in 2020 to 1.7 in 2040; Net migration = 4 million from 2040. D: TFR rises from 1.3 in 2020 to 1.7 in 2040; Net Migration = 0.
Annual net migration of 9 million beginning in 2040 (Scenario B in Figure 2) would be required to keep the number of births near-constant from 2050 to 2120 at around 9.4 million per annum. Under Scenario B, the total population of China would increase a little, leveling off at 1.47 billion. Of course, the notion that 9 million migrants would enter China every year from 2040 to 2120, that is, 720 million migrants over 80 years, is ludicrous.
Now suppose China were able to increase its fertility rate every 5 years by 0.1 births per woman, rising from 1.3 in 2020 to 1.7 in 2040. This may be possible if the current low fertility is a result of delayed births that will take place in the future and/or if economic and cultural change in China were to be much more supportive of childbearing than is the case at present. This fertility assumption is made for Scenario C in Figure 3 which also assumes annual net migration of 4 million per annum from 2040 onwards. Under this scenario, the annual number of births in China would remain near-constant at the 2020 level and the total population would also remain near-constant (Figure 3). This may be an ideal result for China but, again, 4 million migrants per annum entering China is impossible, and China may well struggle to have its fertility rate rise to 1.7 in the next 20 years.
China has been a country of net out-migration for many decades and has had very few in-migrants. It has been extremely difficult for foreigners to obtain permanent residence in China. It has no history of welcoming and integrating migrants. If opposition to permanent residence for foreigners was to loosen, language and cultural obstacles would remain as large deterrents for people to move to China permanently. The most likely future migration scenario for China is that it will continue to be negative and small in relation to the total population.
If China's fertility were to increase to 1.7 by 2040 as in Scenario C and annual net migration was zero, China's demography would follow the course of Scenario D in Figure 3. This scenario would see China's total population falling to around 900 million by 2120 and continuing to fall beyond 2120. However, the percentage aged 65 and over would level off at about 36 per cent from 2060, a much better result than if fertility remained at 1.3 for the next 100 years (47% aged 65+ in 2120). With Scenario D, China would also not face the issue of integration of massive numbers of immigrants. Scenario D has some favorable outcomes, but China would have to adjust to a 40 per cent fall in its total population over the next 100 years and a similar fall in the size of its labor force. This would be a considerable challenge especially given the prospect of continuing falls.
Under all four scenarios, the percentage of the population aged 65 and over would rise rapidly from 12 per cent in 2020 to 27 per cent in 2040 meaning this aging pathway is inevitable for China.
In the context of the present paper, given its massive population size and its migration history, migration is not a feasible option for China in dealing with population aging. A rise in fertility to 1.7 births per woman in the next 20 years is also doubtful.
Japan: Vaguely Feasible With Increased Fertility
If the fertility rate in Japan remains constant at 1.4 births per woman, a constant annual number of births would result with net international migration set at 600,000 per annum from 2020 onwards (Scenario B in Figure 4). Under this scenario, the total population would remain at around 120 million into the future and the percentage aged 65 and over would rise from the current 28 per cent to around 33 per cent. This would be a good result for Japan if it could attract and successfully absorb 600,000 immigrants every year. However, such a result is very unlikely.
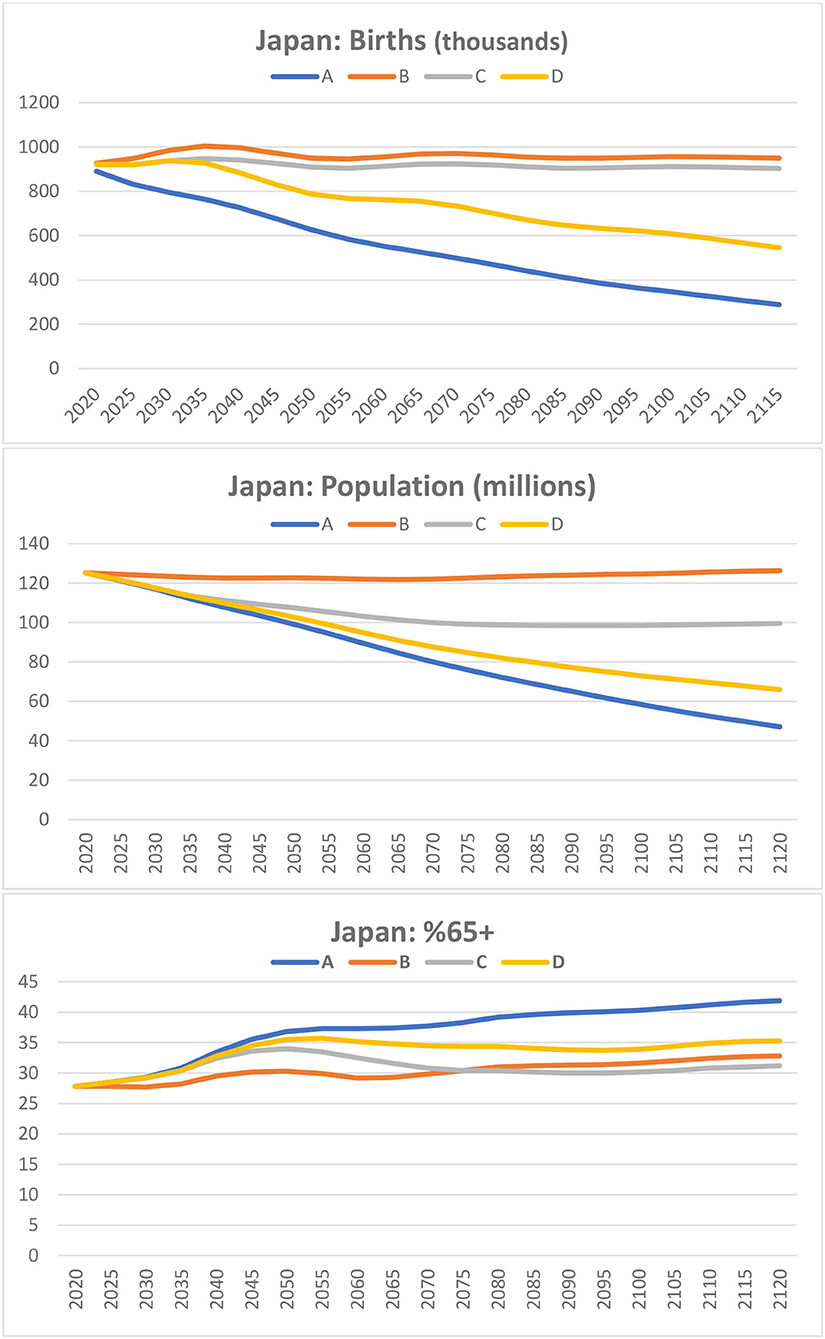
Figure 4. Japan: Projections of births, population and percent of population aged 65+. A: TFR = 1.4; Net migration = 0. B: TFR = 1.4: Net migration = 600,000 from 2020. C: TFR rises from 1.4 in 2020 to 1.7 in 2035; Net migration = 250,000 from 2035. D: TFR rises from 1.4 in 2020 to 1.7 in 2035; Net Migration = 0.
In recent years, annual net migration to Japan has been under 100,000 and the 2019 policy of the Japan Government stipulates the entry of 345,000 immigrants over 5 years (Pollman, 2019). Furthermore, with Scenario B, by 2120, 63 per cent of the population of Japan will derive from the immigrants in the 100 years from 2020 to 2120, a result that would be unacceptable to most Japanese people given even the present level of resistance to immigration (Pollman, 2019). Finally, Japan's current migration policy provides for only five years of residence for most entrants and permanent residence (as distinct from citizenship) for the others. While there are countries where citizenship is reserved for a privileged minority of residents (Brunei and the UAR countries), it would be untenable in a country the size of Japan to have only one third of its population as citizens.
Thus, for Japan to achieve a constant annual number of births, an increase in its fertility rate is required. If the fertility rate were to rise by 0.1 every 5 years to reach 1.7 in 2035, then a constant annual number of births would result if net international migration was zero until 2035 and then 250,000 per annum from 2035 onwards. Under this scenario, the total population size would fall to 100 million before stabilizing at that number and the percentage of the population aged 65 and over would rise to just 31 per cent, considerably below the level of 42 per cent that would result from constant fertility and zero migration (Scenario A in Figure 4). By 2120, only one third of the population would derive from the migrants of the past 100 years. As labor supply pressures mount, the Government of Japan may feel pressure to move to a higher level of permanent migration, but, at present, a low likelihood still attaches to higher fertility and higher migration.
Republic of Korea: Infeasible Without Higher Fertility
If the fertility rate of the Republic of Korea was to remain at its present very low level, annual net migration would need to be 300,000 per annum from 2020 to 2029 increasing to 450,000 from 2030 onwards to achieve a constant future number of births (Scenario B in Figure 5). Under this scenario, the total population of the Republic would increase from 51 million before leveling off at 59 million. Again under Scenario B, by 2120, 80 per cent of the population would be the result of the migrants in the past 100 years; only 20 per cent would derive from today's Korean population.

Figure 5. Republic of Korea: Projections of births, population and percent of population aged 65+. A: TFR = 1.0; Net migration = 0. B: TFR = 1.0; Net migration from 2020 to 2029 = 300,000 and from 2030 onwards = 450,000. C: TFR rises from 1.0 in 2020 to 1.7 in 2040; Net migration, 2020–39 = 50,000, 2040+ = 100,000. D: TFR rises from 1.0 in 2020 to 1.7 in 2040; Net migration = 0.
Net international migration for the Republic of Korea is quite volatile but has averaged 84,000 per annum for the past decade. The main source countries of migrants are China, Vietnam, Thailand and Uzbekistan (Statistics Korea, 2020). However, most of these migrants have only temporary residence meaning that their number does not accumulate across time and only a small number would have births in the Republic. Hence, recent levels of permanent migration are very substantially below the numbers required for Scenario B.
Suppose fertility in the Republic of Korea increased progressively from 1.0 in 2020 to 1.7 in 2040, a constant annual number of births would result from 50,000 annual net migration from 2020 to 2039, stepping up to 100,000 per annum from 2040 onwards (Scenario C in Figure 5). From the perspective of migration, this may be a feasible pathway. Under this scenario, the total population would fall slowly, leveling off at about 40 million and the percentage of the population aged 65+ would settle at around 31 per cent. Only one third of the 2120 population would be derived from the migrants. The issue, of course, is that fertility in the Republic of Korea has remained very low for many years and various policy initiatives have not led to rises in fertility.
Thailand: Approaching Feasibility With Somewhat Higher Fertility
In the case of Thailand, annual net migration of 400,000 from 2030 onwards would lead to a constant number of births, but the population would grow from 70 million to around 84 million before leveling off (Scenario B in Figure 6). Around 33 per cent of the population would be aged 65 and over in the quasi stationary population that results. Like China, however, substantial population aging, from 12.6 per cent aged 65 and over in 2020 to at least 27 per cent by 2045 is inevitable under any demographic scenario. With the Scenario B level of net migration, by 2120, 56 per cent of the total population would be the result of the migrants from 2030 onwards.

Figure 6. Thailand: Projections of births, population and percent of population aged 65+. A: TFR = 1.5; Net migration = 0. B: TFR = 1.5; Net migration = 400,000 from 2030. C: TFR rises to 1.7 by 2040; Net migration = 250,000 from 2020. D: TFR rises to 1.7 by 2040; Net Migration = 0.
Thailand has a history of positive net migration made up almost entirely of people moving across its border from neighboring countries, however, the numbers have never been in the vicinity of 400,000 per annum and very few are afforded permanent residence status. It is estimated that there are close to three million migrants in Thailand (OECD/ILO, 2017). Scenario C assumes that migrants have the same fertility rate as the native population, but this may not be the case given their temporary resident status. However, there seems to be little pressure for temporary migrants to leave Thailand and so they may form partnerships and have children to a greater extent than is the case for temporary migrants in the five other countries in this paper.
Once more, higher fertility is a prerequisite in the achievement of a constant annual number of births. If Thailand's fertility rate were to rise from 1.5 in 2020 to 1.7 in 2040, annual net migration of 250,000 per annum from 2020 onwards would lead to a constant annual number of births (Scenario C in Figure 6). In this scenario, the total population would also increase very gradually from 70 to 80 million, the percentage aged 65 and over would level off at 32 per cent and, by 2120, only 44 per cent of the population would be the result of migration from 2020 onwards. This example is interesting in that it shows that a relatively modest increase in the fertility rate can “replace” a relatively large number of immigrants if the aim is to achieve a constant annual number of births.
If economic development continues to expand in Thailand, it is not unreasonable that migrants would be attracted from Thailand's neighbors especially as population aging in the next 25 years places pressure on the economy and the labor market. In proportional terms, an intake of 250,000 immigrants per year to Thailand (0.35%) is much smaller than the recent levels of migration to Singapore, Australia and New Zealand (all above 1%), but this would still be a challenge for Thailand given its migration history. The issue of permanent residence for migrants is significant.
Singapore: Feasible but Higher Fertility Would Be Preferable
Almost 30 per cent of the 2020 population of Singapore were temporary residents, the large majority having no viable path to permanent residence. Furthermore, the fertility and mortality data published by Statistics Singapore relates only to “Residents,” that is, citizens and permanent residents. For these reasons, the scenarios presented here for Singapore relate only to Singapore Residents. With constant fertility and zero new residents through migration, the Resident population of Singapore would dwindle from just over 4 million in 2020 to 1.2 million by 2120 (Scenario A in Figure 7) and 51 per cent of its population would then be aged 65 years and over.

Figure 7. Singapore: Projections of births, population and percent of population aged 65+. A: TFR = 1.1; Net migration = 0. B: TFR = 1.1; Net migration = 40,000 from 2020. C: TFR rises from 1.1 to 1.7 by 2040; Net migration = 10,000 from 2020. D: TFR rises from 1.1 to 1.7 by 2040; Net migration = 0.
To achieve a constant annual number of births while maintaining the present fertility rate, Singapore would need to have 40,000 new residents every year, that is, people who became citizens or permanent residents (Scenario B in Figure 7). Under this scenario, the population (of residents) would increase very gradually to 5.7 million before leveling off at which point about 34 per cent would be aged 65 and over. Also, under Scenario B, 80 per cent of the 2120 resident population would derive from the migrants arriving after 2020.
In 2019, 33,000 people were granted permanent residence in Singapore (Singapore Department of Statistics, 2020), close to the 40,000 assumed for Scenario B. Most new permanent residents were young and well educated and most came from origins that mirror the ethnic origins of the Singapore population. When Raffles arrived in Singapore in 1819, its population was estimated to have been 150 people. Just 5 years later, at the 1824 Census, its population was 11,000 and it was almost 2 million in 1967 (Saw, 1969). Today, its population is approaching 6 million including temporary residents. Thus, Singapore's history is steeped in its past migration. This history would suggest that the addition of 40,000 new permanent residents each year may not be problematic. While there has been some opposition to permanent migration on the grounds that new permanent residents take the “good” jobs, the Singapore Government appears to be committed to an active immigration programme.
A Scenario C is also examined under which the Singapore fertility rate rises as follows: 1.1 in 2020; 1.25 in 2025; 1.4 in 2030; 1.6 in 2035 and 1.7 in 2040. Under this fertility assumption, a constant annual number of births results if annual net migration was 10,000 from 2020 onwards. Under Scenario C, only 39 per cent of the 2120 population would derive from the post-2020 migrants.
Potentially, therefore, Singapore could achieve a constant annual number of births and a quasi-stationary population through migration. The level of the migration could be adjusted downwards if the fertility rate rises.
The Trade-Off Between Changes in the Level of Fertility and the Annual Number of Migrants
The case of Singapore can be used to illustrate how many fewer migrants would be required each year to achieve the same constant annual number of births if the fertility rate rose across time.
If fertility in Singapore were to remain constant at 1.1 births per woman, a constant annual number of births (approximately 33,000 per annum) would be achieved with annual net migration of 40,000 (as in Scenario B described above). This same constant annual number of births would be achieved with 32,000 migrants annually if fertility rose to 1.2 by 2025 and remained constant thereafter. This means that a nine per cent increase in fertility would be matched by a 20 per cent fall in the number of migrants required. Following the pattern of a 0.1 increase in fertility in every five-year period from 2020 onwards, Table 3 shows how the number of migrants required to achieve a constant 33,000 births per annum falls away reaching just 12,000 when fertility rises to 1.6 by 2045 (a scenario similar to Scenario C described above).
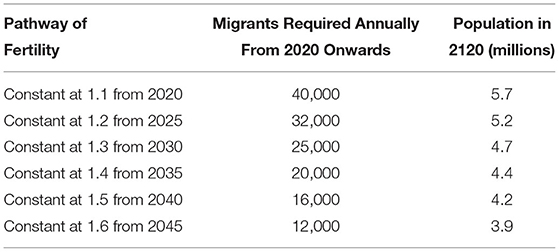
Table 3. Singapore: Annual number of migrants required to achieve a constant annual number of births (~33,000 per annum) when fertility increases across time by increments of 0.1 in each five-year period, and the resultant quasi-stationary population size in 2120.
A very important result, however, is shown in the final column of Table 3. When the quasi-stationary population is achieved by a combination of fertility at 1.1 and annual migration of 40,000, the population rises to 5.7 million before it levels off. At the other end of the spectrum, if fertility were to rise to 1.6 by 2045 and annual migration was 12,000, the population levels off at just 3.9 million. This means that if population growth very close to zero is the aim, a much lower population size will result if this is achieved through a combination of higher fertility and lower migration than vice versa. This is an important consideration for Singapore as a city-state with limited land.
As quasi-stationary populations, all of the combinations of fertility and migration shown in Table 3 lead to relatively young populations (between 32 and 35 per cent aged 65 and over) but the combination of higher fertility (1.6) and lower migration (12,000) leads to the lowest percentage aged 65 and over.
Discussion
The viability of migration as an approach to below replacement fertility is contingent upon three factors:
1 The size of the total population.
2 The level of fertility.
3 The migration history of the country and whether the country will accept new permanent residents in large number.
The analysis for China shows that, because its population is huge, the number of migrants required to offset its below replacement fertility is also huge. Even if the fertility rate were to increase to 1.7 births per woman from the present 1.3, the number of migrants required to offset its low fertility to achieve a quasi-stationary population is still a long way beyond the possible. This is especially the case as China has no history of accepting large numbers of migrants. For China, a substantial increase in fertility (to 1.7) will not stop population decline but it will slow the rate of decline.
Japan, with a population one tenth the size of that of China, is the next largest population considered in the paper. Again, at its current level of fertility (1.4 births per woman), the level of migration that would be required to offset its low fertility is also not possible, especially given opposition to migration in Japan. However, if Japan was able to increase its fertility to 1.7, its lower population size compared with China would enable it to stop population decline so long as it was willing to accept 250,000 new permanent migrants per year from 2035. Under current policy settings, this level of permanent migration seems unlikely, but the Japanese Government has time (to 2035) to change the level of acceptance of such a policy.
Thailand is the next largest country considered here. At 1.5 births per woman, Thailand's relatively higher fertility means that migration is a more viable approach that in China and Japan. Furthermore, Thailand has a long history of migration across its borders from neighboring countries and, while not generally accepting these migrants as permanent residents, it has also not moved to exclude them. Nevertheless, 400,000 new permanent residents for Thailand would be required to attain a quasi-stationary population with its current level of fertility (1.5) and this level of migration is probably not possible for Thailand. With a small increase in fertility (to 1.7), the migration approach comes closer to viability as a policy for Thailand.
The Republic of Korea has a very low fertility rate at present which, combined with its relatively large population, makes a quasi-stable population impossible using migration to balance the low rate of fertility especially given Korean resistance to the acceptance of large numbers of new permanent residents. If Korea's fertility were to rise by 2040 to 1.7 births per woman, migration would then become a viable approach for the Republic.
Singapore's current fertility rate is also very low (1.1) but, in recent times, Singapore has had a policy of large-scale migration of both permanent and temporary migrants. Singapore, of course, has a long history of migration and its new permanent residents have origins that are similar to the origins of the existing population. While this policy has prevented population decline in the short term, its viability in the much longer term is questionable because of the very high level of turnover of the population that it involves. It also leads in the long term to a much larger population size than would be the case if the quasi-stationary state were attained with a higher level of fertility in combination with migration. For these reasons, an increase in fertility from the present low level is a necessary future.
Among the six countries studied, Australia is the only one for which migration without an increase in fertility provides a viable approach to the attainment of a quasi-stationary population. This is because Australia's fertility rate remains relatively high, it has a relatively small population, and it has a long history of accepting new permanent residents. Indeed, the level of migration required to achieve a quasi-stationary population in the future is about half Australia's present level of migration. For Australia, the concern is not population decline but what level of migration best suits the country's future development.
A quasi-stationary population has the desirable features that the population does not decline, the age structure remains near-to-constant and the population does not become excessively old. The analysis here shows that, except for Australia, achievement of a quasi-stationary future requires an increase in fertility in all of the low-fertility Asian countries considered in the paper. All five, China, Japan, the Republic of Korea, Thailand and Singapore, seem to recognize this as all five aspire to fertility that is higher than the present level. However, to this point, all five have been unsuccessful in achieving a higher fertility rate.
It could be said that all five countries have been unable to make the substantial social and economic transformations that are required to maintain fertility at least around the level of 1.7 births per woman that would enable the achievement of a quasi-stable population with a reasonable level of migration. While it is not the purpose of the paper to address the issue of low fertility, the transformations that are required involve reducing the opportunity costs of having children, family-friendly working conditions, employment security for young people, housing costs, and gender equity (McDonald, 2006, 2009; Rindfuss and Cho, 2015; Brinton and Lee, 2016; Poon, 2018; Jeon et al., 2019; Jones, 2019; Ji and Zheng, 2020).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
Both authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fhumd.2022.762199/full#supplementary-material
References
Bijak, J., Kupiszewska, D., and Kupiszewski, M. (2008). Replacement migration revisited: simulations of the effects of selected population and labour market strategies for the ageing Europe, 2002-2052. Populat. Res. Policy Rev. 27, 321–342. doi: 10.1007/s11113-007-9065-2
Brinton, M., and Lee, D. J. (2016). Gender-role ideology, labor market institutions, and postindustrial fertility. Popul. Dev. Rev. 42, 405–433. doi: 10.1111/padr.161
Commonwealth of Australia. (2021). 2021 Intergenerational Report: Australia Over the Next 40 years. Canberra, ACT: Commonwealth of Australia.
Espenshade, T., Bouvier, L., and Arthur, W. B. (1982). Immigration and the stable population model. Demography 19, 125–133. doi: 10.2307/2061132
Feld, S. (2005). Labour force trends and immigration in Europe. Int. Migr. Rev. 39, 637–662. doi: 10.1111/j.1747-7379.2005.tb00283.x
Jeon, S., Lee, M., and Kim, S. (2019). Factors influencing fertility intentions of newlyweds in South Korea: focus on demographics, socioeconomics, housing situation, residential satisfaction, and housing expectation. Sustainability 13, 1534. doi: 10.3390/su13031534
Ji, Y., and Zheng, Z. (2020). China's low fertility rate from the perspective of gender and development. Soc. Sci. China. 41, 169–184. doi: 10.1080/02529203.2020.1806478
Jones, G. (2019). Ultra-low fertility in East Asia: policy responses and challenges. Asian Popul. Stud. 15, 131–149. doi: 10.1080/17441730.2019.1594656
Marois, G., Belanger, A., and Lutz, W. (2020). Population ageing, migration, and productivity in Europe. Proc. Natl. Acad. Sci. 117, 7690–5. doi: 10.1073/pnas.1918988117
McDonald, P. (2006). Low fertility and the state: The efficacy of policy. Popul. Dev. Rev. 32, 485–510. doi: 10.1111/j.1728-4457.2006.00134.x
McDonald, P. (2009). “Explanations of low fertility in East Asia in comparative perspective,” in Ultra-Low Fertility in Pacific Asia: Trends, Causes and Policy Issues, eds Jones, G., Chan, A., and Straughan, P, . (London: Routledge), 23–39.
McDonald, P. (2022). Low fertility and its implications. 20th Professor C. Chandrasekaran Memorial Lecture, Mumbai: International Institute for Population Sciences. Available online at: https://youtu.be/e5SdzqUzlaE (accessed May 20, 2022).
McDonald, P., and Kippen, R. (1999). “Ageing: The social and demographic dimensions,” in Policy Implications of the Ageing of Australia's Population. Canberra, ACT: The Productivity Commission.
McDonald, P., and Kippen, R. (2001). Labour supply prospects in 16 developed countries, 2000-2050. Popul. Dev. Rev. 27, 1–32. doi: 10.1111/j.1728-4457.2001.00001.x
McDonald, P., and Temple, J. (2010). Immigration, Labour Supply and Per Capita Gross Domestic Product: Australia 2010-2050. Canberra, ACT: Department of Immigration. Available online at: http://www.immi.gov.au/media/publications/research/_pdf/labour-supply-gdp-2010-2050.pdf (accessed May 20, 2022).
OECD/ILO. (2017). How Immigrants Contribute to Thailand's Economy, OECD Development Pathways. Paris:L: OECD Publishing. Available online at: http://dx.doi.org/10.1787/XXXXXXXXXXXXX-en (accessed August 21, 2021).
Parr, N. (2021). A new measure of fertility replacement level in the presence of positive net migration. Eur. J. Popul. 37, 243–262. doi: 10.1007/s10680-020-09566-w
Pollman, M. (2019). Is Japan Ready to Welcome Immigrants? The Diplomat. Available online at: https://thediplomat.com/2020/01/is-japan-ready-to-welcome-immigrants/ (accessed January 22, 2020).
Poon, L. (2018). South Korea is Trying to Boost Its Birth Rate. It's not Working. Bloomberg CityLab, 4 August 2018. Available online at: https://www.bloomberg.com/news/articles/2018-08-03/south-korea-is-trying-to-boost-its-birth-rate-it-s-not-working (accessed August 21, 2021).
Rindfuss, R., and Cho, M. K. (2015). Low and Lower Fertility: Variations Across Developed Countries. Dordrecht: Springer.
Saw, S. H. (1969). Population trends in Singapore, 1819-1967. J. Southeast Asian Hist. 10, 36–49. doi: 10.1017/S0217781100004270
Singapore Department of Statistics. (2020). Population in Brief 2020. Singapore: Department of Statistics. Available online at: https://www.strategygroup.gov.sg/files/media-centre/publications/population-in-brief-2020.pdf (accessed August 21, 2021).
Statistics Korea. (2020). International Migration Statistics in 2019. Available online at: http://kostat.go.kr/portal/eng/pressReleases/8/5/index.board (accessed August 21, 2021).
Temple, J., Rice, J., and McDonald, P. (2017). Mature age labour force participation and the life cycle deficit in Australia: 1981-82 to 2009-10. J. Econ. Ageing 10, 21–33. doi: 10.1016/j.jeoa.2017.08.001
United Nations Department of Economic and Social Affairs, Population Division. (2000). Replacement Migration: Is it a Solution to Declining and Ageing Populations?. New York: United Nations.
United Nations Department of Economic and Social Affairs, Population Division. (2019). World Population Prospects 2019. New York: United Nations.
Keywords: population aging, low fertility, immigration, Asia, quasi-stationary population
Citation: McDonald P and Hosseini-Chavoshi M (2022) What Level of Migration Is Required to Achieve Zero Population Growth in the Shortest Possible Time? Asian Examples. Front. Hum. Dyn. 4:762199. doi: 10.3389/fhumd.2022.762199
Received: 21 August 2021; Accepted: 27 May 2022;
Published: 24 June 2022.
Edited by:
Paul Yip, The University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
Xavier Chojnicki, Université de Lille, FranceWolfgang Lutz, University of Vienna, Austria
Copyright © 2022 McDonald and Hosseini-Chavoshi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter McDonald, bWNkb25hbGQucEB1bmltZWxiLmVkdS5hdQ==
 Peter McDonald
Peter McDonald Meimanat Hosseini-Chavoshi
Meimanat Hosseini-Chavoshi