- 1Chemical and Quantum Physics, School of Applied Sciences, RMIT University, Melbourne, VIC, Australia
- 2Australian Research Council Centre of Excellence for Nanoscale BioPhotonics, Melbourne, VIC, Australia
Adiabatic methods are potentially important for quantum information protocols because of their robustness against many sources of technical and fundamental noise. They are particularly useful for quantum transport, and in some cases elementary quantum gates. Here, we explore the extension of a particular protocol, dark state adiabatic passage, where a spin state is transported across a branched network of initialized spins, comprising one “input” spin, and multiple leaf spins. We find that maximal entanglement is generated in systems of spin-half particles, or where the system is limited to one excitation.
1. Introduction
Techniques of adiabatic passage are of interest from fundamental viewpoints, and also for their robustness against many sources of technical noise (Král et al., 2007). The canonical example is stimulated Raman adiabatic passage, STIRAP (Gaubatz et al., 1988), where an electron is transported between two meta-stable states, by applying two laser pulses that couple the meta-stable states to an excited state, or occasionally a continuum (Peters et al., 2005; Dreisow et al., 2009a). By applying the laser pulses adiabatically in the so-called counter-intuitive ordering, where the unpopulated transition is coupled before the laser that addresses the particle to be transferred, the transported particle can move between the two states without ever populating the excited state. In this way, the protocol shows robustness against spontaneous emission, and because the population at any time only goes like the ratio of the Rabi frequencies of the two fields, STIRAP is also robust against fluctuations in the total laser intensity when the fields come from the same source.
A conceptual breakthrough occurred in 2002 when Brandes and Vorrath (2002) reported a method to use STIRAP to transfer electrons between wells in a double quantum dot. This was significant as it was the first time that the use of engineered, as opposed to naturally occurring, systems was considered. Following spatial STIRAP, schemes have been proposed where only the spatial tunneling interaction is varied to affect the counter-intuitive pulse sequence, and these are sometimes termed coherent tunneling adiabatic passage, CTAP. Eckert et al. considered atomic transport through optical potentials (Eckert et al., 2004), Siewert and Brandes proposed transport in superconducting networks (Siewert and Brandes, 2004), and Greentree et al. proposed electronic transport in quantum dot and phosphorus in silicon systems (Greentree et al., 2004). Later proposals included Bose–Einstein condensates (Graefe et al., 2006; Rab et al., 2008), optical waveguides (Paspalakis, 2006; Longhi et al., 2007), Bose–Hubbard systems (Bradly et al., 2012), sonic systems (Menchon-Enrich et al., 2014), polarization (Dimova et al., 2015), and spin chains (Ohshima et al., 2007; Oh et al., 2013; Greentree and Koiller, 2014). Spatial adiabatic passage in spin chains is usually termed dark state adiabatic passage, DSAP, and is the subject of this work.
The combination of designed Hilbert spaces with adiabatic processes leads to interesting new protocols and opportunities. In particular, adiabatic passage enables quantum gates via the method outlined by Unanyan, Shore, and Bergman (Unanyan et al., 1999; Kis and Renzoni, 2002; Devitt et al., 2007; Hope et al., 2015), interferometers (Jong and Greentree, 2010), interaction-free measurements (Hill et al., 2011), and robust splitters (Dreisow et al., 2009b; Chung et al., 2012; Ciret et al., 2012).
Here, we consider the combination of DSAP with branched spin networks to explore how entanglement is generated between the leaf nodes, i.e., end points of the network. We also note that adiabatic passage on lattice networks has been considered (Longhi, 2014). Our aim can be understood with respect to Figure 1A, which shows a simple network where all of the spins are initialized in their lowest spin state, except for the “initial” spin, which is set to some particular state. We perform the counter-intuitive pulse sequence (described explicitly below) with an XX + YY + ZZ Hamiltonian, and explore how the initial spin state is distributed between the leaf nodes. In its simplest form, this case has been considered as a means to create a superposition of a single particle amongst the leaf nodes (Greentree et al., 2006; Hill et al., 2011; Rangelov and Vitanov, 2012), and this case is isomorphic to the spin-half case discussed below. We extend this work by exploring networks of higher spin systems and multiple leaf nodes. We observe more complicated behavior, although such behavior does not appear to lead to entangled states superior to the spin-half case.
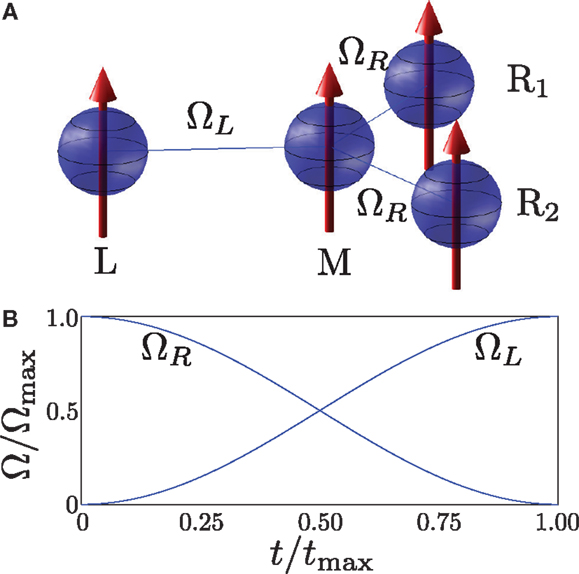
Figure 1. (A) Schematic showing a network for four spin-one particles, with starting node L, central node M, and two leaf nodes R1 and R2. Spin–spin couplings are indicated by the solid lines connecting the spins. (B) Dark state adiabatic passage is achieved by utilizing the counter-intuitive pulse sequence. To transport spin information from L to R1 and R2 requires ΩR(0) ≫ ΩL(0) and ΩL(tmax) ≫ ΩR(tmax). The exact shape of the pulse is of little importance provided that adiabaticity is preserved, and here we have chosen squared sinusoidal coupling for simplicity.
This paper is organized as follows: we first describe the Hamiltonian for DSAP with high-spin systems. We then show results for spin-half, spin-one, and spin-three-half networks. In all cases, we show the adiabatic evolution and quantify the final entanglement generated. Finally, we compare the protocols and offer perspectives.
2. Hamiltonian and Methods
In its most general form, we consider the adiabatic transport of spin information from an initial spin, L, to some entangled state of final (or leaf) spins, R1 to RN, via a middle spin, denoted M, which takes the analogous role of the unpopulated excited state in STIRAP. We assume a uniform, time invariant magnetic field B aligned with the Z direction, which energetically separates manifolds of different numbers of excitations. We assume time-varying inter-site couplings between the spins and the middle spin only, where the L − M coupling strength is ΩL (t) and the M − Rj coupling strength is . The Hamiltonian for our network can be expressed as
where the index i ranges across all spins {L, M, R1 … RN}, and the index j ranges across all leaf spins R1 to RN. Jz, J+, and J− are the Z-projection of the spin operator, spin-raising, and spin-lowering operators respectively. The Hamiltonian preserves the number of excitations meaning that subspaces of different numbers of excitation can be treated separately in the adiabatic passage. α is the coefficient of the always-on ZZ coupling and is to prevent occupation of spin M, and operates in a similar fashion to the role of central state detuning in Bradly et al. (2012). The value of α was set to 1 × 10−2B for all systems. Smaller values create degeneracies, which can create transient population in M. Larger values of α will not alter our results, provided α ≪ B.
DSAP of the spin state from the initial to the final site(s) utilizes the counter-intuitive pulse ordering, i.e., the coupling should be high before ΩL. For our numerical results, for simplicity we have chosen:
where tmax is the total time for the transport, and 0 ≤ t < tmax is the time. This is shown in Figure 1B. In keeping with other adiabatic passage protocols, the exact form of the Ω is relatively unimportant providing that the counter-intuitive ordering is maintained, i.e., as t → 0, as t → tmax, and the variation in the Ω satisfy the adiabaticity criterion, so that for every pair of eigenstates |ψ⟩, |ϕ⟩ with respective eigenenergies E| ψ⟩ and E| ϕ⟩
Although our calculations are performed explicitly as a function of time and without assuming adiabaticity, all of the results we show below are in the adiabatic limit.
While the Hamiltonian and pulse ordering can allow for adiabatic passage of the state in site L to the recipient spins Rj, it is important to stress that DSAP is also dependent on the choice of the initial state of all spins other than L. For simplicity, we will assume a state with all spins M and Rj prepared in their lowest spin projection with respect to the z axis. Another enabling state has all spins in the highest spin projections and yields completely symmetric results. In the case of transport in a linear chain of three spin-one systems, it is possible to observe dark state adiabatic passage with several configurations of the non-L spins (Greentree and Koiller, 2014). It remains an open question as to whether it is possible to realize dark state adiabatic passage in branched networks with any configuration of non-L spins apart from all such spins aligned parallel or antiparallel with the Z axis. Preliminary investigations show that the antisymmetric combination of non-L states, i.e., states of the form where γ is the unknown spin to be transported and zmax () the maximum (minimum) spin projection, do not yield smooth adiabatic transport. Hence, it is uncertain whether or not branched dark state adiabatic passage is possible with other spin configurations. Nevertheless, this is an interesting question for future research.
We quantify the DSAP by two methods. First is to identify the final states for various network configurations. Second, we examine the entanglement that is generated between the Rj nodes. Because we are dealing with multi-partite systems of varying dimensionality, there is no unique way to quantify entanglement. For simplicity, we choose to use the entanglement of formation (Wootters, 1998; Wong and Christensen, 2001), which is an entanglement monotone for pure states, where 0 corresponds to no entanglement and 1 to maximal entanglement for that system. The entanglement of formation for a pure state |ψ⟩ is defined
where is the partial trace of |ψ⟩⟨ψ| over subsystem R2 and is the partial trace of |ψ⟩⟨ψ| over subsystem R1. In the configurations with more than two recipients, we quantify the entanglement of formation as being between one arbitrary leaf spin and all other recipient leaf spins.
3. Results
3.1. Spin-Half Networks
The case of spin-half networks with one excitation is formally equivalent to the case of multi-recipient adiabatic passage (Greentree et al., 2006; Rangelov and Vitanov, 2012), and so we consider it here purely for the purposes of review and to compare with our other results.
We denote the spin projections of the spins with respect to their Jz eigenvalue. We define |1⟩ as the state with spin projection parallel to the external magnetic field, i.e., with spin projection ℏ/2; and as the state antiparallel to the external field, with spin projection −ℏ/2. The middle and leaf (right) spins are assumed initialized in , and we study the adiabatic passage for different initial (left) spin states. The evolution is indicated in Figure 2. The general form of the dark state, i.e., the eigenstate, which defines the adiabatic passage, for n leaf nodes for the case considered above is
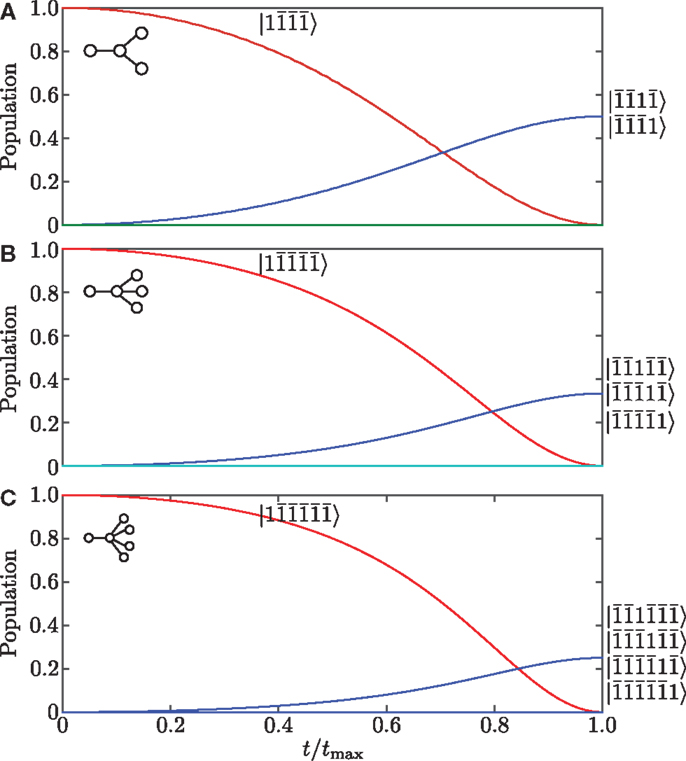
Figure 2. Population evolution for spin-half networks with (A) two leaf nodes, (B) three leaf nodes, and (C) four leaf nodes. The excitation begins at L, i.e., in the state and moves to an equally weighted superposition of all of the leaf nodes, which is a W state across the spins Rj. All initial and final states as well as the quantified entanglement related to each protocol are summarized in Table 1.
Equation (5) shows that for the two leaf configuration, an initial excitation at L (ΩL = 0) is adiabatically transported to an equally weighted, maximally entangled state of the Rj (ΩR = 0). As the number of leaves is increased, we see the formation of W-like states, which have a lower entanglement (as quantified by the entanglement of formation) with increasing n.
3.2. Spin-One Networks
Spin-one networks are more complicated than spin-half, and are no longer isomorphic to the simple case of direct particle transport, although in certain cases a spin-one chain can be treated as a form of particle transport (Haldane, 1983; Affleck et al., 1987). Spin-one DSAP faithfully transmits the state of an arbitrary qutrit from one end of the chain to the single recipient spin at the other end of the chain (Greentree and Koiller, 2014). However, as we will show, the branched geometry maps the doubly excited state partially into product states of two sites with one excitation each, rather than solely an entangled state of both excitations in one or the other site, thereby failing to preserve the integrity of the qutrit.
As before, we define our basis states with respect to the Z projections of the individual spins. The states are corresponding to the spin projections ℏ, 0, and −ℏ. As before, we initialize spins M and Rj to (antiparallel to the Z field). In the spin-one system, transport from L to Rj can be achieved for either one excitation (|0〉) or two excitations (|1〉).
When limiting the system to one excitation, i.e., choosing the initial state of spin L to be |0〉, the transport achieved in all configurations is the equivalent of the spin-half case and the entanglement of formation for both spin-one and spin-half is the same. The evolution for three configurations, with two, three and four leaf nodes, is shown in Figures 3A–C.
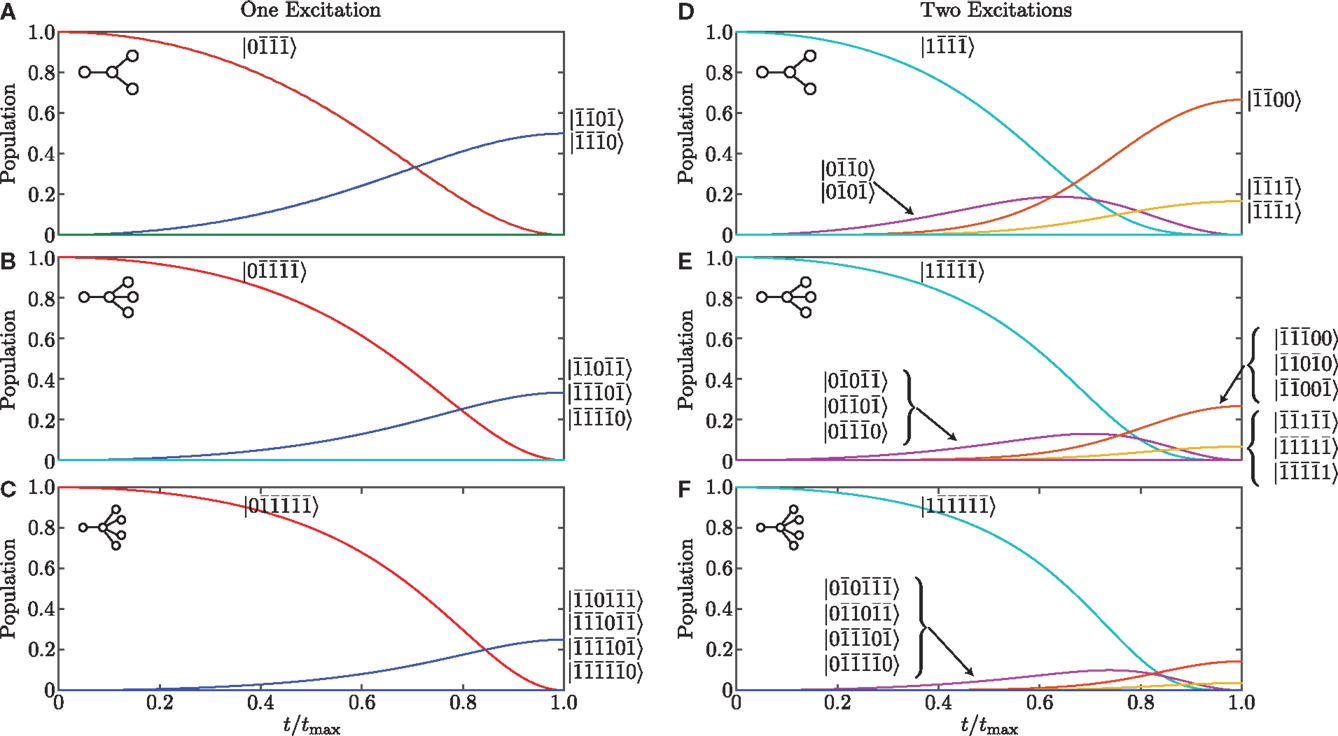
Figure 3. Spin-one networks for DSAP. For the case of one excitation and (A) two leaf nodes, (B) three leaf nodes, and (C) four leaf nodes; we observe results equivalent to those seen for the spin-half networks. For two excitations and (D) two leaf nodes, (E) three leaf nodes, and (F) four leaf nodes, we observe evolution to a more complicated final state, via a transient, W-like state, as shown. The sharing of the population between the states is determined by the egalitarian principle as discussed in the text. Final states for two excitations and four nodes are not given here due to the large number of states involved, but is quantified, along with entanglement of formation, in Table 1.
In the two-excitation subspace for two leaf nodes, the evolution becomes more complicated due to the number of ways the excitations can be shared between the leaf nodes. Figure 3D shows the transport with starting state with two leaf nodes. The counter-intuitive pulse sequence ensures that all of the excitation is transported from L to the Rj without final occupation of M. However, the final state is complicated by the fact that there are more ways for the excitation to be shared between the Rj than in the one-excitation case. The pertinent eigenstate for the DSAP is
This state shows features in common with more conventional adiabatic passage evolution. As ΩR(0) ≫ ΩL(0), we retrieve the starting configuration, i.e., . In the adiabatic limit, the state of M is always , and the final state has excitation only in the leaf nodes. The final state is, however, more complicated in the two-excitation subspace. We observe the formation of a superposition of a W-like state: , and the state , with most of the population in . We find that has less entanglement than a W state (as measured by entanglement of formation), and less entanglement than the state formed from the one-excitation state.
The three and four leaf node configurations with two excitations are more complicated, and we do not show the null states, as these are complicated and do not provide additional insight into the evolution. The final state configuration for the three leaf node configuration gives rise to a superposition of two W-like states:
This entangled state includes all of the possible ways that the two excitations can be shared between the leaf nodes, but the system is more strongly weighted toward configurations where the excitations are shared most evenly. We term this sharing the egalitarian principle, i.e., we expect the adiabatic passage to always favor the configurations where the excitations are most equally shared between the leaf nodes. While the egalitarian principle is phenomenologically observed rather than fundamentally derived, we point out that the coupling , which appears in the Hamiltonian, eq. (1), couples states with a single excitation swapped. A state with multiple excitations in one site, therefore, does not couple directly to a state with the multiple excitations swapped to a different site. This could be an underlying reason for the preferential distribution of excitations due to arguments analogous to statistical reasons for the increase of entropy.
Similarly, the four leaf node configuration with two excitations also obeys the egalitarian principle, with a contribution from a W-like state, and states where the excitations are shared on two of the leaf nodes with an amplitude twice that of the W-like state.
As before, the system is weighted toward configurations where the excitations are shared as evenly as possible, and this results in a state with less entanglement than configurations with fewer leaf nodes.
3.3. Spin-Three-Half Networks
We now consider spin-three-half networks. We again define the eigenstates with respect to the JZ projection, labeling the states corresponding to the eigenvalues +3ℏ/2, +ℏ/2, −ℏ/2, −3ℏ/2, respectively. In the spin-three-half system, transport can be achieved by using one, two, or three excitations. When limiting the system to one excitation, the transport achieved in all configurations is the equivalent of the spin-half case and the entanglement of formation was found to be equal in both cases. When limiting the system to two excitations, Figures 4A–C, the transport produces final states that are equivalent to those obtained in the spin-one case. However, the final states occur with different populations here than they do in the spin-one system. This is due to the additional factor from the J+ and J− spin operators, which also modifies the degree of entanglement produced. Such results are expected to quantitatively affect analogous transport through higher spin networks (i.e., networks with spin >3/2) without modifying the qualitative form of the adiabatic passage or the final entangled states.
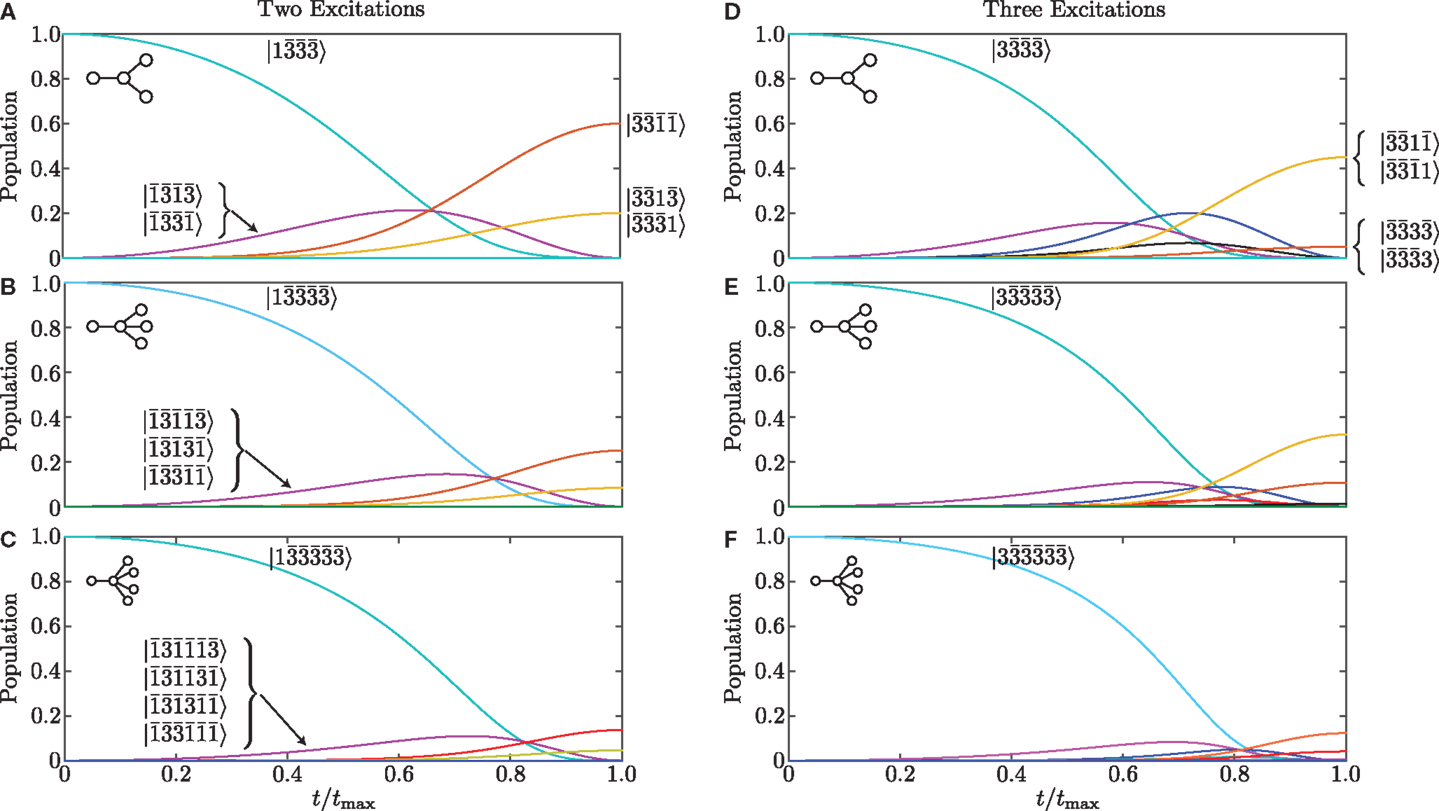
Figure 4. Evolution of systems of spin-three-half particles with two and three excitations. The two-excitation results for (A) two leaf nodes, (B) three leaf nodes and (C) four leaf nodes, are qualitatively similar to the analogous spin-one systems, although quantitatively different due to the different couplings. Three excitations for (D) two leaf nodes, (E) three leaf nodes, and (F) four leaf nodes, exhibit excitation sharing following the egalitarian principle as before, albeit with increased complexity due to the large number of states involved in the transport. Some states are not shown here for reasons of space, but all of the final states can be found in Table 1.
With three excitations () the evolution is more complicated still, as shown in Figures 4D–F. However, we still find that the egalitarian principle holds, with all possible final states represented in the final superposition, but the states with the most equal sharing of the excitation favored. This sharing of excitations reduces the overall entanglement in systems with increasing number of leaf nodes.
4. Discussion
Dark state adiabatic passage can be used to generate entanglement in small networks, and we have shown the properties of the evolution and entanglement in networks of spin-half, spin-one, and spin-three-half systems. Our results for the final state and entanglement of formation for these networks are summarized in Table 1. Networks of spin-half systems show the creation of W-like states across the leaf nodes, and can be understood analogously to particle splitting in spatial adiabatic passage networks (Hill et al., 2011; Rangelov and Vitanov, 2012). However, the higher spin systems exhibit what we term an egalitarian principle, where the excitations are distributed across all possible leaf nodes, but with the states with the most equal distribution of the excitations more strongly represented in the final entangled state. This overrepresentation of states with equal sharing reduces the entanglement of formation observed in the high-spin systems, with the consequence that systems with fewer excitations and fewer leaf nodes exhibit greater entanglement. This result is likely to be significant in the development of quantum protocols for high-spin and qudit systems.
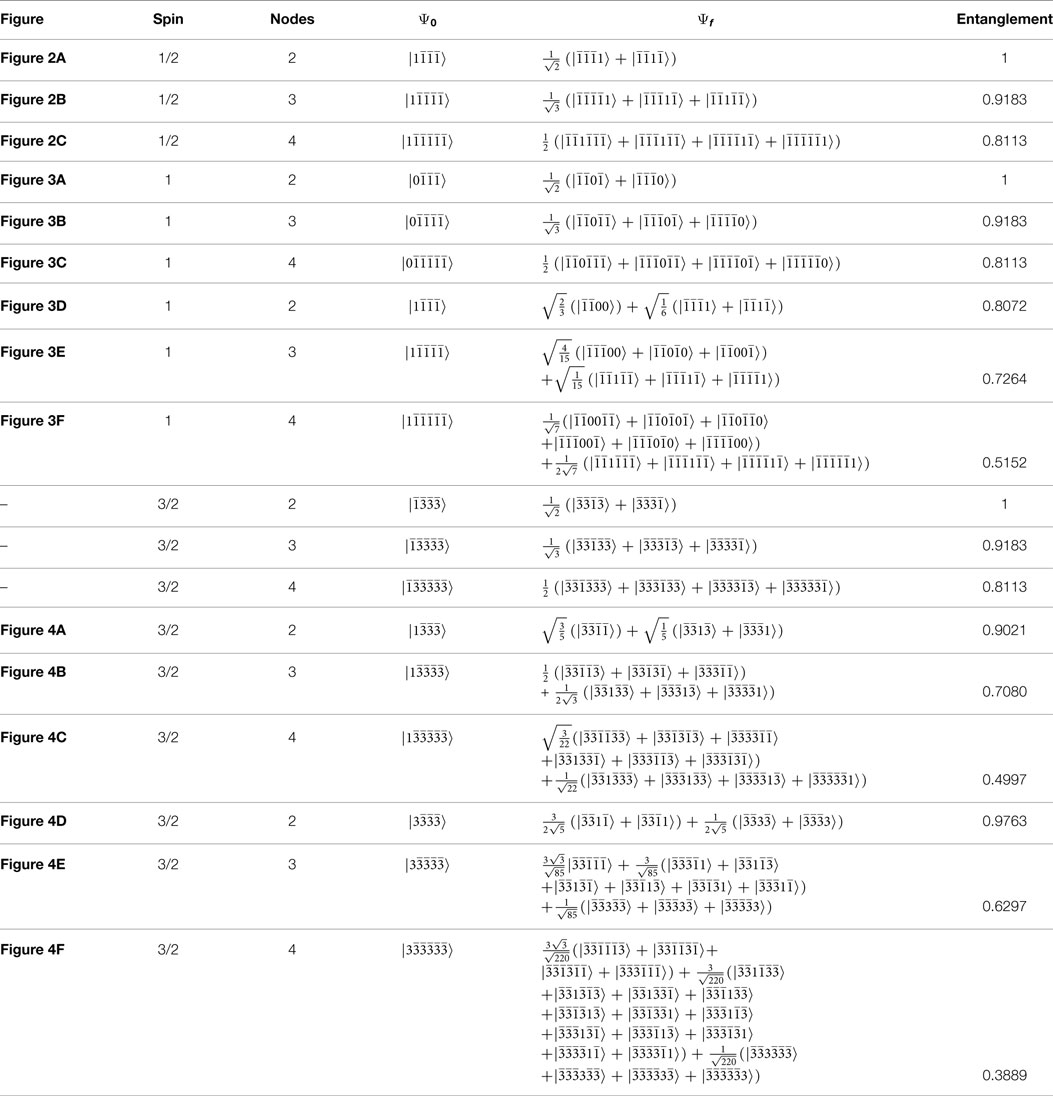
Table 1. Summary of final states following multiple recipient dark state adiabatic passage, and entanglement of formation.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
AG acknowledges the ARC for financial support (DP1301 04381).
References
Affleck, I., Kennedy, T., Lieb, E. H., and Tasaki, H. (1987). Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 59, 799. doi: 10.1103/PhysRevLett.59.799
Bradly, C. J., Rab, M., Greentree, A. D., and Martin, A. M. (2012). Coherent tunneling via adiabatic passage in a three-well Bose-Hubbard system. Phys. Rev. A 85, 053609. doi:10.1103/PhysRevA.85.053609
Brandes, T., and Vorrath, T. (2002). Adiabatic transfer of electrons in coupled quantum dots. Phys. Rev. B 66, 075341. doi:10.1103/PhysRevB.66.075341
Chung, K., Karle, T. J., Rab, M., Greentree, A. D., and Tomljenovic-Hanic, S. (2012). Broadband and robust optical waveguide devices using coherent tunnelling adiabatic passage. Opt. Express 20, 23108. doi:10.1364/OE.20.023108
Ciret, C., Coda, V., Rangelov, A. A., Neshev, D. N., and Montemezzani, G. (2012). Planar achromatic multiple beam splitter by adiabatic light transfer. Opt. Lett. 37, 3789. doi:10.1364/OL.37.003789
Devitt, S. J., Greentree, A. D., and Hollenberg, L. C. L. (2007). Information free quantum bus for generating stabiliser states. Quantum Inf. Process. 6, 229. doi:10.1007/s11128-007-0055-4
Dimova, E., Rangelov, A., and Kyoseva, E. (2015). Broadband and ultra-broadband polarization rotators with adiabatic modular design. [arXiv:1502.04857]
Dreisow, F., Szameit, A., Heinrich, M., Keil, R., Nolte, S., Tünnermann, A., et al. (2009a). Adiabatic transfer of light via a continuum in optical waveguides. Opt. Lett. 34, 2405–2407. doi:10.1364/OL.34.002405
Dreisow, F., Ornigotti, M., Szameit, A., Heinrich, M., Keil, R., Nolte, S., et al. (2009b). Polychromatic beam splitting by fractional stimulated Raman adiabatic passage. Appl. Phys. Lett. 95, 261102. doi:10.1063/1.3279134
Eckert, K., Lewenstein, M., Corbalán, R., Birkl, G., Ertmer, W., and Mompart, J. (2004). Filtering of matter-wave vibrational states via spatial adiabatic passage. Phys. Rev. A 70, 023606. doi:10.1103/PhysRevA.70.023606
Gaubatz, U., Rudecki, P., Becker, M., Schiemann, S., Külz, M., and Bergmann, K. (1988). Population switching between vibrational levels in molecular beams. Chem. Phys. Lett. 149, 463. doi:10.1016/0009-2614(88)80364-6
Graefe, E. M., Korsch, H. J., and Witthaut, D. (2006). Mean-field dynamics of a Bose-Einstein condensate in a time-dependent triple-well trap: nonlinear eigenstates, Landau-Zener models, and stimulated Raman adiabatic passage. Phys. Rev. A 73, 013617. doi:10.1103/PhysRevA.73.013617
Greentree, A. D., Cole, J. H., Hamilton, A. R., and Hollenberg, L. C. L. (2004). Coherent electronic transfer in quantum dot systems using adiabatic passage. Phys. Rev. B 70, 235317. doi:10.1103/PhysRevB.70.235317
Greentree, A. D., Devitt, S. J., and Hollenberg, L. C. L. (2006). Quantum-information transport to multiple receivers. Phys. Rev. A 73, 032319. doi:10.1103/PhysRevA.73.032319
Greentree, A. D., and Koiller, B. (2014). Dark-state adiabatic passage with spin-one particles. Phys. Rev. A 90, 012319. doi:10.1103/PhysRevA.90.012319
Haldane, F. D. M. (1983). Nonlinear field theory of large-spin Heisenberg antiferromagnets: semiclassically quantized solitons of the one- dimensional easy-axis Néel state. Phys. Rev. Lett. 50, 1153. doi:10.1103/PhysRevLett.50.1153
Hill, C. D., Greentree, A. D., and Hollenberg, L. C. L. (2011). Parallel interaction-free measurement using spatial adiabatic passage. New J. Phys. 13, 125002. doi:10.1088/1367-2630/13/12/125002
Hope, A. P., Nguyen, T. G., Mitchell, A., and Greentree, A. D. (2015). Adiabatic two-photon quantum gate operations using a long-range photonic bus. J. Phys. B At. Mol. Opt. Phys. 48, 055503. doi:10.1088/0953-4075/48/5/055503
Jong, L. M., and Greentree, A. D. (2010). Interferometry using spatial adiabatic passage in quantum dot networks. Phys. Rev. B 81, 035311. doi:10.1103/PhysRevB.81.035311
Kis, Z., and Renzoni, F. (2002). Qubit rotation by stimulated Raman adiabatic passage. Phys. Rev. A 65, 032318. doi:10.1103/PhysRevA.65.032318
Král, P., Thanopulos, I., and Shapiro, M. (2007). Coherently controlled adiabatic passage. Rev. Mod. Phys. 79, 53. doi:10.1103/RevModPhys.79.53
Longhi, S. (2014). Coherent transfer by adiabatic passage in two-dimensional lattices. Ann. Phys. (N. Y.) 348, 161. doi:10.1016/j.aop.2014.05.020
Longhi, S., Della Valle, G., Ornigotti, M., and Laporta, P. (2007). Coherent tunneling by adiabatic passage in an optical waveguide system. Phys. Rev. B Condens. Matter 76, 201101(R). doi:10.1103/PhysRevB.76.201101
Menchon-Enrich, R., Mompart, J., and Ahufinger, V. (2014). Spatial adiabatic passage processes in sonic crystals with linear defects. Phys. Rev. B 89, 094304. doi:10.1103/PhysRevB.89.094304
Oh, S., Shim, Y.-P., Fei, J., Friesen, M., and Hu, X. (2013). Resonant adiabatic passage with three qubits. Phys. Rev. A 87, 022332. doi:10.1103/PhysRevA.87.022332
Ohshima, T., Ekert, A., Oi, D. K. L., Kaslizowski, D., and Kwek, L. C. (2007). Robust state transfer and rotation through a spin chain via dark passage. [e-print arXiv:quant-ph/0702019].
Paspalakis, E. (2006). Adiabatic three-waveguide directional coupler. Opt. Commun. 258, 30. doi:10.1016/j.optcom.2005.07.060
Peters, T., Yatsenko, L. P., and Halfmann, T. (2005). Experimental demonstration of selective coherent population transfer via a continuum. Phys. Rev. Lett. 95, 103601. doi:10.1103/PhysRevLett.95.103601
Rab, M., Cole, J. H., Parker, N. G., Greentree, A. D., Hollenberg, L. C. L., and Martin, A. M. (2008). Spatial coherent transport of interacting dilute Bose gases. Phys. Rev. A 77, 061602(R). doi:10.1103/PhysRevA.77.061602
Rangelov, A. A., and Vitanov, N. V. (2012). Achromatic multiple beam splitting by adiabatic passage in optical waveguides. Phys. Rev. A 85, 055803. doi:10.1103/PhysRevA.85.055803
Siewert, J., and Brandes, T. (2004). Adiabatic passage with superconducting nanocircuits. Adv. Solid State Phys. 44, 181. doi:10.1007/978-3-540-39970-4_15
Unanyan, R. G., Shore, B. W., and Bergmann, K. (1999). Laser-driven population transfer in four-level atoms: consequences of non-abelian geometrical adiabatic phase factors. Phys. Rev. A 59, 2910. doi:10.1103/PhysRevA.59.2910
Wong, A., and Christensen, N. (2001). Potential multiparticle entanglement measure. Phys. Rev. A 63, 044301. doi:10.1103/PhysRevA.63.044301
Keywords: adiabatic passage, entanglement, qudits, quantum networks, coupled spins
Citation: Batey C, Jeske J and Greentree AD (2015) Dark state adiabatic passage with branched networks and high-spin systems: spin separation and entanglement. Front. ICT 2:19. doi: 10.3389/fict.2015.00019
Received: 16 June 2015; Accepted: 24 August 2015;
Published: 15 September 2015
Edited by:
Mark Everitt, Loughborough University, UKReviewed by:
Zoltán Zimborás, University College London, UKJacob Dunningham, University of Sussex, UK
Copyright: © 2015 Batey, Jeske and Greentree. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrew D. Greentree, School of Applied Sciences, Melbourne, VIC, Australia,YW5kcmV3LmdyZWVudHJlZUBybWl0LmVkdS5hdQ==
 Caitlin Batey
Caitlin Batey Jan Jeske
Jan Jeske Andrew D. Greentree
Andrew D. Greentree