- 1Alfred Wegener Institute, Bremerhaven, Germany
- 2Climate and Environmental Physics, Physics Institute and Oeschger Centre for Climate Change Research, University of Bern, Bern, Switzerland
- 3National Oceanic and Atmospheric Administration, College Park, MD, USA
- 4CNRS-INSU, Laboratoire d'Océanographie de Villefranche, Villefranche-sur-mer, France
- 5Sorbonne Universités, UPMC Univ Paris 06, Observatoire Océanologique, Villefranche-sur-mer, France
- 6Institute for Sustainable Development and International Relations, Paris, France
The 5th Assessment Report (AR5) of the Intergovernmental Panel on Climate Change (IPCC) states with very high certainty that anthropogenic emissions have caused measurable changes in the physical ocean environment. These changes are summarized with special focus on those that are predicted to have the strongest, most direct effects on ocean biological processes; namely, ocean warming and associated phenomena (including stratification and sea level rise) as well as deoxygenation and ocean acidification. The biological effects of these changes are then discussed for microbes (including phytoplankton), plants, animals, warm and cold-water corals, and ecosystems. The IPCC AR5 highlighted several areas related to both the physical and biological processes that required further research. As a rapidly developing field, there have been many pertinent studies published since the cut off dates for the AR5, which have increased our understanding of the processes at work. This study undertook an extensive review of recently published literature to update the findings of the AR5 and provide a synthesized review on the main issues facing future oceans. The level of detail provided in the AR5 and subsequent work provided a basis for constructing projections of the state of ocean ecosystems in 2100 under two the Representative Concentration Pathways RCP4.5 and 8.5. Finally the review highlights notable additions, clarifications and points of departure from AR5 provided by subsequent studies.
Introduction
Working Groups I and II (WGI and WGII) of the Intergovernmental Panel on Climate Change's (IPCC's) Fifth Assessment Report (AR5) synthesized research regarding observed and projected impacts of climate change on physical and biological processes in the oceans at both global and regional levels. The impacts of these changes on human health and socio-economics were also discussed (reviewed by Cheung et al., submitted). Key findings on physical processes highlighted, with an extremely high certainty, that the upper ocean had warmed over the last 40 years and predicted with very high confidence that this trend would continue over the coming century (Ciais et al., 2013; Rhein et al., 2013). It was considered very likely that this increase in temperature contributed to significant global mean sea level rise (Rhein et al., 2013). High agreement amongst data provided evidence that stratification caused by increasing sea temperatures has caused declining seawater oxygen concentrations (Rhein et al., 2013). The report expressed high confidence that the oceans are absorbing anthropogenic carbon and that the resulting chemical reactions cause ocean acidification (Ciais et al., 2013; Rhein et al., 2013).
Key findings on biological processes highlighted the effect of ocean warming on the geographical distribution of organisms with observations lending evidence to poleward migrations of species (Poloczanska et al., 2014; Pörtner et al., 2014). Temperature has already affected the timing of life history events (phenology) such as reproduction and migration, and caused irreversible regime shifts in warm water coral reef and Arctic ecosystems (medium confidence; Field et al., 2014). Net primary productivity (NPP) was projected to decrease moderately by 2100 in the open ocean under both low- and high-emission scenarios, paralleled by an increase in NPP at high latitudes and a decrease in the tropics (Hoegh-Guldberg et al., 2014; Pörtner et al., 2014). Despite a lack of field observations, ocean acidification was predicted to have a significant effect on many aspects of organisms' physiology, behavior, and population dynamics (Pörtner et al., 2014). There was medium confidence that expansion of suboxic zones would benefit anaerobic microbes and limit oxygen dependent species (Pörtner et al., 2014). There was high confidence that the various environmental drivers would act simultaneously on organisms causing complex, interacting effects (Pörtner et al., 2014).
AR5 also identified key uncertainties regarding potential climate-related impacts on biological and physical systems. In particular, it highlighted the need for an updated understanding regarding the following aspects:
(1) The extent of warming in deep water masses (below 700 m) and limited observational coverage of the ocean, hampering more robust estimates of ocean heat and carbon content.
(2) While acknowledged as a critical process influencing ecosystem productivity, the likelihood of climate-induced changes to major upwelling systems (i.e., increased or decreased upwelling) is still uncertain (Lluch-Cota et al., 2014).
(3) Ways in which climate-induced changes in the physiology and biogeography of an individual species may alter ecosystem structures, species interactions, and food webs (Pörtner et al., 2014).
(4) An improved understanding of climate sensitivity at the ecosystem level that considers multiple drivers (e.g., ocean warming, acidification, and hypoxia) and synergistic impacts (Pörtner et al., 2014; Wong et al., 2014).
(5) The degrees to which species can track changes in climate as well as the influence of multiple stressors on their capacities to respond remained uncertain (Poloczanska et al., 2014).
(6) The capacity for phenotypic and evolutionary adaptation over generations to respond to long-term climate change (Pörtner et al., 2014).
The objective of this review is to draw together the various sections of the AR5 that address the physical and biological impacts of climate change on the ocean. We focus on the physical processes that will have the greatest direct impacts on biota, namely warming, acidification, and deoxygenation. Papers published after the AR5 cutoff dates (15/03/2013 for working group I and 31/08/2013 for working group II) were then reviewed to update the understanding of the observed and projected impacts of climate change on physical and biological processes. The review endeavors to highlight key developments with respect to our scientific understanding of the relationships among different anthropogenic and climatic drivers on marine ecosystems. Lastly, the review calls attention to areas of agreement with, and points of departure from AR5. Throughout the text, where possible, the review strives to employ the same language of certainty as the AR5, summarized in Table 1 and Figure 1.
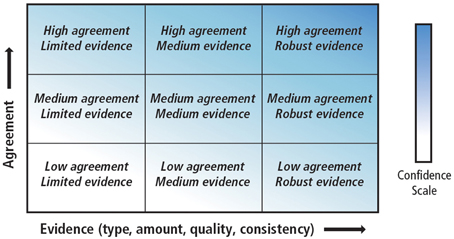
Figure 1. A depiction of evidence and agreement statements and their relationship to confidence. Confidence increases toward the top right corner as suggested by the increasing strength of shading. Generally, evidence is most robust when there are multiple, consistent independent lines of high quality. Source: Stocker et al. (2013).
Physical Science
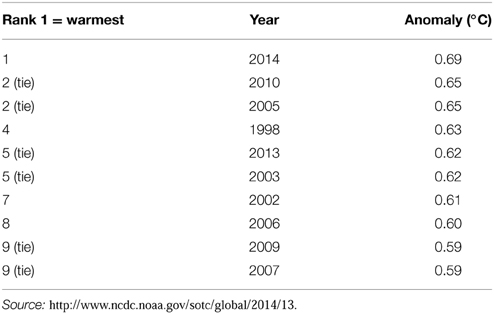
Since the start of the Industrial Era (1750 onwards), anthropogenic activities have resulted in increased concentrations of greenhouse gases and it is now virtually certain that atmospheric concentrations of greenhouse gases are at their highest in the last 800,000 years (Ciais et al., 2013). Concentrations of CO2, CH4 and N2O rose by 40, 150, and 20%, respectively, between 1970 and 2011. Accumulation of these gases in the atmosphere act to increase radiative forcing and, of the three, CO2 has the greatest effect (Ciais et al., 2013). This has resulted in a measureable increase in global air and sea temperatures (Figure 2) with the beginning of the 21st century having the warmest years on record since 1880 (IPCC, 2013; Table 2).
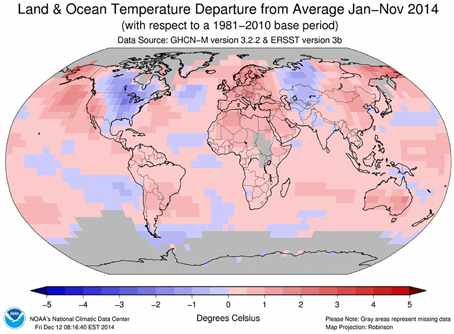
Figure 2. Global temperature anomaly means for January to November 2014 (2014 was the warmest year ever recorded for this period). Source: http://www.ncdc.noaa.gov/sotc/global/2014/11#temp.
Over the last 800,000 years, concentrations of atmospheric CO2 have been relatively stable, oscillating between 180 ppm during glacial periods and 300 ppm during interglacial periods (Ciais et al., 2013). Between 1750 and 2013, atmospheric CO2 levels rose from 278 ppm to 395.31 ppm (Le Quéré et al., 2014), exceeding 400 ppm for much of 2014 (http://www.esrl.noaa.gov/gmd/ccgg/trends/). Total anthropogenic emissions between 1870 and 2014 amounted to 545 ± 55 Pg C (Le Quéré et al., 2014). The AR5 states with very high confidence that burning of fossil fuels and land use changes are the dominant cause of the increase in atmospheric CO2 (Ciais et al., 2013), contributing 395 ± 20 Pg C (including emissions from cement production of 8 Pg C) and 185 ± 65 Pg C, respectively (Le Quéré et al., 2014).
The accumulation of greenhouse gases in the atmosphere and the oceans produces widespread, global, and long-lasting physical changes in the ocean environment. These changes are summarized below, focusing on those that are anticipated to have the greatest effect on organism and ecosystem functioning. It is virtually certain that the oceans have sequestered 155 ± 30 Pg C (28% of total emissions) of anthropogenic CO2 since the Industrial Revolution, very likely at a rate of between 0.1 and 3.2 Pg C yr−1 (Ciais et al., 2013). The increased CO2 absorbed by the ocean is in response to the increasing concentrations of CO2 in the atmosphere. Without ocean uptake, atmospheric CO2 would be much higher, thus the oceans play an important role in mediating global climate change effects (Ciais et al., 2013).
Model projections show that an increase in atmospheric CO2 will always lead to an increase in ocean carbon storage, all other things being held constant (Ciais et al., 2013). The proportion of carbon that remains in the atmosphere will increase with increasing input of carbon in the atmosphere-ocean system as the oceans' buffer capacity diminishes (Ciais et al., 2013). The excess carbon will continue to invade the ocean for centuries, perturbing dissolved inorganic carbon (DIC), the partial pressure of pCO2 in seawater and pH, also in the deep oceans (Ciais et al., 2013). Model projections show a widespread increase of CO2 in the upper mixed layer from 0.1 to 0.2 mol m−3 in year 1990 to 0.2–0.4 mol m−3 in year 2100 under a high emissions scenario (Cocco et al., 2013).
Warming
AR5 Summary
There is high confidence that 93% of the excess heat in Earth's energy inventory from 1971 and 2010 ended up in the oceans (Rhein et al., 2013). The upper ocean has warmed between 1971 and 2010; globally averaged increases from 0 to 200 m between 1971 and 2010 are 0.25°C, accounting for approximately 64% of the total warming occurring in the ocean (Rhein et al., 2013). Warming is most pronounced at the surface; between 1971 and 2010, temperatures in the upper 75 m are estimated to have increased by approximately 0.11°C decade−1 (Rhein et al., 2013). It is also very likely that warming was occurring earlier, between the 1870's and 1971 (Rhein et al., 2013). It is virtually certain that the heat content of the upper oceans has increased; estimates for the heating rate between 1971 and 2010 vary between 74 and 137 TW (Rhein et al., 2013). It is very likely that warming has increased the stratification of upper 200 m of the oceans by about 4% during the period 1971–2010; in turn there is medium confidence that this has reduced the dissolved oxygen concentration and decreased the availability of inorganic nutrients (Rhein et al., 2013).
Regionally, the average sea surface temperature (SST) of the Indian, Atlantic and Pacific Oceans has increased by 0.65, 0.41, and 0.31°C, respectively, between 1950 and 2009 (Hoegh-Guldberg et al., 2014). There is high confidence that sea surface temperatures in sub-tropical gyres of the Atlantic, Pacific, and Indian Oceans have increased (Hoegh-Guldberg et al., 2014). In the Indian Ocean, there is medium confidence that 90% of the warming trend can be attributed to external forcing. Average sea temperatures have increased between 1950 and 2009 by 0.43 and 0.54°C in the Pacific and Atlantic equatorial upwelling systems, respectively (Hoegh-Guldberg et al., 2014). It is likely that North Atlantic surface waters have warmed by 0.07°C decade−1 between 1950 and 2009 (Hoegh-Guldberg et al., 2014), which has been suggested to be a contributing factor to the retreat of the Greenland ice sheet (Straneo and Heimbach, 2013).
Warming can be observed in all the sub-regions of coastal boundary systems (CBS), overall, CBS warmed by 0.14–0.80°C from 1950 to 2009 (Hoegh-Guldberg et al., 2014). Key sub-regions within the CBS such as the Coral Triangle and Western Indian Ocean warmed by 0.79 and 0.60°C, respectively, from 1950–2009 (Hoegh-Guldberg et al., 2014). It is very likely that the Gulf of Mexico and Caribbean Sea have warmed by 0.31 and 0.50°C, respectively from 1982 to 2006 (Hoegh-Guldberg et al., 2014).
Due to undersampling, uncertainties assessing warming in the deep ocean are much higher than for the surface waters; before 2005, the data are too sparse to produce reliable estimates. Studies confirm warming between 0 and 1500 m since 2005 and it is likely that waters between 700 and 2000 m have warmed, on average between 1957 and 2009 (Rhein et al., 2013). Conversely, it is likely that there has been no significant global warming trend between 2000 and 3000 m (1992–2005), although steep vertical gradients and water mass movements confound sparse sampling at mid-depths (Rhein et al., 2013). Globally, waters from 3000 m to the bottom are thought likely to have experienced a warming trend greater than zero (Rhein et al., 2013). Some regions are better sampled than others, allowing a more detailed assessment of temperature changes. It is very likely that N. Atlantic deep waters below 2000 m have a net cooling trend of -4 TW between 1955 and 2005 (Rhein et al., 2013). It is considered likely that waters of Antarctic origin have warmed below 3000 m by 0.01°C decade−1 between 1992 and 2005 and that waters south of the Sub-Antarctic polar front have warmed by 0.03°C decade−1 for the same period (Rhein et al., 2013).
For deep waters, warming of between 0.3°C (RCP2.6) to 0.6°C (RCP8.5) are projected (Figure 3; Ciais et al., 2013). Depending on the emission scenario, global ocean warming between 0.5°C (RCP2.6) and 1.5°C (RCP8.5) will reach a depth of about 1 km by the end of the century (Ciais et al., 2013). There is high confidence that the largest warming of deep waters will occur in the Southern Ocean (Ciais et al., 2013).
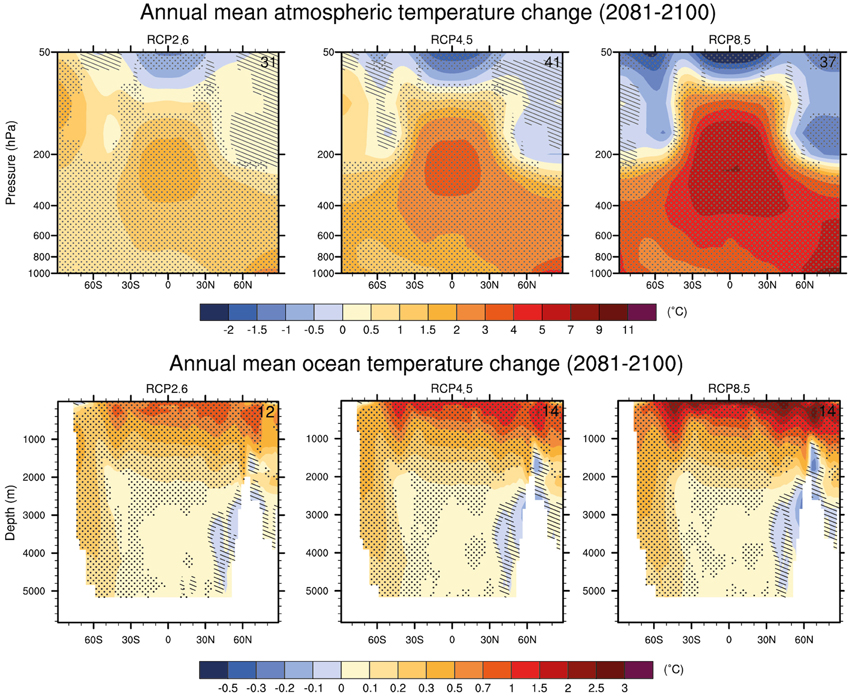
Figure 3. CMIP5 multi-model changes in annual mean zonal mean temperature in the atmosphere and ocean relative to 1986–2005 for 2081–2100 under the RCP2.6 (left), RCP4.5 (center) and RCP8.5 (right) forcing scenarios. Hatching indicates regions where the multi model mean is less than one standard deviation of internal variability. Stippling indicates regions where the multi model mean is greater than two standard deviations of internal variability and where 90% of the models agree on the sign of change Source: Collins et al. (2013).
Updates to AR5
The 2000's were the warmest decade on record and the 1990's the second warmest (Trenberth and Fasullo, 2013; Goddard, 2014). Nonetheless, several estimates used in the AR5 reported that the increase in upper ocean heat content (OHC) has slowed between 2003 and 2010, compared to previous decades (Rhein et al., 2013). Work published since the AR5 suggested that there may be an impact of large scale natural climate variability, a reduced radiative forcing, or a smaller warming response to atmospheric CO2 concentrations (Lewis, 2013). The central and eastern Pacific have exhibited the greatest slowing in warming trend (Trenberth et al., 2014) and it has been suggested that variations in both the Pacific Decadal Oscillation (PDO) and the Atlantic Multidecadal Oscillation may be responsible for this (Trenberth and Fasullo, 2013; Goddard, 2014; Trenberth et al., 2014; Steinman et al., 2015). Two recent studies suggest that the warming hiatus is caused by heat transported to deeper layers in ocean basins, although there is debate as to which basins are the main drivers (Chen and Tung, 2014; Trenberth et al., 2014).
Despite the recent hiatus in the global mean surface air temperature trend, the consensus is that this can be attributed to natural variability (Trenberth and Fasullo, 2013) and OHC continues to increase (Goddard, 2014; Huber and Knutti, 2014; Schmidt et al., 2014b; Trenberth et al., 2014). Data from Argo floats for the period 2006 to 2013 show no warming pause and estimate increases in OHC between 0 and 2000 m depth, at a rate of 0.4–0.6 W m2. The Argo data show that the heat is evenly distributed between the upper 500 m and 500–2000 m with the Southern Hemisphere gaining more heat than the Northern (Roemmich et al., 2015). At the same time, Steinman et al. (2015) combined climate observations and model simulations and found that a modest positive peak in the Atlantic multidecadal variability and a substantially negative-trending Pacific multidecadal variability are seen to produce a slowdown or “false pause” in warming of the past decade.
Durack et al. (2014) argue that the AR5 estimates for increases in OHC might be biased low due to limited sampling of the Southern Hemisphere compared to the Northern Hemisphere. Satellite observations of sea surface height were used as a model parameter to calculate changes in OHC, showing a more homogeneous warming, with larger magnitudes in the South Pacific and South Atlantic basins compared to IPCC estimates. The results yielded an increase in global upper OHC of 2.2 to 7.1 × 1022 J above existing estimates for 1970 to 2004.
Work published since the AR5 has found that the Arctic Ocean has exhibited one of the strongest (but variable) warming trends. In areas where the warming trend is high, a novel study using isotope proxy analysis found up to 3.7°C increase between 1920 and 2011. This is approximately 6 times higher than the observed global warming trend and double the previously suggested rate of warming for the area (Brand et al., 2014). Conversely, SST measurements have decreased in the Southern Ocean, particularly around the sea ice margins, possibly due to runoff from melting shelf ice cooling and freshening surface waters in the surrounding areas (Bintanja et al., 2013).
A recent estimate suggested that, in the last decade, about 30% ocean warming has occurred below 700 m, contributing significantly to an acceleration of the warming trend (Balmaseda et al., 2013). Warming of deep waters is thought to be particularly strong in the Southern Ocean with a rate of up to 0.05°C decade−1 (Patara and Böning, 2014). The warming of deep Antarctic waters, may, in turn, strengthen the large-scale meridional overturning of the Atlantic Ocean (Patara and Böning, 2014).
Results from recent studies agree with the AR5 in predicting high variability for future SSTs: the strongest warming trends are predicted in the Arctic Ocean, the tropics and the North Pacific with increases larger than 4°C in all 3 regions, under scenario RCP8.5 (Figure 3; Bopp et al., 2013). Model projections of surface ocean warming are projected to be +2.73 ±0.72, +1.58 ±0.48, +1.28 ±0.56 and +0.71 ±0.45°C for RCP8.5, RCP6.0, RCP4.5 and RCP2.6, respectively by the end of the 21st century (Figure 3; Bopp et al., 2013).
Upwelling
AR5 Summary
There is considerable debate as to whether climate change will drive a universal intensification of upwelling (Hoegh-Guldberg et al., 2014). There is robust evidence and medium agreement that the California Current has experienced a decrease in the number of upwelling events (23–40%), but high confidence that there has been an increase in the intensity of upwelling events between 1967 and 2010 (Hoegh-Guldberg et al., 2014). In the Canary Current, there is low agreement on whether the strength of the upwelling has intensified over the last 60 years (Hoegh-Guldberg et al., 2014).
It is considered very likely that continued warming would continue to increase thermal stratification (Ciais et al., 2013), potentially decreasing the availability of inorganic nutrients to surface waters. It is likely that the response will vary geographically, as complex systems govern these water mass movements (Ciais et al., 2013). Intensification of upwelling is predicted in the Southern Ocean, however, there is low confidence in the current understanding of how eastern upwelling systems will be altered under future climate change (Ciais et al., 2013). In the Benguela Current there is medium agreement and limited evidence, that upwelling will change as a result of climate change (Hoegh-Guldberg et al., 2014). It is considered likely that warming in the Atlantic equatorial upwelling systems will weaken upwelling (Hoegh-Guldberg et al., 2014).
Updates to AR5
Meta analysis of the last 60 years found intensification of upwelling favorable winds over the California, Benguela, and Humboldt upwelling systems (Sydeman et al., 2014). Jacox et al. (2014) reported an increase in nearshore (≤50 km from the shore) upwelling in the California Current System between 1988 and 2010 but a decrease in off shore (50–200 km) upwelling for the same period. The authors attribute these differences to large-scale climate mode fluctuations.
New model projections predict strong changes in in the intensity, timing and spatial heterogeneity of Eastern Boundary Upwelling Systems (EBUS) by 2100 (Wang et al., 2015). The projections show earlier onset and later end of the upwelling season, as well as an increase in upwelling intensity at higher latitudes. These predictions were consistent for the Benguala, Canary and Humboldt Current systems but not for the California Current System.
Sea Level Rise
AR5 Summary
Sea level varies relative to changes in temperature (thermosteric sea level rise) and fluxes of water between the oceans and the continents and ice sheets (mass sea level rise). Global mean sea level (GMSL) has risen by 0.19 ± 0.02 m over the period 1901–2010 (Rhein et al., 2013). It is very likely that the mean rate was 1.7 ± 0.2 mm yr−1 between 1901 and 2010 and increased to 3.2 ± 0.4 mm yr−1 between 1993 and 2010. Ocean thermal expansion and melting of glaciers have accounted for over 80% of the GMSL rise over the latter part of the time series (Church et al., 2013). Although records for the deep sea are sparser, it is possible to estimate that warming below 2000 m contributed 0.1 [0.0 to 0.2] mm yr−1 to GMSL rise between about 1992 and 2005 (Rhein et al., 2013). The component of sea level rise that is attributed to changes in fluxes of water between the oceans and the continents and ice sheets has been increasing at a rate between 1 and 2 mm yr−1 since 2002 (Rhein et al., 2013).
There is very high confidence that there is high regional variability in sea level rise, with relative sea level rise sometimes exceeding global mean sea level rise by an order of magnitude, reaching more than 10 cm yr−1 (Church et al., 2013). This variation is partly due to fluctuations in ocean circulation, tectonic activity and interactions with climate mode variability such as the ENSO in the Pacific (Church et al., 2013). Anthropogenic activities such as oil and gas extraction and changes to the coastal sediment delivery via damming or consolidation from building work have also contributed to localized changes in relative sea level (Church et al., 2013). Sea level rise in coastal boundary systems is variable but, in some regions, has risen by up to 10 mm yr−1 between 1950 and 2009 (Hoegh-Guldberg et al., 2014). In the Pacific, changes in sea level have been highly variable, in the warm pool of the western Pacific, rates of sea level rise are up to three times higher than the global average (Rhein et al., 2013), while the eastern equatorial Pacific has been declining by −10 mm yr−1 (Hoegh-Guldberg et al., 2014).
It is virtually certain that sea level rise will continue beyond the 21st Century (Church et al., 2013). Future rates of GMSL rise over the 21st century are projected to exceed the observed rate for the period between 1971 and 2010 of 2.0 ± 0.3 mm yr−1 (Church et al., 2013) for all RCP scenarios.
Updates to AR5
The AR5 reports low agreement on the projected magnitude of sea level rise due to the use of different models, some of which take into account ice sheet dynamics (Church et al., 2013). The IPCC AR5 predicts with medium confidence that the mean sea level rise will be 0.44 m under RCP2.6, 0.53 m under RCP4.5, 0.55 m under RCP6.0, and 0.74 m under RCP8.5 (Church et al., 2013). Less conservative estimates of projected sea level rise have been published since and a more recent study suggested it very likely that GMSL would reach 0.5–1.2 m under RCP8.5 and 0.4–0.9 m under RCP4.5 (Kopp et al., 2014; Slangen et al., 2014).
Oxygen
AR5 Summary
Due to the solubility effect, warmer waters contain less dissolved oxygen. Increased stratification, as a result of warming, decreases ventilation of water masses, also causing decreased oxygen concentration. When [O2] are below 60 μmol kg−1 conditions become hypoxic, below 4.5 μmol kg−1, waters are termed suboxic and waters without measurable dissolved oxygen are termed anoxic (Figure 4; Pörtner et al., 2014).
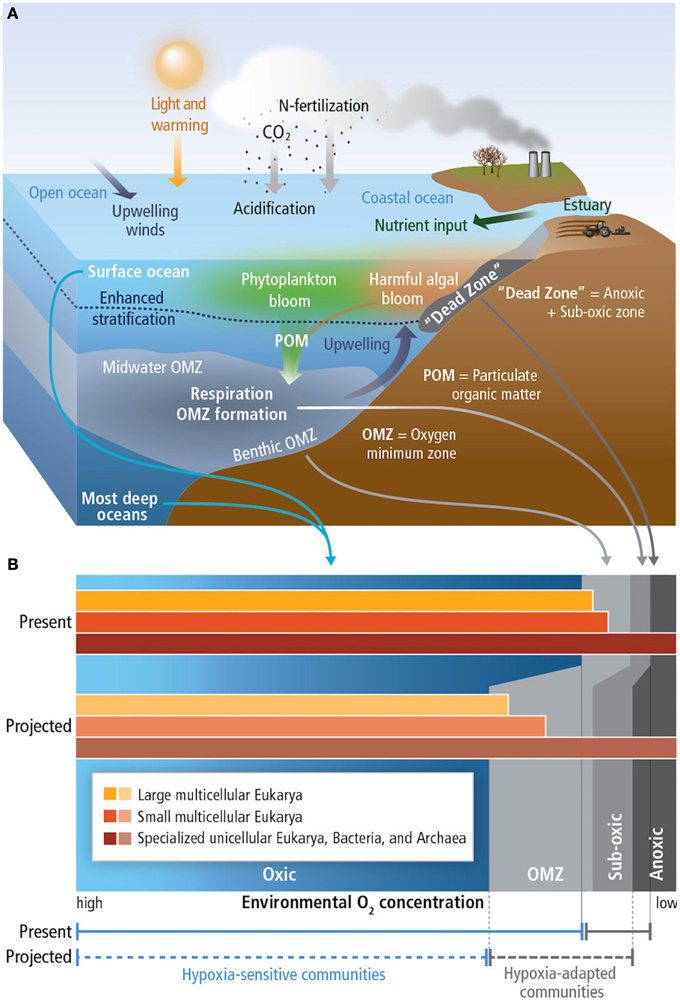
Figure 4. (A) Principal mechanisms underlying the formation of hypoxic conditions and their biological background. The buoyant, fresh input from rivers produces sharp density stratification at the base of the freshened layer (also valid for ice melt and high precipitation) near the surface and, hence, vertical mixing is greatly reduced. In consequence, the nutrient inputs from the river and the atmosphere accumulate in a narrow upper layer, leading to blooms of phytoplankton. The increased oxygen consumption due to aerobic decomposition of sinking particulate organic matter (POM) results in hypoxic conditions of benthic and mid-water oxygen minimum zones (OMZs). Enrichment of nutrients (eutrophication) results in coastal dead zones. In the open oceans, heating of the upper layer increases stratification, while the wind-driven upwelling of hypoxic, nutrient-rich water from deeper layers adds to the formation of the OMZs. (B) Distribution of free-living marine organisms (microbes such as archaea, bacteria), in various water layers. Hypoxia tolerance is enhanced in small compared to large organisms, allowing unicellular species and small animals to thrive in extremely hypoxic habitats. Species richness and body size of animals decrease with falling O2 levels. Source: Pörtner et al. (2014).
There is medium confidence that dissolved oxygen concentrations generally decreased since 1960 but with strong regional variations (Rhein et al., 2013). The mean annual global oxygen loss during 1970–1990 between 100 and 1000 m is calculated as 0.55 ± 0.13 × 1014 mol yr−1 (Rhein et al., 2013). Stratification-induced reduced ventilation is thought to be the major cause of this decline, with solubility effect accounting for only 15% of the decrease (Rhein et al., 2013). Naturally occurring, periodic hypoxic events may be exacerbated by climate change (Rhein et al., 2013).
Decreases in [O2] have been observed over the last 50 years in tropical basins (−2 to −3 μmol kg−1 decade−1), the subpolar North Pacific and below the thermocline in the southern Indian Ocean east of 75°E (Hoegh-Guldberg et al., 2014). Over the same period, [O2] decreased in North Atlantic surface waters but increased in intermediate waters (Hoegh-Guldberg et al., 2014). Conversely, it increased in the thermocline in the Indian Ocean and South Pacific Oceans between the 1990's and 2000's (Hoegh-Guldberg et al., 2014). Results for the Southern Ocean are contradictory depending on region and time period and require further clarification (Rhein et al., 2013). Along the continental shelf, large regions of the Eastern Pacific are low in dissolved oxygen and oxygen minimum zones (OMZ) are found at around 300 m depth (Hoegh-Guldberg et al., 2014).
The shoaling lysocline as a result of ocean acidification means that it is likely that upwelling waters will be both depleted in oxygen and acidified (Rhein et al., 2013). Coastal regions, particularly along the west coast of North America, have exhibited decreases in [O2] due to increased stratification and it has been suggested that oxygen concentrations in coastal areas may be declining approximately 10 times faster than the open ocean, although more data are needed to confirm this hypothesis (Hoegh-Guldberg et al., 2014). Due to the greater solubility of O2 in cold waters and the low microbial activity, deep sea waters are relatively well oxygenated (Hoegh-Guldberg et al., 2014). However, oxygen concentration is decreasing in the deep sea, with the largest decline at intermediate water depths (<1000 m), some deeper waters are also decreasing in O2 (Hoegh-Guldberg et al., 2014).
Ocean warming will very likely lead to further declines in dissolved O2, estimates of global decline range between 6 and 12 μmol kg−1 by 2100, depending on the RCP scenario (Ciais et al., 2013). The regions most affected by decreasing O2 are the intermediate to deep waters of the North Atlantic, North Pacific and Southern Ocean with declines between 20 and 200 μmol kg−1 by 2100 (Hoegh-Guldberg et al., 2014).
Updates to AR5
Recent model projections agree with AR5, suggesting a decrease in oxygen concentration under every RCP scenario. The modeled mean reduction in global ocean [O2] is −3.4, −2.5, −2.3, and −1.8% by the end of the century relative to the 1990s, for RCP8.5, RCP6.0, RCP4.5, and RCP2.6, respectively (Bopp et al., 2013).
Models have been limited in their simulation of present day O2 concentration (Cocco et al., 2013) and as a result there is uncertainty surrounding the expansion of hypoxic and suboxic zones, the AR5 report considers it as likely as it is unlikely that they will expand (Ciais et al., 2013). Cocco et al. (2013) used models representing the interactions between the physical climate system, biogeochemical cycles and ecosystems and predicted a decrease in total ocean dissolved oxygen inventory of 2–4% between 1870 and 2100. The authors found relatively small changes were projected in the volume of hypoxic and suboxic waters. Suboxic waters were projected to decrease in volume by ≤10%. There were discrepancies between model results for more oxygenated waters; the majority of models predict an expansion of between 2 and 16% for regions with less than 80 mmol m−3 and a decrease in volume of between 0.4 and 4.5% for water with less than 50 mmol m−3.
Ocean Acidification
AR5 Summary
CO2 absorbed by the ocean reacts with the seawater and causes a decrease in pH, changing the relative abundances of the dissolved inorganic carbonate species: the concentration of bicarbonate ions (HCO−3) increases while the concentration of carbonate ions (CO2−3) decreases, lowering the saturation state (Ω) of CaCO3. The carbonate system of seawater, including saturation state, is affected by temperature, salinity and pressure and, thus, varies regionally and with depth. The chemical response of the oceans to increasing CO2 is well understood with very high confidence (Rhein et al., 2013). There is high confidence that surface ocean pH has declined by 0.1 pH units since the beginning of the Industrial Era, corresponding to a 26% increase in the concentrations of H+ ions (Rhein et al., 2013). Direct measurements show that the rate of pH decrease is between −0.0014 and −0.0024 units yr−1 in surface waters (Rhein et al., 2013).
Regional estimates vary, with some areas better sampled than others. There is a paucity of time series measurements in the Southern Ocean surface waters; however, the available data suggest rates similar to those seen globally (Rhein et al., 2013). Anthropogenic CO2 has reached at least 1000 m in all three ocean basins and deeper in the Atlantic (Hoegh-Guldberg et al., 2014). As the waters at the bottom of some oceans basins are very old, it will take many centuries for full equilibration of deep ocean waters to recent global warming and CO2 perturbation (Cao et al., 2014; Hoegh-Guldberg et al., 2014). In upwelling areas, upwelled water is high in dissolved CO2, exacerbating ocean acidification driven by anthropogenic activities (Hoegh-Guldberg et al., 2014).
It is virtually certain that the continued uptake of CO2 by the oceans will increase ocean acidification (Ciais et al., 2013). Global decreases in seawater pH are projected to be 0.065 for RCP2.6, 0.145 for RCP4.5, 0.203 for RCP6.0 and 0.31 for RCP8.5 in 2081–2100 compared to 1986–2005 (Ciais et al., 2013). The extent of ocean acidification will vary regionally and seasonally with undersaturated conditions first reached in wintertime (Ciais et al., 2013). The largest decreases in the concentration of CO2−3 will be in warmer low and mid-latitudes, as these areas are naturally high in CO2−3 concentration but high latitudes and coastal upwelling areas are projected to be the first to become undersaturated (Ciais et al., 2013).
Updates to AR5
It has recently been demonstrated that anthropogenic trends in ocean acidification emerge quickly from the background noise of natural variability on the local-to-regional scale. Anthropogenic trends in surface ocean pH (and pCO2) emerge within roughly 12 years, for the majority of the global ocean area, compared to between 10 and 30 years for surface ocean DIC and 45–90 years for SST (Keller et al., 2014). This implies that anthropogenic carbon emissions have already forced surface pH values beyond the range of 20th century natural variability.
Baseline monitoring of the Western Arctic Ocean estimates that 20% of Canadian Basin surface waters are undersaturated with respect to aragonite (Robbins et al., 2013) and that the saturation horizon is shoaling; over 67 and 22% of the bottom water of Hudson Bay was undersaturated with respect to aragonite and calcite, respectively (Azetsu-Scott et al., 2014). In the Arctic, Ω decreases during ice formation and increases during ice melt, resulting in a five times larger seasonal amplitude of the carbonate system in the upper 20 m compared to what is observed in sea ice free systems (Fransson et al., 2013). Calculated pH trends for the North Atlantic Gyre suggest a decrease of −0.0022 ± 0.0004 units yr−1 over the period 1981–2007 (Lauvset and Gruber, 2014). In the North Pacific, a pH decrease of −0.0011 ± 0.0004 units yr−1 from 1997 to 2011 has been calculated (Table 3; Wakita et al., 2013).
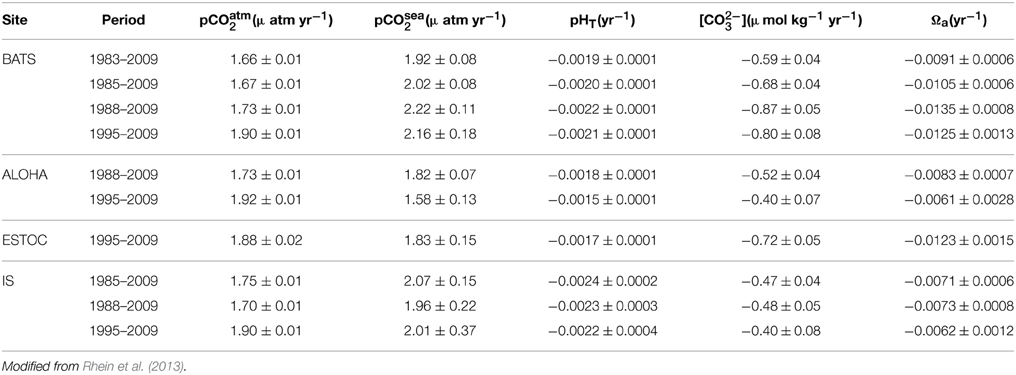
Table 3. Long-term trends of atmospheric (pCO2 atm) and seawater carbonate chemistry (i.e., surface-water pCO2, and corresponding calculated pH, CO2−3 and aragonite saturation state (Ωa) at four ocean time series in the North Atlantic and North Pacific oceans: (1) Bermuda Atlantic Time-series Study (BATS, 31°40′N, 64°10′W) and Hydrostation S (32°10′N, 64°30′W) from 1983 to present; (2) Hawaii Ocean Time series (HOT) at Station ALOHA (A Long-term Oligotrophic Habitat Assessment; 22°45′N, 158°00′W) from 1988 to the present); (3) European Station for Time series in the Ocean (ESTOC, 29°10′N, 15°30′W) from 1994 to the present; and (4) Iceland Sea (IS, 68.0°N, 12.67°W) from 1985 to 2006.
It is unlikely that more than 10% of global surface waters will maintain Ωa higher than 3 if atmospheric CO2 exceeds 550 ppm by 2100 (Steinacher et al., 2013). It is predicted that when atmospheric CO2 reaches four times its pre-industrial level, global mean saturation state of aragonite (Ωa) horizon will shoal from the pre-industrial levels of 1288 m to 143 m (Cao et al., 2014).
Under RCP8.5, pH reductions exceeding 0.2, units are projected in 23% of North Atlantic deep-sea canyons and ~ 8% of seamounts (Gehlen et al., 2014). Recent work has found intermediate waters to be twice as sensitive to increased carbon concentrations as surface waters and project higher rates (−0.0008 to −0.0023 ± 0.0001 units yr−1, the depending on RCP) of acidification in intermediate waters than surface waters over centennial timescales (Resplandy et al., 2013).
Recent projections of future ocean acidification in Polar Regions estimate that increased ice melt in the Arctic would lead to enhanced oceanic uptake of inorganic carbon to the surface layer (Fransson et al., 2013; Reisdorph and Mathis, 2014). Within 10 years, 10% of its waters will be undersaturated with respect to aragonite, and by 2025, under all RCP scenarios, 10% of its waters are projected to be undersaturated with respect to calcite (Popova et al., 2014). It is considered likely that large regions of Antarctic and Sub-Antarctic surface waters will become undersaturated with respect to aragonite by 2030 (Mattsdotter Björk et al., 2014).
Biological Impacts of Climate Change and Ocean Acidification
In the following sections the main findings for the impacts of changes in temperature, dissolved oxygen and ocean acidification are summarized for microbes, plants, animals and ecosystems. Corals and coral reefs are treated separately as they represent a unique and important habitat that is particularly sensitive to the effects of climate change and ocean acidification.
Impacts of Ocean Warming
The AR5 states that all organisms have an optimum range of temperature at which physiological processes are most efficient. The impact of changing temperature depends on the organism's specific window of thermal tolerance and ability to acclimate or adapt to changing conditions, both of which vary greatly among species. Exceeding these limits can have effects on a wide range of physiological processes (Poloczanska et al., 2014; Pörtner et al., 2014).
Organism-specific temperature ranges dictate the distribution of organisms. A common adaptation to changing temperature is the displacement of a species to areas of more favorable temperature (Poloczanska et al., 2014; Pörtner et al., 2014). Hence, under a warming scenario, poleward migrations are expected; however, possibilities for migration are limited for polar organisms. Organisms also respond to temperature-driven changes in the physical environment such as stratification, reduced sea-ice cover and freshening (Pörtner et al., 2014). Unfortunately, for many organisms, poleward movement may be limited by other factors that restrict migration (Pörtner et al., 2014).
According to the AR5 there is high confidence that polar and tropical species are most, and temperate species least vulnerable, to changes in temperature (Pörtner et al., 2014). As ocean temperatures are less variable in the Southern Hemisphere than the Northern Hemisphere, species from the polar regions of the Southern Hemisphere are predicted to be the most vulnerable to increasing temperature (Larsen et al., 2014) and more recent studies add weight to this statement, highlighting the vulnerability of Southern Hemisphere polar organisms to temperature changes (Chambers et al., 2013; Constable et al., 2014; McBride et al., 2014).
Microbes
AR5 summary
According to the AR5, warming will enhance microbial growth. As thermal tolerances are species-specific, continued warming causes changes in species compositions with warmer conditions favoring smaller sized species (Pörtner et al., 2014).
Updates to AR5
Recent work by De Senerpont Domis et al. (2014) supports the assertions of the AR5; showing warming to enhance phytoplankton growth rates (2014). However, several studies find that growth is strongly modulated by nutrient availability, suggesting that under more stratified conditions warming may have a net negative effect on phytoplankton growth (Chust et al., 2014; Lewandowska et al., 2014; Marañón et al., 2014). New model results predict that warming of 2.3°C leads to a 6% reduction in phytoplankton biomass (Chust et al., 2014). Recent work supports the IPCC findings that phytoplankton, including those that cause harmful algal blooms (HABs), are the taxon that has displayed the largest latitudinal range shifts concurrent with climate change, with average distribution shifts of over 400 km decade−1 (Glibert et al., 2014; Poloczanska et al., 2014). In line with the findings of AR5, Calbet et al. (2014) observed shifts in microplankton species compositions, suggesting implications for the global carbon pump, as small size cells are likely to be re-mineralized to inorganic carbon at shallower depths. Recent work has shown that the coccolithophore Emiliania huxleyi is capable of evolutionary adaptation to ocean warming similar to that predicted under RCP8.5 (Benner et al., 2013; Schluter et al., 2014).
Rising temperature has been shown to influence host-pathogen interactions, increasing infectious disease outbreaks with pathogens moving polewards (Baker-Austin et al., 2013; Burge et al., 2014).
Macroalgae and Seagrasses
AR5 summary
There is high confidence that macrophytes are limited in thermal tolerance and, thus, sensitive to warming, especially in lower latitudes (Pörtner et al., 2014). Thermal stress has been shown to affect photosynthesis, growth, reproduction and survival, with subsequent consequences for macrophyte abundance, distribution, and productivity. Sea ice retreat in polar areas has allowed an expansion of macroalgal distribution, via increased habitat availability (Pörtner et al., 2014).
Updates to AR5
Recent publications support the assertions of the AR5, observing different distribution shifts and responses to warming in warm and cold-water species (Brodie et al., 2014; Komatsu et al., 2014) However, there are some inconsistencies in the literature as Brodie et al. (2014) predict, “seagrass will proliferate” in the North Atlantic under future warming. Recent publications add further evidence that, in temperate regions, kelp mortality, spore mortality and germination will be negatively affected by projected temperature increases under RCP8.5 (Brodie et al., 2014; Gaitán-Espitia et al., 2014). Warming has also been found to increase the incidence and/or severity of marine diseases affecting eelgrass (Bockelmann et al., 2013). Increased warming increases the Mg levels in the calcite of crustose coralline algae although, no significant trend was observed in samples collected between 1850 and 2010 (Williamson et al., 2014).
Animals
AR5 summary
There is high confidence that surpassing species-specific heat tolerance limits during warming causes reduced abundance, mortality, shifts in the seasonal timing, and changes in individual growth, development, calcification and immunity (Poloczanska et al., 2014; Pörtner et al., 2014). Although laboratory studies commonly use temperature means, there is evidence that extreme temperatures events illicit greater species response than sustained temperature means, causing mortality and/or latitudinal/depth range distribution shifts that can cause localized extinctions (high confidence; Pörtner et al., 2014). During early life, owing to incomplete development, or as adult spawners, due to large body size, animals can become more sensitive to warming (Pörtner et al., 2014).
Updates to AR5
More recent work continues to strongly support the findings of AR5 that many species are undergoing geographical and phenological shifts as a result of warming (Vehmaa et al., 2013; Goberville et al., 2014; Kamya et al., 2014; Mackenzie et al., 2014a; Church et al., 2013; Mackenzie et al., 2014a,b,c; Queirós et al., 2014; Rice et al., 2014). The AR5 found that zooplankton have exhibited some of the most extreme geographic range shifts of over 100 km decade−1 (Poloczanska et al., 2014). Subsequent work has observed significant distribution shifts of copepod species in the North Sea and North Atlantic in conjunction with warming between 1958 and 2009 (Beaugrand et al., 2014). Latitudinal range shifts have also been observed in benthic cnidarians, molluscs and crustacea, non-bony fish and bony fish (Engelhard et al., 2014; Poloczanska et al., 2014; Potts et al., 2014).
Temperature also governs the distribution and abundance of large pelagic fish in the Indian, Pacific and Atlantic Oceans and the work of Mackenzie et al. (2014a) adds weight to the high confidence of the statement in the AR5 that temperature anomalies caused a major shift in tuna distribution in these areas. This may cause high vulnerability in seasonally spawning fish species (Crozier and Hutchings, 2014; Elettra et al., 2014). There is medium confidence that warming also causes a decrease in the body size of some marine fishes (Rice et al., 2014).
Warming has been shown to increase disease incidence in many marine organisms (reviewed in Burge et al., 2014) and impair immune responses in host organisms, including shellfish (Travers et al., 2009), corals (Harvell et al., 2009), and finfish (reviewed in Bowden, 2008). Recent reemergence of Vibrio tubiashii, a bacterial pathogen of larval Pacific oysters, was linked to warming and upwelling of low pH waters (Elston et al., 2008). In some cases, though, adaptation to warming may reduce disease, as heat-resistant Pacific oysters were more resistant to infection by a herpesvirus (Dégremont, 2011).
Recent work continues to highlight the effects of secondary drivers such as ocean acidification, hypoxia and food availability on the capacity of an organism to adapt to changing temperatures and increasing numbers of recent studies are highlighting the interactive effects of temperature and secondary drivers (Vehmaa et al., 2013; Ko et al., 2014; Mackenzie et al., 2014b,c; Madeira et al., 2014; Pope et al., 2014). A recent study has demonstrated that trans-generational plasticity can mediate the effects of warming in a fish species (Shama et al., 2014); however, there remains low confidence in our understanding of the potential evolutionary adaptation to warming.
Warm and Cold Water Coral Communities
AR5 summary
Thermal tolerance and recovery capacity of the coral host and the symbiotic dinoflagellates varies with geography and among species (Wong et al., 2014). Mass bleaching has more widespread during the last 20 years; 7% of the reef locations exhibited at least one bleaching event between 1985 and 1994 compared to 38% between 1995 and 2004 (Wong et al., 2014). There is very high confidence that bleaching has the potential to cause up to 50% mortality, resulting in declining coral abundance (Figure 5; Wong et al., 2014).

Figure 5. The same coral community (A) before and (B) after a bleaching event in February 2002 at 5 m depth, Halfway Island, Great Barrier Reef. Approximately 95% of the coral community was severely bleached in 2002. Source: Elvidge et al. (2004).
There is high confidence that mass coral bleaching events have occurred in all three sub-tropical gyre (STG) regions, in conjunction with warming (Hoegh-Guldberg et al., 2014). In the Pacific, there has been a steady decline in coral cover on coastal coral reef ecosystems ranging between 0.5 and 2.0% yr−1 (Hoegh-Guldberg et al., 2014). High temperature in the Atlantic STG caused coral mortality in the eastern Caribbean (Eakin et al., 2010a,b), and in the Indian Ocean, coral cover declined by an average of 38% following the 1998 and 2010 temperature extremes (high confidence; Hoegh-Guldberg et al., 2014).
Studies of the thermal sensitivity of cold-water corals are scarce. One species, Lophelia pertusa, responds to 3°C warming with a three-fold increase in metabolic rate, indicating a narrow thermal window (Pörtner et al., 2014).
Updates to AR5
Studies continue to find that thermal tolerance and recovery capacity of the coral host and the symbionts varies geographically and among species (Alemu and Clement, 2014; Cantin and Lough, 2014; Comeau et al., 2014c; Falter et al., 2014; McClanahan and Muthiga, 2014). Nevertheless, mass bleaching events are becoming more predictable due to their relationship with sustained temperature anomalies of 1 to 2°C above the long-term summer maximum (Liu et al., 2014).
Several coral diseases and resultant mortalities have increased with ocean warming (see review in Burge et al., 2014). Population crashes of two key reef-building corals (Acropora cervicornis and Acropora palmata) in the Caribbean (Gladfelter, 1982; Aronson and Precht, 2001) have now been linked to ocean warming (Randall and Van Woesik, 2015) and have had drastic impacts on coral reef ecosystems throughout the region, leading to listing of the species as Threatened under the United States' Endangered Species Act (Weijerman et al., 2014). Temperature increases of 6°C have also been observed to reduce the production of mucous, which may increase susceptibility to coral diseases (Pratte and Richardson, 2014). Dispersal of coral larva is also reduced under high temperatures, which will weaken connectivity among populations, thus potentially slowing recovery if local populations are severely affected (Figueiredo et al., 2014).
Some thermally tolerant species are able to divert cellular energy into mechanisms for survival and recovery of short-term heat stress but at the expense of growth and biomineralization (Maor-Landaw et al., 2014). Studies have shown that repeat bleaching may impact thermal tolerance; some species are able to rapidly acclimatize while others become more susceptible (Grottoli et al., 2014). Models also provide limited evidence that corals have some capacity to acclimatize to high temperatures but even considering possible adaptation, it is projected that under RCP4.5, two thirds of the world's reefs will be subject to long-term degradation (Grottoli et al., 2014; Logan et al., 2014; Palumbi et al., 2014).
Recent work has also suggested that increased temperature and [CO2] may cause cold-water corals to accumulate dimethylsulphoniopropionate (DMSP) from the water column. It has been suggested corals use DMSP in response to environmental challenges, implying an acclimation response to CO2 stress (Burdett et al., 2014).
Ecosystems
AR5 summary
Ecosystems that are built around heat sensitive organisms such as coral reef or kelp forests, may be at increased risk from warming-induced habitat loss. Within ecosystems, different tolerances of individual species can cause changes in inter-specific competition, trophic dynamics and species compositions. There is low confidence in predicting how ecosystems will react to immigration of animals as a result of climate change (Pörtner et al., 2014).
There is medium confidence that in most semi-enclosed seas, temperature induced faunal latitudinal range shifts have occurred and in the Mediterranean, Black, and Baltic Seas, increased temperatures have prompted colonization by invasive warmer water species (Hoegh-Guldberg et al., 2014). There is medium confidence that loss of summer sea ice and increased ocean temperature will enhance secondary pelagic production in some regions of the Arctic). There is high confidence that these changes will alter the species composition and carrying capacity with subsequent effects on fish and shellfish populations (medium confidence; Larsen et al., 2014).
Updates to AR5
New evidence continues to add to the high confidence level that observed changes in distribution, phenology and reproduction of plants and animals in marine ecosystems are, at least partially, temperature induced (Chambers et al., 2013; Beaugrand et al., 2014; Goberville et al., 2014; Hiddink et al., 2014; Jones and Cheung, 2014; Kim et al., 2014; Lambert et al., 2014; Montero-Serra et al., 2014; Rice et al., 2014). As different species and groups have differential responses to warming, effects are seen at every trophic level and can also be amplified up the food chain (Pinsky et al., 2013; Chust et al., 2014). Changes in phenology are not synchronous among phyla and can cause predator-prey mismatches (Arula et al., 2014; Behrenfeld, 2014; Lewandowska et al., 2014), changes to species compositions (Albouy et al., 2014), alterations in food web body size (Gibert and Delong, 2014) and changes in food web composition (Verges et al., 2014). Recent work has suggested that this maybe most pronounced in systems governed by seasonal blooms (Behrenfeld, 2014).
Changes in the frequency, intensity, and geographic distribution of marine diseases have had significant impacts on many ecosystems, particularly if they affect keystone species (Burge et al., 2014).
Sea Level Rise
AR5 Summary
Vegetated habitats such as mangroves, seagrass meadows, intertidal rocky reefs and wetlands are the natural systems most affected by changes in sea level. There is high confidence that these habitats are in decline with the loss estimated to release 0.04–0.28 PgC yr−1 (Wong et al., 2014). Increasing sea levels as a result of warming have also caused reductions and range shifts in seagrass and mangrove systems in the Pacific region (Hoegh-Guldberg et al., 2014).
Updates to AR5
Recent research adds weight to the findings of AR5 by identifying vegetated habitats as being particularly vulnerable to sea level rise (Cazenave and Cozannet, 2014; Di Nitto et al., 2014; Murray et al., 2014b; Saintilan et al., 2014; Thorner et al., 2014). There is medium confidence that some coral reefs will be able to keep up with the projected rate of sea level rise (Hamylton et al., 2014; Woodroffe and Webster, 2014). However, increasing evidence suggests increased erosion and export of land-based sediments and pollutants will exacerbate existing stress to nearshore corals (Storlazzi et al., 2011). Because even small populations of humans in close proximity to coral reefs can be deleterious (Knowlton and Jackson, 2008), evacuation of low-lying islands may reduce stress to some reefs.
Decreasing Dissolved Oxygen Concentration
Under hypoxic conditions, species with higher O2 demands are lost and, if hypoxic conditions are sustained, communities that thrive in low O2 environments replace them (Pörtner et al., 2014). Oxygen demand depends on species, body size, life stage, metabolic activity and temperature. In extreme temperatures, critical O2 concentration is almost the same as fully O2 saturated water, indicating increased sensitivity to hypoxia in increased temperatures (Pörtner et al., 2014).
Microbes
AR5 summary
OMZs form habitat for both anaerobic and aerobic microbes that can utilize very low (<1 μmol kg−1) [O2]. In OMZs, microbial respiration drives O2 concentration down and maintains low concentrations. There is high confidence that microbial life will benefit from expanding OMZs (Pörtner et al., 2014).
Updates to AR5
Storch et al. (2014) observed communities shifting to smaller, multicellular Eukarya, Bacteria and Archaea under diminished O2.
Animals and Plants
AR5 summary
Special adaptations to hypoxia and lower energy demand are present in animals that live permanently in OMZs but this is only possible for animals of small size (<1 mm), in cold temperatures (Pörtner et al., 2014). There is little information on the sensitivity of macrophytes to hypoxia; however, negative responses have been observed in eelgrasses so there is medium confidence that expanding benthic OMZs will constrain the distribution of macrophytes (Pörtner et al., 2014).
Updates to AR5
Few animals have developed strategies to temporarily cope with hypoxic conditions and recent research adds weight to the high confidence level that hypoxia-adapted life forms, such as the jumbo squid, will benefit from expanding OMZs (Stewart et al., 2014). Range expansion of hypoxia adapted squid has been observed (Stewart et al., 2014) and meta-analysis supported the oxygen- and capacity-limited thermal tolerance (OCLTT) theory on the interactive effect of O2 and temperature (Portner, 2010), limiting the depth distributions of non-hypoxia adapted fish and invertebrates (Brown and Thatje, 2014).
Ecosystems
AR5 summary
There is medium confidence that expansions of OMZs, will result in habitat and abundance losses for taxa with high O2 demands (Pörtner et al., 2014). As many pelagic species migrate vertically on a daily and seasonal basis, the shoaling of OMZs will affect migrations and shift microbial and faunal compositions to organisms that can tolerate brief exposure to hypoxia (medium confidence; Pörtner et al., 2014). Larval stages are particularly sensitive, suggesting that the impacts could threaten population survival and affect higher trophic levels (Pörtner et al., 2014). There is high confidence that, as a result of increased energy demand, calcifiers are particularly sensitive to hypoxia (Pörtner et al., 2014). Expansions of OMZs are predicted to compress habitat depth for hypoxia-intolerant fish (Hoegh-Guldberg et al., 2014). Oxidation reactions in OMZs release nitrogen into the atmosphere meaning that less fixed nitrogen is available to primary producers as a result there is medium confidence expansion of OMZs will limit primary productivity (Pörtner et al., 2014).
Updates to AR5
Observed range changes in non-hypoxia tolerant halibut, adds weight to the findings of AR5 (Sadorus et al., 2014). The work of Cheung et al. (2014) supports the assertions of the AR5, finding high sensitivity in the larvae of benthic invertebrates. Decreases in coral photosynthesis observed under hypoxic conditions suggest that decreasing oxygen concentrations could have potential negative implications for reef ecosystems (Wijgerde et al., 2014).
Ocean Acidification
A wide range of organismal functions are affected by ocean acidification including: membrane transport, calcification, photosynthesis, neuronal processes, growth, reproductive success and survival. Due to the direct effect of decreased Ω, calcifying species are thought to be at greatest risk from decreasing pH. Very little is known about the capacity for evolutionary adaptation as most experiments investigating the effects of ocean acidification are run over relatively short time periods (Pörtner et al., 2014). Here, the term ocean acidification primarily refers to the reduction in pH, the reduction in carbonate ion concentration Ω, and the increase in bicarbonate ion concentration and dissolved CO2 concentration in response to carbon dioxide uptake.
Microbes
AR5 summary
Due to insufficient field observations there is limited evidence and low agreement on how future conditions will affect microorganisms. Ocean acidification can drastically alter the species composition of phytoplankton assemblages, and has been linked to increased occurrences of harmful algal blooms (HAB) of diatoms and dinoflagellates. There is low to medium confidence on the effects of ocean acidification on nitrogen (N2) fixing cyanobacteria due to the wide range of N2 fixation responses observed in laboratory experiments. There is medium to high confidence that foraminiferal calcification is negatively affected by acidification (Pörtner et al., 2014).
Updates to AR5
New research suggests that ocean acidification might benefit bacterial communities by elevating growth (Endres et al., 2014) and increased benthic bacterial diversity has been observed along natural CO2 gradients (Taylor et al., 2014). Other studies have found no detectable effects of ocean acidification on natural bacterial communities (Ahrendt et al., 2014; Gazeau et al., 2014). There is low to medium confidence on the effects of ocean acidification on nitrogen (N2) fixing cyanobacteria. A wide range of N2 fixation responses under RCP8.5 conditions have been observed in laboratory experiments (Böttjer et al., 2014; Eichner et al., 2014; Gradoville et al., 2014), possibly due to species-specific differences in the mechanisms of N2 fixation (Eichner et al., 2014).
There is medium evidence and low agreement on how coccolithophore growth and calcification will be affected as they exhibit highly varied responses depending on species, strain and secondary environmental controls such as irradiance, bloom species composition and nutrient availability (Benner et al., 2013; Horigome et al., 2014; Muller and Nisbet, 2014; Poulton et al., 2014; Sett et al., 2014; Young et al., 2014). There is evidence that the coccolithophore, Emiliania huxleyi, has the capacity to evolve genetic adaptions to both warming and ocean acidification expected under RCP8.5 (Benner et al., 2013; Lohbeck et al., 2014; Schluter et al., 2014).
Khanna et al. (2013) adds to the medium to high confidence that foraminiferal calcification is negatively affected by acidification. The severity of effects on benthic foraminifera are species and symbionts-specific (Doo et al., 2014). Planktonic foraminifera are predicted to experience the greatest decrease in diversity and abundance in sub-polar and tropical areas, under RCP8.5 (Roy et al., 2014).
Macroalgae and Seagrasses
AR5 summary
Non-calcifying species generally exhibit positive growth responses to increasing [CO2] (Pörtner et al., 2014). There is high confidence that conditions of 720–1800 μatm CO2 stimulate increases in primary production, shoot density, reproductive output and below ground biomass (Pörtner et al., 2014). There is medium confidence that impacts on calcification and respiration are observed when species-specific pCO2 thresholds are surpassed (Pörtner et al., 2014).
Updates to AR5
Non-calcifying species generally exhibit positive growth responses to increasing [CO2] although these responses are season and species specific (Longphuirt et al., 2013), although these effects can be modulated by nutrient availability (Martínez-Crego et al., 2014). The work of Betancor et al. (2014) adds more evidence to the low confidence levels of the AR5 that ocean acidification can impair the production of grazer-deterrent substances.
Recent work continues to find complex and varied responses to ocean acidification in calcifying macrophytes (James et al., 2014; Johnson et al., 2014b; McMinn et al., 2014). Changes in species composition along natural CO2 gradients have been observed (Ordoñez et al., 2014) but negative effects on calcification can be mediated by inter-specific interactions (Reyes-Nivia et al., 2014; Short et al., 2014) and acclimatization (Johnson et al., 2014a). There is medium confidence that significant dissolution of living and dead maerl beds will occur, both of which provide important habitat for associated fauna (Brodie et al., 2014). Crustose coralline algae display species specific increases in calcification up to 900 μatm and decreases after the species-specific threshold is reached (McCoy and Kamenos, 2015). Greater instances of dissolution and deformities have also been observed in crustose coralline algae populations at natural CO2 vent sites (Brinkman and Smith, 2015).
Animals
AR5 summary
Species-specific responses to ocean acidification are mixed (Pörtner et al., 2014). Amongst benthic invertebrates, calcifying organisms are more sensitive than non-calcifying. There is medium confidence that increased calcification under lowered pH increases energetic costs at the expense of other physiological processes (Pörtner et al., 2014). Early life stages are thought to be more sensitive to ocean acidification drivers and there is high confidence in attributing fatalities at oyster farms to upwelling, CO2 rich waters. Despite experimental observation of ocean acidification effects, the AR5 highlights the lack of field evidence of current ocean acidification effects in natural communities (Pörtner et al., 2014).
Updates to AR5
Recent studies continue to find reduced calcification, reduced rates of repair calcification and weakened calcified structures under acidified conditions (Bressan et al., 2014; Coleman et al., 2014; Fitzer et al., 2014; Pörtner et al., 2014; Wei et al., 2015). Some species have been observed to increase calcification rates at pCO2 ranging from 600 to 900 μatm, before a decrease at higher pCO2 (Collard et al., 2014; Dery et al., 2014; Langer et al., 2014).
More evidence of the negative effects of decreasing pH on fertilization success of invertebrates has been found (Sewell et al., 2013; Bögner et al., 2014; Frieder, 2014; Scanes et al., 2014; Sung et al., 2014) and RCP8.5 acidification has been shown to have negative effects on clam larval dispersal (Clements and Hunt, 2014).
In the California Current System, pteropod shell dissolution due to undersaturated waters can already be observed (Bednaršek et al., 2014). Studies on non-calcifying zooplankton indicate a variety of sub-lethal effects under RCP8.5, including decreased egg production, lower hatch success and decreased survival of nauplii in copepods (Vehmaa et al., 2013; Zervoudaki et al., 2013; Pedersen et al., 2014). The AR5 has high confidence that embryos of Antarctic krill are vulnerable to increased seawater concentrations of CO2 (Larsen et al., 2014) but Atlantic species have been found to be resilient (Sperfeld et al., 2014).
Fish, including some commercially important species such as cod and herring, have been shown to be reasonably resistant to the effects of ocean acidification (Jutfelt and Hedgärde, 2013; Chambers et al., 2014; Maneja et al., 2014). However, deformities in calcified structures (Pimentel et al., 2014) and damage to internal organs continue to be observed under conditions predicted for 2100 under RCP8.5 (Frommel et al., 2014). The strongest effects observed in fish are behavioral, lower pH has been observed to affect predator avoidance, prey detection, odor detection, retinal function, lateralization, boldness and swimming behaviors in fish (Caprio et al., 2014; Chung et al., 2014; Dixson et al., 2014; Domenici et al., 2014; Munday et al., 2014; Murray et al., 2014a; Welch et al., 2014).
Recently published reviews highlight the lack of long-term studies on ocean acidification and the lack of direct experimental evidence of evolutionary adaptation in animals (Reusch, 2014; Sunday et al., 2014). Nevertheless, evidence of a few examples of genetic variations are emerging and have been observed in sea urchins and polychaete worms (Calosi et al., 2013; Kelly et al., 2013; Pespeni et al., 2013), as well as genetic variations in fish that could illicit evolutionary adaptation (Malvezzi et al., 2015). Acclimatization and trans-generational phenotypic plasticity over longer-term experiments have been observed in sea urchins (Dupont et al., 2013) and carry over effects of brief exposure to acidification on growth of oyster larvae (Hettinger et al., 2013).
Warm and Cold Water Corals
AR5 summary
There is high confidence that warm-water corals will be sensitive to future ocean acidification, although the magnitude of response is species specific (Figure 6; Wong et al., 2014). Some species of warm-water and cold-water corals may display resistance to lowered pH and can maintain positive net calcification under aragonite saturation states <1 (Pörtner et al., 2014).

Figure 6. Three CO2 seeps in Milne Bay Province, Papua New Guinea show that prolonged exposure to high CO2 is related to fundamental changes in the ecology of coral reefs. (A) Low pCO2, pHT ~ 8.1, (B) high pCO2, pHT ~ 7.8 to 8.0, (C) very high pCO2, pHT < 7.7. Source: Fabricius et al. (2011).
Updates to AR5
Observations of reductions in calcification continue to demonstrate a species-specific response in both cold and warm water species (Comeau et al., 2014d; Movilla et al., 2014), with fast calcifiers affected more than slow calcifiers (Comeau et al., 2014d). Holcomb et al. (2014) find that response is affected by the internal pH of the calcifying fluid. Despite inter-specific differences in pH tolerance, reef ecosystems may be disproportionately affected if keystone species are lost (Alvarez-Filip et al., 2013). The magnitude of calcification response to acidification is also highly geographically specific, suggesting that secondary factors such as irradiance, nutrient availability and interactions with other ecosystems, such as mangroves, can mediate the effects on calcification (Comeau et al., 2014a,c; Enochs et al., 2014; Gibbin et al., 2014; Tanaka et al., 2014; Wendel, 2014; Yates et al., 2014).
Ocean acidification has been shown to have significant effects on dissolution of warm-water corals, with up to 59% lower net community calcification (Comeau et al., 2014b; Silbiger and Donahue, 2014) observed under RCP8.5 conditions and already resulting in enhanced erosion of reef framework carbonates (Silbiger and Donahue, 2014). There is also evidence that acidified conditions can reduce fertilization and settling success of larvae (Uthicke et al., 2013).
Ecosystems
AR5 summary
As the effects of ocean acidification are complex and species specific, it is difficult to accurately assess the impacts at the ecosystem level. There is high confidence that ocean acidification will have a wide range of direct and indirect effects on ecosystems (Pörtner et al., 2014). There is medium confidence that naturally high CO2 environments are associated with species compositions that favor non-calcifying species, suggesting that calcifiers are outcompeted once pH reaches 7.8–7.7 (Pörtner et al., 2014). There is high confidence that areas prone to low Ω, such as upwelling systems and the polar seas, will be strongly affected by ocean acidification. There is high confidence that Arctic ecosystems are also at high risk due to the exacerbating effects of freshwater from melting sea ice. There is high confidence that elevated CO2 causes losses in diversity, biomass and trophic complexity of benthic marine communities (Pörtner et al., 2014).
Updates to AR5
A variety of recent publications further demonstrate that the severity and the magnitude of effects will vary with the type of ecosystem, geographical location, species composition and the influence of secondary environmental drivers (Garrard et al., 2014; Hendriks et al., 2014; Martínez-Crego et al., 2014; Park et al., 2014; Richier et al., 2014). There is added confidence that ecosystems built around heavily calcified structures such as coral and vermetid reefs or maerl beds are at high risk from ocean acidification (Alvarez-Filip et al., 2013; Brodie et al., 2014; Comeau et al., 2014b; Milazzo et al., 2014).
The Arctic food web is relatively simple, with pteropods acting as an important trophic link (AMAP, 2014). A recent assessment adds to the medium confidence of the AR5 that negative effects on pteropods will have wider consequences for the Arctic ecosystem, potentially affecting important fisheries (AMAP, 2014).
Effects of Multiple Drivers
There is high confidence that the effects of climate change will act on organisms and ecosystems as a suite of simultaneous environmental drivers which will interact with each other to have synergistic or antagonistic effects on the fitness of the individual or ecosystem. There is also growing evidence that the interactions of other environmental factors such as irradiance, nutrient availability geographic location and species community composition can strongly modulate the biological effects of warming, ocean acidification and hypoxia (Ko et al., 2014; Comeau et al., 2014a,c; Poulton et al., 2014; Pörtner et al., 2014).
Microbes
AR5 summary
Experiments and models show mixed responses to multiple drivers on microbial biota in the surface ocean. The effect of RCP8.5 levels of CO2 on growth is species specific and these differences can alter bloom species compositions, with potential impacts on predator-prey interactions. Shifts to different phytoplankton species compositions can alter the sinking rates of particles, as bacteria decompose these particles, it can alter the levels of dissolved oxygen, potentially expanding OMZs (Pörtner et al., 2014).
Updates to AR5
Emiliania huxleyi has demonstrated the ability to adapt to concurrent warming and acidification (Lohbeck et al., 2014; Schluter et al., 2014). Recent work highlights that the effects of RCP8.5 levels of CO2 on growth is species specific with and can be strongly modulated by nutrient availability (Hoppe et al., 2013; Marañón et al., 2014), light conditions and temperature (Errera et al., 2014; Sett et al., 2014).
Plants and Animals
AR5 summary
There is high confidence that the interaction among warming, acidification and hypoxia predicted for 2100 under RCP8.5 can have synergistic negative effects on organisms. There is high confidence that warming acts synergistically with CO2 to decrease calcification and increase sensitivity to bleaching in warm-water corals (Comeau et al., 2014a; Pörtner et al., 2014). Combined warming and ocean acidification in mesocosms following approximately RCP4.5 and RCP8.5 scenarios caused losses of symbionts and corals, and a nocturnal decalcification of the reef community in summer (Pörtner et al., 2014). Hypoxia reduces heat tolerance and vice versa and there is high confidence that warming will expand the area of ecosystems affected by hypoxia, even if oxygen concentrations remain unchanged. This is likely to restrict geographic and depth ranges, particularly in upwelling areas (Pörtner et al., 2014).
Updates to AR5
It has been observed that increasing temperature increases the levels of Mg incorporated into crustose coralline algae calcite, with potentially synergistic negative effects with acidification as high Mg calcite dissolves more readily (Williamson et al., 2014). The combination of warming and high irradiance has been shown to increase bleaching in crustose coralline algae but recovery is possible if favorable conditions resume (McCoy and Kamenos, 2015).
Results continue to show interaction among warming, acidification and hypoxia effects under conditions predicted in 2100 under RCP8.5. Synergistic negative effects have been observed on the growth, survival, fitness, calcification and development of organisms (Padilla-Gamino et al., 2013; Vehmaa et al., 2013; Gaitán-Espitia et al., 2014; Gobler et al., 2014; Hyun et al., 2014; Mackenzie et al., 2014b; Madeira et al., 2014; Maugendre et al., 2014, Rastrick et al., 2014; Roy et al., 2014; Schram et al., 2014; Rosa et al., 2014a,b; Schmidt et al., 2014a). In some cases, hypoxic conditions have been observed to mediate the negative effects of ocean acidification (Mukherjee et al., 2013).
Ecosystems
AR5 summary
There is high confidence that the effects of climate change are already causing changes to the physical and chemical characteristics of habitats and altering food webs (Pörtner et al., 2014). There is high confidence that the indirect effects of climate change, such as shifts in stratification and productivity, expanding OMZs, and the changing composition and biomass of food are exacerbating the effects on ecosystems (Pörtner et al., 2014).
There is high confidence that the combined effects of increased temperature, hypoxia, and ocean acidification will have significant impacts on organisms that act as ecosystem engineers, such as coral or kelp (Dove et al., 2013; Pörtner et al., 2014). Thus, climate change could drastically alter ecosystems by reducing habitat quality and extent.
There is high confidence that species' range distributions and phenologies will be affected by climate change, altering the trophic interactions in a given area (Pörtner et al., 2014). It is likely that some of these changes may be irreversible as the effects of changes at the base of the food web can be amplified up trophic levels and drive the ecosystem to a new regime that may become permanent (Figure 7; Pörtner et al., 2014).
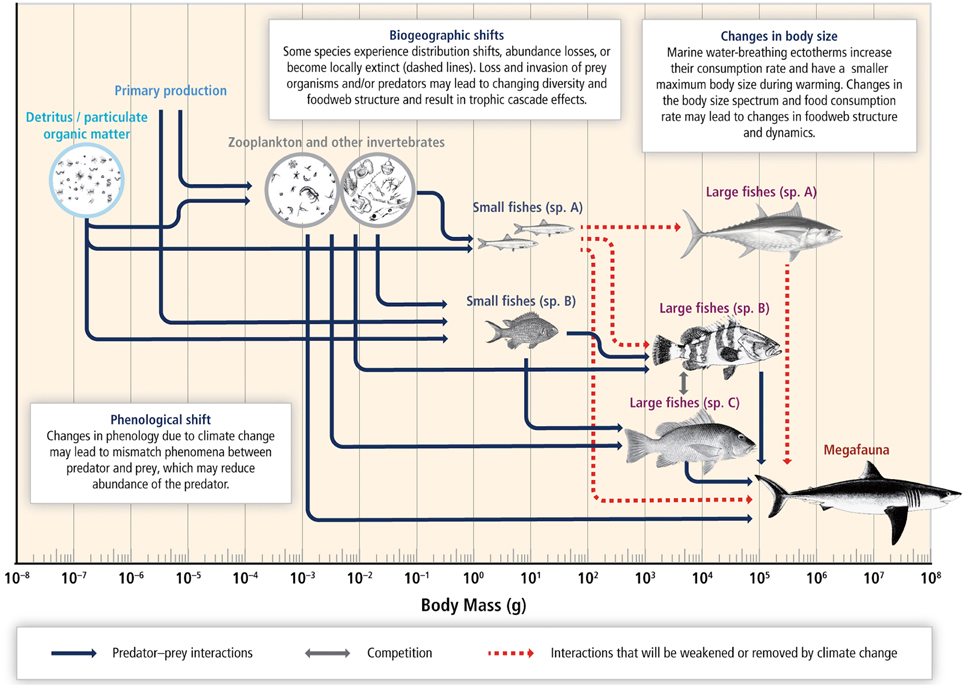
Figure 7. Schematic diagram of expected responses to climate change in a marine food web. A coupled pelagic and benthic food web is structured by the body size spectrum of species. Combined warming, hypoxia, and ocean acidification reduce body size, shift biogeographies, change species composition and abundance, and reconfigure trophic linkages and interaction dynamics. Fishing generally removes large-bodied species and truncates the body-size spectrum of the community. This confounds the detection and attribution of food web responses to climate change. Arrows represent species interactions (e.g., between predator and prey or competitors for food or space). Broken lines reflect the potential loss of populations and trophic linkages due to climate change. Source: Pörtner et al. (2014).
Updates to AR5
Recent studies have modeled the effects of multiple drivers on ecosystems highlighted implications for plankton biomass and trophic functioning (Chust et al., 2014; Guénette et al., 2014). Chust et al. (2014) predicted a global reduction in phytoplankton and zooplankton biomass by 6 and 11%, respectively, with negative tropic amplification of climate change effects for 47% of the ocean. A study focusing on the Scotian Shelf ecosystem found that the effects of climate change could be enhanced or ameliorated by predator–prey interactions and predicted a reduction in biomass of 19–29% by 2100 under RCP8.5 (Guénette et al., 2014).
Future Projections
Due to the relative lack of knowledge on the interacting effects of environmental drivers and the complexity of the marine trophic web, it is difficult to make ecosystem wide projections. It is likely that under both RCP4.5 and 8.5 there will be significant poleward migrations and phenological shifts in many groups of organisms (Pörtner et al., 2014). It is very likely that these effects will be amplified under RCP8.5 compared to RCP4.5 (Figure 8; Pörtner et al., 2014). It has also been suggested that there will be losses in biodiversity, particularly in the tropics (Pörtner et al., 2014). There may also be shifts to smaller body sizes due to thermal stress, exacerbated by interactions with other drivers (Figure 8; Pörtner et al., 2014).
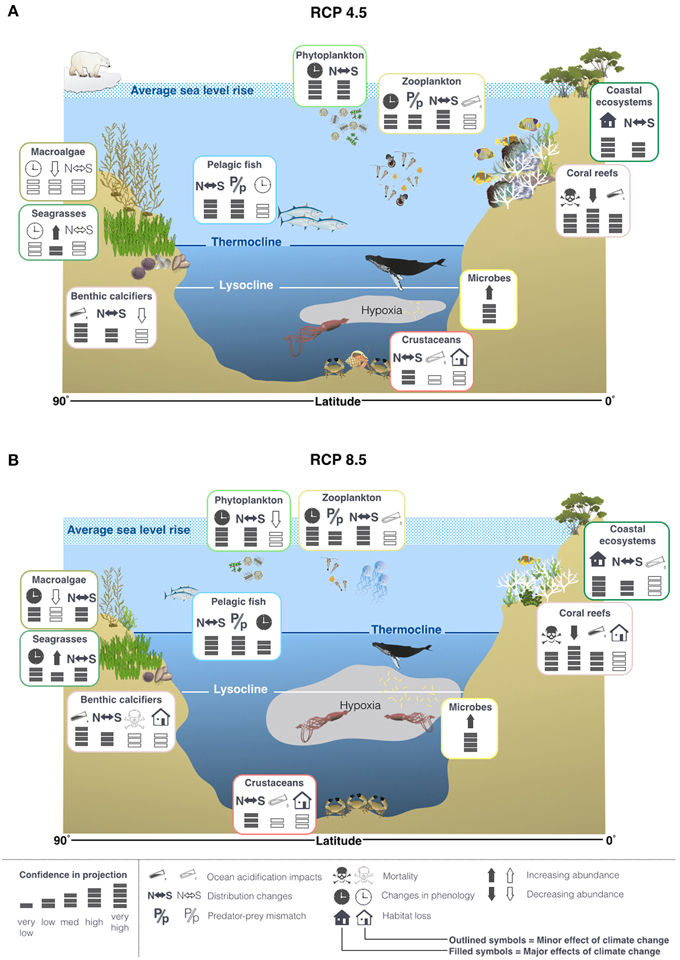
Figure 8. Projected changes to physical features in the oceans and some of the potential impacts on life in the oceans under RCP4.5 (A) and 8.5 (B), based on the findings reported in the IPCC AR5 and literature published since the cut off dates (15/03/2013 for working group I and 31/08/2013 for working group II). It is projected that thermocline and lysocline will shoal to a greater extent and OMZs will expand more under RCP8.5 compared to 4.5. These changes will favor bacteria and hypoxic specialists (Pörtner et al., 2014; Storch et al., 2014) and limit the depth ranges of many species, causing habitat loss (Pörtner et al., 2014). In general, it is predicted that there will be a shift toward smaller body sizes and that many species will exhibit poleward migrations in response to increasing sea temperatures (Pörtner et al., 2014). Icons provided by http://ian.umces.edu/imagelibrary.html.
Possible expansion of OMZs will likely affect trophic interactions, species distribution, migration and composition. Small-bodied (<1 mm) hypoxia-tolerant animals and microbes will benefit at the cost of large bodied, active animals with high metabolic oxygen demands. There will be a loss of biodiversity as communities shift to specialists that are adapted to tolerate hypoxic conditions (Pörtner et al., 2014). Due to the specialized nature of animals living in hypoxic conditions, there is high confidence that expansion of OMZs will decrease biodiversity (Pörtner et al., 2014).
Microbes
New research from Storch et al. (2014) provide evidence that small, less complex eukarya, bacteria and archaea will benefit and proliferate under climate change as they evolve rapidly and can survive anaerobic conditions and higher temperatures (Figure 8).
There is medium to low confidence that the levels of ocean acidification projected under RCP8.5 will be beneficial for most non-calcifying phytoplankton and cyanobacteria (Figure 8; Pörtner et al., 2014). There is medium confidence that coccolithophores are vulnerable to projected end of century pH but new evidence from natural populations found in high CO2 waters and long-term laboratory experiments lends medium confidence that they will be able to adapt to future conditions (Benner et al., 2013; Lohbeck et al., 2014; Pörtner et al., 2014).
Average global primary production is projected to decrease under RCP8.5 due to a lack of nutrients as the result of stratification (Pörtner et al., 2014); however, in high latitude spring blooms systems, photosynthesis is projected to increase. There is high confidence (with added weight from recent studies) that warming is also driving changes in phenology of plankton groups and will continue to do so under RCP8.5 (Behrenfeld, 2014; Hoegh-Guldberg et al., 2014; Poloczanska et al., 2014). From a global perspective, net primary productivity under RCP4.5 will show similar patterns to those projected under RCP8.5, decreasing moderately overall by 2100 but with increases in high latitude systems (Pörtner et al., 2014).
Macrophytes
There is low confidence that seagrasses and non-calcifying macroalgae will benefit under RCP8.5 conditions. As fleshy macroaglae are cool water adapted, it is predicted that under RCP8.5 warming, they will undergo significant changes in their distribution (Figure 8; Brodie et al., 2014). Seagrasses are thought to be more tolerant of increasing temperatures and may proliferate, particularly if they are able to colonize ecological niches provided by the decline of less tolerant groups such as crustose coralline algae (Figure 8; Brodie et al., 2014; Pörtner et al., 2014).
Animals
Temperature increase will lead to poleward migrations and phenological shifts with potential predator prey mismatches. Reduced ocean productivity will reduce the energy available to higher trophic levels and so fishery catches are projected to decrease in temperate and equatorial biomes by 38 and 15%, respectively under RCP8.5 (Figure 8; Pörtner et al., 2014).
Non-calcifying zooplankton are thought to be reasonably resilient to the effects of ocean acidification but sensitive to change in SST (Pörtner et al., 2014). The AR5 and more recent studies find it likely that zooplankton will continue to display large geographic and phenological shifts under increasing temperatures (Figure 8; Chambers et al., 2013; Poloczanska et al., 2014).
New research adds to the high to medium confidence that calcifying invertebrates, including commercially important species such as oysters, mussels and clams, will be vulnerable to end of century ocean acidification (Clements and Hunt, 2014; Scanes et al., 2014). There remains low confidence that crustaceans will be able to tolerate the projected pH decrease (Figure 8; Harms et al., 2014; Pörtner et al., 2014). These projections have profound implications for future trophic interactions and ecosystem function, as it is likely that many calcifiers will be out-competed by non-calcifying species. There is high confidence that elevated CO2 will cause losses of diversity, biomass and trophic complexity in benthic marine communities (Pörtner et al., 2014). The fossil record shows that ocean acidification events in geological history are marked by mass extinctions of calcifying taxa. It is likely that species extinctions will occur under RCP8.5.
Fish are also projected to be vulnerable under RCP8.5 conditions and there is low confidence from model predictions that ocean acidification will generally reduce fish biomass and catch (Pörtner et al., 2014). New projections support the AR5 statement that warming of Arctic waters under RCP8.5 will allow significant distributional shifts and potential interchange of fish species between the North Pacific and the North Atlantic, causing changes to fisheries, trophic dynamics and ecosystem functioning (Jones and Cheung, 2014; Wisz et al., 2015).
There remains low confidence that certain groups of calcifying invertebrates will be tolerant to RCP4.5 conditions, including foraminifers and some pelagic molluscs and medium confidence that crustaceans will also be able to tolerate these conditions (Pörtner et al., 2014). There is also low confidence that many fish species will be resistant under RCP4.5 (Pörtner et al., 2014).
Corals
There is very high confidence that, as warming progresses, coral bleaching and mortality will increase in frequency and magnitude over the next decade. Under A1B emission scenario (approximately RCP6.0), 99% of the reef locations will experience at least one severe bleaching event between 2090 and 2099 (Wong et al., 2014). New studies that take into account potential coral acclimation still predict that more than 50% will experience high frequency bleaching under RCP8.5 (Logan et al., 2014), causing long-term degradation by 2020 (Figure 8; Pörtner et al., 2014). There remains limited evidence and low agreement as to whether corals will be able to acclimate or adapt to increasing temperatures enough to limit bleaching events (Wong et al., 2014). There is high confidence that bleaching events will negatively impact coral community structure and diversity, with medium confidence of bleaching affecting the abundance and species composition of fish communities (Pörtner et al., 2014). New models that account for coral acclimation, predict that fewer than 50% of corals, globally, may experience high frequency bleaching under RCP4.5 throughout the 21st century (Logan et al., 2014), however, there is considerable question as to whether coral adaptive responses can truly keep pace with expected warming. Additionally, while some corals may find geographic refuge due to differential spatial patterns of 21st century warming (Van Hooidonk et al., 2013), opposing spatial gradients in ocean acidification may render them unable to keep pace with erosion as their calcification declines (Van Hooidonk et al., 2014).
There is high confidence that warm-water corals will be vulnerable to decreasing pH under RCP8.5 with widespread dissolution of reefs (medium confidence) and reduced larval dispersal and settlement (low confidence) occurring by 2100 (Wong et al., 2014). This is very likely to reduce habitat and refugia for associated fauna. There is high confidence that calcifying algae, which are associated with coral reefs are also vulnerable under RCP8.5 scenarios, many species are important for reef stability and function, therefore, losses may further impact coral reef health. There is medium confidence that an atmospheric CO2 concentration expected under RCP4.5 (560 ppm) is the threshold at which global dissolution of reefs will occur (Wong et al., 2014). The habitat loss associated with reef dissolution under RCP4.5 will be less severe than for RCP8.5. There is low confidence as to whether RCP4.5 conditions will alter distribution of cold corals (Pörtner et al., 2014).
Ecosystems
It is virtually certain that climate change will cause major changes to ecosystems in high latitude spring bloom systems; warming is a primary driver of ecosystem changes in the North Atlantic (Goberville et al., 2014; Hoegh-Guldberg et al., 2014). There is high confidence that expansion and contraction of faunal ranges have been observed, with an associated increase in diversity as warmer water species colonize new areas (Figure 8; Hoegh-Guldberg et al., 2014; Poloczanska et al., 2014).
There is medium confidence that export of organic matter to the deep sea is controlled by temperature and that warming and changes to primary productivity in the upper ocean will reduce the export of organic matter to the deep sea. This has the potential to affect the distribution, abundance and composition of faunal communities in the deep sea (Hoegh-Guldberg et al., 2014).
The effects of warming will be less severe under the conditions predicted by the end of the century under emissions RCP4.5 than for RCP8.5. Nonetheless, many plants and animals will still be severely affected; however, species distributions and phenological shifts are likely to be less extreme with fewer negative implications on trophic interactions (Pörtner et al., 2014).
Discussion
Research published following AR5 endeavored to address many of the key uncertainties highlighted by the IPCC. Physical and biogeochemical advances include an improved understanding of variability and a growing observational coverage in key environmental drivers such as temperature, carbon and pH. New studies show that ocean heat content continues to increase and anthropogenic climate change continues at high speed. Ecological advances included studies assessing climate-related impacts to different developmental stages of various taxa, as well as an improved understanding of impacts arising from ocean acidification. In most cases the studies published since AR5 agree or add further weight to a growing body of evidence and, therefore, do not significantly alter the projections of future impacts.
The start of this review lists six key uncertainties, identified by the AR5, regarding potential climate-related impacts on biological and physical systems. In light of the new research detailed in this review, these points are revisited and reassessed.
(1) The extent of warming in deep water masses (below 700 m) and limited observational coverage of the ocean, hampering more robust estimates of ocean heat and carbon content.
New studies suggest that the warming hiatus in SST may be caused by heat sequestration in deep ocean basins and natural variability associated with Atlantic and Pacific multi-decadal oscillations. Improved estimates of warming in the deep ocean and southern hemisphere have been proposed (see section Warming).
(2) The likelihood of climate-induced changes to major upwelling systems (i.e., increased or decreased upwelling) is still uncertain (Lluch-Cota et al., 2014).
Models have improved assessment of changes to upwelling systems that have that have already occurred and added weight to the growing body of evidence that predicts regional intensification of upwelling (see section Upwelling).
(3) Ways in which climate-induced changes in the physiology and biogeography of an individual species may alter ecosystem structures, species interactions, and food webs.
Recent studies have identified additional evidence of changes in community size structure (Gibert and Delong, 2014) and food web composition (Chust et al., 2014; Verges et al., 2014), with observed examples of community phase shifts across polar, temperate and tropical marine ecosystems (Beaugrand et al., 2014; Engelhard et al., 2014; Potts et al., 2014; Verges et al., 2014).
(4) An improved understanding of climate sensitivity at the ecosystem level that considers multiple drivers (e.g., ocean warming, acidification, and hypoxia) and synergistic impacts.
Studies have recently begun to investigate ecosystem-level responses to climatic stressors (Chust et al., 2014; Comeau et al., 2014b; Guénette et al., 2014; Silverman et al., 2014; Hendriks et al., 2015), although there is still a paucity of ecosystem level studies that address the impacts of multiple drivers (see section Effects of Multiple Drivers).
(5) The degrees to which species can track changes in climate as well as the influence of multiple stressors on their capacities to respond remained uncertain.
Empirical and theoretical evidence continues to support the role of climate velocity in influencing species range shifts (Pinsky et al., 2013; Hiddink et al., 2014). Shifts in nutrient availability are a key driver for phytoplankton growth, possibly negating the positive growth effects of warming. Increasing numbers of studies examine the impact of multiple stressors on single species (see section Plants and Animals).
(6) The capacity for phenotypic and evolutionary adaptation over generations to respond to long-term climate change.
Increasing numbers of studies have begun to address this question. Trans-generational phenotypic plasticity is observed in response to warming and acidification (see sections Ocean Acidification and Impacts of Ocean Warming), suggesting the potential for genetic adaptation. Two recent studies find evidence of coccolithophores demonstrating evolutionary adaptation under ocean warming and acidification (Lohbeck et al., 2014; Schluter et al., 2014). Despite recent work, there is still a distinct paucity of studies addressing the long-term evolutionary response to climate change stressors, particularly in animals.
Conclusions
Anthropogenic emissions have caused measurable physical changes in the oceans. The oceans absorb 93% of the excess energy produced by global warming and approximately 28% anthropogenic CO2, buffering the effects of climate change (Rhein et al., 2013). This buffering is not without cost and changes in ocean temperature, pH, and oxygen content have been observed over the second half of the 20th century (Rhein et al., 2013). Increasing atmospheric CO2 will always lead to an increase in ocean carbon storage, all other things being held constant (Ciais et al., 2013), thus 21st century emissions will determine the condition of the world's oceans for centuries to come (Ciais et al., 2013). Under both RCP4.5 and 8.5, physical changes are projected to continue but with greater severity under RCP8.5 (Bopp et al., 2013; Ciais et al., 2013).
Impacts of warming on biological processes can already be observed (Poloczanska et al., 2014; Pörtner et al., 2014) as organisms shift their distributions polewards (Poloczanska et al., 2014), alter phenology (Pörtner et al., 2014) and instances of coral bleaching increase in frequency (Wong et al., 2014). Experimental evidence has shown many organisms to be sensitive to projected future levels of ocean acidification, with calcifiers showing the strongest responses. However, observations of the effects of ocean acidification on natural populations are scarce, except in areas with naturally high concentrations of dissolved CO2 (Bednaršek et al., 2014). Changes in dissolved oxygen concentrations are highly variable among regions, but it is predicted that expanding OMZs will favor bacteria and hypoxic specialists whilst reducing habitat for organisms with higher oxygen demands (Pörtner et al., 2014).
The overarching findings of both the AR5, and much of the work published since, is that the effects of anthropogenically produced climate change on organisms are highly species specific. Impacts also varying regionally in response to local drivers and synchronously with other climate change drivers in unpredictable ways. As a result, there is limited ability to project the future for marine ecosystems.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This is a contribution from “The Oceans 2015 Initiative,” an expert group supported by the Prince Albert II of Monaco Foundation, the Ocean Acidification International Coordination Centre through the International Atomic Energy Agency and the BNP Paribas Foundation. FJ acknowledges support by the Swiss National Science Foundation. CME acknowledges support from the National Oceanic and Atmospheric Administration and the National Aeronautics and Space Administration. The contents in this manuscript are solely the opinions of the authors and do not constitute a statement of policy, decision or position on behalf of NOAA or the U.S. Government. Thanks are due to the two reviewers whose comments greatly improved the manuscript.
References
Ahrendt, S., Mobberley, J., Visscher, P., Koss, L., and Foster, J. (2014). Effects of elevated carbon dioxide and salinity on the microbial diversity in lithifying microbial mats. Minerals 4, 145–169. doi: 10.3390/min4010145
Albouy, C., Velez, L., Coll, M., Colloca, F., Le Loc'h, F., Mouillot, D., et al. (2014). From projected species distribution to food-web structure under climate change. Glob. Chang. Biol. 20, 730–741. doi: 10.1111/gcb.12467
Alemu, I. J., and Clement, Y. (2014). Mass coral bleaching in 2010 in the southern Caribbean. PLoS ONE 9:e83829. doi: 10.1371/journal.pone.0083829
Alvarez-Filip, L., Carricart-Ganivet, J. P., Horta-Puga, G., and Iglesias-Prieto, R. (2013). Shifts in coral-assemblage composition do not ensure persistence of reef functionality. Sci. Rep. 3:3486. doi: 10.1038/srep03486
AMAP. (2014). “Acrtic ocean acidification 2013: an overview,” in Arctic Monitoring and Assessment Program (AMAP) (Oslo).
Aronson, R. B., and Precht, W. F. (2001). “White-band disease and the changing face of Caribbean coral reefs,” in The Ecology and Etiology of Newly Emerging Marine Diseases, ed J. W. Porter (Springer), 25–38. doi: 10.1007/978-94-017-3284-0_2
Arula, T., Ojaveer, H., and Klais, R. (2014). Impact of extreme climate and bioinvasion on temporal coupling of spring herring (Clupea harengus m.) larvae and their prey. Mar. Environ. Res. 102, 102–109. doi: 10.1016/j.marenvres.2014.05.001
Azetsu-Scott, K., Starr, M., Mei, Z. P., and Granskog, M. (2014). Low calcium carbonate saturation state in an Arctic inland sea having large and varying fluvial inputs: the Hudson Bay system. J. Geophys. Res. Oceans. 119, 6210–6220. doi: 10.1002/2014jc009948
Baker-Austin, C., Trinanes, J. A., Taylor, N. G., Hartnell, R., Siitonen, A., and Martinez-Urtaza, J. (2013). Emerging Vibrio risk at high latitudes in response to ocean warming. Nat. Clim. change 3, 73–77. doi: 10.1038/nclimate1628
Balmaseda, M. A., Trenberth, K. E., and Källén, E. (2013). Distinctive climate signals in reanalysis of global ocean heat content. Geophys. Res. Lett. 40, 1754–1759. doi: 10.1002/grl.50382
Beaugrand, G., Goberville, E., Luczak, C., and Kirby, R. R. (2014). Marine biological shifts and climate. Proc. Biol. Sci. 281, 20133350. doi: 10.1098/rspb.2013.3350
Bednaršek, N., Feely, R. A., Reum, J. C. P., Peterson, B., Menkel, J., Alin, S. R., et al. (2014). Limacina helicina shell dissolution as an indicator of declining habitat suitability owing to ocean acidification in the California Current Ecosystem. Proc. R. Soc. B Biol. Sci. 281:20140123. doi: 10.1098/rspb.2014.0123
Behrenfeld, M. J. (2014). Climate-mediated dance of the plankton. Nat. Clim. Change 4, 880–887. doi: 10.1038/nclimate2349
Benner, I., Diner, R. E., Lefebvre, S. C., Li, D., Komada, T., Carpenter, E. J., et al. (2013). Emiliania huxleyi increases calcification but not expression of calcification-related genes in long-term exposure to elevated temperature and pCO2. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 368, 20130049. doi: 10.1098/rstb.2013.0049
Betancor, S., Tuya, F., Gil-Díaz, T., Figueroa, F. L., and Haroun, R. (2014). Effects of a submarine eruption on the performance of two brown seaweeds. J. Sea Res. 87, 68–78. doi: 10.1016/j.seares.2013.09.008
Bintanja, R., Van Oldenborgh, G. J., Drijfhout, S. S., Wouters, B., and Katsman, C. A. (2013). Important role for ocean warming and increased ice-shelf melt in Antarctic sea-ice expansion. Nat. Geosci. 6, 376–379. doi: 10.1038/ngeo1767
Bockelmann, A.-C., Tams, V., Ploog, J., Schubert, P. R., and Reusch, T. B. (2013). Quantitative PCR reveals strong spatial and temporal variation of the wasting disease pathogen, Labyrinthula zosterae in northern European eelgrass (Zostera marina) beds. PLoS ONE 8:e62169. doi: 10.1371/journal.pone.0062169
Bögner, D., Bickmeyer, U., and Köhler, A. (2014). CO2-induced fertilization impairment in Strongylocentrotus droebachiensis collected in the Arctic. Helgol. Mar. Res. 68, 341–356. doi: 10.1007/s10152-014-0394-3
Bopp, L., Resplandy, L., Orr, J. C., Doney, S. C., Dunne, J. P., Gehlen, M., et al. (2013). Multiple stressors of ocean ecosystems in the 21st century: projections with CMIP5 models. Biogeosciences 10, 6225–6245. doi: 10.5194/bg-10-6225-2013
Böttjer, D., Karl, D. M., Letelier, R. M., Viviani, D. A., and Church, M. J. (2014). Experimental assessment of diazotroph responses to elevated seawater pCO2 in the North Pacific Subtropical Gyre. Glob. Biogeochem. Cycles 28, 601–616. doi: 10.1002/2013GB004690
Bowden, T. J. (2008). Modulation of the immune system of fish by their environment. Fish Shellfish Immunol. 25, 373–383. doi: 10.1016/j.fsi.2008.03.017
Brand, U., Came, R. E., Affek, H., Azmy, K., Mooi, R., and Layton, K. (2014). Climate-forced change in Hudson Bay seawater composition and temperature, Arctic Canada. Chem. Geol. 388, 78–86. doi: 10.1016/j.chemgeo.2014.08.028
Bressan, M., Chinellato, A., Munari, M., Matozzo, V., Manci, A., Marèeta, T., et al. (2014). Does seawater acidification affect survival, growth and shell integrity in bivalve juveniles? Mar. Environ. Res. 99, 136–148. doi: 10.1016/j.marenvres.2014.04.009
Brinkman, T. J., and Smith, A. M. (2015). Effect of climate change on crustose coralline algae at a temperate vent site, White Island, New Zealand. Mar. Freshw. Res. 66, 360–370. doi: 10.1071/MF14077
Brodie, J., Williamson, C. J., Smale, D. A., Kamenos, N. A., Mieszkowska, N., Santos, R., et al. (2014). The future of the northeast Atlantic benthic flora in a high CO2 world. Ecol. Evol. 4, 2787–2798. doi: 10.1002/ece3.1105
Brown, A., and Thatje, S. (2014). The effects of changing climate on faunal depth distributions determine winners and losers. Glob. Change Biol. 21, 173–180. doi: 10.1111/gcb.12680
Burdett, H. L., Carruthers, M., Donohue, P. J. C., Wicks, L. C., Hennige, S. J., Roberts, J. M., et al. (2014). Effects of high temperature and CO2 on intracellular DMSP in the cold-water coral Lophelia pertusa. Mar. Biol. 161, 1499–1506. doi: 10.1007/s00227-014-2435-5
Burge, C. A., Mark Eakin, C., Friedman, C. S., Froelich, B., Hershberger, P. K., Hofmann, E. E., et al. (2014). Climate change influences on marine infectious diseases: implications for management and society. Ann. Rev. Mar. Sci. 6, 249–277. doi: 10.1146/annurev-marine-010213-135029
Calbet, A., Sazhin, A. F., Nejstgaard, J. C., Berger, S. A., Tait, Z. S., Olmos, L., et al. (2014). Future climate scenarios for a coastal productive planktonic food web resulting in microplankton phenology changes and decreased trophic transfer efficiency. PLoS ONE 9:e94388. doi: 10.1371/journal.pone.0094388
Calosi, P., Rastrick, S. P. S., Lombardi, C., De Guzman, H. J., Davidson, L., Jahnke, M., et al. (2013). Adaptation and acclimatization to ocean acidification in marine ectotherms: an in situ transplant experiment with polychaetes at a shallow CO2 vent system. Proc. R. Soc. B 368:20140444. doi: 10.1098/rstb.2012.0444
Cantin, N. E., and Lough, J. M. (2014). Surviving coral bleaching events: porites growth anomalies on the great barrier reef. PLoS ONE 9:e88720. doi: 10.1371/journal.pone.0088720
Cao, L., Zhang, H., Zheng, M., and Wang, S. (2014). Response of ocean acidification to a gradual increase and decrease of atmospheric CO2. Environ. Res. Lett. 9, 024012. doi: 10.1088/1748-9326/9/2/024012
Caprio, J., Shimohara, M., Marui, T., Harada, S., and Kiyohara, S. (2014). Marine teleost locates live prey through pH sensing. Science 344, 1154–1156. doi: 10.1126/science.1252697
Cazenave, A., and Cozannet, G. L. (2014). Sea level rise and its coastal impacts. Earth's Future 2, 15–34. doi: 10.1002/2013EF000188
Chambers, L. E., Altwegg, R., Barbraud, C., Barnard, P., Beaumont, L. J., Crawford, R. J., et al. (2013). Phenological changes in the Southern Hemisphere. PLoS ONE 8:e75514. doi: 10.1371/journal.pone.0075514
Chambers, R. C., Candelmo, A. C., Habeck, E. A., Poach, M. E., Wieczorek, D., Cooper, K. R., et al. (2014). Effects of elevated CO2 in the early life stages of summer flounder, Paralichthys dentatus, and potential consequences of ocean acidification. Biogeosciences 11, 1613–1626. doi: 10.5194/bg-11-1613-2014
Chen, X., and Tung, K.-K. (2014). Varying planetary heat sink led to global-warming slowdown and acceleration. Science 345, 897–903. doi: 10.1126/science.1254937
Cheung, S., Chan, C., Po, B., Li, A., Leung, J., Qiu, J., et al. (2014). Effects of hypoxia on biofilms and subsequently larval settlement of benthic invertebrates. Mar. Pollut. Bull. 85, 418–424. doi: 10.1016/j.marpolbul.2014.04.051
Chung, W.-S., Marshall, N. J., Watson, S.-A., Munday, P. L., and Nilsson, G. E. (2014). Ocean acidification slows retinal function in a damselfish through interference with GABAA receptors. J. Exp. Biol. 217, 323–326. doi: 10.1242/jeb.092478
Church, J. A., Clark, P. U., Cazenave, A., Gregory, J. M., Jevrejeva, S., Levermann, A., et al. (2013). “Chapter 13: sea level change,” in Climate Change 2013: The Physical Science Basis, eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex, and P.M. Midgley (Cambridge; New York, NY: Cambridge University Press), 1137–1216.
Chust, G., Allen, J. I., Bopp, L., Schrum, C., Holt, J., Tsiaras, K., et al. (2014). Biomass changes and trophic amplification of plankton in a warmer ocean. Glob. Chang. Biol. 20, 2124–2139. doi: 10.1111/gcb.12562
Ciais, P., Sabine, C., Bala, G., Bopp, L., Brovkin, V., Canadell, J., et al. (2013). “Carbon and Other Biogeochemical Cycles,” in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, et al. (Cambridge; New York, NY: Cambridge University Press), 465–570.
Clements, J. C., and Hunt, H. L. (2014). Influence of sediment acidification and water flow on sediment acceptance and dispersal of juvenile soft-shell clams (Mya arenaria L.). J. Exp. Mar. Biol. Ecol. 453, 62–69. doi: 10.1016/j.jembe.2014.01.002
Cocco, V., Joos, F., Steinacher, M., Frolicher, T. L., Bopp, L., Dunne, J., et al. (2013). Oxygen and indicators of stress for marine life in multi-model global warming projections. Biogeosciences 10, 1849–1868. doi: 10.5194/bg-10-1849-2013
Coleman, D. W., Byrne, M., and Davis, A. R. (2014). Molluscs on acid: gastropod shell repair and strength in acidifying oceans. Mar. Ecol. Prog. Ser. 509, 203–211. doi: 10.3354/meps10887
Collard, M., Dery, A., Dehairs, F., and Dubois, P. (2014). Euechinoidea and Cidaroidea respond differently to ocean acidification. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 174, 45–55. doi: 10.1016/j.cbpa.2014.04.011
Collins, M., Knutti, R., Arblaster, J., Dufresne, J.-L., Fichefet, T., Friedlingstein, P., et al. (2013). “Long-term climate change: projections, commitments and irreversibility,” in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, et al. (Cambridge; New York, NY: Cambridge University Press), 1029–1136.
Comeau, S., Carpenter, R. C., and Edmunds, P. J. (2014a). Effects of irradiance on the response of the coral Acropora pulchra and the calcifying alga Hydrolithon reinboldii to temperature elevation and ocean acidification. J. Exp. Mar. Biol. Ecol. 453, 28–35. doi: 10.1016/j.jembe.2013.12.013
Comeau, S., Carpenter, R. C., Lantz, C. A., and Edmunds, P. J. (2014b). Ocean acidification accelerates dissolution of experimental coral reef communities. Biogeosci. Discuss. 11, 12323–12339. doi: 10.5194/bgd-11-12323-2014
Comeau, S., Carpenter, R. C., Nojiri, Y., Putnam, H. M., Sakai, K., and Edmunds, P. J. (2014c). Pacific-wide contrast highlights resistance of reef calcifiers to ocean acidification. Proc. R. Soc. B Biol. Sci. 281:20141339.
Comeau, S., Edmunds, P., Spindel, N., and Carpenter, R. (2014d). Fast coral reef calcifiers are more sensitive to ocean acidification in short-term laboratory incubations. Limnol. Oceanogr 59, 1081–1091. doi: 10.4319/lo.2014.59.3.1081
Constable, A. J., Melbourne-Thomas, J., Corney, S. P., Arrigo, K. R., Barbraud, C., Barnes, D. K., et al. (2014). Climate change and Southern Ocean ecosystems I: how changes in physical habitats directly affect marine biota. Glob. Chang. Biol. 20, 3004–3025. doi: 10.1111/gcb.12623
Crozier, L. G., and Hutchings, J. A. (2014). Plastic and evolutionary responses to climate change in fish. Evol. Appl. 7, 68–87. doi: 10.1111/eva.12135
Dégremont, L. (2011). Evidence of herpesvirus (OsHV-1) resistance in juvenile Crassostrea gigas selected for high resistance to the summer mortality phenomenon. Aquaculture 317, 94–98. doi: 10.1016/j.aquaculture.2011.04.029
Dery, A., Guibourt, V., Catarino, A. I., Compère, P., and Dubois, P. (2014). Properties, morphogenesis, and effect of acidification on spines of the cidaroid sea urchin Phyllacanthus imperialis. Invertebr. Biol. 133, 188–199. doi: 10.1111/ivb.12054
De Senerpont Domis, L. N., Van Der Waal, D., Helmsing, N. R., Van Donk, E., and Mooij, W. M. (2014). Community stoichiometry in a changing world: combined effects of warming and eutrophication on phytoplankton dynamics. Ecology 95, 1485–1495. doi: 10.1890/13-1251.1
Di Nitto, D., Neukermans, G., Koedam, N., Defever, H., Pattyn, F., Kairo, J. G., et al. (2014). Mangroves facing climate change: landward migration potential in response to projected scenarios of sea level rise. Biogeosciences 11, 857–871. doi: 10.5194/bg-11-857-2014
Dixson, D. L., Jennings, A. R., Atema, J., and Munday, P. L. (2014). Odor tracking in sharks is reduced under future ocean acidification conditions. Glob. Change Biol. 21, 1454–1462. doi: 10.1111/gcb.12678
Domenici, P., Allan, B. J. M., Watson, S.-A., McCormick, M. I., and Munday, P. L. (2014). Shifting from right to left: the combined effect of elevated CO2 and temperature on behavioural lateralization in a coral reef fish. PLoS ONE 9:e87969. doi: 10.1371/journal.pone.0087969
Doo, S. S., Fujita, K., Byrne, M., and Uthicke, S. (2014). Fate of calcifying tropical symbiont-bearing large benthic foraminifera: living sands in a changing ocean. Biol. Bull. 226, 169–186.
Dove, S. G., Kline, D. I., Pantos, O., Angly, F. E., Tyson, G. W., and Hoegh-Guldberg, O. (2013). Future reef decalcification under a business-as-usual CO2 emission scenario. Proc. Natl. Acad. Sci. U.S.A. 110, 15342–15347. doi: 10.1073/pnas.1302701110
Dupont, S., Dorey, N., Stumpp, M., Melzner, F. and Thorndyke, M. (2013). Long-term and trans-life-cycle effects of exposure to ocean acidification in the green sea urchin Strongylocentrotus droebachiensis. Mar. Biol. 160, 1835–1843. doi: 10.1007/s00227-012-1921-x
Durack, P. J., Gleckler, P. J., Landerer, F. W., and Taylor, K. E. (2014). Quantifying underestimates of long-term upper-ocean warming. Nat. Clim. Change. doi: 10.1038/nclimate2389
Eakin, C. M., Morgan, J. A., Heron, S. F., Smith, T. B., Liu, G., Alvarez-Filip, L., et al. (2010a). Caribbean corals in crisis: record thermal stress, bleaching, and mortality in 2005. PLoS ONE 5:e13969. doi: 10.1371/journal.pone.0013969
Eakin, C. M., Nim, C. J., Brainard, R. E., Aubrecht, C., Elvidge, C., Gledhill, D. K., et al. (2010b). Monitoring coral reefs from space. Oceanography 23, 118–133. doi: 10.5670/oceanog.2010.10
Eichner, M., Rost, B., and Kranz, S. A. (2014). Diversity of ocean acidification effects on marine N2 fixers. J. Exp. Mar. Biol. Ecol. 457, 199–207. doi: 10.1016/j.jembe.2014.04.015
Elettra, L., Storch, D., Poertner, H.-O., and Mark, F. C. (2014). Effects of ocean acidification and warming on the mitochondrial physiology of Atlantic cod. Biochim. Biophys. Acta 1837(Suppl.), e26. doi: 10.1016/j.bbabio.2014.05.294
Elston, R. A., Hasegawa, H., Humphrey, K. L., Polyak, I. K., and Hase, C. C. (2008). Re-emergence of Vibrio tubiashii in bivalve shellfish aquaculture: severity, environmental drivers, geographic extent and management. Dis. Aquat. Org. 82, 119–134. doi: 10.3354/dao01982
Elvidge, C. D., Dietz, J. B., Berkelmans, R., Andrefouet, S., Skirving, W., Strong, A. E., et al. (2004). Satellite observation of Keppel Islands (Great Barrier Reef) 2002 coral bleaching using IKONOS data. Coral Reefs 23, 123–132. doi: 10.1007/s00338-003-0364-8
Endres, S., Galgani, L., Riebesell, U., Schulz, K.-G., and Engel, A. (2014). Stimulated bacterial growth under elevated pCO2: results from an off-Shore mesocosm study. PLoS ONE 9:e99228. doi: 10.1371/journal.pone.0099228
Engelhard, G. H., Righton, D. A., and Pinnegar, J. K. (2014). Climate change and fishing: a century of shifting distribution in North Sea cod. Glob. Change Biol. 20, 2473–2483. doi: 10.1111/gcb.12513
Enochs, I. C., Manzello, D. P., Carlton, R., Schopmeyer, S., Van Hooidonk, R., and Lirman, D. (2014). Effects of light and elevated pCO2 on the growth and photochemical efficiency of Acropora cervicornis. Coral Reefs 33, 477–485. doi: 10.1007/s00338-014-1132-7
Errera, R. M., Yvon-Lewis, S., Kessler, J. D., and Campbell, L. (2014). Reponses of the dinoflagellate Karenia brevis to climate change: pCO2 and sea surface temperatures. Harmful Algae 37, 110–116. doi: 10.1016/j.hal.2014.05.012
Fabricius, K. E., Langdon, C., Uthicke, S., Humphrey, C., Noonan, S., De'ath, G., et al. (2011). Losers and winners in coral reefs acclimatized to elevated carbon dioxide concentrations. Nat. Clim. Change 1, 165–169. doi: 10.1038/nclimate1122
Falter, J. L., Zhang, Z., Lowe, R. J., McGregor, F., Keesing, J., and McCulloch, M. (2014). Assessing the drivers of spatial variation in thermal forcing across a nearshore reef system and implications for coral bleaching. Limnol. Oceanogr. 59, 1241–1255. doi: 10.4319/lo.2014.59.4.1241
Field, C. B., Barros, V. R., Mach, K. J., Mastrandrea, M. D., Aalst, M. V., Adger, W. N., et al. (2014). “Technical summary,” in Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds C. B. Field, V. R. Barros, D. J. Dokken, K. J. Mach, M. D. Mastrandrea, T. E. Bilir, et al. (Cambridge; New York, NY: Cambridge University Press), 35–94.
Figueiredo, J., Baird, A. H., Harii, S., and Connolly, S. R. (2014). Increased local retention of reef coral larvae as a result of ocean warming. Nat. Clim. Change 4, 498–502. doi: 10.1038/nclimate2210
Fitzer, S. C., Cusack, M., Phoenix, V. R., and Kamenos, N. A. (2014). Ocean acidification reduces the crystallographic control in juvenile mussel shells. J. Struct. Biol. 188, 39–45. doi: 10.1016/j.jsb.2014.08.007
Fransson, A., Chierici, M., Miller, L. A., Carnat, G., Shadwick, E., Thomas, H., et al. (2013). Impact of sea-ice processes on the carbonate system and ocean acidification at the ice-water interface of the Amundsen Gulf, Arctic Ocean. J. Geophys. Res. Oceans 118, 7001–7023. doi: 10.1002/2013JC009164
Frieder, C. A. (2014). Present-day nearshore pH differentially depresses fertilization in congeneric sea urchins. Biol. Bull. 226, 1–7.
Frommel, A. Y., Maneja, R., Lowe, D., Pascoe, C. K., Geffen, A. J., Folkvord, A., et al. (2014). Organ damage in Atlantic herring larvae as a result of ocean acidification. Ecol. Appl. 24, 1131–1143. doi: 10.1890/13-0297.1
Gaitán-Espitia, J. D., Hancock, J. R., Padilla-Gamiño, J. L., Rivest, E. B., Blanchette, C. A., Reed, D. C., et al. (2014). Interactive effects of elevated temperature and pCO2 on early-life-history stages of the giant kelp Macrocystis pyrifera. J. Exp. Mar. Biol. Ecol. 457, 51–58. doi: 10.1016/j.jembe.2014.03.018
Garrard, S. L., Gambi, M. C., Scipione, M. B., Patti, F. P., Lorenti, M., Zupo, V., et al. (2014). Indirect effects may buffer negative responses of seagrass invertebrate communities to ocean acidification. J. Exp. Mar. Biol. Ecol. 461, 31–38. doi: 10.1016/j.jembe.2014.07.011
Gazeau, F., Van Rijswijk, P., Pozzato, L., and Middelburg, J. J. (2014). Impacts of ocean acidification on sediment processes in shallow waters of the Arctic Ocean. PLoS ONE 9:e94068. doi: 10.1371/journal.pone.0094068
Gehlen, M., Séférian, R., Jones, D. O. B., Roy, T., Roth, R., Barry, J., et al. (2014). Projected pH reductions by 2100 might put deep North Atlantic biodiversity at risk. Biogeosci. Discuss. 11, 8607–8634. doi: 10.5194/bgd-11-8607-2014
Gibbin, E. M., Putnam, H. M., Davy, S. K., and Gates, R. D. (2014). Intracellular pH and its response to CO2-driven seawater acidification in symbiotic versus non-symbiotic coral cells. J. Exp. Biol. 217, 1963–1969. doi: 10.1242/jeb.099549
Gibert, J. P., and Delong, J. P. (2014). Temperature alters food web body-size structure. Biol. Lett. 10:20140473. doi: 10.1098/rsbl.2014.0473
Gladfelter, W. B. (1982). White-Band Disease in Acropora palmata: implications for the structure and growth of shallow reefs. Bull. Mar. Sci. 32, 639–643.
Glibert, P. M., Icarus Allen, J., Artioli, Y., Beusen, A., Bouwman, L., Harle, J., et al. (2014). Vulnerability of coastal ecosystems to changes in harmful algal bloom distribution in response to climate change: projections based on model analysis. Glob. Chang Biol. 20, 3845–3858. doi: 10.1111/gcb.12662
Goberville, E., Beaugrand, G., and Edwards, M. (2014). Synchronous response of marine plankton ecosystems to climate in the Northeast Atlantic and the North Sea. J. Mar. Syst. 129, 189–202. doi: 10.1016/j.jmarsys.2013.05.008
Gobler, C. J., Depasquale, E. L., Griffith, A. W., and Baumann, H. (2014). Hypoxia and acidification have additive and synergistic negative effects on the growth, survival, and metamorphosis of early life stage bivalves. PLoS ONE 9:e83648. doi: 10.1371/journal.pone.0083648
Gradoville, M. R., White, A. E., Böttjer, D., Church, M. J., and Letelier, R. M. (2014). Diversity trumps acidification: lack of evidence for carbon dioxide enhancement of Trichodesmium community nitrogen or carbon fixation at Station ALOHA. Limnol. Oceanogr 59, 645–659. doi: 10.4319/lo.2014.59.3.0645
Grottoli, A. G., Warner, M. E., Levas, S. J., Aschaffenburg, M. D., Schoepf, V., McGinley, M., et al. (2014). The cumulative impact of annual coral bleaching can turn some coral species winners into losers. Glob. Change Biol. 20, 3823–3833. doi: 10.1111/gcb.12658
Guénette, S., Araújo, J. N., and Bundy, A. (2014). Exploring the potential effects of climate change on the Western Scotian Shelf ecosystem, Canada. J. Mar. Syst. 134, 89–100. doi: 10.1016/j.jmarsys.2014.03.001
Hamylton, S. M., Leon, J. X., Saunders, M. I., and Woodroffe, C. D. (2014). Simulating reef response to sea-level rise at Lizard Island: a geospatial approach. Geomorphology 222, 151–161. doi: 10.1016/j.geomorph.2014.03.006
Harms, L., Frickenhaus, S., Schiffer, M., Mark, F., Storch, D., Held, C., et al. (2014). Gene expression profiling in gills of the great spider crab Hyas araneus in response to ocean acidification and warming. BMC Genomics 15:789. doi: 10.1186/1471-2164-15-789
Harvell, D., Altizer, S., Cattadori, I. M., Harrington, L., and Weil, E. (2009). Climate change and wildlife diseases: when does the host matter the most? Ecology 90, 912–920. doi: 10.1890/08-0616.1
Hendriks, I. E., Duarte, C. M., Olsen, Y. S., Steckbauer, A., Ramajo, L., Moore, T. S., et al. (2015). Biological mechanisms supporting adaptation to ocean acidification in coastal ecosystems. Estuar. Coast. Shelf Sci. 152, A1–A8. doi: 10.1016/j.ecss.2014.07.019
Hendriks, I. E., Olsen, Y. S., Ramajo, L., Basso, L., Steckbauer, A., Moore, T. S., et al. (2014). Photosynthetic activity buffers ocean acidification in seagrass meadows. Biogeosciences 11, 333–346. doi: 10.5194/bg-11-333-2014
Hettinger, A., Sanford, E., Hill, T. M., Lenz, E. A., Russell, A. D., and Gaylord, B. (2013). Larval carry-over effects from ocean acidification persist in the natural environment. Glob. Change Biol. 19, 3317–3326. doi: 10.1111/gcb.12307
Hiddink, J. G., Burrows, M. T., and García Molinos, J. (2014). Temperature tracking by North Sea benthic invertebrates in response to climate change. Glob. Change Biol. 21, 117–129. doi: 10.1111/gcb.12726
Hoegh-Guldberg, O., Cai, R., Poloczanska, E. S., Brewer, P. G., Sundby, S., Hilmi, K., et al. (2014). “The Ocean,” in Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel of Climate Change, eds V. R. Barros, C. B. Field, D. J. Dokken, M. D. Mastrandrea, K. J. Mach, T. E. Bilir, et al. (Cambridge; New York, NY: Cambridge University Press), 1655–1731.
Holcomb, M., Venn, A. A., Tambutte, E., Tambutte, S., Allemand, D., Trotter, J., et al. (2014). Coral calcifying fluid pH dictates response to ocean acidification. Sci. Rep. 4:5207. doi: 10.1038/srep05207
Hoppe, C. J., Hassler, C. S., Payne, C. D., Tortell, P. D., Rost, B., and Trimborn, S. (2013). Iron limitation modulates ocean acidification effects on Southern Ocean phytoplankton communities. PLoS ONE 8:e79890. doi: 10.1371/journal.pone.0079890
Horigome, M. T., Ziveri, P., Grelaud, M., Baumann, K. H., Marino, G., and Mortyn, P. G. (2014). Environmental controls on the Emiliania huxleyi calcite mass. Biogeosciences 11, 2295–2308. doi: 10.5194/bg-11-2295-2014
Huber, M., and Knutti, R. (2014). Natural variability, radiative forcing and climate response in the recent hiatus reconciled. Nat. Geosci. 7, 651–656. doi: 10.1038/ngeo2228
Hyun, B., Jang, P. G., Lee, W. J., and Shin, K. (2014). Effects of increased CO2 and temperature on the growth of four diatom species (Chaetoceros debilis, Chaetoceros didymus, Skeletonema costatum and Thalassiosira nordenskioeldii) in laboratory experiments.  23, 1003–1012.
23, 1003–1012.
Jacox, M. G., Moore, A. M., Edwards, C. A., and Fiechter, J. (2014). Spatially resolved upwelling in the California Current System and its connections to climate variability. Geophys. Res. Lett. 41, 3189–3196. doi: 10.1002/2014GL059589
James, R., Hepburn, C., Cornwall, C., McGraw, C., and Hurd, C. (2014). Growth response of an early successional assemblage of coralline algae and benthic diatoms to ocean acidification. Mar. Biol. 161, 1687–1696. doi: 10.1007/s00227-014-2453-3
Johnson, M. D., Moriarty, V. W., and Carpenter, R. C. (2014a). Acclimatization of the crustose coralline alga Porolithon onkodes to Variable pCO2. PLoS ONE 9:e87678. doi: 10.1371/journal.pone.0087678
Johnson, M. D., Price, N. N., and Smith, J. E. (2014b). Contrasting effects of ocean acidification on tropical fleshy and calcareous algae. PeerJ 2, e411. doi: 10.7717/peerj.411
Jones, M. C., and Cheung, W. W. L. (2014). Multi-model ensemble projections of climate change effects on global marine biodiversity. ICES J. Mar. Sci. fsu172. doi: 10.1093/icesjms/fsu172
Jutfelt, F., and Hedgärde, M. (2013). Atlantic cod actively avoid CO2 and predator odour, even after long-term CO2 exposure. Front. Zool. 10:81. doi: 10.1186/1742-9994-10-81
Kamya, P. Z., Dworjanyn, S. A., Hardy, N., Mos, B., Uthicke, S., and Byrne, M. (2014). Larvae of the coral eating crown-of-thorns starfish, Acanthaster planci in a warmer-high CO2 ocean. Glob. Change Biol. 20, 3365–3376. doi: 10.1111/gcb.12530
Keller, K. M., Joos, F., and Raible, C. C. (2014). Time of emergence of trends in ocean biogeochemistry. Biogeosciences 11, 3647–3659. doi: 10.5194/bg-11-3647-2014
Kelly, M. W., Padilla-Gamiño, J. L., and Hofmann, G. E. (2013). Natural variation and the capacity to adapt to ocean acidification in the keystone sea urchin Strongylocentrotus purpuratus. Glob. Change Biol. 19, 2536–2546. doi: 10.1111/gcb.12251
Khanna, N., Godbold, J. A., Austin, W. E. N., and Paterson, D. M. (2013). The impact of ocean acidification on the functional morphology of foraminifera. PLoS ONE 8:e83118. doi: 10.1371/journal.pone.0083118
Kim, S., Chung, M., and Park, H.-S. (2014). Tropical fish species thriving in temperate Korean waters. Mar. Biodivers. 1–2. doi: 10.1007/s12526-014-0247-y
Knowlton, N., and Jackson, J. B. (2008). Shifting baselines, local impacts, and global change on coral reefs. PLoS Biol. 6:e54. doi: 10.1371/journal.pbio.0060054
Ko, G. W. K., Dineshram, R., Campanati, C., Chan, V. B. S., Havenhand, J., and Thiyagarajan, V. (2014). Interactive effects of ocean acidification, elevated temperature, and reduced salinity on early-life stages of the Pacific oyster. Environ. Sci. Technol. 48, 10079–10088. doi: 10.1021/es501611u
Komatsu, T., Fukuda, M., Mikami, A., Mizuno, S., Kantachumpoo, A., Tanoue, H., et al. (2014). Possible change in distribution of seaweed, Sargassum horneri, in northeast Asia under A2 scenario of global warming and consequent effect on some fish. Mar. Pollut. Bull. 85, 317–324. doi: 10.1016/j.marpolbul.2014.04.032
Kopp, R. E., Horton, R. M., Little, C. M., Mitrovica, J. X., Oppenheimer, M., Rasmussen, D. J., et al. (2014). Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earth's Future 2, 2014EF000239. doi: 10.1002/2014EF000239
Lambert, E., Pierce, G. J., Hall, K., Brereton, T., Dunn, T. E., Wall, D., et al. (2014). Cetacean range and climate in the eastern North Atlantic: future predictions and implications for conservation. Glob. Change Biol. 20, 1782–1793. doi: 10.1111/gcb.12560
Langer, G., Nehrke, G., Baggini, C., Rodolfo-Metalpa, R., Hall-Spencer, J., and Bijma, J. (2014). Limpets counteract ocean acidification induced shell corrosion by thickening of aragonitic shell layers. Biogeosci. Discuss. 11, 12571–12590. doi: 10.5194/bgd-11-12571-2014
Larsen, J. N., Anisimov, O. A., Constable, A., Hollowed, A. B., Maynard, N., Prestrud, P., et al. (2014). “Polar regions,” in Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel of Climate Change, eds V. R. Barros, C. B. Field, D. J. Dokken, M. D. Mastrandrea, K. J. Mach, T. E. Bilir, et al. (Cambridge; New York, NY: Cambridge University Press), 1567–1612.
Lauvset, S. K., and Gruber, N. (2014). Long-term trends in surface ocean pH in the North Atlantic. Mar. Chem. 162, 71–76. doi: 10.1016/j.marchem.2014.03.009
Le Quéré, C., Moriarty, R., Andrew, R., Peters, G., Ciais, P., Friedlingstein, P., et al. (2014). Global carbon budget 2014. Earth Syst. Sci. Data Discuss. 7, 521–610. doi: 10.5194/essdd-7-521-2014
Lewandowska, A. M., Boyce, D. G., Hofmann, M., Matthiessen, B., Somer, U., and Worm, B. (2014). Effects of sea surface warming on marine plankton. Ecol. Lett. 17, 614–623. doi: 10.1111/ele.12265
Lewis, N. (2013). An objective Bayesian improved approach for applying optimal fingerprint techniques to estimate climate sensitivity. J. Clim. 26, 7414–7429. doi: 10.1175/JCLI-D-12-00473.1
Liu, G., Heron, S. F., Eakin, C. M., Muller-Karger, F. E., Vega-Rodriguez, M., Guild, L. S., et al. (2014). Reef-scale thermal stress monitoring of coral ecosystems: new 5-km global products from NOAA Coral Reef Watch. Remote Sens. 6, 11579–11606. doi: 10.3390/rs61111579
Lluch-Cota, S. E., Hoegh-Guldberg, O., Karl, D., Pörtner, H. O., Sundby, S., and Gatusso, J. P. (2014). “Cross-chapter box on uncertain trends in major upwelling ecosystems,” in Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel of Climate Change, eds C. B. Field, V. R. Barros, D. J. Dokken, K. J. Mach, M. D. Mastrandrea, T. E. Bilir, et al. (Cambridge; New York, NY: Cambridge University Press), 149–151.
Logan, C. A., Dunne, J. P., Eakin, C. M., and Donner, S. D. (2014). Incorporating adaptive responses into future projections of coral bleaching. Glob. Chang. Biol. 20, 125–139. doi: 10.1111/gcb.12390
Lohbeck, K. T., Riebesell, U., and Reusch, T. B. (2014). Gene expression changes in the coccolithophore Emiliania huxleyi after 500 generations of selection to ocean acidification. Proc. R. Soc. B Biol. Sci. 281, 20140003. doi: 10.1098/rspb.2014.0003
Longphuirt, S. N., Eschmann, C., Russell, C., and Stengel, D. B. (2013). Seasonal and species-specific response of five brown macroalgae to high atmospheric CO2. Mar. Ecol. Prog. Ser. 493, 91–102. doi: 10.3354/meps10570
Mackenzie, B. R., Payne, M. R., Boje, J., Høyer, J. L., and Siegstad, H. (2014a). A cascade of warming impacts brings bluefin tuna to Greenland waters. Glob. Change Biol. 20, 2484–2491. doi: 10.1111/gcb.12597
Mackenzie, C. L., Lynch, S. A., Culloty, S. C., and Malham, S. K. (2014b). Future oceanic warming and acidification alter immune response and disease status in a commercial shellfish species, Mytilus edulis L. PLoS ONE 9:e99712. doi: 10.1371/journal.pone.0099712
Mackenzie, C. L., Ormondroyd, G. A., Curling, S. F., Ball, R. J., Whiteley, N. M., and Malham, S. K. (2014c). Ocean warming, more than acidification, reduces shell strength in a commercial shellfish species during food limitation. PLoS ONE 9:e86764. doi: 10.1371/journal.pone.0086764
Madeira, D., Narciso, L., Diniz, M. S., and Vinagre, C. (2014). Synergy of environmental variables alters the thermal window and heat shock response: an experimental test with the crab Pachygrapsus marmoratus. Mar. Environ. Res. 98, 21–28. doi: 10.1016/j.marenvres.2014.03.011
Malvezzi, A. J., Murray, C. S., Feldheim, K. A., Dibattista, J. D., Garant, D., Gobler, C. J., et al. (2015). “Data from: a quantitative genetic approach to assess the evolutionary potential of a coastal marine fish to ocean acidification,” in Dryad Data Repository (Durham, NC).
Maneja, R. H., Dineshram, R., Thiyagarajan, V., Skiftesvik, A. B., Frommel, A. Y., Clemmesen, C., et al. (2014). The proteome of Atlantic herring (Clupea harengus L.) larvae is resistant to elevated pCO2. Mar. Pollut. Bull. 86, 154–160. doi: 10.1016/j.marpolbul.2014.07.030
Maor-Landaw, K., Karako-Lampert, S., Ben-Asher, H. W., Goffredo, S., Falini, G., Dubinsky, Z., et al. (2014). Gene expression profiles during short-term heat stress in the red sea coral Stylophora pistillata. Glob. Change Biol. 20, 3026–3035. doi: 10.1111/gcb.12592
Marañón, E., Cermeno, P., Huete-Ortega, M., Lopez-Sandoval, D. C., Mourino-Carballido, B., and Rodriguez-Ramos, T. (2014). Resource supply overrides temperature as a controlling factor of marine phytoplankton growth. PLoS ONE 9:e99312. doi: 10.1371/journal.pone.0099312
Martínez-Crego, B., Olivé, I., and Santos, R. (2014). CO2 and nutrient-driven changes across multiple levels of organization in Zostera noltii ecosystems. Biogeosci. Discuss. 11, 5239–5274. doi: 10.5194/bgd-11-5239-2014
Mattsdotter Björk, M., Fransson, A., Torstensson, A., and Chierici, M. (2014). Ocean acidification state in western Antarctic surface waters: controls and interannual variability. Biogeosciences 11, 57–73. doi: 10.5194/bg-11-57-2014
Maugendre, L., Gattuso, J.-P., Louis, J., De Kluijver, A., Marro, S., Soetaert, K., et al. (2014). Effect of ocean warming and acidification on a plankton community in the NW Mediterranean Sea. ICES J. Mar. Sci. fsu161. doi: 10.1093/icesjms/fsu161
McBride, M. M., Dalpadado, P., Drinkwater, K. F., Godo, O. R., Hobday, A. J., Hollowed, A. B., et al. (2014). Krill, climate, and contrasting future scenarios for Arctic and Antarctic fisheries. ICES J. Mar. Scie. 71, 1934–1955. doi: 10.1093/icesjms/fsu002
McClanahan, T. R., and Muthiga, N. A. (2014). Community change and evidence for variable warm-water temperature adaptation of corals in Northern Male Atoll, Maldives. Mar. Pollut. Bull. 80, 107–113. doi: 10.1016/j.marpolbul.2014.01.035
McCoy, S. J., and Kamenos, N. A. (2015). Coralline algae (Rhodophyta) in a changing world: integrating ecological, physiological, and geochemical responses to global change. J. Phycol. 51, 6–24. doi: 10.1111/jpy.12262
McMinn, A., Müller, M. N., Martin, A., and Ryan, K. G. (2014). The response of Antarctic sea ice algae to changes in pH and CO2. PLoS ONE 9:e86984. doi: 10.1371/journal.pone.0086984
Milazzo, M., Rodolfo-Metalpa, R., Chan, V. B. S., Fine, M., Alessi, C., Thiyagarajan, V., et al. (2014). Ocean acidification impairs vermetid reef recruitment. Sci. Rep. 4:4189. doi: 10.1038/srep04189
Montero-Serra, I., Edwards, M., and Genner, M. J. (2014). Warming shelf seas drive the subtropicalization of European pelagic fish communities. Glob. Change Biol. 21, 144–153. doi: 10.1111/gcb.12747
Movilla, J., Orejas, C., Calvo, E., Gori, A., López-Sanz, À., Griny,ó, J., et al. (2014). Differential response of two Mediterranean cold-water coral species to ocean acidification. Coral Reefs 33, 675–686. doi: 10.1007/s00338-014-1159-9
Mukherjee, J., Wong, K. K., Chandramouli, K. H., Qian, P.-Y., Leung, P. T., Wu, R. S., et al. (2013). Proteomic response of marine invertebrate larvae to ocean acidification and hypoxia during metamorphosis and calcification. J. Exp. Biol. 216, 4580–4589. doi: 10.1242/jeb.094516
Muller, E. B., and Nisbet, R. M. (2014). Dynamic energy budget modeling reveals the potential of future growth and calcification for the coccolithophore Emiliania huxleyi in an acidified ocean. Glob. Change Biol. 20, 2031–2038. doi: 10.1111/gcb.12547
Munday, P. L., Cheal, A. J., Dixson, D. L., Rummer, J. L., and Fabricius, K. E. (2014). Behavioural impairment in reef fishes caused by ocean acidification at CO2 seeps. Nature Clim. Change 4, 487–492. doi: 10.1038/nclimate2195
Murray, C. S., Malvezzi, A., Gobler, C. J., and Baumann, H. (2014a). Offspring sensitivity to ocean acidification changes seasonally in a coastal marine fish. Mar. Ecol. Prog. Ser. 504, 1–11. doi: 10.3354/meps10791
Murray, N. J., Clemens, R. S., Phinn, S. R., Possingham, H. P., and Fuller, R. A. (2014b). Tracking the rapid loss of tidal wetlands in the Yellow Sea. Fron. Ecol. Environ. 12, 267–272. doi: 10.1890/130260
Ordoñez, A., Doropoulos, C., and Diaz-Pulido, G. (2014). Effects of ocean acidification on population dynamics and community structure of crustose coralline algae. Biol. Bull. 226, 255–268.
Padilla-Gamino, J. L., Kelly, M. W., Evans, T. G., and Hofmann, G. E. (2013). Temperature and CO2 additively regulate physiology, morphology and genomic responses of larval sea urchins, Strongylocentrotus purpuratus. Proc. R.l Soc. B Biol. Sci. 280:20130155. doi: 10.1098/rspb.2013.0155
Palumbi, S. R., Barshis, D. J., Traylor-Knowles, N., and Bay, R. A. (2014). Mechanisms of reef coral resistance to future climate change. Science 344, 895–898. doi: 10.1126/science.1251336
Park, K.-T., Lee, K., Shin, K., Yang, E. J., Hyun, B., Kim, J.-M., et al. (2014). Direct linkage between dimethyl sulfide production and microzooplankton grazing, resulting from prey composition change under high partial pressure of carbon dioxide conditions. Environ. Sci. Technol. 48, 4750–4756. doi: 10.1021/es403351h
Patara, L., and Böning, C. W. (2014). Abyssal ocean warming around Antarctica strengthens the Atlantic overturning circulation. Geophys. Res. Lett. 41, 3972–3978. doi: 10.1002/2014GL059923
Pedersen, S. A., Våge, V. T., Olsen, A. J., Hammer, K. M., and Altin, D. (2014). Effects of elevated carbon dioxide (CO2) concentrations on early developmental stages of the marine copepod Calanus finmarchicus Gunnerus (Copepoda: Calanoidae). J. Toxicol. Environ. Health A 77, 535–549. doi: 10.1080/15287394.2014.887421
Pespeni, M. H., Chan, F., Menge, B. A., and Palumbi, S. R. (2013). Signs of adaptation to local pH conditions across an environmental mosaic in the California current ecosystem. Integr. Comp. Biol. 53, 857–870. doi: 10.1093/icb/ict094
Pimentel, M., Pegado, M., Repolho, T., and Rosa, R. (2014). Impact of ocean acidification in the metabolism and swimming behavior of the dolphinfish (Coryphaena hippurus) early larvae. Mar. Biol. 161, 725–729. doi: 10.1007/s00227-013-2365-7
Pinsky, M. L., Worm, B., Fogarty, M. J., Sarmiento, J. L., and Levin, S. A. (2013). Marine taxa track local climate velocities. Science 341, 1239–1242. doi: 10.1126/science.1239352
Poloczanska, E. S., Hoegh-Guldberg, O., Cheung, W., Pörtner, H. O., and Burrows, M. (2014). “Cross-chapter box on observed global responses of marine biogeography, abundance, and phenology to climate change,” in Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel of Climate Change, eds C. B. Field, V. R. Barros, D. J. Dokken, K. J. Mach, M. D. Mastrandrea, T. E. Bilir, et al. (Cambridge; New York, NY: Cambridge University Press), 123–127.
Pope, E. C., Ellis, R. P., Scolamacchia, M., Scolding, J. W. S., Keay, A., Chingombe, P., et al. (2014). European sea bass, Dicentrarchus labrax, in a changing ocean. Biogeosciences 11, 2519–2530. doi: 10.5194/bg-11-2519-2014
Popova, E. E., Yool, A., Aksenov, Y., Coward, A. C., and Anderson, T. R. (2014). Regional variability of acidification in the Arctic: a sea of contrasts. Biogeosciences 11, 293–308. doi: 10.5194/bg-11-293-2014
Portner, H. O. (2010). Oxygen- and capacity-limitation of thermal tolerance: a matrix for integrating climate-related stressor effects in marine ecosystems. J. Exp. Biol. 213, 881–893. doi: 10.1242/jeb.037523
Pörtner, H.-O., Karl, D., Boyd, P. W., Cheung, W., Lluch-Cota, S. E., Nojiri, Y., et al. (2014). “Ocean sytems,” in Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel of Climate Change, eds C. B. Field, V. R. Barros, D. J. Dokken, K. J. Mach, M. D. Mastrandrea, T. E. Bilir, et al. (Cambridge; New York, NY: Cambridge University Press), 411–484.
Potts, W. M., Henriques, R., Santos, C. V., Munnik, K., Ansorge, I., Dufois, F., et al. (2014). Ocean warming, a rapid distributional shift, and the hybridization of a coastal fish species. Glob. Change Biol. 20, 2765–2777. doi: 10.1111/gcb.12612
Poulton, A. J., Stinchcombe, M. C., Achterberg, E. P., Bakker, D. C. E., Dumousseaud, C., Lawson, H. E., et al. (2014). Coccolithophores on the north-west European shelf: calcification rates and environmental controls. Biogeosciences 11, 3919–3940. doi: 10.5194/bg-11-3919-2014
Pratte, Z., and Richardson, L. (2014). Impacts of temperature increase and acidification on thickness of the surface mucopolysaccharide layer of the Caribbean coral Diploria spp. Coral Reefs 33, 487–496. doi: 10.1007/s00338-013-1115-0
Queirós, A. M., Fernandes, J. A., Faulwetter, S., Nunes, J., Rastrick, S. P. S., Mieszkowska, N., et al. (2014). Scaling up experimental ocean acidification and warming research: from individuals to the ecosystem. Glob. Change Biol. 21, 130–143. doi: 10.1111/gcb.12675
Randall, C. J., and Van Woesik, R. (2015). Contemporary white-band disease in Caribbean corals driven by climate change. Nat. Clim. Change 5, 375–379. doi: 10.1038/nclimate2530
Rastrick, S. P. S., Calosi, P., Calder-Potts, R., Foggo, A., Nightingale, G., Widdicombe, S., et al. (2014). Living in warmer more acidic oceans retards physiological recovery from tidal emersion in the velvet swimming crab Necora puber (L.). J. Exp. Biol. 217, 2499–2508. doi: 10.1242/jeb.089011
Reisdorph, S. C., and Mathis, J. T. (2014). The dynamic controls on carbonate mineral saturation states and ocean acidification in a glacially dominated estuary. Estuar. Coast. Shelf Sci. 144, 8–18. doi: 10.1016/j.ecss.2014.03.018
Resplandy, L., Bopp, L., Orr, J. C., and Dunne, J. P. (2013). Role of mode and intermediate waters in future ocean acidification: analysis of CMIP5 models. Geophys. Res. Lett. 40, 3091–3095. doi: 10.1002/grl.50414
Reusch, T. B. H. (2014). Climate change in the oceans: evolutionary versus phenotypically plastic responses of marine animals and plants. Evol. Appl. 7, 104–122. doi: 10.1111/eva.12109
Reyes-Nivia, C., Diaz-Pulido, G., and Dove, S. (2014). Relative roles of endolithic algae and carbonate chemistry variability in the skeletal dissolution of crustose coralline algae. Biogeosciences 11, 4615–4626. doi: 10.5194/bg-11-4615-2014
Rhein, M., Rintoul, S. R., Aoki, S., Campos, E., Chambers, D., Feely, R. A., et al. (2013). “Observations: ocean,” in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, et al. (Cambridge; New York, NY: Cambridge University Press), 255–316.
Rice, E., Dam, H. G., and Stewart, G. (2014). Impact of climate change on estuarine zooplankton: surface water warming in Long Island Sound is associated with changes in copepod size and community structure. Estuaries Coasts 38, 13–23. doi: 10.1007/s12237-014-9770-0
Richier, S., Achterberg, E. P., Dumousseaud, C., Poulton, A. J., Suggett, D. J., Tyrrell, T., et al. (2014). Carbon cycling and phytoplankton responses within highly-replicated shipboard carbonate chemistry manipulation experiments conducted around Northwest European Shelf Seas. Biogeosci. Discuss. 11, 3489–3534. doi: 10.5194/bgd-11-3489-2014
Robbins, L. L., Wynn, J. G., Lisle, J. T., Yates, K. K., Knorr, P. O., Byrne, R. H., et al. (2013). Baseline monitoring of the Western Arctic Ocean estimates 20% of Canadian Basin surface waters are undersaturated with respect to aragonite. PLoS ONE 8:e73796. doi: 10.1371/journal.pone.0073796
Roemmich, D., Church, J., Gilson, J., Monselesan, D., Sutton, P., and Wijffels, S. (2015). Unabated planetary warming and its ocean structure since 2006. Nat. Clim. Change 5, 240–245. doi: 10.1038/nclimate2513
Rosa, R., Baptista, M., Lopes, V. M., Pegado, M. R., Ricardo Paula, J., Trübenbach, K., et al. (2014a). Early-life exposure to climate change impairs tropical shark survival. Proc. R. Soc. B Biol. Sci. 281:20141738. doi: 10.1098/rspb.2014.1738
Rosa, R., Trübenbach, K., Pimentel, M. S., Boavida-Portugal, J., Faleiro, F., Baptista, M., et al. (2014b). Differential impacts of ocean acidification and warming on winter and summer progeny of a coastal squid (Loligo vulgaris). J. Exp. Biol. 217, 518–525. doi: 10.1242/jeb.096081
Roy, T., Lombard, F., Bopp, L., and Gehlen, M. (2014). Projected impacts of climate change and ocean acidification on the global biogeography of planktonic foraminifera. Biogeosci. Discuss. 11, 10083–10121. doi: 10.5194/bgd-11-10083-2014
Sadorus, L. L., Mantua, N. J., Essington, T., Hickey, B., and Hare, S. (2014). Distribution patterns of Pacific halibut (Hippoglossus stenolepis) in relation to environmental variables along the continental shelf waters of the US West Coast and southern British Columbia. Fish. Oceanogr. 23, 225–241. doi: 10.1111/fog.12057
Saintilan, N., Wilson, N. C., Rogers, K., Rajkaran, A., and Krauss, K. W. (2014). Mangrove expansion and salt marsh decline at mangrove poleward limits. Glob. Change Biol. 20, 147–157. doi: 10.1111/gcb.12341
Scanes, E., Parker, L. M., O'connor, W. A., and Ross, P. M. (2014). Mixed effects of elevated pCO2 on fertilisation, larval and juvenile development and adult responses in the mobile subtidal scallop Mimachlamys asperrima (Lamarck, 1819). PLoS ONE 9:e93649. doi: 10.1371/journal.pone.0093649
Schluter, L., Lohbeck, K. T., Gutowska, M. A., Groger, J. P., Riebesell, U., and Reusch, T. B. H. (2014). Adaptation of a globally important coccolithophore to ocean warming and acidification. Nat. Clim. 4, 1024–1030. doi: 10.1038/nclimate2379
Schmidt, C., Kucera, M., and Uthicke, S. (2014a). Combined effects of warming and ocean acidification on coral reef Foraminifera Marginopora vertebralis and Heterostegina depressa. Coral Reefs 33, 805–818. doi: 10.1007/s00338-014-1151-4
Schmidt, G. A., Shindell, D. T., and Tsigaridis, K. (2014b). Reconciling warming trends. Nat. Geosci. 7, 158–160. doi: 10.1038/ngeo2105
Schram, J. B., Schoenrock, K. M., McClintock, J. B., Amsler, C. D., and Angus, R. A. (2014). Multiple stressor effects of near-future elevated seawater temperature and decreased pH on righting and escape behaviors of two common Antarctic gastropods. J. Exp. Mar. Biol. Ecol. 457, 90–96. doi: 10.1016/j.jembe.2014.04.005
Sett, S., Bach, L. T., Schulz, K. G., Koch-Klavsen, S., Lebrato, M., and Riebesell, U. (2014). Temperature modulates coccolithophorid sensitivity of growth, photosynthesis and calcification to increasing seawater pCO2. PLoS ONE 9:e88308. doi: 10.1371/journal.pone.0088308
Sewell, M. A., Millar, R. B., Yu, P. C., Kapsenberg, L., and Hofmann, G. E. (2013). Ocean acidification and fertilization in the Antarctic sea urchin Sterechinus neumayeri: the importance of polyspermy. Environ. Sci. Technol. 48, 713–722. doi: 10.1021/es402815s
Shama, L. N., Strobel, A., Mark, F. C., and Wegner, K. M. (2014). Transgenerational plasticity in marine sticklebacks: maternal effects mediate impacts of a warming ocean. Func. Ecol. 28, 1482–1493. doi: 10.1111/1365-2435.12280
Short, J., Kendrick, G. A., Falter, J., and McCulloch, M. T. (2014). Interactions between filamentous turf algae and coralline algae are modified under ocean acidification. J. Exp. Mar. Biol. Ecol. 456, 70–77. doi: 10.1016/j.jembe.2014.03.014
Silbiger, N. J., and Donahue, M. J. (2014). Secondary calcification and dissolution respond differently to future ocean conditions. Biogeosci. Discuss. 11, 12799–12831. doi: 10.5194/bgd-11-12799-2014
Silverman, J., Schneider, K., Kline, D. I., Rivlin, T., Rivlin, A., Hamylton, S., et al. (2014). Community calcification in Lizard Island, Great Barrier Reef: A 33 year perspective. Geochim. Cosmochim. Acta 144, 72–81. doi: 10.1016/j.gca.2014.09.011
Slangen, A. B. A., Carson, M., Katsman, C. A., van de Wal, R. S. W., Köhl, A., Vermeersen, L. L. A., et al. (2014). Projecting twenty-first century regional sea-level changes. Clim. Change 124, 317–332. doi: 10.1007/s10584-014-1080-9
Sperfeld, E., Mangor-Jensen, A., and Dalpadado, P. (2014). Effect of increasing sea water pCO2 on the northern Atlantic krill species Nyctiphanes couchii. Mar. Biol. 161, 2359–2370. doi: 10.1007/s00227-014-2511-x
Steinacher, M., Joos, F., and Stocker, T. F. (2013). Allowable carbon emissions lowered by multiple climate targets. Nature 499, 197–201. doi: 10.1038/nature12269
Steinman, B. A., Mann, M. E., and Miller, S. K. (2015). Atlantic and Pacific multidecadal oscillations and Northern Hemisphere temperatures. Science 347, 988–991. doi: 10.1126/science.1257856
Stewart, J. S., Hazen, E. L., Bograd, S. J., Byrnes, J. E., Foley, D. G., Gilly, W. F., et al. (2014). Combined climate- and prey-mediated range expansion of Humboldt squid (Dosidicus gigas), a large marine predator in the California Current System. Glob. Chang. Biol. 20, 1832–1843. doi: 10.1111/gcb.12502
Stocker, T. F., Qin, D., Plattner, G.-K., Alexander, L. V., Allen, S. K., Bindoff, N. L., et al. (2013). “Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change,” in Climate Change 2013: The Physical Science Basis, eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex, and P. M. Midgley (Cambridge; New York, NY: Cambridge University Press).
Storch, D., Menzel, L., Frickenhaus, S., and Portner, H. O. (2014). Climate sensitivity across marine domains of life: limits to evolutionary adaptation shape species interactions. Glob. Chang. Biol. 20, 3059–3067. doi: 10.1111/gcb.12645
Storlazzi, C. D., Elias, E., Field, M. E., and Presto, M. K. (2011). Numerical modeling of the impact of sea-level rise on fringing coral reef hydrodynamics and sediment transport. Coral Reefs 30, 83–96. doi: 10.1007/s00338-011-0723-9
Straneo, F., and Heimbach, P. (2013). North Atlantic warming and the retreat of Greenland's outlet glaciers. Nature 504, 36–43. doi: 10.1038/nature12854
Sunday, J. M., Calosi, P., Dupont, S., Munday, P. L., Stillman, J. H., and Reusch, T. B. (2014). Evolution in an acidifying ocean. Trends Ecol. Evol. 29, 117–125. doi: 10.1016/j.tree.2013.11.001
Sung, C.-G., Kim, T. W., Park, Y.-G., Kang, S.-G., Inaba, K., Shiba, K., et al. (2014). Species and gamete-specific fertilization success of two sea urchins under near future levels of pCO2. J. Mar. Sys. 137, 67–73. doi: 10.1016/j.jmarsys.2014.04.013
Sydeman, W. J., García-Reyes, M., Schoeman, D. S., Rykaczewski, R. R., Thompson, S. A., Black, B. A., et al. (2014). Climate change and wind intensification in coastal upwelling ecosystems. Science 345, 77–80. doi: 10.1126/science.1251635
Tanaka, Y., Iguchi, A., Nishida, K., Inoue, M., Nakamura, T., Suzuki, A., et al. (2014). Nutrient availability affects the response of juvenile corals and the endosymbionts to ocean acidification. Limnol. Oceanogr. 59, 1468–1476. doi: 10.4319/lo.2014.59.5.1468
Taylor, J. D., Ellis, R., Milazzo, M., Hall-Spencer, J. M., and Cunliffe, M. (2014). Intertidal epilithic bacteria diversity changes along a naturally occurring carbon dioxide and pH gradient. FEMS Microbiol. Ecol. 89, 670–678. doi: 10.1111/1574-6941.12368
Thorner, J., Kumar, L., and Smith, S. D. A. (2014). Impacts of climate-change-driven sea level rise on intertidal rocky reef habitats will be variable and site specific. PLoS ONE 9:e86130. doi: 10.1371/journal.pone.0086130
Travers, M. A., Basuyaux, O., Le Goïc, N., Huchette, S., Nicholas, J. L., Koken, M., et al. (2009). Influence of temperature and spawning effort on Haliotis tuberculata mortalities caused by Vibrio harveyi: an example of emerging vibriosis linked to global warming. Glob. Change Biol. 15, 1365–1376. doi: 10.1111/j.1365-2486.2008.01764.x
Trenberth, K. E., and Fasullo, J. T. (2013). An apparent hiatus in global warming? Earth's Future 1, 19–32. doi: 10.1002/2013EF000165
Trenberth, K. E., Fasullo, J. T., Branstator, G., and Phillips, A. S. (2014). Seasonal aspects of the recent pause in surface warming. Nat. Clim. Change 4, 911–916. doi: 10.1038/nclimate2341
Uthicke, S., Pecorino, D., Albright, R., Negri, A. P., Cantin, N., Liddy, M., et al. (2013). Impacts of ocean acidification on early life-history stages and settlement of the coral-eating sea star Acanthaster planci. PLoS ONE 8:e82938. doi: 10.1371/journal.pone.0082938
Van Hooidonk, R., Maynard, J. A., Manzello, D., and Planes, S. (2014). Opposite latitudinal gradients in projected ocean acidification and bleaching impacts on coral reefs. Glob. Change Biol. 20, 103–112. doi: 10.1111/gcb.12394
Van Hooidonk, R., Maynard, J., and Planes, S. (2013). Temporary refugia for coral reefs in a warming world. Nat. Clim. Change 3, 508–511. doi: 10.1038/nclimate1829
Vehmaa, A., Hogfors, H., Gorokhova, E., Brutemark, A., Holmborn, T., and Engström-Öst, J. (2013). Projected marine climate change: effects on copepod oxidative status and reproduction. Ecol. Evol. 3, 4548–4557. doi: 10.1002/ece3.839
Verges, A., Steinberg, P. D., Hay, M. E., Poore, A. G. B., Campbell, A. H., Ballesteros, E., and Wilson, S. K., et al. (2014). The tropicalization of temperate marine ecosystems: climate-mediated changes in herbivory and community phase shifts. Proc. R. Soc. B 281:20140846. doi: 10.1098/rspb.2014.0846
Wakita, M., Watanabe, S., Honda, M., Nagano, A., Kimoto, K., Matsumoto, K., et al. (2013). Ocean acidification from 1997 to 2011 in the subarctic western North Pacific Ocean. Biogeosciences 10, 7817–7827. doi: 10.5194/bg-10-7817-2013
Wang, D., Gouhier, T. C., Menge, B. A., and Ganguly, A. R. (2015). Intensification and spatial homogenization of coastal upwelling under climate change. Nature 518, 390–394. doi: 10.1038/nature14235
Wei, L., Wang, Q., Wu, H., Ji, C., and Zhao, J. (2015). Proteomic and metabolomic responses of Pacific oyster Crassostrea gigas to elevated pCO2 exposure. J. Proteomics 112, 83–94. doi: 10.1016/j.jprot.2014.08.010
Weijerman, M., Birkeland, C., Piniak, G. A., Miller, M. W., Eakin, C. M., McElhany, P., et al. (2014). Endangered Species Act listing: three case studies of data deficiencies and consequences of ESA ‘threatened’listing on research output. Curr. Opin. Environ. Sustainabil. 7, 15–21. doi: 10.1016/j.cosust.2013.11.026
Welch, M. J., Watson, S.-A., Welsh, J. Q., McCormick, M. I., and Munday, P. L. (2014). Effects of elevated CO2 on fish behaviour undiminished by transgenerational acclimation. Nat. Clim. doi: 10.1038/nclimate2400
Wendel, J. (2014). Diverse coral communities thrive in acidified western Pacific waters. Eos, Trans. Am. Geophys. Union 95, 108–108. doi: 10.1002/2014EO120006
Wijgerde, T., Silva, C. I., Scherders, V., van Bleijswijk, J., and Osinga, R. (2014). Coral calcification under daily oxygen saturation and pH dynamics reveals the important role of oxygen. Biol. Open 3, 489–493. doi: 10.1242/bio.20147922
Williamson, C., Najorka, J., Perkins, R., Yallop, M., and Brodie, J. (2014). Skeletal mineralogy of geniculate corallines: providing context for climate change and ocean acidification research. Mar. Ecol. Prog. Ser. 513, 71–84. doi: 10.3354/meps10929
Wisz, M. S., Broennimann, O., Gronkjaer, P., Moller, P. R., Olsen, S. M., Swingedouw, D., et al. (2015). Arctic warming will promote Atlantic-Pacific fish interchange. Nat. Clim. doi: 10.1038/nclimate2500
Wong, P. P., Losada, I. J., Gattuso, J. P., Hinkel, J., Khattabi, A., McInnes, K. L., et al. (2014). “Coastal systems and low-lying areas,” in Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel of Climate Change, eds C. B. Field, V. R. Barros, D. J. Dokken, K. J. Mach, M. D. Mastrandrea, T. E. Bilir et al. (Cambridge; New York, NY: Cambridge University Press), 361–409.
Woodroffe, C. D., and Webster, J. M. (2014). Coral reefs and sea-level change. Mar. Geol. 352, 248–267. doi: 10.1016/j.margeo.2013.12.006
Yates, K. K., Rogers, C. S., Herlan, J. J., Brooks, G. R., Smiley, N. A., and Larson, R. A. (2014). Diverse coral communities in mangrove habitats suggest a novel refuge from climate change. Biogeosciences 11, 4321–4337. doi: 10.5194/bg-11-4321-2014
Young, J. R., Poulton, A. J., and Tyrrell, T. (2014). Morphology of Emiliania huxleyi coccoliths on the northwestern European shelf – is there an influence of carbonate chemistry? Biogeosciences 11, 4771–4782. doi: 10.5194/bgd-11-4531-2014
Zervoudaki, S., Frangoulis, C., Giannoudi, L., and Krasakopoulou, E. (2013). Effects of low pH and raised temperature on egg production, hatching and metabolic rates of a Mediterranean copepod species (Acartia clausi) under oligotrophic conditions. Mediterr. Mar. Sci. 15, 74–83. doi: 10.12681/mms.553
Keywords: oceans and climate change, IPCC AR5, biological processes, physical processes, warming, ocean acidification, anoxia
Citation: Howes EL, Joos F, Eakin CM and Gattuso J-P (2015) An updated synthesis of the observed and projected impacts of climate change on the chemical, physical and biological processes in the oceans. Front. Mar. Sci. 2:36. doi: 10.3389/fmars.2015.00036
Received: 11 March 2015; Accepted: 21 May 2015;
Published: 26 June 2015.
Edited by:
Elvira S. Poloczanska, Commonwealth Scientific and Industrial Research Organisation, AustraliaReviewed by:
Yuri Artioli, Plymouth Marine Laboratory, UKJacqueline L. Padilla-Gamino, California State University Dominguez Hills, USA
Copyright © 2015 Howes, Joos, Eakin and Gattuso. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ella L. Howes, Alfred Wegener Institute, Am Handelshafen 12, Bremerhaven D-27570, Germany,ZWxsYS5sLmhvd2VzQGdtYWlsLmNvbQ==
 Ella L. Howes
Ella L. Howes Fortunat Joos
Fortunat Joos C. Mark Eakin
C. Mark Eakin Jean-Pierre Gattuso
Jean-Pierre Gattuso