- Department of Mechanical Engineering, Universitatea “Dunǎrea de Jos” Galati, Galati, Romania
This work presents a review of the last developments in the numerical wave modeling in the basin of the Black Sea. A wave prediction system, based on the SWAN (Simulating Waves Nearshore) spectral model, has been implemented and focused on the western side of the sea. Various calibrations and validation tests have been performed considering both in situ and remotely sensed measurements. We found that the most critical factors in increasing the reliability of the wave predictions are related to the physical parameterizations of the model that should be adapted to the conditions of the enclosed seas, especially the process of whitecapping, and the accuracy and the resolution of the wind fields considered to force the wave model. Some data assimilation techniques have been also implemented for various computational levels and they were found very effective in improving the reliability of the wave predictions. Up to the present moment, some sequential methods have been applied considering several approaches as Optimal Interpolation, Linear Regression and Kalman Filter. Furthermore, some practical applications of the wave prediction system are also presented and discussed. These are related to the major storms that might be expected in the Black Sea. At this point, it has to be highlighted that an important issue when building an operational wave modeling system in such difficult environments, as the enclosed seas are, would be to implement different model configurations for different events (especially as regards the severe and extreme events). Other important issues concern the use of the wave models as a tool in the effort of preventing the sea and coastal hazards and assessing also the possible coastal impact of the marine energy farms that would operate in the nearshore. Renewable energy evaluations in the Black Sea have been also performed with this system. Finally, the results of the wave predictions were also used as input in some seakeeping studies.
Introduction
The Black Sea is an enclosed basin between Southeastern Europe and Western Asia. This is connected to the Mediterranean Sea via the straits Bosphorus and Dardanelles and with the smaller Sea of Azov by the Strait of Kerch (Figure 1). The surface of the sea, without the Sea of Azov, is about 436,000 square kilometers, while its maximum depth is 2212 m. The water balance of the Black Sea is positive, since it receives significant river waters, Danube River that outflows in the western side of the sea being the most important. There also exists a two-way water exchange with the Mediterranean Sea, which at the surface consists of a net outflow of water, cooler and less saline, from the Black Sea of about 300 km3/year, while the warmer and more saline Mediterranean waters generate a deep sea flow. The sea basin can be divided into two sub-basins, eastern and western separated from the Crimean Peninsula (Rusu, 2009).
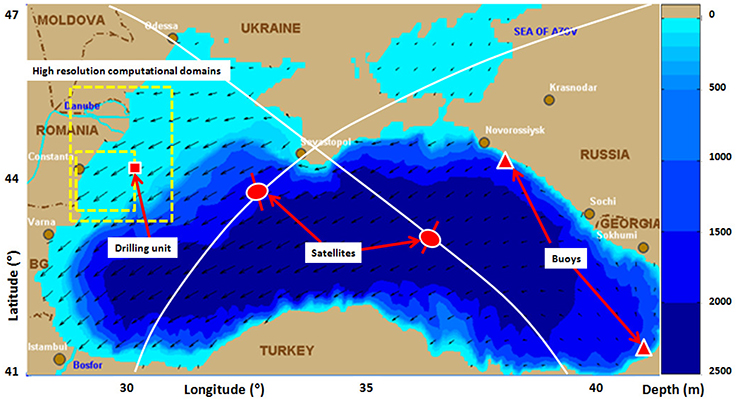
Figure 1. In the background, the bathymetric map of the Black Sea is represented together with the most relevant pattern for the wave propagation, while in the foreground the data sources and the high resolution computational domains are suggested. Results processed from Butunoiu and Rusu (2014) and Rusu (2015).
Although, there is a very long tradition of navigation and human activities in the Black Sea, in the last 25 years the economical activities were continuously enhanced, both offshore and nearshore. This is related to the considerable enlargement of the offshore operations and also to the enhancement of the navigation traffic. The western side of the sea, which it was found to be more energetic, is also subjected to a higher traffic. Here, there are located the two southern gates of the seventh Pan-European transportation corridor, via the Sulina and the Danube-Black Sea canals. The Rhine–Main–Danube Canal system (also called Main-Danube Canal, RMD Canal or Europa Canal), which was previously defined as the seventh Pan-European transportation corridor, links the Black and the North seas and crosses the entire Europe, being the most important inland waterway over the continent. The development of this navigation system represents one of the reasons for increasing, the ship traffic in the Black Sea, in general and in its western side, in special (Gasparotti and Rusu, 2012; Ivan et al., 2012a). At his point, it has to be also highlighted that in the Black Sea the accidents and incidents having as a result, marine and coastal hazards are not at all rare events and that the river ships navigating in the coastal environment of the Black Sea are usually more vulnerable to the harsh environmental conditions (Rusu, 2010).
From this perspective, it became essentially important to be able to provide reliable wave predictions in the sea and coastal environments. Moreover, the climate changes induced sometime in the marine environment rather unusual patterns of the environmental matrix, which means that only a good knowledge of the historical data it is not sufficient. Having in mind all these aspects, the main objective of the present work is to present a review of the advances in the implementation of a wave prediction system in the basin of the Black Sea, including also the Sea of Azov. This provides a comprehensive picture concerning the steps carried out in the implementation, calibration and validation of a system based on numerical spectral wave models, the way in which the accuracy of the wave predictions increases, some data assimilation approaches, and the description of the most significant practical applications of the wave models. Finally, as a conclusion, a brief discussion concerning the results obtained up to now is also employed, followed by some directions considered for the future work.
Implementation of the Wave Prediction System
The most convenient way to provide wave predictions for extended sea surfaces and time intervals is to use numerical wave models based on the spectral approach. The third generation phase averaged models, called also full spectral models, are based on the energy balance equation in a space defined by five dimensions (corresponding to time, geographical and spectral spaces). Very often, instead of the wave energy, the action density is considered (N). This is defined as the wave energy divided by the relative radian frequency (σ) and is because in the presence of the currents the action density is conserved while the wave energy it is not. The governing equation of the spectral wave models is (Holthuijsen, 2007):
() is a derivative operator, which in the case of the spherical coordinates longitude (λ) and latitude (ϕ) (corresponding usually to the large geographical spaces) has the form:
where (θ) represents the wave direction and (c) the propagation velocity.
In the case of the higher resolution computational domains, the Cartesian coordinates are usually considered and the derivative operator has the form:
(S) at the right hand side of equation (1) represents the source term, and in deep water three components are considered more relevant. These correspond to the energy transfer from the wind to the waves (Sin), the nonlinear process of whitecapping dissipation (Sdis) and the nonlinear interactions between four waves denoted also as the quadruplet wave-wave interactions (Snl). In shallow water, some additional terms were also implemented to account for the finite depth effects (Sfd). The processes considered most significant are: wave breaking, bottom friction and triad nonlinear wave interactions. As a result the source term has the expression:
For the ocean scales, the most effective models are considered nowadays WAM (Wave Modeling), (WAMDI group, 1988) and WW3 (Wave Watch 3), (Tolman, 1992). Since for shallow water additional source terms are required, the nearshore spectral models are usually more complex than the ocean scale models (Rusu et al., 2005). Among these coastal models, SWAN (Simulating Waves Nearshore; Booij et al., 1999) is considered the state of the art. Moreover, during the last decade the capacity of this model has been considerably extended, such that the model can be suitably implemented in large geographical spaces, and it seems to be very appropriate for the sea basins as the Black, the Caspian or the Mediterranean seas (Bernardino et al., 2012; Rusu and Onea, 2013).
The first relevant implementation of the SWAN model in the basin of the Black Sea was performed by Guedes Soares and Rusu (2005). Further on, Rusu et al. (2006) performed extended sensitivity analyses in relationship with the most relevant configurations for the main physical processes considering the three sources providing in situ measurements that are indicated in Figure 1. Two buoys, denoted also as B1, which operates in the north eastern side of the basin and B2, located in the south eastern side and the Gloria drilling unit that is placed in the western side of the Black Sea, were considered for in situ validations. In order to create continuous data sets, the gaps in the wave measurements were filled considering the technique indicated by Makarynskyy et al. (2005).
In the spectral wave models, the transfer of energy from wind to the waves is carried out considering the resonance mechanisms of Phillips-Miles (Miles, 1957; Phillips, 1957). The corresponding source term for these mechanisms is commonly described as the sum of linear and exponential growth and two optional expressions for the coefficient corresponding to the exponential grow are considered. The first corresponds to the so called Komen parameterization (Komen et al., 1984), while the second is due to Janssen (1991, 2004) and it is based on the quasi-linear wind-wave theory. In both these two formulations, the whitecapping dissipation is based on the pulse model. An alternative approach to the process of whitecapping is represented by the saturation-based model, denoted also in SWAN as the Westhuysen parameterization (Yan, 1987; Hurdle and van Vledder, 2004), which is based on the apparent relationship between wave groups and the whitecapping dissipation. This approach appears to be more appropriate for the mixed sea-swell conditions and in shallow water (van der Westhuysen et al., 2007).
Following these considerations, and having also in view the fact that this process of whitecapping dissipation is still considered as being the weak link in the deep sea wave modeling process, some early studies related to the implementation of the SWAN based wave modeling system in the Black Sea were focused on the sensitivity tests in relationship with this process. Thus, Table 1 presents some results from Rusu (2009), where the global National Centers for Environmental Prediction (NCEP) re-analysis wind was used as a driver for the regional atmosphere model (REMO). The spatial resolution of the wind model output in the simulations performed at that level was 0.25° and the time step was 1 h. Simulations have been performed in the interval 01/11/1996–06/02/1997 for the comparison with the two buoys (B1 and B2) and for the interval 01/01/2002–31/07/2002 for the comparison at the Gloria drilling unit. The statistical parameters considered are those commonly used to evaluate the wave model output, such as the mean error (Bias) computed as the difference between the average values of the simulated (MedSim) and observed (MedObs) data, the mean absolute error (MAE), the root mean square error (RMSE), the scatter index (SI) defined as the ratio of the standard deviation of the error to the mean observed values, the linear correlation coefficient (R) and the symmetric slope (S, for S > 1 the model overestimates the observations).
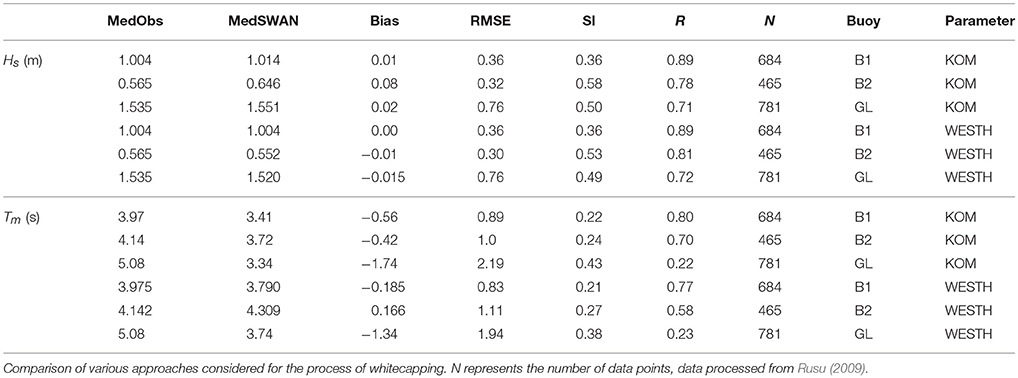
Table 1. Statistical results for the parameters Hs and Tm, SWAN simulations against in situ measurements.
At that moment it was found that the most effective formulations are Komen and Westhuysen and for this reason the study was focused mainly on the performances of these two parameterizations. Nevertheless, it has to be highlighted that during the last decade, SWAN was a very dynamic model and its code was considerably cleaned up and optimized. As a consequence, a significant speedup of the model resulted in the latest versions. Another consequence relates to the Janssen formulation for the wind input, which was considerably improved. Under these circumstances, the present modeling strategy in the Black Sea considers Janssen formulation for the entire sea basin level and Westhuysen formulation for the coastal areas. In this connection, Table 2 presents some results processed from Rusu et al. (2014) concerning the reliability of the SWAN predictions for the entire sea basin computational domain. The wind field considered this time is that provided by NCEP-CFSR (United States National Centers for Environmental Prediction, Climate Forecast System Reanalysis) with a spatial resolution of 0.312° × 0.312° and a temporal resolution of 3 h. Simulations have been performed for the 10-year interval 1999–2008 for the comparison performed in terms of the wave parameter significant wave height with the satellite measurements and for 6-year interval 1999–2004 for the comparison with the measurements at the Gloria drilling unit.

Table 2. Statistical results for the parameter Hs, SWAN simulations against satellite data and in situ measurements.
Another important process in deep water is represented by the quadruplet wave-wave interactions, which dominate somehow the evolution of the wave spectrum (Hasselmann, 1962, 1974). The quadruplets transfer in fact the energy from the spectral peak to both lower and higher frequencies. An analytical representation of the quadruplets is given by the Boltzmann integral, but its full computation is not computationally effective. Nevertheless, in SWAN, an effective computational algorithm has been developed. This is the Discrete Interaction Approximation (DIA) and has been found to be quite successful in describing the essential features of a developing wave spectrum (Herterich and Hasselmann, 1980; Hasselmann et al., 1985; van Vledder and Bottema, 2003). Moreover, in the SWAN model (SWAN, 2015), the quadruplets can be integrated by four different numerical procedures for DIA: semi-implicit computation of the nonlinear transfer with DIA per sweep, fully explicit computation of the nonlinear transfer with DIA per sweep, fully explicit computation of the nonlinear transfer with DIA per iteration, fully explicit computation of the nonlinear transfer with DIA. Various sensitivity tests have been also performed to assess which of these options works better in the basin of the Black Sea (Guedes Soares and Rusu, 2005; Rusu et al., 2006) and up to this moment it was found that the fully explicit computation of the nonlinear transfer with DIA per iteration would be the most appropriate (SWAN, 2015).
As an example illustrating the most relevant patterns for the wave conditions in the Black Sea, Figure 2 presents the field distributions for the significant wave heights and wave vectors corresponding to two representative situations. Thus, Figure 2A presents typical winter conditions, corresponding to the results provided by the wave prediction system for the time frame 08/12/2015/h12 and Figure 2B illustrating regular storm conditions, as for the time frame 21/01/2016/h18. The positions of the maximum values of the significant wave height and wind velocity are also represented.
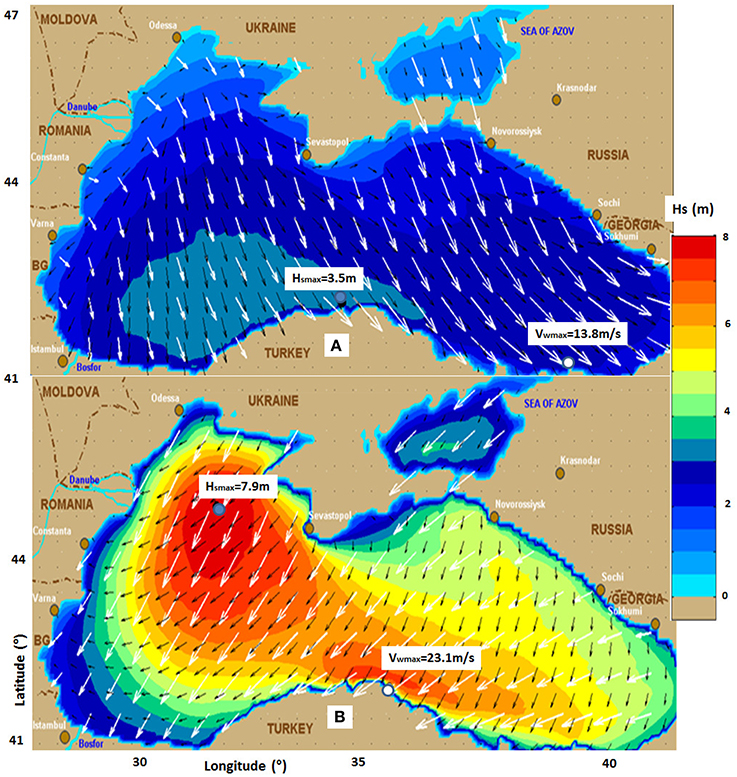
Figure 2. Significant wave height fields and wave vectors. The positions of the maximum values of the significant wave height and wind velocity are also represented. (A) Typical winter wave conditions, results for the time frame 08/12/2015/h12; (B) Regular storm conditions, results for the time frame 21/01/2016/h18. Results processed from Rusu (2016a,c).
Another important issue that was intensively studied is related to the impact of the accuracy and the resolution of the wind fields used to force the wave model (Rusu and Butunoiu, 2014). In fact, it is well known that the quality of the wave predictions is highly dependent on the quality and resolution (in both space and time) of the wind field considered to force the wave model. Nonetheless, in the enclosed seas, as our target area is, this influence is even higher than in open ocean. This is because mainly in such environments the variations in space and time of the wind velocity have much higher gradients. From this perspective, comparisons of various data sources have been carried out against in situ and remotely sensed measurements. Thus, Table 3 presents the U10 statistics, corresponding to the in situ measurements performed at the Gloria drilling unit against NCEP wind data, for the 10-year period 1998–2008, and on the other hand only for the year 2007 for both NCEP and ECMWF wind data. The data presented are processed from Onea et al. (2015) and Onea and Rusu (2014). Table 4, presents the wind statistical evaluations of the NCEP data and of the satellite measurements, corresponding to the total time (TT) and winter time (WT), in four reference points located in the northwest (NW), northeast (NE), east (E) and south (S), respectively. The NCEP data cover the 10–year time interval 1999–2008, while the satellite data the 5–year time interval 2010–2014. For the above mentioned time interval, the Hs measurements are available from multiple satellites whose path crossed the Black Sea, respectively ERS-2, ENVISAT, TOPEX, Poseidon, JASON-1, JASON-2, GEOSAT Follow-On (GFO). The results presented are processed from Onea et al. (2015) and Raileanu et al. (2015b). It has to be highlighted that taking into account the analyses from above, the wind field considered for forcing the wave model in most of the further simulations performed was that provided by NCEP-CFSR, which was found to provide results that can be considered in general reasonable good.

Table 3. U10 statistics, in situ measurements performed at the Gloria drilling unit against NCEP wind data, corresponding to the 10-year period 1998–2008, and only for the year 2007 for both NCEP and ECMWF wind data.
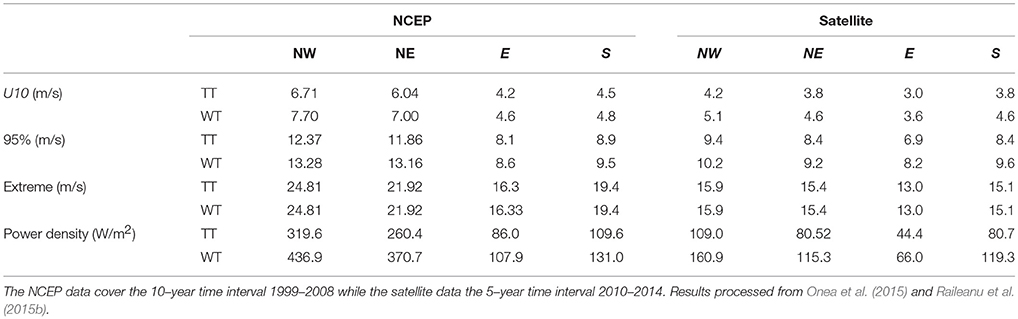
Table 4. Wind statistical evaluations of the NCEP data and of the satellite measurements, corresponding to the total time (TT) and winter time (WT), respectively in four reference points located in the northwest (NW), northeast (NE), east (E) and south (S), respectively.
Finally, at the end of this paragraph, some details related to the architecture of the wave modeling system, SWAN based, that was implemented in the basin of the Black Sea will be also provided. Thus, as shown in Rusu (2010) and Butunoiu and Rusu (2012) although one single wave model is considered, the physics is rather different from one computational level to another. For the generation area, the main physical processes considered are related to the energy transfer from the wind to the waves, whitecapping dissipation and quadruplet interactions. On the other hand, in the higher resolution domains, processes as bottom friction, combined refraction-diffraction, or wave-current interactions, are relevant as well. The nesting process is straightforward when passing from one computational level to another, but considering the same coordinate system (Lalbeharry and Ritchie, 2009). However, when passing from the spherical coordinates to the Cartesian system (in the local areas), in order to connect the high resolution area to the deep water forcing some points are defined on the boundary of the high resolution computational domain. In these points, the wave spectrum is given by the run performed in the spherical coordinates. Further details related to this indirect nesting technique are given in Butunoiu and Rusu (2012).
Assimilation of in situ Measurements and Remotely Sensed Data
We shall focus in this section on another important step in the direction of increasing the reliability of the wave model predictions and in providing reliable nowcast and forecast products. This is to implement some data assimilation techniques. Although, the idea of data assimilation (DA) is very simple, that is to combine the model results with the measurements in order to correct the predictions, the mathematical techniques associated to these are usually rather sophisticated and very often extremely computationally demanding. Having this in mind, it was first started with some simple approaches. Thus, a first idea was to try to improve the wave prediction locally, at the point where we have in situ measurements, that is at the Gloria drilling unit. The first method applied considered the standard linear regression (LR) (Soukissian and Kechris, 2007; Raileanu et al., 2015a), the two regression coefficients being computed considering various training periods, starting with 5 days and continuing with 20, 40, and 60 days. A second approach considered in parallel was a standard Kalman filter (KF), when the training period considered was of only 1 week. Table 5 presents the statistical results SWAN simulations against in situ measurements at the Gloria drilling unit, for the parameters Hs and Tm corresponding to the 9-year period (1999–2007), without and with data assimilation, considering the two different assimilation approaches mentioned (in the case of LR only the results corresponding to training periods of 20 days and 60 days are presented). The data presented are processed from Rusu (2014, 2016b). The explanation of the different number of data points considered in the two approaches is due to the fact that in the case of the linear regression in order to assure a training period of 60 days the interval for effective simulations started in the beginning of March, while for the Kalman Filter the training period considered was of only 1 week. Nevertheless, it has to be also underlined that, while presenting rather similar results from a statistical point of view, the Kalman filter seems to be more effective since requires a considerably smaller training period. Thus, a training period of 1 week was considered satisfactory for KL, while for LR training periods less than 20 days do not provide visible improvements of the wave predictions.
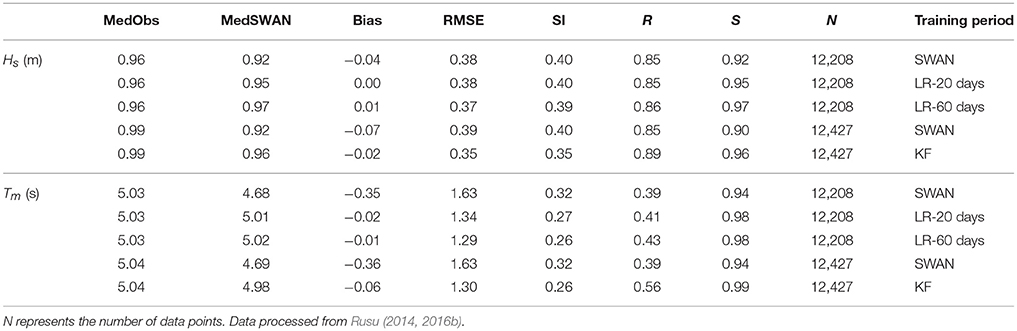
Table 5. Statistical results SWAN simulations against in situ measurements at the Gloria drilling unit, for the parameters Hs and Tm corresponding to the 9-year period (1999–2007), without and with data assimilation, considering two different assimilation approaches, the first is based on the linear regression (LR) and the second on the Kalman Filter (KF).
In order to propagate in space the assimilation results and correct the boundary conditions of the SWAN computational domain, the following approach was considered (Butunoiu and Rusu, 2014). Thus, in a point B (located on the boundary of the high resolution computational domain) the assimilated value of the wave parameter corresponding to the simulation performed for the time moment τ is computed with the following relationship:
is the model predicted value at the point B, the operator Ω(B, τ) was defined as the ratio between the model predicted values in the point B and those corresponding to the point M (at the location of the measurement), respectively of the wave parameter considered:
Finally, ΔZMτ denotes the difference between the measured and the predicted values of the wave parameter at the location of the measurement:
After propagating the information in the geographical space, adequate corrections are also operated in the spectral space.
At the global level, that is for the entire sea basin, the assimilation of the satellite measurements was made considering the Optimal Interpolation (OI) method. Furthermore, for the coastal level subdomain the OI method was combined with LR in order to be able to correct the forecast products. Table 6 presents results of the model simulations for the 10-year time interval (1999–2008). The respective results are processed from Butunoiu and Rusu (2015) for the entire sea level domain and from Raileanu et al. (2015a) for the coastal level. The data assimilation schemes considered for the local computational domains and for the entire sea basin are suggested in Figure 3.

Table 6. Results of the DA schemes considered for the entire Black Sea level, based on the optimal interpolation approach from Butunoiu and Rusu (2015) and for the coastal level, based on a successive correction approach that combines a scheme based on linear regression time propagation with the optimal interpolation (OI) for the space propagation (processed from Raileanu et al., 2015a).
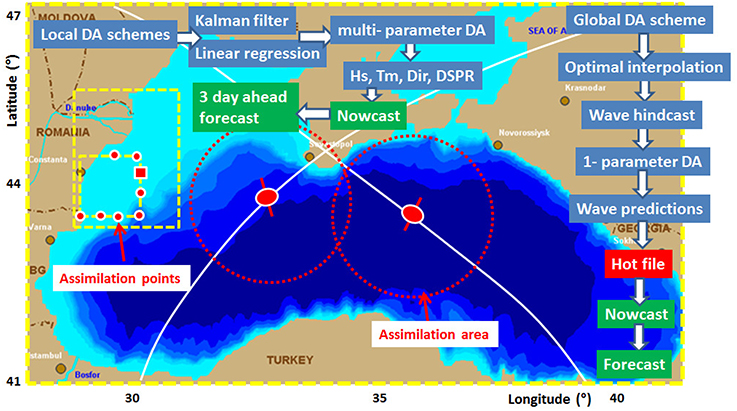
Figure 3. The data assimilation schemes considered for the local computational domains and for the entire sea basin. Results processed from Butunoiu and Rusu (2014), Rusu (2015) and Raileanu et al. (2015a).
At the end of this section, it has to be also highlighted that a MATLAB toolbox was associated with the wave prediction system (Butunoiu and Rusu, 2012). This allows first the visualization and preprocessing of the input data followed by visualizations and post-processing of the output. This is a user friendly GUI (graphical user interface) that helps in global and local analyses, as well as in performing parallel evaluations of the model results for various geographic scales and wave parameters, either vector or scalar fields.
Applications of the Wave Models in the Black Sea
Once implemented and validated in the Black Sea basin, one of the first applications of the wave prediction system was to evaluate the storm conditions. The idea was to start from extended hindcast studies (Rusu et al., 2006, 2014) and, using the experience and the results coming from these, to be able to define the most relevant storm patterns that might affect the marine environment considered. On the other hand, a real challenging objective would be to be able to predict in real time and with a reasonable accuracy the development and impact of the most dangerous storms. The results presented in Tables 1, 2, 5, 6 show that the wave prediction system has performances that are in general in line with those corresponding to similar environments (Lopatoukhin et al., 2004; Valchev et al., 2004; Signell et al., 2005; Cherneva et al., 2008; Bertotti and Cavaleri, 2009).
As we highlighted, the enclosed seas are more difficult environments from the point of view of the wave and wind modeling and that is why it is expected that the results in such areas to be less accurate than in the case of the ocean wave predictions. Another issue to be considered is that the model system calibration was performed for average wave conditions. In such case, for a general under prediction in terms of significant wave height, we may have an over prediction of the most extreme storms, or on the contrary. Having in mind such aspects, probably the best approach would be to design a special model configuration for such storms and when the significant wave height exceeds a certain threshold to start parallel model computations for the duration of the extreme event (Rusu et al., 2014). By analyzing the results obtained in various hindcast studies, we can also define the regular and the extreme storms. Thus, in the case of a regular storm the significant wave height is greater than 7 m over extended regions of the sea. This means that we can expect with a certain regularity, waves of about 14 m or higher in the winter time. An example of such storm is presented in Figure 2B corresponding to the conditions for the time frame 21/01/2016/h18 and we have to underline that such storms may occur several times in a year. A case of extreme storm is illustrated in Figure 4, which presents extreme wave an wind conditions in the Black Sea. The results correspond to the time frame 22/01/2004/h21. Although such a storm is not very common, we can expect such an event at least once in 5 years. In such cases, there are areas in the sea where the significant wave height is greater than 10 m, which means that we may expect maximum wave heights of about 20 m, or even greater.
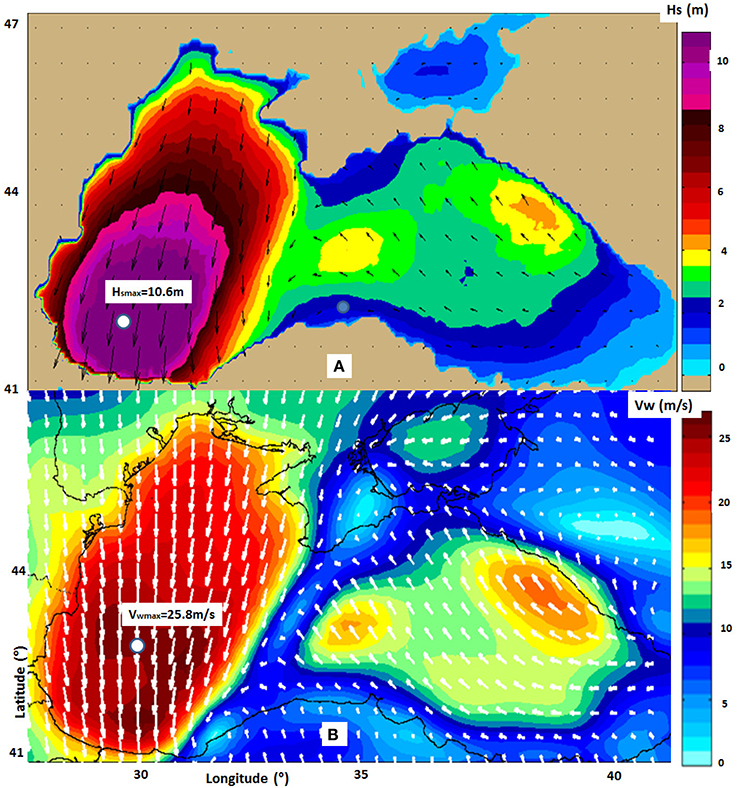
Figure 4. Extreme wind and wave conditions in the Black Sea. Results corresponding to the time frame 22/01/2004/h21, data processed from Rusu et al. (2014). (A) Significant wave height fields and wave vectors; (B) Wind scalar fields and velocity vectors. The positions of the maximum values of the significant wave height and wind velocity are also represented.
The local scale simulations and evaluation of some particular effects represents another important issue where the wave models can play a significant role. Among the local effects, a significant place have the interactions between waves and currents and probably the most relevant effects are those given at the mouths of the Danube River, where the currents, induced by the river outflow, interact with the incoming waves. Detailed descriptions of the very complex phenomena occurring in these areas are presented in Ivan et al. (2012b) and Ivan and Rusu (2015). Some results provided by the modeling system in such local areas are illustrated in Figures 5, 6. Thus, Figure 5 presents high resolution simulations in spherical coordinates, including wave current interactions, at the mouths of the Danube River. The results correspond to the time frame 24/11/2015/h06. The positions of the maximum values of the significant wave height and current velocity are also indicated. On the other hand, Figure 6 presents the next level, that is some high resolution simulations in Cartesian coordinates. The results correspond to the time frame 24/11/2015/h18 and Figure 6A illustrates a simulation in the coastal environment of the Sacalin Peninsula south of the Saint George arm of the Danube, while Figure 6B a simulation at the entrance of the Sulina channel. This is a crucial point for coastal navigation since it represents the main southern entrance in the seventh Pan-European transportation corridor. Besides the common parameters, as significant wave height, wave period and wave direction, relevant information can be provided in such areas by the Benjamin-Feir Index (BFI) or the steepness-over-randomness ratio. This is a spectral shape parameter that can be related to the kurtosis of the wave height distribution. In particular, for Gaussian-shaped spectra the kurtosis of the wave height distribution depends on the square of BFI. Thus, for BFI values of about 0.2–0.3 the maximum wave heights are very well described by the Rayleigh distribution while for values of BFI of 0.9 and 1.2 the ratio Hmax/Hs is substantially underestimated. In fact, greater values of this index show that due to the currents the waves are no longer Rayleigh distributed, which means that the ratio between the maximum and the significant wave height can be considerably higher than 1.86 (which represents the standard value for the Rayleigh distribution). This means also that the existence of the currents does not enhance only the significant wave heights, but freak waves can also occur in such cases. From the results of the simulations performed, it can be noticed that the highest values of the BFI index occur, in general, when the wave approach is normal to the shore (Dir = 90°). As regards the relationship of the magnitude of this index with the values of the significant wave height, it seems that greater values of this index result when the significant wave height is close to the value of 3 m (Rusu and Guedes Soares, 2013). At this point, it has to be highlighted that, as illustrated by Figures 5, 6B, in many coastal environments a key issue is related to the interactions between the waves and the strong opposite currents that may induce very often significant enhancements of the wave heights. Ivan and Rusu (2015) performed several validations SWAN model simulations against tank experiments, especially considering the particular conditions that are usually encountered at the mouths of the Danube. Their results show that the complex phenomena associated with the interactions between waves and strong opposite currents are accounted by the SWAN model in a reasonable way.
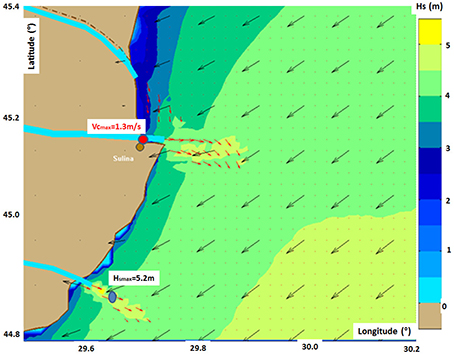
Figure 5. High resolution simulations in spherical coordinates. Wave current interactions at the mouths of the Danube River in the Black Sea, significant wave height scalar fields, wave and current vectors. Results corresponding to the time frame 24/11/2015/h06. The positions of the maximum values of the significant wave height and current velocity are also represented. Results processed from Rusu (2016a).
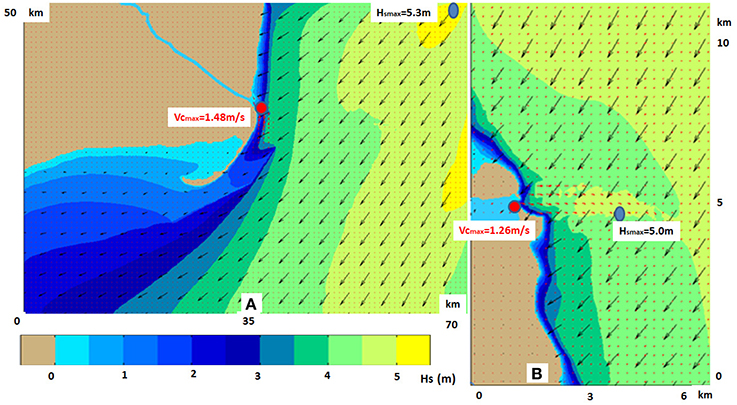
Figure 6. High resolution simulations in Cartesian coordinates. Significant wave height fields, wave and current vectors. Results corresponding to the time frame 24/11/2015/h18. The positions of the maximum values of the significant wave height and current velocity are also represented. (A) Simulation in the coastal environment of the Sacalin Peninsula south of the Saint George arm of the Danube; (B) Simulation at the entrance of the Sulina channel. Results processed from Rusu (2016a).
Another important direction of applicability of the wave models is represented by a reliable assessment of the waves coastal impact. The Black Sea, in general and its western coasts, in special, are subjected to a high dynamics and moreover the climate changes induced very often unusual patterns that might affect in a hazardous way the coastal environment (Ozhan et al., 2004; Yilmaz, 2007; Bilyay et al., 2011). That is why, the wave models represent an appropriate framework to assess the changes expected in the coastal dynamics. Furthermore, since the coastal works are usually extremely expensive (Omer et al., 2015) another possibility explored using the wave models was to take into account the sheltering effect that might be provided by the marine energy farms and several studies have been performed in this direction (Diaconu and Rusu, 2013; Zanopol et al., 2014a,b). If we compare the wind results presented in Tables 2, 3 with the conditions encountered in locations where offshore wind farms already operate, we can notice that the coastal environment of the Black Sea has significant wind energy resources. On the other hand, using the same modeling system (Rusu, 2015) provided an evaluation of the wave energy based on a 15-year wave hindcast and the results show that a hybrid marine farm might be considered as a realistic solution in the western side of the Black Sea. Finally, at the end of this section we can mention also other relevant application of the wave modeling system which is related to the enhancement of the safe navigation by coupling the spectral wave model with a numerical model for seakeeping based on the strip theory (Gasparotti and Rusu, 2014). In relationship with this coupling between the spectral and the seakeeping models and the further application of this approach to increase the navigation safety, an important issue that is targeted for the further work is to assess the relevance of the wave model error on various seakeeping criteria in order to increase the reliability of the model system outputs.
Conclusions
The objective of the present work was to provide a comprehensive picture of the progress in increasing the reliability of the wave predictions in the basin of the Black Sea. The wave prediction system considered is entirely based on the SWAN model. However, the physical settings of the model might present significant differences from one computational level to another.
A first step was to analyze the options available in SWAN for the deep water processes, and among them whitecapping, which is coupled with the energy transfer from the wind to the waves, was considered the most sensitive. Although, initially the most effective parameterization for the basin level appeared to be those of Komen, since the SWAN model development in the last years was quite dynamic, further on the Jansen formulation, recently improved, was found to become better and actually this is the formulation that is used now for the simulations in the entire Black Sea. As regards the coastal computational domain, the saturation based model provided by the formulation of Westhuysen seems to work the best. Another issue that was found particularly essential in enclosed seas is related to the accuracy and resolution of the driving wind fields.
Some data assimilation approaches have been also implemented and evaluated. For the entire basin a scheme for assimilation of the satellite data based on the OI was considered, and the only parameter assimilated at this level was the significant wave height (Hs). For the local scale, in situ measurements performed at the Gloria platform were assimilated, the parameters Hs and Tm (mean period). Two approaches were evaluated in parallel at this level, one based on LR and another on KF, the last one being found more effective. For the coastal level the OI and LR methods were combined (considering the satellite measurements) and the results are promising. As further steps, multi-parameter schemes are being designed for all the computational levels, including, besides Hs and Tm, some other parameters as mean wave direction and directional spreading. Moreover, the optimal interpolation is being combined with the Kalman filter in order to provide more accurate forecast products.
Various applications have been considered for the wave modeling system implemented in the Black Sea basin. Among these, prediction and analysis of the extreme storms, assessment of coastal impact and designing measures for coastal protection, as well as providing the environmental support for the maritime navigation are probably the most relevant. In fact, all of them should have as an effect the prevention of the marine and coastal hazards. The work is still ongoing and besides improving the data assimilation approaches, a real breakthrough would be to implement a coupled system wind-wave-current. Since all these fields are continuously interacting, such approach should provide more accurate predictions of the environmental matrix.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by a grant of the Romanian Ministry of National Education, CNCS – UEFISCDI PN-II-ID-PCE-2012-4-0089 (project DAMWAVE).
References
Bernardino, M. C., Salvação, N., and Rusu, L. C. (2012). “Evaluation of the wind and wave simulations in the Black Sea using satellite altimeter data,” in Maritime Engineering and Technology, eds C. G. Soares, Y. Garbatov, S. Sutulo, and A. Santos (London: Taylor & Francis Group), 467–471.
Bertotti, L., and Cavaleri, L. (2009). Wind and wave predictions in the Adriatic Sea. J. Mar. Syst. 78, S227–S234. doi: 10.1016/j.jmarsys.2009.01.018
Bilyay, E., Ozbahceci, B. O., and Yalciner, A. C. (2011). Extreme waves at Filyos, Southern Black Sea. Nat. Hazards Earth Syst. Sci. 11, 659–666. doi: 10.5194/nhess-11-659-2011
Booij, N., Ris, R. C., and Holthuijsen, L. H. (1999). A third generation wave model for coastal regions. Part 1: model description and validation. J. Geophys. Res. 104, 7649–7666. doi: 10.1029/98JC02622
Butunoiu, D., and Rusu, E. (2014). “Wave modeling with data assimilation to support the navigation in the Black Sea close to the Romanian Ports,” in International Conference on Traffic and Transport Engineering (Belgrade: ICTTE Belgrade 2014).
Butunoiu, D., and Rusu, E. (2012). A Matlab interface associated with modeling surface waves in the nearshore, Protection and Sustainable Management of the Black Sea Ecosystem, Special Issue. J. Environ. Protect. Ecol. 13, 1606–1816.
Butunoiu, D., and Rusu, E. (2015). “A data assimilation scheme to improve the Wave Predictions in the Black Sea,” in Proceedings of OCEAN'15 MTS/IEEE Conference-Discovering Sustainable Ocean Energy for a New World, 18-21 May, (Genova).
Cherneva, Z., Andreeva, N., Pilar, P., Valchev, N., Petrova, P., and Guedes Soares, C. (2008). Validation of the WAMC4 wave model for the Black Sea. Coast. Eng. 55, 881–893. doi: 10.1016/j.coastaleng.2008.02.028
Diaconu, S., and Rusu, E. (2013). The environmental impact of a Wave Dragon array operating in the Black Sea. Sci. World J. 2013:498013. doi: 10.1155/2013/498013
Gasparotti, C., and Rusu, E. (2012). Methods for the risk assessment in maritime transportation in the Black Sea basin. Protection and Sustainable Management of the Black Sea Ecosystem, Special Issue. J. Environ. Protect. Ecol. 13, 1751–1759.
Gasparotti, C., and Rusu, L. (2014). Prediction of the dynamic responses for two containerships operating in the Black Sea. J. Naval Archit. Marine Eng. 11, 55–68. doi: 10.3329/jname.v11i1.17289
Guedes Soares, C., and Rusu, E. (2005). “SWAN Hindcast in the Black Sea,” in Fifth International Symposium - WAVES 2005, 3rd – 7th July 2005 (Madrid).
Hasselmann, K. (1962). On the non-linear energy transfer in a gravity–wave spectrum: Part 1. General theory. J. Fluid Mech. 12, 481–500. doi: 10.1017/S0022112062000373
Hasselmann, K. (1974). On the spectral dissipation of ocean waves due to white-cap. Bound. Layer Meteor. 6, 107–127. doi: 10.1007/BF00232479
Hasselmann, S., Hasselmann, K., Allender, J. H., and Barnett, T. P. (1985). Computations and parameterizations of the nonlinear energy transfer in a gravity wave spectrum. Part II: parameterizations of the nonlinear transfer for application in wave models. J. Phys.Oceanogr. 15, 1378–1391.
Herterich, K., and Hasselmann, K. (1980). A similarity relation for the nonlinear energy transfer in a finite-depth gravity–wave spectrum. J. Fluid Mech. 97, 215–224. doi: 10.1017/S0022112080002522
Holthuijsen, L. H. (2007). Waves in Oceanic and Coastal Waters, Vol. 387. Cambridge: Cambridge University Press.
Hurdle, D. P., and van Vledder, G. P. H. (2004). “Improved spectral wave modelling of white-capping dissipation in swell sea Systems,” in Proceedings of the 23rd International Conference on Offshore Mechanical and Arctic Engineering OMAE2004 (Vancouver, BC).
Ivan, A., Gasparotti, C., and Rusu, E. (2012a). Influence of the interactions between waves and currents on the navigation at the entrance of the Danube Delta. Protection and Sustainable Management of the Black Sea Ecosystem, Special Issue. J. Environ. Protect. Ecol. 13, 1673–1682.
Ivan, A., and Rusu, L. (2015). Validation of the SWAN model for the influence of opposite currents on the wave spectra. Environ. Eng. Manag. J. 14, 751–761.
Ivan, A., Rusu, L., and Măcuţă, S. (2012b). “Validations with experimental data of SWAN simulations for the wave propagation in the presence of strong oposite currents,” in Proceedings of 12th International Multidisciplinary Scientific GeoConference (SGEM2012), 17-23 June (Albena), 1025–1032.
Janssen, P. (2004). The Interaction of the Ocean Waves and Wind. Cambridge, UK: Cambridge University Press.
Janssen, P. A. E. M. (1991). Quasi-linear theory of wind-wave generation applied to wave forecasting. J. Phys. Oceanogr. 21, 1631–1642.
Komen, G. J., Hasselmann, S., and Hasselmann, K. (1984). On the existence of a fully developed wind sea spectrum. J. Phys. Oceanogr. 14, 1271–1285.
Lalbeharry, R., and Ritchie, H. (2009). “Wave simulation using SWAN in nested and unnested mode applications,” in Proceedings of the 11th International Workshop on Wave Hindcasting and Forecasting (Halifax, NS).
Lopatoukhin, L. J., Boukhanovsky, A. V., Chernysheva, E. S., and Ivanov, S. V. (2004). “Hindcasting of wind and wave climate of seas around Russia,” in Proceedings of the 8th International Workshop on Waves Hindcasting and Forecasting (Ohau).
Makarynskyy, O., Makarynska, D., Rusu, E., and Gavrilov, A. (2005). “Filling gaps in wave records with artificial neural networks,” in Maritime Transportation and Exploitation of Ocean and Coastal Resources, Vol. II, eds G. C. Soares, Y. Garbatov, and N. Fonseca (London: Taylor & Francis publications), 1085–1091.
Miles, J. W. (1957). On the generation of surface waves by shear flows. J. Fluid Mech. 3, 185–204. doi: 10.1017/S0022112057000567
Omer, I., Mateescu, R., Rusu, L., Niculescu, D., and Vlasceanu, E. (2015). Coastal works extensions on the romanian touristic littoral, its ecological impacts on the nearshore bathing areas. J. Environ. Protect. Ecol. 16, 424–433.
Onea, F., Raileanu, A., and Rusu, E. (2015). Evaluation of the wind energy potential in the coastal environment of two enclosed seas. Adv. Meteorol. 2015:808617. doi: 10.1155/2015/808617
Onea, F., and Rusu, E. (2014). Wind energy assessments along the Black Sea basin. Meteorol. Applic. 21, 316–329. doi: 10.1002/met.1337
Ozhan, E., Abdalla, S., and Yilmaz, N. (2004). “Long-term and extreme wave climate of the Black Sea,” in Proceedings of the 29th International Conference (ICCE2004), Coastal Engineering 2004, 19–24 September 2004 (Lisbon), 701–713.
Phillips, O. M. (1957). On the generation of waves by turbulent wind. J. Fluid Mech. 2, 417–445. doi: 10.1017/S0022112057000233
Raileanu, A., Onea, F., and Rusu, E. (2015b). “Assessment of the wind energy potential in the coastal environment of two enclosed seas,” in Proceedings of OCEAN'15 MTS/IEEE Conference - Discovering Sustainable Ocean Energy for a New World, 18-21 May (Genova).
Raileanu, A., Rusu, L., and Rusu, E. (2015a). “Wave modelling with data assimilation in the Romanian nearshore,” in Proceedings of 16th International Congress of the International Maritime Association of the Mediterranean, IMAM 2015 - Towards Green Marine Technology and Transport, 21-24 September (Pula).
Rusu, E. (2009). Wave energy assessments in the Black Sea. J. Marine Sci. Technol. Spring. 14, 359–372. doi: 10.1007/s00773-009-0053-6
Rusu, E. (2016a). “Analysis of the effect of a marine energy farm to protect a biosphere reserve,” in Conference: ICACER - 2016, International Conference on Advances on Clean Energy Research Apr. 16-18 (Bangkok).
Rusu, E., and Guedes Soares, C. (2013). “Modelling the effect of wave current interaction at the mouth of the Danube river,” in Developments in Maritime Transportation and Exploitation of Sea Resources, eds C. Guedes Soares and L. Peña (London: Taylor & Francis Group), 979–986.
Rusu, E., and Onea, F. (2013). Evaluation of the wind and wave energy along the Caspian Sea. Energy 50, 1–14. doi: 10.1016/j.energy.2012.11.044
Rusu, E., Rusu, L., and Guedes Soares, C. (2006). “Prediction of extreme wave conditions in the Black Sea with numerical models,” in 9th International Workshop on Wave Hindcasting and Forecasting (Victoria, BC).
Rusu, E., Ventura, S. C., and Rusu, L. (2005). Computational strategies and visualization techniques for the wave modelling in the Portuguese nearshore. Mari. Transport. Exploit. Ocean Coast. Res. 2, 1129–1136. doi: 10.1201/9781439833728.ch136
Rusu, L. (2010). Application of numerical models to evaluate oil spills propagation in the coastal environment of the Black Sea. J. Environ. Eng. Landsc. Manag. 18, 288–295. doi: 10.3846/jeelm.2010.33
Rusu, L. (2014). “A data assimilation scheme to improve the wave predictions in the western side of the Black Sea,” in Proceedings of 14th International Multidisciplinary Scientific GeoConference (SGEM2014), Vol. II (Sofia), 539–545.
Rusu, L. (2015). Assessment of the Wave Energy in the Black Sea, based on a 15-Year Hindcast with Data Assimilation. Energies 8, 10370–10388. doi: 10.3390/en80910370
Rusu, L. (2016b). “Data assimilation method based on the Kalman filter associated with the wave modelling in the western Black Sea,” in Proceedings of 16th International Multidisciplinary Scientific GeoConference (SGEM2016) (Albena: Marine and Ocean Ecosystems).
Rusu, L. (2016c). “Assessment of the renewable energy resources in the Romanian nearshore at the Black Sea,” in Conference: ICACER - 2016, International Conference on Advances on Clean Energy Research Apr. 16-18 (Bangkok).
Rusu, L., and Butunoiu, D. (2014). Evaluation of the wind influence in modeling the Black Sea wave conditions. Environ. Eng. Manag. J. 13, 305–314.
Rusu, L., Butunoiu, D., and Rusu, E. (2014). Analysis of the extreme storm events in the Black Sea considering the results of a ten-year wave hindcast. J. Environ. Protect. Ecol. 15, 445–454.
Signell, R., Carniel, S., Chiggiato, J., Doyle, J., Pullen, J., and Sclavo, M. (2005). Assessment of the wind quality for oceanographic modeling in semi-enclosed basins. J. Mar. Syst. 53, 217–233. doi: 10.1016/j.jmarsys.2004.03.006
Soukissian, T., and Kechris, C. (2007). About applying linear structural method on ocean data: adjustment of satellite wave data. Ocean Eng. 34, 371–389. doi: 10.1016/j.oceaneng.2006.04.002
SWAN (2015). Scientific and Technical Documentation (SWAN Cycle III version 41.01A), Vol. 130. Delft: Delft University of Technology.
Tolman, H. J. (1992). Effects of numerics on the physics in a third-generation wind-wave model. J. Phys. Oceanogr. 22, 1095–1111.
Valchev, N., Pilar, P., Cherneva, Z., and Guedes Soares, C. (2004). “Set-up and validation of a third-generation wave model for the Black Sea,” in Proceedings 7th International Conference “BLACK SEA'2004” (Varna: Scientific and Technical University of Varna), 273–279.
van der Westhuysen, A. J., Zijlema, M., and Battjes, J. A. (2007). Nonlinear saturationbased whitecapping dissipation in SWAN for deep and shallow water. Coast. Eng. 54, 151–170. doi: 10.1016/j.coastaleng.2006.08.006
van Vledder, G. P. H., and Bottema, M. (2003). “Improved modelling of nonlinear four-wave interactions in shallow water,” in Proceedings 28th International Conference Coastal Engineering (Cardiff: ASCE), 459–471.
WAMDI group (1988). The WAM model - a third generation ocean wave prediction model. J. Phys. Oceanogr. 18, 1775–1810.
Yan, L. (1987). An Improved Wind Input Source Term for Third-Generation Ocean Wave Modelling. Scientific Report WR-No 87-8, KNMI, De Bilt.
Yilmaz, N. (2007). Spectral Characteristics of Wind Waves in the Eastern Black Sea. PhD Thesis, Middle East Technical University, Ankara.
Zanopol, A. T., Onea, F., and Rusu, E. (2014a). Coastal impact assessment of a generic wave farm operating in the Romanian nearshore. Energy 72, 652–670. doi: 10.1016/j.energy.2014.05.093
Keywords: Black Sea, numerical wave models, data assimilation, SWAN, Romanian coastal environment
Citation: Rusu E (2016) Reliability and Applications of the Numerical Wave Predictions in the Black Sea. Front. Mar. Sci. 3:95. doi: 10.3389/fmars.2016.00095
Received: 12 April 2016; Accepted: 30 May 2016;
Published: 14 June 2016.
Edited by:
Ananda Pascual, Spanish National Research Council, SpainReviewed by:
Alejandro Orfila, IMEDEA (CSIC-UIB), SpainArthur Capet, Italian National Research Council, Italy
Cláudia Gomes Lucas, Centre for Marine Technology and Ocean Engineering, Portugal
Copyright © 2016 Rusu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eugen Rusu, ZXJ1c3VAdWdhbC5ybw==
 Eugen Rusu
Eugen Rusu