- 1Chemical Oceanography, GEOMAR Helmholtz Institute of Ocean Research, Kiel, Germany
- 2School of Ocean and Earth Science, University of Southampton, Southampton, United Kingdom
- 3Department of Ocean Systems, NIOZ Royal Netherlands Institute for Sea Research, Utrecht University, Texel, Netherlands
In this study we examine the impact of dissolved metal concentrations on the parameters that are commonly determined from complexometric titrations in seawater. We use the non-ideal competitive adsorption (NICA) model within the framework of the chemical speciation program visual MINTEQ with iron as a model metal. We demonstrate that dissolved iron concentrations effect the determined parameters for a heterogeneous binding site distribution with a fixed concentration of dissolved organic carbon. The commonly used terms “ligand concentration” and “binding constant” are therefore dependent on metal concentration, so we adopt the terminology suggested by Town and Filella (2000) and use the terms ligand quotient and stability quotient here. The systematic increase in the ligand quotient with dissolved iron concentration likely contributes toward the trend of increasing ligand quotient with dissolved iron concentration observed in field studies, and makes it hard to assign an objective meaning to the parameter. We suggest that calculation of the side reaction coefficient, a parameter that describes the probability that any added metal will be complexed, could be less prone to bias and misinterpretation than calculation of conditional stability and ligand quotients. We explore the impact of experimental design on side reaction coefficients by applying different detection windows, and multiwindow and reverse titration approaches. We identify the method that results in the best estimates of side reaction coefficients over a range of iron concentrations between 0.1 and 1.5 nmol L−1. We find that single window titrations can only reliably estimate side reaction coefficients over a limited range of iron concentrations. Multiwindow titrations provided estimates of side reaction coefficients within the 99% confidence interval of the values calculated directly from the NICA model at all iron concentrations examined here. We recommend that future reports of speciation measurements consider the potential influence of metal concentrations on the determined parameters and future studies focus on developing and applying experimental designs that improve the robustness and rigor of chemical speciation analysis in the marine environment.
Introduction
Metals that are present at concentrations lower than 1 μmol L−1 in seawater are described as trace metals. They are important as they act as nutrients (e.g., iron, copper, manganese, zinc, cobalt) and/or toxic agents to marine biota (e.g., copper, cadmium, silver). Trace metals influence marine productivity and phytoplankton community composition and therefore ultimately have an impact on the carbon fluxes into the deep ocean and the drawdown of CO2 from the atmosphere. In particular iron, manganese, zinc and cobalt have been shown to be trace nutrients with strong influences on open ocean phytoplankton productivity and community composition (Moore et al., 2013). In coastal environments, elevated inputs of metals result in perturbations of seawater chemistry that can result in ecosystem impacts (Achterberg et al., 1999; Gledhill et al., 1999; Mayer-Pinto et al., 2010). Trace metal availability is directly related to the abundance and lability of chemical species rather than to dissolved metal concentration (Sunda and Guillard, 1976; Buffle et al., 2009; Shaked and Lis, 2012). Furthermore the distribution in the ocean of trace elements like iron cannot be explained without a mechanism that maintains iron in solution at concentrations far beyond its solubility product (Tagliabue et al., 2016; Fitzsimmons et al., 2017).
The inorganic chemistry of metals in seawater is calculated from basic thermodynamic approaches (Turner et al., 1981). Over the last few decades steady improvements have been made to the constants and approaches describing inorganic metal speciation in seawater through incorporation of Pitzer equations to account for the high ionic strength in seawater (e.g., Byrne and Miller, 1985; Pitzer, 1991; Hudson et al., 1992; Millero et al., 1995; Turner et al., 2016). In contrast to our framework for modeling inorganic chemical speciation of trace metals in seawater, we have a simplistic and operational framework for understanding metal organic complexation (Gledhill and Buck, 2012; Pižeta et al., 2015) that limits our ability to identify distinct biogeochemical trends in metal speciation (Hassler et al., 2017). The complexity of DOM in the natural marine environment, coupled with the challenges of analyzing samples of high ionic strength has meant that few specific marine organic compounds have been fully identified (Benner, 2002; Hertkorn et al., 2006), and still fewer specific metal chelators quantified (Gledhill et al., 2004; Mawji et al., 2008, 2011; Velasquez et al., 2011; Boiteau et al., 2016a,b). Total organic carbon concentrations in the open ocean are of the order of 40–100 μmol C L−1, of which the major portion (~90%) is considered to be in the dissolved fraction (DOC, <0.7 μm). In coastal waters, total organic carbon concentrations are enhanced, especially within and close to estuaries (Hoikkala et al., 2014; Avendaño et al., 2016). Despite the challenges associated with the analysis of such a complex mix of components in a highly saline matrix, much progress has been made in recent years in characterizing organic matter. Improvements in extraction techniques (Green et al., 2014) and the application of high resolution mass spectrometry (Ultra high resolution Fourier transform ion cyclotron mass spectrometry, HR-FTICR-MS) has identified thousands of molecules (Koch et al., 2005; Medeiros et al., 2015) and shown that significant differences in molecular composition exist between surface and deep waters that likely relate to DOC aging processes (Hansell et al., 2012; Hansell, 2013; Medeiros et al., 2015). Mass spectrometry coupled to chromatography has also been utilized for the investigation of specific metal complexes in seawater. Specific iron binding complexes produced by bacteria (siderophores) were first determined in the Baltic Sea (Mucha et al., 1999) by capillary electrophoresis with detection by spectrophotometry. However it is becoming increasingly apparent that low concentrations of siderophores can be observed in many regions of the open ocean (Mawji et al., 2008; Velasquez et al., 2011, 2016; Boiteau et al., 2016a). Improved techniques have also recently shown that picomolar concentrations of chromatographically resolvable complexes with copper and nickel can be observed in surface waters of the Equatorial Pacific Ocean (Boiteau et al., 2016b). Furthermore broad unresolved chromatographic humps were identified for Fe, Cu, and Ni supporting the hypothesis that metals also bind with chromatographically unresolvable organic compounds (Boiteau et al., 2016a,b). In tandem with these advances, evidence has emerged that humic like materials and exopolysaccharides play an important role in metal speciation (Laglera et al., 2007; Yang and van den Berg, 2009; Hassler et al., 2011; Whitby and van den Berg, 2015). Thus it is increasingly evident that metal binding to organic matter occurs through complex interactions with many binding sites. Furthermore, such variability in DOM and thus binding site character is highly likely to result in a diverse range of binding site strengths and variable stoichiometry. For example, siderophores alone exhibit denticities of between 2 and 6 and formation constants that vary over 25 orders of magnitude (Hider and Kong, 2010).
Despite this complexity, the binding of metals to organic matter in the marine environment is currently interpreted using an adsorption isotherm that assumes a simple 1:1 stoichiometry and a limited number of binding sites (e.g., Pižeta et al., 2015). Typically, a Langmuir type isotherm is applied to metal titration curves and a conditional stability constant and the apparent ligand concentration of a group of binding sites, i, (Li) derived. The Langmuir type isotherm approach has been useful in showing that organic matter plays an important role in metal biogeochemistry (see e.g., Gledhill and Buck, 2012 and references therein). The conditional approach means results cannot be extrapolated beyond the conditions of analysis (Town and Filella, 2000). The conditions influencing determined and Li are normally considered to be pH, temperature and salinity. However, binding site heterogeneity means that the ratio between the metal and the available binding sites is also a condition that influences the determined “constants,” a factor first pointed out over 15 years ago (Town and Filella, 2000). In practice, this means that if binding site concentrations remain the same but metal concentrations change, then the apparent concentration of Li will vary. Naturally, such behavior makes it challenging to establish links between , Li and the biogeochemical cycle of carbon and this limits our ability to incorporate organic complexation into seawater chemical speciation models (Turner et al., 2016). The dependence of and Li on the ambient conditions of the sample has led to a suggestion that the term “quotient” be used to describe and Li (Town and Filella, 2000), a practice that we adopt in this study. Iron is used as the example metal because an extensive oceanic data set has recently been made available (Caprara et al., 2016). Furthermore, the principles and challenges described here have previously been demonstrated for other trace metals that bind with organic matter in seawater (Town and Filella, 2000). The consequences of variable metal to binding site ratios for and Li quotients for a heterogeneous mix of binding sites are demonstrated through calculations in the speciation program visual MINTEQ (Gustafsson, 2012) using the non-ideal competitive adsorption (NICA) model of fulvic acid (FA). Since trace element concentrations in the open ocean can vary by more than an order of magnitude (De Baar and De Jong, 2001; Morel and Price, 2003), while DOC concentrations only vary by a factor of two (Hansell, 2013), we illustrate the impact of changing metal to binding site ratios by keeping the DOC concentration constant and varying iron concentrations. We simulate titrations employing different experimental designs in an effort to find a strategy capable of reliable determination of metal speciation given heterogeneous binding sites, and thus provide the best estimate of the ratio of bound to inorganic species in a sample. Our overall aim is to improve understanding of how parameters describing metal speciation can be linked to other biogeochemical properties in the ocean, such as pH and DOC concentrations.
Methods and Approach
The principles behind complexometric titration experiments have been described extensively elsewhere (Gerringa et al., 2014; Laglera and Filella, 2015; Pižeta et al., 2015). Conditional stability quotients () describe the apparent strength of a single or group of binding sites (Li), assumed to complex with 1:1 stoichiometry (Town and Filella, 2000). They are related to the concentration of complexed metal ([MeLi]), the concentration of unbound metal ([Me′]) and the concentration of binding sites that are available for complexation by the metal ([]).
In addition to conditional stability quotients, side reaction coefficients are also utilized for describing complex equilibrium processes (Ringbom and Still, 1972). The side reaction coefficient describes the likelihood a particular complex will form given the presence of competing ions within a complex mixture. For the formation of metal complexes with organic binding sites, it can be derived from two expressions
The side reaction coefficient will thus describe the ratio of bound to inorganic metal for a particular sample. An inorganic side reaction coefficient or side reaction coefficient for the unbound metal () likewise describes of the sum of all the concentrations of inorganic ion pairs divided by the free metal concentration.
Adsorptive cathodic stripping voltammetry (AdCSV) is most commonly utilized for complexometric titrations in the marine environment. AdCSV requires the addition of a ligand (the added ligand, AL) that reacts with the metal and allows the metal complex to be adsorbed onto the mercury drop and undergo electrochemical reduction. The electroactive complex redistributes metal species within the sample, lowering the concentration of Me′ and MeLi in the analyzed sample in proportion to the known strength of the MeALx complex, and thus allowing for the calculation of Me′ and MeLi. The relationship between the concentration of MeLi and Me′ is interpreted as a Langmuir adsorption isotherm, and and Li derived. An important assumption of the Langmuir isotherm is that all sites are equal, an assumption known to be incorrect in practice. Application of “multiwindow” methods, that vary the amount of metal bound by AL through varying the AL concentration, with interpretation of data as composite isotherms (i.e., consideration of two or more Li) have been proposed as ways of accounting for the presence of more than one type of binding site, whilst still allowing for the application of the Langmuir isotherm (van den Berg et al., 1990; Buck et al., 2007; Sander et al., 2011). Further improvement to the range of ligands that can be detected has been achieved through unification of multi-window datasets based on mass balance equations (Hudson et al., 2003; Sander et al., 2011; Wells et al., 2013; Pižeta et al., 2015), but this approach has yet to be applied widely in the field. The likelihood that the metal-added ligand complex will form is described by its own side reaction coefficient , which is also thought to define the “detection window” encompassing the spectrum of binding sites that can be detected under the applied conditions. During a titration, is assumed to remain constant, while decreases as a result of adding the metal (Equation 3). Furthermore consideration of Equation (2) makes it clear that when multiple binding sites are present, the initial metal concentration will also determine whether a binding site of a given strength will be detected, since, as any given L′i → Li, αMeL → 0.
In order to illustrate the potential importance of initial metal concentration for and Li the speciation program visual MINTEQ v. 3.0 (Gustafsson, 2012) was used to simulate titrations of diethylenetriaminepentaacetic acid (DTPA) and fulvic acid type organic matter. Binding site heterogeneity was represented using the NICA model. Thermodynamic stability constants for DTPA were from the NIST database (Martell and Smith, 2004). The NICA model is described extensively in Milne et al. (2003) and references therein. Briefly, the NICA model as applied in this study describes a heterogeneous bimodial distribution of binding sites. The two groups of binding sites are generally thought to encompass acidic (carboxylic like) and a basic (phenolic like) functional groups (Kinniburgh et al., 1996; Koopal et al., 2005). Although the NICA model is used in this study to describe heterogeneous binding, the observations are likely valid for any heterogeneous distribution of binding sites as the issue highlighted here relate to the presence of a diverse mix of binding sites of different strengths and are not restricted to a particular binding site distribution (see e.g., Turoczy and Sherwood, 1997; Town and Filella, 2000; Pižeta et al., 2015). Major ions (Na+, K+, Mg2+, Ca2+, Sr2+, Cl−, , Br−, , H3BO3, F−) concentrations, adjusted for a salinity of 35 were used to calculate and correct for ionic strength in visual MINTEQ. Ionic strength corrections were made using the Davies and Debye-Hückel equations. pH was set to 8.05 and temperature 20°C. The solubility and equilibrium constants from Liu and Millero (1999) were used to calculate iron hydroxide concentrations. The NICA parameters derived for Fe3+ for shelf sea waters in Avendaño et al. (2016) and the generic NICA parameters for H+, Ca2+, and Mg2+ described in Milne et al. (2003) were used in the model assuming dissolved organic carbon (DOC, 64 μmol L−1) was present as FA. Although the Donnan model was not excluded from the calculations, the Donnan volume is very small at the ionic strength of seawater and thus no iron was calculated as adsorbed in the Donnan layer. The added ligand, 1-nitroso-2-naphthol (NN), was included in visual MINTEQ for titration simulations (Gledhill and van den Berg, 1994; Avendaño et al., 2016). Three experimental designs for titrations were tested, each incorporating a total of 15–18 data points per titration. (1) single window “forward” titrations at three different detection windows ( = 146, 1,164 and 1.46 × 105, [NN] = 0.5, 1, and 5 μmol L−1), employing iron additions of between 0.5 and 8 nmol L−1. (2) A “reverse” titration, where the added ligand concentration was varied between 0.5 and 150 μmol L−1. (3) A “multiwindow” method, employing reduced resolution forward titrations at two different detection windows ( = 146 and 9,310, [NN] = 0.5 and 2 μmol L−1). A high detection window ( = 9.3 × 106, [NN] = 20 μmol L−1) was included in the simulation as an “overtitration” mechanism for validating the calibration of the slope (Pižeta et al., 2015). The added iron range was extended to cover the range 0.5–30 nmol L−1 (Garnier et al., 2004). Eleven separate titrations were simulated for initial dissolved iron (DFe) concentrations of between 0.05 nmol L−1 and 1.5 nmol L−1.
Simulated concentrations of iron bound to NN calculated in visual MINTEQ were used to calculate and Li whilst making a one or two ligand assumption using the complete fitting approach of Garnier et al. (2004) within the speciation program ProMCC (Omanović et al., 2014). The conditional stability constant for NN was set at log = 21, as this was equivalent to the value calculated from the visual MINTEQ data. This is stronger than the range of values typically given in the literature (17–19) (Hawkes et al., 2013; Gledhill et al., 2015), a factor which is likely related to the ionic strength correction mechanism in visual MINTEQ. For the forward titrations the slope was fitted along with and Li, as is usual for the complete fitting approach (Garnier et al., 2004). Even though the calculated FeNN3 concentration was used to fit the data, the slope did not always equal 1 (especially at lower detection windows), since a small portion of the total metal concentration remained bound to very strong binding sites. For the unified multi-window approach, a slope of 1 was assumed as this approach incorporated an overtitration at a high detection window, when all added iron is calculated to be present as FeNN3.
Simulated reverse titrations (Nuester and van den Berg, 2005; Hawkes et al., 2013) varied the concentration of NN between 0.1 μmol L−1 and 150 μmol L−1. The side reaction coefficient αMeL was determined using non-linear least squares regression of the expression
where [FeNN3]max is the maximum [FeNN3] concentration observed in the titration. The regression fit was carried out within the computer program R (R Development Core Team, 2016).
For the multiwindow method, the unified Sander-Wells method (Sander et al., 2011; Wells et al., 2013) in ProMCC (Omanović et al., 2014) was used to transform the data and derive log() and Li.
Side reaction coefficients in the absence of the added ligand for DFe concentrations between 0.1 and 1.5 nmol L−1 were calculated directly from the visual MINTEQ output obtained when the concentration of [NN] = 0, using Equation (3). The sum of the dominant inorganic species (, Fe(OH)3, and ) were taken to equal [Fe′] and the sum of the organic species (Fe(III)FA1, Fe(III)FA2, where FA1 is the acidic fraction and FA2 is the basic fraction) taken to equal [FeL].
Side reaction coefficients from and Li were calculated using Equation (2). The excess ligand () can be obtained by subtracting DFe from [Li]. However, as [Li] approaches DFe, needs to be calculated by iteration in order to reduce error associated with subtracting two very large numbers in order to obtain a small number. We therefore used R to apply Newton's algorithm (Press et al., 1986) and iteratively resolved the following two equations
to obtain a solution for [Fe′] and , where is the conditional stability quotient with respect to the free iron concentration.
A smaller set of multiwindow titrations were simulated at higher iron concentrations in order to investigate the impact of the existence of an inert colloidal DFe fraction that did not dissolve within the time frame of a typical titration experiment (<24 h). The inert fraction was constrained by solubility—in other words the concentration of the ligand (in this case the hydroxide ion) was not limited, to allow for formation of a solid phase. The inert fraction was thus simulated by adding ferrihydrite as a possible solid in the visual MINTEQ environment and then calculating the speciation of the simulated sample in the absence of NN. The precipitated ferrihydrite concentration was then subtracted from DFe concentrations to give a soluble iron concentration (sFe) and the titration simulated in visual MINTEQ. However, as the inert fraction would still be determined as DFe if it is small enough to be present as a colloid, it was re-added to the sFe concentration prior to transformations of titration data in ProMCC.
Results and Discussion
Influence of the Dissolved Metal Concentration on the Determined Binding Site Concentration and Conditional Stability Constant
The simulated titration data obtained for DFe between 0.05 and 1.5 nmol L−1 is shown in Figure 1. The difference between forward titrations undertaken with a simple single ligand (DTPA) and DOC characterized by a heterogeneous mix of binding sites (NICA-FA) is shown in Figure 1A. It is clear from this figure that the slope of the upper part of the titration curve for DTPA is the same as that observed in the absence of organic matter (slope of linear part (S) = 1), while that obtained for the NICA-FA is lower as a result of the presence of weak binding sites (S = 0.8 for [NN] = 0.5 μmol L−1, = 146). Thus the titration of NICA-FA does not reach a well-defined end point, a problem which is known to cause bias in transformed data (e.g., Turoczy and Sherwood, 1997; Garnier et al., 2004; Pižeta et al., 2015). Forward titration curves of DTPA and NICA-FA using different starting dissolved Fe concentrations all overly each other so that although all 11 simulated titrations are plotted on the graph, only one curve is observed. In Figure 1B, the reverse titration curves simulated at different iron concentrations are visible, but again in the multiwindow method (Figure 1C) data from the 11 different titrations are not distinct since all curves overlie each other. Titration data shown in Figure 1C shows how the slope can be expected to increase (and approach a value of 1) as the applied detection window increases.
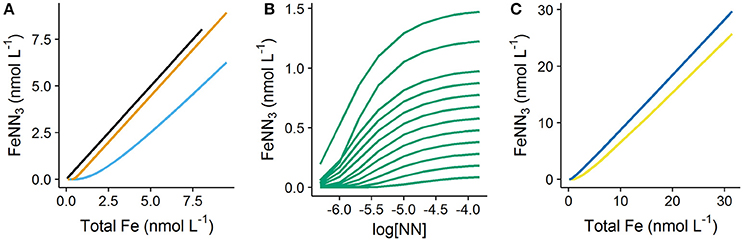
Figure 1. Titrations simulated in visual MINTEQ using 1-nitroso-2-naphthol (NN) as the added ligand. Eleven simulations were undertaken with increasing starting DFe concentrations (0.05–1.5 nmol L−1). (A) Single window forward titrations (iron additions to 8 nmol L−1) of seawater with no organic matter (black line), seawater with 0.5 nmol L−1 diethylenetriaminepentaacetic acid (orange line) and seawater with 64 μmol L−1 dissolved organic carbon as fulvic acid (sky blue line). The graph illustrates titrations simulated with the lowest detection window applied in this study ( = 146). (B) Reverse titrations (NN concentrations increased) of seawater with 64 μmol L−1 dissolved organic carbon as fulvic acid and (C) “Multiwindow” forward titrations of seawater with 64 μmol L−1 dissolved organic carbon as fulvic acid. Two different detection windows were used, = 146 (yellow line) and = 2,348 (dark blue line). The applied initial dissolved iron concentrations are clearly visible in (B), but not visible in (A,C) as the individual titration curves overly each other.
Figure 2 plots log and Li obtained from transformations of the titrations obtained for DFe concentrations. The impact of complexity on log and Li can be observed by comparing results obtained for DTPA and NICA-FA. For DTPA, the expected log of 13.6 and the correct concentration of 0.5 nmol L−1 was obtained irrespective of the NN concentration, although when DTPA was saturated with Fe, a small decrease in log with increasing DFe concentration was observed. Likewise, the fitting error increased at higher DFe concentrations as the number of datapoints (and thus the degrees of freedom) below the equivalence point of the titration decreased.
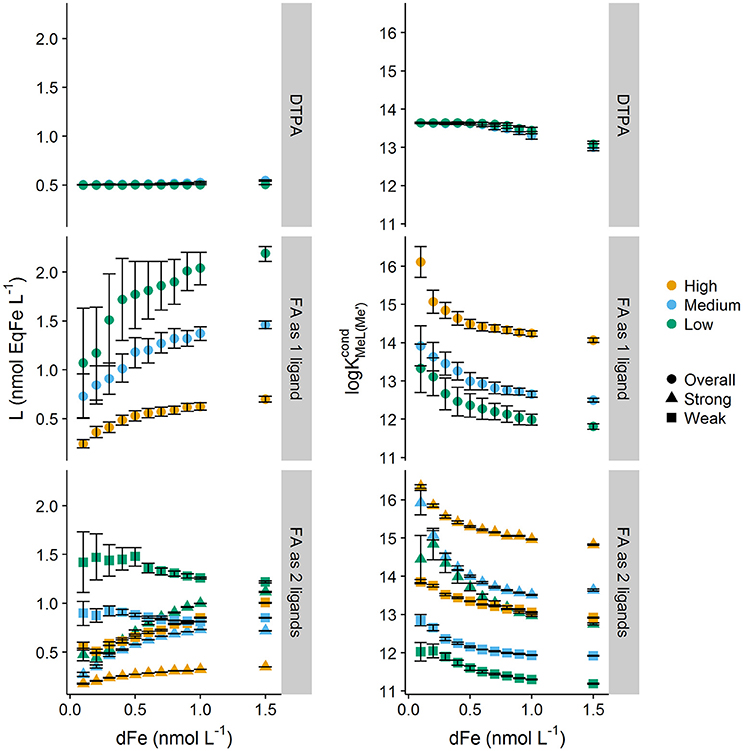
Figure 2. Ligand and conditional stability quotients obtained from simulated forward titrations with different starting dissolved iron concentrations (0.1–1.5 nmol kg−1) of diethylenetriaminepentaacetic acid (DTPA, [L] = 0.5 nM, = 13.6) and a heterogeneous mix of binding sites described by the NICA model of fulvic acid (DOC = 64 μmol L−1) interpreted as only one ligand, and as two ligands. Three different added ligand concentrations were used to simulate titrations applying a high, medium and low detection window. Symbols indicate apparent class of ligand strength, where overall is the ligand class obtained when transformations only considered one ligand class to be present, and strong and weak differentiate the ligand classes for the two ligand transformations. Error bars represent 95% confidence intervals.
For NICA-FA, the determined parameters depended on applied conditions including the dissolved iron concentration. Calculation of log and Li assuming a one ligand model resulted in a trend of increasing Li with metal concentration, coupled with a decrease in log . An assumption of two ligands resulted in a more constant Li concentration across the range of metal concentrations for the weaker of the two assumed ligands, but a marked increase in Li concentration for the stronger ligand, so that the sum of all ligand quotients (Σ Li) still increased with dissolved metal. For both determined ligands log decreased with increased DFe. Overall, it can clearly be seen that categorizing binding sites into “strong” and “weak” in this context becomes rather difficult, since the relative strength and concentration varies according to both the detection window and the dissolved metal concentration (Town and Filella, 2000).
The influence of detection windows on conditional stability constants has been discussed extensively since the concept was introduced by Apte et al. in 1988 (Apte et al., 1988; van den Berg et al., 1990; Town and Filella, 2000; Hudson et al., 2003; Pižeta et al., 2015). Figure 2 also illustrates the impact of changing the detection window on our series of simulated single window iron titrations of NICA-FA. The three detection windows applied were = 146, 1,164 and 1.46 × 105. For a complex mixture of binding sites, log increased at higher detection windows and Li decreased. For the lower detection window coupled with the one ligand model, which is more typical of the approaches adopted for the analysis of field samples (e.g., Buck et al., 2012), varied by less than one order of magnitude over the modeled range of iron concentrations. The observed NICA-FA fitting error distributions were also contrary to that observed for DTPA titrations. For NICA-FA the largest errors for both log and Li were obtained at the lowest DFe concentrations. This most likely arises because it is at these concentrations that the most diverse and heterogeneous range of sites are available for binding, and thus the titration curve deviates most strongly from the Langmuir model.
Results from application of the multiwindow Sander-Wells method are show in Figure 3. Similar trends are observed for the mutliwindow experimental design and Sander-Wells fitting method as are observed for the single window methods, i.e., increasing metal concentrations results in increased Li and decreases in log . Interestingly, for the one ligand assumption, the errors in Li increased with increasing DFe (as for the Langmuir model and DTPA), which suggest that error pattern observed for the multiwindow fit is as would be expected from a reduction in degrees of freedom. The two ligand assumption resulted in a high estimate for the weak ligand quotient, associated with a high error.
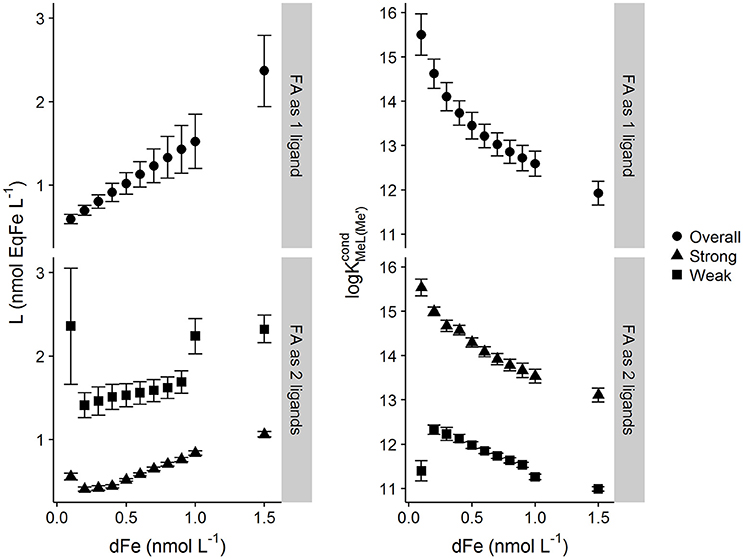
Figure 3. Ligand and conditional stability quotients obtained from simulated multiwindow titrations of a heterogeneous mix of binding sites described by the NICA model of fulvic acid (DOC = 64 μmol L−1) with different starting dissolved iron concentrations (0.05–1.5 nmol kg−1). [Li] and log were calculated using the unified Sander–Wells method within the computer program ProMCC. Titrations were interpreted as one overall ligand and as two ligands (“weak” and “strong”). Error bars represent 95% confidence intervals.
Overall, the results obtained from applying a Langmuir type isotherm to a heterogeneous mix of binding sites across a range of metal concentrations confirm that it is inappropriate to assign an objective meaning to Li and that the dependence of Li on the dissolved metal concentration likely obfuscates meaningful biogeochemical interpretation of complexation quotients in the ocean (Town and Filella, 2000). The trend arising from changing metal concentrations (or more strictly speaking—changing metal to binding site ratio and thus changing ), is associated with the fact that stronger binding sites are filled first, thus at higher metal concentrations, only lower strength binding sites will be available for complexation by the metal added during the titration (Town and Filella, 2000). The side reaction coefficients of competing metals will also impact on the concentration of available sites. The bias is exacerbated by problems associated with calibrating the method, where a priori assumptions are made about the number of ligands present in the sample that influence the estimation of the slope in the titration curve and thus impact on the estimation of bound metal (Turoczy and Sherwood, 1997; Hudson et al., 2003; Gerringa et al., 2014; Pižeta et al., 2015). The determined Li of natural organic binding sites with a heterogeneous distribution thus depends (a) on the number of ligands considered in the data treatment approach and (b) on the relative concentrations of binding sites and competing metals present in the sample. Increasing the detection window results in systematic shift of this bias to the determination of higher log and lower Li, since weaker binding sites cannot be filled by the metal as the added ligand is outcompeting these binding sites.
The result of this bias in for the determination of log and Li in real world samples should be a general trend of increasing Li and decreasing log with DFe as has been reported previously for other metals (Town and Filella, 2000). A trend of increasing Li with iron has been shown in a recently published global ligand compilation (Caprara et al., 2016). The correlation between DFe and Li increases in significance if only deep water samples are selected. DFe and ligand quotients are positively correlated in this data set (>500 m, r = 0.64, n = 669, p < 0.001; Figure 4A), which is interesting as DOC concentrations and composition are known to be relatively constant at depth (Hansell, 2013). Furthermore, fitting errors for Li were highest when Li was high compared to DFe (i.e., high excess Li), as would be expected for a heterogeneous distribution of binding sites (Figure 4 and Supplementary Figure 1). In contrast, the fitting error for log increased as the excess Li decreased (Figure 4 and Supplementary Figure 1), suggesting that the number of data points acquired below the equivalence point (and thus the degrees of freedom) also has an impact of the fitting error for log . Correlations between DFe and Li can also be observed in individual studies such as the data obtained from the Western Atlantic GEOTRACES cruise (r = 0.35, n = 162, p < 0.001; Figure 4B; Gerringa et al., 2015). The potential that such a relationship may in fact result from a methodological bias in combination with variability in binding site concentration arising from changes in DOC concentrations or character is rarely addressed in the literature, but does bring into question the idea that metal concentrations and ligand quotients are somehow biogeochemically tightly coupled (e.g., Gledhill and Buck, 2012; Hassler et al., 2017). The interdependence of Li on DFe almost certainly hinders our ability to link metal speciation to biogeochemical parameters commonly used to quantify changes in DOC concentration or composition (Hassler et al., 2017). This interdependence also means that iron concentrations in the titrated sample should ideally be determined and used in the calculations, since commonly applied sample storage methods (e.g., freezing) may change the dissolved iron concentration in the titrated sample. For example Gerringa et al. (2015) showed a loss of 13% of DFe when samples from the Western Atlantic were frozen as opposed to acidified. Furthermore the proportion of DFe lost could also be dependent on the dissolved iron and binding site concentrations.
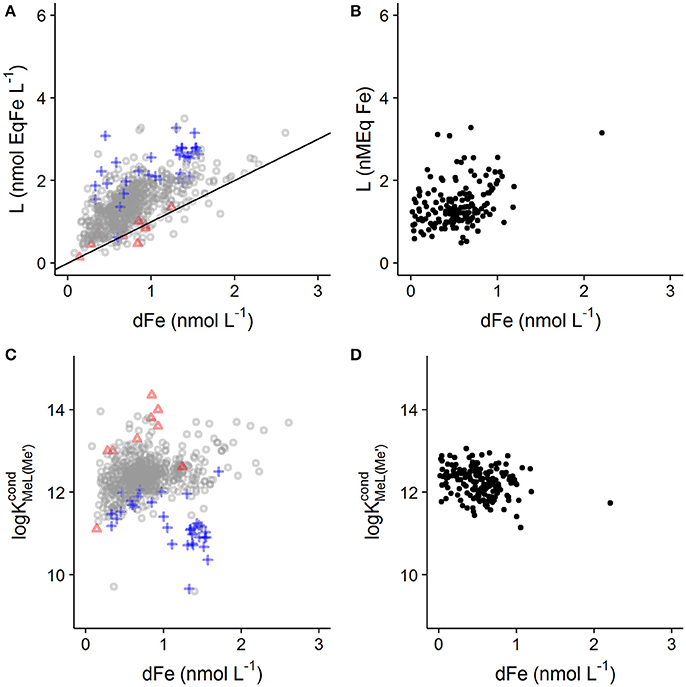
Figure 4. Relationship observed between dissolved iron concentration, Li and log . (A,C) Show Li and log for deep ocean samples (>500 m) from a global compilation (Caprara et al., 2016). Values of Li with 95% confidence intervals >0.4 nmol EqFe L−1 are illustrated with blue crosses, whilst values of log with 95% confidence intervals >1 log unit are displayed as a red triangle. It should be noted that not all values in the data set have associated confidence intervals. (B,D) Show data from the Western Atlantic GEOTRACES cruise (Gerringa et al., 2015). This data set was filtered to remove values of Li with 95% confidence intervals > 0.4 nmol EqFe L−1. A 1:1 line is added to (A) show where concentrations of excess ligand are very low.
Although a weak positive correlation between DFe and log is observed in the deep sea data (r = 0.101, n = 667, p = 0.009; Figure 4C), it is known that individual laboratory practices such as choice of added ligand can strongly influence determined log (Buck et al., 2016). Thus it could be that practices employed by different laboratories influence the global relationship between DFe and log . In support of this, all of the data points with log <11 were obtained using NN as the added ligand, either at pH 6.9 (Witter and Luther, 1998), or using bromate as a catalyst (Boye et al., 2006), whilst weak but significant negative correlations can be apparent in datasets reported from individual laboratories (r = −0.25, n = 162, p = 0.001, Figure 4D, Gerringa et al., 2015).
It is also worth considering here detection limits for the determination of the iron-added ligand complexes and the constraints they impose on the determination of high log at low iron concentrations. Detection limits for the most commonly applied voltammetric methods are given in Table 1 and are typically of the order of 0.1 nmol L−1. Our simulated titrations suggest that a concentration of 0.1 nmol L−1 FeNN3 would not be observed until 0.5 nmol L−1 of total Fe at the higher detection window, and 1.2 nmol L−1 total Fe at the lower detection window. Thus an inability to confidently quantify low MeALx concentrations, will also have a detrimental effect on our ability to observe high log . Any increases in log in the large data set that might arise from decreases in dissolved iron could thus be lost because of variability produced by e.g., use of different added ligand, changing salinity, temperature of titration and titration pH that also influence log.

Table 1. Detection limits reported for the determination of iron by cathodic stripping voltammetry using different added ligands.
The Potential Influence of an Inert Fe Fraction
The discussion of influences on and Li in Section Influence of the Dissolved Metal Concentration on the Determined Binding site Concentration and Conditional Stability Constant above assumes that iron is present only in dissolved forms that are in equilibrium with the added ligand. However it was recently pointed out in Avendaño et al. (2016), that the interpretation of titration data can also be influenced by inert species that do not react with the added ligand on the timescale of the titration experiment. Such inert species could include e.g., aged oxyhydroxides or other colloidal minerals that exceed their solubility product in the sampled seawater and that take a long time (>24 h) to equilibrate with the added ligand (Town and Van Leeuwen, 2005; Fitzsimmons et al., 2017). The kinetics of ligand assisted dissolution can vary considerably from ligand to ligand as a result of ligand solubility, hardness and denticity (Kraemer, 2004), so that although 15 min has been reported to be effective for dissolution of fresh oxyhydroxides by salicylaldoxime (Abualhaija and van den Berg, 2014), such dissolution rates may not be observed for all added ligands used in AdCSV. Inert DFe will not (by definition) be in equilibrium with the added ligand but in titration data such species will manifest as “strong” ligands. Furthermore, if this inert fraction is determined by solubility rather than complexation, then the concentration of the inert fraction will increase with increasing iron concentration (Avendaño et al., 2016). Theoretically, datasets where such behavior occurs can be identified by careful examination of titration curves. In particular examination of equivalent data points (i.e., same concentration of metal added) from separate titration curves from an entire dataset can be illuminating. Figure 5 shows the expected trend in the concentration of FeALx with increasing iron concentration for equivalent titration points (8 nmol L−1 added Fe) obtained for hypothetical samples with increasing DFe, but where binding site concentrations and organic matter composition do not change. In a system in equilibrium, increased iron concentrations will result in increases in both FeALx and FeLi. Importantly an increase is still observed even if the strength of FeLi is much greater than FeALx. However, in the presence of an inert fraction, then FeALx will not increase with total iron, and the equivalent points of the titration curves will simply be shifted to the right (along the blue line in Figure 5). Such a trend was observed for data in Avendaño et al. (2016), and datapoints from this study determined for pH 8, 8 nmol L−1 iron addition are presented along with the theoretical lines in Figure 5. Of course the interpretation of titration data in real data sets has added complexity because binding site concentrations and organic matter composition do vary with sample origin. Nevertheless, the fundamental principle that FeALx should increase in proportion to the total Fe concentration in a system in equilibrium should be kept in mind when considering titration data sets obtained for regions where variability in Fe concentrations far exceed changes in DOC concentration. Such systems include hydrothermal vent fields, or experiments investigating speciation in soluble vs. dissolved phases.
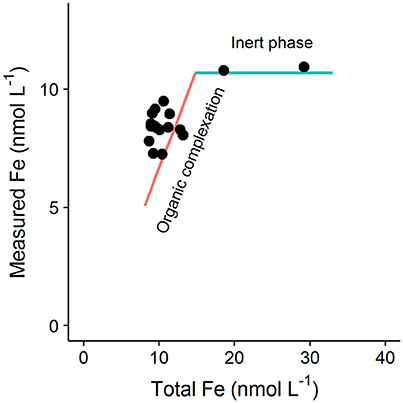
Figure 5. Schematic showing the theoretical change in the concentration of Fe measured for a given titration point (i.e., same added metal concentration) across a dataset if the total Fe concentrations (DFe plus added Fe) vary, but the binding site composition and concentration stay the same. The red line shows the expected behavior for a system in equilibrium, i.e., if DFe is labile to the added ligand and a reaction occurs. If the measured iron concentration fails to increase despite increasing total Fe (blue line) then this is indicative of an inert Fe fraction (e.g., aged oxyhydroxides). Black data points are equivalent titration points (black points) obtained by Avendaño et al. (2016) (8 nmol L−1 iron addition).
What Do We Need to Know?
As with any analysis, it is important to consider the ultimate application of the generated data. In most cases the critical factors are understanding bioavailability and the balance between scavenging and solubility. For both these processes determination of the uncomplexed iron (Fe') concentration could be useful since this is the species that is thought to be most likely to be scavenged and also be the most bioavailable. Fortunately, it is possible to deduce this information from speciation measurements via calculation of side reaction coefficients using Equations (2) or (3).
Figure 6 shows side reaction coefficients obtained from applying Equation (1) to results obtained for discrete ligand approaches with varying detection windows (high, medium, low, multi) and transformation types (1 ligand assumption, 2 ligand assumption). Results are compared to side reaction coefficients obtained by applying equation 2 directly to the species concentrations calculated in vMINTEQ (shown on Figures 6A,B as NICA-FA values). For a one ligand assumption, the high detection window ( = 1.46 × 105) resulted in estimates of within the 99% confidence interval of the NICA-FA side reaction coefficient at DFe < 0.4 nmol L−1 (Figure 6). At DFe concentrations over 0.4 nmol L−1 [Fe′] is no longer determined by the stability quotient obtainable at this detection window and the calculated side reaction coefficient thus deviated strongly from the NICA-FA value. The medium and low detection windows underestimated αMeL at low DFe but converged on the NICA-FA value of as the ligand quotient approached the DFe concentration. These trends corresponded with trends observed for the fitting errors shown in Figure 2, which in turn relate to how much heterogeneity can be observed when applying the single detection window/one ligand assumption approach. The two ligand assumption improved the estimation of for the low and medium windows, although obtaining a good estimate cannot be guaranteed as poor estimates were still obtained for medium and low detection windows at the lowest and highest DFe concentrations. A systematic bias toward an overestimate in was observed for the high detection window at all but the lowest DFe concentration. This is most likely because the high detection window reduces the observable heterogeneity in the sample and this renders a two ligand fit inappropriate.
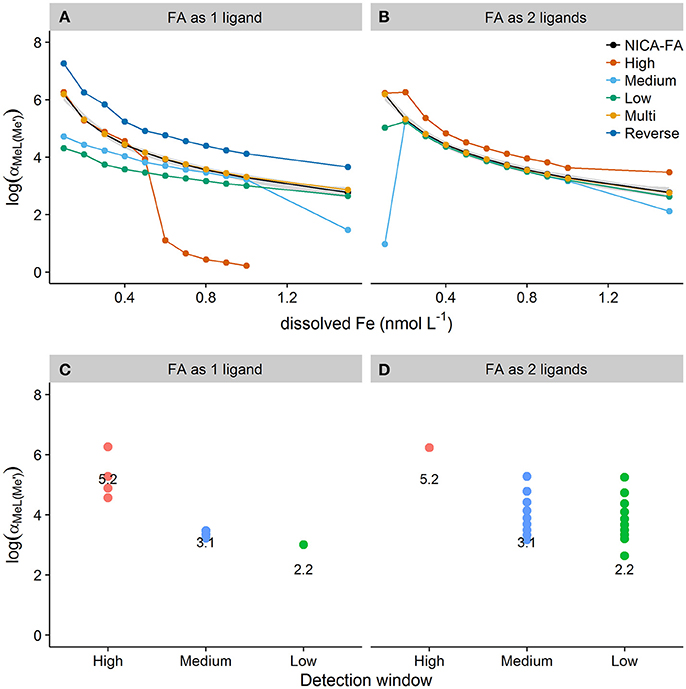
Figure 6. The top panel (A,B) shows side reaction coefficients calculated from the product of the conditional stability quotient and the unbound or excess ligand quotients obtained for simulated titrations of seawater containing a heterogeneous distribution of binding sites and dissolved iron concentrations between 0.1 and 1.5 nmol L−1. Titrations were simulated applying high, medium and low detection windows or reverse and multwindow methods and assuming one (A) or two (B) ligands. Side reaction coefficients calculated directly from the ratio of bound to unbound metal obtained for NICA-FA in visual MINTEQ are shown in black. The 99% confidence interval for the NICA-FA side reaction coefficient is shown as the gray shaded area. The bottom panel (C,D) shows plots of the subset of data from (A,B) where side reaction coefficients determined from log and excess Li were within the 99% confidence interval of NICA-FA side reaction coefficients for the one ligand assumption (C) and the two ligand assumption (D). The value of log() for each detection window is overlaid as text onto the plot.
The relationship between the detection window (i.e., log(αFeNN3(Fe′))) and the range over which log() could be confidently estimated using the one ligand fit was not linear or apparently straightforward (Figures 6C,D), making it difficult to recommend a particular protocol for any given sample. However, it can be seen that for a one ligand fit a higher detection window is required to estimate at low iron concentrations, whilst lower detection windows are more suitable for estimation of at higher DFe concentrations. Application of the two ligand model effectively widens the detection window (to three orders of magnitude above ) and widens the range of DFe concentration that results in agreement (within the 99% confidence interval) with NICA-FA values calculated from vMINTEQ. However, it is the application of mutliwindow titrations in combination with the unified fitting method that results in the best estimates of the side reaction coefficient at all DFe concentrations tested in this study—assuming both 1 and 2 binding sites. As the assumption of one ligand allows log() to be estimated to within the 99% confidence interval of log() for NICA-FA, the accompanying ligand and stability quotients can be thought of as “overall” quotients. Furthermore it appears that whilst a discrimination between two or more ligand classes is not strictly necessary for the confident calculation of (Town and Filella, 2000), provided the multiwindow experimental design is utilized, it is necessary for a single window experimental design. Unfortunately, the two ligand model is often very difficult to apply, as analytical errors particularly at low concentrations of FeALx often result in unsuccessful fits. We therefore suggest that the optimal and most robust experimental approach for metal titrations would be to estimate the side reaction coefficient using a multi-window experimental design with a one ligand model.
Side reaction coefficients can be directly determined via reverse titrations using Equation (4). However, simulation of reverse titrations with subsequent non-linear derivation of shows that this approach results in overestimation of the side reaction coefficient across the range of iron concentrations examined. This is most likely because the method is biased toward the fraction of ligands that are complexed by the metal. This actually results in a significant disadvantage for reverse titrations in the case of iron since it is quite possible that the solubility product will be exceeded before full ligand saturation is achieved, resulting in further complications in interpretation (see Section The Potential Influence of an Inert Fe Fraction above). Furthermore, it is impractical to carry out reverse titrations at low iron concentrations, since the sensitivity of voltammetric methods is not high enough to register a sufficient response for confident fitting of non-linear models.
Determination of the side reaction coefficients and free metal concentrations does not provide information related to the biogeochemistry of the binding sites themselves (Hassler et al., 2017). However, in future it may be better to employ techniques that measure specific properties and concentrations of the ligand pool to investigate these compounds (Mawji et al., 2008; Velasquez et al., 2011, 2016; Boiteau et al., 2016a,b) rather than inferring properties and concentrations from measurements of the metal. It should also be noted here that as this is a simulated study, these results cannot be used to identify the actual optimal conditions for sample analysis—multi-window analysis of real seawater samples are required to show this (Wells et al., 2013; Bundy et al., 2014). However, improved knowledge of how side reaction coefficients vary with metal concentrations, DOC and pH could provide basic information on how probable iron binding is within a sample, and thus allow us to improve our conceptual model of metal speciation in seawater. An understanding of the probability of complexation would allow for testing of the validity of the NICA model for marine DOM and also improve the NICA parametrization for trace metal complexation by marine DOC.
Considerations for Future Studies
The critical importance of determining metal speciation with improved accuracy and robustness is without doubt, yet our analysis suggests that current practices applied to the investigation of this problem are not robust enough to account for the potential complexity of our samples. We have simulated the potential influence of the ambient metal concentration on determined complexation parameters. We have used variation in the concentration of one metal to show how the commonly determined parameters and Li can vary if metal to binding site ratio varies. It should also be noted that changes in the ratio of the metal of interest to other competing metals will also impact on and Li. In addition to these issues, there are other important factors that should be considered when studying metal speciation in natural waters. As already highlighted, a fundamental assumption of our conceptualization of metal complexation in seawater is that the system is at equilibrium. A recent review by Laglera and Filella (2015), has thoroughly covered the subject of ligand exchange processes and their (lack of) investigation in the field of marine metal speciation studies and so this topic is not covered in depth here. Again, this issue is likely to have a particular impact on iron (Laglera and Filella, 2015) and relatively few studies have actually undertaken investigations into the kinetics of metal ligand formation and dissociation (Witter et al., 2000; Gerringa et al., 2007; Croot and Heller, 2012). Nevertheless recent field determinations of hydrothermal derived colloidal and soluble iron in the deep ocean suggest that there are processes, that could be phase changes or reactions, that likely take many years to reach equilibrium (Fitzsimmons et al., 2014, 2017). Thus, there is clearly a need to undertake more kinetic studies in order to improve our mechanistic understanding of the mode of formation and dissociation of metal complexes. As the time scale to reach true equilibrium may be very long, it is likely necessary to combine short term laboratory studies with isotopic observations in order to fully constrain the kinetics of marine trace metal chemistry. In addition, other titration approaches could be employed to improve our understanding of the importance of kinetic processes. Liu and Millero (2002) have shown that organic complexation in seawater only has an impact on solubility between pH 6 and 10. Thus it may be possible to investigate the proportion of DFe that is in short term equilibrium (<24 h) with binding sites by reversibly adjusting sample pH—i.e., undertaking pH titrations. pH titrations could also have the added bonus of allowing for increased certainty in predictions of changes in metal complexation over the pH range observed in contemporary and the future oceans.
Overall, the development of new, more sensitive methods with improved quantification of individual species would be highly beneficial to the determination of the speciation of iron and other metals in seawater. Recent developments (Mawji et al., 2008; Boiteau et al., 2016a,b; Velasquez et al., 2016) suggest we are on the cusp of a proliferation of novel techniques with exciting potential for analyzing specific metal complexes in seawater. Thus, we can look forward to a much improved knowledge base on specific metal complexes in the ocean in the coming years. In order to obtain a prognostic model of metal speciation in seawater however we also require kinetic and thermodynamic information. Electrochemistry is still the method most often employed for such studies in seawater. In this paper we have highlighted how complexation parameters change with changes in the relative concentrations dissolved metal concentration and DOC, and thus raised the question of how to assign objective meaning to the parameters [Li] and log which are commonly determined during titrations. The calculations undertaken as part of this study led to the hypothesize that determination of the side reaction coefficient for a given sample maybe informative as this overcomes potential bias resulting from a priori assumptions about the number of different types of binding sites. Furthermore, this study suggests that the multiwindow method coupled with the determination of overall ligand and conditional stability quotients is required for the determination of accurate side reaction coefficients at all metal concentrations, since use of one detection window will bias results obtained at either high or low metal concentrations, depending on the detection window and data transformation approach adopted. Thus further experimental optimization of the multiwindow approach would be beneficial for application to large scale open ocean campaigns.
A further factor relates both to equilibrium and to the extrapolation of complexation data to in-situ conditions and in particular changes in seawater pH, which is important for modeling both present and future ocean metal biogeochemistry. pH titrations would offer potential improvements in knowledge of the competition of hydrogen ions for binding sites and also allow for the reversibility of the reactions to be assessed, and thus the question of equilibrium to be properly addressed, since pH can be manipulated in both directions.
The application of more sophisticated approaches to the conceptualization of binding with organic matter (e.g., the NICA model) would also greatly benefit our ability to model metal speciation in seawater. The complexity of these approaches poses potential limits for direct incorporation into biogeochemical models. Nevertheless, it is clear from modeling studies that improvements in our understanding of marine iron chemistry (and other metals) are required in order to develop and improve prognostic models predicting the impact of iron and other trace metals on productivity in the ocean under future climate change scenarios. Thus we must continue to seek robust solutions to these issues and continue to keep an open mind with respect to the development of new experimental designs and approaches to investigating metal speciation in seawater.
Author Contributions
MG designed the study and worked on the data, LG worked on the data. Both authors interpreted the results, formulated the concepts and worked on the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling Editor declared a shared affiliation, though no other collaboration with the author MG and states that the process nevertheless met the standards of a fair and objective review.
Acknowledgments
The authors would like to thank the two reviewers for their helpful comments. The authors would like to thank Ying Ye and Christoph Völker for their input during initial discussions and Hans Slagter for the calculation of L′ and Fe′. The work is a contribution to NERC grant NE/K001973/1 (UK) and DFG grant SFB 754 “Climate-Biogeochemistry Interactions in the Tropical Ocean” (Germany) from MG and to a NWO grant (Netherlands Organization for Scientific Research) under contract number 822.01.018 from LG.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fmars.2017.00254/full#supplementary-material
References
Abualhaija, M. M., and van den Berg, C. M. G. (2014). Chemical speciation of iron in seawater using catalytic cathodic stripping voltammetry with ligand competition against salicylaldoxime. Mar. Chem. 164, 60–74. doi: 10.1016/j.marchem.2014.06.005
Achterberg, E. P., Braungardt, C., Morley, N. H., Elbaz-Poulichet, F., and Leblanc, M. (1999). Impact of Los Frailes mine spill on Riverine, estuarine and coastal waters in Southern Spain. Water Res. 33, 3387–3394. doi: 10.1016/S0043-1354(99)00282-1
Apte, S. C., Gardner, M. J., and Ravenscroft, J. E. (1988). An evaluation of voltammetric titration procedures for the determination of trace metal complexation in natural waters by use of computer simulation. Anal. Chim. Acta 212, 1–21. doi: 10.1016/S0003-2670(00)84124-0
Avendaño, L., Gledhill, M., Achterberg, E. P., Rérolle, V. M. C., and Schlosser, C. (2016). Influence of ocean acidification on the organic complexation of iron and copper in Northwest European shelf seas; a combined observational and model study. Front. Mar. Sci. 3:58. doi: 10.3389/fmars.2016.00058
Benner, R. (2002). “Chemical composition and reactivity,” in Biogeochemistry of Marine Dissolved Organic Matter, eds D. A. Hansell and C. Carlson (London: Academic Press), 59–90.
Boiteau, R. M., Mende, D. R., Hawco, N. J., McIlvin, M. R., Fitzsimmons, J. N., Saito, M. A., et al. (2016a). Siderophore-based microbial adaptations to iron scarcity across the eastern Pacific Ocean. Proc. Natl. Acad. Sci. U.S.A. 113, 14237–14242. doi: 10.1073/pnas.1608594113
Boiteau, R. M., Till, C. P., Ruacho, A., Bundy, R. M., Hawco, N. J., McKenna, A. M., et al. (2016b). Structural characterization of natural nickel and copper binding ligands along the US GEOTRACES Eastern Pacific Zonal Transect. Front. Mar. Sci. 3:243. doi: 10.3389/fmars.2016.00243
Boye, M., Aldrich, A., van den Berg, C. M. G., de Jong, J. T. M., Nirmaier, H., Veldhuis, M., et al. (2006). The chemical speciation of iron in the north-east Atlantic Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 53, 667–683. doi: 10.1016/j.dsr.2005.12.015
Buck, K. N., Gerringa, L. J. A., and Rijkenberg, M. J. A. (2016). An intercomparison of dissolved iron speciation at the Bermuda Atlantic Time-series Study (BATS) site: results from GEOTRACES crossover station A. Front. Mar. Sci. 3:262. doi: 10.3389/fmars.2016.00262
Buck, K. N., Lohan, M. C., Berger, C. J. M., and Bruland, K. W. (2007). Dissolved iron speciation in two distinct river plumes and an estuary: implications for riverine iron supply. Limnol. Oceanogr. 52, 843–855. doi: 10.4319/lo.2007.52.2.0843
Buck, K. N., Moffett, J., Barbeau, K. A., Bundy, R. M., Kondo, Y., and Wu, J. (2012). The organic complexation of iron and copper: an intercomparison of competitive ligand exchange-adsorptive cathodic stripping voltammetry (CLE-ACSV) techniques. Limnol. Oceanogr. Methods 10, 496–515. doi: 10.4319/lom.2012.10.496
Buffle, J., Wilkinson, K. J., and van Leeuwen, H. P. (2009). Chemodynamics and bioavailability in natural waters. Environ. Sci. Technol. 43, 7170–7174. doi: 10.1021/es9013695
Bundy, R. M., Biller, D. V., Buck, K. N., Bruland, K. W., and Barbeau, K. A. (2014). Distinct pools of dissolved iron-binding ligands in the surface and benthic boundary layer of the California Current. Limnol. Oceanogr. 59, 769–787. doi: 10.4319/lo.2014.59.3.0769
Byrne, R. H., and Miller, W. L. (1985). Copper(II) carbonate complexation in seawater. Geochim. Cosmochim. Acta 49, 1837–1844. doi: 10.1016/0016-7037(85)90153-X
Caprara, S., Buck, K. N., Gerringa, L., Rijkenberg, M., and Monticelli, D. (2016). A compilation of iron speciation data for open oceanic waters. Front. Mar. Sci. 3:221. doi: 10.3389/fmars.2016.00221
Croot, P. L., and Heller, M. I. (2012). The importance of kinetics and redox in the biogeochemical cycling of iron in the surface ocean. Front. Microbiol. 3:219. doi: 10.3389/fmicb.2012.00219
Croot, P. L., and Johansson, M. (2000). Determination of iron speciation by cathodic stripping voltammetry in seawater using the competing ligand 2-(2-Thiazolylazo)-p-cresol (TAC). Electoanalysis 12, 565–576. doi: 10.1002/(SICI)1521-4109(200005)12:8<565::AID-ELAN565>3.0.CO;2-L
De Baar, H. J. W., and De Jong, J. T. M. (2001). “Distribution, sources and sinks of iron in seawater,” in The Biogeochemistry of Iron in Seawater, eds D. R. Turner and K. A. Hunter (Chichester: Wiley), 123–253.
Fitzsimmons, J. N., Boyle, E. A., and Jenkins, W. J. (2014). Distal transport of dissolved hydrothermal iron in the deep South Pacific Ocean. Proc. Natl. Acad. Sci. U.S.A. 111, 16654–16661. doi: 10.1073/pnas.1418778111
Fitzsimmons, J. N., John, S. G., Marsay, C. M., Hoffman, C. L., Nicholas, S. L., Toner, B. M., et al. (2017). Iron persistence in a distal hydrothermal plume supported by dissolved–particulate exchange. Nat. Geosci. 10, 195–201. doi: 10.1038/ngeo2900
Garnier, C., Pižeta, I., Mounier, S., Benaïm, J. Y., and Branica, M. (2004). Influence of the type of titration and of data treatment methods on metal complexing parameters determination of single and multi-ligand systems measured by stripping voltammetry. Anal. Chim. Acta 505, 263–275. doi: 10.1016/j.aca.2003.10.066
Gerringa, L. J. A., Rijkenberg, M. J. A., Schoemann, V., Laan, P., and de Baar, H. J. W. (2015). Organic complexation of iron in the West Atlantic Ocean. Mar. Chem. 177, 434–446. doi: 10.1016/j.marchem.2015.04.007
Gerringa, L. J. A., Rijkenberg, M. J. A., Thuróczy, C.-E., and Maas, L. R. M. (2014). A critical look at the calculation of the binding characteristics and concentration of iron complexing ligands in seawater with suggested improvements. Environ. Chem. 11:114. doi: 10.1071/EN13072
Gerringa, L. J. A., Rijkenberg, M. J. A., Wolterbeek, H. T., Verburg, T. G., Boye, M., and de Baar, H. J. W. (2007). Kinetic study reveals weak Fe-binding ligand, which affects the solubility of Fe in the Scheldt estuary. Mar. Chem. 103, 30–45. doi: 10.1016/j.marchem.2006.06.002
Gledhill, M., Achterberg, E. P., Li, K., Mohamed, K. N., and Rijkenberg, M. J. A. (2015). Influence of ocean acidification on the complexation of iron and copper by organic ligands in estuarine waters. Mar. Chem. 177, 421–433. doi: 10.1016/j.marchem.2015.03.016
Gledhill, M., and Buck, K. N. (2012). The organic complexation of iron in the marine environment: a review. Front. Microbiol. 3:69. doi: 10.3389/fmicb.2012.00069
Gledhill, M., McCormack, P., Ussher, S., Achterberg, E. P., Mantoura, R. F. C., and Worsfold, P. J. (2004). Production of siderophore type chelates by mixed bacterioplankton populations in nutrient enriched seawater incubations. Mar. Chem. 88, 75–83. doi: 10.1016/j.marchem.2004.03.003
Gledhill, M., Nimmo, M., and Hill, S. J. (1999). The release of copper-complexing ligands by the brown alga Fucus vesiculosus (Phaeophyceae) in response to increasing total copper levels. J. Phycol. 35, 501–509. doi: 10.1046/j.1529-8817.1999.3530501.x
Gledhill, M., and van den Berg, C. M. G. (1994). Determination of complexation of iron (III) with natural organic complexing ligands in sea water using cathodic stripping voltammetry. Mar. Chem. 47, 41–54. doi: 10.1016/0304-4203(94)90012-4
Green, N. W., Perdue, E. M., Aiken, G. R., Butler, K. D., Chen, H., Dittmar, T., et al. (2014). An intercomparison of three methods for the large-scale isolation of oceanic dissolved organic matter. Mar. Chem. 161, 14–19. doi: 10.1016/j.marchem.2014.01.012
Hansell, D. A. (2013). Recalcitrant dissolved organic carbon fractions. Ann. Rev. Mar. Sci. 5, 421–445. doi: 10.1146/annurev-marine-120710-100757
Hansell, D. A., Carlson, C. A., and Schlitzer, R. (2012). Net removal of major marine dissolved organic carbon fractions in the subsurface ocean. Global Biogeochem. Cycles 26:GB1016. doi: 10.1029/2011GB004069
Hassler, C. S., Schoemann, V., Nichols, C. M., Butler, E. C. V., and Boyd, P. W. (2011). Saccharides enhance iron bioavailability to Southern Ocean phytoplankton. Proc. Natl. Acad. Sci. U.S.A. 108, 1076–1081. doi: 10.1073/pnas.1010963108
Hassler, C. S., van den Berg, C. M. G., and Boyd, P. W. (2017). Toward a regional classification to provide a more inclusive examination of the ocean biogeochemistry of iron-binding ligands. Front. Mar. Sci. 4:19. doi: 10.3389/fmars.2017.00019
Hawkes, J. A., Gledhill, M., Connelly, D. P., and Achterberg, E. P. (2013). Characterisation of iron binding ligands in seawater by reverse titration. Anal. Chim. Acta 766, 53–60. doi: 10.1016/j.aca.2012.12.048
Hertkorn, N., Benner, R., Frommberger, M., Schmitt-Kopplin, P., Witt, M., Kaiser, K., et al. (2006). Characterization of a major refractory component of marine dissolved organic matter. Geochim. Cosmochim. Acta 70, 2990–3010. doi: 10.1016/j.gca.2006.03.021
Hider, R. C., and Kong, X. L. (2010). Chemistry and biology of siderophores. Nat. Prod. Rep. 27, 637–657. doi: 10.1039/b906679a
Hoikkala, L., Kortelainen, P., Soinne, H., and Kuosa, H. (2014). Dissolved organic matter in the Baltic Sea. J. Mar. Syst. 142, 47–61. doi: 10.1016/j.jmarsys.2014.10.005
Hudson, R. J. M., Covault, D. T., and Morel, F. M. M. (1992). Investigations of iron coordination and redox reactions in seawater using 59Fe radiometry and ion-pair solvent extraction of amphiphilic iron complexes. Mar. Chem. 38, 209–235. doi: 10.1016/0304-4203(92)90035-9
Hudson, R. J. M., Rue, E. L., and Bruland, K. W. (2003). Modeling complexometric titrations of natural water samples. Environ. Sci. Technol. 37, 1553–1562. doi: 10.1021/es025751a
Kinniburgh, D. G., Milne, C. J., Benedeti, M. F., Pinheiro, J. P., Filius, J., Koopal, L. K., et al. (1996). Metal ion binding by humic acid: application of the NICA-Donnan model. Environ. Sci. Technol. 30, 1687–1698. doi: 10.1021/es950695h
Koch, B. P., Witt, M. R., Engbrodt, R., Dittmar, T., and Kattner, G. (2005). Molecular formulae of marine and terrigenous dissolved organic matter detected by electrospray ionization Fourier transform ion cyclotron resonance mass spectrometry. Geochim. Cosmochim. Acta 69, 3299–3308. doi: 10.1016/j.gca.2005.02.027
Koopal, L. K., Saito, T., Pinheiro, J. P., and van Riemsdijk, W. H. (2005). Ion binding to natural organic matter: general considerations and the NICA–Donnan model. Coll. Surf. A Physicochem. Eng. Asp. 265, 40–54. doi: 10.1016/j.colsurfa.2004.11.050
Kraemer, S. M. (2004). Iron oxide dissolution and solubility in the presence of siderophores. Aquat. Sci. 66, 3–18. doi: 10.1007/s00027-003-0690-5
Laglera, L. M., Battaglia, G., and van den Berg, C. M. G. (2007). Determination of humic substances in natural waters by cathodic stripping voltammetry of their complexes with iron. Anal. Chim. Acta 599, 58–66. doi: 10.1016/j.aca.2007.07.059
Laglera, L. M., and Filella, M. (2015). The relevance of ligand exchange kinetics in the measurement of iron speciation by CLE–AdCSV in seawater. Mar. Chem. 173, 100–113. doi: 10.1016/j.marchem.2014.09.005
Liu, X., and Millero, F. J. (1999). The solubility of iron hydroxide in sodium chloride solutions. Geochim. Cosmochim. Acta 63, 3487–3497. doi: 10.1016/S0016-7037(99)00270-7
Liu, X., and Millero, F. J. (2002). The solubility of iron in seawater. Mar. Chem. 77, 43–54. doi: 10.1016/S0304-4203(01)00074-3
Martell, A. E., and Smith, R. M. (2004). Critically Selected Stability Constants of Metal Complexes. Gaithersburg, MD: Standard Reference Data Program, National Institute of Standards and Technology, U.S. Dept. of Commerce.
Mawji, E., Gledhill, M., Milton, J. A., Tarran, G. A., Ussher, S., Thompson, A., et al. (2008). Hydroxamate siderophores: occurrence and importance in the Atlantic Ocean. Environ. Sci. Technol. 42, 8675–8680. doi: 10.1021/es801884r
Mawji, E., Gledhill, M., Milton, J. A., Zubkov, M. V., Thompson, A., Wolff, G. A., et al. (2011). Production of siderophore type chelates in Atlantic Ocean waters enriched with different carbon and nitrogen sources. Mar. Chem. 124, 90–99. doi: 10.1016/j.marchem.2010.12.005
Mayer-Pinto, M., Underwood, A. J., Tolhurst, T., and Coleman, R. A. (2010). Effects of metals on aquatic assemblages: what do we really know? J. Exp. Mar. Bio. Ecol. 391, 1–9. doi: 10.1016/j.jembe.2010.06.013
Medeiros, P. M., Seidel, M., Powers, L. C., Dittmar, T., Hansell, D. A., and Miller, W. L. (2015). Dissolved organic matter composition and photochemical transformations in the northern North Pacific Ocean. Geophys. Res. Lett. 42, 863–870. doi: 10.1002/2014GL062663
Millero, F. J., Yao, W., and Aicher, J. (1995). The speciation of Fe(II) and Fe(III) in natural waters. Mar. Chem. 50, 21–39. doi: 10.1016/0304-4203(95)00024-L
Milne, C. J., Kinniburgh, D. G., van Riemsdijk, W. H., and Tipping, E. (2003). Generic NICA−Donnan model parameters for metal-ion binding by humic substances. Environ. Sci. Technol. 37, 958–971. doi: 10.1021/es0258879
Moore, C. M., Mills, M. M., Arrigo, K. R., Berman-Frank, I., Bopp, L., Boyd, P. W., et al. (2013). Processes and patterns of oceanic nutrient limitation. Nat. Geosci. 6, 701–710. doi: 10.1038/ngeo1765
Morel, F. M. M., and Price, N. M. (2003). The biogeochemical cycles of trace metals in the oceans. Science 300, 944–947. doi: 10.1126/science.1083545
Mucha, P., Rekowski, P., Kosakowska, A., and Kupryszewski, G. (1999). Separation of siderophores by capillary electrophoresis. J. Chromatogr. A 830, 183–189. doi: 10.1016/S0021-9673(98)00907-8
Nuester, J., and van den Berg, C. M. G. (2005). Determination of metal speciation by reverse titrations. Anal. Chem. 77, 11–19. doi: 10.1021/ac049078e
Obata, H., and van den Berg, C. M. (2001). Determination of picomolar levels of iron in seawater using catalytic cathodic stripping voltammetry. Anal. Chem. 73, 2522–2528. doi: 10.1021/ac001495d
Omanović, D., Garnier, C., and Pižeta, I. (2014). ProMCC: an all-in-one tool for trace metal complexation studies. Mar. Chem. 173, 25–39. doi: 10.1016/j.marchem.2014.10.011
Pitzer, K. S. (ed.). (1991). “Ion interaction approach: theory and data collection,” in Activity Coefficients in Electrolyte Solutions (Boca Raton, FL: CRC Press), 75–153.
Pižeta, I., Sander, S. G., Hudson, R. J. M., Omanovi,ć, D., Baars, O., Barbeau, K. A., et al. (2015). Interpretation of complexometric titration data: an intercomparison of methods for estimating models of trace metal complexation by natural organic ligands. Mar. Chem. 173, 3–24. doi: 10.1016/j.marchem.2015.03.006
Press, W. H., Flanner, B. P., Teukolsky, S. A., and Vetterling, W. T. (1986). “Root finding and nonlinear sets of equations,” in Numerical Recipes, eds W. H. Press, B. P. Flannery, S. A. Teukolsky, and W. T. Vetterling (New York, NY: Cambridge University Press), 347–393.
R Development Core Team (2016). R: A Language and Environment for Statistical Computing. Vienna: R Foundation Statistical Computing.
Ringbom, A., and Still, E. (1972). The calculation and use of a coefficients. Anal. Chim. Acta 59, 143–146. doi: 10.1016/S0003-2670(01)84834-0
Sander, S. G., Hunter, K. A., Harms, H., and Wells, M. (2011). Numerical approach to speciation and estimation of parameters used in modeling trace metal bioavailability. Environ. Sci. Technol. 45, 6388–6395. doi: 10.1021/es200113v
Shaked, Y., and Lis, H. (2012). Disassembling iron availability to phytoplankton. Front. Microbiol. 3:123. doi: 10.3389/fmicb.2012.00123
Sunda, W. G., and Guillard, R. R. L. (1976). The relationship between cupric ion activity and toxicity of copper to phytoplankton. J. Mar. Res. 34, 511–529.
Tagliabue, A., Aumont, O., Death, R., Dunne, J. P., Dutkiewicz, S., Galbraith, E., et al. (2016). How well do global ocean biogeochemistry models simulate dissolved iron distributions? Global Biogeochem. Cycles 30, 149–174. doi: 10.1002/2015GB005289
Town, R. M., and Filella, M. (2000). Dispelling the myths: is the existence of L1 and L2 ligands necessary to explain metal ion speciation in natural waters? Limnol. Oceanogr. 45, 1341–1357. doi: 10.4319/lo.2000.45.6.1341
Town, R. M., and Van Leeuwen, H. P. (2005). Measuring marine iron(III) complexes by CLE-AdSV. Environ. Chem. 2, 80–84. doi: 10.1071/EN05021
Turner, D. R., Achterberg, E. P., Chen, C.-T. A., Clegg, S. L., Hatje, V., Maldonado, M. T., et al. (2016). Toward a quality-controlled and accessible Pitzer model for seawater and related systems. Front. Mar. Sci. 3:139. doi: 10.3389/fmars.2016.00139
Turner, D. R., Whitfield, M., and Dickson, A. G. (1981). The equilibrium speciation of dissolved components in freswater and seawater at 25°C at 1 atm. pressure. Geochim. Cosmochim. Acta 45, 855–882.
Turoczy, N. J., and Sherwood, J. E. (1997). Modification of the van den Berg/Ruzic method for the investigation of complexation parameters of natural waters. Anal. Chim. Acta 354, 15–21. doi: 10.1016/S0003-2670(97)00455-8
van den Berg, C. M. G., Nimmo, M., Daly, P., and Turner, D. R. (1990). Effects of the detection window on the determination of organic copper speciation in estuarine waters. Anal. Chim. Acta 232, 149–159. doi: 10.1016/S0003-2670(00)81231-3
Velasquez, I., Nunn, B. L., Ibisanmi, E., Goodlet, D. R., Hunter, K. A., and Sander, S. G. (2011). Detection of hydroxamate siderophores in coastal and Sub-Antarctic waters off the South Eastern coast of New Zealand. Mar. Chem. 126, 97–107. doi: 10.1016/j.marchem.2011.04.003
Velasquez, I. B., Ibisanmi, E., Maas, E. W., Boyd, P. W., Nodder, S., and Sander, S. G. (2016). Ferrioxamine siderophores detected amongst iron binding ligands produced during the remineralization of marine particles. Front. Mar. Sci. 3:172. doi: 10.3389/fmars.2016.00172
Wells, M., Buck, K. N., and Sander, S. G. (2013). New approach to analysis of voltammetric ligand titration data improves understanding of metal speciation in natural waters. Limnol. Oceanogr. Methods 11, 450–465. doi: 10.4319/lom.2013.11.450
Whitby, H., and van den Berg, C. M. G. (2015). Evidence for copper-binding humic substances in seawater. Mar. Chem. 173, 282–290. doi: 10.1016/j.marchem.2014.09.011
Witter, A. E., Hutchins, D. A., Butler, A., and Luther, G. W. III. (2000). Determination of conditional stability constants and kinetic constants for strong model Fe-binding ligands in seawater. Mar. Chem. 69, 1–17. doi: 10.1016/S0304-4203(99)00087-0
Witter, A. E., and Luther, G. W. III. (1998). Variation in Fe-organic complexation with depth in the Northwestern Atlantic Ocean as determined using a kinetic approach. Mar. Chem. 62, 241–258. doi: 10.1016/S0304-4203(98)00044-9
Yang, R., and van den Berg, C. M. G. (2009). Metal complexation by humic substances in seawater. Environ. Sci. Technol. 43, 7192–7197. doi: 10.1021/es900173w
Keywords: trace element speciation, trace element biogeochemistry, iron, complexometric determination, organic complexation
Citation: Gledhill M and Gerringa LJA (2017) The Effect of Metal Concentration on the Parameters Derived from Complexometric Titrations of Trace Elements in Seawater—A Model Study. Front. Mar. Sci. 4:254. doi: 10.3389/fmars.2017.00254
Received: 14 April 2017; Accepted: 25 July 2017;
Published: 22 August 2017.
Edited by:
Jörg Wiedenmann, University of Southampton, United KingdomReviewed by:
Dario Omanovic, Rudjer Boskovic Institute, CroatiaMarta Plavsic, Rudjer Boskovic Institute, Croatia
Copyright © 2017 Gledhill and Gerringa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martha Gledhill, bWdsZWRoaWxsQGdlb21hci5kZQ==
 Martha Gledhill
Martha Gledhill Loes J. A. Gerringa
Loes J. A. Gerringa