Modeling Fine-Scale Coral Larval Dispersal and Interisland Connectivity to Help Designate Mutually-Supporting Coral Reef Marine Protected Areas: Insights from Maui Nui, Hawaii

Storlazzi, Curt D.; van Ormondt, Maarten; Chen, Yi-Leng; Elias, Edwin P. L.

doi:10.3389/fmars.2017.00381

ORIGINAL RESEARCH article

Front. Mar. Sci., 05 December 2017

Sec. Coral Reef Research

Volume 4 - 2017 | https://doi.org/10.3389/fmars.2017.00381

This article is part of the Research Topic Modelling Corals on Various Scales (from Cells to Reefs to Global) View all 4 articles

Modeling Fine-Scale Coral Larval Dispersal and Interisland Connectivity to Help Designate Mutually-Supporting Coral Reef Marine Protected Areas: Insights from Maui Nui, Hawaii

$\r\nCurt D. Storlazzi*$ Curt D. Storlazzi¹^*

Maarten van Ormondt²

Yi-Leng Chen³

Edwin P. L. Elias⁴

¹Pacific Coastal and Marine Science Center, U.S. Geological Survey, Santa Cruz, CA, United States
²Department of Marine and Coastal Systems, Deltares, Delft, Netherlands
³Meteorology Department, University of Hawai'i, Honolulu, HI, United States
⁴Department of Marine and Coastal Systems, Deltares USA Inc., Silver Spring, MD, United States

Connectivity among individual marine protected areas (MPAs) is one of the most important considerations in the design of integrated MPA networks. To provide such information for managers in Hawaii, USA, a numerical circulation model was developed to determine the role of ocean currents in transporting coral larvae from natal reefs throughout the high volcanic islands of the Maui Nui island complex in the southeastern Hawaiian Archipelago. Spatially- and temporally-varying wind, wave, and circulation model outputs were used to drive a km-scale, 3-dimensional, physics-based circulation model for Maui Nui. The model was calibrated and validated using satellite-tracked ocean surface current drifters deployed during coral-spawning conditions, then used to simulate the movement of the larvae of the dominant reef-building coral, Porites compressa, from 17 reefs during eight spawning events in 2010–2013. These simulations make it possible to investigate not only the general dispersal patterns from individual coral reefs, but also how anomalous conditions during individual spawning events can result in large deviations from those general patterns. These data also help identify those reefs that are dominated by self-seeding and those where self-seeding is limited to determine their relative susceptibility to stressors and potential roadblocks to recovery. Overall, the numerical model results indicate that many of the coral reefs in Maui Nui seed reefs on adjacent islands, demonstrating the interconnected nature of the coral reefs in Maui Nui and providing a key component of the scientific underpinning essential for the design of a mutually supportive network of MPAs to enhance conservation of coral reefs.

Introduction

Larval dispersal commonly controls the spatial distribution of marine organisms that have planktonic larval stages that metamorphose into sessile or highly sedentary adults. A better understanding of the timing and patterns of larval dispersal enhances our understanding of population connectivity (Swearer et al., 2002; Kool and Nichol, 2015; van der Meer et al., 2015) and reef colonization or recolonization after disturbance (Grigg and Maragos, 1974), whether due to natural or anthropogenic (Loya, 1976) factors. Currents that carry larvae also may convey material that is detrimental to marine organisms, including contaminants, excess nutrients, and fine-grained particulates (Fabricius, 2005). Understanding circulation patterns in the vicinity of coral reefs, therefore, has multiple important applications for management and conservation. Despite the importance of fine-scale marine dispersal patterns to resource managers and scientists, they generally remain not well-documented (Gaines et al., 2003; Sale et al., 2005), especially in high-island archipelagos.

A number of previous studies have investigated local or regional-scale coral spawning and larval dispersal using tools such as oceanographic instruments, (Sammarco and Andrews, 1988; Wolanski et al., 1989; Oliver et al., 1992; Tay et al., 2012; Thomas et al., 2014), and/or satellite- or radio-tracked drifters (Lugo-Fernandez et al., 2001; Nadaoka et al., 2002; Storlazzi et al., 2006a). Most of the previous experiments, however, have either been long-term simulations with no field validation or relatively short-term, generally an individual spawning event or two in the same year, thus making it unclear if the short-term model runs and/or drifter trajectories are representative of dominant patterns of dispersal that yield connectivity (Largier, 2003; Oliver et al., 2015) over timescales relevant to management.

Fringing coral reef tracts with high coral coverage (Battista et al., 2007) are found off west Maui, south Molokai, northwest Lanai, and northern Kahoolawe, Hawaii, USA; together, these high volcanic islands are referred to as “Maui Nui,” as they composed one single, large island during previous sea-level low stands caused by glaciation. Most of these reefs, however, have been stressed due to land-based pollution due to poor land-use practices and overfishing (Jokiel and Rodgers, 2007). As demonstrated both in tropical (McClanahan et al., 2006) and higher-latitude settings (Halpern, 2003), marine protected areas (MPAs) have become one of the regulatory tools to protect and preserve benthic and their associated pelagic ecosystems.

Here, we present the results from a physics-based, 3-dimensional coupled ocean-atmosphere numerical model to that provide insights into fine-scale (order of km) patterns in dispersal of coral larvae. Modeling focused on Porites compressa and eight spawning events on 17 reef tracts from 2010 to 2013, with some of the reefs being managed by the State and other tracts being good candidates for protection due to extensive coral cover. These model simulations were validated using satellite-tracked drifters, and they show not only the relatively short timescales of dispersal between the adjacent high islands in Maui Nui, but also the interconnected nature of the islands that has been identified in genetic studies. Together, these results provide some of the fundamental, sound scientific information that is generally lacking (Sale et al., 2005) but needed to help guide the design of mutually-supporting MPAs to protect and preserve coral reefs.

Study Area

Maui Nui is composed of the volcanic islands of Maui, Molokai, Lanai, and Kahoolawe, Hawaii, USA (Figure 1), which range in height from 450 m (Kahoolawe) to 3,050 m (Maui), causing significant wind shadows and topographic steering (Xie et al., 2001; AWS Truewind, 2004). The northeast Trade winds occur throughout the year, but they are most consistent during the boreal summer coral-spawning season (Fletcher et al., 2002). Insolation-driven heating and nocturnal cooling of the islands cause the general Trade wind speeds in the vicinity of the islands to vary from almost negligible at night to more than 15 m s⁻¹ in the afternoon, compared to about 5 m s⁻¹ in the open ocean. These relatively rapid diurnal variations in wind speed result in a very thin (< 1 m) wind-driven surface layer (Storlazzi et al., 2006b) that constrains positively-buoyant particles, such as coral larvae during their planktonic dispersal stage (Storlazzi et al., 2006a), varies greatly over small spatial and temporal scales, and is not captured in larger-scale oceanographic models (Tay et al., 2012; Vaz et al., 2013; Wood et al., 2014). The wave climate in Maui Nui during the period of coral spawning in the boreal summer is dominated by two wave regimes: northeast Trade wind waves and Southern Ocean swell (Moberly and Chamberlain, 1964). The northeast Trade wind waves have heights ~1–4 m and short periods (~4–8 s), whereas Southern swell is characterized by smaller (heights ~1–2 m) waves with longer periods (~14–25 s). Together, the dominant wind and wave directions result in relatively quiescent areas along southwest Maui, south-central Molokai, and southeastern Lanai, as compared to the more energetic areas off northeastern Maui, Lanai, Molokai, and Kahoolawe.

FIGURE 1

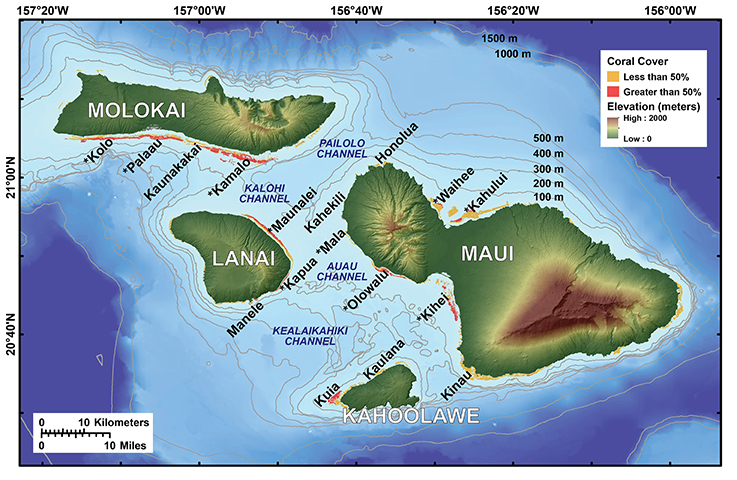
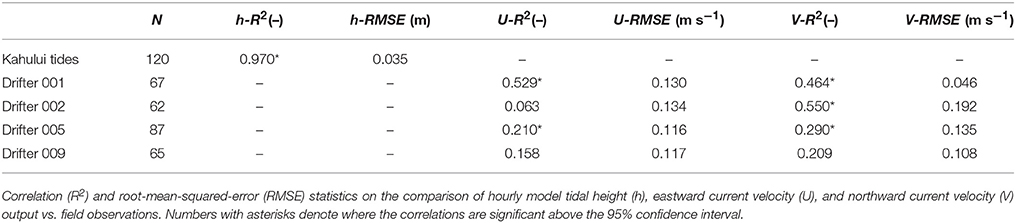
Figure 1. Map of the study area, including the location of major coral reef complexes with high percentages of coral cover that were selected as coral larval sources for the Lagrangian surface current drifter deployments and numerical model simulations. The reefs with asterisks are large reef tracts with high coral cover, whereas those without are existing State of Hawaii MPAs. Note the high topography of the islands that cause orographic effects and the bathymetric structure of the channels that induce hydrodynamic steering of currents.

Satellite altimetry data and a numerical model (Sun, 1996) indicated weak (0.05–0.10 m s⁻¹) long-term mean eastward flow through the Kalohi and Pailolo Channels, and mean southward flow in the Auau Channel driven by differences in sea surface height across the island chain. Flow measured 25 m below the surface in the Pailolo Channel (Flament and Lumpkin, 1996) was primarily oriented east-west at 0.00–1.00 m s⁻¹ (mean = 0.04 m s⁻¹). Previous drifter deployments (Storlazzi et al., 2006a) off west Maui during the summer coral spawning season demonstrated dispersal westward toward Lanai. Those findings, along with others (Storlazzi et al., 2006b), noted that lower frequency motions driven by the northeast trade winds dominated flow, with lesser contributions by diurnal and semi-diurnal tidal currents, especially in the lee of the large West Maui volcano.

Methods

Because of the high spatial and temporal variability in winds and the resulting wave and surface current patterns, it was necessary to replicate such wind forcing to accurately drive surface currents and coral larval dispersal patterns at the scale of the Maui Nui complex. To do this, we utilized a high-resolution 3-dimensional atmospheric model to drive a 3-dimensional hydrodynamic model of the study area, and validated the resulting flow and coral larval dispersal patterns using satellite-tracked Lagrangian current surface drifters.

Wind Modeling

The Weather Research and Forecast's 3-dimensional Advanced Research Weather (WRF-ARW) model (Skamarock and Klemp, 2008) was used as the basis for 7.5 days of daily forecasts after it was initialized at 0000 UTC using the National Centers for Environmental Prediction Global Forecast System (NCEP GFS) data with a 0.5° × 0.5° grid. The GFS model output does not have a resolution capable of producing any meaningful representation of Maui topography. To capture this, three nested domains were employed with a two-way nesting (dynamically-downscaled) at horizontal resolutions of 18, 6, and 2 km, respectively. The 2-km domain covers the entirety of Maui County and the Island of Oahu. It had 38 vertical sigma levels from the surface to the 100-hPa level. Sea surface temperature (SST), which affects near-surface winds, was updated at the time of initialization using the NCEP Real-time, global, 0.5° × 0.5° SST analysis.

The physics options included the cumulus parameterization, planetary boundary layer, microphysics, and rapid radiative transfer schemes. An advanced land surface model (Chen and Dudhia, 2001) was employed using the vegetation cover and soil properties. This model was used to describe the thermally-driven circulations over land and the coastal waters caused by the land-sea thermal contrast that are sensitive to soil moisture and soil temperature input. The 24-h forecasts of the soil moisture and soil temperature of the previous day were used to update the initial conditions for the next day's simulation. The 24-h model forecast (hours 12–35) was used as the simulated diurnal cycle for each day. Winds at 10 m above a 1° × 1° grid applied to the coastal waters were hindcast for a 10-year period (2000–2009) after the model was initialized by data from the NCEP Final Analysis (NCEP FNL), with verification against historical hourly winds recorded by 11 buoys within the 6-km domain (Hitzl et al., 2014).

Wave Modeling

Wave forcing for the circulation model was obtained from NOAA's WAVEWATCH-III (Tolman, 1999) global wave model, which was used, in turn, to drive a SWAN wave model. SWAN is a high-resolution wave model that resolves nearshore coastal dynamics such as refracting, shoaling, and island shadowing. The third generation SWAN model integrates wave effects, such as enhanced bed shear stresses and wave-induced current forcing due to wave breaking, into flow simulations. The SWAN model is based on discrete spectral action balance equations, computing the evolution of random, short-crested waves (Booij et al., 1999; Ris et al., 1999). It includes physical processes such as the generation of waves by wind, dissipation due to whitecapping, bottom friction, depth-induced breaking, and non-linear quadruplet and triad wave-wave interactions. Wave effects, such as enhanced bed shear stresses and wave-induced current forcing due to wave breaking, are integrated into the flow simulations described below.

Circulation Modeling

A Delft3D (Lesser et al., 2004) coupled wave-current numerical circulation model for the Maui Nui complex of Hawaii was constructed to examine the effects of winds, waves, tides, and regional currents on circulation and buoyant transport in and amongst the islands. Delft3D-Flow (Deltares, 2011) forms the core of the model system and simulates water motion due to tidal and meteorologic forcing by solving the unsteady shallow-water equations that consist of the continuity equation, the horizontal momentum equations, and the transport equation under the shallow water and Boussinesq assumptions. By specifying boundary conditions for bed roughness (quadratic friction law), free surface (wind stresses), lateral boundaries (water level, currents, salinity, and water temperature), and closed boundaries with free-slip conditions at the seabed, the equations are solved on a staggered grid by using an Alternating Direction Implicit method (Stelling, 1984; Leendertse, 1987; Deltares, 2011).

It is important to capture both the more slowly varying, large-scale oceanic circulation and the local (wind-and wave-dominated) nearshore flows that generally fluctuate over shorter temporal and spatial scales; therefore, spatial and temporal scales in the models need to match the relevant processes. To achieve this, two Delft3D models were constructed: (1) a coarser Regional Hawaii Model, and (2) a finer-scale Maui Nui Model, which was nested within the larger Regional Hawaii Model (Figure 2). The bathymetric data for these models were obtained by desampling (NOAA's National Geophysical Data Center's, 2009) U.S. Coastal Relief Model 3 arc-s (~90 m) resolution bathymetric dataset. Both of these models consist of the Delft3D-flow and Delft3D-wave modules.

FIGURE 2

Figure 2. The Regional Hawaii Model (blue) and the nested Maui Nui Model (red) grids. One thousand meters isobaths show the regional bathymetry of Main Hawaiian Islands and the southeastern end of the Hawaiian Ridge.

The Regional Hawaii Model is a 3-dimensional, rectangular gridded model consisting of 20 vertical z-layers and a horizontal domain that is 765 × 405 km with 5-km grid resolution. In order to include large-scale oceanic circulation effects, this model was forced using the 3-dimensional global (1/12° resolution) HYbrid Coordinate Ocean Model (HYCOM, http://hycom.org/) model's horizontal current velocities, water temperature, and salinity outputs. HYCOM is a 3-dimensional, data-assimilative, hybrid isopycnal-sigma-pressure coordinate system ocean model that is run operationally. Tidal information at the boundaries of the coarser Delft3D model was provided by the Oregon State University TOPEX/Poseidon global inverse solution (TPXO; http://volkov.oce.orst.edu/tides/global.html). TPXO is a global tide model that uses the Laplace Tidal Equations and incorporates along-track averaged satellite altimetry data (Egbert and Erofeeva, 2002). TPXO uses a global grid with 0.25° resolution, on which the resulting tides are computed as complex amplitudes of the Earth-relative, sea-surface elevations for 13 harmonic tidal constituents. The tidal data from the TPXO global model of ocean tides, which were interpolated to the Regional Hawaii Model boundaries, were also included in the time-series forcing files. A time step of 5 min was used in the Regional Hawaii Model to ensure stable computations on the 20-layer grid schematization.

The Maui Nui Model has a 3-dimensional, curvilinear domain with 19,092 grid cells with a grid cell resolution of 1 km. This model has 20 vertical z-layers, with 2-m resolution at the surface, and decreasing resolution with increasing water depth, and uses a 2-min time step. The water level, temperature, salinity, and horizontal current velocity boundary conditions necessary to accurately model near-surface flows in coastal regions were supplied by the Regional Hawaii Model, using the Delft3D dynamically-downscalling nesting procedure. On the free surface, wind was implemented as a shear stress based on the WRF-ARW wind model data.

For both the Regional Hawaii model and Maui Nui model, wave simulations were performed by the SWAN wave model using the flow grids as spatial domain. The Regional Hawaii model was run in stand-alone mode. In the wave model, default settings were set for the directional space and for frequency space; wave forces were based on the wave energy dissipation rate. Depth-induced breaking was computed by the Battjes and Jansen breaker model with default values and bottom friction was computed with the Jonswap formulation. Diffraction, whitecapping, non-linear triad interactions, and wave setup were not included in the computations. Default accuracy criteria for convergence were applied.

The Maui Nui model used the computed water levels, flow velocities, and wind fields from the Regional Hawaii flow model and was forced by the computed wave spectra from the Regional Hawaii wave model. The default settings for the spectral resolution used were similar to those used for the Regional model; the wave forces are based on the radiation stresses. Processes included are: depth-induced breaking, bottom friction, wind growth, and whitecapping (Komen formulation) with similar settings to the Regional model. Each set of 30-min wave results was coupled to the flow model.

Larval Dispersal and Settling Modeling

MDRIFT is a Matlab-based particle-tracking program that tracks positively-buoyant particles (coral larvae) in the simulation for a certain amount of time as they are transported by the surface currents from natal reefs during their prescribed pelagic stage, after which they are removed from the simulation by settling. To model trajectories of coral larval in the study area, this program was run by releasing 7,200 buoyant particles over a 2-h interval from each natal reef into the time- and space-varying 2-m thick surface velocity current fields in the Maui Nui flow model, which is where the larvae would be contained (Storlazzi et al., 2006b) and logging the resulting transport pathways and settling locations. The tracked coral larvae source and sink locations (Figure 1) were either existing State of Hawaii MPAs or large (>5 km²) reef tracts where coral coverage had been previously mapped to exceed 50% (Battista et al., 2007). The timing of the spawning events of the dominant reef-building coral (Jokiel and Rodgers, 2007), P. compressa, modeled were based on the month and lunar cycle (Table 1) identified in a previous study (Kolinski and Cox, 2003). Particle (larval) diffusion processes (Largier, 2003) were included by adding a random disturbance to the current velocity fields (Peliz et al., 2007), which resulted in dilution increasing exponentially with time.

TABLE 1

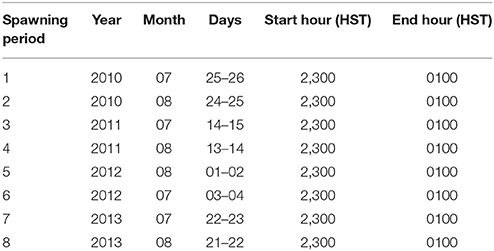
Table 1. Modeled coral larval spawning periods based on Kolinski and Cox (2003).

In this study, the minimum planktonic period was set at 24 h (1 day) and maximum coral-larval dispersal competency was defined at 72 h (3 days) because larval density (Sammarco and Andrews, 1988; Connolly and Baird, 2010) and the competency to settle (Connolly and Baird, 2010) decreases exponentially with time; mortality was set to zero due to this short timescale. The timescale of modeled flow and pelagic larval duration used in this effort was relatively short in comparison to many other studies (Oliver et al., 1992; Vaz et al., 2013; Kool and Nichol, 2015), and it was selected not only because it minimizes the exponential decrease in competency and larval density (due to dilution) but also because the probability of effective connectivity of a substantial number of coral larvae that would need to successfully be transported from one reef to another to support normal mortality decreases exponentially with time and distance. The importance of such dilution in the marine environment is generally greatly underestimated: For example, if 1 million coral larvae that are 1-mm in diameter were evenly distributed in a 1-m thick surface layer that covered a relatively small reef area of 250 m by 250 m, the coral larval density would already be on the order of 1 × 10⁻⁸; once that water mass starts to be advected by currents, dispersion starts and dilution goes up exponentially. So although an extremely small proportion of coral larvae can have long pelagic larval durations, the concentration of larvae and the probability of successful recruitment via the proposed dispersal pathways become so small that they are mathematically insignificant over demographic or management (years) timescales. Such dispersal and longer pelagic larval durations are important over evolutionary (centuries+) timescales, but here we argue they are not significant on timescales relevant to current management needs.

The active settling of coral larvae on a receiving reef was defined to occur if the modeled larvae in the surface layer (Storlazzi et al., 2006b) reached suitable habitat (Battista et al., 2007; Dixson et al., 2014) in water depths less than 30 m, which is the maximum depth of most reefs in the study area (Battista et al., 2007), during the 72-h competency period. This assumption is further supported by the observed patterns of cross-shore velocity shear close to shore over fringing reefs (Storlazzi et al., 2006b; Nickols et al., 2015) that favor increased retention (Largier, 2003) and thus would increase the likelihood of successful settlement.

Ocean Surface Current Drifters

Four satellite-tracked Pacific Gyre Microstar Lagrangian ocean surface current drifters equipped with Differential Global Positioning System (DGPS) were deployed off south-central Molokai and northwest Maui to track surface currents on the nights of 11–12 July 2013 during spring tidal forcing that characterizes coral spawning events. The drifters each had a diamond drogue centered at a depth of 1.75 m (1.0–2.5 depth range) and transmitted their positions every 5 min.

Results

Model Calibration and Validation

Because calibration of the model focused on the thin (< 2 m) surface layer that contained the coral larvae (Storlazzi et al., 2006b), which is typically not resolved by fixed current meters (Andutta et al., 2012) due to waves and the water depths of the channels (often >100 m depth), validation of the model to demonstrate that it was correctly reproducing the relevant processes was done using tide and Lagrangian ocean surface current drifters. Calibration and validation of the Maui Nui model focused on the water levels and dispersal patterns during spring tidal forcing on 11–12 July 2013 when the four drifters were deployed over three coral reefs off Maui and one off Molokai at the time when corals spawn (2300 HST) and tracked for 48 h. The tidal water levels, which are a primary control on water moving amongst the islands and thus driving current velocities (Storlazzi et al., 2006a), needed to be represented accurately. Root-mean squared (RMS) errors between measured and modeled water levels (Figure 3A, Table 2) were significant above the 95% confidence interval, and the RMS errors were 0.035 m, showing very good correspondence between the model and in situ tidal data (NOAA Tides Currents, 2014). The modeled surface (z-layer #1) current velocities were generally on the same order of magnitude and direction as those measured by the drifters (Table 2), with drifters #1 (Figures 3B,C), and #5 (Figures 3F,G) deployed off northwestern Maui and south-central Molokai, respectively, demonstrating statistically significant correspondence with the model, whereas drifters #2 (Figures 3D,E) and #9 (Figures 3H,I), deployed off western Maui and southwestern Maui, did not demonstrate statistically-significant correspondence. The data-model difference for drifter #2 was primarily due to a rapid cross-shore (westerly) advection that was balanced by a longer duration but slower onshore (easterly) flow that resulted in almost the same position after 1.5 days, but that was not captured by the model; the data-model difference for drifter #9 was primarily due to consistent alongshore subtidal flow to the northwest during the deployment that was not accurately captured by the model.

FIGURE 3

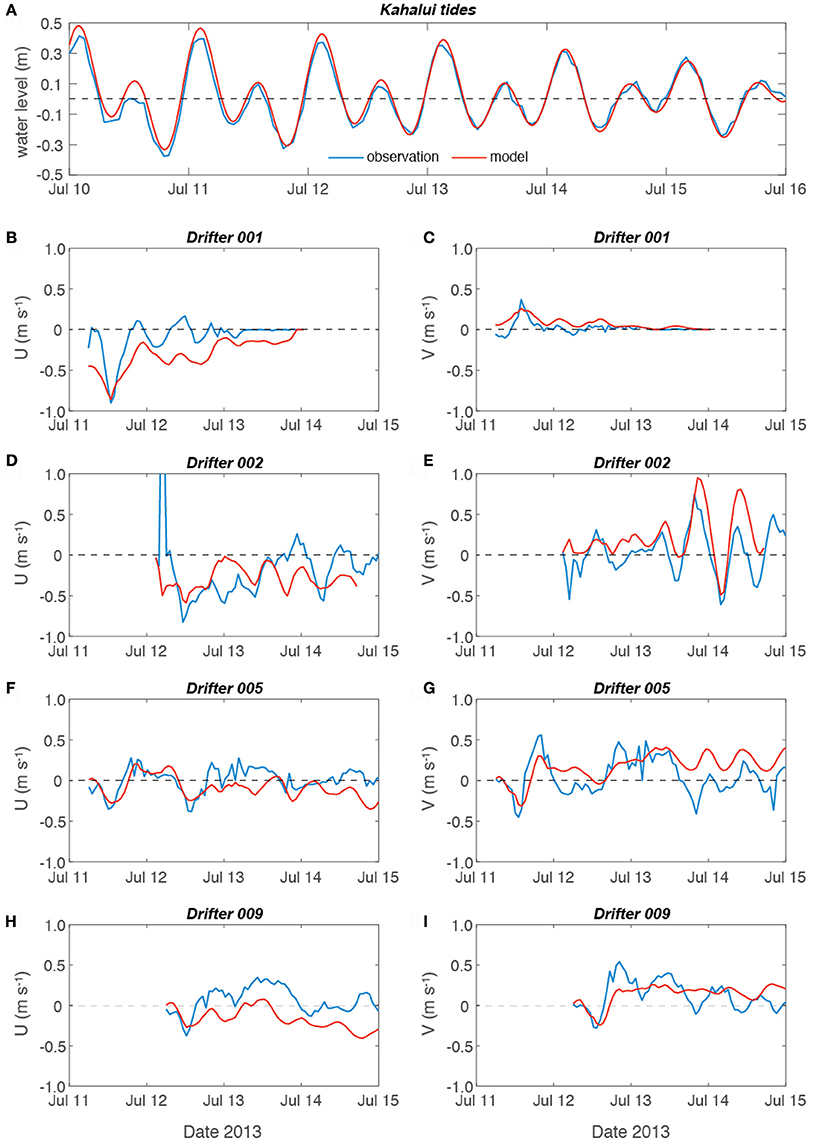
Figure 3. Comparison of model output vs. field observations. (A) Tides at Kahalui Harbor, northern Maui. (B) East-west U-velocity component of drifter 001 deployed off northwest Maui. (C) North-south V-velocity component of drifter 001. (D) U-velocity component of drifter 002 deployed off west Maui. (E) V-velocity component of drifter 002. (F) U-velocity component of drifter 005 deployed off south-central Molokai. (G) V-velocity component of drifter 005. (H) U-velocity component of drifter 009 deployed off southwest Maui. (I) V-velocity component of drifter 009. Note the model not only accurately captured water levels and the majority of the surface velocity patterns, nowhere were there consistent biases in the drifter data, suggesting good model performance in capturing the relevant physical processes and timescales.

TABLE 2

Table 2. Comparison of modeled vs. measured tides and Lagrangian current velocities.

Although data-model RMS velocity errors were on the order of 11 cm s⁻¹, almost two-thirds of the data-model velocities were statistically significant, which is surprising because the drifters' drogues were so tall that they extended across the top two model layers (layer #1 depth = 0–2 m). Vertical velocity shear between the top two model z-layers, due to wind stress driving the top layer whereas the deeper layers responded more to regional and tidal current forcing, therefore likely caused the drifters to reflect a combination of flow from both the model's surface layer (z-layer #1) and uppermost subsurface layer (z-layer #2). Nevertheless, most of the current velocities were statistically significant and showed no significant bias, and the data-model paths coherent. Furthermore, the flow velocities and dispersal patterns for similar forcing conditions are comparable to those previously reported for the study area (Storlazzi et al., 2006a,b). Together, these comparisons provide confidence the model accurately captures the fine-scale processes that occur at the spatial scales being modeled and thus made it possible to conduct inter-model run comparisons to evaluate the influence of the differences in forcing on the resulting dispersal patterns. These promising fine-scale (order~km) model-data comparisons, which have never been conducted in such a complex environment, contrast with numerous modeling efforts focused on larval dispersal patterns where no such model-data comparisons were made (Oliver et al., 1992; Treml et al., 2008; Vaz et al., 2013; Thomas et al., 2014; Kool and Nichol, 2015) and thus model accuracy and the resulting projections and findings are unknown.

Circulation Patterns

Interestingly, despite the regional northeast Trade-wind forcing that dominates the large-scale surface currents around the Hawaiian Archipelago, the primary modeled flow direction within Maui Nui is to the northwest (Figure 4). This pattern resulted in generally stronger flows in the windier areas off Maui's and Molokai's northeastern shores and slower current speeds of southwestern Maui and southern Molokai in the lee of the high islands. Overall, four general residual Lagrangian modeled flow patterns over the course of the 72-h competency periods were observed within Maui Nui. The first flow pattern was characterized by strong westerly flow to the south of Kahoolawe and relatively weak currents amongst the islands Figure 4A. This generated westerly flow north of Kahoolawe, northerly flow between Maui and Lanai, and westerly flow between Lanai and Molokai; more quiescent regions lay to the south and west of Lanai. The second pattern was characterized by weaker westerly flow to the south of Kahoolawe and a slightly more vigorous flow between south Maui and Kahoolawe that extended northwest to between Lanai and west Maui and then west between Lanai and Molokai Figure 4B. The third flow pattern was characterized by strong northerly flow amongst the islands Figure 4C. This resulted in more quiescent areas in the lee of the islands to the north of Maui and Molokai and in the channels between west Maui and Kahoolawe and between Lanai and Molokai. The last pattern was characterized by strong northwesterly flow amongst the islands, causing strong currents between most of the islands and a large eddy between Lanai and Kahoolawe Figure 4D.

FIGURE 4

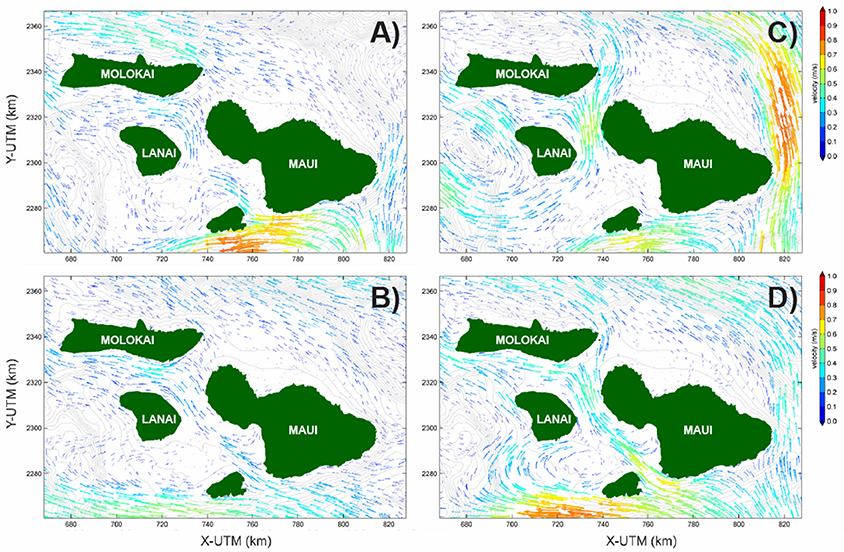
Figure 4. Example modeled Eulerian residual (subtidal) surface current patterns for four coral larval spawning events that demonstrate end-member conditions. (A) 25–27 July 2010. (B) 01–03 August 2012. (C) 03–05 July 2013 (D) 22–25 July 2012. Current vectors are colored-coded by speed. Note that even under regional northeast trade wind forcing, the majority of surface flow in amongst the islands is to the northwest, highlighting the interactions between regional current patterns and the orographic effects of these high islands on the resulting surface current patterns. Together, these result in stagnant zones (short to non-existent arrows) in relatively close proximity to those characterized by rapid advection (long arrows).

Larval Dispersal Patterns

An example of the range of dispersal and settlement patterns resulting from the four dominant flow patterns (Figure 4) is shown in Figure 5. The modeled larval dispersal and settlement patterns generally mimicked the modeled flow direction within Maui Nui. Under weak forcing in the channels between the islands Figure 4A, modeled dispersal distances were generally short and local retention is high, resulting in substantial seeding of adjacent reefs on the same island Figure 5A. When weak westerly flow occurred to the south of Kahoolawe and slightly more vigorous flow occurred between Maui, Lanai, and Kahoolawe Figure 4B, modeled dispersal distances were greater with little local retention, resulting in seeding of reefs on islands to the west and north Figure 5B and a significant portion of larvae lost offshore to the west (e.g., modeled larval pathways did not intersect with suitable substrate within the prescribed competency period). Although some local seeding occurred during strong northerly flow amongst the islands Figure 4C, most larvae were modeled to be lost offshore to the north (Figure 5C). Under strong northwesterly flow amongst the islands Figure 4D, the majority of larvae successfully recruited, either locally to adjacent reefs on the same island or seeding reefs of islands to the west and north (Figure 5D). Overall, there seems to be a general northwesterly predominant directionality in dispersal in Maui Nui; such a predominant directionality in dispersal due to relatively consistent forcing has been observed in other locations (Gaines et al., 2003; Peliz et al., 2007).

FIGURE 5

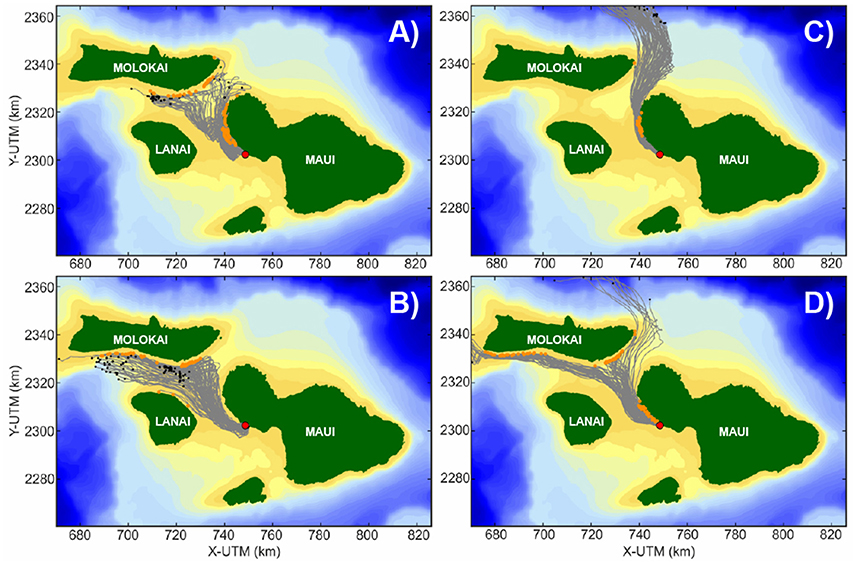
Figure 5. Example modeled Lagrangian coral larval dispersal patterns from the Olowalu reef on west Maui for the four coral larval spawning events that demonstrate end-member conditions shown in Figure 4. (A) 25–27 July 2010. (B) 01–03 August 2012. (C) 03–05 July 2013 (D) 22–25 July 2012. Red dots denote the natal reef from which the larvae were released in the simulation. Gray lines show the modeled larval tracks, with the orange dots denote successful larval recruitment to a new reef, whereas black dots denote where coral larvae did not successfully recruit by the end of the simulation. Note the range of dispersal patterns from a given reef under different meteorologic and oceanographic forcing, demonstrating the potential for a given reef to seed different islands and their respective reefs over relatively short timescales.

The decision to model such a relatively short maximum coral-larval dispersal competency period (72 h) compared to many other studies (Oliver et al., 1992; Vaz et al., 2013; Kool and Nichol, 2015) was demonstrated to be sound because the modeled larvae densities generally decreased more than two orders of magnitude within 24 h (Figure 6). The exponential decrease in density during the initial 24 h is due purely to dispersion, as there is no settling or mortality during this time frame. After 24–48 h, the larvae from most of the reefs were spread across hundreds of km², and due to settling or loss offshore, the larval densities remaining in the water column decreased to dozens or less per km², which is likely insufficient to repopulate impacted reefs over demographic or management timescales.

FIGURE 6

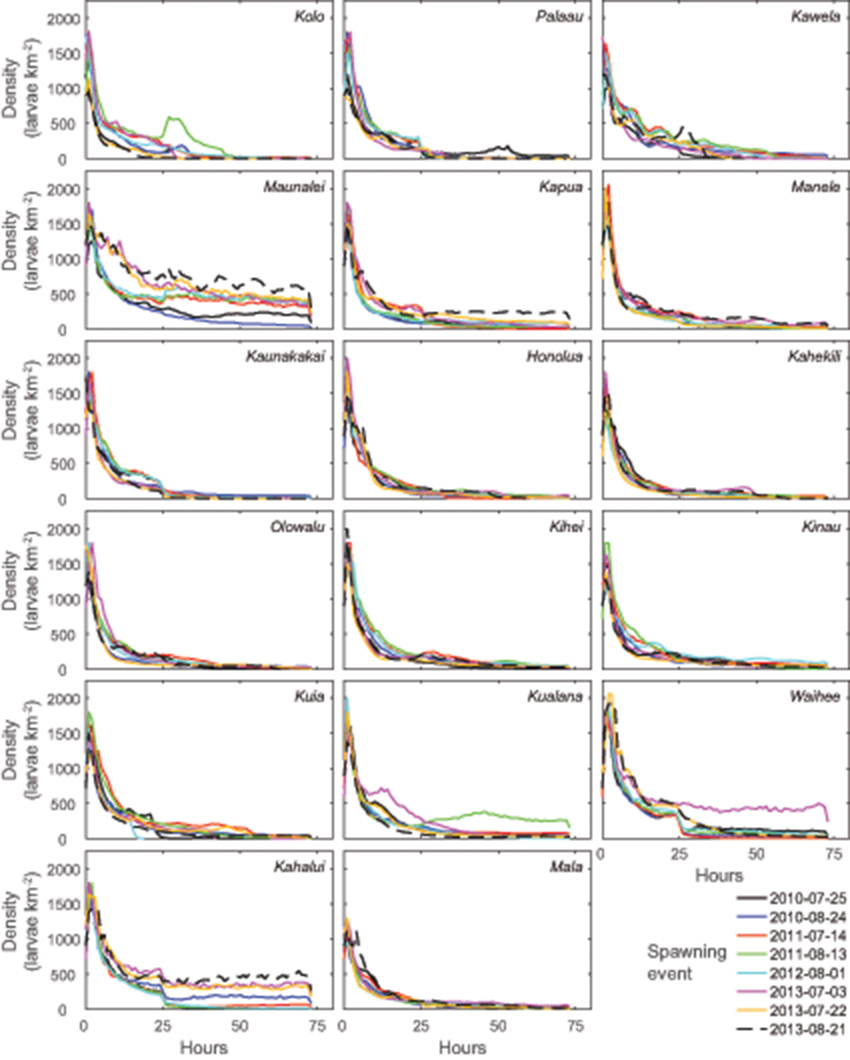
Figure 6. Evolution of coral larval densities from the 13 source reefs through time in the simulations demonstrating the exponential decrease in larval densities due to dispersion in the first 24 h and then further decrease due to settling and movement offshore in the subsequent 48 h.

Reef Connectivity

A connectivity matrix was developed to display the resulting modeled larval connectivity between the different coral reefs in Maui Nui Figure 7. Compared to many studies of much larger regions (Thomas et al., 2014; Kool and Nichol, 2015), the degree of “self-seeding” (recruitment back to the natal reef) that follows the diagonal of the connectivity matrix is intermittent. This demonstrates that many reefs such as Kolo, Kahekili, and Mala retain little measurable larvae under the typical forcing conditions modeled and thus are either sustained primarily from adjacent natal reefs upstream or are seeded infrequently during rare atmospheric and oceanic condition (Moberly and Chamberlain, 1964; Fletcher et al., 2002). On the other hand, reefs such as Maunalei, Waihee, and Kahalui are predominantly self-seeding (defined here as >50% of the modeled larvae settling on a given reef originate from the reef itself). Kinau, Kihei, and Manele are the larval sources for the greatest numbers of reefs in Maui Nui, whereas Kolo and Kahalui are the sources for the least number of reefs.

FIGURE 7

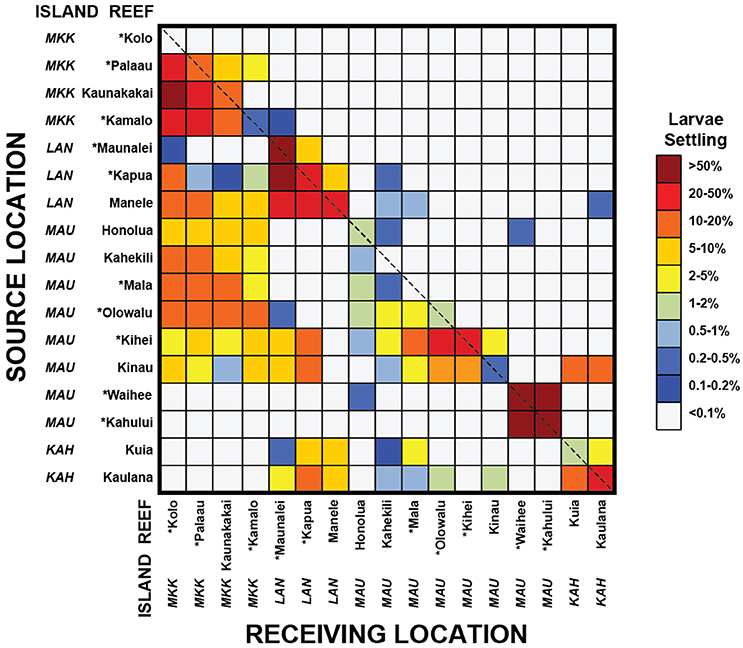
Figure 7. Matrix representation of modeled coral larval connectivity between source reefs and reef sinks in the Maui Nui complex during 8 spawning events in 2010–2013. Colors represent the percentage of larvae spawned from a given source reef settling on another reef (note the non-linear scale); the diagonal dashed line from the top left to bottom right designates self-seeding reefs. Island designations MKK, LAN, MAUI, and KAH are Molokai, Lanai, Maui, and Kahoolawe, respectively. The reefs with asterisks are large reef tracts with high coral cover, whereas those without are existing State of Hawaii MPAs.

Discussion

Coral connectivity in the 8 Main Hawaiian Islands has been documented for specific species using biogeographic (Ziegler, 2002) and genetic methods (Toonen et al., 2011; Conception et al., 2014), but the spatial patterns and time scales over which this occurs have not been clearly demonstrated. The results of this study utilized field observations and km-scale numerical modeling results to infer dispersal patterns and the resulting connectivity of the abundant Hawaiian reef-building coral species P. compressa from numerous reef tracts on adjacent high islands in the Maui Nui complex. Investigation of environmental conditions also revealed consistent patterns of water flow and direction suggesting that the observations in this study are likely representative of annual spawning periods.

The meteorologic and oceanographic data from both this and previous studies (Storlazzi et al., 2006a,b) show that flow in between the islands of Maui Nui is primarily controlled by the winds, tides, and waves. The general flow patterns show greater consistency during the summer months when the forcing by northeast Trade winds is relatively steady, storms occur infrequently, and nearshore surface wave-induced flows are at a minimum. During both the drifter deployment period and the summer coral spawning season, both the forcing (winds and tides) and the resulting flow and environmental patterns were relatively consistent, with Trade wind-driven waves and surface currents overprinted on oscillating tidal currents. Similar forcing and response across multiple spawning periods resulted in comparable models of projected water and coral larvae pathways during the eight spawning seasons in 2010–2013. Furthermore, since P. compressa always spawns the nights following a new moon (Kolinski and Cox, 2003), these spawning events always occur during the transition from spring to neap tides and thus the magnitude of the tidal current forcing during each spawning period is relatively consistent. These coherent patterns, along with the drifters' paths, suggest that the modeled trajectories likely well-characterize the initial larval dispersal patterns in Maui Nui during the summer months when many of the Hawaiian corals spawn.

As the density of coral eggs or developing planula larvae was not measured during the field portion of this study, the results of larvae transport are qualitative in nature. Previous studies (Willis and Oliver, 1988; Wolanski et al., 1989) suggest, however, that ocean surface current drifters can accurately mimic larval dispersal at time scales of up to 5 days. The drifter speeds and trajectories, in conjunction with the model results made over eight spawning periods in four different summer seasons, presented here along with previous genetic studies (Conception et al., 2014), suggest that many of the reef tracts in Maui Nui seed other reefs on their own island and on adjacent islands over relatively short (O~hours to days) time scales. Although larval competency and dispersal potential for many coral species can be quite high (Richmond, 1987; Wilson and Harrison, 1998; Kolinski and Cox, 2003), it has been suggested (Miller and Mundy, 2003) that dispersal of broadcast-spawning corals may be not as great as previously assumed because not only does larval density decrease exponentially with time (Sammarco and Andrews, 1988; Peliz et al., 2007), but so does competency to settle (Peliz et al., 2007). If this is the case, the short time scales of dispersal shown here are important because both larval density (Figure 6) and recruitment success decrease quickly with time and distance (Sammarco and Andrews, 1988) due to mixing and horizontal dispersion (Wolanski et al., 1989; Oliver et al., 1992).

It has been demonstrated (Andutta et al., 2012; Tay et al., 2012) that reefs and islands in close proximity often result in decreased flushing and thus more exposure time in areas where settlement can occur successfully; these features are generally not captured with large-scale models (Vaz et al., 2013; Wood et al., 2014). In this case, the flushing between islands appears to be somewhat offset by areas in the lee of the high islands that result in increased retention that was not captured in previous modeling studies (Andutta et al., 2012; Tay et al., 2012) where topographic steering of winds was not a factor. In addition, as model scale increases, the high cross-shore velocity shear (“coastal boundary layer”) that favors retention of larvae and results in greater self-seeding (Nickols et al., 2015) along many fringing coral reefs (Storlazzi et al., 2006b) is not resolved.

The relatively low number of predominantly self-seeding reefs modeled here contrasts with many other studies in different locations (Treml et al., 2008; Gilmour et al., 2009; Thomas et al., 2014), and is likely due to issues of scale. In most larger-scale studies, local recruitment that defines self-seeding occurs on spatial scales of km to a few 10s of km, whereas in Maui Nui, most of the existing MPAs are smaller than 1 km² and many of the larger reef tracts are separated by distances on the order of km to a few 10s of km. Thus, the finer-scale modeled connectivity patterns that we characterize as reefs with little self-seeding likely, in the larger-scale modeling studies, would be classified as predominantly self-seeding reefs. In general, Maui was the dominant source of larvae for most of the adjacent islands in Maui Nui, with Kahoolawe, and Lanai being lesser sources for adjacent islands. Conversely, Molokai received the most larvae from adjacent islands, with Lanai and Kahoolawe being lesser sinks of larvae (Table 3). Overall, most of Kahoolawe's coral larvae were lost offshore, whereas most of Lanai's larvae were successfully delivered to reefs over these modeled competency period.

TABLE 3

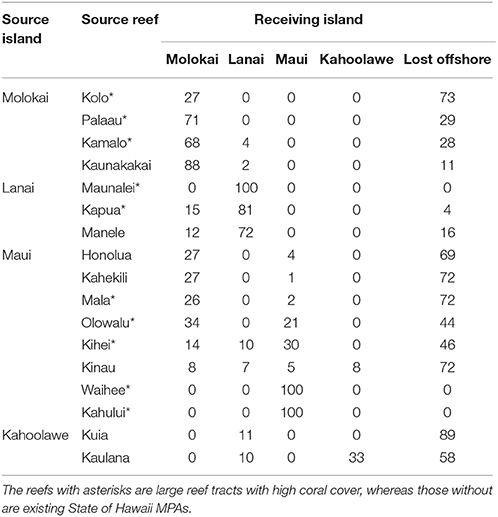
Table 3. Connectivity matrix showing the percentage of modeled coral larvae particles released from each natal reef settling on the different islands or lost at sea in the study area.

Application of Reef Characteristics to Delineating Potential MPAs

One of the more important findings from these simulations, besides distinguishing the modeled coral larvae sources and sinks (Figure 7, Table 3), is the identification of reef tracts where little self-seeding occurs (e.g., Kolo and Kahekili) and those that are dominated by self-seeding (e.g., Maunalei, Waihee, and Kahalui). In locations where relatively little self-seeding occurs, because some corals always die due natural causes, overall decline of the reef can be due to factors solely at other sites that reduce the new input of larvae to a rate too low to offset the local natural loss. On the other hand, such reefs can recover more quickly from local impacts if the local stressors are removed by seeding from healthy source reefs upstream. Reefs characterized by relatively high self-seeding are more at risk from local stressors. Once the reef becomes depauperate, there will be fewer sources for new coral larvae, even if the local stresses are mediated, and therefore the reef becomes more at risk from regional stresses. Identification of reef tracts that are sources of coral larval for other reefs downstream and those reef tracts that are primarily dependent on coral larvae from upstream reefs is therefore important to help direct management for coral reef health and sustainability.

As described above, the prescribed coral larvae source locations and reef tract sinks are existing State of Hawaii MPAs or large reef tracts with high coral cover (Figure 1). All of the State of Hawaii MPAs have limited coral reef tracts (size < 1 km² except for Kuia, which is ~4 km²), whereas none of the large reef tracts are existing MPAs, although they are large enough (>10 km²) not to likely be completely decimated by a single disease outbreak, vessel grounding, etc. These large coral reef tracts modeled as larval sources and receiving reef tracts throughout the Maui Nui complex also are spaced at the scale of kms to 10s of kms, thus meeting a previously-defined spacing criteria (Shanks et al., 2003) that provides a much larger total effective area (= MPA area and downstream area seeded by MPA) than a single MPA of equivalent size (Gaines et al., 2003). Although the km to 10s of km spacing distances previously proposed (Shanks et al., 2003) were based on global review, such spacing is relevant to Maui Nui and other coral reef tracts because it also minimizes the impact of both natural (e.g., storm waves or floods) and anthropogenic (e.g., oil spills or poor land-use practices) stressors to multiple portions of the MPA system.

It therefore appears to be a balance between a number of factors important to MPA network design that can be addressed by coral reef connectivity studies such as presented here. First is identifying the balance between seeding and no self seeding that makes reefs more resilient and able to recover from impacts. Second, there appears to be a need for MPAs to be large enough to have enough habitat to be resilient to local stressors and not be negatively impacted by a single local event, but balancing the need for protection vs. multiple use of waters (and thus only have a proportion, such as 10–30% of an organization's waters, in an MPA). Lastly, MPAs need to be spaced at such as distance that they are not negatively impacted by a local event, but close enough to be supported by large enough concentrations of larvae from adjacent MPAs to sustain populations or recover from impacts (White et al., 2010, 2014; Moffitt et al., 2011).

Based on their size, interconnected nature, and balance between no self-seeding to high self-seeding, the Kamalo, Kapua, Olowalu, and Kihei reef tracts off Molokai, Lanai, west Maui, and east Maui, respectively, best meet the criteria for effective MPA design and thus have the greatest potential to help maintain the health and sustainability of coral reefs in Maui Nui (Figure 7, Table 3). Additional factors that are physical, ecological, political, and economic in nature are important for defining MPAs, and therefore other large reef tracts in Maui Nui also may be viable options for future protection.

This study provides a view of connectivity that complements existing genetic and biogeographic work (Richmond, 1987; Willis and Oliver, 1988; Ziegler, 2002; Toonen et al., 2011; Conception et al., 2014) at time and spatial scales useful for management. Furthermore, the model represents an effective tool for exploring the factors controlling coral reef connectivity and the potential effects of climate change (e.g., Storlazzi et al., 2015) on future connectivity and thus will aid predictions of future reef distributions. Model projections and/or measurements of larval dispersal is but one component of population persistence: population models that can estimate the dynamics of the entire life cycle and actually estimate persistence and sustainability also are needed to assess the effectiveness of potential MPAs (Burgess et al., 2014). Stating that, this effort provides an important component of the scientific underpinning needed for the design of a mutually-supporting network of MPAs in Maui Nui to support coral reef conservation.

Author Contributions

CS: Designed the research program; CS, MvO, Y-LC, and EE: Conducted the research; CS, MvO, and EE: Conducted the analysis; and CS, MvO, Y-LC, and EE: Wrote the manuscript.

Funding

U.S. Geological Survey, Coastal and Marine Geology Program.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was carried out as part of the USGS's Coral Reef Project, an effort in the U.S. and its trust territories to better understand the effect of oceanographic processes on coral reef systems. Joshua Logan (USGS), Tom Reiss (USGS), Susie Cochran (USGS), Darla White (HI-DAR), Linda Castro (HI-DAR), and Kristy Stone (HI-DAR) deserve special credit for their effort on the drifter deployments. We would also like to thank Michael Field (USGS) and Lisa Lucas (USGS), who contributed numerous excellent suggestions and a timely review of our work. This work is dedicated to Paul Jokiel (UH-HIMB), who taught so much about Hawaiian coral reefs to so many. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

References

Andutta, F. P., Kingsford, M. J., and Wolanski, E. (2012). ‘Sticky water' enables the retention of larvae in a reef mosaic. Estuar. Coast. Shelf Sci. 101, 54–63. doi: 10.1016/j.ecss.2012.02.013