- 1Department of Oceanography (OCE), National Institute of Oceanography and Experimental Geophysics (OGS), Sgonico, Italy
- 2International Centre for Theoretical Physics (ICTP), Trieste, Italy
Zooxanthellate corals are known to increase calcification rates when exposed to light, a phenomenon called light-enhanced calcification that is believed to be mediated by symbionts' photosynthetic activity. There is controversy over the mechanism behind this phenomenon, with hypotheses coarsely divided between abiotic and biologically-mediated mechanisms. At the same time, accumulating evidence shows that calcification in corals relies on active ion transport to deliver the skeleton building blocks into the calcifying medium, making it is an energetically costly activity. Here we build on generally accepted conceptual models of the coral calcification machinery and conceptual models of the energetics of coral-zooxanthellae symbiosis to develop a model that can be used to isolate the biologically-mediated and abiotic effects of photosynthesis, respiration, temperature, and seawater chemistry on coral calcification rates and related metabolic costs. We tested this model on data from the Mediterranean scleractinian Cladocora caespitosa, an acidification resistant species. We concluded that most of the variation in calcification rates due to photosynthesis, respiration and temperature can be attributed to biologically-mediated mechanisms, in particular to the ATP supplied to the active ion transports. Abiotic effects are also present but are of smaller magnitude. Instead, the decrease in calcification rates caused by acidification, albeit small, is sustained by both abiotic and biologically-mediated mechanisms. However, there is a substantial extra cost of calcification under acidified conditions. Based on these findings and on a literature review we suggest that the energy aspect of coral calcification might have been so far underappreciated.
Introduction
Marine organisms sensitivity to acidification and warming is a matter of several physiological processes being concomitantly affected, as argued by Pörtner (2008). Despite the huge research effort seen in recent years, biocalcification response to environmental parameters remains an elusive topic, as stated by Allemand et al. (2011) in an extensive review on coral calcification; that review opens with two quotes, written almost one century apart by scientists engaged with coral calcification, both advocating that the key to understand biocalcification lies in the interactions between the living parts of the coral and the skeleton, an aspect that is still sometimes overlooked in many research studies.
Coral calcification is an energy demanding process: Al-Horani et al. (2003) and Venn et al. (2011) demonstrated that scleractinian corals actively regulate the chemical properties (pH, Ca2+ concentration) in the extracellular calcifying medium (ECM, the sub-micrometric interface between coral soft tissue and skeleton, from which the skeleton is secreted) in order to favor calcification, and active regulation requires an energetic investment. Recent studies uncovered several energy demanding physiological processes involved in coral calcification. There is evidence that Ca2+ ions are supplied to the ECM via an active transcellular pathway involving Ca-ATPase active membrane transport proteins that would simultaneously remove protons from the ECM (Barott et al., 2015a; Zoccola et al., 2015). Alternatively, protons may be removed from the ECM by an independent proton pumping mechanism (Jokiel, 2011; Ries, 2011), possibly an H-ATPase of the same kind used to acidify the medium where zooxanthellae are located (Barott et al., 2015b). Carbon, on the other hand, may reach the ECM trough passive bicarbonate anion transports (BAT) of the SLC4 family (Barott et al., 2015a; Zoccola et al., 2015). Barott et al. (2015a) however, also suggest that transport trough BATs may be driven by the co-transport of Sodium that may reach the ECM through an active Na/K-ATPase pump, thus making also carbon delivery costly. However, there is also evidence that not all corals may have evolved the same physiological pathways and mechanisms to control calcification (Barott et al., 2015a; Le Goff et al., 2017), so a complete description of all the processes involved in calcification in corals is still missing.
Corals, through their metabolism, allocate some part of the energy they obtain from heterotrophic feeding and zooxanthellae photosynthesis to calcification (Dubinsky and Jokiel, 1994; Houlbrèque and Ferrier-Pagès, 2009; Tremblay et al., 2012, 2013) and convert it to skeletal material, i.e., calcium carbonate and organic matrix (OM). The ratio of energy invested to skeleton deposited is the [unitary] metabolic cost of calcification. Many studies dealt with proposed metabolic costs of calcification (Anthony et al., 2002; McCulloch et al., 2012; Hohn and Merico, 2015). The exact value of such cost is in fact unknown (Allemand et al., 2011). The only experimental estimate to date was carried out by Palmer (1992) on a mollusc and yielded an estimated cost of 100–200 kJ/mol. More recently the cost of calcification has been identified with the difference in chemical potential between coelenteron and ECM (about 3–6 kJ/mol, McCulloch et al., 2012), the Gibbs free energy of ATP hydrolysis needed to fuel membrane transport proteins (about 30 kJ/mol, Anthony et al., 2002) or the Gibbs free energy of ATP hydrolysis needed to fuel membrane transport proteins, but also with contributions from passive transport mechanisms (about 20 kJ/mol, Hohn and Merico, 2015). Though, these values may be underestimated since they do not account for the inefficiencies that any real life transport process entails. Furthermore, it could be argued that if the cost of building one mole of skeleton was that low [specific enthalpies of combustion of carbohydrates, lipids, and proteins are, by comparison 473, 611, and 543 kJ/mol respectively, (Gnaiger, 1983)], many calcifiers would face little trouble in compensating for acidification effects. Jokiel (2011) proposed that the observed effects of acidified seawater on coral calcification are mediated by diffusion limitation of net H+ transport away from the coral. This is similar to the argument from Cohen and Holcomb (2010) that under acidified conditions corals must spend more energy to remove protons from the calcifying medium in order to maintain calcification rates. These arguments point at an increase in the cost of calcification, or a reduction in efficiency, under acidified conditions.
To understand how calcification is affected by the surrounding environment it is crucial to understand how corals allocate energy to calcification. The problem is not trivial as it involves both the coral host physiological activity and that of its algal symbionts, which are also involved in the phenomenon of light-enhanced calcification (LEC). Higher calcification rates [3x on average, Gattuso et al., 1999; Moya, 2006] are consistently observed during daytime and this effect is believed to be mediated by symbionts photosynthetic activity (Gattuso et al., 1999; Allemand et al., 2011). LEC is an highly debated topic and various non-mutually exclusive hypotheses exist (reviewed in Gattuso et al., 1999; Allemand et al., 2011). All the hypotheses can be coarsely grouped into the two categories of biologically-mediated and abiotic mechanisms.
Abiotic explanations (i.e., directly mediated by inorganic chemistry) concern photosynthesis altering the carbon budget in the coelenteron, producing changes in chemical gradients that eventually affect carbonates deposition (Cyronak et al., 2015; Cohen et al., 2016).
As far as biologically-mediated mechanisms are concerned, photosynthesis would enhance calcification by providing energy and/or material for skeletogenesis. For instance, there is evidence that OM plays a structural role in skeleton formation (Allemand et al., 2004; Puverel et al., 2005; Bertucci et al., 2015; Takeuchi et al., 2016; Von Euw et al., 2017); photosynthesis may thus enhance calcification by providing energy and/or precursors for OM synthesis (Bertucci et al., 2015). Also, some authors mention the energetic coupling between symbionts and host as a possible cause of LEC, either directly as increased ATP production stimulated by the translocation of photosynthate to the host, (Goreau and Goreau, 1959; Chalker and Taylor, 1975) or indirectly as photosynthetic oxygen production enhancing respiration rates (Al-Horani et al., 2007).
Besides light, also other major environmental parameters are believed to play crucial roles in calcification: seawater carbonate chemistry and temperature; and both are believed to act in a 2-fold fashion on the process of calcification, with biologically-mediated and abiotic effects: Temperature is clearly a major determinant of metabolic rates (Coles and Jokiel, 1977), but it also has effects on carbonate chemistry, including calcification rates which are favored at high temperatures. Seawater carbonate chemistry is often considered as a major determinant of chemical gradients within the coral, in fact acidification effects on calcification are mostly ascribed to abiotic mechanisms (Cohen and Holcomb, 2010; Jokiel, 2011); however, carbonate chemistry could also affect photosynthesis (which may be carbon-limited) and respiration (which may be depressed in case of hypercapnia, Pörtner, 2008), although on this matter conflicting evidence is observed, e.g., in Schneider and Erez (2006) vs. Comeau et al. (2017).
Syntrophic symbioses, like the one that happens in many coral species, can be conceptualized in the light of host and symbiont energetics, as done in the syntrophic symbiosis models developed by Dubinsky and Jokiel (1994) and Muller et al. (2009). In these models zooxanthellae produce an excess of photosyntate that is translocated to the coral host and it thus represents additional energy available for whatever metabolic purpose must be fulfilled, whilst (in the Muller et al., 2009 model) the coral host supplies its symbionts with waste material (nutrients) that serve as substrate for algal photosynthesis. The interesting outcome of this setup is that, although the regulation mechanism is entirely passive, it suffices to obtain a stable relationship; furthermore, this relationship shifts from mutualism to parasitism as environmental conditions change, thus providing also a candidate trigger for bleaching events.
We believe the key to understand the mechanisms involved in LEC, and in environmental control of calcification in general, lies in the energetic coupling between coral and zooxanthellae metabolism and calcification. It is however also likely that purely abiotic mechanisms play a major role in determining calcification response. Arguably both abiotic and biological phenomena may be relevant and it would be interesting to be able to discern the effects. The experimental results from Al-Horani et al. (2003) and Venn et al. (2011) and the conceptual model of the calcification physiological machinery from McConnaughey and Whelan (1997) opened the gates to a deeper understanding of the cause and effect mechanisms that regulate coral sensitivity to acidification. Still lot though remains to be understood; the small spatial and temporal scales of the processes involved make many possibly useful experiments impractical: the carbonates system is completely determined with any two of its variables, though measuring such variables in micrometric or sub micrometric spaces (like ECM and coelenteron) is demanding, so that to date not all the details of coral internal chemistry are known.
Models represent a viable way to test existing hypotheses and suggesting new experiments. Hohn and Merico (2012, 2015) compared different conceptual models of coral calcification to determine which one produced the best agreement with the experimental results from Al-Horani et al. (2003). The authors found the model that performed better was the one that incorporated all three of the proposed metabolic pathways (active transport, paracellular diffusion, transcellular diffusion) involved in calcification. Coincidently it was also possible to test hypotheses on the contributions of the different metabolic pathways to calcification: in their model calcium reaches the skeleton mainly through the active pathway and carbon trough transcellular CO2 diffusion, whilst through the paracellular pathway skeleton building blocks diffuse back from ECM to coelenteron.
Nakamura et al. (2013) used a similar model to test the plausibility of the oxygen hypothesis (Allemand et al., 2011) for light-enhanced calcification (LEC), concluding that oxygen-boosted respiration may be responsible for the increase in calcification during daytime.
Here we propose a model of coral calcification built on the conceptual schemes developed in McConnaughey and Whelan (1997), Hohn and Merico (2012, 2015), Nakamura et al. (2013), and implement realistic kinetics of active trans-membrane transport (Smith and Crampin, 2004). The model is applied on an experimental dataset for the Mediterranean coral Cladocora caespitosa (Rodolfo-Metalpa et al., 2010) and used to (1) compare the biologically-mediated and abiotic contributions to calcification due to temperature, metabolic rates (photosynthesis and respiration), and seawater chemistry and (2) assess the cost of calcification and its response to external parameters and physiological rates. In defining biologically-mediated effects we focus here on the energy (or ATP) hypothesis (Goreau and Goreau, 1959; Chalker and Taylor, 1975) and neglect other hypothesizes mechanisms, (e.g., supply of precursors for skeletal organic matter synthesis, oxygen limitation).
Materials and Methods
Case Study
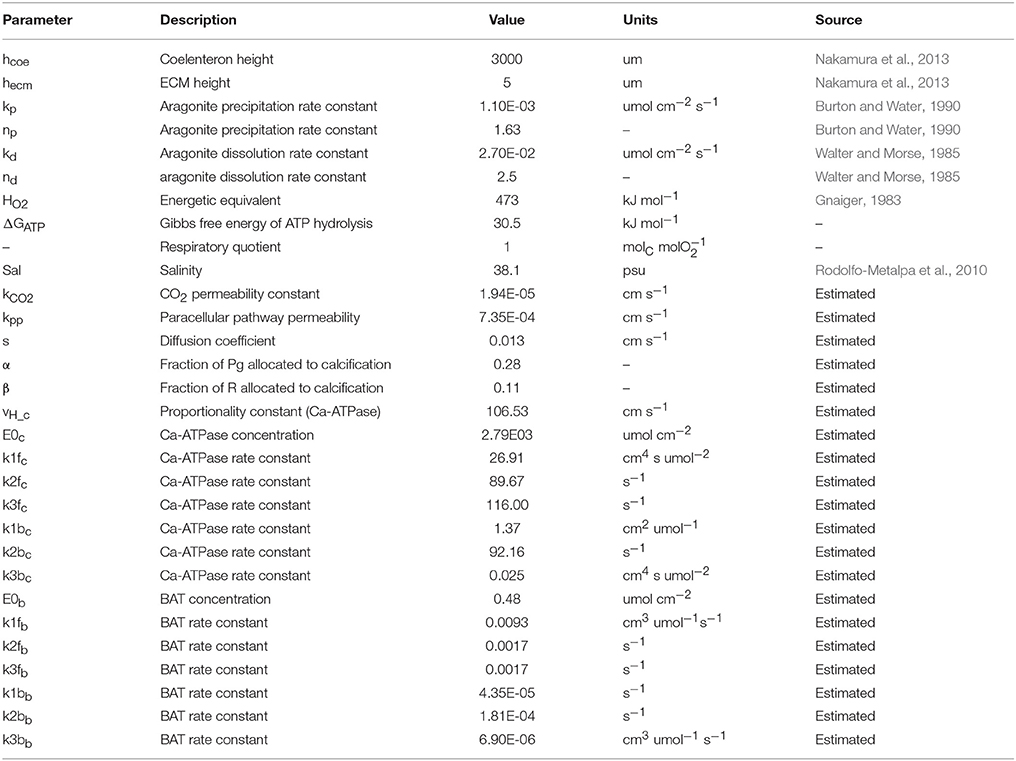
The model is applied on the dataset provided in Rodolfo-Metalpa et al. (2010). This very valuable study assessed the differential influence of temperature and pCO2 on the metabolic rates (gross photosynthesis, dark respiration, calcification) in the Mediterranean coral C. caespitosa. The data set constitutes of four treatments: (1) Baseline temperature (according to replicate) and baseline pCO2 (400 ppm), (2) Baseline temperature and increased pCO2 (700 ppm), (3) Increased temperature (+3°C with respect to the corresponding baseline temperature replicate) and baseline pCO2, (4) Increased temperature and increased pCO2. Each treatment comprises six replicates assessed in different seasons. For this study only the summer and winter replicates were used because both gross photosynthesis and dark respiration were measured. A table of the experimental conditions used in the model is provided in Table 1.
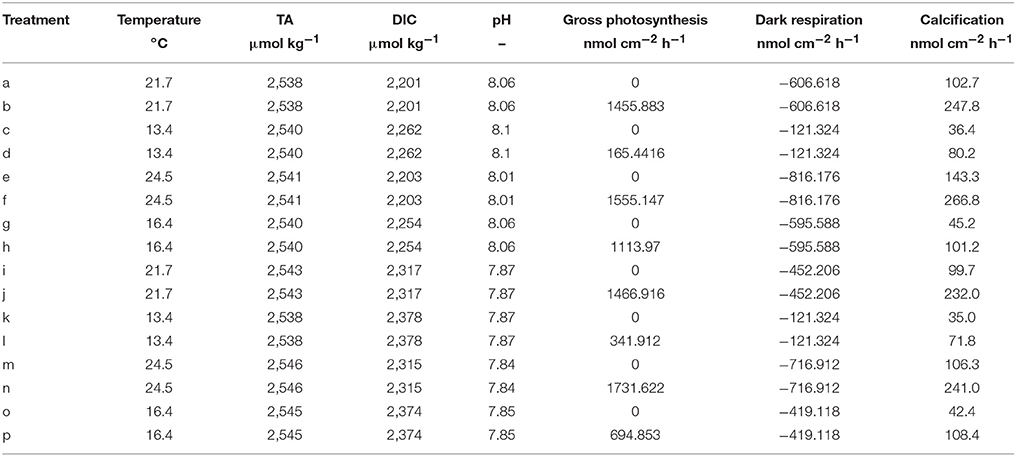
Table 1. Experimental data from Rodolfo-Metalpa et al. (2010) used in this study, calcification rates are measured with the alkalinity anomaly technique.
Model Description
Model Topology, State Variables, and Scales
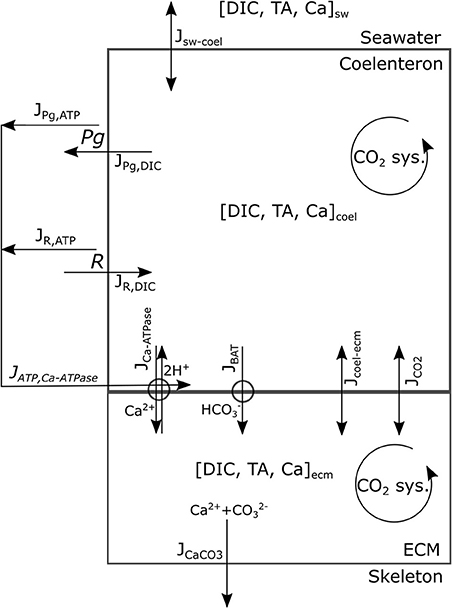
This model's rationale is to follow the transport and reaction of the chemical species and metabolic fluxes physiologically relevant to biocalcification (either in a direct or indirect way) from seawater to coral skeleton trough compartments within the coral living body. We make the simplifying assumption (after Nakamura et al., 2013) that seawater is separated from the skeleton by two consecutive compartments: the coelenteron and the calcifying medium (ECM). Here we hypothesize that (1) mass transfer processes happening through the oral tissue, between seawater and coelenteron, can be neglected because advection rates through the coral mouth should be much larger, and (2) mass transfer processes through various layers within the aboral tissue, between coelenteron and ECM, are in series, hence limited by the least permeable layer which, we assume, is the interface between calicoblastic epitelium and ECM. A scheme of the model is provided in Figure 1, all model parameters and sources are listed in Table 2.
The chemical species considered are the Ca2+ ion and those pertaining to the carbonates system. The reported presence of the enzyme carbonic-anhydrase, which speeds up the equilibration of the carbonates system, in corals' ECM (see (Bertucci et al., 2013) for a review) may hinder the validity of kinetics derived for seawater (Zeebe and Wolf-Gladrow, 2001), whilst, at the same time, suggests that the carbonate system should be reasonably close to equilibrium within the model compartments. Given this reasoning and due to the fact that the whole carbonate system has two degrees of freedom (i.e., is completely determined by any two of the variables involved), we chose as state variables to describe the carbonate system the two conservative quantities dissolved inorganic carbon (DIC) and total alkalinity (TA), as done in Nakamura et al. (2013), and use equilibrium relations (as explained later in this section) to calculate the other (dependent) state variables: H+, OH−, CO2, , and . Whenever some process involves the dependent state variables, the resulting flux is converted in DIC and/or TA fluxes as explained through this section. All transport processes are computed per unit surface area and the growth of the colony is not resolved. As proposed in Galli et al. (2016) the massive growth shape of C. caespitosa would ensure that vital rates do not depend colony size.
Carbonate System Equilibria and Physico-Chemical Constants
The components of the carbonate system, H+, OH−, CO2, , and , are calculated in each compartment from DIC, TA, temperature and salinity, assuming that chemical equilibrium is reached at each time step, according to the equilibrium relations in Zeebe and Wolf-Gladrow (2001). For the sake of simplicity, we consider just the carbonates' contribution to alkalinity and neglect, e.g., borates.
The carbonic acid dissociation constants, K1 and K2, and solubility product of water, Kw, are calculated from temperature and salinity according to Millero (2007). Aragonite solubility product, Kar, is calculated from temperature and salinity according to Zeebe and Wolf-Gladrow (2001). Water density, ρ, is also calculated from temperature and salinity according to Millero and Poisson (1981) and used trough the model to convert volumes to masses when needed.
Photosynthesis and Respiration
Gross photosynthesis, Pg, and respiration, R, are forced in the model with the values measured by Rodolfo-Metalpa et al. (2010) as mol O2 per unit area per unit time. Photosynthesis removes one mol DIC from the coelenteron per mol O2 produced (JPg,DIC flux in Figure 1) whilst respiration increases coelenteron DIC by 1 mol per mol O2 consumed (JR,DIC flux in Figure 1). Contextually, ATP production fluxes (JPg,ATP, JR,ATP) are associated with Pg and R: Pg and R fluxes are converted from O2 to energy with a conversion coefficient (HO2, kJ/molO2) according to Gnaiger (1983) and then to mol ATP by assuming a Gibbs free energy of 30.5 kJ per mol ATP:
JPg,ATP represents the surplus energy budget that is available for the coral host from photosyntate translocation during daytime, whilst JR,ATP represents energy budget from heterotrophic feeding and stored photosynthate.
Passive Transport Processes
The exchanges from seawater to coelenteron are modeled as an advection process governed by concentration gradients:
Where sw−coel is the vector of the fluxes of the state variables from seawater to coelenteron (mass surface−1 time−1), sw and coel are the vectors of the state variables, , in seawater and coelenteron respectively (concentrations), s is the advection coefficient (with units of speed).
The exchanges of state variables between coelenteron and ECM trough the paracellular pathway and the permeation of CO2 trough cell layers are described as advective/diffusive phenomena:
Where coel−ecm is the vector of the fluxes between coelenteron and ECM trough the paracellular pathway, JCO2 is the CO2 flux from coelenteron to ECM trough the living tissue, CO2,coel, and CO2,ecm are CO2 concentrations in coelenteron and ECM respectively, and kpp, kCO2 are permeability coefficients (with units of speed). The JCO2 flux exchanges 1 mol DIC per mol CO2 transported.
Membrane Transport Processes
Two membrane transport proteins are modeled: a Ca-ATPase pump (McConnaughey and Whelan, 1997; Allemand et al., 2004; Barott et al., 2015a) that exchanges 1 mol Ca2+ for 2 mol H+ at the cost of 1 mol ATP (Gattuso et al., 1999) between coelenteron and ECM, and a bicarbonate anion transport [(Furla et al., 2000; Zoccola et al., 2015); BAT, (Barott et al., 2015a)] that exchanges 1 mol between coelenteron and ECM. BAT functioning does not require an ATP supply and may be driven by the co-transport of other ions such as Cl− or Na+ (Barott et al., 2015a; Zoccola et al., 2015), though those have been neglected as they are not relevant for skeletogenesis and unlikely to be rate-limiting due to high seawater concentrations.
Previous modeling studies (Hohn and Merico, 2012, 2015; Nakamura et al., 2013) have dealt differently with membrane transport protein modeling in corals; however, due to the particular aims of this study, we choose to adopt a different solution: in order to relate transport rates to ATP supply as well as concentration gradients, we need to model the co-limitation of transport when two or more substrates are involved (e.g., Ca2+ and H+ on both sides of the membrane, and ATP in the Ca-ATPase). This isn't possible with Michaelis-Menten kinetics, as done, for instance, in Hohn and Merico (2012, 2015). On the other hand, Nakamura et al. (2013) adopted a different formulation, based on the Nernst equation, for membrane transport modeling, that relates fluxes to both ATP supply and concentration gradients. Whereas, this formulation is appealing because it is based on first principles and has only one free parameter (an energy conversion coefficient), we don't think it is entirely realistic because it is linear in ATP supply, whereas enzyme kinetics should saturate.
We chose to model pumps functioning after Smith and Crampin (2004) whom proposed a biophysically-based model of a sodium-potassium antiporter as a four steps cyclic enzymatic reaction comprising both the forward and backward cycles. Such model is based on a reduction scheme from a 15-stage kinetic model that lumps together the fast reactions. To limit the number of unknown parameters we further simplified Smith and Crampin's model by assuming that (1) the binding of two H+ ions in the Ca-ATPase is lumped together in a single reaction, (2) the binding reactions of Ca-ATPase with Ca2+ and of BAT with ions other than are much faster than the other steps due to high Ca2+, Cl−, Na+, etc., concentrations and can therefore be neglected [but see Gutner-Hoch et al. (2017) for evidence that Ca2+ addition can stimulate calcification under light conditions, but not in the dark, hence can be rate-limiting]. This leaves us with two 3-stage reactions that can be written as:
and,
for Ca-ATPase and BAT respectively. Where E1, E2, E3 are the three possible states of Ca-ATPase (subscript c) and BAT (subscript b), whose total concentration is conservative and equals E0i = E1i+E2i+E3i. A graphic scheme of the reactions is presented in Figure 2. In the model we do not compute ATP concentration within the cell but rather we define the ATP flux that is devoted to run the active transports (JATP,Ca−ATPase, see section ATP Flux to Ca-ATPase). Given this constraint we chose, for the Ca-ATPase only, to model reaction kinetics based on fluxes rather than concentrations, as proposed by Kooijman (2010); the fluxes of chemical species reaching the pumps are considered to be linearly proportional to concentrations: with vH a proportionality constant with units of speed. Forward and backward reactions kinetics have reaction constants k1f, k2f, k3f, and k1b, k2b, k3b for the forward and backward cycles respectively. The whole system for the Ca-ATPase can be written as:
At steady state the net production of E1, E2, E3 is zero, hence the flux trough Ca-ATPase equals:
By solving at steady state, the expression for the flux trough Ca-ATPase is derived:
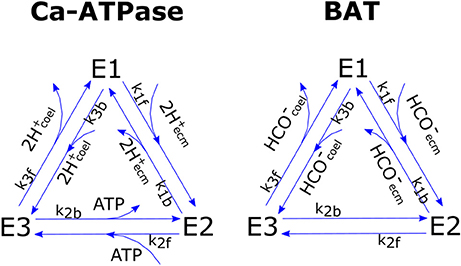
Figure 2. Graphic scheme of the two cyclic enzymatic reactions that were used to model Ca-ATPase and BAT membrane transport proteins.
So that each cycle transports 2 mol protons from ECM to coelenteron and 1 mol Ca2+ from coelenteron to ECM while consuming 1 mol ATP; flow is in opposite direction if the pump functions in reverse. The JCaATPase flux moves 2 mol TA from coelenteron to ECM per mol H+, and vice-versa if the pump functions in reverse.
BAT flux (JBAT) expression is analogous to that of Ca-ATPase and is derived with the same procedure:
The kinetic constants for the two transports are of course different so that the BAT and Ca-ATPase have separate parameterizations. The JBAT flux moves 1 mol DIC and 1 mol TA from coelenteron to ECM under normal functioning and vice-versa if the pump functions in reverse.
ATP Flux to Ca-ATPase
The energetic flux that is used to run the active transports is considered to be a weighted sum of respiration (JR,ATP) and photosynthesis (JPg,ATP) ATP fluxes. Even though zooxanthellae clearly do not directly supply energy to Ca-ATPase, we assume, after Dubinsky and Jokiel (1994) and Muller et al. (2009), they produce some excess photosyntate that is translocated to the host and can be used for whatever purpose, including running ion transport machinery. This mechanism is clearly a simplification, the translocation of photosynthetic energy to the coral host would imply an increase in light respiration and the energy consumed by the active transports will indeed appear solely in the respiratory flux, though it should suffice as a first approximation assuming that the machinery operates at steady state. The ATP flux is:
where α and β are the fractions of JPg,ATP and JR,ATP that are devoted to the active transports.
Aragonite Precipitation and Dissolution
Aragonite precipitation and dissolution kinetics are modeled after Burton and Water (1990) and Walter and Morse (1985) as:
where JCaCO3 is the Aragonite precipitation or dissolution flux (mass per unit time per unit area), kp, np are empirical coefficients for precipitation kinetics, kd, nd are empirical coefficients for dissolution kinetics and Ω is the saturation state of aragonite defined as,
where Kar is the solubility product of aragonite calculated from temperature and salinity according to Zeebe and Wolf-Gladrow (2001) JCaCO3 flux consumes 1 mol DIC and 2 mol TA from the ECM per mol CaCO3 precipitated and vice-versa in case of dissolution.
Model Master Equations and Initialization
Surface based fluxes are converted to concentrations by dividing for the height of the relevant compartment, hcoel and hecm, so that the whole system of differential equations can be written as:
This system is solved with a Runge-Kutta-Fehlberg variable step-size method with error control tolerance 10−6 and initialized with a 0.01 s timestep. The state variables in all compartments are initialized with the relative seawater values (according to experimental setup); after some trials, we determined this does not influence compartments behavior apart for a negligible initial transient.
Model Calibration
The model was run for a simulation time of 500 s, largely sufficient to reach a steady state, with external conditions corresponding to each of the experimental setups (T, Sal, DIC, TA) and vital rates measurements (Pg, R) in Rodolfo-Metalpa et al. (2010) and was calibrated, with a monte-carlo simulation coupled with a genetic algorithm, by minimizing the sum of squared errors between the measured and simulated calcification rates (those measured with the alkalinity anomaly technique, see Rodolfo-Metalpa et al., 2010). We performed several thousands of model runs until we attained a satisfactory fitting of the experimental data. The dataset in Rodolfo-Metalpa et al. (2010) was also used to run simulation experiments (see below).
Cost of Calcification
The instantaneous metabolic cost of calcification can be calculated as the ratio between the ATP flux reaching Ca-ATPase, JATP,Ca−ATPase, and the calcification rate JCaCO3.
Simulation Experiments
After determining the set of parameter values that approximates at best the measured calcification rates, the model was used to run simulation experiments.
Compartments' Behavior Under Light and Dark
To evaluate how the compartments and transport rates behave under light and dark conditions (i.e., in the presence or absence of photosynthesis), the model was run for a total simulation time of 2000 s with alternating light and dark conditions lasting for 500 s each and other conditions as from the (b) setup (see Table 1). Compartments' behavior was then compared with several experimental observations and modeling results as an, albeit qualitative, mean of validation.
Abiotic and Biologically-Mediated Effects on Calcification
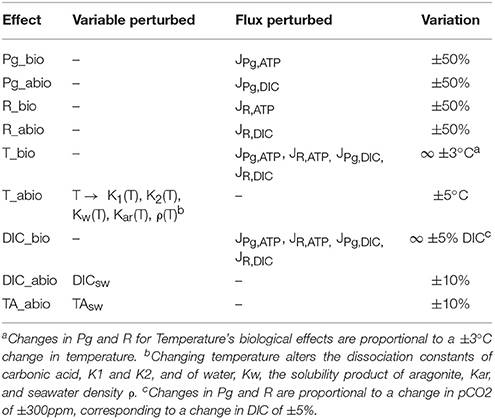
The model was then used to isolate the biologically-mediated and abiotic effects of photosynthesis (light), respiration, seawater chemistry (DIC and TA), and temperature on calcification rates and calcification costs. This was done by perturbing specific state variables or fluxes while leaving the rest unchanged; a scheme with all assessed effects and related perturbed variables and fluxes is presented in Table 3.
We assume that the only effect of light is an increase in photosynthesis (but see Cohen et al., 2016); this in turn alters the DIC balance in the coelenteron (abiotic effect) and the ATP flux to the active transports (biologically-mediated effect). Thus, increasing photosynthesis in the model should simulate the LEC phenomenon. To isolate the biologically-mediated effect of photosynthesis the model was run at all light setups with JPg,ATP fluxes (see Figure 1, Table 3) derived with Pg values in the range ±50% with respect to the baseline setup value. To isolate the abiotic effect of photosynthesis instead, the model was run at all light setups with JPg,DIC fluxes (see Figure 1, Table 3) derived with Pg values in the range ±50% with respect to the baseline setup value. We adopted the same procedure also to separate the biologically-mediated and abiotic effects of respiration, but here both light and dark setups were used. The biologically-mediated effects of respiration were assessed by running the model at all setups with JR,ATP fluxes derived with R values in the range ±50% with respect to the baseline setup value. The abiotic effects of respiration were assessed by running the model at all setups with JR,DIC fluxes derived with R values in the range ±50% with respect to the baseline setup value. The model doesn't incorporate any law of temperature dependence for Pg and R, thus to separate the biologically-mediated effects of temperature the model was run at all setups with Pg and R values from increased temperature setups substituted with Pg and R values from the corresponding baseline temperature setup and vice versa. This method is constrained by the experimental dataset and permits the assessment of two temperature differences only: −3 and +3°C. Please note that here, contrary to what done for Pg and R's effects, the effects of modified rates on coelenteron carbonates budget are included in the biologically-mediated group (i.e., here we are perturbing all of the JPg,DIC, JPg,ATP, JR,DIC, and JR,ATP fluxes simultaneously, see Figure 1, Table 3). In fact, we consider that the abiotic effects of temperature are those for which seawater phyisco-chemical constants, influencing carbonates equilibria and aragonite deposition rates, account for. To isolate the abiotic effects of temperature, the model was run at all setups with all physico-chemical constants (see sections Carbonate System Equilibria and Physico-Chemical Constants and Aragonite Precipitation and Dissolution) calculated with temperatures ranging from −5 to +5°C the baseline setup value. To separate the abiotic effects of different components of carbonate chemistry (DIC, TA) the model was run at all setups with either DIC or TA seawater concentration in the range ±10% with respect to their original setup value. Same as for temperature, the model doesn't incorporate any law that ties Pg nor R to seawater chemistry, also Rodolfo-Metalpa et al. (2010) state no significant correlation emerged in the original experiment between pCO2 and Pg nor pCO2 and R. Nonetheless it is possible to assess potential biologically-mediated effects of pCO2 (Langdon and Atkinson, 2005; Pörtner, 2008) by running the model at each setup with Pg and R values of baseline setups equal to those of the corresponding acidified setup and vice versa. This method is constrained by the experimental setup and permits the assessment of two pCO2 differences only: −300 and +300 ppm, corresponding to a change in DIC of roughly ±5%. Same as for temperature's biological effect, this change affects all of the JPg,ATP, JPg,DIC, JR,DIC, and JR,ATP fluxes simultaneously, see Figure 1, Table 3.
Results
Calibration and Compartments' Behavior
The model correctly simulates the observed calcification rates (that were used for calibration) under all of the experimental conditions (Figure 3). As there is a lack of knowledge about the values, or even ranges of variation, of many of the model parameters, it was not always possible to compare our estimates with experimental evidence. However, we notice that our estimate of the parameter s, diffusion coefficient between seawater and coelenteron, of 0.013 cm/s, is in the range of the clearance rates measured for C. caespitosa in Tremblay et al. (2011) (~0.008: 0.02 cm/s, inferred from the slopes of the regression lines in Figure 6). The model compartments' behavior under alternating light and dark conditions and the direction of the mass fluxes agrees with several experimental observations and modeling results: The ECM pH is always higher than external pH and higher in the light than in the dark (Figure 4D), in agreement with experimental observations (Al-Horani et al., 2003; Raybaud et al., 2017) and modeling results (Hohn and Merico, 2012, 2015; Nakamura et al., 2013); also, the value of the ECM pH in the light (~8.7 at pH 8.06) is in the range of the values calculated for Cladocora in Raybaud et al. (2017) (ca. 8.6–8.7 for a seawater pH of 8.2). ECM Ca2+ concentration is also higher than both the seawater and the coelenteron values and higher in the light than in the dark (Figure 4C), in agreement with Al-Horani et al. (2003), Hohn and Merico (2012, 2015), and Nakamura et al. (2013). Both DIC and TA in the ECM are upregulated with respect to the coelenteron (Figures 4A,B) and seawater. DIC upregulation, though, is smaller (DIC_ecm ~1.2 DIC_sw) than TA's (TA_ecm ~1.4 TA_sw), in agreement with the observations in Cai et al. (2016). Ω in the ECM is also higher than in seawater, ranging from about 12.5 in the light to about eight in the dark (Figure 4E), this reflects on the related calcification rates (Figure 4F).
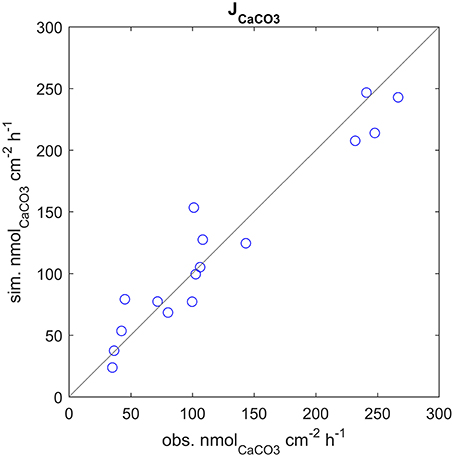
Figure 3. Calcification rates at all experimental setups, observed vs. simulated values. Note that the observed calcification rates were used to calibrate the model.
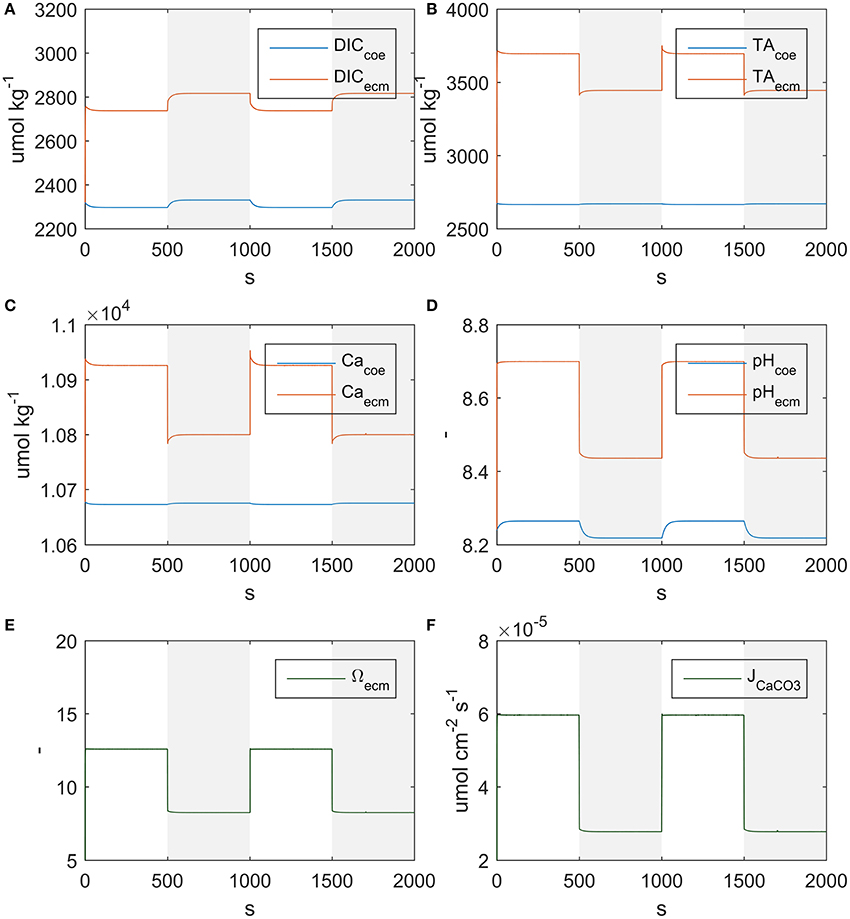
Figure 4. State variables behavior under alternating light and dark conditions. Shaded regions indicate dark conditions. (A) DIC, (B) TA, (C) Ca2+, (D) pH, (E) aragonite saturation, (F) Calcification rate.
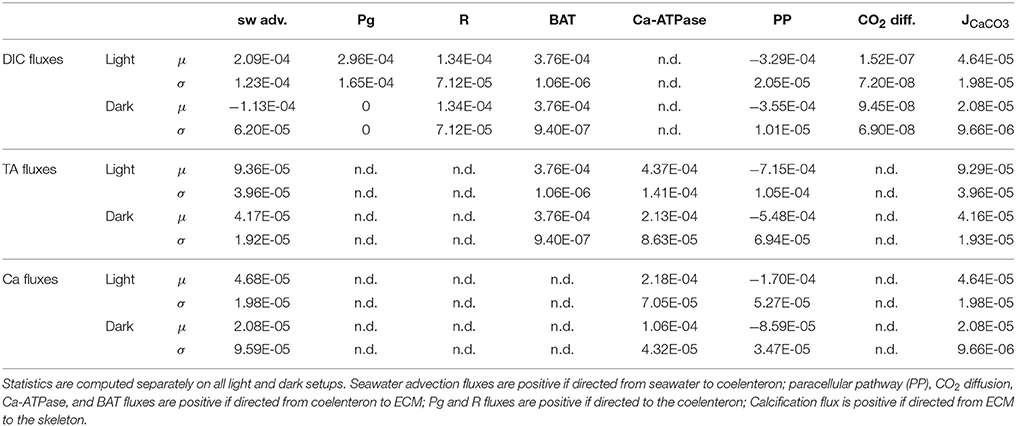
As far as mass fluxes are concerned (see Table 4), under dark conditions respiratory DIC accumulates in the coelenteron due to the absence of the photosynthesis sink, and from there it diffuses back to seawater; on the contrary under light conditions DIC drops in the coelenteron as it is used for photosynthetic activity, so that the diffusive flux is directed from seawater into the coelenteron. Under both light and dark conditions, the skeleton building blocks (DIC and Ca2+) enter the ECM through the membrane transports, whilst through the paracellular pathway they diffuse back to the coelenteron. Transcellular CO2 flux is always directed from coelenteron to ECM but is consistently smaller than the rest of the fluxes and has little overall effect.
In our model, similarly to the one in Nakamura et al. (2013), the compartments' equilibration is almost instantaneous, in opposition with the observations from Al-Horani et al. (2003) that demonstrate equilibration takes indeed several minutes; this discrepancy is due to our simplified assumptions, namely instantaneous translocation of photosynthetic energy to the active transports and equilibration of the carbonates system. Accounting for the time lag of these processes would have introduced additional complexity and it seemed not justified here since all of our analyses are based on the steady state functioning of the system.
Cost of Light and Dark Calcification Under Different Temperatures and pCO2
The estimated costs of calcification under the experimental conditions used in Rodolfo-Metalpa et al. (2010) (Figure 5A), range between about 110 kJ/molCaCO3 or 3.5 molATP/molCaCO3 to about 230 kJ/molCaCO3 or 7.5 molATP/molCaCO3. Dark calcification is generally more cost effective than light calcification; also the costs under acidified conditions are always higher with respect to control, however, extra costs due to acidification decrease with temperature (Figure 5B). Finally, the extra costs of calcification due to acidified conditions are larger in the dark than under the light.
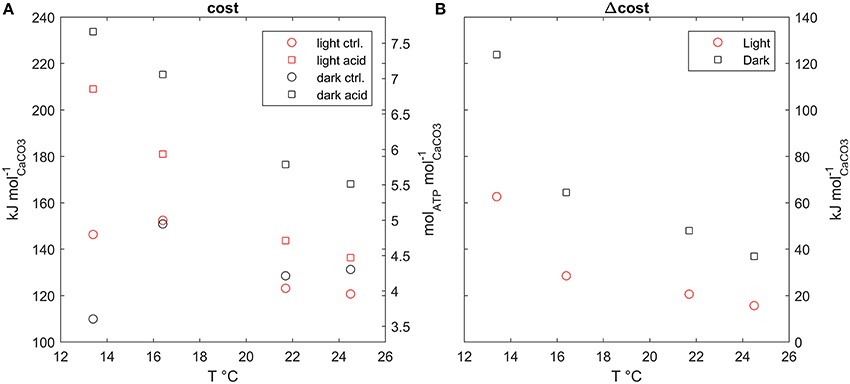
Figure 5. (A) Calcification costs at all model setups plotted against temperature, (B) extra cost of calcification, difference between cost under acidified and control conditions, plotted against temperature.
Contributions to Calcification Rates and Costs
Effects of Photosynthesis (Light) and Respiration
The overall effect of increased photosynthesis is to enhance calcification rates. This LEC effect is for the largest part due to biologically-mediated effects (Figure 6A), which are related to increased photosynthesis boosting Ca-ATPase transport rates. Abiotic mechanisms, related to the carbon budget in the coelenteron, also enhance calcification but to a negligible extent with respect to biologically mediated mechanisms, and a large variability is observed among different setups (Figure 6B). As far as costs are concerned, both biologically-mediated and abiotic mechanisms decrease costs for increased photosynthesis, with comparable magnitude of the effects (Figures 6C,D).
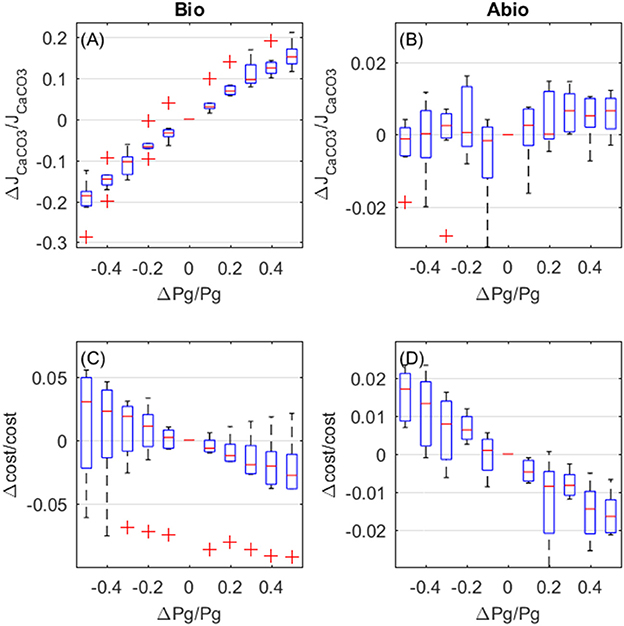
Figure 6. Biologically-mediated (A,C) and abiotic (B,D) effects of photosynthesis, fractional change in calcification rates (top panels) and calcification costs (bottom panels). X and y-axis values are indicative of fractional change. Each boxplot represents all light setups.
Increased respiration also enhances calcification rates and also here biologically mediated effects dominate. However, in opposition to what happens for photosynthsis, biologically-mediated, and abiotic effects are in opposition (Figures 7A,B). Calcification rates increase due to biologically-mediated effects (Figure 7A) in the same way as they increase for photosynthesis, as expected since Pg and R both contribute to the JATP,Ca−ATPase flux. On the contrary, the abiotic effects of increased respiration cause a decrease in calcification (Figure 7B), because respiration has opposite effects, compared to photosynthesis, on the coelenteron carbon budget. As for the costs, biologically-mediated effects of respiration display high variability and it is unclear whether costs increase or decrease for increasing respiration (Figure 7C), abiotic mechanisms, on the other hand, cause an increase in costs for increased respiration rates.
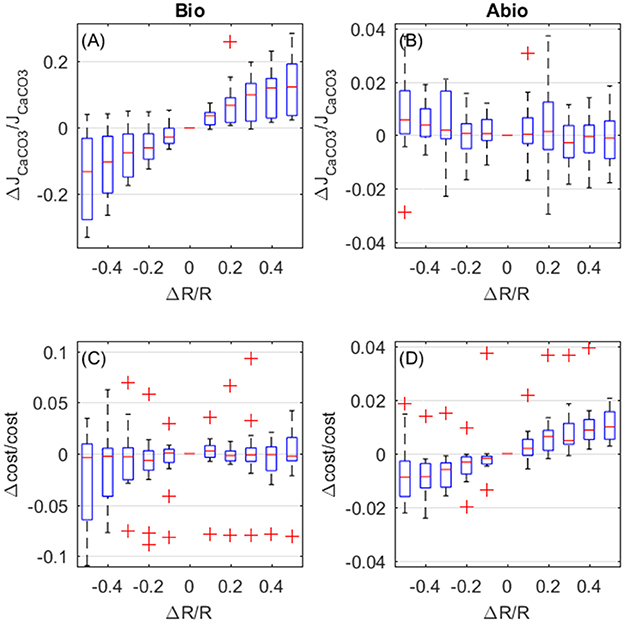
Figure 7. Biologically-mediated (A,C) and abiotic (B,D) effects of respiration, fractional change in calcification rates (top panels) and calcification costs (bottom panels). X and y-axis values are indicative of fractional change. Each boxplot represents all setups.
Effects of Temperature
The overall effect of temperature is to enhance calcification rates. Biologically-mediated and abiotic mechanisms both enhance calcification rates for increasing temperature, with the largest contribution due to biologically mediated effects (Figures 8A,B). As for the costs, the biologically-mediated effects (Figure 8C) are highly variable and it is unclear whether they entail an increase or a decrease in costs for increased temperature. On the contrary, costs decrease with temperature due to abiotic mechanisms (Figure 8D), according to CaCO3 deposition kinetics.
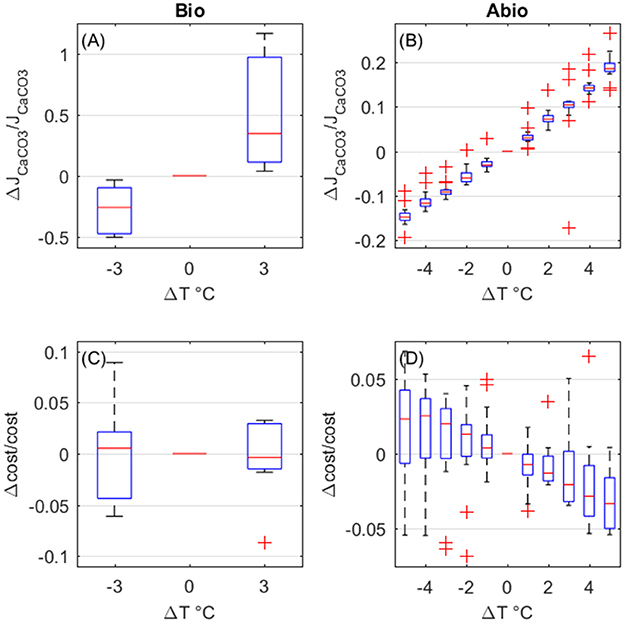
Figure 8. Biologically-mediated (A,C) and abiotic (B,D) effects of temperature, fractional change in calcification rates (top panels) and calcification costs (bottom panels). Y-axis values are indicative of fractional change. Each boxplot represents all setups.
Effects of Seawater Chemistry
The biologically-mediated effects of DIC and the abiotic effects of DIC and TA on calcification rates display similar magnitude. Both biologically-mediated and abiotic mechanisms cause calcifiction rates to decrease for increasing DIC (Figures 9A,B), whilst increased TA causes calcification rates to increase (abiotic effect, Figure 9C). As far as costs are concerned, biologically-mediated mechanisms cause costs to decrease for increasing DIC (Figure 9D), whilst abiotic mechanisms determine an exponential rise in costs for increasing DIC and for decreasing TA (Figures 9E,F).
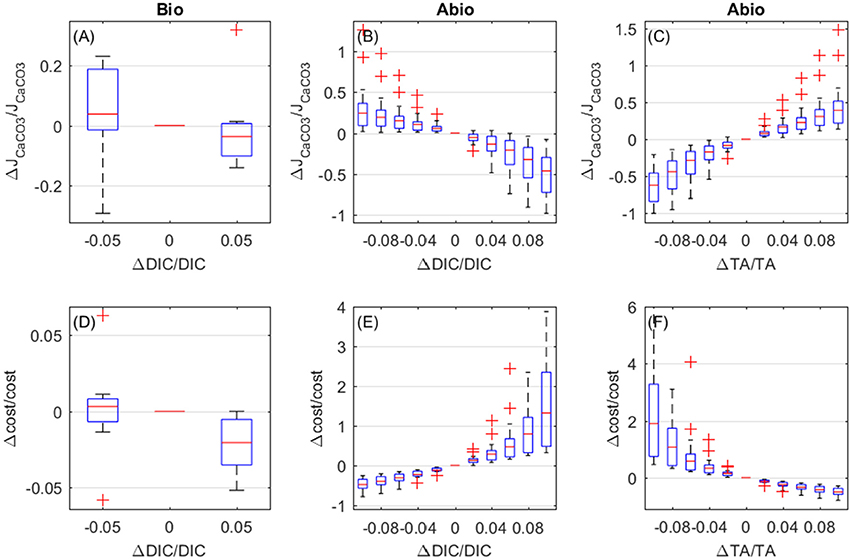
Figure 9. Biologically-mediated (A,D) and abiotic (B,E) effects of DIC and abiotic effects of TA (C,F), fractional change in calcification rates (top panels) and calcification costs (bottom panels). x and y-axis values are indicative of fractional change. Each boxplot represents all setups.
Discussion
Our model successfully simulates the experimental calcification rates determined by Rodolfo-Metalpa et al. (2010), as well as several aspects of the qualitative compartments response to external conditions described in Al-Horani et al. (2003), Hohn and Merico (2012, 2015), and Nakamura et al. (2013). The pH values in the ECM are in the range of measured values for the same species (Raybaud et al., 2017). Our model qualitatively agrees with the observation that the conditions to favor calcification are attained in the ECM more by upregulation of total alkalinity than by upregulation of dissolved inorganic carbon (Cai et al., 2016).
Our model builds on an accredited conceptual model of the physiology of coral calcification (McConnaughey and Whelan, 1997; Hohn and Merico, 2015), already tested for different purposes through similar modeling applications (Hohn and Merico, 2012, 2015; Nakamura et al., 2013), and incorporates realistic kinetics for membrane transport proteins (Smith and Crampin, 2004) that depend both on concentration gradients and available energy. This modeling choice has notable drawbacks in parameter richness and hardly constrainable parameters; however, unlike the solutions adopted in Hohn and Merico (2012, 2015) and Nakamura et al. (2013), it possesses desirable properties for realistic membrane transport modeling, i.e., co-limitation of transport rates when several substrates are involved and saturating behavior. Similar conceptual schemes, based on cyclic enzymatic reactions, for describing complex metabolic fluxes have already been proposed in a bioenergetic modeling framework (Kooijman, 2010; Muller, 2011), and may represent viable solutions for accurate modeling of membrane transport processes also beyond corals. Our coupling between metabolic rates (Pg, R) and the calcification machinery is based on the models of syntrophic symbioses developed in Dubinsky and Jokiel (1994) and Muller et al. (2009); in such models, and in ours as well, the zooxanthellae translocate some excess photosynthate to the coral host that can use it for whatever purpose, and some of this energy is indeed used to run the active transports.
Apart from the treatment of membrane transport proteins, our model's topology and our state variables' choice is indeed very similar to the model developed in Nakamura et al. (2013); here the principal element of novelty is however not in model formulation but rather in its use: the simulation experiments we carried out to isolate biologically-mediated and abiotic effects of external variables and metabolic processes on calcification rates and costs have never been proposed before and, we believe, provide a new and interesting perspective on the mechanisms that control calcification in corals, as well as on highly debated topics like LEC and acidification.
Contribution of the Different Pathways to Calcification
We found that both calcium and carbon enter the ECM through membrane transport proteins; this is in line with the findings from Furla et al. (2000) that found calcification rates in the reef coral Stylophora pistillata to be impaired by both Ca-ATPase and BAT selective inhibitors. As a direct consequence of this, in our model the passive paracellular pathway is a sink rather than a source of carbon and calcium in the ECM (in agreement with Hohn and Merico, 2015 for calcium but not for carbon). Finally, the carbon flux through the transcellular diffusion pathway is small compared to other fluxes. In contrast, Hohn and Merico (2015) demonstrated through a modeling approach that passive carbon diffusion, driven by pH gradients and coupled with active Ca2+ transport and proton removal, can as well explain observed chemical properties of coral's interior compartments, an hypothesis also suggested by other studies (e.g., Cai et al., 2016). The mechanisms of carbon delivery to the ECM and whether they entail an energy cost (either directly or indirectly) remains thus open.
Calcification Cost
Our estimates of the metabolic cost of calcification (ranging around 110–230 kJ/mol) is much larger than the values previously proposed based on theoretical reasoning (in the range 3–30 kJ/mol Anthony et al., 2002; McCulloch et al., 2012; Hohn and Merico, 2015) and more in line with the Palmer (1992) experimental estimate. We obtained such estimates by implementing realistic biophysically-based membrane transport kinetics (Smith and Crampin, 2004) where the transport rates are influenced by both concentration gradients and available energy. Clearly these values are influenced by the model's parameterization, conceptual scheme and variables choice, which are subject to high uncertainty; for instance, Barott et al. (2015a) suggest that transport trough BATs may be driven by the co-transport of Sodium that would reach the ECM trough an active Na/K-ATPase (not included in our model), which the authors identified in the calicoblastic epitelium of two tropical coral species; this suggests also carbon delivery to the ECM may indirectly entail an energetic cost. Also, for the sake of tractability, we neglected the processes happening in the oral epitelium and aboral gastroderm, where active transport proteins have however been identified (Ca-ATPase and H-ATPase Barott et al., 2015a,b). Hence, here we are not considering all the possible sources of energy expense related to ion transport. The identification of energy demanding processes related to calcification in corals is complicated by the fact that not all corals seem to have evolved the same physiological pathways to deliver the skeleton building blocks to the site of calcification (Barott et al., 2015a). Even the up-regulation of pH at the site of calcification appears not to be a universal feature in corals (Le Goff et al., 2017). Finally, here we are not considering the cost for OM synthesis. All of these additional processes may add to our estimate of the calcification cost or may instead lower it in the case a higher yield per unit of energy is achieved through an energy efficient balance of active transport processes: in the model proposed by Hohn and Merico (2015), for instance, several active transport processes are implemented and the estimated calcification cost is ~20 kJ/mol. Bearing all of this in mind, our estimates of the cost of calcification should be interpreted not as exact values, but as indicative of the possibility that the cost of calcification could be much higher than previously assumed. In our opinion, the commonly assumed values for the cost of calcification have a number of limitations as they do not account for transport inefficiencies and/or for the change of transport rates and cost that must follow from a change in chemical gradient; also the values of the calcification cost that have been proposed in previous studies are quite low if compared to common biomass synthesis costs (Gnaiger, 1983). With such low costs many corals would face little trouble in allocating some extra energy to calcification in acidified conditions. Our results are instead indicative of a conspicuous investment into skeleton and may be important to understand the relations between biocalcification and climatic variability. Since, to the best of our knowledge, only one experimental estimate of the cost of calcification is available, and none for corals, we suggest further experiments to test this. Furthermore, the exponential rise of calcification costs that our model simulates for increasing DIC (or equivalently, pCO2) indicates that the calcification process may rapidly become unaffordable even for small changes in seawater chemistry; bioenergetic models may hence be a convenient tool to understand corals' sensitivity to acidification.
LEC, Contributions to Calcification, and Influence of External Parameters
In our model the main factor enhancing calcification is the ATP flux, provided by photosynthesis (LEC) and respiration, that stimulates active transcellular transport activity. The other major contribution to calcification rate is temperature which acts in a similar fashion as light does, by stimulating photosynthesis and respiration. Abiotic contributions are also present but are roughly one order of magnitude smaller with respect to biologically-mediated effects. The effects of seawater chemistry, both abiotic and biologically-mediated, on the other hand, are of similar magnitude and less pronounced than those of temperature and light. This was however expected because the original experiments from Rodolfo-Metalpa et al. (2010) concluded that C. caespitosa is an acidification resistant species.
The adverse effects of acidification on coral calcification is generally attributed to abiotic mechanisms (Cohen and Holcomb, 2010; Allemand et al., 2011; Jokiel, 2011; Cyronak et al., 2015) rather than to biologically-mediated ones. In fact, some studies failed to produce evidence of substantial modification of metabolic rates other than calcification (e.g., photosynthesis, respiration) at the pH levels predicted for the near future (Schneider and Erez, 2006; Rodolfo-Metalpa et al., 2010). Others studies, however, did find a positive correlation between pCO2 and photosynthesis (Langdon and Atkinson, 2005; Marubini et al., 2008); based on this evidence, some authors suggest that photosynthesis and calcification may compete for DIC and that the decline in calcification rates under elevated pCO2 may be due to increased photosynthetic DIC uptake (Langdon and Atkinson, 2005). In contrast, a negative correlation between pCO2 and metabolic rates (photosynthesis, respiration), as well as bleaching response, was found by other studies (Anthony et al., 2008; Kaniewska et al., 2012), thus giving credit also to the alternative hypothesis that acidification response is dictated by CO2-induced metabolic depression (Pörtner, 2008).
In the end, the prevailing mechanism may be species-specific, however, acidification effects on calcification are unequivocally substantial in the case of sensitive species, even to the point of complete skeleton dissolution in some cases (Kvitt et al., 2015). In our model a stronger abiotic response to external pH could be obtained in two ways: (1) by lowering Ca-ATPase and BAT's transport rates, but this would come at the cost of lowering calcification rates even under normal conditions, which is not compatible with the observation that many reef corals are both sensitive to acidification and have very high growth rates, or (2) by making the paracellular transport pathway more permeable. This solution would not substantially affect calcification rates under normal conditions, but would enhance the contribution of abiotic mechanisms under abnormal ones, like in acidified conditions. If our speculation is correct the difference between coral species that are vulnerable or resistant to acidification may lie in the permeability properties of corals' tissues. This also could be tested with experiments.
The hypothesis that calcification in corals is energy limited and that LEC is due to photosynthate translocation from symbionts to host has already been formulated (Goreau and Goreau, 1959; Chalker and Taylor, 1975) but is rather overlooked (e.g., Gattuso et al., 1999; Allemand et al., 2011; and references therein). A positive correlation between photosynthesis and calcification is beyond doubt, but LEC is more often attributed to abiotic mechanisms, i.e., the photosynthetic uptake of CO2 which would increase carbonate ion concentration and facilitate precipitation of CaCO3 (Cohen et al., 2016). However, also increased respiration rates (a source of CO2) are reported to be correlated with enhanced calcification: Holcomb et al. (2014) found that addition of glucose or glycerol, coupled with increased oxygen, stimulated both respiration and dark calcification in bleached S. pystillata micro-colonies (but not in un-bleached ones), and concluded that dark calcification may be oxygen limited in zooxanthellate corals (Anthony et al., 2002) found respiration rates to be the main factor affecting calcification in two reef coral species. Also a reanalysis of the dataset used for this study (Rodolfo-Metalpa et al., 2010) shows how both photosynthesis and respiration rates correlate positively with calcification (R, p = 0.87, 1.3e-5 and 0.61, 0.013 for photosynthesis and respiration respectively). Since photosynthesis consumes carbon whilst respiration produces it, the two processes should instead display opposite effects if the prevailing mechanism was abiotic. In addition to that, Levy et al. (2016) have shown that heterotrophy (a source of energy) can mitigate the stress response in bleached coral colonies and that unfed bleached colonies showed a stress response similar to temperature or acidification stress, including a decrease in the expression of genes related to energy metabolism.
Other proposed hypotheses for LEC share similarities with the energy hypothesis. The oxygen hypothesis, positively tested in Nakamura et al. (2013), shares the same mechanism of action, i.e., enhanced metabolism stimulating active transport rates; In Nakamura et al. (2013) model the coupling between metabolic rates and active transport, as well as their definition of main model compartments and fluxes is substantially equivalent to ours, so that, arguably, a test of the differential contributions of biologically-mediated and abiotic mechanisms to calcification, which the authors did not perform, would lead to results similar to ours. As for the OM hypothesis, recent studies point at a template-mediated nucleation of the mineral phase, rather than a purely geochemical mechanism (Puverel et al., 2005; Bertucci et al., 2015; Takeuchi et al., 2016; Von Euw et al., 2017). However, to date not enough knowledge is available to construct a realistic model, in particular it is still unclear whether in the deposition of skeletal material the deposition of the two fractions, OM and calcium carbonate, obeys some kind of stoichiometric law that can make one of the two fractions rate limiting depending on the conditions. Nonetheless, as far as organism energetics are concerned, the metabolic energy used to synthesize OM must generate from holobiont metabolic activities, i.e., respiration and photosynthesis; hence, also in this case, it should hold that the process of biocalcification is predominantly driven by metabolism.
Evidence is building up that calcification in corals relies on active transport (and new OM synthesis), hence it is an energy demanding process. This suggests calcification should be energy limited under most conditions. Biological processes are indeed renowned for being energy demanding; the practice of studying biocalcification solely from a carbonates chemistry perspective is indeed very popular, perhaps because carbonates chemistry in seawater is rather well-known and all the tools are at hand. This approach undoubtedly led to a much deeper understanding of coral calcification and its relations with environmental parameters, especially in recent years; however ambiguous results are still abundant and many mechanisms have yet to be elucidated. We suggest that the energy limitation of active transport rates in corals may be much more important than often considered and that further experiments should test this hypothesis.
Author Contributions
GG and CS conceived the model. GG coded the model and ran the simulations with the supervision of CS. GG wrote the main text body and CS reviewed it at all stages.
Funding
The research reported in this work was supported by the MedSea project and by OGS and CINECA under HPC-TRES program award number 2015-05. Publication fees were covered by OpenAIRE-FP7-Post-Grant-OA-Pilot.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Dr. Riccardo Rodolfo-Metalpa of IRD for useful discussion and comments on a first draft of this manuscript. We also thank Serena Zunino of OGS for passionate discussion about C. Caespitosa.
References
Al-Horani, F. A., Al-Moghrabi, S. M., and De Beer, D. (2003). The mechanism of calcification and its relation to photosynthesis and respiration in the scleractinian coral Galaxea fascicularis. Mar. Biol. 142, 419–426. doi: 10.1007/s00227-002-0981-8
Al-Horani, F. A., Tambutté, É., and Allemand, D. (2007). Dark calcification and the daily rhythm of calcification in the scleractinian coral, Galaxea fascicularis. Coral Reefs 26, 531–538. doi: 10.1007/s00338-007-0250-x
Allemand, D., Ferrier-pagès, C., Furla, P., Houlbrèque, F., and Darwin, C. (2004). Biomineralisation in reef-building corals: from molecular mechanisms to environmental control. Gen. Palaeontol. 3, 453–467. doi: 10.1016/j.crpv.2004.07.011
Allemand, D., Tambutté, É., Zoccola, D., and Tambutté, S. (2011). “Coral calcification, cells to reefs,” in Coral Reefs: An Ecosystem in Transition, eds Z. Dubinsky and N. Stambler (Dordrecht: Springer Netherlands), 119–150.
Anthony, K. R. N., Connolly, S. R., and Willis, B. L. (2002). Comparative analysis of energy allocation to tissue and skeletal growth in corals. Limnol. Oceanogr. 47, 1417–1429. doi: 10.4319/lo.2002.47.5.1417
Anthony, K. R., Kline, D. I., Diaz-Pulido, G., Dove, S., and Hoegh-Guldberg, O. (2008). Ocean acidification causes bleaching and productivity loss in coral reef builders. Proc. Natl. Acad. Sci. U.S.A. 105, 17442–17446. doi: 10.1073/pnas.0804478105
Barott, K. L., Perez, S. O., Linsmayer, L. B., and Tresguerres, M. (2015a). Differential localization of ion transporters suggests distinct cellular mechanisms for calcification and photosynthesis between two coral species. Am. J. Physiol. Regul. Integr. Comp. Physiol. 309, R235–R246. doi: 10.1152/ajpregu.00052.2015
Barott, K. L., Venn, A. A., Perez, S. O., Tambutté, S., and Tresguerres, M. (2015b). Coral host cells acidify symbiotic algal microenvironment to promote photosynthesis. Proc. Natl. Acad. Sci. U.S.A. 112, 607–612. doi: 10.1073/pnas.1413483112
Bertucci, A., Forêt, S., Ball, E. E., and Miller, D. J. (2015). Transcriptomic differences between day and night in Acropora millepora provide new insights into metabolite exchange and light-enhanced calcification in corals. Mol. Ecol. 24, 4489–4504. doi: 10.1111/mec.13328
Bertucci, A., Moya, A., Tambutté, S., Allemand, D., Supuran, C. T., and Zoccola, D. (2013). Bioorganic & Medicinal Chemistry carbonic anhydrases in anthozoan corals — A review. Bioorg. Med. Chem. 21, 1437–1450. doi: 10.1016/j.bmc.2012.10.024
Burton, E. A., and Water, L. M. (1990). The role of pH in phosphate inhibition of calcite and aragonite precipitation rates in seawater. Geochim. Cosmochim. Acta 54, 797–808. doi: 10.1016/0016-7037(90)90374-T
Cai, W. J., Ma, Y., Hopkinson, B. M., Grottoli, A. G., Warner, M. E., Ding, Q., et al. (2016). Microelectrode characterization of coral daytime interior pH and carbonate chemistry. Nat. Commun. 7:11144. doi: 10.1038/ncomms11144
Chalker, B. E., and Taylor, D. L. (1975). Light-enhanced calcification, and the role of oxidative phosphorylation in calcification of the coral Acropora cervicornis. Proc. R. Soc. Lond. 190, 323–331. doi: 10.1098/rspb.1975.0096
Cohen, A. L., and Holcomb, M. (2010). Why corals care about ocean acidification uncovering the mechanism. Oceanography 22, 118–127. doi: 10.5670/oceanog.2009.102
Cohen, I., Dubinsky, Z., and Erez, J. (2016). Light enhanced calcification in hermatypic corals: new insights from light spectral responses. Front. Mar. Sci. 2:122. doi: 10.3389/fmars.2015.00122
Coles, S. L. L., and Jokiel, P. L. L. (1977). Effects of temperature on photosynthesis and respiration in hermatypic corals. Mar. Biol. 43, 209–216. doi: 10.1007/BF00402313
Comeau, S., Tambutté, E., Carpenter, R. C., Edmunds, P. J., Evensen, N. R., Allemand, D., et al. (2017). Coral calcifying fluid pH is modulated by seawater carbonate chemistry not solely seawater pH. Proc. R. Soc. B Biol. Sci. 284:20161669. doi: 10.1098/rspb.2016.1669
Cyronak, T., Schulz, K. G., and Jokiel, P. L. (2015). The omega myth: what really drives lower calcification rates in an acidifying ocean. ICES J. Mar. Sci. 73, 558–562. doi: 10.1093/icesjms/fsv075
Dubinsky, Z., and Jokiel, P. L. (1994). Ratio of energy and nutrient fluxes regulates symbiosis between zooxanthellae and corals. Pac. Sci. 48, 313–324.
Furla, P., Galgani, I., Durand, I., and Allemand, D. (2000). Sources and mechanisms of inorganic carbon transport for coral calcification and photosynthesis. J. Exp. Biol. 203, 3445–3457.
Galli, G., Bramanti, L., Priori, C., Rossi, S., Santangelo, G., Tsounis, G., et al. (2016). Modelling red coral (Corallium rubrum) growth in response to temperature and nutrition. Ecol. Modell. 337, 137–148. doi: 10.1016/j.ecolmodel.2016.06.010
Gattuso, J. P., Allemand, D., and Frankignoulle, M. (1999). Photosynthesis and calcification at cellular, organismal and community levels in coral reefs: a review on interactions and control by carbonate chemistry. Am. Zool. 39, 160–183. doi: 10.1093/icb/39.1.160
Gnaiger, E. (1983). “Calculation of energetic and biochemical equivalents of respiratory oxygen consumption” in Polarographic Oxygen Sensors, Aquatic and Physiological Applications, eds E. Gnaiger and H. Forstner (Berlin; Heidelberg: Springer-Verlag), 337–345. doi: 10.1007/978-3-642-81863-9
Goreau, T. F., and Goreau, N. I. (1959). The physiology of skeleton formation in corals. II. Calcium deposition by hermatypic corals under different conditions. Biol. Bull. 117, 239–250. doi: 10.2307/1538903
Gutner-Hoch, E., Waldman Ben-Asher, H., Yam, R., Shemesh, A., and Levy, O. (2017). Identifying genes and regulatory pathways associated with the scleractinian coral calcification process. PeerJ 5:e3590. doi: 10.7717/peerj.3590
Hohn, S., and Merico, A. (2012). Modelling coral polyp calcification in relation to ocean acidification. Biogeosciences 9, 4441–4454. doi: 10.5194/bg-9-4441-2012
Hohn, S., and Merico, A. (2015). Quantifying the relative importance of transcellular and paracellular ion transports to coral polyp calcification. Front. Earth Sci. 2:37. doi: 10.3389/feart.2014.00037
Holcomb, M., Venn, A. A., Tambutté, E., Tambutté, S., Allemand, D., Trotter, J., et al. (2014). Coral calcifying fluid pH dictates response to ocean acidification. Nat. Sci. Reports, 4:5207. doi: 10.1038/srep05207
Houlbrèque, F., and Ferrier-Pagès, C. (2009). Heterotrophy in tropical scleractinian corals. Biol. Rev. 84, 1–17. doi: 10.1111/j.1469-185X.2008.00058.x
Jokiel, P. L. (2011). Ocean acidification and control of reef coral calcification by boundary layer limitation of proton flux. Bull. Mar. Sci. 87, 639–657. doi: 10.5343/bms.2010.1107
Kaniewska, P., Campbell, P. R., Kline, D. I., Rodriguez-Lanetty, M., Miller, D. J., Dove, S., et al. (2012). Major cellular and physiological impacts of ocean acidification on a reef building coral. PLoS ONE 7:e34659. doi: 10.1371/journal.pone.0034659
Kooijman, S. A. L. M. (2010). Dynamic Energy Budget Theory for Metabolic Organisation, 3rd Edn. Cambridge: Cambridge University Press.
Kvitt, H., Kramarsky-Winter, E., Maor-Landaw, K., Zandbank, K., Kushmaro, A., Rosenfeld, H., et al. (2015). Breakdown of coral colonial form under reduced pH conditions is initiated in polyps and mediated through apoptosis. Proc. Natl. Acad. Sci. U.S.A. 112, 2082–2086. doi: 10.1073/pnas.1419621112
Langdon, C., and Atkinson, M. J. (2005). Effect of elevated pCO2on photosynthesis and calcification of corals and interactions with seasonal change in temperaSture/ irradiance and nutrient enrichment. J. Geophys. Res. C Ocean. 110, 1–16. doi: 10.1029/2004JC002576
Le Goff, C., Tambutté, E., Venn, A. A., Techer, N., Allemand, D., and Tambutté, S. (2017). In vivo pH measurement at the site of calcification in an octocoral. Sci. Rep. 7:11210. doi: 10.1038/s41598-017-10348-4
Levy, O., Karako-Lampert, S., Waldman Ben-Asher, H., Zoccola, D., Pagès, G., and Ferrier-Pagès, C. (2016). Molecular assessment of the effect of light and heterotrophy in the scleractinian coral Stylophora pistillata. Proc. R. Soc. Lond. B Biol. Sci. 283, 1–10. doi: 10.1098/rspb.2015.3025
Marubini, F., Ferrier-Pagès, C., Furla, P., and Allemand, D. (2008). Coral calcification responds to seawater acidification: a working hypothesis towards a physiological mechanism. Coral Reefs 27, 491–499. doi: 10.1007/s00338-008-0375-6
McConnaughey, T. A., and Whelan, J. F. (1997). Calcification generates protons for nutrient and bicarbonate uptake. Earth Sci. Rev. 42, 95–117. doi: 10.1016/S0012-8252(96)00036-0
McCulloch, M., Falter, J., Trotter, J., and Montagna, P. (2012). Coral resilience to ocean acidification and global warming through pH up-regulation. Nat. Clim. Chang. 2, 623–627. doi: 10.1038/nclimate1473
Millero, F. J. (2007). The marine inorganic carbon cycle. Chem. Rev. 107, 308–341. doi: 10.1021/cr0503557
Millero, F. J., and Poisson, A. (1981). International one-atmosphere equation of state of seawater. Deep Res. 28, 625–629. doi: 10.1016/0198-0149(81)90122-9
Moya, A. (2006). Study of calcification during a daily cycle of the coral Stylophora pistillata: implications for “light-enhanced calcification”. J. Exp. Biol. 209, 3413–3419. doi: 10.1242/jeb.02382
Muller, E. B. (2011). Synthesizing units as modeling tool for photosynthesizing organisms with photoinhibition and nutrient limitation. Ecol. Modell. 222, 637–644. doi: 10.1016/j.ecolmodel.2010.10.008
Muller, E. B., Kooijman, S. A., Edmunds, P. J., Doyle, F. J., and Nisbet, R. M. (2009). Dynamic energy budgets in syntrophic symbiotic relationships between heterotrophic hosts and photoautotrophic symbionts. J. Theor. Biol. 259, 44–57. doi: 10.1016/j.jtbi.2009.03.004
Nakamura, T., Nadaoka, K., and Watanabe, A. (2013). A coral polyp model of photosynthesis, respiration and calcification incorporating a transcellular ion transport mechanism. Coral Reefs 32, 779–794. doi: 10.1007/s00338-013-1032-2
Palmer, A. R. (1992). Calcification in marine molluscs: how costly is it? Proc. Natl. Acad. Sci. U.S.A. 89, 1379–1382. doi: 10.1073/pnas.89.4.1379
Pörtner, H.-O. (2008). Ecosystem effects of ocean acidification in times of ocean warming: a physiologist's view. Mar. Ecol. Prog. Ser. 373, 203–217. doi: 10.3354/meps07768
Puverel, S., Tambutté, E., Zoccola, D., Domart-Coulon, I., Bouchot, A., Lotto, S., et al. (2005). Antibodies against the organic matrix in scleractinians: a new tool to study coral biomineralization. Coral Reefs 24, 149–156. doi: 10.1007/s00338-004-0456-0
Raybaud, V., Tambutté, S., Ferrier-Pagès, C., Reynaud, S., Venn, A. A., Tambutté, É., et al. (2017). Computing the carbonate chemistry of the coral calcifying medium and its response to ocean acidification. J. Theor. Biol. 424, 26–36. doi: 10.1016/j.jtbi.2017.04.028
Ries, J. B. (2011). A physicochemical framework for interpreting the biological calcification response to CO2-induced ocean acidification. Geochim. Cosmochim. Acta 75, 4053–4064. doi: 10.1016/j.gca.2011.04.025
Rodolfo-Metalpa, R., Martin, S., Ferrier-Pages, C., and Gattuso, J.-P. (2010). Response of the temperate coral Cladocora caespitosa to mid- and long-term exposure to pCO2 and temperature levels projected for the year 2100 AD. Biogeosciences 7, 289–300. doi: 10.5194/bg-7-289-2010
Schneider, K., and Erez, J. (2006). The effect of carbonate chemistry on calcification and photosynthesis in the hermatypic coral Acropora eurystoma. Limnol. Oceanogr. 51, 1284–1293. doi: 10.4319/lo.2006.51.3.1284
Smith, N. P., and Crampin, E. J. (2004). Development of models of active ion transport for whole-cell modelling: cardiac sodium-potassium pump as a case study. Prog. Biophys. Mol. Biol. 85, 387–405. doi: 10.1016/j.pbiomolbio.2004.01.010
Takeuchi, T., Yamada, L., Shinzato, C., Sawada, H., and Satoh, N. (2016). Stepwise evolution of coral biomineralization revealed with genome-wide proteomics and transcriptomics. PLoS ONE 11:e0156424. doi: 10.1371/journal.pone.0156424
Tremblay, P., Ferrier-Pagès, C., Maguer, J. F., Rottier, C., Legendre, L., and Grover, R. (2012). Controlling effects of irradiance and heterotrophy on carbon translocation in the temperate coral Cladocora caespitosa. PLoS ONE 7:e44672. doi: 10.1371/journal.pone.0044672
Tremblay, P., Fine, M., Maguer, J. F., Grover, R., and Ferrier-Pagès, C. (2013). Photosynthate translocation increases in response to low seawater pH in a coral-dinoflagellate symbiosis. Biogeosciences 10, 3997–4007. doi: 10.5194/bg-10-3997-2013
Tremblay, P., Peirano, A., and Ferrier-Pagés, C. (2011). Heterotrophy in the Mediterranean symbiotic coral Cladocora caespitosa: comparison with two other scleractinian species. Mar. Ecol. Prog. Ser. 422, 165–177. doi: 10.3354/meps08902
Venn, A., Tambutté, E., Holcomb, M., Allemand, D., and Tambutté, S. (2011). Live tissue imaging shows reef corals elevate pH under their calcifying tissue relative to seawater. PLoS ONE 6:e20013. doi: 10.1371/journal.pone.0020013
Von Euw, S., Zhang, Q., Manichev, V., Murali, N., Gross, J., Feldman, L. C., et al. (2017). Biological control of aragonite formation in stony corals. Science 356, 933–938. doi: 10.1126/science.aam6371
Walter, L. M., and Morse, J. W. (1985). The dissolution kinetics of shallow marine carbonates in seawater: a laboratory study. Geochim. Cosmochim. Acta 49, 1503–1513. doi: 10.1016/0016-7037(85)90255-8
Zeebe, R. E., and Wolf-Gladrow, D. A. (2001). CO2 in Seawater: Equilibrium, Kinetics, Isotopes. Amsterdam: Elsevier Ltd.
Keywords: corals, calcification, light-enhanced calcification, biological control, calcification cost, calcification model, temperature, acidification
Citation: Galli G and Solidoro C (2018) ATP Supply May Contribute to Light-Enhanced Calcification in Corals More Than Abiotic Mechanisms. Front. Mar. Sci. 5:68. doi: 10.3389/fmars.2018.00068
Received: 27 October 2017; Accepted: 14 February 2018;
Published: 01 March 2018.
Edited by:
Sönke Hohn, Leibniz Centre for Tropical Marine Research (LG), GermanyReviewed by:
Virginie Raybaud, University of Nice Sophia Antipolis, FranceAnthony William Larkum, University of Technology Sydney, Australia
Copyright © 2018 Galli and Solidoro. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Giovanni Galli, Z2dhbGxpQGlub2dzLml0
 Giovanni Galli
Giovanni Galli Cosimo Solidoro
Cosimo Solidoro