- 1Chesapeake Biological Laboratory, University of Maryland Center for Environmental Science, Solomons, MD, United States
- 2Department of Chemistry, Whitman College, Walla Walla, WA, United States
Gadolinium diethylenetriaminepentaacetic acid (Gd–DTPA) is widely applied as a contrast enhancer in medical MRI. As Gd–DTPA is only minimally captured in wastewater treatment plants (WTPs) or degraded by UV light and other oxidative processes, concentrations in rivers have increased globally by orders of magnitude following its introduction in 1987. The complex also seems impervious to estuarine scavenging and is beginning to emerge in coastal waters, yet it is unknown how its stability is changed by competition for the DTPA ligand from major seawater cations. We performed potentiometric titrations at seawater ionic strength (0.7 M NaClO4) to determine dissociation constants of the five DTPA carboxylic acid groups, as well as stability constants of Mg, Ca, and Gd complexes with the fully deprotonated and single-protonated ligand. These are in general agreement with literature values at low ionic strength and confirm that complexes with Ca are more stable than with Mg. A new finding, that the DTPA complexes of Mg and Ca appear to be hydrolyzed at elevated pH, implies that their coordination in these chelates is less than hexadentate, enabling additional competition with Gd from dinuclear Mg and Ca species. Side-reaction coefficients for trace-metal-free seawater, calculated from our results, suggest that the higher abundance of Mg and Ca may significantly destabilize Gd–DTPA in coastal waters, causing dissociation and release of as much as 15% of the organically complexed Gd from the ligand. This effect could magnify the particle-reactivity and bioavailability of anthropogenic Gd in sensitive estuarine habitats, indicating an urgent need to further study the fate of this contaminant in marine environments.
Introduction
The rare earth elements (REE) are Sc, Y, and La in group IIIA of the Periodic Table and the 14 elements following La, up to Lu. The term “earth” refers to an old word for oxide minerals, while the term “rare” refers not so much to their abundance, but to the fact that they are rarely found in ore deposits sufficiently enriched to be of economic interest. Actually, their crustal abundance is much higher than that of more familiar elements, like Hg and Pt; it is comparable to that of metals like Cu and Pb for the more abundant light REE, and to that of Cd for the less abundant heavy REE (e.g., Lide and Haynes, 2009; Table 14-18).
Until a few decades ago, the REE were mainly a scientific curiosity, valued by geologists and geochemists for their remarkable chemical coherence as tracers of waters, rocks, and their myriad interactions in a broad range of marine and terrestrial environments (Henderson, 1984). However, in our increasingly technological society, even the REE are finding their way into a multitude of consumer products and industrial processes (Du and Graedel, 2011). These new applications bring with them a number of specific concerns. The unusual ore deposits that contain the most REE-rich minerals, such as bastnäsite, occur in only a few places around the world. This and certain complex market forces have caused the balance of REE supply and demand to be unequally divided among countries with very different economic and political views (Kanazawa and Kamitani, 2006; Showstack, 2012). In addition, the exploding worldwide use of electronic devices like cellular phones and flat-screen displays has led to REE demand rapidly outpacing global production (Du and Graedel, 2011; Izatt et al., 2014). Combined with the high financial and environmental cost of mining, this has prompted a search for ways to minimize losses during manufacturing and to enable recovery through recycling, as well as more efficient extraction from the primary ores and from process waste and landfills (Binnemans et al., 2015; Nancharaiah et al., 2016). Finally, like many industrial chemicals, the REE have started to enter the environment as pollutants, yet we know little about their toxicity and fate. Some organisms are known to incorporate REE in certain enzymes (Chistoserdova, 2016) and they are readily taken up and stored by plants (Chua, 1998; Brioschi et al., 2013). In Asia, REE are routinely applied as fertilizers since they appear to stimulate crop growth (Zhang and Shan, 2001; Xu et al., 2002). On the other hand, there are strong indications that REE ions are toxic to microorganisms (Fuma et al., 2001; d'Aquino et al., 2009) and animals (Shimada et al., 1995; Zhang et al., 2010) on individual to ecosystem scales (González et al., 2014, 2015; Lingott et al., 2016). Release of Gd from MRI contrast agents can lead to accumulation in bone, brain, and kidneys (Rogosnitzky and Branch, 2016) and is the suspected cause of a disabling pathology termed nephrogenic systemic fibrosis in patients with impaired renal function (Port et al., 2008).
A salient feature of the industrial use of REE is that, unlike their natural occurrence as a group, chemical and manufacturing processes often require just a single element. Upon entering the environment, the contrasting geochemical behavior or sheer abundance of these pollutants leads to anomalies against a natural background of otherwise smooth normalized REE patterns, allowing them to be identified as anthropogenic (Kulaksız and Bau, 2007). Anomalies of La, Ce, and Sm have been found in various rivers (Kulaksız and Bau, 2011a, 2013; de Campos and Enzweiler, 2016) and while a distinct source could not always be determined, these elements are critical ingredients of catalysts, car catalytic converters, and rechargeable batteries (Du and Graedel, 2011). Even when used collectively, as in zeolite catalysts for oil cracking, the contaminants often have a unique REE pattern that makes them stand out (Olmez et al., 1991).
One novel application of an REE that has greatly enhanced its release into the environment is the use of gadolinium (Gd) as a contrast enhancer in medical magnetic resonance imaging (MRI) diagnostics. Contrast enhancers are employed for high-resolution tomography of organs where signal gradients are small, such as the brain or other soft tissues. The chemistry of the REE is characterized by the gradual filling of the 4f shell, which can hold a total of 14 electrons. The f shell consists of 7 sub-shells that can each hold a pair of electrons with opposite spin. Starting from La, each sub-shell is initially filled with one electron. At Gd, which is halfway along the REE series, every sub-shell contains a single electron, all with parallel spin. This gives Gd and several other REE unusually high magnetic moments, making it especially suited as an MRI contrast enhancer. Due to its severe toxicity and strong tendency to bind to organic molecules, it is not possible to administer Gd to patients directly. Instead, a number of open-chain and macrocyclic polyaminopolycarboxylic acid ligands has been designed that form highly stable anionic and non-ionic complexes with Gd (Behra-Miellet et al., 1998; Port et al., 2008). In pharmaceutical preparations these are often combined with the aminosugar meglumine for improved uptake and tolerance. The agent is orally or intravenously administered to the patient shortly before the MRI treatment and then excreted again via urination within several hours. A typical dose is 0.1 mmol per kg of bodyweight, amounting to ~1–2 g of Gd for an average patient, whereby it should be noted that background concentrations of Gd in nature range from nanomolar in rivers to picomolar in the ocean (Elderfield et al., 1990).
The same engineered stability that keeps these MRI contrast agents from dissociating inside the human body also prevents their environmental degradation. They appear to be impervious to bacterial attack and removal in wastewater treatment plants (WTPs) (Verplanck et al., 2005, 2010; Lawrence et al., 2009) and to behave conservatively in natural waters, even in estuaries where geogenic REE are extensively scavenged (Elderfield et al., 1990; Kulaksız and Bau, 2007). Consequently, since the introduction of MRI contrast agents in the late 1980s, anthropogenic Gd concentrations have increased by 2–3 orders of magnitude above the natural background in rivers and drinking water throughout Europe (Bau and Dulski, 1996; Möller et al., 2002, 2003; Rabiet et al., 2009; Kulaksız and Bau, 2011b), and more recently in North America (Bau et al., 2006), South America (de Campos and Enzweiler, 2016), Asia (Nozaki et al., 2000; Ogata and Terakado, 2006), and Australia (Lawrence, 2010). Anthropogenic Gd anomalies often completely overwhelm natural Gd anomalies that were previously used as tracers of subtle geochemical fractionation processes (e.g., Garcia-Solsona et al., 2014). At the same time, they are increasingly utilized as a conservative tracer of wastewater effluents, groundwater inputs, and hydrological processes (Fuganti et al., 1996; Möller et al., 2000).
The reputed environmental persistence of Gd-based MRI contrast agents is mostly inferred from geochemical observations, but accurate regional mass balances can be difficult to obtain (Kümmerer and Helmers, 2000) and their ultimate environmental fate is uncertain. Eventually, however, they must dissociate and release Gd into the natural REE cycle. This does not only raise the concern of toxicological effects but also complicates their detection, which is typically based on its distinctive behavior relative to geogenic Gd and the other REE. There are a number of processes that may degrade Gd–polyaminopolycarboxylate complexes, including bacterial attack, UV photo-oxidation, and competition for the ligand from other strongly binding metals (transmetallation). These have been investigated primarily in clinical and pharmacological studies aimed at patient well-being (Idée et al., 2006; Künnemeyer et al., 2009b), yet some studies have taken a broader perspective (Holzbecher et al., 2005; Birka et al., 2016). One process that has received little attention is the effect of increased ionic strength and high concentrations of competing metal ions where rivers meet the salty ocean, notwithstanding the fact that anthropogenic Gd is increasingly being detected in coastal seawater (Zhu et al., 2004; Kulaksız and Bau, 2007; Hatje et al., 2016).
In this study, we focus on potential instability of the anionic Gd–DTPA complex, used as an MRI contrast agent under the brandname Magnevist®, upon mixing of river water with seawater in estuaries. Specifically, we conducted laboratory experiments to investigate displacement of Gd from the complex by high levels of Mg and Ca. The most suitable technique, potentiometric titration, cannot distinguish DTPA complexes with different metals in the same solution and therefore cannot be applied directly to natural or even synthetic seawater samples. Instead, following the approach of our earlier work (Christenson and Schijf, 2011; Schijf and Burns, 2016) on the stability of REE complexes with the siderophore desferrioxamine B (DFOB), we sequentially measured stability constants of DTPA complexes with Mg, Ca, and Gd in an inert medium at seawater ionic strength (0.7 M NaClO4). Using these values in a speciation model, we then calculated the side-reaction coefficient of DTPA in seawater, which in turn permits us to calculate a conditional stability constant for the Gd–DTPA complex. Our results suggest that the effective stability of Gd–DTPA is diminished by almost 6 orders of magnitude, which may cause the release of toxic Gd into the marine food chain and compromises our ability to distinguish anthropogenic from geogenic Gd.
The experiments with DTPA, although conceptually similar to those with DFOB, are considerably more analytically challenging. Unlike DFOB, which can exchange four protons over a limited range of moderately alkaline pH (~8–11), DTPA can exchange as many as eight protons over a pH range from alkaline (~10) to strongly acidic (< 1). Due to the structural symmetry of the DTPA molecule, several of these exchanges occur in closely spaced pairs, making their individual dissociation constants difficult to determine. Moreover, while DFOB is always fully protonated and thus positively charged at pH < 7, DTPA fully protonates only in acidic medium, leading to a solubility minimum around pH 2 (Kragten and Decnop-Weever, 1983), where our titrations normally start. Thirdly, DTPA can potentially form a wider array of mononuclear and polynuclear complexes. And lastly, the stability constants of REE–DTPA complexes are orders of magnitude larger than those of the REE–DFOB complexes (Martell et al., 2004) and at the very edge of the analytical window for our titration method. Conversely, since the stability constants of Mg and Ca complexes are also much larger than for DFOB, these are actually easier to measure and problems with hydrolysis at elevated pH are alleviated.
Materials and Methods
Reagents and Standards
All standards and experimental solutions were prepared with Milli-Q water (18.2 MΩ·cm) inside a class-100 laminar-flow bench and stored in acid-cleaned Teflon containers. Only the titration vessel is fabricated from acid-rinsed high-quality glass. Certified titrants (HCl and carbonate-free NaOH) were supplied by Brinkmann. High-purity magnesium oxide (MgO, 99.995%), calcium oxide (CaO, 99.995%), and gadolinium chloride hexahydrate (GdCl3·6H2O, 99.999%) were purchased from Sigma-Aldrich, as well as diethylenetriaminepentaacetic acid [DTPA; (CH2COOH)2NC2H4N(CH2COOH)C2H4N(CH2COOH)2, ≥99%] and gadolinium DTPA dihydrogen salt hydrate (GdH2DTPA·xH2O, 97%), desferrioxamine B mesylate (DFOB, ≥92.5%), sodium perchlorate hydrate (NaClO4·xH2O, 99.99%), and sodium chloride (NaCl, 99.999%). Concentrated TraceMetal Grade perchloric acid (HClO4) was acquired from Thermo Fisher. All chemicals were used as received.
A pH standard (0.7 M) was prepared by dissolving NaCl in water and setting the pH to 3.000 ± 0.004 with certified HCl. The background electrolyte was prepared by dissolving NaClO4 in water and adjusting the density to obtain a solution of 0.700 ± 0.001 M (Janz et al., 1970). Its pH was then set to 2.0 ± 0.1 with calibrated HClO4 (11.40 ± 0.02 M). An unacidified electrolyte solution was also made for titrations starting at pH > 10. Solutions of about 100 mM Mg or Ca were obtained by dissolving the oxides in the acidified electrolyte and adding excess HClO4. The final pH of these solutions was 1–2. Their exact concentrations were measured via ICP-MS as described by Schijf and Burns (2016). Due to hydration of the oxide, the concentration of the Ca standard and the corresponding metal-to-ligand (M:L) molar ratios of the experimental solutions were somewhat lower than intended, which was accounted for in the calculations.
A solution of about 40 mM DTPA was initially produced by dissolving the solid acid in the acidified electrolyte. At this pH, DTPA remains mostly protonated and is thus rather non-polar and poorly soluble in aqueous solutions. The solubility was improved by adding NaOH solution adjusted to the same ionic strength. In later experiments, DTPA was dissolved in the unacidified electrolyte and titrations were started a high pH, although this approach could not be used for Mg (see section Stability Constants of Mg–DTPA and Ca–DTPA Complexes). A solution of about 40 mM Gd was made by dissolving GdCl3 in the acidified electrolyte. Some titrations were also conducted with a solution of about 40 mM GdH2DTPA, which is quite soluble at pH 2. The exact concentrations of both Gd standards were determined via ICP-MS as described by Christenson and Schijf (2011). Comparison of the exact Gd concentration with the gravimetric value indicates that the GdH2DTPA·xH2O salt is a nonahydrate (x = 9). A full ICP-MS mass spectral scan of the diluted GdH2DTPA standard detected no other REE or metals that are known to bind strongly to DTPA, such as Al and Fe. Some Gd titrations were done in the presence of DFOB. A solution of about 40 mM DFOB was prepared on the day of the experiment by dissolving ~265 mg of the mesylate salt in 10 mL of the acidified electrolyte.
Potentiometric Titrations
Potentiometric titration largely followed the protocols outlined in detail by Christenson and Schijf (2011), Schijf et al. (2015b), and Schijf and Burns (2016). Briefly, experimental solutions of 50 mL were dynamically titrated with certified NaOH or HCl using a Brinkmann Metrohm 809 Titrando autotitrator, generally in the pH window 2–11, but occasionally up to pH ~ 12 or down to pH < 1. The titrations were conducted in a closed glass vessel, maintained at a constant temperature of 25.0 ± 0.1°C, while the solutions were magnetically stirred and continuously sparged with humidified ultrahigh-purity N2 gas to exclude atmospheric CO2. The solution pH was monitored with a glass combination electrode that was calibrated against the pH standard on the free proton concentration scale before each run. Blank titrations were conducted with 50 mL of the acidified background electrolyte. Regressions of the blank titrations with FITEQL4.0 (Herbelin and Westall, 1999) confirm the absence of acid/base contaminants such as bicarbonate, although a slight excess of hydrolysis at high pH indicates the presence, at trace levels (~10 μM), of a metal with a first hydrolysis constant (log ) of −4.5 ± 0.1, possibly Al (Baes and Mesmer, 1981). This is less than 1% of the metal and ligand concentrations in the experiments and Al binds to DTPA nearly as strongly as Gd and much more strongly than Mg or Ca (Taqui Khan and Hussain, 1980), hence it is unlikely to have interfered with the titrations.
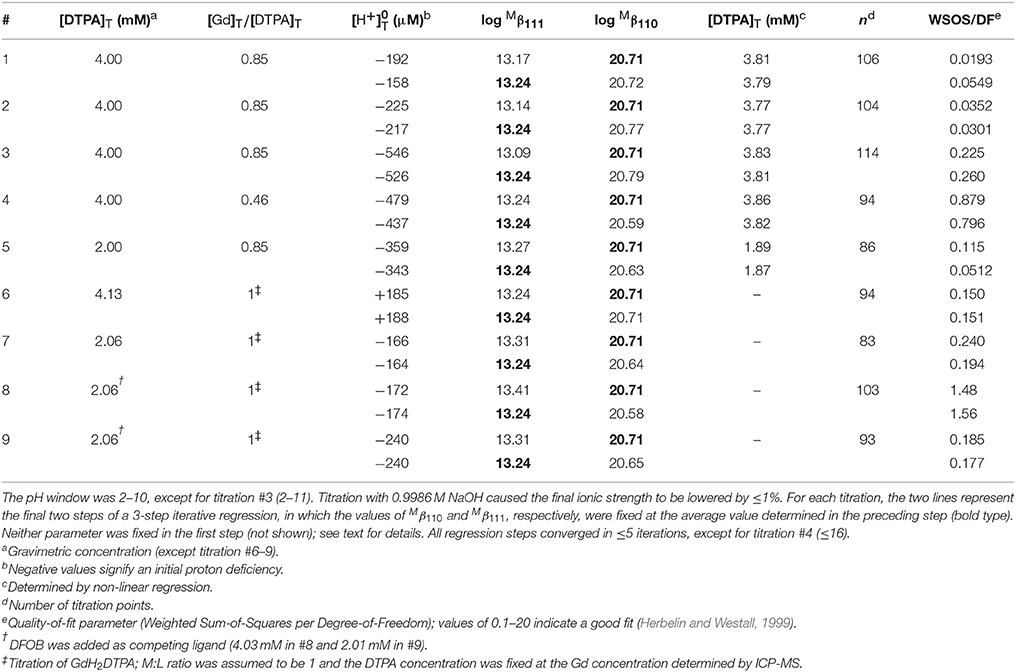
A total of 27 titrations was conducted with DTPA solutions of 1, 2, and 4 mM to determine acid dissociation constants, 14 with 1 M NaOH starting at low pH and 13 with 1 M HCl starting at high pH. Nine titrations were conducted for each of the metals, over a range of M:L ratios, in the presence of 2 mM DTPA for Mg and Ca, and 2 or 4 mM DTPA for Gd. Some early Mg and Ca titrations were done with 0.1 M NaOH as before (Schijf and Burns, 2016) but, due to the lower starting pH and larger number of protons exchanged within the analytical pH window, this was found to cause too much dilution and depression of the ionic strength. All subsequent titrations were therefore conducted with 1 M NaOH for Mg and Gd, or 1 M HCl for Ca. Four Gd titrations were done with 2 mM GdH2DTPA, two of which in the presence of 2 and 4 mM DFOB, respectively. The other five were done using separate metal and ligand standards.
Non-linear Regressions
Non-linear regressions of the data were conducted with FITEQL4.0 as described by Schijf et al. (2015b), selecting the optimal speciation model for each series of titrations. A single FITEQL model was always used for all titrations within a series, although certain adjustable parameters were sometimes fixed in sequential or iterative regressions. Additional details are provided below. Quality-of-fit was assessed from the Weighted Sum-Of-Squares per Degree-of-Freedom (WSOS/DF) parameter (Herbelin and Westall, 1999), where values between 0.1 and 20 are considered acceptable; values lower than 0.1 generally indicate an under-constrained fit. Metal and ligand concentrations were usually fixed at the ICP-MS and gravimetric value, respectively, but the ligand concentration was sometimes used as an adjustable parameter. The initial proton excess, , was always used as an adjustable parameter and negative values were allowed, to accommodate proton deficiencies. The ability of DTPA to exchange protons at very low pH often made its initial degree of protonation difficult to determine. Values of are thus much higher than for DFOB (Christenson and Schijf, 2011), typically several hundred μM. They seem randomly divided between positive and negative values, albeit negative values appear more likely for the metal titrations. The initial proton excess is reported for all titrations, but not further discussed.
The nomenclature for stability constants with protonated organic ligands varies widely in the literature and they will be indexed here in the order L-M-H, following Duffield et al. (1984):
Acid dissociation of the ligand (q = 0) will be described by means of stepwise constants, Kai, as defined in section Deprotonation of DTPA, where β101 = (Ka5)−1, β102 = (Ka5×Ka4)−1, β103 = (Ka5×Ka4×Ka3)−1 etc. To simplify speciation modeling, it is convenient to express stability constants in terms of dissociation of the metal from the protonated ligand, which shall be indicated with a superscript M, where only complexation with a single ligand molecule (p = 1) will be considered:
A more specific list of the equilibrium constants used here is given in Table 1.
Presentation and Discussion of the Experimental Results
Deprotonation of DTPA
The backbone of the DTPA molecule consists of three amine groups separated by two ethylene groups (N–C2H4−N–C2H4–N). The terminal amines each contain two acetate groups (–CH2(C = O)OH), while the central amine contains a fifth (Figure 1). The molecule is essentially an enlargement of the common ligand ethylenediaminetetraacetic acid (EDTA), with one additional amine and one additional acetate group. The longer backbone gives DTPA greater steric freedom and the extra amine and acetate group increase its denticity, improving its binding to larger ions with higher coordination numbers, like the REE.
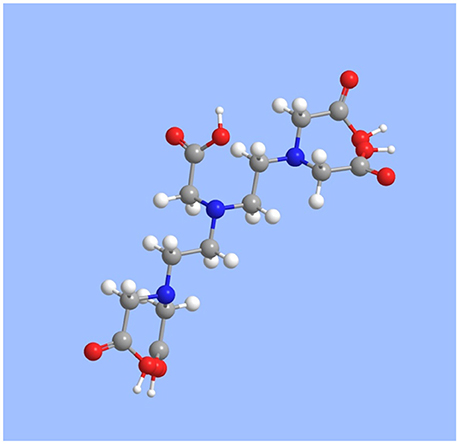
Figure 1. Rendering of the molecular structure of DTPA, produced with ChemDraw v.12.0. Gray = C; white = H; red = O; blue = N.
The protonation of DTPA is complicated. In the neutral molecule, each of the five acetate groups is associated with one exchangeable proton. The acid dissociation constants of these protons are usually numbered Ka1 through Ka5. However, it appears that each of the three amine groups can also accept a proton to form a positively charged molecule at low pH, increasing the number of exchangeable protons to eight, with acid dissociation constants defined as follows (Table 1):
It is possible that, at low pH, one or more of the acetate protons are translocated to the adjacent amines, forming complex zwitterions with multiple positively and negatively charged groups. Harder and Chaberek (1959) show the neutral DTPA molecule with the central and two opposing terminal acetate groups deprotonated and one proton translocated to each of the three amines, making the former negatively and the latter positively charged.
The values of pKa1 and pKa2 are around pH 2–3, pKa3 is just above pH 4, and pKa4 and pKa5 are around pH 8–10 (Martell et al., 2004). There is a good deal of uncertainty about the other three acid dissociation constants. At 25°C, reported values of pKa0 are 1.75 in 0.1 M KNO3 (Letkeman and Martell, 1979) and 1.67 in KCl at I = 1 (Merciny et al., 1978; Mioduski, 1980), while somewhat lower values are found at lower temperature: 1.45 in NaCl (I = 0.11) at 20°C (Matorina et al., 1969) and 1.22 in NaClO4 (I = 1) at 21°C (Kragten and Decnop-Weever, 1983). The same authors report congruent values for pKa−1 under the given conditions: 0.75 (Kragten and Decnop-Weever, 1983), 0.88 (Merciny et al., 1978; Mioduski, 1980), and 0.89 (Matorina et al., 1969), except for Letkeman and Martell (1979), who found a value of 1.45. Only Mioduski (1980) reports a value for pKa−2 (0.81 ± 0.05), but Martell et al. (2004) estimate that it is probably less than zero. It seems that the eight acid dissociation constants form three rather closely spaced pairs separated by two more distinct values (pKa0 and pKa3). In view of the symmetry of the DTPA molecule, it is likely that the three pairs are associated with protonation of the terminal amines and their acetate groups, whereas the two single values are associated with protonation of the central amine and acetate group.
We performed non-linear regressions of 27 titrations of 1, 2, and 4 mM DTPA solutions with 1 M NaOH or HCl. Although acid titrations were conducted to circumvent the poor solubility of DTPA at low pH, they often yielded marginal fits, most commonly caused by a reversal of pKa1 and pKa2, and many were ultimately rejected. Similar to our study of DFOB (Christenson and Schijf, 2011), FITEQL models were initially constructed with all six (de)protonated forms of DTPA (H5−iL(−i)+ with i = 0–5) as the component and, as before, it was found that the model with H3L2− yields pKai values with the highest precision that are least dependent on the ligand concentration. All regressions were subsequently performed with this model. It was also found that titrations of 1 mM DTPA solutions gave persistently bad results and these were rejected. In the end, 10 titrations with NaOH and 3 titrations with HCl were selected to determine the final pKai values (Table 2). Analogous to our titrations of DFOB (Christenson and Schijf, 2011), the regressions were performed with the initial proton excess, , and the pKai values as free parameters. All regressions converged after a small number of iterations and the quality-of-fit parameter, WSOS/DF, was of the order 0.1–1, indicating good fits (Herbelin and Westall, 1999).
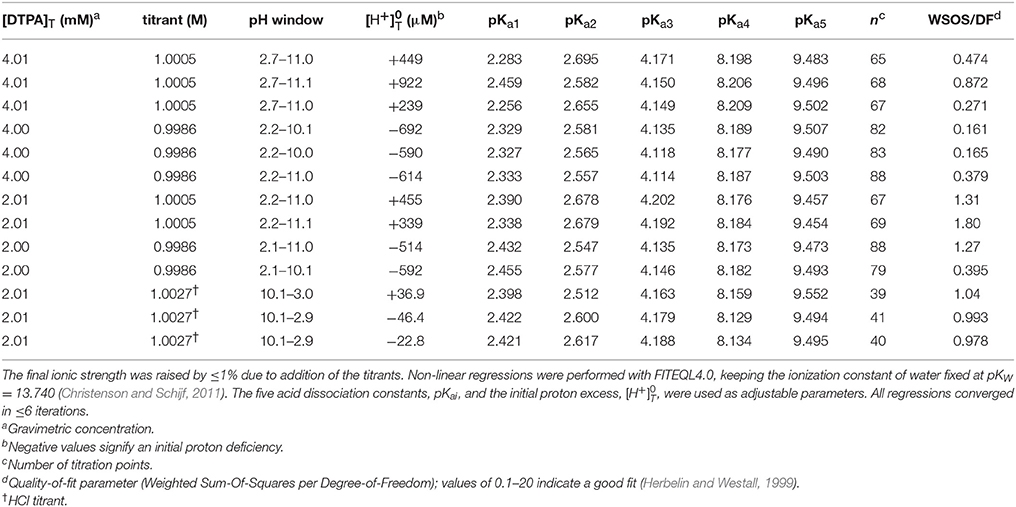
Table 2. Thirteen titrations of diethylenetriaminepentaacetic acid (DTPA) in 50 mL of 0.7 M NaClO4 solution.
The average pKai values are given in Table 3, where they are compared with values from the literature. Relative standard deviations are 2–3% for pKa1 and pKa2 and < 1% for the other three constants, confirming that results are independent of the DTPA concentration and the titrant. The literature contains dozens of studies of DTPA protonation in many different media, using many different techniques. Unlike DFOB (Christenson and Schijf, 2011), it seems that pKai values for DTPA do depend on medium composition and data in NaClO4 were therefore selected for the comparison in Table 3. In studies where different definitions of the acid dissociation constants were used, values were recalculated to match the form of Equation (3). Not all data in Table 3 are internally or mutually consistent. The pKa1 and pKa3 values of Grimes and Nash (2014) (I = 2.0 M) are higher than other literature data for this ionic strength range, although the remaining constants are concordant. The first three pKai values of Nozaki and Koshiba (1967) (I = 0.5) are anomalous as well. Their value for pKa2 is more similar to published values for pKa1. In addition, their values for pKa3 (3.39) and pKa1 (1.13) are remarkably close to, respectively, the average of our values for pKa2 and pKa4 (3.38) at I = 0.7 M and the average of the values for pKa−1 and pKa0 (1.12) at I = 1 (KCl) reported by Merciny et al. (1978) and Mioduski (1980). It seems that pKa3 was not resolved in the regression, causing an upward shift of the lower pKai.
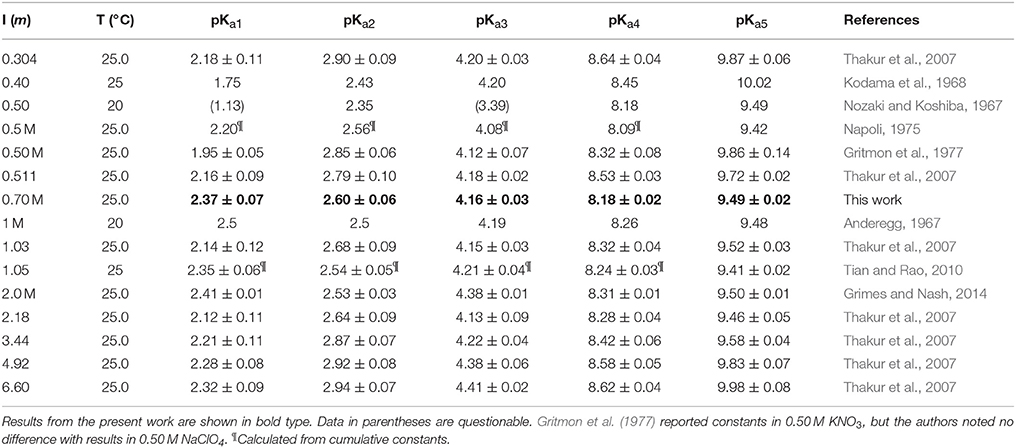
Table 3. Literature values for the five highest DTPA acid dissociation constants in NaClO4 solutions.
The most comprehensive study is that of Thakur et al. (2007), who determined acid dissociation constants over a wide range of ionic strength (I = 0.3–6.6). They found that, again unlike DFOB, the pKai values of DTPA display a definite dependence on ionic strength. In Figure 2, the data in Table 3 are shown for pKa2, pKa3, and pKa5, with extended Debije-Hückel fits through the data of Thakur et al. (2007). For pKa2, the values reported by Thakur et al. (2007) are the highest at each ionic strength for which literature data exist, hence a fit through all data is also shown. Our values are satisfactorily close to these curves.
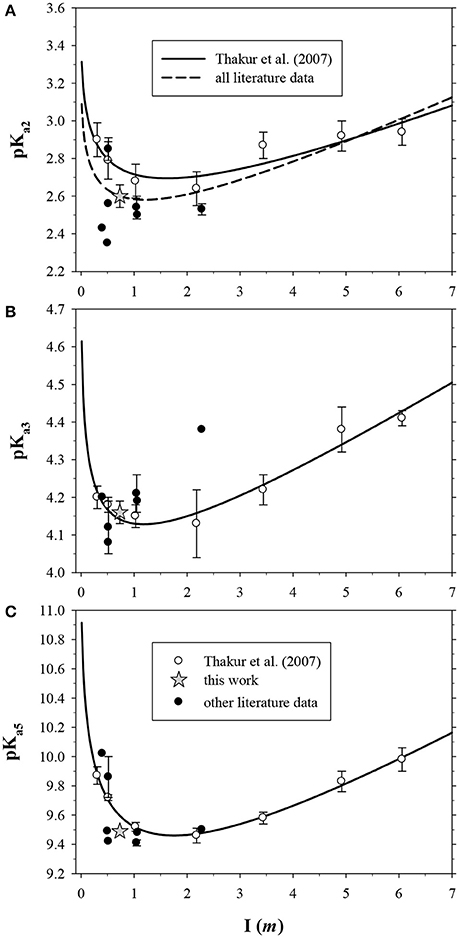
Figure 2. Literature values of three DTPA acid dissociation constants in NaClO4 solutions as a function of ionic strength (Table 3), converted to molal units. Data from Thakur et al. (2007) were fit with extended Debije-Hückel functions. Error bars were not reported for some studies (Table 3), or are within the size of the symbol. (A) pKa2. Additional fit of all data does not include the result from the present work. (B) pKa3. One very low value from Nozaki and Koshiba (1967) is not visible. (C) pKa5. All vertical axes are slightly offset from zero to show the behavior at low ionic strength.
Protonation of the DTPA amine groups occurs outside the pH window of our titrations. Nevertheless, including these reactions in our FITEQL models, with the corresponding pKai fixed at values appropriate for our experimental conditions, might improve the quality of regressions for the metal-ligand titrations. However, our attempts to determine these values were unsuccessful. Four slightly alkaline DTPA solutions of 1 or 2 mM were titrated down to pH ~ 0.9 by adding 1 M HCl in small increments (400–500 shots). Reactions for the protonation of one, two, or all amine groups were added to the FITEQL model, yet despite choosing a range of starting values, or limiting the degrees of freedom by fixing some higher pKai at the average values given in Table 3, the regressions would not converge to reproducible results (data not shown). This may be due in part to poor solubility of the ligand at low pH (Kragten and Decnop-Weever, 1983) or non-linear behavior of the glass electrode, and to a very small degree of proton exchange in a highly acidic matrix, producing inadequate signal-to-noise ratios. Gritmon et al. (1977) emphasized that the response of even high-quality glass electrodes deteriorates at pH < 2. To assess the effect of omitting these protonation reactions from FITEQL models, additional regressions of some Mg and Ca titrations were conducted with pKa−1 and pKa0 fixed at literature values for NaClO4 (I = 1) at 21°C (Kragten and Decnop-Weever, 1983), but excluding pKa−2. The resulting stability constants for Mg–DTPA and Ca–DTPA complexes were not substantially different from those presented in the next section and protonation of the DTPA amine groups was therefore not further considered.
Stability Constants of Mg–DTPA and Ca–DTPA Complexes
We performed 9 titrations each of Mg+DTPA and Ca+DTPA solutions in 0.7 M NaClO4, over a range of M:L ratios. The results are presented in Tables 4, 5. Although Mg and Ca bind more strongly to DTPA than to DFOB (Schijf and Burns, 2016), precipitation of Mg(OH)2 was still observed at M:L ratios around 3 (for 2 mM DTPA). The highest M:L ratio used for Mg was 2.6. Calcium is much less prone to hydroxide precipitation and M:L ratios of up to 3.3 were used. Despite these lower ratios, the titration curves were easily distinguishable from the titration curve for DTPA alone (Figure 3), unlike DFOB (Schijf and Burns, 2016). For Ca, which does not precipitate, titrations could be started at high pH, where DTPA is more soluble, and titrated down with HCl. The results were in good agreement with those obtained from titrations with NaOH (Table 5). Titrations of Mg were all conducted with NaOH (Table 4). The first hydrolysis constants of Mg and Ca were included and their values fixed in the FITEQL model for all regressions (Schijf and Burns, 2016).
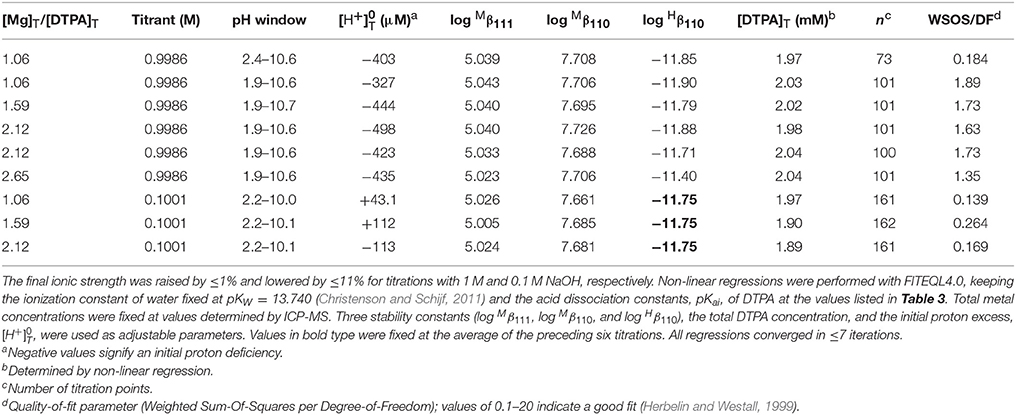
Table 4. Nine titrations of magnesium in 0.7 M NaClO4 solutions containing 2.01 mM DTPA (gravimetric concentration).
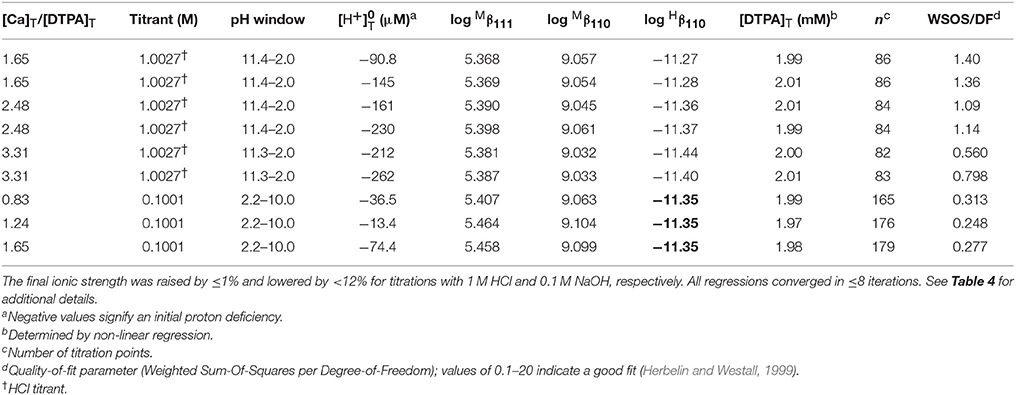
Table 5. Nine titrations of calcium in 0.7 M NaClO4 solutions containing 2.01 mM DTPA (gravimetric concentration).
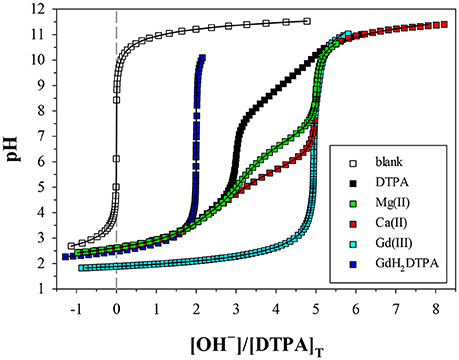
Figure 3. Potentiometric titrations of DTPA and metal+DTPA solutions in 0.7 M NaClO4, where pH is plotted against moles of base (OH−) added per mole of DTPA. The more a metal titration deviates from that of DTPA alone, the higher the stability of the DTPA complexes formed. Symbols are measurements. Solid lines are non-linear regressions performed with FITEQL4.0. The blank consists of the acidified background electrolyte (0.7 M NaClO4/HClO4). All other solutions contain 2 mM DTPA, except the Gd titration (4 mM). The M:L ratios are 1.06 for Mg, 1 for GdH2DTPA, and 1.65 for Ca. The curve for the Gd titration, with an M:L ratio of 0.85, was scaled to overlap the Mg and Ca curves.
Complexes of Mg and Ca with DTPA that have been reported in the literature include those with zero, one, two, and three protons (ML3−, MHL2−, MH2L−, MH3L0), and the dinuclear complex, M2L− (Duffield et al., 1984). The M:L ratios of our titrations (as well as the DTPA concentrations) were too high to detect the double- and triple-protonated forms and too low to detect the dinuclear complex. Nonetheless, it was found that models with only the ML3− and MHL2− complexes did not yield optimal fits, especially in the highest pH region. This was amended by assuming that Mg and Ca can be hydrolyzed inside the fully deprotonated DTPA complex at elevated pH to form the ternary complex, M(OH)L4−. This complex has not been previously reported for Mg or Ca, but it has been observed for more strongly hydrolyzing elements, such as Al, Ga, In (Harris and Martell, 1976; Taqui Khan and Hussain, 1980), and Fe (Vandegaer et al., 1959; Ahrland et al., 1990). The following stability constant was added to the FITEQL model (Table 1):
This constant could not be resolved in titrations with 0.1 M NaOH for either Mg or Ca. In order to have a single FITEQL model for all regressions, values of all three stability constants were first determined from titrations with 1 M NaOH (Mg) or HCl (Ca). Regressions of titrations with 0.1 M NaOH were then performed with fixed at the average of the values so obtained. The values of and were in good agreement for both sets of regressions (Tables 4, 5).
Only a limited number of studies exists on the stability of DTPA complexes with Ca and even fewer for Mg. Table 7 shows only those where more than one constant was measured, most of which also include a value for . One was conducted at physiological conditions (0.150 M NaCl, T = 37°C), while all others were conducted at I = 0.1 and none in NaClO4. Nevertheless, our results for and are generally consistent with literature values, considering the higher ionic strength of our experiments. Our values are lower than those of the careful study by Duffield et al. (1984), which in turn are lower than results at I = 0.1 (except for Mg). This suggests a definite ionic strength dependence for these constants, which is broadly consistent with what is observed for DFOB (Schijf and Burns, 2016), although that finding was essentially based on a single published study. It should be noted that the relative values of our stability constants are also in marked agreement with Duffield et al. (1984). Our values of and are lower by 0.76 and 0.73 log units, respectively, for Ca and by 0.86 and 0.82 log units for Mg. We will use this observation to estimate values of and for our speciation calculations in seawater (sections Calculation of the DTPA Side-Reaction Coefficient and Implications for the Stability of Gd–DTPA Complexes in Seawater). In contrast with DFOB (Schijf and Burns, 2016), DTPA complexes with Ca are more stable than those with Mg. This is clearly illustrated by the titration curves (Figure 3) and by the buffer intensities of the corresponding solutions (Figure 4).
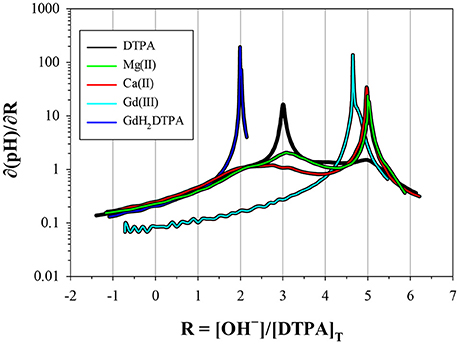
Figure 4. Derivatives of the titration curves in Figure 3, taken with respect to the x-coordinate. Peaks indicate low buffer intensity. The DTPA curve has a prominent peak at R = 3, corresponding to the release of three protons at low pH, and fainter peaks at R = 2, 4, and 5. The metal curves have a prominent peak at R = 5, indicating strong interaction with the fully deprotonated ligand. The fainter peak at R = 3 for Mg is from a higher fraction of free ligand, resulting from the lower stability of its DTPA complexes. The Gd curve (not scaled) has an M:L ratio of 0.85; 15% is present as free DTPA and 85% as virtually inert Gd–DTPA complexes, yielding a peak at 0.15 × 3 + 0.85 × 5 = 4.71. The GdH2DTPA compound has only two protons, producing a single peak at R = 2.
No literature data are available for comparison with our values of . However, they can be compared with first hydrolysis constants of the free metal, log (Table 1), which are −12.04 and −13.00, respectively, for Mg and Ca in 0.7 M NaClO4 (Schijf and Burns, 2016). These constants, while similar in value to , indicate that hydrolysis of the metal inside the complex is thermodynamically distinct from hydrolysis of the free metal and that especially Ca is more readily hydrolyzed inside the complex. It also suggests that Mg and Ca retain at least one water of hydration and are consequently not fully coordinated by DTPA, even when the latter is completely deprotonated. This may explain the unusually high stability of the dinuclear complexes (Table 7 and see section Calculation of the DTPA Side-Reaction Coefficient). The fact that the dinuclear Mg complex was only observed by Duffield et al. (1984) may be due to the low solubility of Mg at elevated pH, which complicates the necessary titrations at high M:L ratios.
Stability Constants of Gd–DTPA Complexes
Nine titrations of Gd+DTPA were performed in 0.7 M NaClO4 and the results are shown in Table 6. Initial runs were conducted with GdH2DTPA. In the regressions, the M:L ratio of this compound was assumed to be 1 and the ligand concentration was fixed and set equal to the Gd concentration measured by ICP-MS. The stability of the Gd–DTPA complex is extremely high and at the very edge of the analytical window for our method (Figures 3, 4). In an attempt to enhance the exchange of protons, two runs were performed in the presence of DFOB as a competing ligand, where the stability constant (log β3 = ) of the hexadentate Gd–DFOB complex is 13.67 in 0.7 M NaClO4 (Christenson and Schijf, 2011). However, this is 7 orders of magnitude less stable than the DTPA complex and the speciation of Gd throughout the titrations was little affected by additions of up to 4 mM DFOB. To allow variation of the M:L ratio, additional titrations were conducted wherein Gd and DTPA were added separately. In the regressions of these data, the DTPA concentration was used as an adjustable parameter. In a few cases this led to under-constrained fits (WSOS/DF < 0.1) and the optimized DTPA concentration was always 4–6% lower than the gravimetric value (Table 6).
Previous studies of Gd have reported the formation of a deprotonated and a single-protonated DTPA complex (Table 7) and both were included in the FITEQL model. The corresponding stability constants could be determined simultaneously for all nine titrations, but the values of were poorly constrained and significantly different for the titrations with GdH2DTPA. For one titration with the lowest M:L ratio (0.46), the values of both stability constants were anomalous. Results were significantly improved by adding two iterative steps to the initial regressions. In the second step, the value of , which was fairly well constrained, was fixed at the average obtained in the first step, excluding the one anomalous run, yielding a more consistent value of for all nine titrations. In the third and final step, the value of was fixed at the average obtained in the second step to yield a final, optimized value of .
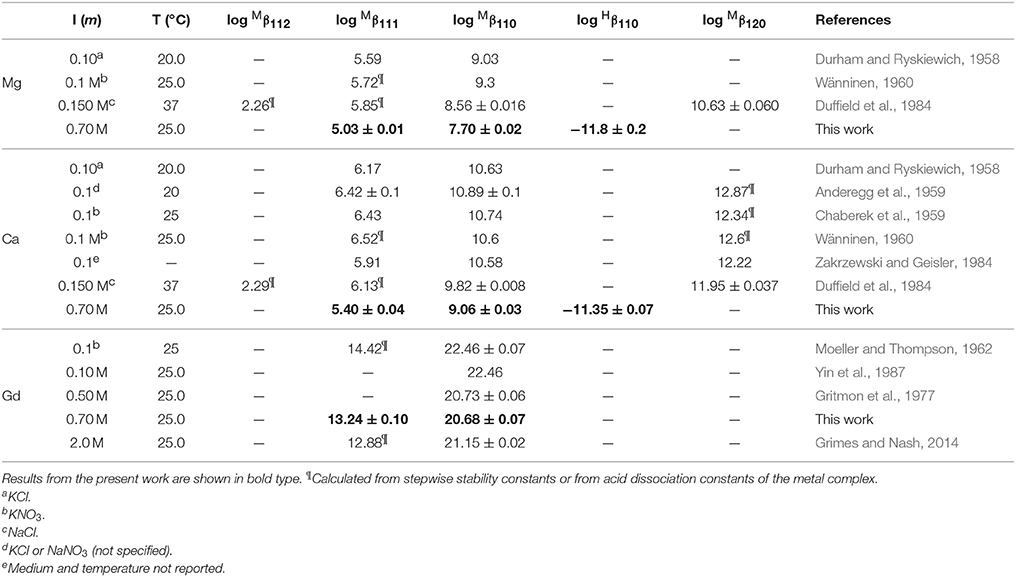
Table 7. Selected literature values of stability constants for DTPA complexes with Mg, Ca, and Gd in NaClO4 solutions, unless otherwise specified.
Studies of DTPA complexation with the REE and actinides are more plentiful in the literature, because of its importance in chemical purification (Baybarz, 1965; Grimes and Nash, 2014), medical diagnostics (Sherry et al., 1988), and the potential treatment of actinide toxicity in humans (Duffield et al., 1984), but most have been conducted at low ionic strength. In Table 7 our results are compared with only three studies conducted in NaClO4, as well as with the widely cited study of Moeller and Thompson (1962), in KNO3. The results of Moeller and Thompson (1962) and Yin et al. (1987) at I = 0.1 are identical, although the latter authors do not report a value for . Our value for at I = 0.7 M is in excellent agreement with the result of Gritmon et al. (1977) at I = 0.5 M. Similar to the behavior of Mg and Ca (Table 7), but unlike REE complexes with DFOB (Christenson and Schijf, 2011), the value of for Gd appears to decrease going from low to intermediate ionic strength. Moreover, its value appears to increase again going on to I = 2.0 M. While this is generally consistent with a Debije-Hückel-type behavior (cf. Figure 2), it should be regarded as a preliminary finding in view of the scarcity of data. A slightly different trend is seen for , which appears to decrease continuously from I = 0.1 to 2.0 M, yet this observation is currently based on just two previously reported values (Table 7). Still, our value falls comfortably between these earlier results and, like , somewhat closer to the value at I = 2.0 M.
Speciation Modeling of the Mg-Ca-Gd-DTPA-H2O-CO2 System in Seawater
Calculation of the DTPA Side-Reaction Coefficient
Strong complexation of DTPA with Mg and Ca can have a significant effect on the stability of the Gd–DTPA complex in seawater, by effectively lowering the amount of available ligand. This is quantified by the side-reaction coefficient, as defined by Ringbom and Still (1972). The calculation of the side-reaction coefficient for polyprotic organic ligands is complicated by the fact that the free ligand may exist in multiple protonated forms. A side-reaction coefficient calculated relative to a particular protonated form is less meaningful if the metal does not form a strong complex with that form of the ligand, or if that form is a minor species in the system of interest. Schijf and Burns (2016) outlined the calculation of a more generic side-reaction coefficient, αf, that converts any thermodynamic stability constant to a conditional constant for a specific system, independent of what protonated forms of the ligand the metal binds to or relative to what form the stability constants are expressed. The coefficient is pH-dependent but does not affect the distribution of the ligand among its various protonated forms. Here, the side-reaction coefficient of DTPA in seawater is calculated using the same approach, as shown in Table 8.
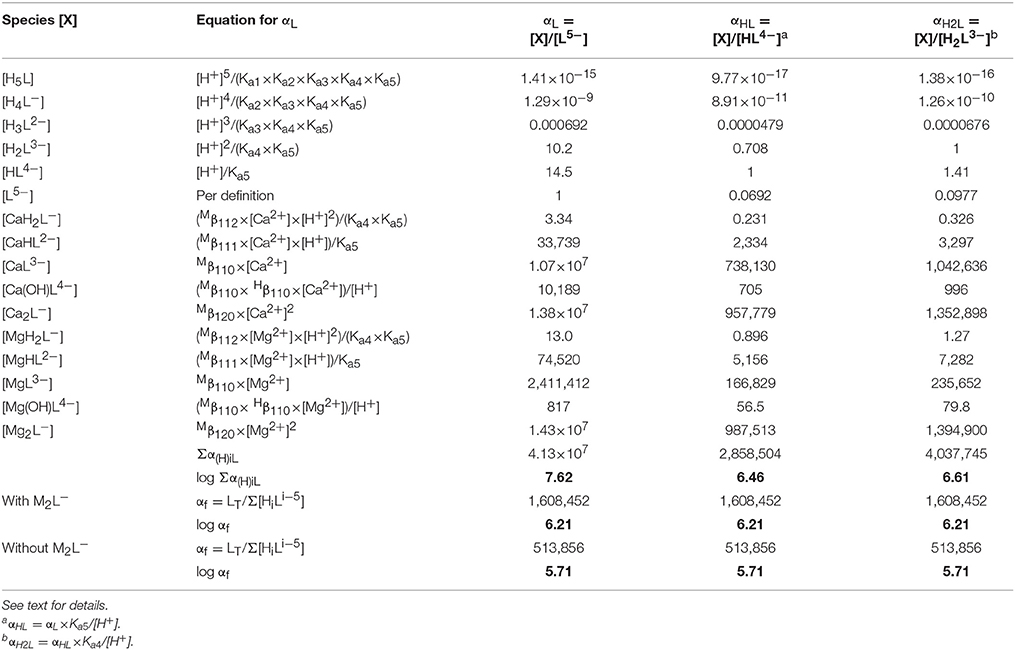
Table 8. Calculation of the side-reaction coefficient in seawater for the three most abundant (de)protonated forms of DTPA, using data from Tables 3, 7.
The coefficient αf was calculated for seawater at S = 35.0 and pH = 8.2 (8.33 on the free proton scale). The concentrations of Mg and Ca are 54.0 and 10.5 mM, respectively, of which about 89% is present as the free cation in each case (Schijf and Burns, 2016). A simple speciation model, using the acid dissociation constants in Table 3, reveals that, ignoring any complexation, only three forms of DTPA are relevant at this pH; about 56.5% is present as the single-protonated species, 39.6% as the double-protonated species, and 3.9% as the deprotonated species, while the other forms are negligible (Figure 5A). To demonstrate some of its behavior, the traditional side-reaction coefficient was calculated for each of these forms, although the coefficient αf is the same for all three (Table 8). To accurately account for the contribution of Mg and Ca to the DTPA speciation, all complexes were included, except for MH3L0, since its stability constant is quite small (Duffield et al., 1984) and H3L2− has very low abundance in seawater. In Table 7, values of the stability constants , , and are presented that are appropriate for seawater. Values of and were reported by Duffield et al. (1984) in NaCl, but at lower ionic strength (Table 7). It was observed in section Stability Constants of Mg–DTPA and Ca–DTPA Complexes that our constants are offset from those of Duffield et al. (1984) by an average of 0.84 log units for Mg and 0.75 log units for Ca. Assuming this to be true for the other constants, we can estimate the values of and in seawater to be 1.55 and 11.21 for Ca, and 1.42 and 9.79 for Mg, respectively.
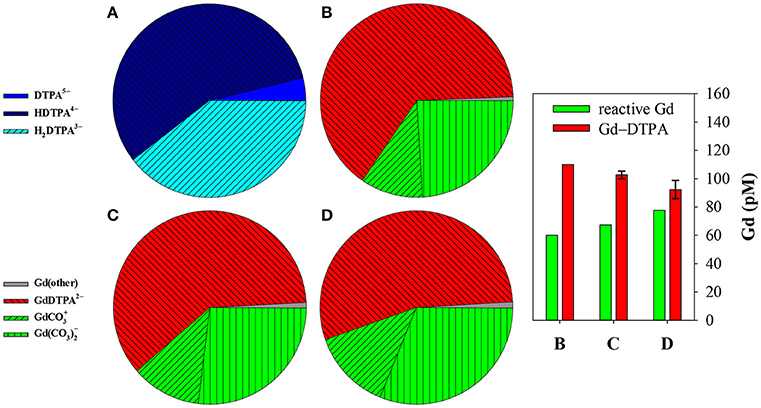
Figure 5. Speciation of Gd and DTPA, calculated with MINEQL, in a seawater sample (S = 35, pHf = 8.33, T = 25°C) containing 60 pM “natural” reactive Gd and 110 pM anthropogenic Gd–DTPA, similar to the 2013 San Francisco Bay sample of Hatje et al. (2016). (A) Depicts the distribution of DTPA among its different protonated forms, in the absence of any complexation. Speciation of Gd in (B) does not account for DTPA complexation with Mg and Ca; 100% of DTPA is complexed with Gd. In (C) some Gd–DTPA has dissociated due to the formation of mononuclear Mg–DTPA and Ca–DTPA complexes. Even more dissociates in (D) when dinuclear Mg–DTPA and Ca–DTPA complexes are included. The destabilization of Gd–DTPA is clearly illustrated in the graph on the right, showing relative concentrations of the two Gd fractions; letters on the x-axis correspond to panels on the left. Uncertainties were estimated by re-running MINEQL after modifying all constants with combinations of added/subtracted 2σ-errors that yield the largest deviations from the model value.
The results in Table 8 show that the speciation of DTPA in seawater is entirely dominated by the ML3− and M2L− complexes for both Mg and Ca, whereas the contribution of the MHL2− complex is comparatively small and that of the MH2L− and M(OH)L4− complexes negligible. The greater uncertainty in the values of and is therefore of minor importance. On the other hand, the high stability and abundance of the dinuclear complexes was not observed for DFOB (Schijf and Burns, 2016) and is somewhat surprising. The importance of the dinuclear complexes can be further stressed by pointing out that the value of the coefficient αf is lowered by 0.5 log units if they are omitted from the calculation (Table 8). This indicates that additional studies are warranted to determine a more accurate value for the stability constant in seawater. Nonetheless, in either case, the value of αf (5.71 or 6.21) implies that the stability of DTPA complexes in seawater, including those with Gd, is about 6 orders of magnitude lower than in freshwater, due to substantial competition from abundant Mg and Ca. In the next section we will illustrate this effect by modeling the Gd speciation in seawater in the presence of DTPA, with and without Mg and Ca complexation, and also with and without the M2L− complexes.
Side-reaction coefficients for DFOB in seawater, calculated relative to different forms of the ligand, increase strongly with decreasing protonation (Schijf and Burns, 2016). This is because the abundance of free ligand species increase with their degree of protonation, whereas the stability of their complexes with Mg and Ca is similar. For DTPA, the deprotonated form of the ligand is a minor species in seawater yet forms very stable complexes with Mg and Ca. The two protonated forms are much more abundant, but their complexes are less stable. The balance of these two effects causes their three side-reaction coefficients to be nearly equal in size, yet the coefficient αHL, corresponding to the single-protonated form of DTPA, is the smallest (Table 8).
Implications for the Stability of Gd–DTPA Complexes in Seawater
Using the side-reaction coefficient αf, calculated in the previous section, we can now model the speciation of Gd and DTPA in a typical seawater sample. A recent survey of archived water samples from San Francisco Bay by Hatje et al. (2016) found that the sample from 2013, the most recent one analyzed, contained about 170 pM dissolved Gd, 110 pM of which was very strongly complexed and probably of anthropogenic origin. We will assume here that this fraction consists of Gd–DTPA. Some of the remaining 60 pM may also be from industrial sources but this fraction is present as reactive species, predominantly complexes with dissolved inorganic and less stable organic complexes (Schijf et al., 2015a). Speciation was calculated with MINEQL2.0 (Westall et al., 1986) for the same standard seawater referred to in the previous section. The sample of Hatje et al. (2016) had a salinity of 28.2, which would lower the side-reaction coefficient as a result of diminished contributions from DTPA complexes with Mg and Ca. However, San Francisco Bay water will eventually enter the open ocean and it is furthermore preferable to keep this exercise consistent with our prior work (Schijf et al., 2015a,b; Schijf and Burns, 2016).
First, the speciation of Gd and DTPA was modeled without any competition from Mg and Ca. All (de)protonated forms of DTPA were included, as well as both Gd–DTPA complexes, using the acid dissociation constants from Table 3 and the stability constants from Table 7. The result is shown in Figure 5B. Since Gd is present in excess, 100% of DTPA is complexed with Gd in the fully deprotonated complex, despite the fact that its stability constant is nearly 2 orders of magnitude lower at the ionic strength of seawater. The contribution of the single-protonated complex is negligible. The reactive Gd fraction displays the usual speciation in standard seawater (Schijf et al., 2015a), dominated by carbonate complexes, where the species makes up nearly 70% and the species nearly 30% of the total. The remaining few percent consist of other Gd species, mainly free and hydrolyzed cations and the sulfate complex. The fraction of Gd–DTPA is essentially unchanged from what Hatje et al. (2016) found based on an interpolation of the shale-normalized pattern to estimate the Gd background concentration, Gd*.
Next, competition from mononuclear complexes with Mg and Ca was included. As explained by Schijf and Burns (2016), these do not have to be explicitly added to the speciation model. Instead, log αf = 5.71 (Table 8) is subtracted from the stability constants of the two Gd–DTPA complexes, resulting in values of 14.97 and 7.53 for and , respectively (Table 7). The values of the pKai stay the same. As shown in Figure 5C, only 93.4% of DTPA is now complexed with Gd, meaning that nearly 7% has dissociated due to competition from Mg and Ca. The rest consists almost entirely of fully deprotonated Mg–DTPA and Ca–DTPA complexes.
Finally, the last calculation was repeated with the inclusion of dinuclear Mg–DTPA and Ca–DTPA complexes. This was done by subtracting log αf = 6.21 (Table 8) from the stability constants of the two Gd–DTPA complexes, resulting in values of 14.47 and 7.03 for and , respectively (Table 7). The contribution of Mg and Ca complexes to the DTPA speciation increases to about 16% (Figure 5D), causing an additional 9% of the Gd–DTPA complex to dissociate. The graph on the right in Figure 5 shows the effect on the anthropogenic and reactive Gd fractions in terms of their relative concentrations. Specifically, the concentration of the reactive fraction increases from 60 to 78 pM, a gain of 30%.
Estuarine scavenging of reactive Gd resulting from salt-induced coagulation of organic colloids is strongest at salinities < 5 (Elderfield et al., 1990). Although Gd–DTPA is expected to progressively destabilize with increasing Mg and Ca concentration i.e., with increasing salinity, each DTPA complex has a unique, non-linear dependence on ionic strength that is as yet poorly constrained (Figure 2) and affects Gd speciation in a non-obvious manner (Table 8 and Figure 5), making it hard to predict where along the salinity gradient most of the decomposition takes place. It is possible that a significant amount of reactive and potentially biotoxic Gd is released well beyond the low-salinity zone of most effective removal and thus reaches the ocean, where it will continue to be scavenged on settling particles (Schijf et al., 2015a). In coastal seas, which are characterized by high productivity, shallow waters, and high settling rates, a sizable fraction of these particles may be transferred to the sediment, thereby making anthropogenic Gd available to the benthic ecosystem.
It should be clear from our investigation that the Gd–DTPA complex, which is generally deemed chemically inert and conservative, can be substantially destabilized upon mixing of river water with seawater in estuaries. We found that, while the increase of ionic strength has a minor effect, as much as 15% of the complex can dissociate due to competition from Mg and Ca. This number should be considered a lower-bound estimate, because several processes that may further destabilize the complex were not considered here and should be the focus of future research: (1) transmetallation with other REE and strongly binding metals like Fe(III) and U, or competition from other strong organic ligands (Bundy et al., 2015) may displace Gd from the DTPA complex; (2) although DTPA complexes with Na+ were inherently accounted for in our experiments, significant differences in protonation constants measured in media containing potassium vs. tetramethylammonium ((CH3)4N+) salts imply that DTPA also forms fairly stable complexes with K+ (Anderegg, 1967); (3) as the released Gd is gradually removed by scavenging, the organically complexed fraction maintains thermodynamic equilibrium by continued dissociation; (4) competition for the DTPA ligand is due in large part to the formation of dinuclear Mg and Ca complexes. The stability constants of these complexes are not well known, but their values are difficult to measure under seawater conditions; and (5) Gd–DTPA is just one of nearly a dozen MRI contrast agents that may well possess a variety of properties and effective stabilities.
Dissociation of complexes like Gd–DTPA will also complicate the interpretation of normalized REE patterns in the coastal environment and the tracking of these anthropogenic and potentially toxic contaminants. Large anthropogenic Gd anomalies may endure, but they will be partly comprised of released Gd that will merge with and behave like the geogenic background. It can then no longer be assumed that anthropogenic Gd anomalies solely represent the chemically inert complex, leaving its concentration uncertain. Although the released Gd is highly particle-reactive and should be quickly transferred to the particulate phase, it may eventually be remobilized by diagenetic processes and rejoin any remnant undissociated Gd complexes that are transported away from the estuary. In this regard, the ongoing development of advanced analytical techniques that can identify and quantify individual organic Gd species directly will be particularly beneficial (Künnemeyer et al., 2009a).
Author Contributions
IC: performed some of the potentiometric titrations; JS: performed the majority of the potentiometric titrations, calculated acid dissociation constants, stability constants, and the side-reaction coefficient, conducted the speciation modeling, and wrote the manuscript.
Funding
The REU project of IC was funded by NSF (OCE-1262374) and administered by the Maryland Sea Grant Program.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Our manuscript was significantly improved by constructive comments of the two reviewers. JS dedicates this work to the late Harry Elderfield, who was a kind and patient member of the examination committee for his Ph.D. defense at the University of Utrecht (The Netherlands) in 1992 and a most gracious host during an earlier visit to Harry's Cambridge laboratory and home. These experiments were partly inspired by the excellent past and present research of Michael Bau and Vanessa Hatje. We are grateful to all the editors of this Research Topic of Frontiers in Marine Science for allowing us to present our results. This is UMCES contribution #5481.
References
Ahrland, S., Dahlgren, Å., and Persson, I. (1990). Stabilities and hydrolysis of some iron(III) and manganese(III) complexes with chelating ligands. Acta Agric. Scand. 40, 101–111.
Anderegg, G. (1967). Komplexone XL. Die Protonierungskonstanten einiger Komplexone in verschiedenen wässerigen Salzmedien (NaClO4, (CH3)4NCl, KNO3). Helv. Chim. Acta 50, 2333–2340.
Anderegg, G., Nägeli, P., Müller, F., and Schwarzenbach, G. (1959). Komplexone XXX. Diäthylentriamin-pentaessigsäure (DTPA). Helv. Chim. Acta 42, 827–836.
Baes, C. F. Jr., and Mesmer, R. E. (1981). The thermodynamics of cation hydrolysis. Am. J. Sci. 281, 935–962.
Bau, M., and Dulski, P. (1996). Anthropogenic origin of positive gadolinium anomalies in river waters. Earth Planet. Sci. Lett. 143, 245–255.
Bau, M., Knappe, A., and Dulski, P. (2006). Anthropogenic gadolinium as a micropollutant in river waters in Pennsylvania and in Lake Erie, northeastern United States. Chem. Erde 66, 143–152. doi: 10.1016/j.chemer.2006.01.002
Baybarz, R. D. (1965). Dissociation constants of the transplutonium element chelates of diethylenetriaminepentaacetic acid (DTPA) and the application of DTPA chelates to solvent extraction separations of transplutonium elements from the lanthanide elements. J. Inorg. Nucl. Chem. 27, 1831–1839.
Behra-Miellet, J., Briand, G., Kouach, M., Gressier, B., Cazin, M., and Cazin, J. C. (1998). On-line HPLC-electrospray ionization mass spectrometry: a pharmacological tool for identifying and studying the stability of Gd3+ complexes used as magnetic resonance imaging contrast agents. Biomed. Chromatogr. 12, 21–26.
Binnemans, K., Jones, P. T., Blanpain, B., van Gerven, T., and Pontikes, Y. (2015). Towards zero-waste valorisation of rare-earth-containing industrial process residues: a critical review. J. Cleaner Prod. 99, 17–38. doi: 10.1016/j.jclepro.2015.02.089
Birka, M., Roscher, J., Holtkamp, M., Sperling, M., and Karst, U. (2016). Investigating the stability of gadolinium based contrast agents towards UV radiation. Water Res. 91, 244–250. doi: 10.1016/j.watres.2016.01.012
Brioschi, L., Steinmann, M., Lucot, E., Pierret, M. C., Stille, P., Prunier, J., et al. (2013). Transfer of rare earth elements (REE) from natural soil to plant systems: implications for the environmental availability of anthropogenic REE. Plant Soil 366, 143–163. doi: 10.1007/s11104-012-1407-0
Bundy, R. M., Abdulla, H. A. N., Hatcher, P. G., Biller, D. V., Buck, K. N., and Barbeau, K. A. (2015). Iron-binding ligand and humic substances in the San Francisco Bay estuary and estuarine-influenced shelf regions of coastal California. Mar. Chem. 173, 183–194. doi: 10.1016/j.marchem.2014.11.005
Chaberek, S., Frost, A. E., Doran, M. A., and Bicknell, N. J. (1959). Interaction of some divalent metal ions with diethylenetriaminepentaacetic acid. J. Inorg. Nucl. Chem. 11, 184–196.
Chistoserdova, L. (2016). Lanthanides: new life metals? World J. Microbiol. Biotechnol. 32:138. doi: 10.1007/s11274-016-2088-2
Christenson, E. A., and Schijf, J. (2011). Stability of YREE complexes with the trihydroxamate siderophore desferrioxamine B at seawater ionic strength. Geochim. Cosmochim. Acta 75, 7047–7062. doi: 10.1016/j.gca.2011.09.022
Chua, H. (1998). Bio-accumulation of environmental residues of rare earth elements in aquatic flora Eichhornia crassipes (Mart.) Solms in Guangdong Province of China. Sci. Total Environ. 214, 79–85. doi: 10.1016/S0048-9697(98)00055-2
d'Aquino, L., Morgana, M., Carboni, M. A., Staiano, M., Antisari, M. V., Re, M., et al. (2009). Effect of some rare earth elements on the growth and lanthanide accumulation in different Trichoderma strains. Soil Biol. Biochem. 41, 2406–2413. doi: 10.1016/j.soilbio.2009.08.012
de Campos, F. F., and Enzweiler, J. (2016). Anthropogenic gadolinium anomalies and rare earth elements in the water of Atibaia River and Anhumas Creek, Southeast Brazil. Environ. Monit. Assess. 188, 1–18. doi: 10.1007/s10661-016-5282-7
Du, X., and Graedel, T. E. (2011). Global in-use stocks of the rare earth elements: a first estimate. Environ. Sci. Technol. 45, 4096–4101. doi: 10.1021/es102836s
Duffield, J. R., May, P. M., and Williams, D. R. (1984). Computer simulation of metal ion equilibria in biofluids. IV. Plutonium speciation in human blood plasma and chelation therapy using polyaminopolycarboxylic acids. J. Inorg. Biochem. 20, 199–214. doi: 10.1016/0162-0134(84)85019-9
Durham, E. J., and Ryskiewich, D. P. (1958). The acid dissociation constants of diethylenetriaminepentaacetic acid and the stability constants of some of its metal chelates. J. Amer. Chem. Soc. 80, 4812–4817.
Elderfield, H., Upstill-Goddard, R., and Sholkovitz, E. R. (1990). The rare earth elements in rivers, estuaries, and coastal seas and their significance to the composition of ocean waters. Geochim. Cosmochim. Acta 54, 971–991.
Fuganti, A., Möller, P., Morteani, G., and Dulski, P. (1996). Gadolinio ed altre terre rare usabili come traccianti per stabilire l'età, il movimento ed i rischi delle acque sotterranee: esempio dell'area di Trento. Geol. Tecn. Ambient. 4, 13–18.
Fuma, S., Takeda, H., Miyamoto, K., Yanagisawa, K., Inoue, Y., Ishii, N., et al. (2001). Ecological evaluation of gadolinium toxicity compared with other heavy metals using an aquatic microcosm. Bull. Environ. Contam. Toxicol. 66, 231–238. doi: 10.1007/s001280000229
Garcia-Solsona, E., Jeandel, C., Labatut, M., Lacan, F., Vance, D., Chavagnac, V., et al. (2014). Rare earth elements and Nd isotopes tracing water mass mixing and particle-seawater interactions in the SE Atlantic. Geochim. Cosmochim. Acta 125, 351–372. doi: 10.1016/j.gca.2013.10.009
González, V., Vignati, D. A. L., Leyval, C., and Giamberini, L. (2014). Environmental fate and ecotoxicity of lanthanides: are they a uniform group beyond chemistry? Environ. Intern. 71, 148–157. doi: 10.1016/j.envint.2014.06.019
González, V., Vignati, D. A. L., Pons, M.-N., Montarges-Pelletier, E., Bojic, C., and Giamberini, L. (2015). Lanthanide ecotoxicity: first attempt to measure environmental risk for aquatic organisms. Environ. Pollut. 199, 139–147. doi: 10.1016/j.envpol.2015.01.020
Grimes, T. S., and Nash, K. L. (2014). Acid dissociation constants and rare earth stability constants for DTPA. J. Solut. Chem. 43, 298–313. doi: 10.1007/s10953-014-0139-6
Gritmon, T. F., Goedken, M. P., and Choppin, G. R. (1977). The complexation of lanthanides by aminocarboxylate ligands—I. Stability constants. J. Inorg. Nucl. Chem. 39, 2021–2023.
Harder, R., and Chaberek, S. (1959). The interaction of rare earth ions with diethylenetriaminepentaacetic acid. J. Inorg. Nucl. Chem. 11, 197–209.
Harris, W. R., and Martell, A. E. (1976). Aqueous complexes of gallium(III). Inorg. Chem. 15, 713–720.
Hatje, V., Bruland, K. W., and Flegal, A. R. (2016). Increases in anthropogenic gadolinium anomalies and rare earth element concentrations in San Francisco Bay over a 20 year record. Environ. Sci. Technol. 50, 4159–4168. doi: 10.1021/acs.est.5b04322
Herbelin, A. L., and Westall, J. C. (1999). FITEQL. A Computer Program for Determination of Chemical Equilibrium Constants from Experimental Data. Version 4.0. Corvallis, OR: Department of Chemistry, Oregon State University.
Holzbecher, E., Knappe, A., and Pekdeger, A. (2005). Identification of degradation characteristics – exemplified by Gd–DTPA in a large experimental column. Environ. Model. Assessm. 10, 1–8. doi: 10.1007/s10666-004-4269-x
Idée, J. M., Port, M., Raynal, I., Schaefer, M., Le Greneur, S., and Corot, C. (2006). Clinical and biological consequences of transmetallation induced by contrast agents for magnetic resonance imaging: a review. Fund. Clin. Pharmacol. 20, 563–576. doi: 10.1111/j.1472-8206.2006.00447.x
Izatt, R. M., Izatt, S. R., Bruening, R. L., Izatt, N. E., and Moyer, B. A. (2014). Challenges to achievement of metal sustainability in our high-tech society. Chem. Soc. Rev. 43, 2451–2475. doi: 10.1039/C3CS60440C
Janz, G. J., Oliver, B. G., Lakshminarayanan, G. R., and Mayer, G. E. (1970). Electrical conductance, diffusion, viscosity, and density of sodium nitrate, sodium perchlorate, and sodium thiocyanate in concentrated aqueous solutions. J. Phys. Chem. 74, 1285–1289.
Kanazawa, Y., and Kamitani, M. (2006). Rare earth minerals and resources in the world. J. Alloys Compd. 408–412, 1339–1343. doi: 10.1016/j.jallcom.2005.04.033
Kodama, M., Noda, T., and Murata, M. (1968). D.C. and A.C. polarographic behavior of thallium(I) ions in diethylenetriaminepentaacetate solutions. Bull. Chem. Soc. Japan 41, 354–358.
Kragten, J., and Decnop-Weever, L. G. (1983). Solubility and protonation of EDTA, DCTA and DTPA in acidic perchlorate medium. Talanta 30, 623–625. doi: 10.1016/0039-9140(83)80145-3
Kulaksız, S., and Bau, M. (2007). Contrasting behaviour of anthropogenic gadolinium and natural rare earth elements in estuaries and the gadolinium input into the North Sea. Earth Planet. Sci. Lett. 260, 361–371. doi: 10.1016/j.epsl.2007.06.016
Kulaksız, S., and Bau, M. (2011a). Rare earth elements in the Rhine River, Germany: first case of anthropogenic lanthanum as a dissolved microcontaminant in the hydrosphere. Environ. Intern. 37, 973–979. doi: 10.1016/j.envint.2011.02.018
Kulaksız, S., and Bau, M. (2011b). Anthropogenic gadolinium as a microcontaminant in tap water used as drinking water in urban areas and megacities. Appl. Geochem. 26, 1877–1885. doi: 10.1016/j.apgeochem.2011.06.011
Kulaksız, S., and Bau, M. (2013). Anthropogenic dissolved and colloid/nanoparticle-bound samarium, lanthanum and gadolinium in the Rhine River and the impending destruction of the natural rare earth element distribution in rivers. Earth Planet. Sci. Lett. 362, 43–50. doi: 10.1016/j.epsl.2012.11.033
Kümmerer, K., and Helmers, E. (2000). Hospital effluents as a source of gadolinium in the aquatic environment. Environ. Sci. Technol. 34, 573–577. doi: 10.1021/es990633h
Künnemeyer, J., Terborg, L., Meermann, B., Brauckmann, C., Möller, I., Scheffer, A., et al. (2009a). Speciation analysis of gadolinium chelates in hospital effluents and wastewater treatment plant sewage by a novel HILIC/ICP-MS method. Environ. Sci. Technol. 43, 2884–2890. doi: 10.1021/es803278n
Künnemeyer, J., Terborg, L., Nowak, S., Telgmann, L., Tokmak, F., Krämer, B. K., et al. (2009b). Analysis of the contrast agent Magnevist and its transmetalation products in blood plasma by capillary electrophoresis/electrospray ionization time-of-flight mass spectrometry. Anal. Chem. 81, 3600–3607. doi: 10.1021/ac8027118
Lawrence, M. G. (2010). Detection of anthropogenic gadolinium in the Brisbane River plume in Moreton Bay, Queensland, Australia. Mar. Pollut. Bull. 60, 1113–1116. doi: 10.1016/j.marpolbul.2010.03.027
Lawrence, M. G., Ort, C., and Keller, J. (2009). Detection of anthropogenic gadolinium in treated wastewater in South East Queensland, Australia. Water Res. 43, 3534–3540. doi: 10.1016/j.watres.2009.04.033
Letkeman, P., and Martell, A. E. (1979). Nuclear magnetic resonance and potentiometric protonation study of polyaminopolyacetic acids containing from two to six nitrogen atoms. Inorg. Chem. 18, 1284–1289.
Lide, D. R., and Haynes, W. M. (2009). CRC Handbook of Chemistry and Physics, 90th Edn. Boca Raton, FL: CRC Press.
Lingott, J., Lindner, U., Telgmann, L., Esteban-Fernández, D., Jakubowski, N., and Panne, U. (2016). Gadolinium-uptake by aquatic and terrestrial organisms-distribution determined by laser ablation inductively coupled plasma mass spectrometry. Environm. Sci. Proc. Imp. 18, 200–207. doi: 10.1039/c5em00533g
Martell, A. E., Smith, R. M., and Motekaitis, R. J. (2004). NIST Critically Selected Stability Constants of Metal Complexes. NIST Standard Reference Database 46 Version 8.0, Gaithersburg, MD.
Matorina, N. N., Shepetyuk, L. V., and Chmutov, K. V. (1969). Thermodynamic functions of the sorption of ethylenediaminetetraacetate and diethylenetriaminepentaacetate by KU-2 cation-exchange resin. Russ. J. Phys. Chem. 43, 1175–1178.
Merciny, E., Gatez, J. M., and Duyckaerts, G. (1978). Constantes de formation des complexes de stoechiométrie 1:1 et 1:2 ainsi que des complexes mixtes formes entre le plutonium(III) et divers acides aminopolyacétiques. Anal. Chim. Acta 100, 329–342.
Mioduski, T. (1980). Protonation constants of 1-hydroxyethylidene-1,1-diphosphonic acid, diethylenetriamino-N,N,N′,N″,N″-penta-acetic acid, and trans-1,2-diaminocyclohexane-N,N,N′,N′-tetra-acetic acid. Talanta 27, 299–303. doi: 10.1016/0039-9140(80)80062-2
Moeller, T., and Thompson, L. C. (1962). Observations on the rare earths—LXXV. The stabilities of diethylenetriaminepentaacetic acid chelates. J. Inorg. Nucl. Chem. 24, 499–510.
Möller, P., Dulski, P., Bau, M., Knappe, A., Pekdeger, A., and Sommer-von Jarmersted, C. (2000). Anthropogenic gadolinium as a conservative tracer in hydrology. J. Geochem. Explor. 69–70, 409–414. doi: 10.1016/S0375-6742(00)00083-2
Möller, P., Morteani, G., and Dulski, P. (2003). Anomalous gadolinium, cerium, and yttrium contents in the Adige and Isarco river waters and in the water of their tributaries (provinces Trento and Bolzano/Bozen, NE Italy). Acta Hydrochim. Hydrobiol. 31, 225–239. doi: 10.1002/aheh.200300492
Möller, P., Paces, T., Dulski, P., and Morteani, G. (2002). Anthropogenic Gd in surface water, drainage system, and the water supply of the city of Prague, Czech Republic. Environ. Sci. Technol. 36, 2387–2394. doi: 10.1021/es010235q
Nancharaiah, Y. V., Mohan, S. V., and Lens, P. N. L. (2016). Biological and bioelectrochemical recovery of critical and scarce metals. Trends Biotechnol. 34, 137–154. doi: 10.1016/j.tibtech.2015.11.003
Napoli, A. (1975). Studies on vanadyl complexes with aminopolycarboxylic acids. I. Vanadyl complexes with EGTA and DTPA. Gazz. Chim. Ital. 105, 1073–1081.
Nozaki, T., and Koshiba, K. (1967). Ultraviolet spectrophotometric determination of the compositions and the stabilities of some aminopolycarboxylate complexes of bismuth(III). Nippon Kagaku Zassi 88, 1287–1291.
Nozaki, Y., Lerche, D., Alibo, D. S., and Tsutsumi, M. (2000). Dissolved indium and rare earth elements in three Japanese rivers and Tokyo Bay: evidence for anthropogenic Gd and In. Geochim. Cosmochim. Acta 64, 3975–3982. doi: 10.1016/S0016-7037(00)00472-5
Ogata, T., and Terakado, Y. (2006). Rare earth element abundances in some seawaters and related river waters from the Osaka Bay area, Japan: significance of anthropogenic Gd. Geochem. J. 40, 463–474. doi: 10.2343/geochemj.40.463
Olmez, I., Sholkovitz, E. R., Hermann, D., and Eganhouse, R. P. (1991). Rare earth elements in sediments off southern California: a new anthropogenic indicator. Environ. Sci. Technol. 25, 310–316. doi: 10.1021/es00014a015
Port, M., Idée, J. M., Medina, C., Robic, C., Sabatou, M., and Corot, C. (2008). Efficiency, thermodynamic and kinetic stability of marketed gadolinium chelates and their possible clinical consequences: a critical review. Biometals 21, 469–490. doi: 10.1007/s10534-008-9135-x
Rabiet, M., Brissaud, F., Seidel, J. L., Pistre, S., and Elbaz-Poulichet, F. (2009). Positive gadolinium anomalies in wastewater treatment plant effluents and aquatic environment in the Hérault watershed (South France). Chemosphere 75, 1057–1064. doi: 10.1016/j.chemosphere.2009.01.036
Ringbom, A., and Still, E. (1972). The calculation and use of α coefficients. Anal. Chim. Acta 59, 143–146.
Rogosnitzky, M., and Branch, S. (2016). Gadolinium-based contrast agent toxicity: a review of known and proposed mechanisms. Biometals 29, 365–376. doi: 10.1007/s10534-016-9931-7
Schijf, J., and Burns, S. M. (2016). Determination of the side-reaction coefficient of desferrioxamine B in trace-metal-free seawater. Front. Mar. Sci. 3:117. doi: 10.3389/fmars.2016.00117
Schijf, J., Christenson, E. A., and Byrne, R. H. (2015a). YREE scavenging in seawater: a new look at an old model. Mar. Chem. 177, 460–471. doi: 10.1016/j.marchem.2015.06.010
Schijf, J., Christenson, E. A., and Potter, K. J. (2015b). Different binding modes of Cu and Pb vs. Cd, Ni, and Zn with the trihydroxamate siderophore desferrioxamine B at seawater ionic strength. Mar. Chem. 173, 40–51. doi: 10.1016/j.marchem.2015.02.014
Sherry, A. D., Cacheris, W. P., and Kuan, K. T. (1988). Stability constants for Gd3+ binding to model DTPA-conjugates and DTPA-proteins: implications for their use as magnetic resonance contrast agents. Magn. Reson. Medic. 8, 180–190. doi: 10.1002/mrm.1910080208
Shimada, H., Kubota, R., Funakoshi, T., and Kojima, S. (1995). Effects of lanthanum, terbium and ytterbium on the absorption of saccharides in the small intestine of mice. Jpn. J. Toxicol. Environ. Health 41, 35–41.
Showstack, R. (2012). U.S. trade dispute with China over rare earth elements. EOS Trans. AGU 93, 134–135. doi: 10.1029/2012EO130002
Taqui Khan, M. M., and Hussain, A. (1980). Aminopolycarboxylic acid complexes of Al(III), Ga(III), and In(III). Indian J. Chem. 19A, 50–57.
Thakur, P., Mathur, J. N., Moore, R. C., and Choppin, G. R. (2007). Thermodynamics and dissociation constants of carboxylic acids at high ionic strength and temperature. Inorg. Chim. Acta 360, 3671–3680. doi: 10.1016/j.ica.2007.06.002
Tian, G., and Rao, L. (2010). Effect of temperature on the protonation of the TALSPEAK ligands: lactic and diethylenetrinitropentaacetic acids. Separ. Sci. Technol. 45, 1718–1724. doi: 10.1080/01496395.2010.494712
Vandegaer, J., Chaberek, S., and Frost, A. E. (1959). Iron chelates of diethylenetriaminepentaacetic acid. J. Inorg. Nucl. Chem. 11, 210–221.
Verplanck, P. L., Furlong, E. T., Gray, J. L., Phillips, P. J., Wolf, R. E., and Esposito, K. (2010). Evaluating the behavior of gadolinium and other rare earth elements through large metropolitan sewage treatment plants. Environ. Sci. Technol. 44, 3876–3882. doi: 10.1021/es903888t
Verplanck, P. L., Taylor, H. E., Nordstrom, D. K., and Barber, L. B. (2005). Aqueous stability of gadolinium in surface waters receiving sewage treatment plant effluent, Boulder Creek, Colorado. Environ. Sci. Technol. 39, 6924–6929. doi: 10.1021/es048456u
Wänninen, E. (1960). Complexometric titrations with diethylenetriaminepenta-acetic acid. Acta Acad. Aboensis 21, 1–110.
Westall, J. C., Zachary, J. L., and Morel, F. M. M. (1986). MINEQL. A Computer Program for the Calculation of the Chemical Equilibrium Composition of Aqueous Systems. Version 1. Corvallis, OR: Department of Chemistry, Oregon State University.
Xu, X., Zhu, W., Wang, Z., and Witkamp, G.-J. (2002). Distributions of rare earths and heavy metals in field-grown maize after application of rare earth-containing fertilizer. Sci. Total Environ. 293, 97–105. doi: 10.1016/S0048-9697(01)01150-0
Yin, J., Jiang, B., Sun, T., and Sun, H. (1987). Determination of heats of coordination for rare-earth ions with aminopolycarboxylate ligands. Wuji Huaxue Xuebao 3, 69–77.
Zakrzewski, A., and Geisler, J. (1984). Stałe trwałości kompleksów Ca i Sm z niektórymi fosfonowymi pochodnymi DTPA. Chemia Analityczna 29, 631–634.
Zhang, H., He, X., Bai, W., Guo, X., Zhang, Z., Chai, Z., et al. (2010). Ecotoxicological assessment of lanthanum with Caenorhabditis elegans in liquid medium. Metallomics 2, 806–810. doi: 10.1039/c0mt00059k
Zhang, S., and Shan, X. (2001). Speciation of rare earth elements in soil and accumulation by wheat with rare earth fertilizer application. Environ. Pollut. 112, 395–405. doi: 10.1016/S0269-7491(00)00143-3
Keywords: gadolinium, DTPA, MRI contrast agent, stability constant, side-reaction coefficient, seawater, magnesium, calcium
Citation: Schijf J and Christy IJ (2018) Effect of Mg and Ca on the Stability of the MRI Contrast Agent Gd–DTPA in Seawater. Front. Mar. Sci. 5:111. doi: 10.3389/fmars.2018.00111
Received: 07 December 2017; Accepted: 15 March 2018;
Published: 10 April 2018.
Edited by:
Antonio Tovar-Sanchez, Consejo Superior de Investigaciones Científicas (CSIC), SpainReviewed by:
Miguel Caetano, Portuguese Sea and Atmosphere Institute, PortugalVanessa Hatje, Universidade Federal da Bahia, Brazil
Copyright © 2018 Schijf and Christy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Johan Schijf, c2NoaWpmQHVtY2VzLmVkdQ==
 Johan Schijf
Johan Schijf Isabel J. Christy
Isabel J. Christy