Metrology of pH Measurements in Brackish Waters—Part 2: Experimental Characterization of Purified meta-Cresol Purple for Spectrophotometric pHT Measurements

Introduction

pH is a master variable of seawater analysis. It allows the tracking of numerous biogeochemical processes, including organic matter production and mineralization, and is the most direct measure for ocean acidification (Byrne et al., 2010; Byrne, 2014). Several methods have been developed to determine pH, ranging from glass electrodes (Easley and Byrne, 2012), to ISFET sensors (Martz et al., 2010) and to pH optodes (Clarke et al., 2015). However, spectrophotometric pH measurements have proven to be the most precise and accurate method and are often considered to be a reference method (Liu et al., 2011; Byrne, 2014). Müller et al. (2018a) recently demonstrated that the method works reliably in the presence of high concentrations of dissolved organic matter and hydrogen sulfide and therefore supports full CO₂ system characterizations even under challenging conditions typical for brackish waters.

Spectrophotometric pH measurements rely on the addition of pH-sensitive indicator dyes, like m-Cresol Purple (mCP), to a water sample. The dye changes its color with sample pH. Those color changes are reflected in the absorbance spectra of the dye as changes in the peak absorbance ratio R, which depends on physico-chemical properties of the dye molecule (Clayton and Byrne, 1993; Liu et al., 2011). The accurate determination of acid-base equilibria in seawater—including the speciation of the CO₂ system—and the determination of long-term acidification trends require knowledge of the dye's dissociation constant and absorbance behavior. In order to ensure comparability of pH measurement results, the determination of the dissociation constant should be traceable to a fully characterized primary pH standard, e.g., by Harned cell measurements (Buck et al., 2002; Dickson et al., 2016).

In previous studies, reliable determinations of the dissociation and absorption behavior of mCP have been established in the salinity range 20–40 (Liu et al., 2011) and for river water conditions (Lai et al., 2016, 2017). The characterization experiments involved measurements of buffer solutions with pH assigned by Harned cell measurements (e.g., DelValls and Dickson, 1998) to determine the dissociation constant. Such buffer solutions were previously not available for salinities between 0 and 20. Mosley et al. (2004) provided an interim solution for this brackish water gap and characterized mCP for the full salinity range. However, the uncertainty of this characterization remained large, mainly due to (i) the interpolation of unknown TRIS buffer pH values between salinity 5 and 20, (ii) the lack of seawater salts in the salinity range 0.06–2, and (iii) the use of non-purified mCP. Further, the characterization was restricted to 298.15 K. Douglas and Byrne (2017b) combined the previous characterizations of purified mCP (Liu et al., 2011; Lai et al., 2016, 2017) with the results of Mosley et al. (2004) and modeled mCP properties over the full salinity and temperature range after correcting for dye impurities (Douglas and Byrne, 2017a). Nevertheless, a direct experimental characterization of purified mCP in brackish waters traceable to a primary pH standard was still missing, making it impossible to quantify the accuracy of spectrophotometric pH measurements in brackish waters. Uncertainties remained especially large at temperatures different from 298.15 K, due to the absence of experimental data.

To overcome these limitations, a concerted series of experiments was performed, which included two work packages:

1. Prior to the experiments presented here, Harned cell measurements of TRIS buffered artificial seawater (ASW) solutions were preformed to determine pH values on the total scale (pH_T) at salinities ranging from 5 to 20, temperatures from 278.15 to 318.15 K and equimolal TRIS/TRIS·H⁺ molalities of 0.01, 0.025, and 0.04 mol·kg-H₂O⁻¹ (Müller et al., 2018b).

2. Here we present the experimental determination of the mCP dissociation behavior in brackish waters based on spectrophotometric measurements performed with the newly available TRIS buffers.

The obtained characterization of mCP in the salinity range 5–20 was combined with previous results at higher and lower salinity, to derive a model for the dissociation behavior covering the full salinity and temperature range. This model was evaluated in comparison to previous characterizations, with special emphasizes to remaining uncertainties for spectrophotometric pH measurements at very low ionic strength.

Materials and Methods

Theory

The basic principles of spectrophotometric pH measurements have been described extensively before (Clayton and Byrne, 1993; Mosley et al., 2004; Liu et al., 2011). In brief, the measurements are based on the addition of a pH-sensitive indicator dye to a water sample. The second dissociation constant, pK₂, of the diprotic dye mCP lies in the pH range typical for seawater. In this case, the solution pH can be expressed as:

$\begin{array}{ll}pH=p{K}_2+{log}_{10}\left(\frac{\left[I^{2-}\right]}{\left[H{I}^{-}\right]}\right)& (1)\end{array}$

where [HI⁻] and [I²⁻] are the concentrations of the monoprotonated and deprotonated species of the indicator dye, respectively. The concentration ratio [HI⁻]/[I²⁻] can be determined by absorbance (A) measurements, because HI⁻ and I²⁻ have two clearly distinguishable absorbance maxima (Figure 1) at wavelength λ₁ = 434 nm and λ₂ = 578 nm, respectively (Clayton and Byrne, 1993). However, the absorbance spectra of both indicator species overlap. Therefore, at both wavelength λ₁ and λ₂ the absorbance A_λ needs to be expressed by the Lambert-Beer-law describing the additive absorbance contribution, $A_{\lambda }(I^{2-})+A_{\lambda }(H{I}^{-})$, of both species as:

$\begin{array}{ll}{A}_{\lambda }=({\epsilon }_{\lambda }(H{I}^{-})·\left[H{I}^{-}\right]+{\epsilon }_{\lambda }(I^{2-})·[I^{2-}])·d& (2)\end{array}$

where ε_λ(X) are the molar extinction coefficients of the indicator species X at wavelength λ, and d is the cuvette length.

FIGURE 1

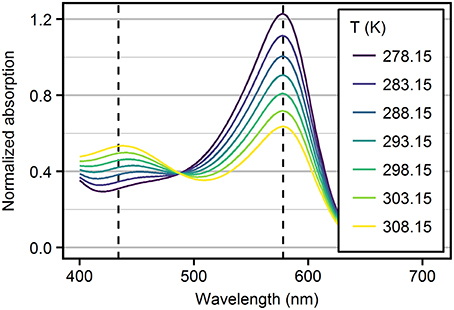
Figure 1. Absorbance spectra of mCP recorded in TRIS ASW solutions (S = 10, $b_{\text{TRIS}/\text{TRIS}·{\text{H}}^{+}}$ = 0.04 mol·kg-H₂O⁻¹) as a function of temperature. Spectra are normalized to the absorption at the isosbestic wavelength at 488 nm. Dashed lines mark the wavelengths of HI⁻ and I²⁻ peak absorbances.

After combining Equations (1) and (2), and with algebraic manipulation, the pH of the solution can be expressed as:

$\begin{array}{ll}pH=p{K}_2+{log}_{10}\left(\frac{R-e_1}{e_2-e_3·R}\right)& (3)\end{array}$

where R = A₅₇₈/A₄₃₄ is the ratio of the absorbance measured at the two peak wavelengths (dashed lines in Figure 1) and e₁ = ε₅₇₈(HI⁻)/ε₄₃₄(HI⁻), e₂ = ε₅₇₈(I²⁻)/ε₄₃₄(HI⁻) and e₃ = ε₄₃₄(I²⁻)/ε₄₃₄(HI⁻) are the molar absorptivity ratios (Clayton and Byrne, 1993; Mosley et al., 2004).

The molar absorptivity ratios e₂ and e₃ include molar extinction coefficients of both mCP species, HI⁻ and I²⁻. Therefore, the separate determination of e₂ and e₃ would require the combination of measurements obtained in high and low pH solutions. Liu et al. (2011) avoided this by rearranging Equation (3) to:

$\begin{array}{ll}pH=p{K}_2{e}_2+{log}_{10}\left(\frac{R-e_1}{1-\frac{e_3}{e_2}·R}\right)& (4)\end{array}$

The salinity and temperature dependence of the term pK₂e₂ can be determined from measurements in buffer solutions with a known pH, provided that e₁ and e₃/e₂ are known. Determined pK₂e₂ values refer to the same pH scale that was assigned to the pH buffer solutions. Currently, the total pH scale (pH_T) is a widely accepted standard in oceanography. According to its definition, $p{H}_T=-lo{g}_{10}\left\{\left[H^{+}\right]·(1+{\left[S{O}_4^{-}\right]}_T/K_{{\text{HSO}}_{\text{4}}^{-}})\right\}$, it accounts for the concentrations of both, the free hydrogen ions, [H⁺], and hydrogen sulfate ions, expressed as the total sulfate concentration ${\left[S{O}_4^{-}\right]}_T$ divided by the dissociation constant of hydrogen sulfate $K_{{\text{HSO}}_4^{-}}$ (Müller et al., 2018b). Previously, the required seawater buffer solutions with pH values assigned on the total scale were only available at salinities ≥ 20 (DelValls and Dickson, 1998).

Buffer Solutions

TRIS buffered ASW solutions were prepared at salinities 5, 10, 15, 20, and at 35 for consistency assessments with previous results, according to Müller et al. (2018b). At each salinity, three buffer solutions contained equimolal TRIS/TRISH⁺ molalities ($b_{\text{TRIS}/\text{TRIS}·{\text{H}}^{+}}$) of 0.01, 0.025, 0.04 mol·kg-H₂O⁻¹. This allows the impact of the solution composition on the pH_T of the buffers and on the dissociation behavior of the dye to be corrected by extrapolation of the determined pK₂e₂ values to zero TRIS/TRISH⁺ molality. The preparation and bottling of the buffer solutions was performed by the national metrological institute of Germany, Physikalisch-Technische Bundesanstalt (PTB), in parallel (same lab, day, stock solutions, and person, but separate weighings) to the preparation of identical buffer solutions for Harned cell pH_T measurements (Müller et al., 2018b). Solutions prepared at PTB were stored in 500 mL glass bottles (Schott DURAN, GL 45 polypropylene screw caps). The headspace was filled with humidified Argon gas (Argon 5.0, 99.999% purity, Linde AG, Pullach, Germany) in order to avoid CO₂ uptake from the atmosphere. Solutions were shipped to the Leibniz Institute for Baltic Sea Research in Warnemünde (IOW) for spectrophotometric measurements. The headspace was refilled with humidified Argon whenever bottles were opened to take subsamples.

Spectrophotometric Measurements

In the buffer solutions described above, absorbance spectra of mCP were recorded at seven temperatures from 278.15 to 308.15 K in intervals of 5 K. Measurements were performed with an instrument set-up as described by Carter et al. (2013). The system consisted of an Agilent 8453 diode array spectrophotometer (Santa Clara, US) and a cylindrical, jacketed, flow-through cuvette (path length 100 mm, inner diameter 5 mm, custom made by Hellma Analytics, Müllheim, Germany). The mantle of the cuvette was permanently flushed with water from a Julabo F30 heating circulator (Seelbach, Germany). Temperature was measured with a Pt resistance thermometer (Burster Kelvimat 4306 equipped with needle probe 42905, Gernsbach, Germany) calibrated at IOW's calibration lab with an uncertainty of 0.02 K. The needle probe was inserted in the water stream just behind the cuvette. Measured temperatures were within ±0.05 K of the target values. Before analysis, buffer solutions were brought to within 1 K of the analysis temperature in a separate temperature bath. The cuvette was filled and emptied with a computer-controlled syringe pump. The Agilent 8453 spectrometer was operated with both the tungsten- and the deuterium lamp switched on. More details on the measurement procedure are given in Carter et al. (2013).

All measurements were performed with purified mCP (Liu et al., 2011) kindly provided by the lab of Robert H. Byrne, Univ. of South Florida. A 2 mM stock solution of the dye was prepared by dissolving 0.08 g mCP in 100 mL deionized water. For better dissolution and pH adjustment, the stock solution was sonicated and 3.25 mL of 0.1 M NaOH were added to achieve a pH of around 8.

Spectrometers are known to behave non-linearly at high and low absorbances. For mCP absorbance spectra, this is critical for the strong absorbance of I²⁻ at 578 nm (Figure 1), especially at high pH in cold TRIS buffer solutions. To avoid non-linear behavior, absorbances at 578 nm were limited to values around 1 by adjusting the added amount of mCP. However, this may result in low absorbance at 434 nm. The most critical conditions were encountered at salinity 35 and 278.15 K with an absorbance ratio around 5 (Figure S1).

The spectrometer performance was verified by running the self-test of the instrument (deuterium lines test for wavelength accuracy and reproducibility; as well as noise-, baseline flatness-, and stability tests). Wavelength accuracy was further verified by measurements of Holmium oxide standards (Certified Reference Materials, Type 667-UV5, Holmium Liquid Filter; Hellma Analytics, Mühlheim, Germany). Furthermore, spectrophotometric comparison measurements were performed under conditions with well-defined solution pH and dye characteristics. This refers to measurements at 298.15 K of TRIS buffer solutions (batch T27 and T30) provided by the lab of Andrew G. Dickson (Univ. of California). Further, measurements performed on own TRIS buffer solutions at salinity 20 and 35 were compared with previous results of Liu et al. (2011), that were obtained in identical experiments, at temperatures from 278.15 to 303.15 K.

Determination of pK₂e₂

pH_T values of TRIS buffer solutions used in this study to calculate pK₂e₂ were assigned by Harned cell measurement (Table S1) according to Müller et al. (2018b). The determination of pK₂e₂ from known pH_T values and corresponding R ratios was obtained from Equation (4) written in the following form:

$\begin{array}{ll}p{K}_2{e}_2=p{H}_T-{log}_{10}\left(\frac{R-e_1}{1-\frac{e_3}{e_2}·R}\right)& (5)\end{array}$

Equation (5) requires knowledge of the absorptivity ratios e₁ and e₂/e₃. As proposed by Douglas and Byrne (2017b), the absorptivity ratios by Liu et al. (2011) according to Equations (6) and (7):

$\begin{array}{ll}{e}_1=-0.007762+4.5174·{10}^{-5}·T& (6)\end{array}$

$\begin{array}{ll}\frac{e_3}{e_2}=-0.020813+2.60262·{10}^{-4}·T+1.0436·{10}^{-4}·(S-35)& (7)\end{array}$

were applied for the salinity range 5–20, although originally determined for salinities >20. Deviations between the salinity-dependent e₂/e₃ of Liu et al. (2011) extrapolated to S = 0, and e₂/e₃ determined by Lai et al. (2016) for freshwater conditions are presumably related to differences in the determination procedure. Only Liu et al. (2011) applied an iterative process to derive e₃/e₂ values that account for all absorbing species in solution, (R.H. Byrne, pers. comm.).

pK₂e₂ values were determined from measured R and pH_T data for all buffer solutions as described above. At each combination of salinity and temperature, the change of pK₂e₂ with TRIS/TRISH⁺ molality was determined by linear regression analysis. The determined slope was used to correct individual pK₂e₂ values to zero TRIS/TRIS·H⁺ molality (Figure S2).

Fitting a pK₂e₂ Model to a Combined Data Set Including Previously Published Results

pK₂e₂ results determined in this study at salinities 5–20 were combined with previously published results to derive a complete characterization of mCP from ocean to river water. In order to include the measurement uncertainty of previous work, we calculated pK₂e₂ values from individual data rather than fitted equations given in the respective publications. The following data were included:

• For salinities 20, 30, 35, and 40 and temperatures from 278.15 to 308.15 K, pK₂e₂ values were calculated from Table S4 in the supporting information of Liu et al. (2011).

• For salinities between 0.06 and 4.03 and 298.15 K, impurity-corrected results based on Mosley et al. (2004) were taken from Table 1 in Douglas and Byrne (2017b). An offset of +0.0065 pH units was observed at S = 5 between the results of Douglas and Byrne (2017b) and this study. This offset was added to all pK₂e₂ values at salinities from 0.06 to 4.03. This correction is smaller than the uncertainty in the data (see discussion) and allows for a pK₂e₂ fit without a discontinuity.

• For salinity 0 and temperatures from 281.2 to 303.2 K, pK₂e₂ was calculated from the measured dissociation constant at infinite dilution, ${\mathrm{pK}}_I^0$ (C. Lai and M. DeGrandpre, pers. comm.), and e₂ (Table 2 in Lai et al., 2016) as ${\mathrm{pK}}_I^0$ – log₁₀(e₂).

The following full model, expressing pK₂e₂ as a function (f) of S, T, was fitted to the combined data set:

$\begin{array}{l}p{K}_2{e}_2=f\{\left(1+S^{0.5}+S+S^{1.5}+S^2+S^{2.5}\right)·\\ \left(1+T+ln\left(T\right)+\frac{1}{T}\right)\}& (8)\end{array}$

Equation (8) includes 24 terms representing all combinations of the terms of a fifth order S^0.5 polynomial and the terms of the physico-chemical expression of the temperature dependence of dissociation constants. The salinity polynomial in Equation (8) is identical to that fitted by Douglas and Byrne (2017b). Expressions with identical temperature dependence were previously fitted to pK₂e₂ results (Liu et al., 2011) and TRIS buffer pH_T data (DelValls and Dickson, 1998).

The fit was obtained by generalized linear modeling with the “stats” package of the statistical programming language “R” (R Core Team, 2014). After fitting the full model (Equation 8), insignificant terms were removed by stepwise variable selection in both directions based on the Akaike information criterion. The removal of terms was performed with the “stepAIC” function from the R package “MASS” and resulted in a pK₂e₂ model with 19 terms (Equation 9).

Results

Extrapolation of pK₂e₂ to Zero Buffer Concentration

At each combination of temperature and salinity, pK₂e₂ was determined at three different TRIS/TRISH⁺ molalities, 0.01, 0.025, and 0.04 mol·kg-H₂O⁻¹. The pK₂e₂ values were extrapolated linearly to zero TRIS/TRISH⁺ molality (Figure S2). The mean slope of this extrapolation ranged from 0.3 to −0.07 mol⁻¹·kg-H₂O at salinities 5 and 35, respectively. For a TRIS/TRISH⁺ molality of 0.04 mol·kg-H₂O⁻¹, this slope corresponds to a mean pK₂e₂ correction ranging from 0.012 to −0.003 at salinities 5 and 35, respectively (Figure S3). The standard deviation of the residuals from the linear extrapolation fit was <0.001 for all combinations of temperature and salinity. The pK₂e₂ value determined at S = 20 and a TRIS/TRISH⁺ molality of 0.025 mol·kg-H₂O⁻¹ deviated from the value interpolated between the results at TRIS/TRISH⁺ molalities of 0.01 and 0.04 mol·kg-H₂O⁻¹ by more than three times the standard deviation of all measurements, and was removed for further analysis without knowing the source of error.

pK₂e₂ Results and Model

The extrapolated pK₂e₂ values of mCP determined in this study at S = 20 and T = 308.15 K and at S = 5 and 278.15 K ranged from 7.57 to 8.08 (Figure 2A). The salinity-dependence of pK₂e₂ increases toward lower salinity. The dependence on temperature is almost linear at constant salinity. The pK₂e₂ model fitted to the combined data set, including results from this study and from that of Douglas and Byrne (2017b), Lai et al. (2016, 2017), and Liu et al. (2011) is given in Equation (9) with respective coefficients given in Table 1.

$\begin{array}{l}p{K}_2{e}_2={\mathrm{\text{a}}}_0+a_1·S^{0.5}+a_2·S^{1.5}+a_3·S^2+a_4·S^{2.5}\\ +b_1·{\mathrm{\text{T}}}^{-1}+b_2·S^{1.5}·{\mathrm{\text{T}}}^{-1}+b_3·S^2·{\mathrm{\text{T}}}^{-1}\\ +b_4·S^{2.5}·{\mathrm{\text{T}}}^{-1}\\ +c_1·ln(\mathrm{\text{T}})+c_2·S^{1.5}·ln(\mathrm{\text{T}})+c_3·S^2·ln(\mathrm{\text{T}})\\ +c_4·S^{2.5}·ln(\mathrm{\text{T}})\\ +d_1·T+d_2·S^{0.5}·T+d_3·S·T+d_4·S^{1.5}·T\\ +d_5·S^2·T+d_6·S^{2.5}·T& (9)\end{array}$

Residuals from the fitted pK₂e₂ model (Figure 2B) are within ±0.005 for the entire salinity and temperature range.

FIGURE 2

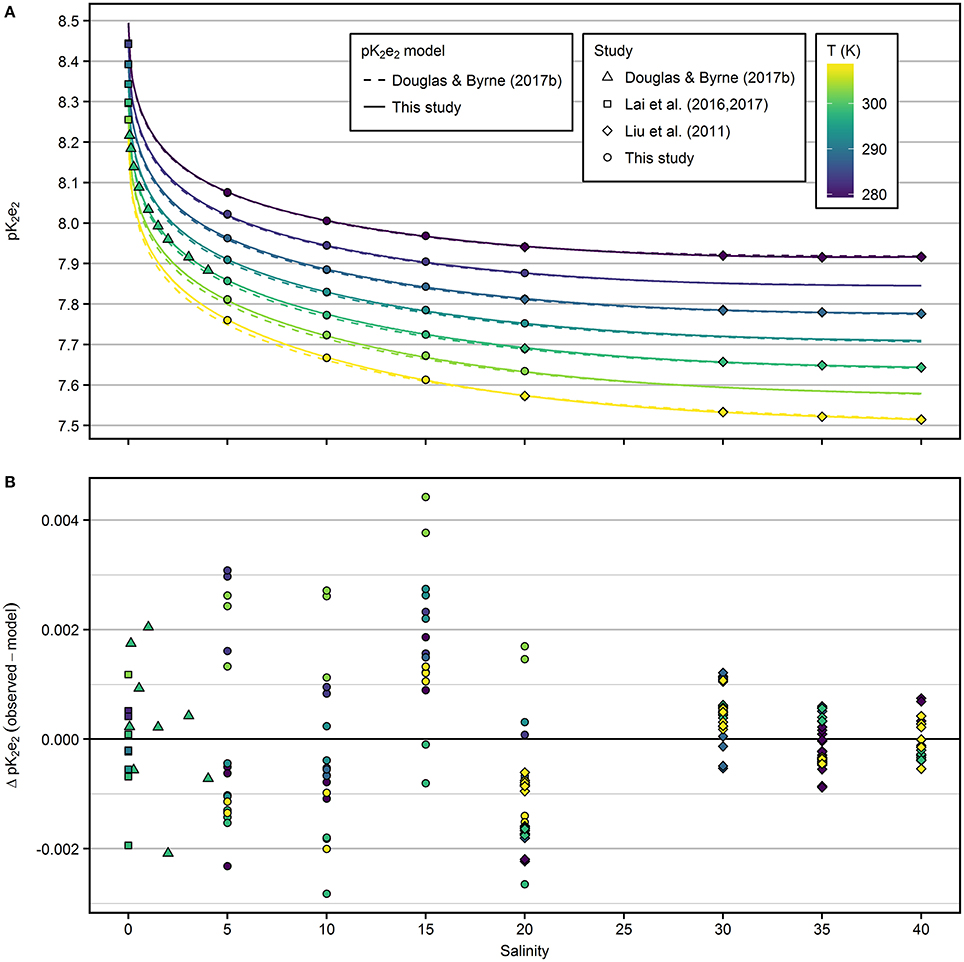
Figure 2. (A) pK₂e₂ of mCP as a function of salinity and temperature. Results from this study (salinity range 5–20) were combined with previous results and fitted to a common pK₂e₂ model (solid lines). Dashed lines represent the pK₂e₂ model by Douglas and Byrne (2017b). (B) Residuals from the model fitted in this study.

TABLE 1

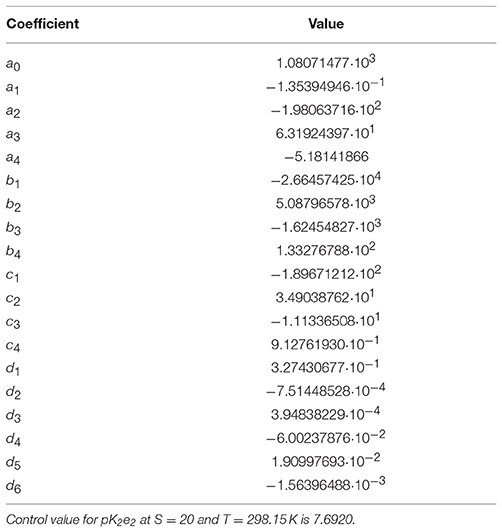
Table 1. Coefficients of equation 9 fitted to the combined data set displayed in Figure 2A.

Agreement With Previous Studies

In the salinity range 5–20, the pK₂e₂ model of Douglas and Byrne (2017b) agrees with the new model presented in this study within 0.008 at 298.15 K (Figure S4). At salinity 20, deviations are within 0.004. At salinity 5 and 308.15 K, the largest offset between both models was observed with 0.013 higher pK₂e₂ values predicted by the model fitted in this study.

In the salinity range 20–40, the pK₂e₂ model of Liu et al. (2011) agrees with the model presented in this study within 0.002 across all temperatures (Figure S4). At freshwater conditions, pK₂e₂ calculated according to Lai et al. (2017) agrees with the model presented in this study within 0.006 across all temperatures (Figure S4).

The residuals from the model (Figure 2B) are larger at salinities ≤20, compared to the residuals at salinities >20. However, the precision achieved within each group of salinity, temperature and TRIS/TRISH⁺ is <0.001 and comparable for the results of this study and those of Liu et al. (2011). The higher residuals at lower salinities reflect the uncertainty in the pH_T determination by Harned cell measurements (compare residuals in Figure 5 of Müller et al., 2018a), which was not included in previous studies when pH_T values of buffer solutions were calculated from fitted models.

For a direct comparison to previous results, spectrophotometric pH_T values calculated according to Liu et al. (2011) were determined in TRIS buffer solutions (batch T27 and T30) purchased from the laboratory of Andrew G. Dickson (Scripps Institution of Oceanography). Results were highly reproducible and consistently 0.005–0.006 pH units lower than TRIS pH_T values calculated according to DelValls and Dickson (1998) at 298.15 K. For own TRIS buffer solutions at salinity 20 and 35, spectrophotometric pH_T values calculated according to Liu et al. (2011) were 0.002 to 0.008 pH units lower than pH_T values determined by Harned cell measurements over the temperature range from 278.15 to 308.15 K.

Discussion

Advantages of a Coordinated Experimental Concept

The experiments presented here were part of a coordinated measurement program covering the preparation of TRIS buffered ASW solutions, pH_T determination by Harned cell measurements and subsequent recording of mCP absorption spectra. This reduces uncertainties included in all previous experiments, in which the required analysis of the buffer solutions (e.g., DelValls and Dickson, 1998) and subsequent mCP characterizations (e.g., Liu et al., 2011) were performed in separate experiments. Nemzer and Dickson (2005) found TRIS buffer pH to vary by up to 0.0034, even when carefully prepared in the same laboratory, and argued that an error of only 0.23% in the TRIS/TRISH⁺ ratio will result in an error of 0.001 in pH. Müller et al. (2018b) and this study reduced this uncertainty by titrating the TRIS- against the HCl-stock solution and subsequently preparing all buffers from the same stock solution. Further, in this study we determined pK₂e₂ based on pH_T values individually assigned by Harned cell measurements to the same batch of buffer solution, whereas previous studies had to rely on pH_T values calculated from fitted models.

Correcting the Contribution of TRIS and HCl to the Ionic Composition of the Buffer Solutions

The ionic composition of buffered ASW solutions differs from that of pure ASW solutions, due to the replacement of seawater salts by TRIS and HCl at a given ionic strength. The relative contribution of the buffer components increases toward lower salinity. This can only to a certain degree be circumvented by lower buffer concentrations, because solutions with lower buffer concentrations are less stable and reproducible. The inevitable difference in solution composition has two effects: (i) The pH_T of the buffer solution changes with the concentration of the buffer and assigned pH_T values do not exactly correspond to the total hydrogen ion concentration scale (see discussion in Nemzer and Dickson, 2005; Dickson et al., 2016; Müller et al., 2018b). (ii) The difference in solution composition affects the pK₂e₂ of mCP. However, both effects (i) and (ii) are corrected when calibration results are extrapolated to zero buffer concentration, as done in this study for the first time.

At salinity 35, we found the pK₂e₂ correction to be < 0.005 for a 0.04 mol·kg-H₂O⁻¹ TRIS/TRISH⁺ molality. Although this effect might be small in comparison to other sources of uncertainty, similar extrapolation experiments as performed in this study are required to accurately determine pH_T at salinities 20–40. More pronounced pK₂e₂ corrections needed to be applied at lower salinity and amounted to as much as 0.02 for a TRIS/TRISH⁺ molality of 0.04 mol·kg⁻¹ at 308.15 K (Figure S3).

Performing the required extrapolation, this study presents the first attempt to determine pK₂e₂ values that allow measurements of pH on a true total hydrogen ion concentration scale referring to the reference ASW composition in the salinity range 5–20. In contrast, the mCP characterization by Mosley et al. (2004) did not account for the ionic strength contribution of TRIS/TRISH⁺, despite covering salinities as low as 0.06. Furthermore, at salinities below 2, TRIS/TRISH⁺ represented the only contribution to ionic strength in the experiments performed by Mosley et al. (2004) but was still interpreted in terms of salinity, based on the results of Bates and Hetzer (1961). In view of these uncertainties, our pK₂e₂ model is strictly valid only for salinities as low as 5 and the reported ASW solutions composition. For salinities below 5, the pK₂e₂ models reported in this study and that of Douglas and Byrne (2017b) are associated with similar uncertainties, going back to the limitations in the study of Mosley et al. (2004).

Spectrophotometric pH Measurements at Very Low Ionic Strength

Similar to the pK₂e₂ extrapolation performed in this study, Lai et al. (2016) determined changes of the dissociation constant of mCP of ~0.02 when decreasing the phosphate buffer concentration by only ~0.005 mol·kg⁻¹ under freshwater conditions. This highlights the potential sensitivity of the dissociation behavior of mCP on the ionic composition of the sample at low ionic strength. It remains to be studied, whether the dissociation behavior of mCP is controlled only by the ionic strength of the solution or whether the ionic composition plays a significant role. If the latter is the case, it would be questionable, whether an accuracy in the order of a few thousands of pH units can ever be achieved at very low ionic strength, without knowing the ionic composition of the sample. This is a consequence of the more general problem to determine salinity from conductivity measurements in low-saline water with variable composition (Feistel et al., 2009; Wright et al., 2011). Lai et al. (2016) started to address this issue by comparing spectrophotometric pH measurements with two different indicator dyes, phenol red and mCP, on seven different freshwater samples. They found pH results that agreed within ±0.01. Those results indicate same ionic interactions of both dyes, i.e., similar activity coefficients in similar media, but do not allow for an independent assessment of the accuracy of the results. Potential approaches to improve the understanding of mCP behavior in very low-saline and river water conditions include: (i) traceable characterization experiments at variable buffer concentrations and ionic composition of the salt matrix, and (ii) estimation of the effects of solution composition changes on the dyes dissociation behavior with Pitzer models (Turner et al., 2016).

Observed offsets in pH_T Comparison Measurements

Performing comparison measurements with TRIS buffers provided by Dickson's laboratory, our pH_T values calculated according to Liu et al. (2011) were consistently lower by 0.005 at 298.15 K. Over the full temperature range, pH_T values determined in own TRIS buffer solutions were 0.002 to 0.008 lower. Similar offsets were reported by Carter et al. (2013), but the reason for this offset could not be determined. Obviously, lower determined pH_T values result from a lower R-ratio in Equation (4). Vice versa, lower R-ratios applied in Equation (5) lead to slightly higher pK₂e₂ values. In accordance with the comparison measurement, we determined slightly higher pK₂e₂ values compared to previous results (Liu et al., 2011) at finite buffer concentration. Interestingly, our extrapolation to zero TRIS/TRISH⁺ molality compensates for this offset to the results of Liu et al. (2011) at salinity 20 (Figure 2). In contrast, at salinity 35 the correction has an opposite sign and observed pH_T differences do not cancel out. Due to the scarce amount of data at salinities >20 obtained in this study, we included only the results by Liu et al. (2011) into our combined data set.

Model Evaluation and Recommendation

The pK₂e₂ model by Douglas and Byrne (2017b) agrees surprisingly well with the results presented in this study, although previous experimental data in the salinity range 5–20, going back to the results of Mosley et al. (2004), were limited to 298.15 K and associated to several uncertainties. However, differences between both models (> 0.01) are larger than the measurement uncertainty of the method (Carter et al., 2013). In addition, the pK₂e₂ model presented in this study fits the results of Liu et al. (2011) almost as well as the original model (residuals within ± 0.002), and therefore better than the model of Douglas and Byrne (2017b), who found residuals > 0.003.

Therefore, we recommend to use the pK₂e₂ model presented in this study for all spectrophotometric pH measurements in brackish water that cover salinities below 20. Due to the excellent agreement with the results of Liu et al. (2011), the pK₂e₂ model presented in this study can also be applied for pH calculations at salinities >20 without constraints. However, the uncertainty of this model is as large as that of Douglas and Byrne (2017b) for salinities well below 5.

Conclusion

In this study, we provided the experimental basis to directly link spectrophotometric pH_T measurements in the salinity range 5–20 to Harned cell pH_T determinations of TRIS buffered artificial seawater solutions. We combined the derived pK₂e₂ estimates of mCP with the results from previous studies and fitted a pK₂e₂ model as a function of temperature and salinity to the combined data set. We recommend using the new pK₂e₂ model for all measurements in brackish waters that include samples with salinities below 20. Measurements under fully marine conditions can be performed without compromise compared to previous pK₂e₂ models. For S < 5, the model faces the same problems as in previous work, but is potentially better suited for pH measurements near 5. For near river water conditions, the impact of ionic composition on spectrophotometric pH determination remains to be studied to answer the question whether spectrophotometric measurements can produce accurate pH results without knowledge of the exact ionic composition of the sample.

Author Contributions

JM: Initiation and concept of the study, experimental work, data analysis and interpretation, manuscript preparation; GR: Coordinator of the research project BONUS PINBAL providing the framework for this work, involved in the outline of the manuscript and the interpretation of the data.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling Editor declared a past collaboration with the authors.

Acknowledgments

The quality of this paper gained from scientific discussions with Bernd Schneider.

The research leading to this manuscript has received funding from BONUS, the joint Baltic Sea research and development programme (Art 185), funded jointly from the European Union's Seventh Programme for research, technological development and demonstration and from the German Federal Ministry of Education and Research through Grant No. 03F0689A (BONUS PINBAL) and Grant No. 03F0773A (BONUS INTEGRAL).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2018.00177/full#supplementary-material

References

Bates, R. G., and Hetzer, H. B. (1961). Dissociation constant of the protonated acid form of 2-amino-2-(hydroxymethyl)- 1, 3-propanediol [tris- hydroxymethyl) -aminomethane] and related thermodynamic quantities from 0 to 50°. J. Phys. Chem. 65, 667–671. doi: 10.1021/j100822a017

CrossRef Full Text | Google Scholar

Buck, R. P., Rondinini, S., Covington, A. K., Baucke, F. G. K., Brett, C. M. A., Camoes, M. F., et al. (2002). Measurement of pH. Definition, standards, and procedures (IUPAC Recommendations 2002). Pure Appl. Chem. 74, 2169–2200. doi: 10.1351/pac200274112169

CrossRef Full Text | Google Scholar

Byrne, R. H. (2014). Measuring ocean acidification: new technology for a new era of ocean chemistry. Environ. Sci. Technol. 48, 5352–60. doi: 10.1021/es405819p

PubMed Abstract | CrossRef Full Text | Google Scholar

Byrne, R. H., Mecking, S., Feely, R. A., and Liu, X. (2010). Direct observations of basin-wide acidification of the North Pacific Ocean. Geophys. Res. Lett. 37:L02601. doi: 10.1029/2009GL040999

CrossRef Full Text | Google Scholar

Carter, B. R., Radich, J. A., Doyle, H. L., and Dickson, A. G. (2013). An automated system for spectrophotometric seawater pH measurements. Limnol. Oceanogr. Methods 11, 16–27. doi: 10.4319/lom.2013.11.16

CrossRef Full Text | Google Scholar

Clarke, J. S., Achterberg, E. P., Rérolle, V. M., Abi Kaed Bey, S., Floquet, C. F. A., and Mowlem, M. C. (2015). Characterisation and deployment of an immobilised pH sensor spot towards surface ocean pH measurements. Anal. Chim. Acta 897, 69–80. doi: 10.1016/j.aca.2015.09.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Clayton, T. D., and Byrne, R. H. (1993). Spectrophotometric seawater pH measurements : total hydrogen results. Deep Sea Res. Part I Oceanogr. Res. Pap. 40, 2115–2129. doi: 10.1016/0967-0637(93)90048-8

CrossRef Full Text | Google Scholar

DelValls, T. A., and Dickson, A. G. (1998). The pH of buffers based on 2-amino-2-hydroxymethyl-1,3-propanediol (“tris”) in synthetic sea water. Deep Sea Res. Part I Oceanogr. Res. Pap. 45, 1541–1554.

Google Scholar

Dickson, A. G., Camões, M. F., Spitzer, P., Fisicaro, P., Stoica, D., Pawlowicz, R., et al. (2016). Metrological challenges for measurements of key climatological observables. Part 3: seawater pH. Metrologia 53, R26–R39. doi: 10.1088/0026-1394/53/1/R26

CrossRef Full Text | Google Scholar

Douglas, N. K., and Byrne, R. H. (2017a). Achieving accurate spectrophotometric pH measurements using unpurified meta-cresol purple. Mar. Chem. 190, 66–72. doi: 10.1016/j.marchem.2017.02.004

CrossRef Full Text | Google Scholar

Douglas, N. K., and Byrne, R. H. (2017b). Spectrophotometric pH measurements from river to sea: calibration of mCP for 0 ≤ S ≤ 40 and 278.15 ≤ T ≤ 308.15 K. Mar. Chem. 197, 64–69. doi: 10.1016/j.marchem.2017.10.001

CrossRef Full Text | Google Scholar

Easley, R. A., and Byrne, R. H. (2012). Spectrophotometric calibration of pH electrodes in seawater using purified m-cresol purple. Environ. Sci. Technol. 46, 5018–5024. doi: 10.1021/es300491s

PubMed Abstract | CrossRef Full Text | Google Scholar

Feistel, R., Weinreben, S., Wolf, H., Seitz, S., Spitzer, P., Adel, B., et al. (2009). Density and Absolute Salinity of the Baltic Sea 2006–2009. Ocean Sci. 6, 3–24. doi: 10.5194/os-6-3-2010

CrossRef Full Text | Google Scholar

Lai, C., DeGrandpre, M. D., Wasser, B. D., Brandon, T. A., Clucas, D. S., Jaqueth, E. J., et al. (2016). Spectrophotometric measurement of freshwater pH with purified meta-cresol purple and phenol red. Limnol. Oceanogr. Methods 14, 864–873. doi: 10.1002/lom3.10137

CrossRef Full Text | Google Scholar

Lai, C., DeGrandpre, M. D., Wasser, B. D., Brandon, T. A., Clucas, D. S., Jaqueth, E. J., et al. (2017). Corrigendum to: spectrophotometric measurement of freshwater pH with purified meta-cresol purple and phenol red: freshwater pH with purified indicators (Limnology and Oceanography: Methods, (2016), 14, 12, (864-873), 10.1002/lom3.10137). Limnol. Oceanogr. Methods 15:903. doi: 10.1002/lom3.10210

CrossRef Full Text

Liu, X., Patsavas, M. C., and Byrne, R. H. (2011). Purification and characterization of meta-cresol purple for spectrophotometric seawater pH measurements. Environ. Sci. Technol. 45, 4862–4868. doi: 10.1021/es200665d

PubMed Abstract | CrossRef Full Text | Google Scholar

Martz, T. R., Connery, J. G., and Johnson, K. S. (2010). Testing the Honeywell Durafet for seawater pH applications. Limnol. Oceanogr. Methods 8, 172–184. doi: 10.4319/lom.2010.8.172

CrossRef Full Text | Google Scholar

Mosley, L. M., Husheer, S. L. G., and Hunter, K. A. (2004). Spectrophotometric pH measurement in estuaries using thymol blue and m-cresol purple. Mar. Chem. 91, 175–186. doi: 10.1016/j.marchem.2004.06.008

CrossRef Full Text | Google Scholar

Müller, J. D., Bastkowski, F., Sander, B., Seitz, S., Turner, D. R., Dickson, A. G., et al. (2018b). Metrology for pH measurements in brackish waters–part 1: extending electrochemical pH_T measurements of TRIS buffers to salinities 5–20. Front. Mar. Sci. 5:176. doi: 10.3389/fmars.2018.00176

CrossRef Full Text | Google Scholar

Müller, J. D., Schneider, B., Aßmann, S., and Rehder, G. (2018a). Spectrophotometric pH measurements in the presence of dissolved organic matter and hydrogen sulfide. Limnol. Oceanogr. Methods 16, 68–82. doi: 10.1002/lom3.10227

CrossRef Full Text | Google Scholar

Nemzer, B. V., and Dickson, A. G. (2005). The stability and reproducibility of Tris buffers in synthetic seawater. Mar. Chem. 96, 237–242. doi: 10.1016/j.marchem.2005.01.004

CrossRef Full Text | Google Scholar

R Core Team (2014). R: A Language and Environment for Statistical Computing. Available online at: http://www.r-project.org/

Turner, D. R., Achterberg, E. P., Chen, C.-T. A., Clegg, S. L., Hatje, V., Maldonado, M. T., et al. (2016). Toward a quality-controlled and accessible pitzer model for seawater and related systems. Front. Mar. Sci. 3:139. doi: 10.3389/fmars.2016.00139

CrossRef Full Text | Google Scholar

Wright, D. G., Pawlowicz, R., McDougall, T. J., Feistel, R., and Marion, G. M. (2011). Absolute salinity, “density salinity” and the reference-composition salinity scale: present and future use in the seawater standard TEOS-10. Ocean Sci. 7, 1–26. doi: 10.5194/os-7-1-2011

CrossRef Full Text | Google Scholar