- 1School of Earth Sciences, University of Western Australia, Perth, WA, Australia
- 2UWA Oceans Institute, University of Western Australia, Perth, WA, Australia
- 3ARC Centre of Excellence for Coral Reef Studies, University of Western Australia, Perth, WA, Australia
- 4Unit of Marine and Coastal Systems, Deltares, Delft, Netherlands
- 5Oceans Graduate School, University of Western Australia, Perth, WA, Australia
- 6Department of Infrastructure Engineering, University of Melbourne, Melbourne, VIC, Australia
- 7Institute of Port, Coastal and Nearshore Engineering, Ocean College, Zhejiang University, Zhoushan, China
Canopies formed by aquatic vegetation, such as mangroves, seagrass, and kelp, play a crucial role in altering the local hydrodynamics in rivers, estuaries, and coastal regions, and thereby influence a range of morphodynamic and biophysical processes. Prediction of the influence of canopies on these hydrodynamic processes requires a fundamental understanding of canopy drag, which varies significantly with both flow conditions and canopy properties (such as density and submergence). Although our knowledge on canopy drag has increased significantly in recent decades, a conclusive, physics-based description for canopy drag that can be applied to both emergent and submerged canopies is currently lacking. Here, we extend a new theoretical canopy drag model (that employs the velocity between canopy elements as the reference velocity) to submerged aquatic canopies. The model is validated for the first time with direct measurements of drag forces exerted by canopies across broad ranges of flow conditions and canopy density and submergence. The skill and broader applicability of the model are further assessed using a comprehensive set of existing experimental data, covering a broad range of natural conditions (including flexible vegetation). The resulting model provides a simple tool to estimate canopy drag forces, which govern hydraulic resistance, sediment transport, and biophysical processes within aquatic ecosystems.
Introduction
It is widely recognized that aquatic vegetation, such as seagrass, reeds, kelp, and mangroves, greatly influences hydrodynamic processes within rivers, estuaries, and coastal regions (e.g., Nepf, 2012). The drag exerted by emergent and submerged vegetation impacts the local hydrodynamics, morphodynamics, and ecology over a range of spatial scales (Koch et al., 2007). The canopies formed by vegetation can affect the local flow environment at the smallest scale (i.e., the plant scale, mm to cm) to the larger-scale (>1 km) flows that occur across benthic ecosystems. Canopy drag forces contribute to reducing flow velocities within canopies (López and García, 2001) and enhancing local turbulence (Nepf and Vivoni, 2000). In areas with significant wave action, such as in coastal regions and large lakes, the rate of work done by canopy drag forces also results in wave energy attenuation (e.g., Fonseca and Cahalan, 1992). The flow reduction induced by canopy drag can, in turn, influence a number of morphodynamic and biophysical processes (Koch et al., 2007). For example, canopies can modify local bed shear stresses (James et al., 2004), thereby affecting sediment transport, deposition (Hendriks et al., 2008, 2010) and resuspension (Widdows et al., 2008). Similarly, canopy drag also indirectly influences other particle dynamics, affecting pollination (Ackerman, 1995), establishment of seedlings (Balke et al., 2013), and recruitment and settlement of larvae, spores, and fauna (Kenyon et al., 1999). The effect of the reduced in-canopy flow on the diffusive boundary layer around plant leaves (Koch et al., 2007) also governs nutrient uptake (Morris et al., 2008) and can influence the growth of epiphytes (Cornelisen and Thomas, 2002). Under strong flow conditions, the drag forces exerted on canopy elements can result in their physical removal from the seabed (Duarte, 2002; Edmaier et al., 2011). Globally, aquatic ecosystems are under increasing pressure from anthropogenic and climate change impacts (Duarte, 2002), and it is crucial we increase our understanding of canopy drag as it directly influences many important biophysical processes in aquatic environments.
To be able to quantify the influence of aquatic canopies on the local hydrodynamics, a comprehensive understanding of the mechanics governing canopy drag is required. Given the diversity of plant morphologies in natural environments, individual plants are often schematized as uniform, rigid cylinders to establish a general knowledge framework for the processes governing drag (see review by Vargas-Luna et al., 2016). The drag force per unit length of a cylinder in isolation is given by:
where ρ is the water density, dc is the cylinder diameter, Cd is the drag coefficient, and Uref is a reference flow velocity (which, in the case of an isolated cylinder, is equal to the upstream velocity). For reference, a Notation table specifying all variables is provided at the end of this manuscript. Predicting the drag coefficient for a cylinder in isolation is historically well-established, and it can be robustly predicted as:
(White, 1991), where the Reynolds number is defined as Re = Urefdc/ν, with ν is the kinematic viscosity. For real-world application, considering plants rather than cylinders, temporal fluctuations in the drag force (due to turbulence) and vertical variation of the drag are often of less interest than the mean drag force, which governs the range of biophysical processes described earlier. As the plant biomass and flow velocity may vary significantly over the height of the plant, the total mean drag force on the plant is usually defined as:
where the drag force is integrated over the vertical dimension (z) and averaged over time (denoted by the overbar), hv is the vegetation (cylinder) height (with z = 0 at the bed), and dv is the vegetation stem (cylinder) diameter.
In the case of a single plant, the upstream velocity is usually weakly vertically-varying over most of the water column and the depth-averaged velocity is an obvious choice for the reference velocity (Uref) needed to estimate the drag force in Equation (3). However, in the case of multiple plants forming a canopy, the flow throughout the canopy (and therefore the “upstream” velocity for each plant) is spatially non-uniform. It is thus unclear which actual velocity governs drag and could be used as the appropriate reference velocity. In emergent canopies (denoted hereafter with the superscript “em”), previous studies have chosen the reference velocity to be either: (1) the bulk velocity (i.e., , where Q is the flow discharge, W is the channel width and h is water depth) (e.g., Wu et al., 1999) or, more commonly, (2) the pore velocity (, where λp is the canopy density that is equivalent to the canopy element plan area per unit bed area) (e.g., Tanino and Nepf, 2008), representing the spatially-averaged velocity inside the fluid spaces within a canopy. However, through Large Eddy Simulation, Etminan et al. (2017) found that the “constricted cross-section velocity,” the average velocity in the constriction between adjacent canopy elements, is the velocity scale that actually governs wake pressure and thus canopy drag. The relationship between the pore velocity and the constricted cross-section velocity () is dependent on the arrangement of canopy elements, and is obtained through conservation of mass []. Here, Sv, l is the lateral spacing between adjacent elements at the same streamwise (x) location, and can only be strictly defined for regular arrays (such as linear or staggered arrangements). This relationship between the constricted cross-section velocity and the pore velocity can be written as a function of the canopy density:
(Stone and Shen, 2002; Etminan et al., 2017). In Equation (4), β represents the ratio between Sv, l and the distance between two rows of canopy elements in the streamwise direction (Sv, s). For random arrays, as can be found in nature, the constricted cross-section velocity can be computed from the bulk velocity:
where Nv is the total number of plants per unit area. Note that this will result in a canopy-average value of , and local values may vary significantly.
In the case of submerged canopies, the shear layer present at the top of the canopy results in strong vertical variations in the spatially-averaged flow, further complicating canopy drag predictions. In many cases, the reference velocity used to predict the drag in submerged canopies is based on the bulk velocity (, where the superscript “sub” refers to a velocity scale used for submerged canopies) (Wu et al., 1999; López and García, 2001). However, this approach does not account for the attenuation of flow within the canopy that will significantly influence canopy drag. An exception is the study of Liu and Zeng (2017) who proposed a more representative in-canopy flow velocity that accounts for vertical variation in the spatially-averaged flow. However, their approach did not account for the local (horizontal) spatial variation in the mean flow inside the canopy.
In emergent canopies, experimental measurements of drag coefficients have most commonly been obtained by measuring the surface slope and assuming a force balance of canopy drag and hydraulic gradient (Liu et al., 2008; Tanino and Nepf, 2008). The drag force of an individual plant within the canopy is then given by:
where g is the gravitational acceleration, and η is the (measured) water surface elevation. By combining Equations (3) and (6), the drag coefficient can be obtained when assuming a depth-uniform velocity profile. For emergent canopies, this is relatively straight-forward, although the choice of reference velocity may greatly affect the calculated Cd values (Etminan et al., 2017). A large range of empirical relations have been established to relate canopy drag coefficients to plant shape, the flow regime (i.e., Reynolds number) and canopy properties (e.g., density). The drag coefficient is generally found to decrease exponentially with increasing Reynolds number (e.g., Liu and Zeng, 2017), following a similar trend to the isolated cylinder case (Equation 2). In terms of canopy geometry, some studies have found that the drag coefficient decreases with increasing canopy density (e.g., Nepf, 1999), while many others obtained conflicting results (e.g., Wu et al., 1999; Tanino and Nepf, 2008; Wang et al., 2014). Relatively few studies have directly measured the forces on canopy elements using force sensors either mounted at the top (e.g., Kothyari et al., 2009) or at the base of a canopy element (e.g., Schoneboom et al., 2010).
Furthermore, the majority of studies have focused on emergent canopies, such that there are still significant knowledge gaps in predicting the drag of submerged canopies. This is largely due to the more complex vertical flow structure within submerged canopies. The in-canopy flow velocity is often significantly lower than the freestream velocity and, as for emergent canopies, horizontal variation in the flow field are expected to play a significant role in canopy drag. Even with accurate measurements of submerged canopy drag forces, it is still unclear how to predict the constricted cross-section velocity within a submerged canopy when velocity measurements are lacking. The main reason for this is that the in-canopy flow velocity is dependent on the drag itself (Lowe et al., 2005), so that Cd is a function of Uref, and vice versa.
This paper aims to reduce the uncertainty in canopy drag estimation through direct measurements of the drag force in aquatic vegetation canopies subject to unidirectional flow. The experimental program includes both emergent and submerged canopies with varying densities, and a range of hydrodynamic conditions covering a broad range of natural conditions that can be found in aquatic systems. In addition, a theoretical canopy drag model for emergent canopies is extended to submerged canopies and validated for the first time using direct force measurements, and then more broadly assessed using a compilation of data reported in previous studies.
Canopy Drag Model
For both emergent and submerged canopies, the mean drag force exerted on a single plant or canopy element is governed by Equation (3). For emergent canopies, the mean horizontal flow velocity is often assumed to be depth-uniform. For submerged canopies, the horizontal flow profile can be approximated as a two-layer flow with depth-uniform velocities both above and inside the canopy (e.g., Lowe et al., 2005; Liu et al., 2008) (see Figure 1 for a definition sketch and relevant velocity definitions).
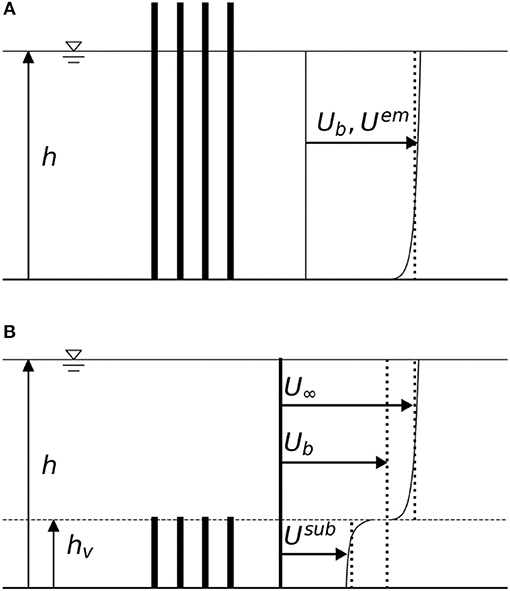
Figure 1. Open channel flows with (A) an emergent canopy and (B) a submerged canopy. In emergent canopies, the depth-averaged velocity () is often used as the representative in-canopy velocity scale (Uem). In submerged canopies, the depth-averaged velocity inside the canopy (Usub) is often substantially reduced from the above-canopy (free stream) velocity (U∞).
Emergent Canopies
For emergent canopies, Etminan et al. (2017) proposed to use the theory of drag for isolated cylinders (i.e., Equation 2) as the basis to compute the drag coefficients associated with emergent canopy. Their model employs the constricted cross-section velocity () as the reference velocity (Uref) to determine the drag coefficient through the Reynolds number (Equation 2) and to compute the drag force (Equation 3), and was validated through Large Eddy Simulation (Etminan et al., 2017).
Submerged Canopies
For a given in-canopy flow, one can hypothesize that an analogous method to emergent canopies can be applied to submerged canopies, i.e., the in-canopy constricted cross-section velocity () can be computed using Equation (4) or (5). However, as discussed in section Introduction, the estimation of is not straight-forward due to the vertical variation in the mean velocity profile (Figure 1); the magnitude of the in-canopy velocity both governs, and depends on, the canopy drag. Here, we propose to use a canopy flow model to predict the in-canopy pore velocity () based on the (undisturbed) above-canopy flow velocity (U∞). This model takes the form:
(Lowe et al., 2005). In Equation (7), Ld is the drag length scale, given by
(Lowe et al., 2005; Ghisalberti, 2009), and represents the flow resistance of the canopy. λf is the canopy element frontal area per unit bed area (= hvdvNv). Ls is the shear length scale, given by
(Lowe et al., 2005) (where Cf is a friction coefficient), which parameterizes the magnitude of the shear stress at the top of the canopy. This shear stress is generated by the velocity difference between the flow within and above the canopy. If velocity measurements are available, the friction coefficient can be estimated based on the peak in the Reynolds stress profile near the top of the canopy (z ≈ hv):
(Lowe et al., 2005), where is the friction velocity and u′ and w′ are the horizontal and vertical turbulent velocity fluctuations, respectively. Data from a wide range of canopies indicates that tends to be consistently O(0.1), which corresponds to Cf = O(0.01) (e.g., Harman and Finnigan, 2007; Lowe et al., 2008; Luhar et al., 2010; Moltchanov et al., 2011; Weitzman et al., 2015). Therefore, for a given canopy geometry and above-canopy flow velocity (U∞), the in-canopy pore velocity can be estimated from Equations (7–10). Subsequently, the constricted cross-section velocity inside a submerged canopy can be obtained through Equations (4) or (5), and is used as the reference velocity (Uref) to calculate the drag coefficient through the Reynolds number (Equation 2) and to compute the drag force (Equation 3).
In summary, the model that is proposed here relies on information on above-canopy flow velocity (U∞) or bulk velocity (for emergent canopies), the local water depth (h), and the canopy properties: height (hv), stem diameter (dv), and canopy density (λp, Nv). It includes one empirical parameter (namely, Cf) in the case of a submerged canopy. It is important to emphasize that given the drag coefficient Cd is also needed in Equation (8) to predict the in-canopy flow (hence the drag forces and in-canopy flow are inherently coupled), for submerged canopies the model involves an iterative process. A flow diagram summarizing the model is provided in Figure 2. In the following sections, the model is validated using newly obtained velocity and drag force data, as well as a large dataset covering a broad range in canopy geometries and flow conditions obtained from literature.
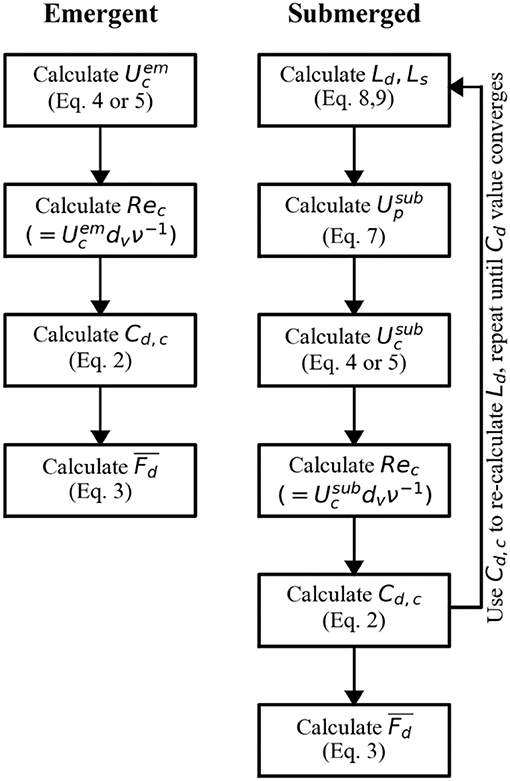
Figure 2. Flow diagram for the canopy drag model. The model can be used to estimate the drag force on an individual element within an emergent or submerged canopy or the bulk canopy drag. As input, it requires above-canopy velocity (U∞) that can be estimated from the flow rate (Q) or bulk velocity (Ub) for submerged and emergent canopies resp., local water depth (h), and the canopy properties: height (hv), stem diameter (dv), and canopy density (λp, Nv). For submerged canopies, an initial value of Cd = 1 (to calculate Ld) is suggested.
Experimental Methods
Experiments were carried out in a 20-m-long, 0.6-m-wide, and 0.6-m-deep recirculating flume using emergent (Table 1) and submerged (Table 2) model vegetation. To accommodate the drag force sensor, a 10-cm-high false bottom was placed over a length of 10 m. Model canopies were constructed using perforated PVC sheets and two sets of 6.4-mm-diameter dowels with heights of 30 cm (emergent) or 9 cm (submerged). Dowels were distributed in a staggered arrangement over the entire width of the flume. The dowel diameter used in this study has been used previously in numerous studies to represent a generic aquatic vegetation canopy (e.g., Nepf, 1999) and was originally based on actual observed stem diameters of cordgrass (Spartina alterniflora, see Zavistoski, 1994). An important design parameter for experimental studies with canopies is the canopy length (Lv). Lowe et al. (2005) found a canopy flow adjustment length (x0) of 3–5 times the drag length scale (Ld) in their experiments. Hence, to ensure fully-developed canopy flow, it was required that Lv >> x0 resulting in Lv ranging between 2.4 m (λp = 0.1) and 3.6 m (λp = 0.025).
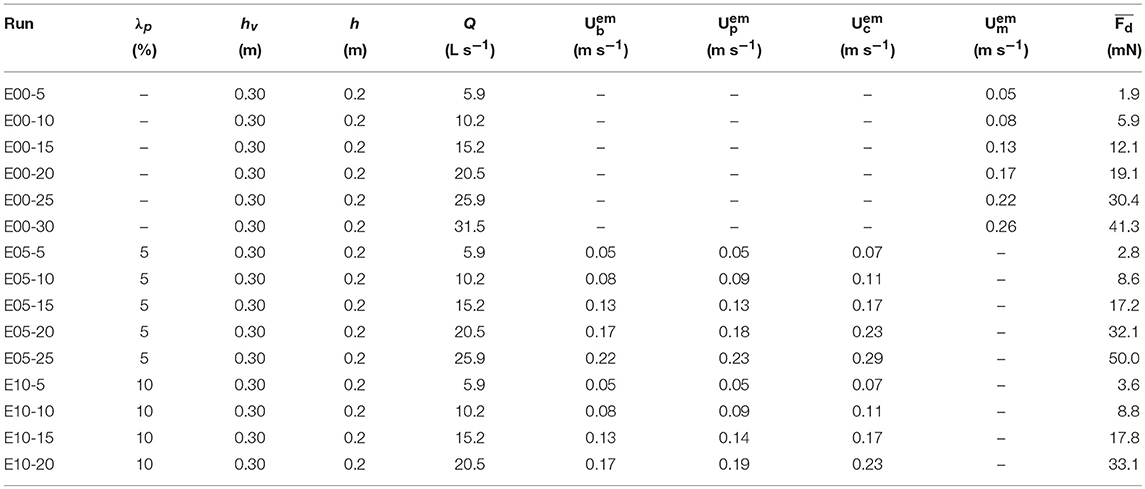
Table 1. Experimental emergent vegetation conditions: canopy density (λp), canopy height (hv), water depth (h), flow rate (Q), bulk velocity (), pore velocity (), constricted cross-section velocity (), measured velocity averaged over the dowel height () and the measured time-averaged drag force acting on a single cylinder ().
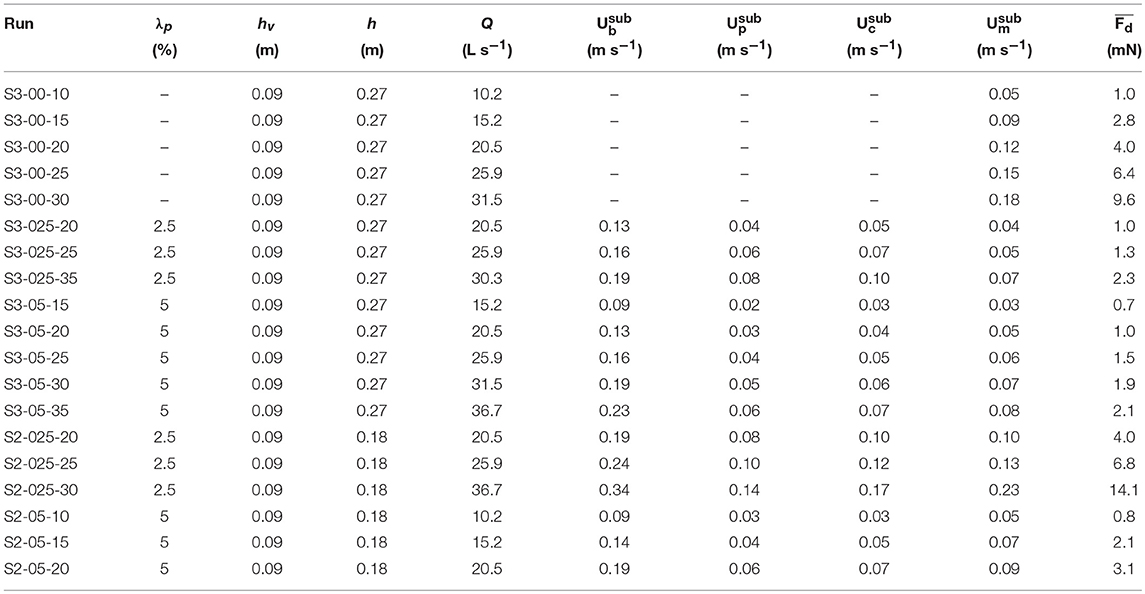
Table 2. Experimental submerged vegetation conditions: canopy density (λp), canopy height (hv), water depth (h), flow rate (Q), bulk velocity (), pore velocity (), constricted cross-section velocity (), measured in-canopy velocity averaged over the canopy/dowel height () and the measured time-averaged drag force acting on a single cylinder ().
The drag force exerted on a representative aluminum dowel (canopy element) was measured using a load cell with 2 N capacity (Uxcell, Hong Kong) connected to a load cell amplifier (RW-ST01A, SMOWO, China). The load cell was mounted vertically onto the underside of the false bottom in the flume, ensuring the bottom end of the load cell was fixed but allowing the upper end to move slightly with the bending moment (MY) generated by the drag force acting on the dowel (Figure 3). Data was obtained from the load cell using a National Instruments data acquisition system (NI-DAQ PCI-6009) and LabVIEW software. This experimental setup relies on the linear relationship between drag force and the instrument voltage output. To confirm the load cell's linearity, the load cell was placed at the edge of a table and the voltage output recorded for cases with both no weight and a weight of (approximately) 1.9 N. The (linear) calibration coefficient was derived by calculating the ratio between the change in voltage output and the change in applied weight. The linear response was subsequently verified using 9 (smaller) weights ranging from 0.01 to 1.2 N (R2 > 0.99). Prior to each individual experimental run, the load cell was re-calibrated using a set of three known weights ranging between 0 and ~0.3 N.
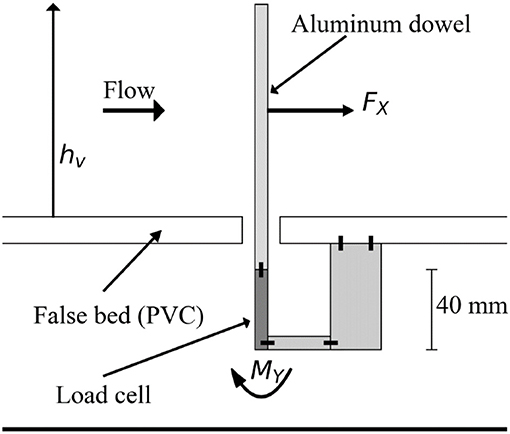
Figure 3. Schematic view of the load cell, which was attached to a single aluminum dowel and placed under the false bed. The drag force (Fx) due to the flow acting on the dowel translates into a moment (My) around the base of the load cell.
For emergent canopies, the water level was measured using a point gauge at three locations both upstream and downstream of the canopy. The water level gradient (dη/dx) was then obtained by averaging the water level in time at the upstream and downstream locations and dividing by the canopy length. To calculate the flow rate, velocity measurements were obtained several meters upstream of the canopy using a Nortek Vectrino II Acoustic Doppler Velocity (ADV) profiler, resulting in 3-cm-tall velocity profiles with 1 mm resolution. The vertical position of the ADV was varied to obtain a full velocity profile extending from the bottom to ~5 cm below the water surface. In a similar manner, the velocity profile in and above the canopy was obtained for the submerged cases, and extended from the base of the canopy up to ~5 cm below the water surface. The ADV was positioned within the constricted cross-section in between two canopy elements at a lateral distance of ~0.25Sv, l from one of the elements. This was based on the modeling of Etminan et al. (2017), who found that the velocity at this point in a staggered canopy was similar to the constricted cross-section value. Experimental runs were repeated several times to obtain the full velocity profile over depth within and above the canopy. Both the load cell and ADV were placed at a distance of ~2/3 of the canopy length downstream from the leading edge, which is at least 10 times the drag length scale (Ld) for all cases.
The experimental program included a range of canopy densities (λp = 0.025, 0.05, and 0.10), canopy submergence ratios (h/hv = 1, 2, and 3, where h is the water depth at still water and hv is the canopy height) and flow rates (Tables 1, 2). The upstream flow velocity ranged between ~0.05 and 0.35 m/s, which in combination with the range in canopy density and submergence ratio covers a broad range of conditions that can be found in aquatic canopies. The drag force and velocity data were processed and the drag coefficient was subsequently computed using Equation (3).
Following Taylor (1997), measurement uncertainties were propagated, with an estimated velocity uncertainty of 0.1 cm/s and drag force uncertainty of 0.4 mN. For the model-data comparison the model skill was quantified using scatter index (SCI), and the relative bias. The scatter index is a relative measure of the scatter between computed (xc) and measured data (xm) and is computed by normalizing the root-mean-square error () with the maximum of the root-mean-square-value of the data () and the absolute value of the mean of the data (). The relative bias is a relative measure of the bias or mean error () and is normalized in the same way as the scatter index.
To date only relatively few studies have used load cells to measure canopy drag, hence a comparison is made between the drag force measured directly using the current methodology (Fd, direct) and the drag force obtained through an indirect measuring method commonly used in previous studies [Fd, momentum, from Equation (6)]. The indirect estimate (Fd, momentum) for the emergent cases (E05 and E10, see Table 1) shows the same trend (R2 = 0.99) as the drag force directly measured with the load cell (Fd, direct, see Figure 4). Although measured drag forces with magnitudes above 0.01 N are very similar for both methods (up to 8% difference), for drag forces < 0.01 N the discrepancy between both methods increases (with an average 22% difference). For these low flow cases the percentage uncertainty associated with the measured water level gradient increases (with the water level dropping only ~3 mm over the length of the canopy) leading to larger errors. Given the high instrument linearity, the force sensor is able to provide more accurate measurements for these cases and is therefore preferred.
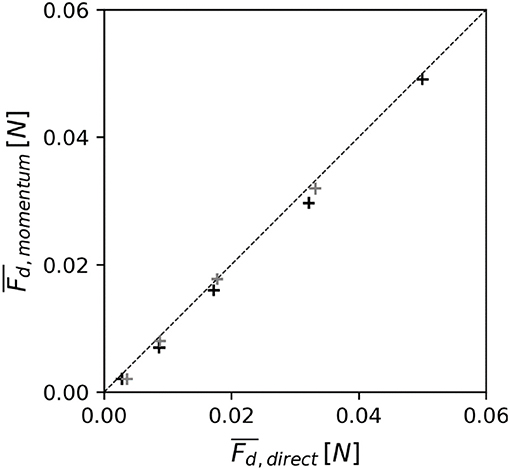
Figure 4. The strong agreement in estimated drag forces on an individual element in an emergent canopy using two methods: (i) measured directly using the force sensor (Fd, direct) and (ii) derived indirectly from the water surface gradient (Fd, momentum). Marker color indicates canopy density (black: λp = 0.05; gray: λp = 0.10). The size of the markers indicates the associated measurement uncertainty. The dashed line represents the line of perfect agreement.
Results and Discussion
Measurement of Drag Coefficients
Isolated Cylinder
Although the focus in this study is on assessing canopy drag, a limited number of experiments were conducted with isolated emergent (Table 1) and submerged (Table 2) cylinders. The isolated cylinder drag coefficients were then compared to theory (Equation 2) to gain confidence in the experimental methodology (particularly the drag force data obtained from the load cell). For the emergent case, there is excellent agreement between the directly-measured drag on an isolated cylinder and Equation (2) (Figure 5, squares). For the submerged case (with same height as the submerged canopy), the value of Cd derived from the measured drag force and measured in-canopy velocity (averaged over the cylinder height) is consistent with isolated cylinder theory (Figure 5, triangles). In other words, despite the single vertical cylinder occupying a fraction of the water column in a boundary layer flow, its forces can be predicted by Equation (2) originally developed for a cylinder in a uniform cross-flow.
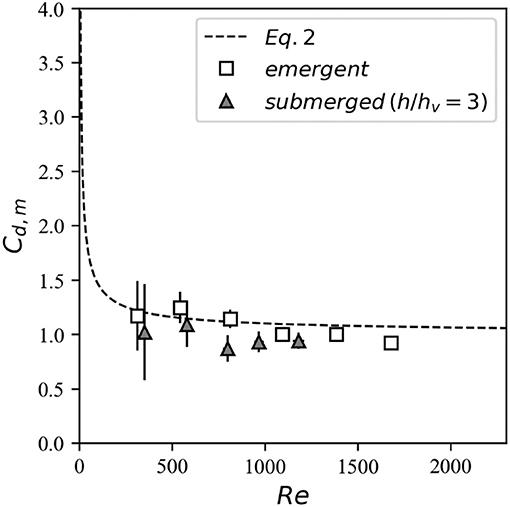
Figure 5. Drag coefficients derived from the velocity and drag force measurements for the isolated cylinder cases.
Emergent Canopies
As discussed in the Introduction, for emergent canopies, both the bulk velocity and pore velocity are often used as the reference velocity in Equation (3) to relate a given flow condition to the canopy drag force through a drag coefficient (i.e., Cd, b and Cd, p, respectively). Here, when using both the bulk velocity () and pore velocity () are used as the drag reference velocity, there are large discrepancies with values for isolated cylinders (Equation 2), similar to results reported in other studies (e.g., Liu and Zeng, 2017). For the highest density canopies (λp = 0.1), there is an exponential decrease in the drag coefficient with Reynolds number using both the bulk velocity (Figure 6A, squares) and pore velocity (Figure 6B). For the 5% density emergent canopies, the drag coefficient shows a slight decrease with Re using both reference velocities. When considering both and , the drag coefficient appears to take an approximately constant value at high Re (i.e., Re >1,000), consistent with other studies (e.g., Tang et al., 2014). Given that the pore velocity accounts for the volume of water being occupied by the canopy, Cd, p is always smaller than Cd, b, but still deviates substantially from isolated cylinder values. To account for these discrepancies, previous studies have arrived at highly empirical Cd, p-Rep relationships that are parameterized as a function of canopy density (Tanino and Nepf, 2008) and (sometimes) stem diameter (Sonnenwald et al., 2018).
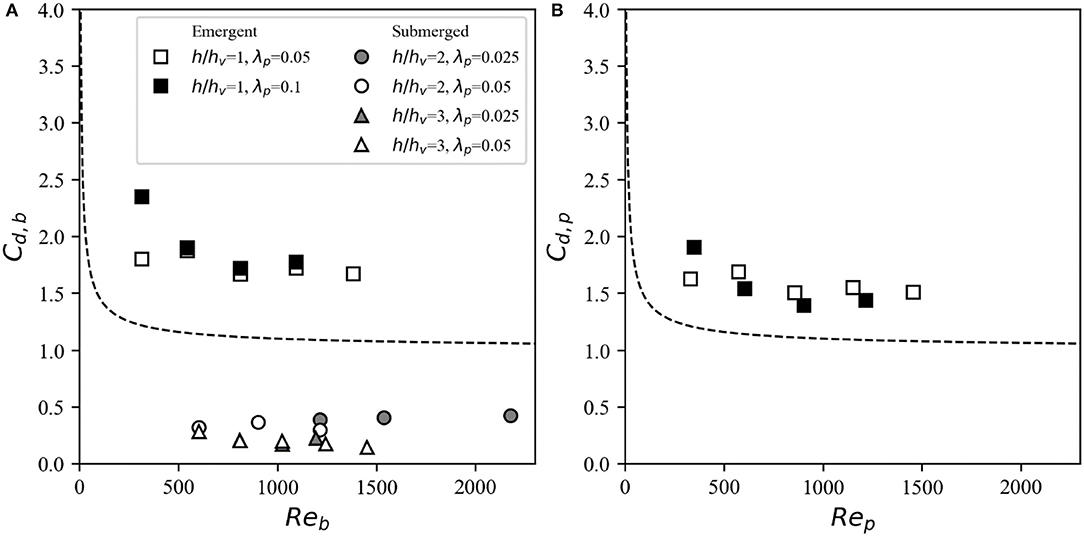
Figure 6. Drag coefficients derived from the drag force measurements using (A) the bulk velocities and and (B) the pore velocity as the reference velocity for the emergent (squares) and submerged (circles: h/hv = 2; triangles: h/hv = 3) cases. The marker color represents the canopy density (black: λp = 0.1; white: λp = 0.05; gray: λp = 0.025), with theoretical values for an isolated cylinder (Equation 2) denoted by the dashed line.
The direct experimental measurements support the canopy drag model proposed by Etminan et al. (2017)–when the constricted cross-section velocity () is used as the reference velocity, calculated drag coefficients closely match the isolated cylinder values (Figure 7, squares). Therefore, while the drag coefficients derived using the bulk and pore velocities exhibit significant scatter (Figure 6), the use of in the drag coefficient (Cd, c) calculations serves to collapse the data onto the isolated cylinder curve. For the range of Reynolds numbers investigated (Rec = 380–1,680), the drag coefficients for the emergent cases show relatively little scatter and approaches a canonical isolated cylinder value of Cd, c ≈ 1.
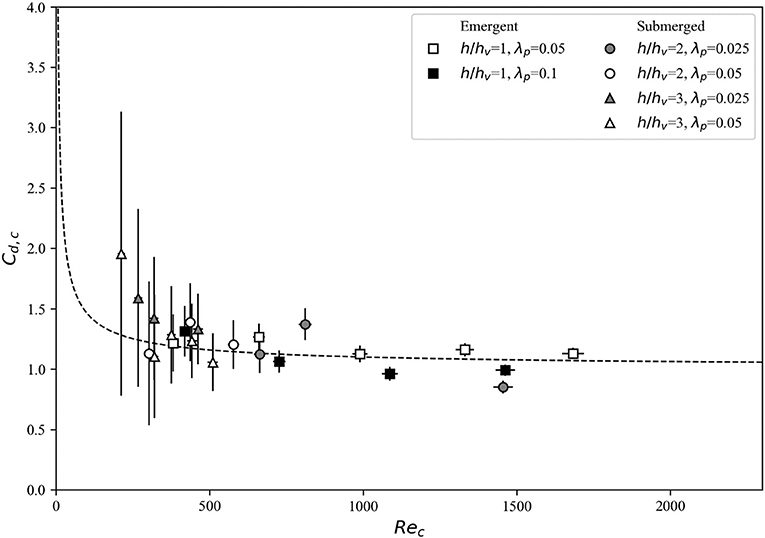
Figure 7. Drag coefficients derived from the drag force measurements for all canopies using the constricted cross-section velocity Uc as the reference velocity for the emergent and submerged cases. Theoretical values for the drag coefficient of an isolated cylinder (Equation 2) are denoted by the dashed line.
Submerged Canopies
The velocity exhibits more vertical variation in submerged canopies than in emergent canopies due the drag discontinuity and resulting shear layer present at the top of the canopy. When using the bulk velocity as the reference velocity to derive Reb and Cd, b, relatively low drag coefficients (that substantially deviate from the isolated cylinder values) are obtained (Figure 6A, circles and triangles). This approach neglects the effect of canopy drag on reducing the in-canopy velocity, which is significant at higher canopy densities. Hence, we use measured obtained approximately within the constricted cross-section area and derive the associated drag coefficients. For the submerged canopy cases, the measured values of Cd, c (i.e., evaluated using the constricted cross-section velocity ) generally follows the isolated cylinder theory curve (Figure 7). There is more scatter at Rec < 500, which can be attributed to the greater uncertainty associated with measuring flow and forces at such low Reynolds numbers. Therefore, analogous to the emergent canopy observations in Figure 6, where Cd evaluated using bulk and pore velocities deviates markedly from isolated cylinder theory, these results indicate that the constricted cross-section velocity is the optimal reference velocity for evaluation of drag of a submerged canopy (Figure 7).
Canopy Drag Model Assessment
Emergent Canopies
The canopy drag model for emergent canopies, based on Equations (2)–(4) using the computed constricted cross-section velocity (see section Canopy Drag Model), was used to predict the drag force on a single canopy element in all experimental cases (Table 1). These predictions were then compared to the time-averaged drag force measured by the force sensor (Figure 8, squares). Using only the bulk flow velocity, which was derived from the known flow rate, and canopy geometry as model input, the canopy drag forces are accurately predicted over the full range of experimental cases. The results provide direct experimental validation of the finding of Etminan et al. (2017) that the constricted cross-section velocity is the most appropriate reference velocity to parameterize canopy drag.
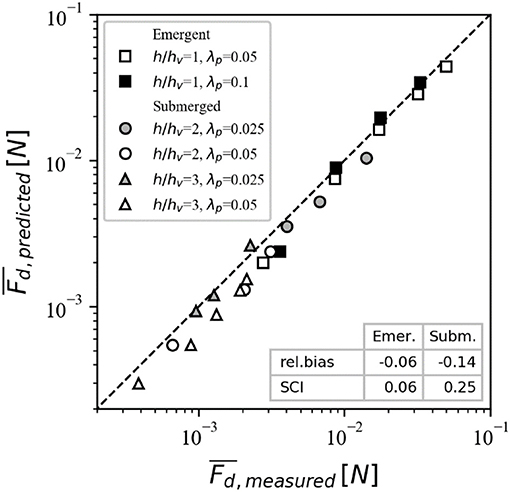
Figure 8. The strong agreement between predicted and measured drag forces, including the line of perfect agreement (dashed). The predictive model skill is described by the relative bias and scatter index (bottom right corner).
Submerged Canopies
To assess the ability of the model to predict the drag of submerged canopies, we first compared the predicted in-canopy velocities with the experimental measurements. Specifically, we compared the measured time-averaged constricted cross-section velocity integrated over the canopy height () with predicted values, which generally reveals good agreement (Figure 9). The model (with above-canopy velocity and canopy geometry as input) is subsequently applied to calculate the drag force for all submerged canopy cases (Table 2). Canopy friction coefficient values were derived for each case through Reynolds stress profiles (Equation 10), resulting in a range of Cf values between 0.01 and 0.04. However, due to the experimental setup in this study, that used a downward facing ADV, the velocity measurement was limited to measuring only ~6 cm below the water surface. The above-canopy velocity is therefore likely underestimated, particularly in the h/hv = 2 cases, and actual Cf values are expected to be lower. Due to this uncertainty, here we opt to use a conventional value of 0.01 for all experimental cases (see section Canopy Drag Model). Compared to emergent canopies, there is greater scatter in the relationship between measured and predicted forces (particularly at low Re), but overall there is still relatively good agreement (Figure 8). Given the complexity involved with submerged canopies (including the uncertainty involved with measurements under low Re), and the range in submergence ratio and density investigated, the model error averages about 11% (SCI = 0.114), and suggests that the whole model outlined in Figure 2 can serve as a useful tool to obtain robust estimates of canopy drag forces.
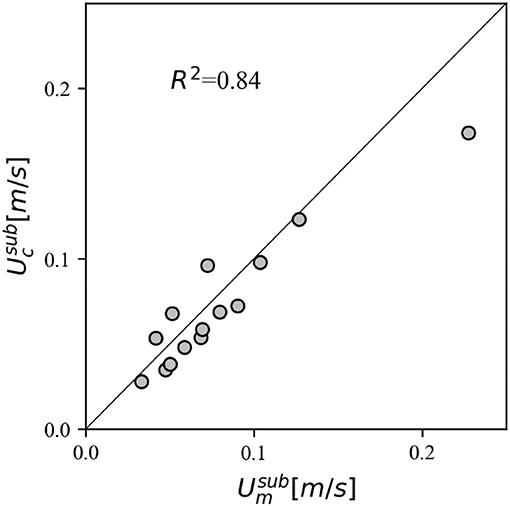
Figure 9. Comparison between the measured depth-averaged in-canopy flow velocity () and the estimated in-canopy constricted cross-section velocity () in submerged canopies.
Model Application to Other Submerged Canopy Data Sets
To date, the canopy drag model has been validated for emergent canopies (Etminan et al., 2017) (albeit using only numerical simulations); here we have provided direct experimental validation for both emergent and submerged canopies for the first time. Nevertheless, the experiments only covered a relatively small range of possible canopy geometry and flow conditions. To further assess the validity of the model across a large range of flow conditions and canopy properties (e.g., density, submergence ratio, flexibility), the model was tested against a large number of existing datasets. Experiments were limited to those with submerged canopies in which the energy slope was reported.
Rigid Vegetation
For rigid vegetation, experiments that employed either staggered (as in the present study), linear or random arrangements were selected here (Table 3). Although on the individual canopy element scale, the velocity distribution may vary significantly among these arrangements, we hypothesize that the model can still be used to estimate bulk canopy drag. Indeed, the work of Etminan et al. (2017) suggested that in the case of randomly-distributed canopy elements, the constricted cross-section velocity can still be considered as the velocity scale governing canopy drag, indicating that the model can be applied here without modification. Hence, using provided values of flow rate and canopy properties, the bulk drag was computed and compared with the measured drag (Figure 10A). Using a constant Cf value of 0.01 (as before), the model shows a similar trend as the measurements (R2 = 0.74) with reasonably low bias and scatter (rel. bias = 0.02, SCI = 0.45). It should be emphasized that the main uncertainty is likely to be attributed to the schematization of relatively complex three-dimensional canopy hydrodynamics into a relatively simple (two-layer) model.
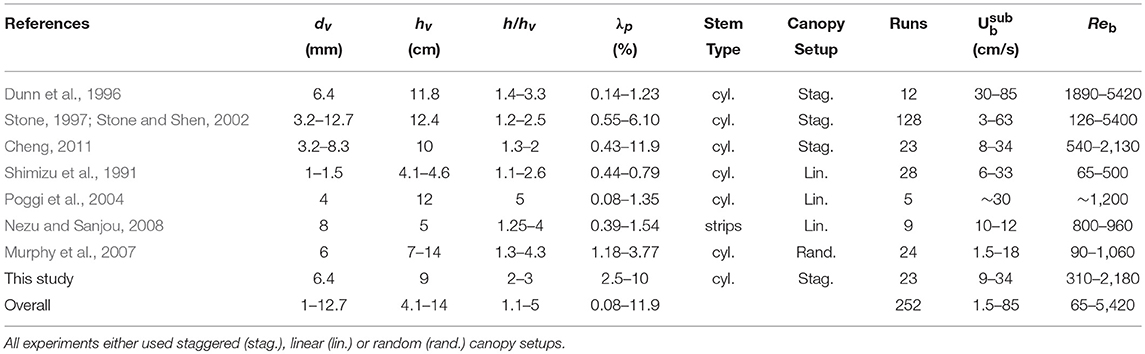
Table 3. Overview of experimental studies on drag in submerged rigid canopies from which data was obtained.
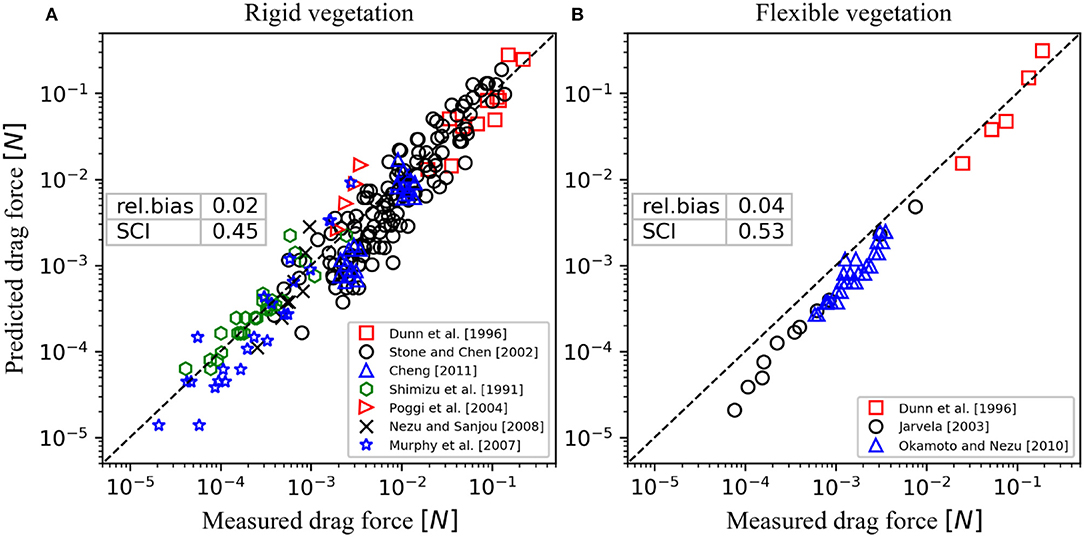
Figure 10. Validation of canopy drag model for submerged canopies against previous experimental results with (A) rigid and (B) flexible vegetation (listed in Tables 3, 4, respectively).
Flexible Elements
Although most studies so far have represented vegetation canopies using rigid elements, aquatic vegetation in natural systems is often flexible (e.g., seagrasses, kelp), adapting its shape and thereby frontal area in response to the flow. Hence, there is now increased experimentation with flexible mimics in hydraulic experiments (e.g., Abdolahpour et al., 2017). The canopy drag model presented in this study does not explicitly account for flexibility, but it is hypothesized that it could still be used as a tool provided the deflected vegetation height (i.e., the height of the vegetation under stationary flow condition) rather than the actual length of the element is used. Hence, data was obtained from three studies that investigated drag in submerged flexible canopies and reported the deflected canopy height (Table 4). From these studies, both Dunn et al. (1996) and Järvelä (2003) observed swaying motions of their flexible plants/(cylindrical) elements, resulting in a time-varying deflected canopy height. Okamoto and Nezu (2010) reported both swaying and the more organized monami-type motions (Ackerman and Okubo, 1993) in their experiments. Here, we use the time-averaged deflected canopy height as input for the model. Furthermore, for the experiments by Okamoto and Nezu (2010) we use the width of the flexible strip as a proxy for dv given that it is equivalent to the frontal area.

Table 4. Overview of experimental studies on drag in submerged flexible canopies from which data was obtained.
For the flexible canopies, the model is able to predict the bulk drag relatively well (Figure 10B, R2 = 0.69, rel. bias = 0.04, SCI = 0.53). This is surprising to some extent, as the complexity associated with flexible elements is only accounted for to some extent by the (deflected) plant height. Both the measurements by Järvelä (2003) and Okamoto and Nezu (2010) are consistently underpredicted, which may be related to the plant geometries that involved flat strips and real plants, respectively. Dunn et al. (1996), on the other hand, used flexible cylinders in their experiments which provide more similarity with rigid cylinders, and may therefore better be represented by model.
Overall, with limited information (above-canopy velocity derived from flow rate, canopy properties) the relatively simple canopy drag model is able to provide reasonably accurate estimates of the bulk canopy drag for both rigid and flexible vegetation canopies. Given the fact that the model performs well over such a broad range of hydrodynamic conditions (Ub = 1.5–85 cm/s, Re = 65–5,430) and canopies (h/hv = 1.1–5, λp = 0.08–11.9%, both rigid and flexible vegetation), and is based on theory rather than empirical relations, it is thus expected the model can robustly predict hydraulic resistance of aquatic canopies, including in field setting with natural vegetation (e.g., where stem diameters are often of order 0.1–1 cm and current velocities of order 0.05–0.5 m/s, which translates to Re ranging between 50 and 5,000).
Summary and Conclusions
In this study we present new direct experimental measurements of canopy drag forces using emergent and submerged canopies with a broad range of flow conditions and canopy properties (i.e., density and submergence ratio). Drag coefficients were derived using direct measurements of the drag force on a dowel within the canopy. We found that if the constricted cross-section velocity is used as the reference velocity, the drag coefficient of both emergent and submerged canopies is equal to that of an isolated cylinder. Comparison between canopy drag model predictions and current and existing experimental data shows that the model is able to robustly and accurately predict canopy drag across the field range of flow conditions and canopy characteristics, including flexible canopies. The model can thus be used to predict drag forces in emergent and submerged canopies and is considered a simple and practical tool for estimating the hydraulic resistance of aquatic canopies.
Data Availability Statement
The datasets analyzed for this study can be obtained by sending a written request to the corresponding author atYXJub2xkLnZhbnJvb2lqZW5AcmVzZWFyY2gudXdhLmVkdS5hdQ==.
Author Contributions
AvR designed the experiments, acquired the data, performed the data analysis, and wrote the manuscript. RL and MG provided support in the experimental design, data interpretation and the development of the manuscript. MC-F and LT provided support in data acquisition during the experiments. All authors revised the draft manuscript and approved the final version for submission.
Funding
This work was supported by an Australian Research Discovery Project Grant (DP170100802) to RL and MG.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was undertaken by AvR as part of a Ph.D. at The University of Western Australia who was funded by a University Postgraduate Award for International Students (UPAIS) and an Australian Government Research Training Program (RTP) Scholarship. LT was supported by the China Scholarship Council (grant number: 201706320274). The authors would like to thank Mr. Carlin Bowyer, Ms. Dianne King, and Mr. Brad Rose for assistance in the lab, Dr. Guido Wager for providing support with the force sensor, Dr. Vahid Etminan for valuable discussions, and the reviewers for their constructive feedback that helped to improve the manuscript.
References
Abdolahpour, M., Hambleton, M., and Ghisalberti, M. (2017). The wave-driven current in coastal canopies. J. Geophys. Res. Oceans 122, 3660–3674. doi: 10.1002/2016JC012446
Ackerman, J. D. (1995). Convergence of filiform pollen morphologies in seagrasses: functional mechanisms. Evol. Ecol. 9, 139–153.
Ackerman, J. D., and Okubo, A. (1993). Reduced mixing in a marine macrophyte canopy. Funct. Ecol. 7, 305–309. doi: 10.2307/2390209
Balke, T., Bouma, T. J., Herman, P. M. J., Horstman, E. M., Sudtongkong, C., and Webb, E. L. (2013). Cross-shore gradients of physical disturbance in mangroves: implications for seedling establishment. Biogeosciences 10, 5411–5419. doi: 10.5194/bg-10-5411-2013
Cheng, N. S. (2011). Representative roughness height of submerged vegetation. Water Resour. Res. 47, 1–8. doi: 10.1029/2011WR010590
Cornelisen, C. D., and Thomas, F. I. (2002). Ammonium uptake by seagrass epiphytes: isolation of the effects of water velocity using an isotope label. Limnol. Oceanogr. 47, 1223–1229. doi: 10.4319/lo.2002.47.4.1223
Duarte, C. M. (2002). The future of seagrass meadows. Environ. Conserv. 29, 192–206. doi: 10.1017/S0376892902000127
Dunn, C., Lopez, F., and Garcia, M. H. (1996). Mean Flow and Turbulence in a Laboratory Channel with Simulated Vegetation. Technical report, Hydraulic Engineering Series No. 51, University of Illinois.
Edmaier, K., Burlando, P., and Perona, P. (2011). Mechanisms of vegetation uprooting by flow in alluvial non-cohesive sediment. Hydrol. Earth Syst. Sci. 15, 1615–1627. doi: 10.5194/hess-15-1615-2011
Etminan, V., Lowe, R. J., and Ghisalberti, M. (2017). A new model for predicting the drag exerted by vegetation canopies. Water Resour. Res. 53, 3179–3196. doi: 10.1002/2016WR020090
Fonseca, M. S., and Cahalan, J. A. (1992). A preliminary evaluation of wave attenuation by four species of seagrass. Estuar. Coast. Shelf Sci. 35, 565–576.
Ghisalberti, M. (2009). Obstructed shear flows: similarities across systems and scales. J. Fluid Mech. 641, 51–61. doi: 10.1017/S0022112009992175
Harman, I. N., and Finnigan, J. J. (2007). A simple unified theory for flow in the canopy and roughness sublayer. Boundary-Layer Meteorol. 123, 339–363. doi: 10.1007/s10546-006-9145-6
Hendriks, I. E., Bouma, T. J., Morris, E. P., and Duarte, C. M. (2010). Effects of seagrasses and algae of the Caulerpa family on hydrodynamics and particle-trapping rates. Mar. Biol. 157, 473–481. doi: 10.1007/s00227-009-1333-8
Hendriks, I. E., Sintes, T., Bouma, T. J., and Duarte, C. M. (2008). Experimental assessment and modeling evaluation of the effects of the seagrass Posidonia oceanica on flow and particle trapping. Mar. Ecol. Prog. Ser. 356, 163–173. doi: 10.3354/meps07316
James, W. F., Barko, J. W., and Butler, M. G. (2004). Shear stress and sediment resuspension in relation to submersed macrophyte biomass. Hydrobiologia 515, 181–191. doi: 10.1023/B:HYDR.0000027329.67391.c6
Järvelä, J. (2003). “Influence of vegetation on flow structure in floodplains and wetlands,” in Proceedings of the 3rd Symposium on River, Coastal and Estuarine Morphodynamics (RCEM). (Madrid), 845–856.
Kenyon, R. A., Haywood, M. D. E., Heales, D. S., Loneragan, N. R., Pendrey, R. C., and Vance, D. J. (1999). Abundance of fish and crustacean postlarvae on portable artificial seagrass units: daily sampling provides quantitative estimates of the settlement of new recruits. J. Exp. Mar. Biol. Ecol. 232, 197–216.
Koch, E. W., Ackerman, J. D., Verduin, J., and van Keulen, M. (2007). “Fluid dynamics in seagrass ecology—from molecules to ecosystems,” in Seagrasses: Biology, Ecology and Conservation, eds A. Larkum, R. Orth, and C. C. Duarte, (Dordrecht: Springer), 193–225. doi: 10.1007/978-1-4020-2983-7_8
Kothyari, U. C., Hayashi, K., and Hashimoto, H. (2009). Drag coefficient of unsubmerged rigid vegetation stems in open channel flows. J. Hydraulic Res. 47, 691–699. doi: 10.3826/jhr.2009.3283
Liu, D., Diplas, P., Fairbanks, J. D., and Hodges, C. C. (2008). An experimental study of flow through rigid vegetation. J. Geophys. Res. Earth Surf. 113, 1–16. doi: 10.1029/2008JF001042
Liu, X., and Zeng, Y. (2017). Drag coefficient for rigid vegetation in subcritical open-channel flow. Environ. Fluid Mech. 17, 1035–1050. doi: 10.1007/s10652-017-9534-z
López, F., and García, M. H. (2001). Mean flow and turbulence structure of open-channel flow through non-emergent vegetation. J. Hydraulic Eng. 127, 392–402. doi: 10.1061/(ASCE)0733-9429(2001)127:5(392)
Lowe, R. J., Koseff, J. R., and Monismith, S. G. (2005). Oscillatory flow through submerged canopies: 1. Velocity structure. J. Geophys. Res. 110, 1–17. doi: 10.1029/2004JC002788
Lowe, R. J., Shavit, U., Falter, J. L., Koseff, J. R., and Monismith, S. G. (2008). Modeling flow in coral communities with and without waves: a synthesis of porous media and canopy flow approaches. Limnol. Oceanogr. 53, 2668–2680. doi: 10.4319/lo.2008.53.6.2668
Luhar, M., Coutu, S., Infantes, E., Fox, S., and Nepf, H. (2010). Wave-induced velocities inside a model seagrass bed. J. Geophys. Res. Oceans 115, 1–15. doi: 10.1029/2010JC006345
Moltchanov, S., Bohbot-Raviv, Y., and Shavit, U. (2011). Dispersive stresses at the canopy upstream edge. Boundary-layer Meteorol. 139, 333–351. doi: 10.1007/s10546-010-9582-0
Morris, E. P., Peralta, G., Brun, F. G., Van Duren, L., Bouma, T. J., and Perez-Llorens, J. L. (2008). Interaction between hydrodynamics and seagrass canopy structure: spatially explicit effects on ammonium uptake rates. Limnol. Oceanogr. 53, 1531–1539. doi: 10.4319/lo.2008.53.4.1531
Murphy, E., Ghisalberti, M., and Nepf, H. (2007). Model and laboratory study of dispersion in flows with submerged vegetation. Water Resour. Res. 43, 1–12. doi: 10.1029/2006WR005229
Nepf, H. M. (1999). Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 35, 479–489. doi: 10.1029/1998WR900069
Nepf, H. M. (2012). Hydrodynamics of vegetated channels. J. Hydraulic Res. 50, 262–279. doi: 10.1080/00221686.2012.696559
Nepf, H. M., and Vivoni, E. R. (2000). Flow structure in depth-limited, vegetated flow. J. Geophys. Res. 105, 28547–28557. doi: 10.1029/2000JC900145
Nezu, I., and Sanjou, M. (2008). Turburence structure and coherent motion in vegetated canopy open-channel flows. J. Hydro-Environ. Res. 2, 62–90. doi: 10.1016/j.jher.2008.05.003
Okamoto, T. A., and Nezu, I. (2010). “Flow resistance law in open-channel flows with rigid and flexible vegetation,” in River flow, Proceedings of the International Conference on Fluvial Hydraulics (Braunschweig), 261–268.
Poggi, D., Porporato, A., Ridolfi, L., Albertson, J. D., and Katul, G. G. (2004). The effect of vegetation density on canopy sub-layer turbulence. Bound. Layer Meteorol. 111, 565–587. doi: 10.1023/B:BOUN.0000016576.05621.73
Schoneboom, T., Aberle, J., and Dittrich, A. (2010). “Hydraulic resistance of vegetated flows: contribution of bed shear stress and vegetative drag to total hydraulic resistance,” in River flow, Proceedings of the International Conference on Fluvial Hydraulics (Braunschweig), 269–276.
Shimizu, Y., Tsujimoto, T., Nakagawa, H., and Kitamura, T. (1991). Experimental study on flow over rigid vegetation simulated by cylinders with equi-spacing. Doboku Gakkai Ronbunshu 1991, 31–40. doi: 10.2208/jscej.1991.438_31
Sonnenwald, F., Stovin, V., and Guymer, I. (2018). Estimating drag coefficient for arrays of rigid cylinders representing emergent vegetation. J. Hydraulic Res. 1–7. doi: 10.1080/00221686.2018.1494050
Stone, B. M. (1997). Hydraulics of Flow in Vegetated Channels. MS thesis, Clarkson University, Potsdam, NY.
Stone, B. M., and Shen, H. T. (2002). Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraulic Eng. 128, 500–506. doi: 10.1061/(ASCE)0733-9429(2002)128:5(500)
Tang, H., Tian, Z., Yan, J., and Yuan, S. (2014). Determining drag coefficients and their application in modelling of turbulent flow with submerged vegetation. Adv. Water Resour. 69, 134–145. doi: 10.1016/j.advwatres.2014.04.006
Tanino, Y., and Nepf, H. M. (2008). Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraulic Eng. 134, 34–41. doi: 10.1061/(ASCE)0733-9429(2008)134:1(34)
Taylor, J. (1997). Error Analysis: The Study of Uncertainties in Physical Measurements, 2nd Edn. Sausalito, CA: University Science Books.
Vargas-Luna, A., Crosato, A., Calvani, G., and Uijttewaal, W. S. (2016). Representing plants as rigid cylinders in experiments and models. Adv. Water Resour. 93, 205–222. doi: 10.1016/j.advwatres.2015.10.004
Wang, H., Tang, H., Yuan, S., Lv, S., and Zhao, X. (2014). An experimental study of the incipient bed shear stress partition in mobile bed channels filled with emergent rigid vegetation. Sci. China Technol. Sci. 57, 1165–1174. doi: 10.1007/s11431-014-5549-6
Weitzman, J. S., Zeller, R. B., Thomas, F. I., and Koseff, J. R. (2015). The attenuation of current-and wave-driven flow within submerged multispecific vegetative canopies. Limnol. Oceanogr. 60, 1855–1874. doi: 10.1002/lno.10121
Widdows, J., Pope, N. D., Brinsley, M. D., Asmus, H., and Asmus, R. M. (2008). Effects of seagrass beds (Zostera noltii and Z. marina) on near-bed hydrodynamics and sediment resuspension. Mar. Ecol. Prog. Ser. 358, 125–136. doi: 10.3354/meps07338
Wu, F. C., Shen, H. W., and Chou, Y. J. (1999). Variation of roughness coefficients for unsubmerged and submerged vegetation. J. Hydraulic Eng. 125, 934–942. doi: 10.1061/(ASCE)0733-9429(1999)125:9(934)
Zavistoski, R. A. (1994). Hydrodynamic Effects of Surface Piercing Plants. MSc Thesis, Massachusetts Institute of Technology.
Notation
Cd = drag coefficient for an isolated cylinder
Cd,c = canopy drag coefficient based on constricted cross-section velocity
Cd,b = canopy drag coefficient based on bulk velocity
Cd,m = canopy drag coefficient based on measured velocity
Cd,p = canopy drag coefficient based on pore velocity
Cf = canopy friction coefficient
dc = cylinder diameter
dv = plant / canopy element diameter
fd = drag force per unit length of a cylinder
Fd = plant / canopy element total drag force
g = gravitational acceleration
h = water depth
hv = plant / canopy height
hvd = deflected plant / canopy height
Lv = canopy length
Ld = canopy drag length scale
Ls = canopy shear length scale
Nv = number of plants / canopy elements per unit bed area
Q = flow rate / discharge
Re = Reynolds number for an isolated cylinder
Rec = Reynolds number (canopy) based on constricted cross-section velocity
Reb = Reynolds number (canopy) based on bulk velocity
Rem = Reynolds number (canopy) based on measured velocity
Rep = Reynolds number (canopy) based on pore velocity
Sv, l = lateral distance between two canopy elements at the same streamwise (x) location
Sv, s = streamwise distance between two canopy element rows
u′ = turbulent velocity fluctuation in x direction
u* = friction velocity based on canopy shear stress
U∞ = free stream flow velocity
, = bulk velocity for emergent or submerged canopy resp.
, = constricted cross-section velocity for emergent or submerged canopy resp.
, = measured depth-averaged velocity for emergent or submerged canopy resp.
, = pore velocity for emergent or submerged canopy resp.
Uref = reference velocity
w′ = turbulent velocity fluctuation in z direction
W = channel width
x = streamwise direction
x0 = canopy flow adjustment length
z = vertical elevation measured from bottom
β = ratio between lateral and streamwise canopy spacing (Sv, l/Sv, s)
η = water surface elevation
λf = canopy (frontal) density / element frontal area per unit bed area
λp = canopy (plan) density / element plan area per unit bed area
ρ = water density
ν = kinematic viscosity
Keywords: ecohydraulics, vegetated flows, flow-plant interaction, drag model, drag coefficient
Citation: van Rooijen A, Lowe R, Ghisalberti M, Conde-Frias M and Tan L (2018) Predicting Current-Induced Drag in Emergent and Submerged Aquatic Vegetation Canopies. Front. Mar. Sci. 5:449. doi: 10.3389/fmars.2018.00449
Received: 27 August 2018; Accepted: 08 November 2018;
Published: 04 December 2018.
Edited by:
Roshanka Ranasinghe, IHE Delft Institute for Water Education, NetherlandsReviewed by:
Tomohiro Suzuki, Flanders Hydraulics Research, BelgiumVanesa Magar, Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE), Mexico
Copyright © 2018 van Rooijen, Lowe, Ghisalberti, Conde-Frias and Tan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arnold van Rooijen, YXJub2xkLnZhbnJvb2lqZW5AcmVzZWFyY2gudXdhLmVkdS5hdQ==
 Arnold van Rooijen
Arnold van Rooijen Ryan Lowe
Ryan Lowe Marco Ghisalberti
Marco Ghisalberti Mario Conde-Frias2,3,5
Mario Conde-Frias2,3,5 Liming Tan
Liming Tan