Effects of Management on the Profitability of Seasonal Fisheries

Ben-Hasan, Abdulrahman; Walters, Carl; Sumaila, U. Rashid

doi:10.3389/fmars.2019.00310

METHODS article

Front. Mar. Sci., 07 June 2019
Sec. Marine Fisheries, Aquaculture and Living Resources
Volume 6 - 2019 | https://doi.org/10.3389/fmars.2019.00310

Effects of Management on the Profitability of Seasonal Fisheries

Abdulrahman Ben-Hasan^*

Carl Walters

U. Rashid Sumaila

Institute for the Oceans and Fisheries, University of British Columbia, Vancouver, BC, Canada

Seasonal fisheries emerge due to a variety of mechanisms: ontogenetic shifts of fish life stages, regulatory initiatives (e. g., fishing seasons) and/or biomass dynamics where there can be a strong seasonal reduction in stock biomass as fisheries harvest a single or double recruiting cohorts each year. The latter mechanism involves targeting species with biological traits including fast growth, high natural mortality and short lifespans; these fisheries have been expanding rapidly over the last 40 years, gaining social and economic importance. In this paper, we underscore the biological and economic dynamics of these fisheries by developing an intraseasonal bioeconomic model to examine the profitability under two situations: open-access and limited entry. We also incorporate the opportunity cost—the earnings that would result from pursuing other lines of work—in our modeling framework. We show that under limited entry situation, profitability is maximized over a given season—when income just balances operating cost per effort. Under open-access, however, net profit per vessel is driven down until it equals the opportunity cost. Biologically, our approach suggests that higher income from alternatives to fishing leads to less biomass depletion than would occur if there were no alternative income sources. To conclude, we discuss several traditional regulatory options and their effects on the distribution of fishing effort and season length.

Introduction

Seasonality in fishing activity, which is described by the temporal structuring of fish populations and fishery dynamics, is evident in numerous fisheries around the world (Clark, 2010; Bjørndal and Munro, 2012). Such a pattern emerges due to a variety of mechanisms, notably: (i) biomass dynamics, as in seasonal fisheries that arise from harvesting a single or a few recruiting cohorts every year (see, for example, Basson et al., 1996; Dichmont et al., 2003; McAllister et al., 2004; Diamond, 2005; Chen et al., 2007); (ii) seasonal availability/catchability, which is associated with the ontogenetic shifts in fish distribution and hence in vulnerability to being captured (e.g., haddock, saithe, and cod; Smith et al., 2016); and (iii) regulatory initiatives, such as fishing seasons, aimed at avoiding overfishing or maximizing the value of the seasonal catch (e.g., commonly implemented in sport fisheries and in jurisdictions like the southeast USA to regulate effort when quotas are unpopular). We focus on the first case, where there can be strong seasonal biomass depletion due to the pursuit of just one or a few fish age cohorts each year; these include species that are short-lived and fast-growing such as Peruvian anchoveta, shrimps, crabs and squids [follows the same references as in point (i) above]. For example, within-season biomass of some major crustacean stocks, such as the Gulf shrimp in the US and the Australian giant mud crab, experience significant reduction throughout the season, where fishing effort rapidly dampens as the stock size becomes economically unviable (Ben-Hasan et al., 2018). Invertebrate fisheries, specifically, have expanded globally over the past 4–6 decades, along with an increasing socioeconomic significance (Anderson et al., 2011; Doubleday et al., 2016). Often such fisheries are regulated by entry limitation programs and seasonal closures; the latter measure is imposed by specifying start dates aimed at preventing growth overfishing while individuals in the recruiting cohort are still small, and closing dates aimed at preventing recruitment overfishing to ensure adequate spawning that produce strong cohorts for later years (e.g., Rosenberg et al., 1990; Watson et al., 1993; Kompas et al., 2004; Rabaoui et al., 2017; Ben-Hasan et al., 2018).

Here, we extend the literature by modeling the economic aspects (income, cost, and profit) of seasonal fisheries using an in-season bioeconomic approach. In our model, we account for the opportunity cost of continuing to fish, since vessel owners that choose to fish also forfeit the potential earnings from doing other gainful activities, such as switching to other types of fisheries or seeking onshore employment. Considering such a cost has significant implications for fisheries management. For instance, Smith et al. (2010) indicated that when planning to implement marine protected areas, decision-makers should be mindful not only of the direct loss of fisher's revenue but also on the opportunity cost if they seek to address concerns of and gain support from the fishing community.

First, we investigate the profitability for cases where total fleet size is either fixed, through limited entry schemes, or increasing between fishing seasons due to lack of regulations (i.e., open-access). We then investigate the sensitivity of the model predictions of catch and biomass to more complex assumptions, namely: heterogeneity in catchability and within-season biomass dynamics. Finally, we explore the temporal distribution of fishing effort under several management options (e.g., ITQs, TACs) using the model framework described below.

Equilibrium Prediction for Fixed Fleet Size

We first examine the economic equilibrium for situations where total fleet size, f, is: (i) fixed by implementing a license limitation program; (ii) there is a fixed fishing season start date, which is set by management agencies; (iii) f is large enough to drive biomass, B, down rapidly through the season, to a biomass level, B_end, where fishers voluntarily stop fishing; (iv) there is no direct interference competition among fishing vessels for favorable fishing sites; (v) there is no spatial variation in the quality of fishing locations; and (vi) the resulting effective fishing season is short enough to ignore biological dynamics (e.g., growth, natural mortality) in predicting in-season biomass change. We show that for this case the end-season biomass, B_end, should depend on price, per-vessel costs, and the relationship between catch per unit effort (cpue) and biomass. Net earnings (annual profit) per vessel should depend on average biomass, B_start, at the beginning of each season, on B_end, on fixed costs for starting to fish, and on fleet size f.

Consider the in-season dynamics of biomass under the above assumptions and assume further that cpue varies with biomass at any time t during the season as a power function of the biomass B_t at that time (0 < t < t_max where t_max < 1.0 is some maximum season length set by either biological or fishing operational factors):

\begin{array}{l} c p u e_{t} = α B_{t}^{β} & (1) \end{array}

where β refers to the density-dependence in catchability q (q increases as biomass decreases if β < 1); and α is expressed as the initial catchability q_o over the initial biomass B_o ( $α = \frac{q_{o}}{B_{o}^{β}}$ ), where q_o is cpue when B = B_o. There is good empirical evidence for this assumption, with the most common case being “hyperstability” β ≪ 1.0 (Hilborn and Walters, 1992; Harley et al., 2001). Indeed, hyperstability arises from a wide range of mechanisms; these mechanisms could be fisheries-related such as improvements in fishing technology or related to the life-history of the harvested species—in particular, species that aggregate for spawning or other purposes like defense (Crecco and Overholtz, 1990; Walters and Maguire, 1996; Sadovy and Domeier, 2005; Erisman et al., 2011). Given equation (1), we expect biomass to decline over time during the season according to the differential equation:

\begin{array}{l} \frac{d B}{d t} = - f (c p u e) = - f α B^{β} & (2) \end{array}

The integral of this rate equation up to time t is given by the relationship:

\begin{array}{l} {B_{t}}^{(1 - β)} = B_{s t a r t}^{(1 - β)} + (β - 1) α f t & (3) \end{array}

(for the case β = 1, the solution reduces to the simple exponential model $B_{t} = B_{s t a r t} e^{- α f t}$ ). Note here that ft is the cumulative fishing effort E_t exerted as of time t. For any fixed value B_t = B_end, end-season effort E_end depends only on the product ft, and fishing season duration t_end is given by:

\begin{array}{l} t_{e n d} = E_{e n d} / f & (4) \end{array}

That is, for any fixed B_end and B_start, t_end is predicted to be simply inversely proportional to fleet size f. It bears noting that the predictions from Equations (3, 4) do not assume effort (and cost) proportional to fleet size. Rather, for all fleet sizes large enough to drive biomass to B_end in t < t_max, the total catch is predicted to remain the same (at B_start − B_end), and fishing mortality rate is predicted to stay at $F = - l n (\frac{B_{e n d}}{B_{s t a r t}})$ , with increases in f resulting in decreasing t_end rather than more harvest.

To predict B_end, we assume that all vessels—being identical—will leave the fishery when the net rate of income (price x cpue) minus the cost per time is brought into equality with the opportunity cost I_o (i.e., the rate of income that the owner can expect to earn by switching to other gainful activities such as fishing for other species or onshore employment), when:

\begin{array}{l} P α B_{t}^{β} - c = I_{o} & (5) \end{array}

where P is price per biomass caught, c is operating cost per time, and I_o is expected income per time for time investment choice other than the fishery (i.e., opportunity cost). Equation (5) immediately implies B_end:

\begin{array}{l} B_{e n d} = {[\frac{I_{o} + c}{α P}]}^{\frac{1}{β}} & (6) \end{array}

Note here that B_end depends on prices, costs, and the cpue parameters, but not on fleet size f; as noted above, f determines only the profitable season length t_end. The sum (I_o+c) in Equation (6) represents “opportunity” plus direct cost of spending time fishing. As we would intuitively expect, B_end should be higher in cases where fishing costs are higher and/or other economic opportunities are good, and should be lower where fishing is more efficient (larger α) and/or prices are higher.

As for the economic quitting time, t_end, the total catch should be equal to B_start − B_end, and the net season profit per vessel (nsp) should be equal to:

\begin{array}{l} n s p = (\frac{B_{s t a r t} - B_{e n d}}{f}) - c t_{e n d} - c_{f i x e d} & (7) \end{array}

where ct_end refers to operating costs that are function of the duration of the fishing season (time to t_end); and c_fixed is the annual fixed cost of entering the fishery (e.g., license fees, carrying costs for loans, etc.). Note here that values of nsp < I_ot_end imply that vessel owners have earned less than they could have by investing time t_end in other gainful activities.

To predict the equilibrium B_start associated with a given economic B_end, we need to use some population dynamics model to predict the average next year's starting biomass as a function of the biomass B_end left after fishing. A realistic and convenient choice for that model is the Schnute-Deriso delay-difference model (Deriso, 1980; Schnute, 1985) for age-structured population dynamics combined with a Beverton-Holt stock-recruitment relationship (Beverton and Holt, 1957), which predicts B_start from B_end as:

\begin{array}{l} B_{s t a r t} = \frac{g B_{e n d} + w_{k} a B_{e n d}}{1 + b B_{e n d}} & (8) \end{array}

where w_k is mean fish weight at recruitment to whatever age k is fully vulnerable to capture, a and b are stock-recruitment parameters, and g is a growth-survival “carryover factor” given by:

\begin{array}{l} g = s (\frac{w_{1}}{\bar{w} + ρ}) & (9) \end{array}

where s is natural annual survival rate, w₁ and ρ are parameters of the body weight growth model (w_a + 1 = w₁ + ρw_a), and w is equilibrium mean body weight of fish aged k and older, given by:

\begin{array}{l} \bar{w} = [s^{*} w_{1} + (1 - s^{*})] / [1 - ρ s^{*}] & (10) \end{array}

where the total annual survival rate $s^{*} = s (B_{e n d} / B_{s t a r t})$ has to be estimated by a simple iterative procedure (since B_start in Equation (8) depends on g which in turn depends on the ratio B_end/B_start through effect of that ratio on w).

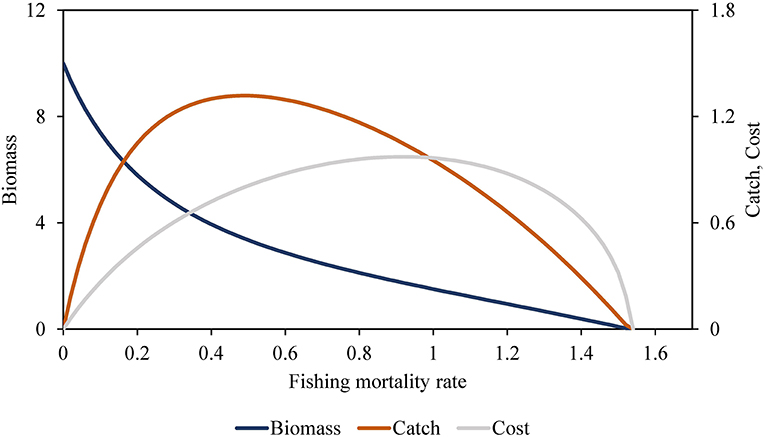
The delay-difference model Equation (8) predicts a monotonic decrease in B_start as B_end decreases, or equivalently monotonic decrease in B_start with increases in the fishing mortality rate, F = −ln(B_end/B_start). As shown in Figure 1, this monotonic relationship predicts a dome-shaped relationship between equilibrium catch (B_start − B_end) and F, with some catch maximum, and also a dome-shaped relationship between F and total profit as measured by (price) (catch) − (ct_end + c_fixed)f. The model can predict both growth overfishing (for low recruitment weight w_k relative to predicted maximum body weight (w₁/(1–ρ)) and recruitment overfishing for low values of B_end (high F).

FIGURE 1

Figure 1. Equilibrium biomass, catch, and cost.

The above model indicates that fishing is lucrative at the start of each season, when the income/effort is positive (i.e., when (price) (cpue) > cost/effort), and vessel owners quit when income/effort = cost/effort (Figures 2A,B). In addition, Figure 2C shows two main trends: accumulation of profit over the fishing season reaching the “profit maximization” point—and a decrease in the difference between net income and cost if fishing were to continue beyond that point.

FIGURE 2

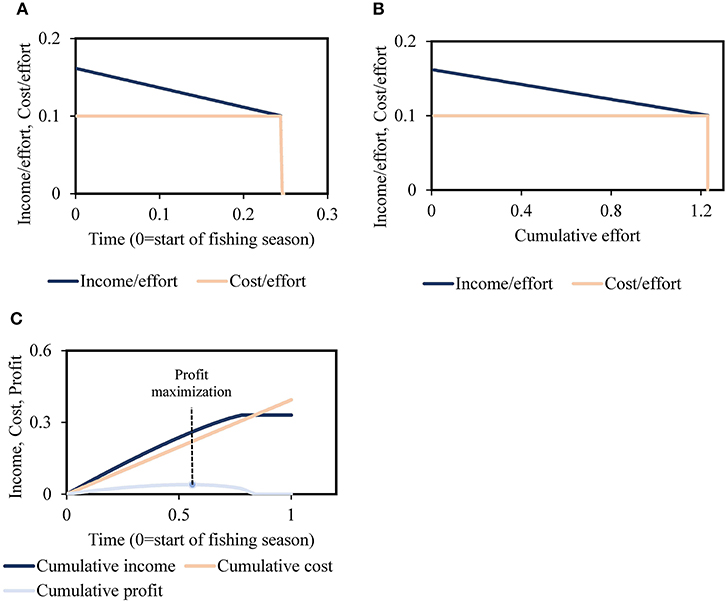
Figure 2. (A) Income/effort and cost/effort as fishing season proceeds, where the fishing season ends at the economic quitting time t_end. (B) Income/effort and cost/effort as fishing effort accumulates. (C) Cumulative income, cost, and profit over a given fishing season.

Prediction of Fleet Size and Profit Under Open-Access

If fishing fleet size f is not fixed through regulation, the existence of relatively high profits as measured by net season profit per vessel, nsp, in Equation (7) exceeding the potential earnings that could be obtained by investing time t_end in other gainful activities, I_ot_end, implies incentive for new vessels to enter the fishery from year to year. That is, fleet size should grow whenever:

\begin{array}{l} P (\frac{B_{s t a r t} - B_{e n d}}{f}) - c t_{e n d} - c_{f i x e d} \geq I_{o} t_{e n d} & (11) \end{array}

But note from Equation (4) that t_end should vary as t_end = E_end/f. Using this relationship, we can predict the fleet size f at which rents per vessel are driven down to just equal expected net income from not fishing, by equating the two sides of Equation (11) and using the E_end prediction of t_end:

\begin{array}{l} f_{e q u i l i b r i u m} = \frac{[P (B_{s t a r t} - B_{e n d}) - E_{e n d} (c + I_{o})]}{c_{f i x e d}} & (12) \end{array}

Note that net total profit for the fleet at this equilibrium is driven down to E_endI_o and profit per vessel is driven down to E_endI_o/f_equilibrium. Also, note that end-season effort E_end depends only on B_start, B_end, and parameters of the cpue biomass relationship where neither B_start or B_end depend on fleet size.

For cases where c_fixed is large, it is possible for the predicted f_equilibrium from Equation (12) to be small enough for the fleet to be unable to drive the stock down to the economic quitting biomass B_end for a season length less than the biological or economic limit t_max. In that case, the fleet should fish until t = t_max, and prediction of f_equilibrium requires a numerical solution scheme because of the highly non–linear dependence of B_start and B_end in Equation (11) on the total effort f_equilibriumt_max. All that we can say in general for such cases is that the overall bionomic equilibrium (B_start, f_equilibrium) will be at a higher B_start (and B_end) than predicted by Equation (12).

Accounting for Seasonal Biomass Dynamics in Annual Species and Variation Among Fishing Vessels in Catchability

In this section, we check two simplifying assumptions made in deriving the model's predictions for seasonal fisheries: (i) we assumed that there is no natural mortality or growth over the season; and (ii) we ignored heterogeneity in individual catchability coefficients (i.e., prediction assumed they all quit at the same seasonal abundance minimum). To examine the effects of more realistic assumptions about the within-season biomass dynamics on the predictions of equilibrium catch and B_end, we predict seasonal dynamics of growth, natural mortality, and harvest for a typical annual penaeid shrimp species, by using growth and mortality rates for the Gulf of Mexico brown shrimp (Farfantepenaeus aztecus; Rothschild and Brunenmeister, 1984). Individuals are assumed to recruit to the fishery at a very small size at the start of the year, then follow a von Bertalanffy growth pattern. They are assumed to die off over the year according to dN/dt = −(F + M)N, where N is numbers of individuals, M is a constant natural mortality rate, and fishing mortality rate F varies with closures and stock biomass. Further, we model the heterogeneity in the catchability of vessels using the approach described in van Poorten et al. (2016), which basically results in a logistic response of total fishing mortality rate (F) to fish biomass over the season, despite hyperstability in cpue caused by increasing mean catchability (fishing skill) of the remaining fishers as those with lower skill—or higher operating cost—stop fishing.

Figures 3A–D compares the unfished biomass, biomass and catch with season-opening time near that giving maximum sustainable yield (corresponding to “Fished biomass” in Figures 3A,B, and “Regulated catch” in Figures 3C,D), and with no restriction so fishers start fishing too early; all panels in Figure 3 include within-season biomass dynamics (growth and natural mortality rates) while (Figures 3B,D) include variation in catchability of fishing vessels (heterogenous fishing fleet). The effects of added realistic assumptions do cause some violations of the within-season assumptions used in the seasonal bioeconomic model; in particular, catches can differ strongly from the simple difference B_start − B_end. But the B_end predictions are robust to the simplifying assumptions (Figures 3A–D), implying the same basic interannual recruitment dynamics and long-term equilibrium as for the simpler model. Further notable information in Figure 3 is the presence of both growth and recruitment overfishing in the “No regulation” case (Figures 3A,B). In addition, we observed that an increase in the variability among fishing vessels causes spawning biomass to decline (i.e., B_end to decline; Figures 3B,D), due to some vessel owners continuing to operate even after most have quit.

FIGURE 3

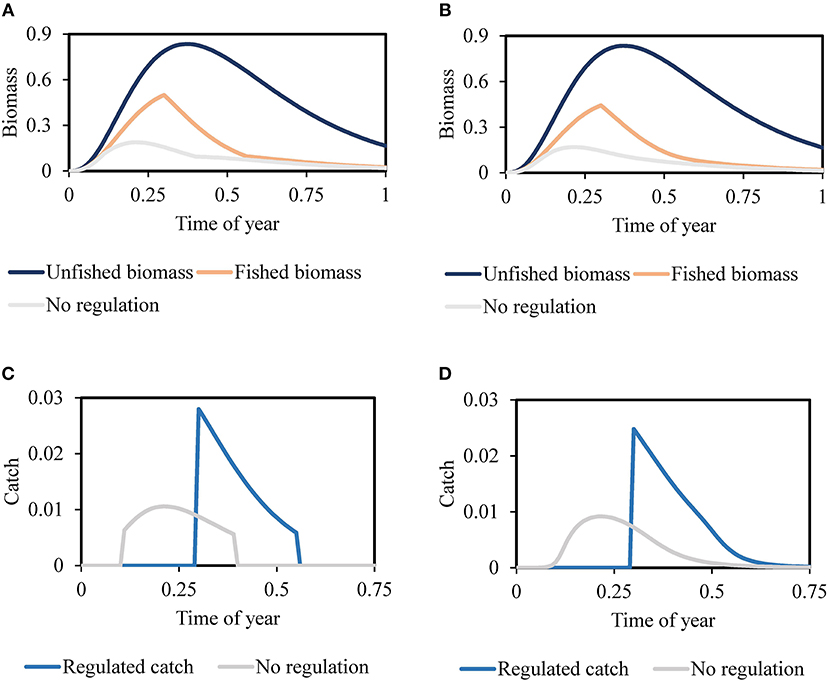
Figure 3. (A) Equilibrium biomass exploited by homogeneous fishing fleet, where “Fished biomass” is the biomass prediction corresponding with season opening time near that giving maximum sustainable yield (Time of year = 0.3) and “No regulation” is the equilibrium biomass pattern under open-access with no season starting date. (B) Equilibrium biomass exploited by a heterogeneous fishing fleet, where “Fished biomass” is the biomass pattern for a season opening time near that giving maximum sustainable yield (Time of year = 0.3) and “No regulation” is the equilibrium biomass pattern under open-access with no season starting date. (C) Equilibrium catch taken by homogeneous fishing fleet, where “Regulated catch” is the catch prediction for season opening time near that giving maximum sustainable yield (Time of year = 0.3) and “No regulation” is the catch prediction under open-access with no season starting date. (D) Equilibrium catch taken by heterogeneous fishing fleet, where “Regulated catch” is the catch prediction for regulated season opening time near that giving maximum sustainable yield (Time of year = 0.3) and “No regulation” reflects the catch estimates under open-access with no season starting date.

Management Policies: Traditional Fisheries Regulatory Options

Suppose that it is ascertained from the analysis of economic B_end and from the population dynamics model behavior (Figure 1) that B_end is likely to involve overfishing. In that case, there should be general support by fishers for regulatory options that move the equilibrium biomass B up to some higher optimal biomass B_opt>B_end, and for use of “harvest control rules” that optimally or at least sensibly vary allowable harvests when (inevitably) there are uncontrollable “stochastic” variations in B_start. These control rule options vary from “fixed escapement” form, where the aim is to allow just enough harvest to end up at a single, time-invariant B_opt every year, to “fixed exploitation rate” options that would set B_opt for each year to a constant fraction of B_start–Hawkshaw and Walters (2015) review the optimization literature that points to these options as the best control rule choices, depending on whether fishers are averse to high interannual variation in catches.

A key prediction from the in-season biomass dynamics model above is that the optimal fishing effort E_opt needed to reduce the stock biomass from any B_start to any target B_opt should vary as:

\begin{array}{l} E_{o p t} = [B_{s t a r t} (1 - β) - B_{o p t} (1 - β)] / [(β - 1) α] & (13) \end{array}

That is, the fishing effort needed to achieve B_opt depends only on the parameters of the cpue-biomass relationship. Modern fisheries managers typically try to avoid direct effort regulation because of concern about increases in catchability (cpue/B) at low stock sizes. Equation (13) directly accounts for that concern through effect of the β parameter; β < 1 implies increasing catchability at low stock sizes. But this does not mean that simple effort regulation, through effort quotas and/or seasonal closures, is the best approach to implementation of harvest control rules. Further, given a management “choice” of B_opt and associated E_opt, along with fleet size f, all of the other equations above involving B_end still apply for calculating quantities—including catch, costs, and net profit.

The ability to predict E_opt from essentially biological expectations or goals along with price and costs does not tell fisheries managers how to equitably distribute that effort. Since E_opt = ft, there are a wide range of choices for regulating f so as to distribute E_opt equitably. That range of choices of course disappears under open-access, though in the open-access case f will increase/decrease until remaining license holders cannot improve their economic position by moving to/from an alternative use of their time (as measured by the opportunity cost I_o). An extreme alternative would be the “sole owner” solution of setting E_opt so as to maximize total profit while setting f to the minimum number of vessels needed by the sole owner to achieve that profit—i.e., by setting the number of vessels so as to minimize the sole owner's fishing cost to achieve the profit. In sum, there are several management choices with different fishing effort and season length distributions:

i) Fix E_opt and vary allowable season length t_opt = E_opt/f as fleet size f changes over time. However, this could result in a pathological decrease in t_opt as f increases. For example, in the British Columbia section of the Pacific halibut fishery, limited entry type program was introduced in 1979, where the management agency strictly limited the number of licensed vessels. However, due to the strong competition among vessel owners for shares of the TAC, the season length was reduced from 60 days per year at the start of the limited entry scheme to 6 days per year by the late 1980s (Knapp, 1996);

ii) Fix E_opt and limit entry (regulate f) so that each license holder's effort share (E_opt/f) results in a “reasonable” profit (e.g., South Australian Spencer Gulf prawn fishery Dixon et al., 2013; Noell and Hooper, 2015);

iii) As in (ii), but implemented by allowing license holders to trade their effort share—such total effort may end up concentrated in the hands of a few efficient owners;

iv) As in (iii), but implemented using tradeable catch shares (ITQs) of the expected allowable catch B_start − B_opt.

Discussion

Our model demonstrated that limited entry fisheries achieve maximum profit from the “seasonal disequilibrium” associated with having a higher stock size (and cpue) at the start of the season than later when vessel owners quit as income per unit effort drops to equal cost per effort. Such dynamics are likely manifested in limited entry fisheries that harvest fast-growing and short-lived species. Owing to the life-history characteristics of the exploited species (e.g., high recruitment variability) and restricted fishing technology, Anderson et al. (2018) indicated that these seasonal fisheries experience minimal capital stuffing, and hence rent dissipation compared with other fisheries operating under limited entry licensing. For example, in Australia's prawn and rock lobster fisheries with restricted entry programs, fishing fleets show strong sensitivity to decreasing income per time fishing when biomass declines, as measured by the difference between the realized and potential fishing efforts represented by multiplying the fleet size f times season length t (Smith and McKelvey, 1986; Walters and Martell, 2004). There are, however, examples where profit has been dissipated: in the Bering Sea/Aleutian Islands crab fisheries and North Carolina brown shrimp, license limitation programs did not actually limit the number of licenses—far too many were issued resulting in derby fisheries (Fina, 2005; Huang and Smith, 2014).

It worth noting that even under optimal license numbers (and when license holders have an individual quota), race for the fish could take place in some seasonal fisheries where fishing opportunities are highly concentrated in space and time (Costello and Deacon, 2007). This occurs because the effort required to take each unit of catch increases as abundance declines, creating an incentive to fish early and to occupy the best fishing spots first. Notable examples are British Columbia and Bristol Bay salmon fisheries, where in the latter example vessel owners compete to situate their nets nearest to the river mouth (Walters, 1998; Anderson et al., 2018).

Assuming unregulated seasonal fishery, our model predicted that profit is driven down until it equals the opportunity cost I_o, which is equivalent to the net income from investing the vessel owners' time in alternative productive activities that earn income rate I_o per time—specifically, until the fleet size is large enough that no owner can improve his/her income (relative to I_o) over the season length by entering the fishery. These dynamics are not uncommon in seasonal open-access fisheries where vessel owners exhibit portfolio diversification: switching from harvesting one species to another—or involve in other non-fishing activities—so as to sustain their economic condition (e.g., Smith and McKelvey, 1986; Olale and Henson, 2012; Ziegler, 2012). Indeed, open-access regimes offer the opportunity to diversify income when fishing is highly seasonal, as opposed to restricted access fisheries where purchasing a permit can be prohibitively expensive (Anderson et al., 2017). Most important, however, implementing limited entry scheme for seasonal fisheries is desirable from the society's point of view—rather than maximizing the profits of fishing firms—because it results in proper allocation of labor and produced capital services for exploiting public natural resources like fish stocks, which ensures a maximum economic return to the public sector income (Anderson, 1986).

We showed that the effects of including more realistic assumptions do not substantially change the prediction of biomass B_end, but do impact the prediction of annual catch. However, further important issues need to be accounted for in future theoretical research; here, our modeling framework provides the initial step in the direction of such research.

For instance, we have not considered in-season price flexibility—notably, in the case where prices are reduced early in the season when daily catches are high, and higher prices later when daily catches plummet. In open-access seasonal fisheries, the expected effects of price flexibility are: (i) reduce overall profitability, since high prices later when cpue is low typically do not make up for lower prices early when catches are high (for example, Burgess et al. (2017) conducted a meta-analysis of price flexibility estimates from about 100 products, where they found that price increases do not make up for catch decreases in terms of revenue); and more important (ii) reduce B_end–make overfishing more likely—by causing fishers to stay out longer when late season prices are higher (Copes, 1970). Additionally, long-term changes in fishing technology, prices, costs, and biological productivity (e.g., recruitment regime shifts) are strongly expected to induce fluctuations in the dynamics of these fisheries.

Data Availability

No datasets were generated or analyzed for this study.

Author Contributions

AB-H, CW, and US: designed the approach and performed the research. AB-H and CW: wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to Matthew Burgess for helpful comments on an earlier version. We also want to thank two reviewers for their constructive comments. AB-H appreciates the financial support from Kuwait University.

References

Anderson, C. M., Krigbaum, M. J., Arostegui, M. C., Feddern, M. L., Koehn, J. Z., Kuriyama, P. T., et al. (2018). How commercial fishing effort is managed. Fish Fish. 25:333. doi: 10.1111/faf.12339

METHODS article

Effects of Management on the Profitability of Seasonal Fisheries

Introduction

Equilibrium Prediction for Fixed Fleet Size

Prediction of Fleet Size and Profit Under Open-Access

Accounting for Seasonal Biomass Dynamics in Annual Species and Variation Among Fishing Vessels in Catchability

Management Policies: Traditional Fisheries Regulatory Options

Discussion

Data Availability

Author Contributions

Conflict of Interest Statement

Acknowledgments

References

People also looked at