Waves and Swells in High Wind and Extreme Fetches, Measurements in the Southern Ocean

The generation and evolution of ocean waves by wind is one of the most complex phenomena in geophysics, and is of great practical significance. Predictive capabilities of respective wave models, however, are impaired by lack of field in situ observations, particularly in extreme Metocean conditions. The paper outlines and highlights important gaps in understanding the Metocean processes and suggests a major observational program in the Southern Ocean. This large, but poorly investigated part of the World Ocean is home to extreme weather around the year. The observational network would include distributed system of buoys (drifting and stationary) and autonomous surface vehicles (ASV), intended for measurements of waves and air-sea fluxes in the Southern Ocean. It would help to resolve the issues of limiting fetches, extreme Extra-Tropical cyclones, swell propagation and attenuation, wave-current interactions, and address the topics of wave-induced dispersal of floating objects, wave-ice interactions in the Marginal Ice Zone, Metocean climatology and its connection with the global climate.

Introduction

The generation and evolution of ocean waves by wind is one of the most complex phenomena in geophysics. Forecasting skill and understanding of these dynamics is critical across a wide range of oceanic applications, including maritime and coastal engineering, air-sea interactions, ocean dynamics, climate, remote sensing. However, the generation and evolution of waves in high-wind conditions and extreme fetches remains poorly understood.

Models are widely inconsistent for large fetch/duration conditions, to a significant extent due to lack of observational guidance. Extreme storms in the North Atlantic and Pacific are seasonal and diverse in their propagation which hinders systematic in situ observations in these regions (e.g., Meucci et al., 2018; Takbash et al., 2018). Also, they usually do not provide extreme fetches. Observations of high-wind conditions with extreme fetch, however, are possible in the Southern Ocean, where these conditions occur regularly and storms move in the same direction (West to East) throughout the year. Swell, which results from such storms in the Southern Ocean radiates into all major ocean basins, but remains poorly predicted by forecast models, both in magnitude and arrival time.

This paper proposes systematic in situ field observations in the Southern Ocean. Understanding the extreme fetch and forcing conditions, and respective advance of the wave models is possible through such observations conducted by means of deployment of a distributed buoy network (drifting and stationary) and autonomous surface vehicles (ASV) in the Southern Ocean. The buoys and ASVs could be deployed from ships of opportunity and through designated efforts of interested countries (e.g., Schulz et al., 2012).

Apart from the extreme fetch and swell problems, such an observational network in the Southern Ocean would address a number of Metocean topics that remain unresolved for decades. The Sections below cover the following unattended problems of Metocean conditions in the World Ocean:

• Wave evolution at extreme fetches;

• Severe extra-tropical cyclones at extreme fetches;

• Swell dynamics and forecasting, with attention to arrival time;

• Wave-driven dispersal of floating objects (search and rescue, transport of microplastic and other pollutants);

• Non-linear wave-current interactions;

• Wave-ice interactions in Marginal Ice Zone subject to extreme storms and waves;

• Metocean climatology in the Southern Ocean.

Wave Evolution at Extreme Fetches

Following the classical paper by Pierson and Moskowitz (1964), it is commonly accepted that there is a limiting condition for wave development such that, for a given wind speed, the significant wave height H_s and peak wavelengths (periods) stop growing. In non-dimensional terms of mean wind speed at standard 10 m height U₁₀ and phase speed of peak waves c_p, the limiting stage of wave development is described by ratio

$$U_{10}/c_p=0.82\left(1\right)$$

which, basically, means that once the dominant waves in a wind-generated field (spectrum) are faster than the wind, the wave development ceases. While intuitively attractive, this concept does not necessarily agree with observations – for example, Young (2006) for Tropical Cyclones and Thomson and Rogers (2014) for lighter winds, demonstrated measurements of wind-generated waves well beyond the PM limit.

Thus, 50+ years after Pierson and Moskowitz, such limit is still in need of validation, clarification, understanding and explaining. While it was purely empirical concept originally, now we can speculate on such a limit from a more advanced physical perception of wind-wave evolution. Such perception includes non-linear interactions which have no regard for the wind and maintain the energy flux to low frequencies (i.e., wave periods larger than the spectral peak), provided the energy flux to the high frequencies continues (e.g., Zakharov and Zaslavskii, 1982). In principle, such behavior would signify no full development, but at some stage the very long waves would be so fast that the friction against the air (no matter how small it is), would balance the weakening non-linear energy influx [e.g., the mechanism for wind-wave interactions when waves overtake the wind in Donelan et al. (2012)].

Not surprisingly, in absence of clear physical guidance, performance of wave-forecast models in the context of full development is contradictory and far from being consistent. While typically tuned to the PM saturation in academic tests, the models hardly ever meet the limiting criteria in realistic simulations. In Figure 1 such comparisons are reproduced from Rogers (2002), for three different physics packages: ST1, ST2, and WAM4, with the first two being from the WAVEWATCH-III model (WW3, Tolman, 2002). In all the cases the mean wind speed is U₁₀ = 15 m/s which, if allowed to persist over unlimited fetch/duration, should lead to ultimate PM wave height of H_s = 5.5 m. None of the models do —they do not even come close — and none reaches another asymptote. This is also true of newer physics packages available in recent versions of WW3 (Wavewatch III^® Development Group, 2016) – ST3, ST4, and ST6 (unpublished). Models in Figure 1 are dissimilar, so at least two are wrong, and probably all three are wrong, but we note that the behavior simulated here is unvalidated, due to scarce observations. Such extreme fetch/duration is a primary “frontier” area for observations, associated with uncertainty in the models.

FIGURE 1

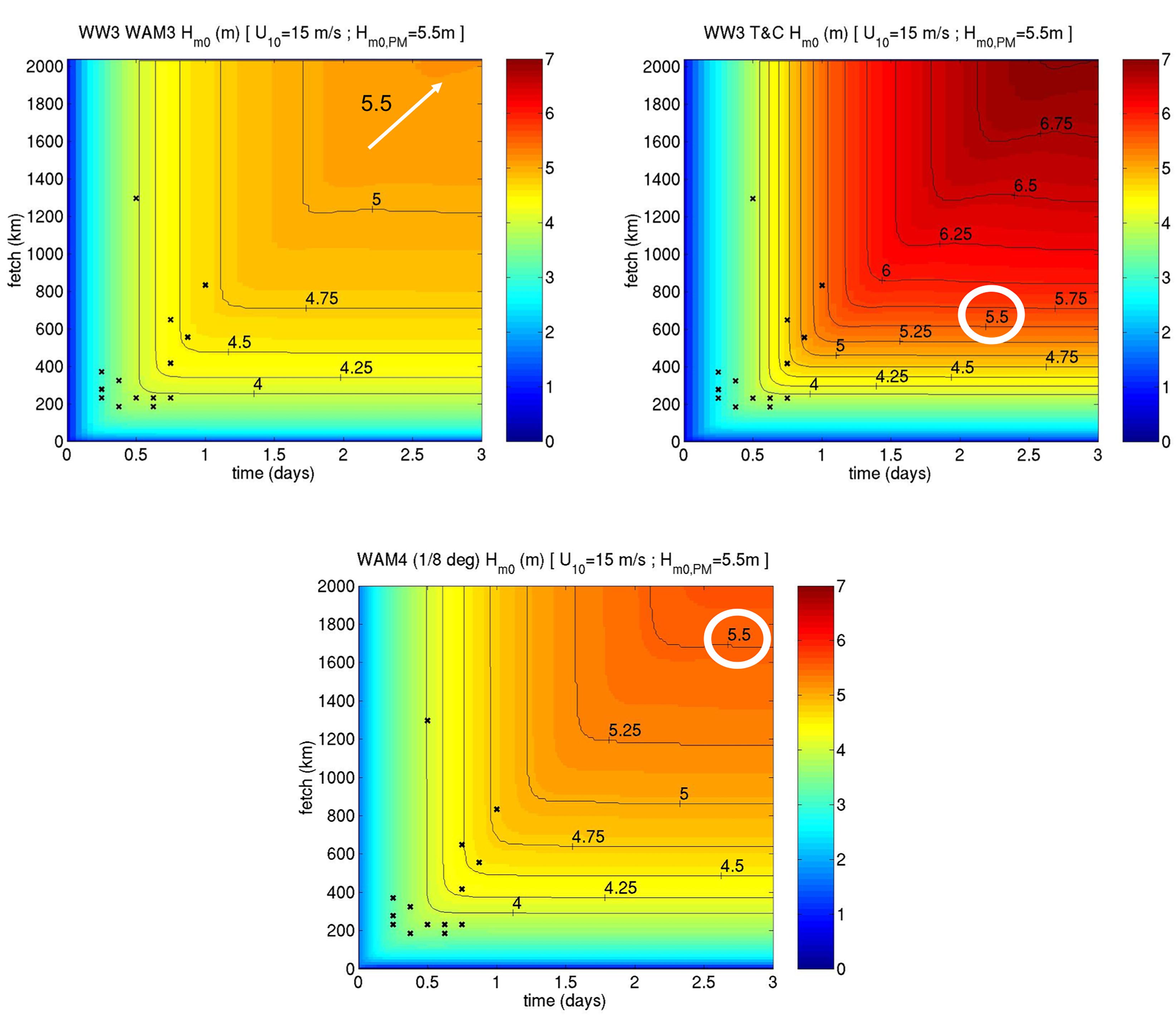
Figure 1. Simulating the PM limit in WW3 (WAM3/ST1, WAM4, ST2 packages from left to right, respectively). U₁₀ = 15 m/s corresponds to PM H_s = 5.5 m. Horizontal scale is duration of wave evolution in days, vertical scale is fetch in kilometers, and color scale is wave height in meters [Figure is reproduced from Rogers (2002)].

In principle, if quasi-full-development exists, it should be easier to reach for lower winds [albeit not in Thomson and Rogers (2014)] than for higher winds. It may never happen for high winds due to very long fetches required, but if it happens anywhere, it would be in the Southern Ocean where, depending on the speed of propagation of extra-tropical cyclones, the fetches can be virtually unlimited. The question of the full development is not hypothetical and/or of pure academic value and interest: lack of understanding of wave evolution at the extreme end of Metocean conditions and wave fetches imposes real limitation on performance of models in circumstances which are most critical for maritime engineering and operations.

Therefore, a network or array of wave buoys (or a set of drifting buoys) in east-west direction in the Southern Ocean would be able to prove or disprove the concept of fully developed limiting stage. Most importantly, such concept, intuitively attractive and most like correct, needs quantification which is only possible on the basis of solid experimental evidence.

Severe Extra-Tropical Cyclones at Extreme Fetches

As a reference point for the extreme Metocean conditions, the hurricane-scale classification is often used: that is a tropical storm becomes a hurricane if the wind speed reaches _U10 ∼ 33 m/s. Babanin (2018) argued that such classification is not arbitrary, and indeed signifies change of physical regimes in all the three environments near the air-sea interface: in the atmospheric boundary layer, at the surface, and through the upper ocean. This threshold is approximately the wind speed at which the drag coefficient was found to saturate in the field observations [U₁₀ ≈ 32–33 m/s, e.g., in Powell et al. (2003)]. This saturation has received a lot of attention lately. Less known are the in situ measurements below the surface, change of the upper-ocean mixing mechanism and of bubble dynamics occur at U₁₀ > 35 m/s (McNeil and D’Asaro, 2007). Directly at the surface, wave dynamics also undergoes essential transformations, from wave breaking (dissipation) being driven by evolution of non-linear waves, to the breaking being forced directly by the winds, at U₁₀ ≈ 34 m/s [Babanin (2011) based on laboratory measurements of Leikin et al. (1995)]. Perhaps related to the wave-breaking change of mechanism is the most striking and abrupt alteration of the gas (CO₂) transfer at U₁₀ = 33.6 m/s in laboratory experiments of Iwano et al. (2013). It is therefore argued that the simultaneous change of physical regime in all the three air-sea environments cannot be coincidental. Such change of the regime means that if we extrapolate our parameterisations from regular conditions into the extreme Metocean environments (which is what we usually do), we will obtain biased or even incorrect results.

It is easy to appreciate the significance of understanding and adequate modeling of waves in such conditions, both for practical and academic purposes, and the associated difficulties which to a large extent are due to lack of respective measurements. What is not appreciated, perhaps due to the lack of observations, is how different are the evolution of such waves in extreme Tropical (TC) and Extra-Tropical (ETC) cyclones. While the waves with H_s in excess of 15 m are not uncommon in both cases [e.g., Young (2006) for TC and Rapizo et al. (2015) for ETC] their directional spectra are very different. Young (2006) based on a large collection of directional spectra in tropical cyclones demonstrated that direction of peak waves does not follow the local wind and, at some quadrants of TCs can be at 90 and even 180 degrees to the wind, whereas in ETCs Rapizo et al. (2015) did not observe unexpected major deviations between wind and wave propagation angles. This means that, while wave evolution in ETC probably follows the direct wind-forcing pattern, in TCs this evolution is different. Young (2006) argued that the presence of large waves propagating perpendicular or even against the wind can only be explained due to the fact that their growth is controlled by non-linear interactions. If so, this is not just an academic curiosity: both the wave-growth dependences and asymptotic behaviors of respective waves will be different (Badulin et al., 2007).

Needless to say, that such differences are not validated and not even accounted for in the current wave forecast. While measurements in Tropical Cyclones are rare, the detailed and consistent measurements in Extreme-Tropical Cyclones are nearly absent. Dedicated effort in the Southern Ocean, where ETCs are continuously present around the year, would be the best observational ground for such extreme Metocean circumstances. Presently, there is only one flux station available at 47 degrees south, 142 degrees East [south of Tasmania Schulz et al. (2012)], and it is proposed that such stations, or air-sea interaction buoys, are deployed south of New Zealand, South America and South Africa. Autonomous surface vehicles (ASV), deployed from ships of opportunity or as a dedicated effort have also proved an efficient way of investigating the air-sea interactions in extreme weather (Schmidt et al., 2017; Thomson and Girton, 2017).

Swell Dynamics and Forecasting, With Attention to Arrival Time

Swell waves are present in most of ocean wave spectra (e.g., Semedo et al., 2011), and provide significant adverse impact on maritime operations and coastal inundation. Their prediction by wave-forecast models, however, is poor, both in terms of wave amplitude and, particularly, arrival time.

The third-generation models, until recently, have entirely based their physics on dynamics and interactions of wind-generated seas. In phenomenological terms, such models simulate the Radiative Transfer Equation [see, e.g., the state-of-the-art review by Cavaleri et al. (2007)]:

$$\frac{dE}{dt}=S_{in}+S_{ds}+S_{nl}\left(2\right)$$

where E is wave spectrum, which changes in space and time and whose integral is the total wave energy, and the right-hand side are sources S_in (from the wind), sinks S_ds (usually due to wave breaking) and redistribution terms S_nl for this energy (more terms are available in specific circumstances, particularly in finite depths). While the forecast based on (2) is applied globally, none of the terms on the right, strictly speaking, applies to the swell: swell is not wind-forced (by definition), swell does not break in deep water because of its low steepness, and the Hasselmann resonant interactions usually employed as S_nl are not applicable to swells because they are unidirectional and therefore cannot satisfy the resonance conditions.

The very definition of ocean swell is ambiguous: while it is usually perceived as former wind-generated waves, in fact it may reconnect with the local wind through non-linear interactions. The visible swell attenuation is driven by a number of dissipative and non-dissipative processes. The dissipative phenomena include interaction with turbulence on the water and air sides (e.g., Babanin, 2006; Ardhuin et al., 2010), with adverse winds or currents (e.g., Donelan, 1999; Babanin et al., 2017, respectively). Non-dissipative contributions to the gradual decline of wave amplitude come from frequency dispersion and directional spreading, refraction by currents, and lateral diffraction of wave energy (e.g., respectively, Ardhuin et al., 2009; Babanin and Waseda, 2015; Rapizo et al., 2018). The interactions with local winds/waves can, on the contrary, cause swell growth (perhaps some observations by Ardhuin et al. (2009) fall into this category).

Swell arrival time is the least understood and the most uncertain problem. Joint analysis of buoy observations and model reanalysis shows that swell can be tens of hours early or late by comparison with model predictions (Jiang et al., 2016), see Figure 2. This is where the lack of model performance incurs the worst consequences: many practical applications related to swell depend not so much on swell height and steepness (which is usually low), but on its presence or absence (operating the tankers, dredging, ports).

FIGURE 2

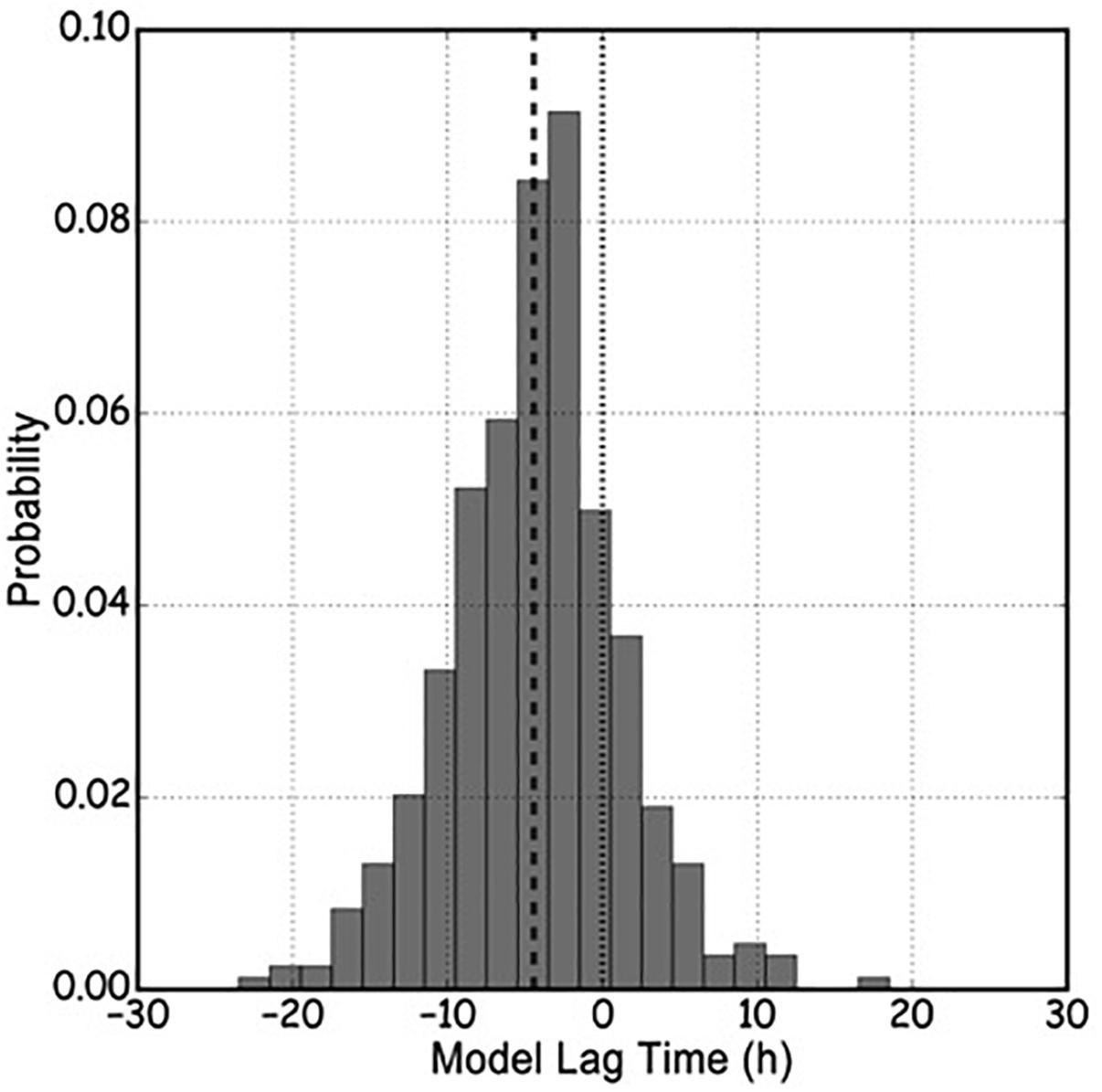
Figure 2. Histogram of relative swell arrival time, model versus buoy observations. Negative values correspond to model predictions being early [Figure is reproduced from Babanin and Jiang (2017)].

Obviously, since the arrival-time error can be both negative and positive, no single physical mechanism can be held responsible for such failure to perform. Rather, this is a combination of various mechanisms, particularly as swells propagate very large distances over vast ocean surfaces and hence even a single swell event can be subject to multiple influences (Babanin and Jiang, 2017). Finite frequency resolution of the initial wave spectrum in a model can be a reason, randomly responsible for early/late arrival, albeit small. For the early arrival, swell has to be accelerating as it moves away from the distant source, such acceleration can be perceived (i.e., short wavelength decaying faster than the longer waves) or real. A real acceleration of waves can be caused, for example, by so-called Raman effect – downshift of wave energy due to modulational instability of non-linear waves in dispersive environments. This effect is well known in non-linear optics (e.g., Gordon, 1986), and has been perceived for the surface waves too (Segur et al., 2005). Interactions of swell with local winds, waves, currents, or a combination of those, can bring about a plethora of accelerating/decelerating effects. For example, adverse currents with horizontal velocity gradient instigate modulational instability and may lead to sudden frequency downshift and propagation acceleration (Babanin et al., 2011). Gradual decrease of wave steepness in the course of wave attenuation should cause slight deceleration of moving swells. Refraction of waves by currents and large-scale eddies, permanent and abundant in the Southern Ocean and at the periphery of other oceans, can bring refraction and sequence of divergence/convergence of swell rays, to result in larger propagation distances and later arrival (e.g., Rapizo et al., 2018). Waves can be trapped by the currents (e.g., Shrira and Slunyaev, 2014) which fact can cause either acceleration or deceleration. Influence of the vertical gradient of surface currents on kinematics of wave orbital motion is likely, but unknown. Shallows and islands, if encountered by swell on its path, should slow it down. Relative to the deep-water value, group velocity is increased in intermediate depth and reduced in shallow depths, and diffraction of waves into the island shade causes reduction of wave energy and hence the velocity.

Field observations of the swell dynamics, however, are even less frequent than those for waves in the tropical cyclones: the three papers by Snodgrass et al. (1966), Ardhuin et al. (2009), and Young et al. (2013) are perhaps close to the exhaustive list. Only the first paper is based on in situ measurements, and the modern studies are remote sensing. The satellites do provide global coverage in nearly real time and are an effective way of estimating swell decay, but they cross the great circles rather than follow swells and, as far as swell arrival time is concerned, in their measurements have to rely on assumptions on the swell propagation speeds, which fact is not helpful since these speeds obviously change as the swell propagates.

Thus, field in situ observations are critical for unveiling the very complex nature of swell problem. A majority of world’s swells are produced by the Southern Ocean storms with its severe weather around the year which radiates swell waves across the Pacific, Indian and South Atlantic Oceans (Aguirre et al., 2017; Portilla-Yandún, 2018, among others). In this regard, it should also be pointed out that, even in its simplest scenario of swell propagation, the main uncertainties in description of swell propagation are within the proximity of ∼4000 km to its source storm (Ardhuin et al., 2009) which fact makes measurements of the Southern Ocean swells close to their origin critical for understanding their nature. Therefore, a network of wave buoys or systematic deployment of drifting wave buoys in the southern parts of the Pacific, Indian and Atlantic Oceans is proposed to address the problem.

Wave-Driven Dispersal of Floating Objects

The spreading of floating objects on the ocean surface is a fundamental problem of fluid mechanics which has a significant practical value, for marine search and rescue, dispersion of pollution. Note that, while mean drift by surface currents and large-scale eddies are well determined nowadays, particularly with implementation of satellite altimetry, random dispersion of surface drifters remains the open problem (e.g., Soomere et al., 2011). In this regard, the impact of ocean waves with random phases and directional spectrum, remains not accounted for or even well-perceived.

The aviation disaster of Malaysian Flight MH370 drew the public attention to the necessity and complexity of oceanic modeling. In particular, it highlighted the fact that, while modeling of the ocean currents is conducted at the top level, there is no coherent and coupled wave-current modeling. Wave orbital velocities can exceed the geostrophic or wind-driven surface currents, and furthermore wave-induced drift and currents can be comparable to the ocean currents, but are unrelated to them both in speed and direction, and therefore search of debris or missing-at-sea people days and even weeks after the incident are essentially impaired without the coupled wave-wind-current approach. Debris (and hence surface pollution and other floating objects) are carried by geostrophic currents, and by wave-induced currents (Stokes drift and momentum passed by wave breaking). The latter cannot be included on average because it is absent if there is no storm in the area and has to be a subject of new modeling development.

Additionally, random waves with directional spectrum would scatter the floating objects. Formally, turbulent dispersion of a passive tracer caused by a random wavefield is similar to the conventional mechanism of the Taylor dispersion (Batchelor and Townsend, 1956), i.e., particle dispersion by a “conventional” turbulent flow, but with the random velocity field is induced by ensemble of random waves (wave turbulence) and not by conventional turbulent flow. This imposes additional analytical and experimental challenges for investigation of this phenomena (e.g., Herterich and Hasselmann, 1982; Balk, 2001; Falkovich, 2009). In some way, this problem is similar to two-dimensional turbulence applications, and hence can borrow from turbulence research, but will also feed back to the fundamental science because the 2D turbulence has received far less attention than its 3D counterpart. And applications of random 2D vorticity, i.e., when vertical scales are much smaller than horizontal scales, range from boundary layers very near the surface to TCs and upper-ocean circulation.

Southern Ocean, if wave buoys with satellite tracking are released as drifters, is the natural body for introducing, developing, investigating, testing and validating the wave-dispersal theories, and implementing them in practice. Innovation due to introduction of the wave scattering can be as big as difference between finding and not finding MH370 and other subjects of search and rescue. Since debris of MH370 have been found along the African coast, location of their origin in the Southern Ocean will require solving the problem of inverse scattering, where new methodology can prove an innovation in its own right. Logistically, this important observational issue can be addresses through deployments of drifting wave buoys in the Southern Ocean as suggested in see Sections “Wave Evolution at Extreme Fetches” and “Severe Extra-Tropical Cyclones at Extreme Fetches.”

Non-Linear Wave-Current Interactions

As far as ocean currents are concerned, these conditions are not common, but are not rare either. Major currents such as Gulf Stream, Kuroshio or Agulhas are well known for harsh seas and high likelihood of abnormal (rogue) waves. Tidal inlets with waves on strong and variable currents are a typical feature of shipping routes in coastal areas. Linear effects of currents on waves, such as refraction, Doppler shift or relative speed with respect to the wind are assumed to be implicitly or explicitly included in wave-forecast models. Our review indicated that in the framework of JCOMM/WMO, since 2001, there is a monthly intercomparison of operational wave model with buoys. Furthermore, operational wave model account for wave/currents interactions by using a surface currents forcing, like the global wave system implemented in Copernicus Marine Service.

Still, absolute majority of the buoys are not located in the Southern Ocean and even the central part of the Atlantic and the Pacific Ocean. So, the validation in the large parts of the ocean, especially at high sea states is mostly missing. Moreover, non-linear effects are usually left out or even unknown. These include changes to non-linear interactions in presence of currents with horizontal or vertical velocity gradients, wave/current energy and momentum exchanges, non-linear modifications of the wave spectrum (Babanin et al., 2017).

Thus the wave-current interactions, along with the topics discussed above and the wave-ice interactions in section below in this article, join the list of the least well performing physics in wave-forecast models. This is largely due to lack of understanding based on observations rather than because of the lack of will to improve the wave forecast in Metocean community. In the meantime, bias in model predictions due to such deficiencies is not negligible, and perhaps somewhat surprisingly is not limited to the specific circumstances of major currents or tidal inlets.

Even such a simple linear effect as refraction-induced convergence and divergence of wave energy have been shown to be important factors in modulating the spatial distribution of wave height on the mesoscale (e.g., Ardhuin et al., 2017). One of the most evident examples of wave refraction is wave trains propagating over mesoscale ocean eddies (Figure 3, left panels). Due to the inverted horizontal current shear, one side of the eddy diverges the incoming wave rays, whereas the other side converges the rays (e.g., Mathiesen, 1987). Rapizo et al. (2018) demonstrated that eddy scales as observed from global current reanalysis can potentially create this effect on Southern Ocean swells, but the main impact of these current on the wave-height bias globally is due to another linear effect – change of relative wind speed for the waves on currents (Figure 3, right panel).

FIGURE 3

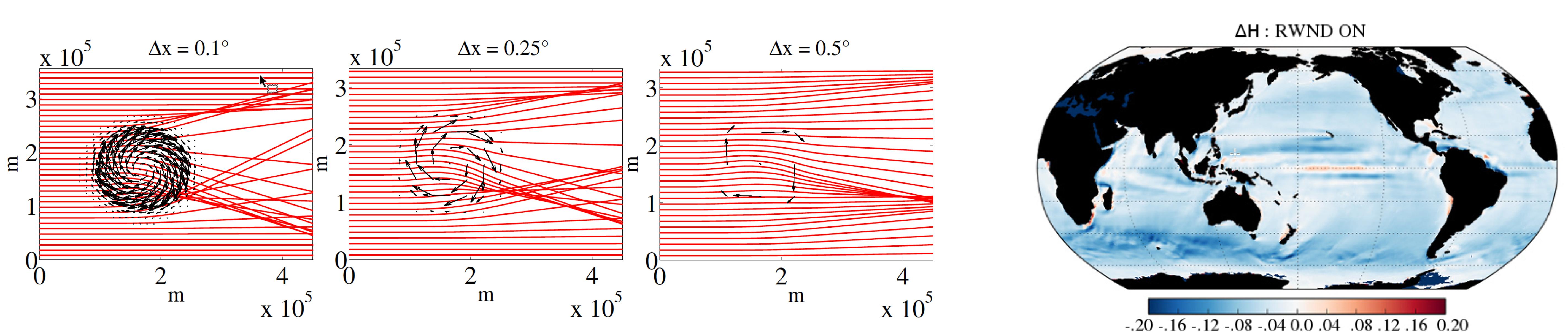
Figure 3. (Left panels) Wave ray refraction on a theoretical eddy. Three different spatial resolutions of the eddy are shown (from left to right): 0.1°, 0.25°, and 0.5°. (Right panel) Difference between H_s fields for the simulations with and without currents, if the option of the relative wind speed with respect to the current is activated [Figure is reproduced from Rapizo et al. (2018)].

Therefore, even linear effects due to currents, which are abundant in the Southern Ocean, have global impact on wave climate and bias of wave modeling. Needless to say that the non-linear wave-current exchanges, which for now not accounted for and not even well understood, can potentially have an enormous influence on the waves due to the very large differences between wave and current kinetic energy. This topic requires a dedicated attention of the community through ongoing satellite observations and through the wave buoy network and drifters proposed in this paper (see sections “Wave Evolution at Extreme Fetches,” “Severe Extra-Tropical Cyclones at Extreme Fetches,” and “Swell Dynamics and Forecasting, With Attention to Arrival Time”).

Wave-Ice Interactions in Marginal Ice Zone

Ice edge and the Marginal Ice Zone in the Southern Ocean, unlike in the Arctic, is subject to continuous wave forcing and extreme storms all round the year and hence is an ideal environment for studying wave-ice interactions. Metocean dynamics of the Antarctic Marginal Ice Zone (MIZ) is a topic of great scientific challenge and practical significance. Until recently, the wave forecast models did not predict waves in MIZ (due to lack of knowledge and capability), and in the large-scale models the waves are mostly not taken into account until now.

In terms of knowledge, the wave forecast models have to describe physical mechanisms of wave energy growth, decay, spectrum transformation and wave propagation – in presence of ice. Even if the wind-wave and non-linear energy exchanges are neglected, as the first step, by comparison with dominant energy process of wave decay in ice, such decay by itself accommodates multiple physical mechanisms of wave attenuation, both conservative (wave scattering, reflection and refraction) and dissipative (viscoelastic, turbulent, among others) – see, e.g., Thomson et al. (2018a). Speed of wave-energy propagation also changes in the ice, and provides a family of new dispersion relationships depending on the ice thickness and other mechanical properties (e.g., Collins et al., 2018). The sea ice is a porous material which consists of solid and liquid (brine) phases, with complex elastic, viscous and flexural behaviors as a function of temperature and water salinity – these behaviors define the wave dissipation and propagation and hence need to be known (Wang and Shen, 2010; Mosig et al., 2015, among others). Ultimately, ice is brittle and subject to fatigue under circulating wave forcing, and waves can break the ice (von Bock und Polac, 2016; Williams et al., 2017; Dolatshah et al., 2018). Once this happens, the waves enter a very different dynamic regime: (a) dissipation is driven by floe collisions, rafting, overwash, depends on distribution of floe sizes, and overall appears orders of magnitude weaker (e.g., Bennetts and Williams, 2015; Squire and Montiel, 2016); (b) wave dispersion (shoaling) adjustment can change sign (e.g., Peters, 1950), and (c) wind-forced growth becomes (possibly) not negligible (e.g., Rogers et al., 2018). Furthermore, the broken ice can melt (and the wave fetches will increase, promoting the wave growth) or can re-freeze (and ice cover will increase, arresting the wave growth) see, e.g., Liu et al. (2016). The former depends, among other processes, on wave-ocean mixing, and the latter on air-sea heat exchange, hence wave forecast in MIZ becomes essentially an air-sea-wave coupled problem (which is less pronounced across the rest of the world’s oceans), see Khon et al. (2014).

Analytical theories for some of the processes outlined above, albeit not all, are available, but quantitative (experimental) guidance is fairly limited: typically, these are case studies rather than non-dimensional parameterisations suitable for global wave modeling in a general case, which conclusion highlights the fact that this kind of measurements are extremely difficult and rare (e.g., Meylan et al., 2014). Thus, advance and even progress in wave forecast is restricted and requires urgent attention, observational in the first place. It should be stressed that the practical problem of wave forecast cannot be approached incrementally – the global wave models are run automatically and require quantitative knowledge of all the above processes, not just some of them or a selection of them, as well as accurate determination of the regime change (ice breakup) – in order to predict waves in MIZ or in the solid ice. For example, if the visco-elastic behavior of ice is known (which it is to some extent), but turbulent dissipation in the water boundary layer below ice is not (which it is not), the wave attenuation cannot be estimated with a reasonable degree of confidence. And if the ice breakup is missed or misplaced by the model, the wave decay, both in time and in space, will be completely off the scale.

In terms of the capability of wave forecast in MIZ, this is not just computing facilities, but mostly operational knowledge on the ice fields which poses predictive limitations. The high-resolution real-time ice information is as essential for modeling wave-ice decay, as good wind fields are for forecasting the wind-wave growth. In this regard, sophisticated analytical theories or precise experimental parameterisations are not helpful if the operational ocean-ice models or satellite observations are not able to provide the relevant properties of ice. Thus, there will always be a gap between research and operational wave modeling, and the practical applications need to balance between exact knowledge and its realistic implementations.

The coupled nature of wave forecast in Antarctica, furthermore, highlights the fact of reciprocal importance of waves for the oceanographic forecast (and, more generally, for air-sea interaction modeling). If waves break the ice and, as a result, it melts faster in spring/summer, this can have significant impact on air-sea fluxes (and not only heat fluxes), even if the ice refreezes in autumn/winter. Note that the first-year ice will be easier to break next summer, and thus the positive feedback loop may accelerate.

Because the presence of waves is more the rule than the exception at the margins of Antarctic ice, this changes the type of ice that forms during the colder months, which can have a profound impact on the heat fluxes and thus the rate of ice growth. Specifically, new ice in the presence of waves will tend to be frazil and pancake ice, and will tend to be sheet ice (starting as nilas) in the case without waves. With pancake and frazil ice, liquid water is directly exposed to the cold air, allowing faster freezing (Doble, 2009). With sheet ice, heat must pass through the insulating ice (thus, slower freezing). The ice type also affects the albedo (so heat flux, again) and the surface roughness (and thus drag on the atmosphere).

Thus, wave-ice interactions, along with the Metocean topics above in this article, is a poorly understood type of ocean-wave dynamics, which, correspondingly, leads to poor performance of wave-forecast models in respective conditions. Like the other topics, the main problem in advancing the fundamental understanding and practical modeling of such conditions is lack of observations, and the most suitable environment for such observations is the Southern Ocean. Necessary observations, in addition to wave and flux observations proposed in see Sections “Wave Evolution at Extreme Fetches,” “Severe Extra-Tropical Cyclones at Extreme Fetches,” and “Swell Dynamics and Forecasting, With Attention to Arrival Time,” will require measurements of wave and ice properties within the Marginal Ice Zone. It is suggested to use Antarctic-going ships of opportunity for this purpose.

Metocean Climatology in the Southern Ocean

The Southern Ocean is the least studied ocean area in terms of in situ oceanographic and Metocean observations. In the meantime, it demonstrates the fastest growth of winds and waves, both in the mean and in extreme percentiles, by comparison with the other Oceans, at least over the era of satellite remote sensing observations, i.e., since mid 1980s (Young et al., 2011). Seasonally, this most dynamic Metocean region is the only one which demonstrates positive trends for the ocean winds well above mean global values over 2/3rds of the year [except Southern spring, see Table 1 and Zieger et al. (2014)].

TABLE 1

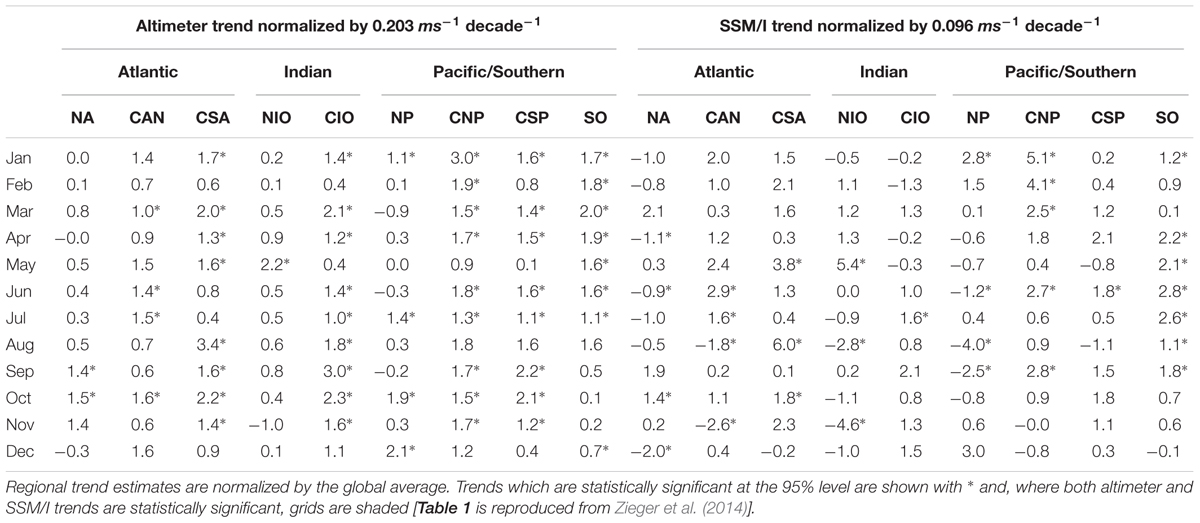
Table 1. Trends in regional average wind speed by calendar month (CNA means Central North Atlantic, SO Southern Ocean, and so on).

Metocean climate, apart from the winds and currents also includes ice-covered area and ice thickness whose trends in the Southern Ocean are different to the Arctic and in need of dedicated investigations. Overall, Metocean characteristics, particularly their consistent trends at large scales in space in time, indicate regional climate changes, which may be also connected to the global climate behaviors. If subject to vigorous measurements, such characteristics and their trends can serve as climate proxies, potentially more robust by comparison with point characteristics (such as temperature) because the nature of Metocean properties is necessarily an integral over large areas.

Thus, major gaps in the global Metocean climatology come from the Southern Ocean where in situ observations, particularly at long-term and systematic basis, are virtually absent. Synergy of the proposed wave and air-sea buoy networks, ice and other Metocean measurements of opportunity (see sections “Wave Evolution at Extreme Fetches,” “Severe Extra-Tropical Cyclones at Extreme Fetches,” “Swell Dynamics and Forecasting, With Attention to Arrival Time,” “Wave-Driven Dispersal of Floating Objects,” “Non-linear Wave-Current Interactions,” and “Wave-Ice Interactions in Marginal Ice Zone”) will help to address this topic of practical and research significance.

Measurements in the Southern Ocean

The paper is proposing a dedicated measurement program for the Southern Ocean, and therefore in this Section we will briefly review available in situ observations. Over the last several years, there have been a number of efforts to start Metocean measurements in the Southern Ocean. Most encouraging are attempts of permanent buoy deployments by the Australian Integrated Marine Observing System (Schulz et al., 2012) and by the Ocean Observatories Initiative of the United States National Science Foundation: https://oceanobservatories.org/array/global-southern-ocean/ (see locations in Figure 4, top panels). A number of moored and drifting buoys were deployed south of New Zealand by the Metocean Solutions and the Royal New Zealand Navy: http://www.metocean.co.nz/southern-ocean/ (Figure 4, bottom left); Metocean observations are conducted by the University of Cape Town in oceanographic voyages of SA Agulhas II in the Southern African sector of the South Ocean all the way to Marginal Ice Zone (Figure 4, bottom right).

FIGURE 4

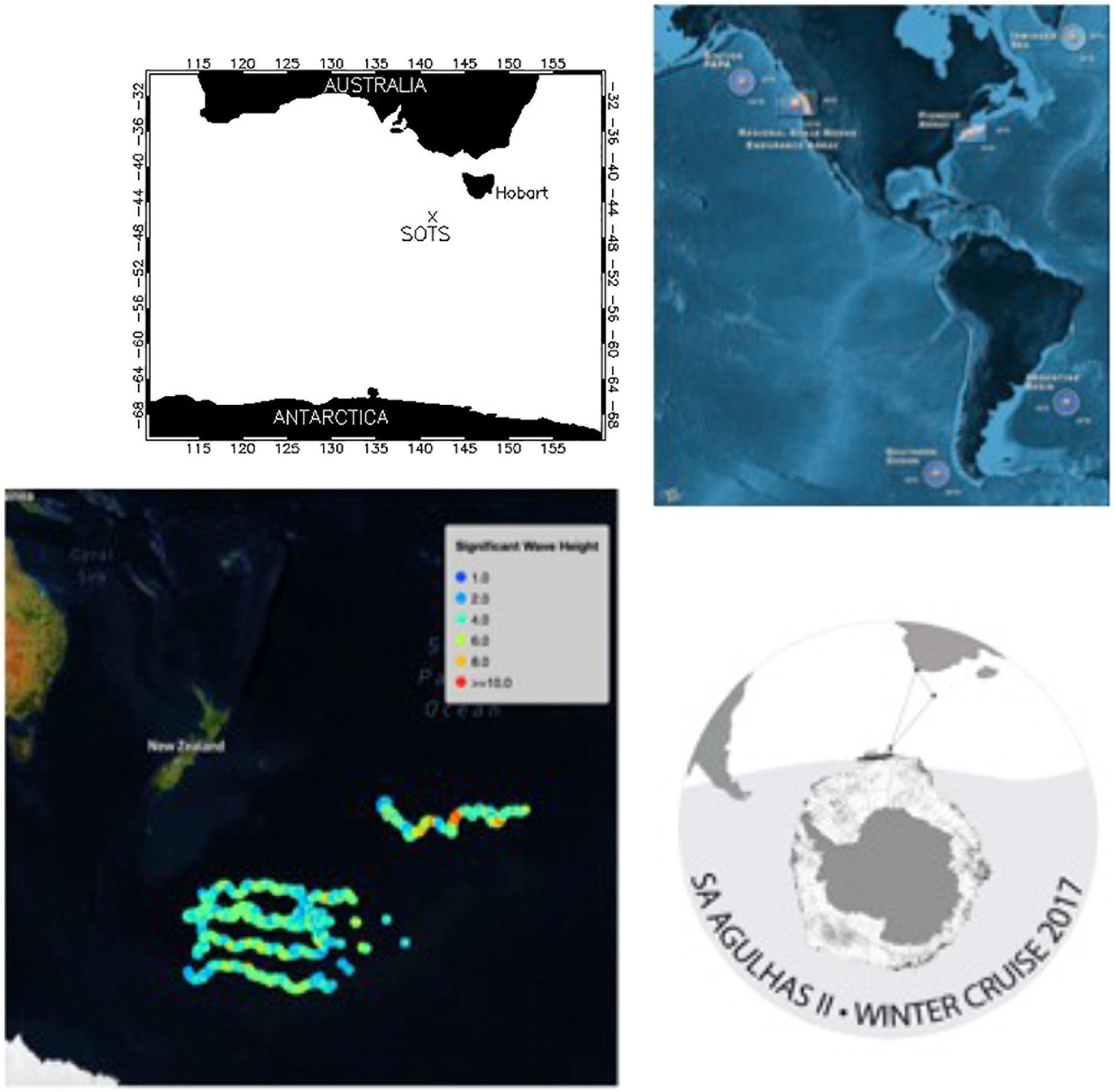
Figure 4. Locations of the Southern Ocean permanent and drifting wave buoys by (top left) Australian Bureau of Meteorology, (top right) United States NSF Ocean Observatories Initiative, (bottom left) Metocean Solutions, New Zealand; (bottom right) SA Agulhas II 2017 winter cruise.

Recently, some investigators have begun using autonomous platforms for Metocean measurements in the Southern Ocean. Thomson and Girton (2017) used a wave glider in the Drake Passage during the austral summer of 2017, with a particular focus on measuring directional wave spectra and wind stress (Thomson et al., 2018b). Schmidt et al. (2017) also use a wave glider to evaluate model winds in the Southern Ocean. These and other mobile platforms continues to operate in 2018–2019. Thus, an expansion of in situ wave observations from autonomous surface platforms in addition to traditional moorings, is also likely.

These few deployments, however, while very promising, is literally a drop in the ocean of the most powerful winds and waves. Hundreds of the wind-wave buoys in the Northern Hemisphere, and very few South of equator such as those off the coast of Brazil in the path of Southern swells (Pereira et al., 2017). Figure 5¹ highlights the importance of the Metocean observations, and the emptiness of the Southern Ocean where most of the actual problems of the modern Metocean science and applications can and need to be solved (Young et al., 2017). While permanent buoy deployments can be a substantial challenge, drifting buoys, wave gliders and other moving platforms can prove feasible and valuable solution of this challenge for a dedicated international effort.

FIGURE 5

Figure 5. Locations of wave (top) and wind (bottom) measurements.

For an area as geographically remote as the Southern Ocean, remote sensing offers obvious benefits in providing wind and wave data. In terms of wind measurements, there are three potential platforms (radiometers, scatterometers and altimeters). For wave data there are also three options (altimeters, synthetic aperture radar and CFOSat). A number of studies have already looked at global climatology of wind speed and wave height, including the Southern Ocean (Zieger et al., 2009; Vinoth and Young, 2011; Young et al., 2011, 2017; Takbash et al., 2018; Young and Donelan, 2018; Ribal and Young, 2019; Young and Ribal, 2019). These studies, however, are limited to wind speed and significant wave height and suffer from very limited possibilities for Southern Ocean Calibrations.

Our capability to measure directional waves, up to the early 1990s with the launch of ERS-1, was restricted to few areas in the world where buoy data, mainly, was available. Synthetic Aperture Radar (SAR) is the only satellite instrument so far capable to measure the directional spectrum, despite some limitations in its high frequency part. SAR data have been available since then, with a myriad of satellites yielding over 25 years of directional spectra with global coverage. Sentinel-1A and its twin 1B are currently operational, sharing the same orbit plane and therefore with a greater revisit rate. Sentinel-1C is scheduled to be launched in the next 3–4 years, which will increase the temporal sample of the constellation. The recent launch of CFOSat, which carries a unique scanning wave scatterometer (SWIM) provides the potential to measure the full directional spectrum for components longer than 80 m. This instrument has great potential to open up a new era of wave measurements in environments such as the Southern Ocean. In the context of the proposed network, directional buoy measurements in the scarcely sampled Southern Hemisphere will contribute to the effort to validate such satellite wave observations.

Conclusion

Metocean measurements in the Southern Ocean – marine winds and currents, surface waves and swells, ice cover and thickness, among others – are either critically important or, at the very least, can contribute to solving and addressing problems of major significance. Without the Southern Ocean in situ observations, it is not possible to resolve the issues of limiting fetches, extreme Extra-Tropical cyclones, swell propagation and attenuation, wave-current interactions. The topics of wave-induced dispersal of floating objects, wave-ice interactions in the Marginal Ice Zone, Metocean climatology and its connection with the global climate cannot be complete in general case without benchmarking the behaviors of these phenomena against observations in this most dynamic area of the global Ocean.

The paper outlines and highlights important gaps in understanding the Metocean processes and suggests a major observational program for this large, but poorly investigated part of the World Ocean. This would include distributed buoy network (drifting and stationary) and autonomous surface vehicles (ASV), intended for measurements of waves and air-sea fluxes in the Southern Ocean.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

MD (Polar Scientific), TD and PM (Oceanum), KE (MetOcean Research), TJ (Spoondrift Technologies), and GW (RPS MetOcean) were employed by their respective companies.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^ https://protect-au.mimecast.com/s/QcHoCZYMPyCgGNqJizxmHV?domain=jcommops.org

References

Aguirre, C., Rutllant, J. A., and Falve, M. (2017). Wind waves climatology of the Southeast Pacific Ocean. Int. J. Climatol. 37, 4288–4301. doi: 10.1002/joc.5084

CrossRef Full Text | Google Scholar

Ardhuin, F., Chapron, B., and Collard, F. (2009). Observation of swell dissipation across oceans. Geophys. Res. Lett. 36:L06607. doi: 10.1029/2008GL037030

CrossRef Full Text | Google Scholar

Ardhuin, F., Gille, S. T., Menemenlis, D., Rocha, C. B., Rascle, N., Chapron, B., et al. (2017). Small-scale open ocean currents have large effects on wind wave heights. J. Geophys. Res. 122, 4500–4517. doi: 10.1002/2016JC012413

CrossRef Full Text | Google Scholar

Ardhuin, F., Rogers, E., Babanin, A., Filipot, J.-F., Magne, R., Roland, A., et al. (2010). Semi-empirical dissipation source functions for ocean waves. part I: definitions, calibration and validations. J. Phys. Oceanogr. 40, 1917–1941.

Google Scholar

Babanin, A. V. (2006). On a wave-induced turbulence and a wave-mixed upper ocean layer. Geophys. Res. Lett. 33:L20605. doi: 10.1029/2006GL027308

CrossRef Full Text | Google Scholar

Babanin, A. V. (2011). Breaking and Dissipation of Ocean Surface Waves. Cambridge: Cambridge University Press, 480.

Google Scholar

Babanin, A. V. (2018). “Change of regime of air-sea dynamics in extreme Metocean conditions,” in Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering OMAE2018, Madrid.

Google Scholar

Babanin, A. V., Hwung, H.-H., Shugan, I., Roland, A., van der Westhuysen, A., Chawla, A., et al. (2011). “Nonlinear waves on collinear currents with horizontal velocity gradient,” in Proceedings of the 12th International Workshop on Wave Hindcasting and Forecasting and 3rd Coastal Hazards Symposium, Big Island.

Google Scholar

Babanin, A. V., and Jiang, H. (2017). “Ocean swell, how much do we know,” in Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering OMAE2017, Trondheim.

Google Scholar

Babanin, A. V., van der Westhuysen, A., Chalikov, D., and Rogers, W. E. (2017). Advanced wave modelling including wave-current interaction. J. Mar. Res. 75, 239–262.

Google Scholar

Babanin, A. V., and Waseda, T. (2015). “Diffraction and instability of short-crested limited-length one-dimensional coherent wave trains,” in Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering OMAE2015, St John’s, NL.

Google Scholar

Badulin, S. I., Babanin, A. V., Zakharov, V. E., and Resio, D. (2007). Weakly turbulent laws of wind-wave growth. J. Fluid Mech. 591, 339–378.

Google Scholar

Balk, A. M. (2001). Anomalous diffusion of a tracer advected by wave turbulence. Phys. Lett. A 279, 370–378.

Google Scholar

Batchelor, G. K., and Townsend, A. A. (1956). “Turbulent diffusion,” in Surveys in Mechanics, eds G. K. Batchelor and H. Bondi (Cambridge: Cambridge University Press), 352–399.

Google Scholar

Bennetts, L. G., and Williams, T. D. (2015). Water wave transmission by an array of floating discs. Proc. R. Soc. A 471:20140698. doi: 10.1098/rspa.2014.0698

CrossRef Full Text | Google Scholar

Cavaleri, L., Alves, J.-H. G. M., Ardhuin, F., Babanin, A., Banner, M., Belibassakis, K., et al. (2007). Wave modelling – the state of the art. Progr. Oceanogr. 75, 603–674.

Google Scholar

Collins, C., Doble, M., Lund, B., and Smith, M. (2018). Observations of surface wave dispersion in the marginal ice zone. J. Geophys. Res. Oceans 123, 3336–3354. doi: 10.1029/2018JC013788

CrossRef Full Text | Google Scholar

Doble, M. J. (2009). Simulating pancake and frazil ice growth in the Weddell Sea: a process model from freezing to consolidation. J. Geophys. Res. 114:C09003. doi: 10.1029/2008JC004935

CrossRef Full Text | Google Scholar

Dolatshah, A., Nelli, F., Bennetts, L. G., Alberello, A., Meylan, M. H., Monty, J. P., et al. (2018). Hydroelastic interactions between water waves and floating freshwater ice. Phys. Fluids 30:091702.

Google Scholar

Donelan, M. A. (1999). “Wind-induced growth and attenuation of laboratory waves,” in Wind-Over-Wave Couplings. Perspective and Prospects, eds S. Sajadi, N. H. Thomas, and J. C. R. Hunt (Oxford: Clarendon Press),183–194.

Google Scholar

Donelan, M. A., Curcic, M., Chen, S. S., and Magnusson, A. K. (2012). Modeling waves and wind stress. J. Geophys. Res. 117:C00J23.

PubMed Abstract | Google Scholar

Falkovich, G. (2009). Could waves mix the ocean? J. Fluid Mech. 638, 1–4. doi: 10.1017/S0022112009991984

CrossRef Full Text | Google Scholar

Gordon, J. P. (1986). Theory of the soliton self-frequency shift. Opt. Lett. 11, 662–664.

Google Scholar

Herterich, K., and Hasselmann, K. (1982). The horizontal diffusion of tracers by surface waves. J. Phys. Oceanogr. 12, 704–712.

Google Scholar

Iwano, K., Takagaki, N., Kurose, R., and Komori, S. (2013). Mass transfer velocity across the breaking air-water interface at extremely high wind speeds. Tellus B 65:21341. doi: 10.3402/tellusb.v65i0.21341

CrossRef Full Text | Google Scholar

Jiang, H., Babanin, A. V., and Chen, G. (2016). Event-based validation of swell arrival time. J. Phys. Oceanogr. 46, 3563–3569.

Google Scholar

Khon, V. C., Mokhov, I. I., Pogarskiy, F. A., Babanin, A. V., Dethloff, K., Rinke, A., et al. (2014). Wave heights in the 21st century Arctic Ocean simulated with a regional climate model. Geophys. Res. Lett. 41, 2956–2961. doi: 10.1002/2014GL059847

CrossRef Full Text | Google Scholar

Leikin, I. A., Donelan, M. A., Mellen, R. H., and McLaughlin, D. J. (1995). Asymmetry of wind generated waves studied in a laboratory tank. Nonlin. Process. Geophys. 2, 280–289.

Google Scholar

Liu, Q., Babanin, A. V., Zieger, S., Young, I. R., and Guan, C. (2016). Wind and wave climate in the Arctic Ocean as observed by altimeters. J. Clim. 29, 7957–7975.

Google Scholar

Mathiesen, M. (1987). Wave refraction by a current whirl. J. Geophys. Res. 92, 3905–3912. doi: 10.1029/JC092iC04p03905

CrossRef Full Text | Google Scholar

McNeil, C., and D’Asaro, E. (2007). Parameterization of air-sea gas fluxes at extreme wind speeds. J. Mar. Sys. 66, 110–121.

Google Scholar

Meucci, A., Young, I. R., and Breivik, O. (2018). Wind and wave extremes from atmosphere and wave model ensembles. J. Clim. 31, 8819–8843. doi: 10.1175/JCLI-D-18-0217.1

CrossRef Full Text | Google Scholar

Meylan, M., Bennetts, L. G., and Kohout, A. (2014). In situ measurements and analysis of ocean waves in the Antarctic marginal ice zone. Geophys. Res. Lett. 41, 5046–5051. doi: 10.1002/2014GL060809

CrossRef Full Text | Google Scholar

Mosig, J. E. M., Montiel, F., and Squire, V. A. (2015). Comparison of viscoelastic-type models for ocean wave attenuation in ice-covered seas. J. Geophys. Res. Oceans 120, 6072–6090.

Google Scholar

Pereira, H. P. P., Violante-Carvalho, N., Nogueira, I. C. M., Babanin, A. V., Liu, Q., de Pinho, U., et al. (2017). Wave observations from an array of directional buoys over the Southern Brazilian Coast. Ocean Dyn. 67, 1577–1591. doi: 10.1007/s10236-017-1113-9

CrossRef Full Text | Google Scholar

Peters, A. S. (1950). The effect of a floating mat on water waves. Commun. Pure Appl. Math. 3, 319–354.

Google Scholar

Pierson, W. J. Jr., and Moskowitz, L. (1964). A proposed spectral form for fully developed wind seas based on the similarity theory of S.A. Kitaigorodskii. J. Geophys. Res. 69, 5181–5190.

Google Scholar

Portilla-Yandún, J. (2018). The global signature of Ocean wave spectra. Geophys. Res. Lett. 45, 267–276. doi: 10.1002/2017GL076431

CrossRef Full Text | Google Scholar

Powell, M. D., Vickery, P. J., and Reinhold, T. A. (2003). Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 422, 279–283.

PubMed Abstract | Google Scholar

Rapizo, H., Babanin, A. V., Schulz, E., Hemer, M. A., and Durrant, T. H. (2015). Observation of wind-waves from a floating buoy in the Southern Ocean. Ocean Dyn. 75, 1275–1288. doi: 10.1007/s10236-015-0873-3

CrossRef Full Text | Google Scholar

Rapizo, H., Durrant, T., and Babanin, A. V. (2018). An assessment of the impact of surface currents on wave modeling in the Southern Ocean. Ocean Dyn. 67, 1577–1591. doi: 10.1007/s10236-018-1171-7

CrossRef Full Text | Google Scholar

Ribal, A., and Young, I. R. (2019). 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 6:77. doi: 10.1038/s41597-019-0083-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers, W. E. (2002). The U.S. Navy’s Global Wind-Wave Models: An Investigation into Sources of Errors in Low-Frequency Energy Predictions. Washington, DC: NRL.

Google Scholar

Rogers, W. E., Posey, P., Li, L., and Allard, R. (2018). Forecasting and Hindcasting Waves In and Near the Marginal Ice Zone: Wave Modeling and the ONR ”Sea State” Field Experiment. Washington, DC: Naval Research Laboratory.

Google Scholar

Schmidt, K., Swart, S., Reason, C., and Nicholson, S. (2017). Evaluation of satellite and reanalysis wind products with in situ Wave Glider wind observations in the Southern Ocean. J. Ocean Atm. Tech. 34, 2551–2568. doi: 10.1175/JTECH-D-17-0079.1

CrossRef Full Text | Google Scholar

Schulz, E., Josey, S. A., and Verein, R. (2012). First air-sea flux mooring measurements in the southern ocean. Geophys. Res. Lett. 39:L16606. doi: 10.1029/2012GL052290

CrossRef Full Text | Google Scholar

Segur, H., Henderson, D., Carter, J., Hammack, J., Li, C.-M., Pheiff, D., et al. (2005). Stabilizing the benjamin-feir instability. J. Fluid Mech. 539, 229–271.

Google Scholar

Semedo, A., Suselj, K., Rutgersson, A., and Sterl, A. (2011). A Global View on the Wind Sea and Swell Climate and Variability from ERA-40. J. Clim. 24, 1461–1479.

Google Scholar

Shrira, V. I., and Slunyaev, A. V. (2014). Nonlinear dynamics of trapped waves on jet currents and rogue waves. Phys. Rev. E 89:041002.

PubMed Abstract | Google Scholar

Snodgrass, F. E., Groves, G. W., Hasselmann, K., Miller, G. R., Munk, W. H., Powers, W. H., et al. (1966). Propagation of ocean swell across the Pacific. Philos. Trans. R. Soc. Lond. A 249, 431–497.

Google Scholar

Soomere, T., Viidebaum, M., and Kalda, J. (2011). On dispersion properties of surface motions in the Gulf of Finland. Proc. Eston. Acad. Sci. 60, 269–279.

Google Scholar

Squire, V., and Montiel, F. (2016). Evolution of directional wave spectra in the marginal ice zone: a new model tested with legacy data. J. Phys. Oceanogr. 46, 3121–3137.

Google Scholar

Takbash, A., Young, I. R., and Breivik, O. (2018). Global wind speed and wave height extremes derived from satellite records. J. Clim. 32, 109–126. doi: 10.1175/JCLI-D-18-0520.1

CrossRef Full Text | Google Scholar

Thomson, J., Ackley, S., Girard-Ardhuin, F., Ardhuin, F., Babanin, A. V., Boutin, G., et al. (2018a). Overview of the Arctic Sea State and Boundary layer physics program. J. Geophys. Res. 123, 8674–8687. doi: 10.1002/2018JC013766

CrossRef Full Text | Google Scholar

Thomson, J., Girton, J., Jha, R., and Trapani, A. (2018b). Measurements of directional wave spectra and wind stress from a wave glider autonomous surface vehicle. J. Atmos. Ocean Tech. 35, 347–363.

Google Scholar

Thomson, J., and Girton, J. (2017). Sustained measurements of Southern Ocean air-sea coupling from a wave glider autonomous surface vehicle. Oceanogr. Magaz. 30, 104–109.

Google Scholar

Thomson, J., and Rogers, W. E. (2014). Swell and sea in the emerging Arctic Ocean. Geophys. Res. Lett. 41, 3136–3140.

Google Scholar

Tolman, H. L. (2002). User Manual and System Documentation of WAVEWATCH-III Version 2.22 Technical Note. Silver Spring: NOAA.

Google Scholar

Vinoth, J., and Young, I. R. (2011). Global estimates of extreme wind speed and wave height. J. Clim. 24, 1647–1665. doi: 10.1175/2010JCLI3680.1

CrossRef Full Text | Google Scholar

von Bock und Polac, R. U. F. (2016). The Mechanical Behavior of Model-Scale Ice: Experiments, Numerical Modeling and Scalability. Helsinki: Aalto University publication. Doctoral Dissertation.

Wang, R., and Shen, H. H. (2010). Gravity waves propagating into an ice-covered ocean: a viscoelastic model. J. Geophys. Res. Oceans 115, 1–12.

Google Scholar

Wavewatch III^® Development Group (2016). User Manual and System Documentation of WAVEWATCH III^® Version 5.16. Tech. Note 329. College Park, MD: NOAA.

Google Scholar

Williams, T. D., Rampal, P., and Bouillon, S. (2017). Wave–ice interactions in the neXtSIM sea-ice model. Cryosphere 11, 2117–2135. doi: 10.5194/tc-11-2117-2017

CrossRef Full Text | Google Scholar

Young, I. R. (2006). Directional spectra of hurricane wind waves. J. Geophys. Res. 111, 1–14.

Google Scholar

Young, I. R., Babanin, A. V., and Zieger, S. (2013). The decay rate of ocean swell observed by altimeter. J. Phys. Oceanogr. 43, 2322–2333.

Google Scholar

Young, I. R., and Donelan, M. A. (2018). On the determination of global ocean wind and wave climate from satellite observations. Remote Sens. Environ. 215, 228–241. doi: 10.1016/j.rse.2018.06.006

CrossRef Full Text | Google Scholar

Young, I. R., and Ribal, A. (2019). Multi-platform evaluation of global trends in wind speed and wave height. Science 364, 548–552. doi: 10.1126/science.aav9527

PubMed Abstract | CrossRef Full Text | Google Scholar

Young, I. R., Sanina, E., and Babanin, A. V. (2017). Calibration and cross-validation of a global wind and wave database of altimeter, radiometer and scatterometer measurements. J. Atmos. Ocean. Technol. 34, 1285–1306. doi: 10.1175/JTECH-D-16-0145

CrossRef Full Text | Google Scholar

Young, I. R., Zieger, S., and Babanin, A. V. (2011). Global trends in wind speed and wave height. Science 332, 451–455. doi: 10.1126/science.1197219

PubMed Abstract | CrossRef Full Text | Google Scholar

Zakharov, V. E., and Zaslavskii, M. M. (1982). Kinetic equation and Kolmogorov’s spectra in a week turbulence theory of wind waves. Izv. Akad. Nauk SSSR, Fiz. Atmos. Okeana 18, 970–979.

Google Scholar

Zieger, S., Babanin, A. V., and Young, I. R. (2014). Changes in ocean surface winds with a focus on trends of regional and monthly mean values. Deep Sea Res. Part 1 86, 56–67.

Google Scholar

Zieger, S., Vinoth, J., and Young, I. R. (2009). Joint calibration of multi-platform altimeter measurements of wind speed and wave height over the past 20 years. J. Atmos. Ocean. Tech. 26, 2549–2564. doi: 10.1175/2009JTECHA1303.1

CrossRef Full Text | Google Scholar