Advancing Observation of Ocean Biogeochemistry, Biology, and Ecosystems With Cost-Effective in situ Sensing Technologies

Advancing our understanding of ocean biogeochemistry, biology, and ecosystems relies on the ability to make observations both in the ocean and at the critical boundaries between the ocean and other earth systems at relevant spatial and temporal scales. After decades of advancement in ocean observing technologies, one of the key remaining challenges is how to cost-effectively make measurements at the increased resolution necessary for illuminating complex system processes and rapidly evolving changes. In recent years, biogeochemical in situ sensors have been emerging that are threefold or more lower in cost than established technologies; the cost reduction for many biological in situ sensors has also been significant, although the absolute costs are still relatively high. Cost savings in these advancements has been driven by miniaturization, new methods of packaging, and lower-cost mass-produced components such as electronics and materials. Recently, field projects have demonstrated the potential for science-quality data collection via large-scale deployments using cost-effective sensors and deployment strategies. In the coming decade, it is envisioned that ocean biogeochemistry and biology observations will be revolutionized by continued innovation in sensors with increasingly low price points and the scale-up of deployments of these in situ sensor technologies. The goal of this study is therefore to: (1) provide a review of existing sensor technologies that are already achieving cost-effectiveness compared with traditional instrumentation, (2) present case studies of cost-effective in situ deployments that can provide insight into methods for bridging observational gaps, (3) identify key challenge areas where progress in cost reduction is lagging, and (4) present a number of potentially transformative directions for future ocean biogeochemical and biological studies using cost-effective technologies and deployment strategies.

Introduction

The biogeochemistry and biology of the ocean play a central role in regulating climate, providing resources for humankind, and shaping the world’s economy. However, over the recent centuries, profound changes, such as ocean acidification, deoxygenation, pollution, habitat loss, and loss of biodiversity, have taken place (Le Quere et al., 2010; IPCC, 2014; Yang et al., 2016; FAO, 2018; Moustahfid et al., 2018). Understanding these changes is critical for maintaining climate stabilization, marine ecosystem health (Brehmer et al., 2011), sustainability of fisheries (Pauly et al., 2002), and other societally relevant issues, thus making ocean biogeochemistry and biology observation a high research priority.

One fundamental challenge for monitoring and studying ocean biogeochemistry and biology is that oceanic signals often have high spatial (millimeters to thousands of kilometers) and temporal (seconds to decades) variability, with long-term trends that can be hidden under large short-term natural variability (Lampitt et al., 2010). The vastness of the ocean makes it economically and logistically challenging to deploy instruments to simultaneously cover both short-term variability and long-term trends in the right locations. In the coastal oceans, the limitation of in situ biogeochemical and biological observational nodes and assets may be even more pronounced due to larger heterogeneity inherent in these dynamic systems. For example, even for the relatively well observed coastal waters of North America, there is still a significant challenge for interpreting and upscaling relatively sparse measurements to a regional or continental scale (Fennel et al., 2019).

In response, regional-to-global scale in situ oceanic observing networks have been developed and deployed, revolutionizing the way that ocean biogeochemistry and biology are studied and providing a new level of understanding of complex global systems. Examples of such networks abound, including the Global Ocean Observing System (GOOS),¹ the U.S. Integrated Ocean Observing System (or IOOS),² the Ocean Observatories Initiative (OOI),³ the African Blue Belt Initiative (BBI),⁴ the Australian Integrated Marine Observing System (IMOS),⁵ the Biogeochemical-Argo (BGC-Argo) program,⁶ the Southern Ocean Carbon and Climate Observations and Modeling (SOCCOM), and the EXPort Processes in the Ocean from Remote Sensing (EXPORTS)⁷. However, cost tradeoffs generally dictate that these networks each are designed to answer a limited set of questions, e.g., long-term vs. short-term variability, spatial or temporal coverage, etc. One common strategy for addressing the physical limitations for achieving high spatial coverage with ocean observatories and the need to understand significant variability of the oceans is to prioritize either (a) a limited number of specific, project-targeted sites for high temporal resolution studies (high temporal coverage with low spatial coverage) or (b) greater spatial coverage that limits shorter temporal resolution. For example, OOI and OceanSITES⁸ aim to characterize long-term changes (e.g., ocean temperature warming, ocean acidification and deoxygenation) and key processes (e.g., exchanges and interactions at the boundaries between interfaces of the ocean) at unique or representative locations, while the Biogeochemical-Argo program aims to measure key biogeochemical parameters – for which robust sensor technologies already exist – across the entire globe, but at a lower temporal resolution.

This review postulates that achieving data collection at the spatial and temporal scales demanded by the big scientific questions currently being pursued in ocean sciences requires a paradigm shift in the way we approach ocean observing. The development of advanced in situ biogeochemical and biological technologies has been a research priority in the oceanographic community for the past decade (e.g., Johnson K.S. et al., 2009; Moore et al., 2009; Byrne et al., 2010; Feely et al., 2010; Moustahfid et al., 2012; Martz et al., 2015). We assert that ocean science and engineering now must focus on dramatically lowering the cost of in situ sensors in order to increase spatiotemporal coverage relevant to high-heterogeneity of many biogeochemical and biological processes. To some extent, the evolution of sensors and deployments becoming cost-effective is already underway, often accelerated by the reduction in cost and size of the actual sensor components (e.g., Mills and Fones, 2012). Low cost electronics and computing solutions, hobby-grade electronics, and fabrication technologies (e.g., 3D printers) are being rapidly developed and advanced for other fields and applications outside of ocean science and are being applied to ocean sensor development. For example, though mostly still at the research stage, while a traditional CTD instrument costs ∼$10k, a new MEMS-based CTD sensor has ∼10-fold lower cost (<$1k). Similarly, a typical oxygen optode may cost upward of $10k, repackaging it using low-cost materials and electronics can decrease cost by 5- to 10-fold. As a field we need to learn from such an initiative to transfer cost savings to other variables of interest in ocean biogeochemistry and biology.

This review, therefore, aims to: (1) provide a review of existing sensor technologies that have already demonstrated a decrease in cost compared to previous sensors and methodologies (section “Existing Cost-Effective Sensing Technologies for Biogeochemical EOVs and Relevant Parameters”), (2) present case studies of cost-effective in situ deployments that can provide insight into methods for bridging observational gaps (section “Cost-Effective Deployments”), (3) identify key challenge areas where progress in cost reduction is lagging (section “Challenging Areas: Technologies Where Innovation Is Needed for Cost Reduction”), and (4) present a number of potentially transformative directions for future ocean biogeochemical and biological studies using cost-effective technologies and deployment strategies (section “Common Themes and Transformative Future Directions”). In this review we include cost-effective sensing technologies for ocean biogeochemistry and biology to provide an interdisciplinary perspective on available cost-effective in situ sensing technologies so the ocean science community can plan and design integrated observing networks using these technologies and because innovations in hardware are likely to be transferable across disciplinary lines.

For the purposes of this analysis we define “low-cost” or “cost-effective” as achieving a decrease in cost of at least threefold or more relative to the cost of established technologies or deployment methods. In other words, we target innovation that theoretically could enable an increase of spatiotemporal resolution by threefold or more, assuming that the lower cost sensor still meets the standards (e.g., accuracy, range, drift) required by specific scientific application. While there is also a need to understand cost in an absolute sense, this relative definition of “cost-effectiveness” provides a lens that is relevant across a wide range of technologies and disciplines. Some biogeochemical sensors may already be “low-cost” (<$1k) while biological sensors are not yet comparable in terms of absolute cost. Although some newly developed biological sensors can be considered to be cost-effective in this context in terms of “cost per data point generated,” it becomes clear through this review that affordability of biological in situ sensors faces more challenges and needs more improvement from developers and the community to catch up. Furthermore, it must be noted that many in situ biogeochemical and biological sensors are first generation sensors, so providing a cost comparison to previous sensors may not possible in all cases.

A complete discussion of all existing cost-effective technologies is beyond the scope of a single review, thus, we aim to present representative sensor technologies that cover important development aspects with respect to cost reduction approaches, including miniaturization, novel sensing modalities, system integration, and unique deployment strategies. By targeting technologies to highlight, we are able to focus primarily on the observational needs and gaps in ocean biogeochemistry and biology, guided by consensus lists of essential ocean variables (EOVs)⁹ (Table 1). Issues that are universal to all sensors, such as packaging, deployment platforms, power supplies, and communication, are discussed in section “Common Themes and Transformative Future Directions.”

TABLE 1

Table 1. List of essential ocean variables (EOVs) and relevant variables identified by the Global Ocean Observing System (GOOS) Expert Panels, based on criteria taking into account relevance, feasibility, and cost effectiveness (adapted from http://www.goosocean.org).

Existing Cost-Effective Sensing Technologies for Biogeochemical EOVs and Relevant Parameters

In this section, we review a sample of available sensor technologies capable of achieving cost-effective measurement of biogeochemical and biological EOVs or related parameters; a summary of included technologies and estimated technology readiness level (TRL) is provided as Table 2 for comparison. Technologies are presented roughly in order of degree of readiness, from those which are already commercialized or in wide use to those which are in the research and development stage.

TABLE 2

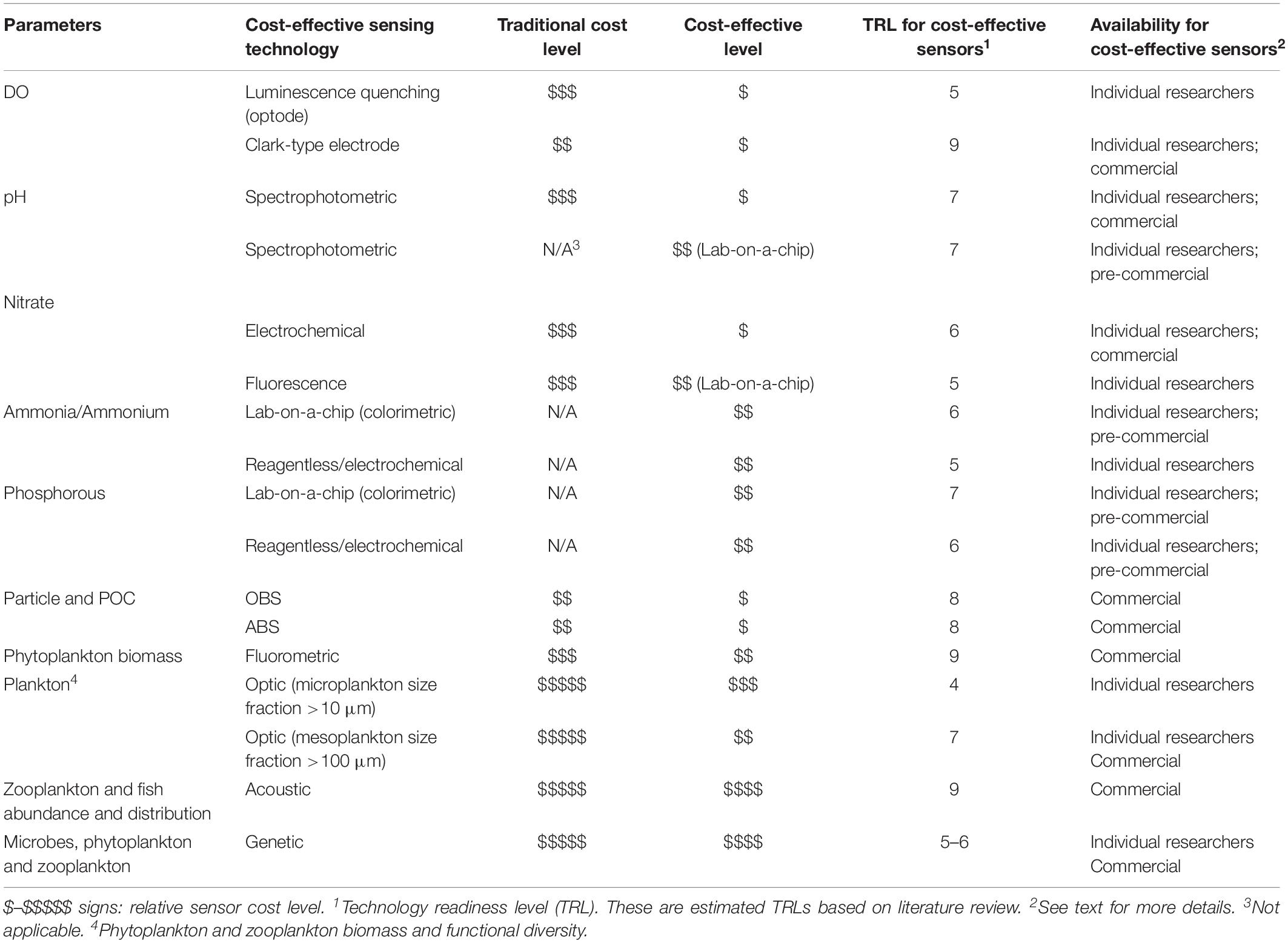
Table 2. Characteristics of cost-effective in situ sensing technologies for biogeochemical and biological parameters.

Dissolved Oxygen

Dissolved oxygen (DO) is a key biogeochemical parameter measured for many oceanographic studies. The required DO measurement uncertainty to detect meaningful changes in the open ocean is about 1–2 μmol kg^–1 (Gruber et al., 2010; Keeling et al., 2010). DO sensors are one of the most mature biogeochemical sensors as a result of advances in detection technology over the last few decades (Bittig et al., 2018). Two commonly used methods for in situ DO sensing are the Clark-type electrochemical detection (DO electrode) (Kanwisher, 1959) and luminescence quenching by oxygen (Kautsky, 1939; Körtzinger et al., 2004, 2005; Lakowicz, 2006; Tengberg et al., 2006). The former is simple to instrumentation, but is generally considered to be less accurate and prone to drift during long-term deployments; the latter is more accurate and has led to the development of the oxygen optode, the technology of which has been widely used on almost all observing platforms for more than a decade (Riser et al., 2016). Furthermore, micro-sensors for in situ DO detection have been available for many years (Sosna et al., 2007; Chipman et al., 2012).

Cost-effective Clark-type DO sensors are already available for seawater measurements. One approach is to use a bare disk electrode design (Sosna et al., 2007) which – with appropriate in situ cleaning – can achieve adequate performance for profiling applications (Sosna et al., 2008). The simplicity of this sensor has also been combined with micro-fabrication techniques and existing lithographic micro-manufactured conductivity (C) and temperature (T) sensors (Huang et al., 2011) to create a combined CT-dissolved oxygen (CT-DO) micro-sensor (Morgan et al., 2014a,b,c,d). The CT-DO device is cost-effective and can be used with pressure balanced, soft or hard potted electronics, obviating the need for pressure cases. This DO sensor has a response time of ∼2 s and current accuracy of ∼5 μmol kg^–1 though additional improvements are foreseen. Another example is the Oxyguard DO profiling sensor,¹⁰ which has a fast response time (∼10 s) and is insensitive to hydrogen sulfide interference. Its measurement uncertainty is 1–2%, allowing it to be useful in dynamic systems, such as coastal sites, where a large variability of DO occurs over different time-scales.

Oxygen optode technology has also matured over the last decade, resulting in robust and sensitive sensors capable of collecting climatology-quality data (Bittig et al., 2018) at moderate a investment (∼$3k per unit). However, further reducing the cost of DO optodes is an active research area. For example, an NSF-funded in situ mini-DO optode sensor has been under development for the last several years, designed for deployment on small marine organisms, such as jellyfish and squid, to 300 m (Figure 1). The sensing element is already commercially available (PreSens, Germany). The use of low-cost components (e.g., synthetic foams and silicone-based epoxy) and improved engineering design allows the cost and power consumption of this mini-O₂ optode to be low (∼$1k, ∼0.2 W). The sensor has a nominal overall uncertainty of ∼±0.5% O₂, a detection limit of 0.1%, and a response time of about 1 min. In situ testing of the sensor is currently underway along with efforts to improve the sensor’s deployment duration and depth. Currently, such a mini-DO optode may be suitable for short-term deployment (days – weeks) on various platforms, such as free-swimming animals, stationary platforms (e.g., buoys), and vehicles (i.e., Autonomous Underwater Vehicles – AUVs).

FIGURE 1

Figure 1. Left: Miniature dissolved oxygen optode assembly (left) in a bio-logging tag platform. The ruler scale is in centimeters. Right: O₂ sensing cube (PreSens, Germany) (courtesy by Dr. Z. A. Wang, WHOI, United States).

These examples of cost-effective in situ DO sensors share two key features: the use of low-cost components and new packaging approaches for submersible deployments. It is expected that the main components and materials of DO sensors will continue to decrease, and such sensors may be among the first biogeochemical parameters that can achieve massively cost-effective deployments with a large number of sensors.

The Carbon Dioxide System

The carbon dioxide (CO₂) system is described by four measurable primary parameters: total dissolved inorganic carbon (DIC), partial pressure of CO₂ (pCO₂) or CO₂ fugacity (fCO₂), pH, and total alkalinity (TA), each of which has its own unique applications in marine biogeochemistry. Measurements of any two of the four parameters are required to fully resolve the carbonate system using seawater acid–base equilibria, including calculation of CaCO₃ saturation states that are highly relevant to OA studies. With continuous efforts invested in developing sensors and instruments for CO₂ parameters in recent decades, significant advancements have been made in this field (Byrne, 2014; Martz et al., 2015). The recent Wendy Schmidt Ocean Health XPRIZE¹¹ has acted as a global catalyst for developing new pH sensor technologies to improve in situ seawater pH measurements. Currently, pCO₂ and pH in situ sensing technologies are relatively more mature, with commercial pCO₂ and pH sensors available for seawater applications, though the need to achieve faster-response and deeper deployment is acknowledged.

Two types of in situ pH sensors are most widely deployed to measure seawater pH: spectrophotometric (Liu et al., 2006; Gray et al., 2011) and ISFET based pH sensors (Martz et al., 2010; Bresnahan et al., 2014; Takeshita et al., 2014). The electrochemistry-based in situ pH electrode is generally considered to be less stable and precise than the other two for seawater applications. SAMI pH (Sunburst Sensors, LLC, United States) and SeaFET (Sea-Bird Scientific, Inc., United States) sensors are, respectively, representative of spectrophotometric and ISFET based in situ pH sensors, which can achieve high-quality measurements if properly calibrated and deployed. However, these commercial sensors still cost more than $10k per unit.

In recent years, there has been progress in the development of low-cost pH sensors to improve marine carbon and OA research. A low-cost (∼75% cost decrease) commercial spectrophotometric pH sensor, iSAMI, is being developed for surface measurements with good measurement quality¹² (Figure 2). In addition, Sunburst Sensors has developed a commercially available handheld pH sensor, pHyter (Figure 3) (<$0.5k). Meanwhile, the pH photometer developed by the University of South Florida (Figure 4) has a “Do-it-yourself” (DIY) design, is low-maintenance, and achieves good quality measurements (±0.01). This sensor is an order of magnitude cheaper than commercial pH sensors that use similar operational principles (Yang et al., 2014, <$0.3k in material and fabrication). Such handheld sensors are particularly attractive tools for engaging citizen scientists and students in OA monitoring, education and research, and the technology has the potential to be further developed for in situ platforms.

FIGURE 2

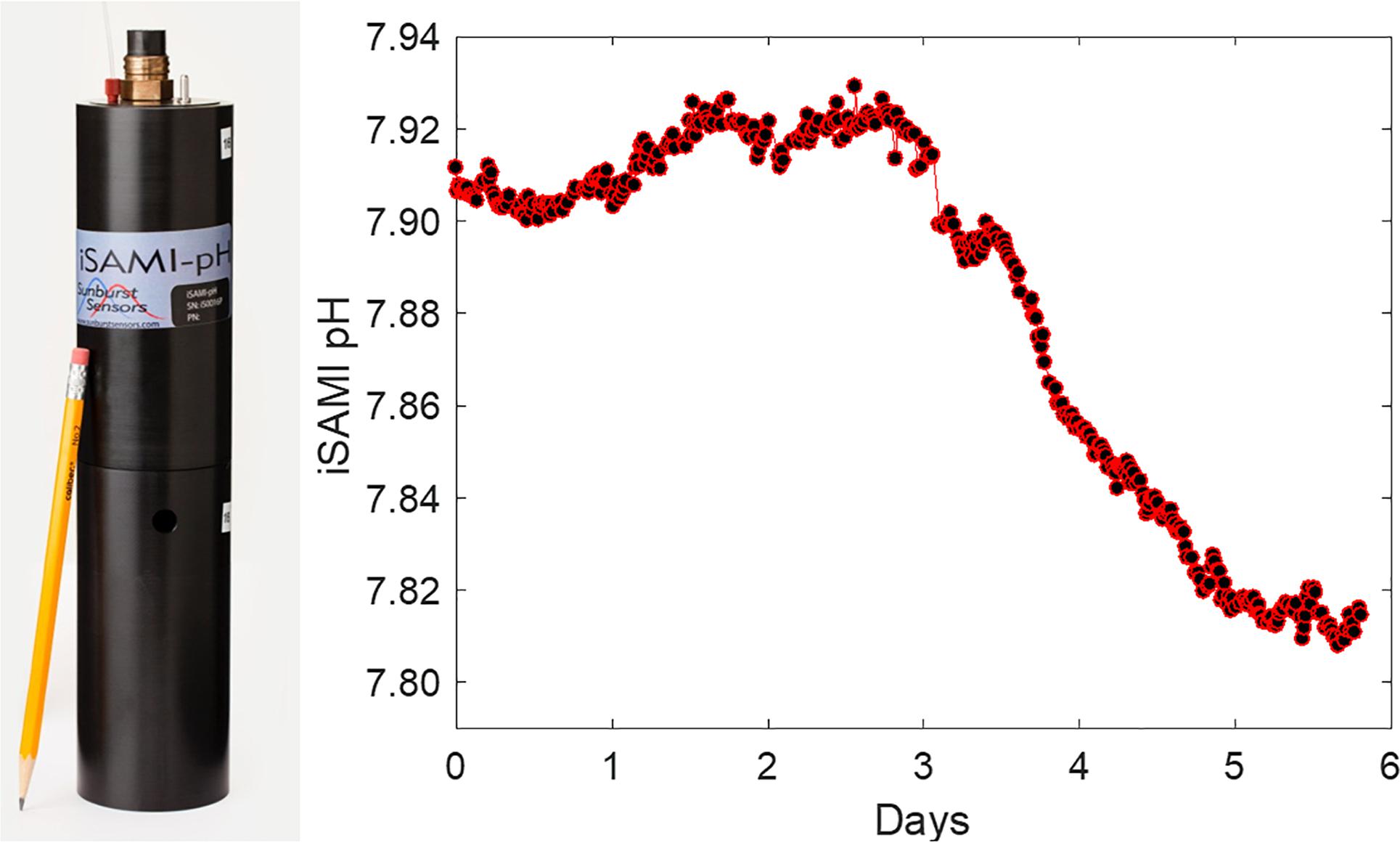
Figure 2. Left: iSAMI pH sensor by Sunburst Sensors, LLC. Right: The in situ testing of iSAMI pH over 6 days (courtesy by Dr. M. DeGrandpre, University of Montana, United States).

FIGURE 3

Figure 3. Sunburst pHyter, a hand-held pH meter, with controlling mobile app (courtesy by Dr. M. DeGrandpre, University of Montana, United States).

FIGURE 4

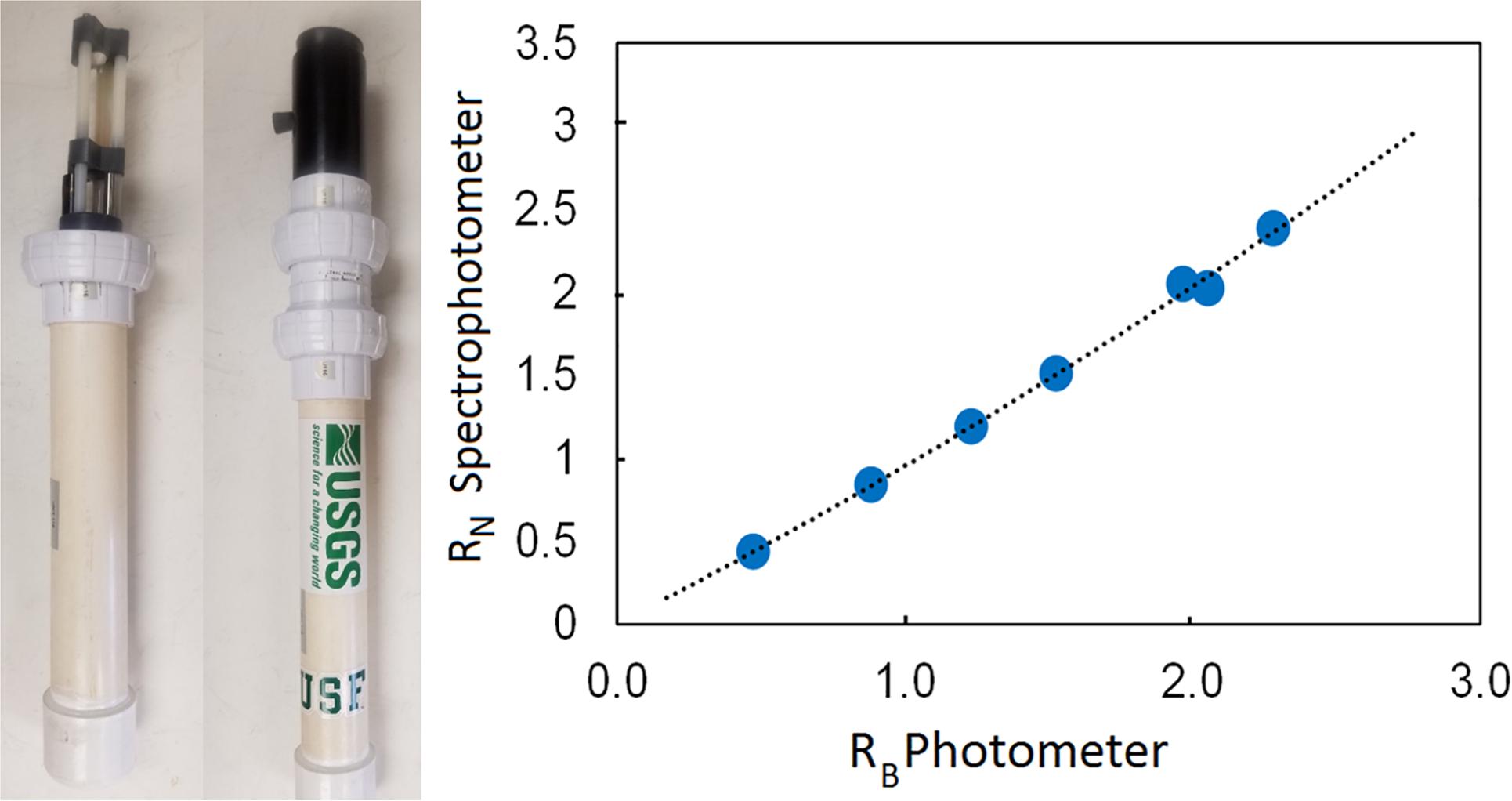
Figure 4. Left: A USF-USGS hand-held pH photometer. Right: Photometer (Unit 115) calibration curve of absorbance ratio R_B against spectrophotometrically determined absorbance ratio R_N (courtesy by Dr. R. H. Byrne, University of South Florida, United States). Absorbance ratio R_B is a function of water pH. The dotted line represents the polynomial best fit, Y = 00679x² + 0.8783x + 0.0021; R² = 0.9971.

In situ pCO₂ sensors in general use either CO₂ equilibration between the sample seawater and a medium (air/gas or reagent such as a pH sensitive dye), followed by infrared or colorimetric spectroscopy of the CO₂-equilibrated medium (e.g., CONTROS HydroC CO₂, Norway; Pro-Oceanus CO₂, Canada; SAMI-pCO₂, Sunburst Sensors, United States). However, these are not typically cost-effective. Miniaturization and cost reduction of these techniques are therefore areas of active research. Over the last decade, the cost of non-dispersive infrared (NDIR) detectors used in pCO₂ sensors has decreased (e.g., a low cost NDIR CO₂ detector is on the order of $100), paving the way for lower cost in situ pCO₂ sensors.

Alternately, a number of groups are now developing pCO₂ optodes (Atamanchuk et al., 2014; Clarke et al., 2017; Staudinger et al., 2018). The method is based on CO₂ equilibration between seawater and a pH sensitive fluorescent dye, followed by fluorescent detection, such as the frequency domain-Dual Lifetime Referencing (f-DLR) method (Atamanchuk et al., 2014) or the time domain-Dual Lifetime Referencing (t-DLR) method (Clarke et al., 2015). The fluorescent dye is reusable, eliminating the need for pumping and replacing reagents, which can reduce the complexity for in situ sensors. These systems in principle operate similarly as DO optodes, thus having the potential to be low cost as DO optodes. However, long-term stability and measurement quality at marine pCO₂ levels remains an area of active assessment.

While measurement of any two of the four parameters allows full resolution of the carbonate system using seawater acid–base equilibria, large calculation errors result when pCO₂ and pH are used due to their strong co-variation (Millero, 2007). The errors are often minimized when the DIC-pH or DIC-pCO₂ pair is used (Byrne et al., 2010). Even when TA contains a significant amount of undefined alkalinity (e.g., organic alkalinity), the DIC-pH or DIC-pCO₂ pair can still accurately calculate carbonate alkalinity and CaCO₃ saturation states. Therefore, development of in situ DIC or TA sensors is of high interest.

In situ sensor technologies for DIC are much less mature (Byrne, 2014; Martz et al., 2015), and currently no commercial in situ DIC sensors are available. Various “research type” in situ sensors and underway instruments for DIC measurements have been emerging in recent years (Sayles and Eck, 2009; Liu et al., 2013; Wang et al., 2013a, b; Fassbender et al., 2015). These proto-type systems have already achieved significant cost-reductions relative to discrete measurements of bottle samples by several folds. In situ DIC detection is based on CO₂ equilibration between an acidified sample and a standard solution through a gas permeable membrane, followed by either spectrophotometric, conductometric, or infrared detection. As lower cost components are developed for other applications, we would expect the costs of these sensors to decrease. For example, built on the technology developed for the Channelized Optical System (CHANOS; Wang et al., 2015), a new miniaturized, lower cost version (CHANOS II) is under field testing, aiming for deployment on profilers, AUVs and remotely operated vehicles (ROVs) with high measurement frequency (1 Hz). In addition, it is designed to make simultaneous measurements of the DIC-pH pair or the DIC-pCO₂ pair based on spectrophotometric principles, thus fully resolving the seawater CO₂ system with less calculation errors in many cases. The target price for the CHANOS II shallow-water version (<500 m) is <$15k per unit with two CO₂ parameters.

Prototype in situ alkalinity sensors, such as spectrophotometric SAMI-Alk (Sunburst Sensors, LLC) (Spaulding et al., 2014) and ISFET-based solid state alkalinity sensors (Briggs et al., 2017), are also emerging, and have the potential to achieve low cost, similar to other pH, pCO₂, and DIC sensors due to the similarity of detection principles (i.e., spectrophotometric and ISFET). These new TA and DIC sensors have all been developed with the goal of climate-quality measurements as defined by the Global Ocean Acidification Observing Network¹³.

While originally applied for nutrient sensing, Lab-on-a-chip (LOC) technology has also been applied to the in situ detection of pH (Rerolle et al., 2018), DIC, and TA. LOC sensors have been developed with a target of being cost-effective, yet high performance in situ sensors suitable for mass deployment on various ocean observing platforms. In the LOC platform designed at the National Oceanography Centre, UK (NOC), the principal engineering choices that enable lower costs are the use of a pressure balanced design which obviates expensive pressure cases, optical windows, and electrical connections. Pressure is equalized inside a low-cost polymer electronics housing using an insulating oil. The sensors use microfluidic technologies to mix the seawater sample with pH indicators to produce a color (for pH and TA) or conductivity (for DIC) change to measure the parameter of interest. The TA sensor is based on the single-point spectrophotometric titration method (Breland and Byrne, 1993). The prototype LOC DIC sensor is based on a conductometric method (Sayles and Eck, 2009). Both the LOC TA and DIC sensors take advantage of a development by Li et al. (2013) who used a gas-permeable Teflon AF 2400 membrane (Wang et al., 2002, 2007) to remove the CO₂ from the sample-titrant mixture. The LOC TA and DIC sensors have been deployed on a benthic lander in the North Sea, through a shipboard underway system, and in an estuary. By 2020, the LOC TA and DIC sensors will be integrated into a single device and, together with the LOC pH sensor, will form a package capable of over determining the carbonate system, to allow the measurements to be validated. Cost is currently dominated by the valve, pump, and electronics components. The goal is to reduce the total component costs to $2.5k in the short term (<1 year) with a target of <$1k beyond that.

In summary, the examples described above highlighted several innovations of lowering the costs for CO₂ parameter sensors, including reagentless detection, simultaneous detections of multiple parameters, low-cost materials and packaging, and microfluidic designs. The encouraging trend in recent developments was to embed system designs with both good measurement quality and cost reduction of the systems starting from the early stage of development.

Nutrients

In the context of marine systems, key nutrients of interest are nitrate, nitrite, ammonium, phosphate, silicate, and a number of trace metals (e.g., iron). Nutrients have historically been more difficult to measure in situ than physical or bulk chemical parameters, due both to cross-sensitivities with other constituents and to challenges with miniaturization of lab instrumentation for field deployment. While there are a number of commercially available multi-parameter instruments for nutrient measurements in the marine environment (comprehensive list in the ACT Technologies Database¹⁴), many of these are now mature technologies that are still relatively costly, unlikely to see further decreases in cost and likely to see only incremental improvements in accuracy. A number of emerging technologies, however, build on insights gained from these instruments and may have the potential to meet decreased size, cost, and/or power demands.

The most common strategy for in situ nutrient measurement is through the use of wet chemical sensors based on standard laboratory and shipboard principles (spectrophotometry or fluorescence), which can achieve detection limits in the micromolar range for most analytes but require reagents (necessitating volume increases and constraining deployment times) and are still moderately large and expensive (>$10k). The logical pathway forward is to take advantage of the specificity and accuracy of spectroscopic methods and miniaturize using methods such as LOC which have lower reagent consumption, power consumption, and cost (3–10× decrease). LOC approaches have already been developed and proven in the lab for colorimetric measurements of nitrate [detection limit of 0.025 μmol kg^–1 (Beaton et al., 2012)] (Figure 5), phosphate [detection limit of 40 nM (Clinton-Bailey et al., 2017)], and silicate [in coastal waters (Cao et al., 2017)]. These sensors have very low power consumption [e.g., 1.8 W for one measurement per 15 min (Clinton-Bailey et al., 2017)], and with LOC systems multiple detection cells can be integrated with little increase of cost. Versions for the measurement of ammonium and iron (Geißler et al., 2017) are in development. Related efforts (e.g., a reflectance sensor using optical fibers and miniaturized flow systems) exist for the measurement of dissolved iron using chelating disks and reagents that complex capture iron (Pons et al., 2005).

FIGURE 5

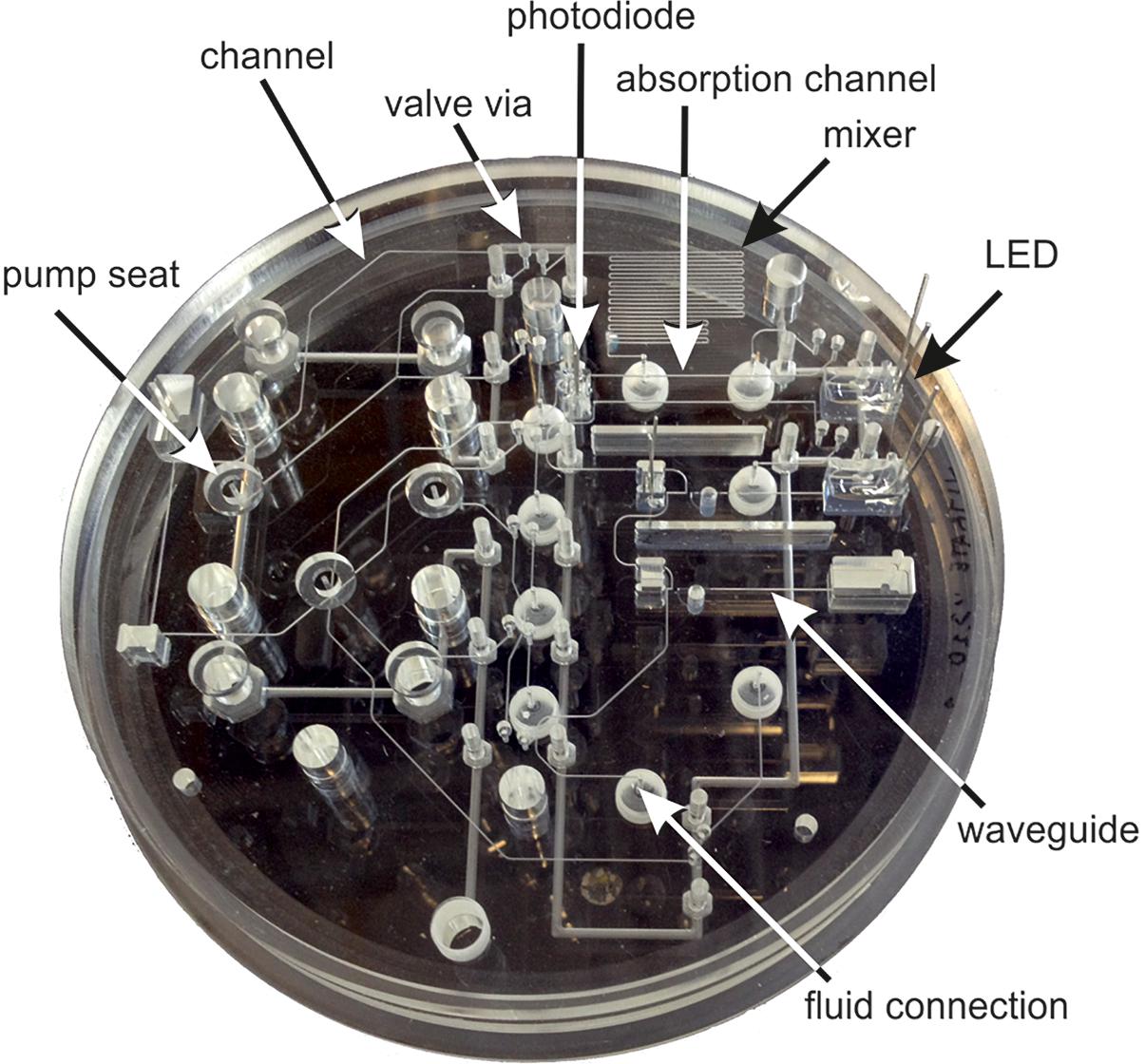
Figure 5. Labeled photograph of a LOC nitrate sensor microfluidic and optofluidic manifold (aka the chip). This 12 cm diameter chip is shown in clear Polymethylmethacrylate (PMMA) to aid visualization. Operational devices are made in tinted PMMA to suppress stray, scattered and ambient light (Ogilvie et al., 2010; Floquet et al., 2011).

Reagentless sensors (e.g., based on direct optical UV absorption measurement) have already been commercialized for the measurement of nitrate in waters with relatively low turbidity and colored dissolved organic carbon (DOC) (Finch et al., 1998; Johnson and Coletti, 2002; Zielinski et al., 2007; Sakamoto et al., 2017; Meyer et al., 2018). While these sensors are at a low enough cost that they are now standard on some profiling floats [e.g., the BGC-Argo and SOCCOM programs (Johnson et al., 2017)], the absolute cost per sensor remains high (order of $10k) and therefore alternate approaches (e.g., reagentless electrochemistry) are also emerging. An indium tin oxide (ITO) sensor was demonstrated in 2017 for detecting ammonia in seawater (Lee et al., 2017) while reagentless measurement of silicate and phosphate in situ has recently been validated for seawater use (Barus et al., 2018). This latter instrument utilizes a two-cell configuration (complexation with molybdenum, detection using gold working and silver reference electrodes) and achieves a micromolar detection limit, has a sampling period of approximately 1 h, is small in size (100 mm diameter, 186 mm height packaged), and has a low power consumption (25 mAh for 1 sample per hour). Finally, while interferences due to the high salt content of marine waters remain high, the consideration of using potentiometric sensors (i.e., ion selective electrodes) for nutrient measurement in marine environments is ongoing, with several already commercially available (e.g., NISE by Hach Lange, EXO by YSI). Successes in pressure compensating semiconductor (ISFET) pH electrodes (Johnson et al., 2016) and progress in membrane specificity [e.g., for Cl^– (Takeshita et al., 2014)] will continue to propel this type of technology forward. Costs for typical ISEs (individual probes, before instrument integration) is on the order of $0.2–$0.9k.

Innovation in both classes of sensors show similar strategies for decreasing costs and improving deployability, particularly miniaturization, which frequently comes with decreasing power consumption. Reagentless sensing strategies, however, rely on continued innovation in material science, including identifying membranes, chelators, and electrodes that have fewer interferences or multi-step processes that can separate target nutrients from potentially interfering signals.

Suspended Particles and Particulate Organic Carbon

Instruments employing backscattering techniques (acoustic and optical backscatter sensors, ABS and OBS) provide a means of sampling suspended particle concentration at a relatively low cost (on the order of $1.3–5k per unit) with a small overall package size. Both ABS and OBS technology may be characterized as mature. The measurement techniques and the cost per unit of the commercial sensors have been essentially static over the last two decades, partially because of their already low cost compared to other oceanic sensors. Because of their wide range of application and low cost, they are relevant for this review, especially when integrating with other sensors to provide more cost-effective deployments.

As ABS instruments do not rely on an optical signal, they are less prone to degradation due to biofouling of the sensor head than an OBS. However, a number of manufacturers offer an OBS with an optical sensor wiper or shutter to cover the sensor head when not taking measurements (e.g., Seabird Sci. ECO Scattering sensor and Campbell Scientific OBS501). A principal distinction between ABS and OBS devices is the range of particle sizes to which they are sensitive. An OBS is most sensitive to fine-grain particles to roughly 40 μm grain size, with the backscatter signal dominated by particles in the 1–10 μm size range (Organelli et al., 2018). By contrast, an ABS is most sensitive to coarser particles, in the 30–400 μm grain-size range. This distinction has prompted some investigators to pair an OBS and ABS to maximize the overall grain size range measured (Hawley, 2004). Seapoint Sensors Inc. has recently developed technology that extends the OBS measurement range to much higher concentrations (well in excess of twice the maximum concentration sensed by the company’s earlier OBS models). The OBS employing this technology (the STM-S) is offered at roughly the same price (∼$1.3k) as the company’s earlier models, equivalent to a cost-reduction with updated capability.

The signal of an OBS can be used to determine the concentration of particulate organic carbon (POC) using a derived POC-concentration vs. OBS-intensity relationship for a given marine area (Briggs et al., 2011; Cetinić et al., 2012; Johnson et al., 2017). This makes an OBS valuable for studying oceanic biogeochemistry, particularly when the OBS is combined with sensors that measure other relevant properties, such as chlorophyll-a and colored dissolved organic matter (CDOM). Instrument packages combining an OBS with CDOM and chlorophyll-a fluorometers are commercially available (at unit cost of order $13k) in sizes suitable for use on moorings and/or mobile platforms (e.g., Seabird Sci. ECO Triplet; Alkire et al., 2014; Roesler et al., 2017).

For observations directed at sediment dynamics in the bottom boundary layer, a profiling ABS offers a useful means of monitoring SPM concentrations at selected distances above the bottom. A number of studies have shown that profiles of SPM concentrations may be obtained with high accuracy using the returns from multi-frequency ABS as well as from a conventional acoustic Doppler current profiler (ADCP) provided that the acoustic return signals are calibrated with coincident measurements of SPM concentration using the sediment characteristic of the measurement site (e.g., Thorne and Hardcastle, 1997; Gartner, 2004; Sahin et al., 2017). Profiling ABS systems employing transducers with a range of frequencies (to provide sensitivity over a range of particle sizes) and suitable for long-term deployment are available at a cost of ∼$15k (e.g., AquaScan 1000 by Aquatec Group Ltd.).

Overall, the commercial sensors in this category are relatively robust. Improvement of cost-effectiveness of their use in comprehensive oceanographic studies, targeting a host of variables, may be expected in the near future, given the trend of sensor integration (i.e., combining particle sensors with sensors for other variables) currently underway. Furthermore, advances in relating the instrument signal to SPC may be expected in the near future. As recently demonstrated by Organelli et al. (2018), the backscattering signal to SPC relationship is sensitive to the structural complexity of the particles measured, revealing the need for further research to optimize in situ detection of marine particles using backscattering techniques. Further cost-reduction of these sensors may be needed to enable large-scale deployment described in this paper.

Fluorescence and Chlorophyll

Quantifying phytoplankton biomass in situ using in vivo chlorophyll fluorescence has been widely employed for more than half a century. It becomes a routine observation because it is fast and adaptable to various deployment platforms (Boss et al., 2018; Lombard et al., 2019). The method is based on the assumption that the fluorescence intensity of chlorophyll-a and its concentration are directly proportional to one another. However, chlorophyll fluorescence measurements in the applicable spectrum range (680–685 nm) have many sources of uncertainty, arising from device hardware (e.g., excitation light and detector) as well as interferences or variability in aquatic environments, such as changes in phytoplankton physiology, photo-acclimation, growth phase, non-photochemical quenching, nutrient limitation, and high CDOM concentration interference (Kiefer, 1973; Cullen, 1982; Xing et al., 2017). To date, the most robust and rigorous procedure to correct the raw data is to compare high pressure liquid chromatography (HPLC) measurements of discrete water samples with sensor observations (Lombard et al., 2019). Existing data must go through vigorous quality checks before use (Boss et al., 2018). For example, Roesler et al. (2017) recommended that the chlorophyll-a values obtained with WET Labs ECO FLBB sensors in the past be corrected by a factor of two in order to produce a global set of data with a relatively small bias compared to global average HPLC measured values.

Because of recent technological advances, miniaturized and/or cost-effective in situ fluorometers are emerging. Leeuw et al. (2013) developed a fluorometer (about $0.15k) which can be deployed in large quantities (e.g., in an array) to detect and monitor the development of phytoplankton blooms over a large spatial scale, such as harmful algal blooms. Blockstein and Yadid-Pecht (2014) also reported proof-of-concept miniature fluorometers (<$0.5k) which can measure chlorophyll and CDOM simultaneously. Another innovation is the T-FLaP technology (Marcelli et al., 2014), which is capable of obtaining vertical profiles of fluorescence of chlorophyll-a or to be used as a stand-alone system for surface mapping. Friedrichs et al. (2017) presented a prototype DIY device, SmartFluo, which consists of a smartphone operation interface, a cuvette adapter, and an illumination source. It is designed for applications in inland and coastal waters, and is useful for citizen science.

In general, these innovations and massive cost decreases have been achieved by capitalizing on mass-produced electronics and miniaturization. Although these new technologies still require regular calibration, and may require additional improvement on detection limit and accuracy before they can be used at scale for oceanographic research, they are a promising proof-of-concept step in the direction of massively increased sensing resolution.

Underwater Bio-Acoustics

Passive and active acoustic sensing are capable of delivering datasets of relevance to several EOVs, including fish abundance and distribution (Simmonds and MacLennan, 2005), marine mammal distributions (Brehmer et al., 2012), diving seabird behaviors (Benoit-Bird et al., 2011; Williamson et al., 2017), habitat type and fine-scale topography (Roberts et al., 2005; Smith and McConnaughey, 2016) and ocean sound (Hildebrand, 2009). Although the absolute price tag may not be comparable with available low-cost biogeochemical sensors, the multi-purposes and high data output per unit cost of bio-acoustic sensors allow them become a cost-effective way of studying a wide range of biological processes and marine organisms, along with their living habitats in the last decade. Technology development and material advancement in recent years also helped to reduce the costs of acoustic systems, allowing more accessibility for ocean research. Here, we focus on active acoustic technologies that have achieved major advances in the last decade for marine biological purposes. Today, fisheries acoustics (Simmonds and MacLennan, 2005) is a central discipline for in situ observations of aquatic organisms extending from plankton to whales (Brehmer, 2006). Acoustics transducer accuracy and reliability are paramount when making biological measurements with acoustic transducers. There exists a wide range of transducers that deliver results of interest for marine scientists, fisheries, and conservation managers, including echosounder and sonar systems. During the last few decades, the main advance is the advent of multibeam (e.g., Guillard et al., 2011) and wideband (Demer et al., 2017; Jech et al., 2017) acoustic systems, although calibration and data treatment are still challenging with existing protocols (e.g., Perrot et al., 2014, 2018; Demer et al., 2015; Korneliussen et al., 2016; Eleftherakis et al., 2018).

Rapid advances in the miniaturization of acoustic sensors (transducers) and the improvement of batteries and computers allow them to be mounted on various mobile platforms, such as gliders and AUVs (Hine et al., 2009; Moline et al., 2015) and buoys (Godo and Totland, 1999; Brehmer et al., 2018), thus rendering this sensing technology cost-effective both in hardware and in deployment compared to traditional shipboard transducers. In the last decade, a new cost-effective multi-purpose scientific echosounder, the Simrad EK15, was designed and validated (Betanzos et al., 2016; Linløkken et al., 2019). Another major development in cost-effective acoustic sensing is the scientific wide band echosounders (Demer et al., 2017) which use a wide band transceiver (WBT) to replace the general purpose transceiver (GPT) that is used for narrow-bandwidth echosounders, e.g., the WBT Miniature wideband transceiver (WBT Mini) (Benoit-Bird et al., 2018), wide-band autonomous transceiver (WBAT), and WBT Tube Subsea transceiver (WBT Tube) (Lavery et al., 2017). Such systems are compact in size and energy efficient, making them useful as a portable echosounder or for installation on a wide range of platforms (e.g., Saildrone by Mordy et al., 2017). This allows long-term deployments in challenging environments (Demer et al., 2017), such as in the arctic, using the Acoustic Zooplankton and Fish Profiler (Ludvigsen et al., 2018).

Multibeam systems such as long-range omnidirectional sonar (Brehmer et al., 2006), multibeam sonar (Korneliussen et al., 2009), and multibeam echosounder (Trenkel et al., 2008) have become more reliable and cost-efficient per unit of data output (e.g., Trygonis et al., 2016; Dunlop et al., 2018). Acoustic cameras have been emerging for fine scale studies of marine organisms in the last decade (Tušer et al., 2014; Martignac et al., 2015), which have provided new detailed knowledge on their living behaviors and physiology. The next step in lowering the overall cost in this field is to capture habitat characteristics at the fine scale (Bertrand et al., 2014) simultaneously with marine organism detections, and applying data processing and analytics from several acoustic sensors (Brehmer et al., 2002). Future concepts for fine scale studies (>20 m) have been presented by Gerlotto et al. (2011) by building and operating a high-frequency, three-dimensional sonar that will allow observation and analysis of fine scale dynamics within marine organism aggregations. Such an approach requires non-conventional concepts as traditional sonars are limited by physical constraints, making observational improvements difficult. Remaining issues of active acoustics systems include relatively high power consumption for autonomous deployment and delivery of large-size data streams generated in a wide range of modulation frequencies.

For systems discussed here, it is a combination of newly available electronics and improvements in battery technologies that have enabled miniaturization of the technologies and particularly, therefore, deployment aboard more cost-effective deployment platforms.

Cost-Effective Deployments

Deployment strategies for cost-effective sensing technologies are a key factor for determining the overall cost of any field effort, and thus the long-term sustainability of ocean observing. For example, small boats and ships of opportunity can provide platforms for deployment and access to flow-through water systems. Lower-cost autonomous surface platforms, such as the JetYak (Kimball et al., 2014) with a <$20k price tag, can become platforms devoted to chemical sensing, as demonstrated by the recent development of the ChemYak (Nicholson et al., 2018) which includes laser-based sensors for dissolved methane and pCO₂ measurements in addition to an oxygen optode and a nitrate sensor. In this section, we describe a few case studies of cost-effective sensor deployments. Although the in situ sensors used in these cases may not all be low cost, the platforms and methodologies are presented as valuable examples for achieving cost-effective deployments.

Democratizing Access to Ocean Observing Technology

Working with a network of traditional Hawaiian Fishpond restoration groups, the group of Dr. B. Glazer at the University of Hawaii (UH) is reducing costs of deploying real-time observing networks of sensors for water level, temperature (accuracy ∼0.1°C), and other environmental variables at high spatiotemporal resolution that are sufficient to characterize streams, tides, and episodic flooding¹⁵. The traditional Hawaiian Fishponds, Loko i‘a, represent a long-lasting example of one of the ancient world’s more significant and successful aquaculture achievements (Keala, 2007); as they are comprised of inputs and outputs over manageable and semi-controlled spatial scales (Figure 6), these fishponds provide ideal natural laboratories for testing new technologies that can improve spatial and temporal resolution of predictive coastal physical, chemical, and ecosystem models (e.g., Briggs et al., 2013).

FIGURE 6

Figure 6. He‘eia Fishpond, Oahu, is an 800-year old, 88-acre coastal walled estuary. Sluice gates (mākāhās) allow for tidal exchange with adjacent Kaneohe Bay. Paepae o He‘eia (PoH) is a local non-profit organization dedicated to the cultural and environmental restoration of the pond (photo courtesy by Paepae o He‘eia).

For the prototype network deployed at He‘eia Fishpond, three styles of low-cost mini-Nodes have been developed: (1) Arduino-controlled telemetry dongles that parse and relay any serial data from industry-standard instruments such as Seabird SBE19+ (node-025), (2) BeagleBone Black-controlled multi-parameter packages that log data from Aanderaa oxygen optodes, Aanderaa conductivity sensors, low-cost MEMS barometric pressure-temperature-humidity sensors, and submersible MEMS piezo-resistive pressure sensors (node-003), and (3) Arduino controlled temperature-compensated ultrasonic sensors mounted on bridges over sluice gates (mâkâhâs) in the Fishpond wall to monitor water level (tidal exchange with Kaneohe Bay). For each configuration, data are telemetered back to a shore-side base station where data are logged into an SQL database, stored, and transferred to a server at UH Mānoa (UHM). At UHM, an x86 Linux server (NUC5i7RYH) performs automatic, first-pass QA/QC data filtering and flags data that is out of expected range or mini-Nodes that have not reported as scheduled. Data are then served on the web via an open-architecture RESTful API (Figure 7).

FIGURE 7

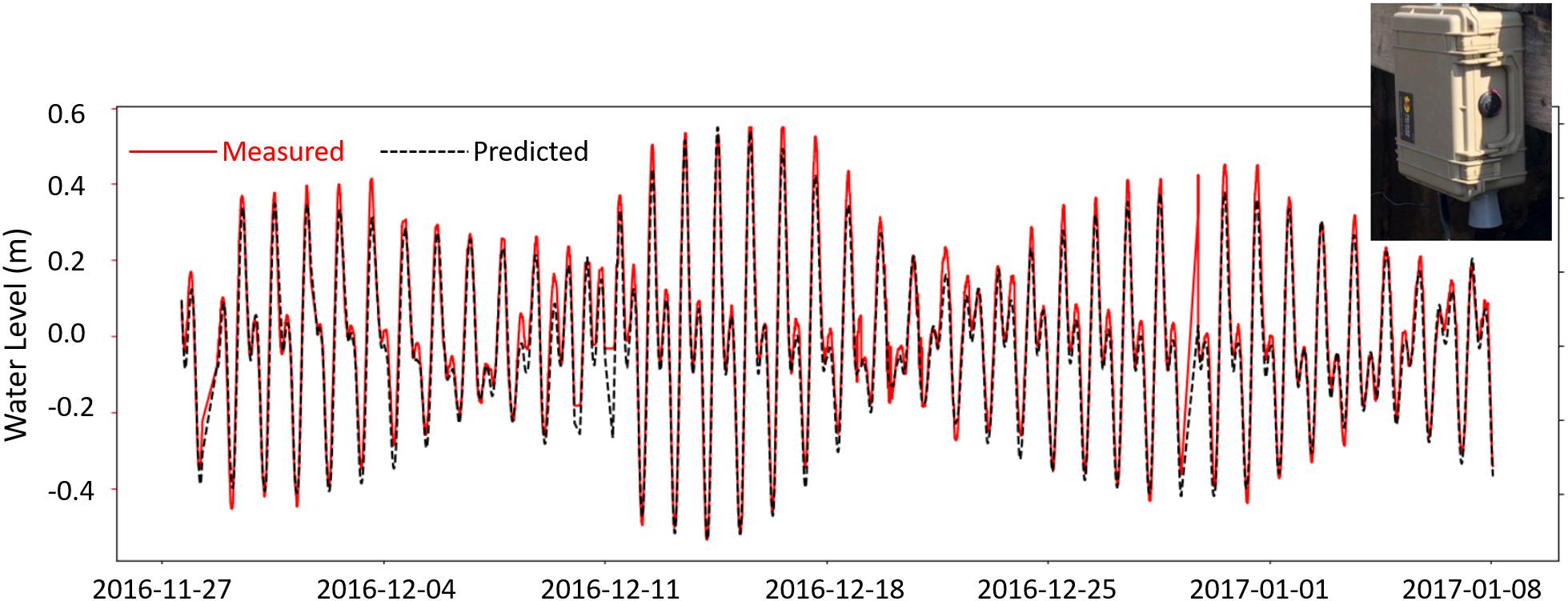
Figure 7. Low-cost temperature compensated ultrasonic sensor mounted above the water level in a He‘eia Fishpond mākāhā (upper right inset) provides near-real-time tidal observations (red, solid line) that compare well with nearby US NOAA tide gauge observations (yellow dashed) and show promise for generating site-specific tide predictions using open-source Python software package, uTide (black, dashed line).

Three specific advances in low-cost electrical components and software tools are making these new deployments possible and timely: (1) the availability of low-cost powerful single-board microcomputers and microcontrollers (e.g., BeagleBone Black, Texas Instruments, $55; ATMEGA32U4, Arduino-compatible, $5), (2) robust low-power radio frequency (RF) wireless mesh network transceivers (XBee Pro 900HP, Digi., $39), and (3) growing popularity and capability of crowd-sourced open-source software tools (i.e., Linux-operating system, Python embedded systems control and visualization libraries, and GitHub coordinated version control development). What once required a team of computer scientists and engineers to implement can now be prototyped, tested, and deployed with a much smaller team and largely open-source hardware and software tools. Such a deployment is representative of combining user-derived low-cost communication and control, sensing packages, data processing, and engagement of citizen science to establish a socially relevant ocean observing network.

Designing Cost-Effective Deployments With Miniaturized Sensors

Miniaturized low-power sensors can enable long deployments with minimal human intervention, particularly in difficult-to-access environments. As was highlighted in several cases in section “Existing Cost-Effective Sensing Technologies for Biogeochemical EOVs and Relevant Parameters,” LOC sensing technology is a new way to miniaturize complex sensing systems and reduce overall device cost. However, their modest size and power consumption also permit cost-effective design of deployments. Low reagent consumption allows for regular recalibration in situ, providing high-quality data over long periods. As examples, the trace metal (Milani et al., 2015; Geißler et al., 2017), nitrate/nitrite (Beaton et al., 2012) and phosphate (Clinton-Bailey et al., 2017) versions of the LOC sensors have been deployed at a coastal observatory in an estuary/fluvial setting providing continuous measurements for up to 18 months with reagent replacement only required every 3 months. This has revealed excellent field metrology and matching to standard water sample data (e.g., nitrate detection limit <25 nM), as well as surprising resilience to fouling.

In the cases of the LOC sensors described above, the rugged pressure balanced design permits their use in extreme environments which are expensive to access regularly. For example, the nitrate/nitrite LOC sensors have been deployed in a proglacial melt stream (Beaton et al., 2017), in the Mauritanian oxygen minimum zone, and offshore of Western Africa (Yucel et al., 2015) where high quality data was successfully collected via profiling (up to 60 m depth) and onboard a lander (to 170 m depth). The deepest deployment of this technology to date has been to 4800 m in trials in the region of the Porcupine Abyssal Plain observatory on a CTD frame where data matched bottle samples.

Another route to cost-effective deployments is through the use of multiple miniature sensors on a single platform. As an example, nitrate, phosphate and pH (Rerolle et al., 2018) LOCs were deployed simultaneously on the NERC Autosub Long Range (ALR) and on a lander (Sonardyne, United Kingdom) to develop monitoring systems for offshore carbon capture and storage reservoir integrity verification systems. Herein the systems on the lander were able to detect the stoichiometric signature of a simulated (deliberate gas release) leak. Other recent examples of deployment on low-power autonomous vehicles include use on a profiling float (PROVOR, NKE, France) as part of the EU SenseOCEAN project¹⁶ and onboard a Kongsberg Seaglider in coastal and shelf systems, measuring nitrate/nitrite (Vincent et al., 2018) and phosphate. These deployments show the ability of the sensor and AUV to capture simultaneous, high spatiotemporal variability of physical parameters and nutrients, revealing previously obscured processes and features.

While often cited as a likely problem for LOC, fouling has not been a significant issue that degraded LOC’s performance. The so-far longest data set obtained without reagent resupply or intervention was >1 year from a nitrate/nitrite sensor deployed on the FixO3 mooring in the Fram Strait. Although the cold and dark conditions in this annually ice covered region (less biofouling) assisted long-term preservation of reagents, other fouling and challenges in low-temperature environments did not degrade sensors’ performance during the deployment period.

Animal Oceanographers

Animal-Borne Sensors (AnBS) have been used for decades to deliver physical oceanographic data and animal behavior observations at a relatively low cost (Roquet et al., 2017). AnBSs are increasingly vital as we seek to observe changing oceans in greater temporal and spatial resolution as they offer a cost-effective strategy for autonomous sampling, with the sensor packages often on the scale of several hundred to a few thousand dollars per tag-package. The ability to affix tags to many animals means there are many tag concurrently making observations. While early AnBSs tended to record relatively basic information such as dive depth, duration, and temperature, innovative use of simple sensors, such as pressure to address ascent or descent rates and particular tracks, provides insight beyond behaviors such as foraging strategies, biological hotspots, occurrence rates (abundances), and relative densities of poorly understood (prey) layers (Johnson M. et al., 2009; Arranz et al., 2011).

AnBSs have typically been applied to large vertebrates that can easily carry the tags. Sharks, tunas, salmon, sturgeon, marine mammals, reptiles, and seabirds have been routinely tagged with sophisticated instruments that sample biological behaviors (diving) and/or oceanographic variables (e.g., pressure, light, temperature, salinity, DO, chlorophyll fluorescence). The horizontal range of measurement is highly variable, depending on the organism outfitted with the AnBS, and can be as small as bays and estuaries but as large as ocean basins when leveraging some large vertebrates. High resolution movement sensors (e.g., gyroscopes, magnetometers, accelerometers) enable observation of the animal’s biological activity and physiology within those conditions) (Wilson et al., 2006). These data on habitat and habitat use are particularly relevant for endangered species (e.g., bluefin tunas), protected taxa (cetaceans), and regions of concern (Block et al., 2011; Fedak, 2013; Roquet et al., 2013).

A major challenge to AnBSs is data storage and transmission. Two general modes of data collection exist to address these challenges. First, data storage tags may record observations in higher resolution but the tag has to be recovered to acquire the data. These sensors may “pop-off” the animal and be recovered at sea, or in the case of elephant seals and other pinnipeds, the AnBSs record high resolution data (often temperature, salinity, oxygen, but also echo sounder data) and the sensor tag is recovered when the animal returns to the rookery or shore (e.g., Lawson et al., 2015). Sometimes the sensors also require recovery for recalibration (as in the case of some oxygen sensors), otherwise assumptions of sensor drift and expected conditions have to be applied, limiting some data resolution or applications. The second general data conveyance method is to relay information through a network (Dragon et al., 2010; Blain et al., 2013). This has long been through the aging ARGOS satellite network. These can be relatively small transmitter-tags but the data is limited by the network thus measurements are often lower-resolution. Iridium hardware is still usually too big for most animals to handle. Cell networks are increasingly being used in areas where service is available (near shore). These methods can be combined, relaying low-resolution data through ARGOS and acquiring high resolution data if/when the AnBS is recovered.

With a cost of a few hundred to a few thousand dollars, AnBSs tend to be relatively cost-effective oceanographic sensor packages. New tag developments are striving to miniaturize sensors which would allow expanded use beyond the large vertebrates. These efforts include AnBSs carried by soft-bodied invertebrates such as jellyfish and squid (Mooney et al., 2015; Fossette et al., 2016) (Figure 8). Many inertial motion sensors are widely available, thus driving down costs. Leveraging these and other “off-the-shelf” sensors would help in further cost-reduction. 3D housing printing would reduce manufacturing costs. Additionally, improving data transfer, perhaps through microsatellites, would help cost-efficiency of gaining the observational data.

FIGURE 8

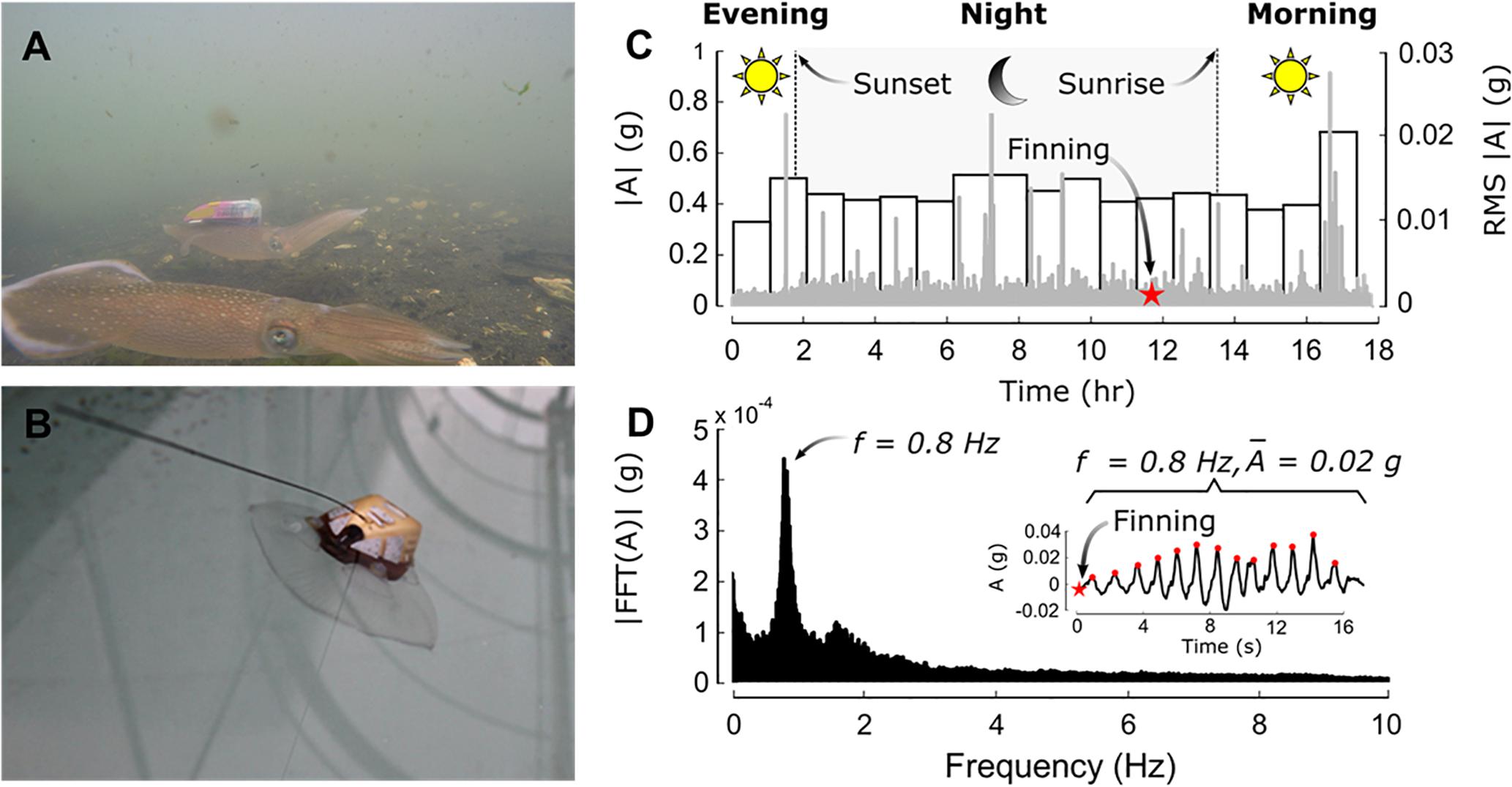
Figure 8. (A) Squid with iTag, a novel biologging ecosensor (midground). A companion squid without an AnBS is seen in the foreground. (B) Jellyfish with a different iTag version. (C–D) iTag data showing general light evaluation from the light sensor, and movement patterns form the 3D accelerometer. Gray is instantaneous peak values and bars are 1 h RMS values. (D) A Fourier transform of accelerometer data showing the occurrence rates of the various accelerometer events with the star shown in the inset [adapted with permission from Mooney et al. (2015)].

Challenging Areas: Technologies Where Innovation Is Needed for Cost Reduction

In this section, we review recent developments of two areas of active research on biological sensors. Although continuous innovations are required to lower the cost of these sensor systems for large-scale deployment, there have been significant advancement in these areas in terms of both technology and cost reduction. Discussion on a more extensive list of biological in situ sensor technologies can be found in the review by Lombard et al. (2019).

Optical Sensors for in situ Plankton Monitoring

Optical monitoring of plankton EOVs (phytoplankton and zooplankton abundances and functional diversity) is challenging and often requires high resolution imaging systems together with dedicated data analysis systems (Picheral et al., 2010), driving up costs (into to $100k range). Various systems have been developed for plankton or particles greater than 10–20 μm, replacing the high-cost laser optical plankton counter (LOPC) (Herman et al., 2004). Rapid advances in electro-optical technology have resulted in new and better ways of illuminating, detecting, and imaging plankton in situ, which has the potential to lower the costs of the systems. Prototypes or commercially available high resolution imaging systems now allow plankton and particles to be detected across a wide range of sizes, up to the centimeter scale. The hardware part of these systems is now mature and additional miniaturization efforts has allowed these sensors to become fully adaptable on autonomous platforms (e.g., floats and gliders) (Boss et al., 2018; Ohman et al., 2019). These technological progresses can be integrated with existing data protocols to allow cross comparison from quantitative data set (Lombard et al., 2019).

For organisms larger than 100 μm, the number of available sensors has increased drastically over the last decade and several are available at reasonable costs (<$100k) with a high capacity of data production. The examples include the FlowCam macro (Sieracki et al., 1998), Video Plankton Recorder I and II (Batten et al., 2003), ZooSCAN (Gorsky et al., 2010), Underwater Vision Profiler (Picheral et al., 2010), and in situ Ichthyoplankton Imaging System (ISIIS) (Cowen and Guigand, 2008) and an onboard system (Colas et al., 2018). However, two identified main limits have high cost associated with operating the instruments, if not in the capital cost itself. The first one is that these organisms are often mixed with non-living particles in this size range. As such, the imaging process for coastal waters is extremely complex. The second limit is the quantity of data production, storage capacities, and analysis tools (Boss et al., 2018; Lombard et al., 2019). The development of shared statistical tools using computing science and artificial intelligence is the current direction to avoid an exponential increase of human resource requirement for data validation.

Organisms smaller than ∼20 μm (pico- to nano-meter range), which includes prokaryotes and protists, are too small for simple and cheaper optical imaging systems. Despite its higher cost, the use of flow cytometry (FC) with fluorescence triggers appears to be the simplest way to automatically access quantitative information of auto- and mixo-trophic cells (<20 μm) whereas measurements of heterotrophic cells are relatively less mature. Assessment of phytoplankton community structure using scanning flow cytometry (SFC) thus showed promising correlations between automated, high-frequency in situ SFC measurements and proxies of community structure from remote sensing (e.g., Thyssen et al., 2015; Mouw et al., 2017). However, currently available commercial systems of SFC are generally bulky, power-hungry, and expensive. Similar to image analyses, the data processing still requires development of automatic clustering to avoid the high demand of human resources.

Despite the associated costs, some novel methods for automated in situ observations are in development by mixing FC and imaging capacities for microphytoplankton. As an example, the Imaging FlowCytobot (IFCB; Olson et al., 2003; Sosik and Olson, 2007; McLane Labs Inc., United States) is one of the most suitable and operational imaging systems for micro-plankton and phytoplankton observations. It is submersible and autonomous and has demonstrated applications as a sentinel for harmful algal taxa (Harred and Campbell, 2014). Underwater holographic systems, such as Holoflow@Sea “DHL” (Sun et al., 2008; Hermand et al., 2013, 2014), are also suitable for in situ imaging of organisms in the size range 2–200 μm and allow species identification and capture of dynamic underwater scenes at very fine scales. Several novel and lower cost methods for automated in situ observations at larger scale are currently in development (Karlson et al., 2017; Lombard et al., 2019). For example, the deployment of the FluoroProbe (Catherine et al., 2012) allows studying phytoplankton community composition at high spatial and temporal resolution, using a phytoplankton quantification method based on fluorescence excitation spectra. These developments of flow cytometers with imaging systems in the last decade represent an order of magnitude of cost reduction compared to traditional shipboard sampling and analysis.

Genetic Sensors for Microbes and eDNA

Many microorganisms perform crucial functions in biogeochemical cycling (e.g., methane or dimethylsulfide production, nitrogen transformations) and toxin production but are not optically distinct. Key groups of bacteria and archaea can only be monitored using analytical DNA and RNA techniques, resulting in the development of “microbe biomass and diversity” as an emerging EOV. Genetic sensors, also referred to as “Ecogenomic” Sensors, bring a wealth of analytical power to existing ocean monitoring instruments through in situ, autonomous detection and enumeration of specific DNA or RNA sequences, providing information on strain and species presence/absence, numbers and activities (Scholin, 2013; McQuillan and Robidart, 2017; Scholin et al., 2018). In cases where direct capture is not possible, the detection and population genetics of microbes, phytoplankton, zooplankton, and larger organisms can be acquired through their environmental DNA or “eDNA” (nucleic acids recovered from lysed or sloughed cells, feces, urine, gametes, mucus, etc.), offering a cost-effective, sensitive, and less invasive opportunity for monitoring organisms across the tree of life (Buxton et al., 2018).

The most advanced and only commercially available ecogenomic sensor is the Environmental Sample Processor (2nd Generation ESP; available through McLane Labs, Woods Hole, MA). The ESP has been demonstrated for monitoring fish (using eDNA signatures), fecal indicator bacteria, other prokaryotes, invertebrates and harmful algae from the water column in real time (Scholin et al., 2018). It is capable of measuring toxins and performing rRNA fingerprinting using ELISA and sandwich hybridization arrays, as well as qPCR using microfluidics (Doucette et al., 2009; Preston et al., 2009, 2011; Robidart et al., 2014). In situ preserved samples have been validated for DNA and RNA analyses, including metatranscriptomics (Ottesen et al., 2011). The ESP was recently deployed in Ocean Observing Buoys (Harmful Algal Bloom “HAB” buoy) in the Gulf of Maine Northeastern Regional Association of Coastal Ocean Observing Systems (NERACOOS) to validate the system for HAB monitoring. However, the up-front cost of such instrumentation is still prohibitively high for it to be widely deployed, despite the fact that ecogenomic sensors can potentially reduce the cost per sample by obviating the need for a specialist operator and decreasing the incidence of human error.

Critically, since they require small (μl scale) reagent volumes, molecular biological techniques are well-suited for miniaturized instrumentation. As an example of the path to a miniaturized system, the third generation ESP is smaller and less complex than the second, now fitting in the nose of a long-range AUV capable of Lagrangian drift (Pargett et al., 2015; Figure 9). Further reducing the size and complexity and improving the robustness of these instruments can significantly reduce operational costs associated with deployment and recovery. A rich innovation pipeline exists within academia and industry, including some key technological advances emerging from the medical “point of care” device sector to merge with miniaturized auto-samplers to advance environmental genetic sensor miniaturization, reducing instrumentation costs (Petralia and Conoci, 2017). Conformance to standards is required, and thus inter-calibration is required for each target organism, which will determine the extent to which these sensors are adopted by diverse sectors.

FIGURE 9

Figure 9. The third Generation ESP fits into the nose of a Glider i.e., Long-Range Autonomous Underwater Vehicle (left photo courtesy of Bill Ussler; right, courtesy of Ben Raanan).

Common Themes and Transformative Future Directions

The vision of this review is to identify strategies for breaking the high-cost barrier of ocean observing over the coming decade by developing cost-effective sensors and deployment strategies. While clear progress is already visible (e.g., as described in sections “Existing Cost-Effective Sensing Technologies for Biogeochemical EOVs and Relevant Parameters” and “Cost-Effective Deployments”), new approaches and technologies are still needed to achieve the order of magnitude increase in spatial and temporal resolution demanded to match the scales of ocean processes. In this final section, we summarize common strategies identified in the case studies presented above and consider how these lessons may recommend promising directions for moving forward toward increasingly cost-effective high resolution sensing of critical oceanographic variables.

Common Strategies and Shared Challenges

To date, common characteristics of successful strategies for cost reduction and increasing data resolution are: (1) miniaturization, (2) use of lower priced materials, (3) innovative approaches for sensing, simultaneous detections, and multi-sensor integration, and (4) engagement of citizen scientists, stakeholders, and the public in deployments. Going beyond the aspects of sensing elements discussed above, there is also a range of other supplementary challenges that are common to all oceanographic sensors in which innovation has the potential to leapfrog progress. For instance, in contrast to typical surface-deployable sensors, packaging considerations for underwater sensors are critical for surviving the high pressure, corrosive environment, both for sensing elements and for the batteries, controllers, and associated peripherals. In recent years, some progress has been made in this area, in part driven by low-cost, hobby-grade robotics initiatives (e.g., low-cost pressure housings, such as those marketed by Blue Robotics¹⁷). However, there remains ample room for standardization in pressure housings and underwater connectors to promote further cost savings. Fouling, both physical and biological, must be considered in oceanographic deployments, and while a wide range of copper-based strategies and physical removal of fouling are in common use, there remains a critical need for innovative non-toxic approaches.

A further common challenge with oceanographic deployments is that the deployment platform places restrictions on the size and weight of the sensor. This can be mitigated by miniaturization of the sensors themselves or by further innovating the platform design itself. Advances to platform design may also allow for longer deployments and there is therefore a critical need for innovation in battery technologies and/or energy efficiency of sensors, as batteries typically represent the majority of the volume and weight of oceanographic deployments. Data collection and transmission by sensors may also be significantly limited by power consumption (see more discussion in section “Remaining Challenges: Power and Data Management”).

Deployment Strategies

As the deployment of sensors can represent a large fraction of the cost of research, innovation in both platform design and deployment strategies play a critical role in enabling higher resolution data collection in ocean observing. Although professional deployments are critical to obtain high-quality data to study ocean biogeochemistry and biology, engagement of citizen scientists, stakeholders, and the public to deploy and use cost-efficient sensors is one emerging way to observe coastal environments on a much larger scale, and it is likely to accelerate as costs of sensors continue to drop. This includes the use of ships of opportunity, sail boats, fishing vessels (fisheries survey), and other private seagoing vessels as well as public/private coastal infrastructure (e.g., piers) as observing platforms for research and ecosystem monitoring (e.g., Doray et al., 2018). Citizen science may also bridge issues of data collection and dissemination to the public through integration with the growing “internet of things” connected by mobile apps and social media. Such strategies have the potential to simultaneously build public engagement in marine science research, resources management, and working toward long-term sustainability. Furthermore, as the number of deployed sensors grows, it may be possible to leverage co-located or proximate sensors to further improve data accuracy (i.e., reduce and better quantify uncertainty) relative to single-sensor deployments. Ultimately this may allow use of low-cost sensor “swarms” to collect data at a quality approaching that of high-cost scientific equipment. To maximize the output of citizen science, however, structured engagements, best practice guides, and practices for data quality control should be developed before the start of a deployment project.

Another novel and potentially cost-effective way of ocean observing is to use marine organisms as observing platforms. In addition to traditional tags deployed on large marine animals and fish species, small tags used on numerically dominant marine species, such as squid and jellyfish, are emerging as a result of sensor miniaturization and advancing of technologies; this has the potential to tap into “unlimited” “bio-observing platforms” that can be deployed with in situ sensors in the ocean. As miniaturization of technologies continues, these tags can be used not only to study fine-scale behaviors of marine organisms but also to record key parameters of their surrounding physical and chemical environment. Because the environment sampled will be limited by the animals’ behaviors, the community may need to explore methods for outfitting multiple species with different behaviors to observe a range of environments of interest.

Remaining Challenges: Power and Data Management

An overarching issue for deploying an increasing number of sensors and platforms is long-term power consumption (Brehmer et al., 2018) and data transmission. This issue may become exponentially more important as more sensors are deployed. In remote deployments where telemetry to shore via Wi-Fi is not an option, non-sensor costs may offset entirely the cost savings in sensor hardware. It is therefore essential that as cost-effective sensors continue to evolve the community consider strategic development of sensing nodes along with (i) networking and (ii) computational demands of the computational models the sensor data will be fed into. For example, sensors of the future could potentially locally process information, e.g., locally aggregate data via a mesh network to feed to an onboard instantiation of the target model, resulting in savings of energy and cost for data transmission by relaying only critical model outputs rather than raw data streams.

Onboard data fusion or feature extraction has already been carried out in many cases for detection of local threats (e.g., onset of harmful algal blooms). As power demand of processors continues to decrease faster relative to power demand for data transmission, local data processing will become increasingly advantageous. As artificial intelligence and data fusion techniques continue to be refined, the types of assessments that can be achieved in situ without losing accuracy or trustworthiness in data products will likely also expand. Such local sensing networks in remote deployments may have the capability to optimize observational assets and sampling strategies, as well as conduct calibrations without human input. If the community can forecast the types of such capabilities that will be most advantageous, we can identify promising pathways forward in underwater communication and networking (e.g., Leonard et al., 2007; Taya et al., 2018; Song et al., 2019) and data fusion (already used for above-water radar applications like (Guerriero et al., 2010).

Roadmapping: Accelerating Transfer of New Technologies to Users

Roadmapping, which has been successfully applied in other fields such as energy systems planning, enables prediction and planning of future characteristics and technologies of complex systems. Recent attempts have jump-started this activity for biogeochemical sensing in ocean observing systems (AtlantOS EU H2020 project, task 6.1¹⁸), contacting biogeochemical sensor and instrumentation technology developers across the globe and requesting their inputs to chart the (projected) availability of instruments over the next decade. Contributors are encouraged to provide links to technical characteristics of the technology and to give a timetable for development of the technology using the TRL framework, with the intention to give ocean technology developers and ocean observers the ability to predict and to plan for the timely use and uptake of state of the art technologies.

To achieve this vision, however, the road mapping needs to be integrated with ocean observing governance entities such as GOOS, JCOMM, and GEO. In addition, it requires frank engagement from the technology development community, which must be promoted by a sense of buy-in from the ocean observing community; this will also incentivize developer involvement through commercial success of products that are a response to the roadmap. The authors hope that this review will drive individuals in the field to consider potential uses for lower-cost sensors in the coming decades and contribute to this roadmap.

Challenges related to road mapping include concerns around disclosure of intellectual property or strategic development plans in what is an increasingly competitive landscape, particularly from the side of industry. However, evidence to date is that developers are keen to reveal their development plans to aid uptake and that the international observing governance bodies are ready and willing to support and sustain this activity beyond the life of short term individual projects (see footnote 18). There is also evidence that inclusion in the roadmap is aiding developers of instrumentation through promoting links to platform and observing systems (see footnote 18). Once new instruments are made available, information databases, such as the one maintained by the Alliance for Coastal Technologies,¹⁹ will be critical in linking global customers to an increasing array of options for studying marine systems.

Conclusion

Further development of cost-effective sensing technologies and deployment strategies can offer innovative solutions and strengthen the observing capabilities to respond to the growing needs for marine biogeochemistry, biology, and ecosystem observation, to inform marine resource management, to ensure the durability of ecosystem services, and to monitor and study global change impacts. A shift toward ocean observing technologies that are significantly lower in cost means new high-resolution applications can be targeted. It is clear that many useful cost-effective biogeochemical sensors are available or will soon become available, and that biological in situ sensors require more attention from the ocean science community and funding agencies in the coming decade to reduce the gap. It is also evident that cost benefits scale when integrated with other traditional and non-traditional deployment strategies. As more sensors can be deployed, we will move from a single point sensor to having arrays of sensors for broader spatial and temporal scale measurements. This will also lead to market scale availability, opening up the possibility for a more diverse group of global scientists and citizen scientists having access to sensors and aiding in the democratization of ocean science.

In closing, we challenge the ocean observing community to consider exploring new ways to fund the ever-growing ocean observing enterprise, particularly those that tie in with new avenues for deployment and inclusion of stakeholders and the community in the scientific endeavor. Traditional routes of research funding may be important but insufficient to support the growing needs of ocean observing, and commercialization of new technologies may have limitations, largely depending on commercial demand and profits. Alternatively, crowd-funding may have the potential to grow significantly if engagement of citizen science using cost-effective sensors grows. In turn, increasing demand for more sensors from non-traditional or non-academic communities, such as citizen scientists, resource management entities, and environmental monitoring groups, may help to reduce the cost of commercialization of a technology.

Author Contributions

ZW led this effort, and contributed to most parts of the work and revision and response to reviewers’ comments. HM co-led the initial initiative of this work, contributed to the biological part of the work, overall structure, and manuscript revision. AVM co-led the initial initiative of this work, contributed to the nutrient sensor section and substantially to the “Future Directions” section, as well as revision, framing, and editing of the complete manuscript. APM co-led the initiative of this work, contributed substantially to the sections “Existing Cost-Effective Sensing Technologies for Biogeochemical EOVs and Relevant Parameters” and “Common Themes and Transformative Future Directions” as well as revision, framing the complete work in addition to final manuscript editing. MM contributed to the sections related to the LOC technology (sections “Dissolved Oxygen,” “The Carbon Dioxide (CO₂) System,” “Nutrients,” and “Designing Cost-Effective Deployments With Miniaturized Sensors”) and roadmapping (section “Roadmapping: Accelerating Transfer of New Technologies to Users”). BG contributed to the section “Democratizing Access to Ocean Observing Technology.” TM contributed to the sections “Animal Oceanographers” and “Common Themes and Transformative Future Directions” and revision of the manuscript. WM contributed to the sections “Underwater Bio-Acoustics” and “Optical Sensors for in situ Plankton Monitoring” on bio-acoustic and optic sensors. JM contributed to the section related to microbes and eDNA, and revision of the manuscript. JR contributed to the section “Genetic Sensors for Microbes and eDNA” related to genetic sensors and revision of the manuscript. JC contributed to the section “Suspended Particles and Particulate Organic Carbon” on sensor technologies for particles and POC, and revision of the manuscript. MS contributed to the sections “Optical Sensors for in situ Plankton Monitoring” and “Common Themes and Transformative Future Directions,” and revision of the manuscript. AD contributed substantially to the section related to Fluorescence and Chlorophyll-a, and revision of the manuscript. AS contributed to sections “The Carbon Dioxide (CO₂) System,” “Nutrients,” and “Designing Cost-Effective Deployments With Miniaturized Sensors,” and revision of the manuscript. SM contributed to the section “The Carbon Dioxide (CO₂) System” and revision of the manuscript. KF contributed to the section “Genetic Sensors for Microbes and eDNA” on eDNA. PB co-led the initial initiative of this work, and contributed to the biological parts of the manuscript, and the manuscript revision.

Funding

The unpublished work related to iTag and mini-DO sensor was supported by the US National Science Foundation (NSF) (DBI-145559). The US NSF (OCE-1233654), the US National Institute of Standards and Technology (NIST) (60NANB10D024), and the NOAA Sea Grant (2017-R/RCM-51) supported the development of the CHANOS sensor. Part of this work was supported by the European Commission via the STEMM-CCS, AtlantOS, SenseOCEAN, TriAtlas, and Preface projects under the European Union’s Horizon 2020 research and innovation program (Grant Nos. 603521, 654462, 633211, 614141, and 817578), as well as the AWA project (IRD and BMBF; 01DG12073E), and the Blue Belt Initiative (BBI). The work on the LOC nutrients and carbonate sensors was supported by the Autonuts and CarCASS projects, part of the UK Natural Environment Research Council capital program OCEANIDS (NE/P020798/1 and NE/P02081X/1). The work on zooplankton and chlorophyll sensors was co-supported by the ROEC program (Reseau d’Observation en Environnement Côtier 2015–2020) and the European Regional Development Fund (ERDF).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to acknowledge the contributions to the LOC elements of this manuscript from the wider OTEG team at the NOC but particularly Socratis Loucaides, Alexander Beaton, Geraldine Clinton-Bailey, Chris Cardwell, and Greg Slavik. The authors would also like to express their gratitude to the development teams of the CHANOS and iTag, particularly Sophie Chu, Mallory Ringham, Kate Morkeski, Alex Shorter, David Mann, Kakani Katija, Fritz Sonnichesen, Steve Lerner, and Glenn McDonald, as well as the IRD and the Ifremer acoustics teams, particularly Lemar, Marbec, Imago, and François Gerlotto, Erwan Josse, Anne Lebourges-Dhaussy, Yannick Perrot, Jeremie Habasque, and Gildas Roudaut.

Footnotes

1. ^ http://www.goosocean.org
2. ^ https://ioos.noaa.gov
3. ^ https://www.oceanobservatories.org
4. ^ http://www.laceinturebleue.org
5. ^ http://www.imos.org.au/
6. ^ http://www.biogeochemical-argo.org
7. ^ http://oceanexports.org
8. ^ http://www.oceansites.org
9. ^ http://www.goosocean.org/eov
10. ^ http://www.oxyguard.dk
11. ^ http://oceanhealth.xprize.org
12. ^ http://sunburstsensors.com/products/isami-ph.html
13. ^ http://goa-on.org/
14. ^ http://www.act-us.info/database.php
15. ^ http://www.smartcoastlines.org
16. ^ https://cordis.europa.eu/project/rcn/110898/factsheet/en
17. ^ http://www.bluerobotics.com
18. ^ https://www.atlantos-h2020.eu/download/deliverables/6.1%20Sensors%20and%20Instrumentation%20Roadmap.pdf
19. ^ http://www.act-us.info

References

Alkire, M. B., Lee, C., D’Asaro, E., Perry, M. J., Briggs, N., Cetinić, I., et al. (2014). Net community production and export from Seaglider measurements in the North Atlantic after the spring bloom. J. Geophys. Res. Oceans 119, 6121–6139. doi: 10.1002/2014JC010105

CrossRef Full Text | Google Scholar

Arranz, P., De Soto, N. A., Madsen, P. T., Brito, A., Bordes, F., and Johnson, M. P. (2011). Following a foraging fish-finder: diel habitat use of Blainville’s beaked whales revealed by echolocation. PLoS One 6:e28353. doi: 10.1371/journal.pone.0028353

PubMed Abstract | CrossRef Full Text | Google Scholar

Atamanchuk, D., Tengberg, A., Thomas, P. J., Hovdenes, J., Apostolidis, A., Huber, C., et al. (2014). Performance of a1 lifetime-based optode for measuring partial pressure of carbon dioxide in natural waters. Limnol. Oceanogr. Methods 12, 63–73. doi: 10.4319/lom.2014.12.63

CrossRef Full Text | Google Scholar

Barus, C., Legrand, D. C., Striebig, N., Jugeau, B., David, A., Valladares, M., et al. (2018). First deployment and validation of in situ silicate electrochemical sensor in seawater. Front. Mar. Sci. 5:60. doi: 10.3389/fmars.2018.00060

CrossRef Full Text | Google Scholar

Batten, S., Clarke, R. A., Flinkman, J., Hays, G., John, E. H., John, A. W. G., et al. (2003). CPR sampling – the technical background, materials and methods, consistency and comparability. Prog. Oceanogr. 58, 193–215. doi: 10.1016/j.pocean.2003.08.004

CrossRef Full Text | Google Scholar

Beaton, A. D., Cardwell, C. L., Thomas, R. S., Sieben, V. J., Legiret, F. E., Waugh, E. M., et al. (2012). Lab-on-chip measurement of nitrate and nitrite for in situ analysis of natural waters. Environ. Sci. Technol. 46, 9548–9556. doi: 10.1021/es300419u

PubMed Abstract | CrossRef Full Text | Google Scholar

Beaton, A. D., Wadham, J. L., Hawkings, J., Bagshaw, E. A., Lamarche-Gagnon, G., Mowlem, M. C., et al. (2017). High-resolution in situ measurement of nitrate in runoff from the Greenland ice sheet. Environ. Sci. Technol. 51, 12518–12527. doi: 10.1021/acs.est.7b03121

PubMed Abstract | CrossRef Full Text | Google Scholar

Benoit-Bird, K. J., Kuletz, K., Heppell, S., Jones, N., and Hoover, B. (2011). Active acoustic examination of the diving behavior of murres foraging on patchy prey. Mar. Ecol. Prog. Ser. 443, 217–235. doi: 10.3354/meps09408

CrossRef Full Text | Google Scholar

Benoit-Bird, K. J., Welch, T. P., Waluk, C. M., Barth, J. A., Wangen, I., McGill, P., et al. (2018). Equipping an underwater glider with a new echosounder to explore ocean ecosystems. Limnol. Oceanogr. Methods 16, 734–749. doi: 10.1002/lom3.10278

CrossRef Full Text | Google Scholar

Bertrand, A., Grados, D., Colas, F., Bertrand, S., Capet, X., Chaigneau, A., et al. (2014). Broad impacts of fine-scale dynamics on seascape structure from zooplankton to seabirds. Nat. Commun. 5:5239. doi: 10.1038/ncomms6239

PubMed Abstract | CrossRef Full Text | Google Scholar

Betanzos, A., Martín, H. A., Tizol, S. V. R., Schneider, P., Hernández, J. L., Brehmer, P., et al. (2016). “Performance of a low cost single beam echosounder: in situ trials in a shallow water coral reef habitat with verification by video,” in Proceedings of the 2015 IEEE/OES Conference on Acoustics in Underwater Geosciences Symposium (RIO Acoustics), Rio de Janeiro.

Google Scholar

Bittig, H. C., Körtzinger, A., Neill, C., van Ooijen, E., Plant, J. N., Hahn, J., et al. (2018). Oxygen optode sensors: principle, characterization, calibration, and application in the ocean. Front. Mar. Sci. 4:429. doi: 10.3389/fmars.2017.00429

CrossRef Full Text | Google Scholar

Blain, S., Renaut, S., Xing, X., Claustre, H., and Guinet, C. (2013). Instrumented elephant seals reveal the seasonality in chlorophyll and light-mixing regime in the iron-fertilized Southern Ocean. Geophys. Res. Lett. 40, 6368–6372. doi: 10.1002/2013gl058065

CrossRef Full Text | Google Scholar

Block, B. A., Jonsen, I. D., Jorgensen, S. J., Winship, A. J., Shaffer, S. A., Bograd, S. J., et al. (2011). Tracking apex marine predator movements in a dynamic ocean. Nature 475, 86–90. doi: 10.1038/nature10082

PubMed Abstract | CrossRef Full Text | Google Scholar

Blockstein, L., and Yadid-Pecht, O. (2014). Lensless miniature portable fluorometer for measurement of chlorophyll and CDOM in water using fluorescence contact imaging. IEEE Photon. J. 6, 1–16. doi: 10.1109/JPHOT.2014.2326665

CrossRef Full Text | Google Scholar

Boss, E., Waite, A., Muller-Karger, F., Yamazaki, H., Wanninkhof, R., Uitz, J., et al. (2018). Beyond chlorophyll fluorescence: the time is right to expand biological measurements in ocean observing programs. Limnol. Oceanogr. Bull. 27, 89–90. doi: 10.1002/lob.10243

CrossRef Full Text | Google Scholar

Brehmer, P. (2006). Fisheries acoustics: theory and practice, 2nd edn. Fish Fish. 7, 227–228. doi: 10.1111/j.1467-2979.2006.00220.x

CrossRef Full Text | Google Scholar

Brehmer, P., Do Chi, T., Laugier, T., Galgani, F., Laloë, F., Darnaude, A. M., et al. (2011). Field investigations and multi-indicators for shallow water lagoon management: perspective for societal benefit. Aquat. Conserv. Mar. Freshw. Ecosyst. 21, 728–742. doi: 10.1002/aqc.1231

CrossRef Full Text | Google Scholar

Brehmer, P., Gerlotto, F., and Rouault, A. (2002). In situ inter-standardization of acoustics data: an integrated database for fish school behaviour studies. Acta Acust. United Acust. 88, 730–734.

Google Scholar

Brehmer, P., Josse, E., and Nøttestad, L. (2012). Evidence that whales (Balaenoptera borealis) visit drifting fish aggregating devices: do their presence affect the processes underlying fish aggregation? Mar. Ecol. 33, 176–182. doi: 10.1111/j.1439-0485.2011.00478.x

CrossRef Full Text | Google Scholar

Brehmer, P., Lafont, T., Georgakarakos, S., Josse, E., Gerlotto, F., and Collet, C. (2006). Omnidirectional multibeam sonar monitoring: applications in fisheries science. Fish Fish. 7, 165–179. doi: 10.1111/j.1467-2979.2006.00218.x

CrossRef Full Text | Google Scholar

Brehmer, P., Sancho, G., Trygonis, V., Itano, D., Dalen, J., Fuchs, A., et al. (2018). Towards an autonomous pelagic observatory: experiences from monitoring fish communities around drifting FADs. Thalassas 35, 177–189. doi: 10.1007/s41208-018-0108-8

CrossRef Full Text | Google Scholar

Breland, J. A., and Byrne, R. H. (1993). Spectrophotometric procedures for determination of sea-water alkalinity using bromocresol green. Deep Sea Res. Part I 40, 629–641. doi: 10.1016/0967-0637(93)90149-w

CrossRef Full Text | Google Scholar

Bresnahan, P. J., Martz, T. R., Takeshita, Y., Johnson, K. S., and LaShomb, M. (2014). Best practices for autonomous measurement of seawater pH with the Honeywell Durafet. Methods Oceanogr. 9, 44–60. doi: 10.1016/j.mio.2014.08.003

CrossRef Full Text | Google Scholar

Briggs, E. M., Sandoval, S., Erten, A., Takeshita, Y., Kummel, A. C., and Martz, T. R. (2017). Solid state sensor for simultaneous measurement of total alkalinity and pH of seawater. ACS Sensors 2, 1302–1309. doi: 10.1021/acssensors.7b00305

PubMed Abstract | CrossRef Full Text | Google Scholar

Briggs, N., Perry, M. J., Cetinić, I., Lee, C., D’Asaro, E., Gray, A. M., et al. (2011). High resolution observations of aggregate flux during a sub-polar North Atlantic spring bloom. Deep Sea Res. I 58, 1031–1039. doi: 10.1016/j.dsr.2011.07.007

CrossRef Full Text | Google Scholar

Briggs, R., Ricardo, A., Ruttenberg, K., and Glazer, B. (2013). Constraining sources of organic matter to tropical coastal sediments: consideration of nontraditional end-members. Aquat. Geochem. 19, 543–563. doi: 10.1007/s10498-013-9219-2

CrossRef Full Text | Google Scholar

Buxton, A. S., Groombridge, J. J., and Griffiths, R. A. (2018). Comparison of two citizen scientist methods for collecting pond water samples for environmental DNA studies. Citiz. Sci. 3, 1–9. doi: 10.5334/cstp.151

CrossRef Full Text | Google Scholar

Byrne, R. H. (2014). Measuring ocean acidification: new technology for a new Era of ocean chemistry. Environ. Sci. Technol. 48, 5352–5360. doi: 10.1021/es405819p

PubMed Abstract | CrossRef Full Text | Google Scholar

Byrne, R. H., DeGrandpre, M. D., Short, R. T., Martz, T. R., Merlivat, L., McNeil, C., et al. (2010). “Sensors and systems for in situ observations of marine carbon dioxide system variables,” in Proceedings of OceanObs’09: Sustained Ocean Observations and Information for Society, eds J. Hall, D. E. Harrison, and D. Stammer, (Paris: ESA Publication).

Google Scholar

Cao, X., Zhang, S. W., Chu, D. Z., Wu, N., Ma, H. K., and Liu, Y. (2017). A design of spectrophotometric microfluidic chip sensor for analyzing silicate in seawater. IOP Conf. Ser. Earth Environ. Sci. 82:012080. doi: 10.1088/1755-1315/82/1/012080

CrossRef Full Text | Google Scholar

Catherine, A., Escoffier, N., Belhocine, A., Nasri, A. B., Hamlaoui, S., Yepremian, C., et al. (2012). On the use of the FluoroProbe (R), a phytoplankton quantification method based on fluorescence excitation spectra for large-scale surveys of lakes and reservoirs. Water Res. 46, 1771–1784. doi: 10.1016/j.watres.2011.12.056

PubMed Abstract | CrossRef Full Text | Google Scholar

Cetinić, I., Perry, M. J., Briggs, N. T., Kallin, E., D’Asaro, E. A., and Lee, C. (2012). Particluate organic carbon and inherent optical properties during 2008 North Atlantic Bloom experiment. J. Geophys. Res. Oceans 117:C06028. doi: 10.1029/2011JC007771

CrossRef Full Text | Google Scholar

Chipman, L., Huettel, M., Berg, P., Meyer, V., Klimant, I., Glud, R., et al. (2012). Oxygen optodes as fast sensors for eddy correlation measurements in aquatic systems. Limnol. Oceanogr. Methods 10, 304–316. doi: 10.4319/lom.2012.10.304

CrossRef Full Text | Google Scholar

Clarke, J. S., Achterberg, E. P., Connelly, D. P., Schuster, U., and Mowlem, M. (2017). Developments in marine pCO2 measurement technology; towards sustained in situ observations. TrAC Trends Anal. Chem. 88, 53–61. doi: 10.1016/j.trac.2016.12.008

CrossRef Full Text | Google Scholar

Clarke, J. S., Achterberg, E. P., Rerolle, V. M. C., Bey, S. A. K., Floquet, C. F. A., and Mowlem, M. C. (2015). Characterisation and deployment of an immobilised pH sensor spot towards surface ocean pH measurements. Anal. Chim. Acta 897, 69–80. doi: 10.1016/j.aca.2015.09.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Clinton-Bailey, G. S., Grand, M. M., Beaton, A. D., Nightingale, A. M., Owsianka, D. R., Slavikt, G. J., et al. (2017). A lab-on-chip analyzer for in situ measurement of soluble reactive phosphate: improved phosphate blue assay and application to fluvial monitoring. Environ. Sci. Technol. 51, 9989–9995. doi: 10.1021/acs.est.7b01581

PubMed Abstract | CrossRef Full Text | Google Scholar

Colas, F., Tardivel, M., Perchoc, J., Lunven, M., Forest, B., Guyader, G., et al. (2018). The zoocam, a new in-flow imaging system for fast onboard counting, sizing and classification of fish eggs and metazooplankton. Prog. Oceanogr. 166, 54–65. doi: 10.1016/j.pocean.2017.10.014

CrossRef Full Text | Google Scholar

Cowen, R. K., and Guigand, C. M. (2008). In situ ichthyoplankton imaging system (ISIIS): system design and preliminary results. Limnol. Oceanogr. Methods 6, 126–132. doi: 10.4319/lom.2008.6.126

CrossRef Full Text | Google Scholar

Cullen, J. J. (1982). The deep chlorophyll maximum - comparing vertical profiles of chlorophyll-A. Can. J. Fish. Aquat. Sci. 39, 791–803. doi: 10.1139/f82-108

CrossRef Full Text | Google Scholar

Demer, D. A., Andersen, L. N., Bassett, C., Berger, L., Chu, D., Condiotty, J., et al. (2017). 2016 USA–Norway EK80 Workshop Report: Evaluation of a Wideband Echosounder for Fisheries and Marine Ecosystem Science. ICES Cooperative Research. Report 336. Copenhagen: International Council for the Exploration of the Sea, 69.

Google Scholar

Demer, D. A., Berger, L., Bernasconi, M., Bethke, E., Boswell, K., Chu, D., et al. (2015). Calibration of Acoustic Instruments. ICES Cooperative Research Report, 326. Copenhagen: International Council for the Exploration of the Sea, 133.

Google Scholar

Doray, M., Petitgas, P., Romagnan, J., Huret, M., Duhamel, E., Dupuy, C., et al. (2018). The PELGAS survey: ship-based integrated monitoring of the Bay of Biscay pelagic ecosystem. Prog. Oceanogr. 166, 15–29. doi: 10.1016/j.pocean.2017.09.015

CrossRef Full Text | Google Scholar

Doucette, G. J., Mikulski, C. M., Jones, K. L., King, K. L., Greenfield, D. I., Marin, I. I. I. R., et al. (2009). Remote, subsurface detection of the algal toxin domoic acid onboard the environmental sample processor: assay development and initial field trials. Harmful Algae 8, 880–888. doi: 10.1016/j.hal.2009.04.006

CrossRef Full Text | Google Scholar

Dragon, A. C., Monestiez, P., Bar-Hen, A., and Guinet, C. (2010). Linking foraging behaviour to physical oceanographic structures: Southern elephant seals and mesoscale eddies east of Kerguelen Islands. Prog. Oceanogr. 87, 61–71. doi: 10.1016/j.pocean.2010.09.025

CrossRef Full Text | Google Scholar

Dunlop, K., Jarvis, T., Benoit-Bird, K., Waluk, M. C., Caress, D., Thomas, H., et al. (2018). Detection and characterisation of deep-sea benthopelagic animals from an autonomous underwater vehicle with a multibeam echosounder: a proof of concept and description of data-processing methods. Deep Sea Res. Part I Oceanogr. Res. Pap. 134, 64–79. doi: 10.1016/j.dsr.2018.01.006

CrossRef Full Text | Google Scholar

Eleftherakis, D., Berger, L., Le Bouffant, N., Pacault, A., Augustin, J. M., and Lurton, X. (2018). Backscatter calibration of high-frequency multibeam echosounder using a reference single-beam system, on natural seafloor. Mar. Geophys. Res. 39, 55. doi: 10.1007/s11001-018-9348-5

CrossRef Full Text | Google Scholar

FAO, (2018). The State of World Fisheries and Aquaculture 2018 - Meeting the Sustainable Development Goals. Licence: CC BY-NC-SA 3.0 IGO. Rome: FAO.

Google Scholar

Fassbender, A. J., Sabine, C. L., De Lawrence-Slavas, N. E., Carlo, H., Meinig, C., and Jones, S. M. (2015). Robust sensor for extended autonomous measurements of surface ocean dissolved inorganic carbon. Environ. Sci. Technol. 49, 3628–3635. doi: 10.1021/es5047183

PubMed Abstract | CrossRef Full Text | Google Scholar

Fedak, M. A. (2013). The impact of animal platforms on polar ocean observation. Deep Sea Res. Part II Top. Stud. Oceanogr. 88, 7–13. doi: 10.1016/j.dsr2.2012.07.007

CrossRef Full Text | Google Scholar

Feely, R. A., Fabry, V. J., Dickson, A. G., Gattuso, J.-P., Bijma, J., Riebesell, U., et al. (2010). “An international observational network for ocean acidification,” in Proceedings of the OceanObs’09: Sustained Ocean Observations and Information for Society, eds J. Hall, D. E. Harrison, and D. Stammer, (Paris: ESA).

Google Scholar

Fennel, K., Alin, S., Barbero, L., Evans, W., Bourgeois, T., Cooley, S., et al. (2019). Carbon cycling in the North American coastal ocean: a synthesis. Biogeosciences 16, 1281–1304.

Google Scholar

Finch, M. S., Hydes, D. J., Clayson, C. H., Weigl, B., Dakin, J., and Gwilliam, P. (1998). A low power ultra violet spectrophotometer for measurement of nitrate in seawater: introduction, calibration and initial sea trials. Anal. Chim. Acta 377, 167–177. doi: 10.1016/s0003-2670(98)00616-3

CrossRef Full Text | Google Scholar

Floquet, C. F., Sieben, V. J., Milani, A., Joly, E. P., Ogilvie, I. R., Morgan, H., et al. (2011). Nanomolar detection with high sensitivity microfluidic absorption cells manufactured in tinted PMMA for chemical analysis. Talanta 84, 235–239. doi: 10.1016/j.talanta.2010.12.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Fossette, S., Katija, K., Goldbogen, J. A., Bograd, S., Patry, W., Howard, M. J., et al. (2016). How to tag a jellyfish? A methodological review and guidelines to successful jellyfish tagging. J. Plankton Res. 38, 1347–1363.

Google Scholar

Friedrichs, A., Busch, J., van der Woerd, H., and Zielinski, O. (2017). SmartFluo: a method and affordable adapter to measure chlorophyll a fluorescence with smartphones. Sensors 17:E678. doi: 10.3390/s17040678

PubMed Abstract | CrossRef Full Text | Google Scholar

Gartner, J. W. (2004). Estimating suspended solids concentrations from backscatter intensity measured by acoustic Doppler current profiler in San Francisco Bay, California. Mar. Geol. 211, 169–187. doi: 10.1016/j.margeo.2004.07.001

CrossRef Full Text | Google Scholar

Geißler, F., Achterberg, E. P., Beaton, A. D., Hopwood, M. J., Clarke, J. S., Mutzberg, A., et al. (2017). Evaluation of a ferrozine based autonomous in situ lab-on-chip analyzer for dissolved iron species in coastal waters. Front. Mar. Sci. 4:322. doi: 10.3389/fmars.2017.00322

CrossRef Full Text | Google Scholar

Gerlotto, F. P., Roux, J., Guillard, E., Josse, R., Fablet, R., Perrot, Y., et al. (2011). Development of real three-dimensional sonar for observing small scale dynamics of fish inside a school. J. Acoust. Soc. Am. 129, 2697–2697. doi: 10.1121/1.3589051

CrossRef Full Text | Google Scholar

Godo, O. R., and Totland, A. (1999). Bergen acoustic buoy (BAB)—A tool for remote monitoring of marine resources. J. Acoust. Soc. Am. 105:1051. doi: 10.1121/1.425005

CrossRef Full Text | Google Scholar

Gorsky, G., Ohman, M. D., Picheral, M., Gasparini, S., Stemmann, L., Romagnan, J.-B., et al. (2010). Digital zooplankton image analysis using the ZooScan integrated system. J. plankton Res. 32, 285–303. doi: 10.1093/plankt/fbp124

CrossRef Full Text | Google Scholar

Gray, S. E. C., DeGrandpre, M. D., Moore, T. S., Martz, T. R., Friederich, G. E., and Johnson, K. S. (2011). Applications of in situ pH measurements for inorganic carbon calculations. Mar. Chem. 125, 82–90. doi: 10.1016/j.marchem.2011.02.005

CrossRef Full Text | Google Scholar

Gruber, N., Doney, S. C., Emerson, S. R., Gilbert, D., Kobayashi, T., Körtzinger, A., et al. (2010). “Adding oxygen to Argo: developing a global in-situ observatory for ocean deoxygenation and biogeochemistry,” in Proceedings of OceanObs’09: Sustained Ocean Observations and Information for Society, Vol. 2, eds J. Hall, D. E. Harrison, and D. Stammer, (Paris: ESA).

Google Scholar

Guerriero, M., Svensson, L., and Willett, P. (2010). Bayesian data fusion for distributed target detection in sensor networks. IEEE Trans. Signal. Proces. 58, 3417–3421. doi: 10.1109/tsp.2010.2046042

CrossRef Full Text | Google Scholar

Guillard, J., Fernandes, P. G., Laloë, T., and Brehmer, P. (2011). Three-dimensional internal spatial structure of young-of-the-year pelagic freshwater fish provides evidence for the identification of fish school species. Limnol. Oceanogr. Methods 9, 322–328. doi: 10.4319/lom.2011.9.322

CrossRef Full Text | Google Scholar

Harred, L., and Campbell, L. (2014). Predicting harmful algal blooms: a case study with Dinophysis ovum in the Gulf of Mexico. J. Plankton Res. 36, 1434–1445. doi: 10.1093/plankt/fbu070

CrossRef Full Text | Google Scholar

Hawley, N. (2004). A Comparison of suspended sediment concentrations measured by acoustic and optical sensors. J. Great Lakes Res. 30, 301–309. doi: 10.1016/s0380-1330(04)70348-2

CrossRef Full Text | Google Scholar

Herman, A. W., Beanlands, B., and Phillips, E. F. (2004). The next generation of Optical Plankton Counter: the Laser-OPC. J. Plankton Res. 26, 1135–1145. doi: 10.1093/plankt/fbh095

CrossRef Full Text | Google Scholar

Hermand, J. P., Guo, L. X., Randall, J., and Brehmer, P. (2014). “Non-destructive optical holographic imaging of microorganisms in situ off the Senegalese coast,” in Proceedings of the OCEANS 2014-TAIPEI, (Taipei), 1–4.

Google Scholar

Hermand, J. P., Randall, J., Dubois, F., Queeckers, P., Yourassowsky, C., Roubaud, F., et al. (2013). “In-situ holography microscopy of plankton and particles over the continental shelf of Senegal,” in Proceedings of the Ocean Electronics (SYMPOL), (Kochi), 1–10.

Google Scholar

Hildebrand, J. A. (2009). Anthropogenic and natural sources of ambient noise in the ocean. Mar. Ecol. Prog. Ser. 395, 5–20. doi: 10.3354/meps08353

PubMed Abstract | CrossRef Full Text | Google Scholar

Hine, R., Willcox, S., Hine, G., and Richardson, T. (2009). “The wave glider: a wave-powered autonomous marine vehicle,” in Proceedings of the OCEANS 2009, (Biloxi, MS).

Google Scholar

Huang, X., Pascal, R. W., Chamberlain, K., Banks, C. J., Mowlem, M., and Morgan, H. (2011). A miniature, high precision conductivity and temperature sensor system for ocean monitoring. IEEE Sensors J. 11, 3246–3252. doi: 10.1109/jsen.2011.2149516

CrossRef Full Text | Google Scholar

IPCC, (2014). Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds V. R. Barros, C. B. Field, D. J. Dokken, M. D. Mastrandrea, K. J. Mach, et al. (Cambridge: Cambridge University Press), 688.

Google Scholar

Jech, J. M., Lawson, G. L., Lavery, A. C., and David Demer, H. (2017). Wideband (15-260 kHz) acoustic volume backscattering spectra of northern krill (Meganyctiphanes norvegica) and butterfish (Peprilus triacanthus). ICES J. Mar. Sci. 74, 2249–2261. doi: 10.1093/icesjms/fsx050

CrossRef Full Text | Google Scholar

Johnson, K. S., Berelson, W. M., Boss, E. S., Chase, Z., Claustre, H., Emerson, S. R., et al. (2009). Observing biogeochemical cycles at global scales with profiling floats and gliders prospects for a global array. Oceanography 22, 216–225. doi: 10.5670/oceanog.2009.81

CrossRef Full Text | Google Scholar

Johnson, M., de Soto, N. A., and Madsen, P. T. (2009). Studying the behaviour and sensory ecology of marine mammals using acoustic recording tags: a review. Mar. Ecol. Prog. Ser. 395, 55–73. doi: 10.3354/meps08255

CrossRef Full Text | Google Scholar

Johnson, K. S., and Coletti, L. J. (2002). In situ ultraviolet spectrophotometry for high resolution and long-term monitoring of nitrate, bromide and bisulfide in the ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 49, 1291–1305. doi: 10.1016/s0967-0637(02)00020-1

CrossRef Full Text | Google Scholar

Johnson, K. S., Jannasch, H. W., Coletti, L. J., Elrod, V. A., Martz, T. R., Takeshita, Y., et al. (2016). Deep-sea DuraFET: a pressure tolerant pH sensor designed for global sensor networks. Anal. Chem. 88, 3249–3256. doi: 10.1021/acs.analchem.5b04653

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, K. S., Plant, J. N., Coletti, L. J., Jannasch, H. W., Sakamoto, C. M., Riser, S. C., et al. (2017). Biogeochemical sensor performance in the SOCCOM profiling float array. J. Geophys. Res. Oceans 122, 6416–6436. doi: 10.1002/2017jc012838

CrossRef Full Text | Google Scholar

Kanwisher, J. (1959). Polarographic oxygen electrode. Limnol. Oceanogr. 4, 210–217.

Google Scholar

Karlson, B., Artigas, F., Créach, V., Louchart, A., Wacquet, G., and Seppälä, J. (2017). JERICO-NEXT. Novel Methods for Automated in Situ Observations of Phytoplankton Diversity. D3.1. Available at: https://archimer.ifremer.fr/doc/00422/53393 (accessed October 4, 2017).

Google Scholar

Kautsky, H. (1939). Quenching of luminescence by oxygen. Trans. Faraday Soc. 35, 216–219. doi: 10.1039/TF9393500216

CrossRef Full Text | Google Scholar

Keala, G. (2007). Loko la: A manual on Hawaiian Fishpond Restoration and Management. Mânoa: University of Hawaii, 76.

Google Scholar

Keeling, R. F., Kortzinger, A., and Gruber, N. (2010). Ocean deoxygenation in a warming world. Annu. Rev. Mar. Sci. 2, 199–229. doi: 10.1146/annurev.marine.010908.163855

CrossRef Full Text | Google Scholar

Kiefer, D. A. (1973). Fluorescence properties of natural phytoplankton populations. Mar. Biol. 22, 263–269. doi: 10.1007/bf00389180

CrossRef Full Text | Google Scholar

Kimball, P., Bailey, J., Das, S., Geyer, R., Harrison, T., Kunz, C., et al. (2014). “The WHOI Jetyak: an autonomous surface vehicle for oceanographic research in shallow or dangerous waters,” in Proceeding of the 2014 IEEE/OES Autonomous Underwater Vehicles (AUV), (Oxford, MS: Institute of Electrical and Electronics Engineers Inc).

Google Scholar

Korneliussen, R. J., Heggelund, Y., Eliassen, I. K., Øye, O. K., Knutsen, T., and Dalen, J. (2009). Combining multibeam-sonar and multifrequency-echosounder data: examples of the analysis and imaging of large euphausiid schools. ICES J. Mar. Sci. 66, 991–997. doi: 10.1093/icesjms/fsp092

CrossRef Full Text | Google Scholar

Korneliussen, R. J., Heggelund, Y., Macaulay, G. J., Patel, D., Johnsen, E., and Eliassen, I. K. (2016). Acoustic identification of marine species using a feature library. Methods Oceanogr. 17, 187–205. doi: 10.1016/j.mio.2016.09.002

CrossRef Full Text | Google Scholar

Körtzinger, A., Schimanski, J., and Send, U. (2005). High quality oxygen measurements from profiling floats: a promising new technique. J. Atmos. Ocean Tech. 22, 302–308. doi: 10.1175/jtech1701.1

CrossRef Full Text | Google Scholar

Körtzinger, A., Schimanski, J., Send, U., and Wallace, D. (2004). The ocean takes a deep breath. Science 306, 1337–1337. doi: 10.1126/science.1102557

PubMed Abstract | CrossRef Full Text | Google Scholar

Lakowicz, J. R. (ed.) (2006). Principles of Fluorescence Spectroscopy. Boston, MA: Springer.

Google Scholar

Lampitt, R. S., Favali, P., Barnes, C. R., Church, M. J., Cronin, M. F., Hill, K. L., et al. (2010). “In situ sustained Eulerian observatories,” in Proceedings of OceanObs’ 09: Sustained Ocean Observations and Information for Society, eds J. Hall, D. E. Harrison, and D. Stammer, (Paris: ESA).

Google Scholar

Lavery, A. C., Bassett, C., Lawson, G. L., and Jech, J. M. (2017). Exploiting signal processing approaches for broadband echosounders. ICES J. Mar. Sci. 74, 2262–2275. doi: 10.1093/icesjms/fsx155

CrossRef Full Text | Google Scholar

Lawson, G. L., Hückstädt, L. A., Lavery, A. C., Jaffré, F. M., Wiebe, P. H., Fincke, J. R., et al. (2015). Development of an animal-borne “sonar tag” for quantifying prey availability: test deployments on northern elephant seals. Anim. Biotelem. 3, 22–38.

Google Scholar

Le Quere, C., Takahashi, T., Buitenhuis, E. T., Rodenbeck, C., and Sutherland, S. C. (2010). Impact of climate change and variability on the global oceanic sink of CO₂. Glob. Biogeochem. Cycle 24:GB4007. doi: 10.1029/2009GB003599

CrossRef Full Text | Google Scholar

Lee, S., Jung, J.-Y., Lee, M., and Chang, J. (2017). An aqueous ammonia sensor based on printed indium tin oxide layer. Sensors Mater. 29, 57–63.

Google Scholar

Leeuw, T., Boss, E. S., and Wright, D. L. (2013). In situ measurements of phytoplankton fluorescence using low cost electronics. Sensors 13, 7872–7883. doi: 10.3390/s130607872

PubMed Abstract | CrossRef Full Text | Google Scholar

Leonard, N. E., Paley, D. A., Lekien, F., Sepulchre, R., Fratantoni, D. M., and Davis, R. E. (2007). Collective motion, sensor networks, and ocean sampling. Proc. IEEE 95, 48–74. doi: 10.1109/jproc.2006.887295

CrossRef Full Text | Google Scholar

Li, Q. L., Wang, F. Z., Wang, Z. A., Yuan, D. X., Dai, M. H., Chen, J. S., et al. (2013). Automated spectrophotometric analyzer for rapid single-point titration of seawater total alkalinity. Environ. Sci. Technol. 47, 11139–11146. doi: 10.1021/es402421a

PubMed Abstract | CrossRef Full Text | Google Scholar

Linløkken, A. N., Næstad, F., Langdal, K., and Østbye, K. (2019). Comparing fish density and echo strength distribution recorded by two generations of single beam echo sounders. Appl. Sci. 9:2041. doi: 10.3390/app9102041

CrossRef Full Text | Google Scholar

Liu, X., Byrne, R. H., Adornato, L., Yates, K. K., Kaltenbacher, E., Ding, X., et al. (2013). In situ spectrophotometric measurement of dissolved inorganic carbon in Seawater. Environ. Sci. Technol. 47, 11106–11114. doi: 10.1021/es4014807

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X. W., Wang, Z. H. A., Byrne, R. H., Kaltenbacher, E. A., and Bernstein, R. E. (2006). Spectrophotometric measurements of pH in-situ: laboratory and field evaluations of instrumental performance. Environ. Sci. Technol. 40, 5036–5044. doi: 10.1021/es0601843

PubMed Abstract | CrossRef Full Text | Google Scholar

Lombard, F., Boss, E., Waite, A. M., Vogt, M., Uitz, J., Stemmann, L., et al. (2019). Globally consistent quantitative observations of planktonic ecosystems. Front. Mar. Sci. 6:196. doi: 10.3389/fmars.2019.00196

CrossRef Full Text | Google Scholar

Ludvigsen, M., Berge, J., Geoffroy, M., Cohen, J. H., De La Torre, P. R., Nornes, S. M., et al. (2018). Use of an autonomous surface vehicle reveals small-scale diel vertical migrations of zooplankton and susceptibility to light pollution under low solar irradiance. Sci. Adv. 4:eaa9887. doi: 10.1126/sciadv.aap9887

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcelli, M., Piermattei, V., Madonia, A., and Mainardi, U. (2014). Design and application of new low-cost instruments for marine environmental research. Sensors 14, 23348–23364. doi: 10.3390/s141223348

PubMed Abstract | CrossRef Full Text | Google Scholar

Martignac, F., Daroux, A., Bagliniere, J. L., Ombredane, D., and Guillard, J. (2015). The use of acoustic cameras in shallow waters: new hydroacoustic tools for monitoring migratory fish population. A review of DIDSON technology. Fish Fish. 16, 486–510. doi: 10.1111/faf.12071

CrossRef Full Text | Google Scholar

Martz, T. R., Connery, J. G., and Johnson, K. S. (2010). Testing the Honeywell Durafet (R) for seawater pH applications. Limnol Oceanogr. Methods 8, 172–184. doi: 10.4319/lom.2010.8.172

CrossRef Full Text | Google Scholar

Martz, T. R., Daly, K. L., Byrne, R. H., Stillman, J. H., and Turk, D. (2015). Technology for ocean acidification research needs and availability. Oceanography 28, 40–47. doi: 10.5670/oceanog.2015.30

CrossRef Full Text | Google Scholar

McQuillan, J. S., and Robidart, J. C. (2017). Molecular-biological sensing in aquatic environments: recent developments and emerging capabilities. Curr. Opin. Biotechnol. 45, 43–50. doi: 10.1016/j.copbio.2016.11.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, D., Prien, R. D., Rautmann, L., Pallentin, M., Waniek, J. J., and Schulz-Bull, D. E. (2018). In situ determination of nitrate and hydrogen sulfide in the Baltic Sea using an ultraviolet spectrophotometer. Front. Mar. Sci. 5:431. doi: 10.3389/fmars.2018.00431

CrossRef Full Text | Google Scholar

Milani, A., Statham, P. J., Mowlem, M. C., and Connelly, D. P. (2015). Development and application of a microfluidic in-situ analyzer for dissolved Fe and Mn in natural waters. Talanta 136, 15–22. doi: 10.1016/j.talanta.2014.12.045

PubMed Abstract | CrossRef Full Text | Google Scholar

Millero, F. J. (2007). The marine inorganic carbon cycle. Chem. Rev. 107, 308–341. doi: 10.1021/cr0503557

PubMed Abstract | CrossRef Full Text | Google Scholar

Mills, G., and Fones, G. (2012). A review of in situ methods and sensors for monitoring the marine environmen. Sensor Rev. 32, 17–28. doi: 10.3390/s17051184

PubMed Abstract | CrossRef Full Text | Google Scholar

Moline, M. A., Benoit-Bird, K., O’Gorman, D., and Robbins, I. C. (2015). Integration of scientific echo sounders with an adaptable autonomous vehicle to extend our understanding of animals from the surface to the bathypelagic. J. Atmos. Ocean. Technol. 32, 2173–2186. doi: 10.1175/jtech-d-15-0035.1

CrossRef Full Text | Google Scholar

Mooney, T. A., Katija, K., Shorter, K. A., Hurst, T., Fontes, J., and Afonso, P. (2015). ITAG: an eco-sensor for fine-scale behavioral measurements of soft-bodied marine invertebrates. Anim. Biotelem. 3, 31–46.

Google Scholar

Moore, T. S., Mullaugh, K. M., Holyoke, R. R., Madison, A. N. S., Yucel, M., and Luther, G. W. (2009). Marine chemical technology and sensors for marine waters: potentials and limits. Annu. Rev. Mar. Sci. 1, 91–115. doi: 10.1146/annurev.marine.010908.163817

PubMed Abstract | CrossRef Full Text | Google Scholar

Mordy, C. W., Cokelet, E. D., De Robertis, A., Jenkins, R., Kuhn, C. E., Lawrence-Slavas, N., et al. (2017). Advances in ecosystem research: Saildrone surveys of oceanography, fish, and marine mammals in the Bering Sea. Oceanography 30, 113–115. doi: 10.5670/oceanog.2017.230

CrossRef Full Text | Google Scholar

Morgan, H., Mowlem, M. C., and Huang, X. (2014a). Apparatus for Sensing Parameters e.g. Conductivity in Sea Water, has Conductivity Sensor and Dissolved Oxygen Sensor Which are Fabricated On Glass Substrate Using Photolithography and Etching. Granted in the US 29/06/2018 and at A1 in Europe 29/07/2015. Patent numbers: WO2014044999-A1; US2015192534-A1; EP2898316-A1; US9983158-US9983152.

Google Scholar

Morgan, H., Mowlem, M. C., Huang, X., and Pascal, R. W. (2014b). Apparatus for Sensing e.g. Dissolved Oxygen in Sea Water for Industrial Applications, has Electrode Based Sensor Including Self-Cleaning Electrode and Reference Electrode, Where Self-Cleaning Electrode is Stable in Water. Granted in the US 14/11/2017 and at A1 in Europe 29/07/2015. Patent numbers: WO2014045001-A1; EP2898320-A1; US2015226697-A1; US9816962-US9816962.

Google Scholar

Morgan, H., Mowlem, M. C., Huang, X., and Pascal, R. W. (2014c). Water Parameter Sensing Apparatus for Determining e.g., Conductivity, Temperature, in Water by Applying Voltage Signal Between Working Electrode and Reference Electrode to Provide Conditioning Waveform, Wait Time, and Measurement Function. Granted in the US 20/09/2016. Patent numbers: WO2014044998-A1; US2015212040-A1; US9448200-US9448202.

Google Scholar

Morgan, H., Mowlen, M. C., Huang, X., and Mowlem, M. C. (2014d). Apparatus for Sensing e.g. Parameter in Sea Water for Industrial and Environmental Applications, has Conductivity Sensor Comprising Electrodes for Current Stimulation Geometrically Bounding and Enclosing Electrodes for Voltage Sensing. Granted in the US 12/12/2017. Patent numbers: WO2014044997-A1; US2015192535-A1; US9841392-US9841392.

Google Scholar

Moustahfid, H., Jech, M. M., Weise, M. J., Horne, J. K., O’Dor, R., and Alexander, C. (2012). “Advancing “bio” sensor integration with ocean observing systems to support ecosystem based approaches,” in Proceeding of the 2012 Oceans, Hampton Roads, VA, 1–7.

Google Scholar

Moustahfid, H., Marsac, F., and Gangopadhyay, A. (2018). “Climate change impacts, vulnerabilities and adaptations: Western Indian Ocean marine fisheries,” in Impacts of Climate Change on Fisheries and Aquaculture: Synthesis of Current Knowledge, Adaptation and Mitigation Options. FAO Fisheries Technical Paper 627, ed. M. Barange, (Rome: FAO).

Google Scholar

Mouw, C. B., Hardman-Mountford, N. J., Alvain, S., Bracher, A., Brewin, R. J. W., Bricaud, A., et al. (2017). A consumer’s guide to satellite remote sensing of multiple phytoplankton groups in the global ocean. Front. Mar. Sci. 4:41. doi: 10.3389/fmars.2017.00041

CrossRef Full Text | Google Scholar

Nicholson, D. P., Michel, A. P. M., Wankel, S. D., Manganini, K., Sugrue, R. A., Sandwith, Z. O., et al. (2018). Rapid mapping of dissolved methane and carbon dioxide in coastal ecosystems using the ChemYak autonomous surface vehicle. Environ. Sci. Technol. 52, 13314–13324. doi: 10.1021/acs.est.8b04190

PubMed Abstract | CrossRef Full Text | Google Scholar

Ogilvie, I. R. G., Sieben, V. J., Floquet, C. F. A., Zmijan, R., Mowlem, M. C., and Morgan, H. (2010). Reduction of surface roughness for optical quality microfluidic devices in PMMA and COC. J. Micromech. Microeng. 20:65016. doi: 10.1088/0960-1317/20/6/065016

CrossRef Full Text | Google Scholar

Ohman, M. D., Davis, R. E., Sherman, J. T., Grindley, K. R., Whitmore, B. M., Nickels, C. F., et al. (2019). Zooglider: an autonomous vehicle for optical and acoustic sensing of zooplankton. Limnol. Oceanogr. Methods 17, 69–86. doi: 10.1002/lom3.10301

CrossRef Full Text | Google Scholar

Olson, R. J., Shalapyonok, A., and Sosik, H. M. (2003). An automated submersible flow cytometer for analyzing pico-and nanophytoplankton: flowCytobot. Deep Sea Res. Part I Oceanogr. Res. Pap. 50, 301–315. doi: 10.1016/s0967-0637(03)00003-7

CrossRef Full Text | Google Scholar

Organelli, E., Dall’Olmo, G., Brewin, R. J. W., Tarran, G. A., Boss, E., and Bricaud, A. (2018). The open-ocean missing backscattering is in the structural complexity of particles. Nat. Commun. 9:5439. doi: 10.1038/s41467-018-07814-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Ottesen, E. A., Marin, R., Preston, C. M., Young, C. R., Ryan, J. P., Scholin, C. A., et al. (2011). Metatranscriptomic analysis of autonomously collected and preserved marine bacterioplankton. ISME J. 5, 1881–1895. doi: 10.1038/ismej.2011.70

PubMed Abstract | CrossRef Full Text | Google Scholar

Pargett, D. M., Birch, J. M., Preston, C. M., Ryan, J. P., Zhang, Y., and Scholin, C. A. (2015). “October. Development of a mobile ecogenomic sensor,” in Proceedings of the OCEANS’15 MTS/IEEE Washington, (Washington, DC: IEEE), 1–6.

Google Scholar

Pauly, D., Christensen, V., Guénette, S., Pitcher, T. J., Sumaila, U. R., Walters, C. J., et al. (2002). Towards sustainability in world fisheries. Nature 418, 689–695. doi: 10.1038/nature01017

PubMed Abstract | CrossRef Full Text | Google Scholar

Perrot, Y., Brehmer, P., Habasque, J., Roudaut, G., Behagle, N., Sarré, A., et al. (2018). Matecho: an open-source tool for processing fisheries acoustics data. Aust. Acoust. 46, 241–248. doi: 10.1007/s40857-018-0135-x

CrossRef Full Text | Google Scholar

Perrot, Y., Brehmer, P., Roudaut, G., Gerstoft, P., and Josse, E. (2014). Efficient multibeam sonar calibration and performance evaluation. Int. J. Eng. Sci. Inovat. Technol. 3, 808–820.

Google Scholar

Petralia, S., and Conoci, S. (2017). PCR technologies for point of care testing: progress and perspectives. ACS Sensors 2, 876–891. doi: 10.1021/acssensors.7b00299

PubMed Abstract | CrossRef Full Text | Google Scholar

Picheral, M., Guidi, L., Stemmann, L., Karl, D. M., Iddaoud, G., and Gorsky, G. (2010). The underwater vision profiler 5: an advanced instrument for high spatial resolution studies of particle size spectra and zooplankton. Limnol. Oceanogr. Methods 8, 462–473. doi: 10.4319/lom.2010.8.462

CrossRef Full Text | Google Scholar

Pons, C., Forteza, R., and Cerda, V. (2005). Optical fibre reflectance sensor for the determination and speciation analysis of iron in fresh and seawater samples coupled to a multisyringe flow injection system. Anal. Chim. Acta 528, 197–203. doi: 10.1016/j.aca.2004.08.023

CrossRef Full Text | Google Scholar

Preston, C., Marin, R. III, Jensen, S., Feldman, J., Massion, E., DeLong, E., et al. (2009). Near real-time, autonomous detection of marine bacterioplankton on a coastal mooring in Monterey Bay, California, using rRNA-targeted DNA probes. Environ. Microbiol. 22, 158–167. doi: 10.1111/j.1462-2920.2009.01848.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Preston, C. M., Harris, A., Ryan, J. P., Roman, B., Marin, R. III, Jensen, S., et al. (2011). Underwater application of quantitative PCR on an ocean mooring. PLoS One 6:e22522. doi: 10.1371/journal.pone.0022522

PubMed Abstract | CrossRef Full Text | Google Scholar

Rerolle, V., Ruiz-Pino, D., Rafizadeh, M., Loucaides, S., Papadimitriou, S., Mowlem, M., et al. (2018). High resolution pH measurements using a lab-on-chip sensor in surface waters of Northwest European shelf seas. Sensors Basel 18:E2622. doi: 10.3390/s18082622

PubMed Abstract | CrossRef Full Text | Google Scholar

Riser, S. C., Freeland, H. J., Roemmich, D., Wijffels, S., Troisi, A., Belbeoch, M., et al. (2016). Fifteen years of ocean observations with the global Argo array. Nat. Clim. Change 6, 145–153.

Google Scholar

Roberts, J. M., Brown, C. J., Long, D., and Bates, C. R. (2005). Acoustic mapping using a multibeam echosounder reveals cold-water coral reefs and surrounding habitats. Coral Reefs 24, 654–669. doi: 10.1007/s00338-005-0049-6

CrossRef Full Text | Google Scholar

Robidart, J. C., Church, M. J., Ryan, J. P., Ascani, F., Wilson, S. T., Bombar, D., et al. (2014). Ecogenomic sensor reveals controls on N 2-fixing microorganisms in the North Pacific Ocean. ISME J. 8, 1175–1185. doi: 10.1038/ismej.2013.244

PubMed Abstract | CrossRef Full Text | Google Scholar

Roesler, C., Uitz, J., Claustre, H., Boss, E., Xing, X., Organelli, E., et al. (2017). Recommendations for obtaining unbiased chlorophyll estimates from in situ chlorophyll fluorometers: a global analysis of WET Labs ECO sensors: unbiased chlorophyll from in situ fluorometers. Limnol. Oceanogr. Methods 15, 572–585. doi: 10.1002/lom3.10185

CrossRef Full Text | Google Scholar

Roquet, F., Boehme, L., Block, B., Charrassin, J.-B., Costa, D., Guinet, C., et al. (2017). Ocean observations using tagged animals. Oceanography 30:139. doi: 10.5670/oceanog.2017.235

CrossRef Full Text | Google Scholar

Roquet, F., Wunsch, C., Forget, G., Heimbach, P., Guinet, C., Reverdin, G., et al. (2013). Estimates of the Southern Ocean general circulation improved by animal-borne instruments. Geophys. Res. Lett. 40, 6176–6180. doi: 10.1002/2013gl058304

CrossRef Full Text | Google Scholar

Sahin, C., Verney, R., Sheremet, A., and Voulgaris, G. (2017). Acoustic backscatter by suspended cohesive sediments: field observations, Seine Estuary, France. Cont. Shelf Res. 134, 39–51. doi: 10.1016/j.csr.2017.01.003

CrossRef Full Text | Google Scholar

Sakamoto, C. M., Johnson, K. S., Coletti, L. J., and Jannasch, H. W. (2017). Pressure correction for the computation of nitrate concentrations in seawater using an in situ ultraviolet spectrophotometer. Limnol. Oceanogr. Methods 15, 897–902. doi: 10.1002/lom3.10209

CrossRef Full Text | Google Scholar

Sayles, F. L., and Eck, C. (2009). An autonomous instrument for time series analysis of TCO₂ from oceanographic moorings. Deep Sea Res. Part I 56, 1590–1603. doi: 10.1016/j.dsr.2009.04.006

CrossRef Full Text | Google Scholar

Scholin, C. A. (2013). “Ecogenomic sensors,” in Encyclopedia of Biodiversity, 2nd Edn, ed. S. A. Levin, (Waltham, MA: Academic Press), 690–700. doi: 10.1016/b978-0-12-384719-5.00408-1

CrossRef Full Text | Google Scholar

Scholin, C. A., Birch, J., Jensen, S., Marin, R. III, Massion, E., Pargett, D., et al. (2018). The quest to develop ecogenomic sensors: a 25-Year history of the environmental sample processor (ESP) as a case study. Oceanography 30, 100–113. doi: 10.5670/oceanog.2017.427

CrossRef Full Text | Google Scholar

Sieracki, C. K., Sieracki, M. E., and Yentsch, C. S. (1998). An imaging-in-flow system for automated analysis of marine microplankton. Mar. Ecol. Prog. Ser. 168, 285–296. doi: 10.3354/meps168285

CrossRef Full Text | Google Scholar

Simmonds, J., and MacLennan, D. N. (2005). Fisheries Acoustics: Theory and Practice, 2nd Edn. Oxford: Wiley-Blackwell, 456.

Google Scholar

Smith, T. A., and McConnaughey, R. A. (2016). The Applicability of Sonars for Habitat Mapping: a Bibliography. Silver Spring, MD: NOAA Tech, 129.

Google Scholar

Song, A., Stojanovic, M., and Chitre, M. (2019). Editorial underwater acoustic communications: where we stand and what is next? IEEE J. Ocean. Eng. 44, 1–6. doi: 10.1109/joe.2018.2883872

CrossRef Full Text | Google Scholar

Sosik, H. M., and Olson, R. J. (2007). Automated taxonomic classification of phytoplankton sampled with imaging-in-flow cytometry. Limnol. Oceanogr. Methods 5, 204–216. doi: 10.4319/lom.2007.5.204

CrossRef Full Text | Google Scholar

Sosna, M., Denuault, G., Pascal, R. W., Prien, R. D., and Mowlem, M. (2007). Development of a reliable microelectrode dissolved oxygen sensor. Sensors Actuat. B Chem. 123, 344–351. doi: 10.1016/j.snb.2006.08.033

CrossRef Full Text | Google Scholar

Sosna, M., Denuault, G., Pascal, R. W., Prien, R. D., and Mowlem, M. (2008). Field assessment of a new membrane-free microelectrode dissolved oxygen sensor for water column profiling. Limnol. Oceanogr. Methods 6, 180–189. doi: 10.4319/lom.2008.6.180

CrossRef Full Text | Google Scholar

Spaulding, R. S., DeGrandpre, M. D., Beck, J. C., Hart, R. D., Peterson, B., De Carlo, E. H., et al. (2014). Autonomous in Situ measurements of seawater alkalinity. Environ. Sci. Technol. 48, 9573–9581. doi: 10.1021/es501615x

PubMed Abstract | CrossRef Full Text | Google Scholar

Staudinger, C., Strobl, M., Fischer, J. P., Thar, R., Mayr, T., Aigner, D., et al. (2018). A versatile optode system for oxygen, carbon dioxide, and pH measurements in seawater with integrated battery and logger. Limnol. Oceanogr. Methods 16, 459–473. doi: 10.1002/lom3.10260

CrossRef Full Text | Google Scholar

Sun, H., Benzie, P. W., Burns, N., Hendry, D. C., Player, M. A., and Watson, J. (2008). Underwater digital holography for studies of marine plankton. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 366, 1789–1806. doi: 10.1098/rsta.2007.2187

PubMed Abstract | CrossRef Full Text | Google Scholar

Takeshita, Y., Martz, T. R., Johnson, K. S., and Dickson, A. G. (2014). Characterization of an ion sensitive field effect transistor and chloride ion selective electrodes for pH measurements in Seawater. Anal. Chem. 86, 11189–11195. doi: 10.1021/ac502631z

PubMed Abstract | CrossRef Full Text | Google Scholar

Taya, M., Tadayon, A., and Stojanovic, M. (2018). “Mobile acoustic communications: real data analysis of partial FFT demodulation with coherent detection,” in Proceedings of the OCEANS 2018 MTS/IEEE Charleston, (Charleston, SC: IEEE), 1–7.

Google Scholar

Tengberg, A., Hovdenes, J., Andersson, H. J., Brocandel, O., Diaz, R., Hebert, D., et al. (2006). Evaluation of a lifetime-based optode to measure oxygen in aquatic systems. Limnol. Oceanogr. Methods 4, 7–17. doi: 10.4319/lom.2006.4.7

CrossRef Full Text | Google Scholar

Thorne, P. D., and Hardcastle, P. J. (1997). Acoustic measurements of suspended sediments in turbulent currents and comparison with in-situ samples. J. Acous. Soc. Am. 101, 2603–2614. doi: 10.1121/1.418501

CrossRef Full Text | Google Scholar

Thyssen, M., Alvain, S., Lefèbvre, A., Dessailly, D., Rijkeboer, M., Guiselin, N., et al. (2015). High-resolution analysis of a North Sea phytoplankton community structure based on in situ flow cytometry observations and potential implication for remote sensing. Biogeosciences 12, 4051–4066. doi: 10.5194/bg-12-4051-2015

CrossRef Full Text | Google Scholar

Trenkel, V. M., Mazauric, V., and Berger, L. (2008). The new fisheries multibeam echosounder ME70: description and expected contribution to fisheries research. ICES J. Mar. Sci. 65, 645–655. doi: 10.1093/icesjms/fsn051

CrossRef Full Text | Google Scholar

Trygonis, V., Georgakarakos, S., Dagorn, L., and Brehmer, P. (2016). Spatiotemporal distribution of fish schools around drifting fish aggregating devices. Fish. Res. 177, 39–49. doi: 10.1016/j.fishres.2016.01

CrossRef Full Text | Google Scholar

Tušer, M., Frouzová, J., Balka, H., Muška, M., Mrkvička, T., and Kubečka, J. (2014). Evaluation of potential bias in observing fish with a DIDSON acoustic camera’. Fish. Res. 155, 114–121. doi: 10.1016/j.fishres.2014.02.031

CrossRef Full Text | Google Scholar

Vincent, A. G., Pascal, R. W., Beaton, A. D., Walk, J., Hopkins, J. E., Woodward, E. M. S., et al. (2018). Nitrate drawdown during a shelf sea spring bloom revealed using a novel microfluidic in situ chemical sensor deployed within an autonomous underwater glider. Mar. Chem. 205, 29–36. doi: 10.1016/j.marchem.2018.07.005

CrossRef Full Text | Google Scholar

Wang, Z. A., Chu, S. N., and Hoering, K. A. (2013a). High-frequency spectrophotometric measurements of total dissolved inorganic carbon in seawater. Environ. Sci. Technol. 47, 7840–7847. doi: 10.1021/es400567k

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z. A., Wanninkhof, R., Cai, W. J., Byrne, R. H., Hu, X. P., and Peng, T. H. (2013b). The marine inorganic carbon system along the Gulf of Mexico and Atlantic coasts of the United States: insights from a transregional coastal carbon study. Limnol. Oceanogr. 58, 325–342. doi: 10.4319/lo.2013.58.1.0325

CrossRef Full Text | Google Scholar

Wang, Z. A., Liu, X. W., Byrne, R. H., Wanninkhof, R., Bernstein, R. E., Kaltenbacher, E. A., et al. (2007). Simultaneous spectrophotometric flow-through measurements of pH, carbon dioxide fugacity, and total inorganic carbon in seawater. Anal. Chim. Acta 596, 23–36. doi: 10.1016/j.aca.2007.05.048

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z. A., Sonnichsen, F. N., Bradley, A. M., Hoering, K. A., Lanagan, T. M., Chu, S. N., et al. (2015). In situ sensor technology for simultaneous spectrophotometric measurements of seawater total dissolved inorganic carbon and pH. Environ. Sci. Technol. 49, 4441–4449. doi: 10.1021/es504893n

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z. A., Wang, Y. H., Cai, W. J., and Liu, S. Y. (2002). A long pathlength spectrophotometric pCO₂ sensor using a gas-permeable liquid-core waveguide. Talanta 57, 69–80. doi: 10.1016/s0039-9140(02)00008-5

CrossRef Full Text | Google Scholar

Williamson, B. J., Fraser, S., Blondel, P., Bell, P. S., Waggitt, J. J., and Scott, B. E. (2017). Multisensor acoustic tracking of fish and seabird behavior around tidal turbine structures in Scotland. IEEE J. Ocean. Eng. 42, 948–965. doi: 10.1109/JOE.2016.2637179

CrossRef Full Text | Google Scholar

Wilson, R. P., White, C. R., Quintana, F., Halsey, L. G., Liebsch, N., Martin, G. R., et al. (2006). Moving towards acceleration for estimates of activity-specific metabolic rate in free-living animals: the case of the cormorant. J. Anim. Ecol. 75, 1081–1090. doi: 10.1111/j.1365-2656.2006.01127.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Xing, X. G., Claustre, H., Boss, E., Roesler, C., Organelli, E., Poteau, A., et al. (2017). Correction of profiles of in-situ chlorophyll fluorometry for the contribution of fluorescence originating from non-algal matter. Limnol. Oceanogr. Methods 15, 80–93. doi: 10.1002/lom3.10144

CrossRef Full Text | Google Scholar

Yang, B., Patsavas, M. C., Byrne, R. H., and Ma, J. (2014). Seawater pH measurements in the field: a DIY photometer with 0.01 unit pH accuracy. Mar. Chem. 164, 126–129. doi: 10.1016/j.marchem.2014.06.007

CrossRef Full Text | Google Scholar

Yang, H., Lohmann, G., Wei, W., Dima, M., Ionita, M., and Liu, J. (2016). Intensification and poleward shift of subtropical western boundary currents in a warming climate. J. Geophys. Res. Oceans 121, 4928–4945. doi: 10.1002/2015jc011513

CrossRef Full Text | Google Scholar

Yucel, M., Beaton, A. D., Dengler, M., Mowlem, M. C., Sohl, F., and Sommer, S. (2015). Nitrate and nitrite variability at the seafloor of an oxygen minimum zone revealed by a novel microfluidic in-situ chemical sensor. PLoS One 10:e0132785. doi: 10.1371/journal.pone.0132785

PubMed Abstract | CrossRef Full Text | Google Scholar

Zielinski, O., Fiedler, B., Heuermann, R., Kortzinger, A., Kopiske, E., Meinecke, G., et al. (2007). “A new nitrate continuous observation sensor for autonomous sub-surface applications: technical design and first results,” in Proceedings of the Oceans 2007—Europe, Aberdeen.

Google Scholar